Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: — полное сопротивление переменному току. | |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: . | |
Сдвиг фаз в цепи переменного тока определяется характером нагрузки: или . |
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): | |
или, переходя к действующим значениям, . | |
Величина наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. | коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии или .
| |
Следовательно, — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. | |
и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, . |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. |
|
При этом если величина , то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! | |
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа . | |
В случае резонанса . |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |
|
Резонансные явления в электрических сетях
Идеальное активное сопротивление от частоты не зависит, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:
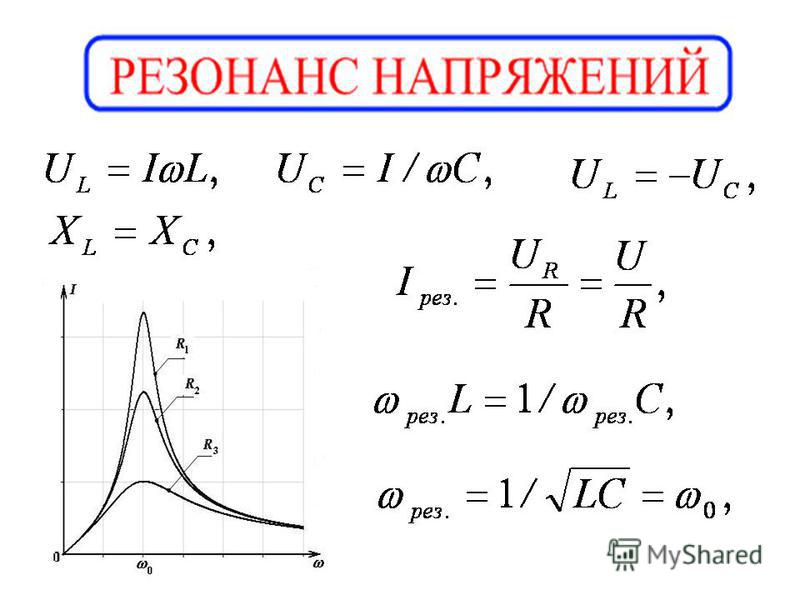
Резонанс напряжений
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю .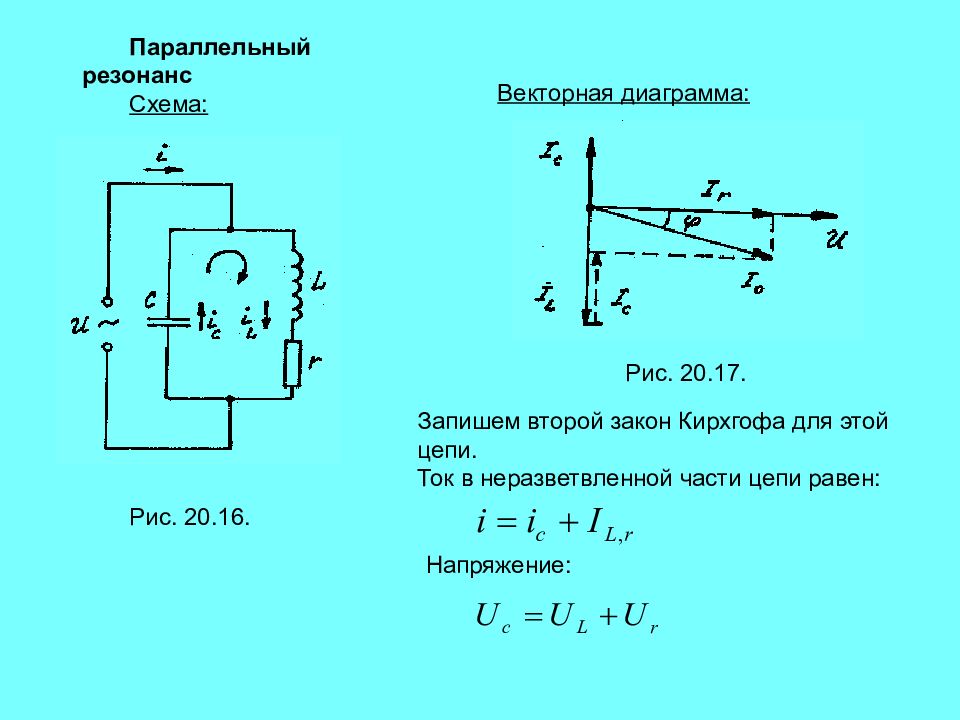 Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.
Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.
При последовательном соединении возникает резонанс напряжения.
Последовательное соединение R, L, C.
Знаменатель данного выражения есть модуль комплексного сопротивления, который зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения по фазе:
Максимальная амплитуда силы тока достигается при условии минимума полного сопротивления, т. е. при
где
— резонансная частота напряжения, определяемая из условия
При последовательном соединении в цепь конденсатора и соленоида силы токов в каждом из участков цепи, как известно, равны. Поэтому, умножив левую и правую части последнего соотношения на силу тока Im, получим
В этом выражении слева — амплитуда напряжения на концах соленоида, а справа — амплитуда напряжения на обкладках конденсатора.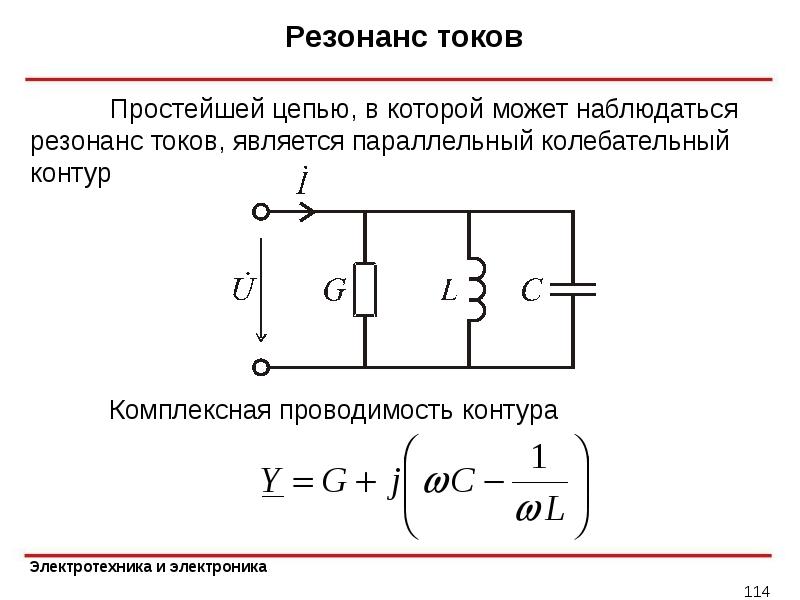
Мы видим, что . Отсюда получаем
Знак минус указывает на то, что колебания напряжения на участках с индуктивностью и емкостью происходят в противофазе.
Режим электрической цепи при последовательном соединении индуктивности и емкости, характеризующийся равенством напряжений на индуктивности и емкости, называют резонансом напряжений.
Волновое или характеристическое сопротивление последовательного контура
Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется добротностью контура:
Добротность контура представляет собой коэффициент усиления по напряжению и в катушках индуктивности может достигать сотен единиц:
При напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике. В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.
Резонанс токов
При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю).
В этом случае:
Параллельное соединение реактивных элементов
тогда
При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость
При ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.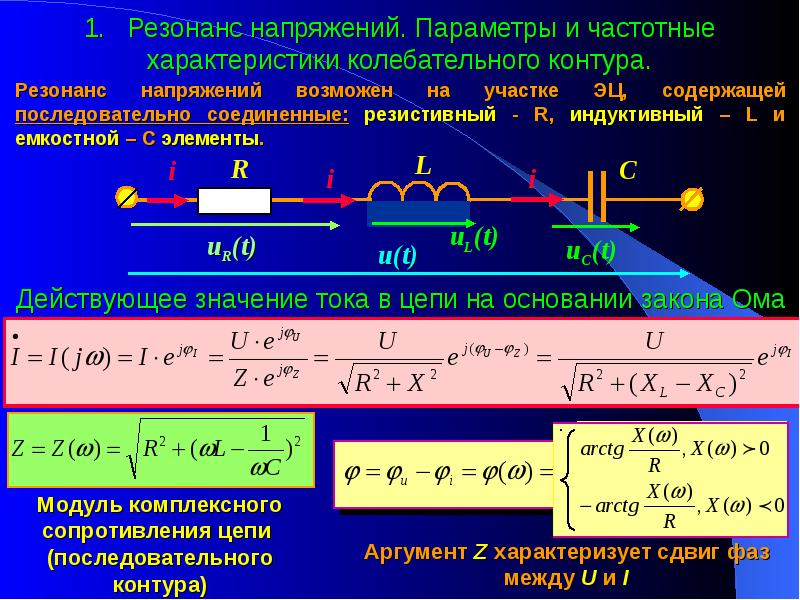
Резонансную частоту тока найдем из условия равенства реактивных проводимостей ветвей.
После ряда преобразований получим:
Из формулы следует, что:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если и больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс невозможен;
3) если , то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии.
§56. Резонанс напряжений и резонанс токов
Явление резонанса.
Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими.
При подсоединении колебательного контура к источнику переменного тока угловая частота источника ω может оказаться равной угловой частоте ω 0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.
В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ω источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ω0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
Резонанс напряжений.
При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL
Z = √( R2 + [ω0L — 1/(ω0C)]2 ) = R
В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис.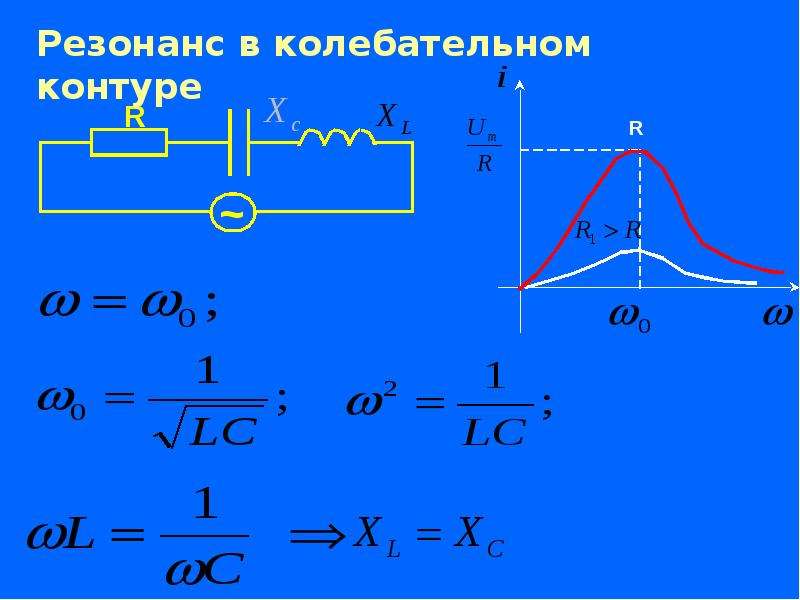 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
Угловая частота ω0, при которой имеют место условия резонанса, определяется из равенства ωoL = 1/(ω0С).
Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений
Отсюда имеем:
ωo = 1/√(LC) (74)
Если плавно изменять угловую частоту ω источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ωo), а затем увеличивается (рис.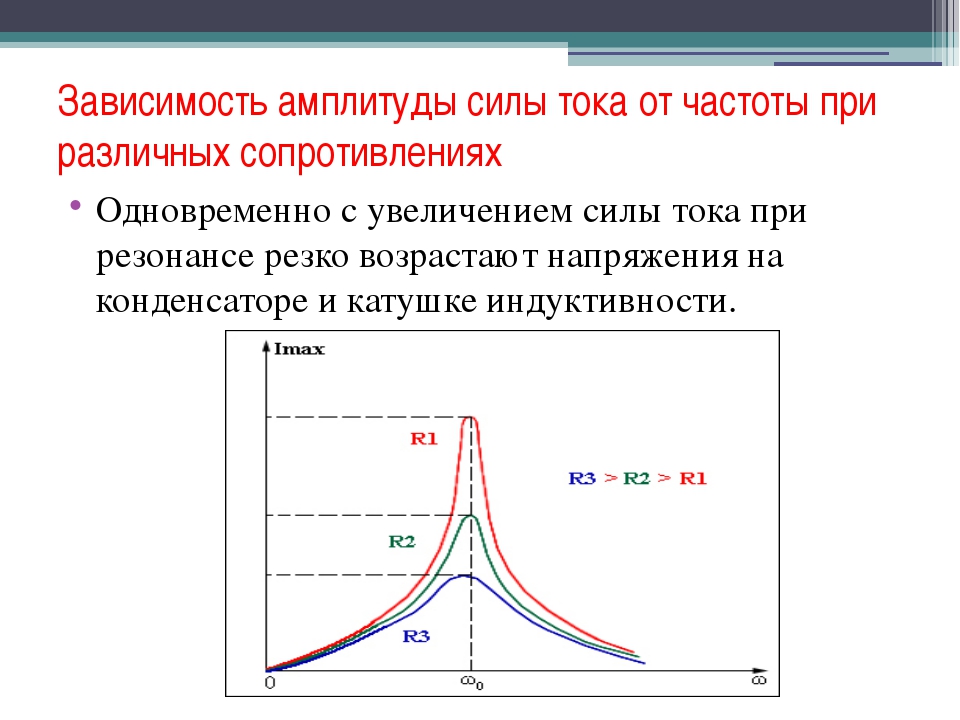 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
Рис. 197. Зависимость тока I и полного сопротивления Z от ω для последовательной (а) и параллельной (б) цепей переменного тока
Резонанс токов.
Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R
Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов
Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части цепи при резонансе I=U √(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).
Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).
Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи I L и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ω0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту.
Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т.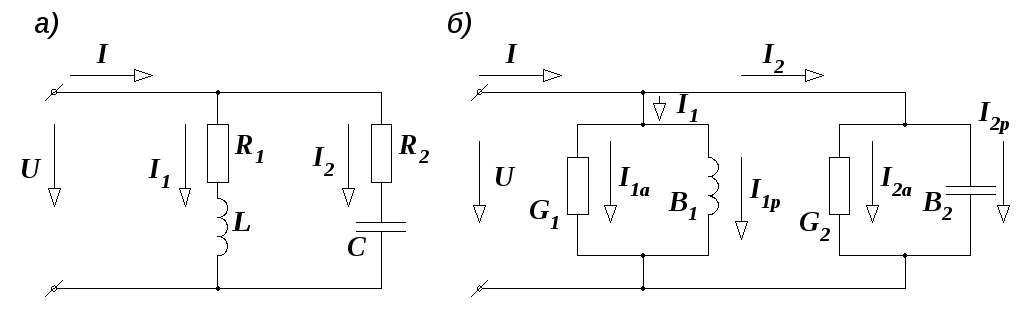 е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс.
е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс.
Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1 и R2, будет равенство реактивных проводимостей BL = BC ветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту ωо источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ω0.
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах.
Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
Понятие резонанса напряжений в электрических цепях переменного тока
Резонанс в электрической цепи возникает при резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определенной резонансной частотой системы. Это происходит тогда, когда два элемента противоположного характера компенсируют эффект друг друга в цепи.
Резонанс токов и напряжений
RLC-цепьСхема RLC – это электрическая цепь с последовательно или параллельно соединенными элементами:
- резистора,
- индуктора,
- конденсатора.

Название RLC связано с тем, что эти буквы являются обычными символами электрических элементов: сопротивления, индуктивности и емкости.
Векторная диаграмма последовательной RLC-цепи представлена в одном из трех вариантов:
- индуктивном,
- емкостном,
- активном.
В последнем варианте при нулевом сдвиге фаз, равенстве индуктивного и емкостного сопротивлений возникает резонанс напряжений.
Электрический резонансВ природе бывают резонанс токов и резонанс напряжений. Наблюдаются они в цепи с параллельным и последовательным соединением элементов R, L и С. Резонансная частота одинакова для обеих цепей, она находится из условия противоположности сопротивлений реактивных элементов и вычисляется по нижеследующей формуле.
Резонансная частота
Векторные диаграммы практически идентичны, только сигналы отличаются. В последовательном контуре резонируют напряжения, в параллельном – ток. Но если отступиться от резонансной частоты такая симметрия естественно нарушится. В первом случае сопротивление возрастет, во втором – уменьшится.
В первом случае сопротивление возрастет, во втором – уменьшится.
Резонанс напряжений, достигающих максимальной амплитуды
На картинке ниже представлена векторная диаграмма цепи последовательного контура, где:
- I – вектор общего тока;
- Ul – опережает I на 900;
- UС – отстает от I на 900;
- UR – синфазно I.
Из трех векторов напряжения (Ul, UС, UR) два первых взаимно компенсируют друг друга. Они между собой:
- противоположны по направлению,
- равны по амплитуде,
- отличаются по фазе на пи.
Получается, что напряжение по второму закону Кирхгофа приложено только к резистору. В этот момент:
- импеданс последовательного контура на резонансной частоте минимален и равен просто R;
- так как сопротивление цепи минимальное, то соответственно ток по амплитуде максимальный;
- также приблизительно максимальны напряжения на индуктивности и на емкости.

Если рассматривать отдельно последовательный контур LC, то он даёт нулевое сопротивление на резонансной частоте:
ZL = -ZC
Резонанс напряжений в цепи переменного тока
Важно! Когда установился гармонический режим c резонансной частотой, в контуре происходит следующее: источник обеспечивает установившуюся амплитуду колебаний; мощность источника расходуется лишь на нагрев резистора.
Резонанс токов через реактивные элементы
Диаграмма параллельного контура на той же частоте. Поскольку все элементы соединены параллельно, то диаграмму лучше начать строить с общего напряжения.
- U – вектор общего тока;
- Ic – опережает U на 900;
- IU – отстает от U на 900;
- Ток в резисторе (IR) синфазен общему напряжению.
Поскольку сопротивления реактивности по модулю равны, то и амплитуды токов Ic и Iu:
- одинаковы;
- достигают максимальной амплитуды.

Получается, что по первому закону Кирхгофа IR равен току источника. Другими словами, ток источника течет только через резистор.
Если рассматривать отдельно параллельный контур LC, то на резонансной частоте его сопротивление бесконечно большое:
ZL = ZC.
Когда установится гармонический режим c резонансной частотой, в контуре происходит следующее:
- источник обеспечивает установившуюся амплитуду колебаний;
- мощность источника тока расходуется лишь на пополнение потерь в активном сопротивлении.
Резонанс токов
Двойственность RLC-контуровТаким образом, можно сделать сравнительный вывод:
- У последовательной RLC цепи импеданс минимален на резонансной частоте и равен активному сопротивлению контура;
- У параллельной RLC цепи импеданс максимален на резонансной частоте и равен так называемому сопротивлению утечки, фактически тоже активному сопротивлению контура.
Для того чтобы предуготовить условия для резонанса тока или напряжения, требуется проверить электрическую цепь с целью предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимую часть необходимо приравнять к нулю.
Для информации. Напряжения в последовательной цепи ведут себя очень похоже токам параллельной цепи на резонансной частоте, в этом проявляется двойственность RLC-контуров.
Резонанс в цепи переменного тока
Применение резонансного явленияХорошим примером применения резонансного явления может служить электрический резонансный трансформатор, разработанный изобретателем Николой Тесла ещё в 1891 году. Тесла проводил эксперименты с различными конфигурациями, состоящими в сочетании из двух, а иногда трех резонансных электрических цепей.
Для информации. Термин «катушки Теслы» применяются к ряду высоковольтных резонансных трансформаторов. Устройства используются для получения высокого напряжения, низкого тока, высокой частоты переменного тока.
В то время как обычный трансформатор предназначен для эффективной передачи энергии с первичной на вторичную обмотку, резонансный трансформатор предназначен для временного хранения электрической энергии. Устройство управляет воздушным сердечником резонансно настроенного трансформатора для получения высоких напряжений при малых токах. Каждая обмотка имеет емкость и функционирует как резонансный контур.
Чтобы произвести наибольшее выходное напряжение, первичный и вторичный контуры настроены в резонанс друг с другом. Оригинальные схемы изобретателя применяются как простые разрядники для возбуждения колебаний с помощью настроенных трансформаторов. В более сложных конструкциях используют транзисторные или тиристорные выключатели.
Для информации. Трансформатор Теслы основан на использовании резонансных стоячих электромагнитных волн в катушках. Своеобразный дизайн катушки продиктован необходимостью достигнуть низкого уровня резистивных потерь энергии (высокая добротность) на высоких частотах, что приводит к увеличению вторичных напряжений.
Резонанс в электрической цепи
Электрический резонанс – одно из самых распространенных в мире физических явлений, без которого не было бы TV, диагностических мед. аппаратов. Одни из самых полезных видов резонанса в электрической цепи – это резонанс токов и резонанс напряжений.
Видео Оцените статью:Резонанс в линейных электрических цепях. Территория электротехнической информации WEBSOR
В том случае, когда электрическая цепь содержит элементы с емкостными, а также с индуктивными свойствами может возникнуть режим резонанса. Кроме того, резонанс в электрической цепи появляется в случае совпадения по фазе тока и напряжения. Реактивное сопротивление и проводимость на входе имеют нулевое значение. Полностью отсутствует сдвиг фаз, и цепь становится активной.
Причины резонанса
Резонанс напряжений появляется в случае последовательного соединения участков, содержащих сопротивления индуктивного и емкостного характера, а также резисторы. Такая простая цепь очень часто носит название последовательного или параллельного контура.
В резонансном контуре вовсе не обязательно присутствие резистивного сопротивления. Тем не менее, его необходимо учитывать при определении сопротивления проводников. Таким образом, резонансный режим полностью зависит от параметров и свойств электрической цепи. На него никак не влияют внешние источники электрической энергии.
Для того, чтобы определить условия, при которых возникает режим резонанса, необходимо проверить электрическую цепь с целью определения ее проводимости или комплексного . Кроме того, её мнимая часть должна быть выделена и приравнена к нулю.
Характеристики резонанса
Все параметры, входящие в цепь, и присутствующие в полученном уравнении, так или иначе, влияют на показатели, характеризующие резонансные явления. В зависимости от параметров, входящих в состав уравнения, решение может иметь несколько различных вариантов. При этом, все решения будут соответствовать собственному варианту и в дальнейшем обретать физический смысл.
В различных видах электро цепей, явление резонанса рассматривается, как правило, при анализе в случае нескольких вариантов. В этих же случаях может проводиться синтез цепи, в котором заранее заданы резонансные параметры.
Электрические цепи которые имеют большое количество связей и реактивных элементов, представляют собой серьезную проблему при проведении анализа. Их никогда не используют при синтезе с заранее заданными свойствами, поскольку далеко не всегда возможно получение желаемого результата. Поэтому, в практической деятельности производится исследование двухполюсных приборов самых простых конструкций и на основании полученных данных проводится создание более сложных цепей с заранее заданными параметрами.
Таким образом, резонанс электрической цепи представляет собой достаточно сложное явление, благодаря использованию в ней определенных элементов. Учет этого явления позволяет наиболее полно определить параметры и прочие характеристики.
Резонансы токов и напряжений
Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер: Z = R; сдвиг фаз отсутствует (φ=0).
Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 27.1, а).
Рис. 27.1 — Векторные диаграммы при резонансе напряжений(а) и токов(б)
Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений:
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.
Из условия выше следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 27.2). Емкость С0, при которой наступает резонанс, можно определить из формулы: С0=1/(ω2L).
Рис. 27.2 — Зависимости параметров режима и емкости
Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C. Векторная диаграмма ее резонансного режима приведена на рис. 27.1, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 27.3, а).
Рис. 27.3 — Разветвленная цепь (а) и ее эквивалентная схема (б)
Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.
Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:
Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:
Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B1 и B2. Заменяя схему на рис. 27.3, а эквивалентной (рис. 27.3, б), параметры которой вычисляем по формулам, и используя условие резонанса (B = B1 – B2 = 0), снова приходим к конечному выражению.
Схеме на рис. 27.3, б соответствует векторная диаграмма, приведенная на рис. 27.4
Рис. 27.4 — Векторная диаграмма резонансного режима разветвленной цепи
Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.
Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет.
Что такое резонанс?
Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.
Признаки резонанса :
- Составляющие реактивных ветвей тока равны между собой IPC = IPL, противофаза образовывается только при равенстве чистой активной энергии на входе;
- Ток в отдельных ветках, превышает весь ток определенной цепи, при этом ветви совпадают по фазе.
Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:
- Последовательный;
- Параллельный.
Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.
Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.
Применение
Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.
Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.
Принцип резонанса токов
Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:
Схема для питания конденсатора
Переключатель будет отвечать за направление колебаний.
Схема: переключатель резонансной схемы
Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.
Схема: ток в резонансной схеме равен нулю
Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.
Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.
Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.
В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.
Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.
Расчет резонансного контура
Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела.
Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом:
R ср = I 2 конт * R = (V 2 конт / Z 2) * R.
При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1
Сама же формула резонанса имеет следующий вид:
ω 0 = 1 / √L*C
Нулевой импеданс в резонансе определяется при помощи такой формулы:
F рез = 1 / 2π √L*C
Резонансная частота колебаний может быть аппроксимирована следующим образом:
F = 1/2 р (LC) 0.5
Где: F = частота
L = индуктивность
C = емкость
Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям:
R = 2 (L / C) 0.5
Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов. При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока.
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Электрические цепи переменного тока Явление резонанса.
Выполнил:
Антропов А. И.
Проверила:
Бородина А. В.
Самара 2009
Электрические цепи переменного тока. Явление резонанса
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением .
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z ]=0 или Im[Y ]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Для определения условий возникновения режима резонанса в электрической цепи нужно:
· найти ее комплексное сопротивление или проводимость;
· выделить мнимую часть и приравнять нулю.
Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.
Уравнение Im[Z ]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.
В электрических цепях резонанс может рассматриваться в задачах:
· анализа этого явления при вариации параметров цепи;
· синтеза цепи с заданными резонансными параметрами.
Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.
Сдвиг фаз между током и напряжением. Понятие двухполюсника
Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром . Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.
Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно
Условием резонанса из выражения (1) будет
Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление x L = wL равно емкостному x C = 1/(wC ) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров — L , C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде
Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать
· изменением индуктивности L при постоянных значениях C и w ;
· изменением емкости C при постоянных значениях L и w ;
· изменением частоты w при постоянных значениях L и C .
Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.
При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Z min = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению .
Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю x C ®µ , x L ® 0 , и j® — 90° (рис. 1 б)). При бесконечном увеличении частоты — x L ®µ , x C ® 0 , а j® 90° . Равенство сопротивлений x L и x C наступает в режиме резонанса при частоте w 0 .
Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i =I m sinwt . Падение напряжения на входе уравновешивается суммой напряжений на элементах
Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура
А при резонансной частоте
величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.
Следовательно, при резонансе
· напряжение на резисторе равно напряжению на входе контура;
· напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура;
· соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений.
Отношение волнового сопротивления к резистивному r /R = Q , называется добротностью контура , а величина обратная D =1/Q — затуханием . Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений .
Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе
U =RI 0
где i =I /I 0 , u k =U k /U , v = w /w 0 — соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I 0 , напряжение на входе U и частота w 0 в режиме резонанса.
Абсолютный и относительный ток в контуре равен
Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q =2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.
На рис. 3 кривые A (v), B (v) и C (v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A (v)=u L (v) и B (v)=u C (v) имеют максимумы, напряжения в которых определяются выражением
, (9)а относительные частоты максимумов равны
(10)При увеличении добротности Q ®µA max = B max ®Q , а v 1 ®1.0 и v 2 ®1.0.
С уменьшением добротности максимумы кривых u L (v) и u С (v) смещаются от резонансной частоты, а при Q 2
Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 4. В целом они дают представление о характере изменения величин, но удобнее делать сопоставление в относительных единицах.
На рис. 5 представлены кривые рис. 4 в относительных единицах. Здесь видно, что увеличение добротности влияет на скорость изменения тока при изменении частоты.
Можно показать, что разность относительных частот, соответствующих значениям относительного тока
, равна затуханию контура D =1/Q =v 2 -v 1 .Перейдем теперь к анализу зависимости фазового сдвига между током и напряжением на входе контура от частоты. Из выражения (1) угол j равен
Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника? может оказаться равной угловой частоте? 0 , с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний? 0 , возникающих в какой-либо физической системе, с частотой вынужденных колебаний?, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота? 0 , при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление X L равно емкостному Х с и полное сопротивление Z становится равным активному сопротивлению R:
Z = ?(R 2 + [? 0 L — 1/(? 0 C)] 2) = R
В этом случае напряжения на индуктивности U L и емкости U c равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = X L -X с становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений U L и U c , причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
Угловая частота?0, при которой имеют место условия резонанса, определяется из равенства ? o L = 1/(? 0 С).
Отсюда имеем
? o = 1/?(LC) (74)
Если плавно изменять угловую частоту? источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при? o), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
Резонанс токов. Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R 1 =R 2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ? o L = 1/(? o C) . Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U?(G 2 +(B L -B C) 2)= 0 . Значения токов в ветвях I 1 и I 2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°). Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи I L и I с, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний? 0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту. Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов I L и I с. Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения
в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R 1 и R 2 , будет равенство реактивных проводимостей B L = B C ветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1 L и I с равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту? о источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения I min = I a при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты? 0 .
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах. Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
Что такое резонанс токов и напряжений. Резонанс в электрической цепи Резонанс в электрических цепях применение
Резонанс является одним из самых распространенных в природе резонанса можно наблюдать в механических, электрических и даже тепловых системах. Без резонанса у нас не было бы радио, телевидения, музыки и даже качелей на детских площадках, не говоря уже об эффективнейших диагностических системах, применяемых в современной медицине. Одним из самых интересных и полезных видов резонанса в электрической цепи является резонанс напряжений.
Элементы резонансной цепи
Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:
- R — резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
- L — индуктивность. Индуктивность в электрических цепях — аналог массы или инерции в механических системах. Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
- С — обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.
Понятие резонансного контура
Ключевыми элементами резонансного контура являются индуктивность (L) и емкость (C). Резистор имеет тенденцию к гашению колебаний, поэтому он удаляет энергию из контура. При рассмотрении процессов, происходящих в колебательном контуре, мы его временно игнорируем, но необходимо помнить, что подобно силе трения в механических системах электрическое сопротивление в цепях невозможно устранить.
Резонанс напряжений и резонанс токов
В зависимости от способа соединения ключевых элементов резонансный контур может быть последовательным и параллельным. При подключении последовательного колебательного контура к источнику напряжения с частотой сигнала, совпадающей с собственной частотой, при определенных условиях в нем возникает резонанс напряжений. Резонанс в электрической цепи с параллельно соединенными реактивными элементами называется резонансом токов.
Собственная частота резонансного контура
Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.
В момент времени «0» вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу). Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя — отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени. Отметим, что T на нашем графике — это время, необходимое для завершения одного колебания, носящего в электротехнике название «период колебания».
Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.
Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина — отрицательный заряд (рисунок внизу).
Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.
Частота колебаний может быть аппроксимирована следующим образом:
где: F — частота, L — индуктивность, C — емкость.
Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.
Исследование резонанса напряжений
В реальных схемах LC всегда присутствует небольшое сопротивление, которое с каждым циклом уменьшает прирост амплитуды тока. После нескольких циклов ток уменьшается до нуля. Этот эффект называется «затухание синусоидального сигнала». Скорость затухания тока до нулевого значения зависит от величины сопротивления в цепи. Тем не менее, сопротивление не изменяет частоту колебаний резонансного контура. Если сопротивление достаточно велико, синусоидальные колебания в контуре не возникнут вообще.
Очевидно, там, где существует собственная частота колебаний, есть возможность возбуждения резонансного процесса. Мы делаем это, включая в последовательную цепь источник питания (АС), как показано на рисунке слева. Термин «переменный» означает, что выходное напряжение источника колеблется с определенной частотой. Если частота источника питания совпадает с собственной частотой контура, возникает резонанс напряжений.
Условия возникновения
Сейчас мы рассмотрим условия возникновения резонанса напряжений. Как показано на последнем рисунке, мы вернули резистор в контур. При отсутствии резистора в контуре ток в резонансной цепи будет нарастать до некоторого максимального значения, определяемого параметрами элементов контура и мощностью источника питания. Увеличение сопротивления резистора в резонансной цепи повышает тенденцию к затуханию тока в контуре, но не влияет на частоту резонансных колебаний. Как правило, режим резонанса напряжений не наступает, если сопротивление цепи резонанса удовлетворяет условию R = 2(L/C) 0,5 .
Использование резонанса напряжений для передачи радиосигнала
Явление резонанса напряжений является не только любопытнейшим физическим феноменом. Оно играет исключительную роль в технологии беспроводных коммуникаций — радио, телевидении, сотовой телефонии. Передатчики, используемые для беспроводной передачи информации, в обязательном порядке содержат схемы, предназначенные для резонирования на определенной для каждого устройства частоте, называемой несущей частотой. При помощи передающей антенны, подключенной к передатчику, он излучает на несущей частоте.
Антенна на другом конце приемо-передающего тракта получает этот сигнал и подает его на приемный контур, предназначенный для резонирования на частоте несущей. Очевидно, что антенна принимает множество сигналов на различных частотах, не говоря уже о фоновом шуме. Благодаря наличию на входе приемного устройства, настроенного на несущую частоту резонансного контура, приемник выбирает единственно правильную частоту, отсеивая все ненужные.
После детектирования амплитудно-модулированного (AM) радиосигнала, выделенный из него низкочастотный сигнал (НЧ) усиливается и подается на звуковоспроизводящее устройство. Это простейшая форма радиопередачи очень чувствительна к шумам и помехам.
Для повышения качества принимаемой информации разработаны и успешно используются другие, более совершенные способы передачи радиосигнала, которые также базируются на использовании настроенных резонансных систем.
Или FM-радио решает многие из проблем радиопередачи с амплитудно-модулированным передающим сигналом, однако это достигается ценой существенного усложнения системы передачи. В FM-радио системные звуки в электронном тракте превращаются в небольшие изменения несущей частоты. Часть оборудования, которое выполняет это преобразование, называется «модулятор» и используется с передатчиком.
Соответственно, к приемнику должен быть добавлен демодулятор для преобразования сигнала обратно в форму, которая может быть воспроизведена через громкоговоритель.
Другие примеры использования резонанса напряжения
Резонанс напряжений как основополагающий принцип заложен также в схемотехнике многочисленных фильтров, широко применяемых в электротехнике для устранения вредных и ненужных сигналов, сглаживания пульсаций и генерирования синусоидальных сигналов.
>> Резонанс в электрической цепи
§ 35 РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса . Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний (позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При механических колебаниях резонанс выражен отчетливо при малых значениях коэфициента трения . В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока но внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном кон-lype должен быть выражен отчетливо при малом активном сопротивлении R.
Мы с вами уже знаем, что если активное сопротивление мало, то собственная циклическая частота колебаний в контуре определяется формулой
При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.
1. Может ли амплитуда силы тока при резонансе превысить силу постоянного тока в цепи с таким же активным сопротивлением и постоянным напряжением, равным амплитуде переменного напряжения!
2. Чему равна разность фаз между колебаниями силы тока и напряжения при резонансе!
3. При каком условии резонансные свойства контура выражены наиболее отчетливо!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Книги и учебники согласно календарному плануванння по физике 11 класса скачать , помощь школьнику онлайн
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиРезонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. B L =B C .
Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Данная схема соответствует цепи, представленной на рис. 8, а , для которойR 2 = 0, а R 1 =R к (здесьR к – активное сопротивление катушки индуктивности). Полная проводимость такой цепиY =.
Условие резонанса токов (B L =B C) можно записать через соответствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивлениеR к, определяется выражениемB L =X L /=L /(R к 2 + 2 L 2), а проводимость конденсатора без учета его активного сопротивления (R C = 0)B C =X C /= 1/X C =C , то условие резонанса может быть записано в виде
L /(+ 2 L 2) = C .
Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров R к,L ,C ипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров.
Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.
В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L , путем изменения емкостиС батареи конденсаторов. С изменением емкостной проводимостиB C =C , пропорциональной емкости конденсатора, происходит изменение полной проводимостиY , общего токаI и коэффициента мощности cos. Указанные зависимости приведены на рис. 10,a . Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (B L =B C) своего минимума, а затем возрастает с увеличениемС , в пределе стремясь к бесконечности. Общий токI =YU , потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости.
Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G /Y . В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями.
a) б)
1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей:
Y = =G .
2. Минимальное значение проводимости обусловливает минимальное значение тока цепи:
I = YU = GU .
3. Емкостный ток I C и индуктивная составляющаяI L тока катушкиI к оказываются при этом равными по величине, а активная составляющая тока катушкиI а1 становится равной токуI , потребляемому из сети:
I р1 = I L = B L U = B C U = I C = I р2 ; I а = I а1 =GU = YU =I .
При этом реактивные составляющие токов I L иI C в зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI , потребляемый электрической цепью из сети.
4. Реактивная составляющая полной мощности цепи при B L =B C оказывается равной нулю:
Q = B L U 2 B C U 2 = Q L Q C = 0.
При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу.
5. Полная мощность цепи при резонансе равна ее активной составляющей:
S = YU 2 = GU 2 = P .
6. Коэффициент мощности всей цепи при резонансе:
cos = P /S = GU 2 /YU 2 = 1.
Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б . В табл. 2 методических указаний по выполнению работы обозначениямI L , I K , I C соответствуют обозначенияI р1 , I 1 , I р2 на векторной диаграмме токов (рис. 10,б ).
Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность. К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах.
Основы > Теоретические основы электротехники
Резонансные явления в электрических цепях
Идеальное активное сопротивление от частоты не зависит, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:
Резонанс напряжений
Резонансом
в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю
. Режим резонанса может быть получен при изменении частоты
питающего напряжения или изменением параметров элементов L и С.
При последовательном соединении возникает резонанс напряжения.
Последовательное соединение
R, L, C.
Знаменатель данного выражения есть модуль комплексного сопротивления, который зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения по фазе:
Максимальная амплитуда силы тока достигается при условии минимума полного сопротивления, т. е. при
где
— резонансная частота напряжения, определяемая из условия
При последовательном соединении в цепь конденсатора и соленоида силы токов в каждом из участков цепи, как известно, равны. Поэтому, умножив левую и правую части последнего соотношения на силу тока
Im
, получим
В этом выражении слева — амплитуда напряжения
на концах соленоида, а справа — амплитуда напряжения
на обкладках конденсатора.
Мы видим, что
. Отсюда получаем
Знак минус указывает на то, что колебания напряжения на участках с индуктивностью и емкостью происходят в противофазе.
Режим электрической цепи при последовательном соединении индуктивности и емкости, характеризующийся равенством напряжений на индуктивности и емкости, называют
резонансом напряжений
.
Волновое или характеристическое сопротивление последовательного контура
Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется
добротностью контура
:
Добротность контура представляет собой коэффициент усиления по напряжению и в катушках индуктивности может достигать сотен единиц:
При напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике. В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.
Резонанс токов
При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю).
В этом случае:
Параллельное соединение реактивных элементов
тогда
При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения.
Такое явление называется
резонансом токов
.
Волновая проводимость
При
ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.
Резонансную частоту тока
найдем из условия равенства реактивных проводимостей ветвей.
После ряда преобразований получим:
Из формулы следует, что:
1)
резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2)
резонанс возможен, если
и
больше или меньше
r
, в противном случае частота будет мнимой величиной и резонанс невозможен;
3)
если
, то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4)
при
резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии
.
В колебательном контуре, обладающем индуктивностью L, емкостью C и сопротивлением R, свободные электрические колебания имеют тенденцию к затуханию. Чтобы колебания не затухали, необходимо периодически пополнять контур энергией, тогда возникнут вынужденные колебания, которые не будут затухать, ведь внешняя переменная ЭДС станет теперь поддерживать колебания в контуре.
Если колебания поддерживать источником внешней гармонической ЭДС, частота которой f очень близка к резонансной частоте колебательного контура F, то амплитуда электрических колебаний U в контуре станет резко возрастать, то есть наступит явление электрического резонанса .
Рассмотрим сначала поведение конденсатора C в цепи переменного тока. Если к генератору, напряжение U на выводах которого меняется по гармоническому закону, присоединить конденсатор C, то заряд q на обкладках конденсатора станет меняться также по гармоническому закону, как и ток I в цепи. Чем больше емкость конденсатора, и чем выше частота f, прикладываемой к нему гармонической ЭДС, тем больше окажется ток I.
С этим фактом связано представление о так называемом емкостном сопротивлении конденсатора XC, которое он вносит в цепь переменного тока, ограничивая ток подобно активному сопротивлению R, но в сравнении с активным сопротивлением, конденсатор не рассеивает энергию в виде тепла.
Если активное сопротивление рассеивает энергию, и таким образом ограничивает ток, то конденсатор ограничивает ток просто из-за того, что в нем не успевает уместиться больше заряда, чем генератор может дать за четверть периода, к тому же в следующую четверть периода конденсатор отдает энергию, которая накопилась в электрическом поле его диэлектрика, обратно генератору, то есть хоть ток и ограничен, энергия не рассеивается (потерями в проводах и в диэлектрике пренебрежем).
Теперь рассмотрим поведение индуктивности L в цепи переменного тока. Если вместо конденсатора присоединить к генератору катушку, обладающую индуктивностью L, то при подаче от генератора синусоидальной (гармонической) ЭДС на выводы катушки, — в ней начнет возникать ЭДС самоиндукции , поскольку при изменении тока через индуктивность, увеличивающееся магнитное поле катушки стремится препятствовать росту тока (закон Ленца), то есть получается, что катушка вносит в цепь переменного тока индуктивное сопротивление XL — дополнительное к сопротивлению провода R.
Чем больше индуктивность данной катушки, и чем выше частота F тока генератора, тем выше индуктивное сопротивление XL и меньше ток I, ведь ток просто не успевает устанавливаться, потому что ЭДС самоиндукции катушки ему мешает. И каждые четверть периода энергия, накопленная в магнитном поле катушки, возвращается к генератору (потерями в проводах пока пренебрежем).
В любом реальном колебательном контуре последовательно соединены индуктивность L, емкость C и активное сопротивление R.
Индуктивность и емкость действуют на ток противоположно в каждую четверть периода гармонической ЭДС источника: на обкладках конденсатора , хотя уменьшается ток, а при нарастании тока через индуктивность ток хоть и испытывает индуктивное сопротивление, но нарастает и поддерживается.
И во время разряда: разрядный ток конденсатора сначала большой, напряжение на его обкладках стремится установить большой ток, а индуктивность препятствует увеличению тока, и чем больше индуктивность, тем меньший разрядный ток будет иметь место. При этом активное сопротивление R вносит чисто активные потери. То есть полное сопротивление Z, последовательно включенных L, C и R, при частоте источника f, будет равно:
Из закона Ома для переменного тока очевидно, что амплитуда вынужденных колебаний пропорциональна амплитуде ЭДС и зависит от частоты. Полное сопротивление цепи будет наименьшим, а амплитуда тока будет наибольшей при условии, что индуктивное сопротивление и емкостное при данной частоте равны между собой, в этом случае наступит резонанс. Отсюда же выводится формула для резонансной частоты колебательного контура :
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой последовательно, то резонанс в такой цепи называется последовательным резонансом или резонансом напряжений. Характерная черта резонанса напряжений — значительные напряжения на емкости и на индуктивности, по сравнению с ЭДС источника.
Причина появления такой картины очевидна. На активном сопротивлении по закону Ома будет напряжение Ur, на емкости Uc, на индуктивности Ul, и составив отношение Uc к Ur можно найти величину добротности Q. Напряжение на емкости будет в Q раз больше ЭДС источника, такое же напряжение окажется приложенным к индуктивности.
То есть резонанс напряжений приводит к возрастанию напряжения на реактивных элементах в Q раз, а резонансный ток будет ограничен ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, сопротивление последовательного контура на резонансной частоте минимально.
Явление резонанса напряжений используют в , например если необходимо устранить из передаваемого сигнала составляющую тока определенной частоты, то параллельно приемнику ставят цепочку из соединенных последовательно конденсатора и катушки индуктивности, чтобы ток резонансной частоты этой LC-цепочки замкнулся бы через нее, и не попал к бы приемнику.
Тогда токи частоты далекой от резонансной частоты LC-цепочки будут проходить в нагрузку беспрепятственно, и только близкие к резонансу по частоте токи — будут находить себе кротчайший путь через LC-цепочку.
Или наоборот. Если необходимо пропустить только ток определенной частоты, то LC-цепочку включают последовательно приемнику, тогда составляющие сигнала на резонансной частоте цепочки пройдут к нагрузке почти без потерь, а частоты далекие от резонанса окажутся сильно ослаблены и можно сказать, что к нагрузке совсем не попадут. Данный принцип применим к радиоприемникам, где перестраиваемый колебательный контур настраивают на прием строго определенной частоты нужной радиостанции.
Вообще резонанс напряжений в электротехнике является нежелательным явлением, поскольку он вызывает перенапряжения и выход из строя оборудования.
В качестве простого примера можно привести длинную кабельную линию, которая по какой-то причине оказалась не подключенной к нагрузке, но при этом питается от промежуточного трансформатора. Такая линия с распределенной емкостью и индуктивностью, если ее резонансная частота совпадет с частотой питающей сети, просто будет пробита и выйдет из строя. Чтобы предотвратить разрушение кабелей от случайного резонанса напряжений, применяют вспомогательную нагрузку.
Но иногда резонанс напряжений играет нам на руку и не только в радиоприемниках. Например, бывает, что в сельской местности напряжение в сети непредсказуемо упало, а станку нужно напряжение не менее 220 вольт. В этом случае явление резонанса напряжений спасает.
Достаточно последовательно со станком (если приводом в нем является асинхронный двигатель) включить по несколько конденсаторов на фазу, и таким образом напряжение на обмотках статора поднимется.
Здесь важно правильно подобрать количество конденсаторов, чтобы они точно скомпенсировали своим емкостным сопротивлением вместе с индуктивным сопротивлением обмоток просадку напряжения в сети, то есть слегка приблизив цепь к резонансу — можно поднять упавшее напряжение даже под нагрузкой.
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой параллельно, то резонанс в такой цепи называется параллельным резонансом или резонансом токов. Характерная черта резонанса токов — значительные токи через емкость и индуктивность, по сравнению с током источника.
Причина появления такой картины очевидна. Ток через активное сопротивление по закону Ома будет равен U/R, через емкость U/XC, через индуктивность U/XL, и составив отношение IL к I можно найти величину добротности Q. Ток через индуктивность будет в Q раз больше тока источника, такой же ток будет течь каждые пол периода в конденсатор и из него.
То есть резонанс токов приводит к возрастанию тока через реактивные элементы в Q раз, а резонансная ЭДС будет ограничена ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, на резонансной частоте сопротивление параллельного колебательного контура максимально.
Аналогично резонансу напряжений, резонанс токов применяется в различных фильтрах. Но включенный в цепь, параллельный контур действует наоборот, чем в случае с последовательным: установленный параллельно нагрузке, параллельный колебательный контур позволит току резонансной частоты контура пройти в нагрузку, поскольку сопротивление самого контура на собственной резонансной частоте максимально.
Установленный последовательно с нагрузкой, параллельный колебательный контур не пропустит сигнал резонансной частоты, поскольку все напряжение упадет на контуре, а на нагрузку придется мизерная доля сигнала резонансной частоты.
Так, основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты.
В электротехнике резонанс токов используется с целью достижения высокого коэффициента мощности нагрузок, обладающих значительными индуктивными и емкостными составляющими.
Например, представляют собой конденсаторы, подключаемые параллельно обмоткам асинхронных двигателей и трансформаторов, работающих под нагрузкой ниже номинальной.
К таким решениям прибегают как раз с целью достижения резонанса токов (параллельного резонанса), когда индуктивное сопротивление оборудования делается равным емкостному сопротивлению подключаемых конденсаторов на частоте сети, чтобы реактивная энергия циркулировала между конденсаторами и оборудованием, а не между оборудованием и сетью; чтобы сеть отдавала энергию только тогда, когда оборудование нагружено и потребляет активную мощность.
Когда же оборудование работает в холостую, сеть оказывается подключена параллельно резонансному контуру (внешние конденсаторы и индуктивность оборудования), который представляет для сети очень большое комплексное сопротивление и позволяет снизиться .
Электрический резонанс и его учет в технике. Резонанс в электрической цепи — Гипермаркет знаний
Резонанс является одним из самых распространенных в природе резонанса можно наблюдать в механических, электрических и даже тепловых системах. Без резонанса у нас не было бы радио, телевидения, музыки и даже качелей на детских площадках, не говоря уже об эффективнейших диагностических системах, применяемых в современной медицине. Одним из самых интересных и полезных видов резонанса в электрической цепи является резонанс напряжений.
Элементы резонансной цепи
Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:
- R — резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
- L — индуктивность. Индуктивность в электрических цепях — аналог массы или инерции в механических системах. Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
- С — обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.
Понятие резонансного контура
Ключевыми элементами резонансного контура являются индуктивность (L) и емкость (C). Резистор имеет тенденцию к гашению колебаний, поэтому он удаляет энергию из контура. При рассмотрении процессов, происходящих в колебательном контуре, мы его временно игнорируем, но необходимо помнить, что подобно силе трения в механических системах электрическое сопротивление в цепях невозможно устранить.
Резонанс напряжений и резонанс токов
В зависимости от способа соединения ключевых элементов резонансный контур может быть последовательным и параллельным. При подключении последовательного колебательного контура к источнику напряжения с частотой сигнала, совпадающей с собственной частотой, при определенных условиях в нем возникает резонанс напряжений. Резонанс в электрической цепи с параллельно соединенными реактивными элементами называется резонансом токов.
Собственная частота резонансного контура
Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.
В момент времени «0» вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу). Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя — отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени. Отметим, что T на нашем графике — это время, необходимое для завершения одного колебания, носящего в электротехнике название «период колебания».
Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.
Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина — отрицательный заряд (рисунок внизу).
Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.
Частота колебаний может быть аппроксимирована следующим образом:
где: F — частота, L — индуктивность, C — емкость.
Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.
Исследование резонанса напряжений
В реальных схемах LC всегда присутствует небольшое сопротивление, которое с каждым циклом уменьшает прирост амплитуды тока. После нескольких циклов ток уменьшается до нуля. Этот эффект называется «затухание синусоидального сигнала». Скорость затухания тока до нулевого значения зависит от величины сопротивления в цепи. Тем не менее, сопротивление не изменяет частоту колебаний резонансного контура. Если сопротивление достаточно велико, синусоидальные колебания в контуре не возникнут вообще.
Очевидно, там, где существует собственная частота колебаний, есть возможность возбуждения резонансного процесса. Мы делаем это, включая в последовательную цепь источник питания (АС), как показано на рисунке слева. Термин «переменный» означает, что выходное напряжение источника колеблется с определенной частотой. Если частота источника питания совпадает с собственной частотой контура, возникает резонанс напряжений.
Условия возникновения
Сейчас мы рассмотрим условия возникновения резонанса напряжений. Как показано на последнем рисунке, мы вернули резистор в контур. При отсутствии резистора в контуре ток в резонансной цепи будет нарастать до некоторого максимального значения, определяемого параметрами элементов контура и мощностью источника питания. Увеличение сопротивления резистора в резонансной цепи повышает тенденцию к затуханию тока в контуре, но не влияет на частоту резонансных колебаний. Как правило, режим резонанса напряжений не наступает, если сопротивление цепи резонанса удовлетворяет условию R = 2(L/C) 0,5 .
Использование резонанса напряжений для передачи радиосигнала
Явление резонанса напряжений является не только любопытнейшим физическим феноменом. Оно играет исключительную роль в технологии беспроводных коммуникаций — радио, телевидении, сотовой телефонии. Передатчики, используемые для беспроводной передачи информации, в обязательном порядке содержат схемы, предназначенные для резонирования на определенной для каждого устройства частоте, называемой несущей частотой. При помощи передающей антенны, подключенной к передатчику, он излучает на несущей частоте.
Антенна на другом конце приемо-передающего тракта получает этот сигнал и подает его на приемный контур, предназначенный для резонирования на частоте несущей. Очевидно, что антенна принимает множество сигналов на различных частотах, не говоря уже о фоновом шуме. Благодаря наличию на входе приемного устройства, настроенного на несущую частоту резонансного контура, приемник выбирает единственно правильную частоту, отсеивая все ненужные.
После детектирования амплитудно-модулированного (AM) радиосигнала, выделенный из него низкочастотный сигнал (НЧ) усиливается и подается на звуковоспроизводящее устройство. Это простейшая форма радиопередачи очень чувствительна к шумам и помехам.
Для повышения качества принимаемой информации разработаны и успешно используются другие, более совершенные способы передачи радиосигнала, которые также базируются на использовании настроенных резонансных систем.
Или FM-радио решает многие из проблем радиопередачи с амплитудно-модулированным передающим сигналом, однако это достигается ценой существенного усложнения системы передачи. В FM-радио системные звуки в электронном тракте превращаются в небольшие изменения несущей частоты. Часть оборудования, которое выполняет это преобразование, называется «модулятор» и используется с передатчиком.
Соответственно, к приемнику должен быть добавлен демодулятор для преобразования сигнала обратно в форму, которая может быть воспроизведена через громкоговоритель.
Другие примеры использования резонанса напряжения
Резонанс напряжений как основополагающий принцип заложен также в схемотехнике многочисленных фильтров, широко применяемых в электротехнике для устранения вредных и ненужных сигналов, сглаживания пульсаций и генерирования синусоидальных сигналов.
Мы убедились в совпадении законов свободных механических и электрических колебаний. Но столь же полное сходство законов имеется и в случае вынужденных колебании, вызываемых действием внешней периодической силы. В случае электрических колебаний роль силы играет, как мы видели в предыдущем параграфе, электродвижущая сила (сокращенно э. д. с). Просмотрите вновь § 12, где мы описали вынужденные колебания, § 13, в котором говорится о явлении резонанса, и § 14, в котором рассмотрено влияние затухания на резонансные явления в колебательной системе. Все сказанное там о механических вынужденных колебаниях целиком относится и к электрическим. И здесь частота вынужденных колебаний в колебательном контуре равна частоте действующей в этом контуре э. д. с. Амплитуда вынужденных колебаний тем больше, чем ближе частота э. д. с. к частоте свободных колебаний в контуре. При совпадении этих частот амплитуда становится наибольшей, получается электрический резонанс: ток в контуре и напряжение на его конденсаторе могут очень сильно превышать те, которые получаются при отстройке, т. е, вдали от резонанса. Резонансные явления выражены тем сильнее и резче, чем меньше сопротивление контура, которое, таким образом, и здесь играет такую же роль, как трение в механической системе.
Все эти явления легко наблюдать, использовав для получения гармонической э. д. с. городской переменный ток и построив колебательный контур, собственную частоту которого можно менять в обе стороны от частоты тока (). Чтобы избежать при этом высоких резонансных напряжений в контуре, которые (при напряжении в городской сети ) могут достичь нескольких киловольт, следует воспользоваться понижающим трансформатором.
На рис. 53 показано расположение приборов и электрическая схема опыта (обозначения на рисунке и на схеме одинаковые). В схему включены понижающий трансформатор 1, конденсатор 2, дроссели 3 и 4, представляющие собой катушки индуктивности с железными сердечниками, которые нужны для получения требуемой большой индуктивности. Для удобства настройки контура индуктивность его составлена из индуктивностей двух отдельных катушек. Настройка осуществляется тем, что у одного из дросселей (4) сердечник имеет воздушный зазор, ширину которого можно плавно менять в пределах , меняя тем самым общую индуктивность. Чем шире зазор, тем меньше индуктивность. В подписи к рис. 53 указаны примерные значения всех величин. Напряжение на конденсаторе измеряется вольтметром переменного тока , а амперметр переменного тока позволяет следить за током в контуре.
Опыт показывает следующее: при малой индуктивности контура напряжение на конденсаторе составляет немногим более, чем наводимая в контуре э. д. с, т. е. несколько вольт. Увеличивая индуктивность, мы увидим, что напряжение растет; это нарастание становится все более и более резким по мере приближения к резонансному значению индуктивности. При тех числовых данных, которые указаны в подписи к рис. 53, напряжение поднимается выше . При дальнейшем увеличении индуктивности напряжение вновь падает. Ток в контуре изменяется пропорционально напряжению на конденсаторе и при резонансе может дойти до .
Этот опыт соответствует механическому опыту с грузом на пружине, который был описан в § 12. Там нам было удобней менять частоту действующей силы, здесь же мы проходим через резонансную настройку, меняя собственную частоту колебательной системы — нашего контура. Сущность явления резонанса от этого не меняется.
Рис. 53. Получение электрического резонанса на частоту городского тока: 1 — трансформатор, понижающий напряжение, например с до , 2 — конденсатор емкости , 3 — дроссель, индуктивность которого , а сопротивление обмотки равно , 4 — дроссель с переменным воздушным зазором, индуктивность которого при ширине и изменяется при изменении ширины зазора на в обе стороны от указанного (резонансного) значения
Роль электрического резонанса в технике огромна. Приведем лишь один пример. По существу на резонансе основана техника радиоприема. Многочисленные радиостанции излучают электромагнитные волны, которые наводят в антенне радиоприемника переменные э. д. с. (электрические колебания), причем каждая радиостанция наводит колебания своей определенной частоты. Если бы мы не умели выделить из этой сложнейшей смеси колебаний колебания, наводимые интересующей нас радиостанцией, то никакой радиоприем не был бы возможен. Здесь и приходит на помощь электрический резонанс.
Мы соединяем с антенной колебательный контур, например через индуктивность, как показано на рис. 54.
Емкость конденсатора можно плавно изменять, меняя тем самым собственную частоту контура. Если мы настроим контур на желательную частоту, например , то э. д. с. с частотой , вызовет в контуре сильные вынужденные колебания, а все остальные э. д. с.- слабые. Следовательно, резонанс позволяет по желанию настраивать приемник на частоту выбранной станции.
Рис. 54. Резонанс позволяет настраиваться на желаемую станцию и отстраиваться от всех остальных. Стрелка на конденсаторе указывает на то, что емкость конденсатора можно менять
Разумеется, в электротехнике, как и в машиностроении, резонанс может явиться величайшим злом там, где его не должно быть. Если электрическая цепь рассчитана на работу в отсутствие резонанса, то возникновение резонанса вызовет аварию: провода раскалятся от чрезмерно сильных токов, изоляция будет пробита из-за высоких резонансных напряжении, и т. п. В прошлом веке, когда электрические колебания были еще недостаточно изучены, такие аварии случались. Теперь же мы умеем в зависимости от условий либо использовать резонанс, либо устранять его.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Резонанс. Его применение
Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
резонанс напряжение электрический медицина
Использование Резонанса
В медицине
Магнитно-резонансная томография, или ее сокращенное название МРТ, считается одним из самых надежных методов лучевой диагностики. Очевидным плюсом использования такого способа проверить состояние организма является то, что оно не является ионизирующим излучением и дает довольно точные результаты при исследовании мышечной и суставной системы организма, помогает с высокой вероятностью диагностировать различные заболевания позвоночника и центральной нервной системы.
Сам процесс обследования довольно прост и абсолютно безболезненный — все, что вы услышите, лишь сильный шум, но от него хорошо защищают наушники, которые выдаст вам перед процедурой врач. Возможны только два вида неудобств, которых не получится избежать. В первую очередь это касается тех людей, которые боятся замкнутых пространств — диагностируемый пациент ложится на горизонтальную лежанку и автоматические реле передвигают его внутрь узкой трубы с сильным магнитным полем, где он находится примерно в течение 20 минут. Во время диагностики не следует шевелиться, чтобы результаты получились как можно точнее. Второе неудобство, которое вызывает резонансная томография при исследовании малого таза, это необходимость наполненности мочевого пузыря.
Если ваши близкие желают присутствовать при диагностировании, они обязаны подписать информационный документ, согласно которому они ознакомлены с правилами поведения в диагностическом кабинете и не имеют никаких противопоказаний для нахождения рядом с сильным магнитным полем. Одной из причин невозможности нахождения в помещении управления МРТ является наличие в организме посторонних металлических компонентов.
Испол ьзование резонанса в радиосвязи
Явление электрического резонанса широко используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур (рис. 4.20). Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот. Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется путем изменения емкости конденсатора. В этом обычно состоит настройка радиоприемника на определенную радиостанцию. Необходимость учета возможности резонанса в электрической цепи. В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии.
Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.
Такого рода аварии нередко случались еще сравнительно недавно, когда плохо представляли себе законы электрических колебаний и не умели правильно рассчитывать электрические цепи.
При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.
Явление резонанса электрических напряжений наблюдается в цепи последовательного колебательного контура, состоящего из емкости (конденсатора), индуктивности и резистора (сопротивления). Для обеспечения энергетической подпитки колебательного контура в последовательную цепь включается также источник электродвижущей силы Е. Источник вырабатывает переменное напряжение с частотой W. При резонансе ток, циркулирующий в последовательной цепи, должен совпадать по фазе с э.д.с. Е. Это обеспечивается, если общее сопротивление схемы Z = R+J(WL — 1/WС) будет лишь активным, т.е. Z=R. Равенство:
(L — 1/WС) = 0 (1),
является математическим условием резонанса в колебательном контуре. При этом величина тока в цепи составит I = E/R. Если преобразовать равенство (1), то получим:
В этом выражении W — является резонансной частотой контура.
Важно то, что в процессе резонанса напряжение на индуктивности равно напряжению на конденсаторе и составляет:
UL = U = WL * I = WLE/R
Общая сумма энергий в индуктивности и емкости (магнитного и электрического полей) постоянна. Это объясняется тем, что между этими полями происходит колебательный обмен энергиями. Суммарное ее количество в любой момент неизменно. При этом обмена энергией между ее источником Е и цепью не происходит. Вместо этого имеет место непрерывное преобразование одного вида энергии в другой.
Для колебательных контуров применятся термин добротность, которая показывает, как соотносятся напряжение на реактивном элемента (емкость или индуктивность) и входное напряжение контура. Добротность вычисляется по формуле:
Для идеальной последовательной цепи с нулевым активным сопротивлением возникновение резонанса сопровождается незатухающими колебаниями. На практике затухание колебаний компенсируется подпиткой контура от генератора колебаний с частотой резонанса.
Применение резонанса напряженийЯвление колебательного резонанса широко используется в радиоэлектронике. В частности, входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, изменяемая с помощью регулировки емкости конденсатора, совпадает с частотой сигнала радиостанции, которую необходимо принять.
В электроэнергетике возникновение резонанса напряжений вследствие сопутствующих ему перенапряжений чревато нежелательными последствиями. Например, в случае подключения к генератору или промежуточному трансформатору длинной кабельной линии (являющейся колебательным контуром с распределенной емкостью и индуктивностью), не соединенной на приемном конце с нагрузкой (это называется режимом холостого хода), весь контур может оказаться в резонансом состоянии. В такой ситуации напряжения, возникающие на некоторых участках цепи, могут оказаться выше расчетных. Это может грозить пробоем изоляции кабеля и выходом его из строя. Такая ситуация предотвращается применением вспомогательной нагрузки.
Размещено на Allbest.ru
…Подобные документы
Биологическое влияние электрических и магнитных полей на организм людей и животных. Суть явления электронного парамагнитного резонанса. Исследования с помощью ЭПР металлсодержащих белков. Метод ядерного магнитного резонанса. Применение ЯМР в медицине.
реферат , добавлен 29.04.2013
Электрические цепи переменного тока, их параметры. Понятие и основные условия явления резонанса. Особенности изменения индуктивного и емкостного сопротивления. Анализ зависимости фазового сдвига между током и напряжением на входе контура от частоты.
контрольная работа , добавлен 16.01.2010
Схема цепи с активным, индуктивным и емкостным сопротивлениями, включенными последовательно. Расчет значений тока и падения напряжения. Понятие резонанса напряжений. Снятие показаний осциллографа. Зависимость сопротивления от частоты входного напряжения.
лабораторная работа , добавлен 10.07.2013
Возбуждение ядер в магнитном поле. Условие магнитного резонанса и процессы релаксации ядер. Спин-спиновое взаимодействие частиц в молекуле. Схема устройства ЯМР-спектрометра. Применение спектроскопии ЯМР 1H и 13CРазличные методы развязки протонов.
реферат , добавлен 23.10.2012
Особенности вынужденных колебаний. Явление резонанса, создание неразрушающихся конструкций. Использование колебаний в строительстве, технике, для сортировки сыпучих материалов. Вредные действия колебаний. Качка корабля и успокоители; антирезонанс.
курсовая работа , добавлен 21.03.2016
Определение влияния активного, индуктивного и емкостного сопротивления на мощность и сдвиг фаз между током и напряжением в электрической цепи переменного тока. Экспериментальное исследование резонансных явлений в параллельном колебательном контуре.
лабораторная работа , добавлен 11.07.2013
Исследование асинхронного трехфазного двигателя с фазным ротором. Схема последовательного и параллельного соединения элементов для исследования резонанса напряжений. Резонанс напряжений, токов. Зависимость тока от емкости при резонансе напряжений.
лабораторная работа , добавлен 19.05.2011
Электрическая цепь при последовательном и параллельном соединении элементов с R, L и C, их сравнительные характеристики. Треугольник напряжений и сопротивлений. Понятие и свойства резонанса токов и напряжений, направления и особенности его регулирования.
реферат , добавлен 27.07.2013
Практическая проверка и определение физических явлений, происходящих в цепи переменного тока при последовательном соединении резистора, индуктивной катушки и конденсатора. Получение резонанса напряжений, построение по опытным данным векторной диаграммы.
лабораторная работа , добавлен 12.01.2010
Квантовая механика как абстрактная математическая теория, выражающая процессы с помощью операторов физических величин. Магнитный момент и ядерный спин, их свойства и уравнение. Условия термодинамического равновесия и применение резонансного эффекта.
>> Резонанс в электрической цепи
§ 35 РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса . Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний (позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При механических колебаниях резонанс выражен отчетливо при малых значениях коэфициента трения . В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока но внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном кон-lype должен быть выражен отчетливо при малом активном сопротивлении R.
Мы с вами уже знаем, что если активное сопротивление мало, то собственная циклическая частота колебаний в контуре определяется формулой
При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.
1. Может ли амплитуда силы тока при резонансе превысить силу постоянного тока в цепи с таким же активным сопротивлением и постоянным напряжением, равным амплитуде переменного напряжения!
2. Чему равна разность фаз между колебаниями силы тока и напряжения при резонансе!
3. При каком условии резонансные свойства контура выражены наиболее отчетливо!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Книги и учебники согласно календарному плануванння по физике 11 класса скачать , помощь школьнику онлайн
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиРезонансом в физике называют явление, при котором амплитуды колебания системы резко возрастают. Это происходит при совпадении собственной и внешней возмущающей частот. В механике примером может служить маятник часов. Подобное поведение характерно и для электрических схем, включающих в себя элементы активной, индуктивной и емкостной нагрузки. Резонанс токов и напряжений очень важен, это явление нашло применение в таких областях науки, как радиосвязь и промышленное электроснабжение.
Векторы и теория
Для понимания смысла процессов, происходящих в цепях, включающих катушки индуктивности, конденсаторы и активные сопротивления, следует рассмотреть схему простейшего колебательного контура. Подобно тому, как обычный маятник попеременно переводит энергию из потенциального в кинетическое состояние, электрический заряд в RCL-цепочке, накапливаясь в емкости, перетекает в индуктивность. После этого процесс происходит в обратном направлении, и все начинается сначала. При этом векторная диаграмма выглядит следующим образом: ток емкостной нагрузки опережает на угол π/2 направление напряжения, индуктивная нагрузка отстает на такой же угол, а активная совпадает по фазе. Результирующий вектор имеет наклон по отношению к абсциссе, обозначаемый греческой буквой φ. Резонанс в цепи переменного тока наступает тогда, когда φ=0, соответственно, cos φ = 1. В переводе с языка математики эта выкладка означает, что ток, проходящий по всем элементам, по фазе совпадает с током в активной составляющей электросхемы.
Практическое применение в системах электроснабжения
Теоретически все эти выкладки понятны, но что они значат для практических вопросов? Очень многое! Всем известно, что полезная работа в любой схеме выполняется активной составляющей мощности. При этом большая часть потребления энергии приходится на электродвигатели, которых на любом предприятии немало, а они содержат в своей конструкции обмотки, представляющие собой индуктивную нагрузку и создающие угол φ, отличный он нуля. Для того чтобы возник резонанс токов, необходимо скомпенсировать реактивные сопротивления таким образом, чтобы их векторная сумма стала нулевой. На практике это достигается включением конденсатора, который создает противоположный сдвиг вектора тока.
Резонанс токов в радиоприемных устройствах
Резонанс токов имеет и другое, радиотехническое применение. Колебательный контур, составляющий основу каждого приемного устройства, состоит из катушки индуктивности и конденсатора. Меняя величину электрической емкости, можно добиться того, что сигнал с требуемой несущей частотой будет приниматься избирательно, а остальные всеволновые составляющие, принимаемые на антенну, включая и помехи, окажутся подавленными. На практике такой переменный конденсатор выглядит как два набора пластин, один из которых при вращении входит или выходит из другого, увеличивая или уменьшая при этом электрическую емкость. При этом создается резонанс токов, а радиоприемник оказывается настроенным на нужную частоту.
Читайте также…
применений резонанса | Резонанс
Пока что явление резонанса кажется бесполезным любопытством или, в лучшем случае, неприятностью, которую следует избегать (особенно, если последовательный резонанс вызывает короткое замыкание в нашем источнике переменного напряжения!). Тем не менее, это не так. Резонанс — очень ценное свойство реактивных цепей переменного тока, используемых в различных приложениях. Одно из применений резонанса — установить условие стабильной частоты в цепях, предназначенных для генерации сигналов переменного тока.Обычно для этой цели используется параллельная (резервуарная) цепь, в которой конденсатор и индуктор напрямую соединены вместе, обмениваясь энергией между собой. Подобно тому, как маятник может использоваться для стабилизации частоты колебаний часового механизма, так и контур резервуара может использоваться для стабилизации электрической частоты цепи генератора переменного тока . Как было отмечено ранее, частота, устанавливаемая контуром резервуара, зависит исключительно от значений L и C, а не от величин напряжения или тока, присутствующих в колебаниях:
Резонансный контур служит источником стабильной частоты.
Другое применение резонанса — в приложениях, где желательны эффекты значительного увеличения или уменьшения импеданса на определенной частоте. Резонансный контур может использоваться для «блокировки» (наличия высокого импеданса) частоты или диапазона частот, таким образом действуя как своего рода частотный «фильтр», чтобы исключить определенные частоты из смеси других. Фактически, эти конкретные схемы называются , фильтрами , и их конструкция сама по себе составляет предмет изучения:
Резонансный контур служит фильтром.
По сути, так работают схемы тюнера аналогового радиоприемника для фильтрации или выбора частоты одной станции из смеси сигналов различных частот радиостанций, перехваченных антенной.
ОБЗОР:
- Резонанс может использоваться для поддержания колебаний цепи переменного тока на постоянной частоте, так же как маятник может использоваться для поддержания постоянной скорости колебаний в механизме хронометража.
- Резонанс можно использовать из-за его свойств импеданса: резкого увеличения или уменьшения импеданса для определенных частот.Схемы, предназначенные для экранирования определенных частот из смеси различных частот, называются фильтрами .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Физика резонанса
Электрические схемы
Трудно понять идею, что электрические цепи могут резонируют, потому что мы этого не видим. Тем не менее, это один из самых полезные и распространенные формы резонанса.
Резонанс может возникать в так называемом RLC схема. Буквы обозначают разные части схемы. р для резистора. Это устройства, преобразующие электрическую энергию. в тепловую энергию. Другими словами, они удаляют энергию из цепь и преобразовать ее в тепло. L обозначает индуктор. (Как они придумали L для индуктора трудно понять.) Индуктивность в электрических цепях подобна массе или инерция в механических системах.Это ничего не значит, пока вы не попытаетесь изменить. В механике изменение — это изменение скорости. В электрическая цепь это изменение тока. Когда это происходит, индуктивность сопротивляется менять. C — для конденсаторов, которые хранят электрическую энергия почти так же, как пружины хранят механическую энергию. Индуктор концентрирует и хранит магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым накапливает электрическую энергию.
Конечно, первый шаг в понимании резонанса в любой системе — найти собственную частоту системы. Здесь индуктор (L) и конденсатор (C) являются ключевыми компонентами. В резистор имеет тенденцию гасить колебания, потому что он забирает энергию из схема. Для удобства мы временно проигнорируем это, но помните, Подобно трению в механических системах, сопротивление в цепях невозможно устранить.
|
| |||||
Мы можем заставить цепь колебаться в естественной частоты, сначала сохраняя электрическую энергию или, другими словами, заряжает свой конденсатор, как показано на рисунке 1.Когда это будет выполнено переключатель переведен в положение, показанное на рисунке 2.
| В момент времени = 0 все электрические энергия накапливается в конденсаторе, и ток равен нулю (см. Рисунок 3). Обратите внимание, что верхняя пластина конденсатора заряжена. положительно и низко отрицательно. Мы не видим электроны колебания в цепи, но мы можем измерить его с помощью амперметра и построить график зависимости тока от времени, чтобы представьте себе, что такое колебание.Обратите внимание, что T на нашем графике — это время, необходимое для завершения одного колебания. |
| ||||
| Ток течет по часовой стрелке (см. Рисунок 4).Энергия перетекает из конденсатора в катушку индуктивности. Сначала может показаться странным, что индуктор содержит энергию, но это подобна кинетической энергии, содержащейся в движущейся массе. |
| ||||
| В конце концов энергия возвращается в конденсатор, но обратите внимание, что полярность конденсатора теперь обратная.В другом словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина отрицательный заряд (см. рисунок 5). |
| ||||
| Теперь ток меняется на противоположный, и энергия течет. из конденсатора обратно в катушку индуктивности (см. рисунок 6).Ну наконец то энергия полностью возвращается в исходную точку, готовая начать Повторите цикл, как показано на Рисунке 3. |
|
Частота колебаний может быть приблизительно равна следует:
| f | = | 1 | |
| 2p (LC) 0.5 |
| Где: | f = частота |
| L = индуктивность | |
| C = емкость |
| Рисунок 7: Резонирующий контур |
В реальных цепях LC всегда есть некоторое сопротивление, которое вызывает рост амплитуды тока меньше с каждым циклом.Через несколько циклов ток уменьшается до нуль. Это называется «затухающей синусоидальной» формой волны. Как быстро ток демпфирования до нуля зависит от сопротивления в схема. Однако сопротивление не меняет частоту синусоидальная волна. Если сопротивление достаточно высокое, ток будет вообще не колеблются.
Очевидно, что там, где есть собственная частота, есть способ возбуждают резонанс.Делаем это, подсоединив переменный ток (AC) источник питания до схемы, показанной на рисунке 7. Термин «чередование» означает, что выходной сигнал источника питания колеблется с определенной частотой. Если частота источника питания переменного тока и цепь, к которой он подключен, являются то же самое, то возникает резонанс. В этом случае мы измеряем амплитуду или величина колебания при измерении тока.
Обратите внимание на рисунок 7, что мы снова вставили резистор в схему.Если нет резистора в цепи амплитуда тока будет увеличиваться, пока цепь не сгорит вверх. Увеличение сопротивления ведет к уменьшению максимального размера амплитуда тока, но не меняет резонансную частоту.
Как показывает практика, цепь не будет колебаться, если сопротивление (R) достаточно низкое, чтобы соответствовать следующему условию:
| R | = | 2 (аккредитив) 0.5 | |
Резонанс в схемах может быть просто любопытством, кроме за его полезность при передаче и приеме беспроводных средства связи, включая радио, телевидение и сотовые телефоны. Передатчики, используемые для отправки сигналов, обычно представляют собой схемы, разработанные резонировать на определенной частоте, называемой несущей частотой.В передатчик затем подключается к антенне, которая излучает электромагнитные волны на несущей частоте.
Антенна на другом конце принимает сигнал и подает его в еще один контур, также предназначенный для резонанса на несущая частота. Очевидно, что антенна принимает много сигналов на разные частоты, не говоря уже о фоновом шуме. Резонирующий схема по существу выбирает правильную частоту из всех нежелательные.
В радиомодулях с амплитудной модуляцией (AM) амплитуда несущая частота изменена так, чтобы она содержала звуки снял микрофон. Это простейшая форма радио передачи, но очень восприимчив к шуму и помехам.
Частотно-модулированное радио или FM-радио решают многие проблемы. проблемы AM-радио, но ценой более высокой сложности в система. В системе FM звуки преобразуются электронным способом в небольшие изменения несущей частоты.Единица оборудования, которая выполняет преобразование, называется модулятором и используется с передатчик. Кроме того, к разъему должен быть добавлен демодулятор. приемник для преобразования сигнала обратно в форму, которую можно воспроизвести на динамик.
- Артикул:
- Физика для ученых и инженеров, 4-е издание Том 2 , Раймонд А.Serway, Saunders College Publishing, стр.949
- Благодарности:
- Этот проект поддержан
Национальный фонд науки
Грант Research
Experience for Teachers в рамках программы Clemson University Лето
Опыт бакалавриата в области беспроводной связи.Особая благодарность д-ру Чалмерсу Батлеру из Университета Клемсона. за его руководство и вклад в подготовку этой страницы.
Для получения дополнительной информации о беспроводной связи и электромагнитном спектре посетите «Скрытый мир электромагнитного спектра».
<предыдущая | содержание | следующий>
Резонансные схемы — обзор
III.B.1 Резонансные преобразователи
При добавлении резонансного контура типа индуктор-конденсатор после переключающих устройств прямоугольные напряжения и токи преобразуются в синусоидальные сигналы.
Резонансный преобразователь постоянного тока состоит из инвертора, резонансного контура, высокочастотного трансформатора и полумостового или мостового выпрямителя, поскольку эти преобразователи используются для высокого уровня мощности.
Наличие синусоидальной формы волны позволяет переключению происходить, когда либо напряжение на переключателе, либо ток через него имеет нулевое значение, что подразумевает теоретические нулевые потери переключения, таким образом, обозначение «мягкое переключение».
Резонансный контур может быть простой последовательной или параллельной цепью LC , или цепью, образованной катушкой индуктивности и двумя конденсаторами (параллельно LCC ), или двумя катушками индуктивности и одним конденсатором (параллельно LLC ), или параллельной цепью . Схема LLCC (рис.12а).
РИСУНОК 12. (a) Параллельный резонансный преобразователь типа LLCC и (b) его характеристики управления. [Воспроизведено с разрешения из Batarseh, I., and Lee, C.Q. (1991). «Стационарный анализ параллельного резонансного преобразователя с коммутационной сетью типа LLCC», IEEE Trans. Силовая электроника 6 , 525–538. © 1991 IEEE.]
Поскольку переключатели должны включаться / выключаться в зависимости от значения соответствующего напряжения / тока, а не в соответствии с решениями цепи обратной связи ШИМ, регулирование рабочего цикла невозможно.Поэтому резонансные преобразователи регулируются с помощью регулятора частоты переключения. На рисунке 12b показаны характеристики управления с точки зрения усиления (выходное напряжение по сравнению с линейным напряжением) в зависимости от отношения частот в градусах (π f r / f s , где f r является резонансным частота), для разных значений нагрузки R 0 ( Q P = R 0 / Z 0 , Z 0 = 2π4 f r L s ).Изменяя f s , можно поддерживать постоянное напряжение нагрузки.
Резонансными преобразователями можно управлять либо в режиме «выше резонанса», когда диапазон частоты переключения всегда выше резонансной частоты резонансного блока, либо в режиме «ниже резонанса», когда частота переключения всегда остается ниже резонансной частоты.
Последний режим имеет то преимущество, что выключатели отключаются, когда ток через них равен нулю, т. Е. Отсутствуют потери на выключение.Эта функция позволяет использовать тиристоры в качестве коммутационных устройств; SCR имеют медленное выключение и большую номинальную мощность. Следовательно, эти преобразователи могут использоваться в приложениях с высокой мощностью. Однако, поскольку для целей регулирования необходимо снизить частоту коммутации ниже ее номинального значения, необходимо спроектировать все магнитные элементы на наименьшую частоту в диапазоне частоты коммутации (в противном случае трансформатор может достичь насыщения), что приведет к больший размер магнитных элементов.Поскольку паразитные емкости переключателей полностью заряжаются перед включением транзисторов, возникают коммутационные потери, и для рассеивания этой энергии необходимы демпферы.
Если преобразователь работает в режиме «выше резонанса», переключатели включаются, когда напряжение на них равно нулю. Следовательно, нет никаких потерь при включении. Эти преобразователи работают с высокой частотой переключения, поэтому размер магнитных элементов и фильтрующих элементов уменьшается. Однако наличие потерь при выключении требует очень быстрого выключения.При небольшой нагрузке частота коммутации должна быть значительно увеличена в целях регулирования; такой большой частотный диапазон затрудняет проектирование схемы управления.
Практическое применение резонанса в схемах
Из этой статьи вы узнаете о практических применениях резонанса в электрических цепях. Эта статья связана с 7 другими статьями, которые могут быть вам интересны:
Пока что явление резонанса кажется бесполезным любопытством или, в лучшем случае, неприятностью, которую следует избегать (особенно, если последовательный резонанс вызывает короткое замыкание в нашем источнике переменного напряжения!).Тем не менее, это не так. Резонанс — очень ценное свойство реактивных цепей переменного тока, используемых в различных приложениях.
Одно из применений резонанса — установить условие стабильной частоты в цепях, предназначенных для генерации сигналов переменного тока. Обычно для этой цели используется параллельная (резервуарная) цепь, в которой конденсатор и индуктор напрямую соединены вместе, обмениваясь энергией между собой. Подобно тому, как маятник может использоваться для стабилизации частоты колебаний часового механизма, так и контур резервуара может использоваться для стабилизации электрической частоты контура генератора переменного тока.Как было отмечено ранее, частота, устанавливаемая контуром резервуара, зависит исключительно от значений L и C, а не от величин напряжения или тока, присутствующих в колебаниях: (рисунок ниже)
Резонансный контур служит источником стабильной частоты.Другое применение резонанса — в приложениях, где желательны эффекты значительного увеличения или уменьшения импеданса на определенной частоте. Резонансный контур может использоваться для «блокировки» (наличия высокого импеданса) частоты или диапазона частот, таким образом действуя как своего рода частотный «фильтр», чтобы исключить определенные частоты из смеси других.Фактически, эти конкретные схемы называются фильтрами, и их конструкция сама по себе является предметом изучения: (рисунок ниже)
По сути, так работают схемы тюнера аналогового радиоприемника для фильтрации или выбора частоты одной станции из смеси сигналов различных частот радиостанций, перехваченных антенной.
Резюме
- Резонанс может использоваться для поддержания колебаний цепи переменного тока на постоянной частоте, так же как маятник может использоваться для поддержания постоянной скорости колебаний в механизме хронометража.
- Резонанс можно использовать из-за его свойств импеданса: либо резкое увеличение, либо уменьшение импеданса для определенных частот. Схемы, предназначенные для экранирования определенных частот из смеси различных частот, называются фильтрами .
Статья извлечена из Урок по электрическим схемам, переменный ток Тони Р. Купхальдт под лицензией на научное проектирование. Заголовок и заголовок изменены / добавлены. Кроме того, содержимое визуально редактируется и переупорядочивается для облегчения просмотра.
Факторы, усложняющие проблему шума | Базовый курс по шумоподавлению
3-1. Введение
В главе 2 описан механизм возникновения электромагнитного шума и, среди прочего, подробно описан шум, который генерируется цифровыми схемами.
Чтобы справиться с шумовыми помехами для электронных устройств, вам необходимо понимать не только источник шума, но и характеристики линий передачи и антенн.В этой главе конкретно описываются линии передачи среди них.
До сих пор возникновение шума объяснялось относительно простыми выражениями (за исключением гармоник). Однако для объяснения механизма передачи и излучения шума вам потребуются термины, которые используются в теории передачи, электромагнетизма и теории антенн, как показано на рис. 3-1-1. Без понимания этих терминов вы не сможете справиться с проблемами шума.
Таким образом, в этой главе будут объяснены эти термины (постарайтесь использовать как можно меньшее количество формул), а также представлены важные темы, касающиеся шума, такие как резонанс и затухание, проводимость и отражение шума, а также сопротивление источника.
3-2. Резонанс и затухание
Резонанс является одним из важных факторов при возникновении шума или индукции шума. Если цепь содержит непредусмотренный резонансный контур, он генерирует очень большой ток или напряжение на резонансной частоте, что повышает вероятность возникновения шумовых помех. Важно максимально устранить резонанс в контуре. Для подавления резонанса используются демпфирующие резисторы.В этом разделе описываются резонансные и демпфирующие резисторы.
3-2-1. Параллельный резонанс и последовательный резонанс
(1) LC резонансный контур
Резонанс означает, что индуктивное реактивное сопротивление и емкостное реактивное сопротивление в цепи взаимно компенсируются на определенной частоте, и конкретная частота называется «резонансной частотой». Хотя типичные части, которые могут генерировать реактивное сопротивление (мнимую составляющую импеданса), включают катушки индуктивности (катушки) и конденсаторы, любые другие части (даже простой провод) могут быть элементом резонанса, поскольку они все еще содержат очень маленькое реактивное сопротивление.(Хотя резонанс в связи с ЭМС может быть вызван антенной, параллельными пластинами, линией передачи и т. Д., Помимо вышеупомянутого, мы сосредоточимся только на ЖК-резонансе индуктора и конденсатора).
(2) Импеданс резонансного контура
Как показано на рис. 3-2-1, существует два типа резонансного контура: последовательный резонанс и параллельный резонанс. Как показано в примере расчета на рис. 3-2-2, последовательный резонанс делает импеданс минимальным (в идеале нулевым), в то время как параллельный резонанс делает его максимальным (в идеале ∞ ).
(3) Реактивность отменена до нуля
Как показано на рис. 3-2-3, понятно, что величины реактивного сопротивления катушки индуктивности и реактивного сопротивления конденсатора становятся одинаковыми на резонансной частоте, компенсируя друг друга и, таким образом, сводя их к нулю.
Хотя рис. 3-2-3 объясняет случай последовательного резонанса, реактивное сопротивление заменяется проводимостью (мнимая составляющая проводимости) в случае параллельного резонанса, что приводит к уменьшению восприимчивости до нуля на резонансной частоте.Поэтому легко понять, что импеданс становится максимальным.
(4) Резонансная частота
Резонансная частота ƒ 0 можно оценить по приведенной ниже формуле как для последовательного, так и для параллельного резонанса. В примере на рис. 3-2-2, ƒ 0 составляет ок. 50 МГц.
(Формула 3-2-1)
(5) Резонанс Q
Сила этого резонанса выражается показателем Q (добротность).Более высокая добротность указывает на более сильный резонанс. Индекс Q также используется в качестве индекса для представления характеристик конденсатора и катушки индуктивности. Существует связь, когда вы используете конденсатор или катушку индуктивности с большой добротностью, вы можете создать резонансный контур с большой добротностью. Как оценить добротность, будет объяснено в разделе 3-2-5.
(6) Собственный резонанс конденсатора и катушки индуктивности
Когда конденсатор или катушка индуктивности используются в высокочастотном диапазоне, сама деталь вызывает резонанс на определенной частоте из-за паразитных компонентов, присущих этой детали.Это называется саморезонансом. Саморезонанс будет более подробно описан в главе 6.
3-2-2. Вопросы по мерам ЭМС для резонансного контура
(1) Резонансный контур усиливает напряжение
Если в электрической цепи возникает непреднамеренный резонанс, импеданс значительно изменяется на резонансной частоте, что приводит к большому току или напряжению, которые могут быть причиной шумовых помех.
Скажем, например, переменный входной сигнал подается извне на последовательный резонансный контур, который был рассчитан на рис.3-2-2 (а). Как показано на рис. 3-2-4, когда генератор сигналов с выходным сопротивлением 50 Ом используется для подачи сигнала с постоянным напряжением (величина 0,5 В), возникает напряжение, которое в несколько раз превышает входной сигнал. на конденсаторе на резонансной частоте 50 МГц. В этом случае напряжение, возникающее на конденсаторе или катушке индуктивности, достигает входного напряжения, умноженного на Q. Как оценить Q, будет объяснено в Разделе 3-2-5. Условия на рис. 3-2-4 указывают Q = 6.3.
(2) Резонансный контур может возникать непреднамеренно
Тестовая схема на рис.3-2-4 содержит конденсатор и катушку индуктивности, где используемые константы являются значениями, которые обычно встречаются в цифровых схемах. Например, входная клемма цифровой ИС имеет плавающую электростатическую емкость в несколько пФ. И проводка имеет индуктивность около 1 мкГн на метр. Следовательно, если кабель длиной около 1 м подключен к входной клемме цифровой ИС (например, для подключения его к внешнему датчику), будет создан резонансный контур, подобный показанному здесь.
Если проводник неправильно подсоединен к этой точке, это может стать причиной появления шума.
(3) Внутреннее напряжение становится высоким даже при небольшом входном напряжении.
Как показано на Рис. 3-2-2 (a), полное сопротивление последовательного резонансного контура становится минимальным на резонансной частоте. Таким образом, вы можете просто предположить, что напряжение становится меньше. Почему напряжение на самом деле становится выше?
На рис. 3-2-5 показана разбивка напряжения. Напряжение на входе (средняя точка между резистором и катушкой индуктивности) резонансного контура резко снижается до очень небольшого напряжения.Однако ток был увеличен из-за пониженного импеданса. Следовательно, внутри резонансного контура возникает напряжение, превышающее приложенное.
Почему напряжение на входе в резонансный контур пропадает, даже если на конденсатор поступает какое-то напряжение? В этот момент на катушку индуктивности подается точно такое же напряжение, как и на конденсатор. Поскольку направление этого напряжения противоположно конденсатору, вы вряд ли увидите какое-либо напряжение на входе в резонансный контур.
(4) Резонансный контур имеет совершенно разное напряжение в зависимости от точки
Когда цепь резонирует, напряжение существенно различается в зависимости от точки. Даже если кажется, что измерение напряжения в какой-то точке указывает на то, что шум уменьшился, измерение общего шумового излучения может остаться неизменным или даже увеличиться. Так что нужно проявлять осторожность.
Приведенный выше пример касается случая последовательного резонансного контура.В случае параллельного резонансного контура ток, протекающий через конденсатор и катушку индуктивности, становится больше, чем входной сигнал. Поскольку этот ток также может быть причиной шума, следует соблюдать осторожность и в случае параллельного резонансного контура.
3-2-3. Когда цифровая цепь подключена к резонансной цепи
(1) Шум более вероятен на резонансной частоте
Как описано выше, если проводник, который может работать как антенна, был подключен к резонансному контуру, он улавливает высокое напряжение резонансной частоты и генерирует сильное излучение, вызывая, таким образом, шум.Кроме того, с точки зрения устойчивости, шум можно легко уловить на резонансной частоте.
Если такой резонансный контур с присоединенной антенной подключен к сигналу, который содержит широкий диапазон частот, например к цифровому сигналу, гармоники на частотах, близких к резонансной частоте, будут иметь сильное излучение. На рисунках 3-2-6 и 3-2-7 показаны примеры измерения изменений формы импульса и излучения, когда описанная выше последовательная резонансная цепь 50 МГц подключена к тактовому сигналу 10 МГц.В качестве примера подавления шума здесь также показаны форма волны и излучение с прикрепленным ферритовым шариком.
(2) Когда цифровой сигнал подключен к резонансному контуру
На рис. 3-2-6 показаны испытательная схема и результаты измерения формы волны напряжения. 74AC00 использовался для цифрового идентификатора, который работает как источник шума. Выход этой ИС подключен к последовательному резонансному контуру с резонансной частотой 50 МГц.Вы можете видеть, что наблюдаемая форма волны указывает на сильный звон в цифровом импульсе 10 МГц, что серьезно искажает форму волны. Считается, что это связано с тем, что среди гармоник, содержащихся в сигнале 10 МГц, была выделена только гармоника 5-го порядка (50 МГц). (Наблюдалась частота звонка 50 МГц)
(3) Демпфирование с использованием ферритовых шариков
Как описано ниже, демпфирующие резисторы и ферритовые шарики эффективны для подавления этого типа резонанса.На рис. 3-2-6 показана форма волны после прикрепления ферритового буртика. Вы можете видеть, что резонанс был подавлен, и сигнал вернулся к исходной форме импульса.
(4) Резонанс подтверждается шумом
На рис. 3-2-7 показаны результаты по шумовому излучению. Напряженность электрического поля измерялась трехметровым методом. Для справки, на рисунке также показан результат измерения без антенны, и было подтверждено, что практически отсутствует шумовое излучение, когда оно состоит только из цифровой ИС и резонансного контура, как указано выше.Линия в нижней части рисунка показывает уровень темнового шума анализатора спектра.
(5) LC-резонанс и резонанс антенны
На рис. 3-2-7 (а) показан случай, когда резонансный контур подключен с помощью 15-сантиметрового провода в качестве антенны для излучения шума. Сильное излучение наблюдалось на резонансной частоте 50 МГц для резонансного контура LC. Помимо частоты, шум также наблюдался на частоте 500 МГц. На этой частоте 15-сантиметровый провод, подключенный как антенна, работает как антенна с длиной волны 1/4.Следовательно, вы можете наблюдать резонансный эффект антенны в дополнение к ЖК-резонансу на рис. 3-2-7 (a). Резонанс антенны будет описан в следующем разделе.
Рис. 3-2-7 (c) показывает результат измерения с прикрепленным ферритовым валиком. Вы можете видеть, что шумовое излучение эффективно подавлено.
3-2-4. Пример возникновения резонанса без катушки индуктивности или конденсатора
(1) Резонансная цепь, создаваемая цифровой сигнальной линией
Чтобы провести измерение с акцентом на эффект резонанса на рис.3-2-6 и 3-2-7, эксперимент проводился путем создания LC-резонансного контура с конденсатором и индуктором. Однако резонанс может возникнуть в реальной цепи без таких частей.
Например, в случае проводки цифрового сигнала, показанной на рис. 3-2-8, провод, соединяющий драйвер и приемник, имеет индуктивность. Кроме того, входной разъем приемника, принимающего сигнал, обладает электростатической емкостью. Считается, что цифровая схема, описанная в разделе 2-4-7, образует резонансный контур с этими факторами.
(2) Проблема становится очевидной, когда резонансная частота становится ниже.
Когда цифровая сигнальная проводка очень короткая, резонансная частота из-за этих факторов становится очень высокой (несколько 100 МГц), и, таким образом, влияние незначительно. Однако, если используется двусторонняя плата, или если индуктивность увеличивается за счет удлинения проводки, или если электростатическая емкость увеличивается за счет подключения нескольких приемников, эффекты (искажение формы импульса или повышенное излучение шума и т. Д.)) от пониженной резонансной частоты больше не будет незначительным.
В рамках подготовки к вышеуказанным случаям, часть вывода сигнала может быть снабжена контактами, позволяющими использовать компонент подавления резонанса, такой как ферритовый шарик, так что меры по подавлению шума могут быть легко реализованы, как описано в Разделе 3-2-6.
(3) Кабель питания и печатная плата могут быть факторами резонанса.
Помимо цифровых сигналов, различные факторы, составляющие схему, могут действовать как конденсатор или катушка индуктивности, которые не были описаны в принципиальной схеме, и вызывать резонанс.Так что нужно проявлять осторожность. На рис. 3-2-9 показан пример.
3-2-5. Демпфирование резистором или ферритовым валиком
(1) Демпфирование последовательного резонансного контура
Резонанс можно подавить, добавив резистор в резонансный контур. Этот резистор называется демпфирующим резистором. На рис. 3-2-10 показан пример добавления демпфирующего резистора (обозначенного как R на рисунке).
Когда демпфирующий резистор используется последовательно с последовательным резонансом, как показано на рис.3-2-10 (a), добротность резонатора определяется следующим образом: [Ссылка 1] .
(Формула 3-2-2)
Например, мы можем включить в эту формулу частичные константы, которые использовались в тесте на рис. 3-2-4. Если выходное сопротивление источника сигнала 50 Ом используется для резистора R , Q = 6.3, что указывает на сильный резонанс. Если резистор R больше, Q становится меньше, тем самым ослабляя резонанс.Таким образом, вы можете видеть, что добавление резистора более 50 Ом к этой точке позволяет ослабить резонанс.
Обычно для подавления резонанса резистор выбирается так, чтобы Q был установлен на 1 или меньше.
(2) Условия отсутствия колебаний последовательного резонансного контура
Чтобы исключить перерегулирование, недорегулирование или звенящий сигнал из импульсной формы волны, такой как цифровой сигнал, используется резистор, который соответствует следующей формуле, чтобы удовлетворить условиям отсутствия колебаний последовательного резонансного контура LCR.
(Формула 3-2-3)
Формула (2) дает Q равным 0,5 или меньше.
(3) Демпфирование параллельного резонансного контура
Напротив, когда демпфирующий резистор используется параллельно с параллельным резонансом, как показано на рис. 3-2-10 (b), добротность резонатора определяется следующим образом:
(Формула 3-2-4)
В этом случае, чем меньше резистор, тем слабее становится резонанс.
3-2-6. Демпфирование цифрового сигнала
(1) Демпфирующий резистор и резистор согласования полного сопротивления
При использовании демпфирующего резистора для предотвращения вызванного резонансом проводки цифровой схемы, показанной на рис. 3-2-8, он обычно используется последовательно с проводкой, как показано на рис. 3-2-11. При этом, чем больше резистор, тем выше становится эффект подавления резонанса. Однако, если демпфирование будет чрезмерным, это вызовет побочные эффекты, такие как затухание сигнала и медленное нарастание формы импульса.Следовательно, соответствующий резистор следует выбирать на основе баланса между подавлением шума и работой схемы. Если проводку можно рассматривать как линию передачи, эту операцию можно выполнить разумно, используя концепцию согласования импеданса, описанную в следующем разделе.
(2) Демпфирование ферритовым валиком
Поскольку примеры показаны в Разделе 2.4.7, Рис. 3-2-6 и Рис. 3-2-7, ферритовые бусины часто используются для демпфирования при измерениях ЭМС.В этом случае деталь следует выбирать так, чтобы сопротивление ( R ) компонент ферритового валика может удовлетворять формуле (2) на резонансной частоте. Поскольку ферритовый шарик имеет частотные характеристики импеданса, резонанс можно подавить, минимизируя влияние на форму сигнала. Кроме того, он может потреблять больший постоянный ток, чем резистор.
«3-2. Резонанс и затухание »- Ключевые моменты
- Резонанс может быть последовательным или параллельным
- Последовательный резонанс делает импеданс минимальным (в идеале нулевым) на резонансной частоте.
- Параллельный резонанс делает полное сопротивление максимальным (в идеале ∞ ) на резонансной частоте
- На резонансной частоте шум может вызвать проблему из-за его максимального напряжения или тока.
- Демпфирующие резисторы или ферритовые шарики используются для подавления резонанса.
Что такое последовательный резонанс? — его эффекты
В последовательной цепи RLC, когда ток схемы находится в фазе с приложенным напряжением, говорят, что цепь находится в последовательном резонансе . Состояние резонанса возникает в цепи последовательного RLC, когда индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
X L = X C или (X L — X C = 0)
Последовательный резонансный контур может потреблять большой ток и мощность от сети; она также называется цепью приемника . Цепь последовательного резонанса RLC показана на рисунке ниже:
В резонансе: X L — X C = 0 или X L = X C
Импеданс будет:
Где Zr — резонансное сопротивление цепи.
Подставив значение X L — X C = 0 в уравнение (1), получим:
Zr =
рэндТок I = V / Zr = V / R
Так как при резонансе противодействием току является только сопротивление (R) цепи. В этом состоянии схема потребляет максимальный ток.
См. Также : Что такое резонансная частота?
Эффекты последовательного резонанса
Следующие эффекты условия последовательного резонанса приведены ниже:
- В условиях резонанса XL = XC полное сопротивление цепи минимально и сводится к сопротивлению цепи.т.е. Zr = R
- В условиях резонанса, поскольку полное сопротивление цепи минимально, ток в цепи максимален. т.е. Ir = V / Zr = V / R
- Поскольку значение резонансного тока Ir является максимальным, следовательно, мощность, потребляемая цепью, также максимальна. т.е. Pr = I 2 Rr
- В условиях резонанса ток, потребляемый цепью, очень велик, или мы можем сказать, что ток потребляется максимальным. Следовательно, падение напряжения на индуктивности L ie (V L = IX L = I x 2πfrL) и емкости C i.e (V C = IX C = I x I / 2πfrC) также будет очень большим.
В энергосистеме, в условиях резонанса, чрезмерное напряжение, создаваемое на индуктивном и емкостном компонентах цепи, таких как автоматический выключатель, реакторы и т. Д., Может вызвать повреждение. Таким образом, в энергосистеме избегается состояние последовательного резонанса.
Однако в некоторых электронных устройствах, таких как антенная цепь радио и ТВ-приемника, схема настройки и т. Д.2}} \
$Эта вторая часть уравнения находится на оси jw и показывает, где координаты полюса будут вдоль этой оси. Первая часть приведенного выше уравнения является действительной частью s на диаграмме полюс-нуль.



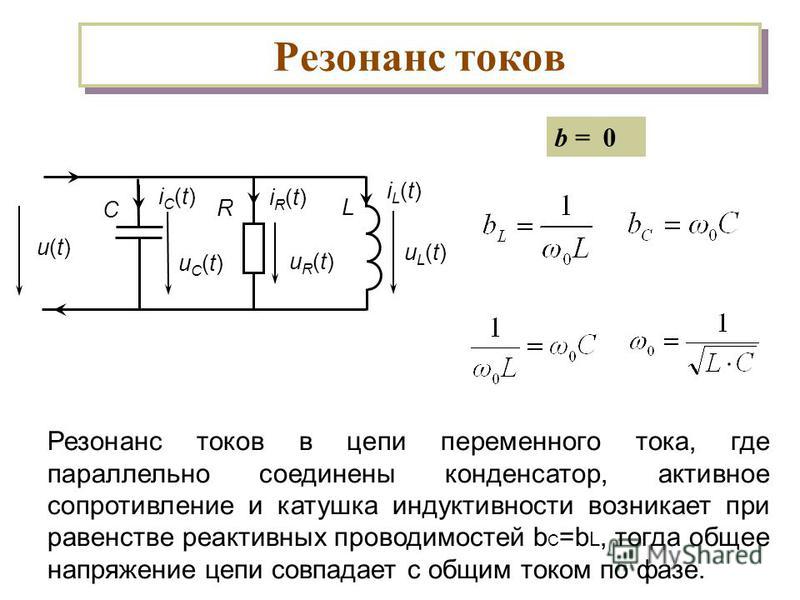 Амплитуда установившихся колебаний тока будет определяться уравнением . В этом и состоит смысл явления резонанса.
Амплитуда установившихся колебаний тока будет определяться уравнением . В этом и состоит смысл явления резонанса. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз.
Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз.