Резонанс в электрической цепи — Класс!ная физика
Резонанс в электрической цепи
«Физика — 11 класс»
В механике резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы.
Резонанс возможен и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При механике резонанс выражен при малом трении.
В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R.
Наличие активного сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника (проводник нагревается).
Поэтому резонанс в электрическом колебательном контуре выражен отчетливо при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная циклическая частота колебаний в контуре:
Сила тока при вынужденных колебаниях достигает максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура:
Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
Амплитуда силы тока при резонансе.
При резонансе в колебательном контуре создаются условия для поступления энергии от внешнего источника в контур.
Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением.
В механике аналогично: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
После включения внешнего переменного напряжения амплитуда колебаний силы тока нарастает постепенно, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
тогда:
ImR = Um
Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением
При R → 0 резонансное значение силы тока неограниченно возрастает: (Im)рез → ∞.
Наоборот, с увеличением R максимальное значение силы тока уменьшается.
Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R1 < R2 < R3):
Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности.
Эти напряжения при малом активном сопротивлении во много раз превышают внешнее напряжение.
Использование резонанса в радиосвязи
Явление электрического резонанса используется в радиосвязи.
На явлении резонанса основана вся радиосвязь.
С антенной индуктивно связан колебательный контур.
Из-за электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот.
Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте.
Настройка контура на нужную частоту ω0 осуществляется путем изменения емкости конденсатора.
В этом обычно состоит настройка радиоприемника на определенную радиостанцию.
Необходимость учета возможности резонанса в электрической цепи
Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии.
Большие напряжения приводят к пробою изоляции.
Итак,
при вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы
class-fizika.ru
Резонанс в электрической цепи
Начнём с основных определений.
Определение 1
Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.
Одними из наиболее полезных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Возникновение резонанса в электрической цепи
Замечание 1
Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:
- емкостной;
- активной;
- индуктивной.
В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.
Резонанс напряжений обычно достигается тремя способами:
- подбором индуктивности катушки;
- подбором емкости конденсатора;
- подбором угловой частоты $w_0$.
При этом все значения емкости, частоты и индуктивности определяются с использованием формул:
$L_0 = \frac{1}{w^2C}$
$C_0 = \frac{1}{w^2L}$
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:
$\frac{U}{r}$
Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
$Q = \frac{U_c0}{U}$
Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.
Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.
Применение явления резонанса
Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.
Замечание 2
Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.
spravochnick.ru
Резонанс в электрических цепях
Резонанс в электрических цепях
Реактивное
сопротивление или проводимость
двухполюсника, в состав которого входят
конденсаторы и катушки индуктивности,
в зависимости от частоты приложенного
напряжения могут принимать как
положительные, так и отрицательные
значения. При определенных условиях
реактивное сопротивление (проводимость)
может оказаться равным нулю, а эквивалентное
сопротивление (проводимость) всей цепи
становится активным. В этом случае ток
и напряжение на входе цепи совпадают
по фазе. Такое явление называют резонансом,
а соотношение 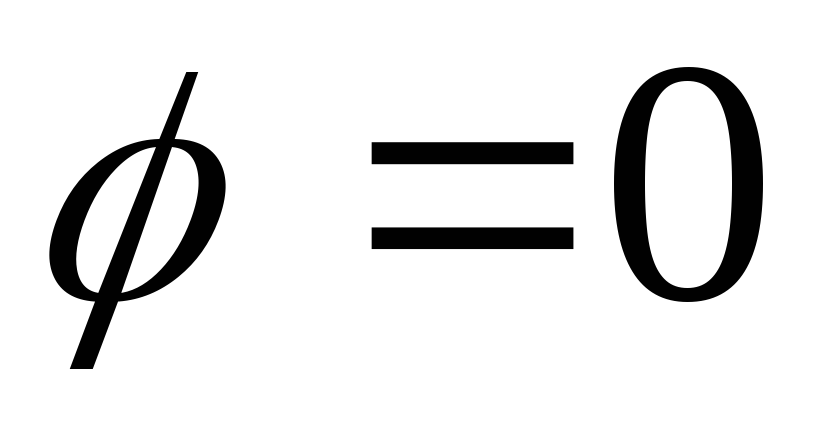 −условием
резонанса.
−условием
резонанса.
Эквивалентные параметры двухполюсника связаны соотношениями
 и
и  ,
,
поэтому
условие  эквивалентно выполнению равенств
эквивалентно выполнению равенств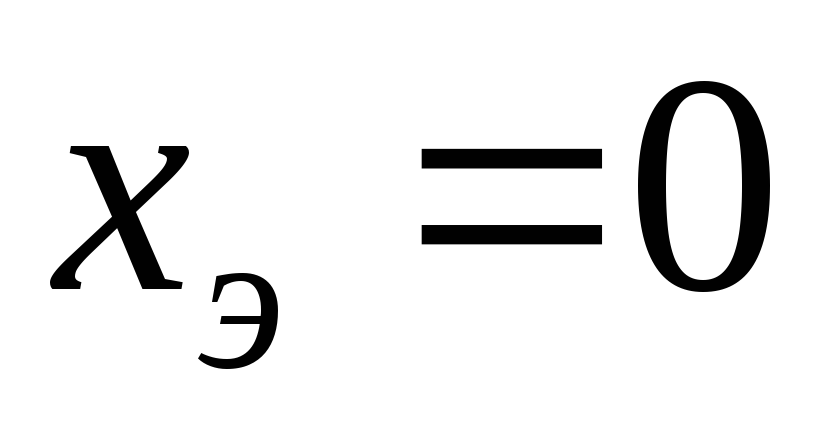 или
или .
.
Из
условий  ,
,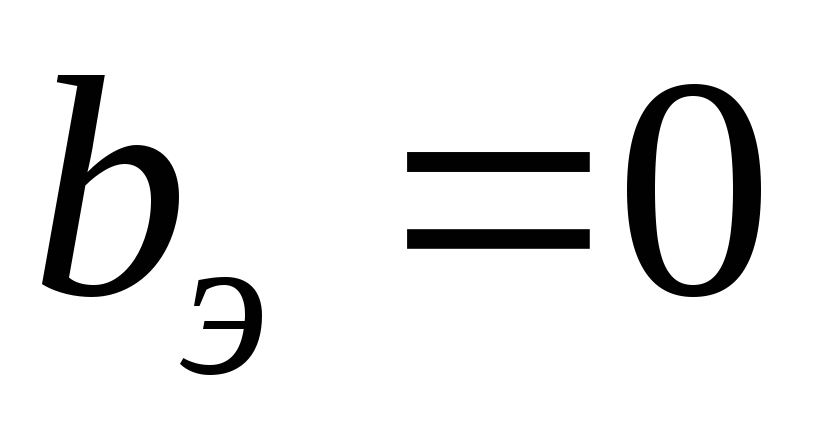 могут быть определены значения параметров
элементов электрической цепи, при
которых наблюдается явление резонанса,
а также значения частотырезонанса.
могут быть определены значения параметров
элементов электрической цепи, при
которых наблюдается явление резонанса,
а также значения частотырезонанса.
Если
для двухполюсника 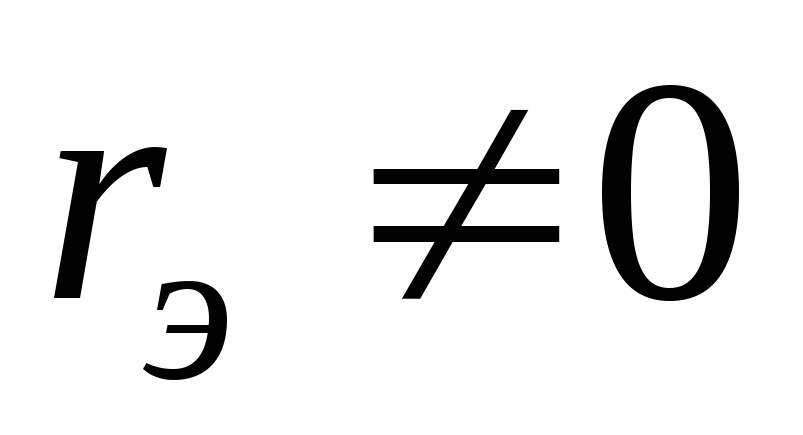 и
и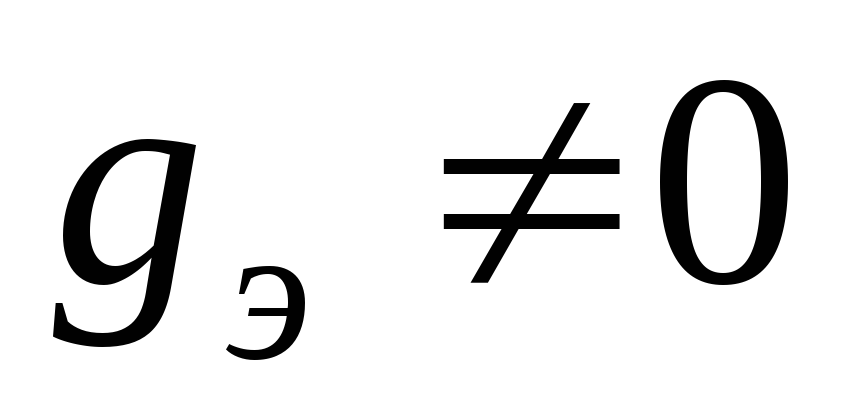 ,
то для определения значений резонансных
частот может быть использовано любое
из условий
,
то для определения значений резонансных
частот может быть использовано любое
из условий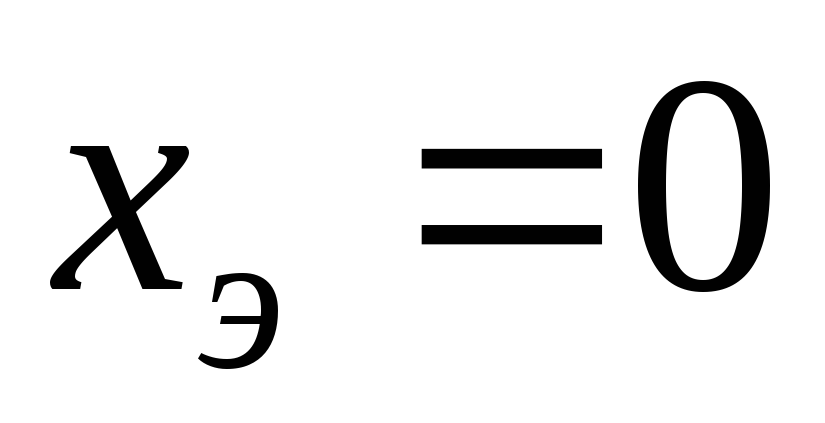 или
или .
.
В
случае, когда активное эквивалентное
сопротивление или активная эквивалентная
проводимость двухполюсника равны нулю,
для определения значений резонансных
частот следует использовать оба условия 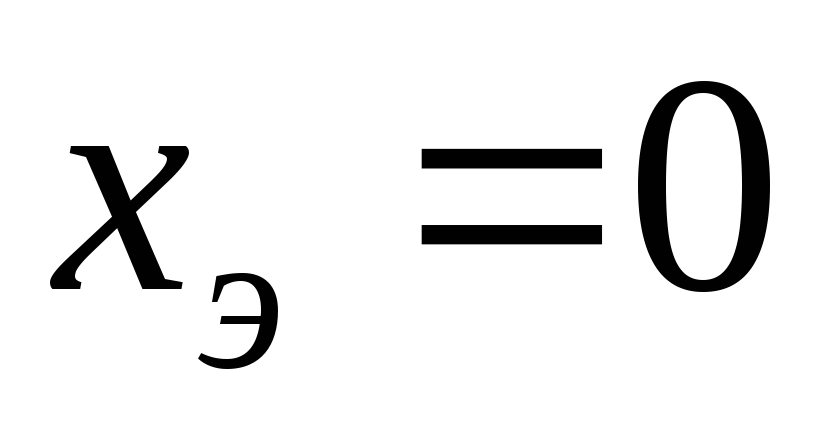 и
и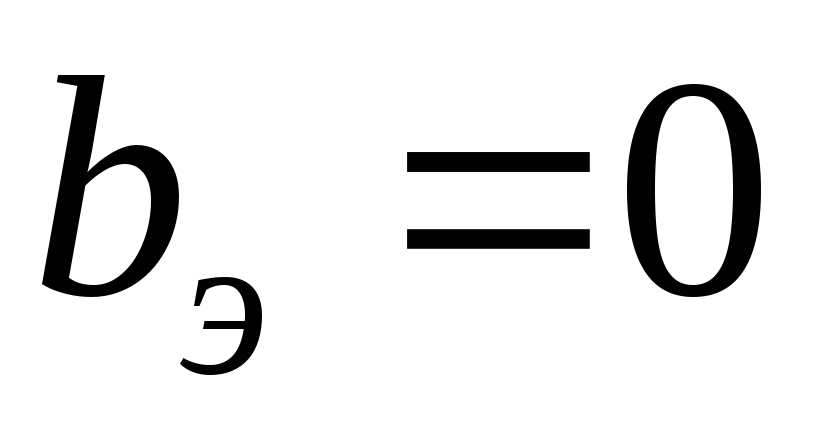 ,
так как при этом
,
так как при этом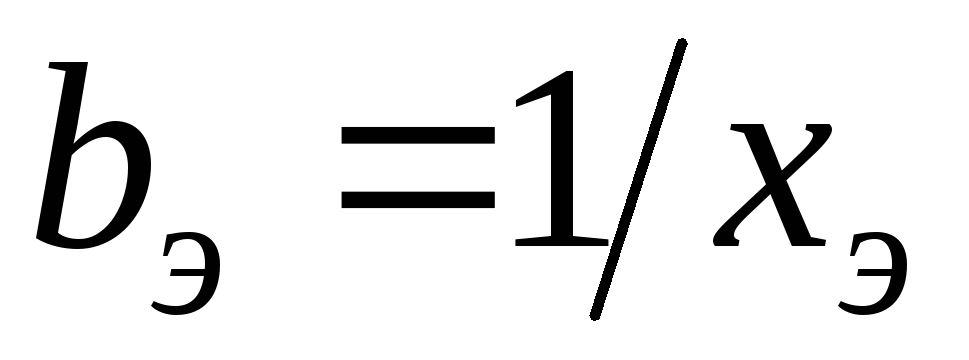 .
Равенства
.
Равенства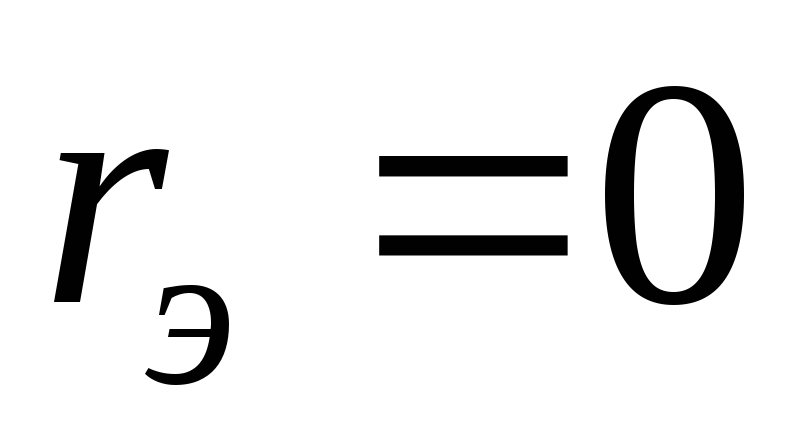 и
и выполняются, в частности, для цепей,
содержащих только катушки индуктивности
и конденсаторы.
выполняются, в частности, для цепей,
содержащих только катушки индуктивности
и конденсаторы.
Для
описания частотных свойств электрических
цепей широко используются частотные
характеристики. Под частотными
характеристиками понимают зависимости
от частоты входных параметров цепи: r , x , z , g , b , y , а также
величин, определяемых этими параметрами 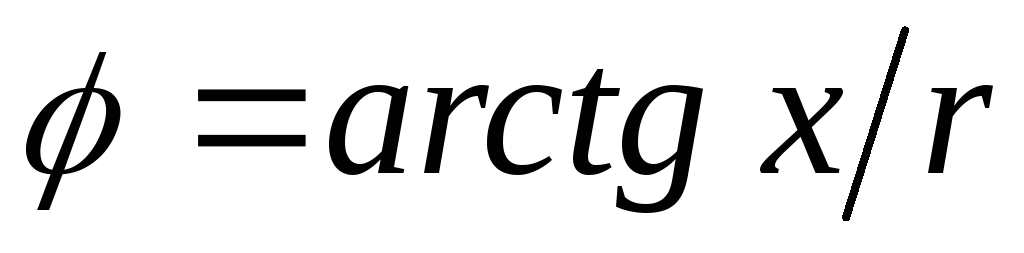 ,
,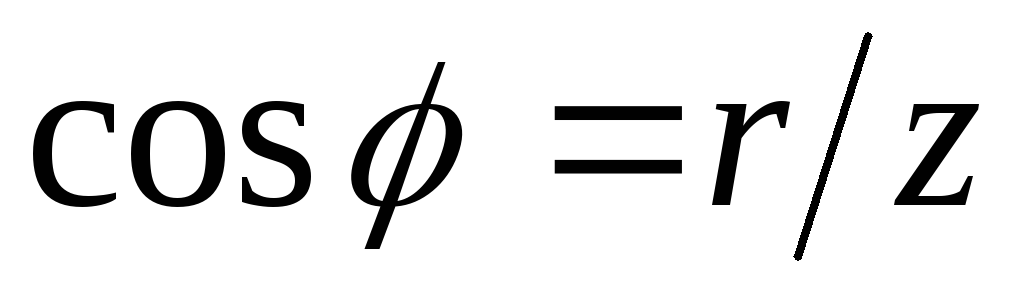 и т.д. Рассмотрим далее частотные
свойства простейших цепей, в которых
возможен резонанс.
и т.д. Рассмотрим далее частотные
свойства простейших цепей, в которых
возможен резонанс.
Резонанс в цепи при последовательном соединении элементов
Рассмотрим цепь, изображенную на рис. 10.1а
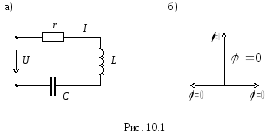
Комплексное сопротивление цепи равно
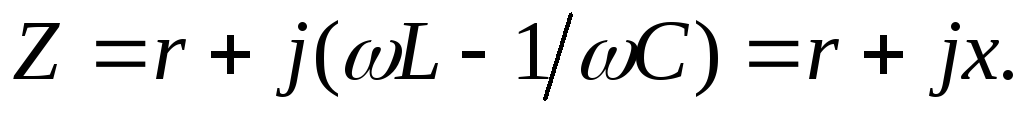
Угол
сдвига между входным током и напряжением 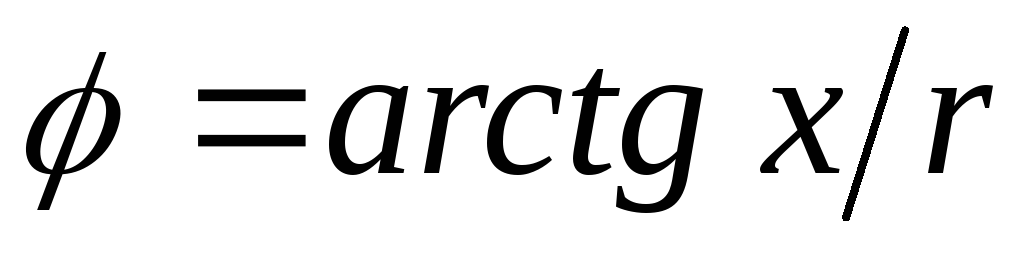 обращается в нуль при равенстве нулю
реактивного сопротивления цепи, то есть
при выполнении условия
обращается в нуль при равенстве нулю
реактивного сопротивления цепи, то есть
при выполнении условия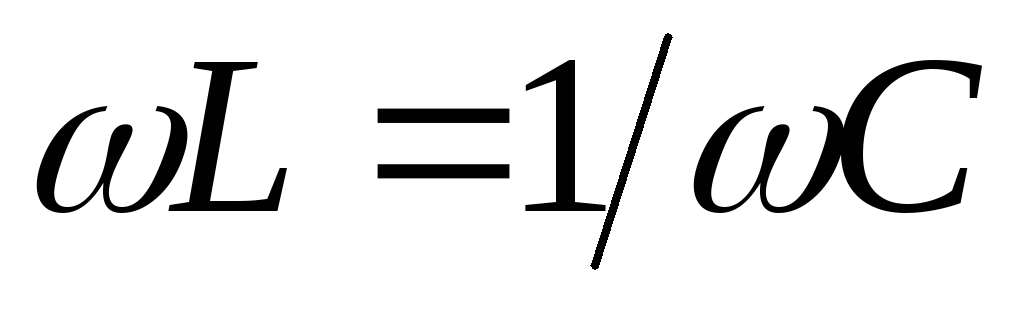 .
Таким образом, состояние резонанса в
цепи наступает при частоте
.
Таким образом, состояние резонанса в
цепи наступает при частоте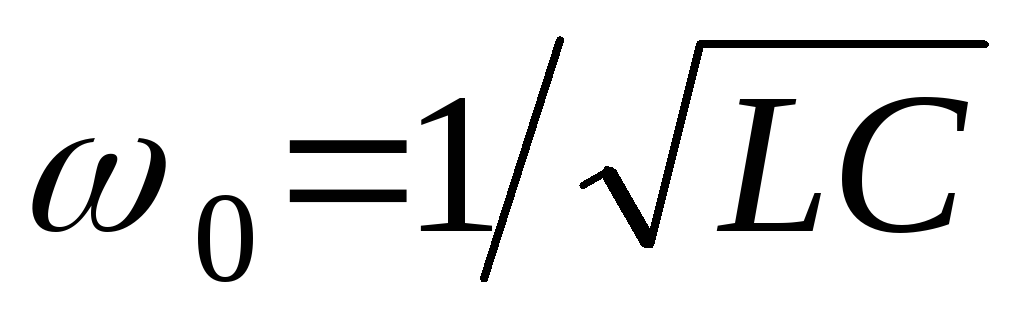 .
Эта угловая частота называетсярезонансной.
Векторная диаграмма для токов и напряжений
в последовательном rLC контуре,
построенная при
.
Эта угловая частота называетсярезонансной.
Векторная диаграмма для токов и напряжений
в последовательном rLC контуре,
построенная при 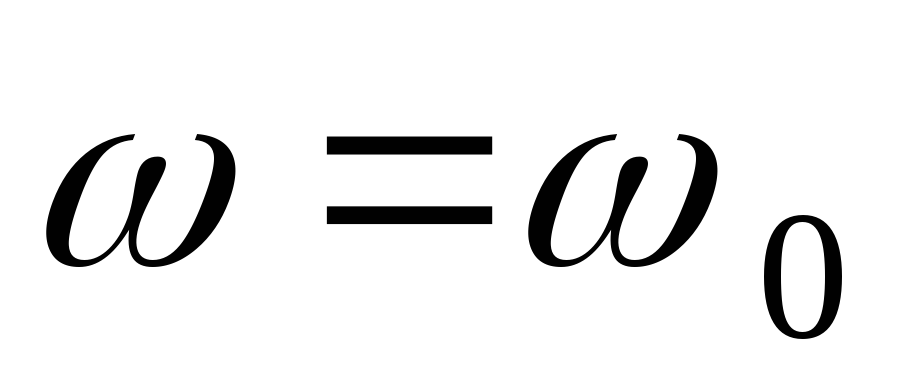 ,
изображена на рис. 10.1б. Как видно из
векторной диаграммы, вектора
,
изображена на рис. 10.1б. Как видно из
векторной диаграммы, вектора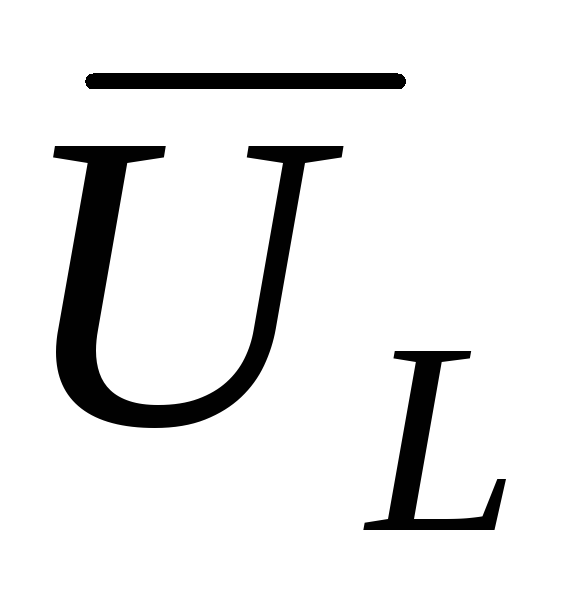 и
и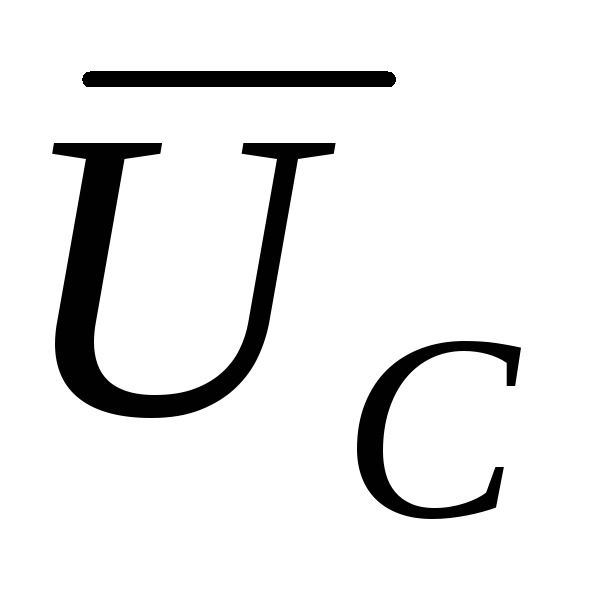 равны по величине и противоположны по
направлению, таким образом, напряжение
равны по величине и противоположны по
направлению, таким образом, напряжение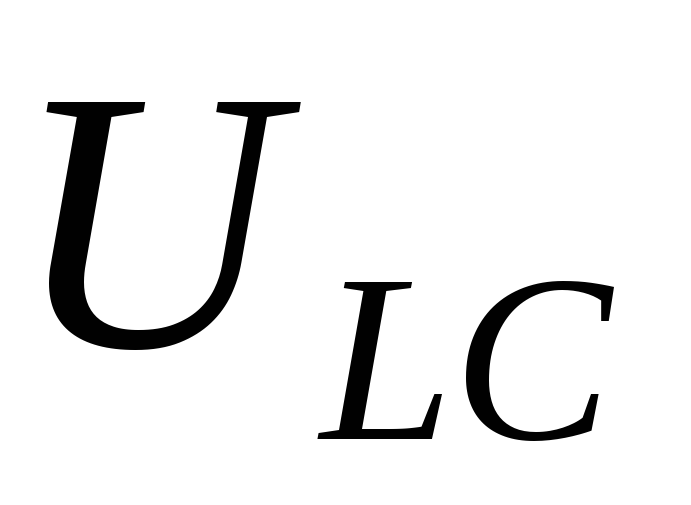 при резонансной частоте равно нулю.
Индуктивное и равное ему емкостное
сопротивление цепи при резонансной
частоте
при резонансной частоте равно нулю.
Индуктивное и равное ему емкостное
сопротивление цепи при резонансной
частоте
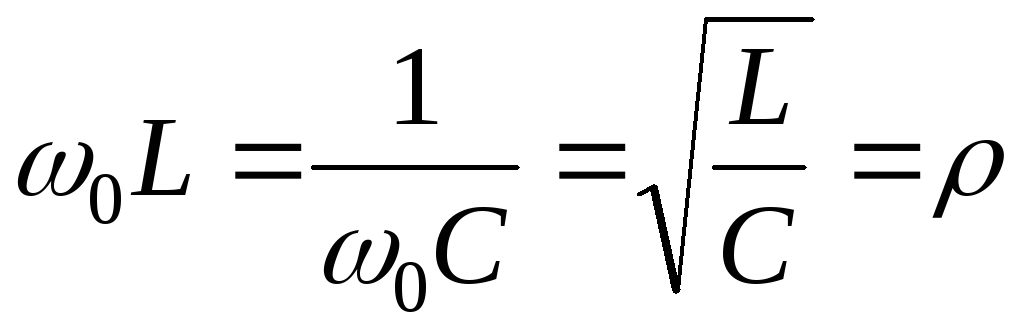 ,
,
обозначаемое
символом  ,
носит названиеволнового
сопротивления колебательного контура и измеряется в
омах.
,
носит названиеволнового
сопротивления колебательного контура и измеряется в
омах.
Отношение волнового сопротивления к активному сопротивлению в последовательном колебательном контуре называется добротностью, а величина, обратная добротности − затуханием:
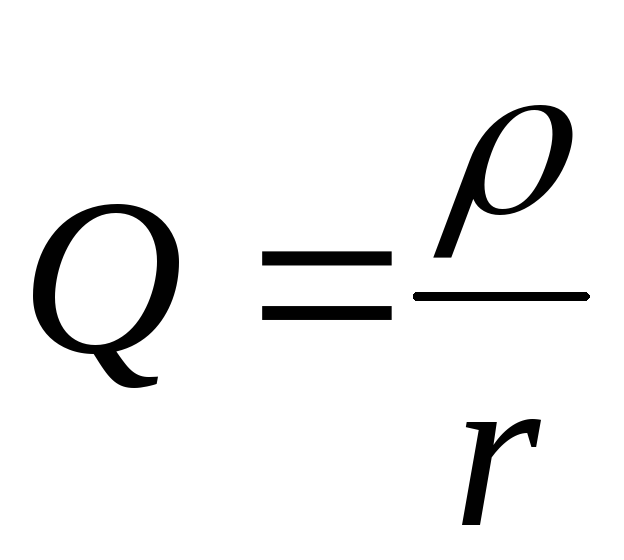 ,
, 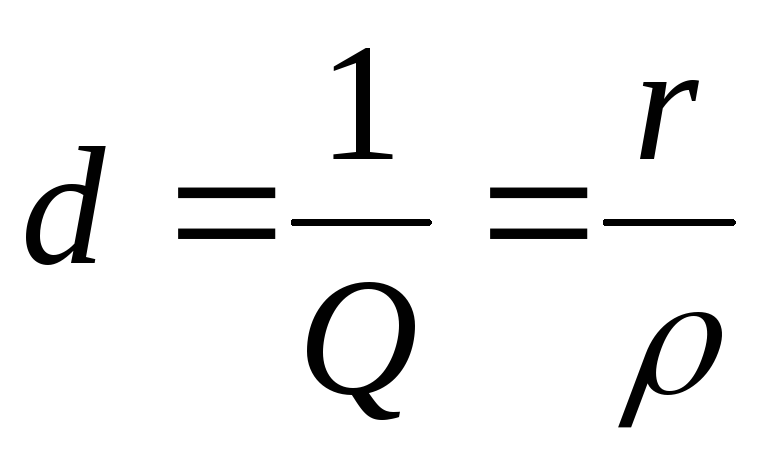 .
.
Как следует из приведенных соотношений, добротность и затухание являются безразмерными величинами. Поскольку во всех элементах цепи, изображенной на рис. 10.1а протекает один и тот же ток, добротность показывает, во сколько раз напряжение на реактивных элементах при резонансе превышает входное напряжение. В реальных колебательных контурах эта величина может достигать значительного уровня. Поэтому резонанс в цепи с последовательным соединением элементов r ,L ,C иногда называютрезонансом напряжений.
При резонансной частоте полное сопротивление z

равно сопротивлению резистора r , ток и входное напряжение совпадают по фазе.
Таким образом, вся мощность, поставляемая в цепь источником, равна активной мощности, потребляемой единственным резистивным элементом, а реактивная мощность цепи равна нулю. Это означает, что в резонансе взаимный обмен энергии происходит только между конденсатором и катушкой индуктивности. Уменьшение энергии электрического поля при разряде конденсатора сопровождается увеличением энергии магнитного поля катушки и наоборот. Обмен энергией между источником и реактивными элементами отсутствует.
Рассмотрим
частотные свойства цепи с последовательно
соединенными элементами r ,L ,C . Будем
считать, что на входе цепи действует
синусоидальное напряжение с постоянной
амплитудой и угловой частотой 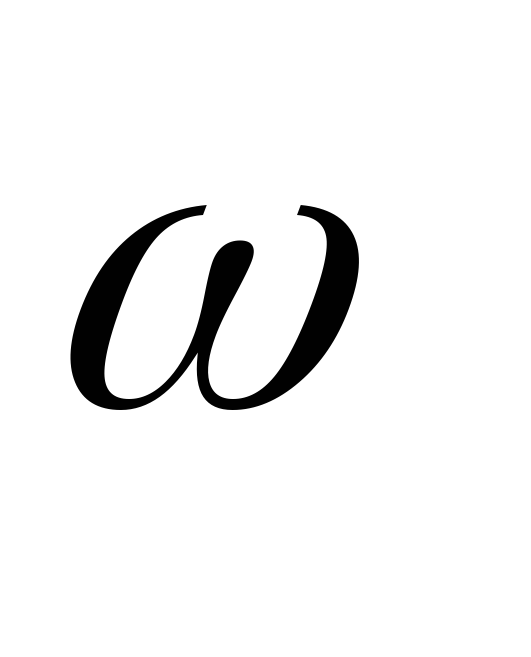
 . На рисунке 10.2 приведены соответствующие
частотные характеристики
. На рисунке 10.2 приведены соответствующие
частотные характеристики 
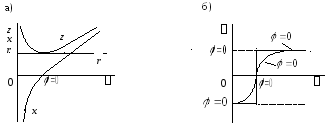 ,
, 
Рис. 10.2
Активное
сопротивление рассматриваемой цепи не
зависит от частоты, а реактивное при
определенных значениях частоты (  )
становится равным либо нулю либо
бесконечности. Эти характерные значения
называют соответственно нулями и
полюсами частотной характеристики.
Важным свойством функции
)
становится равным либо нулю либо
бесконечности. Эти характерные значения
называют соответственно нулями и
полюсами частотной характеристики.
Важным свойством функции
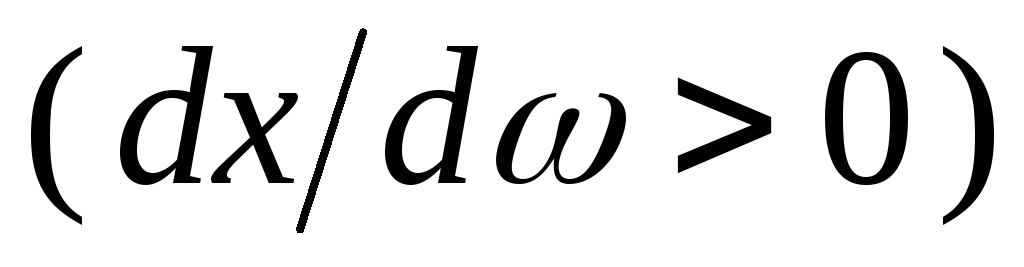 .
В интервале частот
.
В интервале частот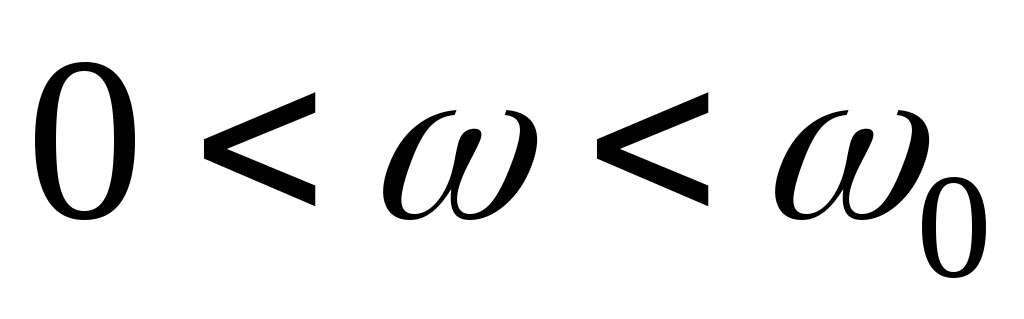 реактивное сопротивление возрастает
от − ∞ до 0 и имеетемкостнойхарактер, при
реактивное сопротивление возрастает
от − ∞ до 0 и имеетемкостнойхарактер, при реактивное сопротивление возрастает
от 0 до ∞ и имеетиндуктивныйхарактер.
реактивное сопротивление возрастает
от 0 до ∞ и имеетиндуктивныйхарактер.Рассмотрим зависимость тока в rLC контуре от частоты приложенного напряжения:
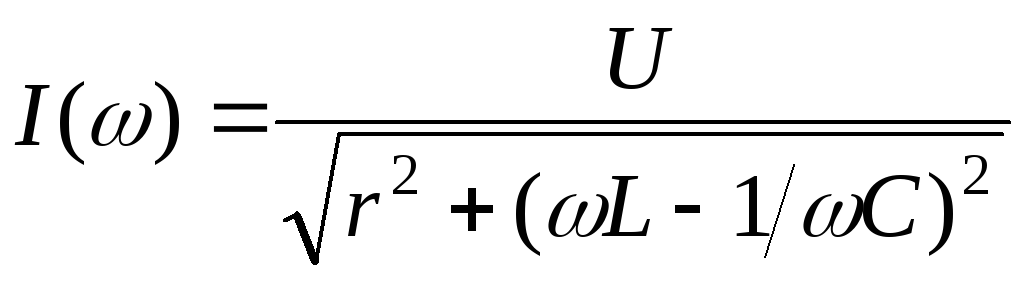 .
.
Анализ этого
выражения показывает, что при 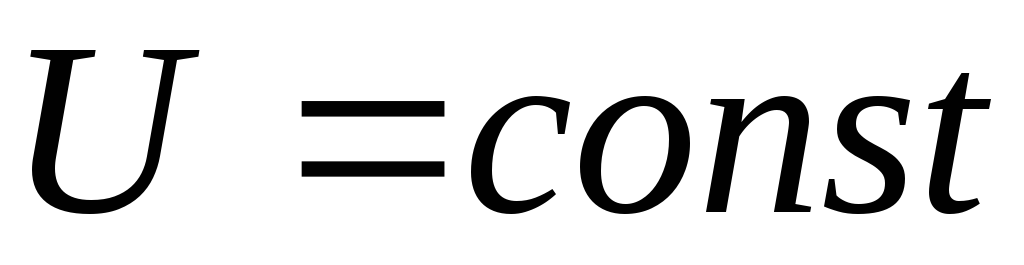 максимального значения
максимального значения ток достигает в точке, соответствующей
резонансной частоте.
ток достигает в точке, соответствующей
резонансной частоте.
Важной характеристикой rLC контура является
ширина резонансной кривой или полоса
пропускания, которую определяют как
разность верхней и нижней
и нижней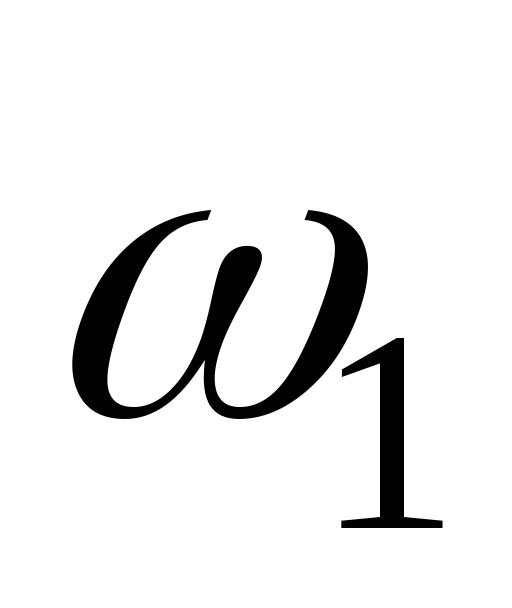 частот, для которых отношение
частот, для которых отношение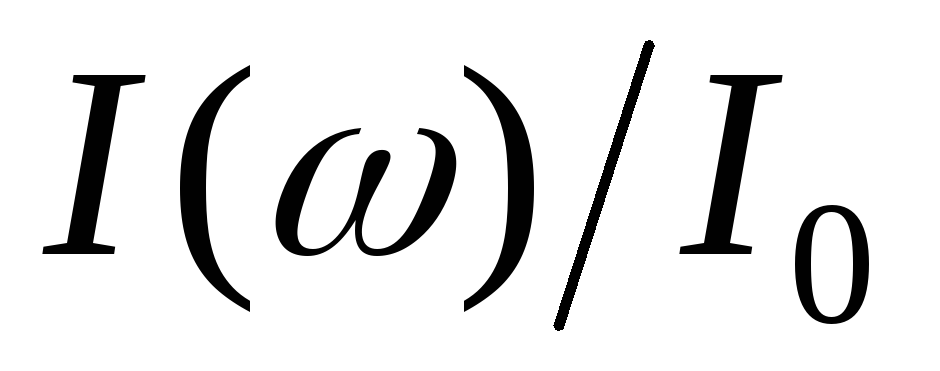 составляет
составляет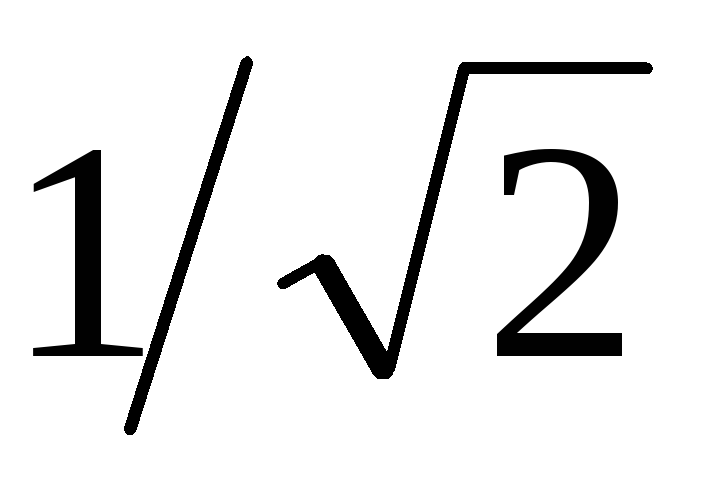 :
:
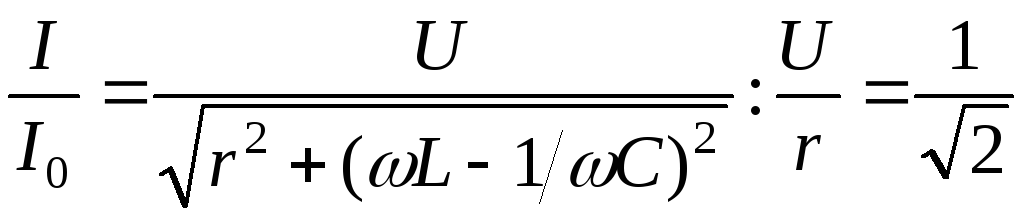 .
.
Частоты  и
и , ограничивающие полосу пропускания,
могут быть определены из соотношения
, ограничивающие полосу пропускания,
могут быть определены из соотношения
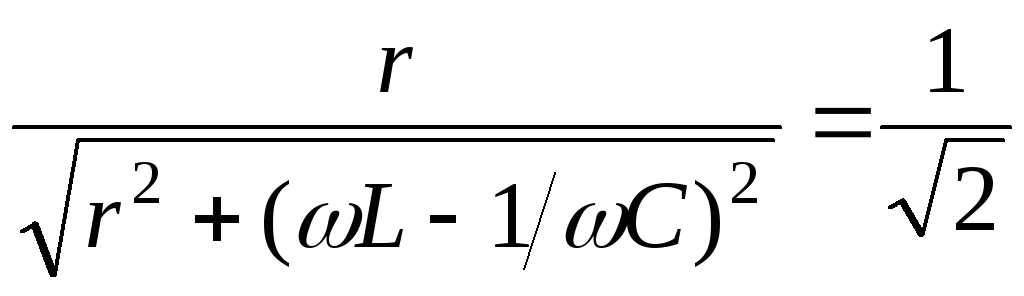 ,
,
откуда следует, что на границах полосы пропускания реактивные сопротивления по абсолютной величине равны активному
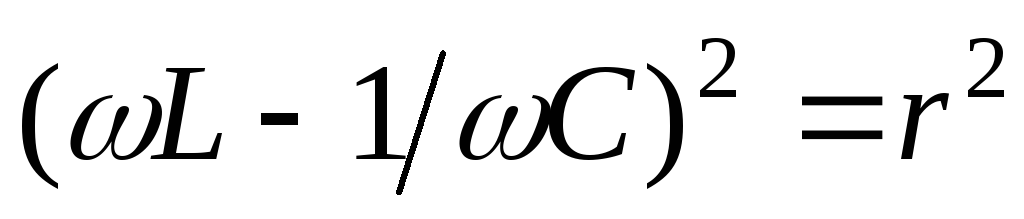 .
.
Последнее соотношение эквивалентно равнству
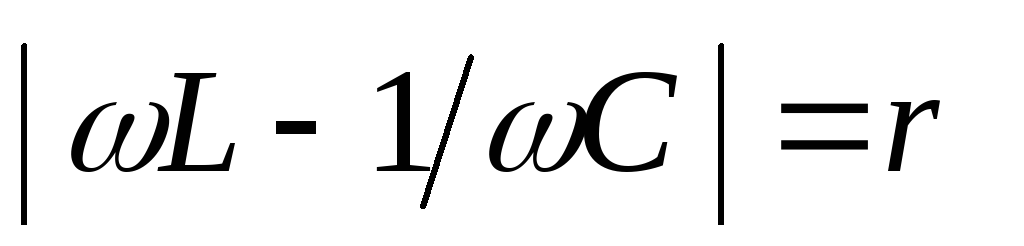 ,
,
Откуда 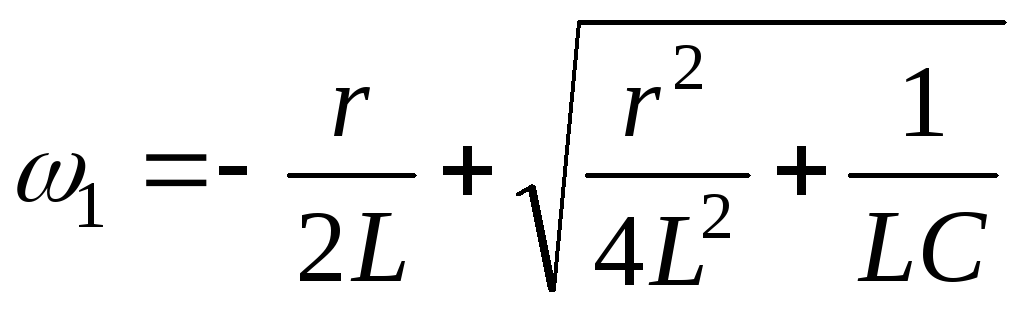 ,
, .
.
Разность
частот 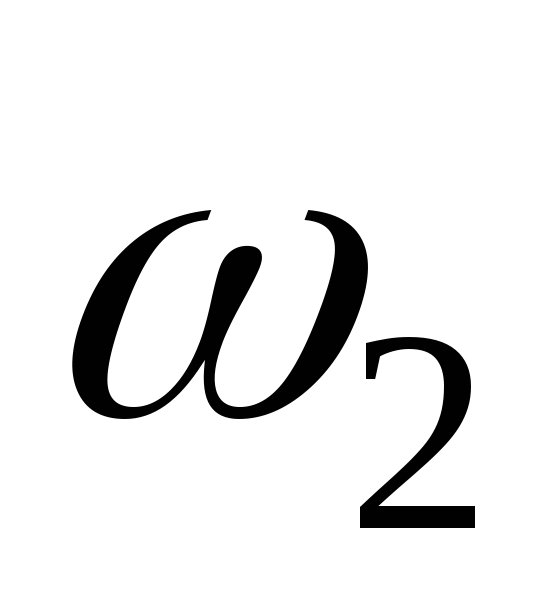 и
и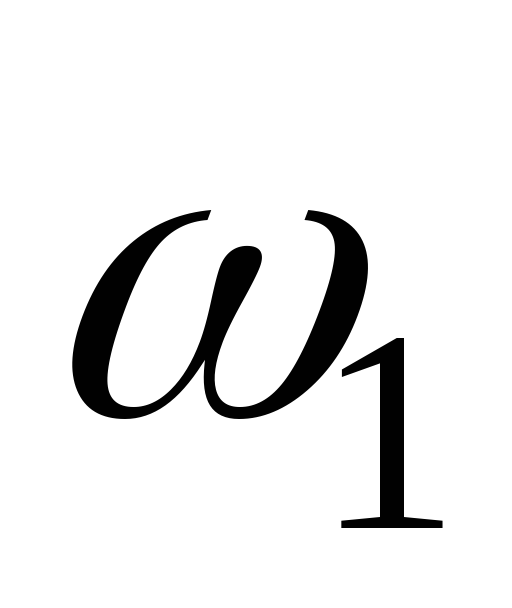 ( полоса пропускания ) определяется
выражением
( полоса пропускания ) определяется
выражением
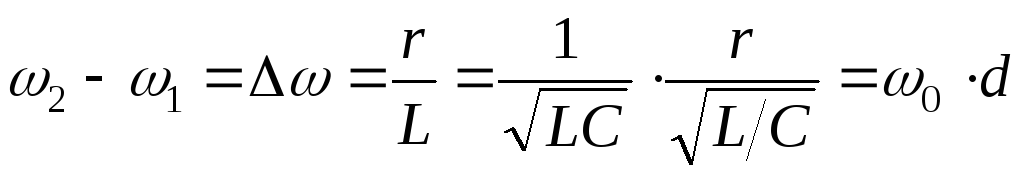
Если построить
зависимость 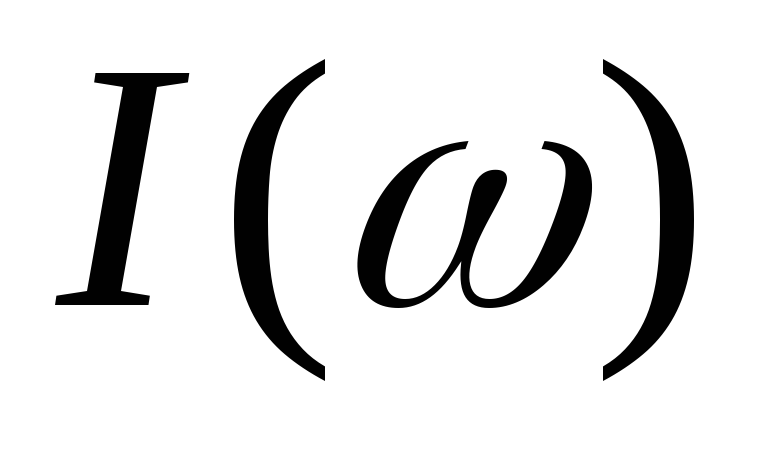 в системе относительных координат,
в системе относительных координат,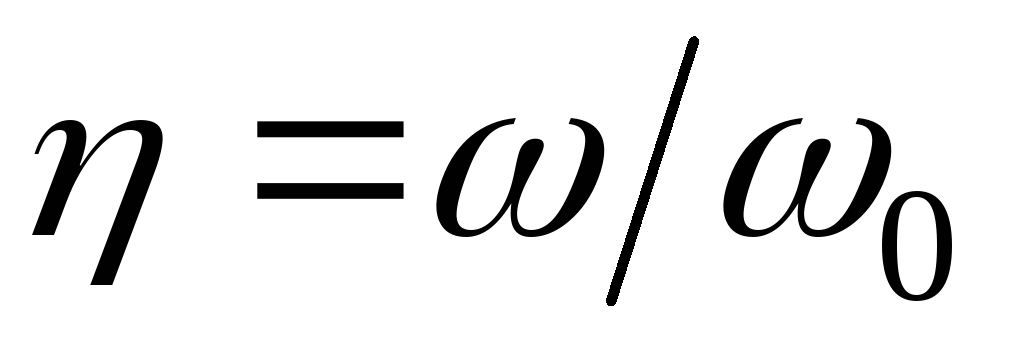 (рис.10.3), то ширина полосы пропускания
оказывается равной затуханию контура.
(рис.10.3), то ширина полосы пропускания
оказывается равной затуханию контура.

В
выражении напряжения на катушке
индуктивности 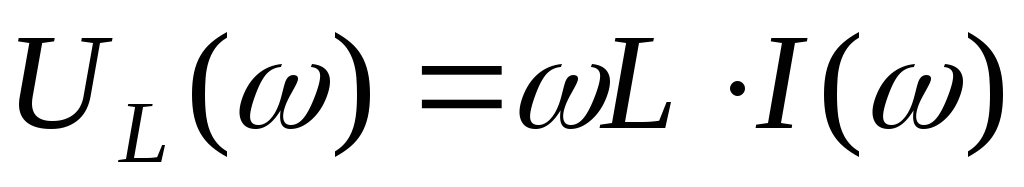 оба сомножителя зависят от частоты.
При
оба сомножителя зависят от частоты.
При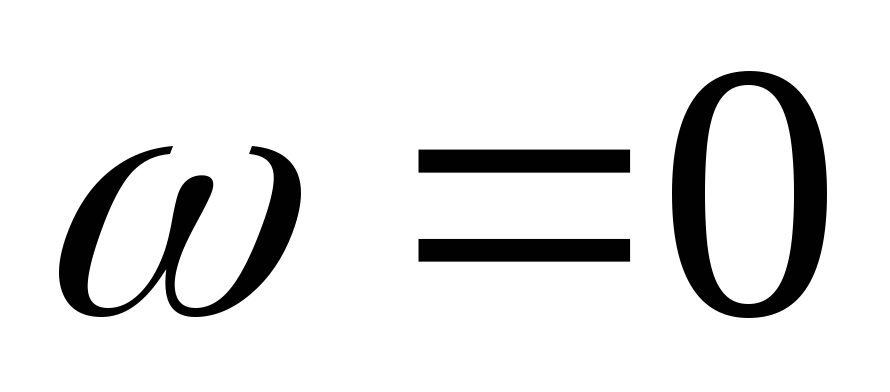 напряжение
напряжение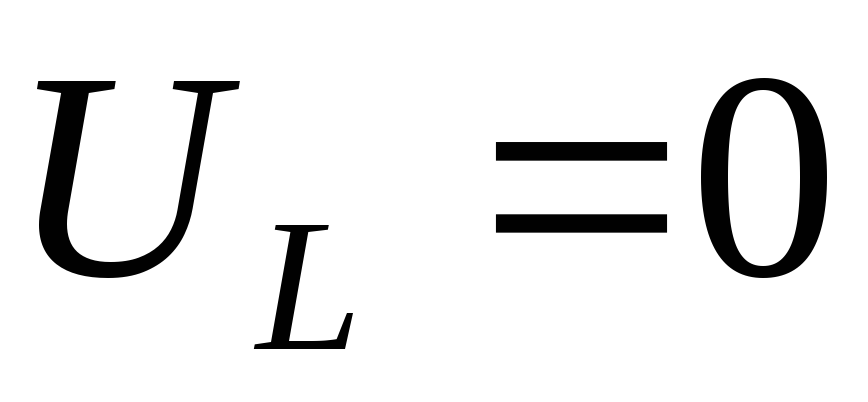 .
С увеличением частоты напряжение
.
С увеличением частоты напряжение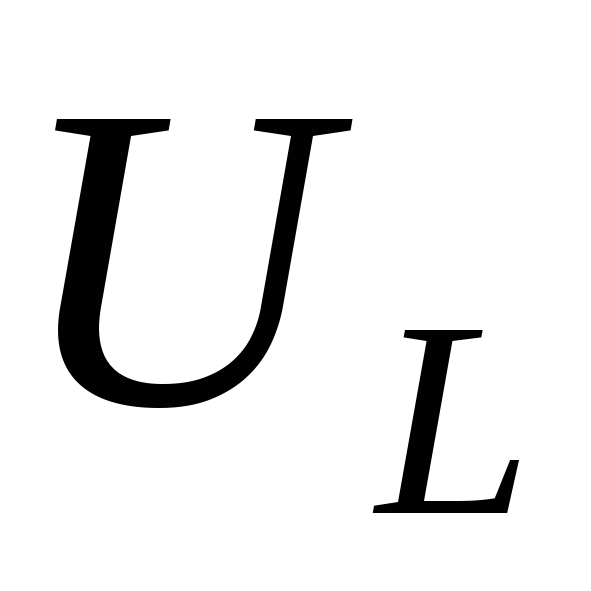 возрастает и стремится к входному при
возрастает и стремится к входному при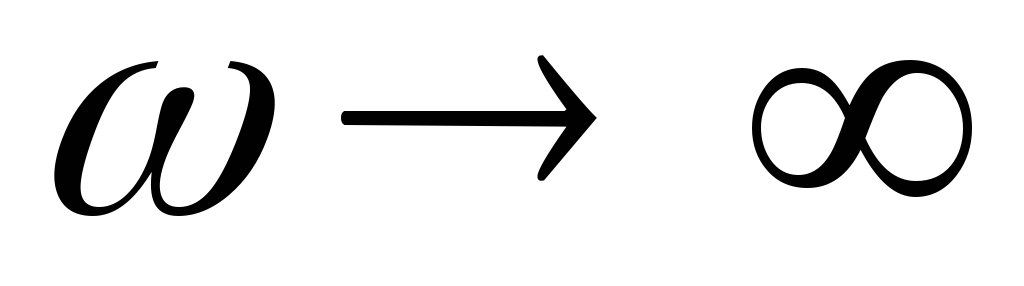 .
Можно показать, что при
.
Можно показать, что при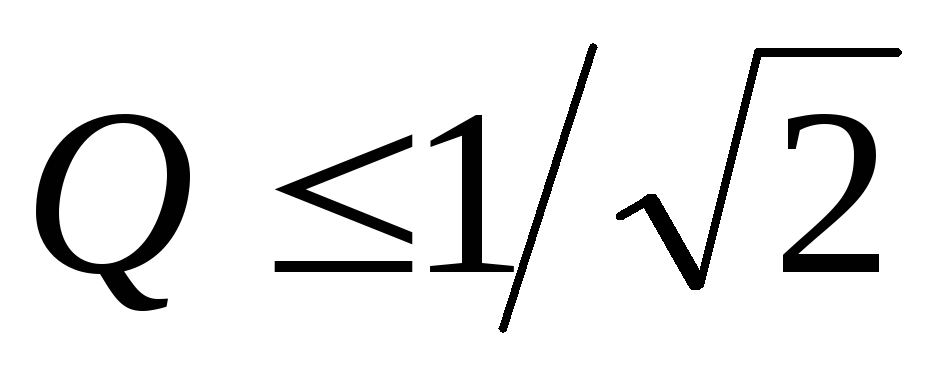 эта зависимость монотонна, а при
эта зависимость монотонна, а при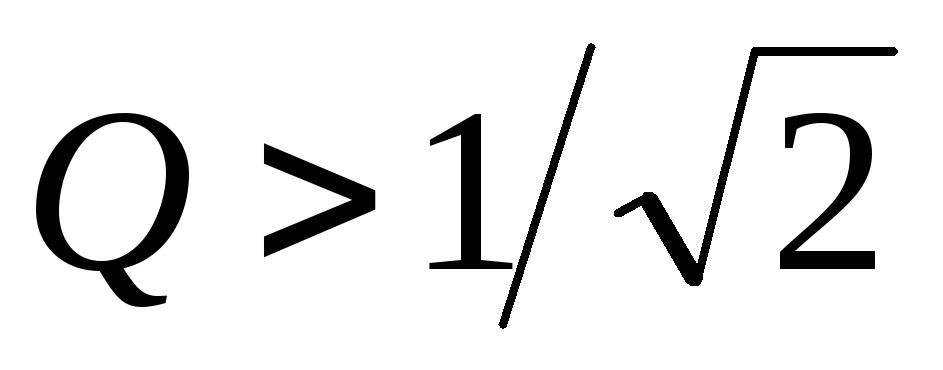 имеет максимум ( рис. 10.4 ).
имеет максимум ( рис. 10.4 ).

Напряжение
на конденсаторе  .
При
.
При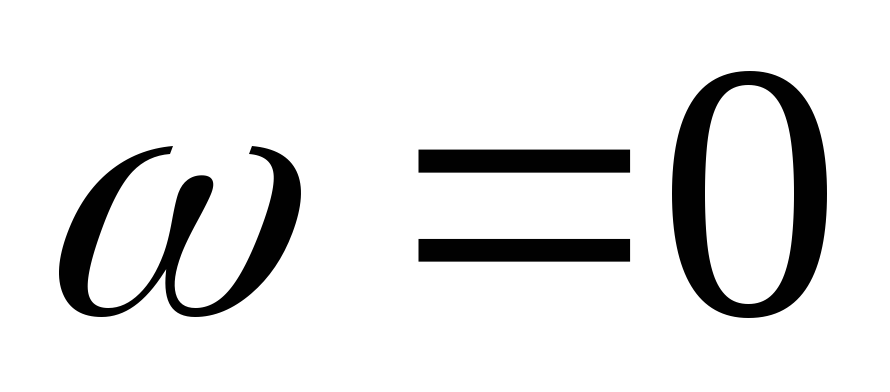 ток в контуре отсутствует и все входное
напряжение оказывается приложенным к
конденсатору. При
ток в контуре отсутствует и все входное
напряжение оказывается приложенным к
конденсатору. При напряжение на конденсаторе стремится
к нулю. Для цепи, добротность которой
превышает
напряжение на конденсаторе стремится
к нулю. Для цепи, добротность которой
превышает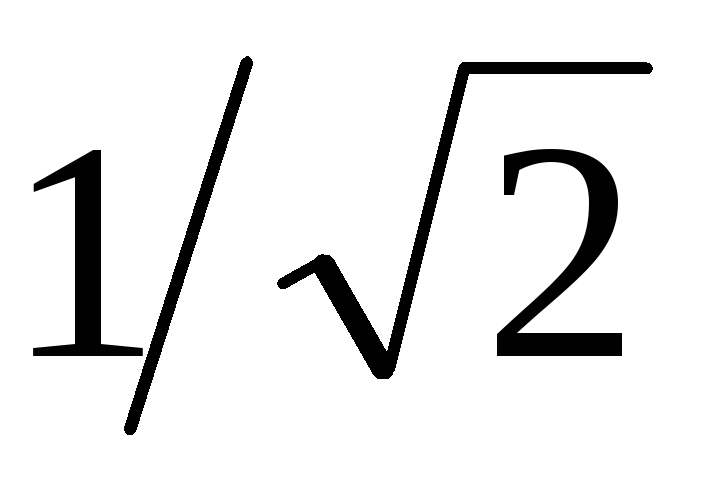 ,
зависимость
,
зависимость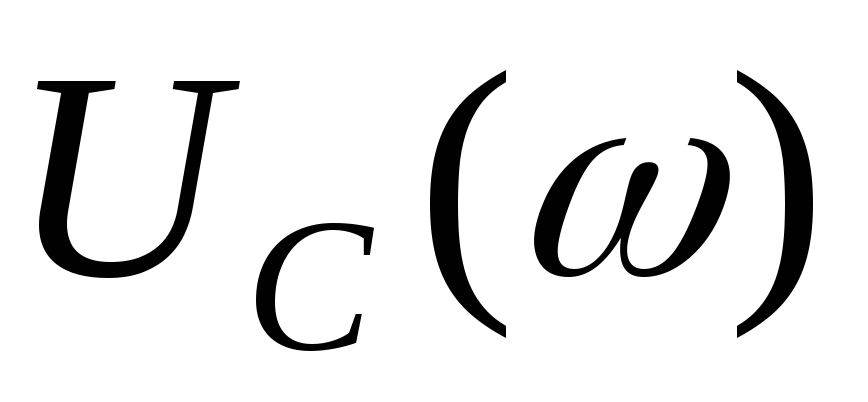 имеет максимум; если
имеет максимум; если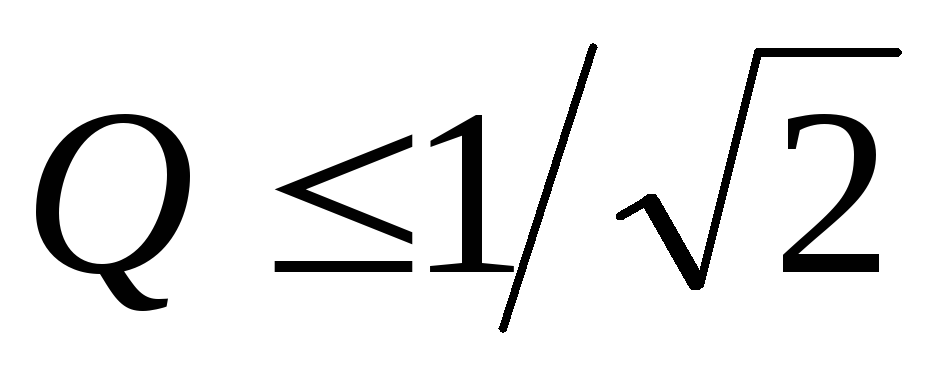 ,
напряжение на конденсаторе монотонно
уменьшается с ростом частоты.
,
напряжение на конденсаторе монотонно
уменьшается с ростом частоты.
studfile.net
ТОЭ Лекции — №27 Явление резонанса в электрических цепях
Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер: Z = R; сдвиг фаз отсутствует (φ=0).
В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным характерами сопротивлений, резонанс называется резонансом напряжений. Рассмотрим простейшую цепь, которую часто называют последовательным контуром. Для нее резонанс наступает при x = xL – xC = 0 или xL = xC, откуда:
Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 27.1, а).
Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений:
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.
Из условия выше следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 27.2). Емкость С0, при которой наступает резонанс, можно определить из формулы: С0=1/(ω2L).
Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C. Векторная диаграмма ее резонансного режима приведена на рис. 27.1, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 27.3, а).
Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.
Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:
Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:
или
Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B1 и B2. Заменяя схему на рис. 27.3, а эквивалентной (рис. 27.3, б), параметры которой вычисляем по формулам, и используя условие резонанса (B = B1 – B2 = 0), снова приходим к конечному выражению.
Схеме на рис. 27.3, б соответствует векторная диаграмма, приведенная на рис. 27.4
Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.
toehelp.com.ua
Понятие резонанса напряжений в электрических цепях переменного тока
Резонанс в электрической цепи возникает при резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определенной резонансной частотой системы. Это происходит тогда, когда два элемента противоположного характера компенсируют эффект друг друга в цепи.
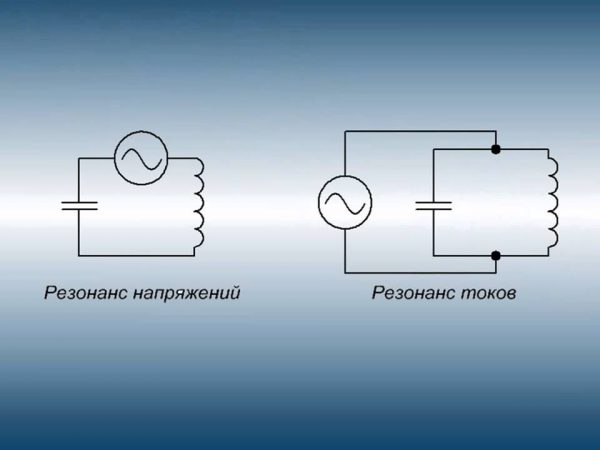
Резонанс токов и напряжений
RLC-цепь
Схема RLC – это электрическая цепь с последовательно или параллельно соединенными элементами:
- резистора,
- индуктора,
- конденсатора.
Название RLC связано с тем, что эти буквы являются обычными символами электрических элементов: сопротивления, индуктивности и емкости.
Векторная диаграмма последовательной RLC-цепи представлена в одном из трех вариантов:
- индуктивном,
- емкостном,
- активном.
В последнем варианте при нулевом сдвиге фаз, равенстве индуктивного и емкостного сопротивлений возникает резонанс напряжений.
Электрический резонанс
В природе бывают резонанс токов и резонанс напряжений. Наблюдаются они в цепи с параллельным и последовательным соединением элементов R, L и С. Резонансная частота одинакова для обеих цепей, она находится из условия противоположности сопротивлений реактивных элементов и вычисляется по нижеследующей формуле.

Резонансная частота
Векторные диаграммы практически идентичны, только сигналы отличаются. В последовательном контуре резонируют напряжения, в параллельном – ток. Но если отступиться от резонансной частоты такая симметрия естественно нарушится. В первом случае сопротивление возрастет, во втором – уменьшится.
Резонанс напряжений, достигающих максимальной амплитуды
На картинке ниже представлена векторная диаграмма цепи последовательного контура, где:
- I – вектор общего тока;
- Ul – опережает I на 900;
- UС – отстает от I на 900;
- UR – синфазно I.
Из трех векторов напряжения (Ul, UС, UR) два первых взаимно компенсируют друг друга. Они между собой:
- противоположны по направлению,
- равны по амплитуде,
- отличаются по фазе на пи.
Получается, что напряжение по второму закону Кирхгофа приложено только к резистору. В этот момент:
- импеданс последовательного контура на резонансной частоте минимален и равен просто R;
- так как сопротивление цепи минимальное, то соответственно ток по амплитуде максимальный;
- также приблизительно максимальны напряжения на индуктивности и на емкости.
Если рассматривать отдельно последовательный контур LC, то он даёт нулевое сопротивление на резонансной частоте:
ZL = -ZC

Резонанс напряжений в цепи переменного тока
Важно! Когда установился гармонический режим c резонансной частотой, в контуре происходит следующее: источник обеспечивает установившуюся амплитуду колебаний; мощность источника расходуется лишь на нагрев резистора.
Резонанс токов через реактивные элементы
Диаграмма параллельного контура на той же частоте. Поскольку все элементы соединены параллельно, то диаграмму лучше начать строить с общего напряжения.
- U – вектор общего тока;
- Ic – опережает U на 900;
- IU – отстает от U на 900;
- Ток в резисторе (IR) синфазен общему напряжению.
Поскольку сопротивления реактивности по модулю равны, то и амплитуды токов Ic и Iu:
- одинаковы;
- достигают максимальной амплитуды.
Получается, что по первому закону Кирхгофа IR равен току источника. Другими словами, ток источника течет только через резистор.
Если рассматривать отдельно параллельный контур LC, то на резонансной частоте его сопротивление бесконечно большое:
ZL = ZC.
Когда установится гармонический режим c резонансной частотой, в контуре происходит следующее:
- источник обеспечивает установившуюся амплитуду колебаний;
- мощность источника тока расходуется лишь на пополнение потерь в активном сопротивлении.

Резонанс токов
Двойственность RLC-контуров
Таким образом, можно сделать сравнительный вывод:
- У последовательной RLC цепи импеданс минимален на резонансной частоте и равен активному сопротивлению контура;
- У параллельной RLC цепи импеданс максимален на резонансной частоте и равен так называемому сопротивлению утечки, фактически тоже активному сопротивлению контура.
Для того чтобы предуготовить условия для резонанса тока или напряжения, требуется проверить электрическую цепь с целью предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимую часть необходимо приравнять к нулю.
Для информации. Напряжения в последовательной цепи ведут себя очень похоже токам параллельной цепи на резонансной частоте, в этом проявляется двойственность RLC-контуров.

Резонанс в цепи переменного тока
Применение резонансного явления
Хорошим примером применения резонансного явления может служить электрический резонансный трансформатор, разработанный изобретателем Николой Тесла ещё в 1891 году. Тесла проводил эксперименты с различными конфигурациями, состоящими в сочетании из двух, а иногда трех резонансных электрических цепей.
Для информации. Термин «катушки Теслы» применяются к ряду высоковольтных резонансных трансформаторов. Устройства используются для получения высокого напряжения, низкого тока, высокой частоты переменного тока.
В то время как обычный трансформатор предназначен для эффективной передачи энергии с первичной на вторичную обмотку, резонансный трансформатор предназначен для временного хранения электрической энергии. Устройство управляет воздушным сердечником резонансно настроенного трансформатора для получения высоких напряжений при малых токах. Каждая обмотка имеет емкость и функционирует как резонансный контур.
Чтобы произвести наибольшее выходное напряжение, первичный и вторичный контуры настроены в резонанс друг с другом. Оригинальные схемы изобретателя применяются как простые разрядники для возбуждения колебаний с помощью настроенных трансформаторов. В более сложных конструкциях используют транзисторные или тиристорные выключатели.
Для информации. Трансформатор Теслы основан на использовании резонансных стоячих электромагнитных волн в катушках. Своеобразный дизайн катушки продиктован необходимостью достигнуть низкого уровня резистивных потерь энергии (высокая добротность) на высоких частотах, что приводит к увеличению вторичных напряжений.

Резонанс в электрической цепи
Электрический резонанс – одно из самых распространенных в мире физических явлений, без которого не было бы TV, диагностических мед. аппаратов. Одни из самых полезных видов резонанса в электрической цепи – это резонанс токов и резонанс напряжений.
Видео
Оцените статью:jelectro.ru
Резонанс токов: применение, принцип резонса тока, расчет контура
Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет.
Что такое резонанс?
Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.
 Соединение двух ветвей при резонансе
Соединение двух ветвей при резонансеПризнаки резонанса:
- Составляющие реактивных ветвей тока равны между собой IPC = IPL, противофаза образовывается только при равенстве чистой активной энергии на входе;
- Ток в отдельных ветках, превышает весь ток определенной цепи, при этом ветви совпадают по фазе.
Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:
- Последовательный;
- Параллельный.
Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.
Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.
Применение
Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.
Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.
Принцип резонанса токов
Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:
 Схема для питания конденсатора
Схема для питания конденсатораПереключатель будет отвечать за направление колебаний.
 Схема: переключатель резонансной схемы
Схема: переключатель резонансной схемыКонденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.
 Схема: ток в резонансной схеме равен нулю
Схема: ток в резонансной схеме равен нулюНаправленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.
Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.
Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.
В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.
Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.
Расчет резонансного контура
Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела.
Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом:
R ср= I2конт * R = (V2конт / Z2) * R.
При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1
Сама же формула резонанса имеет следующий вид:
ω0 = 1 / √L*C
Нулевой импеданс в резонансе определяется при помощи такой формулы:
Fрез = 1 / 2π √L*C
Резонансная частота колебаний может быть аппроксимирована следующим образом:
F = 1/2 р (LC) 0.5
Где: F = частота
L = индуктивность
C = емкость
Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям:
R = 2 (L / C) 0.5
Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов. При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока.
www.asutpp.ru
в цепи переменного тока и напряжения
Многие люди, изучая электронику и все, что с ней связано, сталкиваются с таким понятием как резонанс токов. Что оно собой представляет, при каких условиях возникает резонанс токов, как используется и как его правильно подсчитать? Об этом далее.
Что это такое
Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов
Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия
При каких условиях возникает
Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.
В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает
Как используется
Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.
Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.

Сфера применения
Принцип действия
Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.
Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.

Принцип работы
Как правильно рассчитать
Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.

Формула расчета
Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.

Формула резонансных кривых
Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.

Расчет колебательного контура
Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.
В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.
rusenergetics.ru
