Главная » Разное » Резонансная кривая тока: РЕЗОНАНСНЫЕ КРИВЫЕ ТОКА И НАПРЯЖЕНИЯ — Студопедия

Резонансная кривая тока: РЕЗОНАНСНЫЕ КРИВЫЕ ТОКА И НАПРЯЖЕНИЯ — Студопедия

| – Комментировать

Содержание

РЕЗОНАНСНЫЕ КРИВЫЕ ТОКА И НАПРЯЖЕНИЯ — Студопедия

Рисунок 11.5

Рисунок 11.4

Рисунок 11.3

Рисунок 11.2

Рисунок 11.1

Кривая, которая соединяет концы векторов , носит название годографа передаточной функции (годографом амплитудно-фазовой характеристики). Годограф строят при изменении частоты от нуля к бесконечности.

Пример.Определить комплексный коэффициент передачи по напряжению , АЧХ и ФЧХ для схемы (рис.11.2а).

Согласно с определением: . Задача решается в такой последовательности: 1) задаемся ; 2) определяем комплексное значение выходного напряжения по закону Ома:

;

3) находим ;

4) подаем в показательной форме, находим АЧХ и ФЧХ (рис.11.2б,в):

.

а) б) в)

11.2 Последовательный резонансный контур.

Определение и условия резонанса

Колебательный контур — электрический круг, в котором возможны колебание свободной составной тока. Резонансный контур — электрическая цепь, в которой имеет место явление резонанса (напряжений или токов).

Последовательный резонансный контур — резонансный контур, который состоит из индуктивного и емкостного элементов, соединенных последовательно (рис.11.3а,б). На схеме (рис.11.3в) R, L, C — первичные параметры контура, причем , где — активное сопротивление катушки индуктивности, — сопротивление растекания конденсатора, перерасчитанное в последовательное соединение, — сопротивление проводов (потерь). Чтобы дать определение резонанса, найдем ток в цепи (рис.11.3в):


,

где — реактивное сопротивление контура.

Запишем комплексное действующее значение тока в показательной форме

,

где — полное сопротивление контура.

Итак, резонанс — это явление в электрической цепи, которая имеет участки с индуктивными и емкостными элементами, по которому разница фаз напряжения и тока на входе цепи равняется нулю.

Из этого определения вытекает, что полное сопротивление контура должно быть активным. Тогда реактивное сопротивление или проводимость цепи, в которой наблюдается резонанс, равняются нулю.

а) б) в)

Итак, если в общем случае действительны соотношения

; , то при резонансе:

1) — это условие амплитудного резонанса;

2) ; ; — условие возникновения фазового резонанса.

11.3 Вторичные параметры последовательного резонансного контура

1. Резонансная частота — частота тока (напряжения) во время резонанса в цепи. Обозначается и определяется, исходя из условия резонанса X = 0; :

; .

Значению циклической частоты соответствует резонансная длина волны:

,

где c — скорость распространение электромагнитных волн.

2. Характеристическое (волновое) сопротивление контура — сопротивление каждого из реактивных элементов при резонансе: .

3. Добротность — отношение характеристического сопротивления к активному сопротивлению контура: , где d — затухание — величина, обратная к добротности, которая характеризует интенсивность затухания колебаний в контуре.


Добротность характеризует длительность собственных колебаний в контуре, ее можно определить также как коэффициент качества, который равняется отношению абсолютного значения реактивной мощности к активной мощности.

4. Полное сопротивление — модуль входного комплексного сопротивления контура Z .

,

где — модуль

Z;

— аргумент Z.

Частотные зависимости полного и реактивного сопротивления , изображены на рис.11.4. Из графика видно, что на резонансной частоте реактивное сопротивление контура равняется нулю, а равняется сопротивлению потерь R.

а) б)

5. Фазовая характеристика — зависимость аргумента входного сопротивления последовательного контура от частоты (рис.11.5а): .

6. Резонансная кривая тока — зависимость модуля комплексного действующего (амплитудного) значения тока от частоты (рис.11.5б):

.

Очевидно, что на частоте резонанса , выполняются такие соотношение: , .

11.4 Векторная диаграмма напряжений при резонансе

Запишем для последовательного резонансного контура уравнения по второму закону Кирхгофа:


.

Если частота равняется резонансной частоте , то

,

где — напряжение на сопротивлении R при резонансе;

— напряжение на индуктивности при резонансе;

— напряжение на емкости при резонансе.

В соответствии с полученными выражениями на рис.11.5в изображена векторная диаграмма тока и напряжений при резонансе. Как видно из рисунка, при выполняются такие соотношения:

1) напряжение на сопротивлении R совпадает по фазе с током I, а модуль равняется значению E; напряжения на реактивных элементах равны между собой по модулю и противоположны по направлению;

2) по абсолютной величине напряжения на реактивных элементах последовательного резонансного контура в Q раз превышают значение ЭДС, которая действует на входе: . Итак, в последовательном контуре наблюдается резонанс напряжений.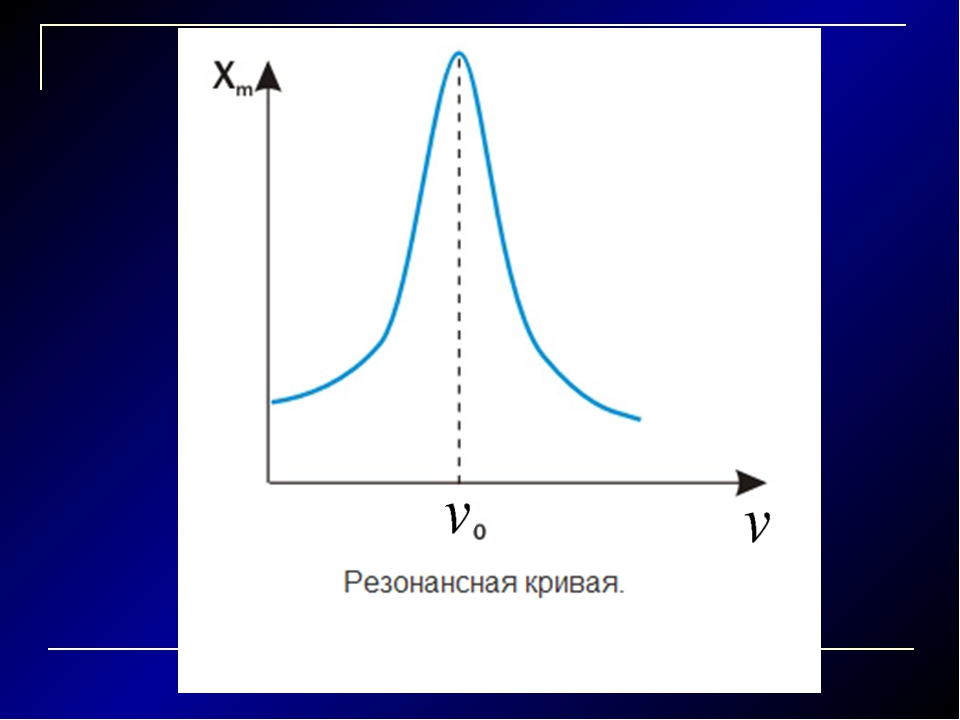

Резонанс напряжений — явление резонанса на участке электрической цепи, в которую входят последовательно соединенные индуктивный и емкостной элементы.

а) б) в)


Частотные характеристики и резонансные кривые последовательного контура

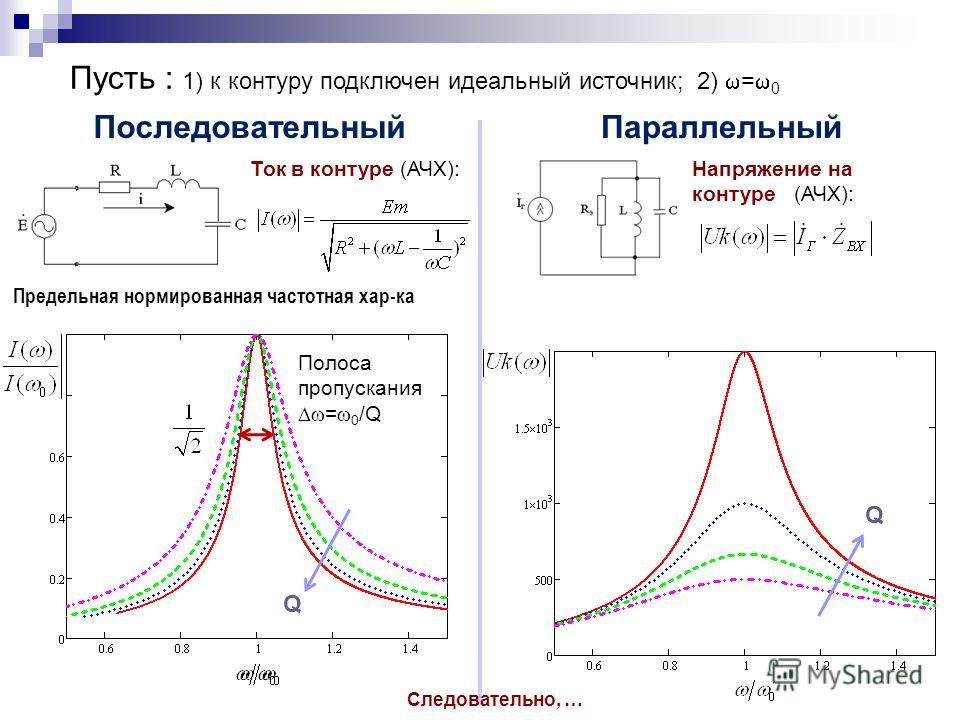
Предположим, что к контуру (см. рис. 3.8) приложено синусоидальное напряжение , амплитуда которого неизменна, а частота может изменяться в пределах от 0 до .
Изменение частоты приводит к изменению параметров контура, изменяется его реактивное, а следовательно, и полное сопротивление, а также угол φ (аргумент комплексного сопротивления). Зависимости от частоты параметров цепи назовем частотными характеристиками цепи, зависимости действующих или амплитудных значений тока и напряжения от частоты резонансными кривыми.
На рис. 5.1 построены частотные характеристики и . Изменение реактивного сопротивления приводит к изменению режима цепи. На рис. 5.2 приведен примерный вид резонансных кривых и кривой для цепи, добротность которой .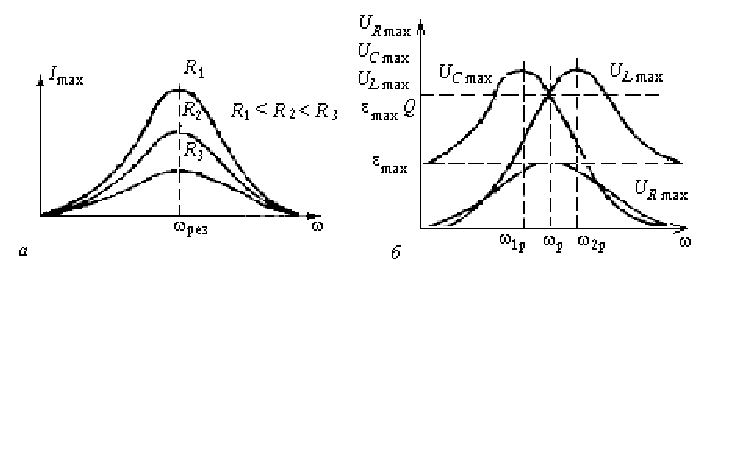 При ω = 0 напряжение, приложенное к цепи, во времени не изменяется, поэтому ток в цепи отсутствует. При изменении частоты от 0 до реактивное сопротивление имеет емкостный характер и изменяется от до 0 (см. рис. 5.1). Вследствие этого ток возрастает от 0 до максимального резонансного значения , а угол сдвига фаз между напряжением и током изменяется от —π/2 до 0. При изменении частоты от до результирующее реактивное сопротивление возрастает от 0 до и имеет индуктивный характер.
Вследствие этого ток уменьшается от наибольшего значения до 0, а угол φ возрастает от 0 до π/2. Напряжение изменяется пропорционально току.

В выражении напряжения на индуктивности оба сомножителя зависят от частоты. При ω = 0 сопротивление , ток I = 0, и, следовательно, . При изменении частоты от 0 до оба сомножителя увеличиваются и возрастает. При дальнейшем увеличении частоты () ток I уменьшается, но за счет роста ωL напряжение продолжает возрастать. Анализ, который здесь не приводится, показывает, что для цепи с добротностью это возрастание продолжается непрерывно до значения U, а для цепи с добротностью напряжение при некоторой частоте достигает максимума , а затем уменьшается. При и , следовательно, .
Теперь рассмотрим зависимость напряжения на емкости от частоты. При ω = 0 тока в цепи нет, поэтому . При возрастании ω, начиная от нуля, непрерывно уменьшается. Анализ показывает, что для цепи с добротностью напряжение непрерывно уменьшается, а при напряжение сначала из-за возрастания тока I увеличивается, достигает при некотором значении частоты максимума , а затем уменьшается.
Уменьшение напряжения с ростом частоты начинается при частоте , меньшей , вследствие непрерывного уменьшения . При как I, так и равны нулю, поэтому . Заметим, что . При , как было отмечено, .
График зависимости тока от частоты показывает, что рассматриваемая цепь обладает «избирательными свойствами». Цепь обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к ее резонансной частоте.

Избирательными свойствами таких цепей широко пользуются в электросвязи и радиотехнике, при этом режим резонанса является нормальным режимом работы. Наоборот, в устройствах, где резонансный режим не предусмотрен, появление резонанса нежелательно, так как возникающие значительные напряжения на катушке и конденсаторе могут оказаться опасными для изоляции.

Рис. 5.1

Рис. 5.2

Выясним влияние параметров цепи на форму резонансной кривой . Для удобства сравнения резонансных кривых друг с другом будем строить их в относительных единицах:

где — действующий ток при резонансе; — относительная частота.
Преобразуем выражение полного сопротивления цепи:

Разность характеризует расстройку контура относительно резонансной частоты. Произведение называется обобщенной расстройкой. С учетом этих обозначений сопротивление

Ток в цепи

Выражение (5.5) показывает, что влияние параметров цепи на вид резонансной кривой полностью учитывается добротностью Q.
На рис. 5.3,а представлен ряд резонансных кривых. Чем больше Q, тем острее резонансная кривая, тем лучше «избирательные свойства» цепи, что и послужило одной из причин назвать Q добротностью контура. Заметим, что наибольшие достигаемые на практике значения Q контуров, состоящих из катушек индуктивности и конденсаторов, лежат в пределах 200-500.
Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосы пропускания контура , которую определяют как разность верхней и нижней частот, между которыми отношение превышает . На рис. 5.3, а проведена горизонтальная линия, соответствующая . Ее пересечение с резонансными кривыми определяет граничные частоты полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.

Рис. 5.3

Высшая и низшая относительные частоты показаны на рис. 5.3,б для контура с известной добротностью Q. На этом же рисунке построена идеальная резонансная кривая, для которой вне полосы пропускания ток равен нулю, т. е. у которой идеальные избирательные свойства. На рис. 5.3, а также проведена горизонтальная линия, соответствующая . Ее пересечение с резонансными кривыми определяет полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.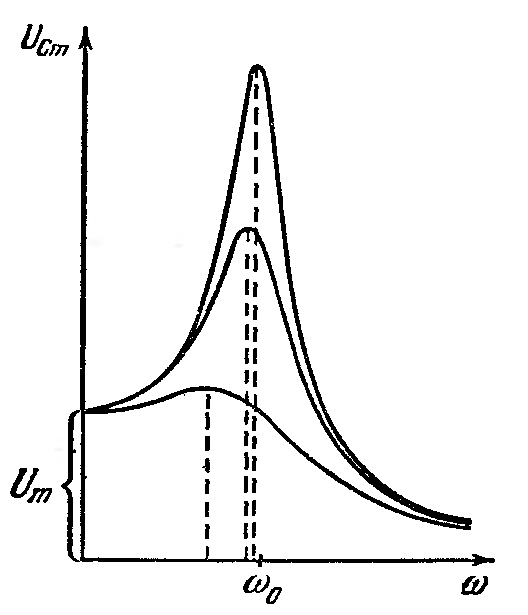
Если диапазон изменения частоты составляет несколько порядков, то часто выбирают для частоты логарифмический масштаб, т. е. или . Интервал частот , для которого , называют декадой (десятикратное изменение частоты). Число декад . Интервал частот, для которого , называют октавой (удвоение частоты), причем 1 декада октавы.

Пример 5.1.
Определить добротность контура по известной резонансной кривой
Решение.
На границах полосы пропускания , т.е. как следует из (5.5), и , откуда

так как и (рис. 5.3, б).
Сложим (а) и (б):

или

т. е должно быть , т. е. .
Вычтем (б) из (а):

или

откуда

Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе

Запишем формулу (5. 68) для амплитуды силы тока в наиболее удобном виде

,

и исследуем эту зависимость для различных значений .

1. ω=0 : , т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.

2. : .

3. Максимум функции наблюдается тогда, когда подкоренное выражение в знаменателе будет минимальным, т.е. первое слагаемое в подкоренном выражении должно быть равным нулю. Поэтому максимум соответствует частоте , а само максимальное значение будет равно

. (5.74)

На рис. 5.18 приведены резонансные кривые в случае идеального колебательного контура () и для двух разных значений сопротивления в нем (, т.е.) при постоянном значении . Как видно, максимум функции с увеличением уменьшается, а его смещение по оси частотне происходит.

Используя табл. аналогий 5.1, можно записать формулы, описывающие резонансные кривые для амплитуды колебаний скорости тела (м.т.) в механической системе:

, (5.75)

: . (5.76)

График для трех значений коэффициента сопротивления () среды приведены на рис. 5. 18,б. Эти графики аналогичны графикам резонансных кривых .

Рис. 5.18

      1. Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые

Перепишем формулы (5.64) для I и в удобном виде

, ,

и добавим к ним формулы для UL и UR:

,. (5.77)

Найдем в соответствии с полученными формулами разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивностии активного сопротивления:

, (5.78)

, (5.79)

. (5.80)

Рис. 5.19

Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.

На ней указаны амплитуды векторов напряжений на отдельных участках электрической цепи. При этом фаза колебания силы тока в контуре принимается равной нулю, т.е. амплитуда вектора силы тока располагается вдоль оси .

На такой диаграмме вектор амплитуды внешнего напряжения, подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений (,,) на разных его участках. Это позволяет записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот, рис. 5.20,а):

, (5.81)

из которой с учетом формул (5.19) и (5.20) () можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения

.

Рис. 5.20

Под фазовыми резонансными кривыми понимают, например, зависимости разности фаз между внешним напряжением и напряжением на конденсаторе, разности фаз между внешним напряжением и силой тока

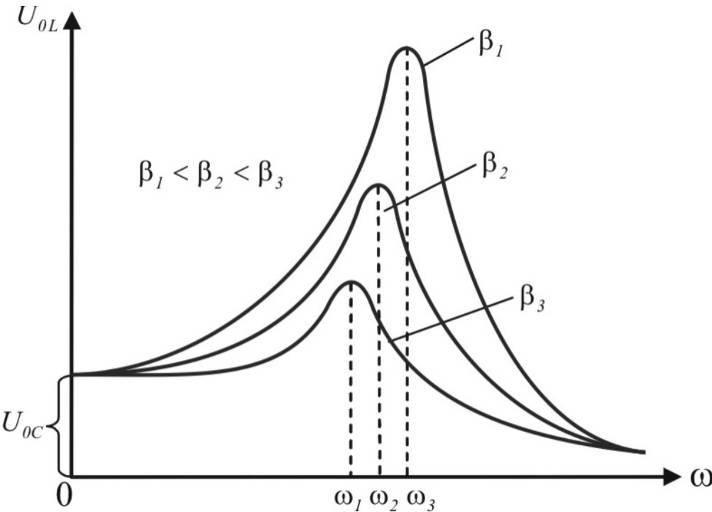I в контуре от частоты внешнего напряжения. Наиболее интересными из них являются зависимости , так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз и можно записать

,. (5.82)

Отметим, что разность фаз для цепей переменного тока обозначают буквой : .

На рис. 5.21 приведены фазовые резонансные кривые и, построенные по формулам (5.66) и (5.82) при значениях параметра : .

Рис. 5.21

Из них следует, что внешнее напряжение опережает по фазе напряжение на конденсаторе на угол . На векторной диаграмме это означает, что вектор амплитуды располагается выше вектора амплитуды(рис. 5.20 а,б,в). Причем угол изменяется от нулевого значения для частоты , равной нулю (), до значения равного при частоте внешнего напряжения стремящегося к бесконечности (, рис.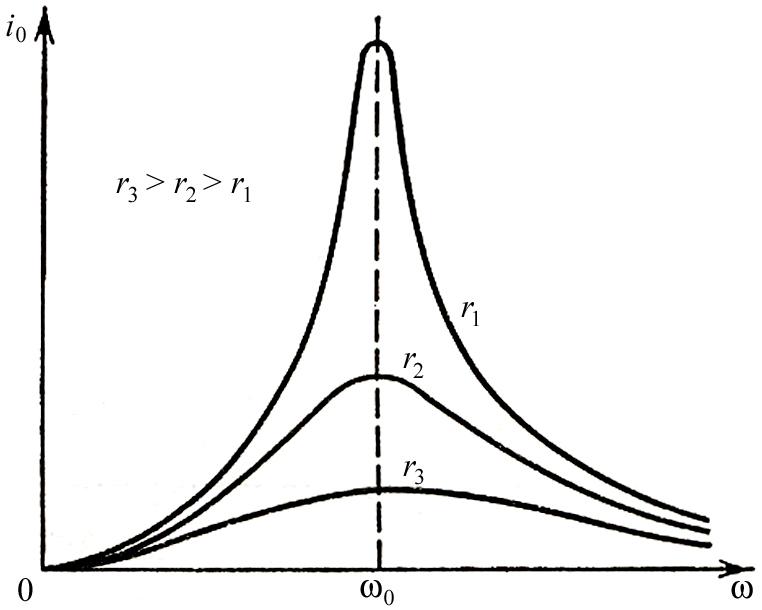 5.21,а). При резонансе амплитуды векторов внешнего напряжения и напряжения на конденсаторевзаимно перпендикулярны (см. рис. 5.20,б), что приводит к разности фаз между ними, равной (, Рис. 5.21,а).

Из другой фазовой резонансной кривой следует, что фаза внешнего напряжения для частот отстает от фазы тока в контуре на угол (рис.5.21,б). Для частот фаза внешнего напряжения опережает на угол фазу колебаний силы тока в контуре и при увеличении частоты стремится к значению, равному . При резонансе (,.) фаза колебаний силы тока и внешнего напряжения совпадают, т.е. и вектора амплитуд инаправлены одинаково, вдоль оси(рис. 5.21,б).

При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q >>1) и формулы (5.64) и (5.66) запишем

: ;

, .

Такое поступление энергии в контур при резонансе приводит к большим амплитудам колебаний, их числовые значения определяются диссипацией (рассеянием) энергии системы, т. е. коэффициентом затухания (формула (5.70)).

При частотах , больших или меньших () амплитуда вынужденных колебаний даже в отсутствии диссипации энергии () будет уменьшаться, она определяется расстройкой резонанса (), т.е. разностью частот и.

Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.

§5. Резонансные кривые.

Чтобы определить резонансную частоту для амплитуды падения напряжения на емкости, нужно найти максимум функции:

(21)

Продифференцировав выражение (21) по и приравняв 0, получим уравнение:

(22)

Решая уравнение (22), можно получить, что максимум амплитуды падения напряжения на емкости достигается при

(23)

Таким образом, резонансная частота для несколько меньше чем собственная частота колебаний в контуре. Если ввести обозначенияи, то выражение (23) перепишется так:

Резонансные кривые для изображены на (рис.7) при различных. В соответствии с (20), (21), чем меньше коэффициент затухания, тем выше и правее лежит максимум данной кривой. По поводу этих резонансных кривых (рис.7) можно сделать следующие замечания. При стремлении частотык нулю кривые стремятся к одному значению, то есть к напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения величиной. При стремлениик бесконечности все кривые асимптотически стремятся к нулю. Чем меньше, тем сильнее изменяется с частотой амплитудавблизи резонанса, тем “острее” максимум резонансной кривой. Остроту резонансных кривых характеризует также добротность, чем больше добротность контура, тем уже и выше максимум на кривой зависимости амплитуды вынужденного колебания от частотывнешнего воздействия. Резонанс напряжений широко используется в радиотехнике, когда нужно усилить колебание напряжения какой-либо определенной частоты, что позволяет выделить из многих сигналов различных радиостанций только одно колебание определенной частоты (настроиться на определенную станцию).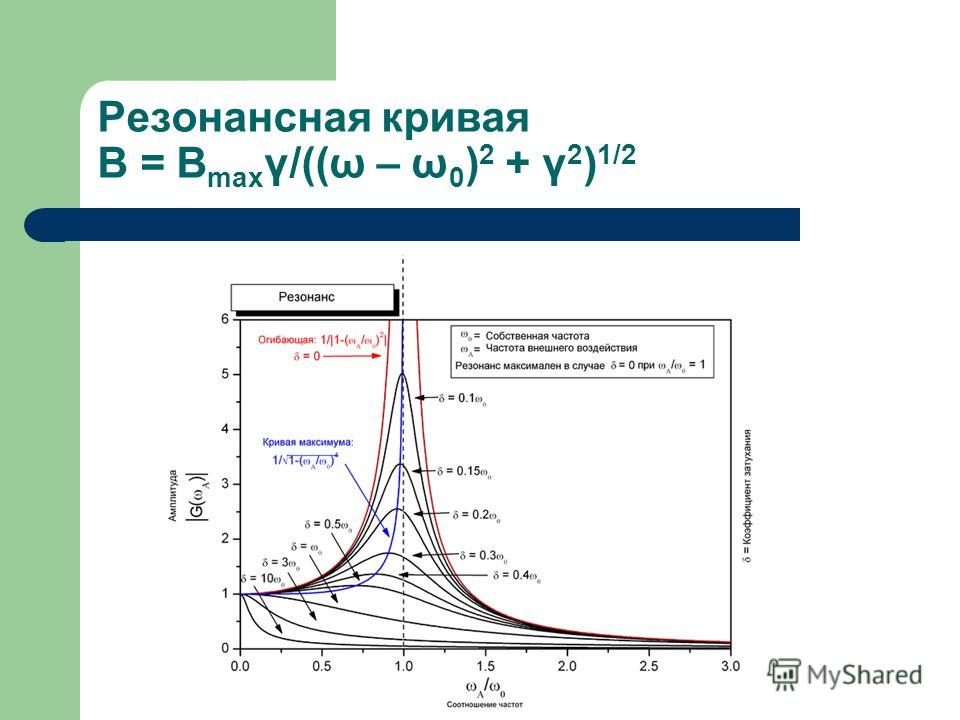

рис.7

Изучение резонанса напряжений.

Приборы и принадлежности:

1. Генератор сигналов звуковой частоты представляет собой источник переменного напряжения звуковой частоты в пределах от 17,7 до 200000 Гц (рис.8).

рис.8

На передней панели звукового генератора находится:

1.1. Тумблер подключения прибора к сети “вкл.” – “откл.”.

1.2. Вольтметр на выходе генератора является индикатором напряжения (Регулятор амплитуды напряжения грубой и тонкой настройки).

1.3. Ручка переключения предела частот (множитель частоты) на четыре положения: 17,7–200 Гц; 177–2000 Гц; 1770–200000 Гц.

1.4. Лимб со шкалой (главный регулятор частоты), поворачивая который избирается нужная частота.

1.5. Клеммы – выход звукового генератора, к которым подключается нагрузка (в данном случае колебательный контур).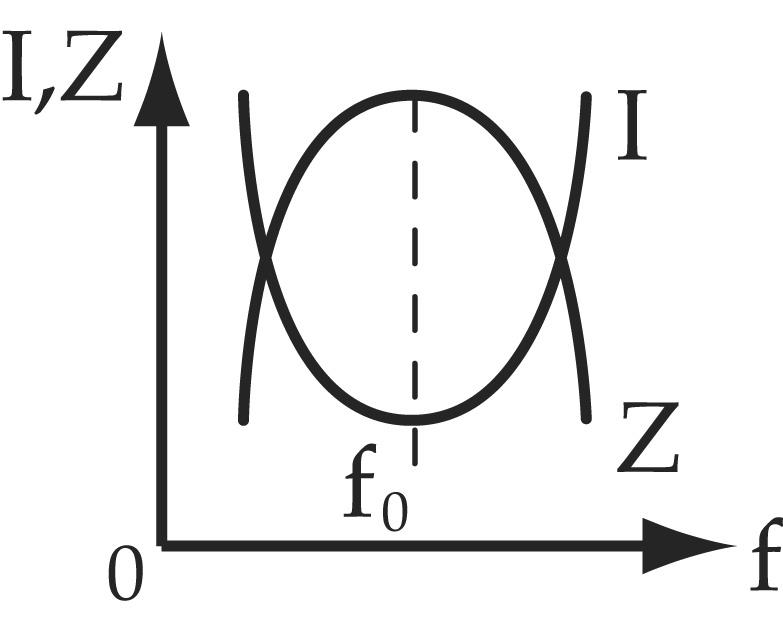

2. Ламповый милливольтметр (предназначен для замеров напряжения в колебательном контуре) (рис.9).

рис.9

На передней панели лампового милливольтметра находится:

2.1. Ручка переключения пределов амплитуды сигнала (замеряемой величины напряжения).

2.2. Клеммы — вход вольтметра.

2.3 Тумблер подключения прибора к сети “вкл.” – “откл.”.

В случае больших или наоборот малых значении напряжения, измеряемого ламповым вольтметром, необходимо изменить предел измерения напряжений ручкой переключения амплитуды сигнала (пределов).

После подключения приборов к сети нужно дать им прогреться 2–3 мин., после чего приступить к работе.

Резонанс напряжений и резонанс токов

В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.

Резонанс напряжений

Резонанс напряжений возникает в последовательной RLC-цепи.

 

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.

При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.

 

С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

 

Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту 

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.

Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.

Резонанс токов

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

 

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.

Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

 

Выразим резонансную частоту 

Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.

Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.

  • Просмотров: 84639

    • РЕЗОНАНСНЫЕ ЯВЛЕНИЯ, КОЛЕБАТЕЛЬНЫЙ КОНТУР

    ТЕОРИЯ: ПОНЕМНОГУ — ОБО ВСЕМ

            1. 8. Резонансные явления. Колебательный контур.

        Цепь, состоящую из последовательно включенных резистора, катушки индуктивности и конденсатора (рис. 8, а), подключим к генератору переменного напряжения, позволяющему регулировать частоту колебаний (предполагается, что генератор напряжения обладает бесконечно малым внутренним сопротивлением и поэтому напряжение на его зажимах практически не зависит от нагрузки). На постоянном токе (нулевая частота) и очень низких частотах ток в цепи практически отсутствует, так как емкостное сопротивление конденсатора велико. Ток будет стремиться к нулю и на очень высоких частотах из-за возрастания индуктивного сопротивления катушки (см. графики на рис. 6,а).

    Рис. 8

        Но есть одна характерная частота, на которой ток в цепи максимален и равен U/R. На этой частоте индуктивное сопротивление равно емкостному, а поскольку у них разные знаки, они компенсируют друг друга и полное сопротивление цепи оказывается активным и равным R. Эта частота называется резонансной, а график зависимости тока в цепи от частоты — резонансной кривой (рис. 8,б). Значение резонансной частоты можно найти, приравняв индуктивное и емкостное сопротивления: pL = 1/рС, следовательно, р2 = 1/LC (резонансная частота). Не забывайте, что угловая, или круговая частота в 2 или в 6,28 раза больше обычной, циклической частоты f, измеряемой в герцах, т.е. = 2f.
        Теперь мы вплотную подошли к понятию добротности, имеющему в радиотехнике очень важное значение. Чем меньше активное сопротивление R цепи, показанной на рис. 8,а, тем острее и выше резонансная кривая и тем больше ток в цепи при резонансе. На самом деле важно не само по себе активное сопротивление R, а отношение реактивного сопротивления r катушки или конденсатора на резонансной частоте р (напомним, что они равны) к активному R. Это отношение называется добротностью колебательного контура: Q = r/R = pL/R = 1/pCR (добротность контура). Аналогично тому, как мы это сделали для резонансной частоты, можно подсчитать, что r2 = L/C.
        Если нужно получить особенно высокую добротность, резистор R в контур, как правило, не устанавливают, а его роль выполняет активное сопротивление провода катушки. Даже у небольших радиочастотных катушек оно составляет единицы, а иногда и десятки ом, поскольку сопротивление провода на высокой частоте больше, чем на постоянном токе. Объясняется это так называемым скин-эффектом, явлением вытеснения тока к поверхности провода. Так, например, в медном проводе на частоте 3 МГц (3 миллиона колебаний в секунду) ток течет в поверхностном слое толщиной не более 0,1 мм.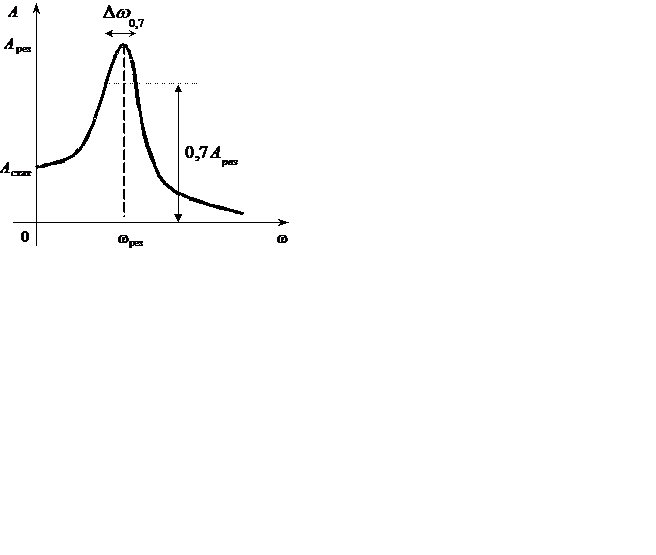
        Для уменьшения активного сопротивления катушек на радиочастотах часто используют многожильный обмоточный провод (литцендрат), скрученный из нескольких (7—21 и более) тонких изолированных проводников. При той же общей площади сечения или общем диаметре провода поверхность у литцендрата (по которой и текут высокочастотные токи) получается значительно больше, а сопротивление меньше, чем у одножильного провода.
        Толщина скин-слоя обратно пропорциональна корню квадратному из частоты, и на частоте 300 МГц она уменьшается до 10 мкм. Здесь и литцендрат уже не помогает, и приходится опять использовать одножильные провода значительного диаметра, благо на таких частотах катушки имеют не более нескольких витков. Окисленные и «шершавые», т.е. плохо обработанные металлические поверхности будут на этих частотах уже плохими проводниками. Для улучшения проводимости поверхностного слоя его часто серебрят, а вместо сплошных круглых проводов используют тонкостенные трубки — и легче, и материал экономится. А сопротивление остается тем же.
        Если выводы цепи рис. 8,а замкнуть накоротко, получится параллельный колебательный контур (рис. 8,в). Он гораздо чаще используется в радиотехнике. Чтобы наблюдать в контуре резонансные явления, к его выводам надо подключить уже не генератор переменного напряжения, а генератор тока, обладающий большим внутренним сопротивлением и поэтому создающий в любой нагрузке ток I, не зависящий от ее сопротивления.
        Генератором тока является, например, короткая (по сравнению с длиной волны) антенна или транзисторный усилительный каскад. В этом случае напряжение на выводах параллельного контура будет изменяться, при изменении частоты, в соответствии с резонансной кривой, показанной на рис.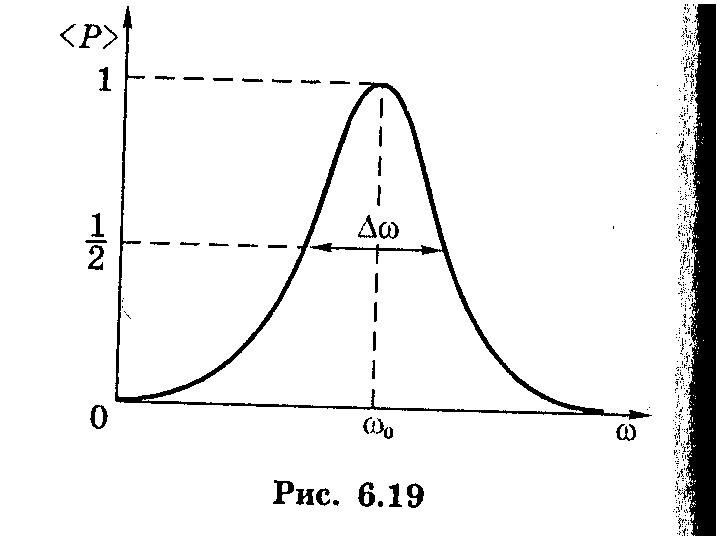 8,б штриховой линией. Как видим, она мало отличается от резонансной кривой для последовательного контура, причем отличия заметны лишь на боковых ветвях, вдали от резонансной частоты.
        Напряжение на выводах контура при резонансной частоте равно IRое, где Roe = r2/R — эквивалентное сопротивление контура на резонансной частоте. Оно тем больше, чем меньше активное сопротивление, включенное последовательно с катушкой, или сопротивление самой катушки. Остается в силе все то, что мы рассказали о контурах с высокой добротностью и о мерах уменьшения сопротивления проводов на высокой частоте.
        Для чего же нужен колебательный контур? Главным образом, для выделения колебаний с нужной нам частотой из множества колебаний с различными частотами. Это чуть ли не основная задача радиотехники. Даже простейший детекторный радиоприемник будет принимать сигналы сразу нескольких наиболее мощных радиостанций, работающих на разных частотах, если его не оснастить колебательным контуром.
        Когда контур настроен на частоту нужной радиостанции, сигналы всех остальных значительно ослабляются, и мы прослушиваем только одну радиопередачу. Чтобы перестраивать контур по частоте, необходимо изменять индуктивность катушки L или емкость конденсатора С (или и то и другое одновременно). С увеличением индуктивности и емкости резонансная частота или частота настройки понижается. Чаще всего используют конденсатор переменной емкости промышленного изготовления и катушку с отводами: переключая отводы, выбирают диапазон частот, а внутри диапазона частоту устанавливают конденсатором.
        Итак, незаметно от рассказа об электротехнике мы перешли к радиотехнике. Но о ней — в следующий раз.

    Радио, 1998

    лабораторная работа 47

    Лабораторная работа № 47

     

    ИЗУЧЕНИЕ
     ВЫНУЖДЕННЫХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ
    И СНЯТИЕ СЕМЕЙСТВА РЕЗОНАНСНЫХ КРИВЫХ

     

    Цель работы — изучение вынужденных электрических колебаний и явления резонанса в электрических цепях; снятие семейства амплитудных резонансных кривых.

    Приборы и принадлежности: звуковой генератор, милливольтметр переменного тока, микроамперметр переменного тока, конденсатор, катушка индуктивности, набор резисторов или магазин сопротивлений, соединительные провода.

     

    Вынужденные электрические колебания

    Пусть к электрической цепи, изображенной на рис. 1 и состоящей из последовательно соединенных конденсатора с электроемкостью С, катушки индуктивностью L и активного сопротивления R, подключен источник переменного тока с ЭДС, изменяющейся по закону

    ,                                  (1)

     

    где — амплитуда ЭДС; — циклическая частота.

     Рис. 1

    В катушке L возникает ЭДС самоиндукции, которая определяется формулой

    ,                                      (2)

     

    где L - индуктивность катушки;  — скорость изменения силы тока в цепи.

    В результате в такой цепи наблюдаются вынужденные электрические колебания и резонанс колебаний.

    Найдем уравнения вынужденных колебаний. Цепь, состоящая из конденсатора С и катушки L, называется к о л е б а т е л ь н ы м    к о н т у р о м (см. работу № 46).

    Используя второй закон Кирхгофа, получим уравнение

    ,

     

    или с учетом того, что напряжение на конденсаторе , а сила тока

     

    , получим

     .                          (3)

     

    Поделив (3) на L и учитывая выражения (коэффициент затухания) и  (циклическая частота собственных колебаний),

     

    формулу (3) можно записать в виде

     .                     (4)

     

    Это дифференциальное уравнение второго порядка вынужденных колебаний.

    Решение уравнения (4) следует искать в виде

    ,                                  (5)

     

    где φ и ω — начальная фаза и циклическая частота вынужденных колебаний; qо - амплитуда заряда на обкладке конденсатора,

    ,

     

     .                          (6)

     

    Сила тока равна , и с учетом

     выражений  (сдвиг фазы между током и ЭДС источника тока)

    и  получим

    ,                                 (7)


    где                  ;                (8)


    .                                      (9)

    Если в (8) и (9) подставим ; , то получим

     

    ;                    (8/)

     

    .                                   (9/)

     

    Напряжения в цепи изменяются по закону:

    — на активном сопротивлении R

    ;                  (10)

     

    — на конденсаторе с учетом , ,  и (4)

     

    .                     (11)

     

    — ЭДС самоиндукции, или напряжение в катушке,

    .                   (12)

     

    В формуле (8/) выражение

                             (13)

     

    называется импедансом, т.е. полным сопротивлением электрической цепи, а

                                                (14)

    и                                                                                  (15)

    называются и н д у к т и в н ы м   и   е м к о с т н ы м сопротивлениями (реактивными сопротивлениями). Тогда с учетом (13) формулу (8/) можно записать

    .                                           (16)

     

    Формула (8/), или (16), соответствует закону Ома для амплитудных значений переменного тока. Амплитудное значение силы тока Io зависит от ω, L, C и R.

    Исследуем зависимость Io от ω.

    При ω→0 Io→0, при ω→∞ Io также стремится к нулю, т.е. Io→0.

    Приравнивая  нулю, найдем резонансную частоту, которая не

    зависит от R и равна

    .                              (17)

     

    При этой частоте из (8) следует, что максимальное значение амплитуды силы тока равно

    .                                         (18)

     

    С ростом R, а следовательно, коэффициента затухания , Iom уменьшается.

    Зависимость резонансных кривых Io от ω показана на рис. 2.

     

    Рис. 2

     

    Резонансные кривые амплитудных значений напряжения отличаются от резонансных кривых силы тока.

    На рис. 3 приведена зависимость изменения резонансных кривых между обкладками конденсатора от частоты ω и коэффициента затухания β.

    Рис. 3

    Из рис. 3 видно, что при ω→0 амплитудное значение напряжения Uoc стремится к Uo=εo. Резонанс колебаний напряжения Uoc наступает при частоте

    .                 (19)

     

    Изучить резонанс колебаний силы тока можно, собрав электрическую цепь по схеме, представленной на рис. 4.

     

    Рис.

    4

     

    Ход работы

    1. Установить на звуковом генераторе начальное значение частоты

    2. С помощью регулятора напряжения установить на выходе звукового генератора напряжение, равное 30 мВ.

    3. Включить в цепь последовательно с катушкой L и конденсатором C сопротивления (сначала R1, затем R2, R3 ).

    4. Измерить значения силы тока I1, I2, I3, изменяя значения частоты в интервале от 200 до 2000 Гц через каждые 200 Гц, поддерживая напряжение в цепи неизменным с помощью регулятора напряжения. Результаты измерений занести в таблицу.

     

    Таблица

    , Гц

    2200

    4400

    6600

    8800

    11000

    11200

    11400

    11600

    11800

    22000

    22500

    33000

    I1, мкА

    R1=

     

     

     

     

     

     

     

     

     

     

     

     

    I2, мкА

    R2=

     

     

     

     

     

     

     

     

     

     

     

     

    I3, мкА

    R3=

     

     

     

     

     

     

     

     

     

     

     

     

     

    4.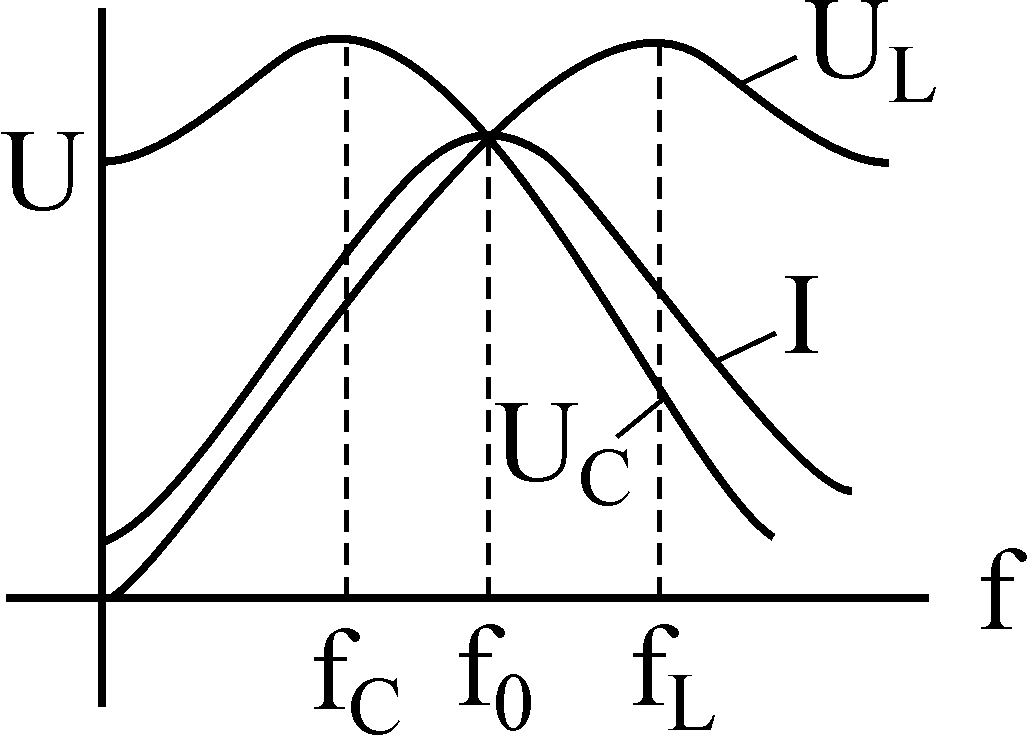 По результатам измерений на миллиметровой бумаге построить семейство амплитудных резонансных кривых.

    5. По полученному графику зависимости Io от () и по максимальному значению силы тока Iom определить резонансную частоту .

    6. По формуле

                                   (20)

     

    рассчитать значение резонансной частоты , подставляя параметры L и C электрической цепи.

    7. Сравнить экспериментальное значение  и рассчитанное по формуле (20) значение .

     

    Вопросы для допуска к работе

    1.      Сформулируйте цель работы.

    2.      Какие колебания называются свободными?

    3.      Какие колебания называются вынужденными?

    4.      Запишите дифференциальное уравнение вынужденных колебаний.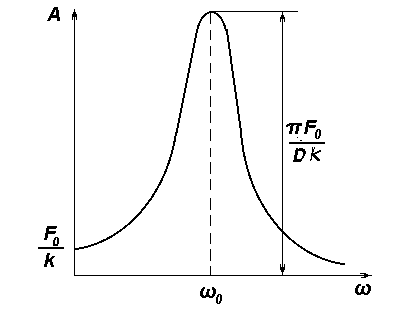

    5.      Что называется резонансом колебаний?

     

    Вопросы для защиты работы

    1.      Что называется колебательным контуром? Объясните возникновение вынужденных электрических колебаний в цепи переменного тока.

    3.      Получите дифференциальное уравнение вынужденных электрических колебаний.

    4.      Выведите формулу для резонансных частот колебаний силы тока и напряжения.

    5.      Изобразите и поясните ход резонансных кривых (амплитудных и фазовых).

    6.      Что такое полное сопротивление (импеданс) переменной электрической цепи?

     

    Резонанс в цепях серии R-L-C (со схемой)

    В этой статье мы обсудим последовательный и параллельный резонанс в цепях R-L-C.

    Резонанс определяется инженерными ситуациями, в которых элементы накопления энергии подвергаются форсирующей функции переменной частоты. В частности, резонанс — это термин, используемый для описания установившейся работы схемы или системы на той частоте, для которой результирующий отклик совпадает по временной фазе с функцией источника, несмотря на наличие элементов накопления энергии.

    Резонанс не может иметь место, когда присутствует только один тип элемента, аккумулирующего энергию, например, емкость или пружина. Должны существовать два типа независимых аккумулирующих энергию элементов, способных обмениваться энергией между собой — например, индуктивность и емкость или масса и пружина. Таким образом, резонанс — это явление, обнаруживаемое в любой системе, включающей два независимых элемента накопления энергии, будь то электрический, механический, пневматический, гидравлический или любой другой.

    Если у нас есть цепь переменного тока, имеющая сопротивление R, индуктивность L и емкость C, соединенные последовательно (рис.6.1) и приложив небольшое напряжение V от источника, который может поддерживать постоянную величину V, но может изменять его частоту, мы обнаруживаем, что величина тока, потребляемого от источника питания, изменяется с изменением частоты источника питания. Будет такое значение частоты, при котором ток будет максимальным. Говорят, что при достижении этого состояния возникает электрический резонанс.

    В этой статье мы обсудим это явление (точнее, последовательный резонанс или резонанс напряжения), а также ситуацию, когда на параллельную цепь подается постоянное напряжение переменной частоты.Самая простая параллельная цепь, встречающаяся на практике, — это катушка, имеющая сопротивление R и индуктивность L, подключенная параллельно конденсатору C. Резонансное состояние в этом случае называется параллельным резонансом, а иногда и антирезонансным. Последнее название подсказано тем, что при резонансе входной ток в параллельную цепь минимален.

    В условиях резонанса такая сеть становится полностью резистивной по своим воздействиям, а напряжение и ток в сети синфазны.Чтобы это произошло, индуктивное реактивное сопротивление и емкостное реактивное сопротивление должны быть уравновешены.

    Серия
    или резонанс напряжения в цепях R-L-C :

    Рассмотрим цепь переменного тока, содержащую сопротивление R, индуктивность L и емкость C, соединенные последовательно, как показано на рис.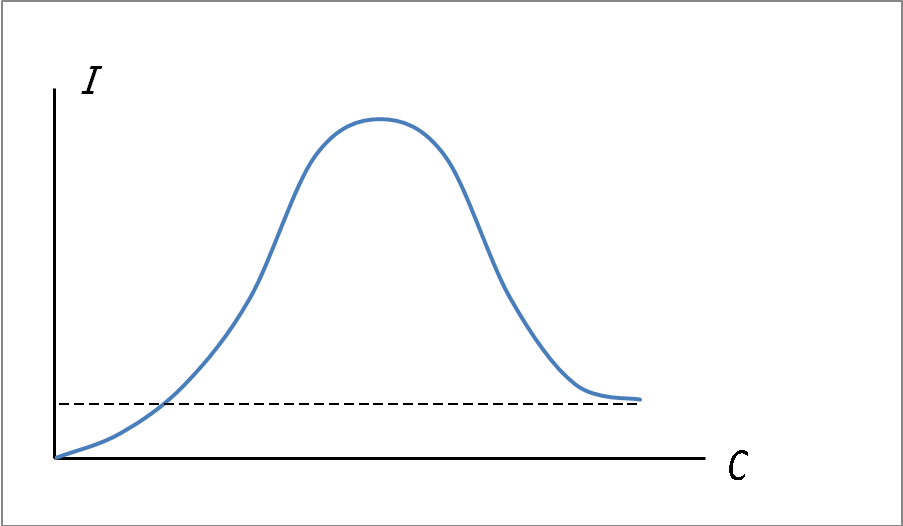 6.1.

    Если для некоторой частоты приложенного напряжения X L = X C по величине, то:

    (i) Чистое реактивное сопротивление равно нулю i.е. Х = 0

    (ii) Импеданс цепи, Z = R

    (iii) Ток, протекающий по цепи, является максимальным и синфазным с приложенным напряжением. Величина тока будет равна V / R

    .

    (iv) Падение напряжения на индуктивности равно падению напряжения на емкости и составляет максимум

    .

    (v) Коэффициент мощности равен единице, а

    (vi) Затраченная мощность = VI Вт.

    Когда это условие существует, считается, что цепь находится в резонансе, а частота, на которой это происходит, называется резонансной частотой.

    Из приведенного выше выражения очевидно, что значение резонансной частоты зависит от параметров двух энергонакопительных элементов.

    Фазорные диаграммы для последовательной цепи RLC, показанной на рис. 6.1, на трех разных частотах, т.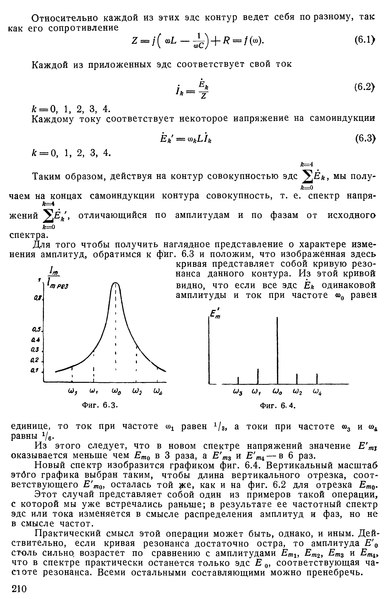 е. (a) f r (b) f = f r и (c) f> f r с L и C сохраняемые постоянными показаны на рис. 6.2 (a), (b) и (c) соответственно.

    Для любой частоты ниже резонансной частоты f r индуктивное реактивное сопротивление X L меньше емкостного реактивного сопротивления X C , поэтому схема ведет себя как емкостная цепь.Точно так же для любой частоты выше резонансной индуктивное реактивное сопротивление больше емкостного реактивного сопротивления, поэтому цепь ведет себя как индуктивная цепь.

    Когда частота приложенного напряжения равна резонансной частоте, индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению, падение напряжения на катушке индуктивности по величине равно падению напряжения на конденсаторе, но противоположно по фазе и, следовательно, ток в цепи I находится в фазе с приложенным напряжением i.е., схема ведет себя как резистивная цепь.

    Когда цепь находится в резонансе, ток слишком велик и вызывает большое падение напряжения на индуктивности и емкости, которые будут равны по величине, но противоположны по фазе, и каждое из них может быть в несколько раз больше, чем приложенное напряжение. Если бы в цепи не было сопротивления R, такая цепь действовала бы как короткое замыкание на токи с частотой, с которой она резонирует.

    Поскольку в этом резонансе напряжение максимальное, он называется резонансом напряжения.Последовательный резонанс также называется цепью акцептора, потому что такая цепь принимает токи на одной конкретной частоте, но отклоняет токи других частот. Такие схемы используются в радиоприемниках.

    Графическое представление резонанса в цепи серии R-L-C:

    Цепь можно сделать резонансной двумя способами, а именно:

    (i) Путем изменения параметров L и C (одного или обоих) при постоянной частоте питания или

    (ii) Изменяя частоту подачи / с постоянными параметрами L и C.В нашем исследовании явления последовательного резонанса мы будем поддерживать напряжение, приложенное к цепи, и параметры L и C постоянными, а частоту будем изменять.

    Сопротивление цепи R не зависит от частоты питания и, следовательно, остается постоянным.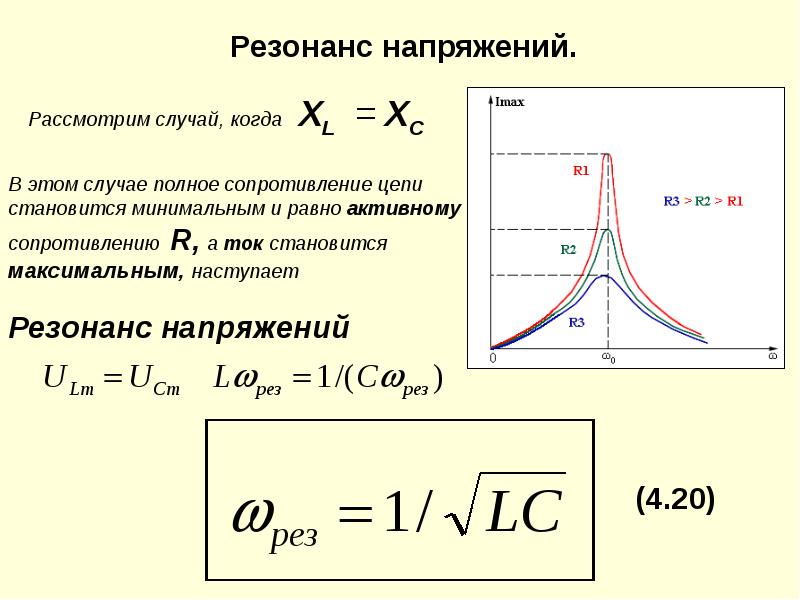 Это было представлено прямой линией, параллельной оси X (или оси частот) на рисунке (рис. 6.3). Индуктивное реактивное сопротивление X L , равное ωL, увеличивается прямо пропорционально частоте питающей сети и представлено прямой линией, проходящей через начало координат (поскольку X L считается положительным, поэтому он лежит в первом квадранте).Емкостное реактивное сопротивление, равное 1 / ωC, уменьшается обратно пропорционально увеличению частоты и представлено прямоугольной гиперболой, лежащей в четвертом квадранте ниже оси частот (емкостное реактивное сопротивление считается отрицательным).

    Чистое реактивное сопротивление — это разница между индуктивным реактивным сопротивлением X L и емкостным реактивным сопротивлением X C , и кривая, проведенная между чистым реактивным сопротивлением (X L ~ X C ) и частотой, будет гиперболой (не прямоугольной). как показано на рис.6.3. Частота, при которой кривая реактивного сопротивления пересекает ось частот, называется резонансной частотой, f r (или f 0 ).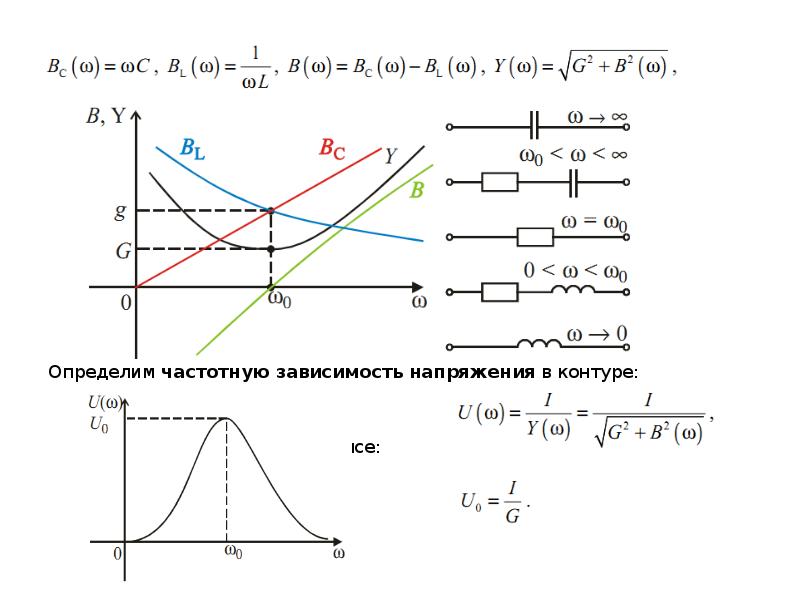

    Полное сопротивление цепи Z, равное √R 2 + (x L — X c ) 2 , минимально на резонансной частоте f r .

    На частотах ниже резонансной частоты f r полное сопротивление Z велико и емкостное, поскольку X C > X L , а коэффициент мощности является опережающим, а на частотах выше резонансной частоты f r полное сопротивление Z равно снова большой, но индуктивный, так как X L > X C и коэффициент мощности отстает.Коэффициент мощности имеет максимальное значение, равное единице на резонансной частоте.

    Резонансная кривая:

    Ток изменяется обратно пропорционально изменению импеданса и, следовательно, он максимален на резонансной частоте, когда импеданс минимален, и уменьшается с изменением частоты по обе стороны от резонансной частоты (поскольку полное сопротивление Z велико), как показано на рис. 6.4.

    Кривая, проведенная между током в цепи и частотой приложенного напряжения, называется резонансной кривой, и ее форма зависит от значения сопротивления цепи R, как показано на рисунке. Для меньших значений R резонансная кривая имеет резкий пик, но для больших значений R кривая пологая (рис.6.4).

    Избирательность и пропускная способность:

    Мы видели, что для цепи с низким сопротивлением резонансная кривая имеет резкий пик, и такая цепь называется резко резонансной или высокоселективной. С другой стороны, цепь с высоким сопротивлением имеет плоскую кривую резонанса и, как говорят, имеет плохую селективность. Селективность различных резонансных контуров сравнивается с точки зрения их ширины полосы частот, которая задается полосами частот, которые лежат между двумя точками по обе стороны от резонансной частоты, где ток в 1 / √2 раза больше максимального тока I max .

    Ширина полосы, Δ f = f 2 — f 1 … (6.2)

    Фактическая потребляемая мощность на частотах f 1 и f 2 :

    Вот почему частоты f 1 и f 2 на границах полосы пропускания называются точками половинной мощности на шкале частот, а соответствующее значение ширины полосы обозначается как ширина полосы половинной мощности (B hp ) или полосы пропускания -3 дБ.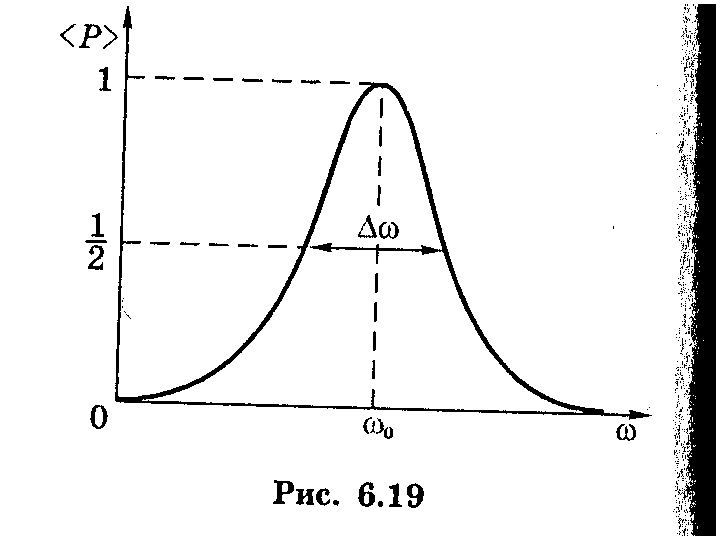

    Следует отметить следующие моменты относительно точек половинной мощности:

    Коэффициент качества последовательной резонансной цепи:

    Добротность последовательной цепи R-L-C может быть определена любым из следующих способов:

    Может быть задано как увеличение напряжения, создаваемое схемой при резонансе.Мы видели, что в резонансе ток в цепи максимален и равен V / R или напряжению питания, V = I max R.

    В случае последовательного резонанса более высокое значение Q-фактора означает не только большее увеличение напряжения, но и более высокую селективность настроечной катушки, поэтому необходимо, чтобы катушка имела высокую индуктивность и низкое сопротивление.

    Фактически, добротность последовательного резонансного контура может быть определена как отношение резонансной частоты к ширине полосы:

    Ток или параллельный резонанс в цепях R-L-C:

    Когда индуктивное реактивное сопротивление и емкостное реактивное сопротивление соединены параллельно, как показано на рис.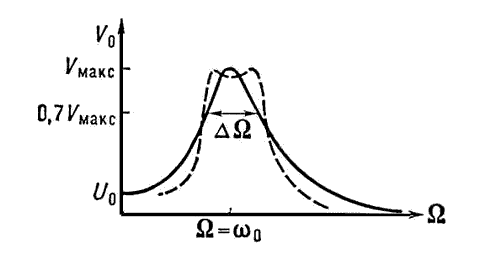 6.8, могут достигаться условия, при которых будет иметь место резонанс тока (также известный как параллельный или антирезонансный). Рассмотрим практический случай подключения змеевика параллельно конденсатору, как показано на рис. 6.8. Пусть катушка имеет сопротивление R Ом и индуктивность L Генри, а конденсатор — сопротивление R Ом и емкость C фарад.

    Считается, что такая цепь находится в электрическом резонансе, когда реактивная (или не имеющая мощности) составляющая линейного тока становится равной нулю. Частота, на которой это происходит, называется резонансной частотой.

    Цепь будет в электрическом резонансе, если реактивная составляющая тока ветви RL, I R — L sin ɸ R — L = Реактивная составляющая тока ветви RC, I R — C sin ɸ R — c

    Резонансный ток:

    Предполагая, что R 1 = 0, как обычно, на резонансной частоте:

    Знаменатель L / CR известен как эффективное или эквивалентное динамическое сопротивление параллельной цепи CR при резонансе.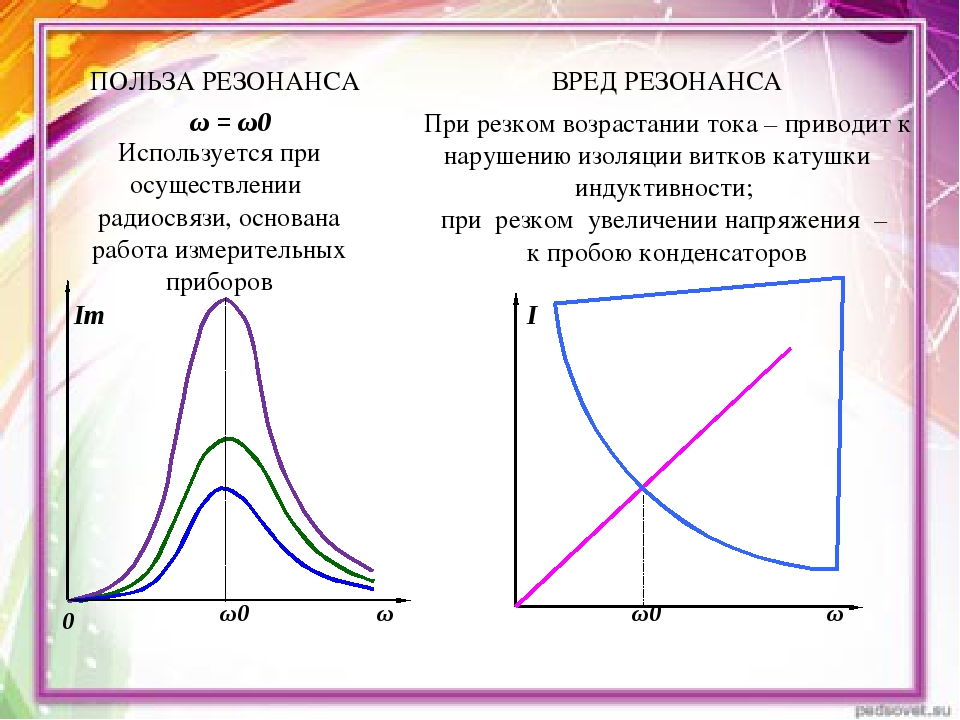

    Важные сведения о токовом или параллельном резонансе :

    1. Подвижность нетто равна нулю, т.е. 1 / X C = X L / X Z или ω r C = ω r L / Z 2 или Z = √L / C

    2. Допуск равен проводимости.

    3. Реактивная составляющая линейного тока равна нулю, следовательно, коэффициент мощности цепи равен единице.

    4. Импеданс чисто резистивный, максимальный по величине и равен L / CR.

    5. Линейный ток минимален, равен величине V / L / CR и находится в фазе с приложенным напряжением.

    6. Частота равна 1 / 2π √1 / LC — R 2 / L 2 Гц.

    Примечание:

    Параллельный резонансный контур иногда называют рефлекторным контуром, потому что на резонансной частоте линейный ток минимален или почти отклоняет его.

    Поскольку в параллельных резонансных цепях циркулирующий ток между ветвями во много раз превышает линейный ток, такой тип резонанса иногда называют токовым резонансом.

    Индуктивная катушка с индуктивностью L, включенная параллельно емкости C, называется баковой цепью.

    Графическое представление тока или параллельного резонанса:

    Теперь мы обсудим влияние изменения частоты на сопротивляемость двух параллельных ветвей. Варианты показаны на рис. 6.10.

    Индуктивная проводимость, равная 1 / ω L или 1 / 2π f L, уменьшается обратно пропорционально увеличению частоты и представлена ​​прямоугольной гиперболой, лежащей в четвертом квадранте ниже оси частот (индуктивная проводимость считается отрицательной).

    Емкостная проводимость, равная ωC или 2π f C, увеличивается прямо пропорционально частоте питающей сети и представлена ​​прямой линией, проходящей через начало координат. Поскольку емкостная восприимчивость считается положительной, значит, она находится в первом квадранте.

    Чистая проводимость B — это разность емкостной и индуктивной проводимости, а кривая, проведенная между чистой проводимостью и частотой приложенного напряжения, представляет собой гиперболу (не прямоугольную), как показано на рис.6.10.

    Частота, при которой кривая чистой проводимости пересекает ось частот, называется резонансной частотой. В этой точке полное сопротивление максимальное или полное сопротивление минимальное и равно G, следовательно, линейный ток минимален.

    Очевидно, что на частоте ниже, чем резонансная, индуктивная проводимость больше, чем емкостная, следовательно, цепь является индуктивной, и линейный ток отстает от приложенного напряжения. Но для частот, превышающих резонансную частоту, преобладает емкостная восприимчивость, следовательно, цепь является емкостной, и линейный ток опережает приложенное напряжение.

    Если сопротивление относительно низкое, ток значительно упадет на резонансной частоте, а если сопротивление велико, уменьшение тока будет менее выраженным, как показано на рис. 6.11.

    Пропускная способность в случае параллельной резонансной цепи:

    Полоса пропускания в случае параллельной цепи определяется так же, как и в случае последовательной цепи. В этом случае также есть верхняя и нижняя точки половинной мощности, где потребляемая мощность составляет половину от резонансной частоты.

    На частотах полосы пропускания чистая проводимость B равна проводимости G. Таким образом, на частоте f 1 чистая проводимость B L1 — B C1 = G и на частоте f 2 , B C2 — B L2 = G. Таким образом, проводимость Y = √G 2 + B 2 = √2 G и фазовый угол ɸ = tan -1 1 = 45˚ или π / 4 радиан.

    Q-фактор или текущий коэффициент увеличения:

    Добротность параллельной цепи определяется как отношение циркулирующего тока к линейному току или как увеличение тока.

    Q-фактор

    и полоса пропускания резонансной цепи | Резонанс

    Коэффициент добротности или качества резонансного контура является мерой «качества» или качества резонансного контура. Более высокое значение этого показателя качества соответствует более узкой полосе пропускания, что желательно во многих приложениях. Более формально Q — это отношение накопленной мощности к мощности, рассеиваемой в реактивном сопротивлении и сопротивлении цепи, соответственно:

    Q = P  сохранено  / P  рассеивается  = I  2  X / I  2  R Q = X / R где: X = емкостное или индуктивное реактивное сопротивление при резонансе R = последовательное сопротивление.

    Эта формула применима к последовательным резонансным цепям, а также к параллельным резонансным цепям, если сопротивление последовательно с индуктором. Так обстоит дело в практических приложениях, поскольку нас больше интересует сопротивление катушки индуктивности, ограничивающее Q.

    Примечание: В некотором тексте могут быть показаны местами X и R в формуле «Q» для параллельного резонансного контура. Это верно для большого значения R параллельно с C и L. Наша формула верна для небольшого R, идущего последовательно с L.

    Практическое применение «Q» состоит в том, что напряжение на L или C в последовательном резонансном контуре в Q раз больше общего приложенного напряжения. В параллельном резонансном контуре ток через L или C в Q раз больше общего приложенного тока.

    Резонансные цепи серии

    Последовательный резонансный контур выглядит как сопротивление на резонансной частоте. Поскольку определение резонанса — X L = X C , реактивные компоненты нейтрализуются, оставляя только сопротивление, чтобы вносить вклад в импеданс.

    Полное сопротивление также минимально в резонансе. Ниже резонансной частоты последовательный резонансный контур выглядит емкостным, поскольку полное сопротивление конденсатора увеличивается до значения, превышающего уменьшающееся индуктивное реактивное сопротивление, оставляя чистое емкостное значение.

    Выше резонанса индуктивное реактивное сопротивление увеличивается, емкостное реактивное сопротивление уменьшается, оставляя чистую индуктивную составляющую.

    ПРИМЕЧАНИЕ:

    При резонансе последовательный резонансный контур выглядит чисто резистивным.Ниже резонанса он выглядит емкостным. Выше резонанса он кажется индуктивным. Ток максимален при резонансе, импеданс минимален. Ток устанавливается величиной сопротивления. Выше или ниже резонанса сопротивление увеличивается.

    Импеданс минимален при резонансе в последовательном резонансном контуре.

    Пик резонансного тока может быть изменен путем изменения последовательного резистора, который изменяет добротность. Это также влияет на ширину кривой.Схема с низким сопротивлением и высокой добротностью имеет узкую полосу пропускания по сравнению с схемой с высоким сопротивлением и низкой добротностью.

    Полоса пропускания по добротности и резонансной частоте:

     BW = f  c  / Q Где f  c  = резонансная частота Q = добротность

    Резонансный контур с высокой добротностью имеет узкую полосу пропускания по сравнению с контуром с низкой добротностью

    Ширина полосы измеряется между точками амплитуды тока 0,707.Точки тока 0,707 соответствуют точкам половинной мощности, поскольку P = I 2 R, (0,707) 2 = (0,5).

    Полоса пропускания Δf измеряется между точками амплитуды 70,7% последовательного резонансного контура. 

     BW = Δf = f  h  -f  l  = f  c  / Q Где: f  h  = край верхней полосы f  l  = край нижней полосы f  l  = f  c  - Δf / 2 f  h  = f  c  + Δf / 2 Где f  c  = центральная частота (резонансная частота)

    На рисунке выше 100% текущая точка составляет 50 мА.Уровень 70,7% составляет 0,707 (50 мА) = 35,4 мА. Верхний и нижний края полосы, считанные с кривой, составляют 291 Гц для f и 355 Гц для f h . Полоса пропускания составляет 64 Гц, а точки половинной мощности составляют ± 32 Гц от центральной резонансной частоты:

    .

     BW = Δf = f  h  -f  l  = 355-291 = 64 f  l  = f  c  - Δf / 2 = 323-32 = 291 f  h  = f  c  + Δf / 2 = 323 + 32 = 355

    Так как BW = fc / Q:

    Q = f c / ЧБ = (323 Гц) / (64 Гц) = 5

    Параллельные резонансные схемы

    Полное сопротивление параллельного резонансного контура максимально на резонансной частоте.Ниже резонансной частоты параллельный резонансный контур выглядит индуктивным, поскольку импеданс катушки индуктивности ниже, и на нее приходится большая часть тока.

    Выше резонанса емкостное реактивное сопротивление уменьшается, потребляя больший ток, таким образом, принимая емкостную характеристику.

    Параллельный резонансный контур является резистивным при резонансе, индуктивным ниже резонанса, емкостным выше резонанса.

    Полное сопротивление является максимальным при резонансе в параллельном резонансном контуре, но уменьшается выше или ниже резонанса.Напряжение достигает пика при резонансе, поскольку напряжение пропорционально импедансу (E = IZ).

    Параллельный резонансный контур: Пики импеданса при резонансе.

    Низкая добротность из-за высокого сопротивления, включенного последовательно с катушкой индуктивности, дает низкий пик на широкой кривой отклика для параллельного резонансного контура. Высокая добротность обусловлена ​​низким последовательным сопротивлением катушки индуктивности. Это дает более высокий пик на более узкой кривой отклика. Высокая добротность достигается за счет наматывания на индуктор большего диаметра (меньшего сечения) провода с меньшим сопротивлением.

    Параллельный резонансный отклик зависит от добротности

    Ширина полосы параллельного резонансного отклика измеряется между точками половинной мощности. Это соответствует точкам напряжения 70,7%, поскольку мощность пропорциональна E 2 . ((0,707) 2 = 0,50) Поскольку напряжение пропорционально импедансу, мы можем использовать кривую импеданса.

    Полоса пропускания, Δf измеряется между 70.Точки полного сопротивления 7% параллельного резонансного контура.

    На рисунке выше точка 100% импеданса составляет 500 Ом. Уровень 70,7% составляет 0707 (500) = 354 Ом. Верхний и нижний края полосы, считываемые с кривой, составляют 281 Гц для fl и 343 Гц для fh. Полоса пропускания составляет 62 Гц, а точки половинной мощности составляют ± 31 Гц от центральной резонансной частоты:

    .

    BW = Δf = f  h  -f  l  = 343-281 = 62 f  l  = f  c  - Δf / 2 = 312-31 = 281 f  h  = f  c  + Δf / 2 = 312 + 31 = 343 
    Q = fc / BW = (312 Гц) / (62 Гц) = 5

    СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

    Пример резонансной кривой TF.Ток TF, представленный как …

    Контекст 1

    … α min — коэффициент поглощения, соответствующий шумовому эквивалентному сигналу, P — мощность оптического возбуждения, а ∆ f — ширина полосы обнаружения. D сильно зависит от процессов передачи энергии в газе, которые будут обсуждаться в разд. 3 подробнее. Однако было обнаружено, что вариации D не превышают двух раз для исследованных оптических переходов в обертонной области. Достижения квантовой электроники предоставили столь же мощные спектроскопические источники, как QC- и IC-лазеры для среднего ИК-диапазона.Основная цель этой работы состояла в том, чтобы изучить применимость QEPAS для обнаружения различных газовых примесей в средней ИК-области основных колебательных полос поглощения. Поскольку молекулярное поглощение в этой области обычно в ~ 100 раз сильнее, чем в ближнем ИК-диапазоне, следует определять концентрации ~ 1-10 частей на миллиард, если D существенно не изменяется. Лазер QC, работающий на 4. 55 мкм было предоставлено Alpes Lasers [5]. Молекулами, выбранными для этого исследования, были N 2 O и CO.Обнаружение следовых концентраций каждого из этих видов имеет практическое значение для ряда приложений. N 2 O вносит важный вклад в глобальный парниковый эффект [6–10]. Фоновая концентрация закиси азота в атмосфере колеблется от 310 до 320 частей на миллиард и увеличивается со средней скоростью 0. 8 ppb / год [11]. CO составляет самую большую часть загрязняющих веществ, содержащихся в промышленной и городской атмосфере. Он образуется в основном в результате неполного сгорания органических материалов, а также является результатом промышленных процессов и выхлопных газов автомобилей [12].Фоновые уровни CO в относительно незагрязненном воздухе колеблются от 0,2 до 1. 0 ppmv [6, 12]. CO в выдыхаемом воздухе человека (400–300 ppbv) является важным биомедицинским маркером для неинвазивной диагностики заболеваний в медицине [13]. Конфигурация лабораторного газового датчика на основе QEPAS показана на рис. 1. В качестве источника фотоакустического возбуждения использовался QC-лазер непрерывного действия (непрерывной) с распределенной обратной связью (DFB). Лазер охлаждался жидким азотом и перекрывал спектральный диапазон 2198. 3– 2195.5 см — 1 при изменении его тока с порогового значения 317 мА до 650 мА. Лазерное излучение собиралось асферической линзой L 1 с фокусным расстоянием 13 мм, расположенной так, чтобы источник отображался на расстоянии 97 см от линзы. Такое большое расстояние перефокусировки уменьшило сферическую аберрацию и позволило выполнить пространственную фильтрацию. Вторая линза L 2 (фокусное расстояние 5 см) повторно отображала источник между зубцами кварцевого камертона (TF). Акустический микрорезонатор, состоящий из двух трубок из кварцевого стекла, каждая по 2 штуки.45 мм длиной с 0. Внутренний диаметр 32 мм был ориентирован перпендикулярно плоскости TF для повышения чувствительности [1–4]. Были приняты меры, чтобы лазерное излучение не освещало стенки микрорезонатора. Было обнаружено, что такое облучение приводит к возникновению фонового фотоакустического сигнала из-за поглощения излучения в кварцевых трубках микрорезонатора. Газовая ячейка объемом ∼ 1 см 3, содержащая ТФ, более подробно описана в [3]. Лазерный луч повторно коллимировался при выходе из ячейки ТФ.Был введен светоделитель для отклонения части излучения к ИК-детектору, в то время как большая часть излучения проходила через измеритель мощности. Контрольная ячейка (l = 13 см) была заполнена высокой концентрацией исследуемого вещества (пиковое поглощение 5-10%) для спектрального сравнения. Длина волны QC-лазера модулировалась на частоте f = f 0/2, где f 0 — резонансная частота ТФ, а регистрация фотоакустического сигнала производилась при f 0, аналогично [1–4]. Модуляция была реализована путем добавления синусоидальной составляющей (обычно ~ 4 мА от пика до пика) поверх постоянного тока лазера.Эксперименты QEPAS проводились в двух режимах: 1. Режим сканирования. В этом режиме постоянная составляющая лазерного тока медленно настраивалась так, чтобы центральная частота лазера охватывала желаемый спектральный диапазон. 2. Режим блокировки. Ток QC-лазера изначально был установлен так, чтобы длина волны лазера была близка к центру линии поглощения. Была измерена 3 f-составляющая сигнала A 3 f ИК-детектора, и периодически производилась пропорциональная поправка на постоянную составляющую лазерного тока ∆ I = const × A 3 f для поддержания A 3 f = 0.Таким образом, длина волны лазера была привязана к центру целевой линии оптического поглощения. Пьезоэлектрический ток, генерируемый ТП, преобразовывался в напряжение с помощью трансимпедансного усилителя с резистором обратной связи R fb = 10 МОм. Выходы двух синхронизированных усилителей и другие аналоговые сигналы, такие как показания измерителей давления и расхода газа, были оцифрованы с помощью карты сбора данных PCMCIA (National Instruments DAQCard-6062E), которая передавала данные на портативный компьютер. Программное обеспечение на основе LabView обеспечивает компьютерное управление генератором функций (который, в свою очередь, управляет током лазера), а также сбор и обработку необходимых данных.Перед каждым запуском фотоакустических измерений определялись резонансная частота f 0 и добротность ТФ. Для этого переменное напряжение от функционального генератора подавалось непосредственно на TF. Ток TF измеряли как функцию частоты приложенного напряжения. Пример резонансной кривой показан на рис. 2. Параметры f 0 и Q зависят от давления газа, основного химического состава газа и температуры. Если давление и состав газа поддерживались постоянными, суточный дрейф f 0 не превышал ± 0.02 Гц. Резонансная кривая позволяет определить импеданс TF как отношение напряжения и тока. Импеданс является чисто резистивным в резонансе, и его значение R связано с тепловым шумом …

    Ошибка разрыва связи

      Приборная панель

      PHYS-2426.P7L

      Перейти к содержанию Приборная панель

      • Авторизоваться

      • Приборная панель

      • Календарь

      • Входящие

      • История

      • Помощь

      Закрывать