Сложение емкостей конденсаторов: Онлайн калькулятор расчета параллельного соединения конденсаторов

Онлайн калькулятор расчета параллельного соединения конденсаторов

В устройствах радиоэлектроники конденсаторы представляют собой один из важнейших элементов, способный накапливать и отдавать электрический заряд. В сравнении с другими элементами, конденсатор обладает такими параметрами как емкость и сопротивление. Сопротивление конденсатора обусловлено изолирующим промежутком, который может выйти со строя из-за скачков напряжения или других аварийных процессов в сети. При необходимости заменить какой-либо конденсатор, многие радиолюбители сталкиваются с трудностью достать модель нужной емкости.

В таком случае на помощь придет правило сложения, позволяющее заменить одно устройство несколькими меньшей емкости, чтобы в суме их хватило для компенсации вышедшего со строя конденсатора. В этом месте многие не могут определить, каким способом вычисляется суммарная мощность параллельно соединенных конденсаторов. Следует отметить, что физически для схемы конденсатор представляет собой разрыв.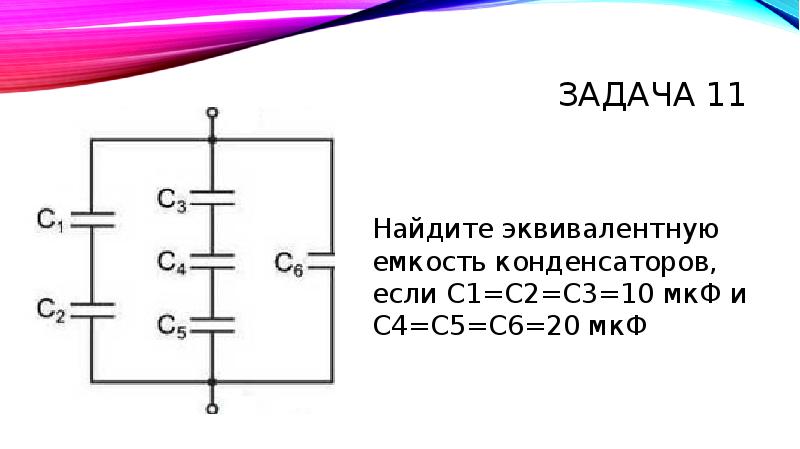

Рис. 1. Параллельное соединение конденсаторов

Посмотрите на рисунок 1, это принципиальная схема параллельного подключения конденсаторов. Как видите, в этом случае одноименные выводы емкостного элемента подводятся к соответствующей точке электрической цепи. Поэтому и емкость между плоскостями двух  и более конденсаторов, соединенных между собой параллельно складывается в одно целое. Исходя из этого, суммарная емкость для параллельно включенных конденсаторов будет вычисляться по формуле:

С₀ = С₁ + С₂ + … + С_n

Где,

• С₀ — общая емкость параллельно соединенных конденсаторов
• С₁ — емкость первого конденсатора;
• С₂ — емкость второго конденсатора.

В данном примере рассматривается ситуация, когда параллельно соединяются только два емкостных элемента, поэтому их результирующая емкость будет равна арифметической сумме емкостей обоих конденсаторов. На практике можно применять и большее число, если вам необходимо получить определенную емкость.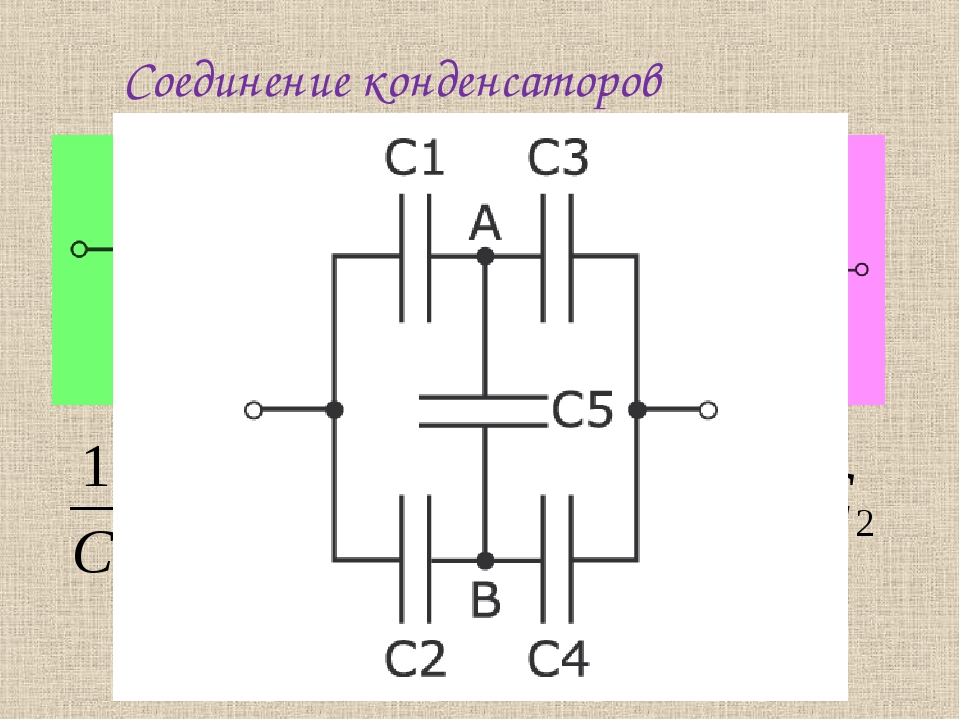

Чтобы рассчитать результирующую емкость при параллельном соединении 2 и более конденсаторов вы можете воспользоваться нашим онлайн калькулятором ниже.

Параллельное и последовательное соединение конденсаторов

Иногда в наличии нет конденсатора с нужными параметрами. В таком случае, можно соединить несколько конденсаторов так, чтобы полученная система обладала необходимой электрической емкостью. Существуют два основных способа соединений:

1. параллельный;
2. последовательный;

Комбинируя эти способы, можно получить смешанное соединение.

Для каждого способа применяют специальные формулы, описывающие распределение заряда и напряжения на конденсаторах, а, так же, получаемую итоговую электроемкость системы.

Параллельное соединение

Этот способ соединения получаем, соединяя каждый вывод одного прибора с соответствующим ему выводом другого (рис. 1).

Рис. 1. Параллельный способ соединения

Емкость для параллельного включения можно определить так:

\[\large \boxed { C_{1} + C_{2} = C_{\text{общ}} } \]

При этом, общая \(\large C_{\text{Общ}} \) электроемкость получится больше самой большой емкости, входящей в соединение.

\(\large C_{1}, C_{2} \left( \text{Ф} \right) \) – электроемкости конденсаторов.

Общая электроемкость включенных параллельно конденсаторов больше емкости большего из них.

Напряжение на конденсаторах

Напряжения, приложенные к параллельно подключенным обкладкам, равны.

\[\large \boxed { U_{1} = U_{2} = U_{\text{общ}} } \]

\(\large U_{1}, U_{2}\left( B\right) \) – напряжения на обкладках.

Рис. 2. Равенство напряжений на параллельно соединенных обкладках

Правило для зарядов

Общий заряд системы разделится на части. Каждая из параллельно соединенных емкостей получит свой заряд.

\[\large \boxed { q_{1} + q_{2} = q_{\text{общ}} } \]

\(\large q_{1}, q_{2}\left( \text{Кл} \right) \) – заряды на конденсаторах.

Рис. 3. Заряды, содержащиеся на каждом параллельно включенном элементе, складываются

При этом, из формулы емкости (ссылка), связывающей ее с напряжением на обкладках и зарядом, следует (рис. 4):

При параллельном соединении меньшая емкость содержит меньший заряд.

Рис. 4. Пример распределения зарядов на конденсаторах при их параллельном включении

Из рисунка 4 следует, в параллельной части цепи конденсатор с наименьшей (0,1 Ф) электроемкостью накапливает меньший (1 Кулон) заряд. А набиольший заряд 4 Кулона содержится на приборе, обладающем максимальной емкостью 0,4 Ф.

Последовательное соединение

Для такого способа соединения складываются величины, обратные емкостям.

\[\large \boxed { \frac {1}{C_{1}} + \frac {1}{C_{2}} = \frac {1}{C_{\text{общ}}} } \]

Примечание: Величина, обратно пропорциональная емкости, измеряется в обратных Фарадах.

\(\large \displaystyle \frac {1}{C} \left( \frac {1}{\text{Ф}} \right) \) – величину, обратную электроемкости в некоторых источниках называют электрической эластичностью (эластансом).

\(\large C_{1}, C_{2}\left( \text{Ф}\right) \) – емкости конденсаторов.

При последовательном включении общая \(\large C_{\text{Общ}} \) электроемкость цепочки окажется меньше самой маленькой емкости включенной в цепочку.

Рис. 5. Последовательный способ соединения емкостей

Общая емкость системы меньше меньшей из включенных последовательно емкостей.

Правило для напряжений

Приложенное к концам последовательной цепочки напряжение распределится между элементами.

\[\large \boxed { U_{1} + U_{2} = U_{\text{общ}} } \]

где \(\large U_{1}, U_{2}\left( B\right) \) — это напряжения на обкладках.

Чем больше емкость конденсатора, тем меньшее напряжение будет наблюдаться на его обкладках при последовательном соединении.

Рис. 6. Способ определить общее напряжение на последовательно включенных емкостях

Общее напряжение разделится на части. Большее напряжение будет на конденсаторе с меньшей электроемкостью.

На рисунке 7 представлена цепочка, состоящая из 4-ех емкостей, соединенных последовательно. На конденсаторе с наименьшей емкостью 0,3 Ф напряжение составляет 4 Вольта.

Рис. 7. Пример распределения напряжений на элементах последовательной цепи

А наименьшее напряжение 1 Вольт, находится на обкладках конденсатора с наибольшей емкостью 1,2 Ф. Общее напряжение на концах цепочки равняется 10-и Вольтам.

Заряд на конденсаторах

Зарядив одну из обкладок конденсатора, мы получим на второй его обкладке такой же (по модулю) заряд противоположного знака. Поэтому, все конденсаторы, соединенные последовательно, будут иметь одинаковые заряды на обкладках.

\[\large \boxed { q_{1} = q_{2} = q_{\text{общ}} } \]

где \(\large q_{1}, q_{2}\left( \text{Кл} \right) \) – заряды, накопленные конденсаторами.

В последовательно включенной цепочке все конденсаторы обладают равными зарядами.

Рис. 8. Равенство зарядов на обкладках последовательно включенных емкостей

Выводы

1. Правила, приведенные в статье, будут справедливы не только для двух, но и для любого количества включенных конденсаторов.
2. Связывающие напряжения и заряды формулы для последовательно и параллельно включенных элементов, можно получить из принципа сложения емкостей и обратных емкостей, а, так же, отношения между приложенным напряжением и зарядом.

Рис. 9. Основные формулы для различных способов соединения

 

Соединение конденсаторов.

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад.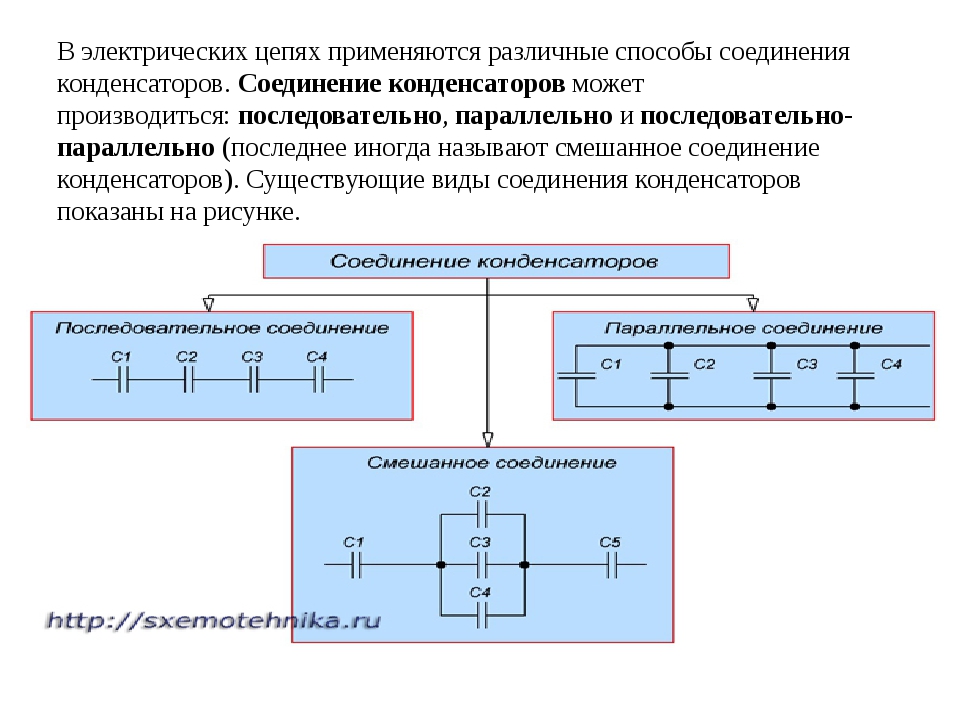

Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С₁ – ёмкость первого;

С₂ – ёмкость второго;

С₃ – ёмкость третьего;

С_N – ёмкость N-ого конденсатора;

C_общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C₁, C₂ в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт.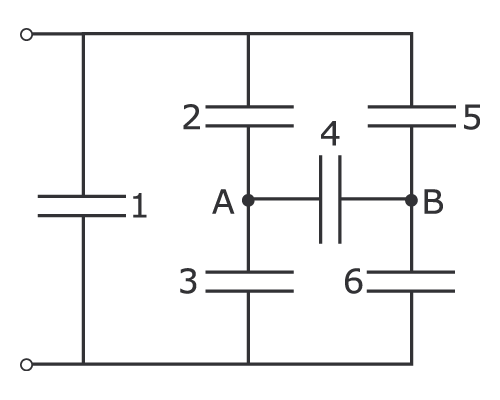

Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C₁ – его ёмкость.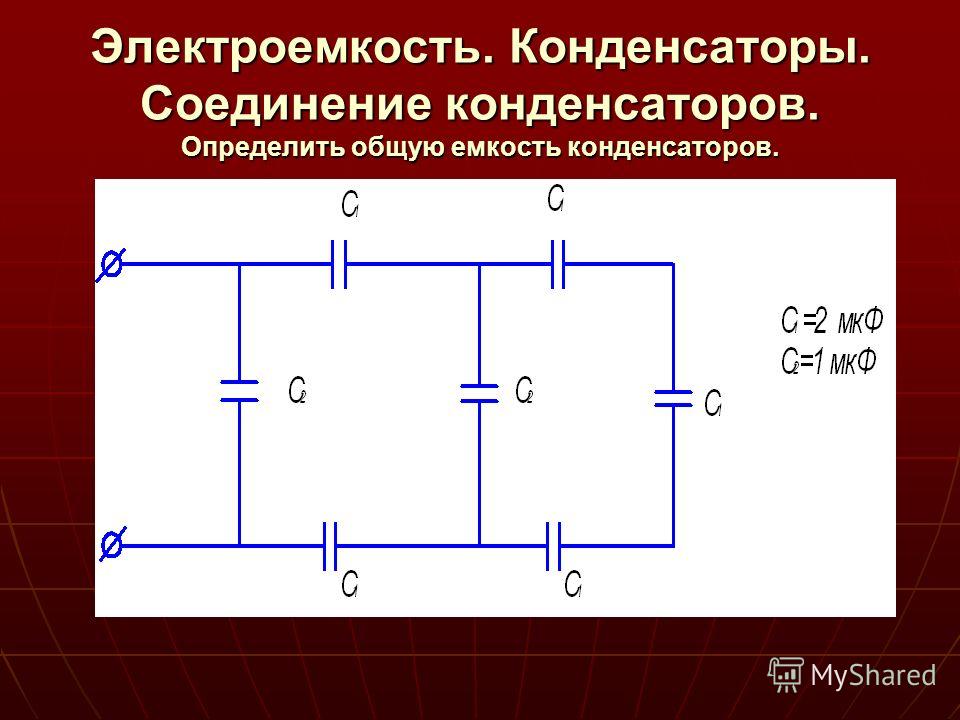

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные).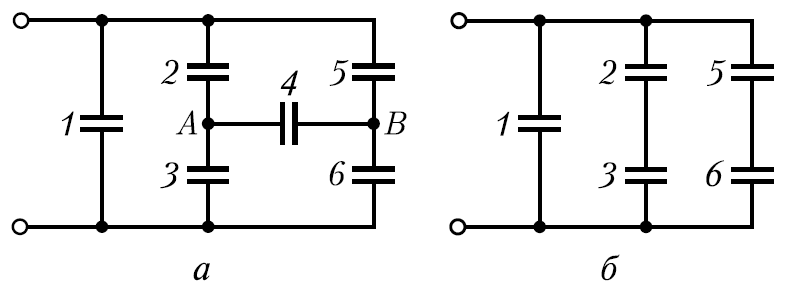 Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

 

Последовательное и параллельное соединение.

 Иногда нужно увеличить ёмкость или сопротивление, а подходящих деталей на нужное сопротивление нет, или размеры конструкции не позволяют вставить один большой конденсатор на 3000 мкф. 

В этом случае можно набрать необходимые ёмкость или сопротивление из нескольких деталей, а вместо конденсатора на 3000 микрофарад вставить 3 штуки по 1000 микрофарад.

Для увеличения ёмкости конденсаторы соединяются параллельно.

Для увеличения сопротивления резисторы соединяются последовательно.
Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.

Последовательное соединение — когда детали стоят друг за дружкой, «в очереди», будто за колбасой, потому оно так и называется.

Не путайте эти соединения, для увеличения ёмкости конденсаторы соединяются параллельно, а резисторы для увеличения сопротивления последовательно !

Со сложением ёмкостей и сопротивлений всё легко.

С параллельным соединением резисторов и последовательным соединением конденсаторов слегка посложнее, но к нашему счастью конденсаторы довольно редко соединяют последовательно, а резисторы параллельно.
Последовательное соединение конденсаторов может понадобиться например в сборке гаусс-гана (электромагнитной стрелялки), когда под рукой конденсаторы только на 400 вольт, а нам нужен 800-вольтовый конденсатор, а их редко где найдёшь и они дорогие.

Параллельное соединение резисторов считается вот по какой формуле:

Через три трубы, в которых в каждой по валенку, вода лучше потечёт, чем через одну трубу с одним валенком. Или если в бочке проковырять три дырки, то вода быстрее выльется, чем если бы мы проковыряли одну дырку.

Последовательное соединение конденсаторов считается по той же формуле.

Если два одинаковых конденсатора по 680uF с максимальным напряжением 400В поставить последовательно, то получится конденсатор на 340 uF с напряжением 800 вольт.
Ёмкость уменьшается, зато вырастает максимальное допустимое напряжение, а запасаемая в обеих конденсаторах энергия остаётся та же самая.

Последовательное соединение конденсаторов распределение напряжений. Последовательное соединение конденсаторов

Содержание:

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .

Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.

Последовательное соединение

Конденсатор, а в просторечии – «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.

Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.

Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество – это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору – он неудачен, т.к.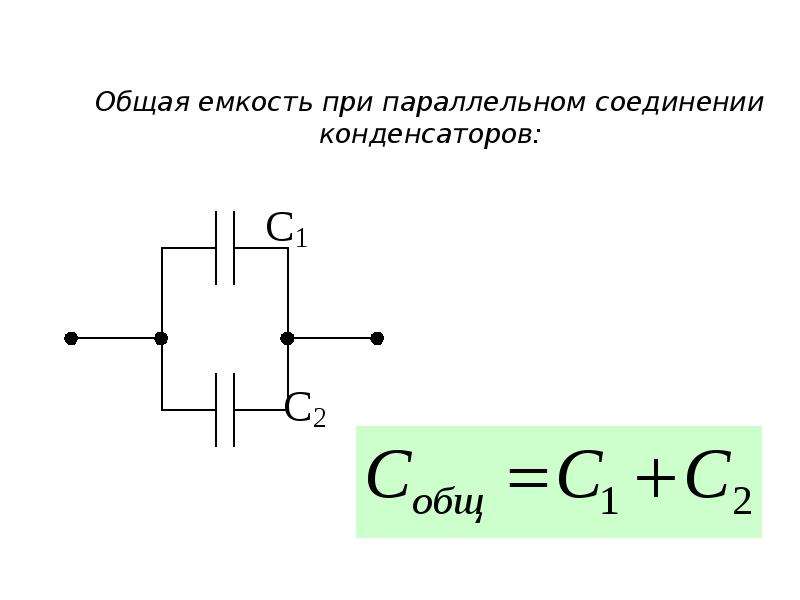 подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.

Чем больше пластины, и меньше расстояние между ними, тем больше . Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.

В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.

Единица измерения ёмкости – 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).

На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.

К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.

Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным – все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.

У радиолюбителей есть способ – через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.

• Rc – емкостное сопротивление, Ом;
• f – частота тока, Гц;
• C – емкость данного конденсатора, Ф;
• 6 – округленное до целой части число 2π.

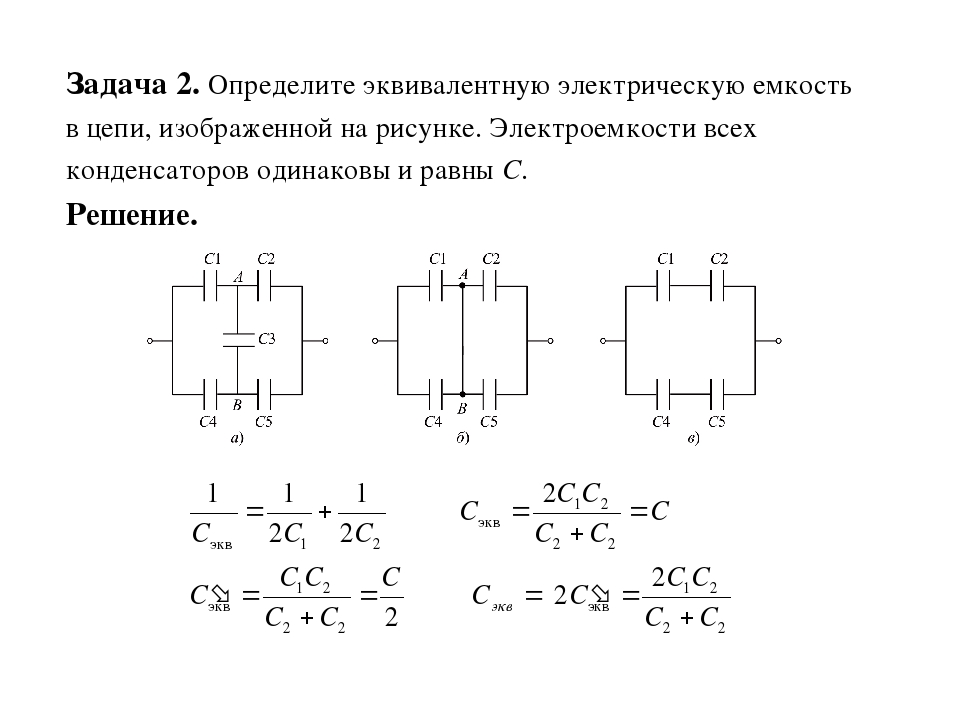
Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.

Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:

Собщ = С1*С2/С1+С2,

Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.

Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.

Параллельное соединение

Накопители электрического заряда постоянной емкости, различают:

• керамические;
• бумажные;
• слюдяные;
• металлобумажные;
• электролитические конденсаторы.

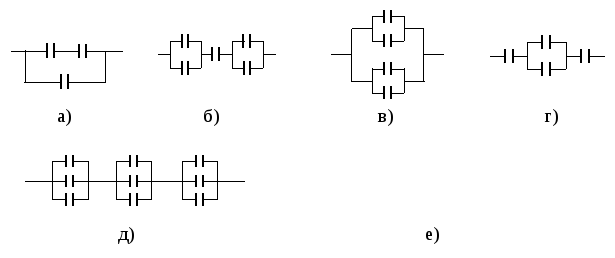
Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.

Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.

Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.

Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.

Для вычисления емкостей конденсаторов формула имеет вид:

Собщ = С1+С2, где С1 и С2 – емкость соответствующих элементов.

Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.

На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.

Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.

Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда – q, а ёмкость – C, можем получим искомое число, подставляя значения. Она имеет вид:

Смешанное соединение

При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.

Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.

Практически на любой электронной плате применяются конденсаторы, устанавливаются они и в силовых схемах. Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.

Выйти из сложившегося положения можно, используя несколько элементов, а необходимые характеристики получают, применяя параллельное и последовательное соединения конденсаторов между собой.

Немного теории

Конденсатор — пассивный электронный компонент, с переменной или постоянной величиной ёмкости, которое предназначено для накопления заряда и энергии электрического поля.

При выборе этих электронных компонентов руководствуются двумя основными характеристиками:

Условное обозначение неполярного постоянного конденсатора на схеме, показано на рис. 1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.

Способы соединения конденсаторов

Составление батарей конденсаторов позволяет изменить суммарную ёмкость или рабочее напряжение. Для этого могут применяться такие способы соединения:

• последовательное;
• параллельное;
• смешанное.

Последовательное соединение

Последовательное подключение конденсаторов показано на рис. 1, в. Применяют такое соединение в основном для увеличения рабочего напряжения. Дело в том, что диэлектрики каждого из элементов расположены друг за другом, поэтому при таком соединении напряжения складываются.

Суммарная ёмкость последовательно соединённых элементов можно рассчитать по формуле, которая для трёх компонентов будет иметь вид, показанный на рис. 1, е.

После преобразования в более привычную для нас форму, формула примет вид рис. 1, ж.

Если, соединённые последовательно, компоненты имеют одинаковые ёмкости, то расчёт значительно упрощается. В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.

Максимально упростить расчёты последовательно соединённых компонентов , позволяет использование онлайн-калькуляторов, которые без проблем можно найти в сети.

Параллельное подключение

Параллельное подключение конденсаторов показано на рис. 1, г. При таком соединении рабочее напряжение не изменяется, а ёмкости складываются. Поэтому для получения батарей большой ёмкости, используют параллельное соединение конденсаторов. Калькулятор для расчёта суммарной ёмкости не понадобится, так как формула имеет простейший вид:

С сум = С 1 + С 2 + С 3.

Собирая батарею для запуска трёхфазных асинхронных электродвигателей, часто применяют параллельное соединение электролитических конденсаторов. Обусловлено это большой ёмкостью этого типа элементов и небольшим временем запуска электродвигателя. Такой режим работы электролитических компонентов допустим, но следует выбирать те элементы, у которых номинальное напряжение минимум в два раза превышает напряжение сети.

Смешанное включение

Смешанное подключение конденсаторов — это сочетание параллельного и последовательного соединений .

Схематически такая цепочка может выглядеть по-разному. В качестве примера рассмотрим схему, изображённую на рис. 1, д. Батарея состоит из шести элементов, из которых С1, С2, С3, соединены параллельно, а С4, С5, С6 — последовательно.

Рабочее напряжение можно определить сложением номинальных напряжений С4, С5, С6 и напряжения одного из параллельно подключённых конденсаторов. Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.

Для определения суммарной ёмкости, схему разбивают на участки с одинаковым соединением элементов, производят расчёт для этих участков, после чего определяют общую величину.

Для нашей схемы последовательность вычислений следующая:

1. Определяем ёмкость параллельно соединённых элементов и обозначаем её С 1-3.
2. Рассчитываем ёмкость последовательно соединённых элементов С 4-6.
3. На этом этапе можно начертить упрощённую эквивалентную схему, в которой вместо шести элементов изображаются два — С 1-3 и С 4-6. Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.

В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям.

Электрические конденсаторы широко используются в радиоэлектронной аппаратуре. Они лидируют по количеству применения в блоках аппаратуры и по некоторым критериям уступают лишь резисторам. Конденсаторы присутствуют в любом электронном устройстве и их потребность в современной электронике постоянно растет. Наряду с имеющейся широкой номенклатурой, продолжаются разработки новых типов, которые имеют улучшенные электрические и эксплуатационные характеристики.

Что такое конденсатор?

Конденсатором называется элемент электрической цепи, который состоит из проводящих электродов, изолированных друг от друга диэлектриком.

Конденсаторы отличают по емкости, а именно по отношению заряда к разности потенциалов, который передается этим зарядом.

В международной системе СИ за единицу емкости принимают емкость конденсатора с возрастанием потенциала на один вольт при сообщении заряда в один кулон. Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).

Группы по виду диэлектрика

Диэлектрики применяют для изоляции пластин друг от друга. Они изготавливаются из органических и неорганических материалов. Нередко, в качестве диэлектрика, применяют оксидные пленки металлов.

По виду диэлектрика элементы делят на группы:

• органические;
• неорганические;
• газообразные;
• оксидные.

Элементы с органическим диэлектриком изготавливают путем намотки тонких лент специальной бумаги или пленки. Также применяют комбинированный диэлектрик с фольговыми или металлизированными электродами. Такие элементы могут быть как высоковольтные (свыше 1600 В), так и низковольтные (до 1600 В).

В изделиях с неорганическим диэлектриком используют керамику, слюду, стекло и стеклокерамику, стеклоэмаль. Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.

В качестве газообразного диэлектрика используют сжатый газ (фреон, азот, элегаз), воздух или вакуум. По характеру изменения емкости и выполняемой функции такие элементы бывают постоянными и переменными.

Наибольшее распространение получили элементы с вакуумным диэлектриком. Они имеют большие удельные емкости (по сравнению с газообразным диэлектриком) и более высокую электрическую прочность. Элементы с вакуумным диэлектриком обладают стабильностью параметров при температурных изменениях окружающей среды.

Область применения – передающие устройства, работающие на коротких, средних и длинных волнах диапазонов с частотой до 30-80 МГц.

Элементы с оксидным диэлектриком бывают:

• общего назначения;
• пусковые;
• импульсные;
• неполярные;
• высокочастотные;
• помехоподавляющие.

Диэлектриком является оксидный слой, который наносится на анод электрохимическим путем.

Условные обозначения

Элементы обозначаются по сокращенной и полной системе.

При сокращенной системе наносятся буквы и цифры , где буквой обозначается подкласс, цифрой — группа в зависимости от применяемого диэлектрика. Третий элемент указывает регистрационный номер типа изделия.

При полном условном обозначении указываются параметры и характеристики в следующей последовательности:

• условное обозначение конструктивного исполнения изделия;
• номинальное напряжение изделия;
• номинальная емкость изделия;
• допустимое отклонение емкости;
• температурная стабильность емкости изделия;
• номинальная реактивная мощность изделия.

Подбор номинала

Конденсаторы могут соединяться друг с другом различными способами.

На практике нередко возникают ситуации, когда при монтаже схемы или замене неисправного элемента, приходится использовать ограниченное количество радиодеталей. Не всегда удается подобрать элементы нужного номинала.

В этом случае приходится применять последовательное и параллельное соединение конденсаторов.

При параллельной схеме соединения, их суммарная величина составит сумму емкостей отдельных элементов. При этой схеме подключения все обкладки элементов соединяются по группам. Один из выводов каждого элемента соединяется в одну группу, а другой вывод в другую группу.

При этом напряжение на всех обкладках будет одинаково , потому что все группы подключены к одному источнику питания. Фактически получается одна емкость, суммарной величины всех емкостей в данной цепи.

Чтобы получить большую емкость, применяют параллельное соединение конденсатора.

Например, необходимо подключить двигатель с тремя фазами к однофазной сети 220 В. Для рабочего режима двигателя необходима емкость величиной в 135 мкФ. Ее найти очень трудно, но можно получить, применив параллельное соединение элементов на 5, 30 и 100 мкФ. В результате сложения получаем необходимую единицу в 135 мкФ.

Последовательно соединение конденсаторов

Последовательное соединение конденсаторов используют, если необходимо получить емкость меньшую емкости элемента. Такие элементы выдерживают более высокие напряжения. При последовательном соединении конденсаторов, обратная величина общей емкости равняется сумме обратных величин отдельных элементов. Для получения требуемой величины нужны определенные конденсаторы, последовательное соединение которых даст необходимую величину.

При последовательном соединении конденсаторов каждый его вывод соединяется с одним выводом другого элемента. Получается некая цепочка из последовательно соединенных конденсаторов, где крайние выводы подключаются к источнику питания.

Емкость общей батареи всегда меньше минимальной емкости элементов, входящих в нее. То есть, половина от емкости каждой из этих емкостей.

При последовательном соединении конденсаторов увеличивается расстояние между обкладками элементов.

Например, при последовательном соединении двух элементов напряжением 200 В можно смело включать в схему напряжением до 1000 В.

Данный метод соединения используется гораздо реже , потому что емкости такой величины и рабочего напряжения можно приобрести в магазинах.

Таким образом, зная принцип общего расчета параллельного и последовательного соединения конденсаторов, всегда можно выйти из затруднительного положения, имея под рукой ограниченное количество номиналов.

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

• ОЕ — общая емкость;
• Н — напряжение;
• КЕ — конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

способы, правила, формулы. Особенности замены конденсаторов

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .

Смешанное соединение конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

Содержание:

Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.

Параллельное включение конденсаторов в цепь

Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.

Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.

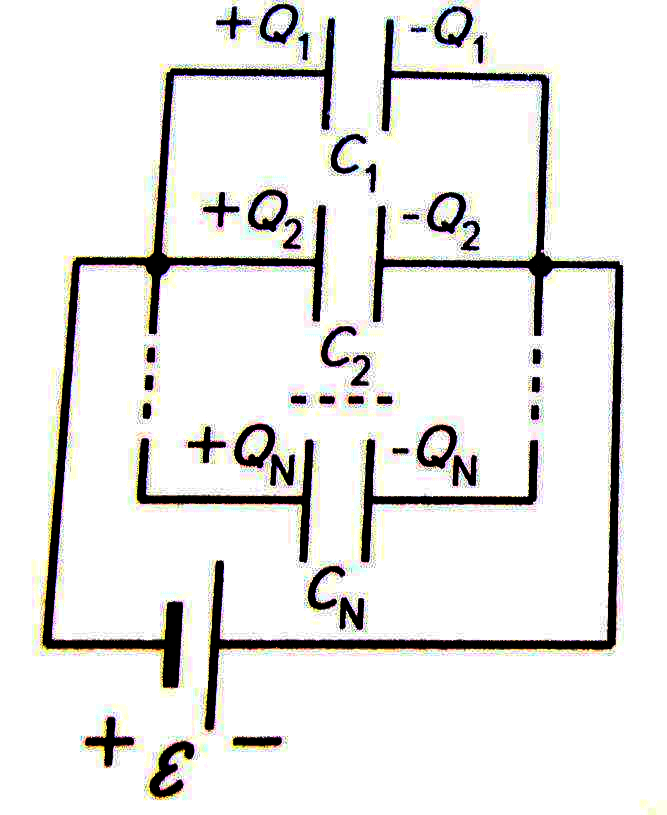
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.

При параллельном соединении конденсаторов емкость равняется:

Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.

Конденсаторы, соединенные параллельно, имеют напряжение:

Последовательное включение конденсаторов в цепь

Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.

Последовательное соединение конденсатора:

При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.

Формула нахождения заряда на конденсаторе, схема подключения конденсатора:

Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.

Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.

Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:

Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:

Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:

Смешанное включение емкостных накопителей в схему

Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.

Участок цепи подсоединенных смешанным включением накопителей емкости:

Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:

• разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
• вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
• проводим нахождение эквивалентной емкости на параллельном участке;
• когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
• рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:

1. Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
2. Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
3. Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.

Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.

Практически на любой электронной плате применяются конденсаторы, устанавливаются они и в силовых схемах. Для того чтобы компонент мог выполнять свои функции, он должен обладать определёнными характеристиками. Иногда возникает ситуация, когда необходимого элемента нет в продаже или его цена неоправданно завышена.

Выйти из сложившегося положения можно, используя несколько элементов, а необходимые характеристики получают, применяя параллельное и последовательное соединения конденсаторов между собой.

Немного теории

Конденсатор — пассивный электронный компонент, с переменной или постоянной величиной ёмкости, которое предназначено для накопления заряда и энергии электрического поля.

При выборе этих электронных компонентов руководствуются двумя основными характеристиками:

Условное обозначение неполярного постоянного конденсатора на схеме, показано на рис. 1, а. Для полярного электронного компонента дополнительно отмечают положительный вывод — рис. 1, б.

Способы соединения конденсаторов

Составление батарей конденсаторов позволяет изменить суммарную ёмкость или рабочее напряжение. Для этого могут применяться такие способы соединения:

• последовательное;
• параллельное;
• смешанное.

Последовательное соединение

Последовательное подключение конденсаторов показано на рис. 1, в. Применяют такое соединение в основном для увеличения рабочего напряжения. Дело в том, что диэлектрики каждого из элементов расположены друг за другом, поэтому при таком соединении напряжения складываются.

Суммарная ёмкость последовательно соединённых элементов можно рассчитать по формуле, которая для трёх компонентов будет иметь вид, показанный на рис. 1, е.

После преобразования в более привычную для нас форму, формула примет вид рис. 1, ж.

Если, соединённые последовательно, компоненты имеют одинаковые ёмкости, то расчёт значительно упрощается. В этом случае суммарную величину можно определить, разделив номинал одного элемента на их количество. Например, если требуется определить, какова ёмкость при последовательном соединении двух конденсаторов по 100 мкФ, то эту величину можно рассчитать, разделив 100 мкФ на два, то есть суммарная ёмкость равна 50 мкФ.

Максимально упростить расчёты последовательно соединённых компонентов , позволяет использование онлайн-калькуляторов, которые без проблем можно найти в сети.

Параллельное подключение

Параллельное подключение конденсаторов показано на рис. 1, г. При таком соединении рабочее напряжение не изменяется, а ёмкости складываются. Поэтому для получения батарей большой ёмкости, используют параллельное соединение конденсаторов. Калькулятор для расчёта суммарной ёмкости не понадобится, так как формула имеет простейший вид:

С сум = С 1 + С 2 + С 3.

Собирая батарею для запуска трёхфазных асинхронных электродвигателей, часто применяют параллельное соединение электролитических конденсаторов. Обусловлено это большой ёмкостью этого типа элементов и небольшим временем запуска электродвигателя. Такой режим работы электролитических компонентов допустим, но следует выбирать те элементы, у которых номинальное напряжение минимум в два раза превышает напряжение сети.

Смешанное включение

Смешанное подключение конденсаторов — это сочетание параллельного и последовательного соединений .

Схематически такая цепочка может выглядеть по-разному. В качестве примера рассмотрим схему, изображённую на рис. 1, д. Батарея состоит из шести элементов, из которых С1, С2, С3, соединены параллельно, а С4, С5, С6 — последовательно.

Рабочее напряжение можно определить сложением номинальных напряжений С4, С5, С6 и напряжения одного из параллельно подключённых конденсаторов. Если параллельно соединённые элементы имеют разные номинальные напряжения, то для расчёта берут меньшее из трёх.

Для определения суммарной ёмкости, схему разбивают на участки с одинаковым соединением элементов, производят расчёт для этих участков, после чего определяют общую величину.

Для нашей схемы последовательность вычислений следующая:

1. Определяем ёмкость параллельно соединённых элементов и обозначаем её С 1-3.
2. Рассчитываем ёмкость последовательно соединённых элементов С 4-6.
3. На этом этапе можно начертить упрощённую эквивалентную схему, в которой вместо шести элементов изображаются два — С 1-3 и С 4-6. Эти элементы схемы соединены последовательно. Остаётся произвести расчёт такого соединения и мы получим искомую.

В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям.

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов при­меняется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов ем­костью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденса­торов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих кон­денсаторов.

При последовательном включении двух конденсаторов их об­щая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конден­саторов емкостью С каждый, то общая емкость этих конденса­торов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. по­следовательное включение конденсаторов приводит к уменьше­нию общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое ра­бочее напряжение U p конденсатора меньше напряжения, на кото­рое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить не­сколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется мень­ше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) кон­денсаторов применяют тогда, когда необходимо увеличить ем­кость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на ниже­приведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым при­ложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохра­нения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего со­противления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Параллельное и последовательное включение конденсаторов. Параллельное и последовательное соединение конденсаторов: способы, правила, формулы

В электрических цепях и схемах используются различные методы соединения конденсаторов. Соединение емкостей в конденсаторные батареи может быть последовательным, параллельным и последовательно-параллельным (смешанным).

Если подключение емкостей в батарею осуществляется в виде цепочки и к точкам включения в цепь присоединены пластины только первого и последнего конденсаторов, то такое соединение называется последовательным .

При последовательном соединение конденсаторов они заряжаются одинаковым количеством электричества, хотя от источника тока заряжаются только две крайние пластины, а остальные пластины заряжаются через влияние электрического поля. При этом заряд пластины 2 будет равен по номиналу, но противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен заряду пластины 2, но также будет противоположной полярности и т. д.

Но если говорить точнее, напряжения на различных емкостных элементах будут отличаться, так как для заряда одним и тем же количеством электричества при различной номинальной емкости всегда необходимы различные напряжения. Чем нижее емкость конденсатора, тем больший уровень напряжение требуется для того, чтобы зарядить радиокомпонент необходимым количеством электричества, и наоборот.

Таким образом, при заряде группы емкостей, соединенных последовательно, на конденсаторах малой емкости напряжения будут выше, а на элементах большой емкости — ниже.

Рассмотрим всю группу емкостей соединенных последовательно, как одну эквивалентную емкость, между пластинами которой существует какой-то уровень напряжения, равный сумме напряжений на всех элементах группы, а заряд которого равен заряду любого компонента из данной группы.

Если более пристально рассмотреть самый меньший номинал емкости в группе, то на нем должно быть самый высокий уровень напряжения. Но фактически, уровень напряжения на нем составляет только часть общего значения напряжения, от общей группы. Напряжение на всей группе всегда выше напряжения на конденсаторе, имеющем самую малую велечину емкости. А поэтому можно сказать, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе .

Для вычисления общей емкости группы, в данном примере воспользуемся следующей формулой:

1 / C общ = 1/C 1 + 1/C 2 + 1/C 3

Для частного случая при двух последовательно соединенных элементов формула примет вид:

C общ = С 1 × С 2 /C 1 + C 2

Для практического примера подключим три радио компонента номиналом 100 мкф на 100 вольт последовательно. Согласно выше приведенной формуле, делим единицу, на емкость. Потом суммируем. Затем единицу делим на получившийся результат.

Итак — (1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03 и наконец 1: 0,03 = 33 мкф на 300вольт (все напряжения суммируем между собой 100+100+100 = 300в). В результате получаем конденсаторную батарею общей емкостью 33 мкф на 300 вольт.

В случае, если при последовательном соединении требуется получить неполярный конденсатор большой емкости, можно соединить два электролитических. При этом желательно выбирать конденсаторы одинакового номинала.

Включаем оба конденсатора последовательно, соединив их отрицательные электроды между собой. В итоге получим емкость равную половине каждого из номиналов

Если группа емкостных элементов включена в схему таким образом, что к точкам непосредственного включения присоединены пластины всех компонентов схемы, то такое соединение называется параллельным соединением конденсаторов.

При заряде группы емкостей, включенных параллельно, между пластинами всех элементов будет одно и тоже напряжение, так как все они заряжаются от одного источника питания. Общее количество электричества на всех элементах будет равно сумме количеств электричества, помещающихся на каждой емкости в отдельности, так как заряд каждой из них осуществляется независимо от заряда других компонентов данной схемы. Исходя из этого, всю систему можно рассматривать как один общий эквивалентный конденсатор. Тогда общая емкость при параллельном соединении конденсаторов равна сумме емкостей всех соединенных элементов.

Обозначим суммарную емкость соединенных в батарею элементов символом С общ , тогда можно записать формулу:

C общ = С 1 + С 2 + C 3

Рассмотрим эту формулу на живом примере. Предположим, что нам для ремонта бытовой техники срочно необходим конденсатор 100 мкф 50в, а у нас имеется только 47мкф на 50в. Если соединить их параллельно (минус к минусу и плюс к плюсу), то суммарная емкость получившейся конденсаторной батареи будет в районе 94 мкф на 50 вольт. Это вполне допустимое отклонение, так что можно без опаски устанавливать эту сборку в электронную технику.

Закрепим полученные знания по параллельному соединению конденсаторов на радиолюбительской практики: допустим для замены вздутого конденсатора на материнской плате персонального компьютера, нам нужна емкость номиналом 2000мкф, а у нас как назло ее не оказалось, а бежать на радиорынок тоже не хочется. Тут на помощь и придет нам знание закона параллельного соединения емкостей.

C общ = С 1 + С 2 = 1000мкф + 1000мкф = 2000мкф

Как видите нет ничего сложного, при параллельном соединении на каждый отдельный емкостной радио компонент действует одно и то же напряжение, а составной конденсатор заряжается в два раза большим количеством электричества.

Последовательно-параллельным соединением конденсаторов называется цепь или схема имеющая в своем составе участки, как с параллельным, так и с последовательным соединением радиокомпонентов.

При расчете общей емкости такой схемы с последовательно-параллельным типом соединения этот участок (как и в случае с ) разбивают на элементарные участки, состоящие из простых групп с последовательным или параллельным соединением емкостей. Дальше алгоритм вычислений принимает вид:

1. Вычисляют эквивалентную емкость участков с последовательным соединением емкостей.
2. Если эти участки состоят из последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей перерисовывают схему. Обычно получается схема из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают общую емкость полученной схемы.

Пример расчета емкости при смешанном соединение конденсаторов

Электрические конденсаторы широко используются в радиоэлектронной аппаратуре. Они лидируют по количеству применения в блоках аппаратуры и по некоторым критериям уступают лишь резисторам. Конденсаторы присутствуют в любом электронном устройстве и их потребность в современной электронике постоянно растет. Наряду с имеющейся широкой номенклатурой, продолжаются разработки новых типов, которые имеют улучшенные электрические и эксплуатационные характеристики.

Что такое конденсатор?

Конденсатором называется элемент электрической цепи, который состоит из проводящих электродов, изолированных друг от друга диэлектриком.

Конденсаторы отличают по емкости, а именно по отношению заряда к разности потенциалов, который передается этим зарядом.

В международной системе СИ за единицу емкости принимают емкость конденсатора с возрастанием потенциала на один вольт при сообщении заряда в один кулон. Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).

Группы по виду диэлектрика

Диэлектрики применяют для изоляции пластин друг от друга. Они изготавливаются из органических и неорганических материалов. Нередко, в качестве диэлектрика, применяют оксидные пленки металлов.

По виду диэлектрика элементы делят на группы:

• органические;
• неорганические;
• газообразные;
• оксидные.

Элементы с органическим диэлектриком изготавливают путем намотки тонких лент специальной бумаги или пленки. Также применяют комбинированный диэлектрик с фольговыми или металлизированными электродами. Такие элементы могут быть как высоковольтные (свыше 1600 В), так и низковольтные (до 1600 В).

В изделиях с неорганическим диэлектриком используют керамику, слюду, стекло и стеклокерамику, стеклоэмаль. Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.

В качестве газообразного диэлектрика используют сжатый газ (фреон, азот, элегаз), воздух или вакуум. По характеру изменения емкости и выполняемой функции такие элементы бывают постоянными и переменными.

Наибольшее распространение получили элементы с вакуумным диэлектриком. Они имеют большие удельные емкости (по сравнению с газообразным диэлектриком) и более высокую электрическую прочность. Элементы с вакуумным диэлектриком обладают стабильностью параметров при температурных изменениях окружающей среды.

Область применения – передающие устройства, работающие на коротких, средних и длинных волнах диапазонов с частотой до 30-80 МГц.

Элементы с оксидным диэлектриком бывают:

• общего назначения;
• пусковые;
• импульсные;
• неполярные;
• высокочастотные;
• помехоподавляющие.

Диэлектриком является оксидный слой, который наносится на анод электрохимическим путем.

Условные обозначения

Элементы обозначаются по сокращенной и полной системе.

При сокращенной системе наносятся буквы и цифры , где буквой обозначается подкласс, цифрой — группа в зависимости от применяемого диэлектрика. Третий элемент указывает регистрационный номер типа изделия.

При полном условном обозначении указываются параметры и характеристики в следующей последовательности:

• условное обозначение конструктивного исполнения изделия;
• номинальное напряжение изделия;
• номинальная емкость изделия;
• допустимое отклонение емкости;
• температурная стабильность емкости изделия;
• номинальная реактивная мощность изделия.

Подбор номинала

Конденсаторы могут соединяться друг с другом различными способами.

На практике нередко возникают ситуации, когда при монтаже схемы или замене неисправного элемента, приходится использовать ограниченное количество радиодеталей. Не всегда удается подобрать элементы нужного номинала.

В этом случае приходится применять последовательное и параллельное соединение конденсаторов.

При параллельной схеме соединения, их суммарная величина составит сумму емкостей отдельных элементов. При этой схеме подключения все обкладки элементов соединяются по группам. Один из выводов каждого элемента соединяется в одну группу, а другой вывод в другую группу.

При этом напряжение на всех обкладках будет одинаково , потому что все группы подключены к одному источнику питания. Фактически получается одна емкость, суммарной величины всех емкостей в данной цепи.

Чтобы получить большую емкость, применяют параллельное соединение конденсатора.

Например, необходимо подключить двигатель с тремя фазами к однофазной сети 220 В. Для рабочего режима двигателя необходима емкость величиной в 135 мкФ. Ее найти очень трудно, но можно получить, применив параллельное соединение элементов на 5, 30 и 100 мкФ. В результате сложения получаем необходимую единицу в 135 мкФ.

Последовательно соединение конденсаторов

Последовательное соединение конденсаторов используют, если необходимо получить емкость меньшую емкости элемента. Такие элементы выдерживают более высокие напряжения. При последовательном соединении конденсаторов, обратная величина общей емкости равняется сумме обратных величин отдельных элементов. Для получения требуемой величины нужны определенные конденсаторы, последовательное соединение которых даст необходимую величину.

При последовательном соединении конденсаторов каждый его вывод соединяется с одним выводом другого элемента. Получается некая цепочка из последовательно соединенных конденсаторов, где крайние выводы подключаются к источнику питания.

Емкость общей батареи всегда меньше минимальной емкости элементов, входящих в нее. То есть, половина от емкости каждой из этих емкостей.

При последовательном соединении конденсаторов увеличивается расстояние между обкладками элементов.

Например, при последовательном соединении двух элементов напряжением 200 В можно смело включать в схему напряжением до 1000 В.

Данный метод соединения используется гораздо реже , потому что емкости такой величины и рабочего напряжения можно приобрести в магазинах.

Таким образом, зная принцип общего расчета параллельного и последовательного соединения конденсаторов, всегда можно выйти из затруднительного положения, имея под рукой ограниченное количество номиналов.

В этой статье мы попытаемся раскрыть тему соединения конденсаторов разными способам. Из статьи про соединения резисторов мы знаем,что существует последовательное, параллельное и смешанное соединение, это же правило справедливо и для этой статьи. Конденсатор (от лат. слова «condensare» — «уплотнять», «сгущать»)– это очень широко распространённый электрический прибор.

Это два проводника (обкладки), между которыми находится изоляционный материал. Если на него подать напряжение (U), то на его проводниках накопится электрический заряд(Q). Основная его характеристика – ёмкость (C). Свойства конденсатора описываются уравнением Q = UC , заряд на обкладках и напряжение прямо пропорциональны друг другу.

Условное обозначение конденсатора на схеме

Пусть на конденсатор подается переменное напряжение. Он заряжается по мере роста напряжения, электрический заряд на обкладках увеличивается. Если напряжение уменьшается, то уменьшается и заряд на его обкладках и он разряжается.

Отсюда следует, что по проводам, соединяющим конденсатор с остальной цепью, электрический ток протекает тогда, когда напряжение на конденсаторе изменяется. При этом не важно, что происходит в диэлектрике между проводниками. Сила тока равна общему заряду, протекшему в единицу времени по подключенному к конденсатору проводу. Она зависит от его емкости и скорости изменения питающего напряжения.

Ёмкость зависит от характеристик изоляции, а также размеров и формы проводника. Единица измерения ёмкости кондёра — фарада (Ф), 1 Ф=1 Кл/В. Однако на практике емкость измеряется чаще в микро- (10-6) или пико- (10-12) фарадах.

В основном используются конденсаторы для построения цепей с частотной зависимостью, для получения мощного короткого электрического импульса, там, где необходимо накапливать энергию. За счёт изменения свойств пространства между обкладками можно использовать их для измерения уровня жидкости.

Параллельное соединение

Параллельное соединение – это соединение, при котором выводы всех конденсаторов имеют две общие точки – назовём их входом и выходом схемы. Так все входы объединены в одной точке, а все выходы – в другой, напряжения на всех конденсаторах равны:

Параллельное соединение предполагает распределение полученного от источника заряда на обкладках нескольких конденсаторов, что можно записать так:

Так как напряжение на всех конденсаторах одинаковое, заряды на их обкладках зависят только от ёмкости:

Суммарная емкость параллельной группы конденсаторов:

Суммарная ёмкость такой группы конденсаторов равна сумме емкостей включенных в схему.

Блоки конденсаторов широко используются для повышения мощности и устойчивости работы энергосистем в линиях электропередач. При этом затраты на более мощные элементы линий можно снизить. Повышается стабильность работы ЛЭП, устойчивость ЛЭП к сбоям и перегрузкам.

Последовательное соединение

Последовательное соединение конденсаторов – это их подключение непосредственно друг за другом без разветвлений проводника. От источника напряжения заряды поступают на обкладки первого и последнего в цепи конденсаторов.

В силу электростатической индукции на внутренних обкладках смежных конденсаторов происходит выравнивание заряда на электрически соединённых обкладках смежных конденсаторов, поэтому на них появляются равные по величине и обратные по знаку электрические заряды.

При таком соединении электрические заряды на обкладках отдельных кондёров по величине равны:

Общее напряжение для всей цепи:

Очевидно, что напряжение между проводниками для каждого конденсатора зависит от накопленного заряда и ёмкости, т.е.:

Поэтому эквивалентная ёмкость последовательной цепи равна:

Отсюда следует, что величина, обратная общей емкости, равна сумме величин, обратных емкостям отдельных конденсаторов:

Смешанное соединение

Смешанным соединение конденсаторов называют такое соединение, при котором присутствует соединение последовательное и параллельное одновременно. Чтобы более подробно разобраться, давайте рассмотрим это соединение на примере:

На рисунке видно,что соединены два конденсатора последовательно вверху и внизу и два параллельно. Можно вывести формулу из выше описанных соединении:

Основой любой радиотехники является конденсатор, он используется в самых разнообразных схемах-это и источники питания и применение для аналоговых сигналов хранения данных, а также в телекоммуникационных связи для регулирования частоты.

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С 1 – ёмкость первого;

С 2 – ёмкость второго;

С 3 – ёмкость третьего;

С N – ёмкость N -ого конденсатора;

C общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.

Последовательное соединение

Конденсатор, а в просторечии – «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.

Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.

Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество – это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору – он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.

Чем больше пластины, и меньше расстояние между ними, тем больше . Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.

В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.

Единица измерения ёмкости – 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).

На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.

К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.

Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным – все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.

У радиолюбителей есть способ – через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.

• Rc – емкостное сопротивление, Ом;
• f – частота тока, Гц;
• C – емкость данного конденсатора, Ф;
• 6 – округленное до целой части число 2π.

Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.

Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:

Собщ = С1*С2/С1+С2,

Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.

Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.

Параллельное соединение

Накопители электрического заряда постоянной емкости, различают:

• керамические;
• бумажные;
• слюдяные;
• металлобумажные;
• электролитические конденсаторы.

Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.

Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.

Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.

Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.

Для вычисления емкостей конденсаторов формула имеет вид:

Собщ = С1+С2, где С1 и С2 – емкость соответствующих элементов.

Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.

На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.

Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.

Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда – q, а ёмкость – C, можем получим искомое число, подставляя значения. Она имеет вид:

Смешанное соединение

При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.

Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.

Серия

и параллельные схемы — learn.sparkfun.com

Добавлено в избранное Любимый 54 Конденсаторы серии

и параллельные

Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?

Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать.Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов. А если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.

Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы к разрядке в друга, сидящего рядом с вами.

Помните, что в последовательной цепи есть только один путь для прохождения тока.Отсюда следует, что количество электронов, выходящих из колпачка внизу, будет таким же, как и количество электронов, выходящих из колпачка наверху. Значит, емкость не увеличилась?

На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора.И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.

Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.

Добавление конденсаторов параллельно похоже на добавление резисторов последовательно: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Простой.

---

← Предыдущая страница
Практические правила для последовательных и параллельных резисторов

Как рассчитать конденсаторы, подключенные последовательно и параллельно — Kitronik Ltd

Параллельные конденсаторы

Когда конденсаторы подключаются друг к другу (бок о бок), это называется параллельным подключением. Это показано ниже. Чтобы рассчитать общую общую емкость ряда конденсаторов, подключенных таким образом, вы складываете отдельные емкости по следующей формуле: CTotal = C1 + C2 + C3 и т. Д. Пример: Чтобы рассчитать общую емкость для этих трех конденсаторов, подключенных параллельно.Cобщ = C1 + C2 + C3 = 10F + 22F + 47F = 79F

---

Задача 1:

Рассчитайте общую емкость следующих конденсаторов, включенных параллельно.

Конденсаторы серии

Когда конденсаторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общую общую емкость двух конденсаторов, подключенных таким образом, вы можете использовать следующую формулу:

Итого =	C1 x C2	и так далее
	C1 + C2

Пример: чтобы рассчитать общую емкость для этих двух последовательно соединенных конденсаторов.

---

Задача 2:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

Три или более конденсатора последовательно

Чтобы рассчитать общую общую емкость трех или более конденсаторов, подключенных таким образом, вы можете использовать следующую формулу: и так далее. Пример: чтобы рассчитать общую емкость для этих трех последовательно соединенных конденсаторов.

---

Задача 3:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

---

ответы

Задача 1

1 = 232.2F 2 = 169,0F 3 = 7,0F

Задача 2

1 = 2,48F 2 = 14,99F 3 = 4,11F

Задача 3

1 = 3,33F 2 = 1,167F 3 = 0,35F Примечание Значения конденсаторов в этом листе поддерживаются высокими (близкими к единице или больше). Это сделано для упрощения процесса обучения. На самом деле типичные значения конденсаторов намного меньше единицы. Загрузите PDF-версию этой страницы здесь. Узнать больше об авторе подробнее »Если вы нашли эту статью полезной и хотели бы получать от нас обновления продуктов и бесплатные электронные ресурсы, зарегистрируйтесь здесь.Мы также ненавидим спам и обещаем никогда не продавать и не сообщать свой адрес электронной почты, и вы можете отказаться от подписки в любое время.

© Kitronik Ltd — Вы можете распечатать эту страницу и ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.

Емкостное реактивное сопротивление

— Как найти последовательные и параллельные конденсаторы

Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1: Найдите общую емкость цепи

Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц. Каково полное емкостное реактивное сопротивление (X _C ) при последовательном или параллельном подключении?

1А. Для конденсаторов серии

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов.Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.

Конденсаторы серии Пример:

1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033

0,083 + 0,050 + 0,033 = 0,166

1 / 0,163 = 6,02 мкФ

Примечание: математические расчеты упрощены для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.

1Б. Для параллельных конденсаторов

При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов. Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.

Параллельные конденсаторы Пример:

12 + 20 + 30 = 62 мкФ

---

Шаг 2: Определите емкостное реактивное сопротивление

Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и, поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X _C ) который измеряется в Ом.

Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока течет. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.

X _C — емкостное реактивное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!

1 мкФ = 0,000001 F

Серия 60 Гц Пример:

6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом

60 Гц Параллельный Пример:

62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом

Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :

Серия 400 Гц Пример:

2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом

Параллельный 400 Гц Пример:

2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом

---

Полезные ссылки

на комментарий.

Конденсаторы последовательно и параллельно с примерами

Последовательные и параллельные конденсаторы

Системы с более чем одним конденсатором имеют эквивалентную емкость. Конденсаторы можно соединять между собой двумя способами. Их можно подключать последовательно и параллельно. Сначала мы увидим конденсаторы, включенные параллельно.

В этой цепи конденсаторы включены параллельно.

Потому что левые стороны конденсаторов подключены к потенциалу a, а правые стороны конденсаторов подключены к потенциалу b.Другими словами, мы можем сказать, что каждый конденсатор имеет одинаковую разность потенциалов. Находим заряд каждого конденсатора как;

Q ₁ = C ₁ .V

Q ₂ = C ₂ .V

Q ₃ = C ₃ .V

Общий заряд системы определяется сложением каждого заряда.

Q _итого = C _экв .V

Q _итого = Q ₁ + Q ₂ + Q ₃ = C ₁ .V + C ₂ .V + C ₃ .V = V. (C ₁ + C ₂ + C ₃ ) = C _экв.

C _экв. = C ₁ + C ₂ + C ₃

Как видите, мы нашли эквивалентную емкость системы как C ₁ + C ₂ + C ₃

Теперь посмотрим последовательно включенные конденсаторы;

В конденсаторах, подключенных последовательно, каждый конденсатор имеет одинаковый поток заряда от батареи.В этой схеме заряд + Q течет от положительной части батареи к левой пластине первого конденсатора и притягивает заряд –Q на правой пластине, с той же идеей заряд -Q течет от батареи к правой пластине. третьего конденсатора и притягивает + Q на левой пластине. Таким же образом заряжаются и другие конденсаторы. Подводя итог, можно сказать, что каждый конденсатор имеет одинаковый заряд с батареей.

C ₁ .V ₁ = Q

С ₂ .V ₂ = Q, V = V ₁ + V ₂ + V ₃ и Q = C _экв .V

C ₃ .V ₃ = Q

Пример: вычислить эквивалентную емкость между точками a и b.

Пример: В приведенной ниже схеме C1 = 60 мкФ, C2 = 20 мкФ, C3 = 9 мкФ и C4 = 12 мкФ.Если разность потенциалов между точками a an b Vab = 120V, найдите заряд второго конденсатора.

Электростатические экзамены и решения

Емкость и конденсаторы <Пред.		Далее> Памятка по электростатике

Конденсатор

в последовательной, параллельной и цепях переменного тока

Конденсатор является одним из наиболее часто используемых электронных компонентов.Он имеет способность накапливать энергию внутри себя в виде электрического заряда, создающего статическое напряжение (разность потенциалов) на его пластинах. Проще говоря, конденсатор похож на небольшую перезаряжаемую батарею. Конденсатор представляет собой просто комбинацию двух параллельных проводящих или металлических пластин, которые электрически разделены хорошим изолирующим слоем (также называемым диэлектриком ) , состоящим из вощеной бумаги, слюды, керамики, пластика и т. Д.

Существует множество применений конденсатора в электронике, некоторые из них перечислены ниже:

• Накопитель энергии
• Кондиционер
• Коррекция коэффициента мощности
• Фильтрация
• Осцилляторы

Теперь дело в , как работает конденсатор ? Когда вы подключаете источник питания к конденсатору, он блокирует постоянный ток из-за изолирующего слоя и позволяет напряжению присутствовать на пластинах в виде электрического заряда.Итак, вы знаете, как работает конденсатор и каково его использование или применение, но вы должны научиться этому, как использовать конденсатор в электронных схемах.

Как подключить конденсатор в электронную схему?

Здесь мы собираемся продемонстрировать вам подключение конденсатора и связанный с ним эффект на примерах.

• Конденсатор серии
• Конденсатор параллельно
• Конденсатор в цепи переменного тока

Конденсатор в последовательной цепи

В схеме, когда вы подключаете конденсаторы последовательно, как показано на изображении выше, общая емкость уменьшается.Ток, проходящий через последовательно соединенные конденсаторы, равен (т.е. i _T = i ₁ = i ₂ = i _{3 =} i _n ). Следовательно, заряд, накопленный конденсаторами, также одинаков (т.е. Q _T = Q ₁ = Q ₂ = Q ₃ ), потому что заряд, накопленный пластиной любого конденсатора, исходит от пластины соседнего конденсатор в цепи.

Применяя Закон Кирхгофа о напряжении (KVL) в цепи, мы получаем

  V  T  = V  C1  + V  C2  + V  C3 … уравнение (1)  

Как известно,

  Q = CV 
  Итак, V = Q / C  

Где, V _C1 = Q / C ₁ ; V _C2 = Q / C ₂ ; V _C3 = Q / C ₃

Теперь, поместив вышеуказанные значения в уравнение (1)

   (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 )  

Для n последовательно подключенных конденсаторов уравнение будет

.

  (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 ) +….+ (1 / Cn)  

Следовательно, приведенное выше уравнение является уравнением конденсаторов серии .

Где, C _T = Общая емкость цепи

C ₁ … n = емкость конденсаторов

Уравнение емкости для двух особых случаев определено ниже:

Случай I: , если два конденсатора соединены последовательно, с разным значением емкость будет выражена как:

  (1 / C  T ) = (C  1  + C  2 ) / (C  1  * C  2 ) 
  Или, C  T  = (C  1  * C  2 ) / (C  1  + C  2 )… уравнение (2)  

Случай II: , если два конденсатора включены последовательно, с одинаковым значением емкость будет выражаться как:

  (1 / C  T ) = 2 / C  2  = 2 / C 
  Или, C  T  = C / 2  

Пример цепи последовательного конденсатора:

Теперь в приведенном ниже примере мы покажем вам, как рассчитать общую емкость и индивидуальное среднеквадратичное падение напряжения на каждом конденсаторе.

Как показано на приведенной выше принципиальной схеме, есть два конденсатора , соединенных последовательно с разными номиналами. Значит, падение напряжения на конденсаторах также неодинаково. Если мы подключим два конденсатора с одинаковым значением, падение напряжения также будет одинаковым.

Теперь для определения общего значения емкости воспользуемся формулой из уравнения (2)

  Итак, C  T  = (C  1  * C  2 ) / (C  1  + C  2 ) 
  Здесь C  1  = 4.7 мкФ и C  2  = 1 мкФ 
  C  T  = (4,7 мкФ * 1 мкФ) / (4,7 мкФ + 1 мкФ) 
  C  T  = 4,7 мкФ / 5,7 мкФ 
  C  T  = 0,824 мкФ  

Теперь падение напряжения на конденсаторе C ₁ составляет:

  VC  1  = (C  T  / C  1 ) * V  T  
  VC  1  = (0,824 мкФ / 4,7 мкФ) * 12 
  VC  1  = 2,103V  

Теперь падение напряжения на конденсаторе C ₂ составляет:

  VC  2  = (C  T  / C  2 ) * V  T  
  VC  2  = (0.824 мкФ / 1 мкФ) * 12 
  VC  2  = 9,88 В  

Конденсатор в параллельной цепи

При параллельном подключении конденсаторов общая емкость будет равна сумме емкостей всех конденсаторов. Потому что верхняя пластина всех конденсаторов соединена вместе, как и нижняя пластина. Таким образом, при соприкосновении друг с другом эффективная площадь пластин также увеличивается. Следовательно, емкость пропорциональна отношению площади и расстояния.

Применяя Текущий закон Кирхгофа (KCL) в вышеупомянутой схеме,

  i  T  = i  1  + i  2  + i  3   

Как известно, ток через конденсатор выражается как;

  i = C (dV /   dt  ) 
  So, i  T  = C  1  (dV /   dt  ) + C  2  (dV /   dt  ) + C  3  (dV /   dt  ) 
  А,
   i    T     = (C  1  + C  2  + C  3 ) * (dV /   dt  ) 
  i  T  = C  T  (dV /   dt  )… уравнение (3)  

Из уравнения (3) уравнение параллельной емкости:

  C  T  = C  1  + C  2  + C  3   

Для числа n конденсаторов, подключенных параллельно, уравнение выше выражается как:

  C  T  = C  1  + C  2  + C  3  +… + Cn  

Пример параллельной цепи конденсатора

На приведенной ниже принципиальной схеме три конденсатора соединены параллельно .Поскольку эти конденсаторы подключены параллельно, эквивалентная или общая емкость будет равна сумме индивидуальных емкостей.

  C  T  = C  1  + C  2  + C  3  
  Где, C  1  = 4,7 мкФ; C  2  = 1 мкФ и C  3  = 0,1 мкФ 
  Итак, C  T  = (4,7 +1 + 0,1) мкФ 
  C  T  = 5,8 мкФ  

Конденсатор в цепях переменного тока

Когда конденсатор подключен к источнику постоянного тока, конденсатор начинает медленно заряжаться.И, когда напряжение зарядного тока конденсатора равно напряжению питания, это считается полностью заряженным. Здесь в этом состоянии конденсатор работает как источник энергии, пока на него подается напряжение. Кроме того, конденсаторы не позволяют току проходить через него после полной зарядки.

Каждый раз, когда на конденсатор подается переменное напряжение, как показано на чисто емкостной схеме выше. Затем конденсатор непрерывно заряжается и разряжается до каждого нового уровня напряжения (заряжается при положительном уровне напряжения и разряжается при отрицательном уровне напряжения).Емкость конденсатора в цепях переменного тока зависит от частоты входного напряжения, подаваемого в цепь. Сила тока прямо пропорциональна скорости изменения напряжения, приложенного к цепи.

  i = dQ /   dt   = C (dV /   dt  )  

Векторная диаграмма конденсатора в цепи переменного тока

Как вы видите на векторной диаграмме конденсатора переменного тока на изображении ниже, ток и напряжение представлены в виде синусоидальной волны.При наблюдении при 0 ° зарядный ток достигает своего пикового значения из-за постоянного увеличения напряжения в положительном направлении.

Теперь при 90 ° ток через конденсатор не протекает, потому что напряжение питания достигает максимального значения. При 180 ° напряжение начинает медленно снижаться до нуля, а ток достигает максимального значения в отрицательном направлении. И снова заряд достигает своего пикового значения на 360 °, потому что напряжение питания находится на минимальном значении.

Таким образом, из приведенного выше сигнала мы можем видеть, что ток опережает напряжение на 90 °.Итак, мы можем сказать, что напряжение переменного тока отстает от тока на 90⁰ в идеальной конденсаторной цепи .

Реактивное сопротивление конденсатора (Xc) в цепи переменного тока

Рассмотрим приведенную выше принципиальную схему, поскольку мы знаем, что входное напряжение переменного тока выражается как

  V = V  м  Sin  вес   

А, заряд конденсатора Q = CV,

Итак, Q = CV _м Sin _wt

А, ток через конденсатор, i = dQ / dt

Итак,

  i = d (CV  м  Sin  wt ) / dt 
  i = C * d (V  m  Sin  wt ) / dt 
  i = C * V  м  Cos  wt  * w 
  i = w * C * V  м  Sin (wt + π / 2) 
  ат, wt = 0 
  sin (вес + π / 2) = 1 
 , следовательно, i  m  = wCV  m  
  V  м  / i  м  = 1 / wC  

Как известно, w = 2πf

Итак,

  Емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC  

Пример емкостного реактивного сопротивления в цепи переменного тока

диаграмма

Давайте рассмотрим значение C = 2.2 мкФ и напряжение питания V = 230 В, 50 Гц

  Теперь емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC 
  Здесь C = 2,2 мкФ и f = 50 Гц 
  Итак, Xc = 1/2 * 3,1414 * 50 * 2,2 * 10 -6  
  Xc = 1446,86 Ом  

Как рассчитать емкость в последовательной и параллельной цепях?

Есть две комбинации конденсаторов: последовательная и параллельная цепи. В последовательных цепях общая емкость меньше наименьшего значения емкости, так как эффективное расстояние между пластинами увеличивается.В параллельных цепях общая емкость складывается из отдельных емкостей.

, когда конденсаторы соединены последовательно, общая емкость меньше наименьшего значения емкости из-за увеличения эффективного расстояния между пластинами. Расчет общей последовательной емкости аналогичен расчету общего сопротивления параллельных резисторов.
Данная комбинация имеет следующие характеристики:

1. У каждого конденсатора одинаковый заряд.Если батарея подает заряд + Q на левую пластину конденсатора C1 из-за индукции, индуцируется заряд -Q на его правой пластине и заряд + Q на левой пластине конденсатора C2, т. Е.

Q = Q ₁ + Q ₂ + Q ₃
2 : Разность потенциалов на каждом конденсаторе разная из-за разных значений емкостей.
3 : Напряжение батареи было разделено между различными конденсаторами, поэтому
В = В ₁ + В ₂ + В ₃
= Q / C ₁ + Q / C ₂ + Q / C ₃
= Q [1 / C ₁ + 1 / C ₂ + 1 / C ₃ ]
V / Q = [1 / C ₁ + 1 / C ₂ +1 / C ₃ ]

4: Эквивалентная емкость

мы можем заменить последовательную комбинацию конденсаторов одним эквивалентным конденсатором емкостью C _экв. i.e,
1 / C _eq = 1 / C ₁ + 1 / C ₂ + 1 / C ₃

Формула для общей емкости в параллельной цепи

При параллельном подключении конденсаторов общая емкость является суммой отдельных емкостей, поскольку эффективная площадь пластины увеличивается. Расчет общей параллельной емкости аналогичен расчету общего последовательного сопротивления.
На приведенном выше рисунке левая пластина каждого конденсатора соединена с положительной клеммой батареи проводящим проводом.Таким же образом правая пластина каждого конденсатора подключается к отрицательной клемме батареи. Этот тип комбинации имеет следующие характеристики.

1. Каждый конденсатор, подключенный к батарее с напряжением V, имеет такую ​​же разность потенциалов, как:

В = В ₁ + В ₂ + В ₃
2. Формирование пластин каждого конденсатора будет разным из-за разной емкости.
3. Общий заряд Q, обеспечиваемый батареей, делится между различными конденсаторами.Следовательно:
Q = Q ₁ + Q ₂ + Q ₃
Или Q = C ₁ V + C ₂ V + C ₃ V
Q = V (C ₁ + C ₂ + C ₃ )
Q / V = ​​C ₁ + C ₂ + C ₃
4. Мы можем заменить параллельную комбинацию конденсаторов одним эквивалентным конденсатором, имеющим емкость C _eq , так что
C _eq = C ₁ + C ₂ + C ₃
В случае n конденсаторов, подключенных параллельно, эквивалентная емкость определяется как:
C _eq = C ₁ + C ₂ + C ₃ + …… + C _n
5.Эквивалентная емкость параллельной комбинации конденсаторов больше любой из отдельных емкостей.
Смотрите также видео

Последовательный и параллельный калькулятор емкости

[1] 2020/11/19 01:33 До 20 лет / Другое / Очень /

Цель использования

Выяснение того, какая комбинация конденсаторов у меня под рукой может создать значение, которое мне нужно в данной схеме

Комментарий / Запрос

Возможность добавления более двух конденсаторов

[2] 2020.08.13 03:32 Уровень 30 лет / Инженер / Полезный /

Назначение Используйте

, чтобы проверить мою собственную работу по созданию проблем, которые должны решить младшие технические специалисты

[3] 2019/11/15 17:26 Уровень 20 лет / Средняя школа / Университет / аспирант / Полезно /

Цель использования

ПОНЯТЬ

Комментарий / запрос

ПОЛУЧИТЬ ЗНАНИЯ

[4] 10.04.2019 15:25 Уровень 30 лет / Самостоятельно занятые люди / Очень /

Цель использования

Генератор Колпитца на УКВ, рассчитать общую емкость e на двойных варикапных диодах, используемых для настройки, а также общая емкость на делителе обратной связи.

[5] 2019/03/08 07:04 60 лет и старше / Пенсионер / Очень /

Цель использования

Помимо того, что я радиолюбитель, я также занимаюсь изготовлением кристаллических радиоприемников.
Для многих конструкций требуется воздушный конденсатор емкостью 500 пФ, но все, что я смог найти, это 630 пФ.
Итак, используя ваш калькулятор, я смог увидеть, сколько емкости мне нужно было добавить последовательно, чтобы снизить емкость конденсатора 630 пФ до 500 пФ.

Отлично сработало, мои искренние благодарности.

[6] 2018/08/27 21:07 Уровень 40 лет / Другое / Очень /

Цель использования

Отсутствие правильных значений на двух крышках.Используется для расчета заменяемых колпачков для старой магнитофонной деки.

Комментарий / запрос

Очень полезно

[7] 2018.08.17 13:15 Уровень 40 лет / Самостоятельно занятые люди / Очень /

Цель использования

Расчет шины питания для лампового усилителя

[8] 2018/08/12 01:16 Возраст 60 лет и старше / Офисный работник / Государственный служащий / Полезно /

Цель использования

Устранение неисправностей источника питания. У меня был счетчик, который показывал максимум 10000 мкФ.Итак, мне пришлось последовательно соединить два одинаковых, чтобы проверить значение крышки фильтра.