Смешанное соединение конденсаторов формула: Смешанное соединение конденсаторов – формула, определение, расчет, схема кратк — Мир Антенн

Содержание

Схемы соединения конденсаторов

При проектировании и построении различных электрических цепей широко используются конденсаторы (емкости). В разрабатываемых схемах они могут соединяться как с другими электронными компонентами, так и между собой. Во втором случае такие соединения подразделяются на последовательные, параллельные, и последовательно-параллельные. Нужно еще отметить, что последовательно-параллельные соединения конденсаторов иначе называются смешанными.

Последовательное соединение конденсаторов

Это способ соединения конденсаторов ( электрических емкостей ) используется тогда, когда то напряжение, которое к ним подводится, выше чем то, на которое они рассчитаны. Используется оно в подавляющем большинстве случаев для того, чтобы избежать пробоев этих элементов устанавливаемых в электронных схемах.

Конденсаторы, соединенные между собой последовательно – это, по сути дела, цепочка.

В ней вторая обкладка первого элемента соединяется с первой обкладкой второго; первая обкладка третьего – со второй второго и так далее.

Последовательное соединение конденсаторов

Напряжение на конденсаторах обратно пропорционально ёмкостям конденсаторов.

C_общ =

C₁ × C₂ × C₃

C₁ + C₂ + C₃

Наибольшее напряжение будет на конденсаторе с наименьшей ёмкостью.

Параллельное соединение конденсаторов

Этот способ соединения конденсаторов используется тогда, когда необходимо существенно увеличить их общую емкость. Суть такого наращивания состоит в том, что значительно возрастает общая площадь пластин по сравнению с той, которую имеет каждый конденсатор в отдельности. Что касается общей емкости всех

конденсаторов, соединенных друг с другом параллельно, то она равняется сумме емкостей каждого из них.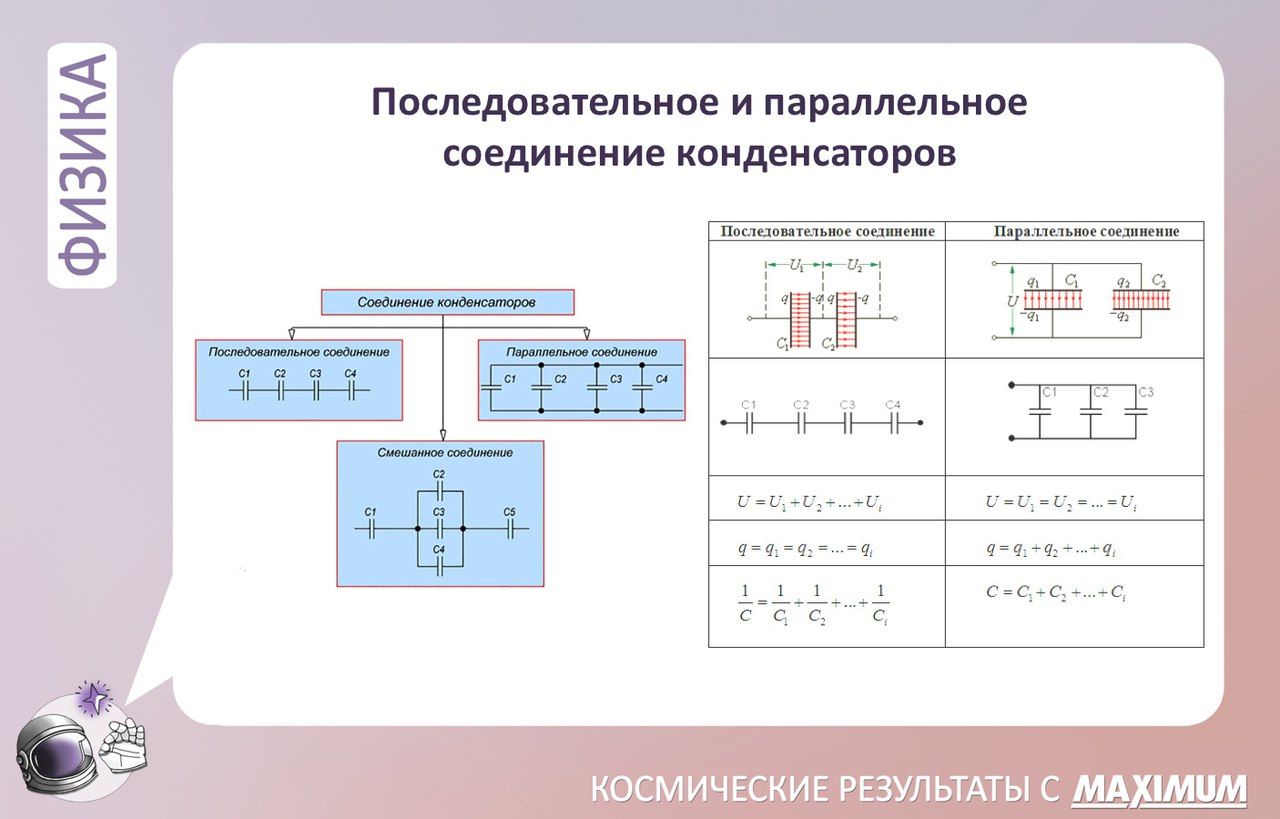

Параллельное соединение конденсаторов

C_общ = C₁ + C₂ + C₃
U_общ = U₁ = U₂ = U₃
q_общ = q₁ + q₂ + q₃

Смешанное соединение конденсаторов

Как нетрудно догадаться из самого названия, этот тип соединения конденсаторов представляет собой ни что иное, как некую комбинацию описанных выше. То есть, смешанное соединение конденсаторов – это сочетание их соединения параллельного и последовательного.

На практике в большинстве случаев оно используется тогда, когда отдельные элементы по таким характеристикам, как емкость и рабочее напряжение, не соответствуют тем параметрам, которые нужны для функционирования электротехнической установки. Когда конденсаторы соединяются между собой именно по такой схеме, то в первую очередь определяются те эквивалентные емкости, которые имеют их параллельные группы, а затем та емкость, которую имеет соединение последовательное.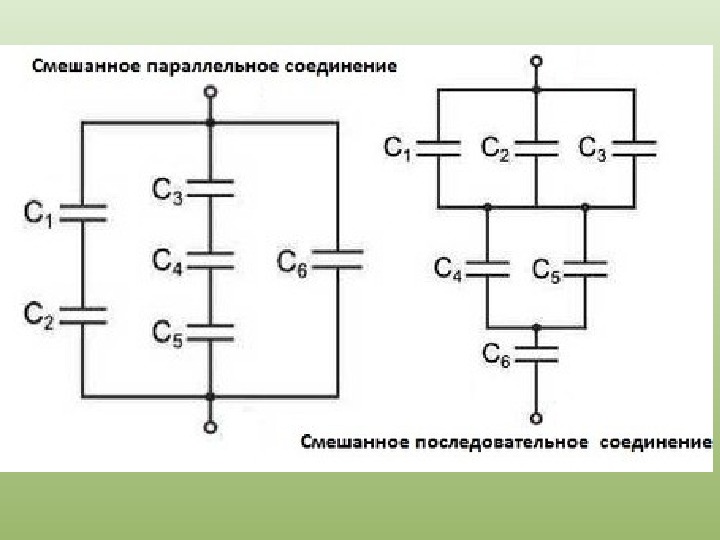

Смешанное соединение конденсаторов

C_2;₃ = C₂ + C₃

C_общ =

C₁ × C_2;₃

C₁ + C_2;₃

Различные виды соединения конденсаторов

Автор Alexey На чтение 4 мин. Просмотров 906 Опубликовано

28.11.2015 Обновлено 10.01.2016

В этой статье мы попытаемся раскрыть тему соединения конденсаторов разными способам. Из статьи про соединения резисторов мы знаем ,что существует последовательное , параллельное и смешанное соединение , это же правило справедливо и для этой статьи. Конденсатор (от лат. слова «condensare» — «уплотнять», «сгущать»)– это очень широко распространённый электрический прибор.

Это два проводника (обкладки), между которыми находится изоляционный материал. Если на него подать напряжение (U), то на его проводниках накопится электрический заряд(Q). Основная его характеристика – ёмкость (C). Свойства конденсатора описываются уравнением Q = UC , заряд на обкладках и напряжение прямо пропорциональны друг другу.

Условное обозначение конденсатора на схеме

Пусть на конденсатор подается переменное напряжение. Он заряжается по мере роста напряжения, электрический заряд на обкладках увеличивается. Если напряжение уменьшается, то уменьшается и заряд на его обкладках и он разряжается.

Отсюда следует, что по проводам, соединяющим конденсатор с остальной цепью, электрический ток протекает тогда, когда напряжение на конденсаторе изменяется. При этом не важно, что происходит в диэлектрике между проводниками . Сила тока равна общему заряду, протекшему в единицу времени по подключенному к конденсатору проводу. Она зависит от его емкости и скорости изменения питающего напряжения.

Ёмкость зависит от характеристик изоляции, а также размеров и формы проводника. Единица измерения ёмкости кондёра — фарада (Ф), 1 Ф=1 Кл/В. Однако на практике емкость измеряется чаще в микро- (10-6) или пико- (10-12) фарадах.

В основном используются конденсаторы для построения цепей с частотной зависимостью, для получения мощного короткого электрического импульса, там, где необходимо накапливать энергию. За счёт изменения свойств пространства между обкладками можно использовать их для измерения уровня жидкости.

Параллельное соединение

Параллельное соединение – это соединение, при котором выводы всех конденсаторов имеют две общие точки – назовём их входом и выходом схемы. Так все входы объединены в одной точке, а все выходы – в другой, напряжения на всех конденсаторах равны:

Параллельное соединение предполагает распределение полученного от источника заряда на обкладках нескольких конденсаторов, что можно записать так:

Так как напряжение на всех конденсаторах одинаковое, заряды на их обкладках зависят только от ёмкости:

Суммарная емкость параллельной группы конденсаторов:

Суммарная ёмкость такой группы конденсаторов равна сумме емкостей включенных в схему.

Блоки конденсаторов широко используются для повышения мощности и устойчивости работы энергосистем в линиях электропередач. При этом затраты на более мощные элементы линий можно снизить. Повышается стабильность работы ЛЭП, устойчивость ЛЭП к сбоям и перегрузкам.

Последовательное соединение

Последовательное соединение конденсаторов – это их подключение непосредственно друг за другом без разветвлений проводника. От источника напряжения заряды поступают на обкладки первого и последнего в цепи конденсаторов.

В силу электростатической индукции на внутренних обкладках смежных конденсаторов происходит выравнивание заряда на электрически соединённых обкладках смежных конденсаторов, поэтому на них появляются равные по величине и обратные по знаку электрические заряды.

При таком соединении электрические заряды на обкладках отдельных кондёров по величине равны:

Общее напряжение для всей цепи:

Очевидно, что напряжение между проводниками для каждого конденсатора зависит от накопленного заряда и ёмкости, т. е.:

Поэтому эквивалентная ёмкость последовательной цепи равна:

Отсюда следует, что величина, обратная общей емкости, равна сумме величин, обратных емкостям отдельных конденсаторов:

https://youtu.be/T4hbcw1o-cw

Смешанное соединение

Смешанным соединение конденсаторов называют такое соединение, при котором присутствует соединение последовательное и параллельное одновременно. Чтобы более подробно разобраться , давайте рассмотрим это соединение на примере :

На рисунке видно ,что соединены два конденсатора последовательно вверху и внизу и два параллельно. Можно вывести формулу из выше описанных соединении:

Основой любой радиотехники является конденсатор, он используется в самых разнообразных схемах-это и источники питания и применение для аналоговых сигналов хранения данных , а также в телекоммуникационных связи для регулирования частоты.

Конденсаторы последовательное калькулятор онлайн. Последовательное соединение конденсаторов. Способы соединения конденсаторов

Содержание:

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .

Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Рис.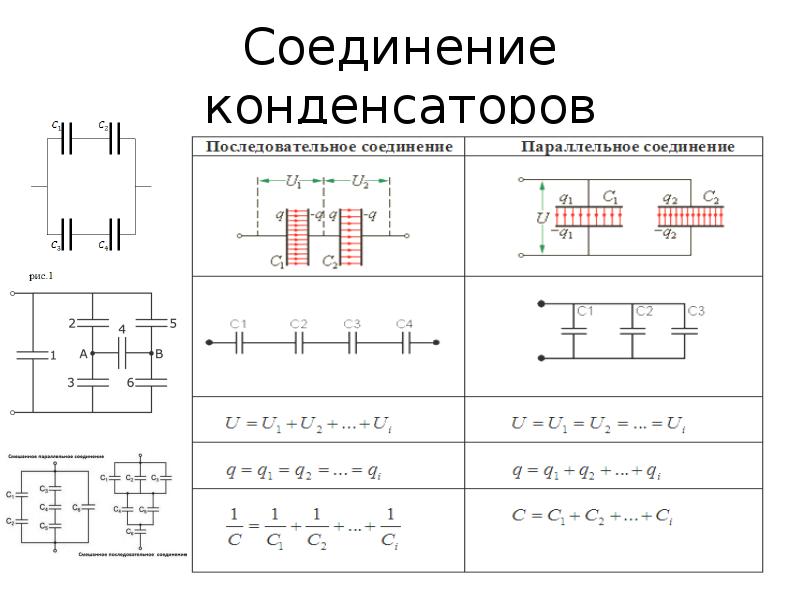 2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6. СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф.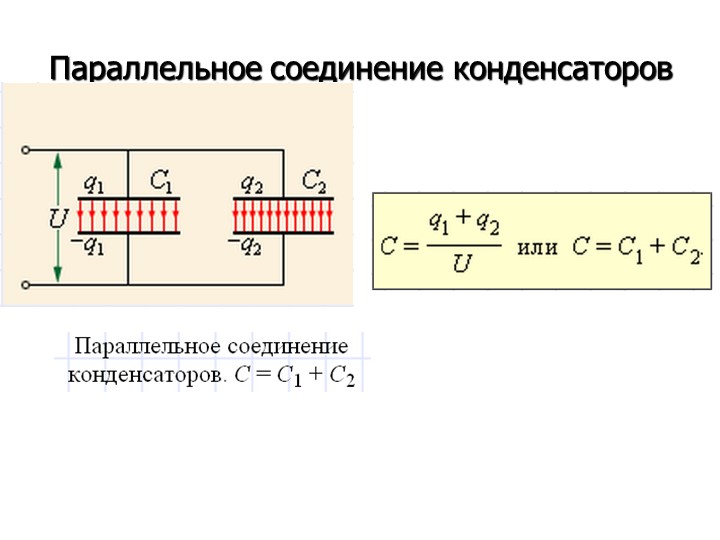 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.

В соответствии со вторым правилом Кирхгофа, падения напряжения V₁ , V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:

По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость C eq всех трех конденсаторов, соединенных последовательно, определяется как

Для группы из n соединенных последовательно конденсаторов эквивалентная емкость C eq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:

Эта формула для C eq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:

Если конденсаторов только два, то их общая емкость определяется по формуле

Если имеется n соединенных последовательно конденсаторов с емкостью C , их эквивалентная емкость равна

Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов .

Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.

Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.

Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.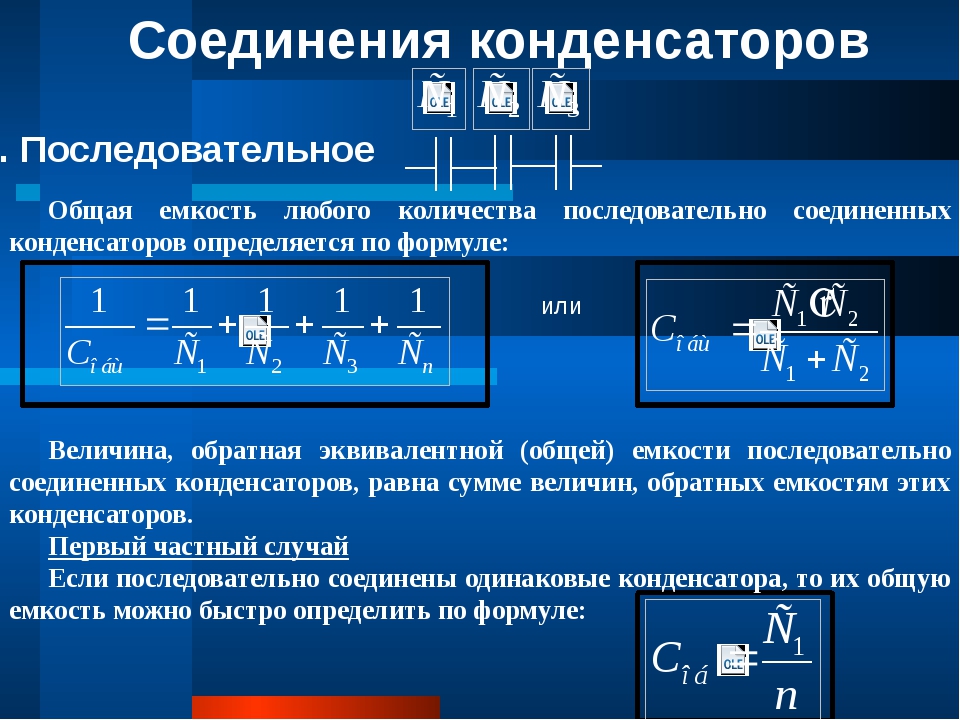

Если несколько конденсаторов соединены параллельно , разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁ , Q₂ and Q₃ тоже будут различными. Общий заряд определяется как

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К 1 =К 2 =К 3 . КЕ — конечная емкость, К — пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ — то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

ОЕ — общая емкость;
Н — напряжение;
КЕ — конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее.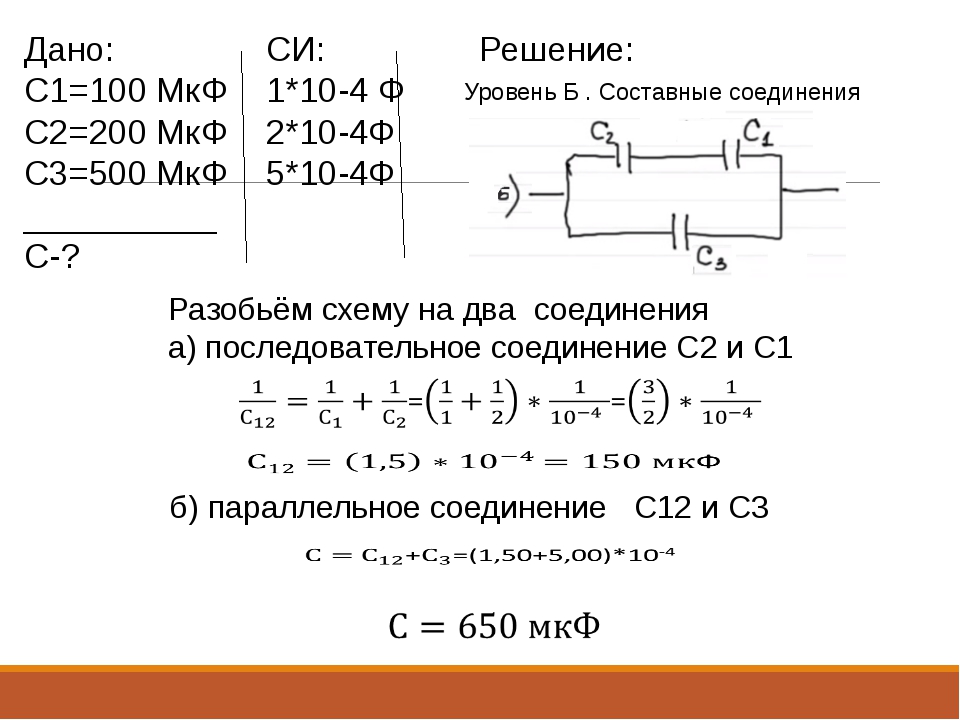 Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними.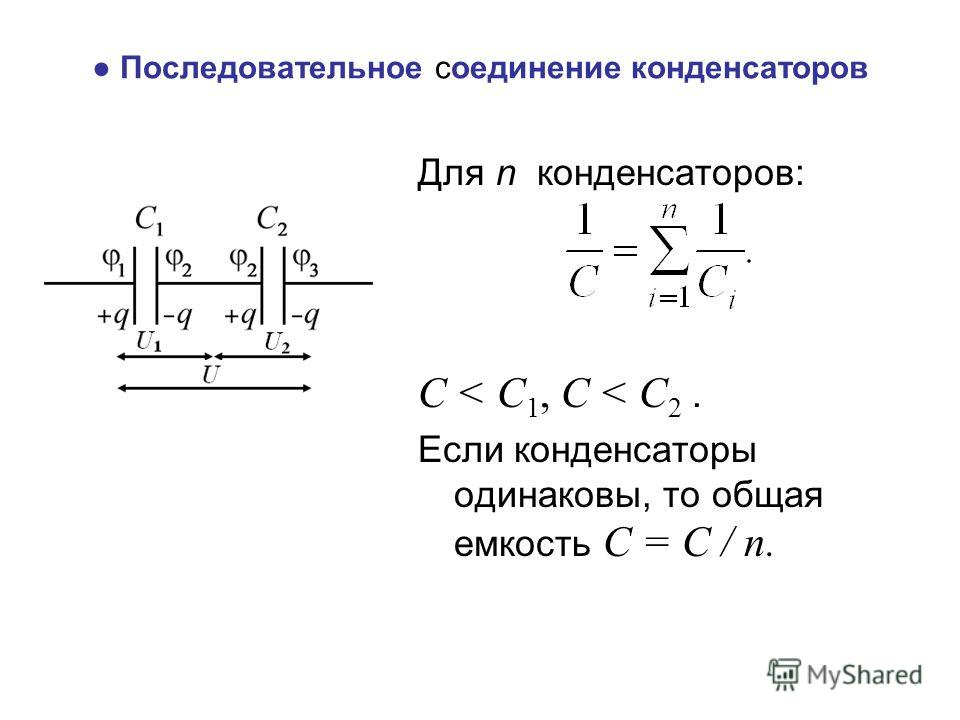 Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

U – напряжение питания схемы;
U1, U2 – падение напряжения на каждом элементе;
С – итоговая емкость схемы;
С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
вторая – С1 = С2 = 400 нФ.

Первый вариант

Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Параллельное и комбинированное соединение

Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:

С = С1 + С2 + С3 + …

Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.

Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.

Особенности замены конденсаторов

К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.

Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.

Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.

Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:

Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.

Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.

Что необходимо учитывать при создании последовательной цепи:

При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.

Включение в последовательную цепь всегда должно происходить с соблюдением «плюса» и «минуса» конденсаторов. Если их соединить одноименными полюсами, то такое сочетание уже теряет поляризованность. При этом емкость созданной группы будет равна половине от емкостного значения одной из деталей. Такие конденсаторы возможно применять в качестве пусковых на электромоторах.

Видео

Способы соединения конденсаторов.

Смешанное включение емкостных накопителей в схему. Схемы замещения элементов электрических цепей

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/1-21-768×410..jpg 260w, https://elquanta.ru/wp-content/uploads/2018/04/1-21.jpg 960w»>

Последовательное соединение конденсаторов

Схема последовательного соединения

q = q1 = q2 = q3 = …

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/2-20-768×476..jpg 120w, https://elquanta.ru/wp-content/uploads/2018/04/2-20.jpg 913w»>

Особенности последовательного соединения

1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
С = 1/27,5 = 0,036 мкФ.

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Png?x15027″ alt=»Емкостной делитель напряжения»>

Емкостной делитель напряжения

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

U – напряжение питания схемы;
U1, U2 – падение напряжения на каждом элементе;
С – итоговая емкость схемы;
С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
вторая – С1 = С2 = 400 нФ.

Первый вариант

Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Параллельное и комбинированное соединение

С = С1 + С2 + С3 + …

Png?.png 600w, https://elquanta.ru/wp-content/uploads/2018/04/4-2-768×350..png 927w»>

Варианты получения эквивалентных схем

Особенности замены конденсаторов

Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.

Что необходимо учитывать при создании последовательной цепи:

При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.

Data-lazy-type=»image» data-src=»http://elquanta.ru/wp-content/uploads/2018/04/5-13-600×259.jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/04/5-13-768×331..jpg 800w»>

Оцените статью:

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .

Смешанное соединение конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С 1 – ёмкость первого;

С 2 – ёмкость второго;

С 3 – ёмкость третьего;

С N – ёмкость N -ого конденсатора;

C общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Могут быть соединены друг с другом различным образом. При этом во всех случаях можно найти емкость некоторого равнозначного конденсатора, который может заменить ряд соединенных между собой конденсаторов.

Для равнозначного конденсатора выполняется условие: если подводимое к обкладкам равнозначного конденсатора напряжение равно напряжению, подводимому к крайним зажимам группы конденсаторов, то равнозначный конденсатор накопит такой же заряд, как и группа конденсаторов.

Параллельное соединение конденсаторов

На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U , Q 2 = C 2U , Q 3 = C 3U , а заряд, полученный от источника Q = Q1 + Q2 + Q3.

Рис. 1. Схема параллельного соединения конденсаторов

Общая емкость равнозначного (эквивалентного) конденсатора:

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3 ,

т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.

Рис. 2. Способы соединения конденсаторов

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q

Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.

Рис. 3. Схема последовательного соединения конденсаторов

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1 , U1 = Q/C 2, U1 = Q/C 3, а общее напряжение U = U1 + U2 + U3

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3 ), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.

Пример 1 . Три конденсатора, емкости которых C1 = 20 мкф, С2 = 25 мкф и С3 = 30 мкф, соединяются последовательно, необходимо определить общую емкость.

Общая емкость определяется из выражения 1/С = 1/С1 + 1/С2 + 1/С3 = 1/20 + 1/25 + 1/30 = 37/300, откуда С = 8,11 мкф.

Пример 2. 100 конденсаторов емкостью каждый 2 мкф соединены параллельно. Определить общую емкость. Общая емкость С = 100 Ск = 200 мкф.

а) параллельно конденсатору большой емкости включать точно такой же конденсатор, но маленькой емкости;

б) вместо одного конденсатора большой емкости включать два-три конденсатора меньшей емкости того же типа;

в) вместо одного конденсатора большой емкости включать много конденсаторов небольшой емкости.

Естественно, включать надо параллельно, при этом емкости суммируются, и общая емкость во всех этих случаях получается одинаковой. Давайте разберемся в данном вопросе (вся необходимая информация есть в таблице 1 и рис. 47).

Вариант а). Говорят, что маленький конденсатор будет помогать работать большому.

Максимальной рабочей частотой конденсатора можно считать ту частоту, на которой его сопротивление минимально. Дальше с ростом частоты полное сопротивление конденсатора начинает расти – это сказывается индуктивность конструкции конденсатора. При этом индуктивное сопротивление перевешивает емкостное, и конденсатор ведет себя как катушка индуктивности. То есть уже и не является конденсатором.

Для конденсатора малой емкости минимум сопротивления действительно наступает на большей частоте, но его сопротивление все равно больше, чем у конденсатора большой емкости (свойства которого на этой частоте уже ухудшаются). А ведь главная задача конденсатора на этих частотах – пропускать через себя ток нагрузки, как можно меньше на него влияя. Поэтому чем у конденсатора сопротивление меньше, тем лучше. И конденсатор малой емкости не очень-то и поможет «большому» конденсатору, слишком уж велико его сопротивление. Только в точке А сопротивления обоих конденсаторов становятся равными, и на более высокой частоте у конденсатора малой емкости сопротивление меньше, чем у «большого». Но посмотрите – в этой точке уже и конденсатор малой емкости работает плохо! В реальности эти графики показаны на рис. 47, где цифрами 1…5 обозначены конденсаторы меньшей емкости, а цифрами 8… 12 – конденсаторы большей емкости.

А вот если в системе присутствует керамический или пленочный конденсатор, то он хорошо работает и на этой частоте, и на более высоких частотах (рис. 48). Только емкость его должна быть достаточно большой,

чтобы на нужных частотах он имел низкое сопротивление.

Вывод: параллельное подключение электролитического конденсатора малой емкости заметной пользы не принесет (хоть и не навредит), гораздо выгоднее шунтирование электролита большой емкости хорошим пленочным конденсатором, который наверняка гораздо более высокочастотный.

Напрашивается вопрос: а для чего же так делают? И даже в промышленной аппаратуре? Ну, во-первых, иногда действительно можно подобрать условия, когда «маленький» конденсатор немного поможет. А главное

– почему бы не поставить такой конденсатор, раз в него верят покупатели? Тем более что он очень дешевый.

Вариант б). Вместо одного конденсатора большой емкости включаем два конденсатора меньшей емкости того же типа. Рассмотрим эту ситуацию для конденсаторов, приведенных в двух последних строках таблицы 1. Допустим, мы ставим два конденсатора 4700 мкФ вместо одного 10000 мкФ. Тогда их сопротивление будет 0,071/2 = 0,0355 Ом, а допустимый ток 3-2=6 ампер. Получается, по ESR примерно то же самое, а по току так даже лучше, чем одиночный конденсатор. Только надо помнить, что у конденсаторов довольно большой разброс, так что можно вместо одного хорошего поставить два плохих. Или наоборот. Более длинные провода, соединяющие два конденсатора, будут иметь большее сопротивление, чем у одиночного. Да и токи заряда конденсаторов будут немного неодинаковыми. В результате это небольшое преимущество от удвоения конденсаторов, скорее всего, будет «съедено» неидеальностью остальных элементов схемы.

Так что в данном случае можно считать эти варианты выбора конденсаторов равноценными. И выбирать тот или иной вариант из каких-либо других соображений. Например, какие конденсаторы поместятся в ваш корпус. Или какие конденсаторы продаются в вашем городе.

Вариант в). Ставим 10 конденсаторов 1000 мкФ вместо одного на 10000 мкФ. Что говорит математика: ESR = 0,199/10 = 0,0199 Ом (по сравнению с 0,033 Ом для конденсатора 10000 мкФ), максимальный ток = 10-1,4= 14А (по сравнению с 5 А конденсатора 10000 мкФ). Вроде бы выигрыш по сопротивлению в 1,5 раза, а по току почти в 3 раза. Судя по полученным цифрам, много конденсаторов лучше, чем один.

Слышали когда-нибудь, как ругают теоретиков, говоря, что на практике получается все совсем не так, как у них в теории? Это про таких горе-теоретиков, которые просто умножат-разделят числа, и не подумают об остальных факторах, влияющих на ситуацию. Посмотрите на рис. 49. Индуктивности и резисторы – это сопротивление и индуктивность проводников, соединяющих всю эту кучу конденсаторов. Поскольку конденсаторов теперь много, то длина проводов существенно увеличивается, растут и индуктивности-сопротивления. Вот тут-то и теряются все преимущества, которые мы насчитали по формулам! Нет, формулы правильные! Только они не учитывают эти вот элементы – ведь мы написали эти формулы без их учета, не подумав про них.

В результате общее сопротивление может получиться даже больше, чем у одиночного конденсатора боль-

шой емкости, а ток распределяется очень неравномерно. Например, при заряде конденсаторов, заряд начинается с самого левого по схеме С1, и в него в самый первый момент времени течет весь максимальный ток (в С2 ток потечет только после того, как С1 уже немного зарядится), а конденсатор-то рассчитан всего на 1,4 ампера! Поэтому может случиться, что этот конденсатор будет перегружаться зарядным током, а значит, долго не проживет. Точно также, разряжается первым самый правый конденсатор СЮ, и он будет перегружаться разрядным током.

В общем, все преимущества обычно получаются только на бумаге. Это как раз та ситуация, когда «слишком хорошо – тоже не хорошо». Все всегда должно быть в разумных пределах, а здесь мы из них вышли. Собственно, «много маленьких» конденсаторов не всегда будет хуже, чем «один большой», но далеко и не всегда будет лучше. Хороший профессионал сможет извлечь пользу из такого включения (когда оно оправданно), а новичок скорее всего все испортит.

На самом деле, есть случай, когда параллельное включение двух-трех конденсаторов принесет пользу. Например, когда конденсатор фильтра установлен возле горячего диода и не удается его отодвинуть. Тогда при нескольких конденсаторов греться будет только один из них.

И еще. При любом наборе электролитов, подключение пленочного конденсатора только приветствуется.

Последовательное и параллельное соединение конденсаторов

На практике часто используются тела, обладающие малыми (и очень малыми) размерами, которые могут накопить большой заряд, при этом имея небольшой потенциал. Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость. Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения. Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).

Последовательное соединение конденсаторов

Последовательное соединение из конденсаторов изображено на рис. 1

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:

где – электрическая емкость i-го конденсатора.

Если емкости конденсаторов при последовательном соединении равны , то емкость последовательного их соединения составляет:

где N – количество последовательно соединенных конденсаторов. При этом предельное напряжение (U), которое выдержит подобная батарея конденсаторов составит:

где – предельное напряжение каждого конденсатора соединения. При последовательном соединении конденсаторов следует следить за тем, чтобы ни на один из конденсаторов батареи не падало напряжение, превышающее его максимальное рабочее напряжение.

Параллельное соединение конденсаторов

Параллельное соединение N конденсаторов изображено на рис. 2.

При параллельном соединении конденсаторов соединяют обкладки, обладающие зарядами одного знака (плюс с плюсом; минус с минусом). В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например, , а другая . Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.

При параллельном соединении конденсаторов суммарная емкость соединения рассчитывается как сумма емкостей отдельных конденсаторов:

При параллельном соединении конденсаторов напряжение равно самой наименьшей величине рабочего напряжения конденсатора из состава рассматриваемого соединения.

Примеры решения задач

Формула подключения конденсатора. Последовательное соединение конденсаторов: формула

В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов в зависимости от потребностей схемы. Давайте их рассмотрим.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов подключены к точкам переключения и образуют батарею.В этом случае во время зарядки конденсаторов каждый из них будет иметь разное количество электрических зарядов с одинаковым количеством подводимой энергии.

Схема параллельной установки

Емкость при параллельной установке рассчитывается на основе емкостей всех конденсаторов в цепи. В этом случае количество электрической энергии, подаваемой на все отдельные двухполюсные элементы схемы, можно рассчитать путем суммирования количества энергии, помещенной в каждый конденсатор. Вся подключенная таким образом цепь рассчитывается как одна двухполюсная.

C всего = C 1 + C 2 + C 3

Схема — накопительное напряжение

В отличие от соединения звездой, на пластины всех конденсаторов подается одинаковое напряжение. Например, на диаграмме выше мы видим, что:

В AB = V C1 = V C2 = V C3 = 20 Вольт

Последовательное соединение

Здесь к точкам включения подключены только контакты первого и последнего конденсатора.

Схема
— Схема последовательного подключения

Основной особенностью схемы является то, что электрическая энергия будет проходить только в одном направлении, а это означает, что ток в каждом из конденсаторов будет одинаковым.В такой схеме для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Следует понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость с последовательным типом может воспроизводиться энергией соседнего накопителя.

Формула, отражающая зависимость тока от подключения конденсаторов, выглядит так:

i = i c 1 = i c 2 = i c 3 = i c 4, то есть токи, проходящие через каждый конденсатор, равны друг другу.

Следовательно, будет такой же не только сила тока, но и электрический заряд. Согласно формуле это определяется как:

Q итого = Q 1 = Q 2 = Q 3

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

1 / C всего = 1 / C 1 + 1 / C 2 + 1 / C 3

Видео: как подключить конденсаторы параллельно и последовательно

Смешанное соединение

Но, следует учитывать, что для подключения различных конденсаторов необходимо учитывать сетевое напряжение.Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых биполей малой емкости будут становиться больше при зарядке, и наоборот, большая электрическая емкость потребует меньшего заряда.

Схема: смешанное соединение конденсаторов

Также существует смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно путем параллельного и последовательного включения электролитических ячеек в цепь.Этот контур имеет несколько участков с разными подключениями конденсационных двухполюсников. Другими словами, на одной цепи цепь включена параллельно, на другой — последовательно. Такая электрическая схема имеет ряд преимуществ по сравнению с традиционными:

Может использоваться для любых целей: подключение электродвигателя, станков, радиоаппаратуры;
Простой расчет. Для монтажа вся схема разбивается на отдельные участки схемы, которые рассчитываются отдельно;
Свойства компонентов не меняются независимо от изменения электромагнитного поля и силы тока.Это очень важно при работе с противоположными двухтерминальными сетями. Емкость постоянна при постоянном напряжении, но в то же время потенциал пропорционален заряду;
Если нужно собрать несколько неполярных полупроводниковых двухполюсных сетей из полярных, то нужно взять несколько однополюсных двухполюсных сетей и соединить их антипараллельно (в треугольник). Минус к минусу, плюс к плюсу. Таким образом, при увеличении емкости меняется принцип работы биполярного полупроводника.

Содержание:

Цепи в электротехнике состоят из электрических элементов, в которых способы подключения конденсаторов могут быть разными. Нужно понимать, как правильно подключить конденсатор. Отдельные участки схемы с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит некоторое количество конденсаторов, но должно быть выполнено условие: когда напряжение, подаваемое на пластины эквивалентного конденсатора, равно напряжению на входе и выходе группы заменяемых конденсаторов, тогда заряд емкости будет равен то же, что и на группе конденсаторов.Чтобы разобраться в вопросе, как подключить конденсатор в любую схему, рассмотрим виды его включения.

Параллельное соединение конденсаторов в цепи

Параллельное соединение конденсаторов — это когда все пластины соединены с точками переключения схемы, образуя батарею конденсаторов.

Разность потенциалов на пластинах емкостных аккумуляторов будет одинаковой, поскольку все они заряжаются от одного источника тока. В этом случае каждый зарядный конденсатор имеет свой заряд с одинаковым количеством энергии, подаваемой на них.

Параллельные конденсаторы, общий параметр количества заряда полученной аккумуляторной батареи, рассчитывается как сумма всех зарядов, размещенных на каждом конденсаторе, потому что каждый заряд конденсатора не зависит от заряда другого конденсатора, включенного в группа конденсаторов, включенных параллельно в цепь.

При параллельном подключении конденсаторов емкость составляет:

Из представленной формулы можно сделать вывод, что всю группу приводов можно рассматривать как один эквивалентный конденсатор.

Параллельно подключенные конденсаторы имеют напряжение:

Последовательное соединение конденсаторов в цепи

При последовательном соединении конденсаторов в цепи это выглядит как цепочка емкостного накопителя, где пластина первого и последнего накопителя конденсатора (конденсатора) подключена к Источник тока.

Последовательное соединение конденсатора:

Когда конденсаторы соединены последовательно, все устройства в этой секции потребляют одинаковое количество электроэнергии, потому что первая и последняя пластинки накопителя участвуют в процессе, а пластины 2, 3 и другие до N заряжаются посредством воздействия. .По этой причине заряд пластины 2 накопительной емкости по величине равен заряду пластины 1, но имеет противоположный знак. Заряд накопительной пластины 3 равен величине заряда пластины 2, но также с противоположным знаком все последующие накопительные устройства имеют аналогичную систему зарядки.

Формула для нахождения заряда конденсатора, схема подключения конденсатора:

Когда конденсаторы соединены последовательно, напряжение на каждом накопителе конденсатора будет разным, поскольку разные емкости участвуют в зарядке с одинаковым количеством электроэнергии.Зависимость емкости от напряжения следующая: чем она меньше, тем большее напряжение необходимо приложить к пластинам накопителя для его зарядки. И обратное: чем больше емкость накопителя, тем меньше напряжения требуется для его зарядки. Можно сделать вывод, что емкость последовательно соединенных запоминающих устройств важна для напряжения на пластинах — чем она ниже, тем больше требуется напряжения, а также запоминающие устройства большой емкости требуют меньшего напряжения.

Основное отличие последовательного подключения емкостных аккумуляторов состоит в том, что электроэнергия течет только в одном направлении, а это значит, что в каждом емкостном аккумуляторе составной батареи ток будет одинаковым.При таком типе подключения конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителя.

Группа емкостных накопителей также может рассматриваться на схеме как эквивалентное запоминающее устройство, на пластины которого подается напряжение, определяемое по формуле:

Заряд общего (эквивалентного) запоминающего устройства последовательной емкостной накопительной группы равен:

Суммарное значение емкости последовательно соединенных конденсаторов соответствует выражению:

Смешанное включение емкостного накопителя в схему

Параллельное и последовательное включение конденсаторов на одном из участков схемы схемы специалисты называют смешанным соединением.

Участок цепи емкостных аккумуляторов, включенных смешанной коммутацией:

Смешанное включение конденсаторов в цепи рассчитывается в определенном порядке, который можно представить следующим образом:

схема разбита на легко вычисляемые участки, это последовательное и параллельное соединение конденсаторов;
рассчитываем эквивалентную емкость для группы конденсаторов, включенных последовательно на участке параллельного включения;
находим эквивалентную мощность в параллельном участке;
при определении эквивалентных мощностей приводов рекомендуется перерисовать схему;
рассчитана емкость эквивалентных аккумуляторов электрической энергии, полученная после последовательного включения.

Емкостные аккумуляторы (двухполюсные устройства) включают в схему по-разному, что дает ряд преимуществ при решении электрических задач по сравнению с традиционными способами переключения конденсаторов:

Использование для подключения электродвигателей и другого оборудования в мастерские, в радиотехнических приборах.
Упрощение расчета значений электрической схемы. Монтаж осуществляется отдельными участками.
Технические свойства всех элементов не меняются при изменении силы тока и магнитного поля, это используется для включения различных запоминающих устройств. Он характеризуется постоянным значением емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Различные типы подключения конденсаторов к схеме используются для решения электрических задач, в частности, для получения полярных накопителей от нескольких неполярных двухполюсных устройств.В этом случае решением будет соединение группы однополюсных накопителей емкости антипараллельным способом (треугольник). В этой схеме минус соединен с минусом, а плюс соединен с плюсом. Емкость хранилища увеличивается, и работа двухпортовой сети изменяется.

Доступные записи не отображаются: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов, емкость.

Фиг.2 U = U 1 = U 2 = U 3

Суммарный заряд Q все конденсаторы

Общая емкость C, или емкость батареи, конденсаторов, подключенных параллельно, равна сумме емкостей этих конденсаторов.

Подключение конденсатора параллельно группе других подключенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Поэтому для увеличения емкости используется параллельное соединение конденсаторов.

4) При параллельном подключении T идентичных конденсаторов емкостью C´ каждый, то общую (эквивалентную) емкость батареи этих конденсаторов можно определить по выражению

Последовательное соединение конденсаторов

Рис. 3

На пластинах последовательно соединенных конденсаторов, подключенных к источнику постоянного тока напряжением U , Появится зарядов одинаковой величины с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкости конденсаторов:

Обратная величина полной емкости последовательно соединенных конденсаторов равна сумме обратной величины емкостей этих конденсаторов.

Когда два конденсатора соединены последовательно, их общая емкость определяется следующим выражением:

Если цепь соединена последовательно NS идентичных конденсаторов емкостью СО каждый, то общая емкость этих конденсаторы:

Из (14) видно, что чем больше конденсаторов НС соединено последовательно, тем меньше их общая емкость будет СО, то есть последовательное соединение конденсаторов приводит к уменьшению общая емкость конденсаторной батареи.

На практике может оказаться, что допустимое рабочее напряжение U p конденсатор меньше напряжения, к которому конденсатор должен быть подключен. Если этот конденсатор подключить к такому напряжению, то он выйдет из строя, так как диэлектрик выйдет из строя. Если же несколько конденсаторов соединены последовательно, то напряжение будет распределяться между ними и на каждом конденсаторе напряжение будет меньше его допустимого рабочего U p . Следовательно, используется последовательное соединение конденсаторов , чтобы напряжение на каждом конденсаторе не превышало его рабочее напряжение U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) конденсаторов используется, когда необходимо увеличить емкость и рабочее напряжение конденсаторной батареи.

Рассмотрим смешанное подключение конденсаторов в приведенных ниже примерах.

Энергия конденсатора

где Q — заряд конденсатора или конденсаторов, на которые подается напряжение U ; С — электрическая емкость конденсатора или батареи подключенных конденсаторов, на которую подается напряжение U .

Таким образом, конденсаторы служат для накопления и хранения электрического поля и его энергии.

15. Дайте определение понятий трехлучевая звезда и треугольник сопротивления. Запишите формулы преобразования трехлучевой звезды сопротивления в треугольник сопротивлений и наоборот. Преобразуйте схему в два узла (Рисунок 5)

Рисунок 5- Электрическая схема

6 СХЕМ ЗАМЕНЫ

Для облегчения расчетов для электрической цепи составлена эквивалентная схема, то есть схема, которая отображает свойства цепи при определенных условиях.

Эквивалентная схема изображает все элементы, влиянием которых на результат расчета нельзя пренебречь, а также указывает электрические связи между ними, находящиеся в схеме.

1.Схемы замены элементов электрических схем

На конструктивных схемах источником энергии может быть ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13) .6).

При r = 0 внутреннее падение напряжения Uо = 0, поэтому

напряжение на выводах источника при любом токе равно

ЭДС: U = E = конст.

В некоторых случаях источник электроэнергии на проектной схеме заменяется другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДС E источник характеризуется своим током короткого замыкания. IK, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимость г = 1 / r .

Возможность такой замены доказывается разделением равенства (3.1) по тел .:

U / р знак равно E / г — Я ,

где U / р знак равно Io — некоторый ток, равный отношению напряжения на выводах источника к внутреннему сопротивлению; E / р знак равно I К — ток короткого замыкания источника;

Вводя новые обозначения, получаем равенство I K знак равно Io + Я , , которому удовлетворяет эквивалентная схема на рис.3.14, а.

В данном случае при любом напряжении на выводах; источника, его ток остается равным току короткого замыкания (рис. 3.14.6):

Источник с постоянным током, не зависящим от внешнего сопротивления, называется источником тока.

Этот же источник электроэнергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Под последовательным соединением мы понимаем случаи, когда два или более элемента образуют цепочку, при этом каждый из них соединяется с другим только в одной точке.Почему конденсаторы так размещены? Как это правильно делать? Что вы должны знать? Какие особенности имеет на практике последовательное соединение конденсаторов? Какая формула результата?

Что нужно знать для правильного подключения?

Увы, здесь не все так просто, как может показаться. Многие новички думают, что если на схеме написано, что нужен элемент на 49 микрофарад, то достаточно просто взять и установить (или заменить на аналог).Но даже в профессиональной мастерской сложно подобрать нужные параметры. А что делать, если необходимых предметов нет? Допустим, есть такая ситуация: нужен конденсатор на 100 мкФ, а их несколько по 47. Ставить не всегда получается. Сходить на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Есть два основных способа: последовательное и параллельное соединение конденсаторов. Поговорим о первом. Но если говорить о последовательном соединении катушки и конденсатора, то особых проблем нет.

Почему они это делают?

При проведении с ними таких манипуляций электрические заряды на пластинах отдельных элементов будут равны: KE = K 1 = K 2 = K 3. KE — конечная емкость, K — пропущенное значение. конденсатора. Это почему? Когда заряды подводятся от источника питания к внешним пластинам, то передача значения, являющегося значением элемента с наименьшими параметрами, может осуществляться на внутренних пластинах.То есть, если вы возьмете конденсатор на 3 мкФ, а затем подключите его к 1 мкФ, то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение 3 мкФ. Но второй элемент так сильно пропустить не сможет, и отрежет все, что больше требуемого значения, оставив большую емкость на исходном конденсаторе. Давайте посмотрим, на что нужно рассчитывать при последовательном соединении конденсаторов. Формула:

OE — общая мощность;
H — напряжение;
KE — конечная мощность.

Что еще нужно знать, чтобы правильно подключить конденсаторы?

Для начала не забываем, что помимо емкости у них есть еще и номинальное напряжение. Почему? При последовательном подключении напряжение распределяется обратно пропорционально их емкости между ними. Поэтому такой подход имеет смысл использовать только в тех случаях, когда любой конденсатор может обеспечить минимально необходимые рабочие параметры. Если используются элементы одинаковой емкости, то напряжение между ними будет делиться поровну.Также небольшая осторожность в отношении электролитических конденсаторов: при обращении с ними всегда внимательно проверяйте их полярность. Ведь если этот фактор не учитывать, последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если все ограничится только разбивкой этих элементов. Помните, что конденсаторы накапливают ток, и если что-то пойдет не так, в зависимости от схемы, может возникнуть прецедент, в результате которого выйдут из строя другие компоненты схемы.

Последовательный ток

Из-за того, что он имеет только один возможный путь потока, он будет иметь одинаковое значение для всех конденсаторов.Причем сумма накопленного заряда везде одинакова. Это не зависит от емкости. Посмотрите на любую схему последовательного подключения конденсаторов. Правая пластина первого соединяется с левой частью второго и так далее. Если используется более 1 элемента, то некоторые из них будут изолированы от общей цепи. Таким образом, эффективная площадь пластин становится меньше и равна параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор заполняется электрическим зарядом, он перестает пропускать ток.И тогда он не может течь по всей цепочке. В этом случае остальные конденсаторы также не смогут зарядиться.

Падение напряжения и общая емкость

Каждый элемент постепенно рассеивает напряжение. Учитывая, что емкость обратно пропорциональна ей, чем она меньше, тем больше будет падение. Как упоминалось ранее, конденсаторы, соединенные последовательно, имеют одинаковый электрический заряд. Следовательно, разделив все выражения на общее значение, можно получить уравнение, которое покажет всю емкость.В этом последовательное и параллельное соединение конденсаторов сильно различаются.

№ примера 1

Воспользуемся формулами, представленными в статье, и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость: C1 = 25 мкФ, C2 = 30 мкФ и C3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую вместимость. Воспользуемся соответствующим уравнением 1 / C: 1 / C1 + 1 / C2 + 1 / C3 = 1/25 + 1/30 + 1/20 = 37/300. Переведем в микрофарады, и общая емкость конденсатора при последовательном включении (а группа в данном случае рассматривается как один элемент) примерно 8.11 мкФ.

Пример №2

Решим еще одну задачу для консолидации нашей работы. Есть 100 конденсаторов. Емкость каждого элемента 2 мкФ. Необходимо определить их общую вместимость. Необходимо их количество умножить на характеристику: 100 * 2 = 200 мкФ. Итак, общая емкость конденсатора при последовательном включении составляет 200 мкФ. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, проанализировали формулы и особенности правильного подключения конденсаторов (последовательно) и даже решили несколько задач.Напоминаю читателям, что нельзя упускать из виду влияние номинального напряжения. Также желательно подбирать однотипные элементы (слюдяные, керамические, металлобумажные, пленочные). Тогда наибольший положительный эффект может дать последовательное соединение конденсаторов.

У многих радиолюбителей, особенно начинающих конструировать электрические схемы, возникает вопрос, как подключить конденсатор необходимой емкости? Когда, например, в каком-то месте схемы нужен конденсатор емкостью 470 мкФ, и такой элемент есть, то проблем не будет.Но когда нужно поставить конденсатор на 1000 мкФ, а есть только элементы несоответствующей емкости, на помощь приходят схемы из нескольких конденсаторов, соединенных вместе. Элементы могут быть соединены путем параллельного и последовательного подключения конденсаторов по отдельности или по комбинированному принципу.

Jpg? .Jpg 600 Вт, https://elquanta.ru/wp-content/uploads/2018/04/1-21-768×410..jpg 260 Вт, https://elquanta.ru/wp-content/uploads/2018/ 04 / 1-21.jpg 960w «sizes =» (max-width: 600px) 100vw, 600px «>

Последовательное соединение конденсаторов

Схема последовательного соединения

Когда применяется последовательная цепь конденсаторов, заряд каждой части эквивалентен .К источнику подключаются только внешние пластины, остальные заряжаются за счет перераспределения электрических зарядов между ними. Все конденсаторы сохраняют на своих пластинах одинаковый заряд. Это связано с тем, что каждый последующий элемент получает заряд от соседнего. Как следствие, справедливо следующее уравнение:

q = q1 = q2 = q3 =…

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора учитывается. в такой электрической схеме рассчитывается иначе.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. При наличии трех конденсаторных элементов в последовательной электрической цепи составляется выражение для напряжения U по закону Кирхгофа:

U = U1 + U2 + U3,

при этом U = q / C, U1 = q / C1, U2 = q / C2, U3 = q / C3.

Подставляя значения напряжений в обе части уравнения, получается:

q / C = q / C1 + q / C2 + q / C3.

Поскольку электрический заряд q является одной и той же величиной, все части полученного выражения можно разделить на него.

Полученная формула для емкостей конденсаторов:

1 / C = 1 / C1 + 1 / C2 + 1 / C3.

Важно! Если конденсаторы подключены в последовательную цепь, величина, обратная величине результирующей емкости, равна совокупности обратных значений единичных емкостей.

Jpg? .Jpg 600 Вт, https://elquanta.ru/wp-content/uploads/2018/04/2-20-768×476..jpg 120w, https://elquanta.ru/wp-content/uploads/2018/ 04 / 2-20.jpg 913w «sizes =» (max-width: 600px) 100vw, 600px «>

Функции последовательного подключения

Пример. Три конденсаторных элемента соединены последовательно и имеют емкости: C1 = 0,05 мкФ, C2 = 0,2 мкФ, C3 = 0,4 мкФ. Рассчитайте общее значение емкости:

1 / C = 1 / 0,05 + 1 / 0,2 + 1 / 0,4 = 27,5;
C = 1 / 27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы соединены последовательно, общая величина емкости не превышает наименьшую емкость отдельного элемента.

Если цепочка состоит только из двух компонентов, формула переписывается следующим образом:

C = (C1 x C2) / (C1 + C2).

В случае создания цепи из двух конденсаторов с одинаковым значением емкости:

C = (C x C) / (2 x C) = C / 2.

Последовательно соединенные конденсаторы имеют реактивное сопротивление, зависящее от от частоты протекающего тока. На каждом конденсаторе падает напряжение из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Png? X15027 «alt =» (! LANG: Емкостной делитель напряжения «>!}

Емкостной делитель напряжения

Формула для емкостного делителя напряжения:

U1 = U x C / C1, U2 = U x C / C2, где :

U — напряжение питания цепи;
U1, U2 — падение напряжения на каждом элементе;
C — полная емкость цепи;
C1, C2 — емкостные индикаторы отдельных элементов.

Расчет падений напряжения на конденсаторах

Например, есть сеть 12 В переменного тока и две альтернативные схемы для подключения последовательных конденсаторных элементов:

первая предназначена для подключения одного конденсатора C1 = 0.1 мкФ, еще C2 = 0,5 мкФ;
второй — C1 = C2 = 400 нФ.

Первый вариант

Суммарная емкость электрической цепи C = (C1 x C2) / (C1 + C2) = 0,1 x 0,5 / (0,1 + 0,5) = 0,083 мкФ;
Падение напряжения на одном конденсаторе: U1 = U x C / C1 = 12 x 0,083 / 0,1 = 9,9 В
На втором конденсаторе: U2 = U x C / C2 = 12 x 0,083 / 0,5 = 1,992 В.

Второй вариант

Результирующая емкость C = 400 x 400 / (400 + 400) = 200 нФ;
Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

По расчетам можно сделать вывод, что если подключены конденсаторы одинаковой емкости, то напряжение делится поровну на обоих элементах, а при разнице емкостных значений напряжение возрастает на конденсаторе с меньшим емкостным значением , наоборот.

Параллельное и комбинированное соединение

Параллельное соединение конденсаторов представлено другим уравнением. Для определения общего емкостного значения вам просто нужно найти набор всех значений по отдельности:

C = C1 + C2 + C3 +…

На каждый элемент будет подаваться одинаковое напряжение. Поэтому для усиления емкости несколько деталей необходимо соединить параллельно.

Если соединения смешанные, последовательно-параллельные, то эквивалентные или упрощенные электрические цепи используются для таких цепей. Каждая область схемы рассчитывается отдельно, а затем, представляя их с рассчитанными емкостями, объединяется в простую схему.

Png? .Png 600w, https://elquanta.ru/wp-content/uploads/2018/04/4-2-768×350..png 927w «sizes =» (max-width: 600px) 100vw, 600px «>

Варианты получения эквивалентных схем

Особенности замены конденсаторов

Например, есть питание от сети 12 В переменного тока и две альтернативные группы конденсаторные элементы включены последовательно.

Конденсаторы подключаются последовательно для увеличения напряжения, при котором они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.

Смешанное соединение конденсаторов часто используется для создания желаемой емкости значение и увеличьте напряжение, которое могут выдержать детали.

Вы можете дать вариант, как соединить несколько компонентов для достижения желаемых параметров. Если требуется конденсаторный элемент 80 мкФ при 50 В, но есть только 40 мкФ при 25 В, должна быть сформирована следующая комбинация:

Подключите два конденсатора 40 мкФ / 25 В последовательно, чтобы в сумме получить 20 мкФ / 50 В;
Теперь в игру вступает параллельное соединение конденсаторов. Пара последовательно соединенных групп конденсаторов, созданная на первом этапе, соединенных параллельно, получается 40 мкФ / 50 В;
Соединяем две собранные в итоге группы параллельно, в итоге получаем 80 мкФ / 50 В.

Важно! Для усиления конденсаторов напряжения их можно объединить в последовательную электрическую цепь. Увеличение общего емкостного значения достигается за счет параллельного включения.

Что следует учитывать при создании гирляндной цепи:

При подключении конденсаторов лучше всего брать элементы с немного разными или с одинаковыми параметрами из-за большой разницы в напряжениях разряда;
Для уравновешивания токов утечки к каждому конденсаторному элементу (параллельно) подключен уравнительный резистор.

Data-lazy-type = «image» data-src = «http://elquanta.ru/wp-content/uploads/2018/04/5-13-600×259.jpg?.jpg 600w, https: // elquanta. ru / wp-content / uploads / 2018/04 / 5-13-768×331..jpg 800w «sizes =» (max-width: 600px) 100vw, 600px «>

Оцените статью:

КОНДЕНСАТОРЫ И ДИЭЛЕКТРИКИ

Конденсатор — это набор проводников, который используется для хранения электрического плата.Очень простой конденсатор представляет собой изолированный металлический шар. Потенциал шара радиусом R и зарядом Q равно

(27,1)

Уравнение (27.1) показывает, что потенциал сферы пропорционален зарядить Q на проводнике. В целом это верно для любой конфигурации проводники. Это отношение можно записать как

(27,2)

где C называется емкостью системы проводников.Единица измерения емкости — фарад (Ф). Емкость металлический шар равен

(27,3)

Другой пример конденсатора — система, состоящая из двух параллельных металлических тарелки. В главе 26 было показано, что разность потенциалов между двумя пластины области A, расстояние разделения d, и с зарядами + Q и -Q, задается по

(27.4)

Используя определение емкости (уравнение (27.2)), емкость этого в системе можно рассчитать:

(27,5)

Уравнение (27.2) показывает, что заряд конденсатора пропорционален емкости C и потенциалу V. Для увеличения количества хранимого заряда на конденсаторе, сохраняя постоянный потенциал (напряжение), емкость конденсатор нужно будет увеличить. Поскольку емкость параллельного пластинчатый конденсатор пропорционален площади пластины А и обратно пропорционален на расстояние d между пластинами, этого можно добиться, увеличив площадь поверхности A и / или уменьшение разделительного расстояния d.Эти большие конденсаторы обычно изготавливаются из двух параллельных листов алюминизированной фольги, несколько дюймов в ширину и несколько метров в длину. Листы располагаются очень близко вместе, но удерживаемый от соприкосновения тонким листом пластика, зажатым между их. Весь бутерброд накрывают еще одним листом пластика и скручивают. вверх, как рулон туалетной бумаги.

Пример: Задача 27.7

Трубка счетчика Гейгера состоит из тонкой прямой проволоки. окружен коаксиальной проводящей оболочкой.Диаметр проволоки 0,0025 см, оболочка — 2,5 см. Длина трубки 10 см. Что такое емкость трубки счетчика Гейгера?
Рисунок 27.1. Схема счетчика Гейгера.
Задача будет решена в предположении, что электрическое поле генерируется бесконечно длинной линией заряда. Схематический вид сбоку трубы показан на рисунке 27.1. Радиус проволоки r _w, радиус цилиндра r _c, длина счетчика L, а заряд на проводе + Q.Электрическое поле в области между проволоку и цилиндр можно рассчитать по закону Гаусса. Электрическое поле в этой области будет иметь радиальное направление и его величина будет зависеть только от на радиальном расстоянии r. Рассмотрим цилиндр длиной L и радиусом r показано на рисунке 27.1. Электрический поток [фи] через поверхность этого цилиндр равен
(27,6)
Согласно закону Гаусса, поток [Phi] равен вложенному заряду, разделенному Автор [epsilon] ₀.Следовательно,
(27,7)
Электрическое поле E (r) можно получить с помощью уравнения (27.7):
(27,8)
Разность потенциалов между проводом и цилиндром может быть получена следующим образом: интегрируя электрическое поле E (r):
(27,9)
Используя уравнение (27.2), можно рассчитать емкость трубки Гейгера:
(27.10)
Подставляя значения для r _w, r _c и L в ур.(27.10) получаем
(27.11)

Символ конденсатора показан на рисунке 27.2. Конденсаторы могут быть соединены вместе; они могут быть подключены последовательно или параллельно. Фигура 27.3 показаны два конденсатора с емкостью C ₁ и C ₂, подключены параллельно. Разность потенциалов на обоих конденсаторах должна быть равно и, следовательно,
(27.12)
Рисунок 27.2. Символ конденсатора. Рисунок 27.3. Два конденсатора подключены параллельно.
Используя уравнение (27.12), можно рассчитать общий заряд обоих конденсаторов
(27,13)
Уравнение (27.13) показывает, что полный заряд конденсаторной системы, показанной на Рисунок 27.3 пропорционален разности потенциалов в системе. В два конденсатора на рисунке 27.3 можно рассматривать как один конденсатор с емкость C, где C относится к C ₁ и C ₂ в следующим образом
(27.14)
На рисунке 27.4 показаны два конденсатора емкостью C ₁ и C ₂, соединены последовательно. Предположим, что разность потенциалов на C ₁ составляет [Delta] V ₁, а разность потенциалов на C ₂ представляет собой [Delta] V ₂. Заряд Q на верхней пластине вызовет заряд -Q на нижней пластине C ₁. Поскольку электрический заряд сохраняется, заряд на верхней пластине C ₂ должен быть равен Q.Таким образом, заряд на нижней пластине C ₂ равен -Q. В разность напряжений на C ₁ определяется как
(27.15)
а разница напряжений на C ₂ равна
(27.16)
Рисунок 27.4. Два конденсатора соединены последовательно. Дана общая разница напряжений на двух конденсаторах. по
(27,17)
Уравнение (27.17) снова показывает, что напряжение на двух конденсаторах, соединены последовательно, пропорциональна заряду Q. Система действует как одиночный конденсатор C, емкость которого может быть получена из следующих формула
(27.18)
Пример: задача 27.10
Многопластинчатый конденсатор, используемый, например, в радиоприемниках, состоит из четырех параллельные пластины, расположенные одна над другой, как показано на рисунке 27.5. Площадь каждой пластины — А, а расстояние между соседними пластинами — d.Что емкость этого устройства?
Рисунок 27.5. Многопластинчатый конденсатор.
Многоканальный конденсатор, показанный на рисунке 27.5, эквивалентен трем идентичным конденсаторы, подключенные параллельно (см. рисунок 27.6). Емкость каждого из три конденсатора равны и равны
(27,19)
Полная емкость многопластинчатого конденсатора может быть рассчитана с помощью уравнение (27.14):
(27.20)
Рисунок 27.6. Схема многопластинчатого конденсатора, показанного на рисунке 27.5. Три конденсатора, емкостью C ₁ = 2,0 мкФ, C ₂ = 5,0 мкФ и C ₃ = 7,0 мкФ, первоначально заряжаются до 36 В подключив каждую на несколько мгновений к батарее на 36 В. Батарея тогда сняты и заряженные конденсаторы включены в замкнутую последовательную цепь, с соединением положительной и отрицательной клемм, как показано на Рисунке 27.7. Что будет окончательный заряд на каждом конденсаторе? Какое будет напряжение на точки PP ‘?
Рисунок 27.7. Проблема 27.13.
Начальные заряды на каждом из трех конденсаторов, q ₁, q ₂ и q ₃, равны
(27.21)
После подключения трех конденсаторов заряд перераспределится. Заряды на трех конденсаторах после того, как система успокоится, равны Q ₁, Q ₂ и Q ₃.Поскольку заряд сохраняется количество, существует связь между q ₁, q ₂ и q ₃, и Q ₁, Q ₂, и Q ₃:
(27.22)
Напряжение между P и P ‘можно выразить через C ₃ и Q ₃, или в терминах C ₁, C ₂, Q ₁ и К ₂:
(27,23)
и
(27.24)
Используя уравнение (27.22), следующие выражения для Q ₁ и Q ₂ можно получить:
(27,25)
(27.26)
Подставляя уравнение (27.25) и уравнение (27.26) в уравнение (27.24), получаем
(27.27)
Комбинируя уравнение (27.27) и уравнение (27.23), Q ₃ можно выразить через известные переменные:
(27.28)
Подставляя известные значения емкости и начальных зарядов, мы получить
(27.29)
Напряжение на P и P ‘можно найти, объединив уравнения (27.29) и уравнение (27.23):
(27.30)
Заряды конденсатора 1 и конденсатора 2 равны
(27.31)
(27.32)

Если пространство между пластинами конденсатора заполнено изолятором, емкость конденсатора будет случайной по сравнению с ситуацией, в которой между пластинами есть вакуум.Изменение емкости вызвано изменение электрического поля между пластинами. Электрическое поле между пластины конденсатора будут создавать дипольные моменты в материале между тарелки. Эти наведенные дипольные моменты уменьшат электрическое поле в область между пластинами. Материал, в котором наведенный дипольный момент равен линейно пропорциональный приложенному электрическому полю называется линейным диэлектрик . В материалах этого типа полное электрическое поле между обкладки конденсатора E связаны с электрическим полем E _free, которое существовал бы без диэлектрика:
(27.33)
где каппа называется диэлектрической проницаемостью. Поскольку финальный электрический поле E никогда не может превышать свободное электрическое поле E _free, диэлектрическая проницаемость [каппа] должна быть больше 1.
Разность потенциалов на конденсаторе пропорциональна электрическому поле между пластинами. Поскольку наличие диэлектрика снижает напряженности электрического поля, это также уменьшит разность потенциалов между обкладками конденсатора (если общий заряд на обкладках сохраняется константа):
(27.34)
Емкость C системы с диэлектриком обратно пропорциональна разность потенциалов между пластинами и связана с емкостью C _{свободный} конденсатора без диэлектрика следующим образом
(27,35)
Поскольку [каппа] больше 1, емкость конденсатора может быть значительно увеличивается за счет заполнения пространства между обкладками конденсатора диэлектрик с большой каппа.
Электрическое поле между двумя пластинами конденсатора представляет собой векторную сумму поля, создаваемые зарядами на конденсаторе, и поле, создаваемое поверхностные заряды на поверхности диэлектрика. Создаваемое электрическое поле зарядами на обкладках конденсатора (плотность заряда [sigma] _{бесплатно}) выдается
(27,36)
Полагая плотность заряда на поверхности диэлектрика равной [sigma] _bound, поле, создаваемое этими связанными зарядами, равно на номер
(27.37)
Электрическое поле между пластинами равно E _free / [каппа] и таким образом
(27.38)
Подставляя уравнение (27,36) и уравнение (27,37) в уравнение (27,38), получаем
(27,39)
или
(27,40)
Пример: задача 27.19
Конденсатор с параллельными пластинами с площадью пластин A и расстоянием разделения d содержит пластину диэлектрика толщиной d / 2 (см. рисунок 27.8) и диэлектрический постоянная каппа. Разность потенциалов между пластинами составляет ΔV.
а) По заданным величинам найти электрическое поле в пустом область пространства между пластинами.
б) Найдите электрическое поле внутри диэлектрика.
в) Найдите плотность связанных зарядов на поверхности диэлектрика.
Рисунок 27.8. Проблема 27.19.
а) Предположим, что электрическое поле в конденсаторе без диэлектрика равно к E ₀.Электрическое поле в диэлектрике E _d равно связано со свободным электрическим полем через диэлектрическую проницаемость [каппа]:
(27,41)
Разность потенциалов между пластинами может быть получена путем интегрирования электрическое поле между пластинами:
(27,42)
Таким образом, электрическое поле в пустой области равно
. (27,43)
б) Электрическое поле в диэлектрике можно найти, комбинируя ур.(27,41) и (27.43):
(27,44)
c) Плотность свободного заряда [сигма] _free равна
(27,45)
Плотность связанного заряда связана с плотностью свободного заряда через следующее отношение
(27,46)
Комбинируя уравнение (27.45) и уравнение (27.46), получаем
(27,47)

Электрическое поле в «пустом» конденсаторе можно получить с помощью закона Гаусса.Рассмотрим идеальный конденсатор (без краевых полей) и интегрирование объем, показанный на рисунке 27.9. Площадь каждой пластины конденсатора — А, а площадь заряды на пластинах +/- Q. Заряд, заключенный в объёме интеграции показанное на рисунке 27.9, равно + Q. Закон Гаусса гласит, что электрический поток [Phi] через поверхность объёма интегрирования относится к приложенному плата:
(27,48)
Если между пластинами вставлен диэлектрик, электрическое поле между пластинами пластины будут меняться (даже если заряд на пластинах остается постоянным).Очевидно, что закон Гаусса, сформулированный в уравнении (27.48), в этом случае не выполняется. Электрическое поле E между обкладками конденсатора связано с поле без диэлектрика E _без:
(27,49)
где [каппа] — диэлектрическая проницаемость материала между пластинами. Теперь закон Гаусса можно переписать как
(27,50)
Закон Гаусса в вакууме является частным случаем уравнения (27.50) с [каппа] = 1.
Рисунок 27.9. Идеальный конденсатор.
Пример: задача 27.25
Металлический шар радиуса R окружен концентрическим диэлектриком. оболочка с внутренним радиусом R и внешним радиусом 3R / 2. Это окружено концентрическая тонкая металлическая оболочка радиуса 2R (см. рисунок 27.10). В диэлектрическая проницаемость оболочки каппа. Какая у этого емкость хитрое изобретение?
Предположим, что заряд на внутренней сфере — Q _{бесплатно}.Электрический поле внутри диэлектрика можно определить, применив закон Гаусса для диэлектрика (уравнение (27.50)) и используя в качестве объема интегрирования сферу радиуса r (где R
(27.51)
Таким образом, электрическое поле в этой области равно
. (27.52)
Рисунок 27.10. Проблема 27.25. Электрическое поле в области между 3R / 2 и 2R может быть полученный аналогичным образом, и равен
(27.53)
Используя электрическое поле из уравнений (27.52) и (27.53), мы можем определить разность потенциалов [Дельта] V между внутренней и внешней сферами:
(27,54)
Емкость системы может быть получена из уравнения (27.54) с использованием определение емкости через заряд Q и потенциал разница [Delta] V:
(27,55)

Электрическая потенциальная энергия конденсатора, не содержащего диэлектрика и имеющего заряд +/- Q на его пластинах равен
(27.56)
где V ₁ и V ₂ — потенциалы двух пластин. Электрическая потенциальная энергия также может быть выражена через емкость С конденсатора
(27,57)
Эта формула также верна для конденсатора с диэлектриком; свойства диэлектрика входит в эту формулу через емкость C.
Пример: задача 27.40
Десять одинаковых конденсаторов емкостью 5 мкФ подключены параллельно к источнику питания 240 В. аккумулятор.Затем заряженные конденсаторы отключаются от аккумулятора и повторно подключены последовательно, положительный вывод каждого конденсатора подключается к отрицательной клемме следующего. В чем разница потенциалов между отрицательный вывод первого конденсатора и положительный вывод последний конденсатор? Если эти клеммы подключены через внешнюю цепь, как много заряда будет течь по этой цепи, поскольку последовательное устройство разряжается ? Сколько энергии выделяется при разряде? Сравните это обвинение и это энергия с зарядом и энергией, хранящейся в исходном, параллельном расположении, и объясните любые неточности.
Заряд на каждом конденсаторе после подключения к батарее 240 В составляет равно
(27,58)
Разность потенциалов на каждом конденсаторе останется равной 240 В после конденсаторы включены последовательно. Общая разность потенциалов по десять конденсаторов, таким образом, равны
(27,59)
Если два концевых вывода конденсаторной сети соединены, заряд 1.2 мкКл будет течь от положительной клеммы к отрицательной (см. Рисунок 27.11).
Рисунок 27.11. Проблема 27.40. Электрическая энергия, запасенная в конденсаторной сети перед разряд равен
(27.60)
Энергия, запасенная в каждом конденсаторе после заряда до 240 В, равна на номер
(27.61)
Очевидно, что при замене конденсатора энергия не теряется. конфигурация с параллельного на последовательный.
Пример: задача 27.39
Подключены три конденсатора, как показано на рисунке 27.12. Их емкости: C ₁ = 2,0 мкФ, C ₂ = 6,0 мкФ, C ₃ = 8,0 мкФ. Если на два свободных клеммы, какой будет заряд на каждом конденсаторе? Что будет электрическая энергия каждого?
Рисунок 27.12. проблема 27.39.
Предположим, что напряжение на конденсаторе C ₁ равно V ₁, а Напряжение на конденсаторе (C ₂ + C ₃) составляет В ₂.Если заряд конденсатора C ₁ равен Q ₁, тогда заряд на параллельном конденсаторе также равен Q ₁. Потенциал разница в этой системе равна
(27,62)
Таким образом, заряд конденсатора 1 определяется разностью потенциалов [Дельта] V
(27,63)
Напряжение V ₂₃ на конденсаторе (C ₂ + C ₃) связано с расходом Q ₁
(27.64)
Заряд конденсатора С ₂ равен
(27,65)
Заряд конденсатора С ₃ равен
. (27,66)
Электрическая потенциальная энергия, запасенная в каждом конденсаторе, равна
. (27,67)
Для трех конденсаторов в этой задаче электрическая потенциальная энергия равна на номер
(27.68)
(27,69)
(27,70)
Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.
Комбинация конденсаторов
Есть два типа комбинаций конденсаторов: конденсаторы, включенные параллельно, и конденсаторы, включенные последовательно. Но возможна и другая комбинация, которая представляет собой комбинацию смешивания, это комбинация последовательного и параллельного подключения конденсатора.Эквивалент комбинации конденсаторов противоположен сопротивлению. Конденсатор сохраняет заряд, а резистор сбрасывает заряд. Последовательное соединение резисторов увеличивает эквивалентное значение, а последовательное соединение конденсатора уменьшает эквивалентное значение. Последовательное соединение выполняется для уменьшения эквивалентной емкости конденсатора, а параллельное соединение используется для увеличения накопительной емкости конденсатора. При параллельном соединении каждый конденсатор может сохранять заряд в соответствии со своей полной емкостью, но при последовательном соединении он не может использовать свою полную емкость, поэтому последовательное соединение используется для понижения значения эквивалентной емкости.
Что такое конденсатор? В котором хранится заряд, называется конденсатор. Конденсатор хранит емкость заряда. Он измеряется в кулонах (C). Комбинированные конденсаторы используются в особых случаях. Расположение множества конденсаторов для одной цели называется комбинацией конденсаторов. Вся комбинация работает как один конденсатор. Есть два типа комбинаций

1. Последовательная комбинация
2. Параллельная комбинация
# Комбинация серий: Обычно последовательные конденсаторы подключаются последовательно.Последовательная комбинация — это такая, при которой все конденсаторы соединены последовательно. Параллельно конденсаторы включаются в параллельную комбинацию. При последовательном соединении вы должны подключить положительный вывод одного конденсатора к отрицательному выводу другого конденсатора, таким образом, последовательная комбинация получается для конденсатора. Между двумя конденсаторами есть только одна общая точка.
Каждый конденсатор имеет заряды + Q и — Q между двумя точками.
Если разность потенциалов каждого конденсатора равна V1, V2, V3
Тогда напряжение конденсаторов
В = V1 + V2 + V3 …………….(i)
Емкость конденсаторов C1, C2 и C3
Теперь
Если мы используем эквивалентный конденсатор вместо конденсаторов, разность потенциалов которых равна V, а заряд равен Q.
Для последовательного конденсатора
Это последовательная формула конденсаторов. Мы используем уравнение, когда конденсаторы включены последовательно.
Комбинация параллельных конденсаторов
Где все конденсаторы Положительные точки соединены в общую точку, а отрицательные точки соединены в общей точке или земля — это конденсаторы, соединенные параллельно.На рисунке показано, где положительные точки конденсаторов соединены с положительной точкой элемента, а отрицательные точки — с отрицательной точкой. Для параллельного соединения между конденсаторами будут две общие точки: все положительные клеммы должны быть закорочены в одной точке, а все отрицательные клеммы должны быть подключены в одной точке, тогда соединение будет параллельным.
Если подается заряд + Q, то конденсаторы получают заряд по своей емкости.
Пусть, заряды конденсатора равны Q1, Q2 и Q3
Общий заряд Q равен
Q = Q1 + Q2 + Q3 ————- (i)
Каждый конденсатор имеет одинаковую разность потенциалов.Потому что их две точки связаны с двумя точками ячейки.
Считаем, напряжение v, емкость каждого конденсатора
С1, С2, С3
Затем напряжение и заряд конденсаторов, Q1 = C1V, Q2 = C2V, Q3 = C3V ————- (ii)
Используя эквивалентный конденсатор с напряжением V и зарядом Q.
Мы можем записать
Cp = Q / V
Или , Q = CpV —————- (iii)
Подставляя значения уравнения (ii) и (iii) в (i)
CpV = C1V + C2V + C3V
Или, Cp = C1 + C2 + C3
Для n параллельных конденсаторов
Cp = C1 + C2 + C3 + ————- + Cn
Итак, можно сказать, что эквивалентный конденсатор
— это сумма емкостей конденсаторов.
Это формула конденсатора при параллельном подключении.
Параллельное соединение конденсаторов. Подключение конденсаторов Как правильно подключить конденсаторы
IN электрические цепи различные способы подключения конденсатора . Конденсаторное соединение может быть выполнено: последовательно , параллельно и последовательно параллельно (последнее иногда называют смешанным соединением конденсаторов). Существующие типы подключения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы подключения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в схему таким образом, что обкладки всех конденсаторов напрямую подключены к точкам переключения, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При зарядке группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одинаковая разность потенциалов, поскольку все они заряжаются от одного источника тока.Общее количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещенного на каждый из конденсаторов, поскольку заряд каждого из их конденсаторов происходит независимо от заряда других конденсаторов этой группы. Исходя из этого, всю систему параллельно включенных конденсаторов можно рассматривать как один эквивалентный (эквивалентный) конденсатор. Тогда общая емкость при параллельном подключении равна сумме емкостей всех подключенных конденсаторов.
Обозначим общую емкость конденсаторов, подключенных к батарее, буквой С tot, емкость первого конденсатора C1, емкость второго C2 и емкость третьего C3. Тогда для параллельного включения конденсаторов будет действительна следующая формула:
Последний знак + и многоточие указывают на то, что эту формулу можно использовать с четырьмя, пятью и, как правило, с любым количеством конденсаторов.
Последовательное соединение конденсаторов.
Если подключение конденсаторов к батарее выполнено в виде цепочки и пластины только первого и последнего конденсаторов напрямую соединены с точками включения в цепи, то это соединение конденсатора называется согласованным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как только крайние пластины (1 и 6) заряжаются непосредственно от источника тока, а остальные пластины (2, 3, 4 и 5) заряжаются. заряжен через влияние.В этом случае заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. Д.
Напряжения на разных конденсаторах, как правило, будут разными, так как разные напряжения всегда требуются для зарядки одним и тем же количеством электричества конденсаторов разной емкости. Чем меньше емкость конденсатора, тем большее напряжение требуется для зарядки этого конденсатора требуемым количеством электричества, и наоборот.
Таким образом, при зарядке группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости будет больше напряжения, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю, мы можем рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого имеется напряжение, равное сумме напряжений на всех конденсаторах группы, и заряд которого равен равен заряду любого из конденсаторов группы.
Возьмите самый маленький конденсатор в группе. Он должен иметь наибольшее напряжение. Но напряжение на этом конденсаторе составляет лишь часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше, чем на конденсаторе с наименьшей емкостью. А это прямо означает, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого маленького конденсатора в группе.
Для расчета общей емкости при последовательном соединении конденсаторов удобнее всего использовать следующую формулу:
Для особого случая двух последовательно соединенных конденсаторов формула для расчета их общей емкости будет:
Последовательно-параллельное (смешанное) соединение конденсаторов
Конденсаторы последовательно-параллельные цепью называют имеющую в своем составе участки как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 показан пример участка схемы со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете суммарной емкости такого участка цепи при последовательно-параллельном соединении конденсаторов этот участок разбивается на простые участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Далее алгоритм расчета имеет вид:
1.Определите эквивалентную емкость секций при последовательном включении конденсаторов.
2. Если эти секции содержат последовательно соединенные конденсаторы, то сначала рассчитывается их емкость.
3. После расчета эквивалентной емкости конденсаторов перерисуйте схему. Обычно цепь состоит из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитайте емкость получившегося контура.
Один из примеров расчета емкости для смешанного подключения конденсаторов показан на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного включения конденсаторов.
У начинающих электронщиков при сборке любого самодельного устройства могут возникнуть проблемы с подключением конденсатора. Ведь даже заядлый энтузиаст электроники может не иметь под рукой конденсатор нужного номинала, особенно когда нужно срочно отремонтировать бытовую технику. Из этой проблемы легко выйти, подключив несколько конденсаторов последовательно или параллельно.
Подготовить:
Конденсаторы
;
вольтметр;
провода
кусачки.
Если два конденсатора с равными емкостями соединены последовательно, то в результате общая емкость будет меньше в 2 раза, а напряжение увеличится. В реальных случаях последовательно соединенные цепи встречаются редко, в основном в высоковольтных источниках питания. Для низковольтных источников питания используется параллельное соединение, так как оно перетекает. Суммарная емкость конденсаторов, соединенных параллельно, будет суммироваться, и напряжение будет равно значению напряжения конденсатора с меньшим параметром.Например, есть три конденсатора по 30 мкФ с напряжением 100 В, соединенные параллельно. Будет рассчитана стоимость всего набора: 90 мкФ * 100.

Существует комбинированный способ подключения — последовательно-параллельный, что встречается крайне редко. Для расчета общей мощности схема разбита на несколько секций, каждая из которых рассчитывается отдельно.

При подключении электролитических конденсаторов необходимо соблюдать полярность. В параллельном методе отрицательный вывод одного конденсатора должен быть подключен к отрицательному выводу другого.По порядку — минус с положительным выводом.

При подключении конденсаторов необходимо учитывать номинальное значение напряжения. Если один из конденсаторов будет с меньшим номинальным напряжением, то, скорее всего, в ближайшее время устройство выйдет из строя.

Подключайте конденсаторы только тогда, когда они полностью отключены от других элементов схемы. Подключение осуществляется изолированными проводами. После любого подключения и отключения проверьте работу с помощью вольтметра.

Для составного конденсатора попробуйте взять конденсаторы того же типа, а если возможно, из одной партии. Конденсаторы керамические, пленочные, металлические, слюдяные.
У многих начинающих энтузиастов электроники в процессе сборки самодельного устройства возникает вопрос: «Как подключить конденсаторы?»
Казалось бы, зачем это нужно, ведь если по концепции указано, что в этом месте схемы должен быть установлен конденсатор на 47 мкФ, то есть берем и ставим необходимый конденсатор.Но, согласитесь, в мастерской даже у заядлого электронщика может не оказаться конденсатора нужного номинала!
Подобная ситуация может возникнуть при ремонте любого устройства. Например, вам нужен электролитический конденсатор емкостью 1000 мкФ, а под рукой всего 2-3 конденсатора на 470 мкФ. Установить конденсатор на 470 мкФ вместо 1000? Нет, это не всегда допустимо. Так что делать? Сходить на радиорынок несколько десятков километров за один конденсатор?
Как выйти из этой ситуации? Можно подключить несколько конденсаторов и в результате получить нужную нам емкость.В электронике есть два способа подключения конденсаторов: параллельно и последовательно .
На самом деле это выглядит так:

Параллельное подключение

Принципиальная схема параллельного подключения

Последовательное подключение
Принципиальная схема последовательного подключения
Также можно комбинировать параллельное и последовательное включение конденсаторов. На практике это вряд ли пригодится.
Как рассчитать общую емкость подключенных конденсаторов?
В этом нам помогут несколько простых формул.Не сомневайтесь, если вы занимаетесь электроникой, то эти простые формулы рано или поздно выручат вас.
Суммарная емкость конденсаторов, соединенных параллельно:
C 1 — емкость первого конденсатора;
С 2 — емкость второго конденсатора;
С 3 — емкость третьего конденсатора;
C N — емкость N -го конденсатора;
C total — общая емкость составного конденсатора.
Как видите, при параллельном подключении конденсаторов нужно просто сложить!
Внимание! Все расчеты необходимо производить в одном блоке.Если считать емкости в микрофарадах, то нужно указать емкость C 1 , C 2 в микрофарадах. Результат тоже получается в микрофарадах. Это правило следует соблюдать, иначе ошибок не избежать!
Во избежание ошибок при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В нем перечислены префиксы, используемые для короткой записи, и коэффициенты, с помощью которых вы можете пересчитать значения количеств.
Емкость двух последовательно соединенных конденсаторов можно рассчитать по другой формуле. Будет немного сложнее:
Внимание! Эта формула действительна только для двух конденсаторов! Для большего количества конденсаторов, подключенных последовательно, потребуется другая формула. Она больше запутана и не всегда полезна.
Или то же самое, но более понятное:
Если вы произведете несколько вычислений, вы увидите, что при последовательном соединении конденсаторов их результирующая емкость всегда будет меньше наименьшей емкости, включенной в эту цепочку.Что это значит? А это значит, что если последовательно подключить конденсатор емкостью 5, 100 и 35 пикофарад, то общая емкость составного конденсатора будет меньше 5.
В том случае, если конденсаторы такой же емкости используются для последовательного подключения эта громоздкая формула упрощается и принимает вид:
Здесь вместо буквы M поставил количество конденсаторов, а С 1 — емкость конденсатора.
Также стоит запомнить простое правило:
Когда два конденсатора с одинаковой емкостью соединены последовательно, результирующая емкость будет равна половине емкости каждого конденсатора.
Таким образом, если последовательно соединить два конденсатора, каждый из которых имеет емкость 10 нанофарад, в результате емкость составного конденсатора будет 5 нанофарад.
Проверяем конденсатор измерением емкости, и на практике подтверждаем правильность приведенных здесь расчетных формул.
Взять двухпленочный конденсатор. Один для 15 нанофарад (0,015 мкФ), другой для 10 нанофарад (0,01 мкФ). Соедините их последовательно. Теперь возьмем мультиметр Victor VC9805 + с функцией измерения емкости конденсаторов и измерения общей емкости двух конденсаторов.Вот что мы получаем (см. Фото).

Измерение емкости последовательно соединенных конденсаторов
Емкость составного конденсатора составила 6 нанофарад (0,006 мкФ)
А теперь сделаем то же самое, но для параллельного соединения конденсаторов. Проверить результат тестером (см. Фото).

Измерение емкости параллельно соединенных конденсаторов
Как видите, при параллельном подключении емкость двух конденсаторов увеличилась и составляет 25 нанофарад (0.025 мкФ).
Что еще нужно знать для правильного подключения конденсаторов?
Во-первых, не забывайте, что помимо емкости у конденсаторов есть еще один важный параметр, например, номинальное напряжение.
Когда конденсаторы соединены последовательно, напряжение между ними распределяется обратно пропорционально емкости этих конденсаторов. Поэтому имеет смысл использовать конденсаторы с номинальным напряжением, равным тому, которое должно быть на конденсаторе, вместо которого мы ставим составной конденсатор.
Если используются конденсаторы одинаковой емкости, то напряжение между ними будет делиться поровну.
Для электролитических конденсаторов.
При подключении электролитических конденсаторов строго соблюдать полярность! При параллельном подключении электролитических конденсаторов всегда подключайте отрицательную клемму одного конденсатора к отрицательной клемме другого. Положительный выход с положительным.

Параллельное соединение электролитических конденсаторов

Схема параллельного соединения
При последовательном соединении электролитических конденсаторов ситуация обратная.Необходимо соединить положительный вывод с отрицательным. Получается что-то вроде последовательного соединения аккумуляторов.

Последовательное подключение электролитических конденсаторов
Также не забываем о номинальном напряжении. При параллельном подключении каждый из задействованных конденсаторов должен иметь это номинальное напряжение, как если бы мы включили в цепь один конденсатор. То есть, если вам необходимо установить в схему конденсатор с номинальным напряжением 35 вольт и емкостью, например, 200 мкФ, то взамен его можно подключить параллельно два конденсатора на 100 мкФ и 35 вольт.Если хотя бы один из этих конденсаторов имеет более низкое номинальное напряжение (например, 25 вольт), то он скоро выйдет из строя.
Желательно, чтобы для составного конденсатора выбирались конденсаторы одного типа (пленочные, керамические, слюдяные, бумажные). Будет лучше, если они будут взяты из одной партии.
Конечно, смешанное (комбинированное) подключение конденсаторов тоже возможно, но на практике оно не используется (не видел). Расчет емкости смешанного соединения конденсаторов обычно дают тем, кто решает задачи по физике и сдает экзамены 🙂
Найдите эквивалентную емкость комбинации класса 12 по физике CBSE
Подсказка: Задача основана на использовании формулы емкости конденсатора.Сначала следует рассчитать последовательную и параллельную емкости конденсатора. Затем чистую емкость следует умножить на заданное значение напряжения, чтобы получить значение заряда, протекающего по цепи.
Используемая формула:
\ [Q = CV \]
Полный пошаговый ответ:
Рассмотрим схему, представляющую соединения компонентов в цепи.
Рассчитаем емкость цепи, учитывая рисунок, одновременно с учетом двух конденсаторов.
Приступим к расчету.
Теперь рассмотрим конденсаторы с маркировкой 5 и 6. Итак, эти конденсаторы включены параллельно. Итак, эквивалентная емкость рассчитывается следующим образом.
\ [\ begin {align}
& {{C} _ {56}} = {{C} _ {5}} + C {} _ {6} \\
& \ Rightarrow {{C} _ {56 }} = 10 + 10 \\
& \ Rightarrow {{C} _ {56}} = 20 \ mu F \\
\ end {align} \]
Теперь рассмотрим конденсаторы, обозначенные 2, 3 и 4. Итак эти конденсаторы включены последовательно. Итак, эквивалентная емкость рассчитывается следующим образом.
\ [\ begin {align}
& \ dfrac {1} {{{C} _ {234}}} = \ dfrac {1} {{{C} _ {2}}} + \ dfrac {1} { {{C} _ {3}}} + \ dfrac {1} {{{C} _ {4}}} \\
& \ Rightarrow \ dfrac {1} {{{C} _ {234}}} = \ dfrac {1} {60} + \ dfrac {1} {60} + \ dfrac {1} {60} \\
& \ Rightarrow {{C} _ {234}} = 20 \, \ mu F \\
\ end {align} \]
Теперь рассмотрим конденсаторы с маркировкой 56 и 234. Итак, эти конденсаторы включены параллельно. Итак, эквивалентная емкость рассчитывается следующим образом.
\ [\ begin {align}
& {{C} _ {23456}} = {{C} _ {234}} + C {} _ {56} \\
& \ Rightarrow {{C} _ {23456 }} = 20 + 20 \\
& \ Rightarrow {{C} _ {23456}} = 40 \ mu F \\
\ end {align} \]
Теперь рассмотрим конденсаторы с маркировкой 23456 и 1.Итак, эти конденсаторы включены последовательно. Итак, эквивалентная емкость рассчитывается следующим образом.
\ [\ begin {align}
& \ dfrac {1} {{{C} _ {123456}}} = \ dfrac {1} {{{C} _ {23456}}} + \ dfrac {1} { {{C} _ {1}}} \\
& \ Rightarrow \ dfrac {1} {{{C} _ {123456}}} = \ dfrac {1} {40} + \ dfrac {1} {40} \\
& \ Rightarrow {{C} _ {123456}} = 20 \, \ mu F \\
\ end {align} \]
Эквивалентная емкость комбинации конденсаторов между точками A и B равна \ [ 20 \, \ mu F \].
Давайте теперь вычислим общий заряд, протекающий в цепи, когда батарея на 100 В подключена между точками A и B.
Диаграмма, представляющая эквивалентную емкость и напряжение между точками A и B, выглядит следующим образом.

Стоимость указана следующим образом.
\ [\ begin {align}
& Q = CV \\
& \ Rightarrow Q = 20 \, \ mu F \ times 100 \, V \\
& \ Rightarrow Q = 2 \, mC \\
\ end {align} \]
Таким образом, эквивалентная емкость комбинации конденсаторов между точками A и B равна \ [20 \, \ mu F \], а общий заряд, протекающий в цепи, когда батарея 100 В подключена между точками А и В — 2 мкСл.
Примечание: Для получения дополнительной информации о решении этих типов проблем необходимо иметь под рукой следующие данные: Формула, используемая для расчета эквивалентной емкости конденсаторов, подключенных параллельно, отличается от формулы, используемой для расчета эквивалентная емкость конденсаторов, соединенных последовательно. Следует позаботиться о единицах измерения параметров.
Как работают конденсаторы | HowStuffWorks
В некотором смысле конденсатор немного похож на батарею.Хотя они работают совершенно по-разному, конденсаторы и аккумуляторы хранят электрическую энергию. Если вы прочитали «Как работают батареи», то знаете, что у батареи есть две клеммы. Внутри батареи химические реакции производят электроны на одном выводе, а другой вывод поглощает их, когда вы создаете цепь. Конденсатор намного проще, чем батарея, поскольку он не может производить новые электроны — он только хранит их. Конденсатор называется так потому, что он обладает «емкостью» для хранения энергии.
В этой статье мы точно узнаем, что такое конденсатор, для чего он нужен и как он используется в электронике.Мы также рассмотрим историю конденсатора и то, как несколько человек помогли сформировать его развитие.
Конденсаторы могут быть изготовлены для любых целей, от самого маленького пластикового конденсатора в вашем калькуляторе до сверхконденсатора, который может питать пригородную шину. Вот некоторые из различных типов конденсаторов и способы их использования.
Воздух: часто используется в схемах настройки радио
Майлар: чаще всего используется для схем таймера, таких как часы, сигнализация и счетчики
Стекло: подходит для высоковольтных приложений
Керамика: используется для высокочастотных целей, таких как антенны, X аппараты для лучевой терапии и МРТ
Суперконденсатор: питает электрические и гибридные автомобили
Внутри конденсатора клеммы подключаются к двум металлическим пластинам, разделенным непроводящим веществом, или диэлектрику .Вы можете легко сделать конденсатор из двух кусков алюминиевой фольги и листа бумаги (и нескольких электрических зажимов). Это не будет особенно хороший конденсатор с точки зрения его емкости, но он будет работать.
Теоретически диэлектриком может быть любое непроводящее вещество. Однако для практических применений используются специальные материалы, которые лучше всего подходят для функции конденсатора. Слюда, керамика, целлюлоза, фарфор, майлар, тефлон и даже воздух — вот некоторые из используемых непроводящих материалов.Диэлектрик определяет, какой это конденсатор и для чего он лучше всего подходит. В зависимости от размера и типа диэлектрика, некоторые конденсаторы лучше подходят для высокочастотных применений, а некоторые — для высоковольтных применений.
Параллельное соединение конденсаторов разной емкости. Параллельное и последовательное соединение конденсаторов
Для получения более широкого диапазона емкостей конденсаторы часто соединяются между собой, получаются так называемые конденсаторные батареи. Подключение может быть параллельным, последовательным или комбинированным (смешанным).Рассмотрим случай с двумя конденсаторами.
Последовательное соединение конденсаторов показано на рис.1
Здесь (рис. 1) пластина одного конденсатора, имеющего отрицательный заряд, соединена с положительной пластиной следующего конденсатора. При последовательном соединении средние пластины конденсаторов за счет воздействия наэлектризованы, поэтому их заряды равны по величине и противоположны по знаку. Заряды на этих конденсаторах одинаковые. При этом добавляются разности потенциалов:
В данном случае имеем:
Получаем, что при последовательном соединении конденсаторов емкость соединения определяется как:
Обобщая формулу (3) для конденсаторов N, получаем:
где — электрическая емкость i-го конденсатора.
Последовательное соединение конденсаторов используется, когда во избежание пробоя конденсатора необходимо распределить разность потенциалов между несколькими конденсаторами.
Последовательное соединение конденсаторов показано на рис. 2
При параллельном соединении разность потенциалов между пластинами конденсаторов одинакова. Общий заряд системы равен сумме зарядов на каждом из конденсаторов:
Из вышесказанного получаем:
Для батареи из N параллельно соединенных конденсаторов имеем:
Параллельное соединение конденсаторов используется, когда необходимо увеличить емкость конденсатора.
Примеры решения проблем
ПРИМЕР 1
Упражнение Получите формулу для расчета емкости многослойного конденсатора.
Решение Конденсатор, называемый слоистым конденсатором, состоит из двух параллельных металлических пластин, разделенных несколькими плоскими слоями различных диэлектриков (рис. 3). Обозначим диэлектрические проницаемости диэлектрических слоев как. Будем считать, что соответствующая толщина диэлектрического слоя в этом случае :.
Предположим, что между слоями диэлектрика вставлены очень тонкие листы проводника. От такой процедуры заряды на пластинах конденсатора и напряженность поля в солях диэлектриков останутся неизменными. Разность потенциалов между пластинами останется неизменной, следовательно, емкость конденсатора не изменится. Но наличие тонких листов проводника превратит слоистый конденсатор в последовательное соединение конденсаторов.
Применяем формулы для емкости плоского конденсатора:
и расчет емкости батареи последовательно соединенных конденсаторов:
получаем:
Ответ
ПРИМЕР 2
Упражнение Какой будет емкость подключения конденсаторов (рис.4), если батарея состоит из одинаковых конденсаторов, емкость каждого из них равна F.
Решение Емкость параллельного соединения конденсаторов обозначается как Она равна:
Под последовательным соединением мы понимаем случаи, когда два или более элемента находятся в виде цепочки, при этом каждый из них соединен с другим. только в одном месте. Почему конденсаторы так размещены? Как это правильно делать? Что вы должны знать? Какие особенности имеет на практике последовательное соединение конденсаторов? Какая формула результата?
Что нужно знать для правильного подключения?
Увы, здесь не все так просто, как может показаться.Многие новички думают, что если на схеме написано, что нужен элемент на 49 микрофарад, то достаточно просто взять и установить (или заменить на аналог). Но даже в профессиональной мастерской сложно подобрать нужные параметры. А что делать, если необходимых предметов нет? Допустим, есть такая ситуация: нужен конденсатор на 100 мкФ, а их несколько по 47. Ставить не всегда получается. Сходить на радиорынок за одним конденсатором? Не обязательно.Достаточно будет соединить пару элементов. Есть два основных способа: последовательное и параллельное соединение конденсаторов. Поговорим о первом. Но если говорить о последовательном соединении катушки и конденсатора, то особых проблем нет.
Почему они это делают?
При проведении с ними таких манипуляций электрические заряды на пластинах отдельных элементов будут равны: KE = K 1 = K 2 = K 3. KE — конечная емкость, K — пропущенное значение. конденсатора.Это почему? Когда заряды подаются от источника питания на внешние пластины, то внутренние могут быть переведены в значение, которое является значением элемента с наименьшими параметрами. То есть, если вы возьмете конденсатор на 3 мкФ, а затем подключите его к 1 мкФ, то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение 3 мкФ. Но второй элемент так сильно пропустить не сможет, и отрежет все, что больше требуемого значения, оставив большую емкость на исходном конденсаторе.Давайте посмотрим, на что нужно рассчитывать при последовательном соединении конденсаторов. Формула:
OE — общая мощность;
H — напряжение;
KE — конечная мощность.
Что еще нужно знать, чтобы правильно подключить конденсаторы?
Для начала не забываем, что помимо емкости у них есть еще и номинальное напряжение. Почему? При последовательном подключении напряжение распределяется обратно пропорционально их емкости между ними.Поэтому такой подход имеет смысл использовать только в тех случаях, когда любой конденсатор может обеспечить минимально необходимые рабочие параметры. Если используются элементы одинаковой емкости, то напряжение между ними будет делиться поровну. Также небольшая осторожность в отношении электролитических конденсаторов: при обращении с ними всегда внимательно проверяйте их полярность. Ведь если этот фактор не учитывать, последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если все ограничится только разбивкой этих элементов.Помните, что конденсаторы накапливают ток, и если что-то пойдет не так, в зависимости от схемы, может возникнуть прецедент, в результате которого выйдут из строя другие компоненты схемы.
Последовательный ток
Из-за того, что он имеет только один возможный путь потока, он будет иметь одинаковое значение для всех конденсаторов. Причем сумма накопленного заряда везде одинакова. Это не зависит от емкости. Посмотрите на любую схему последовательного подключения конденсаторов. Правая пластина первого соединяется с левой частью второго и так далее.Если используется более 1 элемента, то некоторые из них будут изолированы от общей цепи. Таким образом, эффективная площадь пластин становится меньше и равна параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор заполняется электрическим зарядом, он перестает пропускать ток. И тогда он не может течь по всей цепочке. В этом случае остальные конденсаторы также не смогут зарядиться.
Падение напряжения и общая емкость
Каждый элемент постепенно рассеивает напряжение.Учитывая, что емкость обратно пропорциональна ей, чем она меньше, тем больше будет падение. Как упоминалось ранее, конденсаторы, соединенные последовательно, имеют одинаковый электрический заряд. Следовательно, разделив все выражения на общее значение, можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно различаются.
№ примера 1
Воспользуемся формулами, представленными в статье, и рассчитаем несколько практических задач.Итак, у нас есть три конденсатора. Их емкость: C1 = 25 мкФ, C2 = 30 мкФ и C3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую вместимость. Воспользуемся соответствующим уравнением 1 / C: 1 / C1 + 1 / C2 + 1 / C3 = 1/25 + 1/30 + 1/20 = 37/300. Переведем в микрофарады, и общая емкость конденсатора при последовательном включении (а группа в данном случае рассматривается как один элемент) составляет примерно 8,11 мкФ.
Пример №2
Решим еще одну задачу для консолидации нашей работы.Есть 100 конденсаторов. Емкость каждого элемента 2 мкФ. Необходимо определить их общую вместимость. Необходимо их количество умножить на характеристику: 100 * 2 = 200 мкФ. Итак, общая емкость конденсатора при последовательном включении составляет 200 мкФ. Как видите, ничего сложного.
Заключение
Итак, мы проработали теоретические аспекты, проанализировали формулы и особенности правильного подключения конденсаторов (последовательно) и даже решили несколько задач.Напоминаю читателям, что нельзя упускать из виду влияние номинального напряжения. Также желательно подбирать однотипные элементы (слюдяные, керамические, металлобумажные, пленочные). Тогда наибольший положительный эффект может дать последовательное соединение конденсаторов.
Конденсаторы, как и резисторы, могут быть подключены последовательно и параллельно. Рассмотрим подключение конденсаторов: для чего используется каждая из цепей, и их конечные характеристики.

Эта схема самая распространенная.В нем пластины конденсаторов соединены друг с другом, образуя эквивалентную емкость, равную сумме соединяемых конденсаторов.
При параллельном подключении электролитических конденсаторов необходимо, чтобы провода одинаковой полярности были подключены друг к другу.
Особенность такого соединения — одинаковое напряжение на всех подключенных конденсаторах … Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора той группы, в которой оно минимально.
Токи через конденсаторы группы разные: больший ток будет течь через конденсатор большей емкости.
На практике параллельное соединение используется для получения желаемой емкости, когда она выходит за пределы промышленного диапазона или не помещается в стандартный ряд контейнеров. В системах управления коэффициентом мощности (cos ϕ) изменение емкости происходит из-за автоматического включения или отключения конденсаторов параллельно.
При последовательном соединении пластины соединяются конденсатором друг с другом, образуя цепочку.Крайние обкладки подключены к источнику, и ток по всем конденсаторам группы будет течь одинаково.
Эквивалентная емкость последовательно соединенных конденсаторов ограничена наименьшей емкостью в группе. Объясняется это тем, что как только он полностью зарядится, ток прекратится. Вы можете рассчитать общую емкость двух последовательно соединенных конденсаторов по формуле
Но использование последовательного соединения для получения нестандартных значений емкости не так распространено, как параллельное.
При последовательном соединении напряжение питания распределяется между конденсаторами группы. Это позволяет получить на более высокое напряжение конденсаторной батареи , чем номинальное напряжение составляющих ее компонентов. Итак, из дешевых и малогабаритных конденсаторов делаются блоки, выдерживающие высокие напряжения.
Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам; в противном случае напряжение на большем конденсаторе будет высоким.Устройство, работающее на этом принципе, называется емкостным делителем напряжения .
Смешанное соединение конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующих высокой точности получения значения емкости, а также их точной настройки.
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов в зависимости от потребностей схемы.Давайте их рассмотрим.

Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов подключены к точкам переключения и образуют батарею. В этом случае во время зарядки конденсаторов каждый из них будет иметь разное количество электрических зарядов с одинаковым количеством подводимой энергии.
Схема параллельной установки
Емкость при параллельной установке рассчитывается на основе емкостей всех конденсаторов в цепи.В этом случае количество электроэнергии, подаваемой на все отдельные двухполюсные элементы схемы, можно рассчитать, суммируя количество энергии, помещенной в каждый конденсатор. Вся подключенная таким образом цепь рассчитывается как одна двухполюсная.
C всего = C 1 + C 2 + C 3

Схема — накопительное напряжение
В отличие от соединения звездой, на пластины всех конденсаторов подается одинаковое напряжение. Например, на диаграмме выше мы видим, что:
В AB = V C1 = V C2 = V C3 = 20 Вольт
Последовательное соединение
Здесь к точкам включения подключены только контакты первого и последнего конденсатора.
Схема
— Схема последовательного подключения
Основной особенностью схемы является то, что электрическая энергия будет течь только в одном направлении, а это означает, что ток в каждом из конденсаторов будет одинаковым. В такой схеме для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Следует понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость с последовательным типом может воспроизводиться энергией соседнего накопителя.
Формула, отражающая зависимость тока от подключения конденсаторов, выглядит так:
i = i c 1 = i c 2 = i c 3 = i c 4, то есть токи, проходящие через каждый конденсатор, равны друг другу.
Следовательно, будет такой же не только сила тока, но и электрический заряд. Согласно формуле это определяется как:
Q итого = Q 1 = Q 2 = Q 3
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
1 / C всего = 1 / C 1 + 1 / C 2 + 1 / C 3
Видео: как подключить конденсаторы параллельно и последовательно
Смешанное соединение
Но, следует учитывать, что для подключения различных конденсаторов необходимо учитывать сетевое напряжение.Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых биполей малой емкости будут становиться больше при зарядке, и наоборот, большая электрическая емкость потребует меньшего заряда.

Схема: смешанное соединение конденсаторов
Также существует смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно путем параллельного и последовательного включения электролитических ячеек в цепь.Этот контур имеет несколько секций с разными подключениями для конденсационных двухполюсных сетей. Другими словами, на одной цепи цепь включена параллельно, на другой — последовательно. Такая электрическая схема имеет ряд преимуществ по сравнению с традиционными:
Может использоваться для любых целей: подключение электродвигателя, станков, радиоаппаратуры;
Простой расчет. Для монтажа вся схема разбивается на отдельные участки схемы, которые рассчитываются отдельно;
Свойства компонентов не меняются независимо от изменения электромагнитного поля и силы тока.Это очень важно при работе с противоположными двухтерминальными сетями. Емкость постоянна при постоянном напряжении, но в то же время потенциал пропорционален заряду;
Если нужно собрать несколько неполярных полупроводниковых двухполюсных сетей из полярных, то нужно взять несколько однополюсных двухполюсных сетей и соединить их антипараллельно (в треугольник). Минус к минусу, плюс к плюсу. Таким образом, при увеличении емкости меняется принцип работы биполярного полупроводника.
Содержимое:
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае подключение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединены в два узла и не связаны с другими узлами, если это ранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два или более конденсатора включаются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется со следующим только в одной общей точке.Ток (i), заряжающий цепь последовательного конденсатора, будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4.
Из-за того, что через последовательно соединенные конденсаторы протекает одинаковая величина тока, количество заряда, накопленного каждым из них, будет одинаковым, независимо от емкости. Это становится возможным, поскольку заряд, идущий от пластины предыдущего конденсатора, накапливается на пластине следующего элемента схемы.Следовательно, количество заряда в последовательно соединенных конденсаторах будет выглядеть следующим образом: Q total = Q 1 = Q 2 = Q 3.
Если мы рассмотрим три конденсатора C 1, C 2 и C 3, соединенные последовательно, то окажется, что средний конденсатор C 2 при постоянном токе электрически изолирован от общей цепи. В конечном итоге полезная площадь пластин будет уменьшена до площади пластин конденсатора с наименьшими размерами. Полное заполнение пластин электрическим зарядом делает невозможным дальнейшее прохождение через них тока.В результате прекращается движение тока во всей цепи, соответственно, и прекращается зарядка всех остальных конденсаторов.
Общее расстояние между пластинами при последовательном соединении — это сумма расстояний между пластинами каждого элемента. В результате включения в последовательную цепь образуется одиночный конденсатор большой емкости, площадь пластин которого соответствует пластинам элемента с минимальной емкостью. Расстояние между пластинами равно сумме всех расстояний в цепочке.
Падение напряжения на каждом конденсаторе будет разным в зависимости от емкости. Это положение определяется по формуле: C = Q / V, в которой емкость обратно пропорциональна напряжению. Таким образом, при уменьшении емкости конденсатора на него падает большее напряжение. Общая емкость всех конденсаторов рассчитывается по формуле: 1 / C total = 1 / C 1 + 1 / C 2 + 1 / C 3.
Основной особенностью такой схемы является прохождение электрической энергии только в одном направлении.Следовательно, в каждом конденсаторе значение тока будет одинаковым. Каждое запоминающее устройство в последовательной цепи хранит одинаковое количество энергии независимо от емкости. То есть емкость может быть воспроизведена за счет энергии, присутствующей в соседнем накопителе.
Онлайн-калькулятор для расчета емкости конденсаторов, последовательно включенных в электрическую цепь.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельное соединение — это такое соединение, при котором конденсаторы соединены друг с другом двумя контактами.Таким образом, в одной точке можно соединить сразу несколько элементов.
Этот тип подключения позволяет сформировать единый конденсатор больших размеров, площадь пластин которого будет равна сумме площадей пластин каждого отдельного конденсатора. В связи с тем, что она находится в прямой зависимости от площади пластин, общая емкость — это общее количество всех конденсаторных конденсаторов, подключенных параллельно. То есть C total = C 1 + C 2 + C 3.
Поскольку разность потенциалов возникает только в двух точках, одинаковое напряжение будет падать на все конденсаторы, соединенные параллельно. Сила тока в каждом из них будет отличаться в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, используемое в различных схемах, позволяет регулировать различные параметры в определенных областях. Благодаря этому получаются необходимые результаты работы всей системы в целом.
.

Упражнение	Какой будет емкость подключения конденсаторов (рис.4), если батарея состоит из одинаковых конденсаторов, емкость каждого из них равна F.
Решение	Емкость параллельного соединения конденсаторов обозначается как Она равна: