Соединение конденсаторов напряжение – » :

Последовательное соединение конденсаторов: особенности и примеры

Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего.

Физические процессы при последовательном соединении

При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим:

q = q1 = q2 = U1 C1 = U2 C2, откуда запишем:

U1/U2 = C2/C1.

Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы:

C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю:

1/С = 1/С1 + 1/С2.

Вычисление общей емкости батареи

При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:

С = C1C2/(C1 + C2).

Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу.

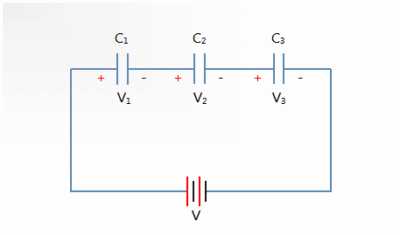
Соединение последовательное конденсаторов

Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта.

Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат. Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством. Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.

Необходимость в последовательном соединении

На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи.

Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример:

Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей.

Решение:

Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом:

1. U1 + U2 + U3 = 12;
2. U1/U2 = 2/1 = 2, откуда запишем: U1 = 2U2;
3. U2/U3 = 4/2 = 2, откуда видно: U2 = 2U

Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее:

4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора. Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение. Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно:

С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ.

Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение. Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.

Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов.

Программные пакеты исследования электрических цепей

Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее. Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы. Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно.

В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей. Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой. Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала.

Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench. Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер. Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка.

И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.

При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата.

Рабочий пример

Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность.

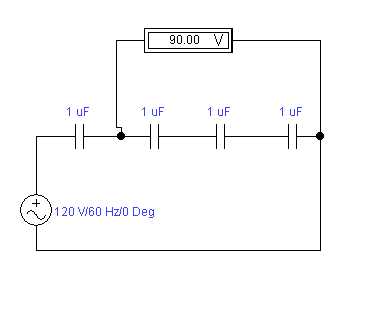
Последовательная батарея конденсаторов

Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить:

1. Частоту (frequency) 50 Гц вместо 60 Гц.
2. Действующее значение напряжения (voltage) 220 вольт вместо 120.
3. Фазу (phase – имитация реактивности) взять согласно своим нуждам.

Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах. Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна. В противном случае результаты заставят надолго поломать голову.

Построение графиков

Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц. При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика. Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу.

Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.

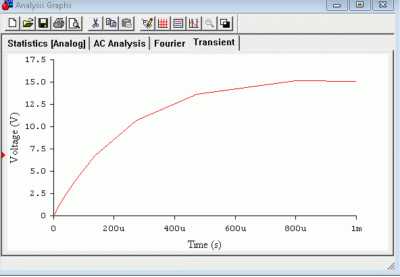
График отклика

Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом:

1. Считается, за три постоянные времени цепи заряд конденсаторов, разряд производится приблизительно на 95%.
2. Легко заметить, точка находится в районе 800 мкс.
3. Следует разделить значение на три, получится постоянная времени батареи последовательно соединенных конденсаторов.

По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи. Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.

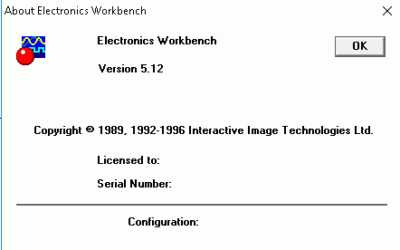
Версия ПО

Раздобыть программный пакет расчета электрики

В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies.

Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim.

Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia.ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:

1. Более 36000 схемных элементов.
2. Возможность разработки печатных плат на основе собранной электрической схемы.
3. Продвинутые опции анализа вместо убогости, демонстрируемой скринам, версии 20-летней давности.

vashtehnik.ru

Последовательное и параллельное соединение.

 Иногда нужно увеличить ёмкость или сопротивление, а подходящих деталей на нужное сопротивление нет, или размеры конструкции не позволяют вставить один большой конденсатор на 3000 мкф. 

В этом случае можно набрать необходимые ёмкость или сопротивление из нескольких деталей, а вместо конденсатора на 3000 микрофарад вставить 3 штуки по 1000 микрофарад.

Для увеличения ёмкости конденсаторы соединяются параллельно.

Для увеличения сопротивления резисторы соединяются последовательно.
Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.

Последовательное соединение — когда детали стоят друг за дружкой, «в очереди», будто за колбасой, потому оно так и называется.

Не путайте эти соединения, для увеличения ёмкости конденсаторы соединяются параллельно, а резисторы для увеличения сопротивления последовательно

!

Со сложением ёмкостей и сопротивлений всё легко.

С параллельным соединением резисторов и последовательным соединением конденсаторов слегка посложнее, но к нашему счастью конденсаторы довольно редко соединяют последовательно, а резисторы параллельно.
Последовательное соединение конденсаторов может понадобиться например в сборке гаусс-гана (электромагнитной стрелялки), когда под рукой конденсаторы только на 400 вольт, а нам нужен 800-вольтовый конденсатор, а их редко где найдёшь и они дорогие.

Параллельное соединение резисторов считается вот по какой формуле:

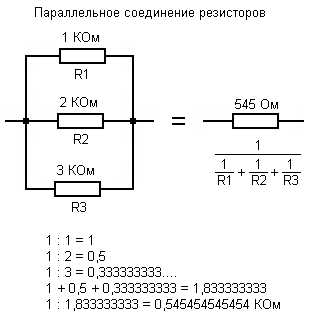
Через три трубы, в которых в каждой по валенку, вода лучше потечёт, чем через одну трубу с одним валенком. Или если в бочке проковырять три дырки, то вода быстрее выльется, чем если бы мы проковыряли одну дырку.

Последовательное соединение конденсаторов считается по той же формуле.

Если два одинаковых конденсатора по 680uF с максимальным напряжением 400В поставить последовательно, то получится конденсатор на 340 uF с напряжением 800 вольт.
Ёмкость уменьшается, зато вырастает максимальное допустимое напряжение, а запасаемая в обеих конденсаторах энергия остаётся та же самая.

shemu.ru

1.4. Способы соединения конденсаторов

Возможны параллельное и последовательное соединения конденсаторов.

П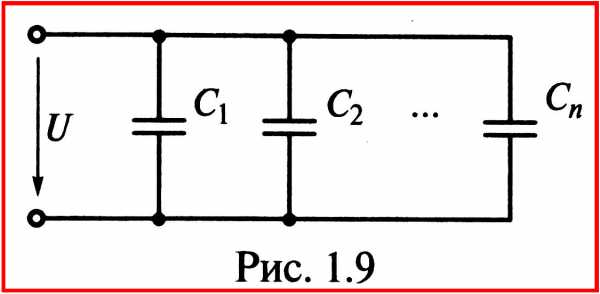рипараллельном соединении (рис. 1.9) все конденсаторы находятся под одним напряжением U, а заряд, который они получают от источника энергии, равен сумме зарядов отдельных конденсаторов

г

деп — число конденсаторов;

к — порядковый номер конденсатора.

Следовательно, общая емкость параллельно соединенных конденсаторов по (1.9)равна сумме емкостей отдельных конденсаторов.

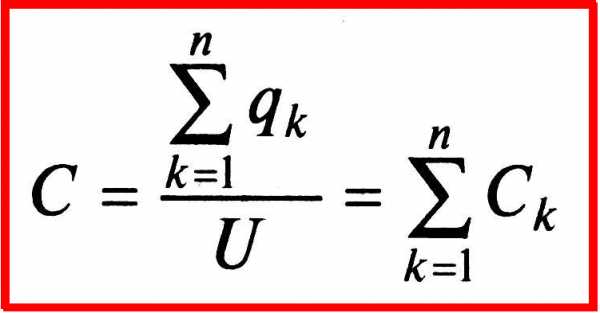
Припоследовательном соединении конденсаторов (рис. 1.10) общее напряжение равно сумме напряжений на отдельных конденсаторах

где п — число конденсаторов;

к — порядковый номер конденсатора.

Но заряд от источника энергии получают лишь внешние электроды двух крайних конденсаторов. На остальных попарно электрически соединенных электродах заряды создаются переносом положительного заряда на один электрод и отрицательного — на второй, которые равны между собой. Таким образом,

при последовательном соединении конденсаторов их заряды одинаковы.

Так как заряд конденсатора равен произведению его емкости на приложенное к нему напряжение

то напряжения на конденсаторах равны

а общая емкость последовательно соединенных конденсаторов — С_общ

Если последовательно соединены n одинаковых конденсаторов каждый емкостью С₀, то их общая емкость будет равна

1.5. Зарядка и разрядка конденсатора

Чтобы изменить скачком энергию конденсатора, необходим источник бесконечной мощности что невозможно.

Поэтому при зарядке и разрядке конденсатора его энергия, а следовательно, и напряжение на нем U_с не могут изменяться скачком. Это условие называется

первым законом коммутации и записывается в виде

(1.16)

где и— моменты времени, непосредственно предшествующий моменту времении непосредственно следующий за моментом времениt, в который начинается зарядка или разрядка конденсатора.

Зарядка конденсатора.

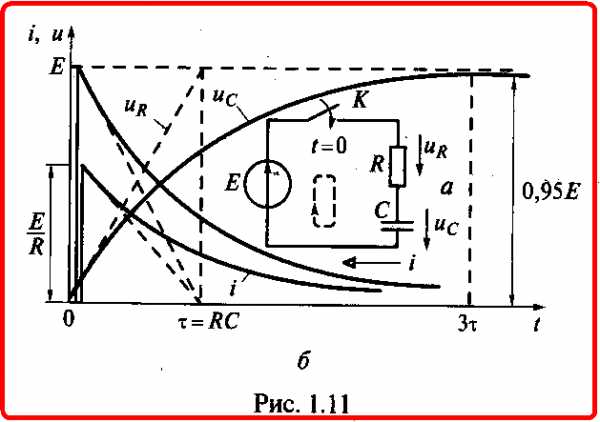
Рассмотрим процесс зарядки конденсатора от источника постоянного напряжения Е=U (см. подразд. 2.7) через резистор сопротивлением R (см. подразд. 2.4) при замыкании в момент времени t=0 ключа К (рис. 1.11, а).

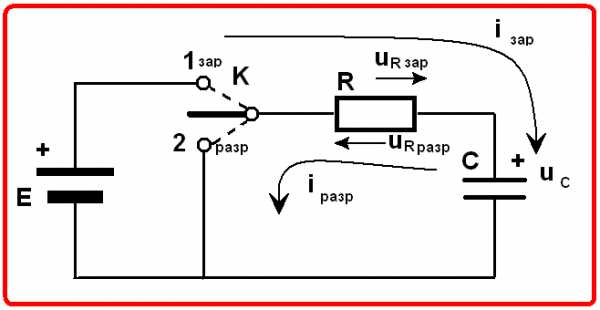
Напряжение источника равно сумме напряжений на резисторе и конденсаторе

или с учетом (2.1) и (1.13)

(1.17)

Разделим переменные в (1.17)

(1.18)

и проинтегрируем (1.18)

(1.19)

где неизвестная постоянная интегрирования записана в виде In А.

Умножив обе части равенства (1.19) на (-1) и заменив разность логарифмов логарифмом частного, после потенцирования получим

или

(1.20)

Для определения постоянной А в (1.20) обратимся к закону коммутации для емкостного элемента (1.16). Примем, что емкостный элемент до замыкания ключа, т. е. и в момент времени /= 0_, не был заряжен. Поэтому

и_с(0_) =

0 = и_с(0₊) = Е+А, откуда А = -Е.

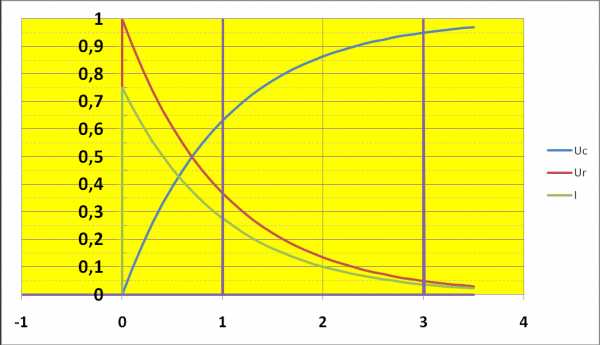
Подставив значение постоянной А в (1.20), найдем напряжение на емкостном элементе во время его зарядки (рис. 1.11, б):

(1.21)

где τ = RC имеет размерность времени (Ом • Ф = Ом • А • с/В = с) и называется постоянной времени цепи. Она определяет скорость переходного процесса.

Напряжение на емкостном элементе (1.21) определяет зависимости от времени тока зарядки и напряжения на резисторе (рис. 1.11,5):

тогда

В

первый момент после замыкания ключа t=0₊ ток заряда в цепи скачком возрастает

от нуля i (0_) = 0

до i (0₊) = E/R.

При малом сопротивлении R в цепи может наблюдаться значительный скачок тока.

Процесс зарядки можно считать практически закончившимся через интервал времени Зτ, (при этом u_c=0,95 E) который может быть достаточно большим, что используется, например, в реле времени — устройствах, срабатывающих по истечении определенного времени.

Разрядка конденсатора.

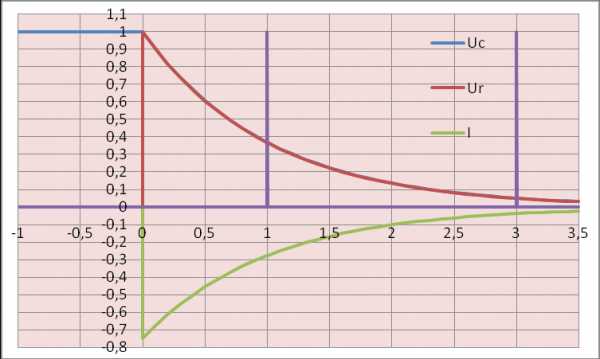
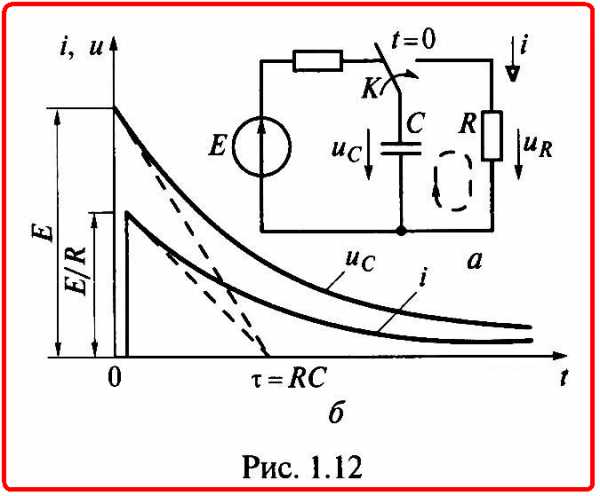
В электрическом поле заряженного емкостного элемента сосредоточена энергия (1.15), за счет которой емкостный элемент в течение некоторого времени сам может служить источником энергии. После подключения емкостного элемента, предварительно заряженного до напряжения и_с= Е, к резистивному элементу сопротивлением R (рис. 1.12, а) ток в цепи будет обусловлен изменением заряда q емкостного элемента (1.13):

(1.22)

где знак минус указывает на то, что ток i — это ток разрядки в контуре цепи, обозначенном на рисунке штриховой линией, направленный навстречу напряжению на емкостном элементе.

Разделим переменные в (1.22)

и проинтегрируем (1.23)

(1.24)

где неизвестная постоянная интегрирования записана в виде (-In А).

После потенцирования (1.24) получим

(1.25)

Для определения постоянной А в (1.25) обратимся к закону коммутации для емкостного элемента (1.16). Так как до коммутации, т.е. и в момент времени t=0_, емкостный элемент был заряжен до напряжения источника, то

и_с (0_) = Е=и_с (0₊)=А.

Подставив значение постоянной А в (1.25), получим зависимость изменения напряжения на емкостном элементе при его разрядке (рис. 1.12,

б):

(1.26)

где τ = RC — постоянная времени цепи.

Ток разрядки найдем по (1.22):

Ток разрядки скачком возрастает от нуля

i(0_) = 0 до i(0+) = E/R, а затем убывает экспоненциально (см. рис. 1.12, б).

Зарядка конденсатора при малых значениях тока и больших значениях ЭДС Ев цепи на рис. 1.12, а позволяет накопить в нем большую энергию, которая может использоваться при разрядке большим током в импульсных источниках.

ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.1. Конденсатор емкостью С = 1 Ф, имеющий заряд q = 1 Кл, в момент времени t= 0 начинает разряжаться через резистор сопротивлением R= 1 Ом (см. рис. 1.12). Определите ток в резисторе в момент времени i=0,5 с.

Ответ: 0,6065 А.

1.2. Сохранив условия задачи 1.1, определите энергию конденсатора в момент времени t=0,5 с.

Ответ: 0,183 Дж.

1.3. Сохранив условия задачи 1.1, определите, какое количество энергии выделится в виде тепла в резисторе к моменту времени t= 0,5 с.

Ответ: 0,317 Дж.

1.4. Плоский конденсатор (см. рис. 1.7, а) состоит из двух листов фольги каждый площадью 20 см², разделенных слоем парафина (см. табл. 1.1) толщиной 0,05 мм с относительной диэлектрической проницаемостью ε_r = 2,1. Определите емкость конденсатора.

Ответ: 0,745 нФ.

5. Дайте определения электрического потенциала и разности электрических потенциалов.

6. Дайте определения линейных и нелинейных емкостных элементов.

7. Определите общую емкость двух конденсаторов, включенных параллельно, емкостью 1 мкФ каждый (см. рис. 1.9).

Ответ: 2 мкФ.

1.8. Определите общую емкость двух конденсаторов, включенных последовательно, емкостью 2 мкФ каждый (см. рис. 1.10).

Ответ: 1 мкФ.

3

studfiles.net

Последовательное и параллельное соединение конденсаторов

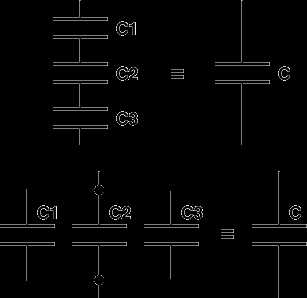
Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
Емкость набора при последовательном соединении конденсаторов будет вычисляться по формуле:

	1	=	1	+	1	+	1	+ …
	C		C1		C2		C3

А общее напряжение будет равняться сумме напряжений всех конденсаторов.
Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.

При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора.

C = C1 + C2 + C3 + C4 + …

Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.

Соединение более двух конденсаторов последовательно редко встречается в реальных схемах. Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления.

Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.

katod-anod.ru

Последовательное соединение конденсаторов: формула :: SYL.ru

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

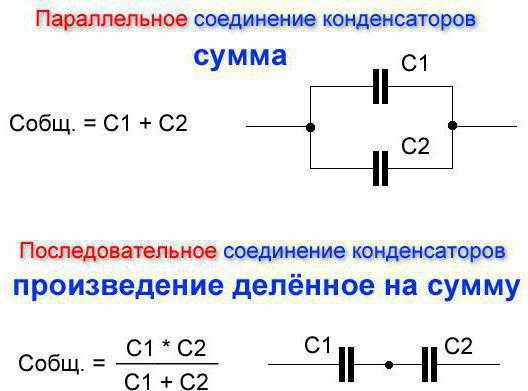
Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

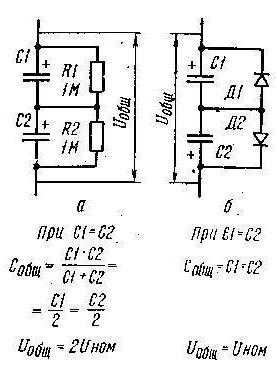Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К₁=К₂=К₃. КЕ – конечная емкость, К – пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ – то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

Н=КЕ/ОЕК

• ОЕ – общая емкость;
• Н – напряжение;
• КЕ – конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

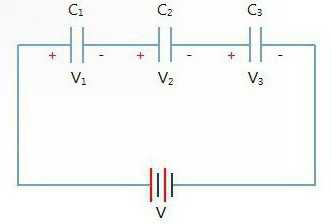Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

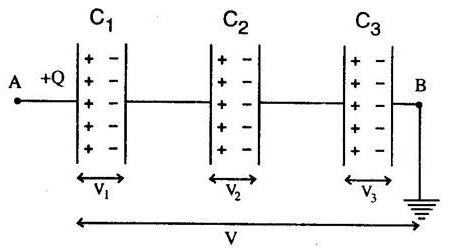Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

www.syl.ru

Параллельное соединение конденсаторов: необходимость и схема

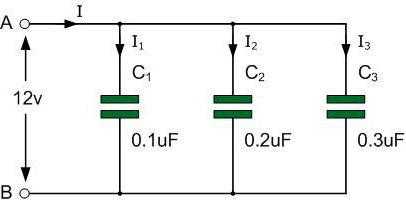
Параллельное соединение конденсаторов – это батарея, где конденсаторы находятся под одинаковым напряжением, а суммарный ток равен полной алгебраической сумме токов указанных элементов.

Основные тезисы

При параллельном включении конденсаторов их ёмкости складываются, позволяя быстро вычислить результат. Рабочее напряжение конденсаторов одинаковое, а заряды складываются воедино. Это следует из формулы, выведенной Вольтой в XVIII веке:

C = q/U, тогда C1 + C2 + … = q1 + q2 + …/U.

Параллельное включение конденсаторов превращается в единственный конденсатор большой ёмкости.

Зачем включать конденсаторы параллельно

• В радиоприёмниках подстройка под частоту волны выполняется коммутацией блоков конденсаторов, обеспечивая ввод резонансного контура в резонанс.
• В фильтрах мощных блоков питания за рабочий цикл предстоит запасать массу энергии. Строить его на индуктивностях экономически нецелесообразно. Применяют параллельный набор из больших электролитических конденсаторов.
• Параллельное включение конденсаторов встречается в измерительных схемах. Эталоны ответвляют на себя часть тока, по величине оценивается номинал — размер ёмкости исследуемого конденсатора.
• Параллельно периодически устанавливаются компенсаторы реактивной мощности. Это устройства, блокирующие выход лишней энергии в питающую сеть. Что предотвращает образование помех, перегрузку генераторов, трансформаторов и избыточный нагрев проводки.

Реактивная мощность сети

Когда работает асинхронный двигатель, происходит расхождение тока и напряжения по фазе. Это отмечается по причине наличия обмотки, показывающей индуктивное сопротивление. Как результат, часть мощности отражается обратно в цепь. Эффект возможно устранить, если индуктивное сопротивление компенсировать ёмкостным. Иной способ – использование синхронных двигателей, эффективен при напряжениях 6 — 10 кВ.

По возможности предприятия должно потреблять всю произведённую собственную реактивную мощность. Но синхронные двигатели не всегда подходят условиям технологических процессов. Тогда ставят конденсаторные установки. Их реактивное сопротивление предвидится равным индуктивностям двигателей. Конечно, в идеале, ведь на производстве условия постоянно меняются и сложно отыскать золотую середину.

Если использовать параллельное соединение конденсаторов и коммутировать при помощи реле должным образом, задача просто решается. Отдельные предприятия за отражённую реактивную мощность тоже платят. При неиспользовании предвидятся экономические потери. Поставщиков энергии можно понять: реактивная мощность забивает линию ЛЭП, нагружает трансформаторы и тогда оборудование не способно выдавать полную нагрузку. Если каждое предприятие станет загружать канал лишним током, экономическое положение энергетиков немедленно пошатнётся.

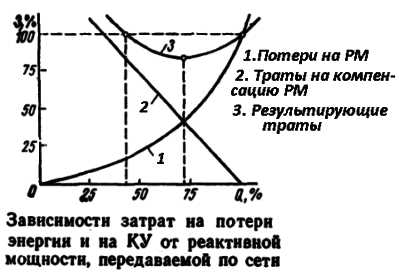
Реле реактивной мощности массово распространены и помогут определить, какую часть конденсаторов включить в работу. Пример графика расчёта затрат приведён на рисунке. Имеется оптимальная точка, перешагивать которую экономически нецелесообразно. Но допускается сделать из-за иных мотивов.

Схема соединения компенсирующих установок

В трёхфазных сетях компенсирующие конденсаторы ставят тройками по двум общеизвестным схемам:

1. Звезда.
2. Треугольник.

Реактивная мощность в этих случаях вычисляется по формулам, представленным на рисунке. Через греческую омегу обозначена круговая частота сети (2 х Пи х 50 Гц). Из соотношений получается, что схема включения конденсаторов треугольником выгоднее: мощность выросла в 3 раза. Объяснение — звезда использует фазное напряжение, в 1,73 раза меньше линейного. Компенсируемая реактивная мощность зависит от квадрата этого параметра.

Из этих соображений трёхфазные конденсаторы всегда изготавливаются треугольником, а под звезду нужно выпросить индивидуальный заказ (три однофазных конденсатора). Есть оборотная сторона медали: на вольтаж 1,05; 3,15; 6,3; 10,5 кВ все конденсаторы однофазные. Допустимо соединять, как заблагорассудится. У звезды, к примеру, меньше рабочее напряжение, значит, каждый конденсатор в отдельности выйдет дешевле. Обе схемы нельзя отнести к параллельным включениям, подобные тройки, впрочем, объединяются в:

• группы;
• секции;
• установки.

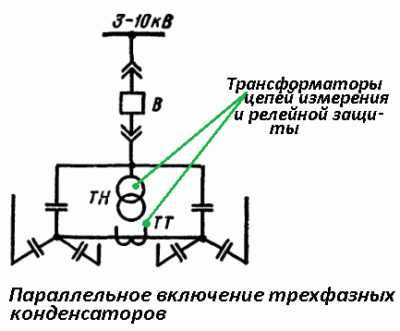
И внутри объединений однофазные конденсаторы могут включаться последовательно и параллельно, а трёхфазные – исключительно параллельно. Рекомендуется номиналы всех отдельных элементов выбирать одинаковы. Это упрощает расчёт, уравнивает нагрузку по частям электрической схемы. Известны установки, где присутствует смешанное соединение по каждой фазе. Образуются параллельные ветви последовательного включения конденсаторов.

Установки выполняют однофазными или трёхфазными. В сетях с напряжением 380 В всегда применяется параллельное соединение конденсаторов. Исключением признаётся случай использования оборудования с одной фазой на 220 В (фазное) и 380 В (линейное). Тогда под прибор ставится индивидуальная установка (или группа), компенсирующая реактивную мощность. В осветительных сетях конденсаторы по большей части ставят уже после выключателя по очевидным причинам. В прочих случаях – в зависимости от особенностей функционирования объекта.

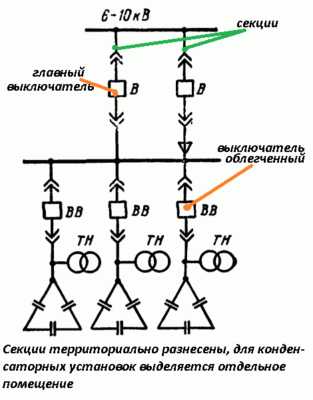
Для напряжений 3, 6 и 10 кВ однофазные конденсаторы включаются обычной или двойной звездой (см. рис.). Один вывод бывает заземлен (глухозаземленная нейтраль). По этой причине допускается использование однофазных конденсаторов, включая с единственным изолированным выводом. В последнем случае нужно убедиться, что нулевой проводник выходит на корпус изделия.

Главный выключатель ставится в определённой секции защищаемого оборудования (территориально) и управляет цепью компенсации в общем, задействует или убирает дополнительное реактивное сопротивление. Если в конкретном секторе технологическое оборудование простаивает, главный выключатель разорвёт цепь компенсации. Конденсаторные установки обычно стоят в выделенном помещении вместе, электрически соединены параллельно. Перед каждой стоит выключатель цепи релейной регуляции для повышения или уменьшения общей ёмкости компенсаторов.

В зависимости от оборудования, используемого предприятием, объем реактивной мощности обусловливает помощь конденсаторных установок, гибко подстраиваемых под имеющиеся нужды. В итоге:

1. Секции оборудования включены параллельно. Это легко понять, если представить бытовые приборы, питаемые одним удлинителем. Все включены параллельно. Но установлены, к примеру, в разных цехах, секторах и пр. Встречаются случаи, когда одна крупная энергетическая установка (допустим, генератор ГЭС) делится на сравнительно независимые секции.
2. Конденсаторные установки включены параллельно, но, как правило, в одном месте, чтобы удавалось автоматически или вручную легко регулировать общую ёмкость посредством коммутации выключателей облегчённого типа. Один конденсатор может работать для компенсации реактивной мощности любой из секций либо сразу обеих.

Особенности конденсаторной защиты

Главные выключатели, как правило, используются при авариях и вырубают сразу целую секцию оборудования. Конденсаторные установки набираются в секции параллельным включением. Тогда главный выключатель сразу вырубит подобную «батарею». А прочие секции конденсаторных установок останутся в действии. Важно понять, что защитное оборудование, как и защищаемое, удаётся группировать разными методами. В зависимости от удобства и экономической обоснованности.

Облегчённые выключатели применяются, как правило, в цепях регуляции. Управляются через реле и повышают или понижают общую ёмкость конденсаторных установок. В качестве главного выключателя выбирается вакуумный или элегазовый.

Особенностью цепей выше 10 кВ считается использование однофазных конденсаторов, собираемых по схеме звезды или треугольника, в каждой ветви которых стоит параллельно-последовательная группа ёмкостей (см. рис.). При наличии изделий с высоким рабочим напряжением допустимо делать наоборот, применять последовательно-параллельно включение. Тогда рабочие напряжения конденсаторов выбираются так, чтобы количество групп, включенных друг за другом оказалось минимальным. Напряжение на каждом из элементов, естественно, увеличивается. Для справки: последовательное соединение конденсаторов.

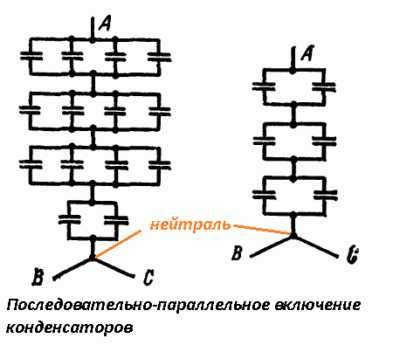
Если сделать все по описанному распорядку, при выходе из строя любого элемента цепи компенсации реактивной мощности прочие продолжат работать в относительно щадящем режиме. Разумеется, параметры цепи нужно контролировать, а эксплуатирующий персонал, согласно методикам, ведёт проверку конденсаторных установок на исправность. При проектировании нужно учесть небольшую особенность:

Чем больше в цепи компенсации последовательных групп конденсаторов, тем сложнее для каждой обеспечить равномерное распределение напряжения. В частности, возможны частые перегрузки определённого сегмента.

Вдобавок сложные электрические соединения непросто проверять обслуживающему персоналу. Витиеватая схема плохо поддаётся монтажу, часты ошибки. Идеальным считается параллельное соединение конденсаторных блоков по каждой фазе. Тогда и монтировать легко, и методика проверки упрощается максимально.

Разряд конденсаторов

Включенные параллельно конденсаторы обладают большой ёмкостью, при прекращении работы на них остаётся заряд. Это возможно прочувствовать, если коснуться штекера только что выключенной старенькой дрели. В новых моделях фильтр устроен так, что цепь разряжается через резистор, и подобного не наблюдается.

Для снижения напряжения допустимо использовать и индуктивности, включенные параллельно конденсаторам. В этом случае сопротивление заземления переменному току весьма велико, а для постоянного — несложно преодолеть этот участок. В период работы оборудования ток здесь мал, потери невелики. После останова технологической линии заряд понемногу сливается через высокоомный резистор или индуктивность. Разумеется, не запрещено поставить в цепи заземления реле, замыкающее контакты только после выключения всех устройств. Конструкция дороже и требует автоматизации.

Процесс разряда цепи важен с точки зрения обеспечения безопасности. Представим: конденсатор, заряжённый от розетки, долго хранит разность потенциалов и представляет опасность для окружающих. В однофазных сетях с напряжением 220 В разряд выполняется через входные фильтры при условии, что корпус правильно заземлён. Сопротивление в цепи, включенной параллельно конденсаторам, определяется по формуле, представленной ниже.

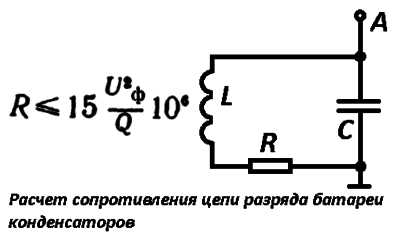
Под Q подразумевается реактивная мощность установки в варах (ВАР), а Uф – фазное напряжение. Легко показать, что формула дана из расчёта времени разряда: Q зависит линейно от ёмкости, будучи перенесена в левую часть формулы, даст постоянную времени RC. За три таких периода батарея разряжается на 97%. Исходя из указанных условий можно найти и параметры индуктивности. А лучше – последовательно с нею включить резистор, как часто и делается в реальных схемах.

vashtehnik.ru

Соединение конденсаторов.

Соединение конденсаторов бывает последовательным и параллельным.

1) Последовательное соединение.

При последовательном соединении заряды на всех конденсаторах одинаковые, а напряжения разные (рисунок).

Рисунок. Последовательное соединение конденсаторов.

Мы имеем:

В итоге получаем

2) Параллельное соединение.

При параллельном соединении напряжения на всех конденсаторах одинаковые =U, а заряды – разные (рисунок ниже).

Рисунок. Параллельное соединение конденсаторов.

В итоге имеем:

Энергия системы неподвижных точечных зарядов.

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рисунок. К определению энергии системы зарядов.

Рассмотрим сначала систему, состоящую из двух точечных зарядов (рисунок). Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q₂ к q₁ либо q₁ к q₂. В обоих случаях совершается одинаковая работа:

В последней формуле — потенциал поля 1-го заряда в том месте, где находится второй заряд;- потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

.

Рисунок. Система трех неподвижных точечных зарядов.

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов (рисунок выше) может быть представлена в виде:

В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле:

Энергия заряженного проводника и заряженного конденсатора.

Поверхность заряженного проводника (рисунок ниже) при равновесии зарядов является эквипотенциальной (φ_i=φ = const). Следовательно, энергия заряженного проводника: , гдеq — заряд проводника.

Рисунок. Заряженный проводник.

Конденсатор представляет собой пару заряженных проводников (рисунок), поэтому имеем:

Рисунок. Заряженный конденсатор.

А поскольку заряд , тоэнергия заряженного конденсатора может быть представлена одной из трех формул:

Энергия электростатического поля.

Выразим энергию заряженного конденсатора через величины, характеризующие электрическое поле, локализованное в пространстве между его обкладками – напряженность поля Е и объем V, занятый полем. Имеем для напряженности поля:

, где .

Воспользовавшись формулой для емкости плоского конденсатора , находим:

, где — объём конденсатора, откуда следует, что

Мы видим, что энергия электрического поля прямо пропорциональна квадрату его напряженности Е и объёму V, занятому полем. Величину энергии поля, отнесенной к единице объема, называют плотностью энергии:

— плотность энергии электрического поля.

studfiles.net