Схема делитель напряжения – Voltage Divider Calculator

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

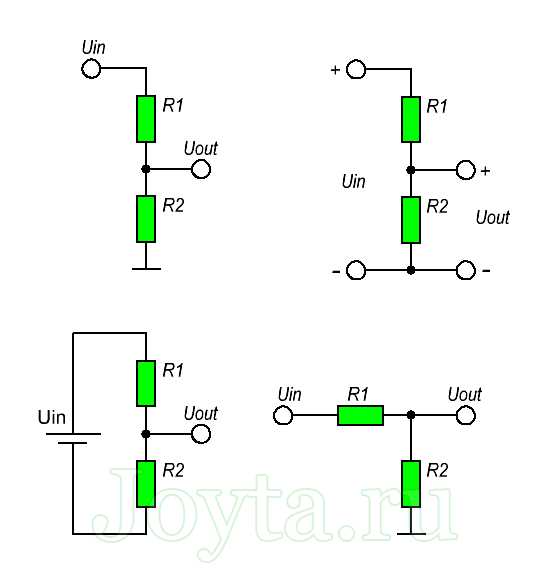Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

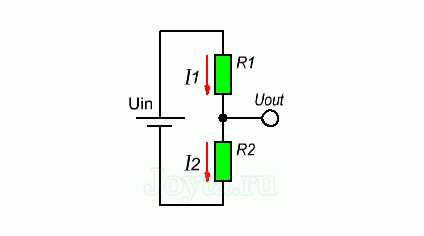Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн



 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

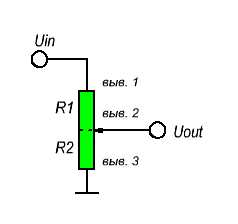
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

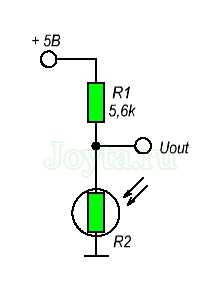
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

www.joyta.ru

схема и расчёт [Амперка / Вики]

Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов.

В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V_out? Или эквивалентный вопрос: какое напряжение покажет вольтметр?

Ток, протекающий через R1 и R2 одинаков пока к выходу V_out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:

Таким образом, сила тока протекающая через резисторы

Теперь, когда нам известен ток в

R2, расчитаем напряжение вокруг него:

Или если отавить формулу в общем виде:

Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.

Применение делителя для считывания показаний датчика

Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.

Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V_out будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.

Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V_out.

Подключение нагрузки

С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):

В этом случае V_out уже не может быть расчитано лишь на основе значений V_in, R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление

В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:

Подставив значение в общую формулу расчёта

V_out, получим:

Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.

Пропорция сохраняется, V_out не меняется:

А потери уменьшатся:

Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.

Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1

равна:

А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.

Применимость

Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.

Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.

Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.

Если потребление тока нагрузкой неравномерно во времени, V_out также будет неравномерным.

wiki.amperka.ru

расчет, теория и принцип действия

Существуют два вида сопротивления – переменное и постоянное, а делитель напряжения на резисторах нужен для защиты электроприборов. Например, светодиодам необходим небольшой ток, в противном случае они могут перегореть. Для ограничения тока в электрическую цепь вставляется резистор, следовательно ток уменьшается и светодиоды работают в штатном режиме. Резистор – радиоэлемент для увеличения сопротивления электрической цепи. Его ставят с целью понижения напряжения или тока.

Постоянное сопротивление – резисторы, которые не изменяют свой номинал. Если подобное происходит, значит резистор вышел из строя. Переменные резисторы могут менять свое сопротивление в процессе своей работы. Они оснащены специальный бегунок, который и регулирует сопротивление. На основе их изготавливают самые различные регуляторы.

В статье будут подробно рассмотрены типы подключения и что такое делитель напряжения. Также в статье содержится видеоролик на данную тему и скачиваемый файл с дополнительной информацией.

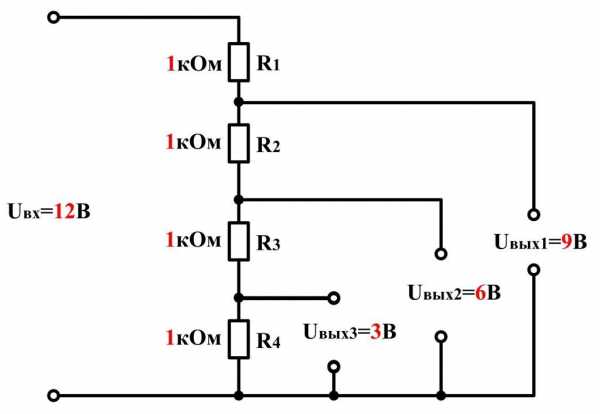
Делитель напряжения.

Соединение резисторов

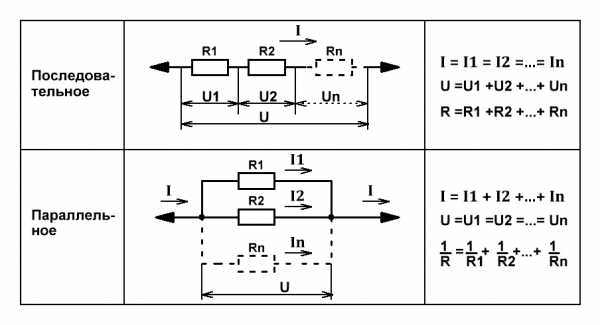
Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно.

Последовательное соединение резисторов

Последовательное соединение.

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее. То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток. Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.

Интересно почитать: принцип действия и основные характеристики варисторов.

Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает. Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле: Rобщ = R1 + R2 + R3+…+ Rn.

Последовательное и параллельное соединение резисторов.

Параллельное соединение резисторов

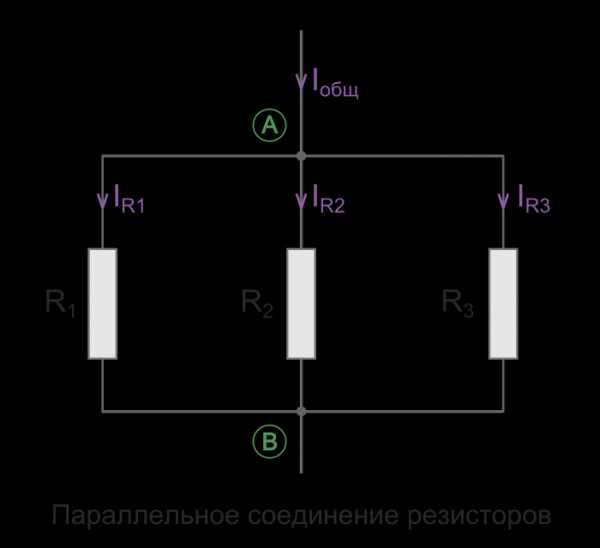Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)

Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn. Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток.

Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.

Каждый вид соединения находится под одинаковым напряжением:

• U = U1 = U2; Суммарная сила тока равняется суммарному значению тока каждого участка
• I = I1 + I2; Сопротивление цепи равно сумме величина обратных сопротивлению участка:
• 1/R = 1/R1 + 17R2 + . . . + 1/Rn; Сила тока пропорциональна сопротивлению каждого участка
• I1/I2=R2/R1.

Примеры расчета

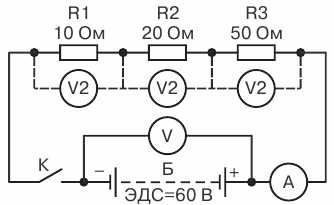
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.  R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В. А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением. На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.

Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:

• Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
• Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
• После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
• Рассчитывают сопротивления полученной схемы.

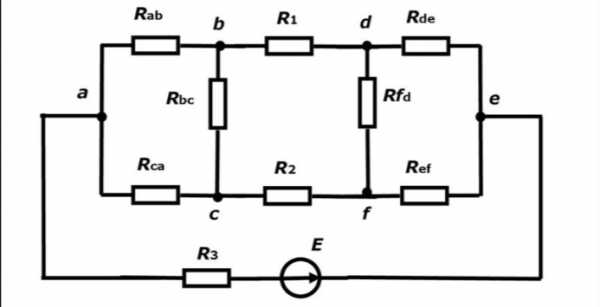
Схема смешанного подключения.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два. Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому: I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.

Параллельное и последовательное соединение резисторов, решение задач

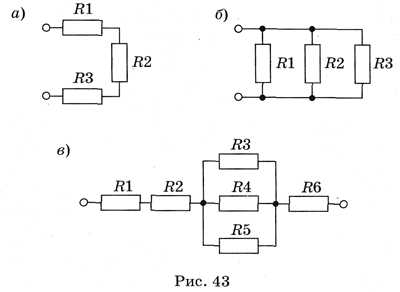Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.

Материал в тему: описание и область применения подстроечного резистора.

Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.

Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Почитать материал по теме: что такое SMD резисторы.

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

• Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
• Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Типы подключений.

Расчет гасящего резистора

В схемах аппаратуры связи часто возникает необходимость подать на потребитель меньшее напряжение, чем дает источник. В этом случае последовательно с основным потребителем включают дополнительное сопротивление, на котором гасится избыток напряжения источника. Такое сопротивление называется гасящим.

Напряжение источника тока распределяется по участкам последовательной цепи прямо пропорционально сопротивлениям этих участков. Рассмотрим схему включения гасящего сопротивления:

1. Полезной нагрузкой в этой цепи является лампочка накаливания, рассчитанная на нормальную работу при величине напряжения Uл= 80 в и тока I =20 ма.
2. Напряжение на зажимах источника тока U=120 в больше Uл, поэтому если подключить лампочку непосредственно к источнику, то через нее пройдет ток, превышающий нормальный, и она перегорит.
3. Чтобы этого не случилось, последовательно с лампочкой включено гасящее сопротивление R гас.

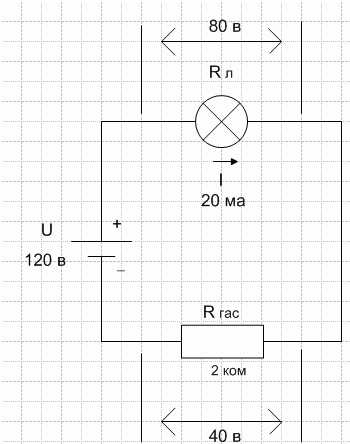
Схема включения гасящего сопротивления резистора.

Расчет величины гасящего сопротивления при заданных значениях тока и напряжения потребителя сводится к следующему:

– определяется величина напряжения, которое должно быть погашено:

Uгас = Uист – Uпотр,

Uгас = 120 – 80 = 40в

определяется величина гасящего сопротивления

Rгас = Uгас / I

Rгас = 40 / 0,020 = 2000ом = 2 ком

Далее необходимо рассчитать мощность, выделяемую на гасящем сопротивлении по формуле

P = I2 * Rгас

P = 0,0202 * 2000 = 0,0004 * 2000 = 0,8вт

Зная величину сопротивления и расходуемую мощность, выбирают тип гасящего сопротивления.

Практическое применение параллельного и последовательного соединения

Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.

Приведем пример работы делителя напряжения на фоторезисторе. Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Диапазон изменения выходного напряжения.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.

Более подробно о делителях напряжения можно узнать из скачиваемого файла правила подключения проводников. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.

Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vк.coм/еlеctroinfonеt. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.elektroznatok.ru

www.themechanic.ru

www.electrono.ru

www.hightolow.ru

www.sxemotehnika.ru

Как вам статья?Poll Options are limited because JavaScript is disabled in your browser.

electroinfo.net

Делитель напряжения | Расчет делителя напряжения

Делитель напряжения (теория)

Для того, чтобы поделить напряжение, нам потребуется два и более резисторов.  Для начала рассмотрим вот такой рисунок:

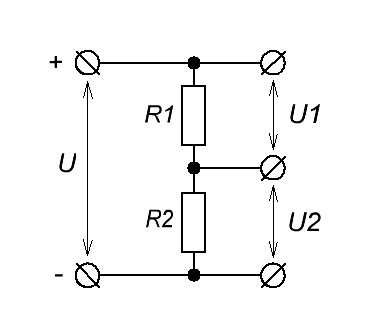
Наш схемка состоит из двух резисторов, подключенных последовательно. На эти резисторы подается напряжение. Оно может быть как переменное, так и постоянное. Назовем его U. Пропуская ток через эти резисторы, у нас сразу же в дело вступит Закон Ома.  Мы знаем, что если резисторы соединены последовательно, то их общее  сопротивление  будет равняться сумме их номиналов. То есть получается, что

R_общее=R1+R2

I=U/R_общее

то есть можно написать

I=U/(R1+R2)

При последовательном соединении резисторов, сила тока – I, проходящая через каждый резистор одинакова – это есть закон последовательного соединения резисторов. Так, разобрались. У нас каждый резистор обладает каким-то своим сопротивлением. Отсюда напрашивается вывод из Закона Ома, что на каждом сопротивлении у нас будет какое-то свое напряжение, которое зависит от сопротивления резистора.

На сопротивлении R1  у нас будет напряжение U1, а на сопротивлении R2  у нас будет напряжение U2

I=U2/R2=U1/R1=U/(R1+R2)

 

Давайте найдем значения U1 и U2. Вы все учились в школе и сможете без проблем решить эту уравнение. Умножаем, сокращаем и в конце концов получаем, что

U1=UxR1/(R1+R2)

U2=UxR2/(R1+R2)

А вы знаете, что если сложить правые части уравнения, получим U ? Не верите? Проверьте! Отсюда получаем, что U=U1+U2.

Короче говоря простым языком чайника: если резисторы включены в цепь последовательно, то на каждом резисторе падает напряжение (падает, значит на концах резистора имеется это напряжение) и сумма падений напряжений на всех резисторах будет равняться напряжению источника (батарейки, блока питания или какого-нибудь источника ЭДС). Мы разделили напряжение источника U на два  разных напряжения U1 и U2.

Для лучшего понимания давайте рассмотрим еще одну цепь, состоящую из n резисторов

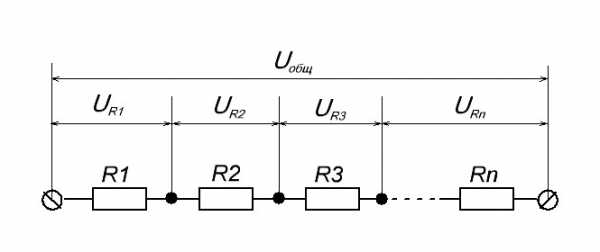
На схеме выше мы видим резисторы, которые соединены последовательно. Чему будет равняться U_общ ? Так как резисторы соединены последовательно, следовательно, на каждом резисторе падает какое-то напряжение. Сумма падений напряжения на всех резисторах будет равняться U_общ . В нашем случае формула запишется как

Делитель напряжения (практика)

Итак у нас имеются вот такие два резистора и наш любимый мультиметр:

Замеряем сопротивление маленького резистора, R1=109,7 Ом.

Замеряем сопротивление большого резистора R2=52,8 Ом.

Выставляем на блоке питания ровно 10 Вольт. Замеряем напряжение с помощью мультиметра (не смотрите на показания блока питания, он обладает бОльшей погрешностью, чем мультиметр).

Цепляемся блоком питания за эти два резистора, запаянные последовательно. Напомню, что на блоке ровно 10 Вольт. Показания амперметра на блоке питания тоже немного неточны. Силу тока мы будем замерять с помощью мультиметра.

Замеряем напряжение на большом резисторе. На нем падает 3,21 Вольт.

Замеряем напряжение на маленьком резисторе. На нем падает 6,77 Вольт

Ну что, с математикой думаю у всех в порядке. Складываем эти два значения напряжения 3,21+6,77 = 9,98 Вольт. А куда делись еще 0,02 Вольта? Спишем на погрешность щупов и средств измерений. Вот наглядный пример того, что мы смогли разделить напряжение на два разных напряжения.

Сила тока при последовательном соединении сопротивлений

Давайте же  убедимся, что сила тока при последовательном соединении резисторов везде одинакова. 0,04 А или 40 мА.

Убедились? 🙂

Переменный резистор в роли делителя напряжения

Для того, чтобы плавно делить напряжение, у нас есть переменный резистор в роли делителя напряжения. Его еще также называют потенциометром.

Его обозначение на схеме выглядит вот так:

Принцип такой: между двумя крайними контактами постоянное сопротивление. Сопротивление относительно среднего контакта по отношению к крайним может меняться  в зависимости от того, куда мы будем крутить крутилку этого переменного резистора. Этот резистор рассчитан на мощность 1Вт и имеет полное сопротивление 330 Ом. Давайте посмотрим, как он будет делить напряжение.

Так как мощность небольшая , всего 1 Вт, то не будем нагружать его большим напряжением. Формула мощности P=IU.  Ток потребления из закона Ома I=U/R. Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого  резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.

Для этого выставляем на блоке напряжение в 1 Вольт и цепляемся к нашему резистору по двум крайним контактам.

Крутим крутилку в каком-нибудь произвольном направлении и останавливаем ее. Замеряем напряжение между левым и средним контактом:

0,34 Вольта

Замеряем напряжение между средним и правым контактом

0,64 Вольта

Суммируем напряжение  и получаем 0,34+0,64=0,98 Вольт. 0,02 Вольта опять где-то затерялись, скорее всего на щупах, так как они тоже обладают сопротивлением.

Заключение

В настоящее время делители напряжения создаются с помощью абсолютно других законов электроники. Это может быть полупроводниковые схемы или даже схемы с использованием микроконтроллеров. Но, если требуется быстро получить делитель напряжения и изменять малую мощность напряжения или сигнала в электронике, то делитель напряжения  на резисторах вам пригодится как нельзя кстати.

www.ruselectronic.com

Делитель напряжения: устройство, принцип работы, назначение

Часто при проектировании электронной схемы возникает необходимость получить точку с определенным уровнем сигнала. Например, создать опорную точку или смещение напряжения, запитать маломощный потребитель, понизив его уровень и ограничить ток. Именно в таких случаях нужно использовать делитель напряжения. Что это такое и как его рассчитать мы расскажем в этой статье.

Определение

Делителем напряжения называется прибор или устройство, которое понижает уровень выходного напряжения относительно входного, пропорционально коэффициенту передачи (он будет всегда ниже нуля). Такое название он получил, потому что представляет собой два и более последовательно соединенных участка цепи.

Они бывают линейными и нелинейными. При этом первые представляют собой активное или реактивное сопротивление, в которых коэффициент передачи определяется соотношением из закона Ома. К ярко выраженным нелинейным делителям относят параметрические стабилизаторы напряжения. Давайте разберемся как устроен это прибор и зачем он нужен.

Виды и принцип действия

Сразу стоит отметить, что принцип работы делителя напряжения в общем одинаков, но зависит от элементов, из которых он состоит. Различают три основных вида линейных схем:

• резистивные;
• емкостные;
• индуктивные.

Наиболее распространен делитель на резисторах, из-за своей простоты и легкости расчетов. На его примере и рассмотрим основные сведения об этом устройстве.

У любого делителя напряжения есть Uвходное и Uвыходное, если он состоит из двух резисторов, если резисторов три, то выходных напряжений будет два, и так далее. Можно сделать любое количество ступеней деления.

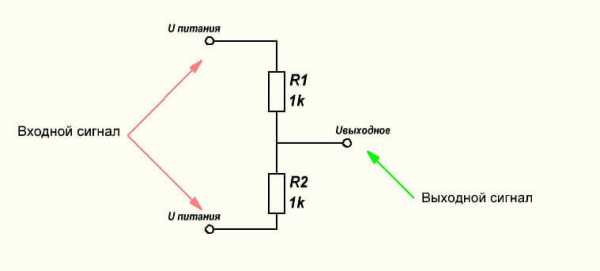
Uвходное равно напряжению питания, Uвыходное зависит от соотношения резисторов в плечах делителя. Если рассматривать схему на двух резисторах, то верхним, или как его еще называют, гасящим плечом будет R1. Нижним или выходным плечом будет R2.

Допустим у нас Uпитания 10В, сопротивление R1 — 85 Ом, а сопротивление R2 — 15 Ом. Нужно рассчитать Uвыходное.

Тогда:

U=I*R

Так как они соединены последовательно, то:

U1=I*R1

U2=I*R2

Тогда если сложить выражения:

U1+U2=I(R1+R2)

Если выразить отсюда ток, получится:

Подставив предыдущее выражение, имеем следующую формулу:

Посчитаем для нашего примера:

Делитель напряжения может быть выполнен и на реактивных сопротивлениях:

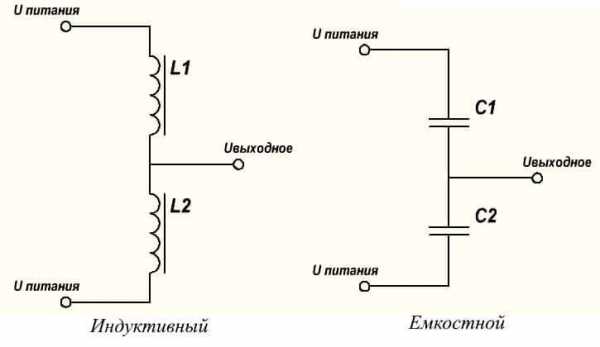
Тогда расчеты будут аналогичны, но сопротивления рассчитывают по нижеприведенным формулам.

Для конденсаторов:

Для индуктивности:

Особенностью и различием этих видов делителей является то, что резистивный делитель может использоваться в цепях переменного и в цепях постоянного тока, а емкостной и индуктивный только в цепях переменного тока, потому что только тогда будет работать их реактивное сопротивление.

Интересно! В некоторых случаях емкостной делитель будет работать в цепях постоянного тока, хорошим примером является использование такого решения во входной цепи компьютерных блоков питания.

Использование реактивного сопротивления обусловлено тем, что при их работе не выделяется такого количества тепла, как при использовании в конструкциях активных сопротивлений (резисторов)

Примеры использования в схеме

Есть масса схем, где используются делители напряжения. Поэтому мы приведем сразу несколько примеров.

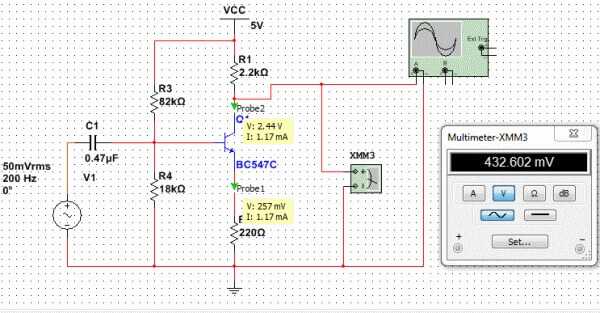
Допустим мы проектируем усилительный каскад, на транзисторе, который работает в классе А. Исходя из его принципа действия, нам нужно задать на базе транзистора такое напряжение смещения (U1), чтобы его рабочая точка была на линейном отрезке ВАХ, при этом чтобы ток через транзистор не был чрезмерным. Допустим нам нужно обеспечить ток базы в 0,1 мА при U1 в 0,6 Вольта.

Тогда нам нужно рассчитать сопротивления в плечах делителя, а это обратный расчет относительно того, что мы привели выше. В первую очередь находят ток через делитель. Чтобы ток нагрузки не сильно влиял на напряжения на его плечах, зададим ток через делитель на порядок выше тока нагрузки в нашем случае 1 мА. Uпитания пусть будет 12 Вольт.

Тогда общее сопротивление делителя равняется:

Rд=Uпитания/I=12/0.001=12000 Ом

R2/R=U2/U

Или:

R2/(R1+R2)=U2/Uпитания

10/20=3/6

20*3/6=60/6/10

R2=(R1+R2)*U1/Uпитания=12000*0.6/12=600

R1=12000-600=11400

Проверим расчеты:

U2=U*R2/(R1+R2)=12*600/12000=7200/12000=0,6 Вольт.

Соответственное верхнее плече погасит

U2=U*R2/(R1+R2)=12*11400/12000=136800/12000=11,4 Вольт.

Но это еще не весь расчет. Для полного расчета делителя нужно определить и мощность резисторов, чтобы они не сгорели. При токе 1 мА на R1 выделится мощность:

P1=11,4*0,001=0,0114 Ватт

А на R2:

P2=0,6*0,001=0,000006 Ватт

Здесь она ничтожно мала, но представьте какой мощности нужны были бы резисторы, если бы ток делителя составлял 100 мА или 1 А?

Для первого случая:

P1=11,4*0,1=1,14 Ватт

P2=0,6*0,1=0,06 Ватт

Для второго случая:

P1=11,4*1=11,4 Ватт

P2=0,6*1=0,6 Ватт

Что уже немалые для электроники цифры, в том числе и для использования в усилителях. Это не эффективно, поэтому в настоящее время используют импульсные схемы, хотя и линейные продолжают использоваться либо в любительских конструкциях, либо в специфичном оборудовании с особыми требованиями.

Второй пример – это делитель для формирования Uопорного для регулируемого стабилитрона TL431. Они применяются в большинстве недорогих блоков питания и зарядных устройств для мобильных телефонов. Схема подключения и расчетные формулы вы видите ниже. С помощью двух резисторов здесь создается точка с Uопорным в 2.5 вольта.

Еще один пример — это подключение всевозможных датчиков к микроконтроллерам. Рассмотрим несколько схем подключения датчиков к аналоговому входу популярного микроконтроллера AVR, на примере семейства плат Arduino.

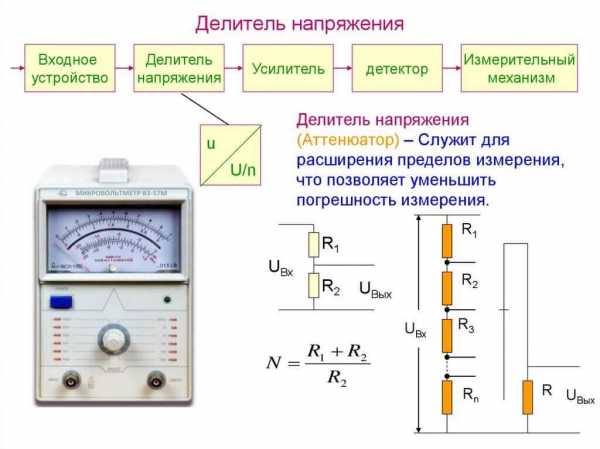
В измерительных приборах есть разные пределы измерения. Такая функция реализуется также с помощью группы резисторов.

Но на этом область применения делителей напряжения не заканчивается. Именно таким образом гасятся лишние вольты при ограничении тока через светодиод, также распределяется напряжение на лампочках в гирлянде, и также вы можете запитать маломощную нагрузку.

Нелинейные делители

Мы упомянули, что к нелинейным делителям относится параметрический стабилизатор. В простейшем виде он состоит из резистора и стабилитрона. У стабилитрона условное обозначение на схеме похоже на обычный полупроводниковый диод. Разница лишь в наличии дополнительной черты на катоде.

Расчет происходит, отталкиваясь от Uстабилизации стабилитрона. Тогда если у нас есть стабилитрон на 3.3 вольта, а Uпитания равно 10 вольт, то ток стабилизации берут из даташита на стабилитрон. Например, пусть он будет равен 20 мА (0.02 А), а ток нагрузки 10 мА (0.01 А).

Тогда:

R=12-3,3/0,02+0,01=8,7/0,03=290 Ом

Разберемся как работает такой стабилизатор. Стабилитрон включается в цепь в обратном включении, то есть если Uвыходное ниже Uстабилизации – ток через него не протекает. Когда Uпитания повышается до Uстабилизации, происходит лавинный или туннельный пробой PN-перехода и через него начинает протекать ток, который называется током стабилизации. Он ограничен резистором R1, на котором гасится разница между Uвходным и Uстабилизации. При превышении максимального тока стабилизации происходит тепловой пробой и стабилитрон сгорает.

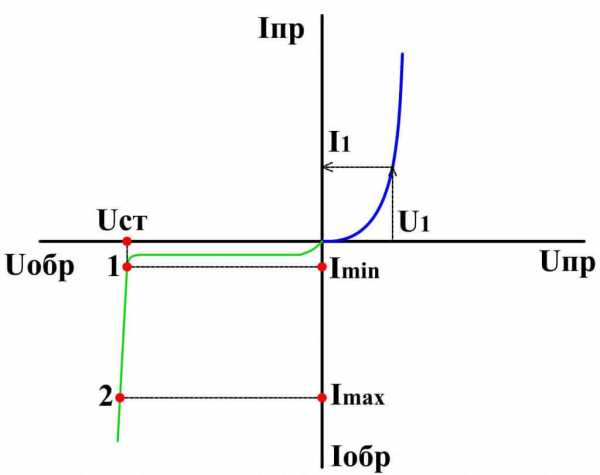
Кстати иногда можно реализовать стабилизатор на диодах. Напряжение стабилизации тогда будет равно прямому падению диодов или сумме падений цепи диодов. Ток задаете подходящий под номинал диодов и под нужды вашей схемы. Тем не менее такое решение используется крайне редко. Но такое устройство на диодах лучше назвать ограничителем, а не стабилизатором. И вариант такой же схемы для цепей переменного тока. Так вы ограничите амплитуду переменного сигнала на уровне прямого падения — 0,7В.

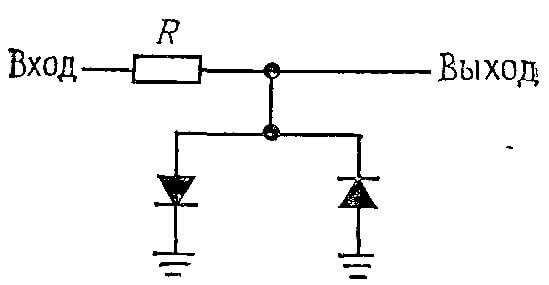
Вот мы и разобрались что это такое делитель напряжения и для чего он нужен. Примеров, где применяется любой из вариантов рассмотренных схем можно привести еще больше, даже потенциометр в сущности является делителем с плавной регулировкой коэффициента передачи, и часто используется в паре с постоянным резистором. В любом случае принцип действия, подбора и расчетов элементов остается неизменным.

Напоследок рекомендуем посмотреть видео, на котором более подробно рассматривается, как работает данный элемент и из чего состоит:

Материалы по теме:

samelectrik.ru

Делитель напряжения на резисторах: онлайн калькулятор расчета

Схема делителя напряжения является простой, но в тоже время фундаментальной электросхемой, которая очень часто используется в электронике. Принцип работы ее прост: на входе подается более высокое входное напряжение и затем оно преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула расчета выходного напряжения основана на законе Ома и приведена ниже.

Классическая формула делителя напряжения

где:

• U_вх. — входное напряжение источника, В;
• U_вых. — выходное напряжение, В;
• R₁ — сопротивление 1-го резистора, Ом;
• R₂ — сопротивление 2-го резистора, Ом.

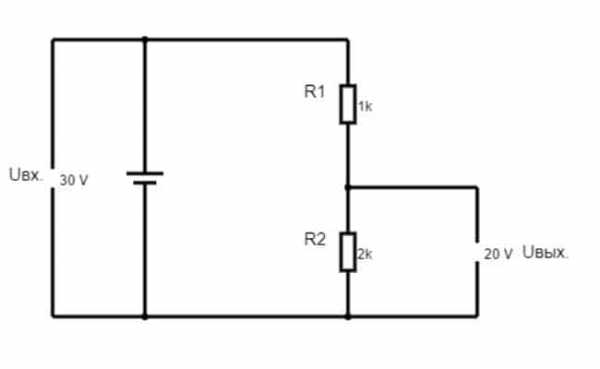Схема классического делителя напряжения на 2 резистора

В калькулятор ниже введите любые три известных значения U_вх., U_вых. и R₁  и нажмите «Рассчитать», чтобы найти значение R₂.

Упрощения

Существует несколько обобщений, которые следует учитывать при использовании делителей напряжения. Это упрощения, которые упрощают оценку схемы деления напряжения.

Во-первых, если R₂ и R₁ равны, то выходное напряжение вдвое меньше входного напряжения. Это верно независимо от значений резисторов.

Итак, если R₁ = R₂, то получаем следующее уравнение:

Формула делителя напряжения, если сопротивления равны

Во-вторых, если R₂ на порядок больше чем R₁, то выходное напряжение U_вых будет очень близко к U_вх., то есть U_вх. ≈ U_вых. А на R₁ будет очень мало напряжения.

Формула делителя напряжения, если R2 на порядок больше R1

Во-третьих, если наоборот R₁ на порядок больше чем R₂, то U_вых будет очень маленьким по сравнению с U_вх, то есть будет стремиться к нулю. Практически все входное напряжение упадет в таком случае на R₁.

Вы можете воспользоваться онлайн калькулятором ниже, чтобы проверить как саму классическую формулу делителя напряжения, представленную на рисунке 1, так и вышеприведенные упрощения этой формулы.

www.asutpp.ru

Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.

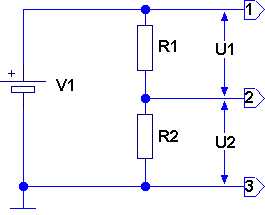
Рис. 1. Схема простейшего делителя напряжения

Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам

U_R1 = I*R1; U_R2 = I*R2       (1)

где U_R1, U_R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U_R1, U_R2 на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:

I = U_пит / (R1 + R2)       (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис.2)

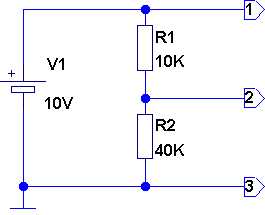
Рис. 2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U_R1 = 0,0002*10000 = 2 В;
U_R2 = 0,0002*40000 = 8 В.

Если из формулы (1) вывести ток:

I = U_R1 / R1       (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U_R1 / R1 = U_пит / (R1 + R2)

Откуда

U_R1 = U_пит * R1 / (R1 + R2)       (4)

Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:

U_R1 = 10 * 10000 / (10000+40000) = 2 В,

и на резисторе R2:

U_R2 = 10 * 40000 / (10000+40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R_c = 1/(2 * π * f * C)

Здесь R_c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U_С1 = U_пит * С2 / (С1 + С2)       (5)

U_С1 = 10 * 40*10^-9 / (10*10^-9+40*10^-9) = 8 В,
U_С2 = 10 * 10*10^-9 / (10*10^-9+40*10^-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R_L = 2 * π * f * L

Здесь R_c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:

U_L1 = U_пит * L1 / (L1 + L2)       (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U_L1 = 10 * 10*10^-6 / (10*10^-6+40*10^-6) = 2 В,
U_L2 = 10 * 40*10^-6 / (10*10^-6+40*10^-6) = 8 В.

В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.

BACK

zpostbox.ru