Ток через катушку: Катушка индуктивности в цепи постоянного и переменного тока

Катушка индуктивности в цепи постоянного и переменного тока

Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?

Катушка индуктивности в цепи постоянного тока

Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.

Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:

Намотать на него лакированного медного провода и зачистить выводы:

Замеряем индуктивность нашей катушки с помощью LC метра:

132 микрогенри.

Теперь собираем все это вот по такой схеме:

где

L – катушка индуктивности

La – лампочка накаливания на напряжение 12 Вольт

Bat – блок питания, с выставленным напряжением 12 Вольт

Лампочка засветилась!

Как вы помните из прошлой статьи, конденсатор у нас не пропускал  постоянный электрический ток:

Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности.

Сопротивлением обладает только сам  провод, из которого намотана катушка.

[quads id=1]

Катушка индуктивности в цепи переменного тока

Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом.  Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него

Собираем все это дело по такой схеме:

Получилось как то так:

Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал – желтым. Следовательно, красная синусоида – это частота, которую нам выдает генератор частоты, а желтая синусоида – это сигнал, который снимается с резистора.

Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.

Опыт N1

Для начала подаем сигнал  с частотой  в 1 Килогерц.

Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой “1” – это замеры “красного”канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой “2”. F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.

Увеличиваем частоту до 10 Килогерц

Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.

Увеличиваем до 100 Килогерц

Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.

Сдвиг фаз – это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Увеличиваем частоту до 200 Килогерц

На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.

Увеличиваем частоту до 300 Килогерц.

Амплитуда  желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.

Увеличиваем частоту до 500 Килогерц

Амплитуда уменьшилась до 480 милливольт.

Добавляем еще частоту до 1 Мегагерц

Амплитуда желтого канала  стала 280 милливольт.

Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца

Амплитуда “желтого” сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.

И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.

[quads id=1]

Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?

С увеличением частоты сопротивление катушки растет,  а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.

Опыт N2

Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.

Итак, прогоняем все по тем же значениям частоты

При  частоте в 1 Килогерц у  нас значение почти не изменилось.

10 Килогерц

Здесь тоже  ничего не изменилось.

100 Килогерц

Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.

200 Килогерц

Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.

300 Килогерц

Сдвиг фаз стал больше и амплитуда просела еще больше

500 Килогерц

Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.

1 Мегагерц

Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉

2 Мегагерца, предел моего генератор частоты

Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.

Обратите внимание на амплитуду в Вольтах  на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.

Отсюда вывод напрашивается сам собой:

При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.

Реактивное сопротивление катушки индуктивности

С помощью нехитрых умозаключений, физиками была выведена формула:

где

Х_L –  реактивное сопротивление катушки, Ом

П – постоянная и равна  приблизительно 3,14

F – частота, Гц

L – индуктивность, Гн

В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда  и мощность  на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.

Видео про катушку индуктивности:

Заключение

Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.

Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:

Катушка индуктивности в цепи постоянного тока

Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.

Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.

Это понятно из формулы: 

Предположим, что ток iL изменился скачком, то есть: 

А значит, что и напряжение в данном случае будет бесконечно велико: 

Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.

На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности  —  “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.

Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.

Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.

Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума. 

Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R =  10 Ом, L = 0,1 Гн.

Скачать файл Multisim 13.0

Рассчитаем время, за которое ток в цепи достигает установившегося значения: 

Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.

Просмотров: 14970

2. Катушка индуктивности в цепи переменного тока | 3. Реактивное сопр. и импеданс — Индуктивность | Часть2

2. Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.

Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:

 

Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:

 

Простая индуктивная цепь: ток катушки отстает от напряжения на 90^o.

Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:

 

Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90^o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.

 

Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:

 

Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения  и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90^o, бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.

Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.

Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: X_L.

Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:

 

Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:

Частота (Гц)	Реактивное сопротивление (Ом)
60	3. 7699
120	7.5398
2500	157.0796

В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360^o. Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360^o. Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.

Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула X_L = 2πfL может быть написана как X_L = ωL.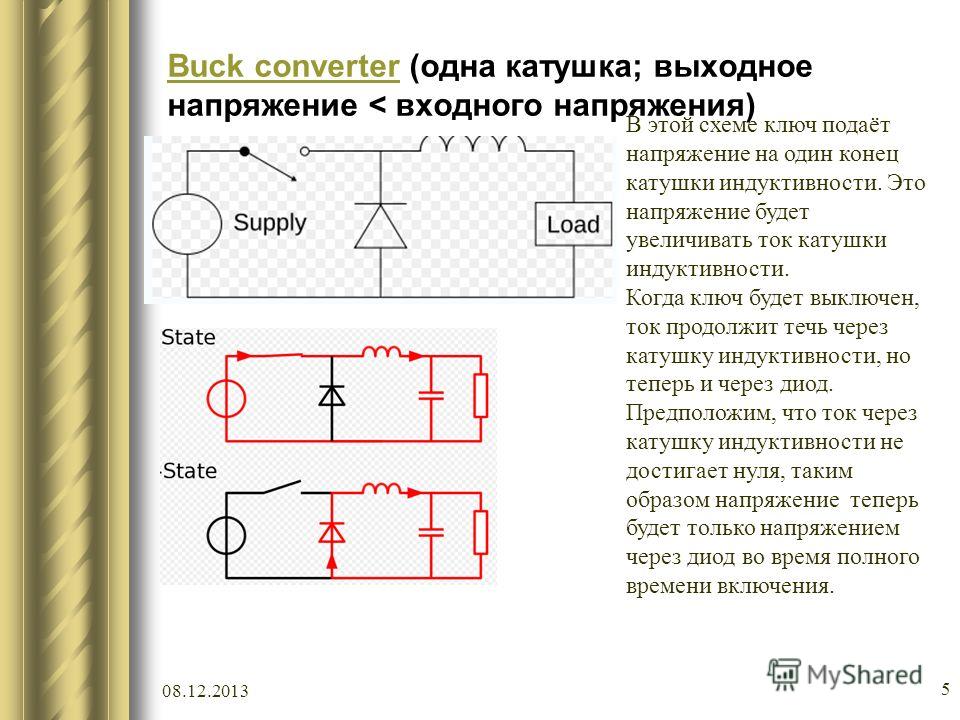

Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.

При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:

 

 

Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90^o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:

 

 

Ток на катушке индуктивности отстает от напряжения на 90^o.

Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90^o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).

Катушка Индуктивности в Цепи Переменного Тока: Принцип Действия

Катушки индуктивности различных модификаций

Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента.

Теоретика

Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.

Что такое катушка индуктивности

Разнообразие размеров катушек

Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:

• Сглаживание биений;
• Подавление помех;
• Ограничение переменного тока;
• Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.

Дроссели на печатной плате

• Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
• Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.

Соленоид

• Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.

Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.

Обмотка с втягивающего реле на стартере

• Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
• Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.

Схема сверхпроводящего индуктивного накопителя

• Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.

Конструкционные особенности

Строение катушки индуктивности

Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.

Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.

Тороидальная катушка

Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.

Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.

Применение

Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.

Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.

Строение трансформатора

Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.

Для справки! Трансформаторы способны функционировать только с переменным током.

Основные характеристики катушек индуктивности

Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.

Определение индуктивности: формула

• Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
• Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
• Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.

Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.

Расчет энергии магнитного поля катушки

• Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии. Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.

Гидротурбина

• Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
• Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
• Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.

При последовательном соединении катушек их индуктивность складывается

• Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия. Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
• Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.

Дроссель сварочного аппарата

• Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств. Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
• Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
• С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.

Паразитная емкость катушки индуктивности

• Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
• ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах. Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
• ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.

Включение катушки индуктивности в цепи с постоянным и переменным током

В целом, мы определили, что такое катушка индуктивности, для чего она нужна, и какие характеристики для расчета ее параметров важны, однако до сих пор неискушенному читателю наверняка не понятно, как будут изменяться параметры протекающего через эту деталь тока.

Цепь, питаемая постоянным током

Катушка индуктивности в цепи постоянного тока

Чтобы упростить изложение, будем проводить очень простой опыт:

• Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.

Стержень из феррита

• Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.

Изготовление катушки индуктивности

• Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
• Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.

Измерение индуктивности собранной катушки

• При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.

Схема с включенной катушкой индуктивности

• Теперь берем все наши детали и соединяем их по приведенной выше схеме.

Схема включена в сеть

• Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.

На данной схеме лампочку заменяет резистор, но это не важно

• Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
• Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
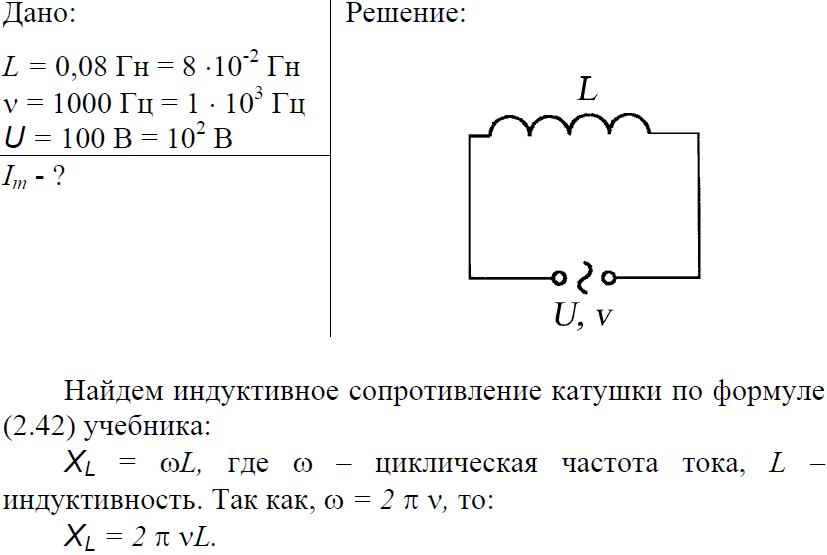
• Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
• Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.

Uвх – входное напряжение питания; Il- изменение величины тока; Ul – напряжение на катушке

• На верхнем графике изображено изменение напряжения входной сети, сразу после включения. Как видим, моментально появляется постоянное значение.
• Дальше показано, как меняется величина тока, протекающего через катушку. Он тоже достигает постоянно значения, но не сразу, а спустя какое-то время.
• Напряжение на катушке (нижний график) также вырастает моментально, но тут же начинает падать. При этом обратите внимание, что графики силы тока и напряжения зеркально противоположны.
• Если все это перенести на наш опыт с лампой, то мы увидим, что после соединения цепи через выключатель, она загорится не сразу, а с некоторой задержкой.

Похожая ситуация будет и при размыкании цепи.

Физические процессы в катушке при размыкании цепи

По графикам видна противоположная ситуация, означающая, что лампочка продолжить гореть еще какое-то время после размыкания цепи.

Дело в том, что при прекращении подачи питания, в катушке снова возникнет ЭДС, однако ток индукции потечет теперь в том же направлении, что и от источника питания, то есть запасенная энергия в катушке, поддержит питание цепи.

Включение в цепь с переменным током

Теперь давайте проведем другой опыт, в котором подключим сделанную ранее катушку к источнику питания переменного тока.

Схема включения катушки индуктивности в цепь переменного тока

• Для создания приведенной схемы и снятия показаний нам потребуются: генератор частоты, осциллограф, резистор на 100 Ом и сама катушка.

Схема в сборе

• На фото выше виден осциллограф, отображающий 2 синусоиды. Это каналы, соответствующие частотам генератора (красная) и резистора (желтая), который включен в цепь уже после катушки индуктивности.
• Опыт с постоянным током показал, что катушка индуктивности при неизменном токе, никак не изменяет параметры тока, то есть не оказывает ему никакого сопротивления, а изменения случаются лишь во время включения и выключения питания.
• Теперь же, при помощи генератора, мы сможем посмотреть, как изменится сопротивление катушки, вследствие увеличения частот.

Ток имеет частоту 1 кГц

• Для начала подадим ток частотой в 1 кГц. Как видно из показаний, сигнал на выходе ничем не отличается от входного – сохранились и частота, и амплитуда.

Частота в 100 кГц

• Наращиваем частоту, останавливаясь на 100 кГц-ах. По графикам видно, что произошло какое-то изменение. А именно, уменьшилась амплитуда (ток стал выравниваться) и желтый график сместился вправо (появилась задержка) – это явление называет сдвигом фаз, то есть разницей между начальными и итоговыми замерами величин.

Интересно знать! Чтобы иметь возможность измерить сдвиг фаз, необходимо чтобы сигналы имели одинаковую частоту. Амплитуда значения не имеет.

Сдвиг фаз

Давайте посмотрим, что произойдет, если частоту увеличить еще.

Частота в 500 кГц

• По графикам видно, что тенденция сохранилась. Фаза сдвинулась еще сильнее, а амплитуда упала до 480 милливольт, хотя изначально равнялась практически 2 Вольтам.

Частота в 2 Мегагерца

• Выставляем максимальную частоту, что способен выдать наш генератор, и видим падение амплитуды до 120 мВ, и смещение фазы практически на 90 градусов.
• Отсюда можно сделать вывод, что с увеличением частоты питающего тока сопротивление катушки индуктивности будет расти. При этом происходит сдвиг фаз, максимальное значение которого составляет 90 градусов.

Сопротивление катушки напрямую зависит от ее индуктивности и рассчитывается по следующей формуле.

Расчет сопротивления катушки индуктивности

Работает при этом катушка все по тому же принципу.

Изменение тока и ЭДС самоиндукции

На графике показана зависимость тока и ЭДС от времени. Почему она выглядит именно так?

• Мы уже выяснили на примере постоянного тока, что ЭДС прямопропорциональна скорости, с которой изменяется сила тока. Собственно на графике и показывается эта зависимость.
• Рассмотрим часть графика. Между точками 1 и 2 ток изменяется, причем вначале изменение весьма резкое, но чем ближе к точке 2, тем оно сильнее замедляется, а в некотором промежутке времени и вовсе остается почти одинаковым.
• Отсюда следует, что скорость изменения тока выше около точки 1, а значит, в тот момент времени ЭДС и будет самым высоким.
• Также мы помним, что направление ЭДС противоположно основному току, то есть принимает отрицательное значение. Вот собственно и показанная зависимость – ток от точки 1 до точки 2 растет, а ЭДС падает, при прямой зависимости от скорости изменения тока.
• Идем дальше – промежуток 2-3. Ток у нас падает – сначала с медленной, а затем быстрой скоростью. ЭДС же, наоборот, растет, принимая положительное значение. И так далее, по аналогии.

Теперь, что касается знаков. На участке 1-2, у тока и ЭДС они противоположные, а значит, ЭДС тормозит ток, препятствуя его возрастанию, из-за того что они направлены навстречу друг другу. Далее идет участок 2-3, на котором ток и ЭДС выравниваются по знакам, а значит ЭДС побежит в ту же сторону, поддерживая убывающий ток.

Вот мы и пришли к тому факту, что току, протекающему в цепи, катушка индуктивности оказывает индуктивное или реактивное сопротивление. Возвращаясь к формуле расчета этого сопротивления, видим, что, так как частота в постоянном токе равно 0, сопротивление не оказывается, и наоборот, высокая частота переменного тока, увеличивает сопротивление катушки.

Так, мы что-то забыли! Да, конечно же! Что будет в это время с напряжением?

Зависимость напряжения и тока от времени

Из графика видно, что ток относительно напряжения сдвинут по фазе на ¼ такта, или на 90 градусов (отстает), что является одним из важнейших свойств цепей переменного тока, с включенной катушкой индуктивности.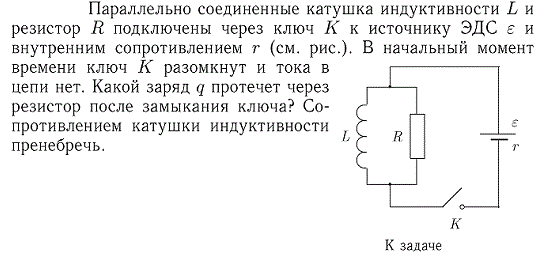

Как все это можно задействовать на практике. Самый банальный пример – это фильтр низких частот (ФНЧ). Мы увидели, что сигнал с высокой частотой проходит намного хуже, тогда как низкочастотный, не испытывает никакого сопротивления. Если включить катушку индуктивности  в цепь, запитывающую динамик, то мы получим обрезку высоких частот, превращая конструкцию в сабвуфер, играющий только басы.

На этом все. Мы разобрали, как меняется ток катушки индуктивности, ЭДС и напряжение. Кто бы мог подумать, что это простое устройство совершает такую работу? Этим то и прекрасен мир электротехники. Изучайте его, и вам откроется много интересного! В дополнение просмотрите лекцию из видео в этой статье. Удачи!

Катушка индуктивности в цепи постоянного тока. — Студопедия.Нет

Устройство и принцип работы катушки индуктивности.

Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса — резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.

Как уже понятно из названия элемента — катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием — витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название Индуктивность — это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:

А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:

В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри — это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:

 

Давайте разберемся, что за величину входят в это выражение:

§ — магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению:

§ — магнитная проницаемость магнитного материала сердечника.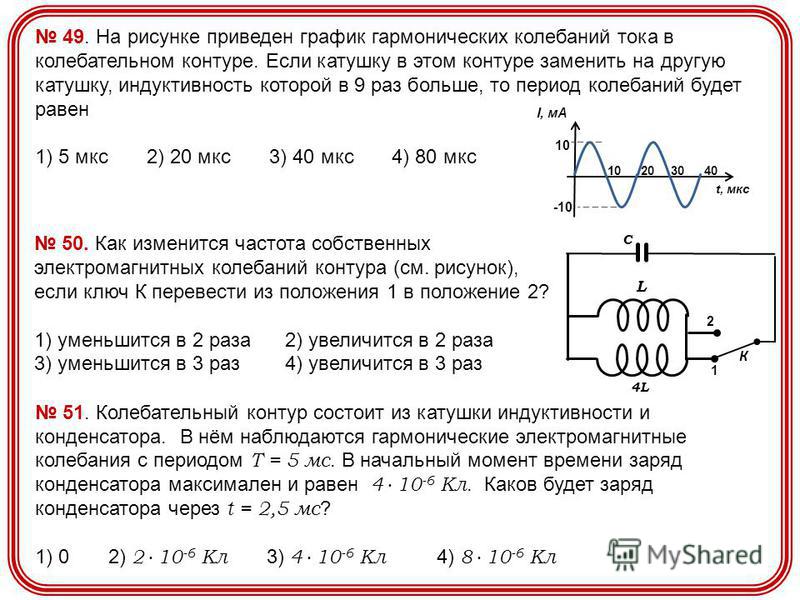 А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами — магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.

§ — площадь поперечного сечения катушки

§ — количество витков

§ — длина катушки

Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины — уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.

С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока.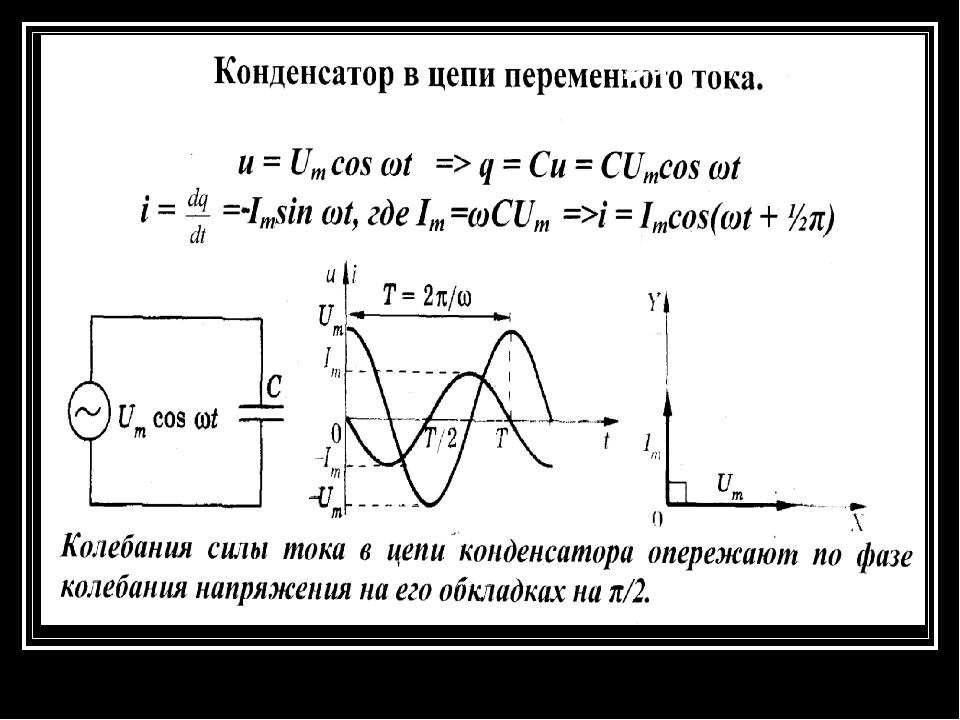 Для этого мы рассмотрим две схемы — в одной будем пропускать через катушку постоянный ток, а в другой -переменный

Катушка индуктивности в цепи постоянного тока.

Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.

Что же произойдет в тот момент когда мы замкнем выключатель?

Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:

 

Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:

На первом графике мы видим входное напряжение цепи — изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).

Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:

После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).

Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:

 

На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим кцепям переменного тока.

Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс

Физика, 11 класс

Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока

Перечень вопросов, рассматриваемых на уроке:

Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;

Устройство и принцип действия генератора переменного тока и трансформатора;

Автоколебания;

Проблемы передачи электроэнергии и способы повышения эффективности её использования.

Глоссарий по теме

Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами.

Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.

Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.

В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:

N- число витков.

Возникает ЭДС индукции который меняется по гармоническому закону.

ЭДС индукции в рамке равна:

Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.

В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.

Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т. к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.

Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.

Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.

Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.

Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.

Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:

Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.

Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.

Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».

k– коэффициент трансформации.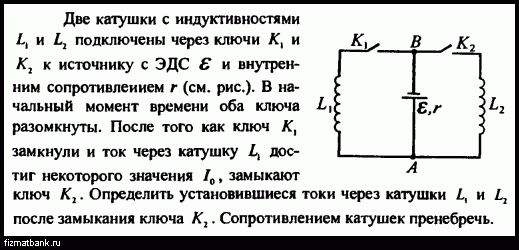

U₁ и_{U2 – напряжения на первичной и на вторичной обмотке.}

N₁ и _{N2— число витков на первичной и на вторичной обмотке.}

Если k < 1 — трансформатор повышающий,

k > 1 — трансформатор понижающий.

КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:

Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.

Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.

Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.

 Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция

Разбор тренировочных заданий

1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м².

Дано:

N=50

ω=180 рад/с

B=0,4 Тл

S=0,02 м²

_________

Ԑ_m=?

Решение:

Ответ: 72 В.

2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.

Дано:

L=0,08 Гн

ν= 1000 Гц

U=100 В

__________

I_m=?

Решение:

Напишем закон Ома для переменного тока

Т.к. Х_C и R равны нулю, то

Учитывая, что , получаем:

Найдем амплитудное значение напряжения:

Подставим числовые данные в формулу для расчета амплитуды силы тока:

Ответ: I_m = 0,3 А.

Катушка индуктивности в цепи переменного тока

 

Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения. Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.

Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.

 Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции

В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.

По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.

Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.

Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.

С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.

В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.

Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.

В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).

Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.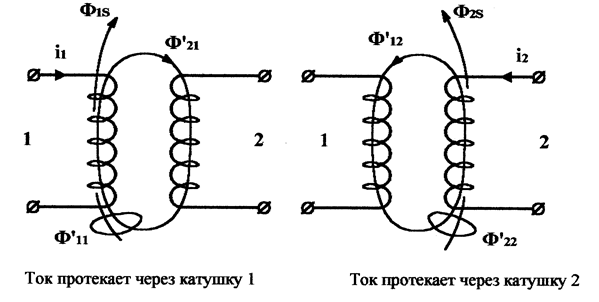

Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.

Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).

Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.

В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис.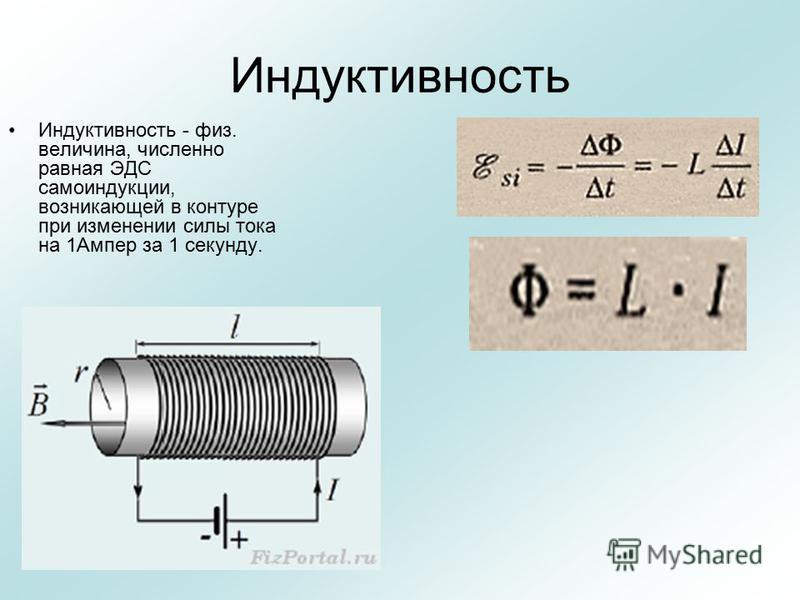 1б), в точности соответствующие графикам рис.1а.

Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.

Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».

Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

 

Добавить комментарий

Катушка тока

| carlingtech.

com

Автоматический выключатель — это электрический выключатель, который автоматически размыкает цепь при соблюдении определенных электрических условий. Как правило, автоматические выключатели размыкаются (срабатывают), когда электрический ток через чувствительное устройство превышает предварительно установленный номинальный ток. Электрический ток измеряется в амперах. — это поток электронов через электрический проводник. Carling Technologies производит гидравлические / магнитные выключатели, в которых в качестве датчика тока используется электромагнитный соленоид или катушка .

Номинальный ток катушки автоматического выключателя Carling — это максимальный ток в амперах, который выключатель может выдерживать непрерывно без отключения. Автоматические выключатели Carling не срабатывают при 100% этого номинального тока, гарантированно срабатывают при 125% — 135% номинального тока (в зависимости от вашего выбора задержки срабатывания) и могут отключаться в диапазоне от 101% до 134% номинального тока. . Для получения дополнительной информации о том, что вызывает срабатывание магнитного прерывателя цепи, см. Страницу Дополнительные сведения — Задержка срабатывания защиты цепи.

Температурный стабильный

Поскольку автоматические выключатели Carling Technologies представляют собой гидравлические / магнитные выключатели, их прецизионные механизмы устойчивы к температуре и не подвержены неблагоприятным изменениям температуры в рабочей среде. Они срабатывают при одинаковом токе независимо от температуры окружающей среды, обеспечивая стабильную работу точки срабатывания в диапазоне температур от -40 ° C до + 85 ° C. При такой стабильности обычно не требуется снижение номинальных характеристик из-за колебаний температуры, и предотвращается отключение из-за перегрева.

Их гидравлическая / магнитная конструкция также обычно более гибкая, поскольку номинальный ток, допуск на пусковой ток и задержка срабатывания могут быть указаны относительно независимо.

Доступные текущие рейтинги

Линия продуктов

Carling Technologies для защиты цепей охватывает широкий диапазон номиналов катушек — от 0,01 до 25 ампер (серия M, серия Q) до 50 ампер (серия A, серия B, серия D) до 100 ампер. (C-Series, E-Series) до 700 А (F-Series).

Рекомендации по выбору

Номинальный ток катушки представляет собой требуемую электрическую нагрузку.Следующие общие рекомендации могут оказаться полезными при определении подходящего номинального тока катушки для вашего приложения:

1. С каким нормальным (стабилизированным) рабочим током столкнется выключатель?
2. Используя приведенный ниже список, каков «коэффициент безопасности» для предотвращения ложного отключения из-за скачка напряжения? Типичные факторы безопасности:
   • 1,20 при нагрузках сопротивления
   • 1,75 на индуктивные и трансформаторные нагрузки
   • 1,5 по цепям линейного питания
   • 2.0 на импульсных цепях питания
   • 1,75 на однофазных асинхронных двигателях
   • 1,25 на другие моторы
3. Конечный номинальный ток = нормальный рабочий ток X коэффициент безопасности.
4. Чтобы свести к минимуму ваши затраты, мы предлагаем выбрать следующий по величине стандартный номинальный ток, указанный в нашем каталоге, для конкретной серии, которая вас интересует. Однако вы также можете связаться с торговым представителем Carling Technologies, чтобы узнать о доступных нестандартных рейтингах, если они вам потребуются.

Номинальное значение отключения по напряжению

Carling Technologies также предлагает номинальное напряжение отключения переменного и постоянного тока для автоматических выключателей серий A, B, C и D. Автоматические выключатели с отключением по напряжению откалиброваны на заводе для отключения при заданном значении напряжения и не рассчитаны на продолжительный режим работы. Номинальные параметры отключения по напряжению часто используются для приложений «Цепь сброса» или «Цепь аварийного отключения», где необходимо размыкать контакты основного питания при малой мощности на входе от одного или нескольких источников.Используйте онлайн-конфигуратор действующего номера детали CONFIGURIT® от Carling Technologies, чтобы узнать о предлагаемых номинальных значениях отключения по напряжению, или обратитесь к торговому представителю Carling Technologies.

Многополюсные выключатели

Также доступны многополюсные выключатели с гальванической развязкой полюсов. Такая многополюсная конструкция позволяет назначать каждому полюсу разный номинальный ток катушки. Это называется конструкцией разнородных полюсов. Чтобы узнать больше о конструкции разнородных полюсов, см. Подробнее — Полюса для защиты цепей.

Для разнородных многополюсных выключателей Carling присваивает специальные каталожные номера, которые выходят за рамки нашей стандартной схемы заказа по каталогу. Тем не менее, вы по-прежнему можете сконфигурировать допустимые конструкции разнородных столбов с помощью нашего онлайн-конфигуратора.

Двойная катушка

Carling Technologies также предлагает автоматические выключатели конструкции с двумя катушками, в которых автоматический выключатель имеет две катушки в пространстве, обычно занимаемом одной катушкой. Комбинируя две электрически независимые катушки в общей магнитной цепи, можно обеспечить размыкание контактов, когда к соответствующим катушкам прикладывается напряжение перегрузки по току или напряжение отключения. Одна катушка будет катушкой отключения по току, работающей в соответствии со стандартными номинальными характеристиками цепи; вторую катушку можно использовать для дистанционного отключения. См. Дополнительные сведения — Схемы для получения дополнительной информации о функциях схем с двойной катушкой или обратитесь к торговому представителю Carling Technologies.

Токовая катушка

— обзор

8.4.1 Создание линейных моделей

Мы предполагаем, что смещения плазменного столба малы и осесимметричны, и игнорируем электрическое сопротивление и вязкость плазмы.Другими словами, мы ограничиваемся рассмотрением идеальной неинерциальной плазмы в рамках классической магнитогидродинамической (МГД) теории. Мы также предполагаем, что плазма устойчива во временном масштабе Альфвена и что наша линейная модель описывает только процессы в масштабе времени, сравнимом с постоянными времени проводящих структур. Наша цель — получить матрицы линейных уравнений (MLE), описывающие поведение плазмы и токов в окружающих проводящих структурах в условиях равновесия. В общем случае интересующая нас эволюция описывается системой нелинейных уравнений в частных производных, а именно уравнением Грэда – Шафранова для равновесия и электротехническими уравнениями для плазмы и токов в цепи. Чтобы решить эту проблему, мы используем численные методы. Для линеаризации используется модель реакции равновесной плазмы со свободной границей на возмущение токов в окружающих проводниках. Здесь мы следуем подходам, описанным в [1, 2].

Чтобы линеаризовать любые уравнения, мы должны определить набор состояний или переменных, которые определяют динамику линейной модели.Положение и изменение формы плазмы зависит от токов в катушках полоидального поля и пассивных цепях.

Поэтому естественно использовать отклонения этих токов относительно начальных (базовых) значений в качестве состояний линейной модели:

(8.1) δIt = It − I0,

, где I ( t ) обозначает токи во времени. t и I ₀ относятся к токам для начальной (базовой) конфигурации ( t = 0).

Динамика токов (состояний) цепи выражается электротехническими уравнениями вида

(8.2) dΨdt + RI = U,

, где ψ — вектор полоидального потока, усредненный по сечению цепи, R — матрица сопротивлений цепей, а U — вектор внешних напряжений, приложенных к цепям. В линейном случае вектор ψ может быть выражен как

(8.3) Ψr, z, t≅Ψr0, z0,0 + ∂Ψ (i) ∂I (j) I = I0δI,

где ∂Ψ (i) ∂I (j) I = I0 — матрица с элементами ( I , j ), определяющая отклонение потока в цепи i при единичном отклонении тока в цепи j в момент времени t = 0 .

Принимая во внимание ур. (8.3), линеаризованное уравнение. (8.2) записывается следующим образом:

(8.4) ddt∂Ψi∂IjI = I0δI + RδI = δU,

для описания динамики отклонений тока в цепях δI ( t ).

Поток ψ представляет собой линейную комбинацию потока через контур, ψ _ext , от внешних токов и собственного тока, и потока от плазмы, ψ _p . Значение ψ _p определяется изменениями формы плазмы и собственным током плазмы (здесь и повсюду изменения формы относятся к движению и деформации плазменного столба). В линейном приближении

(8.5) Ψpr, z, t≅Ψpr0, z0,0 + ∂Ψp∂IpI = I0δI + ∂Ψp∂IpI = I0δIp,

где ∂Ψpi∂IjI = I0 — матрица с элементами ( i , j ), который определяет отклонения потока в цепи i из-за изменения формы плазмы при единичном отклонении тока в цепи j в момент времени t = 0, а ∂Ψp∂IpI = I0 — вектор с элементами ( i ), который определяет изменения отклонения потока в цепи i при единичном отклонении плазменного тока в момент времени t = 0.

Из уравнения. Из (8.5) видим, что линейная модель должна включать в себя состояние δI _p — отклонение плазменного тока от начального значения. Тогда уравнение. (8.4) принимает вид

(8.6) ∂Ψexti∂IjI = I0ddtδI + ∂Ψp∂II = I0ddtδI + ∂Ψp∂IpI = I0ddtδIp + RδI = δU,

где ∂Ψexti∂IjI = I0 — матрица с элементами j ), который определяет отклонение магнитного потока в цепи i при единичном отклонении тока в цепи j в момент времени t = 0 (матрица статической индуктивности). Введем обозначения

L1 = ∂Ψexti∂IjI = I0; L2 = ∂Ψpi∂IjI = I0; Mp = ∂Ψp∂IpI = I0; L3 = L1 + L2

, чтобы получить уравнение. (8.6) образуя

(8.7) L3ddtδI + MpddtδIp + RδI = δU.

Линейная система (8.7) — это на одно уравнение меньше числа состояний. Его следует дополнить уравнением, описывающим изменение тока плазмы δI _p . С этой целью мы предполагаем, в соответствии с теорией МГД, что полоидальный поток «вморожен» в плазму в течение обсуждаемых периодов времени, так что

(8.8) Ψ¯ = 1Ip∫sjΨds = const,

, где j — распределение тока плазмы, а S — поперечное сечение плазменного столба. Мы линеаризуем уравнение. (8.8) относительно состояний δI и δI _p и получаем

(8.9) ∂Ψ¯∂IδI + ∂Ψ¯∂IpδIp = 0,

или

(8.10) δIp = −∂Ψ¯∂IδI / ∂Ψ¯∂Ip.

Путем подстановки Ур. (8.10) в уравнение. (8.7) последнее принимает вид

(8.11) L ∗ ddtδI + RδI = δU,

, где L ∗ = L3 − Mp (∂Ψ¯ / ∂I) / (∂Ψ¯ / ∂Ip). Эта линейная система отражает текущее поведение в активных и пассивных цепях, и уравнение. (8.9) описывает динамику плазменного тока.

Для описания эволюции формы плазмы введем вектор g ( t ), характеризующий параметры формы и положения плазмы. Этот вектор может включать в себя такие параметры, как удлинение и треугольность плазмы, положение точки X , расстояние между границей плазмы и заданными точками на первой стенке и так далее.Тогда

gt = ∂g∂IδI + ∂g∂IpδIp,

, что ведет к формуле. (8.10) до

(8.12) gt = ∂g∂I − ∂g∂Ip∂Ψ¯∂I / ∂Ψ¯∂IpδI.

Обозначим C≡ (∂g∂I − ∂g∂Ip∂Ψ¯∂I / ∂Ψ¯∂Ip) и таким образом получим

(8.13) gt = CδI.

Таким образом, мы получаем требуемую MLE, описывающую динамику токов в цепи и эволюцию формы плазмы:

(8.14) L ∗ ddtδI + RδI = δUgt = CδI.

Ур. (8.14) позволяет анализировать эффективность пассивной стабилизации структур, окружающих плазму.Характеристика, обычно используемая в этом контексте для вертикально вытянутой плазмы, — это скорость роста неустойчивости плазмы (приращение), γ . Он определяется как сингулярное положительное собственное значение матрицы −L * −1R, относящееся к неустойчивой вертикальной моде. Это значение во многом определяет параметры источников питания для управления активными катушками. Как правило, чем выше это значение, тем выше частотные характеристики источника питания и требуемая мощность для управления. Другой характеристикой, обычно используемой в анализе пассивной стабилизации, является запас устойчивости, м _s .Давайте внимательно посмотрим на это.

Для нестабильных плазменных конфигураций τ _γ , обратное инкременту, определяется как сингулярное положительное собственное значение MLE (8.14), то есть

(8.15) −L ∗ xu≡S − L1xu = τγRxu,

где матрица L * ≡L1 − S; матрица S≡− [L2 − Mp (∂Ψ¯ / ∂I) / (∂Ψ¯ / ∂Ip)]; матрица L1 = ∂Ψexti∂IjI = I0; R — это матрица сопротивлений, а x _u — это распределение токов, индуцированных нестабильным режимом, то есть собственный вектор, соответствующий приращению. Из уравнения. (8.15) следует

(8.16) τγ = xuTL1xuxuTRxuxuTSxuxuTL1xu − 1.

Теперь мы вводим «резистивный» запас устойчивости

(8.17) μ = xuTSxuxuTL1xu − 1,

и старшую постоянную времени пассивной структуры

(8.18) τS = xuTL1xuxuTRxu − 1.

Тогда τ _γ = τ _S μ . Из уравнения. Из (8.18) следует, что старшая постоянная времени пассивной структуры является усредненным значением, которое может быть однозначно определено с помощью значений x _и .Отметим, что μ зависит от сопротивления проводников через x _u .

Чтобы перейти к «индуктивной» версии запаса устойчивости, подставим матрицу R в уравнение. (8.15) с матрицей L1 = ∂Ψexti∂IjI = I0 и найти собственные значения m _i и собственные векторы x _i в задаче:

(8. 19) −L * xi≡ S − L1 xi = miL1xi,

, где индекс i пробегает значения от 1 до количества состояний в системе.Из уравнения. (8.19) следует, что

(8.20) m1 = xiTSxixiTL1xi − 1.

Если какая-либо матрица (включая L *) умножается на положительно определенную матрицу (L1−1 или R ), количество положительных или отрицательных собственных значений не изменяется, поэтому остается только одно положительное значение m. _i значение для одного положительного нестабильного режима τ _γ . Обозначим его как запас устойчивости м _с .Если m _s < 0, то плазма либо стабильна по шкале постоянной времени пассивных структур, либо нестабильна по шкале времени Альфвена.

Из уравнения. (8.20) можно показать, что м _s зависит только от геометрии проводников. Собственный вектор x _s , соответствующий запасу устойчивости m _s , определяет внутрипроводное распределение токов из-за мгновенного смещения плазмы в направлении «нестабильности». С физической точки зрения, m _s , если нормировано, отражает разницу между стабилизирующей силой, действующей на плазму токами, индуцированными в идеально проводящих пассивных структурах при мгновенных вертикальных смещениях плазмы, и дестабилизирующей силой, обусловленной плазмой. «удлинение» полоидальным полем. Следовательно, значение m _s определяет, насколько близко должна быть пассивная структура для стабилизации плазмы: чем больше m _s , тем ближе структура к плазме.При проектировании системы управления в настоящее время приемлемо м _с ≈ 0,5. Мы замечаем, что даже при большом m _s параметр τ _γ (более важный для стабилизации плазмы) может быть малым из-за плохой проводимости пассивной структуры. m _s и τ _γ должны быть достаточно высокими, чтобы обеспечить приемлемый уровень стабилизации плазмы. Проще говоря, хорошо проводящая пассивная структура должна быть настолько близка к плазме, насколько это позволяет конструкция.

Линейная модель (уравнение (8.14)) используется в качестве основы для синтеза регуляторов замкнутых систем управления. Таким образом, это позволяет получить матрицу передачи K ( s ), которая связывает сигналы датчиков, идентифицирующих положение, ток и форму плазмы, для управления напряжениями катушки U ( s ) = K ( s ) g ( s ), где s обозначает переменную Лапласа.

При проектировании системы управления положением, током и формой плазмы также важно определить возможные возмущения плазмы, которые должны подавляться системой управления. К ним относятся возмущения внутренней индуктивности плазмы l _i и параметра β _p , вызванные перестройкой профилей температуры и тока при «незначительных нарушениях». Мы вводим такие возмущения в нашу линейную модель. .

Пусть δξ — вектор возмущения. Затем электротехническое уравнение. (8.7) принимает вид

(8.21) L3ddtδI + MpddtδIp + ∂Ψ∂ξddtδξ + RδI = δU.

Ур. (8.9), отражая изменения тока плазмы, принимает вид

(8.22) ∂Ψ¯∂IδI + ∂Ψ¯∂IpδIp + ∂Ψ¯∂ξδξ = 0,

, а уравнение, описывающее геометрию плазмы, принимает вид

(8.23) gt = ∂g ∂IδI + ∂g∂IpδIp + ∂g∂ξδξ.

Замена δI _p из уравнения. (8.22) в уравнения (8.21) и (8.23), получим искомую МДУ, учитывающую возможные возмущения параметров плазмы:

(8.24) L ∗ ddtδI + Mξddtδξ + RδI = δUg = CδI + Fδξ,

, где

Mξ≡∂Ψ∂ξ − Mp∂Ψ¯∂ξ / ∂Ψ¯∂Ip,

и

F≡∂g ∂ξ − ∂g∂Ip∂Ψ¯∂ξ / ∂Ψ¯∂Ip.

В теории синтеза регуляторов уравнения для объекта управления обычно записываются в форме A, B, C, D. Из уравнения. (8.24) следует, что в нашем случае они примут вид

(8.25) ddtδI = AδI + BδU + Eddtδξg = CδI + DδU + Fδξ,

где A≡ − L * −1R, B ≡ (L *) -1, D — нулевая матрица, а E≡ − L * −1Mξ.

Исключая переменную (d / dt) δξ подстановкой x≡δI − Eδξ, получаем уравнение.(8.25) в окончательный вид

(8.26) x˙ = Ax + BδU + AEδξg = Cx + DδU + CE + Fδξ.

Теперь опишем процедуру вычисления матричных коэффициентов линейной модели для заданной конфигурации плазмы. На рис. 8.1 показан пример конфигурации плазмы и положения точек на сепаратрисе, которые используются в качестве мишеней для управления формой плазмы. Пассивная структура схематично представлена ​​комбинацией внутреннего и внешнего осесимметричных колец внутри вакуумного сосуда и двойной оболочкой сосуда.Что касается катушек управления, то в линейной модели они описываются 11 цепями. Внутреннее и внешнее кольца разделены на три петли каждое. Внутренняя и внешняя оболочки вакуумного сосуда разделены на 25 осесимметричных петель каждая. В итоге линейная модель включает 67 состояний (контуров).

Рисунок 8.1. Петли в линейной модели, описывающей плазменную конфигурацию ИТЭР.

(Авторское право организации ИТЭР, 2017 г. ).

После идентификации состояний вычисляем матричные коэффициенты по следующему алгоритму:

a.

Расчет базовой конфигурации плазмы с использованием заданных токов полоидальной катушки и параметров плазмы. Как правило, базовые конфигурации создаются на основе снимков сценариев разряда. Базовая конфигурация рассчитывается с использованием кодов равновесия со свободной границей.

б.

Расчет коэффициентов для матрицы L3 = ∂Ψ¯∂II = I0 (см. Уравнение 8.7)

через соотношение L3i, j≡∂Ψi∂IjI = I0≅ΔΨiΔIj путем изменения j ^th ток цепи относительно базового значения.Здесь Δ ψ _i — это изменение потока в цепи ith , связанное с изменениями тока в цепи jth Δ I _j . Лучшая точность достигается, когда измеряются несколько изменений тока Δ I _j , как положительных, так и отрицательных, и затем усредняются. Изменение тока не должно приводить к качественному изменению конфигурации плазмы. Например, когда решается проблема со свободными границами, плазменная конфигурация X не должна превращаться в конфигурацию ограничителя, и наоборот.Поскольку L ₃ = L ₁ + L ₂ , в принципе достаточно определить коэффициенты матрицы L2 = ∂Ψp∂II = I0. Матрица L1 = ∂Ψext∂II = I0 выражается через статические индуктивности, которые зависят только от геометрии проводников. Поэтому эту матрицу можно рассчитать заранее.

Коэффициенты матрицы Mp = ∂Ψp∂IpI = I0 в уравнении. (8.7) рассчитываются аналогично с той разницей, что варьируется ток плазмы: Mpj≡∂Ψp, j∂IpI = I0≅ΔΨp, jΔIp.Аналогичным образом определяются коэффициенты ∂¯∂IjI = I0≅ΔΨ¯ΔIj, ∂Ψ¯∂IpI = I0≅ΔΨ¯ΔIp (см. Уравнение 8.9) и ∂gi∂IjI = I0≅ΔgiΔIj, ∂gi∂IpI = I0≅ΔgiΔIp (см. Уравнение 8.12).

Коэффициенты матриц для возмущений, учтенных в линейной модели, равны ∂Ψi∂ξjI = I0≅ΔΨiΔξj, ∂Ψi∂ξjI = I0≅ΔgiΔξj, где варьируется параметр возмущения ξ _j . Вариации Δ Ip и Δ ξ также не должны приводить к качественному изменению конфигурации плазмы.

с.

После завершения шага b) выведите желаемую линейную модель в форме уравнения. (8.25) или уравнение. (8.26). Одновременно проанализировать характеристики линейной модели с использованием критериев пассивной или активной стабилизации (путем определения приращения, запаса устойчивости и т. Д.).

Катушки индуктивности ― Часть 2 Основы индукторов ｜ Электроника ABC ｜ Журнал TDK Techno

Поведение индуктора на постоянном токе

Переходная характеристика катушки

Из-за эффекта самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивную электродвижущую силу), которая ориентирована так, чтобы противодействовать изменению тока.Следовательно, когда на катушку подается напряжение, ток не начинает течь сразу, а когда напряжение снимается, ток не прекращается немедленно. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения переключателя, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) подключены параллельно, простое замыкание переключателя батареи (напряжение всего несколько вольт) не приведет к включите неоновую лампу.Но если выключатель разомкнут, когда через катушку протекает ток, загорится неоновая лампа. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI / Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, и поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока большой, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.

Энергия, запасаемая катушкой

В приведенной выше схеме можно зажечь неоновую лампу, потому что катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока. Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу.

Поведение катушки переменного тока

Индуктивное реактивное сопротивление (XL)

Катушка (индуктор) плавно пропускает постоянный ток, но имеет сопротивление переменному току. Сопротивление увеличивается к более высоким частотам. Этот эффект называется индуктивным реактивным сопротивлением (XL) катушки. Между частотой переменного тока (f) и индуктивностью (L) существует следующая зависимость.

Форма кривой напряжения и тока в цепи переменного тока с катушкой

Переменный ток от коммерческой розетки переменного тока имеет синусоидальную форму.Когда катушка подключена к источнику переменного тока, эффект самоиндукции создает электродвижущую силу, ориентированную таким образом, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения.

Намагничивание сердечника и магнитная проницаемость

Кривая намагничивания и магнитное насыщение

Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I).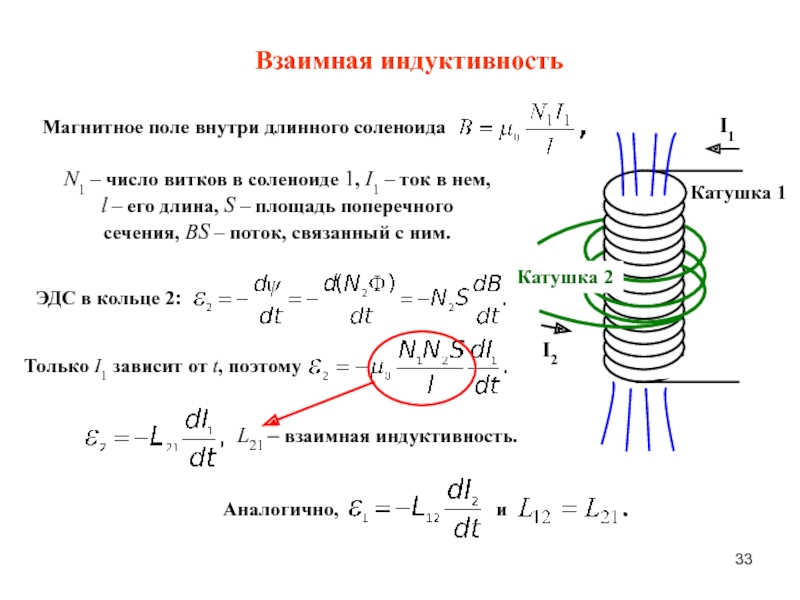 Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и приложение большого тока приведет к созданию более сильного магнитного потока. Однако есть пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).

Процесс намагничивания сердечника и изменение магнитной проницаемости

Когда сердечник намагничивается, магнитная проницаемость сердечника изменяется.Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент около начала кривой — это начальная магнитная проницаемость (μ0). Эта начальная магнитная проницаемость — это то, что обычно называют магнитной проницаемостью, и это также значение, которое указано в каталогах для ферритовых материалов. Увеличение тока в катушке и тем самым увеличение намагниченности в конечном итоге приведет к тому, что магнитная проницаемость достигнет максимально возможного значения.Это называется максимальной магнитной проницаемостью (мкм), после которой значение снова падает.

Потери на вихревые токи в сердечнике

Когда в катушку подается переменный ток, создается электродвижущая сила, которая противодействует изменению магнитного потока, и в сердечнике течет концентрический ток. Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая уходит в виде джоулева тепла.Это называется потерей на вихревые токи. У металлических сердечников с низким электрическим сопротивлением потери на вихревые токи более выражены. Ламинированные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи. Однако потери будут увеличиваться по направлению к более высоким частотам, что приведет к выделению большего количества тепла. Поскольку феррит имеет высокое удельное сопротивление, потери на вихревые токи низкие, что делает этот материал пригодным для многих применений, таких как высокочастотные катушки и высокочастотные трансформаторы.

Форма кривой тока катушки зажигания

Дополнительные указания

Общие принципы

Во всех (индуктивных) системах искрового зажигания используется одна или несколько катушек зажигания. Катушки действуют как аккумулятор для хранения энергии и как повышающий трансформатор для генерации высокого напряжения, необходимого для возникновения электрической искры в камере сгорания.

Катушка зажигания состоит из первичной и вторичной катушек, намотанных друг на друга в непосредственной близости. Вторичная обмотка имеет большое соотношение витков к первичной обмотке. Такое расположение создает условия высокой взаимной индуктивности, то есть изменения магнитного поля в первичной катушке будут вызывать изменения напряжения во вторичной катушке.

Первичная катушка подключена к первичной цепи. Когда ток течет в первичной цепи, энергия накапливается в магнитном поле катушки.Если ток быстро снимается, магнитное поле быстро разрушается и индуцирует высокое напряжение во вторичной катушке. Высокое напряжение подается на свечу зажигания через вторичную цепь.

Время, необходимое катушке для достижения максимальной напряженности магнитного поля (ее насыщение , время ), зависит от пикового тока первичной цепи, который, в свою очередь, зависит от общего сопротивления первичной цепи и способности первичной катушки сопротивляться нарастанию. тока (его индуктивность ).

Период, в течение которого ток течет в первичной цепи, известен как период задержки (или угол задержки, если он соотносится с углом вращения коленчатого вала).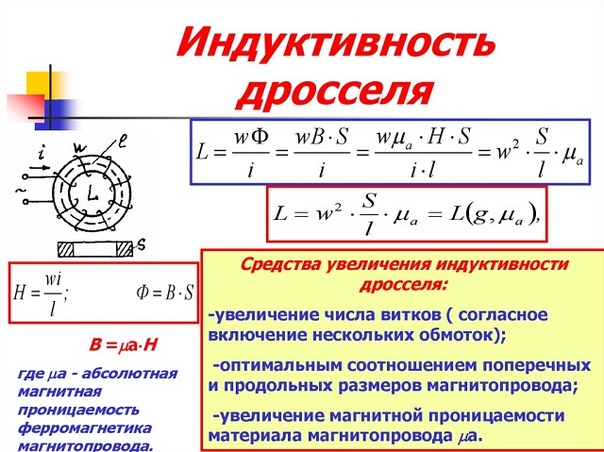 Период выдержки должен быть достаточно длинным (при всех оборотах двигателя), чтобы первичная обмотка могла достичь максимальной напряженности магнитного поля (то есть до насыщения ).

Пиковый ток и период задержки являются ключевыми показателями эффективности (KPI) для управления первичной цепью. Обратитесь к технической информации производителя, чтобы узнать характеристики вашего автомобиля.

Распределитель зажигания

В системах зажигания на базе распределителя используется одна катушка зажигания.

Переключение первичного контура может управляться одним из двух механизмов:

• механически, с помощью прерывателя контактов, приводимого в действие вращающимся кулачком внутри распределителя.
• с использованием транзисторного переключения тока, запускаемого опорным сигналом синхронизации.

Для большинства первичных цепей с механическим запуском требуется балластный резистор для регулирования тока, тогда как транзисторная система может изменять ток более свободно.

Компонент, вращающийся внутри распределителя, ротор, направляет вторичные напряжения на каждую из свечей зажигания двигателя в их порядке зажигания, проходя через периферийные электроды, соединенные с выводами свечей зажигания.

Типичные неисправности катушки

Катушка

подвержена типичным проблемам со схемой как в первичной, так и вторичной обмотке, таким как обрыв, короткое замыкание или высокое сопротивление. Это может быть вызвано поломкой его обмоток (из-за чрезмерного теплового или вибрационного напряжения) или корродированными соединениями.

Типичные симптомы

Признаки неисправности катушки могут быть:

• Множественные, возможно случайные пропуски зажигания в цилиндрах.
• Неуверенность в высоком крутящем моменте.
• Неровная работа при частоте вращения коленчатого вала.
• Затруднение при запуске.

Что такое токовый пробник с катушкой Роговского?

Что такое токовый пробник с поясом Роговского?

Если вы имеете дело с более чем парой десятков ампер переменного тока и хотите проводить гибкие измерения тока, рассмотрите токовый пробник Роговского.

Катушка Роговского — это электрический преобразователь, используемый для измерения токов переменного тока, таких как высокоскоростные переходные процессы, импульсные токи силового устройства или синусоидальные токи линии электропередачи с частотой 50 или 60 Гц. Катушка Роговского имеет гибкую обжимную сенсорную катушку, которую можно легко обернуть вокруг токоведущего проводника для измерения, и она может измерять до пары тысяч ампер очень больших токов без увеличения размера преобразователя.

Как работает пояс Роговского?

Теория работы за поясом Роговского основана на законе Фарадея, который гласит, что полная электродвижущая сила, индуцированная в замкнутой цепи, пропорциональна скорости изменения во времени общего магнитного потока, соединяющего цепь.

Катушка Роговского похожа на трансформатор переменного тока в том, что во вторичной катушке индуцируется напряжение, пропорциональное току, протекающему по изолированному проводнику.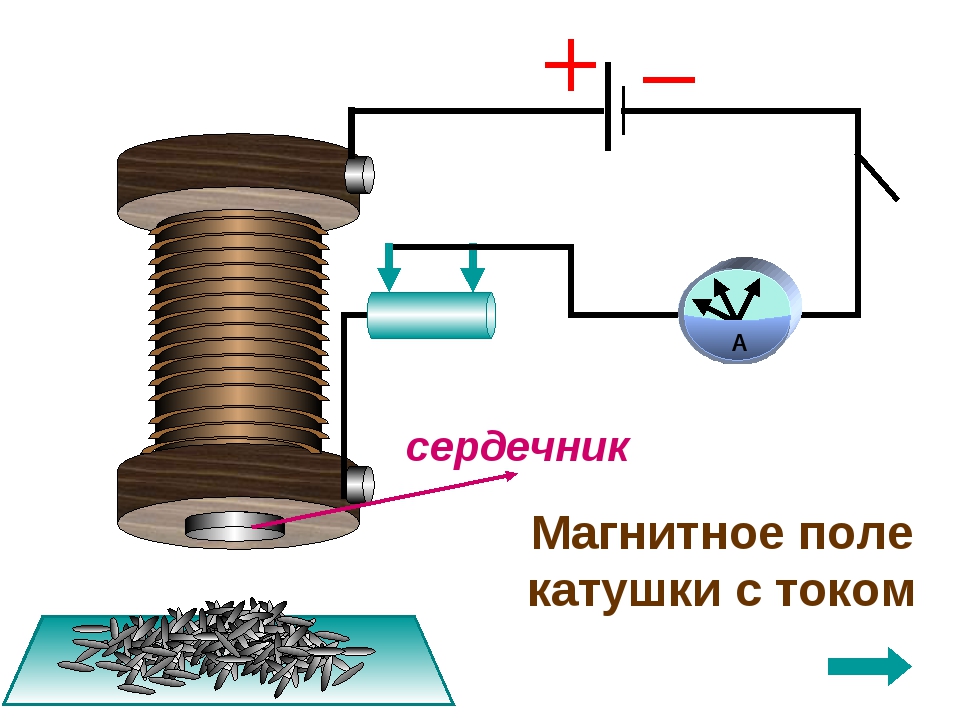 Ключевое отличие состоит в том, что пояс Роговского имеет воздушный сердечник, в отличие от трансформатора тока, который использует стальной сердечник с высокой магнитной проницаемостью для магнитной связи с вторичной обмоткой. Конструкция с воздушным сердечником имеет более низкое вводимое сопротивление, что обеспечивает более быструю реакцию на сигнал и очень линейное напряжение сигнала.

Катушка с воздушным сердечником размещается вокруг токоведущего проводника тороидальным образом, и магнитное поле, создаваемое переменным током, индуцирует в катушке напряжение. Катушка Роговского вырабатывает напряжение, которое пропорционально скорости изменения (производной) тока, заключенного в контуре катушки. Затем напряжение катушки интегрируется, чтобы зонд выдавал выходное напряжение, пропорциональное входному сигналу тока.

Преимущества

Пробники тока с катушкой Роговского

обладают множеством преимуществ по сравнению с различными типами преобразователей тока или измерительными методами.

• Измерение больших токов без насыщения сердечника — Катушки Роговского могут измерять большие токи (в очень широком диапазоне от нескольких мА до нескольких сотен кА) без насыщения сердечника, поскольку в пробнике используется немагнитный » воздух »сердечник. Верхний диапазон измеряемого тока ограничен либо максимальным входным напряжением измерительного прибора, либо пределами пробоя напряжения катушки или элементов схемы интегратора. В отличие от других преобразователей тока, которые становятся все громоздче и тяжелее по мере увеличения диапазона измеряемого тока, пояс Роговского остается той же катушки небольшого размера независимо от амплитуды измеряемого тока.Это делает пояс Роговского наиболее эффективным измерительным инструментом для выполнения нескольких сотен или даже тысяч ампер больших измерений переменного тока.

• Очень гибкий в использовании — Легкая обжимная сенсорная катушка гибкая и легко наматывается на проводник с током. Его можно легко вставить в труднодоступные компоненты схемы. Большинство катушек Роговского достаточно тонкие, чтобы поместиться между ножками корпуса силовых полупроводников T0-220 или TO-247 без необходимости в дополнительной петле провода для подключения токового пробника.Это также дает преимущество в достижении измерения высокой целостности сигнала.
• Широкая полоса пропускания до> 30 МГц — Это позволяет катушке Роговского измерять очень быстро изменяющийся токовый сигнал — например, несколько тысяч А / мкс. Характеристика с высокой полосой пропускания позволяет анализировать гармоники высокого порядка в системах, работающих на высоких частотах переключения, или точно контролировать формы сигналов переключения с быстрым нарастанием или спадом.
• Нет — Интрузивное измерение или измерение без потерь — Катушка Роговского потребляет очень малый ток от ИУ из-за низкого вводимого импеданса.Импеданс, вводимый в ИУ из-за пробника, составляет всего несколько пикогенри, что обеспечивает более быструю реакцию сигнала и очень линейное напряжение сигнала.
• Низкая стоимость По сравнению с датчиком Холла / пробником тока трансформатора, пояс Роговского обычно имеет более низкую цену.

Ограничения

• Только переменный ток — Роговски не может работать с постоянным током. Это только кондиционер.
• Чувствительность — Катушка Роговского имеет более низкую чувствительность по сравнению с трансформатором тока из-за отсутствия магнитопровода с высокой магнитной проницаемостью.

Приложения

Пробники тока с катушкой Роговского

находят широкое применение в различных отраслях энергетики и измерениях мощности. Ниже приведены некоторые примеры применения пояса Роговского:

• Гибкое измерение тока силовых устройств, таких как MOSFET или IGBT, размером с корпус TO-220 или TO-247 или вокруг клемм больших силовых модулей
• Для измерения потерь мощности в силовых полупроводниках
• Для контроля токов в малых индукторах, конденсаторах, демпфирующих цепях и т. Д.
• Для измерения небольшого переменного тока на проводнике с высоким постоянным током или в присутствии сильного постоянного магнитного поля.
• Для измерения высокочастотных синусоидальных, импульсных или переходных токов от частоты линии электропередачи до высокочастотных приложений
• Для измерения тока в моторных приводах и, в частности, измерения качества электроэнергии в цепях VSD, UPS или SMPS
• Для оценки коммутационных характеристик силовых полупроводниковых переключателей (тестер двойных импульсов).
• Мониторинг линии распределения электроэнергии или мониторинг полюсов коммунальных служб
• Приложения для умных сетей
• Измерение тока плазмы

Заключение

Существует ряд различных способов измерения электрического тока, каждый из которых имеет свои преимущества и недостатки.

Катушка Роговского похожа на трансформатор переменного тока в том, что во вторичной катушке индуцируется напряжение, пропорциональное току, протекающему по изолированному проводнику. Однако катушки Роговского способны измерять большие токи (очень широкий диапазон от нескольких мА до нескольких кА) без насыщения из-за своего немагнитного «воздушного» сердечника. Конструкция с воздушным сердечником также имеет более низкий вводимый импеданс, чтобы обеспечить более быструю реакцию сигнала и очень линейное напряжение сигнала, и она очень рентабельна по сравнению с аналогом датчика Холла / трансформатора тока. Это делает пояс Роговского наиболее эффективным измерительным инструментом для измерения нескольких сотен или тысяч ампер переменного тока.

Как работают электромагнитные катушки — Основы схемотехники

Катушка из проволоки — это электрический проводник с одним или несколькими витками, предназначенный для создания магнитного поля. Обычно это используется для увеличения силы магнитного поля. Чем больше витков провода на катушке, тем сильнее будет магнитное поле. Магнитные поля, создаваемые отдельными витками провода, проходят через центр катушки, создавая сильное магнитное поле.

Создание магнитного поля с помощью катушки из проволоки

Движущиеся заряженные частицы создают магнитные поля. Впервые это наблюдалось в начале 19 ^-го века. Во время эксперимента было замечено, что когда электрический ток течет по проводу, ближайший компас меняет направление. Когда ток отключался, компас возвращался в исходное положение север / юг, выровненный по магнитному полю Земли. Таким образом, эксперимент пришел к выводу, что электроны, движущиеся по спиральной проволоке, создают магнитное поле — то, чего не существовало, когда ток был отключен.

Заряженные частицы создают магнитные поля, только когда они движутся. Эксперимент, проведенный в 19, ^и годах, показал, что провод, по которому проходит электрический ток, на самом деле является магнитом. Поскольку все электроны движутся по проводу в одном направлении, вокруг провода создается четко определенное магнитное поле. Сила магнитного поля пропорциональна величине тока, протекающего по проводу. Увеличение тока увеличивает силу магнитного поля.Когда через катушку не течет ток, не будет и магнитного поля.

Количество витков провода также влияет на магнитные поля. Его сила прямо пропорциональна количеству проволочных петель, добавленных к катушке. Другими словами, увеличение проволочных петель приведет к увеличению напряженности магнитного поля.

Если ток течет по катушке по часовой стрелке, то эта сторона катушки будет южным полюсом. С другой стороны, если ток течет вокруг катушки против часовой стрелки, то эта сторона катушки будет северным полюсом.

Катушки из проволоки, которые действуют как стержневые магниты с различными северным и южным полюсами каждый раз, когда через катушку проходит электрический ток, называются электромагнитом.

Магнитные поля, создаваемые проволочной катушкой

Что такое электромагниты?

Электромагниты — это магниты, магнитное поле которых создается электрическим током. Он демонстрирует магнитное притяжение к другим металлическим объектам, когда через них проходит электрический ток. Мы также можем контролировать, включать и выключать силу его магнитного притяжения.

Как сделать электромагнит

Для создания электромагнита потребуется:

Используя материалы выше и следуя простой схеме, сделайте следующее:

1. Оберните магнитную проволоку вокруг железного гвоздя и оставьте 3 дюйма проволоки свободными на конце. Убедитесь, что проволока наматывается плотно, не оставляя промежутков между ними.
2. Обернув гвоздь целиком, обрежьте проволоку, оставив выступ 2–3 дюйма.
3. С помощью устройства для зачистки проводов удалите изоляцию магнитного провода, чтобы обнажить не менее дюйма оголенного провода.Проделайте это с обоих концов проволоки.
4. Присоедините один конец провода к положительной клемме аккумулятора, а другой конец — к отрицательной клемме.
5. Изолентой оберните оба конца провода к клеммам аккумулятора.
6. Проверьте электромагнит, поместив канцелярские кнопки или зажимы рядом с гвоздем, и посмотрите, притягивает ли их гвоздь.

Для изготовления электромагнита необходимо обеспечить более плотную намотку магнитного провода, состоящего из полностью отожженной электролитически очищенной меди.

Что такое магнитный провод?

Магнитный провод или обмоточный провод — это изолированный проводник, используемый для обмена электрической энергии с магнитной энергией. Обычно его покрывают медью или алюминием с тонким слоем изоляции. Он бывает трех типов: эмалированный провод, токопроводящий провод и их комбинация. Они обычно используются для катушек индуктивности, двигателей, потенциометров, электромагнитов и других приложений, требующих плотных витков проволоки.

Повышение напряженности магнитного поля с помощью ферромагнитного сердечника внутри катушки из проволоки

Ферромагнитные материалы — это элементы, которые легко намагничиваются и обычно изготавливаются из стали, кобальта, никелевых сплавов и мягкого железа.Ферромагнитные материалы сильно реагируют на магниты. Включение этих материалов в магнитную цепь приведет к более концентрированному и плотному магнитному потоку, который затем усилит магнитное поле, вызванное током в катушке.

Магнитное поле, создаваемое электроном, может влиять на ориентацию поля, создаваемого соседними электронами, создавая «магнитный домен». Здесь все электроны имеют выровненные магнитные поля. Магнитный домен — это область внутри магнитного материала, где намагниченность имеет однородное направление.Это отвечает за поведение ферромагнитных материалов.

Наведение напряжения и тока с помощью движущегося магнита и неподвижной катушки

Закон индукции Фарадея гласит, что изменяющееся магнитное поле вызывает электродвижущую силу (ЭДС) в проводе контура. Электродвижущая сила заставляет электроны двигаться и образовывать ток. Изменение площади проволочной петли и изменение угла между петлей и магнитным полем может вызвать ток. Это связано с тем, что непосредственно индуцирует ЭДС, известную как магнитный поток.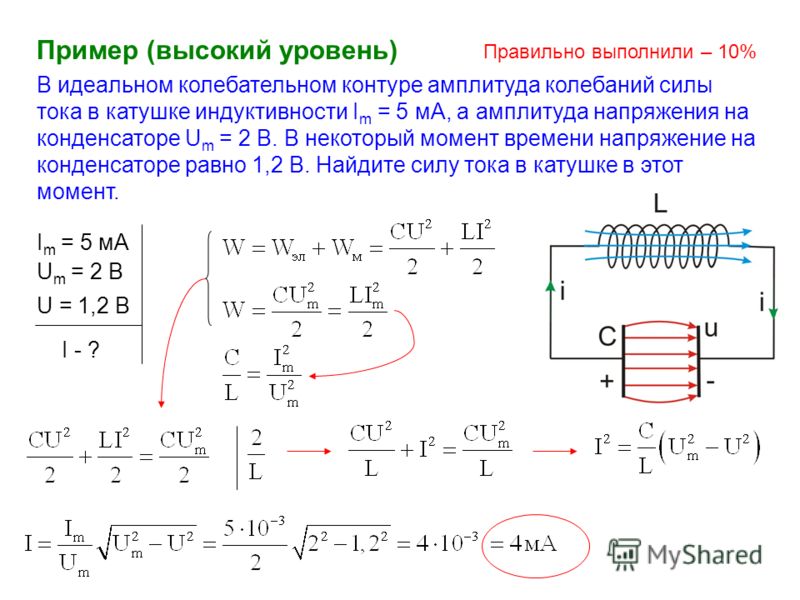 Магнитный поток — это мера общего магнитного поля, которое проходит через проволочную петлю, и когда это поле изменяется, оно индуцирует электродвижущую силу.

Мы можем использовать магнит и катушку с проволокой для генерации электрического тока. На приведенном выше рисунке перемещение магнита внутрь и наружу неподвижной катушки с проволокой вызовет в катушке ток, и это связано с физическим движением магнитного потока. Чем быстрее движется магнит, тем больше вырабатывается ток.Когда магнит неподвижен, в катушке не будет тока. То же самое с неподвижным магнитом и подвижной катушкой. Если мы перемещаем катушку с проволокой вперед и назад внутри неподвижного магнита, в катушке индуцируется электрический ток.

Дроссельная катушка большой силы тока для автомобильного использования — Промышленные устройства и решения

Продукты, описанные на этом веб-сайте, были разработаны и изготовлены для стандартных приложений, таких как общие электронные устройства, офисное оборудование, оборудование для передачи данных и связи, измерительные приборы, бытовая техника и аудио- видеооборудование.

Для специальных применений, в которых требуется качество и надежность, или если отказ или неисправность продуктов могут напрямую угрожать жизни или вызвать угрозу травм (например, для самолетов и аэрокосмического оборудования, дорожного и транспортного оборудования, оборудования для сжигания, медицинского оборудования , устройства для предотвращения несчастных случаев и защиты от кражи, а также защитное оборудование), пожалуйста, используйте только после того, как ваша компания в достаточной степени проверит пригодность наших продуктов для этого применения.

Независимо от области применения, при использовании наших продуктов в оборудовании, для которого ожидается высокий уровень безопасности и надежности, убедитесь, что схемы защиты, схемы резервирования и другие устройства установлены для обеспечения безопасности оборудования при оценке области применения путем независимой проверки безопасности. тесты.

Обратите внимание, что продукты и технические характеристики, размещенные на этом веб-сайте, могут быть изменены без предварительного уведомления в целях улучшения. Независимо от области применения, пожалуйста, подтвердите последнюю информацию и спецификации до окончательного этапа проектирования, покупки или использования.

Техническая информация на этом веб-сайте содержит примеры типичных операций и схем применения продуктов. Он не предназначен для гарантии ненарушения или предоставления лицензии на права интеллектуальной собственности этой компании или любой третьей стороны.

Если какие-либо продукты, спецификации продуктов и техническая информация на этом веб-сайте подлежат экспорту или предоставлению нерезидентам, необходимо соблюдать законы и постановления страны-экспортера, особенно те, которые касаются безопасного экспортного контроля.

Информация, содержащаяся на этом веб-сайте, не может быть перепечатана или воспроизведена полностью или частично без предварительного письменного разрешения Panasonic Corporation.

Инструменты и программы, представленные на этом веб-сайте, должны использоваться по вашему усмотрению. Panasonic не гарантирует каких-либо результатов от использования этих инструментов и программ и не несет ответственности за любые убытки, возникшие в результате использования вами.

<о письме для получения сертификата соответствия директиве ЕС RoHS>
Дата перехода на продукт, соответствующий требованиям RoHS, зависит от номера детали или серии.
При использовании инвентаря, в котором неясно соответствие требованиям RoHS, выберите «Запрос на продажу».
в форме веб-запроса.

Извещение о передаче полупроводникового бизнеса

Полупроводниковый бизнес Panasonic Corporation (далее именуемой «Компания») будет передан 1 сентября 2020 года Nuvoton Technology Corporation (далее именуемой «Nuvoton»). Соответственно, Panasonic Semiconductor Solutions Co., Ltd., которая управляла полупроводниковым бизнесом Panasonic, перейдет под эгидой Nuvoton Group с новым названием Nuvoton Technology Corporation Japan (далее именуемой «NTCJ»).
В соответствии с этой передачей, полупроводниковая продукция, размещенная на этом веб-сайте, после 1 сентября 2020 года будет считаться продукцией производства NTCJ.