Ток формула: Как найти индукционный ток формула — Мир Антенн

Содержание

Как найти индукционный ток формула

Индукционный ток это такой ток, который возникает в замкнутом проводящем контуре, находящемся в переменном магнитном поле. Этот ток может возникать в двух случаях. Если имеется неподвижный контур, пронизываемый изменяющимся потоком магнитной индукции. Либо когда в неизменном магнитном поле движется проводящий контур, что также вызывает изменение магнитного потока пронизывающего контур.

Причиной возникновения индукционного тока является вихревое электрическое поле, которое порождается магнитным полем. Это электрическое поле действует на свободные заряды, находящиеся в проводнике, помещенном в это вихревое электрическое поле.

Также можно встретить и такое определение. Индукционный ток это электрический ток, который возникает вследствие действия электромагнитной индукции. Если не углубляется в тонкости закона электромагнитной индукции, то в двух словах ее можно описать так. Электромагнитная индукция это явление возникновение тока в проводящем контуре под действие переменного магнитного поля.

С помощью этого закона можно определить и величину индукционного тока. Так как он нам дает значение ЭДС, которая возникает в контуре под действие переменного магнитного поля.

Как видно из формулы 1 величина ЭДС индукции, а значит и индукционного тока зависит от скорости изменения магнитного потока пронизывающего контур. То есть чем быстрее будет меняться магнитный поток, тем больший индукционный ток можно получить. В случае, когда мы имеем постоянное магнитное поле, в котором движется проводящий контур, то величина ЭДС будет зависеть от скорости движения контура.

Чтобы определить направление индукционного тока используют правило Ленца. Которое гласит что, индукционный ток направлен навстречу тому току, который его вызвал. Отсюда и знак минус в формуле для определения ЭДС индукции.

Индукционный ток играет важную роль в современной электротехнике. Например, индукционный ток, возникающий в роторе асинхронного двигателя, взаимодействует с током, подводимым от источника питания в его статоре, вследствие чего ротор вращается.

На этом принципе построены современные электродвигатели.

В трансформаторе же индукционный ток, возникающий во вторичной обмотке, используется для питания различных электротехнических приборов. Величина этого тока может быть задана параметрами трансформатора.

И наконец, индукционные токи могут возникать и в массивных проводниках. Это так называемые токи Фуко. Благодаря им можно производить индукционную плавку металлов. То есть вихревые токи, текущие в проводнике вызывают его разогрев. В зависимости от величины этих токов проводник может разогреваться выше точки плавления.

Итак, мы выяснили, что индукционный ток может оказывать механическое, электрическое и тепловое действие. Все эти эффекты повсеместно используются в современном мире, как в промышленных масштабах, так и на бытовом уровне.

Задача 11.4. Рамка сопротивлением r находится в переменном магнитном поле. За время Dt магнитный поток изменился от значения Ф₁ до значения Ф₂. Определите величину тока, считая изменение магнитного потока равномерным.

Ф₁, Ф₂, Dt, R	Решение. В рамке возникла ЭДС индукции
i = ?

ℰ_i .

Рис. 11.25

Для рамки справедлив закон Ома для замкнутой цепи, т.е. рамку в изменяющемся магнитном поле можно заменить на эквивалентную электрическую схему (рис. 11.25), где источник ЭДС имеет нулевое внутреннее сопротивление. Тогда

i = ℰ_i/R = .

Читатель: А что означает знак «минус»?

Автор: Ток может идти как по, так и против согласованного направления обхода контура. Если Ф₂ > Ф₁ (поток возрастает), то ток идет против направления обхода, а если Ф₂ > Ф₁ (поток убывает) – по направлению обхода контура.

СТОП! Решите самостоятельно: А22–А24, В27, В28, С18, С19, D3.

Рис. 11.26

Задача 11.5. Квадратная рамка разделена на две части куском проволоки из такого же материала и помещена в переменное магнитное поле (рис. 11.26). Известно, что в точно такой же рамке без перемычки, помещенной в такое же поле, ЭДС индукции ℰ = 1 В. Сопротивление стороны квадрата R = 1 Ом. Определите индукционный ток в перемычке. Все значения считаются точными.

ℰ = 1 В R = 1 Ом	Решение. В рамке без перемычки возникает ЭДС индукции, по модулю равная \|ℰ\| . (1)
I = ?

В рамке с перемычкой в каждом из контуров (левом и правом) тоже возникает ЭДС индукции:

|ℰ_л| , (2)

|ℰ_п| . (3)

Рис. 11.27

Из равенств (1)–(3) видим, что ℰ_л = ℰ, ℰ_п = ℰ. Теперь можно начертить эквивалентную схему (рис. 11.27).

Для точки А запишем первое правило Кирхгофа:

Для левого и правого контуров запишем второе правило Кирхгофа:

ℰ. (6)

ℰ. (7)

Подставляя численные значения ℰ = 1 В и R = 1 Ом в уравнения (6) и (7), получим:

Теперь в эту систему из уравнения (5) подставим значение I = I_л– I_п:

Подставим значение

I_л из (9) в (8):

Þ А.

А.

Теперь из формулы (5) находим искомый индукционный ток через перемычку:

I = I_л– I_п = А.

Ответ: через перемычку пойдет индукционный ток I = А.

СТОП! Решите самостоятельно: В29, С20, С21, D4.

Дата добавления: 2016-04-11 ; просмотров: 941 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС.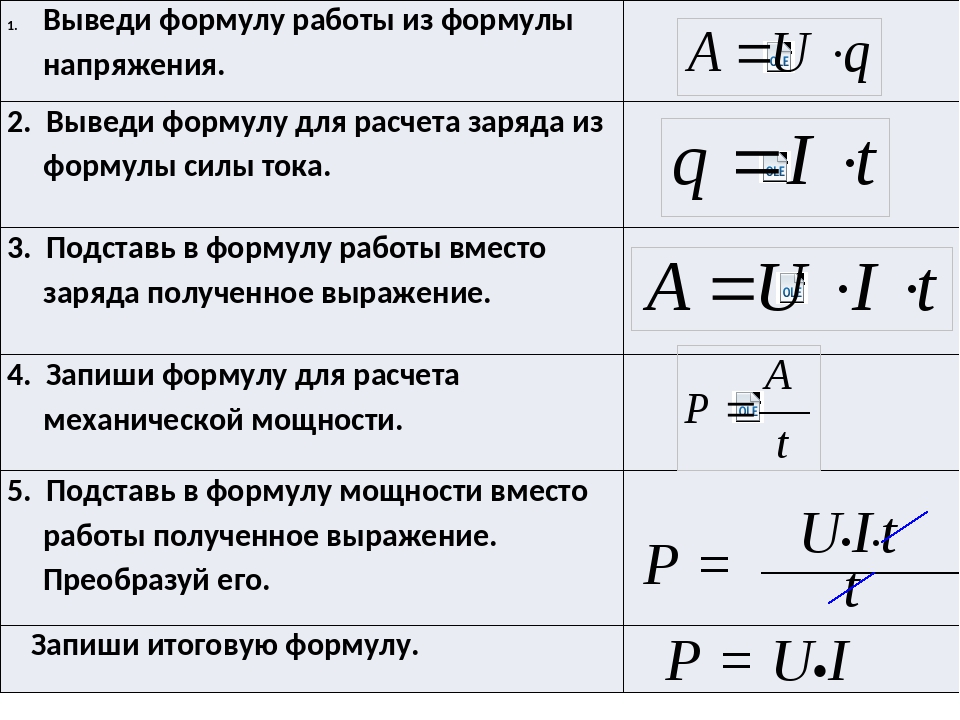

Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока.

Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

L = индуктивность в генри
μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
μ г = относительная проницаемость материала сердечника
N = число витков
A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
l = длина катушки в метрах (м)

Индуктивность прямого проводника:

L = индуктивность в нГн
l = длина проводника
d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

L = индуктивность в мкГн
r = внешний радиус катушки
l = длина катушки
N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

L = индуктивность в мкГн
r = средний радиус катушки
l = длина катушки
N = число витков
d = глубина катушки

Индуктивность плоской катушки:

L = индуктивность в мкГн
r = средний радиус катушки
N = число витков
d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

основные понятия, нахождение через силу тока и сопротивление

При проектировании схем различных устройств радиолюбителю необходимо производить точные расчеты c помощью измерительных приборов и формул. В электротехнике используются формулы для вычислений величин электричества (формулы напряжения, сопротивления, силы тока и так далее).

Общие сведения об электрическом токе

Электрическим током является процесс движения заряженных частиц (свободных электронов), имеющий вектор направленности. Частицы перемещаются под действием напряженности электрического поля, имеющей векторное направление. Это поле совершает работу по перемещению этих частиц. Влияют на работу электрического поля сила тока, напряжение и сопротивление.

Физический смысл

Под физическим смыслом понимается работа тока на участке, соотносящаяся с величиной заряда. Положительный заряд перемещается из одной точки, обладающей одним потенциалом, в другую, причем потенциал в этой точке отличается от предыдущего. В результате этого и возникает разность потенциалов, именуемая напряжением или ЭДС (электродвижущей силой).

Для полного понимания этого физического процесса и выяснения физического смысла напряжения необходимо провести аналогию с трубой. Допустим, труба наполнена водой и к ней прикручен кран для слива воды. Эта труба также оборудована краном для заливания воды с помощью мощного насоса.

Для демонстрации аналогии нужно открыть кран полностью, вода начнет выливаться и можно сделать вывод о незначительном давлении. Во втором случае спускной кран открыт не полностью и происходит набор воды при помощи насоса. В трубе создается давление и напор усиливается. Насос, создающий давление, и является в этом примере напряженностью электрического поля.

Электричество, если его не контролировать и не знать о пагубном влиянии на организм человека, способно создать множество проблем начиная от сгорания приборов и пожаров, и заканчивая угрозой жизни и здоровью человека. Техника безопасности очень важна в любой сфере.

Пагубное влияние на человека

Электричество очень опасно и является причиной несчастных случаев. Радиолюбители подвержены риску поражения электрическим током довольно часто. Некоторые радиолюбители пробуют наличие напряжения пальцами и пренебрегают техникой безопасности. Большинство из них считает опасным для жизни напряжение от 500 В, а 110 и 220 — не наносящими вреда здоровью. Удары от маломощных источников тока (маломощный силовой трансформатор, конденсатор), по их мнению, являются неопасными.

Согласно технике безопасности при работах с электричеством, они ошибаются, но есть и другая сторона этого вопроса: организм каждого человека индивидуален, обладает разными параметрами. Из этого утверждения следует, что смертельные характеристики электричества (напряжение и ток) индивидуальны для каждого человека. Одних может ударить 36 В, а других не пробивает и 220 В.

Действие электричества на организм человека зависит от нескольких факторов: силы и частоты, времени и пути прохождения через организм, сопротивления организма или участка тела, по которому протекает ток.

Исследованиями ученых установлено, что величина смертельного тока, поражающего сердце, составляет более 100 мА. Токи от 50 мА до 100 мА вызывают потерю сознания при кратковременном касании к поверхности, которая проводит ток. Токи до 50 мА могут стать причиной травм, например, падения с лестницы, выпускания из рук токоведущего проводника и т. д.

Влияние на фактор поражения еще оказывает и сопротивление тела человека. Сопротивление для каждого индивида определить сложно и диапазон его составляет от 30 кОм до 200 кОм. Эта величина зависит от множества факторов: толщины кожи, влажности тела и окружающей среды, усталости, нервно-эмоционального состояния, болезни и других факторов. Сопротивление резко уменьшается при повышенной влажности воздуха и работе на влажных участках.

Формула расчета напряжения, опасного для жизни, предполагая, что Rч = 2кОм и I = 60 мА, выглядит так: U = I * R = 0,06 * 2000 = 120 В. В этой ситуации опасным напряжением можно считать 120 В и выше.

Частота тока является еще одной опасной характеристикой, обладающей поражающим действием. При увеличении частоты опасность уменьшается прямо пропорционально. Ток оказывает и тепловое действие, поэтому считать высокочастотные токи безопасными нельзя.

Травмы, происходящие из-за электричества, называются электротравмами. Каждая из них несет в себе меньшую или большую опасность. Наиболее опасными являются травмы, полученные от электрической дуги, которая обладает высокой температурой от 5 тыс. до 12 тыс. градусов по Цельсию. Виды электрических травм:

Электрические ожоги происходят при тепловом воздействии на ткани организма человека, по которым течет ток.
Обожженные участки на коже возникают при прямом контакте ее с токоведущей частью проводника. Пораженный участок приобретает серый или бледно-серый цвет.
Металлизация кожи — пропитывание кожи частицами металла при коротком замыкании или сварке.
Механические повреждения — самопроизвольная судорога мышц, приводящая к падению. При падении происходят переломы, ушибы вывихи суставов и т. д.
Электроофтальмия — воспаление слизистой оболочки глаз при воздействии излучения электрической дуги.

Существует еще один вид поражения — электрический удар. Этот вид поражения можно условно разделить на 5 групп: без потери сознания; с потерей сознания, связанной с нарушением сердечной деятельности или без нее; клиническая смерть и электрический шок.

Единицы измерения

Работа электрического поля по перемещению заряда измеряется в Дж (Джоуль), заряд в Кл (кулон). Вот, как обозначается напряжение или его единица измерения: отношение этих величин (работа по перемещению в Дж к электрическому заряду в Кл) и является разностью потенциалов, измеряется в вольтах (В) и обозначается U. Разность потенциалов бывает:

Переменной (амплитуда и полярность изменяются с течением времени, в зависимости от характерной частоты).
Постоянной (имеет постоянное значение амплитуды и полярность есть величина постоянная).

А также у единиц измерения есть приставки, например, кВ (Киловольт = 1000В) и МВ (мегавольт = 1000000В). Существуют о совсем низкие значения, например, мВ (милливольт = 0,001В).

Цепи переменного и постоянного тока

В цепях постоянного и переменного тока U обладает различными свойствами и производит иные влияния на проводники. Для постоянного напряжения существуют законы по вычислению его характеристик, но для переменного способы вычисления показателей заметно отличаются. Разберем более подробно все различия и сходства.

Расчет и анализ цепей выполняется при помощи закона Ома: сила тока полной цепи прямо пропорциональна напряжению и обратно пропорциональна сумме сопротивлений цепи и источника питания.

Следствие из закона при условии пренебрежения внутренним сопротивлением источника электричества: сила тока участка цепи прямо пропорциональна ЭДС и обратно пропорциональна сопротивлению этого участка.

Запись закона Ома, из которого следует формула напряжения, тока и сопротивления: I = U / (Rц + Rвн), где I — сила тока, U — ЭДС, Rц — сопротивление цепи, Rвн — внутреннее сопротивление источника питания.

Формула силы тока через сопротивление и напряжение: I = U / Rц.

Формула напряжения электрического тока: U = I * Rц.

Для расчета мощности необходимо U умножить на I: P = U * I = U * U / R, где P — мощность.

Переменное однофазное напряжение

В цепях для переменного тока происходят совершенно другие явления и процессы, для них справедливы другие законы. Различают такие основные виды:

Мгновенное (разность потенциалов в конкретный промежуток времени: u = u (t)).
Амплитудное значение (максимальное значение мгновенного U в момент времени: u (t) = Uм * sin (wt + f), где w — угловая частота, t — конкретный момент времени и f — угол начальной фазы напряжения).
Среднее значение (для синусоиды равно нулю).
Среднеквадратичное — Uq (U за весь период колебаний и для синусоиды имеет вид: Uq = 0,707 * Uм).
Средневыпрямленное — Uv (среднее значение модуля U: Um примерно равно 0,9 * Uq).

В цепях 3-фазного тока различают 2 вида напряжений: линейное (фаза-фаза) и фазное (фаза-ноль). При соединении в цепь «треугольником» фазное и линейное U равны. В случае соединения «звездой» — фазное в 1,732050808 раз меньше линейного.

Расчета тока по мощности: формула, онлайн расчет

Чтобы уберечь себя от проблем с электропроводкой в процессе эксплуатации необходимо изначально правильно рассчитать и выбрать сечение кабеля ибо от этого будет зависеть и пожаробезопасность здания. Неправильно выбранное сечение кабеля может привести к короткому замыканию и возгоранию электропроводки, а с ней и всего помещения и здания. Выбор сечения зависит от многих параметров, но, пожалуй, самым главным является сила тока.

Формула расчета мощности электрического тока

Если в уже действующей цепи силу тока можно измерить специальными приборами (амперметром), то как быть при проектировании? Ведь мы не можем измерить силу тока в цепи, которой еще нет.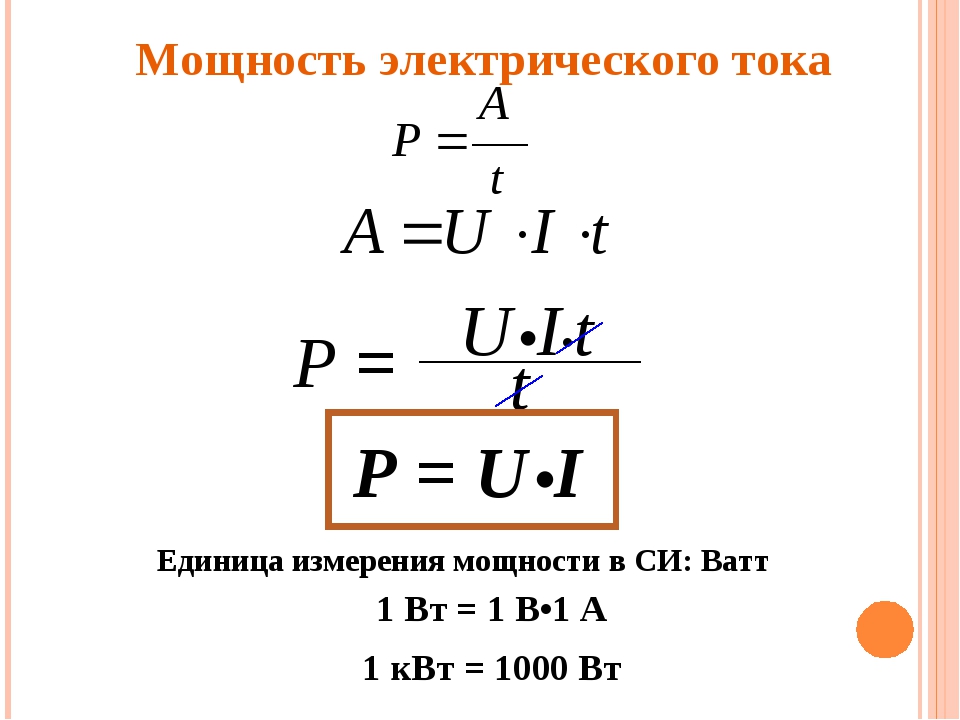 В этом случае пользуются расчетным методом.
При известных параметрах мощности, напряжения в сети и характера нагрузки силу тока можно посчитать используя формулу:

Формула для однофазной сети I=P/(U×cosφ)

Формула для трехфазной сети I=P/(1,73×U×cosφ)

P — электрическая мощность нагрузки, Вт;
U — фактическое напряжение в сети, В;
cosφ — коэффициент мощности.

Мощность определяется, исходя из суммарной мощности всех приборов, планируемых в эксплуатации, подключенных к данной сети, это, как правило, паспортные данные приборов или приблизительные значения для аналогичных приборов. Рассчитывается мощность на этапе планирования электропроводки в квартире.

Коэффициент мощности зависит от характера загрузки, например, для нагревательных приборов, ламп освещения он приближен к 1, но во всякой активной нагрузке есть реактивная составляющая, благодаря чему коэффициент мощности принимают равным 0,95. Это всегда нужно учитывать в разных видах электропроводки.

В мощных приборах и оборудовании (электродвигатели, сварочные аппараты и прочее) доля реактивной нагрузки выше, поэтому для подобных приборов коэффициент мощности принимают 0,8.

Напряжение в сети принимают 220 вольт для однофазного тока и 380 вольт для трехфазного, но для большей точности, если есть такая возможность, рекомендуется использовать для расчета фактические значения напряжения, измеренные приборами.

Форма для расчета мощности тока

Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Физические законы, формулы, переменные

Формулы электричество и магнетизм

Закон Кулона:
где q₁ и q₂ — величины точечных зарядов, ԑ₁ — электрическая постоянная;
ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1),
r — расстояние между зарядами.

Напряженность электрического поля:

где Ḟ — сила, действующая на заряд q₀ , находящийся в данной точке поля.

Напряженность поля на расстоянии r от источника поля:

1) точечного заряда

2) бесконечно длинной заряженной нити с линейной плотностью заряда τ:

3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ:

4) между двумя разноименно заряженными плоскостями

Потенциал электрического поля:

где W — потенциальная энергия заряда q₀ .

Потенциал поля точечного заряда на расстоянии r от заряда:

По принципу суперпозиции полей, напряженность:

Потенциал:

где Ē_iи ϕ_i — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.

Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ₁ в точку с потенциалом ϕ₂ :

Связь между напряженностью и потенциалом

1) для неоднородного поля:

2) для однородного поля:

1)
2)

Электроемкость уединенного проводника:

Электроемкость конденсатора:

где U = ϕ₁ — ϕ₂ — напряжение.

Электроемкость плоского конденсатора:

где S — площадь пластины (одной) конденсатора,

d — расстояние между пластинами.

Энергия заряженного конденсатора:

Сила тока:

Плотность тока:

где S — площадь поперечного сечения проводника.

Сопротивление проводника:

ρ — удельное сопротивление;

l — длина проводника;

S — площадь поперечного сечения.

Закон Ома

1) для однородного участка цепи:

2) в дифференциальной форме:

3) для участка цепи, содержащего ЭДС:

где ε — ЭДС источника тока,

R и r — внешнее и внутреннее сопротивления цепи;

4) для замкнутой цепи:

1)
2)
3)
4)

Закон Джоуля-Ленца

1) для однородного участка цепи постоянного тока:
где Q — количество тепла, выделяющееся в проводнике с током,
t — время прохождения тока;

2) для участка цепи с изменяющимся со временем током:

1)
2)

Мощность тока:

Связь магнитной индукции и напряженности магнитного поля:

где B — вектор магнитной индукции,
μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1),
µ₀ — магнитная постоянная ,
H — напряженность магнитного поля.

Магнитная индукция (индукция магнитного поля):
1) в центре кругового тока
где R — радиус кругового тока,

2) поля бесконечно длинного прямого тока
где r — кратчайшее расстояние до оси проводника;

3) поля, созданного отрезком проводника с током
где ɑ₁ и ɑ₂ — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля;
4) поля бесконечно длинного соленоида
где n — число витков на единицу длины соленоида.

1)
2)
3)
4)

Сила Лоренца:

по модулю
где F — сила, действующая на заряд, движущийся в магнитном поле,
v — скорость заряда q,
α — угол между векторами v и B.

Поток вектора магнитной индукции (магнитный поток через площадку S):
1) для однородного магнитного поля ,
где α — угол между вектором B и нормалью к площадке,
2) для неоднородного поля

1)
2)

Потокосцепление (полный поток):
где N — число витков катушки.

Закон Фарадея-Ленца:
где ԑ_i— ЭДС индукции.

ЭДС самоиндукции:
где L — индуктивность контура.

Индуктивность соленоида:

где n — число витков на единицу длины соленоида,
V — объем соленоида.

Энергия магнитного поля:

Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур:

где ∆Ф = Ф₂ – Ф₁— изменение магнитного потока, R — сопротивление контура.

Работа по перемещению замкнутого контура с током I в магнитном поле:

Зависимость силы тока от напряжения — формула, график и законы

Фундаментальной связью в электричестве является зависимость силы тока от напряжения. Благодаря этому закону, экспериментально установленном Омом в 1826 году, созданы различные измерительные приборы. Удалось исследовать физику короткого замыкания. Формулу можно применять для систем, которые зависят от электросопротивления. Пожалуй, разработка любой электрической сети невозможна без использования этого открытия.

Общие сведения

Любое физическое тело состоит из молекул и атомов. Эти частицы взаимодействуют между собой. Они могут притягиваться друг к другу или отталкиваться. В изолированной системе элементарные частицы являются носителями заряда. В спокойном состоянии, то есть когда на тело не оказывается внешнего воздействия, алгебраическая сумма энергии частиц всегда постоянная величина. Это утверждение называется законом сохранения электрического заряда.

Частицы хаотично могут перемещаться по кристаллической решётке, но их движение компенсируется. Поэтому ток не возникает. Но если к телу приложить внешнюю силу, то свободные электроны начинают двигаться в одну сторону. Это упорядоченное движение заряженных частиц и называют электрическим током. Количественно его можно описать через силу.

Упорядочено заряды заставляет двигаться электрическое поле, вдоль линий которого и происходит перемещение. Впервые этот термин ввёл Фарадей. Он сумел выяснить, что вокруг любого носителя существует особый вид материи, влияющий на поведение других частиц. За силовую характеристику электрического поля было взято отношение действующей силы к величине заряда, помещённого в данную точку: E = F / q. Назвали эту характеристику напряжённостью.

Изучение поля позволило экспериментально открыть принцип суперпозиции. То есть установить, что напряжённость поля, созданного системой зарядов, равна геометрической сумме величин, существующих у отдельных носителей: E = Σ E1 + E2 +…+ En. Напряжённость прямо пропорциональна напряжению, которое, в свою очередь, равняется разности потенциалов между двумя точками.

По сути, это работа электрического поля, совершаемая для переноса единичного заряда из одного места в другое: U = A / q = E * d, где d – расстояние между точками. Значение напряжения зависит от нескольких факторов:

строения тела;
температуры;
сопротивления.

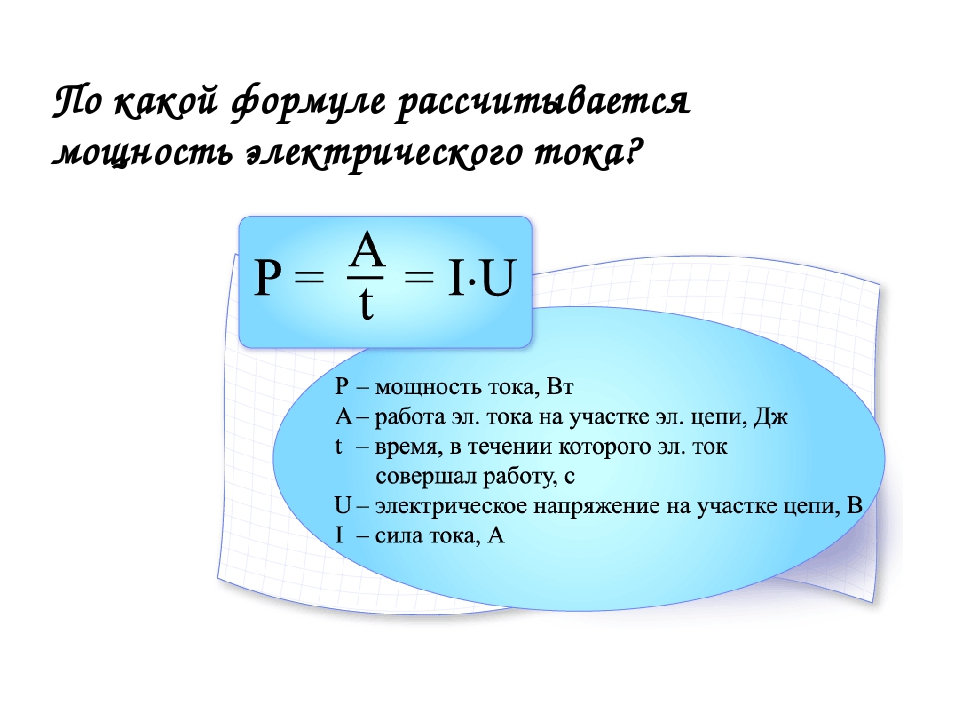
Самое большее влияние оказывает последняя величина. Именно она характеризует способность материала препятствовать прохождению тока, то есть определяет проводимость. Сопротивление зависит от длины проводника и его сечения: R = (p * l) / S, где p – параметр обратный удельной проводимости (справочное значение). Он численно равняется сопротивляемости однородного проводника единичной длины и площади сечения.

Подтверждение закона Ома

Бум исследования электрических явлений пришёлся на конец XVIII – начало XIX веков. Такие учёные, как Фарадей, Ампер, Вольт, Эрстед, Кулон, Лачинов, Ом провели ряд экспериментов, которые позволили Максвеллу создать теорию электромагнитных явлений.

Огромную роль в открытии новых знаний сыграл опыт Ома исследовавшего, от чего зависит сила тока в цепи. Немецкий физик ставил опыты над проводимостью различных материалов. Для этого он использовал электрическую цепь, в разрыв которой подключал проводники разной длины и замерял силу тока.

Изначально учёный не смог установить закономерность. Всё дело в том, что для своих опытов Ом использовал химическую батарею. Друг учёного Поггендорф предложил взять термоэлектрический источник тока. В итоге физик смог проследить зависимость. Описал он её так: частное от a, разделённого на l + b, где b определяет интенсивность воздействия на проводника длиною l, причём a и b — постоянные, зависящие соответственно от действующей силы и сопротивления элементов цепи.

Обычно при изучении закона в седьмом классе средней школы учитель демонстрирует эту зависимость на практических уроках. Для этого чтобы ученики удостоверились в справедливости утверждения, преподаватель собирает электрическую цепь, в состав которой входят:

вольтметр – прибор для измерения напряжения, включается параллельно измеряемому проводнику;
амперметр – устройство для замера тока, подключается последовательно с измеряемым телом;
регулируемый источник электродвижущей силы (ЭДС).

Суть опыта заключается в подключении проводников с разной длиной. Измеренные результаты заносят в таблицу. Она должна иметь примерно следующий вид:

Первое тело		Второе тело		Третье тело
U, В	I, А	U, В	I, А	U, В	I, А

1	0,5	1	0,4	1	0,2
2	1	2	0,6	2	0,3
3	1,5	3	0,8	3	0,4
4	2	4	1	4	0,5

Проведя анализ таблицы, можно сделать вывод. Если для любого тела напряжение разделить на соответствующую ему силу тока, то получится одно и то же число. Следовательно, это отношение является свойством проводника. Для первого оно равно двум, второго – пяти, а третьего – десяти. При одинаковых токах в третьем случае число больше, значит, это тело оказывает большее сопротивление току.

Полученные значения по факту и являются величинами, обратными проводимости. Обозначают их буквой R (resistance).

График зависимости

По результатам эксперимента Ом построил график зависимости силы тока от сопротивления, который напоминает собой левую часть параболы. Современная запись закона Ома имеет вид: I = U / R. Звучит она следующим образом: ток прямо пропорционален напряжению и обратно пропорционален электрическому сопротивлению.

Но при разработке приборов или исследовании участка цепи перед учёными и инженерами стоит задача, прежде всего, выяснить зависимость тока от напряжения. Поэтому ими строится график, в котором по оси абсцисс откладывают значение потенциала, а ординат — силы тока. В итоге если отложить соответствующие точки, то должна получиться прямая линия. Это говорит о том, что зависимость величин линейная. То есть во сколько раз увеличивается напряжение, во столько же возрастает сила тока.

Такого вида график называется вольт-амперной характеристикой (ВАХ). Но при реальных измерениях изменение ток зависит ещё от температуры. Установлено, что при нагреве сопротивление проводника увеличивается. Поэтому прямая на ВАХ будет иметь меньший угол наклона. Кроме того, ток может быть двух видов:

постоянный – сила не изменяется от времени;
переменный – изменяющийся по синусоидальному закону.

Поток носителей заряда для второго вида описывается гармоническим законом: I(t) = Im * cos (wt + f), где: w – циклическая частота, f – сдвиг фаз относительно напряжения, Im – наибольшее значение тока.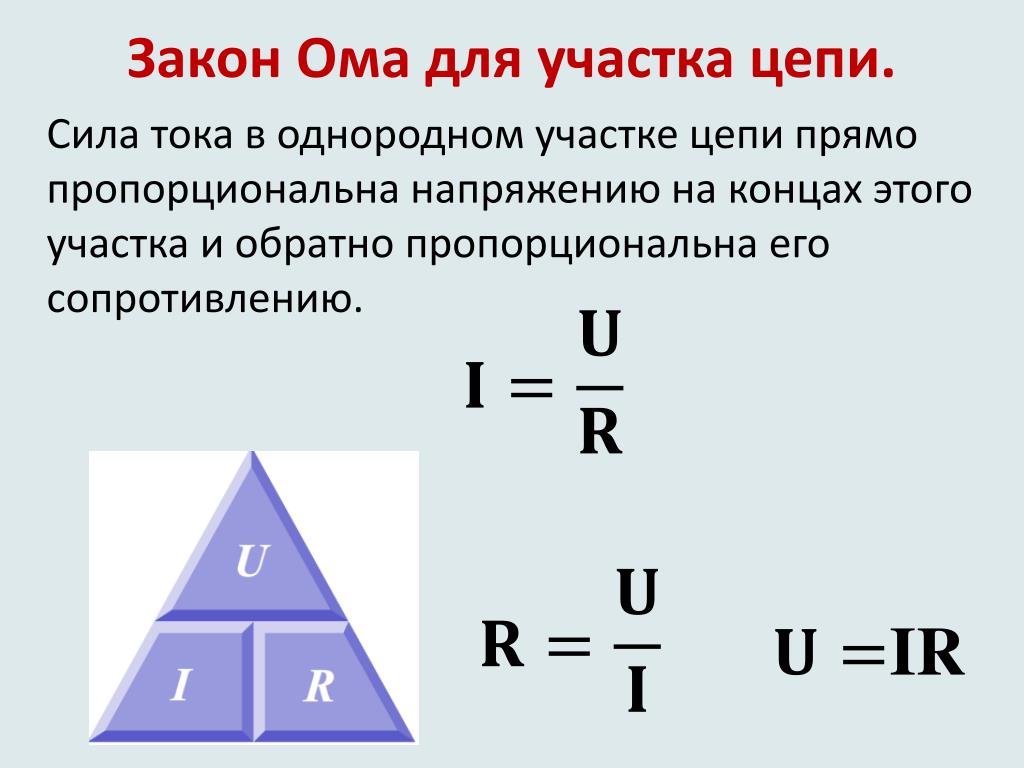 Тогда изменение напряжения во времени можно записать так: U(t) = Um * cos (wt). В этом случае закон Ома примет вид: I = U / Z, где Z – полное сопротивление цепи.

График зависимости силы тока от времени, впрочем, как и напряжения, будет представлять собой синусоиду. Если отложить их на одном рисунке, то при активном сопротивлении (резистор) фазы величин будут совпадать друг с другом. В схеме, содержащей реактивные составляющие, а это ёмкость, и индуктивность, фаза тока соответственно будет опережать и отставать от напряжения. Угол изменения составит девяносто градусов.

Графики зависимости позволяют определить мощность. Сделать это можно, воспользовавшись формулой: P = U * I * cos(f). Чтобы построить график мощности, нужно аппроксимировать на ось t точки синусоиды I(t) и U(t), в которых параметры изменяют свой знак.

Характеристика P(t) будет также описываться по гармоническому закону. Причём в каждой этой точке линя изменит направление.

Простейшие задачи

Зависимость, установленную экспериментальным путём, широко используют при проектировании электронных схем различных устройств. С помощью закона Ома рассчитывают нужное сопротивление резисторов для той или иной цепи, вычисляют значение тока при определённом напряжении.

Вот некоторые из таких заданий:

Пусть имеется схема, подключённая к источнику, выдающему 60 вольт. Определить, какой ток потечёт через резистор 30 Ом. Согласно правилу, связывающему три фундаментальных величины: I = U / R. Так как по условию все нужные данные известны, то необходимо их просто подставить в формулу и выполнить вычисления: I = 60 В / 30 Ом = 2 А. Задача решена. Ответ: через резистор потечёт ток равный двум амперам.

Построить графики зависимости для двух проводников имеющих сопротивление пять и пятнадцать ом.

В задании требуется нарисовать ВАХ. Так как напряжения не указаны, то их можно брать любыми. Используя формулу Ома, нужно определить ток для произвольных значений потенциала. График зависимости – прямая. Значит, нужно отложить две точки. Чтобы правильно разметить значения необходимо выбрать масштаб. Поэтому вначале следует посчитать максимальное значение тока. Пусть за наибольшее напряжение будет принято U = 50 В. Тогда, Im1 = 50 / 5 = 10 А, Im2 = 50 / 10 = 5 А. Теперь останется отложить полученный результат на графике и провести линию через ноль и эти точки.

Определить ток, потребляемый электрочайником, если его спираль имеет сопротивление 40 Ом, а напряжение сети равно 220 вольт. Пример решается по простой формуле: I = U / R = 220 В / 40 Ом = 5, 5 А. Задача решена.

В вольтметре, показывающем 120 вольт, ток составляет 15 миллиампер. Найти сопротивление прибора. Из формулы зависимости можно выразить сопротивление. Оно будет равно: R = U / I. При этом, чтобы получить правильный ответ, миллиамперы следует перевести в амперы.

Решение будет иметь вид: R = 120 В / 15 * 10^-3 А = (120 * 10³) / 15 = 8 * 10³ Ом = 8 кОм. Итак, внутреннее сопротивление вольтметра составит восемь килоом.

Следует отметить, что в школьных задачах не учитываются характеристики источника тока.

По умолчанию считают, что он имеет бесконечно малое внутреннее сопротивление. Но на самом деле это не так. Электродвижущая сила генератора электрической энергии затрачивается как на внутренние, так и внешние потери. Поэтому формула закона Ома для полной цепи имеет вид: I = (U0 + U) / R + r, где: U0 – внутреннее падение напряжения, r0 – сопротивление источника.

ФизикаНаправление электрического тока — условия и причины возникновения

ФизикаУравнение траектории тела — определение и формулы

Формула ЕС

Закон Ома

Импеданс

Фазовый угол

Магнитная
Проницаемость

Где:

Z	=	Импеданс (Ом)
R	=	Сопротивление (Ом)
X _L	=	Индуктивное сопротивление (Ом)

Дополнительная информация

Где:

м	=	Магнитная проницаемость (Генри / метр)
Б	=	Плотность магнитного потока (тесла)
H	=	Сила намагничивания (Ам / метр)

Относительная
Магнитная проницаемость

Электропроводность и удельное сопротивление

Электрический
Электропроводность
(% IACS)

Где:

м _об	=	Относительная магнитная проницаемость (безразмерная)
м	=	Любая заданная магнитная проницаемость (Г / м)
м _или	=	Магнитная проницаемость в свободном пространстве (Г / м), равная 1. 257 x 10 ^-6 В / м

Дополнительная информация

Где:

с	=	Электропроводность Сименс / м
r	=	Удельное электрическое сопротивление (Ом-м)

Дополнительная информация

Когда известно удельное сопротивление

Где:

с _% _IACS	=	Электропроводность (% IACS)
r	=	Удельное электрическое сопротивление (МОм-см)
с _м _{См / см}	=	Электропроводность (мСименс / см)

Дополнительная информация

Если известна проводимость в
См / м или мСм / см или

Где:

с _% _IACS	=	Электропроводность (% IACS)
с _{См / м}	=	Электропроводность (Сименс / метр)
с _м _{См / см}	=	Электропроводность (мСименс / см)

Дополнительная информация

Плотность тока

Стандартная глубина
проникновения

Стандартная глубина проникновения

Стандартная глубина
проникновения

Где:

Jx	=	Плотность тока (ампер / м ²)
Дж _или	=	Плотность тока на поверхности (ампер / м ²⁾
e	=	Базовый натуральный логарифм = 2. 71828
х	=	Расстояние под землей
д	=	Стандартная глубина проникновения

Дополнительная информация

Когда известна электрическая проводимость (См / м).

Где:

д	=	Стандартная глубина проникновения (м)
п	=	3,14
f	=	Тестовая частота (Гц)
м	=	Магнитная проницаемость (Г / м) (1. 257 x 10 ^-6 H / m для немагнитных материалов)
с	=	Электропроводность (Сименс / м)

Дополнительная информация
Калькулятор глубины пера

Если известна электрическая проводимость
(% IACS).

дюйм мм
В дюймах

Где:

д	=	Стандартная глубина проникновения (мм или дюйм)
f	=	Тестовая частота (Гц)
м _r	=	Относительная магнитная проницаемость (безразмерная)
с	=	Электропроводность (% IACS)

Дополнительная информация

Когда известно удельное электрическое сопротивление
(МОм-см).

дюйм мм
В дюймах

Где:

д	=	Стандартная глубина проникновения (мм или дюйм)
r	=	Удельное электрическое сопротивление (МОм-см)
f	=	Тестовая частота (Гц)
м _r	=	Относительная магнитная проницаемость (безразмерная)

Дополнительная информация

Вихретоковый
Задержка фазы поля

Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока

Формулы и уравнения мощности в цепях постоянного и переменного тока 1-Φ и 3-Φ

Возвращаясь к основам, ниже приведены простые формулы электрической мощности для однофазных цепей переменного тока, трехфазных цепей переменного тока и цепей постоянного тока. Вы можете легко найти электрическую мощность в ваттах , используя следующие формулы электрической мощности в электрических цепях .

Базовая формула мощности в цепях переменного и постоянного тока

Формула мощности в цепях постоянного тока

P = V x I
P = I ² x R
P = V ² / R

Формулы мощности в однофазных цепях переменного тока

P = V x I x Cos Ф
P = I ² x R x Cos Ф
P = V ² / R (Cos Ф)

Формулы мощности в трехфазных цепях переменного тока

P = √3 x V _L x I _L x Cos Ф
P = 3 x V _Ph x I _Ph x Cos Ф
P = 3 x I ² x R x Cos Ф
P = 3 (V ² / R) x Cos Ф

Где:

Формулы питания переменного тока в сложных схемах:

Комплексная мощность и полная мощность:

Когда в цепи есть индуктор или конденсатор, wer становится комплексной степенью «S» , что означает, что он состоит из двух частей i. е. реальная и мнимая часть. Величина комплексной мощности называется полной мощностью | S |.

Где

P — активная мощность
Q — реактивная мощность

Активная или реальная мощность и реактивная мощность:

Действительная часть — Комплексная мощность «S» известна как активная или активная мощность «P» , а мнимая часть известна как реактивная мощность «Q» .

S = P + jQ
P = V I cosθ
Q = V I sinθ

Где

θ — фазовый угол между напряжением и током.

Коэффициент мощности:

Коэффициент мощности «PF» — это отношение активной мощности «P» к полной мощности «| S |» . Математически коэффициент мощности — это косинус угла θ между активной и полной мощностью.

Где

| S | = √ (P ² + Q ²)

Другие формулы, используемые для коэффициента мощности, следующие:

Cosθ = R / Z

Где:

Cosθ = коэффициент мощности
R = сопротивление
Z = импеданс (сопротивление в цепях переменного тока i. 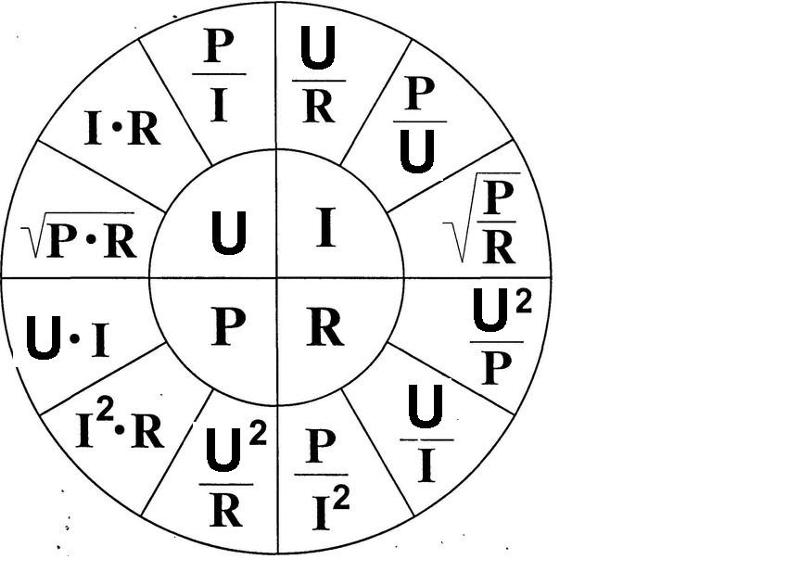е. X _L , X _C и R , известные как Индуктивное реактивное сопротивление , емкостное реактивное сопротивление и сопротивление соответственно).

Cosθ = кВт / кВА

Где

Cosθ = коэффициент мощности
кВт = фактическая мощность в ваттах
кВА = полная мощность в вольт-амперах или ваттах

Для расчета коэффициента мощности используются дополнительные формулы.

Реальная мощность однофазного и трехфазного тока

Где

В _{действующее значение} и I _{среднеквадратичное значение} — это среднеквадратичное значение напряжения и тока соответственно.
В _L-N и I _L-N — это напряжение и ток между фазой и нейтралью соответственно.
V _L-L & I _L-L — это линейное напряжение и ток соответственно.
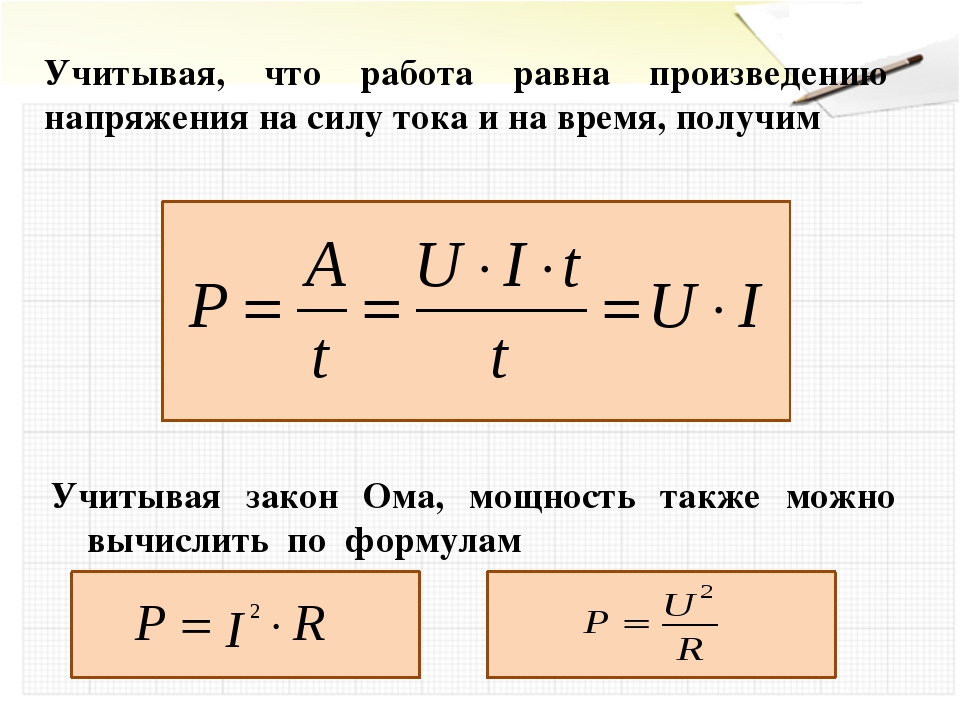
Cosθ — коэффициент мощности PF.

Реактивная мощность однофазного и трехфазного тока:

Где

θ = — фазовый угол, т.е. разность фаз между напряжением и током.

В следующей таблице показаны различные формулы мощности для цепей переменного и постоянного тока.

Количество

пост.

P = V x I
P = I ² x R
P = V ² / R

P = V x I x Cos Ф
P = I ² x R x Cos Ф
P = V ² / R (Cos Ф)

P = √3 x V _L x I _L x Cos Ф
P = 3 x V _Ph x I _Ph x Cos Ф
P = 3 x I ² x R x Cos Ф
P = 3 (V ² / R) x Cos Ф

Сопутствующие формулы Сообщения и уравнения:

Формулы асинхронного двигателя с расчетами

Электродвигатели — это машины, которые преобразуют входную электрическую энергию в механическую энергию. Все двигатели состоят из статора (неподвижная часть) и ротора (вращающаяся часть). Поскольку двигатель работает на электричестве, с его работой связаны различные свойства. Такие свойства включают количество полюсов, скорость, частоту, скольжение, пусковой ток и номинальную мощность. Ранее мы публиковали книгу по двигателям переменного тока, в которой кратко объясняются все эти свойства, этот пост посвящен формулам асинхронных двигателей и примерам расчетов.

Синхронная скорость, частота и полюса

Синхронная скорость, частота и количество полюсов асинхронного двигателя связаны формулой:

η _{синхронизация} = (120 * f _e) / P

η _{синхронизация} = синхронная скорость

f _e = Частота системы

P = количество полюсов, установленных в машине

Расчет: Найдите синхронную скорость 4-полюсного асинхронного двигателя, который работает с частотой 60 Гц.

Решение: η _синхр. = 120 * 60/4 = 1800 об / мин

Мотор скольжения

Скольжение мотора можно найти по формуле:

с = (η _синхр. -η _м) / η _синхр. * 100

η _{синхронизация} = Скорость магнитного поля

η _м = Механическая частота вращения вала

Расчет: Скорость ротора 4-полюсного асинхронного двигателя при 50 Гц составляет 1200 об / мин. Рассчитайте его скольжение.

Решение: Скорость ротора = η _м = 1200 об / мин

Где η _синхр. = 120 * 50/4 = 1500 об / мин

с = (1500 — 1200) / 1500 * 100 = 20

Крутящий момент, мощность и скорость

τ _инд = P / ω _м

τ _ind = Индуцированный крутящий момент в Нм

P = мощность в кВт

ω _м = Скорость в об / мин

Расчет: Найдите крутящий момент на валу асинхронного двигателя мощностью 10 л.с., скорость ротора которого составляет 1500 об / мин.

Решение: τ _ind = (10 л.с. * 746 кВт / л.с.) / (1500 об / мин * 2 π рад / об * 1 мин / 60 с) = 47,49 Нм

Калькулятор пускового тока

I _L = S _начало / (√3 * V _T),

, где S _start = Номинальная мощность двигателя * Кодовый коэффициент

(Кодовый коэффициент — это число, которое зарезервировано для класса) Например, все двигатели класса A имеют фиксированный кодовый коэффициент, который в приведенном выше уравнении следует умножить на номинальную мощность. )

В _T = Номинальное напряжение

Расчет: Найдите пусковой ток 10 л.с., трехфазный двигатель 220 В класса А.

Решение: Максимальное значение кВА / л.с. для двигателя класса A составляет 3,15 (кодовый коэффициент).

S _start = 10 л.с. * 3,15 = 31,5 кВА

I _L = 31,5 кВА / (√3 * 220) = 82,66 А

Возможно, вы захотите узнать: Как рассчитать ток от HP

Формула теста

t — Easy Guides — Wiki

Что такое парный t-тест?

Парный t-критерий Стьюдента используется для сравнения средних значений двух связанных выборок.Это когда у вас есть два значения (пара значений) для одних и тех же образцов.

Например, 20 мышей получали лечение X в течение 3 месяцев. Вопрос состоит в том, чтобы проверить, влияет ли лечение X на вес мышей в конце трехмесячного лечения. Вес 20 мышей измеряли до и после лечения. Это дает нам 20 наборов значений до лечения и 20 наборов значений после лечения на основе измерения удвоенного веса тех же мышей.

В этом случае можно использовать парный t-тест , поскольку два сравниваемых набора значений связаны.У нас есть пара значений для каждой мыши (одно до и другое после лечения).

Формула парного t-критерия

Чтобы сравнить средние значения двух парных наборов данных, сначала необходимо вычислить различия между всеми парами.

Пусть d представляет собой разницу между всеми парами. Среднее значение разницы d сравнивается с 0. Если есть какая-либо значительная разница между двумя парами выборок, то ожидается, что среднее значение d будет далеко от 0.

Статистическое значение теста t можно рассчитать следующим образом:

\ [ t = \ frac {m} {s / \ sqrt {n}} \]

m и s — это среднее значение , и стандартное отклонение разницы (d), соответственно. n — размер d.

После определения значения t вы должны прочитать в таблице t-критерия критическое значение t-распределения Стьюдента , соответствующее выбранному вами уровню значимости альфа (5%). степени свободы (df), использованные в этом тесте:

\ [df = n — 1 \]

Если абсолютное значение статистики t-критерия (| t |) больше критического значения, то разница значительна.В противном случае это не так. Уровень значимости или ( p-значение ) соответствует риску, указанному в таблице t-критерия для вычисленного | t | значение.

Тест можно использовать только в том случае, если разность d распределена нормально.

Функции даты Excel — примеры формул ДАТА, СЕГОДНЯ и т. Д.

Это последняя часть нашего руководства по работе с датами Excel, в которой предлагается обзор всех функций даты в Excel, объясняется их базовое использование и приводится множество примеров формул.

Microsoft Excel предоставляет массу функций для работы с датой и временем. Каждая функция выполняет простую операцию, и, объединив несколько функций в одной формуле, вы можете решать более сложные и сложные задачи.

В предыдущих 12 частях нашего руководства по датам Excel мы подробно изучили основные функции дат Excel. В этой заключительной части мы собираемся обобщить полученные знания и предоставить ссылки на различные примеры формул, которые помогут вам найти функцию, лучше всего подходящую для расчета ваших дат.

Основная функция для расчета дат в Excel:

Получить текущую дату и время:

СЕГОДНЯ — возвращает сегодняшнюю дату
СЕЙЧАС — возвращает текущую дату и время

Преобразование дат в / из текста:

ДАТА ЗНАЧЕНИЕ — преобразует дату в текстовом формате в формат даты
ТЕКСТ — преобразует дату в текстовое значение

Получить даты в Excel:

ДЕНЬ — возвращает день месяца
МЕСЯЦ — возвращает месяц указанной даты
ГОД — возвращает год указанной даты
EOMONTH — возвращает последний день месяца
WEEKDAY — возвращает день недели
WEEKNUM — возвращает номер недели даты

Рассчитать разницу дат:

РАЗНДАТ — возвращает разницу между двумя датами
EDATE — возвращает дату за N месяцев до или после даты начала
YEARFRAC — вычисляет долю года между двумя датами

Расчет рабочих дней:

РАБДЕНЬ — возвращает дату N рабочих дней в будущем или в прошлом
РАБДЕНЬ. INTL — возвращает дату N рабочих дней от начальной даты с настраиваемыми выходными
ЧИСТРАБДНИ — возвращает количество рабочих дней между двумя датами
NETWORKDAYS.INTL — возвращает количество рабочих дней между двумя датами с настраиваемыми выходными

Функция ДАТА в Excel

ДАТА (год, месяц, день) возвращает порядковый номер даты на основе указанных вами значений года, месяца и дня.

Когда дело доходит до работы с датами в Excel, ДАТА является наиболее важной функцией для понимания.Дело в том, что другие функции дат Excel не всегда могут распознавать даты, введенные в текстовом формате. Поэтому при вычислении дат в Excel лучше указывать даты с помощью функции ДАТА, чтобы гарантировать правильные результаты.

Вот несколько примеров формул Excel DATE:

= ДАТА (2015, 5, 20) — возвращает серийный номер, соответствующий 20 мая 2015 года.

= ДАТА (ГОД (СЕГОДНЯ ()), МЕСЯЦ (СЕГОДНЯ ()), 1) — возвращает первый день текущего года и месяца.

= ДАТА (2015, 5, 20) -5 — вычитает 5 дней с 20 мая 2015 года.

На первый взгляд функция Excel DATE выглядит очень простой, однако у нее есть ряд особенностей, указанных в руководстве по Excel DATE.

Ниже вы найдете еще несколько примеров, в которых функция ДАТА в Excel является частью более крупных формул:

Функция Excel СЕГОДНЯ

Функция СЕГОДНЯ () возвращает сегодняшнюю дату, как и предполагает ее название.

СЕГОДНЯ, пожалуй, одна из самых простых в использовании функций Excel, потому что у нее вообще нет аргументов. Всякий раз, когда вам нужно получить сегодняшнюю дату в Excel, введите следующую формулу в ячейке:

= СЕГОДНЯ ()

Помимо этого очевидного использования, функция Excel СЕГОДНЯ может быть частью более сложных формул и вычислений, основанных на сегодняшней дате. Например, чтобы добавить 7 дней к текущей дате, введите в ячейку следующую формулу:

= СЕГОДНЯ () + 7

Чтобы добавить 30 рабочих дней к сегодняшней дате, исключая выходные, используйте это:

= РАБОЧИЙ ДЕНЬ (СЕГОДНЯ (), 30)

Примечание. Дата, возвращаемая функцией СЕГОДНЯ в Excel, обновляется автоматически, когда ваш рабочий лист пересчитывается для отражения текущей даты.

Дополнительные примеры формул, демонстрирующие использование функции СЕГОДНЯ в Excel, см. В следующих руководствах:

Функция Excel СЕЙЧАС

NOW () функция возвращает текущую дату и время. Как и СЕГОДНЯ, у него нет никаких аргументов. Если вы хотите отображать сегодняшнюю дату и текущее время на листе, просто введите в ячейку следующую формулу:

= СЕЙЧАС ()

Примечание. Как и СЕГОДНЯ, Excel СЕЙЧАС — это непостоянная функция, которая обновляет возвращаемое значение каждый раз, когда рабочий лист пересчитывается. Обратите внимание, что ячейка с формулой СЕЙЧАС () не обновляется автоматически в режиме реального времени, только когда книга повторно открывается или лист пересчитывается.
Чтобы принудительно пересчитать электронную таблицу и, следовательно, заставить формулу СЕЙЧАС обновить свое значение, нажмите Shift + F9, чтобы пересчитать только активный рабочий лист, или F9, чтобы пересчитать все открытые книги.
Чтобы функция NOW () автоматически обновлялась каждую секунду или около того, необходим макрос VBA (несколько примеров доступны здесь).
Функция ДАТА ЗНАЧ в Excel
DATEVALUE (date_text) преобразует дату в текстовом формате в порядковый номер, представляющий дату.
Функция DATEVALUE понимает множество форматов даты, а также ссылки на ячейки, содержащие «текстовые даты». DATEVALUE действительно удобен для вычисления, фильтрации или сортировки дат, хранящихся в виде текста, и преобразования таких «текстовых дат» в формат даты.
Ниже приведены несколько простых примеров формулы DATEVALUE:
= ДАТА ЗНАЧЕНИЕ («20 мая 2015 года»)
= ДАТА ЗНАЧЕНИЕ ("20.05.2015")
= ДАТА ЗНАЧЕНИЕ («20 мая 2015 г.»)
И следующие примеры демонстрируют, как функция ДАТАЗНАЧ может помочь в решении реальных задач:
Функция ТЕКСТ в Excel
В чистом смысле функцию ТЕКСТ нельзя отнести к одной из функций даты Excel, поскольку она может преобразовывать любое числовое значение, а не только даты, в текстовую строку.
С помощью функции ТЕКСТ (значение, формат_текста) вы можете изменить даты на текстовые строки в различных форматах, как показано на следующем снимке экрана.
Примечание. Хотя значения, возвращаемые функцией ТЕКСТ, могут выглядеть как обычные даты Excel, они являются текстовыми значениями по своей природе и поэтому не могут использоваться в других формулах и вычислениях.
Вот еще несколько примеров формул ТЕКСТА, которые могут оказаться полезными:
Функция ДЕНЬ в Excel
DAY (serial_number) функция возвращает день месяца как целое число от 1 до 31.
Серийный_номер — это дата, соответствующая дню, который вы пытаетесь получить. Это может быть ссылка на ячейку, дата, введенная с помощью функции ДАТА или возвращенная другими формулами.
Вот несколько примеров формул:
= ДЕНЬ (A2) — возвращает день даты в A2
= DAY (DATE (2015,1,1)) — возвращает день 1 января 2015 г.
= DAY (TODAY ()) — возвращает день сегодняшней даты
Вы можете найти больше примеров формул ДЕНЬ, щелкнув следующие ссылки:
Функция МЕСЯЦ в Excel
MONTH (serial_number) Функция в Excel возвращает месяц указанной даты как целое число от 1 (январь) до 12 (декабрь).
Например:
= МЕСЯЦ (A2) — возвращает месяц даты в ячейке A2.
= МЕСЯЦ (СЕГОДНЯ ()) — возвращает текущий месяц.
Функция МЕСЯЦ редко используется в формулах даты Excel сама по себе. Чаще всего вы будете использовать его вместе с другими функциями, как показано в следующих примерах:
Подробное описание синтаксиса функции МЕСЯЦ и множество других примеров формул можно найти в следующем руководстве: Использование функции МЕСЯЦ в Excel.
Функция ГОД в Excel
YEAR (serial_number) возвращает год, соответствующий заданной дате, в виде числа от 1900 до 9999.
Функция ГОД в Excel очень проста, и вы вряд ли столкнетесь с какими-либо трудностями при ее использовании в расчетах даты:
= ГОД (A2) — возвращает год даты в ячейке A2.
= ГОД («20-мая-2015») — возвращает год указанной даты.
= YEAR (DATE (2015,5,20)) — более надежный способ получить год данной даты.
= ГОД (СЕГОДНЯ ()) — возвращает текущий год.
Дополнительную информацию о функции ГОД см .:
Функция Excel EOMONTH
EOMONTH (start_date, months) функция возвращает последний день месяца через заданное количество месяцев от начальной даты.
Как и большинство функций даты в Excel, EOMONTH может работать с датами, введенными как ссылки на ячейки, введенными с помощью функции ДАТА, или результатами других формул.
Положительное значение в аргументе месяцев добавляет соответствующее количество месяцев к дате начала, например:
= EOMONTH (A2, 3) — возвращает последний день месяца, через 3 месяца после даты в ячейке A2.
Отрицательное значение в аргументе месяцев вычитает соответствующее количество месяцев из начальной даты:
= EOMONTH (A2, -3) — возвращает последний день месяца, 3 месяца перед датой в ячейке A2.
ноль в аргументе месяцев заставляет функцию EOMONTH возвращать последний день месяца начальной даты:
= EOMONTH (DATE (2015,4,15), 0) — возвращает последний день апреля 2015 года.
Чтобы получить последний день текущего месяца , введите функцию СЕГОДНЯ в аргументе start_date и 0 через месяцев :
= EOMONTH (СЕГОДНЯ (), 0)
Вы можете найти еще несколько примеров формул EOMONTH в следующих статьях:
Функция ДЕНЬ НЕДЕЛИ в Excel
WEEKDAY (serial_number, [return_type]) Функция возвращает день недели, соответствующий дате, в виде числа от 1 (воскресенье) до 7 (суббота).
Serial_number может быть датой, ссылкой на ячейку, содержащую дату, или датой, возвращаемой какой-либо другой функцией Excel.
Return_type (необязательно) — число, определяющее, какой день недели считается первым днем.
Вы можете найти полный список доступных типов возвращаемых значений в следующем руководстве: Расчет дней недели в Excel (функция WEEKDAY).
А вот несколько примеров формул ВЫХОДНЫЕ:
= WEEKDAY (A2) — возвращает день недели, соответствующий дате в ячейке A2; 1 ^{-й день недели} — воскресенье (по умолчанию).
= WEEKDAY (A2; 2) — возвращает день недели, соответствующий дате в ячейке A2; неделя начинается в понедельник.
= WEEKDAY (TODAY ()) — возвращает число, соответствующее сегодняшнему дню недели; неделя начинается в воскресенье.
Функция WEEKDAY может помочь вам определить, какие даты в таблице Excel являются рабочими днями, а какие — выходными, а также отсортировать, отфильтровать или выделить рабочие и выходные дни:
Функция РАЗНДАТ в Excel
РАЗНДАТ (start_date, end_date, unit) Функция специально разработана для вычисления разницы между двумя датами в днях, месяцах или годах.
Какой временной интервал использовать для вычисления разницы дат, зависит от буквы, введенной в последнем аргументе:
= РАЗНДАТ (A2, СЕГОДНЯ (), «d») — вычисляет количество дней между датой в A2 и сегодняшней датой.
= РАЗНДАТ (A2, A5, «m») — возвращает полных месяца между датами в A2 и B2.
= РАЗНДАТ (A2, A5, «y») — возвращает число полных лет между датами в A2 и B2.
Это только базовые приложения функции РАЗНДАТ, и она способна на гораздо большее, как показано в следующих примерах:
Excel НЕДЕЛ. Функция
WEEKNUM (serial_number, [return_type]) — возвращает номер недели определенной даты в виде целого числа от 1 до 53.
Например, приведенная ниже формула возвращает 1, потому что неделя, содержащая 1 января, является первой неделей в году.
= WEEKNUM («1 января 2015»)
В следующем руководстве объясняются все особенности функции ЧИСЛО НЕДЕЛИ в Excel: Функция ЧИСЛО НЕДЕЛИ — вычисление номера недели в Excel.
Вы также можете сразу перейти к одному из примеров формул:
Функция EDATE в Excel
EDATE (start_date, months) функция возвращает порядковый номер даты, которая является указанным количеством месяцев до или после даты начала.
Например:
= EDATE (A2; 5) — добавляет 5 месяцев к дате в ячейке A2.
= ДАТА (СЕГОДНЯ (), -5) — вычитает 5 месяцев из сегодняшней даты.
Подробное описание формул EDATE, проиллюстрированных примерами формул, см. В разделе: Добавление или вычитание месяцев к дате с помощью функции EDATE.
Функция ГОДА в Excel
YEARFRAC (start_date, end_date, [base]) Функция вычисляет долю года между двумя датами.
Эта очень специфическая функция может использоваться для решения практических задач, таких как вычисление возраста по дате рождения.
Excel РАБДЕНЬ (функция
)
РАБДЕНЬ (начальная_дата, дни, [праздники]) функция возвращает дату на N рабочих дней до или после начальной даты. Он автоматически исключает из расчетов выходные дни, а также любые указанные вами праздничные дни.
Эта функция очень полезна для расчета вех и других важных событий на основе стандартного рабочего календаря.
Например, следующая формула добавляет 45 рабочих дней к дате начала в ячейке A2, игнорируя праздничные дни в ячейках B2: B8:
= РАБДЕНЬ (A2, 45, B2: B85)
Для подробного объяснения синтаксиса РАБДЕНЬ и других примеров формул, пожалуйста, ознакомьтесь с функцией РАБДЕНЬ — сложение или вычитание рабочих дней в Excel.
Excel РАБДЕНЬ.ИНТЛ (функция
)
РАБДЕНЬ.INTL (начальная_дата, дни, [выходные], [праздники]) — это более мощный вариант функции РАБДЕНЬ, представленный в Excel 2010, а также доступный в Excel 2013 и 2016.
WORKDAY.INTL позволяет рассчитать дату N количество рабочих дней в будущем или в прошлом с настраиваемыми параметрами выходных.
Например, чтобы получить дату через 20 рабочих дней после даты начала в ячейке A2, при этом понедельник и воскресенье считаются выходными, можно использовать любую из следующих формул:
= РАБДЕНЬ.ИНТЛ (A2, 20, 2, 7)
или
= РАБДЕНЬ.INTL (A2, 20, «1000001»)
Конечно, из этого краткого объяснения может быть трудно понять суть, но больше примеров формул, проиллюстрированных скриншотами, упростят задачу: WORKDAY.INTL — расчет рабочих дней с настраиваемыми выходными.
Функция ЧИСТРАБДНИ в Excel
ЧИСТРАБДНИ (начальная_дата, конечная_дата, [праздники]) функция возвращает количество рабочих дней между двумя указанными вами датами.Он автоматически исключает выходные дни и, при необходимости, праздники.
Например, следующая формула вычисляет количество полных рабочих дней между датой начала в A2 и датой окончания в B2, игнорируя субботу и воскресенье и исключая праздничные дни в ячейках C2: C5:
= ЧИСТЫЕ ДНИ (A2, B2, C2: C5)
Вы можете найти исчерпывающее объяснение аргументов функции ЧИСТРАБДНИ, проиллюстрированное примерами формул и снимками экрана в следующем руководстве: Функция ЧИСТРАБДНИ — вычисление рабочих дней между двумя датами.
Excel ЧИСТРАБДНИ.INTL (функция
)
NETWORKDAYS.INTL (start_date, end_date, [выходные], [праздники]) — это более мощная модификация функции NETWORKDAYS, доступная в современных версиях Excel 2010, Excel 2013 и Excel 2016. Она также возвращает количество рабочих дней. между двумя датами, но позволяет указать, какие дни следует считать выходными.
Вот основная формула ЧИСТЫХ ДНЕЙ:
= ЧИСТЫЕ ДНИ (A2, B2, 2, C2: C5)
Формула вычисляет количество рабочих дней между датой в A2 (start_date) и датой в B2 (end_date), исключая выходные воскресенье и понедельник (число 2 в параметре выходных) и игнорируя праздничные дни в ячейках C2: C5.
Для получения полной информации о функции ЧИСТРАБДНИ.INTL см. Функцию ЧИСТРАБДНИ — подсчет рабочих дней с настраиваемыми выходными.
Надеюсь, что это 10-километровое представление функций даты Excel помогло вам получить общее представление о том, как формулы даты работают в Excel. Если вы хотите узнать больше, я рекомендую вам ознакомиться с примерами формул, указанными на этой странице. Я благодарю вас за чтение и надеюсь снова увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Формула процента
Формула для процента следующая, и ее будет легко использовать, если вы будете следовать простым данным инструкциям.Прежде чем рассматривать примеры, внимательно изучите приведенную ниже формулу.
Для иллюстрации рассмотрим несколько примеров. Начнем с формулы слева.
Важно помнить о перекрестном умножении после того, как вы определили различные части формулы.
Перекрестное умножение означает умножение числителя одной дроби на знаменатель другой дроби.
Пример № 1:
25% от 200 составляет ____
В этой задаче из = 200, равно =? И % = 25
Мы получаем:
это /200 = 25/100
Поскольку — это в неизвестном, вы можете заменить его на y, чтобы проблема была более знакомой.
y / 200 = 25/100
Перемножьте крестиком, чтобы получить y × 100 = 200 × 25
y × 100 = 5000
Разделите 5000 на 100, чтобы получить y
Так как 5000/100 = 50, y = 50
Итак, 25% от 200 составляет 50
Пример № 2:
Какое число составляет 2% от 50?
Это просто еще один способ сказать, что 2% от 50 равно ___
Итак, настройте пропорцию как пример # 1:
равно /50 = 2/100
Заменить на y и умножить крестиком, чтобы получить :
y × 100 = 50 × 2
y × 100 = 100
Так как 1 × 100 = 100, y = 1
Следовательно, 1 составляет 2% от 50
Пример # 3:
24 % от ___ равно 36
На этот раз обратите внимание, что равно = 36, но из отсутствует
После настройки формулы вы получите:
36/ из = 24/100
Заменить из на y и умножаем крест-накрест, чтобы получить:
36 / y = 24/100
y × 24 = 36 × 100
y × 24 = 3600
Разделите 3600 на 24, чтобы получить y
3600/24 = 150 , y = 150
Следовательно, 24% от 150 равно 36
Как использовать другую формулу для процента справа.
Теперь мы рассмотрим примеры, чтобы проиллюстрировать, как использовать формулу для процента справа
Пример № 4:
Чтобы использовать другую формулу, которая говорит частично и полностью, просто запомните следующее:
Число после из всегда целиком.
Число после — всегда является частью.
Если проблема говорит, что 25% от ___ равно 60, тогда мы знаем, что целое отсутствует, а часть = 60
Ваша пропорция будет такой:
60/ целое = 25/100
После перекрестного умножения мы получить:
целиком × 25 = 60 × 100
целиком × 25 = 6000
Разделите 6000 на 25, чтобы получить целое
6000/25 = 240, итого целое = 240
Следовательно, 25% от 240 — 60
Пример # 5:
___% от 45 равно 9
Здесь целое = 45 и часть = 9, но % отсутствует
Получаем:
9/45 = % / 100
Замена% на x и перекрестное умножение дает:
9 × 100 = 45 × x
900 = 45 × x
Разделите 900 на 45, чтобы получить x
900/45 = 20, поэтому x = 20
Поехали! Я надеюсь, что формула процентного соотношения была полезной.

Как найти индукционный ток формула

Накопленная энергия в индуктивности

Гидравлическая модель

Индуктивность в электрических цепях

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Последовательное соединение индуктивностей

Добротность катушки индуктивности

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

Индуктивность прямого проводника:

Индуктивность катушки с воздушным сердечником:

Индуктивность многослойной катушки с воздушным сердечником:

Индуктивность плоской катушки:

Конструкция катушки индуктивности

Применение катушек индуктивности

основные понятия, нахождение через силу тока и сопротивление

Общие сведения об электрическом токе

Физический смысл

Пагубное влияние на человека

Единицы измерения

Цепи переменного и постоянного тока

Переменное однофазное напряжение

Рекомендации по выбору прибора

Расчета тока по мощности: формула, онлайн расчет

Формула расчета мощности электрического тока

Форма для расчета мощности тока

Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Зависимость силы тока от напряжения — формула, график и законы

Общие сведения

Подтверждение закона Ома

График зависимости

Простейшие задачи

Формула ЕС

Формулы мощности в однофазных и трехфазных цепях постоянного и переменного тока

Формулы и уравнения мощности в цепях постоянного и переменного тока 1-Φ и 3-Φ

Базовая формула мощности в цепях переменного и постоянного тока

Формула мощности в цепях постоянного тока

Формулы мощности в однофазных цепях переменного тока

Формулы мощности в трехфазных цепях переменного тока

Формулы питания переменного тока в сложных схемах:

Комплексная мощность и полная мощность:

Активная или реальная мощность и реактивная мощность:

Коэффициент мощности:

Реальная мощность однофазного и трехфазного тока

Реактивная мощность однофазного и трехфазного тока:

Формулы асинхронного двигателя с расчетами

Синхронная скорость, частота и полюса

Мотор скольжения

Крутящий момент, мощность и скорость

Калькулятор пускового тока

t — Easy Guides — Wiki

Что такое парный t-тест?

Формула парного t-критерия

Функции даты Excel — примеры формул ДАТА, СЕГОДНЯ и т. Д.

Основная функция для расчета дат в Excel:

Получить текущую дату и время:

Преобразование дат в / из текста:

Получить даты в Excel:

Рассчитать разницу дат:

Расчет рабочих дней:

Функция ДАТА в Excel

Функция Excel СЕГОДНЯ

Функция Excel СЕЙЧАС

Функция ДАТА ЗНАЧ в Excel

Функция ТЕКСТ в Excel

Функция ДЕНЬ в Excel

Функция МЕСЯЦ в Excel

Функция ГОД в Excel

Функция Excel EOMONTH

Функция ДЕНЬ НЕДЕЛИ в Excel

Функция РАЗНДАТ в Excel

Excel НЕДЕЛ. Функция

Функция EDATE в Excel

Функция ГОДА в Excel

Excel РАБДЕНЬ (функция

Excel РАБДЕНЬ.ИНТЛ (функция

Функция ЧИСТРАБДНИ в Excel

Excel ЧИСТРАБДНИ.INTL (функция

Вас также может заинтересовать