Ток в катушке: 42 — магнитный поток в катушке с током • 31415.ru

42 — магнитный поток в катушке с током • 31415.ru

Магнитный поток катушки индуктивности L с током I.

Ф — магнитный поток, Вб (Вебер)
L — индуктивность катушки, Гн (Генри)
I — сила тока, А (Ампер)


Катушка индуктивности состоит из витков изолированного проводника. Обычно это витки медного провода, покрытого краской или любой не проводящей оболочкой. Основная особенность катушки в том, что при пропускании электрического тока, она становится электромагнитом. То есть начинает создавать магнитное поле. При постоянном токе свойства катушки ничем не примечательны — это кусок провода, который можно заменить перемычкой.

При подключении к катушке переменного напряжения начинаются удивительные вещи. Ток меняется, а значит меняется сила магнитного поля, которое создает катушка. Меняется магнитная индукция создаваемая витками и следовательно меняется магнитный поток. А согласно закону электромагнитной индукции — изменение магнитного потока приводит к появлению ЭДС.

Проще говоря, переменный ток превращает катушку в электрогенератор. Причем генерируемый ток направлен противоположно внешнему току. Но стоит отметить, что так можно говорить только с математической точки зрения, с точки зрения формул. На практике, изменение тока в катушке похоже на удар рукой по водной глади: чем медленнее движется рука, тем меньше сопротивление со стороны воды, но чем быстрее движется рука, тем большее сопротивление она испытывает при ударе об жидкость. Это явление в физике называется самоиндукцией. Индуктивность катушки называют также коэффициентом самоиндукции.

Что такое индуктивность, как она зависит от числа витков и других параметров — лучше всего разбирать на практике.
В этом видео, на практических примерах показаны все основные свойства катушки индуктивности.

 

В обычной жизни люди практически не встречаются с измерением индуктивностей и магнитных потоков, поэтому эти термины запоминаются не очень хорошо.

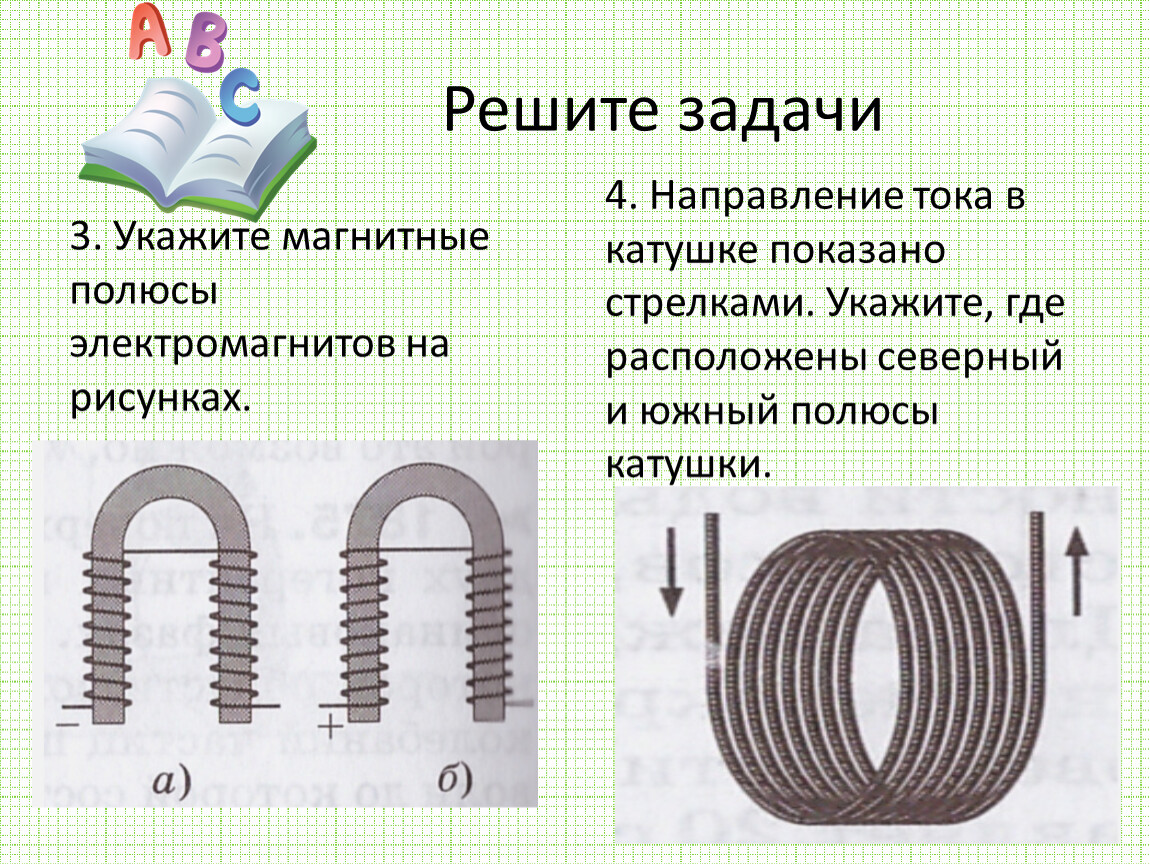Простой способ усвоить эти термины — это разобраться с принципом работы металлоискателей и металлодетекторов. Стойки металлодетекторов можно наблюдать на вокзалах и в торговых центрах. Если вы поймете как они работают, станет понятна важность таких терминов как индуктивность и магнитный поток.

 

Задача 42.
При силе тока 10 А, в катушке возникает магнитный поток 50 мВб. Чему равна индуктивность катушки.
Показать ответОтвет: L=0,005 Гн
 

 

 

Какой ток должен быть на электрической катушке, обмотке – как они работают, их неисправности.

Электрические обмотки в электротехнике используются очень широко. Спектр их применения весьма огромен. Даже людям, совсем не связанных с профессией электрика, хорошо известно, что медную обмотку можно найти в таких устройствах как трансформатор, электродвигатель, электромагнит и т.д. Пожалуй в начале данной статьи стоит напомнить о самой специфике, свойствах и работе любой электрической катушки. Это позволит лучше понять рассматриваемую тему про силу тока обмотки.

Итак, основным материалом, из которого делаются электрические провода и мотаются большинство обмоток, является медь, покрытая сверху изоляционным материалом. Медь является хорошим проводником тока. Из курса физики известно, что если пропустить через провод электрический ток, то вокруг этого провода образуется магнитное поле. Сила поля зависит силы тока (чем он больше, тем сильнее будет и магнитное поле) и кучности (то есть, из максимальной вытянутости провода сделать максимальную сжатость его в объеме) (чем более провод прижат друг к другу, имея форму намотки, тем концентрированей будет и его магнитное поле).

Именно магнитные поля при взаимодействии друг с другом создают эффект притягивания или отталкивания. Внутри электродвигателя это создает механическое движение ротора и вала, что вращает нужные механизмы. Электромагнит же этим полем может притягивать к себе различные металлические предметы. Притягивание металлического язычка, что замыкает электрические контакты, лежит в основе работы обычного реле, контактора, пускателя.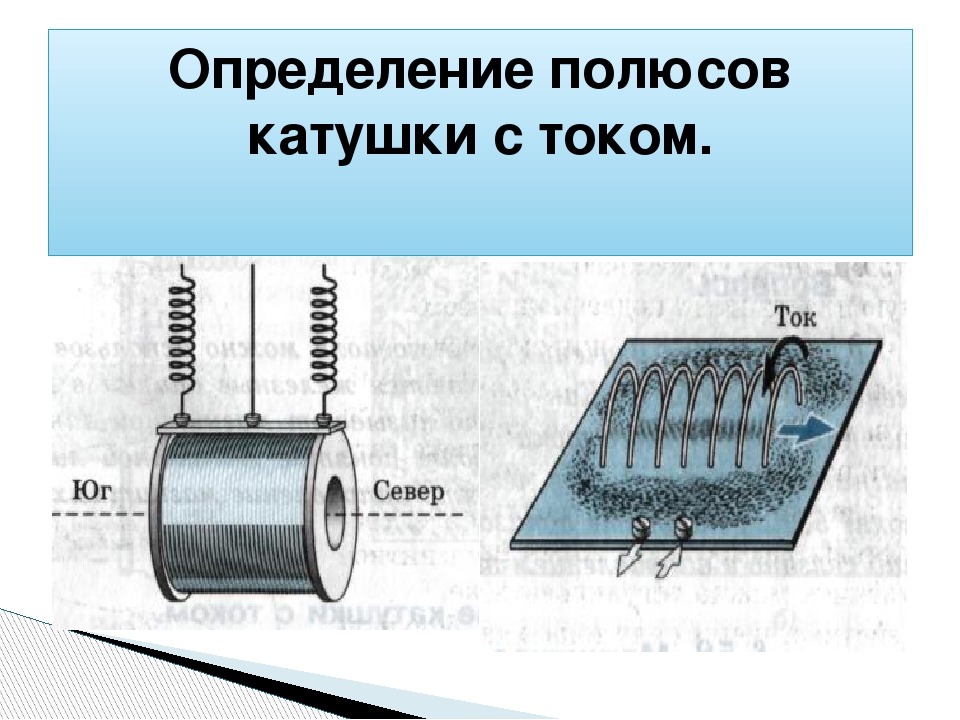 Помимо этого существует и обратный эффект, когда воздействие магнитного поля на электрический проводник приводит к появления электрического тока в этом самом проводнике. Это уже относится к генерации электрической энергии. Ну, и еще стоит упомянуть о таком эффекте как отставание тока катушки от электрического напряжения на ней. Он возникает именно при включении или выключении, а также непосредственно в момент изменения интенсивности электрического питания, что подается на катушку.

Как видно все эффекты, возникающие в электрической катушке, обмотке, непосредственно связаны именно с электрическим током. Для правильной работы устройства, что имеет катушку, обмотку нужны изначально правильные расчеты ее длины, сечения, способа намотки, материала сердечника (если таковой есть). Несоответствие силы тока, протекающего по обмотке, своим номинальным величинам ведет к нарушению правильности работы самого устройства.

Например, слишком большой ток, при несоответствии с нормой, будет способствовать чрезмерному нагреванию обмотки. Высокая температура будет способствовать разрушению изоляции катушки. А это приведет к последующему короткому замыканию и сгоранию этой намотки, или всего устройства в целом. Слишком большие токи в обмотке могут возникнуть по причине, либо появлению в катушке короткозамкнутых витков, либо при подаче на обмотку чрезмерного напряжения, на которое она не рассчитана изначально.

Другим примером может быть случаи, когда сила тока в обмотке меньше, чем должна быть. Это может произойти когда электрические контакты, что связаны с этой катушкой, обмоткой имеют слой окисла, нагара, что сильно ухудшает проводимость этих контактов и увеличивает сопротивление данной электрической цепи. Следовательно, в той обмотке, где имеется недостаточная сила тока, будет меньшая интенсивность магнитного поля. В катушке реле это может приводить к ее не срабатыванию или плохому прижатию контактов. В электродвигателе это снизит его рабочую мощность, а то и вовсе мотор не будет работать. В любом случае варианты переизбытка и недостатка силы тока, протекающий через обмотку ведут к ненормальной работе электротехнического устройства, а то и вовсе к выходу его из строя.

При создании обмотки на конкретное устройство учитываются множество факторов (тип устройства, место и режим его работы, тип тока, величина напряжения, частота, условия эксплуатации, уровень качества и т.д.). Мотать катушку «наобум» скорее всего не «прокатит». Как минимум нужно пользоваться хотя бы основными формулами и упрощенными расчетами. Даже один неучтенный параметр катушки, обмотки может значительно снизить эффективность работы конечного устройства.

Более распространенным случаем бывает когда изначально нормальное, рабочее устройство, содержащее обмотку, вдруг начинает работать ненормально. Тут, естественно, возникает нужда в восстановлении изначальной работоспособности. Прежде всего нужно узнать те основные параметры, характеристики, при которых электрическая обмотка будет работать нормально. Это номинальное напряжение питания, сила тока, мощность, сопротивление, тип тока (переменный или постоянный).

Причиной ненормальной работы электрической обмотки может быть как сама катушка, так и внешняя электрическая цепь. Следовательно, вначале проверяем нужное ли напряжение подается на саму катушку, и способна эта цепь обеспечить достаточную силу тока (нет ли вредного увеличение сопротивления на контактах, клеммах, прочих элементах цепи, ведущие к снижению тока). Для этого берем обычный электронный тестер, мультиметр и меряем напряжение, что должно подаваться на обмотку (сама катушка должна быть отсоединена). Если тестер показал заниженное или завышенное (что бывает гораздо реже) напряжение, то ищем причину во внешней электрической цепи.

Для проверки силы тока, который обеспечивает сама внешняя цепь, нужно взять какую-нибудь подходящую нагрузку (с сопротивлением примерно равным самой обмотке – лампочку, мощный резистор, нагреватель, подходящий кусок нихрома и т.д.). Подсоединяем эту нагрузку вместо обмотки. Переводим мультиметр в режим измерения тока и смотрим на показания. По закону ома легко посчитать силу тока и сравнить ее с измеримым результатом. Допустим, питание у нас 12 вольт, сопротивление мы взяли 12 ом. Чтобы найти силу тока по закону ома нужно напряжение (в вольтах) разделить на сопротивление (в омах), и мы получи ток (в амперах). Если внешняя цепь не может обеспечить нужную силу тока, то при измерении мы увидим заниженный ток, а при измерении напряжения в рабочем режиме будет еще и падение напряжения. Опять же, причины тогда нужно искать во внешней цепи (проверять контакты, клеммы, различные места электрического соединения, прочие электрические элементы, что относятся к этой цепи).

Допустим вы убедились, что с внешней цепью все хорошо. Теперь значит нужно проверить саму обмотку того устройства, которое не работает должным образом. Прежде всего нужно проверить сопротивление катушки.

Далее следует измеренное сопротивление сравнить с тем, что может быть указано на внешней части этой катушки. Если сравнить нес чем, то можно посмотреть в справочных данных, которые относятся именно к вашему устройству. Ну, и совсем крайний вариант, это взять метр провода такого же диаметра (сечение именно медного провода, без изоляции) и измерить на нем сопротивление. После чего приблизительно прикинуть, сколько метров может содержать эта катушка и перемножить измеренное значение на приблизительный метраж вашей катушки. Опытные электрики обычно знают, у каких катушек может быть приблизительное сопротивление, это приходит с практикой.

В большинстве случаев у катушек обычно происходит обрыв. И тут при измерении сопротивление обмотки есть только два варианта, либо сопротивление есть, либо его нет (значит на обмотке есть обрыв, который нужно найти и восстановить). Гораздо реже бываю случаи короткозамкнутых витков. То есть, это когда в целом катушка, как бы исправна, и показывает более или менее нормальное сопротивление, а на деле у нее внутри замкнулись всего несколько витков (где-то повредилась изоляция и произошло короткое замыкание нескольких витков провода). Такие катушки будут работать ненормально. Они потребляют больше тока, будут сильнее греться, их эффективность снижается, а со временем вовсе могут выйти из строя. Искать короткозамкнутые витки задача проблематичная. Тут лучше взять новую, заведомо рабочую катушку, обмотку и заменить ее.

Если для нахождения постоянного тока подойдет обычная формула закона ома (чтобы по известному сопротивлению обмотки и подаваемому напряжению вычислить значение силы тока, протекающего через эту обмотку), то для переменного тока формула будет уже иметь следующий вид:

P.S. С опытом приходит знание. Так опытный электрик скорее всего не будет проделывать ряд лишних операций, при нахождении той или иной поломки. Обычно по некоторым характерным признакам можно уже с большой уверенностью сказать, где именно нужно искать неисправность в нерабочем электрооборудовании. Так же как и приблизительное определение сопротивления обмотки, которое не обязательно измерять, а достаточно увидеть размеры этого катушки и сечение провода.

Катушка индуктивности

Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,

Рис. 4.12. Условное обозначение катушки индуктивности.                         Рис. 4.13           

если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего мак­симального значения.

Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).

Постоянная времени RС-цепи

На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.

Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63

Е, называется постоянной времени контура или цепи.

 

Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.

 

Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.

Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой

где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.

Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна

На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.

 

Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.

 

Постоянная времени RL-цепи

Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе

R станет равным приложенному напряжению Е. Установившееся значение тока равно

E/R = 20 В/1 кОм = 20 мА.

Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем

Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.

Рис. 4.16.

 

Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.

 

Сопротивление по постоянному току

Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего ди­электрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.

 

Векторное представление

Сигнал синусоидальной формы может быть представлен в виде век­тора ОА, вращающегося против часовой стрелки с угловой скоростью

ω= 2πf, где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) со­ответствует одному полному периоду. Половина оборота (180°, или π) со­ответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).

Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами

 

Рис. 4.18. Векторное представление синусоидального сигнала.

Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ

 (или вектор ОВ отстает от вектора ОА) на угол θ.

изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.

Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.

В этом видео рассказывается о катушке индуктивности:

 

Добавить комментарий

Какое сопротивление оказывает катушка постоянному току. Применение в технике

Если катушка индуктивности включена в цепь переменного тока , то в такой цепи, фаза тока всегда отстает от фазы напряжения . Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление , а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.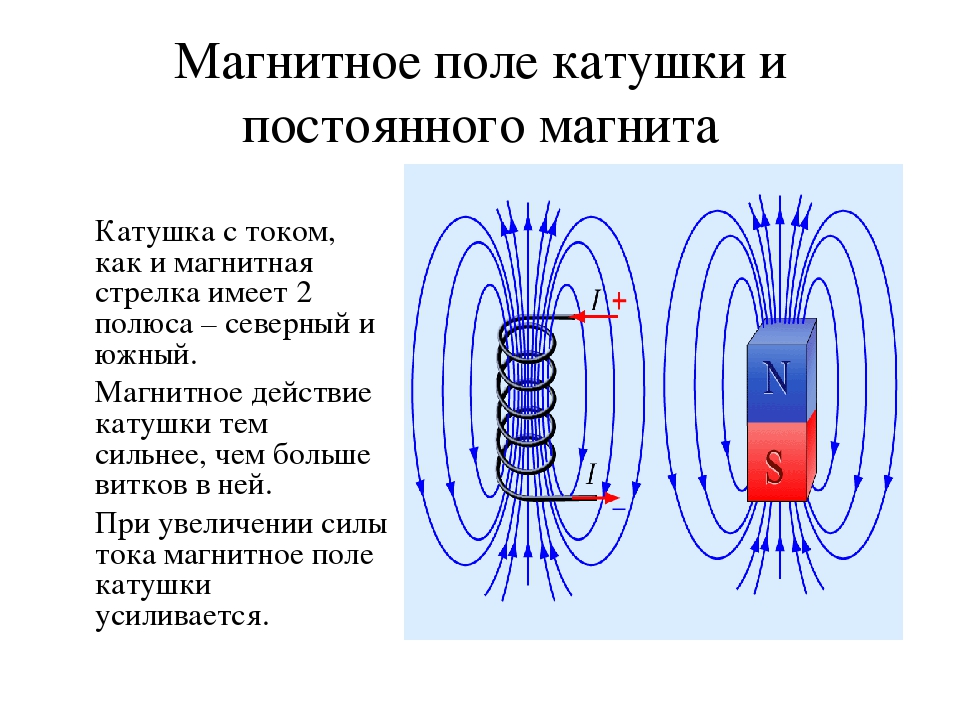

Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.

Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции

В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.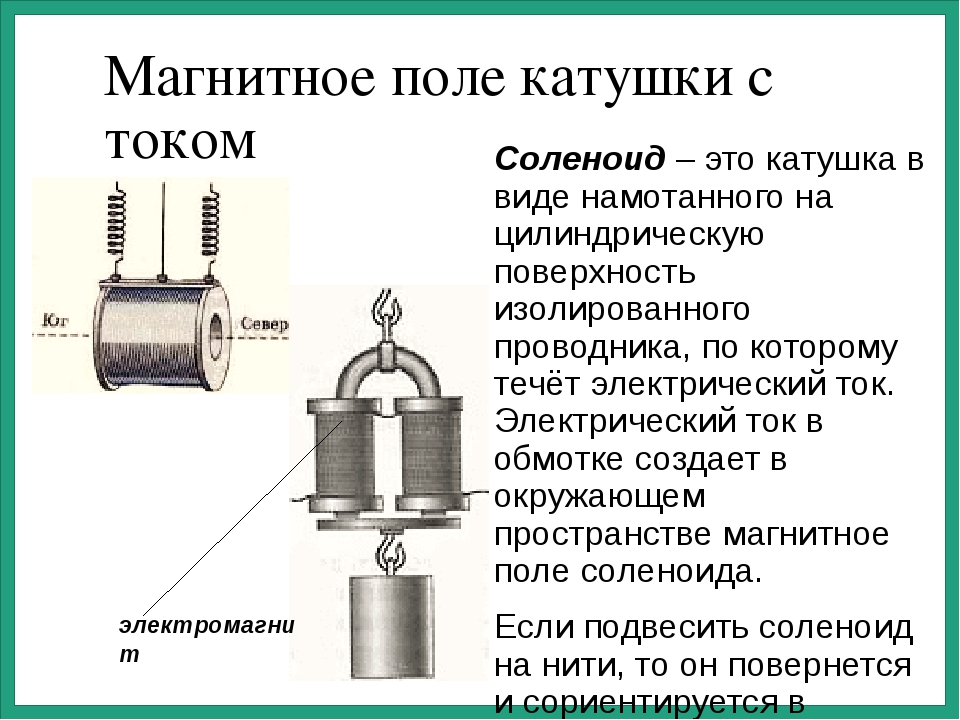

По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.

Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.

Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.

С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.

В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.

Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.

В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).

Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.

Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.

Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).

Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.

В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС , противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции , а скорость вагонетки — электрическому току . Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис. 1б), в точности соответствующие графикам рис. 1а.

Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.

Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».

Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.

Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.

Электрическая цепь и индуктивность

Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Как найти индуктивность

Формула, которая является простейшей для нахождения величины, следующая:

где F — магнитный поток, I — ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.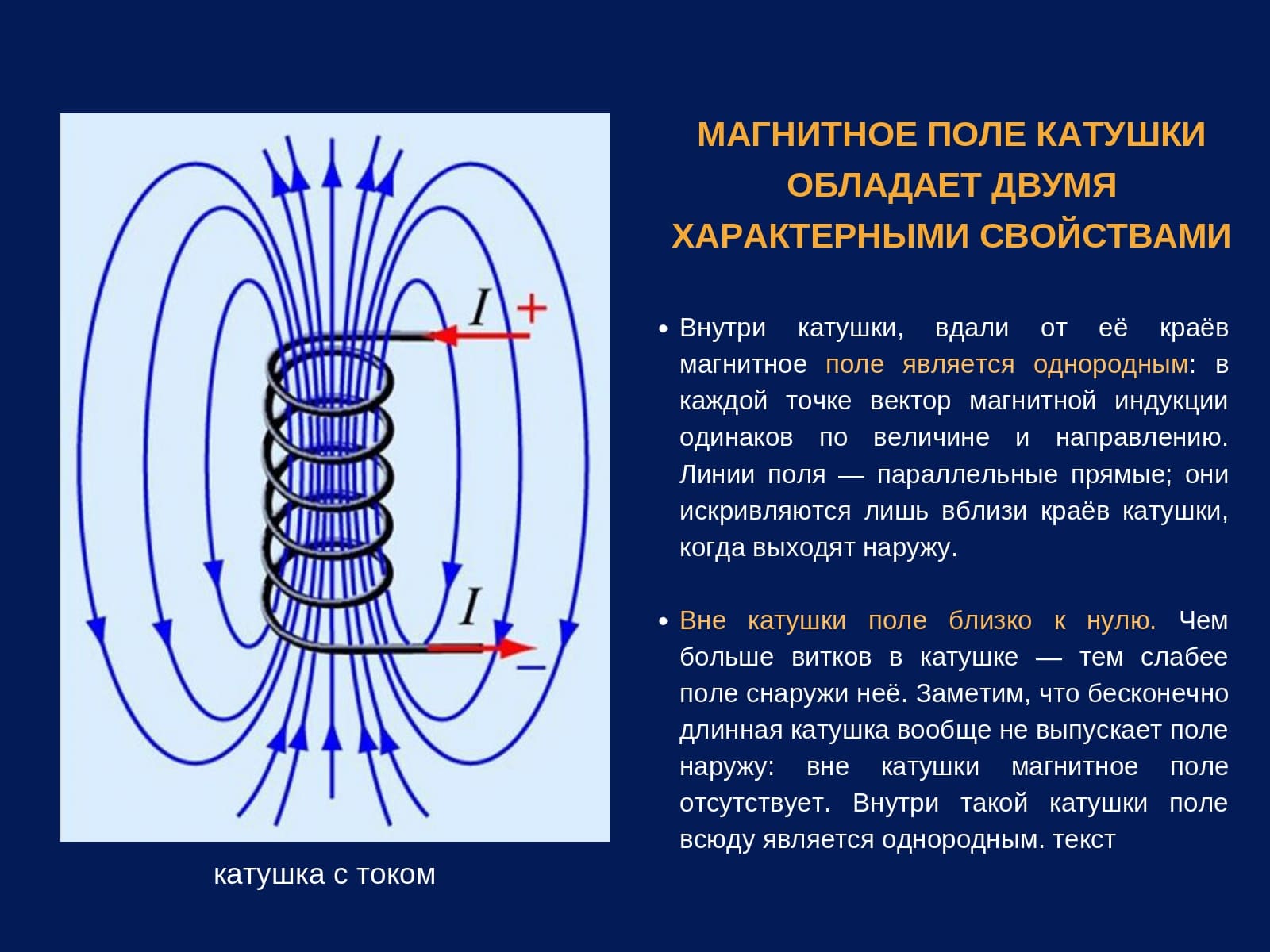

Переменная индуктивность дает возможность найти и энергию магнитного поля:

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк — это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

где I характеризует силу тока, U — показывает напряжение, R — сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка — источник тока», то ЭДС добавится к напряжению.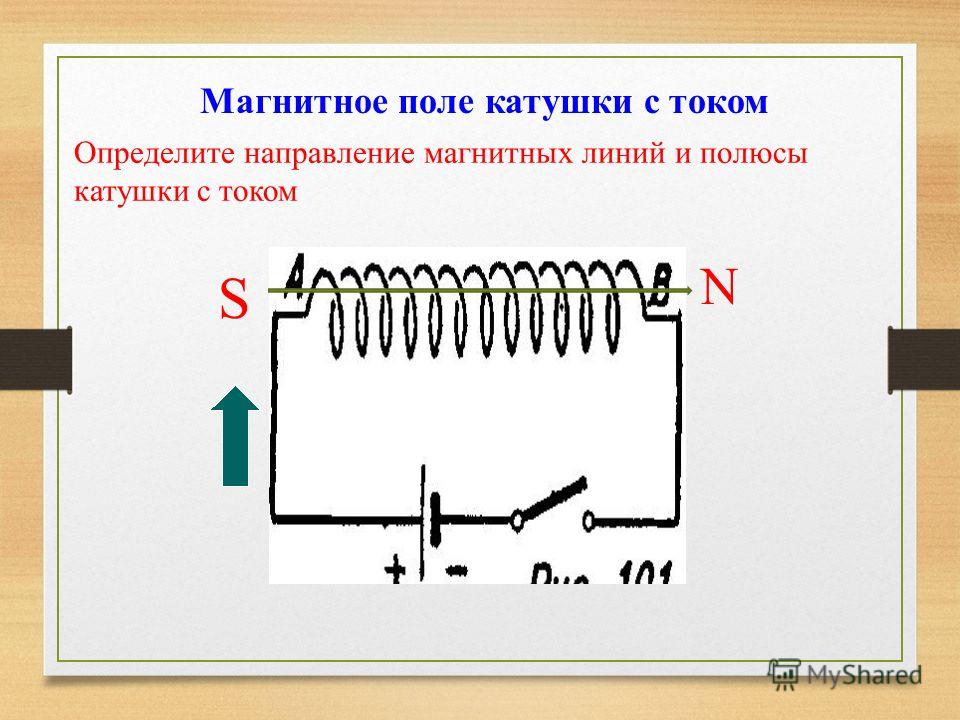 Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN 2 R 2: 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N 2 R 2: 2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
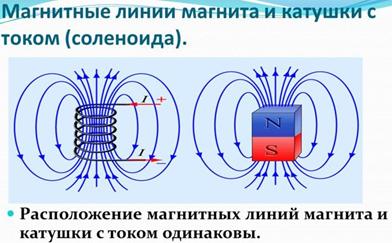
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от «витков в квадрате».
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником.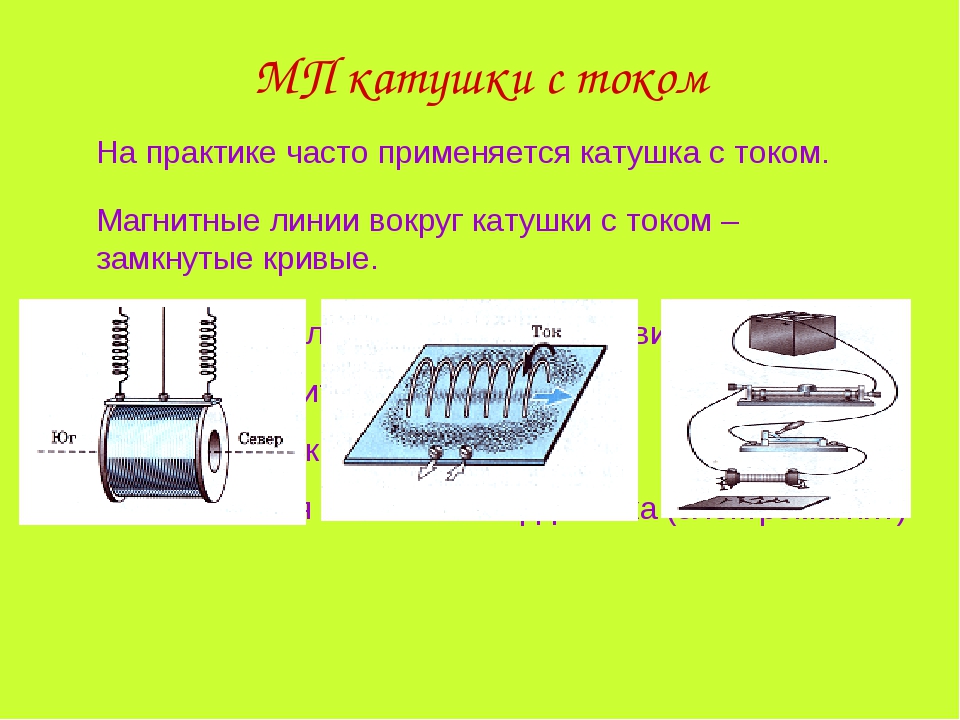 В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом — ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

где µ0 показывает магнитную проницаемость вакуума, n — это число витков, V — объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

где S — это площадь поперечного сечения, а l — длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.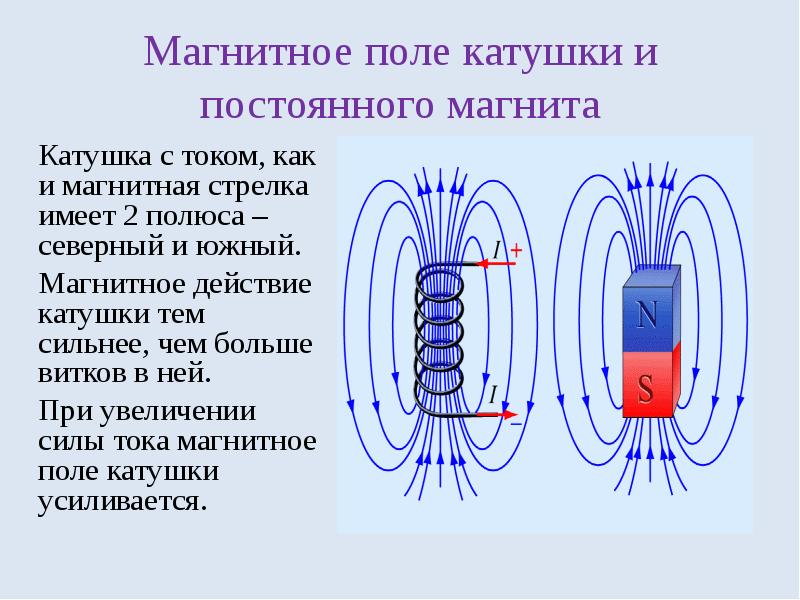

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 — это магнитная проницаемость вакуума, n — это число витков, а I — значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E — запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода.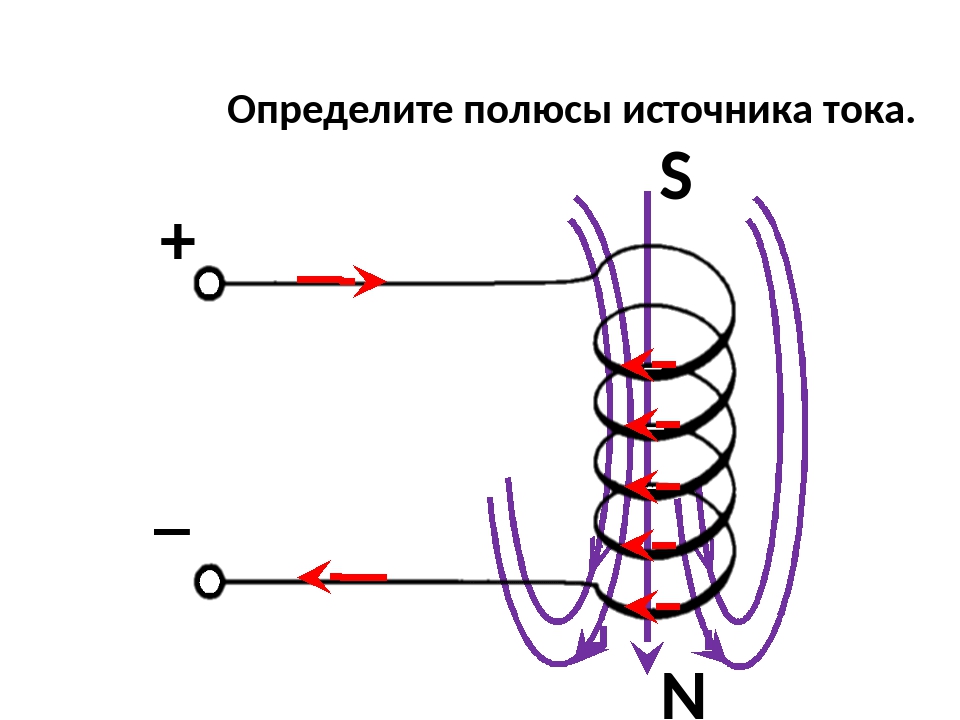 Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для в

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить формула используется следующая:

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное то формула будет выглядеть следующим образом:

Важными характеристиками колебательного контура являются резонансная частота, и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления.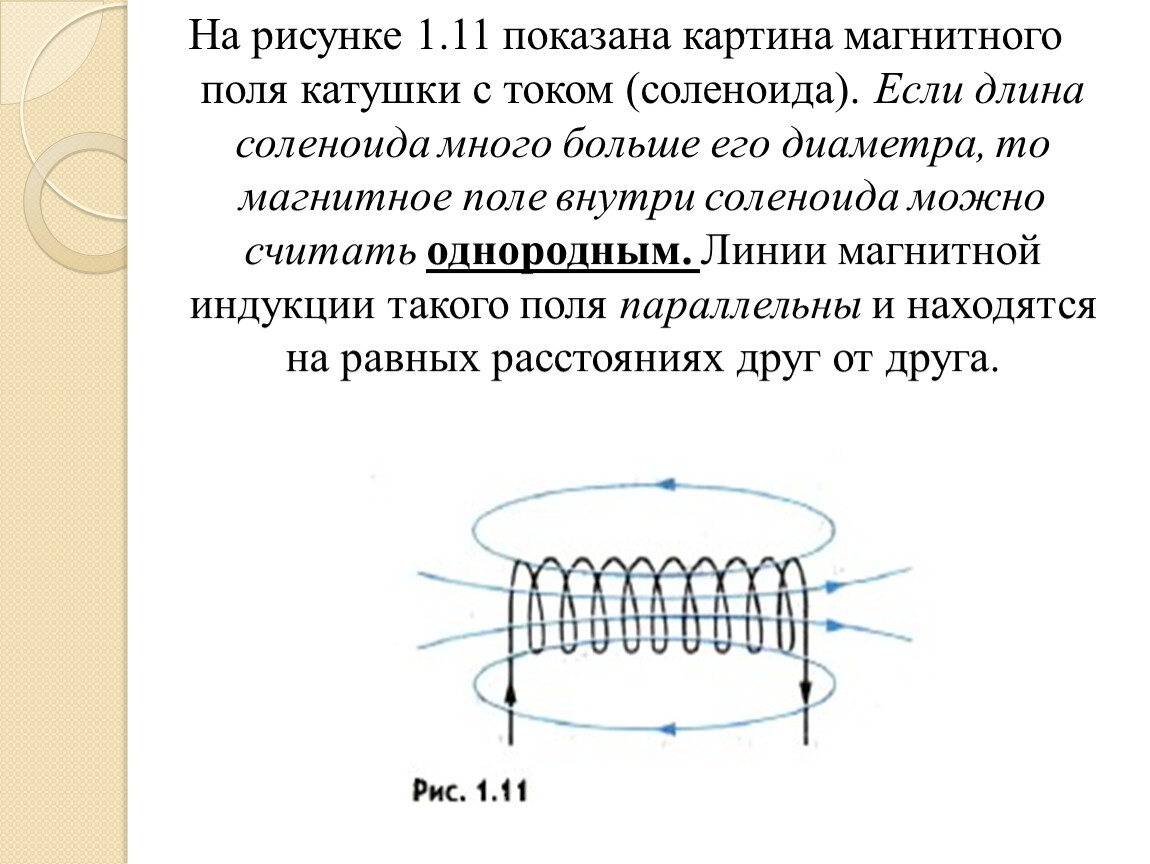 На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

Работа конденсатора

Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.

Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:

1. Конденсаторы с газообразным диэлектриком.
2. Вакуумные.
3. С жидким диэлектриком.
4. С твердым неорганическим диэлектриком.
5. С твердым органическим диэлектриком.
6. Твердотельные.
7. Электролитические.

Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:

1. Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
2. Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
3. Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

• Ce = C: (1 — 4Π 2 f 2 LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f — это частота, L — индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида — апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

где Lk показывает индуктивность устройства, Lp -пакета, Lm — главных шин, а Lb — индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc: n + µ0 l х d: (3b) + Lb,

где l — длина шин, b — ее ширина, а d — расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

Катушка индуктивности. Дроссель Возьмем отрезок медного провода и намотаем его на карандаш, а затем снимем с карандаша полученную спираль. У нас получился очень необходимой в радиоэлектронике элемент под названием катушка индуктивности. В дальнейшем такую спираль будем называть катушкой. Полученная нами катушка в электронике называется «однослойная цилиндрическая катушка без сердечника».

В промышленности катушки наматывают проводами с низким удельным сопротивлением — медь, алюминий, серебро и т.д. Провода покрывают электротехническим лаком для проедотвращения замыкания между витками катушки. В цепях постоянного тока и в цепях переменного тока катушка обладает различными свойствами, о чем в дальнейшем и будет идти речь.
Вспомним, из физики, что вокруг всякого проводника, по которому протекает электрический ток, образуется магнитное поле. Так как катушка — это проводник скрученный в спираль, то вокруг катушки также образуется магнитное поле. При протекании через катушку постоянного тока iL силовые линии магнитного поля направлены так, как показано на рисунке.

Чем больше количество витков и чем больше сила тока через катушку, тем больше величина магнитного поля.
Параметры катушки характеризуются величиной L которая называется: «индуктивность». Индуктивность зависит от геометрических размеров катушки и количества витков намотки. Следовательно, чем больше ток через катушку и больше индуктивность, тем сильнее магнитное поле.
Если в катушку ввести сердечник из магнитного материала (например сталь), то индуктивность катушки возрастет во много раз. Сам сердечник введенный в катушку, при подаче на катушку постоянного напряжения, намагнитится.

Из сказанного следует, что мы можем рассматривать катушку с сердечником как электрический магнит.
Электромагниты широко используются как в промышленности, так и в быту. Свойства электромагнита используются в электродвигателях постоянного тока. Более всего электромагниты распространены в таких приборах, как электромагнитные реле. Реле, это такие приборы, при подаче напряжения на которые включается электромагнит и происходит замыкание или размыкание мощных контактов.

Реле, следовательно могут коммутировать большие токи и напряжения. Реле, так же, широко используют в системах автоматики. При определенном включении реле могут выполнять логические функции.
Несмотря на простоту конструкции, расчёт индуктивности катушки весьма сложен. Приходится учитывать геометрические размеры, форму, количество витков, тип сердечника и т.д.
Для примера приведём формулу расчета индуктивности L простой однослойной цилиндрической катушки диаметром D, длиной намотки l, числом витков W, без сердечника:
L(мкГн) = W 2 * D * 10 -3 *l / (D + 0,45).
Индуктивность катушки измеряется в единицах — генри (Гн). Величина в 1 генри очень большая единица, поэтому на практике часто применяют кратные единицы:
миллигенри (мГн), 1мГн = 1*10 -3 Гн;
микрогенри (мкГн), 1мкГн = 1*10 -6 Гн.

Вернемся к катушке в цепи постоянного тока. Если катушку из нескольких витков, с сердечником, использовать в качестве электромагнита, т.е. подключить ее к источнику тока, то она перегорит (если мощность источника достаточно велика).

Произойдет это потому, что сопротивление катушки постоянному току очень мало, и соответственно ток через катушку и мощность будут максимальны. В связи с этим, для катушек в цепи постоянного тока, важна не индуктивность, а сопротивление катушки постоянному току. У электромагнитных реле, например, в справочниках указывается сопротивление обмотки и рабочее напряжение.
Как получить высокое сопротивление обмотки катушки, если провод которым они наматываются имеет низкое удельное сопротивление? Для этого используют провод с малой площадью поперечного сечения и наматывают большое количество витков в несколько слоев, например распространенное реле РЭС-9 имеет обмотку проводом диаметром 0,1мм и числом витков порядка 2000.
Иначе обстоит дело, когда катушка включена в цепь переменного тока. Так как ток переменный, то и магнитное поле создаваемое катушкой, тоже будет переменным. Переменное магнитное поле будет создавать сопротивление прохождению тока через катушку. Причем, чем больше частота переменного тока, при неизменной индуктивности катушки, тем больше получается сопротивление.

Избавиться от помех можно если в цепи питания поставить фильтр состоящий из катушки и конденсаторов. Так как катушка имеет низкое сопротивление постоянному току, то постоянное напряжение питания проходит через катушку без затухания, а для помехи сопротивление катушки велико и сигнал помехи ослабляется. Сопротивление конденсатора для помехи наоборот мало и помеха заземляется.
Назначение индуктивно-емкостного фильтра не только защита от помех. Фильтры широко используют для частотной селекции (разделения, выделения) сигналов. Например частота звукового сигнала (частота которую в состоянии услышать человеческое ухо) лежит в диапазоне от 20 Гц до 20000 Гц. Для качественного воспроизведения звуковых сигналов в акустических системах применяют 3 динамика — для воспроизведения низких (НЧ), средних (СЧ) и высоких (ВЧ) частот звукового диапазона.

Динамики включаются через фильтры которые выделяют именно тот диапазон частот, какой должен воспроизводить конкретный динамик.

В связи с тем, что конструктивный расчет катушек индуктивности очень сложен, на практике, в основном, применяют готовые (стандартные) катушки индуктивности. Для фильтров применяют катушки которые называют «дроссель». В радиоаппаратуре применяют катушки с изменяемой индуктивностью — сердечник такой катушки делается подвижным и может перемещаться внутри катушки.

В зависимости от применяемого сердечника индуктивность может возрастать или наоборот уменьшаться. Если применен сердечник из магнитного материала — сталь, феррит…, то индуктивность катушки увеличивается; если сердечник из диамагнитного материала — латунь, алюминий…, то индуктивность катушки уменьшается.
Катушки индуктивности, так же, как резисторы и конденсаторы, для получения заданной индуктивности, можно включать как последовательно, так и параллельно. Формулы расчета результирующей индуктивности Lr аналогичны формулам расчета результирующего сопротивления, а именно: для параллельного включения катушек: 1/Lr = 1/L1 + 1/L2 + … + 1/Ln; для последовательного включения — Lr = L1 + L2 + … + Ln.

Трансформаторы Мы знаем, что вокруг катушки, через которую протекает переменный электрический ток, образуется переменное магнитное поле.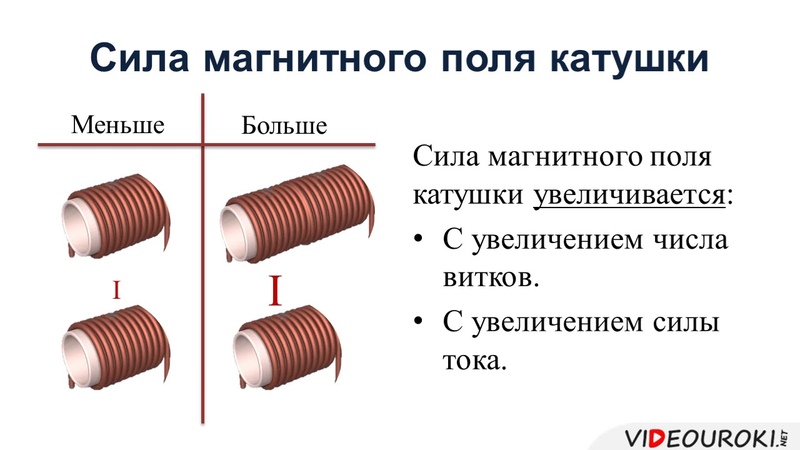 Если рядом с такой катушкой установить еще одну катушку, то магнитное поле первой катушки создаст в второй катушке электродвижущую силу (ЭДС), то есть на выводах второй катушки появится переменное напряжение.

Такое электромагнитное устройство, состоящее из двух (а иногда и более) катушек, одна из которых подключается и источнику переменного тока называется трансформатор. Трансформаторы широко используются в радио и электронике для преобразования одного напряжения в другое той же частоты.

Для усиления индуктивной связи катушки (в трансформаторах они называются «обмотки») размещаются на одном общем сердечнике. Обмотка подключенная к источнику питания называется первичной, а обмотка к которой подключена нагрузка называется вторичной.
Трансформаторы предназначенные для питания радио и электронной аппаратуры называются силовыми. Силовые трансформаторы, обычно, используют для понижения высокого (220V) напряжения осветительной сети в низкое напряжение порядка 9 … 80V.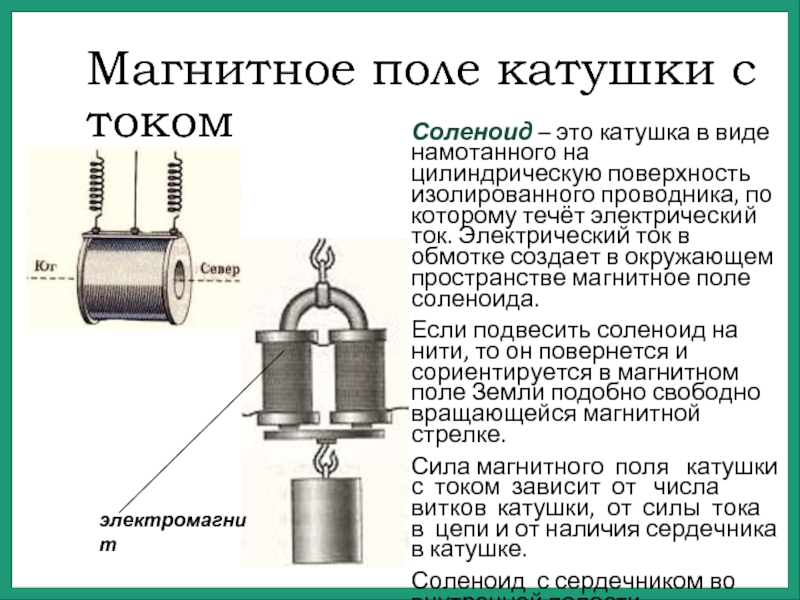 В радиоаппаратуре применяют, обычно, стандартные трансформаторы. Кроме вторичного напряжения, для силовых трансформаторов обязательно указывается мощность которую трансформатор может отдавать в нагрузку. Показанный на рисунке трансформатор типа ТП-200 имеет мощность 200 Ватт.

Отношение (k) числа витков первичной обмотки (W1) к числу витков (W2) вторичной обмотки трансформатора называется коэффициентом трансформации k = W1 / W2. Если k больше 1 то трансформатор является понижающим, т.е. напряжение на вторичной обмотке будет меньше напряжения на первичной обмотке в k раз.

Если k меньше 1 то трансформатор является повышающим и напряжение на вторичной обмотке будет больше напряжения на первичной обмотке в k раз. В общем случае напряжение на вторичной обмотке (U2) будет: U2 = U1/k, где U1 — напряжение на первичной обмотке.

Колебательный контур. Рассмотрим схему показанную на Рис.1. Здесь конденсатор С подключен к источнику питания GB через переключатель SA.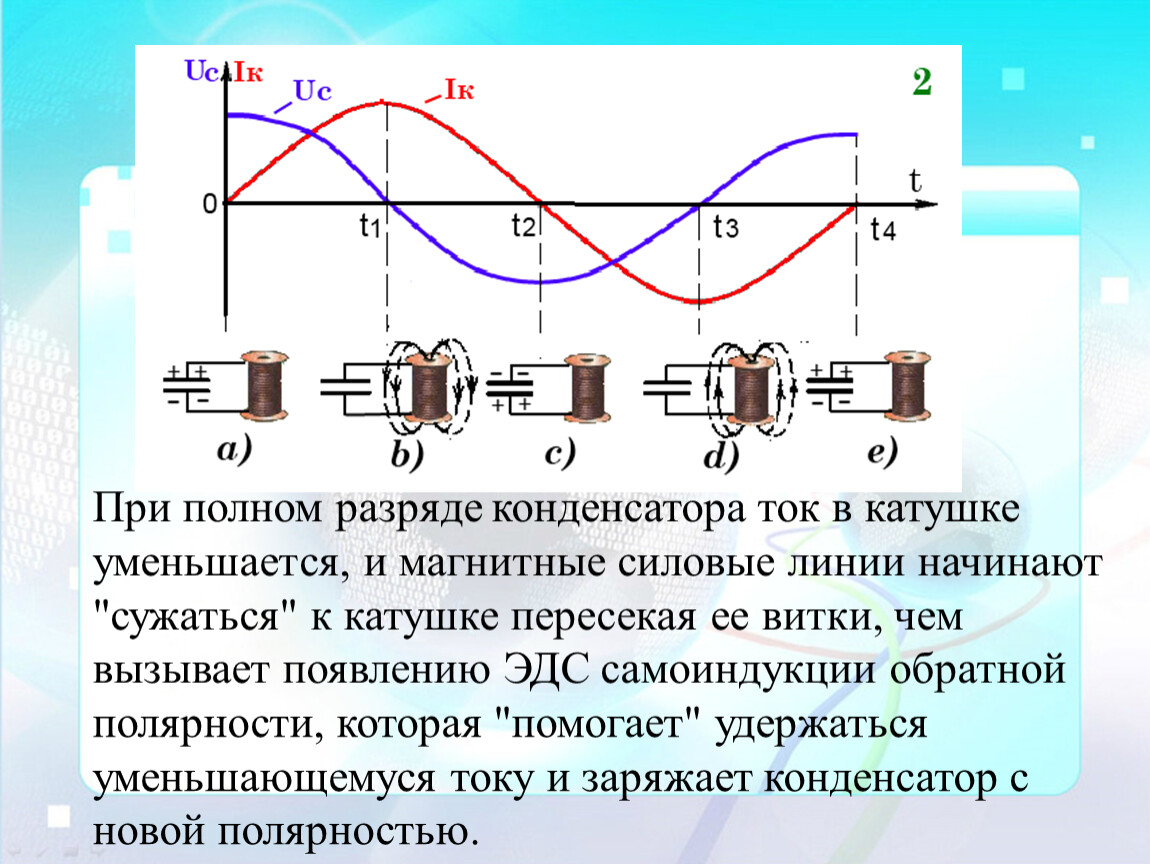

Через определенный промежуток времени конденсатор зарядится. Как только конденсатор зарядится переключим переключатель SA на катушку L (Рис.2). Конденсатор С разрядится через низкое сопротивление катушки L, но на этом процесс в цепи параллельно включенных катушки и конденсатора не закончится.
Вспомним, что при прохождении тока через катушку индуктивности вокруг нее образуется магнитное поле. Как только конденсатор разрядился магнитное поле катушки создает в катушке ЭДС, которая создает ток заряда конденсатора (В данном случае I2. Смотрите рисунок.).

Как видно из рисунка направление тока I2 противоположно току I1. За счет ЭДС катушки конденсатор заряжается. Как только конденсатор зарядился он тут же начинает разряжаться через низкое сопротивление катушки и процесс повторяется. В связи с потерями энергии в катушке и конденсаторе ток заряда — разряда постепенно уменьшается и процесс затухает. На графике этот процесс выглядит так, как показано но рисунке.
Параллельное включение катушки и конденсатора называется: «параллельный колебательный контур» или просто «колебательный контур».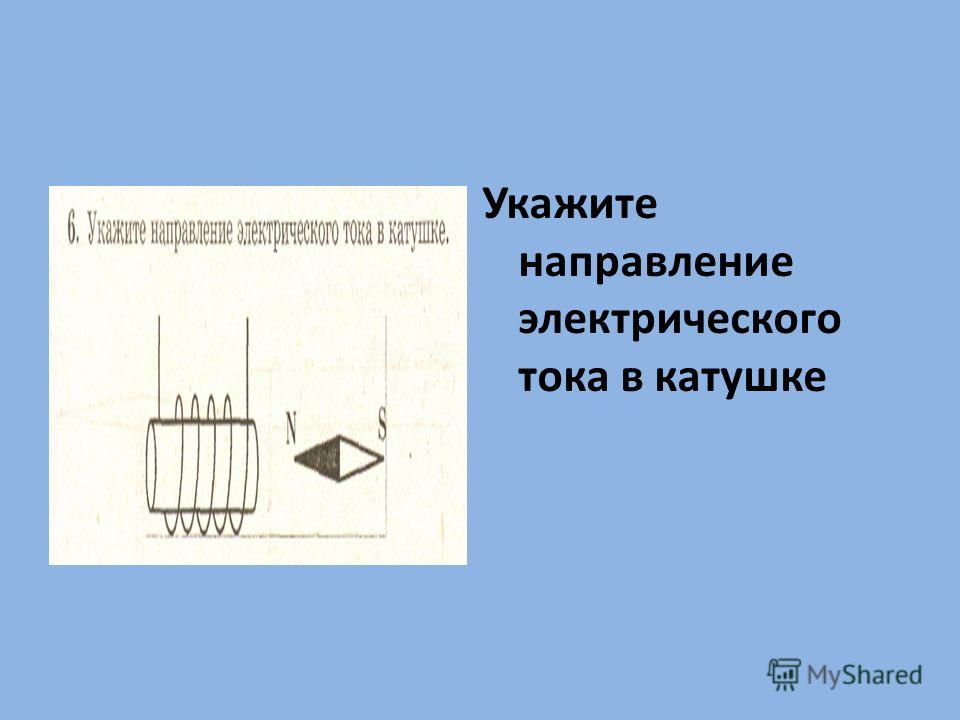 Колебательный контур обладает замечательными свойствами. Одно из свойств колебательного контура, это равенство периодов (Т) колебательного процесса, то есть частота колебаний (f) является постоянной величиной (смотрите график на рисунке).

Частота колебаний зависит от емкости конденсатора и индуктивности катушки. Частота колебательного контура называется «резонансной частотой» (fр). На рисунке показана математическая запись расчета резонансной частоты колебательного контура. Компьютернаязапись той же формулы выглядит так:
fp = 1 / (2 * pi * sqrt(L * C)), где sqrt означает — корень квадратный.
Рассмотрим схему показанную на рисунке.

Здесь к генератору (G) переменного тока подключен колебательный контур (LC). Ток I проходящий через контур измеряет амперметр переменного тока (А). Мы можем плавно изменять частоту генератора от f1 (см. график) которая меньше резонансной частоты колебательного контура до f2 которая больше резонансной частоты. На этих частотах величина тока максимальна. На частоте резонанса контура fp ток через контур резко падает. Это еще одно замечательное свойство колебательного контура. Мы знаем, что чем больше сопротивление цепи, тем меньше ток в этой цепи. Тогда резонансное сопротивление колебательного контура Rp, будет максимальным именно на частоте резонанса.
Свойство колебательного контура, когда резонансное сопротивление контура на частоте резонанса стремится к бесконечности, широко используется на практике. Например, рассмотрим как работает простой радиоприемник. Радиостанции передают радиосигнал в эфир на определенной частоте. За каждой радиостанцией закреплены определенные частоты.

В нашем примере (см. рисунок) радиостанция имеет частоту передающего сигнала 1200 KHz (килогерц). Приемник принимает через антенну радиосигналы. Радиосигналов в эфире очень много и все они имеют разные частоты. Как нам выделить сигнал нужной радиостанции (в нашем примере с частотой 1200 KHz)?
Для настройки радиоприемника на нужную частоту воспользуемся свойствами колебательного контура. Рассмотрим схему показанную на рисунке. Антенна (А) принимает радиосигналы различных частот. Предположим, что колебательный контур (LC) имеет частоту резонанса равную 1200 KHz, именно ту частоту которая нам нужна.

Тогда радиосигналы у которых частоты не равны 1200 KHz практически без помех пройдут через колебательный контур на землю. Для сигнала с частотой 1200 KHz сопротивление колебательного контура велико, поэтому сигнал пойдет не на землю, а на преобразователь радиосигнала высокой частоты в сигнал звуковой частоты (называется «детектор») и далее на усилитель и динамик.
Для настройки на другую частоту, обычно, в колебательном контуре применяют конденсатор переменной ёмкости (рис.1) С изменением емкости конденсатора изменяется и резонансная частота контура fp, то есть изменяется настройка на другую частоту.

В простых приёмниках (например рассмотренного нами) возникает такое явление, как наравне с основной радиостанцией, на частоту которой настроен колебательный контур, прослушивается и другая радиостанция (с меньшей громкостью) имеющая частоту близкую к частоте основной радиостанции. Это явление возникает потому, что частота (fp1) мешающей радиостанции близка к частоте основной радиостанции и резонансное (Rp1) сопротивление колебательного контура велико (Рис. 2).
Относительно высокое сопротивление колебательного контура, не на частоте резонанса, позволяет мешающему сигналу проходить на детектор и соответственно на усилитель и динамик. Поэтому для колебательного контура существует такое понятие как добротность контура.

На графике представлены две кривые зависимости (А и Б) сопротивления контура от частоты сигнала. Очевидно, что сопротивление Rp1 кривой А, на частоте fp1, больше сопротивления Rp2 кривой Б. Из этого следует, что ослабление мешающего сигнала лучше у контура имеющего кривую Б. В радио и электронике принято говорить, что чем острей кривая, тем лучше добротность контура. Добротность контура зависит от качества изготовления катушки индуктивности и качества применяемого конденсатора переменной ёмкости.
Колебательные контуры, в радиоэлектронике применяются не только для настройки на радиостанции. Широкое применение колебательные контуры нашли в радиоэлектронике как фильтры различных сигналов, а так же в качестве стабилизаторов частоты генераторов переменного тока применяемых в передатчиках и других приборах.

Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга . Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индуктивность

Любая катушка индуктивности обладает индуктивностью . Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра .

Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

где

В — магнитное поле, Вб

I —

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение

И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф) . Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:

С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается, то магнитное поле сжимается.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома :

где

I — сила тока в катушке, А

U — напряжение в катушке, В

R — сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником . Снизу на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух — это немагнитный сердечник:-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

Дроссели

Также есть особый вид катушек индуктивностей. Это так называемые . Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей — это . Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Опыты с катушкой

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:

где

1 — это каркас катушки

2 — это витки катушки

3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Обозначение на схемах

Последовательное и параллельное соединение катушек

При последовательном соединении индуктивностей , их общая индуктивность будет равняться сумме индуктивностей.

А при параллельном соединении получаем вот так:

При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.

Резюме

Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.

Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.

Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:

Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:

Простая индуктивная цепь: ток катушки отстает от напряжения на 90 o .

Если мы построим график тока и напряжения для этой простой цепи , то он будет выглядеть примерно так:

Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90 o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.

Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:

Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90 o , бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.

Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.

Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: X L .

Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:

Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:

В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360 o . Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360 o . Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.

Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула X L = 2πfL может быть написана как X L = ωL.

Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.

При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:

Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90 o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:

Ток на катушке индуктивности отстает от напряжения на 90 o .

Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90 o . Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).

Конденсатор и катушка индуктивности в цепи переменного тока

Как мы с вами говорили, в цепи переменного тока, содержащей активное сопротивление, происходят постоянные потери энергии, сопровождающиеся выделением тепла. При этом, количество теплоты, выделяющееся на активном сопротивление при прохождении по нему переменного тока, можно рассчитать, как и в случае с постоянным током, по закону Джоуля — Ленца:

Однако быстрое изменение величины и направления переменного тока обусловливает ряд особенностей, отличающих его действия от действий тока постоянного. Так, например, переменный ток не годится для технических применений электролиза. Дело в том, что величина переменного тока зависит не только от напряжения и сопротивления цепи, но и от индуктивности проводников, включённых в цепь. В этом можно убедиться на следующем опыте. Включим в цепь постоянного тока катушку, содержащую большое количество витков медной проволоки и амперметр.

Снимем показания амперметра. А теперь вдвинем в катушку железный сердечник — ток при этом не изменился.

Посмотрим, что будет происходить в этой же цепи, но при включении в неё источника переменного тока с действующим напряжением, равным напряжению постоянного тока.

Нетрудно заметить, что ток в катушке уменьшился. Введение же в катушку железного сердечника приведёт к ещё большему ослаблению тока. Следовательно, индуктивность цепи переменного тока уменьшает величину тока.

Причиной этого является возникающая в цепях переменного тока ЭДС самоиндукции, которая препятствует нарастанию тока. Вследствие ЭДС самоиндукции в момент, когда напряжение в цепи достигает максимума, ток не успевает достигнуть той величины, которую он достиг бы в отсутствие самоиндукции.

Например, представим, что у нас есть катушка, на которую намотано 600 витков медной проволоки, диаметром 1 мм. Предположим, что на эту катушку пошло 150 метров этой проволоки. Тогда, исходя из определения, её сопротивление примерно равно 3,2 Ом. Но если измерить сопротивление этой катушки в цепи переменного тока частотой 50 Гц, то оно окажется равным примерно 20 Ом.

Это говорит нам о том, что индуктивность в цепи переменного тока действует в отношении величины тока так же, как и активное сопротивление.

Сопротивление, которым обладает цепь вследствие наличия в ней индуктивности, называется индуктивным сопротивлением. Узнаем от чего оно зависит. Итак, пусть в цепи, содержащей катушку индуктивности, протекает переменный ток, сила которого изменяется по гармоническому закону:

Тогда, ЭДС самоиндукции будет равна произведению индуктивности катушки и первой производной силы тока по времени, взятому с обратным знаком:

Если активное сопротивление катушки равно нулю, то и напряжённость электрического поля внутри проводника в любой момент времени должна быть равна нулю. В противном случае сила тока была бы бесконечно большой (это следует из закона Ома). Равенство нулю напряжённости поля оказывается возможным потому, что напряжённость, вихревого электрического поля, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряжённости кулоновского поля, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, удельная работа вихревого поля (то есть ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.

Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение в цепи переменного тока, будет обратно по знаку ЭДС самоиндукции:

Произведение величин, стоящих перед функцией косинуса, является амплитудой напряжения:

Давайте перепишем уравнение для мгновенного напряжения, воспользовавшись введённым обозначением, а также заменим косинус на синус, воспользовавшись формулой приведения:

Отсюда следует, что колебания напряжения на катушке опережают колебания силы тока на π/2:

Давайте выразим из формулы для амплитуды напряжения амплитуду силы тока в катушке:

Величина, равная произведению циклической частоты и индуктивности катушки и есть индуктивное сопротивление:

Тогда можно записать, что амплитудное значение силы тока в цепи переменного тока, содержащую только катушку индуктивности, прямо пропорционально амплитудному напряжению и обратно пропорционально индуктивному сопротивлению.

А теперь давайте определим мгновенную мощность в данной цепи:

Как видим, потребляемая идеальной катушкой, периодически изменяется с двойной частотой, а её среднее значение за период равно нулю, так как равно нулю среднее значение синуса двойного аргумента. Следовательно, так же как активное сопротивление, индуктивное сопротивление ограничивает силу тока в цепи, но в отличие от активного сопротивления на нём электрическая энергия не превращается необратимо в другие виды энергии.

Теперь давайте с вами соберём цепь постоянного тока, содержащую последовательно соединённые конденсатор и лампочку. Замкнув цепь, мы обнаружим, что никакого тока в цепи нет. Это вполне понятно, так как пластины конденсатора отделены друг от друга изолятором. Поэтому через конденсатор постоянный ток течь не может.

А теперь заменим источник постоянного тока на источник переменного напряжения. Лампочка горит. Объясняется это достаточно просто. В цепи переменного тока электроны совершают колебательное движение. Это приводит к тому, что обкладки конденсаторов попеременно заряжаются то положительно, то отрицательно. Электроны же в проводах цепи движутся то в одном, то в другом направлении, нагревая спираль лампы. Если выключить конденсатор из цепи, то лампочка будет гореть ярче. Следовательно, наличие конденсатора в цепи переменного тока увеличивает сопротивление цепи.

Сопротивление, которым обладает цепь вследствие наличия в ней ёмкости, называется ёмкостным сопротивлением.

Выясним, от чего оно зависит. Для этого рассмотрим цепь, состоящую из генератора переменного напряжения, конденсатора и проводов, сопротивление которых пренебрежимо мало.

Пусть напряжение на конденсаторе изменяется синусоидально:

Следовательно, и заряд конденсатора будет изменяться со временем по закону синуса:

Найдём силу тока в цепи, как первую производную заряда по времени:

Произведение величин, стоящих перед функцией синуса, является амплитудой силы тока:

Перепишем предыдущее уравнение с учётом введённых обозначений, и воспользуемся формулой приведения для перехода от функции косинуса к функции синус:

 

Отсюда следует, что колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2:

Теперь давайте перепишем уравнение для амплитуды силы тока так, как это показано на экране:

Величина, обратная произведению ёмкости конденсатора и циклической частоты является ёмкостным сопротивлением:

Подставив данное уравнение в предыдущее равенство, найдём, что амплитудное значение силы тока в цепи переменного тока, содержащую только конденсатор, прямо пропорционально амплитудному напряжению и обратно пропорционально ёмкостному сопротивлению:

Теперь определим мгновенную мощность в данной цепи:

Как и в предыдущем случае, при наличии в цепи только ёмкостного сопротивления частота изменения мощности вдвойне больше частоты изменения силы тока, а её среднее значение за период равно нулю. Следовательно, на ёмкостном сопротивлении электрическая энергия не превращается необратимо в другие виды. Поэтому ёмкостное и индуктивное сопротивления в отличие от активного называют реактивными.

Теперь рассмотрим цепь, содержащую все элементы: резистор, катушку индуктивности, конденсатор и источник переменного напряжения.

Так как электромагнитные взаимодействия распространяются со скоростью света, то во всех последовательно включённых элементах цепи изменения силы тока происходят практически одновременно. Однако колебания мгновенных значений напряжения на каждом из элементов не совпадают по фазе с колебаниями силы тока. Но в любой момент времени сумма мгновенных значений напряжений на последовательно включённых элементах цепи равна ЭДС источника:

Учитывая, что на активном сопротивлении колебания силы тока совпадают, на ёмкостном опережают, а на индуктивном отстают от колебаний напряжения, то последнее равенство можно записать так:

Амплитуду колебаний напряжения в цепи можно выразить через амплитудные значения напряжения на отдельных её элементах, воспользовавшись методом векторных диаграмм.

Амплитудное значение силы тока в цепи совпадает по фазе с амплитудным значением напряжения на резисторе. Из этой диаграммы можно найти амплитуду приложенного напряжения, которая равна геометрической сумме этих амплитуд.

Используя теорему Пифагора, выразим квадрат амплитуды колебаний напряжения в цепи:

Далее, используя закон Ома для участка цепи, выразим амплитудные значения напряжений, стоящих в правой части равенства, через амплитудное значение силы тока и реактивные сопротивления:

Выражая из полученного уравнение амплитудное значение силы тока, получим закон Ома для участка цепи переменного тока:

Величина, стоящая в знаменателе формулы, называется полным сопротивлением цепи:

Величина же, стоящая в скобках под знаком корня, называется реактивным сопротивлением.

Оптимизация расстояния между витками катушки индуктивности

При разработке электромагнитных катушек может потребоваться настроить положение витков, чтобы обеспечить магнитное поле желаемой величины в определенной области в пространстве. Это можно сделать в программном пакете COMSOL Multiphysics® при использовании функционала модулей AC/DC и Оптимизация для совокупной оптимизации параметров и формы. Давайте разберем такую постановку подробнее.При разработке электромагнитных катушек может потребоваться настроить положение витков, чтобы обеспечить магнитное поле желаемой величины в определенной области в пространстве. Это можно сделать в программном пакете COMSOL Multiphysics® при использовании функционала модулей AC/DC и Оптимизация для совокупной оптимизации параметров и формы. Давайте разберем такую постановку подробнее.

Исходная модель катушки и постановка задачи оптимизации

Предположим, что наша задача — разработать такую катушку, при которой величина магнитного поля на отрезке осевой линии будет максимально близка к целевой величине. Как мы уже обсудили в предыдущей статье, этого можно добиться, задав разные значения тока, протекающего по каждому витку катушки. Однако для это подразумевало добавление в физическую модель отдельных элементов управления током для каждого витка. Вместо этого можно использовать источник для всей катушки и менять расстояние между витками катушки в осевом направлении.

Осесимметричная катушка с десятью витками. Цель задачи — изменить магнитное поле на отрезке осевой линии (выделен зеленым цветом).

Исходная геометрия катушки и постановка задачи показаны на рисунке выше. Осесимметричная катушка с десятью витками питается от единого источника тока: по каждому витку идет один и тот же ток. В исходной модели витки катушки диаметром 1 см расположены на одинаковом расстоянии S₀ = 4 см друг от друга. Используем оссеметричную постановку с дополнительной симметрией, т.к. нас интересуют только решения, симметричные на плоскости z = 0.

Схема расчетной области для модели. Мы будем менять положение пяти витков и проходящий через катушку ток.

Цель нашей оптимизации — сделать осевую компоненту магнитного поля (B_z) наиболее близким к целевому значению B₀ вдоль отрезка осевой линии, меняя ток через катушку и z-координаты пяти витков.2 d l \\
& \text{subject to:}
& & -(S_0-G_0)/2 \le \Delta Z_1 \leq \Delta Z_{max}\\
& & & -\Delta Z_{max} \leq \Delta Z_2, \ldots ,\Delta Z_5 \leq \Delta Z_{max}\\
& & & G_0 \le (Z_5-Z_4) \\
& & & G_0 \le (Z_4-Z_3) \\
& & & G_0 \le (Z_3-Z_2) \\
& & & G_0 \le (Z_2-Z_1) \\
& & & 0 \leq I \leq I_{max}\\
\end{aligned}

Решим эту задачу путем совокупной оптимизации параметров и формы с помощью интерфейсов Optimization (Оптимизация) и Deformed Geometry (Деформированная геометрия) в COMSOL Multiphysics.

Настройка и решение задачи оптимизации в COMSOL Multiphysics®

Можно начать с рассмотрения разработанной ранее модели, в которой выполняется схожая оптимизация для достижения определенного значения магнитного поля вдоль оси. Мы также используем аналогичные настройки: интерфейс Optimization (Оптимизация) и опцию Integral Objective (Интегральная целевая функция), назначение которых описано в предыдущей статье. Затем используем два узла Global Control Variable (Глобальные контрольные переменные). В первом описываем пределы для смещений каждого из пяти витков, а с помощью опции Control Variables Scaling (Масштабирование управляющих переменных) перенормируем их так, чтобы они были близки к единице. Во втором узле Global Control Variables аналогичным образом задаем настройки для контрольной переменной тока.

Определения переменных, управляющих положением пяти витков.

Пять управляющих переменных, показанных на снимке экрана выше, определяют смещения витков и небольшой квадратной области вокруг каждого витка, показанной зеленым цветом на следующей иллюстрации. Поскольку эти зеленые области перемещаются вверх и вниз, окружающие их желтые области должны подстраиваться, растягиваясь и сжимаясь, в то время как внешняя окружающая голубая область будет оставаться неизменной. Т.к. нам известно смещение зеленых областей, мы можем задать линейное изменение смещения вдоль всех красных ребер. Эту линейную вариацию смещения удобно определять с помощью математического интерфейса Coefficient Form Boundary PDE, что подробно описано в одной из предыдущих статей корпоративного блога COMSOL о моделировании поступательного движения.

Схематическое деление геометрии на области с различными деформациями.

Сведения об заданных смещениях различных областей задаются с помощью интерфейса Deformed Geometry (Деформированная геометрия), как показано на снимке экрана ниже. Условия типа Prescribed Deformation (Заданная деформация) смещают зеленые области, а желтые области подстраиваются и деформируются из-за наложенного условия Free Deformation (Свободная деформация). Граничные условия Prescribed Mesh Displacement (Заданное смещение сетки) применены к черным и красным ребрам и однозначно доопределяют деформации желтых областей.

Управление смещениями витков катушки с помощью условия Prescribed Deformation (Заданное смещение) в интерфейсе Deformed Geometry (Деформированная геометрия).

С помощью такой настройки через интерфейс Deformed Geometry (Деформированная геометрия) пять управляющих переменных для положений витков теперь определяют задачу оптимизации формы (shape optimization). Ранее мы уже обсуждали задачи оптимизации формы, рассматривая более общую постановку из области механики конструкций. При оптимизации формы можно воспользоваться функционалом COMSOL Multiphysics по анализу чувствительности (Sensitivity-анализу) при изменяющихся геометрических параметрах.

Следует также определить набор Global Inequality Constraints (Глобальных ограничений в виде неравенства), чтобы зеленые области, окружающие витки, не были расположены слишком близко друг к другу и не пересекались. Это показано на следующем снимке экрана. Помните о том, что ограничение масштабируется на величину зазора G₀, поэтому уравнение ограничения мы также сформулируем через нормировку и единицу.

Одно из четырех ограничений, не позволяющих виткам сближаться и накладываться друг на друга.

Ввиду значительных деформаций, которые могут возникнуть в растягивающихся и сокращающихся областях вокруг витков, целесообразно также использовать структурированную сетку типа Mapped.

Структурированная сетка типа Mapped используется в деформируемых областях вокруг витков. Для области c Infinite Element Domain также используется Mapped-сетка.

Теперь можно решить эту задачу с помощью градиентного оптимизационного алгоритма (SNOPT), используя преимущества определения деформаций через Deformed Geometry, что дает возможность использовать аналитические выражения для градиентов. В процессе оптимизации ток, протекающий по катушке, и положения витков меняются, чтобы минимизировать упомянутую выше целевую функцию. Результаты оптимизации показаны на следующем рисунке.

z-компонента плотности магнитной индукции вдоль осевой линии для оптимизированной конструкции катушки.

Оптимальные положения витков.

Заключение

Мы представили модель, в которой сочетается оптимизация формы и параметров для регулировки тока в катушке и интервала между витками в двухмерной осесимметричной катушке. Используя интерфейсы Optimization (Оптимизация) и Deformed Geometry (Деформированная геометрия), мы аналитически рассчитали градиенты для данной задачи и быстро провели оптимизационное исследование.

Дополнительные ресурсы

Катушки индуктивности на ток 5А 6А 8А 10А SMD HP0602, SP6045, HE1040

Катушки индуктивности HP0602 Цены в формате  .pdf,  .xls Купить Упаковка: В блистр-ленте на катушке диаметром 330 мм по 1900 штук экранированных катушек индуктивностей HP 0602 Катушки индуктивности HE0630 Наименование Индуктивность R, Ом Ток, А Ток нас., А Склад Заказ HP0603 R47M2B 0,47мкГн ± 20% 0,004 17A 26A HE0630 1R0MSB 1,0мкГн ± 20% 0,009 11A 22A HE0630 1R5MSB 1,5мкГн ± 20% 0,014 9A 18A HE0630 2R2MSB 2,2мкГн ± 20% 0,018 8A 14A HE0630 3R3MSB 3,3мкГн ± 20% 0,028 6А 13,5А HE0630 4R7MSB 4,7мкГн ± 20% 0,037 5,5A 9,5A HE0630 5R5MSB 5,6мкГн ± 20% 0,052 4,8A 9A HP0603 6R8M2 6,8мкГн ± 20% 0,054 4,5A 8A HE0630 100MSB 10мкГн ± 20% 0,062 4A 5,5A Цены в формате  .pdf,  .xls Купить Упаковка: В блистр-ленте на катушке диаметром 330 мм по 1000 штук экранированных катушек индуктивностей HE 0630 и 1500 штук HP0603. Катушки индуктивности HE1040 Наименование Индуктивность R, Ом Ток, А Ток нас., А Склад Заказ HE1040 1R0MSB 1мкГн ± 20% 0,003 18A 28A HE1040 2R2MSB 2,2мкГн ± 20% 0,0067 12A 22A HE1040 3R3MSB 3,3мкГн ± 20% 0,0108 10A 17A HE1040 4R7MSB 4,7мкГн ± 20% 0,015 9,5A 15A HE1040 6R8MSB 6,8мкГн ± 20% 0,0212 8A 12A HE1040 100M2B 10мкГн ± 20% 0,0332 6,8A 9,5A HE1040 220M2B 22мкГн ± 25% 0,0605 5A 5,5A HE1040 330M2B 33мкГн ± 20% 0,085 4,4 5A HE1040 470M2B 47мкГн ± 25% 0,13 3,5A 4A HE1040 101M2B 100мкГн ± 25% 0,249 3A 2,25A Цены в формате  .pdf,  .xls Купить Упаковка: В блистр-ленте на катушке диаметром 330 мм по 800 штук HE1040. Катушки индуктивности SP6045 Наименование Индуктивность R, Ом Ток, А Ток нас., А Склад Заказ SP6045 1R0YLB 1,0мкГн ± 25% 0,0046 13A 12A SP6045 2R0YLB 2,0мкГн ± 25% 0,0082 9A 8A SP6045 3R0YLB 3,0мкГн ± 25% 0,0133 6,6A 6,3A SP6045 3R9YLB 3,9мкГн ± 25% 0,0147 6,2A 6A SP6045 4R5YLB 4,5мкГн ± 25% 0,016 5,8A 5,4A Цены в формате  .pdf,  .xls Купить Упаковка: В блистр-ленте на катушке диаметром 330 мм по 1000 штук экранированных катушек индуктивностей SP 6045. Размеры экранированных SMD индуктивностей на ток 10А и выше Тип A B C D E F G H HP0602 7,2 мм 6,5 мм 3,0 мм 2,4 мм 1,7 мм 3,4 мм 3,7 мм 7,4 мм HP0603 7,0 мм 6,5 мм 3,0 мм 3,0 мм 1,7 мм 3,4 мм 3,7 мм 7,4 мм HE0630 7,1 мм 6,6 мм 3,0 мм 3,0 мм 1,6 мм 3,4 мм 3,7 мм 7,4 мм SP6045 7,0 мм 6,6 мм 1,4 мм 4,5 мм 1,5 мм 3,4 мм 3,0 мм 7,4 мм HE1040 100(1) 11,5 мм 10,0 мм 2,8 мм 4,0 мм 2,0 мм 3,3 мм 6,0 мм 12,0 мм HE1040 220 11,5 мм 10,0 мм 2,8 мм 4,0 мм 2,5 мм 4,0 мм 6,0 мм 13,0 мм HE1040 470 11,0 мм 10,0 мм 2,8 мм 4,0 мм 2,0 мм 3,3 мм 6,0 мм 12,0 мм HP0602 — новая и наиболее перспективная серия катушек индуктивности. Обеспечивают наименьшие габариты при высоких значениях рабочего тока и индуктивности, благодаря использованию намотки плоским проводом. Новая конструкция ферритового корпуса обеспечивает наименьшие поля рассеивания среди аналогичных изделий компани производителя. Экранированные катушки индуктивности на меньшие токи представлены в типоразмерах SU8030 SU8040 SU1050 и SS0704. Для бюджетных применений доступны не экранированные катушки индуктивности типоразмеров SR0604 SR0805 SR1006. Технические характеристики и маркировка экранированных катушек индуктивности HP0602 Технические характеристики и маркировка экранированных катушек индуктивности SP6045 Технические характеристики и маркировка экранированных катушек индуктивности HP0603 Технические характеристики и маркировка экранированных катушек индуктивности HE0630 Технические характеристики и маркировка экранированных катушек индуктивности HE1040 Технические характеристики и маркировка экранированных катушек индуктивности HE1040101MLB Производитель — ABC

Корзина Корзина пуста

Катушка тока

— определение, важные факторы и применение

Катушка тока — это в основном катушка, например, провод, намотанный вокруг электрического проводника. Обычно катушка изготавливается из изолированной медной проволоки, а проводник представляет собой сердечник из мягкого железа. Когда катушка, намотанная вокруг проводника, проводит ток, было замечено, что катушка начинает вести себя как магнит. Это свойство проводника, намотанного на катушку с током, называется электромагнетизмом. Популярный физический эксперимент проводится с использованием того же явления.Когда гвозди кладут на стол с проводником, намотанным на токоведущий провод, гвозди стола прилипают к катушке. Причина, по которой эти гвозди приклеиваются к проволоке, — электромагнетизм.

Важные факторы для токовой катушки

Существует ряд факторов, от которых зависит сила электромагнетизма.

1. Первым фактором, определяющим силу токовой катушки, является количество витков. Чем больше витков, тем больше ток в амперах.Магнитное поле также умножается на количество витков в катушке.

2. Второй важный фактор — это сила тока, протекающего по проводнику. Чем больше электрический ток, тем больше сила токовой катушки.

3. Третий фактор — это материал, из которого изготовлен проводник. Обычно для улучшения электромагнетизма вокруг катушки с током используются железные или железосодержащие элементы. Кроме того, использование таких сплавов, как алюминий-никель-кобальт, также может создавать сильные магнитные поля.

4. Четвертым и последним фактором, который важен для токовой катушки, является температура. Было обнаружено, что токопроводящая способность улучшается при более низких температурах. Причем самые сильные магниты сделаны из сверхпроводников, охлаждаемых сжиженным азотом или гелием.

Применение токовой катушки

Благодаря своей уникальной способности вызывать электромагнетизм, токовая катушка имеет множество применений в реальном мире.

• Токовая катушка широко известна как Can Crusher.Это приложение основано на электромагнитном поле, которое создается, когда банка помещается в катушку, которая затем получает дополнительную энергию, чтобы изгибать и деформировать банку, сжимая ее в плоский диск.

• Катушки тока также обычно используются в качестве электромагнитов. Также существуют определенные типы электромагнитов, такие как соленоид, катушка Максвелла, звуковая катушка и катушка размагничивания.

• Еще одно распространенное применение токовой катушки — это магнитные краны.На свалках мусор также содержит большое количество металлов, разложение которых может занять годы, или их можно просто переработать и использовать повторно. Здесь может помочь электромагнит. Гигантский электромагнит притягивает и засовывает все металлические детали в мусор на свалках и полигонах. Более того, эти металлические обрезки легко удаляются электромагнитом в обесточенном состоянии. Эта функция была невозможна с постоянными магнитами, и раньше людям приходилось удалять металлические отходы вручную.

Завершение токовой катушки

При изучении физики концепции электричества и магнетизма пересекаются. Пример токовой катушки объясняет совместное возникновение двух вышеупомянутых явлений, которое затем называется электромагнетизмом. Электромагнитное поле, создаваемое при прохождении тока через токовую катушку, может служить нескольким целям. Некоторые из этих реальных применений — это электромагниты, дробилки для жестяных банок и магнитные краны.

Интересные факты

Разница между катушкой тока и катушкой давления.

Катушка давления также известна как катушка напряжения и обычно используется в ваттметрах. Между токовой катушкой и катушкой давления есть заметная разница. Токовая катушка всегда подключается последовательно. При этом катушка давления подключена параллельно нагрузке. Кроме того, катушка тока измеряет ток, а катушка давления измеряет напряжение. Обе катушки используются в шкале ваттметров и для измерения тока или напряжения в линиях передачи напряжения.

Возбуждение катушки

Возбуждение катушки Плотность тока, протекающего в области катушки, вычисляется из сосредоточенной величины, которая составляет возбуждение катушки.Выбор этого количества может быть сделан путем установки параметра возбуждения катушки, при этом значение указывается в соответствующем текстовом поле. Все элементы катушки могут возбуждаться либо током, либо напряжением, либо, в некоторых случаях, силовым возбуждением. Предоставленное значение или выражение преобразуется в плотность тока или электрическое поле, приложенное к области в соответствии с используемой моделью катушки. Функции катушки также могут извлекать значение тока или напряжения из цепи, если для параметра возбуждения катушки установлено значение «Цепь (ток)» или «Цепь (напряжение)» соответственно.

Цепное (токовое) возбуждение работает аналогично токовому возбуждению, но в этом случае входы обеспечиваются схемным подключением. Возбуждение цепи (напряжения) работает аналогично возбуждению напряжением, но в этом случае входы обеспечиваются подключением цепи.

При указании полного тока Icoil катушка прикладывает внешнее электрическое поле в направлении потока тока, рассчитываемое как: (3-2) где L равно толщине физического интерфейса d для 2D-моделей, 2πr для 2D-аксиально-симметричных моделей и длине витка в 3D-моделях.V — неизвестный приложенный потенциал. Потенциал V решается с использованием дополнительного уравнения, которое ограничивает полный интегрированный ток равным заданному значению тока Icoil, действующему как регулятор. При указании общего тока Icoil катушка применяет внешнюю плотность тока в направлении проводов, как в уравнении 3-3, где N — количество заданных витков, а A — общая площадь поперечного сечения области катушки. (3–3) Когда активирован режим Coil Group, в модель добавляются дополнительные уравнения, чтобы обеспечить равенство тока, протекающего в каждом домене или группе доменов.При указании полного тока Icoil, внеплоскостная составляющая плотности тока определяется как: (3-4) где L равно толщине физического интерфейса d для 2D-моделей и 2πr для 2D-аксиально-симметричных моделей, а V — неизвестный приложенный потенциал. Потенциал V вычисляется с использованием дополнительного алгебраического уравнения, которое ограничивает полный интегрированный ток равным заданному значению тока Icoil. При указании общего напряжения Vcoil внешнее электрическое поле рассчитывается как: (3-5) где Vcoil — указанное приложенное напряжение, а L равно толщине физического интерфейса d для 2D-моделей, 2πr для 2D-осесимметричных моделей и длине катушки в 3D-моделях.При указании напряжения Vcoil составляющая плотности тока в направлении проводов определяется, как в уравнении 3-6 и уравнении 3-7. (3-6) где Vcoil — это заданное приложенное напряжение, A — общая площадь поперечного сечения области катушки, N — количество заданных витков, Rcoil — общее сопротивление катушки, рассчитанное как (3-7) где L равно толщине физического интерфейса d для 2D-моделей, 2πr для 2D-аксиально-симметричных моделей и длине катушки в 3D-моделях.Выражение σcoilacoil является произведением объемной проводимости проволоки и площади поперечного сечения проволоки. Vind — индуцированное напряжение, рассчитанное путем интегрирования электрического поля вдоль катушки. Когда активирован режим Coil Group, к модели добавляются дополнительные условия, чтобы ограничить сумму всех напряжений в доменах или группах доменов равными указанному напряжению: где Vcoil — определяемое пользователем падение напряжения на катушке, Vi — индивидуальные приложенные потенциалы, а N — количество витков в группе катушек.При указании общего напряжения Vcoil катушка применяет внешнюю плотность тока вне плоскости, рассчитываемую как: (3-8) где Vcoil — заданное приложенное напряжение, а L равно толщине физического интерфейса d для 2D-моделей и равно 2πr для 2D-моделей с осевой симметрией. В двухмерных и двухмерных осесимметричных моделях мощность является опцией, доступной для параметра возбуждения катушки. Когда выбрано Power, физический интерфейс устанавливает уравнение, как указано в разделе Current Excitation, плюс ограничение между током катушки и напряжением: на стационарных и зависящих от времени этапах исследования, и в частотной области (среднее за цикл).Выберите эту опцию, чтобы указать входную мощность для катушек. С этими настройками проблема становится нелинейной.

Параметр Power недоступен для 3D-моделей из-за большей сложности проблемы по сравнению с 2D-моделями.

Что такое токовый пробник с катушкой Роговского?

Что такое токовый пробник с поясом Роговского?

Если вы имеете дело с более чем парой десятков ампер переменного тока и хотите гибко измерять ток, рассмотрите токовый пробник Роговского.

Катушка Роговского — это электрический преобразователь, используемый для измерения токов переменного тока, таких как высокоскоростные переходные процессы, импульсные токи силового устройства или синусоидальные токи линии электропередачи с частотой 50 или 60 Гц. Катушка Роговского имеет гибкую обжимную сенсорную катушку, которую можно легко обернуть вокруг токоведущего проводника для измерения и может измерять до пары тысяч ампер очень больших токов без увеличения размера преобразователя.

Как работает пояс Роговского?

Теория работы за поясом Роговского основана на законе Фарадея, который гласит, что полная электродвижущая сила, индуцированная в замкнутой цепи, пропорциональна скорости изменения во времени общего магнитного потока, соединяющего цепь.

Катушка Роговского похожа на трансформатор переменного тока в том, что во вторичной катушке индуцируется напряжение, пропорциональное току, протекающему по изолированному проводнику. Ключевое отличие состоит в том, что пояс Роговского имеет воздушный сердечник, в отличие от трансформатора тока, который использует стальной сердечник с высокой магнитной проницаемостью для магнитной связи с вторичной обмоткой. Конструкция с воздушным сердечником имеет более низкое вводимое сопротивление, что обеспечивает более быструю реакцию на сигнал и очень линейное напряжение сигнала.

Катушка с воздушным сердечником размещается вокруг токоведущего проводника тороидальным образом, и магнитное поле, создаваемое переменным током, индуцирует в катушке напряжение. Катушка Роговского вырабатывает напряжение, которое пропорционально скорости изменения (производной) тока, заключенного в кольцевой катушке. Затем напряжение катушки интегрируется, чтобы зонд выдавал выходное напряжение, пропорциональное входному сигналу тока.

Преимущества

Пробники тока с катушкой Роговского

обладают множеством преимуществ по сравнению с различными типами преобразователей тока или измерительными методами.

• Измерение больших токов без насыщения сердечника — Катушки Роговского могут измерять большие токи (в очень широком диапазоне от нескольких мА до более чем нескольких сотен кА) без насыщения сердечника, поскольку в датчике используются немагнитные элементы. воздух »сердечник. Верхний диапазон измеряемого тока ограничен либо максимальным входным напряжением измерительного прибора, либо пределами пробоя напряжения катушки или элементов схемы интегратора. В отличие от других преобразователей тока, которые становятся более громоздкими и тяжелыми по мере увеличения диапазона измеряемого тока, пояс Роговского остается той же катушки небольшого размера независимо от амплитуды измеряемого тока.Это делает пояс Роговского наиболее эффективным измерительным инструментом для выполнения нескольких сотен или даже тысяч ампер больших измерений переменного тока.

• Очень гибкий в использовании — Легкая обжимная сенсорная катушка гибкая и легко наматывается на проводник с током. Его можно легко вставить в труднодоступные компоненты схемы. Большинство катушек Роговского достаточно тонкие, чтобы поместиться между ножками корпуса силовых полупроводников T0-220 или TO-247 без необходимости в дополнительной петле провода для подключения токового пробника.Это также дает преимущество в достижении измерения высокой целостности сигнала.
• Широкая полоса пропускания до> 30 МГц — Это позволяет катушке Роговского измерять очень быстро изменяющийся токовый сигнал — например, несколько тысяч А / мкс. Характеристика с высокой полосой пропускания позволяет анализировать гармоники высокого порядка в системах, работающих на высоких частотах переключения, или точно контролировать формы сигналов переключения с быстрым нарастанием или спадом.
• Не — Интрузивное измерение или измерение без потерь — Катушка Роговского потребляет очень малый ток от ИУ из-за низкого вводимого импеданса.Импеданс, вводимый в ИУ из-за пробника, составляет всего несколько пикогенри, что обеспечивает более быструю реакцию сигнала и очень линейное напряжение сигнала.
• Низкая стоимость По сравнению с датчиком Холла / пробником тока трансформатора, пояс Роговского обычно имеет более низкую цену.

Ограничения

• Только переменный ток — Роговски не может работать с постоянным током. Это только кондиционер.
• Чувствительность — Катушка Роговского имеет более низкую чувствительность по сравнению с трансформатором тока из-за отсутствия магнитопровода с высокой магнитной проницаемостью.

Приложения

Пробники тока с катушкой Роговского

находят широкое применение в различных отраслях энергетики и измерениях мощности. Ниже приведены некоторые примеры применения пояса Роговского:

• Гибкое измерение тока силовых устройств, таких как MOSFET или IGBT, размером с корпус TO-220 или TO-247 или вокруг клемм больших силовых модулей
• Для измерения потерь мощности в силовых полупроводниках
• Для контроля токов в малых индукторах, конденсаторах, демпфирующих цепях и т. Д.
• Для измерения небольшого переменного тока на проводе с высоким постоянным током или в присутствии сильного постоянного магнитного поля.
• Для измерения высокочастотных синусоидальных, импульсных или переходных токов от частоты сети до ВЧ приложений
• Для измерения тока в моторных приводах и, в частности, измерения качества электроэнергии в цепях VSD, UPS или SMPS
• Для оценки коммутационных характеристик силовых полупроводниковых ключей (тестер двойных импульсов).
• Мониторинг линии распределения электроэнергии или мониторинг полюсов электросети
• Приложения для умных сетей
• Измерение тока плазмы

Заключение

Существует ряд различных способов измерения электрического тока, каждый из которых имеет свои преимущества и недостатки.

Катушка Роговского похожа на трансформатор переменного тока в том, что во вторичной катушке индуцируется напряжение, пропорциональное току, протекающему по изолированному проводнику.Однако катушки Роговского способны измерять большие токи (очень широкий диапазон от нескольких мА до нескольких кА) без насыщения из-за своего немагнитного «воздушного» сердечника. Конструкция с воздушным сердечником также имеет более низкий вводимый импеданс, чтобы обеспечить более быструю реакцию сигнала и очень линейное напряжение сигнала, и она очень рентабельна по сравнению с аналогом датчика Холла / трансформатора тока. Это делает пояс Роговского наиболее эффективным измерительным инструментом для измерения больших величин переменного тока в несколько сотен или тысяч ампер.

Электромагнитные клапаны и клапаны высокого давления Clark Cooper

Часто задаваемые вопросы — Катушка и ток

Почему мой клапан Clark Cooper потребляет более высокий ток, чем указано в каталоге / на странице продукта?

Некоторые соленоиды переменного тока измеряются в ваттах, но на самом деле их номинальная мощность в ВА (вольт * ампер) намного выше. ВА — это мера «полной мощности» электрической цепи, которая равна произведению среднеквадратичного (RMS) напряжения и RMS-тока.Это значение следует использовать для определения размеров проводов и предохранителей. Например, номинальная мощность 47 ВА при использовании 120 В переменного тока будет иметь потребляемый ток 0,38 А.

«Реальная мощность» — это мощность в ваттах, которая выполняет работу или выделяет тепло. Это скорость потребления энергии.

В цепях постоянного тока реальная мощность равна указанным ваттам, произведению напряжения и силы тока.

Почему соленоид на моем клапане нагревается во время его использования?

Ожидается повышение температуры при включении соленоида.Например, изоляция класса «H» имеет допустимую температуру 320 ° F. Кроме того, начнется термическое разрушение изоляции провода.
Всегда соблюдайте осторожность при обращении с катушкой под напряжением.

Почему на моем клапане перегорела катушка?

Характеристики наших клапанов основаны на номинальной мощности «удержания», которая описывает потребляемую мощность после подачи питания на соленоид. Когда на соленоид переменного тока в первый раз подается питание, возникает «бросок» тока, который намного превышает нормальный «удерживающий» ток.Если внутренний компонент «застревает» по какой-либо причине, этот пусковой ток будет продолжаться дольше и может сжечь катушку. Это одна из причин, по которой Кларк Купер рекомендует использовать фильтры во всех клапанах, которые могут подвергаться воздействию любых твердых частиц.

Другими причинами возгорания могут быть приложение неправильного напряжения и превышение рабочего цикла для клапанов переменного тока. Более высокая частота циклов означает большее количество рывков и не позволяет адекватно отводить тепло.

Почему существует ограничение для включения катушки переменного тока и нет ограничения для катушек постоянного тока?

Катушка переменного тока ограничена определенным количеством циклов в единицу времени из-за тепловыделения пускового тока.По сути, мы ограничиваем количество рывков в единицу времени. Катушки постоянного тока не имеют этого броска, поэтому они могут иметь высокую тактовую частоту.

Есть ли минимальная температура окружающей среды для змеевиков?

Минимальная температура окружающей среды для змеевиков отсутствует. На самом деле их вредит тепло. Однако покупатель должен знать, что на самом деле больше тока потребляется при очень низких температурах из-за более низкого сопротивления провода.

Рекомендуемая максимальная температура окружающей среды составляет 150 ° F для катушек мощностью 10 Вт и 77 ° F для катушек мощностью 22 Вт.Это предполагает наличие очень горячей жидкости в клапане и частоте цикла. Допускаются более высокие температуры окружающей среды при более низкой температуре жидкости.

Внутренняя температура змеевика не должна превышать значений, указанных в таблице ниже.

Катушки

классифицируются по классам изоляции, которые соответствуют максимально допустимой температуре катушки. Максимально допустимая температура катушки — это температура, при которой катушка может быть подвергнута воздействию без термического разрушения изоляции магнитного провода.Эти классы и соответствующие максимальные уровни температуры:

Класс	Номинальная температура класса	Допустимая температура. методом изменения сопротивления (UL)	Темп. Повышение температуры выше 25 ° C (77 ° F).
А	105 ° С (221 ° F)	110 ° С (230 ° F)	85 ° С (153 ° F)
B	130 ° С (266 ° F)	120 ° С (248 ° F)	95 ° С (171 ° F)
F	155 ° С (311 ° F)	140 ° С (284 ° F)	115 ° С (207 ° F)
H	180 ° С (356 ° F)	160 ° С (320 ° F)	135 ° С (243 ° F)

Змеевики, соответствующие классам F и H, иногда называют «высокотемпературными змеевиками.«

Токовые пробники с поясом Роговского — IWATSU ELECTRIC CO., LTD.

Модель	Внешний вид, технические характеристики
SS-680 Серия		пиковый ток: 600A Максимальная частота: 100 МГц Максимальное напряжение: 1.2кВ Длина кабеля датчика: 1,5 м Рабочая темп. -10ºC ～ 70ºC
SS-660 Серия		пиковый ток: 600A Максимальная частота: 30 МГц Максимальное напряжение: 600 В Длина кабеля датчика: 1.5 мес. Рабочая темп. -40ºC ～ 125ºC
Примеры настройки	Тонкая катушка датчика Urtla, высокое выдерживаемое напряжение (1,2 кВ) Свяжитесь с нами для получения технических характеристик на заказ	Примеры настройки пиковый ток: 1.2кА Максимальная частота: 30 МГц Максимальное напряжение: 1,2 кВ Длина кабеля датчика: 1,5 м Рабочая темп. -40ºC ～ 125ºC
SS-280A-H Серия		пиковый ток: 12кА Максимальная частота: 30 МГц Максимальное напряжение: 1.2кВ Длина кабеля датчика: 1,5 м Рабочая темп. -40ºC ～ 150ºC
SS-280A Серия		пиковый ток: 12кА Максимальная частота: 30 МГц Максимальное напряжение: 1.2кВ Длина кабеля датчика: 1,5 м Рабочая темп. -40ºC ～ 125ºC
Серия SS-620S		пиковый ток: 12кА Максимальная частота: Длина катушки 100 мм Тип: 25 МГц Максимальное напряжение: 5 кВ Длина кабеля датчика: 3 м Рабочая темп.-40ºC ～ 125ºC
SS-620M Серия		пиковый ток: 12кА Максимальная частота: Длина катушки 200 мм Тип: 20 МГц Максимальное напряжение: 5 кВ Длина кабеля датчика: 3 м Рабочая темп.-40ºC ～ 125ºC
SS-290S Серия		пиковый ток: 12кА Максимальная частота: Длина катушки 300 мм Тип: 20 МГц Максимальное напряжение: 10кВ Длина кабеля датчика: 3 м Рабочая темп.-40ºC ～ 125ºC
SS-290L Серия		пиковый ток: 12кА Максимальная частота: Длина катушки 700 мм Тип: 10 МГц Максимальное напряжение: 10кВ Длина кабеля датчика: 3 м Рабочая темп.-40ºC ～ 125ºC

Руководство по проектированию схем для преобразователей постоянного / постоянного тока (4/10)

Выбор катушки

Оптимальное значение L изменяется в зависимости от частоты переключения, поскольку ток катушки пропорционален продолжительности активации полевого транзистора и обратно пропорционален значению L.

Потери в катушке складываются из сопротивления RDC катушки в проволочной обмотке и потерь, возникающих в ферритовом сердечнике.При частотах переключения до 2 МГц считается, что RDC катушки в основном отвечает за потери в катушке. Поэтому сначала выберите катушку с небольшим значением RDC. Однако, если минимизация RDC приводит к выбору слишком малого значения L, текущее значение, когда полевой транзистор активирован, становится слишком большим, увеличивая тепловые потери из полевого транзистора, SBD и катушки и снижая эффективность. Кроме того, пульсация становится больше из-за этого повышенного тока.

Напротив, если значение L слишком велико, значение RDC становится больше, что снижает эффективность во время большой нагрузки, и в ферритовом сердечнике возникает магнитное насыщение, быстро уменьшая значение L.В этом состоянии катушка не может нормально функционировать, и тепло, выделяемое перегрузкой по току, становится опасным. Следовательно, чтобы обеспечить протекание большого тока в катушке с большим значением L, необходимо до некоторой степени увеличить размеры катушки, чтобы избежать магнитного насыщения.

Исходя из вышеизложенного, соответствующее значение L для отдельной частоты переключения определяется с учетом как размеров, так и эффективности.

Таблица 5 показывает стандартные значения L для отдельных частот переключения.Это справочные данные для типичной схемы преобразователя постоянного тока в постоянный, где входное и выходное напряжения (V _IN и V _OUT ) составляют 6,0 В или меньше. Для цепей с более высоким напряжением рекомендуемые значения будут немного другими.

47 мкГн

Таблица 5: Стандартные значения L и номинальные значения тока для частот коммутации

Арт.	Состояние	Рекомендуемые значения
Значение L	Частота переключения	При взвешивании по времени малой нагрузки	Стандартное значение	При высокой нагрузке по времени
	30 кГц, 50 кГц	330 мкГн	220 мкГн	100 мкГн
	100 кГц	220 мкГн	100 мкГн	47 мкГн
	180 кГц	100 мкГн	47 мкГн
	22 мкГн	10 мкГн
	500 кГц	33 мкГн	15 мкГн	6.8 мкГн
	600 кГц	22 мкГн	10 мкГн	4,7 мкГн
	900 кГц	10 мкГн	4,7 мкГн	3,3 мкГн
	1,2 МГц	6,8 мкГн	3,3 мкГн
	2 МГц	3,3 мкГн	2,2 мкГн	1,5 мкГн
	3 МГц	2,2 мкГн	1,5 мкГн	1,0 мкГн
Номинальный ток	Цепь повышения	Прибл.В 2–3 раза больше макс. входной ток
	Понижающая цепь	Прибл. В 1,5–2 раза больше макс. выходной ток

На рисунке 12 показан пример изменения эффективности, соответственно, когда изменяется только значение L в цепи XC9104D093 (повышающей), показанной на рисунке 13.

На рисунках 14 и 15 показаны примеры эффективности и пульсации в схеме XC9220A093 (понижающей), показанной на рисунке 16.

В обоих примерах, если структура катушки идентична, увеличение значения L уменьшает максимальный выходной ток, увеличивает эффективность в условиях малой нагрузки и уменьшает пульсации.Этот результат показывает, что выбор значения L, оптимального для выходного тока, очень важен.

Рисунок 12: Взаимосвязь между значением L и КПД (повышение: XC9104D093)

Рисунок 13: Испытательная схема для XC9104D093, показанная на рисунках 12.

Рисунок 14: XC9220A093 Взаимосвязь между значением L и КПД (понижение)

L VLF10045T （L ： VLF10045T （22µH 33µH 、 47µH）

Рисунок 15: Взаимосвязь между значением L и пульсацией (понижение: XC9220A093)

L ： VLF10045T （22µH 、 33µH 47µH）
CL ： 22 мкФ 、 Tr ： 2SJ616

Рисунок 16: Рисунки 14 и 15 Схема, используемая для измерений, показанных в XC9220A093 (PWM = CE = V _IN )

Следующая страница

Выбор SBD с учетом теплопотерь

Назад к основам: Как работает катушка зажигания

16 февраля 2021 г. | Статья

.

Во всех системах зажигания современных бензиновых двигателей катушки зажигания используются для одной и той же основной функции: для создания высокого напряжения, необходимого для возникновения искры на свече зажигания.Профессионалы послепродажного обслуживания будут знакомы с их назначением и основными характеристиками, но они могут не знать о глубоких научных принципах, на которые они опираются. Здесь мы объясняем, как электромагнетизм лежит в основе важной роли катушки зажигания…

История катушек зажигания

Хотя системы зажигания, безусловно, эволюционировали с течением времени — в частности, включали в себя все больше и больше электроники — они все еще несут отличительные черты оригинальных катушечных систем зажигания, которые были представлены более 100 лет назад.

Первая катушечная система зажигания принадлежит американскому изобретателю Чарльзу Кеттерингу, который разработал катушечную систему зажигания для крупного производителя автомобилей примерно в 1910/1911 годах. Впервые он разработал электрическую систему, которая питала стартер и зажигание одновременно. Аккумулятор, генератор и более полная электрическая система автомобиля обеспечивали относительно стабильное электрическое питание катушки зажигания.

Система Кеттеринга (Рисунок 1) использовала одну катушку зажигания для создания высокого напряжения, которое передавалось на рычаг ротора, который эффективно направлял напряжение на серию электрических контактов, расположенных в узле распределителя (по одному контакту на каждый цилиндр). ).Эти контакты затем соединялись проводами свечей зажигания со свечами зажигания в такой последовательности, которая позволяла распределять высокое напряжение на свечи зажигания в правильном порядке зажигания цилиндров.

Рисунок 1: Основные компоненты системы зажигания Кеттеринга

Система зажигания Kettering стала практически единственным типом системы зажигания для массовых бензиновых автомобилей и оставалась таковой до тех пор, пока в 1970-х и 1980-х годах системы зажигания с электронным переключением и управлением не начали заменять механические системы зажигания.

Основной принцип катушки зажигания

Для создания необходимого высокого напряжения в катушках зажигания используются отношения, существующие между электричеством и магнетизмом.

Когда электрический ток течет через электрический проводник, такой как катушка с проволокой, он создает магнитное поле вокруг катушки (рис. 2). Магнитное поле (или, точнее, магнитный поток) фактически является хранилищем энергии, которая затем может быть преобразована обратно в электричество.

Рисунок 2: Создание магнитного поля путем пропускания электрического тока через катушку

При первоначальном включении электрического тока ток быстро увеличивается до максимального значения. Одновременно магнитное поле или магнитный поток будет постепенно расти до максимальной силы и станет стабильным, когда электрический ток станет стабильным. Когда электрический ток затем отключается, магнитное поле возвращается обратно в катушку с проволокой.

На силу магнитного поля влияют два основных фактора:

1) Увеличение тока, подаваемого на катушку с проволокой, усиливает магнитное поле

2) Чем больше витков в катушке, тем сильнее магнитное поле.

Использование изменяющегося магнитного поля для индукции электрического тока

Если катушка с проволокой подвергается воздействию магнитного поля, а затем магнитное поле изменяется (или перемещается), это создает электрический ток в катушке с проволокой.Этот процесс известен как «индуктивность».

Это можно продемонстрировать, просто перемещая постоянный магнит по катушке. Движение или изменение магнитного поля или магнитного потока индуцирует электрический ток в проводе катушки (Рисунок 3).

Рисунок 3: Изменяющееся или движущееся магнитное поле индуцирует электрический ток в катушке

Есть два основных фактора, которые влияют на то, сколько напряжения индуцируется в катушке:

1. Чем быстрее изменяется (или скорость движения) магнитного поля и чем больше изменение силы магнитного поля, тем больше индуцированное напряжение.
2. Чем больше количество витков в катушке, тем больше индуцированное напряжение.

Использование коллапсирующего магнитного поля для индукции электрического тока

Когда магнитное поле было создано путем приложения электрического тока к катушке с проволокой, любое изменение электрического тока (увеличение или уменьшение тока) вызывает такое же изменение магнитного поля. Если электрический ток выключен, магнитное поле схлопнется.Коллапсирующее магнитное поле индуцирует электрический ток в катушке (рис. 4). Рисунок 4: Если электрический ток, используемый для создания магнитного поля, отключен, магнитное поле схлопывается, что индуцирует другой электрический ток в катушке

.

Точно так же, как увеличение скорости движения магнитного поля по катушке с проволокой увеличивает напряжение, индуцированное в катушке, если коллапсирующее магнитное поле может сжиматься быстрее, это вызовет более высокое напряжение.Кроме того, в катушке может быть индуцировано более высокое напряжение, если количество обмоток в катушке увеличивается.

Взаимная индуктивность и действие трансформатора

Если две катушки провода размещены рядом или вокруг друг друга, и электрический ток используется для создания магнитного поля вокруг одной катушки (которую мы называем первичной обмоткой), магнитное поле также будет окружать вторую катушку (или вторичную обмотку). ). Когда электрический ток отключается, а затем магнитное поле схлопывается, оно индуцирует напряжение как в первичной, так и во вторичной обмотках.Это известно как «взаимная индуктивность» (рис. 5).

Рис. 5: Магнитное поле в первичной обмотке также окружает вторичную обмотку. Коллапс поля индуцирует электрические токи в обеих обмотках

Для катушек зажигания (и многих типов электрических трансформаторов) вторичная обмотка состоит из большего числа обмоток, чем первичная обмотка. Когда магнитное поле схлопывается, оно вызывает более высокое напряжение во вторичной обмотке, чем в первичной обмотке (Рисунок 6).

Рисунок 6: Здесь вторичная обмотка имеет больше катушек, чем первичная. Когда магнитное поле схлопывается, напряжение во вторичной обмотке будет больше, чем напряжение, индуцированное в первичной обмотке

Первичная обмотка катушки зажигания обычно содержит от 150 до 300 витков провода; вторичная обмотка обычно содержит от 15 000 до 30 000 витков провода, что примерно в 100 раз больше, чем первичная обмотка.

Магнитное поле изначально создается, когда электрическая система автомобиля подает примерно 12 вольт на первичную обмотку катушки зажигания.Когда в свече зажигания требуется искра, система зажигания отключает ток в первичной обмотке, что вызывает коллапс магнитного поля. Коллапсирующее магнитное поле вызовет в первичной обмотке напряжение порядка 200 вольт; но наведенное на вторичную обмотку напряжение будет примерно в 100 раз больше, около 20 000 вольт.

Используя эффекты взаимной индуктивности и вторичную обмотку, которая имеет в 100 раз больше обмоток, чем первичная обмотка, поэтому можно преобразовать исходное 12-вольтовое питание в очень высокое напряжение.Этот процесс преобразования низкого напряжения в высокое называется «действием трансформатора».

В катушке зажигания первичная и вторичная обмотки намотаны вокруг железного сердечника, который помогает концентрировать и усиливать магнитное поле и магнитный поток, тем самым делая катушку зажигания более эффективной.

DENSO является давним лидером в области технологий прямого зажигания, и катушки зажигания DENSO доступны на вторичном рынке. Узнайте больше о типах катушек зажигания DENSO и их преимуществах.

Вернуться к обзору .