В какой цепи можно получить резонанс токов: 2.15. Особые явления в цепях переменного тока

2.15. Особые явления в цепях переменного тока

Так как в цепях переменного тока существуют две разновидности реактивных элементов L и С, у которых различны формулы связи напряжения и тока: , то при работе в цепи таких элементов возможно появление резонансных явлений.

Первый вид резонанса – это резонанс напряжений.

Решим задачу:

Дано: u = U_m sin wt, L, C, r соединены последовательно (см. рис. 2.14).

Найти: комплекс тока ; составляющие мощностей: P, Q, S ?

Решение

Мгновенное напряжение переведем в комплексный вид:

.

Параметры нагрузок переведем в комплексный вид:

.

По закону Ома найдем ток:

.

По найденному току определим составляющие мощностей:

.

Суммарная реактивная мощность:

.

Полная или кажущаяся мощность:

.

Мощность в комплексной форме записи:

.

Если X_L – X_C = 0 , то цепь находится в режиме резонанса.

Условиями возникновения резонанса для цепи, содержащей последовательно соединенные LC – элементы является:

,

что соответствует выражению:

.

Если L и C элементы заданы, то можно найти резонансную частоту:

,

которая вводит цепь в резонанс, если же заданы C – элементы, то индуктивность, вводящая цепь в резонанс, равна:

.

Резонансные цепи с последовательно соединенными элементами находятся в состоянии резонанса тогда, когда длины векторов напряжений на

индуктивности и емкости равны:

.

Если угол сдвига между током и напряжением равна нулю (j = 0), то говорят, что цепь находится в режиме резонанса, то есть реактивная мощность равна:

Q =0 и Q_L = Q_C.

Внешний источник при резонансе будет работать, потребляя только активную мощность, не замечая наличия Q_L и Q_C. Такой режим называют более эффективным с точки зрения силовой электротехники.

Параметры резонансных цепей:

индуктивное сопротивление:

.

Его называют волновым сопротивлением индуктивности;

емкостное сопротивление при резонансе:

;

волновое сопротивление:

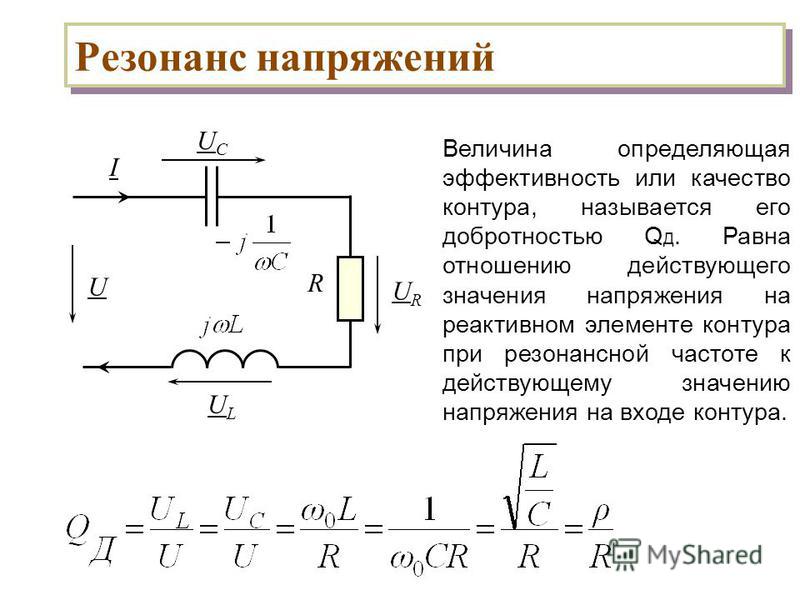
дает основание для определения добротности контура: (добротность – безразмерная величина). Обратную величину добротности называют затуханием: .

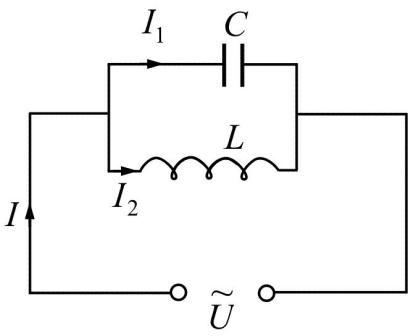
Решим следующую задачу. Пусть те же элементы соединены параллельно (рис. 2.21)

Ток источника равен:

.

Комплексная проводимость имеет вид:

,

где

y – комплексная проводимость; q – активная проводимость; b – мнимая или реактивная проводимость.

Если b_C – b_L = 0 , то цепь находится в режиме резонанса токов, то есть модули токов индуктивности и емкости равны: I_L = I_C.

Условием резонанса будет следующее соотношение:

.

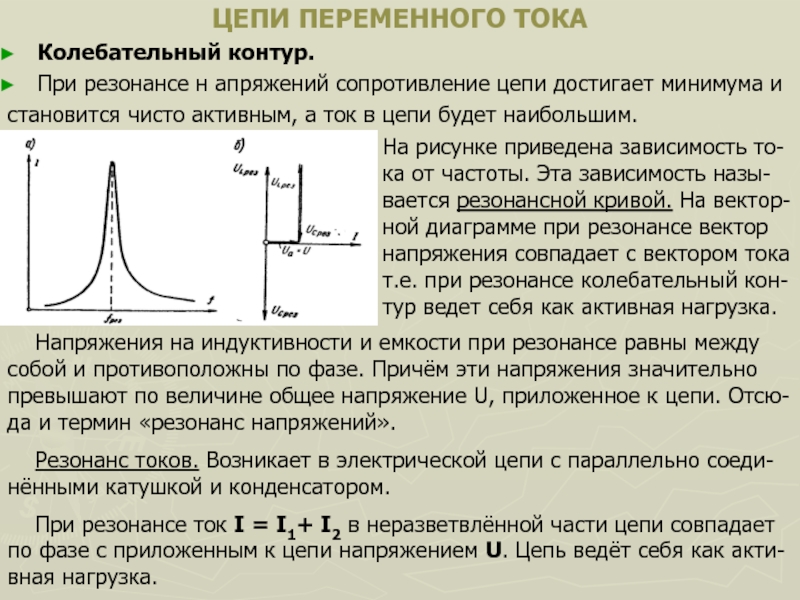
Резонанс в электрической цепи

Начнём с основных определений.

Определение 1

Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.

Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.

Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.

Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.

Одними из наиболее полезных видов резонанса в электрической цепи являются:

• резонанс токов;
• резонанс напряжений.

Возникновение резонанса в электрической цепи

Замечание 1

Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.

Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.

Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:

• емкостной;
• активной;
• индуктивной.

В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.

Резонанс напряжений

При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.

Резонанс напряжений обычно достигается тремя способами:

• подбором индуктивности катушки;
• подбором емкости конденсатора;
• подбором угловой частоты $w_0$.
  2L}$

  Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:

  $\frac{U}{r}$

  Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.

  Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:

  $Q = \frac{U_c0}{U}$

  Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.

  Резонанс токов через реактивные элементы

  Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. 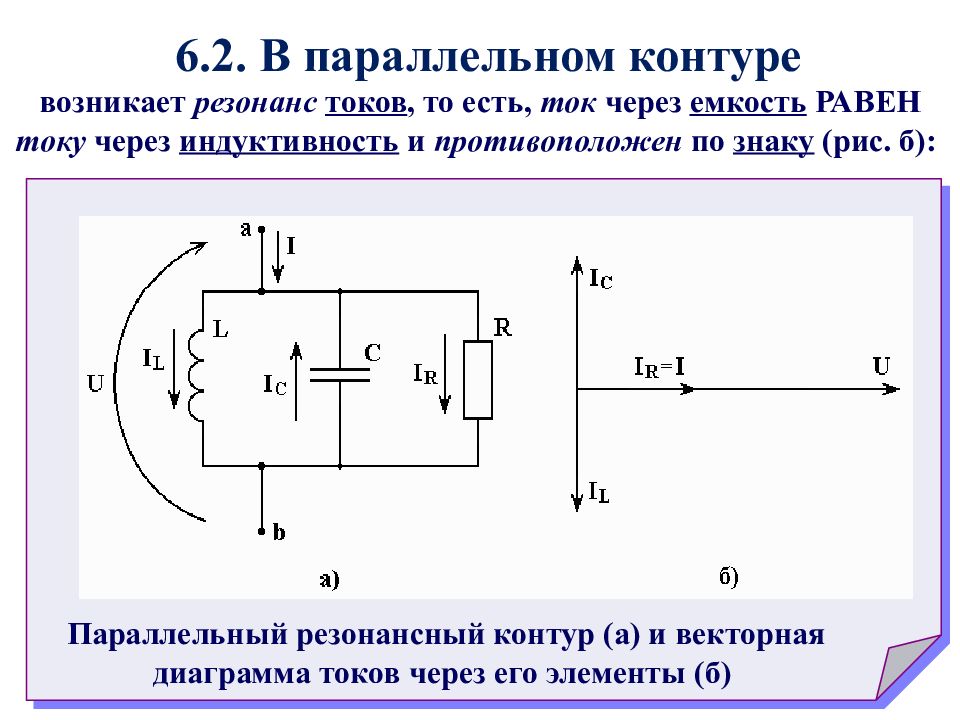В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.

  Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.

  Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.

  Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.

  Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.

  Применение явления резонанса

  Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.

  Замечание 2

  Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.

  Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.

  VI.3. Резонанс в электрических цепях

   

  Резонансом в электрической цепи называется режим участка, содержащего индуктивный и емкостный элементы, при котором угол сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.

  Различают несколько видов резонанса: резонанс напряжений (при
  последовательном соединении элементов), резонанс токов (при параллельном соединении элементов), резонанс в магнитно-связанных цепях и др.

  Резонанс напряжений. Из выражения (6.10) следует, что при последовательном соединении ток в цепи приобретает максимальное значение при , то есть при Этому условию удовлетворяет частота

  (6.15)

  В этом случае , Z = R → min, падения напря-жения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе (рис. 6.15). Таким образом, при резонансе напря-жений

  ,

  и

  (6.16)

  где Q – добротность контура. Так как добротность колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе превышает напряжение U, приложенное к цепи. Из выражения (6.16) следует, что добротность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине
  входного напряжения.

  Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.

  Резонанс токов возможен в цепи с параллельным соединением ветвей
  с параметрами и (рис. 6.16). Между током в неразветвленной части цепи и напряжением имеется некоторый сдвиг фаз . Предположим, что цепь имеет емкостный характер, то есть колебания тока опережают по фазе колебания напряжения. Тогда векторная диаграмма будет иметь вид, приведенный на рис. 6.17.

  Разложим вектор тока на две составляющие: активную , находящуюся в фазе с вектором напряжения на зажимах цепи, и реактивную , перпендикулярную к . Из векторной диаграммы следует

  (6.17)

  Так как

  и

  то, подставляя эти выражения в (6.17), получим

  (6.18)

  (6.19)

  где g и b – активная и реактивная проводимости цепи.

  Найдем соотношение между активной g, реактивной b и полной Y проводимостью цепи. Из векторной диаграммы следует, что модуль действующего значения тока в неразветвленной части цепи равен

  (6.20)

  Так как полная проводимость Y равна обратной величине полного
  сопротивления, то из (6.18) и (6.19) следует

  (6.21)

  В режиме резонанса . Для этого реактивная составляющая тока , а, следовательно, и реактивная проводимость b цепи должны равняться
  нулю. Для схемы на рис. 6.16 общая реактивная проводимость цепи равна сумме реактивных проводимостей и параллельных ветвей. При
  резонансе

  (6.22)

  где

  Тогда условие (6.22) примет вид

  (6.23)

  где – циклическая частота резонанса токов.

  Из (6.23) после преобразования имеем

  (6.24)

  где – характеристическое сопротивление контура.

  Анализ выражения (6. 24) позволяет сделать ряд выводов:

  1. Резонансная частота при резонансе токов зависит не только от
  параметров реактивных элементов, но и от активных сопротивлений и .

  2. Резонанс токов возможен, если сопротивления и или больше , или меньше (в этом случае подкоренное выражение в (6.24) положительное), в противном случае – невозможен ( – мнимая величина).

  3. При и , что справедливо для многих цепей, то есть резонансная частота при резонансе токов равна
  резонансной частоте при резонансе напряжений.

  Рассмотрим контур с малыми омическими потерями в режиме резонанса токов.

  1. Так как и общее сопротивление контура активное, то полная проводимость контура равна активной проводимости и минимальна:

   

   

  2. Ток в неразветвленной части цепи

  минимальный, что позволяет по показаниям амперметра обнаруживать
  резонанс токов в контуре при изменении частоты , параметров L или C.

   

  3. Активные и реактивные составляющие токов

  Так как , то реактивные составляющие токов при резонансе равны
  и находятся в противофазе

  Векторная диаграмма цепи при резонансе токов приведена на рис. 6.18.

  Ток в общей части цепи равен активной составляющей тока

  Токи в ветвях

   

  Если то есть
  и то
  и то есть токи в ветвях значительно превышают по величине ток в неразветвленной части цепи. Это свойство – усиление тока – является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и название этого явления.

   

   

  
  
  

  Читайте также:

   

  Резонансы напряжений и токов. — Студопедия

  Цель работы: исследование резонансных явлений электрических цепях переменного тока при последовательном и параллельном соединениях катушки индуктивности и конденсатора.

  Из элементов (катушек, индуктивности и конденсаторов), иссле­дованных в лабораторных работах №1 и №2, можно составить:

  а) последовательную электрическую цепь (рис.5..I,а), в которой наблюдается резонанс напряжений;

  б) параллельную электрическую цепь (рис.5.1,6), в которой
  наблюдается резонанс токов.

  Рис.5.1. Схемы электрических цепей: а — последовательная; б — параллельная

  XLЭ = Xсэ ,                                 (5.1)

  Условие

  при котором в последовательной схеме на рис.5.1,а достигается резонанс напряжений, и условие

  вLЭ = вСЭ                                                                       (5.2.)

  при котором впараллельной схеме на рис.5.1,6 достигается резонанс токов, могут быть обеспечены за счет использования группы

  из нескольких конденсаторов с общей (эквивалентной) ёмкостью С_э и (или) за счет использования группы из нескольких катушек ин­дуктивности с общей (эквивалентной) индуктивностью L_э.

  
  

  На лабораторном стенде, помимо конденсаторов с емкостями,
  указанными в табл.1.4, имеются еще два точно таких же конденса­тора. Для достижения требуемой величины С_э допускается любое
  (последовательное, параллельное, смешанное) соединение конденса­торов в группе.                                          

  При последовательном соединении m конденсаторов

  
  

   

  при параллельном соединении m конденсаторов

  
  

   

  По величине С_э определяется эквивалентное емкостное сопротивление ХСЭ

  
  

   

  и эквивалентная емкостная проводимость в_сэ

  _{всэ =ωсэ}

  Для обеспечения требуемой величины L_Э в стенде предусмотрены три одинаковые катушки индуктивности. Параметры одной
  из катушек индуктивности (индуктивность, L и сопротивление
  R_K) указаны в табл. 1.4. Катушка имеет сравнительно малую величину индуктивности L , поэтому требуемая для наблюдения резонансных явлений величина L_э может быть получена при последовательном соединении двух или даже трех катушек.

  При последовательном включении m катушек

  
  

  и эквивалентные индуктивная ωLЭ и активная τКЭ проводимости

  По величинам Lэ и R_Kэ определяется эквивалентные индук­тивное х_LЭ и активное τ_КЭсопротивления:

  
  

  группы последовательно соединенных катушек индуктивности.

  Полученные эквивалентные реактивные (емкостные и индуктив­ные) сопротивления Х_сэ и Х_LЭ и проводимости  в_сэ и в_LЭ указаны на рис. 5.1 и входят в условия резонансов (5.1) и (5.2).

  Таким, образом, для реализации в схеме на рис.5.1,а условия резонанса напряжений (5.1) подбирается группа конденсаторов и соответствующая ей (по величине реактивного сопротивления) группа катушек индуктивности. Аналогично, для реализации в схеме на рис.5.1,6 условия резонанса токов. (5.2) подбираются соответствующие друг другу (по величине реактивной проводимости) группа конденсаторов и группа катушек индуктивности.

  Реализация условий (5.1) и (5.2) допускается с погрешнос­тью до 10%.

  а для параллельной схемы (рис.5.1,6)

  При подборе группы катушек индуктивности для последова­тельной схемы (рис.5.1,а) должно выполняться условие (5.3.)

  (5.4.)

  На рис.5.2 даны примеры (отличные от реально получающихся в данной лабораторной работе) электрических цепей, в которых за счет подбора, групп конденсаторов и катушек индуктивности реализованы условия резонансов (5. 1) и (5.2). Здесь же показано включение измерительных приборов, с помощью которых контроли­руется достижение резонансов в рассматриваемых цепях.

   

   

  Рис.5.2. Примеры электрических цепей, в которых могут наблюдаться резонанс напряжений (а) и резонанс токов (б)                                                                 

  Расчетное задание

  I. Резонанс напряжений. Для последовательной электрической цепи, составленной из групп конденсаторов и катушек индуктивности, удовлетворяющих условиям (5.1) и (5.3), определить:

  1) действующее значение I тока ί в последовательной цепи;               

  2) активную мощность Р, потребляемую цепью;

  3) коэффициент мощности цепи соs φ ;

  4) действующие значения U₁и U₂ напряжений u1 и u2 на группе конденсаторов и группе катушек индуктивности соответственно;

   

  5) построить векторную диаграмму, включающую векторы (комплексы) напряжений на входе цепи (Uвх), на группе конденсаторов (U1) и на группе катушек (U2) и тока врассматриваемой последовательной цепи (I)

  По результатам расчета заполняется графа «Расчет» в Taб. 5.1

  Таблица 5.1.

  	Uвх , В	I, A	P, Вт	Cos φ	U1,B	U2 ,B
  Расчет
  Эксперимент
  Погрешность

   

  2. Резонанс токов. Для параллельной электрической цепи, составленной из групп конденсаторов и катушек индуктивности, удовлетворяющих условиям (5.2) и (5.4), определить:

  1) действующее значение I₀тока ί₀ в неразветвленной части цепи;

  2) активную мощность Р , потребляемую цепью;

  3) коэффициент мощности цепи Cos φ;

  4) действующие значения I₁ и I₂ токов ί₁ и ί₂ группы конденсаторов и группы катушек соответственно;

  5) построить векторную диаграмму, включающую в себя век­торы (комплексы) входного тока цепи ( I₀ ), группы конденсато­ров (I₁ ), группы катушек ( I₂ ) и входного напряжения ( U_вх ).

  По результатам расчета заполняется графа «Расчет» в табл. 5.2.

  Таблица 5.2.

  Резонанс токов.

   

  	Uвх , В	I0, A	P, Вт	Cos φ	I1,B	I2 ,B
  Расчет
  Эксперимент
  Погрешность

   

  При выборе параметров конденсаторов и катушек (из табл. 1.4) и величины действующего значения U_вх входного напряжения следует принимать во внимание ограничения (3. 1).

  Эксперимент

  Резонанс напряжений

  На лабораторном стенде собирается последовательная элект­рическая цепь, схема которой была составлена согласно расчетно­му заданию. Катушка индуктивности и конденсатору, входящие в схему, должны иметь параметры, принятые при расчете схемы. В цепь включаются амперметр А и ваттметр W (см.рис.5.2,а). На вход цепи подается напряжение U_вх, действующее значение кото­рого устанавливается равным его расчетной величине.

  Результаты измерений заносятся в табл.5.1 в граф «Эксперимент».

  Величина коэффициента мощности Cos φ определяется по результатам измерений активной мощности Р , действующего значения U_вх входного напряжения и действующего значения I тока в цепи.

  Расхождение экспериментальных и расчетных данных оцениваются по формуле (2.1) и заносятся в графу «Погрешность» в табл.
  5.1.

  Резонанс токов

   На лабораторном стенде собирается параллельная электричес­кая цепь, схема которой была составлена согласно расчетному за­данию. Параметры всех элементов схемы и величина действующего значения U_вх входного напряжения должны быть равны соответ­ствующим значениям, принятым при расчете схемы. В цепь включа­ются амперметры А₀ , А₁, А₂ и ваттметр W (см. рис.5.2,б).

  Результаты измерений заносятся в табл. 5.2 в графу «Эксперимент».

  Величина коэффициента мощности Cos φ определяется по результатам измерений величин Р , U_вх и I₀ (так же, как и при резонансе напряжений).

  Расхождения экспериментальных и расчетных данных оценива­ются по формуле (2.1) и заносятся в графу «Погрешность» в табл. 5.2.

   

  Контрольные вопросы

  1. Каковы основные причины имеющих место в данной лабора­торной работе расхождений расчетных и экспериментальных данных?

  2. Каковы основные проявления резонанса напряжений?

  3. Каковы основные проявления резонанса токов?

  4. Изменением, каких параметров электрической цепи можно обеспечить в ней режим резонанса напряжений (или резонанса токов)?

  5. В чем состоит аналогия между резонансами в электрических цепях и в механических системах?

  6. Для исследованной последовательной электрической цепи построить графики зависимостей:

  а) действующего значения входного тока от частоты входного
  напряжения;                                                                                                      

  б) действующего значения напряжения на группе конденсато­ров от частоты входного напряжения;

  в) действующего значения напряжения на группе катушек индуктивности от частоты входного напряжения.

  На графиках отметить точки, отвечающие резонансу напряжений.

  7. Для исследованной параллельной электрической цепи по-
  строить графики зависимостей:

  а) действующего значения входного тока от частоты входного
  напряжения;

  б) действующего значения тока группы конденсаторов от частоты входного напряжения;

  в) действующего значения тока группы катушек индуктивности
  от частоты входного напряжения.

  На графиках отметить точки, отвечающие резонансу токов.

  8.Дать примеры практического использования резонансных явлений в электрических цепях.

  9.Каково влияние на исследованные резонансные явления ве­личины сопротивления R_K катушки индуктивности?
            Лабораторная работа № 6

  Трехфазные цепи

  Цель работы: приобретение навыков экспериментальных иссле­дований нормальных и аварийных режимов трехфазных цепей при различных способах соединения фаз приемников (звезда и треугольник) и различных нагрузках (симметричной и несимметричной).

  Расчетное задание

  Рассчитываются нормальные и аварийные режимы трехфазных цепей, трехфазная нагрузка которых составлена из элементов, изученных в лабораторных работах №1 и №2. Каждая фаза трехфазной нагрузки состоит в общем случае из набора следующих эле­ментов: резистора, катушки индуктивности и конденсатора.

  В табл. 6.1 для каждого из вариантов расчетного задания
  указаны следующие данные:                                                                          

  1. Схема соединения фаз приемника:

  Y – звезда без нулевого провода;

  Y0 — звезда с нулевым провода;

  Δ – треугольник.

  2. Положения переключателей элементов для каждой фазы. Прочерк в таблице свидетельствует об отсутствии данного элемента. В случае аварийного режима указывается “обрыв” или “короткое замыкание” рассматриваемой фазы.

   

   

  а) Соединение фаз нагрузки в звезду.

  б) Соединение фаз нагрузки в треугольник.

   

  Таблица 6.1.

  Данные по расчетному заданию.

  № Варианта	Схема Соединения фаз	Положение переключателей фаз
  		Фаза А			Фаза В			Фаза С
  		Резистор	Катушка индуктивности	Конденсатор	Резистор	Катушка индуктивности	Конденсатор	Резистор	Катушка индуктивности	Конденсатор
  1	2	3	4	5	6	7	8	9	10	11
  1	Y	-	3	1	-	3	1	-	3	1
  	Y0	ОБРЫВ			-	3	1	-	3	1
  	Δ	3	-	3	-	3	1	-	3	1
  2	Y	-	3	2	-	3	2	-	3	2
  	Y0	ОБРЫВ			-	3	2	-	3	2
  	Δ	-	3	2	-	-	2	-	-	2
  3	Y	-	3	3	-	3	3	-	3	3
  	Y0	КОРОТКОЕ ЗАМЫКАНИЕ			-	3	3	-	3	3
  	Δ	-	3	3	-	3	3	-	3	3
  4	Y	2	2	-	2	2	-	2	2	-
  	Y0	2	2	-	ОБРЫВ			2	2	-
  	Δ	2	2	-	ОБРЫВ			2	2	-
  5	Y	2	2	2	2	2	2	2	2	2
  	Y0	2	2	2	ОБРЫВ			2	2	2
  	Δ	2	-	-	2	2	-	2	-	-
  6	Y	2	3	-	2	3	-	2	3	-
  	Y0	2	3	-	Короткое замыкание			2	3	-
  	Δ	2	-	-	2	3	-	2	3	-
  1	2	3	4	5	6	7	8	9	10	11
  7	Y	2	2	1	2	2	1	2	2	1
  	Y0	2	2	1	2	2	1	ОБРЫВ
  	Δ	2	2	-	2	-	-	-	-	3
  8	Y	3	2	2	3	2	2	3	2	2
  	Y0	3	2	2	-	2	2	3	2	2
  	Δ	2	-	-	2	2	-	2	2	2
  9	Y	3	2	3	3	2	3	3	2	3
  	Y0	3	2	3	3	2	3	Короткое замыкание
  	Δ	3	2	3	-	3	-	3	2	-
  10	Y	3	-	3	3	-	3	3	-	3
  	Y0	ОБРЫВ			3	-	3	3	-	3
  	Δ	1	1	-	3	-	3	3	-	3
  11	Y	1	1	2	1	1	2	1	1	2
  	Y0	ОБРЫВ			1	1	2	1	1	-
  	Δ	1	-	2	-	-	2	1	-	2
  12	Y	1	3	3	1	3	3	1	3	3
  	Y0	Короткое замыкание			1	3	3	-	3	-
  	Δ	1	3	3	1	3	3	-	3	-
  13	Y	-	2	1	-	2	1	-	2	1
  	Y0	-	2	1	ОБРЫВ			-	2	1
  	Δ	-	2	1	2	1	-	3	-	-
  14	Y	-	2	2	-	2	2	-	2	2
  	Y0	-	2	2	ОБРЫВ			-	2	2
  	Δ	-	-	2	-	2	2	-	-	2
  15	Y	1	2	3	1	2	3	1	2	3
  	Y0	1	2	3	Короткое замыкание			1	2	3
  	Δ	1	2	3	-	2	3	-	-	3
  1	2	3	4	5	6	7	8	9	10	11
  16	Y	3	2	1	3	2	1	3	2	1
  	Y0	Короткое замыкание			3	2	1	3	2	1
  	Δ	3	2	1	3	-	-	3	-	-
  17	Y	3	2	-	3	2	-	3	2	-
  	Y0	3	2	1	1	2	3	1	-	3
  	Δ	3	-	2	3	-	2	-	3	-
  18	Y	3	3	3	3	3	3	3	3	3
  	Y0	3	3	3	3	3	3	Короткое замыкание
  	Δ	3	3	3	3	3	-	-	3	3
  19	Y	2	2	2	2	2	2	2	2	2
  	Y0	ОБРЫВ			2	2	2	2	2	2
  	Δ	-	2	2	2	-	2	2	2	-
  20	Y	1	-	3	1	-	3	1	-	3
  	Y0	1	3	-	1	3	-	1	-	3
  	Δ	1	-	3	3	-	1	-	3	1
  21	Y	3	-	1	3	-	1	3	-	1
  	Y0	3	-	1	ОБРЫВ			3	-	1
  	Δ	3	-	1	3	1	-	-	3	1
  22	Y	3	1	-	3	1	-	3	1	-
  	Y0	Короткое замыкание			3	1	-	-	1	3
  	Δ	3	1	-	1	3	-	-	3	-
  23	Y	1	-	3	1	-	3	1	-	3
  	Y0	-	3	-	3	-	-	-	-	3
  	Δ	1	-	3	1	-	3	-	3	-
  24	Y	-	2	3	-	2	3	-	2	3
  	Y0	-	2	3	-	2	3	ОБРЫВ
  	Δ	2	3	-	-	2	3	-	3	-

   

  Для каждой из заданных трех схем необходимо:

  1. Начертить схему соединения фаз приемника с указанием мест включения приборов для определения линейных и фазных токов и напряжений. 

  2. Вычислить, действующие значения фазных и линейных токов и напряжений в каждой из фаз и построить векторную диаграмму токов и напряжений.

  3. Рассчитать полную, активную и реактивную мощности трех­фазной цепи.

  Необходимой для расчетов, величиной действующего значения линейного напряжения источника следует задаться (с учетом ре­альных возможностей лабораторного стенда, отмеченных в Прило­жении). При выборе величины линейного напряжения источника сле­дует также учитывать условия (3.1).

  Результаты расчетов заносятся в графы «Расчет» таблицы 6.2 и 6.3.

   

  Эксперимент

  На лабораторном стенде собираются схемы, которые были рассчитаны в соответствии с расчетным заданием. Резисторы, ка­тушки индуктивности и конденсаторы, включенные в схемы, должны иметь параметры, которые были приняты при расчете, т. е. пере­ключатели элементов должны быть поставлены всоответствующие положения. Переключатель трехфазного источника должен находить­ся в положении, при котором обеспечивается принятое в расчете значение линейного напряжения.  

  По результатам измерений заполняются графы «Эксперимент» таблиц 6.2 и 6.3.

  Расхождения экспериментальных и расчетных данных оценива­ются по формуле (2.1) и заносятся в графы «Погрешность» таблиц
  6.2 и 6.3.                       

              Таблица 6.2.

  Результаты исследования трехфазной цепи, соединенной звездой.

   

  Режим работы

  Напряжение, В

  Токи, А

  Мощность

  линейные

  фазные

  Линейные

  P

  Q

  S

  Uав

  Uвс

  Uса

  Uа

  Uв

  Uс

  Iа

  Iв

  Iс

  Вт

  ВАр

  ВА

  Сим- метрич- ный

  Расчет

  Опыт

  Погрешность

  Несим- метрич- ный

  Расчет

  Опыт

  Погрешность

  Таблица 6. 3.

  Результаты исследования трехфазной цепи, соединенной треугольником.

  Напряжение, В

  Токи, А

  Мощность

  Линейные

  Линейные

  Фазные

  P

  Q

  S

  Uав

  Uвс

  Uса

  Iа

  Iв

  Iс

  Iав

  Iвс

  Iса

  Вт

  ВАр

  ВА

  Расчет

  Эксперимент

  Погрешность

   

  Контрольные вопросы                               

  1. Каковы основные причины имевших место в данной лабораторной работе расхождений расчетных и экспериментальных данных?

  2. Какое соединение фаз трехфазной цепи называется звездой? треугольником?

  3. В каком случае применяют соединение фаз звездой без ну­левого провода?

  4. При какой нагрузке фаз применяют четырех проводную сис­тему и почему?

  5. Будут ли отличаться величины линейных токов при включе­нном и отключенном нулевом проводе, если сопротивления фаз: равны по модулю? равны по фазе? равны по модулю и фазе?

  6. Почему в нулевом проводе не устанавливают предохранитель?

  Как будут отличаться полная, активная и реактивная мощ­ности, потребляемые одним и тем же симметричным трехфазным при­емником при соединении его фаз в первом случае — звездой, во втором — треугольником?

  8. Как будут отличаться линейные токи симметричного трех­фазного приемника при соединении его фаз в первом случае — звездой, во втором — треугольником?

  9. При какой нагрузке и почему для определения токов и на­пряжений во всех фазах достаточно определить токи и напряжения
  в одной фазе?

  10. Какие преимущества трехфазного тока перед однофазным?

  11. Перечислите методы измерения мощности в трехфазной цепи.

  12. Какая нагрузка трехфазной цепи называется симметрич­ной?

  13. Как изменятся токи в фазах симметричного приемника, соединенного звездой, при обрыве линейного провода А?

  14. Когда справедливо соотношение U_л / U_ф =√3 ?

  15. Когда справедливо соотношение I_л / I_ф =√3?

  16. Когда для расчета мощности трехфазной цепи можно ис­пользовать формулу Р = √3 U I соsφ?

  Извините такой страницы Wp-content Uploads 2014 03 Rezonans-na-ladoni Pdf не существует!

  Выбор статьи по меткам03 (1)5 марта 2020 (1)5 мая Статград (2)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 декабря 2020 (1)14 ноября (2)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)16 профильного ЕГЭ (1)16 января Статград (2)17 задача ЕГЭ (1)18 (С5) (2)18 задача ЕГЭ (2)18 мая 2020 физика (1)23 марта (1)25 сентября 2020 (1)31 января (1)2016 (2)140319 (1)14032019 (1)C5 (1)RC-цепь (1)RLC-контур (1)А9 (1)Александрова (2)Ампера (2)Архимед (2)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (2)ГИА физика задания 5 (1)Герона (2)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Деление отрезка (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (26)ЕГЭ по физике (49)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (7)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (9)Каллисто (1)Кельвин (1)Кирхгоф (1)Кирхгофа (1)Койпера (1)Колебания (1)Коши (1)Коэффициенты поверхностного натяжения жидкостей (1)Кулона-Амонтона (1)Ломоносов (2)Лоренца (1)Луна (1)МГУ (1)МКТ (7)МФТИ олимпиада (1)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (3)Менелая (5)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)Нансен (1)НеИСО (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (14)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Плюк (1)Погсона (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Расстояние между скрещивающимися (2)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Савченко (1)Сиена (1)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (2)СпБ ГУ вступительный (1)Средняя кинетическая энергия молекул (1)Статград 14 декабря (1)Статград физика (6)Таблица Менделеева (1)Текстовые задачи (8)Тьерри Даксу (1)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Фобос (1)Френеля (1)Цельсий (1)ЭДС (6)ЭДС индукции (2)Эйлера (1)Электрохимические эквиваленты (1)Эрастофен (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (3)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (2)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)аннуитет (2)апериодический переходной процесс (2)апофема (1)аргумент (1)арифметическая прогрессия (5)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (3)асинхронный (1)атмосферное (2)атмосферном (1)атомная масса (2)афелий (2)афелийное (1)база (1)балка (1)банк (1)без калькулятора (1)без отрыва (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (4)биссектрисы (2)благоприятный исход (1)блеск (4)блеск компонентов (1)блок (2)блоки (3)боковой поверхности (1)большая полуось (1)большем давлении (1)бревно (2)бригада (2)бросили вертикально (1)бросили под углом (3)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)бруски (1)брусок (4)брусок распилили (1)бусинка (1)быстрый способ извлечения (1)ван-обеля (1)вариант (3)вариант ЕГЭ (12)вариант ЕГЭ по физике (18)вариант по физике (1)варианты ЕГЭ (6)вариент по физике (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (3)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)весов (1)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видеоразбор (2)видеоразбор варианта (1)видимая звездная величина (3)виртуальная работа (1)виртуальный банк (1)виртуальных перемещений (1)витка (1)витков (1)виток (1)вклад (2)влажность (3)влажность воздуха (1)влетает (2)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (8)вода (1)вода течет (1)воды (1)возведение в квадрат (1)возвратное уравнение (1)возвратность (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная (1)вписанная окружность (3)вписанная сфера (1)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращается (1)вращение (1)времени (2)время (24)время в минутах (1)время выполнения (1)время движения (2)время минимально (1)время падения (1)все значения а (1)всесибирская олимпиада (1)в стоячей воде (1)встретились (1)встретятся (1)вступительный (1)вступительный экзамен (1)вторая половина пути (1)вторая экваториальная система координат (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон (1)второй закон Кеплера (1)второй закон Ньютона (4)выбор двигателя (1)выборка корней (4)вывод формул тригонометрии (1)выколотая точка (1)выплаты (2)выразить вектор (1)высота (5)высота Солнца (1)высота столба (1)высота столба жидкости (1)высота столбика (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (2)газ (3)газа (1)газов (1)газовая атмосфера (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (4)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (7)гигрометр (1)гидродинамика (1)гидростатика (3)гимназия при ВШЭ (1)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)гонщик (1)горизонтальная сила (1)горизонтальной спицы (1)горизонтальную силу (1)горка (1)гравитационная постоянная (1)градус (1)грани (2)график (2)графики функций (5)графически (1)графический способ (1)графическое решение (3)гроб 2018 (1)груз (2)грузик (2)грузовик (1)грузы (1)группа (1)давление (28)давление жидкости (3)давление пара (1)дальность полета (1)две линзы (1)двигатель с активным ротором (1)движение под углом (2)движение под углом к горизонту (4)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)движется груз (1)двойное неравенство (1)двойной фокус (1)двойным неравенством (1)двугранный угол при вершине (2)девальвация (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (23)делимость чисел (1)делители (1)делитель (2)делится (3)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)диаметру (1)динамика (4)диод (1)диск (2)дискриминант (5)дифракционная решетка (2)дифференцированный платеж (7)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (4)длина вектора (1)длина волны (7)длина медианы (1)длина отрезка (2)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длины поездов (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)долг (1)долг остается равным (1)доля (1)дополнительный угол (2)досок (1)досрочный (2)досрочный вариант (1)дптр (2)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единмтвенное решение (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)желоб (2)жесткость (6)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 4 ЕГЭ (2)задача 9 (1)задача 13 ЕГЭ (1)задача 13 профиль (1)задача 14 профиль (3)задача 15 профиль (1)задача 16 (1)задача 16 ЕГЭ (1)задача 16 профиль (4)задача 17 (1)задача 18 (1)задача 19 (2)задача 26 ОГЭ (2)задача с параметром (7)задачи (1)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задачи с фантазией (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Бернулли (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закон Стефана-Больцмана (1)закона сохранения (1)закон движения (1)закон кулона (7)закон палочки (6)закон сложения классических скоростей (1)закон сохранения импульса (7)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)законы сохранения (1)закрытым концом (1)замена переменной (2)заметаемый сектор (1)замкнутая система (2)зануление (1)запаянная (2)заряд (9)заряда (1)заряд конденсатора (1)заряженная сфера (1)заряженный шар (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (2)знак неравенства (1)знаменатель (1)знаменатель прогрессии (4)значение выражения (1)идеальный блок (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изменение импульса (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (3)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермически (1)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (11)импульса (1)импульс силы (2)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)инвариантность (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (8)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)интерференция (1)иррациональное уравнение (2)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)камешек (1)капилляр (1)карлик (2)касательная (4)касательного (1)касательные (1)касаются (1)катер (2)катет (3)катится (2)катушка (6)качаний (2)квадлратичная зависимость (1)квадрант (1)квадрат (3)квадратичная функция (3)квадратное (1)квадратное уравнение (4)квадратную рамку (1)квазар (1)квант (1)квантов (1)кинематика (2)кинематическая связь (1)кинематические связи (5)кинетическая (12)кинетическая энергия (5)кинетической (1)кинетической энергии (1)кинетическую энегрию (1)кинетическую энергию (1)классический метод (3)классический метод расчета (1)клин (3)ключ (1)кодификатор (1)колебаний (1)колебательный контур (1)колене (1)колесо (1)количество вещества (1)количество теплоты (9)коллектор (1)кольцо (2)комбинаторика (1)комбинированное (1)коммутация (1)комплексное сопротивление (1)комплексное число (1)комплексные числа (1)компонент (1)конвекция (3)конденсатор (10)конденсаторы (1)конденсации (1)конечная скорость (1)конечная температура (1)конечная температура смеси (1)конечный предел (1)консервативные (1)консоль (1)контрольная (1)контрольные (1)контур (5)конус (4)концентрация (7)концентрически (1)концентрическим (1)координата (5)координатный метод (2)координаты (3)координаты вектора (2)координаты середины отрезка (1)координаты точки (1)корабля (1)корень (4)корень квадратный (1)корень кубический (2)корни (3)корни иррациональные (1)корни квадратного уравнения (3)корни уравнения (1)корпоративных (1)косинус (2)косинус разности (1)косинусы (1)котангенс (1)коэффициент (1)коэффициент жесткости (1)коэффициент наклона (3)коэффициент поверхностного натяжения (3)коэффициент подобия (5)коэффициент трансформации (1)коэффициент трения (6)коэффициенты (1)красное смещение (1)красной границы (1)красный (1)кратковременный режим (1)кратные звезды (1)кредит (13)кредитная ставка (4)кредиты (2)криволинейная трапеция (2)кристаллизация (1)критерии оценки (1)круговая частота (1)круговой контур (1)кружок (1)кубическая парабола (1)кулонова сила (1)кульминация (1)кусочная функция (1)левом колене (1)лед (2)лет (1)линейная скорость (2)линейное напряжение (1)линейное уравнение (2)линейный размер (1)линза (2)линзы (2)линии излома (1)линиями поля (1)линия отвеса (1)литров (1)лифт (1)лифта (1)лифте (1)логарифм (11)логарифмические неравенства (3)логарифмические уравнения (1)логарифмическое (1)логарифмическое неравенство (3)логарифмическое с переменным основанием (1)логарифмы (1)лунка (1)лучевая (1)лучевая скорость (1)льда (1)магнитное поле (2)магнитном поле (2)магнитные цепи (1)мажорант (1)максимальная высота (1)максимальная скорость (2)максимальное ускорение (1)максимум (1)малых колебаний (1)масса (24)масса воздуха (1)массе (1)массивная звезда (1)массовое содержание (1)массой (1)массу (1)математика (4)математический маятник (1)математического маятника (2)маятник (4)мгновенный центр вращения (1)мгновенный центр скоростей (3)медиана (2)меридиан (1)мертвая вода (1)мертвая петля (1)металлическая оболочка (1)метод виртуальных (1)метод внутреннего проецирования (1)метод замены множителей (1)метод замены переменной (4)метод интервалов (3)метод комплексных амплитуд (3)метод контурных токов (1)метод координат (1)метод линий (1)методом внутреннего проецирования (1)метод переброски (1)метод переменных состояния (1)метод подстановки (4)метод рационализации (5)метод решетки (1)метод следов (5)метод сложения (4)метод телескопирования (1)метод узловых напряжений (1)методы расчета цепей (2)методы расчета цепей постоянного тока (1)метод эквивалентного генератора (2)механика (1)механическая характеристика (1)механическое напряжение (1)миля (1)минимакс (1)минимальная скорость (1)минимальное (1)минимальной высоты (1)минимальной скоростью (1)минимум (2)мишени (1)мнимая единица (1)мнимая часть (1)многоатомный газ (1)многоугольник (1)многочлены (1)мода (2)модули (1)модуль (13)модуль Юнга (1)модуль средней скорости (1)молекулярно-кинетическая теория (2)моль (2)молярная масса (5)молярная теплоемкость (4)момент (7)момент инерции (2)момент инерции двигателя (1)момент нагрузки (1)момент сил (1)монета (1)монотонная (1)монотонность функции (1)монохроматического (1)московская олимпиада (1)мощности силы тяжести (1)мощность (9)мощностью (1)мяч (1)наблюдатель (1)нагревание (1)нагреватель (1)нагревателя (1)нагрели (1)наибольшее (1)наивысшая точка (1)наименьшая работа (1)наименьшее (1)наименьшее общее кратное (1)наклон (1)наклонная плоскость (2)налог (1)на направление (2)на отрезке (2)на подумать (2)направление (1)направление обхода (3)направлении (1)направляющий вектор (1)напряжение (9)напряжение на зажимах (1)напряжение смещения нейтрали (2)напряженность (4)напряженность поля (6)нарушенная схема (9)насос (2)насоса (1)насыщенный пар (4)натуральное (9)натуральные (10)натуральных (1)натяжение нити (5)натяжения (1)находился в полете (2)начальная температура (1)начальной скоростью (1)недовозбуждение (1)незамкнутая система (2)неизвестное количество лет (1)неизвестный процент банка (1)нелинейное сопротивление (1)необходимо выплатить часть долга (1)неопределенность типа бесконечность на бесконечность (1)неопределенность типа ноль на ноль (1)непериодическая дробь (1)неравенства (8)неравенство (22)неравенство профиль (1)неразрывности струи (1)нерастяжима (3)нерастяжимой (1)нерастяжимой нити (1)нерастяжимость нити (1)нерастянутой резинки (1)несимметричная нагрузка (1)несинусоидальный ток (3)нестандартные задачи (1)нестрогое (1)неупругим (1)нецентральный (1)нечетная функция (2)нечетное (1)нечетность (1)неявнополюсный (1)нити (3)нити паутины (1)нитку (1)нить (2)нить нерастяжима (1)новости (1)нормаль (1)нормальное ускорение (11)нормальной реакции опоры (1)нулевой ток (2)обкладками (1)обкладках (1)обкладки (1)область допустимых значений (9)область значений (1)область определения (8)область определения функции (4)оборот (1)обратные тригонометрические функции (1)обратные функции (1)общая сумма выплат (1)общая хорда (1)общее сопротивление (1)общее сопротивление цепи (1)объем (37)объемный расход (1)объемом (1)объем пара (1)объем параллелепипеда (1)объем пирамиды (1)одинаковые части (1)одновременно (1)одновременно из одной точки (1)однозначное (1)окружность (13)окружность описанная (1)олимпиада (2)олимпиадная физика (1)олимпиады (1)олимпиады по физике (3)они встретятся (1)операторный метод (4)описанная (1)определитель (1)оптика (1)оптимальный выбор (1)оптимизация (1)оптическая разность хода (1)оптический центр (1)орбитам (1)орбитой (1)оригинал (1)осевое сечение (1)оси (1)основание (2)основание логарифма (2)основания трапеции (1)основное тригонометрическое тождество (1)основное уравнение МКТ (2)основной газовый закон (1)основной период (1)основной уровень (1)основные углы (1)остаток (1)остывает (2)ось (1)ось вращения (1)отбор (1)отбор корней (6)ответ (1)отданное (1)отличная (1)относительная (2)относительная влажность (3)относительная скорость (1)относительно (4)относительность движениия (1)относительность движения (2)относительность скоростей (1)отношение (6)отношение времен (1)отношение длин (3)отношение площадей (4)отношение скоростей (2)отрезке (1)отрезок (1)отсечение невидимых граней (1)оценка (1)очки (1)падает (1)падает луч (1)падает под углом (1)падение (3)падение напряжения (2)падения (1)пар (3)парабола (5)параболы (1)параллакс (5)параллелепепед (2)параллелепипед (3)параллелограмм (4)параллелограмм Виньера (1)параллельно (2)параллельно двум векторам (1)параллельное соединение (3)параллельные прямые (1)параллельными граням (1)параметр (33)параметры (1)парообразование (1)парсек (1)парциальное (1)парциальное давление (1)пары (1)паскаль (1)первая треть (1)первичная (1)первый закон Кеплера (1)переброски (1)перевозбуждение (1)перегородка (1)перегрузок (1)перелетит (1)переливания (1)переменная сила (1)переменное магнитное поле (1)переменное основание (2)перемещение (6)перемычка (5)перемычке (1)перемычку (1)переносная (1)переносная скорость (1)пересекает (1)пересечение (1)пересечения (1)переходная проводимость (1)переходное сопротивление (1)переходной процесс (1)переходные процессы (9)перигелий (2)перигельное (1)периметр (3)период (16)периодическая дробь (1)период колебаний (3)период малых колебаний (1)период обращения (2)период функции (1)периоды (1)перпендикулярно (1)песок (1)пион (1)пипетка (1)пирамида (8)пирамида шестиугольная (1)пирамиды (2)пирсона (1)плавание (1)плавкие предохранители (1)плавление (1)план (1)планете (1)планеты (3)планиметрия (14)планиметрия профиль (1)пластинами (1)пластинка (1)платеж (8)плечо (2)плоского зеркала (1)плоскопараллельная (1)плоскость (4)плоскость сечения (1)плотности веществ (1)плотность (23)плотность пара (3)плотность сосуда (1)плотность энергии (1)площади (2)площади фигур на клетчатой бумаге (1)площадь (30)площадь боковой поверхности (1)площадь круга (1)площадь пластин (1)площадь поверхности (1)площадь под кривой (2)площадь проекции (1)площадь проекции сечения (1)площадь сектора (1)площадь сечения (5)площадь треугольника (3)поверхностная плотность заряда (1)поворот (1)повторно-кратковременный режим (1)по гладкому стержню (1)погрешность (1)погружено (1)подвесили (1)подготовка к контрольным (3)под каким углом (1)подмодульное (1)подмодульных выражений (1)подобен (1)подобие (8)подобия треугольников (1)подобны (1)подпереть (1)под углом (2)под углом к горизонту (3)показателем преломления (1)показательное (1)показатель политропы (1)показатель преломления (5)поле (1)полезной работы (1)полезную мощность (1)полигон частот (1)по линиям сетки (1)полное ускорение (1)половина времени (1)половинный угол (1)положение равновесия (1)положительный знаменатель (1)полония (1)полость (1)полуокружность (1)полупроводник (1)полученное (1)понижение горизонта (1)по окружности (1)по переменному основанию (1)поправка часов (1)по прямой (1)поршень (4)поршня (1)порядок максимума (1)порядок решетки (3)последовательно (1)последовательное соединение (3)последовательность (4)по сторонам клеток (1)посторонние корни (4)постоянная Авогадро (1)постоянная Хаббла (1)постоянная времени (1)постоянная скорость (1)постоянная составляющая (2)постоянный ток (5)построение (2)построение графика функции (1)потенциал (6)потенциал сферы (1)потенциал шара (2)потенциальная (13)потенциальная энергия (3)потенциальной (1)потери в стали (2)потеря корней (4)поток (5)по физике (1)правило Саррюса (1)правило левой (1)правило моментов (5)правильная пирамида (3)правильной пирамиде (1)правильную пирамиду (1)правильный многоугольник (1)правом колене (1)предел функции (1)преломляющий угол (1)преобразование графиков функций (1)преобразования (3)преподаватели (2)пресс (2)призма (7)призмы (3)признаки подобия (4)признаки равенства треугольников (3)пробн (1)пробник (217)пробник по физике (23)пробниук (1)пробный (1)пробный ЕГЭ (2)пробный ЕГЭ по физике (4)пробный вариант (25)пробный вариант ЕГЭ (17)пробный вариант ЕГЭ по физике (169)пробный вариант по физике (3)провода (1)проводник (1)проводник с током (1)проводящая оболочка (1)проводящего шара (1)проволока (1)проволоки (1)прогрессия (5)проекции (2)проекции скоростей (2)проекции ускорения (2)проекция (8)проекция перемещения (1)проекция скорости (6)проекция ускорения (2)производительность (2)производная (4)промежутка времени (1)промежуток (1)промежуток знакопостоянства (1)пропорциональны (1)проскальзывает (1)проскальзывания (1)противоположное событие (1)противостояние (1)протона (1)прототипы (1)профиль (2)профильный ЕГЭ (1)процент (5)

  Резонанс напряжений. Что такое резонанс в электрической цепи

  Резонанс является одним из самых распространенных в природе физических явлений. Явление резонанса можно наблюдать в механических, электрических и даже тепловых системах. Без резонанса у нас не было бы радио, телевидения, музыки и даже качелей на детских площадках, не говоря уже об эффективнейших диагностических системах, применяемых в современной медицине. Одним из самых интересных и полезных видов резонанса в электрической цепи является резонанс напряжений.

  Элементы резонансной цепи

  Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:

  • R — резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
  • L — индуктивность. Индуктивность в электрических цепях — аналог массы или инерции в механических системах. Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
  • С – обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют механическую энергию. Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.

  Понятие резонансного контура

  Ключевыми элементами резонансного контура являются индуктивность (L) и емкость (C). Резистор имеет тенденцию к гашению колебаний, поэтому он удаляет энергию из контура. При рассмотрении процессов, происходящих в колебательном контуре, мы его временно игнорируем, но необходимо помнить, что подобно силе трения в механических системах электрическое сопротивление в цепях невозможно устранить.

  Резонанс напряжений и резонанс токов

  В зависимости от способа соединения ключевых элементов резонансный контур может быть последовательным и параллельным. При подключении последовательного колебательного контура к источнику напряжения с частотой сигнала, совпадающей с собственной частотой, при определенных условиях в нем возникает резонанс напряжений. Резонанс в электрической цепи с параллельно соединенными реактивными элементами называется резонансом токов.

  Собственная частота резонансного контура

  Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.

  В момент времени «0» вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу). Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя — отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени. Отметим, что T на нашем графике — это время, необходимое для завершения одного колебания, носящего в электротехнике название «период колебания».

  Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в катушку индуктивности. На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.

  Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина — отрицательный заряд (рисунок внизу).

  Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.

  Частота колебаний может быть аппроксимирована следующим образом:

  где: F — частота, L — индуктивность, C — емкость.

  Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.

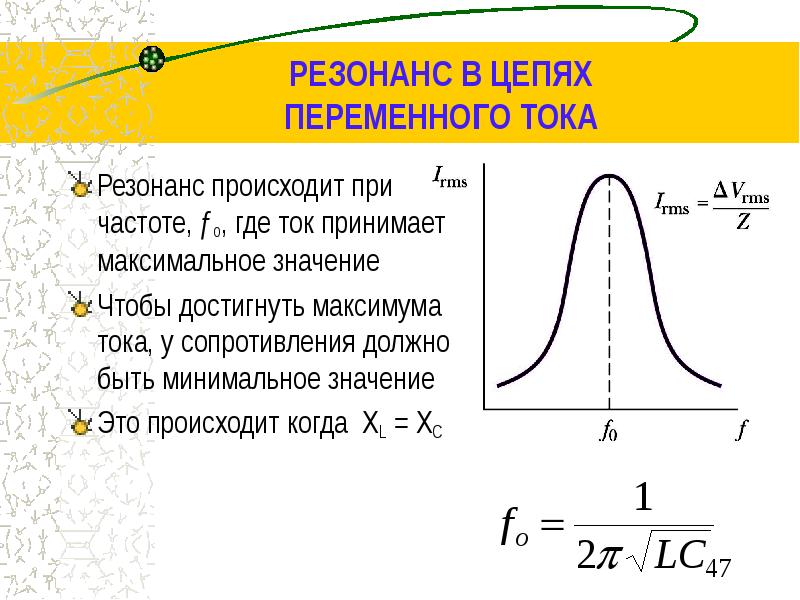
  Исследование резонанса напряжений

  В реальных схемах LC всегда присутствует небольшое сопротивление, которое с каждым циклом уменьшает прирост амплитуды тока.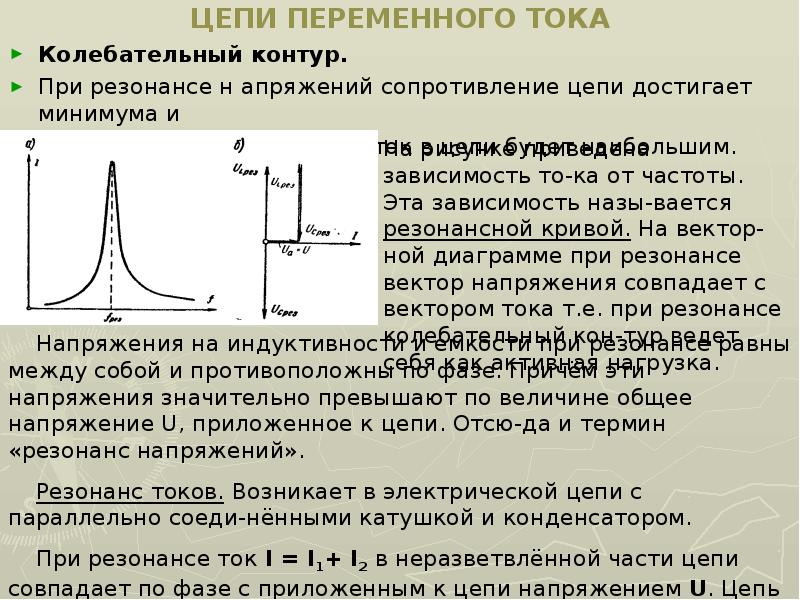 После нескольких циклов ток уменьшается до нуля. Этот эффект называется «затухание синусоидального сигнала». Скорость затухания тока до нулевого значения зависит от величины сопротивления в цепи. Тем не менее, сопротивление не изменяет частоту колебаний резонансного контура. Если сопротивление достаточно велико, синусоидальные колебания в контуре не возникнут вообще.

  Очевидно, там, где существует собственная частота колебаний, есть возможность возбуждения резонансного процесса. Мы делаем это, включая в последовательную цепь источник питания переменного ток (АС), как показано на рисунке слева. Термин «переменный» означает, что выходное напряжение источника колеблется с определенной частотой. Если частота источника питания совпадает с собственной частотой контура, возникает резонанс напряжений.

  Условия возникновения

  Сейчас мы рассмотрим условия возникновения резонанса напряжений. Как показано на последнем рисунке, мы вернули резистор в контур. При отсутствии резистора в контуре ток в резонансной цепи будет нарастать до некоторого максимального значения, определяемого параметрами элементов контура и мощностью источника питания. Увеличение сопротивления резистора в резонансной цепи повышает тенденцию к затуханию тока в контуре, но не влияет на частоту резонансных колебаний. Как правило, режим резонанса напряжений не наступает, если сопротивление цепи резонанса удовлетворяет условию R = 2(L/C)^0,5.

  Использование резонанса напряжений для передачи радиосигнала

  Явление резонанса напряжений является не только любопытнейшим физическим феноменом. Оно играет исключительную роль в технологии беспроводных коммуникаций – радио, телевидении, сотовой телефонии. Передатчики, используемые для беспроводной передачи информации, в обязательном порядке содержат схемы, предназначенные для резонирования на определенной для каждого устройства частоте, называемой несущей частотой. При помощи передающей антенны, подключенной к передатчику, он излучает электромагнитные волны на несущей частоте.

  Антенна на другом конце приемо-передающего тракта получает этот сигнал и подает его на приемный контур, предназначенный для резонирования на частоте несущей. Очевидно, что антенна принимает множество сигналов на различных частотах, не говоря уже о фоновом шуме. Благодаря наличию на входе приемного устройства, настроенного на несущую частоту резонансного контура, приемник выбирает единственно правильную частоту, отсеивая все ненужные.

  После детектирования амплитудно-модулированного (AM) радиосигнала, выделенный из него низкочастотный сигнал (НЧ) усиливается и подается на звуковоспроизводящее устройство. Это простейшая форма радиопередачи очень чувствительна к шумам и помехам.

  Для повышения качества принимаемой информации разработаны и успешно используются другие, более совершенные способы передачи радиосигнала, которые также базируются на использовании настроенных резонансных систем.

  Частотная модуляция или FM-радио решает многие из проблем радиопередачи с амплитудно-модулированным передающим сигналом, однако это достигается ценой существенного усложнения системы передачи. В FM-радио системные звуки в электронном тракте превращаются в небольшие изменения несущей частоты. Часть оборудования, которое выполняет это преобразование, называется «модулятор» и используется с передатчиком.

  Соответственно, к приемнику должен быть добавлен демодулятор для преобразования сигнала обратно в форму, которая может быть воспроизведена через громкоговоритель.

  Другие примеры использования резонанса напряжения

  Резонанс напряжений как основополагающий принцип заложен также в схемотехнике многочисленных фильтров, широко применяемых в электротехнике для устранения вредных и ненужных сигналов, сглаживания пульсаций и генерирования синусоидальных сигналов.

  Резонанс

  в цепях RLC [Analog Devices Wiki]

  Цель:

  Целью этой лабораторной работы является изучение явления резонанса в цепях RLC. Определите резонансную частоту и полосу пропускания данной сети, используя амплитудный отклик на синусоидальный источник.

  Примечания:

  Как и во всех лабораториях ALM, мы используем следующую терминологию при описании подключений к разъему M1000 и настройке оборудования. Зеленые прямоугольники обозначают подключения к разъему аналогового ввода-вывода M1000. Контакты аналогового канала ввода / вывода обозначаются как CA и CB. При настройке принудительного измерения напряжения / измерения тока — В, добавляется, как в CA-, В , или при настройке для принудительного измерения тока / измерения напряжения добавляется -I, как в CA-I. Когда канал настроен в режиме высокого импеданса только для измерения напряжения, -H добавляется как CA-H.

  Кривые осциллографа также обозначаются по каналу и напряжению / току.Например, CA- V , CB- V для сигналов напряжения и CA-I, CB-I для сигналов тока.

  Фон:

  Резонансный контур, также называемый настроенным контуром, состоит из катушки индуктивности и конденсатора вместе с источником напряжения или тока. Это одна из самых важных схем, используемых в электронике. Например, резонансный контур в одной из многих форм позволяет нам в любое время настроиться на желаемую радио- или телевизионную станцию ​​из огромного количества сигналов, которые находятся вокруг нас.

  Сеть находится в резонансе, когда напряжение и ток на входных клеммах сети совпадают по фазе, а входной импеданс сети является чисто резистивным.

  Рисунок 1: Схема параллельного резонанса

  Рассмотрим параллельную RLC-схему на рисунке 1. Установившаяся полная проводимость, предлагаемая схемой, равна:

  Резонанс возникает, когда напряжение и ток на входных клеммах совпадают по фазе. Это соответствует чисто реальной проводимости, так что необходимое условие задается следующим образом:

  Резонансное состояние может быть достигнуто регулировкой L, C или ω.При постоянных L и C резонансная частота ω _o определяется по формуле:

  рад / с (1)

  ИЛИ ЖЕ

  Герц (2)

  Частотная характеристика: это график величины выходного напряжения резонансного контура как функции частоты. Отклик, конечно же, начинается с нуля, достигает максимального значения вблизи собственной резонансной частоты, а затем снова падает до нуля, когда ω становится бесконечным. Частотная характеристика показана на рисунке 2.

  Рисунок 2: Частотная характеристика параллельной резонансной цепи

  Также указаны две дополнительные частоты ω ₁ и ω ₂ , которые называются частотами половинной мощности. Эти частоты определяют те точки на кривой, в которых характеристика напряжения составляет 1 / sqrt (2) или 0,707 от максимального значения. Они используются для измерения ширины полосы кривой отклика. Это называется шириной полосы половинной мощности резонансного контура и определяется как:

  (3)

  Рисунок 3: Схема последовательного резонанса

  Материалы:

  Аппаратный модуль ADALM1000
  Резисторы 100 Ом, 1 кОм
  Конденсаторы 1 мкФ, 0.01 мкФ
  Катушки индуктивности 20 мГн

  Процедура:

  1. Настройте схему RLC, как показано на рисунке 4, на беспаечной макетной плате со значениями компонентов: R _S = 100 Ом, R ₁ = 1 кОм, C ₁ = 1 мкФ и L ₁ = 20 мГн.

  Рисунок 4: Параллельная резонансная схема с последовательным сопротивлением, подключенным к источнику

  Рисунок 5: Соединения макетной платы

  2. Установите минимальное значение AWG канала A равным 0.5 и максимальное значение 4,5 В для подачи синусоидальной волны 4 В (размах) с центром 2,5 В в качестве входного напряжения в схему. В раскрывающемся меню AWG A Mode выберите режим SVMI. В раскрывающемся меню AWG A Shape выберите Sine. В раскрывающемся меню AWG B Mode выберите режим Hi-Z.

  3. В раскрывающемся меню «Кривые ALICE» выберите для отображения CA- V и CB- V . В раскрывающемся меню «Триггер» выберите CA- V и Auto Level. Установите Hold Off на 2 (мсек).Отрегулируйте развертку до тех пор, пока на сетке дисплея не будет примерно двух периодов синусоидальной волны. В раскрывающемся меню Meas CA выберите P-P в CA- V и сделайте то же самое для CB. Также в меню Meas CA выберите A-B Phase.

  4. Измените частоту синусоиды в меню AWG A от 500 Гц до 2,5 кГц с шагом 100 Гц. Для каждой частоты запишите напряжение P-P для каналов A и B, а также для фазы A-B. Обратите внимание, на какой частоте напряжение на выходе цепи на канале B является максимальным.Это будет около резонансной частоты контура. Обратите внимание, что на этой частоте фаза должна быть близка к нулю. Отрегулируйте частоту с шагом 10 Гц около того места, где вы видите максимум напряжения CB P-P, пока фаза A-B не станет точно нулевой.

  5. Повторите эксперимент, используя для последовательной резонансной схемы, показанной на рисунке 3, и используйте L ₁ = 20 мГн, C ₁ = 0,01 мкФ и R ₁ = 1 кОм. Напряжение Vo на резисторе пропорционально последовательному току цепи RLC.

  Вопросы:

  1. Найдите резонансную частоту ω _o , используя уравнение (1), и сравните ее с экспериментальным значением в обоих случаях.

  2. Постройте график зависимости напряжения схемы и получите ширину полосы по частотам половинной мощности, используя уравнение (3).

  Приложение, Графики АЧХ с ALICE-SA

  Программное обеспечение ALICE для настольных ПК может значительно упростить построение графиков частотных и фазовых характеристик. Используя схему параллельного резонанса RLC на рисунке 4, мы можем изменить входную частоту от 10 Гц до 5000 Гц и построить график амплитуды сигнала обоих каналов A и B, а также относительного фазового угла между каналами B и A.

  Со схемой, подключенной к ALM1000, как показано на рисунке 4, запустите программное обеспечение рабочего стола ALICE. Откройте окно построения графика Боде.

  В меню Curves выберите CA-dBV, CB-dBV и Phase B-A.

  В раскрывающемся меню «Параметры» нажмите Cut-DC, чтобы выбрать его.

  Установите минимальное значение канала A AWG на 1,086 и максимальное значение на 3,914. Это будет амплитуда 1 Vrms (0 дБВ) с центром в середине 2,5 В диапазона аналогового входа. Установите режим AWG A на SVMI и Shape на Sine.Установите канал B AWG в режим Hi-Z. Убедитесь, что установлен флажок Sync AWG.

  Используйте кнопку Start Frequency, чтобы установить развертку частоты на 10 Гц, а кнопку Stop Frequency — для остановки развертки на 5000 Гц. В раскрывающемся меню Sweep Gen выберите CHA как канал для развертки. Также используйте кнопку Sweep Steps, чтобы ввести количество шагов частоты, используйте 400 в качестве числа.

  Теперь вы должны иметь возможность нажать зеленую кнопку Run и запустить частотную развертку.После завершения развертки вы должны увидеть что-то вроде снимка экрана на рисунке A1. Вы можете использовать кнопки LVL и дБ, / дел, чтобы оптимизировать графики для наилучшего соответствия экранной сетке.

  Рисунок A1, Развертка частоты от 100 Гц до 20000 Гц

  Ресурсы:

  Для дальнейшего чтения:

  Руководство пользователя настольного ПК ALICE

  Вернуться к разделу «Введение в электротехническую лабораторию». Содержание
  Вернуться к «Электрическая лаборатория».

  университет / курсы / alm1k / circuit1 / alm-cir-7.txt · Последнее изменение: 25 июня 2020 г., 22:07 (внешнее редактирование)

  Параллельный резонанс

  • Изучив этот раздел, вы сможете:
  • • Опишите действие параллельных цепей LCR вверху, внизу и в резонансе.
  • • Опишите увеличение тока и динамическое сопротивление в параллельных цепях LCR
  • • Используйте соответствующие формулы для выполнения расчетов параллельных цепей LCR, включая резонанс, импеданс и динамическое сопротивление.

  Так же, как и в последовательных резонансных цепях, в параллельной цепи есть три основных условия. В зависимости от частоты и значений компонентов, контур будет работать ниже, выше или в резонансе. В этом разделе описываются эти три состояния с использованием векторных диаграмм, включающих векторы тока I _C , I _L и их векторную сумму I _S с эталонным вектором V _S . Обратите внимание, что V _R не показан, но его присутствие в цепи обозначается изменяемым углом I _L , как описано в Модуле 10.2.

  Ниже резонанса

  Рис. 10.3.1 Под резонансом

  Во-первых, если частота источника питания низкая, ниже резонансной частоты ƒ _r , то существует условие, показанное на рис. 10.3.1, и ток I _L через L будет большим (из-за его сравнительно низкого реактивного сопротивления). В то же время ток I _C через C будет сравнительно небольшим. Поскольку I _C меньше, чем I _L , фазовый угол θ будет небольшим.Включение I _S в диаграмму показывает, что он будет отставать от V _S и, следовательно, цепь будет выглядеть ИНДУКТИВНОЙ. (Обратите внимание, что это противоположное положение дел в последовательной цепи, которая имеет емкость ниже резонанса).

  Выше резонанса

  Рис. 10.3.2 Выше резонанса

  На рис. 10.3.2 показано, что происходит на частотах выше резонанса. Здесь ток I _C через C будет больше, чем ток I _L через L, потому что частота выше, а X _C меньше, чем X _L , θ больше, чем на рис.3.1. Это дает нам условие, когда I _S (сумма векторов I _C и I _L ) опережает V _S , и поэтому схема является емкостной.

  При резонансе

  Рис. 10.3.3 При резонансе

  В резонансе идеальная цепь имеет бесконечный импеданс, но это не совсем так в практических параллельных цепях, хотя очень близко. На рис. 10.3.3 показаны условия резонанса в практической параллельной цепи LCR. I _C опережает V _S на 90 °, но I _L не совсем в противофазе (из-за сопротивления в индуктивной ветви цепи). Следовательно, в параллельной схеме резонанс должен определяться как частота, при которой значения I _C и I _L таковы, что I _S находится в ФАЗЕ с V _S .

  Динамическое сопротивление

  В резонансе Рис. 10.3.3 (выше) показывает, что I _S очень маленький, намного меньше, чем I _C или I _L , поэтому полное сопротивление в параллельной цепи должно быть очень высоким при _r и поскольку I _S находится в фазе с V _S , полное сопротивление цепи является чисто резистивным.Это чистое сопротивление, которое возникает только при _r , называется ДИНАМИЧЕСКИМ СОПРОТИВЛЕНИЕМ (R _D ) цепи, и его можно рассчитать (в омах) для любой параллельной цепи, исходя только из значений используемых компонентов, используя формулу:

  Где R — полное сопротивление цепи, включая внутреннее сопротивление L.

  Текущее увеличение

  Другой важный момент, показанный на рис. 10.3.3, — это размер вектора для I _S по сравнению с I _C и I _L .Ток питания намного меньше любого из токов в L- или C-ветвях цепи. Это должно означать, что в цепи протекает больше тока, чем на самом деле подается в нее!

  Это состояние реально и известно как ТОКОВОЕ УВЕЛИЧЕНИЕ. Подобно тому, как увеличение напряжения происходит в последовательных цепях, параллельная цепь LCR увеличивает ток. КОЭФФИЦИЕНТ УВЕЛИЧЕНИЯ (Q) параллельной цепи может быть найден по той же формуле, что и для последовательной цепи, а именно:

  Регулировка резонанса.

  Формула для резонансной частоты параллельной цепи LCR также использует ту же формулу для _r , что и в последовательной цепи, то есть;

  Рис. 10.3.4 Параллельные настроенные схемы LC.

  Но следует отметить, что эта формула игнорирует влияние R на небольшой сдвиг фазы I _L . Фактически формула дает только приблизительное значение для ƒ _r . Однако, поскольку внутреннее сопротивление L обычно довольно мало, его влияние на смещение резонансной частоты контура также невелико.По этой причине одна и та же формула может использоваться для ƒ _r как в последовательной, так и в параллельной цепях. В тех практических LC-схемах, предназначенных для работы на высоких частотах, и там, где требуется точный контроль над _— , значение L или C может быть регулируемым.

  Рис. 10.3.5 Настроенный трансформатор в грохоте

  Окончательные значения для L и C будут достигнуты путем настройки одного из двух компонентов, как показано на рис. 10.3.4, который будет иметь переменный тип, после того как система, содержащая контур LC, будет работать.С помощью этого метода компенсируется не только влияние R, но и любая паразитная индуктивность или емкость в цепи, которые также могут повлиять на конечное значение ƒ _r . Поскольку на высоких частотах магнитные поля легко излучаются от одного компонента в цепи к другому, схемы с LC-настройкой также должны быть экранированы (экранированы) путем помещения их в металлический экран, как показано на рис. 10.3.5.

  6 Что нужно знать о параллельных цепях LCR.

  (и это отличается от последовательной цепи.)

  • 1. ПРИ РЕЗОНАНСЕ (ƒ _r ) V _C не обязательно точно равно V _L , но V _S и I _S находятся в ФАЗЕ
  • 2 .; ПРИ РЕЗОНАНСЕ (ƒ _r ) Импеданс (Z) является максимальным и называется динамическим сопротивлением (R _D )
  • 3. ПРИ РЕЗОНАНСЕ ( _r ) Ток цепи (I _S ) минимален.
  • 4. НА РЕЗОНАНСЕ (ƒ _r ) Цепь полностью резистивная.
  • 5. НИЖЕ РЕЗОНАНСА (ƒ _r ) Цепь индуктивная.
  • 6. ВЫШЕ РЕЗОНАНСА (ƒ _r ) Схема емкостная.

  Схем — Урок — TeachEngineering

  MyTE Переключить навигацию
  • Просмотр
    Учебный план
    • Весь учебный план
    • шт.
    • Уроки
    • Деятельность
    • Осыпает
    • Maker Challenges
    • Living Labs
    • Предметные области
    • Виды учебных программ TE
    • e4usa
  • K-12
    Инженерное дело
    • Что такое инжиниринг?
    • Зачем преподавать инженерное дело в K-12?
    • Виды техники
  • Математика и
    Физика
    • Инженерная физика
    • Инженерная математика
  • 
    NGSS
  • Проектирование
    Проектирование
    • Процесс проектирования
    • Дизайн-мышление
  • Популярные
    темы
  • 
    Стандарты
    • Поиск учебной программы по Стандартам
    • Поиск учебной программы по NGSS
    • Поиск учебной программы по стандартам Common Core
    • Расскажите мне о NGSS
  .