Электрические цепи однофазного тока. Резонанс токов.
Рассмотрим цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью.
Параллельное соединение конденсатора и катушки
Рис. 1
В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z1 и ток I1 определяются по формуле:
Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол φ1 = arctg(R/XL). Покажем это на векторной диаграмме.
Векторная диаграмма для первой ветви
Рис. 2
Спроецируем вектор тока I1 на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I1R, а вертикальная — I1L.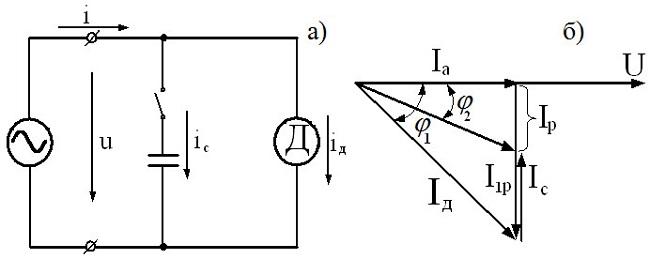 Количественные значения этих составляющих будут равны:
Количественные значения этих составляющих будут равны:
Во вторую ветвь включен конденсатор. Его сопротивление
Этот ток опережает по фазе напряжение на 90°. Для определения тока I в неразветвленной части цепи воспользуемся формулой:
Его значение можно получить и графическим путем, сложив векторы I1 и I2 (рис. 3). Угол сдвига между током и напряжением обозначим буквой φ. Здесь возможны различные режимы в работе цепи. При φ = +90° преобладающим будет емкостный ток, при φ = -90° — индуктивный.
Векторная диаграмма разветвленной цепи
Рис. 3
Резонанс переменного тока. Условие резонанса токов.
Возможен режим, когда φ = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I1L = I2, т.е. при равенстве реактивных составляющих тока в ветвях. Такой режим называется резонансом токов. Также как в случае с резонансом напряжений, он широко применяется в радиотехнике.
Векторная диаграмма в режиме резонанса токов
Рис. 4
Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosφ для электроустановок. Известно, что cosφ является технико-экономическим параметром в работе электроустановок. Определяется он по формуле:
cosφ = P / S, где
Р — активная мощность электроустановок, кВт;
S — полная мощность электроустановок, кВт.
На практике cosφ определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgφ. Далее по таблицам находят и cosφ.
Чем больше cosφ, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosφ приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosφ, в сравнении с низким.
Мероприятия по повышению cosφ:
Кроме этого, на cosφ положительно сказывается подключение к сети статических конденсаторов.
6 Резонансные режимы в электрических цепях синусоидального тока
ЛЕКЦИЯ 6
Резонансные режимы в электрических цепях синусоидального тока.
Резонанс напряжений
Режим работы RLC цепи или LC—цепи, при условии равенства реактивных сопротивлений XC= XL, когда общее напряжение цепи совпадает по фазе с её током , называется резонансом напряжения.
XC= XL – условие резонанса
RLC цепь LC цепь.
Признаки резонанса напряжения:
1.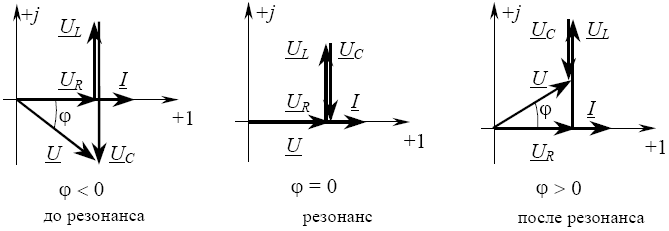 Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
Рекомендуемые файлы
2. Ток в цепи будет наибольшим и как следствие Pmax= I2maxR тоже максимальна, а реактивная мощность равна нулю.
3. Резонансная частота
4.
Резонанс можно достигнуть, изменяя L, C или ω.
Векторные диаграммы при резонансе напряжений
LC цепь RLC цепь
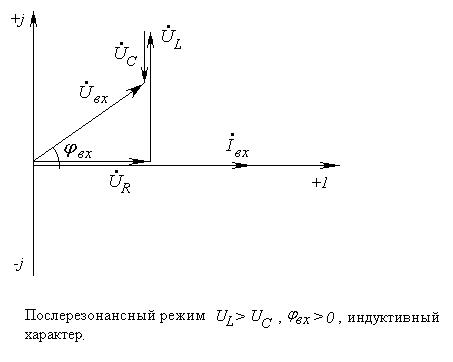
Случаи других режимов работы RLC цепи
- Если XL>XC т.е.
U опережает I, значит цепь имеет активно-индуктивный характер
напряжение на катушке больше напряжения на конденсаторе.
Векторная диаграмма
- Если XL<XC , т.
 е.
е.
U отстает от I, значит цепь имеет активно-емкостной характер
напряжение на конденсаторе больше напряжения на катушке.
Векторная диаграмма
Параллельное соединение элементов в цепи синусоидального тока
На входе параллельной цепи напряжение
Закон Ома
Эквивалентные сопротивления ветвей:
Запишем эквивалентные проводимости:
;
по первому закону Кирхгофа:
где
, где
Треугольники проводимостей и токов
алгебраическая форма
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая.
;
или ;
Треугольник тока
Резонанс токов
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Условие резонанса токов:
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви
Признаки резонанса токов:
- Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
- Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
- и совпадают по фазе
RLC – цепь Векторная диаграмма
LC – цепь Векторная диаграмма
Резонансная частота
Случаи резонансных цепей
цепей
Если R2=0 резонанс наступит, при
Случаи резонанса токов
Случай 1. Один резонанс в цепи, при условии:
Один резонанс в цепи, при условии:
Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов
Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
Частотные характеристики колебательного контура
Баланс мощностей в цепях переменного тока
Коэффициент мощности
• Генератор или электрооборудование энергетически выгодно эксплуатировать, если оно совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.
• Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование
λ=P/S=cosφ≤1
С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .
Способы увеличения коэффициента мощности
Обратите внимание на лекцию «Франко-китайская и японо-китайская войны».
• Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.
• Генератор осуществляет только необратимые преобразования энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем приемников, в режиме максимальной мощности.
• Потребители электрической энергии в основном имеют схему замещения RL элемента, поэтому увеличение коэффициента мощности возможен с помощью компенсации реактивной мощности подключением емкостного элемента (QL—QС), подключение емкостного элемента снижает ток в линии электропередачи, что позволяет уменьшить сечение электропроводов, а это приводит к экономии электропроводящих материалов.
• Значение коэффициента мощности в энергосистемах зависит насколько грамотно эксплуатируется электротехнические установки и приборы.
• сosφ может снижаться, если установки работают в режиме холостого хода, или недогружены.
Резонанс в цепи с параллельно соединенными элементами (резонанс токов), стр.17
Резонанс
в цепи с параллельно соединенными
элементами
(резонанс токов)
Для цепи рис. 4 имеем
,
где
; | (8) |
. | (9) |
В зависимости от соотношения величин и , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
В
цепи преобладает индуктивность, т.е.
,
а следовательно,
. Этому режиму соответствует векторная
диаграмма на рис. 5,а.
Этому режиму соответствует векторная
диаграмма на рис. 5,а.
В цепи преобладает емкость, т.е. , а значит, . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
— случай резонанса токов (рис. 5,в).
Условие резонанса токов или
. | (10) |
При этом, как следует из (8) и (9), . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
Идентичность
соотношений (3) и (5) указывает, что в
обоих случаях резонансная частота
определяется соотношением (4).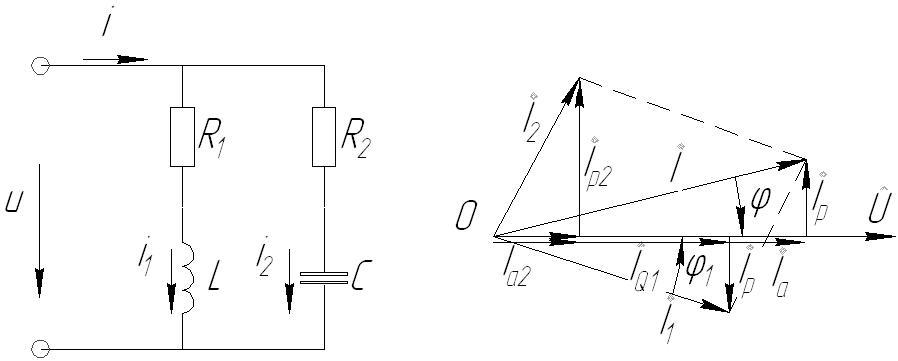 Однако
не следует использовать выражение
(4) для любой резонансной цепи. Оно
справедливо только для простейших
схем с последовательным или параллельным
соединением индуктивного и емкостного
элементов.
Однако
не следует использовать выражение
(4) для любой резонансной цепи. Оно
справедливо только для простейших
схем с последовательным или параллельным
соединением индуктивного и емкостного
элементов.
При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.
Например, для цепи на рис. 6 имеем
Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то условие резонанса имеет вид
,
откуда, в частности, находится резонансная частота.
Резонанс в сложной цепи
Условие
резонанса для сложной цепи со смешанным
соединением нескольких индуктивных
и емкостных элементов, заключающееся
в равенстве нулю мнимой части входного
сопротивления
или
входной проводимости
,
определяет наличие у соответствующих
этому условию уравнений относительно
нескольких
вещественных корней, т. е. таким цепям
соответствует несколько резонансных
частот.
е. таким цепям
соответствует несколько резонансных
частот.
При определении резонансных частот для реактивного двухполюсника аналитическое выражение его входного реактивного сопротивления или входной реактивной проводимости следует представить в виде отношения двух полиномов по степеням , т.е. или . Тогда корни уравнения дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения — значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
В
качестве примера определим резонансные
частоты для цепи рис.
Из решения уравнения получаем частоту , соответствующую резонансу напряжений, а из решения уравнения — частоту , соответствующую резонансу токов.
Литература
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
Что такое резонанс напряжений, чем он характеризуется?
Что такое резонанс токов, чем он характеризуется?
В чем физическая сущность резонансных режимов?
На основании каких условий в общем случае определяются резонансные частоты?
В цепи на рис.
 1 R=1 Ом; L=10 мГн; С=10 мкФ.
Определить резонансную частоту и
добротность контура.
1 R=1 Ом; L=10 мГн; С=10 мкФ.
Определить резонансную частоту и
добротность контура.
Ответ: .
Какие условия необходимы и достаточны, чтобы в цепи на рис. 1 выполнялось соотношение ?
Определить резонансную частоту для цепи на рис. 7, если в ней конденсатор С3 заменен на резистор R3.
Ответ: .
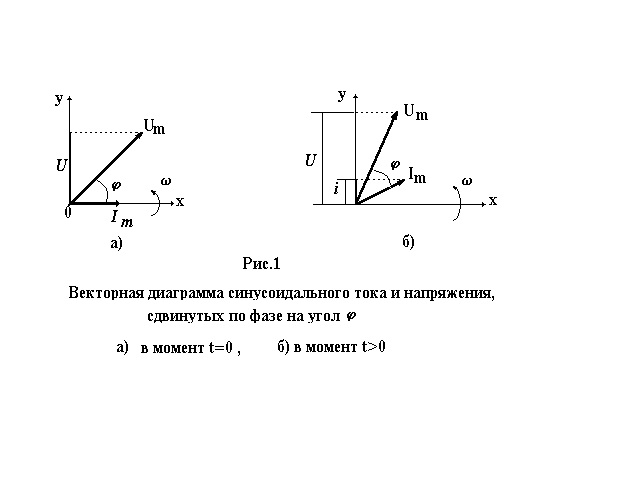
Теория / ТОЭ / Лекция N 9. Векторные и топографические диаграммы. |
Совокупность
радиус-векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения, токи и т. д., называется векторной
диаграммой. Векторные диаграммы наглядно
иллюстрируют ход решения задачи. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях. Для
наглядного определения величины и
фазы напряжения между различными
точками электрической цепи удобно
использовать топографические
диаграммы. В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1). Параметры схемы: При данных параметрах и заданном напряжении на входе схемы найденные значения токов (см. лекцию № 5) равны: ; ; . При
построении векторной диаграммы
зададимся масштабами токов и напряжений
(см. Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости). При
построении топографической диаграммы
обход контуров можно производить по
направлению тока или против. В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС. Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль( ), определим потенциалы этих точек: или Таким
образом, в результате проведенных
вычислений получено, что
.
Но разность потенциалов точек е и а равно напряжению U, приложенному к
цепи, а оно равно 120 В. В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений.
Потенциальная диаграмма Потенциальная
диаграмма применяется при анализе
цепей постоянного тока. Она представляет
собой график распределения потенциала
вдоль участка цепи или контура, при
этом по оси абсцисс откладываются
сопротивления резистивных элементов,
встречающихся на пути обхода ветви
или контура, а по оси ординат –
потенциалы соответствующих точек. Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3. При параметрах схемы ; ; ; ; и токи в ветвях схемы равны: ; ; . Построим потенциальную диаграмму для контура abcda. Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура: после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль: Похожие работы:
|
Графики и векторные диаграммы напряжений и токов. (Лекция 2)
Иркутский филиалМосковского государственного технического
университета гражданской авиации
Ту 144
(первый полет 31.12.1968 г.,
выпущено 18 самолетов)
Экипаж – 4 чел
Дальность — 4 500 км,
Количество пассажиров – 140,
Максимальная скорость -2500 км/ч
Вес топлива – 70 т,
Двигатели — 4×13000 кГс,
Длина – 59,4 м,
Высота – 10,5 м
R
L
Графики и
векторные
диаграммы
C
Z R 2 X C2
Z R 2 X L2
I U / Z
tg X L / R
закон
или
Ома
cos R / Z
I U / Z
закон
tg X C / R
или
Ома
cos R / Z
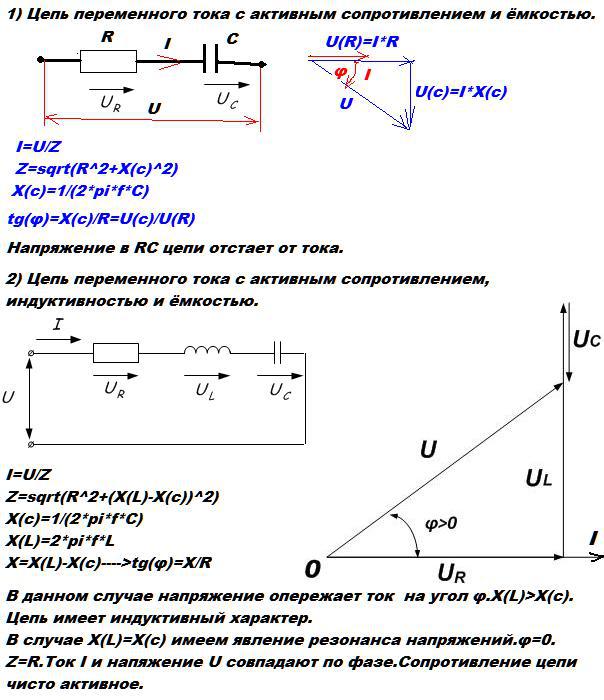
4. 1.8. Цепь с последовательным соединением R, L, С. Векторные диаграммы напряжений и токов
Расчет рассматриваемой цепи произведем для действующих значений величин. В
Вцепи имеются два реактивных элемента, сопротивления которых зависят от частоты
питающего напряжения. Изменяя частоту питающего напряжения, можно добиться
такого положения, когда одно из реактивных сопротивлений будет больше другого
или когда они будут равны
U R U L UC U
i I m sin t
(1)
di 1
idt U m sin( t )
dt C
подставляя(1)в (2)
i r L
(2)
Исходя из рис.,
рассматриваемая цепь
1
может работать в трех
r I m sin t LI m cos t
I m cos t U m sin( t ) или
C
режимах:
1
r I m sin t LI m sin( t 900 )
I m sin( t 900 ) U m sin( t ) XL>XC ;
XL
C
XL = XC .
Сумме мгновенных значений синусоидальных функций соответствует
геометрическая сумма векторов, изображающих эти функции. Построим
векторную диаграмму при XL>XC в следующей последовательности:
U
U r2 (U L2 U C2 ) ,
arctg
UX
U
Цепь для источника создает активноиндуктивный характер нагрузки
1.
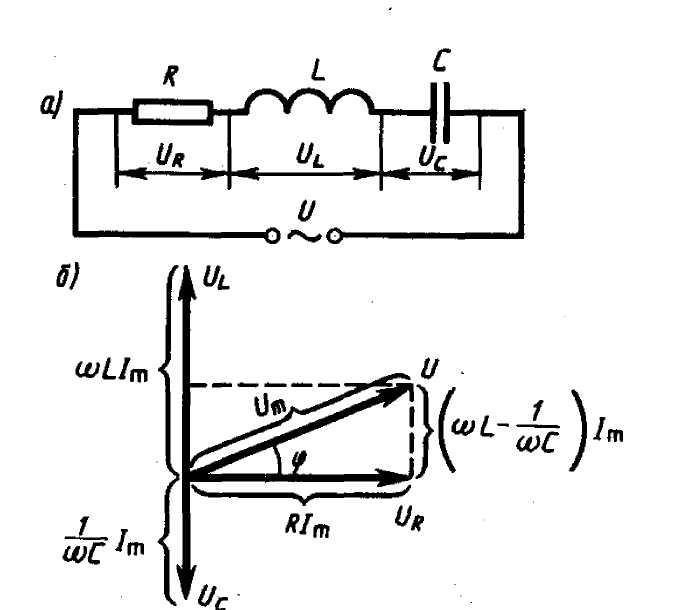 Вектор тока отложим вправо
Вектор тока отложим вправогоризонтально от нулевой точки;
2. Вектор Ur отложим параллельно
вектору тока, т.к. в цепи с резистором ток
и напряжение совпадают по фазе;
3. Вектор UL опережает ток по фазе на
угол 90 , поэтому откладываем его по
отношению к вектору тока против
часовой стрелки;
4. Вектор Uc отстает от тока по фазе
на угол 90 , поэтому откладываем его по
отношению к вектору тока по часовой
стрелке. Так как в цепи ток на всех
участках одинаков, а по условию XL>XC,
то и UL>UC
Наличие сдвига фаз между напряжением источника и током в цепи
указывает на то, что наряду с активной мощностью, расходуемой в активном
сопротивлении, в цепи имеет место и обмен энергиями между реактивными
элементами и источником (реактивная мощность).
Методы расчета разветвленной цепи
А. Метод уравнений Кирхгофа для расчета
разветвленной электрической цепи
Система линейных
уравнений:
Метод Крамера
Определители:
Решение:
Пример
Ветвь, узел и замкнутый контур!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю
Должно быть учтено направление тока по отношению к узлу.

Все токи, направленные к узлу входят в сумму с одним знаком,
а направленные от узла – с противоположным. Первый закон
Кирхгофа может быть сформулирован иначе:
Сумма токов, втекающих в узел, равна
сумме токов вытекающих из узла:
Второй закон Кирхгофа применяется к замкнутым контурам
электрической цепи и формулируется следующим образом:
В любом замкнутом контуре алгебраическая сумма напряжений
на элементах контура равна сумме ЭДС в этом контуре
На основании законов Кирхгофа составляются уравнения для
неизвестных токов в ветвях. Система полученных уравнений
линейна, ее решение позволяет найти неизвестные токи в
ветвях цепи.
1. Обозначим токи во всех
ветвях. Направление токов
выбираем произвольно, но в
цепях с источниками ЭДС
рекомендуется, чтобы
направление токов совпадало с
направлением ЭДС.
2. Составим уравнения по первому закону Кирхгофа. Выбираем 4–1=3 узла
(a, b, c) и для них записываем уравнения:
узел a: I1 — I2 — I3 = 0;
узел b: I2 — I4 + I5 = 0;
узел c: I4 — I5 — I6 = 0.

3. Составим уравнения по второму закону Кирхгофа. Необходимо составить
6–3=3 уравнения. В схеме на рисунке 1 выбираем контура I, II, III и для них
записываем уравнения:
контур I: I1(r01 + R1) + I3R3 = E1;
контур II: I2R2 + I4R4 + I6R7 — I3R3 = 0;
контур III: -I5(r02 + R5 + R6) — I4R4 = -E2.
4. Получаем систему из 6
уравнений с 6 неизвестными:
5. Уравнение можно представить в
матричной форме. Тогда для
заданной электрической цепи
решение системы будет иметь вид
I1 I 2 I 3 0
I I I 0
2 4 5
I 4 I 5 I 6 0
I1 r01 R1 I 3 R3 E1
I 2 R2 I 3 R3 I 4 R4 I 6 R7 0
I 4 R4 I 5 r02 R5 R6 E2
1
1
1
0
0
0
I1
0
0
1
0
1
1
0
I2
0
0
0
0
1
1
1
I3
0
r01 R1
0
R3
0
0
0
0
R2
R3
R4
0
R7
I4
I5
0
0
0
R4
0
I6
r02 R5 R6
E1
0
E2
12.
 Метод контурных токов Суть метода контурных токов: полагают, что в каждом независимом контуре
Метод контурных токов Суть метода контурных токов: полагают, что в каждом независимом контуресхемы течет свой контурный ток. Уравнения составляют относительно
контурных токов, после чего через них определяют токи ветвей. Уравнения
составляются для контура лишь по второму закону Кирхгофа.
Следовательно, метод контурных токов более экономен при вычислительной
работе.
Для трех контуров
Пример: Найти токи в схеме (рис.) методом контурных токов. Числовые
значения сопротивлений в Омах и ЭДС в вольтах указаны на рисунке.
Решение. Выберем направления всех контурных токов I11, I22 и I33 по часовой
стрелке. Определяем:R11 = 5 + 5 + 4 = 14 Ом; R22 = 5 + 10 + 2 = 17 Ом;
R33= 2+ 2+ 1 =5 Ом; R12 = R21 = — 5 Ом; R13 =R31 = 0; R23 = R32 = — 2 Ом;
E11 = -10 В; E33 = -8.
Записываем систему уравнений:
определитель системы
подсчитаем контурные токи
Ток в ветви cm
Icm = I11 — I22 = -0,634-0,224=-0,86 A.
Ток в ветви am
Iam = I22 — I33 = 0,224 + 1,51 = 1,734 A.

14. 1.13. Полная, активная и реактивная электрические мощности. Треугольник электрических мощностей
Активная мощность (Р) определяет среднее значение энергии, поступающей вэлектрическую цепь в единицу времени и превращающуюся там в тепло или в другие
виды энергии.
Р = UIcosφ
Активная мощность всегда положительна, имеет размерность [Ватт].
Реактивной мощностью (Q) называют мощность, которая характеризует
интенсивность обмена энергией между источником и реактивными элементами.
Реактивная мощность рассчитывается по формуле:
Q = UI sinφ
и имеет размерность [ВАр].
Q QL QC X L I 2 X C I 2 ( X L X C ) I 2 XI 2
Полной мощностью (S) называется величина, определяемая S = UI и
характеризующая мощность источников переменного тока. Измеряется полная
мощность в [ВА].
Треугольники мощностей
S
P2 Q2
arctg
Позволяют установить связь
между активной, реактивной и
полной мощностями
cos
Q
,
R
P
S
P 2 (QL QC ) 2 ,
P S cos ,
Q S sin
коэффициен т
мощности
Тема 1.
 Основы символического метода
Основы символического методаЛекция 2 (2 часа)
Изучаемые вопросы:
1.8. Цепь с последовательным соединением R, L, С.
Векторные диаграммы напряжений и токов
1.9. Полное сопротивление цепи. Треугольник
сопротивлений
1.10. Закон Ома, законы Кирхгофа. Комплекс полного
сопротивления цепи
1.11. Резонанс напряжений
1.12. Резонанс токов
1.13. Полная, активная и реактивная электрические
мощности. Треугольник электрических мощностей
Лектор – к.ф.м.н., доцент Кобзарь В.А.
16. 1.9. Полное сопротивление цепи. Треугольник сопротивлений
Если стороны треугольника векторной диаграммы напряжений разделить наодну и ту же величину — ток I , то образуется подобный ему прямоугольный
треугольник сопротивлений, из которого может быть определено полное
сопротивление цепи Z
Расчет электрических цепей с использованием векторных диаграмм
треугольников сопротивлений и мощностей называют методом
сопротивлений.
 Он применим лишь к простым цепям с
Он применим лишь к простым цепям споследовательным соединением пассивных элементов
17. 1.10. Закон Ома в комплексной форме. Полное сопротивления цепи
U U m sin( t U )U R U L UC U
di 1
idt U
(1) интегро дифференциальное
dt C
неоднородное
уравнение
r i L
U m sin( t U ) U
i I m sin( t U ) I m sin( t I ) I
Решение уравнения (1) будем искать не в синусоидальных функциях, а в виде
комплексных амплитуд. При этом операции дифференцирования и интегрирования
заменятся соответственно умножением и делением на jω . Тогда (1) примет вид
r I m j L I m
r I j L I
I
1
Im Um
j C
1
I U
j C
U
U
Z
r j L
1
j C
( 2)
проделив на
2
1
Z r j ( L
) r jx
C
Закон Ома в комплексной форме
18. 1.10.1. Первый и второй законы Кирхгофа в комплексной форме
1r I j L I
I U
j C
1
I UC
j C
j L I U L ,
r I Ur ,
(1)
U r U L UC U
(2)
Соотношение (2) представляет собой уравнение по второму закону
Кирхгофа в комплексной форме.

Алгебраическая сумма комплексных напряжений в
n
m
контуре равна алгебраической сумме комплексных
Uk
Ek
ЭДС в этом же контуре
k 1
k 1
Второй закон Киргофа в
комплексной форме
Первый закон
Киргофа в
комплексной форме
n
I
k 1
k
0
Алгебраическая сумма комплексных токов в узле
равна нулю
19. 1.11. Резонанс напряжений
Резонансом в электрической цепи, содержащей катушку индуктивности иконденсатор, называется явление при котором разность фаз напряжения и тока на
входе цепи равна нулю.
Резонансные явления имеют место, как при последовательном, так и при
параллельном соединении катушек индуктивности и конденсаторов. При этом имеет
место два вида резонанса: резонанс напряжений (в последовательной цепи) и
резонанс токов (в параллельной цепи).
Z r jx r j ( X L X C ) r j ( L
При
1
)
C
резонансе
X X L X C L
1
0
C
(1)
Уравнение (1) — условие возникновения резонанса напряжений.
 Т.е. общее реактивное
Т.е. общее реактивноесопротивление цепи равно нулю
Графики зависимости I и Z от частоты и
p
1
LC
U U
I
Z
r
при резонансе полное
сопротивление цепи минимальное
и равно активному
сопротивлению, т.е. z = r; ток в
цепи при резонансе будет
максимальным
векторная диаграмма при резонансе
20. Добротность последовательного контура
Построим треугольник сопротивлений последовательного контура и найдемсопротивления реактивных элементов при резонансе
ρ- волновое
(характеристическое)
сопротивление [Ом]
Найдем напряжение на индуктивности и емкости
U
U ,
r
U
U Cp I X Cp
U ,
r
/ r добротность контура
U Lp I X Lp
Добротность контура (коэффициент резонанса) показывает во сколько раз
напряжение на индуктивности ULp или на емкости UCp при резонансе больше,
чем напряжение, приложенное к цепи.
Величина, обратная добротности, называется затуханием и обозначается α.
 В
Врадиоаппаратуре, где резонансные явления используются наиболее хорошо,
значение добротности контура равно Θ=5-500.
21. 1.12. Резонанс токов
Если к выводам электрической цепи, состоящей из параллельно соединенныхэлементов приложено синусоидальное напряжение, то синусоидальный ток
проходящий через эту цепь равен алгебраической сумме синусоидальных токов в
параллельных ветвях (первый закон Кирхгофа)
Ток в сопротивлении совпадает по фазе с
r
L
C
напряжением ток в индуктивности отстает, а ток
в емкости опережает напряжение на π/2
следовательно суммарный ток в цепи равен
i i i i
1
1
U m sin t
U cos t CU m cos t
r
L m
1
1
U m sin t (
C ) cos t U m g sin t b cos t
L
r
1
b bL bC
C
реактивная
проводимость
L
1
g
активная
проводимость
r
I m sin( t )
y
g 2 b2
полная
проводимость
(1)
Уравнение (1) представляет
собой тригонометрическую
форму записи первого закона
Киргофа для мгновенных
токов
Явление резонанса в электрической цепи, содержащей параллельно
соединенные индуктивные и емкостные элементы называется резонансом
токов.
 Согласно определению, резонанс в данной цепи имеет место в том
Согласно определению, резонанс в данной цепи имеет место в томслучае, когда напряжение и ток на входе совпадают по фазе, т.е. тогда, когда
проводимость цепи будет чисто активной. Комплексная величина полной
проводимости Y равна: Y 1 j ( 1 C ) g j (bL bC ) g jb y j
r
Y g
L
активная
при b
(
1
C ) 0
L
1
C
L
При резонансе ток в неразветвленной цепи
между током и напряжением равен нулю
I U g , а угол сдвига фаз
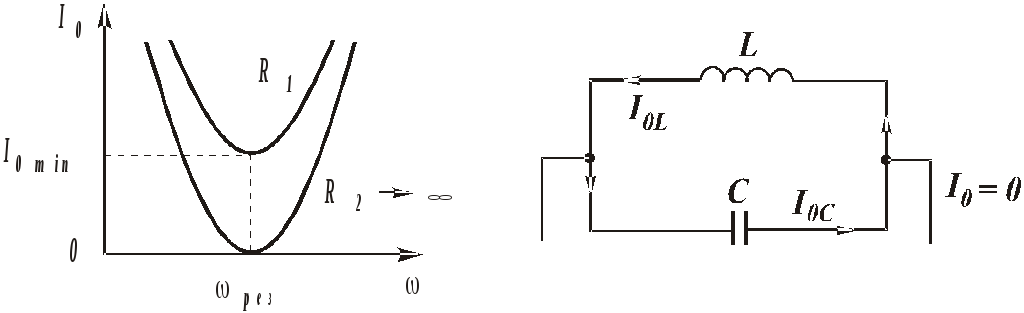
Свойства цепи при резонансе:
— при резонансе полное сопротивление цепи максимальное, т.к. проводимость цепи
минимальная и равна чисто активной проводимости;
— ток в неразветвленной части цепи I будет минимальным
Графики зависимости тока в
неразветвленной части цепи и
полного сопротивления
Векторная диаграмма для
режима резонанса токов
Ток в цепи с L отстает от напряжения на угол
φ1 а ток в цепи с C опережает напряжение на
угол φ2. Вектор тока I в неразветвленной цепи
при резонансе совпадает с вектором
напряжения.
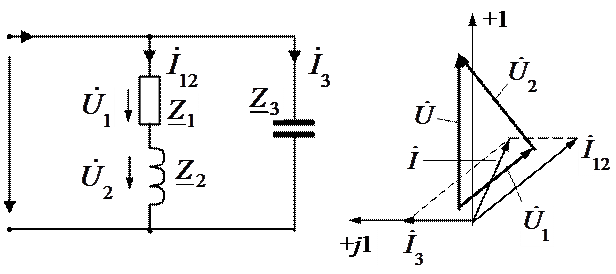 При этом реактивные
При этом реактивныесоставляющие токов IРL и Iрс равны по
величине и противоположно направлены
Реальная схема с учетом активных потерь в ветвях L и С и условие
возникновения резонанса для этой схемы
АНАЛИЗ ωp
1
r12 r22 2
2
r12 r22 2
3
r12 2 è
r22 2
В радиотехнике и электросвязи применяются контуры с малыми
потерями r1
неразветвленной цепи I, и в ветвях I1 и I2 вычисляют по формулам
Добротность контура. Отношение
тока в одной из параллельных ветвей
к току в неразветвленной цепи
называется добротностью контура
при параллельном соединении, а
обратная величина — затуханием
I Lp I ,
I Cp I ,
I Lp I Cp
1
Z r j ( L
)
C
1
L
C
U Lp U ,
U Cp U
1
1
Y j(
C )
r
L
1
C
L
I Lp I ,
I Cp I ,
I Lp I Cp
25. 1.13. Полная, активная и реактивная электрические мощности. Треугольник электрических мощностей
Активная мощность (Р) определяет среднее значение энергии, поступающей вэлектрическую цепь в единицу времени и превращающуюся там в тепло или в другие
виды энергии.

Р = UIcosφ
Активная мощность всегда положительна, имеет размерность [Ватт].
Реактивной мощностью (Q) называют мощность, которая характеризует
интенсивность обмена энергией между источником и реактивными элементами.
Реактивная мощность рассчитывается по формуле:
Q = UI sinφ
и имеет размерность [ВАр].
Q QL QC X L I 2 X C I 2 ( X L X C ) I 2 XI 2
Полной мощностью (S) называется величина, определяемая S = UI и
характеризующая мощность источников переменного тока. Измеряется полная
мощность в [ВА].
Треугольники мощностей
S
P2 Q2
arctg
Позволяют установить связь
между активной, реактивной и
полной мощностями
cos
Q
,
P
P
S
P 2 (QL QC ) 2 ,
P S cos ,
Q S sin
коэффициен т
мощности
26. Методы расчета разветвленных электрических цепей
Метод уравнений Кирхгофа для расчетаразветвленной электрической цепи
Система линейных
уравнений:
Метод Крамера
Определители:
Решение:
Пример
Ветвь, узел и замкнутый контур!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю
Должно быть учтено направление тока по отношению к узлу.

Все токи, направленные к узлу входят в сумму с одним знаком,
а направленные от узла – с противоположным. Первый закон
Кирхгофа может быть сформулирован иначе:
Сумма токов, втекающих в узел, равна
сумме токов вытекающих из узла:
Второй закон Кирхгофа применяется к замкнутым контурам
электрической цепи и формулируется следующим образом:
В любом замкнутом контуре алгебраическая сумма напряжений
на элементах контура равна сумме ЭДС в этом контуре
На основании законов Кирхгофа составляются уравнения для
неизвестных токов в ветвях. Система полученных уравнений
линейна, ее решение позволяет найти неизвестные токи в
ветвях цепи.
1. Обозначим токи во всех
ветвях. Направление токов
выбираем произвольно, но в
цепях с источниками ЭДС
рекомендуется, чтобы
направление токов совпадало с
направлением ЭДС.
2. Составим уравнения по первому закону Кирхгофа. Выбираем 4–1=3 узла
(a, b, c) и для них записываем уравнения:
узел a: I1 — I2 — I3 = 0;
узел b: I2 — I4 + I5 = 0;
узел c: I4 — I5 — I6 = 0.

3. Составим уравнения по второму закону Кирхгофа. Необходимо составить
6–3=3 уравнения. В схеме на рисунке 1 выбираем контура I, II, III и для них
записываем уравнения:
контур I: I1(r01 + R1) + I3R3 = E1;
контур II: I2R2 + I4R4 + I6R7 — I3R3 = 0;
контур III: -I5(r02 + R5 + R6) — I4R4 = -E2.
4. Получаем систему из 6
уравнений с 6 неизвестными:
5. Уравнение можно представить в
матричной форме. Тогда для
заданной электрической цепи
решение системы будет иметь вид
I1 I 2 I 3 0
I I I 0
2 4 5
I 4 I 5 I 6 0
I1 r01 R1 I 3 R3 E1
I 2 R2 I 3 R3 I 4 R4 I 6 R7 0
I 4 R4 I 5 r02 R5 R6 E2
1
1
1
0
0
0
I1
0
0
1
0
1
1
0
I2
0
0
0
0
1
1
1
I3
0
r01 R1
0
R3
0
0
0
0
R2
R3
R4
0
R7
I4
I5
0
0
0
R4
0
I6
r02 R5 R6
E1
0
E2
33.
 Метод контурных токов Суть метода контурных токов: полагают, что в каждом независимом контуре
Метод контурных токов Суть метода контурных токов: полагают, что в каждом независимом контуресхемы течет свой контурный ток. Уравнения составляют относительно
контурных токов, после чего через них определяют токи ветвей. Уравнения
составляются для контура лишь по второму закону Кирхгофа.
Следовательно, метод контурных токов более экономен при вычислительной
работе.
Для трех контуров
Пример: Найти токи в схеме (рис.) методом контурных токов. Числовые
значения сопротивлений в Омах и ЭДС в вольтах указаны на рисунке.
Решение. Выберем направления всех контурных токов I11, I22 и I33 по часовой
стрелке. Определяем:R11 = 5 + 5 + 4 = 14 Ом; R22 = 5 + 10 + 2 = 17 Ом;
R33= 2+ 2+ 1 =5 Ом; R12 = R21 = — 5 Ом; R13 =R31 = 0; R23 = R32 = — 2 Ом;
E11 = -10 В; E33 = -8.
Записываем систему уравнений:
определитель системы
подсчитаем контурные токи
Ток в ветви cm
Icm = I11 — I22 = -0,634-0,224=-0,86 A.
Ток в ветви am
Iam = I22 — I33 = 0,224 + 1,51 = 1,734 A.

35. 1.13. Полная, активная и реактивная электрические мощности. Треугольник электрических мощностей
Активная мощность (Р) определяет среднее значение энергии, поступающей вэлектрическую цепь в единицу времени и превращающуюся там в тепло или в другие
виды энергии.
Р = UIcosφ
Активная мощность всегда положительна, имеет размерность [Ватт].
Реактивной мощностью (Q) называют мощность, которая характеризует
интенсивность обмена энергией между источником и реактивными элементами.
Реактивная мощность рассчитывается по формуле:
Q = UI sinφ
и имеет размерность [ВАр].
Q QL QC X L I 2 X C I 2 ( X L X C ) I 2 XI 2
Полной мощностью (S) называется величина, определяемая S = UI и
характеризующая мощность источников переменного тока. Измеряется полная
мощность в [ВА].
Треугольники мощностей
S
P2 Q2
arctg
Позволяют установить связь
между активной, реактивной и
полной мощностями
cos
Q
,
R
P
S
P 2 (QL QC ) 2 ,
P S cos ,
Q S sin
коэффициен т
мощности
Вектор напряжения — обзор
Кроме того, вектор тока, i * пропорционален вектору напряжения; следовательно, он не имеет ортогональной составляющей по отношению к сетевому напряжению; следовательно, нет передачи реактивной мощности между сетью и РГ.
Пример 8.2
Система DG подключена к распределительной сети через преобразователь постоянного / переменного тока с конфигурацией, показанной на Рисунке 8.19. Система вводит активную мощность 15 кВт с единичным коэффициентом мощности.Напряжение питания 400 В и частота 50 Гц. На PCC подключена нагрузка. Он передает активную мощность 1 МВт и реактивную мощность 0,75 Мвар на номинальное напряжение.
К преобразователю применяется стратегия управления мгновенным единичным коэффициентом мощности. Его работоспособность будет проверена в двух различных ситуациях напряжения:
- •
Синусоидальная, сбалансированная система напряжения.
- •
Несимметричная система сетевого напряжения с составляющей обратной последовательности 20% и несинусоидальная с гармоникой 5-го порядка 15%.
Чтобы проверить работу этой стратегии, система моделируется в MATLAB – Simulink. Система DG подключается к сети с помощью LC-фильтра с индуктивностью 50 мГн и емкостью 0,7 мкФ.
Распределительная сеть моделируется с помощью программируемого трехфазного источника бесконечной мощности. Этот источник позволяет включать в напряжение дисбалансы и гармоники.
Контроллер постоянного тока был опущен, чтобы не влиять на создание текущих ссылок.Как следствие, источники питания постоянного тока используются для подачи необходимого напряжения в цепи постоянного тока. Напряжение звена постоянного тока установлено на 1500 В.
Стратегия управления реализована в соответствии с блок-схемой, показанной на рисунке 8.20, которая является развитием уравнения (8.18). Входными сигналами схемы управления являются вектор фазного напряжения В и активная мощность ДГ P .
Рисунок 8.20. Стратегия управления мгновенным единичным коэффициентом мощности, блок-схема.
В первом случае напряжение синусоидальное со среднеквадратичным значением 400 В и частотой 50 Гц.На рисунке 8.21a показана форма сигнала системного напряжения в PCC. Действующее значение фазного напряжения составляет 230,9 В. Токи, подаваемые системой DG, имеют форму волны, показанную на рисунке 8.21b. Как уже отмечалось, это сбалансированная синусоидальная система. Действующее значение тока составляет 21,5 А.
Действующее значение фазного напряжения составляет 230,9 В. Токи, подаваемые системой DG, имеют форму волны, показанную на рисунке 8.21b. Как уже отмечалось, это сбалансированная синусоидальная система. Действующее значение тока составляет 21,5 А.
Рисунок 8.21. Стратегия управления мгновенным единичным коэффициентом мощности. Балансное и синусоидальное напряжение: (а) напряжение сетки и (б) ток сетки.
Что касается баланса мощности, система DG обеспечивает 14 884 Вт, а распределительная сеть 985 116 Вт, таким образом, активная мощность, потребляемая нагрузкой, составляет 1 МВт.
Во втором случае напряжение распределительной сети имеет составляющую обратной последовательности 20% и гармонику 5-го порядка 15%. Трехфазный источник, моделирующий распределительную сеть, запрограммирован на эти значения. Осциллограммы напряжений показаны на Рисунке 8.22a. Среднеквадратичные значения напряжения для каждой фазы составляют 279, 214 и 214 В.
Рисунок 8.22. Стратегия управления мгновенным единичным коэффициентом мощности. Несимметричное и несинусоидальное напряжение: (а) напряжение сетки и (б) ток сетки.
Несимметричное и несинусоидальное напряжение: (а) напряжение сетки и (б) ток сетки.
Формы сигналов тока, вводимых в систему системой DG, показаны на Рисунке 8.22b. Отмечено, что эти токи не сбалансированы и имеют синусоидальную форму. Текущие среднеквадратичные значения каждой фазы: 23, 20 и 21 A.
Что касается мощности, в этой ситуации DG подает 14 657 Вт, распределительная сеть подает 1 027 676 Вт, а нагрузка потребляет 1 042 333 Вт.
резонанс | вибрация | Британника
резонанс , в физике, относительно большой избирательный отклик объекта или системы, которые колеблются пошагово или фазово, с приложенной извне колебательной силой.Впервые резонанс был исследован в акустических системах, таких как музыкальные инструменты и человеческий голос. Примером акустического резонанса является вибрация, возникающая в струне скрипки или фортепиано с заданной высотой звука, когда рядом поется или играет музыкальная нота той же высоты.
Понятие резонанса было расширено по аналогии на некоторые механические и электрические явления. Известно, что механический резонанс, создаваемый в мостах ветром или марширующими солдатами, достиг размеров, достаточно больших, чтобы быть разрушительными, как в случае разрушения моста Tacoma Narrows Bridge ( кв.v. ) в 1940 году. Космические аппараты, самолеты и надводные аппараты должны быть спроектированы таким образом, чтобы вибрации, вызываемые их двигателями или их движением по воздуху, были сведены к безопасному минимуму.
Известно, что механический резонанс, создаваемый в мостах ветром или марширующими солдатами, достиг размеров, достаточно больших, чтобы быть разрушительными, как в случае разрушения моста Tacoma Narrows Bridge ( кв.v. ) в 1940 году. Космические аппараты, самолеты и надводные аппараты должны быть спроектированы таким образом, чтобы вибрации, вызываемые их двигателями или их движением по воздуху, были сведены к безопасному минимуму.
Подробнее по этой теме
электричество: резонанс
Наиболее интересное состояние, известное как резонанс , возникает, когда фазовый угол равен нулю в уравнении (31) или, что то же самое,…
Резонанс в электрических системах имеет несколько иную природу. Его появление в частотно-чувствительных цепях (переменного тока) позволяет устройствам связи, оборудованным такими цепями, принимать сигналы одних частот и отклонять другие. В телевизионном приемнике, например, резонанс возникает, когда частота одного из входящих сигналов, достигающих цепи, близка к собственной частоте цепи, которая затем реагирует поглощением максимальной энергии из сигнала, когда ток в цепи возвращается назад и вперед в ногу с очень слабым током в антенне.
В ядерном масштабе была обнаружена форма резонанса, отчасти аналогичная определенному виду механического резонанса. Это явление, называемое магнитным резонансом, возникает, когда атомы или их ядра реагируют на приложение различных магнитных полей, испуская или поглощая электромагнитное излучение радио- и микроволнового диапазона. См. Также магнитный резонанс .
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчас% PDF-1.4
%
93 0 объект
>
эндобдж
xref
93 109
0000000016 00000 н.
0000003109 00000 п.
0000003252 00000 н.
0000004201 00000 н.
0000004617 00000 н.
0000005050 00000 н.
0000005086 00000 н.
0000008514 00000 н.
0000011321 00000 п.
0000013974 00000 п.
0000016213 00000 п.
0000016585 00000 п.
0000016979 00000 п.
0000017173 00000 п.
0000017355 00000 п.
0000017497 00000 п.
0000017669 00000 п.
0000017879 00000 п.
0000020885 00000 п.
0000021018 00000 п.
0000021320 00000 н. 0000021606 00000 п.
0000021898 00000 п.
0000024194 00000 п.
0000024487 00000 п.
0000024872 00000 п.
0000025207 00000 п.
0000025372 00000 п.
0000025668 00000 п.
0000025830 00000 п.
0000025995 00000 н.
0000028891 00000 п.
0000032113 00000 п.
0000039794 00000 п.
0000040151 00000 п.
0002265974 00000 п.
0002268044 00000 п.
0002289512 00000 п.
0002298780 00000 п.
0002345085 00000 п.
0002346202 00000 п.
0002371308 00000 п.
0002371337 00000 п.
0002371412 00000 п.
0002371525 00000 п.
0002371802 00000 п.
0002371877 00000 п.
0002371991 00000 п.
0002372269 00000 п.
0002372344 00000 п.
0002372620 00000 п.
0002386076 00000 п.
0002386336 00000 п.
0002386768 00000 п.
0002401237 00000 п.
0002401491 00000 п.
0002401969 00000 п.
0002413539 00000 п.
0002413805 00000 п.
0002414154 00000 п.
0002425953 00000 п.
0002426216 00000 п.
0002426571 00000 п.
0002428810 00000 п.
0002429071 00000 п.
0002429426 00000 п.
0002429516 00000 п.
0002430030 00000 п.
0002430292 00000 п.
0000021606 00000 п.
0000021898 00000 п.
0000024194 00000 п.
0000024487 00000 п.
0000024872 00000 п.
0000025207 00000 п.
0000025372 00000 п.
0000025668 00000 п.
0000025830 00000 п.
0000025995 00000 н.
0000028891 00000 п.
0000032113 00000 п.
0000039794 00000 п.
0000040151 00000 п.
0002265974 00000 п.
0002268044 00000 п.
0002289512 00000 п.
0002298780 00000 п.
0002345085 00000 п.
0002346202 00000 п.
0002371308 00000 п.
0002371337 00000 п.
0002371412 00000 п.
0002371525 00000 п.
0002371802 00000 п.
0002371877 00000 п.
0002371991 00000 п.
0002372269 00000 п.
0002372344 00000 п.
0002372620 00000 п.
0002386076 00000 п.
0002386336 00000 п.
0002386768 00000 п.
0002401237 00000 п.
0002401491 00000 п.
0002401969 00000 п.
0002413539 00000 п.
0002413805 00000 п.
0002414154 00000 п.
0002425953 00000 п.
0002426216 00000 п.
0002426571 00000 п.
0002428810 00000 п.
0002429071 00000 п.
0002429426 00000 п.
0002429516 00000 п.
0002430030 00000 п.
0002430292 00000 п. 0002430755 00000 п.
0002431016 00000 п.
0002441878 00000 п.
0002442141 00000 п.
0002442211 00000 п.
0002442384 00000 п.
0002442411 00000 п.
0002442714 00000 п.
0002454849 00000 п.
0002455102 00000 п.
0002455172 00000 п.
0002455443 00000 п.
0002455470 00000 п.
0002455858 00000 п.
0002456559 00000 п.
0002456834 00000 п.
0002457987 00000 п.
0002458262 00000 п.
0002458594 00000 п.
0002458687 00000 п.
0002459114 00000 п.
0002459378 00000 п.
0002513384 00000 п.
0002562191 00000 п.
0002612278 00000 п.
0002661814 00000 п.
0002715679 00000 н.
0002715708 00000 н.
0002715783 00000 н.
0002715812 00000 н.
0002715887 00000 н.
0002715984 00000 п.
0002716130 00000 n
0002716447 00000 н.
0002716502 00000 н.
0002716618 00000 п.
0002716730 00000 н.
0002716854 00000 п.
0000002939 00000 н.
0000002524 00000 н.
трейлер
] >>
startxref
0
%% EOF
201 0 объект
> поток
x \ KBq
0002430755 00000 п.
0002431016 00000 п.
0002441878 00000 п.
0002442141 00000 п.
0002442211 00000 п.
0002442384 00000 п.
0002442411 00000 п.
0002442714 00000 п.
0002454849 00000 п.
0002455102 00000 п.
0002455172 00000 п.
0002455443 00000 п.
0002455470 00000 п.
0002455858 00000 п.
0002456559 00000 п.
0002456834 00000 п.
0002457987 00000 п.
0002458262 00000 п.
0002458594 00000 п.
0002458687 00000 п.
0002459114 00000 п.
0002459378 00000 п.
0002513384 00000 п.
0002562191 00000 п.
0002612278 00000 п.
0002661814 00000 п.
0002715679 00000 н.
0002715708 00000 н.
0002715783 00000 н.
0002715812 00000 н.
0002715887 00000 н.
0002715984 00000 п.
0002716130 00000 n
0002716447 00000 н.
0002716502 00000 н.
0002716618 00000 п.
0002716730 00000 н.
0002716854 00000 п.
0000002939 00000 н.
0000002524 00000 н.
трейлер
] >>
startxref
0
%% EOF
201 0 объект
> поток
x \ KBq
в параллельных цепях — Инженеры Страница
Резонансный ток
Как показано на рисунке (B), поскольку безваттная составляющая тока равна нулю, ток в цепи равен
Положив значение Z2 = L / C из (i) выше, мы получаем
Знаменатель L / CR известен как эквивалент или динамическое сопротивление параллельной цепи в резонансе. Следует отметить, что сопротивление является только «резистивным». Поскольку ток в резонансе минимален, L / CR должны, следовательно, представлять максимальное сопротивление цепи. Фактически, параллельный резонанс — это условие максимального импеданса или минимальной проводимости.
Следует отметить, что сопротивление является только «резистивным». Поскольку ток в резонансе минимален, L / CR должны, следовательно, представлять максимальное сопротивление цепи. Фактически, параллельный резонанс — это условие максимального импеданса или минимальной проводимости.
Ток в резонансе минимален, поэтому такую схему (при использовании в радиоработах) иногда называют схемой отклонителя, потому что она отклоняет (или принимает минимальный ток) ту частоту , с которой она резонирует. Этот резонанс часто называют токовым резонансом также потому, что ток, циркулирующий между двумя ветвями, во много раз превышает линейный ток, снимаемый с источника питания.
Явление параллельного резонанса имеет большое практическое значение, поскольку оно лежит в основе настраиваемых схем в электронике. Изменения импеданса и тока в зависимости от частоты показаны на рисунке (B). Как видно, на резонансной частоте импеданс максимален и равен L / CR. Следовательно, ток при резонансе минимален и составляет = V / (L / CR). На нерезонансных частотах сопротивление уменьшается и, как следствие, увеличивается ток, как показано.
Следовательно, ток при резонансе минимален и составляет = V / (L / CR). На нерезонансных частотах сопротивление уменьшается и, как следствие, увеличивается ток, как показано.
Альтернативное лечение
Теперь цепь будет в резонансе, когда j-компонент комплексной полной проводимости равен нулю i.е. когда
или X L X C = R 2 + X L 2 = Z 2 –—————— как раньше
Говоря с точки зрения восприимчивости, Вышеуказанные соотношения можно представить в виде: Индуктивная проводимость
емкостная проводимость B C = 1 / X C
Чистая проводимость B = (B C — B L )
∴ Y = G + j (B C — B L ) = G + jB.
Считается, что параллельная цепь находится в резонансе, когда B = 0.
∴ B C — B L = 0 или
Остальная процедура такая же, как и выше. Можно отметить, что в резонансе проводимость равна проводимости .
Можно отметить, что в резонансе проводимость равна проводимости .
Распределение поверхностного тока и электрического поля при резонансе …
Плевральный выпот и отек легких — это состояния, характеризующиеся избыточным накоплением жидкости в плевральной полости и воздушных мешках легких, соответственно. Эти состояния возникают в результате нескольких заболеваний, таких как различные виды рака и сердечная недостаточность.Помимо важности мониторинга этих состояний для лечения первичного источника экссудата, решающее значение имеет диагностика и, следовательно, предотвращение этих проявлений, поскольку избыток жидкости внутри грудной стенки сопровождается серьезными осложнениями дыхания. Таким образом, раннее обнаружение скопления жидкости в грудной клетке и, что более важно, наблюдение за его прогрессированием ценны при управлении многими опасными для жизни ситуациями. Рентген грудной клетки, магнитно-резонансная томография (МРТ) и компьютерная томография (КТ) — обычные методы, используемые для обнаружения избыточной жидкости внутри туловища. Несмотря на свои выдающиеся характеристики, эти устройства не подходят для частого мониторинга из-за воздействия на пациентов ионизирующего излучения, недостаточной чувствительности для обнаружения небольшого количества жидкости и требований к экранированию. Поэтому исследователи предложили альтернативные подходы, такие как системы электромагнитной визуализации (EMI). Скопление жидкости внутри туловища приводит к изменению диэлектрических свойств легочной ткани, что может быть обнаружено с помощью методов электромагнитного излучения. Несмотря на обычные инструменты, системы EMI являются недорогими, низкопрофильными, портативными и безопасными из-за их маломощного неионизирующего излучения, что делает их подходящими альтернативами для целей диагностики и мониторинга.В системах EMI антенны играют важную роль в передаче / приеме электромагнитных сигналов в / из целевой области. Для систем EMI были предложены различные типы широкополосных антенн с фиксированным однонаправленным излучением. Несмотря на их выдающиеся характеристики, их основным ограничением является фиксированная диаграмма направленности.
Несмотря на свои выдающиеся характеристики, эти устройства не подходят для частого мониторинга из-за воздействия на пациентов ионизирующего излучения, недостаточной чувствительности для обнаружения небольшого количества жидкости и требований к экранированию. Поэтому исследователи предложили альтернативные подходы, такие как системы электромагнитной визуализации (EMI). Скопление жидкости внутри туловища приводит к изменению диэлектрических свойств легочной ткани, что может быть обнаружено с помощью методов электромагнитного излучения. Несмотря на обычные инструменты, системы EMI являются недорогими, низкопрофильными, портативными и безопасными из-за их маломощного неионизирующего излучения, что делает их подходящими альтернативами для целей диагностики и мониторинга.В системах EMI антенны играют важную роль в передаче / приеме электромагнитных сигналов в / из целевой области. Для систем EMI были предложены различные типы широкополосных антенн с фиксированным однонаправленным излучением. Несмотря на их выдающиеся характеристики, их основным ограничением является фиксированная диаграмма направленности. Следовательно, для сканирования различных частей туловища необходим массив антенн вдоль туловища или механически подвижная конструкция. Однако это приводит к получению сложной и громоздкой системы, которая подвержена механическим ошибкам перемещения.Чтобы преодолеть это ограничение, в качестве платформы сканирования можно использовать антенны с изменяемой диаграммой направленности.
В этой диссертации представлены различные типы реконфигурируемых антенн, используемых в системах EMI для электронного сканирования всей области грудной клетки человека для обнаружения скопления жидкости внутри легких. Предлагаются различные методологии и теоретический анализ для разработки новых поколений антенн с реконфигурируемой диаграммой направленности, что привело к созданию шести различных типов антенн. Предложенные антенны были реализованы и успешно протестированы в системе EMI с использованием реалистичных фантомов для обнаружения избыточной жидкости внутри грудной клетки.Первый вклад в эту диссертацию посвящен конструкции плоских антенн с петлевым дипольным переключением луча, способных сканировать всю область туловища. Антенна состоит из одноволновой петли, модифицированного полуволнового диполя-бабочки и двух паразитных направляющих. Управление лучом достигается с помощью паразитных направляющих для изменения распределения тока в контуре и, таким образом, позволяет переключать луч.
Второй вклад — разработка поверхностей с высоким импедансом для увеличения усиления и уменьшения обратного излучения.Во-первых, предлагается реконфигурируемая антенна типа бабочка с широкополосной диаграммой направленности на индуктивном отражателе. Антенна может управлять диаграммой направленности в одной плоскости. Затем был разработан другой механизм управления лучом на основе гофрированных поперечно-щелевых излучателей с паразитными щелями на индуктивном отражателе. Антенна способна двумерно (2-D) переключать луч как в азимутальной, так и в наклонной плоскости.
Чтобы добиться низкопрофильных структур и уменьшить общую высоту антенн, отражающие поверхности могут быть заменены передающими метаповерхностями.В результате метаповерхности тщательно исследуются как третий вклад. Метод смещения сначала представлен для проектирования метаповерхности управления лучом. Механизм управления лучом основан на возбуждении каждой элементарной ячейки метаповерхности с разными фазовыми задержками путем изменения положения излучающей щели. Чтобы преодолеть ограничение метода смещения для двумерного управления лучом, предлагается другой механизм управления лучом, основанный на активации / деактивации элементарных ячеек.
Четвертым вкладом в диссертацию является разработка линзовых антенн, согласованных с телом.Метаповерхности эффективны для создания сфокусированного излучения плоской волны внутри области визуализации. Однако они по-прежнему страдают от отражений от кожи, что значительно снижает проникновение волн внутрь туловища человека. Следовательно, существует потребность в структурах, которые могут действовать как согласующая среда при формировании сфокусированного поля в ближней зоне внутри области формирования изображения. С этой целью предлагается антенна с согласованной линзой с градиентным индексом (GRIN), сфокусированная на теле луча в ближнем поле.
Последний, но не менее важный вклад — это проверка способности изготовленных конструкций создавать платформы EMI.Испытательная установка включает в себя предлагаемые антенны в качестве излучающих элементов, искусственный фантом туловища, микроволновый приемопередатчик и блок обработки для обнаружения скопления жидкости внутри грудной клетки. Используется модифицированный алгоритм микроволнового изображения на основе радара, который может успешно обнаруживать скопившуюся жидкость внутри фантома торса человека.
Следовательно, для сканирования различных частей туловища необходим массив антенн вдоль туловища или механически подвижная конструкция. Однако это приводит к получению сложной и громоздкой системы, которая подвержена механическим ошибкам перемещения.Чтобы преодолеть это ограничение, в качестве платформы сканирования можно использовать антенны с изменяемой диаграммой направленности.
В этой диссертации представлены различные типы реконфигурируемых антенн, используемых в системах EMI для электронного сканирования всей области грудной клетки человека для обнаружения скопления жидкости внутри легких. Предлагаются различные методологии и теоретический анализ для разработки новых поколений антенн с реконфигурируемой диаграммой направленности, что привело к созданию шести различных типов антенн. Предложенные антенны были реализованы и успешно протестированы в системе EMI с использованием реалистичных фантомов для обнаружения избыточной жидкости внутри грудной клетки.Первый вклад в эту диссертацию посвящен конструкции плоских антенн с петлевым дипольным переключением луча, способных сканировать всю область туловища. Антенна состоит из одноволновой петли, модифицированного полуволнового диполя-бабочки и двух паразитных направляющих. Управление лучом достигается с помощью паразитных направляющих для изменения распределения тока в контуре и, таким образом, позволяет переключать луч.
Второй вклад — разработка поверхностей с высоким импедансом для увеличения усиления и уменьшения обратного излучения.Во-первых, предлагается реконфигурируемая антенна типа бабочка с широкополосной диаграммой направленности на индуктивном отражателе. Антенна может управлять диаграммой направленности в одной плоскости. Затем был разработан другой механизм управления лучом на основе гофрированных поперечно-щелевых излучателей с паразитными щелями на индуктивном отражателе. Антенна способна двумерно (2-D) переключать луч как в азимутальной, так и в наклонной плоскости.
Чтобы добиться низкопрофильных структур и уменьшить общую высоту антенн, отражающие поверхности могут быть заменены передающими метаповерхностями.В результате метаповерхности тщательно исследуются как третий вклад. Метод смещения сначала представлен для проектирования метаповерхности управления лучом. Механизм управления лучом основан на возбуждении каждой элементарной ячейки метаповерхности с разными фазовыми задержками путем изменения положения излучающей щели. Чтобы преодолеть ограничение метода смещения для двумерного управления лучом, предлагается другой механизм управления лучом, основанный на активации / деактивации элементарных ячеек.
Четвертым вкладом в диссертацию является разработка линзовых антенн, согласованных с телом.Метаповерхности эффективны для создания сфокусированного излучения плоской волны внутри области визуализации. Однако они по-прежнему страдают от отражений от кожи, что значительно снижает проникновение волн внутрь туловища человека. Следовательно, существует потребность в структурах, которые могут действовать как согласующая среда при формировании сфокусированного поля в ближней зоне внутри области формирования изображения. С этой целью предлагается антенна с согласованной линзой с градиентным индексом (GRIN), сфокусированная на теле луча в ближнем поле.
Последний, но не менее важный вклад — это проверка способности изготовленных конструкций создавать платформы EMI.Испытательная установка включает в себя предлагаемые антенны в качестве излучающих элементов, искусственный фантом туловища, микроволновый приемопередатчик и блок обработки для обнаружения скопления жидкости внутри грудной клетки. Используется модифицированный алгоритм микроволнового изображения на основе радара, который может успешно обнаруживать скопившуюся жидкость внутри фантома торса человека.
16.6 Стоячие волны и резонанс — University Physics Volume 1
На протяжении всей этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое.При определенных условиях волны могут подпрыгивать назад и вперед через определенную область, фактически становясь стационарными. Они называются стоячими волнами .
Другой связанный эффект известен как резонанс. В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызывать движение большой амплитуды. Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды.Иногда этот резонанс бывает хорошим — например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
Стоячие волны
Иногда кажется, что волны не двигаются; скорее, они просто вибрируют на месте. Например, вы можете увидеть неподвижные волны на поверхности стакана с молоком в холодильнике.Вибрация двигателя холодильника создает волны на молоке, которые колеблются вверх и вниз, но не движутся по поверхности. (Рисунок) показывает эксперимент, который вы можете попробовать дома. Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны. Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на (Рисунок) для двух идентичных волн, движущихся в противоположных направлениях.Волны движутся друг сквозь друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Рисунок 16.25 Стоячие волны образуются на поверхности миски с молоком, установленной на ящичном веере. Вибрация вентилятора заставляет поверхность молока колебаться. Волны видны из-за отражения света от лампы. рисунок 16.26 Временные снимки двух синусоид. Красная волна движется в направлении -x, а синяя волна движется в направлении + x. Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точкахи обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени. Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию
., а вторая волна имеет волновую функцию
. Волны интерферируют и образуют результирующую волну
Это можно упростить с помощью тригонометрического идентификатора
где
и
, что дает нам
, что упрощается до
Обратите внимание, что результирующая волна представляет собой синусоидальную волну, которая является функцией только положения, умноженной на функцию косинуса, которая является функцией только времени.Графики x ( x , t ) в зависимости от x для различных моментов времени показаны на (Рисунок). Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна является суммой двух волн. По мере того, как красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и деструктивной интерференции.
Первоначально в момент времени
две волны находятся в фазе, и в результате получается волна, которая в два раза превышает амплитуду отдельных волн.Волны также находятся в фазе в момент
.Фактически, волны находятся в фазе в любом целом кратном половине периода:
В остальное время две волны равны
не в фазе, и результирующая волна равна нулю. Это происходит на
Обратите внимание, что некоторые положения результирующей волны x всегда равны нулю, независимо от фазового соотношения. Эти позиции называются узлами .Где возникают узлы? Рассмотрим решение суммы двух волн
Нахождение позиций, в которых функция синуса равна нулю, обеспечивает положение узлов.
Есть также позиции, в которых y колеблются между
. Это пучностей . Мы можем найти их, посчитав, какие значения x дают
.
В результате получается стоячая волна, как показано на (Рисунок), где показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях.Результирующая волна представляет собой синусоидальную волну с узлами в целых кратных половинных длинах волн. Пучности колеблются между
.из-за члена косинуса,
, который колеблется между
.
Результирующая волна кажется неподвижной, без видимого движения в направлении x , хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x .(Рисунок) показывает различные снимки получившейся волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
Рисунок 16.27 Когда две идентичные волны движутся в противоположных направлениях, результирующая волна является стоячей волной. Узлы появляются в целых числах, кратных половине длины волны. Пучности появляются с нечетными числами, кратными четверти длины волны, где они колеблются междуУзлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами. Когда струна защипывается, импульсы проходят по струне в противоположных направлениях. Концы струн фиксируются на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на (Рисунок).
Рисунок 16.28 Лабораторная установка для создания стоячих волн на струне. У струны есть узел на каждом конце и постоянная линейная плотность. Длина между фиксированными граничными условиями равна L. Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f .Другой конец струны проходит над шкивом без трения и привязан к подвешенной массе. Величина натяжения тетивы равна весу подвешенной массы. Струна имеет постоянную линейную плотность (масса на длину)
, а скорость, с которой волна распространяется по струне, равна
.(рисунок). Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны.Начиная с нулевой частоты и медленно увеличивая частоту, первая мода
выглядит так, как показано на (Рисунок). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами
. Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
., где скорость волны
Сохранение постоянного напряжения и увеличение частоты приводит ко второй гармонике или
режим.Этот режим — полная длина волны
, а частота в два раза больше основной частоты:
Рисунок 16.29 Стоячие волны, создаваемые на струне длиной L. Узлы возникают на каждом конце струны. Узлы — это граничные условия, которые ограничивают возможные частоты, возбуждающие стоячие волны. (Обратите внимание, что амплитуды колебаний оставались постоянными для визуализации. Возможные модели стоячих волн на струне известны как нормальные моды.Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды при увеличении частоты.)Следующие две моды или третья и четвертая гармоники имеют длины волн
.и
работает на частотах
и
Все частоты выше частоты
известны как обертоны . Уравнения для длины волны и частоты можно резюмировать как:
Возможные для струны модели стоячей волны, первые четыре из которых показаны на (Рисунок), известны как нормальные моды с частотами, известными как нормальные частоты.Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота
нормальный режим струны — это первый обертон (или вторая гармоника). Частота
нормальный режим — это второй обертон (или третья гармоника) и так далее.
Решения, показанные как (Уравнение) и (Уравнение), предназначены для строки с граничным условием узла на каждом конце.Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. (Уравнение) и (Уравнение) подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример
Стоячие волны на струне
Рассмотрим строку
, прикрепленный к струнному вибратору с регулируемой частотой, как показано на (Рисунок). Волны, создаваемые вибратором, распространяются по струне и отражаются фиксированным граничным условием на шкиве.Струна, имеющая линейную массовую плотность
проходит через шкив без трения с незначительной массой, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые должен быть настроен струнный вибратор, чтобы произвести первые три нормальные моды стоячих волн.
Рисунок 16.30 Струна, прикрепленная к струнному вибратору с регулируемой частотой.Стратегия
- Скорость волны можно найти с помощью
Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет составлять половину волны. Второй можно найти, добавив половину длины волны. Это самая короткая длина, которая приведет к образованию узла на границах.Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на (Рисунок).
- Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны. Рисунок 16.31 (a) На рисунке представлен второй режим строки, который удовлетворяет граничным условиям узла на каждом конце строки. (b) Этот рисунок не может быть нормальным режимом для струны, потому что он не удовлетворяет граничным условиям.На одном конце есть узел, а на другом — пучность.
Решение
- Начните со скорости волны на струне. Натяжение равно весу подвешенной массы. Даны линейная массовая плотность и масса подвешенной массы:
- Первая нормальная мода с узлами на каждом конце — это половина длины волны. Следующие две моды находятся путем добавления половины длины волны.
- Частоты первых трех мод находятся с помощью
Значение
Три режима стоя в этом примере были созданы путем поддержания натяжения струны и регулировки частоты возбуждения.Сохранение постоянного натяжения струны приводит к постоянной скорости. Те же самые режимы можно было бы получить, сохранив постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу).
Проверьте свое понимание
Уравнения для длин волн и частот мод волны, создаваемой на струне:
были получены путем рассмотрения волны на струне, где были симметричные граничные условия узла на каждом конце.Эти режимы являются результатом двух синусоидальных волн с идентичными характеристиками, за исключением того, что они движутся в противоположных направлениях, ограниченных областью L с узлами, необходимыми на обоих концах. Будут ли работать те же уравнения при наличии симметричных граничных условий с пучностями на каждом конце? Как бы выглядели нормальные режимы для среды, которая могла бы свободно колебаться на каждом конце? Не беспокойтесь, если вы не можете представить себе такую среду, просто рассмотрите две синусоидальные волновые функции в области длиной L с пучностями на каждом конце.
Да, уравнения будут одинаково хорошо работать для симметричных граничных условий среды, свободно колеблющейся на каждом конце, где на каждом конце есть пучности. Ниже показаны нормальные режимы первых трех режимов. Пунктирная линия показывает положение равновесия среды.
Обратите внимание, что первая мода составляет две четверти или половину длины волны. Вторая мода — это одна четверть длины волны, за которой следует половина длины волны, за которой следует четверть длины волны или одна полная длина волны.Третья мода — полторы длины волны. Это тот же результат, что и у строки с узлами на каждом конце. Уравнения для симметричных граничных условий одинаково хорошо работают как для фиксированных граничных условий, так и для свободных граничных условий. К этим результатам мы вернемся в следующей главе, когда будем обсуждать звуковую волну в открытой трубке.
Свободные граничные условия, показанные в последнем разделе «Проверьте свое понимание», могут показаться трудными для визуализации. Как может быть система, которая может свободно колебаться на каждом конце? На (Рисунок) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим).В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При соответствующей частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, составляющих четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При соответствующей частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности.Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и примите во внимание (рисунок).
Рисунок 16.32 (a) Металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на каждом конце. При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с узлом на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца.При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с пучностями на каждом конце. Рисунок 16.33 Длину волны можно измерить между двумя ближайшими повторяющимися точками. На волне на веревке это означает одинаковую высоту и наклон. (а) Длина волны измеряется между двумя ближайшими точками, где высота равна нулю, а наклон является максимальным и положительным. (b) Длина волны измеряется между двумя идентичными точками, где высота максимальна, а наклон равен нулю.Обратите внимание, что изучение стоячих волн может стать довольно сложным. На (Рисунок) (а) модель
Показана мода стоячей волны, которая дает длину волны, равную L . В этой конфигурации
Режимтакже был бы возможен с стоячей волной, равной 2 L . Можно ли получить
для конфигурации, показанной в части (b)? Ответ — нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия.Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн. Следует отметить, что когда система приводится в действие с частотой, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, производимый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле. Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, для поиска частот звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте.Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире. Воздух в трубке, например, в музыкальном инструменте, таком как флейта, может вызвать резонанс и произвести приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения дает доказательства наличия условий, подходящих для резонанса, стоячих волн, а также конструктивных и деструктивных помех.Здание может колебаться в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, создавая резонанс, в результате которого одно здание рушится, а соседние — нет. Часто здания определенной высоты разрушаются, в то время как другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто бывает, что спортзалы, супермаркеты и церкви страдают от повреждений, тогда как отдельные дома страдают гораздо меньше.Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Поскольку волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникает конструктивная интерференция. Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше — повреждены.
Как это работает ?: Магнитно-резонансная томография
Магнитно-резонансная томография (МРТ) использует естественные магнитные свойства тела для получения детальных изображений любой части тела.Для визуализации используется ядро водорода (отдельный протон) из-за его большого количества в воде и жире.
Водородный протон можно сравнить с планетой Земля, вращающейся вокруг своей оси с полюсом север-юг. В этом отношении он ведет себя как небольшой стержневой магнит. В нормальных условиях эти водородные протонные «магниты-стержни» вращаются в теле, а их оси случайно выровнены.
Когда тело помещается в сильное магнитное поле, например в МРТ-сканер, оси протонов совпадают.Это равномерное выравнивание создает магнитный вектор, ориентированный вдоль оси сканера МРТ. Сканеры МРТ имеют разную напряженность поля, обычно от 0,5 до 1,5 тесла.
Когда к магнитному полю добавляется дополнительная энергия (в виде радиоволны), магнитный вектор отклоняется. Частота радиоволн (RF), которая вызывает резонанс ядер водорода, зависит от искомого элемента (в данном случае водорода) и силы магнитного поля.
Напряженность магнитного поля может быть изменена электронным способом с головы до ног с помощью ряда градиентных электрических катушек, и, изменяя локальное магнитное поле этими небольшими приращениями, различные части тела будут резонировать при применении разных частот.
Когда радиочастотный источник выключен, магнитный вектор возвращается в состояние покоя, и это вызывает излучение сигнала (также радиоволны). Именно этот сигнал используется для создания МРТ изображений. Катушки приемника используются вокруг рассматриваемой части тела, чтобы действовать как антенны, чтобы улучшить обнаружение излучаемого сигнала. Затем интенсивность принятого сигнала наносится на шкалу серого и строятся изображения поперечного сечения.
Несколько переданных радиочастотных импульсов можно использовать последовательно, чтобы выделить определенные ткани или аномалии.Другой акцент возникает из-за того, что разные ткани расслабляются с разной скоростью, когда переданный радиочастотный импульс выключен. Время, необходимое протонам для полной релаксации, измеряется двумя способами. Первый — это время, необходимое для возврата магнитного вектора в состояние покоя, а второе — время, необходимое для того, чтобы осевое вращение вернулось в состояние покоя. Первый называется релаксацией T1, второй — релаксацией T2.
Таким образом, МРТ состоит из серии импульсных последовательностей.Различные ткани (например, жир и вода) имеют разное время релаксации и могут быть идентифицированы отдельно. Например, используя импульсную последовательность «подавления жира», сигнал от жира будет удален, оставив только сигнал от любых отклонений, лежащих в нем.
Большинство заболеваний проявляются увеличением содержания воды, поэтому МРТ является чувствительным тестом для выявления заболеваний.

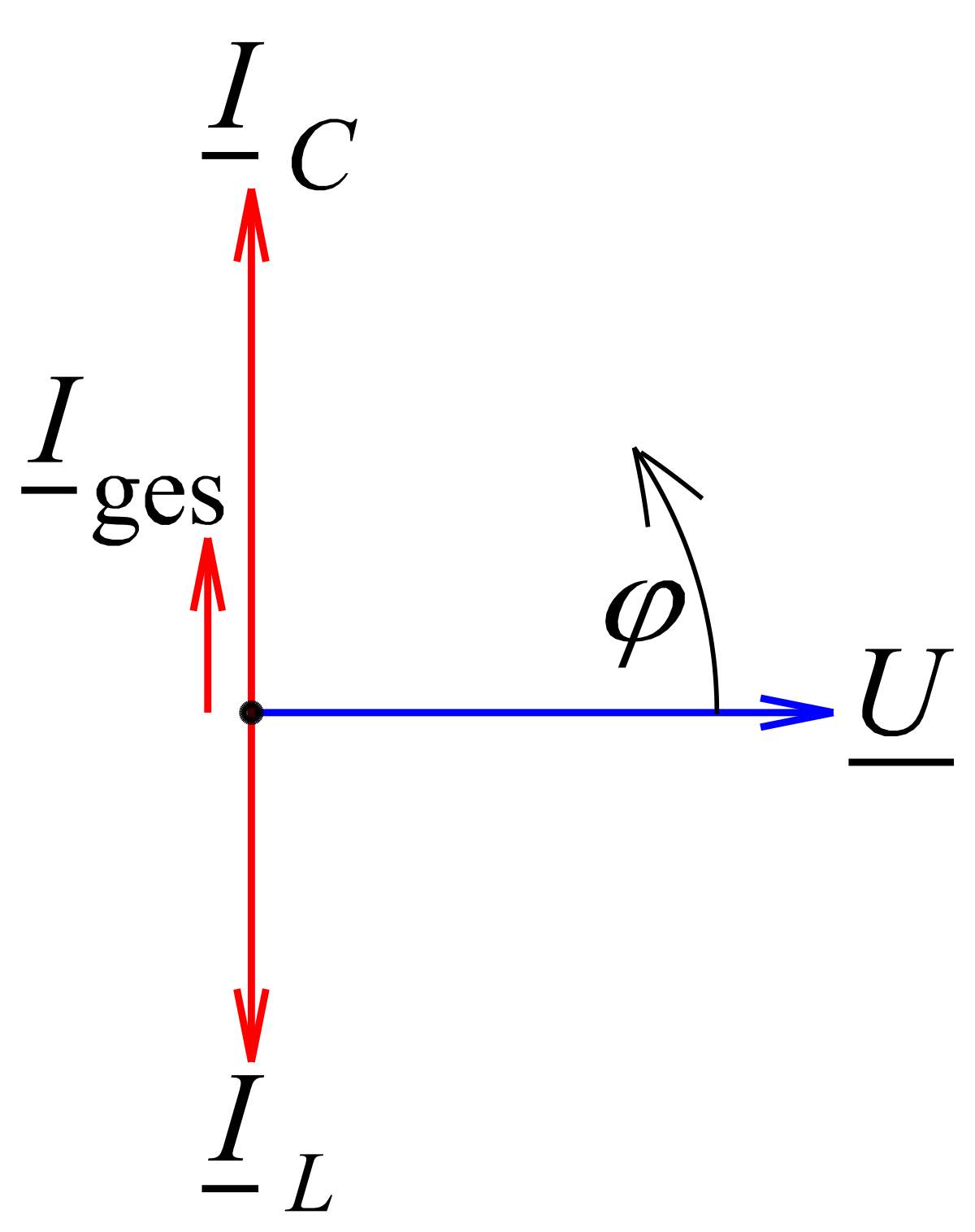 При
точном построении векторов можно
непосредственно из диаграммы определить
амплитуды и фазы искомых величин.
Приближенное (качественное) построение
диаграмм при аналитическом решении
служит надежным контролем корректности
хода решения и позволяет легко
определить квадрант, в котором
находятся определяемые векторы.
При
точном построении векторов можно
непосредственно из диаграммы определить
амплитуды и фазы искомых величин.
Приближенное (качественное) построение
диаграмм при аналитическом решении
служит надежным контролем корректности
хода решения и позволяет легко
определить квадрант, в котором
находятся определяемые векторы. Они представляют собой соединенные
соответственно схеме электрической
цепи точки на комплексной плоскости,
отображающие их потенциалы. На
топографической диаграмме, представляющей
собой в принципе векторную диаграмму,
порядок расположения векторов
напряжений строго соответствует
порядку расположения элементов в
схеме, а вектор падения напряжения
на каждом последующем элементе
примыкает к концу вектора напряжения
на каждом предыдущем элементе.
Они представляют собой соединенные
соответственно схеме электрической
цепи точки на комплексной плоскости,
отображающие их потенциалы. На
топографической диаграмме, представляющей
собой в принципе векторную диаграмму,
порядок расположения векторов
напряжений строго соответствует
порядку расположения элементов в
схеме, а вектор падения напряжения
на каждом последующем элементе
примыкает к концу вектора напряжения
на каждом предыдущем элементе.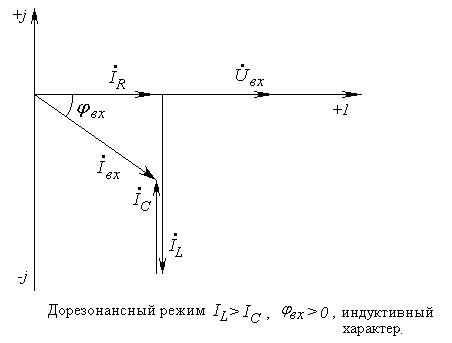 рис. 2). Векторную диаграмму можно
строить, имея запись комплекса в
показательной форме, т.е. по значениям
модуля и фазы . Однако на практике
удобнее проводить построения, используя
алгебраическую форму записи, поскольку
при этом вещественная и мнимая
составляющие комплексной величины
непосредственно откладываются на
соответствующих осях комплексной
плоскости, определяя положение точки
на ней.
рис. 2). Векторную диаграмму можно
строить, имея запись комплекса в
показательной форме, т.е. по значениям
модуля и фазы . Однако на практике
удобнее проводить построения, используя
алгебраическую форму записи, поскольку
при этом вещественная и мнимая
составляющие комплексной величины
непосредственно откладываются на
соответствующих осях комплексной
плоскости, определяя положение точки
на ней.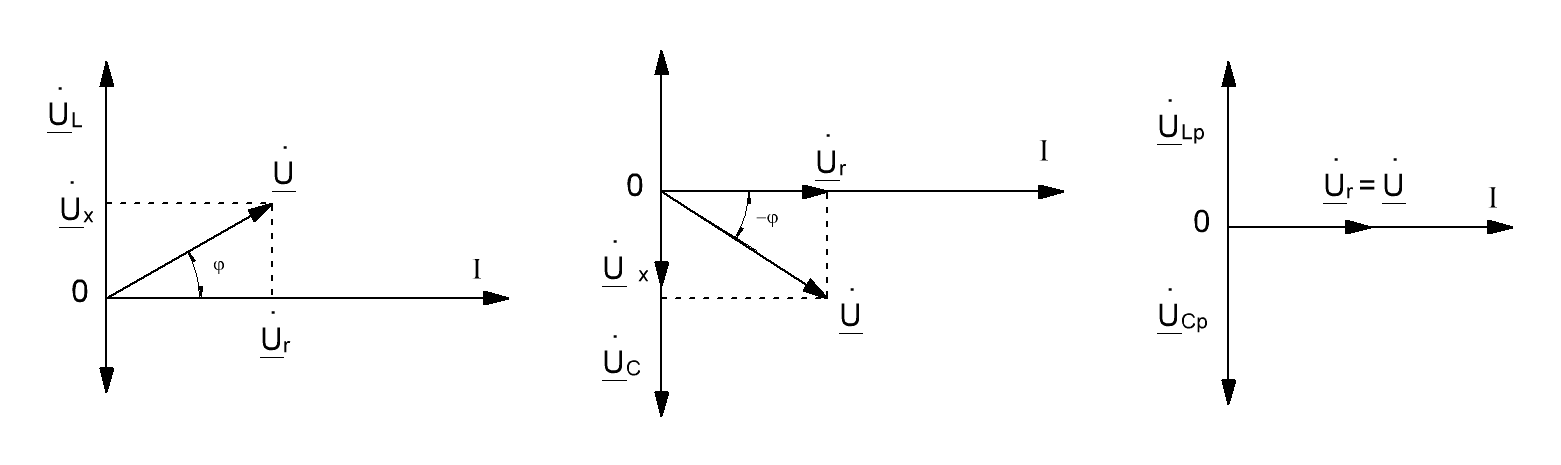 Чаще
используют второй вариант.
Чаще
используют второй вариант. Таким образом,
второй закон Кирхгофа выполняется,
а следовательно, вычисления выполнены
верно. В соответствии с полученными
результатами строится топографическая
диаграмма на рис. 2. Следует обратить
внимание на ориентацию векторов,
составляющих топографическую
диаграмму, относительно векторов
тока: для резистивных элементов
соответствующие векторы параллельны,
для индуктивного и емкостных –
ортогональны.
Таким образом,
второй закон Кирхгофа выполняется,
а следовательно, вычисления выполнены
верно. В соответствии с полученными
результатами строится топографическая
диаграмма на рис. 2. Следует обратить
внимание на ориентацию векторов,
составляющих топографическую
диаграмму, относительно векторов
тока: для резистивных элементов
соответствующие векторы параллельны,
для индуктивного и емкостных –
ортогональны.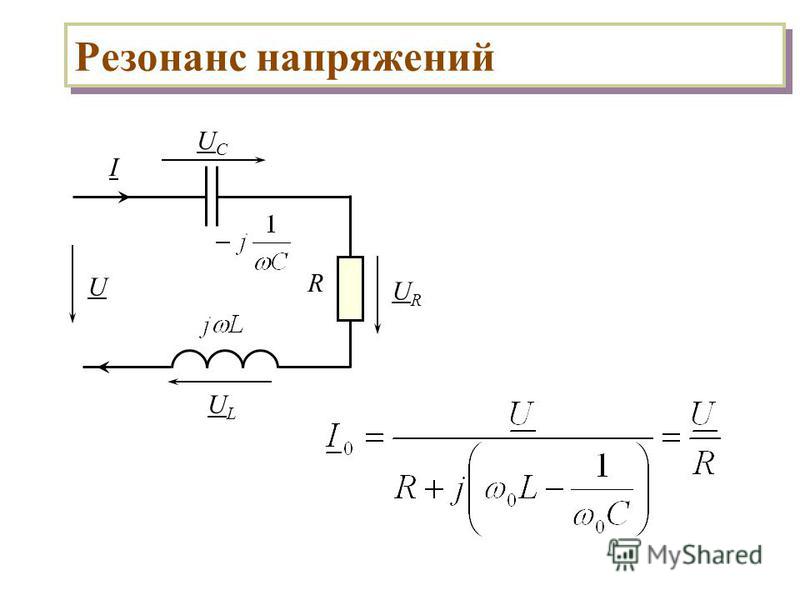 Таким образом, каждой точке
рассматриваемого участка или контура
соответствует точка на потенциальной
диаграмме.
Таким образом, каждой точке
рассматриваемого участка или контура
соответствует точка на потенциальной
диаграмме. .. . С удовольствием вспоминаю лекции В.И. Бакштановского и В. И. Ротницкого. С открытым ртом слушал лекции по эстетике и до сих … -64-2. По окончании института в 1969 году был оставлен на кафедре ТОЭ и электрических …
.. . С удовольствием вспоминаю лекции В.И. Бакштановского и В. И. Ротницкого. С открытым ртом слушал лекции по эстетике и до сих … -64-2. По окончании института в 1969 году был оставлен на кафедре ТОЭ и электрических … .. угодно или — везде. Сегодня читает лекции в Лондоне, завтра отправляется к …
.. угодно или — везде. Сегодня читает лекции в Лондоне, завтра отправляется к …