Генерация второй гармоники 📙 — Физика
1. Теория эффекта
2. Режим генерации второй гармоники
3. Генерация второй гармоники в нелинейном кристалле
С появлением мощных первоисточников согласованного светопреломления оптического объёма применение нелинейных процессов в оптике получилось возможным и несложным. В этих явлениях, в противоположность от простых световых процессов, возникает отступление от принципов суперпозиции оптических волн.
Определение 1
Генерация второй гармоники — нелинейный оптический эффект. В данном эффекте фотоны с идентичной частотой, взаимно действуя с нелинейным веществом, концентрируются для создания новых фотонов с двойной энергией, и, стало быть, с двойной частотой и длиной волны в два раза меньшей изначальной. Это индивидуальный случай нелинейного суммирования частот светоизлучения.
В нынешнее время основной методикой приобретения акустических частот лазерного излучения представляется генерация второй гармоники, которая предполагает создание огромного импульса.
После чего присоединяется доброкачественность вибратора, число фотонов начинается сразу возрастать, что создаёт инициирование пронзительного короткого сигнала. В этой ситуации значительным является время существования элементарной частицы на высоком уровне, каковой обязан быть очень длительным.
Генерация второй гармоники обнаруживается в:
- Сегнетоэлектриках с высокой поляризуемостью.
- Полимерах, которые содержат молекулы с нелинейно-оптическими хромофорами.
- В волновых представлениях со спонтанной поляризацией.
Не нашли что искали?
Просто напиши и мы поможем
Исследования увеличения частоты в два раза в генерации второй гармоники обеспечили возможность специалистам обнаружить новые обоснованности взаимные связи световых потоков с веществом.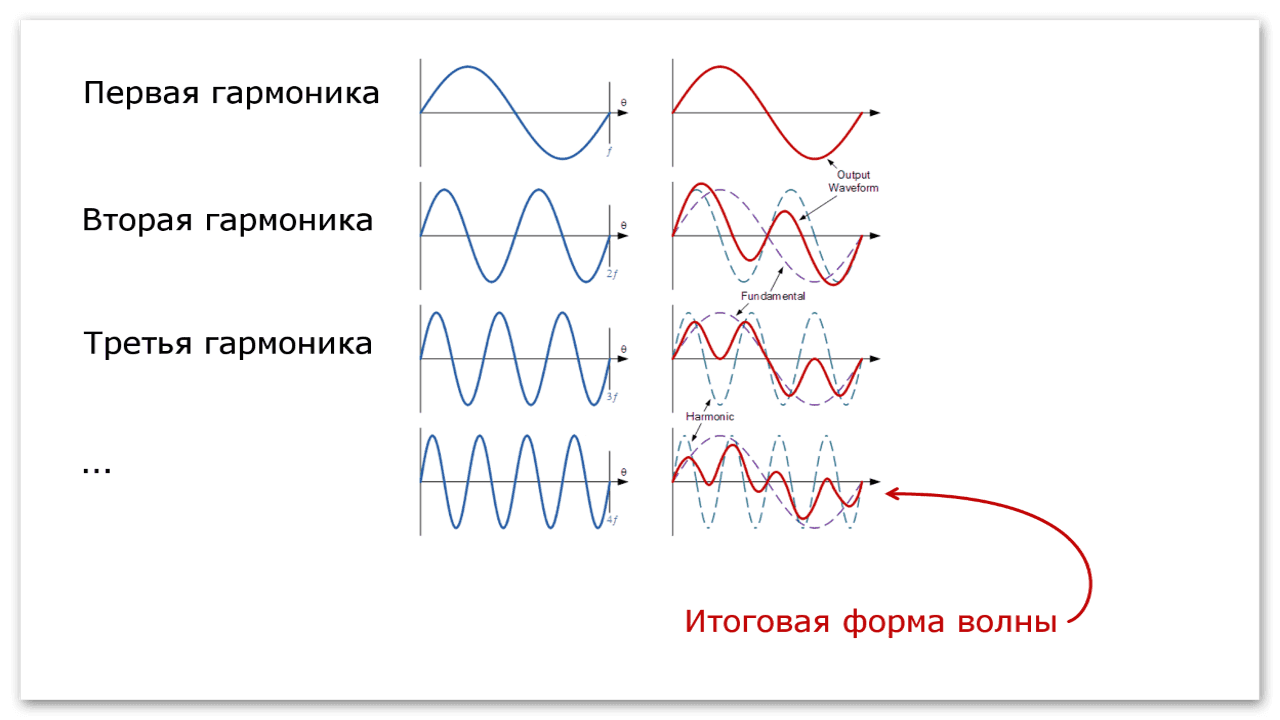
Фактическими результатами изучения оказалась разработка эффективных акселераторов частоты лазерных потоков, в том числе многокаскадных удвоителей на следующую более старшую гармоники. Подобные процессы обретают массовое использование в аппаратуре квантовой электроники.
Замечание 1
Исходя из всеобщих взглядов каждое нелинейное явление может быть охарактеризовано, как выражение отступлений от принципов суперпозиции оптических электромагнитных полей.
Исследование нелинейных процессов возможно проводить на некотором количестве «уровней строгости». Простое представление производится на основании традиционных принципов, в которых передвижение электрона в атоме и взаимодействие с полем воспроизводятся традиционными формулами Ньютона и Максвелла. Гораздо серьезнее определение предполагает применение квантовой механики для действия атома и классических формул для поля.
Для деятельности в пределах традиционной физики, применяют образец атома Томсона, который состоит в том, что плюсовой заряд распространен по всей области конкретного радиуса, а в средине этой структуры находится электрон. Напряженность электрического поля плюсового заряда в данной ситуации ровно возрастает от средины к окончанию области, а воздействующая на электрон сила соответствует закону Гука.
Напряженность электрического поля плюсового заряда в данной ситуации ровно возрастает от средины к окончанию области, а воздействующая на электрон сила соответствует закону Гука.
Нелинейные явления второго уровня, особенно, генерацию второй гармоники, возможно встретить лишь в объектах, которые не изотропных и не имеют центра симметрии. В действительности, если материальный объект изотропен, тогда при трансформации начального направления применённого электрического поля поляризация обязана машинально изменять знак.
Для удовлетворения этого правила, элементы, которые включают чётные степени, не должны присутствовать. Данный процесс вызовет пошаговое пропаданию показателей второго уровня.
Для трансформации в состояние генерации второй гармоники потребуется обеспечить конкретное напряжение на оптико-электрическое вещество. В то же время небольшая порция внутренней энергии излучения основной частоты будет превращаться в данный нелинейный эффект. Во время проектирования полагалось, что интенсивность светопреломления второй гармоники прямо пропорциональна второй степени интенсивности.
Данное аппроксимирование не является допустимым при больших интенсивностях, поскольку соотношение оказывается намного солиднее. В вычислениях специалисты применяют мощности меньше 10 ватт, с каковыми всякое согласие квадратичной необоснованности безусловно исполняется.
Замечание 2
Коэффициент пропорциональности возможно определить, в том случае, когда интенсивность светопреломления пучка света в средине резонатора трансформируется во вторую гармонику.
Для весьма продуктивного применения исходного импульса одно из зеркал работающего резонатора должно быть сделано совершенно просвечивающимся для образования второй гармоники, а второе зеркало должно быть отчасти отсвечивающим. Небольшая фракция внутренней энергии светоизлучения исключается понемногу из резонатора, таким образом, интенсивность светопреломления главной частоты в средине объекта уменьшается.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Данной процесс при имитации предусматривался в установлении прямого соотношения коэффициента отражения, действовавшего в выпускных зеркалах от концентрации лучей фотонов первой гармоник.
В конкретных физических процессах волна нелинейной поляризации создаёт вторую оптическую гармонику. Любопытно, что поляризационная волна передаётся с малым быстродействием, не так, как волна второй гармоники. Чтобы трансформация активного заряда от волны поляризации к излученному световому вектору осуществлялась очень продуктивно, необходимо достичь идентичности скоростей обеих волн.
Определение 2
Это значит, что обязано осуществляться соглашение, называемое в науке волновым синхронизмом.
При данных условиях применяется:
- Соответствие показателя светопреломления от ориентации в кристалле;
- Световая волна, которая имеет различные ускорения;
- Значительная часть кристаллов, называемых одноосными кристаллами.
Коэффициент светопреломления для обычной волны передвигается независимо и не подчиняется направлению расширения электромагнитной волны, в то время как коэффициент светопреломления необыкновенной волны подчиняется направлению распространения света. Когда световая волна распределяется вдоль оптического вектора кристалла, в этом случае она не разделяется на обыкновенную и необыкновенную волны.
Когда световая волна распределяется вдоль оптического вектора кристалла, в этом случае она не разделяется на обыкновенную и необыкновенную волны.
Когда волновая ось организовывает определённый угол, тогда указанное явление возникает. Таким образом, соглашение волнового синхронизма считается исполненным, когда волны светоизлучения передаются в кристалле под конкретным углом к его оптическому вектору. В том числе, когда ложащаяся на кристалл волна в полном объёме поляризована перпендикулярно к поверхности главного профиля.
Таким образом, в качестве базиса предпочтительно принимать кристаллическую модель, в которой волна второй гармоники поляризована, ощущает конкретное отклонение в поперечной ориентации, которая квалифицируется углом, называемым углом анизотропии.Указанное преобразование порождает уменьшение отношения интенсивности второй гармоники к мощности светоизлучения, которое падает на кристалл. Данное отношение специалисты отмечают как эффективность преобразования во вторую гармонику.
Генерация второй гармоники
С возникновением сверхмощных источников когерентного преломления оптического диапазона (лазеров) использование нелинейных явлений в оптике стало реальным и простым. В таких процессах, в отличие от обычных оптических эффектов, происходит нарушение принципов суперпозиции световых волн.
Рисунок 1. Поляризация света. Автор24 — интернет-биржа студенческих работ
Определение 1
Генерация второй гармоники — это нелинейный оптический эффект, который был образован воздействием на вещество ультратонких, лазерных импульсов.
На сегодняшний день главным методом получения звуковых частот лазерного излучения является генерация второй гармоники, предполагающая формирование гигантского импульса. В этом случае накачка осуществляется до тех пор, пока инверсия населенностей не достигнет предела максимального значения. Тогда подключается добротность резонатора, и количество фотонов в нем начинает мгновенно увеличиваться, что приводит к появлению интенсивного короткого сигнала. В данном случае важно значение времени жизни элементарной частиц на верхнем уровне, который должен быть достаточно большим.
В данном случае важно значение времени жизни элементарной частиц на верхнем уровне, который должен быть достаточно большим.
Генерация второй гармоники наблюдается:
- в сегнетоэлектриках с большой поляризуемостью;
- в полимерах, содержащих молекулы с нелинейно-оптическими хромофорами;
- в волновых концепциях со спонтанной поляризацией.
Рисунок 2. Генерация второй оптической гармоники. Автор24 — интернет-биржа студенческих работ
Изучение удвоения частоты в генерации второй гармоники позволили ученым выявить новые закономерности взаимосвязи светового излучения с веществом. Практическим итогом исследований стало создание высокоэффективных ускорителей частоты лазерного излучения, а также каскадных удвоителей на третью, четвертую и более высокие гармоники. Такие явления находят широкое применение в устройствах квантовой электроники.
Теория эффекта
Замечание 1
Из наиболее общих соображений все нелинейные явления могут быть охарактеризованы как проявления нарушений принципа суперпозиции оптических электромагнитных полей.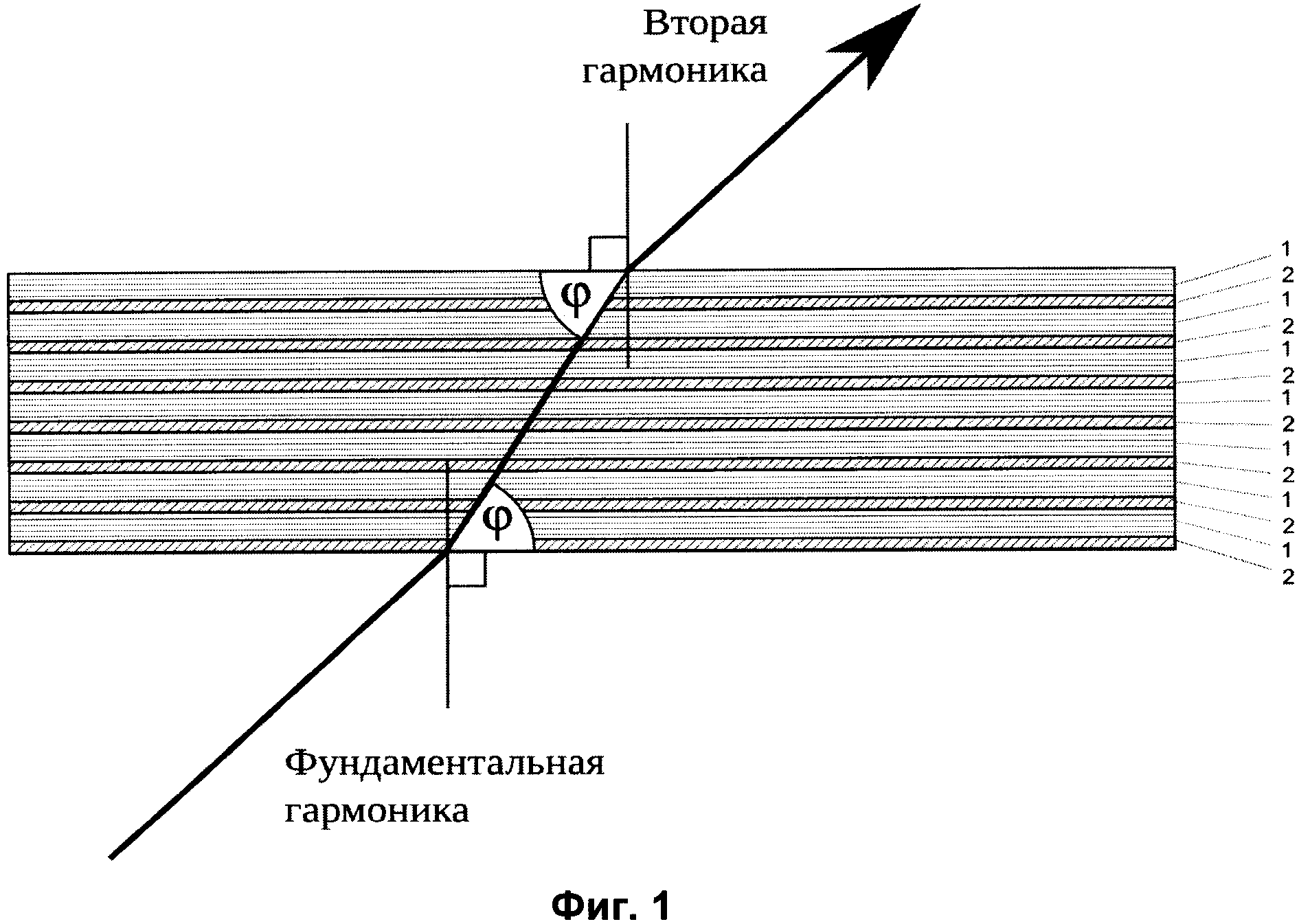
Рассмотрение нелинейных явлений может быть проведено на нескольких «уровнях строгости». Простейшее описание дается на основе классических представлений, в которых движение электрона в атоме и взаимодействие с полем описываются классическими уравнениями Ньютона и Максвелла. Более строгая формулировка подразумевает использование квантовой механики для поведения атома и классических уравнений для поля.
Для работы в рамках классической физики, используют модель атома Томсона, состоящая в том, что положительный заряд размазан по всей сфере некоторого радиуса, а в центре данной системы расположен электрон. Напряженность электрического поля положительного заряда в этом случае линейно растет от центра к краю сферы, а действующая на электрон сила удовлетворяет закон Гука.
Нелинейные эффекты второго порядка, а, в частности, генерацию второй гармоники, могут наблюдать только в веществах не изотропных и не имеющих центра симметрии. Действительно, когда материальное вещество изотропно, при изменении изначального направления приложенного электрического поля поляризация должна автоматически менять знак.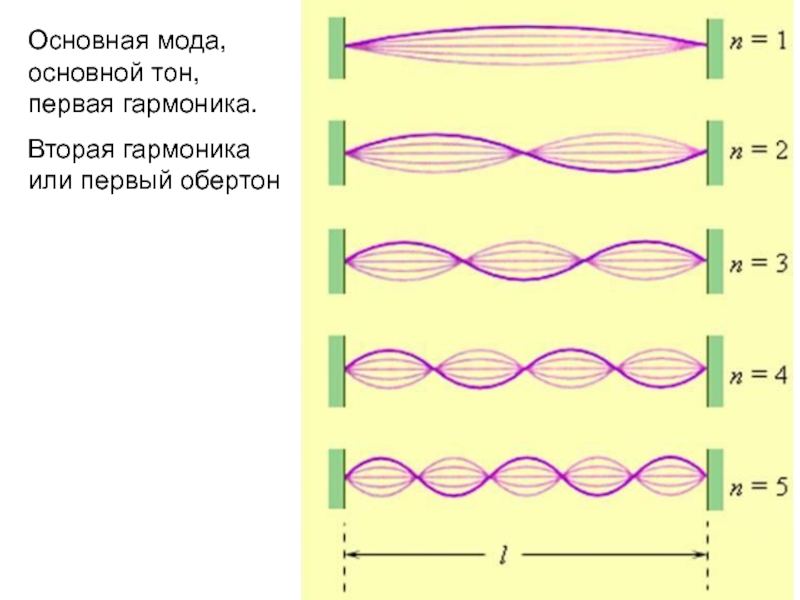 Чтобы удовлетворить это требование, элементы, включающие четные степени, должны отсутствовать. Такой процесс приведет к постепенному исчезновению коэффициентов второго порядка.
Чтобы удовлетворить это требование, элементы, включающие четные степени, должны отсутствовать. Такой процесс приведет к постепенному исчезновению коэффициентов второго порядка.
Режим генерации второй гармоники
Для перехода в режим генерации второй гармоники необходимо предоставить определенное напряжение на электрооптическое вещество. При этом часть внутренней энергии излучения главной частоты будет трансформироваться в этот нелинейный эффект. При конструировании считалось, что интенсивность светового преломления второй гармоники прямо пропорциональна общему квадрату интенсивности.
Такое приближение недопустимо при значительных интенсивностях, так как тогда зависимость становится значительно больше. В расчетах ученые используют мощности меньшие 10 Вт, при которых любое условие квадратичной несостоятельности обязательно выполняется.
Замечание 2
Показатель пропорциональности определяется, если интенсивность преломления пучка света внутри резонатора преобразуется во вторую гармонику.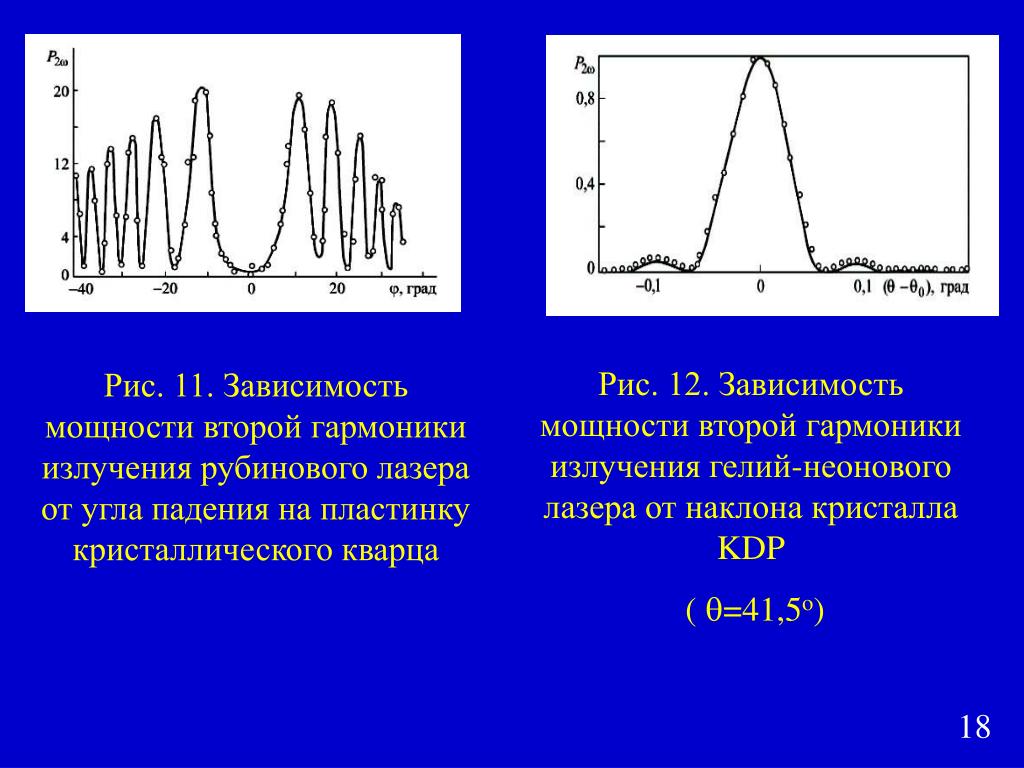
Для более эффективного использования выходного импульса одно из зеркал действующего резонатора необходимо сделать полностью прозрачным для возникновения второй гармоники, а второе – частично отражающим. Часть внутренней энергии излучения света выводится постепенно из резонатора, следовательно, интенсивность преломления основной частоты внутри объекта будет уменьшаться.
Это явление при моделировании учитывался во введении прямой зависимости показателя отражения, который действовал в выходных зеркалах от плотности потока фотонов первой гармоник. Таким образом, чем больше плотность данных элементов в резонаторе, тем больше коэффициент трансформации во вторую гармонику и тем быстрее уменьшается интенсивность светового излучения главной частоты.
Рисунок 3. Схемы внерезонаторной генерации второй гармоники. Автор24 — интернет-биржа студенческих работ
Генер&
Обучение музыки
Что такое гармонические искажения. Хью Робджонс. Аналоговая теплота.
Любая нелинейная звуковая система (такая, как аналоговый магнитофон), до некоторой степени искажает входной сигнал. И поскольку эти искажения изменяют форму звуковой волны, то это обычно приводит к созданию дополнительных гармоник. Чтобы не углубляться в научные дебри, скажем следующее: гармоники – это набор частот, производных от какой-то фундаментальной частоты (так сказать, её копии с увеличенной частотой – высшие гармоники). Эти гармоники обогащают и «усложняют» исходный звук. И не всегда такое обогащение приятно нашему слуху. Гармоники, кратные исходной частоте в отношении 2, 4, 6, 8 и так далее раз, называются чётными. А гармоники, кратные в отношении 3, 5, 7, 9 – называются нечётными. Некоторые нелинейные системы генерируют больше чётных гармоник, чем нечётных, другие же – наоборот. И баланс между чётными и нечётными гармониками очень сильно влияет на звуковое качество.
Словесное описание искажения похоже на попытку описать аромат сыра посредством танца, но я всё-таки попробую. Гармоники (обертоны) – это то, что даёт звуку его тембр и характер. Например, благодаря им звук флейты отличается от звука кларнета. Таким образом, гармоническое искажение – это такое искажение, при котором происходит генерация новых или усиление уже существующих гармоник, что приводит к изменениям в тембре исходного сигнала. C музыкальной точки зрения частоты высших гармоник имеют вполне определенный смысл. Например, вторая гармоника — это та же нота, что и основной тон, только октавой выше, четвертая — двумя октавами выше. Таким образом, чётные гармоники придают звуку объем, делают его сочнее, так как звучат слитно с основным тоном и его подчеркивают. Если мы играем не одну, а несколько нот, то их вторые и четвертые гармоники будут также консонировать (или диссонировать) друг с другом, как и основные тоны, сохраняя читаемость аккорда (или всего комплекса инструментов). Многие приборы, сделанные на основе электронных ламп, имеют тенденцию генерировать, главным образом, чётные гармоники.
Гармоники (обертоны) – это то, что даёт звуку его тембр и характер. Например, благодаря им звук флейты отличается от звука кларнета. Таким образом, гармоническое искажение – это такое искажение, при котором происходит генерация новых или усиление уже существующих гармоник, что приводит к изменениям в тембре исходного сигнала. C музыкальной точки зрения частоты высших гармоник имеют вполне определенный смысл. Например, вторая гармоника — это та же нота, что и основной тон, только октавой выше, четвертая — двумя октавами выше. Таким образом, чётные гармоники придают звуку объем, делают его сочнее, так как звучат слитно с основным тоном и его подчеркивают. Если мы играем не одну, а несколько нот, то их вторые и четвертые гармоники будут также консонировать (или диссонировать) друг с другом, как и основные тоны, сохраняя читаемость аккорда (или всего комплекса инструментов). Многие приборы, сделанные на основе электронных ламп, имеют тенденцию генерировать, главным образом, чётные гармоники.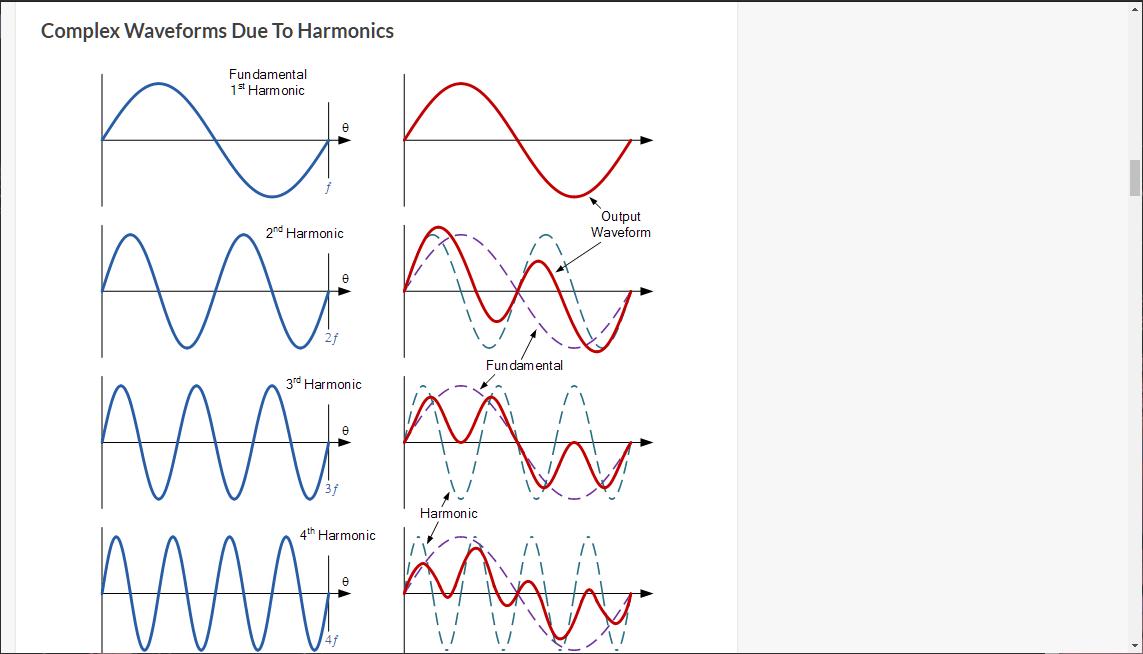 Давайте теперь обратим свой взгляд в сторону нечётных гармоник. К примеру, третья гармоника — это квинта через октаву. Эта гармоника составляет консонанс с основным звуком, но объема уже не придаёт и нота может звучать слишком холодно, стерильно. Если играется более одной ноты, то эти гармоники могут диссонировать друг с другом или с основными тонами, порождая звучание, которое описывается как «скрежещущее», «грубое», «острое» или «песочное». Но умеренное количество таких гармоник часто связывается и с такими понятиями, как «богатство» и «глубина» звука. Многие ранние (1960 – 1970-е годы) транзисторные усилители имели тенденцию генерировать при перегрузке, главным образом, искажения с нечётными гармониками. И это создало для ранних транзисторных устройств не очень хорошую репутацию. В аналоговых магнитофонах главной проблемой, связанной с физическими основами записи на магнитную ленту, является третья гармоника, и потому общепринятым методом оценки нелинейных искажений в процессе записи является измерение коэффициента гармонических искажений третьего порядка.
Давайте теперь обратим свой взгляд в сторону нечётных гармоник. К примеру, третья гармоника — это квинта через октаву. Эта гармоника составляет консонанс с основным звуком, но объема уже не придаёт и нота может звучать слишком холодно, стерильно. Если играется более одной ноты, то эти гармоники могут диссонировать друг с другом или с основными тонами, порождая звучание, которое описывается как «скрежещущее», «грубое», «острое» или «песочное». Но умеренное количество таких гармоник часто связывается и с такими понятиями, как «богатство» и «глубина» звука. Многие ранние (1960 – 1970-е годы) транзисторные усилители имели тенденцию генерировать при перегрузке, главным образом, искажения с нечётными гармониками. И это создало для ранних транзисторных устройств не очень хорошую репутацию. В аналоговых магнитофонах главной проблемой, связанной с физическими основами записи на магнитную ленту, является третья гармоника, и потому общепринятым методом оценки нелинейных искажений в процессе записи является измерение коэффициента гармонических искажений третьего порядка.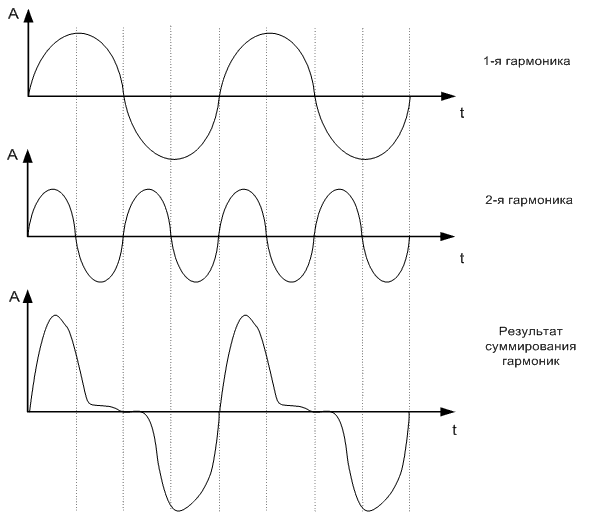 Большинство процедур настройки магнитофона перед записью использует в качестве ссылки уровень этих третьих гармоник.
Большинство процедур настройки магнитофона перед записью использует в качестве ссылки уровень этих третьих гармоник.
Тем не менее, в действительности всё намного сложнее, потому что вид искажения только лишь частично зависит от того, какие активные элементы используются. Как уже было сказано, вид искажения очень сильно связан со схемотехническими особенностями устройства, и ничто не мешает изготовить транзисторную схему, преимущественно производящую чётные гармоники, или ламповую, генерирующую нечётные. И, кроме того, на базе обоих типов активных элементов можно изготавливать очень линейные, с очень малым количеством искажений, устройства. То же самое относится и магнитофонам. Даже если в каком-то аппарате и декларируется наличие чётных гармонических искажений, то они редко являются доминирующими. Обычно они вызываются искажениями в усилительном тракте (обычно в ламповых магнитофонах), или в результате намагниченности головок.
При настройке магнитофона звукоинженер обычно пытается оптимизировать его параметры так, чтобы минимизировать искажения. Минимальное искажение для данного типа ленты будет результатом определённой комбинации уровня записи, корректирующей эквализации и параметров подмагничивания. Из всего этого набора только один параметр легко доступен для пользователя (без углубления в недра магнитофона) – это уровень записи. При подаче на запись сигнала с высоким уровнем, Вы можете перегрузить ленту, и «поощрить» её создать больше искажений и сильнее «плющить» транзиенты. Насколько «горячо» записывать и сколько получать искажений – это, очевидно, вопрос вкуса, но я бы всё равно призвал бы Вас к некоторой осторожности.
Минимальное искажение для данного типа ленты будет результатом определённой комбинации уровня записи, корректирующей эквализации и параметров подмагничивания. Из всего этого набора только один параметр легко доступен для пользователя (без углубления в недра магнитофона) – это уровень записи. При подаче на запись сигнала с высоким уровнем, Вы можете перегрузить ленту, и «поощрить» её создать больше искажений и сильнее «плющить» транзиенты. Насколько «горячо» записывать и сколько получать искажений – это, очевидно, вопрос вкуса, но я бы всё равно призвал бы Вас к некоторой осторожности.
И Вам ещё следует знать, что некоторые магнитные ленты последнего поколения обладают большой перегрузочной способностью, и чтобы добиться от них эффекта сатурации, при записи требуется подать очень высокий уровень сигнала. Однако, не в каждом магнитофоне электроника записывающего тракта способна работать с такими уровнями (да и не каждая головка справляется с ними). К примеру, такая проблема может быть с некоторыми магнитофонами от Revox. Таким образом, подбирайте тип ленты под конкретную модель магнитофона, если намеренно ищите эффекты такой перегрузки.
Таким образом, подбирайте тип ленты под конкретную модель магнитофона, если намеренно ищите эффекты такой перегрузки.
Виды губных гармошек. | Статьи
19-02-2008
Губная гармошка — наиболее распространенный блюзовый инструмент. Она маленькая, недорогая и очень проста в обучении и игре, но тем не менее, предоставляет музыканту поистине колоссальные исполнительские возможности.
Губные гармошки бывает двух видов: диатонические и хроматические. Давайте кратко рассмотрим каждый их них.
Диатонические гармошки
Диатонические и хроматические гармошки принципиально отличаются друг от друга. Диатонические имеют диатонический строй (например: С D E F и так далее) без полутоновых интервалов между нотами (С# D# и так далее). Игра на диатонической гармошке напоминает игру по белым клавишам фортепиано. Полутона (черные клавиши) в ее строе отсутствуют.
В диатонических гармошках используются три способа настройки язычков: одиночный, тремоло и октавный. В первом случае в каждом отверстии располагается один язычок, работающий на вдохе или выдохе. Каждый язычок настраивается на свою высоту звука. В каталоге фирмы «Hohner» существует большое количество моделей подобной конструкции. Бывает, что модель представлена только в тональностях С и G. В такой конструкции четыре отверстия перекрывают диапазон в одну октаву.
В первом случае в каждом отверстии располагается один язычок, работающий на вдохе или выдохе. Каждый язычок настраивается на свою высоту звука. В каталоге фирмы «Hohner» существует большое количество моделей подобной конструкции. Бывает, что модель представлена только в тональностях С и G. В такой конструкции четыре отверстия перекрывают диапазон в одну октаву.
Другие модели могут выпускаться в мажорных тональностях А, В, Вb С, Db, E, Еb, F, F#, G и Аb. На таком инструменте с десятью отверстиями можно играть уже в 3-х октавах.
Есть гармошки с минорным строем С или G. Они также имеют десять отверстий и перекрывают 3 октавы.
Существует модель и для блюзовых музыкантов, которая выпускается в различных тональностях и работает в 3-х октавах.
Отверстия нумеруются слева направо. Отверстия 1-3 и 8-10 используются для извлечения аккордов. А через отверстия 4-7 вы можете полностью исполнить диатоническую гамму. Ноты гаммы играются как последовательность выдохов и вдохов.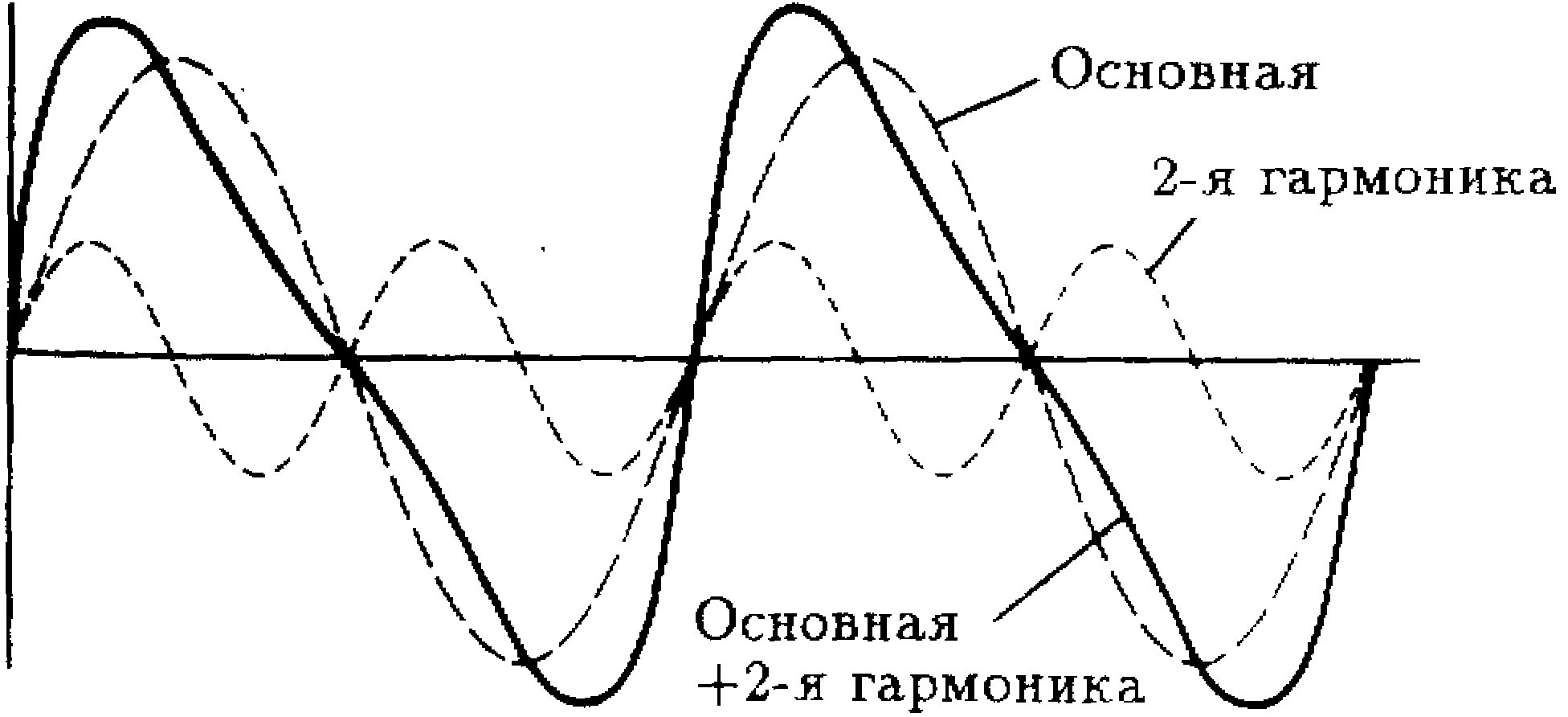 Натуральный до-мажор включает в себя следующие ноты: С(до) D(pe) Е(ми) F(фа) G(соль) А(ля) В(си) С(до). Чтобы исполнить эту восходящую гамму вверх, нужно проделать следующую последовательность действий: выдох (C), вдох (D), выдох (Е), вдох (F), выдох (G), вдох (А), вдох (В) и выдох (C). При нисходящем движении выполните те же действия, но уже в обратном порядке.
Натуральный до-мажор включает в себя следующие ноты: С(до) D(pe) Е(ми) F(фа) G(соль) А(ля) В(си) С(до). Чтобы исполнить эту восходящую гамму вверх, нужно проделать следующую последовательность действий: выдох (C), вдох (D), выдох (Е), вдох (F), выдох (G), вдох (А), вдох (В) и выдох (C). При нисходящем движении выполните те же действия, но уже в обратном порядке.
Второй способ настройки — тремоло. Такие гармошки имеют ряд двойных отверстий. Каждое отверстие оборудовано двумя язычками, настроенными на одну ноту. Однако при этом один из язычков настраивается чуть выше. При звукоизвлечении эта едва заметная разница в настройке создает вибрацию, напоминающую эффект тремоло. Существуют одиночные, двухсторонние, квартетные и секстетные модели подобных гармошек, с диапазоном от двух до четырех октав.
Каждая из моделей выпускается в нескольких тональностях. Одиночная модель представляет собой гармошку с одним рядом двойных отверстий. Двухсторонняя имеет два ряда отверстий с разным строем, располагающихся с противоположных сторон корпуса. Другие модели представляют собой от 4-х до 6-ти гармошек в разных тональностях, закрепленных на едином держателе.
Другие модели представляют собой от 4-х до 6-ти гармошек в разных тональностях, закрепленных на едином держателе.
Третий тип настройки губных гармошек — октавный. Конструктивно он не отличается от предыдущего. Разница лишь в том, что язычки расположенные в двойных отверстиях настраиваются в октавный интервал. Такие модели обладают мощным звуком без всякой вибрации. Гармошки с таким вариантом строя существуют лишь в одиночном или двухстороннем варианте.
Хроматические гармошки
Тип гармошки, который позволяет исполнителю извлекать и полутона, называется хроматической губной гармошкой. Подобный инструмент был предложен фирмой «Hohner» в 1920 году. Существует два типа хроматических гармошек: для игры соло и для аккомпанемента. Первая разновидность, как видно из названия, предназначается для игры соло или в ансамбле. На таком инструменте полутона извлекаются при помощи слайдера, то есть кнопки, располагающейся на одной из боковых сторон корпуса инструмента.
Диапазон хроматических гармошек может составлять от 2-х до 4-х октав.
Существуют модели для начинающих и для профессионалов. 2-х октавная хроматика имеет диапазон от С 1-й октавы до С# 3-й октавы. На профессиональной модели в 2 1/2 октавы можно играть от С 1-й октавы до F# 3-й октавы. 3-х октавные модели также выпускаются как для начинающих, так и для профессионалов. Их диапазон также начинается от С 1-й октавы. 4-х октавные, профессиональные модели имеют диапазон от С малой октавы до D 4-й октавы. Когда слайдер на хроматической гармошке отжат, то исполнитель имеет доступ к диатоническим нотам (белые клавиши ф-но), а когда слайдер зажат — к полутонам (черным клавишам).
Басовые гармошки
Другим типом хроматики является басовая губная гармоника, которая используется в оркестровом аккомпанементе. Эти инструменты работают в басовом регистре, начиная от ноты Е, расположенной в контроктаве. Еще одним аккомпанирующим инструментом является 48-аккордовая гармошка. Этот инструмент используется в ансамблевом аккомпанементе. К примеру, уже историческая модель «Hohner The 48 Chord» представляет собой две соединенные друг с другом гармошки с 12-ю аккордами на вдохе или выдохе в каждой, что в сумме дает 48 аккордов. Причем это могут быть мажорные, минорные, доминантовые, уменьшенные и увеличенные аккорды. Этот инструмент имеет 96 двойных отверстий и 384 язычка. При длине в 58,4 см — это самая длинная губная гармошка в мире.
Этот инструмент используется в ансамблевом аккомпанементе. К примеру, уже историческая модель «Hohner The 48 Chord» представляет собой две соединенные друг с другом гармошки с 12-ю аккордами на вдохе или выдохе в каждой, что в сумме дает 48 аккордов. Причем это могут быть мажорные, минорные, доминантовые, уменьшенные и увеличенные аккорды. Этот инструмент имеет 96 двойных отверстий и 384 язычка. При длине в 58,4 см — это самая длинная губная гармошка в мире.
определение гармоники по The Free Dictionary
Коронер должен сидеть в комнате на первом этаже в Sol’s Arms, где два раза в неделю проходят встречи Harmonic Meetings и где кресло занимает известный профессиональный джентльмен, с которым столкнется Little Swills, комический вокалист, который надеется
Бидл и домовладелец проводят его в конференц-зал Harmonic, где он надевает шляпу на пианино и занимает кресло Windsor во главе длинного стола, состоящего из нескольких коротких столов, соединенных вместе и украшенных клейкими кольцами. в бесконечных инволюциях, сделанных горшками и стаканами.
в бесконечных инволюциях, сделанных горшками и стаканами.
Считается вполне вероятным, что вечером он воспользуется имитацией коронера и сделает это главной особенностью Гармонической встречи.
Бидл очень осторожен, чтобы два джентльмена, не очень аккуратные в манжетах и пуговицах (для размещения которых он предусмотрел специальный столик рядом с коронером в зале заседаний Harmonic), могли видеть все, что можно увидеть.
Прибывает час Гармонической Встречи, джентльмен из профессиональной знаменитости садится в кресло, стоит лицом к лицу.
Звон рояля, наконец, замолкает, и друзья Гармоника собираются вокруг своих подушек.
Фактически, он не принадлежал ни к одному из многочисленных обществ, кишащих в английской столице, от Гармонического до Энтомологов, основанных в основном с целью уничтожения вредных насекомых. Это не шум, который вы слышите, Но Музыка, гармоничная и чистая. Клуб встретил его с транспортом и в тот вечер устроил гармоничное собрание в его честь; в то время как миссис Эти тогда, хотя и незаметно в глубокой ночи, не светят напрасно и не думают, хотя мужчин не было, Что бы не было зрителей, Богу нужна хвала; Миллионы духовных Созданий ходят по Земле Невидимым, как когда мы просыпаемся, так и когда мы спим: Все они с непрекращающейся хвалой Его дела созерцают И днем, и ночью: как часто мы слышим с обрыва Эхом Холма или Чащи мы слышим Небесные голоса до полуночи Воздух, Подошва или отзывчивые друг к другу ноты Пение своего великого Создателя: часто в группах Пока они несут вахту, или ночная прогулка по округе С легким прикосновением инструментальных звуков В полном гармоническом количестве соединяются, три песни Разделяют ночь и поднимают наши мысли к небу. ухо Генделя предсказывает колдовство гармонического звука? Буска, «Анализ гармонического взаимодействия в преобразователе, подключенном к сети, с использованием моделирования в гармоническом пространстве состояний (HSS)», IEEE Transactions on Power Electronics, vol.
ухо Генделя предсказывает колдовство гармонического звука? Буска, «Анализ гармонического взаимодействия в преобразователе, подключенном к сети, с использованием моделирования в гармоническом пространстве состояний (HSS)», IEEE Transactions on Power Electronics, vol.Среднее значение гармоник в R (2 примера)
На этой странице показано, как вычислить среднее гармоническое на языке программирования R.
Я покажу на основе двух воспроизводимых примеров , как вычислить гармоническое среднее значение для числового вектора или столбца кадра данных.
Вы здесь за ответом, так что давайте копаться!
Пример 1: Вычислить среднее гармоническое значение вектора в R
В первом примере я объясню, как вычислить гармоническое среднее числового вектора. Итак, давайте сначала создадим такой числовой вектор:
x <- c (10, 14, 29, 30, 41, 53, 27, 55) # Создать вектор-пример |
x <- c (10, 14, 29, 30, 41, 53 , 27, 55) # Создать вектор-пример
Чтобы получить среднее гармоническое для этого вектора, нам нужно установить и загрузить дополнительный пакет Psy:
установить. |
install.packages ("Psy") # Установить пакет Psy library ("mental") # Загрузить пакет Psy
Теперь мы можем применить функцию Harmonic.mean из пакета Psy для вычисления среднего гармонического вектора нашего примера:
Harmonic.mean (x) # Применить гармонику.средняя функция # 23.68814 |
harmonic.mean (x) # Применить функцию Harmonic.mean # 23.68814
Как вы можете видеть на основе вывода консоли RStudio, среднее гармоническое значение вектора нашего примера составляет 23,68814.
Примечание: Команда Harmonic.mean также может применяться к данным со значениями NA (т. Е. Отсутствующими значениями). По умолчанию такие значения удаляются перед обработкой.
Пример 2: Среднее гармоническое значение столбца кадра данных
Во втором примере мы применим гармонику. означают функцию R пакета Psy к некоторым реальным данным, то есть набору данных Iris Flower. Мы можем загрузить данные следующим образом:
означают функцию R пакета Psy к некоторым реальным данным, то есть набору данных Iris Flower. Мы можем загрузить данные следующим образом:
data (iris) # Загрузить данные диафрагмы головка (диафрагма) # Первые строки данных диафрагмы |
данных (диафрагма) # Загрузить данные диафрагмы head (iris) # Первые строки данных радужной оболочки
Таблица 1: Первые шесть рядов матрицы данных цветков ириса.
Теперь мы используем гармоническое среднее значение для вычисления, например, среднего гармонического значения первого столбца кадра данных:
harmonic.mean (iris $ Sepal.Length) # Применить Harmonic.mean к столбцу # 5.728905 |
harmonic.mean (iris $ Sepal.Length) # Применить Harmonic.mean к столбцу # 5.728905
Среднее гармоническое значение первого столбца - 5,728905.
Дополнительные ресурсы и резюме
Прочитав эту статью, вы сможете рассчитать гармонические средние в R. Однако мы еще не говорили о теоретической исследовательской концепции гармонического среднего. Если вы хотите узнать больше о статистической концепции, лежащей в основе гармонического среднего, вы можете посмотреть следующее видео на YouTube о zedstatistics. Спикер объясняет концепцию гармонического среднего и сравнивает его с другими мерами, которые вычисляют среднее значение, такими как среднее арифметическое или среднее геометрическое.
Однако мы еще не говорили о теоретической исследовательской концепции гармонического среднего. Если вы хотите узнать больше о статистической концепции, лежащей в основе гармонического среднего, вы можете посмотреть следующее видео на YouTube о zedstatistics. Спикер объясняет концепцию гармонического среднего и сравнивает его с другими мерами, которые вычисляют среднее значение, такими как среднее арифметическое или среднее геометрическое.
Пожалуйста, примите файлы cookie YouTube для воспроизведения этого видео. Согласившись, вы получите доступ к контенту YouTube, услуги, предоставляемой третьей стороной.
Политика конфиденциальности YouTube
Если вы примете это уведомление, ваш выбор будет сохранен, и страница обновится.
Принять контент YouTube
Кроме того, вы можете ознакомиться с некоторыми другими учебниками по программированию на R, которые я опубликовал на сайте statisticsglobe.com:
Это все, что я хотел показать вам в этом уроке. Однако, если у вас есть какие-либо вопросы или комментарии, пожалуйста, дайте мне знать в разделе комментариев ниже.
Однако, если у вас есть какие-либо вопросы или комментарии, пожалуйста, дайте мне знать в разделе комментариев ниже.
Мы рекомендуем переместить этот блок и предыдущую ссылку CSS в HEAD вашего HTML-файла. * /
]]>
Harmonic Second Interval - Почему он отличается
Добро пожаловать в GSG Music
- 1 (800) 520 4680
- info @ ultimatemusictheory.com
- Мои курсы
- МАГАЗИН
- БЕСПЛАТНЫЕ ресурсы
- PREP 1 - Prep 1, Prep Level, Level 1
- PREP 1 Rudiments
- Планы уроков для Prep 1
- Свидетельство о достижении
- Экзамен по свободной практике и ответы
- 80 карточек для бесплатного скачивания
- PREP LEVEL - Supplemental
- Изучите PREP LEVEL с Prep 1
- Бесплатные видеоресурсы
- История музыки и оркестровые инструменты
- УРОВЕНЬ 1 - Дополнительный
- Завершить УРОВЕНЬ 1 после УРОВНЯ ПОДГОТОВКИ
- Бесплатные видеоресурсы
- Рассказ через музыку
- PREP 2 - Prep 2, Level 2, Level 3
- PREP 2 Rudiments
- Планы уроков для Prep 2
- Свидетельство о достижении
- Экзамен по свободной практике и ответы
- 80 карточек для бесплатного скачивания
- УРОВЕНЬ 2 - дополнительный
- УРОВЕНЬ 2 с подготовкой 2
- Бесплатные видеоресурсы
- Музыка Моцарта
- УРОВЕНЬ 3 - дополнительный
- Завершить УРОВЕНЬ 3 после УРОВНЯ 2
- Бесплатные видеоресурсы
- Музыка Баха и Петцольда
- BASIC - базовый, уровень 4, уровень 5
- BASIC Rudiments
- Планы уроков для Basic
- Свидетельство о достижении
- Экзамен по свободной практике и ответы
- 80 карточек для бесплатного скачивания
- УРОВЕНЬ 4 - дополнительный
- УРОВЕНЬ 4 с базовым
- Бесплатные видеоресурсы
- Музыка Чайковского и Бриттена
- УРОВЕНЬ 5 - Дополнительный
- Завершить УРОВЕНЬ 5 после УРОВНЯ 4
- Бесплатные видеоресурсы
- Музыка Генделя, Моцарта и Арлена
- INTERMEDIATE - средний, уровень 6, уровень 7
- INTERMEDIATE Rudiments
- Планы уроков для среднего уровня
- Свидетельство о достижении
- Экзамен по свободной практике и ответы
- 80 карточек для бесплатного скачивания
- PREP 1 - Prep 1, Prep Level, Level 1
Возвращает порядки, амплитуды и основную частоту гармоник
[ гармоника Порядок , гармоника Величина , частота гармоники]
знак равно. вычисляет гармонические порядки, величины и основную частоту  .
.
pe_getHarmonics ( loggingNode ) simscape.logging.Node переменного тока или периодической переменной.
Функция находит точки в сигнале i th (valueIdx), где журнал Simscape ™ пересекает порог (offsetOfInterest). Он использует точки пересечения, чтобы найти необходимое количество периодов. (nPeriodOfInterest) до указанного времени (tOfInterest).потом он вводит выбранные вниз данные в алгоритм Герцеля, который вычисляет амплитуды гармоник вплоть до требуемой количество гармоник (nHarmonic).
Вы вводите входные аргументы в определенном порядке. Журнал Simscape
Требуется входной аргумент узла. Все остальные входные аргументы необязательны
и имеют значения по умолчанию. Если вы указываете значение для последующего
необязательный входной аргумент, введите [] , чтобы использовать значение по умолчанию
значение для необязательного входного аргумента.
Вы можете использовать функцию pe_plotHarmonics чтобы получить гистограмму из тех же входных аргументов. Вы можете использовать
выходы этой функции как входы в функцию pe_calculateThdPercent для расчета процента общих гармонических искажений (THD).
[ использует
индекс в данные значения. гармоника Порядок , гармоническая величина , основная частота ]
= ...
pe_getHarmonics ( loggingNode , valueIdx )
[ использует
время моделирования. гармоника Порядок , гармоническая величина , основная частота ]
= ...
pe_getHarmonics ( loggingNode , valueIdx , tOfInterest )
[ использует
количество периодов основной частоты. гармоника Порядок , гармоническая величина , основная частота ]
= ...
pe_getHarmonics ( loggingNode , valueIdx , tOfInterest , nPeriodOfInterest ) 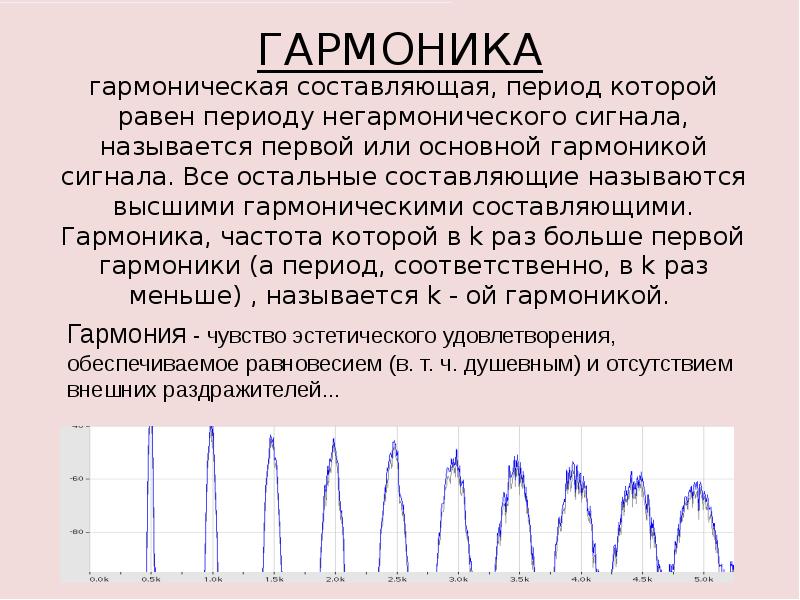
[ использует смещение постоянного тока. гармоника Порядок , гармоническая величина , основная частота ]
= ...
pe_getHarmonics ( loggingNode , valueIdx , tOfInterest , nPeriodOfInterest , ...
offsetOfInterest )
[ гармоника Порядок , гармоническая величина , основная частота ]
= ...
pe_getHarmonics ( loggingNode , valueIdx , tOfInterest , nPeriodOfInterest ,.2 (omega)
Эта интенсивность максимальна для условия согласования фаз Delta k = 0. Если процесс не согласован по фазе, управляющая поляризация на 2 омега входит и не совпадает по фазе с генерируемой волной E (2 омега), и преобразование колеблется как sin {(Delta k l / 2)}. Длина когерентности определяется как l_c = frac {pi} {Delta k}. Не стоит использовать нелинейный кристалл, длина которого намного превышает длину когерентности. (Периодический опрос и квази-фазовое согласование обеспечивают другой подход к этой проблеме.)
(Периодический опрос и квази-фазовое согласование обеспечивают другой подход к этой проблеме.)
Генерация второй гармоники с истощением
Когда преобразование во вторую гармонику становится значительным, становится необходимым включить истощение основной гармоники.2 {(Гамма l)}.
Типы SHG
Генерация второй гармоники бывает двух типов, обозначенных I и II. В SHG типа I два фотона, имеющие обычную поляризацию по отношению к кристаллу, объединятся, чтобы сформировать один фотон с удвоенной частотой и необычной поляризацией. В ГСП типа II два фотона с ортогональной поляризацией объединятся, чтобы сформировать один фотон с удвоенной частотой и необычной поляризацией. Для данной ориентации кристалла возникает только один из этих типов ГВГ.
Общие области применения
Генерация второй гармоники используется энтузиастами лазерной промышленности для создания зеленых лазеров с длиной волны 532 нм из источника 808 нм.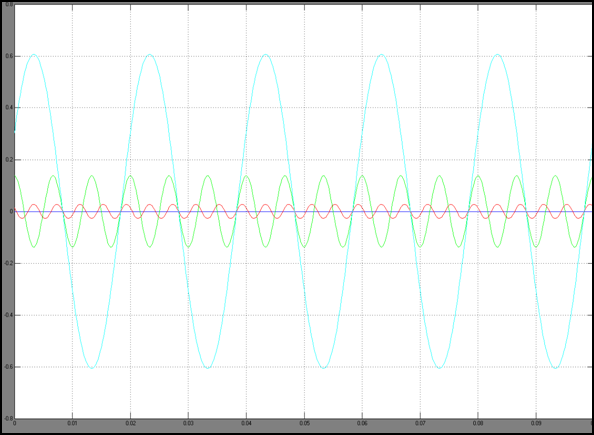 Источник преобразуется в кристалл с длиной волны 1064 нм, затем пропускается через кристалл второй гармоники KDP. Это закрыто инфракрасным фильтром, чтобы предотвратить утечку любого инфракрасного излучения, которое может быть вредным для человеческого глаза.
Источник преобразуется в кристалл с длиной волны 1064 нм, затем пропускается через кристалл второй гармоники KDP. Это закрыто инфракрасным фильтром, чтобы предотвратить утечку любого инфракрасного излучения, которое может быть вредным для человеческого глаза.
Историческая справка
Генерация второй гармоники, часто называемая удвоением частоты, также является процессом в радиосвязи; он был разработан в начале 20 века и использовался с частотами в диапазоне МГц.
Внешние ссылки
Примечания
Статьи о генерации второй гармоники
* Франкен, Пенсильвания, Хилл, А.Е., Питерс, CW, и Вайнрайх, Г. "[ http: // link. aps.org/abstract/PRL/v7/p118 Генерация оптических гармоник ] "," Phys. Rev. Lett. " 7 , стр. 118–119 (1961). DOI: doi | 10.1103 / PhysRevLett.7.118
* Parameswaran, KR, Kurz, JR, Roussev, MM & Fejer, "Наблюдение 99% истощения накачки при однопроходной генерации второй гармоники в волноводе из ниобата лития с периодической полярностью" , «Оптика Письма», 27 , стр. 43-45 (январь 2002 г.).
43-45 (январь 2002 г.).
* cite web | url = http: //www.rp-photonics.com/frequency_doubling.html | title = Удвоение частоты | work = Энциклопедия лазерной физики и технологий | accessdate = 2006-11-04
Компании участвует в производстве и производстве ГВГ
* [ http://www.advr-inc.com/waveguide.html AdvR - Преобразование частоты в волноводах KTP ]
* [ http: //www.radiantis. com Radiantis ]
Гармонические функции: гармонический анализ
Гармонические функции: гармонический анализТеория.com использует файлы cookie. Используя наш сайт, вы соглашаетесь на использование файлов cookie. Прочтите нашу политику конфиденциальности для получения дополнительной информации. Закрыть
Теперь мы воспользуемся обсужденными концепциями, чтобы проанализировать короткое произведение русского композитора Петра Ильича Чайковского (1840–1893) под названием Французская песня .
Первый шаг - определить тональность пьесы. Сначала мы должны взглянуть на подпись ключа. В данном случае тональная подпись (а) имеет две квартиры, так что это си-бемоль мажор или соль минор.Глядя на первый (b) и последний (c) такты, мы видим, что он начинается и заканчивается аккордом G минор. Из этого можно сделать вывод, что произведение написано в тональности соль минор:
.Тональность соль минор также может быть определена с помощью ноты фа-диез в аккорде ре мажор непосредственно перед последним аккордом. Ре мажор - это доминирующий аккорд соль минор.
Как только мы узнаем тональность пьесы, мы можем определить аккорды, инверсии, степени и гармонические функции. Давайте посмотрим на аккорды соль минор.Для мажорных аккордов используются римские цифры в верхнем регистре. Строчная римская цифра для минорных аккордов. o используется для идентификации уменьшенной хорды:
В минорных тональностях обычно изменяются V и VII ступени. В результате у нас может быть больше семи аккордов. В данном случае мы использовали только приподнятую седьмую ступень в аккордах V и VII.
В результате у нас может быть больше семи аккордов. В данном случае мы использовали только приподнятую седьмую ступень в аккордах V и VII.
Давайте сделаем полный анализ:
| Пьеса начинается с тонического аккорда соль минор (i), ноты красного цвета - это ноты аккорда. Ноты синего цвета - негармонических тона , в данном случае проходящих тона . Для получения дополнительной информации см. Негармонические тоны. | ||
| В такте 3 мы находим аккорд до минор (субдоминанту) во второй инверсии. Одна нота (синяя) - это проходящий тон . Возвращаемся к тонизирующему такту 4. | ||
| В тактах 5 и 6 мы снова имеем субдоминантные и тонические аккорды. Мера 7 начинается с vii o градусов, за которыми следует доминирующая (V).  Фраза заканчивается совершенной аутентичной каденцией (V7-i). | ||
| В такте 6 находятся соседняя банкнота (Eb) и appoggiatura (C). В такте 7 G - это предвкушение . Для получения дополнительной информации см. Негармонические тоны. | ||
| На басу воспроизводится педальный тон (G) от такта 1 до 6. | ||
| Фраза повторяется в тактах с 8 по 16. | ||
| Новая фраза в тактах с 17 по 24 заканчивается на полукеденции или полубагадии . i, iv y V. | ||
Этот короткий фрагмент заканчивается повторением первой фразы. | ||

 packages ("Psy") # Установить пакет Psy
библиотека ("Psy") # Загрузить пакет Psy
packages ("Psy") # Установить пакет Psy
библиотека ("Psy") # Загрузить пакет Psy