Высшие гармоники что это: Высшие гармоники — это… Что такое Высшие гармоники?

Высшие гармоники — это… Что такое Высшие гармоники?

Высшие гармоники

Высшие гармоники оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трнсформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счет мощности искажения, вызванной протеканием токов высших гармоник, а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности. Источниками высших гармонических тока и напряжения являются электроприемники с нелинейными нагрузками. Например электродуговые сталеплавильные печи, установки электродуговой сварки, газоразрядные лампы и др.

Wikimedia Foundation. 2010.

• Высшее театральное училище имени Б.В. Щукина
• Высшие Женские Курсы

Смотреть что такое «Высшие гармоники» в других словарях:

• высшие гармоники — — [В. А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN upper harmonics …   Справочник технического переводчика

• коэффициент мощности, не учитывающий высшие гармоники — [Интент] EN displacement power factor DPF The displacement power factor is the power factor due to the phase shift between voltage and current at the fundamental line frequency. For sinusoidal (non distorted) currents, the displacement power… …   Справочник технического переводчика

• коэффициент мощности, учитывающий высшие гармоники — [Интент] EN apparent power factor APF The apparent power factor (APF) is the ratio of real power to apparent power, including harmonics. This includes all harmonics. Harmonic currents decrease the power factor, even when there is no phase angle… …   Справочник технического переводчика

• высшие пространственные гармоники — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г. ] Тематики электротехника, основные понятия EN high space excitation harmonics …   Справочник технического переводчика

• ЗВУК И АКУСТИКА — Звук это колебания, т.е. периодическое механическое возмущение в упругих средах газообразных, жидких и твердых. Такое возмущение, представляющее собой некоторое физическое изменение в среде (например, изменение плотности или давления, смещение… …   Энциклопедия Кольера

• Авиационный тренажёр — Информацию об игровых авиатренажерах смотрите в статье Авиасимулятор. Авиационный (пилотажный) тренажер это имитатор полета, предназначенный для наземной подготовки пилотов. В авиационном тренажере имитируется динамика полета и работа систем ВС с …   Википедия

• Жежеленко И. В. — Игорь Владимирович Жежеленко Дата рождения: 1930 Место рождения: Мариуполь Гражданство: СССР, Украина Научная сфера: электроснабжение промышленных предприятий Место работы: Ждановский металлургический институт / Приазовский государственный… …   Википедия

• Жежеленко, Игорь Владимирович — Игорь Владимирович Жежеленко Дата рождения: 1930 год(1930) Место рождения: Мариуполь Страна: СССР, Украина Научная сфера: электроснабжение промышленны …   Википедия

• Жежеленко Игорь Владимирович — Игорь Владимирович Жежеленко Дата рождения: 1930 Место рождения: Мариуполь Гражданство: СССР, Украина Научная сфера: электроснабжение промышленных предприятий Место работы: Ждановский металлургический институт / Приазовский государственный… …   Википедия

• Жежеленко, И.

  В. — Игорь Владимирович Жежеленко Дата рождения: 1930 Место рождения: Мариуполь Гражданство: СССР, Украина Научная сфера: электроснабжение промышленных предприятий Место работы: Ждановский металлургический институт / Приазовский государственный… …   Википедия

Высшие гармоники | Electric-Blogger.ru

2020-12-17 Статьи  

Как нам хорошо известно, сетевое напряжение имеет синусоидальную форму и частоту равную 50 Гц. Это в идеале, но на практике так бывает далеко не всегда. И дело здесь в гармонических составляющих сети, представляющих из себя частотные сигналы, отличающиеся от основной частоты, и вносящих искажения в синусоидальную форму питающего напряжения, а это в свою очередь становится причиной ухудшения качества электроэнергии, нарушению нормальной работы электропотребителей и т.д.

Откуда же берутся эти гармонические составляющие?

Дело в том, что в цепях с линейной нагрузкой, к которым можно отнести сопротивление, индуктивность, емкость, протекающий через нагрузку ток пропорционален прикладываемому напряжению и следовательно синусоидальной форме сигнала напряжения соответствует токовая синусоида, поэтому разность фаз между ними равна нулю. А вот в случае, если наблюдается нелинейная зависимость протекающего тока от приложенного напряжения, синусоидальная форма сигнала искажается.

Связано это в первую очередь с ростом количества электрооборудования, имеющего нелинейные характеристики, вызванные наличием в схемотехнике полупроводниковых элементов. Наиболее «проблемными» в этом плане являются тиристорные регуляторы, преобразователи частоты, источники бесперебойного питания, электронные балласты, сварочные аппараты, электродуговые печи и другое оборудование с импульсными источниками питания.

Это приводит к возникновению импульсных токов, содержащих большое количество гармонических составляющих, так называемых высших гармоник, отличающихся от основной гармоники, которые затем попадают в электрические сети и вносят искажения. Гармоники образуются на частотах, кратных основной. Так, первая (основная) гармоника имеет частоту 50 Гц, частота гармоники 3-го порядка будет равна 150 Гц, частота гармоники 5-го порядка – 250 Гц и т. д. Получается, что реальное напряжение в сети представляет собой сумму основного синусоидального сигнала и его гармонических составляющих.

Надо учитывать, что полностью избавиться от влияния гармонических составляющих невозможно, и пока уровень гармоник не превышает допустимых норм, в принципе можно не беспокоиться о каких-то серьезным последствиях. Согласно ГОСТ 13109-97, нормально допустимое значение коэффициентов гармонических составляющих напряжения для сетей 0,38 кВ составляет 8 %, а предельно допустимое — 12 %. Также в этом ГОСТ приведены допустимые значения для каждой n-ой гармонической составляющей, например для 3-ей гармоники это 5%, для 5-ой гармоники – 6,0 %, для 7-ой гармоники – 5 % и т.д. Считается, что наибольшие искажения в синусоидальный сигнал вносят гармоники 3, 5, 7 порядка.

Немного расчётов

Параметр, указывающий на уровень влияния нелинейных искажений, или по другому степень отличия формы сигнала от синусоидальной, называется коэффициентом нелинейных искажений Ku (THD — Total Harmonic Distorsions).

U (1) – действующее значение напряжения 1-ой гармоники

U (2), U (3) … U (40) – действующие значения напряжения высших гармоник.

Таким образом можно определить общую долю суммарного напряжения высших гармоник по отношению к напряжению основной частоты.

Еще одним параметром является коэффициент n-ой гармонической составляющей напряжения

n — номер гармонической составляющей, кратной основной частоте

По этой формуле вычисляется вклад конкретной гармоники в общие искажения.

Основные характеристики гармоник

Все гармоники можно разделить по трем основным характеристикам — порядковому номеру, частоте и типу последовательности.

• Порядковый номер гармоники — это число,показывающее во сколько раз частота гармонической составляющей превышает частоту основной гармоники.
• Частота гармоники определяется путем умножения порядкового номера гармоники на значение основной частоты — 50 Гц.
• По типу последовательности разделяют гармоники прямой, обратной и нулевой последовательности. Гармоники 4, 7, 10, 13 и т. д. порядка образуют симметричную систему напряжений прямой последовательности, то есть совпадающей с последовательностью фаз первой гармоники. Гармоники 2, 5, 8, 11, 14 и т.д. образуют системы напряжений обратной последовательности по отношению к основной частоте. Гармоники с порядковым номером, кратным третьей гармоники (3, 6, 9, 12 и.д.) имеют нулевой порядок следования фаз, т.е. совпадают, и, следовательно, образуют симметричные системы нулевой последовательности.

Последствия возникновения

Какие же проблемы приносят гармонические составляющие в случае отклонения от предельно допустимых показателей?

На самом деле негативных воздействий немало, это увеличение потерь в сетях, перегрев трансформаторов,перегрузки на нейтральных проводах, гармонические шумы, искажение формы синусоидальной кривой, перегрузка и следовательно уменьшение срока службы конденсаторов коррекции коэффициента мощности, поверхностный эффект.

И это еще перечислены не все негативные последствия данного эффекта. Все эти факторы приводят в конечном итоге к экономическим, энергетическим потерям и сокращению срока службы оборудования.

Поэтому в случае увеличения количества гармоник и их выхода за допустимые пределы, необходимо задуматься о принятии решений для снижения их уровня, при этом предварительно проводятся измерения гармонических искажений, по результату которых уже определяются необходимые меры .

Измерение показателей гармоник в сети

Для анализа качества электросети и выявления высших гармоник применяются, в частности, многофункциональные измерительные приборы или по другому анализаторы качества электроэнергии.

Они позволяют получать подробную информацию по всем основным характеристикам качества электроэнергии, таким как:

• коэффициент мощности
• коэффициент амплитуды
• среднеквадратичные значения тока и напряжения
• значения активной, реактивной и полной мощности
• активной и реактивной энергии в прямом и обратном направлении
• суммарный коэффициент гармоник THD тока и напряжения
• коэффициент n-й гармонической составляющей напряжения
• дисбаланс напряжения

И целый ряд других параметров, которые по совокупности позволяют получить точную оценку не только гармонических величин, но и провести полный анализ состояния сетей.

Кроме этого, анализаторы имеют дополнительные функции, такие как ведение журнала событий, проверка последовательности чередования фаз, передача данных на верхний уровень по интерфейсу RS-485 или Ethernet, светодиодная индикация, дискретные входы и выходы.

Способы уменьшения гармонических составляющих

На основании полученных данных можно принимать решения о внедрении средств, направленных на уменьшение гармонических составляющих.

К основным способам уменьшения гармоник относятся разделение линейных и нелинейных нагрузок, обеспечение симметричного режима работы трехфазной системы, снижение полного сопротивления распределительной сети за счет увеличения сечения кабелей, применение линейных дросселей, применение изолирующих трансформаторов с обмотками «треугольник» и «звезда», применение пассивных и активных фильтров.

Одним из наиболее простых способов снижения уровня высших гармоник является установка линейных дросселей переменного тока. В частности, такой способ фильтрации широко применяется для подавления помех, возникающих при работе частотных преобразователей.

Дроссель имеет малое значение индуктивного сопротивления на основной частоте 50 Гц и большое значение сопротивления для высших гармоник, что приводит к их ослаблению. Помимо дросселей переменного тока, для частотных преобразователей могут применяться и дроссели звена постоянного тока.

Помимо дросселей широко применяются пассивные и активные фильтры.

Пассивный фильтр гармоник

Пассивные фильтры строятся на основе индуктивно-емкостной схемы (LC-фильтры), состоящей из продольных индуктивностей и поперечной цепи, состоящей из последовательно включенных индуктивности и емкости которые образуют последовательный колебательный контур, настроенный на определенную гармонику. Если необходимо уменьшение коэффициента искажения по нескольким гармоникам, можно использовать несколько параллельно включенных фильтров. Такой метод часто используется в цепях с источниками бесперебойного питания ( UPS).

Недостатком такого метода является его ограниченный только определенными гармониками эффект, поэтому для подавления всего спектра гармонических составляющих в сети используются активные фильтры.

Активный фильтр гармоник

Активный фильтр гармоник (АФГ) представляет собой электронное устройство, можно сказать является управляемым источником тока, подключаемым параллельно с нагрузкой, генерирующей высшие гармоники. Принцип действия основан на анализе гармоник нелинейной нагрузки и генерировании в распределительную сеть таких же гармоник, но противофазе. В результате высшие гармонические составляющие нейтрализуются в точке подключения фильтра и на выходе получается почти синусоидальная форма.

Такой метод благодаря своей эффективности является одним из наиболее действенных способов подавления высших гармоник, но не самым дешевым. Его применение оправдано там, где наблюдается большой уровень искажений.

Доказано: В электросетях существуют высшие гармоники с частотами свыше 2 кГц

Российский стандарт 13109—97 при оценке качества напряжения разрешает учитывать только целочисленные гармоники до 40-го порядка по отношению к основной частоте 50 Гц, то есть до 2 кГц. Это положение стандарта представляется ошибочным.

 

В работе [1] на рис. 3 приводился пример осциллограммы напряжений в сети 10 кВ с вентильным электроприводом прокатного стана. Частота измерений здесь была равна 10 кГц, когда при разложении в ряд Фурье можно выделить предельную 100-ю гармонику частоты 5 кГц. Наблюдались гармоники кратности 60?80 с амплитудой до 15 %, тогда как коэффициент несинусоидальности напряжения, рассчитанный по ГОСТ, равен

Коэффициент несинусоидальности в этой сети, рассчитанный с учетом всех гармоник, равен

,

а долевой вклад высших гармоник кратности >40, составил

(здесь и далее приводятся усредненные по трем фазам значения коэффициентов).

В отклике на статью специалиста ОАО ВНИПИ «Тяжпромэлектропроект» А. К. Красовского приводятся сведения об опасных гармонических возмущениях на еще больших частотах 7.9?8.1 кГц (158?162-я гармоники).

 

Заметим, что возмущения на частотах 9 кГц — 30 МГц традиционно изучаются специалистами по связи, причем CISPR (Интернациональный Комитет по Радиопомехам), накладывает соответствующие нормативные ограничения на напряжения и токи больших частот. Полагается, что диапазон 2?9 кГц должен контролироваться специалистами электрических систем, но это не произошло вследствие, очевидно, относительно малого количества наблюдавшихся экстремальных ситуаций, требующих решения, и явной неподготовленностью парка измерительных приборов.

 

Приведем ряд дополнительных примеров, показывающих на проблемы в работе электрооборудования из-за наличия гармоник с порядковым номером n>40.

На рис. 1 показаны мгновенные значения и гармонические спектры фазных напряжений в одной из сетей 6 кВ, питающей 12-пульсные выпрямители преобразователей частоты мощностью 4 МВт. Высокочастотные колебания напряжения приводят к сбоям в работе находящихся в сети электронных приборов (компьютеров, цифровых реле и электросчетчиков), создают телефонные помехи.

 

Рис. 1. Фазные напряжения в сети с нагрузкой преобразователей частоты и их спектры

 

Спектр напряжений, рассчитанный до частоты 10 кГц (fизм=20 кГц), явно имеет гармоники с частотой более 200-й кратности. Если бы приводились измерения прибором, ориентированным на учет гармоник до 40-й, то пользователь зафиксировал бы коэффициент искажения синусоидальности напряжения KU ГОСТ=4.6 % (близкое к норме ГОСТ значение) с небольшим превышением допустимых уровней для 35 и 37-й гармоник. Но действующее значение коэффициента искажения синусоидальности в действительности составляет

,

а доля гармоник порядков n>40 превышает допустимое по ГОСТ значение для низкочастотного диапазона n=2?40 (KU n>40=10.2 %).

Главной причиной появления столь высокочастотных гармоник (рис 1), подтвержденных математическим моделированием процессов в данной сети, является относительно малая величина емкостной проводимости изоляции в сочетании с наличием высокочастотных возмущений от управляемых тиристорных преобразователей — см. рис.2. При относительно малой в данном случае нагрузке преобразователей (около 25 %) наблюдаются близкие к нулю углы коммутации и большие di/dt. Двенадцать раз на периоде возникают резкие срезы обратных токов тиристоров, в результате чего спектр гармонических возмущений по току не затухает и на 200-й гармонике. Недопустимые гармонические возмущения наблюдались и при нагрузке, приближающейся к номинальной, несмотря на увеличение углов коммутации.

Рис. 2. Токи нагрузки, приводящие к показанным на рис. 1 возмущениям напряжения.

 

На рис. 3 показаны спектры напряжения в сети 6 кВ завода, где работают выполненные с 12-пульсными выпрямителями электропечи высокочастотного нагрева мощностью 5 МВА фирмы АВВ. При изменениях нагрузки печи за счет переключения ступеней регулирования (их всего 14) наблюдаются существенные изменения гармонических спектров токов и напряжений. При относительно невысоких величинах показателя KU ГОСТ имеем недопустимо большие коэффициенты KU и KU n>40, особенно при работе на ступенях с малой нагрузкой. Выполнить такой подробный анализ гармоник оказалось возможным с использованием осциллографа-анализатора «НЕВА-ИПЭ» [1].

Рис. 3. Зависимость спектров напряжений в сети 6 кВ от режима работы электропечи с частотным преобразователем.

 

На основании изложенного можно высказать следующие пожелания.

1. ГОСТ 13109—97 должен быть дополнен разделом, посвященным нормированию гармоник в диапазоне 2?9 кГц. К этой ответственной работе следует приступить как можно скорее.

2. Разработчикам приборов ПКЭ необходимо расширить диапазон измеряемых гармоник.

3. Следует рекомендовать исследователям при возникновении подозрений на существование недопустимых высокочастотных помех использовать для измерений различного рода осциллографы и специализированные алгоритмы обработки измеренных сигналов.

4. Необходимо активизировать исследовательские работы по поиску рациональных путей подавления высокочастотных помех. Над решением этой достаточно сложной задачи работают, в частности, специалисты ЗАО «НПФ «ЭНЕРГОСОЮЗ».

 

Литература

1. Л.А.Кучумов, А.А.Кузнецов, М.В.Сапунов. Исследователи ждут большего от современных измерительных приборов. «Новости электротехники». СПб.: № 4, 2004.-С.64—66

 

Авторы:

Л.А.Кучумов, проф. СПбГПУ;
А.А.Кузнецов, доцент СПбГПУ;
М.В.Сапунов, инженер ЗАО «НПФ «ЭНЕРГОСОЮЗ».

ТОЭ лекции-№53 Высшие гармоники в трехфазных цепях

В симметричном трехфазном режиме токи и напряжения в фазах сдвинуты взаимно во времени на Δt = T/3 в порядке следования фаз А → В → С → А, что в градусной мере составляет: для 1 гармоники Δωtt = = 120°, для 2 гармоники 2Δωt = 2·360°/3 = 240= -120°, для 3 гармоники Δ3ωt = 3·360°/3 = 360° = 0, и т. д.

Из этого следует, что в симметричной трехфазной системе гармоники с порядковым номером к = 3n-2 (n = 1, 2, 3…), т.е. 1-я, 4-я, 7-я и т.д., имеют прямой порядок следования фаз А → В → С → А и, следовательно, образуют сим¬метричные системы прямой последовательности. Гармоники с порядковым номером к = 3n+1 (2-я, 5-я, 8-я и т.д.) имеют обратный порядок следования фаз А → С → В → А и, следовательно, образуют симметричные системы обратной последовательности. Гармоники с порядковым номером к=3n (3-я, 6-я, 9-я и т.д.) имеют нулевой порядок следования фаз, т.е. совпадают, и, следовательно, образуют симметричные системы нулевой последовательности.

Пусть обмотки трехфазного генератора соединены по схеме звезды с выводом нулевой точки, а его фазные напряжения (ЭДС) содержат все возможные гармоники (рис.53.1).

B функциях фазных напряжений будут содержаться все гармоники с соответствующими их номеру сдвигами фаз:

uA(t) = U1msinωt +U2msin2ωt + U3msin3ωt + …

uB(t) = U1msin(ωt — 120°) +U2msin(2ωt + 120°) + U3msin3ωt + …

uC(t) = U1msin(ωt + 120°) +U2msin(2ωt — 120°) + U3msin3ωt + …

Векторные диаграммы напряжений для 1-й, 2-й и 3-й гармоник показаны на рис. 53.2 а, б, в.

Линейные напряжения равны разности соответствующих двух фазных напряжений, например uAB = uA — uB. Как следует из векторных диаграмм амплитуды линейных напряжений для гармоник прямой и обратной последовательностей в √3 раз больше их фазных значений, а гармоники нулевой последовательности (кратные трем) в линейных напряжениях вообще отсутствуют (равны нулю):

uAB(t) = √3U1msin(ωt + 30°) + √3U2msin(ωt — 30°) + 0 +…

uBC(t) = √3U1msin(ωt — 90°) + √3U2msin(ωt + 90°) + 0 +…;

uBC(t) = √3U1msin(ωt + 150°) + √3U2msin(ωt — 150°) + 0 +…;

Действующие значения фазного и линейного напряжения:

Сравнение полученных уравнений показывает, что при наличии в фазных напряжениях генератора гармоник нулевой последовательности (кратных трем) стандартное соотношение Uл/Uф=√3 не соблюдается, а именно Uл≤√3Uф. Из совместного решения этих уравнений получим:

— действующее значение всех гармоник нулевой последовательности. В реальных трехфазных цепях четные гармоники, как правило, отсутствуют вообще, а амплитуда 9-й гармоники незначительна, поэтому можно приближенно считать, что U0 ≈ U3 , и U3m ≈ U0 — амплитуда 3-й гармоники.

Если обмотки трехфазного генератора соединить по схеме треугольника, то гармоники прямой и обратной последовательностей в контуре тре¬угольника складываясь, в сумме дают нуль, а гармоники нулевой последовательности складываются арифметически, и в контуре треугольника будет действовать суммарная ЭДС, равная 3U0. Даже при незначительных амплитудах гармоник нулевой последовательности в фазных ЭДС, вызываемые ими в контуре треугольника токи могут оказаться значительными по величине, так как внутреннее сопротивление обмоток очень мало. Это привело бы к дополнительным потерям энергии в генераторе и снижению его КПД. По этой причине обмотки трехфазных генераторов запрещается соединять по схеме треугольника.

Расчет трехфазной цепи при несинусоидальном напряжении генератора производится так же, как и любой сложной цепи, а именно, по методу наложения в три этапа. На 1-ом этапе выполняется разложение несинусоидального фазного напряжения в гармонический ряд Фурье. На 2-ом этапе выполняется расчет схемы для каждой гармоники в отдельности, при этом учитывается зависимость порядка следования фаз от номера гармоники. Например, гармоники токов нулевой последовательности могут замкнуться только через нулевой провод, поэтому при отсутствии нулевого провода гармоники кратные трем в фазных и линейных токах равны нулю.

На заключительном этапе расчета определяются действующие значения токов, напряжений, активные мощности.

В случае симметричной трехфазной нагрузки расчет токов и напряжений для каждой гармоники можно выполнять только в одной фазе А, а соответствующие токи и напряжения в других фазах определять через поворотные множители “а”, “а2” с учетом порядка следования фаз.

Влияние высших гармоник и их фильтрация

Развитие современных технологий полупроводников ведет все к более возрастающему количеству потребителей, управляемых тиристорами и преобразователями.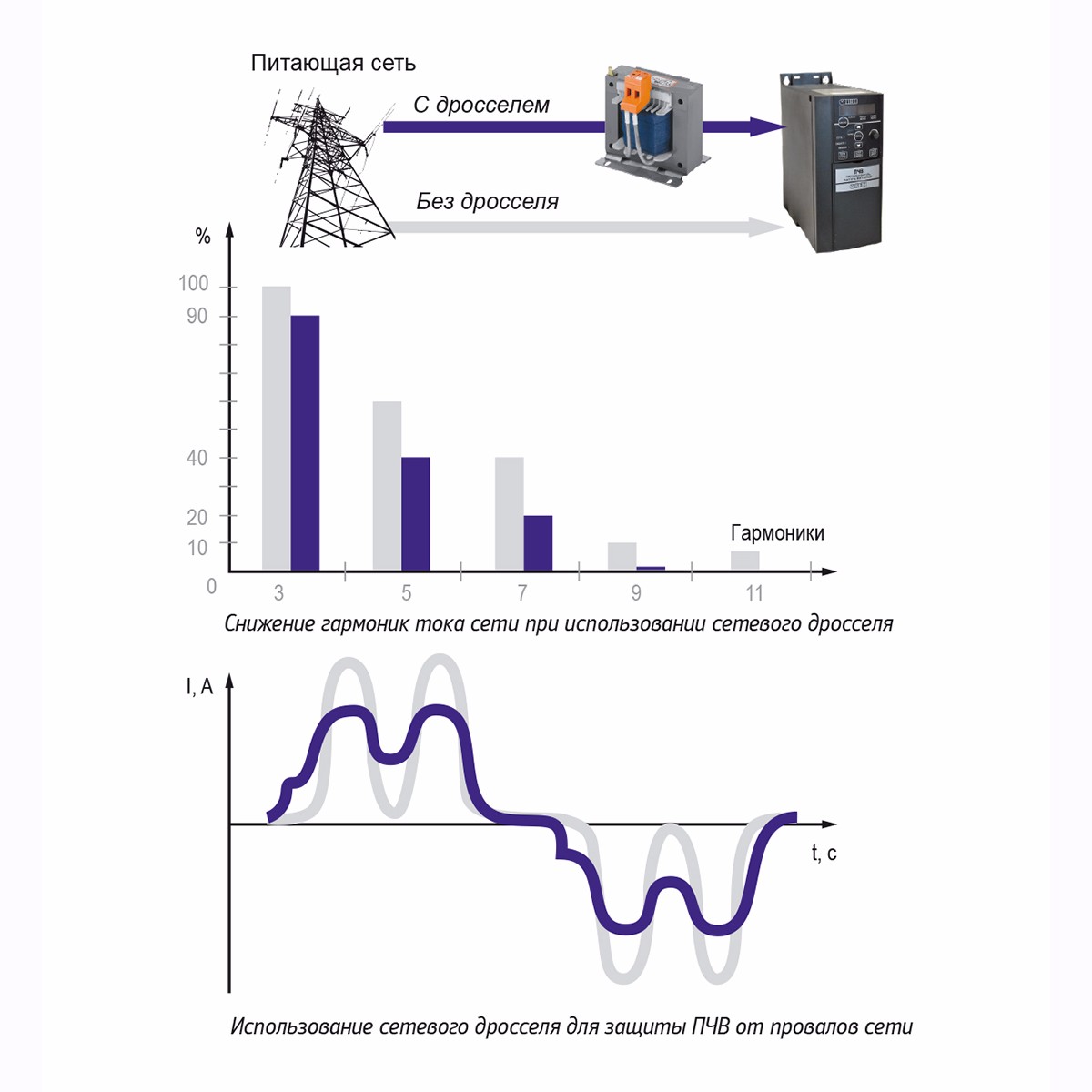 К сожалению, преобразователи увеличивают значение индуктивной реактивной мощности и ухудшают несинусоидальную форму токовой кривой. Эти помехи питаемой сети ведут к повреждениям и ложным срабатываниям оборудования и приборов. Типичный ток преобразователя представляет собой наложения различных синусоидальных составляющих тока, т.е. основной сетевой частоты и определенного числа так называемых высших гармоник (в трехфазной сети в первую очередь гармоники 5-го, 7-го и 11-го порядков). Содержание высших гармоник ведет к повышению тока в конденсаторах, т.к. реактивное сопротивление конденсаторов с возрастанием частоты уменьшается. Параллельно с возрастанием тока в конденсаторах, который можно регулировать с помощью конструктивных мер, в неблагоприятных случаях в сетях могут возникнуть резонансные явления. Компенсационные конденсаторы и индуктивности трансформатора и сети представляют собой резонансный контур. Если собственная частота такого контура совпадет с частотой высших гармоник, то возможно возникновение колебаний со значительными сверхтоками и перенапряжениями. Это ведет к перегрузкам и повреждениям в электрических установках. Загрязнение сетей переменного тока высшими гармониками может вести к следующим последствиям:

• Снижение срока службы конденсаторов
• Преждевременное срабатывание контакторов и других предохранителей
• Выход из строя или ошибочная деятельность компьютеров, приводов двигателей, устройств освещения и др. чувствительных потребителей

Целью подключения дросселя (реактора) к конденсатору служит снижение резонансной частоты сети до значения, величина которого ниже значения наименьшей высшей гармоники данной сети. Этим предотвращается резонанс между конденсаторами и сетью, а значит и возрастание токов высших гармоник. Кроме того, такое включение имеет эффект фильтра, при котором уменьшается степень искажения напряжения. Рекомендуется в тех случаях, когда доля потребителей, загрязняющих сеть высшими гармониками, составляет более 20% всех потребителей сети. Резонансная частота конденсатора, включенного последовательно с дросселем, всегда лежит ниже частоты 5-ой гармоники. Для токов высших гармоник цепь фильтра представляет собой очень низкое полное сопротивление. Поэтому большая часть таких токов направляется в этот контур. Чтобы качественно проанализировать наличие гармонической составляющей необходимо произвести энергоаудит электрических сетей, который наше предприятие успешно осуществляет.

---

Добавить вопрос/отзыв

ОЦЕНКА ВКЛАДА НЕЛИНЕЙНОЙ НАГРУЗКИ В ВЫСШИЕ ГАРМОНИКИ НАПРЯЖЕНИЯ СЕТИ ПРИ НАЛИЧИИ В ПИТАЮЩЕМ НАПРЯЖЕНИИ ВЫСШИХ ГАРМОНИК | Опубликовать статью ВАК, elibrary (НЭБ)

 

ОЦЕНКА ВКЛАДА НЕЛИНЕЙНОЙ НАГРУЗКИ В ВЫСШИЕ ГАРМОНИКИ НАПРЯЖЕНИЯ СЕТИ ПРИ НАЛИЧИИ В ПИТАЮЩЕМ НАПРЯЖЕНИИ ВЫСШИХ ГАРМОНИК

Научная статья

Сысун В.И.^1, *, Олещук О.В.², Соболев Н.В.³,Тихомиров А. А.⁴

^{1, 2, 3, 4} Петрозаводский государственный университет, Петрозаводск, Россия

* Корреспондирующий автор (sasha.82[at]mail.ru)

Аннотация

В настоящей работе предложена методика расчета токовых гармоник генерируемых нелинейной нагрузкой при условии наличия в питающей сети высших гармоник напряжения. Предложена модель нелинейной нагрузки потребителя. Получены условия применения независимых схем для каждой гармоники напряжения. Рассмотрено влияние высших гармоник напряжения нелинейной нагрузки на высшие гармоники тока. Данная методика может быть использована для расчетов показателей качества электроэнергии в сети при наличии нелинейных нагрузок.

Ключевые слова: высшие гармоники, нелинейная нагрузка, электроэнергетика.

EVALUATING THE CONTRIBUTION OF NON-LINEAR LOADS TO HIGHER-ORDER HARMONICS OF NETWORK VOLTAGE IN SUPPLY VOLTAGE OF HIGHER-ORDER HARMONICS

Research article

Sysun V. I.^1, *, Oleshchuk O.V.², Sobolev N.V.³, Tikhomirov A.A.⁴

^{1, 2, 3, 4} Petrozavodsk State University, Petrozavodsk, Russia

* Corresponding author (sasha.82[at]mail.ru)

Abstract

The following paper proposes a method for calculating current harmonics generated by the non-linear load in the supply voltage of higher-order harmonics of the voltage. A model of non-linear consumer load is also proposed. The conditions for the use of independent circuits for each voltage harmonic are obtained. The effect of higher-order harmonics of non-linear load voltage on higher-order harmonics of the current is considered. This method can be used to calculate the quality of electricity in the network in case of non-linear loads.

Keywords: higher harmonics, non-linear load, electric power industry.

Генерация высших гармоник тока различными типами электрооборудования в настоящее время является важным объектом исследования [1], [2], [3], [4].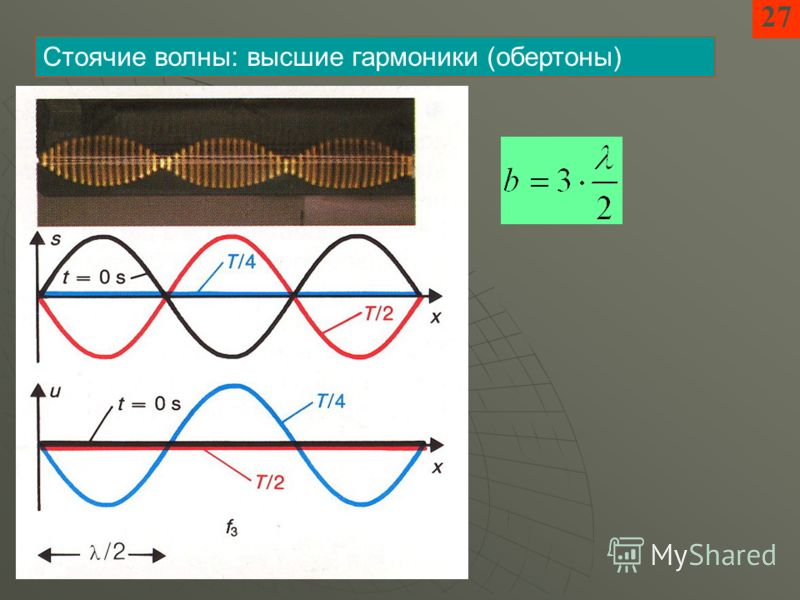 Дополнительной задачей является учёт наличия в напряжении сети своих высших гармоник, что усложняет анализ состояния технических средств и прогноза их ресурса [5], [6]. Показателями качества электроэнергии в сети являются суммарный коэффициент гармонических составляющих напряжения  и коэффициент n-ой гармонической составляющей напряжения . Здесь U_(1)д и U_(n)д действующие значения первой и n-ой гармоники напряжения. Другим показателем нелинейности в узле сети являются искажающая мощность n-ой гармоники D_(n)=U₍₁₎I_П(n), где I_П(n) ток n-ой гармоники потребляемой нагрузкой.

Целью настоящей работы является оценка влияния высших гармоник напряжения на высшие гармоники тока нелинейной нагрузки и методика определения собственных генерируемых гармоник тока по их измерениям при наличии в сети высших гармоник напряжения.

При подаче на нелинейную нагрузку синусоидального напряжения в токе возникают гармоники с кратными частотами обусловленные нелинейной зависимостью тока и напряжения [7, С.495], [8], [9]

  (1)

где  – сдвиг фазы n – ой гармоники тока относительно фазы напряжения в начальный момент времени. Амплитуды гармоник могут быть вычислены при аппроксимации характеристики цепи математической зависимостью, например, степенным полиномом или гиперболическим синусом [10, С. 460], а также измерены и внесены в паспорт нагрузки. Аппроксимация гиперболическим синусом при соответствующем выборе коэффициентов разложения может быть сведена к степенной аппроксимации. При симметричной вольт – амперной характеристике она аппроксимируется нечётными степенями напряжения, а в токе будут только нечётные гармоники

   (2)

Коэффициенты разложения могут зависеть от частоты и представляют собой комплексные проводимости.

При малых значениях нелинейности выполняется условие:

    (3)

Основной вклад в гармонику тока даёт соответствующий член разложения (2):

Тогда условие малой нелинейности (3) запишется в виде

   (4)

Степень неравенства (3) определяется допустимой погрешностью.

В процессе эксплуатации параметры цепи могут изменяться, и требуется контроль генерируемых высших гармоник тока. Однако, напряжение питания сети тоже может содержать высшие гармоники

   (5)

и требуется определение собственных гармоник тока нагрузки по измерениям высших гармоник тока при напряжении сети со своими высшими гармониками.

При оценке вклада нелинейной нагрузки в высшие гармоники напряжения сети [9, 11 – 12] нелинейная нагрузка потребителя моделируется параллельно подсоединёнными эквивалентными проводимостями для каждой гармоники и источниками тока каждой гармоники  (рис.1).

Рис. 1 – Модель нелинейной нагрузки потребителя

 

При этом сеть в точке присоединения потребителя обладает эквивалентной проводимостью для каждой гармоники и может содержать высшие гармоники напряжения  обусловленные высшими гармониками тока, генерируемые как данной нагрузкой, так и другими потребителями сети. Вкладом высших гармоник напряжения из-за их малости в генерацию токов нагрузки   пренебрегают, но учитывают их вклад в ток, потребляемый нагрузкой:

В (5) фазы   отсчитываются от основной гармоники напряжения .

По сути дела приближение (5) и рисунок 1 предполагают учёт для высших гармоник напряжения в (2) только первого линейного члена. Учёт более высоких членов при подстановке (4) в (2) и оставление только наиболее значимых составляющих при условии слабой нелинейности (3) показывает, что для выполнения приближения (5) необходимо дополнительное условие  , что обычно выполняется.

Пусть  – напряжение в сети до подключения нагрузки. После подключения нагрузки напряжение     определяется из соотношения

   (6)

После подстановки в (5) будем иметь:

   (7)

Как видно из (7) проводимость нагрузки (в том числе если она будет линейной) обычно уменьшает напряжение гармоник сети, а вклад от индуцированных высших гармоник тока определяется как амплитудами индуцированных токов, так и их фазами. Это позволяет компенсировать кратные гармоники напряжения взаимной компенсацией индуцированных токов от нескольких нелинейных нагрузок. Искажающая мощность высшей гармоники после подключения нагрузки согласно (5) состоит из двух составляющих: генерирующей искажающей мощности , и поглощаемой искажающей мощности . Таким образом, параметры нелинейной нагрузки  являются определяющими изменения нагрузкой коэффициента высших гармоник  и искажающей мощности сети . Это определяет необходимость текущего контроля над значением их амплитуд и фаз в процессе работы нагрузки.

Определение двух параметров нелинейной нагрузки  требует измерений тока и напряжения гармоники в узле  в двух разных режимах работы сети  на интервале времени, за которое данная нагрузка не изменяется [11]. Изменение режима сети может проходить естественно в течении суток, либо в результате подключения второй нагрузки. Тогда согласно (5):

  (8)

   (9)

При чисто активной нагрузке проводимость  не зависит от частоты и равна проводимости для первой гармоники

   (10)

Фазы генерируемых токов высших гармоник будут совпадающими с фазой первой гармоники тока при учёте их возможных разных знаков. Тогда из (5) будем иметь:

Мнимые части членов правой части (11) должны компенсировать друг друга. Тогда получаем:

   (12)

Здесь сдвиги фаз измеряемых гармоник тока и напряжения относительно основной гармоники. При совпадении фаз гармоник напряжения  также будем иметь  и получим в (12) алгебраическую сумму относительных гармоник тока и напряжения.

Таким образом, соотношения 8, 9, 12 позволяют рассчитывать собственные проводимости нагрузки в процессе её эксплуатации и генерируемые нагрузкой токи высших гармоник при наличии с сети высших гармоник напряжения. Получены условия применения независимых схем для каждой гармоники напряжения. Рассмотрено влияние высших гармоник напряжения нелинейной нагрузки на высшие гармоники тока.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Semwal S. Group control and identification of residential appliances using a nonintrusive method / S. Semwal, M. Singh, R. S. Prasad //  J. Elect. Eng. Comput. Sci. – 2015. – Vol. 23, no. 6. – P. 1805–1816.
2. Jettanasen C. Analytical study of the harmonics issued from LED lamp driver / C. Jettanasen, C. Pothisarn // Proceedings of the International Multiconference of Engineers and computer scientists. – 2014. – Vol. II. – P. 683–686.
3. Большаков О. В. О происхождении и измерении гармонических искажений в электрических сетях / О. В. Большаков, О. А. Васильева // Автоматизация и IT в энергетике. – 2016. – №11(88). – С. 2–11.
4. Фархадзе Э. М. Расчёт показателей несинусоидального режима узла нагрузки / Э. М. Фархадзе, Г. Б. Гулиев // Электричество. – 2002. – №8. – C. 20–25.
5. Шклярский Я. Э. Влияние гармонического состава тока и напряжения на мощность искажения / Я. Э. Шклярский, А. А. Брагин, В. С. Добуш // Нефтегазовое дело. – 2012. – №4. – C. 26–31.
6. Тухас В. А. Инжекция высших гармоник тока в электрическую сеть различными типами светового оборудования общего назначения / В. А. Тухас, О. В. Олещук, А. А. Комбин и др. // Технологии ЭМС. – 2016. – №4 (59). – C. 25–31.
7. Гоноровский В. С. Радиотехнические цепи и сигналы / В. С. Гоноровский. – М. : Радио и связь, 1986. – 512 с.
8. Демирчан Теоретические основы электротехники / К. С. Демирчан, Л. Р. Нейман, Н. В. Коровкин. – М. – Т 2. – 575 с.
9. Харлов Н. Н. Математическое моделирование и идентификация узлов нагрузки с нелинейными электроприёмниками / Н. Н. Харлов // Электричество. – 2006. – №2. – С. 7–12.
10. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи / Л. А. Бессонов. – М. : Гардарики, 2002. – 638 с.
11. Смирнов С. С. Вклад потребителя в уровни напряжения высших гармоник в узлах электрической сети / С. С. Смирнов, Л. И. Коверникова // Электричество. –1996. – №1. – С. 58–64.
12. Смирнов Метод определения фактических вкладов сети и потребителя в коэффициенты высших гармоник напряжения узла / С. С. Смирнов // Электричество. – 2005. – №10. – С. 54-61.

Список литературы на английском языке / References in English

1. Semwal S. Group control and identification of residential appliances using a nonintrusive method / S. Semwal, M. Singh, R. S. Prasad //  J. Elect. Eng. Comput. Sci. – 2015. – Vol. 23, no. 6. – P. 1805–1816.
2. Jettanasen C. Analytical study of the harmonics issued from LED lamp driver / C. Jettanasen, C. Pothisarn // Proceedings of the International Multiconference of Engineers and computer scientists. – 2014. – Vol. II. – P. 683–686.
3. Bolshakov O. V. O proishogdenii i izmerenii garmonicheskih iskagenii v electricheskih setax [About origin of harmonic distortion change] / O. V. Bolshakov, O. A. Vasil’eva // Avtomatizacia i IT v energetike [Automatic and IT in power engineering].– 2016. – №11(88). – P. 2–11. [in Russian]
4. Farharidze A. M. Rashet pokazatelei nesibusoidalnogo regima uzla nagruzki [Estimation of nonsinusoidal mode parameters of load node ] / A. M. Farharidze, G. B. Guliev // Electrishestvo [Electricity]. – 2002. – №8. – P. 20–25. [in Russian]
5. Shklarski Ja. A. Vlianie garmonicheskogo sostava toka i napragenia na moshnost iskagenia [Influence of harmonic current and voltage content on distortion power] / Ja. A. Shklarski, A. A. Bragin, V. S. Dovbush // Neftegazovoe delo [Oil and gas engeneering]. – 2012. – №4. – P. 26–31. [in Russian]
6. Tuhas V. A. Ingekcia vishih garmonic toka v electrisheskuy set razlichnimi tipami svetovogo [Different types lighting equipment current ingection of higher harmonics in electric power system] / V. A. Tuhas, O. V. Oleshuk, A. A Kombin. Tehnologii EMS [Technology of EMS]. – 2016. – №4 (59). – P. 25–31. [in Russian]
7. Gonorovskii V. S. Radiotehnicheskie cepi i signali [Radiotechnical circuit and signal] / V. S. Gonorovskii. – М. : Radio i svaz [Radio and signal], 1986. – 512 P. [in Russian]
8. Demirchan K. S. Teoreticheskie osnovi electrotechiniki [Theoritical basic of electrotechics] / K. S. Demirchan, L. S. Neiman, N. V. Korovkin – М. – V 2. – 575 P. [in Russian]
9. Harlov N. N. Matematicheskoe modelirovanie i indeficatsia uzlov nagruzki c nelineinimi [Mathematical modelling and edification of power node with nonlinear load ] / N. N. Harlov // Electrichestvo [Electricity]. – 2006. – №2. – P. 7–12. [in Russian]
10. Bessonov L. A. Teoreticheskie osnovi electrotechniki. Electricheskie cepi[Theoretical basics of electrotechnics. Electrical circuits ] / L. A. Bessonov – М. : Gardariki, 2002. – 638 P. [in Russian]
11. Smirnov S. S. Vklad potrebitela v urovni napragenia vishih garmonic v uzlax electricheskoi [Load contribution in the level of high harmonic voltage level of node power system ] / S. S. Smirnov, L. I. Kovernikova // Electrichestvo [Electricity].–1996. – №1. – 58–64. [in Russian]
12. Smirnov S. S. Metod opredelenia fakticheskix vkladov seti i potrebitela v koefficienti vishix garmonic napragenia [Method of real contribution power system and load definition in high harmonic node voltage coefficient ] / S. S. Smirnov // Elektrichestvo [Electricity]. – 2005. – №10. – С. 54-61. [in Russian]

1.9. Высшие гармоники в цепях генераторов. 1. Основы теории ламповых генераторов. Устройства генерирования и формирования радиосигналов. Учебное пособие

1.9.1. Умножители частоты

1.9.1.1. Ламповые и транзисторные умножители частоты

1.9.1.2. Варакторные умножители частоты

1.9.2. Понижение КПД генератора из-завысших гармоник

1.9.3. Повышение КПД генератора за счет высших гармоник

1.9.1. Умножители частоты

Умножители частоты в радиопередающих устройствах используются для расширения диапазона передатчика без расширения диапазона задающего генератора и для увеличения стабильности частоты. Последнее связано с тем, что на более низких частотах эталонные свойства колебательных систем выше (при одних и тех же добротности Q и R_э). Наиболее широко умножение частоты используется на коротких волнах, где понижение частоты задающего генератора особенно важно. Кроме указанного выше, применение умножителей частоты в многокаскадных передатчиках уменьшает паразитную связь между отдельными каскадами и, следовательно, повышает устойчивость работы передатчика. В передатчиках с угловой модуляцией умножители используются для увеличения индекса модуляции.

Основными параметрами умножителей являются кратность умножения n, рабочая частота, энергетические показатели (выходная мощность, КПД ) и др.

По типу используемых приборов умножители частоты могут быть разделены на два класса: умножители на нелинейных активных элементах (лампы, транзисторы), и умножители на пассивных нелинейных элементах (диоды, варикапы). При использовании резистивного нелинейного элемента (диод, лампа или транзистор) коэффициент преобразования, или КПД умножителя равен: h_n=Р_нn/ P_вх, где Р_нn — мощность n -ой гармоники в нагрузке, Р_вх — мощность на входе умножителя. Известно, что при использовании резистивного нелинейного элемента (диод, лампа, транзистор) h_n не превышает величину 1/n² , тогда как при использовании реактивного нелинейного элемента при не слишком больших значениях n он может быть близок к 1.

1.9.1.1. Ламповые и транзисторные умножители частоты

Ламповый (транзисторный) умножитель частоты представляет собой генератор с независимым возбуждением, анодный (коллекторный) контур которого настроен на n-ю гармонику частоты напряжения возбуждения. Работа этих умножителей частоты основана на использовании нелинейных свойств электронной лампы или транзистора. Основные отличия умножителя от усилителя заключаются в том, что, во-первых, анодный (коллекторный) контур возбуждается не первой, а n-й гармоникой анодного (коллекторного) тока, и, во-вторых, высокочастотное напряжение на аноде (коллекторе) меняется с частотой в n раз большей, чем частота высокочастотного напряжения возбуждения (n — коэффициент умножения). Режим работы умножителя должен обеспечить максимальное значение той гармоники анодного (коллекторного) тока, которая соответствует степени умножения частоты n. Поэтому угол отсечки q анодного (коллекторного) тока умножителя выбирается так, чтобы амплитуда требуемой гармоники имела максимальное значение. Из рис.1.3 видно, что при косинусоидальной форме импульсов анодного тока амплитуда второй гармоники имеет максимум при q = 60°, а третьей — при q =40⁰ (то есть q_оpt@120⁰/n) . Энергетические показатели умножителей частоты всегда намного хуже, чем усилителей. Действительно, мощность на выходе умножителя и его электронный КПД h_n равны:

P_~n=0,5a_ni_amaxx_nE_a,

,

где .

Здесь — максимальное значение импульса анодного тока лампы в выбранной рабочей точке; -эквивалентное сопротивление анодного контура на n-ой гармонике; a₀, a_n— коэффициенты разложения соответственно постоянной составляющей и n -ой гармоники косинусоидального импульса анодного тока; x_n — коэффициент использования по анодному напряжению лампы умножителя. Если электронная лампа используется по току при умножении частоты так же, как при усилении (т.е. i_amax не изменяется), то для того, чтобы коэффициент использования x_n умножителя был таким же, как x усилителя, эквивалентное сопротивление анодного контура умножителя должно быть больше, чем R_э усилителя в раз, что не всегда возможно осуществить, поскольку величина R_эn= , где r_n — характеристическое сопротивление анодного контура наn-ой гармонике, ограничивается выходной емкостью лампы. Однако, даже в тех случаях, когда удается увеличить в требуемое число раз, мощность на выходе умножителя оказывается все-таки меньше, чем у усилителя, приблизительно в раз и при более низком электронном КПД.

Из-за низких значений электронного КПД умножение частоты производится всегда в маломощных каскадах. Обычно умножители ставят либо после буферного каскада, следующего непосредственно за задающим генератором, либо сразу после задающего генератора. В последнем случае умножитель выполняет функции буферного каскада, то есть работает без сеточных токов.

В умножителях частоты импульс анодного тока, проходящий через лампу один раз за каждый период частоты напряжения возбуждения, возбуждает анодный контур только один раз за n периодов колебаний в нем. По этой причине добротность анодного контура должна быть достаточно высокой. Колебания в анодном контуре умножителя можно считать практически синусоидальными только при выполнении условия Q ³ 5n . При удвоении и утроении частоты это условие обычно хорошо выполняется. При n > 3 его выполнение может оказаться затруднительным. Необходимо также иметь в виду, что при больших значениях n оптимальный угол отсечки анодного тока q_opt=120°/n мал, и амплитуда переменного напряжения на управляющей сетке лампы, обеспечивающая удовлетворительное её использование по току, может оказаться настолько велика, что возникает опасность пробоя в пространстве катод — управляющая сетка

Форма импульсов анодного тока ламповых умножителей отличается от косинусоидальной, однако, поскольку проницаемость ламп мала, при инженерном расчете удвоителей и утроителей допустимо пользоваться соотношениями, полученными для усилителей. Еще более далеки от косинусоидальной формы импульсы коллекторного тока транзисторных умножителей, поэтому в выходной колебательный контур, настроенный на требуемую гармонику, включают шунты, настроенные на наиболее интенсивные гармоники рабочей частоты (в удвоителях — на первую, в утроителях — на первую и на вторую).

1.9.1.2. Варакторные умножители частоты

Варактор представляет собой полупроводниковый диод. В качестве нелинейного элемента используется нелинейная ёмкость p-n-перехода, которая складывается из барьерной и диффузионной емкостей, С_б и С_д. При закрытом переходе емкостью варактора является барьерная емкость С_б, а при открытом к ней добавляется диффузионная емкость С_Д. Известно, что барьерная ёмкость закрытого p-n-перехода нелинейно зависит от приложенного напряжения U (рис.1.13а), но её величина и нелинейность невелики, поэтому умножители, работающие при полностью закрытом переходе используют на частотах выше 10 ГГц в удвоителях и утроителях частоты. На более низких частотах в умножителях с большей кратностью умножения ( n>3) используют режим с отпиранием р-n-перехода, когда доминирующую роль играет диффузионная ёмкость С_д, которая на несколько порядков больше С_б, а её нелинейность очень велика (рис.1.13а). При этом преобразуемая мощность и коэффициент преобразования оказываются достаточно большими при высокой кратности умножения (до n =5-7). Эквивалентная схема варактора изображена на рис.1.13б, где r_р-сопро-тивление рекомбинации, а r_м – сопротивление полупроводникового материала, а также потери, обусловленные конечным временем восстановления закрытого состояния p-n-перехода. Для эффективного умножения необходимо, чтобы при открытом p-n-переходе ток, протекающий через диффузионную емкость С_д существенно превышал ток через сопротивление рекомбинации r_р, для этого рабочая частота должна быть достаточно высокой: w₁>10/r_рС_д . С другой стороны, частота должна быть достаточно низкой, чтобы потери на сопротивлении r_м были относительно малы, т. е. w₂<0,1/r_мС_б. Таким образом, рабочие частоты варакторного умножителя должны находиться в интервале частот w₂ < w_раб < w₁, при этом частота на входе умножителя w_вх > w₂, а частота на его выходе Nw_вз<w₁.

Рис.1.14

Структурная схема варакторного умножителя изображена на рис.1.14, она содержит пассивный нелинейный элемент НЭ, входной и выходной фильтры, Ф_вх и Ф_вых , и цепь смещения. В качестве входного фильтра может быть использован фильтр нижних частот, а в качестве выходного — полосовой фильтр.

1.9.2. Понижение КПД генератора из-за высших гармоник

При изучении лампового генератора предполагалось, что напряжение возбуждения на его управляющей сетке изменяется по косинусоидальному закону, т.е. u_g=U_gmcoswt. В действительности, вследствие импульсного характера анодного и сеточного токов и обусловленных этим высших гармоник в сеточной цепи, форма сеточного возбуждения может сильно исказиться, что повлечёт за собой понижение электронного кпд генератора.

В течение той части периода, когда остаточное напряжение между сеткой и катодом е_g отрицательное, сеточный ток отсутствует, он появляется лишь в ту часть периода, когда это напряжение на сетке становится положительным. Следовательно, для сеточного тока промежуток сетка-катод представляет собой нелинейную цепь, которую при индуктивной связи контура возбудителя c

а) б)

Рис.1.15

сеточной цепью генератора (рис.1.15а) можно представить эквивалентной схемой рис.1.15б, где диод символизирует нелинейный характер сеточной цепи, а r_g — входное сопротивление лампы, которое зависит от ее электронного режима. В сеточной цепи действуют напряжение смещение Е_g и наводимая из контура возбудителя эдсU_gmcoswt. Если бы индуктивности L_g не было, в цепи сетки протекали бы импульсы сеточного тока i_g с углом отсечки q_g= – arccos.

а) б)

Рис.1.16

Индуктивность L_g в сеточной цепи препятствует нарастанию сеточного тока и замедляет его уменьшение, поэтому форма импульсов сеточного тока искажается (рис.1.16а). При решении подобных задач ток, протекающий в нелинейной цепи рис.1.15б, представляют суммой двух токов — свободного i_св и вынужденного i_вын, т.е. i_g= i_св + i_вын.

Свободный ток i_св может быть найден из дифференциального уравнения

Таким образом, уравнение дла тока i_g имеет вид:

i_g = + A .

Рис.1.17

Коэффициент А можно определить из условия, что в момент времени t₁ (рис. 1.16) ток i_g=0, т.е.:

0 = + A ,

откуда

А =- [].

Тогда:

i_g=— [].

На рис.1.16б показаны диаграммы токов и напряжений в сеточной цепи. Импульс сеточного тока начинается при t = t₁ и заканчивается при t = t₃, когда вынужденный ток равен свободному току, но имеет обратное направление. При L_g=0 ток i_g прекратился бы в момент времени t₂, следовательно из-за индуктивности L_g длительность импульса сеточного тока возрастает. Напряжение между сеткой и катодом будет иметь ту же форму, что сеточный ток.

При прекращении сеточного тока в цепи остаются только напряжения смещения E_g и напряжение возбуждения U_gmcoswt, поэтому в момент времени t₃ происходит скачок напряжения, как показано на рис. 1.17. рис.1.17. Результирующее напряжение на сетке е_g показано на рис.1.17 сплошной линией, пунктиром показано напряжение e_g при L_g=0. Чем больше индуктивное сопротивление катушки wL_g и импульс тока i_gmax, тем сильнее искажена форма напряжения сеточного возбуждения. Поскольку проницаемость лампы мала, соответственно искажается и форма импульса анодного тока i_a — он становится уплощенным и более длительным. У такого импульса уменьшается отношение a₁/a₀ и, следовательно, понижается электронный КПД (на рис.1.17 пунктиром показан неискажённый импульс). Эти явления должны сказываться сильнее при работе генератора в перенапряженном режиме, так как тогда сеточные токи больше и, следовательно, сопротивление r_g меньше, чем в недонапряженном режиме.

Искажения импульса анодного тока из-за высших гармоник в сеточной цепи можно также объяснить наличием высших гармоник сеточного тока — I_g2, I_g3 и др. Если бы сеточный ток изменялся по косинусоидальному закону с амплитудой I_g1, напряжение между сеткой и катодом лампы не было бы искажено, оно было бы сдвинуто по фазе относительно наводимой из контура возбудителя эдс U_g, а его амплитуда былабы равна:

Так как сеточный ток имеет форму импульсов, он богат высшими гармониками, которые создают падения напряжения на катушке L_g— I_g22wL_g, I_g33wL_g и т.д., вследствие чего форма сеточного напряжения искажается.

Для устранения этого явления необходимо, чтобы сеточная цепь представляла малое сопротивление для высших гармоник. Наилучшей является ёмкостная связь с предыдущим каскадом, так как конденсатор связи представляет для высших гармоник малое сопротивление.

1.9.3. Повышение КПД генератора за счет высших гармоник

Ранее было установлено, что генератор отдаёт наибольшую мощность при работе генераторной лампы в граничном режиме, т.е. при коэффициенте использования x = x_{к р}= и U_a = U_акр. При x>x_кр режим становится перенапряжённым, в импульсе анодного тока появляется сед­ловина, приводящая к резкому уменьшению первой гармоники анодного тока I_al и уменьшению мощ­ности генератора.

Рис. 1.18

Можно было бы существенно улучшить энергетические показатели гене­ратора, если бы удалось исказить должным образом форму колебательного напряжения на аноде, так, чтобы увеличить x за пре­делы его критического зна­чения без перехода генера­тора в перенапряженный режим (т.е. без искажения формы им­пульса анодного тока). Одним из путей безболезненного увеличения коэффициента использования x является искажение формы переменного анодного напряжения е_а, действующего между анодом и катодом лампы, при котором при значениях wt, близких к 2np (где n = 0; 1, 2…) его мгновенные значения не превышали бы допустимой величины. Этого можно добиться, если последо­следовательно с напряжением первой гармоники U_а1 включить в анодную цепь лампы напряжение третьей гармоники основной частоты U_a3, противофазноенапряжениюU_а1. На рис.1.18 показана форма кривой результирующего напряжения е_а между анодом и катодом лампы, равного сумме всех напряжений, действующих между этими электродами:

e_a = E_a — U_a1coswt + U_a3cos3wt .

Из рисунка видно, что амплитуда первой гармоники переменного напряжения на аноде U_а1 больше U_а1кр, хотя режим не становится перенапряженным. При этом отдаваемая генератором мощность и его КПД увеличиваются. Для того,чтобы выделить напряжение третьей гармоники U_a3 в анодную цепь включают дополнительный контур L₃C₃, настроенный на тре­тью гармонику (рис1.19).

Рис.1.19

Этот контур представляет для неё активное со­противление R_э3=r₃Q₃ и весьма малое реактивное сопротивление для про­чих гармоник, в том числе и для первой. Угол отсечки анодного тока должен быть немного больше 90⁰, при этом фазы составляющих третьей и первой гармоник анодного тока противоположны (рис.1.3). Напряжение между сеткой и катодом е_g, как всегда, равно сумме напряжения смещения и мгновенных значений напряжения возбуждения:

e_g = E_g + U_gcoswt

Расчеты показывают, что при =~ 0,25 можно сохранить у генератора граничный режим при U_a1» Е_а, что совершенно невозможно при косинусоидальном напряже­нии на аноде.

Следует отметить, что изменение в процессе настройки элементов одного из контуров влияет на состояние другого, поэтому бигармонические режимы используют главным образом в неперестраиваемых (или редко перестраиваемых) передатчиках длинных и средних волн.

Исследования показали, что напряжение третьей гармоники может быть противофазным и при угле отсечки анодного тока, меньшем 90°, но при условии, что импульс анодного тока будет упло­щенном, или имеющем седловину. Аналогичный эффект может быть по­лучен также путем использования второй гармоники вместо третьей.

Еще одним способом получения тех же результатов является неболь­шаярасстройка анодного контура генератора, работающего в перенапряженном режиме. При работе лампы в перенапряженном режиме импульс анодного тока из-за седловины имеет относительно большую про­тивофазную составляющую третьей гармоникиI_a3. Хотя анодный контур представляет для неё небольшое ёмкостное сопротивление Z_ЭЗ»R_э/ Q, на нём всё же появляется некоторое напряжение U_а3 = I_a3Z_э3,которое отстаёт по фазе от I_a3 на 90°. Если анодный контур настроен на частоту немного выше рабочей частоты, т.е.w>w_раб, то для последней он представляет собой комплексное сопротивление ин­дуктивного характера, поэтому падение напряжения на нём U_a3 = I_а3Z_э3 опережает по фазе ток I_a1 на 90⁰. В результате напряжение U_a3 оказывается почти противофазным напряжению U_а1. Такое искажение формы колебательного напряжения на аноде при небольшой расстройке анодного контура приводит к увеличению первой гармоники анодного тока I_a1, а вместе с ней и тока в контуре. При этом может заметно повыситься и КПД генератора. Этот метод иногда ис­пользуют в передатчиках с анодной модуляцией, оконечный каскад которых работает в перенапряжённом режиме.

ПОЧЕМУ возникают гармоники? — Музыка: Обмен практическими и теоретическими стеками

Почему гитарная струна не вибрирует только на одной частоте?

Гармоники обычно производятся системами с нелинейным откликом, такими как струна.

---

Один из способов понять гармоники — это взглянуть на математические операции, такие как преобразования Фурье или другие преобразования. Эти операции преобразуют (преобразуют) интегральное уравнение некоторой величины, обычно амплитуда vs.время в сумме другой величины, обычно амплитуды в зависимости от частоты, где гармонические частоты выступают в качестве основных членов суммы.

Другой способ — посмотреть, как нелинейность создает гармоники. Это то, о чем я здесь подробно расскажу. Нелинейность не является чем-то неизвестным для музыкантов, как только усилитель или микрофон являются нелинейными, они создают гармонические искажения, которые представляют собой просто паразитные гармонические частоты, добавленные к усиленной копии аудиовхода. Гармоническим искажением в музыке еще называют… тембр инструмента. Столько разных слов для одного физического эффекта!

Линейность возвращающей силы: Пружина

В качестве примера линейности представьте пружину. Если удлинить пружину, они почувствуют возвращающую силу, чем больше удлинение и больше сила, возможно, до такой степени, что пружина не может быть растянута дальше. Обычно винтовая пружина развивает восстанавливающую силу, точно пропорциональную удлинению:

Такая система называется линейной в отношении ее реакции на возмущение.Дополнительную информацию о линейности пружин и некоторых приложениях можно найти в статье в Википедии о законе Гука.

Линейность восстанавливающей силы: Диапазон

Диапазон — интересный инструмент, потому что он колеблется в основном без гармоник. Колебание зубцов происходит в линейной области упругости металла, где возвращающая сила пропорциональна текущему расстоянию от положения покоя.

Эта (квази) линейная упругость существует для металлического материала, но только при малых смещениях, что означает небольшую энергию, передаваемую воздуху, и ограниченную интенсивность звука.Если бы мы попытались создать более высокие звуки, мы бы вышли из линейной области и появились бы гармоники.

Вернемся к диапазону позже. Давайте сначала посмотрим на действительно нелинейную систему: гитарную струну!

Гитара: большие колебания, в основном нелинейные

Колебательная система, такая как вибрирующая струна, также имеет положение покоя. При перемещении из этого положения он развивает силу в форме натяжения, стремящуюся восстановить состояние покоя, чем больше поперечное расстояние от положения покоя, тем больше продольное натяжение.

Однако гитарная струна не работает в небольшом диапазоне линейной эластичности диапазона, она должна воспроизводить мощные звуки, струна «возбуждается» большими входными сигналами, на которые материал не может реагировать линейно. Натяжение не пропорционально поперечному расстоянию в данной точке струны:

^{(Правый график от Хенрика Б. Педерсена и Йеппе Лангеланда Кнудсена, адаптированный)}

(Примечание: рисунок выше был обновлен после того, как @ user1079505 прокомментировал неправильное значение амплитуды x.Здесь неправильная / оригинальная цифра.)

Амплитуда восстанавливающей силы имеет тенденцию увеличиваться в большей пропорции по мере того, как мы приближаемся к пределу упругости и немного приближаемся к точке остаточной деформации / разрушения. Другие факторы играют роль, в том числе отклик не зависит от времени, отклик также зависит от предыдущего возмущения струны.

Результатом является то, что восстанавливающая сила не является масштабированной копией текущего расстояния струны от ее положения покоя, и, добавляя сложности, в данный момент времени коэффициент масштабирования не является одинаковым для всех сегментов струны.

Эта нелинейность между амплитудой смещения и восстанавливающим натяжением является источником гармоник. Фактический механизм сложен, но мы увидим простой случай, снова посмотрев на диапазон, который, в конце концов, не является полностью линейным …

Вернуться в диапазон с его небольшой нелинейностью

Утверждение, что в диапазоне нет гармоник, было приблизительным. Диапазон обычно развивает вторую гармонику, и подробности того, как это происходит, являются хорошим примером чрезвычайной чувствительности физических колебательных устройств к асимметрии и нелинейности, которые проявляются в действии со струнами.

Обычно зубцы камертона колеблются в своей общей плоскости, как консольные балки, а центр масс, если смотреть сверху, остается неподвижным из-за симметрии смещений. Однако это не относится к его вертикальному положению.

Когда зубцы колеблются, их отдельный центр масс перемещается вверх и вниз на небольшое расстояние по дуге окружности. Это также происходит при 440 Гц (или любой другой частоте, на которую настроена вилка). Это смещение массы вызывает реакцию в вертикальном направлении, шток поднимается и опускается на очень небольшую величину.

Диапазон обычно проводится против другой поддержки, например. стол. При этом колебания зубцов передаются на опору, действующую как усилитель.

Оказывается, шток более эффективно передает вертикальные колебания, а поверхность стола легче сгибать по вертикали, чем перемещать по горизонтали. Из-за этого избирательного усиления столом очень небольшая вертикальная вибрация теперь имеет большее значение.

Если частота поперечной волны и волны центра масс одинаковы, это может пройти без последствий, однако проблема заключается в том, что их форма волны отличается, одна из них является искаженной синусоидой.И угадайте причину этого искажения … Вот и мы: Нелинейность!

^{Источник}

Этот график является частью исследования, которое полезно читать. Он показывает два колебания (шкалы не одного порядка). В то время как поперечная волна почти синусоидальная, вертикальная волна из-за смещения массы имеет пики и спады различной формы. Причина в том, что вертикальные колебания чередуют силы растяжения и сжатия в штоке, на которые металл по-разному реагирует с разными скоростями.Остались две волны, которые естественно интерферируют, создавая гармонику 880 Гц:

Это простой пример гармоник, созданных небольшой нелинейностью, принцип тот же для других материалов и вибрирующих устройств, включая гитарные струны, хотя задействовано больше элементов.

Линейность: более точное определение

Технически мы говорим, что это гомоморфизм, от гомосексуалов- такая же и -морфа формы. Это громкие слова, на практике это линейное преобразование:

^{Источник}

BC и B’C ‘являются линейными преобразованиями друг друга.Определение линейной системы:

• Если вход x дает выход u, то для любого числа k k.x должно производить k.u. Это означает, что выход должен быть пропорционален входу. Если вход увеличивается в k раз, то выход увеличивается в том же раз.

• Если ввод x дает u, а ввод y дает v, то ввод k1.x + k2.y должен давать k1.u + k2.v (k1 и k2 — любые множители). Это означает, что выход, произведенный суммой, совпадает с суммой выходов отдельных входов.

Вот и все. Любая система, не обладающая двумя вышеуказанными свойствами, производит искажения / гармоники. Это может случиться с усилителями, вибрирующими устройствами, космическими волнами или электрической сетью. Гармоники обычно нежелательны, но их бывает трудно удалить.

гармоник и амплитуды — Музыка: практика и теория Stack Exchange

Мы также знаем, что есть падение амплитуды, примерно соответствующее 1 / ч, где h = гармоника.

Даже с оговоркой «примерно», я не уверен, насколько это полезно в качестве практического правила.Некоторые формы волны (например, пилообразная волна) обладают этим свойством, но многие формы волны, которые могут быть созданы как настоящими, так и электронными инструментами, имеют разную относительную силу своих гармоник. Кроме того, относительные силы обычно меняются со временем, в зависимости от техники игры и так далее.

Итак, если 440 — наша основная гармоника, 880 — наша вторая гармоника. Означает ли это, что амплитуда второй гармоники = 440 (880 * 1/2) или = 220 (440 * 1/2)?

Я думаю, вы смешиваете амплитуду с частотой .Если ваша первая гармоника имеет частоту из 440, вторая гармоника имеет частоту (не амплитуду) 880.

Если предположить, что у нас есть пилообразная волна, то есть относительные амплитуды гармоник равны 1 / номер гармоники, и мы предположим, что амплитуда основной гармоники на частоте 440 Гц равна 1 (в некоторой произвольной единице), то у нас будет

амплитуда 2-й гармоники = 1 * (1/2) = 0,5
амплитуда 3-й гармоники = 1 * (1/3) = 0.333 …
амплитуда 4-й гармоники = 1 * (1/4) = 0,25

и так далее.

Поскольку человеческое ухо может слышать от 20 Гц> 20 000 Гц, если первое верно, это будет означать, что в этом случае мы можем слышать до 46-й гармоники (440 * 46 = 20 240), однако, если последнее верно, это предполагает мы можем слышать только до 22-й гармоники (440 * 1/22 = 20).

Опять же, мы должны быть осторожны, чтобы не перепутать частоту с амплитудой.

Самый простой способ вычислить высшую гармонику, которую вы слышите:

.

20000 / (основная частота ноты)

Если ваша нота находится на частоте 440 Гц, то 20000/440 = 45.45 … упрощенно говоря, это правда, что теоретически вы можете услышать до 45-й или 46-й гармоники для ноты на частоте 440 Гц. Для более низких нот вы можете услышать более высокие гармоники. Но помните, что все это зависит от громкости гармоник. Человеческое ухо менее чувствительно на очень высоких частотах, поэтому, если бы амплитуда гармоники составляла всего 1/46 амплитуды основной гармоники, его было бы трудно услышать.

акустика — Значение высших гармоник

Как бы ни был интересен ваш вопрос, возможно, он слишком общий.Когда дело доходит до восприятия (а не просто объективных значений) , эта тема в целом не совсем понятна. Всегда помните, что восприятие любого параметра звука нелинейно и зависит от других параметров (например, вам нужно учитывать высоту тона, когда вы приближаете его воспринимаемую громкость).

Конечно, с этим связана воспринимаемая громкость, но это не то же самое. Для этих целей вместо дБ мы используем устройство под названием Phon с собственной шкалой (на самом деле это исправленный SPL).Хотя, строго говоря, эта поправка сделана для по физиологии , но вам нужна связь с по психологии , а это чертовски сложно.

Я думаю, что ваш метод не совсем ошибочен. Позвольте мне предложить вам еще несколько параметров для рассмотрения.

• Удельная громкость по Цвикеру . Я не буду здесь излагать всю теорию, просто перейдите по ссылке и, возможно, сначала прочтите что-нибудь о лае.
• Громкость как RMS (среднеквадратичное значение).n c_k}
  $

  Вы должны думать обо всем этом как о приближении. Всегда необходимо проводить окончательную проверку с использованием ваших собственных ушей (а лучше — большего количества ушей, чем только ваши — статистика является ключевым моментом).

  • Необходимо учитывать переходные характеристики тона. Особенно важна атакующая часть тона для восприятия громкости. Вы должны быть уверены, что сравниваете два тона без каких-либо неестественных трещин вначале (используйте, например, постепенное появление) и достаточно долго, чтобы быть полностью воспринятыми (около 1 секунды).
  • Нельзя полностью исключить фазу гармоник. Вы представили только амплитудный спектр, и этого может быть недостаточно для восприятия.
  • Вам следует учитывать некоторые особенности, которые могут быть трудно различимы в спектре, такие как субгармоники (здесь явно присутствуют!), Модуляции (удары !!!) или маскирование звука.

  Основные частоты и гармоники — Teach Me Audio

  Музыкальные звуки состоят из основной частоты, гармоник и обертонов.

  Основная частота

  Самая низкая частота любого вибрирующего объекта называется основной частотой . Основная частота обеспечивает звук с самой сильной слышимой опорой pitch — это преобладающая частота в любой сложной форме волны.

  Синусоидальная волна является самой простой из всех форм волны и содержит только одну основную частоту и не содержит гармоник, обертонов или парциальных частот.

  Практически все музыкальные звуки имеют волны, которые бесконечно сложнее синусоидальной волны. Это добавление к волне гармоник и обертонов , что позволяет различать разные звуки и инструменты; тембр.

  Гармоники

  Гармоника — это одна из восходящей серии звуковых компонентов, которые звучат на выше основной слышимой частоты.

  Высшие частотные гармоники, которые звучат выше основной гармоники, составляют гармонический спектр звука.Гармоники может быть трудно отчетливо воспринимать как отдельные компоненты, тем не менее, они есть.

  Гармоники имеют на меньшую амплитуду на , чем основная частота.

  Гармоники — это целые числа, кратные основной частоте. Например, если основная частота равна 50 Гц (также известная как первая гармоника), то вторая гармоника будет 100 Гц (50 * 2 = 100 Гц), третья гармоника будет 150 Гц (50 * 3 = 150 Гц) и так далее.

  Рисунок 1 — Гармоники

  Обертоны

  Обертоны — это частоты формы волны, которые выше, но не связаны напрямую с , основной частотой.

  Результирующий тембр

  Два тона, воспроизводимые разными инструментами, могут иметь одну и ту же основную частоту и, следовательно, одинаковую высоту, например ноту C, но звучать очень по-разному из-за наличия разного количества гармоник и обертонов.

  Это присутствие гармоник и обертонов в звуковой волне, что помогает производить звуки уникального звука.

  Тембр описывает те характеристики звука, которые позволяют уху различать звуки с одинаковой основной высотой .

  Благодаря тембру мы можем отличить один инструмент от другого, например, пианино, играемое в C3, звучит иначе, чем гитара, взятая в C3.

  Тембр часто описывается субъективно, например, тростниковый или золотистый.

  Обновлено 6 мая 2020

  гармоник — звук, частота, основная гармоника и примечание

  Что делает ноты музыкального инструмента насыщенными? объем звука определяется амплитудой колебаний в звуковой волне, расстояние между отдельными молекулами колеблется.Большая амплитуда производит более громкий звук и передает больше энергии . Высота ноты — это частота , частота или количество колебаний в секунду. Чем выше частота, тем выше тон звука. Богатство или качество звука создается гармониками.

  Чистая нота, целиком состоящая из одной частоты, будет казаться скучной. Музыкальный инструмент, который воспроизводил бы только такие чистые ноты, не казался бы приятным. Гармоники отсутствуют. Гармоники кратны основной частоте.Первая гармоника — это основная частота, 264 цикла в секунду для среднего C. Вторая гармоника будет вдвое больше этой частоты, 528 циклов в секунду, что на октаву выше. Третья гармоника будет в три раза больше основной частоты, 792 цикла в секунду и так далее. Эти гармоники также называются обертонами: вторая гармоника — это первый обертон, третья гармоника — второй обертон и так далее.

  Скрипка, фортепиано и гитара создают звуки за счет вибрации струн.Воспроизведение той же ноты, скажем средней C, даст тон с основной частотой 264 цикла в секунду. Но все три инструмента звучат по-разному, потому что имеют разные гармоники. Количество каждой присутствующей гармоники — это то, что придает каждому музыкальному инструменту уникальный звук. Хорошо сделанный инструмент будет звучать богаче, чем плохо сделанный, потому что у него будут лучшие гармоники. Инструмент без гармоник будет звучать как камертон, в котором присутствует только одна основная частота.

  По причинам, которые мы не полностью понимаем, звуки, состоящие из гармоник, частоты которых являются целыми кратными друг другу, кажутся приятными для человеческого уха .Они музыка. С другой стороны, звуки, состоящие из частот, не кратных друг другу, являются диссонирующим шумом для человеческого уха.

  Громкость и спектр

  Громкость и спектры Громкость зависит не только от амплитуды волны, но также от ее частоты и спектра. Это в основном потому, что наши уши не одинаково чувствительны ко всем частотам (подробнее см. Что такое децибел?) На рисунке ниже (взятом с нашей страницы, посвященной акустике из латуни), две верхние цифры — это спектры, снятые по первому и последнему нулю.3 секунды звукового файла. Спектрограмма (нижний рисунок) показывает время по оси x, частоту по вертикальной оси и уровень звука (по шкале децибел) в ложном цвете (синий — слабый, красный — сильный). Обратите внимание на гармоники в спектрах, которые отображаются как компоненты, расположенные на одинаковом расстоянии (вертикальные линии). На спектрограмме гармоники отображаются в виде горизонтальных линий — они имеют постоянную частоту. Мощность каждой гармоники со временем увеличивается, поэтому звук становится громче.Высшие гармоники усиливаются сильнее, чем нижние, что делает тембр «медленнее» или ярче, а также делает его громче. Основная частота увеличивается всего на 8 дБ, но девятая и некоторые более высокие гармоники — в чувствительном диапазоне вашего уха — увеличиваются более чем на 45 дБ. А крещендо играли на тромбоне. Высшие гармоники делают звук ноты громче отчасти потому, что они добавляют дополнительную мощность звуковой волне, но также потому, что наши уши становятся более чувствительными, когда частота увеличивается с увеличением частоты (по крайней мере, примерно до кГц).Более высокий уровень высоких гармоник также делает звучание сильной ноты более насыщенным тембром. Таким образом, добавление более высоких гармоник делает звук более громким. Обычно верно и обратное: когда человек играет громче, он генерирует больше высоких гармоник. Это связано с тем, что инструменты становятся более нелинейными с увеличением амплитуды вибрации. Это обсуждается, например, в этом разделе нашей страницы о кларнете. Флейта представляет собой особенно интересный пример. Если вы посмотрите на спектр ноты флейты C4, сыгранной на разных динамических уровнях, вы заметите, что i) уровень основной гармоники (первая гармоника, для C4 это около 262 Гц) практически не меняется, но ii) появляется больше высших гармоник, и их уровни увеличиваются по мере того, как нота становится громче. Большинство музыкальных инструментов и многие другие колебательные системы демонстрируют аналогичное поведение — по мере того, как вибрация становится больше, появляется больше гармоник. Мы легко можем отличить например, кто-то кричит, а кто-то тихо говорит в систему громкой связи. Для небольших вибраций зависимость между смещением и возвращающей силой линейна — в в случае пружины пропорциональность между двумя называется законом Гука.Поскольку амплитуда вибрации становится равной чем больше, тем хуже линейное приближение представление криволинейной связи между силой и смещение. Линейная зависимость дает линейный дифференциал уравнение, решением которого является простая синусоида. Как отношения становится более нелинейным, решение выглядит искаженным синусоида — обычно пики выравниваются.Эта волна все еще периодический, поэтому он имеет гармонический спектр (см. звук спектр), но более сложная форма волны последовательно больше мощности на высоких гармониках. По сравнению с некоторыми другими инструментами (например, кларнетом, саксофоном и скрипка) флейта имеет относительно небольшой динамический диапазон. Игроки пользуются изменением тембра, чтобы сделать громче ноты в нижнем регистре: они используют чистый тон для фортепиано и насыщенный «гудящий» тон для форте.Они также склонны использовать больше вибрато на громких нотах, потому что изменение ноты более заметно чем устойчивый. Слушайте аудиоклипы Джеффри Коллинза играет C4 на трех разных динамических уровнях. Обратите внимание на другой тембр и различное использование вибрато. Обратите также внимание на то, как он использует изменяет количество вибрато во время ноты, чтобы помочь «придать форму» Это.Сравните это со звуковыми клипами Кэтрин Маккоркилл. играет на E3.

  Анализ высших гармоник в группе сфокусированных волн воды с помощью модели нелинейного потенциального потока

  Основные моменты

  •

  Реализована генерация группы нелинейных сфокусированных волн в числовом волновом резервуаре.

  •

  Нелинейность важна для изменения формы сфокусированной волны при большой крутизне.

  •

  Четырехфазный метод манипуляции эффективен для гармонического разложения нелинейного подъема волны до четвертого порядка.

  •

  Нелинейная группа волн имеет структуру стоксова типа высших гармоник.

  •

  Оценка высших гармоник из линейной волновой группы с помощью коэффициентов гармоник является точной.

  Abstract

  В данной работе анализируются возвышения волн высших гармоник сфокусированных групп волн на основе предположения о нелинейной структуре типа Стокса.Полностью нелинейная модель потенциального потока используется для генерации нелинейных групп волн по теории NewWave, которая представляет собой экстремальное событие в случайном состоянии моря. Мы представляем методологию для генерации высококачественных нелинейных волновых групп узкополосного волнового спектра в числовом волновом резервуаре. Для точного выделения возвышений высших гармоник используется подход фазовой манипуляции. Спектры возвышений показывают четкое разделение первых четырех гармоник. Сравнение с экспериментальными данными показывает удивительно хорошее согласие для высших гармоник.Подтверждаем лежащую в основе нелинейную структуру гармонических возвышений стоксовского типа в сфокусированных волновых группах. Это обнаруживается путем моделирования групп волн с различной крутизной волны и вычисления соответствующих коэффициентов возвышения для высших гармоник. Коэффициенты гармоник практически постоянны при изменении крутизны. Следствием структуры типа Стокса для нелинейных возвышений волн является то, что она позволяет нам оценивать высшие гармоники только на основе линейной составляющей.Это успешно продемонстрировано путем восстановления группы нелинейных сфокусированных волн с использованием линейной модели NewWave и коэффициентов на ее высших гармониках.

  Ключевые слова

  Полностью нелинейное моделирование

  Сфокусированная группа волн

  Высшие гармоники

  Разложение Стокса

  Рекомендуемые статьиЦитирующие статьи (0)

  Полный текст

  © 2019 Elsevier Ltd.