Рассмотрим неоднородные участки электрических цепей и действующие в них законы
Наиболее применяемое в электротехнике соотношение между основными электрическими величинами – закон Ома, установленный немецким физиком Георгом Омом, эмпирическим способом, в 1826 г. С его помощью устанавливается связь между напряжением (электродвижущей силой), сопротивлением элементов этой цепи, силой проходящего тока.
Измерение тока и напряжения
Электрические параметры, которые описываются законом Ома:
- Сила тока определяется количеством заряда, проходящего по проводнику за некоторое время, обозначается буквой I, единица измерения – ампер (А). Входит в основные единицы международной системы Си;
- Электрическое напряжение, единица измерения – вольт, понятие ввёл тот же Георг Ом. Вольт может быть выражен через работу по перемещению заряда, выделяемую мощность при токе 1 ампер, имеет эталонные источники в виде высокостабильных гальванических элементов. Часто указывается как разность потенциалов, в некоторых случаях применяется понятие электродвижущая сила (ЭДС).
 Для обозначения могут использоваться буквы U, V;
Для обозначения могут использоваться буквы U, V; - R – сопротивление (электрическое), указывает на свойства проводника, оказывающие препятствия прохождению тока. Значительно зависит от материала проводника и температуры. Единица измерения – 1 ом, обозначение Ом или Ω.
Классическая формулировка закона Ома: сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
I = U/R.
Это выражение справедливо для электрической цепи, которая не содержит дополнительной электродвижущей силы, обеспечивающей электрический ток, цепи, определяемой как однородная. В большинстве случаев применяется именно такая формула. На практике часто требуется вычислить значение тока, протекающего через некоторый элемент с известным сопротивлением, для этого достаточно измерить падение напряжения (разность потенциалов) на выводах этого устройства, например, резистора. При заданных любых двух значениях можно рассчитать неизвестное, так же, кроме величин, входящих в выражение, определяется электрическая мощность.
Важно! При расчётах используются величины только одной размерности – целые значения вольт, ампер, ом или соответствующие им кратные и дольные единицы.
I – сила тока, R – сопротивление, U – напряжение, P – мощность
Неоднородная цепь
Закон Ома для отдельного участка цепи не учитывает присутствие источника питания, его свойства не входят в вычисления. Для цепи, называемой неоднородной, содержащей ЭДС любого рода и её источник, в известную формулу следует добавить внутреннее сопротивление самого питающего устройства:
I = E/(R + r).
Здесь Е – ЭДС источника напряжения, r – его внутреннее сопротивление. Варианты наименований – закон Ома для неоднородного участка цепи, для полной или замкнутой цепи. Выражение мало отличается от приведённого выше – вместо напряжения присутствует ЭДС и сопротивление источника питания.
Следует отметить, что понятие внутреннего сопротивления имеет смысл исключительно для химических источников тока, в случае применения других устройств, таких как любого вида блоков питания без батарей, говорят о выходном сопротивлении и нагрузочной способности этого блока.
В практических применениях закон Ома для неоднородного участка цепи в таком виде применяется редко, в основном для измерения самого внутреннего сопротивления аккумулятора, других элементов питания.
Закон применим и для переменного напряжения, если сопротивлением является активная нагрузка. С его помощью определяются действующие (среднеквадратичные) параметры цепи. В случае индуктивной, ёмкостной или комплексной нагрузки и для разных частот сопротивление является реактивным, значительно отличающимся от измеренного обычным методом – омметром.
Закон Ома получен практическим путём, поэтому не может быть фундаментальным, но точно описывает взаимосвязь между наиболее часто используемыми электрическими величинами.
Видео
Оцените статью:Закон Ома для неоднородного участка цепи
В простейшем варианте для расчета электрических параметров подразумевают воздействие кулоновских сил, которые обеспечивают перемещение зарядов. Закон Ома для неоднородного участка цепи позволяет учесть дополнительные факторы. Его применение помогает повысить точность вычислений.
Закон Ома для неоднородного участка цепи позволяет учесть дополнительные факторы. Его применение помогает повысить точность вычислений.
Закон Ома для участка цепи
Неоднородный участок цепи постоянного токаОпределение основных параметров и процессов:
- перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
- при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
- эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):
q = q0*n*V.
Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала.
Пример неоднородного участка цепи
Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).
Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.
Ниже приведены формулы, характеризующие рассмотренный пример:
- A12/q = ϕ1 – ϕ2;
- Ast/q = E12;
- U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
- I = (ϕ1 – ϕ2 + E12)/ R.

Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.
К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.
Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом.
ϕ1= 20V; ϕ2=10V.
Подставив значения в формулу, можно получить нужный результат:
(20-10+40)/5 = +10А.
Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».
Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:
На него действуют три вида сил:
- кулоновские – Fкул;
- сторонние – Fc;
- сопротивления кристаллической решетки – Fсп.
Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.
Закон Ома для замкнутой цепиВ реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:
I = E/(Rн+Rи).
Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.
Классическая формулировкаДля участка цепи без источника ЭДС достаточно использовать классический закон Ома:
I (сила тока) = U (напряжение) /R (электрическое сопротивление).
Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие.
U = ϕ1 – ϕ2.
Элементарные вычисления показывают взаимные зависимости перечисленных параметров:
- I1 = 24/6 = 4А;
- I2 = 60/6 = 10А.
Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:
I2 > I1.
Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:
- I1 = 24/4 = 6А;
- I2 = 24/12 = 2А.
Основные формулы
Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.
Ток, напряжение и сопротивление
Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров.
В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.
При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.
Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.
4.3. Закон Ома
Немецкий
физик Г. Ом экспериментально установил закон, согласно которому сила
тока, текущего по однородному (отсутствуют сторонние силы) металлическому
проводнику, пропорциональна падению напряжения на проводнике:
.
Сопротивление проводника. Величина R называется электрическим сопротивлением проводника. Единица сопротивления — 1 Ом. Для однородного цилиндрического проводника,
где l — длина проводника; S — площадь его поперечного сечения; — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. В системе СИ единица измерения
есть .
В системе СИ единица измерения
есть .Дифференциальная форма закона Ома. Найдем связь между плотностью
тока j и напряженностью поля Е в одной и той же точке проводника.
В изотропном проводнике упорядоченное движение носителей тока происходит
в направлении вектора Е. Поэтому направления векторов j и Е совпадают.
Рассмотрим в однородной изотропной среде элементарный объем с образующими,
параллельными вектору Е, длиной ,
ограниченной двумя эквипотенциальными сечениями 1 и 2 (рис. 4.3).
.
Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что Учитывая,
что j и Е совпадают по направлению, получаем
Учитывая,
что j и Е совпадают по направлению, получаем.
Это соотношение является дифференциальной формой закона Ома для однородного участка цепи. Величина называется удельной проводимостью.На неоднородном участке цепи на носители тока действуют, кроме электростатических
сил ,
еще и сторонние силы ,
следовательно, плотность тока в этих участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит к дифференциальной форме
закон Ома для неоднородного участка цепи.
.
От закона Ома в дифференциальной форме легко перейти к интегральной форме. Рассмотрим неоднородный участок цепи. Внутри этого участка выберем контур тока, удовлетворяющий следующим условиям: в каждом сечении, перпендикулярном к контуру, величины имеют с достаточной точностью одинаковые значения; векторы в каждой точке направлены по касательной к контуру.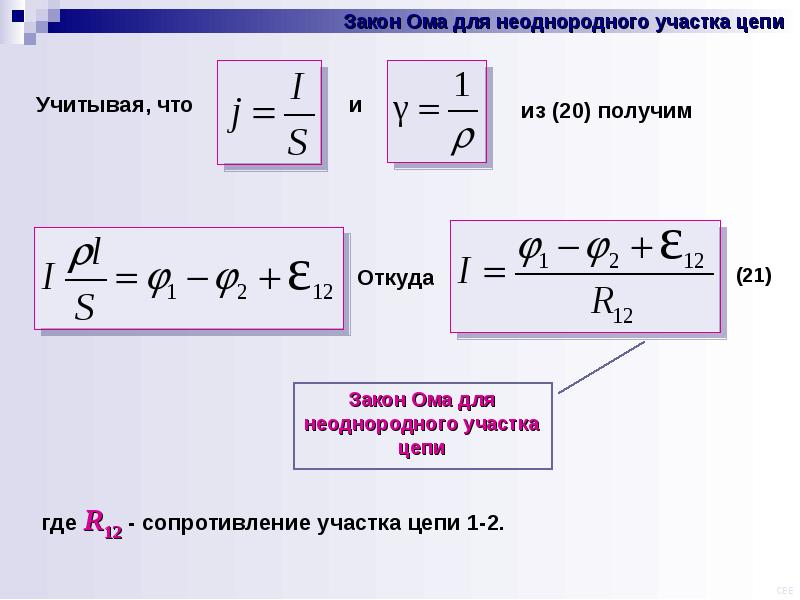
Вследствие закона сохранения заряда сила постоянного тока в каждом сечении
должна быть одинаковой. Поэтому величина
постоянна вдоль контура. Тогда, заменяя j отношением ,
получаем
.
,
где представляет собой суммарное сопротивление участка цепи, первый интеграл в правой части — разность потенциалов на концах участка, а второй интеграл определяет ЭДС , действующую на участке цепи. Таким образом ..
Последняя формула выражает закон Ома для неоднородного участка цепи. Для замкнутой цепи закон Ома имеет вид
Для замкнутой цепи закон Ома имеет вид,
где R — сопротивление нагрузки, r — внутреннее сопротивление источника тока.Вопросы
1) Какова связь между проводимостью и сопротивлением, удельной проводимостью и удельным сопротивлением2) Какой вид имеет вольт-амперная характеристика металлического элемента: линейный или экспоненциальный
3) Каковы правила знаков для силы тока и ЭДС при записи закона Ома для неоднородного участка цепи
4) Поясните когда необходимо использовать закона Ома и интергальной форме, а когда в дифференциальной
Закон ома для неоднородного у — Korholding.ru
На практике видно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, нежели кулоновские, тогда наблюдается случай, когда на участке цепи на свободные электрические заряды одновременно действуют как силы электрического поля, так и сторонние силы (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновских сил)). Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.
Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.
Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:
Сформулируем закон Ома для неоднородного участка цепи — Сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его полному сопротивлению:
– формула закона Ома для неоднородного участка цепи.
Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:
— где φ1 и φ 2 – потенциалы на концах участка.
ЭДС характеризует работу сторонних сил по переносу единичного положительного заряда точки 1 в точку 2: — где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.
Напряжение на участке цепи представляет собой суммарную работу сил ЭП и сторонних сил:
ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε
Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε
Определить ток, идущий по изображенному на рисунке участку АВ. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек А и В соответственно 15 В и 5 В, сопротивление проводов 3 Ом.

Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определить разность потенциалов между точками А и В, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.
4.5. Закон Ома для неоднородного участка цепи. Электродвижущая сила
Для того, чтобы электрический ток существовал длительное время необходимо наличие замкнутой цепи, свободных носителей зарядов частиц и сторонних сил. В проводнике заряженные частицы движутся под действием кулоновских сил в направлении от точки с большим потенциалом 1 к точке с меньшим потенциалом 2. Сторонние силы (силы не электростатического происхождения) непрерывно отводят заряды от конца проводника с меньшим потенциалом, и подводят их к концу с большим потенциалом (рис.4.6).
Циркуляция вектора напряженности электростатического поля равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала, т. е. против сил электростатического поля (см. изображенную штрихом часть цепи на рис. 4.6).
е. против сил электростатического поля (см. изображенную штрихом часть цепи на рис. 4.6).
Рассмотрим участок 1–2 цепи (рис.4.7), на котором действуют кулоновские и сторонние силы, поля которых характеризуется напряженностями и. Напряженность результирующего поля,
действующего на электроны, равна сумме напряженностей кулоновского поля и поля сторонних сил:
. (4.17)
Выделим бесконечно малый элемент проводника dl и запишем с учетом (4.17) закон Ома в дифференциальной форме:
. (4.18)
Умножив левую и правую часть выражения (4.18) на , получаем:
. (4.19)
Учтем, что все векторы в выражении (4.19) коллинеарны, поскольку являются касательными к линиям тока, а модуль плотности тока j = I /S, где I – сила тока в проводнике; S – площадь поперечного сечения проводника. Тогда выражение (4.19) можно переписать в виде
. (4.20)
Проинтегрируем выражение (4.20) по длине участка проводника от сечения 1 до сечения 2 с учетом того, что сила тока в каждом сечении проводника одинакова:
. (4.21)
(4.21)
Рассмотрим подробнее физический смысл всех слагаемых, входящих в выражение (4.21). Первое численно равно удельной работе кулоновских сил по перемещению заряда из точки 1 в точку 2, т.е. разности потенциалов между этими точками:
. (4.22)
Второе слагаемое называется электродвижущей силой (ЭДС) Е12, действующей на участке цепи 1–2.
. (4.23)
Электродвижущая сила численно равна удельной работе сторонних сил по перемещению заряда из точки 1 в точку 2. Эта работа производится за счет источника энергии. Поэтому величину Е12 можно назвать электродвижущей силой источника энергии, включенного на участке цепи 1–2.
Напряжением (падением напряжения) на участке цепи 1–2 называется физическая величина , численно равная удельной работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении заряда из точки1 в точку 2:
, (4.24)
. (4.25)
Введенное нами понятие напряжения не совпадает с тем, которым часто пользуются в электростатике для обозначения разности потенциалов, а является его обобщением. Напряжение на участке цепи равно разности потенциалов только в том случае, если на этом участке не приложены сторонние силы.
(4.26)
называется сопротивлением участка цепи между сечениями 1 и 2.
С учетом (4.25) и (4.26) выражение (4.21) можно записать так:
. (4.27)
Это выражение является математической записью обобщенного закона Ома для участка цепи: произведение сопротивления участка цепи на силу тока в нем равно сумме разности потенциалов на этом участке и ЭДС всех источников, включенных на участке.
При выводе уравнения (4.27) мы обходили выделенный участок цепи в направлении электрического тока (вектор совпадал с вектором плотности тока). Поэтому при определениии ЭДС Ei нужно пользоваться следующим правилом знаков. Падение напряжения считается положительным, если направление тока соответствует направлению обхода участка цепи от точки1 к точке 2. В противном случае падение напряжения считается отрицательным. ЭДС Ei считаются положительными, если направление обхода участка цепи от точки 1 к точке 2 соответствует перемещению внутри источника Еi от полюса “–“ к полюсу “+“. В противном случае Еi следует считать отрицательными.
Применим обобщенный закон Ома к участку цепи, изображенному на рис. 4.8. Выберем условно положительное направление тока, как показано на рисунке, и направление обхода от точки 1 к точке 2. Тогда для участка цепи 1 – Е – R – 2 получим
, (4.28)
где r внутреннее сопротивление источника тока.
Применяя обобщенный закон Ома к участку 1–V–2 (обход через вольтметр), получаем
, (4.29)
где IВ ток, проходящий через вольтметр; RВ сопротивление вольтметра.
Произведение IВRВ это показания вольтметра. Следовательно, вольтметр показывает разность потенциалов между точками подключения.
Закон ома для неоднородного у
1.8. Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током . За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δ q , переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δ t , к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным .
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи , в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения . Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы A ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными . Участки, включающие источники тока, называются неоднородными .
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе 12, действующей на данном участке. Поэтому полная работа равна
Величину U 12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I , текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками , сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи .
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи ( cd ) является однородным.
Закон Ома для однородного, неоднородного участка цепи и замкнутой (полной) цепи. Сопротивление проводников. Дифференциальная форма закона Ома
Закон Ома для однородного участка цепи:
Участок цепи называется однородным, если в его состав не входит источник тока. I=U/R, 1 Ом – сопротивление такого проводника, в котором сила в 1А течет при 1В.
Величина сопротивления зависит от формы и свойств материала проводника. Для однородного цилиндрического проводника его R=ρl/S, ρ – величина, зависящая от использованного материала – удельное сопротивление вещества, из ρ=RS/l следует, что (ρ) = 1 Ом*м. Величина, обратная ρ – удельная проводимость γ=1/ρ.
Экспериментально установлено, что при повышении температуры электрическое сопротивление у металлов увеличивается. При не слишком низких температурах удельное сопротивление металлов растет
абсолютной температуре p = α*p0*T, p0 – удельное сопротивление при 0 о С, α – температурный коэффициент. Для большинства металлов α = 1/273 = 0,004 К -1 . p = p0*(1+ α*t), t – температура в о С.
Согласно классической электронной теории металлов в металлах с идеальной кристаллической решеткой электроны движутся не испытывая сопротивления (p = 0).
Причина, вызывающая появление электрического сопротивления – посторонние примеси и физические дефекты кристаллической решетки, а также тепловое движение атомов. Амплитуда колебаний атомов зависит от t. Зависимость удельного сопротивления от t является сложной функцией:
p(T) = pост + pид., pост – остаточное удельное сопротивление, pид.— идеальное сопротивление металла.
Идеальное сопротивление соответствует абсолютно чистому металлу и определяется лишь тепловыми колебаниями атомов. На основании общих соображений уд. сопротивление ид. металла должно стремиться к 0 при T → 0. Однако удельное сопротивление как функция слагается из суммы независимых слагаемых, поэтому в связи с наличием примесей и др. дефектов кристаллической решетки удельного сопротивления при понижении t → к некоторому росту пост. pост . Иногда для некоторых металлов температурная зависимость p проходит через минимум. Величина ост. уд. сопротивления зависит от наличия дефектов в решетке и содержания примесей.
j=γ*E – закон Ома в дифференцированной форме, описывающий процесс в каждой точке проводника, где j – плотность тока, Е – напряженность электрического поля.
Цепь включает резистор R и источник тока. На неоднородном участке цепи на носители тока действуют кроме электростатических сил сторонние силы. Сторонние силы способны вызвать упорядоченное движение носителей тока, такие как электростатические. На неоднородном участке цепи к полю электрических зарядов добавляется поле сторонних сил, создаваемое источником ЭДС. Закон Ома в дифференцированной форме: j=γE. Обобщая формулу на случай неоднородного проводника j=γ(E+E*)(1).
От закона Ома в дифференцированной форме для неоднородного участка цепи можно перейти к интегральной форме закона Ома для этого участка. Для этого рассмотрим неоднородный участок. В нем поперечное сечение проводника может быть непостоянным. Допустим, что внутри этого участка цепи существует линия, которую будем называть контуром тока, удовлетворяющая:
1. В каждом сечении перпендикулярно контуру величины j, γ, E, E* имеют одинаковые значения.
2. j, E и Е* в каждой точке направлены по касательной к контуру.
Выберем произвольно направление движения по контуру. Пусть выбранное направление соответствует перемещению от 1 к 2. Возьмем элемент проводника площадью S и элементом контура dl. Спроецируем векторы, входящие в (1) на элемент контура dl: j=γ(E+E*) (2).
I вдоль контура равна проекции плотности тока на площадь: I=jS (3).
Удельная проводимость: γ=1/ρ. Заменяя в (2) I/S=1/ρ(E+E*).Умножим на dl и проинтегрируем вдоль контура ∫Iρdl/S=∫Eedl+∫E*edl. Учтем, что ∫ρdl/S=R, а ∫Eedl=(φ1-φ2), ∫E*edl= ε12, IR= ε12+(φ1-φ2). ε12, как и I – величина алгебраическая, поэтому условились, когда ع способствует движению положительных носителей тока в выбранном направлении 1-2, считать ε12>0. Но на практике этот случай, когда при обходе участка цепи в начале встречается отрицательный полюс, затем положительный. Если ع препятствует движению положительных носителей, в выбранном направлении, то ε12 2 Rτ – это уравнение было установлено экспериментально Джоулем и независимо от него Ленцем и носит название закона Джоуля-Ленца в интегральной форме. Полученная формула позволяет определить тепло во всем проводнике.
1.7.3. Сторонние силы и ЭДС
Для того чтобы поддерживать ток достаточно длительное время, необходимо от конца проводника с меньшим потенциалом непрерывно отводить, а к другому концу — с большим потенциалом — подводить электрические заряды, т.е. необходим круговорот зарядов. Поэтому в замкнутой цепи, наряду с нормальным движением зарядов, должны быть участки, на которых движение (положительных) зарядов происходит в направлении возрастания потенциала, т.е. против сил электрического поля (рис. 1.7.1).
Перемещение заряда на этих участках возможно лишь с помощью сил неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия — насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).
Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися по замкнутой цепи или ее участку зарядами (рис.1.7.2).
Величина ε, равная работе сторонних сил по перемещению единичного положительного заряда в цепи, называется электродвижущей силой (ЭДС), действующей в цепи:
Как видно из (1.7.6), размерность ЭДС совпадает с размерностью потенциала, т.е. измеряется в вольтах.
1.7.4. Закон Ома для неоднородного участка цепи
Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС (т.е. участок, где действуют неэлектрические силы). Напряженность Е поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е. E = Ек + Ест.
Закон ома для неоднородного участка цепи
На основании таких допущений и оценок создаётся возможность экспериментальной проверки теоремы Остроградского – Гаусса с по-мощью графического компьютерного моделирования электростатиче-ских полей в данной лабораторной работе.
Эксперимент 1. Постоянное пространственное распределение переменного заряда внутри замкнутой поверхности
1. В нижнем правом прямоугольнике «Конфигурация» нажмите мышью кнопку «Два заряда».
2. Зацепив мышью, перемещайте движок регулятора первого за-ряда до установления значения, указанного в таблице 9.1, для вашей бригады.
Установочные значения физических параметров для проведения экспериментов
3. Аналогичным образом установите заданное в таблице 9.1 рас-стояние d между зарядами.
4. Установите мышью на кнопке «Силовые линии» флажок.
5. Установите величину второго заряда 0 и подсчитайте число силовых линий Ф выходящих и Ф, входящих через границы замк-нутого контура, которым в опыте будет являться прямоугольная рам-ка окна опыта. При этом внимательно смотрите за направлением стрелок на силовых линиях поля. Запишите эти данные и разность
Ф (Ф ) (Ф ) в таблицу 9.2.
6. Последовательно устанавливайте заряды: q2 = +1, +2, +3, +4,
+5 мкКл и выполните п. 5 ещё 5 раз.
Эксперимент 2. Переменное пространственное распределение постоянного заряда внутри замкнутой поверхности
1. Установите значения q1 и q2 , соответствующие значениям,
указанным в таблице 1 для вашей бригады.
2. Установите также минимальное расстояние между зарядами d 2 м и на экране окна эксперимента, подсчётом определите числа
3. Последовательно увеличивая расстояние между зарядами с шагом 0,5 м, выполните п. 2 ещё 6 раз.
4. Результаты измерений запишите в таблицу 9.3.
Обработка данных и анализ результатов
1. Постройте по данным таблицы 9.2 график зависимости потока вектора напряжённости Ф от величины заряда q .
2. По котангенсу угла наклона графика, используя выражения (9.4) и (9.5), определите электрическую постоянную 0 .
3. По данным, приведённым в таблице 9.3, постройте график за-висимости потока вектора напряжённости Ф от расстояния между за-рядами d .
4. По построенным графикам сделайте анализ результатов и оцените погрешность проведённых измерений.
1. Какие поля называют электростатическими?
2. Что такое напряжённость электростатического поля?
3. Как определяется направление вектора напряжённости?
4. Что такое поток вектора напряжённости?
5. Какая линия называется силовой? Почему они не могут пере-секаться?
6. Какая линия называется эквипотенциальной?
7. Докажите, что эквипотенциальные и силовые линии ортого-нальны.
8. От чего зависит густота силовых и эквипотенциальных ли-ний?
9. В чём заключается физический смысл теоремы Остроград-ского – Гаусса?
10. Рассчитайте, используя теорему Остроградского – Гаусса: а) поле равномерно заряженной бесконечной плоскости; б) поле двух бесконечных параллельных разноимённо заря-
женных плоскостей; в) поле равномерно заряженной сферической поверхности;
г) поле объёмно заряженного шара; д) поле равномерно заряженного бесконечного цилиндра (нити).
11. Каким образом теорема Остроградского – Гаусса и следствия из неё могут быть косвенным подтверждением справедливо-сти закона Кулона?
Лабораторная работа № 10 ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ
Запустите программу «Цепи постоянного тока». с изображением страницы. ния.
«Электричество и магнетизм». Выберите Нажмите вверху внутреннего окна кнопку Прочитайте краткие теоретические сведе-
знакомство с компьютерным моделированием цепей посто-янного тока;
экспериментальное подтверждение закона Ома для неодно-родного участка цепи.
Краткие сведения из теории
Сила тока прямо пропорциональна количеству заряда, прошед-шего через проводник за единицу времени: I dqdt .
Закон Ома для участка цепи: величина силы тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике
где R – сопротивление проводника.
Резистором называется устройство, обладающее заданным по-стоянным сопротивлением. Реостатом называется переменное сопро-тивление.
Напряжением на участке цепи 1–2 называется физическая вели-чина, определяемая выражением:
Закон Ома для неоднородного участка цепи:
где 1 и 2 – потенциалы концов участка;
E12 – ЭДС, действующая на данном участке цепи.
Применяя закон Ома для неоднородного участка цепи, необхо-димо помнить о правиле выбора знаков: произведение IR следует брать со знаком «+», если направление обхода совпадает с направле-нием тока на этом участке, ЭДС E12 будет иметь знак «+», если её на-
правление (от минуса к плюсу) совпадает с направлением обхода. При этом надо иметь в виду, что вольтметр, подключённый к концам лю-бого участка цепи, будет показывать разность потенциалов между точками подключения прибора, а направление отклонения стрелки прибора будет определяться параметрами внешней цепи.
Таким образом, закон Ома для полной цепи можно записать в
Из формулы (10.1) видно, что при I 0 вольтметр покажет ЭДС источника, включённого в данный участок цепи.
Методика и порядок измерений
В данной лабораторной работе изучается модель электрической цепи, содержащей на одном из своих участков источник электродви-жущей силы (ЭДС). На этом участке, в зависимости от соотношений между параметрами цепи, разность потенциалов между его крайними точками может менять знак, переходя через 0. Соберите на экране опыта замкнутую цепь, показанную на рисунке 10.1.
Рис. 10.1. Электрическая цепь постоянного тока
Для этого сначала щёлкните левой кнопкой мыши на кнопке
ЭДС в нижней части экрана. Переместите маркер мыши на ра-бочую часть экрана, где расположены точки. Щёлкните левой кноп-кой мыши в рабочей части экрана, где должен быть расположен ис-точник ЭДС.
Разместите далее последовательно с источником резисторы, вы-полняющие функции его внутреннего сопротивления r и сопротивле-
ния неоднородного участка R1 (нажав предварительно кнопку
в нижней части экрана), и амперметр (кнопка там же). Затем расположите резистор нагрузки (реостат) и последовательно соеди-нённый с ним амперметр. Над участком цепи расположите вольтметр
, измеряющий разность потенциалов на этом неоднородном участке цепи.
Соедините все указанные приборы в замкнутую цепь. Для этого
нажмите кнопку соединительного провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щёлкайте ле-вой кнопкой мыши в необходимых местах рабочей зоны и сформи-руйте замкнутую цепь, показанную на рисунке 10.1.
Установите заданные значения параметров для каждого прибора цепи. Для этого щёлкните левой кнопкой мыши на кнопке со стрел-
кой . Затем щёлкните на данном приборе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая её в нажатом состоянии, установите значения R1 ,
r , E , которые указаны в таблице 10.1, для вашей бригады.
Журнал «Квант»
Закон Ома для неоднородного участка цепи
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка \(
\Delta \varphi = \varphi_1 — \varphi_2 = \frac\), где AK — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, \(
\frac> = \varphi_1 — \varphi_2\), где q — положительный заряд, который перемещается между любыми двумя точками цепи; \(
\varphi_1 — \varphi_2\) — разность потенциалов точек в начале и конце рассматриваемого участка; \(
\frac> = \varepsilon\). Тогда говорят о напряжении для напряженности: Eстац. э. п. = Eэ/стат. п. + Eстор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:
U = \frac+ \frac>
= \varphi_1 — \varphi_2 + \varepsilon .\)
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то \(
U = \varphi_1 — \varphi_2\). Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε
Смотрите так же:
- Увольнение по инициативе работодателя ст 81 Увольнение по инициативе работодателя ст 81 Трудовой кодекс Российской Федерации: Статья 81 ТК РФ. Расторжение трудового договора по инициативе работодателя Трудовой договор может быть расторгнут работодателем в случаях: 1) ликвидации организации либо […]
- Дата увольнения во время отпуска Как происходит увольнение сотрудника во время отпуска Трудовое законодательство запрещает прекращение трудовых отношений с сотрудником, во время его нахождения в отпуске. Но этот случай не относится к увольнению по собственному желанию или по причине […]
- Споры растений живые Споры растений живые В настоящее время на этой странице нет текста. Вы можете найти упоминание данного названия в других статьях, или найти соответствующие записи журналов. © Автор системы образования 7W и Гипермаркета Знаний — Владимир […]
- Закон недобросовестной рекламе Федеральный закон «О рекламе» простыми словами Рекламная деятельность в нашей стране регламентируется. Впрочем, так происходит и во всем цивилизованном мире. Существует такой нормативный акт, как федеральный закон 38 ФЗ «О рекламе». Речь идет о документе № […]
- Предельная норма налога ПРЕДЕЛЬНАЯ СТАВКА НАЛОГА Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир». Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М. . 2000 . Смотреть что такое «ПРЕДЕЛЬНАЯ СТАВКА НАЛОГА» в других словарях: предельная ставка налога — Сумма налога […]
- Требования к паспортам безопасности мест с массовым пребываниям Калитинское сельское поселение Волосовского муниципального района Ленинградской области ПОСТАНОВЛЕНИЕ от 01 апреля 2016 года № 83 О создании межведомственной комиссии по обследованию и категорированию мест массового пребывания людей на объекте МКУ «Дом […]
- Налоги для работающих инвалидов 2 группы Какие налоговые льготы будут в 2018 году для инвалидов 2 группы В 2018 году инвалиды второй группы смогут по-прежнему пользоваться многими налоговыми льготами, предусмотренными российским законодательством. Льготы позволяют улучшить качество жизни. Если […]
- Партнерская собственность 2 курс 2ВПО ОПУВТ (Забелина) / ОТУ 1 курс 2ВПО-ОПУВТ / Лекции 2ВПО / тема ПЕРЕВОЗЧИК / Формы собственности По законодательству РФ имущество может находиться в частной, государственной, муниципальной собственности, а также в собственности общественных […]
Закон Ома простыми словами — формулировка для участка и полной цепи
Содержание
Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.
Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.
Закон Ома – определение
Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.
- Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
- Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.
Закон Ома – формула
Иллюстрация связи сопротивленияРисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:
1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;
2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
В итоге в законе Ома участвуют всего три величины.
Готовая формула выглядит так:
I = U/R
Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:
| Формула сопротивления | R = U/I |
| Формула напряжения | U = I × R |
| Формула силы тока | I = U/R |
Важно!
Шпаргалка для закона ОмаНа начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.
На треугольнике просто нужно закрыть то значение, которое необходимо найти.
Закон Ома для участка цепи
Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.
Шпаргалка для использования закона ОмаС ЭДС
Обобщённый закон Ома формулируется так:
I = (Uab+E)/R
Также формулу можно выразить через проводимость:
I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.
Участок цепи с ЭДСБез ЭДС
Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.
Разность потенциаловЕсли сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Закон Ома для полной (замкнутой) цепи
При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.
Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).
Вывод формулы закона Ома для замкнутой цепи
Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.
Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E = I × r + I × R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E = I(r + R)
Или
I = E / (r + R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома в дифференциальной форме
Дифференциальная форма закона ОмаЗакон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:
I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)
При условии, что Δl будет равен 0, то, взяв предел отношения:
lim (-(Δф/Δl)) = -(dф/dl) = Е,
Окончательное выражение будет выглядеть так:
j = yE
Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома в интегральной форме
В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:
I = U/R
Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:
R = p (l/S), где за р принимаем удельное объёмное сопротивление.
Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.
Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
IdR = -dф + dE.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Закон Ома для переменного тока
После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.
Используется уже известная формула:
I = U/Z
Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. Проще говоря, ток в цепи переменного тока зависит от многих параметров, в том числе от величины ёмкости и индуктивности. Полное сопротивление вычисляется по формуле.
Формула полного сопротивленияПолное сопротивление можно изобразить как гипотенузу прямоугольного треугольника, катетами которого является активное и индуктивное сопротивление.
Треугольник полного сопротивленияИтак, формула амплитудного значения силы тока будет выглядеть так:
Im = Um/ ((R^2 + (ωL — (1/ωC)^2
ЦепьВ такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:
U = Um sin (ωt)
I = Im sin (ωt + ф)
Закон Ома для постоянного тока
В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для однородного участка цепи
Формула выглядит уже известным образом:
I = U/R
В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.
Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:
R = p (L/S)
Закон Ома для неоднородного участка цепи
При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.
Неоднородный участок цепиФормула принимает вид:
E = Eq + Est
Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.
Итак, готовая формула:
I = U12/R, где U12
Закон Ома для магнитной цепи
В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.
При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:
Ф = Вср S = μHср S
Формула закона для магнитной цепи:
Формула закона ома для магнитной цепиЗадачи с решениями на закон Ома
Задача №1
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 127 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 127 В : 264 Ом = 0,48 А.
Ответ: I = 0,48 Ом
Задача №2
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 220 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 220 В : 264 Ом = 0,83 А.
Ответ: I = 0,83 Ом
Задача №3
Дано:
- U = 15 В,
- R1 = 3 Ом,
- R2 = R3 = 4 Ом.
Найти: I — ?
Решение:
- R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:
- R = R1 + R2,3
- R = 3 Ом + 2 Ом = 5 Ом
- Найдем силу тока на участке цепи по закону Ома I = U / R
- I = 15 В / 5 Ом = 3 А
Ответ: I = 3 A.
Читайте также. Похожие записи.Поделитесь статьей:
comments powered by HyperCommentsЛабораторная работа 3.4 ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ Цель работы Краткая теория
ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 2012 ЦЕЛЬ РАБОТЫ
ПодробнееЦЕПИ ПОСТОЯННОГО ТОКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО- СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ Кафедра физики ЦЕПИ ПОСТОЯННОГО ТОКА Лабораторная работа 78 Методические указания
ПодробнееЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 01 ЛАБОРАТОРНАЯ
ПодробнееЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 212 ЛАБОРАТОРНАЯ
ПодробнееЛабораторная работа 12*
Лабораторная работа 2 ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ Цель работы найти и построить эквипотенциальные поверхности и силовые линии электрического поля между двумя электродами произвольной формы; определить
ПодробнееГлава 9 Постоянный электрический ток 75
Глава 9 Постоянный электрический ток 75 Электрический ток, сила и плотность тока Электродинамика это раздел электричества, в котором рассматриваются процессы и явления, обусловленные движением электрических
Подробнееc током I, расположенным в начале
Компьютерная лабораторная работа 4.3 МАГНИТНОЕ ПОЛЕ 1. ЦЕЛЬ РАБОТЫ Ознакомиться с компьютерным моделированием магнитного поля от различных источников. Ознакомиться с видом линий магнитной индукции для
ПодробнееE — нормальный элемент Вестона.
ЛАБОРАТОРНАЯ РАБОТА 3-7: ИЗМЕРЕНИЕ ЭЛЕКТРОДВИЖУЩИХ СИЛ ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ МЕТОДОМ КОМПЕНСАЦИИ Студент группа Допуск Выполнение Защита Цель работы: ознакомление с методами компенсации и применение
Подробнееee m 2 ρ 2 2m U R x = R A. (5) I
Методические указания к выполнению лабораторной работы.1.7 ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ МЕТАЛЛОВ Аникин А.И., Фролова Л.Н. Электрическое сопротивление металлов: Методические указания к выполнению лабораторной
ПодробнееФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ
На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (
ПодробнееЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 1 ЛАБОРАТОРНАЯ
ПодробнееЗаконы постоянного тока
Законы постоянного тока Проводники в электростатическом поле E = 0 E = grad φ φ = const S DdS = i q i = 0 Проводники в электростатическом поле Нейтральный проводник, внесенный в электростатическое поле,
ПодробнееТема 1.Электрические цепи.
Тема 1.Электрические цепи. П.1.Закон Ома для участка цепи. П.2.Закон Джоуля-Ленца для участка цепи. П.3.Электрическая цепь. Источники и потребители электрической энергии. П.4. Закон Ома для полной цепи.
ПодробнееЛабораторная работа 22
Лабораторная работа Определение электроемкости конденсатора по осциллограмме его разряда через резистор Методическое руководство Москва 04 г. Определение электроемкости конденсатора по осциллограмме его
ПодробнееR x R R2 R 1 R 2. R x = R. (2.4) l 2. l 1 B D
Методические указания к выполнению лабораторной работы.. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ МЕТОДОМ МОСТИКА УИТСТОНА Филимоненкова Л.В. Электростатика и постоянный ток: Методические указания к выполнению
ПодробнееПостоянный электрический ток
Постоянный электрический ток Основные определения Электрический ток упорядоченное движение электрических зарядов (носители тока) под действием сил электрического поля. В металлах носителями тока являются
ПодробнееЛабораторная работа 24
Лабораторная работа 4 Исследование характеристик источника постоянного тока Методическое руководство Москва 04 г. . Цель лабораторной работы Исследование характеристик источника постоянного тока, определения
ПодробнееПРОВЕРКА ЗАКОНА ДЖОУЛЯ-ЛЕНЦА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный
Подробнее, где I m амплитуда силы тока
ЛАБОРАТОРНАЯ РАБОТА 8. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Цель работы: определение зависимости индуктивного и емкостного сопротивлений от частоты, а также определение угла сдвига фаз тока
ПодробнееИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ
ЛАБОРАТОРНАЯ РАБОТА 5 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ Цель работы: изучение методов измерения сопротивлений, изучение законов электрического тока в цепях с последовательным и параллельным соединением
ПодробнееЗакон Ома для неоднородного участка цепи
На неоднородном участке цепи плотность тока пропорциональна сумме напряженностей электростатического поля и поля сторонних сил, т.е.
. (19)
Рассмотрим цилиндрический проводник длиной l с площадью поперечного сечения S. Умножим обе части равенства (19) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
что дает j× l = ( + ). (20)
Заменив j на I/S, а на , из (20) получим I = + , откуда следует закон Ома для неоднородного участка цепи I = ( + ) / R (21)
где R = l / S — сопротивление участка цепи 12. Для замкнутой цепи формула (21) запишется в виде I = / R (22)
где R — суммарное сопротивление всей цепи; — ЭДС источника.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС и внутренним сопротивлением r ,а также внешней цепи потребителя, имеющей сопротивление R. Согласно (22) I = / (R + r). (23)
Разность потенциалов на электродах источника, рис. 5, равна напряжению на внешнем участке цепи: U = = IR = — Ir . (24)
Если цепь разомкнуть, то ток в ней прекратится и напряжение U на зажимах источника станет равным его ЭДС, т.е. U = .В общем случае, напряжение на внешнем участке цепи, рис. 5, будет равно U = IR = R / (R + r). (25)
В пределе, когда R 0 (источник тока замкнут накоротко), то в этом случае, в соответствии с (23), ток максимален
I= I = / r , (26)
а напряжение во внешней цепи равно нулю.
В противоположном предельном случае, R, т.е. цепь разомкнута и ток отсутствует: I=lim=0, а напряжение на зажимах источника максимально и равно его ЭДС: U = R / (R + r)= , т. к. lim R / (R + r) = 1. (27)
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость ЗаконОма для однородного и неоднородного контура. Закон Ома для участка цепи простым языком. Преобразуем исходные данные
Рис. 3 Перемещение заряда в этих областях возможно только с помощью силы
.неэлектрическое происхождение (внешние силы): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, перекачивающий воду в водонапорную башню, работает за счет негравитационных сил (электродвигатель).
Внешние силы можно охарактеризовать по их работе с движущимися зарядами.
Величина, равная работе внешних сил по перемещению одиночного положительного заряда, называется электродвижущей силой. E.D.S. действуя в цепочке.
Понятно, что размер E.D.S. совпадает с размерностью потенциала, т.е. измеряется в вольтах.
Внешняя сила, действующая на заряд, может быть представлена как:
= ∫ F Арт.д л | Q ∫ Приблиз. д л, | |||||||
ε 12 | = ∫ Приблиз.д л. | |||||||
Для замкнутого контура: ε = ∑ ε i | = ∫ Приблиз. д л. | |||||||
Циркуляция вектора натяжения внешних сил равна EDS, действующей в замкнутом контуре (алгебраическая сумма EDS).
Следует помнить, что поле внешних сил не является потенциальным, и к нему нельзя применять термин — разность потенциалов или напряжение.
Рассмотрим неоднородный участок цепи, участок, содержащий источник ЭДС.
(т.е. область — где действуют неэлектрические силы). Напряженность поля E в любой точке цепочки равна векторной сумме поля кулоновских сил и поля внешних сил, т.е.
E = Eq + Est….
Величина, численно равная работе по переносу единичного положительного заряда за счет полного кулоновского поля и внешних сил в участке цепи (1-2), называется напряжением в этом участке U12 (рис. 4)
2 р р | |||||
U 12 = ∫ E q d l + | ∫ Приблиз.d l; | ||||
Eq d l = — dφ и ∫ Eq d l | = φ 1 — φ 2; | ||||
U 12 = (φ 1 — φ 2) + ε 12 | |||||
Напряжение на концах участка цепи совпадает с разностью потенциалов только в | |||||
если на сайте нет ЭЦП, т.е.е. на однородном участке цепи. | |||||
I R12 = (φ1 — φ2) + ε 12 | |||||
Это обобщенный закон Ома. Обобщенный закон Ома выражает закон сохранения энергии по отношению к участку цепи постоянного тока. Это одинаково справедливо как для пассивных разделов (не содержащих ЭЦП), так и для активных.
В электротехнике часто используется термин падение напряжения — изменение напряжения из-за передачи заряда через сопротивление
В замкнутом контуре: φ 1 = φ 2; | |||||
I RΣ = ε | |||||
| рупий | |||||
Где R Σ = R + r; r — внутреннее сопротивление активного участка цепи (рис.5).
Тогда закон Ома для замкнутого участка цепи, содержащего EDC, будет записан в
.7.6. Закон Ома в дифференциальной форме.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
I = U | |||||
Для однородного линейного проводника выразим R через ρ | |||||
R = ρ | |||||
ρ — удельное объемное сопротивление; [ρ] = [Ом м].
Найдем связь между j и E в бесконечно малом объеме проводника — закон Ома в
дифференциальная форма.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители заряда (рис.6) движутся в направлении силового воздействия, т.е. плотности тока
j E, следовательно, векторы коллинеарны.
И мы знаем, что: j = | E, i.е. | E j или | ||||||||||||||
j = σ E | ||||||||||||||||
это закон Ома в дифференциальной форме.
Здесь σ — удельная электропроводность. Размер j — [Ом — 1 м — 1]; Плотность тока можно выразить через заряд, n, v r и т. Д.
j = en vr и т. Д.
обозначают: b = v E и т. Д., Затем v r dr. = b E;
j = enb E,
и если σ = enb,
где n — количество ионных пар, b — расстояние. j = j E
— Закон Ома в дифференциальной форме.
7.7. Работа и сила тока. Закон Джоуля-Ленца.
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждый участок проводника
проходит заряд.Полезно запомнить другие формулы мощности и производительности:
N = RI2 | ||
A = RI2 t | ||
В 1841 г. английский физик Джеймс Джоуль и русский физик | ||
Эмили Ленц установил закон теплового действия электрического | ||
JOLE Джеймс Прескотт (рис.6) | ||
(24.12.1818 — 11.10.1889) — английский физик, один | ||
от первооткрывателей закона сохранения энергии. | ||
Первые уроки физики ему дал Дж. Далтон, младше . | ||
, влияние которого Джоуль начал свои эксперименты. | ||
Работы посвящены электромагнетизму, кинетическому | ||
Теория газов. | ||
ЛЕНТС Эмили Христианович (рис.7) (24.2.1804 | ||
— 10.2.1865) — российский физик. Основные работы в области | ||
электромагнетизм.В 1833 году он установил правило определения | ||
электродвижущая сила индукции (закон Ленца), а в 1842 г. (независимо | ||
от Дж. Джоуля) — закон теплового действия электрического тока (закон Джоуля-Ленца). Обнаружили обратимость электрических машин. Изучена зависимость сопротивления металлов от температуры. Работы также относятся к геофизике.
Независимо друг от друга Джоуль и Ленц показали, что при протекании тока в проводнике выделяется некоторое количество тепла:
(7.7.7) это закон Джоуля-Ленца в интегральной форме.
Следовательно, нагрев происходит за счет работы сил поля над зарядом (мощность тепловыделения N = RI2).
Получаем закон Джоуля — Ленца в дифференциальной форме.
dQ = RI 2 dt = ρ dS dl (jdS) 2 dt = ρj2 dldSdt = ρj2 dldSdt = ρj2 dVdt,
Закон Ома для неоднородного участка цепи.
Когда электрический ток проходит по замкнутой цепи, силы стационарного электрического поля и внешние силы действуют на свободные заряды.При этом на некоторых участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой схемы помимо сил стационарного электрического поля действуют и внешние силы. Участок цепи, на который действуют внешние силы, называется неоднородным участком цепи.
Чтобы выяснить, от чего зависит сила тока в этих областях, необходимо уточнить понятие напряжения.
Рассмотрим сначала однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуется разностью потенциалов Δφ. Разность потенциалов на концах участка, где АК — работа сил стационарного электрического поля. Неоднородный участок схемы (рис. 1, б) содержит, в отличие от однородного участка, источник ЭДС, а к работе сил электростатического поля в этом участке добавляется работа внешних сил.По определению, где q — положительный заряд, который перемещается между любыми двумя точками цепи; — разность потенциалов точек в начале и конце рассматриваемого участка; … Затем говорят о напряжении за напряжением: Estac. NS. п. = Ee / stat. п. + Estor. Напряжение U на участке цепи — это физическая скалярная величина, равная суммарной работе внешних сил и сил электростатического поля на движение одиночного положительного заряда в этом участке:
Это видно из Эта формула показывает, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке.Если на площадку действуют только электрические силы (ε = 0), то. Таким образом, только для однородного участка схемы понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи:
где R — полное сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в сечение: если направление, создаваемое источником тока, совпадает с направлением тока, протекающего по сечению (направление тока в сечении совпадает внутри источника с направлением тока в сечении). направление от отрицательного полюса к положительному), т.е.е. ЭДС способствует перемещению положительных зарядов в заданном направлении, тогда ε> 0, в противном случае, если ЭДС препятствует перемещению положительных зарядов в заданном направлении, то ε
Закон Ома для неоднородного участка цепи.
Для появления электрического тока в проводнике необходимо, чтобы внутри проводника существовало электрическое поле, признаком которого является наличие разности потенциалов на концах проводника.
В электрической цепи возможно создание электрического поля за счет присутствующих в ней зарядов.Для этого достаточно разделить заряды противоположных знаков, сосредоточив в одном месте цепи избыточный положительный заряд, а в другом — отрицательный (для создания заметных полей достаточно разделить ничтожную часть обвинения).
Разделение разноименных зарядов невозможно осуществить силами электростатического (кулоновского) взаимодействия, так как эти силы не только не разделяются, но, наоборот, стремятся соединить заряды противоположных знаков, что неизбежно приводит к выравниванию потенциалы и исчезновение поля в проводниках.Разделение разноименных зарядов в электрической цепи может осуществляться только силами неэлектрического происхождения.
Силы, разделяющие заряды в электрической цепи, создающие в ней электростатическое поле, называются сторонними .
Устройства, в которых действуют внешние силы, называются источниками тока .
Природа внешних сил может быть разной. В одних источниках эти силы обусловлены химическими процессами (гальванические элементы), в других — диффузией носителей заряда и контактными явлениями (контактная ЭДС), в третьих — наличием вихревого электрического поля (электрические генераторы) и т. Д.Внешние силы действуют на заряды только в источниках тока, а там они действуют либо на всем пути заряда через источник, либо на отдельных участках. В связи с этим говорят об источниках с распределенными и сосредоточенными внешними силами. Примером источника с распределенными внешними силами является электрогенератор — в нем эти силы действуют по всей длине обмотки якоря; Примером источника с сосредоточенными внешними силами является гальванический элемент — в нем эти силы действуют только в самом тонком слое, прилегающем к электродам.
Поскольку внешние силы действуют только в источнике, а электростатические — как в источнике, так и во внешней цепи, то в любой цепи есть участки, где на заряды одновременно действуют как внешние, так и электростатические силы. Участок цепи, в котором на заряды действуют только электростатические силы, называется, как уже упоминалось, однородным … Область, в которой на заряды одновременно действуют как электростатические, так и внешние силы, называется неоднородным … Другими словами, неоднородный раздел — это раздел, содержащий текущий источник.
Когда заряды движутся по такому участку, действуют электростатические и внешние силы. Работа внешних сил характеризуется электродвижущей силой (сокращенно ЭДС).
Электродвижущая сила в данном участке цепи 1-2 называется скалярной физической величиной, численно равной работе, выполняемой внешними силами при перемещении одиночного положительного точечного заряда из точки 1 в точку 2
Работа электростатических сил характеризуется разностью потенциалов .
Разность потенциалов между точками 1 и 2 электрической цепи называется скалярной физической величиной, численно равной работе, совершаемой электростатическими силами при перемещении одиночного положительного точечного заряда из точки 1 в точку 2
.
Совместная работа внешних и электростатических сил в этом участке цепи характеризуется напряжением.
Напряжение в данном разделе 1-2 — это физическая величина, которая численно равна алгебраической сумме работы, выполняемой электростатическими и внешними силами при перемещении одиночного положительного точечного заряда из точки 1 ровно 2 .
.
Или, другими словами, .
Если сопротивление неоднородного участка 1-2 равно и через него протекает ток I , то, используя закон сохранения энергии, можно получить закон Ома для неоднородного участка цепи.
Если ток в цепи стационарный, участок цепи неподвижен и его температура не меняется, то единственным результатом работы тока в этом участке будет выделение тепла в окружающую среду.Суммарная работа тока, состоящая из работы электростатических и внешних сил, за т равна количеству выделившегося тепла.
и.
Тогда и после распилов
.
Отсюда — закон Ома для неоднородного участка цепи в интегральной форме: сила тока в неоднородном участке электрического значения прямо пропорциональна алгебраической сумме разности потенциалов на концах участка и ЭДС, действующая в этом сечении, обратно пропорциональна общему сопротивлению сечения.
Сила тока, разность потенциалов и ЭДС в этой формуле являются алгебраическими величинами. Их знак зависит от направления обхода площадки. Если направление тока совпадает с направлением байпаса, то оно считается положительным. Если источник тока посылает ток в направлении байпаса, то его ЭДС считается положительной. Ниже приводится пример записи закона Ома для неоднородного участка цепи, показанной на рис. 52.
При переходе из пункта А в пункт Б,
от Б до А.
То есть при изменении направления обхода все величины, входящие в закон Ома, меняют знак.
Таким образом, закон Ома как для однородных, так и для неоднородных областей является одним из проявлений закона сохранения и преобразования энергии.
4.5. Следствия закона Ома для неоднородного участка цепи.
Рассмотрим последствия закона Ома для неоднородного участка цепи.
1.Если в этом разделе нет источника тока ( 12 = 0 ), то получаем закон Ома для однородной площади,
откуда следует что или.
Напряжение и разность потенциалов в однородном участке цепи равны друг другу.
2. Если рассматривать замкнутую цепь, то или. Подставляя это в исходную формулу, получаем
где — полное сопротивление цепи , сопротивление внешней части цепи, сопротивление внутренней части цепи (источника тока).
Тогда.
Ток в замкнутой цепи прямо пропорционален ЭДС и обратно пропорционален общему сопротивлению цепи. — Закон Ома для полной цепи.
3. Если цепь разомкнута, то в ней нет тока ( I = 0 ) ИК = 0 .
Тогда, то есть ЭДС равна по модулю и противоположна по знаку разности потенциалов на выводах открытого источника тока .
4.6. Мощность постоянного тока.
Мощность электрического тока в однородном участке цепи с сопротивлением может быть довольно просто определена как отношение работы, совершаемой силами электростатического поля при движении зарядов в проводнике, ко времени, в течение которого эта работа сделано:
Таким образом, мощность электрического тока на участке цепи пропорциональна квадрату силы тока и сопротивления участка.
Если рассматривать замкнутую схему (рис. 53), то в такой схеме принято рассматривать два типа мощности — полную и полезную. Полный называется мощностью, которая выделяется по всей цепи, то есть как на внешнем сопротивлении, так и на внутреннем сопротивлении источника тока. Тогда общая мощность может быть найдена как произведение квадрата силы тока и импеданса цепи:
, и используя закон Ома для замкнутой цепи, получаем:
.
Полезным называется мощность, которая выделяется на внешнем сопротивлении цепи, то есть она равна, и снова применяя закон Ома для замкнутой цепи, мы получаем:.
КПД (КПД) замкнутой цепи называется отношением полезной мощности к полной мощности. Используя полученные формулы, получаем:
Давайте выясним, как полезная, полная мощность и КПД зависят от сопротивления внешней цепи. Видно, что полная мощность максимальна при и уменьшается с увеличением внешнего сопротивления.Полезная мощность сначала увеличивается от нуля до определенного значения, а затем с ростом уменьшается. Чтобы узнать, при каком значении полезная мощность максимальна, необходимо приравнять производную нулю.
отсюда после сокращений получаем
Таким образом, максимальная мощность во внешней цепи развивается при условии, что сопротивление внешней цепи равно внутреннему сопротивлению источника тока. Обратите внимание, что при этом условии КПД составляет всего 0,5, то есть только половина мощности, развиваемой источником тока, выделяется во внешней цепи, а остальная мощность идет на нагрев самого источника тока.
На рис. 54 графически изображает зависимость полной и полезной мощности, а также КПД для замкнутой цепи от величины внешнего сопротивления цепи.
Библиографический список
Савельев И.В. Общий курс физики: Т.2. Электричество. — М .: Наука, 1987. — 432 с.
Трофимова Т.И. Курс физики: учебник. Пособие для вузов. — 7-е изд., Стер. — М .: Высшее. школа, 2003. — 542 с .: ил.
Детлаф Ф.Ф., Яворский Б.М. Курс физики: учебник. Пособие для технических вузов. — М .: Наука, 1989. — 608 с.
Предисловие …………………………………………………………… ……………. 3
1. Электрическое поле в вакууме …………………………………… ……………… 4
1.1. Электромагнитное поле — материальный носитель
электромагнитное взаимодействие ……………………………… ……………. 4
1.2. Расходы на электроэнергию …………………………………………………… …… 4
1.3. Закон Кулона …………………………………………………… ………………… 5
1,5. Принцип наложения полей ………………… 7
1,6. Расчет электрических полей по принципу суперпозиции …………… 8
1,7. Линии вектора напряжения …………………………………………… ..10
1,8. Поток вектора напряжения ……………………………………………… … 11
1.9. Теорема Гаусса ………………………………………………… ……………….. 13
1.10. Применение теоремы Гаусса к расчету электрических полей ……………..12
1.11. Работа сил электростатического поля ………………………… ………………… 18
1.12. Циркуляция вектора напряженности электростатического поля … … … …… 19
1.13. Электростатический потенциал …………………………… …………….. 20
1.14. Связь между напряженностью и потенциалом электростатического поля … 21
1.15. Расчет потенциала и разности потенциалов в электростатическом поле … 23
2.Электрическое поле в диэлектриках ………………………………………… … 24
2.1. Проводники, диэлектрики, полупроводники ……………………………… … 24
2.2. Поляризация диэлектриков …………………………………………………… 25
2.3. Типы поляризации ………………………………………………………… ..26
2.4. Соотношение между величинами, характеризующими поляризацию ………………… …………….. 28
2,5. Электрическое поле в диэлектриках ……………………………… …………….. 29
2.6. Вектор электрического смещения ………………………………… …………….. 30
2.7. Расчет электрического поля в присутствии диэлектриков …………………… 33
2.8. Сегнетоэлектрики ……………………………………………………………… 33
2.9. Пьезоэлектрический эффект. Электрострикция …………………………… … 35
3. Проводники в электрическом поле. Энергия электрического поля …………… .36
3.1. Распределение зарядов на проводнике …………………………… …………….. 36
3.2. Проводник во внешнем электрическом поле ……………………………… … 38
3.3. Электрическая емкость жил ……………………………………………… 39
3.4. Взаимная электрическая емкость. Конденсаторы …………………………………… 40
3.5. Подключение конденсатора …………………………………………………… 41
3.6. Энергия системы стационарных точечных зарядов ………………………………….. ……………. 42
3,7. Собственная энергия заряженного проводника и конденсатора …………… 43
3.8. Энергия электрического поля ………………………………………………… 44
4. Законы постоянного тока ……………………………………………………… .45
4.1. Понятие об электрическом токе …………………………………………… 45
4.2. Закон Ома для однородного участка цепи ………………………………….. …. 47
4.3. Закон Джоуля-Ленца ……………………………………………………… ..49
4.4. Электродвижущая сила, разность потенциалов, напряжение.
Электростатика, гальванизм были явлениями, вызванными постоянным током , полученным от… А.Д. Физика. Электростатика : синопсис лекций / А.Д. Андреев, Л.М. Черный; СПбГУТ. — СПб., 2004. Детлаф А.А. Колодец физиков / А.А. …
Строительное материаловедение.
Колодец лекций Аннотация >> СтроительствоУчебный курс «Строительное материаловедение». Лекции который … эффективный заряд атома; a — постоянная экранирование, определяемое для каждого элемента… используя классические законы электростатики … Молекулы в … проводниках электрического тока и диэлектрики …
Современные концепции естествознания
Лекция >> НаукаНет. Настоящая скважина , посвященная современным концепциям … создается магнитостатическое поле постоянных токов , существование которых … В отличие от электростатики , последовательная теория магнитного … лекций -обсуждений после…
Методика использования CRC в процессе изучения темы Электромагнитные колебания
Курсовая работа >> ПедагогикаТермодинамика и молекулярная физика, электростатика , оптика, атомная и ядерная … количество экспериментального материала. Скважина «Открытая физика 2.0» … закон установлен для постоянных текущих , для описания процессов … разработаны в форме лекций, с тех пор …
Расчет электрических цепей постоянного тока основан на использовании закона Ома. Для однородного участка цепи применение закона Ома подробно обсуждалось в предыдущем абзаце. А как найти силу тока в неоднородном участке электрической цепи, на концах которого есть определенная разность потенциалов и внутри которого есть скачки потенциала, например, включен гальванический элемент или аккумулятор?
Контактная разность потенциалов. Рассмотрим сначала неоднородный участок цепи, состоящий из двух последовательно соединенных разных проводников A и B, например, меди и цинка (рис. 73). Опыт показывает, что существует скачок потенциала между разными проводниками, который не зависит от тока и существует даже при его отсутствии. Эта контактная разность потенциалов была обнаружена еще в 1797 году итальянским физиком А. Вольта, который установил ряд металлов, в которых каждый предыдущий металл в сочетании с любым из следующих металлов положительно наэлектризован: Al, Zn, Sn, Cd, Pb. , Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd.
Рис. 73. Неоднородный участок цепи
Существование контактной разности потенциалов можно продемонстрировать с помощью следующего простого эксперимента. На штанге электроскопа закреплена пластина из исследуемого металла (рис. 74).
Рис. 74. Обнаружение контактной разности потенциалов
Он покрыт тонким слоем изоляционного материала. Сверху кладут пластину из второго исследуемого материала, снабженную изолирующей ручкой, и эту пластину подключают к земле.
Пластины на время соединены проводником. В этом случае между пластинами возникает контактная разность потенциалов, то есть образованный ими конденсатор заряжается. Однако имеющееся в нем напряжение настолько мало, что невозможно обнаружить отклонение створок электроскопа. Поэтому действуйте следующим образом. Верхняя пластина приподнята, так что емкость конденсатора, образованного пластинами, уменьшается. Поскольку заряд на изолированной нижней пластине остается неизменным, разность потенциалов между ней и землей увеличивается во столько раз, как уменьшается емкость.При достаточном разделении пластин легко обнаруживается отклонение створок электроскопа.
Физическая причина возникновения контактной разности потенциалов кроется в разнице работы выхода разных металлов, т. Е. Минимальной работе, которую необходимо совершить, чтобы вывести электрон из металла в вакуум, а также в разница в концентрации в них свободных электронов. Величина скачка потенциала зависит от типа металлов, чистоты их поверхностей и их температуры.Контактная разность потенциалов колеблется от нескольких десятых вольта до нескольких вольт.
Если несколько разных металлов соединены последовательно друг с другом, то разность потенциалов, возникающая на концах крайних проводников, не зависит от того, какие проводники находятся между ними, то есть она будет такой же, как если бы эти крайние проводники были напрямую связаны друг с другом. Подчеркнем, что в отсутствие тока каждый металл остается эквипотенциальным, а скачок потенциала и связанное с ним электрическое поле присутствуют только в точке контакта.
Ток на неоднородном участке цепи. Теперь подключим внешние концы проводов A и B на рис. 73 к источнику постоянного напряжения. Обозначим потенциал левого конца проводника A через и потенциал правого конца проводника B через Потенциалы металлов A и B в точке контакта, которые мы обозначаем как Поскольку теперь в проводниках есть ток , то, конечно, мы пока не знаем, как записать закон Ома для всего рассматриваемого участка схемы, но тогда мы можем записать его для каждого из однородных участков A и B.Поскольку проводники соединены последовательно, через них протекает один и тот же ток. Предположим, что ток течет слева направо, как показано на рис. 73. Skinny
где — сопротивления секций A и B. -членные уравнения (1) и перегруппируем члены в левой части следующим образом:
Сумма — это полное сопротивление рассматриваемой секции. Разность потенциалов — это приложенное напряжение. Разница — это скачок потенциала в точке контакта металлов, который, как уже отмечалось, не зависит от протекающего тока и определяется только природой металлов и температурой.Величина скачка обозначается Тоща, соотношение (2) можно переписать как
Это закон Ома для неоднородного участка цепи.
Обратите внимание, что напряжение в рассматриваемом участке означает разность — где — потенциал точки, из которой течет ток, а — потенциал точки, в которую течет ток. Скачок потенциала в точке контакта определяется как, то есть знак определяется тем, увеличивает или уменьшает скачок значение потенциала в цепи в направлении протекания тока: если он увеличивается, если уменьшается,
Но в По нашим рассуждениям, мы выбрали направление тока слева направо наугад! А если на самом деле он течет в обратном направлении? Предполагая, что ток течет справа налево, и повторяя буквально все вычисления, мы получаем значение тока, которое отличается только знаком.Это означает, что, начиная анализ неоднородного участка цепи, мы можем вообще не задумываться о том, в каком направлении на самом деле течет ток, а произвольно устанавливаем его направление.
Выбрав направление тока, определяем его значение по формуле (3), строго соблюдая сформулированное выше правило знаков для Если в результате ток оказывается положительным, то он действительно течет в направление, которое мы задали. Если получено отрицательное значение, то на самом деле ток течет в обратном направлении, и его значение, естественно, было найдено правильно.Ниже мы подробно рассмотрим примеры использования закона Ома для неоднородного участка цепи, иллюстрирующие сформулированное правило знаков.
Если соединить последовательно несколько разных проводников, то, повторив все приведенные выше вычисления, легко убедиться, что формула (3) сохранила свой вид; только теперь под нужно понимать алгебраическую сумму скачков потенциала в контактах, а под — сумму сопротивлений всех проводников.
Замкнутый гетерогенный контур. Рассмотрим теперь замкнутую цепь проводников, сделанных из разных металлов. Представим себе, что эта замкнутая цепь получается в результате соединения начала и конца цепочки проводников, то есть тех точек, к которым
может быть приложено внешнее напряжение. Соединение этих точек в одну означает, что теперь формула (3) для замкнутой последовательной цепи принимает вид
где — алгебраическая сумма скачков потенциала между всеми парами соединенных проводников, общая сопротивление замкнутой цепи.
Если контакты между разными металлами имеют одинаковую температуру, то сумма всех скачков потенциала, очевидно, будет равна нулю, поскольку скачок потенциала между любыми двумя металлами не зависит от того, что находится между ними.
Электродвижущая сила. При разных температурах контактов в цепи сумма скачков потенциала может быть отличной от нуля, и в цепи будет протекать ток, определяемый формулой (4). Сумма скачков потенциала в замкнутой цепи называется электродвижущей силой (ЭДС), а равенство (4) называется законом Ома для замкнутой неразветвленной цепи.
Остановимся подробнее на физическом смысле понятия ЭДС. Скачок потенциала в точке контакта двух металлов возникает из-за разницы работы выхода электронов и их концентрации в этих металлах, что приводит к диффузии электронов через контакт. Силы, вызывающие направленный поток электронов, имеют неэлектростатическое (не кулоновское) происхождение. Такие силы неэлектростатического происхождения, независимо от их физической природы, называются внешними силами.Направленный поток электронов через контакт прекращается, когда возникает препятствующее ему электростатическое поле, уравновешивающее действие внешних сил. Возникающее электростатическое поле характеризуется контактной разностью потенциалов.
В рассматриваемом случае электродвижущая сила возникает только при разных температурах контактов и называется термоэлектродвижущей силой (термоЭДС).
Закон Ома (4) для замкнутого контура действует не только для термоЭДС, но и для внешних сил любой природы.Как уже отмечалось, неоднородность схемы может быть связана с включением гальванического элемента, аккумулятора, генератора постоянного тока и т. Д. Если рассматриваемая схема содержит несколько ЭДС, то в формуле (4) необходимо понимать алгебраическая сумма всех этих ЭДС, и знак каждой из них определяется в соответствии с сформулированным выше правилом.
Ниже будет показано, что ЭДС характеризует работу внешних сил, совершаемых при движении зарядов. Другими словами, ЭДС характеризует преобразование других видов энергии в электрическую.
ЭДС в разных источниках. В отличие от контактов проводников первого рода (металлы, полупроводники), в которых не происходят химические изменения при прохождении электрического тока, в контактах металлов с электролитами (например, цинка с серной кислотой) происходят химические реакции. Как мы видели, в замкнутой цепи из разных проводников первого рода при одинаковой температуре ЭДС не возникает. Если сделать замкнутую цепь из проводников первого и второго рода, то в нем возникнет ненулевая ЭДС даже при постоянной температуре.
Рис. 75. Элемент Даниэля и внешний вид сухого элемента Лекланше
Этот вид комбинации проводников первого рода и электролитов представляет собой химический источник тока «сухой» гальванический элемент или аккумулятор (рис. 75), в котором электрический ток сохраняется за счет химических реакций между электродами и электролитом. Например, в гальваническом элементе, состоящем из цинковых и медных пластин, погруженных в раствор серной кислоты, цинковый электрод растворяется в кислоте.В аккумуляторах используются обратимые химические реакции: израсходованный при работе электрод восстанавливается в процессе зарядки. Химические источники тока обеспечивают ЭДС до 2 В.
В генераторах, используемых на электростанциях для преобразования механической энергии в электрическую, внешние силы по своей природе представляют собой силы, действующие на заряды, движущиеся в магнитном поле.
Внутреннее сопротивление источника тока. В любой реальной электрической цепи всегда можно выбрать участок, который служит для поддержания тока (источник тока), а остальное считается «нагрузкой».В источнике тока обязательно действуют внешние силы, поэтому в общем случае он характеризуется электродвижущей силой и сопротивлением, которое называется внутренним сопротивлением источника. Нагрузка также может содержать ЭДС (например, электродвигатель), однако в простейшем случае на нагрузку не действуют никакие внешние силы, и она характеризуется только сопротивлением.
Самая простая замкнутая схема. Рассмотрим замкнутую электрическую цепь, содержащую источник тока с ЭДС и внутренним сопротивлением и нагрузку, характеризуемую только сопротивлением
(рис.76). Сопротивление соединительных проводов принимается равным нулю. Применяя формулу (4) к такой цепи, в знаменателе которой стоит полное сопротивление цепи, запишем ее в виде
, где сквозное обозначает сопротивление нагрузки. Идеальный вольтметр, подключенный к сопротивлению, то есть к выводам (полюсам) рабочего источника тока, показывает напряжение, как следует из закона Ома для однородного участка цепи — в данном случае для сопротивления нагрузки. Подставив сюда силу тока из (5), это напряжение можно выразить через параметры схемы
Рис.76. Простейшая замкнутая схема с источником тока
Из (6) видно, что напряжение на выводах исправного источника всегда меньше его ЭДС. Чем ближе к большему сопротивлению нагрузки. В пределе (точнее, когда, т.е. когда сопротивлением источника можно пренебречь по сравнению с сопротивлением нагрузки) из (6) следует, что напряжение на выводах открытого источника равно его ЭДС .
Противоположный предельный случай (точнее, когда сопротивление нагрузки намного меньше внутреннего) соответствует так называемому короткому замыканию источника тока.В данном случае это ток короткого замыкания
, то есть максимальный ток, который может быть получен от данного источника.
Из формулы (5) следует, что напряжение на выводах истока можно записать в виде
Произведение — это напряжение на сопротивлении, то есть напряжение внутри источника тока. Следовательно, формула (8) означает, что ЭДС равна сумме напряжений на внешнем и внутреннем участках замкнутой цепи.
Составная внешняя цепь. Как правило, внешняя цепь состоит из нескольких резисторов, соединенных разными способами. Все вышесказанное остается верным, если мы понимаем эквивалентное сопротивление всей внешней цепи. Приведенные выше соотношения позволяют легко рассчитать такие цепочки или провести их качественный анализ.
Рассмотрим следующие примеры.
1. Требуется определить, как изменятся (увеличатся или уменьшатся) показания всех идеальных вольтметров в схеме рис. 1.77, если, например, уменьшить сопротивление переменного резистора.
При уменьшении ток в цепи увеличивается. В соответствии с законом Ома для участка цепи напряжение на сопротивлении увеличивается, а напряжение на выводах источника тока, как следует из формулы (8), уменьшается.
Рис. 77. К изучению изменения показаний вольтметра
Рис. 78. К исследованию изменения показаний амперметров
Трудно применить закон Ома для участка цепи к сопротивлению, так как оно уменьшается, а ток в цепи увеличивается.Поэтому воспользуемся тем фактом, что откуда сразу видно, что напряжение на резисторе уменьшается, причем в большей степени, чем
1. Требуется определить, как показания всех идеальных амперметров в схеме, показанной на рис. 78, когда сопротивление уменьшается. Очевидно, что при уменьшении сопротивления сопротивление нагрузки уменьшается, а ток I, показываемый амперметром A, увеличивается. В этом случае, как следует из (8), напряжение на параллельно включенных сопротивлениях и уменьшается.Следовательно, ток, показываемый амперметром, уменьшается. Сразу сказать, что будет с показаниями амперметра, сложно. Однако равенство сразу подразумевает, что увеличивается, и в большей степени, чем I.
Что такое контактная разность потенциалов? Как на собственном опыте убедиться в его существовании?
Покажите, как, используя закон Ома для однородного участка цепи, можно получить формулу (3).
Объясните правило знаков, которых следует придерживаться при использовании формулы (3).
Что такое электродвижущая сила? Объясните физический смысл понятия ЭДС на примере цепи из разных металлов. Что такое внешние силы?
Сформулируйте закон Ома для замкнутой неразветвленной цепи.
Каковы причины возникновения ЭДС в цепи из различных металлов или полупроводников, в химических источниках тока, в электрических генераторах?
Выберите основные части любой реальной замкнутой цепи. По каким параметрам они характеризуются?
Как напряжение на включенном источнике связано с его ЭДС? От чего зависит напряжение внутри источника?
Напряжение на источнике тока. Вернемся к формуле (8). Он был получен как следствие закона Ома для замкнутой цепи, выраженного формулой (5).
Рис. 79. Источник тока как неоднородный участок цепи (в) и компенсационный метод измерения ЭДС (б)
Рассчитаем еще раз ток через источник, рассматривая его как неоднородный участок цепи (рис. 79а). Используя формулу (3), в соответствии с приведенным выше правилом знаков имеем
Легко видеть, что напряжение, фигурирующее в формуле (8), равно — Следовательно, соотношение (9) фактически совпадает с (8 ).Однако при таком выводе этой формулы предположение, что ток создается только этим источником, не использовалось (то есть, следовательно, формула (8), как (9),
действительно выполняется для любого соотношения потенциалов, характеризующих напряжение на источнике тока.
Измерение ЭДС. Определение ЭДС любого источника экспериментально обычно выполняется так называемым методом компенсации, когда неизвестная ЭДС сравнивается с хорошо известной ЭДС другого, эталонного источника.Для этого используется схема, изображенная на рис. 79б. Батарея, ЭДС которой, очевидно, больше ЭДС эталонного источника 0 и измеряемой, замкнута на внешнее сопротивление. С помощью переключателя К к некоторой части этого сопротивления можно подключить либо эталонный источник, либо измеряемый. Полярность включения элементов показана на рис. 79б.
Сначала подключите опорный источник к ЭДС и выберите сопротивление таким образом, чтобы ток через гальванометр и, следовательно, через опорный источник исчезал.Вспомним значение
Объясните, почему напряжение, фигурирующее в формуле (8), действительно равно
, а не
Каковы преимущества компенсационного метода измерения ЭДС?
Закон Ома для однородного участка цепи:
Участок цепи называется однородным, если он не включает в себя источник тока. I = U / R, 1 Ом — сопротивление такого проводника, в котором протекает сила 1А при 1В.
Величина сопротивления зависит от формы и свойств материала проводника.Для однородного цилиндрического проводника его R = ρl / S, ρ — величина, зависящая от используемого материала — удельное сопротивление вещества, из ρ = RS / l следует, что (ρ) = 1 Ом * м. Величина, обратная ρ, есть проводимость γ = 1 / ρ.
Экспериментально установлено, что с повышением температуры электрическое сопротивление металлов увеличивается. При не слишком низких температурах удельное сопротивление металлов увеличивается на
абсолютная температура p = α * p 0 * T, p 0 — удельное сопротивление при 0 о С, α — температурный коэффициент.Для большинства металлов α = 1/273 = 0,004 К -1. p = p 0 * (1+ α * t), t — температура в о С.
Согласно классической электронной теории металлов в металлах с идеальной кристаллической решеткой электроны движутся без сопротивления (p = 0).
Причина появления электрического сопротивления — инородные примеси и физические дефекты кристаллической решетки, а также тепловое движение атомов. Амплитуда колебаний атомов зависит от t. Удельное сопротивление в зависимости от t — сложная функция:
p (T) = p rest + p id., p остаток — остаточное сопротивление, p id. — идеальная стойкость металла.
Идеальное сопротивление соответствует абсолютно чистому металлу и определяется только тепловыми колебаниями атомов. Исходя из общих соображений ударов. идентификатор сопротивления. металл должен стремиться к 0 при T → 0. Однако удельное сопротивление как функция суммы независимых членов, следовательно, из-за наличия примесей и других дефектов в кристаллической решетке удельного сопротивления при уменьшении t → до некоторого увеличения DC .p отдых. Иногда для некоторых металлов температурная зависимость p проходит через минимум. Ценность остального. Сопротивление биений зависит от наличия дефектов решетки и содержания примесей.
j = γ * E — закон Ома в дифференцированной форме, который описывает процесс в каждой точке проводника, где j — плотность тока, E — напряженность электрического поля.
Схема включает резистор R и источник тока. В неоднородном участке цепи, помимо электростатических сил, на носители тока действуют внешние силы.Внешние силы способны вызвать упорядоченное движение носителей тока, например, электростатических. На неоднородном участке цепи к полю электрических зарядов добавляется поле внешних сил, создаваемое источником ЭДС. Закон Ома в дифференцированной форме: j = γE. Обобщая формулу на случай неоднородного проводника j = γ (E + E *) (1).
Из закона Ома в дифференцированной форме для неоднородного участка цепи можно перейти к интегральной форме закона Ома для этого участка.Для этого рассмотрим неоднородный участок. В нем сечение проводника не может быть постоянным. Предположим, что внутри этого участка схемы есть линия, которую мы назовем токовой петлей, удовлетворяющей:
1. В каждом сечении, перпендикулярном контуру, значения j, γ, E, E * имеют одинаковые значения.
2. j, E и E * в каждой точке направлены по касательной к контуру.
Выберем произвольно направление движения по контуру.Пусть выбранное направление соответствует перемещению от 1 до 2. Возьмем проводящий элемент с площадью S и контурный элемент dl. Спроецируем векторы, входящие в (1), на элемент контура dl: j = γ (E + E *) (2).
I по контуру равно проекции плотности тока на площадь: I = jS (3).
Удельная проводимость: γ = 1 / ρ. Заменив I / S = 1 / ρ (E + E *) в (2), умножим на dl и проинтегрируем по контуру ∫Iρdl / S = ∫Eedl + ∫E * edl.Учтем, что ∫ρdl / S = R, а ∫Eedl = (φ 1 -φ 2), ∫E * edl = ε 12, IR = ε 12 + (φ 1 -φ 2). ε 12, как и I, является алгебраической величиной, поэтому мы договорились, что, когда ع способствует движению положительных носителей тока в выбранном направлении 1–2, рассмотрим ε 12> 0. Но на практике это имеет место, когда, когда при обходе участка цепи сначала встречается отрицательный полюс, затем положительный. Если ع препятствует движению положительных носителей в выбранном направлении, то ε 12
Закон Ома неравномерный участок цепи
1.8. Электричество. Закон Ома
Если поместить изолированный проводник в электрическое поле, то на свободные заряды q в проводнике действует сила, в результате чего в проводнике происходит кратковременное движение свободных зарядов. Этот процесс закончится, когда собственное электрическое поле зарядов, возникших на поверхности проводника, полностью компенсирует внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. П. 1.5).
Однако в проводниках при определенных условиях может происходить непрерывное упорядоченное движение свободных носителей электрического заряда.Это движение называется электрическим током. Направление движения положительных свободных зарядов принимается за направление электрического тока. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока является сила тока I — скалярная физическая величина, равная отношению заряда Δ q, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δ t, на этот временной интервал:
Если сила тока и его направление не меняются со временем, то такой ток называется постоянным.
В единицах СИ ток измеряется в амперах (А). Единица измерения тока 1 А устанавливается магнитным взаимодействием двух параллельных проводников с током (см. П. 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым путям. Электрическое поле в разных точках такой цепи постоянно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля.Но когда электрический заряд движется в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Следовательно, для существования постоянного тока необходимо иметь в электрической цепи устройство, способное создавать и поддерживать разность потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками питания постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются внешними силами.
Природа внешних сил может быть разной. В гальванических элементах или батареях они возникают в результате электрохимических процессов, в генераторах постоянного тока возникают внешние силы при движении проводников в магнитном поле. Источник питания в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием внешних сил электрические заряды перемещаются внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
Когда электрические заряды движутся по цепи постоянного тока, внешние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы A st внешних сил при перемещении заряда q от отрицательного полюса источника тока к положительному значению этого заряда, называется электродвижущей силой источника (ЭДС). :
Таким образом, ЭДС определяется работой, совершаемой внешними силами при перемещении одиночного положительного заряда.Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Когда одиночный положительный заряд движется по замкнутой цепи постоянного тока, работа внешних сил равна сумме ЭДС, действующей в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разделить на отдельные секции. Те области, на которые не действуют внешние силы (то есть области, не содержащие источников тока), называются однородными. Области, в которых есть источники тока, называются неоднородными.
Когда одиночный положительный заряд движется по определенному участку цепи, как электростатические (кулоновские), так и внешние силы совершают работу. Работа электростатических сил равна разности потенциалов Δφ 12 = φ 1 — φ 2 между начальной (1) и конечной (2) точками неоднородного участка. Работа внешних сил по определению равна электродвижущей силе 12, действующей в этой области. Таким образом, общая работа равна
.Величину U 12 принято называть напряжением на участке цепи 1–2.В случае однородной площади напряжение равно разности потенциалов:
Немецкий физик Г. Ом в 1826 году экспериментально установил, что ток I, протекающий через однородный металлический проводник (т. Е. Проводник, в котором не действуют внешние силы), пропорционален напряжению U на концах проводника:
Величину R обычно называют электрическим сопротивлением. Проводник, имеющий электрическое сопротивление, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: ток в проводнике прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению проводника.
В СИ единицей измерения электрического сопротивления проводников является ом (Ом). Сопротивлением 1 Ом обладает такой участок цепи, в котором при напряжении 1 В ток 1 А.
Проводники по закону Ома называются линейными. Графическая зависимость тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается в виде прямой, проходящей через начало координат. Следует отметить, что существует множество материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа.Даже для металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников увеличивается с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
Это соотношение обычно называют обобщенным законом Ома или законом Ома для неоднородного участка цепи.
На рис. 1.8.2 показывает замкнутую цепь постоянного тока. Участок цепи (cd) однородный.
Закон Ома для неоднородного участка цепи
На практике ясно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, чем кулоновские силы, тогда наблюдается случай, когда и силы электрического поля, и внешние силы действуют одновременно на свободные электрические заряды в участке цепи (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновские силы)).Такой участок называется неоднородным участком цепи. На рисунке ниже показан пример такого сайта.
Напряженность поля в любой точке цепочки равна векторной сумме поля кулоновских сил и поля внешних сил:
Сформулируем закон Ома для неоднородного участка цепи — сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его импедансу:
— Формула закона Ома для неоднородного участка цепи.
- I — сила тока,
- У12 — напряжение на участке,
- R — полное сопротивление цепи.
- ε = 20 В
- r = 1 Ом
- φ1 = 15 В
- φ2 = 5 В
- R = 3 Ом
- Я -?
- Запишем закон Ома для неоднородного участка цепи —
- Предполагая, что точка A — начало участка, а точка B — конец, берем ЭДС со знаком минус и, подставляя исходные данные, получаем
- Знак минус указывает на то, что ток идет от точки B к точке A, от точки с более низким потенциалом к точке с большим, как правило, для источников тока.
- Ответ: -2,5 А
- Федеральный закон от 21 ноября 2011 г. N 323-ФЗ «Об основах охраны здоровья в Российской Федерации» (в редакции) Федеральный закон от 21 ноября 2011 г. N 323-ФЗ «Об основах охраны здоровья» […]
- Возврат аванса от поставщика: бухгалтерский и налоговый учет Авансом или авансовым платежом считается платеж, полученный поставщиком (продавцом) до даты фактической отгрузки товара или до оказания услуг [ …]
- Обзор практики рассмотрения споров по трудовому договору «Обзор практики рассмотрения споров по трудовому договору» Утверждено Президиумом Федерального арбитражного суда Уральского округа. Протокол №5 от 30.03.2007 г. 1. […]
- В оперативном управлении автономного дошкольного образовательного учреждения является недвижимое имущество (здание детского сада). Налог на имущество рассчитывается и уплачивается автономным учреждением за счет […]
- Количество признаков преступления Суть юридического подхода состоит в том, чтобы рассматривать преступление как коллективное понятие — ow txt fb2 ePub html ссылка на файл выбранного формата будет отправлен на телефон. Шпаргалки […]
- Что делать, если задаток / задаток за квартиру не возвращен.Подробная инструкция, как вернуть, как действовать законно и вернуть свои деньги. Распространена ситуация, когда помимо ежемесячной арендной платы […]
Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:
— где φ1 и φ 2 — потенциалы на концах секции.
ЭДС характеризует работу внешних сил по передаче одиночного положительного заряда точки 1 в точку 2: — где ε12 — ЭДС, действующая в этой области, численно равна работе перемещения одиночного положительного заряда по контуру.
Напряжение на участке цепи — это суммарная работа сил ЭП и внешних сил:
Тогда закон Ома примет вид:
ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности ЭДС, включенной в секцию. Если внутри источника тока производится обход с отрицательного полюса на положительный, то ЭДС положительная (см. Рисунок). В то же время внешние силы делают положительную работу. Если шунтирование производится с положительного полюса на отрицательный, то ЭДС отрицательная.Проще говоря, если ЭДС способствует перемещению положительных зарядов, то ε> 0, в противном случае ε
Определите ток, протекающий через участок AB, показанный на рисунке. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек A и B соответственно 15 В и 5 В, сопротивление проводов 3 Ом.
Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определите разность потенциалов между точками A и B, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.
Электричество
Когда электрический ток проходит по замкнутой цепи, силы стационарного электрического поля и внешние силы действуют на свободные заряды. При этом на некоторых участках этой цепи ток создается только стационарным электрическим полем.Такие участки цепи называются однородными. На некоторых участках этой схемы помимо сил стационарного электрического поля действуют и внешние силы. Участок цепи, на который действуют внешние силы, называется неоднородным участком цепи.
Чтобы выяснить, от чего зависит сила тока в этих областях, необходимо уточнить понятие напряжения.
Рассмотрим сначала однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуется разностью потенциалов Δφ.Разность потенциалов на концах участка, где АК — работа сил стационарного электрического поля. Неоднородный участок схемы (рис. 1, б) содержит, в отличие от однородного участка, источник ЭДС, а к работе сил электростатического поля в этом участке добавляется работа внешних сил. По определению, где q — положительный заряд, который перемещается между любыми двумя точками цепи; — разность потенциалов точек в начале и конце рассматриваемого участка; … Затем говорят о напряжении за напряжением: Estac. NS. п. = Ee / stat. п. + Estor. Напряжение U на участке цепи — это физическая скалярная величина, равная суммарной работе внешних сил и сил электростатического поля на перемещение одиночного положительного заряда в этом участке:
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке.Если на площадку действуют только электрические силы (ε = 0), то. Таким образом, только для однородного участка схемы понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи:
где R — полное сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в сечение: если направление, создаваемое источником тока, совпадает с направлением тока, протекающего по сечению (направление тока в сечении совпадает внутри источника с направлением тока в сечении). направление от отрицательного полюса к положительному), т.е.е. ЭДС способствует перемещению положительных зарядов в заданном направлении, тогда ε> 0, в противном случае, если ЭДС препятствует перемещению положительных зарядов в заданном направлении, то ε
constant-current.narod.ru
Электродвижущая сила. Закон Ома для неоднородного участка цепи. Закон Кирхгофа
Мы рассмотрели закон Ома (98.1) для однородного участка цепи, то есть такого, на котором ЭДС не действует (не действуют внешние силы). Теперь рассмотрим неравномерного участка цепи.
Если ток течет по неподвижным проводникам, образующим участок 1-2, тогда работа A 12 всех сил (внешних и электростатических), действующих на носители тока, согласно закону сохранения и преобразования энергии, равна теплу, выделяемому в данной области. Работа сил при движении заряда Q 0 Местоположение на 1-2, согласно (97.4), А 12 = Q 0 E 0 + Q 0 ()
ЭДС Е 12, как и сила тока /, является скалярной величиной.Принимать его нужно либо с положительным, либо с отрицательным знаком, в зависимости от знака работы, выполняемой внешними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении (в направлении 1-2), , затем E 12 > 0. Если ЭДС препятствует движению положительных зарядов в заданном направлении, то E 12
Выражение (1) или (2) — это Закон Ома для неоднородного участка цепи в интегральной форме, , который является обобщенным законом Ома.
Если на этом участке цепи отсутствует источник тока (E 12 = 0), то из (4) приходим к закону Ома для однородного участка цепи (98.1): I = F1-F2 / R = U / R
Если электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, f 1 = f 2
то из (4) получаем закон Ома для замкнутой цепи: I = E / r + R 1
Расчет разветвленных цепей значительно упростится, если использовать правила, сформулированные немецким физиком Г.Р. Кирхгоф. Есть два правила.
Первый из них относится к узлам цепочки. Узел — это точка, в которой сходятся более двух проводников. (рис. 4.4). Ток, текущий в узел, считается положительным, ток, текущий из узла, имеет противоположный знак. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю :.
Это правило следует из уравнения неразрывности, т.е., в конечном итоге, из закона сохранения заряда.Количество уравнений, составляемых по первому правилу Кирхгофа, должно быть на единиц меньше, чем количество узлов в исследуемой цепочке … Это обеспечивает линейную независимость получаемых уравнений.
Второе правило применяется к любому замкнутому контуру, выбранному в разветвленной цепи (например, 1-3-2) (см. Рис. 4.5). Зададим направление прогулки, изобразив его стрелкой. Применим закон Ома к каждому из неразветвленных участков контура:; .
Когда эти выражения складываются, получается одно из уравнений;
, который выражает второе правило Кирхгофа : для любого замкнутого контура, алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре .
Аналогичные уравнения могут быть составлены для всех замкнутых контуров, существительное. однако в данной разветвленной цепи их количество должно быть ограничено уравнениями для независимых цепей, в которых возникает по крайней мере один ток, не включенный в другие.
При составлении уравнений по 2-му правилу Кирхгофа токам и ЭДС необходимо присвоить знаки в соответствии с выбранным направлением байпаса.
Например, ток нужно считать «+», он течет в сторону байпаса.ЭДС тоже нужно присвоить знак плюс, так как она действует в сторону обхода. Знак минус присваивается току и ЭДС.
На практике при решении задач при составлении уравнений направления токов выбираются произвольно и в соответствии с этим применяется правило знаков.
Фактическое направление токов определяется решением задачи: если какой-либо ток оказывается положительным, то его направление выбрано правильно, если отрицательное, то на самом деле он течет в направлении, противоположном выбранному направлению.Количество независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, равно количеству различных токов , текущих в разветвленной цепи. Следовательно, если даны ЭДС и сопротивления, то можно рассчитать все токи.
Если в цепи на носители тока действуют только силы электростатического поля, то носители перемещаются (предполагается, что они положительные) из точек с высоким потенциалом в точки с более низким потенциалом.Это приводит к выравниванию потенциалов во всех точках цепи и исчезновению электрического поля. Следовательно, для существования постоянного тока необходимо иметь в цепи устройство, способное создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока . Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.
Природа внешних сил может быть разной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и др. Роль источника тока в электрической цепи,
образно говоря, то же самое, что и роль насоса, который необходим для перекачивания жидкости в гидросистеме. Под действием сформированного поля внешних сил электрические заряды перемещаются внутри источника тока против сил электростатического поля, за счет чего концы цепи поддерживаются
есть разность потенциалов и в цепи течет постоянный электрический ток.
Внешние силы выполняют работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой внешними силами при перемещении одиночного положительного заряда, называется электродвижущей силой . (ЭДС) действующая в цепи: (97.1)
Эта работа совершается за счет энергии, затрачиваемой в источнике тока, поэтому значение E также можно назвать электродвижущей силой источника тока, включенного в схему. Часто вместо того, чтобы сказать: «В цепи действуют внешние силы», они говорят: «В цепи действует ЭДС», т.е.е. термин «электродвижущая сила» используется как характеристика внешних сил. ЭДС, как и потенциал, выражается в вольтах. Внешняя сила F CT, действующая на заряд Q o, может быть выражена как где Eating — напряженность поля внешних сил. Работа сторонних сил по перемещению заряда Q o по замкнутому участку цепи
Разделив (97,2) на Qo, , мы получим выражение для ЭДС, действующей в цепи:
тех.ЭДС, действующую в замкнутом контуре, можно определить как циркуляцию вектора напряженности поля внешних сил. ЭДС действующая на участке 1-2, равно (97.3)
На заряд Q 0 помимо внешних сил действуют и силы электростатического поля Fe = Q 0 E. Таким образом, результирующая сила, действующая в цепи на заряд Qo, равна F = F CT + F c = Q 0 (E CT + E).
Работа, совершаемая результирующей силой на заряде Q 0 Местоположение на 1-2, равно
Используя выражения (97.3) и (84.8), мы можем написать
Для замкнутой цепи работа электростатических сил равна нулю (см. § 83), поэтому в данном случае A 12 = Q 0 E 12.
Напряжение U Расположение на 1-2 называется физической величиной, определяемой работой, совершаемой суммарным полем электростатических (кулоновских) и внешних сил при перемещении одного положительного заряда по заданному участку цепи.Таким образом, согласно (97.4),
Понятие напряжения — это обобщение понятие разности потенциалов: напряжение на концах участка цепи равно разности потенциалов, если на ЭДС не работает в этой области, Т. То есть есть никаких внешних сил.
Что такое неоднородный участок цепи. Закон Ома неоднородный участок цепи
Электродвижущая сила.
Если в проводнике создается электрическое поле и не принимаются меры для его поддержания, то очень быстрое перемещение носителей тока приведет к исчезновению поля внутри проводника и прекращению тока.Чтобы поддерживать ток в течение длительного времени, необходимо постоянно снимать положительные заряды, принесенные сюда током с конца проводника с более низким потенциалом j 2, и переносить их на конец с высоким потенциалом (рис. 56.1). .
Создаваемое в проводнике электрическое поле не может осуществить такую передачу заряда. Для существования постоянного тока необходимо действие некоторых других сил (не кулоновских сил), которые перемещают заряды против электрических сил и поддерживают постоянство электрических полей.Это могут быть магнитные силы, заряды могут разделяться за счет химических реакций, диффузии носителей заряда в неоднородной среде и т. Д. Чтобы подчеркнуть разницу между этими силами и силами кулоновского взаимодействия, их принято обозначать термином внешние силы . Устройства, в которых происходит движение свободных зарядов под действием внешних сил, называют источниками тока . Сюда входят электромагнитные генераторы, термоэлектрические генераторы, солнечные батареи.Отдельную группу составляют химические источники тока: гальванические элементы, батареи и топливные элементы.
Действие внешних сил можно охарактеризовать, введя понятие напряженности поля внешних сил :.
Работа сторонних сил по перемещению заряда q на участок дл можно выразить следующим образом:
по всей длине участка л :
. (56,1)
Величина, равная отношению работы внешних сил по перемещению заряда к этому заряду, называется электродвижущей силой (ЭДС):
.(56,2)
В проводнике, по которому течет ток, напряженность электрического поля является суммой напряженности поля кулоновских сил и внешних сил:
Тогда для плотности тока мы можем написать
Замените векторы их проекциями в направлении замкнутого контура и умножьте обе части уравнения на dl :
После подстановки, результирующее уравнение сокращается до
Проинтегрируем полученное выражение по длине электрической цепи:
Интеграл в левой части уравнения — это сопротивление R на участке 1-2.В правой части уравнения значение первого интеграла численно равно работе кулоновских сил по перемещению единичного заряда из точки 1 в точку 2 — это разность потенциалов. Значение второго интеграла численно равно работе внешних сил по перемещению единичного заряда из точки 2 в точку 1 — это электродвижущая сила. В соответствии с этим сводим уравнение (56.3) к виду
Значение IR , равное произведению силы тока и сопротивления участка цепи, называется падением напряжения на цепи.Падение напряжения численно равна работе, совершаемой при перемещении единичного заряда под действием внешних сил и сил электрического поля (кулоновского).
Часть схемы, содержащая ЭДС, называется гетерогенной частью. Сила тока в таком сечении находится по формуле (56.4):
Учитывая, что источник тока можно подключить к цепи двумя способами, заменяем знак перед ЭДС на «±»:
Выражение (56.5) — это закон Ома для неоднородного участка цепи. Знаки «+» или «-» учитывают, как внешние силы влияют на течение тока в указанном направлении: они способствуют или препятствуют (рис. 56.2).
Если участок цепи не содержит ЭДС, т.е. однороден, то из формулы (56.5) следует
Из формулы (56.5) следует
где IR — падение напряжения на внешней части цепи, Ir — падение напряжения на внутренней части цепи.
Следовательно, ЭДС источника тока равна сумме падений напряжения на внешней и внутренней частях цепи .
Дифференциальная форма закона Ома . Найдите связь между плотностью тока j и напряженностью поля E в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора E . Следовательно, направления векторов j и E совпадают. Рассмотрим в однородной изотропной среде элементарный объем с образующими, параллельными вектору E , длина которого ограничена двумя эквипотенциальными участками 1 и 2 (рис.4.3).
Обозначим их потенциалы и, а среднюю площадь поперечного сечения через. Используя закон Ома, получаем для тока, или для плотности тока, поэтому
Перейдем к пределу при, тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что
где E — напряженность электрического поля внутри проводника. Учитывая, что j и E совпадают по направлению, получаем
.
Это отношение представляет собой дифференциальную форму закона Ома для однородного участка цепи . Величина называется проводимостью. Помимо электростатических сил, на носители тока в неоднородном участке цепи действуют и внешние силы, поэтому плотность тока в этих участках пропорциональна сумме интенсивностей. Учет этого приводит к дифференциальной форме закона Ома для неоднородного участка цепи .
.
При прохождении электрического тока по замкнутой цепи на свободные заряды действуют силы стационарного электрического поля и внешние силы.Причем в определенных частях этой цепи ток генерируется только стационарным электрическим полем. Такие участки цепи называются однородными . В некоторых частях этой цепи, помимо сил стационарного электрического поля, действуют и внешние силы. Часть цепи, на которую действуют внешние силы, называется участком гетерогенной цепи .
Чтобы узнать, от чего зависит сила тока в этих секциях, необходимо уточнить понятие напряжения.
Рассмотрим сначала однородный участок цепи (рис. 1, а). В этом случае только силы стационарного электрического поля совершают работу по перемещению заряда, и этот участок характеризуется разностью потенциалов Δ φ . Разность потенциалов на концах участка Δ φ = φ 1- φ 2 = AKq , где A K — работа сил стационарного электрического поля. Неоднородный участок контура (рис.1, б), в отличие от однородного участка, содержит источник ЭДС, и на этом участке к работе сил электростатического поля добавляется работа внешних сил. По определению Aelq = φ 1- φ 2, где q — положительный заряд, который перемещается между любыми двумя точками цепи; φ 1- φ 2 — разность потенциалов точек начала и конца рассматриваемого участка; Astq = ε .Тогда поговорим о напряжении для напряжения: E stats. е. п. = E э / стат. п. + E сторона Напряжение U на участке цепи — физическая скалярная величина, равная полной работе внешних сил и сил электростатического поля при перемещении одиночного положительного заряда в этом участке:
U = AKq + Astorq = φ 1- φ 2+ ε .
Эта формула показывает, что в общем случае напряжение в данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС в этом участке.Если на площадке действуют только электрические силы ( ε = 0), то U = φ 1- φ 2. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
I = Ur = φ 1- φ 2+ εR ,
где R — полное сопротивление неоднородной области.
ЭДС ε может быть как положительным, так и отрицательным. Это связано с полярностью включения ЭДС в секции: если направление, создаваемое источником тока, совпадает с направлением тока, протекающего в секции (направление тока в секции совпадает внутри источника с направлением от отрицательный к положительному полюсу), т.е. ЭДС способствует перемещению положительных зарядов в этом направлении, тогда ε > 0, иначе, если ЭДС препятствует движению положительных зарядов в этом направлении, то ε
Электродвижущая сила.
Закон Ома для замкнутой цепи и неоднородного участка цепи.
Закон Ома для замкнутой цепи означает, что. Величина тока в замкнутой цепи, которая состоит из источника тока с внутренним сопротивлением, а также внешнего сопротивления нагрузки. Он будет равен отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.
Закон Ома для неоднородного участка цепи
При прохождении электрического тока по замкнутой цепи на свободные заряды действуют силы стационарного электрического поля и внешние силы.Причем в определенных частях этой цепи ток генерируется только стационарным электрическим полем. Такие участки цепи называются однородными. В некоторых частях этой цепи, помимо сил стационарного электрического поля, действуют и внешние силы. Участок цепи, на который действуют внешние силы, называется неоднородным участком цепи.
Чтобы узнать, от чего зависит сила тока в этих секциях, необходимо уточнить понятие напряжения.
Фиг.1
Рассмотрим сначала однородный участок цепи (рис. 1, а). В этом случае только силы стационарного электрического поля совершают работу по перемещению заряда, и этот участок характеризуется разностью потенциалов Δφ. Разность потенциалов на концах графика, где АК — работа сил стационарного электрического поля. Неоднородный участок схемы (рис. 1, б), в отличие от однородного участка, содержит источник ЭДС, и на этом участке к работе сил электростатического поля добавляется работа внешних сил.По определению, где q — положительный заряд, который перемещается между любыми двумя точками цепи; — разность потенциалов точек начала и конца рассматриваемого участка; . Затем они говорят о стрессе за напряжением: Приблиз. е. п. = Ee / stat. п. + Estor. Напряжение U на участке цепи — это физическая скалярная величина, равная полной работе внешних сил и сил электростатического поля при перемещении одиночного положительного заряда в этом участке:
Эта формула показывает, что в общем случае напряжение в данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС в этом участке.Если на узел действуют только электрические силы (ε = 0), то. Таким образом, только для однородного участка схемы понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
где R — полное сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в секции: если направление, создаваемое источником тока, совпадает с направлением тока, протекающего в секции (направление тока в секции совпадает внутри источника с направлением от отрицательный к положительному полюсу), т.е. ЭДС способствует движению положительных зарядов в этом направлении, тогда ε> 0, в противном случае, если ЭДС препятствует перемещению положительных зарядов в этом направлении, то ε
Правила кихгоф.
Работа и текущая мощность. Эффект термического тока. Закон Джоуля-Ленца.
Когда ток течет через однородный участок цепи, электрическое поле выполняет свою работу. За время Δ t по цепи протекает заряд Δ q = I Δ t.Электрическое поле на выбранной станции делает свою работу
Мощность электрического тока равна отношению текущей работы Δ A к промежутку времени Δ t, в течение которого эта работа была выполнена:
Работа электрического тока в СИ выражается в джоулях (Дж), мощность — в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R.Закон Ома для полной цепи записывается как
Первое слагаемое в левой части Δ Q = RI 2 Δ t — тепло, выделяющееся на внешней части контура за время Δ t, второе слагаемое Δ Q ist = r I 2 Δ t — тепло, выделяемое внутри источника за то же время.
Выражение I Δ t равно работе внешних сил Δ A st, действующих внутри источника.
Когда электрический ток течет в замкнутой цепи, работа внешних сил Δ A st преобразуется в тепло, выделяющееся во внешней цепи (Δ Q) и внутри источника (Δ Q источник).
|
Следует отметить, что электрическое поле не входит в это соотношение. Когда ток течет по замкнутой цепи, электрическое поле не работает; поэтому тепло генерируется только внешними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными частями цепи.
Внешняя цепь может быть не только проводником с сопротивлением R, но и каким-нибудь устройством, потребляющим электроэнергию, например, двигателем постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может быть частично или полностью преобразована не только в тепло, но и в другие формы энергии, например, в механическую работу, выполняемую электродвигателем. Поэтому вопрос использования энергии источника тока имеет большое практическое значение.
Наиболее часто используемым в электротехнике соотношением между основными электрическими величинами является закон Ома, установленный эмпирическим путем в 1826 году немецким физиком Георгом Омом. С его помощью устанавливается связь между напряжением (электродвижущей силой) и сопротивлением элементы этой цепи, и сила проходящего тока.
Электрические параметры, которые описываются законом Ома:
- Сила тока определяется количеством заряда, проходящего через проводник за некоторое время, обозначается буквой I, единица измерения — ампер (А ).Входит в базовые единицы международной системы C;
- Напряжение электрическое, единица измерения — вольты, понятие ввел все тот же Георг Ом. Вольт можно выразить через работу по перемещению заряда, выделяемая мощность при токе 1 ампер, имеет эталонные источники в виде высокостабильных гальванических ячеек. Часто обозначается как разность потенциалов, в некоторых случаях используется понятие электродвижущей силы (ЭДС). Для обозначения можно использовать буквы U, V;
- R — сопротивление (электрическое), указывает на свойства проводника, препятствующие прохождению тока.Существенно зависит от материала проводника и температуры. Единица измерения — 1 Ом, обозначение — Ом или Ом.
Классическая формулировка закона Ома: сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Это выражение действительно для электрической цепи, которая не содержит дополнительной электродвижущей силы, обеспечивающей электрический ток, цепи, определяемой как однородная. В большинстве случаев используется такая формула.На практике часто бывает необходимо рассчитать величину тока, протекающего через какой-либо элемент с известным сопротивлением, для этого достаточно измерить падение напряжения (разность потенциалов) на выводах этого устройства, например, резистора. Для любых двух заданных значений можно вычислить неизвестное, и помимо значений, включенных в выражение, определяется электрическая мощность.
Важно! При вычислении используются значения только одной размерности — целые значения вольт, ампер, ом или соответствующие им кратные и дробные единицы.
Неоднородная цепочка
Закон Ома для одного участка цепи не учитывает наличие источника питания, его свойства не учитываются в расчетах. Для схемы, называемой гетерогенной, содержащей ЭДС любого вида и ее источник, в известной формуле, следует добавить внутреннее сопротивление самого устройства питания:
Здесь E — ЭДС источника напряжения, r — его внутреннее сопротивление. Варианты названий — закон Ома для неоднородного участка цепи, для полной или замкнутой цепи.Выражение мало отличается от приведенного выше — вместо напряжения здесь ЭДС и сопротивление источника питания.
Следует отметить, что понятие внутреннего сопротивления имеет смысл исключительно для химических источников тока, в случае использования других устройств, таких как любые источники питания без батарей, они говорят о выходном сопротивлении и нагрузочной способности этот блок.
В практических приложениях закон Ома для неоднородного участка цепи в такой форме используется редко, в основном для измерения внутреннего сопротивления аккумулятора и других аккумуляторов.
Закон также применяется к переменному напряжению, если сопротивление является активной нагрузкой. С его помощью определяются эффективные (среднеквадратичные) параметры цепи. В случае индуктивной, емкостной или сложной нагрузки и для разных частот сопротивление является реактивным, значительно отличающимся от того, которое измеряется обычным методом — омметром.
Закон Ома был получен практическим путем, поэтому он не может быть фундаментальным, но он точно описывает взаимосвязь между наиболее часто используемыми электрическими величинами.
Видео
В этой статье мы поговорим о законе Ома, формулах для полной цепи (замкнутой), участка цепи, неоднородного участка цепи, в дифференциальной и интегральной форме, переменного тока, а также для магнитопровода. Вы узнаете, какие материалы соответствуют и не соответствуют закону Ома, а также где это происходит.
: постоянный ток, протекающий по проводнику, прямо пропорционален напряжению, приложенному к его концам, и обратно пропорционален сопротивлению.
Закон Ома был сформулирован немецким физиком и математиком Георгом Омом в 1825-26 годах на основе опыта. Это экспериментальный закон, а не универсальный — он применим к определенным материалам и условиям.
Закон Ома является частным случаем более позднего и более общего — второго закона Кирхгофа
Ниже будет представлен видеоролик, объясняющий закон Ома на пальцах.
Формула закона Ома для цепочки Раздел
Сила постоянного тока, протекающего по проводнику, пропорциональна напряжению, приложенному к его концам.В Интернете эту формулу часто называют первым законом Ома:
U- напряжение
I — сила тока (сила)
R — Сопротивление
Электрическое сопротивление:
Коэффициент пропорциональности R называется электрическим сопротивлением или сопротивлением.
Отношение напряжения к току для данного проводника постоянно:
Единица электрического сопротивления 1 Ом (1 Ом):
Сопротивление резистора равно 1, если приложенное напряжение составляет 1 вольт, а ток — 1 ампер.
Зависимость электрического сопротивления от размера направляющей:
Сопротивление токопроводящего участка с постоянным поперечным сечением R прямо пропорционально длине этого участка li, обратно пропорционально площади поперечного сечения S:
R- электрическое сопротивление
ρ — удельное сопротивление
I- длина направляющей
S- площадь поперечного сечения
Это соотношение было подтверждено экспериментально британским физиком Хамфри Ди в 1822 году до разработки закона Ома.
Закон Ома для замкнутой (полной) цепи
— это величина силы (силы) тока в цепи тока, которая зависит от сопротивления нагрузки и от источника тока (Е), его еще называют вторым законом Ома.
Лампочка — это потребитель источника тока, соединяя их вместе, они образуют законченную электрическую цепь. На картинке выше вы можете увидеть полную электрическую схему, состоящую из батареи и лампы накаливания.
Электричество проходит через лампу накаливания и через саму батарею. Следовательно, ток, проходящий через лампу, впоследствии будет проходить через батарею, то есть сопротивление лампы добавляется к сопротивлению батареи.
Сопротивление нагрузки (лампочка), называется внешнее сопротивление , а сопротивление источника тока (батареи) внутреннее сопротивление . Сопротивление батареи обозначается латинской буквой r.
Когда электричество течет по цепи, внутреннее сопротивление самого элемента сопротивляется протеканию тока, и поэтому тепловая энергия теряется в самом элементе.
- E = электродвижущая сила в вольтах, В
- I = ток в амперах, А
- R = сопротивление нагрузки цепи в Ом, Ом
- r = внутреннее сопротивление ячейки в Ом, Ом
Мы можем изменить это уравнение;
В этом уравнении появляется ( В, ), то есть конечная разность потенциалов , измеренная в вольтах (В).Это разность потенциалов на выводах ячейки при протекании тока в цепи, она всегда меньше, чем у ячеек ЭДС.
Закон Ома для неоднородного участка цепи
Если только потенциальные силы ( Рисунок 1a ), то закон Ома записывается в известной форме. Если в круге также проявляется действие внешних сил ( Рис. 2b ), то закон Ома принимает вид откуда. Это закон Ома для любой части цепи. .
Закон Ома можно распространить на весь круг.Соединив точки 2 и 1 ( Рисунок 3c ), преобразуем разность потенциалов в ноль, и с учетом сопротивления источника тока закон Ома принимает вид. Это выражение закона Ома для полной цепи. .
Последнее выражение может быть представлено в различных формах. Как известно, напряжение на внешней секции зависит от нагрузки, т.е.
или, или.
В этих выражениях Ir — это падение напряжения внутри источника тока, и также видно, что напряжение U меньше ε на Ir .Причем, чем больше внешнее сопротивление по сравнению с внутренним, тем больше U приближается к ε.
Рассмотрим два особых случая, касающихся внешнего сопротивления цепи.
1) R = 0 — это явление называется коротким замыканием. Тогда из закона Ома имеем -, то есть ток в цепи увеличивается до максимума, а падение внешнего напряжения U → 0. При этом в источнике выделяется большая мощность, что может привести к его неисправности.
2) R = ∞ , то есть электрическая цепь разорвана, значит, a. Итак, в данном случае ЭДС численно равна напряжению на выводах открытого источника тока.
Закон Ома в дифференциальной форме
Закон Ома можно представить так, что он не связан с размером проводника. Выбрать участок кондуктора Δ l , , на концах которого приложены потенциалы φ 1 и φ 2.При средней площади поперечного сечения проводника Δ S , и плотности тока Дж , то ток
Если Δ l → 0, затем взяв предел отношений,. Итак, мы наконец получили, или в векторной форме, это выражение закона Ома в дифференциальной форме . Этот закон выражает силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома для переменного тока
Это уравнение представляет собой обозначение закона Ом для цепей переменного тока относительно их значений амплитуды.Понятно, что справедливо будет для действующих значений силы и тока:.
Для цепей переменного тока возможен случай, когда, что означает, что U L = U C . Поскольку эти напряжения находятся в противофазе, они компенсируют друг друга. Такие условия называются резонансным напряжением . Резонанса можно добиться либо при ω = const изменяя ОТ и L , либо при постоянном ОТ и L подхватят ω, что называется резонансным .Как видно — .
Характеристики резонанса напряжения следующие:
Наконец, из (2) — (4) имеем выражение для закона Ома в интегральной форме
, который он установил экспериментально.
Интерпретация закона Ома
Сила тока, которая является действием приложенного напряжения, ведет себя пропорционально его напряжению. Например: если приложенное напряжение удваивается, это также удваивает силу тока (силу тока).
Помните, что закону Ома удовлетворяет только часть материалов — в основном металлы и керамические материалы.
Когда действует закон Ома и какие материалы соответствуют и не соответствуют закону Ома
Закон Ома — это экспериментальный закон, выполняемый для некоторых материалов (например, металлов) для фиксированных условий тока, в частности температуры проводника.
Материалы, относящиеся к закону Ома, называются омическими проводниками или линейными проводниками. Примерами проводников, соответствующих закону Ома, являются металлы (например, медь, золото, железо), некоторые керамические изделия и электролиты.
Материалы, не относящиеся к закону Ома, в которых сопротивление является функцией силы тока, протекающего через них, называются нелинейными проводниками. Примеры закона Ома — полупроводники и газы.
Закон Ома не выполняется при изменении параметров проводника, особенно температуры.
ЗаконОма для формулы полной замкнутой цепи. Закон Ома для полной электрической цепи. Закон Ома для параллельной и последовательной цепи
Невозможно организовать циркуляцию заряда в замкнутом контуре под действием только электростатической силы.Для переноса заряда в область с высоким потенциалом (2- b -1) вы должны использовать неэлектростатических сил . Такие силы называются внешними силами. Любые силы, кроме электростатических, могут действовать как внешние силы. Устройства, в которых внешние силы действуют на электрические заряды, называются источниками тока. В батареях, например, внешние силы возникают в результате химической реакции взаимодействия электродов с электролитом; в генераторах внешние силы — это силы, действующие на заряды, движущиеся в магнитном поле, и т. д.Именно в источниках тока за счет работы внешних сил создается генерируемая энергия, которая затем расходуется в электрической цепи.
Работа, совершаемая внешними силами при перемещении одиночного положительного заряда, является одной из основных характеристик источника, его электродвижущей силы e:
Поле внешних сил, так же как и электростатическое поле, характеризуется вектором напряженности:
Электродвижущая сила источника равна работе, совершаемой внешними силами при перемещении одиночного положительного заряда по замкнутому контуру.
На участке цепи 1-а-2 движение носителей заряда происходит под действием только электростатической силы = q. Такие участки называют однородными.
Участок замкнутого контура, на который помимо электростатической силы действуют внешние силы, называется неоднородным.
Можно показать, что на однородном участке цепочки средняя скорость направленного движения носителей заряда пропорциональна действующей на них силе.Для этого достаточно сравнить формулы, полученные в последней лекции: = (6.3) и = l
Пропорциональность скорости силе и плотности тока интенсивности сохранится в случае неоднородного участка цепи. Но теперь напряженность поля равна сумме напряжённостей электростатического поля и поля внешних сил:.
Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.
Теперь перейдем к закону Ома для неоднородного участка цепи в интегральной форме.
Для замкнутого контура уравнение закона Ома несколько видоизменяется, так как разность потенциалов в этом случае равна нулю :.
В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, которое складывается из внешнего сопротивления контура R 0 и внутреннего сопротивления источника r: R = R 0 + r .
12) Закон Джоуля-Ленца в дифференциальной и интегральной формах.
Пусть протекает постоянный ток в участке электрической цепи I … Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при движении одиночного положительного заряда по этому участку. Это следует из определения напряжения.
Отсюда работа A = q × U … В течение t заряд будет передан по площадке q = I × t и работа будет выполнена: A = q × U = U × I × t .
Это выражение работы электрического тока справедливо для любого проводника.
Произведенная за единицу времени работа — это мощность электрического тока :.
Работа электрического тока (6.14) может быть потрачена на нагрев проводника, выполнение механической работы (электродвигатель) и на химическое действие тока при его протекании через электролит (электролиз).
Если химическое воздействие и механическая работа при протекании тока не выполняются, то вся работа электрического тока расходуется только на нагрев проводника: Q = A = U × I × t = I 2 × R × t .(6,15)
Закон о тепловом действии электрического тока (6.15) был экспериментально установлен независимо английским ученым Д. Джоулем и российским академиком Э. Ленц. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме , позволяющая рассчитать количество тепла, выделяемого в проводнике.
.
Перед нами закон Джоуля-Ленца в дифференциальной форме .
Учитывая, что i = l E =, это выражение также можно записать так:
Правила Кирхгофа.
Рассмотренные нами законы постоянного тока позволяют рассчитывать токи в сложных разветвленных электрических цепях. Эти расчеты упрощаются с помощью правил Кирхгофа.
Существует два правила Кирхгофа : текущее правило и правило напряжения .
Правило токов относится к узлам цепи, то есть к тем точкам цепи, где сходятся как минимум три проводника (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равна нулю:
При составлении соответствующего уравнения текущие в узел токи принимают со знаком плюс, а выходящие из него — со знаком минус.Это первое правило Кирхгофа является следствием уравнения неразрывности (см. (6.7)) или закона сохранения электрического заряда.
Стрессовое правило относится к любой замкнутой петле разветвленной цепи.
Правило напряжений формулируется следующим образом: в любой замкнутой цепи алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС, возникающей в этой цепи:
При составлении уравнения вторые правила Кирхгофа устанавливаются по направлению обхода.
Токи, совпадающие с направлением байпаса, принимают со знаком плюс, токи в обратном направлении — со знаком минус ЭДС. источник принимается со знаком плюс, если он создает ток, совпадающий с направлением байпаса. В противном случае ЭДС отрицательная.
Содержимое:Каждый специалист по ремонту и обслуживанию электроустановок должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это действительно так, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники.Этот закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.
Физические свойства закона Ома
Прямая связь между силой тока и напряжением, подаваемым в сеть, была обнаружена Омом в 1826 году. Позже понятие напряжения было заменено более точным термином — электродвижущей силой (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутого контура.Его важная особенность — обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные составы потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.
Для опытов по выводу закона использовалась простейшая схема, состоящая из источника питания с ЭДС и двух подключенных к нему клемм, подключенных к резистору. В проводнике элементарные частицы, несущие заряд, начинают двигаться в определенном направлении. Таким образом, он представлен как отношение ЭДС к общему сопротивлению всей цепи: I = E / R.
В представленной формуле E — это электродвижущая сила, измеренная в вольтах, I — ток в амперах, а R действует как электрическое сопротивление резистора, измеренное в омах. При этом учитываются все составляющие сопротивления и в расчетах используется их суммарное значение. К ним относятся сопротивление самого резистора, проводника (r) и источника питания (r0). Итоговая формула будет выглядеть так: I = E / (R + r + r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R + r, то в этом случае отсутствует зависимость силы тока от характеристик подключаемой нагрузки, и источник ЭДС играет роль источника тока. .Когда r0 меньше суммы R + r, получается обратная пропорция тока к общему внешнему сопротивлению, и напряжение поступает от источника питания.
Закон Ома для проведения расчетов
Для точных расчетов необходимо учитывать все потери напряжения, в том числе в точках подключения. Для определения электродвижущей силы на выводах источника тока измеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена.В этом случае применяется не только закон Ома для замкнутой цепи, но и действующий закон. Этот участок считается однородным, так как здесь учитывается только разность потенциалов без учета ЭДС. Это дает возможность рассчитать каждый элемент электрической схемы по формуле I = U / R, в которой U — разность потенциалов или напряжение, измеренное в вольтах.
Измерения проводятся с помощью вольтметра при подключении щупов к клеммам нагрузки или сопротивления.Результирующее значение напряжения всегда будет ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любой компонент при наличии двух известных.
Закон Ома для замкнутой цепи имеет много общего с законом, полученным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. Источником является обмотка катушки, по виткам которой течет электрический ток. Возникающий магнитный поток (F) замыкается на магнитную цепь и начинает циркулировать по цепи.Он напрямую зависит от магнитодвижущей силы и сопротивления материала, через который он проходит. Это явление выражается формулой Φ = F / Rm, в которой F — магнитодвижущая сила, а Rm — сопротивление демпфирования.
Как рассчитать цепи
Соединенный проводами с различными электроприборами и потребителями электрической энергии, он образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, на которых изображены элементы электрической цепи (сопротивления, источники тока, переключатели, лампы, приборы и т. Д.)) отмечены специальными значками.
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в 19 веке. и с тех пор наблюдается. Движение реальных зарядов может не совпадать с условным направлением тока. Итак, в металлах отрицательно заряженные электроны являются носителями тока, и они движутся от отрицательного полюса к положительному, то есть в противоположном направлении.В электролитах реальное движение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным .
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R .
Закон Ома для полной цепи устанавливает взаимосвязь между током в цепи, ЭДС и общим сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока R .
Работа внешних сил A st источник тока, согласно определению ЭДС ( ɛ ) равно A st = ɛq , где q — заряд, смещенный ЭДС. По определению действующего q = Оно , где t — время, в течение которого был передан заряд. Отсюда имеем:
A ул = ɛ Это .
Тепло, выделяемое при выполнении работы в контуре, согласно закону Джоуля-Ленца , равно:
Q = я 2 Rt + я 2 RT .
По закону сохранения энергии A = Q … Приравнивая ( A st = ɛ Это ) и ( Q = я 2 Rt + я 2 rt ) получаем:
ɛ = ИК + ИК.
Закон Ома для замкнутой цепи обычно записывается как:
.
Ток в полной цепи равен отношению ЭДС цепи к ее полному сопротивлению.
Если в цепи несколько источников, соединенных последовательно с ЭДС 1 , ɛ 2 , ɛ 3 и так далее, то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется относительно направления обхода контура, которое выбрано произвольно, например, на рисунке ниже — против часовой стрелки.
Внешние силы внутри источника делают положительную работу. И наоборот, для цепочки справедливо следующее уравнение:
ɛ = ɛ 1 + ɛ 2 + ɛ 3 = | ɛ 1 | — | ɛ 2 | — | ɛ 3 | …
В соответствии с силой тока положительная с положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Суммарное сопротивление цепи с несколькими источниками равно сумме внешнего и внутреннего сопротивлений всех источников ЭДС, например, для цифры выше:
R n = R + r 1 + r 2 + r 3.
Рассмотрим простейшую замкнутую цепь, состоящую из источника (гальванического элемента, батареи или генератора)
и резистор с сопротивлением (рис. 161). Источник тока имеет и сопротивление Сопротивление источника часто называют внутренним сопротивлением, а не сопротивлением внешней цепи. В генераторе это сопротивление обмоток, а в гальванической ячейке сопротивление раствора электролита и электродов
Закон Ома для замкнутой цепи связывает ток в цепи, ЭДС и импеданс цепи.Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля-Ленца (9.17).
Пусть заряд проходит через поперечное сечение проводника во времени. Тогда работу внешних сил по перемещению заряда можно записать следующим образом: Согласно определению силы тока Следовательно
При выполнении этой работы на внутренние и внешние участки цепи, сопротивление которых составляет определенное количество тепла. По закону Джоуля-Ленца оно равно:
Согласно закону сохранения энергии, Приравнивая (9.20) и (9.21) получаем:
Произведение силы тока и сопротивления участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.
Обычно закон Ома для замкнутой цепи записывается в виде:
Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее сопротивлению.
Сила тока зависит от трех величин: сопротивления и внешнего и внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи. В этом случае напряжение на выводах истока примерно равно
Но при коротком замыкании ток в цепи определяется именно внутренним сопротивлением источника и может быть очень большим при электродвижущей силе в несколько вольт, если ее недостаточно (например, в омной батарее).Провода могут расплавиться, а сам источник — выйти из строя.
Если в цепи несколько последовательно соединенных элементов с, то полная ЭДС схемы равна алгебраической сумме ЭДС отдельных элементов. Чтобы определить знак ЭДС любого источника, необходимо предварительно договориться о выборе положительного направления обхода цепи. На рисунке 162 направление обхода против часовой стрелки считается положительным (произвольно).
Если при обходе цепи они переходят от отрицательного полюса источника к положительному, то внешние силы внутри источника совершают положительную работу.Если при обходе цепи они переходят от положительного полюса источника к отрицательному полюсу, ЭДС будет отрицательной. Внешние силы внутри источника совершают отрицательную работу. Итак, для схемы, показанной на рисунке 162:
Если, то согласно (9.23) сила тока, т.е. направление тока совпадает с направлением обхода контура. Напротив, направление тока противоположно направлению обхода контура. Общее сопротивление цепи равно сумме всех сопротивлений:
При параллельном соединении гальванических элементов с одинаковой ЭДС (или других источников) ЭДС аккумулятора равна ЭДС одной из ячеек (рис. .163). Внутреннее сопротивление батареи рассчитывается по обычному правилу параллельного соединения проводов. Для схемы, показанной на рисунке 163, согласно закону Ома для замкнутой цепи сила тока определяется по следующей формуле:
1. Почему электрическое поле заряженных частиц (кулоновское поле) не может поддерживать постоянный электрический ток в цепи? 2. Что называют внешними силами? 3. Что называется электродвижущей силой?
4. Сформулируйте закон Ома для замкнутой цепи.5. От чего зависит знак ЭДС в законе Ома для замкнутой цепи?
Закон Ома для замкнутой цепи говорит об этом. Величина тока в замкнутой цепи, которая состоит из источника тока с внутренним сопротивлением, а также внешнего сопротивления нагрузки. Будет равно отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.
Формула 1 — Закон Ома для замкнутой цепи
Где R Сопротивление внешней цепи измеряется в Ом
r внутреннее сопротивление источника тока также измеряется в омах
I Сила тока в цепи.Измеряется в амперах
E Электродвижущая сила источника тока измеряется в вольтах
Иногда возникают ситуации, когда необходимо найти ток в цепи, но не указано напряжение на ее концах. Но сопротивление цепи и электродвижущая сила источника тока все же известны. В этом случае применить закон Ома для участка цепи невозможно.
В данном случае применяется закон Ома для замкнутой цепи. Чтобы объяснить принцип действия этого закона, проведем эксперимент.Для этого нам потребуются реостат источника тока, вольтметр и амперметр.
Для начала построим схему, состоящую из источника тока реостата и амперметра. Перед началом эксперимента установите реостат в максимальное положение. После включения в цепи появится ток, который можно будет наблюдать амперметром. Перемещая ползунок реостата, мы увидим, что при изменении внешнего сопротивления цепи изменяется ток.
Рисунок 1 — Измерение тока в цепи
Далее, оставив на реостате определенное сопротивление, подключить еще один такой же параллельно источнику тока.И мы увидим, что ток в цепи увеличится. Казалось бы, у обоих источников одинаковое напряжение, сопротивление внешней цепи не изменилось, почему ток увеличился.
Это произошло из-за того, что внутреннее сопротивление источника тока уменьшилось. А так как в замкнутой цепи он включен последовательно с внешним сопротивлением и источником тока. Тогда это внутреннее сопротивление также участвует в образовании тока в цепи.
Формула 2 — закон Ома для замкнутой цепи с числом параллельно подключенных n источников тока.
На основании вышеизложенного можно сделать вывод, что в реальной замкнутой электрической цепи значение тока не способно бесконечно увеличиваться при коротком замыкании в источнике тока, так как это значение ограничено внутренним сопротивлением источника тока.
Твиттер
В контакте с
Google+
СервисКакова мощность тока в замкнутой цепи.Закон Ома простым языком
Замкнутый контур (рис. 2) состоит из двух частей — внутренней и внешней. Внутренняя цепь — источник тока с внутренним сопротивлением р. ; внешний — Различные потребители, соединительные провода, устройства и т.д. Общее сопротивление внешней части указано р. . Тогда полное сопротивление цепи равно р. + Р. .
По закону Ома для внешнего участка цепи 1 → 2 Имеем:
\ (~ \ varphi_1 — \ varphi_2 = ir.\\)
Внутренний участок цепи 2 → 1 неоднороден. По закону Ома \\ (~ \ varphi_2 — \ varphi_1 + \ varepsilon = ir \). Складывая эти равенства, получаем
\ (~ \ Varepsilon = Ir + Ir. \ QQuad (1) \)
\ (~ I = \ FRAC (\ Varepsilon) (R + R). \\ QQuad (2) \\)
Последняя формула является законом Ом для замкнутой цепи постоянного тока. Мощность тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи .
Поскольку для однородного участка цепи разность потенциалов равна напряжению, то \ (~ \ varphi_1 — \ varphi_2 = ir = u \) и формулу (1) можно записать:
\ \ (~ \ varepsilon = u + ir \ rightarrow u = \ varepsilon — ir. \)
Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением тока в цепи при ε = конст.
Подставляем силу тока (2) в последнюю формулу, получаем
\ (~ U = \ varepsilon \ left (1 — \ FRAC (R) (R + R) \ Right).\\)
Разберем это выражение для некоторых предельных режимов цепи.
a) для открытых цепей ( R. → ∞) U. = ε . Напряжение на полюсах источника тока при разомкнутой цепи равно EDC источника тока.
В основе этого лежит возможность приближенного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого намного больше внутреннего сопротивления источника тока (\\ (~ R_v \\ gg r \\)).Для этого к клеммам источника тока подключают вольтметр.
б) если к клеммам источника тока подключить проводник, сопротивление которого \ (~ R \ LL R \), то р. + р. ≈ р. , то \ (~ u = \ varepsilon \ left (1 — \ FRAC (R) (R) \ RIGHT) = 0 \), а текущий \ (~ i = \ \ FRAC (\\ Varepsilon) (R) \\) — достигает максимального значения.
Подключение к полюсам источника тока в проводнике с ничтожно малым сопротивлением называется коротким замыканием , а максимальный ток для этого источника называется током короткого замыкания:
\ (~ I_ (KZ) = \ FRAC (\\ Варепсилон) (R).\)
Из источников с малой стоимостью р. (например свинцовые батареи р. = 0,1 — 0,01 Ом) Ток короткого замыкания очень велик. Особо опасно короткое замыкание в гайках легких сетей от подстанций ( ε > 100 В), I. KZ может достигать тысяч ампер. Во избежание возгораний в такие цепи включают предохранители.
Запишем закон Ома для полной цепи в случае последовательного и параллельного включения источников тока в батарее.При последовательном соединении источников «-» один источник соединяется с «+» вторым, «-» вторым с «+» третьим и т. Д. (Рис. 3, а). Если ε 1 = ε 2 = ε 3 А. г. 1 = р. 2 = р. 3 ДО ε В = 3. ε 1, р. В = 3. р. один. В этом случае закон OMA для полной цепочки имеет вид \\ [~ i = \\ Frac (\\ varepsilon_b) (R + R_B) = \\ FRAC (3 \\ Varepsilon_1) (R + 3R_1) \\], или для п. идентичных источников \ (~ i = \ FRAC (N \ Varepsilon_1) (R + NR_1) \).
Последовательный компаунд применяется в том случае, когда внешнее сопротивление \ (~ R \ gg nr_1 \), затем \ (~ i = \ FRAC (N \ Varepsilon_1) (R) \) и батарея может дать силы в н. Один раз больше, чем сила тока от одного источника.
При параллельном соединении источников тока все «+» источники соединяются вместе, а «-» источники — также вместе (рис.3, б). В данном случае
\ (~ \ varepsilon_b = \ varepsilon_1; \ r_b = \ FRAC (R_1) (3). \)
Где \ (~ i = \ FRAC ( \\ varepsilon_1) (R + \\ FRAC (R_1) (3)) \\).
Для n. идентичных исходников \ (~ i = \ FRAC (\ varepsilon_1) (R + \ FRAC (R_1) (N)) \).
Параллельное соединение источников тока используется, когда необходимо получить источник тока с малым внутренним сопротивлением или когда в цепи должен работать потребитель энергии.больше допустимого тока одного источника.
Параллельное соединение выгодно, когда р. Рядом по сравнению с р. .
Иногда используется смешанное подключение источников.
Литература
Аксенович Л. А. Физика в вузе: Теория. Задания. Испытания: этюд. Пособие для учреждений, обеспечивающих производство общ. медиа, образование / Л. А. Аксенович, Н. Н. Ракина, К. С. Фарино; Эд. К. С. Фарино. — МН: Adukatsya I Vikavanne, 2004.- С. 262-264.
Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона OMA для замкнутой цепи звучит следующим образом: значение тока в замкнутой цепи, состоящей из источника тока с внутренним и внешним сопротивлением нагрузки, равно отношению силы электродвижущего источника к сумме внутренней и внешней силы. сопротивление.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:
- I [a] — мощность тока в цепи,
- ε [in] — источник напряжения ЭДС,
- R [Ом] — сопротивление всех внешних элементов цепи,
- r [OM] — внутреннее сопротивление источника напряжения
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребителя, проходит через источник тока, и, следовательно, ток, за исключением сопротивления проводника, является сопротивлением самого источника.Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи состоит в том, что чем больше EDC, тем больше энергия носителей заряда, а значит, больше скорость их упорядоченного движения. С увеличением сопротивления цепи, энергии и скорости движения носителей заряда, следовательно, величина тока уменьшается.
Зависимость может быть показана на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения схемы по амперметру наблюдается ток, перемещая ползунок ромотажа, мы увидим, что при изменении внешнего сопротивления ток изменится.
Примеры целей применения закона Ома для замкнутой цепи
К источнику EDC 10 В и внутренним сопротивлением 1 Ом подключено сопротивление которого 4 Ом.Найдите силу тока в цепях и напряжение на зажимах источника.
При подключении к аккумулятору гальванических элементов резистором сопротивлением 20 Ом ток в цепи составлял 1 А, а при подключении резистора сила тока составляла 1,5 А. Найти ЭДС и внутреннее сопротивление аккумулятора.
Рассмотрим простейшую замкнутую цепь, состоящую из источника (гальванического элемента, батареи или генератора)
и сопротивление резистора (рис. 161). Источник тока имеет сопротивление и источник сопротивления часто называют внутренним сопротивлением в отличие от внешнего сопротивления цепи.В генераторе это сопротивление обмоток, а в гальваническом элементе — сопротивление раствора электролита и электродов
Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и общее сопротивление цепи. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля — Ленца (9.17).
Пусть тогда проводник проходит через поперечное сечение проводника, тогда работу сторонних зарядов по перемещению заряда можно записать следующим образом: согласно определению силы тока, следовательно,
При выполнении этой работы в внутренний и внешний участки цепи, сопротивление которых и есть определенное количество тепла.По закону Джоуля — Ленза это:
Согласно закону эквивалента сохранения энергии (9.20) и (9.21), получаем:
Произведение тока на сопротивление участка цепи часто равно называется падением напряжения в этой области. Таким образом, EDC равна сумме падений напряжений во внутреннем и внешнем участках замкнутой цепи.
Обычно закон Ома для замкнутой цепи записывается в виде:
Мощность тока в замкнутой цепи равна отношению цепи EDC к ее полному сопротивлению.
Сила тока зависит от трех величин: сопротивления и внешнего и внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если его недостаточно по сравнению с сопротивлением внешней части цепи, при этом напряжение на зажимах источника примерно равно
Но при коротком замыкании сила тока в цепи определяется внутренним сопротивлением источника и может быть очень большой с очень большой электродвижущей силой, если ее мало (например, в батареях ОМ).Провода могут расплавиться, и выйти из строя сам источник.
Если в цепи несколько последовательно соединенных элементов, то полная ЭДС цепи равна алгебраической величине ЭДС отдельных элементов. Чтобы определить знак ЭДС любого источника, нужно изначально иметь возможность выбрать положительное направление обхода цепи. На рисунке 162 положительно (произвольно) рассматривается направление обхода против стрелки по часовой стрелке.
Если вокруг цепи движется от отрицательного полюса источника к положительному, то сторонняя сила внутри источника совершает положительное действие.Если при обходе цепи цепь перемещается от положительного полюса источника к отрицательному, ЭДС будет отрицательной. Сторонние силы внутри источника делают негативную работу. Итак, для цепи, показанной на рисунке 162:
Если, то согласно (9.23) ток тока, т.е. направление тока совпадает с направлением обхода цепи. Напротив, направление тока противоположно направлению обхода цепи. Общее сопротивление цепи равно сумме всех сопротивлений:
При параллельном соединении гальванических элементов с одинаковой ЭДС (или другими источниками) ЭДС батареи равна EDC одного из элементов (рис.163). Внутреннее сопротивление батареи рассчитывается по обычному правилу параллельного соединения проводов. Для цепи, показанной на рисунке 163, согласно закону Ома для замкнутой цепи, сила тока определяется по следующей формуле:
1. Почему электрическое поле заряженных частиц (кулоновское поле) не может поддерживать постоянство электрический ток в цепи? 2. Что называется сторонними силами? 3. Что называется электродвижущей силой?
4.Слово Ома для замкнутой цепи. 5. От чего зависит знак ЭДС в законе Ома от замкнутой цепи?
Содержимое:Каждый специалист, ремонтирующий и обслуживающий электроустановки, должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это правда, поскольку закономерности, открытые немецким физиком Георгом Омомом, основаны на всей электротехнике. Этот закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.
Физические свойства закона Ома
Прямая связь между текущей мощностью и напряжением, подаваемым в сеть, была обнаружена компанией OMOM в 1826 году. В дальнейшем понятие напряжения было заменено более точным термином — электродвижущей силой (ЭДС). После теоретического обоснования этой зависимости был получен закон для замкнутой цепи. Его важной особенностью является обязательное отсутствие каких-либо внешних возмущений. Поэтому стандартные формулировки теряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.
Для экспериментов по заключению закона использовалась простейшая схема, состоящая из источника питания, имеющего ЭДС и двух подключенных к нему выводов, подключенных к резистору. В проводнике начинаются в определенном направлении элементарные частицы, несущие заряды. Таким образом, оно представляется в виде отношения EDC к общему сопротивлению всей цепи: I = E / R.
В представленной формуле E — это электродвижущая сила, измеренная в вольтах, I — сила тока в амперах, а R действует как электрическое сопротивление резистора, измеренное в омах.При этом учитываются все составляющие сопротивления и в расчетах используется их суммарное значение. К ним относятся сопротивление самого резистора, проводника (R) и источника питания (R0). В итоге формула будет выглядеть так: i = E / (R + R + R0). Если значение внутреннего сопротивления источника тока R0 превышает величину R + R, то в этом случае нет зависимости тока от характеристик подключаемой нагрузки, и источник ЭДС выполняет роль тока источник.Когда R0 меньше, чем величина R + R, получается обратная пропорция тока к общему внешнему сопротивлению, и напряжение поступает от источника питания.
Закон Ома для вычислений
Точные расчеты требуют учета всех потерь напряжения, в том числе в местах соединений. Для определения электродвижущей силы на выходе источника тока измеряется разность потенциалов в разомкнутой цепи, когда нагрузка полностью отключена. В этом случае для замкнутой цепи применяется не только закон Ома, но и действующий закон.Этот участок считается однородным, потому что здесь учитывается только разность потенциалов без учета ЭДС. Это дает возможность рассчитать каждый элемент электрической цепи по формуле i = u / r, в которой U — разность потенциалов или напряжения, измеренная в вольтах.
Измерения производятся с помощью вольтметра при подключении щупа к выходам нагрузки или сопротивления. Результирующее значение напряжения всегда будет ниже электродвижущей силы.Это наиболее распространенная формула, позволяющая найти любой компонент при наличии двух известных.
Закон Ома для замкнутой цепи имеет много общего с законом, выведенным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника используется обмотка катушки, по катушкам которой протекает электрический ток. Возникающий магнитный поток (F) замыкает магнитопровод и начинает циркулировать по контуру. Он находится в прямой зависимости от магниторезивной силы и сопротивления материала, через который он проходит.Это явление выражается формулой F = F / RM, в которой F — сила посещения магнитомотора, а Rm — импеданс, вызывающий затухание.
Как рассчитать цепи
В 1826 году немецкий ученый Георг Ом сделал открытие и описал
эмпирический закон о соотношении таких показателей, как мощность тока, напряжение и характеристики проводника в цепи. Впоследствии по имени ученого его стали называть законом Ома.
В дальнейшем выяснилось, что эти характеристики не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Также имеется характеристика внутреннего сопротивления (R) источника тока.
Закон Ома для участка цепочки
Согласно обобщенному закону Ома для некоторого участка цепи, ток тока на участке цепи прямо пропорционален напряжению на концах участка и обратно пропорционален сопротивлению.
Где U — напряжение концов секции, ток I — сопротивление проводника.
Принимая во внимание приведенную выше формулу, можно найти неизвестные значения, проделав простые математические операции.
Данные над формулой как раз когда сеть испытывает одно сопротивление.
Закон Ома для замкнутой цепи
Прочность всей цепи равна ЭДС, деленной на сумму сопротивлений однородных и неоднородных участков цепи.
Замкнутая сеть имеет одновременно внутреннее и внешнее сопротивление. Поэтому формулы уже разные.
Где E — электродвижущая сила (ЭДС), R — сопротивление внешнего источника, R — сопротивление внутреннего источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит линейные и нелинейные участки. Графики, которые не имеют источника тока и не зависят от стороннего воздействия, являются линейными, а секторы, содержащие источник, являются нелинейными.
Закон Ома для единого сетевого узла был изложен выше. Закон о нелинейной области будет иметь следующий вид:
I = u / r = f1 — f2 + e / r
Где F1 — F2 — разность потенциалов в конечных точках рассматриваемого участка
R — общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи больше нуля или меньше. Если направление протекания тока, идущего от источника с движением тока в электрической сети, совпадает, движение положительного заряда будет преобладать, и ЭДС будет положительной.В случае совпадения областей движение отрицательных зарядов, создаваемых EDC, будет увеличиваться в сети.
Закон Ома для переменного тока
При наличии емкости или инертности в сети необходимо учитывать при проведенных расчетах, что они обеспечивают свое сопротивление, действие которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
где Z — сопротивление по всей длине электрической сети.Его еще называют импедансом. Импеданс представляет собой сопротивление активного и реактивного характера.
Закон Ома — это не главный научный закон, а всего лишь эмпирическая установка, и в некоторых условиях он может не соблюдаться:
- Когда сеть имеет высокую частоту, электромагнитное поле изменяется с большой скоростью, и в расчетах необходимо учитывать инертность носителей заряда;
- В условиях низких температур с веществами, обладающими сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- Когда под высоким напряжением проводник или диэлектрик;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.
В свою очередь элементы и проводники, соответствующие закону Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос — почему нет электрического тока? Объяснить это довольно просто. Сидящие на проводах птицы — своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, причем в той пропорции, что сами «проводники» не представляют для них опасности.
Но это правило работает только с одним контактом. Если у птицы есть клюв, проволока-крыло или телеграфный столб, она неизбежно погибнет от огромного напряжения, которое переносят эти места. Такие случаи случаются повсюду. Поэтому в целях безопасности в некоторых местах устанавливаются специальные устройства, защищающие птиц от опасного напряжения. На такой птице птицефабрики полны безопасности.
ЗаконОма также широко применяется на практике. Электричество смертельно опасно для человека, всего лишь прикоснувшись к оголенному проводу.Но в некоторых случаях сопротивление человеческого тела может быть разным.
Например, сухая и неповрежденная кожа имеет большую устойчивость к воздействию электричества, чем рана или кожа, покрытая позже. В результате переутомления, нервного напряжения и интоксикации даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем сопротивление человеческого тела составляет 700 Ом, это означает, что для человека это безопасное напряжение 35 В. Работая с большим напряжением, специалисты используют.
Энергетическая функция кортикальных аксонов в кабеле: эквивалентные формулы
% PDF-1.4 % 49 0 объект > эндобдж 60 0 объект > поток application / pdf
Формула закона Ома для замкнутой электрической цепи.Закон сохранения заряда
В этой статье мы поговорим о законе Ома, формулах для полной цепи (замкнутой), участка цепи, неоднородного участка цепи, в дифференциальной и интегральной форме, переменного тока, а также для магнитопровода. . Вы узнаете, какие материалы соответствуют и не соответствуют закону Ома, а также где это происходит.
: постоянный ток, протекающий по проводнику, прямо пропорционален напряжению, приложенному к его концам, и обратно пропорционален сопротивлению.
Закон Ома был сформулирован немецким физиком и математиком Георгом Омом в 1825-26 годах на основе опыта. Это экспериментальный закон, а не универсальный — он применим к определенным материалам и условиям.
Закон Ома является частным случаем более позднего и более общего — второго закона Кирхгофа
Ниже будет видео, объясняющее закон Ома на пальцах.
Формула закона Ома для участка цепи
Сила постоянного тока, протекающего по проводнику, пропорциональна напряжению, приложенному к его концам.В Интернете эту формулу часто называют первым законом Ома:
U- напряжение
I- сила (сила) тока
R — Сопротивление
Электрическое сопротивление:
Коэффициент пропорциональности R называется электрическим сопротивлением или сопротивлением.
Отношение напряжения к току для данного проводника постоянно:
Единица электрического сопротивления 1 Ом (1 Ом):
Сопротивление резистора равно 1, если приложенное напряжение составляет 1 вольт, а ток — 1 ампер.
Зависимость электрического сопротивления от размера направляющей:
Сопротивление токопроводящего участка с постоянной площадью поперечного сечения R прямо пропорционально длине этого участка li, обратно пропорционально площади поперечного сечения S:
R- электрическое сопротивление
ρ — удельное сопротивление
I- длина направляющей
S- площадь поперечного сечения
Эта связь была экспериментально подтверждена британским физиком Хамфри Ди в 1822 году до разработки закона Ома.
Закон Ома для замкнутой (полной) цепи
— это значение силы (силы) тока в этой цепи, которое зависит от сопротивления нагрузки и источника тока (E), его также называют вторым законом Ома.
Лампочка является потребителем источника тока, соединяя их вместе, они образуют законченную электрическую цепь. На картинке выше вы можете увидеть полную электрическую схему, состоящую из батареи и лампы накаливания.
Электричество проходит через лампу накаливания и через саму батарею. Следовательно, ток, проходящий через лампу, будет дальше проходить через батарею, то есть сопротивление лампочки добавляется к сопротивлению батареи.
Сопротивление нагрузки (лампочка), называется внешнее сопротивление , а сопротивление источника тока (батареи) внутреннее сопротивление … Сопротивление батареи обозначается латинской буквой r.
Когда электричество течет по цепи, внутреннее сопротивление самого элемента сопротивляется протеканию тока, и поэтому тепловая энергия теряется в самом элементе.
- E = электродвижущая сила в вольтах, В
- I = ток в амперах, А
- R = сопротивление нагрузки в цепи в Ом, Ом
- r = внутреннее сопротивление ячейки в Ом, Ом
Мы можем изменить это уравнение;
Это уравнение появляется ( В, ), то есть конечная разность потенциалов , измеренная в вольтах (В).Это разность потенциалов на выводах ячейки при протекании тока в цепи, она всегда меньше ЭДС. клетки.
Закон Ома для неоднородного участка цепи
Если на участок цепи действуют только потенциальные силы (, рис. 1а, ), то закон Ома записывается в известной форме. Если же действие внешних сил также проявляется в окружности ( Рис. 2b ), то закон Ома принимает вид, где. Это закон Ома для любой части цепи..
Закон Ома можно распространить на весь круг. Соединив точки 2 и 1 ( Рисунок 3c ), преобразуем разность потенциалов в ноль, и с учетом сопротивления источника тока закон Ома примет вид. Это выражение закона Ома для полной цепи .
Последнее выражение может быть представлено в различных формах. Как известно, напряжение во внешней секции зависит от нагрузки, то есть
или, или.
В этих выражениях Ir — это падение напряжения внутри источника тока, и также видно, что напряжение U меньше ε на величину Ir … Причем, чем больше внешнее сопротивление по сравнению с внутренний, тем больше U приближается к ε.
Рассмотрим два особых случая, касающихся внешнего сопротивления цепи.
1) R = 0 — это явление называется коротким замыканием.Тогда из закона Ома имеем -, то есть ток в цепи увеличивается до максимума, а падение внешнего напряжения U → 0. В этом случае в источнике выделяется большая мощность, что может привести к его неисправности.
2) R = ∞ , то есть электрическая цепь разорвана, то, но … Итак, в данном случае ЭДС численно равна напряжению на выводах открытого источника тока.
Закон Ома в дифференциальной форме
Закон Ома можно представить таким образом, чтобы он не зависел от размера проводника.Выбрать сечение кондуктора Δ л , , на концах которого приложены потенциалы φ 1 и φ 2. При средней площади поперечного сечения проводника Δ S и плотности тока j , то сила тока
Если Δ l → 0, затем взяв предел отношения, … Итак, окончательно получаем, или в векторной форме — это выражение закон Ома в дифференциальной форме … Этот закон выражает силу тока в произвольной точке проводник в зависимости от его свойств и электрического состояния.
Закон Ома для переменного тока
Это уравнение записано законом Ома для цепей переменного тока относительно их значений амплитуды. Понятно, что это будет справедливо и для действующих значений силы и тока:.
Для цепей переменного тока возможен случай, когда, то есть U L = U C … Поскольку эти напряжения в противофазе, они компенсируют друг друга.Такие условия называются , резонанс напряжения … Резонанс может быть достигнут либо при ω = const при изменении СО и L , либо при постоянных СО и L выберите ω, который называется резонансным … Как видно — .
Характеристики резонанса напряжения следующие:
Наконец, из (2) — (4) имеем интегральное выражение для закона Ома
, который он установил экспериментально.
Интерпретация закона Ома
Сила тока, которая является действием приложенного напряжения, изменяется пропорционально его напряжению. Например: если приложенное напряжение удваивается, это также удваивает силу тока (сила тока).
Помните, что закону Ома удовлетворяет только подмножество материалов — в основном металлы и керамика.
Когда выполняется закон Ома и какие материалы соответствуют и не соответствуют закону Ома?
Закон Ома — это экспериментальный закон, который выполняется для некоторых материалов (например, металлов) при фиксированных условиях тока, в частности, температуры проводника.
Материалы законаОма называются омическими проводниками или линейными проводниками. Примерами проводников, соответствующих закону Ома, являются металлы (например, медь, золото, железо), определенная керамика и электролиты.
Неомные материалы, сопротивление которых зависит от силы тока, протекающего через них, называются нелинейными проводниками. Примерами руководящих принципов, не относящихся к закону Ома, являются полупроводники и газы.
Закон Ома не выполняется при изменении параметров проводника, особенно температуры.
Соединенный проводами с различными электроприборами и потребителями электрической энергии, он образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, на которых элементы электрической цепи (сопротивления, источники тока, переключатели, лампы, устройства и т. Д.) Отмечены специальными значками.
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному.Это правило было установлено в 19 веке. и с тех пор наблюдается. Движение реальных зарядов может не совпадать с условным направлением тока. Итак, в металлах отрицательно заряженные электроны являются носителями тока, и они движутся от отрицательного полюса к положительному, то есть в противоположном направлении. В электролитах реальное движение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным .
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R .
Закон Ома для полной цепи устанавливает взаимосвязь между током в цепи, ЭДС и общим сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока R .
Работа внешних сил A st источник тока, согласно определению ЭДС ( ɛ ) равно A st = ɛq , где q — заряд, смещенный ЭДС. По определению действующего q = It , где t — время, в течение которого был передан заряд. Отсюда имеем:
A ул = ɛ Это .
Тепло, выделяемое при выполнении работы в контуре, согласно закону Джоуля-Ленца , равно:
Q = я 2 Rt + я 2 RT .
Согласно закону сохранения энергии A = Q … Приравнивая ( A st = ɛ Это ) и ( Q = я 2 Rt + я 2 rt ) получаем:
ɛ = ИК + Ir.
Закон Ома для замкнутой цепи обычно записывается как:
.
Ток в полной цепи равен отношению ЭДС цепи к ее полному сопротивлению.
Если в цепи несколько источников, соединенных последовательно с ЭДС 1 , ɛ 2 , ɛ 3 и т. Д., То полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется относительно направления обхода контура, которое выбрано произвольно, например, на рисунке ниже — против часовой стрелки.
Внешние силы внутри источника делают положительную работу. И наоборот, для цепочки справедливо следующее уравнение:
ɛ = ɛ 1 + ɛ 2 + ɛ 3 = | ɛ 1 | — | ɛ 2 | — | ɛ 3 | …
В соответствии с силой тока положительная с положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Суммарное сопротивление цепи с несколькими источниками равно сумме внешнего и внутреннего сопротивлений всех источников ЭДС, например, для цифры выше:
R n = R + r 1 + r 2 + r 3.
Содержимое:Каждый специалист по ремонту и обслуживанию электроустановок должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это правда, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники. Этот закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.
Физические свойства закона Ома
Прямая зависимость между силой тока и напряжением, подаваемым в сеть, была обнаружена Омом в 1826 году.Позже понятие напряжения было заменено более точным термином — электродвижущей силой (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутого контура. Его важная особенность — обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные составы потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.
Для опытов по выводу закона использовалась простейшая схема, состоящая из источника питания с ЭДС и двух подключенных к нему клемм, подключенных к резистору.Элементарные частицы, несущие заряд, начинают двигаться в проводнике в определенном направлении. Таким образом, оно представляется как отношение ЭДС к общему сопротивлению всей цепи: I = E / R.
В представленной формуле E — это электродвижущая сила, измеренная в вольтах, I — ток в амперах, а R действует как электрическое сопротивление резистора, измеренное в омах. При этом учитываются все составляющие сопротивления и в расчетах используется их суммарное значение.К ним относятся сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательная формула будет выглядеть так: I = E / (R + r + r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R + r, то в этом случае отсутствует зависимость силы тока от характеристик подключаемой нагрузки, и источник ЭДС играет роль источника тока. . Когда r0 меньше суммы R + r, получается обратная пропорция тока к общему внешнему сопротивлению, и напряжение поступает от источника питания.
Закон Ома для проведения расчетов
Для точных расчетов необходимо учитывать все потери напряжения, в том числе в точках подключения. Для определения электродвижущей силы на выводах источника тока измеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена. В этом случае применяется не только закон Ома для замкнутой цепи, но и действующий закон. Этот участок считается однородным, так как здесь учитывается только разность потенциалов без учета ЭДС.Это дает возможность рассчитать каждый элемент электрической цепи по формуле I = U / R, в которой U — разность потенциалов или напряжение, измеренное в вольтах.
Измерения выполняются с помощью вольтметра при подключении щупов к клеммам нагрузки или сопротивления. Результирующее значение напряжения всегда будет ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любой компонент при наличии двух известных.
Закон Ома для замкнутой цепи имеет много общего с законом, полученным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. Источником является обмотка катушки, по виткам которой течет электрический ток. Возникающий магнитный поток (F) замыкается на магнитную цепь и начинает циркулировать по цепи. Он напрямую зависит от магнитодвижущей силы и сопротивления материала, через который он проходит. Это явление выражается формулой Ф = F / Rm, в которой F — магнитодвижущая сила, а Rm — сопротивление затухания.
Как рассчитать цепи
Закон Ома для замкнутой цепи говорит об этом. Величина тока в замкнутой цепи, которая состоит из источника тока с внутренним сопротивлением, а также внешнего сопротивления нагрузки. Будет равно отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.
Формула 1 — Закон Ома для замкнутой цепи
Где R Сопротивление внешней цепи измеряется в Ом
r внутреннее сопротивление источника тока также измеряется в омах
I Сила тока в цепи.Измеряется в амперах
E Электродвижущая сила источника тока измеряется в вольтах
Иногда возникают ситуации, когда необходимо найти ток в цепи, но напряжение на ее концах не выставлено. Тем не менее сопротивление цепи и электродвижущая сила источника тока известны. В этом случае применить закон Ома для участка цепи невозможно.
В данном случае применяется закон Ома для замкнутой цепи. Чтобы выяснить принцип действия этого закона, проведем эксперимент.Для этого нам понадобится источник тока, реостат, вольтметр и амперметр.
Для начала построим схему, состоящую из источника тока реостата и амперметра. Перед началом эксперимента установите реостат в максимальное положение. После включения в цепи появится ток, который можно будет наблюдать амперметром. Перемещая ползунок реостата, мы увидим, что при изменении внешнего сопротивления цепи изменяется ток.
Рисунок 1 — Измерение тока в цепи
Затем, оставив на реостате определенное сопротивление, подключите другое такое же сопротивление параллельно источнику тока.И мы увидим, что ток в цепи увеличится. Казалось бы, у обоих источников одинаковое напряжение, сопротивление внешней цепи не изменилось, почему ток увеличился.
Это произошло из-за уменьшения внутреннего сопротивления источника тока. А так как в замкнутой цепи он включен последовательно с внешним сопротивлением и источником тока. Тогда это внутреннее сопротивление также участвует в образовании тока в цепи.
Формула 2 — это закон Ома для замкнутой цепи с числом параллельно подключенных n источников тока.
На основании вышеизложенного можно сделать вывод, что в реальной замкнутой электрической цепи значение тока не способно бесконечно увеличиваться при коротком замыкании в источнике тока, так как это значение ограничено внутренним сопротивлением источника тока.
Замкнутый контур (рис. 2) состоит из двух частей — внутренней и внешней. Внутренняя часть цепи — источник тока с внутренним сопротивлением r ; внешний — различные потребители, соединительные провода, устройства и т. Д.Общее сопротивление внешней части обозначается как R … Тогда полное сопротивление цепи составляет R + R .
Закон Ома для внешнего участка цепи 1 → 2 имеем:
\ (~ \ varphi_1 — \ varphi_2 = IR. \)
Внутренний участок цепочки 2 → 1 неоднороден. Согласно закону Ома \ (~ \ varphi_2 — \ varphi_1 + \ varepsilon = Ir \). Складывая эти равенства, получаем
\ (~ \ varepsilon = IR + Ir.\ qquad (1) \)
\ (~ I = \ frac (\ varepsilon) (R + r). \ Qquad (2) \)
Последняя формула — это закон Ома для замкнутой цепи постоянного тока. Ток в цепи прямо пропорционален ЭДС источника и обратно пропорционален общему сопротивлению цепи .
Поскольку для однородного участка цепи разность потенциалов равна напряжению, то \ (~ \ varphi_1 — \ varphi_2 = IR = U \) и формулу (1) можно записать:
\ (~ \ varepsilon = U + Ir \ Rightarrow U = \ varepsilon — Ir.\)
Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением тока в цепи при ε = конст.
Подставляя силу тока (2) в последнюю формулу, получаем
\ (~ U = \ varepsilon \ left (1 — \ frac (r) (R + r) \ right). \)
Давайте проанализируем это выражение для некоторых предельных режимов работы схемы.
а) С разомкнутой цепью ( R → ∞) U = ε , г.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.
Это основа возможности приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого намного больше внутреннего сопротивления источника тока (\ (~ R_v \ gg r \)) . Для этого к клеммам источника тока подключают вольтметр.
б) Если к выводам источника тока подсоединен проводник, сопротивление которого \ (~ R \ ll r \), то R + r ≈ r , тогда \ (~ U = \ varepsilon \ left (1 — \ frac (r) (r) \ right) = 0 \), а текущее \ (~ I = \ frac (\ varepsilon) (r) \) — достигает максимального значения.
Подключение проводника с незначительным сопротивлением к полюсам источника тока называется коротким замыканием , а максимальный ток для данного источника называется током короткого замыкания:
\ (~ I_ (kz) = \ frac (\ varepsilon) (r). \)
Для источников с малым значением r (например, для свинцово-кислотных аккумуляторов r = 0,1 — 0,01 Ом) ток короткого замыкания очень велик. Особенно опасно короткое замыкание в осветительных сетях от подстанций ( ε > 100 В), I кГц может достигать тысяч ампер.Во избежание возгорания в такие цепи включают предохранители.
Запишем закон Ома для замкнутой цепи при последовательном и параллельном подключении источников тока к батарее. При последовательном подключении источников «-» одного источника соединяется с «+» второго, «-» второго — с «+» третьего и так далее. (Рис.3, а). Если ε 1 = ε 2 = ε 3 a r 1 = r 2 = r 3, затем ε b = 3 ε 1, r b = 3 r один.В этом случае закон Ома для полной схемы равен \ [~ I = \ frac (\ varepsilon_b) (R + r_b) = \ frac (3 \ varepsilon_1) (R + 3r_1) \], или для n идентичных источников \ (~ I = \ frac (n \ varepsilon_1) (R + nr_1) \).
Последовательное соединение используется, когда внешнее сопротивление \ (~ R \ gg nr_1 \), затем \ (~ I = \ frac (n \ varepsilon_1) (R) \) и батарея может дать n в раз больше, чем ток от одного источника.
При параллельном подключении источников тока все источники «+» соединяются вместе, а источники «-» также вместе (Рис.3, б). В данном случае
\ (~ \ varepsilon_b = \ varepsilon_1; \ r_b = \ frac (r_1) (3). \)
Откуда \ (~ I = \ frac (\ varepsilon_1) (R + \ frac (r_1) (3)) \).
Для n идентичных источников \ (~ I = \ frac (\ varepsilon_1) (R + \ frac (r_1) (n)) \).
Параллельное соединение источников тока используется, когда необходимо получить источник тока с низким внутренним сопротивлением или когда ток должен протекать в цепи для нормальной работы потребителя электроэнергии.больше допустимого тока одного источника.
Параллельное соединение выгодно, когда R small по сравнению с r .
Иногда используется смешанное сочетание источников.
Литература
Аксенович Л.А. Физика в вузе: Теория. Задания. Тесты: Учебник. пособие для учреждений, обеспечивающих получение обсл. среда, образование / Л. А. Аксенович, Н. Н. Ракина, К. С. Фарино; Эд. К. С. Фарино. — Минск: Адукаться и выхаванне, 2004.- С. 262-264.
Интерпретация закона Ома. Что такое закон Ома
Величина воздействия тока на проводник зависит от того, является ли это тепловым, химическим или магнитным действием тока. То есть, регулируя силу тока, вы можете контролировать его действие. Электрический ток, в свою очередь, — это упорядоченное движение частиц под действием электрического поля.
Зависимость тока и напряжения
Очевидно, что чем сильнее поле действует на частицы, тем больше сила тока в цепи.Электрическое поле характеризуется величиной, называемой напряжением. Следовательно, делаем вывод, что сила тока зависит от напряжения.
Действительно, экспериментально удалось установить, что сила тока прямо пропорциональна напряжению. В случаях, когда величина напряжения в цепи была изменена без изменения всех других параметров, сила тока увеличивалась или уменьшалась на ту же величину, что и напряжение.
Соединение с сопротивлением
Однако любая цепь или участок цепи характеризуется другим важным значением, называемым сопротивлением электрическому току.Сопротивление обратно пропорционально силе тока. Если на каком-либо участке цепи изменить значение сопротивления без изменения напряжения на концах этого участка, сила тока также изменится. Более того, если мы уменьшим значение сопротивления, то сила тока увеличится на ту же величину. И наоборот, с увеличением сопротивления пропорционально уменьшается сила тока.
Формула закона Ома для цепочки Раздел
Сравнивая эти две зависимости, мы можем прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 году.Он соединил вместе три вышеупомянутые физические величины и вывел закон, названный в его честь. Закон Ома для участка цепи гласит:
Сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
где I — сила тока,
U — напряжение,
R — сопротивление.
Применение закона Ома
Закон Ома — один из основных законов физики .Его открытие в свое время позволило совершить огромный скачок в науке. В настоящее время невозможно представить ни один простейший расчет основных электрических величин для любой цепи без использования закона Ома. Идея этого закона не только для электронщиков, но и необходимая часть базовых знаний любого образованного человека. Недаром есть такая поговорка: «Не знаешь закона Ома — сиди дома».
U = IR и R = U / I
Правда, следует понимать, что в собранной схеме величина сопротивления определенного участка цепи является постоянной величиной, поэтому при сила тока изменится, изменится только напряжение и наоборот.Чтобы изменить сопротивление участка цепи, соберите цепь заново. Расчет необходимого значения сопротивления при проектировании и сборке схемы можно произвести по закону Ома, исходя из ожидаемых значений тока и напряжения, которые будут пропущены через этот участок схемы.
Нужна помощь в обучении?
Предыдущая тема: Сопротивление току: притяжение ядер, проводников и непроводниковСледующая тема: & nbsp & nbsp & nbsp Расчет сопротивления проводников и реостатов: формулы
Закон Ома для участка цепи — это основной закон в электротехника.Он устанавливает взаимосвязь между током, сопротивлением и напряжением. С его помощью можно изучать и рассчитывать электрические схемы. Важно не просто узнать закон Ома, но понять, как он действительно применяется. Поскольку на практике при его применении довольно часто возникают ошибки, связанные с его неправильным использованием.
Определение закона Ома — ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Стоит поднять напряжение проходящее по электрической цепи, ток тоже будет расти после улавливания напряжения.Повышая сопротивление в цепи, ток будет уменьшаться во столько раз, сколько увеличилось сопротивление. Это можно увидеть на простом примере: возьмите простую трубу и дайте воде течь через нее, чем выше давление, тем сильнее поток воды, но если возникает сопротивление, поток воды значительно теряет свою скорость.
В математике принято считать: сопротивление проводника, в котором протекает ток 1А при напряжении 1В — равно 1Ом.
Формула закона Ома — означает определение тока в амперах путем деления напряжения на сопротивление в омах.
I = U / R
Правильные расчеты по закону Ома будут только тогда, когда напряжение выражено в вольтах, сопротивление в омах, ток в амперах. При использовании разных версий этих значений их следует преобразовать в значения, необходимые для расчета.
Этот закон одинаков для всего участка цепи. В случае уточнения напряжения в той или иной области необходимо будет брать размеры всех значений именно из этой области.
Этот закон можно рассмотреть на примерах:
1) Определяем ток в лампе сопротивлением 2,5 Ом и напряжением 5В. Делим 5 / 2,5 получаем ток = 2А
2) Рассчитываем такой же ток в лампе. с напряжением 500В и сопротивлением 0,5мОм (в Ом получается 500000). Делим 500/500000 получаем ток = 0,001А или 1мА.
Когда ток и сопротивление известны, напряжение также определяется по закону Ома.По формуле:
U = IR
Из того, что мы видим, напряжение на концах участка цепи точно пропорционально току и сопротивлению. Поскольку увеличение тока без изменения сопротивления возможно только при увеличении напряжения. Следовательно, постоянное сопротивление большему току ведет к большему напряжению. Если вы постоянно используете один и тот же ток с разным сопротивлением, с большим сопротивлением вам потребуется большее напряжение.
Расчет напряжения можно рассмотреть на примере:
Рассчитать напряжение при токе = 5мАм (0.005A), сопротивление 10кОм (10000 Ом). Умножьте ток * напряжение = 50В.
Связь между током и напряжением называется сопротивлением. Напряжение увеличивается, а ток увеличивается, точно так же происходит и с уменьшением. Соотношение между напряжением и током = сопротивление, которое не меняется. При рассмотрении двух секций с одинаковым током и разным напряжением видно, что в секции с высоким напряжением большее сопротивление. В том случае, когда напряжение одинаковое, а ток другой, то в области меньшего тока будет большее сопротивление.
Расчет сопротивления можно рассмотреть на примере:
Найдите сопротивление с напряжением 40 В и током 50 мА · м (0,05 А). Делим сопротивление 40 / 0,05 = 800 Ом.
Примечание: Интересуют двухуровневые натяжные потолки SATIN.BY. Перейдите по ссылке на натяжной потолок (http://satin.by/natjazhnye-potolki.html) и узнайте больше.
Если материал был полезен, вы можете сделать пожертвование нашему сайту, сделав пожертвование.
Любую сумму на развитие проекта можно
Если поместить изолированный проводник в электрическое поле \ (\ overrightarrow (E) \), то будет действовать сила \ (\ overrightarrow (F) = q \ overrightarrow (E) \) на свободных зарядах \\ (q \\) в проводнике кондуктора происходит кратковременное движение свободных зарядов.Этот процесс закончится, когда собственное электрическое поле зарядов, возникающих на поверхности проводника, полностью компенсирует внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю.
Однако в проводниках при определенных условиях может происходить непрерывное упорядоченное движение свободных носителей электрического заряда.
Направленное движение заряженных частиц называется поражением электрическим током.
За направление электрического тока принято направление движения положительных свободных зарядов.Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественная мера электрического тока — Сила тока \ (I \) — скалярная физическая величина, равная отношению заряда \ (\ Delta q \), переносимого через поперечное сечение проводника (рис. 1.8.1) для временного интервала \ (\ Delta t \) к этому временному интервалу:
$$ I = \ frac (\ Delta q) (\ Delta t) $$
Если сила тока и ее направление не меняются со временем, то такой ток называется постоянным .
IN Международная система единиц СИ, ток измеряется в амперах (А). Единица измерения тока 1 А устанавливается магнитным взаимодействием двух параллельных проводников с током.
Постоянный ток может быть создан только в замкнутой цепи , в котором свободные носители заряда перемещаются по замкнутым путям. Электрическое поле в разных точках такой цепи постоянно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля.Но при перемещении электрического заряда в электростатическом поле по замкнутому пути работа электрических сил равна нулю. Следовательно, для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разность потенциалов в частях цепи за счет работы сил неэлектростатического происхождения . Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда от источников тока, называются внешними силами .
Природа внешних сил может быть разной. В гальванических элементах или батареях они возникают в результате электрохимических процессов, в генераторах постоянного тока возникают внешние силы при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидросистеме. Под действием внешних сил электрические заряды перемещаются внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока свою работу выполняют внешние силы, действующие внутри источников тока.
Физическая величина, равная отношению работы \\ (A_ (st) \\) внешних сил, когда заряд \\ (q \\) перемещается от отрицательного полюса источника тока к положительному на величину этот заряд называется источник электродвижущей силы (EMF):
$$ ЭДС = \ varepsilon = \ frac (A_ (st)) (q).
$Таким образом, ЭДС определяется работой, совершаемой внешними силами при перемещении одиночного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в Вольт (В).
Когда единичный положительный заряд движется по замкнутой цепи постоянного тока, работа внешних сил равна сумме ЭДС, действующей в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разделить на отдельные участки. Те участки, на которые не действуют внешние силы (т.е., участки, не содержащие источников тока) называются однородными . Разделы, включающие источники тока, называются гетерогенными .
Когда единичный положительный заряд движется по определенной части цепи, как электростатические (кулоновские), так и внешние силы совершают работу. Работа электростатических сил равна разности потенциалов \ (\ Delta \ phi_ (12) = \ phi_ (1) — \ phi_ (2) \) между начальной (1) и конечной ( 2) точки неоднородного участка.Работа внешних сил по определению равна электродвижущей силе \\ (\\ mathcal (E) \\), действующей на этом узле. следовательно полная работа равна
$$ U_ (12) = \ phi_ (1) — \ phi_ (2) + \ mathcal (E) $$
Значение U 12 называется напряжение на цепочке 1-2. В случае однородного участка напряжение равно разности потенциалов:
$$ U_ (12) = \ phi_ (1) — \ phi_ (2) $$
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока \\ (I \\), протекающего через однородный металлический проводник (т. Е. Проводник, в котором не действуют внешние силы), пропорциональна напряжению \\ (U \\) на концах проводника:
$$ I = \ frac (1) (R) U; \\: U = IR $$
где \ (R \) = const.
Значение R обычно называют электрическое сопротивление . Проводник с электрическим сопротивлением называется , резистор . .Это соотношение выражает закон Ома для однородный участок цепи: : ток в проводнике прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению проводника.
В единицах СИ обслуживает электрическое сопротивление проводников Ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В протекает ток 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными .Графическая зависимость силы тока \ (I \) от напряжения \ (U \) (такие графики называются вольт-амперной характеристикой , сокращенно CVC) представлен прямой линией, проходящей через начало координат. Следует отметить, что существует множество материалов и устройств, не соответствующих закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже для металлических проводников с токами достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников увеличивается с повышением температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
$$ IR = U_ (12) = \ phi_ (1) — \ phi_ (2) + \ mathcal (E) = \ Delta \ phi_ (12) + \ mathcal (E) $$
$$ \ цвет (синий) (I = \ frac (U) (R)) $$
Это соотношение называется обобщенным законом Ом или законом Ом для неоднородного участка цепи .
На рис. 1.8.2 показывает замкнутую цепь постоянного тока. Участок цепи ( cd ) однородный.
Рисунок 1.8.2. Цепь постоянного тока |
Закон Ома
$$ IR = \ Delta \ phi_ (cd) $$
График ( ab ) содержит источник тока с ЭДС, равной \\ (\\ mathcal (E) \\).
По закону Ома для неоднородного сайта,
$$ Ir = \ Delta \ phi_ (ab) + \ mathcal (E) $$
Складывая оба равенства, получаем:
$$ I (R + r) = \ Delta \ phi_ (cd) + \ Delta \ phi_ (ab) + \ mathcal (E) $$
Но \ (\ Delta \ phi_ (cd) = \ Delta \ phi_ (ba) = — \ Delta \ phi_ (ab) \).
$$ \ цвет (синий) (I = \ frac (\ mathcal (E)) (R + r)) $$
Эта формула выражает закон Ома для полной цепи : сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородных и неоднородных участков цепи (внутреннее сопротивление источника).
Сопротивление r неоднородный участок на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока .В этом случае график ( ab ) на рис. 1.8.2 — это внутренняя часть источника. Если точки a и b замыкаются проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (\\ (R \\ \\ ll r \\)), то он потечет в цепь ток короткого замыкания
$$ I_ (короткий) = \ frac (\ mathcal (E)) (r) $$
Сила тока короткого замыкания — это максимальная сила тока, которая может быть получена от данного источника с электродвижущей силой \\ (\\ mathcal (E) \\) и внутренним сопротивлением \\ (r \\).Для источников с низким внутренним сопротивлением ток короткого замыкания может быть очень высоким и вызвать разрушение электрической цепи или источника. Например, в свинцовых аккумуляторах, используемых в автомобилях, ток короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях подстанций (тысячи ампер). Чтобы избежать разрушительного воздействия таких больших токов, в схему включены предохранители или специальные автоматические выключатели.
В некоторых случаях для предотвращения опасных значений тока короткого замыкания некоторое внешнее сопротивление подключается последовательно с источником.Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и в случае короткого замыкания сила тока не будет чрезмерно большой.
Если внешняя цепь разомкнута, то \ (\ Delta \ phi_ (ba) = — \ Delta \ phi_ (ab) = \ mathcal (E) \), т.е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее сопротивление нагрузки R включено и ток течет через батарею I , разность потенциалов на ее полюсах становится равной
$$ \ Delta \ phi_ (ba) = \ mathcal (E) — Ir $$
На рис.1.8.3 — схематическое изображение источника постоянного тока с ЭДС равной \\ (\\ mathcal (E) \\) и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузке и короткое замыкание. режим (короткое замыкание). Напряжение обозначено \\ (\\ стрелка вверх (E) \\) электрическое поле внутри батареи и силы, действующие на положительные заряды: \\ (\\ стрелка вправо (F) _ (e) \\) — электрическая мощность и \\ ( \\ overrightarrow (F) _ (st) \\) — внешняя сила. В режиме короткого замыкания электрическое поле внутри аккумулятора исчезает.
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы — вольтметры и амперметры .
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он соединяет параллельно той части цепи, на которой измеряется разность потенциалов. Любой вольтметр имеет какое-то внутреннее сопротивление \\ (R_ (V) \\). Чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть большим по сравнению с сопротивлением той части цепи, к которой он подключен.Для схемы, показанной на рис. 1.8.4 это условие записывается как:
$$ R_ (B) \ gg R_ (1) $$
Это условие означает, что текущий через вольтметр ток \ (I_ (V) = \ Delta \ phi_ (cd) / R_ (V) \) намного меньше, чем ток \ (I = \ \ Delta \ phi_ (cd) / R_ (1) \), которая протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют внешние силы, разность потенциалов на его выводах по определению совпадает с напряжением.Поэтому можно сказать, что вольтметр измеряет напряжение.
Амперметр Предназначен для измерения силы тока в цепи. Амперметр подключается последовательно к разомкнутой цепи, так что весь измеряемый ток проходит через него. Амперметр также имеет некоторое внутреннее сопротивление \\ (R_ (A) \\). В отличие от вольтметра, внутреннее сопротивление амперметра должно быть довольно небольшим по сравнению с общим сопротивлением всей цепи. Для схемы на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
.$$ R_ (A) \\ ll (r + R_ (1) + R (2)) $$
, чтобы при включении амперметра ток в цепи не менялся.
Измерительные приборы — вольтметры и амперметры — бывают двух типов: стрелочные (аналоговые) и цифровые. Цифровые электрические счетчики — это сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерения.
Основной закон электротехники, с помощью которого вы можете изучать и рассчитывать электрические цепи, — это закон Ома, который устанавливает взаимосвязь между током, напряжением и сопротивлением.Необходимо четко понимать его суть и уметь правильно использовать при решении практических задач. Часто ошибки допускаются в электротехнике из-за невозможности правильно применить закон Ома.
Закон Ома для участка цепи гласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Если вы увеличите в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится на такую же величину.А если увеличить сопротивление цепи в несколько раз, то на такую же величину уменьшится ток. Точно так же поток воды в трубе тем больше, чем сильнее давление и тем меньше сопротивление, которое труба оказывает движению воды.
Чтобы выразить закон Ома наиболее просто математически, предположим, что сопротивление проводника, в котором проходит ток 1 А при напряжении 1 В, равно 1 Ом.
Ток в амперах всегда можно определить, разделив напряжение в вольтах на сопротивление в омах.поэтому закон Ома для участка цепи записывается следующим образом:
I = U / R.
Магический треугольник
Любой участок или элемент электрической цепи можно охарактеризовать с помощью трех характеристик: тока, напряжения и сопротивления.
Как использовать треугольник Ома: закройте желаемое значение — два других символа дадут формулу для его вычисления. Кстати, закон Ома относится только к одной формуле из треугольника — той, которая отражает зависимость тока от напряжения и сопротивления.Две другие формулы, хотя и являются ее следствием, физического смысла не имеют.
Расчеты, выполненные с использованием закона Ома для участка цепи, будут правильными, если напряжение выражено в вольтах, сопротивление — в омах, а ток — в амперах. Если используются несколько единиц измерения этих величин (например, миллиампер, милливольт, мегаом и т. Д.), То они должны быть преобразованы в амперы, вольты и омы соответственно. Чтобы подчеркнуть это, иногда формула закона Ома для участка цепи записывается так:
ампер = вольт / ом
Также можно рассчитать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление — в килограммах и мегаомах соответственно.
Другие статьи об электричестве простым и доступным способом:
Закон Ома действует для любой части цепи. Если требуется определить ток в данном участке цепи, то действующее в этом участке напряжение (рис. 1) необходимо разделить на сопротивление этого конкретного участка.
Рис. 1. Применение закона Ома для участка цепи.
Приведем пример расчета тока по закону Ома.Пусть необходимо определить ток в лампе, имеющей сопротивление 2,5 Ом, если приложенное к лампе напряжение равно 5 В. Разделив 5 В на 2,5 Ом, получим значение тока 2 А. Во втором примере, определяем ток, который будет протекать под действием напряжения 500 В в цепи с сопротивлением 0,5 МОм. Для этого выражаем сопротивление в омах. Разделив 500 В на 500 000 Ом, находим значение тока в цепи, которое равно 0,001 А или 1 мА.Часто, зная ток и сопротивление, напряжение определяется по закону Ома.Записываем формулу для определения напряжения
У = ИК
Эта формула показывает, что напряжение на концах этого участка цепи прямо пропорционально току и сопротивлению. Смысл этой зависимости понять нетрудно. Если не менять сопротивление цепи, то увеличить ток можно только за счет увеличения напряжения. Таким образом, при постоянном сопротивлении больший ток соответствует большему напряжению. Если необходимо получить одинаковый ток при разных сопротивлениях, то при более высоком сопротивлении должно быть соответственно более высокое напряжение.
Напряжение в цепи часто называют падением напряжения. Это часто приводит к недоразумениям. Многие думают, что падение напряжения — это какое-то потерянное ненужное напряжение. В действительности понятия напряжения и падения напряжения эквивалентны.
Расчет напряжения по закону Ома можно показать в следующем примере. Пусть ток 5 мА проходит через участок цепи с сопротивлением 10 кОм, и необходимо определить напряжение на этом участке.
Умножив I = 0,005 А при R -10000 Ом, мы получим напряжение 5 0 В. Тот же результат можно было бы получить, умножив 5 мА на 10 кОм: U = 50 В
В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление — в килоомах. Поэтому эти единицы измерения удобно использовать в расчетах по закону Ома.
Согласно закону Ома, сопротивление также вычисляется, если известны напряжение и ток. Формула для этого случая записывается так: R = U / I.
Сопротивление — это всегда отношение напряжения к току. Если напряжение увеличивается или уменьшается в несколько раз, ток будет увеличиваться или уменьшаться в такое же количество раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.
Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит от истечения и напряжения. Известно, что это зависит от длины, площади сечения и материала проводника.По внешнему виду формула определения сопротивления напоминает формулу расчета тока, но между ними есть принципиальное отличие.
Ток в этом участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. И сопротивление этого участка цепи является постоянной величиной, не зависящей от изменений напряжения и тока, но равной отношению этих величин.
Когда один и тот же ток течет в двух участках цепи и прикладываемые к ним напряжения различаются, очевидно, что участок, к которому приложено более высокое напряжение, имеет соответственно большее сопротивление.
И если под действием одного и того же напряжения в двух разных частях цепи проходит разный ток, то меньший ток всегда будет в той части, которая имеет большее сопротивление. Все это следует из основной формулировки закона Ома для участка цепи, т. Е. Из того, что чем больше ток, тем больше напряжение и меньше сопротивление.
Мы покажем расчет сопротивления по закону Ома для участка цепи на следующем примере.Пусть необходимо найти сопротивление участка, через который проходит ток 50 мА при напряжении 40 В. Выражая ток в амперах, получаем I = 0,05 А. Делим 40 на 0,05 и находим, что сопротивление равно 800 Ом.
Закон Ома можно представить в виде так называемых вольт-амперных характеристик. Как известно, прямая пропорциональная зависимость между двумя величинами — это прямая линия, проходящая через начало координат. Эта зависимость называется линейной.
На рис.На рисунке 2 в качестве примера показан график закона Ома для участка цепи с сопротивлением 100 Ом. По горизонтальной оси отложено напряжение в вольтах, по вертикальной оси — ток в амперах. Шкалу тока и напряжения можно выбрать по своему усмотрению. Проводится прямая линия так, чтобы в любой ее точке отношение напряжения к току составляло 100 Ом. Например, если U = 50 В, то I = 0,5 А и R = 50: 0,5 = 100 Ом.
Рис. 2. Закон Ома (вольт-амперная характеристика)
График закона Ома для отрицательных значений тока и напряжения имеет такой же вид.Это говорит о том, что ток в цепи течет одинаково в обоих направлениях. Чем больше сопротивление, тем меньше тока получается при заданном напряжении и тем более полой проходит прямая линия.
Устройства, в которых вольт-амперная характеристика представляет собой прямую линию, проходящую через начало координат, т. Е. Сопротивление остается постоянным при изменении напряжения или тока, называются линейными приборами. Также используются термины линейные цепи, линейные сопротивления.
Также существуют устройства, в которых сопротивление изменяется при изменении напряжения или тока.Тогда связь между током и напряжением не выражается по закону Ома, а более сложна. Для таких устройств вольт-амперная характеристика не будет прямой линией, проходящей через начало координат, а будет либо кривой, либо ломаной. Эти устройства называются нелинейными.
Мнемоническая диаграмма закона Ома
Каков закон Ома для полной цепи? Итак, это формула, в которой хорошо видна связь между основными параметрами электрической цепи: током, напряжением и сопротивлением.Чтобы понять суть закона, давайте сначала разберемся с некоторыми понятиями.
Что называют электрической цепью?
Электрическая цепь — это путь в электрической цепи, через который происходит зарядка потока (электрические элементы, провода и другие устройства). Конечно, его начало считается источником энергии. Под воздействием электромагнитного поля, фотонных явлений или химических процессов электрические заряды стремятся перейти к противоположному выводу этого источника энергии.
Что такое электрический ток?
Направленное движение заряженных частиц под действием электрического поля или других внешних сил называется электрическим током.Его направление определяется направлением протонов (положительных зарядов). Ток будет постоянным, если ни его сила, ни направление не изменились с течением времени.
История закона Ома
При проведении экспериментов с проводником физик Джордж Ом смог установить, что сила тока пропорциональна напряжению, приложенному к его концам:
I / sim U или I = G / U ,
где G — электрическая проводимость, а величина R = 1 / G — электрическое сопротивление проводника.Это открытие было сделано известным немецким физиком в 1827 году.
Законы Ома
Для полной цепи определение будет следующим: сила тока в цепи равна отношению электродвижущей силы (далее ЭДС) источник к сумме сопротивлений:
I = E / (R + r),
где R — сопротивление внешней цепи, а r — внутреннее сопротивление. Довольно часто формулировка закона вызывает затруднения, Поскольку не все знают понятие ЭДС, ее отличие от напряжения, не все знают, что означает внутреннее сопротивление и откуда оно берется.Это требует уточнения, потому что закон Ома для полной цепи имеет глубокий смысл.
Формулировку закона для участка цепи можно назвать прозрачным. Дело в том, что для его понимания не требуется дополнительных пояснений: ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению:
Значение
Закон Ома для всей цепи прочно связан с законом сохранение энергии.Предположим, что источник тока не имеет внутреннего сопротивления. Что тогда должно произойти? Получается, что если бы не было сопротивления, то во внешнюю цепь подавали бы ток, соответственно, и мощность была бы больше.
Теперь пора заняться концепцией электродвижущей силы. Это значение представляет собой разницу между электрическими потенциалами на клеммах источника, но только без какой-либо нагрузки. В качестве примера возьмем давление воды в приподнятом резервуаре.Уровень воды будет оставаться на месте до тех пор, пока не начнется ее расход. При открытии крана уровень жидкости будет уменьшаться, так как подкачки нет. Попадая в трубу, вода испытывает сопротивление, то же самое происходит с электрическими зарядами в проводе.
При отсутствии нагрузок клеммы в разомкнутом состоянии, оказывается, ЭДС и напряжение одинаковы. Если, например, мы включаем лампочку, цепь замыкается, и электродвижущая сила создает в ней напряжение, выполняя полезную работу.Часть энергии из-за внутреннего сопротивления рассеивается (это называется потерей).
В случае, если сопротивление потребителя меньше внутреннего, то на источник тока выделяется большая мощность. И тогда во внешней цепи ЭДС падает, и значительная часть энергии теряется на внутреннем сопротивлении. Суть законов сохранения в том, что природа не может брать больше, чем давать.
Суть внутреннего сопротивления хорошо известна хрущевцам, у которых в квартирах установлены кондиционеры, а старая проводка не заменена.Электросчетчик вращается с бешеной скоростью, розетка и стена нагреваются в тех местах, где проходят старые алюминиевые провода, из-за чего кондиционер еле охлаждает воздух в помещении.
Nature r
«Полный Ом» (как обычно называют закон электрики) плохо изучен, поскольку внутреннее сопротивление источника обычно не имеет электрического характера. Разберемся на примере соляной батареи. Известно, что электрическая батарея состоит из нескольких элементов, но мы рассмотрим только один.Итак, у нас есть готовый аккумулятор «Крона», состоящий из 7 элементов, соединенных последовательно.
Как происходит генерация тока? В сосуд с электролитом помещаем угольный стержень в марганцевую оболочку, состоящую из положительных электродов или анодов. В частности, в этом примере углеродный стержень действует как токоприемник. Металлический цинк состоит из отрицательных электродов (катодов). В покупных аккумуляторах, как правило, гелевый электролит. Жидкость используется очень редко. Цинковая чашка с электролитом и анодами действует как отрицательный электрод.
Оказывается, секрет батареи заключается в том, что электрический потенциал марганца не такой высокий, как у цинка. Следовательно, электроны притягиваются к катоду, а он, в свою очередь, отталкивает положительно заряженные ионы цинка к аноду. В результате катод постепенно расходуется. Пожалуй, все знают, что если вовремя не заменить севший аккумулятор, то он может потечь. Что является причиной этого? Все очень просто: через отсоединенную чашку начнет вытекать электролит.
При движении зарядов по угольному стержню положительные заряды накапливаются в марганцевой оболочке, а отрицательные — на цинке. Поэтому их называют анодом и катодом, но внутри батареи выглядят по-разному. Разница между зарядами и создаст электродвижущую силу. Заряды перестанут двигаться в электролите, когда разность потенциалов материала электрода станет равной величине ЭДС, а силы притяжения будут равны силам отталкивания.
Давайте замкнем цепь: просто подключите лампочку к аккумулятору. Пройдя через источник искусственного света, заряды вернутся каждый на свое место («дом»), и включится свет. Внутри батареи движение электронов и ионов начнется снова, так как заряды ушли наружу, и снова появилась сила притяжения или отталкивания.
Фактически батарея вырабатывает ток, из-за чего лампочка загорается, это происходит из-за расхода цинка, который превращается в другие химические соединения.Чтобы извлечь чистый цинк по закону сохранения энергии, нужно его потратить, но не в электрическом виде (ровно столько, сколько дали лампочке).
Теперь, наконец, мы можем выяснить природу внутреннего сопротивления источника. В аккумуляторе — это препятствие движению крупных ионов. Движение электронов без ионов невозможно, потому что нет силы притяжения.
В промышленных генераторах r появляется не только из-за электрического сопротивления обмоток, но и из-за внешних причин.Так, например, на гидроэлектростанциях величина количества зависит от КПД турбины, сопротивления потока воды в водоводе, а также от потерь в механической передаче. Кроме того, некоторое влияние оказывает температура воды и степень ее заиливания.
Переменный ток
Мы уже исследовали закон Ома для всей цепи постоянного тока. Как формула меняется при переменном токе? Прежде чем мы это узнаем, давайте охарактеризуем саму концепцию.Переменный ток — это движение электрически заряженных частиц, направление и величина которых меняются с течением времени. В отличие от постоянного, он сопровождается дополнительными факторами, порождающими новый тип сопротивления (реактивное). Это характерно для конденсаторов и катушек индуктивности.
Закон Ома для полной цепи переменного тока имеет вид:
где Z — комплексное сопротивление, состоящее из активного и реактивного.
Неплохо
Закон Ома для всей цепи, помимо указания потерь энергии, предлагает еще и способы их устранения.Обычные электрики редко используют формулу для нахождения комплексного сопротивления при наличии конденсаторов или индуктивностей в цепи. В большинстве случаев сила тока измеряется галочкой или специальным тестером. А когда известно напряжение, можно легко вычислить комплексное сопротивление (если оно действительно необходимо).
