формулы и определения / Блог :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.
Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.
Формула закона Ома для полной цепи

- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.
По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
Закон Ома кратко и понятно для чайников
Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.
Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.
Закон Ома – определение
Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.
- Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
- Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.
Закон Ома – формула

 Иллюстрация связи сопротивления
Иллюстрация связи сопротивленияРисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:
1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;
2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
В итоге в законе Ома участвуют всего три величины.
Готовая формула выглядит так:
I = U/R
Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:
| Формула сопротивления | R = U/I |
| Формула напряжения | U = I × R |
| Формула силы тока | I = U/R |
Важно!

 Шпаргалка для закона Ома
Шпаргалка для закона ОмаНа начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.
На треугольнике просто нужно закрыть то значение, которое необходимо найти.
Закон Ома для участка цепи
Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.

 Шпаргалка для использования закона Ома
Шпаргалка для использования закона ОмаС ЭДС
Обобщённый закон Ома формулируется так:
I = (Uab+E)/R
Также формулу можно выразить через проводимость:
I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.

 Участок цепи с ЭДС
Участок цепи с ЭДСБез ЭДС
Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.

 Разность потенциалов
Разность потенциаловЕсли сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Закон Ома для полной (замкнутой) цепи
При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.
Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).
Вывод формулы закона Ома для замкнутой цепи
Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.
Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E = I × r + I × R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E = I(r + R)
или
I = E / (r + R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома в дифференциальной форме

 Дифференциальная форма закона Ома
Дифференциальная форма закона ОмаЗакон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:
I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)
При условии, что Δl будет равен 0, то, взяв предел отношения:
lim (-(Δф/Δl)) = -(dф/dl) = Е,
окончательное выражение будет выглядеть так:
j = yE
Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома в интегральной форме
В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:
I = U/R
Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:
R = p (l/S), где за р принимаем удельное объёмное сопротивление.
Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.
Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
IdR = -dф + dE.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Закон Ома для переменного тока
После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.
Используется уже известная формула:
I = U/Z
Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. Проще говоря, ток в цепи переменного тока зависит от многих параметров, в том числе от величины ёмкости и индуктивности. Полное сопротивление вычисляется по формуле.

 Формула полного сопротивления
Формула полного сопротивленияПолное сопротивление можно изобразить как гипотенузу прямоугольного треугольника, катетами которого является активное и индуктивное сопротивление.

 Треугольник полного сопротивления
Треугольник полного сопротивленияИтак, формула амплитудного значения силы тока будет выглядеть так:
Im = Um/ ((R^2 + (ωL — (1/ωC)^2

 Цепь
ЦепьВ такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:
U = Um sin (ωt)
I = Im sin (ωt + ф)
Закон Ома для постоянного тока
В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для однородного участка цепи
Формула выглядит уже известным образом:
I = U/R
В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.
Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:
R = p (L/S)
Закон Ома для неоднородного участка цепи
При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.

 Неоднородный участок цепи
Неоднородный участок цепиФормула принимает вид:
E = Eq + Est
Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.
Итак, готовая формула:
I = U12/R, где U12
Закон Ома для магнитной цепи
В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.
При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:
Ф = Вср S = μHср S
Формула закона для магнитной цепи:

 Формула закона ома для магнитной цепи
Формула закона ома для магнитной цепиЗадачи с решениями на закон Ома
Задача №1
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 127 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 127 В : 264 Ом = 0,48 А.
Ответ: I = 0,48 Ом
Задача №2
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 220 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 220 В : 264 Ом = 0,83 А.
Ответ: I = 0,83 Ом
Задача №3
Дано:
- U = 15 В,
- R1 = 3 Ом,
- R2 = R3 = 4 Ом.
Найти: I — ?
Решение:
- R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:


- R = R1 + R2,3
- R = 3 Ом + 2 Ом = 5 Ом
- Найдем силу тока на участке цепи по закону Ома I = U / R
- I = 15 В / 5 Ом = 3 А
Ответ: I = 3 A.
Закон Ома для полной цепи
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название “закон Ома для полной цепи”

где
Е – ЭДС источника питания, В
R – сопротивление всех внешних элементов в цепи, Ом
I – сила ток в цепи, А
r – внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
для участка цепи, для полной цепи +ВИДЕО
Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.
Содержание статьи
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.

Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.

Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.
Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.
И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.
Содержание статьи:
Отдельный участок и полная электрическая цепь
Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.
Расчет тока участка электрической схемы
Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.
Поэтому расчетная формула, в данном случае, выглядит просто:
I = U/ R,
Где, соответственно:
- I – сила тока;
- U – приложенное напряжение;
- R – сопротивление.
Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.
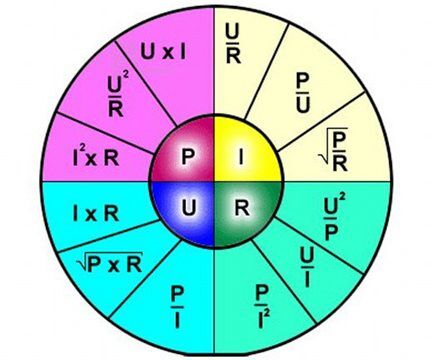

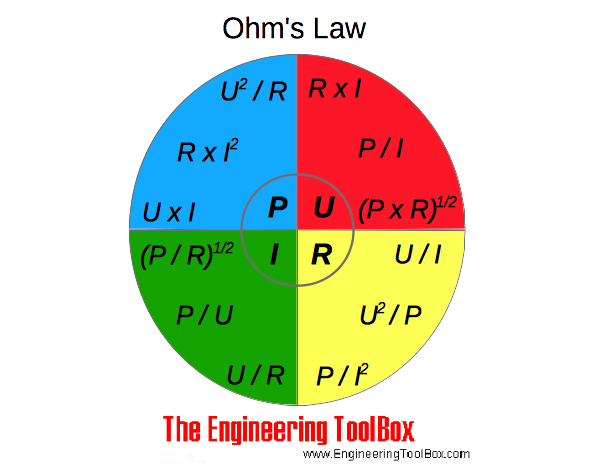
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор “P” – формулы мощности; сектор “U” – формулы напряжения; сектор “I” – формулы тока; сектор “R” – формулы сопротивления
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.
Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.
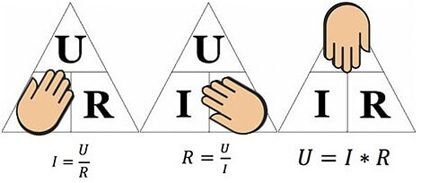

Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 – определение тока; 2 – определение сопротивления; 3 – определение напряжения, где I – сила тока, U – напряжение, R – сопротивление
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.
Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).
Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.
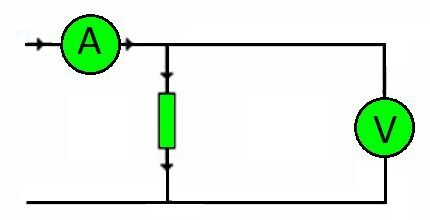

Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.
Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.
У нас на сайте есть подробная инструкция по по мощности и току.
Вариант расчета для полной цепи
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.
Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.
Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
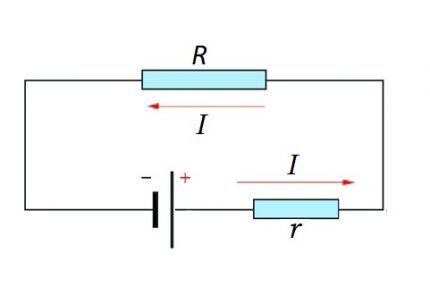

Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I – прохождение тока; R – резистивный элемент внешний; r – резистивный фактор ЭДС (источника энергии)
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.
Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Рассмотрение действия закона к переменной величине
Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).
Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения – синусоидальной величине тока.


Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R – резистивная составляющая; С – емкостная составляющая; L – индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока
Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.
Расчёт подобных явлений ведётся при помощи формулы:
Z = U / I или Z = R + J * (XL – XC)
где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
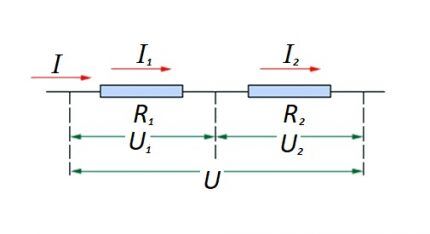

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
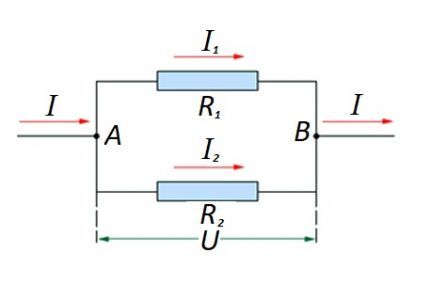

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Выводы и полезное видео по теме
Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.
Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:
Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.
Объёмных знаний по данному вопросу не требуется – достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.
Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.
Принципиальная схема законаОм [Как читать символы] • Закон Ома
Простая принципиальная схема Ома содержит сопротивление, соединенное последовательно с источником постоянного напряжения.
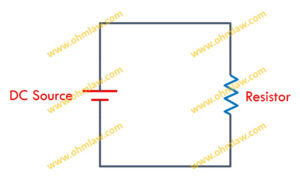
Две параллельные линии, одна из которых имеет сравнительно большую длину, представляют источник постоянного тока, а зигзагообразный символ представляет резистор. В то время как простые линии используются для представления проводов.
Приведенная выше диаграмма верна для общего случая, практически нам нужно добавить амперметр и вольтметр для целей измерения.Теперь наша диаграмма с инструментами будет выглядеть так:
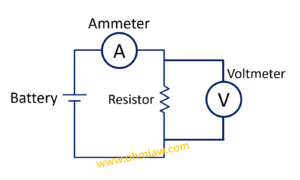
Давайте разберемся в компонентах нашей принципиальной схемы.
Батарея: это источник постоянного напряжения, обеспечивающий питание внутренней цепи. Когда мы изучали утверждение Ома: V = IR. На самом деле, V — это аккумулятор или источник напряжения, который питает всю цепь.
Амперметр: считывает ток, который течет по всей цепи. Помните, что амперметр всегда подключается последовательно к цепи.
Вольтметр: считывает напряжение на резисторе. Помните, что вольтметр всегда включается параллельно компоненту.
Теперь давайте начнем изучать базовую математику права, используя 5 различных примеров.
Пример 1: батарея 10 В подключается последовательно с сопротивлением 20 кОм. Найти ток, протекающий по цепи.
Решение: Использование V 1 = I 1 R 1 .
I 1 = V 1 / R 1 = 0.5 мА
Пример 2: источник 15 В соединяется с неизвестным резистором. Значение тока измеряется как 5 мА. Найдите значение R.
Решение: R 2 = V 2 / I 2 = 15 В / 5 мА = 3 кОм
Пример 3: резистор 50 кОм включается с переменным напряжением 25 В постоянного тока. Найти значение неизвестного тока, который течет через эту цепь.
Решение: I 3 = V 3 / R 3 = 25 В / 50 к = 0,5 мА
Пример 4. Рассеиваемая мощность при сопротивлении 29 кОм составляет 15 Вт.Найти значение тока и входного напряжения, подаваемого источником.
Решение: Здесь будут использоваться формулы: I = SQRT (P / R) и V = SQRT (P * R). Вы можете узнать обо всех этих формулах из Ohmic Wheel.
Пример 5: R5 = 10 Ом и P5 = 20 Вт
Решение: V5 = 14,14 и I5 = 1,414
,ЗаконОм
ЗаконОма показывает линейную зависимость между напряжением и током в электрической цепи.
Падение напряжения и сопротивление резистора задают постоянный ток, протекающий через резистор.
По аналогии с потоком воды мы можем представить электрический ток как ток воды через трубу, резистор как тонкую трубу, которая ограничивает поток воды, напряжение как перепад высот воды, который обеспечивает поток воды.
формула закона Ома
Ток I резистора в амперах (A) равен сопротивлению резистора напряжение V в вольтах (В), деленное на сопротивление R в омах (Ом):
В — падение напряжения на резисторе, измеренное в вольтах (В).В некоторых случаях закон Ома использует букву E для обозначения напряжения. E обозначает электродвижущую силу.
I — электрический ток, протекающий через резистор, измеренный в амперах (A)
R — сопротивление резистора, измеряется в Ом (Ω)
Расчет напряжения
Когда мы знаем ток и сопротивление, мы можем рассчитать напряжение.
Напряжение V в вольтах (В) равно току I в амперах (A), умноженному на сопротивление R в омах (Ом):
Расчет сопротивления
Когда мы знаем напряжение и ток, мы можем рассчитать сопротивление.
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (A):
Поскольку ток определяется значениями напряжения и сопротивления, формула закона Ома может показать, что:
- Если мы увеличим напряжение, ток увеличится.
- Если мы увеличим сопротивление, ток уменьшится.
Пример №1
Найти ток электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.
Решение:
В = 5 В
R = 50Ω
I = В / R = 5 В / 50 Ом = 0,1 А = 100 мА
Пример №2
Найти сопротивление электрической цепи, которая имеет напряжение питания 10 Вольт и ток 5 мА.
Решение:
В = 10 В
I = 5 мА = 0,005A
R = В / I = 10 В / 0,005 А = 2000 Ом = 2 кОм
ЗаконОм для цепи переменного тока
Ток нагрузки I в амперах (A) равен напряжению нагрузки V Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ом):
В — падение напряжения на нагрузке, измеряется в Вольтах (В)
I — электрический ток, измеренный в амперах (A)
Z — полное сопротивление нагрузки, измеряется в Ом (Ω)
Пример № 3
Найти ток в цепи переменного тока с напряжением питания 110 В ± 70 ° и нагрузкой 0.5kΩ∟20 °.
Решение:
В = 110 В∟70 °
Z = 0,5 кОм20 ° = 500 кОм20 °
I = В / Z = 110 В ~ 70 ° / 500 Ом ~ 20 ° = (110 В / 500 Ом) ∟ (70 ° -20 °) = 0,22 А ~ 50 °
Калькулятор закона Ома (краткая форма)
Ом закон калькулятора: рассчитывает соотношение между напряжением, током и сопротивлением.
Введите 2 значений, чтобы получить третье значение, и нажмите кнопку Рассчитать :
закон закона Ома II ►
См. Также
,ЗаконОм Закон
Ом гласит, что
«ток, проходящий через проводник между двумя точками, прямо пропорционален разности потенциалов или напряжению в двух точках, и обратно пропорционален сопротивлению между ними».
Закон Ома можно выразить как
I = U / R (1)
, где
I = ток (ампер, А)
U = электрический потенциал (вольт, В)
R = сопротивление (Ом, Ω )
Пример — закон Ома
Батарея 12 В питает сопротивление 18 Ом .Ток в электрической цепи может быть рассчитан как
I = (12 вольт) / (18 Ом)
= 0,67 ампер
Эквивалентные выражения закона Ома
закон Ома (1) также можно выразить как
U = RI (2)
или
R = U / I (3)

Скачать и распечатать диаграмму закона Ома !
Пример — сопротивление электрической цепи
Ток 1 ампер протекает через электрическую цепь 230 В .Из приведенной выше диаграммы это показывает сопротивление
R ≈ 220 Ом
. Альтернативно это можно рассчитать по закону Ома.
R = (230 В) / (1 А)
= 230 Ом
Пример. — Закон Ома, кратные и кратные
Токи, напряжения и сопротивления в электрических цепях часто могут быть очень маленькими или очень большими — поэтому часто используются кратные и кратные числа.
Требуемое напряжение подается на 3.Резистор 3 кОм для генерации тока 20 мА можно рассчитать как
U = (3,3 кОм) (1000 Ом / кОм) (20 мА) (10 -3 А / мА)
= 66 В
Номограмма электрического сопротивления
 Загрузите и распечатайте номограмму электрического сопротивления вольт и ампер!
Загрузите и распечатайте номограмму электрического сопротивления вольт и ампер!
Значения по умолчанию в номограмме выше указывают 230 В, , сопротивление , 24 Ом, и , ток 10 А, .
Мощность
Электрическая мощность может быть выражена как
P = UI
= RI 2
= U 2 / R (4) 9012
0003P = электрическая мощность (Вт, Вт)
Пример — потребляемая мощность
Мощность, потребляемую в вышеуказанной электрической цепи 12В , может быть рассчитана как
P = (12 вольт) 2 / ( 18 Ом)
= 8 Вт
Пример — мощность и электрическое сопротивление
Электрическая лампочка 100 Вт подключена к источнику питания 230 В .Текущий ток можно рассчитать путем реорганизации от (4) до
I = P / U
= (100 Вт) / (230 В)
= 0,43 ампер
Сопротивление может быть рассчитано путем реорганизации от (4) до
R = U 2 / P
= (230 В) 2 / (100 Вт)
= 529 Ω
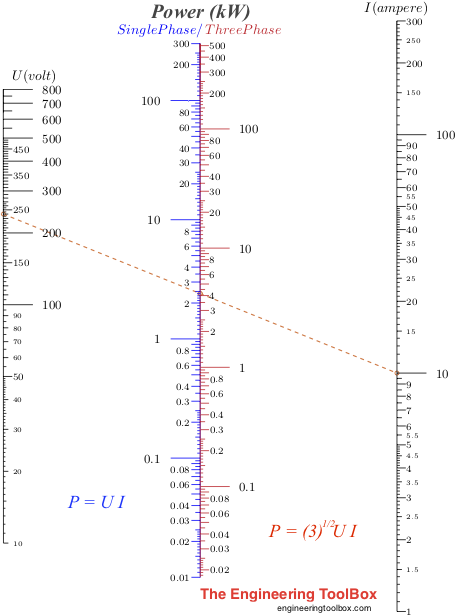
Номограмма электроэнергии
Эта номограмма может использоваться для оценкинапряжение и ампера.
 Загрузите и распечатайте номограмму «Электроэнергия против вольт и ампер»!
Загрузите и распечатайте номограмму «Электроэнергия против вольт и ампер»!
Значения по умолчанию в приведенной выше номограмме указывают 240 вольт , сопротивление 10 ампер и мощность 2,4 кВт для постоянного или однофазного переменного тока — и 4 кВт для трехфазного переменного тока.
ЗаконЗакон Ома гласит, что в электрической цепи ток, проходящий через резистор между двумя точками, связан с разностью напряжений между двумя точками и связан с электрическое сопротивление между двумя точками.
- Пример) р знак равно В я {\ displaystyle R = {\ frac {V} {I}}}
Где I — ток в амперах, В, — это разность потенциалов в вольтах, а R — это постоянная, измеренная в омах, называемая сопротивлением.
Ток прямо пропорционален потере напряжения через резистор. То есть, если ток удваивается, то и напряжение увеличивается. Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение. Закон Ома показывает взаимосвязь между напряжением (V), током (I) и сопротивлением (R). Это можно записать тремя способами:
- я знак равно В р или В знак равно я р или р знак равно В я {\ displaystyle I = {\ frac {V} {R}} \ quad {\ text {or}} \ quad V = IR \ quad {\ text {or}} \ quad R = {\ frac {V} {I }}} ,
Изложение закона Ома. Закон Ома гласит, что «ток, протекающий в проводнике, прямо пропорционален разности потенциалов, приложенной к его концам, при условии, что физические условия и температура проводника остаются постоянными».
Напряжение [изменить | изменить источник]
Напряжение — это количество энергии между двумя точками в цепи. Эти две точки имеют разные заряды, один выше, а другой ниже. Разница между этими двумя точками заряда заключается в том, как мы измеряем напряжение.Единицей «вольт» является имя итальянского физика Алессандро Вольта, который создал первую химическую батарею. Буква «V» обозначает напряжение.
Ток [изменить | изменить источник]
Ток — это скорость заряда. Чем выше заряд, тем быстрее ток. Ток связан с электронами, протекающими по цепи. Текущий измеряет, как быстро идут электроны. Единицей тока является «Ампер», и обычно человек записывает его как «Ампер». Буква «я» может представлять собой ток.
Сопротивление [изменить | изменить источник]
Сопротивление — это то, насколько цепь сопротивляется потоку заряда. Это гарантирует, что заряд не течет слишком быстро и не повредит компоненты. В цепи лампочка может быть резистором. Если электроны протекают через лампочку, лампочка загорится. Если сопротивление высокое, то лампа будет тусклее. Единицей сопротивления является «Ω», которая называется омега, и произносится как «ом», это имя изобретателя закона Ома.18 электронов. [2]
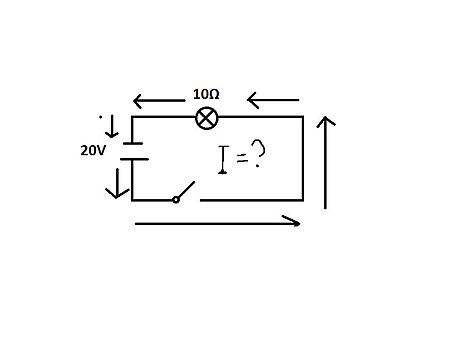
Например, ученый знает, что значение напряжения составляет 20 В. Сопротивление известно, что в лампочке, составляет 10 Ом. Теперь нам нужно найти другую неизвестную переменную, которая является текущей. Формула закона Ома может быть использована для ее решения. С двумя известными переменными, V (напряжение) и R (сопротивление), единственной переменной, которую нужно найти, является I (ток).
20 В = 10 Ом * I
I = 2A
В задаче ученый всегда получает достаточно информации для решения других ценностей, единственное, что ученый должен запомнить — это формула закона Ома.Затем он используется с тем, что дано для решения неизвестной части. В приведенном выше примере ток составляет 2 А.
[1]
- ↑ ссылка, Get; facebook; Twitter; Pinterest; Эл. адрес; Приложения, Другое. «Калькулятор закона Ома | Вычислить напряжение, сопротивление и силу тока». Получено 2019-08-21.
