В цепь последовательно подключены конденсатор: В цепь последовательно подключены конденсатор емкостью 1мкФ, катушка индуктивностью 0,5Гн, резистор сопротивлением 1 кОм. Найти индуктивное сопротивление, емкостное сопротивление и полное сопротивлени… — Мир Антенн

Содержание

StudyPort.Ru — Механические и электромагнитные колебания

Страница 1 из 6

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x

2 оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с^-1. Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

Переменный электрический ток

1 Прямоугольная рамка площади S=100 см2 вращается в горизонтальном однородном магнитном поле с частотой n= 50 об/с (рис. 145). Магнитная индукция поля В = 0,2 Тл. Найти закон изменения магнитного потока через рамку в зависимости от времени t, если в начальный момент времени плоскость рамки: а) расположена горизонтально; б) составляет с горизонтальной плоскостью угол φ = 30°.

Решение:

где Фо=2 мВб. Отсчет начальной фазы j производится от горизонтальной плоскости в сторону вращения рамки.

2 В условиях задачи 1 найти амплитуду э.д.с, индуцируемой в рамке. Как изменится амплитуда э. д. с, если частоту вращения рамки увеличить в три раза?

Решение:
Рамка, занимавшая в начальный момент времени горизонтальное положение, вращаясь с угловой скоростью ω=2πn, в момент времени t будет составлять с горизонтальной плоскостью угол ωt=2πnt (рис. 379). В течение последующего очень малого промежутка времени Δt она повернется еще на малый угол ωΔt. Пусть сторона рамки, параллельная оси 00, равна а и сторона рамки, перпендикулярная к оси, равна b. За время Δt проводник рамки cd переместится в положение c’d’ и «заметет» при этом площадь

где S=ab — площадь рамки. Магнитный поток через площадь, «заметаемую» проводником cd,

где α — угол между нормалью N к плоскости cc’d’d и направлением магнитной индукции В.
Если промежуток времени Δt очень мал, то угол α практически равен углу ωt, так как направление нормали n мало отличается от направления стороны рамки kd, а вектор В по условию направлен горизонтально. Таким образом,

Следовательно, в момент времени t в проводнике cd индуцируется э. д.с.

Вектор В параллелен плоскостям, в которых при вращении рамки движутся проводники kd и lс. Поэтому через «заметаемые» этими проводниками площади магнитный поток равен нулю и э.д.с. не возникает. В проводнике ad, как легко видеть, индуцируется э.д.с. ε₂. равная по модулю ε₁; но направленная так, что при обходе по контуру рамки эти э.д.с. складываются. В результате суммарная э.д.с, индуцируемая в рамке,

Наибольшее значение э.д.с. принимает в те моменты времени, когда cosωt максимален, т. е. равен единице. Поэтому амплитуда э.д.с.

При увеличении частоты вращения рамки в три раза амплитуда э.д.с. также увеличится в три раза, т.е.

3 Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся в однородном магнитном поле с частотой n=10 об/с, если амплитуда индуцируемой в рамке э. д. с. ε₀ = 3 В (рис. 145).

Решение:

4 Найти частоту вращения прямоугольной рамки в однородном магнитном поле с индукцией B= 0,5 Тл, если амплитуда индуцируемой в рамке э. д. с. ε₀= 10 В (рис. 145). Площадь рамки S=200 см2, число витков рамки w = 20.

Решение:

5 Напряжение на концах участка цепи, по которому течет переменный ток, изменяется с течением времени по закону , где φ=π/6— начальная фаза напряжения. В момент времени t=T/12 мгновенное значение напряжения V=10В. Найти амплитуду напряжения Vo, круговую частоту ω и частоту f тока, если период колебаний T=0,01 с. Представить графически зависимость напряжения от времени t.

Решение:
Круговая частота тока

частота тока f=1/T=100 Гц. В момент времени t=T/12 мгновенное значение напряжения

отсюда

График зависимости напряжения от времени представлен на рис. 380.

6 Найти индуктивность катушки, если амплитуда напряжения на ее концах Vo = 160B, амплитуда тока в ней Iо = 10А и частота тока f=50 Гц.

Решение:
Индуктивное сопротивление катушки

где ω=2πf — круговая частота тока. Амплитуда тока

отсюда

7 Индуктивное сопротивление катушки XL = 500 Ом, эффективное напряжение сети, в которую включена катушка, Vэ = 100 В, частота тока f=1 кГц. Найти амплитуду тока в цепи и индуктивность катушки.

Решение:

8 Найти сдвиг фаз φ между напряжением и током для цепи, состоящеи из последовательно включенных резистора с сопротивлением R = 1 кОм, катушки с индуктивностью L = 0,5 Гн и конденсаторах емкостью С= 1 мкФ. Найти мощность, выделяемую в цепи, если амплитуда напряжения Vo = 100 В, а частота тока f=50 Гц.

Решение:
Полное сопротивление

Мощность

9 В цепь последовательно включены резистор с сопротивлением R = 1 кОм, катушка с индуктивностью L = 0,5 Гн и конденсатор с емкостью С= 1 мкФ. Найти индуктивное сопротивление XL, емкостное сопротивление Хc и полное сопротивление Z цепи при частотах тока f1 = 50Гц и f2 = 10кГц.

Решение:
Индуктивное сопротивление

емкостное сопротивление

и полное сопротивление

где ω=2πf — круговая частота тока. При

при

10 К зажимам генератора присоединен конденсатор с емкостью С=0,1 мкФ. Найти амплитуду напряжения на зажимах, если амплитуда тока Io = 2,2 А, а период тока T = 0,2 мс.

Решение:

11 В сеть переменного тока с эффективным напряжением Vэ=127 В последовательно включены резистор с сопротивлением R=100 Ом и конденсатор с емкостью С = 40 мкФ. Найти амплитуду тока в цепи.

Решение:

12 В сеть переменного тока с эффективным напряжением Vэ=120 В последовательно включены проводник с сопротивлением R=15 Ом и катушка с индуктивностью L=50 мГн. Найти частоту тока f, если амплитуда тока в цепи Io = 7 А.

Решение:

13 Найти полное сопротивление цепи, состоящей из последовательно включенных конденсатора с емкостью С=0,1 мкФ и катушки с индуктивностью L= 0,5 Гн, при частоте тока f=1 кГц. При какой частоте fo полное сопротивление цепи равно нулю?

Решение:
Полное сопротивление цепи

Из условия, что при частоте f0 полное сопротивление цепи равно нулю, имеем

отсюда

14 В колебательный контур (рис. 146) включен источник переменного тока с э. д. с. , где амплитуда э. д. с. ε₀ = 2 В. При резонансе амплитуда напряжения на отдельных элементах контура, например на конденсаторе, значительно увеличивается. Найти резонансную амплитуду напряжения на конденсаторе, если известно, что она во столько раз больше амплитуды э.д.с, во сколько раз индуктивное сопротивление XL (или емкостное сопротивление Хс) при резонансе больше сопротивления R. Резонансная частота контура fо = 0,1 МГц, индуктивность катушки L= 1мГн, сопротивление контура R=3 Ом.

Решение:

15 Соленоид с железным сердечником (дроссель), имеющий индуктивность L = 2 Гн и сопротивление обмотки R = 10 Ом, включен сначала в сеть постоянного тока с напряжением V=20 В, а затем в сеть переменного тока с эффективным напряжением Vэ=20 В и частотой тока f=0,4 кГц. Найти ток, текущий через соленоид, в первом случае и амплитуду тока во втором случае.

Решение:
В цепи постоянного тока I=V/R=2 А. Индуктивное сопротивление соленоида

Амплитуда напряжения Так как то амплитуда переменного тока

16 Найти коэффициент мощности cosj электрической цепи, если генератор отдает в цепь мощность N=8 кВт, амплитуда тока в цепи Io=100 А и амплитуда напряжения на зажимах генератора Vo = 200 В.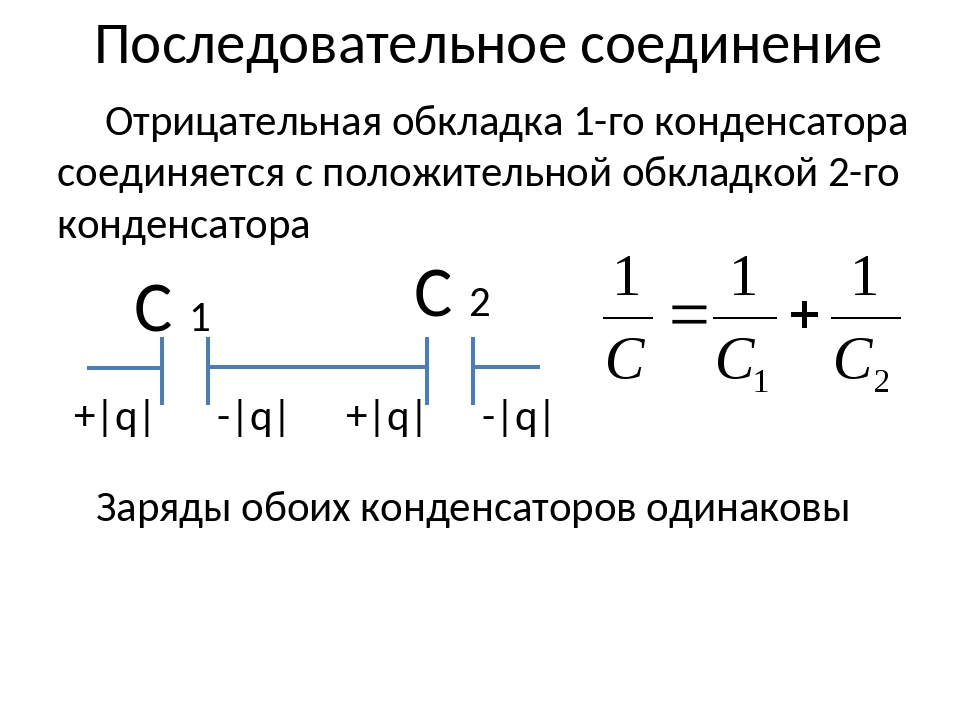

Решение:
Мощность

отсюда

17 От генератора переменного тока питается электропечь с сопротивлением R = 22 Ом. Найти количество теплоты Q, выделяемое печью за время τ = 1 ч, если амплитуда тока Io=10 А.

Решение:
Эффективный ток

Количество теплоты, выделяемое печью,

18 Кипятильник работает от сети переменного тока с эффективным напряжением Vэ=100В. При температуре tо = 20° С сопротивление фехралевой спирали R = 25 Ом. Какая масса кипящей воды превращается кипятильником в пар за время τ = 1 мин? Удельная теплота парообразования воды r = 2,3 МДж/кг. Температурный коэффициент сопротивления фехраля .

Решение:

где t=100° С-температура кипения воды.

19 Неоновая лампа включена в сеть переменного тока с эффективным напряжением Vэ=71 В и периодом T= (1/50) с. Найти промежуток времени Δt, в течение которого длится вспышка лампы, и частоту вспышек лампы n. Напряжение зажигания лампы Vэ=86,7 В считать равным напряжению гашения Vг.

Решение:
В сети с эффективным напряжением Vэ амплитуда напряжения

Принимая начальную фазу напряжения равной нулю, запишем закон изменения напряжения с течением времени:

Зажигания (гашения) лампы происходят в моменты времени когда мгновенное напряжение в сети равно напряжению зажигания (рис. 381):

Наименьшее положительное значение, которое может иметь величина

стоящая под знаком синуса, составляет 60° = π/З. В общем случае

где т=0,1, 2, … Следовательно,

Знак плюс здесь соответствует моментам зажигания лампы (напряжение в эти моменты возрастает по модулю), а знак минус-моментам гашения лампы (напряжение убывает по модулю). В частности, первая вспышка . происходит при tо=T/6 и первое гашение — при

Таким образом, длительность вспышки

Вспышки и гашения, происходят в течение каждой половины периода; следовательно, частота вспышек n= 2/T=100.

20 Найти частоту вспышек неоновой лампы, включенной в сеть переменного тока по схеме, изображенной на рис. 147. Э.д.с. батареи элементов ε = 60 В, эффективное напряжение, снимаемое с автотрансформатора, Vэ= 28,3 В, напряжение зажигания лампы Vз = 86,7 В. Частота переменного тока f=200 Гц.

Решение:
Амплитуда переменного напряжения на выходе автотрансформатора

Это напряжение с течением времени изменяется по закону

Напряжение между электродами лампы

(график зависимости этого напряжения от времени приведен на рис. 382).
При

напряжение V2 принимает наибольшее значение

При

напряжение V2 принимает наименьшее значение

Таким образом, напряжение на электродах лампы становится больше напряжения зажигания лишь один раз в течение периода, поэтому частота вспышек неоновой лампы равна частоте тока f=200 Гц.

21 Ток в первичной обмотке трансформатора I1=0,5 А, напряжение на ее концах V1 = 220 В. Ток во вторичной обмотке трансформатора I2 = 11 А, напряжение на ее концах V2 = 9,5 В. Найти к.п.д. трансформатора.

Решение:
Мощность, подводимая к первичной обмотке (затраченная мощность), N1=I1V1. Мощность, отдаваемая вторичной обмоткой нагрузке (полезная мощность), N2=I2V2. К. п. д. трансформатора

22 Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=8 включена в сеть переменного тока с напряжением V1=220 В. Сопротивление вторичной обмотки r=2 Ом, ток в ней I=3 А. Найти напряжение V2 на зажимах вторичной обмотки.

Решение:
Индуцируемая во вторичной обмотке э.д.с .

Напряжение на ее зажимах

23 Первичная обмотка трансформатора для питания накала радиоприемника имеет w1= 12000 витков и включена в сеть переменного тока с напряжением V1= 120 В. Какое число витков w2 должна иметь вторичная обмотка, если ее сопротивление r=0,5 Ом? Напряжение накала радиоприемника V2 = 3,5 В при токе I=1А.

Решение:
Индуцируемая во вторичной обмотке э.д.с. должна быть равна напряжению накала V2 и падению напряжения на сопротивлении обмотки Ir. Поэтому отношение чисел витков в обмотках

отсюда

24 Первичная обмотка понижающего трансформатора включена в сеть переменного тока с напряжением V1=220 В. Напряжение на зажимах вторичной обмотки V2 = 20 В, ее сопротивление r=1 Ом, ток в ней I=2 А. Найти коэффициент трансформации k и к.п.д. η трансформатора.

Решение:
Индуцируемая во вторичной обмотке э.д.с.

Коэффициент трансформации трансформатора

Ток в первичной обмотке находим из условия

К.п.д. трансформатора (отношение мощности на зажимах вторичной обмотки к мощности, потребляемой первичной обмоткой)

25 Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=10 включена в сеть переменного тока с напряжением V1=120 В. Сопротивление вторичной обмотки r=1,2 Ом, ток в ней I=5 А. Найти сопротивление R нагрузки трансформатора и напряжение V2 на зажимах вторичной обмотки.

Решение:

26 Найти амплитуду и фазу напряжения в сети, питаемой двумя последовательно включенными генераторами переменного тока, напряжения на зажимах которых . Амплитуды напряжения генераторов V10 = 60 В и V20=100 В; частота тока f=50 Гц; начальная фаза напряжения второго генератора φ₀ = 30°.

Решение:
Амплитуда напряжения

Задачи по физике и математике с решениями и ответами

Задача по физике — 4099

В каком случае обмотка электромотора сильнее нагревается проходящим по ней током — когда мотор работает вхолостую или совершает некоторую работу? Напряжение в сети считать постоянным. Подробнее

Задача по физике — 4101

Магнитное поле имеет вертикальную ось симметрии (ось $z$). Проекция вектора магнитной индукции $\vec{B}$ на эту ось $B_{z} = B_{0} \left ( 1 + \frac{z}{h_{0}} \right )$. С большой высоты падает медное кольцо диаметра $d$, имеющее электрическое сопротивление $R$; плоскость кольца все время горизонтальна, а центр движется вдоль оси $z$. Определите установившуюся скорость падения $v$, если масса кольца равна $m$. Подробнее

Задача по физике — 4102

Конденсатор переменной емкости колебательного контура радиоприемника может изменять емкость от $C_{1}$ до $C_{2} > C_{1}$. Какой комплект из $N$ сменных катушек следует использовать, чтобы диапазон длин волн, на которые можно настраивать приемник, был как можно более широким и не содержал «просветов»? Какова верхняя граница $\lambda_{max}$ этого диапазона, если нижняя граница равна
Подробнее

Задача по физике — 4103

Электрический контур состоит из конденсатора постоянной емкости и катушки, в которую можно вдвигать сердечник. Один сердечник — ферритовый, другой изготовлен из меди. Как изменится частота собственных колебаний контура, если вдвинуть в катушку ферритовый сердечник? Медный? Подробнее

Задача по физике — 4104

Почему увеличение дальности радиосвязи с космическими кораблями в три раза требует увеличения мощности передатчика в 9 раз? Во сколько раз следует увеличить мощность передатчика для увеличения в три раза дальности радиолокации? В обоих случаях излучатель радиоволн можно считать точечным.{-1}$, изображение разлагается на $N = 625 строк$.

Подробнее

Задача по физике — 4106

Конденсатор емкостью $C_{1}$ заряжен до напряжения $U_{1}$ а конденсатор емкостью $C_{2}; не заряжен (см. рисунок). Каким будет максимальное значение $I_{m}$ силы, тока в катушке индуктивностью $L$ после замыкания ключа? Конденсаторы, и катушку считайте идеальными.
Подробнее

Задача по физике — 4107

Один из двух одинаковых конденсаторов (см. рисунок) заряжен до напряжения $U_{0}$, другой — не заряжен. Какое напряжение $U$ установится на конденсаторах после замыкания ключа? Как согласуется этот результат с законом сохранения энергии? Рассмотрите, в частности, случай, когда соединительные провода являются сверхпроводящими.

Подробнее

Задача по физике — 4108

В цепь последовательно включены резистор с сопротивлением $R$, конденсатор с емкостью $C$ и катушка с индуктивностью $L$. По цепи протекает переменный ток $i = I_{M} \cos \omega t$. Определите амплитуды напряжения на каждом из элементов цепи и во всей цепи. По какому закону изменяется приложенное к цепи напряжение? Подробнее

Задача по физике — 4109

На рисунке показана схема простейшего выпрямителя, используемого в школьных экспериментах. Емкость конденсатора $C = 500 мкФ$, сопротивление резистора $R = 1,0 кОм$. Каково максимально возможное значение напряжения $U_{вых}$ на выходе выпрямителя? Какое обратное напряжение должен выдерживать диод?
Подробнее

Задача по физике — 4110

Два одинаковых идеальных трансформатора имеют обмотки из $N_{1} = 200$ и $N_{2} = 600$ витков. Они соединены последовательно различными обмотками (см. рисунок) и подключены к источнику переменного напряжения $U = 200 B$. Определите напряжение $U_{AC}$ между точками А и С. Подробнее

Задача по физике — 4111

В ясный безоблачный вечер лучи заходящего солнца попадают в затемненную комнату через узкую горизонтальную щель в ставне. Длина щели $a = 6 см$, расстояние от окна до противоположной стены $l = 3 м$. Какова форма светового пятна на стене, если солнечные лучи падают на нее под прямым углом? Оцените размеры светового пятна. Что произойдет с пятном, если уменьшать ширину щели? Длину?
Подробнее

Задача по физике — 4112

Солнечные лучи, проходя сквозь маленькие отверстия в листве дерева, дают на земле светлые пятна в форме эллипсов одинаковой формы, но разных размеров.{-3} рад$. Подробнее

Задача по физике — 4113

Луч света, идущий из точки А, приходит в точку В, отразившись от плоской пластины CD (см. рисунок). Докажите, что, «подчиняясь» закону отражения, луч «выбирает» кратчайший путь.
Подробнее

Задача по физике — 4114

Три зеркала образуют между собой двугранные прямые углы (см. рисунок). Докажите, что после трех отражений от этой системы зеркал направление любого луча света изменяется на противоположное.
Подробнее

Цепь «резистор – конденсатор включены последовательно»

Цепь «резистор – конденсатор включены последовательно»

Рассмотрим электрическую цепь, изображённую на рис.39,а. В этой цепи последовательно соединены идеальный источник напряжения резистор и конденсатор. Параллельно резистору и конденсатору подключены два вольтметра, и последовательно в цепь включён амперметр.

Рис.39. Последовательно соединённые в электрической цепи

резистор и конденсатор.

Направление тока выбрано совпадающим с положительной полуволной синусоидальной ЭДС Ė. Так как цепь замкнута и не имеет ответвлений (замкнутый контур), то применим второй закон Кирхгофа:

Ė = Ů _R +Ů _C

Заменим, согласно закона Ома, Ů₁и Ů₂на İ· R ₁и İ· X_C , тогда

Ė = İ· R + İ· X_C = İ·Ż.

Предположим, что İ= I · e^j⁰, тогда

Ė = U = I · e^j⁰ · R + I · e^j⁰ · X_C = U_Rm · e^j⁰ + U_Cm · e^j^-90° = U_Rm · sin 0° + U_Cm · sin -90°= U_Rm · sin 0° + U_Cm · cos 0°

(так как напряжение на конденсаторе отстаёт от тока на угол 90°).

Для того, чтобы узнать суммарное напряжение в цепи напряжение просуммируем графически напряжение на резисторе и конденсаторе.

Для этого отложим на оси реальных значений (оси абсцисс) в масштабе величину тока İ, затем на это же оси величинунапряжения Ů _R, так как это напряжение совпадает по фазе с током, протекающим в цепи. Так как напряжение на конденсаторе отстаёт от тока на угол 90° (так как отстаёт, значит — угол -90°), то отложим Ů _C по оси мнимых чисел (оси ординат) вниз (см. Рис.39,б). Помним, что I и II квадранты для положительных мнимых чисел, III и IV квадранты для отрицательных мнимых чисел.

Таким образом, мы видим, что суммарное напряжение Ů отстаёт по фазе на меньший угол, по сравнению с цепью с одним конденсатором.

Что же покажут приборы? Приборы покажут действующие значения напряжений и токов. Вольтметр U_Rпокажет 0,707·I_m · R =0,707·U_Rm , вольтметр U_Cпокажет 0,707·I_m · X_C = 0,707·U_Cm , то есть они покажут значения напряжений без учёта фаз. Вольтметр U покажет U =√( U_R² + U_C² ).

Напряжение U будет равно U =√( U_R² + U_C² ), а угол ψ = arctgX_C / R то есть модуль напряжения U e^j^-ψ.

Определим мощности, выделяемые на резисторе и конденсаторе:

На резисторе будет выделяться активная мощность P = I ² · R и на конденсаторе будет выделяться реактивная мощность Q= I ² · X_C . И тогда полная мощность – Ṡ = S · e^jψ, где: S =√( P ² + Q ² ). При переменном токе также определяют коэффициент мощности — cosφ = = P / Q .

Задача.

Определить ток, падение напряжения, мощность, выделяемую на элементах схемы (см. рис.39), если İ =0,705· e^j⁰ , R =200 Ом, C =30 мкФ, f =50Гц.

Определим модуль реактивного сопротивления X_C =1/(2·π· f · C )=1/([Гц]·[Ф])= [Ом] 1/(2·3,14·50·0,00003)=106 Ом, тогда Ẋ _C=106· e^j^-90°Ом. Здесь величину ёмкости конденсатора перевёл из мкФ в Ф, 30 мкФ=30·0,000001=0,00003 Ф.

Определим действующую величину тока I = I_m ·0,707=0,705·0,707=0,498≈0,5 А.

Определим падения напряжения на элементах:

— на R падение напряжения U_R = I · R = I · R =[А]·[Ом]=[В]=0,5·200=100 В, амплитудное значение U_Rm =1,41·U_R =1,41·100=141 В.

— на C падение напряжения U_C = I · X_C =[А]·[Ом]= [В]=0,5·106=53В, амплитудное значение U_Cm =1,41·U_C =1,41·53=74,7 В. .

— определим модуль результирующего напряжения U =√( U_R² + U_C² )=√(100²+53²) ≈ ≈113,2 В, U_m =√( U_Rm² + U_Cm² )=√(141²+74,7²) ≈159,6 В, ψ = arctg X_C / R = arctg106/200 = arctg 0,53 =31°

Теперь можно построить треугольник напряжений (вектор напряжения на конденсаторе направлен вниз потому, что напряжение на конденсаторе отстаёт от тока на угол 90°). Длина векторов равна амплитудным значениям токов и напряжений.

Рис. 40 Треугольник напряжений.

Определим мощности, выделяемые на элементах цепи:

— мощность на активном резисторе R равна P = I ² · R = [А]²·[Ом]=[Вт]= 0,5²·200=50 Вт;

— мощность на конденсаторе C равна Q =I ² · X_C= [А]²·[Ом]=[вар]=0,5²·106=26,5 вар;

— полная мощность S =√( P ² + Q ² ) =√(50²+26,5²) =56,59 ВА;

— определяем коэффициент мощности cosφ = P / S = 50/56,59=0,88.

цепь «резистор – конденсатор включены последовательно»

Рис.39. Последовательно соединённые в электрической цепи

резистор и конденсатор.

Ė = Ů _R +Ů _C

Заменим, согласно закона Ома, Ů₁и Ů₂на İ· R ₁и İ· X_C , тогда

Ė = İ· R + İ· X_C = İ·Ż.

Предположим, что İ= I · e^j⁰, тогда

Ė = U = I · e^j⁰ · R + I · e^j⁰ · X_C = U_Rm · e^j⁰ + U_Cm · e^j^-90° = U_Rm · sin 0° + U_Cm · sin -90°= U_Rm · sin 0° + U_Cm · cos 0°

(так как напряжение на конденсаторе отстаёт от тока на угол 90°).

Напряжение U будет равно U =√( U_R² + U_C² ), а угол ψ = arctgX_C / R то есть модуль напряжения U e^j^-ψ.

Определим мощности, выделяемые на резисторе и конденсаторе:

Задача.

Определим действующую величину тока I = I_m ·0,707=0,705·0,707=0,498≈0,5 А.

Определим падения напряжения на элементах:

— на R падение напряжения U_R = I · R = I · R =[А]·[Ом]=[В]=0,5·200=100 В, амплитудное значение U_Rm =1,41·U_R =1,41·100=141 В.

— на C падение напряжения U_C = I · X_C =[А]·[Ом]= [В]=0,5·106=53В, амплитудное значение U_Cm =1,41·U_C =1,41·53=74,7 В. .

Рис. 40 Треугольник напряжений.

Определим мощности, выделяемые на элементах цепи:

— мощность на активном резисторе R равна P = I ² · R = [А]²·[Ом]=[Вт]= 0,5²·200=50 Вт;

— мощность на конденсаторе C равна Q =I ² · X_C= [А]²·[Ом]=[вар]=0,5²·106=26,5 вар;

— полная мощность S =√( P ² + Q ² ) =√(50²+26,5²) =56,59 ВА;

— определяем коэффициент мощности cosφ = P / S = 50/56,59=0,88.

В цепи последовательно подключены конденсатор емкостью. Соединение конденсаторов

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Для получения большего спектра емкостей конденсаторы часто соединяют между собой, получают, так называемые батареи конденсаторов. Соединение при этом может быть параллельным, последовательным или комбинированным (смешанным). Рассмотрим случай с двумя конденсаторами.

Последовательное соединение конденсаторов показано на рис. 1

Здесь (рис.1) обкладка одного конденсатора, имеющая отрицательный заряд соединяется с положительной обкладкой следующего конденсатора. При последовательном соединении средние пластины конденсаторов электризуются через влияние, следовательно, их заряды по величине равны и противоположны по знаку. Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:

При этом имеем:

Получаем, что при последовательном соединении конденсаторов емкость соединения находят как:

Обобщив формулу (3) для N конденсаторов, получаем:

где — электрическая емкость i-го конденсатора.

Последовательное соединение конденсаторов используют тогда, когда для избегания пробоя конденсатора необходимо разность потенциалов распределить между несколькими конденсаторами.

Последовательное соединение конденсаторов показано на рис. 2

При параллельном соединении разности потенциалов между обкладками конденсаторов одинаковы. Суммарный заряд системы равен сумме зарядов на каждом из конденсаторов:

Из сказанного выше получим:

Для батареи из N параллельно соединенных конденсаторов имеем:

Параллельное соединение конденсаторов используют тогда, когда необходимо увеличить емкость конденсатора.

Примеры решения задач

ПРИМЕР 1

Задание

Получите формулу для расчета емкости слоистого конденсатора.

Решение

Конденсатор, который называют слоистым, состоит из двух параллельных металлических обкладок, разделенных несколькими плоскими слоями разных диэлектриков (рис.3). Обозначим диэлектрические проницаемости слоев диэлектриков как . Будем считать, что соответствующая толщина слоя диэлектрика при этом: .

Допустим, что между слоями диэлектриков вставлены очень тонкие листы из проводника. От такой процедуры заряды на обкладках конденсатора и напряженности полей в солях диэлектриков останутся неизменными. Останутся без изменений разности потенциалов между обкладками, следовательно, не изменится емкость конденсатора. Но, наличие тонких листов проводника превратит слоистый конденсатор в последовательное соединение конденсаторов.

Применим формулы емкости плоского конденсатора:

и расчета емкости батареи последовательно соединенных конденсаторов:

получаем:

Ответ

ПРИМЕР 2

Задание	Какой будет емкость соединения конденсаторов (рис.4), если батарея составлена из одинаковых конденсаторов, емкость каждого из них равна Ф.
Решение	Емкость параллельного соединения конденсаторов обозначим как Она равна:

Параллельное соединение конденсаторов – это батарея, в которой все конденсаторы находятся под одним и тем же напряжением, а суммарный ток равен полной алгебраической сумме токов этих элементов.

Основные тезисы

При параллельном включении конденсаторов их ёмкости складываются. Это позволяет быстро вычислить результат. Рабочее напряжение для всех конденсаторов одинаковое, а заряды из всех складываются воедино. Это следует из формулы, выведенной Вольтой ещё в XVIII веке:

C = q/U, тогда C1 + C2 + … = q1 + q2 + …/U.

Параллельное включение конденсаторов ведёт себя, как один конденсатор большой ёмкости.

Зачем нужно включать конденсаторы параллельно

В радиоприёмниках подстройка под частоту волны осуществляется коммутацией блоков конденсаторов. Этим осуществляется ввод резонансного контура в резонанс.
В фильтрах мощных блоков питания за каждый рабочий цикл нужно запасать много энергии. Строить его на индуктивностях экономически нецелесообразно. Поэтому применяют параллельный набор из больших электролитических конденсаторов.
Параллельное включение конденсаторов можно встретить в измерительных схемах. Где эталоны ответвляют на себя часть тока, и по этой величине оценивается номинал. То есть размер ёмкости исследуемого конденсатора.
Параллельно время от времени могут устанавливаться компенсаторы реактивной мощности. Это устройства, которые блокируют выход лишней энергии в питающую сеть. Что предотвращает образование помех, перегрузку генераторов, трансформаторов и избыточный нагрев проводки.

Реактивная мощность сети

Когда работает асинхронный двигатель, то происходит расхождение тока и напряжения по фазе. Это наблюдается вследствие наличия обмотки, которая имеет индуктивное сопротивление. Как результат, часть мощности отражается обратно в цепь. Этот эффект можно устранить, если индуктивное сопротивление компенсировать ёмкостным. Имеется и другой способ – использование синхронных двигателей. Он эффективен при напряжениях от 6 до 10 кВ.

По возможности предприятия должно потреблять всю произведённую им самим реактивную мощность. Но синхронные двигатели не всегда подходят условиям технологических процессов. Тогда и ставят конденсаторные установки. Их реактивное сопротивление должно быть равным индуктивностям двигателей. Конечно, в идеале, потому что на производстве условия постоянно меняются. В этом свете становится понятно, почему так сложно отыскать золотую середину.

Но если использовать параллельное соединение конденсаторов и коммутировать их при помощи реле должным образом, то задача достаточно просто решается. Сюда можно добавить, что некоторые предприятия за отражённую реактивную мощность тоже платят. И если её не использовать, то это будут чистой воды экономические потери. Поставщиков энергии тоже можно понять: реактивная мощность забивают линию ЛЭП, нагружает трансформаторы и тогда оборудование не может выдавать полную нагрузку. Если каждое предприятие станет загружать канал лишним током, то экономическое положение энергетиков немедленно пошатнётся.

В то же время реле реактивной мощности широко распространены и помогут определить, какую часть конденсаторов включить в работу. Пример графика расчёта затрат приведён на рисунке. Имеется некая оптимальная точка, перешагивать которую экономически нецелесообразно. Но можно это сделать из каких-либо иных мотивов.

Схема соединения компенсирующих установок

В трёхфазных сетях компенсирующие конденсаторы ставят тройками по двум общеизвестным схемам:

Звезда.
Треугольник.

Реактивная мощность в этих случаях вычисляется по формулам, представленным на рисунке. Через греческую омегу обозначена круговая частота сети (2 х Пи х 50 Гц). Из соотношений получается, что схема включения конденсаторов треугольником более выгодна: мощность выросла в 3 раза. Это происходит от того, что звезда использует фазное напряжение, а оно в 1,73 раза меньше линейного. Компенсируемая реактивная мощность же зависит от квадрата этого параметра.

Из этих соображений трёхфазные конденсаторы обычно всегда изготавливаются треугольником, а под звезду нужно выпросить индивидуальный заказ (фактически три однофазных конденсатора). Есть и другая сторона медали: на вольтаж 1,05; 3,15; 6,3; 10,5 кВ все конденсаторы однофазные. И можно соединять их так, как заблагорассудится. У звезды, например, меньше рабочее напряжение, а значит, и каждый конденсатор в отдельности выйдет дешевле. Ту и другую схему нельзя отнести к параллельным включениям, но такие тройки, в свою очередь, объединяются в:

группы;
секции;
установки.

И внутри объединений однофазные конденсаторы могут включаться последовательно и параллельно, а трёхфазные – только параллельно. При этом рекомендуется номиналы всех отдельных элементов выбирать одинаковы. Это не только упрощает расчёт, но и уравнивает нагрузку по всем частям электрической схемы. Имеются и установки, где присутствует смешанное соединение по каждой фазе. Образуются параллельные ветви .

Установки выполняют однофазными или трёхфазными. В сетях с напряжением 380 В практически всегда применяется параллельное соединение конденсаторов. Исключением является случай использования оборудования с одной фазой как на 220 В (фазное), так и 380 В (линейное). Тогда под прибор ставится индивидуальная установка (или группа), компенсирующая реактивную мощность. В осветительных сетях конденсаторы по большей части ставят уже после выключателя по очевидным причинам. В прочих случаях – в зависимости от особенностей функционирования объекта.

Для напряжений 3, 6 и 10 кВ однофазные конденсаторы могут включаться обычной или двойной звездой (см. рис.). Один вывод здесь может быть заземлены (глухозаземленная нейтраль). По этой причине и допускается использование однофазных конденсаторов, в том числе и одним изолированным выводом. В последнем случае нужно убедиться, что нулевой проводник выходит на корпус изделия.

Обычно главный выключатель ставится в той или иной секции защищаемого оборудования (территориально) и управляет цепью компенсации в общем. То есть задействует или убирает вовсе дополнительное реактивное сопротивление. Если в данном секторе технологическое оборудование простаивает, то и главный выключатель разорвёт цепь компенсации. Конденсаторные установки обычно стоят в выделенном помещении вместе, электрически соединены параллельно. Перед каждой из них стоит выключатель цепи релейной регуляции для повышения или уменьшения общей ёмкости компенсаторов.

Таким образом, в зависимости от того, какое именно оборудование используется предприятием, объем реактивной мощности обусловливает помощь тех или иных конденсаторных установок, гибко подстраиваемых под имеющиеся нужды. В итоге:

Секции оборудования включены параллельно. Это легко понять, если представить бытовые приборы, питаемые одним удлинителем. Все включены параллельно. Но находятся, например, в разных цехах, секторах и пр. Встречаются и случаи, когда одна крупная энергетическая установка (например, генератор ГЭС) делится на сравнительно независимые секции.
Конденсаторные установки также включены параллельно, но находятся, как правило, в одном месте. Это сделано для того, чтобы можно было автоматически или вручную легко регулировать общую ёмкость посредством коммутации выключателей облегчённого типа. Один и тот же конденсатор может работать для компенсации реактивной мощности любой из секций или сразу обеих.

Особенности конденсаторной защиты

Главные выключатели, как правило, используются при авариях и вырубают сразу целую секцию оборудования. Конденсаторные установки также могут набираться в секции параллельным их включением. Тогда главный выключатель может сразу вырубать одну такую «батарею». Тогда как другие секции конденсаторных установок останутся в действии. Важно понять, что защитное оборудование, как и защищаемое можно группировать самыми разными методами. В зависимости от того, как это удобно и экономически обосновано.

Облегчённые выключатели применяются, как правило, в цепях регуляции. Управляются через реле и повышают или понижают общую ёмкость конденсаторных установок. В качестве главного выключателя обычно выбирается вакуумный или элегазовый.

Особенностью цепей выше 10 кВ является использование однофазных конденсаторов, собираемых по схеме звезды или треугольника, в каждой ветви которых стоит параллельно-последовательная группа ёмкостей (см. рис.). При наличии изделий с высоким рабочим напряжением можно делать и наоборот. То есть применять последовательно-параллельно включение. Тогда рабочие напряжения конденсаторов выбираются так, чтобы количество групп, включенных друг за другом было минимальным. Напряжение на каждом из элементов при этом, естественно, увеличивается. Для справки: .

Если сделать все так, как описано выше, то при выходе из строя любого элемента цепи компенсации реактивной мощности прочие будут работать в относительно щадящем режиме. Разумеется, параметры цепи нужно контролировать, а эксплуатирующий персонал согласно имеющимся методикам ведёт проверку конденсаторных установок на исправность. При проектировании нужно учесть одну небольшую особенность:

Чем больше в цепи компенсации последовательных групп конденсаторов, тем сложнее для каждой из них будет обеспечить равномерное распределение напряжения. В частности, возможны частые перегрузки того или иного сегмента.

Вдобавок ко всему сложные электрические соединения непросто проверять обслуживающему персоналу. Витиеватая схема плохо поддаётся монтажу, часты ошибки. Идеальным является параллельное соединение конденсаторных блоков по каждой фазе. Тогда и монтировать легко, и методика проверки упрощается максимально.

Разряд конденсаторов

Включенные параллельно конденсаторы обладают большой ёмкостью, вследствие чего при прекращении работы на них остаётся заряд. Это можно прочувствовать на себе, если коснуться штекера только что выключенной старенькой дрели. В новых моделях фильтр устроен так, что цепь разряжается через резистор, и ничего подобного, описанному выше, не наблюдается.

Для снижения напряжения можно также использовать и индуктивности, включенные параллельно конденсаторам. В этом случае сопротивление заземления переменному току весьма велико, а для постоянного — не сложно преодолеть этот участок. То есть, в период работы оборудования ток здесь весьма мал, и потери невелики. После останова технологической линии заряд понемногу сливается через высокоомный резистор или индуктивность. Разумеется, никто не запрещает поставить в цепи заземления реле, замыкающее контакты только после выключения всех устройств. Но это дороже и требует автоматизации.

Процесс разряда цепи важен с точки зрения обеспечения безопасности. Можно представить это так: конденсатор, заряжённый от розетки, ещё долго хранит разность потенциалов и представляет определённую опасность для окружающих. В однофазных сетях с напряжением 220 В разряд выполняется через входные фильтры при условии, что корпус правильно заземлён. Сопротивление в цепи, включенной параллельно конденсаторам, определяется по формуле, представленной ниже.

Под Q подразумевается реактивная мощность установки в варах (ВАР), а Uф – фазное напряжение. Можно легко показать, что формула дана из расчёта времени разряда. В самом деле: Q зависит линейно от ёмкости, будучи перенесена в левую часть формулы, она даст постоянную времени RC. За три таких периода батарея разряжается примерно на 97%. Исходя, из этих условий можно найти и параметры индуктивности. А ещё лучше – последовательно с нею включить резистор, как часто и делается в реальных схемах.

Содержание:

Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.

Параллельное включение конденсаторов в цепь

Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.

Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.

Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.

При параллельном соединении конденсаторов емкость равняется:

Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.

Конденсаторы, соединенные параллельно, имеют напряжение:

Последовательное включение конденсаторов в цепь

Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.

Последовательное соединение конденсатора:

При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.

Формула нахождения заряда на конденсаторе, схема подключения конденсатора:

Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.

Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.

Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:

Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:

Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:

Смешанное включение емкостных накопителей в схему

Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.

Участок цепи подсоединенных смешанным включением накопителей емкости:

Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:

разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
проводим нахождение эквивалентной емкости на параллельном участке;
когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Последовательное, параллельное и смешанное соединение конденсаторов, расчет емкости:

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:

Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.

Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.

Конденсатор в цепи переменного тока

Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.

Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).

Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.

В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.

После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.

Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.

С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.

Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.

Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.

В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.

Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.

Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны

Емкостное сопротивление конденсатора

Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС

Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.

Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.

Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.

Величина емкостного сопротивления определяется по следующей формуле:

где Хс — емкостное сопротивление конденсатора в ом;

f—частота переменного тока в гц;

ω — угловая частота переменного тока;

С — емкость конденсатора в ф.

При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.

Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.

Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.

Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.

Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.

Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.

Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.

Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.

Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.

В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.

В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.

Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.

Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.

Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.

Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.

И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.

При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.

А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

цепь переменного тока частотой

Задача 13728

В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 20 см и диаметром d = 5 см, содержащая N = 500 витков медного провода площадью поперечного сечения S = 0,6 мм². Определите, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм·м.

Задача 13729

В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см², содержащая N = 1000 витков. Определите активное сопротивление катушки, если известно, что сдвиг фаз φ между напряжением и током составляет 30°.

Задача 13734

В цепь переменного тока частотой ν = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсате емкостью С = 22 мкФ. Определите, какая доля напряжения, приложенного к этой цепи, приходится на падение напряжения на конденсаторе.

Задача 13735

В цепь переменного тока с частотой ν = 50 Гц и действующим значением напряжения U = 300 В последовательно включены конденсатор, резистор сопротивлением R = 50 Ом и катушка индуктивностью L = 0,1 Гн. Падения напряжения U₁:U₂ = 1:2. Определите: 1) емкость конденсатора; 2) действующее значение силы тока.

Задача 13737

В цепи переменного тока с частотой ω = 314 рад/с вольтметр показывает нуль при L = 0,2 Гн. Определите емкость конденсатора.

Задача 13738

В цепи переменного тока с частотой ν = 50 Гц вольтметр показывает нуль при значении С = 20 мкФ. Определите индуктивность катушки.

Задача 60342

Катушка индуктивности, сопротивление которой R = 12 Ом, включена в цепь переменного тока с частотой 50 Гц. Сдвиг фазы между колебаниями тока и напряжения на катушке φ = 60. Определить индуктивность катушки.

Задача 60467

Определите индуктивность катушки, сопротивление которой в цепи переменного тока частотой 50 Гц равно 20 Ом.

Задача 60599

Емкостное сопротивление конденсатора в цепи переменного тока частотой 50 Гц равно Х_С = 5 Ом. Какова его емкость?

Задача 60609

В цепь переменного тока с частотой 4 Гц включена катушка индуктивностью 0,001 Гн. Какой емкости конденсатор надо включить в эту цепь, чтобы осуществился резонанс?

Задача 15593

Конденсатор емкостью С = 20 мкФ и резистор, сопротивление которого R = 150 Ом, включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения U, приложенного к этой цепи, составляют падения напряжения на конденсаторе U_C и на резисторе U_R?

Задача 15597

Конденсатор емкостью С = 1 мкФ и резистор с сопротивлением R = 3 кОм включены в цепь переменного тока частотой ν = 50 Гц. Найти полное сопротивление Z цепи, если конденсатор и резистор включены: а) последовательно; б) параллельно.

Задача 16466

В цепь переменного тока частотой ν = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсатор емкостью С = 22 мкФ. Определить отношение амплитуды колебания напряжения на конденсаторе U_Cm к амплитуде колебания напряжения U_m, приложенного к цепи.

Задача 16567

Конденсатор емкостью в C = 20 мкФ и реостат, активное сопротивление которого равно R = 80,0 Ом, включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения, приложенного к этой цепи, составляет падение напряжения: 1) на конденсаторе; 2) на реостате?

Задача 17202

Катушка длиной l = 25 см и радиусом r = 2 см имеет обмотку из N = 1000 витков медного провода площадью поперечного сечения S = 1 мм². Катушка включена в цепь переменного тока частотой ν = 50 Гц. Какую часть полного сопротивления катушки составляет: 1) активное сопротивление, 2) индуктивное сопротивление?

Задача 17748

В цепь переменного тока с частотой 50 Гц последовательно включены резистор сопротивлением 100 Ом и конденсатор емкостью 22 мкФ. Определите, какая доля напряжения, приложенного к цепи, приходится на падение конденсатора и на резисторе.

Задача 20787

Реостат, активное сопротивление которого равно R = 90 Ом, и катушка индуктивностью L = 0,19 Гн включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения, приложенного к этой цепи, составляет падение напряжения: 1) на катушке. 2) на реостате? Oтвет: 1) 0,56; 2) 0,83.

Конденсаторы серии

и параллельные — Inst Tools

Последовательные конденсаторы объединяются как резисторы, включенные параллельно.

Рисунок 13: Конденсаторы, подключенные в серии

Общая емкость конденсаторов, соединенных последовательно (рисунок 13), C _T, показана в уравнении ниже.

Если последовательно соединены только два конденсатора, приведенное выше уравнение можно упростить, как показано ниже.

Приведенное выше уравнение действительно, когда последовательно соединены только два конденсатора.

Когда все конденсаторы, подключенные последовательно, имеют одинаковое значение, общую емкость можно найти, разделив номинал конденсатора на количество конденсаторов, подключенных последовательно, как указано в уравнении ниже.

где

C = номинал любого последовательно подключенного конденсатора
N = количество последовательно подключенных конденсаторов с одинаковым номиналом.

Параллельно подключенные конденсаторы объединяются как последовательно включенные резисторы. Когда конденсаторы подключены параллельно (Рисунок 14), общая емкость, C _T, является суммой отдельных емкостей, как указано в уравнении ниже.

C

_T = C ₁ + C ₂ + C ₃ …… .. + C _N

Рисунок 14: Конденсаторы, подключенные параллельно

Пример 1:

Найдите общую емкость конденсаторов 3 мкФ, 6 мкФ и 12 мкФ, соединенных последовательно (Рисунок 15).

Рисунок 15: Пример 1 — Конденсаторы, подключенные в серии

1 / К _Т = 1/3 + 1/6 + 1/12

C _T = 12/7 = 1.7 мкФ

Пример 2:

Найдите общую емкость и рабочее напряжение двух последовательно соединенных конденсаторов, когда оба имеют значение 150 мкФ, 120 В (рисунок 16).

Рисунок 16: Пример 2 — Конденсаторы, подключенные в серии

C _T = 150/2 = 75 мкФ

Общее напряжение, которое может быть приложено к группе последовательно соединенных конденсаторов, равно сумме рабочих напряжений отдельных конденсаторов.

рабочее напряжение = 120 В + 120 В = 240 вольт

Пример 3:

Найдите общую емкость трех конденсаторов, включенных параллельно, если значения составляют 15 мкФ — 50 В, 10 мкФ — 100 В и 3 мкФ — 150 В (рисунок 17).Какое было бы рабочее напряжение?

Рисунок 17: Пример 3 — Конденсаторы, подключенные параллельно

C

_T = C ₁ + C ₂ + C ₃

C _T = 15 мкФ + 10 мкФ + 3 мкФ = 28 мкФ

Рабочее напряжение группы конденсаторов, включенных параллельно, равно минимальному рабочему напряжению отдельного конденсатора. Следовательно, рабочее напряжение этой комбинации всего 50 вольт.

Кривая разряда конденсатора, подключенного последовательно с резистором, показана ниже, если…

(а) Конденсатор емкостью 220 мкФ соединен последовательно с резистором 150 кОм, переключателем и амперметром. Постоянный ток источник питания с незначительным внутренним сопротивлением подключен к цепи, как показано …

(а) Конденсатор емкостью 220 мкФ соединен последовательно с резистором 150 кОм, переключателем и амперметром. Постоянный ток Источник питания с незначительным внутренним сопротивлением подключен к схеме, как показано ниже. 1 50 кОм 220HF. Запускается секундомер, и через 10 секунд переключатель S замкнут. Показания амперметра записываются через равные промежутки времени, пока на секундомере не отобразится время 80 с.На графике ниже показано, как ток в …

Полностью разряженный идеальный конденсатор соединен последовательно с резистором и батареей. Как…

Полностью разряженный идеальный конденсатор соединен последовательно с резистором и батареей. Сколько времени нужно, чтобы на резисторе и конденсаторе была одинаковая разность потенциалов? (постоянная времени r = RC) Выберите одно: a. Т б. т / 2 C 2T d 0,697

Резистор 11,4 кОм и конденсатор включены последовательно и затем 12.0 В …

Резистор 11,4 кОм и конденсатор включены последовательно и затем к ним внезапно прикладывается разность потенциалов 12,0 В. Разность потенциалов на конденсаторе возрастает до 4,82 В в 1,48 мкс. (а) Рассчитайте постоянную времени схема. (б) Найдите емкость конденсатор. Резистор 11,4 к2 и конденсатор подключаются последовательно, а затем к ним внезапно прикладывается разность потенциалов 12,0 В. Разность потенциалов на конденсаторе …

29.(10 баллов) Конденсатор и резистор a25 ko подключены последовательно к батарее 10v ….

29. (10 баллов) Конденсатор и резистор 25 кОм подключаются последовательно к батарее 10 В. Напряжение на конденсаторе повысилось до 7,0 В через 4,7 с после начала зарядки конденсатора a. Какова постоянная времени t? (5 баллов)

Конденсатор подключен последовательно к резистору с сопротивлением 1,2 кОм и …

Конденсатор подключен последовательно к резистору с сопротивлением 1.2ko и аккумулятор с ЭДС 12 В. a) Сколько времени, кратное постоянной времени, дает время, необходимое первоначально незаряженному конденсатору для достижения 58% его максимального заряда? б) Какой ток через резистор при этой зарядке? Каков потенциал на конденсаторе при этой зарядке? г) Каков потенциал на резисторе при этой зарядке?

48. Если конденсатор 5,6 пФ, конденсатор 49,3 пФ и 35,5 пФ конденсаторы все подключены в …

48. Если 5.Конденсатор 6 пФ, конденсатор 49,3 пФ и конденсатор 35,5 пФ конденсаторы все подключены последовательно, тогда каков общий емкость этой последовательной комбинации в пикофарадах? 50. Если эквивалентом Тевенина для цепи является напряжение 5 В источник последовательно с резистором 5,3 кОм, тогда что такое Norton эквивалентный ток для этой схемы в миллиамперах? 51. Если эквивалент Norton для цепи составляет 2,2 мА источник, подключенный параллельно резистору 23 кОм, …

10. Резистор и конденсатор подключены последовательно к источнику напряжения.В момент t …

10. Резистор и конденсатор подключены последовательно к источнику напряжения. В момент времени t = 0 конденсатор начинает заряжаться, и заряд конденсатора равен Qc. График ниже отображает Qc в зависимости от t. Наклон графика представляет: Qс CV a) общий заряд конденсатора b) потенциальную энергию, запасенную в конденсаторе c) эквивалентное сопротивление цепи d) мгновенное напряжение на конденсаторе e) мгновенный ток через. ..

(а) Емкость конденсатора 5 мкФ.Объясните, что это означает с точки зрения электрического заряда. (b) Конденсатор емкостью 5 мкФ, показанный на схеме ниже, изначально не заряжен. Схема подключена к компьютеру …

(а) Емкость конденсатора 5 мкФ. Объясните, что это означает с точки зрения электрического заряда. (b) Конденсатор емкостью 5 мкФ, показанный на схеме ниже, изначально не заряжен. Схема подключена к компьютеру и выключатель S замкнут. На мониторе компьютера отображается график зависимости тока от времени по мере зарядки конденсатора, отслеживая зарядный ток / мкА 30 20 10 0.2,3 4 раза в секунду, компьютер Батарея имеет незначительное внутреннее сопротивление. (i) Рассчитать …

Незаряженный конденсатор и резистор подключены последовательно к источник ЭДС. Если…

Незаряженный конденсатор и резистор подключены последовательно к источник ЭДС. Если ЭДС = 9,00 В, емкость = 21,5 мкФ, и сопротивление = 127 Ом, найдите (а) постоянную времени цепи. После 1,30 мс, найти (б) заряд конденсатора, (в) падение напряжения на конденсаторе, (d) падение напряжения на резисторе, и (e) текущее.

Тор заряжается до начального напряжения микроразряда 1OV через резистор 40 кОм. Затем вы берете 10 единиц напряжения в зависимости от времени и записываете объем 10 единиц напряжения, а значение напряжения составляет 47 об.

Тор заряжается до начального напряжения микроразряда 1OV через резистор 40 кОм. Затем вы берете 10 единиц напряжения в зависимости от времени и записываете объем 10 Это напряжение и значение напряжения 47 вольт через 60 через 50 секунд Каков ваш процент.47 вольт через 60 секунд. Ошибка по сравнению с теоретическим значением напряжения после трех постоянных времени? 6% -6% c.60% d. -60% Какое уравнение для …

конденсаторов последовательно и параллельно с их примерами

Существуют различные типы конденсаторов, в зависимости от области применения, которые подразделяются на разные типы. Подключение этих конденсаторов может осуществляться разными способами, которые используются в различных приложениях. Различные соединения конденсаторов работают как один конденсатор.Таким образом, общая емкость этого единственного конденсатора в основном зависит от того, как подключены отдельные конденсаторы. Таким образом, в основном есть два простых и распространенных типа соединений, такие как последовательное соединение и параллельное соединение. Используя эти соединения, можно рассчитать общую емкость. Есть некоторые соединения, которые также могут быть связаны с последовательными и параллельными комбинациями. В этой статье обсуждается обзор конденсаторов, подключенных последовательно и параллельно, с их примерами.

Последовательные и параллельные конденсаторы

Конденсатор в основном используется для хранения электрической энергии, например, электростатической. Когда возникает необходимость увеличить больше энергии для накопления емкости, может потребоваться соответствующий конденсатор с увеличенной емкостью. Конструкция конденсатора может быть выполнена с использованием двух металлических пластин, которые соединены параллельно и разделены диэлектрической средой, такой как слюда, стекло, керамика и т. Д.

Диэлектрическая среда образует непроводящую среду между двумя пластинами и обладает исключительной способностью удерживать заряд.

Когда к пластинам конденсатора подключается источник напряжения, на одной пластине осаждается заряд + Ve, а на следующей пластине — заряд -Ve. Здесь общий накопленный заряд «q» может быть прямо пропорционален источнику напряжения «V».

q = CV

Где «C» — это емкость, и ее значение в основном зависит от физических размеров конденсатора.

C = εA / d

Где

‘ε’ = диэлектрическая проницаемость

‘A’ = площадь эффективной пластины

d = расстояние между двумя пластинами.

Если два или более конденсатора соединены последовательно, общая емкость этих конденсаторов мала по сравнению с емкостью отдельного конденсатора. Точно так же, когда конденсаторы подключаются параллельно, общая емкость конденсаторов является суммой емкостей отдельных конденсаторов. Используя это, выводятся выражения для полной емкости последовательно и параллельно. Также определены последовательные и параллельные части в комбинации соединений конденсаторов.И эффективная емкость может быть рассчитана последовательно и параллельно через отдельные емкости

Конденсаторы серии

Когда несколько конденсаторов соединены последовательно, напряжение, приложенное к конденсаторам, составляет «V». Если емкость конденсатора составляет C1, C2… Cn, тогда соответствующая емкость конденсаторов при последовательном соединении будет «C». Приложенное напряжение на конденсаторах равно V1, V2, V3…. + Vn соответственно.

Конденсаторы серии

Таким образом, V = V1 + V2 + …….. + Вн

Заряд, передаваемый от источника через эти конденсаторы, равен «Q», тогда

V = Q / C, V1 = Q / C1, V2 = Q / C2, V3 = Q / C3 и Vn = Q.Cn

Поскольку заряд, передаваемый в каждом конденсаторе, и ток во всей последовательной комбинации конденсаторов будут одинаковыми, это считается как «Q».

Теперь приведенное выше уравнение «V» можно записать следующим образом.

Q / C = Q / C1 + Q / C2 +… Q / Cn

Q [1 / C] = Q] 1 / C1 + 1 / C2 +… 1 / Cn]

1 / C = 1 / C1 + 1 / C2 + 1 / C3 +… 1 / Cn

Пример

При последовательном подключении конденсаторов рассчитайте их емкость.Последовательное соединение конденсаторов показано ниже. Здесь последовательно подключено два конденсатора.

Конденсаторы в формуле последовательного включения: Ctotal = C1XC2 / C1 + C2

Значения двух конденсаторов: C1 = 5F и C2 = 10F

Cобщ. = 5FX10F / 5F + 10F

50F / 15F = 3,33F

Параллельные конденсаторы

Когда емкость конденсатора увеличивается, тогда конденсаторы подключаются параллельно, когда две связанные пластины соединяются вместе.Эффективная область перекрытия может быть добавлена за счет стабильного расстояния между ними, и поэтому их одинаковое значение емкости превращается в удвоенную индивидуальную емкость. Конденсаторная батарея используется в различных отраслях промышленности, где конденсаторы используются параллельно. После того, как два конденсатора соединены параллельно, напряжение «V» на каждом конденсаторе будет одинаковым, то есть Veq = Va = Vb, а ток «ieq» можно разделить на два элемента, например «ia» и «ib».

Конденсаторы параллельно

i = dq / dt

Подставьте значение «q» в уравнение выше

= d (CV) / dt

i = C dV / dt + VdC / dt

Когда емкость конденсатора постоянна, тогда

i = C dV / dt

Применяя KCL к вышеуказанной схеме, уравнение будет

ieq = ia + ib

ieq = Ca dVa / dt + Cb dVb / dt

Veq = Va = Vb

ieq = Ca dVeq / dt + Cb dVeq / dt => (Ca + Cb) dVeq / dt

Наконец, мы можем получить следующее уравнение

ieq = Ceq dVeq / dt, здесь Ceq = Ca + Cb

Следовательно, как только «n» конденсаторов соединены параллельно, равная емкость всего соединения может быть задана с помощью следующего уравнения, которое выглядит как соответствующее сопротивление резисторов при последовательном соединении.

Ceq = C1 + C2 + C3 +… + Cn

Пример

При параллельном подключении конденсаторов рассчитайте их емкость. Ниже показано параллельное соединение конденсаторов. Здесь конденсаторов, соединенных параллельно, два.

Конденсаторы в параллельной формуле: Ctotal = C1 + C2 + C3

Значения двух конденсаторов: C1 = 10F, C2 = 15F, C3 = 20F

Cобщ. = 10F + 15F + 20F = 45F

Падение напряжения на конденсаторах, подключенных последовательно и параллельно, будет изменяться в зависимости от индивидуальных значений емкости конденсаторов.

Примеры

Конденсаторы последовательно и параллельно, примеры обсуждаются ниже.

Конденсаторы в примерах последовательно и параллельно

Найдите значение емкости трех конденсаторов, включенных в следующую схему, со значениями C1 = 5 мкФ, C2 = 5 мкФ и C3 = 10 мкФ

Емкости конденсаторов: C1 = 5 мкФ, C2 = 5 мкФ и C3 = 10 мкФ

Следующая схема может быть построена с тремя конденсаторами, а именно C1, C2 и C3

Когда конденсаторы C1 и C2 соединены последовательно, емкость можно рассчитать как

1 / C = 1 / C1 + 1 / C2

1 / C = 1/5 + 1/5

1 / C = 2/5 => 5/2 = 2.5 мкФ

Если вышеуказанный конденсатор «C» можно подключить параллельно с конденсатором «C3», то емкость можно рассчитать как

C (Всего) = C + C3 = 2,5 + 10 = 12,5 мкФ

Таким образом, значение емкости можно рассчитать в зависимости от анализа последовательных и параллельных соединений в цепи. Это можно наблюдать, когда значение емкости уменьшается при последовательном включении. При параллельном подключении конденсатора значение емкости можно увеличить.Однако при расчете сопротивления все происходит наоборот.

Таким образом, это все обзор конденсаторов, включенных последовательно и параллельно, с примерами. Из приведенной выше информации, наконец, мы можем сделать вывод, что, используя последовательное и параллельное соединение конденсаторов, можно рассчитать емкость. Вот вам вопрос, а какая у конденсатора единица измерения?

Незаряженный конденсатор соединен последовательно с батареей, переключателем и резистором, как показано на рис.6.1.

Вопрос 3

Незаряженный конденсатор соединен последовательно с батареей, переключателем и резистором, как показано на Рис. 6.1.

Рис. 6.1

Аккумулятор имеет э.д.с. 9,0 В и незначительное внутреннее сопротивление. Емкость конденсатора 4700 мкФ.

Переключатель закрыт в момент времени т = 0.

Во время интервал т = 0 до т = 4.0 с, заряд, проходящий через резистор, составляет 22 мКл.

(а) (i) Рассчитайте передачу энергии в батарее за время интервал т = 0 до т = 4,0 с. [2]

(ii) Определить, для конденсатора в момент времени т. = 4,0 с,

1. разность потенциалов В на конденсаторе, [2]

2. энергия, запасенная в конденсаторе. [2]

(б) Предложите, почему ваши ответы в пунктах (a) (i), и (a) (ii) часть 2 разные.[1]

Ссылка: Документ о прошедшем экзамене — Документы 41 и 43 Q6 за июнь 2014 г.

Решение:

(а) (i)

{Мы хотим найти передача энергии в батарее. Итак, мы используем уравнение, которое связывает энергию с заряд от АКБ. Мы не можем использовать уравнение для конденсаторов.

э.м.ф. E = Работа выполнена / Заряд

E = энергия / Q

Энергия = EQ}

Энергия = EQ = 9.0 × (22 × 10 ^-3)

Энергия = 0,20 Дж

(ii)

Емкость, C = Q / V

Потенциал разность, V = (22 × 10 ^-3) / (4700 × 10 ^-6)

p.d. знак равно 4,7 В

ЛИБО энергия, E = ½ CV ² = ½ × 4700 × 10 ^-6 × 4,7 ² = 5,1 × 10 ^-2 Дж

ИЛИ E = ½ QV = ½ × 22 × 10 ^-3 × 4.7 = 5,1 × 10 ^-2 Дж

ИЛИ E = ½ Q ² / C = ½ × (22 × 10 ^-3) ² / (4700 × 10 ^-6) = 5,1 × 10 ^-2 Дж

(b) Потеря энергии (как тепловая энергия) в сопротивлении / проводах / батарее / резисторе Суперконденсатор

— Энергия, запасенная в конденсаторах, соединенных последовательно Суперконденсатор

— Энергия, запасенная в конденсаторах, соединенных последовательно — Обмен электротехническими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 178 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

0
+0
Авторизоваться Подписаться

Electrical Engineering Stack Exchange — это сайт вопросов и ответов для профессионалов в области электроники и электротехники, студентов и энтузиастов.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 5 лет, 6 месяцев назад

Просмотрено 4к раз

\ $ \ begingroup \ $

Меня сбивает с толку расчет полной энергии, запасенной в последовательно соединенных конденсаторах.Для расчета энергии, хранящейся в одном конденсаторе, в джоулях получается Кл (В * В) / 2 . Я хочу подключить 2,5 В 500 Фарад емкость 20 конденсаторов последовательно к источнику 48 Вольт . поэтому общая запасенная энергия равна 500 (48 * 48) / 2 или 20 (500 (2,5 * 2,5) / 2) ? Который правильный?

Создан 22 мар.

\ $ \ endgroup \ $ \ $ \ begingroup \ $

Даже не зная формулы энергии в конденсаторе, ответ прост: в 20 раз больше энергии, хранящейся в одном конденсаторе.Правила сохранения энергии.

Проблема с вашей первой формулой заключается в том, что общая емкость N конденсаторов C, соединенных последовательно, равна не C, а C / N.

Создан 22 марта 2016 г. в 9: 322016-03-22 09:32

Воутер ван Оойен

47.4k11 золотых знаков6161 серебряный знак133133 бронзовых знака

\ $ \ endgroup \ $ \ $ \ begingroup \ $

Для последовательного подключения конденсатора,

найдите C_total , используя уравнение
c_total = 1 / ((1 / c1) + (1 / c2) +.2`
Создан 22 мар.
\ $ \ endgroup \ $ \ $ \ begingroup \ $
Окей. Я немного запылен, но давайте посмотрим … Конденсаторы — это не что иное, как комплексное сопротивление (Reactance): $$ Z = 1 / jωC = -j / ωC = -j / 2πfC $$ Когда у вас есть резисторы последовательно, вы делаете: \ $ R_s = R_1 + R_2 + R_3 +… \ $
Аналогично, полное сопротивление, если конденсаторы соединены последовательно, составляет: $$ Z_s = Z_1 + Z_2 + … = {-j * 20 \ over 2πfC} = 20 * Z $$ Поскольку все конденсаторы одинаковые, напряжение на каждом из них будет одинаковым (падение напряжения будет одинаковым, поскольку полное сопротивление одинаково и закон Кирхгофа по напряжению верен). Итак, у вас на самом деле есть делитель напряжения для каждого из них: $$ V_c = {Z \ over Z_s} * V_ {in} = {Vin \ over20} $$ Теперь все просто. 2 \ over20} $$ Я вижу, что это не равно энергии, хранящейся в одном конденсаторе.Я считаю, что это связано с нелинейностью, которую конденсаторы вносят в систему, и тем, как они запускают переменный ток. В конце концов, мы просто измеряем СОХРАНЕННУЮ энергию, а не общую энергию. Возможно, я ошибаюсь, но я не вижу ошибки в своей логике. Критика приветствуется.
Создан 26 апр.
\ $ \ endgroup \ $ 2 Электротехнический стек Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Лаборатория 4 — Зарядка и разрядка конденсатора
Введение
Конденсаторы — это устройства, которые могут накапливать электрический заряд и энергию.Конденсаторы имеют несколько применений, например, в качестве фильтров в источниках питания постоянного тока и в качестве аккумуляторов энергии для импульсных лазеров. Конденсаторы пропускают переменный ток, но не постоянный, поэтому они используются для блокировки постоянной составляющей сигнала, чтобы можно было измерить переменную составляющую. Физика плазмы использует способность конденсаторов накапливать энергию. В физике плазмы часто требуются короткие импульсы энергии при чрезвычайно высоких напряжениях и токах. Конденсатор можно медленно заряжать до необходимого напряжения, а затем быстро разряжать для обеспечения необходимой энергии.Можно даже зарядить несколько конденсаторов до определенного напряжения, а затем разрядить их таким образом, чтобы получить от системы большее напряжение (но не больше энергии), чем было вложено. В этом эксперименте используется схема RC , которая является одной из простейших схем, в которой используется конденсатор. Вы изучите эту схему и способы изменения ее эффективной емкости, комбинируя конденсаторы последовательно и параллельно.
Обсуждение принципов
Конденсатор состоит из двух проводов, разделенных небольшим расстоянием.Когда проводники подключены к зарядному устройству (например, к батарее), заряд передается от одного проводника к другому до тех пор, пока разность потенциалов между проводниками из-за их равного, но противоположного заряда не станет равной разности потенциалов между клеммами. зарядного устройства. Количество заряда, накопленного на любом проводнике, прямо пропорционально напряжению, а константа пропорциональности известна как емкость . Это записывается алгебраически как Заряд C измеряется в единицах кулонов (C), напряжение
ΔV
в вольт (В) и емкость C в единицах фарад (F). Конденсаторы — физические устройства; Емкость — это свойство устройства.
Зарядка и разрядка
В простой RC-цепи резистор и конденсатор соединены последовательно с батареей и переключателем. См. Рис.1.
Рисунок 1 : Простая RC-цепь
Когда переключатель находится в положении 1, как показано на рис. 1 (а), заряд на проводниках через некоторое время достигает максимального значения. Когда переключатель переведен в положение 2, как на рис.1 (b), аккумулятор больше не является частью цепи и, следовательно, заряд конденсатора не может быть восполнен. В результате конденсатор разряжается через резистор. Если мы хотим исследовать зарядку и разрядку конденсатора, нас интересует, что происходит сразу же, после того, как переключатель перемещается в положение 1 или положение 2, а не дальнейшее поведение схемы в ее установившемся состоянии. Для схемы, показанной на рис. 1 (а), уравнение петли Кирхгофа можно записать как Решение уравнения.(2) — это
(3)
Q = Q _f
1 — e ^{(−t / RC)}
где
Q _f
представляет собой окончательный заряд на конденсаторе, который накапливается через бесконечный промежуток времени, R — сопротивление цепи, а C — емкость конденсатора. Из этого выражения вы можете видеть, что заряд растет экспоненциально во время процесса зарядки.См. Рис. 2 (а). Когда переключатель перемещается в положение 2, для схемы, показанной на рис. 1 (b), уравнение петли Кирхгофа теперь имеет вид Решение уравнения. (4) является
(5)
Q = Q ₀ e ^{(−t / RC)}
где
Q ₀
представляет начальный заряд на конденсаторе в начале разряда, то есть при
t = 0.
Из этого выражения видно, что заряд экспоненциально затухает при разряде конденсатора, и что для полной разрядки требуется бесконечное количество времени.См. Рис. 2 (b).
Рисунок 2 : График изменения во времени
Постоянная времени
τ Произведение
RC
(имеющее единицы времени) имеет особое значение; это называется постоянной времени цепи. Постоянная времени — это время, необходимое для повышения заряда зарядного конденсатора до 63% от его конечного значения. Другими словами, когда
t = RC,
(6)
Q = Q _f
1 — e ^-1
а также
(7)
1 — е ⁻¹ = 0.632.
Другой способ описать постоянную времени — сказать, что это количество секунд, необходимое для того, чтобы заряд на разряжающемся конденсаторе упал до 36,8%
(e ^-1 = 0,368)
от своего начального значения. Мы можем использовать определение
(I = dQ / dt)
тока через резистор и уравнение. (3) Q = Q _f
1 — e ^{(−t / RC)}
и уравнение. (5)
Q = Q ₀ e ^{(−t / RC)}
, чтобы получить выражение для тока во время процессов зарядки и разрядки.
(8)
зарядка: I = + I ₀ e ^{−t / RC}
(9)
разгрузка: I = −I ₀ e ^{−t / RC}
где в формуле. (8)
зарядка: I = + I ₀ e ^{−t / RC}
и уравнение. (9)
разряд: I = −I ₀ e ^{−t / RC}
— максимальный ток в цепи в момент времени t = 0. Тогда разность потенциалов на резисторе будет выражаться следующим образом.
(10)
зарядка: ΔV = + ΔV _f e ^{−t / RC}
(11)
нагнетание: ΔV = — ΔV ₀ e ^{−t / RC}
Обратите внимание, что во время процесса разрядки ток будет течь через резистор в обратном направлении. Следовательно, I и
ΔV
в уравнении. (9)
разряда: I = −I ₀ e ^{−t / RC}
и уравнение. (11)
разряд: ΔV = — ΔV ₀ e ^{−t / RC}
отрицательны.Это напряжение как функция времени показано на рис.3.
Рисунок 3 : Напряжение на резисторе как функция времени
Полезно описывать зарядку и разрядку в терминах разности потенциалов между проводниками (т.е. «напряжение на конденсаторе»), поскольку напряжение на конденсаторе можно измерить непосредственно в лаборатории. Используя соотношение
Q = C ΔV,
Ур. (3) Q = Q _f
1 — e ^{(−t / RC)}
и уравнение.(5)
Q = Q ₀ e ^{(−t / RC)}
, которые описывают зарядку и разрядку конденсатора, можно переписать в терминах напряжения. Просто разделите оба уравнения на
C,
, и отношения станут следующими.
(12)
зарядка: ΔV = ΔV _f
1 — e ^{(−t / RC)}
(13)
нагнетание: ΔV = ΔV ₀ e ^{(−t / RC)}
Обратите внимание, что эти два уравнения похожи по форме на формулу.(3) Q = Q _f
1 — e ^{(−t / RC)}
и уравнение. 5
Q = Q ₀ e ^{(−t / RC)}
. График зависимости напряжения на конденсаторе от времени показан на рисунке 4 ниже.
Рисунок 4 : Напряжение на конденсаторе как функция времени
Переставив уравнение. (12) зарядка: ΔV = ΔV _f
1 — e ^{(−t / RC)}
получаем Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить
(15)
−ln
=.
График зависимости
−ln ((ΔV _f — ΔV) / ΔV _f)
от времени даст прямолинейный график с наклоном 1/ RC . Точно так же для процесса разряда формула. 13
разрядка: ΔV = ΔV ₀ e ^{(−t / RC)}
можно переписать, чтобы получить Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить
(17)
−ln
=.
График зависимости
−ln (ΔV) / ΔV ₀)
от времени даст прямолинейный график с наклоном 1/ RC .
Использование прямоугольной волны для имитации роли переключателя
В этом эксперименте вместо переключателя мы будем использовать генератор сигналов, который может генерировать периодические волновые формы различной формы, такие как синусоидальная волна, треугольная волна и прямоугольная волна. Также можно регулировать как частоту, так и амплитуду формы волны. Здесь мы будем использовать генератор сигналов для создания изменяющегося во времени напряжения прямоугольной формы на конденсаторе, аналогичного показанному на рис.5.
Рисунок 5 : Прямоугольная волна с периодом Τ
Выходное напряжение генератора сигналов изменяется назад и вперед от постоянного положительного значения до постоянного нуля вольт через равные интервалы времени t . Время
T = 2t
— это период прямоугольной волны. В течение первой половины цикла, когда напряжение положительное, это похоже на то, что переключатель находится в положении 1. Во второй половине цикла, когда напряжение равно нулю, это то же самое, что переключатель находится в положении 2. .Таким образом, прямоугольная волна, представляющая собой напряжение постоянного тока, которое периодически включается и выключается, служит одновременно аккумулятором и переключателем в схеме, показанной на рис.1. Генератор сигналов позволяет выполнять это переключение многократно, и можно оптимизировать сбор данных, регулируя частоту повторения. Эта частота будет зависеть от постоянной времени RC-цепи. Когда время t больше постоянной времени τ RC-цепи, у конденсатора будет достаточно времени для зарядки и разрядки, и напряжение на конденсаторе будет таким, как показано на рис.4.
Цель
В этом эксперименте (смоделированный компьютером) осциллограф будет использоваться для отслеживания разности потенциалов и, следовательно, косвенно заряда конденсатора. Измерения напряжения будут использоваться двумя разными способами для вычисления постоянной времени цепи. Наконец, конденсаторы будут подключены параллельно, чтобы проверить их эквивалентную емкость цепи.
Оборудование
- Печатная плата PASCO
- Сигнальный интерфейс с выходной мощностью
- Соединительные провода
- Программное обеспечение Capstone
Процедура
Распечатайте лист для этой лабораторной работы.Этот лист понадобится вам для записи ваших данных.
Настройка RC-цепи
Печатная плата RLC, которую вы будете использовать, среди других элементов состоит из трех резисторов и двух конденсаторов. См. Рис. 6 ниже. Теоретически вы можете использовать разные комбинации резисторов и конденсаторов. В этом эксперименте вы будете использовать резисторы 33 и 100 Ом и два конденсатора.
Рисунок 6 : Печатная плата RLC
1
Подключите крайнюю правую выходную клемму сигнального интерфейса к резистору 33 Ом в точке 2.
2
Чтобы обойти индуктор, подключите провод от точки 8 к точке 9.
3
Подключите точку 6 ко второй выходной клемме сигнального интерфейса, чтобы замкнуть цепь.
4
Подключите пробник напряжения к аналоговому каналу A.
5
Чтобы измерить напряжение на конденсаторе, подключите черный провод датчика напряжения к точке 6, а красный провод — к точке 9. Убедитесь, что земля интерфейса (вывод «-») подключена к той же стороне конденсатора, что и земля генератора сигналов (выход мощности).Подключение вашей схемы должно выглядеть так, как показано на рис.7.
Рисунок 7 : Принципиальная схема
Контрольная точка 1:
Попросите своего технического специалиста проверить соединения вашей цепи.
Процедура A: Постоянная времени контура
В этом эксперименте мы будем использовать компьютер для эмуляции осциллографа.
6
Откройте файл Capstone, связанный с этой лабораторной работой.Отобразится экран, аналогичный показанному на рис. 8.
Рисунок 8 : Начальный экран файла Capstone
7
Настройте генератор сигналов на создание положительной прямоугольной волны, выбрав положительную прямоугольную волну в окне генератора сигналов, как показано на рисунке 9 ниже.
Рисунок 9 : Окно генератора сигналов
8
Если это еще не было установлено при открытии файла Capstone, настройте генератор сигналов на создание прямоугольной волны амплитудой 5 В с частотой 20 Гц и установите смещение напряжения на 5 В.
9
Включите генератор сигналов, щелкнув ON в окне генератора сигналов.
10
Чтобы контролировать сигнал, нажмите кнопку START в главном окне. Потребуется отрегулировать шкалы времени и напряжения, чтобы получить кривую сигнала, подобную показанной на рис. 10. Это позволит вам наблюдать, как напряжение на конденсаторе изменяется в зависимости от времени. Для этого установите курсор на любое значение вдоль оси, которую вы хотите увеличить, и переместите курсор влево-вправо или вверх-вниз по мере необходимости.При правильном увеличении у вас будет только одна длина волны на графике, как на кривой на рис.10.
Рисунок 10 : Трасса сигнала
Если в любой момент вы захотите удалить записанный набор данных, нажмите кнопку Удалить последний прогон под графиком.
11
Нажмите кнопку Показать координаты из кнопок над графиком. См. Рис.11.
Рисунок 11 : Показать координаты
Когда активна функция отображения координат, показания напряжения и времени отображаются, куда бы вы их ни перетащили, как на рис.11. Используя этот инструмент, определите и запишите время начала (то есть, когда линия начала расти с 0 вольт) на рабочем листе.
12
Вычислите 63,2% максимального напряжения,
ΔV _f,
(которое должно быть 5 В), настройку амплитуды генератора сигналов. Используя Показать координаты , определите и запишите время начала (то есть, когда кривая начиналась вверх с 0 вольт) на рабочем листе.
13
Из этих двух значений времени определите и запишите время, необходимое для перехода сигнала от Δ V = 0 до Δ V = 0.632
ΔV _f.
Это ваше экспериментальное значение для RC .
14
В рабочем листе введите принятые значения сопротивления и емкости, которые напечатаны на печатной плате.
15
Вычислите экспериментальное значение емкости, используя свое экспериментальное значение для RC и принятое значение R . Запишите это на листе.
16
Вычислите ошибку в процентах, используя два значения емкости.См. Приложение Б.
Контрольная точка 2:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Процедура B: Расчет емкости графическими методами
17
Запишите максимальное напряжение на листе.
18
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, при которых Δ V = 1, 2, 3 и 4 вольта на восходящей части кривой.Запишите эту информацию в Таблицу данных 1 на рабочем листе. Примечание : Возможно, вам придется сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента.
19
Выполните необходимые вычисления, чтобы заполнить Таблицу данных 1.
20
Используя Excel, постройте график
−ln ((ΔV _f — ΔV) / ΔV _f)
в зависимости от времени. См. Приложение G.
21
Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.См. Приложение H.
22
По значению крутизны определите постоянную времени и емкость. Запишите эти значения на листе.
23
Вычислите ошибку в процентах между этим значением емкости и принятым значением.
Контрольная точка 3:
Попросите своего технического специалиста проверить ваши данные, график и расчеты, прежде чем продолжить.
Процедура C: Измерение эффективной емкости
Емкость увеличивается непосредственно при параллельном подключении конденсаторов и в обратном порядке при последовательном подключении.Это противоположно правилу для резисторов. Для конденсаторов, подключенных параллельно, эффективная емкость определяется выражением
(18)
C _eff = C ₁ + C ₂ + C ₃ +. . .
а для конденсаторов, включенных последовательно, эффективная емкость равна
24
Подключите второй конденсатор (330 мк Ф) параллельно конденсатору, используемому в процедуре A, подключив провод от точки 6 к точке 7.
25
Переключите резистор на резистор 10 Ом, переместив соединение из точки 2 в точку 1.
26
Запишите другой набор данных, щелкнув START в главном окне. После того, как вы записали второй набор данных, вы можете захотеть отобразить только эти данные на графике и удалить набор данных 1. Для этого удалите первый прогон (см. Примечание к шагу 10). На графике вы будете видеть только одну длину волны.
27
В этой части эксперимента вы будете рассматривать разрядную часть кривой. Теперь начальное напряжение
ΔV ₀
будет наивысшим значением пика перед тем, как график начнет спадать.Запишите это значение на листе.
28
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, при которых Δ V = 1, 2, 3 и 4 вольта на спадающей части кривой. ( Примечание : вам может потребоваться большое увеличение, чтобы получить необходимую точность при использовании интеллектуального инструмента). Запишите эту информацию в Таблицу данных 2 на рабочем листе.
29
Выполните необходимые вычисления, чтобы заполнить Таблицу данных 2.
30
Используя Excel, постройте график зависимости
−ln (ΔV) / ΔV ₀)
от времени.
31
Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.
32
По значению наклона определите постоянную времени и запишите это значение в рабочий лист.
33
Вычислите
C _eff,
эффективную емкость параллельной комбинации, используя принятое значение для R .
34
Сравните это экспериментальное значение с тем, что вы получили из уравнения.18
C _eff = C ₁ + C ₂ + C ₃ +. . .
и принятые значения емкости путем вычисления ошибки в процентах между двумя значениями.
Контрольная точка 4:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Copyright © 2012 Advanced Instructional Systems, Inc. и Государственный университет Северной Каролины | Кредиты
Когда конденсатор хранит больше энергии, последовательное или параллельное соединение?

Эй, в этой статье мы узнаем, когда конденсатор будет хранить больше энергии при последовательном или параллельном подключении.Эта статья расширит ваши знания об основах конденсаторов. Если вы хотите стать гением, сначала очистите свои базовые знания в области электротехники. Однако давайте узнаем.
Конденсатор — это пассивное устройство, которое может накапливать электрическую энергию в виде заряда. Формула накопления энергии конденсатора:

здесь C = емкость
V = приложенное напряжение на конденсаторе
Таким образом, накопление электрической энергии зависит от значения емкости конденсатора и квадрата приложенного напряжения.
При последовательном соединении 4-х конденсаторов общее значение емкости составит
.
При параллельном соединении 4-х конденсаторов общее значение емкости составит:
Так что убирается, что при параллельном подключении значение емкости будет больше.
Поскольку накопление энергии зависит от значения емкости и напряжения, конденсатор будет накапливать гораздо больше энергии при параллельном соединении, чем при последовательном соединении для того же уровня приложенного напряжения, потому что при параллельном соединении значение емкости больше.

Поясним это на примере
. Предположим, мы берем 4 одинаковых конденсатора номиналом 4 фарада, 4 вольта.
Последовательное подключение, накопитель энергии,

При параллельном подключении накопитель энергии,
Итак, теперь вы можете понять, что при параллельном соединении конденсатор может хранить, сколько энергии, чем при последовательном соединении.

Теперь, если мы подумаем практически, когда несколько конденсаторов подключены параллельно, все они будут иметь одинаковое напряжение, поэтому каждый из них будет накапливать энергию в соответствии с их значением емкости, а чистый накопитель энергии будет суммой всех отдельных накопителей энергии. .
Когда несколько конденсаторов соединены последовательно, все они не будут получать одинаковое напряжение, потому что напряжение будет падать в зависимости от распределения номиналов конденсаторов. Таким образом, они не могут заряжаться полностью или не могут хранить максимум энергии.
Таким образом, можно сделать вывод, что конденсатор будет хранить больше энергии при параллельном соединении, чем при последовательном соединении.

StudyPort.Ru — Механические и электромагнитные колебания

Переменный электрический ток

Задачи по физике и математике с решениями и ответами

Задача по физике — 4099

Задача по физике — 4101

Задача по физике — 4102

Задача по физике — 4103

Задача по физике — 4104

Задача по физике — 4106

Задача по физике — 4107

Задача по физике — 4108

Задача по физике — 4109

Задача по физике — 4110

Задача по физике — 4111

Задача по физике — 4112

Задача по физике — 4113

Задача по физике — 4114

Цепь «резистор – конденсатор включены последовательно»

В цепи последовательно подключены конденсатор емкостью. Соединение конденсаторов

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

Примеры решения задач

Основные тезисы

Зачем нужно включать конденсаторы параллельно

Реактивная мощность сети

Схема соединения компенсирующих установок

Особенности конденсаторной защиты

Разряд конденсаторов

Параллельное включение конденсаторов в цепь

Последовательное включение конденсаторов в цепь

Смешанное включение емкостных накопителей в схему

Вывод

Конденсатор в цепи переменного тока

Емкостное сопротивление конденсатора

Похожие материалы:

Добавить комментарий

цепь переменного тока частотой

и параллельные — Inst Tools

C

C

Кривая разряда конденсатора, подключенного последовательно с резистором, показана ниже, если…

Полностью разряженный идеальный конденсатор соединен последовательно с резистором и батареей. Как…

Резистор 11,4 кОм и конденсатор включены последовательно и затем 12.0 В …

29.(10 баллов) Конденсатор и резистор a25 ko подключены последовательно к батарее 10v ….

Конденсатор подключен последовательно к резистору с сопротивлением 1,2 кОм и …

48. Если конденсатор 5,6 пФ, конденсатор 49,3 пФ и 35,5 пФ конденсаторы все подключены в …

10. Резистор и конденсатор подключены последовательно к источнику напряжения.В момент t …

Незаряженный конденсатор и резистор подключены последовательно к источник ЭДС. Если…

конденсаторов последовательно и параллельно с их примерами

Последовательные и параллельные конденсаторы

Конденсаторы серии

Пример

Параллельные конденсаторы

Пример

Примеры

Незаряженный конденсатор соединен последовательно с батареей, переключателем и резистором, как показано на рис.6.1.

— Энергия, запасенная в конденсаторах, соединенных последовательно Суперконденсатор

Сеть обмена стеков

Лаборатория 4 — Зарядка и разрядка конденсатора

Введение

Обсуждение принципов

Зарядка и разрядка

Постоянная времени

Использование прямоугольной волны для имитации роли переключателя

Цель

Оборудование

Процедура

Настройка RC-цепи

Процедура A: Постоянная времени контура

Процедура B: Расчет емкости графическими методами

Процедура C: Измерение эффективной емкости

Когда конденсатор хранит больше энергии, последовательное или параллельное соединение?

Читайте также

Светодиодная лента 220в подключение: Лента RGB 220V — Устройство, монтаж светодиодной RGB ленты 220В

Схема подключения электродвигателя 220 с конденсатором: Схема Подключения Электродвигателя 220 — tokzamer.ru

Как от выключателя провести розетку схема подключения: Как подключить розетку от выключателя: можно ли запитать, последствия

Добавить комментарий Отменить ответ