Мощность в цепи переменного тока
Мощность в цепи переменного тока.
В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теориикомплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ(сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность
Единица измерения — ватт (W, Вт).
Среднее за период
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
studfiles.net
Мощность в цепях переменного тока
В цепях переменного тока различают три вида мощностей: активную Р, реактивную Q и полную S.
Активная мощность вычисляется по формуле:
(2.20)
Активную мощность потребляет резистивный элемент. Единица
измерения активной мощности называется Ватт (Вт), производная единица – килоВатт (кВт), равная 103 Вт.
Реактивная мощностьвычисляется по формуле:
(2.21)
Реактивная мощность потребляется идеальным индуктивным и
емкостным элементами. Единица измерения реактивной мощности называется Вольт-Ампер реактивный (Вар), производная единица – килоВАр (кВАр), равная 103 ВАр.
Полная мощность потребляется полным сопротивлением и обозначается буквой S:
S= (2.22)
Единица измерения полной мощности называется ВА (Вольт-Ампер), производная единица – килоВольт-Ампер (кВА), равная 103 ВА.
По сути, размерность у всех выше перечисленных единиц измерения одинакова – . Разные название этих единиц нужны, чтобы различать эти виды мощности.
Проявляются различные виды мощности по-разному. Активная мощность необратимо преобразуется в другие виды мощности (например, тепловую, механическую). Реактивная мощность обратимо циркулирует в электрических цепях: энергия электрического поля конденсатора преобразуется в энергию магнитного поля, и наоборот. «Извлечь» реактивную мощность с «пользой для дела» невозможно.
Из формул (2.19) – (2.21) следует, что между активной, реактивной и полной мощностью имеет место соотношение:
(2.23)
Соотношение между P, Q и S можно интерпретировать как соотношение сторон прямоугольного треугольника (вспомните треугольник сопротивлений, треугольник напряжений – все эти треугольники подобны).
Рис. 2.10
Из рис. 2.10 видно, что cosφ = (2.24)
Отсюда вытекает определение одной из основных характеристик цепей переменного тока – коэффициента мощности.Специального обозначения он не получил.
Коэффициент мощности показывает, какую долю полной мощности составляет активная мощность.
Желательно, чтобы коэффициент мощности цепи был как можно больше, т.е. приближался к 1. Реально предприятия электрических сетей устанавливают такое ограничение для промышленных предприятий : соs φ = (0,92…..0,95). Достигать значений соs φ >0,95 рискованно, так как разность фаз φ при этом может скачком перейти от положительных значений к отрицательным, что вредно для электрооборудования. Если соsφ < 0,92, предприятия подвергаются штрафу.
Если коэффициент мощности оказывается мал, его необходимо повышать. График функции соs φ имеет вид монотонно убывающей функции в интервале от 00 до 900. Следовательно, увеличить соsφ – значит уменьшить разность фаз , то есть уменьшить (ХL-ХС).
Если влиять на (ХL-ХС), меняя С и L, то это приведет к увеличению тока в последовательной цепи и изменению режима работы оборудования, по этому такой способ практически не применяется. В следующем разделе рассмотрен другой способ повышения коэффициента мощности.
ЛЕКЦИЯ 4.
2.6 Цепь переменного тока с параллельным соединением ветвей.
Рассмотрим электрическую цепь с двумя параллельными
ветвями (рис. 2.11). Полученные выводы распространим на цепь с любым количеством ветвей. К цепи, содержащей две параллельные ветви, включающие активные, индуктивные и емкостные элементы (R1, L1, C1 и R2, L2, C2 cоответственно), подводится переменное напряжение U частоты f.
Прямая задача: Заданы все Обратная задача: Заданы свойства
входящие в цепь элементы. цепи. Найти неизвестные элементы
Найти все токи и разности цепи (эта задача решена в лабора-
фаз. торной работе Ц-5)
Решим прямую задачу, то есть найдем токи I1, I2 и общий ток I .
 |
Рис. 2.11.Электрическая цепь с двумя параллельными
ветвями
Из второго закона Кирхгофа следует, что напряжения на параллельных участках цепи одинаковы :
U1 = U2 = U (2.25)
На основании закона Ома найдем токи I1 и I2 :
; (2.26)
Найдем также разности фаз тока и напряжения для каждой ветви:
(2.27)
На основании первого закона Кирхгофа применительно к узлу А можно записать:
= + (2.28)
Таким образом, для определения тока I необходимо векторно сложить токи I1 и I2. В качестве опорного вектора удобно выбрать вектор напряжения .
Предположим, что при расчете разностей фаз тока и напряжения в ветвях цепи оказалось, что φ1>0, а φ2 <0. Строим вектор под углом φ1 к вектору , и вектор под углом φ2 к вектору . Графически складываем эти векторы (см. рис.2.12). Величина тока определяется длиной полученного вектора с учетом выбранного масштаба. Разность фаз неразветвленного участка цепи определяется углом между векторами и
 |
Рис. 2.12
Активное сопротивление в цепи переменного тока
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.
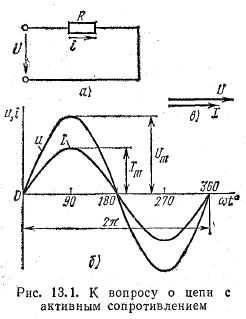

Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R = U2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
electrikam.com
Переменный ток, мощность переменного тока
В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон – что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав.
Вступление
Переменный ток значительно эффективнее использовать для передачи энергии. Обсудим, как вычисляется мощность переменного тока, ведь переменный ток — это мощность, которая передается на расстоянии.

Вычисление мощности
Допустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому закону, а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор.

В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача – установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу:
(U(t) = U(m) cos w t)
Нагрузка – самое произвольное понятие.
Сила тока в нагрузке и, соответственно, в проводах, которые подводят мощность к нагрузке, будет меняться. Частота колебаний тока выйдет такая же, как частота колебаний напряжения, но существует также понятие сдвига фазы в промежутках колебаний тока и напряжения:
(I (t) = I (m) cos w t)
Дальнейшие вычисления
Показатели мощность будут равны произведению:
P (t) = I (t) U (t)
Этот закон остаётся справедливым как для переменного тока с мощностью, которую необходимо было вычислить, так и для постоянного.
(I (t) = I (m) cos (wt + J)
Мощность переменного тока при переменном токе вычисляется при помощи трех формул. Представленные выше расчеты относятся к основной формуле, которая вытекает из определения силы тока и напряжения.
Если участок цепи однородный и можно пользоваться законом Ома для этого участка цепи, здесь такие вычисления использовать нельзя, так как нам неизвестен характер нагрузки.
Определяем результат
Подставим показатели силы тока и напряжения в данную формулу, и тут нам на помощь придет знание тригонометрических формул:
cosa cosb = cos(a +b) + cos(a — b) / 2
Воспользуемся этой формулой и получим вычисления:
P(t) = I(m) U (m) cos (wt + J) cos wt
После упрощения результатов получим:
P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ
Посмотрим на эту формулу. Здесь первое слагаемое зависит от времени, меняясь по гармоническому закону, а второе является величиной постоянной. Мощность переменного тока при переменном токе складывается из постоянной и переменной составляющей.
Если мощность положительна, значит, нагрузка потребляет энергию от генератора. При отрицательной мощности, наоборот, нагрузка раскручивает генератор.
Найдем среднее значение мощности за период времени. Для этого работу, совершенную электрическим током, поделим на величину этого периода.
Мощность трехфазной цепи переменного тока– это сумма переменной и постоянной составляющих.
Активная и реактивная мощность
Многие физические процессы можно представить аналогиями друг друга. На этой базе постараемся раскрыть суть понятий активной мощности цепи переменного тока и реактивной мощности цепи переменного тока.
Стакан представляет собой электростанцию, вода – электроэнергию, трубочка – кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.

Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная – энергия индуктивности и ёмкости.
Покажем это на конденсаторе, ёмкости и стакане. Активными называются те элементы, которые способны преобразовывать энергию в другой вид. К примеру, в тепло (утюг), свет (лампочка), движение (мотор).

Реактивная энергия
При имитации реактивной энергии напряжение увеличивается, и ёмкость заполняется. При уменьшении напряжения накопленная энергия возвращается по проводу обратно в электростанцию. Так повторяется циклически.
Сам смысл реактивных элементов заключается в накоплении энергии, которая потом обратно возвращается или используется для других функций. Но никуда не тратится. Основной минус этой производной в том, что виртуальный трубопровод, по которому как-бы идет энергия, имеет сопротивление, и на нем тратится процент экономии.
Полной мощности цепи переменного тока требуются затраты определенного процента усилий. По этой причине на крупных предприятиях идет борьба с реактивной составляющей полной мощности.
Активная мощность – это та энергия, которая потребляется или преобразуется в другие виды – свет, тепло, движение, то есть в какую-либо работу.
Опыт
Для опыта возьмем стакан, которые служит активной составляющей мощности. Он представляет часть энергии, которую необходимо потребить или преобразовать в другой вид.
Часть энергии воды можно выпить. Полная мощность переменного тока коэффициент мощности — это показатель, который складывается из реактивной и активной составляющих: энергии, текущей по водопроводу и той, которая преобразуется.
Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент – конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это – полная мощность.

Преобразование мощности
Активная мощность преобразовывается в другой вид энергии, к примеру, в механическое движение или нагрев. Реактивная мощность, которая накапливается в реактивном элементе, позднее возвращается назад.
Полная мощность – это геометрическая сумма активной и реактивной мощности.
Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон – это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.
Косинус представлен отношением, которое предопределяет длина прилегающего катета относительно длины гипотенузы.

Синусом угла является вид отношения, которое составляет длина противолежащего катета относительно гипотенузы. Зная угол и длину любой из сторон, можно вычислить все остальные углы и длину.
В данном треугольнике можно взять длину гипотенузы и прилежащего катета и вычислить этот угол с помощью тригонометрической функции косинусов. Мощность постоянного и переменного тока вычисляется с применением таких знаний.
Для вычисления угла можно применять обратную функцию от косинуса. Получим необходимый результат вычислений. Чтобы вычислить длину противолежащего катета, можно вычислить синус и получить соотношение противолежащего катета к гипотенузе.
Вычисление мощности цепи переменного тока по формуле предложено в этом описании.
В цепях постоянного тока мощность равна произведению напряжения на ток. В цепях переменного тока также работает это правило, но его трактовка будет не совсем правильной.
Индуктивность
Помимо активных элементов, действуют реактивные элементы – индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть.
Активная мощность, которую имеет трехфазная цепь переменного тока, может выполнять полезную работу, а реактивная не выполняет никакой полезной работы, а только расходуется на преодоление реактивных сопротивлений индуктивности и ёмкости.
Попытаемся выполнить опыт. Возьмем источник переменного напряжения на 220 Вт с частотой 50Гц, датчик напряжения и тока источника, нагрузка, которая составляет активное 1Ом и индуктивное 1ОМ сопротивление.
Также есть выключатель, который подключится в определенный момент, активно-ёмкостная нагрузка. Запустим такую систему. Для удобства рассмотрения введем коэффициенты поправки напряжения.
Запускаем устройство
При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол – коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах.
Угол зависит от величины индуктивного сопротивления нагрузки. Когда сдвиг уменьшается, увеличивается ток сети. Представим, что сопротивление катушки уменьшить нельзя, но надо улучшить косинус сети. Для этого и нужны конденсаторы, которые, в отличие от индуктивности, опережают напряжение и могут взаимно компенсировать реактивную мощность.
В момент подключения конденсаторной батареи за 0,05 с происходит резкое снижение косинуса, практически до 0. Также идет резкое снижение тока, который без конденсаторной батареи имел амплитудное значение намного ниже, чем при включении конденсаторной батареи.
Фактически подключением конденсаторной батареи удалось снизить мощность тока, потребляемого из сети. Это является положительным моментом и позволяет снижать ток сети и экономить на сечение кабелей, трансформаторах, силовом оборудовании.
Если произойдет отключение индуктивной нагрузки и останется активное сопротивление, произойдет процесс, когда косинус сети после подключения конденсаторной батареи приведет к фазовому сдвигу и большому скачку тока, который идёт в сеть, а не потребляется из неё, что происходит в генераторном режиме реактивной мощности.
Итоги
Активная мощность опять остается постоянной и равна нулю, так как нет индуктивного сопротивления. Начался процесс генерации реактивной мощности в сеть.
Следовательно, компенсировать реактивную мощность на крупных предприятий, потребляемых колоссальные её объёмы из энергосистем, — это приоритетная задача, так как это позволяет экономить не только на электрооборудовании, но и на затратах по оплате самой реактивной мощности.
Такое понятие регламентируется, и предприятие оплачивает и потребляемую, и генерируемую мощность. Здесь устанавливаются автоматические компенсаторы, обеспечивающие поддержку баланса мощности на заданном уровне.
При отключении мощной нагрузки, если не выключить из сети компенсирующее устройство, будет происходить генерация реактивной мощности в сеть, что создаст проблемы в энергосистеме.
В быту компенсация реактивной мощности не имеет смысла, так как потребление мощности здесь значительно ниже.
Активная и реактивная мощность – понятия школьного курса физики.
fb.ru
