Что такое полная, активная и реактивная мощность?
ЧТО ТАКОЕ ПОЛНАЯ, АКТИВНАЯ И РЕАКТИВНАЯ МОЩНОСТЬ? ОТ СЛОЖНОГО К ПРОСТОМУ.
В повседневной жизни практически каждый сталкивается с понятием «электрическая мощность», «потребляемая мощность» или «сколько эта штука «кушает» электричества». В данной подборке мы раскроем понятие электрической мощности переменного тока для технически подкованных специалистов и покажем на картинке электрическую мощность в виде «сколько эта штука кушает электричества» для людей с гуманитарным складом ума :-). Мы раскрываем наиболее практичное и применимое понятие электрической мощности и намеренно уходим от описания дифференциальных выражений электрической мощности.
ЧТО ТАКОЕ МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА?
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для практических расчётов бесполезна. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность (Real Power)
Единица измерения — ватт (русское обозначение: Вт, киловатт — кВт; международное: ватт -W, киловатт — kW).
Среднее за период Τ значение мгновенной мощности называется активной мощностью, и
выражается формулой:
В цепях однофазного синусоидального тока , где υ и Ι это среднеквадратичные значения напряжения и тока, а φ — угол сдвига фаз между ними.Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S, активная связана соотношением .В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность (Reactive Power)
Единица измерения — вольт-ампер реактивный (русское обозначение: вар, кВАР; международное: var).
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними:
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью P соотношением: .Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулойреактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения
Полная мощность (Apparent Power)
Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А, ВА, кВА-кило-вольт-ампер; международное: V·A, kVA).
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; соотношение полной мощности с активной и реактивной мощностями выражается в следующем виде: где P — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q›0, а при ёмкостной Q‹0).Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Визуально и интуитивно-понятно все вышеперечисленные формульные и текстовые описания полной, реактивной и активной мощностей передает следующий рисунок 🙂

Специалисты компании НТС-групп (ТМ Электрокапризам-НЕТ) имеют огромный опыт подбора специализированного оборудования для построения систем обеспечения жизненно важных объектов бесперебойным электропитанием. Мы умеем максимально качественно учитывать множество электрических и эксплуатационных параметров, которые позволяют выбрать экономически обоснованный вариант построения системы бесперебойного электропитанияс применением стабилизаторов напряжения, топливных электростанций, источников бесперебойного питания и др. сопутствующего оборудования.
© Материал подготовлен специалистами компании НТС-групп (ТМ Электрокапризам-НЕТ) с использованием информации из открытых источников, в т.ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org
electrokaprizam.net
Активная и реактивная мощность. За что платим и работа
Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).
Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.
В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.
Активная и реактивная мощность
Активная мощность
Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.
Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность . Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).
Реактивная мощность
Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).
Реактивная емкостная мощность
Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке. Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.
Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.
Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.
Реактивная индуктивная мощность
Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.
На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.
Реальные потребители электрической энергии и полная электрическая мощность
Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи. Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.
Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.
Таинственный «косинус фи»
Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.
В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.
За что платим?
И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».
Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.
Потребитель находит возможность платить меньше
Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.
Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.
Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.
Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.
Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.
Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.
Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.
Похожие темы:
electrosam.ru
2.4. Активная, реактивная и полная мощности. Баланс мощностей
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть напряжение и ток являются синусоидальными функциями времени:
.
Получим выражение для мгновенной мощности: (2.29)
Из
(2.29) следует, мгновенная мощность
изменяется с частотой 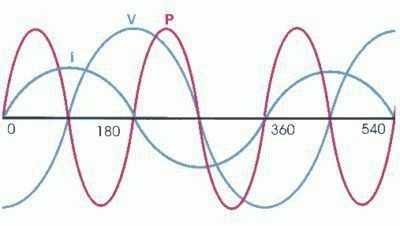 ,
в два раза превышающей частоту тока и
напряжения.
,
в два раза превышающей частоту тока и
напряжения.
Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:
(2.30)
При выводе (2.30) учтено равенство
Учитывая из треугольника сопротивлений (рис.2.15) соотношение и из треугольника проводимостей (рис.2.16), получаем из (2.30) следующие выражения для активной мощности:
(2.31)
Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой.
Множитель  называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения
называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения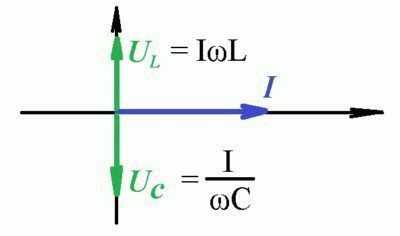 остается одной из основных задач
энергосбережения.
остается одной из основных задач
энергосбережения.
Рассмотрим идеальные реактивные элементы (индуктивность и емкость). Активная мощность в этих элементах равна нулю, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90 o и
В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
Преобразуем выражение (2.29) для мгновенной мощности:
где — мгновенная мощность в активном сопротивлении;
— мгновенная мощность в реактивном элементе (в индуктивности или в емкости).
Максимальное или амплитудное значение мощности p2 называется реактивной мощностью:
Q =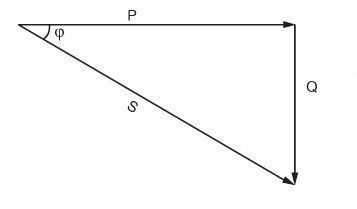 (2.32)
(2.32)
Амплитудное значение суммарной мощности p = p1 + p2 называется полной мощностью. Полная мощность, измеряемая в вольт-амперах (ВА), равна произведению действующих значений напряжения и тока:
. (2.33)
Возьмем треугольник сопротивлений (рис.2.15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 2.17).
Рис. 2.17
Из треугольника мощностей получим соотношения между мощностями P
, Q, S: Q
= ,
,
 .
(2.34)
.
(2.34)
При
расчете электрических цепей комплексным
методом используют выражение комплексной
мощности, равное произведению комплексного
напряжения на сопряженный комплекс
тока. Для цепи, имеющей
активно-индуктивный характер, ток по
фазе отстает от напряжения на угол 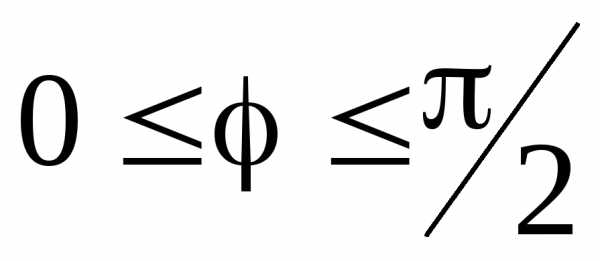
 ,
,
где
—
комплекс напряжения;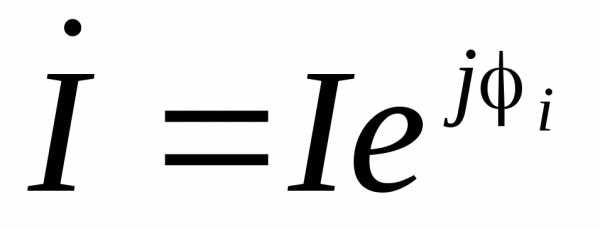 — комплекс тока;
— комплекс тока;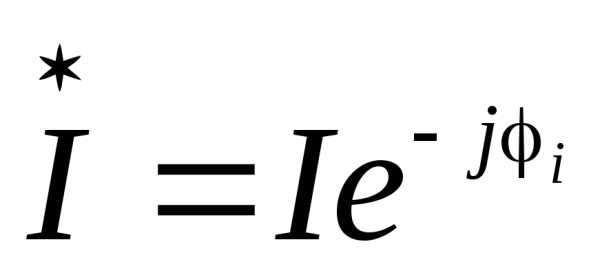 — сопряженный комплекс тока;- сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
— сопряженный комплекс тока;- сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
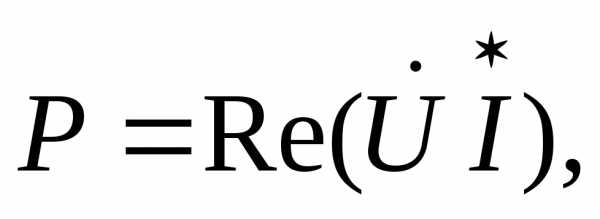 Q =
Q = 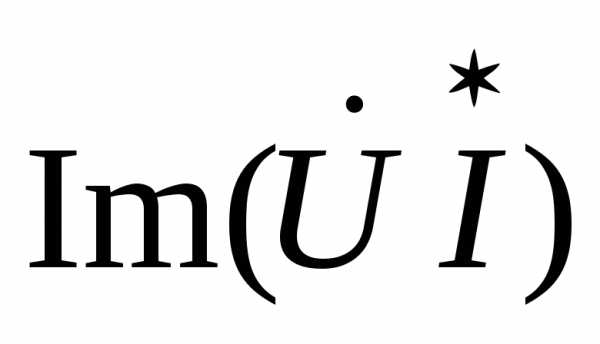 . (2.35)
. (2.35)
Для цепи, имеющей активно-емкостной характер, ток по фазе опережает напряжение .
Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, — положительна, а в цепи с емкостным характером — отрицательна.
При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (2.31)-(2.33), (2.35) для источника имеют следующий вид:
Q=
; 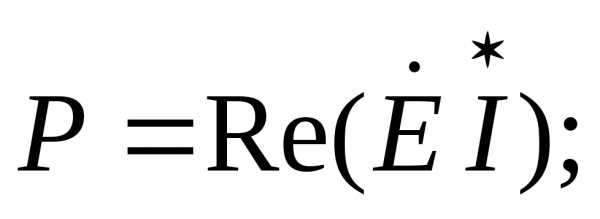 Q =
Q = 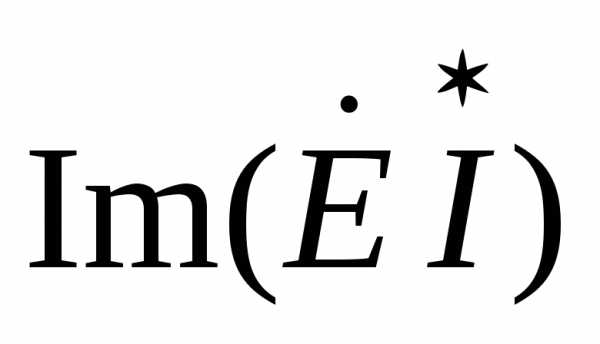 .
(2.36)
.
(2.36)
Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.
Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (рис.2.7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.
Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:
, 
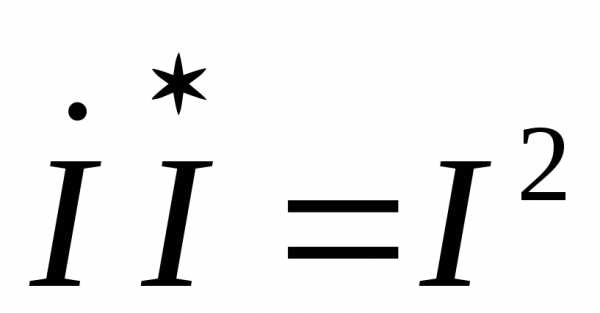 ,
,где — результирующее реактивное сопротивление.
,
где — полная комплексная, активная и реактивная мощности источника питания.
,
где активная и реактивная мощности, потребляемые элементами схемы.
Получим уравнение для комплексных мощностей источника и приемника:
(2.37)
Равенство (2.37) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (2.37) можно записать в следующей форме:
. (2.38)
Из следует (2.38), что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками
.Рассмотрим условие передачи источником максимальной мощности при заданном коэффициенте мощности приемника.
В
схеме на рис. 2.18 обозначены :  — полное, активное и реактивное
сопротивления источника ЭДС,
— полное, активное и реактивное
сопротивления источника ЭДС,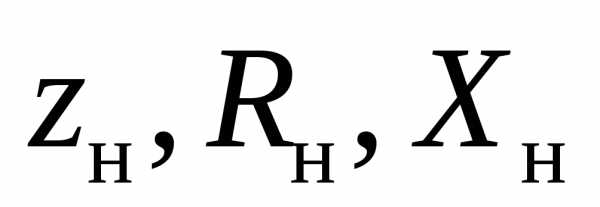 — полное, активное и реактивное
сопротивления нагрузки.
— полное, активное и реактивное
сопротивления нагрузки.

Рис. 2.18
Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке,
. (2.39)
Активная
мощность, развиваемая генератором 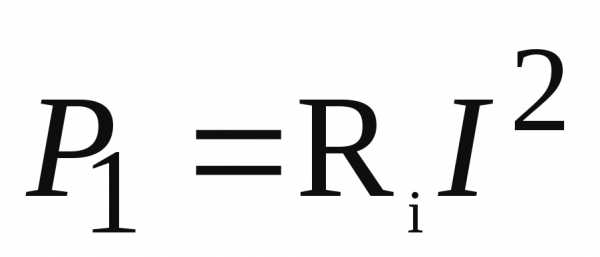
 .
.
Из
(2.39) видно, что выделяемая в нагрузке
мощность будет максимальной, когда
знаменатель минимален. Последнее имеет
место при
,
т.е. при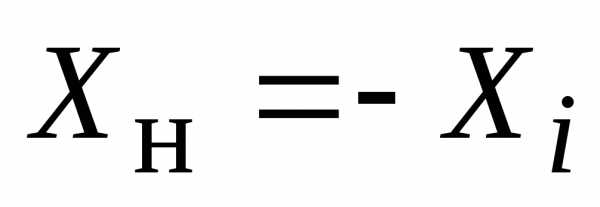 .
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
.
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
 .
(2.40)
.
(2.40)
Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность:
.
отсюда 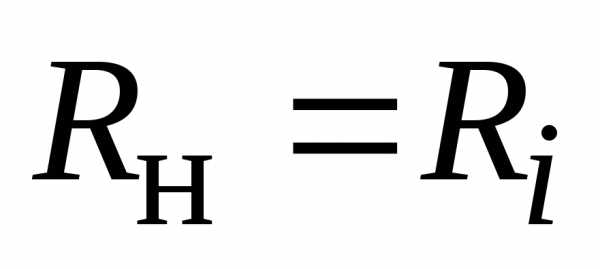
От источника к нагрузке передается наибольшая мощность, когда
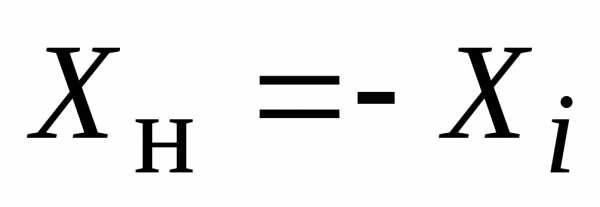 ;
;
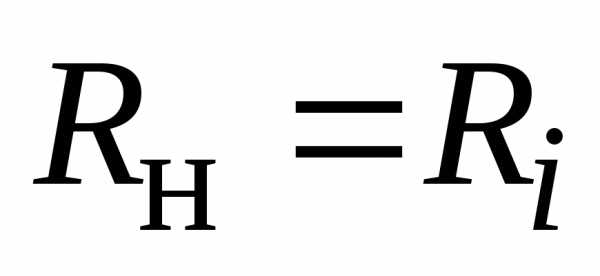 .
(2.41)
.
(2.41)
Величина наибольшей мощности
. (2.42)
Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (2.41) — согласованием нагрузки с источником.
В согласованном режиме величина КПД составляет:
 .
.
Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.
studfiles.net
активная, реактивная, полная (P, Q, S), коэффициент мощности (PF)
Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
 |
 |
Мощность не всех приборов указана в Вт, например:
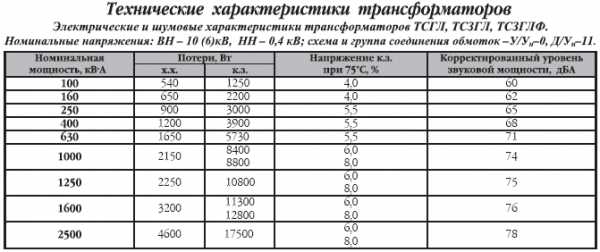
- Мощность трансформаторов указывается в ВА:
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение) - Мощность конденсаторов указывается в Варах:
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение) - Примеры других нагрузок — см. приложения ниже.
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
2. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
|
|
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
| Однофазные автотрансформаторы |
|
||
| TDGC2-0.5 kVa, 2A | АОСН-2-220-82 | ||
| TDGC2-1.0 kVa, 4A | Латр 1.25 | АОСН-4-220-82 | |
| TDGC2-2.0 kVa, 8A | Латр 2.5 | АОСН-8-220-82 | |
| TDGC2-3.0 kVa, 12A | |||
| TDGC2-4.0 kVa, 16A | |||
| TDGC2-5.0 kVa, 20A | АОСН-20-220 | ||
| TDGC2-7.0 kVa, 28A | |||
| TDGC2-10 kVa, 40A | АОМН-40-220 | ||
| TDGC2-15 kVa, 60A | |||
| TDGC2-20 kVa, 80A | |||
http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
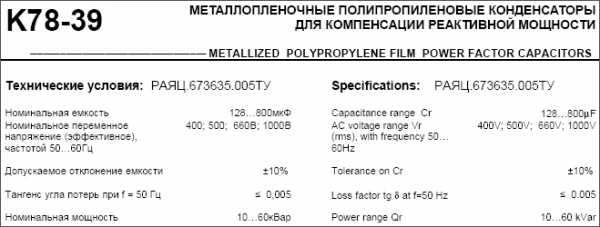 |
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
 |
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
 |
http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ)
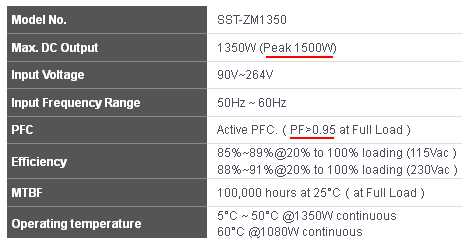 |
http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.
Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др.) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
- К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
- К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик). Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
- Полное сопротивление (импеданс) Z=R+iX
- Полная мощность S=P+iQ
- Диэлектрическая проницаемость e=e’+ie»
- Магнитная проницаемость m=m’+im»
- и др.
Вопрос 2:
На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
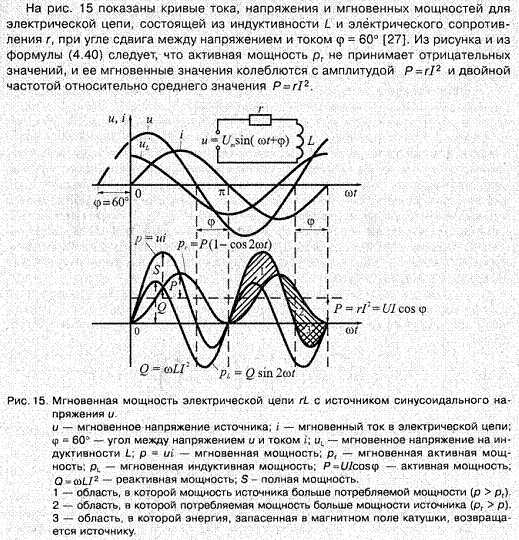 |
Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
 |
См. дополнительную литературу, например:
[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН
www.xn--80aacyeau1asblh.xn--p1ai
Тема 4 Активная, реактивная и полная мощности. Коэффициент мощности
1.
Активная мощность при r
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200 В,
равна
В,
равна
1) P = 2000 Вт 2) Р = 200 Вт
3) Р = 100 Вт 4) Р = 20 Вт
2. Формула
для определения мгновенной мощности  переменного тока
переменного тока
3. Выражение для энергии WL, накопленной в поле индуктивного элемента, имеет вид
4) 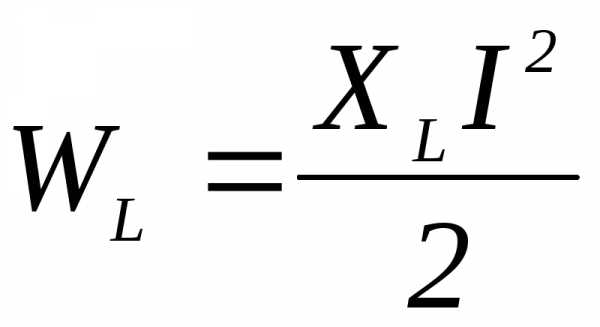
4. Формула полной мощности имеет вид
1) 2)
3) 4)
5. Формула активной мощности цепи имеет вид
1) 2)
3) 4)
6. Полная
комплексная мощность  для цепи из последовательно соединенныхR,L,Cопределяется по формуле
для цепи из последовательно соединенныхR,L,Cопределяется по формуле
1) 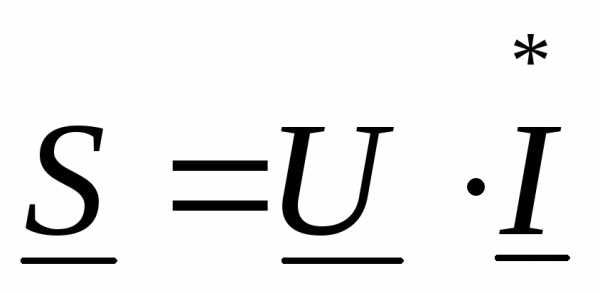 2)
2)
3)4)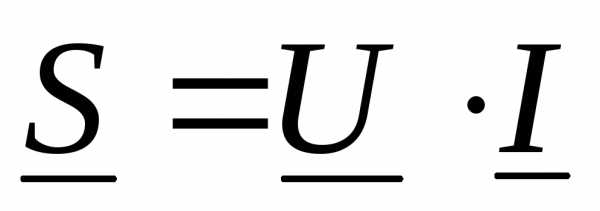
7. Формула реактивной мощности катушки индуктивности имеет вид
1) 2) 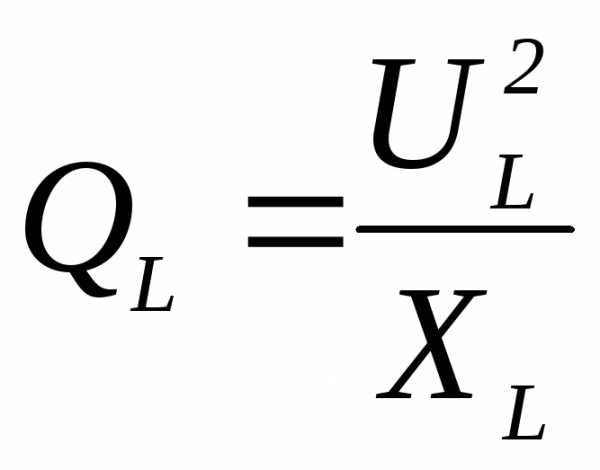
3) 4) 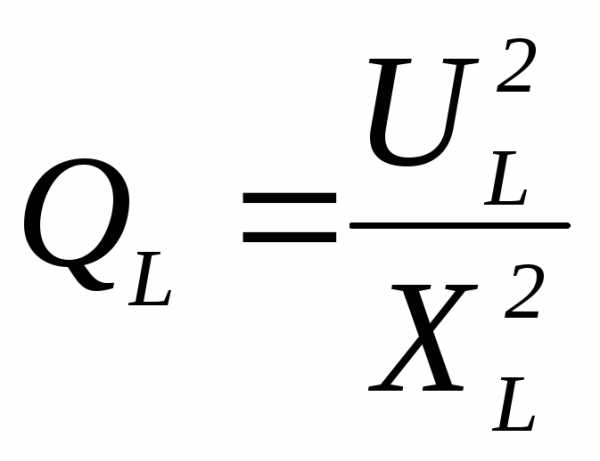
8. Формула реактивной мощности QCконденсатора С в цепи имеет вид
1) 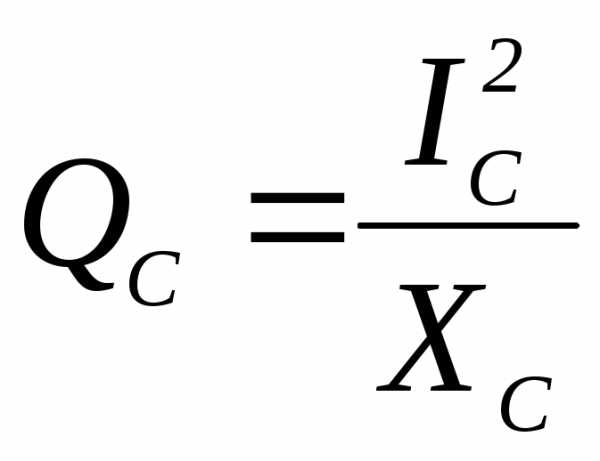 2)
2)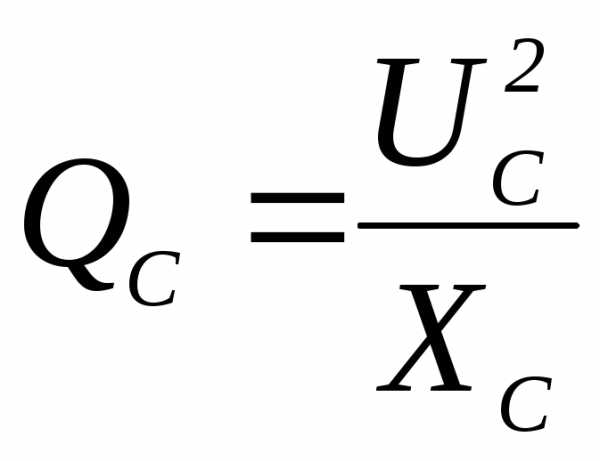
3) 4)
9. Выражение активной мощности Р пассивного двухполюсника в цепи переменного тока имеет вид
1)2)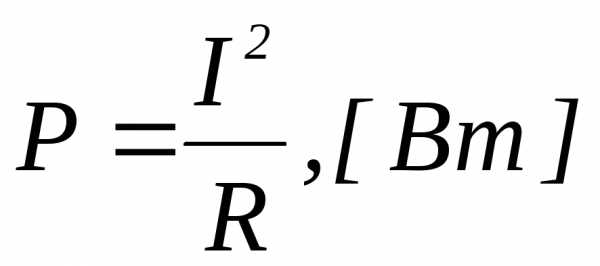
3) 4)
10. Каким свойством обладают индуктивные элементы схем
1) поглощать энергию2) создавать энергию
3) запасать энергию в виде электрического поля
4) запасать энергию в виде магнитного поля
11.Полная мощность цепи переменного тока
1)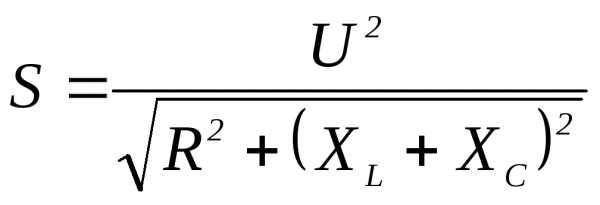 2)
2) 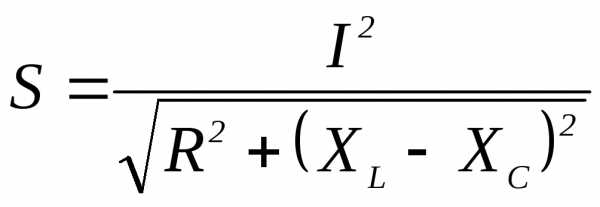
3) 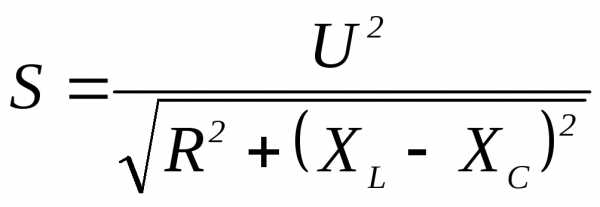 4)
4)
12. Каким свойством обладают резистивные элементы схем
1) создавать энергию
2) запасать энергию в виде электрического поля
3) запасать в виде энергию магнитного поля
4) преобразовывать электрическую энергию
13. Формула для определения реактивной мощности QLна индуктивностиLв цепи переменного тока
1) 2)  3) 4)
3) 4) 
14. Формула, показывающая связь между активной, реактивной и полной мощностью
1) 2)
3) 4)
15. Формула, показывающая связь между реактивной и полной мощностью
1) Q=S tg 2) Q=S/sin 3) Q=S/tg 4) Q=S sin
16. Выражение полной мощности S пассивного двухполюсника в цепи переменного тока имеет вид

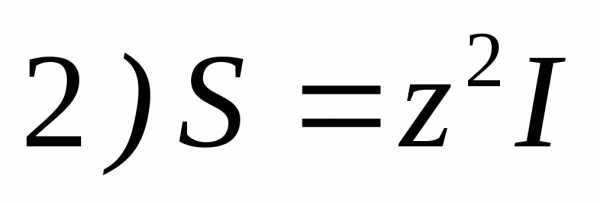
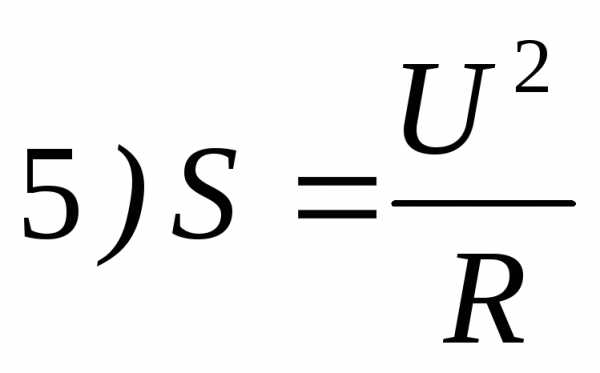
17.
Реактивная мощность при r
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200 В,
равна
В,
равна
1) Q=20 вар 2) Q= 2000 вар
3) Q= 200 вар 4) Q= 2вар
18.
Полная мощность приr
= XC = 20 Ом и показаниях амперметра 10 А,
вольтметра 200 В,
равна
В,
равна
1) S =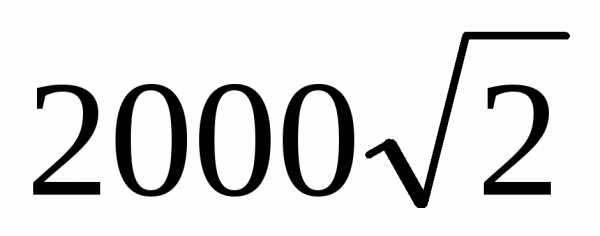 ВА 2)S=
ВА 2)S=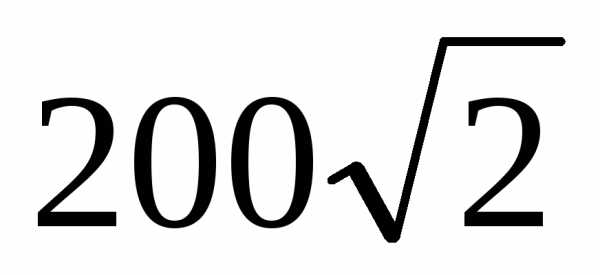 ВА 3) 200 ВА
4) 2000 ВА
ВА 3) 200 ВА
4) 2000 ВА
19. Активная мощность цепи переменного тока
1) 2)
3) 4)
20. Реактивная мощность цепи переменного тока
1) 2)
3) 4)
5. Частотные свойства электрической цепи. Резонанс
1. Резонансная частота0колебательного контура

2. Резонансная частота — 0 колебательного контура
3. В режиме резонанса, приU=90 В,r=5 Ом,ХL =ХC= 20 Ом, амперметр покажет
1) I=18A2)I=2A3)I=4,5A4)I=6A
4. В режиме резонанса, приU=90 В,R=5 Ом,Ом, вольтметр покажет:
1) U=90 В 2) U=10 В 3) U=30 В 4) U=22,5 В
5. В режиме резонанса, при U=90 В,R=5 Ом, 20 Ом, вольтметр покажет:
1) U=360 В 2) U=180 В 3) U=40 В 4) U=120 В
6. В режиме резонанса, приU=90 В,R=5 Ом,Ом, вольтметр покажет
1) U=360 В 2) U=180 В 3) U=40 В 4) U=120 В
7. В режиме резонанса, приU=100 В,R=10 Ом,Ом, амперметр покажет:
1) I=10A2)I=20A3)I=5A4)I=50A
8. Резонансная частота контура при уменьшении активного сопротивления в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
9. Резонансная частота контура при увеличении активного сопротивления в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
10. Резонансная частота контура при увеличении емкости в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
11. Резонансная частота контура при уменьшении емкости в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
12. Резонансная частота контура при увеличении индуктивности в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
13. Резонансная частота контура при уменьшении индуктивности в 4 раза
1) уменьшится в 2 раза 2) увеличится в 2 раза 3) не изменится
14. Условием возникновения резонанса напряжений в линейной электрической цепи является
1) равенство нулю активной составляющей полной мощности
2) равенство нулю активной и мнимой части комплексной проводимости
3) равенство нулю мнимой части комплексного сопротивления
4) равенство нулю активной составляющей комплексного сопротивления
15. Условием возникновения резонанса токов в линейной электрической цепи является
1) равенство нулю мнимой части комплексной проводимости
2)равенство нулю действительной и мнимой части комплексного сопротивления
3) равенство нулю активной мощности
4) равенство нулю разности мнимой и действительной части
16. Резонансом электрической цепи r, L, С называется режим работы, при котором
1) резонансная частота цепи равна частоте напряжения сети
2) активная мощность цепи равна нулю
3) цепь имеет чисто активный характер
4) цепь имеет индуктивный характер
5) цепь имеет емкостной характер
17. Электрическая цепь, в которой возможно возникновение резонанса напряжений, имеет вид
1) 2) 3) 4)
18. Электрическая цепь, в которой возможно возникновение резонанса токов, имеет вид
1) 2) 3) 4)
19. Цепь находится в режиме резонанса, когда
1) IL =IC 2) I = IL + IC 3) IC = I + IL 4) IL = I + IC
20. Цепь находится в режиме резонанса, когда
1) UL =UC 2) U = UL + UC 3) UC = Ur + UL 4) UL = Ur + UC
21.
Резонансные кривые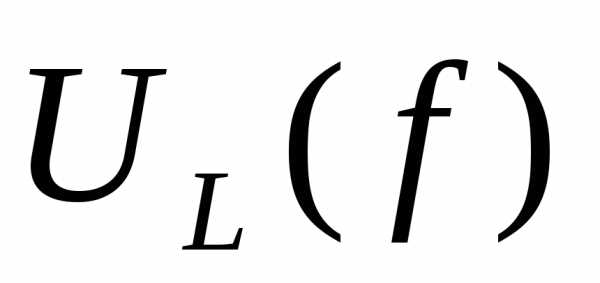 ,
,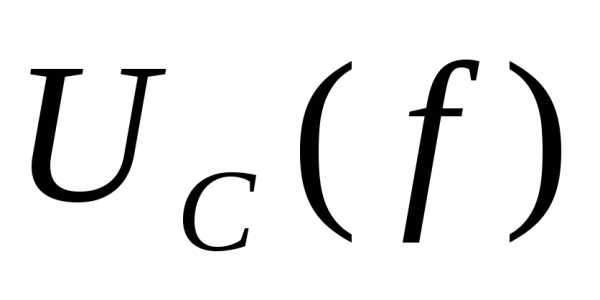 ,
, имеют вид
имеют вид
studfiles.net
12. Активная реактивная, полная мощность.
Р = Ur*I = I^2*r — активная мощность цепи, Вт, кВт; QL = UL*I = I^2*XL —реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар.
QС = UС*I = I^2*XС — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар.
Q = QL — QС = I^2x — реактивная мощность цепи, вар, это та мощность, которой приемник обменивается с сетью;
S = U*I = I^2*Z— полная мощность цепи. В • А;
cos φ = r/z = P/S—коэффициент мощности
Реактивные мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, они оказывают существенное влияние на режим работы электрической цепи. Коэффициент мощности показывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности наряду с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов и других устройств. Ваттметр измеряет активную мощность Р цепи.
14. Закон Ома для цепи синусоидального тока.
Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: I=U/Z;
U = U0eiωt — напряжение или разность потенциалов,
I — сила тока,
Z = Re−iδ — комплексное сопротивление (импеданс),
R = (Ra^2 + Rr^2)^1/2 — полное сопротивление,
Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
Rа — активное (омическое) сопротивление, не зависящее от частоты,
δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
15. Треугольник сопротивлений и проводимостей.
Из выражения Z=R+jX, вытекает, что модуль комплексного сопротивления равен z=(r^2+x^2)^0.5, следовательно z, можно представить, как гипотенузу прямоугольного треугольника, в котором один из катетов= r, а другой =x, а tg(ФИ)=x/r. Аналогично представляется треугольник проводимости, y=(g^2+b^2)^0.5, только в нем tg(ФИ)= b/g.
Треугольник сопротивлений и проводимостей дает графическую интерпретацию связи между полным сопротивление и активного и реактивного сопротивления, а также полной проводимость, и активной и реактивной проводимостью.
№ 16. Законы Кирхгофа в символической форме записи
Первый закон:
Алгебраическая сумма значений токов, сходящихся в любом узле схемы, равна нулю:
Σ Ik= 0
Второй закон:
Алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
Σ Ik*Zk=ΣEk
(Величины в уравнениях являются комплексными (с точками сверху))
№ 12, 17. Активная, реактивная и полная мощности. Коэффициент мощности
Активная мощность P– среднее значение мгновенной мощностиpза период Т:
P= 1 /T*0∫Tpdt, [P] = Вт
Реактивная мощность Q– произведение напряженияUна участке цепи на токIпо этому участку на синус угла φ междуUиI:
Q=U*I*sin(φ), [Q] = ВАр (вольт-амперы реактивные)
Полная мощность: S=U*I, [S] = ВА
P^2 +Q^2 =S^2 – т.е. графически можно представить в виде прямоугольноготреугольника мощности
Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения:
cos(φ) =P/S
№ 18. Мгновенная мощность и колебание энергии в цепи синусоидального тока
Мгновенная мощность– произведение мгновенного значения напряженияuна участке цепи на мгновенное значение токаi, протекающего по этому участку:
p=u*i
Энергия магнитного поля катушки: Wм =L*i^2 / 2
Энергия электрического поля конденсатора: Wэ =C*uC^2 / 2
№ 19. Эквивалентные преобразования в электрических цепях
Теорема компенсации: в любой электрической цепи без изменения токораспределения сопротивление можно заменить ЭДС, численно равной падению напряжения на заменяемом сопротивлении и направленной встречно току в этом сопротивлении.
Несколько параллельно включённых ветвей, содержащих источники ЭДС и тока и сопротивления можно заменить одной эквивалентной ветвью со следующими параметрами:
gэ = Σgk
Eэ = (ΣEk*gk+ ΣIk) / Σgk
№ 20. Метод законов Кирхгофа
1. Произвольно выбрать положительные направления токов в ветвях и направления обхода контуров
2. Составить уравнения по первому закону Кирхгофа для всех узлов, кроме одного
3. Составить уравнения по второму закону Кирхгофа так, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, которая ещё не входила ни в одно из уравнений
№ 21. Метод контурных токов
Применяется для уменьшения числа уравнений в системе и теоретическом анализе схемы. За искомые токи принимают контурные токи и составляется система уравнений по второму закону Кирхгофа, число уравнений равно числу независимых контуров:
I11 * R11 + I22 * R12 + … = E11
I11 * R21 + I22 * R22 + … = E22
…
где I11,I22 – контурные токи;R11,R22 – суммы сопротивлений в контуре;R12,R21 – взаимные сопротивления контуров, взятых с минусом;E11,E22 – сумма ЭДС в контуре. После нахождения контурных токов вычисляют исходные токи
№ 22. Принцип наложения и метод наложения
Принцип наложения: ток вk-цепи равен алгебраической сумме токов, вызываемых каждой из ЭДС:
Ik = E1 * gk1 + E2 * gk2 + … + En * gkn
По методу наложения поочерёдно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя из схемы остальные, затем находят исходные токи в ветвях
№ 23. Входные и взаимные проводимости ветвей
Коэффициенты g(из предыдущего вопроса) имеют размерность проводимости. Коэффициенты с одинаковыми индексами (gmm) называют входными проводимостями ветвей (ветвиm), коэффициенты с разными индексами (gkm) – взаимными проводимостями ветвей (ветвейkиm) (k– ветвь с ЭДС,m– текущая ветвь)
№ 24. Метод узловых потенциалов
За неизвестные принимают потенциалы узлов схемы и составляется система уравнений по первому закону Кирхгофа, число уравнений равно числу узлов минус 1:
φ1 * g11 + φ2 * g12 + … = I11
φ1 * g21 + φ2 * g22 + … = I22
…
где φ1,φ2 – потенциалы узлов;g11,g22 – суммы проводимостей всех ветвей, сходящихся в узле;g12,g21 – сумма проводимостей ветвей между узлами, взятых с минусом;I11,I22 – узловые токи, равные сумме токов, полученных от деления ЭДС, подходящих к узлу, на сопротивление данных ветвей. После решения системы определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС
№ 25. Метод эквивалентного генератора
По отношению к выделенной цепи всю остальную часть схемы можно заменить эквивалентным генератором, состоящим из ЭДС E=Uxxи сопротивленияRвх
1. Ветвь, ток в которой необходимо определить, размыкают и находят напряжение на её зажимах
2. Определяют входное сопротивление Rвх всей схемы относительно зажимов при закороченных источниках ЭДС
3. Рассчитывают ток: I=Uxx/ (R+Rвх)
studfiles.net
Активная мощность
Мгновенная мощность pпроизвольного участка цепи, напряжение и ток которого изменяются по законуu=Umsin(t), i = Imsin(t–), имеет вид
p = ui= Umsin(t)Imsin(t–) = UmIm[cos — cos(2t — )]/2 =
= Uicos — UIcos(2t — ) = (UIcos – UIcos cos2t) – UIsin sin2t. (1)
Активная мощность цепи переменного тока Pопределяется как среднее значение мгновенной мощностиp(t) за период:
P = 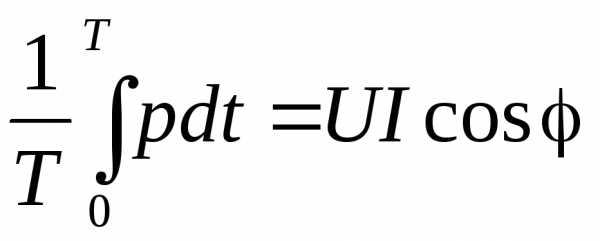 ,
,
так как среднее за период значение гармонической функции равно 0.
Из этого следует, что средняя за период мощность зависит от угла сдвига фаз между напряжением и током и не равна нулю, если участок цепи имеет активное сопротивление. Последнее объясняет ее название активная мощность. Подчеркнем еще раз, что в активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, например в тепловую. Активная мощность может быть определена как средняя за период скорость поступления энергии в участок цепи. Активная мощность измеряется в ваттах (Вт).
Реактивная мощность
При расчетах электрических цепей находит широкое применение так называемая реактивнаямощность. Она характеризует процессы обмена энергией между реактивными элементами цепи и источниками энергии и численно равна амплитуде переменной составляющей мгновенной мощности цепи. В соответствии с этим реактивная мощность может быть определена из (1) как
Q = UIsin.
В зависимости от знака угла реактивная мощность может быть положительной или отрицательной. Единицу реактивной мощности, чтобы отличить ее от единицы активной, называют не ватт, а вольт-ампер реактивныйвар. Реактивные мощности индуктивного и емкостного элементов равны амплитудам их мгновенных мощностейpL иpC. С учетом сопротивленийэтих элементов реактивные мощности катушки индуктивности и конденсатора равныQL=UI=xLI 2иQC=UI= xCI 2, соответственно.
Результирующая реактивная мощность разветвленной электрической цепи находится как алгебраическая сумма реактивных мощностей элементов цепи с учетом их характера (индуктивный или емкостный): Q=QL–QС. ЗдесьQLесть суммарная реактивная мощность всех индуктивных элементов цепи, аQС представляет собой суммарную реактивную мощность всех емкостных элементов цепи.
Полная мощность
Кроме активной и реактивной мощностей цепь синусоидального тока характеризуется полной мощностью, обозначаемой буквой S. Под полной мощностью участка понимают максимально возможную активную мощность при заданных напряженииUи токеI. Очевидно, что максимальная активная мощность получается при cos= 1, т. е. при отсутствии сдвига фаз между напряжением и током:
S = UI.
Необходимость во введении этой мощности объясняется тем, что при конструировании электрических устройств, аппаратов, сетей и т. п. их рассчитывают на определенное номинальное напряжение Uноми определенный номинальный токIноми их произведениеUном Iном= Sномдает максимально возможную мощность данного устройства (полная мощность Sномуказывается в паспорте большинства электрических устройств переменного тока.). Для отличия полной мощности от других мощностей ее единицу измерения называют вольт-ампер и сокращенно обозначают ВА. Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности.
Из приведенных соотношений можно найти связь между различными мощностями:
P = S cos, Q = S sin, S = UI =
и выразить угол сдвига фаз через активную и реактивную мощности:
 .
.
Рассмотрим простой прием, который
позволяет найти активную и реактивную
мощности участка цепи по комплексным
напряжению и току. Он заключается в том,
что нужно взять произведение комплексного
напряжения  и тока
и тока ,
комплексно сопряженного току
,
комплексно сопряженного току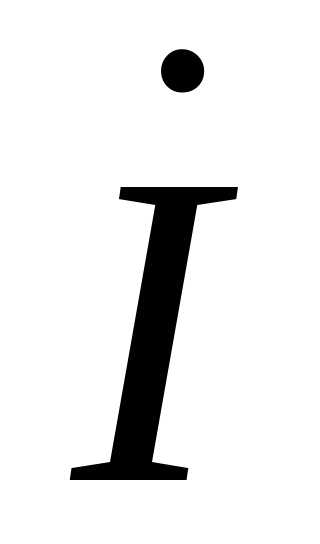 рассматриваемого участка цепи.
Операция комплексного сопряжения
состоит в смене знака на противоположный
перед мнимой частью комплексного числа
либо в смене знака фазы комплексного
числа, если число представлено в
экспоненциальной форме записи. В
результате получим величину, которая
называетсяполной комплексной мощностьюи обозначается
рассматриваемого участка цепи.
Операция комплексного сопряжения
состоит в смене знака на противоположный
перед мнимой частью комплексного числа
либо в смене знака фазы комплексного
числа, если число представлено в
экспоненциальной форме записи. В
результате получим величину, которая
называетсяполной комплексной мощностьюи обозначается .
Если,
то для полной комплексной мощности
получаем:
.
Если,
то для полной комплексной мощности
получаем:
.
Отсюда видно, что активная и реактивная мощности представляют собой вещественную и мнимую части полной комплексной мощности, соответственно. Для облегчения запоминания всех формул, связанных с мощностями, на рис. 7, б(с. 38) построен треугольник мощностей.
studfiles.net