Что называется резонансом: Резонанс — урок. Физика, 9 класс. — Мир Антенн

Содержание

Резонанс — урок. Физика, 9 класс.

если вам случалось путешествовать на поезде, то наверняка вы обратили внимание на заметное, сильное раскачивание железнодорожного вагона при случайном совпадении его собственной частоты колебаний на рессорах с частотой ударов колёс на стыках рельсов.

Ещё один очень яркий пример проявления явления резонанса — это несколько случаев обрушения мостов, когда по ним строевым шагом проходила рота солдат.

Чеканный шаг солдатских сапог совпал с собственной частотой колебаний моста. Мост стал колебаться с такой амплитудой, на которую его прочность не была рассчитана и… развалился. Тогда и родилась новая воинская команда «…не в ногу». Она звучит, когда пешая или конная рота солдат проходит по мосту.

Однако самый яркий пример разрушительного действия резонанса — это рухнувший $7$ ноября $1940$ года почти двухкилометровый Такомский подвесной мост в США (штат Вашингтон).

Данный случай и видео волнообразного раскачивания конструкции даже рекомендованы к просмотру на факультетах физики некоторых университетов как самый хрестоматийный пример такого явления резонанса.

Разрушение подвесного моста под действием ветра — это иллюстрация того, как относительно постоянная сила вызывает резонанс. При этом происходит следующее:

1. порыв ветра отклоняет часть конструкции в сторону движения ветра — внешняя сила способствует возникновению колебаний;

2. при обратном движении конструкции сопротивления воздуха недостаточно, чтобы погасить колебание или значительно снизить его амплитуду;

3. вследствие упругости системы начинается новое движение по ветру, которое он (ветер) и усиливает, продолжая дуть в одном направлении.

Это пример поведения комплексного объекта, где резонанс развивается на фоне высокой добротности и значительной упругости под действием постоянного воздействия силы в одном направлении. К сожалению, Такомский мост — это не единственный пример обрушения конструкций. Случаи, аналогичные описанному, наблюдались и наблюдаются по всему миру, в том числе и в России.

Явление резонанса — Основы электроники

Явления резонанса связаны с периодическим колебательным движением электронов в контуре и состоят в том, что электроны в данном колебательном контуре легче всего «раскачиваются» с какой-то определенной частотой, которую мы называем резонансной. С периодическим колебательным движением мы встречаемся повсеместно. Колебания маятника, дрожание струны, движение качелей — все это примеры колебательного движения.

Для примера рассмотрим колебательную систему, изображенную на рисунке 1. Эта система, как мы увидим дальше, имеет много общего с электрическим колебательным контуром. Состоит она из пружины и массивного шара, закрепленного на стержне.

Рисунок 1. Механическая модель колебательного контура. Масса-индуктивность, гибкость-емкость, трение-сопротивление.

Если мы оттянем шар в низ от положения равновесия, то он под действием пружины немедленно устремится обратно; однако приобретя некоторую скорость шар не остановится в точке равновесия, а по инерции проскочит дальше, чем вызовет новую деформацию (сжатие) пружины. Затем этот процесс повторится в обратном направлении и т. д. Шар будет колебаться в ту и другую сторону до тех пор, пока не израсходуется на трение весь запас энергии, сообщенной пружине при отклонении шара.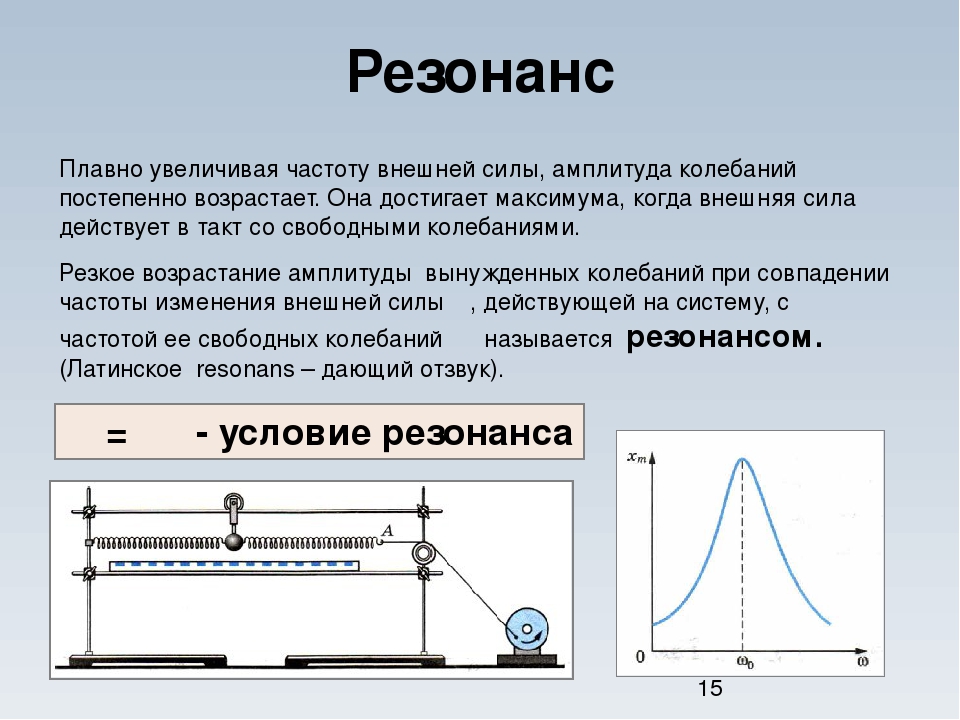

Нетрудно заметить, что при колебаниях шара энергия, сообщенная системе, все время переходит из энергии деформации (сжатия и растяжения) пружины в энергию движения шара и обратно. В механике первый вид энергии называется потенциальной энергией, а второй вид — кинетической.

В то время, когда шар находится в одном из крайних положений, он на мгновение останавливается. В этот момент энергия его движения равна нулю. Зато пружина в этот момент очень сильно деформирована: или сжата или растянута; в ней, следовательно, заключено наибольшее количество энергии. В тот же момент, когда шар с наибольшей скоростью проходит через положение равновесия, он обладает наибольшей энергией, но зато энергия пружины в этот момент равна нулю, так как она не сжата и не растянута.

Отклоняя шар на различные расстояния и наблюдая каждый раз за частотой последующих свободных колебаний системы, мы заметим, что частота колебаний системы остается все время одной и той же. Иными словами, она не зависит от величины начального отклонения.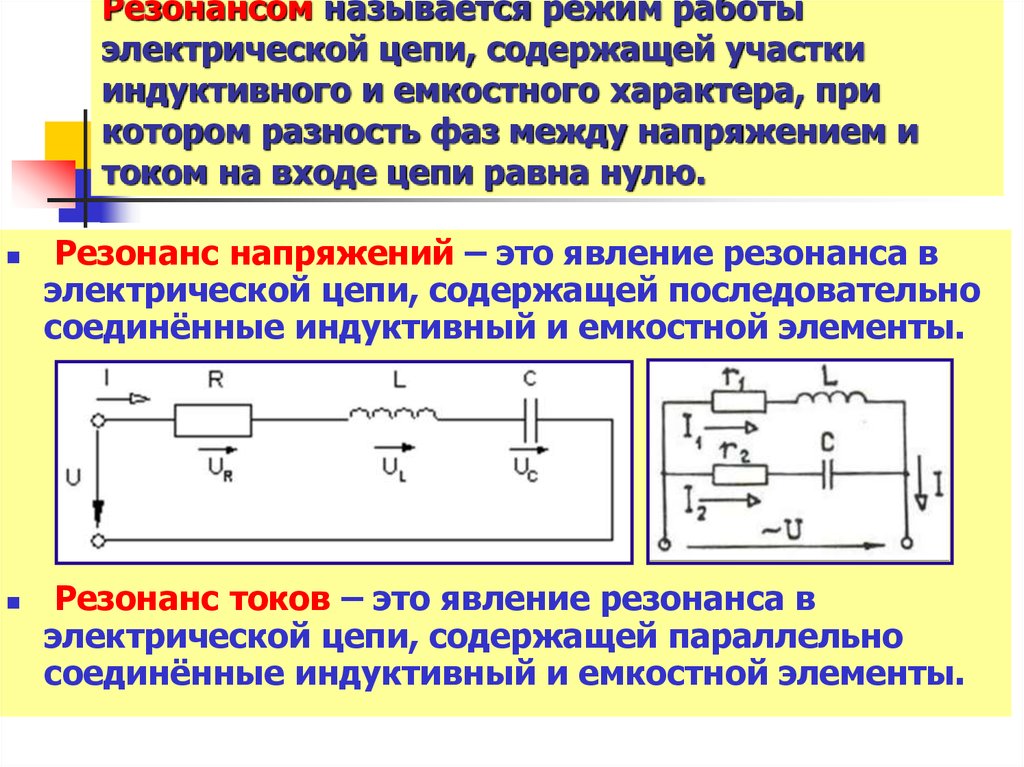 Эту частоту мы будем называть собственной частотой колебаний системы.

Если бы мы имели в своем распоряжении не одну такую систему, а несколько, то мы могли бы убедиться в том, что собственная частота свободных колебаний системы уменьшается с увеличением массы шара и увеличивается с увеличением упругости, т. е. с уменьшением гибкости пружины. Эта зависимость может быть обнаружена и на более простом примере с колеблющимися струнами различной толщины и различной степени натяжения.

Если мы пожелаем раскачать шар с наименьшей затратой усилий, то мы, безусловно, постараемся, во-первых, установить строгую периодичность наших толчков, т. е. постараемся, чтобы толчки следовали друг за другом через определенное время, а во-вторых, постараемся, чтобы промежуток времени между толчками равнялся периоду собственных колебаний системы (Рисунок 2).

Рисунок 2. Механическая модель колебательного контура с незатухающими колебаниями. Частота вынужденной силы равна собсвенной частоте системы (резонанс).

Для того чтобы раскачать колебательную систему с наименьшей затратой усилий, нужно частоту вынуждающей силы сделать равной собственной частоте колебания системы. Это правило очень хорошо известно всем нам еще с детского возраста, когда мы его применяли, раскачиваясь на качелях.

Рисунок 3. Явление резонанса на примере качелей.

Итак, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы, амплитуда колебаний становится наибольшей.

Таким образом, необходимо сказать, что совпадение частоты вынуждающей силы с собственной частотой колебаний системы и является резонансом.

За примерами резонанса ходить далеко не нужно. Оконное стекло, дрожащее с определенной частотой каждый раз, когда мимо проезжает трамвай или грузовая машина; дрожание струны музыкального инструмента после того, как мы прикоснулись к соседней струне, настроенной в унисон с первой, и т. п. — все это явления резонанса.

Зарядим конденсатор некоторым количеством электричества (рис.4, а) и замкнем его после этого на катушку индуктивности (рис.4, б). Конденсатор начнет немедленно разряжаться. Через катушку индуктивности потечет разрядный ток, а появление тока в катушке приведет к возникновению магнитного поля вокруг нее. При этом в катушке возникнет ЭДС самоиндукции, которая будет задерживать разряд конденсатора. Когда конденсатор разрядится, то ток в катушке не прекратится, так как он будет теперь поддерживаться ЭДС самоиндукции за счет энергии, запасенной в магнитном поле катушки во время разряда конденсатора. Этот продолжающийся ток перезарядит конденсатор в обратном направлении, т. е. та пластина, которая была прежде положительной, станет отрицательной, и наоборот (рис.4, в).

Рисунок 4. Свободные колебания. Вверху — электрические, внизу — механические.

После этого конденсатор снова начнет разряжаться, снова перезарядится (рис.

4, г, д) и т. д. Колебания тока в контуре будут продолжаться до тех пор, пока вся электрическая энергия, сообщенная контуру при заряде конденсатора, не превратится в тепловую энергию. Это произойдет тем скорее, чем больше активное сопротивление контура.

Итак, разряд конденсатора через катушку индуктивности является колебательным процессом. Во время этого процесса конденсатор несколько раз заряжается и разряжается, энергия поочередно переходит из электрического поля конденсатора в магнитное поле катушки и обратно.

Рисунок 5. Колебания в колебательном контуре.

Колебания тока, имеющие место при этом разряде, носят затухающий характер (рис.6).

Рисунок 6. Затухающие колебания в контуре.

Частота колебаний при выбранных величинах емкости и индуктивности является величиной вполне определенной и называется собственной частотой контура. Собственная частота контура будет тем больше, чем меньше величины емкости и индуктивности контура.

Если в колебательный контур ввести источник переменного тока, частота которого совпадает с собственной частотой контура, то колебания в контуре достигнут наибольшей величины, т. е. будет иметь место явление резонанса.

Между электрическими и механическими колебаниями может быть проведена далеко идущая параллель.

В табл. 1 слева даны электрические величины и явления, а справа аналогичные им величины и явления из области механики применительно к нашей механической модели колебательного контура.

**Аналогия электрических и механических величин**
Электрические величины	Механические величины
Индуктивность колебательного контура	Масса шара;
Емкость колебательного контура	Гибкость пружин
Активное сопротивление контура	Механическое трение
Пластины конденсатора	Пружины
Заряд конденсатора	Деформация (сжатие и растяжение) пружин
Положительный заряд пластин	Сжатие пружины
Отрицательный заряд пластины	Растяжение пружины
Сила тока	Скорость движения шара
Направление тока	Направление движения шара
Электродвижущая сила самоиндукции	Сила инерции шара
Амплитуда (наибольшее мгновенное значение тока)	Амплитуда (наибольшее отклонение шара от положения равновесия)
Частота (число циклов в секунду)	Частота (число колебаний в се¬кунду)
Резонанс (совпадение частоты внешней ЭДС с собственной частотой конура)	Резонанс (совпадение частоты толчков вынуждающей силы с собственной частотой колебаний шара)

Различные моменты электрического колебания и соответствующие им моменты колебания нашей механической модели колебательного контура изображены на рис.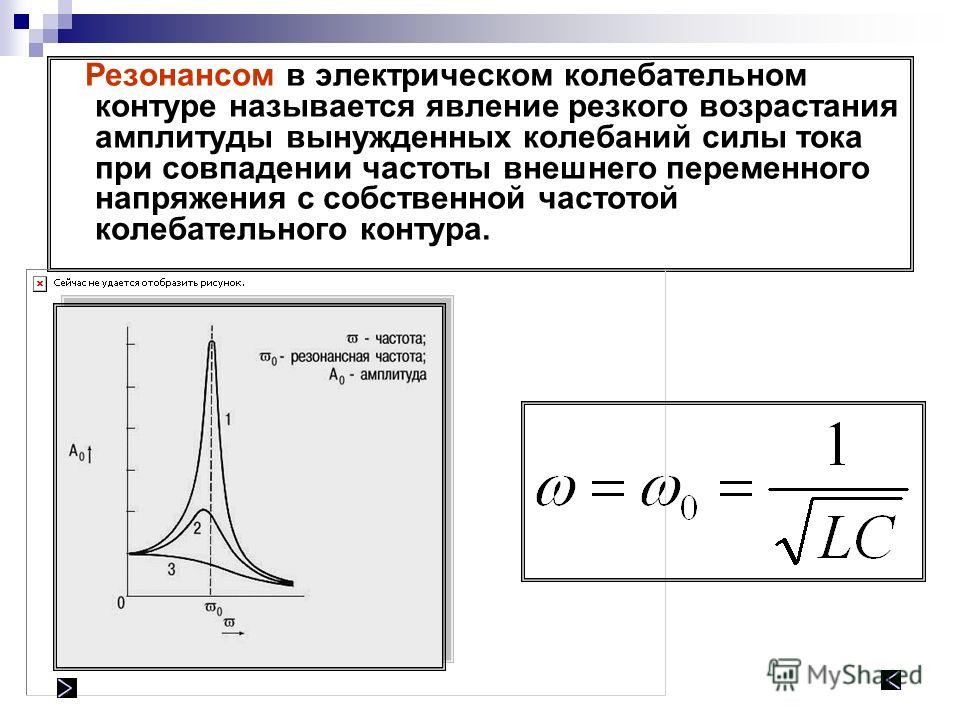 4.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Резонансные явления в электрических сетях

Идеальное активное сопротивление от частоты не зависит, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

Резонанс напряжений

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю . Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.
При последовательном соединении возникает резонанс напряжения.

Последовательное соединение R, L, C.

Знаменатель данного выражения есть модуль комплексного сопротивления, который зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения по фазе:

Максимальная амплитуда силы тока достигается при условии минимума полного сопротивления, т. е. при

где
— резонансная частота напряжения, определяемая из условия

При последовательном соединении в цепь конденсатора и соленоида силы токов в каждом из участков цепи, как известно, равны. Поэтому, умножив левую и правую части последнего соотношения на силу тока Im, получим

В этом выражении слева — амплитуда напряжения на концах соленоида, а справа — амплитуда напряжения на обкладках конденсатора.
Мы видим, что . Отсюда получаем

Знак минус указывает на то, что колебания напряжения на участках с индуктивностью и емкостью происходят в противофазе.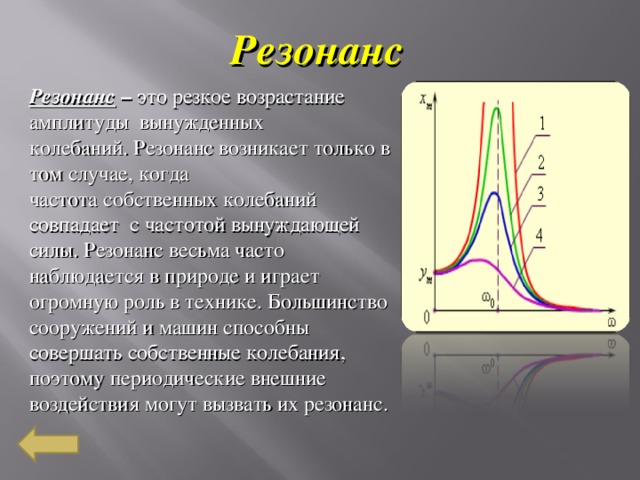
Режим электрической цепи при последовательном соединении индуктивности и емкости, характеризующийся равенством напряжений на индуктивности и емкости, называют резонансом напряжений.

Волновое или характеристическое сопротивление последовательного контура

Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется добротностью контура:

Добротность контура представляет собой коэффициент усиления по напряжению и в катушках индуктивности может достигать сотен единиц:

При напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике. В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.

Резонанс токов

При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю).
В этом случае:

Параллельное соединение реактивных элементов

тогда

При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость

При ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.
Резонансную частоту тока найдем из условия равенства реактивных проводимостей ветвей.

После ряда преобразований получим:

Из формулы следует, что:

1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если и больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс невозможен;
3) если , то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при резонансная частота напряжения равна резонансной частоте тока.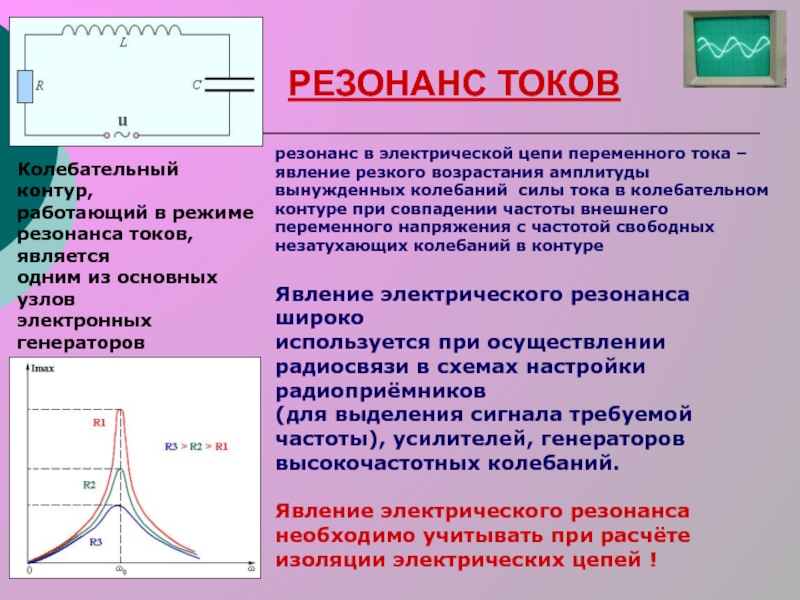

Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии.

Резонансная частота — это… Что такое Резонансная частота?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем.

Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.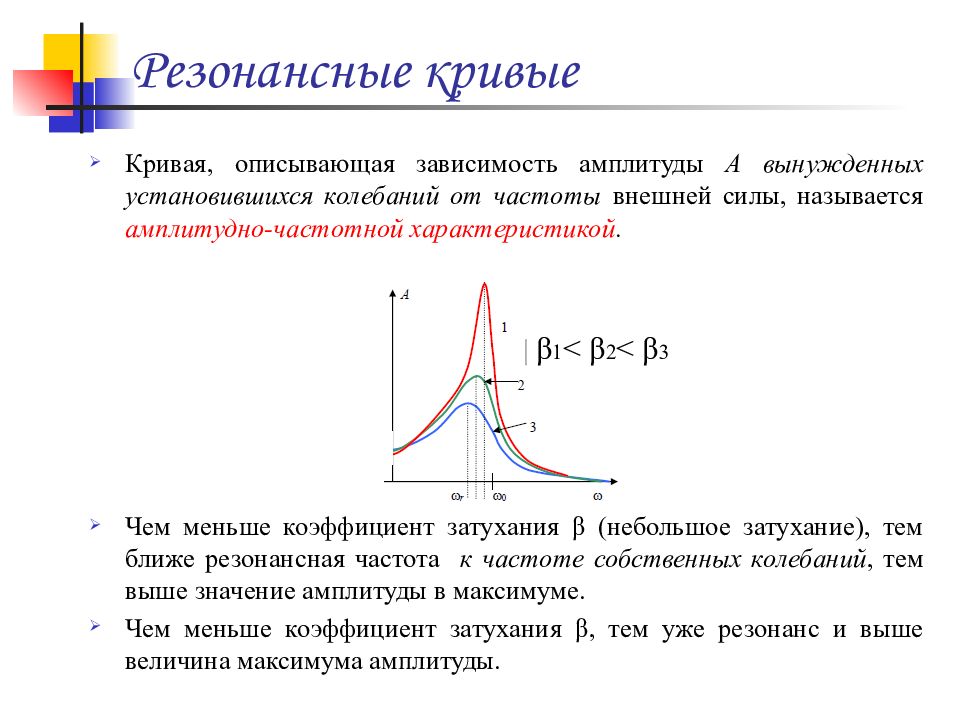

Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Примечания

См. также

Ссылки

Richardson LF (1922), Weather prediction by numerical process, Cambridge.

Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.

Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.

Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.

Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.

Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.

Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.

Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука

Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.: Наука — 232 с.

Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука

Wikimedia Foundation. 2010.

РЕЗОНАНС • Большая российская энциклопедия

В книжной версии
Том 28. Москва, 2015, стр. 336-337
Скопировать библиографическую ссылку:

Авторы: В. В. Клиньшов, В. И. Некоркин

РЕЗОНА́НС (франц. resonance, от лат. resono – откликаться), избирательный отклик колебат. системы на внешнее периодич. воздействие определённой частоты. Явление Р. происходит при приближении частоты внешнего воздействия ω к частоте собств. колебаний системы ω₀ и заключается в резком возрастании амплитуды её вынужденных колебаний. В этом случае частота воздействия называется резонансной (ω_р). Её величина определяется свойствами колебат. системы. Впервые Р. описан Г. Галилеем для механич. систем. От Р. при внешнем воздействии следует отличать параметрический резонанс, возникающий при периодич. изменении параметров колебат. системы.

Суть эффекта Р. можно понять на примере раскачивания качелей путём их периодич. подталкивания. Для эффективного раскачивания качелей частота внешнего подталкивания должна совпадать с частотой их собств. колебаний. В этом случае каждый толчок происходит в одной и той же фазе движения качелей, способствуя увеличению размаха колебаний. При неправильно выбранной частоте подталкивания толчки происходят в разных фазах движения, то ускоряя, то замедляя качели, и существенной раскачки колебаний не происходит.

Рис. 1. Резонансная кривая линейной системы.

Осн. свойства Р. можно наблюдать при воздействии внешнего гармонич. сигнала на линейную систему с одной степенью свободы, такую как колебат. контур или математич. маятник. Зависимость амплитуды A вынужденных колебаний такой системы от частоты внешнего сигнала ω (резонансная кривая) имеет чётко выраженный максимум на резонансной частоте ω_р (рис. 1). Для описания резонансных свойств линейной колебат. системы часто используют понятие добротности, характеризующее степень затухания колебаний в системе. Величина добротности определяет форму резонансной кривой: чем больше добротность, тем меньше ширина пика резонансной кривой, т. е. тем более избирательной является колебат. система. С ростом добротности увеличивается высота пика и уменьшается разница между резонансной и собств. частотами.

Рис. 2. Резонансная кривая нелинейной системы.

В нелинейных системах Р. имеет существенные особенности по сравнению с линейными. Во-первых, резонансная частота нелинейной системы зависит от амплитуды внешнего воздействия. Во-вторых, при достаточно сильных воздействиях исчезает однозначное соответствие амплитуды вынужденных колебаний параметрам внешнего сигнала. При одной и той же частоте внешней силы возможны режимы колебаний с разл. амплитудами (рис. 2). Штриховой кривой на рисунке показана ветвь, соответствующая неустойчивому режиму колебаний. Переключение между разл. режимами при перестройке частоты происходит в виде скачков амплитуды и имеет гистерезисный характер.

Для линейных систем с несколькими степенями свободы и для распределённых систем, в которых собств. колебания могут происходить на разных частотах, Р. наблюдается при приближении частоты внешнего сигнала к одной из этих частот. В этом случае резонансная кривая характеризуется наличием нескольких максимумов, и внешнее воздействие распределяется по отд. координатам системы.

Р. играет важную роль в природе, науке и технике. В некоторых случаях он является нежелательным, т. к. приводит к негативным последствиям. Напр., при совпадении частоты набегающих на корабль волн с собств. частотой килевой качки возникает резкое увеличение амплитуды колебаний корабля, при которых его нос «зарывается» в волну. Р. может вызывать сильные колебания и последующие разрушения при работе вибрирующих станков, машин, двигателей внутр. сгорания. Известны случаи разрушения мостов под действием ритмич. толчков от проходящих по ним войск. С др. стороны, на явлении Р. основана работа мн. приборов и устройств. Напр., настройка частоты колебат. контура радиоприёмника на частоту электромагнитного сигнала позволяет осуществлять его приём. Явление Р. лежит в основе принципа действия СВЧ электронных приборов, напр. клистронов, использующих высокодобротные объёмные резонаторы для усиления СВЧ-сигналов.

Российские ученые обнаружили новый физический парадокс

https://ria.ru/20200706/1573854536.html

Российские ученые обнаружили новый физический парадокс

Российские ученые обнаружили новый физический парадокс — РИА Новости, 06.07.2020

Российские ученые обнаружили новый физический парадокс

Ученые Санкт-Петербургского политехнического университета Петра Великого (СПбПУ) обнаружили и теоретически объяснили новый физический эффект, суть которого… РИА Новости, 06.07.2020

2020-07-06T09:00

2020-07-06T15:50

наука

университетская наука

навигатор абитуриента

санкт-петербургский политехнический университет петра великого

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdn22.img.ria.ru/images/07e4/07/06/1573952487_0:127:1280:847_1920x0_80_0_0_e3ea427eb33597688ce1ce9267fc7ad1.jpg

МОСКВА, 6 июл — РИА Новости. Ученые Санкт-Петербургского политехнического университета Петра Великого (СПбПУ) обнаружили и теоретически объяснили новый физический эффект, суть которого заключается в возможности роста амплитуды механических колебаний объекта без внешнего воздействия. Кроме того, они предложили свой вариант устранения парадокса Ферми — Паста — Улама — Цингу.В СПбПУ это объяснили на простом примере: чтобы раскачать качели, их нужно постоянно подталкивать. Считалось, что без постоянного внешнего воздействия добиться колебательного резонанса невозможно.Однако научная группа Высшей школы теоретической механики Института прикладной математики и механики СПбПУ обнаружила новое физическое явление — баллистический резонанс, при котором механические колебания могут возбуждаться исключительно за счет внутренних тепловых ресурсов системы.Ключом к пониманию стали экспериментальные работы научных групп по всему миру, показавшие, что в сверхчистых кристаллических материалах на нано- и микроуровне тепло распространяется с аномально высокой скоростью. Это явление назвали баллистической теплопроводностью.Научная группа под руководством члена-корреспондента РАН Антона Кривцова вывела уравнения, описывающие это явление, и существенно продвинулась в понимании тепловых процессов на микромасштабах. В исследовании, опубликованном в научном журнале Physical Review E, ученые рассмотрели поведение систем при начальном периодическом распределении температуры в кристаллическом материале.Обнаруженное явление заключается в том, что процесс выравнивания тепла приводит к возникновению механических колебаний с возрастающей со временем амплитудой. Эффект получил название баллистического резонанса.Эти открытия также дают возможность разрешения парадокса Ферми — Паста — Улама — Цингу. В 1953 году научная группа, возглавляемая Энрико Ферми, провела ставший впоследствии знаменитым компьютерный эксперимент. Ученые рассмотрели простейшую модель колебаний цепочки частиц, соединенных пружинками. Предполагалось, что механическое движение постепенно затухнет, превратившись в хаотические тепловые колебания, однако результат оказался неожиданным: колебания в цепочке сначала почти затухли, но затем возродились и практически достигли начального уровня. Система пришла в начальное состояние, и цикл снова повторился. Причины появления механических колебаний из тепловых в рассмотренной системе уже на протяжении десятков лет являются предметом научных исследований и споров.Амплитуда механических колебаний, вызванная баллистическим резонансом, не возрастает бесконечно, а достигает максимума, после чего начинает постепенно уменьшаться до нуля. Со временем механические колебания затухают полностью, а температура выравнивается вдоль всего кристалла. Этот процесс называется термализацией. Для механиков и физиков данный эксперимент важен по той причине, что цепочка частиц, соединенных пружинками, является хорошей моделью кристаллического материала.Исследователи Высшей школы теоретической механики СПбПУ показали, что переход механической энергии в тепло происходит необратимо, если рассматривать процесс при конечной температуре.»Обычно не учитывается, что в реальных материалах, наряду с механическими, присутствует тепловое движение, энергия которого на несколько порядков выше. Мы воссоздали эти условия в компьютерном эксперименте и показали, что именно тепловое движение гасит механическую волну и препятствует возрождению колебаний», — пояснил директор Высшей школы теоретической механики СПбПУ, член-корреспондент РАН Антон Кривцов.По мнению экспертов, теоретический подход, предложенный учеными СПбПУ, позволяет по-новому взглянуть на то, что понимается под теплом и температурой, и может иметь основополагающее значение при разработке наноэлектронных устройств будущего.

https://ria.ru/20200601/1572124337.html

https://ria.ru/20191029/1560312152.html

https://ria.ru/20191024/1560122244.html

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2020

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

Новости

ru-RU

https://ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

https://cdn23.img.ria.ru/images/07e4/07/06/1573952487_6:0:1145:854_1920x0_80_0_0_0c9643ea2890b5eeea2c2e34b32e0523.jpg

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

РИА Новости

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

университетская наука, навигатор абитуриента, санкт-петербургский политехнический университет петра великого

МОСКВА, 6 июл — РИА Новости. Ученые Санкт-Петербургского политехнического университета Петра Великого (СПбПУ) обнаружили и теоретически объяснили новый физический эффект, суть которого заключается в возможности роста амплитуды механических колебаний объекта без внешнего воздействия. Кроме того, они предложили свой вариант устранения парадокса Ферми — Паста — Улама — Цингу.

В СПбПУ это объяснили на простом примере: чтобы раскачать качели, их нужно постоянно подталкивать. Считалось, что без постоянного внешнего воздействия добиться колебательного резонанса невозможно.

1 июня 2020, 09:00НаукаРоссийские ученые усовершенствовали аккумулятор для сенсоров

Однако научная группа Высшей школы теоретической механики Института прикладной математики и механики СПбПУ обнаружила новое физическое явление — баллистический резонанс, при котором механические колебания могут возбуждаться исключительно за счет внутренних тепловых ресурсов системы.

Ключом к пониманию стали экспериментальные работы научных групп по всему миру, показавшие, что в сверхчистых кристаллических материалах на нано- и микроуровне тепло распространяется с аномально высокой скоростью. Это явление назвали баллистической теплопроводностью.

Научная группа под руководством члена-корреспондента РАН Антона Кривцова вывела уравнения, описывающие это явление, и существенно продвинулась в понимании тепловых процессов на микромасштабах. В исследовании, опубликованном в научном журнале Physical Review E, ученые рассмотрели поведение систем при начальном периодическом распределении температуры в кристаллическом материале.

Обнаруженное явление заключается в том, что процесс выравнивания тепла приводит к возникновению механических колебаний с возрастающей со временем амплитудой. Эффект получил название баллистического резонанса.

«Последние несколько лет наша научная группа занимается исследованием механизмов распространения тепла на микро- и наноуровне. В процессе работы мы обнаружили, что на этих уровнях тепло распространяется совсем не так, как мы ожидали, — например, тепло может течь от холодного к горячему. Такое поведение наносистем приводит к новым физическим эффектам, таким как баллистический резонанс», — отметил доцент Высшей школы теоретической механики СПбПУ Виталий Кузькин. По его словам, в дальнейшем ученые хотят понять, как это можно использовать в таких перспективных материалах, как, например, графен.

Эти открытия также дают возможность разрешения парадокса Ферми — Паста — Улама — Цингу. В 1953 году научная группа, возглавляемая Энрико Ферми, провела ставший впоследствии знаменитым компьютерный эксперимент. Ученые рассмотрели простейшую модель колебаний цепочки частиц, соединенных пружинками. Предполагалось, что механическое движение постепенно затухнет, превратившись в хаотические тепловые колебания, однако результат оказался неожиданным: колебания в цепочке сначала почти затухли, но затем возродились и практически достигли начального уровня. Система пришла в начальное состояние, и цикл снова повторился. Причины появления механических колебаний из тепловых в рассмотренной системе уже на протяжении десятков лет являются предметом научных исследований и споров.

29 октября 2019, 03:00НаукаВ России впервые в мире систематизировали холестерические жидкие кристаллы

Амплитуда механических колебаний, вызванная баллистическим резонансом, не возрастает бесконечно, а достигает максимума, после чего начинает постепенно уменьшаться до нуля. Со временем механические колебания затухают полностью, а температура выравнивается вдоль всего кристалла. Этот процесс называется термализацией. Для механиков и физиков данный эксперимент важен по той причине, что цепочка частиц, соединенных пружинками, является хорошей моделью кристаллического материала.

Исследователи Высшей школы теоретической механики СПбПУ показали, что переход механической энергии в тепло происходит необратимо, если рассматривать процесс при конечной температуре.

«Обычно не учитывается, что в реальных материалах, наряду с механическими, присутствует тепловое движение, энергия которого на несколько порядков выше. Мы воссоздали эти условия в компьютерном эксперименте и показали, что именно тепловое движение гасит механическую волну и препятствует возрождению колебаний», — пояснил директор Высшей школы теоретической механики СПбПУ, член-корреспондент РАН Антон Кривцов.

По мнению экспертов, теоретический подход, предложенный учеными СПбПУ, позволяет по-новому взглянуть на то, что понимается под теплом и температурой, и может иметь основополагающее значение при разработке наноэлектронных устройств будущего.

24 октября 2019, 09:00НаукаУченые работают над созданием мельчайших наноэлектронных устройств в мире

Resonance | Protocol (Translated to Russian)

9.10: Резонанс

Структура Льюиса нитрит аниона (NО₂⁾ может быть начерчена двумя различными способами, отличаемыми расположением связей N-O и N=O.

Если ионы нитритов действительно содержат одну и двойную связь, то ожидается, что две длины связи будут разными. Двойная связь между двумя атомами короче (и сильнее), чем одна связь между двумя атомами. Однако эксперименты показывают, что и связи N–O в_{^{No2 имеют} одинаковую прочность и длину и идентичны по всем другим свойствам. Невозможно создать единую структуру Льюиса для NО₂^, в которой азот имеет октет, и обе связи эквивалентны.}

Вместо этого используется понятие резонанса: Если для молекулы или иона могут быть записаны две или более структуры Льюиса с одинаковым расположением атомов, фактическое распределение электронов является средним значением, показанным различными структурами Льюиса. Фактическое распределение электронов в каждом из азотно-кислородных связей NО₂^— это среднее значение двойной связи и одной связи.

Отдельные структуры Льюиса называются резонансными формами. Фактическую электронную структуру молекулы (среднее от резонансных форм) называют резонансным гибридным из отдельных резонансных форм. Двуглавая стрелка между структурами Льюиса указывает на то, что они являются резонансной формой.

Карбонат анион, CO3₂^—, является вторым примером резонанса.

Один атом кислорода должен иметь двойную связь с углеродом, чтобы завершить октет на центральном атоме.
Однако все атомы кислорода эквивалентны, и двойная связь может образоваться от любого из трех атомов. Это приводит к появлению трех резонансных форм карбонатного иона.
Поскольку можно записать три идентичные резонансные структуры, фактическое расположение электронов в карбонатномионе, как известно, является средним из трех структур.
Опять же, эксперименты показывают, что все три связи с-о абсолютно одинаковы.

Всегда помните, что молекула, описанная как резонансный гибрид, никогда не обладает электронной структурой, описанной ни по резонансной форме. Он не колеблется между резонансной формой; скорее, фактическая электронная структура всегда является средним значением, показанным всеми резонансными формами.

Джордж Веланд, один из пионеров теории резонанса, использовал историческую аналогию для описания взаимосвязи между резонансными формами и резонансными гибридами. Средневековый путешественник, никогда ранее не видел носорога, описал его как гибрид дракона и единорога, потому что он имел много общих с ними свойств. Так же как носорог не является ни драконом, ни единорогом в другое время, резонансный гибрид не является ни его резонансной формой в данный момент времени.

Как и носорог, это реальный объект, существование которого показали экспериментальные данные. У него есть некоторые общие характеристики с его резонансными формами, но сами резонансные формы представляют собой удобные воображаемые изображения (например, единорог и дракон).

Этот текст адаптирован к Openstax, Химия 2е изд., раздел 7.4: Формальные сборы и резонанс.

Что такое вибрационный резонанс?

Резонанс вибрации возникает, когда оборудование или продукт подвергаются внешней вынужденной вибрации, возникающей на одной или нескольких собственных частотах. Возникающая в результате вибрация продукта усиливается и может быть огромной! Вибрационные резонансы могут серьезно повредить изделия и значительно сократить срок их службы. Примеры вибрационных резонансов можно увидеть ниже и на нашей странице видео.

Собственная частота — это частота, с которой система будет колебаться после приложения внешней силы, а затем ее удаления.Все объекты имеют собственную частоту вибрации. Большинство продуктов имеют много собственных частот.

Во время вибрационных испытаний с использованием вибрационных шейкеров для изучения резонансов в продуктах используется сканирование резонанса синусоидальной вибрации или поиск резонанса. При выполнении резонансного сканирования вибростол подвергает продукт контролируемым вынужденным колебаниям в диапазоне частот, чтобы изучить ответные колебания продукта. Уровни вынужденной вибрации низкие (обычно ½ G) и считаются не повреждающими.Ускорение реакции продукта сравнивается с контролируемым ускорением стола. Любое усиление, равное или большее 2: 1, обычно считается резонансным. Частота, при которой это происходит, называется резонансной частотой . DES видел очень серьезные резонансные пики, превышающие 20 к 1! Типичный график резонансного сканирования показан ниже. Например, ускорение отклика продукта (DUT) составляет 2,288 G при 688,1 Гц. Ускорение стола (Control) составляет ½ G при 688.1 Гц. Таким образом, 688,1 Гц считается резонансной частотой, потому что отношение ускорения продукта к столу составляет 2,288G / 0,5G = 4,576, что больше 2: 1.

Некоторые спецификации испытаний на случайную вибрацию, такие как RTCA DO-160 (Условия окружающей среды и процедуры испытаний для бортового оборудования), требуют сканирования резонанса синусоидальной вибрации до и после испытания вдоль каждой оси. Любое значительное изменение результатов резонансного сканирования может быть признаком повреждения или поломки продукта.

Самым известным провалом, вызванным резонансом, было катастрофическое обрушение моста Tacoma Narrows Bridge, как видно из статьи нашего блога «Вибрационная реакция продуктов». Когда изделия подвергаются вибрациям, близким к их собственным частотам, могут возникнуть усталостные разрушения из-за вибрационного резонанса. Компрессоры и двигатели являются примерами оборудования, которое может создавать значительные вибрации. Продукты, установленные рядом с таким оборудованием, не должны иметь собственных частот, близких к их скорости движения.

Чтобы предотвратить ранние отказы вашего продукта из-за усталости, DES может тестировать и анализировать вибрационный отклик вашего продукта, используя свои обширные знания и программное обеспечение для анализа вибрации.

14.4 Звуковые помехи и резонанс — Физика

Задачи обучения разделу

К концу этого раздела вы сможете делать следующее:

Опишите резонанс и удары
Определите основную частоту и ряд гармоник
Контрастность резонатора открытого и закрытого типа
Решение проблем, связанных с гармоническими сериями и частотой биений

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:

(7) Научные концепции.Студент знает характеристики и поведение волн. Ожидается, что студент:
(D) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.

Кроме того, Руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием: Звуковые волны, а также следующие стандарты:

(7) Научные концепции. Студент знает характеристики и поведение волн.Ожидается, что студент:
(D) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.

Раздел Ключевые термины

удар	частота биений	демпфирование	основной	гармоники
собственная частота	обертон	резонанс	резонировать

Поддержка учителя

[BL] Перед началом этого раздела было бы полезно рассмотреть свойства звуковых волн и то, как они связаны друг с другом, стоячие волны, суперпозиция и интерференция волн.

Резонанс и биения

Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту, нажимая на педаль сустейна. Он пропоет вам ту же ноту — струны, которые имеют те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Это хороший пример того факта, что объекты — в данном случае струны фортепиано — можно заставить колебаться, но лучше всего они колеблются на своей собственной частоте.

Движущая сила (например, ваш голос в примере) вводит энергию в систему с определенной частотой, которая не обязательно совпадает с собственной частотой системы.Со временем энергия рассеивается, а амплитуда постепенно уменьшается до нуля — это называется затуханием. Собственная частота — это частота, с которой система будет колебаться, если бы не было движения и демпфирующей силы. Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.

Большинство из нас играли с игрушками, в которых объект подпрыгивает на резинке, что-то вроде шарика, подвешенного на пальце на рисунке 14.18. Сначала вы держите палец неподвижно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете. По мере того, как частота возбуждения постепенно становится выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.

Рис. 14.18 Шарик на своей резиновой ленте перемещается в ответ на палец, поддерживающий его. Если палец движется с собственной частотой мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.

Другой пример: когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на частоте вещания (движущей силы) желаемой радиостанции.Кроме того, ребенок на качелях приводится в движение (толкается) родителем на собственной частоте качелей для достижения максимальной амплитуды (высоты). Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.

Рисунок 14.19 В некоторых типах наушников для подавления посторонних шумов используются явления конструктивных и деструктивных помех.

Поддержка учителя

[BL] [OL] [AL] Камертоны и трубы могут использоваться для демонстрации концепции резонанса.Используйте любую трубу или трубку, закрытую с одного конца. Закрепите его так, чтобы он стоял вертикально открытым концом вверх. Выберите камертон и ударьте по нему, чтобы он завибрировал. Поднесите его к горлышку трубы и послушайте звук. Теперь наполните трубу водой и повторите. При изменении уровня воды изменяется длина резонирующего столба воздуха. Продолжайте это делать. При достижении определенной длины звук камертона будет резонировать через колонку.

Все звуковые резонансы вызваны конструктивными и деструктивными помехами.Только резонансные частоты конструктивно интерферируют, образуя стоячие волны, тогда как другие интерферируют деструктивно и отсутствуют. От звука, издаваемого надуванием бутылки, до узнаваемости голоса великого певца, резонанс и стоячие волны играют жизненно важную роль в звуке.

Помехи случаются со всеми типами волн, включая звуковые волны. Фактически, один из способов подтвердить, что что-то является волной , — это наблюдать эффекты интерференции. На рис. 14.19 показан набор наушников, в которых для подавления шума используется умное использование звуковых помех.Чтобы получить деструктивную интерференцию, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.

Помимо резонанса, суперпозиция волн также может создавать биения. Биения производятся наложением двух волн с немного разными частотами, но одинаковой амплитудой. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне амплитуду, которая изменяется во времени.(См. Результирующую волну на рисунке 14.20).

Эта волна колеблется по амплитуде или биениям с частотой, называемой частотой биений. Уравнение для частоты биений:

fB = | f1 − f2 |, fB = | f1 − f2 |,
14,13
, где f ₁ и f ₂ — частоты двух исходных волн. Если две частоты звуковых волн похожи, то мы слышим среднюю частоту, которая становится громче и тише с частотой биений.
Советы для успеха
Не путайте частоту биений с обычной частотой волны, возникающей в результате наложения.Хотя частота биений задается приведенной выше формулой и описывает частоту биений, фактическая частота волны, полученная в результате наложения, является средним значением частот двух исходных волн.
Рисунок 14.20 Биения возникают в результате наложения двух волн немного разных частот, но одинаковых амплитуд. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне изменяющуюся во времени амплитуду.
Виртуальная физика
Волновые помехи
Для этого упражнения перейдите на вкладку «Звук». Включите параметр «Звук» и поэкспериментируйте с изменением частоты и амплитуды, а также с добавлением второго динамика и барьера.
Проверка захвата
Согласно графику, что происходит с амплитудой давления с течением времени. Как называется это явление и что его вызывает?
Амплитуда со временем уменьшается. Это явление называется затуханием.Это вызвано рассеянием энергии.
Амплитуда со временем увеличивается. Это явление называется обратной связью. Это вызвано накоплением энергии.
Амплитуда колеблется со временем. Это явление называется эхом. Это вызвано колебаниями энергии.
Основная частота и гармоники
Предположим, мы держим камертон возле конца трубки, которая закрыта на другом конце, как показано на рисунке 14.21, Рис. 14.22 и Рис. 14.23. Если камертон имеет правильную частоту, столб воздуха в трубке громко резонирует, но на большинстве частот он очень мало вибрирует. Это означает, что столб воздуха имеет только определенные собственные частоты. На рисунках показано, как формируется резонанс на самой низкой из этих собственных частот. Возмущение движется по трубке со скоростью звука и отскакивает от закрытого конца. Если трубка правильной длины, отраженный звук возвращается на камертон ровно через полцикла и конструктивно мешает продолжающемуся звуку, производимому камертоном.Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.
Рисунок 14.21 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение движется по трубе.
Рисунок 14.22 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение отражается от закрытого конца трубки.
Рис. 14.23 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Если длина трубки L подходящая, помеха возвращается к камертону через полцикла и конструктивно мешает продолжающемуся звуку камертона.Эта интерференция образует стоячую волну, и столб воздуха резонирует.
Стоячая волна, сформированная в трубе, имеет максимальное смещение воздуха (пучность) на открытом конце и отсутствие смещения (узел) на закрытом конце. Вспомните из предыдущей главы о волнах, что движение неограничено в пучности и останавливается в узле. Расстояние от узла до пучности составляет одну четвертую длины волны, и это равно длине трубки; следовательно, λ = 4Lλ = 4L. Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубки или около него, как показано на рисунке 14.24.
Рис. 14.24 Такая же стоячая волна создается в трубке из-за вибрации, вносимой около ее закрытого конца.
Поскольку максимальное смещение воздуха возможно на открытом конце, а не на закрытом, существуют другие, более короткие длины волн, которые могут резонировать в трубке (см. Рис. 14.25). Здесь стоячая волна имеет в трубке три четверти своей длины волны, или L = (3/4) λ′L = (3/4) λ ′, так что λ ′ = 4L / 3λ ′ = 4L / 3. Существует целый ряд коротковолновых и высокочастотных звуков, резонирующих в трубке.
Мы используем определенные термины для обозначения резонансов в любой системе. Самая низкая резонансная частота называется основной, а все более высокие резонансные частоты — обертонами. Все резонансные частоты кратны основной и называются гармониками. Основная гармоника — это первая гармоника, первый обертон — это вторая гармоника и так далее. На рисунке 14.26 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.
Рис 14.25 Еще один резонанс для трубки, закрытой с одного конца. Он имеет максимальное вытеснение воздуха на открытом конце и полное отсутствие на закрытом конце. Длина волны короче: три четверти λ′λ ′ равны длине трубки, так что λ ′ = 4L / 3λ ′ = 4L / 3. Эта высокочастотная вибрация — первый обертон.
Рис. 14.26 Основной и три нижних обертона закрытой с одного конца трубки. У всех есть максимальные вытеснения воздуха на открытом конце и нет — на закрытом конце.
Основной тон и обертоны могут присутствовать одновременно в различных комбинациях.Например, средняя до ноты на трубе звучит очень иначе, чем средняя до на кларнете, хотя оба инструмента представляют собой в основном модифицированные версии закрытой с одного конца трубки. Основная частота такая же (и обычно самая интенсивная), но обертоны и их сочетание интенсивностей различны. Этот микс — это то, что придает музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струнные или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для регулировки основных и сочетания обертонов.
Открытые и закрытые резонаторы
Резонансные частоты закрытой с одного конца трубки (известной как резонатор с закрытой трубкой): fn = nv4L, n = 1,3,5 …, fn = nv4L, n = 1,3,5 … ,
, где f ₁ — основной тон, f ₃ — первый обертон и т. Д. Обратите внимание, что резонансные частоты зависят от скорости звука v и от длины трубки L .
Другой тип трубки — это трубка, открытая на , с обоих концов (известная как открытый резонатор).Примеры — органные трубы, флейты и гобои. Воздушные столбы в трубках, открытых с обоих концов, имеют максимальное вытеснение воздуха с обоих концов. (См. Рисунок 14.27). Стоячие волны формируются, как показано на рисунке.
Рис. 14.27. Показаны резонансные частоты трубки, открытой с обоих концов, включая основной тон и первые три обертона. Во всех случаях максимальное смещение воздуха происходит на обоих концах трубы, что дает ей собственные частоты, отличные от собственных частот трубы, закрытой с одного конца.
Резонансные частоты открытого резонатора
fn = nv2L, n = 1,2,3…, fn = nv2L, n = 1,2,3 …,
, где f ₁ — основной обертон, f ₂ — первый обертон, f ₃ — второй обертон и т. Д. Обратите внимание, что трубка, открытая с обоих концов, имеет основную частоту вдвое больше, чем она была бы, если бы закрылась с одного конца. Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны.
Например,
Middle C будет звучать богаче при игре на открытой трубе, поскольку в ней больше обертонов. Резонатор с открытой трубкой имеет больше обертонов, чем резонатор с закрытой трубкой, потому что он имеет четные кратные основной и нечетной частоты, тогда как закрытая трубка имеет только нечетные кратные.
В этом разделе мы рассмотрели резонансные и стоячие волны для духовых инструментов, но вибрирующие струны на струнных инструментах также резонируют и имеют основы и обертоны, аналогичные таковым для духовых инструментов.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Другие инструменты также используют воздушный резонанс по-разному для усиления звука. Например, у скрипки и гитары есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат. Чем сложнее форма звуковой коробки, тем выше ее способность резонировать в широком диапазоне частот.Тип и толщина дерева или других материалов, используемых для изготовления звуковой коробки, также влияют на качество звука. Попросите учащихся привести еще несколько примеров того, как различные музыкальные инструменты используют явление резонанса.
Решение проблем, связанных с рядом гармоник и частотой биений
Рабочий пример
Определение длины трубы для замкнутого трубного резонатора
Если звук распространяется по воздуху со скоростью 344 м / с, какой длины должна быть закрытая с одного конца трубка, чтобы основная частота составляла 128 Гц?
Стратегия
Длину L можно найти, переставив уравнение fn = nv4Lfn = nv4L .
Решение
(1) Определите известных.
Основная частота 128 Гц.
Скорость звука 344 м / с.
(2) Используйте fn = nvw4Lfn = nvw4L, чтобы найти основную частоту ( n = 1).
(3) Решите это уравнение относительно длины.
(4) Введите значения скорости звука и частоты в выражение для L .
L = v4f1 = 344 м / с4 (128 Гц) = 0,672 мл = v4f1 = 344 м / с4 (128 Гц) = 0.672 м
14,16
Обсуждение
Многие духовые инструменты представляют собой модифицированные трубки с отверстиями для пальцев, клапанами и другими устройствами для изменения длины резонирующего столба воздуха и, следовательно, частоты проигрываемой ноты. Для рожков, воспроизводящих очень низкие частоты, таких как тубы, нужны лампы такой длины, чтобы они были свернуты в петли.
Рабочий пример
Обнаружение третьего обертона в открытом резонаторе
Если лампа, открытая с обоих концов, имеет основную частоту 120 Гц, какова частота ее третьего обертона?
Стратегия
Поскольку нам уже известно значение основной частоты (n = 1), мы можем найти третий обертон (n = 4), используя уравнение fn = nv2Lfn = nv2L.
Решение
Поскольку основная частота (n = 1) равна
и
f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц. f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц.
14,18
Обсуждение
Чтобы решить эту проблему, не нужно было знать длину трубки или скорость воздуха из-за взаимосвязи между основным и третьим обертоном. В этом примере был резонатор с открытой трубой; обратите внимание, что для резонатора с закрытой трубой третий обертон имеет значение n = 7 (не n = 4).
Рабочий пример
Использование частоты ударов для настройки фортепиано
Настройщики фортепиано постоянно используют биты в своей работе. Сравнивая ноту с камертоном, они прислушиваются к ударам и регулируют струну, пока удары не исчезнут (до нулевой частоты). Если тюнер пианино слышит два удара в секунду, а камертон имеет частоту 256 Гц, каковы возможные частоты фортепиано?
Стратегия
Поскольку мы уже знаем, что частота биений f _B равна 2, а одна из частот (скажем, f ₂) равна 256 Гц, мы можем использовать уравнение fB = | f1 − f2 | fB = | f1 − f2 | найти частоту фортепиано f ₁.
Решение
Так как fB = | f1 − f2 | fB = | f1 − f2 |,
мы знаем, что либо fB = f1 − f2fB = f1 − f2, либо −fB = f1 − f2 − fB = f1 − f2.
Решение для f ₁,
f1 = fB + f2 или f1 = −fB + f2.f1 = fB + f2 или f1 = −fB + f2.
14,19
Подставляя значения,
f1 = 2 + 256 Гц или f1 = −2 + 256 Гц f1 = 2 + 256 Гц или f1 = −2 + 256 Гц
14,20
Итак,
f1 = 258 Гц или 254 Гц. f1 = 258 Гц или 254 Гц.
14,21
Обсуждение
Настройщик пианино может изначально не определить, просто слушая, является ли частота пианино слишком высокой или слишком низкой, и должен настроить ее методом проб и ошибок, сделав настройку, а затем снова протестировав.Если после настройки ударов еще больше, то тюнер знает, что пошел не в том направлении.
Практические задачи
21.
Две звуковые волны имеют частоты 250 \, \ text {Гц} и 280 \, \ text {Гц}. Какова частота биений при их наложении?
290 \, \ text {Гц}
265 \, \ text {Гц}
60 \, \ text {Гц}
30 \, \ text {Гц}
22.
Какова длина трубы, замкнутой с одного конца с основной частотой 350 \, \ text {Гц}? (Предположим, что скорость звука в воздухе 331 \, \ text {м / с}.)
26 \, \ text {см}
26 \, \ text {m}
24 \, \ text {m}
24 \, \ text {см}
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся по целям обучения раздела.Если учащиеся борются с определенной целью, эти вопросы помогут определить ее и направить учащихся к соответствующему содержанию.
23.
Что такое демпфирование?
Со временем энергия увеличивается, а амплитуда постепенно уменьшается до нуля. Это называется демпфированием.
Со временем энергия рассеивается, а амплитуда постепенно увеличивается. Это называется демпфированием.
Со временем энергия увеличивается, а амплитуда постепенно увеличивается.Это называется демпфированием.
Со временем энергия рассеивается, и амплитуда постепенно уменьшается до нуля. Это называется демпфированием.
24.
Что такое резонанс? Когда можно сказать, что система резонирует?
Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
Явление возбуждения системы с частотой выше, чем ее собственная частота, называется резонансом, и система, работающая на собственной частоте, не резонирует.
Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, и система, работающая на собственной частоте, не резонирует.
Явление возбуждения системы с частотой выше, чем ее собственная частота, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
25.
В эксперименте с камертоном и трубкой, в случае образования стоячей волны, в какой точке трубки наблюдается максимальное возмущение от камертона? Напомним, что трубка имеет один открытый конец и один закрытый конец.
В середине трубы
Оба конца трубки
На закрытом конце трубки
На открытом конце трубки
26.
В эксперименте с камертоном и лампой, когда столб воздуха будет издавать самый громкий звук?
Если камертон вибрирует с частотой, вдвое превышающей собственную частоту столба воздуха.
Если камертон вибрирует с частотой ниже собственной частоты столба воздуха.
Если камертон вибрирует с частотой выше, чем собственная частота столба воздуха.
Если камертон вибрирует с частотой, равной собственной частоте столба воздуха.
27.
Что такое резонатор с закрытой трубой?
Труба или цилиндрическая воздушная колонна, закрытая с обоих концов
Труба с пучностью на закрытом конце
Труба с узлом на открытом конце
Труба или цилиндрическая воздушная колонна, закрытая с одного конца
28.
Приведите два примера открытых резонаторов.
фортепиано, скрипка
барабан, таблица
электрогитара, акустическая гитара
флейта, гобой
Определение резонанса по Merriam-Webster
Res · o · nance | \ ˈRe-zə-nən (t) s , ˈRez-nən (t) s \ 1а : качество или состояние резонанса
б (1) : — вибрация большой амплитуды в механической или электрической системе, вызванная относительно небольшим периодическим воздействием того же или почти такого же периода, что и период собственных колебаний системы.
(2) : состояние регулировки, вызывающее резонанс в механической или электрической системе.
2а : усиление и обогащение музыкального тона дополнительной вибрацией.
б : качество, придаваемое озвученным звукам за счет вибрации в анатомических резонирующих камерах или полостях (например, во рту или носовой полости).
c : качество богатства или разнообразия
d : качество вызова ответа какой резонанс, похоже, вызывает скандал — U.S. News & World Report
3 : звук, возникающий при перкуссии грудной клетки.
4 : концептуальное чередование химического вещества (например, молекулы или иона) между двумя или более эквивалентными разрешенными структурными представлениями, различающимися только размещением электронов, что помогает понять фактическое состояние химического вещества как объединение его возможных структур. и обычно более высокая, чем ожидалось, стабильность вида
5а : усиление реакции атома, ядра или частицы или событие рассеяния за счет возбуждения внутреннего движения в системе
6 : чрезвычайно короткоживущая элементарная частица.
7 : — синхронная гравитационная взаимосвязь двух небесных тел (таких как луны), вращающихся вокруг третьего (например, планеты), которое может быть выражено как простое соотношение их орбитальных периодов.
Захватывающая физика резонанса
На прошлое Рождество мой двоюродный брат подарил мне массажер для головы.Мало ли она знала о его потрясающей физике, которую я собирался раскрыть… и научить ее! На самом деле, я был настолько поражен этим подарком, что решил показать его гораздо большему количеству людей:

Магия массажеров для головы
Итак, позвольте мне быстро объяснить захватывающую физику массажеров головы. Любопытно, что когда длинная струна натягивается, а затем отпускается, это заставляет все длинные струны вибрировать. Однако короткие строки — нет.
В самом деле? А как насчет того, чтобы тянуть за короткие ниточки?
Это то же самое! Отпускание короткой струны заставляет все короткие струны вибрировать, а длинные почти не двигаются!
Почему?
Совершенно верно! Почему???
В видео вы сказали что-то о резонансе…
Да.Но прежде чем перейти к резонансу, мне нужно поговорить о частотах.
Что это?
Частота — подсчет количества повторений движения за заданный промежуток времени. Другими словами, чем выше частота, тем чаще вы будете ощущать дрожь. Важно отметить, что струна, как и в музыкальных инструментах, имеет определенную собственную частоту, которую мы обычно называем ее высотой тона или музыкальной нотой. И то же самое действительно для всех объектов.
Значит, каждая струна массажера для головы имеет собственные частоты?
Да! И, как и в музыке, эти собственные частоты зависят от формы струн и их материалов.Следовательно, все длинные струны имеют одинаковую собственную частоту, которая отличается от обычной собственной частоты коротких струн. Теперь, когда вы отпускаете длинную струну, эта длинная струна будет вибрировать с собственной частотой. За счет резонанса это будет возбуждать все окружающие объекты с одинаковой собственной частотой. Вот почему при колебаниях одной длинной струны будут колебаться все другие длинные струны, и только они.
Ужасающий резонанс
Меня больше всего поражает универсальность феномена, который раскрывают массажеры для головы.Резонанс вездесущ! И это имеет ужасающие последствия.
Как обрушение моста, о котором интервьюировали в видео?
Совершенно верно! Они имели в виду обрушение моста в Анже в 1850 году. Этот подвесной мост сломался, когда по нему прошел батальон солдат. Хотя износ моста и плохая погода в тот день определенно сыграли свою роль, считается, что именно резонанс их марша действительно спровоцировал обрушение моста.(Изображение из Викимедиа)
Фактически, в то время явление резонанса было уже хорошо известно военачальникам, поскольку им требовалось, чтобы батальоны ломали ступеньки при переходе мостов. Но этого явно было недостаточно, чтобы не дать Анжескому мосту обрушиться…
Неужели инженеры-строители не могут что-то сделать, чтобы предотвратить резонанс?
Это не так просто. Каждая искусственная конструкция имеет собственные частоты, и резонанс с непредвиденными вибрациями может быть внушительно устрашающим.Один особенно вопиющий пример произошел с небоскребами в Японии, вскоре после землетрясения силой 9 баллов:
.

О боже… Боже! Надеюсь, они приняли меры по противодействию резонансу в современных огромных небоскребах!
Есть! Забавно, что решение, данное для предотвращения колебаний в ранее самом высоком здании в мире Taipei 101, состоит в том, чтобы позволить некоторым массивным объектам внутри здания колебаться без него. Точнее, инженеры поместили внутрь Taipei 101 огромные маятники.Эти маятники естественным образом улавливают колебания всего здания.
Не знаю, почему это работает…
Упрощенный взгляд на это выглядит следующим образом. С точки зрения вибраций важны колебания центра масс. В случае землетрясения все здание должно будет вибрировать. Однако, позволяя некоторой части его массы вибрировать независимо от самого здания, вибрации самого здания уменьшаются. Вот видео простого эксперимента, демонстрирующего феномен так называемого массового демпфера путем сравнения первого случая без массового демпфера и второго с массовым демпфером:

Предотвращение резонанса или, по крайней мере, уменьшение его эффектов — важная часть других начинаний гражданского строительства.Производители судов предотвращают резонанс между волнами и кораблем, производители автомобилей избегают шумного резонанса между двигателем и корпусом автомобиля, а строители железных дорог ограничивают резонанс между воздушными линиями. Чтобы вернуться к зданиям, прежде чем перейти к полезному резонансу, вот более полное видео TedEds:

Восхитительный резонанс
Но резонанс — это не всегда плохо. Во-первых, он позволяет проводить зрелищные шоу с катушками Тесла, как блестяще объясняется в следующем потрясающем видео от Gentleman Physicist:

Вау! Вы собираетесь здесь объяснять катушку Тесла?
Извините… нет.Вы можете проверить отличное объяснение в этом видео Дрю Колпурса. Вместо этого я хочу поговорить о еще более важных приложениях резонанса.
Как что?
Нравится радио. Вы когда-нибудь задумывались об этом? Когда вы слушаете 100 AM, вы слышите только 100 AM. Вам не кажется, что это взорвало?
Я никогда не думал об этом … Но ДА !!! Это потрясающе!
И это благодаря резонансу!
В самом деле? Какое отношение радио имеет к резонансу?
Ключ — это цепь RLC.
Что такое цепь RLC?
Я не хочу вдаваться в подробности, но в основном схема RLC состоит из трех компонентов: сопротивления, катушки индуктивности и конденсатора. Важно отметить, что эта схема имеет собственную частоту, которая в основном зависит от катушки индуктивности и конденсатора.
В цепи есть собственная частота? Что это обозначает?
Это означает, что если вы подаете электрический ток сразу в цепь RLC, то напряжение в точке будет колебаться с этой собственной частотой.Но что еще более важно, если вы вводите альтернативный электрический ток, частота которого совпадает с собственной частотой цепи RLC, то за счет резонанса электрический ток в цепи RLC будет значительно усилен.
Тем не менее, я не понимаю, какое это имеет отношение к радио…
Вместо классического источника переменного тока радиостанции используют электромагнитную радиоволну для запуска токов в своих цепях RLC. И, что особенно важно, из-за резонанса ток, индуцируемый в цепи RLC электромагнитными радиоволнами, представляет собой только ток радиоволн той же частоты, что и собственная частота цепи RLC! Вот почему, когда мы слушаем 100 AM, мы слышим только 100 AM.4 $ герц, что равняется 1 МГц. Это означает, что сигнал 100 AM колеблется один миллион раз в секунду.
Подождите … Когда мы слушаем 100 AM, разве мы не слышим реальный звук, а не звук, соответствующий частоте 100 AM?
Мы делаем! Это потому, что сигнал с частотой 1 МГц — это просто несущая волна . Чтобы отправить фактический сигнал через несущую волну, вам нужно смодулировать несущую волну. Это можно сделать, умножив несущую волну на реальный речевой сигнал, который имеет гораздо более низкую частоту.Это соответствует рисунку справа, где первая кривая, помеченная как «сигнал», является фактическим отправляемым сообщением.
Есть небольшая разница между амплитудной модуляцией (AM) и частотной модуляцией (FM). В первом случае колебания фактического сообщения умножаются на колебания несущей волны, тогда как во втором случае именно частота уменьшается, когда фактический сигнал, который должен быть отправлен, имеет низкую амплитуду, следовательно, уменьшается резонанс.
Сигнал AM выглядит знакомо…
Если вы когда-либо работали со звуковыми сигналами, то определенно должны! Просто взгляните на результаты поиска Google Image по запросу «Звук».
Что это значит? Есть ли модуляция голосовых сигналов?
Удивительно, да. Когда вы говорите, вы в основном модулируете высоту своего голоса, которая действует как волновой носитель, умножая ее на звук слов, которые содержат фактическое сообщение! Очевидно, небольшое отличие от радио состоит в том, что вместо электромагнитной волны вы используете механическую волну давления воздуха.
Вы хотите сказать, что наши уши работают как радиоприемники?
Да! Разве это не потрясающе?
Но как они это делают? Я имею в виду … У ушей нет внутренних цепей RLC, не так ли?
№Давайте заглянем нам в уши с помощью тизера шоу BBC:
.

Что особенно важно, внутри наших ушей находится набор крошечных волосковых клеток разной высоты, погруженных в жидкость. Эти волосковые клетки в точности похожи на струны наших массажеров для головы. Они будут вибрировать только в том случае, если жидкость, в которую они погружены, колеблется с их собственной частотой. Теперь, поскольку эта жидкость находится в контакте с давлением воздуха прямо за пределами наших ушей, она вибрирует в соответствии со звуковыми волнами.Итак, что удивительно, обнаруживая, какие волосковые клетки вибрируют, наши нейронные системы могут различать частоты, составляющие звуковые волны, которые мы слушаем! Разве это не удивительно?
Уау! Это так круто!
Так что на самом деле массажеры для головы — это просто макроскопическая копия того потрясающего физического окружения, которое имеет место в наших ушах! Это потрясающе! Теперь я должен упомянуть, что есть и другие применения резонанса в медицине. В первую очередь это знаменитый магнитно-резонансный томограф (МРТ), который позволяет отслеживать активность мозга.Еще одним интересным приложением может быть лечение рака.
Музыка и несколько частот
Настоящие звуки на самом деле являются сложением множества разных частот. Фактически, удивительным и в то же время фундаментальным результатом анализа Фурье является тот факт, что все сигналы представляют собой композиции разных частот. Но на самом деле то же самое и с собственными частотами.
Что ты имеешь в виду?
Я имею в виду, что объекты на самом деле имеют несколько собственных частот. Конечно, некоторые из них более « натуральный », чем другие, но тот факт, что они имеют несколько из этих частот, является феноменом, который имеет важное значение для музыки.Оказывается, причина, по которой несколько разных музыкальных нот называются одним и тем же именем, –, сильно зависит от этого факта!
В самом деле? Вы хотите сказать, что между двумя нотами и существует сильная связь?
Да! На это прекрасно указал замечательный Маркус дю Сотуа в шоу BBC Story of Math:
.

Но что это за сильная связь? Какое отношение к гармонии звука имеет деление струны пополам?
Важно отметить, что у струны не только одна собственная мода колебаний.Конечно, основной режим колебаний соответствует вибрации струны, в которой остаются только две конечные точки. Но есть также колебания со средней точкой, называемые второй модой. Или, когда остаются первая и вторая третьи точки, это называется третьим режимом. И так далее… Прекрасная визуализация этого явления была создана великим Брайаном Коксом в вечернем шоу BBC:

Частоты различных форм колебаний соответствуют собственным частотам колебаний струны.Таким образом, когда мы возбуждаем гитарную струну, она будет вибрировать во всех различных режимах вибрации (хотя первый режим является основным). Теперь, что очень важно, многие из этих режимов вибрации для полной струны являются общими для полусуны! Фактически, все четные моды колебаний являются модами колебаний полуструны. Итак, удивительно, что октава от до содержит все колебания октавы от до . Вот почему они звучат так гармонично!
Вы хотите сказать, что когда мы слушаем до верхней октавы, мы слышим ее до нижней октавы?
Это именно то, что я говорю! При переключении с одного на другой некоторые волосковые клетки наших ушей все еще вибрируют, как раньше.Вот почему в нашем построении музыки есть такая важная гармония!
Отлично!
Я знаю!
Немного математики
Теперь, как математик, я не могу оставить у вас впечатление, что резонанс работает благодаря какой-то необъяснимой магии. Итак, в этом последнем разделе я объясню универсальный основной феномен. Для этого нам нужно обобщить этот паттерн, который соответствует математике.
Возможно, это прозвучит странно, поскольку я опишу резонанс с очень математической точки зрения, вместо того, чтобы выводить уравнения из физического моделирования.Моя статья о личности Эйлера является предпосылкой для этого раздела.
Итак, как вы используете математику для описания резонанса?
Во-первых, нам нужно описать частоты.
Как вы это описываете?
Частота описывает повторяющееся явление, поскольку подсчитывает, сколько раз начальное состояние происходит в единицу времени. Какая самая простая математическая структура соответствует этому?
Хм … не знаю …
Что-то, что возвращается в исходное состояние… Как это звучит?
Как петля?
В точности как петля! На самом деле, давайте рассмотрим простейший вид петли: круг! Я утверждаю, что зацикливание по кругу — это простейшая ситуация, в которой понятие частоты начинает обретать смысл.{i \ tau k} = 1 $. Между моментами времени $ t = 0 $ и $ t = 1 $ это происходит для целых чисел $ k $ от $ f t = 0 $ до $ f t = f $. Таким образом, это происходит $ f $ раз, что означает, что за 1 единицу времени происходит $ f $ колебаний. Итак, да, $ f $ действительно частота. {i \ tau f t} = i \ tau f z $.{i \ tau F t} $, окончательно получаем уравнение $ i \ tau a (F — f) = A $. В частности, амплитуда колебаний физического объекта имеет абсолютное значение $ | a | $, равное:
Эта формула означает, что амплитуда вращения вагона пропорциональна амплитуде $ A $ внешнего источника, что неудивительно. Но, что более важно, она обратно пропорциональна разнице частот. Итак, что поразительно, если частота источника полностью совпадает с частотой нашего физического объекта, амплитуда колебаний нашего физического объекта бесконечна! Это крайний резонанс!
И я полагаю, что это почти всегда разрушает физический объект!
Да, конечно! В реальной жизни очень маловероятно, что $ F = f $.2} $, который никогда не взорвется, если $ r> 0 $.
Честно говоря, я не очень доволен собой для этого раздела, поскольку я не могу получить интуицию резонанса без использования дифференциальных уравнений, таких как $ z-i \ tau f z = Z $. Прошу прощения за это … Если у вас есть идеи, как добиться большего успеха, я хотел бы это услышать!
Заключение
Феномен резонанса поражает своей вездесущностью в окружающем нас мире. Как сказал Никола Тесла: «, если вы хотите понять вселенную, подумайте об энергии, частоте и вибрации ».В этой вселенной вибраций резонанс играет центральную роль.
Вы не преувеличиваете?
Не думаю. Современные теории физики, такие как квантовая механика, наполнены волнами. Концепция частоты имеет важное значение для этих теорий, а резонанс — это очень противоречивый, но ключевой аспект для понимания этих теорий. А ключ к истинному пониманию волн лежит в мощном анализе Фурье. Но прежде чем читать об этом больше, я предлагаю вам сделать паузу еще на 3 минуты, чтобы взглянуть на удивительный эксперимент Brussup с пластиной Хладни, который раскрывает некоторые впечатляющие резонансные явления, возникающие на трясущейся пластине:

Здесь происходит то, что песок падает на не колеблющиеся участки плиты.Участки пластины, которые резонируют с центральными колебаниями, избавляются от песка из-за своих колебаний.
Собственная частота: хорошее, плохое и катастрофическое
Крошащиеся мосты, разбитое стекло, кричащие дети, тяжелые басы — тот, кто считает, что у этих вещей нет ничего общего, ошибается. Все они создаются вибрациями, и, в частности, сильные вибрации создаются собственными частотами. Читайте дальше, пока мы объясним науку, лежащую в основе этого принципа, и что такое резонансные катастрофы, а также рассмотрим игру резонанса крена, когда дело касается громкоговорителей.
Все вибрирует, но как?
Вибрация наушников всегда является реакцией на импульс энергии. Рука может запустить маятник в движение, ветер может раскачать небоскреб, а катушка с помощью магнита может сдвинуть мембрану громкоговорителя. Насколько сильно что-то вибрирует, зависит от приложенной мощности вибрации, а также от материала, включая конструкцию колебательной системы. С другой стороны, большое значение имеет частота, с которой действуют импульсы энергии.Ведь если частота подаваемой энергии совпадает с собственной частотой тела, тело вибрирует с особенно высокой амплитудой.
Как явление резонансной частоты выглядит на практике, можно понять с помощью маятника: если пружинный маятник является периодическим, то есть через регулярные промежутки времени получает энергию, соответствующую собственной частоте маятника, отклонение маятника составляет его величайший. Если импульсы энергии имеют более низкую или более высокую частоту, чем собственная частота, отклонение маятника будет меньше.

На качелях вы можете попробовать на себе, как работает резонансная частота. Когда вы ударяете качелями в наивысшую точку, подача энергии точно соответствует собственной частоте системы. Вот почему качели имеют такой большой импульс качания. Если вы ударите до или после того, как замах достигнет своей наивысшей точки, сила передается менее эффективно или даже никуда не денется.
От хороших к плохим колебаниям
Корпус акустической гитары, качелей, стекла или моста может вибрировать с соответствующей резонансной частотой.Но это не везде желательно и даже может нанести большой ущерб. Это связано с тем, что системы могут так сильно вибрировать, что конструкция не может выдержать нагрузку.
Это явление можно наблюдать, когда человек направляет голос на бокал с вином с небольшого расстояния. Если высота голоса в точности соответствует собственной частоте стекла, оно через относительно короткое время разбивается — происходит так называемая резонансная катастрофа. Если голосовые связки заставляют молекулы воздуха колебаться с большей или меньшей частотой, стекло остается неповрежденным.Собственную частоту стекла можно услышать, когда вы ударите его каким-либо предметом.
Одна из самых известных резонансных катастроф произошла в США в 1940 году, когда из-за ветра мост Tacoma Narrows Bridge так сильно затрясся, что он рухнул.

Чтобы избежать резонансных катастроф, дорожный кодекс запрещает группам людей, например, военным частям, шагать по мостам.
С другой стороны, для музыкальных инструментов резонанс — это преднамеренный эффект для увеличения громкости звука.В акустической гитаре корпус действует как механический усилитель звуковых волн, которые запускаются струнами. Корпус гитары устроен таким образом, что резонансная частота возникает даже на разных тонах.
Громкоговорители Teufel
Резонансные эффекты в громкоговорителях нежелательны — за одним исключением
Резонансная частота в громкоговорителях не приветствуется. Громкоговорители сконструированы таким образом, что различные компоненты не вибрируют на своей резонансной частоте.Это означало бы, что звуки в том же частотном диапазоне, что и отдельные компоненты, будут воспроизводиться намного громче, чем другие. Именно здесь вступает в игру кроссоверная сеть: в многоканальных системах она направляет сигналы на динамики в соответствии с их частотой.
Резонансные эффекты также не должны возникать в корпусе громкоговорителя. Это может произойти, когда мембрана на задней стороне излучает звук внутрь громкоговорителя. Этот звук может вызвать вибрацию корпуса и, таким образом, негативно повлиять на звуковой образ.Чтобы предотвратить это, корпус громкоговорителя снабжен демпфером, который поглощает звуковые волны, излучаемые внутрь.
Исключением из этого правила являются фазоинверторные колонки. Эти шкафы имеют трубчатое отверстие, через которое излучаемый внутрь звук на определенных низких частотах может выходить в комнату. Это работает по принципу резонатора Гельмгольца, который мы объяснили в нашем тексте о сабвуферах.
Нам нужны басы: бас Teufel для более глубоких вибраций
Der Subwoofer der Kombo 42 BT Power Edition verleiht den Regallautsprechern ordentlich Wumms
▶ Моно-сабвуфер US 2106/1 SW: Этот сабвуфер для новичков предлагает мощные басы, не нарушая шума потока, несмотря на его компактные размеры.Это достигается с помощью двух ламп фазоинвертора.
▶ Ultima 40/20 «2.0> 5.1 Extension Set Surround»: акустические системы Ultima 40/20 HiFi — настоящая дьявольская классика для дома. С помощью этого набора вы можете расширить свою стереосистему до объемного звука 5.1. Сабвуфер T 10 обеспечивает хороший резонанс в диапазоне низких частот.
Еще товары от Teufel
Вывод: резонансная частота полезна
На резонансной частоте собственная частота колебательной системы совпадает с частотой подводимой энергии.
В случае резонанса отклонение колебаний увеличивается.
В акустике более высокая амплитуда звуковых волн означает более высокое звуковое давление и, следовательно, большую громкость.
Резонансные частоты обычно нежелательны для громкоговорителей.
Акустические системы с фазоинвертором являются исключением. Они усиливают низкие частоты по принципу резонатора Гельмгольца.
Наконец, классика «Багз Банни» на эту тему:

Значение, характеристики, преимущества и недостатки
Наука> Физика> Стационарные волны> Резонанс
В этой статье мы изучим явление резонанса, его характеристики, достоинства и недостатки.
Свободные колебания:
Тело или система, способные колебаться, при смещении из положения покоя колеблются с определенной определенной частотой. Эта частота характерна для тела или системы. Такие колебания называются свободными колебаниями или свободными колебаниями, а частота таких колебаний называется собственной частотой тела или системы.
Пример — 1: Когда натянутую проволоку, закрепленную на концах, выщипывают и отпускают, она вибрирует с частотой, которая зависит от длины струны, ее массы на единицу длины и натяжения струны. .
Пример — 2: Когда качель простого маятника колеблется, его частота колебаний зависит от длины маятника.
В связи с сила трения, амплитуда колебаний непрерывно уменьшается и наконец, тело перестает вибрировать.
Характеристики свободных колебаний:
Они образуются, когда тело, способное к вибрации, отклоняется от его нормального положения равновесия, а затем отпускается.
Частота вибрации зависит от тела и называется собственной частотой.
Частота вибрации такая же, как собственная частота тела.
Амплитуда вибрации большая.
Вибрация продолжается еще немного после снятия внешней силы.
Пример: Колебания опоры маятника
Вынужденные колебания:
Принудительный вибрации — это колебания, производимые в теле при применении внешнего периодическая сила, имеющая частоту, обычно отличную от естественной частота тела.
Тело или систему, способную вибрировать, также можно заставить вибрировать при любом желании. частота. Тело можно заставить вибрировать с той же частотой, что и частота приложенной периодической силы. Предположим, что собственная частота металлический сосуд — 200 Гц. Если настроен камертон с частотой 256 Гц вибрации, и его шток соприкасается с сосудом, затем судно будет вынуждено вибрировать с частотой 256 Гц. В таком В этом случае говорят, что сосуд совершает вынужденные колебания.
Первоначально, тело имеет тенденцию вибрировать с собственной частотой. Но очень скоро собственные колебания затухают, и он начинает колебаться с частотой приложенная периодическая сила.
амплитуда вынужденных колебаний зависит от:
Разница частот внешней силы и собственная частота тела.
Амплитуда приложенной силы.
Характеристики принудительного Вибрации:
Они образуются при воздействии на тело внешней периодической силы.
Частота вибрации такая же, как частота внешней периодической силы.
Частота вибрации отличается от собственной частоты тела.
Амплитуда вибрации мала.
Амплитуда становится равной нулю, как только снимается внешняя сила.
Пример: вибрирующий камертон на деревянном ящике, музыкальный инструмент с декой или ящиком.
Резонанс:
амплитуда вынужденных колебаний зависит от разницы между собственная частота тела и частота приложенной периодической силы.Когда разница между двумя частотами большая, отклик тела плохая или вынужденные колебания малой амплитуды. Когда частота разница становится меньше, тело вибрирует быстрее или амплитуда вынужденные колебания возрастают. Наконец, когда частота (f) применяемого периодическая сила становится такой же, как собственная частота fo тела, амплитуда вынужденных колебаний становится максимальной и явление известно как резонанс.
Если кого-то заставляют вибрировать внешней периодической силой с частотой, которая совпадает с собственной частотой тела, тело начинает вибрировать с очень большой амплитудой.Это явление называется резонансом.
Различие между вынужденными колебаниями и резонансом:
Вынужденные колебания Резонанс
Они возникают под действием внешней периодической силы любой частоты. Они создаются внешней периодической силой, частота которой равна собственной частоте тела.
В частота вибрации отличается от собственной частоты тела. Частота вибрации такая же, как собственная частота тела.
Амплитуда вибрации мала. Амплитуда вибрации большая.
Вибрация прекращается, как только снимается внешняя сила. Вибрация продолжается еще немного после снятия внешней силы
Преимущества резонанса:
Резонанс используется для определения неизвестной частоты.
Резонанс используется для увеличения интенсивности звука музыкальных инструментов.
Резонанс полезен для настройки радиоприемника на любую желаемую частоту.
Резонанс полезен для анализа музыкальных нот.
Недостатки резонанса:
Солдатам предлагается сломать ступеньки при переходе через мост. Это можно объяснить следующим образом
Солдаты маршируя по мосту, делайте шаги с определенной частотой и заставляйте мост вибрировать с частотой шагов.
Если вынужденная частота на мосту равна собственной частоте вибрации моста, мост приводится в резонансные колебания.
Благодаря резонанс, мост вибрирует с большей амплитудой и из-за этого может крах.
Из-за ритмичных хлопков публики крыша стадиона может обрушиться. Это можно объяснить следующим образом
Когда публика ритмично хлопает в ладоши, они делают это с определенной частотой и заставляют крышу стадиона вибрировать с частотой хлопков.
Если вынужденная частота на крыше стадиона равна собственной частоте вибрация крыши стадиона, крыша стадиона установлена в резонансную вибрации.
Из-за резонанса крыша стадиона вибрирует с большей амплитудой и из-за этого может обрушиться.
Когда скорость самолета увеличивается, различные части вынуждены вибрировать. что опасно для конструкции самолета.
Эксперимент с резонансной трубкой для определения Скорость звука в воздухе:
Металл Трубка, открытая с обоих концов, погружается в высокую стеклянную банку, наполненную водой.Таким образом, между открытым концом металлической трубки и трубкой образуется столб воздуха. поверхность воды. Длина столба воздуха, который закрывается поверхность воды на нижнем конце, можно изменять, поднимая или опуская металл трубка. Камертон приводится в колебания и удерживается возле устья трубка так, чтобы ее плечи колебались параллельно оси трубки. В продольная волна, начиная от камертона, распространяется по длине столб воздуха и отражается обратно от поверхности воды.В падающая и отраженная волны интерферируют, создавая стационарную волну.
Молекулы воздуха, соприкасаясь с поверхностью воды, остаются в покое. Следовательно, закрытый становится узлом. Молекулы воздуха около горловины трубки колеблются с максимальной амплитудой. Таким образом, открытый конец становится пучностью. Частоту воздушного столба можно изменять, регулируя его длину. Когда его частота становится такой же, как частота вилки, возникает резонанс и слышен громкий звук.
Если длина столба воздуха увеличена с небольшого значения, первый резонанс возникает, когда есть узел на закрытом конце и пучность на открытом конце, без каких-либо других узлов или пучностей между ними. Следовательно, длина воздуха колонка л = λ / 4
∴ λ = 4 л
Из-за резонанса частота столба воздуха такая же, как у вилки. Теперь скорость звука определяется выражением v = nλ
.
∴ v = 4 n l
Конечная поправка:
Это было Реньо показал, что пучность образуется не точно на открытом конце, а на расстоянии 0.3 d над открытым концом, где d — внутренний диаметр трубка. Это дополнительное расстояние, называемое конечной коррекцией, необходимо, поскольку волна слегка распространяется, чуть выше открытого конца, и частицы воздуха просто вне открытого конца также находятся в вибрации.
∴ исправлено длина = л + 0,3d
Следовательно, скорость звука в воздухе при комнатной температуре
В = nλ = 4n ( л + 0,3d)
Следовательно, зная n, l, и d, определяется скорость звука в воздухе.
Предыдущая тема: Колебания столба воздуха
Для получения дополнительных тем по физике щелкните здесь
Наука> Физика> Стационарные волны> Резонанс
Резонанс спагетти: физическая наука
Вы можете заставить объект вибрировать разными способами. Вы можете дотронуться до него ручкой камертона. Вы можете петь под нее. По нему можно натереть смычок, как скрипку. Вы даже можете жужжать при этом, как в трубе.Или, что наиболее очевидно, вы можете схватить его рукой и встряхнуть. Но это не единственный способ, которым объект может вибрировать. Многие объекты имеют собственную частоту, а это означает, что, когда они вытягиваются или смещаются из своего исходного положения, они подпрыгивают и какое-то время вибрируют сами. Гитарные струны, камертоны, фужеры, здания, трубки с воздухом и многие другие предметы будут вибрировать с определенной частотой, если часть объекта потянуть назад, а затем отпустить.
Если совместить обе эти ситуации вместе, произойдет нечто удивительное.Если вы заставите объект вибрировать с его собственной частотой, он начнет вибрировать с очень большой амплитудой. Чтобы понять, почему, представьте, что спагетти и зефир раскачиваются взад и вперед. Если вы толкнете спагетти пальцем в самый подходящий момент — когда они снова начинают раскачиваться, зефир уйдет чуть дальше, чем в прошлый раз, получив большую амплитуду. Если вы нажмете на спагетти в неподходящее время — например, когда зефир возвращается к вам, — вы замедляете зефир, а не ускоряете его, и его амплитуда будет меньше, чем была раньше.Следовательно, чтобы зефир раскачивался вперед и назад на все большее и большее расстояние, вы должны нажимать на спагетти синхронно с тем, как они уже раскачиваются. Другими словами, чтобы зефир имел большую амплитуду, вы должны заставить его вибрировать с собственной частотой. На этой частоте самый маленький толчок может составить достаточно большой взмах, чтобы разбить спагетти.
Каждый кусок спагетти с зефиром имеет собственную частоту, которая зависит от жесткости спагетти, их массы и зефира и расстояния до каждой массы.Чем длиннее или плотнее паста или зефир, тем ниже собственная частота. Чем гуще паста, тем выше собственная частота. В зависимости от этих факторов, каждый вид макаронных изделий будет иметь свою собственную частоту.
Короткий кусок макаронных изделий будет иметь другую собственную частоту, чем длинный кусок макаронных изделий. Когда вы кладете их в одну руку, вы заставляете их вибрировать с одинаковой частотой. Если собственная частота одного куска макаронных изделий совпадает с этой частотой, то этот кусок будет резонировать, но не другой.Поскольку они имеют разные собственные частоты, им нужны разные частоты вынужденных колебаний, чтобы они входили в резонанс.
.

Вынужденные колебания	Резонанс
Они возникают под действием внешней периодической силы любой частоты.	Они создаются внешней периодической силой, частота которой равна собственной частоте тела.
В частота вибрации отличается от собственной частоты тела.	Частота вибрации такая же, как собственная частота тела.
Амплитуда вибрации мала.	Амплитуда вибрации большая.
Вибрация прекращается, как только снимается внешняя сила.	Вибрация продолжается еще немного после снятия внешней силы

Резонанс — урок. Физика, 9 класс.

Явление резонанса — Основы электроники

Похожие материалы:

Добавить комментарий

Резонансные явления в электрических сетях

Резонанс напряжений

Резонанс токов

Резонансная частота — это… Что такое Резонансная частота?

Механика

Электроника

Акустика

Струна

Примечания

См. также

Ссылки

РЕЗОНАНС • Большая российская энциклопедия

Российские ученые обнаружили новый физический парадокс

Resonance | Protocol (Translated to Russian)

9.10: Резонанс

Что такое вибрационный резонанс?

14.4 Звуковые помехи и резонанс — Физика

Задачи обучения разделу

Поддержка учителей

Поддержка учителей

Раздел Ключевые термины

Поддержка учителя

Поддержка учителя

Резонанс и биения

Поддержка учителя

Поддержка учителя

Советы для успеха

Виртуальная физика

Волновые помехи

Проверка захвата

Основная частота и гармоники

Открытые и закрытые резонаторы

Поддержка учителя

Поддержка учителя

Решение проблем, связанных с рядом гармоник и частотой биений

Рабочий пример

Определение длины трубы для замкнутого трубного резонатора

Стратегия

Рабочий пример

Обнаружение третьего обертона в открытом резонаторе

Стратегия

Рабочий пример

Использование частоты ударов для настройки фортепиано

Стратегия

Практические задачи

Проверьте свое понимание

Поддержка учителей

Поддержка учителей

Определение резонанса по Merriam-Webster

Захватывающая физика резонанса

Магия массажеров для головы

Ужасающий резонанс

Восхитительный резонанс

Музыка и несколько частот

Немного математики

Заключение

Собственная частота: хорошее, плохое и катастрофическое

Все вибрирует, но как?

От хороших к плохим колебаниям

Громкоговорители Teufel

Резонансные эффекты в громкоговорителях нежелательны — за одним исключением

Нам нужны басы: бас Teufel для более глубоких вибраций

Еще товары от Teufel

Вывод: резонансная частота полезна

Значение, характеристики, преимущества и недостатки

Резонанс спагетти: физическая наука

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ