Последовательное и параллельное соединение конденсаторов
Последовательное соединение более двух конденсаторов редко встречается в реальных схемах. Хотя для увеличения общего напряжения такую комбинацию можно найти в высоковольтных источниках питания. Однако для низковольтных приложений довольно часто используется несколько параллельно включенных конденсаторов для сглаживания эффектов пульсаций после выпрямления при больших токах.
Содержание
Последовательное и параллельное соединение конденсаторов
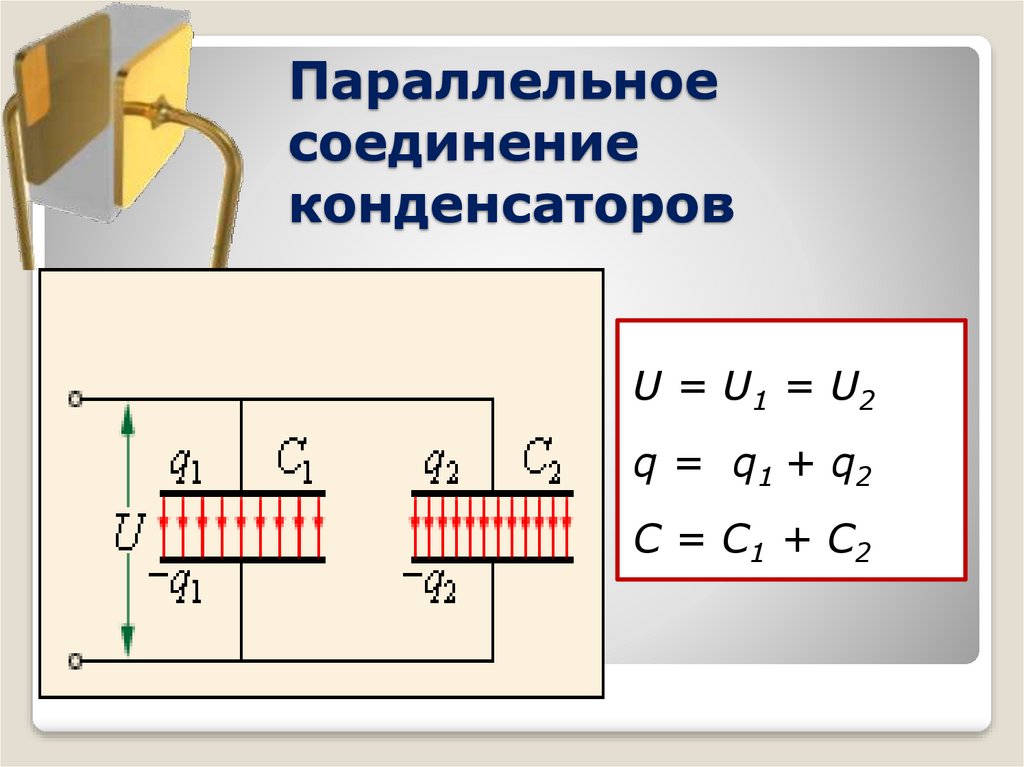
При параллельном соединении суммарная емкость конденсатора складывается, и допустимое напряжение всего комплекта будет равно напряжению конденсатора с наименьшим допустимым напряжением из всего комплекта.
C = C1 + C2 + C3 + C4 + .
Например: у нас есть три конденсатора 30 мкФ x 100 В, соединенных параллельно. Параметры всего набора конденсаторов в этом случае составят 90 мкФ x 100 В.
Последовательное соединение более двух конденсаторов редко встречается в реальных схемах. Хотя для увеличения общего напряжения такую комбинацию можно найти в высоковольтных источниках питания. Однако в низковольтных источниках питания довольно распространено параллельное подключение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах.
Хотя для увеличения общего напряжения такую комбинацию можно найти в высоковольтных источниках питания. Однако в низковольтных источниках питания довольно распространено параллельное подключение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах.
Обратите внимание, что формулы для расчета емкости последовательных и параллельных конденсаторов точно такие же, как и формулы для расчета сопротивления последовательных и параллельных резисторов.
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-параллельным (смешанным). Если провести аналогию между подключением конденсаторов и подключением резисторов, то стоит отметить, что формулы для расчета общей емкости и общего сопротивления идентичны, просто между разными типами соединений: Формула Cвсего При параллельном соединении конденсаторов = Rобщий При последовательном соединении резисторов.
Последовательное и параллельное соединение конденсаторов
Конденсаторы в электрической цепи могут быть соединены последовательно, параллельно и последовательно-параллельно (смешанно). Чтобы провести аналогию между подключением конденсатора и подключением резистора, стоит отметить, что формулы для расчета общей емкости и общего сопротивления идентичны, просто между разными типами соединений: Формула Cвсего при параллельном соединении конденсаторов = Rвсего при последовательном соединении резисторов.
Чтобы провести аналогию между подключением конденсатора и подключением резистора, стоит отметить, что формулы для расчета общей емкости и общего сопротивления идентичны, просто между разными типами соединений: Формула Cвсего при параллельном соединении конденсаторов = Rвсего при последовательном соединении резисторов.
- Cобщий – общая емкость.
- Rвсего – общее сопротивление.
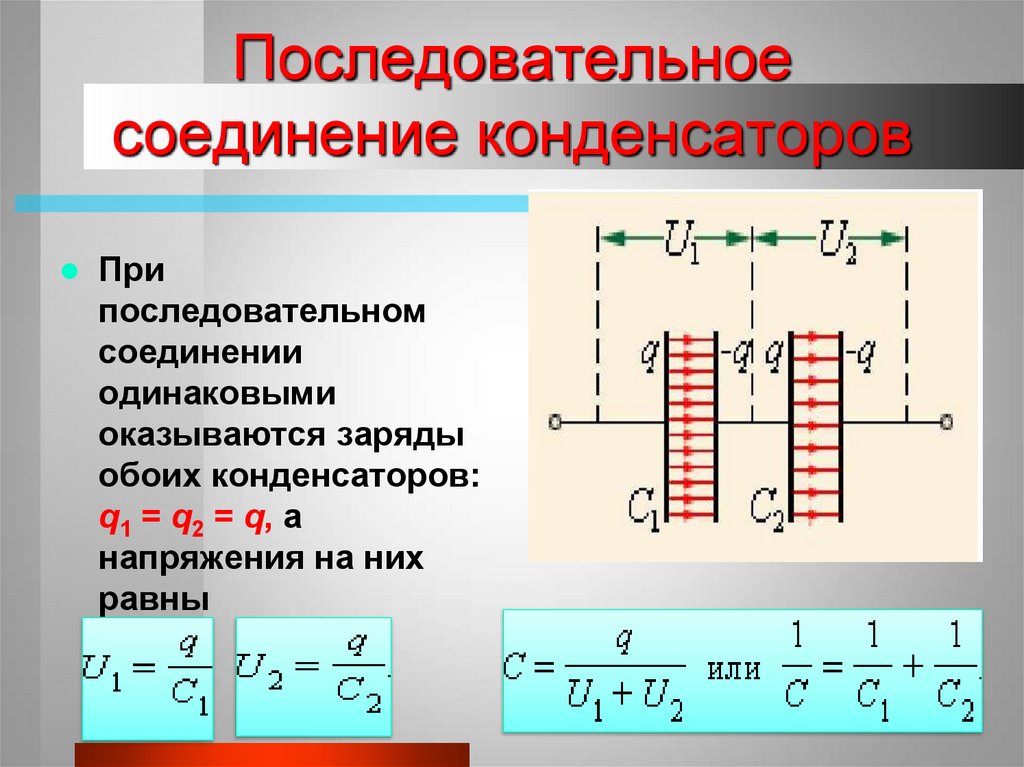
Когда конденсаторы соединены последовательно (рис. 3), электрические заряды на выводах отдельных конденсаторов равны по величине: Q1 = Q2 = Q3 = Q. Действительно, от сети заряды достигают только внешних обкладок цепи конденсаторов, а на соединенные между собой внутренние обкладки соседних конденсаторов передается только заряд одинаковой величины от одной обкладки к другой (электростатическая индукция), поэтому на них имеются одинаковые и разные электрические заряды.
Напряжение между стенками отдельных конденсаторов в последовательном соединении зависит от емкости отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3. Общая емкость эквивалентного конденсатора C = Q / U = Q / (U1 + U2 + U3), т.е. если конденсаторы соединены последовательно, то обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Формулы для эквивалентных емкостей аналогичны формулам для эквивалентных проводимостей.
Общая емкость эквивалентного конденсатора C = Q / U = Q / (U1 + U2 + U3), т.е. если конденсаторы соединены последовательно, то обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Формулы для эквивалентных емкостей аналогичны формулам для эквивалентных проводимостей.
_________________
| Страница 5 Со страницы 6 | [Новости: 104 ] | На предыдущую страницу. 1 , 2 , 3 , 4 , 5 |
Объяснить, почему емкость уменьшается, когда конденсаторы одного номинала соединены последовательно, очень просто На этом сказка заканчивается, и хорошо тому огурцу, который слушал. _________________ JLCPCB, всего $2 за прототип платы! Любой цвет по вашему желанию! Подпишитесь и получите два купона на $5 каждый: https://jlcpcb. Сегнетокерамика и имеет проницаемость около 10000. Керамические конденсаторы имеют низкую емкость, потому что между диэлектриком и пластиной есть микроскопический слой воздуха, а воздух имеет проницаемость = 1. У нас конденсаторы соединены последовательно, или субж. В электролите удалили один из слоев и емкость увеличилась, а в суперконденсаторе удалили и другой слой и получили гигант (на пальцах). Если электролиты соединены последовательно, то нет необходимости в диодах, внутреннее сопротивление таких электролитов в обратном режиме в любом случае довольно низкое. Поэтому первоначально один конденсатор действительно будет заряжаться в обратной полярности, но затем напряжение на нем упадет, а на другом вырастет. Такие цепи не используются при больших токах – в основном они применяются для развязки цепей по постоянной составляющей. В тех же схемах можно нагрузить средний отвод конденсаторов резистором на землю (если подключен к минусу) или на питание (если подключен к плюсу), тогда оба конденсатора будут иметь положительную полярность и срок их службы немного увеличится. _________________ Сборка печатной платы от $30 + БЕСПЛАТНАЯ доставка по всему миру + шаблон Согласно закону сохранения заряда, если центральная точка никуда не подключена, то ни один из конденсаторов не поляризован, они оба вращаются вокруг нулевой точки и каждый получает полупериод обратного заряда. либо диоды, либо резистор, оба дадут центральную точку, поляризованную в нужном направлении – диоды, как и резистор, не работают непрерывно, ток через них течет только в начале, при включении нельзя, но необходимо – обратное смещение будет постепенно разрушать оксидный слой даже при малых токах Модули Navigator позволяют значительно сократить время разработки программного обеспечения. Во время вебинара 17 ноября вы сможете узнать о новых семействах Teseo-LIV3x, Teseo-VIC3x и Teseo-LIV4F. Вы узнаете, как легко добавить функцию позиционирования с повышенной точностью, используя двухдиапазонный приемник и навигационную функцию MEMS-датчика. _________________ Компания Infineon представила семейство 40-вольтовых МОП-транзисторов OptiMOS 5. Эти транзисторы относятся к МОП-транзисторам нормального уровня с более высоким пороговым напряжением (по сравнению с другими низковольтными МОП-транзисторами) для защиты от ложных срабатываний в шумной обстановке. Это уже обсуждалось в другом месте, при подключении привода переменного тока. _________________ _________________ _________________ _________________ _________________ _________________ _________________ Конденсатор имеет паразитную проводимость, она же ток утечки, она же саморазряд. Если два одинаковых конденсатора соединены последовательно, и общее напряжение на них одинаково, ток утечки будет вдвое меньше (потому что напряжение на каждом конденсаторе будет вдвое меньше; а сопротивление последовательно соединенных конденсаторов суммируется). _________________ _________________ _________________ Часовой пояс: UTC + 3 часа Кто в настоящее время находится на форумеСейчас этот форум просматривают: нет зарегистрированных пользователей или гостей: 17 Рисунок 5: Пример расчета последовательно-параллельного соединения конденсаторов. Последовательно-параллельное (смешанное) соединение конденсаторовПараллельно-последовательное соединение конденсаторов представляет собой цепь с последовательно и параллельно соединенными секциями конденсаторов. На рисунке 4 показан пример схемы со смешанным соединением конденсаторов. Рисунок 4: Последовательно-параллельное соединение конденсаторов. При расчете общей емкости такого участка цепи с последовательно-параллельными конденсаторами участок разбивается на простые секции, состоящие только из групп последовательных или параллельных конденсаторов. Алгоритм расчета следующий: 1. определить эквивалентную емкость секций с последовательно-параллельными конденсаторами. 2. если в этих секциях есть последовательно соединенные конденсаторы, сначала рассчитайте их емкости. 3. рассчитав эквивалентные емкости конденсаторов, перерисуйте схему. Обычно получается схема последовательно соединенных эквивалентных конденсаторов. 4 Вычислите емкость полученной цепи. Один из примеров расчета емкости в смешанном конденсаторном соединении показан на рисунке 5. Рисунок 5: Пример расчета последовательно-параллельного соединения конденсаторов. Подробнее о расчете соединений конденсаторов вы можете узнать в мультимедийном учебнике по основам электротехники и электроники: ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Пример 2. 100 конденсаторов по 2 мкФ каждый соединены параллельно. Определите общую емкость. Общая емкость C = 100 кф = 200 мкф. Параллельное и последовательное соединение конденсаторовОтдельные конденсаторы могут быть соединены вместе различными способами. Во всех случаях для замены серии конденсаторов, соединенных вместе, можно найти емкость некоторого эквивалентного конденсатора. Для эквивалентного конденсатора выполняется условие: если напряжение, приложенное к выводам эквивалентного конденсатора, равно напряжению, приложенному к крайним выводам группы конденсаторов, то эквивалентный конденсатор будет накапливать такой же заряд, как и группа конденсаторов. Параллельное соединение конденсаторов На рисунке 1 показано параллельное соединение нескольких конденсаторов. В этом случае напряжения, приложенные к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на выводах отдельных конденсаторов равны Q1 = C1U , Q 2 = C 2 U , Q 3 = C 3 U , а заряд, поступающий от источника Q = Q1 + Q2 + Q3. Рисунок 1: Схема параллельного соединения конденсаторов Общая емкость эквивалентного конденсатора: C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3 , т.е. При параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. Последовательное подключение конденсаторов При последовательном соединении конденсаторов (рис. 3) электрические заряды на выводах отдельных конденсаторов равны по величине: Q1 = Q2 = Q3 = Q Действительно, источник электрических зарядов приложен только к внешним катушкам цепи конденсаторов, а на внутренних катушках соединенных конденсаторов происходит только перенос электрических зарядов одинаковой величины с одной катушки на другую (электростатическая индукция), поэтому на них имеются одинаковые и разные электрические заряды. Рис. 3 Схема последовательного соединения конденсаторов Напряжение между выводами отдельных конденсаторов в последовательном соединении зависит от емкости отдельных конденсаторов: U1 = Q/C1 , U1 = Q/C 2, U1 = Q/C 3, а общее напряжение U = U1 + U2 + U3 Общая емкость эквивалентного конденсатора C = Q / U = Q / ( U1 + U2 + U3 ), т.е. если конденсаторы соединены последовательно, то обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Формулы для эквивалентных емкостей аналогичны формулам для эквивалентных проводимостей. Пример 1. Три конденсатора емкостью C1 = 20 мкФ, C2 = 25 мкФ и C3 = 30 мкФ соединены последовательно, определите их общую емкость. Общая емкость определяется из выражения 1/C = 1/C1 + 1/C2 + 1/C3 = 1/20 + 1/25 + 1/30 = 37/300, где C = 8,11 мкф. Пример 2: 100 конденсаторов по 2 мкФ каждый соединены параллельно. Определите общую емкость. Общая емкость C = 100 Ck = 200 мкф. Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Параллельное соединение конденсаторов. 25.04.2016 Lega95 0 комментариев Привет всем. Этот небольшой пост посвящен теме подключения конденсаторов. На практике часто случается, что у нас нет конденсатора с нужным номиналом для установки, а технику требуется срочный ремонт. Именно для таких случаев нам необходимо знать правила подключения конденсаторов. Существует только два способа подключения конденсаторов. Это последовательное соединение и параллельное соединение. Теперь мы рассмотрим оба метода более подробно. Параллельное соединение конденсаторов. Это наиболее распространенный способ подключения конденсаторов. При параллельном соединении емкость конденсатора увеличивается, а напряжение остается прежним. Формула для параллельного соединения конденсаторов: C= C1+C2+C3… Давайте рассмотрим пример. Предположим, вам нужен конденсатор 100 мкФ 50 Ви у тебя есть только 47 мкФ при 50 В. Параллельное подключение конденсаторов Конденсаторы соединены последовательно. При таком подключении общая емкость уменьшается, а рабочее напряжение конденсатора увеличивается. Конденсаторы соединяются последовательно в соответствии со следующей формулой: Формула расчета для последовательного соединения конденсаторов Например, подключим 3 конденсатора со следующими номиналами (1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03 далее 1 : 0,03 = 33 мкф для 300 В (напряжение добавить 100 + 100 + 100 = 300в). В общей сложности 33 мкФ для 300 В. |
Читайте далее:
- Принцип работы транзисторов Мосфета.
- Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.
- Расчет цепи постоянного тока с конденсаторами.
- Биполярные транзисторы.
- Как работает транзистор.
- Конденсаторы.
- Расчет понижающего конденсатора.
Напряжение конденсаторов при последовательном соединении
Для получения нужной емкости или при напряжении сети, превышающем номинальное напряжение конденсатора, они соединяются последовательно, параллельно или смешанно. При последовательном соединении рис. Последовательное соединение конденсаторов. Параллельное соединение конденсаторов. Обозначив заряд одного электрода конденсатора через Q, можно написать для двух последовательно соединенных конденсаторов т.
Поиск данных по Вашему запросу:
Напряжение конденсаторов при последовательном соединении
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Соединение конденсаторов
- Емкость конденсатора при последовательном соединении – советы электрика
- Параллельное и последовательное соединение конденсаторов: способы, правила, формулы
- Последовательное и параллельное соединение
- Последовательное соединение конденсаторов, онлайн расчет
- Конденсаторы в электрических цепях
- Параллельное и последовательное соединение конденсаторов
- При последовательном соединении конденсаторов их суммарная емкость – советы электрика
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как увеличить напряжение конденсатора.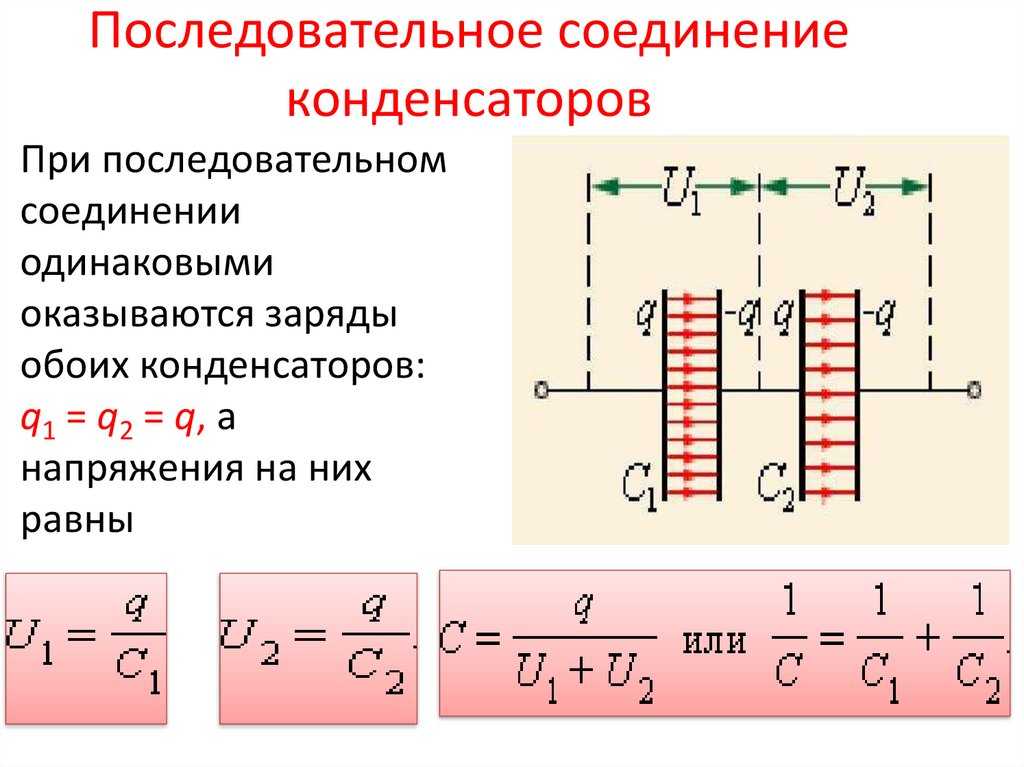
Соединение конденсаторов
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей.
Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения. Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
Формула и расшифровка. Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор. Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости конденсатора подключены к источнику тока.
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния.
По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак.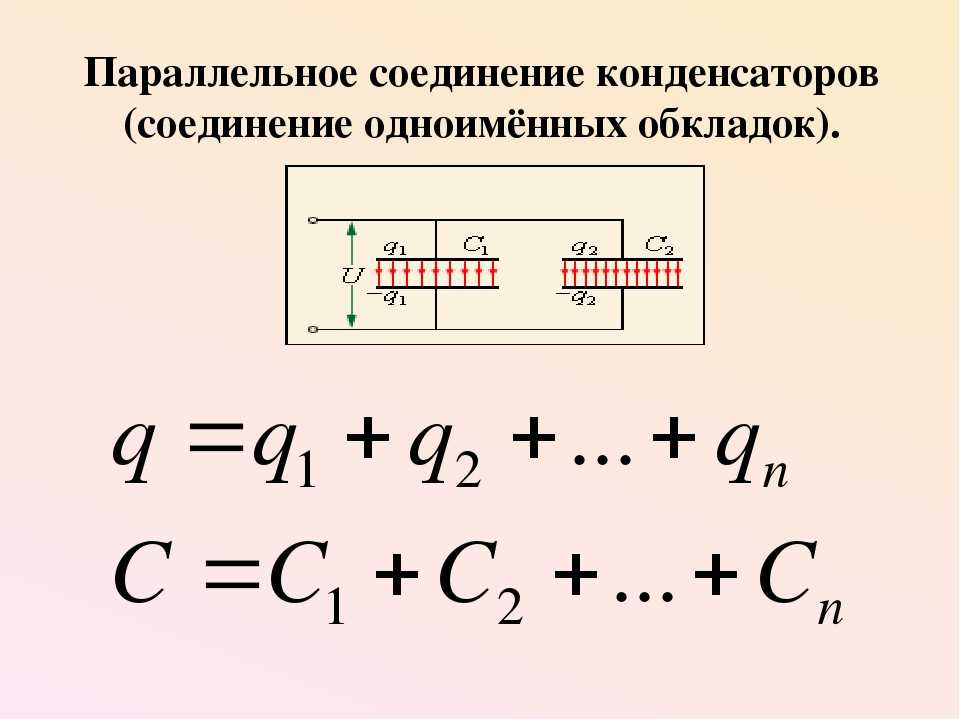 Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда. Последовательное соединение конденсаторов. Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.
Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда. Последовательное соединение конденсаторов. Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.
Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки.
Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения. Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым.
В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей. Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:. Основные моменты. Заряд общего эквивалентного накопителя группы емкостных накопителей последовательного соединения равен:. Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Схема подключения конденсаторов. Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:. Последовательное, параллельное и смешанное соединение конденсаторов. Накопители емкостей двухполюсники включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:. Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников.
В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу треугольником. В этой схеме минус соединяется с минусом, а плюс — с плюсом.
Происходит увеличение емкости накопителя, и меняется работа двухполюсника. Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость. В электротехнике существуют различные варианты подключения электрических элементов.
Рассмотрим их. Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи.
В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии. Схема параллельного крепления. Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор.
При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор.
Вся схема, подключенная таким образом, рассчитывается как один двухполюсник. Схема — напряжение на накопителях. В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:.
Схема — схема последовательного соединения. Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:. Следовательно, одинаковой будет не только сила тока, но и электрический заряд.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд.
По формуле это определяется как:. А так определяется общая суммарная емкость конденсаторов при последовательном соединении:.
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов. Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь.
Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом — последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:. Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов. Способов соединения конденсаторов существуют всего два.
Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:. Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов. Способов соединения конденсаторов существуют всего два.
Это последовательное и параллельное соединение. Сейчас более детально рассмотрим оба способа. Это наиболее частый вид соединения конденсаторов. При подключении параллельно, емкость конденсатора увеличивается, а напряжение остается прежним. Рассмотрим на примере. Предположим, что необходим конденсатор мкф 50в , а у Вас в наличии только 47мкф на 50в.
При подключении, таким образом, общая емкость уменьшается, а напряжение работы конденсатора растёт. Согласно формуле, делим единицу, на емкость конденсаторов. Потом суммируем. Далее единицу делим на результат.
Итого 33мкф на в. Весь инструмент и расходники, которые я использую в ремонтах находится здесь. Если у Вас возникли вопросы по ремонту телевизионной техники, вы можете задать их на нашем новом форуме. Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно.
Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга.
При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно.
Следовательно, и общая емкость батареи конденсаторов меньше. Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов.
В случае батареи из двух конденсаторов:. А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов. По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Параллельное и последовательное соединение конденсаторов. Параллельное включение конденсаторов в цепь Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей. Параллельное соединение конденсаторов : Параллельное соединение конденсаторов Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока.
Параллельное включение конденсаторов в цепь Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей. Параллельное соединение конденсаторов : Параллельное соединение конденсаторов Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока.
При параллельном соединении конденсаторов емкость равняется: Формула и расшифровка Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор. Конденсаторы, соединенные параллельно, имеют напряжение: Формула Последовательное включение конденсаторов в цепь Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости конденсатора подключены к источнику тока.
Последовательное соединение конденсатора: Формула При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. Формула нахождения заряда на конденсаторе, схема подключения конденсатора: Последовательное соединение конденсаторов Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора: Последовательное соединение конденсаторов Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой: Основные моменты Заряд общего эквивалентного накопителя группы емкостных накопителей последовательного соединения равен: Формула Общему значению емкости последовательно соединенных конденсаторов соответствует выражение: Формула Смешанное включение емкостных накопителей в схему Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости: Схема подключения конденсаторов Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом: разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов; вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения; проводим нахождение эквивалентной емкости на параллельном участке; когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать; рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.
Последовательное, параллельное и смешанное соединение конденсаторов Накопители емкостей двухполюсники включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов: Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах. Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей.
Емкость конденсатора при последовательном соединении – советы электрика
Любая электроника в доме может выйти из строя. Однако сразу бежать в сервис не стоит — простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь.
При последовательном соединении конденсаторов заряд каждого равноценен. Напряжения меж конденсаторами распределяются обратно.
Параллельное и последовательное соединение конденсаторов: способы, правила, формулы
Изучите соединения конденсаторов — последовательные и параллельные. Как выглядят последовательно и параллельно соединенные конденсаторы, емкость, схемы. Посмотрим на схему, где конденсаторы соединены последовательно. Обратная общая емкость достигает суммы обратных значений емкости каждого отдельного конденсатора:. Суммарная емкость в параллельном соединении конденсаторов находится при обычном добавлении отдельных емкостей каждого конденсатора. Бывает так, что схема вмещает сразу два типа соединения параллельное и последовательное соединение конденсаторов. Чтобы отыскать общую емкость, нужно разделить цепочку на отдельные сегменты. Задачу можно сделать проще, если сначала решить проблему с последовательным соединением, а потом заняться параллельным. В а расположены последовательные конденсаторы, выступающие параллельными C3.
Последовательное и параллельное соединение
Господа, как-то раз чудесным летним деньком я взял ноутбук и вышел из дома на дачный участок. Там, усевшись в кресле-качалке в тени яблонь, я и решил написать данную статью. Ветерок шумел в ветвях деревьев, раскачивая их из стороны в сторону, и в воздухе была та самая атмосфера, благоприятствующая течению мыслей, которая так порой необходима…. Впрочем, хватит лирики, пора переходить непосредственно к существу обозначенного в заголовке статьи вопроса. Итак, параллельное соединение конденсаторов… Что вообще такое параллельное соединение?
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт.
Последовательное соединение конденсаторов, онлайн расчет
Отдельные конденсаторы могут быть соединены друг с другом различным образом. При этом во всех случаях можно найти емкость некоторого равнозначного конденсатора, который может заменить ряд соединенных между собой конденсаторов. Для равнозначного конденсатора выполняется условие: если подводимое к обкладкам равнозначного конденсатора напряжение равно напряжению, подводимому к крайним зажимам группы конденсаторов, то равнозначный конденсатор накопит такой же заряд, как и группа конденсаторов. На рис. При последовательном соединении конденсаторов рис. Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую наблюдается электростатическая индукция , поэтому и на них по- являются равные и разноименые электрические заряды.
Для равнозначного конденсатора выполняется условие: если подводимое к обкладкам равнозначного конденсатора напряжение равно напряжению, подводимому к крайним зажимам группы конденсаторов, то равнозначный конденсатор накопит такой же заряд, как и группа конденсаторов. На рис. При последовательном соединении конденсаторов рис. Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую наблюдается электростатическая индукция , поэтому и на них по- являются равные и разноименые электрические заряды.
Конденсаторы в электрических цепях
В предыдущих статьях были рассмотрены вопросы работы и характеристики конденсаторов. Сейчас Я расскажу о всех методах соединения конденсаторов для подключения в схему. Сразу скажу, что в жизни практически везде, за исключением редких случаев используется только параллельная схема подключения. Следует знать , что в цепи переменного тока конденсатор выступает еще как емкостное сопротивление. При чем с увеличением величины емкости конденсатора- уменьшается сопротивление в цепи переменного тока. При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема на картинке.
Следует знать , что в цепи переменного тока конденсатор выступает еще как емкостное сопротивление. При чем с увеличением величины емкости конденсатора- уменьшается сопротивление в цепи переменного тока. При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема на картинке.
При последовательном соединении конденсаторов — Всё о электрике в доме Параллельное и последовательное соединение конденсаторов.
Параллельное и последовательное соединение конденсаторов
Напряжение конденсаторов при последовательном соединении
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным смешанным. Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:. Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При последовательном соединении конденсаторов их суммарная емкость – советы электрика
ВИДЕО ПО ТЕМЕ: Последовательное соединение конденсаторов (видео 16) — Цепи — Физика
Категории Справочная Статьи для новичков. Как раз для таких случаев нам необходимы знания о правилах соединения конденсаторов. Способов соединения конденсаторов существуют всего два. Это последовательное и параллельное соединение. Сейчас более детально рассмотрим оба способа.
Не всегда удаётся подобрать конденсатор нужного номинала.
В электротехнике существуют различные варианты подключения электрических элементов. Рассмотрим их. Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии. Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор.
В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии. Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор.
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом.
Конденсаторы последовательно и параллельно — Конденсаторы
Конденсаторы
Конденсаторы могут быть соединены последовательно или параллельно, чтобы получить результирующее значение, которое может быть либо
сумма отдельных значений (параллельно) или значение меньше, чем у наименьшей емкости
(последовательно).
Конденсаторы серии
Цепь, состоящая из нескольких последовательно соединенных конденсаторов, в некоторых отношениях похожа на одну. несколько последовательно соединенных резисторов. В последовательной емкостной цепи один и тот же ток смещения протекает через каждую часть цепи, и приложенное напряжение будет делиться на отдельные конденсаторы. На рисунке ниже показана схема, содержащая источник и три последовательных конденсатора.
Конденсаторы последовательно.
Сумма напряжений на конденсаторе должна равняться напряжению источника (закон напряжения Кирхгофа).
Заряды на всех конденсаторах должны быть одинаковыми, так как конденсаторы соединены последовательно и любые движение заряда в одной части цепи должно происходить во всех частях последовательной цепи. Решение уравнения C = Q / V для напряжения через емкость и заряд ( В = Ом / C ), для каждой из серий получены следующие результаты конденсаторы и общая емкость ( C t )
Подставив эти результаты в приведенное выше уравнение закона Кирхгофа для напряжения
Разделив обе части приведенного выше уравнения на общий множитель Q
Взяв обратную величину обеих сторон и предполагая любое количество конденсаторов
Это уравнение является общим уравнением, используемым для расчета общей емкости конденсаторов. соединены последовательно. Обратите внимание на сходство между этим уравнением и тем, которое использовалось для нахождения эквивалента.
сопротивление параллельных резисторов. Если в цепи всего два конденсатора, произведение превышает
можно использовать формулу суммы
соединены последовательно. Обратите внимание на сходство между этим уравнением и тем, которое использовалось для нахождения эквивалента.
сопротивление параллельных резисторов. Если в цепи всего два конденсатора, произведение превышает
можно использовать формулу суммы
Из приведенных выше формул должно быть видно, что суммарная емкость конденсаторов при последовательном соединении меньше емкости любого из отдельных конденсаторов.
Пример:
Определите общую емкость последовательной цепи, содержащей три конденсатора, номиналы которых
составляют 10 нФ, 0,25 мкФ и 50 нФ соответственно.
Решение:
Общая емкость 8 нФ немного меньше самого маленького конденсатора (10 нФ).
Параллельные конденсаторы
При параллельном соединении конденсаторов (см. рисунок ниже) одна пластина каждого конденсатора подключается напрямую.
к одной клемме источника, а другая пластина каждого конденсатора подключена к
другой терминал источника. На рисунке ниже все отрицательные пластины конденсаторов
соединены вместе, и все положительные пластины соединены вместе.
Суммарная (эквивалентная) емкость Кл t , следовательно, выступает как емкость с пластиной
площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее,
емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов
увеличивает площадь пластины и тем самым увеличивает общую емкость.
На рисунке ниже все отрицательные пластины конденсаторов
соединены вместе, и все положительные пластины соединены вместе.
Суммарная (эквивалентная) емкость Кл t , следовательно, выступает как емкость с пластиной
площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее,
емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов
увеличивает площадь пластины и тем самым увеличивает общую емкость.
Параллельные конденсаторы.
Полную емкость можно рассчитать математически. Применяя уравнение C = Q / V на каждый конденсатор и на общую емкость
Общий заряд Q t есть сумма зарядов на каждом конденсаторе
Из уравнения C = Q / V следует, что Q = C V , а если заряд записывается в этой форме и подставляется в приведенное выше уравнение, это уравнение приводит к
Разделив обе части приведенного выше уравнения на общий множитель В и приняв любое количество конденсаторов
Это уравнение математически утверждает, что общая емкость ряда конденсаторов
параллельно сумма отдельных емкостей.
Пример:
Определите общую емкость в параллельной емкостной цепи, содержащей три конденсатора.
значения которых составляют 30 нФ, 2 мкФ и 0,25 мкФ соответственно.
Решение:
Конденсаторы, включенные последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Выводить выражения для полной емкости при последовательном и параллельном подключении.
- Определите последовательное и параллельное соединение конденсаторов.
- Рассчитайте действующую емкость при последовательном и параллельном подключении по отдельным емкостям.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9. 0143 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
0143 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
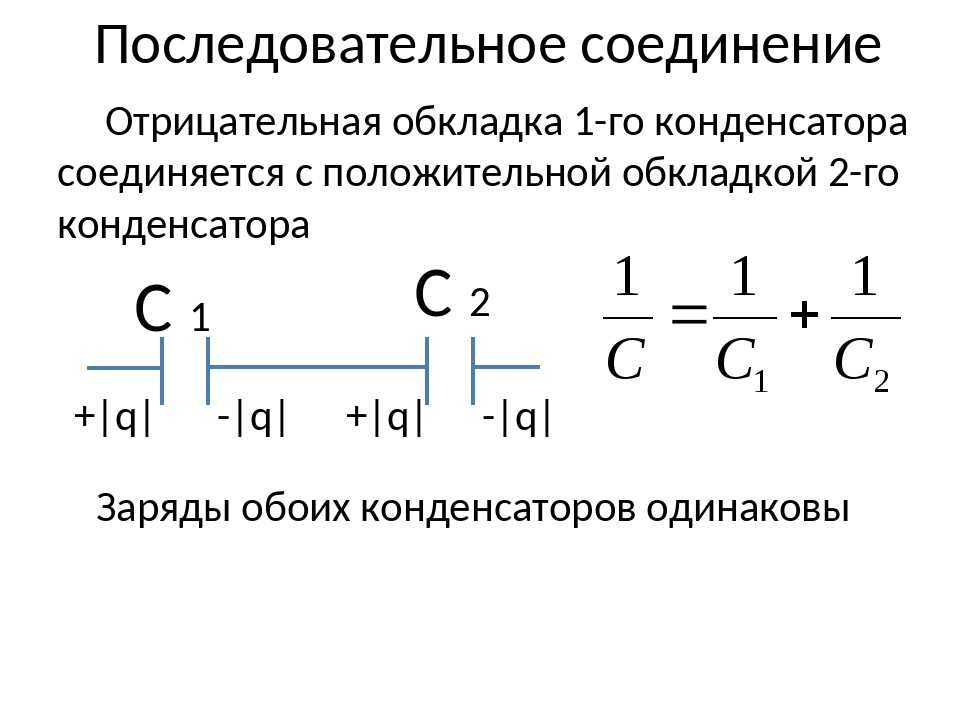
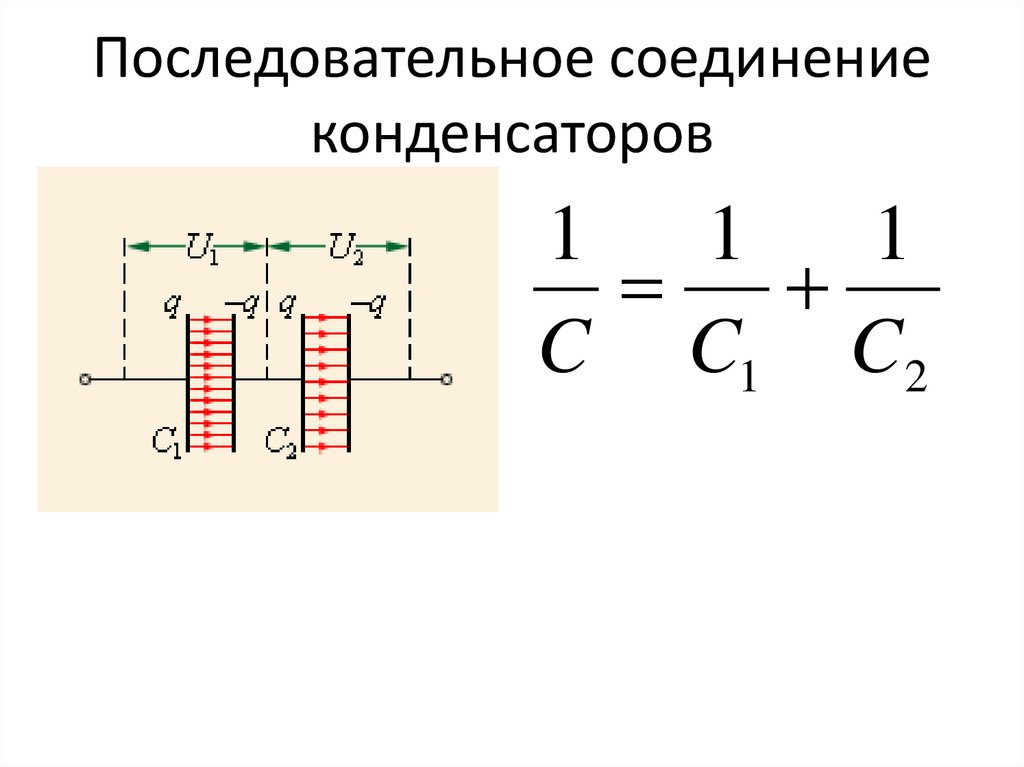
Емкость в серии
На рис. 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]C=\frac{Q}{V}\\[/latex].
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов, когда приложено напряжение V . Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1b.) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
(См. рис. 1b.) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанное на рисунке 1. Решение [latex]C=\frac{Q}{V}\\[/latex] для В дает [ латекс]V=\frac{Q}{C}\\[/латекс]. Таким образом, напряжения на отдельных конденсаторах равны [latex]V_1=\frac{Q}{C_1},V_2=\frac{Q}{C_2},\text{ и }V_3=\frac{Q}{C_3}\\ [/латекс].
Общее напряжение равно сумме отдельных напряжений:
В = В 1 + В 2 + В 3 3
Теперь, назвав общую емкость C S для последовательной емкости, учтите, что
[латекс]V=\frac{Q}{C_{\text{S}}}=V_1+V_2+V_3\\ [/латекс].
Ввод выражений для В 1 , В 2 и В 3 , получаем
[латекс]\frac{Q}{C_{\text{S}}}=\frac{Q}{C_{1}}+\frac{Q}{C_{2} }+\frac{Q}{C_{3}}\\[/latex].
Отменив Q с, получим уравнение для полной емкости в ряду C S равной
[латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots,\\[/latex]
, где «…» означает что выражение справедливо для любого числа последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к полной емкости C S меньше любой из отдельных емкостей C 1 , C 2 , …, как показано в Примере 1.
Полная последовательная емкость,
C сПолная последовательная емкость:
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1 }}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots\\[/latex]
Пример 1.
 Что такое последовательная емкость?
Что такое последовательная емкость?Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.
Решение
Ввод данных емкостей в выражение для [латекс]\фракция{1}{С_{\текст{S}}}\\[/латекс] дает [латекс]\фракция{1}{С_{\ text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex].
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{1,000 \mu\text{F}}+\frac{1}{5,000 \mu\text{F }}+\frac{1}{8.000 \mu\text{F}}=\frac{1.325}{\mu\text{F}}\\[/latex]
Инвертирование для нахождения C S дает [латекс] C _ {\ text {S}} = \ frac {1,325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [ /латекс].
Обсуждение
Суммарная ёмкость серии C s меньше, чем наименьшая индивидуальная ёмкость, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
[латекс]\frac{1}{C_{\text{S}}}=\frac{40}{40 \mu\text{F}}+\frac{8}{40 \mu\text{F }}+\frac{5}{40 \mu\text{F}}=\frac{53}{40\mu\text{F}}\\[/latex]
, так что
[latex]C_ {\text{S}}=\frac{40\mu\text{F}}{53}=0,755\mu\text{F}\\[/latex]
Параллельные конденсаторы
На рисунке 2a показана параллель соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную полную емкость C p , сначала отметим, что напряжение на каждом конденсаторе равно В , такое же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения. ) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q представляет собой сумму отдельных сборов: Q = Q 1 + Q 2 + Q 3 .
) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q представляет собой сумму отдельных сборов: Q = Q 1 + Q 2 + Q 3 .
Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.
Используя отношение Q = CV , we see that the total charge is Q = C p V , and the individual charges are Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V 444444444444444444444444. Ввод их в предыдущее уравнение дает
Ввод их в предыдущее уравнение дает
C p В = В 1 В + В 2 В + В 3
Отмена V Из уравнения мы получаем уравнение для общей емкости в параллельной
C P : C P = C 31131++1313131313131414141414141414141414141414 3931 2 . C 3 + ….
Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … ” указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в примере 1 были соединены параллельно, их емкость была бы
C p = 1,000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ.
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рисунке 2b.
Суммарная емкость при параллельном подключении,
C PОбщая емкость в параллельной C P = C 1 + C 2 ++ C 2 ++ C 2 ++ C 2 ++ C 2 ++ C 2 +. быть комбинациями последовательного и параллельного. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.
Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (б) C 1 и C 2 последовательно; их эквивалентная емкость C S меньше любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме C S и C 3 .
Таким образом, общая емкость равна сумме C S и C 3 .
Пример 2. Смесь последовательных и параллельных емкостей
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ( C 1 = 1,000 мкФ, C 2 = 3,000 мкФ и C 3 = 8,000 мкФ), и округлите ответ до трех знаков после запятой.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы С 1 и С 2 включены последовательно. Их комбинация, обозначенная на рисунке C S , параллельна С 3 .
Решение
Поскольку C 1 и C 2 соединены последовательно, их общая емкость определяется выражением [латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex]. Ввод их значений в уравнение дает
Ввод их значений в уравнение дает
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2} }=\frac{1}{1.000\mu\text{F}}+\frac{1}{5.000\mu\text{F}}=\frac{1.200}{\mu\text{F}}\\ [/латекс].
Инвертирование дает C S = 0,833 мкФ.
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общее количество равно сумме
[латекс]\begin{array}{lll}C_{\text{tot}}&=&C_{\text{S}}+C_{\text{S}}\\\ текст { }&=&0,833\мю\текст{F}+8,000\мю\текст{F}\\\текст{ }&=&8,833\мю\текст{F}\конец{массив}\\[ /latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.
Резюме раздела
- Суммарная емкость последовательно [латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{ 2}}+\frac{1}{C_{3}}+\dots\\[/latex]
- Суммарная емкость при параллельном соединении C p = C 1 + C 2 + C 3 + …
- Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.

Концептуальные вопросы
- Если вы хотите хранить большое количество энергии в конденсаторной батарее, вы бы соединили конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
- Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Сочетание последовательного и параллельного соединения конденсаторов.
- Предположим, вам нужна батарея конденсаторов общей емкостью 0,750 Ф, и у вас имеется множество конденсаторов емкостью 1,50 мФ. Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
- Какую общую емкость можно получить, соединив вместе конденсаторы емкостью 5,00 мкФ и 8,00 мкФ?
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Сочетание последовательного и параллельного соединения конденсаторов.
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.


 Электроны бегут от плюсовой стороны источника питания к плюсовой стороне конденсатора. Почему они убежали? Ток течет от плюса к минусу. Откуда берется минус? Минусовая клемма конденсатора подключена к минусу, поэтому он принимает минусовой потенциал. Электроны “увидели”, что за диэлектрическим слоем находится отрицательный заряд, и все вместе побежали к плюсовому концу конденсатора, чтобы там, собравшись вместе, перейти к минусовому концу. Но этого не произошло! Диэлектрический слой настолько прочен, что электроны не перейдут на минусовую сторону, как бы им этого ни хотелось. Диэлектрический слой отвечает за то, насколько сильно электроны “чувствуют” противоположную стенку конденсатора, и, следовательно, сколько их может на ней накопиться.
Электроны бегут от плюсовой стороны источника питания к плюсовой стороне конденсатора. Почему они убежали? Ток течет от плюса к минусу. Откуда берется минус? Минусовая клемма конденсатора подключена к минусу, поэтому он принимает минусовой потенциал. Электроны “увидели”, что за диэлектрическим слоем находится отрицательный заряд, и все вместе побежали к плюсовому концу конденсатора, чтобы там, собравшись вместе, перейти к минусовому концу. Но этого не произошло! Диэлектрический слой настолько прочен, что электроны не перейдут на минусовую сторону, как бы им этого ни хотелось. Диэлектрический слой отвечает за то, насколько сильно электроны “чувствуют” противоположную стенку конденсатора, и, следовательно, сколько их может на ней накопиться. 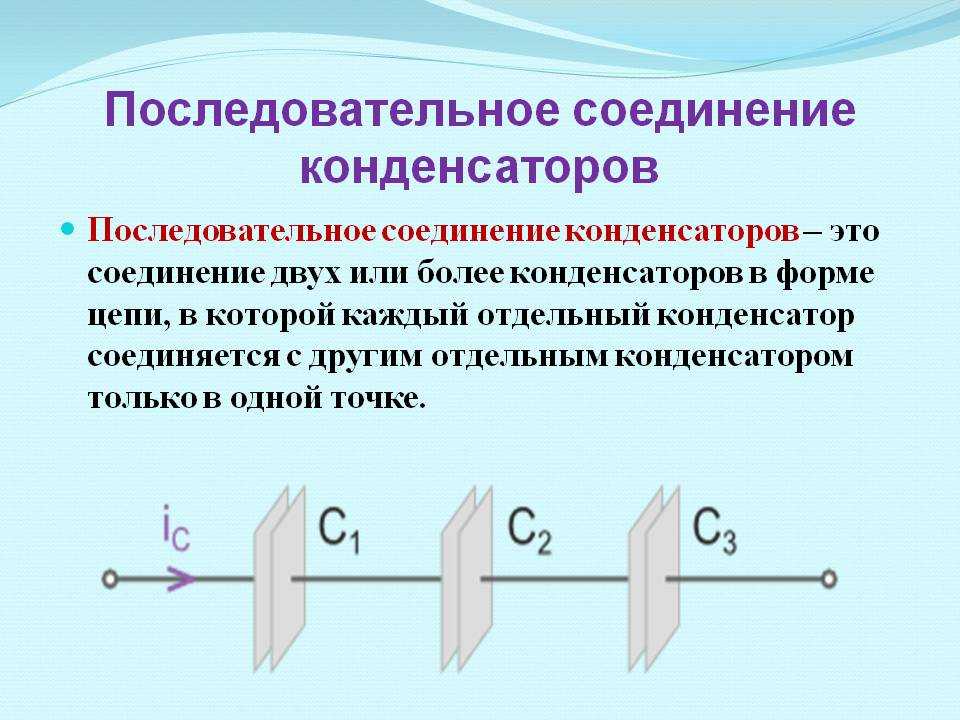 Но что происходит с емкостью? Подключаем источник питания. Электроны бегут к положительной стороне конденсатора. И что они там видят? Они увидели, что есть одна диэлектрическая стена и другая, которую они действительно хотят преодолеть. Но какова толщина этих стен? Бедные электроны не знают. Они могут ощущать противоположный заряд (минус) только через эти стенки. Минус кричит на них: “Эй, собирайтесь вместе! У меня есть потенциал, и мне нужно так много вас!”.
Но что происходит с емкостью? Подключаем источник питания. Электроны бегут к положительной стороне конденсатора. И что они там видят? Они увидели, что есть одна диэлектрическая стена и другая, которую они действительно хотят преодолеть. Но какова толщина этих стен? Бедные электроны не знают. Они могут ощущать противоположный заряд (минус) только через эти стенки. Минус кричит на них: “Эй, собирайтесь вместе! У меня есть потенциал, и мне нужно так много вас!”.  com/cwc
com/cwc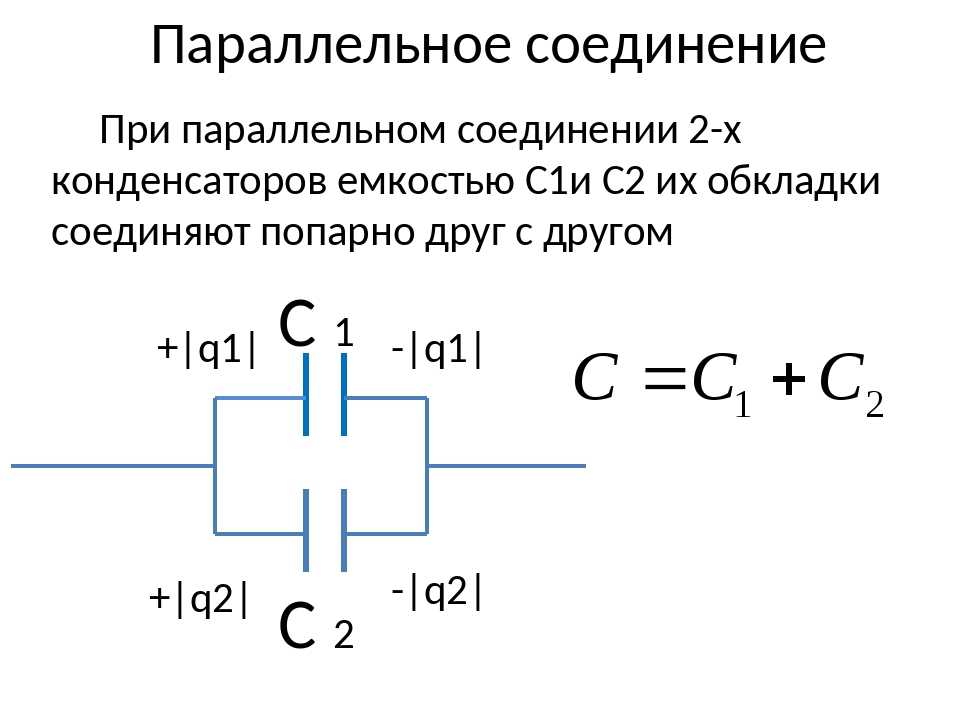 Но обычно так не поступают.
Но обычно так не поступают. Давайте поработаем с Teseo Suite и посмотрим на результаты полевых испытаний.
Давайте поработаем с Teseo Suite и посмотрим на результаты полевых испытаний.




 Если мы соединим эти конденсаторы параллельно (плюс к плюсу и минус к минусу), общая емкость составит ок. 94 мкФ при 50 В. Это приемлемый допуск, чтобы его можно было свободно установить в технике.
Если мы соединим эти конденсаторы параллельно (плюс к плюсу и минус к минусу), общая емкость составит ок. 94 мкФ при 50 В. Это приемлемый допуск, чтобы его можно было свободно установить в технике.