Формула расчета энергии конденсаторов, как зарядить плоский конденсатор
Конденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими.
Конденсаторы различных типов
В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит.
Определение понятия энергии
Наиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика.
Плоский конденсатор
Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее:
- На разделение зарядов по обкладкам электрическим полем затрачивается определенная работа. В соответствии с законом сохранения энергии, эта работа равняется энергии заряженного конденсатора;
- Разноименно заряженные обкладки притягиваются друг к другу.
Энергия заряженного конденсатора в этом случае равняется работе, затраченной на сближение пластин друг к другу вплотную.
Энергия заряженного конденсатора в этом случае равняется работе, затраченной на сближение пластин друг к другу вплотную.Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами.
Вывод формулы
Энергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок.
Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной:
F=q0E.
В данном выражении q0 – величина заряда, E – напряженность поля обкладки.
Поскольку напряженность электрического поля определяется из выражения:
E=q/(2ε0S), где:
- q – величина заряда,
- ε0 – электрическая постоянная,
- S – площадь обкладок,
формулу силы притяжения можно записать как:
F=q0 q/(2ε0S).
Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет:
F=q2/(2ε0S).
Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением:
W=A=Fd.
Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0.
С учетом предыдущих выражений можно записать:
W=d q2/(2ε0S).
Известно, что емкость плоского конденсатора определяется из такого выражения:
C=d/(ε0S).
В результате энергия определяется как:
W=q2/(2С).
Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь:
q = С U.
Теперь выражение принимает полностью понятный вид:
W=CU2/2.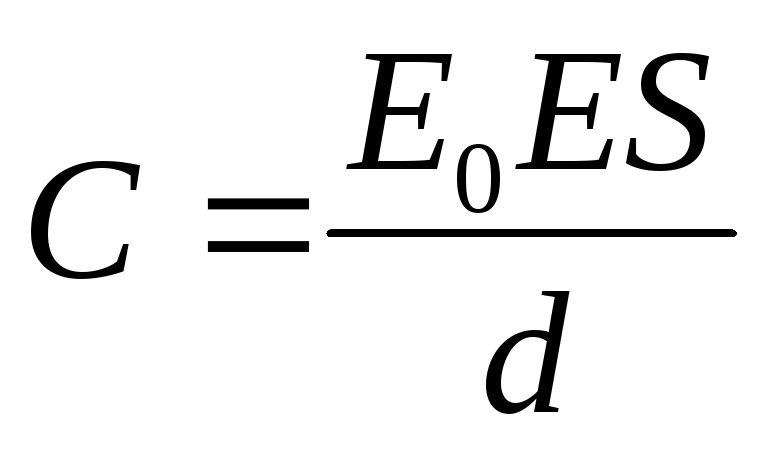
Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию.
Для чего необходимо знать энергию
В большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопительном конденсаторе энергия источника питания накапливается сравнительно медленно – несколько секунд, но разряд происходит практически мгновенно через электроды импульсной лампы.
Конденсатор, подобно аккумулятору, служит для накопления электрического заряда, но между этими элементами есть много различий. Емкость аккумулятора несравненно выше, чем у конденсатора, но последний способен отдать ее практически мгновенно. Лишь недавно, с появлением ионисторов, это различие несколько сгладилось.
Ионистор
Какова же ориентировочная величина энергии? Можно для примера вычислить ее для уже упомянутой фотовспышки. Пускай, напряжение питания составляет 300 В, а емкость накопительного конденсатора – 1000 мкФ. При полном заряде величина энергии составит 45 Дж. Это довольно большая величина. Прикосновение к выводам заряженного элемента может привести к несчастному случаю.
Конденсатор фотовспышки
Важно! Принудительный разряд путем закорачивания выводов металлическими предметами чреват выходом устройства из строя. Накопленная энергия конденсатора способна за долю секунды расплавить выводы внутри элемента и вывести его из строя.
Видео
Оцените статью:Энергия конденсатора формула в чем измеряется
В заряженном конденсаторе обкладки име-ют разноименные заряды и взаимодейст-вуют между собой благодаря электричес-кому полю, которое сосредоточено в прост-ранстве между обкладками. О телах, между которыми существует взаимодействие, гово-рят, что они имеют потенциальную энер-гию. Следовательно, можно говорить и об энергии заряженного конденсатора .
Обкладки заряженного конден-сатора взаимодействуют между собой.
Наличие энергии у заряженного конден-сатора можно подтвердить опытами.
Возьмем конденсатор достаточно боль-шой емкости, источник тока, лампочку на-кала и составим электрическую цепь, схема которой изображена на рис.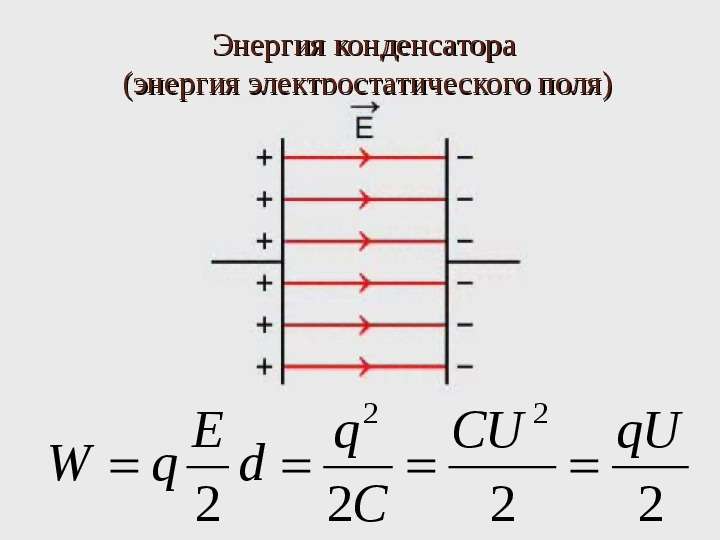
4.82. Переведем переключатель S в положение 1 и зарядим конденсатор до определенной разности по-тенциалов от источника GB. Если после этого перевести переключатель в положение 2, то можно наблюдать кратковременную вспышку света вследствие накала нити лам-почки. Наблюдаемое явление можно объяс-нить тем, что заряженный конденсатор имел
В соответствии с законом сохранения энер-гии работа, выполненная при разрядке кон-денсатора, равняется работе, выполненной при его зарядке. Расчет этой работы и, соответственно, потенциальной энергии кон-денсатора осложнен особенностями процес-са зарядки конденсатора. Пластины его за-ряжаются и разряжаются постепенно. Зави-симость заряда Q конденсатора от времени при зарядке показана на графике (рис. 4.83). Заряд не только увеличивается постепенно, но и скорость его изменения не остается постоянной. Итак, вести расчеты на осно-вании формулы A = qEd нельзя, поскольку напряженность электрического поля не остается постоянной.
Разность потенциалов также изменяется от нуля до максимально-го значения. На рис. 4.84 показано, что разность потенциалов изменяется про-порционально заряду конденсатора. Такая зависимость характерна для силы упругос-ти, которая зависит от удлинения пружины (рис. 4.85).
Воспользовавшись таким подобием, мож-но сделать вывод, что энергия заряженного конденсатора будет равна
W = Q Δφ / 2. Материал с сайта
Эта энергия равна работе по зарядке конденсатора, которая численно равна пло-щади заштрихованного треугольника на гра-фике рис. 4.84.
Учитывая, что Q = C Δφ , получим
W = C(Δφ) 2 / 2.
А если учесть связь разности потенциалов с зарядом Δφ = Q / C , то потенциальная энер-гия конденсатора может быть вычислена по формуле
W = (Q / 2) . (Q / C) = Q 2 / 2 C.
На этой странице материал по темам:
Энергия заряженного конденсатора шпора
Энергия заряженного конденсатора
Какие физические величины определяют энергию конденсатора
Самостоятельная работа по теме электроемкость плоского конденсатора
Як визначити енергію конденсатора за допомогою графіка
Вопросы по этому материалу:
Электроемкостью
(емкостью) C уединенного изолированного
проводника называется физическая
величина, равная отношению изменения
заряда проводника q к изменению
его потенциала f:
C = Dq/Df.
Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) — это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон. 1 Ф = 1 Кл/1 В.
Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом). Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U: C = Q/U.
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
Соединение
конденсаторов в батареи.
На практике
конденсаторы часто соединяют в батареи —
последовательно или параллельно.
При параллельном соединении напряжение на всех обкладках одинаковое U1 = U2 = U3 = U = e, а емкость батареи равняется сумме емкостей отдельных конденсаторов C = C1 + C2 + C3.
При последовательном соединении заряд на обкладках всех конденсаторов одинаков Q1 = Q2 = Q3, а напряжение батареи равняется сумме напряжений отдельных конденсаторов U = U1 + U2 + U3.
Емкость всей системы последовательно соединенных конденсаторов рассчитывается из соотношения: 1/C = U/Q = 1/C1 + 1/C2 + 1/C3.
Емкость
батареи последовательно соединенных
конденсаторов всегда меньше, чем емкость
каждого из этих конденсаторов
в отдельности.
Энергия электростатического
поля.
Энергия заряженного плоского
конденсатора Eк равна работе A, которая
была затрачена при его зарядке, или
совершается при его разрядке.
A =
CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку
напряжение на конденсаторе может
быть рассчитано из соотношения:
U =
E*d,
где E — напряженность поля между
обкладками конденсатора,
d —
расстояние между пластинами
конденсатора,
то энергия заряженного
конденсатора равна:
Eк = CU2/2 =
ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2,
где V —
объем пространства между обкладками
конденсатора.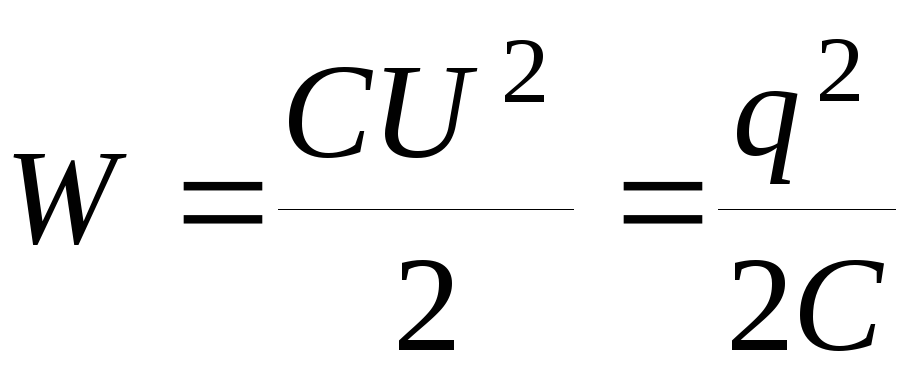
Тип конденсатора | Формула для расчета емкости | Примечания | Схематическое изображение |
Плоский конденсатор | S — площадь пластины; d — расстояние между пластинами. | ||
Сферический конденсатор | C = 4pee0R1R2/(R2 — R1) | R2 и R1 — радиусы внешней и внутренней обкладок. | |
Цилиндрический конденсатор | C = 2pee0h/ln(R2/R1) | h — высота цилиндров. |
Как
и любая система заряженных
тел, конденсатор обладает
энергией. Вычислить энергию заряженного
плоского конденсатора с однородным
полем внутри него несложно. Энергия
заряженного конденсатора. Для
того чтобы зарядить конденсатор, нужно
совершить работу по разделению
положительных и отрицательных зарядов.
Согласно закону сохранения энергии эта
работа равна энергии конденсатора. В
том, что заряженный конденсатор обладает
энергией, можно убедиться, если разрядить
его через цепь, содержащую лампу
накаливания, рассчитанную на напряжение
в несколько вольт (
Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна Е/2 , где Е -напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q , распределенный по поверхности другой пластины (рис.14.38 ). Согласно формуле (14.14) для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
где q — заряд конденсатора, а d — расстояние между пластинами. Так как Ed=U , где U — разность потенциалов между обкладками конденсатора, то его энергия равна:
Эта
энергия равна работе, которую совершит
электрическое поле при сближении пластин
вплотную.
Пусть потенциал обкладки конденсатора, на которой находится заряд равен а потенциал обкладки, на которой находится заряд , равен Тогда каждый из элементарных зарядов на которые можно разделить заряд находится в точке с потенциалом а каждый из зарядов, на которые можно разделить заряд , в точке с потенциалом .
Согласно формуле (28.
1) энергия такой системы зарядов равна
Воспользовавшись соотношением (27.2), можно написать три выражения для энергии заряженного конденсатора:
Формулы (29.2) отличаются от формул (28.3) только заменой на
С помощью выражения для потенциальной энергии можно найти силу, с которой пластины плоского конденсатора притягивают друг друга. Допустим, что расстояние между пластинами может меняться. Свяжем начало оси х с левой пластиной (рис. 29.1). Тогда координата х второй пластины будет определять зазор d между обкладками. Согласно формулам (27.3) и (29.2)
Продифференцируем это выражение по х, полагая заряд на обкладках неизменным (конденсатор отключен от источника напряжения). В результате получим проекцию на ось х силы, действующей на правую пластину:
Модуль этого выражения дает величину силы, с которой обкладки притягивают друг друга:
Теперь попытаемся вычислить силу притяжения между обкладками плоского конденсатора как произведение напряженности поля, создаваемого одной из обкладок, на заряд, сосредоточенный на другой.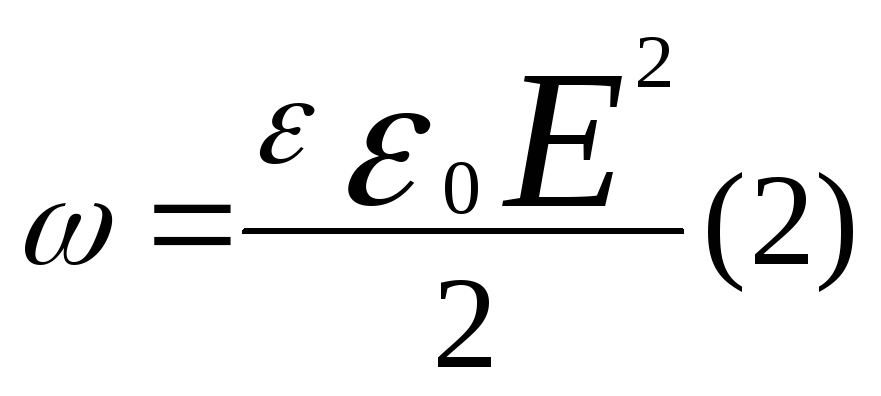
Согласно формуле (14.3) напряженность поля, создаваемого одной обкладкой, равна
Диэлектрик ослабляет поле в зазоре в раз, но это имеет место только внутри диэлектрика (см. формулу (20.2) и связанный с нею текст). Заряды на обкладках располагаются вне диэлектрика и поэтому находятся под действием поля напряженности (29.4).
Умножив заряд обкладки q на эту напряженность, получим для силы выражение
Формулы (29.3) и (29.5) не совпадают. С опытом согласуется значение силы (29.3), получающееся из выражения для энергии. Это объясняется тем, что, кроме «электрической» силы (29.5), на обкладки действуют со стороны диэлектрика механические силы, стремящиеся их раздвинуть (см. § 22; отметим, что мы имеем в виду жидкий или газообразный диэлектрик). У края обкладок имеется рассеянное поле, убывающее по величине при удалении от краев (рис. 29.2). Молекулы диэлектрика, обладая дипольным моментом, испытывают дйствие силы, втягивающей их в область более сильного поля (см. формулу (9.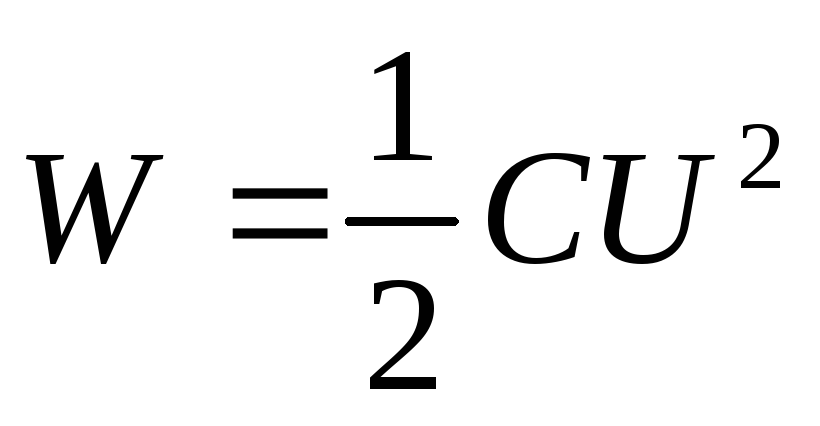
16)). В результате давление между обкладками повышается и появляется сила, ослабляющая действие силы (29.5) в раз.
Если заряженный конденсатор с воздушным зазором частично погрузить в жидкий диэлектрик, наблюдается втягивание диэлектрика в пространство между пластинами (рис. 29.3). Это явление объясняется следующим образом. -Диэлектрическая проницаемость воздуха практически равна единице. Поэтому до погружения пластин в диэлектрик емкость конденсатора можно считать равной а энергию равной При частичном заполнении зазора диэлектриком конденсатор можно рассматривать как два параллельно включенных конденсатора, один из которых имеет площадь обкладки, равную — относительная часть зазора, заполненная жидкостью), и заполнен диэлектриком с второй с воздушным зазором имеет площадь обкладки, равную При параллельном включении конденсаторов емкости складываются:
Поскольку энергия будет меньше, чем (заряд q предполагается неизменным — перед погружением в жидкость конденсатор был отключен от источника напряжения).
Следовательно, заполнение зазора диэлектриком оказывается энергетически выгодным. Поэтому диэлектрик втягивается в конденсатор и уровень его в зазоре поднимается. Это в свою очередь приводит к возрастанию потенциальной энергии диэлектрика в поле сил тяжести. В конечном итоге уровень диэлектрика в зазоре установится на некоторой высоте, соответствующей минимуму суммарной энергии (электрической и гравитационной). Рассмотренное явление сходно с капиллярным поднятием жидкости в узком зазоре между пластинками (см. § 119 1-го тома).
Втягивание диэлектрика в зазор между обкладками можно яснить также и с микроскопической точки зрения. У краев пластин конденсатора имеется неоднородное поле. Молекулы диэлектрика обладают собственным дипольным моментом либо приобретают его под действием поля; поэтому на них действуют силы, стремящиеся переместить их в область сильного поля, т. е. внутрь конденсатора. Под действием этих сил жидкость втягивается в зазор до тех пор, пока электрические силы, действующие на жидкость у края пластин, не будут уравновешены весом столба жидкости.
Энергия поля конденсатора — Основы электроники
Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую.
При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q.
Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.
Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.
Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q.
Полученный результат мы можем записать в виде следующей математической формулы:
W = UQ/2 (1)
Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:
W = CU2/2 (2)
Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами.
Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Конденсатор. Энергия электрического поля — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара, — его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Энергия конденсатора
Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!
В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.
Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.
Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:
Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:
То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.
Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля. Это позволяет использовать формулу работы без векторов:
Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.
Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать
Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.
Рисунок 1 – Плоский конденсатор
Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.
Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать
Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем
Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:
Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.
Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:
Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем
Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:
Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем
Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.
Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии
Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.
Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор
Рисунок 2 – Конденсатор
И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:
Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.
Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!
Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Электроемкость. Энергия электрического поля | Физика
1. Электроемкость
В курсе физики основной школы вы уже познакомились с конденсатором – устройством, предназначенным для накопления электрических зарядов.
Например, плоский конденсатор (рис. 54.1) состоит из двух параллельных пластин, расстояние между которыми намного меньше их размеров. Эти пластины называют обкладками конденсатора.
Между обкладками конденсатора находится диэлектрик. Им может быть, например, воздух. Но чаще пространство межу обкладками заполняют жидким или твердым диэлектриком.
Если сообщить обкладкам конденсатора равные по модулю, но противоположные по знаку электрические заряды, то поле, созданное этими зарядами, будет сосредоточено практически полностью между обкладками (см. рис. 51.6).
Зарядом конденсатора называют модуль заряда любой из го обкладок (напомним, что разноименные заряды на обкладках конденсатора равны по модулю).
Если увеличить заряды обкладок конденсатора, скажем, 3 раза, то при этом напряженность поля между обкладками увеличится также в 3 раза. Значит, в 3 раза увеличится и работа поля по перемещению заряда с одной обкладки на другую. Следовательно, напряжение между обкладками увеличится тоже в 3 раза.
Это рассуждение показывает, что напряжение между обкладками конденсатора прямо пропорционально заряду конденсатора. Поэтому отношение заряда q конденсатора к напряжению U между его обкладками не зависит ни от заряда, и от напряжения. Следовательно, это отношение является характеристикой самого конденсатора.
Отношение заряда конденсатора к напряжению между его обкладками называют электроемкостью:
C = q/U. (1)
Единица электроемкости. Единицей электроемкости является 1 фарад (Ф). Эта единица названа в честь английского ученого Майкла Фарадея.
1Ф = 1 Кл / 1 В.
Если конденсатор имеет электроемкость 1 Ф, то при заряде 1 Кл напряжение между его обкладками равно 1 В. Это очень большая электроемкость, поэтому для практических целей используют такие единицы электроемкости как микрофарад (10-6 Ф) и пикофарад (1 пФ = 10-12 Ф).
? 1. Чему равен заряд конденсатора, если его электроемкость равна 5 мкФ, а напряжение между его обкладками 200 В?
? 2. Как изменится электроемкость конденсатора, если:
а) заряд конденсатора увеличить в 2 раза?
б) напряжение между обкладками конденсатора уменьшить в 3 раза?
От чего зависит электроемкость плоского конденсатора?
Поставим опыт
Соединим одну из обкладок школьного демонстрационного конденсатора с корпусом электрометра, а другую – с его стержнем (рис. 54.2, а).
Зарядим конденсатор и начнем сближать обкладки. Мы увидим, что показания электрометра уменьшаются (рис. 54.2, б). Это означает, что разность потенциалов (напряжение) между обкладками уменьшается.
Поскольку заряд обкладок остается при этом неизменным, из формулы C = q/U следует, что при уменьшении расстояния между обкладками электроемкость конденсатора увеличивается.
Если при неизменном расстоянии между пластинами конденсатора внести между ними диэлектрик (например, лист органического стекла), то разность потенциалов между пластинами уменьшится. Это указывает на то, что емкость конденсатора увеличилась.
Изменяя площадь пластин конденсатора, мы увидим, что при увеличении площади пластин емкость конденсатора увеличивается.
Более точные опыты и расчеты показывают, что электроемкость плоского конденсатора выражается формулой
C = (εε0S)/d, (2)
где S – площадь одной из обкладок, d – расстояние между ими, ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между ними, ε0 = 8,85 * 10-12 Кл2 / (Н * м2) (так называемая электрическая постоянная).
? 3. Как изменится электроемкость конденсатора, если:
а) площадь его обкладок увеличить в 3 раза?
б) расстояние между обкладками уменьшить в 2 раза?
в) заполнить пространство между обкладками диэлектриком с диэлектрической проницаемостью ε = 4?
Соотношение между напряжением на конденсаторе и напряженностью поля между его обкладками. В пространстве между обкладками плоского конденсатора электрическое поле можно считать практически однородным. Поэтому если расстояние между ними обозначить d, получим следующее соотношение (см. § 53):
E = U/d.
? 4. Чему равен заряд плоского конденсатора, если его электроемкость 20 пФ, напряженность поля между обкладками 50 кВ/м, а расстояние между обкладками равно 5 мм?
? 5. Расстояние между обкладками плоского конденсатора увеличили в 3 раза при неизменном заряде. Как изменились напряжение между обкладками и напряженность поля?
2. Энергия заряженного конденсатора
Поставим опыт
Замкнем обкладки заряженного конденсатора через лампочку накаливания. Мы увидим, что при разрядке конденсатора лампочка вспыхнет. Это означает, что заряженный конденсатор обладает энергией.
Предположим, что мы раздвигаем обкладки заряженного конденсатора, начальное расстояние между которыми практически равно нулю. Раздвигая пластины, мы совершаем положительную работу, потому что разноименно заряженные обкладки притягиваются. При этом согласно закону сохранения энергии потенциальная энергия конденсатора возрастает. Расчет показывает, что она увеличивается на
Wp = qU/2, (3)
где q – модуль заряда обкладки (заряд конденсатора), U – напряжение между его пластинами. Это и есть энергия заряженного конденсатора.
Множитель ½ в формуле (3) обусловлен тем, что, раздвигая пластины конденсатора, мы перемещаем каждую из них в поле, созданном зарядом одной (другой) пластины. А напряженность поля, создаваемого одной обкладкой, в 2 раза меньше модуля напряженности поля между обкладками.
? 6. Докажите, что энергия заряженного конденсатора выражается также формулами
Wp = q2/2C, (4)
Wp = CU2/2. (5)
Подсказка. Воспользуйтесь формулой C = q/U.
Из формулы (4) следует, что энергия заряженного конденсатора обратно пропорциональна его электроемкости, а из формулы (5) следует, что она, наоборот, прямо пропорциональна электроемкости. Не противоречат ли эти формулы одна другой?
Чтобы ответить на этот вопрос, рассмотрим, как изменяется энергия конденсатора при изменении его электроемкости. Конденсаторы, электроемкость которых можно изменять, широко используются, особенно в радиотехнике: например, с их помощью настраивают радиоприемник на волну той или иной радиостанции (подробнее мы расскажем об этом в курсе физики 11-го класса). Такие конденсаторы называют конденсаторами переменной емкости.
Например, в описанном выше опыте (см. рис. 54.2) электроемкость конденсатора увеличивалась при сближении его пластин.
Исследуя зависимость энергии конденсатора от его электроемкости, очень важно учитывать, какая величина остается неизменной при изменении электроемкости: заряд конденсатора или напряжение между его пластинами.
? 7. Электроемкость конденсатора увеличивают в 3 раза при неизменном заряде.
а) Найдите изменение энергии конденсатора, используя формулу (4).
б) Как изменилось напряжение между обкладками конденсатора?
в) Найдите изменение энергии конденсатора, используя формулу (5).
? 8. Электроемкость конденсатора увеличивают в 3 раза при неизменном напряжении между обкладками.
а) Найдите изменение энергии конденсатора, используя формулу (5).
б) Как изменился заряд конденсатора?
в) Найдите изменение энергии конденсатора, используя формулу (4).
Таким образом, мы видим, что противоречия между формулами (4) и (5) нет: обе эти формулы дают одинаковое значение энергии конденсатора, если принять во внимание, что заряд конденсатора и напряжение между его обкладками связаны соотношением C = q/U.
3. Энергия электрического поля
Потенциальную энергию зарядов в электрическом поле важно рассматривать также как энергию электрического поля. При перемещении зарядов друг относительно друга энергия созданного этими зарядами электрического поля изменяется.
Например, раздвигая заряженные обкладки конденсатора, мы совершаем положительную работу, потому что обкладки притягиваются друг к другу. Согласно закону сохранения энергии совершенная работа равна увеличению энергии электрического поля. Увеличивая расстояние между пластинами, мы увеличиваем объем пространства, занятый электрическим полем: на рисунке 54.3, а, б занятая электрическим поем область пространства для наглядности выделена светлым.
Расчеты показывают, что для однородного поля энергия электрического поля в заданной области пространства пропорциональна объему этой области и квадрату напряженности поля.
Дополнительные вопросы и задания
9. Все размеры воздушного конденсатора уменьшили в 2 раза и затем заполнили пространство между его обкладками диэлектриком.
а) Как изменилась электроемкость конденсатора вследствие уменьшения его размеров?
б) Чему равна диэлектрическая проницаемость диэлектрика, если после заполнения им пространства между обкладками значение электроемкости конденсатора стало равно первоначальному?
10. Маленький заряженный шарик подвешен на нити между вертикально расположенными пластинами воздушного конденсатора. Масса шарика 0,2 г, заряд 30 нКл, расстояние между пластинами 5 см. Нить отклонена на угол 30º от вертикали.
а) Изобразите на чертеже все силы, действующие на шарик.
б) Чему равна сила, действующая на шарик в электростатическом поле?
в) Чему равна напряженность поля между пластинами конденсатора?
г) Чему равна разность потенциалов между пластинами конденсатора?
11. Пространство между пластинами плоского конденсатора заполнено диэлектриком, диэлектрическая проницаемость которого равна 7. Заряды пластин конденсатора остаются неизменными. Как изменится при удалении диэлектрика:
а) электроемкость конденсатора?
б) разность потенциалов между его пластинами?
в) энергия конденсатора?
12. Пространство между пластинами воздушного конденсатора заполняют диэлектриком с диэлектрической проницаемостью ε и уменьшают расстояние между пластинами в 2 раза. При этом разность потенциалов между пластинами поддерживают неизменной.
а) Как изменяется электроемкость конденсатора?
б) Как изменяется заряд конденсатора?
в) Как изменяется энергия конденсатора?
Энергия конденсатора. Энергия заряженного конденсатора
Электрическая емкость проводника.
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд . В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
Конденсатор. Емкость плоского конденсатора.
Соединение конденсаторов.
Параллельное соединение конденсаторов | |
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора | |
Вывод: При параллельном соединении конденсаторов а) заряды складываются, б) напряжения одинаковые, в) емкости складываются. Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов | |
Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С 1 другая от конденсатора С 2 — играют роль обкладок нового конденсатора. | |
Вывод: При последовательном соединении конденсаторов а) напряжения складываются, б) заряды одинаковы, в) складываются величины, обратные емкости. Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов. |
Энергия, накопленная в конденсаторе.
При заряде конденсатора внешний источник расходует энергию на разделение зарядов на положительные и отрицательные. Которые будут находиться на обкладках конденсатора. Следовательно, исходя из закона сохранения энергии, она никуда не пропадает, а остается в конденсаторе. Энергия в конденсаторе запасается в виде силы взаимодействия положительных и отрицательных зарядов находящихся на его обкладках. То есть в виде электрического поля. Которое сосредоточено между пластинами. Это взаимодействие стремится притянуть одну обкладку к другой, поскольку, как известно разноименные заряды притягиваются.
Как известно из механики F=mg , аналогично в электрике F=qE , роль массы играет заряд, а роль сили притяжения напряжённость поля.
Работа по перемещению заряда в электрическом поле выглядит так:A=qEd1-qEd2=qEd
C другой же стороны работа также равна разнице потенциальных энергий A=W1-W2=W.
Таким образом используя эти два выражения можно сделать вывод что потенциальная энергия накопленная в конденсаторе равна:
Формула 1 — Энергия заряженного конденсатора
Не трудно заметить, что формула очень похожа на потенциальную энергию из механики W=mgh .
Если провести аналогию с механикой: Представим камень, находящийся на крыше здания. Здесь взаимодействует масса земли с массой камня посредством силы тяжести, а здание высотой h противодействует силе гравитации. Если здание убрать камень упадет, следовательно, потенциальная энергия перейдет в кинетическую.
В электростатике же есть два разноименных заряда стремящихся притянутся друг к другу им противодействует диэлектрик толщиной d находящийся между обкладками. Если обкладки замкнуть между собой то потенциальная энергия заряда перейдет в кинетическую то есть в тепло.
В электротехнике формула для энергии в таком виде не применяется. Ее удобно выразить через емкость конденсатора и напряжение, до которого он заряжен.
Так как заряд конденсатора определяется зарядом одной из его пластин то напряжённость поля, создаваемая ею, будет равна E/2 . Поскольку общее поле складывается из полей создаваемых обеими обкладками заряжении одинаково, но с противоположным знаком.
Следовательно, энергия конденсатора будет иметь вид: W=q(E/2)d
Поскольку напряжение можно выразить через напряжённость и расстояние(U=Ed) подставим его в нашу формулу получим: W=qU/2
А теперь используя выражение для емкости, C=q/U получим окончательный результат.
Энергия заряженного конденсатора имеет вид:
Энергия электрического поля.
Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Частное U / d равно напряженности поля в зазоре; произведение S · d представляет собой объем V , занимаемый полем. Следовательно,
Для того, чтобы правильно представлять работу конденсатора, необходимо точно знать о поведении в . Именно их свойства являются основой работы этих специальных устройств. Одним из показателей работы служит энергия заряженного конденсатора, формула которой достаточно точно описывает этот процесс. Кроме того, нужно знать, что вообще представляет собой обычный стандартный конденсатор.
Устройство и принцип работы конденсатора
Название конденсатора имеет латинские корни, означающие сгущение или уплотнение. Он имеет два полюса и обладает емкостью с переменным или постоянным значением. Отличительной чертой конденсатора является его незначительная проводимость. Это устройство выполняет основную функцию, связанную с накоплением определенного заряда и электрической энергии.
Конденсатор относится к категории пассивных электронных компонентов. Типовая конструкция включает в себя два электрода в виде пластин, разделяемых с помощью диэлектрика. Его толщина значительно меньше, чем у пластин, которые называются обкладками. В конденсаторах, применяемых на практике, пластины и электроды состоят из множества слоев. Как правило, происходит их чередование в виде лент, сворачиваемых в форму параллелепипеда или цилиндра.
При постоянном токе, зарядка и перезарядка производится при включении конденсатора в цепь. После отключения, ток через него уже не проходит. В цепях переменным током, колебания проводятся при циклической перезарядке, а замыкание осуществляется с помощью тока смещения.
Значение энергии конденсатора
Прежде всего, необходимо рассмотреть такое понятие, как электрическая емкость. В обычном проводнике этот параметр почти не используется. Более всего он подходит к заряженному конденсатору, который, по своей сути, также является проводником или даже системой проводников. В зависимости от емкости, определяется и энергия заряженного конденсатора, формула которой отражает ее величину.
Практически каждый конденсатор после его заряда, начинает обладать энергией. Достаточно подключить лампочку, чтобы увидеть, как она загорится на короткое время. Это показывает наличие определенных запасов энергии, выделение которой происходит во время разрядки. Она возникает, как потенциальная энергия, с которой взаимодействуют между собой обкладки конденсатора. Эти обкладки имеют разноименные заряды, способные притягиваться между собой.
Значение энергии зависит от величины заряда, напряжения в сети и других факторов. Чем больше , тем более высокой энергией он обладает.
«Физика — 10 класс»
«Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22).
Задача 1.
Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C 1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.
Р е ш е н и е.
Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С 2 — C)U = (nC 1 — C 1)U = (п — 1)С 1 U = 10 -8 Кл.
Изменение энергии электрического поля
Задача 2.
Заряд конденсатора q = 3 10 -8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона
Р е ш е н и е.
Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А — работа электрического поля конденсатора:
Следовательно,
Окончательно
Задача 3.
Четыре конденсатора ёмкостями С 1 = С 2 = = 1 мкФ, С 3 = 3 мкФ, С 4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов.
Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С 2,3 = С 2 + С 3 а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С 1 , С 2,3 , С 4 , найдём из соотношения
1/Cэкв = 1 /С 1 + 1/С 2,3 + 1 /С 4 , Сэкв = (4/7) 10 -6 Ф.
Заряды на этих конденсаторах одинаковы:
q 1 = q 2,3 = q 4 = Сэкв = 8 10 -5 Кл.
Следовательно, заряд первого конденсатора q 1 = 8 10 -5 Кл, а разность потенциалов между его обкладками, или напряжение, U 1 = q 1 /С 1 = 80 В.
Для четвёртого конденсатора аналогично имеем q 4 = 8 10 -5 Кл, U 4 = q 4 /C 4 = 40 В.
Найдём напряжение на втором и третьем конденсаторах: U 2 = U 3 = q 2,3 /C 2,3 = 20 В.
Таким образом, на втором конденсаторе заряд q 2 = C 2 U 2 = 2 10-5 Кл, а на третьем конденсаторе q 3 = C 3 U 3 = 6 10 -5 Кл. Отметим, что q 2,3 = q 2 + g 3 .
Задача 4.
Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны.
Р е ш е н и е.
Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов.
В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φ A ≠ φ B в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и С экв определим по формуле 1/С экв = 1/2С 1 + 1/2С 2 , откуда
Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно,
Эквивалентные конденсаторы с С» экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:
Задача 5.
Энергия плоского воздушного конденсатора W 1 = 2 10 -7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если:
1) конденсатор отключён от источника питания;
2) конденсатор подключён к источнику питания.
Р е ш е н и е.
1) Так как конденсатор отключён от источника питания, то его заряд q 0 остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком после заполнения где С 2 = εС 1 .
Как и любая система заряжен-ных тел, конденсатор обладает энер-гией. Вычислить энергию заряжен-ного плоского конденсатора с одно-родным полем внутри него не-сложно.
Энергия заряженного конденса-тора.Для того чтобы зарядить конденсатор, нужно совершить рабо-ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра-бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со-держащую лампу накаливания, рас-считанную на напряжение в не-сколько вольт (рис. 4). При раз-рядке конденсатора лампа вспыхи-вает. Энергия конденсатора пре-вращается в другие формы: тепло-вую, световую.
Выведем формулу для энергии плоского конденсатора .
Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру-гой пластины (рис. 5). Согласно формуле W p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
Можно доказать, что эти форму-лы справедливы для энергии любого конденсатора, а не только для плос-кого.
Энергия электрического поля.Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче-ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря-женность.
Так как напряженность электри-ческого поля прямо пропорциональ-на разности потенциалов
(U = Ed), то согласно формуле
энергия конденсатора прямо пропор-циональна напряженности электри-ческого поля внутри него: W p ~ E 2 . Детальный расчет дает следующее значение для энергии поля, приходя-щейся на единицу объема, т.е. для плотности энергии:
где ε 0 — электрическая постоянная
Применение конденсаторов.Энер-гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку-муляторы в качестве источников электрической энергии.
Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при-менения. Они имеют одно важное свойство: конденсаторы могут на-капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.
Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря-жаемого предварительно специаль-ной батареей. Возбуждение кванто-вых источников света — лазеров осу-ществляется с помощью газораз-рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем-кости.
Однако основное применение кон-денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.
Энергия конденсатора пропор-циональна его электроемкости и квадрату напряжения между плас-тинами. Вся эта энергия сосредото-чена в электрическом поле. Плот-ность энергии поля пропорциональна квадрату напряженности поля.
Рис. 1 Рис. 2
ЗАКОНЫ ПОСТОЯННОГО ТОКА.
Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды слу-жить нам, их нужно привести в движение — создать электрический ток. Электрический ток освещает квартиры, приводит в дви-жение станки, создает радиоволны, циркулирует во всех электрон-но-вычислительных машинах.
Мы начнем с наиболее простого случая движения заряжен-ных частиц — рассмотрим постоянный электрический ток.
ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА
Дадим строгое определение тому, что называют электрическим током.
Напомним, какой величиной ха-рактеризуется ток количественно.
Найдем, как быстро движутся электроны по проводам в вашей квартире.
При движении заряженных час-тиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не про-исходит (рис.1). Электриче-ский заряд перемещается через по-перечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис. 2). В этом случае говорят, что в проводнике устанавливается электрический ток.
Из курса физики VIII класса вы знаете, что электрическим током называют упорядоченное (направ-ленное) движение заряженных частиц.
Электрический ток возникает при упорядоченном перемещении свобод-ных электронов или ионов.
Если перемещать нейтральное в целом тело, то, несмотря на упо-рядоченное движение огромного чис-ла электронов, и атомных ядер, электрический ток не возникает. Полный заряд, переносимый через любое сечение проводника, будет при этом равным нулю, так как заряды разных знаков с одинаковой средней скоростью.
Электрический ток имеет определенное направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению дви-жения частиц.
Действия тока. Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем дей-ствиям или явлениям, которые его сопровождают.
Во-первых, проводник, по которо-му течет ток, нагревается.
Во-вторых, электрический ток мо-жет изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).
В-третьих, ток оказывает силовое воздействие на соседние токи и на-магниченные тела. Это действие то-ка называется магнитным. Так, маг-нитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химиче-ского и теплового является основ-ным, так как проявляется у всех без исключения проводников. Хими-ческое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсут-ствует у сверхпроводников.
Сила тока.Если в цепи уста-навливается электрический ток, то это означает, что через поперечное сечение проводника все время пере-носится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной ха-рактеристикой тока, называемой си-лой тока.
Таким образом, сила тока равна отношению заряда q, переносимого через поперечное сечение провод-ника за интервал времени t, к этому интервалу времени. Если сила тока со временем не меняется, то ток на-зывают постоянным.
Сила тока, подобно заряду, — ве-личина скалярная. Она может быть как положительной, так и отрица-тельной. Знак силы тока зависит от того, какое из направлений вдоль проводника принять за положитель-ное. Сила тока / > 0, если направ-ление тока совпадает с условно вы-бранным положительным направле-нием вдоль проводника. В против-ном случае /
Сила тока зависит от заряда, переносимого каждой частицей, кон-центрации частиц, скорости их направленного движения и площади поперечного сечения проводника. По-кажем это.
Пусть проводник (рис. 3) имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление сле-ва направо. Заряд каждой частицы равен q 0 . В объеме проводника, ограниченном поперечными сечениям-и 1 и 2, содержится nSl частиц, где п — концентрация частиц. Их общий заряд q = q Q nSl. Если частицы движутся слева направо со средней скоростью υ, то за время
Все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:
формуле (2) где е — модуль заряда электрона.
Пусть, например, сила тока I = 1 А, а площадь по-перечного сечения проводника S = 10 -6 м 2 . Модуль заряда электрона е = 1,6 — 10 -19 Кл. Число электронов в 1 м 3 меди равно числу атомов в этом объеме, так как один из ва-лентных электронов каждого атома меди коллективизирован и является свободным. Это число есть п = 8,5 · 10 28 м -3 Следовательно,
Рис №1. Рис №2 Рис №3
УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
Что необходимо для создания электрического тока? Подумайте над этим сами и только потом прочтите этот параграф.
Для возникновения и существо-вания постоянного электрического тока в веществе необходимо, во-первых, наличие свободных заряжен-ных частиц. Если положительные и отрицательные заряды связаны друг с другом в атомах или молекулах , то их перемещение не приведет к по-явлению электрического тока.
Наличия свободных зарядов еще недостаточно для возникновения то-ка. Для создания и поддержания упорядоченного движения, заряжен-ных частиц необходима, во-вторых, сила, действующая на них в опре-деленном направлении. Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за сопротив-ления, оказываемого их движению ионами кристаллической решетки металлов или нейтральными молеку-лами электролитов .
На заряженные частицы, как мы знаем, действует электрическое поле с силой . Обычно именно электрическое поле внутри провод-ника служит причиной, вызываю-щей и поддерживающей упорядочен-ное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.
Если внутри проводника имеется электрическое поле, то между конца-ми проводника в соответствии с фор-мулой существует разность потенциалов. Когда разность потен-циалов не меняется во времени, то в проводнике устанавливается по-стоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минималь-ного — на другом. Это уменьшение потенциала можно обнаружить на простом опыте.
Возьмем в качестве проводника не очень сухую деревянную палку и подвесим ее горизонтально. (Такая палка хотя и плохо, но все же про-водит ток.) Источником напряжения пусть будет электростатическая ма-шина, Для регистрации потенциала различных участков проводника от-носительно земли можно использо-вать листочки металлической фоль-ги, прикрепленные к палке. Один полюс машины соединим с землей, а второй — с одним концом проводни-ка (палки). Цепь окажется незамк-нутой. При вращении рукоятки ма-шины мы обнаружим, что все лис-точки отклоняются на один и тот же угол (рис. 1).
Значит, потен-циал всех точек проводника отно-сительно земли одинаков. Так и должно быть при равновесии заря-дов на проводнике. Если теперь дру-гой конец палки заземлить, то при вращении рукоятки машины карти-на изменится. (Так как земля — проводник, то заземление провод-ника делает цепь замкнутой.) У за-земленного конца листочки вообще не разойдутся: потенциал этого кон-ца проводника практически равен потенциалу земли (падение потен-циала в металлической проволоке мало). Максимальный угол расхож-дения листочков будет у конца про-водника, присоединенного к машине (рис. 2). Уменьшение угла рас-хождения листочков по мере удале-ния от машины свидетельствует о падении потенциала вдоль провод-ника.
Электрический ток может быть получен только в веществе, в котором имеются свободные заряженные частицы. Чтобы они пришли в движение, нужно создать в проводнике электрическое поле.
Рис №1 Рис №2
ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ
В VIII классе изучался закон Ома . Этот закон прост, однако столь важен, что его необходимо повторить.
Вольт — амперная характеристика.В предыдущем параграфе было уста-новлено, что для существования то-ка в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяет-ся этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряженность электриче-ского поля в проводнике и, следо-вательно, тем большую скорость на-правленного движения приобретают заряженные частицы. Согласно фор-муле, это означает увеличение силы тока.
Для каждого проводника — твер-дого, жидкого и газообразного — существует определенная зависи-мость силы тока от приложенной разности потенциалов на концах про-водника. Эту зависимость выражает так называемая вольт — амперная ха-рактеристика проводника. Ее нахо-дят, измеряя силу тока в проводнике при различных значениях напряже-ния. Знание вольт — амперной характе-ристики играет большую роль при изучении электрического тока.
Закон Ома.Наиболее простой вид имеет вольт — амперная характеристи-ка металлических проводников и растворов электролитов. Впервые (для металлов) ее установил немец-кий ученый Георг Ом, поэтому зависимость силы тока от напря-жения носит название закона Ома. На участке цепи, изображенной на рисунке 109, ток направлен от точки 1 к точке 2. Разность потен-циалов (напряжение) на концах проводника равна: U = φ 1 — φ 2. Так как ток направлен слева направо, то напряженность электрического поля направлена в ту же сторону и φ 1 > φ 2
Согласно закону Ома для участка цепи сила тока прямо пропорцио-нальна приложенному напряжению U и обратно пропорциональна сопро-тивлению проводника R:
Закон Ома имеет очень простую форму, но доказать эксперименталь-но его справедливость довольно трудно. Дело в том, что разность по-тенциалов на участке металлическо-го проводника даже при большой силе тока мала, так как мало сопро-тивление проводника.
Электрометр, о котором шла речь, непригоден для измерения столь малых напряжений: его чув-ствительность слишком мала. Нужен несравненно более чувствительный прибор. Тогда, измеряя силу тока амперметром, а напряжение чув-ствительным электрометром, можно убедиться в том, что сила тока пря-мо пропорциональна напряжению. Применение же обычных приборов для измерения напряжения — вольт-метров — основано на использовании закона Ома.
Принцип устройства, вольтметра такой же, как и ампер-метра. Угол поворота стрелки прибо-ра пропорционален силе тока. Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он под-ключен. Поэтому, зная сопротивле-ние вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в воль-тах.
Сопротивление. Основная элек-трическая характеристика проводни-ка — сопротивление. От этой вели-чины зависит сила тока в провод-нике при заданном напряжении. Со-противление проводника представля-ет собой как бы меру противо-действия проводника установлению в нем электрического тока. С помощью закона Ома можно определить сопротивление проводника:
Для этого нужно измерить напря-жение и силу тока.
Сопротивление зависит от мате-риала проводника и его геометри-ческих размеров. Сопротивление про-водника длиной l с постоянной пло-щадью поперечного сечения S равно:
где р — величина, зависящая от рода вещества и его состояния (от тем-пературы в первую очередь). Вели-чину р называют удельным сопро-тивлением проводника. Удельное со-противление численно равно сопро-тивлению проводника, имеющего форму куба с ребром 1 м, если ток направлен вдоль нормали к двум противоположным граням куба.
Единицу сопротивления провод-ника устанавливают на основе зако-на Ома и называют ее ом. Провод-ник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А.
Единицей удельного сопротивле-ния является 1 Ом?м. Удельное со-противление металлов мало. Диэлектрики обладают очень большим удельным сопротивлением. В табли-це на форзаце приведены примеры значений удельного сопротивления некоторых веществ.
Значение закона Ома.Закон Ома определяет силу тока в электриче-ской цепи при заданном напря-жении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротив-ления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Закон Ома — основа всей элект-ротехники постоянных токов. Формулу — надо хорошо понять и твердо запомнить.
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
От источника тока энергия может быть передана по проводам к устрой-ствам, потребляющим энергию: Элек-трической лампе, радиоприемнику и др. Для этого составляют электри-ческие цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, по-требляющих электрическую энергию, соединительных проводов и выклю-чателей для замыкания цепи. Часто и электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участ-ках цепи, — амперметры и вольт-метры.
К наиболее простым и часто встречающимся соединениям провод-ников относятся последовательное и параллельное соединения.
Последовательное соединение проводников.При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. На рисунке 1 показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R 1 , и R 2 . Это могут быть две лампы, две обмотки элект-родвигателя и др.
Сила тока в обоих проводниках одинакова, т. е. (1)
так как в проводниках электриче-ский заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.
Напряжение на концах рассмат-риваемого участка цепи складывает-ся из напряжений на — первом и вто-ром проводниках:
Надо надеяться, что с доказатель-ством этого простого соотношения вы справитесь сами.
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно до-казать, что полное сопротивление всего участка цепи при последова-тельном соединении равно:
Это правило можно применить для любого числа последовательно соединенных проводников.
Напряжения на проводниках и их сопротивления при последователь-ном соединении связаны соотноше-нием:
Докажите это равенство.
Параллельное соединение про-водников.На рисунке 2 показано параллельное соединение двух про-водников 1 и 2с сопротивлениями R 1 и R 2 . В этом случае электриче-ский ток 1 разветвляется на две час-ти. Силу тока в первом и втором про-водниках обозначим через I 1 и I 2 . Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не на-капливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно, I = I 1 + I 2
Напряжение U на концах про-водников, соединенных параллельно, одно и то же.
В осветительной сети поддержи-вается напряжение 220 или 127 В. На это напряжение рассчитаны при-боры, потребляющие электрическую энергию. Поэтому параллельное сое-динение — самый распространенный способ соединения различных потре-бителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размы-кает цепь.
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных провод-ников:
Сила тока в каждом из провод-ников и сопротивления проводников при параллельном соединении свя-заны соотношением
Различные проводники в цепи соединяются друг с другом после-довательно или параллельно. В пер-вом случае сила тока одинакова во всех проводниках, а во втором слу-чае одинаковы напряжения на про-водниках. Чаще всего к осветитель-ной сети различные потребители тока подключаются параллельно.
ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Как измерить силу тока ампер-метром, а напряжение вольтметром, должен знать каждый.
Измерение силы тока.Для изме-рения силы тока в проводнике ам-перметр включают последовательно с этим проводником (рис. 1). Но нужно иметь в виду, что сам ампер-метр обладает некоторым сопротив-лением R a . Поэтому сопротивление участка цепи с включенным ампер-метром увеличивается, и при неиз-менном напряжении сила тока умень-шается в соответствии с законом Ома. Чтобы амперметр оказывал как можно меньшее влияние на силу тока, измеряемую им, его сопротив-ление делают очень малым. Это нужно помнить и никогда не пытать-ся измерять силу тока в освети-тельной сети, подключая амперметр к розетке. Произойдет короткое за-мыкание; сила тока при малом со-противлении прибора достигнет столь большой величины, что обмотка ам-перметра сгорит.
Измерение напряжения.Для того чтобы измерить напряжение на участке цепи с сопротивлением R, к нему параллельно подключают вольтметр. Напряжение на вольтметре совпа-дает с напряжением на участке цепи (рис. 2).
Если сопротивление вольтметра R B , то после включения его в цепь сопротивление участка будет уже не R, а . Из-за этого измеряемое напряжение на участ-ке цепи уменьшится. Для того чтобы вольтметр не вносил заметных иска-жений в измеряемое напряжение, его сопротивление должно быть большим по сравнению с сопротивлением участка цепи, на котором измеряется напряжение. Вольтметр можно вклю-чать в сеть без риска, что он сгорит, если только он рассчитан на напря-жение, превышающее напряжение сети.
Амперметр включают последова-тельно с проводником, в котором измеряют силу тока. Вольтметр включают параллельно проводнику, на котором измеряют напряжение.
РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА
Электрический ток получил такое широкое применение потому, что он несет с собой энергию. Эта энергия может быть превращена в любую форму.
При упорядоченном движении за-ряженных частиц в проводнике электрическое поле совершает ра-боту; ее принято называть работой тока. Сейчас мы напомним сведения о работе и мощности тока из курса физики VIII класса.
Работа тока.Рассмотрим произ-вольный участок цепи. Это, может быть однородный проводник, напри-мер нить лампы накаливания, обмот-ка электродвигателя и др. Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу A = qU.
Так как сила тока , то эта работа равна:
Работа тока на участке цепи равна произведению силы тока, на-пряжения и времени, в течение ко-торого совершалась работа.
Согласно закону сохранения энергии эта работа должна быть рав-на изменению энергии рассматри-ваемого участка цепи. Поэтому энер-гия, выделяемая на данном участке цепи за время At, равна работе тока (см. формулу (1)).
В случае если на участке цепи не совершается механическая рабо-та и ток не производит химических действий, происходит только нагре-вание проводника. Нагретый про-водник отдает теплоту окружающим телам.
Нагревание проводника происхо-дит следующим образом. Электриче-ское поле ускоряет электроны. После столкновения с ионами кристалличе-ской решетки они передают ионам свою энергию. В результате энергия беспорядочного движения ионов око-ло положений равновесия возраста-ет. Это и означает увеличение внут-ренней энергии. Температура про-водника при этом повышается, и он начинает передавать теплоту окру-жающим телам. Спустя небольшое время после замыкания цепи процесс устанавливается, и температура пе-рестает изменяться со временем. К проводчику за счет работы элект-рического поля непрерывно поступа-ет энергия. Но его внутренняя энер-гия остается неизменной, так как проводник передает окружающим те-лам количество теплоты, равное ра-боте тока. Таким образом, формула (1) для работы тока определяет количество теплоты, передаваемое проводником другим телам.
Если в формуле (1) выразить либо напряжение через силу тока, либо силу тока через напряжение с помощью закона Ома для участка цепи, то получим три эквивалентные формулы:
(2)
Формулой A = I 2 R t удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При парал-лельном соединении удобна формула , так как напряжение на всех проводниках одинаково.
Закон Джоуля — Ленца.Закон, определяющий количество теплоты, которое выделяет проводник с то-ком в окружающую среду, был впервые установлен эксперименталь-но английским ученым Д. Джоу-лем (1818-1889) и русским ученым Э. X. Ленцем (1804-1865). Закон Джоуля — Ленца был сформулиро-ван следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квад-рата силы тока, сопротивления про-водника и времени прохождения то-ка по проводнику:
(3)
Мы получили этот закон с по-мощью рассуждений, основанных на законе сохранения энергии. Формула (3) позволяет вычислить количе-ство теплоты, выделяемое на любом участке цепи, содержащем какие угодно проводники.
Мощность тока.Любой электри-ческий прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу вре-мени. Поэтому наряду с работой то-ка очень важное значение имеет по-нятие мощность тока. Мощность то-ка равна отношению работы тока за время t к этому интервалу времени.
Согласно этому определению
(4)
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если исполь-зовать закон Ома для участка цепи:
На большинстве приборов ука-зана потребляемая ими мощность.
Прохождение по проводнику электрического тока сопровождается выделением в нем энергии. Эта энер-гия определяется работой тока: про-изведением перенесенного заряда и напряжения на концах проводника.
ЭЛЕКТРОДВИЖУЩАЯ СИЛА.
Любой источник тока характеризуется электродвижущей силой, или ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?
Соедините проводником два ме-таллических шарика, несущих за-ряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис. 1). Но этот ток будет очень кратковремен-ным. Заряды быстро нейтрализуют-ся, потенциалы шариков станут одинаковыми, и электрическое поле ис-чезнет.
Сторонние силы.Для того чтобы ток был постоянным, надо поддер-живать постоянное напряжение меж-ду шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со сто-роны электрического поля шариков. В таком устройстве на заряды, кро-ме электрических сил, должны дей-ствовать силы не электростатического происхождения (рис. 2). Одно лишь электрическое поле заряжен-ных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.
Любые силы, действующие на электрически заряженные частицы, за исключением сил электростати-ческого происхождения (т. е. кулоновских), называют сторонними си-лами.
Вывод о необходимости сторон-них сил для поддержания посто-янного тока в цепи станет еще оче-виднее, если обратиться к закону сохранения энергии. Электростатиче-ское поле потенциально. Работа это-го поля при перемещении заряжен-ных частиц вдоль замкнутой электри-ческой цепи равна нулю. Прохож-дение же тока по проводникам сопровождается выделением энер-гии — проводник нагревается. Сле-довательно, в любой цепи должен быть какой-то источник энергии, по-ставляющий ее в цепь. В нем, по-мимо кулоновских сил, обязательно должны действовать сторонние не- потенциальные силы. Работа этих сил вдоль замкнутого контура долж-на быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энер-гию и отдают ее затем проводникам электрической цепи.
Сторонние силы приводят в дви-жение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальваниче-ских элементах, аккумуляторах и т.д.
При замыкании цепи создается электрическое поле во всех провод-никах цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрица-тельному), а во всей остальной цепи их приводит в движение электриче-ское поле (см. рис. 2).
Аналогия между электрическим током и течением жидкости.Чтобы лучше понять механизм возникнове-ния тока, обратимся к сходству меж-ду электрическим током в провод-нике и течением жидкости по трубам.
На любом участке горизонталь-ной трубы жидкость течет за счет разности давлений на концах участ-ка. Жидкость перемещается в сторо-ну уменьшения давления. Но сила давления в жидкости — это вид сил упругости, которые являются потен-циальными, подобно кулоновским силам. Поэтому работа этих сил на замкнутом пути равна нулю и одни эти силы не способны вызвать длительную циркуляцию жидкости по трубам. Течение жидкости сопро-вождается потерями энергии вслед-ствие действия сил трения. Для цир-куляции воды необходим насос.
Поршень этого насоса действует на частички жидкости и создает по-стоянную разность давлений на вхо-де и выходе насоса (рис. 3). Благодаря этому жидкость течет по трубе. Насос подобен источнику тока, а роль сторонних сил играет сила, действующая на воду со стороны движущегося поршня. Внутри на-соса жидкость течет от участков с меньшим давлением к участкам с большим давлением. Разность дав-лений аналогична напряжению.
Природа сторонних сил.Природа сторонних сил может быть разнооб-разной. В генераторах электростанций сторонняя сила — это сила, дей-ствующая со стороны магнитного поля на электроны в движущемся проводнике. Об этом кратко гово-рилось в курсе физики VIII класса.
В гальваническом элементе, на-пример элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кис-лоте. В раствор переходят положи-тельно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной — кислоте.) Между цинковым и мед-ным электродами появляется раз-ность потенциалов, которая обуслов-ливает ток в замкнутой электриче-ской цепи.
Электродвижущая сила.Дейст-вие сторонних сил характеризуется важной физической величиной, на-зываемой электродвижущей силой (сокращенно ЭДС).
Электродви-жущая сила в замкнутом контуре представляет собой отношение рабо-ты сторонних сил при перемещении заряда вдоль контура к заряду:
Электродвижущую силу выража-ют в вольтах.
Можно говорить об электродви-жущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единич-ного заряда) не во всем контуре, а только на данном участке. Электро-движущая сила гальванического эле-мента есть работа сторонних сил при перемещении единичного положи-тельного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть вы-ражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при переме-щении заряда между клеммами ис-точника тока вне самого источника равна нулю.
Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совер-шают работу 1,5 Дж при переме-щении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС
Рис №1 Рис №2 Рис №3
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ
Электродвижущая сила опреде-ляет силу тока в замкнутой электри-ческой цепи с известным сопротив-лением.
Спомощью закона сохранения энергии найдем зависимость силы тока от ЭДС и сопротивления.
Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или гене-ратора) и резистора сопротивле-нием R (рис. 1). Источник тока имеет ЭДС εи сопротивление r. Сопротивление источника часто на-зывают внутренним сопротивлением в отличие от внешнего сопротивле-ния R цепи. В генераторе r — это сопротивление обмоток, а в гальва-ническом элементе — сопротивление раствора электролита и электродов.
Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление R + r цепи. Эта связь может быть установлена теоретически, если использовать за-кон сохранения энергии и закон Джоуля — Ленца.
Пусть за время t через попе-речное сечение проводника пройдет электрический заряд q. Тогда рабо-ту сторонних сил при перемещении заряда?qможно записать так: А ст = ε · q. Согласно определению силы тока q = It. Поэтому
(1)
При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых r и R, выделяется некоторое количество теплоты. По закону Джоуля — Лен-ца оно равно:
Q = I 2 R · t + I 2 r · t. (2)
Согласно закону сохранения энергии A = Q. Приравнивая (1) и (2), получим:
ε = IR + Ir (3)
Произведение силы тока и сопро-тивления участка цепи часто назы-вают падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внут-реннем и внешнем участках замкну-той цепи.
Обычно закон Ома для замкну-той цепи записывают в форме
(4)
энергии в конденсаторах | Физика
Цели обучения
К концу этого раздела вы сможете:
- Перечислите некоторые варианты использования конденсаторов.
- Выразите в уравнении энергию, запасенную в конденсаторе.
- Объясните функцию дефибриллятора.
Большинство из нас видели инсценировки, в которых медицинский персонал использовал дефибриллятор , чтобы пропустить электрический ток через сердце пациента, чтобы заставить его нормально биться.(Просмотрите рис. 1.) Часто реалистичный в деталях, человек, применяющий электрошок, просит другого человека «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, накапливается в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ — джоули. Менее драматично использование конденсаторов в микроэлектронике, например в некоторых портативных калькуляторах, для подачи энергии при зарядке аккумуляторов. (См. Рис. 1.) Конденсаторы также используются для питания ламп-вспышек на камерах.
Рис. 1. Энергия, накопленная в большом конденсаторе, используется для сохранения памяти электронного калькулятора, когда его батареи заряжены. (Источник: Kucharek, Wikimedia Commons)
Энергия, запасенная в конденсаторе, представляет собой электрическую потенциальную энергию, и, таким образом, она связана с зарядом Q и напряжением В, на конденсаторе. Мы должны быть осторожны при применении уравнения для электрической потенциальной энергии ΔPE = q Δ V к конденсатору. Помните, что ΔPE — это потенциальная энергия заряда q , проходящего через напряжение Δ В .Но конденсатор начинает с нулевого напряжения и постепенно достигает своего полного напряжения по мере зарядки. Первый заряд, помещенный на конденсатор, испытывает изменение напряжения Δ В, = 0, поскольку конденсатор имеет нулевое напряжение в незаряженном состоянии. Последний заряд, помещенный на конденсатор, испытывает Δ В, = В, , поскольку теперь на конденсаторе имеется полное напряжение В, . Среднее напряжение на конденсаторе во время процесса зарядки составляет [латекс] \ frac {V} {2} \\ [/ latex], поэтому среднее напряжение, испытываемое при полной зарядке q , равно [latex] \ frac {V} {2} \\ [/ латекс].Таким образом, энергия, запасенная в конденсаторе E cap , равна [latex] E _ {\ text {cap}} = \ frac {QV} {2} \\ [/ latex], где Q — это заряд на конденсаторе приложено напряжение В . (Обратите внимание, что энергия не QV , а [latex] \ frac {QV} {2} \\ [/ latex].) Заряд и напряжение связаны с емкостью C конденсатора как Q = CV , поэтому выражение для E cap можно алгебраически преобразовать в три эквивалентных выражения:
[латекс] \ displaystyle {E} _ {\ text {cap}} = \ frac {QV} {2} = \ frac {CV ^ 2} {2} = \ frac {Q ^ 2} {2C} \\ [/ латекс],
, где Q, — это заряд, а В, — напряжение на конденсаторе C, .2} {2C} \\ [/ latex],
, где Q, — заряд, В, — напряжение, а C, — емкость конденсатора. Энергия выражается в джоулях для заряда в кулонах, напряжения в вольтах и емкости в фарадах.
В дефибрилляторе доставка большого заряда коротким импульсом к набору лопастей на груди человека может быть спасением. Инфаркт у человека мог возникнуть в результате быстрого, нерегулярного сердцебиения — фибрилляции сердца или желудочков.Применение сильного разряда электрической энергии может прекратить аритмию и позволить кардиостимулятору тела вернуться к нормальному режиму работы. Сегодня в машинах скорой помощи обычно есть дефибриллятор, который также использует электрокардиограмму для анализа сердечного ритма пациента. Автоматические внешние дефибрилляторы (AED) можно найти во многих общественных местах (рис. 2). Они предназначены для использования непрофессионалами. Устройство автоматически диагностирует состояние сердца пациента, а затем применяет разряд с соответствующей энергией и формой волны.Во многих случаях перед использованием АВД рекомендуется СЛР.
Рис. 2. Автоматические внешние дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства предоставляют устные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (Источник: Оуайн Дэвис, Wikimedia Commons)
Пример 1. Емкость дефибриллятора сердца
Дефибриллятор сердца вырабатывает 4,00 × 10 2 Дж энергии, разряжая конденсатор первоначально на 1.{-6} \ text {F} \\\ text {} & = & 8.00 \ mu \ text {F} \ end {array} \\ [/ latex]
Обсуждение
Это довольно большая, но управляемая емкость при 1,00 × 10 4 В.
Сводка раздела
- Конденсаторы используются в различных устройствах, включая дефибрилляторы, микроэлектронику, такую как калькуляторы, и импульсные лампы для подачи энергии.
- Энергия, запасенная в конденсаторе, может быть выражена тремя способами: [латекс] {E} _ {\ text {cap}} = \ frac {\ text {QV}} {2} = \ frac {{\ text {CV }} ^ {2}} {2} = \ frac {{Q} ^ {2}} {2C} \\ [/ latex], где Q — это заряд, В, — напряжение, а С — емкость конденсатора.Энергия выражается в джоулях, когда заряд — в кулонах, напряжение — в вольтах, а емкость — в фарадах.
Концептуальные вопросы
- Как изменяется энергия, содержащаяся в заряженном конденсаторе, когда вставлен диэлектрик, если конденсатор изолирован и его заряд постоянен? Означает ли это, что работа была сделана?
- Что происходит с энергией, накопленной в конденсаторе, подключенном к батарее, когда вставлен диэлектрик? Была ли проделана работа в процессе?
Задачи и упражнения
- (a) Какая энергия хранится в 10.0 мкФ конденсатор дефибриллятора сердца заряжен до
9,00 × 10 3 В? (b) Найдите количество накопленного заряда. - При операции на открытом сердце гораздо меньшее количество энергии вызывает дефибрилляцию сердца. (а) Какое напряжение приложено к конденсатору 8,00 мкФ дефибриллятора сердца, который накапливает 40,0 Дж энергии? (b) Найдите количество сохраненного заряда.
- Конденсатор емкостью 165 мкФ используется вместе с двигателем. Сколько энергии в нем хранится при подаче 119 В?
- Предположим, у вас есть 9.Батарея 00 В, конденсатор 2,00 мкФ и конденсатор 7,40 мкФ. (а) Найдите заряд и запасенную энергию, если конденсаторы подключены к батарее последовательно. (б) Сделайте то же самое для параллельного подключения.
- Нервный физик опасается, что две металлические полки его книжного шкафа с деревянным каркасом могут получить высокое напряжение, если они заряжены статическим электричеством, возможно, вызванным трением. (а) Какова емкость пустых полок, если они имеют площадь 1,00 × 10 2 м 2 и равны 0.200 м друг от друга? (б) Какое напряжение между ними, если на них помещены противоположные заряды величиной 2,00 нКл? (c) Чтобы показать, что это напряжение представляет небольшую опасность, рассчитайте запасенную энергию.
- Покажите, что для данного диэлектрического материала максимальная энергия, которую может хранить конденсатор с параллельными пластинами, прямо пропорциональна объему диэлектрика (Объем = A · d ). Обратите внимание, что приложенное напряжение ограничено диэлектрической прочностью.
- Создайте свою проблему. Рассмотрим дефибриллятор сердца, аналогичный описанному в примере 1. Постройте задачу, в которой вы исследуете заряд, накопленный в конденсаторе дефибриллятора, как функцию накопленной энергии. Среди факторов, которые необходимо учитывать, — это приложенное напряжение и то, должно ли оно меняться в зависимости от подаваемой энергии, диапазон задействованных энергий и емкость дефибриллятора. Вы также можете рассмотреть гораздо меньшую энергию, необходимую для дефибрилляции во время операции на открытом сердце, как вариант решения этой проблемы.
- Необоснованные результаты. (a) В определенный день для запуска двигателя грузовика требуется 9,60 × 10 3 Дж электроэнергии. Вычислите емкость конденсатора, способного хранить такое количество энергии при напряжении 12,0 В. (б) Что неразумного в этом результате? (c) Какие допущения ответственны?
Глоссарий
дефибриллятор: устройство, используемое для электрического разряда в сердце пострадавшего от сердечного приступа, чтобы восстановить нормальный ритмический паттерн сердца
Избранные решения проблем и упражнения
1.(а) 405 Дж; (б) 90,0 мС
2. (а) 3,16 кВ; (б) 25,3 мС
4. (а) 1.42 × 10 −5 C, 6.38 × 10 −5 Дж; (б) 8.46 × 10 −5 C, 3.81 × 10 −4 J
5. (а) 4,43 × 10 –12 F; б) 452 В; (в) 4.52 × 10 –7 Дж
8. (а) 133 F; (б) Такой конденсатор был бы слишком большим для перевозки в грузовике. Размер конденсатора был бы огромным; (c) Неразумно предполагать, что конденсатор может хранить необходимое количество энергии.
Калькулятор энергии конденсатора
Это калькулятор энергии конденсатора, простой инструмент, который поможет вам оценить количество энергии, хранящейся в конденсаторе. Вы также можете узнать, сколько заряда накопилось в конденсаторе. Читайте дальше, чтобы узнать, какая энергия хранится в конденсаторе и каково уравнение энергии конденсатора.
Какая энергия хранится в конденсаторе?
Конденсатор — это электронный компонент, обычно используемый в схемах. Его функция — накапливать электрический заряд . В стандартных конденсаторах с параллельными пластинами на соседних пластинах присутствуют заряды равной, но противоположной величины (для сферических конденсаторов вместо пластин используются концентрические сферы). Эти заряды создают между собой электрическое поле, состоящее из определенного количества энергии контура. Поскольку мы говорим о накопленных зарядах, это пример потенциальной энергии.
Формула энергии конденсатора
Как вы оцениваете энергию E , запасенную в конденсаторе с емкостью C и приложенным напряжением В ? Это эквивалентно работе, выполняемой батареей по перемещению заряда Q на конденсатор.В результате получается уравнение:
E = 1/2 * C * V² .
Используя общую формулу для емкости, C = Q / V , мы можем переписать уравнение энергии емкости в двух других аналогичных формах:
E = 1/2 * Q² / C или E = 1/2 * Q * V .
Электрическая энергия в конденсаторе — пример
Сколько энергии может храниться в конденсаторе емкостью C = 300 мкФ , когда мы подключаем его к источнику напряжения В = 20 В ? Давайте вместе разберемся!
- Чтобы облегчить нашу жизнь, используйте научное обозначение емкости:
C = 3 · 10⁻⁴ F - В соответствии с формулой мощности емкости результат оценивается как:
E = 1/2 * 3 · 10⁻⁴ F * (20 В) ² = 6 · 10⁻² Дж - Энергия, запасенная в конденсаторе, также может быть записана как
0.06 Джили60 мДж - Кроме того, мы можем оценить общий заряд, накопленный в конденсаторе:
Q = C * V = 3 · 10⁻⁴F * 20 V = 6 · 10⁻³ C = 6 мКл - … или вы можете просто сэкономить свое время, используя этот калькулятор энергии конденсатора, который автоматически выполняет все вычисления за вас!
Кстати, если у вас есть система с более чем одним конденсатором, вам лучше проверить наши конденсаторы последовательно или конденсаторы в параллельных калькуляторах, чтобы быстро найти общую емкость, потому что это значение, которое вы должны использовать в формуле для энергия конденсатора.
Преобразования энергии в LC-цепи
LC-цепь — это система, состоящая из катушки индуктивности и конденсатора. На практике это может быть обобщено как цепь RLC из-за некоторого сопротивления в системе. Как только схема обрабатывает сигнал резонансной частоты, потенциальная энергия конденсатора непрерывно преобразуется в магнитную энергию, создаваемую током, протекающим через катушку. Эти виды схем широко используются при обработке сигналов или при отправке и приеме радиоволн.
Энергия, запасенная в конденсаторе — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как энергия хранится в конденсаторе
- Использование соотношений энергии для определения энергии, запасенной в конденсаторной сети
Большинство из нас видели, как медицинский персонал использует дефибриллятор, чтобы пропустить электрический ток через сердце пациента, чтобы заставить его нормально биться.Часто реалистичный в деталях, человек, применяющий электрошок, просит другого человека «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, накапливается в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ — джоули. Менее драматично использование конденсаторов в микроэлектронике для подачи энергии при зарядке аккумуляторов ((рисунок)). Конденсаторы также используются для питания импульсных ламп на камерах.
Конденсаторы на печатной плате электронного устройства следуют соглашению о маркировке, при котором каждый из них обозначается кодом, начинающимся с буквы «C.”(Источник: Винделл Оскей)
Энергия, запасенная в конденсаторе, является электростатической потенциальной энергией и, таким образом, связана с зарядом Q и напряжением В между пластинами конденсатора. Заряженный конденсатор накапливает энергию в электрическом поле между пластинами. По мере зарядки конденсатора нарастает электрическое поле. Когда заряженный конденсатор отсоединяется от батареи, его энергия остается в поле в пространстве между пластинами.
Чтобы понять, как можно выразить эту энергию (в терминах Q и В ), рассмотрим заряженный пустой конденсатор с параллельными пластинами; то есть конденсатор без диэлектрика, но с вакуумом между пластинами.Пространство между его пластинами имеет объем Ad и заполнено однородным электростатическим полем E . Полная энергия конденсатора содержится в этом пространстве. Плотность энергии в этом пространстве просто делится на объем Ad . Если мы знаем плотность энергии, ее можно найти как. В книге «Электромагнитные волны» (после завершения изучения уравнений Максвелла) мы узнаем, что плотность энергии в области свободного пространства, занятой электрическим полем E , зависит только от величины поля и составляет
Если мы умножим плотность энергии на объем между пластинами, мы получим количество энергии, хранящейся между пластинами конденсатора с параллельными пластинами :.
В этом выводе мы использовали тот факт, что электрическое поле между пластинами однородно, так что и Поскольку, мы можем выразить этот результат в других эквивалентных формах:
Выражение (рисунок) для энергии, запасенной в конденсаторе с параллельными пластинами, в общем, справедливо для всех типов конденсаторов. Чтобы убедиться в этом, рассмотрим любой незаряженный конденсатор (не обязательно с параллельными пластинами). В какой-то момент мы подключаем его к батарее, давая ему разность потенциалов между пластинами.Первоначально заряд на пластинах равен По мере того, как конденсатор заряжается, заряд постепенно накапливается на его пластинах и через некоторое время достигает значения Q . Чтобы переместить бесконечно малый заряд dq с отрицательной пластины на положительную (от более низкого к более высокому потенциалу), объем работы dW , который должен быть выполнен на dq , составляет.
Эта работа становится энергией, запасенной в электрическом поле конденсатора. Чтобы зарядить конденсатор до заряда Q , требуется общая работа
.Поскольку геометрия конденсатора не указана, это уравнение справедливо для любого типа конденсатора.Общая работа Вт, , необходимая для зарядки конденсатора, представляет собой запасенную в нем электрическую потенциальную энергию, или. Когда заряд выражается в кулонах, потенциал выражается в вольтах, а емкость выражается в фарадах, это соотношение дает энергию в джоулях.
Зная, что энергия, запасенная в конденсаторе, равна, теперь мы можем найти плотность энергии, запасенную в вакууме между пластинами заряженного конденсатора с параллельными пластинами. Нам просто нужно разделить на объем Ad пространства между его пластинами и учесть, что для конденсатора с параллельными пластинами мы имеем и.Следовательно, получаем
Мы видим, что это выражение для плотности энергии, запасенной в конденсаторе с параллельными пластинами, соответствует общему соотношению, показанному на (Рисунок). Мы могли бы повторить этот расчет либо для сферического конденсатора, либо для цилиндрического конденсатора — или для других конденсаторов — и во всех случаях мы бы получили общее соотношение, представленное (рисунок).
Проверьте свое понимание Разность потенциалов на конденсаторе 5,0 пФ составляет 0,40 В.а) Какая энергия хранится в этом конденсаторе? (b) Теперь разность потенциалов увеличена до 1,20 В. В какой раз увеличивается запасенная энергия?
а .; б. 9 раз
При неотложной сердечной недостаточности портативное электронное устройство, известное как автоматический внешний дефибриллятор (AED), может быть спасением. Дефибриллятор ((Рисунок)) подает большой заряд в виде короткого импульса или разряда в сердце человека, чтобы исправить нарушение сердечного ритма (аритмию). Сердечный приступ может возникнуть в результате быстрого, нерегулярного сердцебиения, называемого фибрилляцией сердца или желудочков.Применение большого разряда электрической энергии может прекратить аритмию и позволить естественному кардиостимулятору организма вернуться к своему нормальному ритму. Сегодня машины скорой помощи носят с собой AED. AED также можно найти во многих общественных местах. Они предназначены для использования непрофессионалами. Устройство автоматически диагностирует сердечный ритм пациента, а затем применяет разряд с соответствующей энергией и формой волны. Во многих случаях перед использованием дефибриллятора рекомендуется сердечно-легочная реанимация.
Автоматические внешние дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства предоставляют устные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (кредит: Оуайн Дэвис)
Емкость дефибриллятора сердца Дефибриллятор сердца доставляет энергию путем первоначального разряда конденсатора. Какова его емкость?
Стратегия Нам дается В и , и нас просят найти емкость C .Решаем (рисунок) вместо C и подставляем.
Решение Решение этого выражения для C и ввод данных значений дает
Сводка
- Конденсаторы используются для подачи энергии к различным устройствам, включая дефибрилляторы, микроэлектронику, такую как калькуляторы, и лампы-вспышки.
- Энергия, запасенная в конденсаторе, — это работа, необходимая для зарядки конденсатора, начиная с нулевого заряда на его пластинах. Энергия накапливается в электрическом поле в пространстве между пластинами конденсатора.Это зависит от количества электрического заряда на пластинах и от разности потенциалов между пластинами.
- Энергия, запасенная в конденсаторной сети, представляет собой сумму энергий, сохраненных на отдельных конденсаторах в сети. Его можно вычислить как энергию, запасенную в эквивалентном конденсаторе сети.
Концептуальные вопросы
Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Глоссарий
- плотность энергии
- энергия, запасенная в конденсаторе, деленная на объем между пластинами
энергии в конденсаторах
энергии в конденсаторахДалее: Рабочие примеры Up: Емкость Предыдущий: Последовательные конденсаторы и Рассмотрим зарядку изначально незаряженной параллельной пластины. конденсатор путем передачи заряда от одного пластину к другой, оставив прежнюю пластину заряженной, а более позднюю с зарядом.Конечно, как только мы передали некоторый заряд, между пластины, которые препятствуют дальнейшей передаче заряда. Чтобы полностью зарядить конденсатор, мы должны сделать работать против этого поля, и эта работа становится энергия, запасенная в конденсаторе. Подсчитаем это энергия.
Предположим, что обкладки конденсатора несут заряд и что
разность потенциалов между пластинами составляет. Работа, которую мы делаем по передаче бесконечно малая величина заряда от отрицательного к отрицательному
положительная пластина — это просто
| (117) |
Чтобы оценить общую работу, проделанную при переводе полный заряд от одной пластины к другой, мы можем разделить этот заряд на множество мелких приращения, найдите дополнительную работу сделано при переводе этого дополнительного заряда, используя приведенную выше формулу, и затем просуммируйте все эти работы.Единственная сложность заключается в том, что потенциал разница между пластинами является функцией от общего количества переданных заряжать. На самом деле, так
| (118) |
Интеграция дает
| (119) |
Обратите внимание, что работа, выполняемая при зарядке конденсатора, такая же, как энергия, запасенная в конденсаторе. Поскольку мы можем запишите эту накопленную энергию в одной из трех эквивалентных форм:
| (120) |
Эти формулы верны для любого типа конденсатора, поскольку использованные нами аргументы их получение не зависит от каких-либо особых свойств параллельной пластины конденсаторы.
Где энергия в параллельной пластине конденсатор реально хранится? Хорошо, если мы подумаем о это единственное место, где он может храниться, — это электрическое поле, генерируемое между пластинами. Это понимание позволяет нам вычислить энергию (или, скорее, плотность энергии) электрического поля.
Рассмотрим заполненный вакуумом конденсатор с параллельными пластинами, пластины которого имеют площадь поперечного сечения,
и расположены на некотором расстоянии друг от друга. Электрическое поле между пластинами
является
приблизительно равномерный и по величине
, где, — заряд, накопленный на пластинах.В остальном электрическое поле примерно равно нулю. Разница потенциалов
между пластинами есть. Таким образом, энергия, запасенная в конденсаторе
можно написать
| (121) |
где использовалась формула. (108). Теперь — объем заполненной полем области между пластинами, поэтому, если энергия хранится в электрическом поле, тогда энергия на единицу объема, или плотность энергии , поля должна быть
| (122) |
Оказывается, это довольно общий результат.Таким образом, мы можем вычислить энергию содержание любого электрического поля, разделив пространство на маленькие кубики, применяя формула выше, чтобы найти энергосодержание каждого куба, а затем суммируя полученные таким образом энергии для получения полной энергии.
Легко показать, что плотность энергии в диэлектрике
средний
| (123) |
где — диэлектрическая проницаемость среды. Эта плотность энергии состоит из двух элементов: плотности энергии удерживается в электрическом поле, а плотность энергии удерживается в диэлектрической среде (это представляет собой работу, проделанную на составляющие молекулы диэлектрика чтобы поляризовать их).
Далее: Рабочие примеры Up: Емкость Предыдущий: Последовательные конденсаторы и Ричард Фицпатрик 2007-07-14
Энергия, запасенная в конденсаторе
Пример 6.4: Энергия, запасенная в конденсатореДалее: Электрический ток Up: Емкость Предыдущий: Пример 6.3: Эквивалентная емкость Вопрос: Конденсатор с параллельными пластинами, заполненный воздухом, имеет емкость пФ.Потенциал 100 В подается на пластины, которые находятся на расстоянии в см друг от друга, используя аккумуляторная батарея. Какая энергия хранится в конденсаторе? Предположим, что аккумулятор отключается, и пластины перемещаются до тех пор, пока они не сантиметры. отдельно. Какая сейчас энергия хранится в конденсаторе? Предположим вместо этого, что аккумулятор остается подключенным, и пластины снова перемещают, пока они не будут см друг от друга. Какая энергия в этом случае хранится в конденсаторе?
Ответ: Начальная энергия, запасенная в конденсатор
При увеличении расстояния между пластинами в два раза емкость конденсатора
уменьшается вдвое до пФ.Если аккумулятор отключен, то этот процесс
происходит при постоянной зарядке. Таким образом, из
формула
что энергия, запасенная в конденсаторе, удваивается. Итак новая энергия J. Между прочим, повышенная энергия конденсатора учитывается работой, проделанной при вытягивании пластины конденсатора (поскольку эти пластины заряжены противоположно, они притягиваются друг к другу).
Если аккумулятор оставить подключенным, то емкость все равно уменьшится вдвое, но теперь
процесс происходит при постоянном напряжении.Это следует из
формула
что энергия, запасенная в конденсаторе, уменьшается вдвое. Итак, новая энергия J. Между прочим, энергия потеряла конденсатором поступает в аккумулятор (по сути, идет на подзарядку аккумулятор). Точно так же работа, выполняемая при разделении пластин, является тоже отдано на аккумулятор.
Далее: Электрический ток Up: Емкость Предыдущий: Пример 6.3: Эквивалентная емкость Ричард Фицпатрик 2007-07-14
электричество — Расчет энергии для конденсатора
Это проблема, которая часто вызывает концептуальные трудности.2} {2} = \ frac {Q_1 V_1} {2} + \ frac {Q_2 V_2} {2} \ tag {1} $$ Затем вы соединяете их параллельно. Заряды складываются в $ Q_1 + Q_2 $, емкости складываются в $ C = C_1 + C_2 $, и устанавливается общее напряжение $ V $ $$ V = \ frac {Q} {C} = \ frac {Q_1 + Q_2 } {C_1 + C_2} = \ frac {C_1V_1 + C_2V_2} {C_1 + C_2} \ tag {2} $$ $ V $ — это средневзвешенное значение напряжений $ V_1 $ и $ V_2 $. 2} {2} = \ frac {VQ} {2} = \ frac {(C_1V_1 + C_2V_2) (Q_1 + Q_2)} {2 (C_1 + C_2)} \ tag {4} $$ Можно легко проверить что электростатическая потенциальная энергия $ U_B $ конденсаторов, соединенных параллельно, всегда меньше или равна сумме потенциальных энергий $ U_A $ разделенных конденсаторов $$ U_B \ le U_A $$ Это довольно сбивает с толку, потому что закон в этом случае также должно выполняться сохранение энергии.Так куда же пропала разница в энергии $$ W = U_A-U_B $$?
Чтобы понять это, важно сначала, рассматривать это как чисто электростатическую задачу перемещения зарядов в консервативном электростатическом поле от одного проводника с потенциалом $ V_1 $ к другому проводнику с более низким потенциалом $ V_2 $, пока оба проводника не окажутся на тот же потенциал $ V $, заданный формулой (2). При перемещении небольшого элемента заряда $ dQ $ от проводника с потенциалом $ V_1 $ к проводнику с более низким потенциалом $ V_2 $ выделяется энергия $ dW $ $$ dW = dQ [V_1 (Q_1) -V_2 (Q_2) ] $$, что соответствует работе, выполняемой над зарядом при его обратном перемещении.Эта энергия $ dW $ может быть выдана в любой форме, совместимой с законом сохранения энергии. Таким образом, это может быть механическая кинетическая энергия, передаваемая объекту, который передает заряд, это может быть другая форма потенциальной механической энергии, такая как пружина, или подъем массы в гравитационном поле, это также могут быть другие формы электромагнитной энергии, такие как электромагнитные волны. , или химическая энергия. Это, конечно, тоже может быть тепло, но это только один из множества вариантов!
Поскольку поле консервативно, путь переноса заряда совершенно произвольный.Таким образом, вы можете переместить $ dQ $ в первом конденсаторе от электрода с потенциалом $ V_1 $ к другому с потенциалом $ 0 $, а затем переместить его в другом конденсаторе от электрода с потенциалом $ 0 $ к электроду с потенциалом $ V_2 $. И вы можете продолжать делать это до тех пор, пока напряжение (потенциал) первого конденсатора не станет $ V_1 = V $, а напряжение второго не станет $ V_2 = V $. Таким образом, в конце повторяющихся перемещений небольших зарядов $ dQ $ вы можете соединить пластины (электроды) двух конденсаторов параллельно без дальнейшей передачи заряда, поскольку потенциалы пластин равны $ V_1 = V_2 = V $.2} {2} $$, который согласно уравнениям (1) и (4) равен $$ W = U_A-U_B $$
Вывод состоит в том, что соединение двух заряженных конденсаторов параллельно соответствует ситуации, когда электростатическая потенциальная энергия высвобождается за счет переноса зарядов от проводника с более высоким потенциалом к проводнику с более низким потенциалом. Это уменьшение потенциальной энергии может быть преобразовано в любую другую (кинетическую или потенциальную) форму энергии, не только в тепло, в соответствии с законами сохранения энергии.
Добавлено позже: В двух конденсаторах, соединенных резистором, энергия $ W $ будет в основном преобразована в тепло Джоуля.Если вы соедините два пластинчатых конденсатора (или коаксиальных конденсатора) с идеальными проводниками, вы получите две соединенные линии передачи с фронтами электромагнитных волн ТЕМ, отражающимися назад и вперед в поперечном направлении между концами конденсатора с небольшим демпфированием радиационными потерями. С хорошими проводниками вы также получаете такие волны с дополнительным резистивным джоулевым демпфированием токами в проводниках. В искрах происходит частичное превращение в световую энергию.
Энергия конденсатора — AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.