Энергия запасенная в конденсаторе: Энергия поля конденсатора — Основы электроники — Мир Антенн

Содержание

Энергия поля конденсатора — Основы электроники

Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую.

При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q.

Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.

Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.

Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q.

Полученный результат мы можем записать в виде следующей математической формулы:

W = UQ/2 (1)

Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:

W = CU²/2 (2)

Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами.

Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Энергия конденсатора

Details: 01 February 2017

Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!

В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.

Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.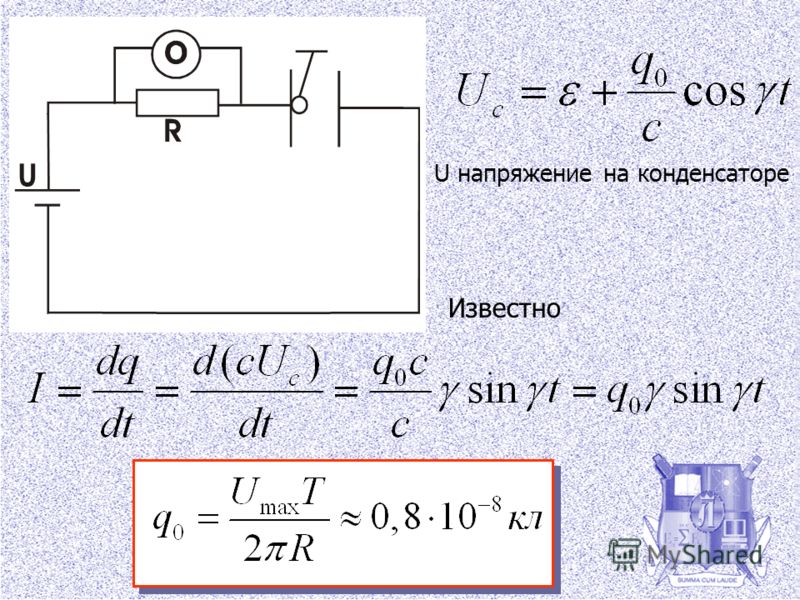

Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:

Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:

То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.

Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля. Это позволяет использовать формулу работы без векторов:

Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются

потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.

Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу

А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать

Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.

Рисунок 1 – Плоский конденсатор

Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q

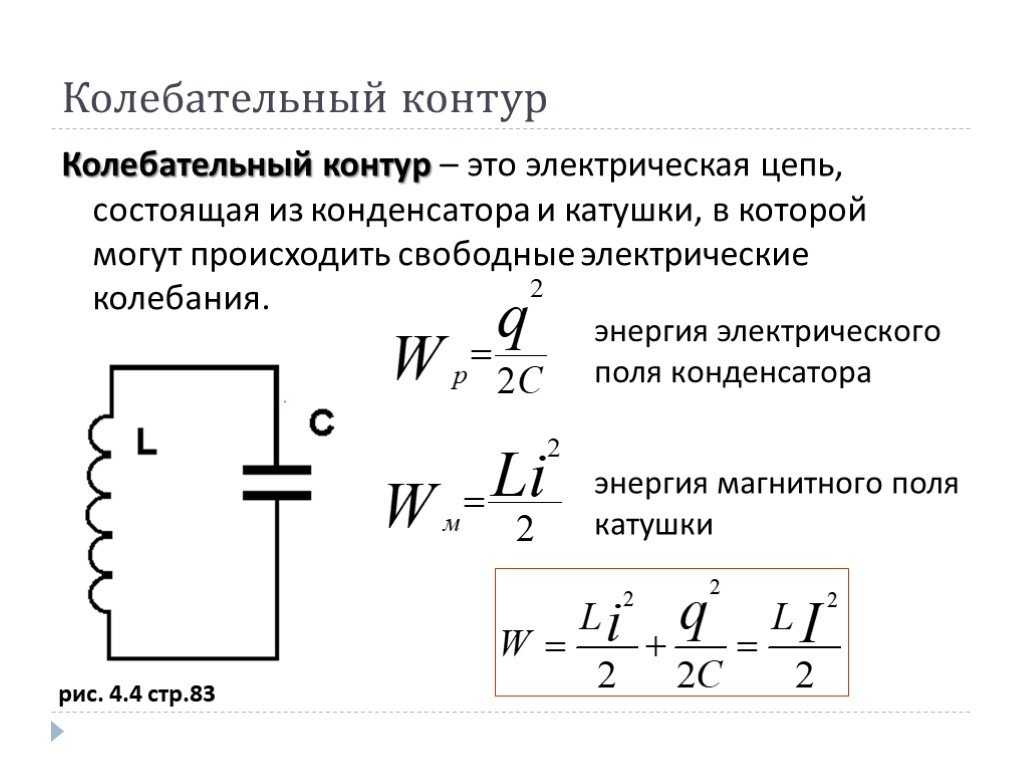Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.

Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать

Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем

Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть

энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:

Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.

Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:

Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем

Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:

Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем

Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.

Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии

Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.

Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор

Рисунок 2 – Конденсатор

И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:

Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.

Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!

Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

8.3 Энергия, запасенная в конденсаторе — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

Объясните, как энергия накапливается в конденсаторе
Использование энергетических соотношений для определения энергии, запасенной в конденсаторной сети

Большинство из нас видели инсценировку медицинского персонала, использующего дефибриллятор для пропускания электрического тока через сердце пациента, чтобы заставить его нормально биться. Часто реалистичный в деталях, человек, применяющий разряд, приказывает другому человеку «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике для подачи энергии при зарядке батарей (рис. 8.15). Конденсаторы также используются для питания ламп-вспышек на камерах.

Рисунок 8.15 Конденсаторы на печатной плате электронного устройства соответствуют соглашению по маркировке, согласно которому каждый из них идентифицируется кодом, начинающимся с буквы «C». (кредит: Windell Oskay)

Энергия UCUC, хранящаяся в конденсаторе, представляет собой электростатическую потенциальную энергию и, таким образом, связана с зарядом Q и напряжением V между пластинами конденсатора. Заряженный конденсатор запасает энергию в электрическом поле между своими пластинами. Когда конденсатор заряжается, электрическое поле нарастает. При отключении заряженного конденсатора от батареи его энергия остается в поле в пространстве между его пластинами.

Чтобы понять, как эта энергия может быть выражена (в терминах Q и V ), рассмотрим заряженный пустой конденсатор с параллельными пластинами; то есть конденсатор без диэлектрика, но с вакуумом между его пластинами. Пространство между его пластинами имеет объем Ad и заполнено однородным электростатическим полем E . Полная энергия UCUC конденсатора заключена в этом пространстве. Плотность энергии uEuE в этом пространстве равна просто UCUC, деленной на объем Объявление . Если мы знаем плотность энергии, то энергию можно найти как UC=uE(Ad)UC=uE(Ad). В «Электромагнитных волнах» мы узнаем (после завершения изучения уравнений Максвелла), что плотность энергии uEuE в области свободного пространства, занятого электрическим полем E , зависит только от величины поля и составляет

uE=12ε0E2. uE=12ε0E2.

8,9

Если мы умножим плотность энергии на объем между пластинами, мы получим количество энергии, запасенной между пластинами плоского конденсатора: UC=uE(Ad)=12ε0E2Ad=12ε0V2d2Ad=12V2ε0Ad=12V2CUC=uE(Ad) =12ε0E2Ad=12ε0V2d2Ad=12V2ε0Ad=12V2C.

В этом выводе мы использовали тот факт, что электрическое поле между пластинами однородно, так что E=V/dE=V/d и C=ε0A/d.C=ε0A/d. Поскольку C=Q/VC=Q/V, мы можем выразить этот результат в других эквивалентных формах:

UC=12V2C=12Q2C=12QV.UC=12V2C=12Q2C=12QV.

8.10

Выражение в уравнении 8.10 для энергии, запасенной в конденсаторе с плоскими пластинами, в целом справедливо для всех типов конденсаторов. Чтобы убедиться в этом, рассмотрим любой незаряженный конденсатор (не обязательно пластинчатый). В какой-то момент мы подключаем его к батарее, придавая ему разность потенциалов V=q/CV=q/C между его пластинами. Первоначально заряд на пластинах равен Q=0.Q=0. По мере заряда конденсатора заряд на его обкладках постепенно накапливается и через некоторое время достигает значения В . Чтобы переместить бесконечно малый заряд dq с отрицательной пластины на положительную (от более низкого потенциала к более высокому), количество работы dW , которое необходимо совершить над dq , равно dW=Vdq=qCdqdW=Vdq= qCdq.

Эта работа превращается в энергию, запасенную в электрическом поле конденсатора. Чтобы зарядить конденсатор до заряда Q , общая необходимая работа составляет

Вт=∫0W(Q)dW=∫0QqCdq=12Q2C.W=∫0W(Q)dW=∫0QqCdq=12Q2C.

Поскольку геометрия конденсатора не указана, это уравнение верно для любого типа конденсатора. Полная работа Вт , необходимая для зарядки конденсатора, представляет собой запасенную в нем электрическую потенциальную энергию UCUC, или UC=WUC=W. Когда заряд выражается в кулонах, потенциал — в вольтах, а емкость — в фарадах, это соотношение дает энергию в джоулях.

Зная, что энергия, запасенная в конденсаторе, равна UC=Q2/(2C)UC=Q2/(2C), теперь мы можем найти плотность энергии uEuE, запасенной в вакууме между пластинами заряженного плоского конденсатора.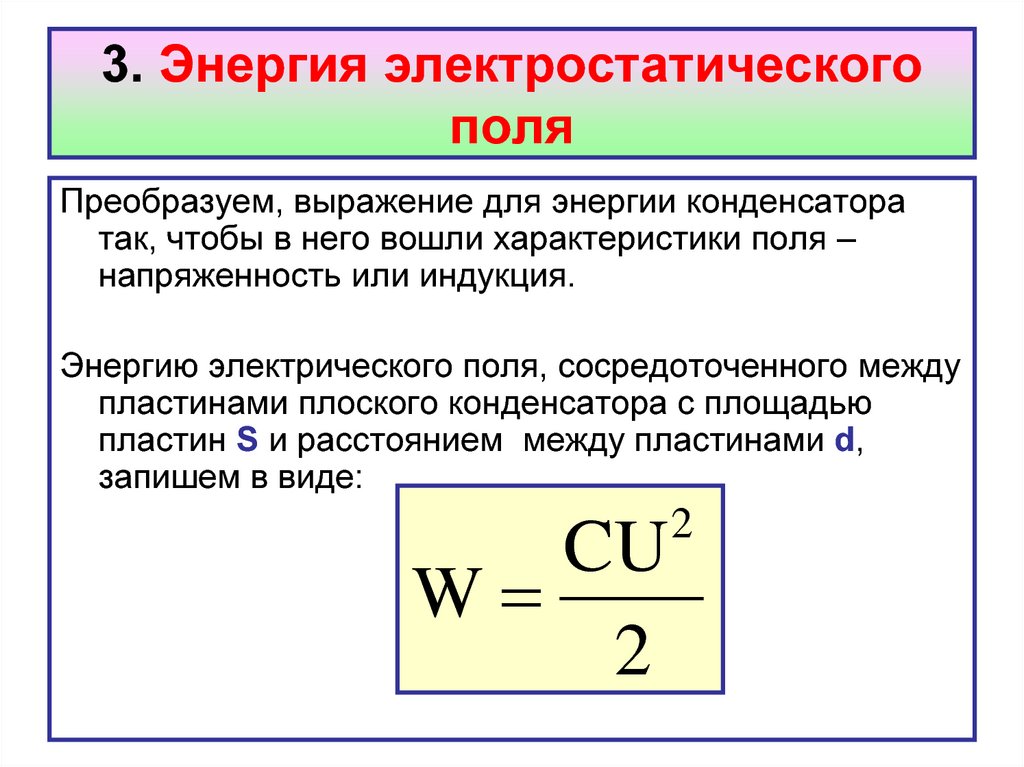 Нам просто нужно разделить UCUC на объем Ad пространства между его пластинами и учесть, что для плоского конденсатора имеем E=σ/ε0E=σ/ε0 и C=ε0A/dC=ε0A/d. Таким образом, получаем Eε0)22ε0=ε02E2.

Мы видим, что это выражение для плотности энергии, запасенной в плоском конденсаторе, соответствует общему соотношению, выраженному в уравнении 8.9. Мы могли бы повторить этот расчет либо для сферического конденсатора, либо для цилиндрического конденсатора, либо для других конденсаторов, и во всех случаях мы пришли бы к общему соотношению, заданному уравнением 8.9..

Пример 8,8

Энергия, запасенная в конденсаторе

Рассчитайте энергию, накопленную в цепи конденсаторов на рис. 8.14(a), когда конденсаторы полностью заряжены и когда емкости C1=12,0 мкФ, C2=2,0 мкФ, C1=12,0 мкФ, C2=2,0 мкФ и C3=4,0 мкФ. ,C3=4,0 мкФ соответственно.

Стратегия

Мы используем уравнение 8. 10, чтобы найти энергию U1U1, U2U2 и U3U3, хранящуюся в конденсаторах 1, 2 и 3 соответственно. Полная энергия есть сумма всех этих энергий.

Решение

Мы идентифицируем C1 = 12,0 мкФ1 = 12,0 мкФ и V1 = 4,0 В V1 = 4,0 В, C2 = 2,0 мкФС2 = 2,0 мкФ и V2 = 8,0 В V2 = 8,0 В, C3 = 4,0 мкФС3 = 4,0 мкФ и V3 = 8,0 В. V3 = 8,0 В. Энергия, запасенная в этих конденсаторах,

U1=12C1V12=12(12,0 мкФ)(4,0 В)2=96 мкДж,U2=12C2V22=12(2,0 мкФ)(8,0 В)2=64 мкДж,U3=12C3V32=12(4,0 мкФ)(8,0 В)2 =130 мкДж.U1=12C1V12=12(12,0 мкФ)(4,0 В)2=96 мкДж,U2=12C2V22=12(2,0 мкФ)(8,0 В)2=64 мкДж,U3=12C3V32=12(4,0 мкФ)(8,0 В) 2=130 мкДж.

Суммарная энергия, накопленная в этой сети, равна

UC=U1+U2+U3=96 мкДж + 64 мкДж + 130 мкДж = 0,29 мДж. UC = U1 + U2 + U3 = 96 мкДж + 64 мкДж + 130 мкДж = 0,29 мДж.

Значение

Мы можем проверить этот результат, рассчитав энергию, запасенную в одном конденсаторе емкостью 4,0 мкФ4,0 мкФ, который оказывается эквивалентным всей сети. Напряжение в сети составляет 12,0 В. Полная энергия, полученная таким образом, согласуется с нашим ранее полученным результатом: V)2=0,29 мДж.

Проверьте свое понимание 8,6

Проверьте свои знания Разность потенциалов на конденсаторе емкостью 5,0 пФ составляет 0,40 В. (a) Какова энергия, запасенная в этом конденсаторе? б) Разность потенциалов увеличилась до 1,20 В. Во сколько раз увеличилась запасенная энергия?

При неотложной сердечной деятельности портативное электронное устройство, известное как автоматический внешний дефибриллятор (АНД), может спасти жизнь. Дефибриллятор (рис. 8.16) подает большой заряд короткой вспышкой или разрядом в сердце человека для коррекции аномального сердечного ритма (аритмии). Сердечный приступ может возникнуть в результате быстрого, нерегулярного сокращения сердца, называемого сердечной или желудочковой фибрилляцией. Применение сильного разряда электрической энергии может остановить аритмию и позволить естественному водителю ритма вернуться к своему нормальному ритму. Сегодня машины скорой помощи обычно несут AED. AED также можно найти во многих общественных местах. Они предназначены для использования мирянами. Устройство автоматически диагностирует сердечный ритм пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР (сердечно-легочная реанимация) рекомендуется во многих случаях перед использованием дефибриллятора.

Рисунок 8.16 Автоматические наружные дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства дают словесные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (кредит: Оуайн Дэвис)

Пример 8,9

Емкость сердечного дефибриллятора

Сердечный дефибриллятор выдает 4,00×102 Дж4,00×102 Дж энергии, разряжая конденсатор первоначально при 1,00×104 В. 1,00×104 В. Какова его емкость?

Стратегия

Нам даны UCUC и V , и нас просят найти емкость C . Решаем уравнение 8.10 для C и подставляем.

Раствор

Решение этого выражения для C и ввод заданных значений дает C=2UCV2=24,00×102 Дж(1,00×104 В)2=8,00 мкФ. C=2UCV2=24,00×102 Дж(1,00×104 В)2=8,00 мкФ.