Фазные и линейные токи и напряжения: Линейные и фазные токи и напряжения в трехфазных цепях — Мир Антенн

Содержание

Линейные и фазные токи и напряжения в трехфазных цепях

Трехфазная система электроснабжения принята в качестве стандарта в большинстве стран мира, Россия не исключение. Каждый дом в стране подключен именно к такой сети, но в отдельную квартиру заходит, как правило, один фазный провод. При желании можно провести и еще две фазы, что часто делается на участках, предназначенных для ИЖС. Они нужны для работы оборудования, содержащего электродвигатель. При подключении к трехфазной цепи часто возникают вопросы, связанные с такими понятиями, как фазный и линейный ток, а также с соответствующими показателями напряжений.

Цепи переменного тока

Как известно, электроснабжение в России осуществляется с помощью цепей переменного тока с частотой 50 Гц. За одну секунду совершается 50 циклов. Полный цикл представляет собой круг, угловой размер которого можно измерить в градусах и радианах — 360 градусов радиан или 2π радиан. Соответственно, половина этого цикла будет 180 или π радиан, треть — 120 или 2 π/3 и т.

д. Конкретный момент этого цикла и называется фазой. Цепи в стране синхронизированы в единую систему.

Сдвиг по фазе в цепи

Это выражение не имеет ничего общего со здоровьем головного мозга. Таким термином объясняют несовпадение графиков тока и напряжения, что бывает на участках с катушками или конденсаторами, а также сравнение фаз в разных проводах. При трехфазной системе электроснабжения сдвиг составляет 120 градусов или 2 π/ 3 радиан.

Вот так выглядит наложение графиков напряжений в трех проводах, идущих от трансформаторной будки. Слева даже наглядно показано, как такое можно получить от простой турбины.

Возможно, некоторые помнят подобное упражнение при составление графика функции y=sin (x), когда рисовали ее от круга.

Действующие показатели тока и напряжения

Максимальная амплитуда напряжения в цепи, идущей от трансформаторной подстанции во дворе, составляет 310 В.

За 1 с она бывает 100 раз — внизу и вверху графика. Мгновенные значения этого параметра зависят от фазы, в которой находится график. Естественно, для потребителей такое представление крайне неудобно, поэтому в обиходе используется понятие действующего напряжения.

Его формула была выведена экспериментально на основе закона Джоуля-Ленца. Суть вывода этой формулы заключается в том, что действующее значение переменного тока эквивалентно значению постоянного при одинаковом выделении теплоты. Коэффициент, который используется при вычислении, равен √2. Зная это, можно воспользоваться правилом:

I=I m/ √2, U=Um/√2,

где I m и Um — амплитуда. Если подставить во вторую формулу значение амплитуды, то получается, что действующее напряжение фазного провода относительно земли в квартире составит 230 В. Оно еще называется фазным. Ну, а величина тока будет зависеть от нагрузки, согласно закону Ома:

I=U/R.

Ток в фазном проводе тоже будет называться фазным.

Соединения звезда и треугольник

В домашней розетке помимо фазы обязательно присутствует ноль. Правильное его название — нейтраль. Некоторые путают его с заземлением, но на самом деле у него иная функция. Чтобы ее лучше понять, нужно ознакомиться с таким понятиями, как «звезда» и «треугольник».

Роль нейтрали в цепи

На подстанции, откуда в квартиру идет питающий провод, все три фазы одним концом соединены. Второй конец одной из фаз идет в одну квартиру, другой — в другую, третий — в третью. Если в каждой квартире в качестве второго провода использовать заземление, может возникнуть неприятная ситуация.

Но равновесие в этой системе возможно лишь тогда, когда все три потребителя одновременно включают одинаковую нагрузку — она называется симметричной. В реальности же один может включить телевизор, а другой — электрическую духовку. Итогом этого станет перекос фаз, когда у владельца телевизора в розетке будет 380, а у обладателя духовки 30 с небольшим.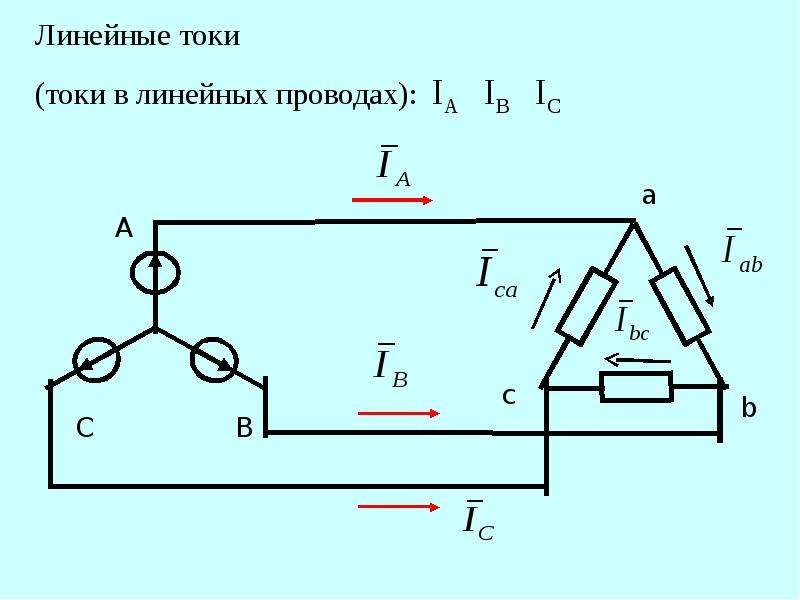

Чтобы такого не случилось, с места соединения концов фазных проводов выводят нейтраль, которая и идет в каждую квартиру. Для пущей осторожности ее тоже заземляют.

Нейтраль (нулевой провод) является компенсатором несимметричности нагрузки в такой цепи, которую назвали «звездой». В таком соединении между одной из фаз и нейтралью напряжение приблизительно равно 220 В, а между двумя фазами — 380. Это самое межфазное напряжение и называется линейным.

Его значение вычисляется исходя из действующего фазного и значения угла сдвига между ними. Вспомнив уроки геометрии в школе можно вывести:

AB=2x230x√3/2=230х√3=400.

Учитывая, что в цепь постоянно что-то включено, и в чистом виде ЭДС дома не измерить, получим:

220х√3=380.

Таким образом, фазные и линейные напряжения и токи при соединении звездой подчиняются следующим закономерностям:

U (l)=√3U (f), I (l)=I (f) — линейный ток равен фазному.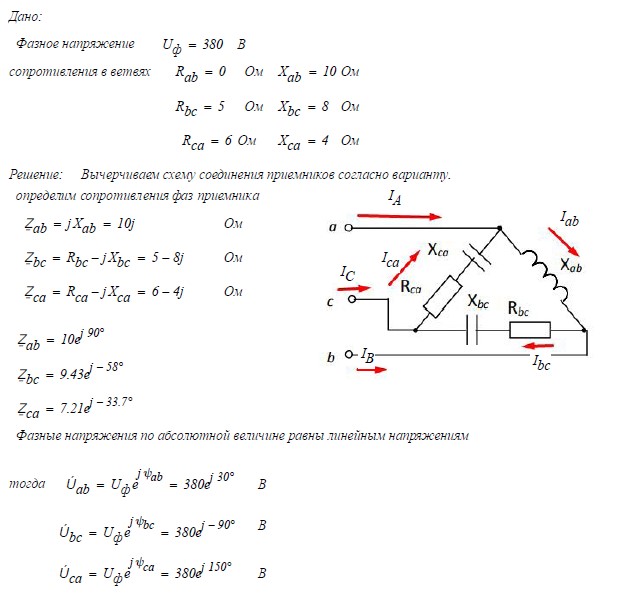

Соединение звездой с нейтралью очень удобно для распределения проводки по разным потребителям. Его преимущества можно перечислить:

устойчивость режима работы электроприборов в условиях разных нагрузок;
двигатели, обмотки которых подключены таким методом, не перегреваются;
из-за невозможности увеличить ток — пуск двигателя осуществляется плавно;
возможность использования как линейного, так и фазного напряжения.

Схема треугольник и максимум мощности

Такая необходимость возникает при желании по максимуму использовать КПД электродвигателя. Это можно достигнуть путем соединения фазных проводов в треугольник. Фазное и линейное напряжение в трехфазных цепях такого типа будут совпадать и равняться 380 В. А вот линейный ток, протекающий в подведенных к двигателю фазах, будет отличаться от того, что протекает через обмотки. Фазный ток можно вычислить, зная сопротивление и напряжение в обмотках, это величины известные. А вот линейный ток вычисляется по такой же диаграмме, как и напряжение в схеме «звезда»:

I (l)=I (f)x√3, U (f)=U (l).

Стоит ли делать такое переключение — отдельный вопрос. Для этого нужно учесть ряд важных моментов:

Мощность, конечно, увеличится в 1,5 раза. Возможность перегрева — тоже.

Если у двигателя тяжелый ротор, то при раскрутке ток будет раз в 7 выше, чем при устойчивой работе.
То же самое будет наблюдаться при попытке дать физическую нагрузку на вращающуюся часть, например, при пилке чего-то жесткого, при подъеме тяжести (если двигатель используется в качестве лебедки).

Поэтому перед проведением экспериментов стоит хорошо ознакомиться с паспортом двигателя и возможностями вашей сети.

Вполне возможно, что лучше будет приобрести электродвигатель с реостатной регулировкой пускового тока.

Линейное и фазное напряжение — соотношение и формулы, схема соединения звездой и треугольником

Одним из видов систем с множеством фаз, представлены цепи, состоящие из трех фаз.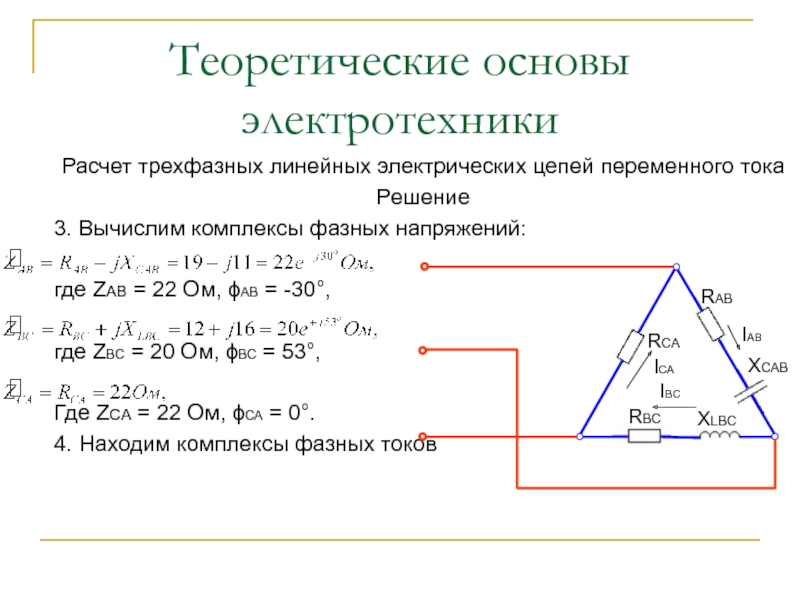 В них действуют электродвижущие силы синусоидального типа, возникающие с синхронной частотой, от единого генератора энергии, и имеют разницу в фазе.

Электрическое напряжение трехфазных сетей

Под фазой, понимаются самостоятельные блоки системы с множеством фаз, имеющие идентичные друг другу параметры тока. Поэтому, в электротехнической области, определение фазы имеет двойное толкование.

Во-первых, как значение, имеющее синусоидальное колебание, а во-вторых, как самостоятельный элемент в электросети с множеством фаз. В соответствии с их количеством и маркируется конкретная цепь: двухфазная, трехфазная, шестифазная и т.д.

Сегодня в электроэнергетике, наиболее популярными являются цепи с трехфазным током. Они обладают целым перечнем достоинств, выделяющих их среди своих однофазных и многофазных аналогов, так как, во-первых, более дешевы по технологии монтажа и транспортировки электроэнергии с наименьшими потерями и затратами.

Во-вторых, они имеют свойство легко образовывать движущееся по кругу магнитное поле, которое является движущей силой для асинхронных двигателей, которые используются не только на предприятиях, но и в быту, например, в подъемном механизме высотных лифтов и т. д.

Электрические цепи, имеющие три фазы, позволяют одновременно пользоваться двумя видами напряжения от одного источника электроэнергии – линейным и фазным.

Виды напряжения

Знание их особенностей и характеристик эксплуатации, крайне необходимо для манипуляций в электрощитах и при работе с устройствами, питаемыми от 380 вольт:

Линейное. Его обозначают как межфазный ток, то есть проходящий между парой контактов или идентичными клеймами разных фаз. Оно определяется разностью потенциалов пары фазных контактов.
Фазное. Оно появляется при замыкании начального и конечного выводов фазы. Также, его обозначают как ток, возникающий при замыкании одного из контактов фазы с нулевым выводом. Его величина определяется абсолютным значением разности выводов от фазы и Земли.

Отличия

В обычной квартире, или частном доме, как правило, существует только однофазный тип сети 220 вольт, поэтому, к их щиту электропитания, подведены в основном два провода – фаза и ноль, реже к ним добавляется третий – заземление.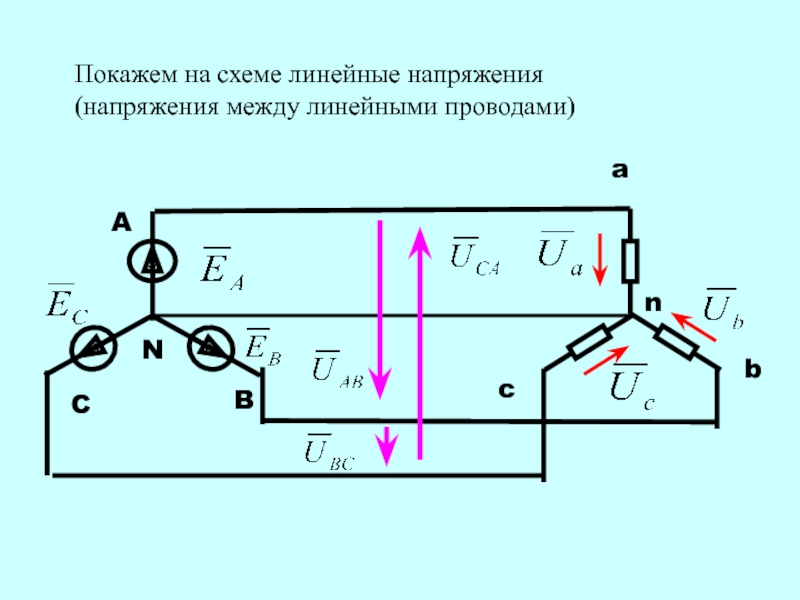

К высотным многоквартирным зданиям с офисами, гостиницами или торговыми центрами, подводится сразу 4 или 5 кабелей электропитания, обеспечивающих три фазы сети 380 вольт.

Почему такое жесткое разделение? Дело в том, что трехфазное напряжение, во-первых, само отличается повышенной мощностью, а во-вторых, оно специфически подходит для питания особых сверхмощных электродвигателей трехфазного типа, которые используются на заводах, в электролебедках лифтов, эскалаторных подъемниках и т.д.

Такие двигатели при включении в трехфазную сеть вырабатывают в разы большее усилие, чем их однофазные аналоги тех же габаритов и веса.

Проводить разводку проводки такого типа можно без использования профессионального оборудования и приборов, достаточно обычных отверток с индикаторами.

Соединяя проводники не нужно монтировать нулевой контакт, ведь вероятность пробоя очень мала, благодаря не занятой нейтрали.

Но такая схема сети имеет и свое слабое место, так как в линейной схеме монтажа крайне сложно найти место повреждения проводника в случае аварии или поломки, что может повысить риск возникновения пожара.

Таким образом, главным отличием между фазным и линейным типами являются разные схемы подключения проводов обмоток источника и потребителя электроэнергии.

Соотношение

Значение напряжения фазы равняется около 58% от мощности линейного аналога. То есть, при обычных эксплуатационных параметрах, линейное значение стабильно и превосходит фазное в 1,73 раза.

Оценка напряжения в сети трехфазного электрического тока, в основном производится по показателям его линейной составляющей. Для линий тока этого типа, подающегося с подстанций, оно, как правило, равняется 380 вольтам, и идентично фазному аналогу в 220 В.

В электросетях с четырьмя проводами, напряжение трехфазного тока маркируется обоими значениями – 380/220 В. Это обеспечивает возможность питания от такой сети устройств, как с однофазным потреблением электроэнергии 220 вольт, так и более мощных агрегатов, рассчитанных на ток 380 В.

Самой доступной и универсальной стала система трехфазного типа 380/220 В, имеющая нулевой провод, так называемое заземление. Электрические агрегаты, работающие на одной фазе 220 В., могут быть запитаны от линейного напряжения при подключении к любой паре фазных выводов.

Электрические агрегаты трехфазного питания работают только при подключении сразу к трем выводам разных фаз.

В этом случае, применение нулевого вывода в качестве заземления, не является обязательным, хотя в случае повреждения изоляции проводов, его отсутствие серьезно повышает вероятность удара током.

Схема

Агрегаты трехфазного тока имеют две схемы подключения в сеть: первая – «звезда», вторая – «треугольником». В первом варианте, начальные контакты всех трех обмоток генератора замыкаются вместе по параллельной схеме, что, как и в случае с обычными щелочными батарейками не даст прироста мощности.

Вторая, последовательная схема подключения обмоток источника тока, где каждый начальный вывод подключается к конечному контакту предыдущей обмотки, дает трехкратный прирост напряжения за счет эффекта суммирования напряжений при последовательном подключении.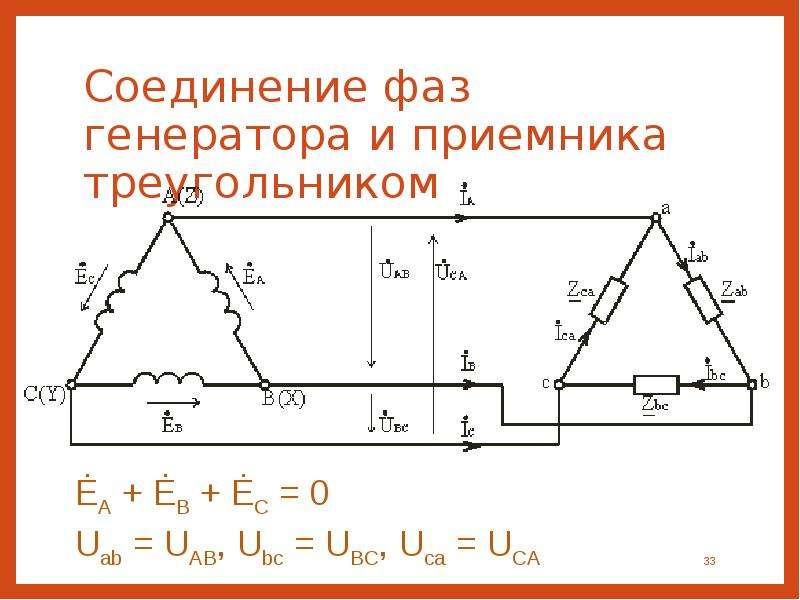

Кроме того, такие же схемы подключения имеют и нагрузку в виде электродвигателя, только устройство, подключенное в трехфазную сеть по схеме «звезда», при токе в 2,2 А будет выдавать мощность 2190Вт, а тот же агрегат, подключенный «треугольником», способен выдать в три раза большую мощность – 5570, за счет того, что благодаря последовательному подключению катушек и внутри двигателя, сила тока суммируется и доходит до 10 А.

Имея источник трехфазного напряжения и двигатели, имеющие аналогичную схему подключения, можно получить в разы больше мощности просто за счет эффективного подключения всех агрегатов.

Расчет линейного и фазного напряжения

Сети с линейным током нашли широкое применение за счет своих характеристик меньшей травмоопасности и легкости разведения такой электропроводки. Все электрические устройства в этом случае соединены только с одним фазным проводом, по которому и идет ток, и только он один и представляет опасность, а второй – это земля.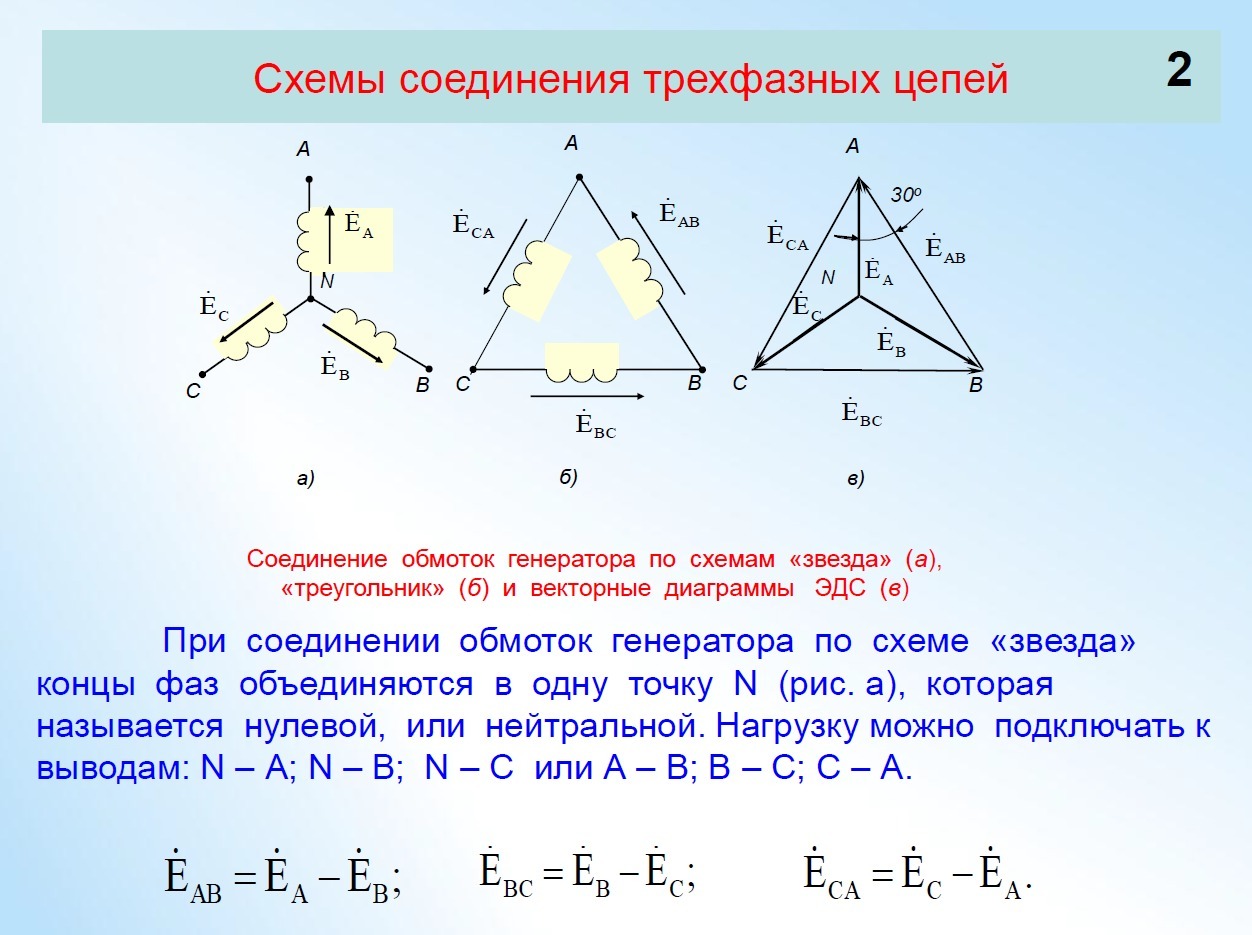

Рассчитать такую систему несложно, можно руководствоваться обычными формулами из школьного курса физики. Кроме того, для измерения этого параметра сети, достаточно использовать обычный мультиметр, в то время как для снятия показаний подключения фазного типа, придется задействовать целую систему оборудования.

Для подсчета напряжения линейного тока, применяют формулу Кирхгофа:

Уравнение которой гласит, что каждой из частей электрической цепи, сила тока равна нулю – k=1.

И закон Ома:

Используя их, можно без труда произвести расчеты каждой характеристики конкретного клейма или электросети.

В случае разделения системы на несколько линий, может появиться необходимость рассчитать напряжение между фазой и нулем:

Эти значения являются переменными, и меняются при разных вариантах подключения. Поэтому, линейные характеристики идентичны фазовым.

Однако, в некоторых случаях, требуется вычислить чему равно соотношение фазы и линейного проводника.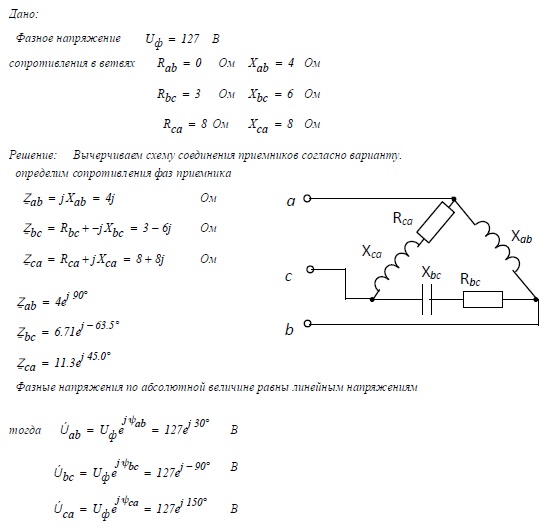

Для этого, применяют формулу:

Uл – линейное, Uф – фазовое. Формула справедлива, только если – I_L = I_F.

При добавлении в электросистему дополнительных отводящих элементов, необходимо и персонально для них рассчитывать фазовое напряжение. В этом случае, значение Uф заменяется на цифровые данные самостоятельного клейма.

При подключении промышленных систем к электросети, может появиться необходимость в расчете значения реактивной трехфазной мощности, которое вычисляется по следующей формуле:

Идентичная структура формулы активной мощности:

Примеры расчета:

Например, катушки трехфазного источника тока подключены по схеме «звезда», их электродвижущая сила 220В. Необходимо вычислить линейное напряжение в схеме.

Линейные напряжения в этом подключении будут одинаковы и определяются как:

U1=U2=U3= √3 Uф=√3*220=380 В.

Соотношение между фазными и линейными напряжениями

Напряжение фаз нагрузки отличны от значения ЭДС генератора из-за падения напряжения на линии от генератора к потребителю.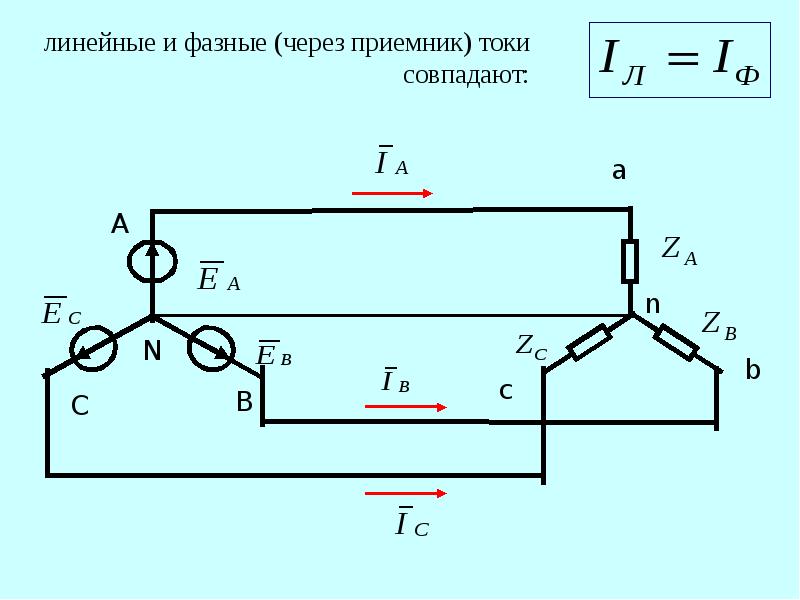 Длина этих линий может составлять несколько метров, а может и пару сотен метров, также возможна длина и в тысячи километров. Вопросы о падении напряжений на линиях электрических передач ЛЭП, снабжающих потребителей энергией электрической от электрических станций будут рассматриваться чуть позже, в последующих статьях. Для упрощения расчетов указанным значением падений напряжений можно пренебречь.

Соединение звездой

При принятых допущениях для соединенных источников звездой:

применив второй закон Кирхгофа получим:

Из выражения (1) можно сделать вывод, что при симметричной системе ЭДС генератора его фазные напряжения также симметричны, и, соответственно, их векторная диаграмма:

не будет отличатся от векторной диаграммы ЭДС:

Исходя из уравнений, составленных по второму закону Кирхгофа для контуров (схема соединения в звезда указана выше):

Исходя из этих уравнений можно составить следующие уравнения, которые связывают линейные и фазные напряжения:

Использовав выражение (2) при наличии векторов фазных напряжений можно построить векторы линейных напряжений U_ab, U_bc, U_ca.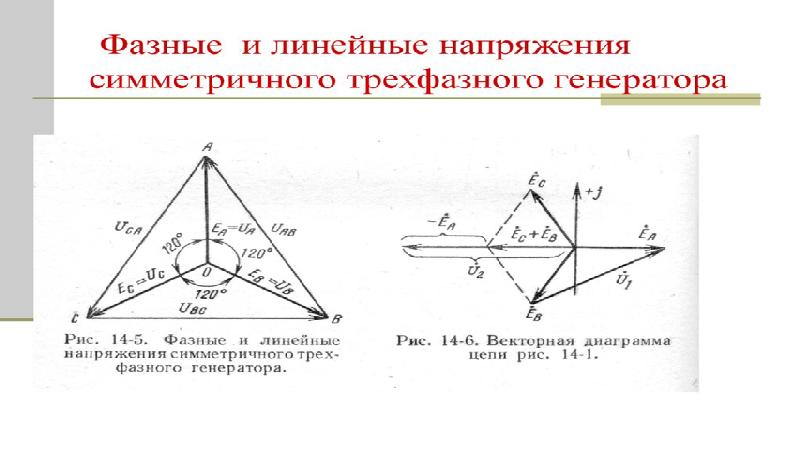

Исследовав векторную диаграмму при соединении звездой можно сделать вывод, что линейные напряжения будут равны и, как и фазные, сдвинуты друг относительно друга на угол 120⁰ или 2π/3. Векторы линейных напряжений чаще всего показывают как соединенные фазные направления:

Из этого следует:

Соответственно такие же соотношение и между остальными фазными и линейными значениями:

Соединение треугольником

Выражения (1) будут правильны и при соединении в треугольник источника. Из формул (2) следует равенство фазных и линейных напряжений при соединении треугольником, и это можно представить в таком виде:

Или можно записать как Uл = Uф.

Векторная диаграмма при соединении треугольником для линейных и фазных напряжений:

Номинальные напряжения

Из выше перечисленного можно сделать такие выводы как – трехфазная сеть имеет два напряжения, а именно фазные и линейные. При соединении звездой линейные напряжения больше фазных, а при соединении треугольником равны. Этот фактор необходимо учитывать при подключении нагрузки, чтоб не произошло аварийных ситуаций и выхода оборудования из строя.

Линейные напряжения тоже сдвинуты друг относительно друга на угол 120⁰ или 2π/3.

Номинальные напряжения – напряжения, на которые рассчитываются потребители электроэнергии, и которые соответствуют их нормальной работе.

Наиболее распространенными напряжениями в сетях до 1000 В являются 380В, 220В, 127В. 380 В и 220 В наиболее распространены в промышленности, а 220 В и 127 В в бытовых электросетях. Также при четырехпроводной электросети (соединения звезда с нулевым проводом) существует возможность получения фазного напряжения, которые при линейном 380 В будут равны , а при линейном 220 В будут равны . Такое соединение дает плюс в виде возможности при наличии четырехпроводной сети производить подключение как трехфазных потребителей 380 В, так и однофазных с номиналом в 220 В.

Линейные и фазные токи при соединении треугольником.

Соединение обмоток генератора и потребителей электрической энергии треугольником

При соединении обмоток трехфазного генератора треугольником (рис. 7-8) конец первой обмотки X соединяется с началом второй обмотки В, конец второй обмотки У соединяется с началом третьей обмотки С и конец третьей обмотки Z с началом первой А.

Рис. 7-8. Схема соединения обмоток генератора треугольником.

Рис. 7-9. Векторная диаграмма э. д. с. при соединении генератора треугольником.

Три линейных провода, идущих к приемникам энергии, присоединяются к началам фаз А, В и С.

Из рис. 7-8 ясно, что при таком соединении обмоток фазные напряжения равны линейным, т. е.

При соединении треугольником три фазы генератора образуют замкнутый контур с весьма малым сопротивлением. Очевидно, такое соединение возможно только в том случае, если сумма э. д. с., действующих в этом контуре, будет равна нулю, так как в противном случае в контуре даже при отсутствии нагрузки возникнет значительный ток, могущий вызвать перегрев генератора.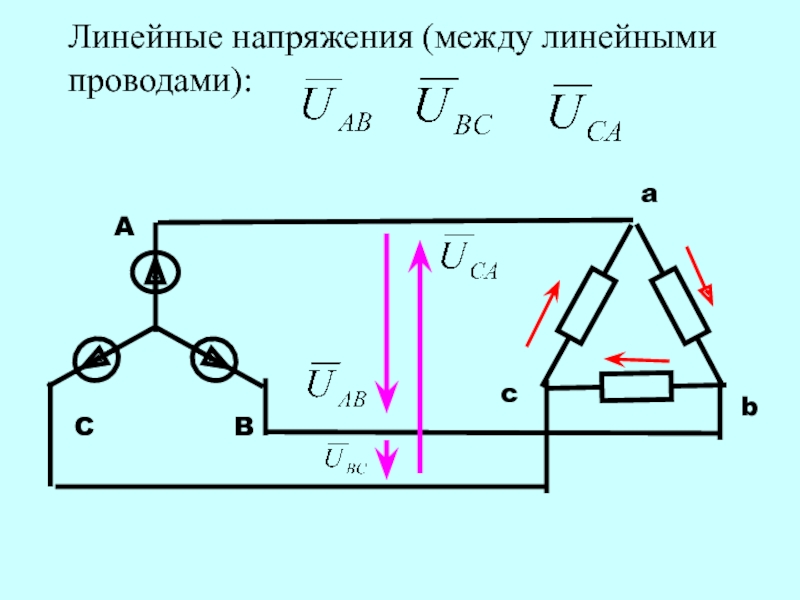

Сумма трех симметричных э. д. с., действующих в обмотках генератора, равна нулю. В этом легко убедиться, складывая векторы э. д. с.

На рис. 7-9 даны три вектора э. д. с. Складывая и получаем вектор, равный и противоположный вектору т. е.

а следовательно, сумма трех векторов э. д. с. равна нулю, т. е.

Опасно неправильное соединение обмоток генератора треугольником.

Рис. 7-10. Неправильная схема соединения, обмоток генераторй треугольником.

Рис. 7-11. Векторная диаграмма э. д. с. генератора, соединенного по схеме рис. 7-10.

На рис. 7-10 дана одна из возможных неправильных схем соединения, в которой конец первой фазы X правильно соединен с началом второй фазы В, но конец второй фазы Y соединен не с началом третьей фазы С, а с ее концом Z, и начало третьей фазы С соединено с началом первой фазы А, вследствие чего э. д. с. не складывается с остальными э. д. с., а вычитается из их суммы. Результирующая э. д. с. может быть определена из векторной диаграммы рис.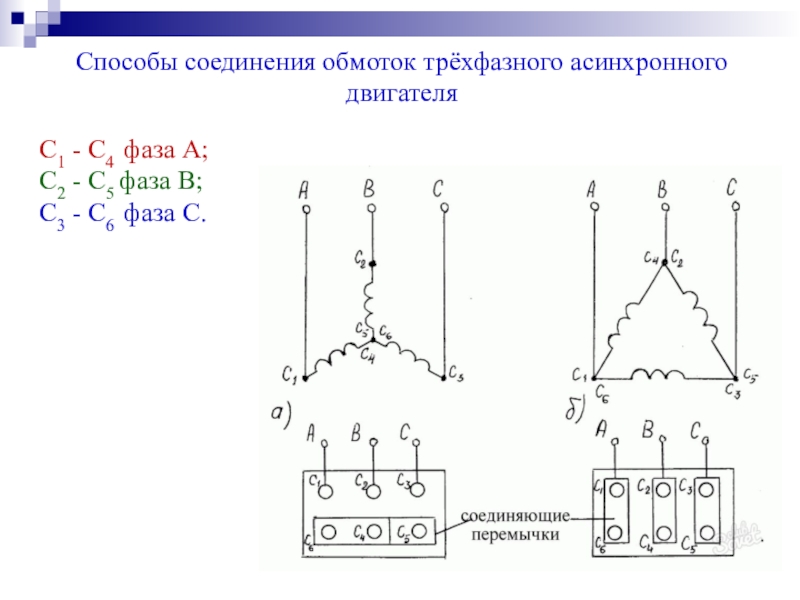 7-11, на которой произведено сложение векторов Сумма этих трех векторов, как видно из диаграммы, равна удвоенному вектору т. е.

Таким образом, в этом случае э. д. с. замкнутого контура по абсолютной величине равна удвоенному значению фазной э. д. с., что при малом сопротивлении контура (обмоток генератора) равносильно короткому замыканию.

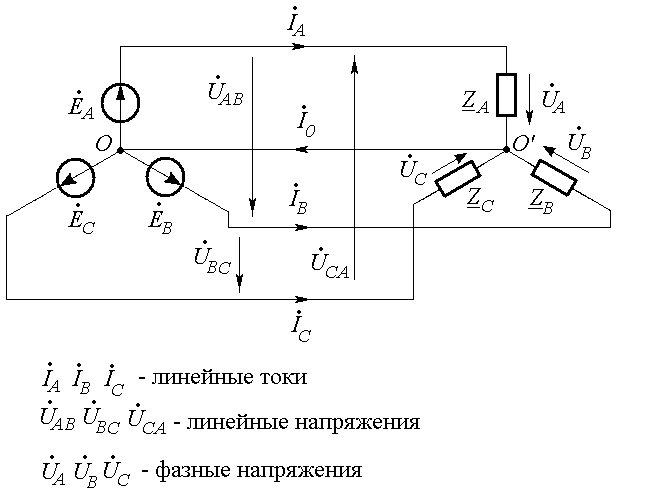
Если фазные обмотки генератора или потребителя соединить так, чтобы были соединены в одну общую точку, а начала обмоток присоединены к линейным проводам, то такое соединение называется соединением звездой и обозначается условным знаком Y. На рис. 1 обмотки генератора и потребителя соединены звездой. Точки, в которых соединены концы фазных обмоток генератора или потребителя, называются соответственно нулевыми точками генератора (0) и потребителя (0’). Обе точки 0 и 0’ соединены проводом, который называется нулевым, или нейтральным проводом. Остальные три провода трехфазной системы, идущие от генератора к потребителю, называются линейными проводами.

Таким образом, генератор соединен с потребителем четырьмя проводами. Поэтому эта система называется четырехпроводной системой трехфазного тока.

Рис. 1. Соединение звездой

Сравнивая несвязанную и четырехпроводную системы трехфазного тока, видим, что в первом случае роль обратного провода выполняют три провода системы, а во втором – один нулевой провод. По нулевому проводу протекает ток, равный геометрической сумме токов:

IA, IB и IC, т. е. Ī0= ĪA + ĪB + ĪC .

Напряжения, измеренные между началами фаз генератора (или потребителя) и нулевой точкой (или нулевым проводом), называются фазными напряжениями и обозначаются UA, UB и UC, или в общем виде Uф. Часто задаются величины э.д.с. фазных обмоток генератора. Они обозначаются ЕA, ЕB и ЕC, или Еф. Если пренебречь сопротивлениями обмоток генератора, то можно записать:

ЕA= UA, ЕВ= UВ, ЕC= UС.

Напряжения, измеренные между началами двух фаз: А и В, В и С, С и А – генератора или потребителя, называются линейными напряжениями и обозначаются UАВ, UВС, UСА, или в общем виде Uл.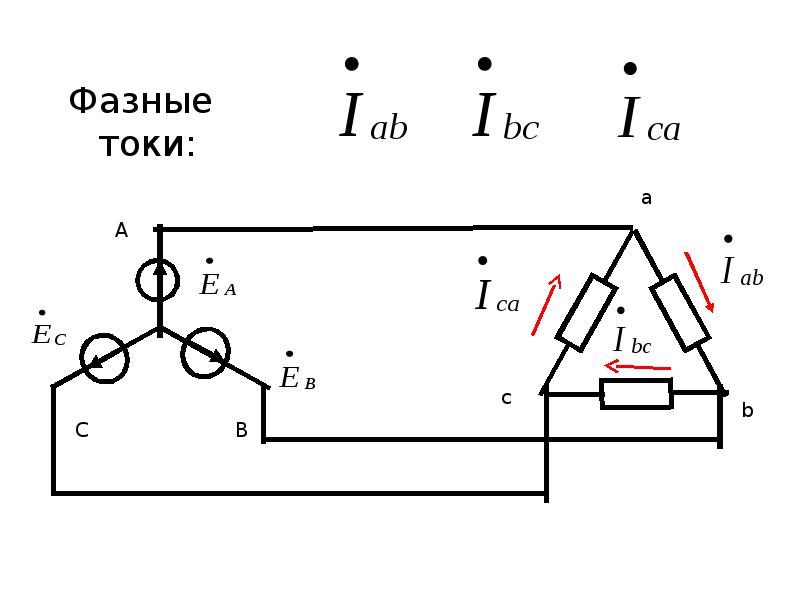 На рис. 1 стрелки показывают выбранное положительное направление тока, которое в линейных проводах принято от генератора к потребителю, а в нулевом проводе – от потребителя к генератору.

Если присоединить зажимы вольтметра к точкам А и В, то он покажет линейное напряжение UАВ. Так как положительные направления фазных напряжений UA, UB и UC выбраны от начал фазных обмоток к их концам, то вектор линейного напряжения UАВ будет равен геометрической разности векторов фазных напряжений UA и UB:

ŪAВ=ŪA- ŪВ.

Аналогично можно записать:

ŪВС=ŪВ- ŪС;

ŪСА=ŪС- ŪА.

Иначе можно сказать, что мгновенное значение линейного напряжения равно разности мгновенных значений соответствующих фазных напряжений. На рис. 2 вычитание векторов заменено сложением векторов:

UA и — UB; UВ и — UС; UС и — UА.

Из векторной диаграммы видно, что векторы линейных напряжений составляют замкнутый треугольник.

Рис. 2. Фазные и линейные напряжения при соединении звездой

Зависимость между линейным и фазным напряжениями:

UBС=2UBcos30o, так как cos30o=√3/2, то UBС=√3UB,
или в общем виде Uл=√3Uф.

Следовательно, при соединении звездой линейное напряжение в √3 раз больше фазного напряжения.
Ток, протекающий по фазной обмотке генератора или потребителя, называется фазным током и обозначается в общем виде Iф. Ток, протекающий по линейному проводу, называется линейным током и обозначается в общем виде Iл. На рис. 1 видно, что при соединении звездой линейный ток равен фазному току, т. е.

Iл=Iф .

Рассмотрим случай, когда нагрузка в фазах потребителя одинакова как по величине, так и по характеру. Такая нагрузка называется равномерной, или симметричной. Это условие выражается равенством.

z1= z2= z3.

Нагрузка не будет равномерной, если, например, z1= r1=0,5ом; z2=ωL2=0,5ом и z3=1/ωC3=0,5ом , так как здесь выполнено лишь одно условие – равенство сопротивлений фаз потребителя по величине, в то время как характер сопротивлений различен (r1 — активное сопротивление, ωL2 — индуктивное сопротивление, 1/ωC3 — емкостное сопротивление) .

При симметричной нагрузке:

IА=UА/zА; IВ=UВ/zВ; IС=UС/zС; IА=IВ=IС.

Фазные коэффициенты мощности вследствие равенства сопротивлений и одинаковости их характера будут одинаковы:

cosφ1=rА/zА; cosφ2=rB/zB; cosφ3=rC/zC; cosφ1=cosφ2=cosφ3.

В нулевом проводе должна протекать геометрическая сумма токов всех трех фаз. Если посмотреть на кривые изменения токов при симметричной нагрузке трехфазной системы, то увидим, что максимальные значения для всех трех синусоид тока одинаковы. Поскольку при симметричной нагрузке сумма мгновенных значений токов трехфазной системы равна нулю, следовательно, ток в нулевом проводе будет равен нулю.
Отбрасывая нулевой провод в четырехпроводной системе, переходим к трехпроводной системе трехфазного тока. Если имеется симметричная нагрузка, как, например, трехфазного тока, трехфазные печи, трехфазные трансформаторы и т. п., то к такой нагрузке подводятся только три провода. Потребители, включенные звездой с несимметричной нагрузкой фаз, нуждаются в нулевом проводе.
При симметричной нагрузке фазные напряжения отдельных фаз равны между собой. При несимметричной нагрузке трехфазной системы симметрия токов и напряжений нарушается. Однако в четырехпроводных цепях часто пренебрегают незначительной несимметрией фазных напряжений. В этих случаях между линейными и фазными напряжениями существует зависимость:

Uл=√3Uф.

Кроме соединения звездой, генераторы, трансформаторы, двигатели и другие потребители трехфазного тока могут включаться треугольником. Если объединить попарно провода несвязанной шестипроводной системы и соединить фазы, как показано на рисунке 1, получим трехфазную трехпроводную систему, соединенную треугольником.

Рис. 1. Несвязанная трехфазная схема.

Рис. 2. Связанная трехфазная схема, соединенная треугольником .

Соединение треугольником выполняется таким образом (рис. 2), чтобы конец фазы А был соединен с началом фазы В, конец фазы В соединен с началом фазы С и конец фазы С соединен с началом фазы А. К местам соединения фаз присоединяют линейные провода. Если обмотки генератора соединены треугольником, то линейное напряжение создает каждая линейная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному: Uл=Uф.
Определим зависимость между фазными и линейными токами при соединении треугольником, если нагрузка фаз будет одинакова по величине и характеру. Составляем уравнения токов по первому закону Кирхгофа для трех узловых точек А1, B1 и C1 потребителя:

ĪA+ ĪСА= ĪАВ;
ĪВ+ ĪАВ= ĪВС;
ĪС+ ĪВС= ĪСА;

откуда

ĪA= ĪАВ-ĪСА;
ĪВ= ĪВС-ĪАВ;
ĪС= ĪСА-ĪВС.

Отсюда видно, что линейные токи равны геометрической разности фазных токов. При симметричной нагрузке фазные токи одинаковы по величине и сдвинуты один относительно другого на 120o. Производя вычитание векторов фазных токов согласно полученным уравнениям, получаем линейные токи. Зависимость между фазными и линейными токами при соединении в треугольник:

Iл=2Iфcos30o=2Iф√3/2=√3Iф .

Следовательно, при симметричной нагрузке, соединенной треугольником, линейный ток в √3 раз больше фазного тока.
У двигателей и у других потребителей трехфазного тока в большинстве случаев наружу выводят все . Обычно к трехфазной машине крепится доска из изоляционного материала (клеммная доска), на которую и выводят все шесть концов.
Если у нас есть двигатель, на паспорте которого написано 127/220 в, значит, этот двигатель можно использовать на два напряжения 127 и 220 в.
Если линейное напряжение сети равно 127 в, то обмотки двигателя необходимо включить треугольником. Тогда на обмотку каждой фазы двигателя будет подано напряжение 127 в. При напряжении 220 в обмотки двигателя нужно включить звездой, тогда обмотка каждой фазы также будет под напряжением 127 в.

Обмотки трехфазного генератора могут быть соединены и другим способом: если конец первой обмотки соединить с началом второй, конец второй обмотки — с началом третьей и конец третьей — с началом первой, получим соединение треугольником (рис6).

Рассматривая рис.6, мы видим, что обмотки генератора образуют замкнутую последовательную цепь. На первый взгляд создается впечатление, что они замкнуты накоротко, однако фактически короткого замыкания нет, так как сумма э. д. с, действующих в этом замкнутом контуре, в любой момент времени равна нулю, что показано на векторной диаграмме (рис.6). Другое дело, если при соединении спутать концы одной из обмоток (рис.7), тогда фаза соответствующего фазного напряжения опрокинется на 180°и результирующее напряжение, действующее внутри треугольника обмоток, будет равно удвоенной величине фазного напряжения:

векторная сумма Uф1 + Uф3 = Uф2

И общее напряжение U= Uф1+ Uф2+ Uф3=2Uф2

Линейные провода при соединении треугольником отводятся от точек соединения обмоток. Очевидно, что напряжение между линейными проводами в этом случае равно напряжению фазы, включенной между этими проводами. Таким образом, если обмотки генератора соединены треугольником, линейное напряжение равно фазному, т. е.

Рассмотрим теперь зависимость между линейными и фазными токами. Если нагрузка равномерна (т. е. если комплексы сопротивлений, включенных на стороне потребителя в каждую из фаз, равны), то фазные токи в каждой из фаз генератора будут равны по величине и сдвинуты относительно друг друга на 120°. На рис.8 показаны обмотки трехфазного генератора, соединенные треугольником, и векторная диаграмма напряжений и токов для данного случая. Примем за положительное направление тока в обмотке направление против часовой стрелки, а за положительное направление тока в линии- направление от генератора к потребителю

Напишем в комплексной форме уравнения первого закона Кирхгофа для узлов I, II и III:

Iл1=Iф1-Iф3; (7)

Iл2=Iф2-Iф1; (8)

Iл3=Iф3-Iф1, (9)

т. е. линейный ток равен геометрической разности токов двух фаз, сходящихся в точке включения данного линейного провода. Произведем вычитание комплексов токов на векторной диаграмме. Фазные токи, как мы уже условились, взяты равной величины и сдвинуты от своих фазных напряжений на одинаковые, углы (φ). Техника вычитания не отличается от рассмотренной нами при определении величины линейного напряжения для системы с соединением обмоток генератора звездой. Для того чтобы не усложнять рисунок, мы показали на нем только определение линейного тока Iл1
Из построения очевидно, что величина , т. е. при соединении обмоток генератора треугольником величина линейного, тока больше величины фазного тока в раз.
Необходимо подчеркнуть, что эта зависимость имеет место только при равномерной нагрузке фаз. При неравномерной нагрузке необходимо находить линейные токи в каждом отдельном случае по уравнениям (7), (8) и (9) графически или аналитически (пользуясь символическим методом).
Из сравнения двух способов соединения обмоток генераторов следует, что при соединении звездой увеличивается напряжение между проводами линии передачи, но (при одинаковой нагрузке) уменьшаются линейные токи. При соединении обмоток треугольником не может быть проложен нулевой провод между генератором и потребителем, что создает значительные неудобства при неравномерной нагрузке фаз. Поэтому в распределительных сетях низкого напряжения вторичные обмотки силовых трансформаторов, как правило, соединяются звездой.

Линейное и фазное напряжение: трехфазные цепи

Линейное и фазное напряжение – отличие и соотношение

В этой краткой статье, не вдаваясь в историю сетей переменного тока, разберемся в соотношениях между фазными и линейными напряжениями. Ответим на вопросы о том, что такое фазное напряжение и что такое линейное напряжение, как они соотносятся между собой и почему эти соотношения именно таковы.

Ни для кого не секрет, что сегодня электроэнергия от генерирующих электростанций подается к потребителям по высоковольтным линиям электропередач с частотой 50 Гц. На трансформаторных подстанциях высокое синусоидальное напряжение понижается, и распределяется по потребителям на уровне 220 или 380 вольт. Где-то сеть однофазная, где-то трехфазная, однако давайте разбираться.

Действующее значение и амплитудное значение напряжения

Прежде всего отметим, что когда говорят 220 или 380 вольт, то имеют ввиду действующие значения напряжений, выражаясь математическим языком – среднеквадратичные значения напряжений . Что это значит?

Это значит, что на самом деле амплитуда Um (максимум) синусоидального напряжения, фазного Umф или линейного Umл, всегда больше этого действующего значения. Для синусоидального напряжения его амплитуда больше действующего значения в корень из 2 раз, то есть в 1,414 раза.

Так что для фазного напряжения в 220 вольт амплитуда равна 310 вольт, а для линейного напряжения в 380 вольт амплитуда окажется равной 537 вольт. А если учесть, что напряжение в сети никогда не бывает стабильным, то эти значения могут быть как ниже, так и выше. Данное обстоятельство всегда следует учитывать, например выбирая конденсаторы для трехфазного асинхронного электродвигателя.

Фазное сетевой напряжение

Обмотки генератора соединены по схеме «звезда», и объединены концами X, Y и Z в одной точке (в центре звезды), которая называется нейтралью или нулевой точкой генератора. Это четырехпроводная трехфазная схема. К выводам обмоток A, B и C присоединяются линейные провода L1, L2 и L3, а к нулевой точке — нейтральный провод N.

Напряжения между выводом A и нулевой точкой, B и нулевой точкой, С и нулевой точкой, – называются фазными напряжениями, их обозначают Ua, Ub и Uc, ну а поскольку сеть симметрична, то можно просто написать Uф — фазное напряжение.

В трехфазных сетях переменного тока большинства стран стандартное фазное напряжение равно приблизительно 220 вольт — напряжение между фазным проводом и нейтральной точкой, которая обычно заземляется, и ее потенциал принимается равным нулю, потому она и называется еще нулевой точкой .

Линейное напряжение трехфазной сети

Напряжения между выводом A и выводом B, между выводом B и выводом C, между выводом C и выводом A, – называются линейными напряжениями, то есть это напряжения между линейными проводниками трехфазной сети. Их обозначают Uab, Ubc, Uca, или можно просто написать Uл.

Стандартное линейное напряжение в большинстве стран равно приблизительно 380 вольт. Легко заметить в данном случае, что 380 больше 220 в 1,727 раза, и, пренебрегая потерями, ясно, что это квадратный корень из 3, то есть 1,732. Безусловно, напряжение в сети все время в ту или другую сторону колеблется в зависимости от текущей загруженности сети, но соотношение между линейными и фазными напряжениями именно таково.

Откуда взялся корень из 3

В электротехнике часто применяют векторный метод изображения синусоидально изменяющихся во времени величин напряжений и токов.

График зависимости величины проекции от времени есть синусоида. И если амплитуда напряжения — это длина вектора U, то проекция, которая меняется со временем — это текущее значение напряжения, а синусоида отражает динамику напряжения.

Так вот, если теперь изобразить векторную диаграмму трехфазных напряжений, то получится, что между векторами трех фаз одинаковые углы по 120°, и тогда если длины векторов — это действующие значения фазных напряжений Uф, то чтобы найти линейные напряжения Uл, необходимо вычислить РАЗНОСТЬ любой пары векторов двух фазных напряжений. Например Ua – Ub.

Выполнив построение методом параллелограмма, увидим, что вектор Uл = Uа + (-Ub), и в результате Uл = 1,732Uф. Отсюда и получается, что если стандартные фазные напряжения равны 220 вольт, то соответствующие линейные будут равны 380 вольт.

Особенности линейного напряжения

Электрические цепи характеризуются наличием различных типов напряжения. Линейное напряжение (ЛН) возникает между фазовыми проводами трёхфазной цепи. У всех частей (фаз) многофазной цепи характеристика тока идентична. Название цепей (шести-, трёх- или 2-фазные) обуславливаются числом фаз. Наибольшее распространение получили трёхфазные электроцепи, так как являются наиболее экономичными в сравнении с многофазными или 2-фазными. А также позволяют на одном агрегате получить ЛН и фазное напряжение (ФН).

Какое напряжение называется линейным, а какое фазным

Линейным называется напряженье между 2-мя фазами линии или когда определяется величина между 2-мя проводами различных фаз.

Напряжение между любой фазой и нулём — фазное. Оно меряется между начальной и конечной стадией фазы. Практически ФН от ЛН отличается на 58-60 процентов.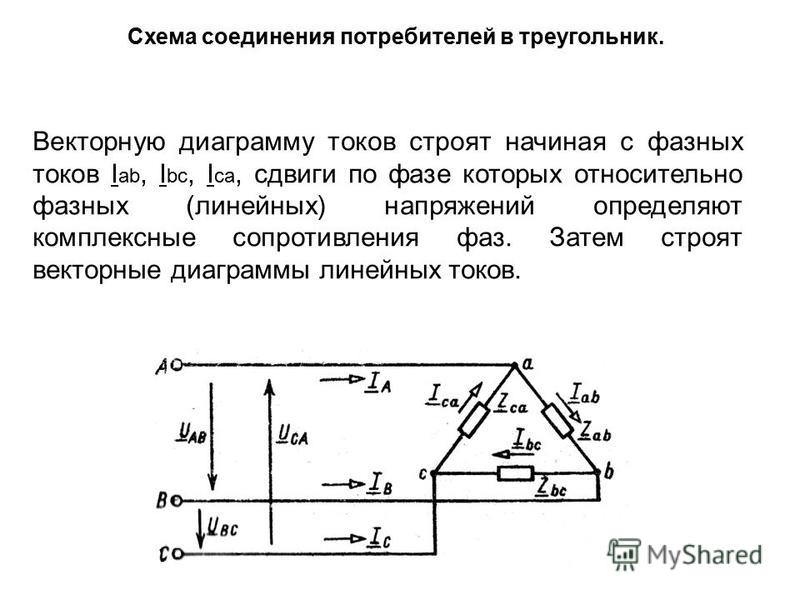 То есть, величины ЛН в 1,73 раза больше величин ФН.

Трёхфазные цепи имеют 380В ЛН, что позволяет получить 220В фазного.

Отличия

Специфика ЛН — это показатель, по которому производится расчёт токов и остальных величин трёхфазной цепи. Подобная схема позволяет подключать одно- и трёхфазные контакты. Номинальное равно 380В и меняется при изменениях в ограниченной сети, к примеру, вследствие скачков.

Популярнейшей является цепь с нейтралью и заземлением. Подключение в такой системе производится по схеме:

к фазным проводам подсоединяются однофазные провода;
к 3-фазным — 3-фазные.

Широта применения ЛН обуславливается его безопасностью и комфортностью разветвления цепи. Оборудование в таком случае подключается к фазному выводу, и лишь он не безопасен.

Расчёт системы несложен, при этом действуют стандартные физические формулы. Параметры ЛН сети замеряются мультиметром, а ФН — спецустройствами, например, вольтметром, датчиком тока, тестером.

Разводка подобной проводки не нуждается в применении профессионального оборудования. Достаточно отвёрток, которые имеют индикаторы.
Вероятность удара током очень мала. Подобное объясняется присутствующей в цепи свободной нейтралью. Соединение проводников не требует подключения 0-вого вывода.
Схема подходит для всех видов тока.

Важно! К 3-фазной цепи можно подключить 1-фазную. Наоборот сделать нельзя.

Подобная схема подключения пригодна для многих устройств, которым необходима высокая мощность, чтобы работать. ЛН позволяет увеличить КПД двигателя на33%.

При переключении обмоток генератора к треугольнику со звезды обуславливает увеличение в 1,73 раза величины ЛН.

Важно! Сложность обнаружения повреждений в линейном соединении является немаловажным недостатком цепи, так как вследствие этого может случиться пожар.

Отличие между ЛН и ФН состоит в различии соединяемых проводов обмоток.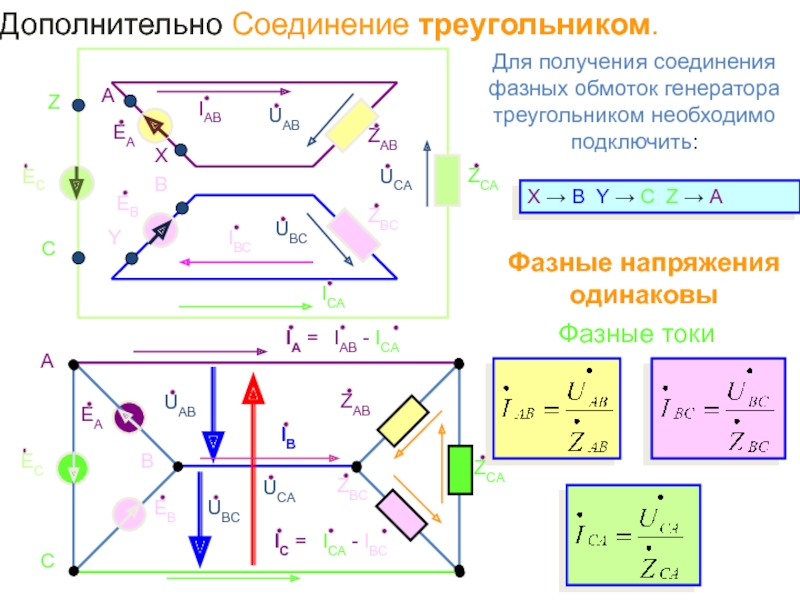 Чтобы проконтролировать параметры ЛН и ФН потребуется импульсный стабилизатор, по-другому — линейный стабилизатор. Этот прибор даёт возможность, сохраняя показатель на одном уровне, приводить в норму напряжение, если оно резко выросло. Прибор можно подключить к контактам электорооборудования, обычной розетке.

Соотношения фазного и линейного напряжения

Соотношение между напряжением линейным и фазным составляет 1,73. То есть при ста процентах мощности ЛН, напряжение фазы будет 58%. То есть, ЛН превышает ФН в 1,73 раза и при этом стабильно.

Напряжение в трёхфазной цепи оценивается по параметрам линейной составляющей. Обычно оно 380 вольт и тождественно 220 вольтам фазной компоненты сети трёхфазного электротока. В электрических сетях, где имеется четыре провода, напряжение 3-фазного тока обозначается 380/220В. Это позволяет подключить к подобной сети оборудование с 1-фазным потреблением электричества 220В и мощных приборов, которые могут работать от 380В.

Универсальной и приемлемой в большинстве случаев является трёхфазная цепь 380/220В 0-вым проводом. Электроприборы, которые функционируют от однофазного напряженья 220В, могут при подсоединении к паре проводов ФН питаться от ЛН.

Электрооборудование, которое запитывается от трёхфазной сети может работать, только если имеется подсоединение одновременно к 3-м выводам различных фаз. Тогда заземление не обязательно, но если изоляционный материал провода будет повреждён, то отсутствие 0-ого значительно увеличивает опасность удара электрическим током.

Важно! При понижении ЛН меняются величины ФН. При уже выясненном значении междуфазного напряжения определить величину ФН труда не составит.

Чему равно линейное напряжение

В большей части стран мира стандартное ЛН составляет примерно 380В.

В трёхфазных цепях фазное и линейное напряжение находятся в соотношении 220В/380В соответственно.

В чем измеряется

Согласно ГОСТ 13109 норма напряжения в электрической сети варьирует в диапазоне от 198В до 242В (то есть 220В плюс или минус 10 процентов). При частой поломке бытовой техники, ламп или их мигании потребуется измерение напряжения в электрической проводке. Подобная проверка делается мультиметром или вольтметром. Ночью, когда электроприборы используются по минимуму, полученные значения будут максимальными.

Мультиметром измеряется напряжение в трёхфазной сети так:

Между рабочим 0 и каждой из фаз: А-N, В-N, С-N.
Линейные напряжения: А-В, А-С, В-С.

Всего должно получиться шесть измерений. Иногда делается ещё один замер — между заземляющим и нулевым рабочим проводником: N-PE.

Как измерить

Измерить подобную систему можно мультиметром или применив физические формулы.

ЛН рассчитывается по формуле Кирхгофа: ∑ Ik = 0. Здесь сила тока равняется нулю во всех частях электроцепи, то есть к=1. Используется также закон Ома: I=U/R. Применив обе формулы можно высчитать параметры клейма или электросети.

В системе из несколько линий, потребуется найти напряжение между 0 и фазой IL = IF. Значения IL и IF непостоянные и меняются при разных вариациях подключения. Потому линейные параметры точно такие же, как и фазные.

Фазное

Для того чтобы получить показания подключения фазного вида, потребуется специальное оборудование, например, мультиметр, вольтметр. Для того чтобы измерить токи и напряжения в трёхфазных цепях обычно достаточно знать данные одного линейного тока и одного ЛН.

ФН измеряется при проседании (падении) линейного. Из линейных величин извлекается Квадратный корень из трёх. Полученный показатель и есть параметры ФН.

Линейное

Для расчёта соотношения линейного проводника и фазы применяется формула: Uл=Uф∙√3, Uф — фазовое, Uл — линейное.

Важно! Формула справедлива, только если IL = IF. Когда в цепь добавлены другие отводящие элементы, то для них потребуется сделать персональный расчёт фазового напряжения. Тогда Uф нужно заменить цифровыми величинами самостоятельного клейма.

Реактивная трёхфазная мощность рассчитывается по формуле: Q = Qа + Qb + Qс. Значение активной мощности можно найти, используя аналогичную формулу: P = Pа + Pb + Pс. Необходимость в подобных расчётах возникает, если к электрической сети подключается промышленная система.

Распространённость сетей с линейным током объясняется их относительной безопасностью и несложностью разведения электропроводки. Электрооборудование присоединено исключительно к одному фазному проводу (по нему проходит ток) и только он может быть опасен, второй — это заземление. ЛН возникает в трёхфазной цепи и даёт увеличение приблизительно на 73%.

Фазное и линейное напряжение

Одним из вариантов систем многофазных электрических цепей является трехфазная цепь. В многофазных электрических цепях происходит действие синусоидальных электродвижущих сил с одинаковой частотой. Они отличаются друг от друга по фазе и создаются от общего источника энергии. В трехфазных цепях важными параметрами являются фазное и линейное напряжение, отличающиеся своими электрическими характеристиками.

Что такое фаза

Каждая часть многофазной системы, имеющая одинаковую характеристику тока, называется фазой. Поэтому определение фазы имеет двоякое значение в электротехнике. Во-первых, как величина, изменяющаяся синусоидально, а во-вторых, как отдельная часть в системе многофазных электрических цепей. Количество фаз определяет наименование цепей: двухфазные, трехфазные, шестифазные и т.д.

Самыми распространенными цепями в современной энергетике являются трехфазные. Они имеют ряд преимуществ перед другими видами цепей, как однофазными, так и многофазными. Они более экономичны при производстве и передаче электроэнергии. Трехфазное напряжение возникает в результате вращения магнита внутри катушки. С его помощью достаточно просто образуется вращающееся круговое магнитное поле, обеспечивающее работу асинхронных двигателей. Данное явление известно, как ЭДС или по-другому, электродвижущая сила индукции.

Вращающийся магнит называется ротором, а катушки, расположенные вокруг него, образуют статор. Переменное напряжение получается путем преобразования постоянного напряжения, когда прямая линия принимает синусоидальную конфигурацию с изменяющимися положительными и отрицательными значениями.

Изменение магнитного потока происходит за счет вращения ротора, что и приводит к образованию переменного напряжения. В статоре имеется три катушки, в каждой из которых присутствует собственная отдельная электрическая цепь. Каждая катушка сдвинута относительно друг друга на 120 градусов по окружности. Под действием вращающегося магнита во всех катушках возникает одинаковое переменное напряжение между фазами в трехфазной сети.

Трехфазные цепи дают возможность получать два эксплуатационных напряжения на одной установке – фазное и линейное.

Фазное и линейное напряжение в трехфазных цепях

Фазное напряжение – возникает между началом и концом какой-либо фазы. По другому его еще определяют, как напряжение между одним из фазных проводов и нулевым проводом.

Линейное – определяется как межфазное или между фазное – возникающее между двумя проводами или одинаковыми выводами разных фаз.

Рассматривая фазные и линейные напряжения и токи, следует отметить, что показатель фазного напряжения составляет примерно 58% от параметров линейного. Таким образом, при нормальных условиях эксплуатации показатели линейных одинаковы и превышают фазные в 1,73 раза. То есть, если линейное напряжение 380, чему равно фазное можно определить с помощью этого коэффициента.

В трехфазной сети напряжение, как правило, оценивают по данным линейного напряжения. Для трехфазных линий, которые отходят от подстанции, устанавливается линейное напряжение номиналом 380 вольт. Это соответствует фазному в 220 вольт. В трехфазных четырех проводных сетях номинальное напряжение указывается с обозначением обеих величин – 380/220 В. Это означает, что в такую сеть подключаются как приборы с 380 вольт, так и однофазные – на 220 вольт.

Наибольшее распространение получила трехфазная система 380/220 вольт с заземленным нулевым проводом. Однофазные электроприборы на 220 вольт подключаются к линейному напряжению между любой парой фазных проводов. Трехфазные электроприборы подключаются к трем различным проводам фаз. В последнем случае не требуется использование нулевого провода, при этом отсутствие заземления повышает риск поражения током, когда нарушена изоляция.

Отличие линейного напряжения от фазного

Прежде чем рассматривать практическое значение этих параметров, необходимо точно знать, чем различаются между собой линейное и фазное напряжения. Определенное межфазное напряжение в трехфазной цепи может возникнуть либо между двумя фазами, либо между одной из фаз и нулевым проводом. Подобное взаимодействие становится возможным из-за использования в схеме четырехпроводной трехфазной цепи. Ее основными характеристиками являются напряжение и частота.

Напряжение, возникающее между двумя фазными проводниками, считается линейным, а между фазным и нулевым возникает фазное. Линейное напряжение используется для расчета токов и других параметров трехфазной цепи. К таким схемам возможно подключение не только трехфазных контактов, но и однофазных, например, различных бытовых приборов. Номинальное значение линейного напряжения составляет 380 В. Иногда оно изменяется под действием различных факторов, появляющихся в локальной сети. Таким образом, все основные различия между обоими видами напряжений заключаются в способах соединения обмоток.

Наибольшее распространение получило линейное напряжение, из-за безопасного использования и удобного распределения сетей. Для его замеров достаточно мультиметра, тогда как определение характеристик фазного напряжения требует использования вольтметров, датчиков тока и других специальных приборов.

Контроль и выравнивание данного параметра осуществляется с помощью линейного стабилизатора напряжения. Этот прибор обеспечивает поддержание этого показателя на нормативном уровне, в том числе он нормализует и повышенное напряжение.

Использование линейного и фазного напряжения

Классическим примером использования линейного и фазного напряжения считаются соединения, используемые при запуске трехфазного генератора. В его конструкцию входят первичные и вторичные обмотки, которые могут соединяться звездой или треугольником.

Схема «треугольник» предполагает соединение конца первой фазы с началом второй. Кроме того, каждый фазный проводник соединяется с линейными проводами источника тока. В результате, происходит выравнивание токов, а фазное напряжение становится равным линейному. По такой же схеме подключаются электродвигатели и трансформаторы.

Другим вариантом является схема «звезда». В этом случае начала всех обмоток подключаются к одной сети при помощи перемычек. Таким образом, в обмотки будет поступать ток с характеристиками этой сети, а межфазное напряжение вступит во взаимодействие со всеми активными контактами.

В чем главные отличия линейного и фазного напряжения?

Электрическое напряжение трехфазных сетей

Виды напряжения

Линейное. Его обозначают как межфазный ток, то есть проходящий между парой контактов или идентичными клеймами разных фаз. Оно определяется разностью потенциалов пары фазных контактов.
Фазное. Оно появляется при замыкании начального и конечного выводов фазы. Также, его обозначают как ток, возникающий при замыкании одного из контактов фазы с нулевым выводом. Его величина определяется абсолютным значением разности выводов от фазы и Земли.

Отличия

Соотношение

Схема

Расчет линейного и фазного напряжения

Для подсчета напряжения линейного тока, применяют формулу Кирхгофа:

Уравнение которой гласит, что каждой из частей электрической цепи, сила тока равна нулю – k=1.

И закон Ома:

Используя их, можно без труда произвести расчеты каждой характеристики конкретного клейма или электросети.

Однако, в некоторых случаях, требуется вычислить чему равно соотношение фазы и линейного проводника.

Для этого, применяют формулу:

Uл – линейное, Uф – фазовое. Формула справедлива, только если – I_L = I_F.

Идентичная структура формулы активной мощности:

Примеры расчета:

Линейные напряжения в этом подключении будут одинаковы и определяются как:

Что такое линейное и фазное напряжение, каково их соотношение?

Переменное напряжение и его величины

Напряжение различают по роду тока: переменное и постоянное. Переменное может быть разной формы, основная суть в том, что с течением времени изменяется его знак и величина. У постоянного знак всегда одной полярности, а величина может быть стабилизированной или нестабилизированной.

В наших розетках напряжение переменное синусоидальной формы. Выделяют разные его значения, чаще всего используются понятия мгновенное, амплитудное и действующее. Как понятно из названия, мгновенное напряжение — это количество вольт в конкретный момент времени. Амплитудное – это размах синусоиды относительно нуля в вольтах, действующее — это интеграл от функции напряжения по времени, соотношение между ними такое: действующее в √2 или 1,41 раз меньше амплитудного. Вот как это выглядит на графике:

Напряжение в трехфазных цепях

В трёхфазных цепях выделяют два вида напряжения – линейное и фазное. Чтобы разобрать их отличия нужно взглянуть на векторную диаграмму и график. Ниже вы видите три вектора Ua, Ub, Uc – это вектора напряжений или фаз. Угол между ними 120°, иногда говорят 120 электрических градусов. Этот угол соответствует таковому в простейших электрических машинах между обмотками (полюсами).

Если отразить вектор Ub так, чтобы сохранился его угол наклона, но начало и конец поменялись местами, его знак изменится на противоположный. Тогда установим начала вектора –Ub в конец вектора Ua, расстояние между началом Ua и концом –Ub будет соответствовать вектору линейного напряжения Uл.

Простыми словами мы видим, что величина линейного напряжения больше чем фазного. Давайте разберем график напряжений в трёхфазной сети.

Красной вертикальной линией выделено линейное напряжение межу фазой 1 и фазой 2, а желтой линией выделено фазное амплитудное фазы 2.

КРАТКО: Линейное напряжение измеряется между фазой и фазой, а фазное между фазой и нулём.

С точки зрения расчетов, разница между напряжениями обуславливается решением этой формулы:

Линейное напряжение больше фазного в √3 или в 1,73 раза.

Нагрузка к трёхфазной сети может быть подключена по трём или четырем проводам. Четвертый проводник – нулевой (нейтральный). В зависимости от типа сеть может быть с изолированной нейтралью и глухозаземленной. Вообще при равномерной нагрузке три фазы можно подать и без нулевого провода. Он нужен для того, чтобы напряжения и токи распределялись равномерно и не было перекоса фаз, а также в качестве защитного. В глухозаземленных сетях, при пробое на корпус выбьет автоматический разъединитель или перегорит предохранитель в щите, так вы избежите опасности поражения электрическим током.

Отлично то, что в такой сети у нас одновременно есть два напряжения, которые можно использовать исходя из требований нагрузки.

Для примера: обратите внимание на электрический щиток в подъезде вашего дома. К вам приходит три фазы, а в квартиру заведена одна из них и ноль. Таким образом, вы получаете в розетках 220В (фазное), а между фазами в подъезде 380В (линейное).

Схемы подключения потребителей к трём фазам

Все двигателя, мощные нагреватели и прочая трёхфазная нагрузка может быть подключена по схеме звезды или треугольника. При этом большинство электродвигателей в борно имеют набор перемычек, которые в зависимости от их положения формируют звезду или треугольник из обмоток, но об этом позже. Что такое соединение звездой?

Соединение звездой предполагает соединение обмоток генератора таким образом, когда концы обмоток соединяются в одну точку, а к началам обмоток подключается нагрузка. Звездой же соединяются и обмотки двигателя и мощных нагревателей, только вместо обмоток в них выступают ТЭНы.

Давайте рассуждать на примере электродвигателя. При соединении его обмоток звездой линейное напряжение 380 В приложено к двум обмоткам, и так с каждой парой фаз.

На рисунке A, B, C – начала обмоток, а X, Y, Z – концы, соединенные в одну точку и эта точка заземлена. Здесь вы видите сеть с глухозаземленной нейтралью (провод N). На практике это выглядит так, как на фото борно электродвигателя:

Красным квадратом выделены концы обмоток, они соединены между собой перемычками, такое расположение перемычек (в линию) говорит о том, что они соединены по звезде. Синим цветом – питающие три фазы.

На этом фото промаркированы начала (W1, V1, U1) и концы (W2, V2, U2), обратите внимание на то, что они сдвинуты относительно начал, это нужно для удобного соединения в треугольник:

При соединении в треугольник к каждой обмотке приложено линейное напряжение, это приводит к тому, что протекают большие токи. Обмотка должна быть рассчитана на такое подключение.

У каждого из способов включения есть свои достоинства и недостатки, некоторые двигателя вообще в процессе пуска переключаются со звезды на треугольник.

Нюансы

В продолжение разговора о двигателях нельзя оставить без внимания вопрос выбора схемы включения. Дело в том, что обычно двигателя на своем шильдике содержат маркировку:

В первой строке вы видите условные обозначения треугольника и звезды, обратите внимание, треугольник идет первым. Далее 220/380В – это напряжение на треугольнике и звезде, значит, что при соединении треугольником нужно, чтобы линейное напряжение было равно 220В. Если в вашей сети напряжение равно 380 – значит нужно подключать двигатель в звезду. В то время как фазное всегда на 1,73 меньше, не зависимо от величины линейного.

Отличным примером является следующий двигатель:

Здесь номинальные напряжения уже 380/660, это значит, что его для линейного 380 нужно подключать треугольником, а звезда предназначена для питания от трёх фаз 660В.

Если в мощных нагрузках чаще оперируют с величинами межфазного напряжения, то в осветительных цепях в 99% % случаев используют фазное напряжение (между фазой и нулем). Исключением являются электрокраны и подобное, где может использоваться трансформатор с вторичными обмотками с линейным 220 В. Но это скорее тонкости и специфика конкретных устройств. Новичкам запомнить проще так: фазное напряжение – это то, которое в розетке между фазой и нулем, линейное – в линии.

Линейное и фазное напряжение: трехфазные цепи

Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.

Таким образом, понятие «фаза» имеет в электротехнике два различных значения:

фаза как аргумент синусоидально изменяющейся величины;
фаза как составная часть многофазной электрической системы.

Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.

Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.

Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на рад. (см. рис. 2).

Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:

– экономичность передачи электроэнергии на большие расстояния;

– самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;

– возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;

– уравновешенность симметричных трехфазных систем.

Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.

Система ЭДС (напряжений, токов и т.д.) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.


Рис.3	Рис.4

Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).

Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).

Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.

Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.

Схемы соединения трехфазных систем

Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.

Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.

Соединение в звезду

На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.

Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).

Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.

Все величины, относящиеся к фазам, носят название фазных переменных, к линии – линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.

Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; – фазные напряжения нагрузки.

Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать

;

(1)

;

(2)

(3)

Отметим, что всегда – как сумма напряжений по замкнутому контуру.

На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае

(4)

Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .

Соединение в треугольник

В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).

Для симметричной системы ЭДС имеем

Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.

Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.

Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями

Аналогично можно выразить линейные токи через фазные токи генератора.

На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов

(5)

В заключение отметим, что помимо рассмотренных соединений «звезда – звезда» и «треугольник – треугольник» на практике также применяются схемы «звезда – треугольник» и «треугольник – звезда».

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

Какой принцип действия у трехфазного генератора?
В чем заключаются основные преимущества трехфазных систем?
Какие системы обладают свойством уравновешенности, в чем оно выражается?
Какие существуют схемы соединения в трехфазных цепях?
Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
На диаграмме на рис. 10 (трехфазная система токов симметрична) . Определить комплексы остальных фазных и линейных токов.
Какие схемы соединения обеспечивают автономность работы фаз нагрузки?

Фазное и линейное напряжение

В том случае, если обмотки генератора трехфазного тока соединить между собой специальным образом («звездой» или треугольником), то у такого тока возникают свойства, которые удобны в применении.

Векторная диаграмма напряжений для соединения «звезда»

Схема соединения звездой (рис.1(а)) и соответствующая векторная диаграмма напряжений на обмотках (рис.1(в)) изображены на рис.1. Здесь имеется точка $О$, которая называется точкой одинакового потенциала. Напряжение на каждой обмотке называется фазным (его амплитуда $U_{mf}$). Проводник, который соединен с точкой одинакового потенциала называют нулевым проводом. Проводники, которые соединены со свободными концами обмоток, называются фазными проводами. Получается, что фазные напряжения — это напряжения между нулевым и фазными проводами. Напряжения между фазными проводами называют линейным (его амплитуда $U_{ml}$). Линейное напряжение между проводами 1-2 могут обозначать как $U_{12}$, между проводами 1-3 — $U_{13}$ и так далее.

Рисунок 1.

Векторная диаграмма показывает, что амплитуды $U_{ml}\ $и $U_{mf}$находятся в соотношениях:

Ток, который течет через обмотки генератора называют фазным током ($I_f$), ток который течет в линиях называется током линии ($I_l$). В соединении звездой фазные токи равны токам в линии. Если сопротивления нагрузок не равны нулю, а $R_1=R_2=R_2=R$, то суммарная сила тока через нулевой провод равна нулю:

так как из векторной диаграммы видно, что $\sum\limits_i{U_i=0.}$

Векторная диаграмма напряжений для соединения «треугольник»

Схема соединения обмоток генератора треугольник изображена на рис.2. В этом случае амплитуды напряжений фазного и линейного равны ($U_{mf}=U_{ml}$).

Рисунок 2.

Готовые работы на аналогичную тему

Из векторной диаграммы токов (рис.2(в)) запишем амплитудных значений тока:

В соединении обмоток генератора треугольником ток замыкания в обмотках равен нулю. Однако это справедливо только для основной гармоники. Токи высших гармоник, появляющиеся из-за нелинейности колебаний, в обмотках есть.

Соединение нагрузок тоже может быть в виде звезды и в виде треугольника. На рис. 1 и рис.2 изображены соединения одного типа, как для генератора, так и для нагрузок. Но совсем не обязательно, что соединения обмоток генератора и нагрузок совпадают. Так, можно реализовать четыре возможные комбинации соединения генератора и нагрузок: «звезда» — «звезда», треугольник — треугольник, «звезда» — треугольник, треугольник — «звезда». Каждое из перечисленных соединений имеет свои особенности.

Пример 1

Задание: В чем состоят особенности соединений «звезда» — «звезда» и «звезда» — треугольник?

Решение:

При соединении «звезда» — «звезда» (рис.1) на всех нагрузках имеется разное напряжение. При одинаковых сопротивлениях ($R_1=R_2=R_3$) (или примерно равных) сила тока по нулевому проводу равна нулю (или очень мала). Теоретически нулевой провод можно убрать, но без него на каждую из пар нагрузок действует линейное напряжение, амплитудное значение которого равно:

\[U_{ml}=\sqrt{3}U_{mf}\left(1.1\right).\]

Это напряжение распределяется между нагрузками в соответствии с величиной их сопротивлений. Такая зависимость напряжений от нагрузок крайне не удобна, поэтому нулевой провод сохраняют.

При соединении «звезда» — треугольник (рис.3). На каждое сопротивление действует линейное напряжение равное:

\[U_{ml}=\sqrt{3}U_{mf}\left(1.2\right).\]

Это линейное напряжение не зависит от величины сопротивления.

Рисунок 3.

Пример 2

Задание: Определите, чему равно фазное напряжение, если линейное $U_{ml}=220\ В$. Чему будет равно линейное напряжение, если 220 В считать фазным напряжением? Считать, что соединение обмоток генератора — «звезда».

Решение:

В том случае, если обмотки генератора соединены звездой, и это соединение имеет нулевой провод, в линии существует две системы напряжений (линейное и фазное), что является достоинством такого соединения.

Для соединения «звезда» мы имеем соотношение:

\[U_{ml}=\sqrt{3}U_{mf}\left(2.1\right).\]

Следовательно, для фазного напряжение имеем:

\[U_{mf}=\frac{U_{ml}}{\sqrt{3}}=\frac{220}{\sqrt{3}}\approx 127\ \left(В\right).\]

Если дано фазное напряжение, то:

\[U_{ml}=\sqrt{3}U_{mf}=\sqrt{3}\cdot 220\approx 380\ (В)\left(2.2\right).\]

Ответ: 1. $U_{mf}=127\ В.$ $U_{ml}=380\ В.$

Линейное напряжение — Asutpp

В электрических цепях бывают разные типы напряжения. Линейное напряжение можно наблюдать в трехфазной сети, где оно возникает между двумя фазовыми проводами. В большинстве случаев его уровень достигает 380 Вольт.

Отличие линейного от фазного напряжения

Если представить трехфазную цепь, то четко понятно, что в ней есть определенное напряжение между фазными контактами и фазным и нулевым проводом. Это происходит из-за того, что в этой схеме используется четырёхпроводная трехфазная цепь. Главные её характеристики – напряжение и частота. Напряжение, возникающее в цепи между двумя фазными проводами – это линейное, а то, что появляется между фазным и нулевым – фазным.

4-проводная сеть

Примечательной особенностью линейного напряжения является то, что именно по нему рассчитываются токи и другие параметры трехфазной цепи. Кроме того, к такой схеме можно подключать не только стандартные трехфазные контакты, но и однофазные (это различные бытовые приборы, приемники). Номинальное равняется 380 вольт, при этом оно может изменяться в зависимости от скачков или других перемен в локальной сети.

Существует несколько вариантов такого соединения, скажем, система с нейтралью под заземлением является самой популярной. Она характеризуется тем, что подключение к ней производится по особой схеме:

Однофазные отводы подключаются к фазным проводам;
Трехфазные – к трехфазным, соответственно.

Линейное напряжение имеет очень широкое использование благодаря своей безопасности и удобства разветвления сети. Электрические приборы подключаются только к одному- фазному проводу, опасность представляет он один. Расчет системы очень прост, в нем руководствуются стандартными формулами из физики. При этом, чтобы измерить этот параметр сети, достаточно воспользоваться простым мультиметром, для того, чтобы замерить характеристики фазового подключения потребуется несколько специальных устройств (датчики тока, вольтметры и прочие).

Некоторые особенности сети:

При разводке такой проводки не требуется использовать профессиональные приборы- все измерения проводятся отвертками с индикаторами;
При соединении проводников нет необходимости подключать нулевой провод, т. к. благодаря свободной нейтрали, риск поражения током крайне мал;
Электротехника использует такую схему подключения для различных электродвигателей и других устройств, требующих высокую мощность для работы. Дело в том, что используя этот тип напряжения есть возможность повысить КПД на треть, что является весьма полезным свойством, в особенности, для асинхронного двигателя;
Схема используется как для переменного тока, так и для постоянного;
Нужно помнить, что однофазное соединение можно подключить к трехфазной сети, но не наоборот;
Но, у такой цепи есть и определенные недостатки. В линейном соединении проводников очень сложно обнаружить повреждения. Это способствует повышенной пожарной опасности.

Соответственно, основная разница между фазовым и линейным напряжением заключается в разности подсоединяемых проводов обмоток.

Для контроля и выравнивания этого параметра часто используется специальный прибор — линейный стабилизатор напряжения. Он позволяет поддерживать показатель на определённом уровне, при этом нормализуя повышенное. Еще одно его определение – импульсный стабилизатор. Устройство может подключаться к розетке, контактам электрических приборов и т. д.

Расчет

Соединение

Линейное и фазное напряжение часто используется для запуска генератора. Рассмотрим, какие бывают соединения проводов на примере трехфазного генератора. Он состоит из первичных и вторичных обмоток. Их можно соединить звездой или треугольником.

Схема звезда и треугольник

Соединяя проводники в «треугольник» начало второй фазы соединяется с концом первой. Помимо этого, к каждому фазному проводнику подключаются линейные провода источника. Это выравнивает токи, исходя из чего, фазовое напряжение становится равным линейному. Аналогичная схема и для подключения трансформатора и двигателя.

Такое соединение также позволяет обеспечить нулевую электрическую движущую силу и постоянную частоту. Токи обмоток сдвигаются на 120 градусов, благодаря чему в общей схеме это соединение имеет вид трех отдельных токов, которые относительно друг друга сдвинуты на 2/3 периода. Это соотношение может изменяться в зависимости от типа подключаемого устройства и характеристик сети.

Формулы для расчета двигателей

Аналогично можно подсоединить трехфазный асинхронный двигатель, стабилизатор или усилитель в сеть 220 вольт «звездой». Эта схема подразумевает подключение начала обмоток к сети. Тогда от входа начнет двигаться ток с характеристиками сети. Контакты выхода (концы обмоток), соединятся с началом при помощи специальных перемычек. Таким образом, межфазное напряжение будет протекать через все активные контакты.

В изолированной сети используются различные пусковые конденсаторы для запуска системы. Аналогично соединяются клеммы на обмотках. Это подключение часто используется для понижающих трансформаторов и различных двигателей, предусмотренных для работы в однофазной сети.

Стабилизатор напряжения с защитой от перегрузок

Расчет

Для того чтобы рассчитать линейное напряжение используется формула Киргофа:

∑ Ik = 0;, которая говорит о том, что в любом узле цепи сила тока равна нулю.

_k=1

И закон Ома:

I = U / R . Зная эти законы можно без проблем рассчитать любую характеристику определенного контакта или сети.

При разветвлении системы может понадобиться вычислить напряжение между фазовым проводом и нейтральным:

I_L = I_F – эти параметры могут изменяться в зависимости от подключения. Отсюда следует, что линейные параметры равняются фазовым.

Но, в определенных ситуациях, необходимо рассчитать, чем равно соотношение напряжения между фазовым и линейным проводниками.

Для этого используется формула: Uл=Uф∙√3, где:

Uл –линейное, Uф – фазовое. Формула справедлива только если I_L = I_F.

При включении в сеть дополнительных отводов, нужно отдельно вычислять фазовое напряжение каждого из подключений. Тогда вместо Uф подставляются данные этого конкретного отвода.

При работе с промышленными установками может потребоваться расчет реактивной трехфазной мощности. Он производится по формуле:

Q = Qа + Qb + Qс

Аналогичный вид имеет формула активной:

P = Pа + Pb + Pс

Разница между линейным напряжением и фазным напряжением с решенными примерами

Линейное напряжение в трехфазной системе — это разность потенциалов между любыми двумя линиями или фазами, присутствующими в системе, обозначенная как V line или V L-L. Присутствующие здесь фазы являются проводниками или обмотками катушки. Если R, Y и B — три фазы (красная фаза, желтая фаза, синяя фаза), то разница напряжений между R и Y, Y и B или B и R образует линейное напряжение. С другой стороны, фазовое напряжение — это разность потенциалов между одной фазой (R, Y или B) и точкой соединения нейтрали, обозначенная как V фаза = VR (напряжение в красной фазе) = VY (напряжение в желтой фазе) = VB ( напряжение в синей фазе).

(изображение будет загружено в ближайшее время)

Точно так же линейный ток — это ток в одной фазе, а фазный ток — это ток внутри трехфазного соединения.

Чтобы понять соотношение линейного напряжения и фазного напряжения, первое, что нам нужно понять, это различные типы трехфазных систем подключения.

Соотношение между линейным напряжением и фазным напряжением при соединении звездой

Рассмотрим три катушки провода или обмотки трансформатора, соединенные общей точкой соединения.Три провода, идущие от каждой катушки к нагрузке, называются линейными проводами, а сами проводники являются фазами. Эта система представляет собой типичную трехфазную трехпроводную систему соединения звездой. Если нейтральный провод присоединяется к общей средней точке, это называется трехфазной четырехпроводной системой соединения звездой.

Термины линейное напряжение и фазное напряжение уже объяснялись ранее, и они связаны следующим образом:

\ [V_ {line} = \ sqrt {3} V_ {phase} \];

Пока линейный ток = фазный ток.

(изображение будет загружено в ближайшее время)

Соотношение между линейным напряжением и фазным напряжением при соединении треугольником

При соединении треугольником все три конца фаз соединены в замкнутый треугольник шлейф, и у него нет общей нейтральной точки, как при соединении звездой. Здесь линейное и фазное напряжение связаны следующим образом:

\ [V_ {line} = V_ {phase} \];

Пока линейный ток = √3 × фазный ток.

(изображение будет загружено в ближайшее время)

Разница между фазным напряжением и линейным напряжением определяется следующим образом:

Разница между линейным напряжением и фазным напряжением

Sl No.	Напряжение сети	Напряжение фазы
1.	Напряжение линии выше, чем напряжение фазы при соединении звездой.	Фазное напряжение меньше линейного напряжения при соединении звездой.
2.	Линейное напряжение — это разность потенциалов между двумя фазами или линиями.	Фазное напряжение — это разность потенциалов между фазой и нейтралью
3.	При соединении звездой линейное напряжение в √3 раз больше фазного напряжения.	При соединении звездой фазное напряжение в 1 / √3 раза больше линейного напряжения.

При соединении треугольником линейное и фазное напряжение равны.

(изображение будет загружено в ближайшее время)

Решенные примеры

1. Рассчитайте фазное напряжение, если линейное напряжение составляет 460 вольт, учитывая, что система представляет собой трехфазную сбалансированную систему, соединенную звездой.

Ответ: Мы знаем,

Vphase = Vline / √3 = 460 / √3 = 265,59 вольт.

2. В какой из следующих цепей линейное и фазное напряжение равны? А как насчет соотношения линейного напряжения и фазного напряжения в другой цепи?

(изображение скоро будет загружено)

Ответ: Как мы знаем, при соединении треугольником (второй рисунок) линейное и фазное напряжение равны. В то время как для соединения звездой линейное напряжение выше, чем фазное напряжение, которое определяется соотношением: Vline = √3 Vphase.

Интересные факты

В любой проблеме или вопросе обычно указывается напряжение сети. В случае фазного напряжения следует упомянуть. Если не указано иное, считайте это линейным напряжением.
Наш бытовой трехфазный источник питания или 440 вольт — это сетевое напряжение.
Однофазный источник переменного тока 230 В — это разность напряжений между фазой и нейтральным переходом или, скорее, фазное напряжение.
Многофазная система, в которой все линейные напряжения и линейные токи равны, известна как трехфазная сбалансированная система.В случае несимметричных нагрузок система, как правило, неуравновешенная.

Что такое трехфазное напряжение | Тихоокеанский источник энергии

Однофазное переменное напряжение

Большинство из нас знакомы с однофазным напряжением в наших домах, обеспечиваемым местными коммунальными предприятиями. Для США это обычно 120 В. Для однофазного напряжения напряжение выражается как напряжение между фазой и нейтралью между двумя силовыми проводниками (плюс защитное заземление). Нейтральный провод обычно имеет потенциал земли, а линейный провод — синусоидальное переменное напряжение со среднеквадратичным значением 120 В переменного тока.Это означает, что пик переменного напряжения меняется от + 169,7 В до -169,7 В каждые 16,667 мс на частоте сети 60 Гц в США. Для многих других стран эти номинальные значения составляют 230 В среднеквадратического значения при 50 Гц (20 мс).

Рисунок 1: Форма волны синусоидального напряжения 120 В среднеквадратического значения для однофазной сети

Пауэр Лимитед

Однофазное напряжение может выдавать только столько мощности, сколько вся мощность должна передаваться через линейный и нейтральный проводники. Это не проблема для домашнего использования, но для промышленного использования может потребоваться больший ток для работы машин, двигателей, освещения и других мощных нагрузок.В таких ситуациях часто бывает желательно увеличить как напряжение, так и ток, чтобы получить более высокую мощность. Один из вариантов — использовать две фазы, как в некоторых домах в США, для работы электрических сушилок. Это называется соединением с разделением фаз, когда две фазы 120 В среднеквадратического значения разнесены по фазе на 180 °, обеспечивая удвоенное межфазное напряжение 120 В или 240 В. Это удваивает доступную мощность. Разделенная фаза обычно не используется в Европе или Азии, поскольку нормальное напряжение однофазной сети уже составляет от 220 В до 240 ЛН.

Трехфазное переменное напряжение

Если пойти дальше, то мощные нагрузки обычно получают питание от трех фаз.Это распределяет ток по трем, а не по одному набору проводов, что позволяет использовать меньшую и, следовательно, менее дорогую проводку. Три источника напряжения сдвинуты по фазе на 120 ° друг относительно друга, чтобы уравновесить токи нагрузки. Это показано на рисунке 2.

Рисунок 2: Кривые трехфазного напряжения с разным вращением

Фазовый сдвиг на 120 ° между каждой формой сигнала может быть выполнен в одном из двух чередований фаз — A -> B -> C или A -> C -> B. Чередование фаз не влияет на большинство нагрузок, за исключением трехфазных двигателей переменного тока, которые будут поверните в обратном направлении, если чередование фаз изменилось.Изменить чередование фаз можно, поменяв местами любые два из трех фазных соединений. При использовании программируемого источника питания переменного тока, такого как серия AFX, фазовые углы для фаз B и C можно запрограммировать на 120 ° и 240 ° или 240 ° и 120 ° соответственно, чтобы изменить чередование фаз. AFX также позволяет программировать фазовый дисбаланс для изучения влияния фазовых изменений на тестируемое устройство.

Осторожно при определении межфазных напряжений

В то время как «нормальное» соотношение трехфазного треугольника и звездочки легко уловить в простой формуле, это применимо только к равным линейным и нейтральным напряжениям, идеальному фазовому балансу и синусоидальным напряжениям.В этом идеальном случае соотношение между линейным и нейтральным среднеквадратичным напряжением и линейным среднеквадратичным напряжением может быть выражено следующей формулой:

Это соотношение между фазой и нейтралью и линейным напряжением показано на фазовой диаграмме на Рисунке 3.

Рисунок 3: Трехфазная фазовая диаграмма

На рисунке 4 ниже показаны два типичных примера трехфазных конфигураций напряжения электросети, используемых в Соединенных Штатах. В Европе и Азии вместо этого обычно используются конфигурации 220/380 В или 230/400 В.120VLN на фазу эквивалентно векторной сумме 208VLL:

В _LL = 120 В _LN * 1,732 = 207,84 В _LL

Обратите внимание, что конфигурация сети, соединенная треугольником 480 В, не имеет нейтрального соединения и называется соединением 3 провода + земля треугольник. Чтобы смоделировать этот тип сети с источником питания переменного тока, трехфазная нагрузка подключается по схеме треугольника только между тремя выходными фазами без подключения к выходной клемме нейтрали.

Рисунок 4: Типичные конфигурации трехфазного напряжения, используемые в США

Это соотношение √3 важно при использовании программируемого трехфазного источника питания переменного тока, поскольку все источники переменного тока типа T&M программируются только на линейное и нейтральное напряжение.Таким образом, если какое-либо из указанных условий не выполняется, вы не можете просто полагаться на эту формулу для определения межфазного напряжения:

Идентичные напряжения VLN на всех трех фазах
Сбалансированные углы фаз на фазах B и C
Низкие искажения, чистый синусоидальный сигнал

Небольшой фазовый сдвиг на одной или нескольких из трех фаз может иметь значительное влияние на напряжения V _LL, что также приводит к дисбалансу тока нагрузки.

Искаженное напряжение, вызванное нелинейной нагрузкой на одной или нескольких фазах, также может сбрасывать линейные напряжения.

Почему это важно?

Программируемые трехфазные источники питания переменного тока имеют регулируемые углы фаз и часто поддерживают сигналы произвольной формы. Это означает, что соотношение между фазой и нейтралью и линейным напряжением не обязательно «фиксированное». Как правило, все трехфазные программируемые источники питания переменного тока программируются на среднеквадратичное значение от линии до нейтрали, независимо от типа нагрузки (треугольник или звезда). Таким образом, может потребоваться фактически измерить результирующее линейное напряжение, так как его расчет недействителен, если эти условия не выполняются.

Заключение

При тестировании трехфазных нагрузок обращайте особое внимание на параметры напряжения и фазы, делая предположения о напряжениях между фазами, приложенных к тестируемому устройству.

Трехфазная терминология: фаза против линии?

«Фаза» и «Линия» — как они определяются

, 2019 г.

Два основных термина, которые часто вызывают путаницу при изучении трехфазных систем переменного тока : « фаза » и « линия ».В этом нет ничего удивительного, ведь зачастую термины употребляются совершенно неправильно, не только в полевых условиях, но, к сожалению, очень часто, к сожалению, и в учебниках!

Часто, например, мы слышим, как кто-то называет три проводника, свисающие с распределительной линии, « фазными проводниками » или « фазами ». Это совершенно неверно . Правильная терминология — « линейных проводников » или « линий ».

Три находящихся под напряжением проводника , которые подключают трехфазную нагрузку к трехфазному источнику питания, называются «линиями ».Напряжение между любыми двумя линейными проводниками называется « линейных напряжений », а ток, который проходит по каждому линейному проводнику, называется «линейным током ». Клеммы трехфазного источника (генератора или трансформатора) или трехфазной нагрузки, к которым подключены линейные проводники, называются « линейные клеммы ».

‘ Фазы ‘, , с другой стороны, подключены между любой парой линейных клемм (соединение «треугольник»), или между любыми отдельными линейными клеммами и нейтралью («звезда» или «звезда» связь’). Независимо от того, подключены ли они по схеме «треугольник» или «звезда» (звезда), три обмотки генератора или трансформатора и три сопротивления нагрузки являются « фазами ». Напряжение, возникающее на любой фазе, называется «фазным напряжением », а ток, проходящий через любую фазу, называется «фазным током ».

В системе , соединенной треугольником, , даже несмотря на то, что линейное напряжение численно равно соответствующему фазному напряжению , мы должны всегда сохранять правильные термины, в соответствии с ГДЕ эти напряжения измеряются.

В системе , соединенной звездой , даже несмотря на то, что линейный ток численно равен соответствующему фазному току , мы всегда должны сохранять правильные значения в соответствии с ГДЕ эти токи измеряются — как показано ниже:

Идентификационные линии

Линейные провода и линейные клеммы (НЕ фазы) идентифицируются в соответствии с национальными стандартами. В Европе, например, цвета коричневый , черный и серый используются для обозначения линий и линейных клемм.В других странах используются другие цвета. Однако в международном масштабе принято использовать буквы A , B и C — например, на принципиальных схемах (как указано выше). Использование букв имеет дополнительное преимущество, заключающееся в том, что высоковольтных линий (или клемм ) могут быть идентифицированы с использованием заглавных букв : A , B и C, в то время как низковольтных линий (или клемм ) можно идентифицировать с помощью строчных букв : a , b и c .

Британский стандарт, касающийся трансформаторов, например, использует буквы A , B и C для обозначения клемм высоковольтных трансформаторов и строчные буквы a , b и c , для обозначения клемм низкого напряжения.

Важно понимать, что эти цвета или буквы используются для обозначения линии ( проводников) или клемм , НЕ фаз.

Определение фаз

Фазовые обмотки или , сопротивление нагрузки сами по себе не идентифицируются. Вместо этого они обозначены в терминах линейных клемм , между которыми они соединены. Например, в случае соединения треугольником фазная обмотка, подключенная между линейными выводами A, и B , обозначается как ‘ Phase A-B ‘ ; фазная обмотка, подключенная между линейными выводами B и C , обозначена как ‘ Phase B-C ‘ ; фазная обмотка, подключенная между линейными выводами C и A , обозначена как ‘ Phase C-A ‘ .То же самое применимо, если мы используем цвета вместо букв: например, «Фаза коричнево-черная» и др.

В случае соединения звездой каждая фаза идентифицируется с точки зрения линейного вывода, к которому она подключена, и нейтральной точки, то есть ‘ Phase AN ‘, ‘ Phase BN ‘, и ‘ Фаза CN ‘ .

Нет никакого смысла ссылаться, например, на ‘ коричневая фаза ‘ или ‘ фаза A ‘ и т. Д., поскольку эти цвета или буквы обозначают линий (или клемм ), , а не фазы.

Соединение звездой в трехфазной системе — связь между фазой и линией, напряжением и током

В соединении звездой одинаковые концы (начало или конец) трех обмоток подключены к общей точке, называемой звездой или нейтральной точкой. Трехлинейные проводники отходят от оставшихся трех свободных клемм, называемых линейными проводниками .

Провода подводятся к внешней цепи, образуя трехфазные трехпроводные системы, соединенные звездой. Однако иногда четвертый провод проводится от точки звезды к внешней цепи, называемый нейтральным проводом , образуя трехфазные четырехпроводные системы, соединенные звездой.

Состав:

Соединение звездой показано на схеме ниже:

Учитывая приведенный выше рисунок, оконечные клеммы a ₂, b ₂ и c ₂ трех обмоток соединены так, чтобы образовать звезду или нейтраль.Три проводника, обозначенные как R, Y и B, отходят от оставшихся трех свободных клемм, как показано на рисунке выше.

Ток, протекающий через каждую фазу, называется Фазный ток I _ph , а ток, протекающий через каждый линейный провод, называется Line Current I _L . Точно так же напряжение на каждой фазе называется Phase Voltage E _ph , а напряжение на двух линейных проводниках известно как Line Voltage E _L.

Зависимость между фазным напряжением и линейным напряжением при соединении звездой

Подключение звездой показано на рисунке ниже:

Поскольку система сбалансирована, сбалансированная система означает, что во всех трех фазах, то есть R, Y и B, через них протекает равное количество тока. Следовательно, три напряжения E _NR, E _NY и E _NB равны по величине, но электрически смещены друг от друга на 120 °.

Фазорная диаграмма звездообразного соединения показана ниже:

Стрелки на ЭДС и токе указывают направление, а не их фактическое направление в любой момент.

Сейчас,

Между любыми двумя линиями есть двухфазные напряжения.

По следам петли НРИН

Чтобы найти векторную сумму ENY и –ENR, мы должны перевернуть вектор ENR и сложить его с ENY, как показано на векторной диаграмме выше.

Следовательно,

Аналогично

Следовательно, при соединении звездой линейное напряжение в 3 раза больше фазного напряжения.

Соотношение между фазным током и линейным током при соединении звездой

Тот же самый ток течет через фазную обмотку, а также в линейный провод, поскольку он включен последовательно с фазной обмоткой.

Где будет фазный ток:

Линейный ток будет:

Следовательно, в трехфазной системе звездообразного соединения линейный ток равен фазному току.

9.3: Трехфазные соединения — Engineering LibreTexts

Можно сконфигурировать системы, использующие источники, подключенные треугольником или Y, с нагрузками, подключенными треугольником или Y. Следует отметить, что системы с треугольным соединением всегда представляют собой трехпроводные системы, в то время как системы с соединением по схеме Y могут использовать четвертый нейтральный провод (общая точка, к которой подключаются все три источника).

Однородные системы

Самые простые системы — это дельта-дельта и Y-Y. Мы будем называть их однородными системами, поскольку конструкции генератора и нагрузки схожи. Примеры показаны на рисунках \ (\ PageIndex {1} \) и \ (\ PageIndex {2} \) соответственно.

Рисунок \ (\ PageIndex {1} \): генератор, подключенный по схеме треугольник, с нагрузкой, подключенной по схеме треугольник (треугольник-треугольник). Рисунок \ (\ PageIndex {2} \): генератор с подключением по схеме Y и нагрузкой с подключением по схеме Y (ГГ). Показан дополнительный четвертый нейтральный провод от центра к центру.

В этих конфигурациях каждая ветвь нагрузки соответствует соответствующей ветви генератора. В конфигурации дельта-треугольник на рисунке \ (\ PageIndex {1} \) должно быть очевидно, что напряжение на любом плече нагрузки должно равняться напряжению соответствующего плеча генератора. Например, импеданс нагрузки, подключенной между \ (A ‘\) и \ (B’ \), должен соответствовать напряжению, подаваемому генератором, расположенным между \ (A \) и \ (B \), потому что \ (A \) непосредственно соединен с \ (A ‘\) так же, как \ (B \) с \ (B’ \).Точно так же для конфигурации YY на рисунке \ (\ PageIndex {2} \) ток через любую ветвь нагрузки должен быть равен току, протекающему через связанную ветвь генератора, поскольку нет других путей для тока между \ (A \) и \ (A ‘\), \ (B \) и \ (B’ \), а также \ (C \) и \ (C ‘\).

Поскольку нагрузка уравновешена и ветви генератора идентичны, за исключением их фазы, напряжение и ток (и, следовательно, мощности) для каждой ветви нагрузки должны быть одинаковыми, за исключением фаза.Это верно как для конфигурации Y-Y, так и для конфигурации дельта-дельта. Сложность здесь заключается в разнице между током или напряжением источника (или нагрузки) и линейным током или напряжением.

\ [\ text {Напряжение линии — это величина напряжения между любыми двумя проводниками, соединяющими источник с нагрузкой, за исключением земли или общего провода.} \ Nonumber \]

\ [\ text {Линейный ток — это величина тока, протекающего в любом проводнике, соединяющем источник с нагрузкой, за исключением земли или общего провода.} \ nonumber \]

Рассмотрим систему дельта-дельта на рисунке \ (\ PageIndex {1} \). Мы уже установили, что напряжение, развиваемое генератором \ (A, B \), должно быть таким же, как напряжение на нагрузке \ (A ‘, B’ \). Таким образом, напряжение, измеренное от проводника A, A ‘к проводнику B, B’, должно быть таким же, как напряжения источника и нагрузки. Другими словами, в конфигурации треугольник-треугольник все напряжения источника, нагрузки и линии одинаковы.

Мы также обнаружили, что токи источника и нагрузки должны быть одинаковыми для конфигурации треугольник-треугольник, однако это не означает, что ток, протекающий через провод, соединяющий \ (A \) с \ (A ‘\), должен быть такой же, как ток, протекающий через генератор или нагрузку.В конце концов, к \ (A ‘\) подключаются два провода нагрузки, а не только один. По определению, ток, протекающий через этот провод, является линейным током, и поэтому в конфигурации треугольник-треугольник линейный ток не совпадает с токами источника или нагрузки. Чтобы избежать путаницы, напряжение или ток, связанные с одной ветвью, называют фазным напряжением или током в зависимости от линейного напряжения или тока.

Обращаясь к конфигурации Y-Y на рисунке \ (\ PageIndex {2} \), мы видим противоположную ситуацию.Источник, нагрузка и линейный ток будут одинаковыми. С другой стороны, линейное напряжение состоит из двух генераторов, а не одного (например, от \ (A \) до \ (B \) или от \ (B \) до \ (C \)). Таким образом, для конфигурации Y-Y напряжения источника и нагрузки одинаковы, но они не равны линейному напряжению (и не в два раза, благодаря фазовому сдвигу).

Определение линейного напряжения и тока

Чтобы определить линейное напряжение для генератора, подключенного по схеме Y (и аналогично, линейный ток для генератора, подключенного по схеме треугольника), полезно изучить векторную диаграмму напряжений отдельных генераторов.Это показано на рисунке \ (\ PageIndex {3} \). У нас есть три напряжения одинаковой амплитуды, единственная разница между ними — их фаза. Каждый вектор отделен от других на 120 градусов. Далее, каждый отдельный генератор соединен из общей точки с одной из внешних точек \ (A \), \ (B \) и \ (C \). Линейное напряжение определяется как потенциал, существующий между любыми двумя этими тремя точками. Хотя можно просто вычесть напряжение одного генератора из другого, чтобы получить разницу, есть хорошее графическое решение, из которого мы можем вывести точную формулу для линейного напряжения с учетом напряжения генератора.

Рисунок \ (\ PageIndex {3} \): фазорная диаграмма Y-связного генератора

Мы начнем с сосредоточения внимания на втором и третьем квадрантах векторной диаграммы. Этот раздел перерисован на рисунке \ (\ PageIndex {4} \). В действительности для следующего доказательства можно использовать любые два вектора, но эта пара оказывается особенно удобной по ориентации.

Рисунок \ (\ PageIndex {4} \): Решение для линейного напряжения генератора с Y-соединением.

Для удобства использования приведем величину напряжения генератора к единице.Мы видим, что векторы \ (B \) и \ (C \) идеально разделяются горизонтальной осью; то, что находится над осью, идеально отражается под ней. В верхней части мы находим прямоугольный треугольник с гипотенузой единицы (темно-красный). Угол, который он образует с горизонталью, должен составлять половину угла между ним и вектором \ (C \). Это половина 120 градусов или 60 градусов. Поскольку сумма внутренних углов треугольника должна составлять 180 градусов, это означает, что третий угол должен составлять 30 градусов. Горизонтальный отрезок треугольника (темно-желтый или, может быть, «острая горчица») может быть определен, потому что мы знаем и гипотенузу, и противоположный угол.2} \ nonumber \]

\ [\ text {vertical} = \ sqrt {\ frac {3} {4}} \ nonumber \]

\ [\ text {vertical} = \ frac {1} {2} \ sqrt {3} \ nonumber \]

Вертикальная ножка идеально отражается под горизонтальной осью. Следовательно, интервал от \ (B \) до \ (C \) должен быть в два раза больше этого значения, или \ (\ sqrt {3} \). Поскольку напряжение, развиваемое на каждой ножке генератора, называется фазным напряжением генератора, мы можем сказать:

\ [\ text {Линейное напряжение для генератора, подключенного по схеме Y, в} \ sqrt {3} \ text {умножено на его фазное напряжение.} \ label {9.1} \]

Например, если фазное напряжение генератора, подключенного по схеме Y, составляет 120 вольт, линейное напряжение будет в \ (\ sqrt {3} \) раз больше, или примерно 208 вольт.

Для генератора, соединенного треугольником, то же самое верно для фазных и линейных токов, с доказательством, оставленным в качестве упражнения. То есть

\ [\ text {Линейный ток генератора, соединенного треугольником, равен} \ sqrt {3} \ text {умноженному на его фазный ток.} \ Label {9.2} \]

Те же самые отношения справедливы как для нагрузок, так и для источников, e.g., ток в ветви нагрузки, подключенной по схеме Y, будет таким же, как и линейный ток, а его фазное напряжение будет в \ (\ sqrt {3} \) раз меньше, чем линейное напряжение.

\ [\ text {В итоге: для конфигураций треугольником (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного тока на} \ sqrt {3} \ text {. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение} \ sqrt {3} \ text {больше, чем фазное напряжение.} \ nonumber \]

Для однородных систем, поскольку генератор и нагрузка используют одну и ту же конфигурацию, фазные напряжения и токи нагрузки должны быть идентичны таковым у генератора. Полезное средство запоминания состоит в том, что мощность, рассеиваемая в системе, должна равняться генерируемой мощности.

Пример \ (\ PageIndex {1} \)

Генератор с трехфазным соединением треугольником питает нагрузку с трехфазным соединением треугольником, как в системе, показанной на рисунке \ (\ PageIndex {1} \). Предположим, что фазное напряжение генератора составляет 120 В переменного тока (среднеквадратичное значение).Груз состоит из трех одинаковых ножек по 50 \ (\ Omega \) каждая. Определите линейное напряжение, напряжение фазы нагрузки, ток фазы генератора, линейный ток, ток фазы нагрузки и общую мощность, подаваемую на нагрузку.

Поскольку это однородная система (треугольник-треугольник), напряжение и ток фазы нагрузки такие же, как у генератора. Следовательно, напряжение фазы нагрузки также должно быть 120 вольт. Во-вторых, в конфигурации треугольником линейное напряжение равно фазному напряжению, снова 120 вольт.Ток фазы нагрузки определяется по закону Ома и будет среднеквадратичным значением, так как напряжение равно среднеквадратичному значению:

\ [i_ {phase} = \ frac {v_ {phase}} {Z_ {load}} \ nonumber \]

\ [i_ {phase} = \ frac {120 V} {50 \ Omega} \ nonumber \]

\ [i_ {phase} = 2,4 A \ nonumber \]

Фазный ток генератора должен быть одинаковым, поскольку генератор и нагрузка имеют одинаковую конфигурацию. Для дельта-конфигураций линейный ток в \ (\ sqrt {3} \) раз больше, чем фазный ток, таким образом,

\ [i_ {line} = \ sqrt {3} \ times i_ {phase} \ nonumber \]

\ [i_ {line} = \ sqrt {3} \ times 2.2 \ раз 50 \ Омега \ nonumber \]

\ [P_ {total} = 864 Вт \ nonumber \]

Это эквивалентно примерно 1,2 л.с. Мы также могли бы вычислить фазную мощность нагрузки, используя квадрат фазного напряжения, деленный на сопротивление нагрузки, или умножая фазное напряжение на фазный ток. Поскольку это чисто резистивная нагрузка, здесь нет фазового угла и, следовательно, нет коэффициента мощности, о котором нужно было бы беспокоиться.

Пример \ (\ PageIndex {2} \)

Трехфазный генератор с Y-подключением питает трехфазную нагрузку с Y-подключением, аналогично системе, показанной на рисунке \ (\ PageIndex {2} \).Предположим, что фазное напряжение генератора составляет 220 В переменного тока (среднеквадратичное значение). Груз состоит из трех одинаковых ножек по 100 \ (\ Omega \) каждая. Определите линейное напряжение, напряжение фазы нагрузки, ток фазы генератора, линейный ток, ток фазы нагрузки и общую мощность, подаваемую на нагрузку.

Это однородная (Y-Y) система, поэтому напряжение и ток фазы нагрузки такие же, как у генератора. Следовательно, напряжение фазы нагрузки должно быть 220 вольт. В конфигурации Y линейное напряжение равно фазному напряжению, умноженному на \ (\ sqrt {3} \).

\ [v_ {строка} = \ sqrt {3} \ times v_ {фаза} \ nonumber \]

\ [v_ {line} = \ sqrt {3} \ times 220V \ nonumber \]

\ [v_ {line} \ приблизительно 381 V \ nonumber \]

Ток фазы нагрузки определяется по закону Ома и будет среднеквадратичным значением, поскольку напряжение является среднеквадратичным. Это то же самое, что и фазный ток генератора, и линейный ток.

\ [i_ {phase} = \ frac {v_ {phase}} {Z_ {load}} \ nonumber \]

\ [i_ {phase} = \ frac {220 V} {100 \ Omega} \ nonumber \]

\ [i_ {phase} = 2.2A \ nonumber \]

Общую мощность можно найти, используя базовый степенной закон, поскольку нагрузка является чисто резистивной, и у нас есть среднеквадратичные значения. В этом случае мы будем использовать ток, умноженный на напряжение, для изменения темпа.

\ [P_ {total} = 3 \ times i_ {фаза} \ times v_ {фаза} \ nonumber \]

\ [P_ {total} = 3 \ times 2.2 A \ times 220 V \ nonumber \]

\ [P_ {total} = 1452 Вт \ nonumber \]

Это всего-навсего 2 ХП. Опять же, это чисто резистивная нагрузка и фазовый угол отсутствует.Таким образом, коэффициент мощности равен единице, причем действительная и кажущаяся мощности одинаковы.

Пример \ (\ PageIndex {3} \)

Для системы, показанной на рисунке \ (\ PageIndex {5} \), определите общую полную и активную мощность, подаваемую на нагрузку. Также найдите напряжение в сети. Фазовое напряжение источника составляет 240 вольт (среднеквадратичное значение) при 60 Гц.

Рисунок \ (\ PageIndex {5} \): Схема для примера \ (\ PageIndex {3} \).

Учитывая тот факт, что все три опоры груза находятся вместе в одной общей точке (земле), это должна быть система Y-Y.Следовательно, мы знаем, что линейное напряжение должно быть в \ (\ sqrt {3} \) раз больше фазного напряжения генератора.

\ [v_ {строка} = \ sqrt {3} \ times v_ {фаза} \ nonumber \]

\ [v_ {line} = \ sqrt {3} \ times 240 В \ nonumber \]

\ [v_ {line} \ приблизительно 416 В RMS \ nonumber \]

Это однородная система (Y-Y), поэтому мы также знаем, что напряжение нагрузки равно напряжению генератора или 240 вольт RMS. Отсюда мы можем найти ток нагрузки (линейный ток должен быть того же значения, потому что это нагрузка, подключенная по схеме Y).2 \ times R_ {load} \ nonumber \]

\ [P = 3 \ times 4.8A 2 \ times 40 \ Omega \ nonumber \]

\ [P = 2765W \ nonumber \]

Компьютерное моделирование

Схема примера \ (\ PageIndex {3} \) достойна моделирования. Первое, что нужно сделать, это определить подходящее значение индуктивности для достижения реактивного сопротивления \ (j40 \ Omega \). Учитывая частоту источника 60 Гц, получается примерно 80 мГн. Схема построена, как показано на рисунке \ (\ PageIndex {6} \).Среднеквадратичное фазовое напряжение источника 240 вольт эквивалентно пиковому напряжению приблизительно 340 вольт. Положения катушки индуктивности и резистора в каждой ножке поменялись местами по причине, которая вскоре станет очевидной.

Рисунок \ (\ PageIndex {6} \): Эквивалентная система, показанная на рисунке \ (\ PageIndex {5} \) в симуляторе.

Непосредственный интерес представляет проверка временных сдвигов и амплитуд фазных напряжений. Они соответствуют узлам 1, 2 и 3. В этой конфигурации напряжение фазы нагрузки равно напряжению фазы генератора, поэтому они должны быть пиковыми 340 вольт и разделены на 120 градусов или 1/3 цикла.

Выполняется анализ переходных процессов, вычерчивая интересующие узловые напряжения. Результат показан на рисунке \ (\ PageIndex {7} \). Напряжения в точности такие, как ожидалось, и график отлично согласуется с теоретическим графиком на рис. 9.2.4.

Рисунок \ (\ PageIndex {7} \): три напряжения нагрузки, смоделированные из рисунка \ (\ PageIndex {6} \).

Теперь проверяем сетевое напряжение. Было рассчитано, что это среднеквадратичное значение 416 вольт, или примерно 588 вольт пикового значения. Постпроцессор используется для отображения результата: напряжение узла 1 минус напряжение узла 2.Это показано на рисунке \ (\ PageIndex {8} \). Опять же, результаты такие, как ожидалось, с пиком чуть ниже 600 вольт.

Наконец, мы исследуем истинную мощность нагрузки. Возможно, самый простой способ сделать это — определить напряжение на резистивной части нагрузки. Из предыдущих работ мы знаем, что истинная мощность связана только с сопротивлением, а не с реактивным сопротивлением. Таким образом, все, что нам нужно сделать, это измерить пиковое напряжение на резисторе. Отсюда мы находим его эквивалент RMS, возводим его в квадрат и делим на номинал резистора.Это дает нам истинную мощность нагрузки на одну ногу. Для общей мощности просто утроим результат. Получить напряжение на резисторе легко, если резистор заземлен. В этом случае это просто напряжение на узле, к которому подключен резистор. Вот почему позиции индуктора и резистора были поменяны местами при моделировании. Поскольку они подключены последовательно, это не влияет на общий импеданс нагрузки, однако новая схема позволяет нам получать напряжение резистора напрямую, вместо того, чтобы полагаться на дифференциальное напряжение, полученное через постпроцессор.

Выполняется еще один анализ переходных процессов, на этот раз строится график напряжения на одном из нагрузочных резисторов; а именно узел 4. Результат показан на рисунке \ (\ PageIndex {9} \). Пик этой формы волны составляет 271,5 вольт, или около 192 вольт (среднеквадратичное значение). Если возвести это в квадрат и разделить на 40 \ (\ Omega \), получим чуть более 921 ватт на каждую ногу, то есть в общей сложности около 2765 ватт, как и ожидалось.

Рисунок \ (\ PageIndex {8} \): одно из линейных напряжений, смоделированное из рисунка \ (\ PageIndex {6} \). Рисунок \ (\ PageIndex {9} \): моделируемое напряжение на одном из нагрузочных резисторов на рисунке \ (\ PageIndex {6} \).

Гетерогенные системы

Системы, настроенные как дельта-Y и Y-дельта, кажутся немного более сложными, чем однородные системы. Мы будем называть их гетерогенными системами, так как структуры генератора и нагрузки противоположного типа. Примеры показаны на рисунках \ (\ PageIndex {10} \) и \ (\ PageIndex {11} \) соответственно.

Рисунок \ (\ PageIndex {10} \): генератор, подключенный по схеме треугольник, с нагрузкой, подключенной по схеме Y (треугольник-Y). Рисунок \ (\ PageIndex {11} \): генератор с подключением по схеме Y и нагрузкой, подключенной треугольником. (Ydelta).

Эти системы вовсе не так сложны, как думают некоторые; все, что вам нужно сделать, это запомнить операторы \ ref {9.1} и \ ref {9.2}. Действительно, здесь стоит повторить суммирование:

\ text {Для конфигураций треугольником (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного тока на} \ sqrt {3} \ text {. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение} \ sqrt {3} \ text {больше, чем фазное напряжение.} \ nonumber \]

Анализ этих систем можно рассматривать как двухэтапный процесс. Сначала определите линейное напряжение и ток от генератора или нагрузки; и во-вторых, переход от линии к другой стороне (нагрузке или генератору). Если возникнет путаница, помните, что генерируемая мощность должна равняться мощности рассеиваемой или доставленной.

На рисунке \ (\ PageIndex {10} \) линейное напряжение равно фазному напряжению генератора. Нагрузка подключена по схеме Y, поэтому на каждой ветви напряжение линии делится на \ (\ sqrt {3} \).Исходя из этого, можно вычислить каждое плечо тока нагрузки. Обратите внимание, что линейный ток равен току нагрузки. Фазный ток генератора равен линейному току, деленному на \ (\ sqrt {3} \).

На рисунке \ (\ PageIndex {11} \) линейное напряжение равно \ (\ sqrt {3} \), умноженному на фазное напряжение генератора. Нагрузка соединена треугольником, поэтому на каждой ножке отображается линейное напряжение. Зная это, можно вычислить каждое плечо тока нагрузки. Кроме того, линейный ток равен фазному току генератора, а фазный ток нагрузки будет равен линейному току, деленному на \ (\ sqrt {3} \).{\ circ} \) \ (\ Omega \), определяет фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и общую мощность, подаваемую на нагрузку.

Генератор подключен по схеме треугольника, поэтому линейное напряжение равно фазному напряжению генератора, или 230 вольт. Нагрузка, подключенная по схеме Y, будет видеть фазное напряжение, уменьшенное в \ (\ sqrt {3} \) раз.

\ [v_ {load} = \ frac {v_ {line}} {\ sqrt {3}} \ nonumber \]

\ [v_ {load} = \ frac {230 В} {\ sqrt {3}} \ nonumber \]

\ [v_ {load} \ около 132.{\ circ} \ Omega} \ nonumber \]

\ [i_ {load} \ приблизительно 0,664 A RMS \ nonumber \]

При Y-соединении линейный ток должен быть таким же, как ток фазы нагрузки, или 0,664 ампера. Для соединений треугольником линейный ток в \ (\ sqrt {3} \) раз больше, чем фазный ток, поэтому фазный ток генератора должен быть в \ (\ sqrt {3} \) раз меньше.

\ [i_ {gen} = \ frac {i_ {line}} {\ sqrt {3}} \ nonumber \]

\ [i_ {gen} = \ frac {0.664A} {\ sqrt {3}} \ nonumber \]

\ [i_ {gen} \ около 0.2 \ times 200 \ Omega \ nonumber \]

\ [P_ {total} = 264 Вт \ nonumber \]

В качестве перекрестной проверки вырабатываемая мощность составляет:

\ [P_ {total} = 3 \ times i_ {gen} \ times v_ {gen} \ nonumber \]

\ [P_ {total} = 3 \ times 0,383A \ times 230 V \ nonumber \]

\ [P_ {total} = 264 Вт \ nonumber \]

Выработанная мощность равна рассеиваемой мощности.

Пример \ (\ PageIndex {5} \)

Система Y-треугольник, подобная показанной на рисунке \ (\ PageIndex {11} \), имеет фазное напряжение генератора 100 В (среднеквадратичное значение) при 60 Гц.Если нагрузка имеет величину 50 \ (\ Omega \) с запаздывающим коэффициентом мощности 0,8, определите ток фазы генератора, линейное напряжение, напряжение фазы нагрузки, ток фазы нагрузки и общую истинную мощность, подаваемую на нагрузку. .

Генератор, соединенный по схеме Y, создает линейное напряжение, равное фазному напряжению генератора, умноженному на \ (\ sqrt {3} \). Это также напряжение фазы нагрузки, поскольку оно соединено треугольником.

\ [v_ {строка} = \ sqrt {3} \ times v_ {фаза} \ nonumber \]

\ [v_ {line} = \ sqrt {3} \ times 100 V \ nonumber \]

\ [v_ {line} \ около 173.2В RMS \ nonumber \]

Нагрузка, подключенная по схеме треугольника, будет видеть фазное напряжение, такое же, как линейное напряжение, или 173,2 вольт. Отсюда мы можем определить ток нагрузки.

\ [i_ {load} = \ frac {v_ {phase}} {Z_ {load}} \ nonumber \]

\ [i_ {load} = \ frac {173.2V} {50 \ Omega} \ nonumber \]

\ [i_ {load} \ приблизительно 3,464A RMS \ nonumber \]

Поскольку нагрузка подключена по схеме треугольника, линейный ток равен времени тока нагрузки \ (\ sqrt {3} \). Фазный ток генератора будет таким же, как и линейный ток.2 \ times 40 \ Omega \ nonumber \]

\ [P_ {total} = 1440 Вт \ nonumber \]

Мы также можем найти полную мощность и использовать коэффициент мощности.

\ [P_ {total} = 3 \ times v_ {load} \ times i_ {load} PF \ nonumber \]

\ [P_ {total} = 3 \ умножить на 173,2 В \ умножить на 3,464 А \ умножить на 0,8 \ nonumber \]

\ [P_ {total} = 1440 Вт \ nonumber \]

Для перекрестной проверки сравните рассеиваемую мощность с генерируемой.

\ [P_ {total} = 3 \ times v_ {gen} \ times i_ {gen} \ times PF \ nonumber \]

\ [P_ {total} = 3 \ умножить на 100В \ умножить на 6А \ умножить на 0.8 \ nonumber \]

\ [P_ {total} = 1440 Вт \ nonumber \]

Еще раз о расчетах трехфазного переменного тока — Dataforth

Преамбула

Это примечание по применению является продолжением Указания по применению AN109, которые содержат систему переменного тока определения и основные правила расчетов с примерами. Читателю предлагается ознакомиться с AN109, Ссылки 3, 4 и 5 в качестве фона для данной инструкции по применению.

Трехфазная система напряжения

Системы трехфазного напряжения состоят из трех синусоидальные напряжения равной величины, равной частоты и разделены на 120 градусов.

На рисунке 1 показаны функции косинуса в реальном времени и соответствующее обозначение вектора для трехфазного межфазного система напряжения с линейным напряжением V12 в качестве эталона.

Обзор свойств системы трехфазного напряжения

Трехфазные питающие напряжения и системы нагрузки имеют два базовые комплектации; 4-проводная звезда и 3-проводная «Дельта». На рисунке 2 показан базовый трехфазный четырехпроводной звездой. сконфигурированная система напряжения с V1N в качестве эталона и На рисунке 3 показана трехпроводная система напряжения, настроенная по схеме «треугольник». с V12 в качестве ссылки соответственно.

Важные определения, условные обозначения и правила вычислений как для 3-фазной 4-проводной схемы «звезда», так и для 3-проводной схемы «треугольник» сконфигурированные системы напряжения описаны в следующих список без «беспорядочной» векторной математики.

Ориентация фазора:
По определению, все синусоидальные векторы вращаются в против часовой стрелки с {1-2-3} или {3-2-1} последовательность и углы измеряются как положительные в против часовой стрелки.4-проводная 3-фазная система звезды показан на рисунке 2 с V1N, выбранным в качестве эталона. В линейные напряжения составляют V12, V23 и V32 с линейно- нейтральные напряжения показаны как V1N, V2N и V3N. Фигура 3 показаны правильные линейные векторные напряжения для 3-х фазного преобразователя. фаза 3-проводная конфигурация треугольника с выбранным вектором V12 в качестве ссылки. Примечание: любой вектор может быть выбран как ссылка, выбор совершенно произвольный.

Чередование фаз:
Последовательность фаз определяет последовательную синхронизацию, по которой каждый вектор линейного напряжения отстает друг от друга линейное напряжение вектор против часовой стрелки. Рисунки 1, 2 и 3 показана последовательность фаз {1-2-3}. Последовательность {1-2-3} означает, что V12 опережает V23 на 120 градусов, а V23 опережает V31 на 120 градусов. Кроме того, V1N опережает V2N на 120 градусов, а V2N опережает V3N на 120 градусов.это необходимо установить последовательность фаз перед выполнением любые вычисления для того, чтобы вычисленный вектор вектора углы могут быть правильно расположены друг относительно друга.

Есть только две допустимые последовательности фаз; {1-2-3} последовательность и последовательность {3-2-1}. Обе эти фазы последовательность определяется тем, как 3-фазный трансформатор линии питания (L1, L2, L3) подключены и промаркированы.На рисунке 4 показана последовательность {3-2-1} относительно {1-2-3} последовательность. Примечание: последовательность фаз может быть можно изменить, просто поменяв местами соединения любых двух из трех (L1, L2, L3) линий питания; однако это следует делать только в соответствии со всеми надлежащими нормы и правила, а также одобрение заводского инжиниринга сотрудники.

Индексы:
Соблюдение правильного порядка нижних индексов для всех векторов количество — один из важнейших ключей к успеху 3-х фазные расчеты.На рисунке 4 показан правильный нижний индекс порядок для каждой из двух различных последовательностей фаз. Для последовательность {1-2-3}, правильный порядок индексов [12], [23] и [31]; тогда как правильный порядок нижнего индекса для последовательность {3-2-1} — это [32], [21] и [13].

Нижний индекс:
После определения последовательности фаз и правильного индексы обозначены, расчеты по этим индексов вместе с условными обозначениями, принятыми для Версия закона Ома для переменного тока предотвратит угловые ошибки.

По соглашению, V12 — это падение напряжения вектора плюс (1) к минус (2) в направлении тока, протекающего из точки (1) к точке (2) и равен этому току, умноженному импедансом переменного тока между точками (1) и (2). Для пример в векторной записи;

Сложение / вычитание фазора:
Правильная запись в нижнем индексе устанавливает правильный метод для векторного сложения / вычитания векторов.На рисунке 2 фазоры линейного напряжения в этой трехфазной {1-2-3} Последовательная 4-проводная система «звезда» состоит из линейно-нейтральной векторные напряжения следующим образом;

Если среднеквадратичные напряжения между фазой и нейтралью равны (стандарт сбалансированной системы), то приведенные выше уравнения показывают, что все линейные напряжения питания фазора — фаза-нейтраль. напряжения, умноженные на 3, и подводят фазу к нейтрали векторы напряжения на 30 градусов .Например, стандартный 4-проводная трехфазная система звездой с фазным напряжением 120 вольт и V1N, выбранный в качестве опорного вектора на ноль градусов имеет линейное напряжение;

V12 = 208∠ 30 °; V23 = 208∠ -90 °; V31 = 208∠ 150 °.

Важная концепция: Конфигурация трехфазного трехпроводного треугольника система уравновешивания напряжений фактически не имеет линейно- нейтральные напряжения, такие как звездочка.Однако дельта-фазное напряжение, как показано на Рисунке 3, все еще может быть построенный из теоретического набора сбалансированных 3-фазных линейные напряжения, как показано выше. В отношения с этими теоретическими напряжениями чрезвычайно полезно для определения углов дельта-фазора.

Процедуры, инструкции и формулы расчетов

Следующий список процедур, рекомендаций и формул проиллюстрировать схему расчета трехфазного фазора количества с использованием типовых данных на паспортной табличке, взятых из отдельные единицы нагрузки.

Расчеты производятся следующим образом;

Идентификация чередования фаз; {1-2-3} или {3-2-1}
Определить индексы; [12], [23], [31] или [32], [21], [13]
Предположим, что линейные токи L1, L2, L3 текут к нагрузкам. и нейтральный (обратный) ток течет к источнику питания.
Протекает ток нагрузки и падение напряжения должно соответствовать обозначения подстрочных индексов, как определено ранее.
Используйте «Закон Ома для переменного тока» для расчета величин и углы каждой отдельной однофазной нагрузки Текущий. Просмотрите AN109 Dataforth, ссылка 1.
Важные понятия: Линейные токи как звезды, так и звезды. 3-фазные нагрузки, сбалансированные по схеме треугольника, рассчитываются с использованием следующие отношения;
1. Входная мощность переменного тока = 3 x (Vline) x (Iline) x PF
2. PF — косинус угла, на который прямая токи опережают или отстают от линейного напряжения.Фактическое трехфазное напряжение фаза-нейтраль существуют в конфигурациях звезды; тогда как они теоретически в дельта-конфигурациях. Например, принять любую сбалансированную 3-фазную нагрузку на 10 ампер линейного тока и коэффициент мощности запаздывания 0,866 (30 °). Если системная последовательность {1-2-3} и V12 является справочным, тогда I1 = 10∠ -60 °; I2 = 10∠ 180 °; I3 = 10∠ 60 °.
Определите количество треугольников мощности; Вт «P» и VAR «Q» для каждой нагрузки. Ссылка на обзор 1.
Суммировать ранее рассчитанную индивидуальную нагрузку токи с использованием правильной записи индекса для определения каждая отдельная строка тока
Наконец, просуммируйте все отдельные треугольники мощности нагрузки. количества (Вт «P» и VAR «Q») для определения количество треугольников мощности системы; P, Q и PF.Это этот последний шаг, который определяет, как загружается система население ведет себя.

Примеры расчетов

В следующих примерах предполагается типичное напряжение 208–120 вольт. трехфазная конфигурация 4 звезды с чередованием фаз из {1 2 3}, и V12 выбран в качестве ссылки. Это звёздочка система; однако нагрузки, подключенные между каждым из три отдельные линии питания (L1, L2, L3) составляют 208-вольтная 3-проводная конфигурация, треугольник.Три категории однофазные нагрузки предполагаются для следующих расчеты. Эти категории идентичны тем определено в Руководстве по применению AN109 (Ссылка 1) и перечисленные ниже с необходимыми данными паспортной таблички.

Выходные киловатты; КВт, КПД (опция), PF = 1
лошадиных сил на выходе; HP, КПД, P
Входная кВА; КВА, ПФ, КПД 100%.

В таблице 1 приведены расчетные значения для предполагаемого население этих нагрузок. Читатели должны проверить эти расчеты. Dataforth предлагает интерактивный Excel рабочая книга, аналогичная таблице 1, которая автоматически рассчитывает все параметры трехфазной системы. Видеть Ссылка 2 для загрузки загрузите этот файл Excel.

Пример расчета для нагрузок от линии к нейтрали
Трехфазные звездообразные системы с нейтралью могут иметь одинаковые или неравные отдельные однофазные нагрузки, подключенные между любой из линий питания (L1, L2, L3) и нейтраль.Системы сбалансированы, если все нагрузки между фазой и нейтралью идентичны.

На рисунке 5 показаны три группы однофазных линейно-нейтральных нагрузки, подключенные по трехфазной системе «звезда». Эта конфигурация однофазных нагрузок может быть рассматривается как составная несбалансированная звездообразная нагрузка

На рисунке 6 показаны три группы однофазных межфазных нагрузки, подключенные по трехфазной системе «звезда».Этот конфигурацию однофазных нагрузок можно рассматривать как композитная несбалансированная дельта-нагрузка

На рисунке 7 показаны группа сбалансированных нагрузок звездой и группа. сбалансированных дельта-нагрузок, обе из которых (могут быть) подключен по трехфазной системе звездой.

Таблица 1 представляет собой составной набор расчетных результатов для конфигурации, показанные на рисунках 5, 6 и 7.Эти расчеты предполагают произвольную популяцию типа загружает ранее определенные и использует все правила, процедуры и определения, как показано выше. В Результаты системы из расчетов Таблицы 1 показаны ниже. в таблицах 2 и 3.

Напряжение сети V12 (208 при нулевом градусе) является опорным для указанные выше текущие углы.

Читателям предлагается проверить эти расчеты.

Как упоминалось выше, Dataforth предоставляет интерактивный Файл Excel, предназначенный для энтузиастов-исследователей. при расчете системных токов и сопутствующей мощности уровни. Этот файл позволяет исследователю ввести паспортную табличку. данные по всем системным нагрузкам; после этого все линии тока векторов и мощности рассчитываются автоматически. «Интерактивная рабочая тетрадь Excel для трех- Расчет фаз переменного тока »можно загрузить с Веб-сайт Dataforth, см. Ссылку 2.

Рисунок 8 — иллюстрация изолированного истинного значения Dataforth. Модуль ввода RMS, SCM5B33. Эта функция также доступен в упаковке на DIN-рейку; DSCA33. Dataforth имеет набор модулей преобразования сигналов, спроектированных специально для измерения высоковольтных среднеквадратичных значений переменного тока параметры с использованием встроенного затухания. Читатель рекомендуется посетить ссылки 1, 6, 7 и 8.Ссылки на Dataforth Читателю предлагается посетить веб-сайт Dataforth и изучить их полную линейку изолированного преобразования сигнала модули и соответствующие примечания по применению, см. ссылки показано ниже.

Dataforth Corp., http://www.dataforth.com
Dataforth Corp., AN110 Excel Интерактивная работа Книга для расчета трехфазного переменного тока
Dataforth Corp., Примечание по применению AN109, Измерения однофазного переменного тока
Dataforth Corp., AN109 Excel Интерактивная работа Книга для расчетов однофазного переменного тока
контролируется Национальной пожарной службой Агентство по охране, NFPA
Dataforth Corp., Система аттенюатора напряжения SCMVAS,
Dataforth Corp., серия модульных формирователей сигналов с истинным среднеквадратичным значением SCM5B33
Dataforth Corp., серия DSCA33 формирователей сигналов True RMS для монтажа на DIN-рейку

Типы электрических услуг и напряжения

На этой странице описаны различные типы коммунальных электросетей и напряжения питания.Номинальное напряжение питания системы, указанное ниже, может изменяться на ± 10% или более. Модели счетчиков WattNode ^® доступны в семи различных версиях, которые охватывают весь диапазон типов электрических услуг и напряжений. Новый WattNode Wide-Range Modbus охватывает 100-600 В переменного тока, звезда и треугольник, однофазный и трехфазный с одной моделью. Измерители и трансформаторы тока предназначены для использования в системах с частотой 50 или 60 Гц.

Классификация электрических услуг

Системы распределения электроэнергии переменного тока можно классифицировать по следующим признакам:

Частота: 50 Гц или 60 Гц
Количество фаз: одно- или трехфазное
Количество проводов: 2, 3 или 4 (без учета защитного заземления)
Нейтраль присутствует:
- Система, соединенная звездой , имеет нейтраль
- Системы, подключенные по схеме Delta , обычно не имеют нейтрали
Классы напряжения: (ANSI C84.1-2016)
- Низкое напряжение: 1000 В или менее
- Среднее напряжение: более 1000 В и менее 100 кВ
- Высокое напряжение: больше 100 кВ, но равно или меньше 230 кВ
- Сверхвысокое напряжение : более 230 кВ, но менее 1000 кВ
- Сверхвысокое напряжение : не менее 1000 кВ

Линия-нейтраль, звезда	Линейное напряжение звезды или треугольника
120	208
120 ¹	240
230	400
240	415
277	480
347	600

Линейное напряжение в трехфазных системах обычно равно 1.В 732 раза больше напряжения между фазой и нейтралью:
В симметричной трехфазной электрической системе напряжения между фазой и нейтралью должны быть одинаковыми, если нагрузка сбалансирована.
Примечание: 120 ¹ Относится к трехфазной четырехпроводной схеме подключения по схеме «треугольник».

Общие электрические услуги и нагрузка

На следующих чертежах символы катушек представляют вторичную обмотку сетевого трансформатора или другого понижающего трансформатора. Нормы электрических правил в большинстве юрисдикций требуют, чтобы нейтральный проводник был соединен (подключен) с заземлением на входе в электрические сети.

Однофазный трехпроводной

Также известна как система Эдисона, с расщепленной фазой или нейтралью с центральным отводом. Это наиболее распространенная услуга по проживанию в Северной Америке. Линия 1 к нейтрали и линия 2 к нейтрали используются для питания 120-вольтного освещения и подключаемых нагрузок. Линия 1 — линия 2 используется для питания однофазных нагрузок на 240 вольт, таких как водонагреватель, электрическая плита или кондиционер.

Трехфазная четырехпроводная звезда

Наиболее распространенное электрическое обслуживание коммерческих зданий в Северной Америке — это звезда на 120/208 В, которая используется для питания 120-вольтных нагрузок, освещения и небольших систем отопления, вентиляции и кондиционирования воздуха.В более крупных объектах напряжение составляет 277/480 вольт и используется для питания однофазного освещения на 277 вольт и больших нагрузок HVAC. В западной Канаде распространено напряжение 347/600 В.

Трехфазный трехпроводной, треугольник

Используется в основном на промышленных предприятиях для обеспечения питания нагрузок трехфазных электродвигателей, а также в системах распределения электроэнергии. Номинальное рабочее напряжение составляет 240, 400, 480, 600 и выше.

Загрузить: Типы электрических служб и напряжение (AN-129) (PDF, 3 страницы)

Необычные электрические услуги

Трехфазный, четырехпроводной, треугольник

Также известна как система дельт с высоким или диким концом.Используется на старых производственных предприятиях с нагрузкой в основном трехфазными двигателями и примерно 120-вольтовым однофазным освещением и розетками. Подобно трехфазной трехпроводной схеме, описанной выше, но с центральным ответвлением на одной из обмоток трансформатора для создания нейтрали для однофазных нагрузок на 120 вольт. Двигатели подключены к фазам A, B и C, а однофазные нагрузки подключены к фазе A или C и к нейтрали. Фаза B, высокий или дикий полюс, не используется, так как напряжение на нейтрали составляет 208 вольт.

Трехфазный двухпроводной, заземленный в угол треугольник

Используется для снижения затрат на электромонтаж за счет использования служебного кабеля только с двумя изолированными проводниками, а не с тремя изолированными проводниками, используемыми в обычном трехфазном служебном входе.

Международные системы распределения электроэнергии

Описание	L – N Vac	L – L Vac	Страны	Модели с ватт-узлом (звезда или треугольник)
1-фазный, 2-проводный 120 В с нейтралью	120	–	США	3Y-208
1-фазный, 2-проводный 230 В с нейтралью	230	–	ЕС, прочие	3Y-400
1-фазный, 2-проводный 208 В (без нейтрали)	–	208	США	3D-240
1-фазный, 2-проводный 240 В (без нейтрали)	–	240	США	3D-240
1-фазный, 3-проводный 120/240 В	120	240	США	3Y-208
3-фазный, 3-проводный, 208 В, треугольник (без нейтрали)	–	208	США	3D-240
3-фазный, 3-проводный 230 В, треугольник (без нейтрали)	–	230	Норвегия	3D-240
3-фазный, 3-проводный, 400 В, треугольник (без нейтрали)	–	400	ЕС, прочие	3D-400
3-фазный, 3-проводный 480 В, треугольник (без нейтрали)	–	480	США	3D-480
3-фазный, 3-проводный, 600 В, треугольник (без нейтрали)	–	600	США, Канада	нет ¹
3-фазный, 4-проводный 208Y / 120 В	120	208	США	3Y-208, 3D-240
3 фазы, 4 провода 400Y / 230 В	230	400	ЕС, прочие	3Y-400, 3D-400
3-фазный, 4-проводный 415Y / 240 В	240	415	Австралия	3Y-400, 3D-400
3-фазный, 4-проводный 480Y / 277 В	277	480	США	3Y-480, 3D-480
3-фазный, 4-проводный 600Y / 347 В	347	600	США, Канада	3Y-600
3-фазный 4-проводный Delta 120/208/240 Wild Phase	120, 208	240	США	3D-240
3-фазный 4-проводный треугольник 240/415/480 Wild Phase	240, 415	480	США	3D-480
Трехфазное соединение, заземленное треугольником 208/240	–	240	США	3D-240
Трехфазное соединение, заземленное треугольником 415/480	–	480	США	3D-480

¹ Используя трансформаторы напряжения (ТН), счетчики WattNode могут измерять дельта-сигналы 600 В, а также сети среднего и высокого напряжения.