Формула мощности через напряжение и сопротивление: Закон ома | Онлайн калькулятор

формула, расчёт силы тока, напряжения и сопротивления

Напряжение, сопротивление, ток и мощность.

Электричество само по себе невидимо, хотя от этого его опасность ничуть не меньше. Даже наоборот: как раз потому и опаснее. Ведь если бы мы его видели, как видим, например, воду, льющуюся из крана, то наверняка бы избежали множества неприятностей.

Вода. Вот она, водопроводная труба, и вот закрытый кран. Ничего не течет, не капает. Но мы точно знаем: внутри вода. И если система исправно работает, то вода эта там находится под давлением. 2, 3 атмосферы, или сколько там? Неважно. Но давление там есть, иначе система бы не работала. Где-то гудят насосы, гонят воду в систему, создают это самое давление.

А вот наш провод электрический. Где-то далеко, на другом конце тоже гудят генераторы, вырабатывают электричество. И в проводе от этого тоже давление. Нет-нет, не давление, конечно, тут в этом проводе напряжение. Оно тоже измеряется, но в своих единицах: в вольтах.

Давит в трубах на стенки вода, никуда не двигаясь, ждет, когда найдется выход, чтобы ринуться туда мощным потоком. И в проводе молча ждет напряжение, когда замкнется выключатель, чтобы потоки электронов двинулись выполнять свое предназначение.

И вот открылся кран, потекла струя воды. По всей трубе течет, двигаясь от насоса к расходному крану. А как только замкнулись контакты выключателя, в проводах потекли электроны. Что это за движение? Это ток. Электроны текут. И это движение, этот ток тоже имеет свою единицу измерения: ампер.

И еще есть сопротивление. Для воды это, образно говоря, размер отверстия в выпускном кране. Чем больше отверстие, тем меньше сопротивление движению воды. В проводах почти также: чем больше сопротивление провода, тем меньше ток.

Вот, как-то так, если образно представлять себе основные характеристики электричества. А с точки зрения науки все строго: существует так называемый закон Ома. Гласит он следующим образом: I = U/R.
I – сила тока. Измеряется в амперах.
U – напряжение. Измеряется в вольтах.
R – сопротивление. Измеряется в омах.

Есть еще одно понятие – мощность, W. С ним тоже просто: W = U*I. Измеряется в ваттах.

Собственно, это вся необходимая и достаточная для нас теория. Из этих четырех единиц измерения в соответствии с вышеприведенными двумя формулами можно вывести некоторое множество других:

№	Задача	Формула	Пример
1	Узнать силу тока, если известны напряжение и сопротивление.	I = U/R	I = 220 в / 500 ом = 0.44 а.
2	Узнать мощность, если известны ток и напряжение.	W = U*I	W = 220 в * 0.44 а = 96.8 вт.
3	Узнать сопротивление, если известны напряжение и ток.	R = U/I	R = 220 в / 0. 44 а = 500 ом.
4	Узнать напряжение, если известны ток и сопротивление.	U = I*R	U = 0.44 а * 500 ом = 220 в.
5	Узнать мощность, если известны ток и сопротивление.	W = I 2 *R	W = 0.44 а * 0.44 а * 500 ом = 96.8 вт.
6	Узнать мощность, если известны напряжение и сопротивление.	W = U 2 /R	W = 220 в * 220 в / 500 ом = 96.8 вт.
7	Узнать силу тока, если известны мощность и напряжение.	I = W/U	I = 96.8 вт / 220 в = 0,44 а.
8	Узнать напряжение, если известны мощность и ток.	U = W/I	U = 96.8 вт / 0.44 а = 220 в.
9	Узнать сопротивление, если известны мощность и напряжение.	R = U 2 /W	R = 220 в * 220 в / 96.8 вт = 500 ом.
10	Узнать сопротивление, если известны мощность и ток.	R = W/I 2	R = 96.8 вт / (0,44 а * 0,44 а) = 500 ом.

Ты скажешь: – Зачем мне это все надо? Формулы, цифры. Я ж не собираюсь заниматься расчетами.

А я так отвечу: – Перечитай предыдущую статью Электроснабжение. Основы.. Как можно быть уверенным, не зная простейших истин и расчетов? Хотя, собственно, в бытовом практическом плане наиболее интересна только формула 7, где определяется сила тока при известных напряжении и мощности. Как правило, эти 2 величины известны, а результат (сила тока) безусловно необходим для определения допустимого сечения провода и для выбора защиты.

Есть еще одно обстоятельство, о котором следует упомянуть в контексте этой статьи. В электроэнергетике используется так называемый “переменный” ток. То есть, те самые электроны движутся в проводах не всегда в одном направлении, они постоянно меняют его: вперед-назад-вперед-назад. И эта смена направления движения – 100 раз в секунду.

Погоди, но ведь везде говорится, что частота 50 герц! Да, именно так и есть. Частота измеряется в количестве периодов за секунду, но в каждом периоде ток меняет свое направление дважды. Иначе сказать, в одном периоде две вершины, которые характеризуют максимальное значение тока (положительное и отрицательное), и именно в этих вершинах происходит смена направления.

Не будем вдаваться в подробности более глубоко, но все же: почему именно переменный, а не постоянный ток?

Вся проблема в передаче электроэнергии на большие расстояния. Тут как раз вступает в силу неумолимый закон Ома. При больших нагрузках, если напряжение 220 вольт, сила тока может быть очень большой. Для передачи электроэнергии с таким током потребуются провода очень большого сечения.

Выход здесь только один: поднять напряжение. Седьмая формула говорит: I = W/U. Совершенно очевидно, что если мы будем подавать напряжение не 220 вольт, а 220 тысяч вольт, то сила тока уменьшится в тысячу раз. А это значит, что сечение проводов можно взять намного меньше.

В этой статье уже не раз я обмолвился о зависимости сечения проводника от силы протекаемого тока. О том, как определить допустимое значение, узнаем в следующей статье Допустимый длительный ток..

Как найти мощность: формула, расчёт силы тока, напряжения и сопротивления

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая – мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая – метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Как рассчитать мощность электрического тока?

Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.

Понятие электрической мощности и способы ее расчета

С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.

В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.

Через напряжение и ток

Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I

• P – активная мощность;
• U – напряжение приложенное к участку цепи;
• I — сила тока, протекающего через соответствующий участок.

Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.

Через напряжение и сопротивление

Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:

I = U/R

Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:

P = U*(U/R)=U 2 /R

• P – величина нагрузки;
• U – приложенная разность потенциалов;
• R – сопротивление нагрузки.

Через ток и сопротивление

Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.

Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:

U=I*R

после того как выражение подставить в формулу мощности, получим:

P = (I*R)*I =I 2 *R

Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.

Полная мощность в цепи переменного тока

Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

• S – полная мощность
• P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
• Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.

Также составляющие вычисляются через тригонометрические функции, так:

P = U*I*cosφ

Q = U*I*sinφ

что активно используется в расчете электрических машин.

Рис. 1. Треугольник мощностей

Пример расчета полной мощности для электродвигателя

Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.

Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:

В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:

Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.

Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.

Рис. 2. Шильд электродвигателя

Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:

• полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
• коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
• тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
• напряжение, при соединении обмоток треугольником составит 220 В;
• сила тока при том же способе соединения – 13,3 А.

С таким перечнем характеристик можно воспользоваться несколькими способами:

S = 1,732*220*13,3 = 5067 Вт

Чтобы найти искомую величину, сначала определяем активную составляющую:

P = P_{полезная} / КПД = 3000/0.8 = 3750 Вт

Далее полную по способу деления активной на коэффициент cos φ:

S = P/cos φ = 3750/0.74 = 5067 Вт

Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.

Примеры задач

Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.

Рис. 3. Последовательная расчетная цепь

Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:

P = U 2 /R = 81 / (10+20+30) = 1.35 Вт

Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:

Рис. 4. Параллельная схема подключения

Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:

Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:

Формула напряжения тока

Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.

Электрический ток

Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.

Электрическое напряжение

Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.

Сопротивление

Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам.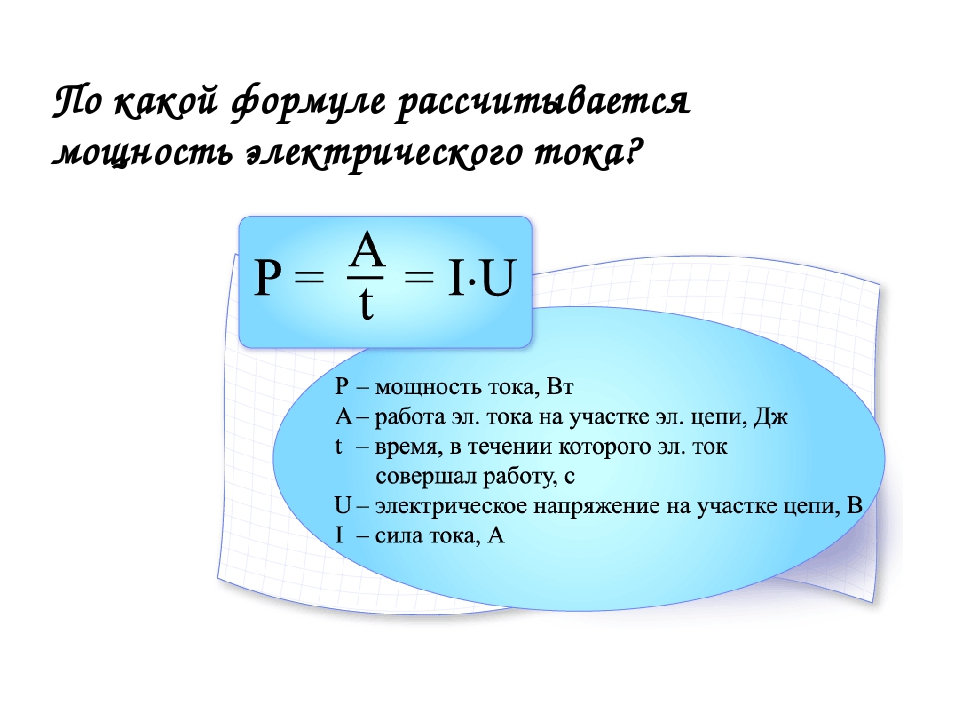 Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.

Мощность

Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.

Взаимосвязь параметров электрической цепи

Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.

К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.

Формула напряжения тока закона Ома выглядит следующим образом:

Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.

Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:

• I – сила тока;
• U – напряжение;
• R – сопротивление.

Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.

Кроме закона Ома, используется формула расчета мощности:

Символом P здесь обозначена мощность тока.

Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.

Единицы измерения в формуле

Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:

• Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
• Сила тока – Ампер. Обозначается символом А;
• Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
• Электрическая мощность – Ватт. Обозначается как Вт или W.

Как работает закон в реальной жизни

Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.

Сила тока формула через мощность:

Сопротивление:

Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:

Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.

Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:

Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.

Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.

Облегчить расчеты можно, используя онлайн калькулятор.

Пример с обычной водой

Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.

Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.

По какой формуле определяется напряжение

Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:

• Ток и сопротивление – U=I∙R;
• Ток и мощность – U=P/I;
• Мощность и сопротивление – U=√P∙R

Различные используемые величины

Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:

• Кило – 1000;
• Мега – 1000000;
• Гига – 1000000000;
• Милли – 0.001.

Таким образом, получается:

• Киловольт (кВ) – тысяча вольт;
• Мегаватт (Мвт) – миллион ватт;
• Миллиом (мОм) – одна тысячная Ом;
• Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.

Как найти напряжение

Формула нахождения напряжения как разности потенциалов в электрическом поле:

U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.

Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:

U=A/q, где q – величина заряда.

Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.

Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.

Гидравлическая аналогия

Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:

• Источник питания – насос;
• Проводники – трубы;
• Электроток – движение воды.

Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.

Измерительные приборы

Для измерения параметров электрических цепей служат измерительные приборы:

Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.

Типичные напряжения

Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:

• Бытовая сеть –220В;
• Бортовая сеть автомобиля – 12 или 24В;
• Батареи и аккумуляторы – 1.5, 3 или 9В.

Потенциал Гальвани

В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.

Видео

Особенности расчета мощности по току и напряжению

Чтобы электропроводка и все электрическое оборудование, которое имеется в доме, работало исправно и правильно, необходимо правильно сделать вычисление мощности по току и электронапряжению, поскольку при неправильно подобранных показателях может возникнуть короткое замыкание или возгорание. Как сделать расчёт потребляемой мощности по току и напряжению, как вычисляется сила тока, формула через мощность и напряжение и другое, далее.

Как узнать силу тока, зная мощность и напряжения

Чтобы ответить на вопрос, как определить ток, необходимо поделить электронапряжение на общее число ватт. При этом сделать все необходимые вычисления можно самостоятельно, а можно прибегнуть к специальному онлайн-калькулятору.

Узнать потребление электроэнергии по токовой силе резистора можно умножением первой на сопротивление, выражаемое в Омах. В итоге, получится значение, представленное в вольтах, перемноженных на ом. Получится ампер.

Обратите внимание! Если нет сопротивления, нужно поделить ваттный показатель на токовую энергию, то есть следует поделить ватты на амперы и получится значение электроэнергии в вольтах. Понять мощностное показание через величину электричества с электронапряжением, можно умножив соответствующие показания с устройства.

Формулы для расчета тока в трехфазной сети

Подсчитать токовую энергию в трехфазной сети сложно, поскольку вместе одной фазы есть три. К тому же, сложность заключается в использовании нескольких схем соединения. Трудность состоит в симметрии или ее отсутствии во время распределения нагрузки по фазам.

Для определения силы тока в трехфазной сети, нужно общее число ватт поделить на показатель 1,73, перемноженный на напряжение и косинус мощностного коэффициента, который отражает активную и реактивную составляющую сопротивления нагрузки. Что касается однофазной сети, то из выражения для подсчета убирается показатель 1,73. Остается формула I = P/(U*cos φ).

Как рассчитать ампераж

Ампераж является значением электротока, которое выражена в амперах. Рассчитать ампераж можно так: I=P/U.

Расчет потребляемой мощности

Электромощность является величиной, которая отвечает за факт скорости изменения или передачи электрической энергии. Есть полная и активная мощностная нагрузка, а также активная и реактивная. Полная вычисляется так: S = √ (P2 + Q2), где P является активной частью, а Q реактивной. Для нахождения потребляемого мощностного показателя необходимо знать число электротока, которое потребляется нагрузкой, а также питательное напряжение, которое выдается при помощи источника.

Что касается бытового определения потребляемой электрической энергии, необходимо вычислить общее количество ватт питания электрических приборов и паспортные данные номинальной силы электротока котла. Как правило, все электрические приборы работают с переменным током и напряжением в 220 вольт. Для вычисления тока проще всего воспользоваться амперметром. Зная первый и второй параметры, реально узнать величину потребляемой энергии.

Стоит указать, что измерить мощность через напряжение или сделать расчет мощности по сопротивлению и напряжению возможно не только формулой, но и прибором. Для этого можно воспользоваться мультиметром с токоизмерительными клещами или специализированным измерителем — ваттметром.

Обратите внимание! Оба работают по одному и тому же принципу, указанному в руководстве по их эксплуатации.

Мощность, ток и напряжение — три составляющие расчета проводки в доме. Узнать все необходимые параметры в любой сети просто при помощи формул, представленных выше. От этих значений будет зависеть исправность работы всей домашней электрики и безопасность ее владельца.

Как найти мощность тока — формулы с примерами расчетов

Определение

Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:

P=dA/dt

Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.

Электрическая мощность равна произведению тока на напряжение или:

P=UI

Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.

Формулы для расчётов цепи постоянного тока

Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:

P=UI

Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:

P=U 2 /R

Также можно выполнить расчет, зная ток и сопротивление:

P=I 2 *R

Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.

Для переменного тока

Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.

Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:

S=UI

Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.

P=UIcosФ

Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.

Q=UIsinФ

Или выразить из этого выражения:

И отсюда вычислить искомую величину.

Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:

А зная Uлинейное:

1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.

Тогда по аналогии чтобы найти P активную:

Определить реактивную мощность можно:

На этом теоретические сведения заканчиваются и мы перейдём к практике.

Пример расчёта полной мощности для электродвигателя

Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.

Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:

Тогда найти активную электрическую мощность можно по формуле:

P=P_{на валу}/n=160000/0,94=170213 Вт

Теперь можно найти S:

Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.

Расчет для параллельного и последовательного подключения

При расчете схемы электронного устройства часто нужно найти мощность, которая выделяется на отдельном элементе. Тогда нужно определить, какое напряжение падает на нём, если речь идёт о последовательном подключении, или какая сила тока протекает при параллельном включении, рассмотрим конкретные случаи.

Здесь Iобщий равен:

На каждом резисторе R1 и R2, так как их сопротивление одинаково, напряжение падает по:

И выделяется по:

P_{на резисторе}=UI=6*0,6=3,6 Ватта

Тогда при параллельном подключении в такой схеме:

Сначала ищем I в каждой ветви:

И выделяется на каждом по:

Или через общее сопротивление, тогда:

Все расчёты совпали, значит найденные значения верны.

Заключение

Как вы могли убедиться найти мощность цепи или её участка совсем несложно, неважно речь идёт о постоянке или переменке. Важнее правильно определить общее сопротивление, ток и напряжение. Кстати этих знаний уже достаточно для правильного определения параметров схемы и подбора элементов – на сколько ватт подбирать резисторы, сечения кабелей и трансформаторов. Также будьте внимательны при расчёте S полной при вычислении подкоренного выражения. Стоит добавить лишь то, что при оплате счетов за коммунальные услуги мы оплачиваем за киловатт-часы или кВт/ч, они равняются количеству мощности, потребленной за промежуток времени. Например, если вы подключили 2 киловаттный обогреватель на пол часа, то счётчик намотает 1 кВт/ч, а за час – 2 кВт/ч и так далее по аналогии.

Напоследок рекомендуем просмотреть полезное видео по теме статьи:

Также читают:

Ток, напряжение, сопротивление

Электрический ток ( I ) — это упорядоченное движение заряженных частиц. Первая мысль, которая приходит в голову из школьного курса физики — движение электронов. Безусловно.

Однако электрический заряд могут переносить не только они, а, например, еще ионы, определяющие возникновение электрического тока в жидкостях и газах.

Хочу предостеречь также от сравнения тока с протеканием воды по шлангу. (Хотя при рассмотрении Закона Кирхгофа такая аналогия будет уместна). Если каждая конкретная частица воды проделывает путь от начала до конца, то носитель электрического тока так не поступает.

Если уж нужна наглядность, то я бы привел пример переполненного автобуса, когда на остановке некто, втискиваясь в заднюю дверь, становится причиной выпадения из передней менее удачливого пассажира.

Условиями возникновения и существования электрического тока являются:

• Наличие свободных носителей заряда
• Наличие электрического поля, создающего и поддерживающего ток.

Будем считать, что теперь про электрический ток Вы знаете все. Это, конечно, шутка. Тем более что еще ничего не сказано про электрическое поле, которое у многих ассоциируется с напряжением, что не верно.

Электрическое поле — это вид материи, существующей вокруг электрически заряженных тел и оказывающее на них силовое воздействие. Опять же, обращаясь к знакомому со школы «одноименные заряды отталкиваются, а разноименные притягиваются» можно представить электрическое поле как нечто это воздействие передающее.

Это поле, равно как любое другое непосредственно ощутить нельзя, но существует его количественная характеристика — напряженность электрического поля.

Существует множество формул, описывающих взаимосвязь электрического поля с другими электрическими величинами и параметрами. Я ограничусь одной, сведенной к примитиву: E=Δφ.

Здесь:

• E — напряженность электрического поля. Вообще это величина векторная, но я упростил все до скаляра.
• Δφ=φ1-φ2 — разность потенциалов (рисунок 1).

Поскольку условием существования тока является наличие электрического поля, то его (поле) надо каким либо образом создать. Хорошо знакомые опыты электризации расчески, натирания тканью эбонитовой палочки, верчения ручки электростатической машины по вполне очевидным причинам на практике неприемлимы.

Поэтому были изобретены устройства, способные обеспечивать разность потенциалов за счет сил неэлектростатического происхождения (одно из них — хорошо всем известная батарейка), получившие название источник электродвижущей силы (ЭДС), которая обозначается так: ε.

Физический смысл ЭДС определяется работой, которую совершают сторонние силы, перемещая единичный заряд, но для того, чтобы получить первоначальное понятие что такое электрический ток, напряжение и сопротивление нам не нужно подробное рассмотрение этих процессов в интегральной и иных не менее сложных формах.

Напряжение ( U ).

Наотрез отказываюсь продолжать заморачивать Вам голову сугубо теоретическими выкладками и даю определение напряжения как разности потенциалов на участке цепи: U=Δφ=φ1-φ2, а для замкнутой цепи будем считать напряжение равным ЭДС источника тока: U=ε.

Это не совсем корректно, но на практике вполне достаточно.

Сопротивление ( R ) — название говорит само за себя — физическая величина, характеризующая противодействие проводника электрическому току. Формула, определяющая зависимость напряжения, тока и сопротивления называется закон Ома. Этот закон рассматривется на отдельной странице этого раздела.

Кроме того, сопротивление зависит от ряда факторов, например, материала проводника. Данные эти справочные, приводятся в виде значения удельного сопротивления ρ, определяемого как сопротивление 1 метра проводника/сечение. Чем меньше удельное сопротивление, тем меньше потери тока в проводнике.

Соответственно сопротивление проводника длиной L и площадью сечения S, будет составлять R=ρ*L/S.

Непосредственно из приведенной формулы видно, что сопротивление проводника также зависит от его длины и сечения. Температура тоже оказывает влияние на сопротивление.

Несколько слов про единицы измерения тока, напряжения, сопротивления. Основные единицы измерения этих величин следующие:

Ток — Ампер (А)
Напряжение — Вольт (В)
Сопротивление — Ом (Ом).

Это единицы измерения интернациональной системы (СИ) не всегда удобны. На практике применяются из производные (милиампер, килоом и пр.). При расчетах следует учитывать размерность всех величин, содержащихся в формуле. Так, если Вы, в законе Ома умножите ампер на килоом, то напряжение получите совсем не вольтах.

© 2012-2020 г. Все права защищены.

Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Расчет электрической мощности

Добавлено 1 октября 2020 в 09:01

Сохранить или поделиться

Формула расчета мощности

Мы видели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на ток в «амперах», мы получаем ответ в «ваттах». Давайте применим ее на примере схемы:

Рисунок 1 – Пример электрической схемы

Как использовать закон Ома для определения силы тока

В приведенной выше схеме мы знаем, что у нас напряжение батареи 18 В и сопротивление лампы 3 Ом. Используя закон Ома для определения силы тока, мы получаем:

\[I = \frac{E}{R} = \frac{18 \ В}{3 \ Ом} = 6 \ А\]

Теперь, когда мы знаем силу тока, мы можем взять это значение и умножить его на напряжение, чтобы определить мощность:

\[P = IE = (6 \ А)(18\ В) = 108 \ Вт\]

Это говорит нам о том, что лампа рассеивает (выделяет) 108 Вт мощности, скорее всего, в виде света и тепла.

Увеличение напряжения батареи

Давайте попробуем взять ту же схему и увеличить напряжение батареи, чтобы посмотреть, что произойдет. Интуиция подсказывает нам, что с увеличением напряжения ток в цепи будет увеличиваться, а сопротивление лампы останется прежним. Таким же образом, увеличится и мощность:

Рисунок 2 – Пример электрической схемы

Теперь напряжение аккумулятора составляет 36 вольт вместо 18 вольт. Лампа по-прежнему обеспечивает для прохождения тока электрическое сопротивление 3 Ом. Теперь сила тока равна:

\[I = \frac{E}{R} = \frac{36 \ В}{3 \ Ом} = 12 \ А\]

Это понятно: если I = E/R, и мы удваиваем E, а R остается прежним, сила тока тоже должна удвоиться. Так и есть: теперь у нас сила тока 12 ампер, вместо 6 А. А что насчет мощности?

\[P = IE = (12 \ А)(36\ В) = 432 \ Вт\]

Как повышение напряжения батареи влияет на мощность?

Обратите внимание, что мощность, как мы могли догадаться, увеличилась, но она увеличилась немного больше, чем ток. Почему? Поскольку мощность является функцией напряжения, умноженного на ток, а значения напряжения и силы тока увеличились в два раза по сравнению с их предыдущими значениями, мощность увеличится в 2 х 2, или в 4 раза. Вы можете проверить это, разделив 432 Вт на 108 Вт и увидев, что соотношение между ними действительно равно 4. Снова воспользовавшись алгеброй для манипуляции формулами, мы можем взять нашу исходную формулу мощности и изменить ее для случаев, где мы не знаем одновременно и напряжение, и силу тока, а знаем только напряжение (E) и сопротивление (R):

\[Если \qquad I=\frac{E}{R} \qquad и \qquad P=IE\]

\[То \qquad P=\frac{E}{R}E \qquad или \qquad P=\frac{E^2}{R}\]

Если мы знаем только ток (I) и сопротивление (R):

\[Если \qquad E=IR \qquad и \qquad P=IE\]

\[То \qquad P=I(IR) \qquad или \qquad P=I^2R\]

Закон Джоуля и закон Ома

Историческая справка: именно Джеймс Прескотт Джоуль, а не Георг Симон Ом, первым открыл математическую связь между рассеиваемой мощностью и током через сопротивление.2R\]

Резюме

• Мощность измеряется в ваттах, которые обозначается как «Вт».
• Закон Джоуля: P = I²R; P = IE; P = E²/R

Оригинал статьи:

Теги

Закон ДжоуляЗакон ОмаМощностьОбучениеРассеиваемая мощностьСхемотехникаЭлектрический токЭлектрическое напряжениеЭлектричество

Сохранить или поделиться

формула формула мощности электрического тока

Электрический ток является физическим процессом. Если говорить упрощенно, то это упорядоченное движение заряженных частиц. Его протекание можно измерить и соответственно выразить в символьном и цифровом виде. Формула электрического тока, представляет собой выражение качественных и количественных параметров через сопротивление проводника, напряжение или разность потенциалов, а также через его силу. Так как любое перемещение чего-либо, подразумевает под собой совершение работы, то дополнительно можно вести разговор об электричестве используя формулу мощности электрического тока.

Основные понятия и формулы характеризующие электрический ток

Количественным параметром электрического тока является его сила, представляющая собой скалярную величину и выражающуюся в отношении заряда (принято обозначать буквой 

q) к периоду времени (t), за которое он пересекает сечение проводника. Следовательно, формула электрического тока, а если говорить правильно его сила, будет выглядеть следующим образом — I=q/t. Измеряется данный параметр в амперах. Так как скалярные величины являются действительными числами и определяются только значением, сила тока не может иметь отрицательный знак. С учетом того, что величина заряда не является постоянным параметром для разных электрических цепей, было введено понятие – плотность электрического тока (j), формула которой выглядят так – j=I/S, где S – площадь, пересекаемая зарядами. Следовательно, при увеличении силы тока и уменьшении поперечного сечения проводника плотность тока возрастает и наоборот. Как отмечалось выше, важными параметрами электричества, вернее электрической цепи являются напряжение в ней и сопротивление проводящих ток элементов.

Формула выражения силы электрического тока через сопротивление и напряжение

В отличие от фундаментальных исследований, в основе которых лежат теоретические выкладки данная зависимость была выведена практическим путем. Автором открытия является физик Ом, в честь которого закон и получил свое имя. По результатам своих опытов и экспериментов Ом пришел к выводу что сила тока (I) напрямую зависит от величины напряжения (U)и имеет обратную зависимость от сопротивления (R) элементов и деталей, включенных в электрическую цепь. Эту связь можно представить в виде – I=U/R. Путем несложных преобразований, формулы сопротивления и напряжения, выраженные через силу тока, будут выглядеть следующим образом – R=U/I и U=IxR, соответственно.

Формула силы электрического тока

Сопротивление электрического тока: формула
Формула напряжения электрического тока

Работа и мощность электрического тока

Формула мощности (Р) электрического тока напрямую зависит от его работы (

А). Под работой тока подразумевается преобразование электрической энергии в механический, тепловой, световой или иной ее вид. Величина данного процесса напрямую зависит от времени его протекания, силы тока и напряжения в сети. Это можно выразить следующей формулой – А=IxUxt. Произведение (IxU) является ничем иным как мощностью. Следовательно, чем выше напряжение или сила тока в сети, тем большую мощность имеет электрический ток и большую работу он может совершить за единицу времени. Формула мощности электрического тока имеет следующий вид – Р=А/t или Р=IxU.

Работа электрического тока формула
Формула мощности электрического тока

Поэтому, если необходимо вычислить, какую работу производит ток, протекая по цепи в течение определенного времени, необходимо умножить мощность на временной промежуток, выраженный в секундах. Рассмотрим применение формул расчета работы и мощности электрического тока на примере электрического двигателя, подключенного к сети 220 В, а сила тока, измеренная амперметром для этого участка, составила 10А.

Р (мощность двигателя) = 10А (сила тока) х 220В (напряжение в сети) = 2200 Вт = 2,2 кВт.

Зная данный показатель, а также реальное или предполагаемое время функционирования электродвигателя можно определить какую работу он совершит за этот отрезок времени или другим словами сколько будет потрачено электроэнергии. Если двигатель был включен, например, 1 час, то можно найти искомое значение.

А (работа, совершенная двигателем) = 2,2 кВт (мощность) х 1 (время работы в часах) = 2,2 кВт ч. Именно этот показатель будет отражен на приборе учета расхода электроэнергии.

Исходя из того, что электрический ток является физическим процессом, то какой-либо его неизвестный параметр можно определить, зная его остальные характеристики. Приведем наиболее распространенные формулы для определения характеристик электрической цепи применяемые в электротехнике.

Напряжение или разность потенциалов

• U = RxI
• U = P/I
• U = (P*R)^1/2

Сила электрического тока

Сопротивление

• R = U / I
• R = U²/ P
• R = P / I²

Мощность

В заключение отметим, что приведенная информация справедлива для цепей с постоянным электрическим током. Формулы, применяемые для расчета характеристик переменного тока, будут отличаться за счет введения дополнительных переменных и характеристик свойственных данному типу электричества.

Формула электрического сопротивления для новичков

Не у всех хорошо ладится с физикой, а особенно когда дело доходит до решения задач. Но как говорят все учителя: «Учить и понимать — разные вещи». Так давайте лучше один раз  во всём разберёмся, чем просто заучить непонятный текст, при этом не зная, как его применить. Ну и ответим на главный вопрос  Как рассчитать сопротивление, и как найти мощность тока.

Единицы и размерности

Начнем с того, кто придумал данный закон. Установлен Георгом Омом.

В честь его и назван — закон Ома.

Вы, наверное, слышали такое понятие, как единица (СИ). В каждой физической формуле она присутствует. В законе Ома её очень легко запомнить, т.к. его фамилия и является единицей сопротивления и обозначается «Ом».

Какие существуют виды сопротивлений

Их немного, одно из которых мы уже разобрали:

• омическое;
• активное;
• индуктивное;
• ёмкостное.

Формулы расчёта электрического сопротивления для переменного тока простыми словами.

К сожалению, наш друг-физик решил не идти нам навстречу и вывел несколько формул по нахождению всех трёх величин. Электрическое сопротивление обозначается буквой R.

Но перед тем как пойти дальше, совет: всегда придумывайте какие-нибудь ассоциации, чтобы запомнилось на всю жизнь, например:

1. R (сопротивление). Можете запомнить что R, как рюмка. Нужно сопротивляться, чтобы не выпить ещё одну рюмку.
2. I (сила тока). Латинская «I», как проводок, по которому идёт ток.
3. U (напряжение). Эта буква, как дуга. И напряжение разносится с одного конца на другой по дуге.

Ну и, конечно, формула закона Ома для участка цепи.

1. R=U/I  т.е., чтобы найти сопротивление(рюмку) надо напряжение (дугу) разделить на ток (проводок).
2. U=IR, хотите найти напряжение (дугу), умножьте проводок на рюмку.
3. I=U/R чтобы найти чему равен проводок, нужно напряжение разделить на сопротивление.

Ну а теперь главное, для чего мы все здесь собрались: «Зачем нужен этот закон? Что он даёт?»

Представьте перед собой электрическую цепь, по которой проходит ток, напряжение и сопротивление. И встаёт вопрос, как понять где что и в каких размерах. Для этого вывели формулу.

Также не забывате, если вдруг вас спросят от чего зависит сопротивление — отвечайте: » От напряжения и мощности».

Формула активного сопротивления

Ну что сказать? Придется запастись терпением и потратить время на все эти законы и определения.

Но к счастью, активное сопротивление, так и осталось большой буквой R. Просто немного поменялась формула и ее предназначение.

Подключим к нашей цепи проводник. Проводником может выступать лампа.

Понятно, что по нему тоже будет проходить ток. Это как танец «волна». Все 5 человек берутся за руки и начинают по очереди создавать колебания. Сопротивление уже известно на всех. Так же и здесь.

Мы ищем полное сопротивление. Обозначается большой буквой Z.

Если посмотреть, то можно найти сходство танца «волны» с этой буквой. Так и запомните.

Формула, как рассчитать силу тока:

I=U/Z

О том, как найти общее сопротивление мы поговорим ниже.

Формула индуктивного сопротивления

Боюсь, что когда вы увидите данную формулу, то она вам точно не понравится. Но нет слова «не хочу», есть слово «надо».

Начнем с обозначения:

• XL (индуктивное сопротивление). Прямо как размер в одежде. Но почему именно так? L — это цепь переменного тока;
• f — частота, в Гц;
• сопротивление с частотой взаимосвязаны, так, если возрастает одно — увеличивается и другое;
• единица СИ индуктивного сопротивления: [XL] = Ом;
• запомните, что индуктивное сопротивление отличается от омического тем, что у первого нет потери мощности;
• XL=2π×f×L;
• формула расчета мощности по напряжению: P = U×I;
• мощность электрического тока вычисляется в Ватах.

Формула ёмкостного сопротивления Xc

Ёмкостное сопротивление — это проводник, который подключен к цепи. Он не имеет сопротивление, но есть ёмкость. Обозначается это ёмкостное сопротивление буквами Xc.

Единица измерения сопротивления неизменно остается Ом.

 

• Xc = 1/ωC;
• ω — циклическая частота;
• С — ёмкость.

Формула полного сопротивления

Как говорилось выше — полное сопротиление что-то на подобии танца «волны». Нужно узнать R (сопротивление) всех.

Чтобы определить полное сопротивление цепи:

R = R1 +R2 (проводников может быть несколько).

Теперь, если у вас спросят как определить общее сопротивление цепи, вы знаете что делать.

Что такое вольтамперная характеристика

Какое страшное название. Глаза боятся, а голова запоминает.

Говоря простыми словами, это когда напряжение находится в зависимости от тока, протекающего в электрической цепи.

Также, такую характеристику подразделяют на линейную и нелинейную. В чем разница и что это вообще такое?

1. Линейная, так же, как и нелинейная — это цепь.
2. Линейная цепь — это та, которая содержит элементы напряжения и тока, от которых зависит сопротивление.
3. У нелинейной элементами является зависимость напряжения на зажимах. Она не подчиняется закону Ома.

Формула электрического сопротивления по свойсвам среды: научный подход

• Сущесвует такое понятие как удельное сопротивление. Это способность материала припятствовать прохождению электрического тока.

• Существует таблица металлов, где указаны эти силы сопротивления.

Формула:

• R = p×L/S;
• R — электрическое сопротивление;
• p — удельное сопротивление;
• S — площадь.

Для вычисления сопротивления вы можете воспользоваться специальным калькулятором, который можно найти в интернете.

Учитесь, узнавайте много нового. И понимайте пройденный материал.

Прописные истины для новичков. — Начинающим — Теория

Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.

Закон Ома.

Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm,  1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.

Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.

Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.
Выглядит она следующим образом:

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Электрические измерения.

Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.

Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Поэтому категорически нельзя измерять «ток приходящий на нагрузку» путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать — закоротить цепь.
Если источник питания обладает хорошей мощностью — будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.

Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра — сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.

На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.

Постоянный и переменный ток.

Кратко напомню — постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) — это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.

На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие — «Действующее (или эффективное) значение» переменного тока.

Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) — то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.

Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.

Что такое «Амплитудное значение» переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно — лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.

Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря — если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, — то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).

Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.

Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).

Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.

Для действующего значения переменного синусоидального напряжения (тока) — справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений — приведённые выше в Законе Ома для постоянного тока.

Ответим на вопросы в начале статьи;

Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
Нам стало известно две величины, а именно — необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).

Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного — надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) — амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт — до которых и заряжаются электролитические конденсаторы фильтра.

Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля — Ленца) для первой магнитолы, которую она выдаст теоретически — будет 10,6 ватта, для второй — 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.

В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными «цешками» или бытовыми «цифровиками», так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт — это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.

 

Калькулятор законов Ома и Джоуля — Ленца • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Определения и формулы

Электрическая схема простейшей цепи, иллюстрирующая параметры U, I и R закона Ома

Мы окружены электронными устройствами и электрическими цепями. От компьютеров, планшетов, смартфонов и автомобилей до кредитных карточек, ключей к автомобилям и домам — во всех этих устройствах используются электрические цепи. И работа всех этих цепей основана на законе Ома:

Все мы помним (ладно, не все, только некоторые) эту простую формулу из уроков физики, а некоторые знают ее даже с раннего детства. Европейцы знают первую формулу, а те, кто живет в Северной Америке, привыкли ко второй. Европейцы предпочитают обозначать напряжение буквой U, а американцы предпочитают V. Поэтому мы можем смело заявить, что закон Ома — везде. Попробуем понять его чуть лучше.

Закон Ома

Георг Симон Ом (1789–1854)

Закон Ома назван в честь немецкого физика и математика Георга Симона Ома (1789–1854), который, будучи школьным учителем в школе с хорошо оборудованной физической лабораторией, исследовал недавно изобретенный Вольтов столб (в 1799 г.) и термопару, изобретенную в 1821 г. Он обнаружил, что ток в проводнике был прямо пропорционален разности потенциалов на концах проводника. Ом опубликовал результаты своих исследований в 1827 г. в знаменитой книге Die galvanische Kette, mathematisch bearbeitet (Математическое исследование гальванической цепи). Это соотношение между током, напряжением и сопротивлением, известное теперь под названием закона Ома, является фундаментом всей электроники. Единица сопротивления ом также названа в честь ученого. Работы ученого были признаны не сразу и ему пришлось много лет бороться за признание на своей родине.

Элемент электрических цепей, основной целью которого является ввод в цепь электрического сопротивления, называется резистором. На принципиальных схемах он обозначается двумя символами, один из которых используется в Европе и стандартизован Международной электротехнической комиссией (МЭК), а другой — в Северной Америке и стандартизован Институтом инженеров электротехники и электроники (IEEE).

Резисторы и их символы — европейский, стандартизованный МЭК (слева), и американский, стандартизованный IEEE (справа)

В законе Ома сопротивление, измеренное в омах — просто коэффициент пропорциональности между током и напряжением:

где I — ток, V и U — напряжение и R — сопротивление. Отметим, что в этом выражении R ≥ 0. Отметим также, что в этой формуле предполагается, что резистор имеет постоянное сопротивление, не зависящее от приложенного напряжения или протекающего тока. Если величина R или отношение U/I постоянны, то можно построить график зависимости тока от напряжения, который будет иметь вид прямой линии.

В резистивных цепях, например, в проводах и резисторах, ток и напряжение линейно пропорциональны. В математике линейной функцией называется такая функция, график которой представляет собой прямую линию (см. рисунок ниже). Например, функция y = 2x — линейная. Если две величины связаны линейным соотношением, то при увеличении или уменьшении одной величины, скажем, в три раза, вторая величина также увеличивается или уменьшается в то же самое число раз. В приложении к закону Ома это означает, что, если напряжение на резисторе увеличится втрое, ток через него также увеличится втрое. Однако, это справедливо только в предположении, что сопротивление резистора постоянно.

График, показывающий соотношение между током и напряжением для определенного электронного элемента, называется его вольт-амперной характеристикой. Резисторы имеют линейную вольт-амперную характеристику.

Более подробную информацию о резисторах и других электронных компонентах вы найдете в наших Электротехнических и радиотехнических калькуляторах, а также в Электротехнических конвертерах.

Нелинейные элементы

Графики вольт-амперных характеристик некоторых электронных элементов: 1 — резистор, 2 — диод, 3 — лампа накаливания, 4 — полупроводниковый стабилитрон; как мы видим, только резистор имеет линейную характеристику

Несмотря на то, что при изучении закона Ома мы всегда предполагаем, что вольт-амперные характеристики резисторов линейные, важно отметить, что многие очень нужные электрические и электронные элементы, такие как лампы накаливания, диоды и транзисторы, широко применяемые в электрических схемах, имеют нелинейные характеристики сопротивления. То есть, их вольт-амперные характеристики не являются прямыми линиями, проходящими через начало координат.

В этой цепи повышение напряжения не приведет к пропорциональному увеличению тока, так как сопротивление горячей лампы накаливания при подаче на нее номинального напряжения 12 В выше, чем оно было при 4 или 6 В. Вольт-амперная характеристика становится более пологой при повышении напряжения, что означает увеличение сопротивления лампы (см. рисунок выше)

Во многих случаях предположение о линейности резисторов неверное. Возьмем, например, схему с лампой накаливания и источником переменного напряжения. Эту схему можно найти во многих школьных учебниках, где обсуждается зависимость тока от напряжения в предположении, что сопротивление лампы накаливания постоянное. Там объясняют, что, если напряжение, приложенное к 12-вольтовой лампе, увеличивать, ток также пропорционально увеличивается. Однако это совсем не так! Если включить амперметр и измерить ток, мы увидим, что он не прямо пропорционален напряжению. Это связано с тем, что сопротивление ламы изменяется — оно растет, когда нить накаливания начинает светиться, так как лампа имеет нелинейную вольт-амперную характеристику.

Когда молодые люди начинают изучать электротехнику, законы Ома и Джоуля — Ленца будут, скорее всего первыми законами, которые нужно будет понять. Однако, когда они увидят эти законы в форме «колеса закона Ома», они могут испугаться, особенно если они поймут, что им придется зазубрить все эти формулы — потому что их учителям намного проще проверить память своих учеников, чем разобраться в том, понимают они предмет или нет. Поэтому многие преподаватели заставляют студентов зазубривать 12 формул вместо того, чтобы получше объяснить и показать на опыте суть закона и попросить их запомнить, а еще лучше, понять всего две из них:

и

Несмотря на то, что этот круг чаще всего называют «колесом закона Ома», здесь объединены два закона: Ома и Джоуля — Ленца.

Недорогой набор для изучения школьниками законов электротехники

Остальные 10 «страшных» формул можно просто вывести их этих двух. И даже эти две формулы не нужно запоминать. Запомнить и понять нужно то, что ток через элемент прямо пропорционален разности потенциалов, приложенной к этому элементу, и обратно пропорционален его сопротивлению. Это и есть закон Ома. А также то, что мощность прямо пропорциональна току и напряжению — это закон Джоуля — Ленца.

Эти два закона очень интуитивны, если студенты понимают что такое ток, напряжение, сопротивление и мощность. А понять это можно, если поиграть с батарейкой, несколькими резисторами и мультиметром. Можно также поиграть и с этим калькулятором.

Для понимания закона Ома удобно использовать гидравлический аналог с водяным насосом (представляющим источник питания), обеспечивающим давление жидкости (представляющее напряжение), которое толкает воду (ток) по трубе (цепи) с узким местом (сопротивление). Все остальные формулы, показанные в «колесе», выводятся из этих двух формул и, если они используются ежедневно, их в конце концов не трудно будет запомнить без лишних усилий.

Закон Джоуля — Ленца

Джеймс Прескотт Джоуль (1818–1889)

Для молодого Джеймса Джоуля, который работал менеджером в пивоварне, занятия наукой были просто хобби. Его отец был богатым пивоваром и Джеймс начал работать в пивоварне в 15 лет. Именно там, в 23 года, Джеймс Джоуль открыл закон, который теперь носит его имя. Его интересовало какой привод более эффективен в его работе: привычный паровой двигатель или недавно изобретенный электродвигатель. Этим экспериментам он посвящал много времени. В результате Джоуль установил соотношение между током, текущим через электрическое сопротивление (провод), и теплом, которое выделялось при этом.

Закон Джоуля утверждает, что мощность выделяемого в проводнике тепла P при прохождении через него электрического тока I пропорциональна произведению квадрата тока на сопротивление проводника R:

Если объединить этот закон с законом Ома, получается несколько полезных формул, которые можно использовать для расчета мощности, рассеиваемой резистором, определять сопротивление по известным току и напряжению, определять ток, текущий через резистор, а также приложенное к резистору напряжение. Эти формулы часто изображают в виде «колеса закона Ома» (вид довольно устрашающий) или не такого страшного «треугольника закона Ома». Ниже приведены примеры использования этих формул. Примеры кликабельные и результат расчетов можно посмотреть в калькуляторе. Нагрев провода при протекании через него тока иногда называют также омическим или резистивным нагревом.

Эмилий Ленц (1804–1865)

Выделение тепла в проводнике при прохождении через него электрического тока было независимо исследовано также русским физиком Эмилием Ленцем, который изучал электромагнетизм с 1831 г. Ленц известен прежде всего правилом о направлении индукционного тока в проводнике в изменяющемся магнитном поле, носящим его имя. Он также независимо от Джоуля открыл закон о выделении тепла в проводнике, поэтому он носит и его имя — закон Джоуля-Ленца.

Следует отметить, что в некоторых учебниках на английском языке закон Джоуля-Ленца неправильно называют законом Уатта, особенно если используется формула P = UI.

Закон Ома для цепей переменного тока

Закон Ома используется не только для анализа описанных выше цепей постоянного тока. Если напряжение имеет форму изменяющейся во времени функции, например, к цепи приложено синусоидальное напряжение, то закон Ома не прекращает свое действие. Если к резистору приложено синусоидальное напряжение, то через него течет синусоидальный ток. Этот ток находится в фазе с приложенным напряжением, так как при изменении полярности напряжения, в тот же момент изменяет полярность и ток. Когда напряжение проходит через максимум, ток делает то же самое.

При использовании закона Ома для анализа цепей переменного тока всегда необходимо выражать ток и напряжение единообразно. Это означает, что ток и напряжение нужно выражать в виде или среднеквадратичных значений, или пиковых значений, или двойной амплитуды. Если закон Джоуля — Ленца используется для определения рассеиваемой резистором мощности, действует аналогичное правило: ток и напряжение должны быть выражены одинаковым образом, например:

Здесь индекс RMS означает среднеквадратичное значение (англ. root mean square). Или

Здесь индекс p означает пиковое (англ. peak) значение. Если цепь переменного тока содержит реактивные элементы, такие как конденсаторы или катушки индуктивности, или обмотки двигателей, то закон Ома применим и к ним. В этом случае вместо активного сопротивления используется реактивное сопротивление:

Здесь X может быть реактивным сопротивлением конденсатора X_C или катушки индуктивности X_L, которые рассчитываются по известным формулам:

и

Подробную информацию о реактивном сопротивлении различных элементов электронных схем, а также об их параллельном и последовательном соединении вы найдете в наших электротехнических и радиотехнических калькуляторах и конвертерах.

Что касается мощности, потребляемой реактивными элементами, они не преобразуют энергию в тепло и, следовательно, энергия на их нагрев не теряется и рассеиваемая на них в виде тепла активная мощность P равна нулю. Мгновенная мощность (точнее, энергия) перемещается туда-сюда между конденсатором или катушкой и источником питания (помним, что соединительные провода при этом нагреваются и энергия теряется!). Скорость, с которой реактивный элемент сохраняет или возвращает энергию, называется реактивной мощностью Q и определяется по следующим формулам:

Реактивная мощность измеряется в вольт-амперах реактивных (вар) и эту единицу можно использовать со всеми десятичными приставками, например: квар, Мвар, и т. д.

Параллельная RLC-цепь

Чтобы применить законы Ома и Джоуля-Ленца для цепей с реактивными и активными компонентами нужно использовать комплексные величины импеданса Z, напряжения U и тока I. В связи с тем, что при расчетах по этим законам нужно выполнять умножение и деление комплексных чисел, удобно представлять их в полярной форме. Для конвертирования величин тока, напряжения, комплексной мощности и импеданса из алгебраической формы в тригонометрическую и наоборот можно воспользоваться нашим калькулятором. Для определения импеданса различных параллельных и последовательных цепей с активными и реактивными компонентами пользуйтесь нашими Электротехническими и радиотехническими калькуляторами.

Формулы закона Ома для переменного тока

Вначале отметим, что оригинал этой статьи написан на английском языке для англоязычной аудитории. В учебниках по теоретическим основам электротехники и основам теории цепей на английском языке, в отличие от учебников на русском языке, широко используется анализ с помощью векторных диаграмм на комплексной плоскости в полярной системе координат, который здесь и рассматривается. Причем, в отличие от учебников на русском языке, где в таких случаях обычно используется формула Эйлера, в англоязычной (особенно американской) литературе принято обозначение комплексных числе в полярной системе координат с углом (∠), который обычно обозначается в градусах:

Здесь U∠φ — сокращение для Ue^jφ.

Ниже приведены формулы, используемые в этом калькуляторе. Расчёты выполняются с комплексными величинами, представленными в тригонометрической форме и в соответствии с правилами умножения и деления комплексных чисел в тригонометрической (векторной) форме.

где φ_U, φ_I и φ_Z — соответственно фазовые углы напряжения, тока и импеданса.

Все комплексные величины вводятся в калькулятор в алгебраической или в тригонометрической форме. Несмотря на то, что импеданс и комплексная мощность не являются векторами, как напряжение и ток, их можно представлять в комплексной форме, потому что они являются комплексными числами, как ток и напряжение. Если они вводятся в алгебраической форме, то для удобства вычислений они преобразуются в тригонометрическую форму по формулам, описанным в нашем Калькуляторе преобразования алгебраической формы комплексного числа в тригонометрическую.

В качестве примера рассчитаем общий ток I_T, в параллельной RLC-цепи с R = 10 Ом, L = 100 мкГн и C = 1 мкФ. Источник переменного тока подает в цепь синусоидальное напряжение 0,5 В с частотой 10 кГц (щелкните для просмотра результата вычислений).

Величина модуля импеданса этой RLC-цепи равна

Фазовый угол (аргумент):

Положительный фазовый угол означает, что нагрузка имеет индуктивный характер и ток отстает от напряжения. Полный импеданс в тригонометрической форме:

Для расчета полного тока воспользуемся законом Ома и правилом деления чисел в тригонометрической форме (модули делятся, углы вычитаются):

Мощность в цепях переменного тока

В нашем калькуляторе мощности переменного тока показано, что активную P, реактивную Q, полную |S| и комплексную S мощность можно рассчитать по следующим формулам:

и

Еще раз напомним, что, поскольку при расчете мощности нужно выполнять умножение и деление комплексных чисел, это удобно делать в тригонометрической форме. Можно показать, что комплексная мощность равна произведению комплексного значения напряжения и сопряженного комплексного значения тока, то есть

Здесь U и I — напряжение в комплексной форме, а I*, U* и Z* — сопряженные комплексные значения тока, напряжения и импеданса соответственно. Полужирным шрифтом выделены комплексные значения. Отметим, что здесь комплексная мощность S измеряется в вольт-амперах (ВА). В тригонометрической форме имеем:

Здесь φ_U — фазовый угол напряжения и φ_I — фазовый угол тока. Эти формулы использованы для «колеса закона Ома для переменного тока». Его удобно использовать в качестве шпаргалки для вычислений.

«Колесо закона Ома»; полужирный шрифт показывает комплексные значения тока, напряжения, мощности и индуктивности. Звездочкой в I* показано, что это сопряженное комплексное значение тока I.

Подробную информацию о расчете мощности переменного тока вы найдете в нашем Калькуляторе мощности переменного тока. Ниже приведено несколько примеров расчетов с использованием данного калькулятора.

Примеры расчетов

Пример 3. Нагреватель с сопротивлением 10 Ом подключен к розетке с напряжением 120 В. Рассчитайте потребляемую мощность и протекающий через нагреватель ток.

Пример 4. Установленная в холодильнике маломощная лампа накаливания с сопротивлением 2300 Ом подключена к напряжению питания 120 В. Рассчитайте потребляемую лампой мощность и протекающий через нее ток.

Пример 5. Ток 0,15 А от солнечной батареи протекает через резистор сопротивлением 220 Ом. Рассчитайте напряжение на резисторе и мощность, которую он рассеивает.

Пример 6. Рассчитайте сопротивление галогенной лампы и потребляемую ею мощность, если она потребляет ток 1,5 А от автомобильной аккумуляторной батареи напряжением 12 В.

Пример 7. Рассчитайте ток, протекающий через 12-килоомный резистор и падение напряжения на нем, если на резисторе рассеивается мощность 1 Вт.

Последовательная RC-цепь (см. Пример 6). Дано: R = 10 Ом, C = 0,1 мкФ, I = 0,2∠0°. Определить: U

Пример 8. 10-омный резистор и конденсатор ёмкостью 0,01 мкФ, соединенные последовательно, подключены к источнику переменного напряжения частотой 1 МГц. Определите напряжение источника в тригонометрической форме, если потребляемый от источника ток равен I = 0,2∠0° А. Подсказка: используйте Калькулятор импеданса последовательной RC-цепи для определения импеданса в тригонометрической форме (Z = 18.8 ∠–57.86°), затем используйте этот калькулятор для определения напряжения источника питания (V = 3.76∠–57.8° V).

Автор статьи: Анатолий Золотков

Закон

Ома … взаимосвязь между напряжением, током и сопротивлением

Время чтения: 5 минут

Теоретические термины и определения

Следующие определения относятся к основной теории электричества. Важно, чтобы установщики и инспекторы обладали практическими знаниями теории электричества. Такие знания часто имеют жизненно важное значение для определения правильного сечения проводов для цепей с различной нагрузкой.

Вольт — единица электрического давления — это давление, необходимое для того, чтобы заставить один ампер пройти через сопротивление в один Ом; сокращенно «E», первая буква термина электродвигатель сила .

Ампер — это единица измерения электрического тока, который протекает через один Ом под давлением в один вольт за одну секунду; сокращенно «I», первая буква термина сила тока .

Ом — единица электрического сопротивления — это сопротивление, через которое один вольт заставит один ампер; сокращенно «R», первая буква термина сопротивление .

Вт — это единица измерения энергии, протекающей в электрической цепи в любой данный момент.Это также объем работы, выполняемой в электрической цепи. Термины ватт или киловатт использовались чаще для выражения объема работы, выполняемой в электрической цепи, а не джоулей . Ватты — это произведение вольт и ампер, которое иногда называют вольт-ампер. Одна тысяча вольт-ампер упоминается как один киловольт-ампер или одна кВА.

Закон Ома

Джордж Саймон Ом обнаружил взаимосвязь между током, напряжением и сопротивлением в электрической цепи в 1826 году.Он обнаружил экспериментально, что давление равно произведению силы тока и сопротивления; это соотношение называется законом Ома. Этот закон является практической основой большинства электрических расчетов. Формула может быть выражена в различных формах и ее использовании, как в трех примерах, показанных на рисунке 1.

Рис. 1. Основные примеры и применение закона Ома

Если известны любые два значения, третье можно найти с помощью формулы. Например, если известны сопротивление и напряжение, ток можно определить, разделив напряжение на сопротивление.Это может быть полезно при определении величины тока, который будет протекать в цепи, для правильного определения размеров проводников, а также устройств перегрузки по току.

л.с. Механическая мощность обычно выражается в лошадиных силах, а электрическая мощность — в ваттах. Термин лошадиных сил возник как объем работы, которую сильная лондонская тягловая лошадь могла выполнять за короткий промежуток времени. Он также использовался для измерения мощности паровых двигателей. Одна лошадиная сила, сокращенно «HP», равна работе, необходимой для поднятия 33 000 фунтов на один фут (33 000 фут-фунтов) за одну минуту.Это то же самое, что поднимать один фут на 550 фунтов за секунду.

Часто необходимо преобразовать мощность от одного устройства к другому, и уравнение на рисунке 2 используется для преобразования мощности в ватты или ваттов в лошадиные силы.

Рисунок 2. Базовая формула HP

Формула л.с. применима к лабораторным условиям, поскольку двигатели потребляют больше мощности, чем доставляют. Это связано с тем, что мощность, потребляемая двигателем в виде тепла, преодолевает трение в подшипниках, сопротивление ветру и другие факторы.Например, двигатель мощностью 1 л.с. (746 Вт) может потреблять почти 1000 Вт, причем разница расходуется на преодоление уже указанных факторов. Для определения истинной мощности однофазных двигателей необходимо учитывать коэффициент полезного действия двигателя (см. Рисунок 3).

Рисунок 3. Основные формулы коэффициента мощности

Колесо Ватт

Колесо Ватта было разработано и опубликовано во многих руководствах и в нескольких вариантах для иллюстрации ватт или мощности и их связи с элементами закона Ома.Как показано в этом тексте, это верно для цепей постоянного тока и для резистивных нагрузок цепей переменного тока, где коэффициент мощности близок к 100 процентам или единице (см. Рисунок 4). Не пытайтесь использовать его для нагрузки двигателя, так как в формулу необходимо учесть коэффициент мощности и КПД двигателя (см. Рисунок 3).

Рисунок 4. Колесо Ватта и закон Ома

В цепях переменного тока мы используем термин импеданс , а не Ом для обозначения сопротивления цепи. Импеданс — это полное сопротивление току в цепи переменного тока; он измеряется в омах.Импеданс включает сопротивление, емкостное реактивное сопротивление и индуктивное реактивное сопротивление. Последние два фактора уникальны для цепей переменного тока и обычно могут игнорироваться в цепях, таких как лампы накаливания и цепи нагревателя, состоящие из резистивных нагрузок. Подробное объяснение емкостного реактивного сопротивления и индуктивного реактивного сопротивления выходит за рамки этого текста, но его можно найти во многих прекрасных текстах по теории электричества.

Закон Ома и основная электрическая теория

Электрический ток, протекающий через любую электрическую цепь, можно сравнить с водой под давлением, протекающей через пожарный шланг.Вода, протекающая через пожарный шланг, измеряется в галлонах в минуту (GPM), а электричество, протекающее через контур, измеряется в амперах (A).

Вода течет по шлангу, когда на него оказывается давление и открывается клапан. Давление воды измеряется в фунтах на квадратный дюйм (psi). Электрический ток течет по электрическому проводнику, когда к нему прикладывается электрическое давление, и создается путь для прохождения тока. Подобно тому, как «фунты на квадратный дюйм» (давление) вызывают поток галлонов в минуту, так «вольт» (давление) заставляет течь «амперы» (ток).

Чтобы пропустить такое же количество воды через маленький шланг, требуется большее давление, чем через шланг большего размера. Маленький шланг, к которому приложено такое же давление по сравнению с большим шлангом, будет пропускать гораздо меньше воды за определенный период. Отсюда следует, что маленький шланг оказывает большее сопротивление потоку воды.

В электрической цепи большее электрическое давление (вольт) заставляет заданное количество тока (амперы) проходить через небольшой проводник (сопротивление), чем то, которое требуется для протекания того же количества тока (в амперах) через проводник большего размера (сопротивление). .Проводник меньшего размера позволит проходить меньшему току (в амперах), чем проводник большего размера, если к каждому проводнику в течение того же периода приложить одинаковое электрическое давление (вольт). Можно предположить, что меньший проводник имеет большее сопротивление (Ом), чем провод большего размера. Таким образом, мы можем определить сопротивление как «свойство тела, которое сопротивляется или ограничивает поток электричества через него». Сопротивление измеряется в Ом — термин, аналогичный трению в шланге или трубе.

Выдержка из Электрические системы для одно- и двухквартирных домов , 8 ^{-е издание} . Эта книга доступна по адресу www.iaei.org/web/shop или Amazon.com .

Знать взаимосвязь между мощностью и сопротивлением

Чтобы представить себе соотношение мощности и сопротивления, представьте себе источник постоянного напряжения или батарею. Когда в цепи большое сопротивление, может протекать очень небольшой ток, поэтому батарея выдает очень мало энергии, и резистор не будет слишком горячим из-за меньшей мощности.{2} R \]

Где I — электрический ток, измеренный в Амперах или А.

Что такое мощность?

Мы определяем мощность как способность тела выполнять работу за единицу времени. Например, человек A выполняет 30 Дж работы за 2 часа, а другой человек B выполняет такой же объем работы за 3 часа, поэтому здесь, если мы воспользуемся следующей формулой:

Мощность = Работа / время

Случай 1: 30 / 2 = 15 Вт

Случай 2: 30/2 = 10 Вт

Мы видим, что мощность человека A больше, чем мощность человека B.Таким образом, мощность A больше, чем мощность B.

Однако с точки зрения электричества мощность определяется как произведение тока и напряжения.

P = VI

Где

В — разность потенциалов, измеряемая в вольтах.

I измеряется в амперах.

Что такое сопротивление?

При движении автомобиля на высокой скорости мы должны замедлить нашу машину на некотором расстоянии до ограничителей скорости, иначе наша машина будет прыгать с большим рывком.Итак, здесь наш высокоскоростной автомобиль — это максимальный ток, протекающий по цепи (дороге), а выключатель скорости — это сопротивление, позволяющее избежать аварий или коротких замыканий в наших домах.

Итак, сопротивление — это препятствие, подключенное к цепи, чтобы избежать перетекания заряда через цепь. Он измеряется в Ом, где мы обозначаем его омегой или Ом.

Формула мощности и сопротивления

Мы заметили, что приведенные выше формулы описывают соотношение между мощностью и сопротивлением. {2}} {R} \]

Отсюда мы видим, что мощность P обратно пропорциональна сопротивлению R .

Отсюда мы можем сделать следующие выводы:

Для любой постоянной разницы потенциалов

• Когда мощность в цепи высокая, сопротивление будет меньше.

• Однако, если мощность низкая, сопротивление будет высоким.

Формула сопротивления мощности

Вывод формулы мощности и сопротивления поможет нам понять концепцию связи мощности и сопротивления.

В физике мощность и сопротивление можно связать с помощью двух формул, которые мы подробно обсудим в этой статье.

Мы знаем, что электрическая мощность или P — это мера электрического тока I с q кулонами заряда, проходящими через разность потенциалов V (в вольтах) за время t секунд. Математически мы можем выразить это утверждение как:

P = Vq / t = VI… . {2}} {R} \]

Из приведенных выше выводов мы получили следующий вывод:

Мощность и сопротивление в электронике

В электронике мы определяем мощность как скорость выполнения работы.Итак, какие работы ведутся в области электроники? Это обычная повседневная работа или что-то еще? Опишем это простым утверждением:

Мы определяем сопротивление как сопротивление потоку электронов в цепи. Это означает, что чем больше препятствие, тем больше работы выполняется в единицу времени, чтобы заставить их течь, т.е. тем больше энергии требуется, чтобы сделать их легким течением.

Из приведенного выше утверждения мы не можем отрицать тот факт, что соотношение между мощностью и сопротивлением пропорционально.

Законы Ома и Ватта | SpazzTech

Что такое закон Ома и закон Ватта ?:

Закон Ома определяет одно из самых фундаментальных соотношений в электронике. Это соотношение между напряжением, током и сопротивлением. Закон Ватта определяет еще одно из самых фундаментальных соотношений в электронике. Это соотношение между мощностью и величинами, определенное законом Ома. Мы не сможем углубиться в электронику, пока эти концепции не будут поняты.

Вольт:

Единицей измерения параметра напряжения является вольт. Символ, который используется для обозначения вольт, — это буква «V». В зависимости от ситуации используются как верхний, так и нижний регистры. Символом параметра напряжения также является буква «V». Если бы электрическая цепь представляла собой садовый шланг, напряжение было бы аналогично давлению в шланге. Единица V равна количеству энергии в Джоулях, необходимой для перемещения одного кулона электронов между двумя точками.Напряжение иногда называют «потенциалом», потому что оно способно перемещать эти электроны.

Ампер или Ампер:

Единицей измерения параметра тока является ампер. Ампер часто сокращают до ампер. Символ, используемый для обозначения усилителя, — это буква «А». В зависимости от ситуации используются как верхний, так и нижний регистр. Символ, используемый для представления параметра тока, — это буква «I». Если бы электрическая цепь представляла собой садовый шланг, ток был бы подобен скорости потока воды в шланге.Единица A равна количеству кулонов, проходящих через контур за одну секунду.

Ом:

Единицей измерения параметра сопротивления является ом. Для обозначения сопротивления используется символ Ω. Символ, используемый для обозначения параметра сопротивления, — это буква «R». Если бы электрическая цепь была садовым шлангом, сопротивление было бы любым клапаном или другим ограничением в шланге. Единица Ω равна сопротивлению, которое существует, когда 1 А протекает между двумя точками с напряжением 1 В между этими двумя точками.Это составляет основу форм закона Ома, приведенных в следующем разделе.

Формы закона Ома:

Мощность:

Единицей измерения мощности в электронике чаще всего является ватт. Символ, используемый для обозначения ватта, — это заглавная буква «W». По сути, мощность — это скорость выполнения работы. Фактически, один ватт равен одному джоулю в секунду. Из определений, данных для вольт и ампер, приведенных выше, мы можем сказать, что один ватт также равен одному вольту, умноженному на один ампер, потому что вольт — это мера джоулей на кулон, а ампер — мера кулонов в секунду.Кулоны сокращаются, и у нас остаются джоули в секунду.

Формы закона Ватта:

Настенная диаграмма комбинированных соотношений закона Ома и закона Ватта:

Объединив закон Ома и закон Ватта, нам нужно знать только две величины, чтобы определить две другие. Эти величины представляют собой напряжение (В) в вольтах, ток (I) в амперах, сопротивление (R) в омах и мощность (P) в ваттах. Все отношения между этими количествами приведены в таблице ниже.

© SpazzTech LLC, 2014-2017. Все права защищены

Закон

Ома: определение и взаимосвязь между напряжением, током и сопротивлением — Видео и стенограмма урока

Закон Ома

Взаимосвязь между напряжением, током и сопротивлением описывается законом Ома . Это уравнение, i = v / r , говорит нам, что ток, i , протекающий по цепи, прямо пропорционален напряжению, v , и обратно пропорционален сопротивлению, r .Другими словами, если мы увеличим напряжение, то увеличится и ток. Но, если увеличить сопротивление, то ток уменьшится. Мы увидели эти концепции в действии с садовым шлангом. Увеличение давления привело к увеличению потока, но изгиб шланга увеличил сопротивление, что привело к уменьшению потока.

Эта диаграмма — простой способ решать уравнения.

Как здесь написано уравнение, было бы легко использовать закон Ома, чтобы вычислить ток, если бы мы знали напряжение и сопротивление.Но что, если бы мы вместо этого захотели вычислить напряжение или сопротивление? Один из способов сделать это — переставить члены уравнения для решения других параметров, но есть более простой способ. Приведенная выше диаграмма даст нам соответствующее уравнение для решения любого неизвестного параметра без использования алгебры. Чтобы использовать эту диаграмму, мы просто закрываем параметр, который пытаемся найти, чтобы получить правильное уравнение. Это станет более понятным, когда мы начнем его использовать, поэтому давайте рассмотрим несколько примеров.

Закон Ома в действии

Ниже представлена ​​простая электрическая схема, которую мы будем использовать для выполнения наших примеров. Наш источник напряжения — это аккумулятор, подключенный к лампочке, которая обеспечивает сопротивление электрическому току. Для начала предположим, что наша батарея имеет напряжение 10 вольт, электрическая лампочка имеет сопротивление 20 Ом, и нам нужно вычислить ток, протекающий по цепи. Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, то есть ток, или i , и это оставляет нам напряжение v над сопротивлением r .Другими словами, чтобы найти ток, нам нужно разделить напряжение на сопротивление. Делая математические вычисления, 10 вольт, разделенные на 20 Ом, дают половину ампера тока, протекающего в цепи.

Чтобы найти ток, разделите напряжение (20 вольт) на сопротивление (20 Ом).

Теперь давайте увеличим напряжение, чтобы посмотреть, что происходит с током. Мы будем использовать ту же лампочку, но перейдем на 20-вольтовую батарею.Используя то же уравнение, что и раньше, мы разделим 20 вольт на 20 Ом, и мы получим 1 ампер тока. Как мы видим, удвоение напряжения привело к удвоению тока. Это имеет смысл, когда мы думаем о садовом шланге. Если бы мы увеличили давление в шланге, можно было бы ожидать, что поток воды также увеличится. Всегда полезно перепроверить свою работу, спросив, соответствуют ли результаты тому, что вы ожидали.

Если бы мы увеличили сопротивление лампочки, что бы вы ожидали, что произойдет с током? Чтобы выяснить это, давайте поменяем существующую лампочку на другую с сопротивлением 40 Ом.Поскольку мы все еще ищем ток, мы используем то же уравнение, что и раньше. Разделив 20 вольт на 40 Ом, мы получим половину ампера тока. Этот результат говорит нам, что удвоение сопротивления уменьшило ток вдвое. Вы этого ожидали? Если вспомнить наш шланг, логично предположить, что перегиб в шланге уменьшит поток воды, точно так же, как увеличение сопротивления в цепи уменьшит ток.

До сих пор мы только рассчитали ток в цепи, но что, если бы кто-то поменял нашу лампочку, когда мы не смотрели, и нам нужно было вычислить сопротивление новой? Что ж, мы знаем, что напряжение нашей батареи составляет 20 вольт, и мы можем измерить ток в цепи с помощью инструмента, называемого амперметром, поэтому все, что осталось, — это выполнить некоторые вычисления.Используя нашу диаграмму, мы скрываем параметр, который мы пытаемся найти, а именно сопротивление, r . Схема теперь показывает нам, что нам нужно разделить напряжение на ток. Если наш амперметр измерил ток в 5 ампер, протекающий по цепи, то сопротивление будет равно 20 вольт, разделенным на 5 ампер, что составляет 4 Ом

Чтобы определить напряжение, умножьте силу тока (3 ампера) на сопротивление (4 Ом).

Наконец, представьте, что кто-то заменил нашу батарею, и нам нужно выяснить ее напряжение.Процесс почти такой же. Мы знаем, что наша новая лампочка имеет сопротивление 4 Ом, и мы можем измерить ток в цепи с помощью амперметра. Используя диаграмму, мы покрываем напряжение v , которое говорит нам, что нам нужно умножить ток на сопротивление. Если бы амперметр измерял ток в 3 ампера, тогда напряжение было бы 3 ампера, умноженным на 4 Ом, что составляет 12 вольт. Это все, что нужно сделать. Зная любые два из трех параметров, мы всегда можем вычислить третий, используя закон Ома.

Краткое содержание урока

Закон Ома определяет соотношение между напряжением, током и сопротивлением в электрической цепи: i = v / r . Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Это означает, что увеличение напряжения приведет к увеличению тока, а увеличение сопротивления приведет к уменьшению тока. Зная любые два из трех параметров, мы можем вычислить третий, неизвестный параметр.Мы можем сделать это, переставив члены в уравнении закона Ома или используя диаграмму, приведенную выше в уроке. Скрытие параметра, который мы пытаемся найти, показывает нам соответствующее уравнение с использованием двух известных параметров.

Результаты обучения

По завершении этого урока вы сможете:

• Описывать взаимосвязь между напряжением, током и сопротивлением, используя закон Ома
• Напишите уравнение закона Ома
• Объясните, как можно найти любую из трех переменных в уравнении закона Ома, если вам известны две другие
• Рассчитайте любую из трех переменных, используя уравнение закона Ома

Изучение закона Ома | BCHydro Power Smart для школ

Вы построите схему и проведете демонстрацию, чтобы ваши ученики могли наблюдать взаимосвязь между напряжением, током и сопротивлением.

Инструкции

Представьте тему

Настройте схему, как показано здесь:

Просмотрите рабочий лист «Изучение закона Ома» со студентами.

Проведите демонстрацию

• Используя амперметр и вольтметр, покажите учащимся, как считывать значения тока и напряжения в цепи. Пока вы проводите измерения, запишите данные на доске и попросите учащихся записать данные на своих рабочих листах.Напомните им преобразовать мА в А; 1 ампер = 1000 миллиампер.
• Последовательно добавьте сухую ячейку и повторите измерения.
• Если у вас больше сухих ячеек, добавляйте их последовательно по одной и повторяйте измерения каждый раз.

Постройте график сопротивления

Используя данные из таблицы, попросите учащихся построить график зависимости напряжения от тока (V от I). Убедитесь, что они помечают все части своего графика. Объясните, какая линия лучше всего подходит, и попросите учащихся нарисовать ее на своем графике.

Попросите учащихся вычислить наклон линии по наиболее подходящей линии:

• Выберите две точки на прямой (точка A и точка B).
• Рассчитайте разницу между напряжениями в двух точках (НАРАЩИВАНИЕ наклона).
• Вычислите разницу между током в двух точках (ПЕРЕДАЧА НАКЛОНА).
• Разделите ПОДЪЕМ на БЕГ. Это наклон линии.

Сопротивление цепи математически отображается в виде алгебраического уравнения:

• Сопротивление = напряжение / ток.

Интерпретация данных

Сравните наклон графиков, созданных вашими учениками, с заявленным сопротивлением резистора, который вы использовали. Цифры должны быть похожими (разные числа являются результатом индивидуальных различий в выборе наиболее подходящей линии).

Связь между напряжением и током — это закон Ома, а наклон линии на графике этих двух величин является значением сопротивления в цепи. Уравнение закона Ома можно представить тремя способами:

• R = V / I (сопротивление = напряжение, деленное на ток)
• V = I x R (напряжение = ток x сопротивление)
• I = V / R (ток = напряжение, деленное на сопротивление)

Работа, напряжение и мощность

Люблю на работать на ламповых усилителях.Требуется работы, , чтобы заставить их работать, но как только они работают, вся эта тяжелая работа 1 действительно окупается. Это лишь некоторые из определений , работа , которые не имеют значения для физика вроде Георга Симона Ома. Ему требуется работа, чтобы переместить объект против силы, противодействующей его движению. Так что подъем Hiwatt DR103 с пола на рабочий стол требует работы, потому что вы перемещаете усилитель вверх против силы тяжести, которая ему противостоит. С другой стороны, носить Twin Reverb вокруг блока — это совсем не работа, потому что усилитель движется горизонтально — гравитация не препятствует движению в этом направлении.(Так что, когда дорожная бригада жалуется, просто вернитесь к этому руководству и объясните им, почему здесь нет никакой работы.)

Перемещение усилителя с испытательного стенда на пол требует работы, в данном случае отрицательной работы, потому что направление движения поддерживается силой тяжести. Если все это уже звучит странно, просто добавьте к этому концепцию: работа не зависит от времени. Чтобы поднять DR103 на верстак, требуется определенная работа. Неважно, дерните ли вы его вверх за доли секунды или потратите 20 минут, чтобы поднять его по тому же пути.Это такой же объем работы.

Когда противодействующая сила измеряется в ньютонах, а расстояние, пройденное против противодействующей силы, измеряется в метрах, тогда работа, измеряемая в джоулях, представляет собой силу, умноженную на расстояние:

W = Fd

Вопрос: 30-килограммовый ламповый усилитель — сколько килограммов на Луне? Ответ: 30 килограмм. Получается, что килограмм — это единица массы. Сила, о которой мы думаем, когда пытаемся поднять этот параллельный двухтактный якорь, равна массе, умноженной на ускорение свободного падения, которое равно 9.8 метров на секунду в квадрате. Когда мы умножаем количество килограммов на 9,8, мы получаем силу земного притяжения, измеряемую в ньютонах.

Проблема

Выходной трансформатор для вашего Traynor YGA-1 установлен в перевернутом виде и весит 6,6 фунтов. Какая сила тяжести тянет его вниз?

Amp Books®

Раствор

6,6 фунтов — это 6,6 / 2,2 = 3 кг. Тогда сила тяжести в ньютонах равна

(3 кг) (9,8 м / с ² ) = 29N

---

---

Проблема

Ваш винтаж 6.6-фунтовый выходной трансформатор лежит на полу, когда вы внезапно решаете, что он идеально подойдет для переиздания вашего JTM45. Верх вашей скамейки находится на высоте 1,2 метра от пола. Сколько работы потребуется, чтобы подобрать трансформатор и поставить его на скамейку? Что делать, если трансформатор стоит на полу в соседней комнате, которая находится в 20 метрах?

Решение

В предыдущей задаче мы определили, что сила тяжести на объекте весом 6,6 фунта составляет 29 ньютонов. Тогда объем работы в джоулях равен

(29N) (1.2 м) = 35 Дж

Боковому движению не препятствует сила тяжести, и трансформатор в соседней комнате проходит такое же вертикальное расстояние. Следовательно, требуется такой же объем работы — 35 джоулей.

Напряжение

Противоположные обвинения привлекают. Вроде обвинения отталкивают. Если мы перемещаем отрицательный электрон к другому электрону, мы совершаем работу, потому что движемся против противоположной силы. Перемещение двух электронов к двум другим электронам требует больше работы, потому что существует большая противодействующая сила.Нам часто нужен удобный способ описать, сколько работы требуется для перемещения заряда из одной точки в другую. Это понятие напряжения.

Если перемещение положительного заряда из точки B в точку A требует положительной работы, то говорят, что точка A имеет положительное напряжение по отношению к B. Напряжение в вольтах равно требуемой работе в джоулях, деленной на количество заряда в кулонах:

V = W / Q

Поскольку W и Q могут быть положительными или отрицательными, понятно, что V также может быть положительным или отрицательным.

---

---

Проблема

Требуется 1,6 кДж (1600 джоулей) энергии, чтобы переместить 1×10 ²⁰ электронов от источника питания пластины (точка A) через нагрузочный резистор пластины к пластине (точка B) вашего предусилителя JTM45. (Обратите внимание, что это противоположно реальному потоку электронов. показано здесь.) Какое напряжение V на резисторе?

— V + BA300VDC

Решение

1×10 ²⁰ электронов представляют

(1×10 ²⁰ ) (- 1.6х10 ^-19 ° С) = -16 ° С

заряда. Таким образом, требуется + 1,6 кДж работы, чтобы разогнать -16C из точки A в точку B. Это означает, что потребуется + 1,6 кДж работы, чтобы передать положительный заряд 16C из точки B в точку A. Таким образом, мы заключаем, что напряжение в точке A положительна по отношению к B на величину, равную

V = 1,6 кДж / 16C = 100 В

Таким образом, между питанием пластины и пластиной на резисторе падает 100 вольт.

---

---

Мощность

Мощность — это мера количества работы или энергии, затрачиваемой с течением времени.При измерении в течение одной секунды количество джоулей звуковой энергии, создаваемой Ampeg SVT с шестью двухтактными силовыми трубками, работающими на полную мощность, будет намного больше, чем у Champ 5E1. По той же концепции для быстрого физического подъема Hiwatt не требуется дополнительной работы, но требуется больше энергии, поскольку работа выполняется в течение более короткого периода времени. Когда работа измеряется в джоулях, а время измеряется в секундах, тогда мощность в ваттах равна общей работе, деленной на общее время:

P = Вт / т

Проблема

Вам потребуется 2 секунды, чтобы стабильно поднять свой 6.6-фунтовый выходной трансформатор от пола до верха скамьи, общее расстояние по вертикали 1,2 метра. Какое среднее количество энергии вы тратите, когда поднимаете его?

Решение

Ранее мы определили, что для подъема трансформатора требуется 35 джоулей работы. Вы расходуете эту энергию за 2 секунды, поэтому средняя мощность в ваттах, передаваемая на трансформатор вашими руками и квадрицепсами, равна

P = 35Дж / 2с = 17Вт

Связь между напряжением, током и мощностью

Мы видели, что напряжение между двумя точками является показателем количества работы, необходимой для перемещения заряда между двумя точками.В противоположность этой концепции, работу можно определить как напряжение между двумя точками, умноженное на величину заряда, который был перемещен между ними:

W = VQ

Мы можем использовать эти концепции, чтобы вывести очень важную формулу для гитарных усилителей. Соотношение между напряжением, током и мощностью

P = W / t = (VQ) / t = V (Q / t) = VI

где переменная «I» используется для обозначения силы тока. Когда I в амперах, а V в вольтах, тогда P в ваттах.

---

---

Проблема

При отсутствии сигнала гитары через дроссель Fender Bassman 5F6-A протекает постоянный ток 11 мА.Дроссель не является идеальным индуктором, потому что его внутренние обмотки имеют сопротивление постоянному току, которое вызывает падение на нем 1,2 В. Какую мощность дроссель выделяет в виде тепла?

Решение

Поскольку напряжение на дросселе и ток через него стабильны (ну, может быть, небольшая пульсация переменного тока), выделяемая мощность в виде тепла, измеряемая в милливаттах, равна

(1,2 В) (11 мА) = 13 мВт

Проблема

Катодный резистор на 47 Ом в усилителе мощности вашего Vox AC30 рассчитан на максимальную мощность 10 Вт.На холостом ходу напряжение на нем обычно составляет 10 вольт. Каким должен быть средний ток через резистор, чтобы произвести 10 ватт тепла?

СЛЕДУЮЩАЯ СТРАНИЦА

Закон ужасного ома

В предыдущей статье мы рассмотрели формулу мощности и обсудили взаимосвязь между мощностью, напряжением и током. Посмотрев на формулу мощности, теперь есть только одна формула, необходимая для решения практически всех электрических расчетов, это ужасный закон Ома.Мы не будем вдаваться в вывод формулы, но уделите минуту, чтобы прочитать следующую иллюстрацию:

Когда вы откроете кран, подключенный к садовому шлангу без насадки, вы увидите, что вода вытекает из другого конца. Поток воды через шланг подобен потоку электрического тока — электрический ток — это поток электронов через провод.

Если теперь вы положите большой палец на конец шланга и попытаетесь перекрыть поток воды, давление воды, которое вы почувствуете, будет похоже на напряжение.Напряжение — это давление, которое толкает электроны через провод. Что интересно, если ваш большой палец полностью перекрывает поток воды, давление (напряжение) воды все равно остается. Наличие сопла на конце шланга и прекращение потока воды похоже на то, что к розетке в стене ничего не подключено — нет воды / тока, но давление / напряжение все еще есть. Следует отметить, что напряжение присутствует, даже если нет тока. Другой пример — автомобильный аккумулятор — на любой подключенный к нему провод всегда подается 12 Вольт, независимо от того, какой ток идет.

Вернемся к садовому шлангу. Если теперь переместить большой палец на конец шланга, можно изменить количество выходящей воды. То есть, изменяя сопротивление воде, вы меняете и поток. То же самое и в электрической цепи — измените сопротивление, и ток изменится соответственно. Давайте определим электрическое сопротивление как «сопротивление, блокирующее, препятствующее или ограничивающее ток, протекающий по цепи». Примеры сопротивления в цепи — электрическая лампочка или электрический прибор.

Если напряжение (давление воды) остается прежним, ток будет зависеть от сопротивления. Чем больше сопротивление, тем меньше ток. И наоборот, чем меньше сопротивление, тем больше ток. Это похоже на то, что чем больше вы перекрываете конец шланга, тем больше уменьшается поток воды, уменьшение сопротивления увеличивает поток воды.

Если сопротивление остается прежним, ток можно увеличивать или уменьшать, увеличивая или уменьшая напряжение (давление воды).

Георг Симон Ом

В 1827 году немец по имени Георг Симон Ом опубликовал книгу, описывающую взаимосвязь между напряжением, током и сопротивлением. Эта связь теперь известна как закон Ома. Закон Ома гласит, что ток прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Математически это выглядит так:

Ток = напряжение / сопротивление

Символы и единицы измерения напряжения и тока такие же, как и в формуле мощности.Обратите внимание на стандартные термины сопротивления.

Имя	Символ	Единицы измерения
Текущий	я	ампер или ампер (A)
Напряжение	В	вольт (В)
Сопротивление	р	Ом (Ом)

Следовательно, мы можем быстро записать эту формулу как:

I =

^В / _R

Популярный способ запомнить эту формулу и ее производные — это показанный здесь треугольник.Какую бы характеристику вы ни искали, прикройте ее пальцем, и формула, которая вам нужна, останется.

Пример 1. Чтобы найти напряжение в цепи, зная сопротивление и ток, коснитесь пальцем буквы «V», и формула будет I x R.

Пример 2: Чтобы найти ток в цепи, зная напряжение и сопротивление, приложите палец, чтобы закрыть «I», и формула: ^В / _R

Пример 3: Чтобы найти сопротивление цепи, зная напряжение и ток, коснитесь пальцем буквы «R», и формула будет ^В / _I

Другими словами, формула в трех возможных формах:

В = I x R I =

^В / _R R = ^В / _I

Используя эти формулы и следующую схему, можно увидеть взаимосвязь между сопротивлением и током, при условии, что напряжение остается прежним.

Пример 1: Учитывая, что напряжение составляет 220 В, а сопротивление составляет 110 Ом (Ом), мы можем рассчитать ток по формуле:

I = ^В / _R = ²²⁰ / ₁₁₀ = 2 А

Пример 2: То же напряжение (220 В), но теперь сопротивление всего 2 Ом.

I = ^В / _R = ²²⁰ / ₂ = 110 А

То есть, чем больше сопротивление, тем меньше ток может протекать.Кроме того, чем меньше сопротивление, тем больший ток может протекать.

Может оказаться полезным снова использовать аналогию с водой. Если у вас есть водопроводная труба большого диаметра, то через нее может протекать много воды (тока), потому что «сопротивление» низкое (отсутствие засоров). Если есть закупорка в трубе (сопротивление), то (текущий) поток уменьшается. Чем больше засорение (чем выше сопротивление), тем меньше (ток) протекания.

Этот принцип проиллюстрирован в примерах выше.В примере 1 сопротивление 110 Ом позволяло проходить через цепь только 2 ампера. В примере 2 небольшое сопротивление (2 Ом) позволяло протекать по цепи большому току в 110 ампер.

Сопротивление — это все, что сопротивляется току, протекающему по цепи. Лампочка — это сопротивление, как утюг, кухонный комбайн или плита. В электронике есть небольшие компоненты, называемые резисторами, которые имеют фиксированное известное значение. Даже простой кабель имеет некоторое сопротивление, на самом деле причина использования толстых кабелей заключается в том, чтобы уменьшить сопротивление и позволить большему току проходить через него (например, пожарный шланг больше, чем садовый шланг, поэтому через него может течь больше воды) .

P.S .: мы только что рассмотрели основные принципы закона Ома, но шшш, никому не говори.

Если вы находите математику запутанной, попробуйте простой калькулятор закона Ома.

Последовательный или параллельный

Часто вы не знаете, какое сопротивление в цепи, и вам не нужно это знать. Однако эти формулы по-прежнему очень полезны, но в основном для того, что на их основе выводится, а не для их непосредственного вычисления. Это длинный способ сказать: «Пожалуйста, примите, что следующие концепции вытекают из приведенной выше формулы, и нам не нужно тратить время и силы на ее доказательство».

Концепция 1:

Рассмотрим схему из шести лампочек. Поскольку они подключаются друг за другом, говорят, что они подключены последовательно.

Интересно, что происходит с напряжением, током и сопротивлением.

Напряжение: «Входное напряжение» — это сумма напряжений на всех отдельных лампах. В этом примере индивидуальное напряжение на каждом источнике света составляет 40 вольт, поэтому общее напряжение составляет 240 вольт.

Ток: Ток через каждый отдельный светильник такой же, как ток во всей цепи.Если ток, идущий в цепь, составляет 1 ампер, то ток через каждую отдельную лампу также составляет 1 ампер.

Сопротивление: Общее сопротивление равно сумме всех отдельных «последовательных» сопротивлений.

На практике этот тип цепи редко используется в доме. Это связано с тем, что если в дом поступает 240 вольт, и в нем шесть последовательно соединенных ламп, то каждый свет будет получать только одну шестую от этого напряжения, то есть 40 вольт. Тем не менее, этот тип схемы часто используется для гирлянды елки e.грамм. 20 лампочек по 12 вольт каждая равны 240 вольт. Проблема с этой схемой в том, что если горит одна лампочка, то погаснут и все остальные. Это связано с тем, что проводное соединение со следующим светом оборвано, поэтому цепь не завершена.

Часто используется последовательная цепь с батареями. Когда батареи включены последовательно, общее напряжение равно сумме всех отдельных напряжений, а общий ток, протекающий по всей цепи, такой же, как ток, протекающий через любую одну батарею.Например: четыре батареи на 1,5 В 500 мА, соединенные последовательно друг с другом, составляют батарею на 6 В (4 x 1,5) при 500 мА.

КОНЦЕПЦИЯ 2:

Рассмотрим схему из шести лампочек. Поскольку они соединены друг с другом или параллельно друг другу, говорят, что они соединены параллельно.

То, что происходит с напряжением, током и сопротивлением в этом типе цепи, отличается от того, что происходит в последовательной цепи.

Напряжение: напряжение на каждом индикаторе такое же, как «напряжение на входе».Если в цепь поступает 220 вольт, значит, 220 вольт на каждой отдельной лампе.

Ток: Ток, протекающий в цепи, представляет собой сумму токов в каждом отдельном источнике света. Если ток через каждую лампу составляет 1 ампер, то общий ток, поступающий в эту схему, будет 6 ампер (6 x 1 ампер).

Сопротивление: общее сопротивление рассчитывается по сложной формуле, которую нам не нужно изучать на данном этапе. Достаточно сказать, что общее сопротивление меньше наименьшего индивидуального сопротивления.Вот формула для тех, кому действительно нужно знать:

На практике этот тип схемы используется в жилых домах. например Если у вас в доме 220 вольт, то все светильники и розетки (розетки) тоже 220 вольт, потому что они соединены параллельно.

Батареи также можно подключать параллельно. Выходное напряжение двух параллельно включенных батарей такое же, как у одной из батарей, но текущая емкость удваивается. Например: две автомобильные батареи на 12 вольт 100 ампер / час, подключенные параллельно, составляют эквивалент 12-вольтовой батареи 200 ампер / час.Те же две батареи, соединенные последовательно, будут эквивалентны батарее на 24 вольта и 100 ампер / час.

Собираем все вместе

Некоторые люди в восторге от того, как формулу закона Ома можно подставить в нашу формулу Силы для создания новых формул. Те из вас, кто любит играть с формулами, могут понять, как это делается; в остальном просто согласитесь, что эта таблица показывает различные комбинации этих формул.

В этой таблице показаны все возможные комбинации с использованием двух изученных нами основных формул.Попробуйте использовать калькулятор и следующие значения, чтобы проверить это:

В = 12 В I = 2 А R = 6 Ом P = 24 Вт

Вы можете распечатать таблицу и прикрепить ее к футляру мультиметра или стене мастерской для использования в будущем.

Простой калькулятор для вычисления всех этих комбинаций доступен здесь.