Как подключить конденсаторы чтобы увеличить емкость: Как подключить конденсаторы для увеличения емкости

Как соединить конденсаторы? Последовательное и параллельное соединение конденсаторов

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой. Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

1. Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
2. Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
3. Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно.

Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов. Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства.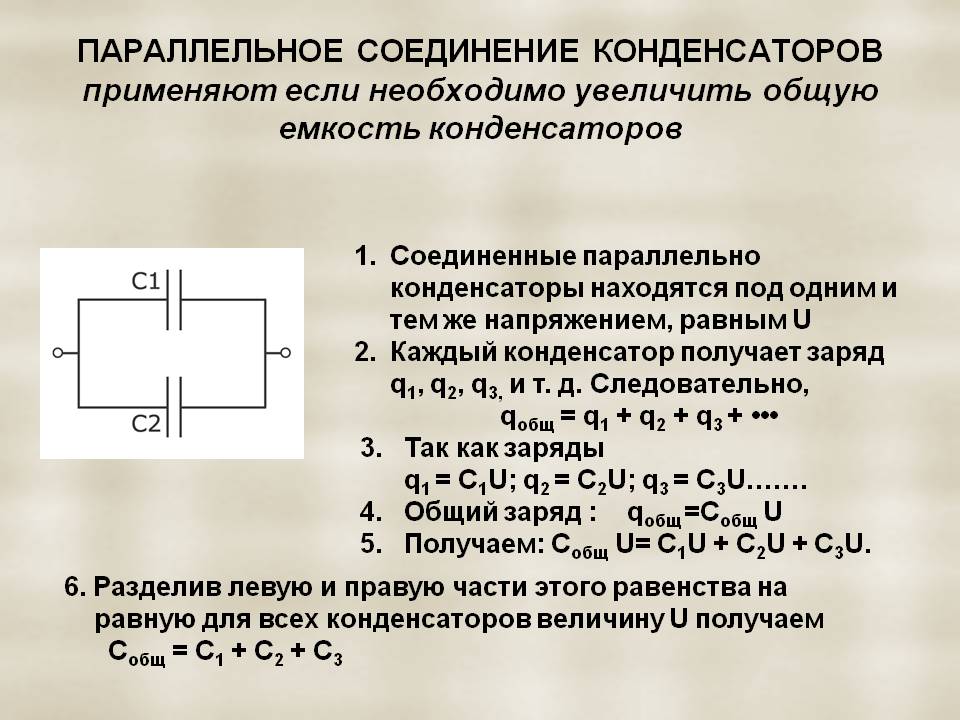 Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

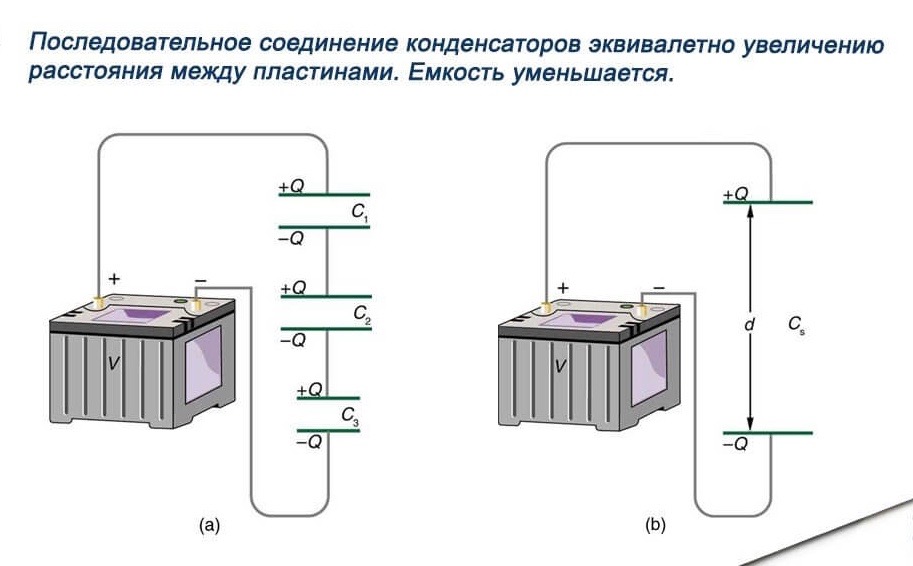
Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.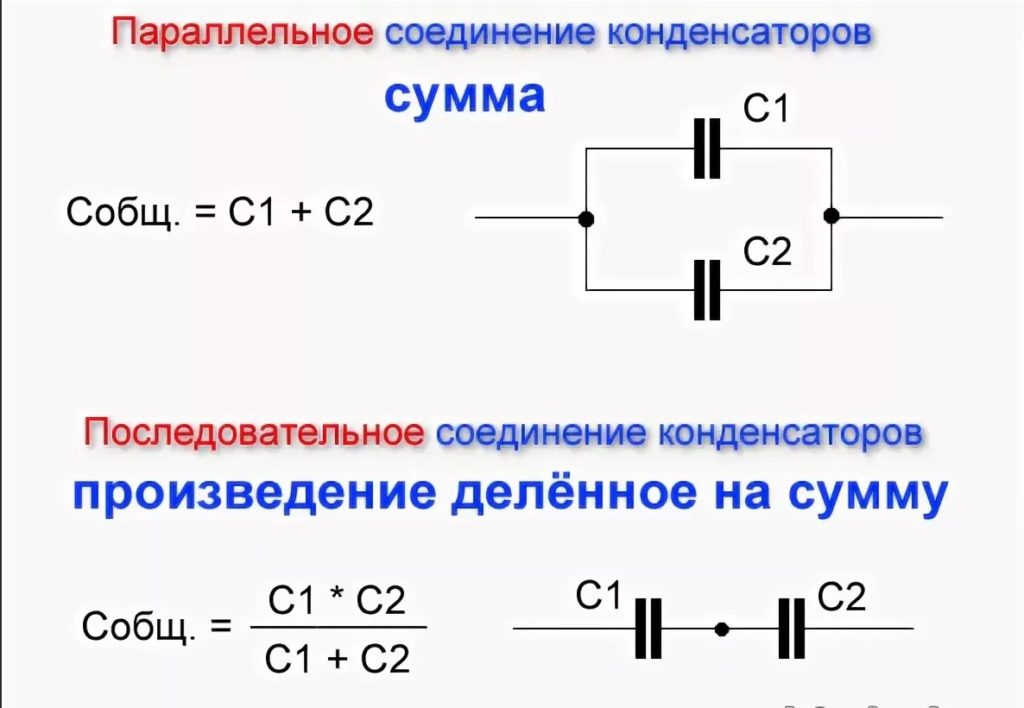

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

Добавить отзыв

Электроемкость конденсатора — формула и определение

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Электроемкость C = q/φ С — электроемкость [Ф] q — электрический заряд [Кл] φ — потенциал [В]

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух или более проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Зарядка конденсатора — это процесс накопления заряда на двух его обкладках. Заряды на них равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

Электроемкость конденсатора C = q/U С — электроемкость [Ф] q — электрический заряд [Кл] U — напряжение (разность потенциалов) [В]

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо сквозь диэлектрик. Такой конденсатор больше работать не будет.

Виды конденсаторов

Особенность электроемкости в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости.

Проще всего вычислить электроемкость плоского конденсатора. Плоский конденсатор состоит из двух металлических пластин, между которыми помещают диэлектрическое вещество.

Электроемкость плоского конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — площадь пластин [м2] — расстояние между пластинами [м]

Самый популярный конденсатор — цилиндрический. Он состоит из двух металлических цилиндров, вложенных друг в друга, и диэлектрика, которым заполнено пространство между ними. Рассмотрим формулу электроемкости такого конденсатора.

Электроемкость цилиндрического конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — длина цилиндров [м] — радиусы цилиндров [м] — функция натурального логарифма, которая зависит от радиусов цилиндров

Сферический конденсатор состоит из двух проводящих сфер, вложенных друг в друга, и непроводящей жидкости, которой заполнено пространство между ними.

Электроемкость сферического конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — радиусы сфер [м]

Подытожим все, что узнали, на картинке-шпаргалке:

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля Wp = qEd Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] E — напряженность электрического поля [В/м] d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора Wp = qU/2 Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] U — напряжение на конденсаторе [В]

Энергия конденсатора Wp = q2/2C Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] C — электроемкость конденсатора [Ф]

Энергия конденсатора Wp = CU2/2 Wp — энергия электростатического поля [Дж] C — электроемкость конденсатора [Ф] U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.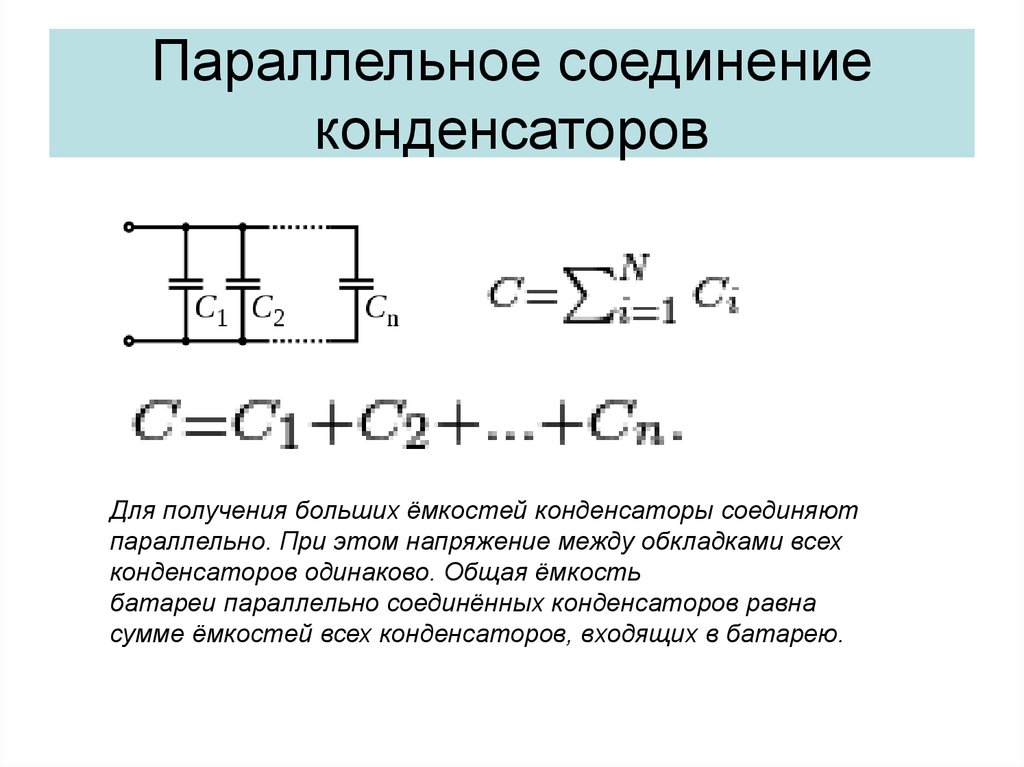

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Изучать физику на примерах из реальной жизни может быть очень даже интересно.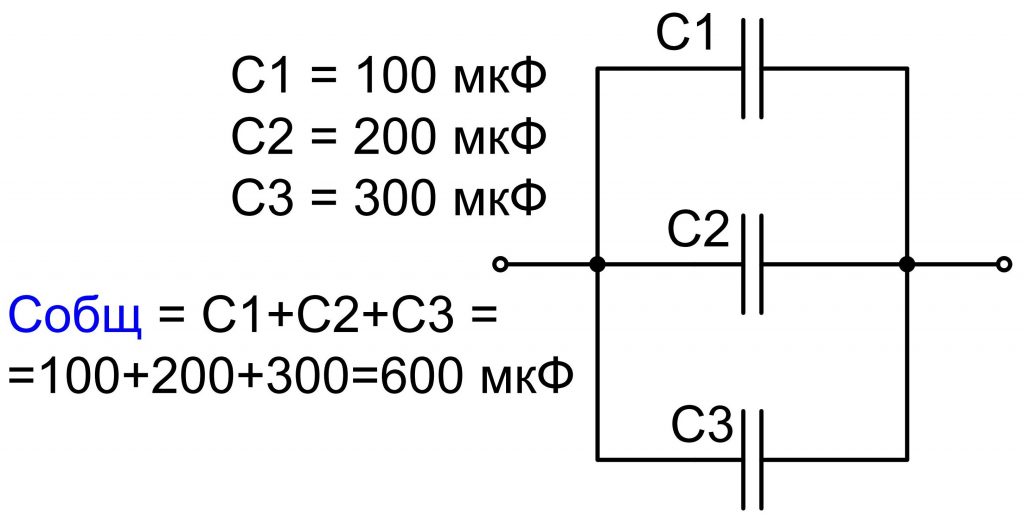 Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.

Electronics Components: Конденсаторы в параллельном и последовательном соединении

Вы можете комбинировать конденсаторы в последовательные или параллельные сети, чтобы создать любое значение емкости, которое вам нужно в электронной схеме. Например, если вы соедините три конденсатора по 100 мкФ параллельно, общая емкость цепи составит 300 мкФ.

Соединение конденсаторов параллельно

Рассчитать общую емкость двух или более конденсаторов, включенных параллельно, очень просто: просто сложите значения отдельных конденсаторов, чтобы получить общую емкость.

Это правило имеет смысл, если задуматься. Когда вы соединяете конденсаторы параллельно, вы, по сути, соединяете пластины отдельных конденсаторов. Таким образом, параллельное соединение двух одинаковых конденсаторов существенно удваивает размер пластин, что фактически удваивает емкость.

Здесь две цепи имеют одинаковые емкости. Первая схема выполняет работу с одним конденсатором, вторая — с тремя. Таким образом, схемы эквивалентны.

Всякий раз, когда вы видите два или более конденсатора, подключенных параллельно в цепи, вы можете заменить их одним конденсатором, емкость которого является суммой отдельных конденсаторов. Точно так же каждый раз, когда вы видите один конденсатор в цепи, вы можете заменить два или более конденсаторов параллельно, если их значения в сумме совпадают с исходным значением.

Суммарная емкость параллельно включенных конденсаторов всегда больше емкости любого из отдельных конденсаторов. Это потому, что каждый конденсатор добавляет к общей емкости свою емкость.

Соедините конденсаторы последовательно

Вы также можете объединить конденсаторы последовательно для создания эквивалентных емкостей. Однако, когда вы это сделаете, математика немного усложнится. Получается, что расчеты, необходимые для конденсаторов, соединенных последовательно, такие же, как для расчета резисторов, соединенных параллельно.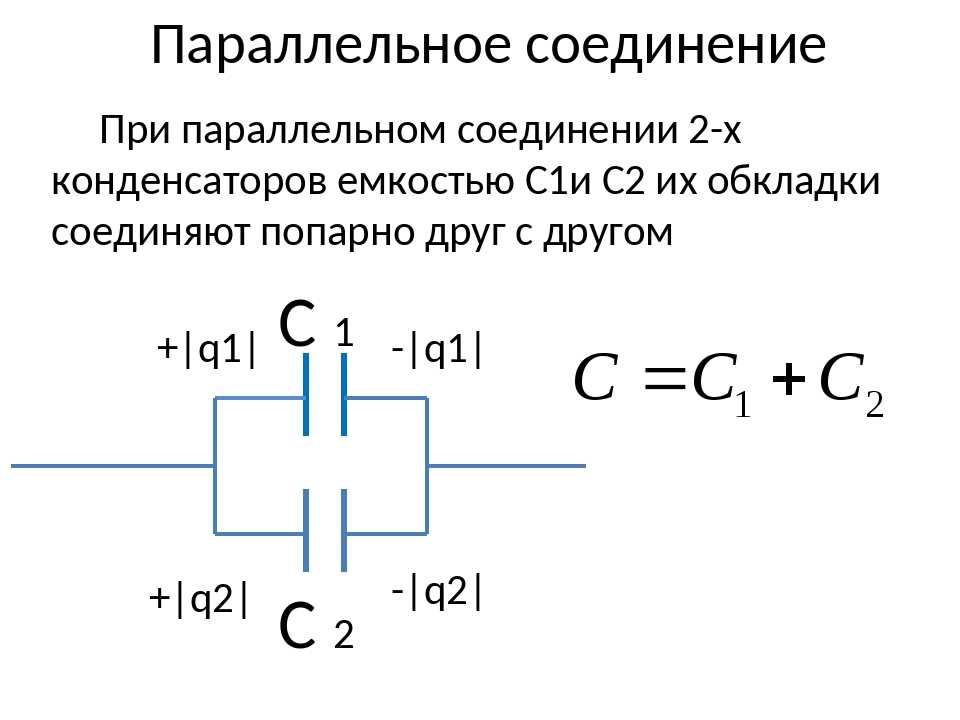

Вот правила расчета емкостей последовательно:

• Если конденсаторы одинаковые, вам повезло. Все, что вам нужно сделать, это разделить емкость одного из отдельных конденсаторов на количество конденсаторов. Например, общая емкость двух конденсаторов по 100 мкФ составляет 50 мкФ.

• Если используются только два конденсатора, используйте следующий расчет:

  В этой формуле C1 и C2 — номиналы двух конденсаторов.

  Вот пример на основе последовательно соединенных конденсаторов 220 мкФ и 470 мкФ:

• Для трех или более последовательно соединенных конденсаторов формула следующая:

  Обратите внимание, что многоточие в конце выражения означает, что вы продолжаете складывать обратные величины емкостей для всех имеющихся у вас конденсаторов.

  Вот пример для трех конденсаторов емкостью 100 мкФ, 220 мкФ и 470 мкФ:

  Как видите, конечный результат равен 59,9768 мкФ. Если только вас не зовут Спок, вас, вероятно, не волнует точность ответа, так что вы можете смело округлить его до 60 мкФ.

Формулы для расчета общей емкости сети конденсаторов обратны правилам, которым вы следуете при расчете сетей резисторов. Другими словами, формула, которую вы используете для резисторов, соединенных последовательно, применима к конденсаторам, включенным параллельно, а формула, которую вы используете для резисторов, соединенных параллельно, применима к конденсаторам, соединенным последовательно. Разве не забавно, как наука иногда любит возиться с вашим разумом?

Об этой статье

Эту статью можно найти в категории:

• Схема,

Электростатика. Можно ли увеличить емкость конденсатора, поместив материал с высокой диэлектрической проницаемостью между двумя прочными изоляторами?

$\begingroup$

Мои очень ограниченные исследования диэлектрических материалов показали, что чем выше диэлектрическая проницаемость материала, тем менее он изолирует. Так почему бы просто не зажать какой-нибудь материал с чрезвычайно высокой диэлектрической проницаемостью между двумя чрезвычайно прочными изоляторами? Не должно ли это привести к большему увеличению значения абсолютной диэлектрической проницаемости по сравнению с увеличением расстояния (в отношении конденсатора с плоскими пластинами), что, следовательно, приведет к большей общей емкости, как указано в уравнении:

C = ε(A/d)

Верно ли также, что считается, что проводящие материалы имеют бесконечную диэлектрическую проницаемость? Если да, то почему он не используется так, как я предложил выше?

Я считаю, что в моем понимании того, что происходит, есть ошибка, и был бы признателен за некоторые разъяснения.

• электростатика
• емкость
• диэлектрик

$\endgroup$

$\begingroup$

Добавление дополнительных слоев в диэлектрический пакет, независимо от того, имеет ли он высокую диэлектрическую проницаемость или нет, не приведет к увеличению емкости.