Резистор. Падение напряжения на резисторе. Мощность. Закон Ома — МикроПрогер
Итак, резистор… Базовый элемент построения электрической цепи.
Работа резистора заключается в ограничении тока, протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока. То есть, без резистора по цепи течет большой ток, встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.
Пример с лампочкой
Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток, проходящий через цепь. И Резистор. Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток, например, 0,75А. Лампочка горит ярко.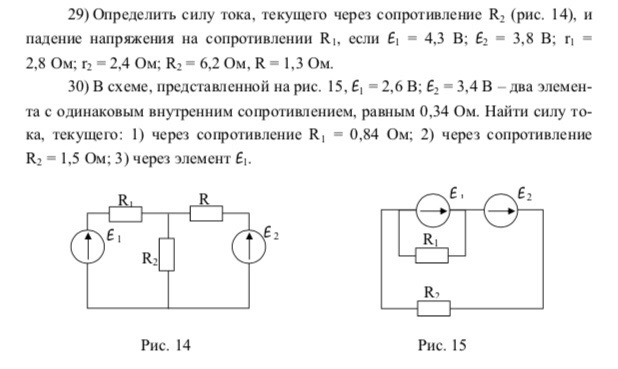
Кроме того, на резисторе происходит падение напряжения. Барьер не только задерживает ток, но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор. Включаем цепь без резистора(слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.
Падение напряжение на резисторе Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе.
Основная характеристика резистора — сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.
Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока(I) и Сопротивление(R).
V=I*R
Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором
V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом
Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи, будет составлять 0,2А.
Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи, будет составлять 0,2А.
Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.
Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.
При протекании тока через резистор совершается работа по ограничению электрического тока. При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.
Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.
Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток, проходящий по цепи(а значит и через резистор), равный 0,2А. Падение напряжения на резисторе
Соединение резисторов
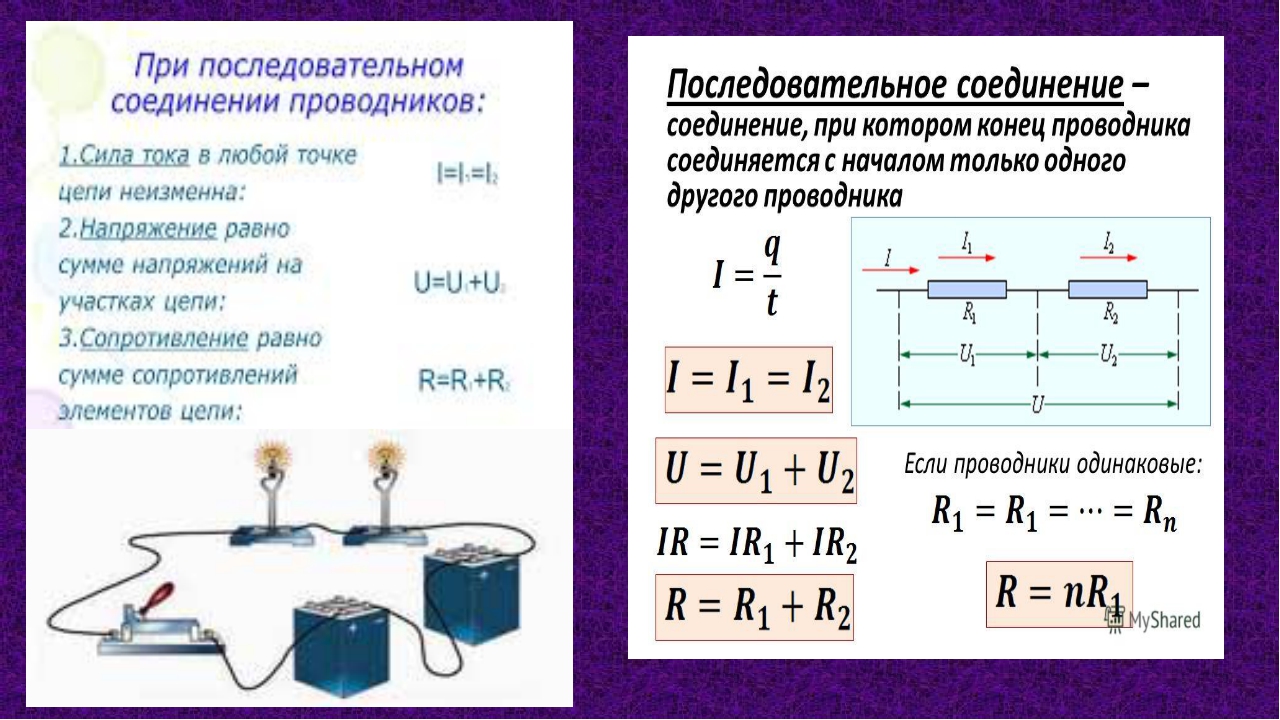
Резисторы в цепях электрического тока имеют последовательное и параллельное соединение.
Последовательное соединение резисторов
При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:
Последовательное соединение резисторов
Параллельное соединение резисторов
При параллельном соединении общее сопротивление резисторов
рассчитывается по формуле: Параллельное соединение резисторов
Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)
Автор публикации
не в сети 9 месяцев
wandrys
877 Комментарии: 0Публикации: 27Регистрация: 17-03-2016Вычислить падение напряжения на резисторе. Падение напряжения
В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Представление об электричестве
Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.
Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.
Резистор
Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах . Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего.
Закон Ома
Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.
Последовательное и параллельное соединение резисторов
Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:
В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:
В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:
Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.
Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R 3 =R 1 +R 2
Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R 3 =R 1 +R 2
В интернете есть удобные он-лайн калькуляторы для расчета и соединения резисторов.
Токоограничивающий резистор
Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.
Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так:
I=(V 1 -V 2)/R
где (V 1 -V 2) является разностью напряжений до и после резистора.
Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).
Математически это запишется так:
Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.
Вы можете воспользоваться он-лайн калькулятором для .
Резисторы как делитель напряжения
Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его.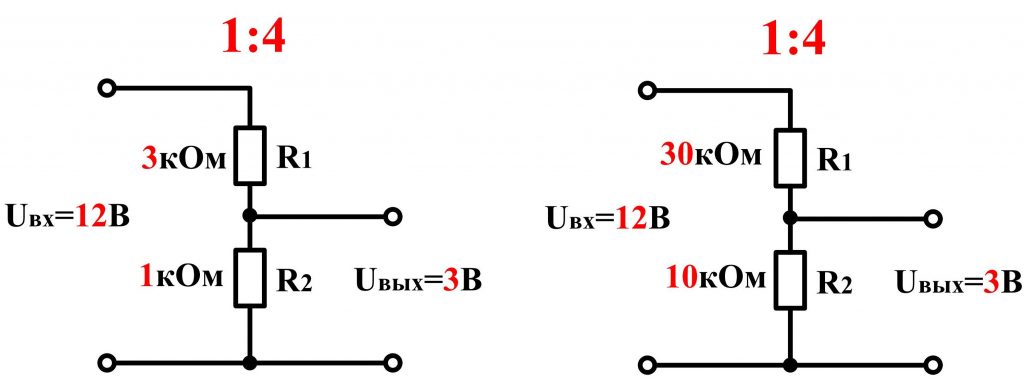 Формула:
Формула:
Если оба резистора имеют одинаковое значение (R 1 =R 2 =R), то формулу можно записать так:
Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B.
Заменив Vb на 0 в формуле 6А, получаем:
Узловой анализ
Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.
Упрощенные правила узлового анализа
Определение узла
Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.
Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.
Определение ветви
Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.
Все напряжения обычно измеряются относительно земли напряжение на которой всегда равно 0 вольт.
Ток всегда течет от узла с более высоким напряжением на узел с более низким.
Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы:
V 1 -V 2 =I 1 *(R 1)
Перенесем:
V 2 =V 1 -(I 1 *R 1)
Где V 2 является искомым напряжением, V 1 является опорным напряжением, которое известно, I 1 ток, протекающий от узла 1 к узлу 2 и R 1 представляет собой сопротивление между 2 узлами.
Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно:
I 1 =(V 1 -V 2)/R 1
Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I 1 + I 3 =I 2
Важно, чтобы вы были в состоянии понимать смысл этих простых формул.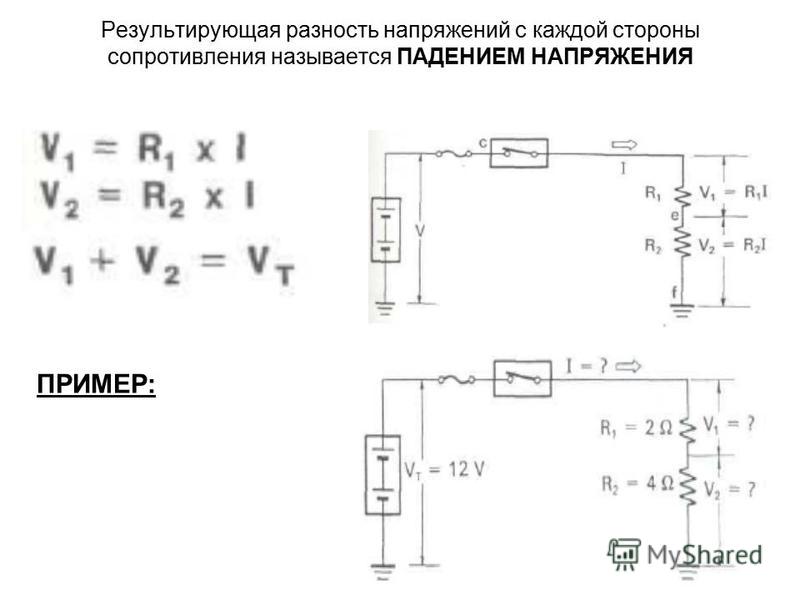 Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.
Расчет необходимой мощности резистора
При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными.
Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I):
P=I*V
где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)
На фото предоставлены резисторы различной мощности, в основном они отличаются размером.
Разновидности резисторов
Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.
Переменный резистор (потенциометр)
На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.
Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb.
Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.
Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.
LDR (светочувствительные резисторы) и термисторы
Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.
Фоторезистор (LDR)
Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны.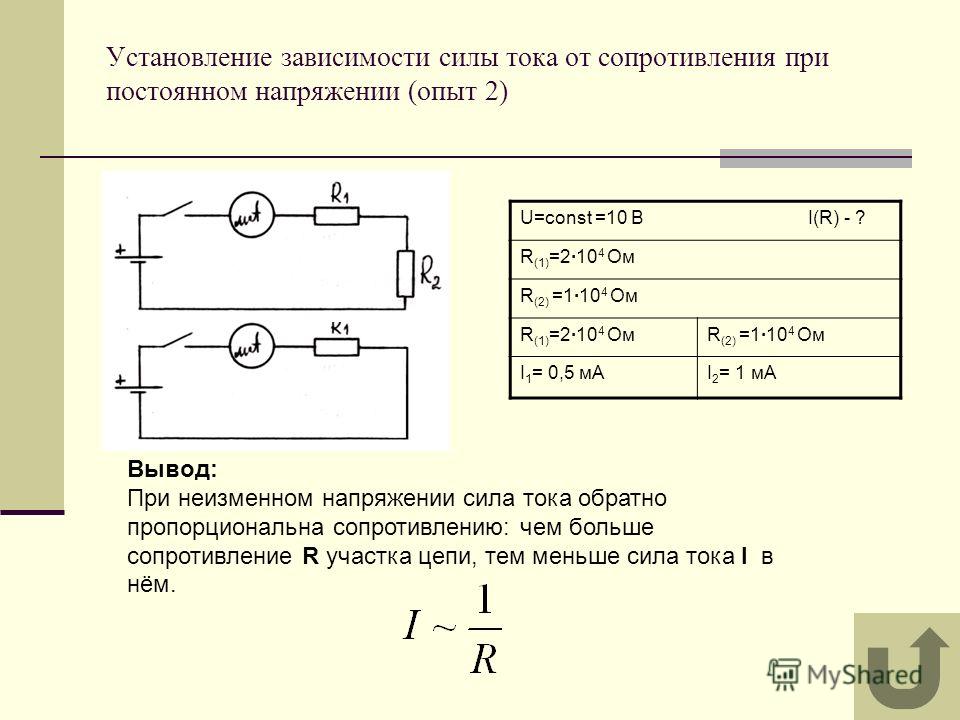 Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.
Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.
Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:
Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то V out будет соответственно от 0.005В до 4.975В.
Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.
Про определение номинала резистора используя цветовую маркировку можно почитать .
Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.
Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Расчет делителя напряжения на резисторах
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.
Зная эти величины, мы можем рассчитать выходное напряжение.
Формула делителя напряжения
Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на .
Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:
Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:
Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:
И, на какое-то время, мы можем упростить схему:
Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:
Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:
А так как I1 равно I2, то:
Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.
Делитель напряжения — калькулятор онлайн
Примечание: десятичные значения вводите через точку
Применение делителя напряжения на резисторах
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометры
Представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.
Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Резистивные датчики
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Пример работы делителя напряжения на фоторезисторе.
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.
Каждый уважающий себя радио-мастер обязан знать формулы для расчета различных электрических величин. Ведь при ремонте электронных устройств или сборке электронных самоделок очень часто приходится проводить подобные расчеты. Не зная таких формул очень сложно и трудоемко, а порой и невозможно справиться с подобного рода задачей!
Первое, что нужно усвоить – ВСЕ ВЕЛЕЧИНЫ В ФОРМУЛАХ УКАЗЫВАЮТЬСЯ В АМПЕРАХ, ВОЛЬТАХ, ОМАХ, МЕТРАХ И КИЛОГЕРЦАХ.
Закон Ома.
Известный из школьного курса физики ЗАКОН ОМА. На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:
На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:
Где: I – сила тока (А), U – напряжение (В), R– сопротивление, имеющееся в цепи (Ом).
Теперь рассмотрим на практике применение формул в радиолюбительских расчетах.
Сопротивление гасящего резистора рассчитывают по формуле: R= U /I
Где: U – излишек напряжения, который необходимо погасить (В), I – ток потребляемый цепью или устройством (А).
Расчет мощности гасящего резистора проводят по формуле: P=I 2 R
Где I – ток потребляемый цепью или устройством (А), R– сопротивление резистора (Ом).
Напряжение падения на сопротивлении можно рассчитать по формуле: U пад =RI
Где R– сопротивление гасящего резистора (Ом), I– ток потребляемый устройством или цепью (А).
Где P– мощность устройства (Вт), U– напряжение питания устройства (В).
Где I– ток потребляемый устройством (А), U– напряжение питания устройства (В).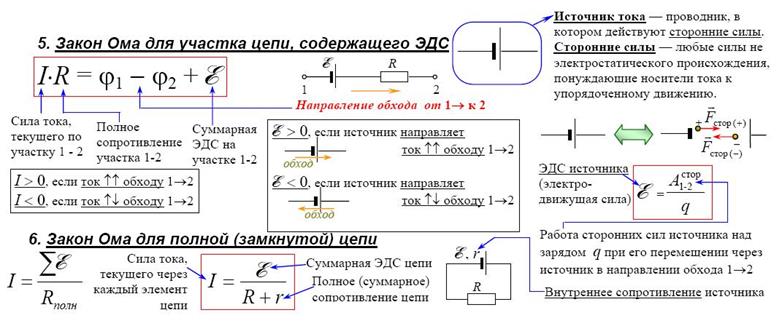
Где ƒ-частота в килогерцах ƛ- длинна волны в метрах.
Где ƛ- длинна волны в метрах, ƒ – частота в килогерцах.
Рассчитать номинальную выходную мощность звуковоспроизводящего устройства (усилитель, проигрыватель и т.п.) можно по формуле: P=U 2 вых. / R ном .
Где U 2 – напряжение звуковой частоты на нагрузке, R– номинальное сопротивление нагрузки.
И в завершении еще несколько формул. По этим формулам, ведут расчет сопротивления и емкости резисторов и конденсаторов в тех случаях, когда возникает необходимость в параллельном или последовательном их соединении.
Расчет соединенных параллельно двух резисторов производят по формуле: R=R 1 R 2 /(R 1 +R 2)
Где R 1 и R 2 — сопротивление первого и второго резистора соответственно (Ом).
Расчет сопротивления включенных параллельно более чем двух резисторов проводят по формуле: 1/R=1/R 1 +1/R 2 +1/R n…
Где R 1 , R 2 , R n … — сопротивление первого, второго и последующих резисторов соответственно (Ом).
Расчет емкости соединенных параллельно нескольких конденсаторов проводят по формуле: C=C 1 + C 2 +C n …
Где C 1 , C 2 и C n – емкость первого, второго и последующих конденсаторов соответственно (мФ).
Расчет емкости двух соединенных последовательно конденсаторов проводят по формуле: C=C 1 C 2 /C 1 +C 2
Где C 1 и C 2 – емкость первого и второго конденсаторов соответственно (мФ).
Расчет емкости включенных последовательно более чем двух конденсаторов проводят по формуле :
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1 Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r = 0,5 Ом. Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей .
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2Общий ток цепи, содержащей два соединенных параллельно резистора R 1 =70 Ом и R 2 =90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала
Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала
Закон Ома (страница 3)
Решение:
Падения напряжения на резисторах R1 и R2, а также на резисторах 2R1 и 2R2 пропорциональны их сопротивлениям. Поэтому падение напряжения на резисторе R равно нулю и ток через него не проходит. Через резистор R2 течет ток
18 Один полюс источника тока с э. д. с. ε = 1400 В и внутренним сопротивлением r = 2,2 Ом подключен к центральной алюминиевой жиле кабеля (диаметр жилы D1 = 8мм), другой — к его свинцовой оболочке (наружный диаметр D2 =18 мм, внутренний — d2 = 16 мм). На каком расстоянии l от источника кабель порвался и произошло замыкание жилы с оболочкой, если начальный ток короткого замыкания I=120 А? Удельные сопротивления алюминия и свинца ρ1 =0,03 мкОм·м и ρ2 = 0,2 мкОм·м.
Решение:
Полное сопротивление цепи R= R1 + R2 + r, где сопротивления жилы и оболочки до места замыкания
Ток в цепи I= e/R; отсюда
19 Найти ток I, текущий через резистор с сопротивлением R1 в схеме, параметры которой даны на рис. 107, в первый момент после замыкания ключа, если до этого напряжение на конденсаторе было постоянным.
Решение:
Напряжение на конденсаторе V=ε. Это же напряжение будет в первый момент после замыкания ключа на резисторе R1. Поэтому текущий через него в этот момент ток I=ε/R1.
20 Найти напряжения V1 и V2 на конденсаторах с емкостями С1 и С2 в схеме, параметры которой даны на рис. 108.
Решение:
После включения источника тока с э. д. с. ε конденсаторы зарядятся, и, когда ток прекратится, все их обкладки, соединенные с резистором R, будут иметь одинаковый потенциал. Конденсаторы с емкостями С+С1 и С+С2 включены последовательно с источником тока. Общее напряжение на них V1+V2 =ε, а заряд на них
отсюда
21 Найти заряды q1, q2 и q3 на каждом из конденсаторов в схеме, параметры которой даны на рис. 109.
Решение:
Обкладки конденсатора C1 замкнуты через резисторы R1 и R2. Поэтому заряд на этом конденсаторе q1=0 (после прекращения зарядки конденсаторов С2 и С3). Так как после зарядки конденсаторов токи в схеме не протекают, то напряжения на конденсаторах С2 и С3 равны ε. Следовательно,
22 В цепь, питаемую источником тока с внутренним сопротивлением r = 3 Ом, входят два резистора с одинаковыми сопротивлениями R1 = R2 = 28 Ом, включенные параллельно, и резистор с сопротивлением R3 = 40 Ом (рис.110). Параллельно резистору R3 подключен конденсатор емкости С=5 мкФ, заряд которого q=4,2 Кл. Найти э. д. с. ε источника.
Решение:
Падение напряжения на резисторе R3 будет V=q/C=IR3; отсюда ток, текущий через этот резистор, I=q/CR3. Полное сопротивление цепи и э. д. с. источника тока
23 Два резистора с одинаковыми сопротивлениями R1 =25 Ом и резистор с сопротивлением R2 = 50 Ом подключены к источнику тока по схеме, изображенной на рис. 111. К участку ab подключен конденсатор емкости С = 5 мкФ. Найти э. д. с. ε источника тока, если заряд на конденсаторе q = 0,11 мКл.
Решение:
24 Найти заряд на конденсаторе емкости С в схеме, параметры которой даны на рис. 112.
Решение:
Сопротивление конденсатора постоянному току бесконечно велико. Поэтому после зарядки конденсатора по резистору R3 ток протекать не будет. Не будет и падения напряжения на этом резисторе. Следовательно, точка а и верхняя обкладка конденсатора будут иметь одинаковый потенциал. Потенциал же точки b будет равен потенциалу нижней обкладки конденсатора. Таким образом, напряжение на конденсаторе будет равно падению напряжения на резисторе R2. Ток в цепи
отсюда заряд на конденсаторе
25 Найти напряжение на конденсаторе емкости в схеме, параметры которой даны на рис. 113.
Решение:
26 Источник тока с внутренним сопротивлением r=10м замкнут на резистор с сопротивлением R. Вольтметр, подключенный к зажимам источника, показывает напряжение V1=20 B. Когда параллельно резистору с сопротивлением R присоединен резистор с таким же сопротивлением R, показание вольтметра уменьшается до V2 = 15 B. Найти сопротивление резистора R, если сопротивление вольтметра велико по сравнению с R.
Решение:
Напряжения на зажимах источника тока в первом и во втором случаях V1=I1R и V2=I2R/2. Токи в общей цепи в этих случаях
отсюда
27 К источнику тока с э. д. с. ε = 200 В и внутренним сопротивлением r = 0,5 Ом подключены последовательно два резистора с сопротивлениями R1 = 100Ом и R2 = 500 Ом. К концам резистора R2 подключен вольтметр. Найти сопротивление R вольтметра, если он показывает напряжение V=160 В.
Решение:
Падение напряжения на резисторе R2 (и на вольтметре) V=IRо (рис. 358), где R0 = R2R/(R2 + R)-сопротивление параллельно включенных вольтметра и резистора R2. Ток в общей цепи равен
Решая совместно эти уравнения, получим
Тот же результат можно получить, решая систему уравнений
28 Проволока из нихрома изогнута в виде кольца радиуса а=1 м (рис.114). В центре кольца помещен гальванический элемент с э. д. с. ε = 2 В и внутренним сопротивлением r=1,5 0м. Элемент соединен с точками с и d кольца по диаметру с помощью такой же нихромовой проволоки. Найти разность потенциалов между точками cad. Удельное сопротивление нихрома ρ=1,1мкОм⋅м, площадь сечения проволоки S= 1 мм2.
Решение:
В эквивалентной схеме резисторы R1 соответствуют проволокам, соединяющим элемент с кольцом, а резисторы R2-двум половинам кольца (рис. 359). Полное внешнее сопротивление цепи
Ток в общей цепи
Разность потенциалов между точками с и d
29 К источнику тока с внутренним сопротивлением r = 1 Ом подключены два параллельно соединенных резистора с сопротивлениями R1 = 10 Ом и R2 = 2 Ом. Найти отношение токов, протекающих через резистор R1 до и после обрыва в цепи резистора R2.
Решение:
30 Два резистора с сопротивлениями R1 = R2 = 1 Ом и реостат, имеющий полное сопротивление R3 = 2 Ом, присоединены к источнику тока с внутренним сопротивлением r = 0,5 Ом (рис. 115). К разветвленному участку цепи подключен вольтметр. Когда движок реостата находится на его середине (точка а), вольтметр показывает напряжение Va=13 В. Каково будет показание вольтметра, если движок передвинуть в крайнее правое положение на реостате? Сопротивление вольтметра велико по сравнению с R1 и R2.
Решение:
31 Шесть проводников с одинаковыми сопротивлениями R0 = 2 Ом соединены попарно параллельно. Все три пары соединены последовательно и подключены к источнику тока с внутренним сопротивлением r=1 Ом. При этом по каждому проводнику течет ток I0 = 2,5А. Какой ток будет течь по каждому проводнику, если один из них удалить?
Решение:
Сопротивление каждой пары проводников равно R0/2. Полное внешнее сопротивление цепи до удаления одного из проводников R1=3R0/2. По закону Ома для полной цепи
отсюда э. д. с. источника тока
После удаления одного из проводников полное внешнее сопротивление цепи
Ток в общей цепи
Через проводник, оставшийся без пары, будет идти ток
а через остальные проводники будут идти токи I2/2 = 2 А.
32 Источник тока с э. д. с. ε = 100 В и внутренним сопротивлением r = 0,2 Ом и три резистора с сопротивлениями R1 = 3 Ом, R2 = 2 Ом и R3 = 18,8 Ом включены по схеме, изображенной на рис. 116. Найти токи, текущие через резисторы R1 и R2.
Решение:
33 К источнику тока с э. д. с. e=120 В и внутренним сопротивлением r=10 Ом подключены два параллельных провода с сопротивлениями R1 =20 Ом. Свободные концы проводов и их середины соединены друг с другом через две лампы с сопротивлениями R2 = 200 Ом. Найти ток, текущий через источник тока.
Решение:
Верхняя лампа и провода, идущие к ней, начиная от места присоединения нижней лампы (рис. 360), образуют последовательную цепочку с сопротивлением R3=R1+R2. Эта цепочка соединена параллельно с нижней лампой и вместе с ней образует сопротивление
Полное внешнее сопротивление цепи
Через источник тока течет ток
34 При замыкании источника тока на резистор с сопротивлением R1=5 Ом в цепи идет ток I1 = 5 А, а при замыкании на резистор с сопротивлением R2 = 2 Ом идет ток I2 = 8 А. Найти внутреннее сопротивление r и э. д. с. источника тока ε.
Решение:
Если ε и r — э. д. с. и внутреннее сопротивление источника тока, то
Из этих уравнений имеем
35 При замыкании источника тока на резистор с сопротивлением R1 = 14 Ом напряжение на зажимах источника V1 = 28 В, а при замыкании на резистор с сопротивлением R2 = 29 Ом напряжение на зажимах V2 = 29 В. Найти внутреннее сопротивление r источника.
Решение:
36 Амперметр с сопротивлением R1 = 2 Ом, подключенный к источнику тока, показывает ток I1 = 5 А. Вольтметр с сопротивлением R2 = 150 Ом, подключенный к такому же источнику тока, показывает напряжение V=12B. Найти ток короткого замыкания Iк источника.
Решение:
При подключении к источнику тока амперметра через него течет I1=ε/(R1+r), где ε — э. д. с. батареи, а r — ее внутреннее сопротивление; при подключении к источнику тока вольтметра через него течет ток I2=ε/(R2+r), и вольтметр показывает напряжение
отсюда
Ток короткого замыкания (при равном нулю внешнем сопротивлении)
37 Два параллельно соединенных резистора с сопротивлениями R1=40 Ом и R2 = 10 Ом подключены к источнику тока с э. д. с. ε=10 В. Ток в цепи I=1 А. Найти внутреннее сопротивление источника и ток короткого замыкания.
Решение:
38 Аккумулятор с э. д. с. ε = 25 В и внутренним сопротивлением r = 1 Ом заряжается от сети с напряжением V=40 В через сопротивление R = 5 Ом. Найти напряжение Vа на зажимах аккумулятора.
Решение:
При зарядке аккумулятор включается навстречу источнику тока. Во время зарядки ток внутри аккумулятора течет от положительного полюса к отрицательному. Напряжение сети V=ε+I(R+r), где I-ток зарядки; отсюда I=(V-ε)/(R+r). Напряжение на зажимах аккумулятора
Какое напряжение после резистора. Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор
Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.
Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов.
Весь смысл состоит в том, что при протекании тока через диод на нем падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.
На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включают соответствующее количество диодов.
Чтобы понизить напряжение на 6 В необходимо приблизительно включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.
Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором. Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?
На Рис 1 — добавочное сопротивление — резистор (проволочное сопротивление), Рис 2 — добавочное сопротивление — диод.
У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во столько же раз увеличится и падение напряжения на резисторе.
Из примера 1: если мы к лампочке подключим параллельно еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом *0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.
Совсем другая картина будет если вместо резистора будет цепочка диодов.
Зависимость между током протекающем через диод и падающем на нем напряжении нелинейная. Ток может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.
Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше увеличивается его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.
Диоды в такой цепи выполняют роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.
Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.
В цепях переменного тока, в качестве добавочного сопротивления можно использовать конденсатор, индуктивность, динистор или тиристор (с добавлением схемы управления).
Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.
Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид — это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.
На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.
Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:
где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.
Электрическая энергия — это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.
Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.
Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.
Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.
Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:
R = (R1*R2) / (R1+R2)
Определяем сопротивление всей цепи через сумму R4 = R+R3.
Рассчитываем ток:
Остается узнать значение падение напряжения на выбраном элементе:
Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.
Итак, резистор … Базовый элемент построения электрической цепи.
Работа резистора заключается в ограничении тока , протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока . То есть, без резистора по цепи течет большой ток , встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.
Пример с лампочкойРассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток , проходящий через цепь. И Резистор . Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток , например, 0,75А. Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.
Кроме того, на резисторе происходит падение напряжения . Барьер не только задерживает ток , но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт. На всякий случай амперметр, два вольтметра про запас, лампочку и резистор . Включаем цепь без резистора (слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В. На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.
Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе .
Основная характеристика резистора — сопротивление . Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление , тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.
Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока (I) и Сопротивление(R).
Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора , при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.
V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом
Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи , будет составлять 0,2А.
Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.
Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.
При протекании тока через резистор совершается работа по ограничению электрического тока . При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.
Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.
Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток , проходящий по цепи(а значит и через резистор ), равный 0,2А. Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе ). Это значит, что мощность тока через резистор равна P=I*V=0,2А*5В=1Вт. Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.
Соединение резисторовРезисторы в цепях электрического тока имеют последовательное и параллельное соединение .
При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:
При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:
Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r = 0,5 Ом. Сопротивления резисторов R 1 = 20 и R 2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей .
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2Общий ток цепи, содержащей два соединенных параллельно резистора R 1 =70 Ом и R 2 =90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала
Расчет падения напряжения на транзисторе
Во-первых: ток течет в базу, через излучатель. во-вторых, ток течет через коллектор и выходит из излучателя. Суммарный ток через излучатель равен току через основание плюс ток через коллектор.
Вам потребуется таблица данных, чтобы определить точное падение напряжения. Однако также следует помнить, что нет двух идентичных транзисторов.
Таблица данных будет содержать графики, которые вы можете использовать для поиска ожидаемых значений. Для некоторых вычислений полезно предположить, что Vbe обычно составляет около 0,7v. Соединение база-эмиттер по сути является диодом, поэтому оно зажимает напряжение на себе примерно до 0,7 В. Используя этот факт, легко вычислить ток, поступающий в базу: напряжение на R составляет приблизительно 5-0,7 = 4,3 В. Таким образом, ток, идущий в базу, должен быть примерно:
I = V / R = 4,3 / R
Так что, если вы знаете R, вы можете приблизить ток, текущий в базу. Это даст вам один фактор, который поможет вам прочитать графики из таблицы данных транзистора. Скажем, R составляет 10 кОм, ток, протекающий в базу, будет приблизительно 0,43 мА.
Теперь с этим базовым током вы можете рассчитать ток, протекающий через коллектор — просто умножьте его на коэффициент усиления тока транзистора. Но имейте в виду, что они могут сильно различаться в первую очередь между транзисторами одной модели, а также при разных условиях работы этой модели. Скажем, если 50, то ток, протекающий через коллектор, будет приблизительно 22,5 мА.
Используя приведенную выше схему, предположим, что падение напряжения на светодиоде составляет 2 В при 22,5 мА, что означает, что значение Vbe должно составлять 5-2 = 3 В. Однако, опять же, падение напряжения светодиода при данном токе будет незначительно отличаться между светодиодами одной и той же модели, и некоторые светодиоды, такие как белые светодиоды, имеют тенденцию иметь более высокое падение напряжения, например, 4v.
Чтобы попытаться получить точное значение Vbe, есть формула, которую вы можете использовать, однако, учитывая различия между отдельными транзисторами, гораздо проще просто использовать графики. Поскольку вы знаете приблизительное напряжение Vce и приблизительный базовый ток Ib, вы можете посмотреть Vbe на графике.
И учитывая диапазон возможных значений hfe, указанных в таблице, (обычно они предоставляют три значения: минимальное, типичное и максимальное). Используя верхнюю и нижнюю границы hfe, вы можете рассчитать верхнюю и нижнюю границы тока, который будет проходить через коллектор. Исходя из этого и таблицы данных светодиода, вы можете рассчитать верхнюю и нижнюю границу Vce. Это значение будет полезно при уточнении возможных значений Vbe, поскольку часто Vbe существенно зависит от Vce и Ice; это может иметь значение +/- 0,2 В или около того.
Другие соображения, которые также могут быть весьма значительными, это температура перехода транзистора. Итак, сколько энергии протекает через него, как долго, а также насколько хорошо он отдает тепло в окружающую среду, и температура этой среды будет определять температуру перехода транзистора, что, в свою очередь, повлияет на такие значения, как hfe, Vbe и так далее.
Для вашей схемы выше, вы можете использовать транзистор, такой как NP54 BC547, который является BJT NPN транзистором общего назначения. Эта таблица должна быть достаточной для того, чтобы вы могли понять, как она будет себя вести. Значения hfe, которые я изложил выше, будут разными в BC547; в техническом описании указано минимальное значение 110, максимальное — 800. Таким образом, ваша схема даст очень широкий диапазон значений потенциального льда, поэтому будьте осторожны, чтобы не перегореть светодиод. Вы можете определить hfe любого отдельного транзистора, подав небольшой ток через базу, и измерить ток через коллектор; затем разделите Ic на Ib, и это то, что нужно для этой ситуации. (Если транзистор не «насыщен», то есть светодиод или что-то на его месте в вашей цепи имеет почти 5 В через него, что означает, что транзистор не может еще больше увеличить Ic, поскольку он уже действует как короткое замыкание.) чтобы рассчитать hfe одного конкретного BC547, можно предположить, что он не будет иметь hfe меньше 110, а затем рассчитать резистор для замены R и светодиода (назовем его Rled) на. Сделайте R в 800 раз больше Rled, затем измерьте ток через Rled. (Vbe / kt) -1) не применяется, когда транзистор насыщен , поскольку Ie будет ограничено. (Смотри ниже). Во-вторых, решение включает в себя построение пересечения двух графиков: напряжение на R против Ir в соответствии с законом Ома и Vbe против Ib с уравнением Эберса-Молла, решение, где Ir и Ib равны. Ir против Vr будет прямой линией, а Ib против Vbe будет экспоненциальной.
График в вашем ответе выглядит правильно, если предположить, что он взят из схемы, которую вы разместили в своем вопросе? (То есть со светодиодом?) Причина, по которой он может перестать быть линейным, заключается в том, что напряжение на светодиоде становится близким к 5 В, что означает, что транзистор насыщается. Таким образом, больший базовый ток приводит лишь к немного большему току, проходящему через светодиод, из-за немного уменьшенных насыщенных значений Vce. Это отражается в следующем:
Если вы посмотрите на эту таблицу данных для 2N3904 , она сведет в таблицу эти два значения:
VBE (sat) Напряжение насыщения базового излучателя:
- С IC = 10 мА и IB = 1,0 мА, тогда Vbe = 0,65
- При IC = 50 мА и IB = 5,0 мА, тогда Vbe = 0,85
Схемы включения светодиодов
Светодиод — полупроводниковый прибор с электронно-дырочным переходом, создающий оптическое излучение при пропускании через него электрического тока в прямом направлении.
Светодиод является прибором токовым, т.е. ток через него должен быть ограничен с помощью резистора. Как рассчитать этот резистор, было уже рассказано, повторяться здесь не будем, но формулу, на всякий случай, приведем еще раз.
Рисунок 1.
Здесь Uпит. – напряжение питания, Uпад. – падение напряжение на светодиоде, R – сопротивление ограничивающего резистора, I – ток через светодиод.
Однако, несмотря на всю теорию, китайская промышленность выпускает всевозможные сувениры, брелоки, зажигалки, в которых светодиод включен без ограничительного резистора: просто две-три дисковых батарейки и один светодиод. В этом случае ток ограничивается внутренним сопротивлением батареи, мощности которой просто не хватает, чтобы спалить светодиод.
Но тут, кроме перегорания, есть и еще одно неприятное свойство – деградация светодиодов, более всего присущее светодиодам белого и синего цветов: через некоторое время яркость свечения становится совсем незначительной, хотя ток через светодиод протекает вполне достаточный, на уровне номинального.
Нельзя сказать, что не светит вовсе, свечение еле заметно, но это уже не фонарик. Если при номинальном токе деградация происходит не ранее, чем через год непрерывного свечения, то при завышенном токе дождаться этого явления можно через полчаса. Такое включение светодиода следует назвать плохим.
Подобную схему можно объяснить лишь стремлением сэкономить на одном резисторе, припое, и трудозатратах, что при массовых масштабах производства, видимо, оправдано. Кроме того, зажигалка или брелок вещь одноразовая, копеечная: кончился газ или села батарейка — сувенир просто выкинули.
Рисунок 2. Схема плохая, но применяется достаточно часто.
Очень интересные вещи получаются (конечно, случайно), если по такой схеме подключить светодиод к блоку питания с выходным напряжением 12В и током не менее 3А: происходит ослепительная вспышка, раздается достаточно громкий хлопок, дымок, и остается удушливый запах. Так и вспоминается вот такая притча: «Можно ли посмотреть на Солнце в телескоп? Да, но только два раза. Один раз левым глазом, другой правым». Кстати, подключение светодиода без ограничительного резистора наиболее распространенная ошибка у начинающих, и о ней хотелось бы предупредить.
Чтобы исправить это положение, продлить срок службы светодиода, схему следовало бы чуточку изменить.
Рисунок 3. Хорошая схема, правильная.
Именно такую схему следует считать хорошей или правильной. Чтобы проверить, правильно ли указан номинал резистора R1, можно воспользоваться формулой, показанной на рисунке 1. Будем считать, что падение напряжения на светодиоде 2В, ток 20мА, напряжение питания 3В обусловлено применением двух пальчиковых батареек.
А вообще не надо стремиться ограничить ток на уровне предельно допустимых 20мА, можно запитать светодиод меньшим током, ну, хотя бы, миллиампер 15…18. При этом произойдет совсем незначительное уменьшение яркости, который глаз человека, в силу особенностей устройства, не заметит совсем, а вот срок службы светодиода намного увеличится.
Еще один пример плохого включения светодиодов можно встретить в различных фонариках, уже более мощных, нежели брелоки и зажигалки. В этом случае некоторое количество светодиодов, иногда достаточно большое, просто включено параллельно, и тоже без ограничительного резистора, в роли которого опять же выступает внутреннее сопротивление батареи. Такие фонарики достаточно часто попадают в ремонт именно по причине выгорания светодиодов.
Рисунок 4. Совсем плохая схема включения.
Казалось бы, исправить положение может схема, показанная на рисунке 5. Всего один резистор, и дело, казалось бы, пошло на поправку.
Рисунок 5. Так уже немного лучше.
Но и такое включение поможет мало. Дело в том, что в природе просто не найти двух одинаковых полупроводниковых приборов. Именно поэтому, например, транзисторы одного типа имеют различный коэффициент усиления, даже если они из одной производственной партии. Тиристоры и симисторы тоже бывают разные. Некоторые открываются легко, а другие настолько тяжко, что от их применения приходится отказаться. То же можно сказать и о светодиодах – двух абсолютно одинаковых, тем более трех или целой кучи, найти просто невозможно.
Замечание на тему. В DataSheet на светодиодную сборку SMD-5050 (три независимых светодиода в одном корпусе) включение, показанное на рисунке 5, не рекомендуется. Мол, из-за разброса параметров отдельных светодиодов, может быть заметна разница в их свечении. А казалось бы, в одном корпусе!
Никакого коэффициента усиления у светодиодов, конечно же, нет, зато есть такой важный параметр, как прямое падение напряжения. И если даже светодиоды взяты из одной технологической партии, из одной упаковки, то двух одинаковых в ней просто не будет. Поэтому ток у всех светодиодов будет разный. Тот светодиод, у которого ток будет больше всех, и рано или поздно превысит номинальный, сгорит раньше всех.
В связи с этим прискорбным событием весь возможный ток пойдет через два оставшихся в живых светодиода, естественно, превышая номинальный. Ведь резистор-то рассчитывался «на троих», на три светодиода. Повышенный ток вызовет и повышенный нагрев кристаллов светодиодов, и тот, который окажется «слабее», тоже сгорает. Последнему светодиоду также не остается ничего иного, как последовать примеру своих товарищей. Такая вот цепная реакция получается.
В данном случае под словом «сгорит» подразумевается просто разрыв цепи. Но может произойти, что в одном из светодиодов получится элементарно короткое замыкание, шунтирующее остальные два светодиода. Естественно, что они обязательно погаснут, хотя и останутся в живых. Резистор при такой неисправности будет усиленно греться и в конце концов, может быть, сгорит.
Чтобы такого не произошло, схему надо немного изменить: для каждого светодиода установить свой резистор, что и показано на рисунке 6.
Рисунок 6. А вот так светодиоды прослужат очень долго.
Здесь все, как требуется, все по правилам схемотехники: ток каждого светодиода будет ограничен своим резистором. В такой схеме токи через светодиоды не зависят друг от друга.
Но и это включение не вызывает особого восторга, поскольку количество резисторов равно количеству светодиодов. А хотелось бы, чтобы светодиодов было побольше, а резисторов поменьше. Как же быть?
Выход из этого положения достаточно простой. Каждый светодиод надо заменить цепочкой последовательно включенных светодиодов, как показано на рисунке 7.
Рисунок 7. Параллельное включение гирлянд.
Платой за такое усовершенствование будет увеличение напряжения питания. Если для одного светодиода достаточно всего трех вольт, то даже два светодиода, включенных последовательно, от такого напряжения уже не зажечь. Так какое же напряжение понадобится для включения гирлянды из светодиодов? Или по-другому, сколько светодиодов можно подключить к источнику питания с напряжением, например, 12В?
Замечание. Под названием «гирлянда» здесь и далее следует понимать не только елочное украшение, но также любой осветительный светодиодный прибор, в котором светодиоды соединены последовательно или параллельно. Главное, что светодиод не один. Гирлянда, она и в Африке гирлянда!
Чтобы получить ответ на этот вопрос, достаточно напряжение питания просто разделить на падение напряжения на светодиоде. В большинстве случаев при расчетах это напряжение принимается 2В. Тогда получается 12/2=6. Но не надо забывать, что какая-то часть напряжения должна остаться для гасящего резистора, хотя бы вольта 2.
Получается, что на светодиоды остается только 10В, и количество светодиодов станет 10/2=5. При таком положении дел, чтобы получить ток 20мА, ограничительный резистор должен иметь номинал 2В/20мА=100Ом. Мощность резистора при этом составит P=U*I=2В*20мА=40мВт.
Такой расчет вполне справедлив, если прямое напряжение светодиодов в гирлянде, как было указано, 2В. Именно это значение часто принимается при расчетах, как некоторое среднее. Но на самом деле это напряжение зависит от типа светодиодов, от цвета свечения. Поэтому при расчетах гирлянд следует ориентироваться на тип светодиодов. Падения напряжения для светодиодов разных типов приведены в таблице, показанной на рисунке 8.
Рисунок 8. Падение напряжения на светодиодах разных цветов.
Таким образом, при напряжении источника питания 12В, за вычетом падения напряжения на токоограничивающем резисторе, всего можно подключить 10/3,7=2,7027 белых светодиодов. Но кусочек от светодиода не отрежешь, поэтому подключить возможно только два светодиода. Такой результат получается если из таблицы взять максимальное значение падения напряжения.
Если же в расчет подставить 3В, то совершенно очевидно, что подключить возможно три светодиода. При этом каждый раз придется кропотливо пересчитывать сопротивление ограничительного резистора. Если реальные светодиоды окажутся с падением напряжения 3,7В, а может выше, три светодиода могут и не зажечься. Так что лучше остановиться на двух.
Принципиально не важно, какого цвета будут светодиоды, просто при расчете придется учитывать разные падения напряжений в зависимости от цвета свечения светодиода. Главное, чтобы они были рассчитаны на один ток. Нельзя собрать последовательную гирлянду из светодиодов, часть которых с током 20мА, а другая часть из 10-ти миллиамперных.
Понятно, что при токе 20мА светодиоды с номинальным током 10мА попросту сгорят. Если же ограничить ток на уровне 10мА, то 20-ти миллиамперные засветятся недостаточно ярко, примерно как в выключателе со светодиодом: ночью видно, днем нет.
Чтобы облегчить себе жизнь, радиолюбители разрабатывают различные программы-калькуляторы, облегчающие всевозможные рутинные расчеты. Например, программы для расчета индуктивностей, фильтров различного типа, стабилизаторов тока. Есть такая программа и для расчета светодиодных гирлянд. Скриншот такой программы приведен на рисунке 9.
Рисунок 9. Скриншот программы «Расчет_сопротивления_резистора__Ledz_».
Программа работает без установки в системе, просто ее надо скачать и пользоваться. Все настолько просто и понятно, что никаких пояснений к скриншоту совсем не требуется. Естественно, что все светодиоды должны быть одного цвета и с одинаковым током.
Ограничительные резисторы это, конечно, хорошо. Но только тогда, когда известно, что вот эта гирлянда будет питаться от стабилизированного источника постоянного напряжения 12В, и ток через светодиоды не превысит расчетного значения. А как быть, если просто нет источника с напряжением 12В?
Такая ситуация может возникнуть, например, в грузовом автомобиле с напряжением бортовой сети 24В. Выйти из такой кризисной ситуации поможет стабилизатор тока, например, «SSC0018 — Регулируемый стабилизатор тока 20..600мА». Его внешний вид показан на рисунке 10.
Рисунок 10. Регулируемый стабилизатор тока SSC0018
Технические характеристики стабилизатора показаны на рисунке 11.
Рисунок 11. Технические характеристики стабилизатора тока SSC0018
Изначально стабилизатор тока SSC0018 был разработан для применения в светодиодных светильниках, но может также применяться для зарядки малогабаритных аккумуляторов. Пользоваться устройством SSC0018 достаточно просто.
Сопротивление нагрузки на выходе стабилизатора тока может быть нулевым, попросту можно замкнуть накоротко выходные клеммы. Ведь стабилизаторы и источники тока не боятся коротких замыканий. При этом ток на выходе будет номинальным. Уж если установили 20мА, то столько и будет.
Из сказанного можно сделать вывод, что к выходу стабилизатора тока можно «напрямую» подключить миллиамперметр постоянного тока. Начинать такое подключение следует с самого большого предела измерений, ведь какой там отрегулирован ток никому не известно. Далее простым вращением подстроечного резистора установить требуемый ток. При этом, конечно, не забыть подключить стабилизатор тока SSC0018 к блоку питания. На рисунке 12 показана схема включения SSC0018 для питания светодиодов, соединенных параллельно.
Рисунок 12. Подключение для питания светодиодов, соединенных параллельно
Здесь все понятно из схемы. Для четырех светодиодов с током потребления 20мА на каждый на выходе стабилизатора надо выставить ток 80мА. При этом на входе стабилизатора SSC0018 потребуется напряжение чуть большее, чем падение напряжения на одном светодиоде, о чем было сказано выше. Конечно, подойдет и большее напряжение, но это приведет только к дополнительному нагреву микросхемы стабилизатора.
Замечание. Если для ограничения тока с помощью резистора напряжение источника питания должно превышать общее напряжение на светодиодах незначительно, всего вольта на два, то для нормальной работы стабилизатора тока SSC0018 это превышение должно быть несколько выше. Никак не меньше, чем 3…4В, иначе попросту не откроется регулирующий элемент стабилизатора.
На рисунке 13 показано подключение стабилизатора SSC0018 при использовании гирлянды из нескольких последовательно соединенных светодиодов.
Рисунок 13. Питание последовательной гирлянды через стабилизатор SSC0018
Рисунок взят из технической документации, поэтому попробуем рассчитать количество светодиодов в гирлянде и постоянное напряжение, потребное от блока питания.
Указанный на схеме ток, 350мА, позволяет сделать вывод, что гирлянда собрана из мощных белых светодиодов, ведь как было сказано чуть выше, основное назначение стабилизатора SSC0018 это источники освещения. Падение напряжения на белом светодиоде находится в пределах 3…3,7В. Для расчета следует взять максимальное значение 3,7В.
Максимальное входное напряжение стабилизатора SSC0018 составляет 50В. Вычитаем из этого значения 5В, необходимых для работы самого стабилизатора, остается 45В. Этим напряжением можно «засветить» 45/3,7=12,1621621… светодиодов. Очевидно, что это надо округлить до 12.
Количество светодиодов может быть и меньше. Тогда входное напряжение придется уменьшить (при этом выходной ток не изменится, так и останется 350мА как был отрегулирован), зачем на 3 светодиода, пусть даже мощных, подавать 50В? Такое издевательство может закончиться плачевно, ведь мощные светодиоды отнюдь недешевы. Какое потребуется напряжение для подключения трех мощных светодиодов желающие, а они всегда найдутся, могут посчитать сами.
Регулируемый стабилизатор тока SSC0018 устройство достаточно хорошее. Но весь вопрос в том, всегда ли оно нужно? Да и цена девайса несколько смущает. Каков же может быть выход из создавшегося положения? Все очень просто. Прекрасный стабилизатор тока получается из интегральных стабилизаторов напряжения, например, серии 78XX или LM317.
Для создания такого стабилизатора тока на базе стабилизатора напряжения потребуется всего 2 детали. Собственно сам стабилизатор и один единственный резистор, сопротивление и мощность которого поможет рассчитать программа StabDesign, скриншот которой показан на рисунке 14.
Рисунок 14. Расчет стабилизатора тока с помощью программы StabDesign.
Особых пояснений программа не требует. В выпадающем меню Type выбирается тип стабилизатора, в строке Iн задается требуемый ток и нажимается кнопочка Calculate. В результате получается сопротивление резистора R1 и его мощность. На рисунке расчет проведен для тока 20мА. Это для случая, когда светодиоды соединены последовательно. Для параллельного соединения ток подсчитывается так же, как показано на рисунке 12.
Светодиодная гирлянда подключается вместо резистора Rн, символизирующего нагрузку стабилизатора тока. Возможно даже подключение всего одного светодиода. При этом катод подключается к общему проводу, а анод к резистору R1.
Входное напряжение рассмотренного стабилизатора тока находится в пределах 15…39В, поскольку применен стабилизатор 7812 с напряжением стабилизации 12В.
Ранее ЭлектроВести писали, что в городе Эссен (Германия) возле городской филармонии и театра Аалто установили 15 интеллектуальных уличных фонарей, которые позволят подзарядить автомобиль, а также предоставлять данные о качестве окружающего воздуха и доступ в Интернет.
По материалам: electrik.info.
Помогите рассчитать сопротивление.
← →Дмитрий С © (2010-06-12 17:20) [0]
Нужно рассчитать сопротивление, которое нужно включить последовательно с светодиодом, чтобы тот работал от 12V.
Параметры светодиода:
• Потребляемый ток (I): 20 mA;
• Рабочее напряжение (U) от 2.8 до 3.6 V (возьмем 3 V).
Я рассуждаю так:
1. Сопротивление диода (по закону Ома)
R = U / I = 3 / 0.020 = 150 Ом
2. От 12 V нормально будут работать 4 светодиода подключенных последовательно (по какому закону не помню, но помню что это так). Поэтому для подключения 1 светодиода нужно добавить в цепь сопротивление 3х светодиодов.
R3 = 3 * R = 450 Ом.
3. Получаем схему:
(+) —|◄—|450Ом|— (-)
С пониманием физики электрического тока у меня плохо, а тут, как известно знают всё. Поправьте меня, если где ошибся.
← →
Владислав © (2010-06-12 17:33) [1]
Не-не-не.
По закону Ома берем подаваемое напряжение (12 В), берем необходимый ток (20 мА), считаем сопротивление. R = 12/0.020 = 600 (Ом).
Подключаем, наслаждаемся.
← →
Дмитрий С © (2010-06-12 17:35) [2]
> Владислав © (12.06.10 17:33) [1]
600 Ом — это сопротивление всей цепи, диода вместе с резистором, разве нет?
← →
Anatoly Podgoretsky © (2010-06-12 17:50) [3]
> Дмитрий С (12.06.2010 17:35:02) [2]
Если твое рассуждение насчет 3 вольт правильно, то расчет верный, надо
погасить 9 вольт, что ток был 20 ма
← →
Pavia © (2010-06-12 17:53) [4]
450Ом хватит можно меньше и больше.
> • Рабочее напряжение (U) от 2.8 до 3.6 V (возьмем 3 V).
Скорее всего диапозон гораздо шире.
Главное что-бы он на обратное не светился и напряжение постоянно.
← →
Дмитрий С © (2010-06-12 18:01) [5]
> Anatoly Podgoretsky © (12.06.10 17:50) [3]
Так по закону Ома тоже получается 450 Ом, что логично. Спасибо
> Pavia © (12.06.10 17:53) [4]
> Скорее всего диапозон гораздо шире.
Такой диапазон указан в описании светодиода.
> Главное что-бы он на обратное не светился и напряжение постоянно.
Что значит «на обратное не светился»?
Кстати, это хорошее замечание. Напряжение может меняться от 10 до 14,5 V (бортовая сеть авто). В этом случае нужно рассчитать сопротивление для максимального напряжения?
← →
Владислав © (2010-06-12 18:07) [6]
Вспоминаем физику и диод.
В нормальных условиях в одну сторону сопротивление близко к нулю, в другую близко к бесконечности.
именно это свойство диода применяется в диодном мосте для преобразования переменного тока в постоянный.
← →
Anatoly Podgoretsky © (2010-06-12 18:08) [7]
> Дмитрий С (12.06.2010 18:01:05) [5]
> Что значит «на обратное не светился»?
Что бы дым с него не шел, и сам он не светился при этом.
← →
NailMan © (2010-06-12 18:11) [8]
Чтобы не разрывать себе мозг есть интернет
http://www.novomoskovsk.ru/andreev/led_calc.html
← →
Дмитрий С © (2010-06-12 20:03) [9]
> Anatoly Podgoretsky © (12.06.10 18:08) [7]
ну примерно понял:)
> NailMan © (12.06.10 18:11) [8]
Спасибо.
Еще один вопрос встал, подскажите хороший интернет магазин для радиолюбителей, где можно заказать необходимые принадлежности и радиодетали?
← →
begin…end © (2010-06-12 20:26) [10]
Uпит — напряжение источника питания (12 В)
Uраб — рабочее напряжение светодиода (3 В)
I — ток в цепи (0,02 А — через светодиод, сопротивление и источник питания ток течёт одинаковый)
R — сопротивление светодиода
R» — искомое сопротивление
Падение напряжения на светодиоде и резисторе, вместе взятых:
I * (R + R») = Uпит
Падение напряжения на светодиоде:
I * R = Uраб
Вычитая из 1-го уравнения 2-е, получим: I * R» = Uпит — Uраб, отсюда:
R» = (Uпит — Uраб) / I = (12 — 3) / 0,02 = 450 Ом
Мощность, выделяемая на резисторе:
P» = R» * Sqr(I) = 450 * Sqr(0,02) = 0,18 Вт
← →
begin…end © (2010-06-12 20:28) [11]
> Дмитрий С © (12.06.10 20:03) [9]
http://chip-dip.ru/
← →
Дмитрий С © (2010-06-12 21:07) [12]
> http://chip-dip.ru/
Тоже то что нужно.
> Мощность, выделяемая на резисторе:
> P» = R» * Sqr(I) = 450 * Sqr(0,02) = 0,18 Вт
Резистор можно брать мощнее, в случае если нет точно такого?
И еще такой вопрос. В том же магазине есть, например,
— Резисторы постоянные выводные 0.25Вт 5-10%
А что означают эти 5-10% ? (ссылка: http://www.chip-dip.ru/search.aspx?tmpl=results&searchtext=%F0%E5%E7%E8%F1%F2%EE%F0 )
В рамках этой же темы хотелось бы спросить, как подбирать сопротивление резистора для подключения транзистора.
Хочу собрать по схеме «индикатор мощности для звуковой колонки».
Нашел вот такую схему:
http://cxem.net/sound/raznoe/indikators2-2.gif
(источник с описанием: http://www.remexpert.com/ipb/topic907.html?mode=threaded&pid=3695)
Для нее по описанию подобрал такой транзистор: Макс. напр. к-б при заданном обратном токе к и разомкнутой цепи э.(Uкбо макс),В 60
Макс. напр. к-э при заданном токе к и разомкнутой цепи б.(Uкэо макс),В 40
Максимально допустимый ток к ( Iк макс.А) 0.1
Статический коэффициент передачи тока h31э мин 110
Граничная частота коэффициента передачи тока fгр.МГц 150
Максимальная рассеиваемая мощность ,Вт 0.25
http://www.chip-dip.ru/product1/35670756.aspx
На схеме указаны резисторы сопротивлением 470 Ом, но там транзистор кт315в — не такой, какой я выбрал. На российском меня смутил маленький «Статический коэффициент передачи тока h31э мин», равный 30, тогда как в описании рекомендовался более 100.
До диодов и конденсаторов пока не дошел.
← →
Anatoly Podgoretsky © (2010-06-12 21:16) [13]
> Дмитрий С (12.06.2010 21:07:12) [12]
Ни одна деталь не критично, можно практически использользовать близкие
детали.
← →
Дмитрий С © (2010-06-12 21:54) [14]
> Anatoly Podgoretsky © (12.06.10 21:16) [13]
>
> > Дмитрий С (12.06.2010 21:07:12) [12]
>
> Ни одна деталь не критично, можно практически использользовать
> близкие
> детали.
Это хорошо.
Про конденсаторы вопрос:
У них есть параметр «Рабочее напряжение». Какое выходное напряжение усилителя я, естественно, не знаю. Можно использовать с заведомо большим параметром, например 35В ? Нормальный ли Допуск номинальной емкости, равный 20%?
И какой лучше выбрать «Алюминиевый электролитический» или «Танталовый электролитический»?
← →
инспектор (2010-06-12 21:55) [15]
У светодиода нет сопротивления. У него есть падение напряжения при заданном токе.
> На российском меня смутил маленький «Статический коэффициент
> передачи тока h31э мин», равный 30, тогда как в описании
> рекомендовался более 100
Так это min. На этот коэффициент не стоит рассчитывать, он меняется во время работы. Хотя скорее вместо буквы в лучше взять букву г
← →
NailMan © (2010-06-12 22:54) [16]
> [9] Дмитрий С © (12.06.10 20:03)
> Еще один вопрос встал, подскажите хороший интернет магазин
> для радиолюбителей, где можно заказать необходимые принадлежности
> и радиодетали?
Если нужны ценики с «номерами телефонов» — в чипдип. а я как разработчик-любитель беру детали в www.megachip.ru или www.smd.ru посредством инет-покупок. Паяльное оборудование итрасходники в чипедипе или в www.radiodelo.ru. Детальки в чипедипе брать — разоришься. Правда я беру десятками-сотнями — все равно дешевле чем в чиподипе взять даже десятками-штуками %-)
← →
KilkennyCat © (2010-06-12 22:58) [17]
> http://chip-dip.ru/
питерская версия данного магазина отличается мерзостным обслуживанием и дикими ценами.
http://www.micronika.ru/
http://www.terraelectronica.ru/
http://www.megachip.ru
← →
гость (2010-06-13 03:18) [18]
Последнее, что я паял руками был игрушечный светофор на светодиодах для 5-ти летнего сына… Светофор работал, как на автомате, так и в ручном режиме. Сынишка вжигал на игрушечных авто вокруг этого светофора…
А щаз… Уже начал забывать, как держать в руках паяльник. Дешевле купить китайский ширпотреб… 🙁
Вот значит какие сложности сейчас возникают… включить светодиод в бортовую сеть авто… Проценты на резисторах обозначают возможный процент отклонения сопротивления от номинала. Самые грубые и самые дешевые 20%. т.е. конкретный экземпляр резистора может быть от 360 до 540 Ом. Наиболее часто ювелирное соответствие номиналу резистора не требуется. В вашем случае тоже т.к. напряжение бортовой сети «гуляет». Главное чтобы при пиковых значениях напряжения ток не превысил максимально допустимого для светодиода (20 мА)
Но если уж приспичило подобрать с точностью до ома… берите тестер и подбирайте нужный резистор из партии. Или покупайте претезенционный (0,1%) который к тому же еще имеет небольшой температурный коэффициент изменения сопротивления (такие детали применяются например в измерительных приборах, где требуется высокая точность).
Кстати! Не забудьте расчитать рассееваемую на резисторе мощность. Р = падение напряжения на резисторе * ток = 9 * 0,02 = 0,18 Вт. т.е. нужно брать 0,25 Вт-ный, а не 0,125 Вт-ный.
Совершенно аналогично и с конденсаторами. Напряжение электролита всегда должно быть выбрано с запасом, берите как минимум с 50% запасом по напряжению, а там ставьте хоть на 1500 вольт если место позволяет.
А «какой выбрать алюминиевый или танталовый?» Если критично время наработки на отказ схемы (надо лет экак 20 кряду при круглосуточной эксплуатации) — ставьте танталовые, если таких требований к надежности нет — ставьте что есть под рукой или что дешевле.
А там ставьте в схему то, к чему душа лежит… у меня же при мысли о танталовых конденсаторах и претезенционных резисторах для того, чтобы погасить 9 вольт на светодиоде сразу возникла ассоциация использования золотых гвоздей для столярных работ. 🙂
← →
Германн © (2010-06-13 03:36) [19]
> Параметры светодиода:
> • Потребляемый ток (I): 20 mA;
> • Рабочее напряжение (U) от 2.8 до 3.6 V (возьмем 3 V).
>
Бред.
Или я очень отстал от жизни.
У диода (любого диода включая светодиод нет и не может быть такого параметра. Точнее «таких параметров»)!
Боже, куда мы катимся!?
← →
silver © (2010-06-13 09:48) [20]
Удалено модератором
← →
Virgo_Style © (2010-06-13 18:22) [21]
> Или я очень отстал от жизни.
Похоже на то 🙂
—
Чип-и-дип и у меня оставил неприятные впечатления. Хотя в конечном итоге я все получил, но времени это заняло — словно из Китая везли.
← →
Германн © (2010-06-14 02:21) [22]
> Virgo_Style © (13.06.10 18:22) [21]
>
>
> > Или я очень отстал от жизни.
>
>
> Похоже на то 🙂
>
И в чём именно? Если не секрет. 🙂
> Чип-и-дип и у меня оставил неприятные впечатления. Хотя
> в конечном итоге я все получил, но времени это заняло —
> словно из Китая везли.
>
Во всех магазинах можно нарваться на подобную ситуацию. Все они в своих прайс листах стараются публиковать всё что могут найти в И-нете. Но всегда нужно интересоваться сроками поставки конкретной продукции. Ибо она (продукция) может:
1. быть на складе магазина;
2. быть заказана у поставщика;
3. вообще не существовать, ибо производитель только анонсировал такой продукт.
← →
Virgo_Style © (2010-06-14 11:22) [23]
> И в чём именно? Если не секрет. 🙂
в том, что
> нет и не может быть такого параметра. Точнее «таких параметров»
🙂
Не, если Земля не имеет форму шара — то эти параметры будут называться, наверное, «номинальный ток» и «падение напряжения на диоде при номинальном токе».
Это если «по науке». А если хочется продать побольше — тогда «потребляемый ток» и «напряжение питания» — самое оно 🙂
> Но всегда нужно интересоваться сроками поставки конкретной
> продукции.
В практически всех подобных магазинах сроки поставки написаны на страничке товара.
Вот только иногда они не имеют ничего общего с реальностью 🙁
← →
абизяна (2010-06-14 12:45) [24]
> Virgo_Style © (14.06.10 11:22) [23]
Нормальный, не перегретый диод, почти, не потребляет ток, так-что такая характеристика, как «потребляемый ток» для диода представляет этот самый диод в виде электроплиты. Кстати, падение напряжения на диоде почти не зависит от протекающего через него тока — это одно из отличительных свойств полупроводниковых приборов от пассивных сопротивлений — резисторов. Когда-то, за отсутствием стабилитронов на малые напряжения использовали диоды при прямом включении по несколько штук последовательно и они отлично справлялись со стабилизацией напряжения, что, определённо, доказывает независимость падения напряжения на диоде от величины протекающего через него тока.
← →
Virgo_Style © (2010-06-14 23:55) [25]
> абизяна (14.06.10 12:45) [24]
Все это очень интересно и познавательно, но не имеет к светодиодам ровно никакого отношения.
Потребление 3Вт — норма жизни (а бывает и 30), и ВАХ параболическая.
← →
Дмитрий С © (2010-06-15 07:27) [26]
> почти, не потребляет ток
А за счет чего он светиться должен тогда?
← →
Inovet © (2010-06-15 07:47) [27]
> [25] Virgo_Style © (14.06.10 23:55)
> параболическая
Эээ. Может не совсем? Сравним наш диод (или для пущей наглядности стабилитрон, как говорилось выше) с вакуумным диодом (подкинем там резисторами напруги) и куском провода на одной установке из одного генератора напряжения и трёх осциллографов (опять же для пущей наглядности).
← →
Inovet © (2010-06-15 07:48) [28]
> [26] Дмитрий С © (15.06.10 07:27)
> А за счет чего он светиться должен тогда?
А вот и заметим это ещё на четвёртом.
← →
Inovet © (2010-06-15 07:52) [29]
Да. Наш генератор напряжения будет нам выдавать +- относительно 0 — который будет масса, хе. По-моему школьный курс физики, но могу чуть ошибаться.
← →
Inovet © (2010-06-15 08:06) [30]
Сформулирую точнее постановку эксперимента.
Есть: четыре коробочки (возможно чёрных), на каждой написана сила тока +-. Задача: снять ВАХ со всех. Выоводы: сравнить и сделать предположения о содержимом. Работа: сделать измерительную установку для решения задачи.
← →
Inovet © (2010-06-15 08:10) [31]
> [30] Inovet © (15.06.10 08:06)
> сила тока +-.
И напряжение, пожалуй не лишним будет.
← →
Virgo_Style © (2010-06-15 09:20) [32]
> Может не совсем?
Ну, если быть точным — то скорее экспонента. Однако рабочий участок настолько невелик, что imho вполне сойдет за параболу 🙂
← →
Anatoly Podgoretsky © (2010-06-15 09:38) [33]
http://www.lumenhouse.ru/index.php?option=com_content&task=view&id=59&Itemid=21
← →
Jeer © (2010-06-15 10:35) [34]
Мда.. инженерами и не пахнет, увы.
Диод, как впрочем и любой другой двухполюсный электроэлемент, имеет такую двухпараметрическую зависимость, как вольт-амперная характеристика.
Кроме того, имеются предельные параметры напряжения и тока.
Для простейшего расчета ( без учета дестабилизирующих факторов ), достаточно знать номинальный ток и падение напряжения на светодиоде — это и есть рабочая точка на ВАХ.
Разность напряжения питания и падения напряжения на светодиоде в рабочей точке, поделенная на рабочий ток, дает значение сопротивления резистора.
← →
Inovet © (2010-06-15 12:07) [35]
> [34] Jeer © (15.06.10 10:35)
> Мда.. инженерами и не пахнет, увы.
Мы тут уже перешли к исследованию неизвестного прибора с двумя клеммами. Будем считать, что образцы есть в запасе, иначе значительно сложнее исследовать, хотя начнём тогда от нуля на нашем генераторе напряжения что ли, и будем по чуть-чуть добавлять в обе стороны на каждом замере, пока не увидим неповторяющиеся показания, тут сделаем вывод о разрушении образца и его предельных параметрах — тогда и надписей не надо на корбках.
> [33] Anatoly Podgoretsky © (15.06.10 09:38)
Там не показаны ещё несколько важных участков, но для сабжа, естественно, даже больше чем надо.
> [34] Jeer © (15.06.10 10:35)
> в рабочей точке
Вот
Смайликов выше, как обычно, не наставил.:)
← →
абизяна (2010-06-15 18:20) [36]
> Virgo_Style © (14.06.10 23:55) [25]
>
> > абизяна (14.06.10 12:45) [24]
>
>
> Все это очень интересно и познавательно, но не имеет к светодиодам
> ровно никакого отношения.
>
> Потребление 3Вт — норма жизни (а бывает и 30), и ВАХ параболическая.
>
> <Цитата>
Вот сходи по ссылке в [33]. Ну и гду здесь парабола на рабочем участке?
И, как писали выше «ток потребления 0,02А при 3В». Каким это образом получается 3Вт?
ВАХ светодиода отличается от обычного диода тем, что рабочий участок сдвинут вправо и несколько более пологая, т.е. падение напряжения на светодиоде раз в 10 больше чем на диоде, но, всё-таки слабо зависит от величины тока.
http://www.radiodetali.com/article/all/led-faq.htm
> Дмитрий С © (15.06.10 07:27) [26]
>
> > почти, не потребляет ток
>
> А за счет чего он светиться должен тогда?
почти Т.е. светит так же, как и протребляет. Хотя, конечно, есть и помощнее, к примеру, как утверждал Чубайс:»На основе нанотехнологий российские учёные … .» Просто речь шла о 20мА и 3В, что означает 60мВ.
← →
Jeer © (2010-06-15 18:26) [37]
> почти Т.е. светит так же, как и протребляет
Ерунда. КПД обычных светодиодов 20..50%
← →
абизяна (2010-06-15 18:44) [38]
http://moto.w6.ru/obshee/poleznoe/199-svetodiody-i-ikh-primenenie.html
Как рассчитать падение напряжения на резисторе подробное объяснение
Если вы ищете, как рассчитать падение напряжения на резисторе, то SoManyTech предлагает вам полную теорию и практические примеры падения напряжения на резисторе. Перед этим давайте освежим в памяти закон Ома: (Прокрутите вниз, если вы профессиональный пользователь)
- Распространенный способ показать поведение схемного устройства — это его характеристика.
Это график зависимости тока «I» через устройство от приложенного к нему напряжения «V».Это устройство, резистор, имеет простую линейную характеристику В – I , показанную на рис. . выше. - Эта линейная зависимость устройства выражается законом Ома :
V = IR - Константа пропорциональности R известна как сопротивление устройства и равна наклону кривой I. –V характеристика. Единица измерения сопротивления — Ом, символ Ом . Любое устройство с линейной ВАХ называется резистором.
Какое падение напряжения на резисторе?
- Падение напряжения на резисторе — это не что иное, как значение напряжения на резисторе. Иногда его также называют «напряжение на резисторе» или просто «падение напряжения».
- Обычно обозначается как:
‘V (drop ) ‘ или ‘Vr’ или ‘Vd’
Для нескольких резисторов это записывается как Vr1, Vr2, Vr3 и т. Д.
Как мы все знаем, резистор — это устройство, которое оказывает сопротивление протекающему через него току.Затем, применяя закон Ома, резистор будет предлагать падение напряжения на резистивном устройстве, которое определяется как:
В ( падение ) = I × R
, где I = ток через резистор в (А) в амперах
R = сопротивление в (Ом) Ом
В ( падение ) = падение напряжения в (В) вольтах
Как рассчитать падение напряжения по сопротивлению пошагово:
Шаг 1: Упростим данную схему.Если, скажем, схема заполнена резисторами, включенными последовательно и параллельно, то повторно подключите ее, чтобы упростить. (проверьте практический пример ниже)
Step2: Затем найдите эквивалентный резистор.
Для параллельного подключения: 1 / Треб. = 1 / R1 + 1 / R2…
Для серии: Треб. = R1 + R2 +. . .
Step3: Найдите ток через каждый резистор. (Ток через последовательный резистор одинаков, а ток через параллельные резисторы отличается и зависит от его значения)
Step4 : Примените формулу закона Ома для расчета падения напряжения.
В = IR
Напряжение в последовательной цепи — Практические примеры:
Случай I:
Если есть только один резистор последовательно с батареей или источником питания, как показано в этой схеме.
В этой схеме падение напряжения на резисторе такое же, как и в цепи питания. Это связано с тем, что оба компонента имеют общие потенциальные точки, разделенные между ними (точка A и точка B)
∴ Vs = Vdrop = 5 вольт (скажем)
Случай II:
Если есть два или несколько резисторов, включенных последовательно с батареей, как показано на этой схеме.
В этой схеме мы должны вычислить полный ток «I», протекающий через цепь.
I (общий) = V (питание) / R (эквивалент)
∴ I (общий) = 5/30 = 0,166 A
Тогда падение напряжения на R1 будет: Vr1 = I × R1
Падение напряжения на R2 будет: Vr2 = I × R2
Падение напряжения на Rn будет: Vrn = I × Rn
- Vr1 = I × R1 = 0,166 × 10 = 1,66 В & Vr2 = I × R2 = 0.166 × 20 = 3,33 вольт
Напряжение на параллельных резисторах:
Случай I:
Два резистора включены параллельно батарее или источнику питания, как показано на этой схеме.
В этой схеме падение напряжения на этих параллельных резисторах такое же, как у источника питания.
Это связано с тем, что оба резистора имеют общие потенциальные точки, разделенные между ними (точка A и точка B), поэтому напряжение будет одинаковым, но ток будет другим.
Vs = Vdrop = Vr1 = Vr2 = 5 вольт (скажем)
Случай II:
Один резистор включен последовательно и два резистора с источником питания, как показано на этой схеме.
В этой схеме нам нужно вычислить ток «I» через каждый компонент.
- i1 = I (всего) = Is = V (питание) / R (эквивалент)
где, R (эквивалент) = R1 + Rp
, где 1 / Rp = 1 / R2 + 1 / R3∴ Rp = 12 Ом и R ( эквивалент ) = 22 Ом
- i2 = i1 * (R3 / (R2 + R3))
i3 = i1 * (R2 / (R2 + R3))
- Падение напряжения на R1 будет Vr1 = R1 * i1
Падение напряжения на R2 будет Vr2 = R2 * i2
Падение напряжения на R3 будет Vr3 = R2 * i3
Положив значения, которые мы имеем,
Теперь i1 = V (поставка) / R (эквивалент) = 5/22 = 0.227 ампер
∴ i1 = 0,227 A
Падение напряжения на 10 Ом -> Vr1 = 10 * i1 = 10 × 0,227 вольт
∴ Vr1 = 2,27 вольт
∴ i2 = 0,1362 A
Падение напряжения на 20 Ом -> Vr2 = 20 * i2 = 20 × 0,1362 В
∴ Vr2 = 2,724 В
Теперь i3 = i1 * (R2 / (R1 + R2))
∴ i3 = 0.09 A
Падение напряжения на 30 Ом -> Vr2 = 30 * i2 = 30 × 0,09 В
∴ Vr3 = 2,7 В
000 Метод 2:
i1 = В (питание) / R (эквивалент) = 0,227 AТогда падение напряжения на R1 будет В r1 = R1 * i1 = 10 × 0,227 = 2,27 В
∴ Эквивалентное напряжение в точке ‘A’ будет равно
Veq = Va = Vs — Vr1
∴ Va = 5 — 2.27 = 2,73 В
Следовательно, мы получаем равное значение потенциала на R2 и R3.
Метод 3:
В этом методе мы используем цифровой мультиметр или, можно сказать, вольтметр. Все, что вам нужно, это установить мультиметр в режим напряжения.
Теперь с помощью двух щупов проверьте напряжение на требуемом резисторе, подключив к нему щупы. (на рис. показания вольтметра только для справки)
Вуаля !! Ты понял.
Это самый простой способ найти падение напряжения на резисторе в любой цепи.
ток — Падение напряжения на одном резисторе и на двух резисторах
Сначала я скажу, что вопрос ОП и все ответы здесь (включая последний, сделанный минуту назад) отличные, и я оцениваю их на +1 🙂 Я только дополню их еще несколькими экстравагантными, но «заставляющими задуматься» «соображения …
«Возникает вопрос, почему падение напряжения на резисторах с одинаковым сопротивлением меняется от первой цепи ко второй? Имеет ли это какое-либо отношение к току? Почему это происходит? Я пытаюсь найти интуитивное объяснение: почему это происходит.»
«Что мне действительно нужно, так это ответ на вопрос, почему падение напряжения во второй цепи на каждом резисторе составляет половину, хотя они имеют такое же сопротивление, как и в первой цепи».
Если вы действительно хотите, чтобы падение напряжения на резисторах с одинаковым сопротивлением было одинаковым, я могу предложить вам решение — всего замените источники напряжения на источники тока . Это не просто шутка, а вполне реальная конфигурация схемы, которую мы можем наблюдать в некоторых хорошо известных электронных схемах (например,например, в так называемом «каскаде с общим эмиттером с вырождением эмиттера» или «фазоделителе»).
Но вернемся к схемам ОП с 1 и 2 резисторами, питаемыми от источников напряжения, и сделаем несколько интересных выводов.
Во-первых, нас может не интересовать ток, протекающий через резисторы, и их сопротивление. В обеих цепях напряжение не зависит ни от тока, ни от сопротивления. Во второй схеме падение напряжения на резисторе зависит только от отношения его сопротивления к общему сопротивлению.
Второй интересный вывод, который мы можем сделать в отношении потенциометра транзистора . Хотя это переменный резистор, когда мы поворачиваем его стеклоочиститель, мы фактически ничего не меняем — ни сопротивление … ни ток … ни напряжение. Мы просто измеряем (выбираем) напряжение в одной точке на его внутреннем резистивном слое … но все остальные точки имеют линейно убывающие напряжения.
Wikimedia Commons
Конечно, мы можем представить, что при вращении стеклоочистителя одно частичное сопротивление увеличивается, когда другое уменьшается, поэтому их сумма остается постоянной… и, как следствие, постоянный ток. Такие «электронные потенциометры» мы можем видеть в каскадах CMOS, усилителях с обратной связью по току (CFA) и т. Д.
ЗаконОм — Как я могу рассчитать ток (I), если я не знаю падения напряжения
Но что, если я передумаю и не хочу, чтобы на моем резисторе 1k упало 7,1 В, а 7,2 В вместо
Если вы используете источник питания 9 В и светодиод 1,9 В, то на любой резистор всегда будет 7,1 В.
Возможно, вы не знакомы с концепцией «делителя напряжения»? 9 вольт блока питания автоматически распределяются по цепочке подключенных к нему компонентов.Если у нас есть светодиод на 1,9 В и резистор, на резисторе всегда будет 7,1 В, где 7,1 плюс 1,9 В в сумме составляют 9,0 В, то же самое, что и напряжение источника питания.
Другими словами, вы не можете передумать и вместо этого получите 7,2 В. Светодиод должен решать, а не вы. (Ну, я думаю, вы могли бы вместо этого поднять источник питания до 9,1 В вместо 9,0 В. Или вместо этого используйте светодиод 1,8 В с исходным источником питания 9 В.)
Обратите внимание, что все вышесказанное описывает упрощенный случай.Он использует идеальный светодиод: идеальный светодиод, который всегда показывает 1,9 В на своих выводах, даже при нулевом токе. Настоящий светодиод не будет иметь фиксированного напряжения, но вместо этого будет демонстрировать экспоненциальную кривую V-I, как любой реальный диод. Настоящий светодиод может иметь 1,9 В при 10 или 20 мА … но это напряжение будет намного ниже при микроамперном токе и намного выше при 500 мА. Если вы хотите, чтобы действительно понимал все, что происходит, вам придется склониться и изучить уравнение экспоненциального диода для зависимости напряжения от тока.
Это, или поиграйте с симулятором схемы, который использует полномасштабную математическую модель светодиода, а не просто упрощенное приближение, в котором светодиод Vd имеет фиксированное значение 1,9 В.
можно ли сбросить все 9 В с резистора 1 кОм, чтобы светодиод получил 0 В
Просто замените 1K резистором с бесконечным сопротивлением! Другими словами, открытый переключатель. Но это не сработает для упрощенного идеального светодиода, где напряжение на нем навсегда останется 1,9 В, даже если аккумулятор удален.:)
Анализ цепи— Определение напряжения на резисторе
Назовем нижний узел «землей» и обозначим его как 0 В. Тогда верхний узел можно назвать напряжением \ $ V_x \ $. Вы знаете, что ток в узле должен быть равен току, текущему обратно (ток не накапливается в узле). Таким образом, должно выполняться следующее:
$$ (1) ~~~~~~~~~~~~ 30 \ textrm {A} = \ frac {V_x} {2.4 \: \ Omega} + \ frac {V_x} {1.6 \: \ Omega + 8 \: \ Omega} $$
На приведенном выше рисунке вы можете видеть два тока ответвления, перечисленные справа, и входящий ток 30 А слева.Они должны быть равны.
Приведенное выше уравнение преобразуется в:
$$ (2) ~~~~~~~~~~~~~~~~~~~~~ V_x = \ frac {30 \ textrm {A}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} $$
Но вас не волнует \ $ V_x \ $. Просто нужно выражение, которое является самым правым в первом уравнении, указанном выше, а именно ток через ветвь с двумя резисторами. Таким образом, вы можете подключить один к другому, чтобы получить:
$$ I = \ frac {\ left (\ frac {30 \ textrm {A}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} \ right)} {1.6 \: \ Omega + 8 \: \ Omega} = \ frac {30 \ textrm {A}} {\ frac {1.6 \: \ Omega +8 \: \ Omega} {2.4 \: \ Omega} + 1} = \ frac {30 \ textrm {A}} {\ frac {1.6 \: \ Omega + 8 \: \ Omega + 2.4 \: \ Omega} {2.4 \: \ Omega}} = 30 \ textrm {A} \ frac {2.4 \: \ Omega} {1.6 \: \ Omega + 8 \: \ Omega + 2.4 \: \ Omega} $$
Это просто подтверждает то, что вам уже сказали. Но это не дает интуиции.
В делителе напряжения напряжение на последовательном элементе равно общему напряжению за вычетом всех падений напряжения на других последовательных элементах.n_1 G_i} \ end {align *} $$
Симметрия должна быть очевидной. В вашем случае у вас есть только две проводимости: \ $ G_1 = \ frac {1} {2.4 \: \ Omega} \ $ и \ $ G_2 = \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega } \ $. И в этом случае \ $ G_x = G_2 \ $.
Если вы используете те, которые входят в нижнее уравнение (4), вы получите правильный ответ. Однако это не похоже на то, что написал учитель. Но если вы подключите что-то, вы поймете, почему:
$$ \ begin {align *} (5) ~~~~~~~~~ I_x & = I_T \ cdot \ frac {\ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} {\ frac {1} {2.4 \: \ Omega} + \ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} \\ \\ & = I_T \ cdot \ frac {\ frac {1} {1.6 \: \ Omega + 8 \: \ Omega}} {\ frac {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} { 2.4 \: \ Omega \ cdot \ left (1.6 \: \ Omega + 8 \: \ Omega \ right)}} \\ \\ & = I_T \ cdot \ frac {\ frac {1} {1}} {\ frac {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} {2.4 \: \ Omega}} = I_T \ cdot \ frac {2.4 \: \ Omega} {2.4 \: \ Omega + 1.6 \: \ Omega + 8 \: \ Omega} \ end {align *} $$
Однако это НЕ общий подход. В этом случае это просто работает. Так что, возможно, ваша интуиция права насчет того, что вы запутались в классе.n R_j} \ end {align *} $$
Имейте в виду, что в приведенном выше примере каждый \ $ R_i \ $ равен , а не каждому из ваших резисторов, бесполезно. Эти сопротивления являются эффективными сопротивлениями ветвей. Итак, в одной из ваших веток это значение представляет собой сумму. Не забывай и об этом.
Уравнение (6) намного уродливее, чем вы могли представить, исходя из решения вашего учителя. Но это правильный вариант. Итак, если вы хотите что-то запомнить, используйте метод проводимости. Как видите, использование сопротивлений не сразу интуитивно понятно.
Если вы должны использовать сопротивления в текущем случае ветвления, как это, тогда вы должны следовать (6) выше и НЕ просто пытаться расширить то, что ваш учитель сделал каким-то невежественным образом. Это не сработает.
Это означает, что я не согласен с ответом, предполагающим: «Ваш профессор дал формулу для текущего делителя».
Неправильно!
Обычно люди делают то, что предлагают некоторые другие ответы — вычисляют последовательное и параллельное сопротивление до одного значения (если возможно), а затем вычисляют напряжение.Затем проработайте детали самой ветки, чтобы получить ток. Это в значительной степени то, как большинство подошло бы к этому. (Или используйте узловой анализ, если схема более сложная.)
Формула вашего учителя не является расширяемой формулой . Это как раз то, что выпало в данном случае.
Цепи делителя напряжения| Делительные схемы и законы Кирхгофа
Давайте проанализируем простую последовательную схему и определим падение напряжения на отдельных резисторах:
Из приведенных значений отдельных сопротивлений мы можем определить общее сопротивление цепи, зная, что сопротивления складываются последовательно:
Определите полное сопротивление цепи
Отсюда мы можем использовать закон Ома (I = E / R) для определения общего тока, который, как мы знаем, будет таким же, как ток каждого резистора, при этом токи одинаковы во всех частях последовательной цепи:
Использование закона Ома для вычисления тока
Теперь, зная, что ток в цепи равен 2 мА, мы можем использовать закон Ома (E = IR) для расчета напряжения на каждом резисторе:
Должно быть очевидно, что падение напряжения на каждом резисторе пропорционально его сопротивлению, учитывая, что ток одинаков на всех резисторах.Обратите внимание, что напряжение на R 2 вдвое больше, чем напряжение на R 1 , так же как сопротивление R 2 вдвое больше, чем R 1 .
Если бы мы изменили общее напряжение, мы бы обнаружили, что эта пропорциональность падений напряжения остается постоянной:
Решение для коэффициентов падения напряжения
Напряжение на R 2 все еще в два раза больше, чем падение R 1 , несмотря на то, что напряжение источника изменилось.Пропорциональность падений напряжения (соотношение между ними) строго зависит от значений сопротивления.
При более внимательном рассмотрении становится очевидным, что падение напряжения на каждом резисторе также является фиксированной пропорцией напряжения питания. Напряжение на R 1 , например, составляло 10 вольт при питании от батареи 45 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза больше), падение напряжения на R 1 также увеличилось в 4 раза (с 10 до 40 вольт).Однако соотношение между падением напряжения R 1 и общим напряжением не изменилось:
Аналогичным образом, ни один из других коэффициентов падения напряжения не изменился с увеличением напряжения питания:
Формула делителя напряжения
По этой причине последовательную схему часто называют делителем напряжения из-за ее способности пропорционально или делить общее напряжение на дробные части постоянного отношения. Приложив немного алгебры, мы можем вывести формулу для определения падения напряжения на последовательном резисторе, учитывая не что иное, как общее напряжение, отдельное сопротивление и общее сопротивление:
Отношение отдельного сопротивления к общему сопротивлению такое же, как отношение отдельного падения напряжения к общему напряжению питания в цепи делителя напряжения.Это известно как формула для делителя напряжения , и это сокращенный метод определения падения напряжения в последовательной цепи без проведения расчетов тока по закону Ома.
Пример использования формулы делителя напряжения
Используя эту формулу, мы можем повторно проанализировать падение напряжения на примере схемы за меньшее количество шагов:
Напряжение — разделяющие компоненты
Делители напряжениянаходят широкое применение в схемах электросчетчиков, где определенные комбинации последовательных резисторов используются для «деления» напряжения на точные пропорции как часть устройства измерения напряжения.
Потенциометры как компоненты деления напряжения
Одним устройством, часто используемым в качестве компонента деления напряжения, является потенциометр , который представляет собой резистор с подвижным элементом, перемещаемым ручкой или рычагом. Подвижный элемент, обычно называемый скребком , контактирует с резистивной полосой материала (обычно называемой направляющей , если она сделана из резистивной металлической проволоки) в любой точке, выбранной ручным управлением:
Контакт стеклоочистителя — это обращенная влево стрелка, нарисованная в центре вертикального резисторного элемента.При перемещении вверх он контактирует с резистивной полосой ближе к клемме 1 и дальше от клеммы 2, уменьшая сопротивление клеммы 1 и повышая сопротивление клеммы 2. При перемещении вниз возникает противоположный эффект. Сопротивление, измеренное между клеммами 1 и 2, постоянно для любого положения стеклоочистителя.
Поворотные и линейные потенциометры
Здесь показаны внутренние иллюстрации двух типов потенциометров: поворотного и линейного.
Потенциометры линейные
Некоторые линейные потенциометры приводятся в действие прямолинейным движением рычага или ползунковой кнопки.Другие, подобные изображенному на предыдущем рисунке, приводятся в действие поворотным винтом для возможности точной регулировки. Последние единицы иногда называют подстроечными элементами , потому что они хорошо работают в приложениях, требующих «подгонки» переменного сопротивления до некоторого точного значения.
Следует отметить, что не все линейные потенциометры имеют такое же назначение клемм, как показано на этом рисунке. У некоторых клемма стеклоочистителя находится посередине между двумя концевыми клеммами.
Поворотный потенциометр
На изображении ниже показана конструкция корпуса поворотного потенциометра.
На следующей фотографии показан реальный поворотный потенциометр с открытым стеклоочистителем и проводом для удобного просмотра. Вал, который перемещает скребок, повернут почти полностью по часовой стрелке, так что скребок почти касается левого конечного конца скользящей проволоки:
Вот тот же потенциометр с валом стеклоочистителя, перемещенным почти до упора против часовой стрелки, так что стеклоочиститель находится около другого крайнего конца хода:
Влияние регулировки потенциометра в цепи
Если постоянное напряжение приложено между внешними клеммами (по всей длине скользящей проволоки), положение стеклоочистителя будет отводить часть приложенного напряжения, измеряемого между контактом стеклоочистителя и любой из двух других клемм.Дробное значение полностью зависит от физического положения дворника:
Важность применения потенциометров
Так же, как и фиксированный делитель напряжения, коэффициент деления напряжения потенциометра строго зависит от сопротивления, а не от величины приложенного напряжения. Другими словами, если ручка потенциометра или рычаг перемещается в положение 50 процентов (точное центральное положение), падение напряжения между стеклоочистителем и любой внешней клеммой будет ровно 1/2 от приложенного напряжения, независимо от того, с чем это напряжение происходит. быть, или каково сквозное сопротивление потенциометра.Другими словами, потенциометр работает как переменный делитель напряжения, где коэффициент деления напряжения устанавливается положением стеклоочистителя.
Это применение потенциометра является очень полезным средством получения переменного напряжения от источника постоянного напряжения, такого как аккумулятор. Если для схемы, которую вы строите, требуется определенное количество напряжения, которое меньше значения доступного напряжения батареи, вы можете подключить внешние клеммы потенциометра к этой батарее и «набрать» любое необходимое вам напряжение между потенциометром. стеклоочиститель и один из внешних выводов для использования в вашей цепи:
При таком использовании название потенциометра имеет смысл: они измеряют (контролируют) приложенный к ним потенциал (напряжение), создавая переменное отношение делителя напряжения.Такое использование трехполюсного потенциометра в качестве переменного делителя напряжения очень популярно в схемотехнике.
Образцы малых потенциометров
Здесь показаны несколько небольших потенциометров, которые обычно используются в бытовом электронном оборудовании, а также любителями и студентами при конструировании схем:
Меньшие блоки слева и справа предназначены для подключения к макетной плате без пайки или для пайки в печатную плату.Средние блоки предназначены для установки на плоской панели с проводами, припаянными к каждой из трех клемм. Вот еще три потенциометра, более специализированных, чем только что показанный набор:
Большой блок «Helipot» представляет собой лабораторный потенциометр, предназначенный для быстрого и легкого подключения к цепи. Блок в нижнем левом углу фотографии представляет собой потенциометр того же типа, только без корпуса и без 10-поворотного счетного диска. Оба этих потенциометра являются прецизионными блоками, в которых используются многооборотные спиралевидные резистивные ленты и грязесъемные механизмы для выполнения небольших регулировок.Блок в правом нижнем углу представляет собой потенциометр для монтажа на панели, предназначенный для работы в тяжелых промышленных условиях.
ОБЗОР:
- Пропорция цепей серии
- , или делят , общее напряжение питания между отдельными падениями напряжения, пропорции строго зависят от сопротивлений: ERn = ETotal (Rn / RTotal)
- Потенциометр — это компонент переменного сопротивления с тремя точками подключения, часто используемый в качестве регулируемого делителя напряжения.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
резисторов последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Contrast Способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, соединенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, тогда R 1 на Рисунке 1 (a) может быть сопротивлением вала отвертки, R 2 сопротивлением ее ручки , R 3 сопротивление тела человека и R 4 сопротивление его обуви.На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный шнур с высоким сопротивлением, прибор, уменьшающий рабочий ток.)
Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на рис. 2. Согласно закону Ома падение напряжения В на резистор, когда через него протекает ток, рассчитывается по формуле V = IR , где I равно току в амперах (A), а R — сопротивление в омах (Ω).Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R 1 составляет В 1 = IR 1 , что на R 2 составляет В 2 = IR 2 , и что для R 3 это V 3 = IR 3 .Сумма этих напряжений равна выходному напряжению источника; то есть
В = В 1 + В 2 + В 3 .
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — это электрический заряд, а V, — напряжение. Таким образом, энергия, отдаваемая источником, составляет кв.кв. , а энергия, рассеиваемая резисторами, составляет
.qV 1 + qV 2 + qV 3 .
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV 1 + qV 2 + qV 3 . Плата q аннулируется, давая V = V 1 + V 2 + V 3 , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает
V = IR 1 + IR 2 + IR 3 = I ( R 1 + R 2 + R 3 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R с , мы имеем
В = ИК с .
Это означает, что полное или эквивалентное последовательное сопротивление R s трех резисторов составляет R s = R 1 + R 2 + R 3 .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R с последовательного соединения составляет
R с = R 1 + R 2 + R 3 +…,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
Стратегия и решение для (b)Ток определяется по закону Ома: В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Стратегия и решение для (c)Напряжение — или падение IR — на резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает
.В 1 = IR 1 = (0,600 A) (1,0 Ом) = 0,600 В.
Аналогично
В 2 = IR 2 = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR 3 = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)Три капли IR добавляют к 12.0 В, прогноз:
В 1 + В 2 + В 3 = (0,600 + 3,60 + 7,80) В = 12,0 В.
Стратегия и решение для (d)Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома В = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
.P 1 = I 2 R 1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт
Аналогично
P 2 = I 2 R 2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
P 3 = I 2 R 3 = (0.{2}} {R} \\ [/ latex], где В, — это падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.
Стратегия и решение для (e)Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e)Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, как мощность, выдаваемая источником. То есть
P 1 + P 2 + P 3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт.
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Последовательные сопротивления добавить: R с = R 1 + R 2 + R 3 +….
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рис. 3 показаны резисторы, подключенные параллельно и , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления R p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I 1 + I 2 + I 3 .
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R p параллельного соединения связано с отдельными сопротивлениями на
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: В = 12.0 В, R 1 = 1,00 Ом, R 2 = 6,00 Ом и R 3 = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R p . Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Суммарное сопротивление с правильным количеством значащих цифр составляет R p = 0,804 Ом
Обсуждение для (а)R p , как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)Полный ток можно найти из закона Ома, заменив полное сопротивление R p . Это дает
[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б)Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
Обсуждение для (c)Общий ток складывается из отдельных токов:
I 1 + I 2 + I 3 = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (д)Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (e)Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
P 1 + P 2 + P 3 = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждениеОбратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов- Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
- На каждый параллельно включенный резистор подается такое же полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя технику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R 1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R 2 и R 3 могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепейНа рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения.Мы можем считать R 1 сопротивлением проводов, ведущих к R 2 и R 3 . (а) Найдите полное сопротивление. (b) Что такое падение IR в R 1 ? (c) Найдите текущие значения с I 2 по R 2 . (d) Какую мощность рассеивает R 2 ?
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация последовательно с R 1 .
Стратегия и решение для (а)Чтобы найти полное сопротивление, отметим, что R 2 и R 3 находятся параллельно, и их комбинация R p находится последовательно с R 1 . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.R итого = R 1 + R p .
Сначала находим R p , используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.R до = R 1 + R p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)Чтобы найти падение IR в R 1 , отметим, что полный ток I протекает через R 1 . Таким образом, падение IR составляет
.В 1 = ИК 1
Мы должны найти I , прежде чем сможем вычислить V 1 .Полный ток I находится с помощью закона Ома для схемы. То есть
[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, мы получаем
В 1 = IR 1 = (2,35 А) (1,00 Ом) = 2,35 В.
Обсуждение для (б)Напряжение, приложенное к R 2 и R 3 , меньше общего напряжения на величину В 1 .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R 2 и R 3 .
Стратегия и решение для (c)Чтобы найти ток через R 2 , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R 2 , так и к R 3 , уменьшается на величину В 1 , и поэтому оно составляет
В p = В — В 1 = 12.0 В — 2,35 В = 9,65 В.
Теперь ток I 2 через сопротивление R 2 находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)Ток меньше, чем 2,00 А, которые протекали через R 2 , когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)Мощность, рассеиваемая R 2 , равна
P 2 = ( I 2 ) 2 R 2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт
Обсуждение для (д)Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное номером R 3 , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, представленных R 1 , уменьшая напряжение на лампочке (которое составляет R 2 ), которое затем заметно гаснет.
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему. Стратегии решения проблем для последовательных и параллельных резисторов- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, сокращайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при обнаружении R необходимо соблюдать осторожность.
- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, которое почти равно нулю в замкнутом состоянии и очень велико в разомкнутом состоянии, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рис. 7. Переключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в лаборатории физики по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он потрясен им? Объяснять.
7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводящими? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкают накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10. Предположим, вы проводите физическую лабораторию, которая просит вас вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?
Задачи и упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 2 Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6.(a) Учитывая батарею на 48,0 В и резисторы на 24,0 и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I 3 двумя следующими способами: (a) по известным значениям I и I 2 ; (б) используя закон Ома для R 3 . В обеих частях явно показано, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация последовательно с R 1 .
8. Ссылаясь на рисунок 5: (a) Вычислите P 3 и обратите внимание на его сравнение с P 3 , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 2 , подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 9 Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Явно покажите, как вы следуете шагам, описанным выше в стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 2 подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 9 Ом каждый.
11. Покажите, что если два резистора R 1 и R 2 объединены, и один из них намного больше другого ( R 1 >> R 2 ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R 1 .(b) Их параллельное сопротивление почти равно меньшему сопротивлению R 2 .
12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
- серия:
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор:
- компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь
- сопротивление:
- вызывает потерю электроэнергии в цепи
- Закон Ома:
- соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
- напряжение:
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения:
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- текущий:
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля:
- соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]
- параллельно:
- разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.(а) 2,75 кОм (б) 27,5 Ом
3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
, так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения.Когда все устройства в цепи соединены последовательным соединением, эта схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда схема называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной и той же цепи.В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям. Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы.Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии
| Параллельные схемы
|
Каждое из приведенных выше понятий имеет математическое выражение.Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных цепейОсновная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом.Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно.Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи.Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
. R до = 1 + R 2 + R 3 +…Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.
Пример 1:Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление.Цель анализа — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 .Таким образом, общее сопротивление составляет
. R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR общ = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (60 В) / (15 Ом)I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи.Тем не менее, резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
I до = I 1 = I 4 = 4 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению.Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 А.
I 2 = I 3 = 2 АТеперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)ΔV 1 = 20 ВΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 ВΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 ВΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое значение сопротивления. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:
1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …1 / R экв = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 3 Ом + R 4 = 5 Ом + 3 Ом + 8 ОмR общ = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I общ = ΔV общ / R общ = (24 В) / (16 Ом)I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Тем не менее, резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 АДля параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно быть равно 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)ΔV 1 = 7,5 ВΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и R 4 . Таким образом,
ΔV 2 = V 3 = 4,5 ВЗная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)I 2 = 1,125 АI 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 A
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегииДва приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте условные обозначения, такие как те, что показаны в примере выше.
- При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например I до , I 1 , R 3 , ΔV 2 и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (по вашему мнению) параллельную секцию одним резистором, имеющим значение сопротивления, равное эквивалентному сопротивлению параллельной секции.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с ним взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) ток в точке B.
г. Сила тока в точке B равна _____ (больше, равна, меньше) тока в точке E.
г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.
