Как вычислить индуктивность катушки: Определение и формулы для расчета и измерения индуктивности

Расчёт индуктивности. Часть 2 | HomeElectronics

Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Виды катушек индуктивности

Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности

Расчёт индуктивности катушки.

Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:

D₁ – внутренний диаметр, D₂ – внешний диаметр, D_ср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить

Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:

если l > D_ср – длинная катушка,

если l < D_ср – короткая катушка,

если l << D_ср – очень короткая катушка,

если l = 0 – плоская катушка,

если t ≈ D_ср – толстая катушка,

если t << D_ср – тонкая катушка,

если t = 0 – соленоид.

Особенности расчёта катушек индуктивности

Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением

где L_Р – расчётная индуктивность;

∆L – поправка на «изоляцию», ∆L = ∆₁L + ∆₂L;

∆₁L – поправка учитывающая влияние индуктивности витков;

∆₂L – поправка учитывающая влияние взаимной индуктивности витков.

В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности L_Р, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.

Особенности расчёта круговых катушек индуктивности состоят в следующем:

1. При определении расчётной индуктивности L_P, средний диаметр принимается равным среднему диаметру реальной катушки;

2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении

3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.

4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.

5. Так как величина поправки на взаимную индуктивность ∆₂L в несколько раз меньше, чем поправка на индуктивность витков ∆₁L, то при расчётах можно учитывать только ∆₁L.

Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.

Расчёт индуктивности соленоида

Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.

Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

d – диаметр соленоида, м;

Φ – коэффициент, который зависит от отношения α = l/D;

l – длина соленоида, м;

Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d

Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит

Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит

Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.

Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.

Индуктивность плоской катушки

Определение индуктивности плоской катушки, D₁ – внутренний диаметр, D₂ – внешний диаметр, D – средний диаметр, t – толщина намотки.

В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D – средний диаметр катушки, м;

Ψ – коэффициент, который зависит от отношения ρ = t/D­;

t – толщина намотки катушки.

Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D

При небольшой толщине намотки, когда ρ < 0,5

При большой толщине намотки, когда ρ > 0,5

где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки

Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.

Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.

Индуктивность круговой катушки прямоугольного сечения

Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник

Индуктивность прямоугольной катушки.

Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.

Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле

где L₀ – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/D_cp;

l – длина катушки, м;

D_cp – средний диаметр катушки, м;

∆ — поправка на форму катушки.

В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру D_cp, можно разделить на несколько типов:

1. Длинная катушка, у которой α > 0,75.

2. Короткая катушка, имеющая α < 0,75 и γ < 1.

3. Очень короткая катушка, имеет α << 1 и γ > 1.

где

Рассмотрим каждый случай по отдельности.

Индуктивность длинной катушки

Длинная катушка.

Для длинной катушки (α > 0,75) величина L₀ рассчитывается также как для длинного соленоида, где l – длина соленоида, D_cp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

где D₁ – внутренний диаметр, D₂ – внешний диаметр.

Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром D_CP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.

Индуктивность короткой катушки

Короткая катушка.

Для короткой катушки (α < 0,75, t < l) величина L₀ рассчитывается также как для короткого соленоида, где l – длина соленоида, D_СР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром D_СР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.

Индуктивность очень короткой катушки

Очень короткая катушка.

Для очень короткой катушки (α << 1, t > l) величина L₀ рассчитывается также как для плоской катушки, где t – толщина намотки, D_cp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром D_CP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.

Расчёт поправки на собственную индуктивность витков

Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности L_P и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆₁L и поправки на взаимную индуктивность витков ∆₂L

Данные поправки зависят от взаимного расположения витков в катушке.

Для провода круглого сечения возможны следующие варианты заполнения катушки

Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.

В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности L_P

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

где p – шаг намотки по длине катушки, s_p – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

где q – шаг намотки по толщине катушки, s_p – диаметр голого провода (без изоляции).

Расчёт поправки на взаимную индуктивность витков

В общем случае поправка на взаимную индуктивность витков ∆₂L катушки определяется выражением

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

J – коэффициент, зависящий формы катушки и от числа витков катушки.

1. Для катушки выполненной в один слой по длине катушки (соленоид):

а) при определении расчётной индуктивности L_P толщина намотки t принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит

где ω – количество витков катушки.

2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):

а) при определении расчётной индуктивности L_P длина катушки l принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит

где ω – количество витков катушки.

На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.

 

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Пример 1. Расчёт катушки индуктивности

Создадим 2D-модель катушки. При создании геометрии учтём тот факт, что в плоскопараллельной модели сечения катушек — это бесконечные проводники. Подразумевается, что на торцах они виртуально соединены друг с другом (см. рисунок П.1.1). Рисунок П.1.1 – Плоскопараллельная модель катушки в 2D В нашем же случае необходимо строить тело вращения. Для этих целей необходимо изменить тип геометрии в окне Solution Type, установить параметр Geometry Mode в значение: Cylindrical about Z (осевая симметрия). После чего создадим геометрию с учётом того, что модель строится вращением тела вокруг оси Z. Получим геометрию, изображённую на рисунке П.1.2 Рисунок П.1.2 – Цилиндрическая модель геометрии 2D (a) и её представление в 3D(б) Зададим параметры катушки. Выделяем объект-катушку, указываем значение тока равным 1 амперу (Assign Excitation > Current…) Т.к. мы считаем индуктивность катушки на постоянном токе, не важно, какова будет величина тока, т.к. поток будет расти пропорционально току. Не забываем указать, что катушка распределённая (Stranded). Создадим матрицу для расчета индуктивности катушки (ПКМ на пункт Parameters > Assign > Matrix…) Далее выбираем созданную катушку (Current1). На вкладке Post Processing задаём число витков катушки (Рисунок П.1.3). Внешней границе полукруга задаём граничное условие (ПКМ на внешней линии окружности > Assign Boundary > Balloon. .), линию, лежащую на оси Z, не трогаем. Переключение в режим выбора линий производится ПКМ на пустом месте Select Edges… Далее создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… ) Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup) Запускаем задачу на расчёт. Результат расчёта можно посмотреть в окне Solution Data на вкладке Matrix, предварительно установив галочку PostProcessing (Рисунок П.1.4). Рисунок П.1.3 — Задание элемента Matrix. Рисунок П.1.4 — Результаты расчёта модели Итого, индуктивность, рассчитанная МКЭ, составила Lм = 1,053 мкГн. Сравнивая с результатами, полученными по формуле Виллера (L = 1,152 мкГн), можно сделать вывод, что задача посчитана правильно, и расхождение двух методов расчета составляет менее 10%. Автор материалов: Drakon (С) 2014. Редактор: Админ

формула расчета. Измерение индуктивности. Индуктивность контура

Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.

Электрическая цепь и индуктивность

Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Как найти индуктивность

Формула, которая является простейшей для нахождения величины, следующая:

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.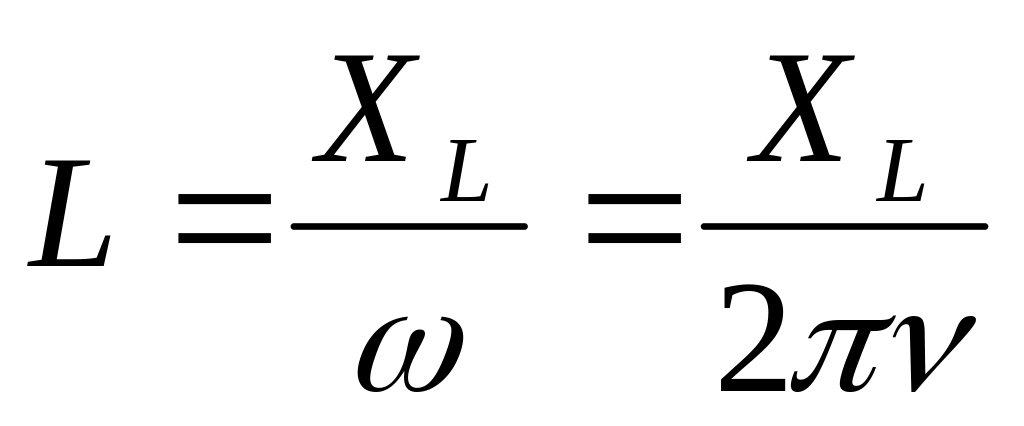

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN²R² : 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N²R² :^{2Π(6R + 9l + 10w).}

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от «витков в квадрате».
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:

Xc = 1 : W х C.

Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

Работа конденсатора

Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.

Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.

Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:

1. Конденсаторы с газообразным диэлектриком.
2. Вакуумные.
3. С жидким диэлектриком.
4. С твердым неорганическим диэлектриком.
5. С твердым органическим диэлектриком.
6. Твердотельные.
7. Электролитические.

Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:

1. Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
2. Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
3. Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

Расчет индуктивности катушки

Coil32 – прекрасная программа для всевозможных расчетов, связанных с катушками индуктивности

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

Сегодня я хочу познакомить вас с очередной радиолюбительской программой.

Программа называется Coil32 и предназначена для расчета индуктивности катушек. Перед тем как мы рассмотрим эту программу, хочу выразить благодарность ее автору и создателю. К сожалению я не нашел его имени-отчества, да и фамилии тоже (даже в разделе “Об авторе программы”). Сайт создателя программы – coil32.narod.ru. Если у вас будут какие-либо замечания по работе программы, предложения, или вы захотите поблагодарить автора (возможно и материально – пожертвовав один рубль на развитие проекта) вы всегда сможете сделать это на сайте создателя программы.

Вот что пишет автор о своей программе:
Довольно часто перед радиолюбителем встает вопрос: “Как рассчитать индуктивность катушки?“. Катушки используются и в высокочастотной связной аппаратуре, и при конструировании акустических систем, и даже взглянув на материнскую плату компьютера, Вы и там обнаружите индуктивные элементы. С помощью программы Coil32 можно быстро рассчитать индуктивность катушки. В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки можно “не отходя от кассы” рассчитать емкость конденсатора в колебательном контуре.
Программа предназначена для расчета индуктивности катушек на разных каркасах: одно и многослойных, на ферритовых кольцах, в броневом сердечнике, плоских катушек на печатной плате, а также колебательных контуров. Имеется набор плагинов к программе для расчета дополнительных видов индуктивности. Список плагинов имеется на странице загрузки (в конце этой страницы вы сможете скачать последнюю версию программы с уже установленными всеми доступными плагинами). Также можно воспользоваться онлайн расчетом индуктивности (на сайте автора).

Программа бесплатна и свободна для использования и распространения.

В последней версии Coil32 v7.3 доступны:
♦ Расчет числа витков катушки при заданной индуктивности
♦ Расчет индуктивности катушки для заданного числа витков
♦ Расчет добротности для однослойных катушек
♦ Расчет индуктивности многослойной катушки по ее омическому сопротивлению
♦ Расчет длины провода, необходимого для намотки многослойной катушки
♦ Расчет длины провода, необходимого для намотки катушки на ферритовом кольце

Программа позволяет производить расчет следующих типов катушек индуктивности:
♦ Одиночный круглый виток
♦ Однослойная виток к витку
В качестве начальных параметров при расчете катушки можно выбрать два варианта:
◊ Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
◊ Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
♦ Однослойная катушка с шагом
♦ Катушка с не круглой формой витков
♦ Многослойная катушка
В качестве начальных параметров при расчете катушки можно выбрать два варианта:
◊ Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки (“сколько надо отрезать”).
◊ Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.
♦ Тороидальная однослойная катушка
♦ Катушка на ферритовом кольце
♦ Катушка в броневом сердечнике
(Ферритовом и карбонильном)
♦ Тонкопленочная катушка
(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)

В чем преимущества программы перед аналогами?
◊ Программа рассчитывает индуктивность многих типов катушек. Можно подобрать оптимальный вариант, либо пересчитать катушку под имеющийся каркас.
◊ Результаты всех расчетов выводятся в текстовое поле, откуда их можно сохранить в файл. В дальнейшем Вы можете их просмотреть, чтобы не пересчитывать заново. Можно открыть этот файл в “MS Word” и распечатать.
◊ Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
◊ Можно рассчитать длину провода для намотки многослойной катушки и на ферритовом кольце
◊ Для катушек в броневых сердечниках есть возможность выбрать один из нескольких стандартных, что позволяет рассчитать катушку несколькими щелчками мыши.
◊ Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
◊ В Сети часто встречаются программы для расчета индуктивности, работающие под DOS, о преимуществах Windows-интерфейса, думаю, говорить не приходится.
◊ Программа имеет возможность расширения функционала с помощью дополнительных плагинов для расчета индуктивностей
◊ Программа имеет мультиязычный интерфейс и скины, дополнительные наборы скинов можно найти на странице загрузки.
◊ Программа распространяется в стиле “Portable” и не имеет установщика. Для установки программы распакуйте файл Coil32.zip в любой каталог и запустите на выполнение файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.

Программа очень проста в использовании и разобраться в ней совершенно несложно. Кроме того, все ее возможности подробно описаны в разделе “Help”, там-же указаны формулы, по которым производится каждый расчет.
В разделе “Plugins” вы можете воспользоваться дополнительными возможностями программы (плагинами):
— meandr_PCBv0.3 – Расчет плоской печатной катушки в форме меандра.
– square_loop – Расчет индуктивности прямоугольной рамки
– screen – Учет влияния экрана на величину индуктивности
– multiloop – Расчет индуктивности многовитковой круглой рамки круглого сечения (для металлоискателей)
– Ferrite – Расчет индуктивности на ферритовом стержне.
– Precise Helix – Точный расчет однослойной катушки с произвольным шагом намотки.
– MLC Precise – Точный расчет многослойной катушки с любой геометрией намотки по эллиптическим интегралам Максвелла.

У нас на сайте вы сможете скачать последнюю версию программы, с уже установленными всеми плагинами (а на сегодняшний день – их всего восемь):

  Программа для расчета индуктивности катушки Coil32_v7.3.7 (5.1 MiB, 13,791 hits)

---

---

Урок 46. Лабораторная работа № 12. Измерение индуктивности катушки.

Тема: Измерение индуктивности катушки

Цель: вычисление индуктивного сопротивления катушки и ее индуктивности по результатом измерений напряжений на катушке и силы тока в цепи.

Оборудование: источник переменного напряжения; катушка школьного разборного трансформатора; вольтметр и миллиамперметр переменного тока; соединительные провода.

Теория.

   Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току. Она препятствует его возрастанию и, наоборот, поддерживает его при убывании. Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки, то и называется оно индуктивным сопротивлением.

   Индуктивное сопротивление обозначается через Х_L и измеряется, как и активное сопротивление, в омах. Индуктивное сопротивление цепи тем больше, чем больше частота тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле:

 Х_L=ωL , где ω — круговая частота, определяемая произведением 2πν, L — индуктивность цепи в генри (Гн).

   Т.е.

   Тогда индуктивность катушки можно выразить:

   Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна  индуктивному сопротивлению цепи, т. е

   , где I и U  — действующие значения тока и напряжения, а Х_L — индуктивное сопротивление цепи. 

Выполнение работы:

1. Подготовить таблицу для результатов измерений и вычислений:

Напряжение U, В	Сила тока I, мА	Индуктивное сопротивление XL, Ом	Частота ν, Гц	Индуктивность L, мГн

2. Собрать электрическую схему согласно рисунка 1 и перечертить её в тетрадь:

3. Спомощью регулятора напряжения подать на схему напряжение 1,5 В и установить частоту переменного тока 80 Гц. Записать показания миллиамперметра.

4. Увеличивая частоту в 2,3,4 и 5 раз каждый раз записывать показания миллиамперметра в таблицу.

5. Вынуть сердечник из катушки и, не изменяя напряжения и частоты переменного тока, записать показания миллиамперметра в таблицу.

Напряжение U, В	Сила тока I, мА	Индуктивное сопротивление XL, Ом	Частота ν, Гц	Индуктивность L, мГн
1,5	0,345		80
1,5	0,178		160
1,5	0,121		240
1,5	0,090		320
1,5	0,072		400
1,5	0,284		400

6. В каждом опыте рассчитать индуктивное сопротивление катушки по формуле:

7. Вычислить в каждом опыте индуктивность катушки L, используя формулу:

8. Сравнивая индуктивности катушек, сделайте вывод, от чего и как зависит индуктивность.

9. Ответьте письменно на контрольные вопросы.

Контрольные вопросы.

1. Чем вызвано индуктивное сопротивление у катушки при подключении её в цепь переменного тока?

2. От чего зависит индуктивное сопротивление?

3. Почему уменьшается индуктивное сопротивление при удалении из катушки железного сердечника?

4. Почему на постоянном токе индуктивное сопротивление катушки равно нулю?

5. Чему равно индуктивное сопротивление в цепи переменного тока?

6. Как связаны между собой действующие значения силы тока и напряжения на катушке индуктивности?

    

Задачи по физике и математике с решениями и ответами

Задача по физике — 7616

Катушку индуктивности $L = 300 мГ$ и сопротивления $R = 140 мОм$ подключили к источнику постоянного напряжения. Через сколько времени ток через катушку достигнет $\eta = 50$% установившегося значения? Подробнее

Задача по физике — 7617

Вычислить постоянную времени $\tau$ прямого соленоида длины $l = 1,0 м$, имеющего однослойную обмотку из медного провода массы $m = 1,0 кг$. Предполагается, что диаметр сечения соленоида значительно меньше его длины.
Примечание. Постоянной времени $\tau$ называют отношение где $L$ — индуктивность, $R$ — активное сопротивление. Подробнее

Задача по физике — 7618

Найти индуктивность единицы длины кабеля, представляющего собой два тонкостенных коаксиальных металлических цилиндра, если радиус внешнего цилиндра в $\eta = 3,6$ раза больше, чем радиус внутреннего. Магнитную проницаемость среды между цилиндрами считать равной единице. Подробнее

Задача по физике — 7619

Определить индуктивность тороидального соленоида из $N$ витков, внутренний радиус которого равен $b$, а поперечное сечение имеет форму квадрата со стороной $a$. Пространство внутри соленоида заполнено однородным парамагнетиком с магнитной проницаемостью $\mu$. Подробнее

Задача по физике — 7620

Вычислить индуктивность единицы длины двухпроводной ленточной линии (рис.), если расстояние между лентами $h$ значительно меньше их ширины $b$, а именно, $b/h = 50$.
Подробнее

Задача по физике — 7621

Найти индуктивность единицы длины двухпроводной линии, если радиус каждого провода в $\eta$ раз меньше расстояния между их осями. { \circ}$ в положение, перпендикулярное к полю. Найти:
а) ток в кольце после поворота; б) работу, совершенную при этом. Подробнее

Задача по физике — 7623

Ток $I_{0} = 1,9 А$ течет по длинному замкнутому соленоиду, проволока которого находится в сверхпроводящем состоянии. Найти ток в соленоиде после того, как его растянули, увеличив длину на $\eta = 5$%. Подробнее

Задача по физике — 7624

Кольцо радиуса $a = 50 мм$ из тонкой проволоки радиуса $b = 1,0 мм$ поместили в однородное магнитное поле с индукцией $B = 0,50 мТ$ так, что плоскость кольца оказалась перпендикулярной к вектору $\vec{B}$. Затем кольцо охладили до сверхпроводящего состояния и выключили магнитное поле. Найти ток в кольце после этого. Иметь в виду, что индуктивность тонкого кольца, вдоль которого течет поверхностный ток, $L = \mu_{0}a \left ( ln \frac{2a}{b} — 2 \right )$. Подробнее

Задача по физике — 7625

Замкнутая цепь состоит из последовательно включенных источника постоянной э. д. с. $\mathcal{E}$ и дросселя индуктивности $L$. Активное сопротивление всей цепи равно $R$. В момент $t = 0$ индуктивность дросселя скачком уменьшили в $\eta$ раз. Найти ток в цепи как функцию времени $t$.
Указание. При скачкообразном изменении индуктивности полный магнитный поток (потокосцепление) остается неизменным. Подробнее

Задача по физике — 7626

Найти закон изменения во времени тока, текущего через индуктивность $L$ в схеме (рис. ) после замыкания ключа К в момент $t = 0$.
Подробнее

Задача по физике — 7627

В схеме (рис.) известны э. д. с. $\mathcal{E}$ источника, сопротивление $R$ и индуктивности катушек $L_{1}$ и $L_{2}$. Внутреннее сопротивление источника и сопротивления катушек пренебрежимо малы. Найти установившиеся токи в катушках после замыкания ключа К.
Подробнее

Задача по физике — 7628

Вычислить взаимную индуктивность длинного прямого провода и прямоугольной рамки со сторонами $a$ и $b$. Рамка и прямой провод лежат в одной плоскости, причем ближайшая к проводу сторона рамки длиной $b$ параллельна проводу и отстоит от него на расстояние $l$. Подробнее

Задача по физике — 7629

Определить взаимную индуктивность тороидальной катушки и проходящего по ее оси бесконечного прямого провода.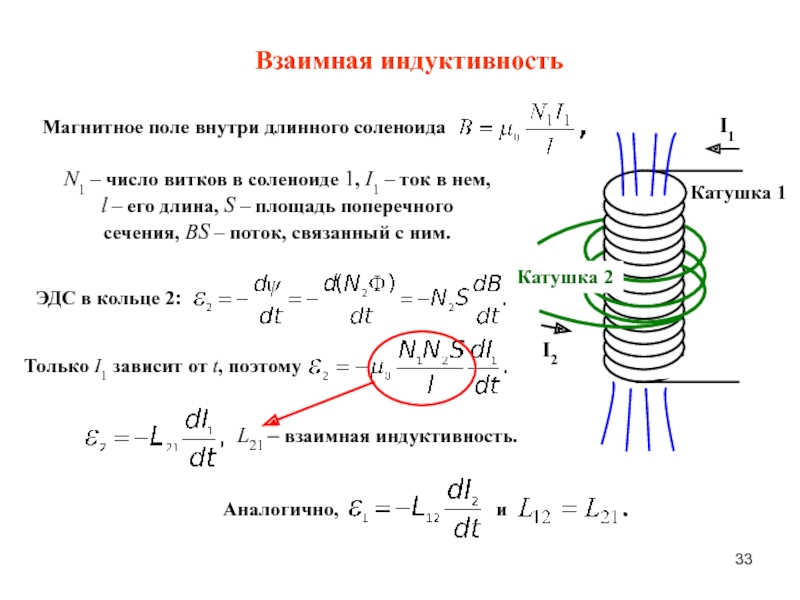 Катушка имеет прямоугольное сечение, ее внутренний радиус $a$, внешний $b$. Длина стороны поперечного сечения тора, параллельная проводу, равна $h$. Число витков катушки $N$. Система находится в однородном магнетике с проницаемостью $\mu$. Подробнее

Задача по физике — 7630

Два концентрических тонких проводника в форме окружностей с радиусами $a$ и $b$ лежат в одной плоскости. Имея в виду, что $a \ll b$, найти:
а) их взаимную индуктивность;
б) магнитный поток, который пронизывает поверхность, натянутую на внешний проводник, когда по внутреннему проводнику течет ток $I$. Подробнее

Расчёт катушки индуктивности под динамик

Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.

На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.

высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.

Пример расчета

Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.

Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.

1. откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
2. далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
3. длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
4. количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
5. диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
6. масса намотки: m = (h³ х 10^-3) / 21,4 = (26,96³ х 10^-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.

Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.

Итак имеем данные, которые понадобятся для расчета будущей катушки:

1. высота намотки h = 26,96 мм;
2. значит внутренний диаметр a = 53,92 мм;
3. соответственно внешний: b = 107,84 мм;
4. длинна жилы: 34,3 м;
5. количество витков: 135;
6. диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).

Статья специально подготовлена для сайта ldsound.ru

Как рассчитать индуктивность катушки (однослойные индукторы с цилиндрическим сердечником)

Индуктивность катушки зависит от ее геометрических характеристик, количества витков и способа намотки катушки. Чем больше диаметр, длина и большее количество витков обмотки, тем больше ее индуктивность.

Если катушка намотана плотно, от поворота к витку, то она будет иметь большую индуктивность, чем катушка с неплотной намоткой, с промежутками между витками. Иногда вам нужно намотать катушку с заданной геометрией, а у вас нет провода с требуемым диаметром, тогда, если вы используете более толстую проволоку, вам следует немного увеличить количество витков, а если использовать более тонкую проволоку, это нужно для уменьшения витков катушки, чтобы получить требуемую индуктивность.

Все вышеперечисленное относится к обмоткам без ферритовых сердечников.

Индуктивность однослойных катушек на цилиндрических формах обмоток можно рассчитать по формуле:

L = ( D /10) ² * n ² /( 4.5 * D + 10 * l ) (1)

Где
L — индуктивность катушки, мкГн;
D — диаметр бухты (диаметр формовки), мм;
l — длина змеевика, мм;
n — количество витков обмоток.

В расчете может быть две задачи:

А. Дана геометрия катушки, найти индуктивность;
B. Дана индуктивность катушки, посчитайте количество витков и диаметр провода.

В случае «А» все данные указаны, индуктивность найти несложно.

Пример 1. Рассчитаем индуктивность катушки, показанной на рисунке выше. Подставьте значения в формулу 1:

L = (18/10) ² * 20 ² / (4.5 * 18 + 10 * 20) = 4,6 мкГн

Во втором случае известны диаметр катушки и длина намотки. Длина намотки зависит от количества витков и диаметра проволоки. Поэтому рекомендуется производить расчет именно в таком порядке. Исходя из геометрических соображений, определите размер катушки, диаметр и длину намотки, а затем подсчитайте количество витков по формуле:

n = 10 * (5 * L * (0,9 * D + 2 * л )) ^1/2 / D (2)

После того, как вы нашли количество витков, определите диаметр провода с изоляцией по формуле:

d = l / n (3)

Где
d — диаметр проволоки, мм;
l — длина намотки, мм;
n — количество витков.

Пример 2. Нам нужно сделать катушку диаметром 10 мм и длиной намотки 20 мм, катушка должна иметь индуктивность 0,8 мкГн. Обмотка однослойная, от поворота к повороту.

Подставляем значения в формулу 2, получаем:
n = 10 * (5 * 0,8 * (0,9 * 10 + 2 * 20)) ^1/2 /10 = 14

Диаметр проволоки: d = 20/14 = 1,43 мм

Для намотки катушки проводом меньшего диаметра необходимо расположить полученные расчетом 14 витков по всей длине катушки (20 мм) с равными интервалами между витками (шаг намотки).Индуктивность катушки будет на 1-2% меньше номинальной, это следует учитывать при изготовлении этих катушек. Чтобы намотать катушку проволокой толще 1,43 мм, новый расчет следует производить с увеличенным диаметром или длиной обмотки катушки. Вам также может потребоваться увеличить диаметр и длину одновременно, пока не получите желаемые размеры катушки для данной индуктивности.

Следует отметить, что приведенные выше формулы предназначены для расчета катушек с длиной намотки l равной половине диаметра или более.Если длина намотки меньше половины диаметра намотки D /2, более точные результаты можно получить, используя следующие формулы:

L = (D /10) ² * n ² / ((4 D +11 l )) (4)

и

n = (10 L * (4 D +11 l )) ^1/2 / D (5)

Артикул: «300 практических советов»

Взаимная индуктивность и самоиндукция | Формула и пример

Электромагнитная индукция возникает, когда магнитный поток, движущийся относительно одиночного проводника или катушки, индуцирует ЭДС в проводнике или катушке.Поскольку рост или уменьшение тока через катушку генерирует изменяющийся поток, ЭДС индуцируется в катушке из-за ее собственного изменения тока. Тот же эффект может вызвать ЭДС в соседней катушке. Уровень наведенной ЭДС в каждом случае зависит от самоиндукции катушки или от взаимной индуктивности между двумя катушками. Во всех случаях полярность наведенной ЭДС такова, что она противодействует первоначальному изменению, вызвавшему ЭДС.

Компоненты, называемые индукторами или дросселями, сконструированы с заданными значениями индуктивности.Индукторы могут работать последовательно или параллельно. Даже самый короткий проводник имеет индуктивность. Обычно это нежелательная величина, называемая паразитной индуктивностью.

Самоиндуктивность

Катушка и индуктивность проводника

Было показано, что ЭДС индуцируется в проводнике, движущемся через магнитное поле, и что рост тока в катушке может индуцировать ЭДС в другом магнитном поле. спаренная катушка. Катушка также может индуцировать в себе напряжение при изменении уровня тока.Это явление известно как самоиндукция, и его принцип показан на рисунке 1.

Рисунок 1: Токопроводящая катушка и ее площадь поперечного сечения

Магнитный поток, растущий наружу вокруг витков катушки, разрезает (или задевает) другая катушка поворачивается и индуцирует ЭДС в катушке.

Катушка и ее площадь поперечного сечения показаны на рисунке 1, концы стрелок и точки указывают направления тока в каждом витке. Каждый виток катушки имеет магнитный поток вокруг него, создаваемый током, протекающим через катушку.Однако для удобства на рисунке показано увеличение потока только вокруг одного витка катушки. Видно, что по мере роста тока поток расширяется наружу и срезает (или сметает) другие витки. Это вызывает индукцию токов в других витках, и направление индуцированных токов таково, что они создают поток, противодействующий индуцирующему их потоку.

Помня, что ток через катушку вызывает рост потока вокруг всех витков одновременно, видно, что поток от каждого витка индуцирует ток, который противодействует ему на каждом втором витке.

Чтобы установить встречные потоки, индуцированный ток в катушке должен быть противоположен току, протекающему через катушку от внешнего источника питания. Наведенный ток, конечно же, является результатом наведенной ЭДС. Таким образом, видно, что самоиндукция катушки создает наведенную ЭДС, которая противодействует внешней ЭДС, которая пропускает ток через катушку. Поскольку эта наведенная ЭДС противоположна напряжению питания, ее обычно называют противоэдс или противоэдс .Противоэдс возникает только тогда, когда ток в катушке растет или уменьшается. Когда ток достигает постоянного уровня, поток больше не меняется, и противоэдс не генерируется.

Даже один проводник имеет самоиндукцию. На рис. 2 показано, что при нарастании тока в проводнике поток может расти наружу от центра проводника. Этот поток разрезает другие части проводника и вызывает противоэдс.

Рис. 2: поперечное сечение проводника

Рост тока внутри проводника индуцирует ЭДС на других участках проводника.

На рисунке 3 полярность противоэдс, наведенная в катушке, проиллюстрирована для данной полярности напряжения питания. На рисунке 3 (а) переключатель замкнут, и ток I начинает расти с нуля. Полярность противоэдс (e _L ) такова, что она противодействует росту I, поэтому она последовательно противостоит напряжению питания. Когда переключатель разомкнут (рис. 3 (b)), ток стремится к нулю. Но теперь полярность e _L такова, что противостоит закату I.это последовательно с питающим напряжением. Фактически, e _L может вызвать искрение на выводах переключателя, поскольку это зависит от индуктивности катушки.

Рис.3: Полярность наведенной ЭДС

Противоэдс, наведенная в катушке, всегда противодействует увеличению или уменьшению тока.

Единицей индуктивности в системе СИ является Генри (Гн).

Индуктивность цепи равна одному Генри, когда ЭДС 1 В индуцируется изменением тока со скоростью 1 А / с.

Таким образом, соотношение между индуктивностью, наведенным напряжением и скоростью изменения тока будет следующим:

\ [\ begin {matrix} L = \ frac {{{e} _ {L}}} {{\ Delta i} / {\ Delta t} \;} & {} & \ left (1 \ right) \\\ end {matrix} \]

Где L — индуктивность в Генри, e _L — наведенная противоэдс в вольтах. и — скорость изменения тока в А / с. знак минус иногда ставится перед e _L , чтобы показать, что наведенная ЭДС противоположна приложенной ЭДС.Когда e _L = 1 В и = 1 А / с, L = 1H. Если скорость изменения тока составляет 2 А / с и e _L = 1 В, индуктивность составляет 0,5 Гн.

Катушка, сконструированная так, чтобы иметь определенную индуктивность, обычно называется индуктором или дросселем. Обратите внимание на графические символы для катушки индуктивности, показанные на рисунке 3.

Формула самоиндуктивности

Выражение для индуктивности может быть получено с учетом размеров катушки и количества витков [см. Рисунок 4].

Рис.4: Количество витков в катушке

Индуктивность катушки зависит от количества витков, а также от магнитного потока и изменений тока.

Из уравнения (2):

\ [\ begin {matrix} {{e} _ {L}} = N \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left ( 2 \ right) \\\ end {matrix} \]

Подстановка e _L в уравнение (1) дает

\ [L = N \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]

Или

\ [\ begin {matrix} L = N \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (3 \ right) \\\ end {matrix} \]

Также

\ [\ phi = B \ times A \]

и

$ B = {{\ mu} _ {o }} \ times {{\ mu} _ {r}} \ times H = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {IN} {l} $

Следовательно,

$ \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times IN \ times \ frac {A} {l} $

Поскольку I — максимальный уровень тока, он также представляет изменение тока (∆i) от нуля до максимального уровня.{A} / {} _ {l} & {} & \ left (4 \ right) \\\ end {matrix} \]

Обратите внимание, что, как показано на рисунке 5, индуктивность пропорциональна поперечному сечению площадь катушки и квадрат числа витков. Он также обратно пропорционален длине катушки. Таким образом, максимальная индуктивность достигается при использовании короткой катушки с большой площадью поперечного сечения и большим количеством витков.

Рис.5: Размеры катушки

Индуктивность катушки можно рассчитать, исходя из ее размеров и проницаемости сердечника.

Уравнение (4) теперь позволяет вычислить индуктивность катушки известных размеров. В качестве альтернативы его можно использовать для определения требуемых размеров катушки с заданной индуктивностью. Однако его не так просто применить к катушкам с железным сердечником, потому что проницаемость ферромагнитного материала изменяется при изменении плотности потока. Следовательно, индуктивность катушки с железным сердечником постоянно изменяется по мере увеличения и уменьшения тока катушки.

Неиндуктивная катушка

Во многих случаях желательно иметь неиндуктивную катушку; например, прецизионные резисторы обычно не являются индуктивными.Чтобы построить такую ​​катушку, обмотка сделана из двух расположенных бок о бок проводников, как показано на рисунке 6. Каждый виток катушки имеет соседний виток, несущий ток в противоположном направлении. Магнитные поля, создаваемые соседними витками, нейтрализуют друг друга. Следовательно, противоэдс не генерируется, и катушка не индуктивна.

Рис.6: Неиндуктивная катушка

Пример самоиндуктивности

Соленоид с 900 витками имеет общий поток 1,33 X 10 ^-7 Вт через воздушный сердечник при токе катушки 100 мА.{-3}}} = 1,6 мВ \]

Взаимная индуктивность

Когда поток от одной катушки разрезает другую соседнюю (или магнитно связанную) катушку, во второй катушке индуцируется ЭДС. Следуя закону Ленца, ЭДС, индуцированная во второй катушке, создает поток, противодействующий исходному потоку из первой катушки. Таким образом, наведенная эдс снова является противоэдс, и в этом случае индуктивный эффект называется взаимной индуктивностью. На рисунке 7 показаны графические символы, используемые для катушек с взаимной индуктивностью, также называемых связанными катушками.

Рис.7: Графические символы для катушек с воздушным и железным сердечником

Как и самоиндукция, взаимная индуктивность измеряется в Генри (H) .

Формула взаимной индуктивности

Две катушки имеют взаимную индуктивность 1 Гн, когда ЭДС 1 В индуцируется в одной катушке за счет изменения тока со скоростью 1 А / с в другой катушке.

Это определение приводит к уравнению, связывающему взаимную индуктивность с наведенным напряжением и скоростью изменения тока:

\ [\ begin {matrix} M = \ frac {{{e} _ {L}}} {{{ \ Delta i} / {\ Delta t} \;} & {} & \ left (5 \ right) \\\ end {matrix} \]

Где M — взаимная индуктивность по Генри, e _L — ЭДС в вольтах, индуцированная во вторичной катушке, и представляет собой скорость изменения тока в первичной катушке в А / с.

Катушка, через которую проходит ток от внешнего источника, называется первичной, а катушка, в которой наведена ЭДС, называется вторичной.

Уравнение для ЭДС, индуцированной во вторичной катушке, можно записать как:

\ [\ begin {matrix} {{e} _ {L}} = {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left (6 \ right) \\\ end {matrix} \]

Здесь ∆ϕ — полное изменение магнитного потока во вторичной обмотке, N _с — количество витков вторичной обмотки, а ∆t — время, необходимое для изменения магнитного потока.

Подстановка e _L из уравнения (6) в уравнение (5) дает

\ [M = {{N} _ {s}} \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]

Следовательно,

\ [\ begin {matrix} M = {{N} _ {s}} \ frac {\ Delta \ phi } {\ Delta i} & {} & \ left (7 \ right) \\\ end {matrix} \]

Рисунок 8 (a) иллюстрирует тот факт, что когда две катушки намотаны на один ферромагнитный сердечник, эффективно весь поток, создаваемый первичной обмоткой, соединяется с вторичной обмоткой.Однако, когда катушки имеют воздушный сердечник, только часть потока от первичной обмотки может соединяться с вторичной (см. Рисунок 8 (b)). В зависимости от того, какая часть первичного потока пересекает вторичную, катушки могут быть классифицированы как слабо связанные или сильно связанные. Один из способов обеспечить плотное соединение показан на Рисунке 8 (c), где каждый виток вторичной обмотки находится рядом с одним витком первичной обмотки. Катушки, намотанные таким образом, называют бифилярными.

Рис.8: Потоковые связи в первичной и вторичной обмотках

Величина магнитного потока от первичной обмотки, которая связана со вторичной, зависит от того, насколько тесно связаны катушки. Коэффициент сцепления определяет сцепление.

Величина магнитной связи между первичной обмоткой и вторичной обмоткой также определяется в терминах коэффициента связи, k. Если весь первичный поток связан с вторичной обмоткой, коэффициент связи равен 1. Когда только 50% первичного потока соединяется с вторичной обмоткой, коэффициент связи равен 0.5. Таким образом,

\ [k = \ frac {flux \ text {} связей \ text {} между \ text {} primary \ text {} и \ text {} \ sec ondary} {total \ text {} fluxproduced \ text {} by \ text {} primary} \]

Возвращаясь к уравнению (7). Когда ∆ϕ — полное изменение магнитного потока в первичной обмотке, магнитная связь с вторичной обмоткой равна k∆ϕ. Следовательно, уравнение для M

\ [\ begin {matrix} M = k {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (8 \ right ) \\\ end {matrix} \]

Также, заменив $ \ Delta \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ times N \ times \ frac {A} {l} $ в уравнение (8) дает

\ [M = \ frac {k {{N} _ {s}}} {\ Delta i} \ times {{\ mu } _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ times {{N} _ {p}} \ times \ frac {A} {l} \]

или

\ [\ begin {matrix} M = k \ times {{N} _ {p}} \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (9 \ right) \\\ end {matrix} \]

Каждая рассматриваемая обмотка сама по себе имеет самоиндукцию, которая может рассчитывается по уравнению (4).{2}} $

или

\ [\ begin {matrix} \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = {{N} _ {p} } \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (10 \ right) \\\ end {matrix} \]

Сравнивая уравнения 9 и 10, видно, что

\ [\ begin {matrix} M = k \ sqrt {{{L} _ { 1}} \ times {{L} _ {2}}} & {} & \ left (11 \ right) \\\ end {matrix} \]

Пример взаимной индуктивности

Две одинаковые катушки намотаны железный сердечник кольцевой формы с относительной проницаемостью 500.{-2}}} \ cong 9.42mH \\\ end {align} \]

Поскольку катушки намотаны на один и тот же железный сердечник, k = 1. Уравнение (11):

$ M = k \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = \ sqrt {9.42 \ times 9.42} = 9,42 мГн $

Калькулятор индуктивности соленоида

Калькулятор индуктивности соленоида находит самоиндуктивность соленоида. Прочитав текст ниже, вы узнаете, как работает соленоид в электрических цепях и какова его индуктивность.

Как работает соленоид

Соленоиды и катушки в целом являются важными элементами электрических цепей (попробуйте RLC Circuit Calculator, чтобы увидеть индуктивный элемент в действии).Их характеристика — индуктивность L , и они действуют как инерционные элементы: катушки сопротивляются изменению тока. Изменение тока, протекающего через катушку, приводит к самоиндуцированной разности потенциалов. Индуктивность L устанавливает соотношение между потенциалом и скоростью изменения тока

.

В = - L * dI / dt

Минус показывает резистивный характер индуктивности; разность потенциалов препятствует изменению тока.Магнитное поле внутри соленоида вызывает такое поведение. Если мы изменим ток, мы изменим это магнитное поле. В свою очередь, это вызывает разность потенциалов в соленоиде. Чтобы узнать больше о магнитном поле внутри соленоида и явлениях индуктивности, проверьте Калькулятор магнитного поля соленоида и Калькулятор закона Фарадея.

Индуктивность соленоида

Соленоид — это длинная туго намотанная катушка. Мы можем описать соленоид с помощью трех параметров:

• число витков N ,
• длина л ,
• площадь поперечного сечения А .-6 Т * м / А . С помощью нашего калькулятора индуктивности соленоида вы можете легко найти индуктивность соленоида для различных конфигураций. Вместо указания площади поперечного сечения A можно задать радиус r . Затем калькулятор вычисляет площадь, принимая круглое поперечное сечение.

  Формула и расчеты индуктивного сопротивления

  Любая катушка индуктивности сопротивляется изменениям переменного тока, и это приводит к возникновению у нее импеданса.

  ---

  Учебное пособие по индуктивности и трансформатору Включает:
  Индуктивность Символы Закон Ленца Собственная индуктивность Расчет индуктивного реактивного сопротивления Теория индуктивного реактивного сопротивления Индуктивность проволоки и катушек Трансформеры

  ---

  Катушка индуктивности препятствует прохождению переменного тока за счет своей индуктивности.Любая катушка индуктивности сопротивляется изменению тока в результате закона Ленца.

  Степень, в которой индуктор препятствует прохождению тока, обусловлена ​​его индуктивным реактивным сопротивлением.

  Индуктивное реактивное сопротивление зависит от частоты — возрастает с частотой, но его можно легко вычислить с помощью простых формул.

  Индуктивное реактивное сопротивление

  Эффект, за счет которого уменьшается протекание переменного или изменяющегося тока в катушке индуктивности, называется ее индуктивным реактивным сопротивлением.Любое изменение тока в катушке индуктивности будет затруднено в результате связанной с ней индуктивности.

  Причину этого индуктивного реактивного сопротивления можно просто увидеть, исследуя самоиндуктивность и ее влияние в цепи.

  Когда изменяющийся ток подается на катушку индуктивности, самоиндукция вызывает индуцированное напряжение. Это напряжение пропорционально индуктивности, и в результате закона Ленца индуцированное напряжение противоположно приложенному напряжению.Таким образом, индуцированное напряжение будет работать против напряжения, вызывающего протекание тока, и, таким образом, будет препятствовать протеканию тока.

  Формулы индуктивного реактивного сопротивления

  Хотя идеальных катушек индуктивности не существует, полезно представить себе, чтобы взглянуть на формулы и расчеты, связанные с катушками индуктивности и индуктивностью. В этом случае идеальный индуктор — это тот, который имеет только индуктивность, а не сопротивление или емкость. Если на эту идеальную катушку индуктивности подается изменяющийся сигнал, такой как синусоида, реактивное сопротивление препятствует протеканию тока и подчиняется закону Ома.

  Где:
  X _L = индуктивное реактивное сопротивление, Ом, Ом
  В = напряжение в вольтах
  I = ток в амперах

  Индуктивное реактивное сопротивление катушки индуктивности зависит от ее индуктивности, а также от применяемой частоты. Реактивное сопротивление линейно увеличивается с частотой. Это можно выразить в виде формулы для расчета реактивного сопротивления на определенной частоте.

  Где:
  XL = индуктивное реактивное сопротивление в Ом, Ом
  π = греческая буква Пи, 3.142
  f = частота в Гц
  L = индуктивность в генри

  
  

  Суммируя индуктивное реактивное сопротивление и сопротивление

  Настоящая катушка индуктивности будет иметь некоторое сопротивление, или индукторы могут быть объединены с резисторами для создания комбинированной сети. В любом из этих случаев необходимо знать полное сопротивление цепи.

  Поскольку ток и напряжение внутри индуктора сдвинуты по фазе на 90 ° (ток отстает от напряжения), индуктивное реактивное сопротивление и сопротивление нельзя складывать напрямую.

  Добавление индуктивного реактивного сопротивления и сопротивления постоянному току

  Добавление индуктивного реактивного сопротивления и сопротивления постоянному току достигается векторным образом

  Из диаграммы видно, что две величины необходимо сложить векторно. Это означает, что необходимо возвести в квадрат индуктивное реактивное сопротивление и сопротивление, а затем извлечь квадратный корень:

  VTotal2 = VL2 + VR2

  Это можно переписать в более удобный формат:

  
  VTotal = VL2 + VR2

  Результирующая комбинация сопротивления и индуктивного реактивного сопротивления называется импедансом, который снова измеряется в омах.

  При использовании и проектировании цепей, содержащих катушки индуктивности, часто необходимо посмотреть на индуктивное реактивное сопротивление, рассчитать его по формулам выше, а затем прибавить его к чистому сопротивлению, чтобы получить общее сопротивление. Как таковые, эти формулы особенно полезны.

  Другие основные концепции электроники:
  Напряжение Текущий Мощность Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность Радиочастотный шум
  Вернуться в меню «Основные понятия электроники».. .

  Катушки индуктивности в серии

  Катушка индуктивности — это пассивный элемент, который используется в электронных схемах для временного хранения электрической энергии в виде магнитного потока или просто магнитного поля. Индуктивность — это свойство любой катушки, которая может создавать магнитный поток, когда через нее проходит ток.

  Любое устройство, обладающее свойством индуктивности, можно назвать индуктором. Обычно индуктор построен в виде катушки из медного материала вокруг сердечника из магнитной (железо) или немагнитной среды (например, воздуха).

  Катушки индуктивности могут быть подключены последовательно или параллельно в зависимости от характеристик, требуемых схемой. Эти комбинации используются для проектирования более сложных сетей. Общая индуктивность цепи зависит от способа подключения катушек индуктивности, может быть последовательным или параллельным.

  Кроме того, способ подключения индукторов таким образом, что одна индуктивность не влияет на другую, также изменяет общую индуктивность по сравнению с эффектом магнитной связи между индукторами.

  Следовательно, индукторы располагаются на основе их взаимной индуктивности или магнитной связи в последовательной или параллельной комбинации.

  Катушки индуктивности, подключенные последовательно

  Предположим, что индукторы, подключенные в цепь, не имеют связи между собой. Это означает, что нет никаких магнитных линий от одного индуктора, соединенного с другим, и, следовательно, не будет взаимного потока между катушками.

  Соединение двух или более индукторов «конец в конец» называется «последовательным соединением индукторов».В этой связи индукторы соединены последовательно, так что эффективное количество витков индуктора увеличивается. Последовательное соединение катушек индуктивности показано на диаграмме ниже.

  Индуктивность последовательно соединенных катушек индуктивности рассчитывается как сумма индивидуальных индуктивностей каждой катушки, поскольку изменение тока через каждую катушку одинаково.

  Это последовательное соединение аналогично последовательному соединению резисторов, за исключением того, что резисторы заменены индукторами.Если ток I протекает в последовательном соединении, а катушки L1, L2 и т. Д., Общий ток в последовательных индукторах определяется как

  I _Всего = I _L1 = I _L2 = I _Л3 . . . = I _n

  Если отдельные падения напряжения на каждой катушке в этом последовательном соединении равны VL1, VL2, V¬L3 и т. Д., Общее падение напряжения между двумя клеммами VT будет равно

  В _Всего = V _L1 + V _L2 + V _L3 ….+ V _n

  Поскольку мы знаем, что падение напряжения может быть представлено в терминах собственной индуктивности L, это означает

  В = L di / dt.

  Это также можно записать как

  LT di / dt = L1 di / dt + L2 di / dt + L3 di / dt +. . . + Ln di / dt

  Следовательно, общая индуктивность составляет

  L _Всего = L ₁ + L ₂ + L ₃ +… .. + L _n

  Это означает, что общая индуктивность последовательное соединение — это сумма индивидуальных индуктивностей всех катушек индуктивности.Вышеупомянутое уравнение верно, когда нет влияния взаимной индуктивности между катушками в этой последовательной конфигурации.

  Взаимная индуктивность катушек индуктивности приведет к изменению значения общей индуктивности в последовательной комбинации катушек индуктивности.

  Предположим, что есть две катушки индуктивности, подключенные последовательно к источнику переменного напряжения, который может генерировать переменный ток в цепи, как показано на рисунке выше.

  Если в цепи нет взаимной индуктивности, то общая индуктивность задается как

  L _T = L ₁ + L ₂

  Важно помнить, что общая индуктивность всегда больше, чем самый большой индуктор в последовательном расположении индукторов.

  Катушки индуктивности, соединенные последовательно Пример

  Пример 1: Если в цепи последовательно соединены 3 катушки индуктивности по 60 Генри, 30 Генри и 20 Генри, какова будет общая индуктивность серии?

  Sol: Мы знаем, что формула для полной индуктивности серии L _Total = L ₁ + L ₂ + L ₃ +… .. + L _n

  Учитывая, что L ₁ = 60 Генри

  L ₁ = 30 Генри

  L ₁ = 20 Генри

  Общая индуктивность, L _Всего = 60 + 30 + 20 = 110 Генри.

  Последовательно соединенные между собой индукторы

  Теперь представьте, что индукторы соединены таким образом, что магнитное поле одной катушки влияет на другую. Когда две или более катушки индуктивности соединены последовательно, на индуктивность одной катушки индуктивности будет влиять магнитное поле, создаваемое другой катушкой.

  Это называется взаимной индуктивностью, а катушки — «взаимно подключенными индукторами». Эта взаимная индуктивность может увеличивать или уменьшать общую индуктивность последовательной цепи.

  Фактором, влияющим на взаимную индуктивность последовательно соединенных катушек индуктивности, является расстояние между катушками и их ориентация.

  Взаимосвязанные катушки индуктивности могут быть двух типов

  1) Кумулятивно связанные или последовательные

  2) Дифференциально связанные или последовательно встречные

  Кумулятивно связанные индукторы последовательно

  Если магнитные потоки, создаваемые индукторами, одинаковы направление протекания тока через них, тогда катушки известны как «кумулятивно связанные».

  В этой последовательной вспомогательной или кумулятивно связанной схеме ток входит или покидает клеммы катушек в любой момент времени в одном направлении.

  На рисунке ниже показано последовательное соединение двух индукторов.

  Если мы пропустим ток через кумулятивно связанные катушки (между узлами A и D) в одном направлении, падение напряжения каждой отдельной катушки повлияет на общую индуктивность серии.

  Пусть собственная индуктивность катушки 1 равна L ₁ , собственная индуктивность катушки 2 равна L ₂ , а взаимная индуктивность между катушкой 1 и катушкой 2 равна M.

  Самоиндуцированная ЭДС в катушке-1 составляет

  e1 = — L ₁ di / dt

  Взаимная наведенная ЭДС в катушке-1 из-за изменения тока в катушке-2 составляет

  eM1 = — M di / dt

  Точно так же самоиндуцированная ЭДС в катушке-2 составляет

  e2 = — L ₂ di / dt

  Взаимная наведенная ЭДС в катушке-2 из-за изменения тока в катушке-1 составляет

  eM2 = — M di / dt

  Следовательно, полная наведенная ЭДС в последовательной вспомогательной цепи задается как

  e = — L ₁ di / dt– L ₂ di / dt– 2M di / dt

  = — (L ₁ + L ₂ + 2M) di / dt

  Если L _T — полная индуктивность цепи, общая наведенная ЭДС будет эквивалентна

  e = — L _T di / dt

  Подстановка в приведенном выше уравнении мы получаем

  — L _T di / dt = — (L ₁ + L ₂ + 2M) di / dt

  Следовательно, L _T = (L ₁ + L ₂ + 2M)

  Пример последовательного подключения кумулятивно связанных индукторов

  Пример: Если две катушки с индуктивностью 70 мГн и 30 мГн соединены последовательно, найдите общую кумулятивную индуктивность последовательно соединенных катушек индуктивности.Учтите, что взаимная индуктивность комбинации двух катушек составляет 40 мГн.

  Sol:

  Учитывая, что L ₁ = 70 мГн

  L ₂ = 30 мГн

  M = 40 мГн

  Применяя формулу для кумулятивно подключенных катушек индуктивности, LT = L1 + L2 + 2M

  L _T = 70 + 30 + 2 (40)

  = 100 + 80

  = 180 мГн

  Следовательно, совокупная индуктивность катушки составляет 180 милли Генри.

  Дифференциально связанные индукторы серии

  Если магнитные потоки, создаваемые индукторами, имеют противоположное направление, то катушки известны как «дифференциально связанные».

  В этом дифференциально-связанном или последовательном оппозиционном соединении ток входит или выходит из клемм катушек в любой момент времени в противоположном направлении.

  На рисунке ниже показано соединение двух катушек индуктивности в последовательном оппозиционном расположении.

  В дифференциально связанных катушках поля магнитного потока могут создаваться в том же или противоположном направлении. Пусть собственная индуктивность катушек равна L1 и L2, а взаимная индуктивность равна M.

  Здесь взаимная индуктивность будет добавлена ​​к собственной индуктивности каждой катушки из-за конфигурации цепи.
  Таким образом, полная наведенная ЭДС в последовательной встречной цепи задается как

  e = — L ₁ di / dt– L ₂ di / dt + 2M di / dt

  = — (L ₁ + L ₂ — 2M) di / dt

  Если L _T — это полная индуктивность цепи, общая наведенная ЭДС будет эквивалентна

  e = — L _T di / dt

  Подставив указанное выше уравнение, получаем

  — L _T di / dt = — (L ₁ + L ₂ — 2M) di / dt

  Следовательно, L _T = (L ₁ + L ₂ — 2M)

  Пример последовательного соединения индукторов с дифференциальной связью

  Пример: если две катушки индуктивности 70 мГн и 30 мГн соединены последовательно, найдите общую дифференциальную индуктивность последовательно соединенных индукторов.Учтите, что взаимная индуктивность комбинации двух катушек составляет 40 мГн.

  Sol:

  Учитывая, что L ₁ = 70 мГн

  L ₂ = 30 мГн

  M = 40 мГн

  Применяя формулу для дифференциально подключенных индукторов, LT = L1 + L2 — 2M

  L _T = 70 + 30-2 (40)

  = 100-80

  = 20 мГн

  Следовательно, дифференциальная индуктивность катушки составляет 20 миллигенри.

  Резюме

  • Катушка индуктивности — это пассивный элемент, который используется в электронных схемах для хранения энергии в виде магнитного потока.Индуктивность измеряется в Генри.
  • Количество рассеиваемой фактической мощности с током, протекающим в цепи, называется «индуктивным реактивным сопротивлением». Измеряется в омах. X _L = 2  f L
  • Самоиндукция — это свойство электрической цепи или контура, в котором собственное магнитное поле противодействует любому изменению тока
  • Взаимная индуктивность — это способность катушки индуктивности, которая вызывает индукцию ЭДС в другой индуктор помещается очень близко к нему, когда ток в первом индукторе изменяется.
  • Соединение двух или более индукторов «конец в конец» называется «последовательным соединением индукторов». Формула для общей индуктивности в серии: L _T = L ₁ + L ₂
  • Общая индуктивность последовательно соединенных катушек индуктивности всегда больше, чем самая большая индуктивность в этой серии.
  • Если магнитные потоки, создаваемые катушками индуктивности, совпадают с направлением тока через них, то катушки известны как «кумулятивно связанные».L _T = L ₁ + L ₂ + 2M
  • Если магнитные потоки, создаваемые индукторами, имеют противоположное направление, то катушки известны как «дифференциально связанные». L _T = L ₁ + L ₂ — 2M

  Пример расчета индуктивности

  Индуктивность Пример расчета

  Дэвид Микер

  [email protected]

  Сопутствующий файл: index1a.fem

  Введение

  Распространенной задачей, к которой можно применить FEMM, является расчет индуктивности индуктора с зазором. Хотя индуктивность можно оценить с помощью простого магнитного Теория схем, схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ методом конечных элементов может быть заняты. Цель настоящего пример — показать, как рассчитывается индуктивность в моделировании FEMM, и сравните этот результат с приближением, полученным через магнитную цепь подход.

  Пример геометрии

  Примерная геометрия состоит из ламинированного EI с зазором. сердечник с поперечным сечением, как показано на рисунке 1. Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного возвратного тракта воздушным зазором. Толщина 0,025 дюйма.

  Рисунок 1: Пример геометрии

  Обмотка, которая лежит в пазах E, состоит из 66 витки толстой изоляции провода 18 AWG, примерно для 66% меди заполните фракцию в окне змеевика.это Предполагается, что сердцевина расширяется на 1 дюйм в направлении страницы. В данной модели материал считается линейным ферромагнитным материалом с относительной проницаемостью из 2500.

  Теория цепей Индуктивность

  Для приблизительной оценки индуктивности мы можем предположить, что нет подтеков и окантовки, и что вклад железа секций на сопротивление магнитной цепи тривиально по сравнению с вклады с воздуха.Затем, поток, текущий в магнитной цепи, получается путем решения уравнения цепи:

  за ф , всего поток связан катушкой. Модель R представляет собой сопротивление магнитной цепи, которое согласно нашим предположениям можно записать как:

  , где g = 0,025 дюйма , a _полюс = 0.5 в ² и м _o = 4 p (10 ^-7 ) H / м. Так как общий поток, связывающий катушку, тогда:

  , а общая самоиндукция равна потоку, умноженному на общее количество витков:

  так, чтобы самоиндуктивность была:

  Так как в нашем случае витков 66, индуктивность работает из:

  L = 1.39 мГн

  Мы ожидаем, что индуктивность получена из конечных элементов. вычисления должны быть в районе 1,39 мГн.

  Индуктивность конечного элемента (I)

  В целях создания решения методом конечных элементов индуктор помещается в центр коробки размером 2 на 2,5 дюйма. На границах области граница условие A = 0 определено. Для Для выполнения анализа методом конечных элементов ток 1 А является допустимым. несколько произвольно применяется к катушкам.Достаточно грубая плотность сетки с ограничением размера ячейки больше 0,05 дюйма определяется везде. Сетка проблемной области изображена на рисунке 2.

  Рисунок 2: Проблемная область, нарисованная в FEMM.

  После выполнения анализа и запуска постпроцессора, индуктивность можно определить, нажав кнопку «Свойства схемы» в постпроцессор:
  Появляется диалоговое окно с рядом свойств обмотки, если смотреть со стороны выводов обмотки.Диалоговое окно «Свойства схемы» для этого примера показано ниже на рисунке 3.

  Рисунок 3: Схема Диалог результатов свойств.

  При отсутствии постоянных магнитов или других катушек, Результат потока / тока можно интерпретировать напрямую как собственную индуктивность:

  L = 1,73 м вод. Ст.

  Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и окантовки пренебрежение схемным подходом приводит к небольшому увеличению индуктивности.

  Индуктивность конечного элемента (II)

  Альтернативный подход — получение энергии через Интеграл «Энергия магнитного поля». Для этого подхода энергия получается через:

  , где этот интеграл взят по всей задаче домен, а не просто над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в режим интегрального блока, нажав кнопку на панели задач.Затем выберите каждый регион в проблеме с помощью щелчки левой кнопкой мыши. Когда выделена вся проблемная область, нажмите кнопку Integral и выберите Интеграл энергии магнитного поля из выпадающего списка объемных интегралов. Если W представляет собой интегральный результат, результирующая индуктивность:

  Для примера задачи результат из энергии интеграция:

  Вт = 0.000865042 Джоули

  Что при подстановке в формулу дает то же результат как метод (I):

  L = 1,73 м вод. Ст.

  Выводы

  Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получена из двух методы сравнивались друг с другом и с «проверкой работоспособности» оценка индуктивности по теории магнитной цепи.

  Хотя результаты двух подходов конечных элементов для получения одинаковых индуктивностей в этом случае обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( т.е. асимптотическое граничное условие, используемое для аппроксимации «открытой граничной» задачи) подразумевают, что некоторая энергия хранятся вне смоделированной проблемной области. Внутренне FEMM вычисляет поток связь с использованием метода, который учитывает эту дополнительную энергию, тогда как интегрирования B * H по всем элементам нет.

  Строго говоря, один коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с учитывались только линейные материалы.

  Если проблема связана с нелинейными материалами и есть значительная насыщенность, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному Текущий.В этом случае гармонический анализ может быть запущен в FEMM (, т.е. , когда частота, отличная от нуля, указанные в Определении проблемы). FEMM реализует нелинейную формулировку гармоники времени, которая вычисляет амплитуда и фаза основной части магнитного поля для времени гармонические задачи с нелинейными материалами. Для нелинейных задач гармоники по времени свойство Circuit Properties Диалог снова может быть использован для сбора различных свойств терминала катушек.

  Измерение индуктивности с помощью мультиметра и резистора

  Предпосылки

  С самого раннего возраста я всегда интересовался повторным использованием, переработкой и изобретением способов использования вещей, а также расширением их текущего использования или поиском новых целей. Моим основным направлением всегда была электроника (звуковая электроника, если быть точнее, электрогитара, если быть точным). Когда я построил свой первый ламповый усилитель, я использовал 90% переработанных деталей, и это звучало УБИЙСТВЕННО !.

  Если вы работали с электронными компонентами, вы знаете, что большинство из них (резисторы, конденсаторы, электронные лампы и т. Д.) Легко идентифицировать. На них проштампован их номинал или стоимость, они имеют цветовую кодировку, или вы можете напрямую измерить их с помощью мультиметра.

  Проблема связана с индукторами и трансформаторами. Когда вы повторно используете их из старого оборудования, вы не можете быть уверены в их ценности. Даже если вы используете новый, без таблицы вы застряли.

  Я использовал простой метод, который собираюсь описать, и он сработал для моего приложения.

  Моя идея состоит в том, что, хотя сегодня люди в более развитых местах на земле могут очень легко купить оборудование (у кого нет осциллографа или генератора сигналов, верно?). Большая часть этого «материала» была недоступна, когда я росла, и до сих пор недоступна в других местах на земле. Раньше у меня не было ни осциллографа, ни аудиогенератора, поэтому я обойдусь без них.Мы должны стремиться делать все, что в наших силах, с тем, что у нас есть под рукой.

  Допущения

  Эта инструкция предполагает, что читатель имеет базовые представления об электронике и ее основных управляющих законах: Ома и Кирхгофа.

  Хотя я изложу некоторые принципы, используемые для расчетов, я рекомендую прочитать теорию электрических цепей для более глубокого понимания их.

  Objective

  Цель данного руководства — представить простой и проверенный метод косвенного определения индуктивности дросселя фильтра (индуктора).

  Ожидания

  Ожидание состоит в том, чтобы получить значение компонента, которое можно использовать в ваших проектах. Он будет определять только значение L индуктора. Этот метод не будет определять максимальный ток, максимальные значения диэлектрической изоляции, максимальное входное напряжение, мощность и т. Д. Размер индуктора и приложение, из которого вы берете его для повторного использования, могут дать вам представление о максимуме мощность и ток, но я не собираюсь этого делать в этой инструкции.

  Соображения

  Расчетный результат будет очень близким приближением к реальному значению, мы не ищем до 5-й самой значащей цифры, хорошо? 🙂

  Подавляющее большинство используемых компонентов имеют допуск 5%. Еще лучше: большинство индукторов фильтров (дросселей) рассчитаны на плюс / минус 20% от номинального значения в соответствии с техническими описаниями производителя. В итоге: методических ошибок, лежащих в пределах +/- 20% от расчетного значения, считаю приемлемыми для меня .

  Например: при добавлении двух величин, если одно из них имеет значение меньше 10% другого, я отброшу его как «несущественное для каких-либо практических целей».

  Во время вычислений я укажу на это, сказав: Из-за того, что A более чем в 10 раз больше, чем B, если A + B = C, я предполагаю, что C приблизительно равно A, поэтому отбрасываю B в расчетах.

  Инструменты, инструменты, материалы и т. Д.

  Для этих измерений нам потребуется:

  • известный понижающий трансформатор (от 120/240 В до 6/12 В или любой другой, имеющийся под рукой).