Калькулятор делителя напряжения на резисторах онлайн: Онлайн-калькулятор делителя напряжения на резисторах

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.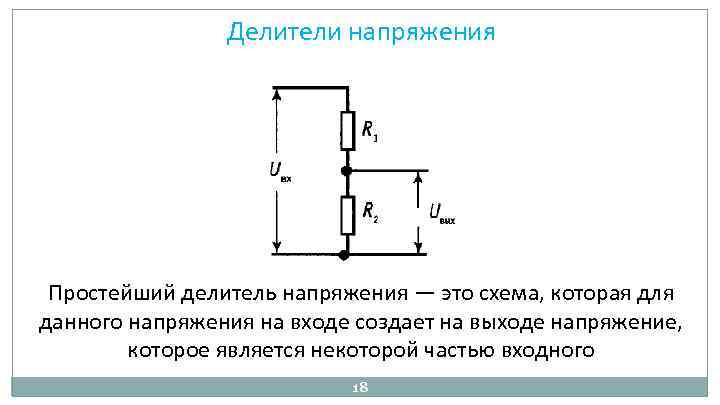

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Цифровой мультиметр AN8009

Большой ЖК-дисплей с подсветкой, 9999 отсчетов, измерение TrueRMS.

..

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн





 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Делитель напряжения на резисторах: онлайн калькулятор расчета

Схема делителя напряжения является простой, но в тоже время фундаментальной электросхемой, которая очень часто используется в электронике. Принцип работы ее прост: на входе подается более высокое входное напряжение и затем оно преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула расчета выходного напряжения основана на законе Ома и приведена ниже.

Классическая формула делителя напряжения

где:

• U_вх. — входное напряжение источника, В;
• U_вых. — выходное напряжение, В;
• R₁ — сопротивление 1-го резистора, Ом;
• R₂ — сопротивление 2-го резистора, Ом.

Схема классического делителя напряжения на 2 резистора

В калькулятор ниже введите любые три известных значения U_вх., U_вых. и R₁  и нажмите «Рассчитать», чтобы найти значение R₂.

Упрощения

Существует несколько обобщений, которые следует учитывать при использовании делителей напряжения.  Это упрощения, которые упрощают оценку схемы деления напряжения.

Во-первых, если R₂ и R₁ равны, то выходное напряжение вдвое меньше входного напряжения. Это верно независимо от значений резисторов.

Итак, если R₁ = R₂, то получаем следующее уравнение:

Формула делителя напряжения, если сопротивления равны

Во-вторых, если R₂ на порядок больше чем R₁, то выходное напряжение U_вых

будет очень близко к U_вх., то есть U_вх. ≈ U_вых. А на R₁ будет очень мало напряжения.

Формула делителя напряжения, если R2 на порядок больше R1

Во-третьих, если наоборот R₁ на порядок больше чем R₂, то U_вых будет очень маленьким по сравнению с U_вх, то есть будет стремиться к нулю. Практически все входное напряжение упадет в таком случае на R₁.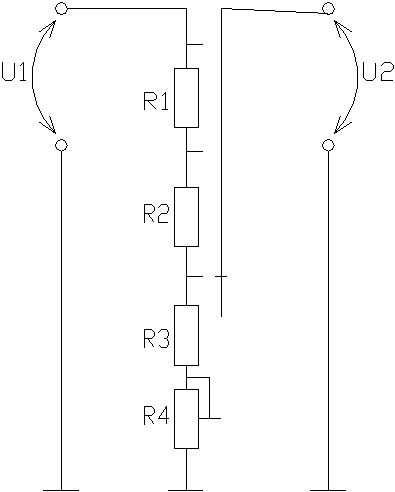

Вы можете воспользоваться онлайн калькулятором ниже, чтобы проверить как саму классическую формулу делителя напряжения, представленную на рисунке 1, так и вышеприведенные упрощения этой формулы.

Резисторный делитель напряжения: расчёт-онлайн, формулы и схемы

Резисторный делитель напряжения — одна из основополагающих конструкций в электронике, без которой не обходится ни одно устройство. Подбор сопротивлений задаёт нужные режимы работы. Как правило, эта конструкция содержит два резистора. Один ставится между входом и выходом схемы. Второй резистор одним концом подключается к общему проводу, а вторым — к выходу схемы, тем самым его шунтируя. Он также играет роль нагрузки источника, подключённого ко входу.

Формула делителя напряжения

Расчёт можно осуществить, используя формулы, вытекающие из закона Ома. Можно узнать, каким будет U на выходе устройства, если известно входное, а также сопротивления обоих резисторов. Можно также решить обратную задачу, например, вычислить напряжение, которое получится на выходе при известных сопротивлениях резисторов.

Чтобы выполнить расчет резистивного делителя, необходимо:

• Обозначить резистор, находящийся ближе ко входу делителя, как R1.
• Обозначить резистор, находящийся ближе к выходу делителя, как R2.
• Протекающие через резисторы токи обозначаются, как I1 и I2, а входное и выходное напряжения — UВХ и UВЫХ, соответственно.
• Промежуточная формула примет следующий вид: UВЫХ=I2*R2.
• Если предположить, что силы обоих токов равны, то формула для определения протекающего через схему тока станет выглядеть так: I=UВХ/R1+R2.
• Окончательная формула принимает такой вид: UВЫХ=R2*(UВХ/R1+R2).

Из неё становится ясно, что выходное напряжение всегда будет меньше, чем входное.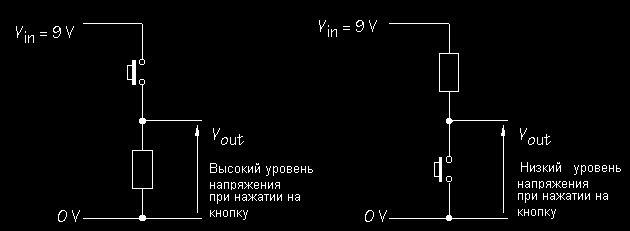 Оно зависит от самих резисторов. Чем больше сопротивление R1 и сила протекающего тока, тем меньше будет UВЫХ. Напротив, чем больше сопротивление R2, включённое между выходом и общим проводом, тем больше будет UВЫХ. Если упомянутое сопротивление стремится к бесконечности, то UВЫХ будет почти равным входному. Чем больше ток, который проходит по резисторам, тем меньше будет UВЫХ. Таким образом при больших токах делитель на резисторах становится малоэффективным, ввиду сильного падения напряжения.

Онлайн-калькуляторы

С их помощью можно рассчитать делитель напряжения на резисторах онлайн. Входными данными в этом случае могут являться: входное напряжение и оба сопротивления. Калькулятор «Делитель напряжения — онлайн» произведёт все необходимые операции по обозначенной формуле, и выведет значения искомых параметров. Расчет делителя напряжения на резисторах онлайн облегчает процесс разработки многих электронных схем, позволяет добиться достижения требуемых режимов и правильной работы устройств.

Разновидности делителей

Самая распространенная и характерная из них — это потенциометр. Он представляет собой стандартный переменный резистор. Внутри его находится дужка, на которую нанесен токопроводящий слой. По ней скользит контакт, делящий сопротивление на две части. Таким образом, потенциометр имеет три вывода, два из которых подключены к самому резистору, а третий — к перемещаемому движку.

Источник тока подключается к двум крайним выводам потенциометра, а UВЫХ будет сниматься с вывода движка и общего провода. По такой схеме устроены, например, регуляторы громкости и тембра звука в различной аудиоаппаратуре. При перемещении движка в крайнее нижнее положение UВЫХ станет равным нулю, а в противоположной ситуации будет равно входному. Если же перемещать движок, то напряжение будет плавно изменяться от нуля до входного.

Свойства делителей также используются при конструировании резистивных датчиков.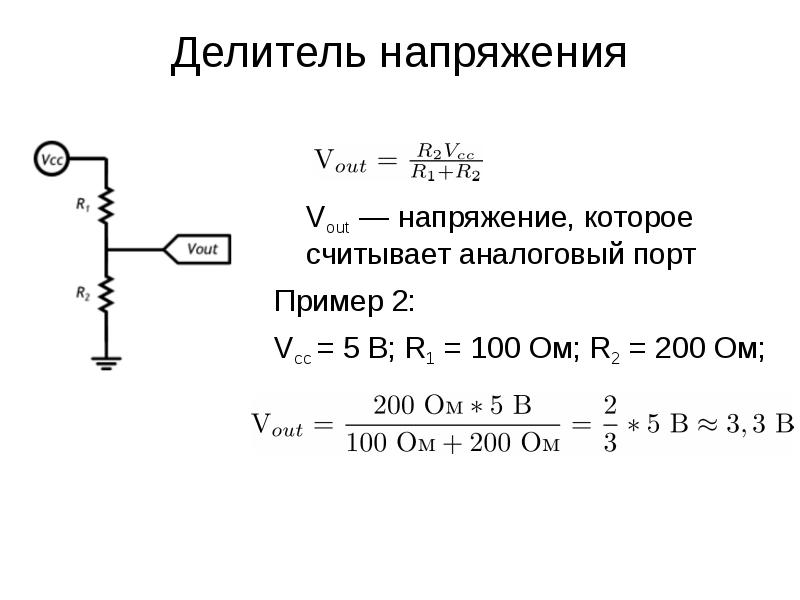 Например, одним из их элементов может являться фоторезистор, изменяющий свое сопротивление в зависимости от освещённости. Есть и другие датчики, преобразующие физические воздействия в изменение сопротивления: терморезисторы, датчики давления, ускорения. Созданные на их основе делители используются совместно с аналого-цифровыми преобразователями для измерения и отслеживания самых различных величин в промышленности и быту: температуры, скорости вращения.

В качестве примера можно привести схему для определения уровня освещенности. Последняя деталь включается между выходом и общим проводом (R2 в формуле). Для расширения пределов изменения напряжения схема дополняется постоянным сопротивлением (R1 в формуле). К её выходу присоединяется микроконтроллер аналого-цифрового преобразователя. Чем сильнее освещённость фоторезистора, тем ниже UВЫХ, так как он включён между выходом конструкции и «массой», шунтируя его.

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Hantek 2000 — осциллограф 3 в 1

Портативный USB осциллограф, 2 канала, 40 МГц….

Подробнее

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.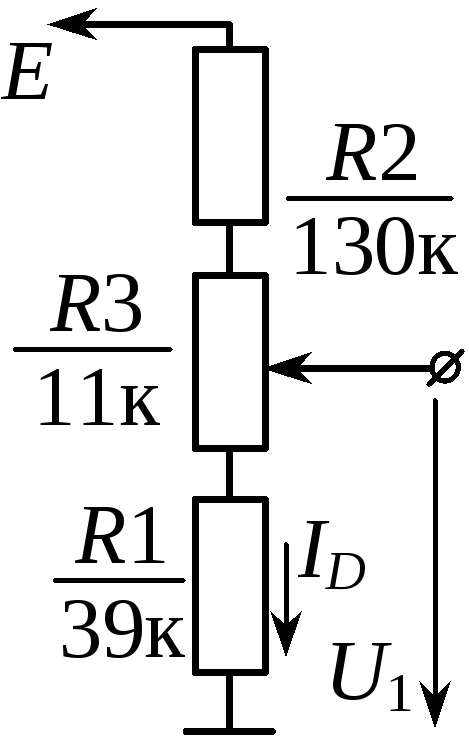

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Практическое применение параллельного и последовательного соединения

Составные элементы прибора соединяют в цепь, чтобы получить из сети нужную для устройства часть энергии.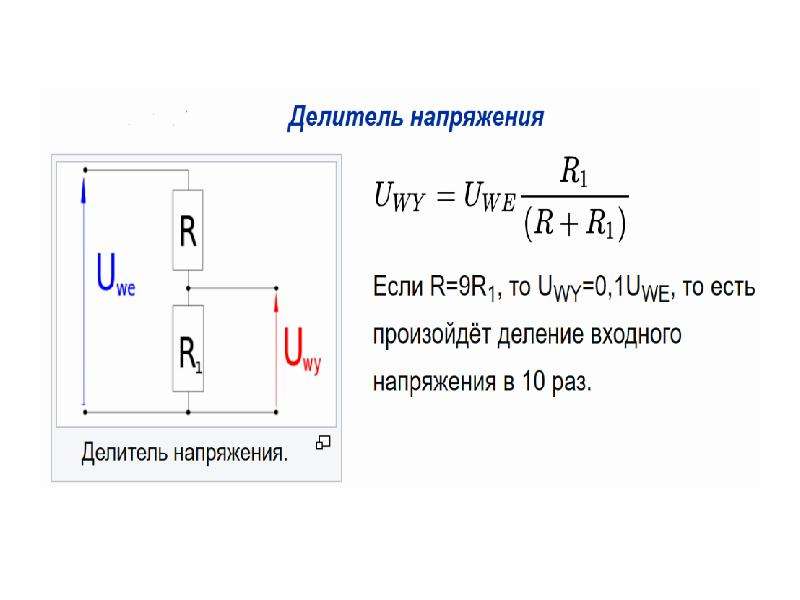

Пример работы делителя напряжения на фоторезисторе.

Исходное сопротивление меняется от 1кОм в момент полного освещения до 10кОм при отсутствии света, то можно увеличить диапазон сопротивления. При добавлении резисторов с R=5,6кОм, исходящее напряжение меняется следующим образом:

Освещённость	R1 (кОм)	R2(кОм)	R2/(R1+R2)	U выходное (В)
Яркая	5,6	1	0,15	0,76
Тусклая	5,6	7	0,56	2,78
Темнота	5,6	10	0,67	3,21

Таким образом, увеличивается диапазон выходного напряжения, и оно становится подходящим для большинства сетей.

Потенциометры

Потенциометры используют в качестве делителя в системе с постоянным током. Их применяют в основном для изменения отдельных параметров в механизме.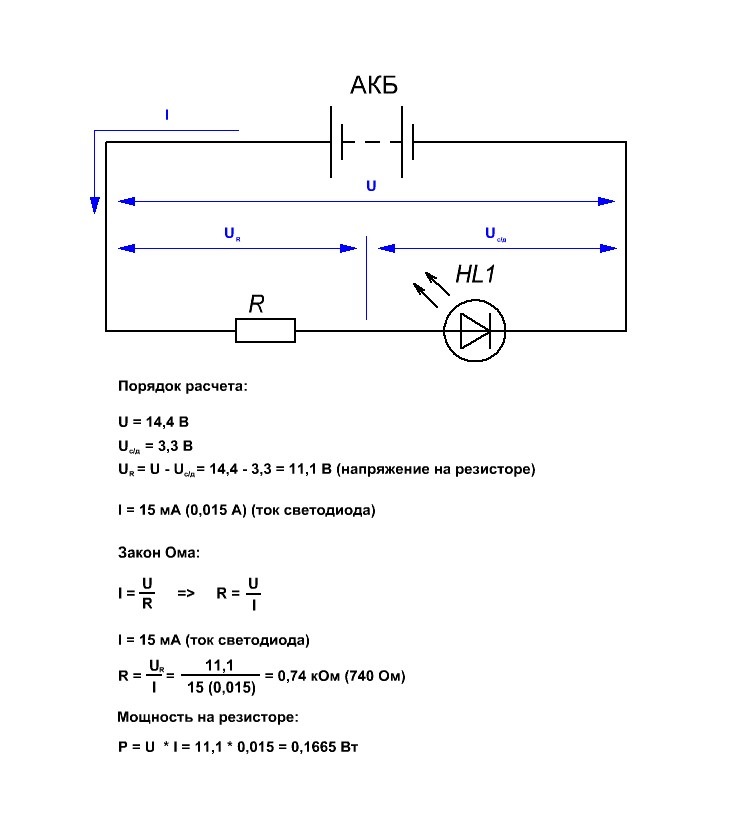

На потенциометр подается напряжение, регулируемое подвижным контактом, который действует, когда крутят ручку, в результате оно может меняться от нуля до исходного значения. Потенциометры используют в быту, как регулятор громкости, и в электронике, например, в качестве датчика.

Резистивные датчики

Резистивные датчики также называют омическими. Это приборы, в которых изменяется сопротивление, если изменяется длина, площадь сечения или удельное сопротивление. Их используют в устройствах для изменения сопротивления, а также при помощи микроконтроллера с его помощью вы можете измерить напряжение. Существуют различные датчики, одним из некоторых является фоторезистор — переменный резистор, сопротивление которого зависит от попадающего на него света.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов.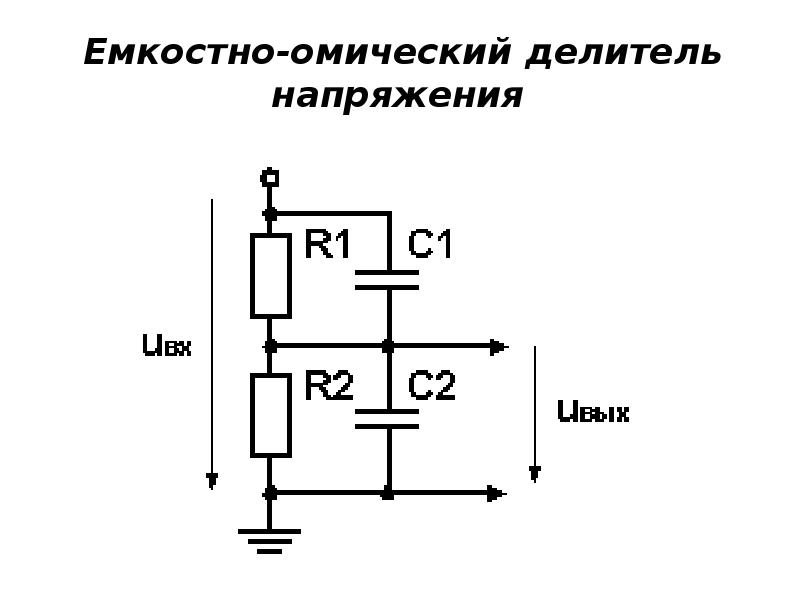 Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Блок питания 0…30 В / 3A

Набор для сборки регулируемого блока питания…

Подробнее

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом виде: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Соединение резисторов

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике. Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов. Соединение резисторов может производиться последовательно, параллельно и смешанно.

Последовательное соединение резисторов

Последовательное соединение.

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее.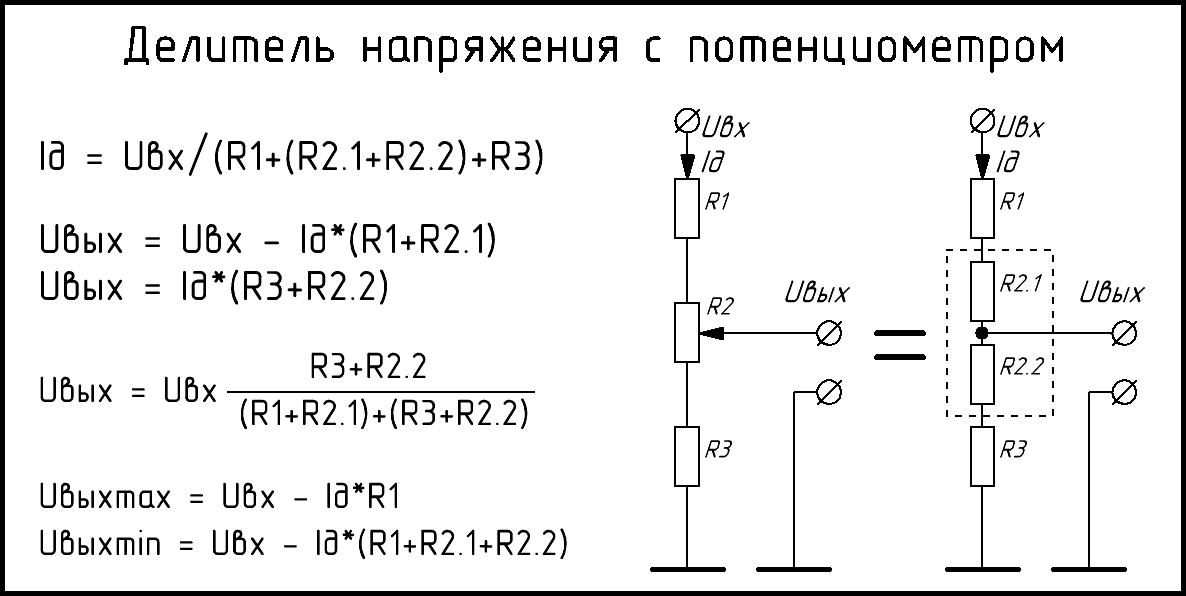 То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток. Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.

Интересно почитать: принцип действия и основные характеристики варисторов.

Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает. Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле: Rобщ = R1 + R2 + R3+…+ Rn.

Последовательное и параллельное соединение резисторов.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)

Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn. Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток.

Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.

Каждый вид соединения находится под одинаковым напряжением:

• U = U1 = U2; Суммарная сила тока равняется суммарному значению тока каждого участка
• I = I1 + I2; Сопротивление цепи равно сумме величина обратных сопротивлению участка:
• 1/R = 1/R1 + 17R2 + . . . + 1/Rn; Сила тока пропорциональна сопротивлению каждого участка
• I1/I2=R2/R1.

Будет интересно➡ Что такое терморезистор?

Примеры расчета

Давайте рассмотрим пример.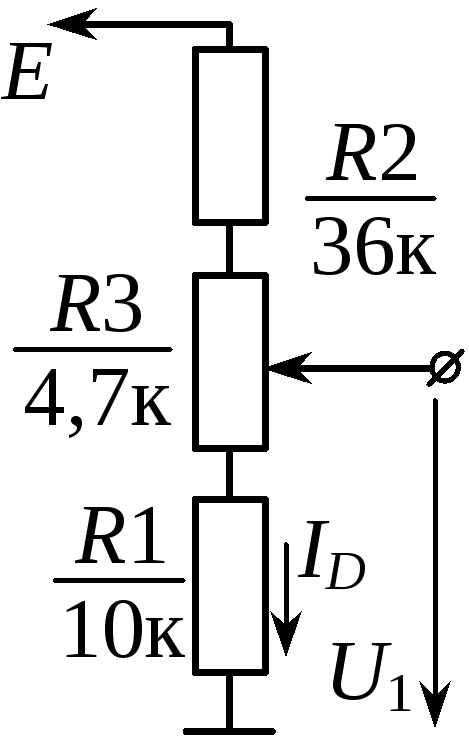 Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В. А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения.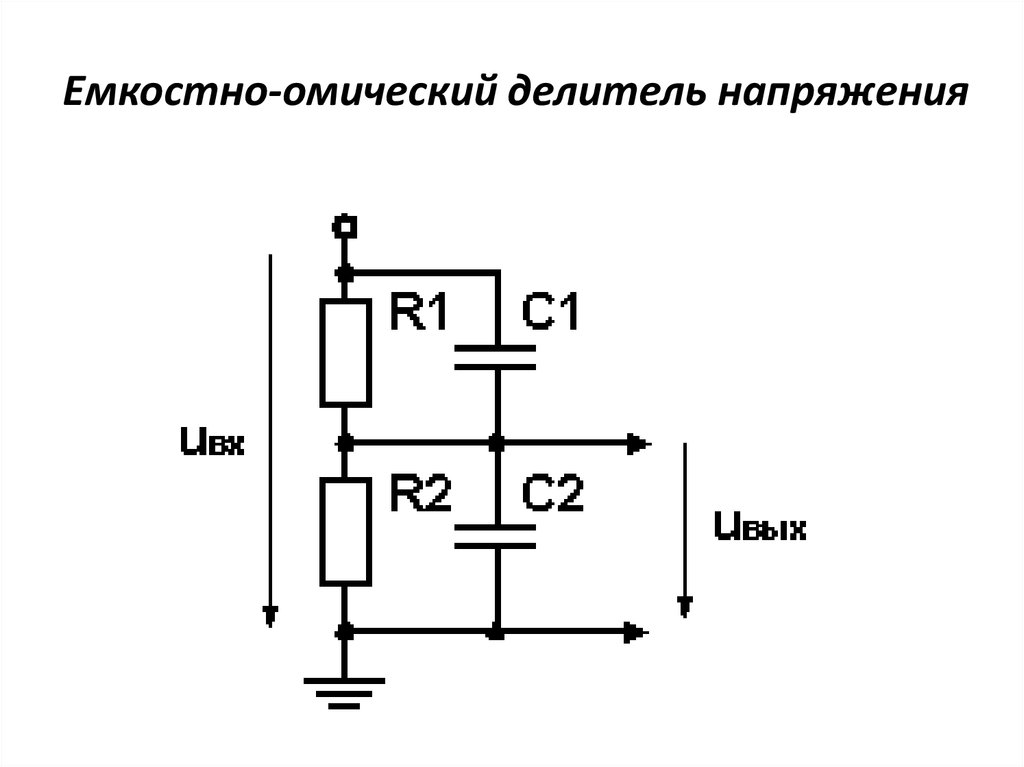 Иногда подобную комбинацию называют последовательно-параллельным соединением. На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.

Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:

• Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
• Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
• После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
• Рассчитывают сопротивления полученной схемы.

Схема смешанного подключения.

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Расчет гасящего резистора

В схемах аппаратуры связи часто возникает необходимость подать на потребитель меньшее напряжение, чем дает источник.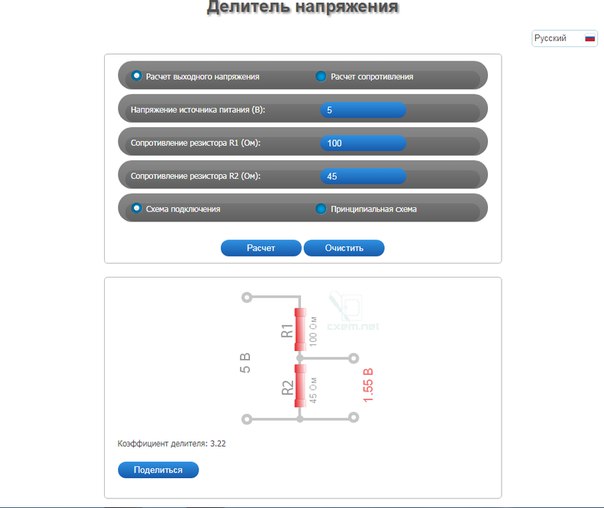 В этом случае последовательно с основным потребителем включают дополнительное сопротивление, на котором гасится избыток напряжения источника. Такое сопротивление называется гасящим.

Будет интересно➡ Как отличается параллельное и последовательное соединение резисторов?

Напряжение источника тока распределяется по участкам последовательной цепи прямо пропорционально сопротивлениям этих участков. Рассмотрим схему включения гасящего сопротивления:

1. Полезной нагрузкой в этой цепи является лампочка накаливания, рассчитанная на нормальную работу при величине напряжения Uл= 80 в и тока I =20 ма.
2. Напряжение на зажимах источника тока U=120 в больше Uл, поэтому если подключить лампочку непосредственно к источнику, то через нее пройдет ток, превышающий нормальный, и она перегорит.
3. Чтобы этого не случилось, последовательно с лампочкой включено гасящее сопротивление R гас.

Схема включения гасящего сопротивления резистора.

Расчет величины гасящего сопротивления при заданных значениях тока и напряжения потребителя сводится к следующему:

– определяется величина напряжения, которое должно быть погашено:

Uгас = Uист – Uпотр,

Uгас = 120 – 80 = 40в

определяется величина гасящего сопротивления

Rгас = Uгас / I

Rгас = 40 / 0,020 = 2000ом = 2 ком

Далее необходимо рассчитать мощность, выделяемую на гасящем сопротивлении по формуле

P = I2 * Rгас

P = 0,0202 * 2000 = 0,0004 * 2000 = 0,8вт

Зная величину сопротивления и расходуемую мощность, выбирают тип гасящего сопротивления.

Калькулятор делителей напряжения — электротехнические и электронные инструменты

Калькулятор делителя напряжения

Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.

Выходы

Выходное напряжение (V _out )

Вольт (V)

Как найти выходное напряжение цепи делителя

Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов. Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами.

Уравнение

$$ V_ {out} = V_ {in} * \ frac {R_ {2}} {R_ {1} + R_ {2}} $$

Где:

$$ V_ {out} $$ = Выходное напряжение. Это уменьшенное напряжение.

$$ V_ {in} $$ = Входное напряжение.

$$ R_ {1} $$ и $$ R_ {2} $$ = значения резистора. Отношение $$ \ frac {R_ {2}} {R_ {1} + R_ {2}} $$ определяет масштабный коэффициент.

Приложения

Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.

потенциометры

Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:

«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.

Уровневые сдвиги

Другая область, в которой используются делители напряжения, — это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:

Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:

$$ V_ {out} = 5 * \ frac {2k \ Omega} {2k \ Omega + 1k \ Omega} = 3.33 V $$

Этот уровень напряжения теперь безопасен для работы датчика. Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания.

Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:

Комбинация резисторов	использование
4, 7 кОм и 6, 8 кОм	От 12 В до 5 В
4, 7 кОм и 3, 9 кОм	9V до 5V
3, 6 кОм и 9, 1 кОм	От 12 В до 3, 3 В
3, 3 кОм и 5, 7 кОм	От 9 В до 3, 3 В

Чтение резистивного датчика

Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:

Термистор — это датчик, сопротивление которого изменяется пропорционально температуре.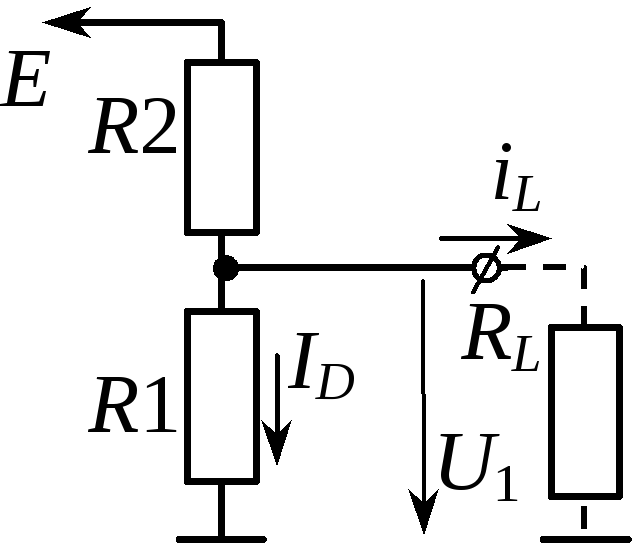 Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.

Когда термистор находится при комнатной температуре, выходное напряжение:

$$ V_ {out} = 5 * \ frac {350 \ Omega} {350 \ Omega + 350 \ Omega} = 2.5V $$

Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:

$$ V_ {out} = 5 * \ frac {350.03 \ Omega} {350 \ Omega + 350.03 \ Omega} = 2.636V $$

Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.

Дальнейшее чтение

Техническая статья — Разделители напряжения и тока: что это такое и что они делают

Учебник — Глава 6 — Цепи Divider и законы Кирхгофа

Учебник — Потенциометр в качестве делителя напряжения

Рабочий лист — Цепь делителя напряжения

Расчёт делителя напряжения на резисторах онлайн

Р/л технология

---

Схема такого делителя предназначена для получения заданного выходного напряжения, которое будет ниже, чем входное. Например, источник напряжения 24 Вольта, в нужно получить 6 Вольт. Самым простым способом решить этот вопрос – это применить делитель напряжения, состоящий из двух споротивлний.

Он применяется, как при проектировании схем, так и по прямому назначению. Для его расчета используются формулы, которые основаны на законе Ома. Эти формулы позволяют подобрать нужный номинал сопротивлений. Потребуется лишь знать сопротивление нагрузки, входное и выходное напряжения. От этого сопротивления зависит, насколько точно удастся рассчитать весь делитель и получить точно указанное выходное напряжение. Как правило, сопротивление нагрузки выше, чем сопротивление делителя напряжения.

Если неизвестно выходное напряжение, но известно сопротивление и входное напряжения, то неизвестную величину можно вычислить по указанной формуле.

 

 

 

 

Для того чтобы не считать постоянно по формулам эти величины, были придуманы онлайн-калькуляторы, которые позволяют точно определить значения резисторов или выходного напряжения. Потребуется лишь внести известные величины. Такой расчет можно производить, как на компьютере, с доступом в сеть Интернет, так и при помощи смартфона. Это значительно экономит время и дает стабильную точность расчетов. 

Стоит отметить, что современные калькуляторы-онлайн могут рассчитать и мощность, на которую должен быть установлен резистор. 

В радиоэлектронике делители напряжения представлены и в готовых конструктивных решениях. Ими служат, к примеру, переменные резисторы и фоторезисторы, которые имеют возможность менять значение сопротивления, при повороте ручки потенциометра или попадании света. В переменном резисторе присутствуют три вывода, с которых можно получить два сопротивления. 

Автор: RadioRadar

Мнения читателей

Нет комментариев. Ваш комментарий будет первый.

Вы можете оставить свой комментарий, мнение или вопрос по приведенному выше материалу:

Поля, обязательные для заполнения

Добавить

Очистить

Радио для всех — Лаборатория

В разделе представлены on-line калькуляторы

Цветовая маркировка резисторов
Расчет индуктивности
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Расчёт резистивного и ёмкостного делителей
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Компенсация реактивной мощности
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
Расчет элементов J антенны
Расчет резонансной частоты LC-контура
Расчет резистивного Пи аттенюатора
Делитель напряжения
Цветовой код конденсаторов
Стабилизация напряжения
Дроссели, намотанные на резисторах МЛТ
Реактивное сопротивление конденсатора
Реактивное сопротивление катушки индуктивности
Калькулятор определения номинала SMD-резистора
Расчет значения резистора для LM317
Онлайн калькулятор таймер 555
Расчет «Cantenna» (баночной антенны) для Wi Fi
Расчет усилителя на биполярном транзисторе
Калькулятор расчета компактных монолитных усилителей
Расчет силового трансформатора
Расчет дискоконусной антенны
Сопротивления для согласующего трансформатора
Расчет для тороидальных (ферритовых) сердечников Amidon
Расчет петлевого вибратора
Калькулятор DC-DC преобразователя MC34063A
Расчет выпрямителя для блока питания
Расчет гасящего конденсатора в блоке питания
Расчет резистора для подключения светодиода

Цветовая маркировка резисторов

 

Расчет индуктивности

 
Расчёты электронных цепей.

Вписываем значения и кликаем мышкой в таблице

Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L

Реактивное сопротивление ёмкости Xc = 1/(2πƒC)

Реактивное сопротивление индуктивности XL = 2πƒL

Расчёт параллельного соединения резисторов и последовательного конденсаторов

Параллельное соединение двух сопротивлений R =R1*R2/(R1+R2)

Последовательное соединение двух ёмкостей C = C1*C2/(C1+C2)

---

Расчёт резистивного и ёмкостного делителей

Расчёт резистивного делителя напряжения U1 = U*R1/(R1+R2)

Расчёт ёмкостного делителя напряжения U1 = U*C2/(C1+C2)

---

---

Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ

Частота резонанса колебательного контура LC F = 1/(2π√(LC))

Пост. времени τ RC и частота среза RC-фильтра τ = RC ;   Fср = 1/(2πτ)

---

---

Компенсация реактивной мощности

Реактивная мощность Q = √((UI)²-P²) Реактивное сопротивление X = U²/Q Компенсирующая ёмкость C = 1/(2πƒX)

---

---

Закон Ома. Расчёт напряжения, сопротивления, тока, мощности

После сброса ввести два любых известных параметра I=U/R;   U=IR;   R=U/I;   P=UI   P=U²/R;   P=I²R;   R=U²/P;   R=P/I²   U=√(PR)   I= √(P/R)

 

Расчет элементов J антенны

 

Дополнение: Арифметические калькуляторы и конвертеры величин
Расчет делителя напряжения

Просмотрите схему делителя напряжения, представленную здесь, и рассчитайте выходное напряжение с помощью калькулятора делителя напряжения по следующей формуле делителя напряжения:

V _выход = (V _дюйм x R ₂ ) / ( _{R 1} + R ₂ )

Здесь:

• В _в входное напряжение
• R1 — сопротивление 1-го резистора,
• R2 — сопротивление 2-го резистора,
• V _out — выходное напряжение.

В качестве альтернативы вы также можете использовать этот калькулятор делителя напряжения, чтобы получить любые 3 известных значения в цепи и вычислить 4-е.

---

Схема делителя потенциала — очень распространенная схема, используемая в электронике, где входное напряжение должно быть преобразовано в другое напряжение, меньшее, чем оно. Эта схема очень полезна для всех аналоговых схем, где требуются переменные напряжения, поэтому важно понимать, как эта схема работает и как рассчитывать значения резисторов.

Схема делителя напряжения — это очень простая схема, состоящая всего из двух резисторов (R1 и R2), как показано выше. Требуемое выходное напряжение (Vout) можно получить на резисторе R2. Используя эти два резистора, мы можем преобразовать входное напряжение в любое требуемое выходное напряжение, это выходное напряжение определяется значением сопротивления R1 и R2. Формулы для расчета Vout показаны ниже.

V _выход = (V _дюйм x R ₂ ) / (R ₁ + R _{2 9000}

Где, Vout = выходное напряжение Vin = входное напряжение и R1 = верхний резистор R2 = нижний резистор

Мы можем использовать вышеупомянутый калькулятор делителя напряжения для вычисления любого из значений, упомянутых в формулах делителя напряжения , но теперь давайте узнаем, как были получены эти формулы.Рассмотрим схему ниже, которую можно использовать для преобразования входного сигнала 5 В в выходное напряжение 3,3 В для анализа

.

Чтобы понять, как выводятся формулы потенциального дайвера, нам нужен калькулятор закона Ома, согласно закону Ома падение напряжения в любом месте является произведением тока, протекающего по цепи, и сопротивления в ней.

Напряжение = Ток, протекающий через × Сопротивление на напряжении

Давайте воспользуемся этим, чтобы вычислить входное напряжение (Vin) для вышеуказанной схемы.Здесь есть два резистора на входном напряжении Vin, следовательно,

Входное напряжение = ток × (сопротивление 1 + сопротивление 2)

Vin = I × (R1 + R2) ( 1)

Аналогичным образом рассчитаем выходное напряжение (Vout), здесь есть только один резистор (R2), следовательно,

Выходное напряжение = ток × сопротивление R2

Vout = I × R2 ( 2)

Если мы посмотрим на уравнения 1 и 2, мы можем заметить, что значение тока одинаковое, поэтому давайте перепишем

Уравнение 1 как, I = Vin / (R1 + R2)

Уравнение 2 как, I = Vout / R2

Поскольку ток, протекающий по цепи, постоянен, ток I останется одинаковым для обоих уравнений, поэтому мы можем приравнять их как

Вин / (R1 + R2) = Vout / R2

V _выход = (V _дюйм x R ₂ ) / (R ₁ + R _{2 9000}

Давайте проверим эту формулу делителя напряжения для указанной выше схемы, где Vin = 5 В, R1 = 1000 Ом и R2 = 2000 Ом.

Выход = (5 × 2000) / (1000/2000)

Выход = (10000) / (3000)

Выход = 3,3333 В

Еще одним важным фактором, который следует учитывать при выборе номиналов резистора, является его номинальная мощность (P) . Как только вы узнаете значения I (в зависимости от нагрузки), Vin, R1 и R2, сложите R1 и R2 вместе, чтобы получить R _ИТОГО , и используйте калькулятор закона Ома, чтобы узнать номинальную мощность (в ваттах), необходимую для резисторов. Или просто используйте формулы P = VI, чтобы определить номинальную мощность вашего резистора.Если не выбрана правильная номинальная мощность, резистор будет перегреваться и также может сгореть.

Онлайн калькулятор делителя напряжения

с формулой

Калькулятор делителя напряжения:

Введите сопротивление резистора в омах и напряжение источника в вольтах, затем нажмите кнопку вычисления, чтобы получить напряжение на этом конкретном резисторе. Наш калькулятор делителя напряжения работает на основе модели с тремя резисторами, как указано в схеме. Здесь третье сопротивление необязательно.По крайней мере, вы должны ввести два значения резистора.

Калькулятор делителя напряжения для цепи с тремя сопротивлениями

Напряжение на этом конкретном сопротивлении равно напряжению источника, умноженному на это сопротивление, деленное на сумму всех сопротивлений.

Таким образом, вы можете рассчитать напряжение на трех резисторах одновременно, и формула будет

Формула делителя напряжения

Делитель потенциала — это электрическая цепь, используемая для пошагового уменьшения напряжения с помощью резистора.Ниже приведена формула для расчета напряжения на любой цепи сопротивления.

Возьмем простую схему, состоящую из трех сопротивлений,

Многократный резистор

R1 => Сопротивление 1-го резистора в Ом (Ом).

R2 => Сопротивление 2-го резистора в Ом (Ом).

Ri => Сопротивление резистора i ^th в Ом (Ом).

В _выход => Выходное напряжение на резисторе R2 в вольтах.

Vin => Напряжение источника в вольтах.

Vi => Напряжение на резисторе i ^th .

Для расчета напряжения на резисторе i ^th формула принимает вид

делитель напряжения для нескольких резисторов

Для расчета напряжения на нескольких резисторах просто используйте вышеупомянутую формулу.

Пример:

R1 = 10 Ом, R2 = 20 Ом, R3 = 10 Ом, входное напряжение = 24 В, Рассчитайте напряжение на резисторе R3.

Используйте нашу формулу,

В ₃ = 24 x 10 / (10 + 20 + 10)

В ₃ = 6 В

В ₃ = Напряжение на третьем сопротивлении равно 6 В

Калькулятор делителя напряжения

| Good Calculators

Вы можете использовать этот калькулятор делителя напряжения для определения любой из четырех переменных, связанных с простым двухрезисторным делителем напряжения, когда доступны значения трех других переменных.

Четыре переменные, участвующие в двухрезисторном делителе напряжения: входное напряжение ( _{В на} ), выходное напряжение ( _{В на выходе} ), сопротивление 1 (R1) и сопротивление 2 (R2).

Калькулятор также строит принципиальную схему и генерирует значения компонентов.

Как использовать калькулятор делителя напряжения:

1. Введите три известные переменные
2. Нажмите кнопку «Рассчитать»
3. Калькулятор отобразит оставшееся значение и принципиальную схему.

Дополнительная информация

Инженеры очень часто используют схему двухрезисторного делителя напряжения. Делитель напряжения, который также часто называют делителем потенциала, предлагает явное преимущество, заключающееся в том, что он может поляризовать другие элементы в цепи, включая интегральные схемы и транзисторы, с напряжением, отличным от напряжения основного источника напряжения.

Основная причина, по которой используется эта схема, — это масштабирование входного напряжения до более низкого значения в соответствии с соотношением двух резисторов.

Это достигается следующим образом:

1. Соотношение резисторов (R1 и R2) снижает входное напряжение до более низкого выходного напряжения.
2. Выходное напряжение представляет собой часть входного напряжения. Эта дробь принимает форму R2, деленного на сумму R1 + R2.
3. Основная формула, которая используется для определения выходного напряжения, основана на законе Ома и выглядит следующим образом:

V _out = V _in * R2 / (R1 + R2)

Например, скажем, мы работаем со схемой, которая имеет вход 12 В.Однако одной из микросхем в схеме нужно 9 вольт, а другой — всего 3 вольта. Делитель напряжения может использоваться для распределения напряжения между различными микросхемами в соответствии с их требованиями.

Если один резистор имеет значение 2 кОм, а другой — 6 кОм, вход 12 В будет разделен на 3 В и 9 В.

Обратите внимание: Никогда не используйте делитель напряжения для высоких напряжений, потому что полный ток должен пройти через резисторы, и это может привести к повреждению.В этом случае лучшим вариантом будет стабилизатор напряжения.

Пример:

Допустим, мы хотели бы определить выходное напряжение, если сопротивление резистора R1 составляет 5 кОм, сопротивление резистора R2 равно 10 кОм, а входное напряжение — 9 В.

Решение:

V _out = V _in * R2 / (R1 + R2) = (9V) (10KΩ) / (5KΩ + 10KΩ) = 6V

V _out = 6 Volts.

Формулы

В этом калькуляторе делителя напряжения используются следующие формулы:

V _out = V _in * R2 / (R1 + R2)

V _in = V _out * (R1 + R2) / R2

R1 = R2 * (V _вход — V _выход ) / V _выход

R2 = R1 * V _выход / (V _вход — V _выход )

Где, В _выход = выходное напряжение (вольт), В _вход = входное напряжение (вольты), R1 и R2 = значения резистора (Ом).

Вас также может заинтересовать наш Калькулятор цветовой маркировки резистора или Калькулятор трансформатора

Делитель напряжения под нагрузкой, онлайн-калькулятор и формулы

Онлайн-калькулятор для расчета значений на нагруженном делителе напряжения

Рассчитать нагруженный делитель напряжения

Эта функция вычисляет напряжения, токи и сопротивления на нагруженном делителе напряжения.

На выходе схемы можно указать значения напряжения U ₂ или сопротивления нагрузки R ₃ . Вход напряжения U ₂ задан.

Rechner, Belasteten Spannungsteiler

Формулы для нагруженного делителя напряжения

Делитель напряжения представляет собой последовательную цепь, состоящую из двух резисторов, которые делят электрическое напряжение.Когда делитель напряжения нагружен, дополнительный резистор (нагрузочный резистор) подключается параллельно второму резистору. Соотношение парциальных напряжений соответствует соотношению резисторов R ₁ и сопротивление параллельного включения (R ₂ и R _L ).

Поэтому для расчета необходимо сначала рассчитать общее сопротивление R ₂ и R _L . по следующей формуле:

\ (\ Displaystyle U_ {2L} = \ гидроразрыва {R_2 · R_L} {R_2 + R_L} \)

Тогда напряжение U ₂ рассчитывается по формуле:

\ (\ Displaystyle U_2 = U · \ гидроразрыва {R_ {2L}} {R_1 + R_ {2L}} \)

Эта страница полезна? да Нет Спасибо за ваш отзыв! Прошу прощения за это Как мы можем это улучшить? послать

---

Калькулятор делителя напряжения

Это калькулятор делителя напряжения — всеобъемлющий, но простой инструмент, который поможет вам оценить выходной сигнал (т.е.е. напряжение), которое получается в одном делителе напряжения. Прочтите, чтобы узнать, что такое делитель напряжения, узнайте основную формулу делителя напряжения и как она распространяется на различные уравнения для разных типов делителей напряжения, а также узнайте, как можно получить некоторую долю входного напряжения, применяя правило делителя напряжения. Кроме того, ознакомьтесь с многочисленными применениями делителя напряжения как в базовых, так и в невероятно сложных системах и убедитесь, что электронные схемы не о чем беспокоиться!

Что такое делитель напряжения?

Простой делитель напряжения — это часть линейной схемы, которая преобразует входное напряжение ( В ) в выходное напряжение ( В ) , которое представляет собой другое значение.Поскольку схема является пассивной, отношение В₂ / В₁ никогда не превышает 1. Общий делитель напряжения представлен на этой простой диаграмме:

, где Z₁ и Z₂ — некоторые импедансы. Полные сопротивления могут быть связаны с сопротивлением R , емкостью C или индуктивностью L . Можно выделить несколько основных типов делителей напряжения, к которым применимо правило делителей напряжения:

1. Делитель резистивный, RR
2. Делитель емкостный, CC
3. Индуктивный делитель, LL
4. Делители RC и CR (также известные как фильтры RC, CR)
5. Делители RL и LR (также известные как фильтры RL, LR)
6. Делители CL и LC (также известные как фильтры CL, LC)

линейка делителя напряжения

Принцип действия делителей напряжения заключается в том, что ток, проходящий через несколько последовательно соединенных элементов, является постоянным, но напряжение распределяется между ними каким-то образом .Чтобы найти точные значения, мы должны применить к нашей схеме закон Ома. Перед тем как это сделать, необходимо отметить один важный момент:

Состав RR — единственный, применимый к цепям постоянного тока . В этих случаях любой импеданс можно рассматривать как провод с нулевым сопротивлением, а емкости работают как разрыв в цепи, поэтому они имеют бесконечное сопротивление. В остальном все они используются в цепях переменного тока, и правило делителя напряжения применяется для максимального значения разности потенциалов.Также может быть полезно найти фазовый сдвиг для этих напряжений.

Формула делителя напряжения

Общее уравнение (или формула) делителя напряжения для импедансов выглядит следующим образом:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ .

Напоминание: в целом, В₁ и В₂ соответствуют амплитудам сигналов , например синусоидальные. Если рассматривать только сопротивления, формула делителя напряжения естественным образом меняется на:

V₂ = R₂ / (R₁ + R₂) * V₁ .

Поскольку сопротивление не влияет на фазу сигнала, формула одинакова как для переменного, так и для постоянного тока. Сравниваются значения напряжения в данный момент. Как упоминалось ранее, остальные типы делителей предназначены для цепей переменного тока, поэтому давайте рассмотрим несколько примеров.

Уравнения емкостного и индуктивного делителя напряжения

Для делителя CC нам нужно использовать импедансы конденсаторов: Z = 1 / (j * ω * C) , где j — мнимое число, а ω — угловая частота переменного напряжения. .Подставляя исходное уравнение делителя напряжения этим выражением, получаем:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = (1 / (jωC₂)) / (1 / (jωC₁) + 1 / (jωC₂)) * V₁ ,

и умножая каждый член на jωC₁C₂ , получаем:

V₂ = C₁ / (C₁ + C₂) * V₁ .

Аналогичная процедура может быть проделана для делителей LL, где Z = j * ω * L . На этот раз выходное напряжение:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = jωL₂ / (jωL₁ + jωL₂) * V₁ .

Разделив числитель и знаменатель на jω , окончательная формула будет:

V₂ = L₂ / (L₁ + L₂) * V₁ .

В обоих случаях выходное напряжение синфазно относительно входной фазы .

Фильтры RC и CR

Цепи делителя напряжения, состоящие более чем из одного типа элементов, не так просто оценить, как предыдущие примеры. Нам приходится иметь дело с алгеброй комплексных чисел, но, поверьте, это выглядит более пугающим, чем есть на самом деле.

Для RC-делителя формулу делителя напряжения можно расширить до:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = (1 / (jωC)) / (R + 1 / (jωC)) * V₁ = V₁ / (jωRC + 1) .

Результат — комплексное число, поэтому, чтобы оценить амплитуду выходного напряжения, мы должны найти его модуль:

| V₂ | = | V₁ / (jωRC + 1) | = | V₁ | / √ ((ωRC) ² + 1) .

Если частота увеличивается, выходная амплитуда напряжения уменьшается, поэтому эту схему также называют фильтром нижних частот .Сдвиг фазы можно вычислить как арктангенс мнимой части, деленной на действительную часть нашего комплексного числа:

Δφ = атан (-ωRC) .

Аналогично можно найти амплитуду и фазовый сдвиг для цепи CR. Первый шаг — вычислить общую формулу выходного напряжения:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = R / (R + 1 / (jωC)) * V₁ = jωRC / (jωRC + 1) * V₁ .

Его амплитуду можно определить как:

| V₂ | = | jωRC / (jωRC + 1) * V₁ | = ωRC / √ ((ωRC) ² + 1) * | V₁ | ,

, а фазовый сдвиг задается как:

Δφ = атан (1 / ωRC) .

На этот раз мы видим, что если частота стремится к 0, то же самое происходит с амплитудой В , а для высоких значений ω она остается такой же, как входное напряжение. Вывод состоит в том, что CR можно рассматривать как фильтр верхних частот .

Фильтры RL и LR

Цепи, содержащие резистивные и индуктивные элементы, мало чем отличаются от RC и CR, когда дело доходит до расчетов, но стоит повторять каждый шаг, чтобы понять все тонкие различия.

В случае фильтра RL мы можем начать, как обычно, с общей формулы делителя напряжения:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = jωL / (R + jωL) * V₁ .

Чтобы найти амплитуду выходного напряжения, нам нужно оценить модуль этого значения:

| V₂ | = | jωL / (R + jωL) * V₁ | = ωL / √ (R² + (ωL) ²) * | V₁ | ,

и его фазовый сдвиг:

Δφ = атан (R / ωL) .

Для делителя LR мы просто заменяем эти элементы, поэтому уравнение делителя напряжения дает:

V₂ = Z₂ / (Z₁ + Z₂) * V₁ = R / (R + jωL) * V₁ .

Еще раз, мы можем определить амплитуду выходного напряжения и фазовый сдвиг:

| V₂ | = | R / (R + jωL) * V₁ | = R / √ (R² + (ωL) ²) * | V₁ | ,

Δφ = атан (-ωL / R) .

Взгляните на результаты; амплитуда В для фильтра RL очень похожа на CR, а амплитуда LR похожа на амплитуду напряжения RC. Как и их фазовые сдвиги. Это очень ценный результат, потому что оказывается, что фильтры RC и RL могут использоваться взаимозаменяемо, если они спроектированы в соответствующей конфигурации, а значения проводимости и индуктивности правильно настроены .Это особенно полезно для схем, размер которых должен быть доведен до нанометрового масштаба, поскольку применение действительно небольших конденсаторов намного проще, чем создание крошечных катушек.

В любом случае, если у вас возникнут проблемы с вычислением свойств выходного сигнала, вы всегда можете вернуться к этим главам или просто попробовать наш калькулятор делителя напряжения! Выберите подходящий вариант, и результат отобразится моментально.

Выше было описано несколько пассивных фильтров, но правило делителя напряжения также может применяться к активным.

CL и LC как резонансные контуры

Мы могли бы выполнить те же вычисления для систем CL и LC, однако некоторые нелепые результаты могут произойти, если мы просто применим правило делителя напряжения. Мы можем заставить амплитуду выходного напряжения уходить в бесконечность! Это вызвано тем, что подключенные LC-элементы иногда называют резонансными контурами . Они используются для генерации и приема радиоволн, что наиболее эффективно на резонансной частоте , представленной как:

ω = 1 / √ (L * C) .

В более реалистичной картине мы должны учитывать также некоторое ненулевое сопротивление, поэтому проблема резонатных цепей описана в калькуляторе цепей RLC.

Применение делителя напряжения в более сложных схемах

То, что мы уже сделали, показывает, как делители напряжения работают в простейших возможных системах. Очевидно, вы можете представить, что в реальной жизни они практически нигде не используются, и, как правило, применяются более сложные схемы. Однако все полученные выше результаты могут быть полезны при упрощении более сложных.Например, всякий раз, когда вы можете обнаружить резисторы, включенные последовательно или параллельно, вы можете рассматривать их как единое сопротивление. Точно так же работают конденсаторы и соленоиды. Для смешанных компонентов он оценивается практически так же, но мы должны учитывать импеданс Z вместо R , C или L .

Применение делителя напряжения

1. Одним из наиболее часто используемых устройств, которое работает благодаря концепции делителя напряжения, является потенциометр .Другое слово, описывающее этот элемент, — реостат. Обычно они состоят только из резистивных компонентов. Мы можем различать как аналоговые, так и цифровые, но, в любом случае, сопротивление можно выставить с высокой точностью . Некоторые из самых популярных типов потенциометров — это скользящие горшки, ножницы или подставки для большого пальца, и они различаются по размеру и структуре. Ключевым элементом является скользящий контакт, позволяющий регулировать выходное сопротивление .

2. Приборы для измерения высокого напряжения — Оказывается, можно измерить высокое напряжение, даже если прямое измерение может быть разрушительным для прибора.В таком случае удобно использовать делитель напряжения, чтобы понизить напряжение до безопасной области . Для исключительно высоких напряжений (скажем, выше 100 кВ) лучше использовать емкостные, а не резистивные.

3. Поиск неизвестного сопротивления — Можно ли найти какое-либо неизвестное сопротивление, если у вас есть только источник напряжения и другой резистор с известным сопротивлением? Вам повезло, если вы можете прочитать его цветовой код, но что, если его нет? Что ж, вы можете просто создать простую схему с обоими резисторами, расположенными последовательно, установить входное напряжение и измерить напряжение на желаемом резисторе .После этого просто вставьте все эти значения в калькулятор делителя напряжения, и все — тайна раскрыта. Вы всегда можете преобразовать общее уравнение делителя напряжения, чтобы найти R₂ как неизвестный параметр:

R₂ = V₂ / (V₁ - V₂) * R₁ .

Плюсы и минусы делителей напряжения

Некоторым из вас может быть интересно, почему люди измеряют неизвестное сопротивление с помощью делителя напряжения, когда они могут просто прочитать значение силы тока, протекающей через резистор при приложении внешнего напряжения — просто закон Ома.Что ж, в общем, для этих методов не должно быть значительной разницы, но мы должны знать, что сопротивление подавляющего большинства материалов зависит от температуры . Хуже того, эти зависимости различны для металлов, полупроводников или изоляторов.

Принимая во внимание металлы, их сопротивление увеличивается с повышением температуры, поэтому для определения сопротивления при некоторой стандартизированной температуре, например T = 25 ° C , мы должны найти тепловой коэффициент (TCR) материала.Это требует точного измерения температуры окружающей среды и выполнения некоторых расчетов, при этом надеясь, что за это время не было допущено никаких ошибок. Однако мы можем сделать это гораздо проще! Как вы уже догадались, можно использовать простой делитель напряжения!

В базовой версии у нас два резистора, и если они сделаны из одного материала, это означает, что их температурные зависимости сопротивления примерно такие же, как у . Независимо от того, насколько велика разница температур, эти сопротивления изменяются примерно на один и тот же процент, скажем, на 5% на каждые 20 ° C.Но, , поскольку в общем случае формула делителя напряжения имеет отношение импедансов, любое относительное изменение будет отменено, и выходное напряжение должно быть независимым от температуры (или, по крайней мере, его влияние должно быть значительно уменьшено). Более того, если мы посмотрим на уравнение из предыдущего раздела, мы получим значение сопротивления, такое же, как первое при данной температуре — никаких дополнительных расчетов не требуется!

Во-вторых, делители напряжения удобно использовать при проектировании сложных электрических схем.Вместо использования нескольких отдельных источников напряжения, каждый из которых создает разный потенциал в системе, мы можем реализовать один источник и применить столько делителей напряжения, сколько нам нужно.

С другой стороны, мы должны помнить о том, что чем длиннее провода в нашей цепи, тем больше вероятность падения напряжения. Что ж, это далеко не так для длинных промышленных кабелей, но все же, если нам нужно провести действительно точные измерения, этот фактор следует принять во внимание и, в идеале, уменьшить как можно больше.

Делитель тока

До сих пор мы были сосредоточены на обработке сигнала — в основном, на изменениях напряжения. Тем не менее, мы можем использовать аналогичную концепцию, которая рассматривает проблему с другой точки зрения — это называется текущим делителем.

Идея почти такая же, но вместо разделения входного напряжения на более мелкие части мы хотим разделить начальную силу тока и получить какое-то конкретное значение на выходе. Отличий всего несколько: во-первых, нам нужен источник тока вместо источника напряжения.Во-вторых, все импедансы (в простом случае, как обычно, два) должны быть расположены параллельно, а не последовательно. Собственно, все это принципиальные отличия. В этой схеме мы снова можем использовать закон Ома. Полученная формула:

Iₓ = Z / (Z + Zₓ) * Iᵢ .

Мы можем заметить интересный и ценный объект. Для делителя напряжения, чем выше выходное сопротивление, тем больше выходное напряжение, в то время как для делителя тока результат имеет обратное значение для .

Точно так же мы можем производить различные типы делителей тока, включая катушки и конденсаторы, и все они применимы для переменного тока, тогда как для постоянного тока работает только состав резисторов. В общих случаях можно оценить как амплитуду, так и фазовый сдвиг протекающего тока. Мы уверены, что после прочтения пошаговых решений этого калькулятора делителя напряжения вам не составит труда выполнить аналогичные вычисления.

Бесплатный онлайн-калькулятор делителя напряжения

Калькулятор делителя напряжения: вычисляет падение напряжения на каждой резисторной нагрузке при последовательном подключении.

Для цепи постоянного тока с источником постоянного напряжения В _T и Если резисторы включены последовательно, падение напряжения V _i на резисторе R _i определяется по формуле:

---

В настоящее время у нас есть около 1975 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.

На этой странице вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитов и калькуляторы лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и ​​инструментах (как писать смайлы в Интернете и т. Д.)

В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.

Это наиболее часто используемые пользователями во всем мире.

И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.

Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите даже малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.

Делитель потенциала — онлайн-калькулятор

Делитель потенциала — это самый простой способ получения источника с более низкой ЭДС. от источника с более высокой э.д.с.

Выходное напряжение делителя потенциала можно рассчитать как

U _out = U _in R ₂ / (R ₁ + R ₂ ) (1)

где

U _выход = выходное напряжение (В)

R = сопротивление (Ом, Ом)

U _дюймов = входное напряжение (В)

Пример — потенциальный делитель — Высокое энергопотребление

Выходное напряжение делителя потенциала с двумя резисторами R ₁ = 10 Ом и R ₂ = 20 Ом и входное напряжение 12 В можно рассчитать как

U _вых = (12 В) (20 Ом) / ((10 Ом) + (20 Ом))

= 8 (В)

Ток через делитель потенциала R ₁ и 900 рандов 06 2 (напр.выходной ток) можно рассчитать по закону Ома

I = U / R

= (12 В) / ((10 Ом) + (20 Ом))

= 0,4 А

можно рассчитать потребляемую мощность делителя

P = UI

= (12 В) (0,4 A)

= 4,8 Вт

Пример — Делитель потенциала — более низкая потребляемая мощность

Выходное напряжение от делителя потенциала с двумя резисторами R ₁ = 1000 Ом и R ₂ = 2000 Ом и входное напряжение 12 В можно рассчитать как

U _out = (12 В) ( 2000 Ом) / ((1000 Ом) + (2000 Ом))

= 8 (В)

Ток через делитель потенциала R ₁ и R ₂ (пример.выходной ток) можно рассчитать по закону Ома

I = U / R

= (12 В) / ((1000 Ом) + (2000 Ом))

= 0,004 А

можно рассчитать потребляемую мощность делителя

P = UI

= (12 В) (0,004 A)

= 0,048 Вт

Потребляемую мощность в делителе потенциала можно уменьшить за счет увеличения сопротивления .