Калькулятор параллельного соединения резисторов онлайн: Онлайн-калькулятор расчета последовательного и параллельного соединения резисторов

Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Параллельное соединение: общая информация

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь

потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчёта

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=

1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте

определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Видео: Правильное подключение светодиодов

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.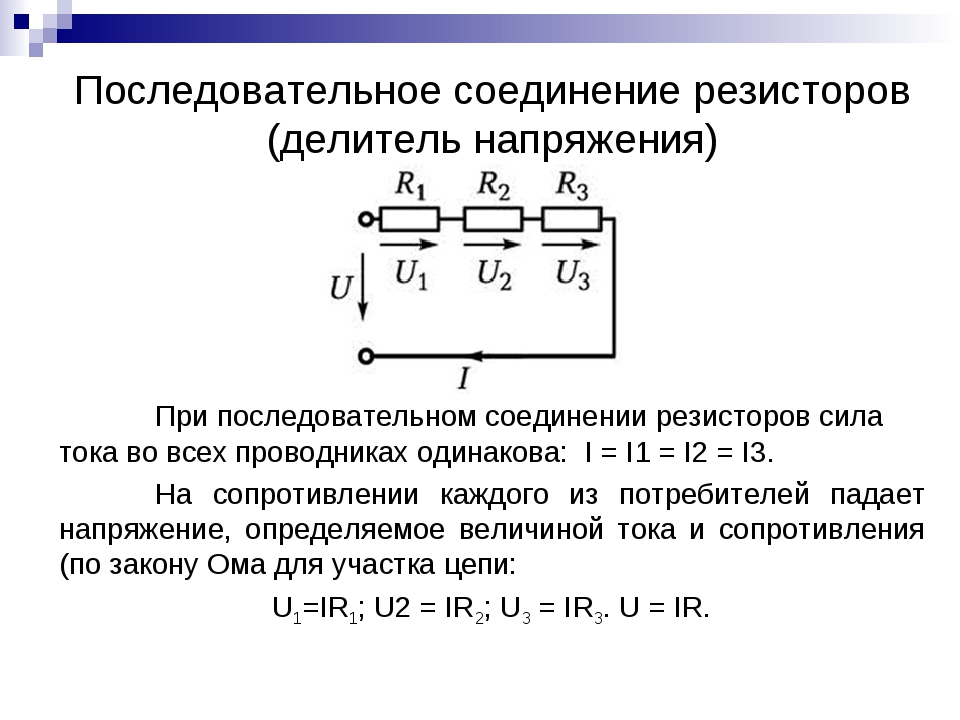 Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.

Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

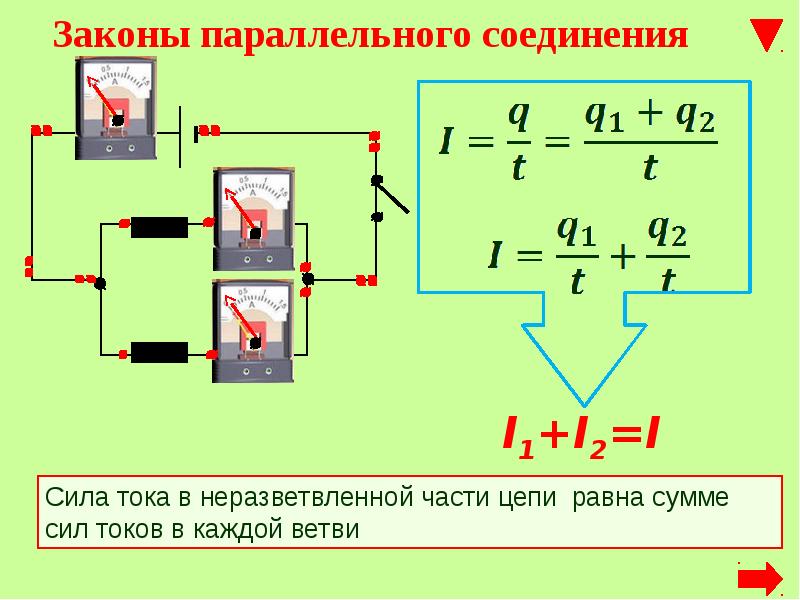
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется

n соединенных параллельно одинаковых резисторов R , то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений.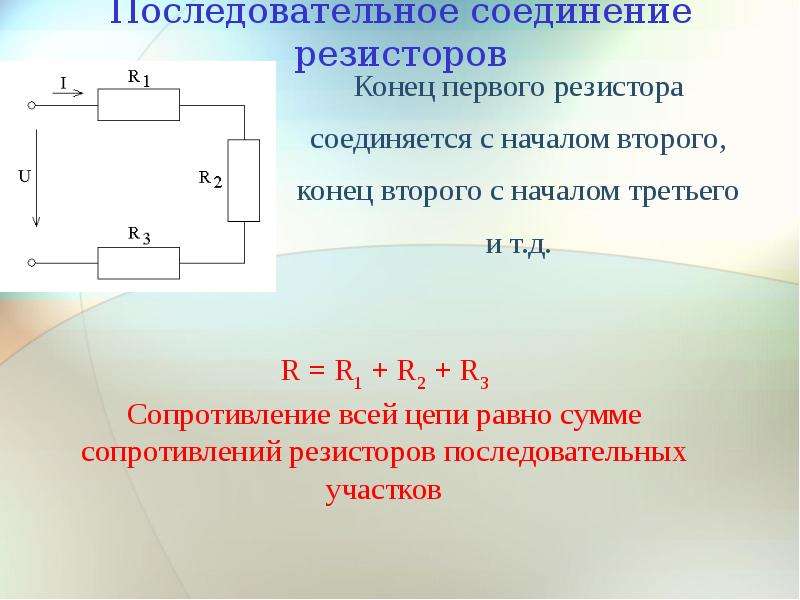 Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства . Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку.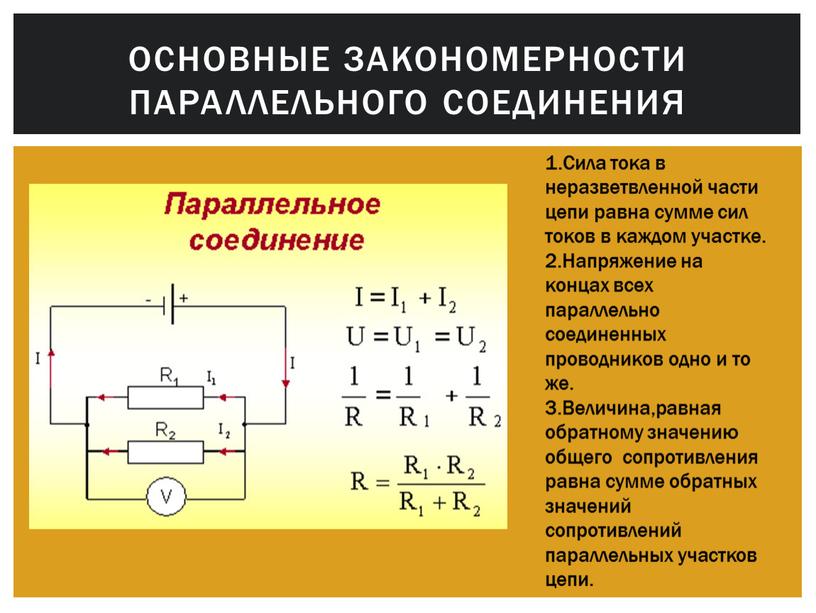 Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.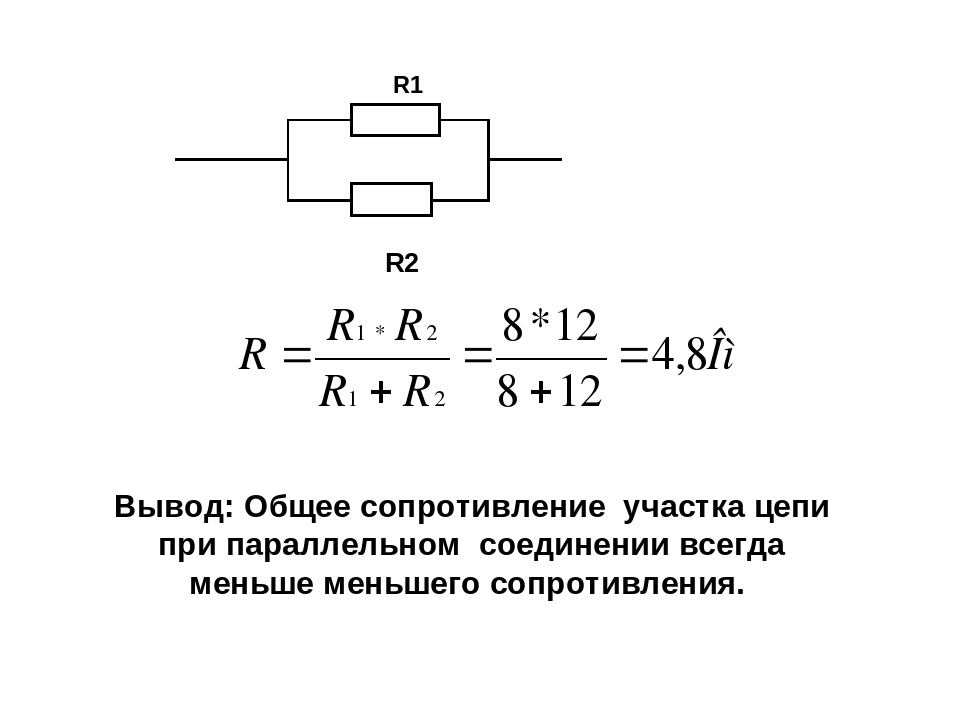

Расчет общего сопротивления при параллельном соединении резисторов

В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:

Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.

Сила тока и напряжение

При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.

Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.

Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.

Пример расчета

В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:

По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного.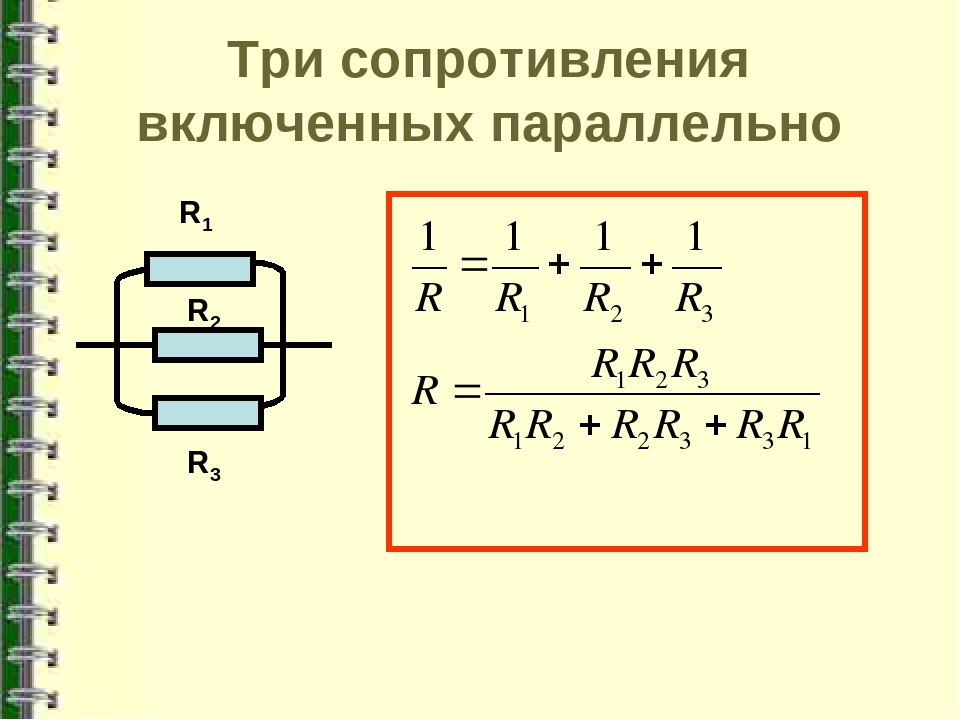 А также прекрасно соотносится с увеличением проводимости в два раза.

Второй пример

Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:

Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.

Пример смешанного соединения

Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.

Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.

Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.

Применение параллельной схемы

Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.

Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.

Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.

Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.

Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.

Итог

При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.

Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.

Параллельное соединение резисторов калькулятор для расчета

Уникальнvй софт / Калькулятор соединения резисторов

Калькулятор соединения резисторов v.1.0 – предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного). Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе.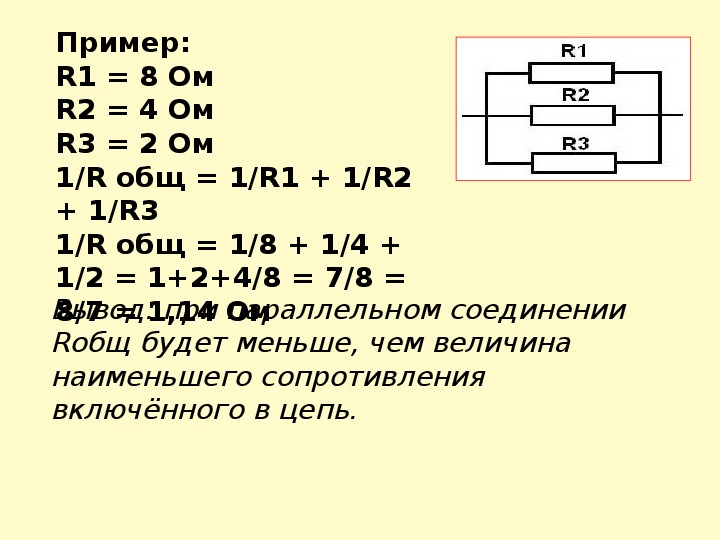 Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».

Скачать программу Объём 167 кБ Всего загрузок: 1181

Из закона Ома и первого и второго правил Кирхгофа следует:

При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.

При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.

Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются

Параллельное соединение двух сопротивлений

При параллельном соединении двух сопротивлений формула (1) упрощается

Параллельное соединение двух сопротивлений

При параллельном соединении двух сопротивлений формула (1) упрощается

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.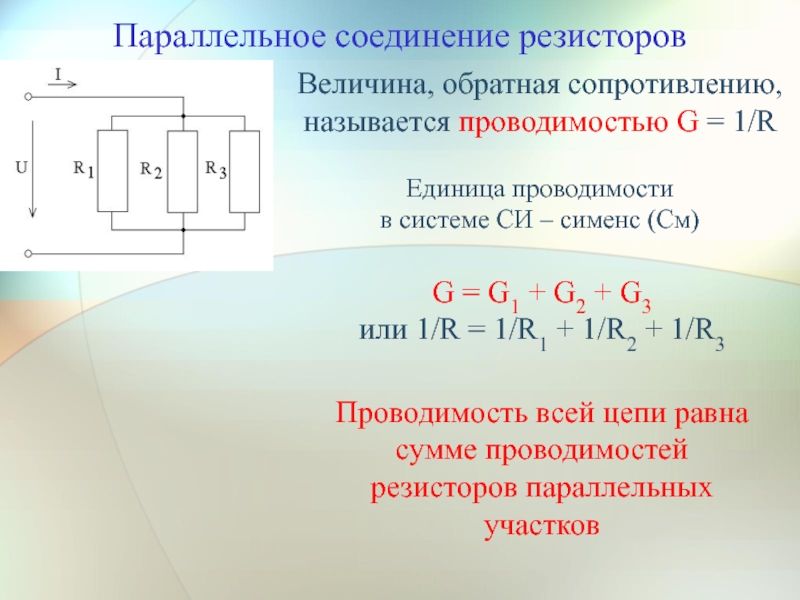

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно.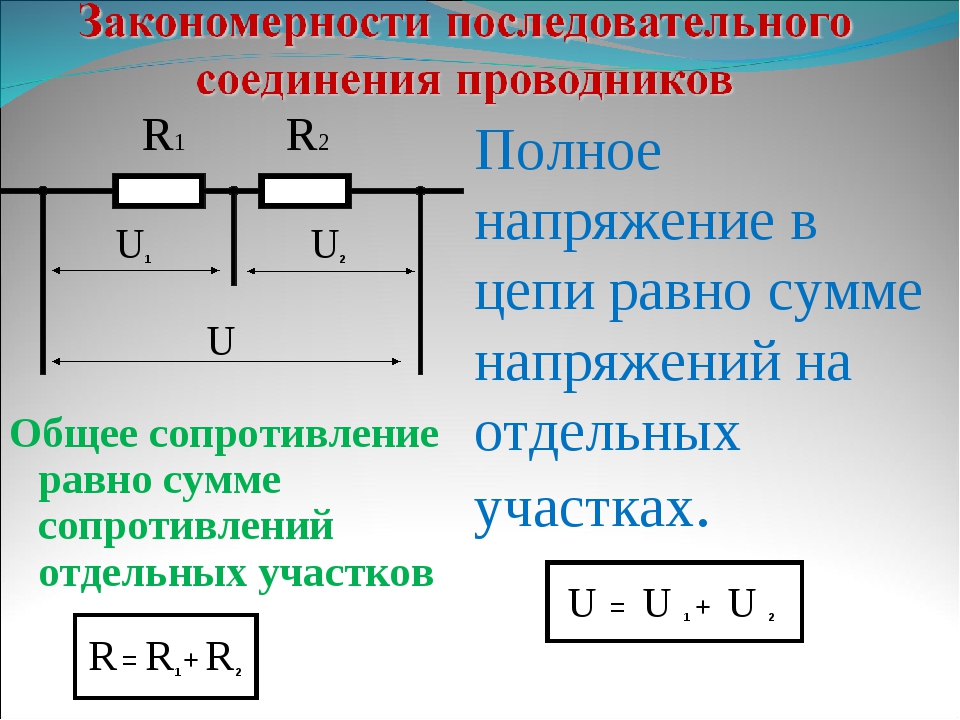 Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор расчёта параллельного соединения резисторов

Уникальнvй софт / Калькулятор соединения резисторов

Калькулятор соединения резисторов v.1.0 – предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного). Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе. Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».

Скачать программу Объём 167 кБ Всего загрузок: 1182

Интернет калькулятор для расчета параллельного сопротивления R1 + R2 в цепи. Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.

Калькулятор параллельного соединения резисторов

Формула параллельных резисторов :

• R_p = Параллельное сопротивление
• R_{1 и} R₂ = Параллельно соединенные резисторы

8 комментариев

• Новые
• Старые
• Лучшие

• Приветствуем гость

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

Примитивно. По тексту:»Вы можете определить общее эквивалентное сопротивление (R) до 2 резисторов параллельно.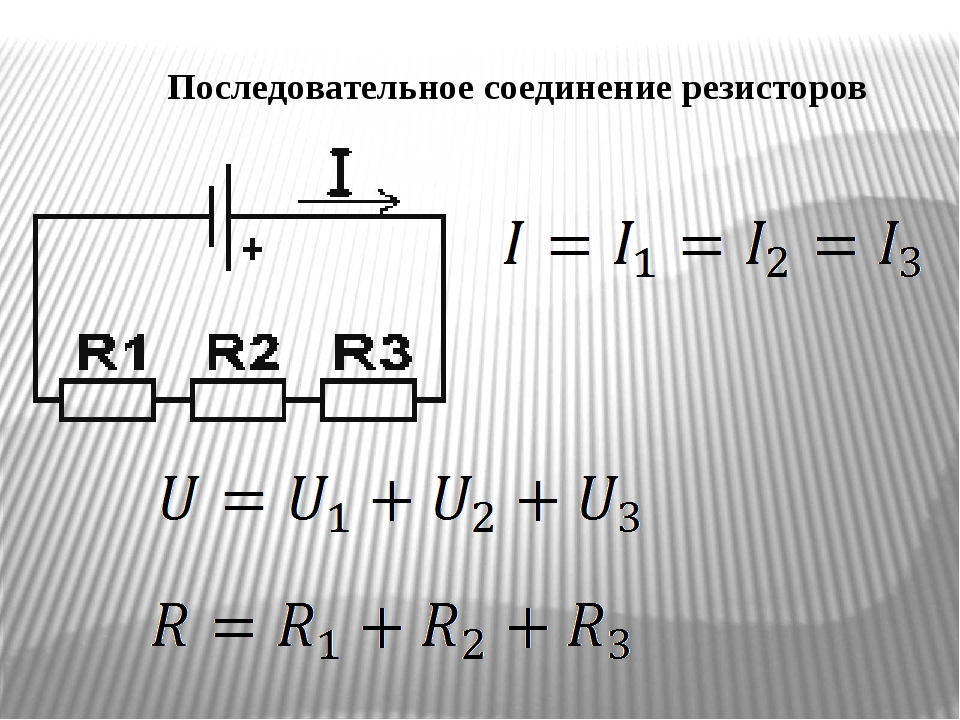 »А что параллельно бывает 1 резистор или 1,5 штуки?А что 3-4-5-…резисторов рассчитать нельзя?

• Маркер комментария
• Delete comment

А чего неработает?

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

До обыденного примитивно.Вот пример.
У меня есть R1=1500 омМне нужно Rобщее= 1250 омНу и какое сопротивление нужно добавить?R2= .
Если что-то делать, так делать.

• Маркер комментария
• Delete comment

• Маркер комментария
• Delete comment

когда-то уменя был график общего R при двух параллельном подключении резисторов где можно увидеть такое повторение

• Маркер комментария
• Delete comment

в любом калькуляторе .которых в сети немеряно.

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Калькулятор расчёта параллельного соединения резисторов — MOREREMONTA

Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)

Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.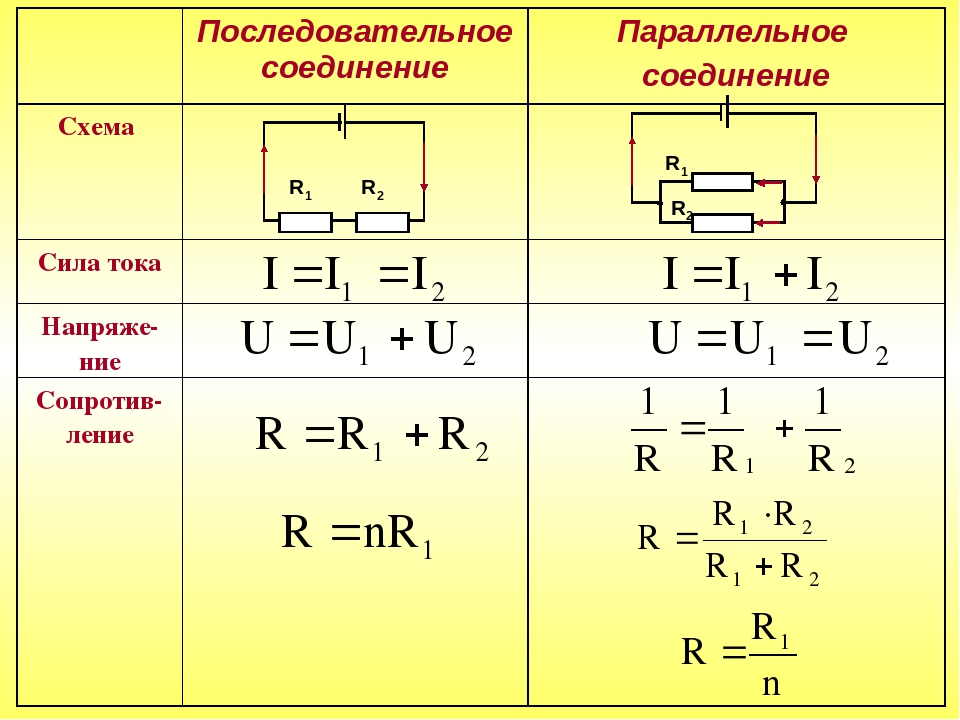

Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

• Указать в графе «количество резисторов» их число, в нашем примере их три;
• После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
• Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

• R_сум — суммарное сопротивление параллельно соединенных элементов
• R₁ — сопротивление первого резистора;
• R₂ — сопротивление второго резистора;
• R₃ — сопротивление третьего резистора;
• R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.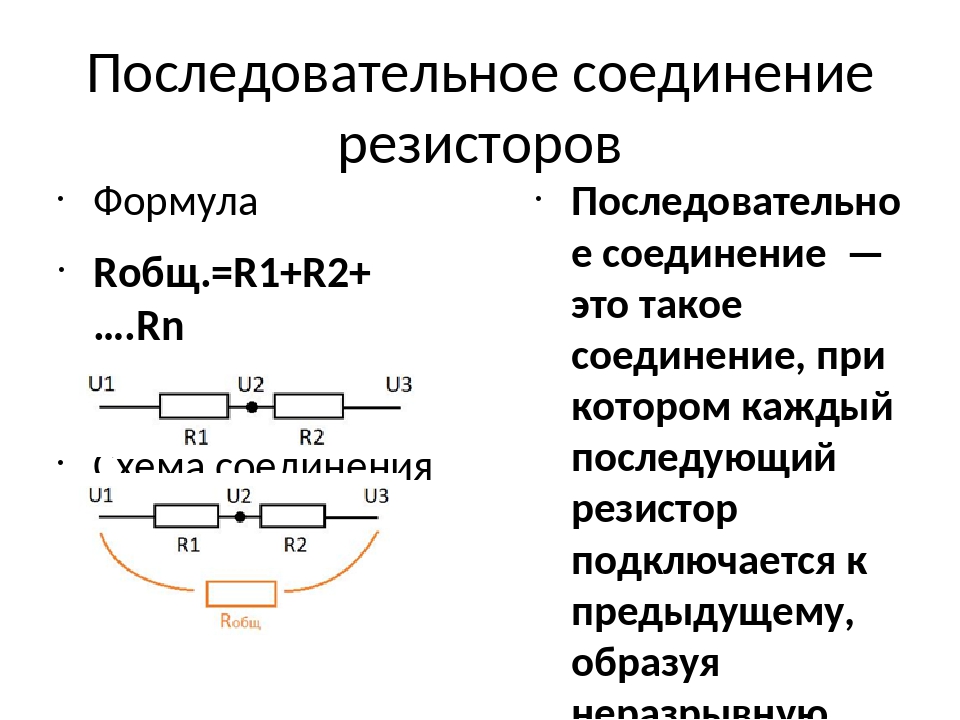

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Суммарное сопротивление при последовательном соединении. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов. Сопротивление параллельной цепи

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга.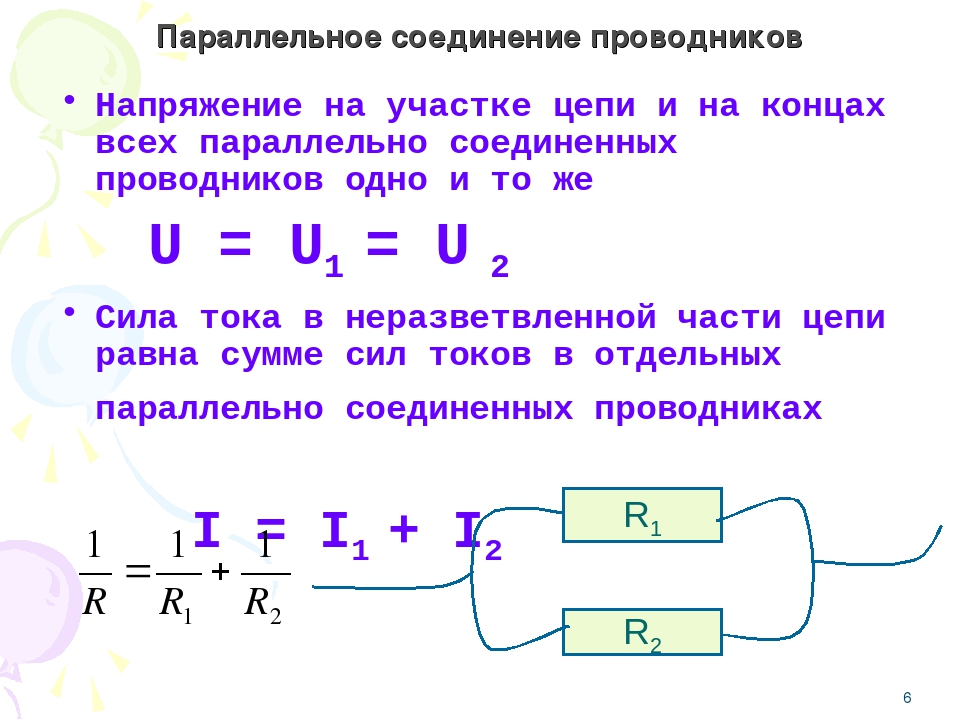 В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2.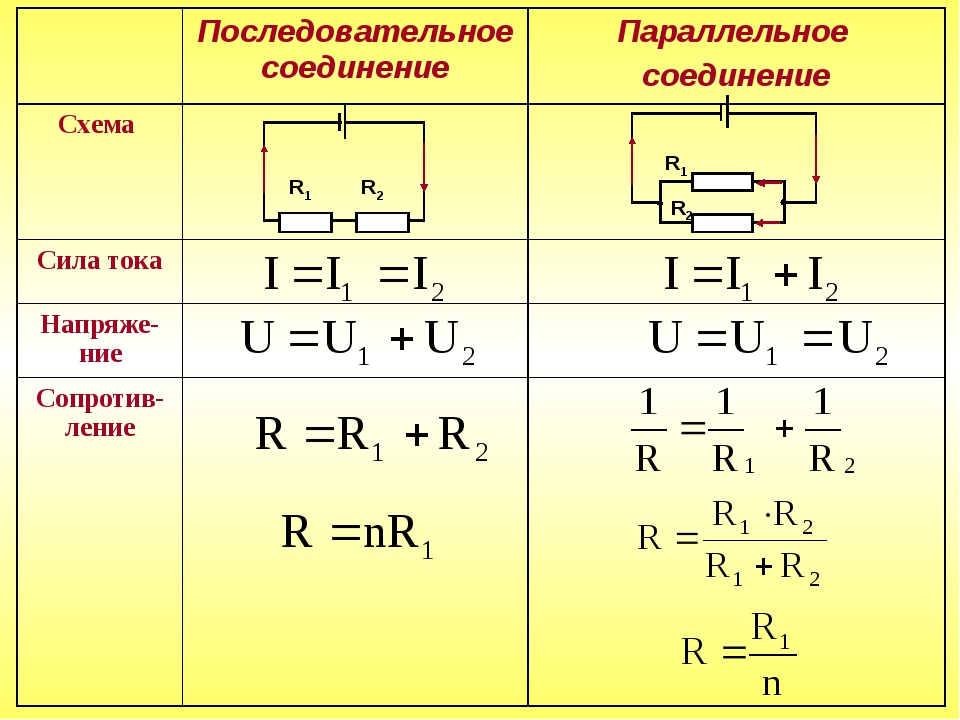 При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.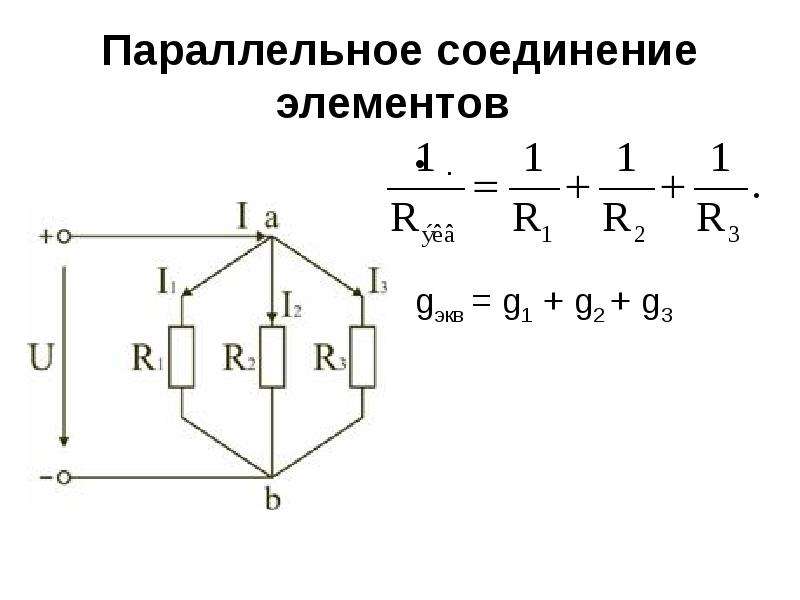

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение

т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I 1 и I 2 в формулу (2), получим.

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

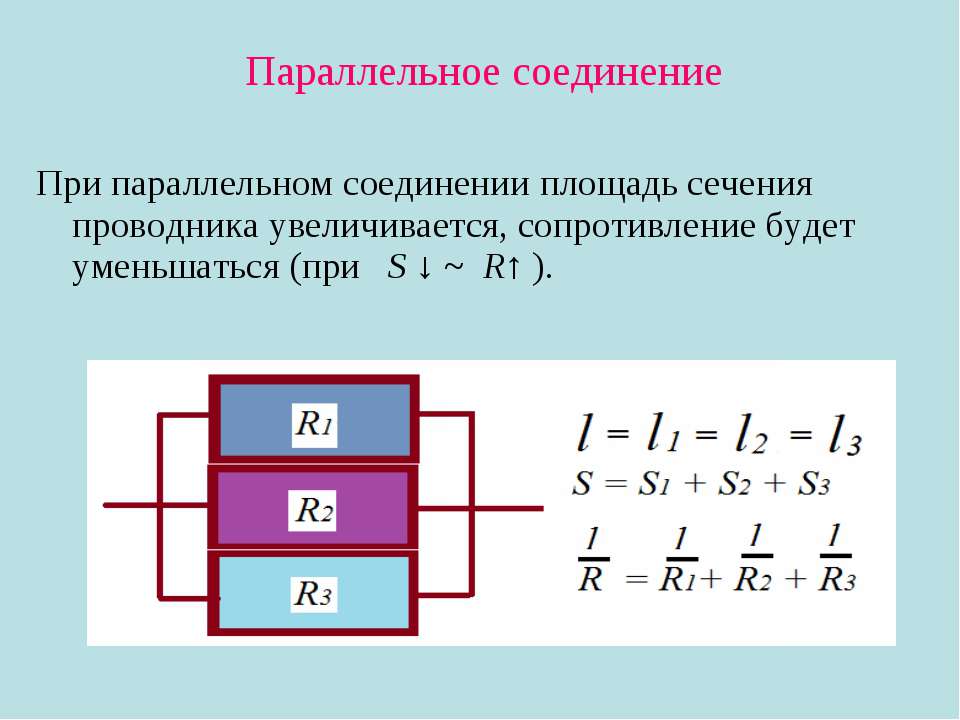
Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

калькулятор параллельного соединения резисторов онлайн

Вы искали калькулятор параллельного соединения резисторов онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и онлайн калькулятор параллельного соединения резисторов, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор параллельного соединения резисторов онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор параллельного соединения резисторов онлайн,онлайн калькулятор параллельного соединения резисторов,онлайн калькулятор последовательное соединение резисторов,онлайн калькулятор расчет сопротивления,онлайн калькулятор резисторов последовательное соединение,онлайн расчет параллельного соединения резисторов,онлайн расчет сопротивления,онлайн расчет сопротивления цепи,параллельное соединение резисторов калькулятор онлайн,последовательное соединение резисторов калькулятор онлайн,последовательное соединение резисторов онлайн калькулятор,рассчитать сопротивление онлайн,расчет онлайн сопротивления,расчет параллельного соединения резисторов онлайн,расчет сопротивления калькулятор онлайн,расчет сопротивления онлайн,расчет сопротивления онлайн калькулятор,расчет сопротивления цепи онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор параллельного соединения резисторов онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, онлайн калькулятор последовательное соединение резисторов).

Где можно решить любую задачу по математике, а так же калькулятор параллельного соединения резисторов онлайн Онлайн?

Решить задачу калькулятор параллельного соединения резисторов онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С₁+ С₂+….+ С_n   и   1/L = 1/L₁+ 1/L₂ +…+ 1/L_n    для параллельных цепей и
L = L₁ + L₂ +….+ L_n   и   1/С = 1/С₁+ 1/С₂+…+ 1/С_n    для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

 

Калькулятор параллельного / последовательного резистора

| Детали с усилением

Используйте этот калькулятор для определения общего сопротивления сети. Этот калькулятор может давать результаты для последовательного, параллельного и любого их сочетания. Схема создается автоматически по мере добавления резисторов в сеть в качестве наглядного пособия.

Сложные резистивные схемы часто можно упростить до одного резистора эквивалентного номинала. В процессе упрощения используются два уравнения: резисторы в последовательном уравнении и резисторы в параллельном уравнении.

Резисторы серии

Резисторы включены последовательно при соединении в одну линию. Текущий ток является общим для всех резисторов в этой цепи. Это связано с тем, что ток, протекающий через первый резистор, проходит по одному пути через каждый из следующих резисторов в цепи. Общее сопротивление должно равняться сумме номиналов каждого резистора, используемого в цепи.

$$ R _ {\ text {Equiv}} = R_1 + R_2 + R_3 + \ ldots R_n $$

Мы можем рассматривать всю эту цепочку резисторов как один резистор со значением ~ R _ {\ text {Equiv}} ~.

Параллельные резисторы

Резисторы включены параллельно, если они используют одни и те же два узла. Падение напряжения на каждом резисторе в этой конфигурации обычное. Теперь ток имеет несколько путей и может не быть одинаковым для каждого резистора. Общее сопротивление резисторов, подключенных параллельно, является суммой, обратной величине каждого используемого резистора.

$$ \ frac {1} {R _ {\ text {Equiv}}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ ldots \ frac { 1} {R_n} $$

Мы можем рассматривать эти параллельные резисторы как один резистор со значением ~ R _ {\ text {Equiv}} ~

Обратите внимание, что информация, представленная в этой статье, предназначена только для справочных целей.Amplified Parts не делает никаких заявлений, обещаний или гарантий относительно точности, полноты или адекватности содержания этой статьи и прямо отказывается от ответственности за ошибки или упущения со стороны автора. В отношении содержания данной статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, права собственности, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.

Калькулятор параллельных резисторов — [100% бесплатно]

Расчет эквивалентного сопротивления или REQ параллельных резисторов вручную может быть довольно утомительным. К счастью, этот калькулятор параллельных резисторов может помочь вам в расчетах независимо от того, сколько резисторов у вас параллельно. Вы также можете выполнить вычисления вручную, а затем использовать калькулятор параллельной схемы, чтобы проверить свой ответ.

Как использовать параллельный калькулятор резисторов?

Каким бы пугающим ни казался расчет параллельных резисторов, использование этого калькулятора параллельных резисторов является полной противоположностью.Этот онлайн-инструмент очень прост в использовании и понимании. Вот шаги, которые необходимо выполнить для использования этого калькулятора эквивалентного сопротивления или параллельного калькулятора сопротивления:

• Сначала введите значение резистора 1.
• Затем введите значения резистора 2, резистора 3, резистора 4 и резистора 5.
• После ввода всех требуемых значений калькулятор параллельной цепи автоматически сгенерирует нужный вам результат. Поскольку единицей измерения для всех значений резистора является Ом, конечный результат также имеет ту же единицу измерения.

Что такое параллельный резистор?

Когда вы соединяете обе клеммы резисторов вместе параллельно, это означает, что вы соответственно подключили каждую клемму к другому резистору или резисторам. В отличие от других схем, вы также можете классифицировать схему с параллельными резисторами как делитель тока.

Это связано с тем, что параллельные резистивные цепи могут проходить более одного пути, поскольку они имеют несколько путей, через которые может проходить ток.Поскольку этот тип схемы обеспечивает несколько путей для прохождения источника тока, сила тока может быть неодинаковой во всех ответвлениях или путях.

Но падение напряжения, которое возникает на всех резисторах в параллельной цепи, остается неизменным. Это означает, что параллельные резисторы имеют общее напряжение, и этот факт применим ко всем элементам, соединенным параллельно.

По определению, параллельная резистивная цепь — это цепь, в которой резисторы имеют параллельные соединения или совместно используют одни и те же узлы или точки соединения.Кроме того, этот тип схемы имеет более одного пути, подключенного к одному источнику напряжения.

Как рассчитать сопротивление в параллельной цепи?

Основной характеристикой параллельной цепи является общая разность напряжений или потенциалов на концах всех резисторов. Даже без использования калькулятора эквивалентного сопротивления, вы можете рассчитать эквивалентное сопротивление для этого типа цепи по следующей формуле:

1 / R = 1 / R1 + 1 / R2 +… + 1 / Rn

где:

R относится к эквивалентному параллельному сопротивлению
R1, R2,… Rn относится к сопротивлениям отдельных резисторов с номерами 1… n .2) в базовых единицах СИ

Вот несколько шагов, которые необходимо выполнить для расчета параллельного сопротивления без использования параллельного калькулятора сопротивления:

• Сначала определите значения сопротивления всех резисторов, подключенных параллельно. Например, у нас есть три номинала резистора: 4 Ом , 3 Ом и 6 Ом .
• Подставьте эти значения в приведенную выше формулу:

1 / R = 1/4 + 1/3 +1/6

, следовательно, , 1 / R = 0.75, а R = 1,33

• Чтобы проверить точность вашего ответа, введите значения в калькулятор параллельного резистора.

Как рассчитать сопротивление?

Прежде чем вы сможете выполнить расчет, вы должны хорошо разбираться в параллельных цепях. Помните, что такая схема делится на несколько путей, а затем снова соединяется. Также имейте в виду, что ток течет по каждому из отдельных путей цепи.

Если в схеме есть резисторы на главном ответвлении или если в одном ответвлении имеется более одного резистора, следует выполнить другой расчет.Найдите общее сопротивление, используя значение сопротивления каждой из ветвей. Каждый из резисторов замедляет ток, проходящий через одну ветвь.

Но резисторы не так сильно влияют на общее сопротивление цепи. Следовательно, вы должны использовать формулу общего сопротивления:

1 / RT = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4… 1 / Rn

где:

R1 относится к сопротивлению 1-й ветви
R2 относится к сопротивлению 2-й ветви
R3 относится к сопротивлению 3-й ветви
R4 относится к сопротивлению 4-й ветви
и так далее, пока не дойдете до конечной ветки Rn .

Это самый простой способ рассчитать сопротивление. Но в некоторых случаях у вас может не быть значений отдельных сопротивлений. В таком случае вам нужно вместо этого использовать напряжение и ток. Вот шаги, которые необходимо выполнить:

• В параллельных цепях напряжение на одной ветви имеет то же значение, что и общее напряжение, протекающее по всей цепи. Если вам известно значение напряжения одной из ветвей, вы можете выполнить расчет.
• Вы также можете найти значение общего напряжения, равное источнику питания схемы, например, батарее. В параллельных цепях токи различаются от ветви к ветви. Вы должны знать значение общего тока. Без него вы не сможете рассчитать общее сопротивление.
• Как только у вас есть общее напряжение и ток, вы можете вычислить полное сопротивление по закону Ома:

R = V / I.

• Обратите внимание на любые ветви, у которых есть ноль. сопротивление.Если параллельная цепь имеет одну такую ​​ветвь, весь ток течет через эту ветвь, и сопротивление становится равным нулю.

Почему при параллельном подключении эквивалентное сопротивление меньше?

По мере того, как вы продолжаете добавлять резисторы в параллельную цепь, это уменьшает эквивалентное сопротивление всей цепи. Однако это также увеличивает общий ток цепи. Это происходит потому, что добавление резисторов параллельно предоставляет схемам больше путей для прохождения тока.

Калькулятор параллельного и последовательного сопротивления

Параллельный и последовательный

Сопротивление Сопротивление серии

Параллельное сопротивление	XXXX Ом
	XXXX Ом

Рассчитать Прозрачный
⚠️ Сообщить о проблеме

Сопротивление — это электрический элемент, который не позволяет легко протекать через него току.В нашей повседневной жизни сопротивление используется во многих электрических цепях и устройствах. Внутри этих электрических устройств сопротивления расположены в различных конфигурациях.

Вы также, должно быть, наблюдали, выполняя соединения на макетной плате в своей лаборатории электроники, как резисторы подключаются по-разному. В зависимости от способа соединения их концов различают два основных типа цепей сопротивления:

Цепи серии
• Параллельные схемы

По мере продвижения в этом посте мы будем понимать работу, сравнение, вычисления и различия между этими последовательными цепями и параллельными цепями.

Цепи серии

Два или более резистора считаются подключенными последовательно, если ток, протекающий через них, одинаков. Другими словами, ток, исходящий от источника, или общий ток не будут разветвляться по какому-либо другому пути, а будут двигаться только по одному прямому пути.

При последовательном соединении сопротивлений чистое сопротивление цепи является суммой всех сопротивлений цепи.

На следующей принципиальной схеме показаны три последовательно соединенных сопротивления R ₁ , R ₂ и R ₃ .Общее сопротивление этой последовательной цепи составляет R _{, нетто} = R ₁ + R ₂ + R ₃ .

Как правило, если «n» сопротивлений соединены последовательно, общее сопротивление будет R _net = R ₁ + R ₂ +…. Р _№ .

Например, если в цепи есть три последовательно подключенных резистора по 10 Ом, и источник напряжения 30 В, то ток, протекающий в цепи и через каждый из них, определяется выражением I = V / R = 10/30 = 0. .33 А.

Параллельные цепи

Два или более резистора считаются подключенными параллельно, если они соединены головками на одной стороне и выводами на другой стороне цепи. В параллельной цепи ток, исходящий от источника, или полный ток будет ветвиться в месте соединения, где головки сопротивлений встречаются, а затем течет в разных количествах в каждом резисторе, а затем снова объединяется в точке встречи хвостов резисторы и течет к источнику.

При параллельном соединении сопротивлений сопротивление цепи, обратное сопротивлению цепи, является суммой значений, обратных сопротивлению всех сопротивлений цепи.

На следующей принципиальной схеме показаны три сопротивления R ₁ , R ₂ и R ₃ , соединенных параллельно. Общее сопротивление этой параллельной цепи составляет 1 / R _net = 1 / R = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ .

Как правило, если «n» сопротивлений подключены параллельно, общее сопротивление составляет:

1 / R _net = 1 / R = 1 / R + 1 / R ₂ + 1 / R ₃ +….+ 1 / R _n

Например, если три резистора 4 Ом, 8 Ом и 8 Ом соединены параллельно в цепи с питанием 10 В, то общее сопротивление цепи определяется как: 1 / Rnet = 1/4 + 1/8 + 1/8 = ½ или Rnet = 2 Ом

Тогда ток, протекающий по цепи, равен V / I = 10/2 = 5 ампер.

Если вы хотите рассчитать ток в каждом резисторе, вы можете использовать закон Ома:

Ток через резистор 4 Ом I ₁ = 10/4 = 2.5 А

Ток через резистор 8 Ом I ₁ = 10/8 = 1,25 A

Ток через резистор 4 Ом I ₁ = 10/8 = 1,25 A

Обратите внимание: если вы сложите отдельные токи через каждый резистор, вы получите общий ток, протекающий в цепи.

Комбинация последовательных и параллельных резисторов

Если вы найдете схему, в которой резисторы включены последовательно и параллельно, то вам нужно решить комбинацию резисторов шаг за шагом, учитывая, находятся ли они последовательно или параллельно с соседними, и затем прийти к окончательному сопротивлению цепи.

Пункты о последовательном и параллельном соединении резисторов:

• Эффективное сопротивление последовательной цепи всегда больше, чем у каждого резистора в цепи.
• Эффективное сопротивление параллельной цепи всегда меньше, чем сопротивление каждого резистора в цепи.
• Ток в каждом из последовательно соединенных резисторов одинаков, а напряжение на каждом параллельном резисторе одинаково.
• В цепи последовательных резисторов, если одно сопротивление повреждается, вся цепь разрывается и ведет себя как разомкнутая цепь.
• В схеме параллельных резисторов, если один резистор поврежден, ток продолжает течь в других резисторах, и схема будет продолжать работать, но с другим значением сопротивления цепи.

Как вам помогает калькулятор последовательного и параллельного сопротивления CalculatorHut?

В повседневной жизни мы сталкиваемся с последовательным и параллельным сочетанием резисторов во многих местах. Например, для цепей освещения мы используем параллельное соединение, а для приборов, которые работают непосредственно от сети, дается последовательное соединение.

CalculatorHut, универсальный центр научных и ненаучных онлайн-калькуляторов, предлагает бесплатный онлайн-калькулятор последовательного и параллельного сопротивления, который решит все ваши потребности в онлайн-калькуляторе бесплатно. Вы можете рассчитать до десяти резисторов, которые подключены последовательно или параллельно, с помощью этого удобного онлайн-калькулятора последовательного и параллельного сопротивления. Это очень удобный инструмент для студентов, который помогает им проверить правильность расчетов сопротивления.

CalculatorHut также предлагает широкий выбор более 100 калькуляторов по различным темам — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, физические калькуляторы, химические калькуляторы, математические калькуляторы и многие другие бесплатные онлайн-калькуляторы для научных расчетов.

Наши читатели также могут получить бесплатный виджет любого калькулятора из нашего широкого диапазона калькуляторов для встраивания в качестве виджетов на свои веб-сайты. Для этого они могут написать нам на [адрес электронной почты]

.

Мы пропустили какой-нибудь бесплатный онлайн-калькулятор? Пожалуйста, дайте нам знать.Мы будем более чем счастливы удовлетворить ваши потребности в бесплатном онлайн-калькуляторе бесплатно и всегда!

Вот еще одна фантастическая новость! Вы можете бесплатно носить с собой в кармане наш широкий ассортимент онлайн-калькуляторов. Да! Бесплатное приложение CalculatorHut — ваш друг, который упрощает и упрощает любые вычисления! Удачных расчетов!

Добавьте параллельные резисторы в схему

Если комбинация резисторов обеспечивает несколько путей для прохождения тока, она называется параллельными резисторами.Эквивалентное сопротивление всегда уменьшается, когда мы добавляем параллельные резисторы. Воспользуйтесь онлайн-калькулятором параллельных резисторов здесь.

Параллельная комбинация:

Комбинация резисторов будет называться , параллельные резисторы , если к одному узлу в цепи подключено более двух компонентов.

Предположим, у нас есть три резистора, подключенных друг к другу в точке b, головка первого резистора подключена к головке второго и третьего резистора.Предполагая, что ток течет сверху вниз. В отличие от последовательной комбинации, положительный вывод R ₁ соединен с положительным выводом R ₂ и R ₃ . Комбинация приведет к трем различным путям для тока.

Обратите внимание, что в узле a и узле b присутствуют четыре компонента; источник, R ₁ , R _2, и R ₃ , как показано на диаграмме.

Параллельная цепь обеспечивает более одного пути для тока.

Онлайн-калькулятор параллельных резисторов:

Для расчета общего сопротивления резисторов, которые соединены параллельно, используйте следующий калькулятор параллельных резисторов. $ R_1, R_2 $ и $ R_3 $ — это три резистора, соединенных параллельно, а $ R_ {Total} $ — эквивалентное сопротивление.

Калькулятор тока параллельной цепи

После расчета общего сопротивления параллельных резисторов теперь вы можете рассчитать общий ток. Поместите общее сопротивление из онлайн-калькулятора параллельных резисторов, указанного выше.Также введите напряжение цепи, чтобы рассчитать ток.

Решающие резисторы в параллельной цепи:

Мы хотим знать несколько типов параметров для вышеуказанной схемы, как мы это сделали для последовательной комбинации.

Общее эквивалентное сопротивление:

Каков общий ток, обеспечиваемый источником?

Чтобы ответить на вопрос, нам нужно вычислить полное или эквивалентное сопротивление цепи. И формула для этого:

$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $

Если мы используем те же номиналы резисторов, которые мы использовали в последовательной схеме i.е. R $ _ {1} $, R $ _ {2,} $ и R $ _ {3} $ равны 20, 40 и 10 $ \ Omega $ соответственно. И поместите эти значения в приведенную выше формулу, тогда:

$ \ frac {1} {R_ {Eq}} = \ frac {1} {20} + \ frac {1} {40} + \ frac {1} { 10} = \ frac {7} {40} $
$ R_ {Eq} = \ frac {40} {7} = 5.714 \ Omega $

Вышеупомянутая сложная схема теперь сведена к этой схеме с одним резистором. Теперь мы можем легко определить полный ток, потребляемый схемой, по закону Ома, как показано ниже:

$ I_ {T} = \ frac {V} {R_ {Eq}} = \ frac {140 v} {5.714 \ Omega } $
$ I_ {T} = 24.5 A $

Общее сопротивление намного меньше, чем у последовательной цепи, а общий ток намного больше, чем у последовательной цепи.

Напряжение на каждом резисторе:

Какое напряжение на каждом резисторе?

Прежде всего, взгляните на схему, и вы поймете, что каждый резистор подключен к источнику напряжения. Напряжение на каждом резисторе совпадает с напряжением источника. Формула для напряжения:

$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $

В нашем случае напряжение для R $ _ {1} $, R $ _ {2} $ и R $ _ {3} $: V $ _ {1} $ = 140 v, V $ _ {2} $ = 140 v и V $ _ {3} $ = 140 v соответственно.

Ток каждого резистора:

Какой ток каждого резистора?

Мы можем использовать закон Ома для определения силы тока. Предположим, что ток для R $ _ {1} $, R $ _ {2,} $ и R $ _ {3} $ равен I $ _ {1} $, I $ _ {2,} $ и I $ _ {3} $ соответственно. Итак, применяя закон Ома к каждому резистору, мы получаем

$ I_ {1} = \ frac {V_ {1}} {R_ {1}} = \ frac {140 v} {20 \ Omega} = 7 A $
$ I_ {2} = \ frac {V_ {2}} {R_ {2}} = \ frac {140 v} {40 \ Omega} = 3,5 A $
$ I_ {3} = \ frac {V_ {3} } {R_ {3}} = \ frac {140 v} {10 \ Omega} = 14 A $

А что, если мы сложим все эти отдельные токи? Давай сделаем это.

$ I_ {T} = I_ {1} + I_ {2} + I_ {3}
$ I_ {T} = 7 A + 3,5 A + 14 A $
$ I_ {T} = 24,5 A $

Такой же ток может быть подтвержден с помощью вычислителя параллельных резисторов выше.

Наконец-то! Мы получили полный ток, потребляемый всеми этими резисторами, так как мы нашли первое место. Это означает, что полный ток цепи равен сумме токов отдельных резисторов. Мы можем обобщить формулу следующим образом:

$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $

Индивидуальный ток каждого резистора можно найти с помощью правила делителя тока. (CDR).

Формула для добавления параллельных резисторов:

В приведенном выше обсуждении мы наблюдали три параметра: первое общее сопротивление при параллельном подключении, второе, индивидуальное напряжение каждого резистора и, наконец, индивидуальный ток каждого резистора. Все эти формулы представлены здесь для вашей простоты с общей применимостью до n резисторов.

Полное сопротивление параллельной цепи:

$ \ frac {1} {R_ {Equivalent}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ ldots + \ frac {1} {R_ {n}} $

Отдельное напряжение резисторов такое же, как и напряжение источника:

$ V_ {T} = V_ {1} = V_ {2} = \ ldots = V_ {n} $

Суммарный ток складывается из всех индивидуальных токов:

$ I_ {T} = I_ {1} + I_ {2} + \ ldots + I_ {n} $

Добавить параллельные резисторы То же значение:

Предположим, что в цепи, в которой все резисторы имеют одинаковое значение и все они подключены параллельно, каково будет общее сопротивление?

Предположим, что $ n $ количество параллельно подключенных резисторов с одинаковым сопротивлением.Общее сопротивление цепи будет

$ R_ {Total} = \ frac {R} {n} $

$ R $ — это значение сопротивления, которое одинаково для всех резисторов, а $ n $ равно количество резисторов, включенных параллельно.

Какой будет ток в каждом резисторе?

Ток каждого резистора будет

$ I = \ frac {I_ {Total}} {n} $

Вывод:

• Деление тока в параллельной цепи
• Добавьте параллельные резисторы, чтобы увеличить пути прохождения тока
• Общий ток равен индивидуальному току параллельных цепей
• Напряжение остается неизменным в параллельных цепях электрической цепи
• Общее сопротивление уменьшается в параллельной цепи по сравнению с сопротивлением отдельных параллельных цепей

Невероятный мощный калькулятор сопротивления : 7 шагов (с картинками)

Эти 2 схемы не самые интересные, но с них можно начать.

Чтобы использовать калькулятор, наберите текст в «записной книжке». Это немного похоже на текстовый процессор, в котором вы можете печатать то, что хотите. Разница в том, что он разделен не на абзацы, а на «ячейки». Когда вы закончите с ячейкой, вы можете «выполнить» ее, и ее результат появится чуть ниже ячейки. Ниже у вас может быть еще одна ячейка. Ячейку можно изменить, а затем выполнить снова, возможно, с немного другим содержанием. Блокнот можно сохранить как файл.

Это может показаться немного громоздким, но действительно полезно, поскольку у вас всегда есть запись о том, что вы сделали, и вы можете копировать и вставлять старые работы или образцы работ.Вы также можете добавлять комментарии, чтобы задокументировать свою работу. Я покажу вам содержимое ячейки с большим количеством комментариев (так что объяснение находится внутри ячейки), а затем покажу вам результат ячейки. Обратите внимание, что когда вы делаете свои вычисления, вам не нужно быть настолько многословным. (Строки, начинающиеся с символа «#», являются для вас просто комментариями и ничего не делают в калькуляторе. Я напишу некоторые из этих инструкций, используя комментарии в коде, пожалуйста, прочтите их. Только 4 строки действительно выполняют вычисления, остальное объяснение.)

Вот и

 -------------------- код начала --------------------
# Для первого расчета получим полное сопротивление резистора
# 1 кОм последовательно с одним из 10 кОм
# (и да, я знаю, что если вы разбираетесь в электронике, вы можете сделать это в своей голове)
print «Первый расчет - последовательно добавьте резистор 1 кОм к резистору 10 кОм:»
Распечатать

# Шаг 1
# сделать резистор, который является калькулятором, LRC означает индуктивность, сопротивление,
# Емкость, и # используется, потому что калькулятор может сделать все из них.# Я буду использовать длинное имя «aResistor», чтобы напомнить вам, что оно означает,
# но вы можете использовать просто «r»
# Следующая строка создает "aResistor" без значения (технически со значением None)

# Шаг 1
aResistor = LRC ()
print "игнорировать распечатку о частоте, это используется только в более сложных расчетах"

# Шаг 2
# теперь мы добавляем новое сопротивление нашему "резистору"

aResistor.add_series_r (1000) # добавить резистор 1 кОм
# это приведет к выводу, что мы сделали

# Шаг 3
# теперь добавьте второе сопротивление последовательно с первым

Резистор.add_series_r (10000) # 10000 = 10 КБ

# это снова вызовет вывод, который сообщает, что мы сделали


# Шаг 4
# получить окончательное значение сопротивления (обратите внимание, что z - общий символ сопротивления)

Распечатать
print "Конечное значение комбинированного сопротивления =", aResistor.get_z ()

# показывает текущее значение сопротивления, просто сумму сопротивлений

# последний комментарий подавляет печать по умолчанию в конце ячейки

-------------------- начало вывода --------------------

Первый расчет - последовательно добавьте резистор 1 кОм к резистору 10 кОм:

LRC () с использованием внутренней частоты lrc_freq в Гц
игнорируйте распечатку о частоте, это используется только в более продвинутых
расчеты
LRC.add_series_r () 1000
LRC.add_series_r () 10000

Конечное значение комбинированного сопротивления = 11000
-------------------- конец вывода -------------------- 

Мы можем сделать такую ​​же сортировку для двух параллельных резисторов мы снова будем использовать 1 кОм и 10 кОм, вот и:

-------------------- стартовый код ---------------------------- ----
напечатать "Второй расчет - добавить резистор 1 кОм к резистору 10 кОм параллельно:"
Распечатать

# -----
# создаем "aResistor", который является калькулятором

aResistor = LRC ()

# -----
# теперь мы добавляем сопротивление нашему "резистору"

Резистор.add_parallel_r (1000)

# это вызовет вывод, который сообщает, что мы сделали, и текущий
# значение импеданса = сопротивление

# -----
# теперь добавляем второе сопротивление параллельно первому

aResistor.add_parallel_r (10000)

# это снова вызовет вывод, который сообщает, что мы сделали, и

# -----

Распечатать
print "Конечное значение комбинированного сопротивления =", aResistor.get_nz ()
# nz в функции выше переводит полную числовую оценку в десятичное значение

# этот комментарий подавляет печать конца ячейки по умолчанию

-------------------- начать вывод ---------------------------- ----

Второй расчет - добавьте резистор 1 кОм к резистору 10 кОм параллельно:

LRC () с использованием внутренней частоты lrc_freq в Гц
LRC.add_parallel_r () 1000
LRC.add_parallel_r () 10000

Конечное значение комбинированного сопротивления = 909,090909090909
-------------------- конец вывода ---------------------------- ----
 

Пара замечаний о том, что здесь происходит.

• Это объектно-ориентированное программирование. Такие выражения, как lrc = LRC () — вот как Python создает объект.

• Первый резистор, добавленный к объекту, на самом деле не включен последовательно или параллельно, не имеет значения, добавляете ли вы параллельно или последовательно, сопротивление перед добавлением равно «Нет».

• Каждый раз, когда вы добавляете сопротивление, объект находит сопротивление, эквивалентное его старому значению в сочетании с добавленным вами значением. Он (вы) можете добавлять резисторы столько, сколько захотите, конечно, не ограничиваясь двумя резисторами.

Hippy’s Happy Калькулятор резисторов

Используя только резисторы в E12, E6, E3 и E1 диапазоны резисторов, калькулятор найдет пару резисторов, которые можно использовать для создать сопротивление, наиболее близкое к требуемому, а также сообщайте о любом лучшем совпадении, которое может быть получено с использованием трех резисторов (или с использованием четыре резистора для серий E1 и E3).

Обычно предпочтение отдается ближайшему решению, в котором используются резисторы в последовательно, а не параллельно, согласованные пары резисторов и резисторы Значение 1К, 10К и 100К.

Возможные комбинации резисторов, используемых при расчете, не исчерпывающий (поскольку время обработки может стать чрезмерно большим), но является Достаточно всеобъемлющий, чтобы найти подходящие пары практически для любого необходимого сопротивления.

Вы можете ввести необходимое сопротивление практически в любом формате; 1234, 1234R, 1.234К, 1K234, M001234 и 0M001234 имеют одинаковое сопротивление.

Вы также можете ввести уравнения сопротивления, используя ‘+’ для резисторов, включенных последовательно, и ‘|’ для резисторов параллельно. Сопротивление можно умножить и разделить на используя ‘*’ и ‘/’ соответственно. Круглые скобки ‘(‘ и ‘)’ могут использоваться для группировки резисторы устанавливаются вместе.

Например; необходимое сопротивление 24K5 можно ввести как «24K5», «24,5K», ’24 .5E3 ‘,’ 24K + 500R ‘,’ (48K | 48K) + (1K | 1K) ‘,’ 12K25 * 2 ‘,’ 98K / 4 ‘и многие другие способами.

Калькулятор не создаст решение, использующее одну стандартную серию E. резистор, указанный в поле Требуемое сопротивление, поскольку предполагается, что это значение недоступно; иначе зачем вам искать альтернативу решение использовать стандартное значение?

Фактический резистор допуски не учитываются при выполнении расчеты.

Результаты расчетов представлены в одном из следующих форматов …

9020 + R4

R1		Одиночный резистор
R1 + R2		Два последовательно подключенных резистора
R1 + R2 + R3		Три резистора последовательно	Четыре последовательно соединенных резистора
R1 | R2		Два резистора, включенных параллельно
R1 | R2 | R3		Три резистора параллельно
R1 | R2 | R3 | R4		Четыре резистора, включенных параллельно
R1 + (R2 | R3)		Один резистор, включенный последовательно с параллельной парой
R1 | (R2 + R3)		Один резистор, включенный параллельно с последовательной парой
R1 + R2 + (R3 | R4)		Два резистора, включенных последовательно с параллельной парой
R1 | R2 | (R3 + R4)		Два резистора, включенных параллельно последовательной паре
(R1 | R2) + (R3 | R4)		Две последовательно соединенные пары резисторов
(R1 + R2) | (R3 + R4)		Две пары резисторов, включенных параллельно

Например, сопротивление 24 кОм может быть сформировано из резисторов в E6 или E3. диапазон следующим образом…

2K2 + 22K		с ошибкой -1,22%, или
1K + (47K | 47K)		точное совпадение

Решение с тремя или четырьмя резисторами дается только в том случае, если они лучше, чем два. резистор можно найти, и его стоит проверить.

---

Допуски резистора

Хотя можно найти комбинацию резисторов, которая создаст любое произвольное значение сопротивления, в этом нет необходимости.

Все сопротивления имеют производственный допуск, который обычно +/- 1%, но может быть и +/- 10% в зависимости от типа резистора.

Исходные значения серии E были выбраны, чтобы воспользоваться преимуществами этого производства. неточность, поскольку любое специально требуемое значение обычно соответствует допустимому диапазону доступных номиналов резисторов. Обычно вполне приемлемо выбрать номинал резистора ближайший к требуемому, не создавая проблем с работа проектируемой схемы; вот почему имея только E3 или E1 диапазон значений приемлем во многих случаях.

Обычно бессмысленно создавать комбинацию резисторов, которая соответствует необходимое сопротивление именно тогда, когда используемые резисторы имеют широкий сами допуски, хотя найдено идеальное соответствие, допуски Фактические резисторы, используемые в решении, часто делают результат меньше, чем идеально.

Несмотря на проблему допуска, счетчик резисторов по-прежнему чрезвычайно полезно для тех, кто хранит в инвентаре только Е1, Значения резисторов E3 или E6 и необходимость чтобы обеспечить значение сопротивления, которое недоступно.

Калькулятор комбинации резисторов

Эта страница не работает с отключенным JavaScript

Введите необходимое сопротивление резистора в Ом (извините, сейчас нет синтаксического анализа / преобразования единиц измерения), выберите максимальное количество резисторов в комбинации, выберите номиналы резисторов, доступные для создания комбинации (вы даже можете выбрать собственные подмножества E12 или E24), отрегулируйте тип комбинации (только параллельный, только последовательный или оба), нажмите кнопку «Вычислить».
Имейте в виду, близость значения комбинации к требуемой не гарантирует, что вы действительно получите это значение, используя резисторы с допуском ± 10% (E12) или ± 5% (E24).

Каждый дополнительный резистор в комбинации улучшит качество полученных значений примерно на два порядка. Однако запрашиваются комбинации из большего количества резисторов. вызовет более длительный поиск комбинаций (экспоненциальный рост). Калькулятор ограничит максимальное количество резисторов в комбинации в зависимости от количества доступных значений входного резистора.

Желаемое значение
Набор резисторов Пользовательское подмножество E12E24E12 Пользовательское подмножество E24
Макс. # В комбинации 123456
Комбинированный тип Последовательный и параллельный только параллельный Только серия
Compute

• Для наборов входов до 24 значений вы можете запросить комбинации до 6 резисторов.
• Для наборов входов до 36 значений максимальное количество резисторов в комбинации составляет 5
• Для 72 входных значений (включая полный E12) могут быть запрошены комбинации до 4 резисторов
• Для более чем 72 значений будут рассматриваться только комбинации из 3 резисторов

Даже с этими ограничениями полное сканирование всех комбинаций может занять довольно много времени; нажмите кнопку «Отмена» раньше, если вы видите достаточно хороший результат

Комбинация (*: параллельно, +: последовательно)	Значение	Отн.err (% от целевого)	Мин. Значение (% от целевого)	Максимальное значение (% от целевого)

---

Код

доступен на github под CC-BY- NC — это творческое сообщество, совместное использование, указание авторства, некоммерческое использование.
Пока вы используете калькулятор на этой странице, ничего страшного.