Мощность цепи переменного тока: Мощность в цепи переменного тока и коэффициент мощности (косинус φ)

Содержание

Мощности в цепях переменного тока

Расчетные формулы для цепей однофазного тока

1. Мгновенное значение мощности в цепи с активным сопротивлением r, Вт:

Среднее значение активной мощности в цепи с активным сопротивлением г, Вт:

2. Цепи с чисто индуктивным сопротивлением: ток в цепи i=Im sinωt, тогда ЭДС самоиндукции

т.е. ЭДС отстает от тока, ее вызвавшего, на угол

Падение напряжения на катушке

Мгновенная мощность катушки

Средняя за период мощность идеальной катушки:

Это означает, что в течение периода идеальная катушка дважды получает от источника энергию, преобразуя ее в магнитное поле, и дважды возвращает ее.

Емкостное сопротивление, Ом,

ействующее значение тока, А,

Мгновенная мощность

Средняя мощность

В течение периода конденсатор дважды получает от источника энергию для заряда (создания электрического поля в диэлектрике) и дважды возвращает ее источнику (разряжается).

Реактивная мощность конденсатора, вар,

Из изложенного следует важный для практики вывод: токи индуктивности и емкости в цепи переменного тока в каждый момент времени направлены в

противоположные стороны. Другими словами, в каждый момент времени, когда катушка получает от источника электромагнитную энергию, конденсатор возвращает ее источнику и наоборот.

4. Цепь, содержащая последовательно включенные активное, индуктивное и емкостное сопротивления (рис. 1.9).

Реактивное сопротивление цепи, Ом,

Полное сопротивление цепи, Ом,

Угол сдвига фаз между векторами напряжения и тока

Коэффициент мощности цепи

Мгновенное значение приложенного напряжения равно сумме мгновенных значений падений напряжений на участках цепи:

Мгновенное значение мощности для этой цепи, Вт,

Среднее значение мощности равно активной мощности, Вт:

Реактивная мощность, вар,

Полная мощность, В-А,

При xL = xc имеет место резонанс напряжения, цепь ведет себя как чисто активная, а ток имеет наибольшее (при U = const) значение.

5. Цепь, содержащая параллельно включенные активное, индуктивное и емкостное сопротивления (рис. 1.10).

В такой цепи все элементы находятся под одинаковым напряжением источника

Проводимости элементов цепи:

активная, См,

емкостная,См,

индуктивная, См,

Угол сдвига фаз тока и напряжения

Полная проводимость цепи, содержащей элементы R, L, С, См:

Значения мощностей рассчитываются по приведенным выше формулам.

При вс= Bl имеет место резонанс токов. Общий ток в цепи имеет минимальное значение и активный характер.

На практике параллельное включение конденсаторов в однофазной и трехфазной цепях широко используется для разгрузки питающих линий (проводов, кабелей, шин) от реактивной (индуктивной) составляющей тока. Это позволяет уменьшить потери электроэнергии в передающих линиях, и тем самым экономить ее, выбирать меньшие сечения проводов и кабелей для питания тех же самых электроприемников.

Мощность переменного тока — Основы электроники

Мы знаем, что в цепях переменного тока между током и напряжением может возникнуть разность фаз.

Как же вычислить мощность переменного тока в этом случае, когда направления радиусов-векторов тока и напряжения не совпадают?

Представим себе, что мы тянем вагонетку с грузом, катящуюся по рельсам. Но наши усилия направлены не как обычно, вдоль рельсов, а под некоторым углом к ним. Угол между направлением движения вагонетки и направлением наших усилий обозначим буквой φ (фи).

Ясно, что при таком способе передвижения вагонетки часть наших сил будет затрачиваться бесполезно, не производя работы, то есть работа не будет равна произведению приложенной силы на пройденный путь, как обычно (работа = сила * путь),

а будет меньше этого произведения.

Для того чтобы вычислить количество произведенной работы, нужно силу, приложенную к вагонетке, разложить на две части или на две составляющие. Это разложение силы сделано на рисунке 1. Составляющая силы, направленная вдоль движения, которая называется проекцией силы на направление движения, будет полезной силой, а, составляющая, направленная под прямым углом к направлению движения, будет силой бесполезной.

Если стрелка (вектор), изображающая силу, вычерчена в масштабе, то, измерив полезную составляющую силы, мы можем определить количество работы: работа = полезная сила * путь.

Теперь обратимся к радиусам-векторам тока и напряжения. Здесь полностью применим тот же самый метод.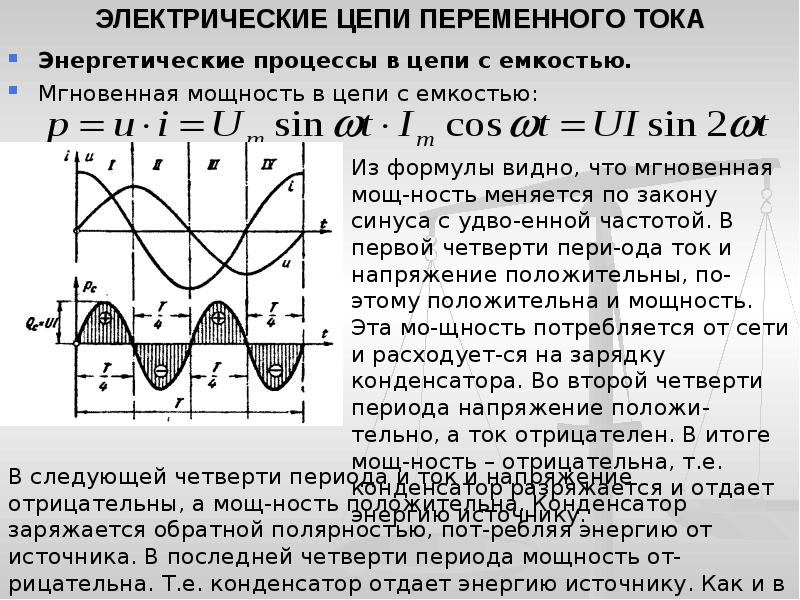 Мощность переменного тока при разности фаз φ = 0° будет равна половине произведения вектора напряжения Um и вектора тока Im.

Тогда мощность переменного тока, при разности фаз φ не равной нулю, будет равна половине произведения вектора напряжения Um и проекции вектора тока Imп, проецируемого на вектор напряжения (рисунок 2). Как нетрудно видеть, величина проекции зависит, во-первых, от длины проецируемого вектора, а во-вторых, от угла между ним и направлением, на которое он проецируется.

Если обозначить этот угол буквой φ, то длина проекции будет равна длине проецируемого вектора, умноженной на особый коэффициент, характеризующий этот угол, называемый косинусом угла (cos φ ). Значения косинусов различных углов приведены в таблице.

Итак, проекция радиуса-вектора равна длине радиуса-вектора, умноженной на cos φ.

И, следовательно, мощность переменного тока равна:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Мощность в цепи переменного тока

«Природа так обо всём позаботилась,

что повсюду ты находишь, чему учиться».

Леонардо да Винчи

Задача 1. В цепь переменного тока последовательно с лампочкой включен конденсатор с переменной ёмкостью. Как изменится накал лампы, если: а) не меняя частоту, уменьшить ёмкость конденсатора б) не меняя ёмкости, уменьшить частоту?

РЕШЕНИЕ:

Накал лампы напрямую зависит от мощности, поэтому, чтобы понять, как изменится накал, нам нужно узнать, как изменится мощность. Запишем формулу, по которой вычисляется мощность в цепи переменного тока.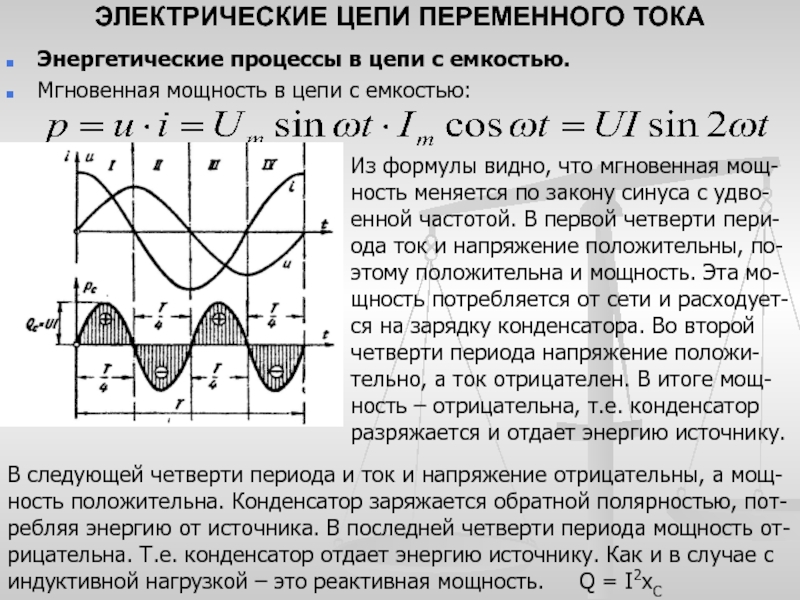

Сопротивление лампочки никак не зависит от частоты. Установим, как зависит сила тока от указанных параметров. Для этого, в первую очередь, вспомним связь между амплитудными значениями заряда и напряжения, а затем – связь между амплитудными значениями заряда и силы тока.

Исходя из этих двух соотношений, выведем зависимость амплитудного значения силы тока от амплитудного значения напряжения.

Запишем теперь общее уравнение для гармонических колебаний силы тока и преобразуем это уравнение в соответствии с выведенной зависимостью.

Амплитудное напряжение остаётся неизменным, поскольку оно задано источником переменного тока. Поэтому, исходя из полученного уравнения, накал лампы уменьшится и при уменьшении ёмкости конденсатора, и при уменьшении частоты.

Ответ

: а) накал лампы уменьшится; б) накал лампы уменьшится.

Задача 2. В цепи без активного сопротивления действующие значения силы тока и напряжения равны 2 А и 50 В соответственно.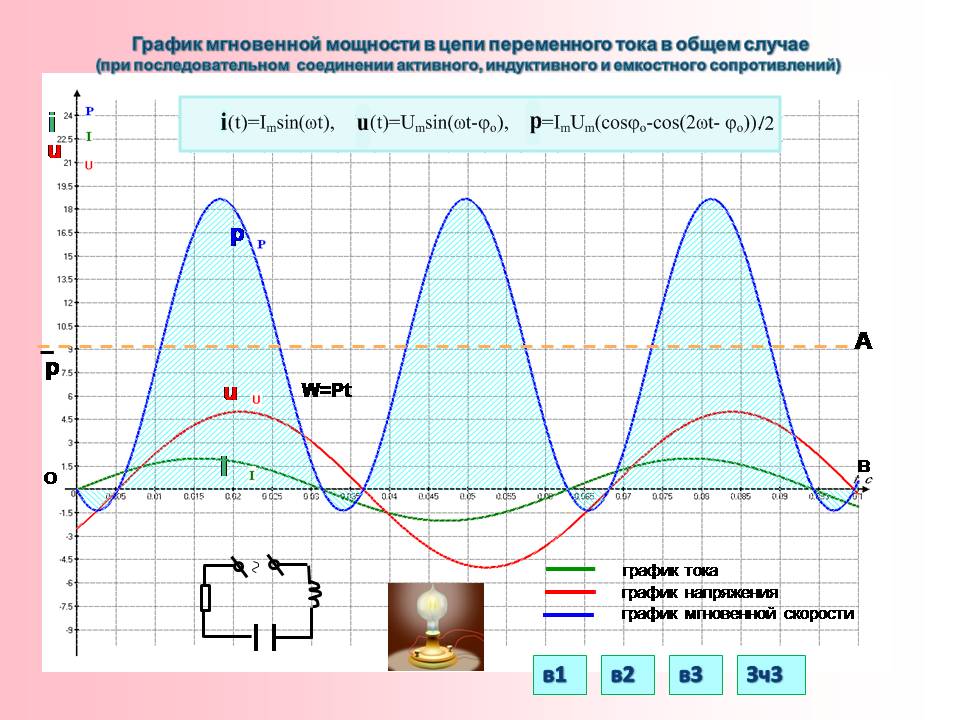 Найдите разность фаз между колебаниями тока и напряжения, если средняя мощность цепи равна 70,7 Вт.

ДАНО:

РЕШЕНИЕ

Мощность в цепи переменного тока определяется по формуле

Тогда

Ответ: ток отстаёт от напряжения на рад.

Задача 3. В цепь переменного тока последовательно включены резистор с сопротивлением 50 Ом, конденсатор с ёмкостью 50 мкФ и катушка с индуктивностью 2 мГн. Амплитудное напряжение на зажимах равно 220 В, частота колебаний равна 100 Гц. Найдите активную мощность цепи.

ДАНО:

СИ

РЕШЕНИЕ

Запишем закон Ома для цепей переменного тока

Полное сопротивление цепи определяется по формуле

Тогда сила тока равна

Активная мощность определяется по формуле

Действующие значения напряжения и силы тока определяются по формулам

Тогда активная мощность равна

С учётом того, что активная мощность равна

активная мощностьравна

Ответ: 352 Вт.

Задача 4. В сеть переменного тока последовательно включен конденсатор ёмкостью 50 мкФ и катушка с индуктивностью 20 мГн. Активное сопротивление цепи равно 80 Ом. Известно, что за один период колебаний током совершается работа, равная 10 Дж. Действующее значение напряжения равно 100 В. Найдите среднюю мощность цепи и действующее значение силы тока. Частота колебаний равна 50 Гц.

ДАНО:

СИ

РЕШЕНИЕ

Мощность – это работа в единицу времени

Мощность в цепи переменного тока определяется по формуле

Запишем формулу, с помощью которой можно вычислить разность фаз

Индуктивное и ёмкостное сопротивления определяются по формуле

Циклическую частоту можно найти по выражению

Тогда разность фаз

Действующее значение силы тока равно

Мощности в цепях переменного тока

Мощности в цепях переменного тока

Категория:

Сварка металлов

Мощности в цепях переменного тока

В электрических цепях переменного тока с реактивными сопротивлениями различают три вида мощности: полную, активную и реактивную.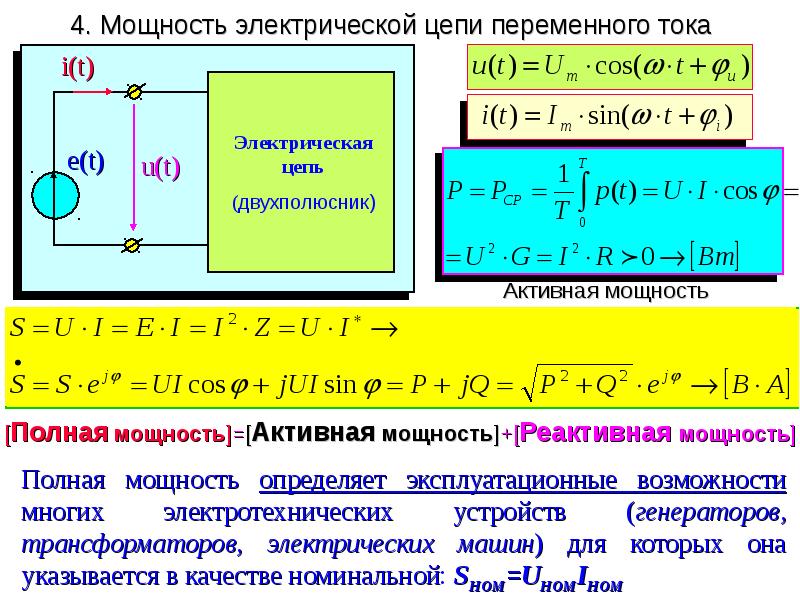 Полная мощность электроустановки переменного тока состоит из мощности, расходуемой в активном сопротивлении и реактивной части мощности (геометрическая сумма).

Размеры электроустановок переменного тока (генераторы, трансформаторы, электродвигатели) определяются полной мощностью, на которую они рассчитаны. Это связано с тем, что толщина изоляции этих устройств рассчитывается на определенное номинальное напряжение, а сечение проводов обмоток их — на определенный номинальный ток. Номинальными величинами отдельно ограничиваются напряжение и ток, причем эти ограничения не зависят от сдвига по фазе между напряжением и током.

Единицами полной мощности служат вольт-ампер (ВА) и киловольт-ампер (кВА). На табличках генераторов и трансформаторов указывается полная мощность. На табличках электродвигателей указывается активная (полезная) мощность, которую они могут развить. Полную мощность электродвигателя, которую он потребляет от электрической сети, можно определить расчетным способом, Полная мощность цепи переменного тока определяется произведением напряжения на ток.

Рис. 1. Емкость в цепи переменного гока

Реактивная часть полной мощности обусловлена колебаниями энергии при возникновении и исчезновении магнитных и электрических полей. В электрической цепи переменного тока с реактивными сопротивлениями происходит «перекачивание» энергии от источника к реактивным сопротивлениям и обратно. Реактивные токи, протекающие между источником (генератором) и реактивными приемниками, бесполезно загружают генератор, трансформаторные подстанции, линии передачи и этим вызывают дополнительные потери энергии.

Реактивная мощность измеряется в вольт-амперах реактивных и киловольт-амперах реактивных.

Статьи по теме:

Открытая Физика. Закон Ома для цепи переменного тока. Мощность

В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности: RIR=UR; 1ωCIC=UC; ωLIL=UL.

Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.

Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R, 1ωC и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.

При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J ċ u. Практический интерес представляет среднее за период переменного тока значение мощности P=Pср=I0 U0cosωtcos(ωt+φ)¯.

Здесь I₀ и U₀ – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0: PR=IRURcos2ωt¯=IRUR2=IR2R2.

Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения: Iд=I02; Uд=U02.

Средняя мощность переменного тока на участке цепи, содержащем резистор, равна PR=IдUд.

Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением φ=π2. Поэтому PC=ICUCcosωtcos(ωt+π2)¯=ICUCcosωt( -sin ωt)¯=0.

Аналогично можно показать, что P_L = 0.

Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.

Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать J (t) = I₀ cos ωt; e (t) = ℰ₀ cos (ωt + φ).

Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна P=I0ℰ0cosωtcos(ωt+φ)¯=I0ℰ02cosφ=Iдℰдcosφ.

Как видно из векторной диаграммы, U_R = ℰ₀ · cos φ, поэтому P=I0UR2. Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.

В § 2.3 было выведено соотношение между амплитудами тока I₀ и напряжения ℰ₀ для последовательной RLC-цепи: I0=ℰ0R2+(ωL-1ωC)2.

Величину Z=R2+(ωL-1ωC)2 называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде ZI₀ = ℰ₀.

Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).

Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).

Параллельный RLC-контур

При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.

Векторная диаграмма для параллельного RLC-контура

Из диаграммы следует: I0=ℰ0(1R)2+(ωL-1ωC)2.

Поэтому полное сопротивление параллельного RLC-контура выражается соотношением Z=1(1R)2+(ωL-1ωC)2.

При параллельном резонансе (ω² = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора: Z = Z_max = R.

Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.

Мощность цепи переменного тока — Энциклопедия по машиностроению XXL

Мощность цепи переменного тока полная (ВА) S = Ul активная (Вт) Р = UJ os (р = г, реактивная (вар) ( = t// sin ф = Р tg ф.

[c.113]

Мощность цепи переменного тока активна ) [c.341]

При измерении мощности цепей переменного тока высокого напряжения включение обмоток ваттметров производится через измерительные трансформаторы. Например, схема Арона при высоком напряжении будет выглядеть так, как это показано на фир. 75. [c.374]

Мощность цепи переменного тока полная [c.224]

Мощность цепи переменного тока (активная) [c.460]

Мощность цепи переменного тока полная S = UI ва активная Р == I/7 os ф = ЛГд вш реактивная [c.113]

Для цепей, не содержащих стали, при промышленных частотах активное сопротивление можно принимать равным омическому г. Мощность цепи переменного тока (активная) [c.208]

Фиг. 1. Схема соединений для измерения мощности цепи переменного тока с измерительными трансформаторами

Отсюда средняя мощность на участь е цепи переменного тока равна произведению квадрата действующего значения силы тока lia активное сопротивление R участка цепи [c.241]

Найдите среднюю мощность, выделяющуюся на активном сопротивлении в цепи переменного тока при амплитудном значении силы тока 2 А и амплитудном значении напряжения 310 В. [c.296]

Найдите активное сопротивление электрической лампы накаливания, включенной в цепь переменного тока с действующим напряжением 220 В, при этом выделяется средняя мощность 100 Вт. [c.296]

На выходе электронного реле мод. 238 — 2 установлено реле типа РЭН-18, износоустойчивость выходных контактов которого 1 млн. срабатываний при индуктивной нагрузке не более двух генри и разрывной мощности не более 50 вт в цепи постоянного тока, не более 500 вт в цепи переменного тока (величина тока через контактную пару допускается не более 5 а). [c.41]

Мощность в цепи переменного тока. [c.520]

Измерение мощности в цепях переменного тока производится с помощью ваттметра. Схема включения ваттметра приведена на фиг. 22. Коэфициент мощности ( os (у) подсчитывается из выражения [c.526]

Аварийный винтовой насос служит для подачи масла в систему в случае разрыва цепи переменного тока. Насос приводится от электродвигателя постоянного тока мощностью 2,5 л. с. [c.113]

Средняя мощность, выделяемая в цепи переменного тока, возникающего в колебательном контуре, [c. 221]

Величина нагрузки контролировалась по прибору К-50, который предназначен для измерения потребляемой мощности в однофазных и трехфазных цепях переменного тока при равномерной и неравномерной нагрузке фаз. Предварительно зубчатые пары прирабатывались (с маслом) без нагрузки в течение 3 ч. Испытания проводились с указанной выше нагрузкой в течение 120 ч. Износ определялся через каждые 20 ч работы редуктора измерением толщины зубьев в трех сечениях по ширине. Измерения проводились на шести зубьях, расположенных равномерно по окружности. Температура масла в редукторах в процессе испытания не превышала 50 °С. [c.118]

Полной мощностью 5 цепи переменного тока называется величина, равная произведению действующих значений напряжения U и силы тока I [c.306]

Магнитный усилитель представляет собой электромагнитное устройство, в котором с помощью сигнала постоянного тока осуществляется управление значительно большей мощностью переменного тока. На рис. 31, а представлен магнитный усилитель на двух сердечниках 2 и 3 с общей управляющей обмоткой 5, намотанной на оба сердечника. Обмотка 5 присоединена к цепи постоянного тока, а обмотки 4п 1 — к цепи переменного тока. Небольшие изменения силы постоянного тока в обмотке 5 меняют индуктивное сопротивление и силу тока в обмотках 4и I. Магнитные усилители виброустойчивы, дешевы, имеют большой коэф- [c.163]

Предельный коэффициент эффективности акустического излучения. В цепях переменного тока с последовательным соединением мощность, расходуемая источником э.д. с., идет на нагревание активного сопротивления. Индуктивная нагрузка накапливает энергию в форме энергии магнитного поля и периодически обменивается ею с источником напряжения. Аналогичный процесс осуществляется и в поле при излучении акустических волн мощность источника энергии излучателя поглощается в виде потока энергии аку- [c.200]

Высокая частота вводится в цепь переменного тока (127/220 В и 50 Гц), питающую дуговой разряд (контур I на рис. II.8) с помощью индукционной катушки Трь которая связана с высокочастотным контуром II. Контур питается от трансформатора небольшой мощности Тр2, напряжение которого регулируется сопро-тивление.м Rz- Цепь вторичной обмотки замкнута через конденсатор Сг и сопротивление Rz. По мере повышения напряжения сети переменного тока в начале каждого полупериода (т. е. 100 раз в секунду) конденсатор заряжается. Зарядка продолжается до тех пор, пока напряжение на нем не достигнет напряжения пробоя вспомогательного разрядного промежутка Разг. В этом контуре [c.133]

Из сказанного ясно, что мощность, связанная с компонентой скорости, отстающей на 90° от давления, является реактивной мощностью, аналогичной мощности, потребляемой индуктивностью в цепи переменного тока. [c.67]

Таким образом, мощность, связанная с реактивной частью импеданса, аналогична мощности, потребляемой индуктивностью в цепи переменного тока, а сама реактивная часть 1т 2 — индуктивному сопротивлению катушки. Активная же часть Не 2 = р с ЗоЯ определяет мощность, необратимо теряемую источником на излучение в среду, и она эквивалентна активному сопротивлению электрической цепи. Поэтому эквивалентная схема акустического импеданса пульсирующей сферы может быть представлена параллельно соединенными катушкой и омическим сопротивлением. [c.208]

Максимальная мощность для размыкания контактов реле в цепи постоянного тока 50 вт, в цепи переменного тока—500 вт. [c.73]

ВКЛЮЧЕНИЕ АКТИВНЫХ, ИНДУКТИВНЫХ И ЕМКОСТНЫХ ПРИЕМНИКОВ В ЦЕПЬ ПЕРЕМЕННОГО ТОКА. МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА И КОЭФФИЦИЕНТ МОЩНОСТИ [c.35]

При наличии в цепи переменного тока всех трех сопротивлений величина сдвига фаз между током и напряжением будет зависеть от соотношений между отдельными сопротивлениями. Мощность переменного тока выражается формулой [c.35]

Если цепь переменного тока содержит только активную нагрузку, то полная мощность является активной мощностью и в этом случае коэффициент мощности равен I.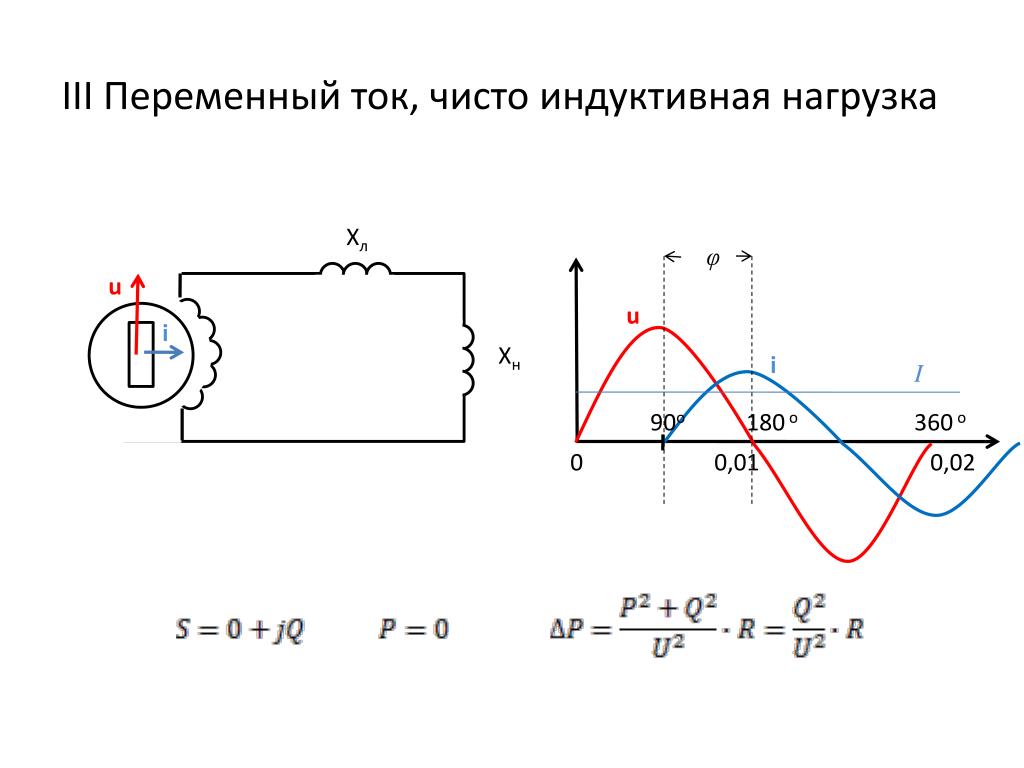 [c.36]

Электродвижущая сила в проводнике, вращающемся в магнитом поле. Основные понятия о переменном токе. Понятие о периоде и частоте. Эффективный ток и эффективное напряжение. Самоиндукция и емкость в цепи переменного тока. Понятие о фазе. Трехфазный ток. Соединение звездой и треугольником. Мощность трехфазного тока. [c.507]

Обозначения h(H) — высота оси вращения i3jj — наружный диаметр сердечников статоров (для асинхронных двигателей) Р — номинальная мощность 7 — номинальное напряжение питания /ц —номинальное значение силы тока — номинальная частота вращения вала — номинальный момент max — максимальная частота вращения вала т — коэффициент полезного действия Ля — сопротивление якорной обмотки Лд — сопротивление дополнительных полюсов (на дополнительных полюсах располагается компенсационная обмотка, которая включается последовательно с обмоткой якоря и предназначена для улучшения процесса коммутации в щеточно-коллекторном узле) — сопротивление обмотки возбуждения — индуктивность обмотки якоря J — момент инерции якоря S — номинальное скольжение М ах> — максимальный и пусковой момент на валу соответственно (для асинхронных двигателей) — пусковой ток os ф — коэффициент мощности (отношение активной мощности цепи переменного тока к полной мощности, чем ближе к единице, тем лучше). [c.194]

В цепях переменного тока рассеяние мощности в катушках индуктивности иногда оценивают тангенсом угла магнитных потерь. Тороидальную катушку индуктивности с сердечником из магнитного материала, собственной емкостью и сопротивлением обмотки 1чОторой можно пренебречь, представим в виде схемы, состоящей из последовательно соединенных индуктивности L и сопротивления 1квивалентн0г0 всем видам потерь мощности в магнетике (рис. 9-10) для этого случая из векторной диаграммы получим [c.273]

В электростатической форме удается запасти небольшое количество энергии, например в 1 м при технически осуществимом значении Е = 10 В всего 0,440 кДж. Эта энергия может играть значительную роль при включении конденсаторов в цепь переменного тока, меняющего 100 раз в секунду свое напряжение, когда конденсатор заряжается и разряжается в течение V200 с так, что отдаваемая при разрядке или требующаяся при зарядке средняя мощность составит значительную величину. Запас энергии в электретах ничтожен. [c.118]

Концевые и путевые выключатели и микровыключателн муфты ограничения крутящего момента должны работать в цепи переменного тока напряжением 220 В. Разрывная мощность контактов не менее 100 Вт. [c.78]

С учётом потерь в баластном дросселе световая отдача флюоресцентных ламп превышает световую отдачу ламп накаливания соответствующих мощностей в 3—3,5 раза. Это свойство флюоресцентных ламп, несмотря на некоторые их недостатки (сложность пуск0В010 устройства, зависимость световой отдачи от температуры окружающего воздуха, непостоянство светового потока во времени при включении ламп в цепь переменного тока), обеспечило внедрение их в практику промышленного освещения. [c.525]

РПИБ-М Регулирование электрической активной мощности в трехфазных цепях переменного тока Переменный, частота 50 Гц 2 Первичный прибор с дифференциально — трансформаторным датчиком производства завода Манометр и датчиком трансформатора тока ДТТ-58 производства МЗТА Вместо указанного прибора с дифференциально — трансформаторным датчиком могут применяться Первичные приборы с ферродинамиче-скими, индукционными или реостатными датчиками [c. 771]

Диэлектрические потери представляют собой часть энергии электрического поля, которая превращается в диэлектрике в теплоту и нагревает его. При частотах свыше 20 кГц их величина становится одним из самых важных параметров диэлектрика. Для определения потерь диэлектрик удобно рассматривать как конденсатор в цепи переменного тока (рис. 18.24). У идеального конденсатора угол сдвига фаз между током / и напряжением U равен 90°, поэтому активная мощность Na, = IU osy равна нулю. Диэлектрик не является идеальным конденсатором, и угол сдвига фаз у него меньше 90° на угол 6, называемый углом диэлектрических потерь. Тангенс угла S и диэлектрическая постоянная е характеризуют удельные потери (на единицу объема диэлектрика), Вт/м [c.602]

Микропроцессорное управляющее устройство ПРОЛОГ 101 (ОАО МЗТА ) предназначено для автоматического управления паровыми и водогрейными газомазутными одногорелочными каналами небольщой мощности. Основные функции управление пуском, остановом котла автоматическое регулирование параметров автоматическая защита от недопустимых состояний котла и его оборудования. Входные сигналы аналоговые от датчиков температуры, давления, уровня и т.д. по девяти каналам дискретные — по 24 каналам. Выходные сигналы импульсные для управления по ПИ-алгоритму двумя ЭИМ, дискретные (контакты реле для коммутации цепей переменного тока 24,250 В) — по 18 каналам. Габаритные размеры (ширина, высота, глубина) 300x320x350 мм. масса — 12 кг [c.557]

Алюминиевые фольговые конденсаторы выпускаются и для цепей переменного тока (К50-19). В таких конденсаторах обе обкладки делаются на одинаково заформованных алюминиевых лент — анодов, разделенных бумагой, пропитанной электролитом, т. е. фактически мы имеем два электролитических конденсатора, включенных последовательно емкость такого неполярного конденсатора в 2 раза меньше обычного полярного. Неполярные конденсаторы выпускаются на напряжение до 320 В (действующее значение) и емкость до 750 мкФ. Они чаще всего применяются в пусковых цепях однофазных асинхронных двигателей малой мощности, в качестве фильтров в цепях низких и звуковых частот. Для длительного включения в цепи переменного тока такие конденсаторы целесообразно применять при низких рабочих напряжениях, когда сохраняются их габаритные преимущества по сравне- [c.261]

Изменение тока в электрической цепи (включение, выключение) вызывает появление в ней ЭДС самоиндукции, препятствующей этому изменению. При увеличении тока она направлена против ЭДС источника напряжения, а при уменьшении тока, она мешает ему исчезнуть. Сопротивление в цепи, возникающее в результате действия ЭДС самоиндукции, называется индуктивным, а сопро-тивл 1ние проводников цепи—активным. Вся мощность, получаемая цепью переменного тока, называется кажущейся и состоит из активной и реактивной — мощностей. Активная мощность расходуется на нагрев. В двигателях переменного тока большая часть активной мощности превращается в механическую. Реактивная мощность обусловлена наличием магнитных и электрических полей в индуктивностях и емкостях цепей. В цепи с индуктивной нагрузкой нельзя избежать наличия реактивной мощ- [c.31]

Контакторы переменного тока делают трехполюсными. Обозначают их буквами КТ. Контакторы переменного тока с магнитной системой постоянного тока типов КТП и КТПВ, предназначенные для переключения цепей переменного тока, не имеют недостатков магнитных систем переменного тока и отличаются меньшими габаритными размерами. Мощность, необходимая для питания катушек контакторов, значительно меньше мощности двигателей, управляемых контакторами. Поскольку токи в управляющих цепях контакторов незначительны, они могут замыкаться кнопками или контактами электромагнитных реле. [c.116]

Электрические цепи переменного тока

Переменный ток получил гораздо большее распространение в промышленности и в быту, чем постоянный, так как упрощается конструкция электродвигателей, а синхронные генераторы могут быть выполнены на значительно большие мощности и более высокие напряжения, чем генераторы постоянного тока. Переменный ток позволяет легко изменять величину напряжения с помощью трансформаторов, что необходимо при передаче электроэнергии на большие расстояния.

Электрический ток, возникающий под действием э. д. с, которая изменяется по синусоидальному закону, называют переменным. По существу, переменный ток — это вынужденные колебания тока в электрических цепях.
Амплитудой переменного тока называется наибольшее значение, положительное или отрицательное, принимаемое переменным током.
Периодом называется время, в течение которого происходит полное колебание тока в проводнике.
Частота — величина, обратная периоду.
Фазой называется угол или , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
Периодический режим: . К такому режиму может быть отнесен и синусоидальный:

где
— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f=50Гц T= 1/f=0,02 с, 314рад/с.

График синусоидальной функции называется волновой диаграммой.

Расчет цепей переменного тока с использованием мгновенных значений тока, напряжения и ЭДС требует громоздкой вычислительной работы. Поэтому изменяющиеся непрерывно во времени токи, напряжения и ЭДС заменяют эквивалентными во времени величинами.
При расчете электрических цепей синусоидальную функцию выражают по формуле Эйлера через экспоненциальные функции:

где

Тогда

где

— поворотный множитель;
— комплексная амплитуда напряжения;
— сопряженная комплексная амплитуда напряжения.

Таким образом, синусоидальное напряжение можно представить на комплексной плоскости вращающимся вектором. Тогда амплитудное значение напряжения будет представлять собой модуль или длину вектора напряжения.

Вектор напряжения на комплексной плоскости
Так как в цепи с синусоидальным напряжением ток тоже будет подчиняться этому закону, то аналогично можно записать

где
— комплексная амплитуда тока; *
— сопряженная комплексная амплитуда тока.
Разделив напряжение на ток, получим закон Ома в комплексном виде:

При напряжение на сопротивлении согласно закону Ома . Таким образом, следует отметить, что на активном сопротивлении напряжение и ток совпадают по фазе и (см. рисунок).

Кривые напряжения и тока в активном сопротивлении

Величину переменного напряжения или тока можно оценить значением амплитуды или средним значением за полупериод или действующим значением. При изменении напряжения или тока по закону синуса среднее значение напряжения определяется:

При большой частоте вращения ротора генератора, т. е. при большой частоте колебаний э. д. с. и силы тока, измерять их амплитуды на практике крайне неудобно. По этой причине ввели величины, названные действующими значениями э. д. с, силы тока и напряжения.
Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.

откуда

При синусоидальном законе действующие значения тока и напряжения:

Приборы электромагнитной системы, применяемые для измерений напряжений и токов на переменном токе, регистрируют действующие значения. Соответственно градуируются и шкалы этих приборов

Кривые напряжения и тока в индуктивном сопротивлении

Напряжение на индуктивности определяется выражением

где

-индуктивное сопротивленияе
Индуктивное сопротивление выражают в омах, оно играет роль сопротивления в цепи переменного тока с катушкой индуктивности.
В идеальной индуктивности ток отстает от напряжения на 90°.

Если напряжение на емкости меняется по закону синуса , то

-емкостное сопротивление.
Емкостное сопротивление выражается в омах, оно играет роль сопротивления в цепи переменного тока с конденсатором.
Кривые напряжения и тока в емкостном сопротивлении
В идеальной емкости ток опережает напряжение на 90°

Режим — состояние электрической цепи переменного тока описывается дифференциальными уравнениями, представляющими собой уравнения с постоянными коэффициентами и правой частью, например:

Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов:

где
— ток принужденного режима при di/dt=0
— ток свободного режима.
Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать. Принужденный и свободный режимы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому.
При установившемся режиме ток и напряжение сохраняют в течение длительного времени амплитудные значения.
В цепях постоянного тока токи и напряжения остаются неизменными, а в цепях переменного тока остаются неизменными кривые изменения токов и напряжений.

Мощность цепи переменного тока

В периодическом синусоидальном режиме

Используя известное тригонометрическое преобразование

и обозначив , получим

Среднее за период значение гармонической функции удвоенной частоты равно нулю.
Измерение мгновенного значения мощности переменного тока затруднено из-за сравнительно большой частоты колебаний (v = 50 Гц). Поэтому на практике принято пользоваться средней мощностью тока. Средняя мощность — это отношение энергии, потребляемой за один период, к периоду:

где
— энергетическое значение коэффициента мощности,

Потребляемая на участке цепи с резистором средняя мощность получила название активной мощности. Она необратимо преобразуется в джоулеву теплоту и другие виды энергии. Мощность, потребляемую на участках цепи с емкостным и индуктивным сопротивлениями, называют реактивной мощностью.
При передаче электрической энергии по цепи переменного тока ее необратимые преобразования происходят только на тех участках цепи, которые содержат резисторы. Такие участки цепи называют активной нагрузкой. На активной нагрузке электроэнергия превращается в теплоту или механическую работу.
Участок цепи с индуктивностью или емкостью называют реактивной нагрузкой. На участках цепи, которые состоят из чистых емкостных или индуктивных сопротивлений, электроэнергия не потребляется. В цепи с реактивными нагрузками происходит только перекачка энергии от генератора к нагрузке и обратно с неизбежными потерями в подводящих проводах.

При заданных Р и U ток является функцией cosj. Потери мощности на сопротивлении
В цепи с резистором j=0.

Коэффициент мощности cosj показывает, какая часть полной мощности, вырабатываемой генератором и передаваемой нагрузке, необратимо используется нагрузкой. Он играет важную роль в электротехнике. В самом деле, если в цепи имеется значительный сдвиг по фазе между колебаниями тока и э. д. с, то коэффициент мощности мал и нагрузка потребляет от генератора малую активную мощность. Вместе с тем генератор должен вырабатывать полную мощность S. Эту же мощность должен отдавать генератору первичный двигатель. Таким образом, при низком коэффициенте мощности нагрузка потребляет лишь часть энергии, которую вырабатывает генератор. Оставшаяся часть энергии перекачивается периодически от генератора к потребителю и обратно и рассеивается в линиях электропередачи.
Максимально благоприятные условия передачи электроэнергии создаются в цепи, работающей в режиме резонанса. В самом деле, при приближении к резонансу амплитуда силы тока оказывается максимальной и коэффициент мощности стремится к единице. В этом случае активная мощность приближается к полной мощности, т. е. достигает максимума.
Повышение к. м. является важной народнохозяйственной задачей, от решения которой зависит эффективность использования вырабатываемой электроэнергии.
Уменьшение к. м. в промышленных цепях происходит в основном за счет содержащихся в них трансформаторов и асинхронных электродвигателей, имеющих значительные индуктивные сопротивления. Поэтому повысить к. м. при таких нагрузках можно путем подключения параллельно основной цепи компенсирующих конденсаторов, позволяющих приблизиться к режиму резонанса токов.
С целью повышения к. м. и экономии электроэнергии не следует допускать холостого хода (т. е. работы без нагрузки) трансформаторов и асинхронных электродвигателей, ибо в этом случае они представляют собой чисто индуктивные сопротивления и вызывают дополнительные потери мощности.
Коэффициент мощности (к. м.) ни в коем случае нельзя путать с коэффициентом полезного действия (к. п. д.). Так, например, при определенном соотношении емкости и индуктивности коэффициент мощности в данной цепи может оказаться равным единице. Коэффициент же полезного действия цепи всегда меньше единицы.

Мощность цепи переменного тока

Мощность в активном сопротивлении

Мгновенное значение мощности для цепи с резистором:

Из рисунка видно, что потребляемая резистором мгновенная мощность остается все время положительной, но пульсирует с удвоенной по отношению к силе тока и э. д. с. частотой.

Действующее значение мощности:

Активная мощность в цепи с идеальной катушкой индуктивности и конденсатором равна 0. Реактивная мощность определяется выражением:

Аналогично можно проделать для цепи с идеальным конденсатором:

В произвольной цепи переменного тока потребляемая одновременно активной и реактивной нагрузками суммарная мощность

Но так как , следовательно, . Мы приходим к выводу, что суммарная средняя мощность, потребляемая полной цепью переменного тока, равна активной мощности.

где S — полная мощность, вырабатываемая генератором переменного тока, ВА;
a — сдвиг по фазе между колебаниями э. д. с. и силы тока.

15.5: Питание в цепи переменного тока

Цели обучения

К концу раздела вы сможете:

Опишите, как можно записать среднюю мощность от цепи переменного тока в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения.
Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности

Элемент схемы рассеивает или производит мощность в соответствии с \ (P = IV \), где I — ток через элемент, а \ (V \) — напряжение на нем.Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность \ (p (t) = i (t) v (t) \) также зависит от времени. График \ (p (t) \) для различных элементов схемы показан на рисунке \ (\ PageIndex {1} \). Для резистора \ (i (t) \) и \ (v (t) \) синфазны и, следовательно, всегда имеют один и тот же знак. Для конденсатора или катушки индуктивности относительные знаки \ (i (t) \) и \ (v (t) \) меняются в течение цикла из-за разницы фаз. Следовательно, \ (p (t) \) в одни моменты времени положительно, а в другие — отрицательно, что указывает на то, что емкостные и индуктивные элементы вырабатывают энергию в одни моменты и поглощают ее в другие.

Рисунок \ (\ PageIndex {1} \): График мгновенной мощности для различных элементов схемы. (a) Для резистора \ (P_ {ave} = I_0V_0 / 2 \), тогда как для (b) конденсатора и (c) катушки индуктивности \ (P_ {ave} = 0 \). (d) Для источника \ (P_ {ave} = I_0V_0 (cos \, \ phi) / 2 \), который может быть положительным, отрицательным или нулевым, в зависимости от \ (\ phi \).

Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью .T \ sin \ omega t \, \ cos \, \ omega t \, dt = 0. \ nonumber \]

Следовательно, средняя мощность, связанная с элементом схемы, равна

\ [\ boxed {P _ {\ mathrm {ave}} = \ frac {1} {2} I_ {0} V_ {0} \ cos \ phi.} \ Label {eq5} \]

В инженерных приложениях \ (\ cos \ phi \) известен как коэффициент мощности , который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за отсутствия напряжения и тока. фазы.{2} R. \ label {eq10} \]

Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения. Оба уравнения \ ref {eq5} и \ ref {eq10} верны для средней мощности, но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.

Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна \ (110 \ sqrt {2} \, V = 156 \, V \).Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, типичный вольтметр переменного тока, установленный на бытовой розетке, будет показывать 110 В.

Для конденсатора и катушки индуктивности, \ (\ phi = \ pi / 2 \) и \ (- \ pi / 2 \, rad \), соответственно. Поскольку \ (\ cos \, \ pi / 2 = cos (- \ pi / 2) = 0 \), мы находим из уравнения \ ref {eq5}, что средняя мощность, рассеиваемая любым из этих элементов, равна \ (P_ {ave } = 0 \). Конденсаторы и катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода.Это поведение проиллюстрировано на графиках на рисунках \ (\ PageIndex {1b} \) и \ (\ PageIndex {1c} \), которые показывают, что \ (p (t) \) колеблется синусоидально около нуля. 2}} = \ dfrac {R} {Z}.{-6} F \) и \ (R = 5.00 \, \ Omega \).

Какое действующее значение напряжения на генераторе?
Какое сопротивление цепи?
Какая средняя выходная мощность генератора?

Стратегия

Действующее значение напряжения — это амплитуда напряжения, умноженная на \ (1 / \ sqrt {2} \). Импеданс цепи включает сопротивление и реактивные сопротивления конденсатора и катушки индуктивности. Средняя мощность рассчитывается по формуле \ ref {eq30}, потому что у нас есть полное сопротивление цепи \ (Z \), среднеквадратичное напряжение \ (V_ {rms} \) и сопротивление \ (R \).2 / R \), где В заменяет действующее значение напряжения.

Упражнение \ (\ PageIndex {1A} \)

Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.

Ответ: \ (v (t) = (10.0 \, V) \, \ sin \, 90 \ pi t \)

Упражнение \ (\ PageIndex {1B} \)

Покажите, что среднеквадратичные значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток равен \ (I_ {rms} \), выражаются как \ (I_ {rms} R, \, I_ {rms} X_C \) и \ (I_ {rms} X_L \) соответственно.Определите эти значения для компонентов цепи RLC по формуле \ ref {eq5}.

Ответ: 2,00 В; 10,01 В; 8.01 В

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (by 4.0).

Мощность в цепи переменного тока — Circuit Globe

Мощность трехфазной цепи переменного тока используется в крупных отраслях промышленности для работы тяжелых машин. Питание от однофазной сети переменного тока используется для управления малой бытовой техникой. Величина мощности трехфазной цепи переменного тока в три раза больше, чем мощность однофазной цепи.

Рассмотрим, если P — мощность однофазной цепи, то 3P — это мощность трехфазной симметричной цепи переменного тока.Мощность несимметричной трехфазной цепи определяется суммированием мощности отдельной фазы.

Как рассчитать мощность цепи переменного тока?

В цепи постоянного тока значение напряжения и тока становится постоянным. Но в цепи переменного тока мгновенные значения тока и напряжения и, следовательно, мощность источника питания непрерывно меняются со временем. Поэтому для измерения мощности цепей переменного и постоянного тока используются разные методы.

Мгновенная мощность цепи переменного тока непрерывно изменяется при изменении их напряжения и тока.Мгновенная мощность — это мощность цепи в определенный момент времени. Пусть p — мощность в любой момент, v — напряжение, а «i» — ток цепи.

Если синусоидальный ток и напряжение протекают по цепи переменного тока и ток отстает от напряжения на угол Φ, в этом случае значение мгновенной мощности определяется выражением

Если напряжение и ток не совпадают по фазе друг с другом, то значение тока и напряжения становится равным

Мгновенная мощность цепи выражается как

Пусть, Θ = ωt

Средняя мощность схемы

Член cosΦ в данном выражении показывает, что ваттметр необходим для измерения мощности цепи переменного тока.

Как мощность цепи переменного тока зависит от коэффициента мощности?

Коэффициент мощности определяет общие потоки полезной мощности в цепи. Для понимания роли коэффициента мощности в цепи переменного тока рассмотрим три условия.

Питание переменного тока в чисто резистивной цепи

Резистор — это электрический компонент, потребляющий электрическую мощность цепи переменного тока.

В чисто резистивной цепи ток, протекающий через резистор, находится в фазе с напряжением питания, т.е.е., формы волн напряжения и тока синфазны друг с другом. Разность фаз нулевого градуса возникает между формой волны напряжения и тока.

Электропитание переменного тока в чисто индуктивной цепи

В чисто индуктивной цепи значения напряжения и тока не совпадают по фазе друг с другом. Напряжение и ток растут и падают вместе при фазовом сдвиге 90º. Выражение дает мощность чисто индуктивной цепи. Вышеприведенное уравнение показывает, что катушка индуктивности не потребляет и не рассеивает электрическую мощность.

Питание переменного тока в чисто емкостной цепи

В чисто емкостной цепи переменного тока формы сигналов напряжения и тока не совпадают по фазе друг с другом. Ток в цепи опережает их напряжение под углом 90º. Несмотря на рассеивание энергии, конденсатор сохраняет электрическую энергию.

Мгновенная и средняя мощность — Wira Electrical

Формула мгновенной и средней мощности является важным расчетом в электрической цепи.

Мгновенная мощность p (t) , потребляемая элементом, является произведением мгновенного напряжения v (t) на элементе и мгновенного тока i (t) через него.

Обязательно сначала прочтите, что такое цепь переменного тока.

Обязательно прочтите:

Что такое вектор
Импеданс и проводимость
Законы Кирхгофа для цепи переменного тока
Трехфазная цепь переменного тока

И ее приложения:

Схема фазовращателя
и формула
мост
ОУ переменного тока
Схема умножения емкости
Генератор моста Вина

В цепи переменного тока есть несколько типов мощности:

Максимальная средняя передаваемая мощность
Среднеквадратичное значение напряжения и тока
Коэффициент мощности и полная мощность
Треугольник мощности и комплекс мощности
Энергосбережение переменного тока

Формула мгновенной и средней мощности

Принимая условное обозначение пассивного знака,

000

(1)

9312 (в ваттах) — мощность в любой момент времени.

Это скорость, с которой элемент поглощает энергию.

Рассмотрим общий случай мгновенной мощности, потребляемой произвольной комбинацией элементов схемы при синусоидальном возбуждении, как показано на рисунке (1).

Рисунок 1. Синусоидальный источник и пассивная линейная схема

Пусть напряжение и ток на выводах схемы равны

03 (2a)

(2a) 90

(2b)

где V _m и I _m — амплитуды (или пиковые значения), а θ _{v _{и θ _v — фазовые углы напряжения и тока соответственно.}}

Мгновенная мощность, потребляемая цепью, составляет

(3)

Мы применяем тригонометрическую идентичность

(4) выразить уравнение (3) как

(5)

Это показывает нам, что мгновенная мощность состоит из двух частей. Первый постоянный или не зависящий от времени.Его величина зависит от разности фаз между напряжением и током.

Вторая — синусоидальная функция, частота которой равна 2ω, что в два раза больше угловой частоты напряжения или тока.

Эскиз p (t) в уравнении (5) показан на рисунке (2), где T = 2π / ω — период напряжения или тока.

Мы видим, что p (t) является периодическим, p (t) = p ( t + T ₀ ) и имеет период T ₀ = T /2, так как его частота вдвое больше напряжения или тока.

Мы также видим, что p (t) положительно для некоторой части каждого цикла и отрицательно для остальных.

Когда p (t) положительный, мощность потребляется схемой.

Когда p (t) отрицательно, мощность поглощается источником; то есть мощность передается от схемы к источнику.

Это возможно из-за накопительных элементов (конденсаторов и катушек индуктивности) в цепи.

Рисунок 2.Мгновенная мощность p (t) , поступающая в цепь

Мгновенная мощность изменяется со временем, и поэтому ее трудно измерить.

Средняя мощность удобнее измерять. Фактически, ваттметр, прибор для измерения мощности, реагирует на среднюю мощность.

Средняя мощность в ваттах — это среднее значение мгновенной мощности за один период.

Таким образом, средняя мощность определяется как

(6)

Хотя уравнение.(6) показывает усреднение, выполненное по T , мы получили бы тот же результат, если бы мы выполняли интегрирование за фактический период p (t) , что составляет T ₀ = T /2.

Подстановка p (t) в уравнение (5) на (6) приводит к

(7)

Первое подынтегральное выражение является постоянным, а среднее значение константы равно та же константа. Второе подынтегральное выражение — синусоида.

Мы знаем, что среднее значение синусоиды за ее период равно нулю, потому что площадь под синусоидой во время положительного полупериода компенсируется площадью под синусоидой в течение следующего отрицательного полупериода.

Таким образом, второй член в уравнении (7) исчезает, и средняя мощность становится

(8)

Поскольку cos (θ _v — θ _i) = cos (θ _v — θ _i), важна разница фаз напряжения и тока.

Обратите внимание, что p (t) зависит от времени, а P не зависит от времени. Чтобы найти мгновенную мощность, мы обязательно должны иметь v (t) и i (t) во временной области.

Но мы можем найти среднюю мощность, когда напряжение и ток выражены во временной области, как в уравнении (8), или когда они выражены в частотной области.

Форма вектора v (t) и i (t) в уравнении (2): V = V _m ∠θ _v и I = I _m ∠θ _i соответственно.

P вычисляется с использованием уравнения (8) или векторов V и I . Чтобы использовать векторы, мы замечаем, что

(9)

Мы распознаем действительную часть этого выражения как среднюю мощность P согласно уравнению (8). Следовательно,

(10)

Рассмотрим два частных случая уравнения.(10). Когда θ _v = θ _i, напряжение и ток синфазны. Это подразумевает чисто резистивную цепь или резистивную нагрузку R, и

(11)

где | I | ² = I x I * . Уравнение (11) показывает, что чисто резистивная цепь постоянно поглощает мощность. Когда θ _v — θ _i = ± 90 ^o, мы имеем чисто реактивный контур, а

(12)

, показывающий, что чисто реактивный контур не поглощает средняя мощность.Таким образом,

Резистивная нагрузка ( R ) постоянно поглощает мощность, в то время как реактивная нагрузка ( L или C ) потребляет нулевую среднюю мощность.

Примеры формул мгновенной и средней мощности

Для лучшего понимания рассмотрим приведенные ниже примеры

1. Учитывая, что
v (t) = 120 cos (377 t + 45 ^o) V и i (t) = 10 cos (377 t — 10 ^o) A

найти мгновенную мощность и среднюю мощность, потребляемую пассивной линейной сетью на рисунке.(1)

Решение:
Мгновенная мощность определяется как

Применение тригонометрического тождества

дает

или

Средняя мощность составляет

, что является постоянной частью p (t) выше.

2. Рассчитайте среднюю мощность, потребляемую импедансом Z = 30 — Дж 70 Ом при приложении напряжения V = 120 ∠0 ^o

Решение:
Ток через полное сопротивление

Средняя мощность

3.Для схемы на рисунке (3) найдите среднюю мощность, подаваемую источником, и среднюю мощность, потребляемую резистором.

Рисунок 3

Решение:
Ток I задается

Средняя мощность, подаваемая источником напряжения через резистор

равно

, а напряжение на нем

Средняя мощность, потребляемая резистором, составляет

, что соответствует средней подаваемой мощности.Конденсатор поглощает нулевую среднюю мощность.

4. Определите среднюю мощность, генерируемую каждым источником, и среднюю мощность, потребляемую каждым пассивным элементом в схеме, показанной на рисунке (4a).

Рисунок 4

Решение:
Мы применяем анализ сетки, как показано на рисунке (4b). Для сетки 1

Для сетки 2

или

Для источника напряжения ток, протекающий от него, равен I ₂ = 10.58∠79,1 ^o A, а напряжение на нем составляет 60-30 ^o В, так что средняя мощность составляет

Согласно условию пассивного знака, эта средняя мощность поглощается источником с учетом направления I ₂ и полярность источника напряжения.

То есть схема передает среднюю мощность источнику напряжения.

Для источника тока ток через него составляет I ₁ = 4∠0 ^o, а напряжение на нем составляет

Средняя мощность, подаваемая источником тока, составляет

Это отрицательное значение в соответствии с соглашение о пассивном знаке, означающее, что источник тока подает питание на схему.

Для резистора ток через него составляет I ₁ = 4∠0 ^o, а напряжение на нем составляет 20 I ₁ = 80∠0 ^o, так что потребляемая мощность на резисторе

Для конденсатора ток через него I ₂ = 10,58∠79,1 ^o и напряжение на нем — Дж 5 I ₂ = (5∠- 90 ^o) (10,58∠79,1 ^o) = 52,9∠79,1 — 90 ^o.

Средняя мощность, потребляемая конденсатором, составляет

Для катушки индуктивности ток через нее составляет I ₁ — I ₂ = 2 — Дж 10,39 = 10,58∠-79,1 ^o.

Напряжение на нем составляет Дж 10 ( I ₁ — I ₂) = 10,58∠-79,1 ^o + 90 ^o. Таким образом, средняя мощность, потребляемая катушкой индуктивности, составляет

. Обратите внимание, что катушка индуктивности и конденсатор поглощают нулевую среднюю мощность и что общая мощность, подаваемая источником тока, равна мощности, потребляемой резистором и источником напряжения, или

, что указывает на то, что власть сохраняется.

Мощность в цепи переменного тока — уравнение, коэффициент мощности и решаемые примеры

В зависимости от направления тока, протекающего в цепи, она подразделяется на два типа. Один — это переменный ток, а другой — постоянный ток. Когда электрический ток периодически меняет свое направление на противоположное при протекании через электрическую цепь, это называется переменным током (AC). С другой стороны, когда ток течет только в одном направлении, это называется постоянным током (DC).

Основным преимуществом переменного тока является то, что напряжение переменного тока может быть легко преобразовано с более высокого уровня на более низкий и наоборот.Благодаря этому качеству мощность высокого напряжения от электростанций может быть снижена до более безопасного напряжения для домашнего использования. Только переменный ток совместим с конденсаторами и индукторами. Используя их в цепях переменного тока, можно повернуть электрический ток. Это свойство помогает настраивать радиостанции. По этим причинам для бытовой техники наиболее предпочтительно использовать переменный ток.

Мощность, потребляемая в цепи переменного тока

Электрическая цепь вырабатывает мощность, которая определяется выражением P = I V.

Где, I — ток, протекающий по цепи, а

В — напряжение в ней.

Цепи переменного тока всегда имеют реактивное сопротивление, поэтому есть две составляющие мощности: составляющая мощности из-за магнитного поля и другая из-за электрического поля. Средняя мощность, потребляемая схемой, становится суммой энергии, накопленной и возвращенной в течение одного полного цикла. Таким образом, средняя мощность, потребляемая схемой, будет мгновенной мощностью за один цикл.

Поскольку ток, протекающий по цепи, и напряжение зависят от времени, мгновенная мощность также зависит от времени t. Это определяется как,

p (t) = I (t) x v (t).

Изображение будет загружено в ближайшее время.

Рассмотрим схему LCR, как показано на рисунке, напряжение V приложено к цепи. Напряжение V определяется как,

V = Vm × sinωt

Ток в этом случае записывается как:

I = Im × sin (ωt + Φ)

Где, Vm — амплитуда напряжения

Im — Амплитуда тока

ω- Угловая частота.{2}} \]

\ [Tan \ Phi \] = \ [\ frac {X_ {L} — X_ {C}} {R} \]

\ [\ Phi = arctan \ frac {x_ {L } — x_ {C}} {R} \]

Используя все приведенные выше уравнения, чтобы найти потребление энергии в цепи переменного тока,

Мы знаем, P = IV

P = (\ [V_ {m} \] × sin⍵t) × (\ [1_ {m} \] × sin (⍵t + \ [\ Phi \]))

Чтобы найти среднее значение мощности

\ [P_ {avg} \] = ( \ [V_ {m} \] × sin⍵t) × (\ [1_ {m} \] × sin (⍵t + \ [\ Phi \]))

Использование тригонометрической формулы,

2 sin A sin B = cos (A- B) — cos (A + B)

Получаем,

\ [P_ {avg} = Среднее \: of \: \ frac {V_ {m} I_ {m} [cos \ Phi \: — \: cos (2 \ omega t + \ Phi)]} {2} \]

\ [P_ {avg} = \ frac {V_ {m} I_ {m} cos \ Phi} {2} \ ]

\ [Среднее \: из \: \ frac {V_ {m} I_ {m} cos (2 \ omega t + \ Phi)} {2} \] = 0

\ [P_ {avg} = \ гидроразрыв {V_ {m} I_ {m}} {2} cos \ Phi \]

\ [P_ {avg} = V_ {rms} × I_ {rms} × cos \ Phi \]

Для резистивной цепи Φ = 0, что дает cosΦ = 1

Следовательно, Pavg = Vrms x Irms

Для индуктивной цепи Φ = 900, (напряжение на катушке индуктивности опережает ток на 900)

, поэтому cosΦ = 0

Следовательно, Pavg = 0

Для емкостной цепи Φ = -900.Это означает, что cosΦ = 0 (это означает, что в случае конденсаторов напряжение отстает от тока на 900)

Следовательно, Pavg = 0

Средняя мощность цепи переменного тока называется истинной мощностью цепи.

Коэффициент мощности

Коэффициент мощности переменного тока определяется как отношение истинной мощности, протекающей через цепь, к полной мощности, присутствующей в цепи.
Обычно находится в интервале от -1 до 1 и безразмерен.

Коэффициент мощности = Истинная мощность / Полная мощность

Также cosΦ = R / Z

R- сопротивление в цепи

Z- полное сопротивление цепи.

Интересные факты

Закон Ома для среднеквадратичного значения переменного тока вычисляется путем деления среднеквадратичного напряжения на импеданс.
Средняя мощность, подаваемая в цепь LCR, зависит от фазового угла.

Решенные примеры

1.Генератор переменного тока, ЭДС которого определяется выражением v (t) = [4,00 В] sin [(1,00 x 104 рад / с) t],

, подключен к цепи LCR, для которой L = 2,00 x 10-3H, C = 4,00 x 10-6 Ф и R = 5 Ом

Какое среднеквадратичное значение напряжения на генераторе?
Какое сопротивление цепи LCR?
Какова средняя выходная мощность генератора?

Решение —

Среднеквадратичное значение напряжения на генераторе в 1 / √2 раз больше амплитуды напряжения.{2}} \] = 0,801Вт

2. Две нагрузки мощностью 10кВт каждая работают с коэффициентом мощности 0,8 (каждая из них отстает). Каков суммарный коэффициент мощности для обеих нагрузок?

Решение — мы знаем, полная мощность = истинная мощность / коэффициент мощности

Для нагрузки 1

Полная мощность = 10 кВт / 0,8

Полная мощность = 12,5 кВА

Для нагрузки 2

Полная мощность = 12,5 кВА

Комбинированный коэффициент мощности = Общая истинная мощность / полная полная мощность

= (10 + 10) / (12.5 + 12,5)

Комбинированный коэффициент мощности = 0,8 (запаздывания)

Цепь переменного тока — обзор

18.4 Краткое описание решения проблем

Проблемы в цепях переменного тока идентифицируются автоматически. Наиболее распространенные цепи переменного тока возбуждаются синусоидальной переменной ЭДС, Δ v = V sinω t , которую удобно представить в виде вращающегося вектора длиной V , вращающегося с угловой скоростью ω. В таких цепях переменного тока компоненты R, L и C имеют мгновенные значения разности потенциалов Δ v _R, Δ v _L, и Δ v _C , векторы которых V _R, V _L, и V _C имеют разные фазовые соотношения (фазовые углы) с соответствующими токами, i _R, i _L, и i _C .В частности, Δ v _R и i _R находятся в фазе, Δ v _L выводов i _L на 90 ° и Δ v _C отстает i _C на 90 °.

В цепи переменного тока реактивное сопротивление емкости C или индуктивности L является мерой способности этого компонента препятствовать прохождению заряда в этой цепи. Реактивное сопротивление зависит от частоты v переменного тока.Реактивное сопротивление X _C емкости C равно 1 / ω C = 1/2 (π vC ). Реактивное сопротивление X _L индуктивности L равно ω L = 2π vL . Чистое реактивное сопротивление X цепи переменного тока определяется как X = X _L — X _C .

Мы начинаем анализ последовательной цепи переменного тока, комбинируя аналогичные компоненты, когда это необходимо.Если эквивалентные компоненты находятся в цепи последовательного RLC , то в каждом компоненте в любой момент будет одинаковый ток. Поэтому удобно соотносить векторы компонентов схемы с вектором тока I . В частности, вектор разности потенциалов, V _R = IR , для сопротивления R находится в фазе с I , а вектор V _R находится в том же направлении, что и ток вектор I .Вектор разности потенциалов В _L = IX _L, для индуктивности L выводов I на 90 °, а вектор разности потенциалов В _C = IX _C, для емкостных отставаний I на 90 °. Затем мы можем построить векторную диаграмму с I , нарисованным в произвольный момент времени t , так что I образует угол ω t с осью, соответствующей направлению I при t = 0.Затем, нарисовав вектора V _R , V _L, и V _C, в соответствующих направлениях, мы можем построить вектор разности потенциалов V ЭДС. Величина и направление вектора V равны векторной сумме векторов, V _R, V _L и V _C. Фазовый угол ϕ между ЭДС и током в цепи — это угол между векторами V и I , а величина ϕ определяется как ϕ = tan ^-1 ( X / R ).

Полное сопротивление Z = В / I цепи переменного тока играет ту же роль, что и сопротивление цепи в цепи постоянного тока. Для данной последовательной цепи переменного тока полное сопротивление Z = R2 + (XL-XC) 2 зависит от сопротивления и реактивного сопротивления цепи. Поскольку X _L и X _C зависят от частоты ЭДС, импеданс зависит от частоты. Частота, при которой импеданс минимален, называется резонансной частотой v _o контура.Резонанс возникает, когда частота такова, что чистое реактивное сопротивление, X _L — X _C, равно нулю, то есть когда X _L = X _C . Резонансная частота v _o может быть выражена через индуктивность L и емкость C цепи как v _o = 1 / (2π√ LC ). На резонансной частоте ток в цепи переменного тока достигает максимальной амплитуды.

Измерения мощности в цепях переменного тока удобно описывать в терминах среднеквадратичных (среднеквадратичных) значений ЭДС и тока. Используя В _{среднеквадратичное значение} = В / √2 и I _{среднеквадратичное значение} = I / √2, мы можем выразить среднюю мощность P _av , подаваемую в цепь переменного тока с помощью P _av = V _rms I _rms cosϕ, где cosϕ называется коэффициентом мощности цепи. И снова ϕ — это фазовый угол между вектором ЭДС V и вектором тока I .Величина ϕ связана с общим сопротивлением R и полным сопротивлением Z цепи переменного тока соотношением cosϕ = R / Z .

Электромагнитные (ЭМ) волны состоят из взаимно перпендикулярных электрических и магнитных полей, которые распространяются в свободном пространстве со скоростью света ( c = 3,0 × 10 ⁸ м / с). Как электрическое поле E , так и магнитное поле B электромагнитной волны перпендикулярны направлению распространения волны.Направление распространения — в каждой точке волны в направлении, указанном E × B . Вектор Пойнтинга, S = (1 / μ _o) E × B , дает величину и направление энергии, переносимой электромагнитной волной через единицу площади за единицу времени. Таким образом, величина S представляет мощность, которую электромагнитная волна передает через единицу площади.

Длина волны λ электромагнитной волны — это расстояние между соседними максимумами электрического поля (или магнитного поля), измеренное вдоль направления распространения волны.Длина волны λ и частота v электромагнитной волны в свободном пространстве связаны со скоростью распространения c соотношением c = v λ. Таким образом, указание длины волны ЭМ волны, по сути, определяет ее частоту; аналогично, указав его частоту, вы получите длину волны.

Диапазон известных длин (или частот) электромагнитных волн называется электромагнитным спектром. Радио- и телевизионные волны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи и гамма-лучи составляют электромагнитный спектр.Хотя эти излучения возникают по-разному и очень по-разному взаимодействуют с веществом, существенное различие между этими электромагнитными излучениями заключается в их длине волны (или частоте).

Цепи переменного тока и системы питания на практике

Предисловие xiii

Благодарности xvii

Часть I 1

1 Энергетические системы: общий обзор 3

1.1 Трехфазная система переменного напряжения 3

1.2 Распределение низкого напряжения 6

1.3 Примеры распределительных трансформаторов 8

1.4 Практические пределы значений для низковольтных нагрузок 10

1.5 Сеть среднего напряжения 11

1.6 Передающие и вспомогательные сети передачи 24

1.7 Производство электроэнергии 32

1.8 Источники 41

Дополнительная литература 41

2 Обзор теории цепей переменного тока и применение векторных диаграмм 43

2.1 Представление напряжений и токов переменного тока 43

2.2 Измерение RMS изменяющихся во времени величин переменного тока 44

2.3 Обозначение векторов (анализ фазорной диаграммы) 45

2.4 Компоненты пассивной цепи: резисторы, конденсаторы и индукторы 49

2.5 Обзор условных обозначений и сетевых теорем 55

2.6 Анализ цепей переменного тока Примеры 61

2.7 Резонанс в цепях переменного тока 74

2.8 Проблемы 83

2.9 Практический эксперимент 88

3 Активная мощность, реактивная мощность и коэффициент мощности 91

3.1 Однофазное питание переменного тока 91

3.2 Активная мощность 92

3.3 Реактивная мощность 93

3.4 Полная мощность или вольт-амперный продукт, S 96

3.5 Трехфазное питание 97

3,6 Коэффициент мощности 99

3.7 Коррекция коэффициента мощности 100

3.8 Типичные профили промышленной нагрузки 105

3.9 Направленные потоки мощности 107

3.10 Розничная торговля энергией 110

3.11 Проблемы 111

4 Магнитные цепи, индукторы и трансформаторы 115

4.1 Магнитные цепи 115

4.2 Модель магнитной цепи 116

4.3 Сердечники с зазорами и эффективная проницаемость 119

4.4 Расчеты индуктивности 120

4.5 Материалы сердечников 121

4.6 Магнитные характеристики GOSS 122

4.7 Энергия, запасенная в воздушном зазоре 125

4.8 Уравнение ЭДС 126

4.9 Топологии магнитных цепей 127

4.10 Потери на намагничивание 129

4.11 Работа двухобмоточного трансформатора 131

4.12 Номинальные характеристики и КПД трансформатора 133

4.13 Эквивалентная схема трансформатора с двумя обмотками 134

4.14 Помещенная на единицу система 137

4.15 Тесты короткого замыкания и обрыва трансформатора 138

4.16 Фазорная диаграмма трансформатора 140

4.17 Ток Трансформаторы 142

4.18 Проблемы 144

4.19 Источники 153

5 Симметричные компоненты 155

5.1 Теория симметричных компонентов 156

5.2 Последовательные сети и анализ неисправностей 160

5.3 Соединения при отказе сети 163

5.4 Измерение компонентов нулевой последовательности (остаточный ток и напряжение) 170

5.5 Токи замыкания на землю, отраженные от звезды к обмотке, соединенной треугольником 171

5.6 Компоненты последовательности, удаленные от неисправности 173

5.7 Проблемы 175

5.8 Источники 185

6 Потоки мощности в сетях переменного тока 187

6.1 Направления потоков мощности 188

6.2 Синхронный конденсатор 188

6.3 Синхронный двигатель 191

6.4 Обобщенный анализ потока мощности 192

6.5 Низкий X / R Сети 197

6.6 Предел стабильности стабильной передачи 201

6.7 Падение напряжения в энергосистемах 202

6,8 Проблемы 207

6,9 Источники 209

Часть II 211

7 Трехфазные трансформаторы 213

7,1 Полное сопротивление положительной и отрицательной последовательности 213

7.2 Импеданс нулевой последовательности трансформатора 219

7.3 Векторные группы трансформатора 221

7.4 Регулировка напряжения трансформатора 222

7.5 Гармоники тока намагничивания 228

7.6 Методы переключения ответвлений 233

7.7 Параллельное соединение трансформаторов 245

Паспортная табличка трансформатора 249,8

7.9 Шаговый регулятор напряжения 251

7.10 Проблемы 264

7.11 Источники 272

8 Трансформаторы напряжения 273

8.1 Индуктивные и емкостные трансформаторы напряжения 273

8.2 Ошибки трансформатора напряжения 276

8.3 Эквивалентная схема трансформатора напряжения 281

8.4 Линии ошибок трансформатора напряжения 284

8.5 Изменение номинальных значений трансформаторов напряжения 288

8.6 Классы точности для защитных трансформаторов напряжения 289

8.7 Двухобмоточные трансформаторы напряжения 292

8.8 Заземление и защита трансформаторов напряжения 292

8.9 Нетрадиционные трансформаторы напряжения 297

8.10 Проблемы 299

8.11 Источники 301

9 Трансформаторы тока 303

9.1 Вторичные токи и коэффициенты трансформатора тока 304

9.2 Ошибки и стандарты трансформатора тока 306

9.3 IEEE C57.13 Класс измерений

Ошибки амплитуды и фазы

9.4 Эквивалентная схема трансформатора тока 312

9.5 Методы изменения адмиттанса намагничивания и компенсации трансформатора тока 315

9.6 Общая ошибка 319

9.7 Фактор безопасности прибора для измерения ТТ 322

9.8 Защитные трансформаторы тока 324

9.9 Номинальные параметры межвиткового напряжения 337

9.10 Нетрадиционные трансформаторы тока 338

9.11 Проблемы 341

9.12 Источники 349

10 Измерение энергии

10.1 Интервалы измерения 353

10.2 Общий анализ измерений с использованием симметричных компонентов 361

10.3 Ошибки измерения 367

10.4 Поправочные коэффициенты коэффициента 373

10,5 Ошибка измерения реактивной мощности 378

10.6 Оценка общей погрешности установки 379

10.7 Ввод в эксплуатацию и аудит измерительных установок 381

10,8 Проблемы 383

10,9 Источники 388

110002 Системы 391

11.1 Воздействие электричества на человеческое тело 391

11.2 Устройства остаточного тока 399

11.3 Низковольтные системы заземления 402

11.4 системы низковольтного заземления, используемые во всем мире 413

11.5 Системы заземления среднего напряжения 413

11.6 Заземление высокого напряжения 423

11,7 Упражнение 423

11,8 Проблемы ( Конструкция заземляющей сети ) 425

11,9 Введение от 9000 до 434

Защита энергосистемы 437

12.1 Основные принципы защиты 437

12.2 Защитные реле 438

12.3 Первичная и резервная защита (двойная защита) 439

12.4 зоны защиты 441

12,5 Защита от перегрузки по току 443

12,6 Дифференциальная защита 451

12,7 Защита шин от утечек корпуса и дуги 462

12,8 Дистанционная защита (защита по сопротивлению) 464

12,9 Проблемы 469

9143 Источники 13 Гармоники в энергосистемах 477

13.1 Измерение гармонических искажений 479

13.2 Разложение нелинейного тока или напряжения на его гармонические составляющие (серия Фурье) 480

13.3 последовательности гармонических фаз 484

13,4 Тройные гармонические токи 487

13,5 Гармонические потери в трансформаторах 487

13,6 Фактор мощности при наличии гармоник 492

13,7 Управление гармониками 495

13,8 514

13.10 Проблемы 515

13.11 Источники 519

14 Производственные аспекты энергетики 521

14.1 Номера устройств 521

14.2 Однолинейная схема (СТАРАЯ) 523

14.3 Топологии распределительного устройства 526

14.4 Планы переключения, изоляция оборудования и процедуры разрешения на работу 537

14.5 Электробезопасность 542

14.6 Измерения с неправильно настроенным мультиметром 549

14.7 Источники 551

Индекс 553

Цепь переменного тока: применение, типы и характеристики

Цепи переменного тока или цепи переменного тока — это просто цепи, питаемые от источника переменного тока, либо тока, либо напряжения.Переменное напряжение или ток — это напряжение, в котором величина либо напряжения, либо тока изменяется относительно определенного среднего значения и периодически меняет направление на обратное.

Большинство бытовых и промышленных систем и устройств в настоящее время питаются от переменного тока. Все устройства на базе перезаряжаемых аккумуляторных батарей на базе постоянного тока технически работают на переменном токе. Все устройства постоянного тока используют мощность постоянного тока, полученную от переменного тока, для зарядки своей системы питания и батарей.

Схема переменного тока была впервые создана в 1980-х годах, когда Tesla стремилась решить проблему многочисленных неработоспособностей генераторов постоянного тока Томаса Эдисона. Он попытался представить способ передачи электричества под высоким напряжением. Затем, используя трансформаторы для увеличения или уменьшения мощности для распределения, мы сможем минимизировать потери мощности на больших расстояниях, что в то время было центром проблем постоянного тока.

Постоянный ток и переменный ток (переменный и постоянный)

AC и DC во многом различаются от передачи к генерации и распределению.Существенная разница между постоянным и переменным током, которая также является основой их разнообразных характеристик, заключается в направлении потока электричества. В постоянном токе электроны движутся непрерывно в определенном направлении или вперед, но в системе переменного тока электроны меняют направление своего движения с периодическими интервалами. Этот переменный ток также приводит к изменению значения напряжения, поскольку оно изменяется с отрицательного на положительное в соответствии с током.

Сравнение переменного и постоянного тока (Ссылка: circuitdigest.com)

Что такое цепь переменного тока?

Электрические и электронные схемы включают в себя множество различных соединительных компонентов, образующих замкнутую и законченную цепь. Основными пассивными компонентами, используемыми в любой схеме, являются конденсатор , резистор и индуктор . Все три названных пассивных компонента имеют одну общую черту; они ограничивают электрический ток в цепи, но совершенно разными способами.

Электрический ток может проходить через цепь двумя способами.Если он проходит только в одном направлении, он называется постоянным током (DC). Если электрический ток чередуется в разных направлениях вперед и назад, он называется переменным током (AC). Поскольку они обеспечивают сопротивление внутри цепи, пассивные компоненты в цепях переменного тока действуют совершенно иначе, чем компоненты в цепях постоянного тока.

Пассивные компоненты в цепи потребляют электрическую энергию. Следовательно, они не могут усиливать или увеличивать мощность подаваемых на них электрических сигналов. Просто все потому, что они пассивны и всегда будут иметь меньший выигрыш.Пассивные компоненты, размещенные в электрической и электронной схеме, могут быть объединены в бесконечное количество конструкций, как показано ниже, при этом рабочие характеристики этих схем основаны на взаимодействии между их различными электрическими свойствами.

Пример сложной цепи переменного тока (Ссылка: allaboutcircuits.com)

Что такое реагент и импеданс?

Тип цепей, в которых ток пропорционален напряжению, называется линейными цепями.В резисторе отношение напряжения к току является его сопротивлением. Сопротивления не имеют независимости от частоты и имеют две фазы. Тем не менее, схемы только с резисторами не очень интересны и применимы.

Обычно частота не влияет на отношение напряжения к току, и существует разность фаз. Таким образом, общее название отношения напряжения к току — импеданс. Символ импеданса — Z. Сопротивление — это частный случай импеданса. Другой частный пример: ток и напряжение сдвинуты по фазе на 90 °; это важный случай, потому что при этом не происходит потери мощности в цепи.В этом случае, когда ток и напряжение не совпадают по фазе на 90 °, мы называем реактивным сопротивлением отношение напряжения к току, и его символ — X.

Терминология

Для сжатия мы обозначим разность электрических потенциалов как напряжение. Мы будем рассматривать напряжения и токи как функцию, которая изменяется синусоидально со временем, и будем использовать строчные буквы i и v для тока и напряжения при явном анализе их изменения. Мы представим амплитуду или пикового значения синусоидального изменения через Vm и I _м, в то время как V = V _м / √2 и I = I _м / √2 без нижних индексов относятся к их Значения RMS.Чтобы понять источник синусоидально изменяющегося напряжения и то, как мы их используем, см. Этот пост.

Напряжение и ток, которые мы используем в переменном токе, можно представить в виде следующих уравнений:

v = v (t) = V_m sin (\ omega t)

i = i (t) = I_m sin (\ omega t + \ varphi)

где:

\ omega = 2πf = угловая частота

f = обычная или циклическая частота = количество полных колебаний в секунду.

\ varphi = разность фаз между напряжением и током.

Синусоидальное напряжение и ток в цепи переменного тока (Ссылка: electronics-tutorials.ws)

Пассивные компоненты в цепях переменного тока

Мы можем назвать R сопротивлением, C емкостью и L индуктивностью. Независимо от того, используем ли мы резисторы в цепях постоянного или переменного тока, они всегда имеют одинаковое значение сопротивления в системе независимо от частоты питания.Это все потому, что резисторы идентифицируются как чистые, имеющие паразитные характеристики, такие как нулевая индуктивность L = 0 и бесконечная емкость C = ∞. Кроме того, для полностью резистивной схемы у нас всегда есть синфазное напряжение и ток, поэтому мы можем найти мощность, потребляемую в любой момент, умножив напряжение на ток.

С другой стороны, конденсаторы и катушки индуктивности имеют отдельный тип сопротивления переменному току, известный как реактивное сопротивление , как упоминалось перед (X _L и X _C).Реактивное сопротивление также блокирует прохождение тока, но значение реактивного сопротивления не является фиксированной величиной для одного конденсатора или катушки индуктивности по сравнению с резистором с фиксированным значением сопротивления. Величина реактивного сопротивления катушки индуктивности или конденсатора зависит от частоты тока питания и величины постоянного тока самого элемента.

Кроме того, существует часто используемый список пассивных компонентов в цепях переменного тока и соответствующие им уравнения, которые можно применять для определения их импеданса и значения реактивного сопротивления тока цепи.Следует отметить, что здесь мы представили теоретически совершенную (чистую) катушку индуктивности или конденсатор, не имеющую сопротивления. Но в реальном мире у нас всегда есть комбинация компонентов, упомянутых ранее, включая сопротивление.

Полностью резистивная цепь

Резисторы препятствуют, регулируют или задают прохождение тока по определенному пути, или вызывают отключение напряжения в электрической цепи на основе этого потока. {\ circ} = 0-jX_C

I_S = \ frac {V_S} {X_S}

Полностью индуктивная цепь

Катушка индуктивности включает катушку с проволокой, которая индуцирует магнитное поле внутри себя или в центральном сердечнике из-за тока, протекающего через катушку.{2}}

\ поэтому Z = X_C-X_L или X_L-X_C

Z = \ угол (\ phi _1 + \ phi _2) = 0 + jX_L-jX_C

f_r = \ frac {1} {2 \ pi \ sqrt {LC}}

I_S = I_L = I_C

Схема LC серии

(Ссылка: electronics-tutorials.ws)

Параллельные цепи переменного тока

Мы можем соединять пассивные компоненты вместе последовательно в цепях переменного тока, чтобы сформировать цепи RC, RL и LC, как описано ниже.

Параллельная RC-цепь

Принципиальная схема и уравнение для параллельной RC-цепи:

I_R = \ frac {V_s} {R}, I_C = \ frac {V_S} {X_C}

I_S = \ sqrt {I_R ^ {2} + I_C ^ {2}}

\ phi = tan ^ {- 1} (\ frac {I_C} {I_R})

Y = \ frac {1} {Z} = \ sqrt {G ^ {2} + B_c ^ {2}}

V_S = V_C = V_R

Параллельная RC-схема (Ссылка: electronics-tutorials.{2}}

V_S = V_L = V_R

Параллельная цепь RL (Ссылка: electronics-tutorials.ws)

Параллельный контур LC

Принципиальная схема и уравнение для параллельной LC-цепи:

B_L = \ frac {1} {X_L}, B_C = \ frac {1} {X_C}

Y = \ frac {1} {Z} = B_L + B_C

f_R = \ frac {1} {2 \ pi \ sqrt {LC}}

V_S = V_L = V_C

Параллельная LC-схема (Ссылка: electronics-tutorials.{2}}

f_R = \ frac {1} {2 \ pi \ sqrt {LC}}

V_S = V_C = V_R = V_L

Параллельная цепь RLC (Ссылка: electronics-tutorials.ws)

Выше было показано, что в цепях переменного тока пассивные компоненты ведут себя совершенно иначе, чем при использовании в цепи постоянного тока, из-за наличия частоты ( ). В полностью резистивной цепи у нас есть синфазные ток и напряжение. В полностью емкостной цепи ток в конденсаторе составляет -90 ^o с напряжением, в то время как он составляет 90 ^o для полностью индуктивной цепи.

В последовательных схемах векторная сумма напряжений на компонентах схемы эквивалентна напряжению питания (V _S) . С другой стороны, в параллельной схеме сумма векторов протекающих токов в каждом элементе равна току питания (I _S).

Как для последовательного, так и для параллельного соединения цепей RLC, резонанс возникает при XL = XC, когда ток источника «синфазен» с напряжением питания цепи. Резонанс последовательной цепи идентифицируется как цепь приемника , а цепь параллельного резонанса идентифицируется как цепь отклоняющего устройства .

Питание в цепи переменного тока

В цепях постоянного тока мощность компонентов — это просто выходное напряжение постоянного тока, умноженное на ток в ваттах. Однако для цепи переменного тока с реактивными элементами мы должны оценивать потребляемую мощность по-другому.

Электрическая мощность — это энергия, потребляемая в цепи. Все электрические и электронные элементы и устройства имеют ограничение на количество электроэнергии, с которой они могут безопасно работать. Например, у нас есть резистор на 1/4 Вт или усилитель на 20 Вт.

Количество мощности в цепях в любой момент называется мгновенной мощностью и известно из известного соотношения мощности, равной амперам, умноженным на вольт (P = VI). В результате один ватт будет равен результату вольт-ампер, умноженному на один вольт на один ампер (один ватт — это скорость потребления энергии из расчета один джоуль в секунду).

Итак, мощность, потребляемая или обеспечиваемая элементом схемы, представляет собой напряжение на элементе и ток, протекающий внутри него. Предположим, у нас есть сопротивление в цепи постоянного тока R Ом.{2}} {R}

где:

В: напряжение постоянного тока

I: постоянный ток

R: значение сопротивления.

Электроэнергия в цепи переменного тока

В цепях постоянного тока напряжения и токи постоянны и не меняются во времени, так как нет функции синусоидальной формы волны, связанной с питанием. Напротив, мгновенные значения тока, напряжения и результирующей мощности в цепи переменного тока постоянно меняются под действием источника питания. Следовательно, мы не можем рассчитать мощность в цепях переменного тока так же, как в предыдущем методе.Тем не менее, мы все же можем предположить, что мощность равна амперам (i), умноженным на напряжение (v).

Еще одним важным моментом является то, что цепи переменного тока имеют реактивное сопротивление, поэтому компоненты создают магнитные и / или электрические поля. В отличие от чисто резистивного элемента, мощность накапливается, а затем возвращается обратно в схему, когда синусоидальная форма волны проходит за один полный периодический цикл.

В результате средняя мощность, потребляемая схемой, представляет собой сумму накопленной энергии и мощности, возвращаемой за один полный цикл.Средняя потребляемая мощность схемы — это средняя мгновенная мощность в течение одного полного цикла. Мгновенная мощность (p) может быть определена как мгновенное напряжение (v), умноженное на мгновенный ток (i).

Если принять синусоидальные формы сигналов напряжения и тока, мы имеем:

Форма волны синусоидального напряжения (Ссылка: electronics-tutorials.ws)

P = v \ раз i

В = V_msin (\ omega t + \ phi _v)

i = I_msin (\ omega t + \ phi _i)

p = [V_msin (\ omega t + \ theta _v) \ times I_msin (\ omega t + \ theta _i)]

\ поэтому V_mI_m (sin (\ omega t + \ theta _i) \ times sin (\ omega t + \ theta _v))

Тригонометрическое произведение на сумму:

sin (A + B) = \ frac {1} {2} [cos (A-B) -cos (A + B)]

Где \ theta = \ theta _v- \ theta _i, и, поместив в приведенное выше уравнение, мы имеем:

p = \ frac {V_mI_m} {2}) (cos (\ theta) -cos (2 \ omega t + \ theta))

\ frac {V_mI_m} {2} = \ frac {V_m} {\ sqrt {2}} \ times \ frac {I_m} {\ sqrt {2}} = V_ {RMS} \ times I_ {RMS}

, где V _RMS и I _RMS — среднеквадратические значения синусоидальных сигналов для v и i , соответственно.Поэтому мы можем отобразить мгновенную мощность как:

P = VIcos \ theta — cos (2 \ omega t + \ theta))

Это уравнение показывает нам, что мгновенная мощность переменного тока включает две разные части и является суммой двух членов. Вторая часть представляет собой синусоидальную функцию времени с частотой, вдвое превышающей угловую частоту источника питания. Однако первый член — это константа, значение которой основано на разности фаз θ между напряжением и током.

Поскольку мгновенная мощность постоянно изменяется в зависимости от синусоидальной функции во времени, ее трудно измерить.{2} Zcos \ theta

Мощности в цепях переменного тока

Мощность переменного тока — Основы электроники

Похожие материалы:

Добавить комментарий

Мощность в цепи переменного тока

Мощности в цепях переменного тока

Реклама:

Читать далее:

Статьи по теме:

Открытая Физика. Закон Ома для цепи переменного тока. Мощность

Мощность цепи переменного тока — Энциклопедия по машиностроению XXL

Электрические цепи переменного тока

Мощность цепи переменного тока

15.5: Питание в цепи переменного тока

Авторы и авторство

Мощность в цепи переменного тока — Circuit Globe

Как рассчитать мощность цепи переменного тока?

Как мощность цепи переменного тока зависит от коэффициента мощности?

Питание переменного тока в чисто резистивной цепи

Электропитание переменного тока в чисто индуктивной цепи

Питание переменного тока в чисто емкостной цепи

Мгновенная и средняя мощность — Wira Electrical

Формула мгновенной и средней мощности

Примеры формул мгновенной и средней мощности

Мощность в цепи переменного тока — уравнение, коэффициент мощности и решаемые примеры

Цепь переменного тока — обзор

18.4 Краткое описание решения проблем

Цепи переменного тока и системы питания на практике

Цепь переменного тока: применение, типы и характеристики

Добавить комментарий Отменить ответ

Мощности в цепях переменного тока

Мощность переменного тока — Основы электроники

Похожие материалы:

Добавить комментарий

Мощность в цепи переменного тока

Мощности в цепях переменного тока

Реклама:

Читать далее:

Статьи по теме:

Открытая Физика. Закон Ома для цепи переменного тока. Мощность

Мощность цепи переменного тока — Энциклопедия по машиностроению XXL

Электрические цепи переменного тока

Мощность цепи переменного тока

15.5: Питание в цепи переменного тока

Авторы и авторство

Мощность в цепи переменного тока — Circuit Globe

Как рассчитать мощность цепи переменного тока?

Как мощность цепи переменного тока зависит от коэффициента мощности?

Питание переменного тока в чисто резистивной цепи

Электропитание переменного тока в чисто индуктивной цепи

Питание переменного тока в чисто емкостной цепи

Мгновенная и средняя мощность — Wira Electrical

Формула мгновенной и средней мощности

Примеры формул мгновенной и средней мощности

Мощность в цепи переменного тока — уравнение, коэффициент мощности и решаемые примеры

Цепь переменного тока — обзор

18.4 Краткое описание решения проблем

Цепи переменного тока и системы питания на практике

Цепь переменного тока: применение, типы и характеристики

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ