Общие сведения
Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
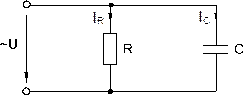
Рис. 6.2.1
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в резисторе IR(активная составляющая).
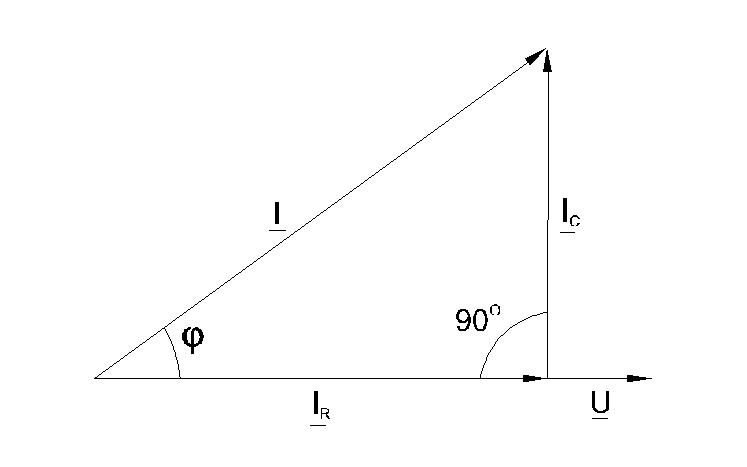
Между токами I, IC и IR существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением XC конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
| 
|
| Рис. 6.2.2 | Рис. 6.2.3 |
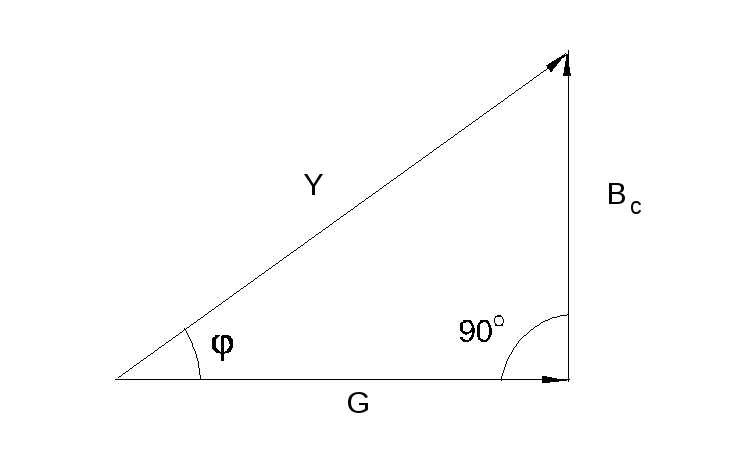
Фазовый сдвиг между напряжением U цепи и током в резисторе IRотсутствует, тогда как между этим напряжением и током в конденсаторе IC равен –900 (т.е. ток опережает напряжение на 900). При этом сдвиг между полным током Iи напряжением U цепи определяется соотношением междупроводимостями BC и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).
В треугольнике проводимостей G=1/R, BC=1/XC, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а BC– реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = IR +IC.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи
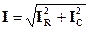; I = U ¤ Z = UY.
Полная проводимость цепи
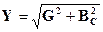
гдеZ— полное сопротивление цепи.
Угол сдвига фаз
j = arctg (I C ¤ IR) = arctg (BC ¤ G).
Активная и реактивная проводимости
G = Y cosj; BC = Y sinj.
Экспериментальная часть
Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе I C, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и емкостную реактивную проводимость BC.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.
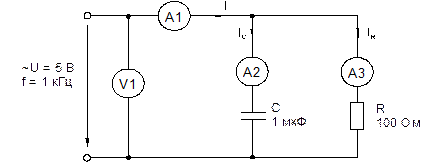
Рис. 6.2.4
· Выполните измерения U, I, IC, IR и занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте также R, j, XC, Z.
Таблица 6.2.1
| U, B | I, мА | IС, мА | IR, мА | j, град | R, Ом | XC, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
· Вычислите и запишите в таблицу:
Фазовый угол
j = arctg (I C ¤ I R) =
Активные проводимость цепи и сопротивление цепи
G = IR ¤ U ; R = U ¤ IR.
Емкостные реактивные проводимость и сопротивление цепи
BC = IC ¤ U ; XC = U ¤ IC.
Полные проводимость и сопротивление цепи
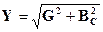; Z = 1 ¤ ÖY.
· Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
· Постройте векторную диаграмму токов (рис. 6.2.5) и треугольник проводимостей (рис. 6.2.6).
Рис. 6.2.5 Рис. 6.2.6
Автор Aluarius На чтение 5 мин. Просмотров 325 Опубликовано
Для чего предназначены резисторы и конденсаторы
Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.
Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.
Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд. Величина, которую способно накопить устройство, называют «ёмкость».
Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.
После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.
Особенности соединения резистора и конденсатора в цепи
Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.
Параллельное соединение резистора и конденсатора
Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.
При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.
Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.
Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.
Последовательное соединение
Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.
Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/Собщ = 1/С1 + 1/С2 + … + 1/Сn.
Как рассчитать импеданс в цепи
Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.
Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.
К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.
Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.
Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.
Практические расчеты импеданса чаще всего выполняются по следующей формуле:
Z = Um/Im.
Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.
Энергия будет храниться и выделяться в двух типах:
- Магнитного поля. Реактивная часть является индуктивной.
- Электрического поля.
Как рассчитать время разряда и заряда конденсатора через резистор
Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.
Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.
Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.
Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток. Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.
По мере того как конденсатор станет заряжаться, величина R на нём будет падать.
Время процесса зарядки будет зависеть от следующих величин:
- Внутреннее сопротивление электрического генератора.
- Способность конденсатора принять количество тока.
Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.
Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.
В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.
Продолжительность разряда устройства имеет зависимость от:
- Отношению заряда к разности потенциалов;
- Удельному электрическому сопротивлению.
Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.
Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.
Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.
6.2.1. Общие сведения
Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
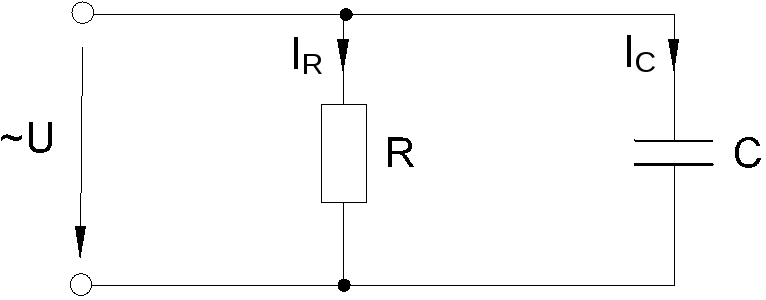
Рис. 6.2.1
Общий ток цепи Iразветвляется на ток в конденсатореIC (емкостная составляющая общего тока) и ток в резистореIR (активная составляющая).
Между токами I, ICиIRсуществуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлениемXCконденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
|
|
Рис. 6.2.2 | Рис. 6.2.3 |
Фазовый сдвиг между напряжением Uцепи и током в резистореIR отсутствует, тогда как между этим напряжением и током в конденсатореICравен –900(т.е. ток опережает напряжение на 900). При этом сдвиг между полным токомI и напряжениемUцепи определяется соотношением между проводимостямиBCиG. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).
В треугольнике проводимостей G=1/R,BC=1/XC, аYпредставляет собой так называемую полную проводимость цепи в См, тогда какG– активная, аBC – реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = IR +IC.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи
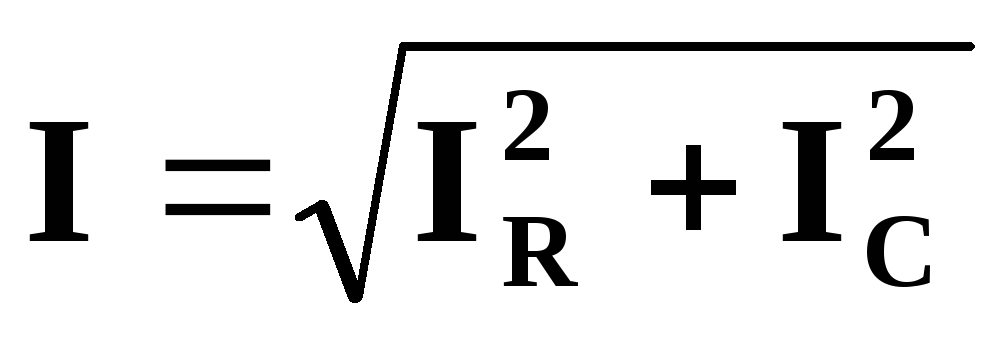; I = U Z = UY.
Полная проводимость цепи
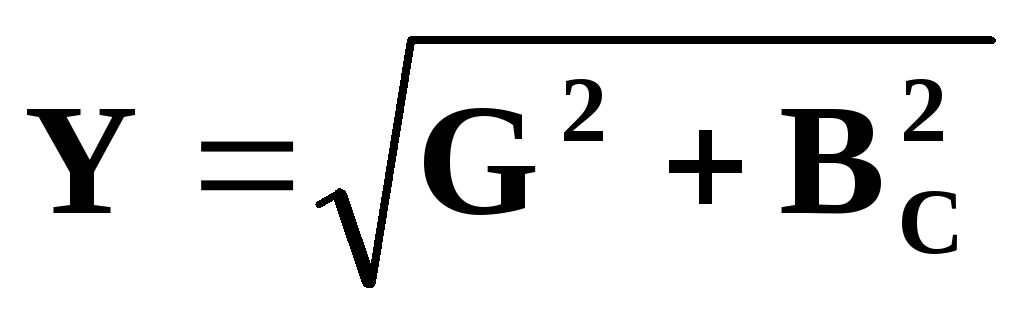; Y = I U = 1/Z ,
где Z — полное сопротивление цепи.
Угол сдвига фаз
= arctg (I C IR) = arctg (BC G).
Активная и реактивная проводимости
G = Y cos; BC=Ysin.
6.2.2. Экспериментальная часть Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IRи конденсатореI C, полный токIи вычислите угол сдвига фаз, полное сопротивление цепиZи емкостную реактивную проводимостьBC.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 1 кГц.
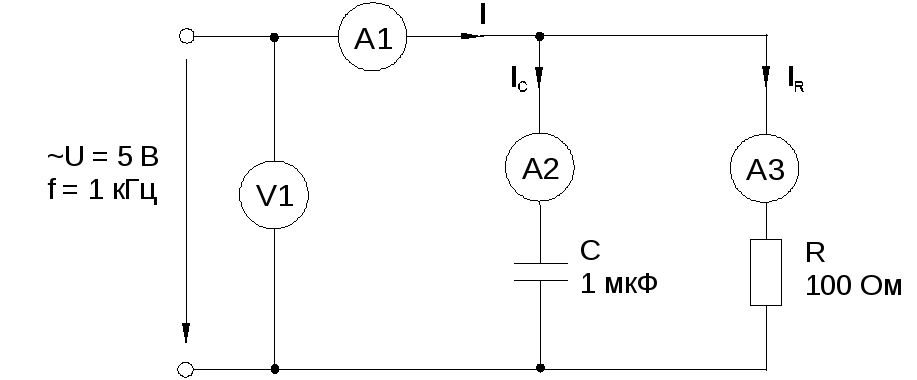
Рис. 6.2.4
Выполните измерения U,I,IC,IRи занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте такжеR, , XC, Z.
Таблица 6.2.1
U,B | I, мА | IС, мА | IR, мА | , град | R, Ом | XC, Ом | Z, Ом | Примечание |
Расчет | ||||||||
Вирт. Изм |
Фазовый угол
= arctg (I C I R) =
Активные проводимость цепи и сопротивление цепи
G = IR U ; R = U IR.
Емкостные реактивные проводимость и сопротивление цепи
BC = IC U ; XC = U IC.
Полные проводимость и сопротивление цепи
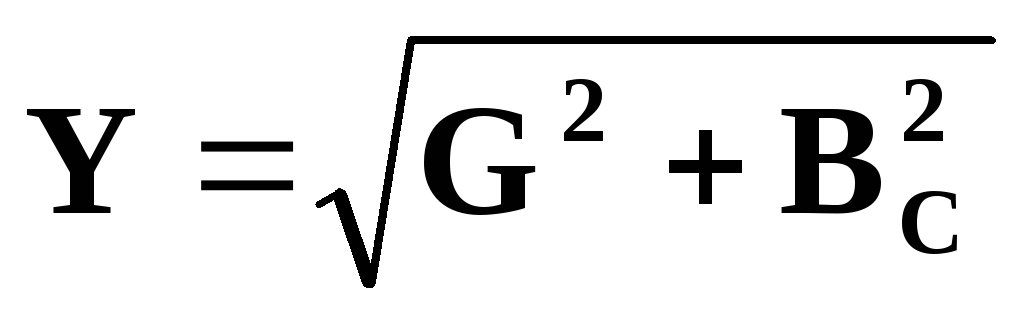; Z = 1 Y.
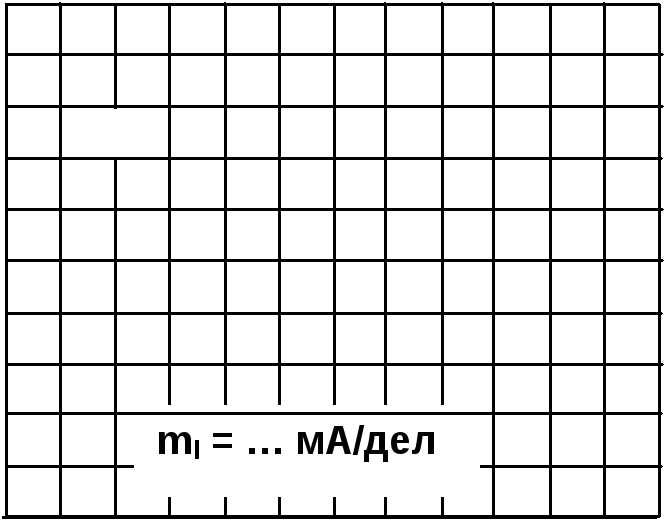
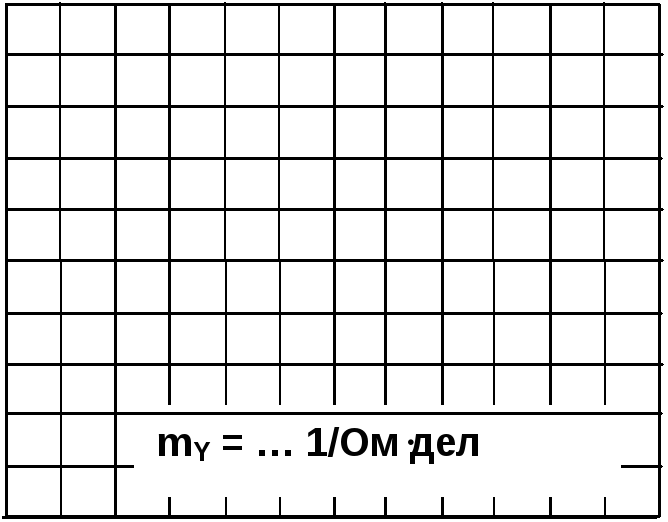
Рис. 6.2.5 Рис. 6.2.6
Конденсатор и RC цепочка | Электроника для всех
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!
Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.
Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.
Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.
Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.
Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.
А у этого закона есть пара характерных величин:
- Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
- 3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C.
Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.
Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10-6 * 103 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.
Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.
Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:
Видишь как колбасится 🙂 Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!
А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.
А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!
Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.
Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.
Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.
Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?
Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.
Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T
Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая. Они же фильтр низких частот и фильтр высоких частот.
Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.
Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.
Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.
А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.
- На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
- На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
- На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
- Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.
А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:
Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.
Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.
А если загнать в дифференциатор пилу, то на выходе получим…
прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.
Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер 🙂 Препод будет в шоке 🙂
Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:
И вот что получилось на осциллографе:
Вот, чуть покрупней один участок:
| > |
Как видишь, на одном срезало постоянную составляющую, на другом переменную.
Ладно, что то мы отвлеклись от темы.
Как еще можно применить RC цепь?
Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:
При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0
Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.
Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.
Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.
Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.
По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!
Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.
Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами 🙂
На нашем сайте вышел обновленный курс по электронике! Мы рады предложить Вам новые версии статей по этой теме:
Итак, продолжаем изучать основы электроники и сегодня мы рассмотрим еще один основополагающий элемент – а именно конденсатор. Также в этой статье мы рассмотрим дифференцирующую и интегрирующую RC-цепи.
Упрощенно можно сказать, что конденсатор – это резистор, но не обычный, а зависящий от частоты. И если в резисторе ток пропорционален напряжению, то в конденсаторе ток пропорционален не просто напряжению, а скорости его изменения. Конденсаторы характеризуются такой физической величиной как емкость, которая измеряется в Фарадах. Правда 1 Фарад – это очень большая емкость, обычно емкости измеряются в нанофарадах (нФ), микрофарадах (мкФ), пикофарадах (пФ) и т. д.
Как и в статье про резисторы, давайте сначала рассмотрим параллельное и последовательное соединения конденсаторов.
- Параллельное соединение конденсаторов:
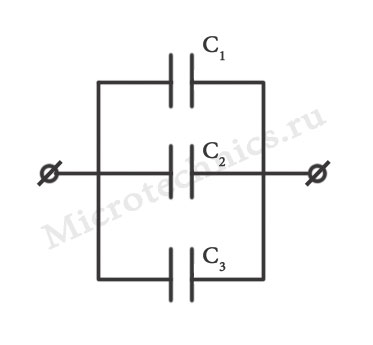
Общая емкость в случае параллельного соединения конденсаторов будет равна: C_0 = C_1 + C_2 + C_3.
- Последовательное соединение конденсаторов:
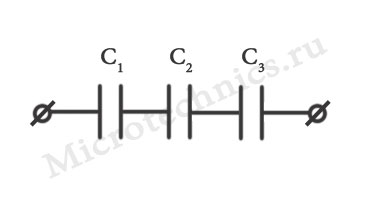
Общая емкость в случае последовательного соединения конденсаторов будет такой: \frac{1}{C_0} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}.
С соединениями конденсаторов между собой, в принципе, все понятно, особо нечего пояснять, так что двигаемся дальше! А дальше мы будем рассматривать соединение резистора и конденсатора, именуемое RC-цепочкой. Простейшая RC-цепь имеет вид:
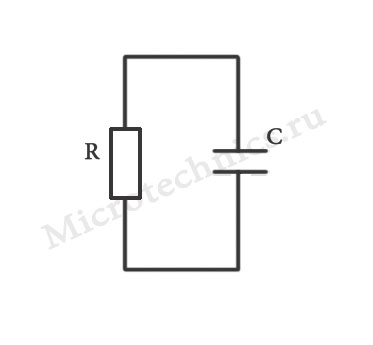
Если записать дифференциальное уравнение, связывающее ток и напряжение в этой схеме, а затем его решить, то получим выражение, в соответствии с которым происходит заряд и разряд конденсатора. Не буду тут нагружать математическими выкладками, просто посмотрим на конечный результат:
U = Ae^{-t\medspace/\medspace RC}
То есть разряд и заряд конденсатора происходит по экспоненциальному закону, вот смотрите на графики:
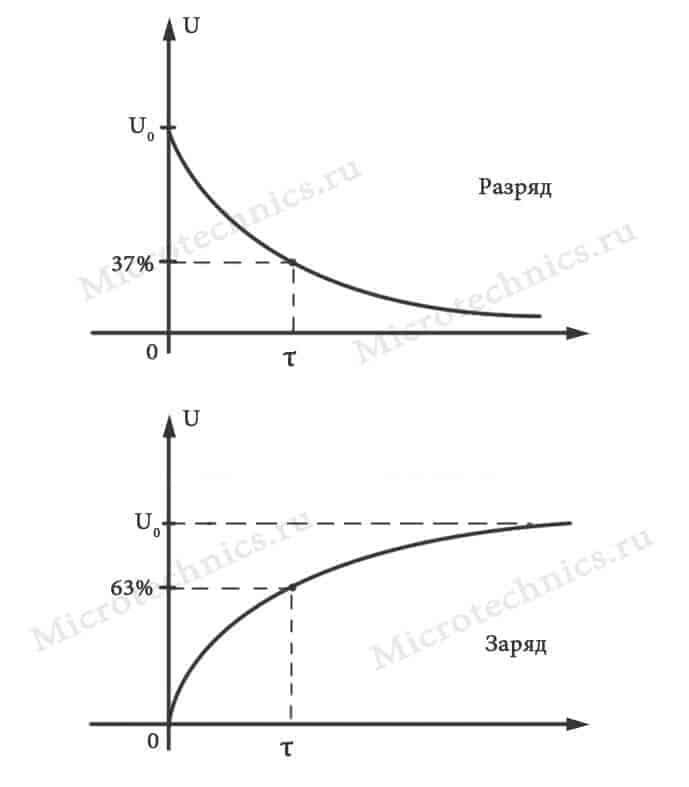
Как видите, тут отдельно отмечено значение времени τ. Запомните обязательно эту величину – это постоянная времени RC-цепи и равна она: \tau = RC. На графиках обозначено, на сколько процентов заряжается/разряжается конденсатор за это время. Есть, кстати, полезное практическое правило – за время, равное пяти постоянным времени RC-цепи, конденсатор заряжается или разряжается на 99%, ну то есть можно считать, что полностью.
Что же все это значит и в чем фишка конденсаторов?
А все просто, дело в том, что если на конденсатор подать постоянное напряжение, то он просто зарядится и все, а вот если приложенное напряжение будет переменным, тут то все и начнется. Конденсатор будет то разряжаться, то заряжаться, соответственно в цепи будет бегать ток. А в итоге мы получаем важный вывод – через конденсатор легко протекает переменный ток, а вот постоянный не может. Поэтому одно из самых важных предназначений конденсатора – разделить постоянную и переменную составляющие тока в цепи.
С этим разобрались, а теперь пара слов о дифференцирующих и интегрирующих RC-цепях.
Дифференцирующая RC-цепь.
Дифференцирующую цепочку еще называют ФВЧ – фильтром высоких частот, ее схема представлена ниже:
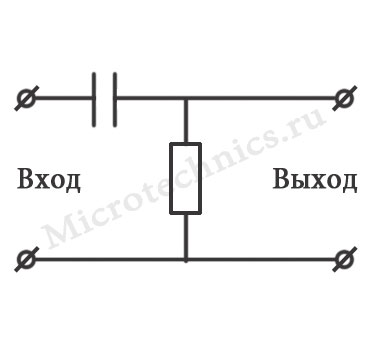
Как следует из названия, да, собственно, это видно и по схеме – RC-цепь не пропускает постоянную составляющую, а переменная преспокойно себе проходит через конденсатор на выход. Опять же название намекает, что на выходе мы будем получать дифференциал входной функции. Давайте попробуем подать на вход дифференцирующей цепи прямоугольный сигнал и посмотрим, что будет на выходе:
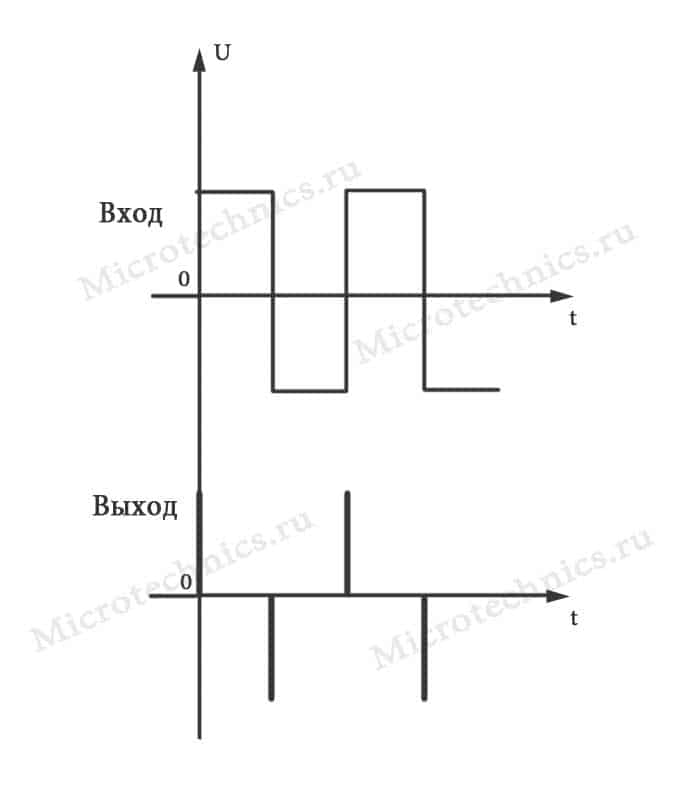
Когда на входе напряжение не меняется – на выходе ноль, так как дифференциал есть не что иное, как скорость изменения функции. Во время скачков напряжения на входе производная велика и на выходе мы наблюдаем всплески. Все логично 🙂
А что же нам подать на вход данной RC-цепи, если мы хотим получить на выходе прямоугольные импульсы? Правильно – пилообразное напряжение. Так как пила состоит из линейных участков, каждый из которых на выходе даст нам постоянный уровень, соответствующий скорости изменения напряжения, то в совокупности на выходе дифференцирующей RC-цепочки мы получим прямоугольные импульсы.
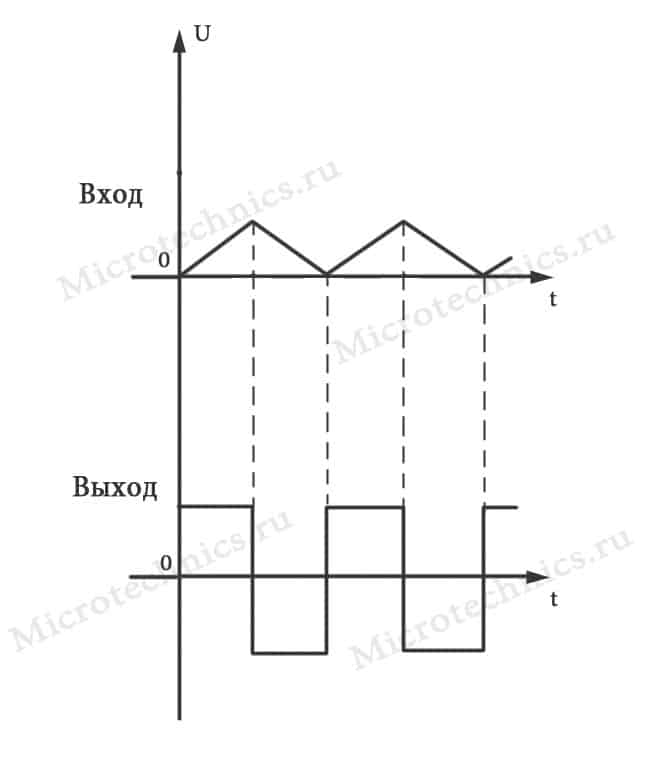
Интегрирующая RC-цепь.
Теперь пришло время интегрирующей цепочки. Также ее называют фильтром низких частот. По аналогии несложно догадаться, что интегрирующая цепь пропускает постоянную составляющую, а переменная уходит через конденсатор и не проходит на выход. Схема имеет следующий вид:
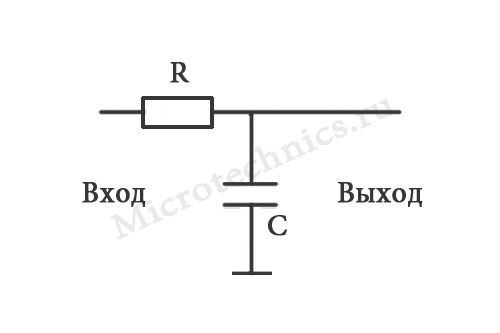
Если немножко вспомнить математику и записать выражения для напряжений и токов, то окажется что напряжение на выходе представляет собой интеграл входного напряжения. Из-за этого цепь и получила свое название 🙂
Итак, мы рассмотрели очень важные и на первый взгляд, несложные схемы. Важно сразу понять, как все это работает и зачем все это вообще надо, чтобы впоследствии при решении конкретных задач сразу видеть подходящее схемотехническое решение. И на этом на сегодня заканчиваем, до скорой встречи в следующих статьях, если возникли какие-либо вопросы, обязательно спрашивайте, постараюсь помочь!
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью. »
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо. », а заодно набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
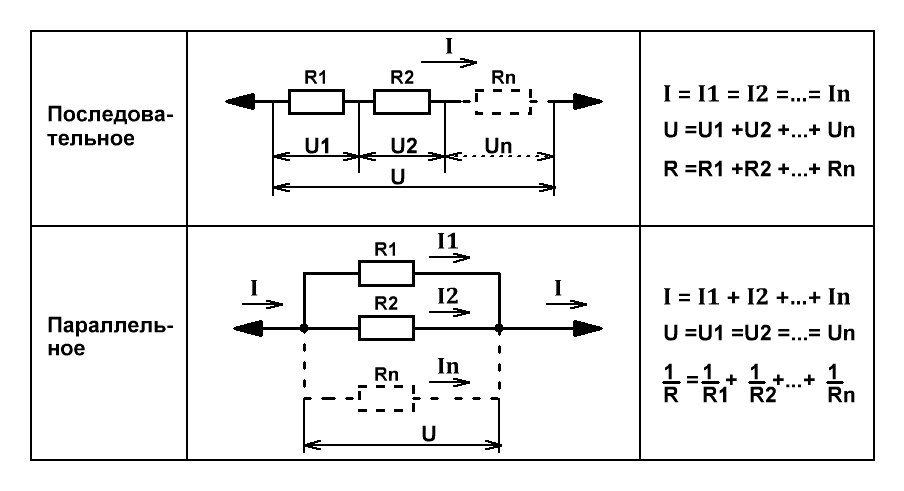
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить.
Короче, все вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С 1 + С 2 +. + С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и
L = L 1 + L 2 +. + L n и 1/С = 1/С 1 + 1/С 2 +. + 1/С n для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.
Общие сведения
Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
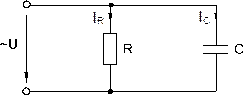
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в резисторе IR(активная составляющая).
Между токами I, IC и IR существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением XC конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).
| | |
| Рис. 6.2.2 | Рис. 6.2.3 |
Фазовый сдвиг между напряжением U цепи и током в резисторе IRотсутствует, тогда как между этим напряжением и током в конденсаторе IC равен –90 0 (т.е. ток опережает напряжение на 90 0 ). При этом сдвиг между полным током Iи напряжением U цепи определяется соотношением междупроводимостями BC и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).
В треугольнике проводимостей G=1/R, BC=1/XC, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а BC– реактивная (емкостная) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = IR +IC.
Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:
Действующее значение полного тока цепи
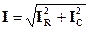; I = U ¤ Z = UY.
Полная проводимость цепи
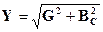; Y = I ¤U = 1/Z ,
гдеZ— полное сопротивление цепи.
Угол сдвига фаз
j = arctg (I C ¤ IR) = arctg (BC ¤ G).
Активная и реактивная проводимости
G = Y cosj; BC = Y sinj.
Экспериментальная часть
Задание
Для цепи с параллельным соединением резистора и конденсатора измерьте действующие значения тока в резисторе IR и конденсаторе I C, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и емкостную реактивную проводимость BC.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.
· Выполните измерения U, I, IC, IR и занесите результаты в табл. 6.2.1. Если измерения производите виртуальными приборами, то измерьте также R, j, XC, Z.
| U, B | I, мА | IС, мА | IR, мА | j, град | R, Ом | XC, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
· Вычислите и запишите в таблицу:
j = arctg (I C ¤ I R) =
Активные проводимость цепи и сопротивление цепи
G = IR ¤ U ; R = U ¤ IR.
Емкостные реактивные проводимость и сопротивление цепи
Полные проводимость и сопротивление цепи
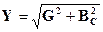; Z = 1 ¤ ÖY.
· Сравните результаты вычислений с результатами виртуальных измерений (если они есть).
· Постройте векторную диаграмму токов (рис. 6.2.5) и треугольник проводимостей (рис. 6.2.6).
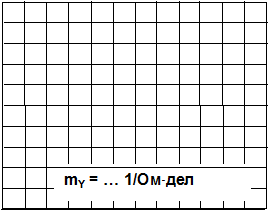
Рис. 6.2.5 Рис. 6.2.6
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Автор Aluarius На чтение 7 мин. Просмотров 548 Опубликовано
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.
Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.
Считаем сопротивление Rобщ1 = R2+R3+R4.
Выделяем вторую группу из последовательных элементов R1, R5, R6.
Считаем сопротивление Rобщ2 = R1+R5+R6.
Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Сопротивление R и C параллельно Калькулятор
- Цель использования
- Сравнить результаты с пользовательской конструкцией анализатора импеданса ,
[1] 2020/04/17 00:06 Мужской / 20-летний уровень / Инженер / Очень /
- Цель использования
- Убедитесь, что я правильно рассчитываю полное сопротивление для параллельная цепь переменного тока для класса электроники.
[2] 2020/04/13 06:49 Женский / 50-летний уровень / Высшая школа / Университет / Аспирант / Очень /
- Назначение
- Определить значения R, C для желаемого гистерезиса, используемого с операционным усилителем (Horowitz & Hill стр. 134-5)
[3] 2020/03/14 09:14 Мужской / 40-летний уровень / Инженер / Очень /
- Назначение
- bangin ur mom
[4] 2019/12/13 05:07 Мужчина / 30-летний уровень / Инженер / Очень /
- Цель использования
- проверить свою интуицию по задаче домашнего задания
[5] 2019/10/04 01:42 Мужской / 20-летний уровень / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- Проверка прибора Fluke RCL, чтобы убедиться, что он все еще функционирует ОК
действительно оценил вашу прекрасную программу
[6] 2019/09 / 10 05:36 Мужчина / 60 лет или старше / Учитель / Исследователь / Очень /
- Назначение Используйте
- Регулятор вентилятора
- Комментарий / Запрос
- Дайте мне принципиальную схему с номинальным компонентом конденсаторной базы регулятора вентилятора
[7] 2018/03/21 16:15 Женщина / Уровень 30 лет / Инженер / — /
- Цель использования
- расчет устойчивости плода
- Комментарий / запрос
- Я считаю, что плод может быть представлен RC-цепью, и я хотел бы провести измерение с известной частотой.Я могу измерить «Z» и фазовый сдвиг в градусах.
Я хотел бы извлечь » R » и » C ».Уточнение: Наличие: » F », » Z », » Phase », необходимо извлечь: » R » и » C ».
[8] 2018/02/05 18:41 Мужчина / 60 лет или старше / Self- занятые люди / очень /
- Назначение
- Очень удобно для быстрого выполнения расчетов по широкому кругу предметов. Спасибо, что сделали его доступным.
[9] 2018/01/08 08:46 Мужчины / 50 лет / Пенсионеры / Очень /
- Назначение
- Разработка контуров обратной связи в регулируемых источниках питания
- Комментарий / запрос
- Отрицательный знак для фазы правильный, так как определение «задержка тока от напряжения».Поскольку ток опережает напряжение в этой цепи, «задержка» является отрицательной.
[10] 2016/09/26 04:20 Мужчина / 60 лет или старше / Инженер / Очень /
параллельных резисторов и конденсаторов
Введение
В этом последнем разделе мы рассмотрим частотную характеристику цепей, содержащих резисторы и конденсаторы в параллельных комбинациях. Как и в предыдущем разделе, мы можем использовать анализ постоянного тока параллельных цепей резисторов в качестве отправной точки, а затем учитывать фазовое соотношение между током, протекающим через резистор и компоненты конденсатора.
Анализ RC параллельных цепей
Как мы видели ранее в параллельной цепи, у тока есть несколько альтернативных путей, и выбранный маршрут зависит от относительного «сопротивления» каждой ветви.На рисунке ниже показана параллельная комбинация одного резистора и конденсатора между точками A, и B, .
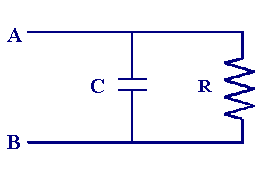
Для расчета полного сопротивления (сопротивления) этой цепи мы снова используем емкостное реактивное сопротивление Xc в качестве эквивалентного сопротивления конденсатора. Затем мы используем те же правила, которые были введены для суммирования резисторов в серии, помня, что теперь мы имеем дело с векторными величинами. Напомним, что правило для суммирования резисторов параллельно задается
, рассматривая R2 и выше как емкостное реактивное сопротивление и немного алгебры комплексных чисел, мы можем показать, что величина импеданса и фазовый угол задаются следующими
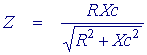
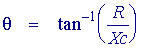
Теперь рассмотрим реакцию цепи, как указано выше, с емкостным сопротивлением 50 Ом и сопротивлением 100 Ом.
| Z = 100 x 50 / (100 2 + 50 2) ½ = 44.7 ° |
и угол составляет -63,4 °. АЧХ этого типа схемы показан ниже в виде векторов и форм Боде.
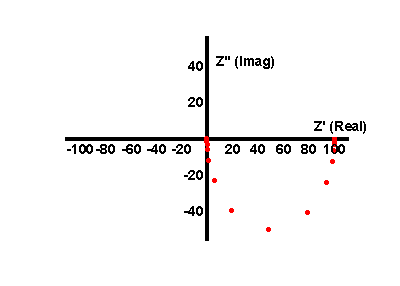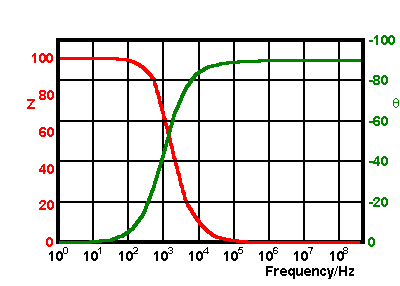
Видно, что фазовый угол изменяется от 0 ° на низких частотах, где ток протекает почти полностью через плечо резистора, до -90 ° на высоких частотах, где ток протекает через ветвь, содержащую конденсатор.
,Серияи параллельные цепи — learn.sparkfun.com
Избранные любимец 48 Серияи параллельные цепи
Простые схемы (с несколькими компонентами) обычно довольно просты для начинающих. Но вещи могут становиться липкими, когда другие компоненты приходят на вечеринку. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, отважный читатель.Ценная информация следует.
В этом руководстве мы сначала обсудим разницу между последовательными и параллельными цепями, используя схемы, содержащие самые основные компоненты — резисторы и батареи — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы объединяете различные типы компонентов, таких как конденсаторы и катушки индуктивности.
В этом уроке
- Как выглядят конфигурации последовательных и параллельных цепей
- Как действуют пассивные компоненты в этих конфигурациях
- Как источник напряжения будет действовать на пассивные компоненты в этих конфигурациях
Рекомендуемое Чтение
Возможно, вы захотите посетить эти учебные пособия по основным компонентам, прежде чем углубляться в построение схем в этом учебном пособии.
Видео
Схемы серии
узлов и ток
Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел . Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема смоделирована на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя одноцветными узлами.
Это полдела, чтобы понять разницу между сериями и параллелями. Нам также необходимо понять , как ток протекает через цепь . Ток течет от высокого напряжения к более низкому напряжению в цепи. Некоторое количество тока будет протекать через каждый путь, по которому можно добраться до точки наименьшего напряжения (обычно называемой заземлением). Используя приведенную выше схему в качестве примера, вот как будет течь ток при его прохождении от положительной клеммы аккумулятора к отрицательной:
Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же схеме, что и выше.Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток поступает так же, как и при выходе. В других узлах (в частности, в трехстороннем соединении между R 2 , R 3 и R 4 ) основной (синий) ток разделяется на два разных. Это ключевое различие между серией и параллелью!
Схемы серииопределены
Два компонента соединены последовательно, если они совместно используют общий узел и если через них протекает один и тот же ток , то .Вот пример схемы с тремя последовательными резисторами:
Есть только один способ протекания тока в вышеуказанной цепи. Начиная с положительного полюса аккумулятора, ток вначале встретится с R 1 . Оттуда ток протекает прямо к R 2 , затем к R 3 и, наконец, обратно к отрицательному выводу батареи. Обратите внимание, что существует только один путь для текущего. Эти компоненты в серии.
параллельных цепей
Определены параллельные цепи
Если компоненты совместно используют двух общих узлов, они расположены параллельно.Вот пример схемы трех резисторов параллельно с батареей:
От положительной клеммы аккумулятора ток течет до R 1 … и R 2 и R 3 . Узел, который соединяет батарею с R 1 , также соединен с другими резисторами. Другие концы этих резисторов аналогичным образом связаны друг с другом, а затем снова связаны с отрицательным выводом батареи. Есть три различных пути, по которым ток может пройти до возвращения в батарею, и связанные резисторы, как говорят, параллельны.
Если все последовательные компоненты проходят через одинаковые токи, параллельные компоненты имеют одинаковое падение напряжения на них — серия: ток :: параллель: напряжение.
Серияи параллельные цепи, работающие вместе
Оттуда мы можем смешивать и сочетать. На следующем рисунке мы снова видим три резистора и батарею. С положительной клеммы аккумулятора ток сначала сталкивается с R 1 . Но по другую сторону от R 1 узел разделяется, и ток может доходить до R 2 и R 3 .Токовые пути через R 2 и R 3 затем снова связываются вместе, и ток возвращается к отрицательной клемме батареи.
В этом примере R 2 и R 3 параллельны друг другу, а R 1 последовательно с параллельной комбинацией R 2 и R 3 .
Расчет эквивалентных сопротивлений в последовательных цепях
Вот некоторая информация, которая может быть вам более полезна.Когда мы соединяем резисторы вместе, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть 10 В на 10 кОм; резистор, закон Ома гласит, что у нас течет ток 1 мА.
Если мы тогда поставим еще 10 кОм; последовательно с первым резистором и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление удвоилось.
Другими словами, есть только один путь для прохождения тока, и мы только усложнили его для прохождения тока.Насколько сложнее? 10k & Ом; + 10кОм; = 20 кОм. И вот как мы рассчитываем резисторы последовательно — только добавляют их значения .
Чтобы сформулировать это уравнение более широко: общее сопротивление N — произвольное число резисторов — это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
А как насчет параллельных резисторов? Это немного сложнее, но не намного.Рассмотрим последний пример, где мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавим еще 10 кОм; параллельно вместо серии. Теперь есть два пути для тока. Так как напряжение питания не изменилось, закон Ома гласит, что первый резистор все еще будет потреблять 1 мА. Но, так же, как и второй резистор, и теперь у нас есть 2 мА от источника, удваивая первоначальный 1 мА. Это означает, что мы сократили общее сопротивление вдвое.
Пока можно сказать, что 10кОм; || 10k & Ом; = 5 кОм; («||» примерно означает «параллельно с»), у нас не всегда будет 2 одинаковых резистора.Что тогда?
Уравнение для добавления произвольного числа резисторов параллельно:
Если взаимные переходы не для вас, мы также можем использовать метод под названием «произведение на сумму», когда у нас есть два резистора параллельно:
Однако этот метод подходит только для двух резисторов в одном расчете. С помощью этого метода мы можем объединить более 2 резисторов, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (опять же как произведение на сумму), но обратный метод может быть менее трудоемким.
Время эксперимента — часть 1
Что вам нужно:
Давайте попробуем простой эксперимент, чтобы доказать, что эти вещи работают так, как мы говорим.
Во-первых, мы собираемся подключить около 10 кОм; резисторы в серии и смотреть, как они добавляются самым таинственным образом. Используя макет, поместите один 10 кОм; резистор, как указано на рисунке и измерьте с помощью мультиметра. Да, мы уже знаем, что это будет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Как только мы убедимся в том, что мир не сильно изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогичным образом, но с выводом от каждого резистора, электрически подключенного через макет, и проведите измерения снова. Теперь счетчик должен сказать что-то близкое к 20 кОм.
Вы можете заметить, что измеренное вами сопротивление может не совпадать с сопротивлением, которое, по словам резистора, должно быть. Резисторы имеют определенное значение с допуском , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10,01 кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читатель должен продолжать это упражнение до тех пор, пока не убедится, что он знает, каким будет результат, прежде чем делать это снова, или у него закончатся резисторы, чтобы прилипнуть к макету, в зависимости от того, что наступит раньше.
Время эксперимента — часть 2
Теперь давайте попробуем это с резисторами в параллельной конфигурации .Поместите один 10 кОм; резистор в макете, как и раньше (мы будем полагать, что читатель уже полагает, что один резистор 10 кОм будет измерять что-то близкое к 10 кОм на мультиметре). Теперь поместите вторую 10 кОм; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора были в электрически соединенных рядах. Но прежде, чем измерить комбинацию, рассчитайте с помощью суммирования по продукту или взаимных методов, каким должно быть новое значение (подсказка: оно будет 5 кОм).Тогда измерить. Это что-то близкое к 5 кОм? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.
Повторите упражнение сейчас с 3, 4 и 5 резисторами. Расчетные / измеренные значения должны составлять 3,33 кОм; 2,5 кОм; и 2кОм соответственно. Все получилось как запланировано? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Пойди попей молочный коктейль, прежде чем мы продолжим. Ты заслужил это.
Полезные правила для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать некоторых творческих комбинаций резисторов.Например, если мы пытаемся создать очень специфический источник опорного напряжения вы почти всегда необходимо очень специфическое соотношение резисторов, значения которых вряд ли будут «стандартные» значения. И хотя мы можем получить очень высокую степень точности значений резисторов, нам, возможно, не захочется ждать X дней, которые требуются для доставки чего-либо, или платить цену за нестандартные значения. Таким образом, в крайнем случае, мы всегда можем построить наши собственные значения резисторов.
Совет №: Равные резисторы в параллельном соединении
Если добавить резисторов N с одинаковым номиналом R параллельно, мы получим R / N Ом.Допустим, нам нужно 2,5 кОм; резистор, но все, что у нас есть, это ящик, заполненный 10 кОм. Параллельное объединение четырех из них дает нам 10 кОм / 4 = 2,5 кОм.
Совет №: допуск
Знай, какую толерантность ты можешь терпеть. Например, если вам нужно 3,2 кОм; резистор, можно было бы поставить 3 10 кОм; резисторы параллельно. Это даст вам 3,3 кОм, что примерно на 4% меньше допустимого значения. Но, если схема, которую вы строите, должна быть с допустимым отклонением более 4%, мы можем измерить наш тайник в 10 кОм, чтобы увидеть, какие значения являются самыми низкими, потому что они тоже имеют допуск.По идее если заначка 10кОм; все резисторы имеют допуск 1%, мы можем получить только до 3,3 кОм. Но производители деталей, как известно, допускают именно такие ошибки, поэтому стоит немного поковыряться.
Совет№ 3: Номинальная мощность в серии / параллельно
Этот вид последовательных и параллельных комбинаций резисторов также подходит для номинальной мощности. Допустим, нам нужно 100 Ом. резистор рассчитан на 2 Вт (Вт), но все, что мы получили, это группа 1 кОм; резисторы четверть ватта (¼W) (а сейчас 3 часа ночи, вся Mountain Dew ушла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 кОм; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень, но это поможет нам завершить проект и даже может дать нам дополнительные очки за способность думать на ногах.
Нам нужно быть немного более осторожными, когда мы объединяем резисторы разного значения параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Это должно быть совершенно очевидно для читателя, но …
Совет №: Различные резисторы параллельно
Совместное сопротивление двух резисторов разных значений всегда меньше, чем резистор наименьшего значения.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и достигает значения, которое находится на полпути между двумя резисторами (1 кОм; || 10 кОм; НЕ равняется чему-то около 5 кОм!). Общее параллельное сопротивление всегда будет перемещаться ближе к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет № 4 10 раз.
Совет №: Рассеяние мощности параллельно
Мощность, рассеиваемая в параллельной комбинации разнородных значений резисторов, не разделяется равномерно между резисторами, потому что токи не равны.Используя предыдущий пример (1k & ome; || 10k & ohm;), мы можем видеть, что 1 k & ohm; будет в 10 раз больше тока 10 кОм. Так как закон Ома гласит, что мощность = напряжение х ток, из этого следует, что 1 кОм; резистор рассеивает в 10 раз мощность 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем, когда параллельно объединяем резисторы разной величины. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.
серии и параллельные конденсаторы
Объединение конденсаторов похоже на объединение резисторов … только наоборот. Как бы странно это ни звучало, это абсолютно верно. С чего бы это?
Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.И если пластины раздвигаются дальше, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы разрядиться в друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для тока. Отсюда следует, что число электронов, которые разряжаются из крышки на дне, будет таким же, как число электронов, выходящих из крышки наверху.Значит, емкость не увеличилась?
На самом деле, это даже хуже, чем это. Размещая конденсаторы последовательно, мы эффективно расположили пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается вместе. Таким образом, у нас нет 20 мкФ или даже 10 мкФ. У нас есть 5 мкФ. В результате мы добавляем значения последовательных конденсаторов так же, как добавляем значения параллельных резисторов. Как суммируемый, так и взаимный методы действительны для последовательного добавления конденсаторов.
Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое больше напряжения (или номинальное напряжение). Как и батареи, когда мы последовательно соединяем конденсаторы, напряжение накапливается.
Параллельное добавление конденсаторов похоже на последовательное добавление резисторов: значения просто складываются, никаких хитростей. Почему это? Размещение их параллельно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Просто.
Время эксперимента — часть 3
Что вам нужно:
Давайте посмотрим, как работают последовательно и параллельно подключенные конденсаторы. Это будет немного сложнее, чем примеры с резисторами, потому что измерять емкость непосредственно с помощью мультиметра сложнее.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается от нуля вольт. Когда ток начинает идти в одном из выводов, равное количество тока выходит из другого.И если нет последовательного сопротивления с конденсатором, это может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, медленнее сбегает до тех пор, пока напряжения не станут равными, когда поток тока полностью прекратится.
Как указано выше, потребление тока может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). В этом эксперименте мы хотим иметь возможность следить за зарядом конденсатора, поэтому мы будем использовать 10 кОм; резистор последовательно, чтобы замедлить действие до точки, где мы можем легко его увидеть.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в Фарадах. Просто? Нет? Мы продемонстрируем на следующей странице.
Время эксперимента — часть 3, продолжение …
Для первой части этого эксперимента мы собираемся использовать один резистор 10 кОм и один 100 мкФ (что соответствует 0,0001 фарадам). Эти две части создают постоянную времени в 1 секунду:
При зарядке нашего конденсатора емкостью 100 мкФ через 10 кОм; Резистор, мы можем ожидать, что напряжение на крышке возрастет примерно до 63% от напряжения питания за 1 постоянную времени, что составляет 1 секунду.Через 5 временных констант (в данном случае 5 секунд) крышка заряжается примерно на 99% до напряжения питания, и она будет следовать кривой заряда, как показано на рисунке ниже.
Теперь, когда мы знаем этот материал, мы собираемся подключить схему на схеме (убедитесь, что полярность правильно установлена на этом конденсаторе!).
С нашим мультиметром, настроенным на измерение вольт, проверьте выходное напряжение блока при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5 В (это будет немного больше, если батареи новые). Теперь подключите цепь, следя за тем, чтобы выключатель аккумуляторного блока находился в положении «ВЫКЛ», прежде чем подключать его к макету. Также позаботьтесь о том, чтобы красный и черный провода шли в правильные места. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного развести эти ножки, чтобы было легче).
Как только мы убедимся, что схема выглядит правильно и наш прибор включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ON».Примерно через 5 секунд индикатор должен показывать значение, близкое к напряжению аккумуляторной батареи, что показывает, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще хорошо держит это напряжение, не так ли? Это потому, что нет пути для тока разрядить конденсатор; у нас есть разомкнутая цепь. Чтобы разрядить крышку, вы можете использовать другой резистор 10K параллельно. Примерно через 5 секунд он вернется почти к нулю.
Время эксперимента — часть 3, даже больше…
Теперь перейдем к интересным деталям, начиная с последовательного подключения двух конденсаторов. Помните, что мы сказали, что результат будет аналогичен соединению двух резисторов параллельно. Если это правда, мы можем ожидать (используя перерасход)
Что это будет делать с нашей постоянной времени?
Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает нулевое напряжение (или около того), и установите переключатель в положение «ON».Заряжалось ли примерно вдвое меньше времени, чтобы зарядиться до напряжения аккумуляторной батареи? Это потому, что емкость вдвое меньше. Электронный газовый баллон стал меньше, поэтому для его зарядки требуется меньше времени. Для этого эксперимента предлагается третий конденсатор, чтобы доказать это, но мы держим пари, что читатель увидит надпись на стене.
Теперь мы попробуем конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на последовательное добавление резисторов. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
Это означает, что теперь потребуется около 10 секунд, чтобы увидеть зарядку параллельных конденсаторов до напряжения питания 4.5V.
Для доказательства начните с нашей оригинальной схемы в 10 кОм; резистор и один конденсатор емкостью 100 мкФ последовательно, как показано на первой диаграмме для этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно через 5 секунд. Теперь добавьте второй конденсатор параллельно. Убедитесь, что показания счетчика близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и установите переключатель на батарейном блоке в положение «ON». Это займет много времени, не так ли? Конечно же, мы сделали электронный газовый баллон больше, и теперь для его заполнения требуется больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и наблюдать, как он заряжается в течение длительного времени.
Серияи параллельные индукторы
Серияи параллельные индукторы
Случаи, когда катушки индуктивности необходимо добавлять последовательно или параллельно, встречаются довольно редко, но не случайно. В любом случае, давайте обратимся к ним, чтобы быть полными.
Короче говоря, они добавляют так же, как и резисторы, то есть они добавляют со знаком плюс, когда в серии, и с перерасходом продукта, когда параллельно.Сложная часть возникает, когда они расположены близко друг к другу, чтобы иметь взаимодействующие магнитные поля, умышленно или нет. По этой причине предпочтительно иметь один компонент, а не два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они добавляют, как резисторы. Больше информации, чем то, что касается индукторов, выходит за рамки данного руководства.
Ресурсы и дальнейшее развитие
Теперь, когда вы знакомы с основами последовательных и параллельных цепей, почему бы не проверить некоторые из этих руководств?
- Делители напряжения
- . Делителем напряжения является одна из самых основных и повторяющихся цепей.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
- Что такое Arduino? — Теперь, когда вы ознакомились с основами микросхем, вы можете приступить непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino. Основы коммутатора
- . Мы говорили о некоторых элементах схемы в этом руководстве, но это не был один из них. Переключатели являются критически важным компонентом практически для каждого проекта в области электроники.Узнайте все о переключателях в этом уроке
- Шитье с проводящей нитью — цепи не обязательно должны быть макетами и проволокой. Электронный текстиль использует проводящую нить, чтобы шить огни и другую электронику в одежду или другую ткань.