Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис. 2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
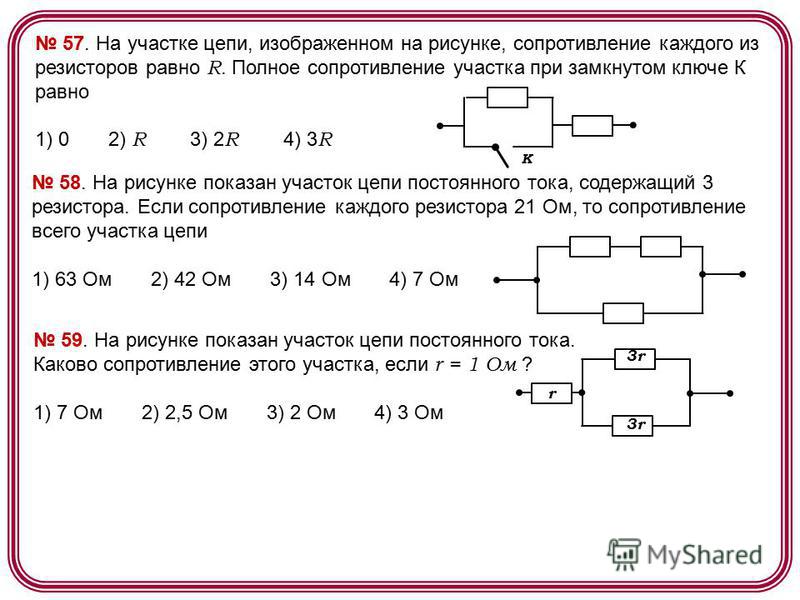
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
в момент, когда опоздавший пассажир вбежал на платформу, мимо него за 10 с проехал предпоследний вагон, последний проехал за 8с на сколько времени опоздал пассажир
Молекулярная физика
Колебательный контур состоит из конденсатора емкостью С=2. 5 мкФ
5 мкФ
Решено
Чему равна энергия теплового движения…
Решено
Пользуйтесь нашим приложением
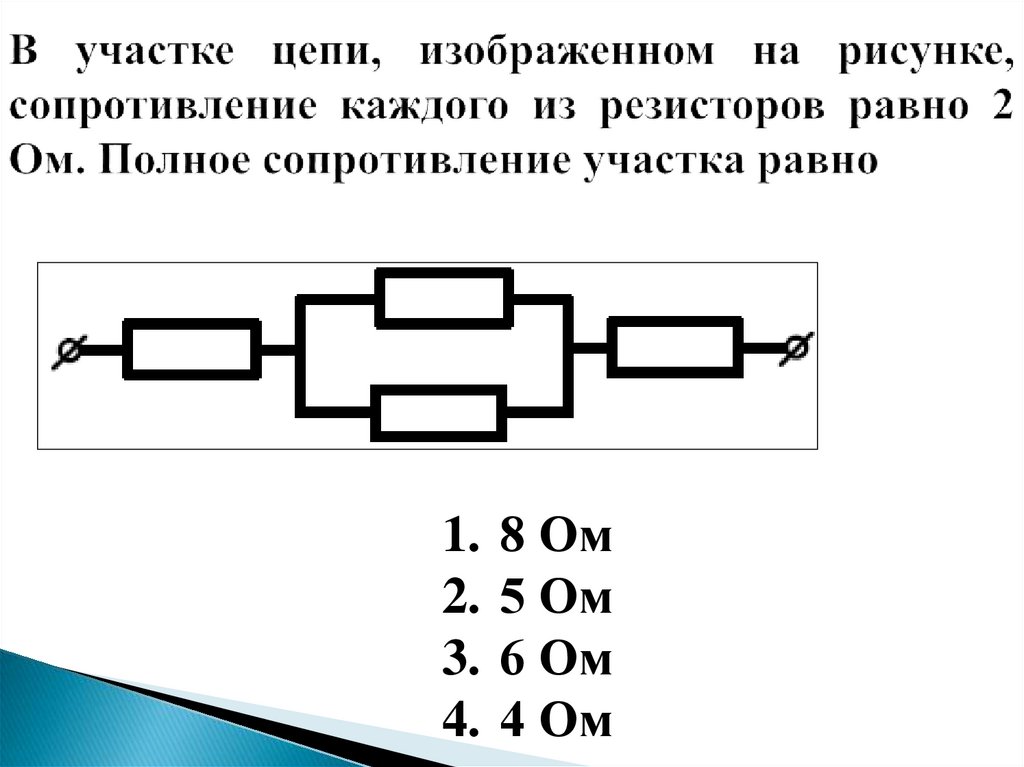
Объяснение урока: Анализ комбинированных цепей
В этом объяснении мы научимся определять токи через и напряжения на участках цепей, содержащих резисторы как последовательно, так и параллельно.
Напомним, что последовательно соединенные резисторы соединяются в один проводящий путь. На приведенной ниже схеме показаны три последовательно соединенных резистора.
В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=𝑅+𝑅+𝑅.
Распространяется на любое количество последовательно соединенных резисторов: 𝑅=𝑅+𝑅+⋯+𝑅.
С другой стороны, резисторы параллельно соединены вдоль нескольких
токопроводящие пути. На приведенной ниже схеме показаны три резистора, соединенные последовательно.
параллельно.
На приведенной ниже схеме показаны три резистора, соединенные последовательно.
параллельно.
В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=1𝑅+1𝑅+1𝑅.
Это распространяется на любое количество резисторов, включенных параллельно: 𝑅=1𝑅+1𝑅+⋯+1𝑅.
Комбинированная схема содержит секции резисторов, соединенных последовательно и параллельно. На приведенной ниже схеме показаны два резистора, соединенные последовательно с двумя резисторы параллельно.
В приведенном выше примере часть схемы, содержащая 𝑅 и 𝑅 последовательно, а участок цепи, содержащий 𝑅 и 𝑅 параллельны.
Для анализа этой схемы каждый набор резисторов можно преобразовать в их
эквивалентный резистор. На приведенной ниже диаграмме показано, как последовательно подключить два резистора.
и два резистора параллельно могут быть преобразованы в один эквивалентный
резисторы, которые затем могут быть преобразованы в окончательный эквивалентный резистор для
вся цепь.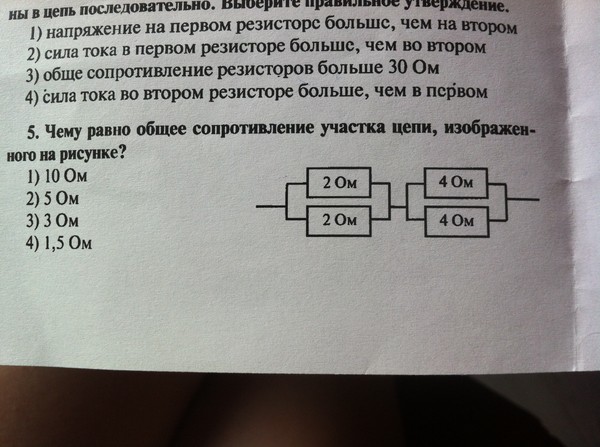
Раздел серии, содержащий 𝑅 и 𝑅 можно преобразовать в его эквивалентный резистор, 𝑅: 𝑅=𝑅+𝑅.
Параллельная секция, содержащая 𝑅 и 𝑅 можно преобразовать в эквивалентный ему резистор, 𝑅: 𝑅=1𝑅+1𝑅.
Тогда, наконец, эквивалентное сопротивление всей цепи, 𝑅, это 𝑅=𝑅+𝑅.
Давайте рассмотрим примерный вопрос.
Пример 1. Определение эквивалентного сопротивления комбинированной цепи
Показанная схема содержит как последовательные, так и параллельные комбинации резисторов.
- Какова общая сила тока в показанной цепи? Дайте свой ответ на один десятичный знак.
- Какова общая мощность, рассеиваемая цепью? Дай свой ответ до одного десятичного знака.
Ответ
Часть 1
В первой части этого вопроса мы должны рассчитать общий ток в
схема. Для этого необходимо найти эквивалентное сопротивление
схема.
Мы начнем с обозначения компонентов на электрической схеме.
Первый шаг в расчете эквивалентного сопротивления цепи: найти эквивалентное сопротивление параллельного участка, состоящего из 𝑅 и 𝑅. Обозначим эквивалентное сопротивление этого параллельного участка на 𝑅: 𝑅=1𝑅+1𝑅.
Подставляя известные значения для 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩ
Теперь мы можем рассчитать эквивалентное сопротивление всей цепи, 𝑅: 𝑅=𝑅+𝑅+𝑅.
Подставляя известные значения для 𝑅=1,6Ω и 𝑅=1,5Ом и значение 𝑅, которое мы рассчитали как 1,40 Ом дает нам 𝑅=1,6+1,5+1,4𝑅=4,5.ΩΩΩΩΩ
Тогда мы можем использовать закон Ома для расчета полного тока в цепи, при 𝑉=5,5 В: 𝐼=𝑉𝑅𝐼=5,54,5.VΩ
Полный ток в цепи с точностью до одного десятичного знака равен 𝐼=1.2.A
Часть 2
Полная мощность, рассеиваемая в цепи, может быть рассчитана путем умножения
ток в цепи на полное падение потенциала на
схема:
𝑃=𝐼𝑉𝑃=1,2×5,5. AV
AV
Полная мощность, рассеиваемая в цепи, с точностью до одного десятичного знака равна 𝑃=6.7.W
Эти методы анализа комбинированных цепей также можно использовать для анализировать схемы, содержащие компоненты, отличные от резисторов. Мы сейчас проработайте пример вопроса об этом.
Пример 2. Анализ цепей, содержащих компоненты, отличные от Резисторы
Ток измеряется амперметром в цепи, показанной на схеме. Амперметр имеет сопротивление 2,5 мкОм.
- Какие показания будут на амперметре? Дай свой ответ до одного десятичного знака.
- Какими были бы показания амперметра, если бы он был подключен к параллельно Резистор 3,5 Ом? Отдай свое ответ до одного десятичного знака.
Ответ
Часть 1
В первой части вопроса нам предлагается рассчитать сумму текущего
через цепь. Для этой цели мы можем заменить амперметр на
резистор эквивалентного сопротивления.
Мы можем обобщить это на диаграмме, где каждый резистор помечен. 𝑅 — эквивалентное сопротивление для амперметра.
Общее сопротивление цепи равно 𝑅=𝑅+𝑅+𝑅𝑅=2,5+3,5+2,5×10𝑅=6,0000025.ΩΩΩΩΩ
Ток в цепи можно рассчитать по закону Ома: 𝐼=126,0000025𝐼=1,9999991.VΩA
Амперметр будет показывать до одного десятичного знака 2,0 А. Давайте сравните это с идеальным амперметром, который имеет нулевое внутреннее сопротивление.
Общее сопротивление цепи будет точно равно сумме из двух резисторов: 𝑅=2,5+3,5𝑅=6,0.ΩΩΩΩ
Это означает, что ток в цепи равен 𝐼=126.0𝐼=2.0.VΩA
Таким образом, амперметр покажет точно
2,0 А. Это
подчеркивает, насколько важно иметь амперметр с очень низким
внутреннее сопротивление. Если внутреннее сопротивление достаточно низкое, т.
в данном примере, им можно пренебречь при расчетах.
Часть 2
Во второй части вопроса нам предлагается рассмотреть, что произойдет, если амперметр будет подключен параллельно Резистор 3,5 Ом.
Заменив амперметр его эквивалентным резистором, мы можем нарисуй на схеме.
Теперь мы должны рассчитать эквивалентное сопротивление, 𝑅, параллельного участка цепи: 𝑅=13,5+12,5×10𝑅=(0,28+400000)𝑅=400000,28𝑅=2,499998×10,ΩΩΩ
3 амперметр такой низкий по сравнению до 3,5 Ом резистора, что он полностью доминирует над эквивалентным сопротивлением два.
Общее сопротивление цепи равно 𝑅=2,5+2,499998×10𝑅=2,5000025,Ω
Тогда ток в цепи можно рассчитать по закону Ома: 𝐼=122,5000025𝐼=4,799995.VΩA
Итак, с точностью до десятых, амперметр показывает 4,8 А.
Рассчитаем показание тока, если эквивалентное сопротивление
параллельным сечением в расчете пренебрегают:
𝐼=122,5𝐼=4,8. VΩA
VΩA
Как видно, внутреннее сопротивление амперметра настолько мало, что эквивалентным сопротивлением параллельного участка можно пренебречь.
В то время как эквивалентное сопротивление позволяет нам анализировать многие комбинированные схемы, есть некоторые, которые нельзя решить, используя только эквивалентное сопротивление.
Цепь, показанная на следующей принципиальной схеме, не может быть проанализирована с помощью только эквивалентное сопротивление.
Поскольку есть две батареи, мы не можем рассчитать эквивалентное сопротивление из 𝑅 и 𝑅.
Для анализа таких цепей мы можем использовать законы Кирхгофа.
Первый закон Кирхгофа гласит, что ток в переходе или узле в цепь должна быть такой же, как и ток, выходящий из перехода или узла.
Определение: Первый закон Кирхгофа
Первый закон Кирхгофа утверждает, что сумма токов в
соединение/узел в цепи, 𝐼+𝐼+⋯()()inin,
должно быть таким же, как сумма токов из узла/узла,
𝐼+𝐼+⋯()()outout:
𝐼+𝐼+⋯=𝐼+𝐼+⋯. ()()()()ininoutout
()()()()ininoutout
Например, предположим, что в следующем соединении цепи есть токи 𝐼 и 𝐼 на перекрестке и 𝐼 с перекрестка.
Первый закон Кирхгофа гласит, что сумма токов в переходе, 𝐼+𝐼, должны равняться сумме токов из перекресток, 𝐼: 𝐼+𝐼=𝐼.
Второй закон Кирхгофа позволяет нам анализировать разность потенциалов на различных точках комбинационной цепи.
Второй закон Кирхгофа гласит, что сумма всех разностей потенциалов между компонентами в цикле должны быть равны нулю.
На следующей принципиальной схеме показано последовательное подключение трех резисторов к батарее.
Определение: Второй закон Кирхгофа
Сумма разностей потенциалов на каждом компоненте контура равна нуль: 𝑉+𝑉+⋯+𝑉=0,
В приведенной схеме разность потенциалов на ячейке равна 𝑉, а на трех резисторах разность потенциалов равна 𝑉, 𝑉 и 𝑉 соответственно.
Закон Кирхгофа гласит, что сумма разностей потенциалов по всем
компоненты в цикле равны нулю. То есть,
𝑉+𝑉+𝑉+𝑉=0,
То есть,
𝑉+𝑉+𝑉+𝑉=0,
В этом случае разность потенциалов на ячейке положительна и равна по модулю равна полной разности потенциалов на трех резисторы.
Законы Кирхгофа можно использовать для сравнения цепей. Мы будем работать через пример вопрос об этом сейчас.
Пример 3. Анализ нескольких похожих цепей
Схемы (a) и (b) очень похожи, но немного отличаются друг от друга. Другой. Какова разница в полном токе между цепью, показанной на рис. схеме (а) и цепи, показанной на схеме (б)? Дайте ответ с точностью до одного десятичного знака.
Ответ
Начнем с анализа схемы (б).
Мы можем использовать второй закон Кирхгофа для петли, образованной цепью. Отзывать что второй закон Кирхгофа гласит, что сумма разностей потенциалов по каждому компоненту в цикле должен равняться нулю.
Обозначим разность потенциалов на
800 мОм
резистор как 𝑉 и разность потенциалов на
Резистор 960 мОм как
𝑉.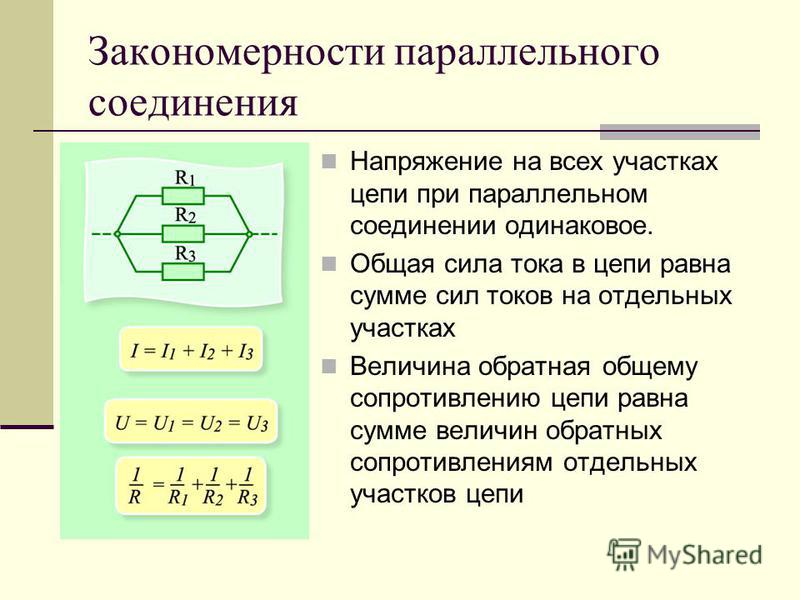
Два резистора можно преобразовать в один эквивалентный резистор, который мы будет коллировать 𝑅 со следующим сопротивлением: 𝑅=880+960𝑅=1840.мОммОммОм
Разность потенциалов на этом эквивалентном резисторе равна 𝑉 и равно 𝑉=𝑉+𝑉.
Сумма разностей потенциалов на каждом компоненте в цепи (b) можно записать как 2,5+1,4−𝑉−𝑉=0,ВВВ или, учитывая эквивалентный резистор, 𝑅, это можно записать как 2,5+1,4−𝑉=0𝑉=3,9.VVVV
Итак, разность потенциалов на этом эквивалентном резисторе равна 3,9 В.
Ток в цепи (b), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=3,91,84𝐼=2,12.VΩA
Теперь проанализируем схему (а).
Схема (а) почти идентична схеме (б), за исключением того, что
Батарея 1,4 В есть
перевернулся. Когда мы на этот раз применим второй закон Кирхгофа, эта батарея
вносит в уравнение отрицательную разность потенциалов.
Объединение резисторов в эквивалентный резистор, как мы это делали ранее, мы можем написать 2,5−1,4−𝑉=0𝑉=1,1.VVVV
Итак, разность потенциалов на этом эквивалентном резисторе равна 1,1 В.
Ток в цепи (a), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=1,11,84𝐼=0,60.VΩA
Тогда разница токов между двумя цепями равна 𝐼−𝐼=2,12−0,06𝐼−𝐼=1,52.AAA
Разница в общем токе между цепью, показанной на схеме (а) и схема, показанная на диаграмме (б), поэтому 1,5 А до одного десятичного знака.
Законы Кирхгофа также можно использовать для анализа комбинационных цепей. Когда мы учитывая комбинированную схему, мы должны идентифицировать петли и соединения/узлы.
Например, следующая принципиальная схема содержит несколько резисторов и аккумуляторы в разных цепях цепи.
Мы можем идентифицировать два узла в этой цепи и три петли. Это
проиллюстрировано на следующей диаграмме.
Это
проиллюстрировано на следующей диаграмме.
Теперь мы рассмотрим пример вопроса, в котором мы должны использовать метод Кирхгофа. законы для анализа комбинационной цепи.
Пример 4. Использование законов Кирхгофа для анализа комбинационных цепей
На схеме показана схема, содержащая несколько ячеек.
- Какой ток через Резистор 20 Ом?
- Какой ток на минусовой клемме Батарея 5,0 В?
- Какой ток на отрицательной клемме Аккумулятор 10,0 В?
Ответ
Часть 1
Начнем с обозначения принципиальной схемы.
Токи в каждой ветви цепи маркируются в соответствии с
узел в нижней части цепи. Ток от
Ячейка 10,0 В к узлу
помечен 𝐼 и считается током в
узел. Ток от узла к
20 Ом помечено
𝐼 и считается вне узла. Электрический ток
от узла к
Ячейка 5,0 В помечена
𝐼 и считается вне узла.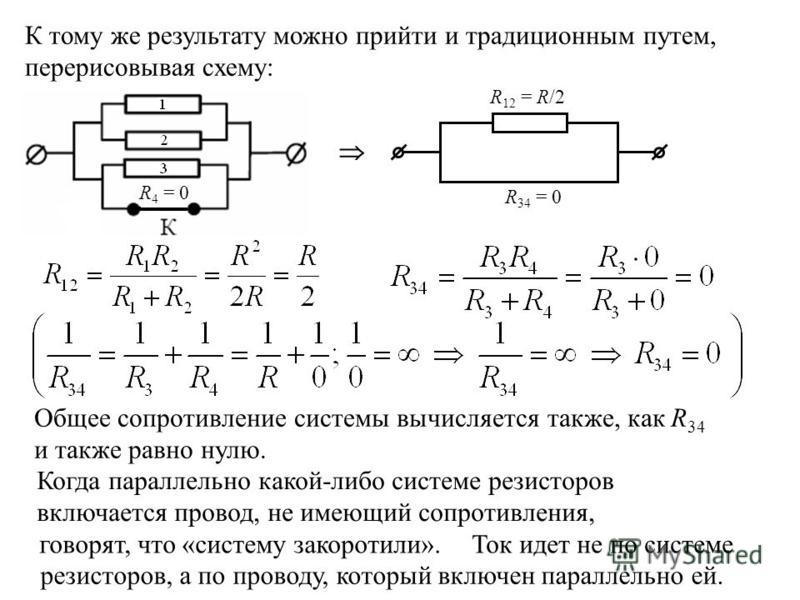
Мы можем применить второй закон Кирхгофа к каждому контуру цепи, чтобы найти разность потенциалов на каждом резисторе.
Начиная с цикла, содержащего 𝑉 и 𝑅, имеем 𝑉−𝑉=0,В поэтому разность потенциалов на 𝑅 равна 𝑉=10.0.V
Используя закон Ома, мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=10,020𝐼=0,5.VΩA
Это равно 𝐼. Ток через Резистор 20 Ом 𝐼 и, следовательно, равно 0,5 А.
Часть 2
Далее мы можем посмотреть на цикл, содержащий 𝑉, 𝑉 и 𝑅: 𝑉+𝑉−𝑉=05,0+10,0−𝑉=0,VVVV
Итак, разность потенциалов на 𝑅 равна 𝑉=15,0.V
По закону Ома мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=15,015𝐼=1,0.VΩA
Это равно 𝐼. Ток на минусе терминал 5,0 А аккумулятор 𝐼 и, следовательно, равно 1,0 А.
Часть 3
Используя первый закон Кирхгофа, мы можем вычислить 𝐼 из
узел в нижней части схемы:
𝐼=𝐼+𝐼𝐼=1. 0+0.5=1.5.A
0+0.5=1.5.A
Ток на минусовой клемме Батарея 10,0 В есть 𝐼 и поэтому равно 1,5 А.
Пример 5. Использование законов Кирхгофа для анализа комбинационных цепей с Unknown Components
В показанной схеме сопротивление одного из резисторов неизвестно. Общая ток в цепи есть 0,25 А.
- Найти текущий 𝐼. Отдай свое ответ до двух знаков после запятой.
- Найти текущий 𝐼. Дайте ответ на два десятичные знаки.
- Найдите разность потенциалов на неизвестном резисторе. Дайте свой ответ на Ближайшая вольт.
Ответ
Часть 1
Начнем с маркировки компонентов схемы.
В первой части вопроса нам предлагается найти 𝐼, ток через 𝑅. Для этого нам нужно найти разность потенциалов на параллельном участке цепи.
Мы можем преобразовать параллельный участок цепи в эквивалентный
резистора по следующей формуле:
𝑅=1𝑅+1𝑅.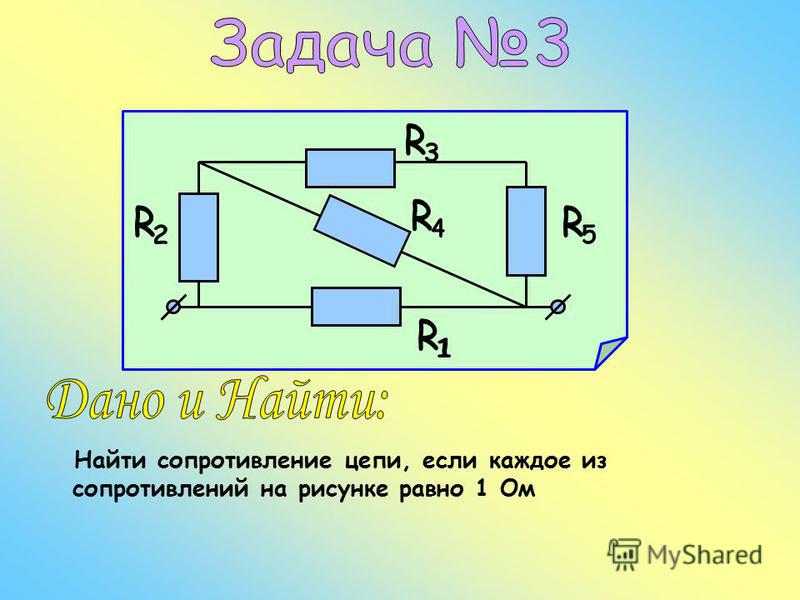
Вставка значений 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩ
Зная, что ток в цепи 0,25 А, потенциал разницу между эквивалентным резистором можно рассчитать, используя сопротивление Ом. закон: 𝑉=𝐼𝑅𝑉=0,25×1,40𝑉=0,35.AΩV
Эта разность потенциалов одинакова на обеих ветвях параллельного участок цепи. Тогда ток 𝐼 может быть рассчитывается по закону Ома: 𝐼=𝑉𝑅𝐼=0,352,5𝐼=0,14.VΩA
Часть 2
Во второй части вопроса нам предлагается рассчитать текущий 𝐼.
Мы уже рассчитали разность потенциалов на параллели участок цепи, поэтому мы можем применить закон Ома к 𝑅: 𝐼=𝑉𝑅𝐼=0,353,2𝐼=0,11.VΩA
Часть 3
В третьей части этого вопроса нам предлагается рассчитать потенциал разница на неизвестном резисторе.
Мы можем использовать второй закон Кирхгофа, чтобы решить эту задачу. Кирхгофа
Второй закон гласит, что сумма разностей потенциалов на каждом
отдельная компонента в цикле равна нулю. Для этой схемы мы
запишет разность потенциалов через 𝑅 как
𝑉, по параллельному сечению как 𝑉, а поперек
𝑅 как 𝑉:
12−𝑉−𝑉−𝑉=0,V
Кирхгофа
Второй закон гласит, что сумма разностей потенциалов на каждом
отдельная компонента в цикле равна нулю. Для этой схемы мы
запишет разность потенциалов через 𝑅 как
𝑉, по параллельному сечению как 𝑉, а поперек
𝑅 как 𝑉:
12−𝑉−𝑉−𝑉=0,V
Мы уже рассчитали 𝑉=0,35В. 𝑉 можно рассчитать по закону Ома: 𝑉=𝐼𝑅𝑉=0,25×2,2𝑉=0,55.AΩV
Мы можем подставить их в уравнение для второго закона Кирхгофа, помня, что это уменьшение потенциала, поэтому они отрицательны: 12−𝑉−0,55−0,35=0,VVV
Затем мы можем изменить это, чтобы получить значение разности потенциалов через 𝑅 неизвестный резистор: 𝑉=11,1.V
Итак, разность потенциалов на неизвестном резисторе с точностью до вольт, 11 В.
Давайте обобщим то, что мы узнали из этого объяснения, в следующем ключевые моменты.
Ключевые точки
- В комбинированных цепях мы можем идентифицировать части цепей, соединенные параллельно
и цепи последовательно.
 Мы можем рассчитать эквивалентное сопротивление этих
разделы для анализа комбинированной схемы.
Мы можем рассчитать эквивалентное сопротивление этих
разделы для анализа комбинированной схемы. - Первый закон Кирхгофа гласит, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно совпадать с сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout
- Второй закон Кирхгофа гласит, что сумма разности потенциалов по каждому компоненту, 𝑉,𝑉,…𝑉, в цикле равно нулю: 𝑉+𝑉+⋯+𝑉=0.
- В комбинированных схемах мы можем идентифицировать петли и узлы, которые позволяют нам применять законы Кирхгофа для анализа цепи.
и параллельные цепи — обучение — ScienceFlip0332
Цепь серии имеет только один путь для протекания электрического тока. Электрические компоненты подключаются один за другим. Если одна лампочка сломается или разомкнется выключатель в последовательной цепи, остальные лампочки погаснут, так как цепь не замкнута.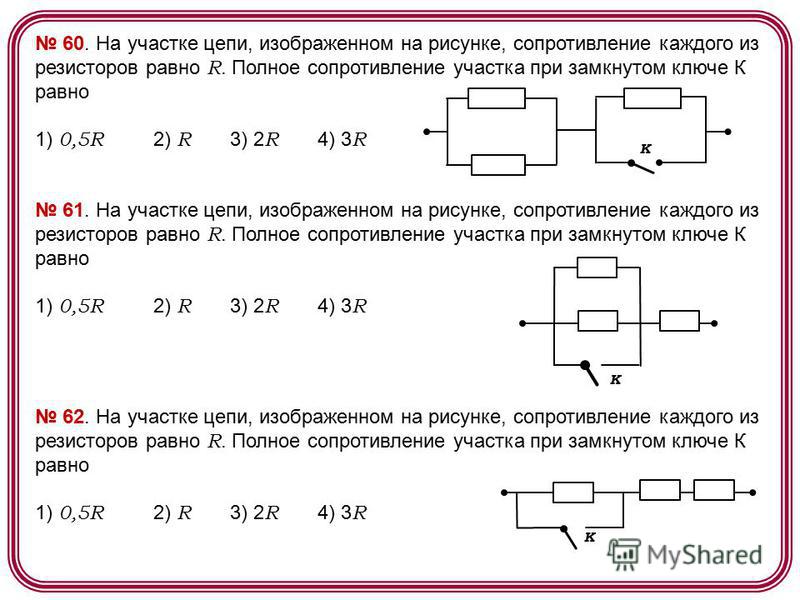 Чем больше ламп добавляется в последовательную цепь, тем светлее становится свет.
Чем больше ламп добавляется в последовательную цепь, тем светлее становится свет.
Параллельная цепь содержит более одного пути для протекания электрического тока. Если погаснет одна лампочка или разомкнется выключатель, ток может продолжать течь по другому пути. Параллельные цепи позволяют включать и выключать отдельные компоненты, не затрагивая другие компоненты. Добавление или удаление световых шаров не влияет на яркость каждого шара.
Когда цепь содержит более одного резистора, Закона Ома недостаточно для расчета тока, протекающего через резистор, и разности потенциалов на каждом резисторе. Цепи с более чем одним резистором необходимо анализировать по частям. Расчеты также будут зависеть от того, является ли цепь последовательной или параллельной.
Анализ последовательных цепей
При последовательном соединении резисторов применяются следующие правила:
- Ток через все резисторы одинаков.
- Сумма разностей потенциалов на каждом резисторе равна разности потенциалов (напряжению), подаваемой на всю цепь. Это также известно как закон напряжения Кирхгофа .
- Общее сопротивление цепи равно сумме отдельных сопротивлений. Это демонстрируется следующим уравнением и известно как эквивалентное эффективное сопротивление : .
Анализ параллельных цепей
При параллельном соединении резисторов применяются следующие правила:
- Напряжение на каждом резисторе одинаково.
- Ток распределяется между резисторами. Это также известно как действующий закон Кирхгофа .
- Инверсия общего сопротивления цепи равна сумме инверсий отдельных сопротивлений. Эквивалентное эффективное сопротивление параллельной цепи определяется по формуле:
Сложные проблемы могут быть связаны с цепями, которые имеют как последовательные, так и параллельные участки.

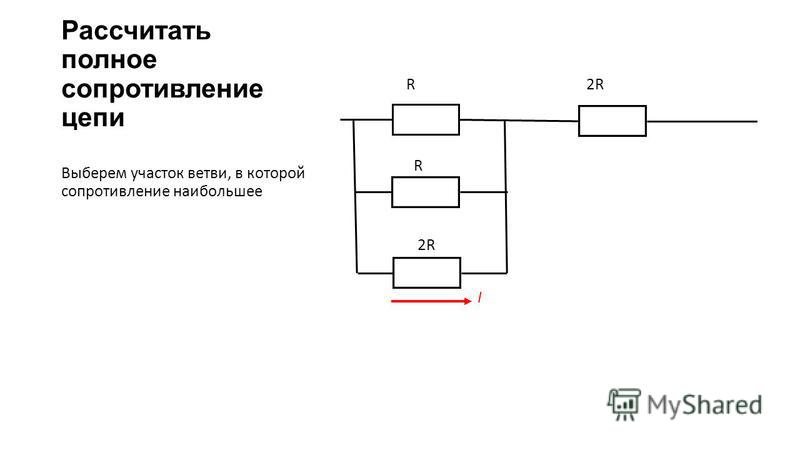 04.13
04.13 04.13
04.13