Поток рассеяния — Энциклопедия по машиностроению XXL
Сварочные трансформаторы, как правило, имеют падающую внешнюю характеристику, их используют для дуговой ручной сварки и автоматической сварки под флюсом. Широко применяют трансформаторы с увеличенным магнитным рассеянием и подвижной вторичной обмоткой (типов тс и ТД). В этих трансформаторах (рис. 5.5, о) первичная I и вторичная 2 обмотки раздвинуты относительно друг друга, что обусловливает их повышенное индуктивное сопротивление вследствие появления магнитных потоков рассеяния. [c.188]Для плавного регулирования сварочного тока изменяют расстояние между обмотками трансформатора. При сближении обмоток (рис. 5.5, б) происходит частичное взаимное уничтожение противоположно направленных потоков рассеяния и что уменьшает индуктивное сопротивление вторичной обмотки и увеличивает сварочный ток. Минимальный сварочный ток соответствует наибольшему расстоянию между обмотками и максимальным потоком рассеяния (рис.

Магнитные методы контроля основаны на обнаружении полей магнитного рассеяния, образующихся в местах дефектов при намагничивании контролируемых изделий. Изделие намагничивают, замыкая им сердечник электромагнита или помещая внутрь соленоида. Требуемый магнитный поток можно создать пропусканием тока по виткам (3— витков) сварочного провода, заматываемого на контролируемую деталь. В зависимости от способа обнаружения потоков рассеяния различают следующие методы магнитного контроля метод магнитного порошка, индукционный и магнитографический. [c.149]
Часть полного магнитного потока Ф, проходящая через рабочий зазор 8, называется рабочим магнитным потоком н обозначается Фг. Этот поток обусловливает силы, под действием которых совершается перемещение якоря. Часть потока Ф, которая не замыкается через рабочий воздушный зазор, называется потоком рассеяния, или утечки, и обозначается Фу (рис. 26.1). Значение рабочего потока Ф , зависит от конфигурации магнитной цепи и размера 8 зазора.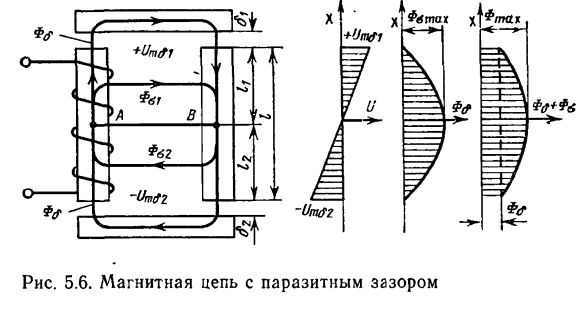
Здесь (г ) — пространственное распределение источников у-квантов -й энергетической группы ц — линейный коэффициент ослабления этих у-квантов — фактор накопления потока рассеянных у-квантов /-й энергетической группы от источника, испускающего у-кванты -й группы. [c.57]
При использовании небольших интенсивностей, характерных для источников некогерентного излучения, интенсивность спонтанного комбинационного рассеяния невелика. Даже для очень интенсивных линий поток рассеянного света составляет 10 — 10 часть возбуждающего света. [c.312]
Рассмотрим схемы замещения 6-4, бив применительно к индуктору с магнитопроводом. Из рис. 6-5 видно, что путь обратного замыкания рабочего магнитного потока Ф 2, сцепленного как с нагреваемым объектом, так и с индуктирующим проводом, проходит через воздушные зазоры /г и через магнитопровод, в то время как путь обратного замыкания потока рассеяния пролегает только через магнитопровод, где эти потоки и объединяются.
Поток рассеяния, проходящий через воздушное пространство вне зазора, обычно учитывается введением коэффициента q [c.199]
Будем считать, что все тот же магнитный поток Ф дит по нагреваемому объекту и индуктору в виде двух составляющих (поток рассеяния) и Ф (поток в нагреваемом объекте), а на остальном пути — одним общим потоком Ф . [c.79]
Для ограничения потоков рассеяния применяются экраны из короткозамкнутых витков или магнитопроводы из расслоенного железа. Наиболее эффективным способом экранирования является использование магнито-провода из трансформаторной стали на средних частотах и из ферритов на высоких частотах. Располагая маг-нитопровод таким образом, чтобы магнитный поток на всем своем пути проходил или в нагреваемой детали, или в магнитопроводе, ограничивая его путь по воздуху минимальным зазором между нагреваемой поверхностью и магнитопроводом, можно сосредоточить нагрев только там, где он требуется.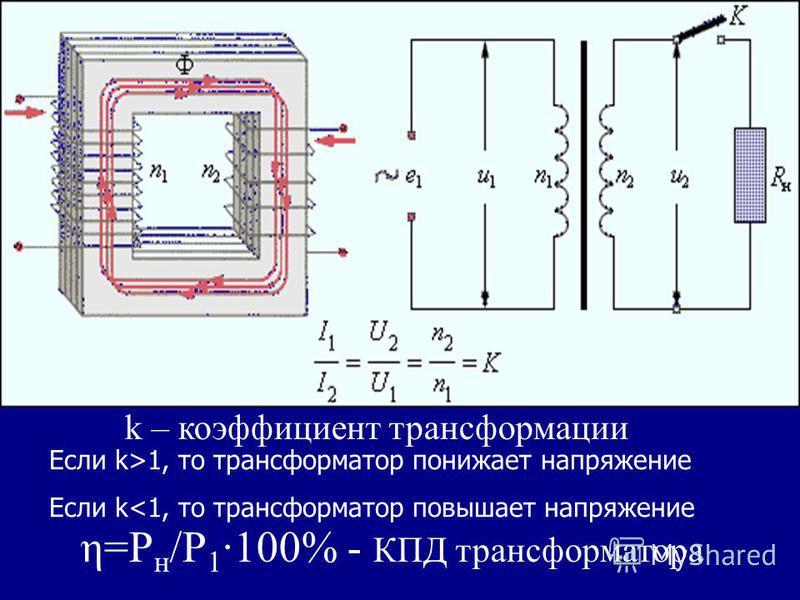 Во всех индукторах с магнито-проводами, описанных выше, используется этот прием. Коротко-замкнутые витки из медных полос или трубок в энергетическом отношении менее выгодны, так как на нагревание их расходуется
[c.164]
Во всех индукторах с магнито-проводами, описанных выше, используется этот прием. Коротко-замкнутые витки из медных полос или трубок в энергетическом отношении менее выгодны, так как на нагревание их расходуется
[c.164]
В некоторых случаях уменьшение влияния кривизны поверхности достигается специальным магнитопроводом, уменьшающим или ограничивающим поток рассеяния. При этом следует учесть, что уменьшение площадки контактирования приводит к уменьшению чувствительности прибора.
Выявление скрытых дефектов в стальных закаленных деталях и в сварных соединениях (трещин, непроваров, шлаковых включений, газовых пор) является основной задачей магнитного контроля. Обнаружение дефектов магнитными методами основано на возникновении над дефектом местного магнитного потока рассеяния. [c.301]
При намагничивании продольным магнитным полем испытуемого ферромагнитного тела (например, наплавленной стальной пластины) внутри тела возникает магнитный поток. Величина этого потока будет тем больше, чем меньше магнитное сопротивление намагничиваемого тела или чем выше его магнитная проницаемость. Небольшая часть магнитного потока, проходящего вне испытуемого тела, носит название потока рассеяния (фиг. 103), который усиливается возле дефектных мест.
[c.301]
Величина этого потока будет тем больше, чем меньше магнитное сопротивление намагничиваемого тела или чем выше его магнитная проницаемость. Небольшая часть магнитного потока, проходящего вне испытуемого тела, носит название потока рассеяния (фиг. 103), который усиливается возле дефектных мест.
[c.301]
| Фиг. 103. Прохождение магнитною потока при наличии де-фектов в металле а — поток рассеяния. |
Ixs — индуктивное падение напряжения, вызванное потоком рассеяния /г—активное падение напряжения. [c.534]
В случае учёта потока рассеяния соответствующее уменьшение используемой индукции может быть представлено в виде наклонной линии ОК и полезно используемая индукция будет [c.184]
Магнитные способы контроля сварных швов. Магнитные способы испытания сварных швов основаны на следующем всякие дефекты (непровар, трещины и т. д.) в намагниченном шве изменяют распределение ма нитного потока, образуя на поверхности шва местные потоки рассеяния, которые обнаруживаются при помощи магнитного порошка (железа или его окислов) или индукционными катушками. [c.439]
Индукционный способ. Образование местных потоков рассеяния над дефектом [c.439]
Наличие полей рассеяния над дефектами обусловливается типом, размерами, ориентацией дефектов относительно потока намагничивания (рис.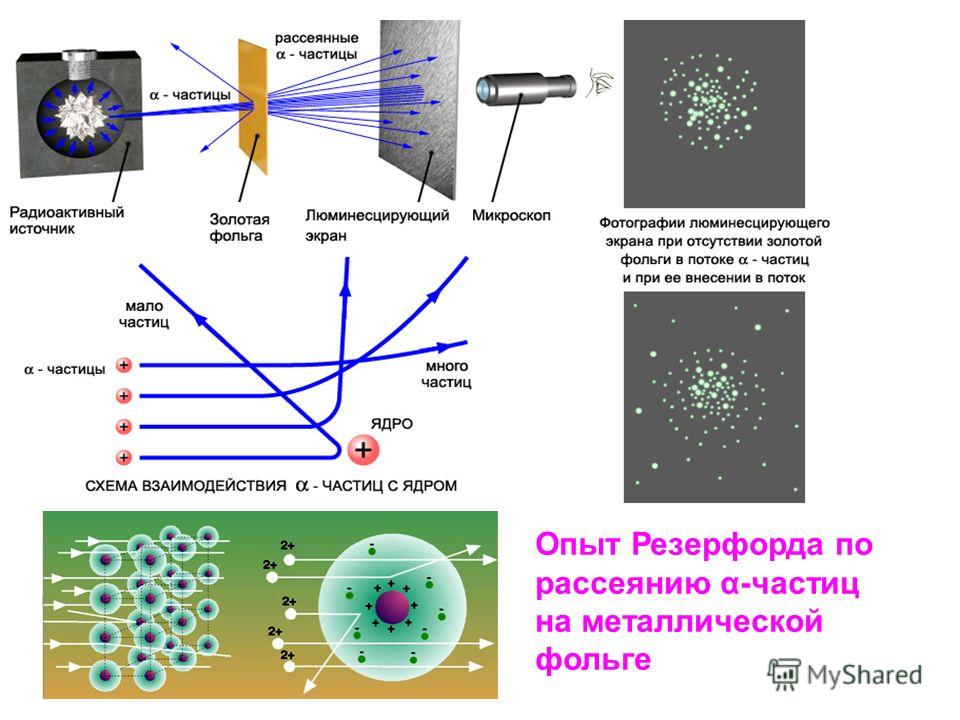 5.59, в,г,д), местом расположения, размерами и конфигурацией сварного соединения, состоянием поверхности и определяет выявляемость дефектов методами магнитного контроля. Местные потоки рассеяния могут вызываться также изменением структуры металла, величины зерна, твердости и т. д.
[c.556]
5.59, в,г,д), местом расположения, размерами и конфигурацией сварного соединения, состоянием поверхности и определяет выявляемость дефектов методами магнитного контроля. Местные потоки рассеяния могут вызываться также изменением структуры металла, величины зерна, твердости и т. д.
[c.556]
Индукционный метод контроля основан на обнаружении местных потоков рассеяния в подмагниченном сварном соединении при помощи индукционной катушки, в которой наводится электродвижущая сила при перемещении ее з магнитном потоке рассеяния над дефектом. [c.560]
Несмотря на противоречивость экспериментальных данных плотность потока рассеянного излучения вблизи высокоэнергетических ускорителей удовлетворительно описывается эмпирическим соотношениемТрансформаторы могут быть с увеличенным магнитным рассеянием их выполняют с подвижными обмотками или с магнитными шунтами.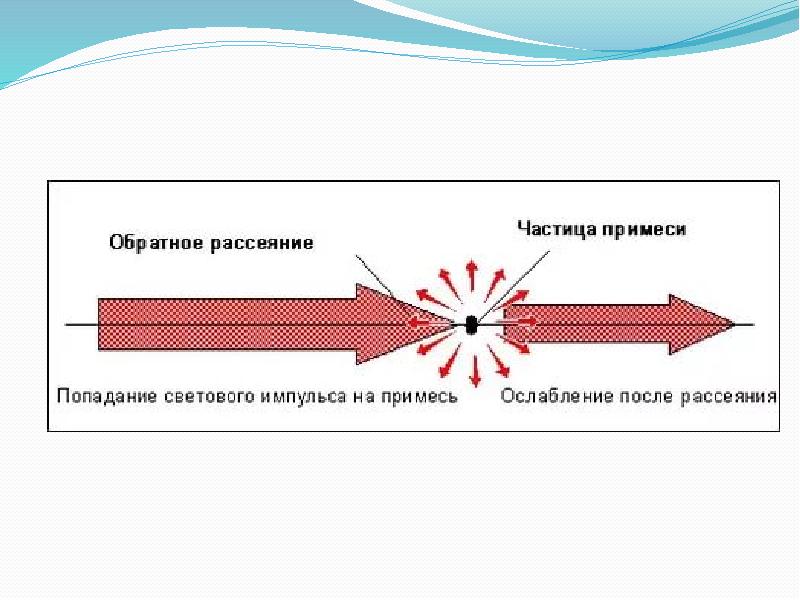 Режим сварки регулируют с помощью механизма, перемещаюн1,его одну обмотку относительно другой или магнитный пгупт, в результате чего изменяется величина потока рассеяния.
[c.132]
Режим сварки регулируют с помощью механизма, перемещаюн1,его одну обмотку относительно другой или магнитный пгупт, в результате чего изменяется величина потока рассеяния.
[c.132]
При работе трансформатора основной магнитный поток Фо, создаваемый первичной и вторичной обмотками, замыкается через магннтопровод 3. Часть магнитного потока ответвляется и замыкается вокруг обмоток через воздушное пространство, образуя потоки рассеяния и s2- Потоки рассеяния индуктируют в обмотках электродвижущую силу, противоположную основному напряжению. С увеличением сварочного тока увеличиваются потоки рассеяния и, следовательно, возрастает индуктивное сопротивление вторичной обмотки, что и создает внешнюю падающую характеристику трансформатора. [c.189]
Применительно к ЭМУ системная модель включает в себя универсальные детерминированные модели электромеханических преобразований, нагрева, деформаций и магнитных проявлений, блоки реализации статистических испытаний, автоматизации перестройки исходных моделей, моделирования условий производства и эксплуатации (рис. 5.(2). Детерминированная часть ее предполагает наличие моделей разных версий для анализа влияющих физических процессов, примеры построения которых даны в 5.1,2 и 5.1.3. Часть входных параметров являются общими для всех блоков, другими блоки обмениваются между собой в процессе работы, в том числе за счет использования обратных связей (земпературы, магнитных потоков рассеяния, изменения момента сопротивления в опорах и нр.). Изложенные
5.(2). Детерминированная часть ее предполагает наличие моделей разных версий для анализа влияющих физических процессов, примеры построения которых даны в 5.1,2 и 5.1.3. Часть входных параметров являются общими для всех блоков, другими блоки обмениваются между собой в процессе работы, в том числе за счет использования обратных связей (земпературы, магнитных потоков рассеяния, изменения момента сопротивления в опорах и нр.). Изложенные
Интенсивное движение расплавленного металла из каналов в ванну и в обратном направлении имеет важнейшее значение, так как почти все тепло выделяется в каналах. В возникновении циркуляции металла некоторую роль играет конвекция, связанная с перегревом металла в каналах, но основным фактором является электродинамическое взаимодействие тока в канале с магнитным потоком рассеяния, нроходягцим между каналом и индуктором. [c.278]
Сварочные трансформаторы — это понижающие трансформаторы (вторичное напряжение U. = 60 ч- 80 В), падающая характеристика которых создается за счет повышенного магнитного рассеяния или включения в сварочную цепь индуктивного сопротивления (дросселя). Электрическая схема сварочного трансформатора с повышенным магнитным рассеянием представлена на рис. 2.10, а. Катушки первичной / и вторичной 2 обмоток расположены попарно на обоих стержнях сердечника трансформатора 3. Первичная обмотка неподвижна и закреплена в нижней части сердечника, вторичная перемещается по нему с помощью винтового механизма. При прохождении тока по обмоткам возникают магнитные потоки основной Фт, создаваемый намагничивающей силой обмоток 1 и 2, и потоки рассеяния этих же обмоток Фр1 и Фр , дающие суммарный ноток Фр, который наводит в трансформаторе реактивную ЭДС, определяющую его индуктивное сопротивление XПри рабочей нагрузке трансформатора его ЭДС уравновешивается падением напряжения дуги U, и реактивной ЭДС Ер, а при коротком замыкании — t/д /кяХ следовательно, такой ИП имеет падающую характеристику.
= 60 ч- 80 В), падающая характеристика которых создается за счет повышенного магнитного рассеяния или включения в сварочную цепь индуктивного сопротивления (дросселя). Электрическая схема сварочного трансформатора с повышенным магнитным рассеянием представлена на рис. 2.10, а. Катушки первичной / и вторичной 2 обмоток расположены попарно на обоих стержнях сердечника трансформатора 3. Первичная обмотка неподвижна и закреплена в нижней части сердечника, вторичная перемещается по нему с помощью винтового механизма. При прохождении тока по обмоткам возникают магнитные потоки основной Фт, создаваемый намагничивающей силой обмоток 1 и 2, и потоки рассеяния этих же обмоток Фр1 и Фр , дающие суммарный ноток Фр, который наводит в трансформаторе реактивную ЭДС, определяющую его индуктивное сопротивление XПри рабочей нагрузке трансформатора его ЭДС уравновешивается падением напряжения дуги U, и реактивной ЭДС Ер, а при коротком замыкании — t/д /кяХ следовательно, такой ИП имеет падающую характеристику.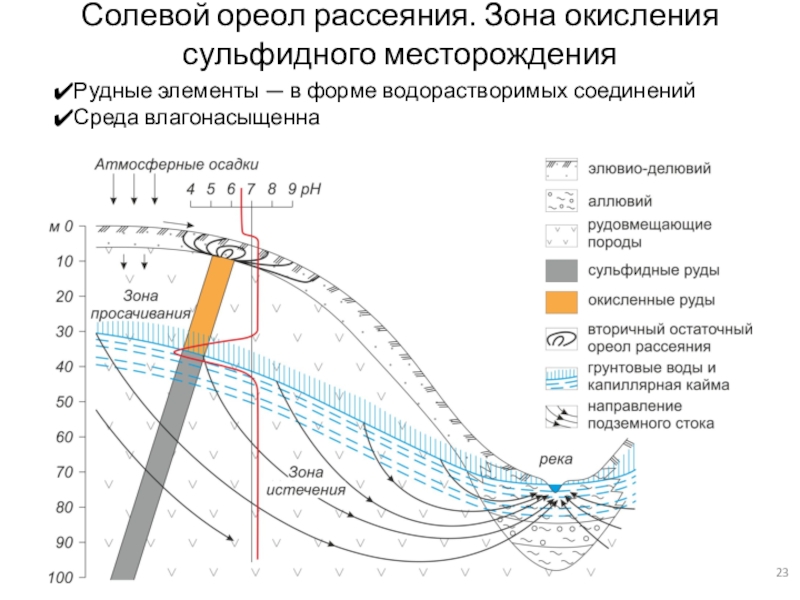 Сварочный ток регулируется изменением расстояния между обмотками / и 2 (при его увеличении поток Ф растет, а сварочный ток уменьшается).
[c.53]
Сварочный ток регулируется изменением расстояния между обмотками / и 2 (при его увеличении поток Ф растет, а сварочный ток уменьшается).
[c.53]
Схематически вариант а) первого типа дефектов представлен на рис. 2, а. Анализ показывает, что в этом случае над поверхностью, к которой примыкает дефект, магнитный поток рассеяния должен образоваться при меньшей средней намагниченности листа, чем над противоположной поверхностью. Объясняется это тем, что бесконечно тонкий слой металла (как это можно считать) между дефектом и верхней поверхностью намагнитится до касыщения при незначительной средней намагниченности лис-та. Специальными же исследованиями установлено, что магнитный поток рассеяния, обусловленный к. д. м. с., начинает улавливаться на обеих поверхностях одновременно при одной и той же средней намагниченности листа. Следовательно, вариант а) не может служить моделью расположения квазидефектов в листах трансформаторной стали. [c.187]
Реакция якоря. При работе генератора вхолостую в нём существует только поток полюсов. При протекании тока по обмотке статора вокруг проводников с током образуется магнитный поток. Часть этого потока сцеплена только с обмоткой якоря — поток рассеяния другая часть вступает в полюс и взаимодействует с потоком полюсов— поток реакции якоря. Магнитные потоки фазных обмоток статора образуют результирующий магнитный поток, равный полуторному значению ыаксимал ьного потока одной фазы Ф =
[c.534]
При работе генератора вхолостую в нём существует только поток полюсов. При протекании тока по обмотке статора вокруг проводников с током образуется магнитный поток. Часть этого потока сцеплена только с обмоткой якоря — поток рассеяния другая часть вступает в полюс и взаимодействует с потоком полюсов— поток реакции якоря. Магнитные потоки фазных обмоток статора образуют результирующий магнитный поток, равный полуторному значению ыаксимал ьного потока одной фазы Ф =
[c.534]
Часть стержня, лежащая в глубине паза, сцепляется с большим потоком рассеяния, чем верхняя. При пуске двигателя в ход повышенное реактивное сопротивление нижней части стержня вызывает вытеснение тока ротора в верхнюю часть сечения стержня. Это эквивалентно увеличению активного сопротивления обмотки ротора. Увеличение активного сопротивления повышает начальный момент двигателя, а увеличение реактивного сопротивления уменьшает пусковой ток.
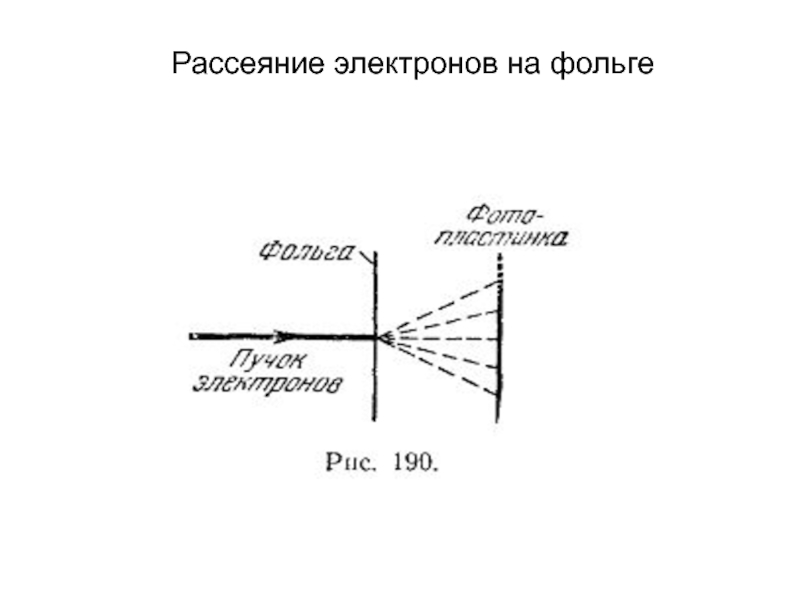 При нормальной скорости двигателя реактивное сопротивление становится незначительным благодаря уменьшению частоты, ток распределяется по сечению стержня почти равномерно и двигатель работает как обычный короткозамкнутый. Характеристики двигателя приведены на фиг. 62, б. Двигатели с глубоким пазом проще в производстве и дешевле двигателей Бушеро.
[c.539]
При нормальной скорости двигателя реактивное сопротивление становится незначительным благодаря уменьшению частоты, ток распределяется по сечению стержня почти равномерно и двигатель работает как обычный короткозамкнутый. Характеристики двигателя приведены на фиг. 62, б. Двигатели с глубоким пазом проще в производстве и дешевле двигателей Бушеро.
[c.539]Контролируемый сварной шов подмагничивается переменным полем, создаваемым электромагнитом, работающим от сети переменного тока. Переменные потоки рассеяния над дефектами улавливаются индукционной катушкой. Наведенная в искательной катушке электродвижущая сила через усилитель может фиксироваться с помощью телефона, гальванометра или осциллографа. [c.560]
Двигатели с двойной клеткой Доливо-Добровольского. П 1ч ротора показан па фиг. 22. Стержни верхней клеткн ротора выполняются из материала с большим удельным сопротивлением — латуни, алюминиевой бронзы и т. д. Нижняя клетка, которая выполняется из красной мели, охватывается большим числом линий потока рассеяния. Поэтому при пуске (при больших скольжениях) ток идет главным образом по стержням верхней клетки, имеющей большее сопротивление. Это равносильно включению внешнего реостата в двигателе с контактными кольцами и приводит к одновременному уменьшению пускового тока и увеличению пускового момента. В нормальном режиме (при малых скольжениях) ток проходит главным образом по нижней клетке, имеющей малое сопротивление.
[c.396]
Поэтому при пуске (при больших скольжениях) ток идет главным образом по стержням верхней клетки, имеющей большее сопротивление. Это равносильно включению внешнего реостата в двигателе с контактными кольцами и приводит к одновременному уменьшению пускового тока и увеличению пускового момента. В нормальном режиме (при малых скольжениях) ток проходит главным образом по нижней клетке, имеющей малое сопротивление.
[c.396]
Если принять, что магнитный поток рассеяния мало изменяется при колебаниях якоря, а индуктивное со-протиеление мало по сравнению с омическим, то силу [c.72]
Эксперименты показали, что существует корреляция между значениями плотности потока рассеянных быстрых нейтронов (Фа/пр) и нейтронов, замедливщихся до промежуточных энергий (Фм»). При изменении границы между этими двумя группами соответственно изменяются количественные соотношения, которые приведены в табл. 1. [c.297]
Магнитный поток в трансформаторах
Сухие, тороидальные и масляные трансформаторы работают по принципу магнитной индукции, которая позволяет им преобразовывать ток одной величины в другую.
Принцип формирования магнитного потока
Магнитная индукция непосредственно связана с формированием магнитного потока на первичной обмотке трансформатора. Рассмотрим этот процесс подробнее.
После подключения первичной обмотки к источнику переменного тока, по ней начинает протекать электрический ток, который создает магнитное поле. Обмотка обычно представляет собой медную проволоку, с помощью которой обматывается магнитный сердечник. Образующиеся магнитные линии пронзают витки не только первичной, но и вторичной обмоток.
Часть из них замыкается в немагнитной среде, формируя рассеивающий поток на первичной обмотке. Рассеивающий поток пронизывает исключительно первичную обмотку, поэтому не используются для трансформации электроэнергии.
Когда вторичная обмотка подключается к приемнику питания, то по ней начинает протекать иной ток, формирующий собственное магнитное поле. Магнитный поток пронзает обе обмотки. Часть магнитных линий также замыкается в немагнитной среде, формируя рассеивающий поток вторичной обмотки, который сцеплен только с ее витками.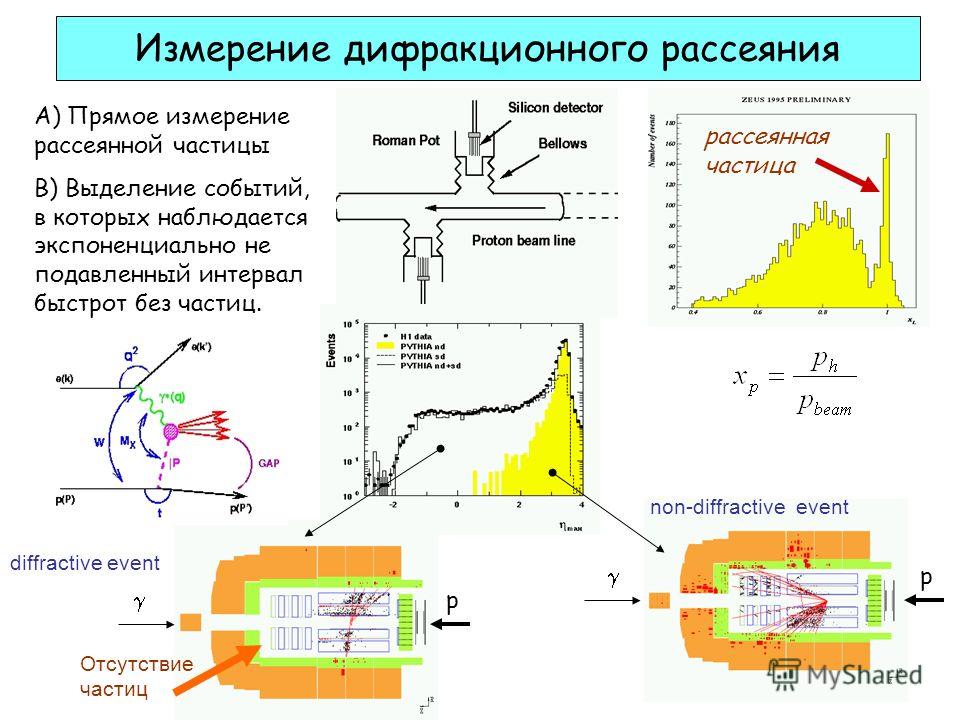
Потоки рассеяния
Потоки рассеяния первичной и вторичной обмоток трансформатора ТМП и других разновидностей в сравнении с основным магнитным потоком значительно ниже, поскольку замыкаются через изоляцию и сталкиваются с высоким сопротивлением. Основной поток замыкается в стальном сердечнике и поэтому встречает на пути низкое сопротивление.
Величина рассеивающих потоков на обеих обмотках приблизительно равная. Оба потока сдвигаются по фазе на угол, равный 180°.
Если рассматривать активную нагрузку, то:
- Рассеивающие потоки обмоток будут представлять по форме синусоиды с одинаковыми амплитудами, но расположенные в противофазе.
- Той же синусоидой изображается основной магнитный поток, который относительно синусоид рассеивающего потока сдвигается на четверть периода.
Амплитуда основного потока существенно выше рассеивающих.
Особенности расчета индуктивностей рассеяния трансформаторов с развитыми магнитными потоками рассеяния / Calculation features of leakage inductances for transformers with heightened magnetic fluxes of a dispersion
Пентегов И. В. Особенности расчета индуктивностей рассеяния трансформаторов с развитыми магнитными потоками рассеяния / И.В. Пентегов, С.В. Рымар // Електротехніка і електромеханіка. – 2004. – № 2. – С. 38-45.
Трансформаторы с развитыми магнитными потоками рассеяния, помимо традиционной области их применения в сварочной технике, можно использовать в преобразовательных устройствах с выпрямителями и в источниках вторичного электропитания, совмещая их с фильтрами высших гармоник тока, заменяя традиционные источники питания с автономными фильтрами высших гармоник тока. При этом масса такой системы уменьшается приблизительно на 30%. Создание источников питания, трансформаторы которых совмещены с фильтрами высших гармоник тока, актуально, поскольку такие источники существенно улучшают качество электрической энергии питающих сетей.
Получены уточненные формулы для расчета индуктивностей рассеяния основных типов трансформаторов с развитыми магнитными потоками рассеяния: однофазного трансформатора с развитыми поперечными потоками рассеяния; однофазного трансформатора с развитыми поперечными потоками рассеяния и магнитным шунтом; однофазного трансформатора с развитыми яремными потоками рассеяния; трехфазного трансформатора с развитыми поперечными потоками рассеяния.
В. Особенности расчета индуктивностей рассеяния трансформаторов с развитыми магнитными потоками рассеяния / И.В. Пентегов, С.В. Рымар // Електротехніка і електромеханіка. – 2004. – № 2. – С. 38-45.
Трансформаторы с развитыми магнитными потоками рассеяния, помимо традиционной области их применения в сварочной технике, можно использовать в преобразовательных устройствах с выпрямителями и в источниках вторичного электропитания, совмещая их с фильтрами высших гармоник тока, заменяя традиционные источники питания с автономными фильтрами высших гармоник тока. При этом масса такой системы уменьшается приблизительно на 30%. Создание источников питания, трансформаторы которых совмещены с фильтрами высших гармоник тока, актуально, поскольку такие источники существенно улучшают качество электрической энергии питающих сетей.
Получены уточненные формулы для расчета индуктивностей рассеяния основных типов трансформаторов с развитыми магнитными потоками рассеяния: однофазного трансформатора с развитыми поперечными потоками рассеяния; однофазного трансформатора с развитыми поперечными потоками рассеяния и магнитным шунтом; однофазного трансформатора с развитыми яремными потоками рассеяния; трехфазного трансформатора с развитыми поперечными потоками рассеяния. Формулы позволяют с погрешностью от 3 до 10%, по сравнению с опытными данными, рассчитывать индуктивности рассеяния в рассмотренных типах трансформаторов.
Ключевые слова: трансформаторы, развитые магнитные потоки рассеяния, индуктивности рассеяния, методики расчета, источники питания, фильтры высших гармоник тока.
/
Pentegov I.V., Rymar S.V. Calculation Features of Leakage Inductances for Transformers With Heightened Magnetic Fluxes of a Dispersion. Electrical Engineering & Electromechanics, 2004, no. 2, pp. 38-45. (Rus).
Transformers with heightened magnetic fluxes of a dispersion, besides traditional field of their application in welding engineering, it is possible to use them in transforming devices with rectifiers and in sources of the secondary power supplies, combining them with filters of higher harmonics of a current, substituting traditional power supplies with independent filters of higher harmonics of a current. Thus the mass of such system is diminished approximately by 30%.
Формулы позволяют с погрешностью от 3 до 10%, по сравнению с опытными данными, рассчитывать индуктивности рассеяния в рассмотренных типах трансформаторов.
Ключевые слова: трансформаторы, развитые магнитные потоки рассеяния, индуктивности рассеяния, методики расчета, источники питания, фильтры высших гармоник тока.
/
Pentegov I.V., Rymar S.V. Calculation Features of Leakage Inductances for Transformers With Heightened Magnetic Fluxes of a Dispersion. Electrical Engineering & Electromechanics, 2004, no. 2, pp. 38-45. (Rus).
Transformers with heightened magnetic fluxes of a dispersion, besides traditional field of their application in welding engineering, it is possible to use them in transforming devices with rectifiers and in sources of the secondary power supplies, combining them with filters of higher harmonics of a current, substituting traditional power supplies with independent filters of higher harmonics of a current. Thus the mass of such system is diminished approximately by 30%.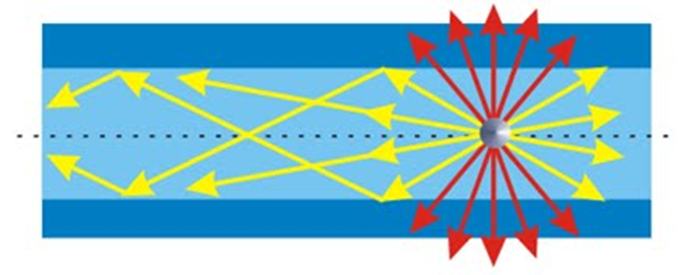 Making of power supplies, which transformers are combined with filters of higher harmonics of a current, is actual; as such source supplies essentially improve quality of electrical energy in networks.
Improved formulas for calculation of leakage inductances of the basic types of transformers with heightened magnetic fluxes of a dispersion are obtained: the single-phase transformer with heightened cross flows of a dispersion; the single-phase transformer with heightened cross flows of a dispersion and the flux shunt; the single-phase transformer with heightened yokes streams of a dispersion; the three-phase transformer with heightened cross flows of a dispersion. Using obtained formulas you can have a margin error from 3 up to 10%, as contrasted to experimental data to calculate leakage inductances in surveyed types of transformers.
Key Words: Transformers, Heightened Magnetic Fluxes of a Dispersion, Leakage Inductance, Design Procedure, Power Supplies, Filters of Higher Harmonics of a Current.
Making of power supplies, which transformers are combined with filters of higher harmonics of a current, is actual; as such source supplies essentially improve quality of electrical energy in networks.
Improved formulas for calculation of leakage inductances of the basic types of transformers with heightened magnetic fluxes of a dispersion are obtained: the single-phase transformer with heightened cross flows of a dispersion; the single-phase transformer with heightened cross flows of a dispersion and the flux shunt; the single-phase transformer with heightened yokes streams of a dispersion; the three-phase transformer with heightened cross flows of a dispersion. Using obtained formulas you can have a margin error from 3 up to 10%, as contrasted to experimental data to calculate leakage inductances in surveyed types of transformers.
Key Words: Transformers, Heightened Magnetic Fluxes of a Dispersion, Leakage Inductance, Design Procedure, Power Supplies, Filters of Higher Harmonics of a Current.
All figure content in this area was uploaded by Sergii Rymar
Content may be subject to copyright.
10.1. Конструкция трансформатора Трансформатор представляет собой
электромагнитный аппарат,
предназначенный для преобразования величин токов и напряжений без изменения
частоты. Рис. 10.1 Рис. 10.2 10.2. Работа трансформатора в режиме холостого хода Под холостым ходом трансформатора
понимается режим его работы при разомкнутой вторичной обмотке. Рис. 10.3 W1 — число витков первичной обмотки;W2— число витков вторичной обмотки; R1 — активное сопротивление первичной обмотки. Определим ЭДС, индуктированную
в первичной обмотке трансформатора основным магнитным потоком. . Основной магнитный поток изменяется по синусоидальному закону , где Фm — максимальное или амплитудное значение основного магнит-ного потока; ω = 2πf — угловая частота; f — частота переменного напряжения. Мгновенное значение ЭДС . Максимальное значение . Действующее значение ЭДС в первичной обмотке . Для вторичной обмотки можно получить аналогичную формулу . Электродвижущие силы E1 и E2, индуктированные в обмотках трансформатора основным магнитным потоком, называются трансформаторными ЭДС. Трансформаторные ЭДС отстают по фазе
от основного магнитного потока на 90°. Трансформаторные ЭДС отстают по фазе
от основного магнитного потока на 90°. Магнитный поток рассеяния индуктирует в первичной обмотке ЭДС рассеяния , где L1s — индуктивность рассеяния в первичной обмотке.Запишем уравнение по второму закону Кирхгофа для первичной обмотки , откуда. (10.1) Напряжение на первичной катушке имеет три слагаемых: падение напряжения, напряжение, уравновешивающее трансформаторную ЭДС, напряжение, уравновешивающее ЭДС рассеяния. Запишем уравнение (10.1) в комплексной форме . (10.2) где индуктивное сопротивление рассеяния первичной обмотки.  На рис. 10.4 изображена векторная диаграмма трансформатора, работающего в режиме холостого хода. Векторы трансформаторных ЭДС и отстают на 90° от вектора основного магнитного потока . Вектор напряжения параллелен вектору тока , а вектор опережает вектор тока на 90°. Вектор напряжения на зажимах первичной обмотки трансформатора равен геометрической сумме векторов — , , Рис. 10.4 . На рис. 10.5 изображена схема замещения трансформатора, соответствующая уравнению (10.2).
XЭ — индуктивное сопротивление, пропорциональное
реактивной мощности, затрачиваемой на создание основного магнитного
потока. Рис. 10.5 Коэффициент трансформации экспериментально определяется из опыта холостого хода. 10.3. Работа трансформатора под нагрузкой Если к первичной обмотке
трансформатора подключить напряжение U1, а вторичную обмотку
соединить с нагрузкой, в обмотках появятся токи I1 и I2.
Эти токи создадут магнитные потоки Ф1 и Ф2, направленные
навстречу друг другу. Суммарный магнитный поток в магнитопроводе уменьшается.
Вследствие этого индуктированные суммарным потоком ЭДС E1
и E2 уменьшаются. , , где X2S — индуктивное сопротивление рассеяния вторичной обмотки.Для первичной обмотки можно записать уравнение . , (10.4) где R2 — активное сопротивление вторичной обмотки;ZН — сопротивление нагрузки. Основной магнитный поток трансформатора есть результат совместного действия магнитодвижущих сил первичной и вторичной обмоток. . Трансформаторная ЭДС E1, пропорциональная
основному магнитному потоку, приблизительно равна напряжению на первичной
катушке U1. Действующее значение напряжения постоянно. Поэтому
основной магнитный поток трансформатора остается неизменным при изменении
сопротивления нагрузки от нуля до бесконечности. . (10.5) Уравнение (10.5) называется уравнением равновесия магнитодвижущих сил.Уравнения (10.3), (10.4), (10.5) называются основными уравнениями трансформатора. Из уравнения (10.5) получим формулу . (10.6) Согласно формуле (10.6), ток в первичной обмотке складывается из тока холостого хода, или намагничивающего тока, и тока, компенсирующего размагничивающее действие вторичной обмотки.Умножим левую и правую части уравнения (10.4) на коэффициент трансформации KT . (10.7) где приведенное активное сопротивление вторичной обмотки;приведенное индуктивное сопротивление вторичной обмотки; приведенное напряжение на нагрузке;
приведенное сопротивление нагрузки. . (10.8) Уравнению (10.8) соответствует упрощенная схема замещения трансформатора, изображенная на рис. 10.6.
индуктивное
сопротивление короткого замыкания. Параметры упрощенной схемы замещения определяются из опыта короткого замыкания. Для этого собирается схема рис. 10.7.
Затем вычисляют . где ZK — полное сопротивление короткого замыкания.
На рис. 10.8 изображена векторная диаграмма трансформатора,
соответствующая упрощенной схеме замещения. Нагрузкой трансформатора
является активное сопротивление RH. Рис. 10.8 10.4. Специальные типы трансформаторов Наиболее часто в электротехнических
установках используются следующие специальные типы трансформаторов:
автотрансформаторы, многообмоточные и трехфазные трансформаторы.
Режим холостого хода автотрансформатора, когда I2
= 0, ничем не отличается от режима холостого хода обычного трансформатора.
Рис. 10.9 Вторичное напряжение где коэффициент трансформации. Автотрансформаторы выгодно использовать в тех случаях, когда коэффициент трансформации близок к единице.Многообмоточные (одна первичная и несколько вторичных) трансформаторы используются в радиотехнических схемах для получения нескольких напряжений. В режиме холостого хода работа таких трансформаторов не отличается от двухобмоточных. В трехфазной сети переменного тока преобразование напряжений осуществляется с помощью трехфазного трансформатора с общим для трех фаз сердечником. В трехфазном трансформаторе с общим магнитопроводом магнитный поток любой из фаз может замыкаться через стержни, на которых расположены обмотки двух других фаз. Затраты стали на трехфазный трансформатор значительно меньше, чем на три однофазных трансформатора. |
рассеяние
рассеяниеЭтот материал рассматривается в Гасиорович Глава 23 .
Рассеяние одного объекта от другого, возможно, наш лучший способ наблюдать и изучать микроскопический мир. На самом деле это рассеяние света от предметов и последующее обнаружение рассеянного света нашими глазами. это дает нам лучшую информацию о макроскопическом мире. Мы можем узнать формы объектов, а также некоторые свойства цвета, просто наблюдая за рассеянным светом.
Есть предел тому, что мы можем узнать с помощью видимого света. В квантовой механике мы знаем, что мы не можем различить детали микроскопических систем (например, атомов), которые меньше чем длина волны рассеиваемой частицы. Поскольку минимальная длина волны видимого света составляет около 0,25 микрона , мы не можем видеть атомы или что-либо меньшее даже при использовании оптических микроскопов. Физика атомов, ядер, субатомных частиц, фундаментальных частиц и взаимодействий в природе должна быть изучается путем рассеяния частиц большей энергии, чем фотоны видимого света.
Рассеяние — это тоже то, с чем мы знакомы по нашему повседневному опыту. Например, бильярдные шары предсказуемо разлетаются друг от друга. Мы можем довольно легко вычислить, как бы разбегались бильярдные шары, если бы столкновения были упругими. но с некоторой потерей энергии и возможностью передачи энергии спину расчет становится более трудным.
В качестве примера для изучения возьмем макроскопический пример рассеяния ББ на бильярдных шарах .Мы будем мотивировать некоторые термины, используемые в макроскопическом рассеянии. Предположим, мы стреляем BB по бильярдному шару. При пропуске ББ не разлетается. Если мы попали, BB отскакивает от мяча и улетает в направлении, отличном от первоначального. Предположим, что наша цель плохая и что BB имеет равномерное распределение вероятностей по площади вокруг бильярдного шара. Площадь проекции бильярдного шара в два измерения составляет всего если это радиус бильярдный шар. Предположим, что BB намного меньше, поэтому его радиусом пока можно пренебречь.
Тогда мы можем сказать что-то о вероятности того, что рассеяние произойдет, если нам известна площадь проекции бильярдного шара.
и количество снятых нами ББ на единицу площади.
Где это количество снятых нами ББ, это площадь, на которой они распространены, и — радиус бильярдного шара.
В экспериментах по нормальному рассеянию у нас есть пучок частиц и
мы знаем количество частиц в секунду.
Измеряем количество скаттеров в секунду
поэтому мы просто разделим приведенное выше уравнение на период времени
получить ставки.
Падающий поток — это количество частиц на единицу площади в единицу времени в пучке. Это хорошо определенная величина в квантовой механике, . Поперечное сечение — площадь проекции бильярдного шара в этом случае. В других случаях может быть сложнее. Например, если не пренебрегать радиусом ЗБ сечение рассеяния равно
Очевидно, что по рассеянию доступно больше информации, чем по тому, рассеивается частица или нет.Например, Резерфорд обнаружил, что атомное ядро , увидев, что иногда альфа-частицы высокой энергии
обратное рассеяние от фольги, содержащей атомы.
Атомная модель того времени не позволяла этого, поскольку положительный заряд был распределен по большому объему.
Мы измеряем вероятность разлететься в разные стороны.
То же самое произойдет и с ББ и бильярдным шаром.
Полярный угол рассеяния будет зависеть от « прицельного параметра » падающего ББ.
Мы можем измерить рассеяние на некоторый небольшой телесный угол
.Часть поперечного сечения
который рассеивается в этот телесный угол, можно назвать сечение дифференциала .
Интеграл по телесному углу вернет нам полное сечение.
Идея сечений и падающих потоков хорошо переносится в используемую нами квантовую механику. Если входящий пучок представляет собой плоскую волну , то есть пучок частиц с определенным импульсом или волновым числом, мы можем описать это просто с помощью числа частиц на единицу площади в секунду, падающего потока.Рассеянная частица также является плоской волной , идущей в направлении, определяемом . Остается взаимодействие между целевой частицей и частицей луча, которое вызывает переход от начального состояния плоской волны к конечному состоянию плоской волны.
Мы уже изучили один приближенный метод рассеяния, называемый парциальный волновой анализ. Это хорошо для потенциалов рассеяния ограниченного диапазона и для рассеяния низкой энергии. Он разделяет набегающую плоскую волну на частичные волны с определенным угловым моментом.Компоненты волны с высоким угловым моментом не будут рассеиваться (сильно), потому что они находятся на большом расстоянии от рассеивающего потенциала, где этот потенциал очень мал. Затем мы можем иметь дело только с несколькими первыми терминами (или даже только с срок) в расширении. Мы показали, что приходящая парциальная волна и уходящая волна могут отличаться только фазовым сдвигом при упругом рассеянии. Если мы вычислим этот фазовый сдвиг , тогда мы можем определить дифференциальное сечение рассеяния.
Давайте рассмотрим некоторые уравнения.Плоскую волну можно разложить на сумму сферических волн с определенными угловыми моментами
который сводится к простой сумме входящих и исходящих сферических волн на больших
.
Потенциал, вызывающий упругое рассеяние, изменит фазы исходящих сферических волн.
Мы можем вычислить дифференциальное сечение упругого рассеяния.
Полезно записать это через амплитуды рассеянных волн.
Например, это использовалось для
вычислить сечение рассеяния от сферической потенциальной ямы
предполагая только
фазовый сдвиг был значительным.Согласовав граничные условия на границе сферической ямы, мы определили фазовый сдвиг.
Дифференциальное сечение
который будет иметь нули, если
Мы можем вычислить полное сечение рассеяния, используя соотношение .
Интересно, что полное сечение можно связать с амплитудой рассеяния при , для которого .
Полное сечение связано с мнимой частью амплитуды упругого рассеяния вперед.Это, казалось бы, странное соотношение известно как оптическая теорема . Это можно понять с точки зрения удаления потока от набегающей плоской волны. Помните, что у нас есть приходящая плоская волна плюс рассеянные сферические волны. Полное сечение соответствует снятию потока с плоской волны. Единственный способ сделать это — деструктивная интерференция рассеянных волн. Поскольку плоская волна находится на это только рассеянная амплитуда при что может мешать. Поэтому разумно, что соотношение, подобное оптической теореме, верно даже тогда, когда возможны упругие и неупругие процессы.
Мы не рассматривали неупругое рассеяние. Неупругое рассеяние может быть сложным и интересным процессом.
Именно при высокоэнергетическом неупругом рассеянии электронов на протонах была « видна » кварковая структура протона.
Фактически оказалось, что электроны рассеиваются на по существу свободных кварках внутри протона.
Протон иногда распадается на множество частиц в процессе, но данные можно было просто проанализировать с помощью рассеянного электрона.
При анализе фазового сдвига неупругое рассеяние удаляет поток исходящих сферических волн.
Здесь , где 0 означает полное поглощение парциальной волны, а 1 — чисто упругое рассеяние. Интересным примером эффекта поглощения (или неэластичного образования другого состояния) является черный диск . Диск имеет определенный радиус и поглощает парциальные волны на . Если решить эту задачу, то обнаружится, что существует сечение неупругого рассеяния . Несколько удивительно полное сечение упругого рассеяния .Диск поглощает часть луча, а также наблюдается дифракция вокруг острых краев. То есть удаление исходящих сферических частичных волн модифицирует плоскую волну, чтобы включить в нее рассеянные волны.
Для высоких энергий относительно обратного диапазона потенциала анализ парциальных волн бесполезен, и гораздо лучше использовать теорию возмущений. Приближение Борна справедливо для высоких энергий и слабых потенциалов. Если потенциал слабый, необходимо вычислить только один или два члена в ряду возмущений.
Если мы работаем в обычной системе центра масс, у нас возникает проблема с рассеянием одной частицы в потенциале.
Набегающую плоскую волну можно записать как
Рассеянная плоская волна равна
Мы можем использовать золотое правило Ферми для вычисления скорости перехода к первому порядку теории возмущений.
Дельта-функция выражает сохранение энергии для упругого рассеяния, которое мы предполагаем на данный момент. Если необходимо рассчитать неупругое рассеяние, энергия атомного состояния изменяется, и это изменение должно быть включено в дельта-функцию и изменение атомарного состояния должно быть включено в матричный элемент.
Элемент матрицы упругого рассеяния равен
куда . Мы замечаем, что это прямо пропорционально преобразованию Фурье потенциала.
Предполагая пока что нерелятивистские частицы в конечном состоянии, мы вычисляем
Теперь нам нужно преобразовать эту скорость перехода в поперечное сечение. Наши волновые функции нормированы на одну частицу на единицу объема, и мы должны изменить это так, чтобы поток составлял одну частицу на квадрат. сантиметр в секунду, чтобы получить поперечное сечение.Для этого мы устанавливаем громкость на . Относительная скорость — это просто количество движения, деленное на приведенную массу.
Это очень полезная формула для рассеяния на слабом потенциале или для рассеяния при высокой энергии для задач, в которых сечение становится маленьким, потому что преобразование Фурье потенциала уменьшается при больших значениях . Он не подходит для рассеяния из-за сильного взаимодействия, поскольку сечения большие и обычно не уменьшаются при высоких энергиях.Отметим, что матричные элементы и, следовательно, амплитуды рассеяния, вычисленные в борновском приближении, являются действительными и поэтому не удовлетворяют оптической теореме. Это недостаток приближения.
Подразделы Джим Брэнсон 2013-04-22
kCARTA: быстрый алгоритм псевдострочного переноса излучения с аналитическими якобианами, потоками, нелокальным термодинамическим равновесием и рассеянием для инфракрасного излучения
Ауман, Х., Шахин, М., Готье, К., Голдберг, М., Калнай, Э., Макмиллин, Л., Revercomb, H., Rosenkranz, P., Smith, W., Staelin, D., Strow, L., и Сасскинд, Дж .: AIRS / AMSU / HSB о миссии Aqua: дизайн, наука Цели, продукты данных и системы обработки, IEEE T. Geosci. Remote, 41, 253–264, 2003. a
Buehler, S., Eriksson, P., and Lemke, O .: Справочные таблицы поглощения в модель переноса излучения ARTS, J. Quant. Spectrosc. Ра., 112, 1559–1567, https://doi.org/10.1016/j.jqsrt.2011.03.008, 2011. a
Чжоу, М.-Д., Ли, К.-Т., Цай, С.-К., Фу, Q .: Параметризация для облака Длинноволновое рассеяние для использования в моделях атмосферы, J. Climate, 12, 159–169, 1999. a, b, c, d
Clerbaux, C., Boynard, A., Clarisse, L., George, M., Hadji-Lazaro, J., Herbin, H., Hurtmans, D ., Pommier, M., Razavi, A., Turquety, S., Wespes, C., and Coheur, P.-F .: Мониторинг состава атмосферы с использованием теплового инфракрасного зонда IASI / MetOp, Atmos. Chem. Phys., 9, 6041–6054, https://doi.org/10.5194/acp-9-6041-2009, 2009.а
Клаф С. и Яконо М. Дж .: Построчное вычисление атмосферных потоков. и скорости охлаждения, 2. Применение к двуокиси углерода, озону, метану, Закись азота и галоидоуглероды, J. Geophys. Рес.-Атмос., 100, 16519–16535, 1995. a
Клаф, С., Кнейзис, Ф., Дэвис, Р., Гамаш, Р., и Типпинг, Р.: Теоретические исследования. форма линии для водяного пара; Приложение к континууму, в: Атмосферное водяной пар, отредактированный: Дипак, А., Вилкерсон, Т., и Рунке, Л., Academic Press, Нью-Йорк, 25–46, 1980.а, б
Клаф, С., Шепард, М., Млавер, Э., Деламер, Дж., Яконо, М. Дж., Кади-Перейра, К., Букабара, С., Браун, П .: Атмосферное излучение. моделирование передачи: сводка кодов AER, J. Quant. Spectrosc. Ra., 91, 233–244, DOI: 10.016 / j.qsrt2004.05.058, 2005. a, b
Клаф, С. А., Кнейзис, Ф. X., Дэвис, Р. У .: Форма линии и вода Континуум пара, атмосфера. Res., 23, 229–241, 1989. a
Клаф, С. А., Яконо, М. Дж., И Монсе, Дж. Л .: Построчное вычисление атмосферные потоки и скорость охлаждения: применительно к водяному пару, Дж.Geophys. Res., 97, 15761–15785, 1992. a, b, c, d
Де Соуза-Мачадо, С. и Строу, Л.Л .: UMBC_LBL, доступно по адресу: https://github.com/sergio66/UMBC_LBL (последний доступ: 12 января 2020 г.), 8.00, 2000. a
Де Соуза-Мачадо, С., Строу, Л. Л., Тобин, Д., Моттелер, Х., Хэннон, С .: UMBC-LBL: алгоритм для вычисления линейных спектров, Tech. Респ., Университет штата Мэриленд, округ Балтимор, факультет физики, доступно по адресу: http://asl.umbc.edu/pub/rta/umbclbl/lbl.ps (последний доступ: 12 января 2020 г.), 2002 г.a, b
Де Соуза-Мачадо, С., Строу, Л. Л., Моттелер, Х., Хэннон, С., Лопес-Пуэртас, М., Функе Б. и Эдвардс Д. Моделирование переноса излучения 4,3 мкм Нелокальные эффекты термодинамического равновесия для Aqua / AIRS Инфракрасный датчик температуры, Geophys. Res. Lett., 34, L01802, https://doi.org/10.1029/2006GL026684, 2007. a
Де Соуза-Мачадо, С., Строу, Л. Л., Имбириба, Б., Макканн, К., Хофф, Р., Хэннон , С., Мартинс, Дж., Танре, Д., Деузе, Дж., Дюко, Ф., и Торрес, О.: Инфракрасное извлечение пыли с помощью AIRS: сравнение оптических глубин и высоты, полученные для пыльной бури в Северной Африке, по другим расположенным вместе EOS A-Train и наземные наблюдения, J. Geophys. Res., 115, D15201, https://doi.org/10.1029/2009JD012842, 2010. a
Де Соуза-Мачадо, С., Строу, Л. Л., Моттелер, Х., и Хэннон, С. Э .:, kCARTA Matlab, доступно по адресу: https://github.com/strow/kcarta-matlab (последний доступ: 12 января 2020 г.), 1.00, 2012. a
DeSouza-Machado, S., Strow, L. L., Tangborn, A., Huang, X., Chen, X., Liu, X., Wu, W. и Yang, Q .: Получение одного отпечатка для AIRS с использованием быстрой модели облачного представления TwoSlab и SARTA all -небо алгоритм передачи инфракрасного излучения, Атмос. Измер. Tech., 11, 529–550, https://doi.org/10.5194/amt-11-529-2018, 2018. a
De Souza-Machado, S., Strow, LL, Motteler, H., and Хэннон, ЮВ: kCARTA F90, доступно по адресу: https://github.com/sergio66/kcarta_gen (последний доступ: 12 января 2020 г.), 1.21, 2019. a
Дудхия, А.: Reference Forward Model (RFM), J. Quant. Spectrosc. Ra., 186, 243–253, 2017. a, b, c, d
Edwards, D.: GENLN2: Общая построчная атмосферная проницаемость и Модель сияния, Техническая нота NCAR 367 + STR, Национальный центр Атмосферные исследования, Боулдер, Коломбо, 1992. a, b, c, d
Эдвардс, Д. П., Лопес-Пуэртас, М., и Лопес-Вальверде, М .: Без LTE. Исследования 15 мкм полос CO 2 для атмосферного дистанционного зондирования, J. Geophys. Res., 98, 14955–14977, 1993.а
Эдвардс, Д. П., Лопес-Пуэртас, М., и Гамаш, Р.: Исправление без LTE к колебательная составляющая внутренней суммы раздела для атмосферного Расчеты, J. Quant. Spectrosc. Ra., 59, 423–436, 1998. а
Фармер, К. Б. и Нортон, Р.: Атлас инфракрасного спектра Солнца и Атмосфера Земли из космоса, Том I, Солнце, публикация NASA JPL 1224, НАСА, Пасадена, Калифорния, 1989. a
Фармер К. Б., Рэпер О. и О’Каллаган Ф .: Заключительный отчет о первом полете. прибора ATMOS во время миссии Spacelab 3 с 29 апреля по 6 мая 1985 г., публикация JPL, Лаборатория реактивного движения, Пасадена, Калифорния, 87–32, 1987.a
Gambacorta, A .: Уникальная система обработки данных CrIS / ATMS NOAA (NUCAPS): Документация по теоретическим основам алгоритмов, Tech. Представитель, NCWCP, доступно по адресу: http://www.ospo.noaa.gov/Products/atmosphere/soundings/nucaps/docs/NUCAPS_ATBD_20130821.pdf (последний доступ: 2 января 2020 г.), 2013. а
Гуди, Р. и Юнг, Й .: Атмосферное излучение: теоретические основы, Оксфорд. University Press, 519 pp., 1989. a, b
Gordon, I., Rothman, L., Hill, C., Kochanov, R., and Tan, Y.E.A .: The База данных молекулярной спектроскопии HITRAN 2016, J.Quant. Spectrosc. Ra., 203, 3–69, https://doi.org/10.1016/j.jqsrt.2017.06.038, 2017. a
Han, Y., Revercomb, H., Cromp, M., Strow, L ., Чен, Ю., и Тобин, Д .: Суоми Измерения АЭС КРИС, алгоритм записи данных датчиков, калибровка и деятельность по проверке достоверности данных и качество записи данных, J. Geophys. Res., 118, 12734–12748, https://doi.org/10.1002/2013JD020344, 2013. a
Hartmann, J.-M., Boulet, C., Tran, D., Tran, H., and Baranov, Y .: Эффект влажность на континууме поглощения CO 2 и N 2 около 4 мкм: расчеты, сравнения с измерениями, последствия для атмосферных спектров, Дж.Chem. Phys, 148, 54304, https://doi.org/10.1063/1.5019994, 2018. a
Hoffmann, L. и Alexander, M .: Получение стратосферных температур из Измерения яркости атмосферного инфракрасного эхолота для исследования гравитационных волн, J. Geophys. Res., 114, D07105, https://doi.org/10.1029/2008JD011241, 2009. a
Husson, N., Armante, R., Scott, N., Chedin, A., Crepeau, L., Boitammine , C., Bouhdaoui, A., Crevoisier, C., Capelle, V., Boone, C., Poulet-Croviser, N., Барбе, А., Беннер, К., Будон, В., Браун, Л., Булдырева, Дж., Кампарг, А., Л. Х., К., Маки, А. и др.: Издание GEISA 2015 г. спектроскопическая база данных, J. Mol. Спектр., 327, 31–72, https://doi.org/10.1016/j.jms.2016.06.007, 2015. a
Ламуру, Дж., Тран, Х., Ларайя, А. Л., Гамаш, Р. Р., Ротман, Л. С., Гордон, И. Э. и Хартманн Дж.-М .: Обновленная база данных плюс программное обеспечение для микширования линий в инфракрасных спектрах CO 2 и их проверка с использованием лабораторных спектров в Область 1,5–2,3 мкм, J. Quant. Spectrosc.Ра., 111, 2321–2331, https://doi.org/10.1016/j.jqsrt.2010.03.006, 2010. a
Ламуру, Дж., Рогалия, Л., Томас, X., Вандер Аувера, Дж., Гамаш, Р., и Hartmann, J.-M .: CO 2 база данных микширования линий и обновление программного обеспечения и его тесты в областях 2,1 мкм и 4,3 мкм, J. Quant. Spectrosc. Ра., 151, 88–96, https://doi.org/10.1016/j.jqsrt.2014.09.017, 2015. а, б
Лиу, К .: Введение в атмосферное излучение, Academic Press, 583 стр., 1980. a, b, c
Лю, X., Смит, В., Чжоу, Д., и Ларар, А.: на основе основных компонентов модель переноса излучения для гиперспектральных датчиков: теоретические концепции, Прил. Опт., 45, 201–209, 2006. а
Лопес-Пуэртас, М. и Тейлор, Ф .: Перенос излучения NONLTE в Атмосфера, World Scientific Publishing, 471 стр., 2001. a
Матрикарди, М .: Включение аэрозолей и облаков в RTIASI, ECMWF модель быстрого переноса излучения для инфракрасного зондирования атмосферы интерферометр, Тех. Отчет 474, 55 с., 2005. a
Млауэр, Э. Дж., Пейн, В. Х., Монсе, Ж.-Л., Деламер, Дж., Альварадо, М., и Тобин, Д .: Разработка и недавняя оценка модели MT_CKD континуальное поглощение, П. Рой. Soc. A-Math. Phy., 370, 1–37, doi: 10.1098: rsta.2011.0295, 2012. a, b
Nalli, N., Smith, W., and Liu, Q .: Угловой эффект необнаруженных облаков в Наблюдения за яркостью в инфракрасном окне: экспериментальный анализ с самолета, J. Atmos. Sci., 73, 1987–2011, https://doi.org/10.1175/JAS-D-15-0262.1, 2016.a
Ниро, Ф., Джакс, К. У., и Хартманн, Дж. М .: Расчеты спектров в центральных и области крыльев CO 2 ИК-диапазоны от 10 до 20 мкм: программное обеспечение и база данных для расчета атмосферных спектров, J. Quant. Spectrosc. Ra., 95, 469–481, 2005. а
Роджерс, Ч .: Обратные методы зондирования атмосферы, Мир Scientific, Сингапур, 256 стр., 2000. a, b
Ротман, Л.С., Гордон, И., Бабиков, Ю., Барб, А., Беннер, Д., и Бернат, П.Е.А .: База данных молекулярной спектроскопии HITRAN 2012, J.Quant. Spectrosc. Ра., 130, 4–50, 2013. а
Сондерс, Р., Матрикарди, М., и Брунель, П .: Улучшенный быстрый радиационный модель передачи для усвоения спутниковых наблюдений яркости, В. Дж. Рой. Метеор. Soc., 125, 1407–1425, 1999. a
Шрайер, Ф., Гарсия, С., Хедельт, П., Гесс, М., Мендрок, Дж., Васкес, М., и Сюй, Дж .: ЧЕСНОК — перенос атмосферного излучения общего назначения построчный инфракрасно-микроволновый код: реализация и оценка, J. Quant. Spectrosc. Ра., 137, 29–50, 2014. a
Стамнес, К., Цай, С.-К., Вискомб, В., и Джаявира, К.: численно стабильный Алгоритм метода дискретных ординат. рассеивающие и излучающие слоистые среды, Прил. Опт., 27, 2502–2509, 1988. а
Строу, Л., Моттелер, Х., Бенсон, Р., Хэннон, С., и Де Соуза-Мачадо, С.: Fast Расчет монохроматического инфракрасного пропускания атмосферы с использованием Сжатые справочные таблицы, J. Quant. Spectrosc. Ра., 59, 481–493, г. 1998. а, б, в, г, д
Строу, Л., Хэннон, С., ДеСуза-Мачадо, С., Тобин, Д., и Моттелер, Х .: An Обзор модели переноса излучения AIRS, IEEE T. Geosci. Remote, 41, 303–313, 2003. a, b
Строу, Л. и Пайн, А. С .: Смешивание линий Q-ветви в N 2 O: Влияние Удвоение ℓ-типа, J. Chem. Phys., 89, 1427–1434, https://doi.org/10.1063/1.455142, 1988. a
Сасскинд, Дж., Барнет, К., и Блейсделл, Дж .: Атмосфера и поверхность. Параметры из смоделированных данных зондирования AIRS / AMSU / HSB: поиск и облако Методология клиринга, Adv.Космос. Наук, 21, с. 369–384, https://doi.org/10.1016/S0273—1177(97)00, 1998. a
Tjemkes, S., Patterson, T., Rizzi, R., Shephard, M., Clough, S., Matricardi , М., Хей, Дж., Хопфнер, М., Паян, С., Троценко, А., Скотт, Н., Райер, П., Тейлор, Дж., Клербо, К., Строу, Л., ДеСуза-Мачадо, С., Тобин, Д., и Кнутесон, Р .: The ISSWG Line-by-line Intercomparison Experiment, J. Quant. Spectrosc. Ra., 77, 433–453, https://doi.org/10.1016/S0022-4073(02)00174-7, 2002. a
Tobin, D. C., Strow, L.Л., Лафферти, У. Дж., И Олсон, У. Б .: Экспериментальная Исследование само- и N 2 -разорванного континуума в пределах ν 2 Полоса водяного пара, прим. Opt., 35, 4724–4734, https://doi.org/10.1364/AO.35.004724, 1996. a
Tran, H., Flaud, P.-M., Gabard, T., Hase, F. , Фон Кларманн, Т., Ками-Пейре, К., Пайан С. и Хартманн Дж. Х .: Модель, программное обеспечение и база данных для эффекты линейного смешения в полосах v3 и v4 канала CH 4 и тесты с использованием лабораторных и планетарные измерения, I.N2 (и воздушное) уширение и Земля атмосфера, J. Quant. Spectrosc. Ra., 101, 284–305, 2006. a, b
Тран, Х., Турбет, М., Челин, П., и Ландшир, X .: Измерения и моделирование поглощения смесями CO 2 + H 2 O в спектральной области за пределами CO 2 v3 bandhead, Icarus, 306, 116–121, 2018. а
Тернер, Д.: Свойства арктических облаков со смешанной фазой по данным AERI-лидарных наблюдений: Алгоритм и результаты SHEBA, J. Appl. Мет., 44, 427–444, 2005.а
Тернер Д., Акерман С., Баум Б., Реверкомб Х. и Янг П .: Фаза облака. Определение с использованием наземных наблюдений AERI в SHEBA, J. Appl. Встретились., 42, 701–715, 2003. a
Ван Флек, Дж. Х. и Хубер, Д. Л .: Поглощение, излучение и ширина линий: A полуисторическая перспектива, Rev. Mod. Phys., 49, 939–959, https://doi.org/10.1103/RevModPhys.49.939, 1977 г. a
Видот, Дж., Баран, А., и Брюнель, П .: Новая параметризация ледяного облака для моделирование переноса инфракрасного излучения облачного излучения: оценка и оптимизация с помощью БИХ-наблюдений и продуктов для восстановления профиля ледяных облаков, Дж.Geophys. Res., 120, 6937–6951, https://doi.org/10.1002/2015JD023462, 2015. a
Винсент Р. и Дудхия А. Быстрый перенос излучения с использованием монохроматического справочные таблицы, J. Quant. Spectrosc. Ра., 186, 254–264, https://doi.org/10.1016/j.jqsrt.2016.04.011, 2017. a, b, c
Zorn, S., von Clarmann, T., Echle, G., Funke, B ., Хазе, Ф., Хопфнер, М., Кемницер, Х., Кунц, М., Стиллер, Г .: КОПРА: Аналитические выражения для моделирование переноса излучения и инструментальных эффектов, Тех. Rep., Карлсруэ Университет, Германия, доступно по адресу: https://www.imk-asf.kit.edu/downloads/SAT/kopra_docu_part02.pdf (последний доступ: 2 января 2020 г.), 2002 г.
иллюстраций Евгения Деримиана, Олега Дубовика и др.
Аннотация
Оценка радиационного воздействия аэрозоля на широкополосный полусферический солнечный поток часто выполняется с использованием упрощенных спектральных и направленных характеристик рассеяния атмосферного аэрозоля и отражательной способности подстилающей поверхности. В этом исследовании мы представляем строгий, но быстрый вычислительный инструмент, который точно учитывает детальную изменчивость как спектральных, так и угловых характеристик рассеяния аэрозоля и отражательной способности поверхности при расчете прямого радиационного эффекта аэрозоля.Инструмент разработан в рамках проекта GRASP (Generalized Retrieval of Aerosol and Surface Properties). Мы используем этот инструмент для оценки мгновенной и среднесуточной радиационной эффективности (радиационный эффект на единицу оптической толщины аэрозоля) нескольких ключевых моделей атмосферных аэрозолей над различными типами поверхности. Затем мы исследуем различия, обусловленные пренебрежением анизотропией отражения поверхности, несферичностью формы аэрозольных частиц и учетом только асимметрии углового рассеяния аэрозоля вместо использования полной фазовой функции.Например, показано, что пренебрежение несферичностью аэрозольных частиц приводит в основном к завышению эффекта охлаждения аэрозоля, и что величина этой завышенной оценки значительно изменяется в зависимости от зенитного угла Солнца (SZA), если параметр асимметрии используется вместо детальной фазовой функции. Было также обнаружено, что несферические и сферические различия в рассчитанном аэрозольном радиационном эффекте не претерпевают значительных изменений, если вместо ламбертовского приближения отражательной способности поверхности используется подробный BRDF (функция распределения двунаправленной отражательной способности).Кроме того, расчеты показывают, что использование только угловой асимметрии рассеяния даже для сферических аэрозолей изменяет зависимость мгновенного радиационного воздействия аэрозоля от SZA. Этот эффект можно отменить для среднесуточных значений, но только если солнце достигнет зенита; в противном случае сохраняется систематическая предвзятость. Поскольку среднесуточный радиационный эффект получается путем интегрирования по диапазону SZA, ошибки меняются в зависимости от широты и сезона. Таким образом, настоящий анализ показал, что использование упрощенных допущений вызывает систематические ошибки, а не случайные неопределенности при расчетах как мгновенного, так и среднесуточного радиационного воздействия аэрозолей.Наконец, мы проиллюстрируем применение строгих расчетов радиационного эффекта аэрозолей, выполненных в рамках извлечения аэрозолей GRASP из реальных спутниковых наблюдений POLDER / PARASOL.
Название публикации
Химия и физика атмосферы
Рекомендуемое цитирование
Деримиан Ю.,
Дубовик О.,
Хуанг, X.,
Лапёнок Т.,
Литвинов, П.,
Костинский, А.,
Дюбюиссон П.,
&
Дюко, Ф.
(2016).
Комплексный инструмент для расчета радиационных потоков: иллюстрация чувствительности коротковолнового аэрозольного радиационного воздействия к деталям в аэрозоле и характеристикам подстилающей поверхности. Химия и физика атмосферы,
16 , 5763-5780.
http://doi.org/10.5194/acp-16-5763-2016
Получено с https: // digitalcommons.mtu.edu/physics-fp/172
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера на прием файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
сечений рассеяния нейтрино заряженным током на 132Xe для обнаружения сверхновых
Полные сечения, а также скорости нейтринных событий рассчитаны в рассеянии нейтрино заряженного тока и антинейтрино на изотопе 132 Xe при энергии нейтрино МэВ.Переходы в возбужденные состояния ядра рассчитаны в рамках приближения квазичастичных хаотических фаз. Показаны вклады от разных мультиполей для разных энергий нейтрино. Усредненные по потоку сечения получены путем свертки сечений с двухпараметрическим распределением Ферми-Дирака. Усредненные по потоку сечения также рассчитываются с использованием наземных источников нейтрино, основанных на традиционных источниках (распад мюона в состоянии покоя) или на бета-пучках низкой энергии.
1.Введение
Обнаружение нейтрино и их свойств — один из главных приоритетов современной ядерной физики и физики элементарных частиц, а также астрофизики. Среди зондов, использующих нейтрино, нейтрино-ядерные реакции занимают видное место. Детальные предсказания нейтринно-ядерных сечений (NNCS) имеют решающее значение для обнаружения или различения нейтрино разного аромата и исследования базовой структуры слабых взаимодействий [1–14]. Зарезервированные сечения рассеяния нейтрино на ядре при энергиях нейтрино, которые актуальны для нейтрино от сверхновых, доступны только в нескольких случаях, то есть для [15], [15, 16] и дейтрона [17].Поэтому использование микроскопических моделей ядерной структуры необходимо для количественного описания нейтринно-ядерных реакций. К ним относятся модель ядерной оболочки [18, 19], приближение случайных фаз (RPA), релятивистская RPA [20, 21], континуальная RPA (CRPA) [22], квазичастичная RPA (QRPA) [23–26], проектируемая квазичастичный RPA (PQRPA) [27], гибридные модели CRPA, оболочечная модель [28, 29] и модель ферми-газа [30]. Модель оболочки обеспечивает очень точное описание волновых функций основного состояния.Однако описание высоколежащих возбуждений требует использования пространств больших моделей, что часто приводит к вычислительным трудностям, что делает подход применимым по существу только к легким и средним ядрам. Следовательно, для систематических исследований скоростей слабого взаимодействия для соответствующих тяжелых ядер с массовым числом вокруг, микроскопические расчеты должны выполняться с использованием моделей, основанных на RPA [23, 25].
Признак взаимодействия нейтрино сверхновой, имеющий место в различных детекторах, — это наблюдение электронов, позитронов, фотонов и других частиц, которые образуются в результате взаимодействий заряженного и нейтрального тока.Два процесса, которые влияют на общую частоту событий в детекторах, — это реакции заряженного тока (CC). и реакции нейтрального тока (NC) Нейтрино (или антинейтрино) не имеют достаточной энергии для производства соответствующих лептонов в реакциях с заряженным током и взаимодействуют только через взаимодействия нейтрального тока и, следовательно, имеют более высокую среднюю энергию, чем и, которые взаимодействуют через заряженный ток, а также взаимодействия нейтрального тока.Численное моделирование дает следующие значения средней энергии для различных ароматов нейтрино, то есть МэВ, МэВ и МэВ, и согласуются со спектром нейтрино сверхновой, заданным распределением Ферми-Дирака [31, 32]: где — температура нейтрино, — параметр вырождения, принимаемый равным 0 или 3. обозначает нормировочный коэффициент, зависящий от заданного из для . Следуя [33], среднюю энергию нейтрино через функции (4) можно записать как В большинстве расчетов нейтринно-ядерных сечений принимались значения.Однако в астрофизических приложениях может быть важно провести исследования скоростей реакций для различных значений в зависимости от выполняемого моделирования и от конкретной рассматриваемой фазы сверхновой [29, 34]. В нашем исследовании это значение также использовалось. Средние значения энергии для различных типов нейтрино означают, что для, значения температуры составляют 3,5 МэВ (2,75 МэВ) для, 5 МэВ (4 МэВ) для и 8 МэВ (6 МэВ) для (). Недавние теоретические исследования предсказывают меньшее значение температуры, которое ближе к [34–37].
Систематические измерения взаимодействия нейтрино с ядром могут быть идеальным инструментом для исследования слабого ядерного отклика. В настоящее время предлагаются новые эксперименты с различными ядрами на новой установке, использующей распад мюонов в состоянии покоя [38]. Другая возможность может быть предложена бета-лучами. Это новый метод получения чистых и хорошо известных пучков электронных нейтрино, использующий бета-распад усиленных радиоактивных ионов [39]. Идея создания установки для низкоэнергетического бета-пучка была впервые предложена в [40] и обсуждалась в исследованиях ядерной структуры, физике сверхновых с коллапсом ядра и изучении фундаментальных взаимодействий [40–49].
Детектор, активная цель которого состоит из благородного жидкого ксенона, может предложить уникальные возможности обнаружения в области физики нейтрино [47, 50], а также способность обнаруживать сигналы очень низкой энергии в контексте поиска темной материи [51 , 52]. Новая концепция сферического детектора TPC, заполненного ксеноном высокого давления, также была предложена как устройство, способное обнаруживать нейтрино низкой энергии, исходящие от галактической сверхновой. В частности, детектор TPC может быть использован для наблюдения когерентного NC, а также CC-рассеяния нейтрино-ядром [37, 53–58].
В этой статье мы представляем микроскопические расчеты CC сечения реакции. Соответствующие приведенные матричные элементы в области низких и промежуточных энергий нейтрино рассчитаны в рамках приближения квазичастичных случайных фаз (QRPA). Мы представляем полные нейтринно-ядерные сечения, а также вклад различных мультиполей и обсуждаем, как их важность меняется в зависимости от энергии нейтрино. Приведено также сравнение сечений КК и сечений когерентных НК [37, 55].Наконец, мы даем усредненные по потоку сечения, связанные с распределением Ферми-Дирака, а также с распределениями, основанными на земных источниках нейтрино, таких как низкоэнергетические бета-пучки или обычные источники (распад мюона в состоянии покоя).
2. Формализм для расчетов нейтрино-ядерных сечений
Рассмотрим нейтринно-ядерное взаимодействие с нейтральным или заряженным током, при котором нейтрино с низкой или средней энергией (или антинейтрино) неупруго рассеивается от ядра.Предполагается, что исходное ядро является сферически-симметричным, имеющим основное состояние — состояние.
Соответствующий эффективный гамильтониан ток-токового взаимодействия стандартной модели можно записать как где — константа слабой связи Ферми для реакции с заряженным током и для реакции с нейтральным током. и обозначают лептонный и адронный токи соответственно. Согласно теории V-A, лептонный ток принимает вид где спиноры нейтрино / антинейтрино.
С точки зрения ядерной физики важен только адронный ток. Структура для процессов нейтрального тока (NC) и заряженного тока (CC) как векторной, так и аксиально-векторной составляющих (без учета псевдоскалярных вкладов) записывается как где — масса нуклона, а — спиноры нуклона. Форм-факторы и определяются как и форм-факторы нейтрального тока, а как Здесь — оператор изоспина нуклона, а — угол Вайнберга ().Подробные выражения нуклонных формфакторов приведены в [59]. Аксиально-векторный форм-фактор определяется выражением [60] где ГэВ — масса диполя, а — статическое значение (at) аксиального форм-фактора.
В соглашении, которое мы использовали в данной статье, квадрат переданного импульса записывается как где — энергия возбуждения ядра. обозначает энергию входящего нейтрино и обозначает энергию выходящего лептона., — соответствующие 3-импульсы. В (11) мы не учитывали вклады странных кварков в формфакторы. В рассматриваемой в нашей работе реакции рассеяния участвуют только малые передачи импульса, а вкладом странности можно пренебречь [61].
Дифференциальное сечение нейтрино / антинейтрино-ядро после применения мультипольного анализа слабого адронного тока записывается как где обозначает угол рассеяния лептона.Суммирования в (14) содержат вклады кулоновского и продольного, а также поперечного электрического и магнитного мультипольных операторов [62]. Эти операторы включают как полярно-векторную, так и аксиально-векторную компоненты слабого взаимодействия. Вклады и записываются как где, и. В (16) знак соответствует рассеянию нейтрино, а знак — антинейтрино. Абсолютное значение трех переданных импульсов определяется выражением Для реакций с заряженным током в уравнение сечения (14) необходимо внести поправку на искажение выходной волновой функции лептона кулоновским полем дочернего ядра.Сечение можно либо умножить на функцию Ферми, полученную из численного решения уравнения Дирака для расширенного ядерного зарядового распределения [29, 63], либо, при более высоких энергиях, влияние кулоновского поля можно описать эффективным импульсное приближение (EMA) [63–65]. В этом приближении импульс и энергия лептона модифицируются как где — эффективный кулоновский потенциал. В недавнем исследовании с использованием точных волновых функций Дирака было показано, что точное приближение для эффективных импульсов электронов получается с использованием среднего значения кулоновского потенциала, где соответствует электростатическому потенциалу, вычисленному в центре ядра [ 66, 67].- заряд дочернего ядра; — его радиус в предположении сферического распределения заряда. обозначает постоянную тонкой структуры. В расчетах с EMA исходные импульс лептона и энергия, фигурирующие в выражении для сечения, заменяются указанными выше эффективными величинами.
3. Энергии и волновые функции
Для реакций, индуцированных нейтрино-ядром с нейтральным током, основное состояние и возбужденные состояния четно-четного ядра создаются с использованием приближения квазичастичных случайных фаз (QRPA), включающего два квазинейтрона и два квазипротонных возбуждения в матрице QRPA [68] (далее обозначаемые pp-nn QRPA).Мы начнем с записи гамильтониана A-фермионов в представлении числа заполнения в виде суммы двух членов. Один представляет собой сумму одночастичных энергий (spe), которая проходит по всем значениям квантовых чисел, а второй член включает в себя взаимодействие двух тел, то есть где двухчастичный член содержит антисимметричный матричный элемент взаимодействия двух тел, определяемый как. Операторы и обозначают обычные операторы рождения и разрушения нуклонов в состоянии.
Для сферических ядер с частично заполненными оболочками наиболее важным эффектом двухчастичной силы является создание парных корреляций. Для учета парного взаимодействия используется теория БКШ [69]. Самый простой способ ввести эти соотношения в волновую функцию — выполнить преобразование Боголюбова-Валатина: где, и. Амплитуды заполнения и определяются с помощью вариационной процедуры минимизации энергии основного состояния БКШ отдельно для протонов и нейтронов.В подходе BCS основное состояние четно-четного ядра описывается как сверхпроводящая среда, где все нуклоны образовали пары, которые эффективно действуют как бозоны. Основное состояние BCS определяется как где представляет собой ядро ядра (эффективный вакуум частиц).
После преобразования (20) гамильтониан можно записать в квазичастичном представлении как где первый член дает энергии одиночных квазичастиц, а второй включает различные компоненты остаточного взаимодействия.
В настоящих расчетах мы используем параметр перенормировки, который можно настроить, решая уравнения БКШ. Элементы монопольной матрицы двухчастичного взаимодействия умножаются на коэффициент. Корректировка может быть выполнена путем сравнения результирующей энергии наименьшей квазичастицы с феноменологической энергетической щелью, полученной из энергий разделения соседних дважды четных ядер для протонов и нейтронов по отдельности.
Возбужденные состояния четно-четного эталонного ядра построены с использованием QRPA.В QRPA оператор создания возбужденного состояния имеет вид где операторы рождения и уничтожения пар квазичастиц определены как где и являются индексами протона (p) или нейтрона (n), маркируют магнитные подсостояния и нумеруют состояния для определенного углового момента и четности.
Амплитуды прямого и обратного направления определяются из матричного уравнения QRPA. где обозначает энергии возбуждения ядерного состояния.Матрицы QRPA, и, выводятся матричными элементами двойных коммутаторов и с ядерным гамильтонианом, определенным как куда . Наконец, двухчастичные матричные элементы каждой мультиполярности, встречающиеся в матрицах QRPA и, умножаются на две феноменологические константы масштабирования, а именно, прочность частицы-дырки и сила частицы-частицы. Эти значения параметров определяются путем сравнения полученной энергии самого низкого фонона с соответствующим самым низким коллективным колебательным возбуждением дважды четного ядра и путем воспроизведения некоторых гигантских резонансов, которые играют решающую роль.
Для нейтринно-ядерных реакций заряженного тока возбужденные состояния нечетно-нечетного ядра генерируются с помощью протон-нейтронной QRPA (pnQRPA). QRPA в своей протон-нейтронной форме содержит фононы, состоящие из пар протон-нейтрон, а именно: Матрицы и, определенные в каноническом базисе, равны где и — энергии двухквазичастичного возбуждения, и — p-h и p-p матричные элементы остаточного нуклон-нуклонного взаимодействия соответственно.Для реакций с заряженным током матричные элементы любого оператора перехода между основным состоянием и возбужденным можно разложить на множители следующим образом: где — приведенные матричные элементы, вычисленные независимо для данного одночастичного базиса [70, 71].
4. Результаты и обсуждение
Элементы матрицы перехода типа, входящего в (15) и (16), могут быть вычислены в рамках pnQRPA. Исходное ядро считалось сферически-симметричным с основным состоянием.Основные оболочки с двумя осцилляторами (и), плюс орбиталь вторжения от следующей основной оболочки с более высоким осциллятором, использовались как для протонов, так и для нейтронов в качестве валентного пространства исследуемых ядер. Соответствующие одночастичные энергии (SPE) были получены с помощью скорректированного по кулону потенциала Вудса-Саксона с использованием параметров Бора и Моттельсона [72].
Матричные элементы двухчастичного взаимодействия были получены из Боннского потенциала однобозонного обмена с использованием методов G-матрицы [73]. Сильное парное взаимодействие между нуклонами можно регулировать, решая уравнения БКШ.Монопольные матричные элементы двухчастичного взаимодействия масштабируются по параметрам силы спаривания и отдельно для протонов и нейтронов. Регулировка может быть сделана путем сравнения полученной энергии наименьшей квазичастицы, чтобы воспроизвести феноменологическую щель спаривания [74]. Результаты этой процедуры приводят к параметрам силы спаривания и. Матричные элементы частица-частица, а также матричные элементы частица-дырка перенормируются с помощью параметров и, соответственно. Эти параметры были настроены для каждого мультипольного состояния отдельно, чтобы воспроизвести некоторые из экспериментально известных энергий низколежащих состояний в ядре и соответственно.Полученные значения соответствующих параметров лежат в диапазоне и. В частности, для многополярности использовались значения и, в то время как для многополярности использовались значения и. Более того, для, использовались значения и, за исключением многополярности, для которой использовались и. Включены все состояния.
На рисунке 1 мы представляем численные результаты полного сечения рассеяния (14) в зависимости от энергии падающего нейтрино для реакций и, соответственно.Значения реакций составляют 2,12 МэВ и 3,58 МэВ соответственно. Здесь мы рассмотрели гибридный рецепт, уже использованный в предыдущих расчетах [19, 75, 76], где функция Ферми для кулоновской поправки используется ниже области энергий, в которой оба подхода предсказывают одинаковые значения, в то время как EMA принимается выше этого энергетический регион.
Вклад различных мультиполей в полное сечение падающих энергий нейтрино показан на рисунке 2.Когда полное сечение в основном приписывается переходам Гамова-Теллера () и Ферми (). Другие переходы составляют всего несколько процентов от общего сечения. По мере увеличения энергии нейтрино мультипольные состояния также становятся важными. Наконец, за пределами 80 МэВ все состояния вносят вклад, и сечение распространяется по многим мультиполям.
На рис. 3 показаны сечения когерентных процессов нейтрального и заряженного тока в зависимости от энергии нейтрино.Как видно, процесс когерентного нейтрального тока () [55] имеет сечения, которые на порядок больше, чем сечения заряженного тока электронного нейтрино (). Оба они даже больше, чем из событий сечения тока заряда электронного антинейтрино (). При МэВ разница между и оказывается в 5. Это можно понять с точки зрения энергетического порога и ядерных эффектов реакций. Поскольку значение для реакций на 1,46 МэВ больше единицы, это уменьшает энергию падающего нейтрино и, следовательно, уменьшает сечение для данной энергии.В таблице 1 полные (анти) нейтринные сечения указаны в см 2 .
| ||||||||||||||||||||||||||||||||||||||||||||||||
Общий поток сечения могут быть вычислены путем складывания сечений, показанных на рисунке 3, со спектром Ферми-Дирака, заданным формулой (3), следующим образом: В таблице 2 приведены усредненные по потоку полные сечения для различных значений температуры.Параметры химического потенциала и использовались для описания спектра сверхновых [32]. Соответствующая средняя энергия нейтрино была рассчитана с помощью (4) и (5). Как видно, рассчитанное усредненное по потоку сечение увеличивается с увеличением средней энергии нейтрино. Введение химического потенциала в спектр при фиксированной температуре нейтрино увеличивает среднюю энергию нейтрино. На рисунке 4 контурный график используется для отображения линий усредненных по постоянному потоку поперечных сечений (в единицах см 2 ) реакции как функции от и.При более низких температурах сечения, усредненные по потоку, очень слабо зависят от. Однако уже выше МэВ сечения, усредненные по потоку, растут гораздо быстрее при более высоких значениях химического потенциала.

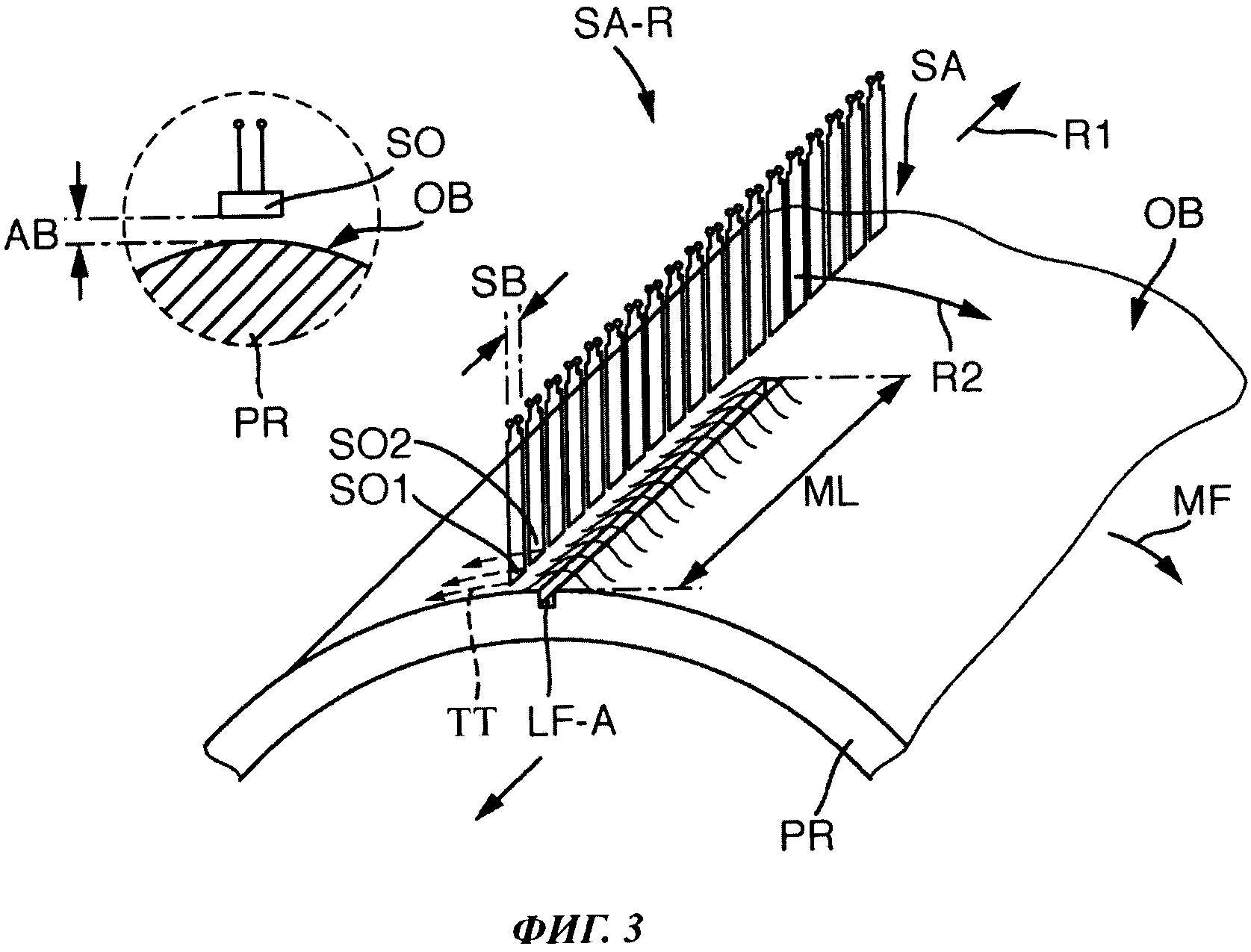 Отдельные листы стали изолируют слоем лака, после
чего стягивают болтами. Такое устройство применяется для уменьшения
вихревых токов, индуктируемых в стали переменным потоком.
Отдельные листы стали изолируют слоем лака, после
чего стягивают болтами. Такое устройство применяется для уменьшения
вихревых токов, индуктируемых в стали переменным потоком. 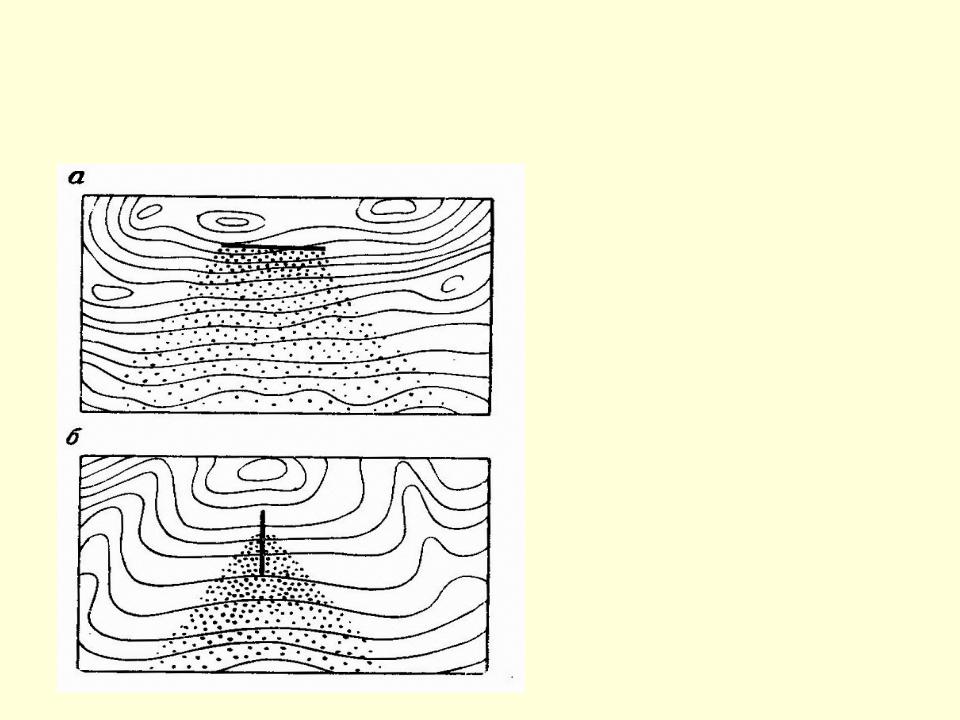


 Действующее значение напряжения U1
остается неизменным. Уменьшение E1, согласно (10.2),
вызывает увеличение тока токи I1. При увеличении тока I1
поток Ф1 увеличивается ровно настолько, чтобы скомпенсировать
размагничивающее действие потока Ф2. Вновь восстанавливается
равновесие при практически прежнем значении суммарного потока.
Действующее значение напряжения U1
остается неизменным. Уменьшение E1, согласно (10.2),
вызывает увеличение тока токи I1. При увеличении тока I1
поток Ф1 увеличивается ровно настолько, чтобы скомпенсировать
размагничивающее действие потока Ф2. Вновь восстанавливается
равновесие при практически прежнем значении суммарного потока. 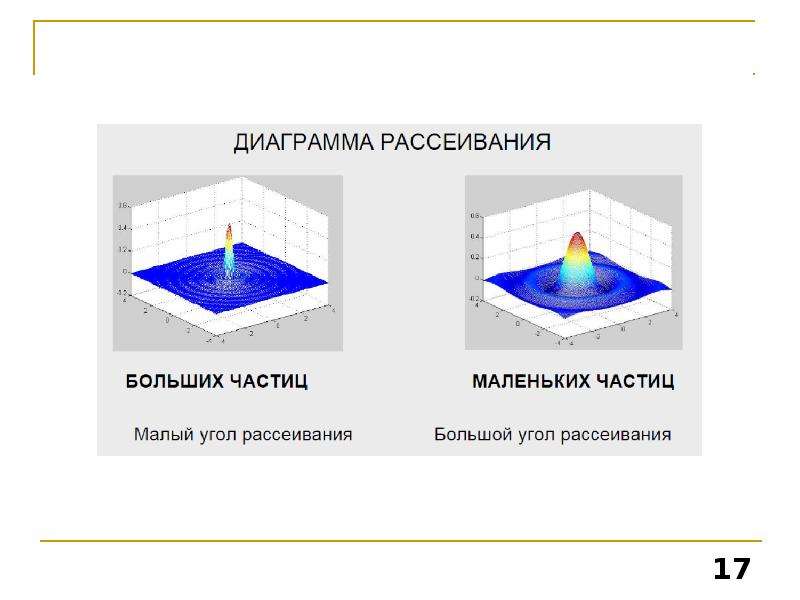 (10.3)
(10.3)