При параллельном соединении конденсатор равен const: способы, правила, формулы. Вычисление падений напряжения на конденсаторах — Мир Антенн

Содержание

способы, правила, формулы. Вычисление падений напряжения на конденсаторах

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

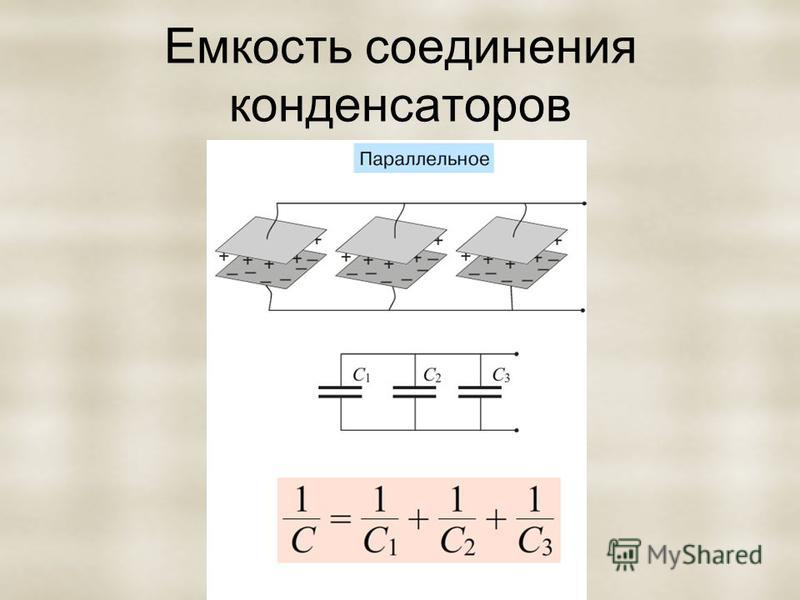
Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

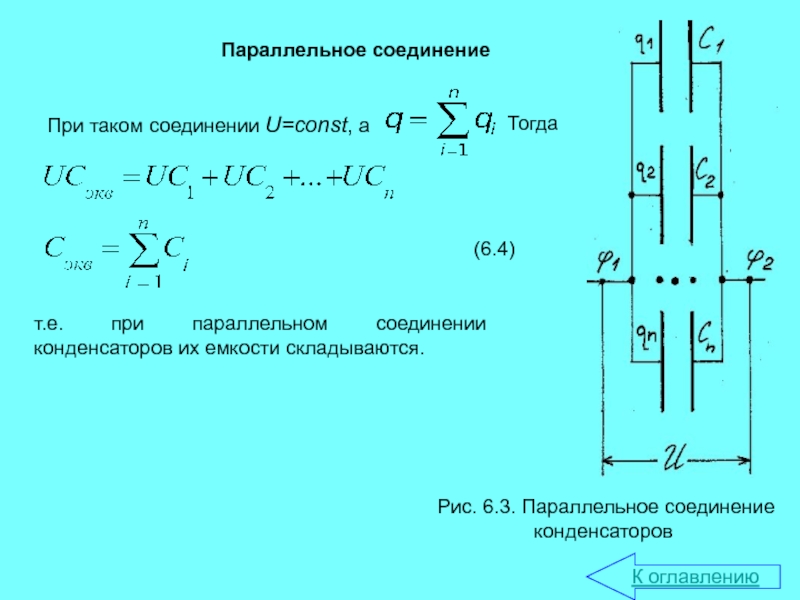
При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить

батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов.

Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .

Смешанное соединение конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.

В соответствии со вторым правилом Кирхгофа, падения напряжения V₁ , V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:

По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость C eq всех трех конденсаторов, соединенных последовательно, определяется как

Для группы из n соединенных последовательно конденсаторов эквивалентная емкость C eq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:

Эта формула для C eq и используется для расчетов в этом калькуляторе.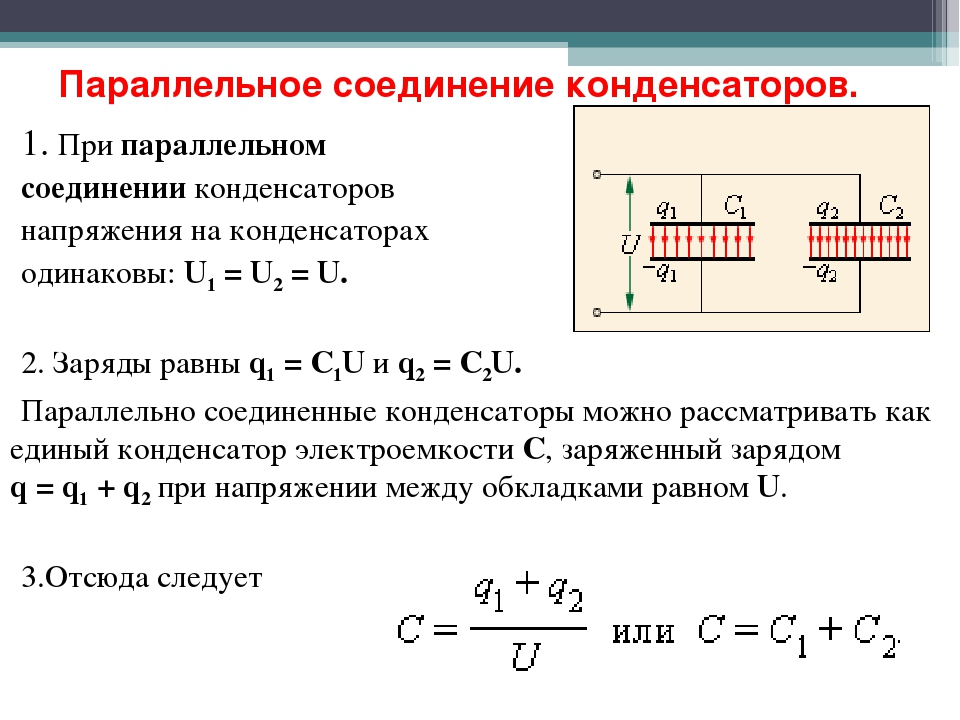

Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:

Если конденсаторов только два, то их общая емкость определяется по формуле

Если имеется n соединенных последовательно конденсаторов с емкостью C , их эквивалентная емкость равна

Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов .

Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.

Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки.

На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.

Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.

Если несколько конденсаторов соединены параллельно , разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах

Q₁ , Q₂ and Q₃ тоже будут различными. Общий заряд определяется как

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С 1 – ёмкость первого;

С 2 – ёмкость второго;

С 3 – ёмкость третьего;

С N – ёмкость N -ого конденсатора;

C общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см.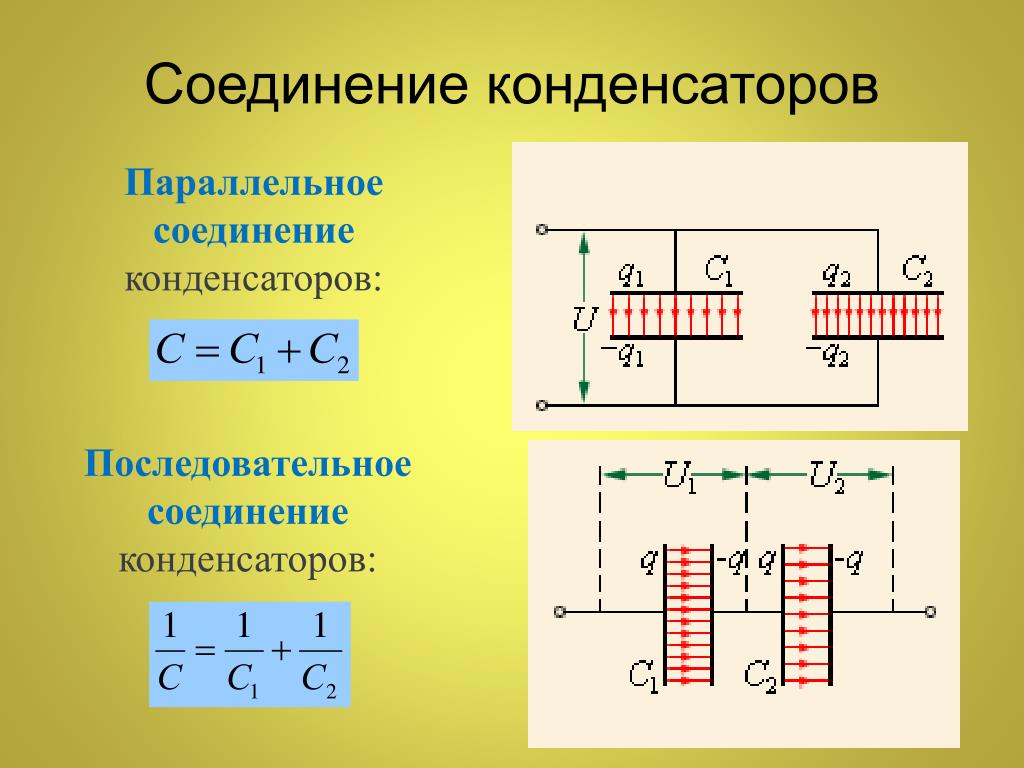 фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор.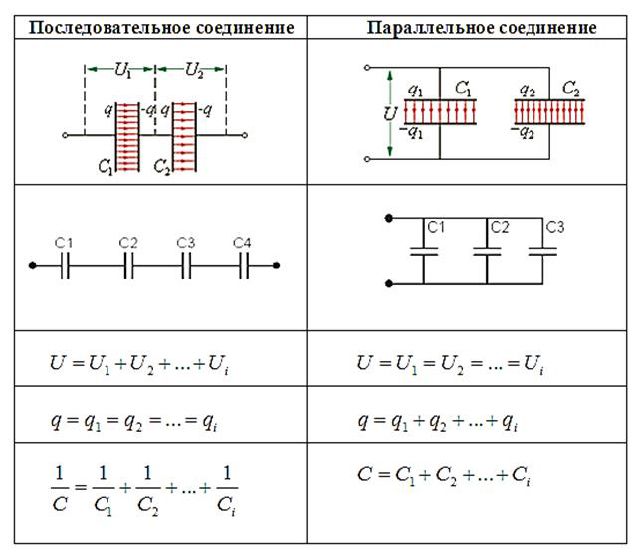 То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы , могут соединяться последовательно или параллельно.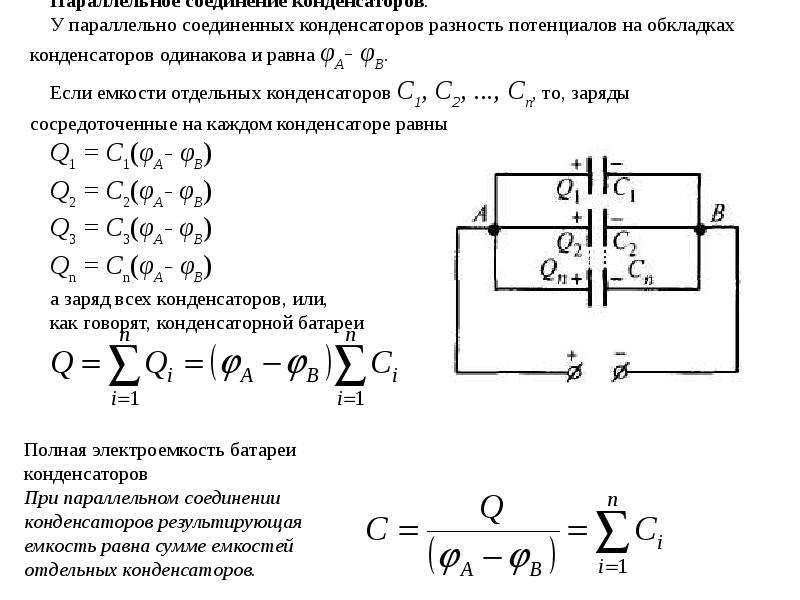 Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

Пример 1

Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С 1 = 10 мкФ, C 2 = 2 мкФ, C 3 = 5 мкФ, а C 4 = 1 мкФ?

При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2

Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С 1 = 7 мкФ, С 2 = 2 мкФ, С 3 = 1 мкФ.

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.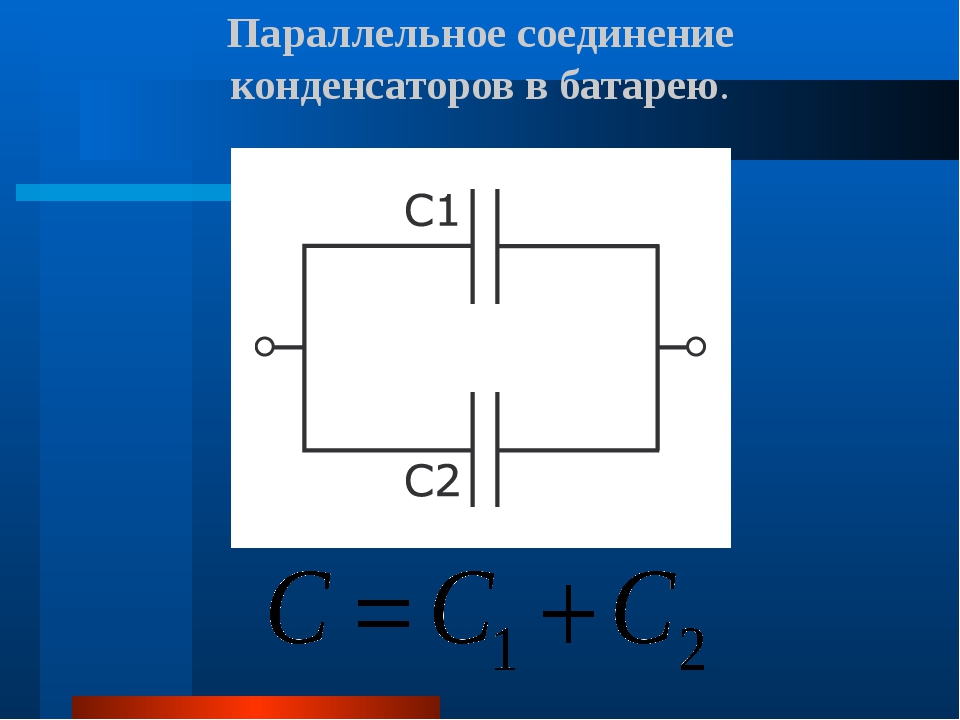

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Соединение конденсаторов Параллельное соединение конденсаторов

При параллельном соединении конденсаторов к каждому конденсатору приложено одинаковое напряжениеU, а величина заряда на обкладках каждого конденсатора Q пропорциональна его емкости (рис. 2).

Рис.2 U=U₁=U₂=U₃

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.

Q=Q₁=Q₂=Q₃

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

На практике может оказаться , что допустимое рабочее напряжение U_p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U_p. Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U_p.

Смешанное соединение конденсаторов

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

1.Схемы замещения элементов электрических цепей

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U=E=const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI_K, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg=1/r.

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U/r = E/r—I,

где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = I_K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I_K = Io + I, которому удовлетворяет эквивалентная схема рис. 3.14,а.

I=I_к=const.

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

3.6. Примеры решения задач к разделу 3

Пример 1.
Плоский конденсатор заряжен и отключен от источника. Определите силу притяжения пластин конденсатора.
Ответ: отключенный конденсатор — электрически замкнутая система (Q = const), поэтому , где .

Пример 2.
Вычислите силу взаимодействия обкладок сферического конденсатора, если он заполнен диэлектриком с проницаемостью = 6, а радиусы R₁ и R₂ равны соответственно 6 и 8 см. Конденсатор подключен к источнику с разностью потенциалов

Решение

Потенциальная энергия сферического конденсатора , подставляя выражение для емкости конденсатора получаем . Сила, действующая, например, на внешнюю обкладку составит

; F = 3 ·10^-3 Н.

Пример 3.
Цилиндрический конденсатор с радиусами обкладок соответственно R₁ = 10 и R₂ = 15 см, заполненный диэлектриком с проницаемостью = 4, подключен к источнику с разностью потенциалов = 3·10² В. Определите силу взаимодействия обкладок на единицу h = 1 м длины конденсатора.

Решение

Погонная энергия заряженного цилиндрического конденсатора есть

Сила взаимодействия обкладок ; F = 4,1 10^-4 Н / м.

Пример 4.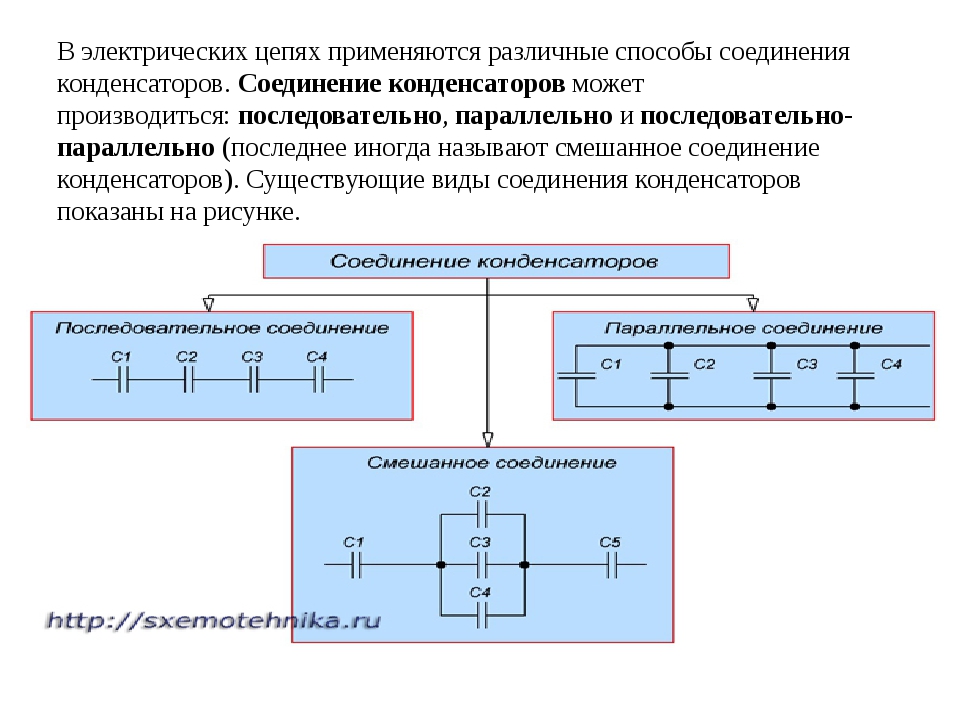
Потенциал наэлектризованного металлического шара и напряженность ЭСП на расстоянии а = 5 см от его поверхности составляют = 1,2·10⁴ В; Е = 6·10⁴ В / м. Определите энергию W шара.

Решение

Для определения энергии необходимо найти радиуса R шара и заряд Q на его поверхности. Находим их из известных соотношений: и . Тогда ; W = 4·10^-4 Дж.

Пример 5.
1) Сферическую тонкостенную оболочку радиуса R₁, равномерно заряженную по поверхности зарядом Q, расширили до радиуса R₂. Определите работу А₁₂, совершенную при расширении силами ЭСП.
Ответ: .
2) В центре сферической тонкостенной оболочки, по поверхности которой равномерно распределен заряд Q = 5 мкКл, расположен точечный заряд Q₀ = 1,5 мкКл. Определите работу сил ЭСП при расширении оболочки, т.е. при увеличении ее радиуса от R₁ = 50 мм до R₂ = 0,1 м.
Ответ: ; А₁₂ = 1,8 Дж.

Пример 6.
Система проводников состоит из двух концентрических тонкостенных металлических оболочек радиусов R₁ и R₂ и зарядами на оболочках соответственно Q₁ и Q₂. Определите полную энергию W системы.

Решение

Полная энергия системы двух сфер есть сумма их собственных энергий и потенциальной энергии взаимодействия , каждое из слагаемых есть:

; ; .
.

Пример 7.
1) У плоского конденсатора с площадью пластин S и расстоянием d между ними одна из пластин заземлена. Конденсатор заряжен и отключен от источника.

Определите энергию 2-ой обкладки в ЭСП первой.

Решение

Потенциал ЭСП, создаваемого 1-ой (заземленной) обкладкой в месте расположения элементарных зарядов на 2-ой обкладке, равен . Потенциальная энергия элементарных зарядов на 2-ой обкладке в ЭСП первой составит

2) Плоский конденсатор с пластинами площадью S = 0,02 м2 каждая и расстоянием между ними d = 0,5 см заполнен диэлектриком с = 4. Конденсатор заряжается до разности потенциалов = 0,1 кВ после чего отключается от источника. Какую работу необходимо затратить, чтобы удалить диэлектрик из конденсатора?

Решение

Энергия конденсатора с диэлектриком , после извлечения диэлектрика . Искомая работа есть

; А = 2·10^-8 Дж.

3) Пусть имеется плоский воздушный конденсатор с площадью обкладок S.

Какую работу А₁₂ против сил ЭСП надо совершить, чтобы медленно увеличить расстояние между обкладками от d₁ до d₂, если при этом поддерживать неизменными заряд Q на обкладках.

Решение

Работа внешних сил расходуется на изменение внутренней энергии конденсатора. Здесь существенно, что по условию Q = const, поэтому энергию удобно вычислять по формуле , тогда .

Пример 8.
1) Максимальная электроемкость конденсатора настройки в радиоэлектронном устройстве равна 100 пФ (1 пФ = 1·10^-12 Ф). Путем поворота подвижных пластин электроемкость конденсатора может быть уменьшена до 10 пФ. Предположим, что конденсатор подключен к источнику с разностью потенциалов = 0,3 кВ, когда его емкость максимальна. Затем ручка настройки поворачивается, и электроемкость конденсатора становится минимальной. Какая работа совершается при повороте ручки настройки?

Решение

Энергия заряженного конденсатора с электроемкостью С равна . Искомая работа (здесь внешней силы) равна разности энергий конденсатора после и до поворота ручки настройки, т. е. ; А = -4,1·10^-6 Дж.
2) Максимальная электроемкость плоского конденсатора переменной электроемкости С₁ = 400 пФ, минимальная — С₂ = 2 пФ. Изменение электроемкости в этих пределах достигается поворотом рукоятки ротора на 180⁰, при этом подвижные пластины остаются параллельными неподвижным. Момент сил трения в подшипниках ротора М = 5,00 10^-6 Н м. Какую работу надо совершить, чтобы изменить электроемкость конденсатора от максимальной до минимальной, если конденсатор подключен к источнику с разностью потенциалов = 100 В?
Ответ: ; А=13,8 10^-6 Дж.

Пример 9.
Пластины плоского многопластинчатого конденсатора площадью S = 20 см² каждая разделены слюдяным диэлектриком ( = 6) толщиной d = 5 10^-5 м. При разности потенциалов на конденсаторе = 0,33 кВ энергия ЭСП в нем W = 7,7·10^-4 Дж. Определите электроемкость конденсатора и число N пластин.
Ответ: ; С=3,21·10^-8 Ф; ; ; N = 17.

Пример 10.
Число удаленных друг от друга ртутных капелек N = 100, радиусом r = 1 мм каждая заряжены до одинакового потенциала = 9 В. Капельки соединяются в одну большую радиуса R. Определите изменение W электростатической составляющей энергии капель.

Решение

Заряд на каждой капельке , и энергия всех удаленных друг от друга капелек . После слияния капель в одну заряды и объемы складываются, поэтому и , откуда .

Энергия большой капли составит . Изменение энергии ; = 8,2·10^-9 Дж.

Пример 11.
1) Заряды на обкладках двух конденсаторов с электроемкостями С₁ и С₂ равны соответственно Q₁ и Q₂. Конденсаторы соединяют параллельно одноименными обкладками. Проанализируйте ситуацию и покажите, что при соединении конденсаторов энергия батареи уменьшается. Укажите на возможные «каналы» потери энергии. На основе полученного результата проанализируйте, возможна ли ситуация, при которой энергия не теряется.

Решение

Энергия конденсаторов до их соединения равна При параллельном соединении электроемкости конденсаторов складываются, поэтому энергия ЭСП батареи составит Изменение энергии при этом составит
Уменьшение энергии произошло за счет ее излучения во внешнее пространство и превращения во внутреннюю энергию соединительных проводов (при перераспределении зарядов).

Потери энергии не происходит, если Q₁C₂ = Q₂C₁. Иначе, это отвечает условию
2) Конденсатор с электроемкостью С₁ = 1 мкФ, заряженный до разности потенциалов = 0,3 кВ, подключили параллельно к незаряженному конденсатору электроемкостью С₂ = 2 мкФ. Вычислите изменение энергии системы конденсаторов после соединения их в батарею и установления в ней равновесия.

Решение

После соединения конденсаторов в батарею ее электроемкость увеличится до значения С = (С₁ + С₂), но заряд останется неизменным. Следовательно, изменение энергии составит
3) Два конденсатора с электроемкостями С₁ = 6 и С₂ = 4 мкФ соединены последовательно и вся батарея заряжена до разности потенциалов = 1·10⁴ В.

Затем конденсаторы отключаются от источника и соединяются в новую батарею параллельно одноименными обкладками. Определите изменение энергии батареи.

Решение

При последовательном соединении энергия . После параллельного соединения конденсаторов заряд на батарее , а ее электроемкость станет , поэтому энергия .
Изменение энергии:

; = — 5 Дж.

Пример 12.
Точечный заряд Q = 3,0 мкКл находится в центре сферического слоя из диэлектрика с проницаемостью = 3,0. Внутренний радиус R₁ cлоя составляет 0,25 см, внешний R₂ = 0,5 м. Вычислите энергию W ЭСП в таком слое.

Решение

В тонком сферическом слое толщиной dr и радиуса содержится энергия

Интегрируем далее это выражение по r в пределах от R₁ до R₂, получаем

; W = 27 мДж.

Пример 13.
Металлическому шару радиуса R₁ сообщен заряд Q. Шар окружен сферическим диэлектрическим слоем из материала с проницаемостью ; наружный радиус слоя R₂. Вся система находится в неограниченной однородной среде с проницаемостью . Определите энергию ЭСП заряженного шара. Определите энергетическую массу m ЭСП, заключенного в слое.

Решение

Разбиваем мысленно все пространство вокруг шара на сферические слои радиусов r, толщиной dr, объемом . Энергия ЭСП, заключенного в таком слое, составит , где есть объемная плотность энергии ЭСП.
Используя результаты исследования структуры напряженности E(r) такой системы и после интегрирования, получаем .
Для массы m ЭСП в слое согласно формуле Эйнштейна , имеем , где с₀ = 3,0·10⁸ м / с — скорость электромагнитных волн в вакууме.

Поучительны цифровые оценки: если Q = 2·10^-6 Кл, R₁ = 0,1 м, R₂ = 0,2 м, = 2, то m = 1·10^-18 кг. Это намного больше, чем массы покоящихся электрона, протона, и др.

Пример 14.
Вычислите энергию W_p ЭСП между двумя эквипотенциальными поверхностями на расстояниях R₁ = 5 и R₂ = 10 см от весьма тонкого металлического провода длиной h = 1 м, линейная плотность заряда которого = 5·10^-8 Кл / м.

Решение

Предполагаем здесь проводник достаточно длинным, поэтому краевыми эффектами пренебрегаем. В тонком воображаемом цилиндрическом слое радиуса r и толщиной dr, расположенном соосно с проводником, ЭСП обладает элементарной энергией . Интегрируя эти элементарные энергии в пределах от R₁ до R₂, получаем ; W_p = 1,6·10^-5 Дж.

Конденсатор / Хабр

Конденсатор имеет следующее схематическое изображение

Рассмотрим водопроводную модель конденсатора. Ранее мы говорили о том, что ток может течь только ~~в трубе, соединенной в кольцо~~ в замкнутой цепи. Но можно представить пустую емкость, в которую можно заливать воду, пока емкость не заполнится. Это и есть конденсатор — емкость, в которую можно заливать заряд.

Для большей аналогии лучше представить себе водонапорную башню, в модели — трубу бесконечной длины поставленную вертикально. Вода насосом закачивается в эту трубу с нижнего торца и поднимается на высоту. Чем больше воды закачали и чем выше она поднялась — тем сильнее столб воды давит на днище и выше там давление. Так-то в эту бесконечную трубу можно сколько угодно воды (электрического заряда) закачать, но при этом противодавление столба воды будет расти. Если качать заряд генератором напряжения, то когда противодавление сравняется с давлением (напряжением), создаваемым генератором — закачка остановится.

Если характеристикой резистора является сопротивление, то электрической характеристикой конденсатора является емкость.

С=Q/U

Емкость говорит, сколько заряда можно в конденсатор закачать, чтобы напряжение там поднялось до величины U. Можно сказать, что емкость характеризует диаметр трубы. Чем ýже труба, тем быстрее поднимается уровень воды при закачке и растет давление на дне трубы. Давление же зависит только от высоты водяного столба, а не от массы закачанной воды.

В электрических терминах, чем меньше емкость конденсатора, тем быстрее растет напряжение при закачке туда заряда.

Напомню, что электрический ток I равен количеству протекающего заряда Q в секунду. То есть I=Q/T, где T — время. Это все равно, что поток воды исчисляемый кубометрами в секунду. Или килограммами в сек, потом проверим по размерности).

Поэтому конденсатор с маленькой емкостью заполняется зарядом быстро, а с большой емкостью — медленно.

Рассмотрим теперь электрические цепи с конденсатором.

Пусть конденсатор подключен к генератору напряжения.

рис 9. Подключение конденсатора к генератору напряжения.

«Главный инженер повернул рубильник» S1 и.. тыдыщ!!! Что произошло?

Идеальный генератор напряжения имеет бесконечную мощность и может выдавать бесконечный ток. Когда замкнули рубильник в нашу емкость хлынуло бесконечное количество заряда в секунду и она мгновенно заполнилась и напряжение на ней выросло до U.

Теперь рассмотрим более реальную цепь.

Это Вторая Главная Цепь в жизни инженера-электронщика (после делителя напряжения) —
RC–цепочка.

RC–цепочка

RC -цепочки бывают интегрирующего и дифференцирующего типа.

RC–цепочка интегрирующего типа

рис 10. Подключение RC -цепочки интегрирующего типа к генератору напряжения.

Что произойдет в этой схеме, если замкнуть выключатель S1?

Конденсатор С исходно разряжен и напряжение на нем рано 0. Поэтому ток в первый момент будет равен I=U/R. Затем конденсатор начнет заряжаться, напряжение на нем увеличивается, и ток через резистор начнет уменьшаться. I=(U-Uc)/R. Этот процесс будет продолжаться, конденсатор будет заряжаться уменьшающимся током до напряжения источника U. Напряжение на конденсаторе при этом будет расти по экспоненте.

рис 11. График роста напряжения на конденсаторе при подаче напряжения величиной U (ступеньки).

Вопрос: А если запитать такую цепочку от генератора тока, как будет расти напряжение на конденсаторе?

Почему цепочка называется — «интегрирующего типа»?

Как выше было отмечено, ток в первый момент после подачи напряжение будет равен I=U/R, так как конденсатор разряжен, и напряжение на нем равно 0. И какое-то время, пока напряжение на конденсаторе Uc мало по сравнению с U, ток будет оставаться почти постоянным. А при заряде конденсатора постоянным током напряжение на нем растет линейно.

Uc=Q/C, а мы помним, что ток это количество заряда в секунду, то есть скорость протекания заряда. Другими словами, заряд это интеграл от тока.

Q = ∫ I * dt =∫ U/R * dt

то есть

Uc=1/RC * ∫ U * dt

Но все это близко к истине в начальный момент, пока напряжение на конденсаторе малó.

На самом деле все сводится к тому, что конденсатор заряжается постоянным током.
А постоянный ток выдает генератор тока. (См. вопрос выше)
Если источник напряжения выдает бесконечно большое напряжение и сопротивление R также имеет бесконечно большую величину, то по факту мы имеем уже идеальный генератор тока, и внешние цепи на величину этого тока влияния не оказывают.

RC–цепочка дифференцирующего типа

Ну тут все то же самое, что в интегрирующей цепочке, только наоборот.

рис 12. Дифференцирующая цепочка.

Более подробно свойства RC цепей хорошо освещены в интернете.

Параллельное и последовательное соединение конденсаторов

Так же как резисторы, конденсаторы можно соединять последовательно и параллельно.

При параллельном соединении емкости складываются — ну это и понятно, это как заполнять сообщающиеся сосуды, общий объем получается равным сумме объемов. При последовательном же соединении получится так, что конденсатор с маленькой емкостью заполнится зарядом быстрее, чем конденсатор с большой емкостью.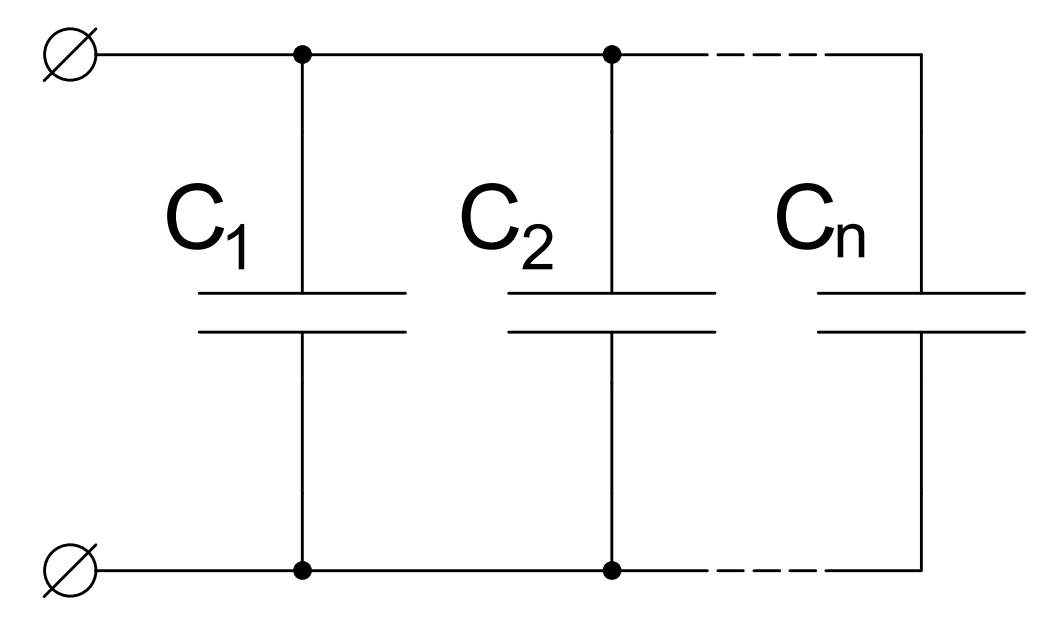 Напряжение на маленьком конденсаторе быстро вырастет почти до напряжения источника ( ну и остальные конденсаторы внесут свой вклад) , ток в общей цепи уменьшится до нуля, и процесс заряда конденсаторов прекратится. Таким образом емкость последовательно соединенных конденсаторов получается меньше емкости самого маленького из них.

Upd.
Рассмотрим более подробно процесс заряда конденсатора на схеме рис.10 (по мотивам учебника И.В.Савельева «Курс общей физики», том II. «Электричество» )
Как было сказано в предыдущей статье О природе электрического тока электрический ток — это движение заряженных частиц. В проводниках ( в отличие от диэлектриков-изоляторов) часть электронов является свободными и такие электроны могут перескакивать от одного атому к другому. В целом проводник электрически нейтрален — отрицательный заряд электронов компенсируется положительным зарядом ядер атомов. Чтобы заставить электроны двигаться нужно создать их избыток на одном конце проводника и недостаток на другом. Этот избыток электронов на одном полюсе создает батарейка вследствие протекающих в ней электрохимических реакций. Когда проводник присоединяется к полюсам батарейки электроны от полюса, где их избыток начинают двигаться к другому полюсу, потому что одноименные заряды отталкивают друг друга. Эти свободные электроны движутся внутри проводника по всему объему.
Движение электронов в RC цепи на рис. 3 имеет другой характер. Поскольку цепь не замкнута (обкладки конденсатора не соединены друг с другом) постоянный ток в цепи идти не может. Поэтому поступающий избыток электронов с полюса батарейки приводит к тому, что проводник теряет электрическую нейтральность. Избыточный заряд q, распределяется по поверхности проводника так, чтобы напряженность поля внутри проводника была равна нулю. Ну это понятно, одноименные заряды отталкиваются и стремятся расположиться подальше друг от друга, то есть на поверхности. Если бы не было резистора R, то перераспределение зарядов по поверхности происходило бы мгновенно. Однако резистор ограничивает ток ( движение зарядов) поэтому перераспределение происходит постепенно. По мере зарядки конденсатора напряжение на нем растет и ток через резистор уменьшается. Избыточные электроны концентрируются на одной обкладке и создают электрическое поле. Это поле отталкивает электроны, находящиеся на другой обкладке и «проталкивает» их дальше по проводнику к отрицательному полюсу батареи. (Знаки + и — в данном случае берем условно). Таким образом в незамкнутой цепи протекает ток заряда конденсатора. Этот ток не постоянный и уменьшается со временем. Однако, если в какой-то момент поменять полярность батареи, то ток потечет уже в обратную сторону. Если это переключение делать достаточно часто, так чтобы конденсатор не успевал полностью зарядиться, то в цепи все время будет течь ток, то в одну, то в другую сторону. Это и происходит, когда говорят, что «конденсатор проводит переменный ток».
Для плоского конденсатора емкость равна С=ε0*ε*S/d , где d – зазор между обкладками, ε – диэлектрическая проницаемость вещества, заполняющего зазор, S — площадь обкладок.
То есть на емкость влияет не только площадь обкладок и расстояние между ними, но и материал диэлектрика, который между обкладками помещен. Причем на емкость конденсатора материал диэлектрика может влиять достаточно сильно, с разными дополнительными эффектами, см. например статью «Поляризация диэлектрика»

Литература
«Драма идей в познании природы», Зельдович Я.Б., Хлопов М.Ю., 1988
«Курс общей физики», том II. «Электричество» И.В.Савельев
Википедия — статьи про электричество.

Как соединить электролитические конденсаторы для увеличения напряжения. Последовательное и параллельное соединение конденсаторов

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Смешанное соединение конденсаторов

В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии

Схема параллельного крепления

Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме.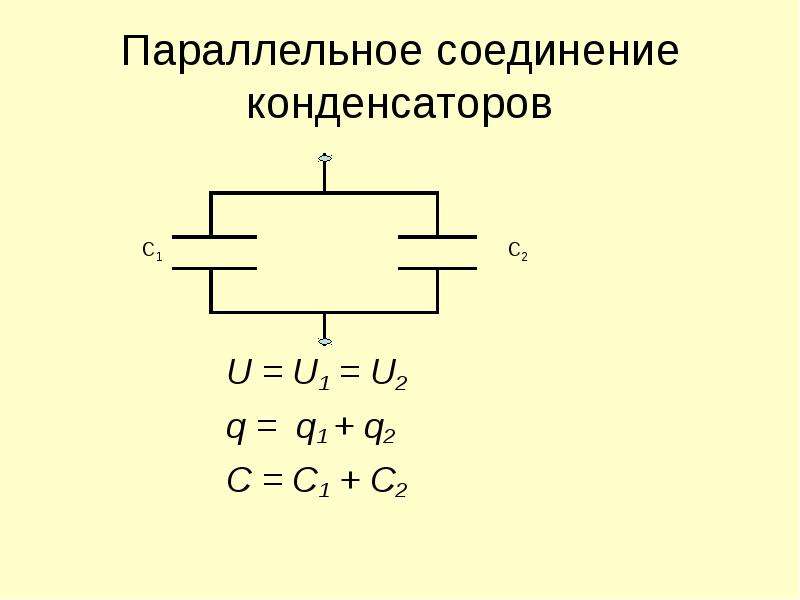 При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.

C общ = C 1 + C 2 + C 3

Схема – напряжение на накопителях

В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:

V AB = V C1 = V C2 = V C3 = 20 Вольт

Последовательное соединение

Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.

Схема – схема последовательного соединения

Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.

Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:

i = i c 1 = i c 2 = i c 3 = i c 4 , то есть токи проходящие через каждый конденсатор равны между собой.

Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:

Q общ = Q 1 = Q 2 = Q 3

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

1/C общ = 1/C 1 + 1/C 2 + 1/C 3

Видео: как соединять конденсаторы параллельным и последовательным методом

Смешанное подключение

Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Схема: смешанное соединение конденсаторов

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:

Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.

Содержание:

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке.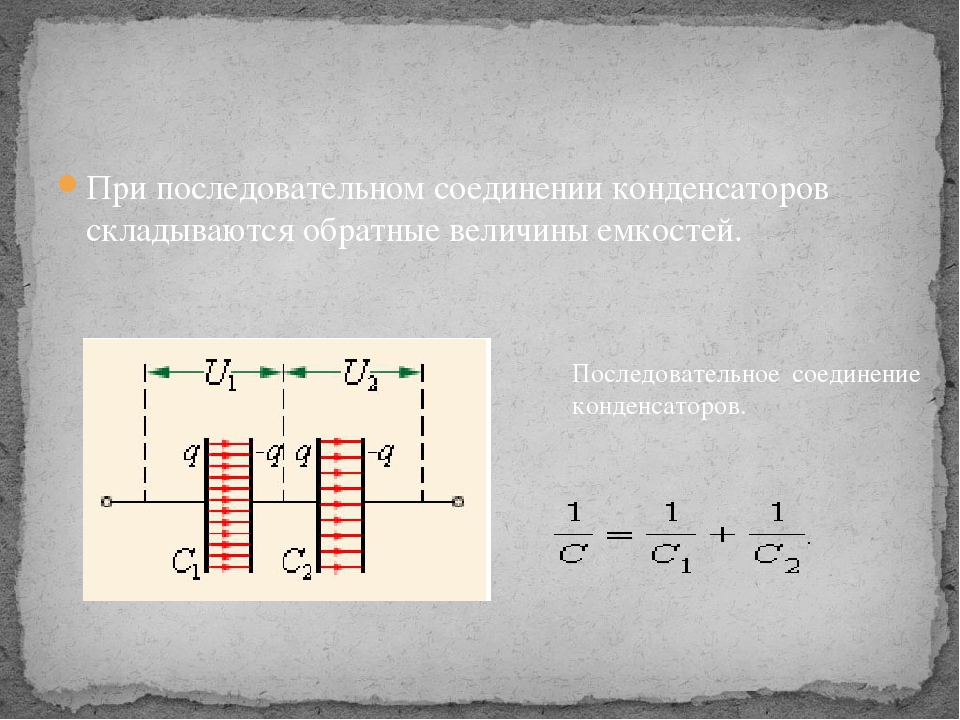 Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .

Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами.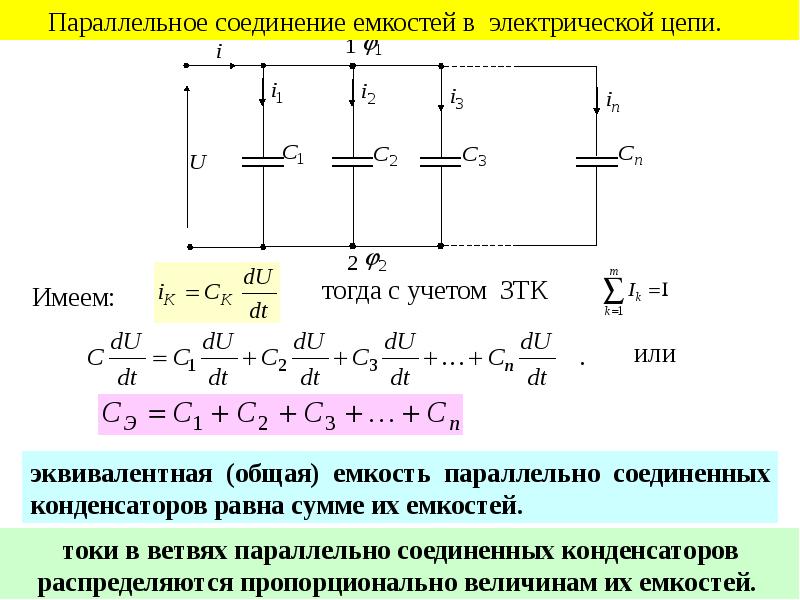 Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, С общ = С 1 + С 2 + С 3 .

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Последовательное соединение конденсаторов

Рис.3

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Смешанное соединение конденсаторов

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

1.Схемы замещения элементов электрических цепей

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой . Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно. Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов . Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства. Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.

Параллельное соединение конденсаторов — Мегаобучалка

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

q₁ + q₂ + q₃ + … +q_n = const.

Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности^[1]^[2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.

2)Закон Кулона

Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. Точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. Их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. Расположение зарядов в вакууме.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда

3) То́чечный заря́д — идеализация, вводимая для упрощения описания поля заряженного тела или системы тел. Иногда также определяется как электрически заряженная материальная точка.

Более простыми словами, точечный заряд — заряд, размерами носителя которого по сравнению с расстоянием, на котором рассматривается электростатическое взаимодействие, можно пренебречь.

Именно для точечных зарядов сформулирован закон Кулона

Для потенциалов относительно слабых электростатических полей выполняется принцип суперпозиции. Если электростатическое поле создаётся системой неподвижных электрических зарядов , ,…, и поле каждого заряда в отсутствие других зарядов описывается некоторым потенциалом, то потенциал суммарного поля всей системы зарядов есть сумма потенциалов полей всех зарядов системы по отдельности , где — потенциал заряда , , 2, …, . Если потенциал электростатического поля задан, то можно найти вектор напряжённости электростатического поля. Рассмотрим разность потенциалов в бесконечно близких точках пространства и . Согласно (3.10) или . В формулах (3.15) используются частные производные потенциала по координатам x, y и z точки наблюдения. Система точечных зарядов благодаря кулоновскому взаимодействию обладает потенциальной энергией. Эта энергия определяется той минимальной работой, которую необходимо совершить для создания рассматриваемой системы зарядов при условии, что в начальном состоянии заряды находились на бесконечном расстоянии друг от друга, где кулоновское взаимодействие между ними можно считать равным нулю. Рассмотрим сначала систему из двух точечных зарядов и , находящихся на расстоянии друг от друга в вакууме. Допустим, что заряд покоится в точке 1, а заряд под действием силы , где ,

4) Напряженность электростатического поля является векторной силовой характеристикой поля и численно равна силе, с которой поле действует на единичный пробный заряд, внесенный в данную точку поля:

Единицей напряженности является 1 Н/Кл — это напряженность такого электростатического поля, которое на заряд в 1 Кл действует с силой в 1 Н. Напряженность также выражают в В/м.

Для графического изображения электростатического поля используют линии напряженности вектора (силовые линии). Эти линии проводятся таким образом, чтобы касательные к ним в каждой точке поля совпадали с направлением вектора напряженности в этой точке.

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля.

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^{в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).}

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В Международной системе единиц (СИ) ёмкость измеряется в фарадах, в системе СГС — в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):

Конденсатор – это два проводника, называемые обкладками, расположенные близко друг к другу

.1. Емкость плоского конденсатора

Напряженность поля внутри конденсатора

2. Емкость цилиндрического конденсатора

Разность потенциалов между обкладками цилиндрического конденсатора, может быть рассчитана по формуле:

где λ – линейная плотность заряда,R₁ иR₂ – радиусы цилиндрических обкладок,l– длина конденсатора, .

Параллельное соединение конденсаторов

При параллельном соединении двух конденсаторов ёмкостями С₁ и С₂ напряжения на них одинаковы и равны U, а заряды q₁ и q₂ различны. Понятно, что общий заряд батареи равен сумме зарядов конденсаторов q = q₁ + q₂, а её ёмкость:

Параллельное включение конденсаторов калькулятор. Соединение конденсаторов параллельное соединение конденсаторов

Параллельное соединение конденсаторов – это батарея, в которой все конденсаторы находятся под одним и тем же напряжением, а суммарный ток равен полной алгебраической сумме токов этих элементов.

Основные тезисы

При параллельном включении конденсаторов их ёмкости складываются. Это позволяет быстро вычислить результат. Рабочее напряжение для всех конденсаторов одинаковое, а заряды из всех складываются воедино. Это следует из формулы, выведенной Вольтой ещё в XVIII веке:

C = q/U, тогда C1 + C2 + … = q1 + q2 + …/U.

Параллельное включение конденсаторов ведёт себя, как один конденсатор большой ёмкости.

Зачем нужно включать конденсаторы параллельно

В радиоприёмниках подстройка под частоту волны осуществляется коммутацией блоков конденсаторов. Этим осуществляется ввод резонансного контура в резонанс.
В фильтрах мощных блоков питания за каждый рабочий цикл нужно запасать много энергии. Строить его на индуктивностях экономически нецелесообразно. Поэтому применяют параллельный набор из больших электролитических конденсаторов.
Параллельное включение конденсаторов можно встретить в измерительных схемах. Где эталоны ответвляют на себя часть тока, и по этой величине оценивается номинал. То есть размер ёмкости исследуемого конденсатора.
Параллельно время от времени могут устанавливаться компенсаторы реактивной мощности. Это устройства, которые блокируют выход лишней энергии в питающую сеть. Что предотвращает образование помех, перегрузку генераторов, трансформаторов и избыточный нагрев проводки.

Реактивная мощность сети

Когда работает асинхронный двигатель, то происходит расхождение тока и напряжения по фазе. Это наблюдается вследствие наличия обмотки, которая имеет индуктивное сопротивление. Как результат, часть мощности отражается обратно в цепь. Этот эффект можно устранить, если индуктивное сопротивление компенсировать ёмкостным. Имеется и другой способ – использование синхронных двигателей. Он эффективен при напряжениях от 6 до 10 кВ.

По возможности предприятия должно потреблять всю произведённую им самим реактивную мощность. Но синхронные двигатели не всегда подходят условиям технологических процессов. Тогда и ставят конденсаторные установки. Их реактивное сопротивление должно быть равным индуктивностям двигателей. Конечно, в идеале, потому что на производстве условия постоянно меняются. В этом свете становится понятно, почему так сложно отыскать золотую середину.

Но если использовать параллельное соединение конденсаторов и коммутировать их при помощи реле должным образом, то задача достаточно просто решается. Сюда можно добавить, что некоторые предприятия за отражённую реактивную мощность тоже платят. И если её не использовать, то это будут чистой воды экономические потери. Поставщиков энергии тоже можно понять: реактивная мощность забивают линию ЛЭП, нагружает трансформаторы и тогда оборудование не может выдавать полную нагрузку. Если каждое предприятие станет загружать канал лишним током, то экономическое положение энергетиков немедленно пошатнётся.

В то же время реле реактивной мощности широко распространены и помогут определить, какую часть конденсаторов включить в работу. Пример графика расчёта затрат приведён на рисунке. Имеется некая оптимальная точка, перешагивать которую экономически нецелесообразно. Но можно это сделать из каких-либо иных мотивов.

Схема соединения компенсирующих установок

В трёхфазных сетях компенсирующие конденсаторы ставят тройками по двум общеизвестным схемам:

Звезда.
Треугольник.

Реактивная мощность в этих случаях вычисляется по формулам, представленным на рисунке. Через греческую омегу обозначена круговая частота сети (2 х Пи х 50 Гц). Из соотношений получается, что схема включения конденсаторов треугольником более выгодна: мощность выросла в 3 раза. Это происходит от того, что звезда использует фазное напряжение, а оно в 1,73 раза меньше линейного. Компенсируемая реактивная мощность же зависит от квадрата этого параметра.

Из этих соображений трёхфазные конденсаторы обычно всегда изготавливаются треугольником, а под звезду нужно выпросить индивидуальный заказ (фактически три однофазных конденсатора). Есть и другая сторона медали: на вольтаж 1,05; 3,15; 6,3; 10,5 кВ все конденсаторы однофазные. И можно соединять их так, как заблагорассудится. У звезды, например, меньше рабочее напряжение, а значит, и каждый конденсатор в отдельности выйдет дешевле. Ту и другую схему нельзя отнести к параллельным включениям, но такие тройки, в свою очередь, объединяются в:

группы;
секции;
установки.

И внутри объединений однофазные конденсаторы могут включаться последовательно и параллельно, а трёхфазные – только параллельно. При этом рекомендуется номиналы всех отдельных элементов выбирать одинаковы. Это не только упрощает расчёт, но и уравнивает нагрузку по всем частям электрической схемы. Имеются и установки, где присутствует смешанное соединение по каждой фазе. Образуются параллельные ветви .

Установки выполняют однофазными или трёхфазными. В сетях с напряжением 380 В практически всегда применяется параллельное соединение конденсаторов. Исключением является случай использования оборудования с одной фазой как на 220 В (фазное), так и 380 В (линейное). Тогда под прибор ставится индивидуальная установка (или группа), компенсирующая реактивную мощность. В осветительных сетях конденсаторы по большей части ставят уже после выключателя по очевидным причинам. В прочих случаях – в зависимости от особенностей функционирования объекта.

Для напряжений 3, 6 и 10 кВ однофазные конденсаторы могут включаться обычной или двойной звездой (см. рис.). Один вывод здесь может быть заземлены (глухозаземленная нейтраль). По этой причине и допускается использование однофазных конденсаторов, в том числе и одним изолированным выводом. В последнем случае нужно убедиться, что нулевой проводник выходит на корпус изделия.

Обычно главный выключатель ставится в той или иной секции защищаемого оборудования (территориально) и управляет цепью компенсации в общем. То есть задействует или убирает вовсе дополнительное реактивное сопротивление. Если в данном секторе технологическое оборудование простаивает, то и главный выключатель разорвёт цепь компенсации. Конденсаторные установки обычно стоят в выделенном помещении вместе, электрически соединены параллельно. Перед каждой из них стоит выключатель цепи релейной регуляции для повышения или уменьшения общей ёмкости компенсаторов.

Таким образом, в зависимости от того, какое именно оборудование используется предприятием, объем реактивной мощности обусловливает помощь тех или иных конденсаторных установок, гибко подстраиваемых под имеющиеся нужды. В итоге:

Секции оборудования включены параллельно. Это легко понять, если представить бытовые приборы, питаемые одним удлинителем. Все включены параллельно. Но находятся, например, в разных цехах, секторах и пр. Встречаются и случаи, когда одна крупная энергетическая установка (например, генератор ГЭС) делится на сравнительно независимые секции.
Конденсаторные установки также включены параллельно, но находятся, как правило, в одном месте. Это сделано для того, чтобы можно было автоматически или вручную легко регулировать общую ёмкость посредством коммутации выключателей облегчённого типа. Один и тот же конденсатор может работать для компенсации реактивной мощности любой из секций или сразу обеих.

Особенности конденсаторной защиты

Главные выключатели, как правило, используются при авариях и вырубают сразу целую секцию оборудования. Конденсаторные установки также могут набираться в секции параллельным их включением. Тогда главный выключатель может сразу вырубать одну такую «батарею». Тогда как другие секции конденсаторных установок останутся в действии. Важно понять, что защитное оборудование, как и защищаемое можно группировать самыми разными методами. В зависимости от того, как это удобно и экономически обосновано.

Облегчённые выключатели применяются, как правило, в цепях регуляции. Управляются через реле и повышают или понижают общую ёмкость конденсаторных установок. В качестве главного выключателя обычно выбирается вакуумный или элегазовый.

Особенностью цепей выше 10 кВ является использование однофазных конденсаторов, собираемых по схеме звезды или треугольника, в каждой ветви которых стоит параллельно-последовательная группа ёмкостей (см. рис.). При наличии изделий с высоким рабочим напряжением можно делать и наоборот. То есть применять последовательно-параллельно включение. Тогда рабочие напряжения конденсаторов выбираются так, чтобы количество групп, включенных друг за другом было минимальным. Напряжение на каждом из элементов при этом, естественно, увеличивается. Для справки: .

Если сделать все так, как описано выше, то при выходе из строя любого элемента цепи компенсации реактивной мощности прочие будут работать в относительно щадящем режиме. Разумеется, параметры цепи нужно контролировать, а эксплуатирующий персонал согласно имеющимся методикам ведёт проверку конденсаторных установок на исправность. При проектировании нужно учесть одну небольшую особенность:

Чем больше в цепи компенсации последовательных групп конденсаторов, тем сложнее для каждой из них будет обеспечить равномерное распределение напряжения. В частности, возможны частые перегрузки того или иного сегмента.

Вдобавок ко всему сложные электрические соединения непросто проверять обслуживающему персоналу. Витиеватая схема плохо поддаётся монтажу, часты ошибки. Идеальным является параллельное соединение конденсаторных блоков по каждой фазе. Тогда и монтировать легко, и методика проверки упрощается максимально.

Разряд конденсаторов

Включенные параллельно конденсаторы обладают большой ёмкостью, вследствие чего при прекращении работы на них остаётся заряд. Это можно прочувствовать на себе, если коснуться штекера только что выключенной старенькой дрели. В новых моделях фильтр устроен так, что цепь разряжается через резистор, и ничего подобного, описанному выше, не наблюдается.

Для снижения напряжения можно также использовать и индуктивности, включенные параллельно конденсаторам. В этом случае сопротивление заземления переменному току весьма велико, а для постоянного — не сложно преодолеть этот участок. То есть, в период работы оборудования ток здесь весьма мал, и потери невелики. После останова технологической линии заряд понемногу сливается через высокоомный резистор или индуктивность. Разумеется, никто не запрещает поставить в цепи заземления реле, замыкающее контакты только после выключения всех устройств. Но это дороже и требует автоматизации.

Процесс разряда цепи важен с точки зрения обеспечения безопасности. Можно представить это так: конденсатор, заряжённый от розетки, ещё долго хранит разность потенциалов и представляет определённую опасность для окружающих. В однофазных сетях с напряжением 220 В разряд выполняется через входные фильтры при условии, что корпус правильно заземлён. Сопротивление в цепи, включенной параллельно конденсаторам, определяется по формуле, представленной ниже.

Под Q подразумевается реактивная мощность установки в варах (ВАР), а Uф – фазное напряжение. Можно легко показать, что формула дана из расчёта времени разряда. В самом деле: Q зависит линейно от ёмкости, будучи перенесена в левую часть формулы, она даст постоянную времени RC. За три таких периода батарея разряжается примерно на 97%. Исходя, из этих условий можно найти и параметры индуктивности. А ещё лучше – последовательно с нею включить резистор, как часто и делается в реальных схемах.

Для получения большего спектра емкостей конденсаторы часто соединяют между собой, получают, так называемые батареи конденсаторов. Соединение при этом может быть параллельным, последовательным или комбинированным (смешанным). Рассмотрим случай с двумя конденсаторами.

Последовательное соединение конденсаторов показано на рис. 1

Здесь (рис.1) обкладка одного конденсатора, имеющая отрицательный заряд соединяется с положительной обкладкой следующего конденсатора. При последовательном соединении средние пластины конденсаторов электризуются через влияние, следовательно, их заряды по величине равны и противоположны по знаку. Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:

При этом имеем:

Получаем, что при последовательном соединении конденсаторов емкость соединения находят как:

Обобщив формулу (3) для N конденсаторов, получаем:

где — электрическая емкость i-го конденсатора.

Последовательное соединение конденсаторов используют тогда, когда для избегания пробоя конденсатора необходимо разность потенциалов распределить между несколькими конденсаторами.

Последовательное соединение конденсаторов показано на рис. 2

При параллельном соединении разности потенциалов между обкладками конденсаторов одинаковы. Суммарный заряд системы равен сумме зарядов на каждом из конденсаторов:

Из сказанного выше получим:

Для батареи из N параллельно соединенных конденсаторов имеем:

Параллельное соединение конденсаторов используют тогда, когда необходимо увеличить емкость конденсатора.

Примеры решения задач

ПРИМЕР 1

Задание

Получите формулу для расчета емкости слоистого конденсатора.

Решение

Конденсатор, который называют слоистым, состоит из двух параллельных металлических обкладок, разделенных несколькими плоскими слоями разных диэлектриков (рис.3). Обозначим диэлектрические проницаемости слоев диэлектриков как . Будем считать, что соответствующая толщина слоя диэлектрика при этом: .

Допустим, что между слоями диэлектриков вставлены очень тонкие листы из проводника. От такой процедуры заряды на обкладках конденсатора и напряженности полей в солях диэлектриков останутся неизменными. Останутся без изменений разности потенциалов между обкладками, следовательно, не изменится емкость конденсатора. Но, наличие тонких листов проводника превратит слоистый конденсатор в последовательное соединение конденсаторов.

Применим формулы емкости плоского конденсатора:

и расчета емкости батареи последовательно соединенных конденсаторов:

получаем:

Ответ

ПРИМЕР 2

Задание	Какой будет емкость соединения конденсаторов (рис.4), если батарея составлена из одинаковых конденсаторов, емкость каждого из них равна Ф.
Решение	Емкость параллельного соединения конденсаторов обозначим как Она равна:

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Последовательное соединение конденсаторов

Рис.3

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Смешанное соединение конденсаторов

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

1.Схемы замещения элементов электрических цепей

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r — I ,

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

конденсаторов последовательно и параллельно

конденсаторов последовательно и параллельно
Далее: Энергия в конденсаторах Up: Емкость Предыдущая: Диэлектрики Конденсаторы — один из стандартных компонентов электронных схем. Кроме того, часто встречаются сложные комбинации конденсаторов. в практических схемах. Это, поэтому полезно иметь набор правил для определения эквивалентной емкости некоторого общего расположения конденсаторов.Оказывается, всегда можно найти эквивалентная емкость при повторном применение двух простых правил . Эти правила относятся к подключенным конденсаторам. последовательно и параллельно.

**Рисунок 15:** *Два конденсатора подключены параллельно.*

Рассмотрим два конденсатора, подключенных параллельно : , т. Е. , с положительно заряженные пластины подключены к общему « входному » проводу, а отрицательно заряженные пластины присоединены к общему « выходному » проводу — см. рис.15. Какая эквивалентная емкость? между входным и выходным проводами? В этом случае потенциал разница между двумя конденсаторами одинакова и равна разность потенциалов между входным и выходным проводами. Общий заряд однако, хранящиеся в двух конденсаторах делятся между конденсаторы, так как он должен распределяться так, чтобы напряжение на два то же самое. Поскольку конденсаторы могут иметь разную емкость, и, и сборы тоже могут быть разными.Эквивалентная емкость пары конденсаторов — это просто соотношение, где — общий накопленный заряд. Это следует из того

(113)

давая

(114)

Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех конденсаторы. Таким образом, правило таково:

Эквивалентная емкость двух конденсаторов, соединенных параллельно представляет собой сумму отдельных емкостей.

Для конденсаторов, соединенных параллельно, уравнение. (114) обобщает на .

**Рисунок 16:** *Два конденсатора, соединенных последовательно.*

Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что положительная пластина одного прикреплена к отрицательной пластине другого — см. Рис.16. Фактически, предположим, что положительная обкладка конденсатора 1 подключена к проводу « вход » отрицательная обкладка конденсатора 1 подключается к положительная пластина конденсатора 2 и отрицательная пластина конденсатора 2 подключается к проводу « выход ».Какая эквивалентная емкость между входными и выходными проводами? В этом случае важно понимать, что заряд, хранящийся в два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть « внутренние » пластины: , т.е. , отрицательная пластина конденсатора 1 и положительная пластина конденсатора 2. Эти пластины физически отключены. от остальной части схемы, поэтому общий заряд на них должен Остаются неизменными. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд когда к двум конденсаторам приложена нулевая разность потенциалов, следует что при наличии ненулевой разности потенциалов заряд на положительном пластина конденсатора 2 должна быть сбалансирована равным и противоположным зарядом на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина Конденсатор 1 несет заряд, положительная пластина должна нести заряд. Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд, отрицательная пластина должна нести заряд. В итоге оба конденсатора обладают таким же накопленным зарядом. Потенциал падает, и два конденсатора, как правило, разные. Однако сумма этих падение равняется общему падению потенциала, приложенному на входе и выходе провода: т.е. ,. Эквивалентная емкость пары конденсаторы снова .Таким образом,

(115)

давая

(116)

Здесь мы воспользовались тем фактом, что заряд является общим для всех трех конденсаторы. Следовательно, правило таково:

Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в серия — это сумма обратных величин отдельных емкостей.

Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на

Далее: Энергия в конденсаторах Up: Емкость Предыдущая: Диэлектрики

Ричард Фицпатрик 2007-07-14

Конденсатор

Игра с конденсатором

Возьмите конденсатор с параллельными пластинами и подключите его к источнику питания. Блок питания устанавливает разность потенциалов между пластинами конденсатора.

Расстояние между пластинами конденсатора можно изменять.Пока конденсатор все еще подключен к источнику питания, расстояние между пластинами увеличивается. Когда это происходит, что происходит с Q, C и ΔV?

Разность потенциалов на конденсаторе:

увеличений
убавляется
остается прежним

Емкость:

увеличений
убавляется
остается прежним

Заряд на конденсаторе:

увеличений
убавляется
остается прежним

Поскольку конденсатор все еще подключен к источнику питания, разность потенциалов не может измениться.Дальнейшее раздвижение пластин уменьшает емкость, а также снижает заряд, накопленный конденсатором.

Теперь конденсатор заряжается от источника питания, а затем соединения с источником питания отключены. Когда расстояние между пластинами теперь увеличивается, что происходит с Q, C и ΔV?

Разность потенциалов на конденсаторе:

увеличений
убавляется
остается прежним

Емкость:

увеличений
убавляется
остается прежним

Заряд на конденсаторе:

увеличений
убавляется
остается прежним

В этом случае заряд остается постоянным, потому что ему некуда деваться.Емкость все еще уменьшается, а разность потенциалов увеличивается, потому что
ΔV = Q / C

Другой аргумент в пользу увеличения разности потенциалов заключается в том, что разность потенциалов — это поле, умноженное на расстояние между пластинами. Если заряд постоянен, поле постоянно, поэтому увеличение расстояния между пластинами увеличивает ΔV.

Практические задачи: решения емкости — Physics-prep.com

Практические проблемы: Конденсаторные решения

1.(легко) Определите количество заряда, накопленного на любой пластине конденсатора (4×10 ^-6 F) при подключении к 12-вольтовой батарее.
C = Q / V
4×10 ^-6 = Q / 12
Q = 48×10 ^-6 C

2. (легко) Если расстояние между пластинами конденсатора составляет 2,0×10 ^-3 м, определите площадь пластин, если емкость равна точно 1 F.
C = ε _o A / d
1 = ( 8,85×10 ^-12) A / (2,0×10 ^-3)
A = 2,3×10 ⁸ м ²

3.(умеренное) Рассчитайте напряжение батареи, подключенной к конденсатору с параллельными пластинами с площадью пластин 2,0 см ² и расстоянием между пластинами 2 мм, если заряд, накопленный на пластинах, составляет 4,0 пКл.
Площадь = 2,0 см ² (1 м / 100 см) ² = 2,0×10 ^-4 м ²
C = ε _o A / d
C = (8,85×10 ^-12) ( 2,0×10 ^-4) / (2,0×10 ^-3)
C = 8,85×10 ^-13
C = Q / V
8,85×10 ^-13 = 4.0×10 ^-12 / В
В = 4,5 В

4. (простой) Конденсатор с параллельными пластинами состоит из металлических пластин, каждая площадью 0,2 м ². Емкость 7,9 нФ. Определите расстояние между пластинами.
C = ε _o A / d
7,9×10 ^-9 = 8,85×10 ^-12 (0,2) / d
d = 2,2×10 ^-4 м = 0,22 мм

5. (легко) Конденсатор (параллельная пластина) заряжается от батареи постоянного напряжения. Как только конденсатор достигает максимального заряда, аккумулятор удаляется из цепи.Опишите любые изменения, которые могут произойти в перечисленных здесь количествах, если пластины будут сдвинуты ближе друг к другу.
а. Заряд (Заряд, отложившийся на пластинах, не меняется, когда аккумулятор извлекается, и, таким образом, заряд и плотность заряда остаются такими же, когда пластины перемещаются ближе друг к другу.)
b. Емкость (Поскольку емкость составляет C = ε _— А / день, а площадь не меняется, любое уменьшение расстояния между пластинами (d) приведет к увеличению емкости.)
c.Напряжение (поскольку C = Q / V и заряд не меняется, увеличение емкости означает уменьшение напряжения.)
d. E-поле (Поскольку ΔV = -Ed, E-поле останется таким же, как и напряжение, и расстояние уменьшатся пропорционально.)

6. (умеренно) Чипы оперативной памяти используются в компьютерах для хранения двоичной информации в виде «единиц» и «нулей». Один из распространенных способов сохранить «единицу» — зарядить очень маленький конденсатор. Конечно же, тот же конденсатор без заряда представляет собой «ноль».Микросхема памяти содержит миллионы таких конденсаторов, каждый из которых соединен с транзистором (который действует как переключатель), образуя «ячейку памяти». Типичный конденсатор в ячейке памяти может иметь емкость 3×10 ^-14 F. Если напряжение на конденсаторе, показывающее «единицу», составляет 0,5 В, определите количество электронов, которые должны двигаться по конденсатору, чтобы зарядить его.
C = Q / V
3×10 ^-14 = Q / (0,5)
Q = 1,5×10 ^-14 C
# электроны = Полный заряд / заряд на один электрон
# электронов = 1.5×10 ^-14 / 1,6×10 ^-19
#electrons = 93750 электронов

7. (легко) C ₁ = 10 F и C ₂ = 5 F. Определите эффективную емкость для C ₁ и C ₂, соединенных последовательно и параллельно.
Последовательно:
1 / C = 1 / C ₁ + 1 / C ₂
1 / C = 1/10 + 1/5
C = 3,3 F
Параллельно:
C = C ₁ + C ₂
C = 10 + 5 = 15 F

8. (умеренно) Если два рассматриваемых конденсатора №7 были подключены к 50-вольтовой батарее, определите напряжение на конденсаторах для каждого типа подключения.
Для последовательного соединения:
Заряд каждого конденсатора равен заряду эффективной емкости.
C = Q / V
3,3 = Q / 50
Q = 165 C
Для конденсатора 10F:
10 = 165 / V
V = 17 В
Для конденсатора 5 F:
5 = 165 / V
V = 33 В
Для параллельного подключения:
Напряжение на каждом конденсаторе одинаковое (50 В).

9. (средний) Оцените схему, показанную ниже, чтобы определить эффективную емкость, а затем заряд и напряжение на каждом конденсаторе.

Эквивалентная емкость 4 мкФ. Напряжение на эквивалентном конденсаторе составляет 20 вольт.
Это напряжение также присутствует на обоих конденсаторах по 2 мкФ, которые были созданы последовательными комбинациями в каждой ветви.
Найдите заряд на каждом конденсаторе 2 мкФ:
C = Q / V
2 мкФ = Q / 20
Q = 40 мкК
Конденсаторы 4 мкФ в каждой ветви имеют такой же заряд, как и конденсаторы 2 мкФ. Используйте это, чтобы найти напряжение на каждом из них:
C = Q / V
4 мкФ = 40 мкКл / В
V = 10 вольт
Таким образом, каждый из исходных конденсаторов 4 мкФ имеет заряд 40 мкКл и напряжение 10 вольт.

10. (средний) Оцените схему, показанную ниже, чтобы определить эффективную емкость, а затем заряд и напряжение на каждом конденсаторе.

Эффективная емкость составляет 6 мкФ при напряжении 100 В.
Напряжение на конденсаторах 4 мкФ и 2 мкФ также равно 100 В.
Заряд на конденсаторе 4 мкФ:
C = Q / V
4 мкФ = Q / 100
Q = 400 мкКл
Заряд конденсатора 2 мкФ:
C = Q / V
2 мкФ = Q / 100
Q = 200 мкКл
Все три конденсатора по 6 мкФ также имеют заряд 200 мкКл.
Найдите напряжение для конденсаторов 6 мкФ:
C = Q / V
6 мкФ = 200 мкКл / В
V = 33,3 В

11. (умеренное) Оцените схему, показанную ниже, чтобы определить эффективную емкость, а затем заряд и напряжение на каждом конденсаторе.

Эквивалентная емкость 6 мкФ. Напряжение на эквивалентной емкости равно 40 В, как и напряжение на конденсаторах 3 мкФ, и такое же, как на конденсаторах 1 мкФ и 2 мкФ.
Найдите заряд конденсатора 1 мкФ:
C = Q / V
1 мкФ = Q / 40
Q = 40 мкК
Найдите заряд конденсатора 2 мкФ:
C = Q / V
2 мкФ = Q / 40
Q = 80 мкКл
Найдите заряд конденсаторов 3 мкФ:
C = Q / V
3 мкФ = Q / 40
Q = 120 мкКл
Это одинаковый заряд на каждом из конденсаторов 6 мкФ.
Найдите напряжение на каждом из конденсаторов 6 мкФ:
C = Q / V
6 мкФ = 120 мкКл / В
V = 20 В

8,2 Последовательные и параллельные конденсаторы — University Physics Volume 2

Learning Objectives

К концу этого раздела вы сможете:

Объясните, как определить эквивалентную емкость конденсаторов, соединенных последовательно и параллельно
Вычислить разность потенциалов на пластинах и заряд на пластинах конденсатора в сети и определить полезную емкость сети конденсаторов

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

Рисунок 8.11 иллюстрирует последовательную комбинацию трех конденсаторов, расположенных в ряд внутри схемы. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 8.1. Когда эта последовательная комбинация подключена к батарее с напряжением В, , каждый из конденсаторов получает идентичный заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен + Q + Q, а заряд на пластине, подключенной к отрицательной клемме, равен −Q − Q.Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1 = Q / C1V1 = Q / C1 на одном конденсаторе может отличаться от падения потенциала V2 = Q / C2V2 = Q / C2 на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как -Q-Q), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как + Q), + Q) и так далее.

Рисунок 8.11 (a) Три конденсатора подключены последовательно.Величина заряда на каждой пластине — Q . (b) Сеть конденсаторов в (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (a), а заряд на его пластинах составляет Q .

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, V1 = Q / C1V1 = Q / C1, V2 = Q / C2V2 = Q / C2 и V3 = Q / C3V3 = Q / C3.Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:

Потенциал В измеряется на эквивалентном конденсаторе, который держит заряд Q и имеет эквивалентную емкость CSCS. Вводя выражения для V1V1, V2V2 и V3V3, получаем

QCS = QC1 + QC2 + QC3. QCS = QC1 + QC2 + QC3.

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость, CSCS, трех последовательно соединенных конденсаторов:

1CS = 1C1 + 1C2 + 1C3.1CS = 1C1 + 1C2 + 1C3.

Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, является суммой обратных величин индивидуальных емкостей:

1CS = 1C1 + 1C2 + 1C3 + ⋯. 1CS = 1C1 + 1C2 + 1C3 + ⋯.

8,7

Пример 8.4

Эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000 мкФ, 1.000 мкФ, 5.000 мкФ, 5.000 мкФ и 8.000 мкФ, 8.000 мкФ.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.7 с тремя членами.

Решение

Мы вводим данные емкости в уравнение 8.7: 1CS = 1C1 + 1C2 + 1C3 = 11,000 мкФ + 15,000 мкФ + 18,000 мкФ 1CS = 1,325 мкФ 1CS = 1C1 + 1C2 + 1C3 = 11,000 мкФ + 15,000 мкФ + 18,000 мкФ 1CS = 1,325 мкФ.

Теперь мы инвертируем этот результат и получаем CS = μF1,325 = 0,755 мкФ, CS = μF1,325 = 0,755 мкФ.

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, проиллюстрирована на рисунке 8.12 (a). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:

В левой части этого уравнения мы используем соотношение Q = CPVQ = CPV, которое выполняется для всей сети.В правой части уравнения мы используем соотношения Q1 = C1V, Q2 = C2V, Q1 = C1V, Q2 = C2V и Q3 = C3VQ3 = C3V для трех конденсаторов в сети. Таким образом получаем

CPV = C1V + C2V + C3V. CPV = C1V + C2V + C3V.

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

CP = C1 + C2 + C3 + ⋯.CP = C1 + C2 + C3 + ⋯.

8,8

Рисунок 8.12 (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример 8.5

Эквивалентная емкость параллельной сети

Найдите чистую емкость для трех конденсаторов, соединенных параллельно, учитывая, что их отдельные емкости составляют 1,0 мкФ, 5,0 мкФ и 8,0 мкФ. 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.8 с тремя членами.

Решение

Ввод заданных емкостей в уравнение 8.8 дает CP = C1 + C2 + C3 = 1,0 мкФ + 5,0 мкФ + 8,0 мкФ CP = 14,0 мкФ. CP = C1 + C2 + C3 = 1,0 мкФ + 5,0 мкФ + 8,0 мкFCP = 14,0 мкФ.

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке 8.13. Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок 8.13 (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) C1C1 и C2C2 включены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно с C3.C3. Таким образом, эквивалентная емкость всей сети является суммой CSCS и C3.C3.

Пример 8.6

Эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 8.13. Предположим, что емкости известны с точностью до трех десятичных знаков (C1 = 1.000 мкФ, C2 = 5.000 мкФ, (C1 = 1.000 мкФ, C2 = 5.000 мкФ, C3 = 8.000 мкФ). C3 = 8.000 мкФ). Округлите ответ до трех десятичных знаков.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы C1C1 и C2C2 включены последовательно. Их комбинация, обозначенная CS, CS, параллельна C3.C3.

Решение

Поскольку C1 и C2C1 и C2 включены последовательно, их эквивалентная емкость CSCS получается с помощью уравнения 8.7: 1CS = 1C1 + 1C2 = 11.000 мкФ + 15 000 мкФ = 1 200 мкФ⇒ CS = 0,833 мкФ. 1 CS = 1C1 + 1C2 = 11 000 мкФ + 15 000 мкФ = 1 200 мкФ⇒ CS = 0,833 мкФ. Емкость

CSCS подключается параллельно третьей емкости C3C3, поэтому мы используем уравнение 8.8, чтобы найти эквивалентную емкость C всей сети:

C = CS + C3 = 0,833 мкФ + 8,000 мкФ = 8,833 мкФ. C = CS + C3 = 0,833 мкФ + 8,000 мкФ = 8,833 мкФ.

Пример 8.7

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке 8.14, когда емкости C1 = 12.0 мкФ, C2 = 2,0 мкФ, C1 = 12,0 мкФ, C2 = 2,0 мкФ и C3 = 4,0 мкФ FC3 = 4,0 мкФ. Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок 8.14 (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.

Стратегия

Сначала мы вычисляем чистую емкость C23C23 параллельного соединения C2C2 и C3C3. Тогда C, — это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C = Q / VC = Q / V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.

Решение

Эквивалентная емкость для C2C2 и C3C3 равна C23 = C2 + C3 = 2,0 мкФ + 4,0 мкФ = 6,0 мкФ. C23 = C2 + C3 = 2,0 мкФ + 4,0 мкФ = 6,0 мкФ.

Вся комбинация из трех конденсаторов эквивалентна двум последовательным конденсаторам,

1C = 112,0 мкФ + 16,0 мкФ = 14,0 мкФ⇒C = 4,0 мкФ. 1C = 112,0 мкФ + 16,0 мкФ = 14,0 мкФ⇒C = 4,0 мкФ.

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 8.14 (b). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, Q1 = Q23Q1 = Q23. Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому

12.0 В = V1 + V23 = Q1C1 + Q23C23 = Q112.0 мкФ + Q16.0 мкФ⇒Q1 = 48.0 мкКл. 12.0 В = V1 + V23 = Q1C1 + Q23C23 = Q112.0 мкФ + Q16.0 мкФ⇒Q1 = 48.0 мкКл.

Теперь разность потенциалов на конденсаторе 1 равна

. V1 = Q1C1 = 48,0 мкКл 12,0 мкФ = 4,0 В. V1 = Q1C1 = 48,0 мкКл 12,0 мкФ = 4,0 В.

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

V2 = V3 = 12,0 В-4,0 В = 8,0 В. V2 = V3 = 12,0 В-4,0 В = 8,0 В.

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

Q2 = C2V2 = (2,0 мкФ) (8,0 В) = 16,0 мкКл, Q3 = C3V3 = (4,0 мкФ) (8,0 В) = 32.0 мкКл. Q2 = C2V2 = (2,0 мкФ) (8,0 В) = 16,0 мкКл, Q3 = C3V3 = (4,0 мкФ) (8,0 В) = 32,0 мкКл.

Значение

Как и ожидалось, чистый заряд параллельной комбинации C2C2 и C3C3 составляет Q23 = Q2 + Q3 = 48,0 мкКл. Q23 = Q2 + Q3 = 48,0 мкКл.

Проверьте свое понимание 8.5

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что C1 = 1.0pFC1 = 1.0pF, C2 = 2.0pFC2 = 2.0pF, C3 = 4.0pFC3 = 4.0pF и C4 = 5.0pFC4 = 5.0pF. Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Конденсаторы — несколько конденсаторов

< >

Как следует подключить нескольких конденсаторов ? Что происходит с общей емкостью в серийный и параллельных контура? Как можно увеличить всего номинальное напряжение ? Будет ли серийный или параллельный магазин больше общей энергии ?

Параллельные конденсаторы

Параллельно подключенные конденсаторы добавят к их . емкость вместе.

C _всего = C ₁ + C ₂ + … + C _n

Параллельная цепь — самый удобный способ увеличить общее хранилище электрический заряд.

Общее напряжение рейтинг не меняется. Каждый конденсатор будет «видеть» одно и то же напряжение. Они все должно быть рассчитано, по крайней мере, на напряжение вашего источника питания. И наоборот, вы не должны прикладывать больше напряжения, чем наименьшее значение напряжения среди параллельных конденсаторов.

Конденсаторы серии

Конденсаторы, соединенные последовательно, будут иметь нижних общая емкость, чем любая отдельная в цепи.

Если у вас есть только два конденсатора последовательно, это уравнение можно упростить до:

Если у вас есть два одинаковых конденсатора , соединенных последовательно, это дополнительно упрощается до:

Эта последовательная схема предлагает более высокий общий уровень напряжения.Падение напряжения на каждом конденсаторе складывается из общее приложенное напряжение.

Осторожно: Если конденсаторы разные, напряжение разделится так, что конденсаторы меньшего размера подбросьте больше напряжения! Это потому, что все они получают тот же зарядный ток, а напряжение обратно пропорционально пропорционально емкости.

Еще хуже , если один конденсатор немного негерметичен, он будет постепенно передавать свое напряжение другим, возможно превышение их номинального напряжения в свою очередь.И если один из них пробивает диэлектрический барьер и может повредить другие каскадно. Вот почему конденсаторы серии обычно избегают в силовых цепях.

Сеть резисторов для последовательных конденсаторов

Но серийная сеть просто слишком привлекательна, когда у вас ограниченные деньги и запасные части. Как ты можешь встроить какую-нибудь безопасность ?

При последовательном подключении конденсаторов любые расхождения в значениях заставляет каждый заряжаться с разной скоростью и с разным Напряжение.Разница может быть довольно большой для электролитов. Наверху из этого, как только батарея заряжена, утечка каждого конденсатора ток также вызывает * различное * напряжение на каждом конденсаторе.

Если вы полностью заряжаете банк серии, некоторые крышки всегда недозаряженные и некоторые завышенные (не хорошо). Чтобы помочь им поделиться напряжение равно, добавляешь балансировочных резисторов . В основном резисторы действуют как большой делитель напряжения и противодействуют эффектам изменения емкости и тока утечки.А если нет ток утечки, конденсаторы должны со временем зарядиться в соответствии со значениями делителя напряжения.

Используйте это уравнение со стр.13 этого отличного руководства, предоставленного Корнелл Дубилье, «Алюминий Руководство по применению электролитических конденсаторов »для расчета балансировочные резисторы:

Для 2 конденсаторов последовательно:	R = (2V _м — V _b) / (0.0015 C V _b)
Для конденсаторов Н> 2 :	R = (NV _м — V _b) / (0,0015 C V _b)

где	R = сопротивление в МОм В _м = максимальное напряжение, которое вы разрешаете на любом конденсаторе В _b = максимальное напряжение на всей батарее из двух (или N) конденсаторов N = количество конденсаторов в серии C = емкость в мкФ

Пример: Предположим, у вас есть два одинаковых 1000uf конденсаторы, и соедините их последовательно, чтобы удвоить напряжение номинал и уменьшить вдвое общую емкость.Предположим также, что они рассчитаны на 100 Вт постоянного тока (рабочее напряжение) и максимальное перенапряжение 125 В. Решите уравнение, используя V _м = 125 и V _b = 200.

Решение: R = (2×125 — 200) / (0,0015 x 1000 x 200) = 50/300 = 0,167 M = 167 кОм

Некоторые связанные последствия в этом примере:

Резисторы в этом примере будут давать нагрузку I = 200В / (2 * 167К) = 0,6 мА на системе зарядки.Здесь нет проблем, скорее всего, это незначительно к мощной системе зарядки койлганов.
Балансировочные резисторы будут стекать по крышке заряд с постоянной времени RC 2мин 47сек, что означает вы должны держать зарядное устройство подключенным до момента выстрела. Они действуют как предохранительный резистор для удаления воздуха, который гарантирует, что колпачки не остаются заряженными на следующий день (или неделю, или месяц!). Кроме того, это предотвращает зарядку конденсаторов до несколько вольт из-за эффекта диэлектрической памяти.
Каждый резистор выделяет тепло ( P = I ² R ) в этом примере номинал 60 мВт, худший случай 120 мВт. Так что вы следует использовать резистор на 1 Вт или больше. Ладно, резистор на 1/2 ватта тоже подойдет, но может сильно нагреться.
Термин «0,0015 C V _b» означает оценка (в микроамперах) разницы токов утечки в двух конденсаторах, включенных последовательно при номинальной температуре.
Неисправный конденсатор с током утечки более примерно 1 мА собирается перезарядить другую шапку.Так что будь осторожен, и периодически проверяйте актуальные напряжения!
Неисправный конденсатор с внутренним коротким замыканием перезаряжается другие конденсаторы (если он не открывается) независимо от того, что резисторы, которые вы используете.

Общая энергия серии по сравнению с параллельной

Давайте посмотрим, может ли последовательная или параллельная цепь хранить больше полная энергия.

Напомним, что энергия в одном конденсаторе пропорциональна квадрат напряжения.Заманчиво использовать последовательные конденсаторы для получить прирост энергии, используя «квадрат напряжения» в наших интересах. Но давайте посмотрим внимательнее …

Предположим, у вас есть два одинаковых конденсатора, емкостью C и номинальное напряжение В . (Конденсаторы не должны быть идентичны, но результаты верны для общего случая, и математика таким образом намного проще.) Давайте посчитаем запасенную энергию E для обеих схем.

Накопленная энергия в двух параллельных конденсаторах, заряженных до напряжения В:
Накопленная энергия в двух последовательных конденсаторах, заряженных до напряжения 2 В:

Нет разницы ! Обе схемы хранят одно и то же количество энергии. Это должно подтвердить здравый смысл, это говорит о том, что вы не можете увеличить общий запас энергии только за счет повторное подключение одних и тех же конденсаторов в разных схемах.

Выводы

Параллельные конденсаторы безопаснее безопаснее и надежнее последовательного соединения.

Нет преимущества в общем накоплении энергии, чтобы выбрать один из этих цепей над другой. Но! Вполне может быть время когда вам нужна более низкая емкость (например, более быстрый синхронизирующий импульс) и более высокое напряжение, чем может обеспечить имеющаяся у вас деталь.

Источник тока и включенные конденсаторы параллельно — Рубен Санчес

Конденсатор — это электронное устройство, способное накапливать электрическую энергию в электрическом поле. Обычно конденсатор определяется в самом простом варианте как устройство с двумя пластинами площадью \ (A \), разделенными воздухом (или любым другим диэлектрическим материалом) на расстояние \ (d \).

По индуктивной нагрузке — собственный рисунок, выполненный в Inkscape 0.44, Public Domain, ссылка

Если источник тока пропускается через конденсатор, электроны (заряд) осаждаются на одной из пластин, создавая, в свою очередь, электрическое поле на них. Не будет никакого эффективного переноса заряда от одной пластины к другой, потому что пространство между ними заполнено диэлектрическим материалом (непроводящим). Однако электрическое поле через него может вызвать отталкивание или притяжение заряда на другой стороне пластины.

Папа Ноябрь — самодельная SVG-версия Image: Dielectric.png, включающая Image: Capacitor schematic.svg в качестве основы., CC BY-SA 3.0, Link

Конденсатор характеризуется своей емкостью. Емкость измеряется в фарадах (Ф) и определяет соотношение между количеством заряда, необходимого для увеличения одного вольта на выводах конденсатора.

\ [C = \ frac {Q} {V} \]

Следовательно, конденсатору с 1 Ф потребуется 1 кулон (1 Кл) заряда, чтобы установить 1 В на его выводах.Помните, что 1 C представляет собой количество энергии, переносимое постоянным током 1 А за 1 секунду.

Поведение конденсатора, подключенного к источнику постоянного тока

Давайте посмотрим, что произойдет, когда мы подключим источник постоянного тока к конденсатору. {- 12} ~ C \]

Теперь, каким было бы значение напряжения \ (V_1 \), если в момент времени \ (t_1 = 1 ~ ns \) второй конденсатор \ (C_2 \) (разряженный) емкостью \ (2 ~ пФ \) связаны?

В тот самый момент, когда второй конденсатор подключен параллельно, заряд в \ (C_1 \) будет распределен между \ (C_1 \) и \ (C_2 \).{-12} ~ C \]

Если \ (C_2 \) отключен, заряд, хранящийся в нем, будет утерян и не будет перераспределен в сторону \ (C_1 \). Следовательно, общее количество заряда в системе на \ (t_2 = 2 ~ нс \) будет только на \ (C_1 \).

Теперь напряжение увеличивается с той же скоростью, что и в периоде \ (0

Следовательно, если мы построим график напряжения от \ (t = 0 ~ ns \) до \ (t_3 = 3 ~ ns \), мы получим следующий профиль напряжения для \ (V_1 \):

постоянных времени RC в RC параллельно, а не последовательно?

параллельный разряд ж / д

Привет,
Да, разница есть.В расчетах, показанных Буналмисом, предполагается, что ток i (s) через R и C одинаков, что неверно для параллельной цепи. Изначально конденсатор потребляет весь ток, и Ir через R будет равен нулю, но по мере того, как конденсатор заряжается в соответствии с Vc (t) = (1 / C) ic (t) dt, резистор начинает отводить ток. Ir (t) через него так, что Ir (t) = Vc (t) ÷ R. и этот процесс продолжается до тех пор, пока конденсатор не зарядится полностью до приложенного напряжения Vi. Таким образом, с течением времени конденсатор заряжается все медленнее и медленнее, и именно так постоянная времени проявляется.

Здесь мы должны отметить, что, предполагая конечное значение i (t), мы неявно включили внутреннее сопротивление для нашего источника напряжения, поскольку в противном случае бесконечный ток мгновенно зарядил бы конденсатор до приложенного напряжения Vi. Таким образом, чтобы вычислить постоянную времени, вы должны также учитывать это сопротивление источника. Как только вы включите сопротивление источника Rs, вы заметите, что сам ток i (t) зависит от времени и определяется выражением i (t) = (Vi-Vc) ÷ Rs, которое продолжает уменьшаться по мере увеличения напряжения Vc на конденсаторе.

способы, правила, формулы. Вычисление падений напряжения на конденсаторах

Смешанное соединение конденсаторов

Как рассчитать общую ёмкость соединённых конденсаторов?

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Для электролитических конденсаторов.

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

Соединение конденсаторов Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

3.6. Примеры решения задач к разделу 3

Конденсатор / Хабр

RC–цепочка

RC–цепочка интегрирующего типа

RC–цепочка дифференцирующего типа

Параллельное и последовательное соединение конденсаторов

Как соединить электролитические конденсаторы для увеличения напряжения. Последовательное и параллельное соединение конденсаторов

Смешанное соединение конденсаторов

Параллельное соединение

Последовательное соединение

Смешанное подключение

Последовательное соединение

Смешанное соединение

Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Смешанная схема

Параллельное соединение конденсаторов — Мегаобучалка

Параллельное включение конденсаторов калькулятор. Соединение конденсаторов параллельное соединение конденсаторов

Основные тезисы

Зачем нужно включать конденсаторы параллельно

Реактивная мощность сети

Схема соединения компенсирующих установок

Особенности конденсаторной защиты

Разряд конденсаторов

Примеры решения задач

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

конденсаторов последовательно и параллельно

Конденсатор

Игра с конденсатором

Практические задачи: решения емкости — Physics-prep.com

8,2 Последовательные и параллельные конденсаторы — University Physics Volume 2

Learning Objectives

Серия конденсаторов

Пример 8.4

Эквивалентная емкость последовательной сети

Стратегия

Решение

Значение

Параллельная комбинация конденсаторов

Параллельная комбинация

Пример 8.5

Эквивалентная емкость параллельной сети

Стратегия

Решение

Значение

Пример 8.6

Эквивалентная емкость сети

Стратегия

Решение

Пример 8.7

Сеть конденсаторов

Стратегия

Решение

Значение

Конденсаторы — несколько конденсаторов

Параллельные конденсаторы

Сеть резисторов для последовательных конденсаторов

Общая энергия серии по сравнению с параллельной

Выводы

Источник тока и включенные конденсаторы параллельно — Рубен Санчес

Поведение конденсатора, подключенного к источнику постоянного тока

постоянных времени RC в RC параллельно, а не последовательно?

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей