Расчет импеданса — Прототип PCB быстро и легко
С помощью калькулятора импеданса PCBWay вы можете рассчитать приблизительный импеданс вашей печатной платы / высокочастотной печатной платы. Поверхностная обработка игнорируется. Мы рекомендуем программное обеспечение от Polar Instruments, если вы хотите получить точный расчет импеданса.
Примечание: результаты приведены только для аппроксимации и грубой оценки, окончательные значения и конструкция соответствующего слоя должны быть рассчитаны нами. Проверьте информацию о стеке.
Инструкции: Пожалуйста, выберите значение, которое будет определено. Затем вы можете настроить другие параметры в соответствии с вашими потребностями.
Поверхностная микрополоска
mmcmmiluminch
Ширина дорожки
t Cu
mmcmmiluminch
Высот дорожки
hmmcmmiluminch
Высот изоляция
Er
Диэлектрическая постоянная
(FR4 — Стандарт: 4.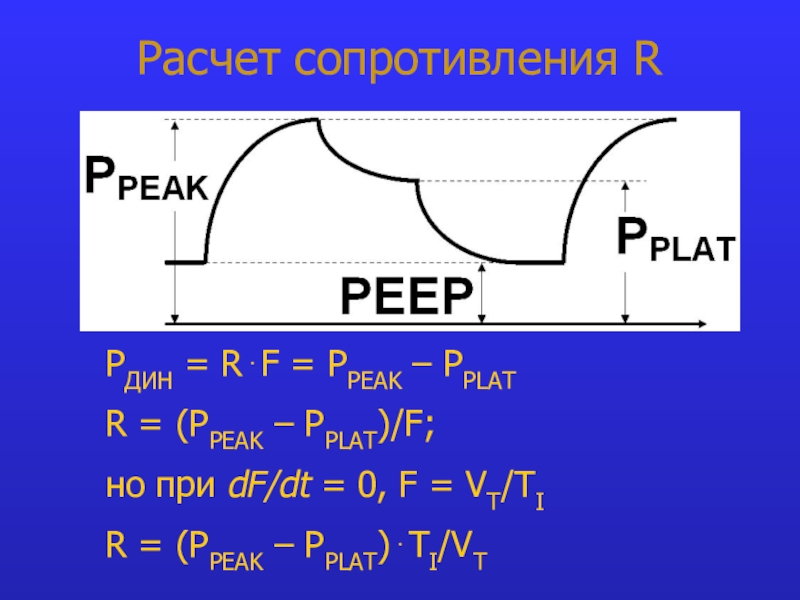 3)
3)
Ω
Расчет импеданса
Микрополосковая поверхность с краевой связью
s
mmcmmiluminch
Track spacew
mmcmmiluminch
Ширина дорожки
t Cu
mmcmmiluminch
Высот дорожки
mmcmmiluminch
Высот изоляция
Er
Диэлектрическая постоянная
(FR4 — Стандарт: 4.
Z0
Ω
Расчет импеданса
ZDiff
Ω
Разница импеданса
Симметричная полоска
mmcmmiluminch
Track space
w
mmcmmiluminch
Ширина дорожкиh
mmcmmiluminch
Высот изоляция
Er
Диэлектрическая постоянная
(FR4 — Стандарт: 4.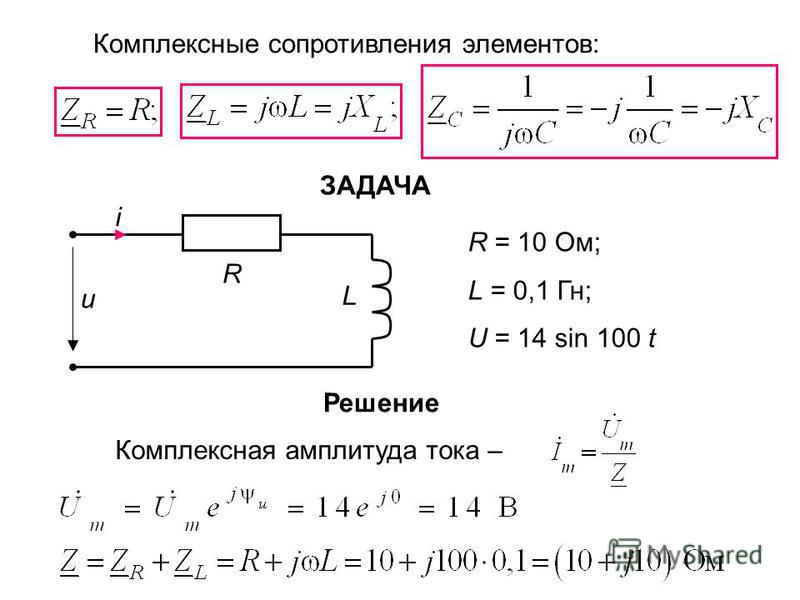
Z0
Ω
Расчет импеданса
Калькулятор импеданса последовательной RLC-цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет импеданс и фазовый сдвиг для соединенных последовательно резистора, катушки индуктивности и конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота.
Пример. Рассчитать импеданс катушки индуктивности 1 Гн, конденсатора 100 мкФ и резистора 100 Ом на частоте 16 Гц. Калькулятор показывает импеданс около 100,006 Ом. Это почти резонанс. Можно проверить импеданс при почти полном резонансе, если ввести 15,9154 Гц вместо 16 Гц. При этой частоте импеданс получается емкостным. Однако, если ввести емкость чуть большую частоту 15,9155 Гц, импеданс станет индуктивным и вы увидите, что фазовый угол, который был чуть меньше нуля, стал положительным.
Входные данные
Сопротивление, R
миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)
Индуктивность, L
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Емкость, С
фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)
Частота, f
герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)
Выходные данные
Угловая частота ω= рад/с
Емкостное реактивное сопротивление XC= Ом
Индуктивное реактивное сопротивление XL= Ом
Полный импеданс RLC |ZRLC|= Ом
Фазовый сдвигφ = ° = рад
Добротность Q=
Резонансная частота
f0= Гц ω0= рад/сВведите значения сопротивления, емкости, индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.
Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.
Для расчетов используются указанные ниже формулы:
φ = 90° если 1/2πfC < 2πfL и R = 0
φ = –90° если 1/2πfC > 2πfL и R = 0
φ = 0° если 1/2πfC = 2πfL и R = 0
Здесь
ZLC — импеданс цепи LC в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
R сопротивление в омах (Ом),
L — индуктивность в генри (Гн),
C — емкость в фарадах (Ф),
Q — добротность последовательной RLC-цепи (безразмерная величина),
ω0 — резонансная угловая частота в радианах в секунду (рад/с),
f0 — резонансная частота в герцах (Гц),
φ — фазовый сдвиг между полным напряжением VT и полным током IT в градусах (°) и радианах и
j — мнимая единица.
Для расчета введите сопротивление, индуктивность, емкость, частоту и выберите единицы измерения. Импеданс RLC –цепи будет показан в омах, сдвиг фаз в градусах и радианах. Также будут рассчитаны добротность, индуктивное и емкостное реактивные сопротивления и резонансная частота. С помощью ссылки Установить резонансную частоту можно рассчитать величины при резонансе.
Последовательная RLC-цепь состоит из резистора R, катушки индуктивности L и конденсатора C, соединенных последовательно. Как и в идеальной последовательной LC-цепи без сопротивления, в RLC-цепи могут возникать колебания с частотой резонанса, которые, однако, затухают из-за наличия сопротивления.
Резонанс возникает на частоте, при которой импеданс цепи минимален, то есть, при нулевом реактивном сопротивлении цепи. Иными словами, он возникает, если импеданс только резистивный, без реактивной составляющей, то есть его мнимая часть равна нулю. Явление резонанса происходит в том случае, когда реактивные сопротивления катушки индуктивности и конденсатора равны и, поскольку они имеют противоположный знак, они гасят друг друга. Как это происходит — показано ниже на векторной диаграмме.
Как это происходит — показано ниже на векторной диаграмме.
Калькулятор определяет резонансную частоту RLC-цепи, и можно ввести эту частоту или значение чуть-чуть меньше или чуть-чуть больше резонансной частоты, чтобы посмотреть, как будут себя вести рассчитываемые величины при резонансе и около него.
Калькулятор рассчитывает также добротность Q последовательной RLC-цепи — параметр, который используется для характеристики электрических резонансных цепей и устройств, а также механических резонаторов. Чем выше сопротивление цепи, тем больше потерь и тем выше затухание в RLC-цепях и ниже их добротность. Добротность Q последовательной RLC-цепи рассчитывается по приведенной выше формуле.
Слева приведен график зависимости импеданса ZRLC последовательной RLC-цепи от частоты f при заданных значениях сопротивления, индуктивности и емкости. Видно, что при резонансе импеданс резистивный и реактивная составляющая отсутствует. При повышении частоты реактивное сопротивление катушки индуктивности увеличивается, а конденсатора — уменьшается. Если же частота уменьшается до нуля (то есть источник выдает постоянное напряжение), реактивное сопротивление катушки индуктивности уменьшается до нуля, а конденсатора — становится бесконечно большим. То есть, при нулевой частоте (на постоянном токе) последовательная RLC-цепь представляет собой просто разомкнутую цепь с бесконечно большим импедансом. На правом графике показана зависимость импеданса и разности фаз последовательной RLC-цепи от частоты. Справа от резонанса импеданс имеет индуктивный характер, а слева — емкостной.
Если же частота уменьшается до нуля (то есть источник выдает постоянное напряжение), реактивное сопротивление катушки индуктивности уменьшается до нуля, а конденсатора — становится бесконечно большим. То есть, при нулевой частоте (на постоянном токе) последовательная RLC-цепь представляет собой просто разомкнутую цепь с бесконечно большим импедансом. На правом графике показана зависимость импеданса и разности фаз последовательной RLC-цепи от частоты. Справа от резонанса импеданс имеет индуктивный характер, а слева — емкостной.
На векторной диаграмме последовательной RLC-цепи показан емкостной импеданс (слева), индуктивный импеданс (в центре) и резистивный импеданс при резонансе (справа). Векторы напряжения на графике образуют прямоугольный треугольник с гипотенузой VT, вертикальным катетом VL– VC и горизонтальным катетом VR. Видно, что при емкостном характере импеданса ток опережает напряжение, а при индуктивном — отстает от него.
В последовательной RLC-цепи один и тот же ток протекает через резистор, конденсатор и катушку индуктивности, однако падения напряжения на элементах этой цепи различны. На векторной диаграмме показано напряжение VT идеального источника напряжения. В связи с наличием сопротивления, на схеме показан горизонтальный вектор напряжения на резисторе в фазе с текущим через него током. Вектор напряжения на индуктивности VL отстает от вектора тока на 90°, поэтому он направлен вверх (+90°). Вектор напряжения на емкости опережает вектор тока на 90°, поэтому он направлен вниз (–90°). Векторная сумма двух векторов, направленных в противоположные стороны, может быть направлена вниз и вверх в зависимости от того, на чем больше падение напряжения — на индуктивности или на емкости. Вектор полного напряжения в цепи VT определяется по теореме Пифагора.
На векторной диаграмме показано напряжение VT идеального источника напряжения. В связи с наличием сопротивления, на схеме показан горизонтальный вектор напряжения на резисторе в фазе с текущим через него током. Вектор напряжения на индуктивности VL отстает от вектора тока на 90°, поэтому он направлен вверх (+90°). Вектор напряжения на емкости опережает вектор тока на 90°, поэтому он направлен вниз (–90°). Векторная сумма двух векторов, направленных в противоположные стороны, может быть направлена вниз и вверх в зависимости от того, на чем больше падение напряжения — на индуктивности или на емкости. Вектор полного напряжения в цепи VT определяется по теореме Пифагора.
На частоте резонанса емкостное и индуктивное реактивные сопротивления равны и, если посмотреть на приведенное выше уравнение для |Z|, мы увидим, что эффективный импеданс будет определяться только величиной сопротивления и будет минимальным. Через катушку индуктивности и конденсатор, течет одинаковый ток, а падения напряжения на них равны и противоположны по знаку, так как их реактивные сопротивления тоже равны. Поэтому на резонансной частоте от источника потребляется ток, определяемый лишь резистором, так как идеальная последовательная LC-цепь при резонансе представляет собой для источника питания короткое замыкание. При наличии в цепи резистора, последовательная RLC-цепь при резонансе представляет собой чисто резистивную нагрузку.
Поэтому на резонансной частоте от источника потребляется ток, определяемый лишь резистором, так как идеальная последовательная LC-цепь при резонансе представляет собой для источника питания короткое замыкание. При наличии в цепи резистора, последовательная RLC-цепь при резонансе представляет собой чисто резистивную нагрузку.
Резонансная частота последовательной RLC-цепи определяется с учетом, что
Умножая обе стороны уравнения на частоту f, получаем:
Если разделить обе части уравнения на 2πL, извлечь из обеих частей квадратный корень и упростить получившееся выражение, получаем значение резонансной частоты:
Режимы отказа элементов
А что если в этой схеме отказал один из элементов? Нажмите на соответствующую ссылку, чтобы посмотреть соответствующие режимы отказа:
Особые режимы работы цепи
Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Различные режимы работы на постоянном токе
Короткое замыкание
Обрыв цепи
Чисто емкостная цепь
Цепь при резонансе
Чисто индуктивная цепь
Индуктивная цепь
Примечания
- Нулевая частота в объяснениях поведения этой цепи означает постоянный ток.
 Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения. - При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
- При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.
Катушки индуктивности в высокочастотном модуле телевизионного приемника
Автор статьи: Анатолий Золотков
Расчет волнового сопротивления в Altium Designer и взаимодействие с производителем печатных плат
Как рассчитать волновое сопротивление в Altium Designer и какие требования предъявлять к производителю плат.
В быстродействующих устройствах, для которых величина фронта сигнала составляет 1 нс и менее, требуется применение печатных плат с контролируемым импедансом для предотвращения искажений сигнала при его передаче по проводникам.
Проводники такой печатной платы (одиночные или дифференциальные) для которых важен параметр импеданса, являются линиями передачи и сигналы должны проходить через них с минимальными потерями формы, амплитуды и скорости.
При проектировании платы, разработчик должен учитывать множество нюансов, связанных с контролем импеданса, в том числе правильно выбрать структуру печатной платы и выбрать материалы с требуемыми свойствами. Необходимо определить в каких слоях будут располагаться проводники с контролем импеданса, а в каких слоях – опорные полигоны земли или питания.
Геометрические параметры печатных проводников высокоскоростных цепей должны быть рассчитаны в соответствии с выбранной структурой печатной платы (необходимо учесть свойства диэлектриков печатной платы, а в некоторых случаях свойства паяльной маски и шероховатость медных слоев).
Калькулятор импеданса Altium Designer
Калькулятор импеданса Altium Designer поддерживает различные структуры линий передач, учитывает множество параметров конструкции платы, а также геометрию печатных проводников. Также калькулятор напрямую взаимодействует с библиотекой материалов. Чтобы получить доступ к калькулятору импеданса, необходимо открыть Layer Stack Manager. В нижней части открывшегося окна необходимо перейти во вкладку Impedance:
В правой части экрана появится кнопка, позволяющая создать новый профиль импеданса для текущего проекта печатной платы (Add impedance profile):
Для работы с калькулятором должна быть активна панель Properties. Подробнее о работе калькулятора можно узнать по ссылке.
Особенности производства плат быстродействующих устройств
Контроль импеданса на печатной плате не только усложняет процесс проектирования, но и предъявляет дополнительные требования к производителю. Квалифицированный производитель печатных плат должен запросить у разработчика печатной платы информацию о том, в каких слоях будут расположены линии передачи с контролируемым импедансом, а в каких будут расположены опорные полигоны.
Квалифицированный производитель печатных плат должен запросить у разработчика печатной платы информацию о том, в каких слоях будут расположены линии передачи с контролируемым импедансом, а в каких будут расположены опорные полигоны.
Производитель может провести моделирование для подтверждения расчетов разработчика или внесения корректировки с учетом технологических нюансов (компенсации подтрава и допуска на металлизацию) из-за этого разработчику печатной платы рекомендуется закладывать 10% погрешность на целевое значение импеданса для реальной печатной платы.
Чрезвычайно важен правильный выбор материала — тип плетения стекловолокна, процент содержания смолы и ее текучесть, так как эти параметры напрямую влияют на диэлектрическую проницаемость, и определяют значение импеданса. При повторном изготовлении печатных плат очень важно использовать точно такие же материалы, как и при первом запуске, так как при замене материалов может потребоваться повторный расчет импеданса.
Качество изготовленных печатных плат с контролируемым импедансом, необходимо подтверждать измерениями методом рефлектометрии, которые подтверждают, что значения волновых сопротивлений находятся в пределах допуска. Для этого на панели с платами размещаются специальные тестовые купоны, на которых выполняются печатные проводники заданной ширины в тех же слоях что и линии передач на платах.
Для этого на панели с платами размещаются специальные тестовые купоны, на которых выполняются печатные проводники заданной ширины в тех же слоях что и линии передач на платах.
Используя специальный прибор, производитель проверяет соответствие волновых сопротивлений на купоне для каждой панели, тем самым получая подтверждение тому, что печатные платы на этой панели выполнены со значением целевого импеданса в пределах допуска. Панели с некорректными значениями импеданса отбраковываются.
Вместе с изготовленными печатными платами предоставляется отчет о контроле импеданса (Impedance Test Report). Узнать нюансы производства печатных плат с контролируемым импедансом можно перейдя по ссылке на сайт производителя печатных плат.
Измерение импедансов для цепей распределения питания
Измерительная задача
Токопроводящие дорожки на печатной плате, подключающие модуль регулятора напряжения (VRM или преобразователь постоянного тока) ко входу источника питания одного или нескольких контуров, обычно называются шиной питания. Совокупность таких дорожек характеризует цепь (систему) распределения питания (PDN) печатной платы.
Совокупность таких дорожек характеризует цепь (систему) распределения питания (PDN) печатной платы.
В соответствии с целевым назначением цепь PDN должна иметь характеристический импеданс (волновое сопротивление) в диапазоне миллиом (мОм). В идеале импеданс не должен ни увеличиваться, ни уменьшаться при изменении частоты относительно своего номинального значения. Анализ частотной характеристики PDN имеет большое значение, так как ток, который течет от VRM к обслуживаемым цепям, проходит переходные фазы (например, при включении питания, динамических нагрузках и т. д.), что расширяет его спектр до несколько сотен мегагерц.
На этих частотах любое межсоединение PDN начинает играть активную роль в процессе передачи энергии, так как оно ведет себя как катушка индуктивности или конденсатор в зависимости от своих физических свойств. Шины питания сами по себе функционируют в качестве линий передачи данных, каждая из которых характеризуется собственными индуктивностью и емкостью. Ток, протекающий через эти резонирующие конструкции, часто вызывает проблемы в обслуживаемых цепях (например, проблемы с целостностью сигнала, электромагнитными излучениями и т. д.). В связи с этим точное определение импеданса PDN имеет первостепенное значение, например, при испытаниях и поиске и устранении неисправностей печатных плат.
Ток, протекающий через эти резонирующие конструкции, часто вызывает проблемы в обслуживаемых цепях (например, проблемы с целостностью сигнала, электромагнитными излучениями и т. д.). В связи с этим точное определение импеданса PDN имеет первостепенное значение, например, при испытаниях и поиске и устранении неисправностей печатных плат.
Не каждый прибор способен выполнять измерения импеданса: одни устройства не могут измерять низкие импедансы из-за ограниченного динамического диапазона, другие не поддерживают развертку на необходимой частоте и гармониках, а третьи не имеют соответствующего интерфейса для взаимодействия с печатной платой. Векторные анализаторы цепей (ВАЦ) обладают всеми указанными выше функциональными возможностями, но точность измерения импеданса пропорциональна качеству согласования прибора и точности измерения параметров отражения или передачи.
Обратите внимание, что для PDN ошибка на уровне 1 мОм может влиять на результат испытания по критерию «годен/не годен» . В связи с этим выбор соответствующего ВАЦ и надлежащей схемы измерения позитивно влияет на выход продукции за счет обеспечения низкой погрешности измерения, снижая вероятность ложных положительных результатов.
В связи с этим выбор соответствующего ВАЦ и надлежащей схемы измерения позитивно влияет на выход продукции за счет обеспечения низкой погрешности измерения, снижая вероятность ложных положительных результатов.
Контроль импеданса на печатной плате | ООО «ПСБ технологии
Мы поставляем печатные платы с контролем волнового сопротивления (импеданса) проводников и дифференциальных пар. Стандартный допуск на волновое сопротивление проводника составляет ±10%, по особому заказу возможно обеспечение более жесткого допуска – до ±5%.
Все больше электронных устройств сегодня имеют дело с высокими скоростями передачи информации. Это требует применения печатных плат с контролируемым импедансом – для предотвращения искажений сигнала при передаче по проводникам. Проводник на печатной плате – это уже не просто дорожка, связывающая контактные площадки и переходные отверстия, а скорее линия передачи, которая передает сигнал на высоких скоростях с малыми потерями формы, амплитуды и скорости.
Контролируемый импеданс поднимает на новый уровень сам процесс проектирования, выбора материала, структуры, а также процесс производства печатных плат. Даже диэлектрические свойства паяльной маски могут повлиять на значение волнового сопротивления.
Как сделать заказ с контролем волнового сопротивления
В конструкторской документации на печатную плату разработчик должен указать, в каких слоях имеются проводники (или дифференциальные пары) с контролем импеданса, а в каких слоях — опорные планы земли и питания. Задача разработчика — провести предварительный расчет структуры печатной платы и спроектировать ее с учетом рассчитанных значений ширины проводника в заданных слоях.
При получении заказа с контролем импеданса мы проводим моделирование, чтобы проверить, что результирующие значения импедансов действительно попадут в заданный допуск ±10%. Если значения, рассчитанные заказчиком, не совпадут с результатами моделирования, мы запрашиваем разрешения заказчика, чтобы провести небольшие корректировки структуры или ширины проводников для более точного обеспечения заданного импеданса, с учетом компенсации подтравов и допусков металлизации на производстве.
Чрезвычайно важен выбор материала — тип стеклянной сетки, содержание смолы и ее текучесть влияют на диэлектрическую проницаемость, которая определяет величину импеданса. При повторном изготовлении плат особенно важно использовать такие же материалы, как при первом запуске.
Измерение импеданса при изготовлении печатных плат
Платы с контролем импеданса требуют выполнения измерений (методом рефлектометрии), которые подтверждают, что значения волновых сопротивлений находятся в пределах допуска. Для этого на специальном тестовом купоне, который располагается на заводской заготовке, выполняются отрезки проводников заданной ширины и в заданных слоях. Используя специальный прибор, мы проверяем соответствие волновых сопротивлений на купоне для каждой заготовке, тем самым получая подтверждение тому, что печатные платы на этой заготовке выполнены с корректным импедансом в пределах допуска. Заготовки с некорректным импедансом отбраковываются. Вместе с изготовленными печатными платами мы предоставляем отчет о контроле импеданса (Impedance Test Report). Заметим, что мы не несем ответственности за возможные некорректности в дизайне самой печатной платы, и не измеряем волновое сопротивление проводников собственно на каждой плате.
Заметим, что мы не несем ответственности за возможные некорректности в дизайне самой печатной платы, и не измеряем волновое сопротивление проводников собственно на каждой плате.
Параметры материала
Типовой материал FR4 для изготовления печатных плат имеет значение диэлектрической постоянной (Er) около 4,5…4,7 на низкой частоте (1 МГц), но с ростом частоты до 1 ГГц оно линейно уменьшается до Er=3,8…4,2 >(в зависимости от марки материала и вида плетения). Реальные значения Er могут колебаться в пределах ±25%. Существуют специальные, «нормированные» виды материала FR4, у которых значение Er нормируется и гарантируется изготовителем, и они ненамного дороже обычных, но производители печатных плат не обязаны использовать «нормированные» виды FR4, если это специально не указано в заказе на печатную плату.
При расчете импеданса линий на печатной плате надо брать значение диэлектрической постоянной для максимальной частоты спектра сигнала. При работе с цифровыми сигналами длительность фронта составляет единицы наносекунд, что соответствует максимальным частотам порядка 1 ГГц и диэлектрической проницаемости порядка 4,0.
При работе с цифровыми сигналами длительность фронта составляет единицы наносекунд, что соответствует максимальным частотам порядка 1 ГГц и диэлектрической проницаемости порядка 4,0.
Толщина диэлектрика
Производители печатных плат работают с диэлектриками стандартных толщин («препреги» и «ядра»), и их толщина в каждом слое должна быть определена перед запуском платы в производство, с учетом допусков на толщину (около ±10%). Разработчик печатной платы не должен подбирать конкретную комбинацию ядер и препрегов. Достаточно указать требуемую общую толщину диэлектрика в нужных слоях, и мы сами подберем нужные материалы.
Высокочастотные материалы
Для сигналов частотой выше 1 ГГц может оказаться необходимым применение более высокочастотных материалов, с лучшей стабильностью и другими диэлектрическими параметрами (такими как Duroid фирмы Rogers и т. д.).
Алгоритм прогонки для расчета импеданса твердого электролита
Please use this identifier to cite or link to this item: https://elib. belstu.by/handle/123456789/12196
belstu.by/handle/123456789/12196
| Title: | Алгоритм прогонки для расчета импеданса твердого электролита |
| Authors: | Бокун, Георгий Станиславович Гапанюк, Дмитрий Владимирович |
| Keywords: | расчет импеданса токопроводящая керамика электрический импеданс метод прогонки линейные алгебраические уравнения |
| Issue Date: | 2014 |
| Publisher: | БГТУ |
| Citation: | Бокун, Г. С. Алгоритм прогонки для расчета импеданса твердого электролита / Г. С. Бокун, Д. В. Гапанюк // Труды БГТУ. — Минск : БГТУ, 2014. — № 6 (170). — С. 110-112. |
| Abstract: | Предложен новый метод прогонки, пригодный, в отличие от известного, для решения систем линейных алгебраических уравнений с матрицами, имеющими ненулевые элементы на 2n +1 диагоналях. Суть метода состоит в том, что выбираются пробные значения n неизвестных и по невязкам последних n уравнений системы находится ее точное решение. Показано, что новый алгоритм решения систем уравнений содержит ряд преимуществ, реализованных на примере построения программы расчета электрического импеданса токопроводящей керамики. Показано, что новый алгоритм решения систем уравнений содержит ряд преимуществ, реализованных на примере построения программы расчета электрического импеданса токопроводящей керамики. |
| URI: | https://elib.belstu.by/handle/123456789/12196 |
| Appears in Collections: | 2014, № 6 |
Files in This Item:
| File | Description | Size | Format | |
|---|---|---|---|---|
| 33.pdf | 569.87 kB | Adobe PDF | View/Open |
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
Вопросы контроля импеданса при изготовлении печатных плат
Требования о контроле импеданса часто сопровождают изготовление сложных многослойных печатных плат. Понимание особенностей обеспечения этих требований помогает не только сократить срок запуска плат в производство, но также способствует получению лучшего результата.
Контроль импеданса на заводе по производству печатных плат можно условно разделить на несколько этапов:
Подбор структуры, если она не задана заказчиком, и расчет уточненных толщин диэлектриков в соответствии с особенностями проводящего рисунка конкретного проекта;
Расчет оптимальных параметров проводников в соответствии со структурой, реальными параметрами используемых материалов и заданными заказчиком требованиями к импедансам;
Согласование расчетных данных с разработчиком платы;
Изготовление плат и выполнение тестирования.
Если в исходных данных задана структура платы, то завод изготовитель из имеющихся на складе материалов подбирает структуру платы, наиболее близкую к заданной. Если структура платы изначально не задана, то на основе предварительных расчетов подбирается структура платы, обеспечивающая наименьшее отклонение фактически полученных на готовой плате значений импедансов от заданных в проекте заказчика. Для подобранной структуры платы выполняется уточненный расчет ширины проводников и зазоров, при которых значения импедансов будут обеспечиваться наиболее точно. Сформированная заводом структура платы и оптимальные параметры ширины проводников и зазоров могут быть согласованы с разработчиком по электронной почте.
Для подобранной структуры платы выполняется уточненный расчет ширины проводников и зазоров, при которых значения импедансов будут обеспечиваться наиболее точно. Сформированная заводом структура платы и оптимальные параметры ширины проводников и зазоров могут быть согласованы с разработчиком по электронной почте.
Стандартная точность, с которой заводы контролируют импеданс, составляет ±10%. В некоторых случаях, по согласованию с заводом, точность контролируемого импеданса может быть повышена до ±7% или даже до ±5%. При разработке и изготовлении плат с контролем импеданса у некоторых разработчиков иногда возникает желание «строго» обеспечить заданные ими требования к импедансам.
Как же выбрать оптимальный вариант изготовления, и будут ли ожидания соответствовать действительности?
На импеданс влияет несколько факторов: параметры проводников, свойства материалов, точность изготовления, внутренние особенности проекта. Попробуем рассмотреть эти факторы подробнее.
Факторы, влияющие на импеданс
При расчете уточненных толщин препрегов в готовой плате должно учитываться заполнение пространства между проводниками проводящего слоя, которое определяется процентным содержанием меди на соседних проводящих слоях и толщинами фольги. Эти величины, используемые при расчете, должны быть близки к реальным значениям в готовой плате.
Эти величины, используемые при расчете, должны быть близки к реальным значениям в готовой плате.
Процентное содержание меди на проводящем слое по отношению к площади платы может быть рассчитано с помощью программы проверки и обработки Gerber-файлов, например, CAM350 или других программ.
Финишная толщина фольги в готовой плате зависит от ее стартовой (базовой) толщины, а также от расположения — внешний или внутренний слой в структуре платы. Для платы, имеющей только сквозные металлизированные отверстия (без слепых и скрытых переходных отверстий и без дополнительных этапов металлизации), среднюю финишную толщину фольги можно определить с помощью таблицы 1.
Таблица 1. Толщины меди в слоях многослойной платы
* Фольга 12 мкм обычно не применяется на внутренних слоях
** Указанные значения даны для примера. Минимальные ширина проводника / зазор могут отличаться как для разных производств, так и для разных участков платы в пределах одного проводящего слоя.
При указанных в таблице предельных минимальных параметрах отдельных проводников и зазоров, минимальные расстояния проводник/полигон и контактная площадка/полигон могут составлять до 0,15-0,2 мм и более, даже для самой тонкой стартовой фольги. Мы не рекомендуем применять указанные в таблице предельные параметры без особой необходимости, особенно для всего проводящего рисунка. Лучше использовать предельные параметры только в «узких местах», упрощая нормы в целом по печатной плате, что повысит выход годных плат и сократит сроки и стоимость их производства.
Одним из важных параметров, которые необходимо учитывать при расчете импеданса, является диэлектрическая константа. Диэлектрическая константа для одного типа материала не всегда имеет строго одно единственное и неизменное значение. Так, для обычного стеклотекстолита типа FR4 она зависит от процентного содержания смолы в материале. Чем больше содержание смолы, тем сравнительно меньше диэлектрическая константа. И наоборот, чем больше процентное содержание стекловолокна, тем сравнительно больше диэлектрическая константа. Для примера приведем данные на стеклотекстолит EM-827B фирмы Elite Material, см. рис. 1
Для примера приведем данные на стеклотекстолит EM-827B фирмы Elite Material, см. рис. 1
Из данных Рис.1 также видно, что с увеличением рабочей частоты диэлектрическая константа материала имеет склонность к снижению. Эту особенность также важно учитывать при расчете параметров критичных проводников.
У материалов разных производителей значение диэлектрической константы и некоторые характеристики материалов могут отличаться, даже для препрегов, имеющих одинаковый тип (например, 1080), поскольку могут отличаться как состав смол, так и наполнитель.
При запуске в производство платы с контролем импеданса можно дополнительно указать рабочую частоту, при которой должен обеспечиваться нужный импеданс. В этом случае завод изготовитель сможет не только рассчитать оптимальные параметры проводников, но и проверить соответствие параметров материала заданной частоте. Если частота не задана, как правило, заводы проводят тестирование импеданса на 1 ГГц.
К точности изготовления можно отнести несколько параметров: точность соблюдения ширины проводника и зазора, толщин фольги и диэлектриков. Стандартная точность при выполнении ширины проводника и зазора для зарубежного производства составляет ±20%. Точность толщин фольги и диэлектриков в готовой плате в большей степени определяется допусками на толщины исходных материалов, которая обычно составляет ±10% от номинала. Достаточно большие допуски на толщины исходных материалов и стандартный допуск на ширину проводников объясняют сложности в обеспечении допуска на импедансы менее 10%.
Структура платы формируется на основе материалов со стандартным рядом толщин. Толщина слоя диэлектрика, хотя и может быть подобрана с достаточно небольшим шагом, для точного получения нужных значений импедансов этого подбора бывает недостаточно. Простым методом обеспечения нужных значений импедансов является уточненный расчет и последующая подстройка ширины критичных проводников. Если расчеты на этапе проектирования были выполнены достаточно точно, то изменения, которые необходимо внести при коррекции ширины проводников, могут не превысить 10% от их исходного значения.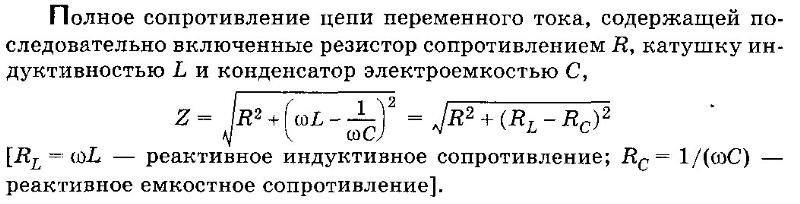 По запросу разработчика завод изготовитель может согласовывать с ним рабочую структуру платы и расчетные параметры контроля импедансов перед началом изготовления. Многие продвинутые САПР печатных плат, такие как Cadence Allegro, позволяют менять трассировку выбранных «классов» цепей групповым образом, задавая им новые значения ширины проводников и зазора в дифференциальной паре, что позволяет почти мгновенно подстроить готовый проект печатной платы под рекомендации завода-производителя.
По запросу разработчика завод изготовитель может согласовывать с ним рабочую структуру платы и расчетные параметры контроля импедансов перед началом изготовления. Многие продвинутые САПР печатных плат, такие как Cadence Allegro, позволяют менять трассировку выбранных «классов» цепей групповым образом, задавая им новые значения ширины проводников и зазора в дифференциальной паре, что позволяет почти мгновенно подстроить готовый проект печатной платы под рекомендации завода-производителя.
При заказе плат с контролем импеданса необходимо знать некоторые особенности их производства. Платы на заводах изготавливаются на технологических панелях. На одной такой панели размещается максимально возможное количество плат. Тестирование импедансов выполняется на заводе не индивидуально для каждого проводника на каждой плате, а на специальных тест-купонах. Тест-купон похож на небольшую плату, на которой моделируют параметры критичных проводников изготавливаемых плат. Он размещается на технологических полях заводской панели, обычно по одному тест-купону на панель. Тест-купон, расположенный на краю панели, находится в наиболее неблагоприятных условиях с точки зрения соблюдения геометрии проводников и зазоров. Таким образом, если импедансы проводников расположенных на тест-купоне соответствуют заданным, то импедансы проводников всех плат на заводской технологической панели тем более соответствуют заданным значениям. Безусловно, тест-купон занимает некоторую полезную площадь заводской панели, поэтому на ней можно разместить меньше печатных плат, чем обычно. Это приводит к удорожанию на 3-5% при серийном изготовлении плат с контролем импеданса.
После того, как уточненные значения ширины проводника и зазоры определены, необходимые изменения должны быть внесены в данные для производства. Ширина каждого типа проводника, требующего контроля импеданса, должна быть скорректирована в соответствии с ранее вычисленным расчетным значением.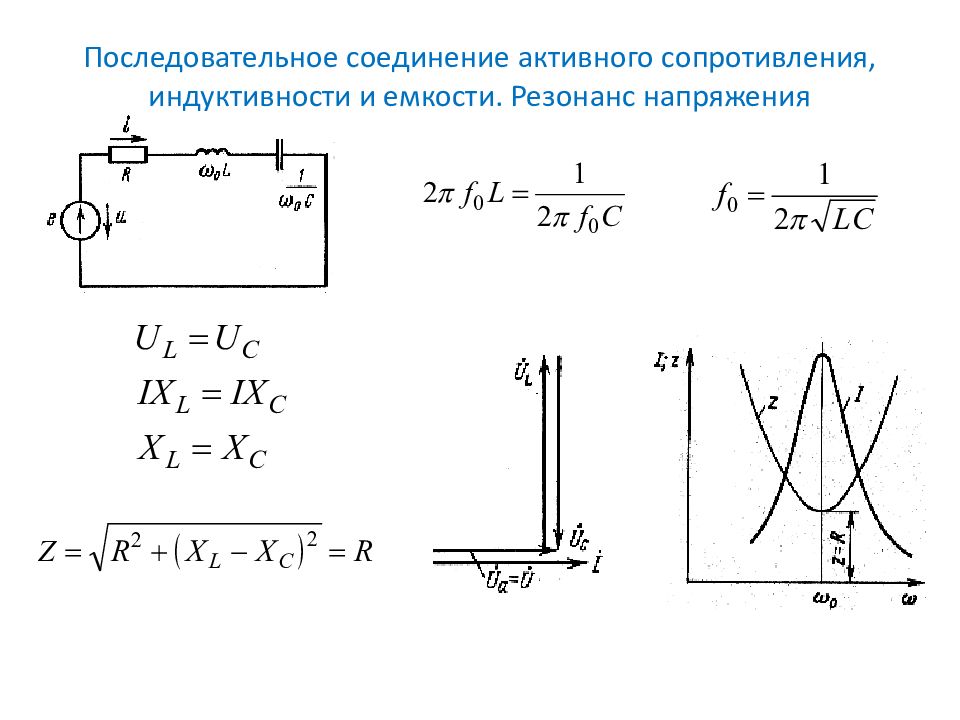
В связи с этим важно понимать некоторые особенности, связанные с выполнением на производстве коррекции ширины проводников:
Производство принимает в работу проекты преимущественно в формате Gerber RS-274-X (со встроенным описанием апертур) плюс сверловка в формате Excellon. Формат Gerber не поддерживает информацию о цепях и их названиях в исходном проекте. По этой причине требования к импедансам, заданные в виде списка названий цепей исходного проекта, будут не совсем корректны с точки зрения производства, поскольку исходные данные содержат информацию в неудобном или неподдерживаемом для Gerber-формата виде.
Программы подготовки плат к производству, используемые на заводах, преимущественно работают с такими свойствами графических объектов, как тип объекта, форма и размер. Такой параметр, как «D-код» графического объекта (то есть «апертура» или «засветка» для фотоплоттера в файлах Gerber), практически не доступен для работы и не применяется. Это значит, что, если проводники разных типов, например, единичные проводники и дифф-пары прорисованы линиями с разными номерами D-кодов, но имеют одинаковую геометрическую форму и размер, на производстве не смогут отличить проводники одного типа от проводников другого типа.
 Например, невозможно отличить единичные проводники 0,1 мм, дифф-пары 0,1/0,1 мм и дифф-пары 0,1/0,12 мм и выполнить раздельно оптимальную подстройку их ширины на заводе. Это означает, что одновременно для нескольких видов проводников можно будет достичь импедансов, только приближенных к номинальным значениям, но не в точности им соответствующих. Настройка параметров и расчетных импедансов для одного типа проводников будет приводить к отклонению импедансов других типов проводников, и наоборот.
Например, невозможно отличить единичные проводники 0,1 мм, дифф-пары 0,1/0,1 мм и дифф-пары 0,1/0,12 мм и выполнить раздельно оптимальную подстройку их ширины на заводе. Это означает, что одновременно для нескольких видов проводников можно будет достичь импедансов, только приближенных к номинальным значениям, но не в точности им соответствующих. Настройка параметров и расчетных импедансов для одного типа проводников будет приводить к отклонению импедансов других типов проводников, и наоборот.
Описанные факторы затрудняют достижение заданных значений импедансов и заданной точности при изготовлении плат на заводе. Они же, в свою очередь, тесно связаны с такой важной группой факторов, которую можно условно назвать «влиянием особенностей проекта».
Во многих проектах печатных плат, поступающих от российских заказчиков в нашу компанию на изготовление, в трассировке зачастую встречаются особенности, влияющие на отклонение импедансов от номинальных значений. Некоторые из них не похожи на то, что разработчик хотел выполнить намеренно, но больше похоже на ошибки проектирования. Например, в некоторых случаях цепи, требующие контроля импеданса, выполнены без экранного полигона на отдельных участках (см. рис.3).
Например, в некоторых случаях цепи, требующие контроля импеданса, выполнены без экранного полигона на отдельных участках (см. рис.3).
Понятно, что ширина проводников и зазор в дифф-парах, за исключением отдельных узких мест, должны строго соответствовать заданным номинальным значениям. В противном случае локальные изменения импеданса могут создать недопустимые искажения сигналов. Тем не менее, в отдельных проектах встречаются дифф-пары с разной шириной проводника или зазором на разных участках (Рис.4).
Рис.4 Примеры дифф-пар с разной шириной проводника на разных участках а) Единичные проводники 0,112 мм, дифф-пары 0,11/0,14 с участками 0,112/0,14 мм б) дифф-пары 0,11/0,14 с участками 0,112/0,14 мм и дифф-пары 0,127/0,127 мм с участком 0,112/0,127 ммИногда встречаются проекты с заметно разным зазором на разных участках дифф-пар, см. рис.5.
рис.5.
Разные зазоры в дифф-парах не способствуют высокой точности при обеспечении импеданса. В данном случае для дифф-пар явно требуется коррекция зазоров перед изготовлением. Без этого изготовление платы даже с минимальным допуском на импеданс ситуацию вряд ли спасет.
Подобное явление не всегда является невнимательностью разработчика. Некоторые программы проектирования сами допускают небольшие отклонения зазора от номинала (например, программы Altium P-CAD200х немного увеличивают зазоры дифф-пар на диагональных участках).
Также отклонения по зазору дифф-пар могут возникнуть при формировании Gerber-файлов для производства, когда проект, сформированный в миллиметрах, переносится в Gerber в формате дюймов с невысокой точностью координат после запятой. Отклонения могут показаться сравнительно небольшими, но в некоторых случаях даже они могут вызывать заметные отклонения расчетных значений импедансов от номинальных.
Еще один важный фактор, влияющий на отклонения импеданса – это неоднородность структуры диэлектрика, состоящего из переплетенных стеклянных нитей и смолы. Один проводник может располагаться над стеклянной нитью в диэлектрике, а соседний проводник – над областью, где преимущественно находится смола. Диэлектрическая проницаемость смолы и стекла отличаются более чем на 30%, и это приводит, во-первых, к отклонению импеданса, а во-вторых, к фазовым задержкам в дифференциальной паре (в одном плече дифф-пары сигнал будет распространяться медленнее, чем в другом). На скоростях передачи сигнала более чем 1 Гбит/c этот фактор может привести к серьезным проблемам. Для того, чтобы уменьшить его влияние, разработчики применяют диэлектрические материалы с более плотным плетением стекловолокна, а также используют диагональное размещение проводников – в этом случае за счет ухода от горизонтали и вертикали, по которым располагается плетение стеклянных нитей, происходит «усреднение» импеданса по длине проводника.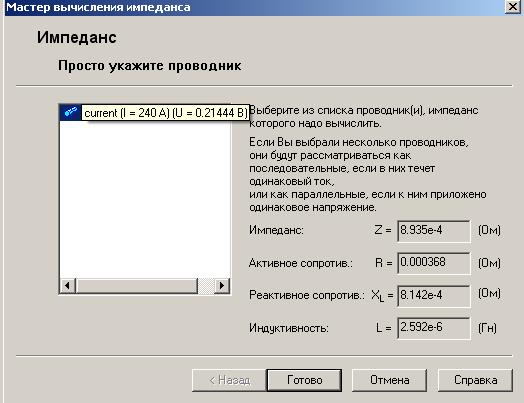
Фактическое волновое сопротивление проводников на печатной плате не всегда соответствует предварительным расчетам или измеренным заводом значениям. Вычисленные с высокой точностью расчетные значения импедансов могут получиться с отклонениями, как вследствие особенностей проекта, так и вследствие неточности изготовления. Простое уменьшение допуска на импеданс при заказе изготовления платы может не привести к ожидаемому результату. Лучшие результаты по импедансам на плате могут быть достигнуты по результатам совокупности факторов — высокого качества изготовления и тщательности трассировки. В ответственных случаях для плат может применяться предварительное моделирование целостности сигналов, например, в системах типа Sigrity и аналогичных.
Стандартное отклонение в пределах ±10% к расчетному значению в большинстве случаев является вполне приемлемым результатом изготовления плат с контролем импеданса.
Рекомендации от производителя печатных плат по размещению заказов с контролем импедансаПроводники, требующие контроля импеданса, расположенные на одном проводящем слое, но принадлежащие разным классам цепей (единичные проводники и дифф-пары, дифф-пары(1) и дифф-пары(2)), должны отличаться по ширине, хотя бы на 1 мкм. Это позволит наиболее точно подобрать на заводе оптимальные расчетные параметры для каждого класса цепей, независимо от других классов.
Это позволит наиболее точно подобрать на заводе оптимальные расчетные параметры для каждого класса цепей, независимо от других классов.
Гербер-файлы проекта, передаваемые на производство, должны по возможности иметь максимальную точность координат графических объектов, которую может позволить пакет проектирования. Наибольшую точность передачи координат можно достичь, работая в миллиметрах. Для проектов, спроектированных в миллиметрах, рекомендуемая точность координат составляет «4:4» (четыре знака после запятой минимум) или «4:5». В дюймах точность координат может составлять «2:5» или «3:6».
Уменьшение влияния отклонений ширины проводников на их импеданс достигается при увеличении их ширины и увеличении толщин диэлектриков. И наоборот, при уменьшении толщины диэлектрика до 0,1 мм и меньше даже небольшое отклонение ширины проводника может привести к заметным изменениям импеданса. Для цепей, требующих максимальной точности импеданса можно рекомендовать применять толщину диэлектрика до опорного слоя 0,15-0,2 мм минимум.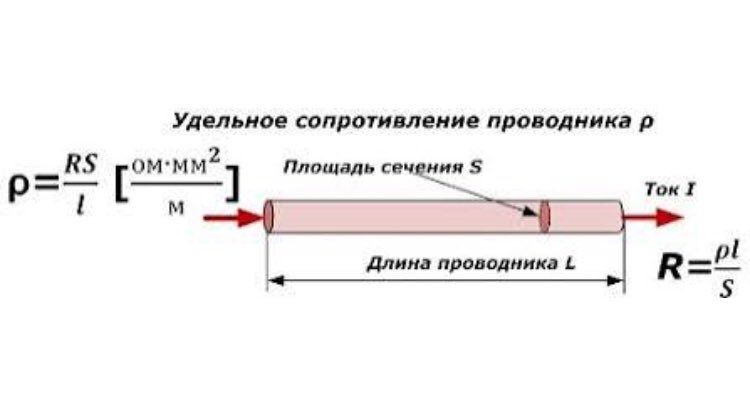
В ситуациях, когда требуется увеличить толщину диэлектрика от микрополосковой линии до опорного слоя, но структура многослойной печатной платы не позволяет это сделать, вы можете локально, только под требуемыми микрополосковыми линиями в слое Top, сделать опорный слой не в слое 2, а в слое 3 или 4, соответственно освободив от трассировки и от медных полигонов промежуточные слои. В этом случае надо дополнительно указать производителю, что для этих проводников в указанной области выбран другой опорный слой, а также дополнительно дать запрет на добавление элементов топологии в этой области в промежуточных слоях. В противном случае производитель может по своей инициативе добавить технологическое медное заполнение в пустых областях внутренних слоев, что может привести к проблемам с целостностью сигналов в готовом электронном узле.
При передаче проекта производителю рекомендуем сопроводить его не только структурой слоев с указанием толщин диэлектрика и меди, но и таблицей с описанием требований к импедансу проводников. В этой таблице надо указать для каждого «класса» проводников с контролем импеданса следующие параметры:
В этой таблице надо указать для каждого «класса» проводников с контролем импеданса следующие параметры:
Номер слоя
Ширина проводника
Ширина проводника и зазор, если это дифф.пара
Опорные слои для этого типа проводников
Требуемый импеданс
Допуск на импеданс
Комментарии и особенности
Пример описания требований к импедансу печатной платы приведен в таблице 2. В верхнем слое имеются проводники шириной 0.155 мм с импедансом 50 Ом относительно опорного слоя 2, требования по допуску 10%. Также есть дифф.пары с проводниками 0.1 мм и зазором 0.15 мм, с импедансом 100 Ом. Кроме того, с обеих сторон платы имеются СВЧ-микрополосковые линии шириной 0.48 мм, имеющие импеданс 50 Ом относительно опорного слоя 3. Под этими микрополосками в проекте не должно быть меди в соседнем слое, и должен присутствовать полигон аналоговой земли в третьем слое относительно поверхности. За счет увеличенной ширины проводника можно повысить точность выполнения ширины этих линий, а значит, улучшить допуски на выполнение импеданса с 10% до 7%. В таблицу добавлен комментарий, запрещающий размещение технологических медных заполнений в этой зоне платы.Также имеются проводники шириной 0.127 мм в слое 3, с опорными слоями в слоях 2 и 4, имеющие импеданс 50 Ом.
В таблицу добавлен комментарий, запрещающий размещение технологических медных заполнений в этой зоне платы.Также имеются проводники шириной 0.127 мм в слое 3, с опорными слоями в слоях 2 и 4, имеющие импеданс 50 Ом.
Таблица 2. Пример технического задания на изготовление печатной платы с контролем импеданса.
Передача такой таблицы при заказе печатных плат позволит производителю плат четко определить, какие именно проводники следует проконтролировать, а также позволит осуществить их «тонкую подстройку», по ширине или по структуре слоев, с целью оптимального выполнения требований по импедансу.
Пример расчета импеданса проводников для такой печатной платы в САПР печатных плат OrCAD Standard показан на рис.6. В данном расчете мы не стали задавать точные значения диэлектрической константы раздельно для каждого слоя, поставив везде ориентировочное «предварительное» значение 4.0, характерное для типовых диэлектриков FR4. В дальнейшем производитель плат может уточнить эти значения, отдельно для каждого слоя, в зависимости от выбранного типа препрегов и бренда материала.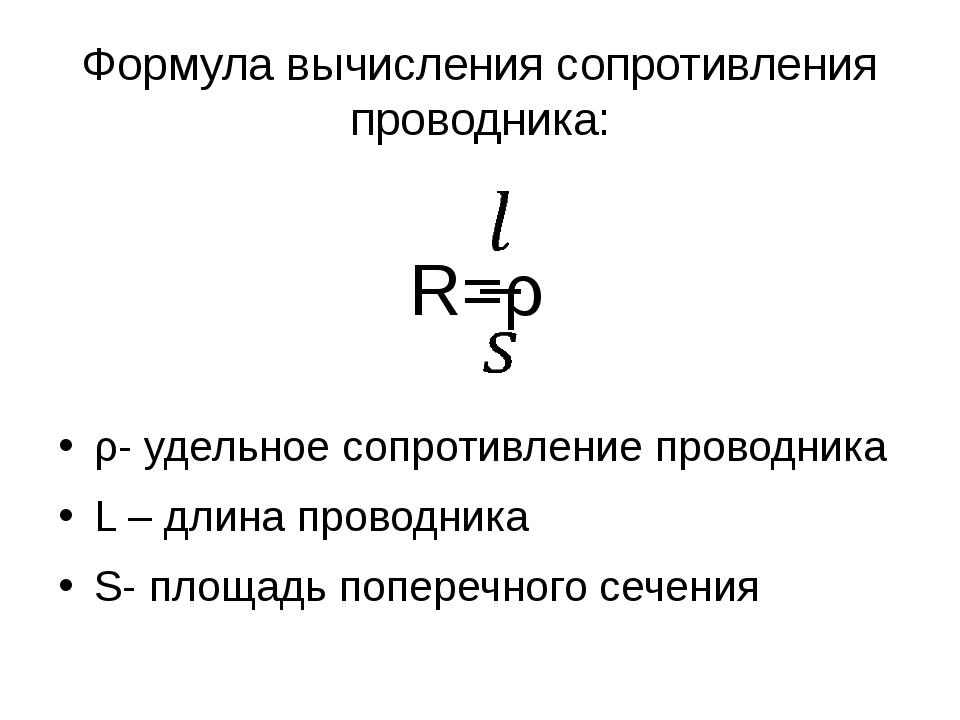
Отметим, что структура получилась «как бы» несимметричной с точки зрения размещения слоев Conductor и Plane, т.к. это требовалось для расчета микрополосковой линии на слое Bottom с опорным слоем 6, и мы назначили слою 6 тип Plane, а слою 7 тип Conductor, что требовалось для корректного выполнения расчета. Но в принципе расположение этих микрополосковых линий может быть ограничено только некоторыми областями на плате, а в остальных областях мы можем разместить полигоны цифровой земли в слое 7, что обеспечивает симметрию структуры (симметричная заливка медью слоя 2 и слоя 7) и повышает качество изготовления печатной платы, улучшая ее плоскостность.
Автор — Андрей Чернышов, [email protected] (инженер по подготовке заказов печатных плат к производству)
Как рассчитать импеданс — Как выполнить
В то время как закон Ома применяется непосредственно к резисторам в цепях постоянного или переменного тока, форма отношения тока к напряжению в цепях переменного тока в целом изменяется на форму:
, где I и V — среднеквадратичные или «эффективные» значения. Величина Z называется импедансом. Для чистого резистора Z = R. Поскольку фаза влияет на импеданс, а вклад конденсаторов и катушек индуктивности отличается по фазе от резистивных компонентов на 90 градусов, такой процесс, как сложение векторов (векторов), используется для разработки выражений для импеданса.Более общим является метод комплексного импеданса.
Величина Z называется импедансом. Для чистого резистора Z = R. Поскольку фаза влияет на импеданс, а вклад конденсаторов и катушек индуктивности отличается по фазе от резистивных компонентов на 90 градусов, такой процесс, как сложение векторов (векторов), используется для разработки выражений для импеданса.Более общим является метод комплексного импеданса.
Импедансы могут быть объединены с использованием метода комплексного импеданса.
Единицы измерения всех величин — Ом. Отрицательный фазовый угол подразумевает, что импеданс является емкостным, а положительный фазовый угол подразумевает чистую индуктивность.
Импеданс — это величина сопротивления, которое компонент оказывает протеканию тока в цепи на определенной частоте.
В этой статье мы поговорим о том, чем импеданс похож и чем он отличается от простого сопротивления.
Во-первых, не будем рассматривать их сходство. Импеданс, как и сопротивление, представляет собой величину, которая показывает величину сопротивления, которое компонент оказывает протеканию электрического тока. И, как и сопротивление, единицей измерения импеданса являются омы (Ом).
И, как и сопротивление, единицей измерения импеданса являются омы (Ом).
Однако, в отличие от сопротивления, импеданс отличается тем, что величина сопротивления компонента сигналу зависит от его частоты. Это означает, что сопротивление компонента изменяется в зависимости от частоты сигнала, входящего в компонент.Сопротивление — это величина и мера, не зависящая от частоты. Он не учитывает частоту проходящего через него сигнала, потому что частота не влияет на сопротивление нереактивных компонентов. Однако реактивные компоненты (которые мы обсудим ниже) изменяют величину сопротивления, которую они предлагают в цепи, в зависимости от частоты входного сигнала. Но импеданс меняется в зависимости от частоты входящего в него сигнала. В этом разница между сопротивлением и импедансом.
Итак, следующий шаг, на который нужно ответить, — какие компоненты зависят от частоты и имеют разное сопротивление в зависимости от частоты, а какие компоненты не изменяются в зависимости от входящей частоты?
Ответ таков: нереактивные компоненты не заботятся о частоте сигнала, поступающего в компонент. Они не изменяют значения сопротивления в зависимости от входной частоты. Одним из таких компонентов является резистор, который работает независимо от частоты. Независимо от того, проходит ли через него напряжение постоянного или переменного тока, это не влияет на величину сопротивления, которое он предлагает.То же самое для сигналов постоянного и переменного тока.
Они не изменяют значения сопротивления в зависимости от входной частоты. Одним из таких компонентов является резистор, который работает независимо от частоты. Независимо от того, проходит ли через него напряжение постоянного или переменного тока, это не влияет на величину сопротивления, которое он предлагает.То же самое для сигналов постоянного и переменного тока.
Однако реактивные компоненты, двумя основными из которых являются конденсаторы и катушки индуктивности, изменяют значения сопротивления в зависимости от частоты входящего в них сигнала. Конденсаторы — это реактивные устройства, которые имеют высокий импеданс на низких частотах и низкий импеданс на высоких частотах. С увеличением частоты реактивное сопротивление уменьшается. Индукторы — это устройства, которые имеют низкий импеданс на низких частотах и более высокий импеданс на высоких частотах. С увеличением частоты увеличивается сопротивление.Они называются индуктивным реактивным сопротивлением и емкостным реактивным сопротивлением.
Импеданс — очень важная концепция, которую необходимо понять, поскольку в большинстве электронных схем используются конденсаторы и катушки индуктивности. Главное понять, что они зависят от частоты.
Как рассчитать импеданс
Теперь мы рассмотрим, как рассчитать импеданс двух основных реактивных компонентов, конденсаторов и катушки индуктивности.
Для каждого импеданса конденсаторов и катушек индуктивности используются отдельные формулы, поэтому для каждого из них необходимо применять правильную формулу.
Импеданс конденсатора
Для расчета полного сопротивления конденсатора используется следующая формула:
, где X C — импеданс в единицах Ом, f — частота сигнала, проходящего через конденсатор, а C — емкость конденсатора.
Чтобы использовать наш онлайн-калькулятор, который автоматически рассчитает импеданс конденсатора, посетите ресурс «Калькулятор импеданса конденсатора».
Импеданс индуктора
Для расчета полного сопротивления катушки индуктивности используется следующая формула:
, где X L — импеданс в единицах Ом, f — частота сигнала, проходящего через катушку индуктивности, а L — индуктивность катушки индуктивности.
Чтобы использовать наш онлайн-калькулятор, который автоматически рассчитает импеданс катушки индуктивности, посетите ресурс «Калькулятор импеданса катушки индуктивности».
Если в цепи присутствуют и конденсаторы, и катушки индуктивности, общий импеданс можно рассчитать, сложив все отдельные импедансы:
Этот инструмент вычисляет реактивное сопротивление конденсатора для заданного значения емкости и частоты сигнала.
Выход
Обзор
Наш калькулятор емкостного реактивного сопротивления поможет вам определить полное сопротивление конденсатора, если заданы его значение емкости (C) и частота сигнала, проходящего через него (f).Вы можете ввести емкость в фарадах, микрофарадах, нанофарадах или пикофарадах. Для частоты доступны следующие единицы измерения: Гц, кГц, МГц и ГГц.
Уравнение
$$ X _ $$ = реактивное сопротивление конденсатора в Ом (Ом)
$$ omega $$ = угловая частота в рад / с = $$ 2 pi f $$, где $$ f $$ — частота в Гц
$$ C $$ = емкость в фарадах
Реактивное сопротивление (X) показывает сопротивление компонента переменному току. Импеданс (Z) показывает сопротивление компонента как постоянному, так и переменному току; это выражается как комплексное число, т.е.е., Z = R + jX. Импеданс идеального резистора равен его сопротивлению; в этом случае действительная часть импеданса — это сопротивление, а мнимая часть равна нулю. Импеданс идеального конденсатора по величине равен его реактивному сопротивлению, но эти две величины не идентичны. Реактивное сопротивление выражается обычным числом с единицей измерения Ом, тогда как импеданс конденсатора — это реактивное сопротивление, умноженное на -j, то есть Z = -jX. Член -j учитывает фазовый сдвиг на 90 градусов между напряжением и током, который возникает в чисто емкостной цепи.
Импеданс (Z) показывает сопротивление компонента как постоянному, так и переменному току; это выражается как комплексное число, т.е.е., Z = R + jX. Импеданс идеального резистора равен его сопротивлению; в этом случае действительная часть импеданса — это сопротивление, а мнимая часть равна нулю. Импеданс идеального конденсатора по величине равен его реактивному сопротивлению, но эти две величины не идентичны. Реактивное сопротивление выражается обычным числом с единицей измерения Ом, тогда как импеданс конденсатора — это реактивное сопротивление, умноженное на -j, то есть Z = -jX. Член -j учитывает фазовый сдвиг на 90 градусов между напряжением и током, который возникает в чисто емкостной цепи.
Приведенное выше уравнение дает вам реактивное сопротивление конденсатора. Чтобы преобразовать это в импеданс конденсатора, просто используйте формулу Z = -jX. Реактивность — более простое значение; он сообщает вам, какое сопротивление будет иметь конденсатор на определенной частоте. Однако для всестороннего анализа цепей переменного тока необходимо полное сопротивление.
Как видно из приведенного выше уравнения, реактивное сопротивление конденсатора обратно пропорционально как частоте, так и емкости: более высокая частота и большая емкость приводят к более низкому реактивному сопротивлению.Обратное соотношение между реактивным сопротивлением и частотой объясняет, почему мы используем конденсаторы для блокировки низкочастотных компонентов сигнала, позволяя проходить высокочастотным компонентам.
Импеданс трансформатора в процентах — это измеренное значение, указанное на паспортной табличке и фактически являющееся измерением напряжения. Это проверенное значение, которое производители применяют для силовых распределительных трансформаторов, и оно используется при расчете тока короткого замыкания. Это важно для координации устройств защиты от сверхтоков (OCPD), анализа короткого замыкания, гармонического анализа и исследований вспышки дуги.
Импеданс в процентах — это процент от номинального напряжения, необходимого для протекания номинального тока при коротком замыкании вторичных обмоток при номинальном отводе напряжения и частоте.
Щелкните изображение, чтобы увидеть паспортную табличку.
Пример процентного сопротивления
Если трансформатор имеет полное сопротивление 6,33%, потребуется 6,33% входного первичного напряжения, чтобы вызвать 100% номинального тока на вторичных обмотках при возникновении наихудшего случая отказа.В электрических распределительных системах наихудший случай неисправности возникает, когда металлическая шина с низким сопротивлением замыкает линии и называется неисправностью с болтовым креплением.
Теперь, если 100% напряжения приложено к первичному входу, то приблизительно 100 / 6,33 = 15,8-кратный номинальный ток будет течь во вторичной обмотке в худшем случае. Это максимальный ток короткого замыкания, который может быть в вашей системе.
Тестирование процентного сопротивления
При наихудшем случае неисправности вторичные выводы трансформатора скреплены болтами, фактически скреплены медными шинами с последовательно включенным амперметром.
Очень осторожно, напряжение на первичных линиях повышается до тех пор, пока не будет достигнут вторичный ток полной нагрузки.
Например, этот трансформатор 2500 кВА, 12,47 кВ на 600/347 В, показанный на фото:
Когда вторичный ток достигает 2406А, на первичной обмотке снимается показание напряжения, чтобы увидеть, какое входное напряжение требуется для достижения этого номинального тока полной нагрузки на вторичной обмотке. В этом случае техник прочитал бы 789,35 В.
.Выполнение простого расчета:
Важное примечание для инженеров-электриков:
Всегда считывайте измеренный% импеданса с паспортной таблички, а не с техпаспорта.На этом трансформаторе в Эдмонтоне, Альберта, на паспортной табличке было указано 6,33, в то время как в сопроводительной литературе указано только 6%. Это была небольшая разница, но при электрических оценках важна точность.
Типичные значения импеданса в процентах
Как инженеры-консультанты по электротехнике, это типичные уровни импеданса, которые мы видели на трансформаторах.
Простой неразрушающий тест импеданса трансформатора в процентах дает точные показания для расчета неисправностей.
Позвоните нам: Ванкувер (604) 283-2784 | Эботтсфорд (604) 283-2521 | Келоуна (778) 738-2172 | Эдмонтон (780) 851-5166 | Калгари (403) 879-4446
Электронная почта: [адрес электронной почты защищен]
© Copyright 2020, Paralynx Engineering Inc.
Все права защищены.
Калькулятор импеданса катушки индуктивности вычисляет полное сопротивление катушки индуктивности на основе значения индуктивности L индуктора и частоты f сигнала, проходящего через катушку индуктивности, в соответствии с формулой X L = 2πfL .
Пользователь вводит индуктивность L и частоту f, и результат будет автоматически рассчитан и показан. Результат импеданса, отображаемый выше, выражается в единицах Ом (Ом).
Вычисленное сопротивление — это мера сопротивления катушки индуктивности проходящему через нее сигналу. Катушки индуктивности имеют более высокое сопротивление для сигналов более высокой частоты; и, наоборот, они имеют меньшее сопротивление для сигналов более низкой частоты. Это означает, что сигналы с более низкой частотой будут иметь более низкий импеданс (или сопротивление), проходя через катушку индуктивности, в то время как сигналы с более высокой частотой будут иметь более высокий импеданс, проходящий через катушку индуктивности.Это означает, что в нашем калькуляторе выше, чем выше частота, которую вы вводите, тем выше будет импеданс. И чем ниже частота, которую вы вводите, тем меньше будет импеданс. Тот же эффект, что и частота сигнала, имеет и индуктивность катушки индуктивности. Чем выше индуктивность катушки индуктивности, тем выше сопротивление. И наоборот, чем ниже индуктивность, тем меньше сопротивление.
Рассчитайте время заряда, энергию и характеристическую частоту или импеданс, реактивное сопротивление и угловую частоту цепи резистор-конденсатор.
- Расчет энергии и времени зарядки
- Расчет импеданса и реактивного сопротивления
Расчет энергии и времени зарядки
Расчет импеданса и реактивного сопротивления
Результатов:
На этой странице:
- Калькулятор
- Формулы RC-цепей
- Формула постоянной времени
- Энергетическая формула
- Формула заряда
- Текущая формула
- Формула характеристической частоты
- Формула угловой частоты
- Формула импеданса
- Формула емкостного реактивного сопротивления
- Формула разности фаз
Цепь резистор-конденсатор, или RC-цепь, представляет собой цепь с последовательно соединенными резистором и конденсатором.Конденсатор в цепи накапливает энергию, а резистор изменяет скорость заряда и разряда конденсатора. Эти схемы чаще всего используются для фильтрации формы волны и используются для создания фильтров нижних, верхних и полосовых частот.
Схема, показывающая цепь резисторного конденсатора.
Формулы RC-цепей
ЦепиRC имеют несколько характеристик, включая постоянную времени, накопление энергии, заряд, импеданс, емкостное реактивное сопротивление, характеристическую частоту и угловую частоту.Расчет каждой из этих характеристик схемы можно выполнить по следующим формулам.
Формула постоянной времени
Постоянная времени, выраженная как tau (τ), — это время в секундах, в течение которого конденсатор в RC-цепи достигает заряда 63,2%. Формула для расчета постоянной времени:
Постоянная времени τ равна сопротивлению R в омах, умноженному на емкость C в фарадах. Конденсатор достигнет заряда 63,2% за τ, 86,5% за 2τ и 99,3% за 5τ.
Энергетическая формула
Энергия, запасенная в полностью заряженном конденсаторе в RC-цепи, может быть найдена по формуле:
Энергия E в джоулях равна емкости C в фарадах, умноженной на квадрат напряжения V, деленной на два.
Формула заряда
Максимальный заряд в цепи конденсатора резистора можно найти по формуле:
Заряд Q в кулонах равен емкости C в фарадах, умноженной на напряжение V.
Текущая формула
Максимальный ток RC-цепи можно найти с помощью закона Ома.Формула:
Ток I в амперах равен напряжению V, деленному на сопротивление R в омах.
Формула характеристической частоты
Характеристическая частота цепи, часто называемая обычной или циклической частотой, может быть найдена по следующей формуле:
Частота f в герцах равна 1, деленному на 2, умноженное на π, умноженное на сопротивление R в омах, умноженное на емкость C в фарадах.
Формула угловой частоты
Угловая частота цепи может быть найдена по формуле:
Угловая частота ω в радианах в секунду равна удвоенной π-кратной характеристической частоте f в герцах.
Формула импеданса
Импеданс RC-цепи можно найти с помощью нескольких формул:
Z = R + 1 jωC
| Z | = √ (R 2 + 1 (ωC) 2)
Где j — мнимая единица, Z — импеданс в омах, R — сопротивление в омах, C — емкость в фарадах, а ω — угловая частота в рад / с.
Формула емкостного реактивного сопротивления
Емкостное реактивное сопротивление RC-цепи можно найти по формуле:
Емкостное реактивное сопротивление X равно 1, деленному на угловую частоту ω, умноженную на емкость C.
Формула разности фаз
Эта формула выражает разность фаз между полным напряжением и полным током.
φ = тангенс -1 (- 1 ωCR)
φ — разность фаз, ω — угловая частота, C — емкость, R — сопротивление.
Калькулятор импеданса емкости вычисляет полное сопротивление конденсатора на основе значения емкости C конденсатора и частоты f сигнала, проходящего через конденсатор, в соответствии с формулой X C = 1 / (2πfC) .
Пользователь вводит емкость C и частоту f, и результат будет автоматически рассчитан и показан. Результат импеданса, отображаемый выше, выражается в единицах Ом (Ом).
Вычисленное сопротивление — это мера сопротивления конденсатора проходящему через него сигналу. Конденсаторы имеют более высокое сопротивление для сигналов более низкой частоты; и, наоборот, они имеют меньшее сопротивление для сигналов более высокой частоты. Это означает, что сигналы с более низкой частотой будут иметь больший импеданс (или сопротивление), проходящий через конденсатор, в то время как сигналы с более высокой частотой будут иметь меньшее или меньшее сопротивление, проходящее через конденсатор.Это означает, что в нашем калькуляторе выше, чем выше частота, которую вы вводите, тем ниже будет импеданс. И чем ниже частота, которую вы вводите, тем выше будет импеданс. То же влияние, что и частота сигнала, имеет и емкость конденсатора. Чем выше емкость конденсатора, тем меньше сопротивление. И наоборот, чем меньше емкость конденсатора, тем выше сопротивление.
Следующие ниже калькуляторы вычисляют различные базовые и единичные величины, обычно используемые инженерами энергосистем в системе анализа на единицу.
Известные переменные: Базовая трехфазная мощность, базовое линейное напряжение
Формулы и переменные
Изменение базовой формулы
Расчет блоков конденсаторов
Расчет двигателя на единицу
Где:
| Z BASE = Базовый импеданс |
| кВ LL = базовое напряжение (в киловольтах между фазами) |
| МВА 3Ф = Базовая мощность |
| A BASE = Base Amps |
| Z PU = Импеданс на единицу |
| Z PU GIVEN = дано на единицу импеданса |
| Z = полное сопротивление элемента схемы (т.е.е. Конденсатор, реактор, трансформатор, кабель и т. Д.) |
| X C = Импеданс конденсаторной батареи (Ом) |
| X C-PU = Группа конденсаторов на единицу импеданса |
| MVAR 3ɸ = 3-фазный номинал конденсаторной батареи |
| X ”= переходное реактивное сопротивление двигателя |
| LRM = Множитель при заторможенном роторе |
Система расчета на единицу — это метод, с помощью которого системные импедансы и величины нормализуются по разным уровням напряжения к общей базе.Устранение влияния переменных напряжений упрощает необходимые расчеты.
Чтобы использовать метод на единицу, мы нормализуем все системные импедансы (и проводимости) в рассматриваемой сети к общей базе. Эти нормированные импедансы называются импедансами на единицу. Любой импеданс на единицу будет иметь одинаковое значение как на первичной, так и на вторичной обмотке трансформатора и не зависит от уровня напряжения.
Сеть с импедансом на единицу может быть затем решена с помощью стандартного сетевого анализа.
Существует четыре основных величины: базовая МВА, базовая КВ, базовое сопротивление и базовый ампер. Когда любые два из четырех назначены, два других могут быть получены. Обычной практикой является присвоение базовых значений исследования MVA и KV. Затем вычисляются базовые амперы и базовые сопротивления для каждого из уровней напряжения в системе. Назначенный MVA может быть рейтингом MVA одного из преобладающих элементов системного оборудования или более удобным числом, например 10 МВА или 100 МВА. Выбор последнего имеет некоторое преимущество общности, когда проводится много исследований, в то время как первый выбор означает, что импеданс или реактивное сопротивление по крайней мере одного значимого компонента не нужно будет преобразовывать в новую базу.Номинальные линейные системные напряжения обычно используются в качестве базовых напряжений, а трехфазное питание используется в качестве базового питания.
Ресурсы для исследований в области энергетики
- Энергетика
- Приводы переменного тока
- Качество энергии
- Инженерные калькуляторы
- Калькулятор индуктивности
- Калькулятор емкости
- Калькулятор единиц
- Калькулятор трансформатора
- Калькулятор линейного реактора
- Расчет размеров токоограничивающего реактора
- Калькулятор коэффициента мощности
- Мотор-калькулятор
- Параметры формы сигнала
- Калькулятор небаланса напряжений
- Расчет делителя напряжения на 3 резистора
- Падение переменного напряжения с коэффициентом мощности
- Калькулятор резонанса
- Калькулятор запуска двигателя
- Калькулятор преобразования дельта-звезда
- Калькулятор фильтра гармоник
- Расчет коэффициента PT
- Энергетика
- Приводы переменного тока
- Качество энергии
- Инженерные калькуляторы
- — Калькулятор индуктивности
- — Калькулятор емкости
- — Калькулятор единиц
- — Трансформаторный калькулятор
- — Калькулятор линейного реактора
- — Расчет размеров токоограничивающего реактора
- — Калькулятор коэффициента мощности
- — Мотор-калькулятор
- — Параметры формы волны
- — Калькулятор небаланса напряжений
- — Расчет делителя напряжения на 3 резистора
- — Падение переменного напряжения с коэффициентом мощности
- — Калькулятор резонанса
- — Калькулятор запуска двигателя
- — Калькулятор преобразования треугольника в звезду
- — Калькулятор фильтра гармоник
- — Расчет коэффициента PT
РАСЧЕТ ИМПЕДАНСА ИСТОЧНИКА В ЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ
Данные от операторов энергосистемы (энергосистемы) часто предоставляются в одном из следующих форматов при заданном напряжении системы:
- Ток короткого замыкания, отношение X / R
- Короткое замыкание MVA, отношение X / R
- Фактическое полное сопротивление прямой последовательности
Часто нам нужно преобразовать данные из одного формата в другой.В этой статье подробно описано, как преобразовать из одного формата в другой, и представлены калькуляторы, которые могут выполнить эту операцию. Калькуляторы представлены в конце статьи.
Основы
Вот некоторые основы концепции единицы. Ключевым моментом является понимание того, что есть два основных параметра, которые необходимо знать при работе с единичными количествами. Это базовое напряжение и базовое МВА.
Базовое напряжение (кВ B ) : Часто в качестве базового напряжения используется напряжение питания.Если напряжение питания энергокомпании составляет 13,2 кВ, базовое напряжение, вероятно, будет 13,2 кВ, если не указано иное. Напряжения всегда линейные или фазо-фазные.
Базовая МВА или Базовая кВА : широко используемая база — 100 МВА. Но по желанию оператора можно выбрать любую другую базу.
БазакВА, базовый ток I B (A) и полное сопротивление базы Z B (Ом) задаются следующими уравнениями:
Теперь, когда определены базовые параметры, давайте посмотрим, как определяются параметры на единицу:
Если полное сопротивление желательно в омах, можно использовать следующую формулу:
Для преобразования тока короткого замыкания в МВА:
Где V ll — линейное напряжение, а V ln — линейное напряжение, при котором обеспечивается значение короткого замыкания.
Расчет отношения X / RКоэффициент X / R — это отношение индуктивности к сопротивлению электросети до точки повреждения. Вблизи крупных генерирующих станций и крупных подстанций это соотношение будет высоким. В конце длинных распределительных линий и для систем низкого напряжения коэффициент будет ниже. Если соотношение X / R равно 10, это означает, что индуктивность системы в 10 раз больше, чем сопротивление системы.
X / R может быть нанесен на плоскость импеданса с R на оси x и X на оси y.
Гипотенуза образованного таким образом треугольника дает полное сопротивление (Z) цепи. Различные уравнения, относящиеся к расчету отношения X / R:
Обратитесь к разделу «Компоненты последовательности», если вам нужна дополнительная информация о параметрах прямой, отрицательной и нулевой последовательности.
Калькулятор преобразования тока короткого замыкания Case1: Заданный ток короткого замыкания (кА), отношение X / RЕсли данные доступны в этом формате, преобразуйте ток короткого замыкания в эквивалентный MVA короткого замыкания, используя приведенные ниже уравнения.
Используйте линейное напряжение и трехфазный ток короткого замыкания на болтах для MVA
sc3 ø , а также линейное напряжение и ток короткого замыкания между фазой и землей для MVA sclg.После преобразования в эквивалентную MVA короткого замыкания используйте калькулятор, приведенный ниже для случая 2, чтобы получить полное сопротивление сети в формате R + jX.
Случай 2: Учитывая короткое замыкание, MVA, отношение X / RЧтобы получить параметры короткого замыкания, когда указаны значения MVA короткого замыкания и отношение X / R, используйте калькулятор ниже.
Случай 3: Заданный импеданс прямой и обратной последовательностиЧтобы получить параметры короткого замыкания, когда задано полное сопротивление прямой и обратной последовательности, используйте калькулятор ниже.
Дополнительная литература: компоненты последовательности
Внутреннее сопротивление усилителя мощности
| «Измерение выходного сопротивления с помощью нагрузки»: предположим, что имеется усилитель 100 Вт . Тогда выходное напряжение при половинной мощности составит P = 50 Вт = В 2/ R .Импеданс динамика = 8 Ом. В = √ ( P × R ) = √ (50 × 8) = 20 вольт. (Вы также можете использовать 10 В.) Подайте синусоидальное напряжение 1 кГц на вход усилителя, пока на выходе мы не получим 20 вольт. Теперь мы применяем «метод 90%», то есть когда устанавливаем выходное сопротивление R , пока не появится 90% напряжения холостого хода, в данном случае 18 вольт. Затем рассчитывается внутреннее сопротивление методом 90%: |
| Метод 90% R внутренний = R /9 |
| На выходе закрепите осциллограф, так как форма волны не должна показывать никаких искажений. Например, если R измеряется 1 Ом, то R внутренний = 0,11 Ом. |
Измерение и вычисление входного импеданса
| Измерение напряжения в точках IN или OUT: В 1 = Напряжение сигнала генератора (при R с = 0 Ом, то есть без последовательного резистора R с ) |
| Когда напряжение В 2 равно половине В 1 , тогда измеренное значение сопротивления R с ( R тест ) равно входу сопротивление Z нагрузка . |
Z нагрузка = входное сопротивление = сопротивление нагрузки = внешнее сопротивление = терминатор
| Входное и выходное сопротивление четырехполюсной сети можно определить путем измерения силы переменного тока в амперах и напряжения переменного тока в вольтах. Измерение входного импеданса обычно происходит следующим образом: напряжение измеряется на входных клеммах IN. Затем ток в цепи создается устройством, включенным последовательно с генератором сигналов.Для цепей с высоким входным сопротивлением ток очень мал и его трудно измерить. R = U / I . Поэтому для измерения цепей с высоким импедансом мы выбрали лучший метод. Он ставит во входную цепь последовательный резистор R s . Сначала измеряем вход устройства в точке IN с В 1 , напряжение переменного тока, если резистор R с = 0 Ом. Затем мы измеряем резистор серии R S , напряжение В 2 .Затем эти найденные значения V 1 , R s и V 2 вводятся в вышеуказанный калькулятор, чтобы найти входной импеданс, который необходимо рассчитать. Найдите подходящее значение сопротивления для измерения R s . Для типичного аудиооборудования это будет от 10 до 100 кОм. Вы можете использовать цифровой вольтметр вместо точки измерения IN и |
Влияние входного и выходного сопротивления студийного оборудования
для моста в аудиотехнике — Z источник Z нагрузка
Импедансы аналоговой аудиотехники для моста с импедансом
или моста по напряжению Z источник Z нагрузка
Выходное сопротивление Z вых = входное сопротивление Z дюймов / коэффициент демпфирования DF
Введите два значения , будет рассчитано третье значение.
Не пропустите.
Импеданс
Полное сопротивление цепи — это полное эффективное сопротивление потоку тока комбинацией элементов схемы.
Суммарное напряжение на всех 3 элементах (резисторах, конденсаторах и катушках индуктивности) записывается как
Чтобы найти это общее напряжение, мы не можем просто сложить напряжения В R , В L и В C .
Поскольку V L и V C считаются мнимыми величинами, мы имеем:
Теперь величина (размер или абсолютное значение) Z определяется как:
Фазовый угол
Угол θ представляет собой фазовый угол между током и напряжением.
Сравните это с фазовым углом, который мы встречали ранее на графиках y = a sin ( bx + c ).
Пример 1
Цепь имеет последовательное сопротивление «5 Ом» и реактивное сопротивление на катушке индуктивности «3 Ом». Представьте импеданс комплексным числом в полярной форме.
В этом случае `X_L = 3 Ω` и` X_C = 0`, поэтому `X_L- X_C = 3 Ω`.
Итак, в прямоугольной форме импеданс записан:
Используя калькулятор, величина для Z определяется как: `5,83`, а угол` θ` (разность фаз) определяется как: `30.@ `, как показано на схеме.
Представляя Z как комплексное число (в полярной форме), получаем:
Пример 2 (а)
Конкретная цепь переменного тока имеет резистор 4 Ом, реактивное сопротивление катушки индуктивности 8 Ом и реактивное сопротивление конденсатора 11 Ом. Выразите полное сопротивление цепи в виде комплексного числа в полярной форме.
В данном случае имеем: `X_L- X_C = 8-11 = -3 Ом`
Итак, `Z = 4 — 3j Ω` в прямоугольной форме.@ `.]
Интерактивный график RLC
Ниже представлен интерактивный график, с которым можно поиграть (это не статичное изображение). Вы можете изучить влияние резистора, конденсатора и катушки индуктивности на полное сопротивление в цепи переменного тока.
Действия для этого интерактивного элемента
- Во-первых, просто поиграйте с ползунками. Вы можете:
Перетащите верхний ползунок влево или вправо, чтобы изменить импеданс резистора, `R`,
Перетащите ползунок X L вверх или вниз, чтобы изменить импеданс индуктора,` X_L `и
Перетащите ползунок X C вверх или вниз, чтобы изменить импеданс конденсатора,` X_C`.- Обратите внимание на влияние различных импедансов на значения X L — X C и Z .
- Обратите внимание на влияние различных импедансов на θ, угол, который красная «результирующая» линия образует с горизонталью (в радианах).
- Рассмотрим графики напряжения и тока в интерактиве. Обратите внимание на величину отставания или опережения при смене ползунков.
- Что вы узнали, играя с этим интерактивом?
Пример 2 (б)
Обращаясь к примеру 2 (a) выше, предположим, что у нас есть ток 10 А в цепи.Найдите величину напряжения на
ii) индуктор ( V L )
iii) конденсатор ( V C )
iv) комбинация ( V RLC )
i) | V R | = | IR | = 10 × 4 = 40 В
ii) | V L | = | IX L | = 10 × 8 = 80 В
iii) | V C | = | IX C | = 10 × 11 = 110 В
iv) | V RLC | = | IZ | = 10 × 5 = 50 В
Импеданс R, C и L параллельно Калькулятор
[1] 2021/10/08 18:25 Уровень 30 лет / Инженер / Очень /
- Цель использования
- Схема
[2 ] 2021/09/17 04:50 До 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Полезно для выполнения расчетов, которые помогают мне понять мою домашнюю работу
[3] 2021 / 08/23 23:35 20 лет уровень / средняя школа / университет / аспирант / очень /
- Цель использования
- помог с заданием
[4] 2021/08/15 13:45 60 лет старый уровень или выше / пенсионер / очень /
- Цель использования
- Предварительные знания
- Комментарий / запрос
- параллельная цепь RCL.Две формулы для фазового угла дают одинаковую величину, но противоположный знак для угла.
[5] 2021.01.22 01:59 Уровень 20 лет / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- помогает проверить мои ответы на мои задания
[6] 2020/12/07 21:02 Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- цель двойной проверки моих ответов и лучшего понимания импеданса
[7] 2020/11/18 16:27 До 20 лет / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Понимание работы в колледже
- Комментарий / запрос
- Довольно полезно, как и я изучаю инженерное дело и изо всех сил пытаюсь учиться дома в условиях текущих ограничений Covid-19.Если бы шаги были включены, это тоже было бы очень полезно.
[8] 2020/10/26 08:08 До 20 лет / Старшая школа / Университет / аспирант / Полезно /
- Цель использования
- Двойная проверка ответов
- Комментарий / запрос
- Очень полезно использовать.
[9] 2020/10/23 03:22 50-летний уровень / учитель / исследователь / полезный /
- Цель использования
- проверка ответов на практические задачи
[10] 2020/07 / 25 16:54 Уровень 60 и старше / Инженер / Полезно /
- Цель использования
- хобби
Расчет импеданса на единицу и базовый импеданс
Расчет единичного и базового импеданса Веб-страница не работает, так как JavaScript не включен.Скорее всего, вы просматриваете с помощью веб-сайта Dropbox или другой ограниченной среды браузера.Следующие ниже калькуляторы вычисляют различные базовые и единичные величины, обычно используемые инженерами энергосистем в системе анализа на единицу.
Calculator-1
Известные переменные: Базовая трехфазная мощность, базовое линейное напряжение
Формулы и переменные
Изменение базовой формулы
Единичные расчеты конденсаторных батарей
00000 9273
000 9273
000 9273
Где:
Z BASE = Базовое сопротивление KV LL = Базовое напряжение (в киловольтах между фазами) MVA 3Ф = Базовая мощность A = Базовый ток Z PU = Импеданс на единицу Z PU ДАННЫЙ = Указанный на единицу импеданс Z = Импеданс элемента схемы (т.е.е. Конденсатор, реактор, трансформатор, кабель и т. Д.) X C = Импеданс блока конденсаторов (Ом) X C-PU = Импеданс блока конденсаторов 295 3 = 3-фазный номинал конденсаторной батареи X «= Субпереходное реактивное сопротивление двигателя LRM = Множитель заторможенного ротора Предпосылки
Система расчета на единицу — это метод, посредством которого системные импедансы и величины нормализуются по разным уровням напряжения к общей базе.Устранение влияния переменных напряжений упрощает необходимые расчеты.
Чтобы использовать метод на единицу, мы нормализуем все системные импедансы (и проводимости) в рассматриваемой сети к общей базе. Эти нормированные импедансы называются импедансами на единицу. Любой импеданс на единицу будет иметь одинаковое значение как на первичной, так и на вторичной обмотке трансформатора и не зависит от уровня напряжения.
Сеть с импедансом на единицу может быть затем решена с помощью стандартного сетевого анализа.
Существует четыре основных величины: базовая МВА, базовая КВ, базовое сопротивление и базовый ампер. Когда любые два из четырех назначены, два других могут быть получены. Обычной практикой является присвоение базовых значений исследования MVA и KV. Затем вычисляются базовые амперы и базовые сопротивления для каждого из уровней напряжения в системе. Назначенный MVA может быть рейтингом MVA одного из преобладающих элементов системного оборудования или более удобным числом, например 10 МВА или 100 МВА. Выбор последнего имеет некоторое преимущество общности, когда проводится много исследований, в то время как первый выбор означает, что импеданс или реактивное сопротивление по крайней мере одного значимого компонента не нужно будет преобразовывать в новую базу.Номинальные линейные системные напряжения обычно используются в качестве базовых напряжений, а трехфазное питание используется в качестве базового питания.
Расчет импеданса в OnScale | OnScale
Профили электрического импеданса являются одним из основных показателей для анализа характеристик преобразовательных устройств и обычно являются первым показателем, исследуемым при сравнении с экспериментальными данными.
Извлечение импеданса в зависимости от частоты — это очень простой процесс в OnScale.Традиционно это выполнялось путем ручного манипулирования хронологией в Review, однако теперь этот процесс стал намного проще с введением расчета импеданса в постпроцессоре.
Как рассчитать импеданс в OnScale
Чтобы рассчитать электрическое сопротивление устройства, вы должны убедиться, что вы настроили пьезоэлектрическое моделирование с активным и заземляющим электродами в правильном месте, чтобы создать разность потенциалов и, следовательно, заряд в материале.
Отсюда вы должны запросить хронологию в pout для сигналов напряжения и заряда на электродах для выполнения расчетов импеданса, например:
надуть электрод histname vq allПосле запуска моделирования вы можете рассчитать импеданс либо с помощью обзора, либо с помощью постпроцессора. Вот статья, в которой рассматриваются оба этих метода.
Теория
Три основных уравнения, используемых для расчета импеданса:
В уравнении 1 V — это напряжение, I — ток, а Z — полное сопротивление.Уравнение 2 показывает отношение заряда к току — производная заряда по времени, поэтому уравнение 3, показывающее интеграл заряда по времени, также верно.
Затем вычисляется частотная область электрического импеданса с использованием уравнения 4, которое делит БПФ напряжения на БПФ тока. Точки на графике электрического импеданса разделены небольшим шагом по частоте ∆f. Если вы назовете общее количество частотных точек на графике NF, уравнения 5, 6 и 7 покажут, как рассчитываются NF, ∆f и f MAX :
В OnScale размер N F составляет половину размера временных выборок N T (Найквист Терем).Шаг частоты в результате БПФ рассчитывается с использованием уравнения 6. Максимальная частота на графике электрического импеданса определяется путем взятия значения, обратного шагу по времени из временных диаграмм. Процесс БПФ обычно дополняет N T , чтобы обеспечить степень 2, 3 или 5 для эффективности (например, NT 1000 увеличивается до 1024 точек).
Когда добавляется заполнение нулями, как NF, так и ∆f изменяются для любой заданной временной истории. Если заполнение равно 3, NT увеличивается в 3 раза; то есть в сигнале временной области в три раза больше точек, но ∆t остается неизменным.Для приведенных выше уравнений NF будет в 3 раза больше; f MAX останется прежним, поскольку он зависит только от начального временного шага ∆t, который является постоянным; и ∆f уменьшится в 3 раза, так как NT увеличится на столько же.
Таким образом, несмотря на то, что теперь точек в 3 раза больше, шаг по частоте между точками уменьшается, что дает более плавный выходной сигнал в частотной области.
На рис. 1 показан пример истории заряда. На рисунках 2 и 3 показано сравнение БПФ с заполнением нулями и без него.
Если у вас есть вопросы, напишите нам на [email protected]!
Калькулятор импеданса Z, формула и таблица согласно IEC
Этот калькулятор импеданса вычисляет Z в переменных токах с учетом сопротивления и индуктивного сопротивления нагрузки.
Он также показывает формулу импеданса, используемую в этом инструменте, определение импеданса и таблицу импеданса трансформаторов в соответствии со стандартом IEC.
Формула для расчета импеданса:
Электрический импеданс (Z) — это полное сопротивление цепи переменному току. Импеданс измеряется в омах и может включать сопротивление (R), индуктивное реактивное сопротивление (XL) и емкостное реактивное сопротивление (XC). Емкостное реактивное сопротивление обычно не может быть представлено в вихретоковых испытаниях, поэтому этот термин не включается в уравнение.
Полный импеданс — это не просто алгебраическая сумма сопротивления и индуктивного реактивного сопротивления.Поскольку индуктивное реактивное сопротивление сдвинуто по фазе на 90 градусов с сопротивлением и, следовательно, его максимальные значения возникают в разное время, для расчета импеданса необходимо использовать векторную сумму. Это показано на изображении справа.
Если величина сопротивления представлена длиной горизонтальной линии, а величина индуктивного реактивного сопротивления представлена длиной вертикальной линии; тогда величина импеданса представлена длиной диагональной линии.
Поскольку линии образуют прямоугольный треугольник, теорему Пифагора можно использовать для определения длины (значения) линии импеданса.
Теорема Пифагора записана: c 2 = a 2 + b 2
Для этого приложения переменная a равна сопротивлению, b равно индуктивному сопротивлению, а c равно к импедансу. Тогда уравнение принимает следующий вид:
Z 2 = R 2 + X L 2
Когда это уравнение переписывается для решения относительно Z, уравнение импеданса появляется в представленной форме.
Где:
- X L = Индуктивное реактивное сопротивление (Ом)
- R = Сопротивление в Ом
- Z = Импеданс
054 Определение сопротивления Z:
понять электрический импеданс? Скорее всего, если вы уже затрагивали эту тему в прошлом, у вас будет некоторый жаргон, такой как фазоры, фазовые отношения и даже воображаемое сопротивление. Что все это значит?Не все инженеры-электрики родились в университете.Некоторые из нас просто играют с электроникой в свободное время и никогда не находят строгой математики, которую можно найти в колледже. Но это не означает, что понимание импеданса должно быть трудным. Если вы планируете работать с электронными устройствами, питаемыми от сети переменного тока, то вам нужно знать, каков импеданс и что он делает в цепи.
Лучший способ понять электрический импеданс — сравнить его с тем, с чем вы уже знакомы: сопротивление . И здесь мы собираемся предложить краткое изложение импеданса в предложении в нескольких словах:
Электрический импеданс — это всего лишь одна из форм сопротивления, которая зависит от частоты.
Вот. Вы можете уйти прямо сейчас и добавить еще одно слово в свой словарь по электротехнике или продолжить чтение. Говоря об импедансе, предоставляется форма сопротивления току в соответствии с рабочей частотой цепи. Но это еще не все.
Резисторы довольно легко работают в цепи постоянного тока; Они сопротивляются току, протекающему через металл определенного типа, например медь. Если вы добавите сопротивление 220 кОм в цепь постоянного тока, вы получите определенное уменьшение тока между одной стороной сопротивления и другой.Резисторы, как и другие нереактивные компоненты, могут меньше беспокоиться о таких вещах, как частота источника питания. Они просто будут продолжать делать то, что делают, все время сопротивляясь одной и той же силе тока.
Но что будет, если вы начнете работать с электроникой с питанием от переменного тока? В случае переменного тока это не просто 5 В, питающее цепь. Вместо этого у него есть новые переменные, которые следует рассматривать как конкретную частоту переменного тока. Здесь переменный ток движется вверх и вниз со скоростью 60 циклов в секунду (60 Гц).
Центральным моментом всего этого является то, что в электронике, питаемой от переменного тока, нужны не только нереактивные компоненты, такие как резисторы, чтобы противостоять току. Также необходимы компоненты, которые могут реагировать на изменения тока и частоты, такие как конденсаторы и катушки индуктивности; в противном случае ваша схема не будет работать должным образом. Сложите все это вместе, и вы можете почти думать об импедансе как о старшем брате сопротивления. Импеданс включает в себя как сопротивление, так и реактивное сопротивление. Или выражается в виде отношения:
Импеданс = Сопротивление + Реактивное сопротивление
Но что такое реактивное сопротивление?
Реактивное сопротивление бывает двух разных видов, в зависимости от того, какой реактивный компонент вы используете, к ним относятся:
Индуктивный балласт:
Вы увидите это в виде электромагнитов, которые изменяют магнитное поле в цепи, также называемой индуктор.Катушки индуктивности будут иметь низкий импеданс на низких частотах и высокий импеданс на высоких частотах.
Емкостное реактивное сопротивление:
Вы увидите это в виде электрического поля заряда между двумя проводящими поверхностями, также называемыми проводниками. Драйверы имеют высокий импеданс на низких частотах и низкий импеданс на высоких частотах.
Поместите резисторы, катушки индуктивности и конденсаторы в цепь переменного тока, и они не только будут иметь возможность противостоять электричеству, но также будут иметь возможность накапливать и отдавать энергию.В то время как резистор будет поддерживать постоянное сопротивление независимо от меняющихся условий, катушки индуктивности и конденсаторы изменят свое сопротивление в зависимости от частоты подаваемого на них сигнала. А когда конденсаторы и катушки индуктивности сопротивляются и накапливают / высвобождают энергию, тогда у вас есть показатель импеданса.
Стандартные единицы реактивного сопротивления:
Название префикса Сокращение Вес Эквивалентный Фарад .000000000001 F Нано фарад нФ 10 -9 0.000000001 F Микрофарад мкФ 10 -6 10 -3 0,001 F Кило Фарадио кФ 10 3 1000 F Таблица полных сопротивлений, рекомендованных в соответствии со стандартом IEC 5 для трансформаторов 955, в соответствии со стандартом 955 IEC 60076-5: 2000 «Силовые трансформаторы», рекомендуется минимальное сопротивление для трансформаторов
Сопротивление короткого замыкания при номинальном токе кВА Минимальное сопротивление короткого замыкания% Свыше 630 4.0 631 до 1250 5,0 1 251 до 2500 6,0 2501 до 63015 9501 6 301 до 25000 8,0 25001 до 40 000 10,0 40 001 до 063001 до 100000 12,5 Более 100000 > 12,5 Примечание 1: Значения для номинальной мощности более 100 000 кВА обычно при условии соглашения между производителем и покупателем.
Примечание 2: В случае однофазных блоков, подключенных для образования трехфазной батареи, значение номинальной мощности применяется к номинальной мощности трехфазной батареи.В отличие от других стандартов, таких как IEEE или AS, которые рекомендуют типичные значения, IEC рекомендует минимальные значения.
Поскольку это минимальные значения, это не означает, что вы, как проектировщик электрооборудования, можете выбрать очень высокие импедансы для своих трансформаторов. Например, IEC рекомендует минимальное сопротивление 4% Z для трансформатора на 300 кВА. Однако это не означает, что у вас может быть Z 6,5%. Хотя остановить это может некому, но% Z трансформатора прямо пропорционален стоимости, размеру и весу трансформатора.
Почему за трансформатор нужно платить больше, если его можно купить дешевле, уменьшив% Z? Единственный раз, когда вы выберете более высокое сопротивление для трансформатора, — это уменьшить ток повреждения в трансформаторе.
[kkstarratings]
3.3: Параллельный импеданс — разработка LibreTexts
Возможно, первым делом необходимо определить эквивалентные значения импеданса для некоторого набора параллельных компонентов. Напомним, что реактивное сопротивление, обратное реактивному сопротивлению, равно , восприимчивость ,
.\ [S = \ dfrac {1} {X} \ label {3.2} \]
, а полное сопротивление равно , проводимость ,
\ [Y = \ dfrac {1} {Z} \ label {3.3} \]
Единицы измерения указаны в сименсах. Также стоит отметить, что из-за разделения знаки меняются местами. Например, емкостная проводимость имеет угол +90 градусов, а если комплексная проводимость имеет отрицательный угол, то соответствующий импеданс является индуктивным.
«Правило проводимости» для параллельных комбинаций, изученное в случае постоянного тока, остается в силе для случая переменного тока, хотя мы обобщаем его для импедансов:
\ [Z_ {total} = \ dfrac {1} {\ dfrac {1} {Z_1} + \ dfrac {1} {Z_2} + \ dfrac {1} {Z_3} + \ dots + \ dfrac {1} { Z_N}} \ label {3.4} \]
Каждый из индивидуальных импедансов, представленных в уравнении \ ref {3.4} (т.е. \ (Z_1 \), \ (Z_2 \) и т. Д.), Может представлять простое сопротивление, чистое реактивное сопротивление или комплексное сопротивление. Кроме того, ярлык правила произведения суммы для двух компонентов также остается действительным для компонентов переменного тока:
\ [Z_ {total} = \ dfrac {Z_1 \ times Z_2} {Z_1 + Z_2} \ label {3.5} \]
Есть один особый случай, когда уравнение \ ref {3.5} может быть «проблемным», и это когда два импеданса состоят из чистого емкостного реактивного сопротивления и чистого индуктивного реактивного сопротивления, оба одинаковой величины.Эти два элемента фактически отменяют друг друга, оставляя знаменатель равным нулю и неопределенным результатом. Хотя теоретическая комбинация «взрывается» и приближается к бесконечности, в действительности она ограничена соответствующими сопротивлениями, такими как \ (R_ {катушка} \), и достигает некоторого конечного значения. Эта ситуация подробно изучается в главе 8, которая охватывает понятие резонанса.
Пример \ (\ PageIndex {1} \)
Определите полное сопротивление сети, показанной на рисунке \ (\ PageIndex {1} \).{\ circ} \ Omega \ nonumber \]
Такой результат может немного удивить проницательного. Обратите внимание, что общая величина больше, чем величина наименьшего компонента (индуктивность в \ (j12 k \ Omega \)). Этого никогда не было бы, если бы все три компонента были резисторами: результат должен был бы быть меньше, чем самый маленький элемент в группе.
Причина этого в том, что емкостное реактивное сопротивление частично компенсирует индуктивное реактивное сопротивление. Если правило произведения-суммы (Уравнение \ ref {3.{\ circ} \) или \ (j16 k \ Omega \). Размещение его параллельно с резистором 20 к \ (\ Omega \) (снова с использованием уравнения \ ref {3.5}) приводит к результату, вычисленному выше.
Диаграмма проводимости показана на рисунке \ (\ PageIndex {2} \). Векторное суммирование проводимости компонентов и сопротивлений хорошо проверено.
Значения отдельных компонентов:
\ [S_L = \ dfrac {1} {j 12k \ Omega} \ приблизительно — j 83.33E-6S \ nonumber \]
\ [S_C = \ dfrac {1} {- j 48k \ Omega} \ приблизительно j 20.{\ circ} S \ nonumber \]
В прямоугольной форме \ (Y_ {total} = 50E − 6 — j62.5E − 6 S \).
Рисунок \ (\ PageIndex {2} \): Диаграмма пропускной способности для сети, показанной на рисунке \ (\ PageIndex {1} \).Пример \ (\ PageIndex {2} \)
Определите полное сопротивление сети, показанной на рисунке \ (\ PageIndex {3} \), на частоте 10 кГц. Повторите это для частоты 1 кГц.
Рисунок \ (\ PageIndex {3} \): Схема для примера \ (\ PageIndex {2} \).Сначала найдите реактивные сопротивления при 10 кГц. Для индуктора находим:
\ [X_L = j 2 \ pi f L \ nonumber \]
\ [X_L = j 2 \ pi 10 кГц 680 \ mu H \ nonumber \]
\ [X_L \ около 42.73 \ Omega \ nonumber \]
А для конденсатора:
\ [X_C = — j \ dfrac {1} {2 \ pi f C} \ nonumber \]
\ [X_C = — j \ dfrac {1} {2 \ pi 10 кГц 470 nF} \ nonumber \]
\ [X_C \ приблизительно — j 33,86 \ Omega \ nonumber \]
Теперь используйте уравнение \ ref {3.4}, чтобы объединить элементы.
\ [Z_ {total} = \ dfrac {1} {\ dfrac {1} {Z_1} + \ dfrac {1} {Z_2} + \ dfrac {1} {Z_3}} \ nonumber \]
\ [Z_ {total} = \ dfrac {1} {\ dfrac {1} {j 42.73 \ Omega} + \ dfrac {1} {1.8k \ Omega} + \ dfrac {1} {- j 33.{\ circ} \ Omega \ nonumber \]
В прямоугольной форме это \ (14.68 — j161.9 \ Omega \). Поскольку реактивное сопротивление конденсатора является наименьшим из трех компонентов, оно преобладает над эквивалентным импедансом на этой частоте. Работая по формуле емкостного реактивного сопротивления в обратном порядке, можно показать, что реактивная часть \ (- j161.9 \ Omega \) может быть достигнута на этой частоте при использовании емкости 98,3 нФ. Это означает, что на частоте 10 кГц эта параллельная сеть имеет тот же импеданс, что и резистор 14,68 \ (\ Omega \), соединенный последовательно с резистором 98.Конденсатор 3 нФ. На любой другой частоте это уже не так, как будет показано ниже.
При 1 кГц частота уменьшается в десять раз. Следовательно, \ (X_L \) будет в десять раз меньше, или примерно \ (j4.273 \ Omega \). Далее \ (X_C \) будет в десять раз больше, или примерно \ (- j338.6 \ Omega \). Индуктивное реактивное сопротивление теперь будет преобладающим.
Новое сопротивление:
\ [Z_ {total} = \ dfrac {1} {\ dfrac {1} {Z_1} + \ dfrac {1} {Z_2} + \ dfrac {1} {Z_3}} \ nonumber \]
\ [Z_ {total} = \ dfrac {1} {\ dfrac {1} {j 4.{\ circ} \ Omega \ nonumber \]
В прямоугольной форме это \ (10.4E − 3 + j4.328 \ Omega \). Результат индуктивный, противоположный тому, что мы видели на частоте 10 кГц. Используя формулу индуктивного реактивного сопротивления, можно показать, что на частоте 1 кГц эта параллельная сеть имеет такое же полное сопротивление, как резистор 10,4 миллиом, соединенный последовательно с катушкой индуктивности 689 \ (\ mu \) H.
Расчет импеданса линии передачис помощью Altium Designer 20
Винсент Мазур| & nbsp Создано: 25 февраля 2020 г. & nbsp | & nbsp Обновлено: 12 апреля 2021 г.
Введение
Многие современные печатные платы работают с высокоскоростными сигналами, поэтому многие дорожки на типичной плате будут действовать как линии передачи.Объедините это с повышенными тактовыми частотами и скоростью передачи данных, и в результате возникнет критическая проблема для высокоскоростного проектирования. Пренебрежение этой динамикой может подорвать разработку продукта, поставив под угрозу производительность, энергопотребление, соответствие требованиям EMC / EMI и многое другое, что приведет к задержкам в циклах проектирования и появлению пробелов, которые могут быть использованы вашими конкурентами.
Оттачивайте свои навыки высокоскоростного проектирования, присоединяясь к нам, когда мы обсуждаем типичные линии передачи, встречающиеся в сегодняшних проектах, переменные печатной платы, влияющие на импеданс, а также способы создания, расчета и проектирования линий передачи в Altium Designer.Вы узнаете, как максимально использовать встроенный двигатель SIMBEOR® от Simberian для создания профилей импеданса для линий передачи в ваших проектах. Мы начнем со стандартной модели для расчета импеданса линии передачи и покажем, как включить расчет импеданса в качестве правил проектирования для функций интерактивной трассировки в Altium Designer.
Профили импеданса
Мы начнем с обсуждения текущих тенденций развития электроники. Представляем простую концепцию модели линии передачи и то, как полное сопротивление этих линий передачи намеренно или случайно проявляется на печатных платах.Мы собираемся продолжить обсуждение очень важной темы, называемой обратным током. Затем мы собираемся рассмотреть конструкцию печатной платы, некоторые ключевые правила проектирования печатной платы и то, как они влияют на импеданс.
Современные тенденции развития электроники
Всем известно, что с каждым годом все становится быстрее, и от нас ожидается, что мы сделаем это в более короткие сроки, занимая меньше места и потребляя меньше энергии. Прекрасным примером является скорость передачи данных Ethernet, которая в наши дни резко выросла, достигнув 100 гигабит и даже больше.В то же время мы видим рост тактовой частоты. Это увеличение приводит к уменьшению на фронтов, сигнала и на более коротких времен нарастания и спада.
Скорость передачи данных по Ethernet по годам
Импеданс линии передачи Модель
Линия передачи образована парой проводников, по которым проходит волна тока. Ток, передаваемый по линии передачи, создает электрическое поле и магнитное поле.Примеры линий передачи — это кабель, который вы используете для спутникового или наземного кабельного телевидения. Все проводники имеют некоторое сопротивление ( R, ), но это не единственный фактор, определяющий импеданс. Поскольку два проводника, образующие линию передачи, образуют замкнутый контур, линия имеет некоторую индуктивность ( L ). Затем, когда мы смотрим на рисунок, показывающий расстояние между сигнальной линией и ее обратным путем, две части линии разделены диэлектриком, который создает некоторую емкость ( C ).Наконец, диэлектрик между двумя участками проводника имеет свою собственную проводимость по постоянному току и потери ( G ), что снижает энергию, переносимую сигналом в линии передачи. Это основные факторы, влияющие на работу линии передачи.
Когда мы говорим об импедансе линии передачи на печатной плате, мы часто видим микрополоски с проводником на верхнем слое и плоскостью возврата на соседнем слое, разделенных диэлектрической подложкой.На приведенной выше принципиальной схеме значения R, L, C и G не являются реальными элементами схемы, они распределены по длине линии передачи. Эти термины относятся к значениям на единицу длины, поэтому мы используем модель распределенной цепи для описания того, как сигнал распространяется по линии передачи. По мере распространения сигнала обратный ток индуцируется вдоль линии в обратную плоскость как ток смещения. Это схематично показано ниже.
Когда у вас есть несоответствие импеданса на каждом конце линии передачи, вы получаете отражения, которые можно увидеть на изображениях осциллографа.В левой части примера изображения ниже показан исходный сигнал, который мы ожидаем увидеть на приемнике, а правая часть показывает пример реального сигнала, который может быть виден на приемнике. На приемнике возникает много отражений из-за несоответствия импеданса, но есть и другие источники искажения сигнала в печатной плате, которые можно увидеть при измерениях реальных сигналов.
Уравнение импеданса линии передачи
Из приведенной выше модели с элементами распределенной цепи уравнение для полного сопротивления линии передачи составляет:
Идеальная линия передачи для печатной платы и контакты имеют сопротивление от 40 до 120 Ом.Следует помнить, что, поскольку мы используем постоянное поперечное сечение или так называемую однородную линию передачи , это важное соотношение является постоянным по всей линии, и нам нужно беспокоиться только об импедансе, а не о длине линии. .
Вот пример правил маршрутизации. Я помню, когда я смотрел правила маршрутизации. Часто это была просто компоновка посадочного места, возможно, некоторые стратегии выхода. Что ж, в наши дни, мы все должны беспокоиться о дифференциальном импедансе, несимметричном разносе импеданса между дифференциальными парами и высокоскоростных периодических сигналах.
Типы линий передачи в печатной плате
Давайте поговорим еще немного о типах линий передачи, которые мы видим на сегодняшних печатных платах:
- Однородные линии передачи имеют поперечное сечение линии передачи, а также среду, в которой оно постоянно по всей ее длине.
- Компланарные устройства имеют сигнальный и обратный тракты на одном слое с диэлектриком под ним.Круговой характер магнитных полей зависит от диэлектрика, а также диэлектрической проницаемости воздуха.
- У нас аналогичная ситуация с микрополосковой линией . Вот где проводник находится на внешнем слое, а обратный путь — это земля.
- Фактически вы можете погрузить эту микрополоску, одинаково встроенную в этот диэлектрик, и получить улучшенные характеристики с помощью встроенной микрополосковой линии . Мы видим это на третьем изображении сверху.
- Симметричная полосковая линия — это место, где проводник идеально центрирован в диэлектрике и окружен двумя заземляющими плоскостями. Это отличная линия передачи, но их сложно изготовить, потому что вы действительно хотите, чтобы они были точно равноудаленными.
- Асимметричная полосковая линия имеет одну сторону диэлектрика, которая больше другой. Итак, я снова упоминал об этом ранее, но опять же, это важная концепция, которую мы хотим использовать эти однородные линии передачи, у которых поперечное сечение одинаково по длине.
Теперь мы упоминали здесь симметричную линию передачи . — это прямой и обратный проводники одинаковой длины. У них одинаковая форма и сечение. Примером тому является дифференциальная пара. И, конечно же, мы сталкиваемся с тем, что оба они реализованы на печатных платах.
Обратный ток
Поговорим об обратном токе! У нас есть две настройки на 1 кГц и 10 МГц.
Начнем с представления обратного тока на частоте 1 кГц.Ток ищет путь наименьшего сопротивления. В случае 1 кГц длинные волны приводят к прямолинейному пути из-за емкостного реактивного сопротивления.
Когда мы переходим к более высоким частотам, как видно из сигнала 10 МГц, путь приближается к этому сигнальному пути также из-за емкостного реактивного сопротивления. Как составляющая импеданса, когда мы смотрим на их взаимосвязь, мы сразу видим, что по мере увеличения этой частоты преобладает емкостная составляющая, и эти типы конструкций в большинстве случаев будут приводить к более низкому импедансу.Вот почему, когда частота повышается, мы увидим, что ответный сигнал, который на самом деле является электромагнитным полем, очень, очень близко расположен к этому проводнику.
Теперь давайте посмотрим на различия между однородными линиями и гетерогенными линиями передачи .
Разрывы в опорном слое не рекомендуется! Маршрутизация через зазор в плоскости отсчета создает большую индуктивность контура в линии передачи, что означает, что линия может испытывать больше перекрестных помех и создавать больше электромагнитных помех.
Мы видим на однородной линии передачи, что обратный ток течет, как и следовало ожидать, вблизи проводника. Однако на неоднородной линии передачи слот заставляет сигнал идти обходным путем, чтобы вернуться к этому источнику. Например, этот обратный маршрут может проходить через некоторые другие сигнальные проводники, и это создает перекрестные помехи . Вы также можете создать отражений возле края прорези, если прорезь достаточно длинная. Настоятельно рекомендуется избегать любых типов прорезей или любых других разрывов на обратном пути.Я знаю, что это простая ошибка, которую я совершал в прошлом, действительно приводила к странному поведению.
Как геометрия проводника влияет на импеданс
Теперь давайте поговорим о типичных правилах проектирования и о том, как они влияют на импеданс. Мы обсудим четыре параметра: Ширина проводника , Толщина диэлектрика , Диэлектрическая постоянная и Толщина меди .
Ширина проводника — увеличение на сильно зависит от уменьшения импеданса.
Толщина диэлектрика — увеличивается на , что обычно увеличивает импеданс.
Диэлектрическая постоянная — средняя зависимость , поскольку ее влияние не так велико, как толщина. По мере увеличения диэлектрической проницаемости сопротивление немного уменьшается.
Вес меди или толщина меди — Существует меньшая зависимость от толщины меди, поскольку в линии передачи присутствует индуктивность, но, как правило, она не так велика, как емкость.По мере увеличения толщины меди сопротивление немного уменьшается.
Некоторые грубые приближения
Есть несколько полезных приближений, которые помогут быстро настроить линии передачи на импеданс 50 Ом. Правила, показанные ниже, являются грубым приближением, и вы всегда должны проверять приближение с помощью калькулятора импеданса или решателя поля.
Сначала рассмотрим микрополоску . Если ширина следа равна двум умноженным на , высотой диэлектрика (для FR4 Dk от 4 до 4.6) полное сопротивление будет примерно 50 Ом .
Если вы используете симметричную полосковую линию на FR4, импеданс будет примерно 50 Ом, если высота диэлектрика , в два раза умноженная на , ширины проводника и для FR4.
Расчет импеданса линии передачи в Altium Designer
Мы рассмотрели предысторию и теорию линий электропередачи. Теперь мы посмотрим, как мы на самом деле проводим расчет импеданса линии передачи в Altium Designer. Layer Stack Manager (LSM) — это ваш концентратор для определения профилей импеданса. Очень важно, чтобы панель свойств была открыта при использовании LSM, поскольку он активно используется в этих операциях. После того, как вы определите свой стек слоев, вы должны определить свои профили импеданса на вкладке LSM. Вы можете думать о профиле импеданса как об определении определенного типа линии передачи. Например, когда мы увидели спецификацию USB, мы увидели, что существуют определенные линии дифференциальной передачи с сопротивлением 90 Ом.Мы можем создать профили дифференциального импеданса 90 Ом, чтобы обеспечить создание соответствующих трасс для вашей конструкции.
В этом случае мы создали несимметричный сигнал с обратным каналом по умолчанию с именем по умолчанию S50 (несимметричный сигнал 50 Ом). Давайте подробнее рассмотрим определение профиля импеданса в проекте. Когда вы создаете свои профили импеданса, вы выделяете различные слои для изменения параметров слоя с помощью панели свойств, чтобы уточнить импеданс для обеспечения выравнивания со стеком слоев.
Затем вы можете применить эти профили импеданса к своему проекту и индивидуальным правилам проектирования. Прежде чем мы это сделаем, мы хотим поговорить о типах линий передачи, которые в настоящее время поддерживаются в Altium Designer.
Типы линий передачи, доступные в Altium Designer
Несимметричные конструкции имеют проводник с обратным путем. У вас может быть обратный путь на другом слое или на том же слое, который называется копланарным.Обратите внимание, что учитывается даже паяльная маска, поскольку она обладает диэлектрическими свойствами, которые могут влиять на распространение сигнала. У нас также есть компланарные несимметричные структуры, в которых обратный путь находится в одном слое по обе стороны от проводника.
Точно так же у нас есть дифференциальная структура и копланарные дифференциальные сигналы.
Настройка профиля импеданса линии передачи
Когда вы выделяете свой слой в своем профиле импеданса, вы сразу видите составляющие его слои в указанном профиле.В данном случае у нас есть по одному диэлектрику 1 и 2 с внутренним заземлением и питанием с обеих сторон. Импеданс на этом слое будет автоматически рассчитан с этим профилем, и вы увидите поперечное сечение, которое будет генерировать система. Когда вы настраиваете импеданс, вы можете определить значение импеданса, а целевой допуск дает вам больше возможностей для маневра, чтобы иметь ширину трасс и топологию, которая будет лучше всего работать для вашего проекта. Результат мы видим в параметрах линии передачи в Панели свойств.Если мы хотим, мы можем позволить системе просто генерировать трассировку, которую она рекомендует для данных параметров, или мы можем трассировать ширину, которую мы хотим для нашего слоя. Например, определите ширину следа 0,1 и нажмите кнопку f x , и он рассчитает все параметры.
Назначьте профиль импеданса цепям
После завершения профилей импеданса вы можете перейти к правилам проектирования, чтобы назначить профили импеданса связанным цепям.Здесь вы убедитесь, что созданный вами профиль импеданса используется во время трассировки, чтобы ваши трассы имели правильный импеданс.
Что действительно приятно в использовании этих правил и профилей импеданса, так это то, что если вы решите, что вам нужно изменить профиль импеданса, вы измените профиль один раз в диспетчере стека слоев, и он будет отражен во всех связанных правилах, которые на него ссылаются. Это невероятно мощно по сравнению с существующими подходами, в которых используются внешние калькуляторы и индивидуально аннотируются, потому что у вас есть возможность быстро и единообразно обновлять данные.Лучше всего, что функция retrace route обновит любые существующие маршруты до надлежащей толщины трассы для вашего нового определения профиля импеданса.
В окне редактора правил и ограничений для печатных плат вы можете назначить профиль импеданса для определенных цепей, перейдя в раздел Routing -> Width и создав новое правило. В рамках этого нового правила вы можете выбрать конкретную цепь или использовать запрос, чтобы указать несколько цепей и назначить этой цепи профиль импеданса.
Вы также можете организовать группы цепей в классы цепей (в том числе в классы цепей дифференциальных пар), что позволит вам применять профили импеданса к группам цепей сразу.Это поможет вам оставаться продуктивным, так что вам не нужно просматривать длинный список трассировок и применять к каждой из них одно и то же правило проектирования.
Если вам надоели другие калькуляторы импеданса или вы все еще занимаетесь формулами импеданса вручную, попробуйте использовать функции расчета импеданса линии передачи в Altium Designer®. У вас будет полная платформа для проектирования, макета, маршрутизации и проверки правил в одной программе.
