Расчет соединения катушек индуктивности смешанное: 16. Смешанное соединение резистора, катушки индуктивности и конденсатора. — Мир Антенн

Содержание

16. Смешанное соединение резистора, катушки индуктивности и конденсатора.

Рис. 16.1.

Рассмотрим двухполюсник, состоящий из смешанного соединения резистора, катушки индуктивности и конденсатора (рис. 16.1). Он подключен к источнику синусоидального напряжения, амплитуда которого постоянна.

Будем понимать эту цепь как модель энергетической системы, состоящей из источника напряжения е, соединенного линией электропередач с нагрузкой в виде последовательно соединенных резистораRи катушки индуктивностиL. Такая модель выбрана, потому что в энергетике большую долю нагрузки составляют электродвигатели и трансформаторы, которые необратимо отбирают электрическую энергию из сети (так, как это делает резистор), а также периодически запасают энергию в магнитном поле своих индуктивностей и отдают ее обратно в цепь (так, как это делает катушка индуктивности).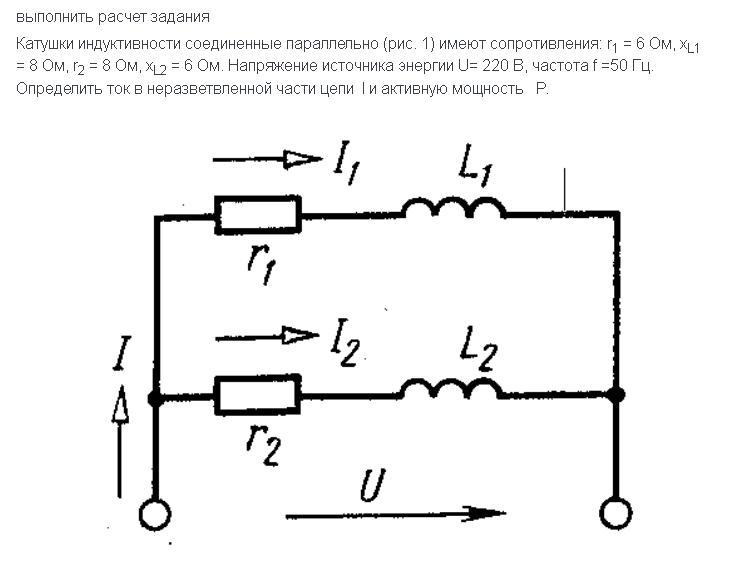

Емкость С рассчитаем так, чтобы токIв линии электропередач был минимальным. Это позволит свести к минимуму потери энергии в проводах линии электропередач, соединяющей источник энергии и нагрузку (см. п.14, а также лабораторную работу №3 по общей электротехнике). Такой режим часто называют компенсацией реактивной мощности нагрузки.

Согласно определению полной проводимости двухполюсника (см. п.13),

то есть, при заданном напряжении Uминимум токаIдостигается при минимуме полной проводимостиy. Найдем эту проводимость, используя эквивалентные преобразования сопротивлений.

Комплексное сопротивление последовательно включенных резистора и катушки будет равно сумме комплексных сопротивлений этих элементов (см. п. 13):

Комплексная проводимость ветви с резистором и катушкой будет обратна к комплексному сопротивлению этой ветви:

При параллельном соединении проводимости складываются, поэтому

Чтобы найти у, удобно выделить действительную и мнимую частьY. Сделаем это, умножив числитель и знаменатель дроби на выражение, комплексно сопряженное знаменателю:

Используем принятые в электротехнике обозначения: – активная проводимость двухполюсника,– реактивная проводимость двухполюсника (см. п.13).

Согласно определению полной проводимости (см. п.13).

Так как gне зависит от емкости конденсатораС, тоукак функция отСдостигает минимума при. Отсюда получаем формулу для емкости конденсатора:

Обратим внимание на то, что – это условие фазового резонанса (см. п.15). Так как при этом сопротивление двухполюсника максимально, то это в данном случае фазовый резонанс совпадает с резонансом токов.

Построим векторную диаграмму напряжений и токов. Вначале нарисуем комплекс напряжения (рис. 16.2). Его фазу будем считать нулевой, поэтому векторнаправим вдоль действительной оси. Затем найдем сдвиг фаз между напряжением и током ветвиRL(см. пример п. 13):- это угол между действительной осью и вектором, изображающим комплекс тока ветвиRL.

Найдем значение тока ветви RL:- это длина вектора, изображающего комплекс тока ветвиRL(в некотором графическом масштабе).

Нарисуем на диаграмме комплекс тока ветви RL (рис. 16.2).

Ток всего двухполюсника равен сумме тока ветвиRLи тока конденсатора:. Ток конденсатора сдвинут по фазе относительно напряжения на. Нарисуем комплекс тока конденсатора и сложим его с комплексом тока ветви

RL, получим ток (рис. 16.3).

Рис. 16.2.

Напряжение и ток ветви RL.

Рис. 16.3. Векторная диаграмма напряжения и тока смешанного соединения RLC (частичная компенсация реактивного тока).

Рис. 16.4. Полная компенсация реактивного тока (резонанс токов).

На рис. 16.3 видно, что наличие в цепи тока конденсатора приводит к уменьшению тока в линии электропередачпо сравнению с током нагрузки. На рис. 16.4 показан случай, когда токподобран так, что он обеспечивает минимум тока.

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

Метод свёртывания цепи

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

I = I1 = I2 =…= IN (2),
U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

Rэкв = (U1 + U2 + …+ UN)/I,
Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

Параллельное соединение

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2 + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

Rобщ = U/(I1 + I2 + …+ IN),
1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

R1 = 1Ом,
R2 = 2Ом,
R3 = 3Ом,
R4 = 6Ом,
R5 = 9Ом,
R6 = 18Ом,
R7 = 2,8Ом,
U = 32В.

Электрическая схема

Из закона Ома имеем:

I = U/R,

где R – суммарное сопротивление всех приборов.

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

Эквивалентная схема

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
R4,5,6 = 3Ом,
Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.

На участке R2,3 напряжение находим по формуле:

U2,3 = I2,3·R2,3,
U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

I2 = U2 / R2,
I2 = 4,8В / 2Ом = 2,4А,
I3 = U3 / R3,
I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

I2,3 = I2 + I3,
I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

U4,5,6 = I4,5,6·R4,5,6,
U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

I4 = U4 / R4,
I4 = 12В / 6Ом = 2А,
I5 = U5 / R5,
I5 = 12В / 9Ом » 1,3А,
I6 = U6 / R6,
I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Видео

Оцените статью:

Соединение источников питания | Электрикам

К химическим источникам питания относятся источники эдс, в которых энергия протекающих химических реакций преобразуется в электрическую энергию.

К химическим источникам относятся гальванические элементы, аккумуляторы и «батарейки» и пр.

Необходимость соединения элементов питания возникает в том случае, когда требуемое напряжение и ток потребителя превышают соответствующие значения источника питания.

Важным условием соединения химических источников питания в единую цепь, является равенство их эдс и внутреннего сопротивления.

Существует три способа подключения химических источников питания:

- последовательно;
- параллельно;
- смешанно.

Соединенные между собой любым способом источники питания образуют так называемую батарею, рассматриваемую в цепи как единое целое.

Последовательное соединение источников питания

При последовательном подключении химических источников питания отрицательный полюс одного источника соединяется с положительным полюсом следующего источника и т.д. Положительный и отрицательный полюсы последнего и первого источника батареи подключаются к нагрузке внешней цепи (рисунок 1).

Рис. 1. Последовательное соединение источников питания

Общая эдс батареи при последовательном соединении химических источников питания равна сумме эдс всех входящих в нее элементов

Если учесть, что эдс всех источников одинаковая, предыдущее выражение может быть записано в виде

где E_i – эдс каждого источника питания в батарее.

При последовательном соединении внутренне сопротивление полученной батареи будет равно сумме сопротивлений каждого источника питания

или

где R_i – внутреннее сопротивление каждого источника питания в батарее.

При последовательном соединении источников питания, емкость батареи будет равна емкости каждого из источников питания.

Последовательное соединение химических источников питания применяется в том случае, когда ток нагрузки не превышает номинальный ток одного элемента, а напряжение – больше эдс одного источника.

Параллельное соединение источников питания

При параллельном соединении положительные полюсы источников питания соединяются в один общий узел, а отрицательные – в другой узел (рисунок 2).

Рис. 2. Параллельное соединение источников питания

При данном способе соединения эдс батареи равна эдс одного любого источника, включенного в ее состав

где E_i – эдс каждого источника питания в батарее.

Внутреннее сопротивлении батареи уменьшается во столько раз, сколько источников входит в ее состав, и вычисляется по формуле

где R_i – внутреннее сопротивление каждого источника питания в батарее.

Параллельное соединение химических источников питания применяется в том случае, когда напряжение потребителя равно напряжению одного источника питания, а сила тока потребителя (нагрузки) значительно превосходит разрядный ток источника.

Смешанное соединение источников питания

При смешанном соединении элементы объединяются в группы последовательно соединенных элементов с равным числом источников питания. Положительные контакты каждой группы источников питания соединяются в один общий узел, а отрицательные – в другой узел (рисунок 3).

Рис. 3. Смешанное соединение источников питания

Смешанное соединение применяется тогда, когда необходимо обеспечить нагрузку напряжением и током, большим чем у входящих в состав батареи источников питания.

Параллельное соединение конденсатора и катушки индуктивности. Понятие о резонансе тока

Составитель: Н.Н. Муравлева

ИССЛЕДОВАНИЕ ВЫПРЯМИТЕЛЬНОГО ДИОДА. ПРИНЦИП ДЕЙСТВИЯ P-N ПЕРЕХОДА. Методические указания к самостоятельной виртуальной практической работе по дисциплине «Электротехника и электроника» для студентов всех

Подробнее Резонанс «на ладони».
Резонанс «на ладони». Резонансом называется режим пассивного двухполюсника, содержащего индуктивные и ёмкостные элементы, при котором его реактивное сопротивление равно нулю. Условие возникновения резонанса
Подробнее С.А. Иванская ЭЛЕКТРОТЕХНИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКОГО КРАЯ ГОУ СПО «Минераловодский колледж железнодорожного транспорта» С.А. Иванская ЭЛЕКТРОТЕХНИКА Методические рекомендации по освоению теоретического материала и
Подробнее А.С. КАЛИНИН ЭЛЕКТРОТЕХНИКА
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технологический университет» МИРЭА Филиал МИРЭА в г. Фрязино Кафедра общенаучных дисциплин
Подробнее РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА Методические указания к практическим занятиям для студентов специальности 464 «Электропривод
Подробнее Виртуальный практикум
Федеральное агентство по образованию «Уральский государственный технический университет УПИ имени первого Президента России Б. Н. Ельцина» В.С. Проскуряков, С.В. Соболев ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ СИНУСОИДАЛЬНОГО
Подробнее «КРАСНОДАРСКИЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Государственное бюджетное профессиональное образовательное учреждение Краснодарского края «КРАСНОДАРСКИЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ» Учебно-методический кабинет Хамула А.А. МЕТОДИЧЕСКИЕ УКАЗАНИЯ к расчетно-графической
Подробнее ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ 1/63
ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ 1/63 1 Закон Ома в комплексной форме основан на символическом методе и справедлив для линейных цепей с гармоническими напряжениями и токами Этот закон следует из физической
Подробнее Тема 4.2. Цепи переменного тока
Тема 4.. Цепи переменного тока Вопросы темы.. Цепь переменного тока с индуктивностью.. Цепь переменного тока с индуктивностью и активным сопротивлением. 3. Цепь переменного тока с ёмкостью. 4. Цепь переменного
Подробнее Лабораторная работа 5 Резонанс напряжений
Лабораторная работа 5 Резонанс напряжений В механической системе онанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания
Подробнее 10. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
44 0 ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕКИЙ ТОК 0 Основные понятия и определения Переменным называется ток, который с течением времени изменяет свою величину Квазистационарным называется переменный ток, который во всех
Подробнее 1. Основные положения теории
. Основные положения теории…. Предварительная подготовка… 5 3. Задание на проведение эксперимента… 8 4. Обработка результатов экспериментов. .. 3 5. Вопросы для самопроверки и подготовке к защите
Подробнее «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
1А Лист 1 из 25 2А Лист 2 из 25 1. Паспорт фонда оценочных средств В результате освоения учебной дисциплины Электротехника обучающийся должен обладать предусмотренными ФГОС по специальности 11.02.01 Радиоаппаратостроение,
Подробнее ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Тамбовский государственный технический университет»
Подробнее ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ФЕДЕРАЛЬНОЕ АГЕНТСТО ПО ОБРАЗОАНИЮ Государственное образовательное учреждение высшего профессионального образования «Пензенский государственный университет» ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ Методические указания
Подробнее Лекция 4 ПЕРЕМЕННЫЙ ТОК
Сегодня: среда, 18 сентября 213 г. Лекция 4 ПЕРЕМЕННЫЙ ТОК Содержание лекции: 1. Сопротивление в цепи переменного тока 2. Емкость в цепи переменного тока 3. Индуктивность в цепи переменного тока 4. Закон
Подробнее ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Министерство образования Республики Беларусь Учреждение образования «Гомельский государственный университет имени Франциска Скорины» ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРОВЕРОЧНЫЕ ТЕСТЫ Для студентов первого курса
Подробнее Исследование резонанса токов
1 Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 447 Курортного района Санкт-Петербурга Исследование резонанса токов (виртуальная лабораторная работа) Подготовил
Подробнее Колебательные контуры
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Мордовский Государственный университет им. Н.
Подробнее Лабораторная работа 2-32
Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре. Цель работы:
Подробнее Тема 1. Линейные цепи постоянного тока.
МЕТОДИЧЕСКОЕ УКАЗАНИЕ 2 системы и технологии» Тема 1. Линейные цепи постоянного тока. 1. Основные понятия: электрическая цепь, элементы электрической цепи, участок электрической цепи. 2. Классификация
Подробнее ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
Федеральное агентство по образованию Уральский государственный технический университет УПИ имени первого Президента России Б.Н. Ельцина В.В. Муханов, А. Г. Бабенко ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР Учебное
Подробнее Как рассчитать сердечник и витки самодельных катушек индуктивности > Флэтора
Умный дом — создаем автономную систему
Перечень функций которые выполняет умный дом, варианты применяемого оборудования, а также проектирование умного дома.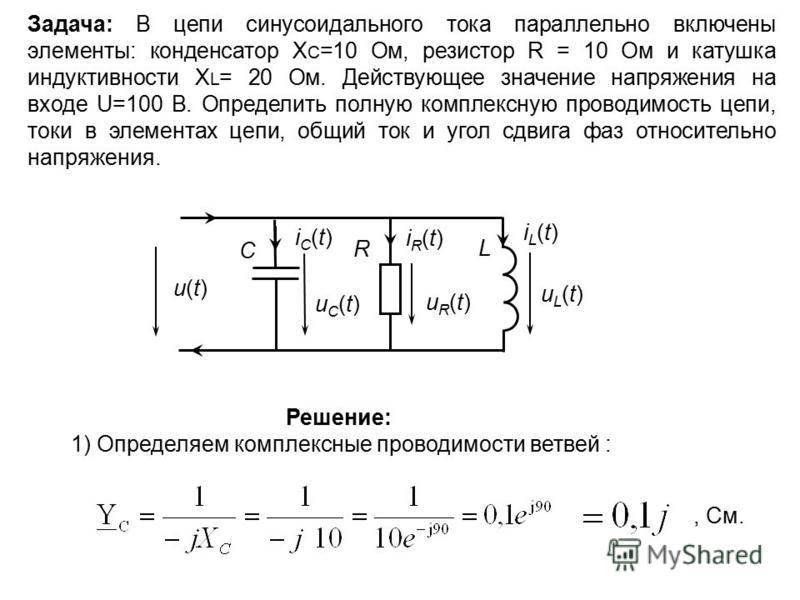 Как работает система….
02 05 2021 18:46:21
Защита IP: стандарт по ГОСТ (степени защит)
От чего защищается электрооборудование. Государственный стандарт ( Г О С Т) степеней защиты IP. Интерпретация кодов. Применение устройств с конкретными индексами. Расшифровка дополнительных букв в кодах. Особенности использования IP-кодировки…
01 04 2021 2:40:17
Определяем прямую и обратную полярности аккумуляторов
Разница между прямой и обратной полярностью. Что будет, если перепутать полярность аккумулятора? Определение полярности А К Б без маркировки. Рекомендации по определению и обслуживанию аккумуляторов в зависимости от полярностей….
25 03 2021 17:23:21
Проверка сопротивления резистора с помощью мультиметра
Признаки повреждения резисторов. Проверка сопротивления мультиметром. Порядок проверки «подозрительного» резистора. Переменный резистор: правила проверки (прозвона). Измеряем позистор. Мультиметр: правила эксплуатации….
02 02 2021 7:44:40
Формула для расчета вектора напряженности электрических полей
Как направлен вектор электрического поля. Правила вычерчивания силовых линий. Определение электрической силы с помощью закона Кулона. Вычисление модуля напряженности. Напряженность электрического поля. Закон обратных квадратов. Формула для расчета вектора напряженности электрических полей….
12 01 2021 9:37:29
Указатели напряжений: однополюсные двухполисные, до 1000в и свыше
Назначение и виды указателей напряжений. Низковольтное и высоковольтное напряжение и приборы для их определения. Высоковольтные устройства и особенности их применения. Порядок работы с указателем высокого напряжения У В Н 10. Указатели напряжения для проверки совпадения фаз….
10 01 2021 21:45:58
Схемы светодиодных ламп на 220 вольт: советы по ремонту
Принцип действия светодиодных ламп 220 в. Типы светодиодов использующихся в диодных лампах. Устройство LED-диодов: преимущества и недостатки. Драйвера и источники питания. Самостоятельный ремонт светодиодной лампы….
04 01 2021 7:27:33
Отопление электрическими конвекторами: энергосберегающие модели
Принцип работы электрического конвектора. Электрический конвектор: устройство и детали конструкции. Нагреватели игольчатые и трубчатого и монолитного типа: преимущества и недостатки. Выбор типа нагревателя (электроконвектора) и места для установки….
31 12 2020 8:28:23
Напряжение при параллельном соединении двух резисторов. Формула для расчета параллельного соединения сопротивлений. Мощность при паралл ельном соединение
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычисляют общее сопротивление для каждого отдельного участка.
o Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно — складывать.
o Если резисторы соединяются параллельно — использовать условное обозначение «||». o Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Эквивалентные преобразования электрических схем.
Определение последовательного соединения элементов
Последовательное соединение элементов электрической цепи — это такое соединение, когда вывод одного элемента подключен к выводу другого элемента. В этом месте подключения нет узлов. Следующий элемент так же подключен к выводу другого элемента и т.д…
На рисунке ниже показано последовательное подключение четырех сопротивлений.
Формулы для расчета эквивалентного сопротивления при последовательном подключении элементов
При последовательном подключении сопротивлений их эквивалентное сопротивление равно сумме сопротивлений.
R экв =ΣR i =R1 + R2 + R3 +…+Rn
При последовательном соединении индуктивностей их эквивалентное сопротивление равно сумме индуктивностей (без учета взаимной индуктивности).
L экв =ΣL i =L1 + L2 + L3 +…+Ln
При последовательном подключении емкостей обратная величина от эквивалентной емкости равна сумме обратных величин емкостей.
1/С экв =Σ(1/C i)=1/С1+1/С2+1/С3+…+1/Cn
Свойства последовательного соединения элементов
При последовательном подключении элементов через них протекает одинаковый ток.
Согласно закону Ома и второму закону Кирхгофа экивалентное (суммарное) напряжение на участке последовательно соединенных сопротивлений равно сумме напряжений на каждом элементе. U общ = U1+U2+U3+U4 = I·(R1+R2+R3+R4). На данном принципе построены простейшие делители напряжения.
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Смешанное соединение . Это сочетание последовательного и параллельного соединения элементов.
Эквивалентное сопротивление для последовательно-параллельного соединения элементов:
R экв = R 1 +R 2 R 3 / (R 2 +R 3)
Сложное соединение . Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.
Формулы преобразования треугольника сопротивлений в эквивалентную трехлучевую звезду имеют вид:
Формулы обратного преобразования ветвей трехлучевой звезды в эквивалентный треугольник:
,
РЕЖИМЫ РАБОТЫ ИСТОЧНИКОВ ПИТАНИЯ
Различают четыре режима работы источников питания. Е
Режим холостого хода . В режиме холостого хода концы источника разомкнуты: (R х = ∞).
Этот режим используют для измерения ЭДС источника. Параметры режима холостого хода: I х = 0; R х = ∞; U х = E; (U х =E-Ir; r= 0; U х = E)
Режим короткого замыкания . В режиме короткого замыкания концы источника соединены накоротко: (R к = 0).
Номинальный режим . Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения приводятся в паспорте источника питания.
Согласованный режим . Это режим работы источника питания с максимальной мощностью Р=Р mах. Такое возможно при условии, когда R вн =R вш. Формула мощности для согласованного режима:
P max = I 2 R = E 2 / 4R.

Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
Внешняя часть цепи, где заряды движутся, увлекаемые полем.
Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
При последовательном включении суммируются сопротивления, при параллельном — проводимости:
Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).

Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).

Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Задачи с конденсаторами: сборная солянка
В эту статью вошли задачи всех типов: здесь и определение эквивалентных емкостей, и напряжений между определенными точками схемы, и бесконечные цепочки, и даже исчезновение конденсаторов из схем (бесследное и без последствий).

Задача 1. Плоский конденсатор разрезают на равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторов соединяют последовательно. Чему равна емкость полученной батaреи конденсаторов, если емкость исходного конденсатора мкФ?
К задаче 1
Площадь исходного конденсатора:

Площадь нового конденсатора (одного) – в 4 раза меньше исходного (так как площадь меньше):

Теперь соединяем последовательно:

Ответ: 1 мкФ.
Задача 2. Два плоских конденсатора, емкостью каждый, соединили параллельно. В один из них вставили диэлектрическую пластину с проницаемостью , заполнившую весь объем конденсатора. Какой емкости и как необходимо подключить третий конденсатор, чтобы емкость системы стала равной ?
Так как первые два конденсатора соединены параллельно, то их емкости надо сложить, чтобы получить эквивалентную емкость:

После введения пластины емкость такого конденсатора стала равна , а эквивалентная емкость стала равна

Теперь к этой конструкции будем присоединять еще один конденсатор. Попробуем присоединить параллельно, тогда

Так как , то , .
Теперь присоединяем последовательно, тогда:

Решим неравенство:

Решение – – это решение не имеет смысла, .
Ответ: , при , параллельно.
, при , последовательно.
Задача 3. Разность потенциалов между точками А и В равна . Емкости конденсаторов известны. Определить заряды конденсаторов и разность потенциалов между точками А и D.
К задаче 3
Так как емкости и соединены параллельно, то напряжение на них одинаковое. Кроме того, заряды на емкостях и системе конденсаторов одинаковы, так как они соединены последовательно. Поэтому

Эквивалентная емкость , поэтому эквивалентная емкость всей схемы – произведение на сумму – .
Тогда заряд

Но вследствие (1)

Тогда

Находим :

Определим заряды и :

Ответ: , , , .
Задача 4. Определить емкость батареи конденсаторов, показанной на рисунке, если мкФ, мкФ, мкФ.
К задаче 4
Сначала два конденсатора подключены параллельно, при этом емкости складываются: . В конце параллельное соединение и : . Теперь имеем последовательное соединение емкостей , и . Тогда

Можно подставить числа и довести решение до конца:

Ответ: мкФ.
Задача 5. Найти емкость системы конденсаторов, изображенной на рисунке.
К задаче 5
На рисунке a) емкость оказывается незаряженной, так как схема совершенно симметрична и , поэтому .
Рисунок 2 (задача 5)
Поэтому конденсатор не заряжен – разность потенциалов на его выводах нулевая. Следовательно, имеем две веточки, включенные в параллель: в каждой последовательное соединение и .
Рисунок 3 (к задаче 5)
Сопротивление одной ветки (емкость двух последовательно включенных конденсаторов – произведение, деленное на сумму):

А двух таких веток в параллель (емкости, включенные параллельно, складываются): .
На рисунке б) – если приглядеться, та же самая ситуация:
К задаче 5 – рисунок 4
Так что, аналогично первой схеме, сопротивление одной ветки с двумя последовательно включенными конденсаторами – , а две такие емкости в параллель дадут .
Ответ: а) ; б) .
Задача 6. Определить емкость Сх бесконечно длинной системы одинаковых конденсаторов, емкостью С каждый, соединенных друг с другом, как показано на рисунке.
К задаче 6, рисунок 1
Выделим в этой цепи повторяющийся элемент:
К задаче 6, рисунок 2
Эти элементы соединены параллельно. Так как емкость цепи бесконечна, то от нее не убудет, если мы один элемент удалим, или выделим. Тогда справа от выделенного элемента цепь с емкостью , и слева – тоже.
К задаче 6, рисунок 3
Можем записать для последовательно включенных емкостей:

Задача 7. Найти разность потенциалов между точками А и В в схеме, изображенной на рисунке. Емкость мкФ, мкФ, мкФ. Напряжение источника В.
К задаче 7
Емкость верхней ветки:

Емкость нижней ветки:

Заряд верхней ветви (мкКл):

Заряд нижней ветви (мкКл):

Но соединен последовательно с , поэтому , и

Аналогично в нижней ветви:

В сумме .
Найдем разность потенциалов между точками и :

Ответ: B.

Преобразование параллельных цепей RL в последовательные эквиваленты
В четвертой части нашей серии «Советы практикующим техникам» мы рассмотрим простой метод, который можно использовать для упрощения анализа цепей при работе с последовательными и параллельными цепями RL. Одна из проблем, с которыми сталкиваются технические специалисты, работающие с параллельными цепями RL, — это необходимость работать со значениями, которые являются обратными значениям более часто используемых стандартных единиц. Использование проводимости, восприимчивости и допуска вместо сопротивления, реактивного сопротивления и импеданса часто может вызвать путаницу или неуверенность при работе с этими менее используемыми единицами.Этот подход или метод преобразования могут быть особенно полезны при работе со схемами, имеющими несколько резисторов и катушек индуктивности в смешанной последовательной / параллельной конфигурациях. Сокращение такой сети со смешанной топологией до нескольких последовательно включенных катушек индуктивности и резисторов значительно упрощает расчет общего сопротивления и индуктивности в данной цепи или сети. В последовательном формате это просто добавление при вычислении общего индуктивного реактивного сопротивления, общего сопротивления для получения общего импеданса.
Ниже приведены основные уравнения для создания последовательного представления данной параллельной цепи RL.
Выполнение преобразования …
Шаг 1 : Рассчитать эквивалентное значение сопротивления
рупий
Шаг 2 : Вычислить эквивалентное индуктивное реактивное сопротивление Xs
Шаг 3 : Рассчитайте необходимое значение индуктивности, которое обеспечит соответствующее последовательное индуктивное реактивное сопротивление для данной частоты.Используйте L = XL / (2 * Pi * freq), чтобы получить значение индуктивности.
Шаг 4 : Перерисуйте схему в последовательной конфигурации, используя полученные значения компонентов для катушки индуктивности и резистора.
Правильное выполнение вышеуказанных шагов приведет к последовательному представлению параллельной цепи RL, которая ведет себя идентично в отношении напряжения, тока и фазового соотношения между ними. С точки зрения точек A и B выше, обе схемы приведут к одинаковому поведению.
Использование методов преобразования топологии, таких как преобразование параллельной схемы в последовательную RL, преобразования треугольника в звезду для резисторных цепей или простых преобразований источников (преобразование источников тока с параллельными сопротивлениями в источники напряжения с последовательными сопротивлениями) является распространенной тактикой упрощения, которая может быть чрезвычайно полезной. в сокращении схем и анализе на техническом уровне. Чем больше у вас, как у техника, инструментов, тем проще будет упростить и свести сложные схемы к простым представлениям.Это, в свою очередь, поможет снизить вероятность ошибок при выполнении анализа схемы на уровне технического специалиста.
В приведенной ниже анимации пример выполнения преобразования из параллельной цепи RL в эквивалентную последовательную цепь RL проиллюстрирован шаг за шагом, когда для данной параллельной цепи RL известны сопротивление и индуктивное реактивное сопротивление.

Если вам понравился этот пост, ознакомьтесь с нашими предыдущими статьями в серии «Практикующий техник»;
Использование функции Natural Log или «ln» в анализе цепей.
Как создать правильные уравнения KCL-ветвлений закона Ома для узлового анализа
Как решить одновременные уравнения с несколькими неизвестными
Мы надеемся, что это было полезно для вас как практикующего специалиста или студента. Мы ищем другие идеи для этой продолжающейся серии «Практикующий техник». Пожалуйста, дайте нам знать, о чем вы хотите, чтобы мы написали, отправив нам свои мысли и вопросы по адресу [email protected].
Основные сведения об индуктивности в реальном мире
Как только ток течет по металлическим проводникам, возникает индуктивность.
Брюс Аршамбо, Ph.D.
Заслуженный инженер IBM, IBM, Research Triangle Park, Северная Каролина, США
Понятие индуктивности — одно из наиболее неправильно понимаемых понятий в электротехнике. Такие термины, как «самоиндуктивность», «индуктивность контура», «частичная индуктивность», «взаимная индуктивность» используются без особого внимания к истинной физике, лежащей в основе эффектов и причин индуктивности.
Индуктивность важна при проектировании EMI / EMC, поскольку она является одним из основных ограничивающих факторов в высокочастотной конструкции.Когда есть металл, и ток течет через этот металл, присутствует индуктивность, которая влияет на ток. На высоких частотах эта собственная индуктивность доминирует над всеми компонентами, дорожками и металлическими поверхностями. Даже конденсаторы и резисторы становятся индукторами.
Полное исследование индуктивности заняло бы как минимум одну целую книгу. Цель этой статьи — помочь читателю лучше понять концепции индуктивности, взаимной индуктивности и частичной индуктивности в том, что касается проектирования EMI / EMC, особенно на печатных платах (ПК).

Где петля?
Одна из первых вещей, которую мы узнали в нашем первом классе схем, это то, что ток должен всегда возвращаться к своему источнику. Обычно мы сначала изучаем это для цепей постоянного тока, а затем переходим к цепям переменного тока. Однако к тому времени, когда мы начнем проектировать высокоскоростные печатные платы, многие из нас, кажется, забывают этот фундаментальный принцип. Ток всегда должен течь по замкнутому контуру, независимо от частоты. Как разработчик печатных плат, разработчик корпуса или системный разработчик, вы всегда должны задавать вопрос: «Как ток возвращается к своему источнику?» Ток должен течь в замкнутом контуре.Текущий будет течь в замкнутом контуре. Единственный реальный вопрос заключается в том, пойдет ли он по пути, который поможет снизить выбросы EMI, или по пути, который приведет к увеличению выбросов EMI. Гораздо лучше спроектировать путь обратного тока «специально», чем «по ошибке». Без этой преднамеренной конструкции пути обратного тока инженеры также должны спросить себя: «Вам сегодня повезло?»
Когда кто-то говорит об индуктивности переходного отверстия или прямого куска провода, петли нет, значит, нет и индуктивности.В случае переходного отверстия, если нет преднамеренного обратного тока через переходное отверстие, то обратный ток будет распространяться и течь через диэлектрик как ток смещения. Чем дальше проходит ток, тем больше петля и, следовательно, больше индуктивность. Если рядом с сигнальным переходом находится обратное переходное отверстие, то индуктивность изменится из-за изменения площади контура. По мере того, как мы приближаем обратный переходник, площадь контура изменяется, как и индуктивность исходного проходного отверстия. Ясно, что сам по себе сквозной сигнал не может иметь много значений индуктивности.Значение индуктивности контура, в котором переходное отверстие является частью этого контура, определяет «индуктивность переходного отверстия».
Закон Фарадея
Когда ток в контуре изменяется во времени, магнитное поле, связанное с этим током, также изменяется. Когда это изменяющееся магнитное поле прорезает проводник, оно индуцирует напряжение в цепи этого проводника. Это происходит независимо от того, прорезают ли линии магнитного поля другой проводник или тот же проводник, что и исходный ток.Напряжение, индуцированное в однопроводной петле, равно скорости изменения магнитного потока, проходящего через проволочную петлю, во времени. [1] [2] Это описано в законе электромагнитной индукции Фарадея как:
Рис. 1. Квадратная петля.
Часто уравнения, подобные (1), не исследуются тщательно для интуитивного понимания основ физики. Закон Фарадея не так сложен, как может показаться на первый взгляд. Правая часть (1) описывает величину изменяющегося во времени магнитного поля в некоторой области.Левая часть (1) — это определение напряжения (электрического поля вдоль пути). И в этом случае путь представляет собой замкнутый контур. Знак минус справа указывает на то, что напряжение будет противодействовать потоку тока, который в первую очередь создал магнитное поле. Это основное определение индуктивности. Обратите внимание, что левосторонний интеграл — это интеграл с обратной связью. Также обратите внимание, что правая часть — это величина (изменяющегося во времени) магнитного поля, содержащегося в области.Естественно, чтобы рассчитать «площадь», нам нужна замкнутая окружность. Таким образом, обе стороны этого уравнения ясно указывают на то, что для определения индуктивности требуется замкнутый контур. Кроме того, чем больше площадь контура (правая сторона), тем больше тормозящий эффект индуктивности.
Мы можем упростить (1), рассмотрев случай простой квадратной петли (показанной на рисунке 1). Если петля мала по сравнению с длиной волны интересующей частоты, то можно предположить, что магнитный поток постоянен в области A, и уравнение (1) может быть уменьшено до
Величину напряжения, индуцированного изменяющимся во времени магнитным полем, можно найти для любой геометрии с помощью уравнения (1) и для простой прямоугольной петли с помощью (2).Опять же ясно, что чем больше площадь в (2), тем больше тормозящая индуктивность.
Теперь, когда мы рассмотрели основное определение индуктивности, мы можем использовать несколько простых уравнений, чтобы найти значение индуктивности на основе физических размеров контура. Предполагая, что площадь петли намного меньше длины волны в интересующем частотном диапазоне, магнитное поле аппроксимируется как постоянное. Примерная индуктивность для нескольких простых форм [3] приведена ниже.
Простая круглая петля
Для простой изолированной токовой петли, где радиус провода r ₀ намного меньше, чем радиус петли a , тогда индуктивность петли приблизительно равна
Если используется несколько витков проволочной петли, то индуктивность просто умножается на количество витков, чтобы найти общую индуктивность числа витков.Обратите внимание на (3), что индуктивность прямо пропорциональна площади контура a , но минимально зависит от радиуса провода r ₀ (из-за функции естественного логарифма). Еще раз, важность площади контура для индуктивности очевидна.
Простая квадратная петля
Для изолированной квадратной петли (с длиной стороны = w ) в свободном пространстве, где радиус провода намного меньше площади петли ( r ₀ << w ² ), индуктивность может быть найдена с помощью
Простая прямоугольная петля
Для однооборотной прямоугольной петли в свободном пространстве индуктивность может быть найдена из
где
w = ширина прямоугольника (широкий размер)
высота прямоугольника = короткий размер), и
r ₀ = радиус проволоки.
Хотя эти формулы выглядят сложными, их можно легко вычислить с помощью программы для работы с электронными таблицами. И снова, в каждой из этих формул ясно, что площадь контура значительно больше влияет на значение индуктивности, чем размер проводника.
Почему нам важна индуктивность контура?
Одной из основных проблем EMI / EMC является индуктивность, особенно индуктивность компонентов фильтра. Например, конденсаторы используются на печатных платах (PCB) для развязки плоскостей питания / заземления, компонентов фильтра ввода-вывода и других высокочастотных целей.Индуктивность, связанная с физическим подключением конденсатора (установленного вверху / внизу печатной платы) к соответствующим плоскостям, будет преобладать над импедансом конденсатора на высоких частотах и сделает конденсатор неэффективным на высоких частотах. Эта индуктивность должна быть включена в любой анализ.
Для точного расчета индуктивности подключения конденсатора требуется сложная формула [4]. Однако, поскольку индуктивность прямо пропорциональна площади контура, мы можем получить относительную добротность, просто преобразовав эту сложную задачу в простой прямоугольный контур и вычислив площадь прямоугольного контура для каждого варианта.Если один вариант имеет меньшую площадь контура, он будет иметь меньшую индуктивность и будет предпочтительным вариантом конструкции.
На рисунках 2 и 4 показано подключение развязывающего конденсатора с низкой индуктивностью, а на рисунках 3 и 5 показано подключение развязывающего конденсатора с высокой индуктивностью.
Рисунок 2. Низкоиндуктивное соединение с конденсатором, установленным на верхней части платы. Рисунок 3. Высокоиндуктивное соединение с конденсатором, установленным наверху платы. Рисунок 4. Низкоиндуктивное соединение с конденсатором, установленным на нижней части платы.Рисунок 5. Соединение с высокой индуктивностью с конденсатором, установленным наверху платы.
На рисунках 2 и 3 площадь петли сильно различается, при этом петля на рисунке 3 значительно больше. В этом примере, где панель питания / заземления находится ближе к низу платы, чем к верху, площадь контура будет меньше (Рисунок 4), а индуктивность соединения будет ниже, если конденсатор будет установлен на задней стороне платы. доска, а не верхняя сторона доски. Обратное верно, если пара плоскости питания / заземления находится рядом с верхней частью печатной платы, как показано на рисунках 2 и 5.
В таблице 1 показаны некоторые примерные значения индуктивности подключения, связанной с установленным на печатной плате развязывающим конденсатором для некоторых типичных размеров. Более сложная формула более точна, но даже значения простой прямоугольной формулы достаточно точны для большинства приложений.
Таблица 1. Типовые значения индуктивности развязывающего конденсатора.
Из уравнения 5 важно отметить, что радиус провода очень мало влияет на индуктивность контура, а высота и ширина (площадь контура) имеют большое влияние на значение индуктивности контура.
Этот тип анализа также применим для определения того, оправдывают ли специальные технологии платы, например, скрытая емкость, затраты на конфигурацию стека плат. Если слой скрытой емкости находится глубоко в плате (ближе к низу), тогда площадь прямоугольной петли между выводами питания / заземления ИС и слоем скрытой емкости будет большой, что сводит к минимуму любые положительные эффекты от слоя скрытой емкости. В качестве альтернативы, если слой скрытой емкости находится рядом с верхом печатной платы, площадь прямоугольного контура, связанная с индуктивностью соединения, мала, в результате чего ИС получает преимущество слоя скрытой емкости без значительной индуктивности соединения.
Взаимная индуктивность
Взаимную индуктивность цепей в реальном мире часто трудно вычислить, поскольку контуры редко имеют простую геометрию, а другие металлы в окружающей среде будут влиять на поведение полей. Если предположить, что две петли расположены в свободном пространстве (электрически далеко от других проводников), тогда проблема упрощается и может быть сделана разумная оценка. В этих условиях взаимная индуктивность между двумя контурами определяется как
, где:
I ₁ = ток, протекающий в контуре № 1,
B = магнитный поток, создаваемый током в контуре №1, и
S ₂ = поверхность контура №2.
В уравнении (6) магнитный поток от тока в первом контуре интегрируется по поверхности второго контура, чтобы найти взаимную индуктивность. Если петли достаточно малы, чтобы мы могли предположить, что магнитное поле постоянно на лицевой стороне петли, то взаимная индуктивность — это просто количество магнитного потока от первого витка, содержащегося в области второго витка, и деленное на ток в первом шлейфе. Таким образом, очевидно, что взаимная индуктивность определяется размером двух контуров и тем, как они ориентированы относительно друг друга.Петли большего размера будут иметь большую взаимную индуктивность. Петли, расположенные ближе друг к другу, будут иметь большую взаимную индуктивность (поскольку магнитный поток от первого витка будет сильнее). Петли с одинаково ориентированными гранями также будут иметь большую взаимную индуктивность (поскольку магнитный поток будет максимальным).
Почему мы заботимся о взаимной индуктивности?
Когда развязывающий конденсатор размещается рядом с выводами питания ИС, область взаимной индуктивности может эффективно снизить индуктивность контура тракта.Чтобы это было значительным, конденсатор и ИС должны располагаться близко друг к другу.
На рис. 6 показан пример ИС и развязывающего конденсатора, установленных на печатной плате. Когда переходные соединения показаны на рисунке 6, направление тока в двух ближайших друг к другу переходных отверстиях приводит к возникновению магнитного потока в противоположном направлении в области взаимного потока между плоскостями питания / земли, как показано на рисунке 6. Этот эффект противоположной взаимной индуктивности снижает полное сопротивление пути.Это уменьшение общей индуктивности из-за этого эффекта наблюдается только тогда, когда конденсатор расположен очень близко к ИС.
Рисунок 6. Взаимная индуктивность между развязывающим конденсатором и ИС.
Частичная индуктивность
Основное определение индуктивности требует, чтобы в контуре протекал ток . Без замкнутого контура не может быть индуктивности . Однако практические соображения заставляют нас обсудить индуктивность части полного токового контура, например индуктивность конденсатора.Идея обсуждения индуктивности только части контура в целом называется частичной индуктивностью [4] [5]. Частичные индуктивности можно объединить, чтобы найти общую индуктивность, используя уравнение (7).
Почему нам важна частичная индуктивность?
Концепция частичной индуктивности особенно полезна, когда физическая геометрия является сложной или когда ток неоднороден по всему поперечному сечению металла. Например, на рисунке 7 показан конденсатор для поверхностного монтажа (SMT) на печатной плате с переходными отверстиями, дорожками и т. Д.В то время как простая формула прямоугольной петли может использоваться для определения приблизительной индуктивности петли, различные поперечные сечения проводников делают расчет только приблизительным. Концепция частичной индуктивности позволяет найти частичную индуктивность каждого компонента и объединить их в конце, чтобы найти полную индуктивность контура, как в уравнении (8).
Рис. 7. Пример геометрии установки развязывающего конденсатора с разбивкой на составляющие частичной индуктивности.
Используя частичные индуктивности, общая индуктивность контура будет равна
, где
Lp — частичная индуктивность компонента
Lpm — частичная взаимная индуктивность параллельных компонентов Примечание
структура может быть проанализирована с возможной целью уменьшения общей индуктивности контура.Каждый из отдельных сегментов может быть изменен (например, путем увеличения диаметра), чтобы увидеть влияние на конечную индуктивность. С помощью этого анализа можно быстро проанализировать многие конфигурации «что, если».
РЕЗЮМЕ
Основной принцип, согласно которому индуктивность требует протекания тока в контуре, является важным понятием. Это не является необоснованным, поскольку текущий должен течь в цикле. Размер токовой петли определяет величину индуктивности.
Индуктивность — это основной строительный блок в электронных схемах. То есть, как только используются металлические проводники и по ним течет ток, возникает индуктивность. Эта индуктивность становится ограничивающим фактором во всех высокочастотных цепях. Например, когда конденсаторы используются в качестве фильтрующих элементов или разделительных конденсаторов, индуктивность контура, связанная с подключением этого конденсатора к печатной плате, будет ограничивать частотный диапазон, в котором конденсатор является эффективным компонентом.
Также дается краткое обсуждение взаимной индуктивности и частичной индуктивности. Однако идея о том, что для оценки индуктивности требуется замкнутый контур, также верна для расчетов взаимной индуктивности и частичной индуктивности.
Это было очень краткое введение в индуктивность. Более полное изучение этой темы можно найти в справочной литературе.
ССЫЛКИ
[1] J.D. Kraus and K.R. Carver, Electromagnetics , 2 ^nd Edition, McGraw-Hill, 1973
[2] F.М. Теще, М.В. Ианоз и Т. Карлссон, Методы анализа ЭМС и вычислительные модели , Wiley-Interscience, 1997 г.
[3] Ф. У. Говер, Расчет индуктивности , Dover Publications, Нью-Йорк, 1946 г.
[4] А. a Complex Integrated Circuit Environment », IBM J. Research and Development , 16, стр 470-481, 1972 г.
[5] CR Paul, Analysis of Multiconductor Transmission Lines, Wiley, 1994
ОБ АВТОРЕ
Брюс Аршамбо , Ph.Д. — заслуженный инженер IBM в IBM в Research Triangle Park, NC. Он получил степень BSEE в Университете Нью-Гэмпшира в 1977 году и степень MSEE в Северо-Восточном университете в 1981 году. Он получил докторскую степень в Университете Нью-Гэмпшира в 1997 году. Его докторские исследования были в области прикладной вычислительной электромагнетизма. к реальным проблемам ЭМС. В 1981 году он присоединился к Digital Equipment Corporation и в течение 1994 года выполнял различные задания: от проектирования и тестирования продуктов EMC / TEMPEST до разработки программных инструментов, связанных с электромагнитной электромагнитной совместимостью.В 1994 году он присоединился к SETH Corporation, где продолжил разрабатывать программные инструменты, связанные с вычислительной электромагнитной электромагнитной совместимостью, и использовал их в качестве инженера-консультанта в различных отраслях промышленности. В 1997 году он присоединился к IBM в Роли, Северная Каролина, где он является ведущим инженером EMC, отвечающим за разработку инструментов EMC и их использование в различных продуктах. Во время своей карьеры в ВВС США он отвечал за внутреннюю безопасность связи и за проекты исследований и разработок, связанные с TEMPEST / EMC. ДокторАршамбо является автором или соавтором ряда статей в области вычислительной электромагнетизма, в основном применяемых в реальных приложениях ЭМС. В настоящее время он является членом совета директоров IEEE EMC Society и бывшим членом совета директоров Applied Computational Electromagnetics Society (ACES). В прошлом он был заслуженным лектором IEEE / EMCS и младшим редактором журнала IEEE Transactions по электромагнитной совместимости. Он является автором книги «Проектирование печатных плат для управления электромагнитными помехами в реальном мире» и ведущим автором книги «Справочник по вычислительному моделированию электромагнитных помех и электромагнитной совместимости».”
4.4: Параллельные цепи резистора-конденсатора — Workforce LibreTexts
Последнее обновление
Сохранить как PDF
Параллельная цепь RC.
Резистор и конденсатор параллельно
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Теперь это параллельная схема, и мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт ∠ 0 ^o) во все столбцы:
Расчет с использованием закона Ома
Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам в таблице, вычислив ток через резистор и ток через конденсатор:
Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего».Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно. Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле.И снова формула параллельного импеданса выглядит так:
Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами. Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:
Обзор
Импедансом (Z) управляют так же, как и сопротивлением (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме! Z _Итого = 1 / (1 / Z ₁ + 1 / Z ₂ +.. 1 / Z _n)
Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
Когда резисторы и конденсаторы смешаны вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ^o и -90 ^o. Ток в цепи будет иметь фазовый угол где-то между 0 ^o и +90 ^o.
Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
Упрощение расчета потерь в сердечнике композитных катушек индуктивности
Упрощение расчета потерь в сердечнике композитных катушек индуктивности
Определение потерь в сердечнике для получения повышения температуры и обеспечения правильного выбора компонентов
НИКОЛАЙ Ж.SCHADE
Vishay Intertechnology
Malvern, PA
http://www.vishay.com
Точно предсказать потери в сердечнике в магнитных компонентах сложно, и не менее сложно в композитных катушках индуктивности. Доступно несколько моделей потерь в сердечнике, каждая из которых имеет свои достоинства.
Эта статья адаптирует существующую модель для оценки потерь в сердечнике композитных катушек индуктивности. Цель состоит в том, чтобы упростить процесс определения потерь в сердечнике и позволить разработчикам как рассчитать общие потери в катушке индуктивности, суммируя потери в сердечнике и меди, так и выбрать подходящий катушку индуктивности для своего применения в зависимости от повышения температуры.В этой статье будут учтены факторы, влияющие на определение потерь в сердечнике, поскольку они немного отличаются для этого типа индуктора.
Наиболее заметное различие заключается в геометрии компонента, которая, как мы увидим позже, требует различных постоянных сердечника для каждого размера и номинала индуктора. Будут представлены примеры, иллюстрирующие расчет потерь в сердечнике и выбор компонентов.
Проблемы с определением потерь в сердечнике
Расчет потерь в сердечнике катушек индуктивности на основе стандартных промышленных стилей сердечников, предлагаемых многочисленными поставщиками, представляет собой простой процесс.Это связано с тем, что стандартные базовые наборы имеют фиксированную геометрию с соответствующими установленными базовыми константами; все, что нужно, — это характеристики материала.
Когда геометрические характеристики известны, легко определить потери в сердечнике для всей серии катушек индуктивности на основе одного размера сердечника. Единственная переменная, которую необходимо учитывать, — это количество витков.
Это не относится к композитным индукторам. Из-за конструкции индукторов геометрические параметры каждой части различаются даже в пределах одного размера индуктора.Композитный индуктор по сути построен в обратном направлении от обычного.
В обычном индукторе магнитный провод наматывается либо непосредственно на сердечник, как в тороиде, либо на бобину со вставленными в него половинками сердечника, как в сердечниках типа «Е».
Составной индуктор изготавливается путем сначала намотки воздушной катушки из медной проволоки. Затем два конца этой воздушной катушки привариваются к раме с выводами, выступы которой служат ее монтажными площадками. Затем порошковое железо прижимается к узлу катушки, образуя индуктор.Прижатие магнитного сердечника к катушке — вот что определяет составной индуктор. Поскольку каждая катушка отличается по диаметру и высоте, каждый индуктор имеет разные геометрические параметры. Это означает, что постоянные сердечника должны быть рассчитаны для каждой катушки индуктивности.
Единственным постоянным элементом в серии индукторов будет железный порошок; следовательно, постоянные потерь в сердечнике для этого материала останутся прежними. Однако существуют различные порошки железа, используемые в различных производственных линиях, которые охватывают широкий диапазон рабочих условий.В этих производственных линиях одинаковые значения индуктивности не используют одну и ту же воздушную катушку, что означает, что константы потребуются не только для геометрии, но и для материала. Все сводится к тому, что каждая катушка индуктивности имеет свои уникальные параметры, даже в пределах одного и того же семейства.
Композитные индукторы часто используются в неизолированных преобразователях постоянного / постоянного тока. Это не проблема, но связанные с ними формы сигналов. Характеристики потерь в сердечнике и результирующие данные часто определяются с использованием синусоидального возбуждения.С другой стороны, преобразователи постоянного / постоянного тока. не работайте с синусоидальными волнами, вместо этого используйте импульсную форму волны постоянного тока. Это означает, что форма волны тока в катушке индуктивности, определяющая потери в сердечнике, будет треугольной, а не синусоидальной. Эту разницу необходимо будет компенсировать при расчетах потерь в сердечнике.
Преобразователи постоянного тока в постоянный все чаще просят работать при более высоких температурах окружающей среды. Это, в свою очередь, требует, чтобы индуктор работал при более высокой температуре в дополнение к его собственному повышению температуры из-за потерь мощности.
Известно, что железный порошок проявляет эффекты старения при более высоких температурах в виде повышенных потерь в сердечнике. Эти потери необходимо учитывать в процессе проектирования, чтобы композитный индуктор можно было использовать при температурах выше 125 ° C. Эффекты термического старения можно свести к минимуму, просто ограничив максимальную температуру индуктора 125 ° C или ниже.
Определение потерь в сердечнике
Хорошей отправной точкой является определение наихудших рабочих условий для задействованной цепи.Как только эти условия будут созданы, можно определить потери в сердечнике, и индуктор будет работать во всем рабочем диапазоне источника питания. Параметры, необходимые для расчета потерь в сердечнике, — это произведение вольт-микросекунд, рабочий цикл и рабочая частота цепи. Остальные значения можно рассчитать по этим трем параметрам.
При проектировании катушек индуктивности потери в сердечнике часто характеризуются уравнением Штейнмеца в мВт / см3:
Уравнение 1
Однако это уравнение было разработано на основе возбуждения синусоидальной волны.Что необходимо, так это уравнение, которое учитывает несинусоидальные формы сигнала, связанные с преобразователями постоянного / постоянного тока. Для расчета потерь в сердечнике с несинусоидальной формой волны было введено модифицированное уравнение Штейнмеца (MSE):
Уравнение 2
В этом уравнении используется «эффективная частота» несинусоидальной формы волны вместе с рабочей частотой цепи, при этом используются параметры Штейнмеца.
Уравнение потерь в сердечнике, показанное ранее, имеет несколько связанных с ним констант, которые необходимо определить.Это постоянная сердечника K0, постоянная частоты Kf и постоянная плотности потока Kb. Эти константы определяются путем подбора кривой экспериментальных данных о потерях в сердечнике, полученных в результате лабораторных испытаний. Константы уникальны для материала, для которого они установлены, и не изменяются от значения индуктивности к значению индуктивности. Конечно, они будут меняться от материала к материалу.
Эффективная частота (fe) — это частота, отличная от частоты повторения схемы, используемой для коррекции несинусоидальных сигналов.Эффективную частоту сигналов, наблюдаемых в индукторах преобразователей постоянного / постоянного тока, можно охарактеризовать следующим образом:
Уравнение 3
Этот метод приравнивает частоту к сумме изменений наклона плотности потока, деленной на изменения амплитуды, деленной на 2 π.
Метод расчета потерь в сердечнике
Чтобы использовать уравнение потерь в сердечнике, необходимо определить эффективную частоту (fe) и максимальную плотность потока (Bpk).Затем эти элементы подключаются к MSE для определения потерь в сердечнике на единицу объема.
Так как произведение вольт-микросекундной схемы известно или может быть вычислено, мы воспользуемся этим для определения Bpk. Композитные индукторы можно охарактеризовать с точки зрения их способности обрабатывать определенное вольт-микросекундное произведение, соответствующее 100 Гаусс. Этот параметр называется константой ET100. Как и раньше, эта константа будет разной для каждого размера и значения индуктивности. Эта константа может использоваться для определения Bpk следующим образом:
Уравнение 4
, где ETckt — произведение вольт-микросекундной цепи, а единицы измерения выражены в гауссах.Произведение вольт-микросекунды для схемы может быть взято из технических описаний и указаний по применению производителя ИС или рассчитано на основе Vout, частоты и рабочего цикла.
Можно показать, что эффективная частота зависит от рабочего цикла цепи и рабочей частоты:
Уравнение 5
Изменения плотности потока в магнитной цепи пропорциональны изменениям тока индуктора, при условии, что индуктивность остается постоянной.Потери в сердечнике вызваны этой пульсацией в соответствии с уровнями плотности потока. На индуктор действует входное напряжение во время включения и напряжение противоположной полярности во время выключения. Результирующий график плотности потока состоит из двух прямолинейных участков, которые соответствуют интегрированию этих двух напряжений во времени.
Когда эффективная частота и максимальная плотность потока известны, потери в сердечнике можно оценить с помощью MSE. Результат этого уравнения будет измеряться в мВт / см3, но для упрощения расчетов объем сердечника превращается в константу K0, что дает окончательную версию MSE для потерь в сердечнике (Pfe) в ваттах:
Уравнение 6
Это приводит к разной постоянной сердечника для каждого индуктора, которую можно найти в технических данных приложения.Константы потерь в сердечнике и соответствующие параметры для неполного списка продуктов индуктивности из композитных материалов IHLP перечислены в таблице 1, разделенные по значению индуктивности и типу материала.
Таблица 1. Константы потерь в сердечнике и соответствующие параметры для неполного списка продуктов индуктивности из композитных материалов IHLP
Выбор подходящего композитного индуктора
Начните процесс выбора индуктора, установив критерии выбора для детали. Композитные индукторы имеют рекомендованную максимальную температуру компонентов 125 ° C.Вычитание температуры окружающей среды даст нам максимально допустимое повышение температуры детали, хотя, если это число превышает 40 ° C, рекомендуется использовать 40 ° C для допустимого повышения температуры. Потери в сердечнике должны быть ограничены до 1/3 от общих потерь, чтобы уменьшить любые эффекты старения, связанные с порошкообразным железом в сердечнике при повышенных температурах.
В технических паспортах
указан номинальный ток нагрева (Iheat) в качестве параметра, который представляет ток, необходимый для определенного повышения температуры, указанного в техническом паспорте.Проблема в том, что это повышение температуры обычно измеряется с использованием постоянного тока и связано только с потерями в меди и не учитывает потери в сердечнике. Однако эта информация полезна, поскольку ее можно использовать для определения максимальных потерь мощности, допускаемых в индукторе, путем умножения сопротивления индуктора с поправкой на температуру на квадрат тока нагрева. Это будет потеря мощности (Pheat), вызывающая повышение температуры, связанное с параметром Iheat.
Для определения потерь в сердечнике разработчик может рассчитать пиковую магнитную индукцию, используя произведение вольт-микросекундной формы волны напряжения на катушке индуктивности во время работы.Используя эту оценку потерь в сердечнике, разработчик может сбалансировать комбинацию потерь в сердечнике и меди, чтобы общие потери и связанный с ними рост температуры не превышали максимальную рабочую температуру композитного индуктора 125 ° C. Необходимо соблюдать осторожность, чтобы гарантировать точные потери в меди, учитывая увеличение сопротивления меди из-за изменения температуры от комнатной температуры (где указан DCR) до максимальной рабочей температуры и потерь из-за компонентов переменного тока, таких как скин-эффект.Наконец, убедитесь, что Ipeak — это Isat (см. Техническое описание). Из-за функции мягкого насыщения композитных индукторов IHLP, Ipeak может превышать Isat без серьезного снижения индуктивности, как это наблюдается в индукторах ферритового типа.
Некоторые примеры
Рассмотрим катушку индуктивности для следующей «понижающей» цепи: Vin = 12 В, Vout = 3,3 В, Iout = 5 A, частота = 500 кГц, температура окружающей среды 50 ° C и коэффициент пульсации приблизительно 0,4, где определяется коэффициент пульсации. как отношение компонентов постоянного и переменного тока.Коэффициент пульсации 0,4 — хороший компромисс между размером индуктора и среднеквадратичным током выходного конденсатора. Принимая во внимание расчетное падение коммутируемого напряжения 0,5 В и падение на диоде 0,5 В, вышеуказанные условия производят следующие проектные требования: рабочий цикл = 0,317, произведение вольт-микросекунды, равное 5,19, и требуемая индуктивность 2,60 мкГн. Поскольку мы хотим сохранить коэффициент пульсации около 0,4, а индуктивность 2,60 мкГн не является стандартным значением, мы выберем стандартное значение выше и ниже расчетной индуктивности.
Ток нагрева композитных катушек индуктивности указан исходя из повышения температуры на 40 C только за счет тока; поэтому нам нужно будет уменьшить постоянный ток, чтобы учесть рост тепла из-за потерь в сердечнике. Мы хотим выбрать катушку индуктивности с более высоким током нагрева, чем те 5 А, которые требует схема. Просматривая спецификации, мы обнаруживаем, что индуктор IHLP-2525CZ-01 2,2 мкГн выдерживает ток 8 А при максимальном DCR 20 мОм, а компонент IHLP-2525CZ-01 3,3 мкГн выдерживает 6 А при максимальном DCR 30 мОм. мОм.Вопрос в том, какой из них будет лучшим выбором для условий эксплуатации?
Начнем с сравнения потерь в сердечниках двух катушек индуктивности. Технические характеристики двух катушек индуктивности приведены в таблице 2.
Таблица 2. Технические характеристики IHLP-2525CZ-01 2.2-мкГн и IHLP-2525CZ-01.3-мкГн
Начните с определения Bpk с помощью уравнения (4). Подключение продукта цепи ET и ET100 индуктора дает нам Bpk 519.3 Г для части 2,2 мкГн и 339,4 Г для части 3,3 мкГн. Эффективная частота из (5) будет одинаковой для обеих катушек индуктивности при 367,752 кГц. Это то же самое, потому что рабочий цикл и рабочая частота одинаковы для обеих частей. Результирующие потери в сердечнике с использованием (6) составляют:
и
Этот результат может заставить вас поверить в то, что часть 3,3 мкГн — лучший выбор, но, как мы увидим, в данном случае это не так.
Чтобы продолжить процесс выбора, нам необходимо определить общие потери, и для этого нам потребуются потери в меди.Чтобы рассчитать потери в меди, мы должны сначала определить рабочее сопротивление (Roper), ток пульсаций цепи (∆I) и постоянный ток индуктора (Idc). Ропер — это сопротивление индуктора в цепи с поправкой на температуру, которое можно найти, предполагая повышение температуры на 40 ° C, с помощью
Уравнение 7
Delta I (∆I) для понижающего дросселя зависит от выходного напряжения, индуктивности в мкГн, частоты в Гц и рабочего цикла в соответствии с
.
Уравнение 8
Результирующий ∆I для схемы равен 2.36 А для индуктора на 2,2 мкГн и 1,57 А для индуктора на 3,3 мкГн. Потери мощности, связанные с воздействием переменного тока в обмотке, можно определить с помощью следующего уравнения, где K1 — постоянная потерь на переменном токе в зависимости от конструкции каждого компонента:
Уравнение 9
Потери мощности постоянного тока — это просто потери, где Idc равно выходному постоянному току в понижающей цепи. Это означает, что потери в меди составят 0,743 Вт для части 2,2 мкГн и 1,008 Вт для части 3,3 мкГн.Добавление этих результатов к потерям в сердечнике дает общие потери 0,919 Вт и 1,113 Вт соответственно. Повышение температуры можно найти, умножив общие потери на тепловое сопротивление (Rth). Тогда повышение температуры для каждого индуктора составит
.
и
Можно увидеть, добавив повышение температуры к температуре окружающей среды, что ни одна из катушек индуктивности не превысит максимальную температуру компонентов 125 ° C. Исходя из этого, индуктор HLP-2525CZ-01 2,2 мкГн является лучшим выбором для этой схемы.
Последний пункт, который нужно проверить, — это увидеть, меньше ли пиковый ток индуктора (Ipeak), чем ток насыщения катушки индуктивности. Пиковый ток можно определить по
.
Уравнение 10
Таким образом,
Ipeak равно 6,18 А, что меньше, чем указано в спецификации 14,0 А для этой катушки индуктивности.
Упростив расчет потерь в сердечнике в композитных индукторах и применив эту информацию как часть общих потерь при определении превышения температуры и правильном выборе компонентов для данного набора конструктивных параметров, можно сделать следующие выводы относительно композитных индукторов:
Геометрия сердечника каждого индуктора различается даже внутри каждого семейства индукторов.Это связано с их конструкцией, которая существенно отличается от традиционных катушек индуктивности.
Константы потерь в сердечнике, связанные с каждым значением индуктивности, также различны. Это происходит из-за разной геометрии.
Композитные индукторы изготавливаются из различных смесей железного порошка. У этих разных смесей также есть свои уникальные константы.
В прошлом потери в сердечнике часто оценивались с использованием синусоидального возбуждения.Композитные индукторы используются в схемах, работающих с несинусоидальными сигналами, которые требуют учета потерь в сердечнике.
Композитные индукторы чувствительны к эффектам термического старения и должны работать при температуре компонентов ниже рекомендованной 125 ° C, если только не учитываются повышенные потери в сердечнике.
Приложение
Расчет необходимой индуктивности
Чтобы рассчитать необходимую индуктивность для понижающей цепи, начните с соотношения
Во время включения преобразователя V будет равно Vin — Vsw — Vout, что дает нам выражение:
, где D — рабочий цикл, а T — период формы сигнала.
Решая L и подставляя 1 / f вместо T, получаем:
Подключив параметры цепи, требуемая индуктивность
Список литературы
1) К. Стейнмец, «О законе гистерезиса», AIEE Transactions, Vol. 9, pp 3-64, 1892, перепечатано под заголовком «Вклад Штейнмеца в революцию в области электроснабжения», введение Дж. Э. Бриттена, в Proceedings of the IEEE 72 (2), 1984, pp. 196-221.
2) Дж. Рейнарт, А. Брокмайер, Р.В. Де Донкер, «Расчет потерь в ферро- и ферромагнитных материалах на основе модифицированного уравнения Штейнмеца», Труды ежегодного собрания Общества отраслевых приложений транзакций IEEE, 1999 г., стр. 2087-2092, т. 3.
3) Джели Ли, Т. Абдалла и К.Р. Салливан, «Улучшенный расчет потерь в сердечнике с несинусоидальными формами волны», Ежегодное собрание Общества промышленных приложений IEEE, 2001 г., стр. 2203-2210. ■
Индуктивность
Ваш браузер не поддерживает Java-апплеты
ИНДУКТОРЫ И ИНДУКТИВНОСТЬ
Конденсаторы способны накопление заряда в электростатическом поле.Индукторы способны хранить заряд в электромагнитном поле.
Способность вызывать напряжение между собой при изменении тока известно как самоиндукция или просто индуктивность. Индуктивность также препятствует изменению тока.
У индукторов нет оппозиции для постоянного постоянного тока.
L — символ индуктивность. Базовая единица индуктивности — Генри, названная в честь американского физик Джозеф Генри.
Индуктивность в электрическом схемы похожи на инерцию в механических операциях. Требуется больше энергии для запуска или остановки тока в катушке индуктивности, чем для поддержания его протекания.
ОСНОВЫ ИНДУКТОРА
Индуктор представляет собой катушку с проволокой. Катушка с проволокой становится электромагнитной, когда через нее проходит ток.
Катушки индуктивности еще называют дроссели, катушки сопротивления и реакторы.
Сердечник индуктора может быть магнитный материал, такой как железо или изолированный материал. Термин «воздушное ядро» используется для любых катушек индуктивности, не имеющих магнитного сердечника.
Индуктивность больше с больше катушек, больше площадь поперечного сечения и меньшая длина катушек.
САМОИНДУКЦИЯ
Любой проводник имеет некоторую индуктивность, потому что он производит магнитное поле вокруг него. При изменении тока изменяется магнитное поле.Когда магнитное поле изменяется, электродвижущая сила индуцируется в дирижер. Полярность этой индуцированной силы противоположна приложенной напряжение проводника. Эффект состоит в том, что индуктивность препятствует изменению текущая величина.
Об этом говорится в законе
Ленца. Индуцированная ЭДС в любой цепи равна всегда в направлении, противодействующем эффекту, который его произвел.
Когда переменный ток (переменный ток) проходит через катушку индуктивности происходит постоянное изменение тока.Эффект противостояния текущему тогда непрерывно.
Когда DC (постоянный ток) проходит через катушку индуктивности, противодействие току присутствует только тогда, когда есть изменение, такое как запуск, остановка или изменение тока.
Самоиндуцированное напряжение Уравнение
1 Гн (Генри) индуктивности составляет наблюдается, когда изменение тока на 1 А в секунду вызывает индуцированное напряжение 1 В.
ФАКТОРЫ, ВЛИЯЮЩИЕ НА КАТУШКУ ИНДУКТИВНОСТЬ
Чем больше число витков, тем выше индуктивность
Катушка большего диаметра имеет большую индуктивность
Индуктивность уменьшается с увеличением длины катушки
Сердечник с высокой магнитной проницаемостью увеличивает индуктивность
L = (мкН2А / л)
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность — это когда два катушки расположены так, что магнитный поток от одной катушки связан с витками другой катушки.Катушки называются связанными.
Трансформатор для переменного тока схемы — распространенный пример взаимной индуктивности.
Факторы, влияющие на взаимную индуктивность
Плотная муфта относится к высокая степень взаимной индуктивности, например, трансформатор с двумя намотанными катушками вокруг того же магнитопровода.
Слабая связь — это когда два катушки расположены далеко друг от друга или под прямым углом друг к другу.
Воздушное ядро
Катушки с полыми или Немагнитные сердечники называются катушками с воздушным сердечником.У них низкие значения индуктивности и обычно используются для высокочастотных приложений.
Железный сердечник
В индукторах с железным сердечником используется железо или сплав для сердечника. Возможны большие значения индуктивности. Гистерезис и потери на вихревые токи ограничивают стальной сердечник низкими частотами, такими как линии электропередач и аудио. Ламинированный листовой материал часто используется для уменьшения вихревых токов. Мягкое железо материал, такой как кремнистая сталь, может быть использован для уменьшения потерь на гистерезис.
Сердечник из порошкового железа
Порошковое железо смешивают с непроводящее связующее снижает потери на вихревые токи. Более высокий ток возможно до насыщения индуктора.
Ферритовый сердечник
Ферриты хорошие магнитные проводники, но плохие электрические проводники. Это снижает потери на вихревые токи.
Тороидальный сердечник
Из-за формы большинство поток течет внутри сердечника, что приводит к очень небольшим потерям на утечку потока.
Подвижный (переменный) сердечник
Это переменные индукторы который можно повернуть.
Ядро печатной платы
Спираль из меди на печатная плата может использоваться как катушка. Только небольшие значения индуктивности возможно, что ограничивает его полезность для высокочастотных приложений.
СОЧЕТАНИЯ ИНДУКТОРОВ
Катушки индуктивности серии
Когда индуктивность не соединены (достаточно далеко друг от друга, чтобы не влиять друг на друга) и соединены последовательно общая индуктивность — это сумма индивидуальных индуктивностей.
L _T = L ₁ + L ₂ + L ₃ + + L _N
Когда два взаимно связаны катушки соединены последовательно, общая индуктивность зависит от их полей либо помогающие друг другу, либо противостоящие друг другу.
L _T = L ₁ + L ₂ +/- 2л _м
Параллельные индукторы
Когда индукторы не соединены и соединены параллельно, общая индуктивность находится в аналогичном способ измерения полного сопротивления параллельно включенных резисторов.
L _T = 1 / (1 / л ₁ + 1 / л ₂ + + 1 / л _N)
Взаимосвязанные индукторы параллельно:
Вспомогательные поля: 1 / L _T = 1 / (L ₁ + L _M) + 1 / (Л ₂ + L _M)
Противоположные поля: 1 / L _T = 1 / (L ₁ — L _M) + 1 / (Л ₂ — L _M)
ЭНЕРГИЯ, СОХРАНЕННАЯ В ИНДУКТОРЕ
Открытие цепи
Когда цепь с индуктор открыт, магнитное поле схлопывается и возникает напряжение.В напряжение со временем рассеивается из-за I ² R потеря.
РАСХОДНАЯ ИНДУКТИВНОСТЬ
Все проводники в цепи обладают некоторой индуктивностью. На высоких частотах паразитная индуктивность может стать равной. значительный.
Для уменьшения паразитной индуктивности длина проводов должна быть короткой. Углеродные резисторы предпочтительнее проволочные резисторы. Однако некоторые резисторы с проволочной обмоткой сделаны неиндуктивными. путем намотки рядом, так что магнитные поля нейтрализуют друг друга.
ПОТЕРИ И НЕИСПРАВНОСТИ ИНДУКТОРА
Потери в индукторе
Потери в индукторе гистерезис и вихревые токи.
Утечка флюса — другое тип потери. Это магнитный поток за пределами пути, для которого он пригодится. Работа.
Скин-эффект — другое причина потери. Большая часть тока течет по внешней стороне проводника или кожа. Для минимизации скин-эффекта можно использовать полую проволоку.
Поиск и устранение неисправностей индуктора Неисправности
Индукторы могут изменять значение (в том числе открытые) и короткое замыкание между обмотками.
Шорты обычно не могут быть обнаруживается омметрами, потому что изменение сопротивления очень мало. Звон можно использовать тест, который создает магнитное поле, а затем проверяет количество звенит, когда поле схлопывается.
Оптимизируйте индукторы коррекции коэффициента мощности
Чрезмерное потребление электроэнергии и низкий КПД больше недопустимы.Устранение низкого коэффициента мощности приведет к увеличению электрического КПД и уменьшит общее потребление электроэнергии. До сих пор большинство катушек индуктивности, используемых для коррекции коэффициента мощности, были специально разработаны для их применения, что приводило к более высоким затратам и увеличению времени выполнения заказа. Используя онлайн-инструменты проектирования и правильно сгруппировав параметры цепи, можно использовать стандартные индукторы для решения проблем с коэффициентом мощности.
Устранение проблем с коэффициентом мощности можно решить разными способами.Однако не все коррекции коэффициента мощности работают для каждой проблемы, связанной с коэффициентом мощности. Без правильного понимания того, что такое коэффициент мощности и что на него влияет, может привести к еще более неэффективным проектам.
КОЭФФИЦИЕНТ МОЩНОСТИ
Коэффициент мощности — это показатель того, насколько эффективно или неэффективно используется электроэнергия. Коэффициент мощности выражается дробью от 0 до 1 и представляет собой соотношение между активной и полной мощностью.
Полная мощность является функцией полного импеданса (Z) цепи и представляет собой векторную сумму реальной и реактивной мощности. На рис. 1 показаны векторные отношения.
Для дальнейшего определения двух составляющих полной мощности, реальная мощность состоит из рассеивающих элементов схемы, обычно сопротивлений (R), а реактивная мощность состоит из реактивных элементов схемы (X) (конденсаторов и катушек). Поскольку полная мощность является произведением напряжения цепи и тока без привязки к фазовому углу, она измеряется в вольт-амперах (ВА).
Коэффициент мощности
— это практическая мера эффективности использования энергии в цепи.Цепи, содержащие чисто резистивные элементы, имеют коэффициент мощности 1,0. Цепи, содержащие индуктивные или емкостные элементы, имеют коэффициент мощности ниже 1,0. Для двух цепей, использующих одинаковое количество реальной мощности, система с более низким коэффициентом мощности будет иметь более высокие циркулирующие токи из-за энергии, которая возвращается к источнику из накопителя энергии в нагрузке. Эти более высокие токи вызывают более высокие потери и снижают общий КПД. Схема с более низким коэффициентом мощности будет иметь более высокую кажущуюся мощность и более высокие потери при том же количестве активной мощности.
Коррекция коэффициента мощности приближает коэффициент мощности в силовой цепи переменного тока к единице, добавляя к цепи равную и противоположную нагрузку, чтобы нейтрализовать влияние реактивного сопротивления нагрузки. Могут быть добавлены конденсаторы и катушки индуктивности, которые нейтрализуют индуктивные или емкостные эффекты нагрузки. Емкостное реактивное сопротивление может быть отменено только добавлением индуктивного реактивного сопротивления; индуктивное реактивное сопротивление может быть отменено только добавлением емкостного реактивного сопротивления. Эффект противоположных реактивных сопротивлений сводится к тому, чтобы общий импеданс схемы был равен ее общему сопротивлению.Другими словами, активная мощность и полная мощность совпадают, в результате чего коэффициент мощности приближается (или равен) к 1.
Еще одна причина для решения проблем с коэффициентом мощности — соблюдение международных норм, особенно если вы собираетесь продавать свое оборудование в Европе. Европейский Союз (ЕС) установил ограничения на гармонические токи, которые могут возникать в сети (линии переменного тока) импульсных источников питания. EN61000-3-2 применяется к источникам питания с входной мощностью 75 Вт или более, которые потребляют до 16 ампер от сети.Источники питания со схемами коррекции коэффициента мощности, соответствующие стандарту EN61000-3-2, по своей природе имеют высокий коэффициент мощности, который обычно составляет 0,97 или выше.
Производители
ИС разрабатывают свои схемы в соответствии с европейскими правилами и ожидают, что аналогичные правила будут разработаны для других частей мира. При разработке своих схем большинство производителей ИС инициировали множество конструкций катушек индуктивности для удовлетворения требований своих схем. Эти конструкции, как правило, представляют собой «готовые» индукторы, не предназначенные для удовлетворения требований коррекции коэффициента мощности или дорогостоящих индукторов, разработанных специально для них.
ВАРИАЦИИ ИНДУКТОРА
Катушка индуктивности или реактор — это пассивный электрический компонент, который может накапливать энергию в магнитном поле, создаваемом проходящим через него электрическим током. Способность индуктора накапливать магнитную энергию измеряется его индуктивностью в единицах генри. Обычно индуктор представляет собой провод, имеющий форму катушки; петли помогают создать сильное магнитное поле внутри катушки из-за закона Ампера. Из-за изменяющегося во времени магнитного поля внутри катушки индуцируется напряжение согласно закону электромагнитной индукции Фарадея, который по закону Ленца противодействует изменению тока, создавшего его.Индукторы являются одним из основных компонентов, используемых в электронике, где ток и напряжение меняются со временем из-за способности катушек индуктивности задерживать и изменять форму переменного тока. Индукторы, называемые дросселями, используются как части фильтров в источниках питания или для блокировки прохождения сигналов переменного тока через цепь.
Практически любой тип силового индуктора может использоваться для коррекции коэффициента мощности, но для этого анализа используются тороидальные индукторы. Тороидальные индукторы обладают более высокими характеристиками, чем другие типы индукторов.Тороидальные индукторы имеют меньший объем, меньше весят и излучают меньше электромагнитных помех (EMI). Теплопередача обмотки более эффективна, поскольку для охлаждения доступна пропорционально большая площадь поверхности меди. Тороидальная геометрия приводит к почти полному гашению магнитного поля за пределами его катушки, позволяя тороидальной катушке индуктивности иметь меньше электромагнитных помех (EMI) по сравнению с другими катушками индуктивности такой же номинальной мощности. Однослойная обмотка и полная намотка на 360 градусов вокруг сердечника обеспечивают отличную межвитковую связь и более низкую индуктивность рассеяния.
Тороидальные индукторы могут использоваться в любых индукторах, которые могут адаптироваться к их форме. Несмотря на то, что тороидальные индукторы применимы, они не всегда применимы для некоторых приложений.
Тороидальные сердечники индуктора доступны из многих материалов: кремнистой стали, никелевого железа, порошка молиберпермаллоя, порошкового железа, аморфного железа, ферритов и других. Кремнистая сталь и никелевое железо доступны в виде сердечников, намотанных на ленту, или в виде ламинированных деталей. Немагнитные тороиды также доступны для изготовления тороидальных индукторов с воздушным сердечником.Для приложений коррекции коэффициента мощности порошковое железо, Kool-mu (Sendust), Hi Flux, молибденовый пермаллой и XFlux — каждый предлагает свои собственные уникальные решения для требований к частоте, управлению мощностью и смещению. Таблица 1 показывает общие рекомендации и компромиссы при выборе материала.
Еще одним полезным критерием выбора материала является диапазон частот, для которого предназначен материал. Решения по рабочей частоте включают компромисс между потерями в сердечнике и обмотке индуктора. С намотанными магнитными компонентами и общедоступными материалами сердечника изучение этих компромиссов приводит к выводу, что работа на частотах до 300-400 кГц возможна, но это уменьшение в ответ примерно через 125 кГц. Таблица 2 дает некоторые общие рекомендации по максимальным частотным диапазонам для некоторых материалов.
Оптимально, индуктор должен быть маленьким и недорогим. Однако нельзя жертвовать надежностью или производительностью индуктора. Чтобы избежать внезапного насыщения, керн должен иметь относительно низкую проницаемость, чтобы поддерживать постоянную составляющую работы. Если в материале с высокой проницаемостью используется зазор, необходимо учитывать, где он размещается и каковы его потери.Эти соображения свидетельствуют в пользу материалов с распределенным зазором, таких как порошковое железо, MPP, сендуст, KoolMu, и против феррита.
Установка тороидального индуктора стала проще, поскольку промышленность стандартизировала несущие элементы и схемы посадки. В зависимости от размера тороида он может быть дополнительно закреплен с помощью эпоксидной смолы, монтажных винтов или даже стяжек. Разработчику схем доступны варианты горизонтального и вертикального монтажа в зависимости от доступной монтажной области платы (или корпуса).Например, размещение тороида на плате может занять слишком много места на плате, в то время как в некоторых случаях установка тороида вертикально будет мешать ограничению по высоте. На рис. 2 показан тороидальный индуктор с улучшенными монтажными характеристиками.
Одна из причин, по которой схемы PFC могут быть трудными при проектировании, заключается в том, что инженеры должны полностью понимать рабочие характеристики катушки индуктивности PFC и ее влияние на схему PFC при изменении критериев проектирования. Выбор индуктора по-прежнему является исключительно индивидуальным, в зависимости от выбора разработчика схемы рабочего режима, диапазона частот, максимальной выходной мощности, эффективности, максимального и минимального напряжения переменного тока, выходного напряжения и тока пульсаций.Как правило, наиболее важными факторами при окончательном выборе являются размер и стоимость, а не самый оптимальный. Разработчик магнитных систем должен уравновесить эти требования, даже если большинство этих параметров движутся в противоположных направлениях, работая друг против друга. Связь между проектировщиком схем и разработчиком магнитных цепей помогает определить приоритетность того, какой параметр более важен для удовлетворения проектных требований.
По запросу клиентов несколько компаний разработали стандартные конструкции индукторов, специально предназначенные для коррекции коэффициента мощности при проектировании источников питания.При этом эти компании стандартизировали общие параметры работы. Линия индукторов с коррекцией коэффициента мощности одной компании основана на методе работы CCM (режим непрерывной проводимости), 100 кГц, КПД 92%, V _IN от 85 до 265 и V _OUT из 385. При стандартизации индуктора , они также упростили процесс выбора индуктора.
Во время APEC 2010 Велли Чоу из Precision, Inc. представил свою разработку инструмента PL Product.Чоу разработал интерактивную модель под названием PL Product, которая будет использоваться инженерами-конструкторами для оценки и ускорения выбора катушек индуктивности PFC в схемах. Традиционно индукторы PFC разрабатываются на основе набора параметров схемы, т. Е. Минимального линейного напряжения, частоты переключения, тока пульсаций, выходного напряжения постоянного тока и т. Д. Хотя такой подход, ориентированный на конкретное приложение, оптимизирует конструкцию индуктора, он затрудняет понимание взаимосвязи. и компромиссы между параметрами схемы и катушкой индуктивности.Продукт PL упрощает это, отделяя выходную мощность (P) и индуктивность (L), необходимые для желаемого пульсирующего тока, от параметров схемы PFC, оставляя разработчикам простой расчет для получения минимального необходимого PL, не вникая в тонкости индуктора. . На рис. 3 показаны характеристики выбранного индуктора. Ожидаемая пульсация выбранного индуктора показана на Рис. 4 .
Для поддержки расчета продукта Чжоу PL, Precision, Inc.разработала онлайн-калькулятор PL Product — управляемое пользователем программное обеспечение, используемое для определения характеристик катушек индуктивности PFC в диапазоне выходной мощности. Основываясь на желаемых рабочих параметрах схемы, разработчики могут рассчитать продукт PL, необходимый для их применения, и сопоставить его с кривыми PL различных катушек индуктивности PFC. Это не только упростит процесс проектирования, упростив выбор индуктора, но также позволит реализовать характеристики схемы и индуктивности PFC в различных рабочих условиях.Продукт PL упрощает разработчикам схем понимание взаимосвязи и компромиссов между параметрами схемы и катушкой индуктивности.
Низкий коэффициент мощности продолжает оставаться проблемой. Европейский Союз уже выявил эту ситуацию и разработал правила для коррекции коэффициента мощности. По мере появления новых правил коррекция коэффициента мощности станет необходимой почти во всех приложениях. Разработчики схем будут по-прежнему сталкиваться с трудным выбором дизайна, в том числе между стоимостью и стоимостью.выбор производительности в магнитных компонентах. Использование надлежащих инструментов, стандартных конструкций индукторов и посадочных мест является ключом к экономичным решениям для схемотехники. Понимание правильных методов коррекции коэффициента мощности поможет повысить электрический КПД.
Большое спасибо Лайлу Шоу и Дэвиду Андерсону из Precision, Inc. и Марку Свихарту из Magnetics, Inc. за поддержку этой статьи.
ССЫЛКА:
Практический подход к усовершенствованию конструкции корректора коэффициента мощности CCM — D.Michael Shields
PL product tool — Welly Chou
Wikipedia
ТАБЛИЦА 1. РЕКОМЕНДАЦИИ ПО ВЫБОРУ МАГНИТНОГО СЕРДЕЧНИКА
PERFORM САМАЯ НИЗКАЯ СТОИМОСТЬ МЯГКОЕ НАСЫЩЕНИЕ ТЕПЛОВАЯ СТАБИЛЬНОСТЬ
Best High Flux Феррит с зазором Феррит с зазором High Flux Железный порошок Kool Mu High Flux
3rd Best Ламинированное кремниевое железо Ламинированное аморфное Kool Mu MPP MPP
MPP MPP
MPP MPP
XFlux Железный порошок
Полоса
ТАБЛИЦА 2.ДИАПАЗОН ЧАСТОТ МАГНИТНЫХ МАТЕРИАЛОВ
ОСНОВНОЙ МАТЕРИАЛ ДИАПАЗОН ЧАСТОТ
Высокий поток
До 200 кГц
Порошковое железо До 25 кГц
Ламинированная сталь До 10 кГц
Феррит с зазорами Полоска от 20 Гц до 2 МГц
от 10 кГц до 100 кГц
XFlux До 25 кГц
(PDF) Прогнозный расчет коэффициента связи между многослойными катушками индуктивности малой площади на кристалле
0.0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
0,008
0,010
0,012
Случай B
: рассчитано k
: смоделировано k
dout1 = dout2 = 39um, x0 = y0 = 7 мкм
S1 = S2 = 0,4 мкм, n1 = n2 = 3, l1 = l2 = 3
Относительная погрешность
Коэффициент связи, k
Ширина металла, w1 (w2) / мкм
0,008
0,010
0,012
0,014
0,016
0,018
0,020
0.022
: относительная ошибка
Рис. 8. Расчетные и смоделированные значения в зависимости от ширины металла
и соответствующих относительных ошибок
случаев. Расчетные и смоделированные значения также хорошо совпадают. Можно видеть, что с увеличением числа витков
значение k уменьшается, тогда как при увеличении числа слоев
значение k увеличивается. На рисунке
8 показаны рассчитанные и смоделированные значения в зависимости от ширины металла
в случае B, при этом dout и расстояние между индукторами x0 (y0)
являются фиксированными.Значение k уменьшается с увеличением ширины металла
. Относительные погрешности также показаны на рисунке.
Дальнейший всесторонний анализ показывает, что значение k
менее чувствительно к количеству слоев l, количеству витков n
и ширине металла w, чем к диаметру dout и расстоянию между индукторами
x0 (y0).
Как упоминалось ранее, при симметричном приближении
переходные отверстия и металлические соединения, вероятно, могут вносить вклад в общую ошибку, особенно для небольших катушек индуктивности.
Однако, как показано на рисунках, все рассчитанные значения
очень хорошо согласуются с смоделированными, даже для
малых dout 15 мкм. Более того, как показано на рисунках 5 и 8,
интересно, что относительные ошибки кажутся
«случайными» и не показывают корреляции с k. Согласно
, описанию в разделе 2, расчеты самоиндукции L
и взаимной индуктивности M
выполняются в симметричном приближении.
Следовательно, вполне естественно, что переходные отверстия и металлические соединения
имеют одинаковое влияние на расчет L
и M и определенно вызывают ошибки. Однако из (1),
, когда дело доходит до вычисления k, ошибки в L и
M фактически в некоторой степени противодействуют, и в конечном итоге ошибка
k остается в пределах 4%, как указано ранее.
Еще одна проблема — различие между конструкциями катушек индуктивности
.Следует отметить, что в данной работе исследуются только
катушек индуктивности, как в [6].
Как правило, многослойный индуктор имеет больше межслойных отверстий
и меньше межвитковых металлических соединений, чем миниатюрный 3-D индуктор
в [7], что приводит к примерно одинаковой ошибке расчета
для обоих типов индукторов. . Структура
трехмерного соленоидного индуктора в [3] аналогична конструкции
миниатюрного трехмерного индуктора.Таким образом, новый метод
считается применимым и эффективным для всех типов многослойных катушек индуктивности
малой площади при вычислении k.
4. Резюме
В этой статье предлагается новый метод расчета коэффициента связи
встроенных в микросхему многослойных катушек индуктивности
малой площади. Симметричная аппроксимация и сопровождающий метод
«кольцо за кольцом» могут значительно упростить процесс вычисления
по сравнению с традиционным способом
«сегмент за сегментом».Было доказано, что
предложенный метод является точным и эффективным для оценки
перекрестных помех между катушками индуктивности на кристалле, которые могут быть
очень критичными для проектирования схем. Следует отметить
, что предложенный метод действительно подходит для
катушек индуктивности, расположенных на разных микросхемах, хотя в этой статье не так много относительного материала.
Благодарности
Эта работа была частично поддержана Национальным естественным
научным фондом Китая (NSFC) в рамках гранта
60976027.
Ссылки
[1] К. Хидзиока, А. Танабэ, Ю. Амамия и Ю.
Хаяси, «Трехмерный сверхмалый размер
Катушка индуктивности в форме соленоида, интегрированная в высокоскоростную систему обработки сигналов
. КМОП сверхбольшие интегрированные схемы
”, Японский журнал прикладной физики, Vol. 47,
№4, стр. 2477–2483 (2008).
[2] Н. Миура, Т. Сакураи, Т. Курода, «Меры противодействия перекрестным помехам
для массива каналов с высокой плотностью индуктивной связи
», IEEE J.Твердотельные схемы, т. 42, вып.
2, с. 410-421 (2007).
[3] К. Хидзиока, А. Танабе, Ю. Амамия, Ю.
Хаяси, «Метод анализа перекрестных помех трехмерного соленоида
Индукторы на кристалле для высокоскоростных CMOS SoC»,
Interconnect Конференция по технологиям, стр.186–188 (2008).
[4] Х. М. Гринхаус, «Проектирование плоских прямоугольных
микроэлектронных индукторов», IEEE Trans. Детали, гибриды,
Упаковка.том 10, вып. PHP – 6, с.101–109 (1974).
[5] Саман Асгаран, «Новые точные выражения в замкнутой форме на основе физики
для компактного моделирования и
проектирования спиральных индукторов на кристалле», 14-я Международная конференция по микроэлектронике
,
с.247- 250 (2002).
[6] А. Золфагари, А. Чан и Б. Разави, «Сгруппированные
индукторов и трансформаторов в КМОП-технологии», IEEE
J. Solid-State Circuits, vol.36, p.620-628 (2002).
[7] К. Тан, К. Ву и С. Лю, «Миниатюрные 3-D индукторы
в стандартном процессе КМОП», IEEE J.
твердотельные схемы
, том 37, стр.

PERFORM	САМАЯ НИЗКАЯ СТОИМОСТЬ	МЯГКОЕ НАСЫЩЕНИЕ	ТЕПЛОВАЯ СТАБИЛЬНОСТЬ
Best	High Flux	Феррит с зазором	Феррит с зазором		High Flux	Железный порошок	Kool Mu	High Flux
3rd Best	Ламинированное кремниевое железо	Ламинированное аморфное	Kool Mu	MPP	MPP
MPP	MPP
MPP	MPP
XFlux	Железный порошок

ОСНОВНОЙ МАТЕРИАЛ	ДИАПАЗОН ЧАСТОТ
Высокий поток
До 200 кГц
Порошковое железо	До 25 кГц
Ламинированная сталь	До 10 кГц
Феррит с зазорами	Полоска от 20 Гц до 2 МГц
от 10 кГц до 100 кГц
XFlux	До 25 кГц

16. Смешанное соединение резистора, катушки индуктивности и конденсатора.

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Соединение источников питания | Электрикам

Последовательное соединение источников питания

Параллельное соединение источников питания

Смешанное соединение источников питания

Параллельное соединение конденсатора и катушки индуктивности. Понятие о резонансе тока

Составитель: Н.Н. Муравлева

Резонанс «на ладони».

С.А. Иванская ЭЛЕКТРОТЕХНИКА

А.С. КАЛИНИН ЭЛЕКТРОТЕХНИКА

РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

Виртуальный практикум

«КРАСНОДАРСКИЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ»

ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ 1/63

Тема 4.2. Цепи переменного тока

Лабораторная работа 5 Резонанс напряжений

10. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Основные положения теории

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Лекция 4 ПЕРЕМЕННЫЙ ТОК

ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Исследование резонанса токов

Колебательные контуры

Лабораторная работа 2-32

Тема 1. Линейные цепи постоянного тока.

ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

Как рассчитать сердечник и витки самодельных катушек индуктивности > Флэтора

Напряжение при параллельном соединении двух резисторов. Формула для расчета параллельного соединения сопротивлений. Мощность при паралл ельном соединение

Определения

Использование параллельного и последовательного соединения проводников

Термины, применяемые к электрическим цепям

Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников

Посчитать сопротивления элементов при последовательном и параллельном соединении

Задачи с конденсаторами: сборная солянка

Преобразование параллельных цепей RL в последовательные эквиваленты

Основные сведения об индуктивности в реальном мире

4.4: Параллельные цепи резистора-конденсатора — Workforce LibreTexts

Резистор и конденсатор параллельно

Расчет с использованием закона Ома

Обзор

Упрощение расчета потерь в сердечнике композитных катушек индуктивности

Индуктивность

Факторы, влияющие на взаимную индуктивность

Воздушное ядро ​​

Железный сердечник

Сердечник из порошкового железа

Ферритовый сердечник

Тороидальный сердечник

Подвижный (переменный) сердечник

Ядро печатной платы

Оптимизируйте индукторы коррекции коэффициента мощности

КОЭФФИЦИЕНТ МОЩНОСТИ

ВАРИАЦИИ ИНДУКТОРА

ССЫЛКА:

(PDF) Прогнозный расчет коэффициента связи между многослойными катушками индуктивности малой площади на кристалле

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ

Воздушное ядро