Расчет заряда конденсатора: конденсатор в цепи постоянного тока

Онлайн калькулятор расчета запасаемой энергии в конденсаторе

Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.

Устройство конденсатора

Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.

Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.

Для этого выполните такую последовательность действий:

• Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
• Укажите во втором поле величину емкости элемента в микрофарадах;
• Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.

Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:

Где,

• W – это количество запасаемой энергии в конденсаторе;
• U – величина напряжения, приложенного к конденсатору;
• C – емкость конденсатора.

Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: T

зар = R*C

Где

• T_зар  — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
• R – величина омического сопротивления конденсатора;
• C – емкость конденсатора.

 

Калькулятор резистивно-емкостной цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Данный калькулятор позволяет рассчитывать максимальный ток I_max в начале заряда конденсатора, максимальную энергию E_max и максимальный заряд конденсатора Q_max, когда он полностью заряжен при данном напряжении, а также постоянную времени RC-цепи.

Пример. Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи.

Входные данные

Напряжение V

микровольт (мкВ)милливольт (мВ)вольт (В)киловольт (кВ)мегавольт (МВ)

Емкость C

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Сопротивление R

миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)

Выходные данные

Постоянная времени

τ с

Макс. энергия

E Дж

Макс. ток

I А

Макс заряд

Q Кл

Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать.

Постоянная времени определяется по формуле

где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.

Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой

где C — емкость в фарадах и V — напряжение в вольтах.

Максимальный ток I определяется по закону Ома:

Максимальный заряд Q определяется по формуле

где C — емкость в фарадах и V — напряжение в вольтах.

Фильтрующие электролитические конденсаторы на системной плате компьютера

Применение

Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе

Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.

Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.

Резистивно-емкостные фильтры нижних частот

Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра

Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.

Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале. У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.

Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.

На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.

В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки. В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.

Простой пассивный RC-фильтр верхних частот

RC-фильтры верхних частот

Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.

Активный фильтр верхних частот с операционным усилителем

Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна. Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю. В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка. Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.

Простой полосовой фильтр, собранный из двух каскадов — фильтра нижних частот (C2, R2) и фильтра высоких частот (C1, R1)

Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках. В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот. Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.

Расчет заряда конденсатора. Энергия заряженного конденсатора. применение конденсаторов. Определение понятия энергии

Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).

Так как в момент включения конденсатор еще не заряжен, то напряжение на нем Поэтому в цепи в начальный момент времени падение напряжения на сопротивлении R равно U и возникает ток, сила которого

Рис. 16-4. Зарядка конденсатора.

Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение и падение напряжения на сопротивлении R уменьшается:

как и следует из второго закона Кирхгофа. Следовательно, сила тока

уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи

С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности — напряжений

Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.

Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю — процесс зарядки конденсатора заканчивается.

Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд.

Скорость протекания процесса характеризуют постоянной времени цепи

чем больше , тем медленнее процесс.

Постоянная времени цепи имеет размерность времени, так как

Через интервал времени с момента включения цепи, равный , напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал процесс зарядки конденсатора можно считать закончившимся.

Напряжение на конденсаторе при зарядке

т. е. оно равно разности постоянного напряжения источника питания и свободного напряжения убывающего с течением времени по закону показательной функции от значения U до нуля (рис. 16-5).

Зарядный ток конденсатора

Ток от начального значения постепенно уменьшается по закону показательной функции (рис. 16-5).

б) Разряд конденсатора

Рассмотрим теперь процесс разряда конденсатора С, который был заряжен от источника питания до напряжения U через резистор с сопротивлением R (рис. 16-6, Где переключатель переводится из положения 1 в положение 2).

Рис. 16-6. Разряд конденсатора на резистор.

Рис. 16-7. График изменения тока и напряжения при разрядке конденсатора.

В начальный момент, в цепи возникнет ток и конденсатор начнет разряжаться, а напряжение на нем уменьшаться. По мере уменьшения напряжения будет уменьшаться и ток в цепи (рис. 16-7). Через интервал времени напряжение на конденсаторе и ток цепи уменьшатся при мерно до 1% начальных значений и процесс разряда конденсатора можно считать закончившимся.

Напряжение на конденсаторе при разряде

т. е. уменьшается по закону показательной функции (рис. 16-7).

Разрядный ток конденсатора

т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).

Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.

Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.

Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора не зависит от формы обкладок и расстояния между ними.

Процессы зарядки и разряда конденсатора называются переходными процессами.

Одними из наиболее часто используемых электронных компонентов являются конденсаторы . И в этой статье нам предстоит разобраться, из чего они состоят, как работают и для чего применяются 🙂

Давайте, в первую очередь, рассмотрим устройство конденсаторов , а затем уже плавно перейдем к их основным видам и характеристикам, а также к процессам зарядки/разрядки. Как видите, нам сегодня предстоит изучить много интересных моментов 😉

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором , а пластины – обкладками конденсатора . Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле, изображенное стрелками на нашей схеме. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит 🙂

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

Здесь – это поверхностная плотность заряда: .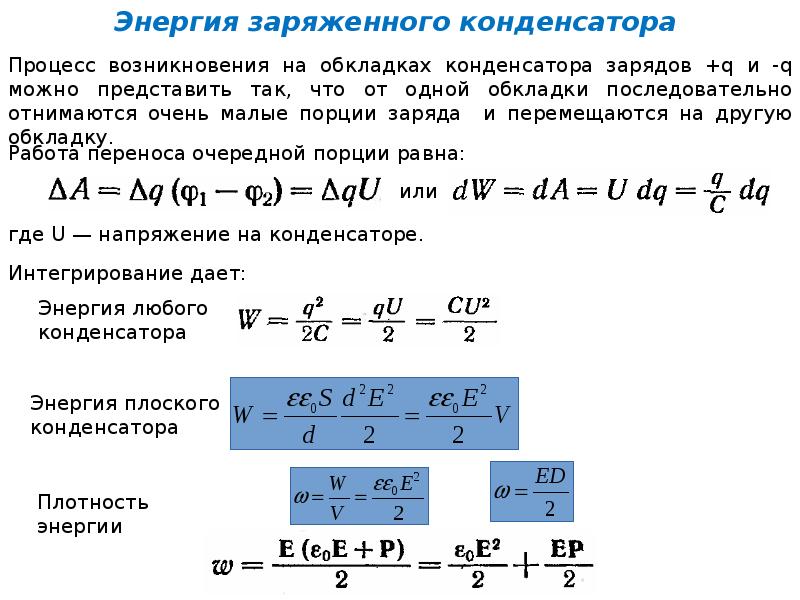 А – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную . Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора , а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного 🙂

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора – физическая величина, которая определяется как отношение заряда конденсатора одного из проводников к разности потенциалов между проводниками:

Емкость изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость конденсаторов измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ).

А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

Здесь у нас – это расстояние между пластинами конденсатора, а – заряд конденсатора. Подставим эту формулу в выражение для емкости конденсатора:

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить

Для запасенной энергии конденсатора справедливы следующие выражения:

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение – то есть величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

В общем, мы рассмотрели сегодня основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений конденсаторов, так что заходите на наш сайт снова!

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.2}$

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т.2$ — электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика.2}/{2}$

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

$I={∆q}/{∆t}$

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$.2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи . Математически закон Ома записывается в виде следующей формулы:

Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:

1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.{-1}$. Для растворов электролитов $α

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Параллельное и последовательное соединение проводников

Для параллельного соединения проводников справедливы следующие соотношения:

1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом ), равен сумме токов в каждом из элементов цепи:

3) при параллельном соединении проводников складываются их обратные сопротивления:

${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$

4) сила тока и сопротивление в проводниках связаны соотношением:

${I_1}/{I_2}={R_2}/{R_1}$

Для последовательного соединения проводников в цепи справедливы следующие соотношения:

1) для общего тока $I$:

где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т. е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;

2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:

4) также справедливо соотношение:

${U_1}/{U_2}={R_1}/{R_2}$

Работа электрического тока. Закон Джоуля-Ленца

Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:

где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Закон Джоуля-Ленца

Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А.2}/{R}$

Из соотношения для ЭДС легко получить мощность источника тока:

В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом

$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:

$Р=10А·220В=2200Вт=2.2кВт.$

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).

$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.

Заряд конденсатора

Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.

Генератор обладает внутренним сопротивлением. При замыкании ключа конденсатор зарядится до напряжения между обкладками, равного э. д. с. генератора: Uс = Е. При этом обкладка, соединенная с положительным зажимом генератора, получает положительный заряд (+q ), а вторая обкладка получает равный по величине отрицательный заряд (-q ). Величина заряда q прямо пропорциональна емкости конденсатора С и напряжению на его обкладках: q = CUc

P ис. 1

Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.

Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.

Рис. 2. Графики напряжения и тока при заряде конденсатора

Пока конденсатор заряжается, по цепи проходит зарядный ток. График зарядного тока показан на рис. 2,б. В начальный момент зарядный ток имеет наибольшую величину, потому что напряжение на конденсаторе еще равно нулю, и по закону Ома io зар = E/ Ri , так как вся э. д. с. генератора приложена к сопротивлению Ri.

По мере того как конденсатор заряжается, т. е. возрастает напряженно на нем, для зарядного тока уменьшается. Когда напряженно па конденсаторе уже имеется, падение напряжения на сопротивление будет равно разности между э. д. с. генератора и напряжением на конденсаторе, т. е. равно Е — U с. Поэтому i зар = (E-Uс)/Ri

Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.

Продолжительность процесса заряда конденсатора зависит от двух величии:

1) от внутреннего сопротивления генератора Ri ,

2) от емкости конденсатора С.

На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением Ri = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: Ri = 5 Ом.

Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.

Рис. 2. Графики зарядных токов при разных сопротивлениях

На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э. д. с. Е = 100 В и внутренним сопротивлением Ri = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).

Величина начального зарядного тока io зар = Е/Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.

Рис. 3. Графики зарядных токов при разных емкостях

Разряд конденсатора

Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.

На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.

Ток идет от положительной обкладки конденсатора через сопротивление к отрицательной обкладке. Это соответствует переходу избыточных электронов с отрицательной обкладки на положительную, где их недостает. Процесс рам ряда происходит до тех пор, пока потенциалы обеих обкладок не сравняются, т. е. разность потенциалов между ними станет равном нулю: Uc=0 .

На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.

На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc /R

Рис. 4. Графики напряжения и токов при разряде конденсатора

В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.

Продолжительность разряда зависит:

1) от емкости конденсатора С

2) от величины сопротивления R , на которое конденсатор разряжается.

Чем больше сопротивление R , тем медленнее будет происходить разряд. Это объясняется тем, что при большом сопротивлении сила разрядного тока невелика и величина заряда на обкладках конденсатора уменьшается медленно.

Это можно показать на графиках разрядного тока одного и того же конденсатора, имеющего емкость 10 мкф и заряженного до напряжения 100 В, при двух разных величинах сопротивления (рис. 5): кривая 1 — при R = 40 Ом, i оразр = Uc о/R = 100/40 = 2,5 А и кривая 2 — при 20 Ом i оразр = 100/20 = 5 А.

Рис. 5. Графики разрядных токов при разных сопротивлениях

Разряд происходит медленнее также тогда, когда емкость конденсатора велика. Получается это потому, что при большей емкости на обкладках конденсатора имеется большее количество электричества (больший заряд) и для стекания заряда потребуется больший промежуток времени. Это наглядно показывают графики разрядных токов для двух конденсаторов раиной емкости, заряженных до одного и того же напряжения 100 В и разряжающихся на сопротивление R =40 Ом (рис. 6 : кривая 1 — для конденсатора емкостью 10 мкф и кривая 2 — для конденсатора емкостью 20 мкф).

Рис. 6. Графики разрядных токов при разных емкостях

Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток проходит только в моменты заряда и разряда, когда напряжение на обкладках меняется.

Объясняется это тем, что при изменении напряжения изменяется величина заряда на обкладках, а для этого требуется перемещение зарядов по цепи, т. е. по цепи должен проходить электрический ток. Заряженный конденсатор не пропускает постоянный ток, так как диэлектрик между его обкладками размыкает цепь.

Энергия конденсатора

В процессе заряда конденсатор накапливает энергию, получая ее от генератора. При разряде конденсатора вся энергия электрического поля переходит в тепловую энергию, т. е. идет на нагрев сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его обкладках, тем больше будет энергия электрического поля конденсатора. Величина энергии, которой обладает конденсатор емкостью С, заряженный до напряжения U, равна: W = W с = СU 2 /2

Пример. Конденсатор С=10 мкф заряжен до напряжении U в = 500 В. Определить энергию, которая выделится в вило тепла на сопротивлении, через которое разряжается конденсатор.

Решение. Пpи разряде вся энергия, запасенная конденсатором, перейдет в тепловую. Поэтому W = W с = СU 2 /2 = (10 х 10 -6 х 500)/2 = 1,25 дж.

Содержание:

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица — фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q — заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов используется формула:
в которой ε 0 = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε — является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S — означает площадь обкладки, а d — зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как . После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I зар = Е/R i , поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора — способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I ут = U/R d , где I ут, — это ток утечки, U — напряжение, прилагаемое к конденсатору, а R d — сопротивление изоляции.

Расчет электролитического конденсатора в сетевом выпрямителе



Расчет электролитического конденсатора в сетевом выпрямителе

Расчет сглаживающего конденсатора в сетевом выпрямителе.

Входной выпрямитель является неотъемлемым элементом большинства преобразователей, питающихся от переменного сетевого напряжения. После диодного моста напряжение на конденсаторе будет иметь вид пилы, верхняя точка которой равна амплитудному напряжению сети (минус падение напряжения на диодах моста, что несущественно для устройств, питающихся от 220В), а нижняя зависит от емкости конденсатора и тока потребления нагрузки выпрямителя. В этой статье приведен пример расчета емкости сглаживающего конденсатора выпрямителя. Более полная информация приведена в статье А.И. Колпакова.

 

В качестве примера приведен расчет конденсатора для реального преобразователя, разработка которого была доведена до практического воплощения,  Pвых=1200Вт (выходное напряжение 60В, ток 20А, КПД около 90%)

 

Исходные данные для расчета:

Uвх = 220В       (напряжение сети)

f = 50Гц             (частота сетевого напряжения)

Задаваемые параметры:

Umin =260В     (минимальное напряжение — задается минимальное значение пилообразного напряжения на конденсаторе)

Iнагр = 5.13А           (ток потребления нагрузки выпрямителя, если известна мощность нагрузки, то ток можно вычислить как I=Pвх/Uмин, в моем случае Pвх=Pвых/КПД, т.е I=(1200/0.9)/260=5.13А )

1. Вычисляется время заряда конденсатора (в течение которого ток потребляется от сети). Так как напряжение изменяется по синусоидальному закону, используем для расчета формулу тригонометрии:

   t(зар) = (arccos(Umin/Umax))/(2*pi*f)

   Для синусоиды Umax = Uвх*1.41=220*1.41= 310 В (амплитудное сетевое напряжение), т.е.

   t(зар) = (arccos(260/310))/(2*3.141*50) = 0.00183 c

2. Вычисляется время разряда конденсатора:

   t(раз) = T-t(зар)

   в двухполупериодном выпрямителе T = (1/f)/2 = 1/50/2=0.01с (частота сети в двухполупериодном выпрямителе удваивается)

   t(раз) = 0.01-0.00183 = 0.0082 с

3. Находится емкость конденсатора, на которой за время t(раз) при токе нагрузки Iнагр напряжение с Umax уменьшится до Umin:

     C = Iнагр*dt/dU,

    в нашем случае dt это  t(раз), а dU является разница (Umax-Umin)

   C = 5.13*0.0082/(310-260) = 0.00084Ф = 840 мкФ

4. Находим пиковый зарядный ток:

   Ipic = C*dU/dt,

   где dU = Umax-Umin, а dt — это время заряда конденсатора, т.е. t(зар)

   Ipic = 0.00084*(310-260)/0.00183 = 23А

5. Находим среднеквадратичное значение импульсного тока через конденсатор по формуле:

   Irms = √(I(зар)²+I(разр)²),

   где  I(зар)-среднеквадратичный ток через конденсатор на цикле заряда, а I(разр) — среднеквадратичный ток через конденсатор на цикле разряда.

   Считаем, что ток заряда конденсатора имеет треугольную форму, тогда

   I(зар) = Ipic*√((t(зар)/T)/3) = 23*√((0.00183/0.01)/3) = 5.7A

   На интервале разряда через конденсатор течет ток нагрузки, поэтому

   I(разр) = Iнагр*t(раз)/T = 5.13*0.0082/0.01 = 4.2А

   Итак,  Irms = √(5.7²+4.2²) = 7.1А

   Полученное  Irms используется при выборе конденсатора (для электролитических конденсаторов обычно указывается допустимое значение импульсного тока для частоты 100Гц). Если у выбранного конденсатора допустимое значение импульсного тока меньше, необходимо набирать конденсаторы с меньшей емкостью и соединять в параллель исходя из условия: суммарная емкость не меньше рассчитанной, а ток, приходящийся на каждый из конденсаторов (ток по конденсаторам с одинаковой емкостью разделится равномерно), не более допустимого.

    

Расхождение теоретического расчета с практикой.

В заключение скажу, насколько вышеизложенная теория разошлась с практикой, и решайте сами, стоит ли применять эту методику.

Суммарная реальная емкость конденсаторов в моем преобразователе составила 1020мкФ, при этом измеренные осциллографом параметры были следующие:

• Umin   равнялось примерно 265-275В (близко к расчетному)

• t(зар) составляло около 3мс (приличная погрешность — по расчету 1.8мс, а учитывая, что емкость выше расчетной, должно быть еще меньше)

• Ipic составило 21А (близко к расчетному)

Формула заряда конденсатора, q

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

   

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

   

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

   

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

   

где – радиусы обкладок конденсатора.

Заряд конденсатора связан с энергией поля (W) внутри него:

   

Из формулы (6) следует, что заряд можно выразить как:

   

Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).

   

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

   

Примеры решения задач по теме «Заряд конденсатора»

Конденсатор в цепи переменного тока

Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.

Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).

Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.

 

В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.

После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.

Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.

С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.

Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.

Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.

В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.

Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.

Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны

 

Емкостное сопротивление конденсатора

Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС

Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.

Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.

Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.

Величина емкостного сопротивления определяется по следующей формуле:

где Хс — емкостное сопротивление конденсатора в ом;

f—частота переменного тока в гц;

ω — угловая частота переменного тока;

С — емкость конденсатора в ф.

При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.

Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.

Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.

Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.

Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.

Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.

Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.

Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.

Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.

В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.

В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.

Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.

 

Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.

Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.

Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.

И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.

При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.

А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Постоянная времени RC

Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e^-t/RC * e^Const.
Решение примет вид:

U = e^-t/RC * Const.

Здесь Const — константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e^-t/RC.

Экспонента — функция exp(x) = e^x
e – Математическая константа, приблизительно равная 2.718281828…

---

Постоянная времени

τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

U_C = U(1 — e^-t/RC)

При t = RC, напряжение на конденсаторе составит U_C = U(1 — e^-1) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e³)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e⁵)*100% ≈ 99% значения U.

---

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue^-t/τ = U/e^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e³)*100% ≈ 5% от значения U.
За время 5τ до (1/e⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

---

Замечания и предложения принимаются и приветствуются!

Заряд, разделение пластин и напряжение

Dynamics Track Наклонная плоскость Импульс Конденсатор Пластина Sep Пластина Sep / Вольт Диэлектрики Цепи Закон Ом Последовательность / Параллель Wave Tank Частота / длина волны Two Pt Interf. Оптическая скамья Рефракция Фокусное расстояние

Конденсатор с параллельной пластиной Заряд конденсаторов, разделение пластин и напряжение Конденсатор используется для хранения электрического заряда.Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда нагнетается в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больший заряд будет вызван данным напряжением. Это соотношение описывается формулой q = CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение. Глядя на эту формулу, можно спросить, что бы произошло, если бы заряд оставался постоянным, а емкость изменялась. Ответ, разумеется, таков, что напряжение изменится! Именно этим вы и займетесь в этой лаборатории. Лабораторный конденсатор Конденсатор с параллельными пластинами — это устройство, используемое для изучения конденсаторов. Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно скручены по спирали в небольших корпусах, поэтому конденсатор с параллельными пластинами значительно упрощает привязку функции к устройству. Этот конденсатор работает, накапливая противоположные заряды на параллельных пластинах, когда напряжение подается с одной пластины на другую.Количество заряда, который перемещается в пластины, зависит от емкости и приложенного напряжения в соответствии с формулой Q = CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт. Конденсаторы накапливают энергию Если напряжение подается на конденсатор, а затем отключается, заряд, накопленный в конденсаторе, сохраняется до тех пор, пока конденсатор каким-либо образом не разрядится.Между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже. От чего зависит емкость? Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними. Чем больше пластины и чем ближе они расположены, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами.Заряд, накопленный на приложенный вольт, представляет собой емкость, измеряемую в фарадах. Может ли изменение емкости заряженного конденсатора изменить его напряжение? Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с емкостью и напряжением. Если конденсатор имеет постоянный заряд, изменение емкости должно вызвать изменение напряжения. Раздвигание пластин приведет к уменьшению емкости, поэтому напряжение должно увеличиться. Как можно математически определить емкость нашего конденсатора? Для конденсатора с параллельными пластинами емкость определяется по следующей формуле: C = ε 0 А / сут Где C — емкость в Фарадах, ε 0 — постоянная диэлектрической проницаемости свободного пространства (8.85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах. Фарада — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6F или пикофарадах (пФ), что составляет 1,0×10 -12F. 1.0F = 1,000,000 мкФ = 1,000,000,000,000 пФ! Будьте очень внимательны с расчетами! Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора.Однако есть и другие факторы, которые вносят ошибки в реальные измерения емкости и напряжения. Вам нужно внимательно учитывать эти факторы. Лабораторное оборудование: Для получения хороших результатов эта лабораторная деятельность требует специального оборудования. Вам нужен хороший стабилизированный источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым при каждом испытании. Вам также понадобится очень точный способ измерения напряжения между пластинами без резистивной нагрузки на конденсатор.Количество накопленного заряда очень мало, поэтому обычный вольтметр не подойдет. Мельчайший заряд, накопленный в конденсаторе, просто разрядится через измеритель, делая любые измерения бесполезными. Вы будете использовать специальный прибор для измерения напряжения, называемый электрометром, который измеряет напряжение без разряда конденсатора. Одна из проблем электрометра состоит в том, что у него есть собственная емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена ​​к емкости конденсатора. Назначение: Целью данной лабораторной работы является исследование взаимосвязи между разделением пластин и напряжением в конденсаторе с параллельными пластинами, который поддерживается постоянным зарядом. Оснащение: Конденсатор переменной емкости Электрометр Регулируемый источник питания Поводки для перемычек Выводы для электрометра Осторожно: Это хрупкое оборудование.Все должно сочетаться с легчайшими прикосновениями. Ничего не заставляйте! Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе. Теоретические расчеты: Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самая сложная часть этого — правильно настроить юниты.Проще всего поставить все в метрах для расчетов: Измерьте диаметр пластин конденсатора в сантиметрах. Ваш размер должен быть около 17,8 см Разделите диаметр на 100, чтобы получить размер в метрах. Результат — 0,178 м. Разделите это на два, чтобы получить радиус: 0,089 м Площадь пластины определяется по общей формуле A = πr 2. Подставьте числа, чтобы получить A = π (0,089) 2 = 0.0249м 2 Преобразуйте расстояние между пластинами (1 мм) в метры, разделив на 1000. 1/1000 = 0,001 м. Используйте это число в формуле C = ε 0A / d, чтобы определить расчетную емкость, таким образом: C = 8,85×10 -12 (0,0249) / 0,001 = 2,20×10 -10. Это равно 220×10 -12F или 220pF Добавьте встроенную емкость электрометра (50 пФ) к теоретической емкости, чтобы получить 270 пФ. Запишите этот результат (270 пФ) в столбец «Расчетная емкость» и в строку 1 мм. Повторите этот процесс для других расстояний между пластинами. Обратите внимание, что площадь пластины одинакова для всех, поэтому все, что вам нужно сделать, это повторить шаги 5, 6 и 7, вставляя правильные значения для интервала в каждом случае. Теперь вы рассчитаете теоретическое напряжение для каждого интервала. Предположим, что для шага 1,0 мм напряжение составляет 10 В, поэтому вы можете просто указать это значение в таблице. Во-первых, вы определяете количество заряда в конденсаторе при таком расстоянии и напряжении.Используйте формулу Q = CV, чтобы определить заряд, таким образом: Q = 270×10 -12F (10V) = 2700×10 -12C. Этот заряд остается неизменным на всех расстояниях между пластинами, поэтому вы можете ввести одно и то же значение во весь столбец Расчетный заряд! Теперь используйте это значение заряда, чтобы определить рассчитанное напряжение на всех других расстояниях. Например, при расстоянии 5 мм используйте формулу V = Q / C, таким образом: V = 2700×10 -12C / 94,0×10 -12F = 28,7V. Введите это значение в столбец «Расчетное напряжение» в строке 5 мм. Повторите тот же расчет напряжения для оставшихся расстояний между пластинами.Используйте рассчитанную емкость и постоянный заряд для каждого промежутка и введите значение напряжения в столбец «Расчетное напряжение» таблицы. Поздравляем! Вы закончили предварительные расчеты! Все, что вам нужно сделать сейчас, это провести фактические измерения! В следующих разделах вы проведете реальный эксперимент для проверки (или, возможно, не проверки!) Ваших теоретических расчетов. Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!) Поместите переменный конденсатор в середину лабораторного стола так, чтобы отметка 0 см находилась слева от вас. Не ставьте конденсатор слишком близко к краю стола! Разместите блок питания за конденсатором переменной емкости. Подключите блок питания, но не включайте его. Подключите красный и черный перемычки к красной и черной клеммам источника питания. Просто прикрепите зажим «крокодил» к отверстию и оставьте другой конец проводов свободным. Поместите электрометр слева от конденсатора. Присоедините плоские клеммы выводов электрометра к клеммам на задней стороне каждой пластины конденсатора.Красный провод идет к правой пластине, черный провод идет к левой пластине. Вставьте разъем BNC в электрометр. Разместите пластины на расстоянии не менее 1 мм. Белые бамперы предотвращают сближение пластин. Если пластины не параллельны друг другу, используйте регулировочные ручки в центре правой опоры, чтобы выровнять пластины. Левый край пластикового язычка, выступающий в сторону шкалы, должен быть совмещен с отметкой 1 мм. Сбор экспериментальных данных Убедитесь, что оборудование настроено правильно и полностью. Поверните все четыре регулятора на блоке питания против часовой стрелки до упора. Поверните крайнюю левую ручку (Fine Current) в положение на 12 часов (прямо вверх!) Включите источник питания. Дисплеи должны загореться. Используйте ручки Fine и Coarse Voltage (две крайние правые ручки), чтобы установить напряжение на 10.0V. Установите пластины на минимальное значение Установите электрометр на шкалу 30 В. Нажмите кнопку питания на электрометре. Должен загореться светодиод 30 В. Нажмите кнопку нуля на электрометре. Это обнуляет счетчик и обеспечивает нулевое напряжение на пластинах относительно друг друга. На мгновение прикоснитесь к проводам от источника питания к пластинам, черный к левой пластине и красный к правой пластине. Электрометр должен показывать 12 вольт в этот момент (12 В — это первая маленькая отметка над «1» на нижней шкале. Если он не проверит вашу настройку, попробуйте еще раз. Иногда вам приходится дотрагиваться выводами до пластин несколько раз. чтобы получить правильное значение 12 В. С этого момента вы должны быть осторожны, чтобы не прикасаться к пластинам. Прикоснувшись к ним, вы измените заряд в пластинах и испортите данные! Следите за электрометром, чтобы убедиться, что заряд сохраняется.Если вы видите падение напряжения более чем на вольт за 30 секунд, остановитесь и выясните, что не так, прежде чем продолжить. Переключите электрометр на настройку 100 В. Счетчик должен по-прежнему показывать 12 В, но по шкале 100 В. Осторожно раздвиньте пластины до 5 мм. Снимите показание электрометра и запишите его в таблицу под столбцом «Измеренное напряжение». Повторите два предыдущих шага для других расстояний между пластинами и запишите соответствующие данные. Разделение пластин (мм) Расчетная емкость (пФ) Расчетный сбор (пКл) Расчетное напряжение (В) Измеренное напряжение (В) 1 5 10 15 20 25 30 35 40 Анализ данных: На миллиметровой бумаге постройте расчетную емкость по оси x (горизонтальная) в зависимости от напряжения по оси y (вертикальная).Нанесите на график рассчитанное и измеренное значение напряжения, используя разные цвета или стили линий, чтобы различать две кривые. Убедитесь, что вы выбрали подходящие масштабы и четко обозначили оси и масштабы. Лучше всего ориентировать бумагу длинной осью в горизонтальном направлении («альбомный режим»). Изучите свой график и ответьте на следующие вопросы: Подтверждают ли ваши измеренные данные измеренные значения? Две кривые имеют одинаковую форму? Если да, то на что это указывает? Что бы вы сделали, чтобы повысить точность собираемых данных? Формула для энергии, запасенной в конденсаторе, U e = ½CV 2.Сохраняется ли энергия, запасенная в конденсаторе, постоянной при изменении расстояния между пластинами? Он идет вверх или вниз? Обсудите, откуда пришла или куда ушла энергия.

Как рассчитать заряд конденсатора — Onlinecomponents.com

Конденсатор — это устройство, которое используется для хранения электрического заряда и электрической энергии. Основной конденсатор состоит из двух металлических пластин, разделенных некоторым изолятором, называемым диэлектриком. Способность конденсатора удерживать заряд называется емкостью.

Когда клеммы батареи соединены через конденсатор, потенциал батареи перемещает заряд, и он начинает накапливаться на пластинах конденсатора. Клемма конденсатора, подключенная к катоду батареи, будет заряжена положительно (+ Q), а клемма, подключенная к аноду батареи, будет заряжена отрицательно (-Q). Конденсатор в целом остается нейтральным, но заряды разделены на противоположных пластинах, которые находятся на заданном расстоянии друг от друга с расстоянием (d).Базовый конденсатор показан на рис. 1

.

Фиг.1

Заряд, накопленный на пластинах конденсатора, прямо пропорционален приложенному напряжению, поэтому [1]

В α Q

Где

В = Напряжение

Q = Заряд

Конденсаторы с разными физическими параметрами могут удерживать разное количество заряда, когда на конденсаторы подается одинаковое напряжение. Эта способность конденсатора называется емкостью.Емкость конденсатора можно определить как отношение количества максимального заряда (Q), который конденсатор может хранить, к приложенному напряжению (V).

V = C Q

Q = C / V

Таким образом, количество заряда конденсатора можно определить по вышеупомянутой формуле.

Конденсаторы заряжаются предсказуемым образом, и для зарядки конденсатора требуется время. Рассматривая зарядку как функцию времени, мы также можем определить количество заряда конденсатора через определенный период времени, когда он подключен к батарее, как показано на рис.2

Рис.2 Конденсатор, включенный в RC-цепочку

Предположим, что конденсатор (C) полностью разряжен, а переключатель разомкнут, конденсатор не заряжается. Эта ситуация представляет собой сценарий, когда при t = 0, I = 0, и заряд, накопленный на конденсаторе C, также будет равен нулю.

Теперь, как только переключатель замкнут, ток начнет течь по цепи, максимальное количество тока, которое будет протекать по цепи, ограничено резистором (R), который подключен последовательно с конденсатором.Ток, который будет протекать по цепи, можно найти с помощью закона напряжения Кирхгофа [2]

V = I (t) R + V _C Q = C / V _C и V _C = Q / C

где

В = Напряжение

I (t) = Ток в цепи в любой момент времени

Vc = напряжение на конденсаторе

Q = Заряд

C = Емкость, включенная в цепь

R = Сопротивление, подключенное в цепи

В = I (t) R + Q / C

Q = CV [1-e ^{-t / RC} ]

Количество заряда в любой момент можно найти с помощью вышеупомянутого уравнения.График зарядки конденсатора показан на рис. 3

.

Рис. 3 Заряд конденсатора по времени

Из графика можно сказать, что первоначально зарядный ток будет максимальным, и конденсатор начнет быстро меняться, а после одноразовой постоянной, равной T = RC, конденсатор будет заряжаться примерно на 63% от своего общего значения. Конденсатор продолжит заряжаться, зарядный ток будет уменьшаться, и скорость, с которой заряжался конденсатор, также уменьшится.

После пятикратной постоянной времени конденсатор будет полностью заряжен и зарядный ток будет равен нулю. Рассматривая заряд конденсатора как функцию времени, когда он включен в цепь, можно определить количество заряда в любой момент времени.

Номер ссылки

[1] Основы электротехники В.К. Мехта, Рохит Мехта, стр. 296

[2] Конденсаторы от Р.П. Дешпанде, стр. 29

Формулы простых конденсаторов для аккумулирования энергии

У вас есть конденсатор, или вам нужно его выбрать, вы хотите рассчитать некоторые вещи с точки зрения его использования для хранения / доставки энергии ( в отличие от фильтрации), вы хотели бы знать немного больше, чем онлайн-калькулятор, но не слишком много, потому что математика заставляет ваш мозг болеть.Эта страница для вас.

ln () (натуральный логарифм) часто встречается в уравнениях, натуральный логарифм — это обратное преобразование e в степень чего-либо (то есть ln (e ^x ) = x), в электронных таблицах это функция » ln () «, в коде (например, C / C ++ [Arduino!]), это обычно функция» log () «.
Все формулы предполагают «идеальный» конденсатор, без учета ESR или других неидеальных характеристик. Достаточно хорошо, чтобы попасть в бейсбольный стадион.
Вы можете изменить поля в каждом разделе, чтобы выполнить свой собственный расчет.

Помните, что ваше напряжение питания для зарядки конденсатора не должно превышать максимальное номинальное напряжение ваших конденсаторов (говоря в общих чертах).

У меня есть неизвестный конденсатор, известный резистор и секундомер, рассчитываю емкость.

C = (0 — секунды) / R / ln (1- (VCharged / VSupply))

Где Секунды — это количество секунд, за которые начисляется оплата; R — резистор в Ом; VCharged — напряжение конденсатора в секундах; VSupply — это напряжение питания.

Вам не нужно заряжать конденсатор полностью, чтобы измерить его, если вы начинаете с разряда, рассчитываете период зарядки и записываете напряжение, которое вы достигли за этот период, вы можете выполнить расчет — но чем дольше (медленнее) вы заряжаете тем более точным будет ваш результат, потому что ваши ошибки и т. д. будут менее значимыми. Когда самая маленькая цифра на вашем счетчике, измеряющая напряжение конденсатора, изменяется один раз в секунду, это было бы разумным моментом для остановки.Имейте в виду также, что конденсаторы имеют заведомо большой допуск (+/- 30% вполне нормально для некоторых типов конденсаторов).

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Сколько ампер-часов (Ач) в этом конденсаторе?

Ач = (C * (VCharged — VDepleted)) / 3600

Где VCharged — это напряжение заряда конденсатора, VDepleted — это опустошенное напряжение, а C — это емкость.

Здесь вы можете видеть, что если вы используете конденсатор для замены батареи, вам действительно нужно подключить его к преобразователю постоянного / постоянного тока с подходящим диапазоном входного напряжения, чтобы вы могли разрядить свой конденсатор до очень низкого напряжения, взяв наш В приведенном выше примере, если бы вместо напряжения отключения 3,3 В у нас было напряжение отключения 0,5 В, мы получили бы 10 мАч вместо жалких 2,5 мАч.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Конденсатор 10F, который был заряжен до 4,2 В, разряжен до 3,3 В, сколько там мАч?

(10 * (4,2 — 3,3)) / 3600 = 0,0025 Ач = 2,5 мАч

Сколько ватт-часов (Втч) в этом конденсаторе?

Вт · ч = (VCharged ² — VDepleted ² ) / (7200 / C)

Здесь вы можете видеть, что если вы используете конденсатор для замены батареи, вам действительно нужно подключить его к повышающему преобразователю с подходящим диапазоном входного напряжения, чтобы вы могли разрядить свой конденсатор до очень низкого напряжения, взяв наш пример выше. , если вместо 3.Напряжение отключения 3 В, у нас было напряжение отключения 0,5 В, мы получили бы 0,024 Вт-ч вместо мизерных 0,009 Вт-ч

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Конденсатор 10F, который был заряжен до 4,2 В, разряжен до 3,3 В, сколько в нем Wh?

((4,2 ² ) — (3,3 ² )) / (7200/10) = 0,009375 Вт · ч

Сколько времени потребуется, чтобы зарядить этот конденсатор постоянным сопротивлением?

секунд = 0 — (R * C * ln (1 — (VCharged / VSupply)))

Где VCharged — это напряжение, измеренное на конденсаторе, а VSupply — это напряжение источника питания, C — емкость в Фарадах, а R — резистор в Ом.

VCharged должно быть ниже, чем VSupply — помните, что по мере того, как конденсатор заряжается больше, его сопротивление зарядке увеличивается, оно никогда не может достичь того же уровня, что и напряжение питания, даже если оно на неизмеримо меньше, оно всегда меньше.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Сколько времени потребуется, чтобы разрядить этот конденсатор через постоянное сопротивление?

секунд = 0 — (R * C * ln (VDepleted / VCharged))

Где VCharged — начальное напряжение конденсатора, VDepleted — конечное напряжение, которое вы определите как разряженное, R — сопротивление, C — емкость.

VDepleted должно быть больше нуля — помните, что ваша реальная схема, вероятно, не может много сделать с чем-либо, даже отдаленно близким к нулю.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Сколько времени потребуется, чтобы зарядить / разрядить этот конденсатор постоянным током?

секунд = (C * (VCharged — VDepleted)) / Amps

Где C в фарадах, VCharged — это начальное напряжение на конденсаторе, VDepleted — это напряжение завершения разряда, а Amps — это ток в амперах.Для постоянного тока формула одинакова, независимо от того, разряжаете ли вы или заряжаете, разница в напряжении имеет значение, сколько напряжения должно нарастать или падать.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Конденсатор 10Ф разряжается с 5В до 4В при постоянном токе 500мА, сколько времени это занимает?

(10 * (5-4)) / 0,5 = 20 секунд (калькулятор)

Сколько времени потребуется, чтобы зарядить / разрядить этот конденсатор постоянной мощностью (Вт)?

секунд = 0.5 * C * ((VCharged ² — VDepleted ² ) / Вт)

Где C — в фарадах, VS — это начальное напряжение на конденсаторе, VC — это напряжение завершения разряда, а P — мощность разряда в ваттах.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Конденсатор 10Ф разряжается с 5В до 4В при постоянной мощности 2Вт, сколько времени это занимает?

0.5 * 10 * ((5 ² — 4 ² ) / 2) = 22,5 секунды

У меня есть батарея / элемент на несколько ампер-часов. Сколько емкости мне нужно для прямой замены?

C = (Ач * 3600) / (VCharged — VDepleted)

Наивно мы можем предположить, что VCharged совпадает с номинальным напряжением вашей батареи, а VDepleted равно нулю, или, точнее говоря, VCharged — это максимальный заряд для вашей батареи, а VDepleted — это минимальное напряжение, которое ваша цепь может использовать.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Щелочной элемент емкостью 1250 мАч с полным напряжением 1,5 В и пустым напряжением 0,8 В должен быть заменен конденсатором, какого размера он должен быть?

(1,25 * 3600) / (1,5 — 0,8) = 6428 F

Очевидно, что это непрактично, поэтому см. Следующий раздел …

Если у меня есть батарея / элемент на несколько ампер-часов, какой емкости мне нужно заменить, если я использую преобразователь постоянного тока в постоянный?

C = 7200 / ((VCharged ² — VDepleted ² ) / ((Ah * VBattery) / 0.75))

Где Ah — это емкость батареи в Ач, VBattery — номинальное напряжение батареи, 0,75 — (наихудший случай) КПД преобразователя постоянного / постоянного тока, VCharged — это заряженное напряжение конденсатора, VDepleted — это наименьшее напряжение конденсатора вашего постоянного / постоянного тока. Преобразователь постоянного тока справится.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Щелочной элемент емкостью 1250 мАч с номинальным напряжением 1.5 В следует заменить конденсатором (батареей), который будет заряжаться до 10,8 В и приводится в действие понижающим преобразователем, который принимает входное напряжение до 1,6 В.

7200 / ((10,8 ² -1,6 ² ) / ((1,25 * 1,5) / 0,75)) = 157F

Я хочу рисовать x ампер в течение t секунд, какая емкость мне нужна?

C = (Амперы * секунды) / (VCharged — VDepleted)

Где C — требуемая емкость, Amps — это требуемый ток, VCharged — это начальное напряжение, до которого вы заряжали конденсатор, а VDepleted — это минимальное напряжение, которое вы будете принимать.Помните, как только вы потребляете ток из конденсатора, его напряжение падает, вот как это работает, поэтому вы не можете просто сказать: «Я хочу 1 ампер при X вольт», вы должны сказать, что я нарисую усилитель и может сделать это между этим и этим напряжением.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Вы хотите потреблять 500 мА от конденсатора, заряженного до 12 В, в течение 5 секунд, и после этого конденсатор будет измерять 9 В. Какого размера должен быть конденсатор?

(0.5 * 5) / (12 — 9) = 0,83F

Я хочу получать x Вт в течение t секунд, какая емкость мне нужна?

C = (секунды * 2) / ((VCharged ² — VDepleted ² ) / Watts)

Где C — емкость, Watts — мощность в ваттах, VCharged — это начальное напряжение, до которого вы заряжали конденсатор, а VDepleted — это минимальное напряжение, которое вы будете принимать. Помните, как только вы потребляете ток из конденсатора, его напряжение падает, вот как это работает, поэтому вы не можете просто сказать: «Я хочу 1 Вт при X Вольт», вы должны сказать, что я возьму ватт и может сделать это между этим и этим напряжением.

Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.

Пример

Вы хотите подавать 10 Вт в течение 5 секунд от конденсатора, первоначально заряженного до 12 В, а затем измеряя 9 В, какого размера должен быть конденсатор?

(5 * 2) / ((12 ² — 9 ² ) / 10) = 1,6F

Как вы пришли к этой формуле?

В представленной формуле нет ничего особенного. Хорошей ссылкой для упрощения работы является этот документ от ELNA, производителя суперконденсаторов, он охватывает основные уравнения для постоянного тока, мощности и разряда сопротивления.

Electronics-Tutorials.ws обеспечивает разряд с постоянным сопротивлением, и заряд с постоянным сопротивлением также задается в виде Vc = Vs (1-e ^{-t / RC} ), которым можно управлять, чтобы найти t (см. Видео ниже) .

Это видео от Пола Уэсли Льюиса помогло моему лишенному математики мозгу научиться управлять манипуляциями.

Следующие ниже онлайн-калькуляторы были полезны при подтверждении моей работы Must Calculate, Circuits.dk, bitluni.net (ВНИМАНИЕ, расчет Wh на сайте bitluni неверен, если у вас минимальное напряжение> 0)

На основе этих уравнений и ресурсов получены следующие данные.

Вывод для ампер-часов

Начните с данной формулы для разряда при постоянном токе, установите t = 3600 секунд и решите, чтобы I было любым током, необходимым для разрядки конденсатора за это время и, следовательно, ампер-часов

секунд = (C * (VCharged — VDepleted)) / I

3600 = (C * (VCharged — VDepleted)) / I

I * 3600 = (C * (VCharged — VDepleted))

I = (C * (VCharged — VDepleted)) / 3600

(I = Ач)

Вывод для ватт-часов

Это выводится из формулы для разряда постоянной мощности, где t = 3600 секунд, вычисленных для P — любых ватт, необходимых для разряда конденсатора за это время, и, следовательно, ватт-часов.

секунды = 0,5 * C * ((VCharged ² — VDepleted ² ) / P)

3600 = ((VCharged ² — VDepleted ² ) / P) * C * 0,5

3600 / 0,5 = ((VCharged ² — VDepleted ² ) / P) * C

7200 = ((VCharged ² — VDepleted ² ) / P) * C

7200 / C = (VCharged ² — VDepleted ² ) / P

P * (7200 / C) = (VCharged ² — VDepleted ² )

P = (VCharged ² — VDepleted ² ) / (7200 / C)

(P = Wh)

Вывод для эквивалентности батареи в ампер-часах

Это просто решение уравнения ампер-часов для емкости

Ач = (C * (VCharged — VDepleted)) / 3600

Ач * 3600 = C * (VCharged — VDepleted)

(Ач * 3600) / (VCharged — VDepleted) = C

Вывод для эквивалентности батареи в ампер-часах с преобразователем постоянного тока в постоянный

Мы используем полученное выше уравнение ватт-часов, заменяя ватт-часы заданными ампер-часами и эквивалентным напряжением батареи, скорректированным на 75% кпд повышающего преобразователя.

Вт · ч = (VCharged ² — VDepleted ² ) / (7200 / C)

((Ач * VBattery) / 0,75) = (VCharged ² — VDepleted ² ) / (7200 / C)

7200 / C = (VCharged ² — VDepleted ² ) / (Ah * VBattery)

7200 = C * ((VCharged ² — VDepleted ² ) / (Ah * VBattery))

7200 / ((VCharged ² — VDepleted ² ) / (Ah * VBattery)) = C

Вывод для отрисовки ампер X для секунд T

Простое решение данного уравнения постоянного тока, решение для C

секунд = (C * (VCharged — VDepleted)) / I

секунд * I = C * (VCharged — VDepleted)

(секунды * I) / (VCharged — VDepleted) = C

Вывод для рисования X Вт в течение T секунд

Простое решение данного уравнения постоянной мощности, решение для C

секунд = 0.5 * C * ((VCharged ² — VDepleted ² ) / P)

секунд = C * ((VCharged ² — VDepleted ² ) / P) * 0,5

секунды * 2 = C * ((VCharged ² — VDepleted ² ) / P)

(секунды * 2) / ((VCharged ² — VDepleted ² ) / P) = C

Заряд конденсатора и постоянная времени, онлайн-калькулятор

Онлайн-калькулятор для расчета постоянной времени и напряжения зарядки

Онлайн калькулятор

На этой странице вы можете рассчитать зарядное напряжение конденсатора. в цепи ПДУ (проход нижних частот) в определенный момент времени.

Помимо номиналов резистора и конденсатора, приложенное входное напряжение и время даны для расчета.

Результат показывает напряжение зарядки в указанное время и постоянную времени τ (тау) RC-цепи. Конденсатор через время 5 τ ок. Заряжено 99,33%. Это означает, что в заданные моменты времени, значительно превышающие 5 τ входное напряжение всегда близко к напряжению зарядки.{- \ frac {t} {τ}} \ right) \)

\ (\ Displaystyle τ = R · С \)

Legende

\ (\ Displaystyle R \)	Резистор (& Ом;)
\ (\ Displaystyle С \)	Конденсатор (F)
\ (\ Displaystyle т \)	Постоянная времени (сек)
\ (\ Displaystyle U_0 \)	Приложенное напряжение (В)
\ (\ Displaystyle U_C \)	Напряжение заряда на конденсаторе (В)

Эта страница полезна? да Нет Спасибо за ваш отзыв! Извините за это Как мы можем это улучшить? послать

---

Простое уравнение для зарядки конденсатора с помощью RC-цепей — Wira Electrical

Ищете способ зарядить конденсатор? Если это так, то ваше самое простое решение — это RC-цепь.Мы также найдем уравнение для зарядки конденсатора.

Схема этого типа довольно проста. Последовательное соединение резистора, конденсатора и источника напряжения позволит зарядить конденсатор (C) через резистор (R).

Временная задержка или RC-цепь постоянной времени

Перед тем, как перейти к RC-схеме зарядки и уравнению для зарядки конденсатора, было бы разумно понять этот термин, называемый постоянной времени. Мы найдем эту временную задержку или постоянную времени в каждой электрической и электронной схеме.

Вскоре в электрической цепи между входом и выходом будет некоторая «задержка по времени», когда на цепь подается напряжение или сигнал постоянного тока (DC) или переменного тока (AC).

Далее, эта постоянная времени представляет временную характеристику первого порядка цепи, питаемой сигналом или напряжением. Это значение постоянной времени зависит от реактивных компонентов, таких как конденсатор и катушка индуктивности в цепи.

Мы найдем постоянную времени много, если попытаемся решить уравнение для заряда конденсатора.

Единицами постоянной времени является тау с символом — 𝜏

Во-первых, предположим, что у нас есть цепь с «пустым» конденсатором. Мы можем назвать это «разряженным» конденсатором. Затем мы прикладываем к цепи постоянное напряжение, и ток начинает течь. Этот ток потребляется конденсатором, и мы называем его «током зарядки».

Конденсатор начинает «заряжаться», пока подключен источник постоянного напряжения. Как только напряжение снижается, конденсатор начинает «разряжаться» в направлении, противоположном источнику напряжения.

Вы можете спросить: «Почему это так?».

Что ж, если мы попробуем поискать это в Google, мы сразу найдем ответ, предоставленный Википедией. Но позвольте нам записать это здесь, чтобы вам не нужно было открывать новую вкладку.

Проще говоря, конденсатор — это устройство, обеспечивающее емкость цепи. Физическая форма конденсатора состоит из двух электрических проводников. Это может быть пара металлических пластин или поверхностей, разделенных диэлектрической средой.

Существует уравнение для расчета накопленного электрического заряда между токопроводящими пластинами:

Q = C.V

Для зарядки и разрядки конденсатора требуется время. Здесь мы используем термин «постоянная времени» для расчета необходимого времени.

Это также будет действовать как уравнение для зарядки конденсатора.

Резюме: постоянная времени — это время, необходимое для зарядки конденсатора через резистор от начального напряжения заряда, равного нулю, до примерно 63,2% от приложенного источника постоянного напряжения. Постоянная времени также используется для расчета времени разряда конденсатора через тот же резистор, которое составляет около 36.8% от начального напряжения заряда.

RC-цепь образована последовательным соединением резистора, конденсатора и источника напряжения, как указано выше. Конденсатор будет постепенно заряжать свое напряжение заряда до тех пор, пока значение не станет таким же, как и у источника напряжения в идеальном предположении.

Интервал времени для полной зарядки конденсатора также известен как время переходного процесса 𝜏. Мы можем найти значение из произведения сопротивления и емкости. Следовательно,

𝜏 = R x C

 Где: 

 𝜏 = постоянная времени, измеренная в секундах (с) 
 R = сопротивление, измеренное в омах (омах) 
 C = емкость, измеренная в фарадах (Ф) 

RC-схема зарядки конденсатора

Чтобы зарядить конденсатор самым простым способом, мы будем использовать конденсатор (C), резистор (R) и источник постоянного напряжения.Мы подключаем все эти компоненты последовательно с добавлением переключателя.

В начальный момент времени или нулевой момент времени переключатель замкнут, и конденсатор начинает заряжаться. Конденсатор будет заряжаться, пока его напряжение не достигнет напряжения источника.

Когда переключатель замкнут, конденсатор будет пытаться поддерживать свои переменные значения до переходного состояния переключателя. Это значение будет использоваться в качестве «начального значения», когда мы будем проводить анализ схемы.

Его устойчивое состояние или окончательное значение будет через бесконечное время, когда значение больше не будет меняться.

Предположим, что конденсатор находится в начальной или начальной точке, когда конденсатор «пустой» или «полностью разряжен». В этом состоянии конденсатор действует как короткое замыкание, и ток течет с максимальным значением.

Его конечное состояние или «установившееся состояние» — это когда конденсатор «полностью заряжен», ток не течет и конденсатор действует как разомкнутая цепь.

Что нам нужно найти дальше?

Нам нужна «постоянная времени», чтобы рассчитать, как долго конденсатор должен быть полностью заряжен.Эта переменная также важна для расчета того, насколько конденсатор заряжается через некоторое время.

В RC-цепи мы получаем постоянную времени (тау -), умножая сопротивление R и емкость C. Следует отметить, что одна постоянная времени — это количество времени, за которое напряжение на конденсаторе достигает 63%. ближе к источнику напряжения.

Теперь давайте проанализируем уравнение для процесса зарядки конденсатора из рисунка выше. Предположим, что конденсатор (C) находится в «полностью разряженном» состоянии после размыкания переключателя (S).Значит, в нем нет напряжения.

Мы называем этот первый шаг начальными условиями, где t = 0 с, i = 0 (разомкнутая цепь) и q = 0 (нет заряда, полностью разряжена).

Когда мы замыкаем переключатель, время начинается с отметки времени t = 0, и ток начинает течь к конденсатору через резистор.

Напряжение заряда в конденсаторе все еще равно нулю (Vc = 0), потому что он был полностью разряжен первым при t = 0. В этом состоянии конденсатор имеет «короткое замыкание».Общий ток ограничен только резистором.

С помощью закона напряжения Кирхгофа (KVL) мы можем рассчитать падение напряжения в цепи как:

Теперь, когда переключатель замкнут, ток свободно течет в цепи. Этот ток будет называться током зарядки. Этот ток можно измерить с помощью простого закона Ома:

I = V / R

Уравнение для анализа диаграммы RC-цепи заряда конденсатора

Повышение напряжения конденсатора и падение тока конденсатора имеют экспоненциальную кривую. .Это означает, что значения быстро меняются вначале и стабилизируются через заданный промежуток времени.

Как мы упоминали выше, для каждой постоянной времени (1𝜏) значение будет на 63% ближе к желаемому значению.

Теперь давайте посмотрим на график напряжения заряда конденсатора и тока заряда конденсатора ниже:

График выше объясняет, как напряжение конденсатора увеличивалось с течением времени, пока не достигло источника напряжения. Наклон начала более крутой, потому что в это время конденсатор начинает заряжаться полным током.

Проходит больше времени, и наклон начинает приобретать стабильную кривую. Скорость зарядки снижается, когда разница напряжений между конденсатором и источником уменьшается.

Разность потенциалов между пластинами увеличивается с течением времени, при этом фактическое время, необходимое для того, чтобы электрический заряд конденсатора достиг 63,2% от его максимально возможного напряжения (источника напряжения).

Из приведенной выше кривой вы снова найдете постоянную времени -.

Эта точка напряжения 0.63Vs или 63,2% Vs обозначают одну постоянную времени или 1.

Кривая выше показывает нам наклон зарядного тока конденсатора. Значения можно рассчитать из уравнения для зарядки конденсатора, приведенного ниже.

По сравнению с кривой напряжения все наоборот. Чем больше времени требуется на зарядку, тем больше ток в цепи уменьшается, пока не достигнет нуля.

Почему?

Прокрутите немного вверх, и вы найдете ответ с точки зрения напряжения.Поскольку разница напряжений между конденсатором и источником уменьшается, также уменьшается ток, необходимый для зарядки конденсатора.

Более заряженный конденсатор означает большее сопротивление в цепи, потому что полностью заряженный конденсатор действует как разомкнутая цепь.

Конденсатор достигает своего предела, когда затраченное время превышает постоянную времени десять (5𝜏). Из уравнения для зарядки конденсатора, напряжение конденсатора составляет 98% от напряжения источника.

На этот раз конденсатор считается полностью заряженным и t = ∞, i = 0, q = Q = CV.

Когда время больше 5𝜏, ток уменьшается до нуля, и конденсатор имеет бесконечное сопротивление или, говоря электрическими терминами, разомкнутую цепь. Напряжение конденсатора Vc = Vs.

Ниже мы начнем использовать уравнение для зарядки конденсатора.

Уравнение для зарядки конденсатора

Если смотреть на кривую слишком сложно, мы можем вычислить постоянную времени с помощью простого уравнения для зарядки конденсатора. В принципе, мы можем выразить одну постоянную времени (1𝜏) в уравнении для заряда конденсатора как

𝜏 = R x C

Где:
𝜏 = постоянная времени
R = сопротивление (Ом)
C = емкость ( C)

Мы можем записать математическое уравнение процента изменения в виде уравнения для зарядки конденсатора, приведенного ниже:

Где:
e = математическая константа Эйлера (около 2.71828)
t = затраченное время, в секундах
𝜏 = постоянная времени, в секундах

После того, как время достигнет одной постоянной времени или 1 the, процент изменения от начального значения до желаемого значения с использованием уравнения для заряда конденсатора равен :

После того, как время достигнет двух постоянных времени или 2𝜏, процент изменения от начального значения до желаемого значения с использованием уравнения для зарядки конденсатора составит:

После того, как время достигнет пяти постоянных времени или 5𝜏, процент изменения от начального значения до желаемого значения с использованием уравнения для зарядки конденсатора составляет:

После того, как время достигнет десяти постоянных времени или 10𝜏, процент изменения от начального значения к желаемому значению с использованием уравнения для конденсатора начисление:

Указанные выше процентные значения изменений поясняют значения, которые мы помещаем в таблицу в следующем разделе.

Мы знаем, что источник напряжения V отвечает за заряд конденсатора. Напряжение конденсатора Vc можно измерить делением Q / C. Напряжение конденсатора Vc в любой момент процесса зарядки может быть выражено как:

Где:
Vc = напряжение на конденсаторе
Vs = источник напряжения
t = время, затрачиваемое с момента подключения источника напряжения к резистору и конденсатору
RC = постоянная времени RC-цепи

На двух графиках выше есть две части периодов.Мы называем их:

• Переходное состояние
• Устойчивое состояние

Переходное состояние — это период, когда переменные системы или схемы менялись с течением времени. Система все еще находится в переходном состоянии, пока система не достигла установившегося состояния.

Время, необходимое для перехода схемы из одного устойчивого состояния в другое устойчивое состояние, называется переходным временем .

Устойчивое состояние — это период, когда переменные системы или цепи достигли стабильного состояния.Переменные больше не меняются во времени.

Глядя на графики, мы можем сделать вывод, когда схема находится в переходном и установившемся состоянии, даже если мы удалим текстовое объяснение над кривой.

Переходный период начинается от начального нуля до постоянной времени 4 (5𝜏). Напряжение конденсатора в этой RC-цепи достигло примерно 98% от максимально возможного напряжения источника напряжения.

Итог, время, необходимое RC-цепи для зарядки конденсатора, пока его напряжение не достигнет 0.98Vs — это переходное состояние, постоянная времени около 4 (4𝜏).

После того, как время достигнет 5 °, говорят, что конденсатор находится в установившемся режиме. Конденсатор полностью заряжен, и напряжение конденсатора (Vc) равно напряжению источника (Vs).

Поскольку конденсатор полностью заряжен, конденсатор действует как разомкнутый контур. Следовательно, в цепи больше нет тока.

Кривая графиков имеет экспоненциальные значения. Это означает, что на практике напряжение на конденсаторе никогда не достигает 100% от источника напряжения.

Время после 5𝜏 все еще является периодом установившегося состояния конденсатора, когда напряжение конденсатора составляет около 99,3% источника напряжения. Тем не менее, мы все еще можем сказать, что конденсатор полностью заряжен.

Формула универсальной постоянной времени

Мы можем умножить полученный процент изменения на разницу между начальным и желаемым значением. Мы можем использовать эту универсальную формулу для определения взятого времени, значений напряжения и тока, а также процента изменения:

Где:
Final = Желаемое значение или значение через бесконечное время
Initial = Начальное значение переменная
e = постоянное число Эйлера (около 2.71828)
t = Время в секундах
𝜏 = Постоянная времени в секундах

Это уравнение также считается уравнением для заряда конденсатора.

Давайте попробуем применить приведенное выше уравнение к приведенной ниже схеме.

RC-цепь выше имеет резистор 10 кОм, конденсатор 100 мкФ и источник напряжения 15 В. Мы знаем, что постоянная времени () — это произведение сопротивления (R) и емкости (C), поэтому

𝜏 = R x C
= 10 кОм x 100 мкФ
= 1 секунда

Предположим, что конденсатор полностью разряжен, то начальное значение равно 0 вольт.Желаемое значение составляет 15 В, так как мы хотим полностью зарядить конденсатор.

Тогда математическое уравнение:

Давайте попробуем установить время в 7,25 секунды. Следовательно, через 7,25 секунды после включения переключателя значение напряжения конденсатора увеличилось на:

Это означает, что мы зарядим конденсатор до 14,989 вольт через 7,25 секунды.

Не только это, но мы также можем использовать это уравнение для зарядки конденсатора для расчета тока, поскольку уравнение универсально.Давай попробуем сейчас.

Имейте в виду, что у конденсатора есть характеристика для заряженного или разряженного:

• Разряженный конденсатор действует как короткое замыкание, поэтому начальный ток максимален.
• Заряженный конденсатор работает как разомкнутая цепь, поэтому конечный ток минимален.

Из этих характеристик можно сделать вывод, что:

• Начальный ток: I = V / R = 15 В / 10 кОм = 1,5 мА
• Конечный ток: 0A

Используя то же значение t = 7.25 с, поэтому ток после 7,25 с будет:

Обратите внимание, что значение тока отрицательное. Это означает, что ток уменьшается с течением времени от начала до 7,25 с. Начальный ток составляет 15 мА, а разница после 7,25 составляет (-1,4989 мА).

Резюме, у нас будет (1,5 мА — 1,4989 мА) 0,0011 мА или 1,1 мкА через 7,25 с.

Или, может быть, нам не нужно уравнение постоянной времени, чтобы найти конечный ток. Мы можем просто использовать простой закон Ома, используя разницу между начальным и конечным напряжением, деленную на сопротивление.

Удобно, что уравнение зарядки конденсатора хорошо согласуется с другими основными законами, такими как закон Ома.

Уравнение для таблицы зарядки конденсаторов

Мы можем превратить графики зарядки конденсаторов и уравнение для зарядки конденсаторов в одну простую таблицу зарядки RC ниже.

Постоянная времени (𝜏)	Напряжение (%)	Ток (%)
0	0	100
1	63.213	36,787
2	86,467	13,533
3	95,022	4,978
4	98,169	5,831
98,169	1 831
6	99,753	0,247
7	99,909	0,091
8	99,967	0,033
9	99.988	0,012
10	99,996	0,004

Уравнение для зарядки конденсаторов

Давайте применим уравнение для зарядки конденсаторов на практике. Найдите постоянную времени 𝜏 для RC-цепи ниже.

Мы можем использовать приведенную выше формулу постоянной времени, где 𝜏 = R x C, измеряемая в секундах.

Следовательно, постоянная времени равна 𝜏 = R x C = 47 кОм x 1000 мкФ = 47 с.

а) Рассчитайте напряжение конденсатора при 0.7 постоянная времени.

Ровно при 7𝜏 напряжение конденсатора Vc равно 0,5Vs.

Следовательно,

Vc = 0.5Vs = 0.5 x 5V = 2.5V

b) Рассчитайте напряжение конденсатора при 1 постоянной времени.

Ровно при 7𝜏 напряжение конденсатора Vc равно 0,63Vs. Следовательно,

В = 0,63 В = 0,5 x 5 В = 3,15 В

c) Рассчитайте время, необходимое для полной зарядки конденсатора.

Мы прочитали график выше, что нам нужно 5 для полной зарядки конденсатора.Мы уже получили постоянную времени из точки «а».

Следовательно,

5𝜏 = 5 x 47s = 235s

d) Рассчитайте напряжение конденсатора через 100 секунд.

Формула напряжения конденсатора Vc = V (1 — e (-t / RC)).

Следовательно,

Vc = 5 (1 — e (-100/47))
= 5 (1 — e-2.1277)
= 5 (1 — 0,1191)
= 4,4 В

Резюме уравнения для зарядки конденсатора

Из длинного объяснения выше, мы можем суммировать уравнение для зарядки конденсатора в следующие шаги:

1. Найдите постоянную времени (𝜏 = R x C).
2. Установите начальное и конечное значения.
3. Используйте универсальную формулу постоянной времени и поместите каждую полученную переменную в уравнение.
4. Решите уравнение.
5. Вы можете либо рассчитать время, необходимое для достижения окончательного значения, либо рассчитать окончательное значение через заданный промежуток времени.
6. Теперь мы увидели использование уравнения для зарядки конденсатора.

Уравнение заряда конденсатора Часто задаваемые вопросы

Давайте рассмотрим наиболее часто задаваемые вопросы по уравнению заряда конденсатора ниже:

Как рассчитать заряд конденсатора?

Электрический заряд Q в конденсаторе (измеренный в кулонах или C) равен произведению емкости C конденсатора (измеренной в фарадах или F) и напряжения V на выводе (измеренного в вольтах или V).Математически Q = C x V. Если C = 10uF и V = 10V, то Q = 10u x 10 = 100u Кулонов.

Что такое зарядка конденсатора?

Если мы подключим последовательно конденсатор, резистор и источник напряжения, конденсатор будет заряжаться до тех пор, пока его значение напряжения не станет равным источнику напряжения. Зарядка конденсаторов означает, что мы накапливаем энергию в конденсаторе в форме электрического поля между пластинами конденсатора.

Сколько времени нужно для зарядки конденсатора?

Около 10 постоянной времени.
Одна постоянная времени, равная произведению сопротивления и емкости в RC-цепях. Конденсатор будет заряжен примерно на 99,995% от источника напряжения.

Что происходит, когда конденсатор полностью заряжен?

Конденсатор перестанет заряжаться, если конденсатор «полностью заряжен». В это время ток перестанет течь в цепи, потому что конденсатор действует как разомкнутый контур. Напряжение конденсатора Vc равно Vs, и соединение с источником напряжения отключено.

домашнее задание и упражнения — Как правильно рассчитать заряд конденсатора?

домашнее задание и упражнения — Как правильно рассчитать заряд конденсатора? — Обмен физическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 9 лет назад

Просмотрено 54k раз

$ \ begingroup $ Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.

---

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.

Закрыт 4 года назад.

Сколько заряда на каждой пластине 4.-5 С

Почему?

Дэвид З

72.2k2424 золотых знака165165 серебряных знаков275275 бронзовых знаков

задан 3 мая ’12 в 19: 182012-05-03 19:18

Ястреб

89722 золотых знака1818 серебряных знаков3232 бронзовых знака

$ \ endgroup $ 0 $ \ begingroup $

Заряд на двух пластинах противоположен и равен ключевому ответу.Параметр Q — это заряд одной пластин, а не сумма абсолютных значений двух зарядов. Емкость определяется как заряд на единицу напряжения, так что $ Q = CV $, поэтому 4F умножить на 12 В — это 48 единиц заряда, что для единицы «F» составляет миллионные доли кулоновского C. Это дает ответ в книге.

Создан 03 мая 2012, 19:27.

$ \ endgroup $ 0 $ \ begingroup $

Чистый заряд конденсатора всегда равен нулю, потому что на пластинах одинаковые и различающиеся заряды.-6 * 12 кулонов т.е. q = 48 микрокулонов

Создан 03 мая 2013, в 9:13

$ \ endgroup $ $ \ begingroup $

Формула $ V = \ frac {Q} {C} $ дает количество заряда, которое находится на одной из пластин. Общая сумма заряда на обеих пластинах, вместе взятых, равна нулю! Оба они заряжены противоположно.

Создан 05 мая 2013, 11:40:56

$ \ endgroup $ Очень активный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос.Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Physics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

10.6: RC-схемы — Physics LibreTexts

При использовании камеры со вспышкой зарядка конденсатора, питающего вспышку, занимает несколько секунд.Световая вспышка разряжает конденсатор за крошечные доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и несколько других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.

Цепи сопротивления и емкости

Схема RC — это цепь, содержащая сопротивление и емкость. Как показано в разделе «Емкость», конденсатор — это электрический компонент, который накапливает электрический заряд, накапливая энергию в электрическом поле.

На рисунке \ (\ PageIndex {1a} \) показана простая схема RC , в которой используется источник постоянного напряжения \ (ε \), резистор \ (R \), конденсатор \ (C \), и двухпозиционный переключатель. Схема позволяет конденсатору заряжаться или разряжаться в зависимости от положения переключателя. Когда переключатель перемещается в положение \ ( A \) , конденсатор заряжается, в результате получается схема, показанная на рисунке \ (\ PageIndex {1b} \). Когда переключатель перемещается в положение B , конденсатор разряжается через резистор.

Рисунок \ (\ PageIndex {1} \): (a) Схема RC с двухполюсным переключателем, который можно использовать для зарядки и разрядки конденсатора. (b) Когда переключатель перемещается в положение A , схема сводится к простому последовательному соединению источника напряжения, резистора, конденсатора и переключателя. (c) Когда переключатель перемещается в положение B , схема сводится к простому последовательному соединению резистора, конденсатора и переключателя. Источник напряжения снят с цепи.

Зарядка конденсатора

Мы можем использовать правило петли Кирхгофа, чтобы понять заряд конденсатора. Это приводит к уравнению \ (\ epsilon — V_R — V_C = 0 \). Это уравнение можно использовать для моделирования заряда как функции времени при зарядке конденсатора. Емкость определяется как \ (C = q / V \), поэтому напряжение на конденсаторе равно \ (V_C = \ frac {q} {C} \). Согласно закону Ома падение потенциала на резисторе равно \ (V_R = IR \), а ток определяется как \ (I = dq / dt \).

\ [\ epsilon — V_R — V_C = 0, \]

\ [\ epsilon — IR — \ frac {q} {C} = 0, \]

\ [\ epsilon — R \ frac {dq} {dt} — \ frac {q} {C} = 0.{- \ frac {t} {\ tau}} \ right). \]

График зависимости заряда конденсатора от времени показан на рисунке \ (\ PageIndex {2a} \). Сначала обратите внимание, что по мере приближения времени к бесконечности экспонента стремится к нулю, поэтому заряд приближается к максимальному заряду \ (Q = C \ epsilon \) и имеет единицы кулонов. {- t / \ tau } \).{-t / \ tau}) \).

Разрядка конденсатора

Когда переключатель на рисунке \ (\ PageIndex {3a} \) перемещается в положение B , схема сокращается до схемы в части (c), и заряженному конденсатору позволяют разрядиться через резистор. График зависимости заряда конденсатора от времени показан на рисунке \ (\ PageIndex {3a} \). Использование правила петли Кирхгофа для анализа цепи при разряде конденсатора приводит к уравнению \ (- V_R -V_C = 0 \), которое упрощается до \ (IR + \ frac {q} {C} = 0 \).{-t / \ tau}. \]

Знак минус показывает, что ток течет в направлении, противоположном току, наблюдаемому при зарядке конденсатора. На рисунке \ (\ PageIndex {3b} \) показан пример графика зависимости заряда от времени и тока от времени. График зависимости разности напряжений на конденсаторе и разницы напряжений на резисторе от времени показан на рисунках \ (\ PageIndex {3c} \) и \ (\ PageIndex {3d} \). Обратите внимание, что величины заряда, тока и напряжения экспоненциально уменьшаются, приближаясь к нулю с увеличением времени.

Рисунок \ (\ PageIndex {3} \): (a) Заряд конденсатора в зависимости от времени, когда конденсатор разряжается. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.

Теперь мы можем объяснить, почему вспышка камеры , упомянутая в начале этого раздела, требует гораздо больше времени для зарядки, чем для разрядки: сопротивление при зарядке значительно больше, чем при разрядке. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки.По мере старения аккумулятора возрастающее внутреннее сопротивление делает процесс зарядки еще медленнее.

Пример \ (\ PageIndex {2} \): Осциллятор релаксации

Одним из применений схемы RC является релаксационный генератор, как показано ниже. Релаксационный генератор состоит из источника напряжения, резистора, конденсатора и неоновой лампы. Неоновая лампа действует как разомкнутая цепь (бесконечное сопротивление), пока разность потенциалов на неоновой лампе не достигнет определенного напряжения.При таком напряжении лампа действует как короткое замыкание (нулевое сопротивление), и конденсатор разряжается через неоновую лампу и производит свет. В показанном релаксационном генераторе источник напряжения заряжает конденсатор до тех пор, пока напряжение на конденсаторе не станет 80 В. Когда это происходит, неон в лампе выходит из строя и позволяет конденсатору разряжаться через лампу, создавая яркую вспышку. После того, как конденсатор полностью разрядится через неоновую лампу, он снова начинает заряжаться, и процесс повторяется.{-t / \ tau}) = ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right), \]

\ [t = — \ tau ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right) = -5.05 \, s \ cdot ln \ left (1 — \ frac {80 \, V } {100 \, V} \ right) = 8.13 \, s. \]

Значение

Одним из применений генератора релаксации является управление световыми индикаторами, которые мигают с частотой, определяемой значениями для R и C . В этом примере неоновая лампа будет мигать каждые 8,13 секунды с частотой \ (f = \ frac {1} {T} = \ frac {1} {8.13 \, s} = 0,55 \, Гц \). Осциллятор релаксации имеет много других практических применений. Он часто используется в электронных схемах, где неоновая лампа заменяется транзистором или устройством, известным как туннельный диод. Описание транзистора и туннельного диода выходит за рамки этой главы, но вы можете рассматривать их как переключатели, управляемые напряжением. Обычно это разомкнутые переключатели, но при подаче правильного напряжения переключатель замыкается и проводит ток. «Выключатель» можно использовать для включения другой цепи, включения света или запуска небольшого двигателя.Осциллятор релаксации может быть использован для того, чтобы заставить мигать поворотники вашего автомобиля или ваш мобильный телефон вибрировать.

Цепи RC находят множество применений. Их можно эффективно использовать в качестве таймеров для таких приложений, как стеклоочистители прерывистого действия, кардиостимуляторы и стробоскопы. В некоторых моделях стеклоочистителей прерывистого действия используется переменный резистор для регулировки интервала между движениями стеклоочистителя. Увеличение сопротивления увеличивает постоянную времени RC , что увеличивает время между срабатываниями дворников.

Еще одно приложение — кардиостимулятор . Частота сердечных сокращений обычно контролируется электрическими сигналами, которые заставляют сердечные мышцы сокращаться и перекачивать кровь. Когда сердечный ритм ненормален (сердцебиение слишком высокое или слишком низкое), для исправления этого нарушения можно использовать кардиостимуляторы. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время физических нагрузок, таким образом удовлетворяя повышенную потребность в крови и кислороде, а схема синхронизации RC может использоваться для контроля времени между сигналами напряжения, подаваемыми на сердце.

Забегая вперед к изучению цепей переменного тока (цепей переменного тока), напряжения переменного тока изменяются как синусоидальные функции с определенными частотами. Ученые часто регистрируют периодические изменения напряжения или электрических сигналов. Эти сигналы напряжения могут исходить от музыки, записанной с помощью микрофона, или от атмосферных данных, собранных радаром. Иногда эти сигналы могут содержать нежелательные частоты, известные как «шум». RC Фильтры могут использоваться для фильтрации нежелательных частот.

В области изучения электроники популярное устройство, известное как таймер 555, выдает синхронизированные импульсы напряжения. Время между импульсами контролируется схемой RC . Это лишь некоторые из бесчисленных применений схем RC .

Пример \ (\ PageIndex {2} \): прерывистые работы дворников

Осциллятор релаксации используется для управления парой дворников. Релаксационный генератор состоит из конденсатора емкостью 10,00 мФ и переменного резистора (10,00 кОм), известного как реостат.Ручка, подключенная к переменному резистору, позволяет регулировать сопротивление от \ (0.00 \, \ Omega \) до \ (10.00 \, k \ Omega \). Выход конденсатора используется для управления переключателем, управляемым напряжением. Переключатель обычно разомкнут, но когда выходное напряжение достигает 10,00 В, переключатель замыкается, запитывая электродвигатель и разряжая конденсатор. Двигатель заставляет дворники один раз подметать лобовое стекло, и конденсатор снова начинает заряжаться. На какое сопротивление нужно регулировать реостат при периоде работы щеток стеклоочистителя 10.3 \, \ Omega) ln \ left (1 — \ frac {10 \, V} {12 \, V} \ right) = 179,18 \, s = 2,98 \, мин. \]

Схема RC имеет тысячи применений и очень важна для изучения. Его можно не только использовать для измерения времени в цепях, но и для фильтрации нежелательных частот в цепи и в источниках питания, например, в вашем компьютере, чтобы преобразовать переменное напряжение в постоянное.

Авторы и авторство

• Сэмюэл Дж.