Резонанс при параллельном соединении: Резонанс в параллельном контуре

Резонанс в параллельном контуре

Рассмотрим цепь с двумя параллельными ветвями: параметры одной — сопротивление и индуктивность L, а другой — сопротивление и емкость С (рис. 5.5). Такую цепь часто называют параллельным контуром. Резонанс наступает, если у входной проводимости

реактивная составляющая

или

где

— реактивные проводимости ветвей.
При противоположные по фазе реактивные составляющие токов равны (рис. 5.6, а), поэтому резонанс в рассматриваемой цепи получил название резонанса токов. Из векторной диаграммы видно, что при резонансе ток I на входных выводах контура может быть значительно меньше токов в ветвях.

Рис. 5.5

Рис. 5.6

В теоретическом случае при токи и сдвинуты по фазе относительно напряжения на углы и (рис. 5.6, б) и суммарный ток . Входное сопротивление цепи при этом бесконечно велико.
Подставив в соотношение (5.12), т. е. в условие резонанса, значения и , выраженные через параметры цепи и частоту, получим

Изменением одной из величин () при остальных четырех постоянных не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины при ее определении из уравнения (5.13) получается мнимым или комплексным. Для L или С могут получаться и по два различных действительных значения, удовлетворяющих уравнению (5.13). В таких случаях изменением L и С можно достичь двух различных резонансных режимов.
Решив уравнение (5.13) относительно ω, найдем следующее значение для резонансной угловой частоты:

Резонанс возможен, если сопротивления и оба больше или оба меньше r. Если же это условие не выполнено, получается мнимая частота , т. е. не существует такой частоты, при которой имел бы место резонанс.
При резонансная частота , т. е. такая же, как и при резонансе в последовательном контуре.
При резонансная частота имеет любое значение, т. е. резонанс наблюдается на любой частоте. Действительно, при входное сопротивление контура

т. е. входное сопротивление контура активное и не зависит от частоты. Следовательно, ток совпадает по фазе с напряжением при любой частоте и его действующее значение равно .
Заметим, что в радиотехнике и электросвязи часто применяются контуры с малыми потерями, т. е. в них и малы по сравнению с ρ. В таких условиях резонансную частоту можно вычислять по формуле

Анализ, который здесь не приводится, показывает, что в общем случае сумма энергий электрического и магнитного полей при резонансе не остается постоянной. Эта сумма постоянна только в теоретическом случае, т. е. при .

Пример 5.2.
Угловая частота ω и действующее значение I синусоидального тока, подводимого к цепи (рис. 5.7, а), поддерживаются неизменными. Емкость конденсатора без потерь изменяется до тех пор, пока при некотором значении С напряжение U, измеряемое вольтметром, не достигнет максимального значения Umax. По известным величинам ω, I, С, Umax и R требуется определить параметры ωL и r катушки, присоединенной к выводам 1 и 2.
Решение.
Проще всего задача решается путем преобразования схемы в эквивалентную, состоящую из переменного емкостного элемента с проводимостью , двух параллельно соединенных элементов — активной g, индуктивной проводимостей (рис.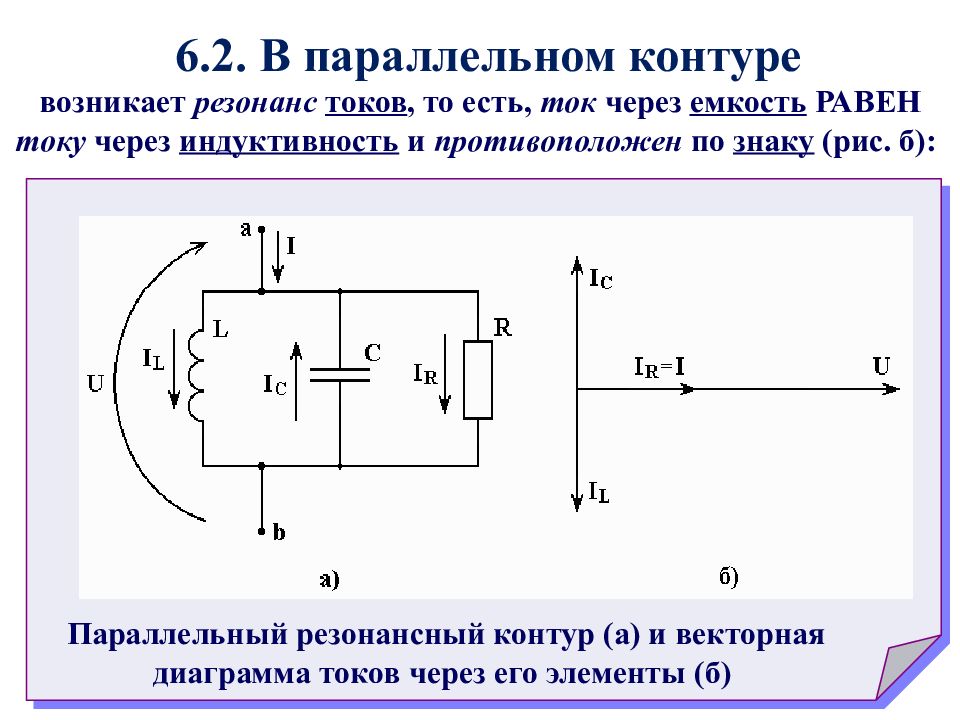 5.7, в) и с источником тока подсоединенным к выводам 3 и 4.
В этой схеме при неизменном действующем токе и изменении емкости максимум напряжения, измеряемого вольтметром, будет наблюдаться при резонансе токов, так как входное сопротивление цепи при этом максимально.
В соответствии с намеченным путем решения приступаем к преобразованию схемы. Питание цепи (рис. 5.7, а) заданным током может рассматриваться как питание от источника тока (показан штриховой линией). Заменим источник тока источником ЭДС (рис. 5.7, б), а от источника ЭДС перейдем к новому источнику тока, подключенному к выводам 3 и 4. Ток этого источника

где .
Последовательное соединение элементов R, r и ωL заменим параллельным (рис. 5.7, в) с проводимостями



Максимум напряжения между выводами 3 и 4 наблюдается при резонансе токов, т. е.



и



Из последнего равенства найдем связь между неизвестными g и z:



где для сокращения записи отношение известных величин обозначено a.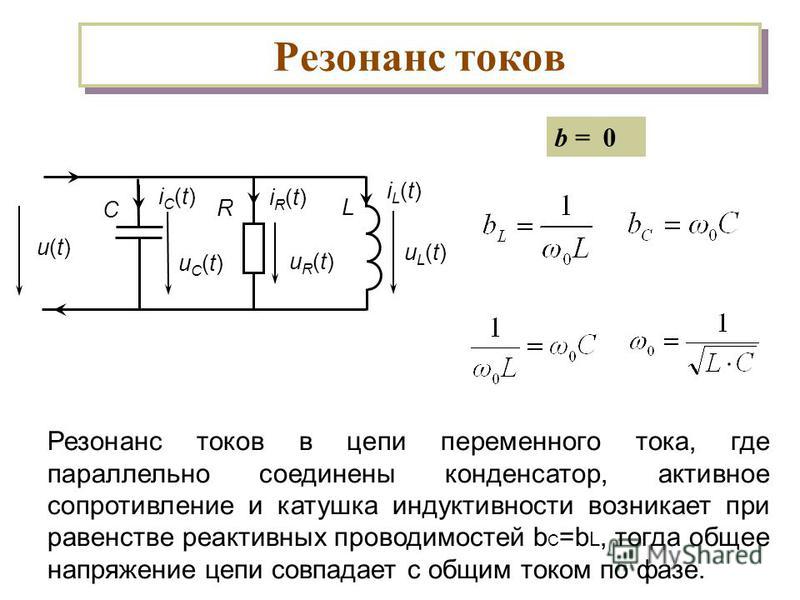
Подставив (б) и (в) в выражение , получим



откуда



Наконец, из (а) найдем, что

 

Рис. 5.7

Резонанс токов в параллельном колебательном контуре

  

Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.

Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.

При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).

Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.

 

Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру.

При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.

Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.

Сопротивление колебательного контура при параллельном резонансе равно:

где L выражено в гн, С—в ф, R_L—в ом.

Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.

Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.

Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.

 

При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.

Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Параллельный колебательный контур | Практическая электроника

В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы  рассмотрим параллельный колебательный контур, в котором катушка и конденсатор  соединяются параллельно.

Параллельный колебательный контур

Идеальный колебательный контур

На схеме идеальный колебательный контур выглядит вот так:

где

L – индуктивность, Генри

С – емкость, Фарад

Реальный колебательный контур

В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема

реального колебательного контура примет вот такой вид:

где

R – это сопротивление потерь контура, Ом

L – индуктивность, Генри

С – емкость, Фарад

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки X_L и конденсатора X_C уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

Резонанс параллельного колебательного контура

Очень интересное свойство параллельного колебательного контура заключается в том, что при Х_L = Х_С   у нас колебательный контур войдет в

резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

где

R_рез  – это сопротивление контура на резонансной частоте

L – собственно сама индуктивность катушки

C – собственно сама емкость конденсатора

R – сопротивление потерь катушки

Формула резонанса

Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

где

F – это резонансная частота контура, Герцы

L – индуктивность катушки, Генри

С – емкость конденсатора, Фарады

Как найти резонанс параллельного колебательного контура на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно.

Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура R_кон.

Упрощенная схема будет выглядеть вот так:

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение.

Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление R_кон будет максимальным, вследствие чего у нас на этом сопротивлении “упадет” бОльшее напряжение.

[quads id=1]

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

200 Герц.

Как вы видите, на колебательном контуре “падает” малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление R_кон

Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что  сопротивление  колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

723 Килогерца

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом.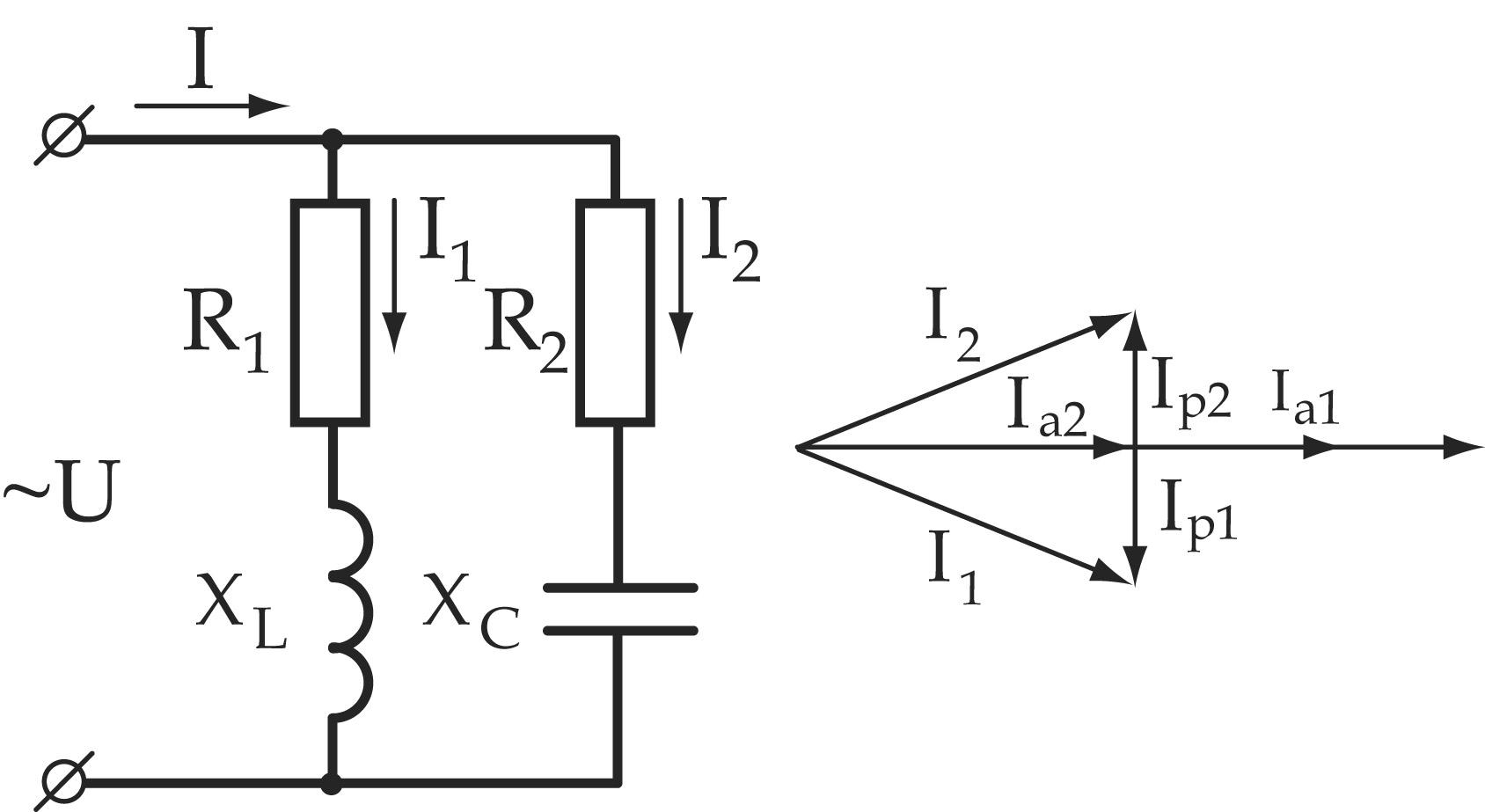 Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Что происходит на резонансной частоте в параллельном колебательном контуре

 Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?

Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое  высокое сопротивление R_кон. На этой частоте Х_L = Х_С. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток  I_рез ? Считаем по закону Ома:

I_рез = U_ген /R_рез  , где  R_рез = L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток I_кон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Добротность параллельного колебательного контура

Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз.  Q – это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила  тока в контуре  I_кон  больше сила тока в общей цепи I_рез

Или формулой:

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:

где

Q – добротность

R – сопротивление потерь на катушке, Ом

С – емкость, Ф

L – индуктивность, Гн

Применение параллельного колебательного контура

Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.

Также смотрите видео:

физический смысл и применение, формулы и способы расчета

Физическое явление параллельного резонанса широко применяется в радиоэлектронике.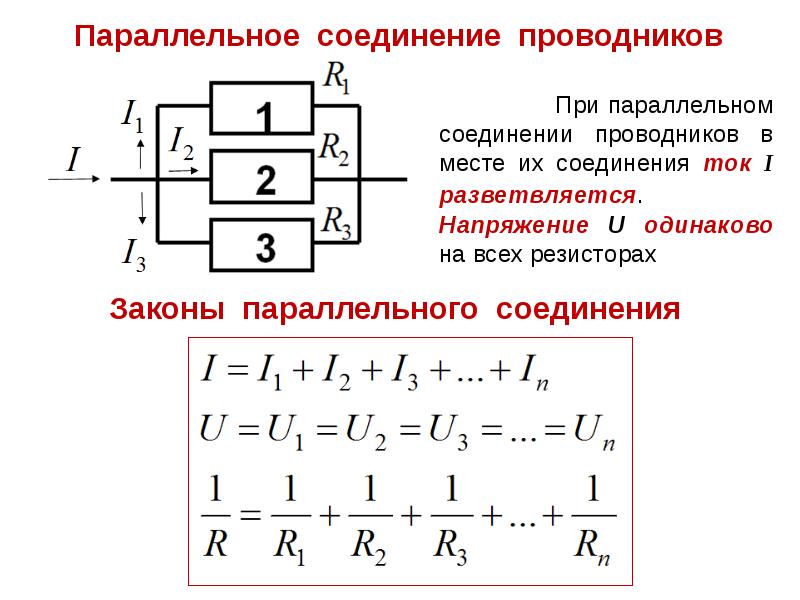 Для построения колебательных контуров, состоящих из активного и реактивного сопротивлений, следует собрать цепь из сопротивления, емкости, а также индуктивности. Для этого необходимо разобраться в назначении резонанса, нахождении сопротивления радиокомпонентов, его основном применении в радиотехнике, а также условии его возникновения.

Общие сведения

Электрическим сопротивлением проводника является свойство проводить электрический ток. Для построения и расчета колебательного контура необходимо знать способы нахождения активного и реактивного сопротивлений. Сопротивление для цепей, питающихся от переменного тока (ЦПТ), бывает следующих видов: активное, реактивное и полное.

Активным сопротивлением ® является обыкновенный резистор. Реактивное состоит из следующих типов нагрузки: индуктивное и емкостное. Индуктивное (Xl) — сопротивление катушки индуктивности в цепи переменного тока, а емкостное (Xc) определяется наличием емкости в цепи (конденсатора).

При сложении активного и реактивного сопротивлений получается полное сопротивление участка электрической цепи, которое обозначается литерой Z.

Активное сопротивление

Активным сопротивлением в ЦПТ называется наличие любой нереактивной нагрузки. Его можно рассчитать следующими способами: при помощи измерения величины сопротивления и расчетным методом. Для измерения R применяется прибор, который называется омметром. Омметр входит в состав комбинированных приборов измерения электрических величин, которые называются мультиметрами. Он подключается параллельно нагрузке, причем для проведения измерений следует выключить электрическую цепь, поскольку наличие тока приведет прибор к выходу из строя.

Существует еще один способ, который является расчетным, однако он требует знаний в области физики. При вычислении величины R следует произвести измерения силы тока и напряжения, а точнее, их амплитудных значений (Uм и Iм соответственно). Это возможно сделать при помощи соответствующих приборов.

Для измерения величины напряжения применяется вольтметр, а силу тока можно измерить при помощи амперметра. Кроме того, эти приборы измеряют только действующие значения напряжения (Uд) и силы тока (Iд). Для расчета амплитудных значений следует воспользоваться следующими формулами:

1. Uм = Uд * sqrt (2).
2. Iм = Iд * sqrt (2).

​Для расчета R, которое можно найти, используя закон Ома для участка цепи (Iм = Uм / R): R = Uм / Iм. Воспользовавшись соотношениями зависимостей амплитудных значений от действующих, возможно рассчитать R: R = Uд * sqrt (2) / Iд * sqrt (2) = Uд / Iд. На практике применяют способ измерения сопротивления омметром.

Другие виды нагрузок

При наличии в ЦПТ катушки индуктивности возникает Xl, которую необходимо только рассчитывать. Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.

Циклическая частота рассчитывается по следующей формуле, для которой необходимо только знать частоту переменного тока (f) и число ПИ (3,1416): w = 2 * 3,1416 * f. Индуктивность катушки рассчитывается, исходя из значений диаметра катушки (D в мм), числа витков (n) и длины намотки (l): L = (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l). Если подставить в формулу расчета индуктивного сопротивления все соотношения, то получается: Xl = 2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l).

Если в ЦПТ присутствует конденсатор с емкостью C, то добавляется еще и емкостное сопротивление — Xl, которое рассчитывается по следующей формуле: Xc = 1 / (w * C) = 1 / (2 * 3,1416 * f * C). Полное сопротивление в ЦПТ обозначается литерой Z и рассчитывается по формуле: Z = sqrt [sqr® +sqr (Xс — Xl)]. Если подставить в формулу полного сопротивления соотношения, по которым находятся R, Xl и Xc, то получается следующая формула: Z = sqrt [sqr (Uд / Iд) +sqr ((1 / (2 * 3,1416 * f * C)) — (2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l))]. Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.

Понятие о резонансе

Резонанс в цепи переменного тока происходит при образовании резонансной частоты, при которой некоторые сопротивления компенсируют друг друга. Основными признаками резонанса являются:

1. Совпадения по фазе U и I в цепи.
2. Значение активного и полного сопротивлений совпадают: Z = R.
3. Сила тока является максимальной.
4. Падение величины U на R равно U, которое приложено к контуру LC.
5. Выполняется равенство падений U на индуктивности и емкости, а также противоположность по фазе и больше приложенного напряжения: Ul > U, Ul = I * Xl = I * Xc и U = I * R.

В последнем случае коэффициент усиления по напряжению рассчитываются следующим способом: Ku = Ul / U = sqrt (L/C) / R = p / R. Этот коэффициент называется добротностью контура и обозначается литерой Q. Волновое сопротивление контура обозначается p, которое вычисляется по формуле: p = sqrt (L/C).

Резонанс в ЦПТ бывает двух видов: последовательный и параллельный. Для последовательного резонанса условием является минимальное сопротивление и нулевая фаза. В основном он применяется в схемах с реактивными составляющими L и C. При параллельном типе резонанса происходит равенство емкостных и индуктивных сопротивлений, которые компенсируют друг друга. Этот тип соединения должен постоянно быть равен расчетной величине. Он получил широкое применение, благодаря резкому минимуму импеданса. Импеданс — полное сопротивление в цепи переменного тока, который обозначается Z.

Контур является схемой, в которой подключены параллельно или последовательно следующие элементы: резистор, катушка индуктивности и конденсатор.

Эта схема образует осциллятор для тока с гармонической составляющей. Наличие сопротивления в схеме приводит к затуханию и уменьшает резонансную пиковую частоту.

Во всей силовой радиоэлектронике применяются колебательные контуры. Примером его является силовой трансформатор. Кроме того, контур используется для настройки телевизоров, согласования антенн. Возможно применение в качестве полосового и режекторного фильтров, которые применяются в датчиках для распределения низких и высоких частот. Эффект резонанса применяется и в медицине при микротоковой терапии, и при проведении биорезонансной диагностики.

Случаи для тока и напряжения

В радиоэлектронике применяется резонанс напряжений и токов. Они отличаются друг от друга и применяются в определенных случаях. Резонанс напряжений возникает при последовательном соединении в RLC-цепи (схема 1):

Схема 1 — Последовательное соединение элементов.

Основным условием возникновения резонанса является равенство частот источника питания и колебательного контура. Кроме того, Xc = Xl, они являются противоположными величинами (по знаку) и равны 0. Напряжения Uc и Ul противоположны по фазам и компенсируют друг друга, следовательно, Z = R. В результате этого происходит увеличение тока, так как при уменьшении сопротивления по закону Ома происходит увеличение I. Вырастает не только I, но и значения U на элементах схемы. При резонансе значения напряжений на конденсаторе и катушке индуктивности могут быть больше относительно напряжения источника питания.

При увеличении частоты значение Xl увеличивается, а Xc — уменьшается. При равенстве частот резонансной и источника питания значение Z будет уменьшаться. Резонансная частота находится по формуле: w = sqrt (1 / (L * C)). Резонанс в ЦПТ зависит от следующих величин: частоты источника питания — f, параметров L и C. Обмен электрической энергией осуществляется между катушкой и конденсатором через источник питания.

Резонанс токов в цепи переменного тока возникает при параллельном включении активных и реактивных нагрузок. На схеме 2 изображен контур с параллельным соединением:

Схема 2 — Параллельное соединение в RLC-контуре.

В этом случае резонанс возникает при равенстве частот источника питания и резонансной, а также равенства проводимостей конденсатора (Bc) и катушки (Bl). Проводимость — величина, обратная сопротивлению. При увеличении частоты источника питания происходит рост полного сопротивления, при котором ток уменьшается. В результате этого, ток уменьшается и равняется активной составляющей. Для определения резонансной частоты следует воспользоваться алгоритмом нахождения этой величины:

1. Удельные проводимости для резистора, катушки индуктивности и конденсатора: G = 1 / R, Bl = 1 / (w * L) и Bc = w * C соответственно.
2. 1 / (w * L) = w * C.
3. Резонансная частота вычисляется по формуле: w = sqrt (1 / (L * C)).

Явление резонанса может привести к выходу из строя элементов схемы, приборов или устройств. Для того чтобы избежать этого, необходимо производить точные расчеты колебательных контуров.

Расчет параллельного контура

Необходимо сделать параллельный контур, частота резонанса которого равна 1,5 МГц. Для его изготовления нужно осуществить расчет, исходя из которого возможно будет его изготовить. Рассчитывать контур следует точно, поскольку любая неточность может привести к негативным последствиям. Основной задачей является расчет нужных индуктивности катушки и емкости конденсатора. Расчет осуществляется по следующему алгоритму:

1. Вычислить необходимую индуктивность в мкГн при заданной емкости и частоте: L = sqr (159,12 / f) / C.
2. Рассчитать количество витков (n) и диаметр каркаса (d в мм) катушки: n = 32 * sqrt (L / d).

Пусть С = 2000 пФ, тогда L = sqr (159,12 / 2) / 2000 = 5,6 мкГн. Количество витков для катушки с d = 3 мм: n = 32 * sqr (5,6 / 3) = 112.

Этот метод является приближенным, поскольку не учитывается межвитковое пространство катушки. Радиолюбители часто применяют уже готовые катушки, имеющие длину 15 мм с диаметром d = 3 мм. Вычислить можно, используя другую формулу: n = 8,5 * sqrt (L) = 8,5 * 2,3664 = 21.

Таким образом, явление резонанса применяется при построении различной радиоаппаратуры и требует выполнения верных расчетов, поскольку даже при незначительных ошибках могут выйти из строя дорогостоящие детали.

Резонанс токов в цепи: пример с решением

Резонанс токов

Резонанс при параллельном соединении индуктивности и емкости называется резонансом токов. Схема цепи с резонансом токов показана на рисунке 5.

Дано:

входное напряжение

; параметры цепи: причем .

Найдем:

1) собственную частоту цепи

;

2) полную входную проводимость цепи при резонансе

;

3) полное входное сопротивление цепи при резонансе

;

4) входной ток в момент резонанса

;

5) токи в индуктивной

и емкостной ветвях при резонансе;

6) сдвиг фаз между током и напряжением в момент резонанса

;

7) входную мощность в момент резонанса

.

Полные сопротивления ветвей схемы в комплексной форме можно записать так:

Проводимости ветвей будут такими:

Полная входная проводимость цепи при параллельном соединении ветвей является суммой проводимостей отдельных ветвей

или

Найдем собственную частоту цепи. На основании общего положения о резонансах, имеем

откуда

Если учесть (6) в (18), то получим:

где

волновое сопротивление цепи.

Таким образом, и здесь, при резонансе токов, собственная частота цепи зависит только от параметров цепи и от схемы их соединения и совершенно не зависит ни от токов, ни от напряжений.

Регулирование собственной частоты производится теми же способами, что и при резонансе напряжений.

Если считать, что

то

Собственная частота при резонансе токов, в случае равенства

близка к собственной частоте при резонансе напряжений. В момент резонанса входная проводимость будет

Так как

то

Ранее мы определили, что

Тогда получаем:

или окончательно

Собственно входное сопротивление будет

Поскольку, активные сопротивления ветвей считаются малыми, то

Таким образом, при резонансе токов входная проводимость цепи стремится к нулю, а входное сопротивление к бесконечности.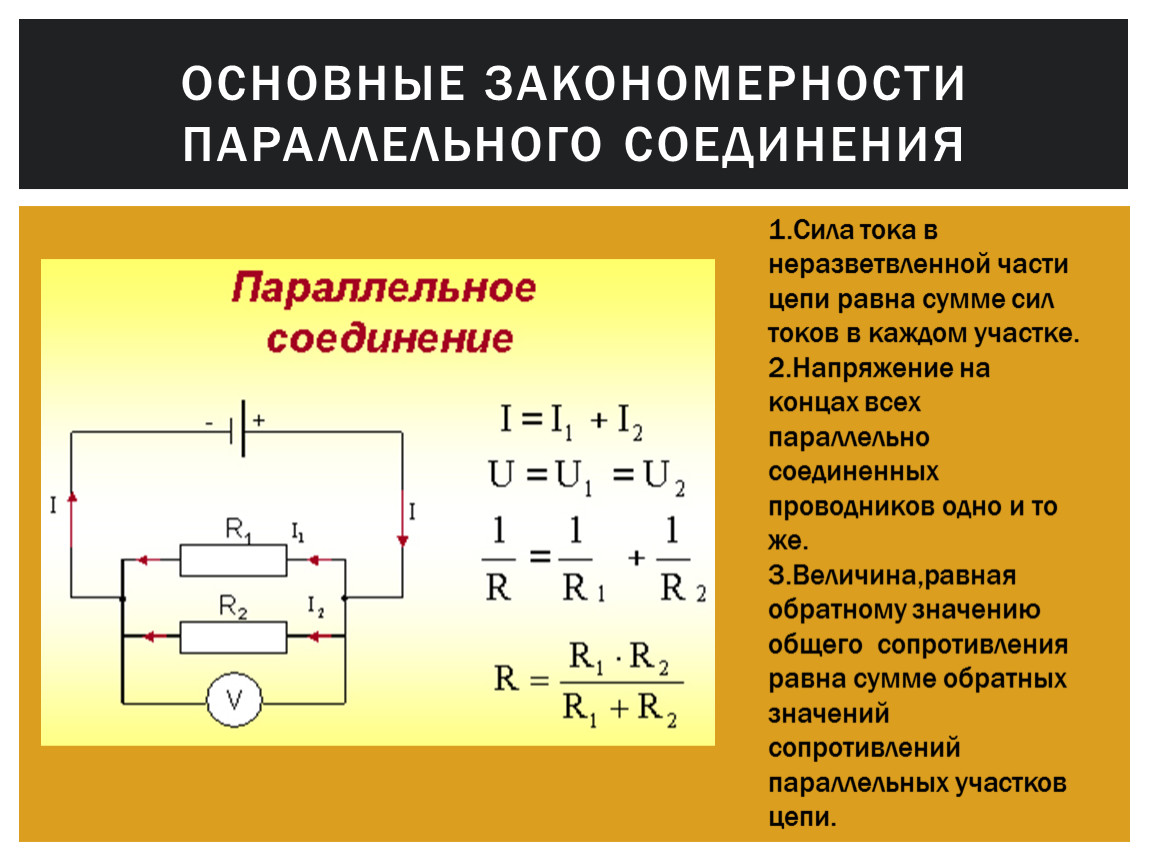 Определим входной ток всей цепи

При резонансе токов входной ток предельно мал, так как сопротивление цепи стремится к бесконечности.

Это свойство широко используется на практике — резонанс токов является заградительным фильтром, непрозрачной преградой, пробкой для
токов резонансной частоты, рисунок 6.

Найдем теперь токи, протекающие в ветвях схемы в момент резонанса.

Поскольку

и , имеем:

Реактивные проводимости будут равны:

Так как

то получим:

Токи при резонансе равны по абсолютной величине и противоположны по фазе.

Выражения (30) получены в предположении, что активные сопротивления ветвей равны нулю. При этом общий входной ток цепи, равный сумме токов текущих в ветвях получится

В действительности, так как

, то общий ток существует, но весьма малой величины.

Выясним, как относятся токи ветвей к входному току.

где

— добротность контура.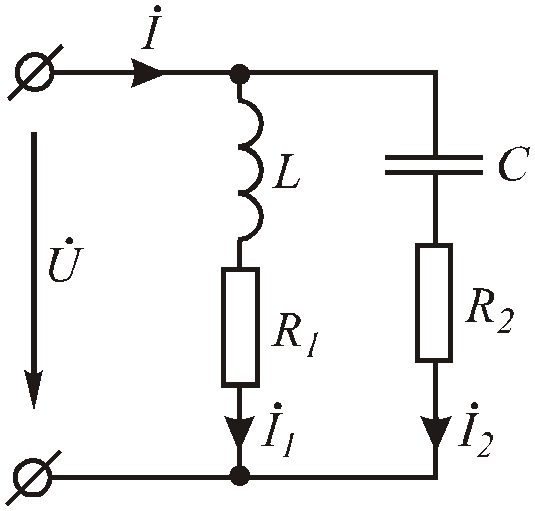

На основании полученных выражений можно сформулировать главное свойство резонанса токов.

При резонансе токов, токи в ветвях равны по абсолютной величине, противоположны по фазе и могут во много раз превышать входной ток цепи.

Следовательно,

Определим фазовый сдвиг на входе цепи.

Входной ток и напряжение при резонансе токов совпадают по фазе.

Коэффициент мощности на входе цепи при резонансе токов максимален и равен единице. Следовательно, цепь работает в самом экономичном режиме.

Входная мощность цепи при резонансе будет

поскольку

то

Видим, что цепь потребляет от источника только активную мощность. Причем весьма малую.

Потребляемая мощность будет тем меньше, чем выше добротность цепи. Поэтому данный тип резонанса широко применяют в радиотехнике, электронике, и автоматике.

Внутри цепи существует и реактивная мощность в виде магнитного и электрического полей, но она не выходит за пределы цепи.

Векторная диаграмма резонанса токов показана на рисунке 7.

Графики частотных характеристик для резонанса токов показаны на рисунке 8.

В виду того, что мощность, потребляемая резонансной цепью при резонансе токов минимальна, и стремится к нулю, данный тип резонанса широко применяется в радиоэлектронике, приборостроении и автоматике.

Эта страница взята со страницы контрольной работы по электротехнике:

Контрольная работа по электротехнике

Возможно эти страницы вам будут полезны:

Резонанс токов: применение, принцип резонса тока, расчет контура

Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет.

Что такое резонанс?

Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.

Соединение двух ветвей при резонансе

Признаки резонанса:

1. Составляющие реактивных ветвей тока равны между собой IPC = IPL, противофаза образовывается только при равенстве чистой активной энергии на входе;
2. Ток в отдельных ветках, превышает весь ток определенной цепи, при этом ветви совпадают по фазе.

Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:

1. Последовательный;
2. Параллельный.

Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.

Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.

Применение

Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.

Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.

Принцип резонанса токов

Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:

Схема для питания конденсатора

Переключатель будет отвечать за направление колебаний.

Схема: переключатель резонансной схемы

Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.

Схема: ток в резонансной схеме равен нулю

Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.

Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.

Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.

В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.

Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.

Расчет резонансного контура

Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела.

Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом:

R _ср= I²_конт * R = (V²_конт / Z²) * R.

При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1

Сама же формула резонанса имеет следующий вид:

ω₀ = 1 / √L*C

Нулевой импеданс в резонансе определяется при помощи такой формулы:

F_рез = 1 / 2π √L*C

Резонансная частота колебаний может быть аппроксимирована следующим образом:

F = 1/2 р (LC) 0. 5

Где: F = частота

L = индуктивность

C = емкость

Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям:

R = 2 (L / C) 0.5

Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов. При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока.

Электрические цепи однофазного тока. Резонанс токов.

Рассмотрим цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью.

Параллельное соединение конденсатора и катушки

Рис. 1

В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z₁ и ток I₁ определяются по формуле:

Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол φ₁ = arctg(R/X_L). Покажем это на векторной диаграмме.

Векторная диаграмма для первой ветви

Рис. 2

Спроецируем вектор тока I₁ на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I_1R, а вертикальная — I_1L. Количественные значения этих составляющих будут равны:

Во вторую ветвь включен конденсатор. Его сопротивление

Этот ток опережает по фазе напряжение на 90°. Для определения тока I в неразветвленной части цепи воспользуемся формулой:

Его значение можно получить и графическим путем, сложив векторы I₁ и I₂ (рис. 3). Угол сдвига между током и напряжением обозначим буквой φ. Здесь возможны различные режимы в работе цепи. При φ = +90° преобладающим будет емкостный ток, при φ = -90° — индуктивный.

Векторная диаграмма разветвленной цепи

Рис. 3

Резонанс переменного тока. Условие резонанса токов.

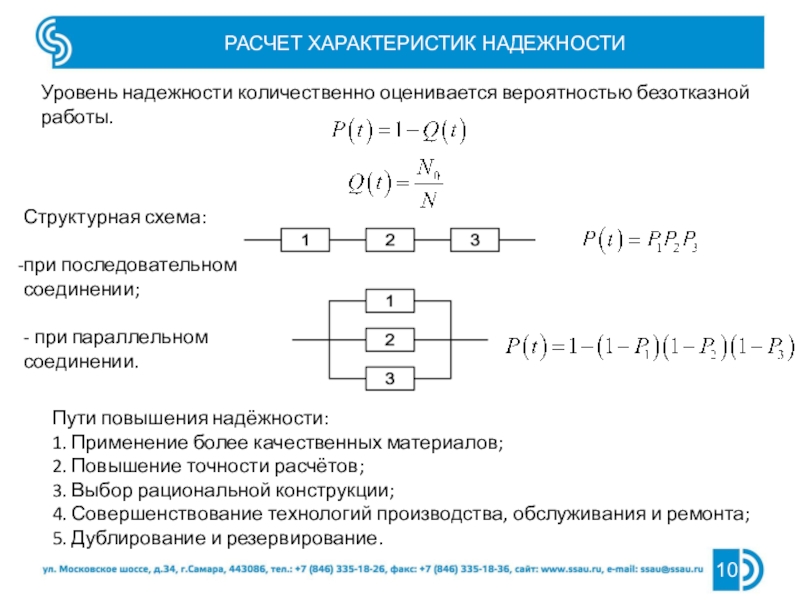
Возможен режим, когда φ = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I_1L = I₂, т.е. при равенстве реактивных составляющих тока в ветвях. Такой режим называется резонансом токов. Также как в случае с резонансом напряжений, он широко применяется в радиотехнике.

Векторная диаграмма в режиме резонанса токов

Рис. 4

Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosφ для электроустановок. Известно, что cosφ является технико-экономическим параметром в работе электроустановок. Определяется он по формуле:

cosφ = P / S, где

Р — активная мощность электроустановок, кВт;
S — полная мощность электроустановок, кВт.

На практике cosφ определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgφ. Далее по таблицам находят и cosφ.

Чем больше cosφ, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosφ приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosφ, в сравнении с низким.

Мероприятия по повышению cosφ:

Кроме этого, на cosφ положительно сказывается подключение к сети статических конденсаторов.

8.3: Параллельный резонанс — разработка LibreTexts

Если три компонента RLC разместить параллельно, как показано на рисунке \ (\ PageIndex {1} \), может возникнуть параллельный резонансный контур. Обычно он приводится в действие источником тока, как показано на рисунке, хотя это не является требованием для резонанса. Параллельный резонанс немного сложнее последовательного резонанса из-за того, что сопротивление последовательной катушки не может быть объединено с остаточным сопротивлением цепи, как это может быть в последовательном случае. Другими словами, на практике у нас есть последовательно-параллельная цепь, в которой катушка индуктивности, по сути, представляет собой последовательную комбинацию индуктивности и сопротивления катушки. Оказывается, обычно это сопротивление нельзя игнорировать, даже если оно очень мало. Чтобы решить эту проблему, можно найти параллельный эквивалент для последовательного индуктивного реактивного сопротивления и соответствующего сопротивления катушки. То есть нам нужна серия для параллельного преобразования.

Рисунок \ (\ PageIndex {1} \): Идеальный параллельный резонансный контур.

8.3.1: преобразование последовательного индуктора в параллельный

Рисунок \ (\ PageIndex {2} \): Реалистичный параллельный резонансный контур.

Во-первых, давайте посмотрим, что у нас есть на практике. Реалистичный параллельный резонансный контур показан на рисунке \ (\ PageIndex {2} \). Эта схема добавляет внутреннее сопротивление катушки индуктивности к идеальной схеме, показанной на рисунке \ (\ PageIndex {1} \). Что мы хотели бы сделать, так это найти способ найти параллельный эквивалент катушки индуктивности с ее сопротивлением катушки.Конечно, это должно быть возможно. В конце концов, сделать обратное упражнение — тривиальное занятие; а именно, взяв параллельную комбинацию катушки индуктивности и резистора и найдя ее последовательный эквивалент (т. е. выражение результирующего импеданса в прямоугольной форме). После завершения процесса у нас должна быть эквивалентная схема, подобная показанной на рисунке \ (\ PageIndex {3} \). В этой эквивалентной схеме \ (R \) и \ (C \) — значения из исходной схемы, а \ (L _ {(p)} \) и \ (R_ {coil (p)} \) — параллельные эквиваленты преобразованные значения, полученные из исходной катушки индуктивности.В этой версии легко объединить \ (R \) параллельно с \ (R_ {coil (p)} \), чтобы создать единственный резистор и, таким образом, вернуться к нашей идеальной схеме на рисунке \ (\ PageIndex {1 } \).

Рисунок \ (\ PageIndex {3} \): преобразованная (эквивалентная) версия реалистичного параллельного резонансного контура.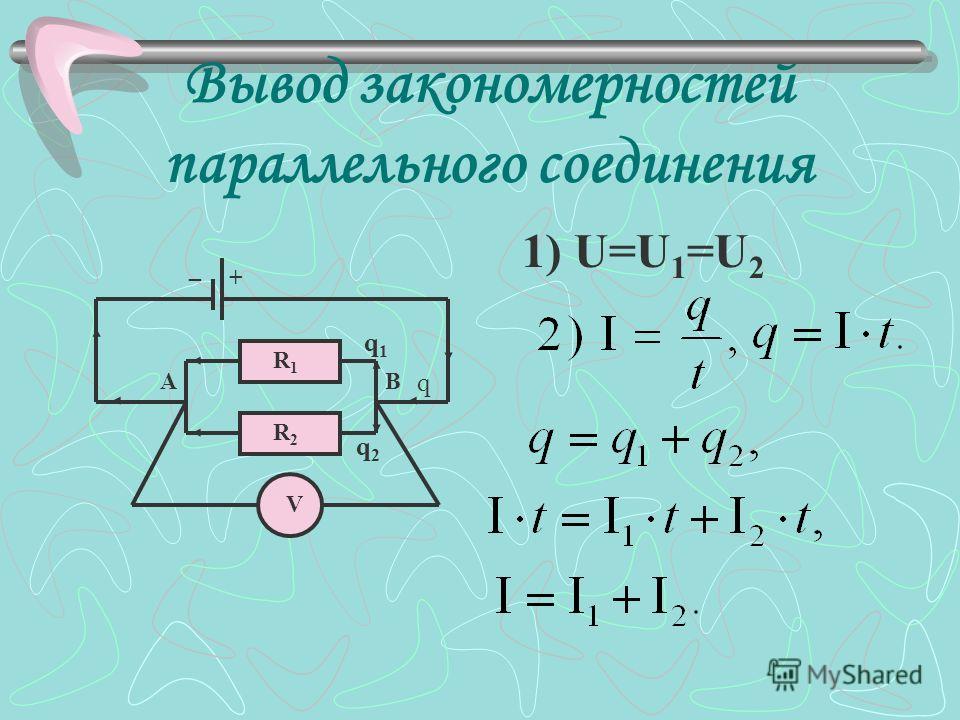

Эквивалентное преобразование показано на рисунке \ (\ PageIndex {4} \). Начнем с практической катушки, состоящей из последовательной комбинации сопротивления и индуктивного реактивного сопротивления, \ (R_s + jX_s \).Мы найдем параллельный эквивалент, \ (R_p || jX_p \).

Рисунок \ (\ PageIndex {4} \): последовательные и эквивалентные параллельные комбинации RL.

Начнем с правила взаимной проводимости / сопротивления:

\ [R_s + jX_s = \ frac {1} {\ frac {1} {R_p} + \ frac {1} {jX_p}} \\ \ frac {1} {R_s + jX_s} = \ frac {1} { R_p} + \ frac {1} {jX_p} \ label {8.14} \]

Следующий шаг — выделить действительную и мнимую части серийной версии. Мы можем сделать это, умножив левый член уравнения \ ref {8.2} {X_s} = jX_s \ label {8.18} \]

Таким образом, для высокого значения \ (Q_ {coil} \) параллельное эквивалентное реактивное сопротивление не отличается от последовательного значения, а параллельное эквивалентное сопротивление равно последовательному сопротивлению, умноженному на \ (Q \) катушки в квадрате.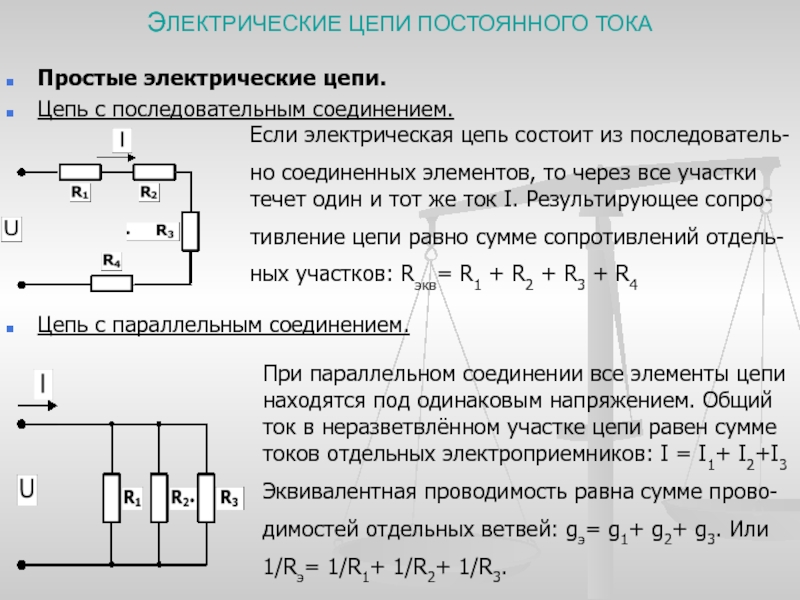 Интересно, что уравнение \ ref {8.17} показывает, что меньший \ (R_S \) (который дает пропорционально больший \ (Q_ {coil} \)) приводит к большему \ (R_P \). Таким образом, идеальная катушка индуктивности, не имеющая сопротивления катушки, дает \ (R_p \) бесконечности. Из-за этой резистивной «инверсии» последовательно-параллельного преобразования параллельная цепь \ (Q \) определяется как:

\ [Q_ {parallel} = \ frac {R_T} {X_L} \ label {8.19} \]

Где

\ (Q_ {parallel} \) — это \ (Q \) параллельного резонансного контура (т.е. \ (Q_ {circuit} \) для параллельного),

\ (R_T \) — полное параллельное сопротивление \ ((R_p || R) \),

\ (X_L \) — реактивное сопротивление при \ (f_0 \).

На основе уравнения \ ref {8.19} и развития уравнения \ ref {8.13} можно показать, что:

\ [Q_ {parallel} = R_T \ sqrt {C} {L} \ label {8.20} \]

Для более высоких цепей \ (Q \) (\ (Q_ {parallel} \ geq 10 \)) \ (f_0 \) находится как в последовательном случае (повторение):

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {LC}} \ label {8.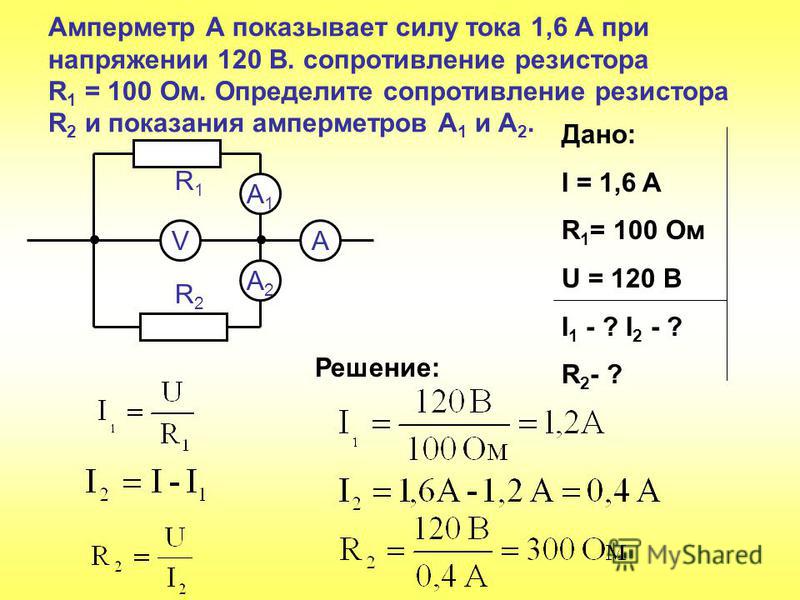 2} \]

Для нижних \ (Q \) цепей \ (f_0 \) будет немного уменьшено из-за того, что преобразованное сопротивление зависит от частоты. Подробнее об этом в следующем разделе.

8.3.2: Импеданс параллельного резонанса

График параллельного импеданса показан на рисунке \ (\ PageIndex {5} \). Эффект обратный последовательному случаю. На низких частотах небольшое индуктивное реактивное сопротивление приводит к низкой величине импеданса с положительным (индуктивным) фазовым углом. На высоких частотах малое емкостное реактивное сопротивление приводит к низкому импедансу с отрицательным (емкостным) фазовым углом.При резонансе реактивные значения отменяются. Остается только значение параллельного сопротивления, которое дает характеристический пик импеданса. Фазовый угол равен нулю, что соответствует единице коэффициента мощности.

Рисунок \ (\ PageIndex {5} \): График импеданса для параллельного резонансного контура.

Если параллельный резонансный контур приводится в действие источником тока, то напряжение, создаваемое на резонансном контуре (иногда называемом контуром с резервуаром), будет отражать форму величины импеданса. Другими словами, он будет эффективно различать высокие и низкие частоты и сохранять только те сигналы, которые находятся вблизи резонансной частоты. Это один из способов создания полосового фильтра. Нижняя и верхняя частоты половинной мощности, \ (f_1 \) и \ (f_2 \), находятся так же, как и в последовательном резонансе.

Повторяю для удобства:

\ [BW = f_2 — f_1 \ label {8.3} \]

\ [Q_ {circuit} = \ frac {f_0} {BW} \ label {8.4} \]

\ [f_0 = \ sqrt {f_1 f_2} \ label {8.2} +1} \ label {8.7} \]

\ [f_1 = \ frac {f_0} {k_0} \ label {8.8} \]

\ [f_2 = f_0 \ times k_0 \ label {8.9} \]

Для более высоких схем \ (Q \) (\ (Q_ {circuit} \ geq 10 \)) мы можем аппроксимировать симметрию, и, таким образом,

\ [f_1 \ приблизительно f_0 — \ frac {BW} {2} \ label {8.10} \]

\ [f_2 \ приблизительно f_0 + \ frac {BW} {2} \ label {8.11} \]

Наконец, стоит повторить, что для относительно низких значений \ (Q \) будет некоторое смещение резонансных частот и частот половинной мощности из приведенных выше уравнений.

Между параллельным и последовательным резонансами есть некоторое сходство. Как и в случае серии, по мере увеличения параллельности \ (Q \) кривая импеданса становится более резкой, а изменение фазы — более резким. Кроме того, мы также видим явный эффект «усиления \ (Q \)» в параллельных резонансных цепях, однако здесь будут увеличиваться реактивные токи относительно тока источника, а не последовательные составляющие напряжения.

Обратите внимание, что параллельный резистор можно использовать для понижения системы \ (Q \) и, таким образом, расширения полосы пропускания, однако система \ (Q \) никогда не может быть выше, чем \ (Q \) самой катушки индуктивности.Индуктор устанавливает верхний предел для системы \ (Q \) и, следовательно, насколько узкой может быть полоса пропускания. Другими словами, \ (Q_ {схема} \ leq Q_ {катушка} \). То же самое мы видели для последовательного резонанса.

Пример \ (\ PageIndex {1} \)

Для схемы на рисунке \ (\ PageIndex {6} \) определите резонансную частоту, угловые частоты \ (f_1 \) и \ (f_2 \), полосу пропускания и систему \ (Q \). Также найдите напряжение цепи на резонансной частоте. \ (R_ {катушка} = 100 \ Омега \).

Рисунок \ (\ PageIndex {6} \): Схема для примера \ (\ PageIndex {1} \).

Во-первых, предположим, что это схема с высоким значением \ (Q (\ geq 10) \).

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {LC}} \ nonumber \]

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {50 м вод. Ст. 910 пФ}} \ nonumber \]

\ [f_0 = 23,6 кГц \ nonumber \]

\ [X_L = 2 \ pi f L \ nonumber \]

\ [X_L = 2 \ pi 23,6 кГц 50 мГн \ nonumber \]

\ [X_L = 7.41k \ Omega \ nonumber \]

\ [Q_ {катушка} = \ frac {X_L} {R_ {катушка}} ​​\ nonumber \]

\ [Q_ {катушка} = \ frac {7.2 \ nonumber \]

\ [R_p = 549,5 к \ Омега \ nonumber \]

Нет другого резистора, подключенного параллельно катушке индуктивности и конденсатору, поэтому эквивалентное параллельное сопротивление \ (R_p \) — это полное сопротивление цепи \ (R_T \). Следовательно, \ (Q \) схемы должен быть таким же, как \ (Q_ {coil} \). Мы можем проверить это следующим образом:

\ [Q_ {parallel} = \ frac {R_T} {X_L} \ nonumber \]

\ [Q_ {parallel} = \ frac {549,5 k \ Omega} {7,41 k \ Omega} \ nonumber \]

\ [Q_ {parallel} = 74.1 \ nonumber \]

Наше первоначальное предположение о высоком уровне цепи \ (Q \) выполнено.

\ [BW = \ frac {f_0} {Q_ {parallel}} \ nonumber \]

\ [BW = \ frac {23,6 кГц} {74.1} \ nonumber \]

\ [BW = 318 Гц \ nonumber \]

\ [f_1 \ приблизительно f_0 — \ frac {BW} {2} \ nonumber \]

\ [f_1 \ приблизительно 23,6 кГц — \ frac {318 Гц} {2} \ nonumber \]

\ [f_1 \ приблизительно 23,44 кГц \ nonumber \]

\ [f_2 \ приблизительно f_0 + \ frac {BW} {2} \ nonumber \]

\ [f_2 \ около 23.6 кГц + \ frac {318 Гц} {2} \ nonumber \]

\ [f_2 \ приблизительно 23,76 кГц \ nonumber \]

Чтобы найти напряжение цепи при \ (f_0 \), просто умножьте резонансный импеданс 549,5 к \ (\ Omega \) на источник 2 мА. Это дает примерно 1100 вольт.

Компьютерное моделирование

Схема из примера \ (\ PageIndex {1} \) фиксируется в имитаторе, как показано на рисунке \ (\ PageIndex {7} \).

Рисунок \ (\ PageIndex {7} \): Схема, показанная на рисунке \ (\ PageIndex {6} \) в симуляторе.

В цепи выполняется частотный анализ или анализ переменного тока, отображающий величину напряжения источника (узел 1) в диапазоне от 2 кГц до 200 кГц. Это даст нам примерно десять раз по обе стороны от резонансной частоты. Результат показан на рисунке \ (\ PageIndex {8} \). График показывает четкий и резкий пик в области низких 20 кГц. Обратите внимание, что пиковое напряжение составляет чуть более 1000 вольт, как и предполагалось. На рисунке \ (\ PageIndex {9} \) показана увеличенная версия этого графика, чтобы мы могли точно проверить пиковое напряжение вместе с \ (f_1 \) и \ (f_2 \).

Рисунок \ (\ PageIndex {8} \): Напряжение источника схемы, показанной на рисунке \ (\ PageIndex {7} \).

Рисунок \ (\ PageIndex {9} \) показывает, что пик действительно составляет примерно 1100 вольт. Частоты \ (f_1 \) и \ (f_2 \) находятся в 0,707 раза выше этого пика, или около 778 вольт. Для этой задачи используются два измерительных курсора. Значения Y — это напряжения в точке пересечения курсора с кривой, а значения X — соответствующие частоты. Видно, что результаты хорошо согласуются с расчетами.На уровнях от 777 до 780 вольт мы получаем значения \ (f_1 \) и \ (f_2 \) примерно 23,44 кГц и 23,75 кГц соответственно.

Рисунок \ (\ PageIndex {9} \): Увеличенный пик графика на рисунке \ (\ PageIndex {8} \).

Пример \ (\ PageIndex {2} \)

Для схемы на рисунке \ (\ PageIndex {10} \) определите резонансную частоту, угловые частоты \ (f_1 \) и \ (f_2 \), полосу пропускания и систему \ (Q \). Также найдите напряжение цепи на резонансной частоте.\ (R_ {катушка} = 100 \ Омега \).

Рисунок \ (\ PageIndex {10} \): Схема для примера \ (\ PageIndex {2} \).

Эта схема идентична схеме в предыдущем примере, за исключением добавленного нагрузочного резистора 100 кОм. Это должно снизить систему \ (Q \) и, таким образом, расширить полосу пропускания. Пиковое сопротивление также будет уменьшено, что вызовет уменьшение напряжения системы при резонансе. Некоторые параметры не изменятся. В их числе:

\ [f_0 = 23.6 кГц \ nonumber \]

\ [X_L = 7,41 к \ Омега \ nonumber \]

\ [Q_ {катушка} = 74,1 \ nonumber \]

\ [R_p = 549,5 к \ Омега \ nonumber \]

Предположим, что это схема с высоким \ (Q (\ geq 10) \).

Rp параллельно нагрузочному сопротивлению \ (R \), что дает эффективное параллельное сопротивление \ (549,5 кОм \ Омега || 100 кОм \ Омега \) или 84,6 кОм \ (\ Омега \).

\ [Q_ {parallel} = \ frac {R_T} {X_L} \ nonumber \]

\ [Q_ {parallel} = \ frac {84.6 к \ Omega} {7.41k \ Omega} \ nonumber \]

\ [Q_ {parallel} = 11.4 \ nonumber \]

Цепь \ (Q \) значительно сокращена, но наше первоначальное предположение о высоком уровне цепи \ (Q \) все еще выполняется. Теперь мы можем найти полосу пропускания и угловые частоты.

\ [BW = \ frac {f_0} {Q_ {parallel}} \ nonumber \]

\ [BW = \ frac {23,6 кГц} {11.4} \ nonumber \]

\ [BW = 2,07 кГц \ nonumber \]

\ [f_1 \ приблизительно f_0 — \ frac {BW} {2} \ nonumber \]

\ [f_1 \ около 23.6 кГц — \ frac {2.07 кГц} {2} \ nonumber \]

\ [f_1 \ приблизительно 22,56 кГц \ nonumber \]

\ [f_2 \ приблизительно f_0 + \ frac {BW} {2} \ nonumber \]

\ [f_2 \ приблизительно 23,6 кГц + \ frac {2,07 кГц} {2} \ nonumber \]

\ [f_2 \ приблизительно 24,64 кГц \ nonumber \]

Напряжение цепи на \ (f_0 \) снижается до 84,6 к \ (\ Omega \) раз 2 мА, или 169,2 вольт.

Компьютерное моделирование

Результаты моделирования соответствуют результатам в Примере \ (\ PageIndex {1} \) и показаны на Рисунке \ (\ PageIndex {11} \).Результаты согласуются с расчетными значениями. Пиковое напряжение было снижено примерно до 170 вольт, а \ (f_1 \) и \ (f_2 \) (найденные при 0,707 пикового значения, или примерно 120 вольт) составляют примерно 22,5 кГц и 24,6 кГц соответственно.

Рисунок \ (\ PageIndex {11} \): результаты моделирования для схемы из примера \ (\ PageIndex {2} \).

Пример \ (\ PageIndex {3} \)

Рассмотрим схему на рисунке \ (\ PageIndex {12} \) со следующими параметрами: \ (L \) = 2 мГн, \ (C \) = 10 нФ и \ (Q_ {coil} \) = 25.Определите резонансную частоту и такое значение для \ (R \), чтобы полоса пропускания системы составляла 3 кГц.

Рисунок \ (\ PageIndex {12} \): Схема для примера \ (\ PageIndex {3} \).

Как обычно, мы предполагаем, что это схема с высоким значением \ (Q (\ geq 10) \). Это, безусловно, верно для катушки, хотя мы должны определить резонансную частоту, чтобы определить \ (Q \) цепи.

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {LC}} \ nonumber \]

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {2mH 10 nF}} \ nonumber \]

\ [f_0 = 35.59 кГц \ nonumber \]

\ [Q_ {parallel} = \ frac {f_0} {BW} \ nonumber \]

\ [Q_ {parallel} = \ frac {35,59 кГц} {3 кГц} \ nonumber \]

\ [Q_ {parallel} = 11.86 \ nonumber \]

У нас высокий \ (Q \), и мы можем продолжить ¹ . В конечном итоге нам нужно определить полное параллельное сопротивление, необходимое для достижения этого \ (Q \). Прежде чем мы сможем это сделать, нам нужно определить \ (X_L \).

\ [X_L = 2 \ pi f L \ nonumber \]

\ [X_L = 2 \ pi 35,59 кГц 2 мГн \ nonumber \]

\ [X_L = 447 \ Omega \ nonumber \]

\ [R_T = Q_ {параллельно} \ times X_L \ nonumber \]

\ [R_T = 11.86 \ times 447 \ Omega \ nonumber \]

\ [R_T = 5.3k \ Omega \ nonumber \]

\ (R_T \) — это параллельная комбинация \ (R \) и \ (R_p \) (параллельный эквивалент \ (R_ {coil} \)), поэтому сначала нам нужно найти \ (R_ {coil} \ ).

\ [R_ {катушка} = \ frac {X_L} {Q_ {катушка}} ​​\ nonumber \]

\ [R_ {coil} = \ frac {447 \ Omega} {25} \ nonumber \]

\ [R_ {катушка} = 17.9 \ Omega \ nonumber \]

Параллельное эквивалентное сопротивление \ (R_ {катушка} \) составляет:

\ [R_p = R_ {катушка} Q_ {катушка} ^ 2 \ nonumber \]

\ [R_p = 17.2 \ nonumber \]

\ [R_p = 11,18 к \ Омега \ nonumber \]

Используя правило проводимости, мы можем найти необходимое значение \ (R \).

\ [R = \ frac {1} {\ frac {1} {R_T} — \ frac {1} {R_p}} \ nonumber \]

\ [R = \ frac {1} {\ frac {1} {5.3k \ Omega} — \ frac {1} {11.18 k \ Omega}} \ nonumber \]

\ [R = 10,08 к \ Омега \ nonumber \]

Таким образом, нам нужно использовать резистор 10,08 кОм \ (\ Omega \), чтобы понизить схему \ (Q \) настолько, чтобы получить полосу пропускания 3 кГц. Без этого резистора полоса пропускания будет меньше половины требуемой.

Компьютерное моделирование

На рисунке \ (\ PageIndex {13} \) показан завершенный дизайн предыдущего примера, захваченный в симуляторе. Для удобства расчетов используется источник тока 1 мА.

Рисунок \ (\ PageIndex {13} \): Схема примера \ (\ PageIndex {3} \) в симуляторе.

Учитывая, что \ (R_T \) составляет 5,3 кОм \ (\ Omega \), источник тока 1 мА должен выдавать 5,3 вольт на резонансной частоте 35,59 кГц. Результаты анализа переменного тока показаны на рисунке \ (\ PageIndex {14} \).{\ circ} \) на этой частоте, причем последнее указывает на полную компенсацию между катушкой индуктивности и конденсатором (т. е. полное сопротивление цепи является чисто резистивным и достигает единичного коэффициента мощности). Курсоры используются для получения точных значений для \ (f_1 \) и \ (f_2 \). Эти частоты достигаются при 0,707 пика 5,3 вольт, или около 3,75 вольт. Частоты составляют приблизительно 34,15 кГц и 37,15 кГц, что позволяет достичь желаемой полосы пропускания 3 кГц.

8.3.3: Параллельный резонанс с низкой добротностью

Есть некоторые изменения в вычислениях, когда \ (Q_ {parallel} \) мало.Как правило, это означает значения ниже 10, хотя мы можем рассматривать значения от 5 до 10 как переходную область, где в игру вступают отклонения в два процентных пункта или меньше. Как только схема \ (Q \) падает ниже 5, отклонения от высоких уравнений \ (Q \) быстро растут и быстро увеличиваются до двузначных процентов. Главный интерес здесь — смещение \ (f_0 \).

Рисунок \ (\ PageIndex {15} \): Параллельная сеть RLC с эквивалентом точного последовательного преобразования.

Эти отклонения вызваны тем, что приближения, используемые для уравнений \ ref {8.17} и \ ref {8.18}, больше не верны. То есть с низкими значениями \ (Q_ {coil} \) мы больше не можем предполагать, что преобразованный \ (X_L \) такой же, как исходный \ (X_L \) (т.е. \ (X_p \) и \ ( X_s \) на рисунке \ (\ PageIndex {4} \)). Учитывая этот факт, мы можем пересмотреть базовую параллельную схему RLC, но на этот раз используя точное значение преобразования последовательно-параллельной индуктивности. Это показано на рисунке \ (\ PageIndex {15} \).{\ circ} \), и по этому определению у нас больше нет резонансного контура.

Мы исследуем реальность этой ситуации, начав с простой параллельной схемы с высоким \ (Q \), а затем исследуем изменения амплитуды и фазовой характеристики при уменьшении \ (Q \). Начнем со схемы на рисунке \ (\ PageIndex {16} \).

Рисунок \ (\ PageIndex {16} \): Базовая параллельная сеть.

Предполагая, что у нас высокий контур \ (Q \), резонансная частота равна:

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {LC}} \ nonumber \]

\ [f_0 = \ frac {1} {2 \ pi \ sqrt {1 mh200 nF}} \ nonumber \]

\ [f_0 = 15.92 кГц \ nonumber \]

\ [X_L = 2 \ pi f L \ nonumber \]

\ [X_L = 2 \ pi 15,92 кГц 1 мГн \ nonumber \]

\ [X_L = 100 \ Omega \ nonumber \]

\ [Q_ {катушка} = \ frac {X_L} {R_ {катушка}} ​​\ nonumber \]

\ [Q_ {катушка} = \ frac {100 \ Omega} {5 \ Omega} \ nonumber \]

\ [Q_ {катушка} = 20 \ nonumber \]

В цепи нет других сопротивлений, поэтому \ (Q_ {circuit} = Q_ {coil} \) и наше первоначальное предположение верно. Схема фиксируется в симуляторе, и выполняется анализ переменного тока.{\ circ} \) дает 15,89 кГц. Оказывается, это даже ближе, чем кажется. Несмотря на высокую схему \ (Q \), \ (k_p \) было вычислено и, как и ожидалось, очень близко к единице, а именно 0,99875. {\ circ} \).{\ circ} \). В этом отношении мы все же можем сказать, что уравнение \ (k_p \) остается точным предсказателем.

Рисунок \ (\ PageIndex {19} \): Результаты моделирования с использованием сопротивления катушки 100 \ (\ Omega \) (\ (Q \) из 1).

8.3.4: Альтернативное определение для параллельной резонансной частоты

Вместо определения параллельной резонансной частоты как точки, в которой коэффициент мощности равен единице, т. Е. Где \ (X_L \) и \ (X_C \) имеют одинаковую величину, ее можно определить в терминах частоты, в которой величина сопротивление максимальное.Для цепей с высоким \ (Q \) два определения дают по существу одинаковую частоту, однако по мере того, как цепь \ (Q \) уменьшается до однозначных цифр, частота максимального импеданса начинает отклоняться от обоих высоких значений \ (Q \). идеализация и определение общего единства коэффициента мощности. Фактически, частота максимальной величины находится между ними. Мы будем называть эту частоту \ (f_ {Z-max} \), чтобы избежать путаницы. 2 }} \ label {8.{\ circ} \) не достигается. Кроме того, частота пика ниже, чем в случае с высоким значением \ (Q \). Уравнение \ ref {8.25} предсказывает пик на частоте 13,6 кГц, что согласуется со значением, полученным в результате моделирования.

8.3.5: Последовательное сочетание и параллельный резонанс

Завершая обсуждение резонанса, мы можем спросить, существуют ли практические повседневные примеры систем, демонстрирующих последовательный и параллельный резонанс в последовательно-параллельных цепях. Ответ положительный. Хорошим примером является базовый динамик с подвижной катушкой типа, рассмотренного в главе 2.Это электромеханическая система, и поэтому подходящая модель должна включать эффекты таких элементов, как механические потери в системе, масса конуса и тому подобное. Одна из возможностей показана на рисунке \ (\ PageIndex {20} \). \ (L_ {vc} \) и \ (R_ {vc} \) — индуктивность и сопротивление звуковой катушки. Остальные компоненты моделируют другие аспекты электромеханической системы. График импеданса типичного громкоговорителя показан на рисунке \ (\ PageIndex {21} \).

Рисунок \ (\ PageIndex {20} \): Эквивалентная электрическая сеть одного динамического громкоговорителя.По материалам Р. Х. Смолла, «Анализ системы громкоговорителей с прямым излучателем», Журнал Общества инженеров аудио, июнь 1972 г.

Рисунок \ (\ PageIndex {21} \): Величина и фаза импеданса типичного динамического громкоговорителя. Предоставлено Dayton Audio

.

Громкоговоритель на рисунке \ (\ PageIndex {21} \) представляет собой низкочастотный динамик среднего размера с номинальным сопротивлением 8 \ (\ Omega \). Во-первых, обратите внимание на большое изменение фазы и величины импеданса. Параллельные элементы модели дают очевидный пик импеданса чуть ниже 30 Гц.{\ circ} \) в \ (f_s \), и что фаза положительная (индуктивная) ниже резонансной частоты и отрицательная (емкостная) выше нее. Такое поведение ожидается от параллельной резонансной системы. Последовательные элементы модели создают нарастающий импеданс, который наблюдается после падения. Обратите внимание, что фазовый угол продолжает увеличиваться с ростом частоты, что указывает на растущее преобладание последовательного индуктивного элемента.

Список литературы

¹ Обратите внимание, что если бы это значение было больше 25, мы бы застряли по другой причине; а именно, что нам нужно получить катушку индуктивности более высокого качества, потому что \ (Q_ {circuit} \) не может быть выше, чем \ (Q_ {coil} \).

² Для получения доказательств, не связанных с исчислениями, см. K. Картрайт, Э. Джозеф, Э. Камински, «Нахождение точной максимальной резонансной частоты импеданса практической параллельной резонансной цепи без исчисления», Международный журнал Technology Interface, vol. 11, вып. 1, осень / зима 2010. [Интернет-сериал]. Доступно: http://tiij.org/issues/issues/winter…inter_2010.htm [по состоянию на 15 февраля 2020 г.].

Простой параллельный резонанс (контур резервуара) | Резонанс

Резонанс в контуре резервуара

Состояние резонанса возникает в цепи резервуара, когда реактивные сопротивления конденсатора и катушки индуктивности равны друг другу.Поскольку индуктивное реактивное сопротивление увеличивается с увеличением частоты, а емкостное реактивное сопротивление уменьшается с увеличением частоты, будет только одна частота, на которой эти два реактивных сопротивления будут равны. Пример:

Простой параллельный резонансный контур (контур резервуара).

В приведенной выше схеме у нас есть конденсатор 10 мкФ и катушка индуктивности 100 мГн. Поскольку мы знаем уравнения для определения реактивного сопротивления каждого из них на заданной частоте, и мы ищем ту точку, где два реактивных сопротивления равны друг другу, мы можем установить две формулы реактивного сопротивления равными друг другу и решить для частоты алгебраически :

Итак, у нас есть это: формула, которая сообщает нам резонансную частоту контура резервуара, учитывая значения индуктивности (L) в Генри и емкости (C) в Фарадах.Подставляя значения L и C в схему нашего примера, мы получаем резонансную частоту 159,155 Гц.

Расчет индивидуальных импедансов

Интересно, что происходит при резонансе. Когда емкостное и индуктивное реактивные сопротивления равны друг другу, полное сопротивление увеличивается до бесконечности, а это означает, что цепь резервуара не потребляет ток от источника переменного тока!

Мы можем рассчитать отдельные импедансы конденсатора 10 мкФ и индуктора 100 мГн и использовать формулу параллельного импеданса, чтобы продемонстрировать это математически:

Как вы могли догадаться, я выбрал эти значения компонентов, чтобы получить резонансные импедансы, с которыми было легко работать (даже 100 Ом).

Формула параллельного импеданса

Теперь мы используем формулу параллельного импеданса, чтобы увидеть, что происходит с общим Z:

Участок моделирования SPICE

Мы не можем разделить любое число на ноль и прийти к значимому результату, но мы можем сказать, что результат приближается к значению бесконечности , когда два параллельных импеданса становятся ближе друг к другу.

На практике это означает, что полное сопротивление цепи резервуара бесконечно (ведет себя как разомкнутая цепь ) в резонансе.Мы можем изобразить последствия этого в широком диапазоне частот источника питания с помощью короткого моделирования SPICE.

Резонансная схема, подходящая для моделирования SPICE.

Резистор 1 пикоом (1 пОм) помещен в этот анализ SPICE, чтобы преодолеть ограничение SPICE, а именно то, что он не может анализировать цепь, содержащую прямую петлю источника напряжения индуктивности. (Рисунок ниже) Было выбрано очень низкое значение сопротивления, чтобы минимизировать влияние на поведение цепи.

Это моделирование SPICE отображает ток цепи в частотном диапазоне от 100 до 200 Гц с двадцатью четными шагами (100 и 200 Гц включительно). Текущая величина на графике увеличивается слева направо, а частота увеличивается сверху вниз.

Ток в этой цепи резко падает вокруг точки анализа 157,9 Гц, которая является ближайшей точкой анализа к нашей предсказанной резонансной частоте 159,155 Гц. Именно в этот момент общий ток от источника питания падает до нуля.

Графический постпроцессор «Мускатный орех»

Приведенный выше график создается из указанного выше файла схемы spice (* .cir), команда (.plot) в последней строке создает текстовый график на любом принтере или терминале. Более красивый сюжет создается графическим постпроцессором «мускатный орех», входящим в состав пакета специй.

Указанная выше специя (* .cir) не требует команды plot (.plot), хотя и не причиняет вреда. Следующие команды создают график ниже:

специя -b -r резонансная.необработанный резонансный. цир
 (-b пакетный режим, -r необработанный файл, ввод - резонансный.cir)
 мускатный орех резонансный. сырье
 

Из подсказки о мускатном орехе:

> setplot ac1 (setplot {ввод} для списка графиков)
 > дисплей (для списка сигналов)
 > сюжетный журнал (v1 # ветка)
 (величина комплексного вектора тока v1 # ветвь)
 

Nutmeg создает график тока I (v1) для параллельного резонансного контура.

Участки Боде

Между прочим, выходной график, полученный в результате компьютерного анализа SPICE, более известен как график Боде .Такие графики отображают амплитуду или фазовый сдвиг по одной оси и частоту по другой. Крутизна кривой графика Боде характеризует «частотную характеристику» схемы или ее чувствительность к изменениям частоты.

ОБЗОР:

• Резонанс возникает, когда емкостное и индуктивное реактивные сопротивления равны друг другу.
• Для контура резервуара без сопротивления (R) резонансная частота может быть рассчитана по следующей формуле

• Общий импеданс параллельной LC-цепи приближается к бесконечности, когда частота источника питания приближается к резонансу.
• График Боде — это график, отображающий амплитуду или фазу сигнала по одной оси и частоту по другой.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Резонанс

в последовательно-параллельных цепях | Резонанс

В простых реактивных цепях с небольшим сопротивлением или без него эффекты радикально измененного импеданса будут проявляться на резонансной частоте, предсказанной уравнением, приведенным ранее. В параллельном (резервуарном) LC-контуре это означает бесконечное сопротивление при резонансе.В последовательной LC-цепи это означает нулевой импеданс при резонансе:

Однако, как только в большинство контуров LC вводятся значительные уровни сопротивления, этот простой расчет резонанса становится недействительным.

На этой странице мы рассмотрим несколько LC-цепей с добавленным сопротивлением, используя те же значения емкости и индуктивности, что и раньше: 10 мкФ и 100 мГн соответственно.

Расчет резонансной частоты цепи с высоким сопротивлением

Согласно нашему простому уравнению, приведенному выше, резонансная частота должна быть 159.155 Гц. Однако посмотрите, где ток достигает максимума или минимума в следующих анализах SPICE:

Параллельная LC-цепь с сопротивлением последовательно с L.

резонансный контур
 v1 1 0 ac 1 грех
 c1 1 0 10u
 г1 1 2 100
 l1 2 0 100м
 .ac lin 20 100 200
 .plot ac i (v1)
 .конец
 

Результатов:

Сопротивление, включенное последовательно с L, дает минимальный ток на 136.8 Гц вместо расчетных 159,2 Гц

Минимальный ток при 136,8 Гц вместо 159,2 Гц! 

Параллельный LC с сопротивлением в серии с C.

Здесь требуется дополнительный резистор (Rbogus), чтобы SPICE не столкнулся с проблемами при анализе. SPICE не может работать с индуктором, подключенным напрямую параллельно любому источнику напряжения или любому другому индуктору, поэтому добавление последовательного резистора необходимо, чтобы «разорвать» контур источника напряжения / индуктора, который в противном случае образовался бы.

Значение этого резистора выбрано с очень низким значением , чтобы минимизировать влияние на поведение схемы.

резонансный контур
 v1 1 0 ac 1 грех
 г1 1 2 100
 c1 2 0 10u
 rbogus 1 3 1e-12
 l1 3 0 100м
 .ac lin 20 100 400
 .plot ac i (v1)
 .конец
 

Минимальный ток примерно при 180 Гц вместо 159,2 Гц! 

Результатов:

Сопротивление последовательно с C сдвигает минимальный ток от расчетного 159.От 2 Гц до примерно 180 Гц.

Цепи LC серии

Обращая внимание на последовательные LC-цепи, мы экспериментируем с размещением значительных сопротивлений параллельно L или C. В следующих примерах последовательной цепи резистор 1 Ом (R1) включен последовательно с катушкой индуктивности и конденсатором для ограничения общего тока. при резонансе.

«Дополнительным» сопротивлением, вставленным для влияния на эффекты резонансной частоты, является резистор R2 на 100 Ом. Результаты показаны на рисунке ниже.

Резонансный контур серии LC с сопротивлением параллельно L.

резонансный контур
 v1 1 0 ac 1 грех
 г1 1 2 1
 c1 2 3 10u
 l1 3 0 100м
 г2 3 0100
 .ac lin 20 100 400
 .plot ac i (v1)
 .конец
 

Максимальный ток примерно при 178,9 Гц вместо 159,2 Гц! 

Результатов:

Последовательный резонансный контур с сопротивлением, параллельным L, сдвигает максимальный ток с 159.От 2 Гц до примерно 180 Гц.

И, наконец, последовательный LC-контур со значительным сопротивлением параллельно конденсатору. Сдвинутый резонанс показан ниже.

Резонансный контур серии LC с сопротивлением, включенным параллельно цепи C.

резонансный контур
 v1 1 0 ac 1 грех
 г1 1 2 1
 c1 2 3 10u
 г2 2 3 100
 l1 3 0 100м
 .ac lin 20 100 200
 .plot ac i (v1)
 .конец
 

 Максимальный ток при 136.8 Гц вместо 159,2 Гц! 

Результатов:

Сопротивление параллельно с C в последовательном резонансном контуре смещает максимум тока с расчетных 159,2 Гц примерно до 136,8 Гц.

Антирезонанс в LC-цепях

Тенденция увеличения сопротивления к перекосу точки, в которой полное сопротивление достигает максимума или минимума в цепи LC, называется антирезонансом . Проницательный наблюдатель заметит закономерность между четырьмя приведенными выше примерами SPICE с точки зрения того, как сопротивление влияет на резонансный пик цепи:

Параллельный («резервуар») LC-контур:

• R последовательно с L: резонансная частота смещена на вниз
• R последовательно с C: резонансная частота смещена вверх

Последовательный контур LC:

• R параллельно с L: резонансная частота смещена вверх
• R параллельно с C: резонансная частота смещена на вниз

Опять же, это иллюстрирует взаимодополняющий характер конденсаторов и катушек индуктивности: как сопротивление, включенное последовательно с одним, создает антирезонансный эффект, эквивалентный сопротивлению, подключенному параллельно с другим.Если вы посмотрите еще ближе к четырем приведенным примерам SPICE, вы увидите, что частоты сдвинуты на и ту же величину , и что форма дополнительных графиков является зеркальным отображением друг друга!

Антирезонанс — это эффект, о котором разработчики резонансных цепей должны знать. Уравнения для определения «сдвига» антирезонанса сложны и не будут рассматриваться в этом кратком уроке. Начинающему электронике должно быть достаточно понять, что эффект существует и каковы его общие тенденции.

Кожный эффект

Добавленное сопротивление в цепи LC не имеет академического значения. Хотя можно производить конденсаторы с незначительным нежелательным сопротивлением, индукторы обычно имеют значительное сопротивление из-за большой длины проводов, используемых в их конструкции.

Более того, сопротивление провода имеет тенденцию увеличиваться с увеличением частоты из-за странного явления, известного как скин-эффект , когда переменный ток имеет тенденцию исключаться из прохождения через самый центр провода, тем самым уменьшая эффективную площадь поперечного сечения провода.

Таким образом, индукторы имеют не только сопротивление, но и изменяющееся, частотно-зависимое, сопротивление.

Добавленное сопротивление в цепях

Как будто сопротивления провода индуктора недостаточно, чтобы вызвать проблемы, мы также должны бороться с «потерями в сердечнике» индукторов с железным сердечником, которые проявляются как дополнительное сопротивление в цепи.

Поскольку железо является проводником электричества, а также проводником магнитного потока, изменение потока, создаваемого переменным током через катушку, будет иметь тенденцию индуцировать электрические токи в самом сердечнике ( вихревые токи ).

Этот эффект можно представить, как если бы железный сердечник трансформатора был своего рода вторичной обмоткой трансформатора, питающей резистивную нагрузку: неидеальная проводимость металлического железа. Этот эффект можно свести к минимуму с помощью ламинированных сердечников, высококачественных материалов с хорошей конструкцией сердечника, но полностью устранить их невозможно.

Цепи RLC

Одним заметным исключением из правила сопротивления цепи, вызывающего сдвиг резонансной частоты, является случай цепей последовательно резистор-индуктор-конденсатор («RLC»).Пока все компоненты соединены последовательно друг с другом, сопротивление не будет влиять на резонансную частоту цепи. Полученный график показан ниже.

Серия LC с последовательным сопротивлением.

последовательная цепь rlc
 v1 1 0 ac 1 грех
 г1 1 2 100
 c1 2 3 10u
 l1 3 0 100м
 .ac lin 20 100 200
 .plot ac i (v1)
 .конец
 

 И снова максимальный ток при 159,2 Гц! 

Результатов:

Сопротивление в последовательном резонансном контуре оставляет максимальный ток равным расчетному 159.2 Гц, расширяя кривую.

Обратите внимание, что пик на графике тока не изменился по сравнению с более ранней последовательной LC-схемой (той, в которой было сопротивление токена 1 Ом), даже несмотря на то, что сопротивление теперь в 100 раз больше. Единственное, что изменилось, — это «резкость» кривой.

Очевидно, что эта схема не резонирует так сильно, как схема с меньшим последовательным сопротивлением (она называется «менее избирательной»), но, по крайней мере, она имеет такую ​​же собственную частоту!

Антирезонансный эффект демпфирования

Примечательно, что антирезонанс имеет эффект гашения колебаний автономных LC-контуров, таких как контуры резервуара.В начале этой главы мы увидели, как конденсатор и катушка индуктивности, соединенные напрямую вместе, будут действовать как маятник, обмениваясь пиками напряжения и тока, точно так же, как маятник обменивается кинетической и потенциальной энергией.

В идеальном контуре резервуара (без сопротивления) это колебание будет продолжаться вечно, точно так же, как маятник без трения продолжит вечно качаться на своей резонансной частоте. Но машины без трения трудно найти в реальном мире, как и схемы танков без потерь.

Энергия, потерянная через сопротивление (или потери в сердечнике индуктора, или излучаемые электромагнитные волны, или …) в контуре резервуара, вызовет затухание колебаний по амплитуде, пока они не исчезнут. Если в контуре резервуара присутствует достаточное количество потерь энергии, он вообще не сможет резонировать.

Эффект демпфирования

Антирезонанса — это больше, чем просто любопытство: его можно довольно эффективно использовать для устранения нежелательных колебаний в схемах, содержащих паразитные индуктивности и / или емкости, как это делают почти все схемы.Обратите внимание на следующую схему задержки времени L / R: (рисунок ниже)

Цепь задержки времени L / R

Идея этой схемы проста: «заряжать» катушку индуктивности при замкнутом переключателе. Скорость зарядки индуктора будет установлена ​​отношением L / R, которое представляет собой постоянную времени цепи в секундах.

Однако, если вы построите такую ​​схему, вы можете обнаружить неожиданные колебания (переменного тока) напряжения на катушке индуктивности, когда переключатель замкнут.(Рисунок ниже) Почему это? В цепи нет конденсатора, так как же мы можем получить резонансные колебания с помощью только катушки индуктивности, резистора и батареи?

Звон индуктора из-за резонанса паразитной емкости.

Все катушки индуктивности содержат определенную паразитную емкость из-за межвитковых и межвитковых изоляционных промежутков. Кроме того, размещение проводников схемы может создать паразитную емкость. Хотя чистая компоновка схемы важна для устранения большей части этой паразитной емкости, всегда будут такие, которые вы не сможете устранить.

Если это вызывает резонансные проблемы (нежелательные колебания переменного тока), дополнительное сопротивление может быть способом борьбы с ними. Если резистор R достаточно велик, это вызовет состояние антирезонанса, рассеивая достаточно энергии, чтобы индуктивность и паразитная емкость не могли поддерживать колебания в течение очень длительного времени.

Интересно, что принцип использования сопротивления для устранения нежелательного резонанса часто используется при проектировании механических систем, где любой движущийся объект с массой является потенциальным резонатором.

Очень распространенное применение этого — использование амортизаторов в автомобилях. Без амортизаторов автомобили будут сильно подпрыгивать на своей резонансной частоте после столкновения с любой неровностью на дороге. Работа амортизатора заключается в создании сильного антирезонансного эффекта за счет гидравлического рассеивания энергии (таким же образом, как резистор рассеивает энергию электрически).

ОБЗОР:

• Дополнительное сопротивление LC-цепи может вызвать состояние, известное как антирезонанс , когда эффекты пикового импеданса возникают на частотах, отличных от тех, которые дают равные емкостные и индуктивные реактивные сопротивления.
• Сопротивление, присущее реальным катушкам индуктивности, может в значительной степени способствовать возникновению антирезонанса. Одним из источников такого сопротивления является скин-эффект , вызванный исключением переменного тока из центра проводников. Другой источник — это потерь в сердечнике в индукторах с железным сердечником.
• В простой последовательной LC-цепи, содержащей сопротивление (цепь «RLC»), сопротивление , а не , создает антирезонанс. Резонанс все еще возникает, когда емкостное и индуктивное реактивные сопротивления равны.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Параллельный резонанс — обзор

Для наблюдения эффекта нелинейной нагрузки предполагается, что источник гармонического напряжения (представляющий искаженное напряжение электросети) закорочен. Гармонический ток, вводимый в конденсатор из-за нелинейной нагрузки, составляет

(E5.3-3) I ~ C, hdueNL = Zsys, hZsys, h + ZC, hI ~ NL, h.

Параллельный резонанс возникает, когда знаменатель приближается к нулю. Частота параллельного резонанса

(E5.3-4) fparallel = 12πLsysC = 12π0.11m⋅1300μ≈420Гц.

Это условие приведет к подаче большого гармонического тока в конденсаторную батарею. Величина инжектируемого гармонического тока может в несколько раз превышать номинальный ток конденсатора и может привести к возникновению значительных гармонических напряжений на конденсаторе. Следовательно, параллельный резонанс может привести к разрушению конденсатора из-за перенапряжения или перегрузки по току.

Чтобы исследовать влияние искаженного сетевого напряжения на конденсатор, предполагается, что источник гармонического тока (аппроксимирующий нелинейную нагрузку) идеален, то есть его полное сопротивление стремится к бесконечности и ведет себя как разомкнутая цепь.Гармонический ток, вводимый в конденсатор из-за искаженного сетевого источника, составляет

(E5.3-5) I ~ C, hduesys = 1Zsys, h + ZC, hV ~ sys, h.

Последовательный резонанс возникает, когда знаменатель приближается к нулю. Следовательно, для этой системы частоты последовательного и параллельного резонансов идентичны:

(E5.3-6) fseries = fparallel = 12πLsysC≈420 Гц.

Ввод гармонического тока в силовой конденсатор будет увеличиваться, если напряжение сети содержит гармонические составляющие вблизи резонансных частот.

Суммарный гармонический ток, вводимый в силовой конденсатор, составляет

(E5.3-7) I ~ C, h = I ~ C, hdueNL + I ~ C, hduesys = Zsys, hZsys, h + ZC, hI ~ NL , h + 1Zsys, h + ZC, hV ~ sys, h.

Следовательно, 5-я гармоническая составляющая подаваемого в конденсатор тока составляет

I ~ C, 5 = I ~ C, 5dueNL + I ~ C, 5duesys, I ~ C, 5dueNL = Zsys, 5Zsys, 5 + ZC, 5I ~ NL, 5, = 0.06 + j52π⋅60⋅0.11⋅10−3I ~ NL, 50.06 + j52π⋅60⋅0.11⋅10−3] — [j / 52π⋅60⋅1300⋅10−6, = 0,06 + j0.20740.06 + j0.2074 − j0.408I ~ NL, 5, = 0,06 + j0.20740.06 − j0.2I ~ NL, 5 = 0.2159∠73.87 ° 0.2∠ − 73,3 ° I ~ NL, 5, = 1,08∠147,17 ° I ~ NL, 5, = 1,08∠147,17 °) 20,3∠0 ° A, = 20,324∠147,17 ° A.

(E5.3-8) I ~ C, 5duesys = 1Xsys, 5 + ZC, 5V ~ sys, 5 = 10,2∠ − 73,3 ° V ~ sys, 5, = 5∠73,3 ° V ~ sys, 5 = 5 73,3 ° 23∠0 ° A, = 215∠73,3 ° A, ⇒⇒I ~ C, 5 = I ~ C, 5dueNL + I ~ C, 5duesys, = 20,324∠147,17 ° + (215∠73,3 ° A, = 24,04 + j14,54 = 215,1∠74,47 ° A.

7-я гармоническая составляющая тока, подаваемого в силовой конденсатор, составляет

(E5.3-9) I ~ C, 7 = I ~ C, 7dueNL + I ~ C, 7duesys, I ~ C, 7dueNL = Zsys, 7Zsys, 7 + ZC, 7I ~ NL, 7, = 0,06 + j72π⋅60⋅0.11⋅10−3I ~ NL, 70.06 + j72π⋅60⋅0.11⋅10−3 −j / 72π⋅60⋅1300⋅10−6, = 0.06 + j7⋅0.041470.06 + j7⋅0.04141 − j2.040 / 7I ~ NL, 7, = 0,06 + j0.2

.06 − j0.0011I ~ NL, 7 = 0,2964∠78.32 ° 0,06∠ − 1.05 ° I ~ NL, 7, = 4.964∠79.37 ° I ~ NL, 7, = 4.964∠79.37 ° 20.2∠0 ° A, = 20.993∠79.39 ° AI ~ C, 7duesys = 1Zsys, 7 + ZC, 7V ~ sys, 7 = 10.06∠− 1.05 ° V ~ sys, 7, = 16.7∠1.05 ° V ~ sys, 7, = 16.7∠1.05 ° 52∠0 ° A, = 233.4∠1.05 ° A, ⇒⇒I ~ C, 7 = I ~ C, 7dueNL + I ~ C, 7duesys, = 20,993∠79,37 ° + 233,4∠1,05 ° A, = 233,58 + 1,59A, = 233,62∠2,7 ° A.

Параллельный резонанс

• Изучив этот раздел, вы сможете:
• • Опишите действие параллельных цепей LCR вверху, внизу и в резонансе.
• • Опишите увеличение тока и динамическое сопротивление в параллельных цепях LCR
• • Используйте соответствующие формулы для выполнения расчетов параллельных цепей LCR, включая резонанс, импеданс и динамическое сопротивление.

Как и в последовательном резонансном контуре, в параллельном контуре есть три основных условия. В зависимости от частоты и значений компонентов, контур будет работать ниже, выше или в резонансе.В этом разделе описываются эти три состояния с использованием векторных диаграмм, включающих векторы тока I _C , I _L и их векторную сумму I _S с эталонным вектором V _S . Обратите внимание, что V _R не показан, но его присутствие в цепи обозначается изменяемым углом I _L , как описано в Модуле 10.2.

Ниже резонанса

Рис. 10.3.1 Ниже резонанса

Во-первых, если частота питающей сети низкая, ниже резонансной частоты ƒ _r , то выполняется условие, показанное на рис.3.1 существует, и ток I _L через L будет большим (из-за его сравнительно низкого реактивного сопротивления). В то же время ток I _C через C будет сравнительно небольшим. Поскольку I _C меньше, чем I _L , фазовый угол θ будет небольшим. Включение I _S в диаграмму показывает, что он будет отставать от V _S , и поэтому цепь будет выглядеть ИНДУКТИВНОЙ. (Обратите внимание, что это противоположное состояние для последовательной цепи, которая имеет емкость ниже резонанса).

Выше резонанса

Рис.10.3.2 Выше резонанса

На рис. 10.3.2 показано, что происходит на частотах выше резонанса. Здесь ток I _C через C будет больше, чем ток I _L через L, потому что частота выше, а X _C меньше, чем X _L , θ больше, чем на рис. 10.3.1. Это дает нам условие, когда I _S (сумма векторов I _C и I _L ) опережает V _S , и поэтому схема является емкостной.

При резонансе

Рис. 10.3.3 При резонансе

В резонансе идеальная цепь имеет бесконечный импеданс, но это не совсем так в практических параллельных цепях, хотя и очень близко. На рис. 10.3.3 показаны условия резонанса в практической параллельной цепи LCR. I _C опережает V _S на 90 °, но I _L не совсем в противофазе (из-за сопротивления в индуктивной ветви цепи). Следовательно, в параллельной схеме резонанс должен быть определен как частота, при которой значения I _C и I _L таковы, что I _S находится в ФАЗЕ с V _S .

Динамическое сопротивление

В резонансе рис. 10.3.3 (выше) показывает, что I _S очень маленький, намного меньше, чем I _C или I _L , поэтому полное сопротивление параллельной цепи должно быть очень высоким при _r и поскольку I _S находится в фазе с V _S , полное сопротивление цепи является чисто резистивным. Это чистое сопротивление, которое возникает только при _r , называется ДИНАМИЧЕСКИМ СОПРОТИВЛЕНИЕМ (R _D ) схемы, и его можно рассчитать (в омах) для любой параллельной цепи, исходя только из значений используемых компонентов, используя формулу:

Где R — полное сопротивление цепи, включая внутреннее сопротивление L.

Текущее увеличение

Другой важный момент, показанный на рис. 10.3.3, — это размер вектора для I _S по сравнению с I _C и I _L . Ток питания намного меньше любого из токов в L- или C-ответвлениях цепи. Это должно означать, что в цепи протекает больше тока, чем на самом деле подается в нее!

Это состояние реально и известно как ТОКОВОЕ УВЕЛИЧЕНИЕ. Подобно тому, как увеличение напряжения происходит в последовательных цепях, параллельная цепь LCR увеличивает ток.КОЭФФИЦИЕНТ УВЕЛИЧЕНИЯ (Q) параллельной цепи может быть найден по той же формуле, что и для последовательных цепей, а именно:

Регулировка резонанса.

Формула для резонансной частоты параллельной цепи LCR также использует ту же формулу для ƒ _r , что и в последовательной цепи, то есть;

Рис. 10.3.4 Параллельные настроенные схемы LC.

Но следует отметить, что эта формула игнорирует влияние R на небольшой сдвиг фазы I _L .Фактически формула дает только приблизительное значение для ƒ _r . Однако, поскольку внутреннее сопротивление L обычно довольно мало, его влияние на смещение резонансной частоты контура также невелико. По этой причине одна и та же формула может использоваться для ƒ _r как в последовательной, так и в параллельной цепях. В тех практических LC-схемах, предназначенных для работы на высоких частотах, и там, где требуется точное управление в диапазоне ƒ _— , нормально, что либо L, либо C могут регулироваться по значению.

Рис. 10.3.5 Настроенный трансформатор в грохоте

Окончательные значения для L и C будут достигнуты путем настройки одного из двух компонентов, как показано на рис. 10.3.4, который будет иметь переменный тип, когда система, содержащая контур LC, будет работать. С помощью этого метода компенсируется не только влияние R, но и любая паразитная индуктивность или емкость в цепи, которые также могут повлиять на конечное значение ƒ _r . Поскольку на высоких частотах магнитные поля легко излучаются от одного компонента в цепи к другому, схемы с LC-настройкой также должны быть экранированы (экранированы) путем помещения их в металлический экран, как показано на рис.10.3.5.

6 Что нужно знать о параллельных цепях LCR.

(и которые отличаются от последовательной цепи.)

• 1. В РЕЗОНАНСЕ (ƒ _r ) V _C не обязательно точно равно V _L , но V _S и I _S находятся в ФАЗЕ
• 2 .; ПРИ РЕЗОНАНСЕ ( _r ) Импеданс (Z) является максимальным и называется динамическим сопротивлением (R _D )
• 3. ПРИ РЕЗОНАНСЕ (ƒ _r ) Ток цепи (I _S ) минимален.
• 4. НА РЕЗОНАНСЕ (ƒ _r ) Цепь полностью резистивная.
• 5. НИЖЕ РЕЗОНАНСА (ƒ _r ) Цепь индуктивная.
• 6. ВЫШЕ РЕЗОНАНСА (ƒ _r ) Схема емкостная.

Поставщики и ресурсы беспроводной связи RF

О компании RF Wireless World

Веб-сайт RF Wireless World является домом для поставщиков и ресурсов радиочастотной и беспроводной связи.На сайте представлены статьи, руководства, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тестирование и измерения, калькуляторы, новости, книги, загрузки и многое другое.

Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, волоконная оптика, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. Д. Эти ресурсы основаны на стандартах IEEE и 3GPP.Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и MBA.

Статьи о системах на основе Интернета вещей

Система обнаружения падений для пожилых людей на основе Интернета вещей : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей. В нем упоминаются преимущества или преимущества системы обнаружения падений Интернета вещей. Читать дальше➤
Также обратитесь к другим статьям о системах на основе Интернета вещей следующим образом:
• Система очистки туалетов самолета. • Система измерения столкновений • Система отслеживания скоропортящихся продуктов и овощей • Система помощи водителю • Система умной торговли • Система мониторинга качества воды. • Система Smart Grid • Система умного освещения на базе Zigbee • Интеллектуальная система парковки на базе Zigbee. • Система умной парковки на основе LoRaWAN

---

Статьи о беспроводной радиосвязи

В этом разделе статей представлены статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE / 3GPP и т. Д. .стандарты. Он также охватывает статьи, относящиеся к испытаниям и измерениям, по тестированию на соответствие, используемым для испытаний устройств на соответствие RF / PHY. УКАЗАТЕЛЬ СТАТЬИ ДЛЯ ССЫЛКИ >>.

---

Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP. Читать дальше➤

---

Основы повторителя и типы повторителей : В нем объясняются функции различных типов ретрансляторов, используемых в беспроводных технологиях.Читать дальше➤

---

Основы и типы замирания : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные, быстрые и т. Д., Используемые в беспроводной связи. Читать дальше➤

---

Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона. Читать дальше➤

---

Основы помех и типы помех: В этой статье рассматриваются помехи в соседнем канале, помехи в одном канале, Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. Д.Читать дальше➤

---

5G NR Раздел

В этом разделе рассматриваются функции 5G NR (New Radio), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. Д. 5G NR Краткий указатель ссылок >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • 5G NR CORESET • Форматы DCI 5G NR • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Эталонные сигналы 5G NR • 5G NR m-последовательность • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • Уровень MAC 5G NR • Уровень 5G NR RLC • Уровень 5G NR PDCP

---

Учебные пособия по беспроводным технологиям

В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводной связи.Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, WLAN, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. Д. См. УКАЗАТЕЛЬ >>

---

Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы по технологии 5G:
Учебное пособие по основам 5G. Частотные диапазоны руководство по миллиметровым волнам Волновая рама 5G мм Зондирование в волновом канале 5G мм 4G против 5G Испытательное оборудование 5G Сетевая архитектура 5G Сетевые интерфейсы 5G NR канальное зондирование Типы каналов 5G FDD против TDD Разделение сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G TF

---

В этом руководстве GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения, Типы пакетов GSM, структура или иерархия кадров GSM, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM, установка вызова или процедура включения питания, MO-вызов, MT-вызов, VAMOS, AMR, MSK, модуляция GMSK, физический уровень, стек протоколов, основы работы с мобильным телефоном, Планирование RF, нисходящая линия связи PS-вызовов и восходящая линия связи PS-вызовов.
➤Подробнее.

LTE Tutorial , охватывающий архитектуру системы LTE, охватывающий основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он обеспечивает связь с обзором системы LTE, радиоинтерфейсом LTE, терминологией LTE, категориями LTE UE, структурой кадра LTE, физическим уровнем LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, передача голоса по LTE, расширенный LTE, Поставщики LTE и LTE vs LTE продвинутые.➤Подробнее.

---

RF Technology Stuff

Эта страница мира беспроводной радиосвязи описывает пошаговое проектирование преобразователя частоты RF на примере преобразователя RF UP от 70 МГц до диапазона C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, колодки аттенюатора. ➤Подробнее.
➤Проектирование и разработка радиочастотного трансивера ➤Конструкция RF-фильтра ➤Система VSAT ➤Типы и основы микрополосковой печати ➤ОсновыWaveguide

---

Секция испытаний и измерений

В этом разделе рассматриваются контрольно-измерительные ресурсы, испытательное и измерительное оборудование для тестирования DUT на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.УКАЗАТЕЛЬ испытаний и измерений >>
➤Система PXI для T&M. ➤ Генерация и анализ сигналов ➤Измерения слоя PHY ➤Тест на соответствие устройства WiMAX ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤Тест на соответствие TD-SCDMA

---

Волоконно-оптическая технология

Оптоволоконный компонент , основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д.Эти компоненты используются в оптоволоконной связи. Оптические компоненты INDEX >>
➤Учебное пособие по оптоволоконной связи ➤APS в SDH ➤SONET основы ➤SDH Каркасная конструкция ➤SONET против SDH

---

Поставщики беспроводных радиочастотных устройств, производители

Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.

Поставщики радиочастотных компонентов, включая радиочастотный изолятор, радиочастотный циркулятор, радиочастотный смеситель, радиочастотный усилитель, радиочастотный адаптер, радиочастотный разъем, радиочастотный модулятор, радиочастотный трансивер, PLL, VCO, синтезатор, антенну, генератор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексор, дуплексер, микросхема резистора, микросхема конденсатора, индуктор микросхемы, ответвитель, оборудование ЭМС, программное обеспечение для проектирования радиочастот, диэлектрический материал, диод и т. д.Производители радиокомпонентов >>
➤Базовая станция LTE ➤RF Циркулятор ➤RF Изолятор ➤Кристаллический осциллятор

---

MATLAB, Labview, встроенные исходные коды

Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. ИНДЕКС ИСХОДНОГО КОДА >>
➤3-8 декодер кода VHDL ➤Код MATLAB для дескремблера ➤32-битный код ALU Verilog ➤T, D, JK, SR триггеры labview коды

* Общая информация о здоровье населения *

Выполните эти пять простых действий, чтобы остановить коронавирус (COVID-19).
ДЕЛАЙ ПЯТЬ
1. РУКИ: часто мойте их.
2. КОЛЕНО: Закашляйтесь
3. ЛИЦО: Не трогай
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВОВАТЬ: Болен? Оставайся дома

Используйте технологию отслеживания контактов >>, соблюдайте >> рекомендации по социальному дистанцированию и установить систему видеонаблюдения >> чтобы спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таким странам, как США и Китай, остановить распространение COVID-19, поскольку это заразное заболевание.

---

RF Беспроводные калькуляторы и преобразователи

Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц. Сюда входят такие беспроводные технологии, как GSM, UMTS, LTE, 5G NR и т. Д. СПРАВОЧНЫЕ КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR ➤5G NR ARFCN против преобразования частоты ➤Калькулятор скорости передачи данных LoRa ➤LTE EARFCN для преобразования частоты ➤ Калькулятор антенн Яги ➤ Калькулятор времени выборки 5G NR

---

IoT-Интернет вещей Беспроводные технологии

Раздел IoT охватывает беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth Low Power (BLE), NFC, RFID, INSTEON, X10, KNX, ANT +, Wavenis, Dash7, HomePlug и другие.Он также охватывает датчики Интернета вещей, компоненты Интернета вещей и компании Интернета вещей.
См. Главную страницу IoT >> и следующие ссылки.
➤ НИТЬ ➤EnOcean ➤Учебник по LoRa ➤Учебник по SIGFOX ➤WHDI ➤6LoWPAN ➤Zigbee RF4CE ➤NFC ➤Lonworks ➤CEBus ➤UPB

СВЯЗАННЫЕ ЗАПИСИ

RF Wireless Учебники

Датчики разных типов

Поделиться страницей

Перевести страницу

Сопротивление

— Почему полное сопротивление в параллельном резонансном контуре максимально при резонансе?

Другие ответы касались концепции, я сосредоточусь на математике.

Вы спросите, похоже ли это на параллельное соединение двух резисторов, ответ будет да , но формула, которую вы используете при работе с импедансом, требует комплексных чисел, и это загвоздка.

Если два двухконтактных элемента импеданса \ $ Z_1 \ $ и \ $ Z_2 \ $ параллельны, они эквивалентны одному импедансу, значение которого рассчитывается по той же формуле, которую вы используете для параллельных резисторов:

\ [ Z_ {eq} = \ dfrac {1} {\ dfrac 1 Z_1 + \ dfrac 1 Z_2} = \ dfrac {Z_1 \ cdot Z_2} {Z_1 + Z_2} \]

проблема в том, что если два импеданса являются комплексными числами.

Рассмотрим интересующий вас случай: параллельный резонансный контур, то есть конденсатор, подключенный параллельно катушке индуктивности, где я представлю резистивные компоненты как резисторы, параллельные этим двум элементам (для упрощения математики, иначе вы могли бы представить последовательное сопротивление катушки индуктивности и ESR конденсатора с двумя резисторами, подключенными последовательно к реактивным элементам, если хотите). В этом случае вы получите:

\ [ Z_1 = \ dfrac {1} {j 2 \ pi C f} \ qquad Z_2 = j 2 \ pi L f \ qquad Z_3 = R \]

Их эквивалентное сопротивление:

\ [ Z_ {eq} = \ dfrac {1} {\ dfrac 1 Z_1 + \ dfrac 1 Z_2 + \ dfrac 1 Z_2} = \ dfrac {1} {j 2 \ pi C f + \ dfrac {1} {j 2 \ pi L f} + \ dfrac 1 R} \]

Чтобы упростить математику, я использую эквивалентную проводимость \ $ Y_ {eq} = \ dfrac 1 Z_ {eq} \ $ и покажу вам, что при резонансе его величина минимальна, что означает, что величина импеданса максимальна.2 = 0 \ quad \ Leftrightarrow \ quad f = \ dfrac 1 {\ sqrt {2 \ pi L C}} = f_r \]

где \ $ f_r \ $ — резонансная частота контура.