Ркшм это: Диагностика доброкачественных заболеваний шейки матки в Минске

Диагностика доброкачественных заболеваний шейки матки в Минске

Цервикальная эктопия (ЦЭ) – доброкачественное состояние шейки матки, при котором слизистая оболочка цервикального канала распространяется на влагалищную часть шейки матки. В норме это состояние встречается у молодых нерожавших женщин до 23-25 лет и, как правило, в лечении не нуждается. Очень часто это состояние называется «эрозия шейки матки» и широко распространено в бытовом общении. Не редко такая терминология используется некоторыми медицинскими работниками, хотя «эктопия» и «эрозия» не имеют ничего общего. Эрозия – это временное состояние эпителия, можно сказать «дефект» эпителия, или ссадина, которые самостоятельно восстанавливаются в течение 10-12 дней.

Рубцовая деформация шейки матки (РДШМ) – состояние шейки, обусловленное травмой шейки матки в родах или во время прерывания беременности. Нередко это сопровождается выворотом цилиндрического эпителия на влагалищную часть шейки матки с формированием эктропиона.

Ретенционные кисты шейки матки (РКШМ) – состояние, при котором в шейке матки  в результате травмы и воспалительного процесса закрываются выводные протоки цервикальных желез. Железы переполняются своим секретом и формируются кисты. Чаще всего это небольшие округлые образования до 5-7 мм в диаметре, но встречаются РКШМ и до 5 см.

Как правило, эти состояния не имеет клинических проявлений, если не осложняются инфекционным процессом.

Эндометриоз шейки матки – проявление системного гормонального заболевания, при котором ткань, сходная по своему функциональному состоянию с тканью эндометрия, развивается в шейке матки. Чаще всего это связано с термическими повреждениями шейки матки (электрокоагуляция, лазерная-, криодеструкция и др.)  на фоне имеющихся гормональных нарушений. Клинически проявляется наличием «шоколадных выделений» накануне месячных.

Цервицит – воспалительный процесс шейки матки, обусловленный специфической (герпес, вирус папилломы человека, хламидиоз, уреа-микоплазмоз, трихомоноз, кандидоз и др. ) или неспецифической инфекцией (кокковая флора, анаэробная инфекция и др.). Цервицит может сопровождать любое из описанных выше состояний и осложнять его течение. Именно наличие цервицита определяет клиническую картину и жалобы пациенток: зуд, жжение, избыточные выделения, специфический запах и др.

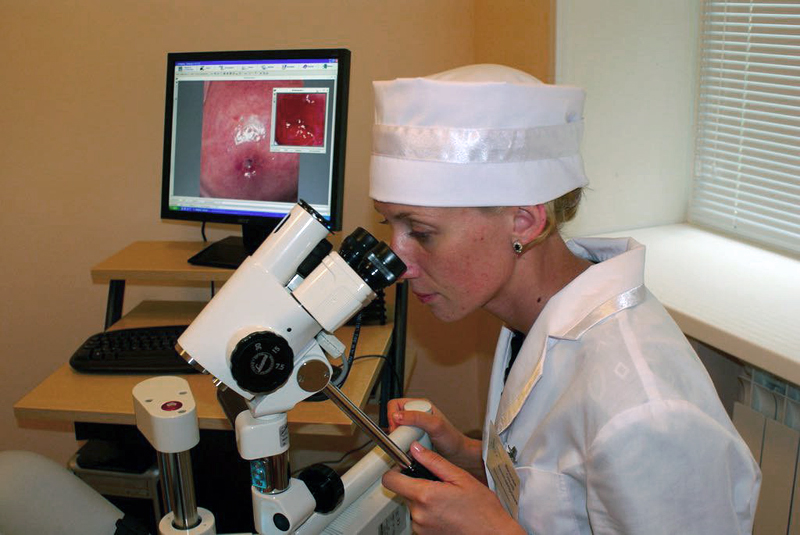
• Кольпоскопия – метод обследования шейки матки с применением оптического прибора кольпоскопа. При исследовании в качестве маркера используется 3-5% раствор уксусной кислоты, который ватным шариком наносится на шейку матки с целью оценки качества эпителия, покрывающего влагалищную часть шейки матки. Исследование безболезненно и не требует специальной подготовки пациентки, сопровождается видео- и фоторегистрацией, во время которой можно детально обсудить все имеющиеся изменения шейки матки в первый и последующие осмотры.
  
• Исследование мазков из шейки матки на наличие атипичных изменений — онкоцитология. В настоящее время выполняются как традиционные мазки, применяющиеся для профилактических осмотров, так и более современные методы – жидкостная онкоцитология. Преимуществом жидкостной цитологии является исследование клеток шейки матки в монослое взятого образца и специфическая окраска клеток, что позволяет более четко дифференцировать имеющиеся изменения.
• Молекулярно-генетические (ПЦР) и бактериологические методы исследования – позволяют обнаружить возбудителя инфекции и назначить комплексное противовоспалительное лечение с учетом выявленной патологии.
• Гистологическое исследование – это вид морфологического исследования фрагмента ткани шейки матки, которое выполняется после взятия биопсии под контролем кольпоскопии.

Вопрос-ответ

Как записаться на диагностику доброкачественных заболеваний шейки матки?

Записаться можно по телефону или оставить заявку через форму на сайте

Возможен ли срочный прием генеколога в вашем центре?

Да, свяжитесь с нами по телефону и мы примем вас в неотложном порядке.

Где можно просмотреть цены на улуги диагностики доброкачественных заболеваний шейки матки вашего центра?

Посмотреть цены на услуги генекологии можно на нашем сайте, на странице «Цены».

Какое оборудование используется в «Роден»?

В распоряжении врачей новейший высокоточное оборудование, позволяющее диагностировать заболевание на раннем этапе развития.

Другие услуги

Отзывы об услуге

Была на приеме у гинеколога Галины Владимировны, лучше гинеколога я не встречала, Просто специалист с большой буквы. Настолько внимательна, аккуратна, вникает во все тонкости и подробности общего состояния женского здоровья, Именно благодаря ей удалось обнаружить образование, которое не видели другие врачи. Здоровья крепкого Галине Владимировне, спасибо за ваш бесценный труд.

Спасибо, Галине Владимировне Костевич за профессионализм, компетентность и бережное отношение. Именно таким я представляю настоящего врача.

Выражаю благодарность доктору Костевич Галине Владимировне за высочайший профессионализм и самоотверженную борьбу за мое здоровье. Спасибо ей за бесконечное терпение, отзывчивость, чуткость и поддержку. Галина Владимировна, вы не только Врач с большой буквы, вы и Человек с большой буквы. Спасибо ВАМ. Также выражаю благодарность администраторам центра за любезное и вежливое обращение, внимательное и уважительное отношение к посетителям в любой ситуации.

Мне не хватит слов, чтобы выразить свой восторг и благодарность врачу-гинекологу Костевич Г.В. которая всегда готова помочь, за профессионализм, чуткость и доброту, бесценные советы, открытость, безграничное тепло и отзывчивость. Спасибо Вам за огромный труд, за терпение и бережное отношение к каждому посетителю. Своим знакомым рекомендую попасть именно к ней.

Ретенционные кисты шейки матки. Диагностика и лечение ретенционных кист шейки матки в Москве – клиника гинекологии Гинеко

Кисты шейки матки (наботовы кисты, ретенционные кисты) — это закрытые и расширенные железы со скопившимся в них секретом. Если в результате воспалительного процесса происходит закупорка выводных протоков желез шейки матки, вырабатывающих слизь, они могут увеличиться в объеме и превратиться в кисты.

Сами кисты не опасны: они не относятся к предраковым заболеваниям, не влияют на гормональный фон, не вызывают задержку менструации или выкидыш. Однако, кисты могут стать очагами инфекций и привести к развитию хронических воспалительных процессов в женских половых органах, которые часто являются причинами внематочной беременности и бесплодия.

Причины возникновения кист шейки матки

Главной причиной возникновения наботовых кист является воспалительный процесс в шейке матки и в цервикальном канале, который развивается вследствие травм и инфекций, полученных во время абортов, родов, неправильного введения внутриматочного средства (ВМС) и недостаточно квалифицированных инструментальных обследований (гистероскопии, диагностического выскабливания).

Симптомы кисты ШЕЙКИ матки

Сложность диагностики кист шейки матки заключается в том, что они не вызывают кровянистых выделений, не приводят к нарушениям менструального цикла или каким-либо другим беспокоящим пациенток проявлениям. Заболевание протекает бессимптомно и чаще всего обнаруживается во время планового осмотра у гинеколога.

Диагностика кисты шейки матки

При обнаружении кисты шейки матки обследование проводится в целях выявления инфекции различной локализации и профилактики повторного возникновения кисты и включает в себя:

• кольпоскопическое исследование;
• бактериоскопическое исследование мазков из влагалища, шейки и канала шейки матки на флору;
• исследование мазков методом ПЦР на хламидию, уреаплазмы, микоплазмы, трихомонаду и гарднереллу.

Лечение кисты шейки матки

В нашей клинике лечение кист шейки матки осуществляется радиоволновым методом амбулаторно. Радиоволновое удаление кисты на аппарате «Сургитрон» занимает 1-2 секунды. Процедура не требует обезболивания. После радиоволнового удаления кист шейки матки иногда, в течение 1-3 дней, могут наблюдаться скудные выделения желтого цвета. Полное заживление шейки матки происходит в течение двух недель после радиоволнового вскрытия и дренирования кист. Осложнений и рецидивов не бывает. Методика разрешена Минздравом к применению и нерожавшим женщинам, так как не вызывает ожогов и рубцов и относится к разряду щадящих методов хирургического лечения. При обнаружении в мазках возбудителей инфекции, требуется соответствующее предварительное лечение.

Врачи гинекологического отделения клиники Гинеко считают, что вопрос о необходимости лечения кисты и выборе метода лечения должен решаться индивидуально, исходя из особенностей заболевания. В распоряжении наших специалистов находятся самые современные и эффективные методы диагностики и лечения, которые позволяют полностью восстановить функции шейки матки и вернуть пациентке способность забеременеть, выносить и родить ребенка.

Middle Atlantic ESUR-HM 60″ DESK&OB W/2X4 RKSHM — Falcon Technologies, Inc.

Middle Atlantic ESUR-HM 60″ DESK&OB W/2X4 RKSHM — Falcon Technologies, Inc.

«Позвоните нам, мы ответим на телефон 314-994-9066» — Джон Бараджола | Президент

Отправить быстрое предложение

60″ DESK&OB W/2X4 RKSHM

Заказы с товарами в наличии, полученные до 16:00 по центральному поясному времени, будут отправлены в тот же день с нашего склада в Сент-Луисе, штат Миссури.   Заказы, размещенные в выходные, будут обработаны на следующий рабочий день. Как только ваш заказ будет обработан, вы получите информацию об отслеживании по электронной почте.Для товаров, которых нет в наличии, сообщите нам, когда они вам понадобятся, и мы организуем доставку в соответствии с вашими требованиями с помощью наиболее экономичного способа доставки.

Если у вас есть какие-либо вопросы или комментарии к нам, всегда не стесняйтесь звонить нам по телефону 1-866-958-4499 . Мы готовы принять ваш звонок с 7:30 до 17:00 CST с понедельника по пятницу.

American ExpressApple PayDiscoverMeta PayGoogle PayMastercardPayPalShop PayVenmoVisa

Ваша платежная информация надежно обрабатывается. Мы не храним данные кредитной карты и не имеем доступа к информации о вашей кредитной карте.

Наша политика заключается в том, чтобы удовлетворить вас, клиента, и мы приложим все усилия, чтобы предоставить вам продукт и услугу, которые вам нужны. Если возврат приемлем на основании критериев, указанных ниже, и спецификаций производителя, будет выдан номер RMA, а форма запроса на возврат материалов будет отправлена ​​по факсу/электронной почте покупателю с информацией о применимой плате за пополнение запасов, если требуется, и сроке оплаты.

вернуть перечисленные материалы.

Товары со склада

Товары со склада, приобретенные в течение последних 90 дней, подлежат возврату в отдел продаж без присвоения номера RMA. Товары должны быть возвращены с копией оригинального счета-фактуры/заказа на продажу Falcon Tech для выдачи кредита. При возврате в течение 30 дней с даты покупки взимается комиссия в размере 10 %. Все товары должны быть в оригинальной упаковке в пригодном для продажи состоянии.

Отсутствующие на складе товары/специальные заказы/специальные товары

Отсутствующие на складе товары стоимостью менее 75 долларов США возврату не подлежат. Возврат товаров, которых нет в наличии, должен быть инициирован в течение 20 дней с момента получения продуктов в Falcon Technologies, Inc. За товары, которых нет в наличии, взимается комиссия. Специальные заказы и индивидуальные заказы ВОЗВРАТУ НЕ ПОДЛЕЖАТ.

Дефектные изделия

Возврат дефектных изделий допускается, если они не функционируют в соответствии со спецификациями, установленными производителем. Прежде чем может быть выдан номер RMA, требуется объяснение дефекта. Любой дефектный товар, срок действия которого превышает 30 дней с даты выставления счета, потребует от клиента взаимодействия напрямую с производителем.

Как запросить RMA:

• Через веб-сайт. Щелкните ссылку формы запроса RMA ниже. Ваш запрос будет обработан, и вы должны получить подтверждение в течение 24-48 часов.
• Через торгового представителя — просто позвоните или напишите своему торговому представителю, чтобы сообщить, какие товары вам нужно вернуть. Укажите номер заказа на продажу или счет-фактуру и причину возврата.
• Форма запроса RMA

Доставка возвращаемых товаров

К возвращаемому товару должна прилагаться копия формы RMA вместе с копией оригинального счета/заказа на продажу. Это относится к возвратам, поступающим на прилавок, а также к возвратам, поступающим через UPS и т. д. Все возвраты, отправляемые в Falcon Technologies, должны четко указывать номер RMA на внешней упаковке.

ВОЗВРАТ МАТЕРИАЛОВ ПО: 2631 METRO BLVD., MARYLAND HEIGHTS, MO 63043

 

 

Тарифы со скидкой

Товары в наличии, отправка в тот же день*

Освобождение от налога с продаж

Если вы освобождены от налога с продаж, мы вернем налог

Первоклассная поддержка

Свяжитесь с нами в чате, по электронной почте , телефон

Безопасные платежи

Visa, Mastercard, Amex, PayPal

Применение метода гильбертова пространства воспроизводящего ядра для решения одного класса нелинейных интегральных уравнений

На этой странице

АннотацияВведениеПредварительные выводыЗаключениеКонфликты интересовБлагодарностиСсылкиАвторские праваСтатьи по теме

Предлагается новый подход, основанный на методе гильбертова пространства воспроизводящего ядра, для аппроксимации решения нелинейных интегральных уравнений второго рода. В этом случае процесс Грама-Шмидта заменяют другим процессом, чтобы получить удовлетворительный результат. В этом методе решение выражается в виде ряда. Кроме того, доказана сходимость предложенной методики. Для иллюстрации эффективности и действенности метода по данному алгоритму решаются четыре примерных интегральных уравнения, возникающих в электромагнетизме.

1. Введение

Электромагнетизм — явление, связанное с электрическими и магнитными полями и их взаимодействием, которое вообще является одной из важнейших наук. Внешнее исчисление дано в [1, 2] внутри некоторых учебников. К способу преподавания электромагнетизма можно подойти через использование дифференциальных форм, которые приведены в [3]. В соответствии с проблемами электромагнитного поля, возникшими много лет назад, были даны некоторые решения с помощью линейных и нелинейных интегральных уравнений (НИУ), которые могут быть полезны в полевых условиях. В таких методах, как блочно-импульсные функции (BPF), Galerkin и коллокация, наиболее важными способами являются базовые функции и соответствующая проекция. На основе метода воспроизводящего ядра гильбертова пространства был найден подход к решению некоторых электромагнитных проблем.

Нелинейные интегральные уравнения встречаются в различных областях науки и в многочисленных приложениях, таких как упругость, пластичность, тепломассоперенос, теория колебаний, гидродинамика, теория фильтрации, электростатика, электродинамика, биомеханика, теория игр, управление, теория массового обслуживания, электротехника , экономика и медицина, среди прочего. Существуют различные типы NIE, которые обычно не могут быть проработаны в явном виде, поэтому к ним следует подходить приблизительно.

Поэтому многие исследователи изучили и сосредоточили внимание на различных численных методах, которые могут работать с этими интегральными уравнениями. Например, в [4, 5] авторы представили метод гомотопического анализа для решения второго рода нелинейных интегральных уравнений Фредгольма и Вольтерра. Линейные многошаговые методы применялись в [6] для получения численного решения сингулярного нелинейного интегрального уравнения Вольтерра. В [7] применялся асимптотический метод численного подхода к нелинейному интегральному уравнению Абеля-Вольтерра.

Гильбертово пространство воспроизводящего ядра (RKHS) было введено Minggen et al. [8, 9], и она развивалась в разных областях, включая теорию приближения, статистику, теорию машинного обучения, теорию представления групп и различные области комплексного анализа. Метод воспроизводящего ядра гильбертова пространства (RKHSM) представляет собой метод ядерной аппроксимации, который применялся для решения нелинейных краевых задач [7–12], обобщенных сингулярных нелинейных уравнений типа Лейна-Эмдена [13], интегродифференциальных уравнений [14–16], интегродифференциальных дробные уравнения [17], задача Братуса [18] и т.д.

Рассмотрим следующее нелинейное интегральное уравнение: где , — вещественные константы, — неизвестная функция, которую можно определить, — непрерывная функция на , — непрерывная функция на , — непрерывный член в as , , и — Пространство ядра воспроизведения. Уравнение (1) имеет непрерывное решение на [19]. Условия существования и единственности решения уравнения (1) обсуждались в [19–23]. Будем считать, что решение (1) единственно.

На протяжении нескольких десятилетий численные методы в задачах электромагнетизма являются одним из важнейших предметов обширных исследований [1–4]. С другой стороны, многие задачи электромагнетизма могут быть смоделированы интегральными уравнениями, упомянутыми в [24–26], например, интегральное уравнение электрического поля (EFIE) и интегральное уравнение магнитного поля (MFIE). В последние годы было представлено несколько численных методов решения линейных и нелинейных интегральных уравнений. В представленной статье подразумеваются применимые уравнения электромагнетизма.

В предыдущих работах, таких как [13–15], рассматривался процесс ортогонализации Грама-Шмидта для реализации RKHSM. Так как этот процесс численно нестабилен и может потребоваться много времени для запуска алгоритма, здесь мы откладываем этот процесс и действуем другим путем. Наш подход объединяет методы, упомянутые в [13–17]. А именно, в отличие от [13–15], без использования процесса ортогонализации РКШМ успешно применяется для решения нелинейной задачи (1).

Структура этого документа может быть описана следующим образом. В разделе 2 описаны основные определения, предположения и предварительные сведения о RKHS. Основная идея и сходимость предложенной схемы обсуждаются в разделе 3. Раздел 4 содержит численные эксперименты. Наконец, раздел 5 посвящен краткому заключению.

2. Предварительные сведения

В этом разделе упоминаются некоторые основные определения и важные свойства воспроизводящих ядерных гильбертовых пространств (RKHS) [8, 9]., 27–29].

Определение 1. Гильбертово пространство — это пространство со скалярным произведением, полное и сепарабельное относительно нормы, определяемой скалярным произведением. Полнота пространства имеет место при условии, что всякая последовательность точек Коши в этом имеет предел, который также находится в и отделим от, допускает счетный ортонормированный базис.

Определение 2. Для абстрактного множества пусть будет гильбертовым пространством действительных или комплекснозначных функций на множестве . Мы говорим, что является гильбертовым пространством с воспроизводящим ядром, если существует линейный и ограниченный оценочный функционал над , или, что то же самое,

Теорема Рисса о представлении подразумевает, что для всех в существует уникальная функция с воспроизводящим свойством, для каждого где представляют скалярный продукт гильбертова пространства .

Определение 3. Пространство интерпретируется как Скалярное произведение и норма в форме

Лемма 4 (см. [9, 29]). Функциональное пространство – это внутреннее пространство.

Теорема 5 (см. [9, 29]). Функциональное пространство является гильбертовым пространством.

Теорема 6 (см. [9, 29]). Функциональное пространство воспроизводит гильбертово пространство ядра.

Теперь эта форма выражения функции Воспроизводящего ядра удалена.

На основании эссе легко доказать, что это ответ следующего обобщенного дифференциального уравнения [9, 29]: где – дельта-функция Дирака. При этом , является ответом следующего постоянного линейного однородного дифференциального уравнения порядка: с граничными условиями. Уравнение (7) является характеристическим . Тогда общее решение уравнения (7) есть где коэффициенты и , , могут быть рассчитаны путем решения следующих линейных уравнений:0003

3. Основная идея и теоретическое обсуждение

Условия единственности для нелинейных задач приведены в [21–23]. В данной работе предполагается единственное решение уравнения (1). Решение (1) дано в пространстве. Рассмотрим (1) как где . Очевидно, что является ограниченным линейным оператором to . Положить и , где – сопряженный оператор . В самом деле, для имеем и .

Ортонормированная система из пространства может быть получена из ортогонального процесса Грама-Шмидта:

Определение 7. В топологическом пространстве подмножество называется плотным, если .

Теорема 8. Если плотно на то является полной системой функций пространства и , где нижний индекс t в операторе указывает, что оператор применим к функции .

Доказательство. У нас есть Ясно . Для каждого фиксированного , пусть , , что означает Предположим, что плотно на и так . Отсюда следует, что из существования . Теперь теорема доказана.

Теорема 9. Если плотно на и решение (12) единственно, то решением (12) является

Доказательство. Используя (13), имеем С другой стороны, и , , — разложение в ряд Фурье по нормальной ортогональной системе и — гильбертово пространство. Таким образом, ряд сходится в смысле и доказательство будет завершено.

Теперь приближенное решение может быть получено путем пересечения -членом точного решения и

Теорема 10. Если существует такое, что .

Доказательство. У нас есть , для любого . Мы знаем . Таким образом .

Теорема 11. Приближенное решение равномерно сходится.

Доказательство. Предполагая , по теоремам 9 и 10 можно доказать, что

В дальнейшем представлен новый итерационный метод для достижения решения (12). Если то (16) можно записать в виде Теперь предположим, что для некоторого известно . Нет проблем, если предположить. Положим и определим аппроксимацию -члена посредствомгде В дальнейшем будет доказано, что приближенное решение в итерации (22) сходится к точному решению (12) равномерно.

Теорема 12. Предположим, что ограничено в (22). Если плотно на тогда -член приближенное решение в итерации (22) сходится к точному решению (12) и , тогда как дается (23).

Доказательство. Прежде всего, была бы доказана сходимость из (22). Мы заключаем, что подпоследовательность ортогональна, и отсюда следует, что очевидно, что последовательность монотонно возрастает. Так как ограничено и сходится, то ограничено и отсюда следует, что .
Если то так . Следовательно, как . Для доказательства его полноты требуется , где то как . Теперь мы можем доказать, что это решение (12).
Если взять предел из (22), то будет , значит . Пусть , и тогда из (23) и (29) следует, что .
плотно на . Для каждого существует подпоследовательность, которая как . Следовательно, когда имеем , что указывает на решение (12).

Указанная выше схема является эффективным методом решения нелинейных уравнений [31–33]. Однако при реализации этого алгоритма на компьютере он не совсем ортогонален из-за ошибок округления. Другими словами, процесс Грама-Шмидта численно нестабилен, а вычислительная стоимость алгоритма высока. Поэтому предложен следующий процесс, аналогичный для линейных задач в [20, 34]. Это предмет следующей теоремы, где используются следующие обозначения:

Теорема 13 (). Приближенное решение, полученное из (22), находится следующим образом: где

Доказательство. Предположим, что . Поскольку , и () линейно независимы, и поэтому уравнение (12) влечет . Поскольку у нас есть Обе части (33) обеспечивают Из (32) и (35) может быть получено следующее уравнение: Уравнение (32) влечет . Что доказывает теорему.

Алгоритм 14. Существуют следующие шаги для аппроксимации решения без применения ортогонального процесса Грама-Шмидта:  Шаг  1 . Исправить и . Если , установите . Остальное установить. Шаг  2 . Для набора. Установлен . Шаг  3 . Установлен . Шаг  4 . Для набора. Шаг  5 . . Шаг  6 . Установлен . Шаг  7 . Установлен . Шаг  8 . Если затем установите и перейдите к шагу 6. ​​В противном случае остановитесь.

Алгоритм 15. Существуют следующие шаги для аппроксимации решения путем применения ортогонального процесса Грама-Шмидта:  Шаг  1 . Исправить и . Если , установите . Остальное установить. Шаг  2 . Для набора. Установлен . Шаг  3 . Для и , если тогда установить и . Еще . Еще . Шаг  4 . Для набора. Шаг  5 . Установлен . Шаг  6 . Установлен . Шаг  7 . Установлен . Шаг  8 . Установлен . Шаг  9 . Если затем установите и перейдите к шагу 7. В противном случае остановитесь.

4. Численные эксперименты

В этой части решаются четыре численных примера для проверки эффективности и полезности настоящего метода. Все расчеты выполняются пакетом MAPLE. Результаты, полученные этим методом, хорошо согласуются с точным решением. Комплексная применимость этого метода обусловлена ​​стабильностью и состоятельностью представленного метода. Надежность метода и повышение точности делают этот метод более применимым.

Пример 1. В качестве первого применимого примера мы предлагаем нелинейные интегральные уравнения Фредгольма [26, 30]: Точное решение этого уравнения есть . Согласно (38) можно принять начальное приближение . Численные результаты приведены в таблице 1 при принятии и . В табл. 1 приведено сравнение абсолютных погрешностей нашего метода и вейвлет-метода Хаара [30]. На рис. 1 показано приближенное решение и его погрешности.

Пример 2. Во втором применимом примере электромагнитная задача решается представленным методом. Это смоделировано в модели нелинейных интегральных уравнений Вольтерра [26, 30]: Точное решение этого уравнения есть . Согласно (39) можно принять начальное приближение . Численные результаты приведены в табл. 2 с учетом , и . В табл. 2 приведено сравнение абсолютных погрешностей предложенного метода и метода BPFs [26]. На рис. 2 показано приближенное решение и его погрешности. В таблице 3 дано сравнение времени выполнения алгоритмов 14 и 15.

Пример 3. Электромагнитная задача решена с помощью нашего метода для другого применимого примера. Это смоделировано в модели нелинейных интегральных уравнений Фредгольма [26, 30]: Точное решение этого уравнения есть . В соответствии с (40) выбирается начальное приближение. Численные результаты приведены в таблице 4, принимая , и . В табл. 4 приведено сравнение абсолютных погрешностей предлагаемого метода и метода BPFs [26]. На рис. 3 показано приближенное решение и его погрешность. В таблице 5 дано сравнение времени выполнения алгоритмов 14 и 15.

Пример 4. Нелинейная интегральная задача Фредгольма [26, 30] решается с помощью нашего метода для этого применимого примера: Точное решение этого уравнения . Согласно (41) рассмотрим начальное приближение как . Численные результаты приведены в таблице 6, принимая , и . В табл. 6 приведено сравнение абсолютных погрешностей предложенного метода и вейвлет-метода Хаара [30]. На рис. 4 показано приближенное решение и его погрешность.

5. Заключение

В соответствии с этим эссе был введен и применен дополнительный итеративный метод воспроизводящего ядра гильбертова пространства для получения приближенного решения некоторого нелинейного интегрального уравнения. В этом методе, в отличие от других подобных методов, не используется ортогональный процесс. Однако время увеличивается, и точность также увеличивается. Основным моментом, который отмечается в данной статье, является то, что алгоритм 14 имеет большее время выполнения по сравнению с алгоритмом 15, но приближенное решение в алгоритме 14 точнее, чем в алгоритме 15. Сформулирован и доказан текущий метод равномерной сходимости. Полученные численные результаты подтверждают, что это хороший кандидат для решения нелинейного интегрального уравнения.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Авторы хотели бы поблагодарить профессора Haipeng Peng за поучительные комментарии и рекомендации по улучшению качества этой работы, а также Научно-исследовательский отдел Исламского университета Азад, Тегеран, за поддержку этого проекта.

Ссылки

1. K. Meetz and W. Engi, Electromagnetische Felder , Springer, Berlin, Germany, 1979.

2. W. Thirring, Lehrbuch der Mathematischen Physik , vol. 2, Springer, Vienna, Austria, 1978.

   Просмотр по адресу:

   Сайт издателя

3. К. Ф. Варник, Р. Х. Селфридж и Д. В. Арнольд, «Обучение теории электромагнитного поля с использованием дифференциальных форм», IEEE Transactions on Education, . об. 40, нет. 1, стр. 53–68, 1997.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

4. С. Аббасбанди, «Метод гомотопического анализа для уравнений теплового излучения», International Communications in Heat and Mass Transfer , vol. 34, нет. 3, стр. 380–387, 2007 г.

   Посмотреть по адресу:

   Сайт издателя | Google Scholar

5. Х. Восуги, Э. Шиванян и С. Аббасбанди, «Новый аналитический метод решения интегральных уравнений Вольтерры», Mathematical Methods in the Applied Sciences , vol. 34, нет. 10, стр. 1243–1253, 2011.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

6. Ж.-П. Каутен, «Обзор сингулярно возмущенных уравнений Вольтерра», Applied Numerical Mathematics. Журнал IMACS , том. 24, нет. 2–3, стр. 95–114, 1997.

   Посмотреть по адресу:

   Сайт издателя | ученый Google | MathSciNet

7. А. А. Килбас и М. Сайго, «О решении нелинейного интегрального уравнения Абеля-Вольтерра», Journal of Mathematical Analysis and Applications , vol. 229, нет. 1, стр. 41–60, 1999.

   Просмотр:

   Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

8. C. Minggen и D. Zhongxing, «О лучшем операторе интерполяции», Mathematica Numerica Sinica , vol. 8, нет. 2, стр. 209–216, 1986.

   Посмотреть по адресу:

   Google Scholar

9. C. Minggen and L. Yingzhen, Nonlinear Numerical Analysis in the Reproducing Kernel Space , Nova Science, New York, NY, США, 2009.

10. С. Аббасбанди, Б. Азарнавид, М. С. Алхутали, «Метод гильбертова пространства с воспроизводящим ядром для множественных решений нелинейных краевых задач», Журнал вычислительной и прикладной математики , том. 279, стр. 293–305, 2015.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

11. Н. Шавагфех, О. Абу Аркуб и С. Момани, «Аналитическое решение нелинейной периодической краевой задачи второго порядка с использованием метода воспроизводящего ядра», Journal of Computational Analysis and Applications , vol. 16, нет. 4, стр. 750–762, 2014.

    Посмотреть по адресу:

    Google Scholar | Zentralblatt МАТЕМАТИКА | MathSciNet

12. Ф. Гэн и М. Цуй, «Решение нелинейной системы краевых задач второго порядка», Журнал математического анализа и приложений , том. 327, нет. 2, стр. 1167–1181, 2007.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

13. Б. Азарнавид, Ф. Парванех и С. Аббасбанди, «Метод гильбертова пространства с ядром, воспроизводящим Пикара, для решения обобщенных сингулярных нелинейных уравнений типа Лейна-Эмдена», Математическое моделирование и анализ , том. 20, нет. 6, стр. 754–767, 2015 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

14. О. А. Аркуб, М. Аль-Смади и Н. Шавагфе, «Решение интегро-дифференциальных уравнений Фредгольма с использованием метода гильбертова пространства с воспроизводящим ядром», Applied Mathematics and Computation , vol. 219, нет. 17, стр. 8938–8948, 2013.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

15. Л. Ян и М. Цуй, «Новый алгоритм для класса нелинейных интегро-дифференциальных уравнений в воспроизводящем пространстве ядра», Прикладная математика и вычисления , том. 174, нет. 2, стр. 942–960, 2006 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

16. О. Абу Аркуб, М. Аль-Смади и С. Момани, «Применение метода воспроизводящего ядра для решения нелинейных интегродифференциальных уравнений Фредгольма-Вольтерра», Реферативный и прикладной анализ , том. 2012 г., идентификатор статьи 839836, 16 страниц, 2012 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

17. S. Bushnaq, B. Maayah, S. Momani, and A. Alsaedi, «Метод гильбертова пространства с воспроизводящим ядром для решения систем дробных интегродифференциальных уравнений», Abstract and Applied Analysis , vol. 2014 г., идентификатор статьи 103016, 6 страниц, 2014 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

18. М. Инк, А. Акгюль и Ф. Генг, «Метод гильбертова пространства воспроизводящего ядра для решения проблемы Брату», Бюллетень Малазийского общества математических наук , том. 38, нет. 1, стр. 271–287, 2015.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

19. А.-М. Wazwaz, A First Course in Integral Equations , World Scientific, 1997.

    Просмотр по адресу:

    MathSciNet

20. С. Джавади, Э. Баболян и Э. Моради, «Новая реализация воспроизводящего ядра метода гильбертова пространства для решения класса функциональных интегральных уравнений» Связь в численном анализе , vol. 2014 г., идентификатор статьи cna-00205, 7 страниц, 2014 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

21. В. Цзян и З. Чен, «Решение системы линейных интегральных уравнений Вольтерра с использованием нового метода воспроизводящего ядра», Applied Mathematics and Computation , vol. 219, нет. 20, стр. 10225–10230, 2013.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

22. А.-М. Wazwaz, Linear and Nonlinear Integral Equations, Methods and Applications , Springer, Berlin, Germany, 2011.

23. И. Л. Эль-Калла, «Сходимость метода Адомиана, примененного к классу нелинейных интегральных уравнений», Прикладная математика Буквы. Международный журнал Rapid Publication , vol. 21, нет. 4, стр. 372–376, 2008 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

24. Г. Гума, К. Моади, М. Аль-Смади и И. Хашим, «Решения неопределенных интегральных уравнений Вольтерра с помощью метода подобранного воспроизводящего ядра гильбертова пространства», Journal of Function Spaces , vol. 2016 г., идентификатор статьи 2920463, 11 страниц, 2016 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | MathSciNet

25. Сизиков В., Сидоров Д. Обобщенные квадратуры для решения сингулярных интегральных уравнений типа Абеля в приложении к инфракрасной томографии, Прикладная вычислительная математика. Журнал IMACS , том. 106, стр. 69–78, 2016 г.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

26. Э. Баболиан, З. Масури и С. Хатамзаде-Вармазьяр, «Новый прямой метод решения нелинейных интегральных и интегро-дифференциальных уравнений Вольтерра-Фредгольма с использованием операционной матрицы с блочно-импульсными функциями», в Progress in Исследование электромагнетизма B , том. 8, стр. 59–76, EMW Publishing, Кембридж, Массачусетс, США, 2008 г.

    Посмотреть по адресу:

    Google Scholar

27. D. Alpay, Ed., Воспроизведение пространств ядра и приложений , vol. 143 of Operator Theory: Advances and Applications , Birkhäuser Basel, 2003.

    Посмотреть по адресу:

    Сайт издателя | MathSciNet

28. С. Сайтох, Д. Алпай, Дж. А. Болл и Т. Осава, Воспроизведение ядер и их приложений , том. стр. 11, Springer Science & Business Media, Берлин, Германия, 2013 г.

29. С. Сайтох, Интегральные преобразования, воспроизведение ядер и их приложения , том. 369 из Pitman Research Notes in Mathematics Series , Longman, Harlow, UK, 1997. с использованием вейвлетов Хаара», Journal of Computational and Applied Mathematics , vol. 225, нет. 1, стр. 87–9. 5, 2009.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

30. Р. Кетабчи, Р. Мохтари и Э. Баболиан, «Некоторые оценки погрешности решения интегральных уравнений Вольтерра с использованием метода воспроизводящего ядра», Journal of Computational and Applied Mathematics , vol. 273, стр. 245–250, 2015.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

31. А. Альванди, М. Парипур и З. Рошани, «Метод воспроизводящего ядра для решения класса интегро-дифференциальных уравнений Фредгольма», в Труды 46-й ежегодной иранской математической конференции (AIMC 46) , с. 505, Yazd University, 2015.

    Посмотреть по адресу:

    Google Scholar

32. Комашинская И. , Аль-Смади М. Итеративный метод воспроизводящего ядра для решения интегродифференциальных уравнений второго порядка типа Фредгольма. Прикладная математика , вып. 2014 г., идентификатор статьи 459509, 11 страниц, 2014 г.

    Посмотреть по адресу:

    Сайт издателя | Академия Google

33. Э. Баболиан, С. Джавади и Э. Моради, «Анализ ошибок воспроизводящего ядра методом гильбертова пространства для решения функциональных интегральных уравнений», Журнал вычислительной и прикладной математики , том. 300, стр. 300–311, 2016.

    Посмотреть по адресу:

    Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet

Copyright

Copyright © 2017 Sedigheh Farzaneh Javan et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.