Сколько ватт в ампере, соотношение и определение.
В большинстве электроприборов техническая информация относительно работы от электрической сети представлена в ваттах и киловаттах. Однако электрические счетчики, розетки и автоматические выключатели маркируются с помощью Амперов. В связи с этим для человека, не знакомого с деталями работы электрических сетей и оборудования, могут возникнуть сложности в понимании того, соответствует ли фактическая нагрузка расчетной и, как следствие, в выборе подходящего предохранителя.
Ватты в амперы или наоборот
Ампер – это единица измерения силы тока, а ватт – мощности (тепловой, механической или электрической). В связи с тем, что работа электрических приборов тесно связана с обоими понятиями и величинами, они выражаются в определенных соотношениях друг к другу. Однако это не значит, что можно напрямую перевести ватты в амперы или наоборот. Однозначного, прямого коэффициента на который можно было бы умножить, или разделить имеющееся число, нет.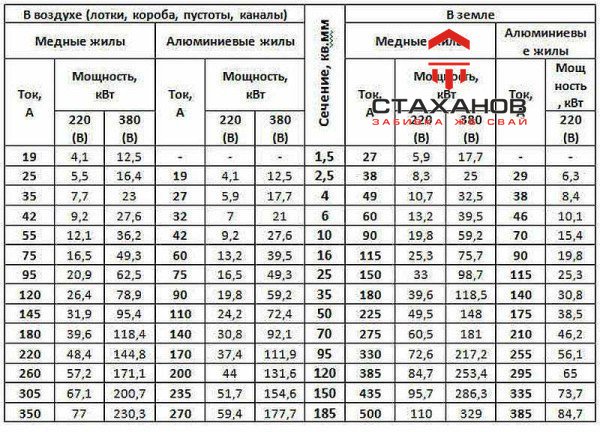
Как переводить
Основная формула, отражающая зависимость показателей электрического тока друг от друга выглядит следующим образом: P = U*I, где U обозначает напряжение в вольтах, I – силу тока в амперах, а P – мощность в ваттах. Всем известное соотношение из школьной физики, которое иногда люди забывают. Собственно зная это соотношение, можно провести все дальнейшие операции самостоятельно, однако есть некоторые тонкости, о которых мы расскажем ниже.
Выражение мощности
Теоретически для получения той или иной величины необходимо лишь преобразовать формулу. К примеру, для нахождения напряжения: U=P/I. К примеру, в России бытовые электросети находятся под напряжением в 220 В.
Если мы переводим амперы в ватты в сети с переменным напряжением, следует использовать его фактическое, действующее значение. Чаще всего именно и указывается в качестве номинального. Если известно только амплитудное значение, его следует привести к действующему с помощью деления на 1,41 (округленное число, но его достаточно для бытовых расчетов, квадратный корень из двух). А затем, используя формулу, вычислить мощность.
Выражение силы тока
Часто при выборе подходящей розетки, вилки, автоматического выключателя, счетчика и другого аналогичного оборудования, возникает необходимость найти силу тока в сети. Для этого формула преобразуется к следующему виду: I=P/U. Учитывая, что мощность зачастую указывается в киловаттах, этот показатель следует перевести в ватты, умножив на 1000.
Если напряжение указано в киловольтах, его не всегда можно преобразовать в вольты путем умножения.
Это связано с тем, что этот показатель нередко округляется. К примеру, значение 0,4 кВ используется как в России, так и в Европе, однако обозначает фактическое напряжение в 380 В и 400 В соответственно. Это значит, что европейские нагрузки сохранят работоспособность в российских сетях при сниженном напряжении, но обратное – не гарантируется.
Инструкция по переводу амперов в ватты (киловатты)
Вроде на первый взгляд, перевод амперов в ватты, кажется простой задаче, начинаешь изучать предмет и понимаешь, что не все так просто. Но стоит начать это делать, как вы поймете, что все опять становится простым и понятным.
Для проведения этой несложной операции необходимо (это конечно в идеале, так сказать по учебнику) наличие:
- тестера;
- электротехнического справочника;
- токоизмерительных клещей;
- калькулятора.

Порядок действий (стоит помнить, что механизм для переменного и постоянного тока отличается, в нашем же случае рассказывается об электрике в доме, где используется переменный ток):
- Узнайте напряжение рабочей сети с помощью тестера.
- В сети с переменным током, измерьте величину тока с помощью токоизмерительных клещей (существуют токоизмерительные клещи и для постоянного тока).
- Для сетей с однофазным переменным напряжением нужно умножить величину U на силу тока и коэффициент мощности. Результат произведения – потребляемая мощность прибора в ваттах.
Исходя из силы тока, протекающей по проводке, необходимо подбирать кабель с учетом сечения.
Слишком тонкие провода будут нагреваться при перегрузке, что может, в лучшем случае, привести к выходу их из строя, а в худшем – к возникновению пожара. Медные провода выдерживают значительно большую нагрузку в сравнении с алюминиевыми, однако и это не причина для того, чтобы подавать на них предельную нагрузку.
Обратите пожалуйста должное внимание на технику безопасности. Электрика это может и не очень сложно, но чрезвычайно ответственно и потенциально опасно. Так что еще раз вдумчиво прочитайте выделенный текст выше, а после этого, добро пожаловать в отзывы и комментарии.
4.5. Мощность тока. Закон Джоуля
Рассмотрим
произвольный участок цепи постоянного тока, к концам которого приложено
напряжение U. За время t через каждое сечение проводника
проходит заряд .
Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.
При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу . Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке .
Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.
В случае, когда проводник неподвижен и химических превращений в нем
не совершается, работа тока затрачивается на увеличение внутренней энергии
проводника, в результате чего проводник нагревается. Принято говорить,
что при протекании тока в проводнике выделяется тепло
(4.1)
Это соотношение называется законом Джоуля — Ленца. Оно было
экспериментально установлено английским физиком Д. П. Джоулем и подтверждено
точными опытами Э. Х. Ленца.
Х. Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся
в проводнике за время t, вычисляется по формуле
.
От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля — Ленца, за время d t, в этом объеме выделится количество теплоты,
где — dV элементарный объем. Разделив это выражение на dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени:.
Величину называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля — Ленца.Вопросы
1) В чем заключается физический смысл удельной тепловой мощности тока2) Напишите закон Джоуля-Ленца в интегральной и дифференциальной формах
4.
 Расчет электрической мощности | 2. Закон Ома | Часть1
Расчет электрической мощности | 2. Закон Ома | Часть14. Расчет электрической мощности
Расчет электрической мощности
В прошлой статье мы с вами вывели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на силу тока в «амперах», мы получаем мощность в «ваттах». Давайте применим ее к следующей схеме:
В этой схеме есть две известные нам величины: напряжение батареи составляет 18 вольт, а сопротивление лампы — 3 ома. Используя Закон Ома мы определим третью величину — силу тока:
Теперь, зная силу тока, мы можем умножить ее значение на напряжение и получить мощность:
Это означает что лампа рассеивает 108 ватт энергии в форме сета и тепла.
Давайте в этой же схеме увеличим напряжение батареи и посмотрим что произойдет. Интуиция подсказывает нам, что при увеличении напряжения и неизменном сопротивлении, сила тока в цепи также увеличится. А это значит, что увеличится и мощность:
В этой схеме напряжение батареи изменено и составляет 36 вольт вместо прежних 18. Сопротивление лампы не изменилось, и равно 3 омам. Сила тока теперь будет равна:
Давайте обсудим полученное значение. Если I=U/R, и мы удваиваем значение напряжения (U), оставляя неизменным сопротивление, то по логике вещей сила тока у нас тоже должна удвоиться. Действительно, сила тока в данной схеме имеет значение 12 ампер вместо прежних 6. А сейчас давайте вычислим мощность:
Обратите внимание, что мощность у нас также увеличилась по сравнению с предыдущим примером, и увеличилась она значительнее, чем увеличилась сила тока.
Используя математику мы можем преобразовать формулу мощности применительно к тем случаям, когда нам не известно значение напряжения или силы тока:
Историческая справка: первым математическую связь между рассеиваемой мощностью и силой тока через сопротивление открыл не Георг Симон Ом, а Джеймс Прескотт Джоуль. Это открытие, опубликованное в 1841 году и содержащее формулу P=I2R, стало известно как Закон Джоуля. Однако очень часто эти уравнения причисляются к Закону Ома.
Краткий обзор:
Цепь переменного тока с активным сопротивлением
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как
В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде:
Активное сопротивление
i = Im sin ωt
При этом
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.
Мощность, ток, напряжение
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается:
I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.
Электрическая мощность
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt. Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
Коэффициент мощности— обзор
2.4 Стандарт IEEE 1459
В 1998 и 1999 годах появились две статьи Эмануэля [10,12] по этой теме. В этой работе автор принимает предложение Depenbrock и переопределяет результаты рабочей группы IEEE в соответствии с видением трехфазной системы с нейтральным проводником как четырехпроводной системы. Таким образом, Стандарт установил общее определение полной мощности, определил так называемое эффективное напряжение и эффективный ток, а затем предположил разложение эффективной полной мощности в терминах мощности, предложенных рабочей группой IEEE [5,6].
Определение полной мощности, которое обрабатывает Std 1459, выглядит следующим образом: полная мощность — это максимальная мощность, которая может быть передана в идеальных условиях (синусоидальная однофазная или синусоидальная сбалансированная трехфазная система) при одинаковом влиянии напряжения (на изоляция и потери холостого хода) и такое же влияние тока (или потери в линии) системы по сети.
Для этого определения действующее значение напряжения и действующего тока характеризуют влияние нагрузки на энергосистему, т.е.е. какое значение тока передается по линии, какая изоляция необходима и какие потери нагрузки ожидаются. Явное выражение кажущейся мощности зависит от воздействия, вызывающего напряжение и ток в нагрузке. Таким образом, чтобы определить полную мощность, как определено выше, мы должны определить эквивалентный ток и эквивалентное напряжение сбалансированной системы прямой последовательности, оказывающие такое же влияние на сеть, как и фактические токи и напряжения в системе.
На рисунке 2.2 показана общая трехфазная система, в которой несимметричная нагрузка обеспечивается четырехпроводной системой.
Рисунок 2.2. Четырехпроводная трехфазная система, в которой сопротивление линейного и нулевого проводов одинаково.
Потери мощности в линиях составляют,
(2,46) ΔP = rIa2 + Ib2 + Ic2 + In2
Идеальная система должна рассеивать точно такую же мощность в линиях, Рисунок 2.3,
Рисунок 2.3. Эквивалентная трехфазная цепь для определения I e .
Нагрузка образована тремя равными резисторами, и линии работают тремя равными токами I e , затем
(2.47) ΔP = 3rIe2
Равенство выражений (2.46) и (2.47), эквивалентный или эффективный ток получается,
(2.48) Ie = 13Ia2 + Ib2 + Ic2 + In2
Следующий шаг — найти эквивалент напряжение В e . Это учитывает потери холостого хода в магнитных сердечниках трансформаторов и изолирует «перед нагрузкой» [6,13,14].
В первой версии Стандарта предполагается, что потери, зависящие от напряжения (без нагрузки), P Y , которые возникают из-за напряжений между фазой и нейтралью, и потери, зависящие от напряжения (без нагрузки), P Δ , которые из-за линейных напряжений равны, рисунок 2.4.
Рисунок 2.4. Проводимость, представляющая потери, зависящие от напряжения.
Это
(2.49) PΔ = 3GΔ3Ve2 = 3GYVe2 = PY ⇒ GΔ = 13GY
, где проводимости G Δ и G Y представлены для представления потерь, которые зависят от напряжения, P Δ и P Y соответственно. Эквивалентное напряжение дается формулой (2.50):
(2.50) GΔVab2 + Vbc2 + Vca2 + GYVan2 + Vbn2 + Vcn2 = 9GΔVe2 + 3GYVe2
Если учесть, как было сказано, что обе мощности равны, или что то же самое, что говоря G Δ = (1/3) G Y , тогда
(2.51) GΔVab2 + Vbc2 + Vca2 + 3GΔVan2 + Vbn2 + Vcn2 = 18GΔVe2
, откуда следует (2.52),
(2.52) Ve = 1183Van2 + Vbn2 + Vcn2 + Vab2 + Vbc2 + Vca2
трехпроводной -фазная система, где I n = 0, Стандарт рекомендует упрощенные выражения,(2,53) Ve = Vab2 + Vbc2 + Vca29; Т.е. = Ia2 + Ib2 + Ic23
, называемый Бухгольцем – Гудхью, и предложения по оригинальным работам рабочей группы IEEE, (2.14), (2.15).
Наконец, разделение эффективной полной мощности включено и опубликовано в стандарте IEEE 1459 в виде сводки,
(2.54) Se2 = P1 + 2 + Q1 + 2 + SU12 + DeI2 + DeV2 + Ph3 + Deh3
Это семь терминов мощности, которые были представлены в предыдущих разделах.
Напоминаем, что эти параметры мощности определяются на основе основных и гармонических эффективных составляющих напряжения и тока, и, следовательно, в среде стандарта IEEE они теперь принимают форму:
(2,55) Ie12 = 13Ia12 + Ib12 + Ic12 + In12; Ieh3 = Ie2 + Ie12
для тока и,
(2,56) Ve12 = 1183Va12 + Vb12 + Vc12 + Vab12 + Vbc12 + Vca12; Veh3 = Ve2 − Ve12
для напряжения.
2.4.1 После Стандарта: Std 1459-2010
Несомненно, влияние Эмануэля доминировало в разработке и распространении Стандарта. Именно он председательствовал на рабочих заседаниях рабочей группы IEEE и, как признано в [15], взял на себя моральную ответственность за теоретическое и техническое содержание Стандарта. Стандарт отражает изменения, касающиеся принятия значений эквивалентного напряжения и тока, которым следовал только Эмануэль. В случае эквивалентного тока ясно, что предложения Depenbrock были приняты, а не в том случае, если эквивалентное напряжение менее наклонно и связано с потерями, от которых зависит напряжение.После того, как первое издание Стандарта было опубликовано, Эмануэль переопределил эквивалентное напряжение и ток в результате сотрудничества со Школой европейской энергетики, на этот раз с участием Виллемса [14]. Далее мы обсудим новые определения I e и V e по той же схеме, что и в предыдущем разделе.
Чтобы определить эквивалентный ток, трехфазная система, состоящая из несимметричной нагрузки, питаемой по четырехпроводной системе, где каждая из линий имеет сопротивление , а нейтральный провод принимает сопротивление, № .Рассеиваемая мощность линии составляет,
(2,57) ΔP = rIa2 + Ib2 + Ic2 + rnIn2
Идеальная система, состоящая из трех равных резисторов, питаемых системой сбалансированного напряжения нагрузки, подтверждает, что I a = I b = I c = I e , I n = 0 и, следовательно, должен рассеивать в линии точно такую же мощность, что и исходная система,
(2,58) ΔP = 3rIe2
Равенство двух выражений для Δ P — значение эквивалентного или действующего тока, I e ,
(2.59) Ie = 13Ia2 + Ib2 + Ic2 + ρIn2; ρ = rnr
Стандартное 1459 предполагает ρ = 1. В установках для типичного среднего и низкого напряжения ρ = 0,2 — 4. Сегодня цифровые приборы могут разработать оборудование для регулировки ρ для любого заданного значения.
Чтобы определить эквивалентное напряжение, В e , предполагается, что нагрузка состоит из группы резисторов, подключенных в Y, и остаточной группы, подключенных в Δ. Эквивалентное сопротивление R Y и R Δ , соответственно, характеризует каждую группу.Критерий эквивалентности основан на идентичных электротермических эффектах, то есть
(2.60) Van2 + Vbn2 + Vcn2RY + Vab2 + Vbc2 + Vca2RΔ = 3Ve2RY + 9Ve2RΔ
Если вы определите соотношение мощностей (2.61),
1
(2.60) ) ξ = PΔPY = (9Ve2 / RΔ) (3Ve2 / RY) = 3RYRΔ
и подставляется в выражение (2.60), it (2.62),
(2.62) Van2 + Vbn2 + Vcn2RY + Vab2 + Vbc2 + Vca23RYξ = 3Ve2RY + 9Ve23RYξ
наконец произведено (2,63),
(2,63) Ve = 3Van2 + Vbn2 + Vcn2 + ξVab2 + Vbc2 + Vca291 + ξ
Это новое определение V e представляет собой важное концептуальное изменение Emanuel .Фактически, как явно указано в [15], концепция потерь, зависящих от напряжения, была оставлена в пользу подхода нагрузки, которая передает эквивалентную активную мощность; именно так это было отражено в стандарте редакции 2010 г. [5].
Электрическое значение, связанное с этими понятиями, кратко изложено в следующем утверждении; Система обеспечивает максимальную передачу мощности идеально сбалансированную и симметричную с линейным током I e и фазным напряжением В, , и .На рисунках 2.5 и 2.6 показаны компенсированная трехфазная система и ее эквивалентная схема соответственно.
Рисунок 2.5. Компенсация тока для трехфазной системы по схеме стандарта IEEE.
Рисунок 2.6. Эквивалентная схема для трехфазной системы согласно подходу IEEE.
Полная мощность, эквивалентное напряжение и ток также могут быть выражены с помощью симметричных составляющих. Если обозначены нижними индексами +, — и 0, компоненты положительной, отрицательной и нулевой последовательности, соответственно, имеют
(2.64) Ie = I + 2 + I − 2 + 1 + 3ρI02
(2.65) Ve = V + 2 + V − 2 + 11 + ξV02
Соотношения значений мощностей, ξ , приводят к различным ситуациям; четыре из них представляют интерес:
- 1.
P Δ = 0, ξ = 0, R Δ → ∞, R e = R Y ;
Нагрузки не соединяются по треугольнику:
(2.66) Ve = 13Van2 + Vbn2 + Vcn2
- 2.
P Y = 0, ξ → ∞, R Y → ∞ , R e = R Δ /3;
Нагрузка из трех проводов:
(2.67) Ve = Vab2 + Vbc2 + Vca29
- 3.
P Δ = P Y , ξ = 1, R Δ = 3 R Y , R e = R Y /2 = R Δ /6;
Ситуация, рекомендованная стандартом 1459:
(2,68) Ve = 1183Van2 + Vbn2 + Vcn2 + Vab2 + Vbc2 + Vca2
- 4.
P Δ = 3 P ξ = 3, R Δ = R Y , R e = R Y /4 = R Δ /4;
Случай, когда все сопротивления четырех проводников равны и дают то же выражение, что и в европейском подходе:
(2.69) Ve = 112Van2 + Vbn2 + Vcn2 + Vab2 + Vbc2 + Vca2
Различия между четырьмя ситуациями можно легко понять из выражений V e и I e на основе симметричных компонентов ( 2.55), (2.56). Таким образом, установлено, что основная причина несоответствия между четырьмя случаями связана с напряжением нулевой последовательности, В 0 , и отношением ξ . Только когда ξ → ∞, не влияет на напряжение нулевой последовательности.В энергосистемах V 0 обычно очень мало, так что ξ имеет очень небольшое влияние на значение V e .
LearnEMC — Введение в представление децибел
Если вы хотите эффективно общаться с инженерами EMC, важно привыкнуть к децибелам (дБ). Обозначение в децибелах — удобный способ выразить отношения величин, которые могут охватывать или не охватывать многие порядки величины. Он также используется для выражения амплитуды различных параметров сигнала, таких как напряжение или ток, относительно заданного опорного уровня.
Коэффициент мощности, P 2 : P 1 , в дБ рассчитывается просто как,
Коэффициент мощности в дБ = 10log (P2P1) (1)
Например, если мы сравниваем полученную мощность 10 Вт со спецификацией 5 Вт, мы могли бы сказать, что полученная мощность превысила спецификацию на
10log (10 Вт 5 Вт) = 3 дБ (2)
Если импеданс, связанный с двумя уровнями мощности, постоянен, то мощность пропорциональна квадрату напряжения (или тока).В этом случае мы также можем выразить отношения напряжения (или тока) в дБ,
10log (P2P1) = 10log (V2V1) 2 = 20log (V2V1) (3)
или,
20log (3 В / м1 В / м) ≈10 дБ (5)
Коэффициент усиления антенны или усилителя обычно указывается в дБ. То же самое и с потерями в кабеле или фильтре. Усилитель, который принимает сигнал мощностью 1 Вт и производит сигнал мощностью 100 Вт, имеет коэффициент усиления
.10log (1001) = 20 дБ (6)
Кабель, входной сигнал которого имеет амплитуду 3,0 В, а выходной сигнал имеет амплитуду 2.8 вольт показывает усиление
20log (2,83,0) = — 0,6 дБ (7)
или потеря
20log (3,02,8) = 0,6 дБ (8)
Обратите внимание, что обратное значение любого отношения выражается изменением его знака в дБ. Коэффициент 1 равен 0 дБ. Комплексные числа, фаза или отрицательные значения не могут быть выражены в дБ.
Контрольный вопрос
Сигнал, проходящий по коаксиальному кабелю на один километр, теряет половину своего напряжения. Экспресс,
- Отношение входного напряжения к выходному
- Соотношение входной и выходной мощностей
- Отношение входного напряжения к выходному в дБ
- Отношение входной и выходной мощностей в дБ.
Конечно, отношение входного напряжения к выходному составляет 2: 1, в то время как отношение входной мощности к выходной мощности равно (2) 2 : (1) 2 = 4: 1. Отношение напряжений, выраженное в дБ, составляет 20 log (2/1) = 6 дБ. Коэффициент мощности составляет 10 log (4/1) = 6 дБ. Это иллюстрирует одно из основных преимуществ выражения прироста или потерь в дБ. Пока импеданс постоянен, нет необходимости указывать, является ли соотношение мощностью или напряжением, когда оно выражается в дБ. Усиление на 6 дБ однозначно означает, что мощность увеличилась в четыре раза, независимо от того, было ли исходное измерение напряжением, током или мощностью.С другой стороны, если бы мы просто сказали, что один сигнал был вдвое сильнее , чем другой, было бы неясно, имеет ли он вдвое большую мощность или вдвое большую амплитуду.
Пример 1-1: Определение отношений в дБ
Укажите следующие коэффициенты в дБ:
| 200 мкВ / м : 100 мкВ / м | 20log (200100) = 6 дБ |
| 300 мВ : 100 мВ | 20log (300100) = 9.5 дБ≈10 дБ |
| 400 мА : 100 мА | 20log (400100) = 12 дБ |
| 500 мкА / м : 100 мкА / м | 20log (500100) = 14 дБ |
| 2 мкВт : 1 мкВт | 10log (21) = 3 дБ |
| 3 мВт : 1 мВт | 10log (31) = 4,8≈5 дБ |
| 5 мВт : 1 мВт | 10log (51) = 7 дБ |
Выражение амплитуд сигналов в дБ
Амплитуды сигнала также могут быть выражены в децибелах как отношение амплитуды к заданному эталону.Например, амплитуда сигнала 100 мкВ также может быть выражена как
20log (100 мкВ1 мкВ) = 40 дБ (мкВ) (9)
Контрольный вопрос
Выразите следующие амплитуды сигнала или поля в их нормальных единицах:
- 6 дБ (мкВ)
- 20 дБ (мкА)
- 20 дБ (A)
- 100 дБ (мкВ / м)
- 100 дБ (мкВт)
Единицы измерения в скобках после «дБ» указывают на то, что выражаемая величина является амплитудой.
Каждое из вышеуказанных количеств просто конвертируется следующим образом:
- 6 дБ (мкВ) = 20log (X1 мкВ) → X = 10620 мкВ = 2 мкВ
- 20 дБ (мкА) = 20log (X1 мкА) → X = 102020 мкА = 10 мкА
- 20 дБ (A) = 20log (X1 A) → X = 102020 A = 10 A
- 100 дБ (мкВ / м) = 20log (X1 мкВ / м) → X = 1010020 мкВ / м = 105 мкВ / м
- 100 дБ (мкВт) = 10log (X1 мкВт) → X = 1010010 мкВт = 1010 мкВт
В децибелах
Зачем выражать амплитуды сигналов в дБ? В конце концов, никогда не возникает двусмысленности относительно того, является ли величина мощностью или напряжением, если указаны амплитуда и ее единицы.Реальная мощность работы в дБ — это расчетные отношения.
Ранее мы упоминали сравнение 10-ваттного приемника с 5-ваттным приемником. В уравнении (2) мы показали, что приемник был на 3 дБ выше спецификации. В этом случае, если мощность была выражена в дБ (Вт),
10 Вт = 10log (10 Вт1 Вт) = 10 дБ (Вт) (15)
5 Вт = 10log (5 Вт1 Вт) = 7 дБ (Вт). (16)
Мы могли бы рассчитать соотношение как,
10 дБ (Вт) −7 дБ (Вт) = 3 дБ. (17)
Вместо того, чтобы делить амплитуды для определения отношения, мы можем просто вычесть амплитуды, выраженные в дБ (·).Опять же, пока импеданс постоянен, не имеет значения, работаем ли мы с единицами измерения мощности, напряжения или тока.
Пример 1-2: Указание коэффициентов в дБ
Укажите следующие коэффициенты в дБ:
| 46 дБ (мкВ / м) : 40 дБ (мкВ / м) | → | 46 дБ (мкВ / м) — 40 дБ (мкВ / м) = 6 дБ |
| 50 дБ (мВ) : 40 дБ (мВ) | → | 50 дБ (мВ) — 40 дБ (мВ) = 10 дБ |
| 52 дБ (мА) : 40 дБ (мА) | → | 52 дБ (мА) — 40 дБ (мА) = 12 дБ |
| 54 дБ (мкА / м) : 40 дБ (мкА / м) | → | 54 дБ (мкА / м) — 40 дБ (мкА / м) = 14 дБ |
| 3 дБ (мкВт) : 0 дБ (мкВт) | → | 3 дБ (мкВт) — 0 дБ (мкВт) = 3 дБ |
| 7 дБ (мВт) : 0 дБ (мВт) | → | 7 дБ (мВт) — 0 дБ (мВт) = 7 дБ |
дБм
Одной из наиболее распространенных единиц измерения в децибелах является дБ (мВт) или дБ относительно 1 милливатта.Это почти всегда записывается в сокращенной форме, дБм (т. Е. Без буквы «W» и скобок). Многие осциллографы и анализаторы спектра дополнительно отображают амплитуды напряжения в дБмВт. Поскольку дБм — это единица измерения мощности, мы должны знать импеданс измерения, чтобы преобразовать дБм в вольты. Например, напряжение, выраженное как 0 дБмВт на 50-омном анализаторе спектра, равно
0 дБм = 10log (X1 мВт) ⇒ X = 1 мВт X = | V | 250 Ом V = (1 мВт) (50 Ом) = 0,2236 В. (18)
Пример 1-3: Указание напряжений в дБм
Укажите следующие напряжения в дБм, предполагая, что они были измерены с помощью осциллографа с сопротивлением 50 Ом:
1 мкВ → (1 мкВ) 250 = 2 × 10−11 мВт → 10log (2 × 10−111) = — 107 дБм
2 мкВ → (2 мкВ) 250 = 8 × 10-11 мВт → 10log (8 × 10-111) = — 101 дБм
10 мкВ → (10 мкВ) 250 = 2 × 10−9 мВт → 10log (2 × 10−91) = — 87 дБм
1 В → (1 В) 250 = 20 мВт → 10log (201) = 13 дБм
2 В → (2 В) 250 = 80 мВт → 10log (801) = 19 дБм
10 В → (10 В) 250 = 2000 мВт → 10log (20001) = 33 дБм
В этом примере мы видим, что удвоение напряжения добавляет 6 дБ (т.е.грамм. 13 дБм + 6 дБ = 19 дБм), а увеличение напряжения в 10 раз добавляет 20 дБ. Это верно независимо от того, какие единицы напряжения используются, и является примером того, почему часто удобно работать с децибелами.
2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ КОЛИЧЕСТВА
2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ КОЛИЧЕСТВА2.1 Прямое электрическое соединение Ток (постоянный)
2.2 Переменный Электрический ток (переменный ток)
2.3 Среднеквадратичное значение (rms) Значения
2.4 Акустическое давление и интенсивность
2,5 децибел
2,6 скорость и Поглощение акустических волн
2.7 Частота и длина волны
2.8 Акустические волны и рыба
Для правильного понимания акустики, используемой в рыболовстве, необходимо иметь некоторые знания о простом электричестве, электромагнитных и акустических волнах.
Важной целью этой главы является объяснение термина мощность , который имеет решающее значение для электрических и акустических измерений.Мощность определяется как количество потока энергии в единицу времени или просто «работа, выполненная» за данный момент времени. Это хорошо известный закон физики, согласно которому энергия не может быть ни создана, ни разрушена, а преобразуется из одной формы в другую. Процесс преобразования формы, которую мы имеем, например, электрической энергии, в желаемую форму, возможно, акустическую, не может быть на 100% эффективным, и, следовательно, некоторые из них могут превратиться в нежелательную форму, часто в тепловую. Жизненно важно, чтобы измерения в акустике рыболовства основывались на истинной мощности сигналов, и чтобы полностью объяснить это, мы сначала рассмотрим постоянный электрический ток, а затем переменный ток, который, в свою очередь, связан с акустическими факторами в разделе 2.4.
Электрическая энергия может храниться разными способами, но самым простым для данной цели является химическая форма в батарее элементов, из которых получается постоянный ток (DC) (ток означает поток электронов в цепи). Законы, регулирующие электрические вопросы, легче всего понять, применив постоянный ток к простым электрическим цепям.
Рис. 1.
Аккумулятор имеет постоянную разность потенциалов (pd) или напряжение (В) на своих выводах Рис.1, и если, например, лампа подключена к клеммам, постоянный ток будет течь как через цепь, так и через батарею. Работа выполняется, потому что электрическая энергия преобразуется в свет при прохождении тока через нить накала лампы. Количество энергии , перешедшее от электричества к свету, при измерении в течение определенного периода времени известно как рассеиваемая мощность (Вт, ватты), и это контролируется напряжением (В) батареи и величиной тока (А). который течет. На самом деле небольшая часть энергии «тратится» в виде тепла, но это не важно для настоящего объяснения.
Мощность — это произведение В, вольт и А, ампер.
Мощность, (Вт, Вт) = В x A (1)
Ток A прямо пропорционален V, но регулируется сопротивлением R (Ом) нити накала лампы.
А = V / R (2)
Если мы заменим уравнение 2 на A в уравнении 1
Мощность = V x V / R = V 2 / R Вт (3)
Соотношение мощности к работе и энергии приведено в Приложении I под производными единицами.Особенно важно помнить, что мощность пропорциональна квадрату напряжения.
Источники постоянного тока используются для обеспечения питания электронных устройств и систем, но не имеют другой полезной функции. Постоянный ток может вырабатываться вращающимися машинами (генераторами), но естественным выходом любой такой машины является волна переменного тока, описание которой дается в следующем разделе.
Рисунок 2.
Рисунок 3.
Электронные и акустические системы, которые распространяют и получают энергию, делают это с помощью электромагнитных или акустических волн. Характерные свойства волн одинаковы для воздуха, твердых тел или воды. Волна определяется как прогрессирующее возмущение в любой из этих сред. Он образуется в результате распространения переменного напряжения и давления без постоянного смещения самой среды.
Переменная электрическая волна может создаваться вращением прямоугольной проволочной петли с постоянной скоростью в магнитном поле.Это схематично показано на рисунке 2 (а). С помощью законов электромагнитной индукции можно продемонстрировать, что ток в петле будет изменяться в зависимости от угла петли относительно магнитного поля. Если за точку отсчета взять клемму P, вращающуюся от 0 ° до 360 °, направление тока и его амплитуду можно отобразить в зависимости от угла поворота, как показано на рисунке 2 (b). Для удобства используются интервалы 30 °.
Хорошо видно, что волна идет в одном направлении в течение первых 180 °, затем проходит через ноль и меняет направление (полярность) на следующие 180 °.Максимальные значения в каждом направлении происходят через 90 ° после прохождения нулей. В чистом (неискаженном) состоянии амплитуду и другие характеристики синусоиды можно легко измерить, но необходимо соблюдать особую осторожность, чтобы избежать путаницы. Например, необходимо быть абсолютно ясным, заявляя, что значения от нуля до максимума в одном направлении (пик) или, если цитируется от крайнего пика в одном направлении до крайнего пика в другом направлении (от пика до пика). см. рисунок 3.
Хотя пиковые значения или значения размаха должны быть записаны, это просто потому, что они являются распознаваемыми точками синусоиды, их необходимо преобразовать перед выполнением любых расчетов мощности.Причина в том, что нас интересует фактическое количество задействованной энергии, но, в то время как с постоянным током это может быть получено как произведение напряжения V и тока A, в данном случае эти величины непрерывно чередуются, поэтому не даст правильного ответа. (среднее значение фактически равно нулю). Мы должны найти значение переменного тока, который выполняет ту же «работу», что и постоянный ток, если он протекает в той же цепи.
Мы уже видели в 2.1, как рассчитывается мощность в цепи постоянного тока,
экв.1 | Вт = В x А | |
и транспонирование ур. 2 | V = AR | |
заменяя V в ур. 1 | Вт = A 2 R | (4) |
, что является более удобной формой для наших нынешних целей.
Если постоянный ток силой 3 А протекает через резистор 1 Ом, рассеиваемая мощность составляет
Вт = 3 2 x 1 = 9 Вт
, и это представлено на рисунке 4 (а) областью OX на XX ‘.
На этом же рисунке изображена синусоида 3А максимум .
Рисунок 4. (a)
Рисунок 4. (b)
Рисунок 4. (c)
Синусоиду можно определить как A max sin w t
, где A max — пиковая амплитуда в каждом направлении формы волны.
w t = 2p или 360 ° в конце одного цикла, см. Рисунок 3.
Мгновенное значение тока i = A max sin w t.
Если это протекает в цепи с сопротивлением 1 Ом, мгновенная скорость рассеиваемой мощности составляет
i 2 x 1 Вт = i 2 Вт.
Таким образом, мы можем возвести в квадрат из мгновенных значений синусоиды и, используя наш пример с максимумом 3А, получим пунктирную кривую на рисунке 4 (b).Легко увидеть или вычислить, что площадь под пунктирной кривой составляет половину площади OX на XX ‘, то есть, когда постоянный ток имеет амплитуду , равную максимальному переменному току, мощность, рассеиваемая за счет переменный ток составляет половину рассеиваемого постоянным током.
По-прежнему используя значения на Рисунке 4, можно определить пропорцию значения AC max , которая дает такое же рассеивание мощности, как и постоянный ток.
Постоянный ток, который дает такую же мощность , рассеиваемую мощность , что и максимальное значение переменного тока , как видно из рисунка 4 (b), составляет 9/2 = 4.5А.
Итак, 4.5 =
Тогда т.е. 3 разделить на квадратный корень из 2, но значение AC max равно 3, поэтому мы можем сказать 1/2 1/2 раз 3.
(5)
Подводя итог, мы можем сказать, что среднеквадратичное значение напряжения или тока представляет собой квадрат корень среднего (среднего) всех мгновенных величин энергии в квадрате, среднеквадратичное значение также известно как действующее значение , или виртуальное значение переменного тока.
Чтобы найти среднеквадратичное значение, умножьте значение пика на 0,707.
Чтобы найти среднеквадратичное значение из числа размаха до пика , сначала разделите на два, затем умножьте на 0,707. Электрические мощности и напряжения могут быть обременительными для манипулирования и расчета, поэтому обычной практикой является преобразование их в более удобную форму. Это децибел (дБ), описанный в разделе 2.5.
2.4.1 Давление
2.4.2 Интенсивность
2.4.1 Давление
Давление легче всего рассматривать как механическую силу. Это может быть вызвано движением поршня, как показано на рисунке 5. Если вращение вала с постоянной скоростью передается шатунной шейкой на поршень, как показано на рисунке, результатом является синусоидальное движение. Это создает волну акустического давления в виде синусоидальных колебаний в воде с областями сжатия и разрежения относительно среднего давления, см. Рис. 5. В акустике мы имеем дело с синусоидальными волнами аналогично электрическим синусоидальным волнам, обсуждаемым в разделе 2.2, т. Е. Выполненная работа или использованная мощность — это среднеквадратичное значение. Любое практическое измерение акустических волн производится путем наблюдения за электрическим выходным сигналом (синусоидальными волнами) чувствительного к давлению устройства (преобразователя). Другими словами, синусоидальная волна давления преобразуется в эквивалентную электрическую синусоиду, по которой могут быть определены акустические свойства.
Рис. 5.
Акустические волны — это форма энергии, которая может распространяться через среду с распределенной массой и упругостью, такую как вода.В любой точке, где эти волны находятся в воде, энергия присутствует в виде изменения в нормальном состоянии напряжения и деформации. Энергия вызывает силу, и колебания частиц, составляющих среду, передаются от точки к точке в воде со скоростью, зависящей от факторов, указанных в разделе 2.6.1.
Связь между давлением, скоростью частиц и величиной r c аналогична той, которая существует в электричестве между напряжением, током и сопротивлением (импедансом), разделы 2.1 и 2.2. Акустический импеданс rc определяется в терминах констант среды, где r — плотность в кг / м 3 , а c — скорость акустических волн в м / с, поэтому rc = кг / м 3 xm / s = кг / м 2 . с. Единица акустического импеданса известна как Рейл (в честь лорда Рэлея), и для морской воды она составляет приблизительно 1,54 x 10 6 Рейля.
Давление измеряется в микропаскалях (м Па). Один м Па равен 10 -6 Ньютон / м 2 .Микропаскали используются в качестве стандартной эталонной единицы, потому что Паскаль (1 Ньютон / м 2 ) всего в 10 раз отличается от предыдущего стандарта, шкалы m, которую можно увидеть в старых учебниках. Чтобы преобразовать любые цифры, указанные в дБ / 1 м b, необходимо добавить 100, например 120 дБ / 1 м b = 220 дБ / 1 м Па и -100 дБ / 1 В / 1 м b = -200 дБ / 1 В / 1 м Па. См. Приложение I и раздел 2.5.
2.4.2 Интенсивность
Рис. 6.
Интенсивность звука (I) определяется как количество энергии в секунду (мощность), проходящая через единицу площади перпендикулярно направлению распространения акустической волны.Эта концепция проиллюстрирована на рисунке 6.
В разделе 2.4.1 было указано, что давление, скорость частиц и r c аналогичны электрическим величинам напряжения, тока и сопротивления соответственно. Сила звука аналогична электрической мощности в зависимости от количества энергии и времени, в течение которого она течет или используется. Таким образом, уравнение 3 можно представить в акустических терминах как
Интенсивность (I) = p 2 / r c (6)
, то есть интенсивность пропорциональна квадрату давления, деленному на акустический импеданс.
Интенсивность акустической волны относится к плоской волне со среднеквадратичным давлением, равным 1 м Па, на расстоянии 1 м от источника. С точки зрения акустики рыболовства плоская волна может быть описана как волна, у которой не наблюдается значительной кривизны своего волнового фронта по длине или протяженности цели.
2.5.1 Мощность и интенсивность Соотношения
2.5.2 Напряжение и давление Передаточные числа
Децибел (дБ) — это одна десятая бел, единица, названная в честь Александра Грэхема Белла, известного изобретателя.Впервые он был использован в связи с телефонными линиями передачи (Мартин, 1929), но теперь является общим для всех отраслей электроники и акустики.
Децибел НЕ является единицей измеряемой величины, такой как метры, килограммы или секунды. Это логарифм с основанием 10 отношения, определяющего соотношение между величинами. В электронике часто наблюдаются очень большие различия или изменения в мощности или напряжении между одной частью системы и другой. В подводной акустике большие различия возникают в интенсивности и давлении, например, из-за потерь при распространении.Преобразуя эти изменения в децибелы с помощью логарифмов, можно упростить цифры и расчеты выигрышей или потерь. Поскольку децибел основан на логарифмах, умножение и деление преобразуются в сложение и вычитание.
2.5.1 Коэффициенты мощности и интенсивности
Электрическая мощность (Вт, ватт) аналогична разделу 2.4 акустической интенсивности (I), и для обоих используется тот же коэффициент 10 log 10 , далее в руководстве будет использоваться 10 log. Обозначение в децибелах для мощности W:
N = 10 log Вт / Wo дБ
, где Wo — выбранная эталонная мощность, аналогично для интенсивности I
N = 10 log I / Io дБ (7)
, где Io — выбранная эталонная интенсивность.
Логарифмическое соотношение между двумя величинами, одна из которых в два раза больше другой, может быть log 2/1 или log 1/2 в зависимости от ссылки. В логах соотношение становится +0,3010 и -0,3010 соответственно. При изменении их на децибелы в случае мощности или интенсивности отношения умножаются на 10.
10 log 2/1 = +3 дБ и 10 log 1/2 = -3 дБ
Другими словами, +3 дБ означает, что величина вдвое больше эталона, а -3 дБ означает, что это только половина эталона.сходным образом
10 log 10/1 = +10 дБ и 10 log 1/10 = -10 дБ
10 log 100/1 = +20 дБ и 10 log 1/100 = -20 дБ.
В таблице 1 показано количество децибел, эквивалентное отношениям мощности и интенсивности. Коэффициент, относящийся к числу децибел, не указанному в таблице, можно найти с помощью
соотношение = Antilog (ndB / 10) или 10 n / 10
в качестве альтернативы числа могут быть выбраны из таблицы дБ, чтобы составить число, которое нужно преобразовать, например 75,5 дБ — это 70 + 3 + 2 + 0.5 и соответствующие отношения равны 10 7 , 2, 1,58 и 1,12, что при умножении на вместе = 2 x 1,58 x 1,12 x 10 7 = 3,539 x 10 7 .
В таблице 1 показано количество децибел, эквивалентное отношениям мощности и интенсивности.
Таблица 1.
Количество децибел | Соотношение мощности (Вт) и интенсивности (I) | |
+ дБ | -дБ | |
0.1 | 1,02 | 0,98 |
0,5 | 1,12 | 0,89 |
1 | 1,26 | 0.79 |
2 | 1,58 | 0,63 |
3 | 2,00 | 0,5 |
6 | 3.98 | 0,25 |
10 | 10,00 | 0,10 |
20 | 10 2 | 0,01 |
30 | 10 3 | 10 -3 |
40 | 10 4 | 10 -4 |
50 | 10 5 | 10 -5 |
60 | 10 6 | 10 -6 |
70 | 10 7 | 10 -7 |
80 | 10 8 | 10 -8 |
90 | 10 9 | 10 -9 |
100 | 10 10 | 10 -10 |
2.5.2 Коэффициенты напряжения и давления
В разделе 2.1 было показано, что мощность пропорциональна квадрату напряжения; такая же взаимосвязь между интенсивностью звука и давлением (раздел 2.4).
Следовательно, обозначение децибел
10 log (V 2 / R) / (Vo 2 / R) = 20 log V / Vo (8)
и (9)
, где Vo и p 0 — соответствующие контрольные величины, а rc — удельное акустическое сопротивление воды (аналогично сопротивлению в электрической цепи, (r — плотность в кг / м) 3 и c = скорость акустической волны в м / с).
Из примера, приведенного в предыдущем разделе, было показано, что логарифмическое соотношение между двумя величинами мощности или интенсивности, одно из которых в два раза больше другого, составляет +3,010 и -3,010 в зависимости от того, какая величина берется в качестве эталонной. .
При изменении их на децибелы напряжения или давления , логарифмы соотношений должны быть умножены на 20
20 log 2/1 = +6 дБ и 20 log 1/2 = -6 дБ.
В таблице 2 показано количество децибел, эквивалентное отношениям напряжения и давления.
Таблица 2.
Количество децибел | Напряжение и коэффициент давления | |
+ дБ | -дБ | |
0,1 | 1.01 | 0,99 |
0,5 | 1,06 | 0,98 |
1 | 1,122 | 0,84 |
2 | 1.26 | 0,79 |
3 | 1,41 | 0,71 |
6 | 2,0 | 0,50 |
10 | 3.16 | 0,316 |
20 | 10,00 | 0,1 |
30 | 31,62 | 0,0316 |
40 | 10 2 | 10 -2 |
50 | 316.0 | 0,00316 |
60 | 10 3 | 10 -3 |
70 | 3162 | 3,162 x 10 -3 |
80 | 10 4 | 10 -4 |
90 | 31622 | 3.162 х 10 -4 |
100 | 10 5 | 10 -5 |
Опорное значение дБ для напряжения часто составляет 1 Вольт, и в этом случае измерение менее 1 В должно быть -n дБ / 1 Вольт.
10 -5 Вольт = 20 x — 5 = -100 дБ относительно 1 В
1 м В = 10 -6 Вольт = 20 x — 6 = -120 дБ относительно 1 В.
На рисунке 7 показана эта взаимосвязь в полезном диапазоне напряжений.
Рисунок 7.
2.6.1 Поглощение Акустические волны
Скорость акустических волн в море обозначается символом c и измеряется в метрах в секунду (м / с). Это переменная, зависящая от температуры, солености и глубины воды, хотя фактор глубины не имеет значения для акустики рыболовства.
Глубину можно измерить правильно, только если известна скорость акустической волны для исследуемой области. На рисунке 8 показано изменение скорости в зависимости от температуры и для ряда соленостей. Из этого рисунка видно, что между летом и зимой могут происходить изменения порядка 2 1/2 %, но обычно этого считают недостаточным, чтобы оправдать корректировку системы синхронизации эхолота.
Рисунок 8.
Скорость акустической волны равна
c = fl (10)
где
c в м / с
f в Гц
l — длина волны (см. Раздел 2.7) в метрах.
Частота f фиксирована в эхолоте, но длина волны изменяется в зависимости от скорости волны.
l = п / ш (11)
, предполагая скорость 1500 м / с (наиболее часто используемый показатель) и частоту 38000 Гц, то есть 38 кГц, длина волны равна
l = 1500/38000 = 0,0395 м или 39,5 мм
Если скорость увеличивается на 20 м / с до 1520 м / с, длина волны увеличивается на 0,5 мм до 40 мм, незначительное изменение. Хотя термоклины (слои воды, температура в которых резко меняется с глубиной) возникают часто по разным причинам, последующее изменение скорости акустических волн не имеет значения для целей эхолокации. I.е. разница в акустическом импедансе r c слишком мала, чтобы ее можно было обнаружить.
2.6.1 Поглощение акустических волн
Когда акустические волны проходят через воду, часть энергии поглощается химическими процессами. Доля преобразованной энергии должна рассматриваться как акустические потери и приниматься во внимание при расчете результатов. Потери линейны с расстоянием, т. Е. На каждый пройденный метр теряется постоянная часть акустической энергии.
Поглощение обозначается символом a и выражается в децибелах на километр (дБ / км), оно увеличивается с увеличением частоты, как показано на рисунке 9.
Рисунок 9.
Имеется заметная температурная зависимость, но она имеет другие характеристики; в нижней части шкалы частот ниже 70 кГц, где есть отрицательный градиент, повышение температуры приводит к уменьшению a. На частоте 120 кГц градиент сначала положительный, затем отрицательный, как на рисунке 10 (а). Эти цифры рассчитаны по формуле, полученной Фишером и Симмонсом (1977) после серии экспериментов, и, как полагают, дают наиболее точные результаты, доступные в настоящее время для акустических работ в рыболовстве.Необходимы дальнейшие исследования, чтобы подтвердить достоверность результатов для всех условий температуры и солености, которые могут встретиться при практических исследованиях. Тем не менее, рекомендуется использовать графики на рисунках 9 и 10 (a) (b) (c) для выбора значения a для опросов, пока не появятся дальнейшие результаты. Вариация значений поглощения для изменений солености на обычно используемых частотах акустической съемки показана на Рисунке 10 (b) (c).
Рисунок 10. (а)
Рисунок 10.(b)
Рисунок 10. (c)
Частота синусоиды определяется как количество пиков одной полярности, возникающих за одну секунду. Частота измеряется в циклах, то есть в количестве полных синусоидальных циклов за одну секунду, но теперь единицей измерения частоты является герц (Гц) после имени физика с таким именем. Таким образом, на рисунке 11 синусоида имеет частоту 5 Гц.
Термин w использовался без объяснения причин в разделе 2.3. Он обозначает угловую скорость волны, то есть скорость, с которой частица движется через цикл, и равна 2p f. Для частоты 5 Гц угловая скорость составляет 31,416 радиан / сек.
Периодическое время (t) — это время , необходимое для завершения цикла или появления соседних пиков, см. Также рисунок 11. Синусоида в разделе 2.3 была определена как A max sin wt и завершение цикл, когда wt = 2p, поэтому t = 2p / 2p f = 1 / f, поэтому периодическое время волны 5 Гц составляет 1/5 секунды.
Рис. 11.
В акустике рыболовства нас интересует ограниченное количество точечных частот, и большая часть работы была сосредоточена на одной из них или близкой к ней, то есть 38 кГц. Хотя удобно говорить об одной частоте, эхолот не может работать, если он не работает в пределах полосы частот, а та, которая всегда указывается, номинально является центральной частотой полосы. Таким образом, мощность передается одновременно на всех частотах в пределах полосы пропускания, и это обсуждается более подробно позже в 3.1.2.
Частота синусоидального сигнала не зависит от среды, в которую он вводится, т. Е. Количество циклов для прохождения фиксированной точки за одну секунду является постоянным. Но другая характеристика синусоиды, длина волны (l), полностью зависит от физических свойств среды, в которой распространяется волна. Это связано с тем, что скорость волны определяется плотностью и модулем объемной упругости среды.
Длина волны определяется как расстояние между соседними пиками или впадинами синусоиды, рисунок 12, т.е.е. физическое измерение в метрах (м), относящееся к этому расстоянию, чем быстрее распространяется волна, тем больше l. Когда мы выбираем частоту работы эхолота, мы знаем, что среда, в которой он будет работать, — это вода, поэтому можно рассчитать длину волны в довольно близких пределах, если скорость акустических волн в определенном объеме воды равна известный. Это связано с тем, что скорость (c) распространения волны связана с частотой (f) и длиной волны (l), как показано в уравнении. 11 то есть l = c / f.
Важность длины волны станет очевидной в следующем разделе, где мы обсудим некоторые эффекты взаимодействия акустических волн с рыбами.
Рисунок 12.
Когда акустическая волна поражает рыбу, часть энергии отражается, и это называется эхом. Факторы, от которых зависит эта величина, не совсем понятны, но в этом разделе мы рассмотрим некоторые из основных теорий.
Когда плоская волна встречается с границей двух различных сред e.грамм. вода и тело рыбы могут частично отражаться. Если рыба имеет размеры того же порядка, что и длина акустической волны, интенсивность, отраженная в любом конкретном направлении, зависит от соотношения импеданса воды и рыбы, а также формы и ориентации рыбы.
Для начала предположим, что рыба остается той же формы, пока происходит ее взаимодействие с акустической волной. Таким образом, мы можем смотреть на диаграмму направленности , когда ориентация рыбы изменяется со временем.Если произвольная опорная ось проходит через рыбу, ориентация которой изменяется, и амплитуда эхо-сигнала измеряется как функция направления этой оси, результат может быть отображен в виде полярной диаграммы. Гипотетический график показан на рисунке 13 (а), но, конечно, это только для одной плоскости, вся диаграмма трехмерна и будет выглядеть примерно как шар с выступающими шишками. На следующем рисунке 13 (b) показан тот же результат, что и раньше, но в линейном угловом масштабе.
Рисунок 13.(a)
Рис. 13. (b)
Если бы рыба постоянно вращалась в плоскости, для которой был нарисован Рис. 13, амплитуда эхо-сигнала будет колебаться, и эффект будет таким, что модулирует эхо-волна. Модуляция означает «запечатлеть информацию», и это видно на рисунке 14, где колебания амплитуды высокочастотной акустической волны обусловлены информацией «о количестве и относительном размере комков или лепестков диаграммы направленности».
Рис. 14.
Фундаментальным свойством таких шаблонов является близость лепестков и, следовательно, скорость, с которой последовательные максимумы и минимумы эхо-сигнала возникают при вращении рыбы, то есть угловая частота доли. Шаблоны с разными угловыми частотами показаны на рисунках 15a и b, и ясно, что (b) имеет гораздо более высокую угловую частоту, чем (a), что приведет к более быстрым колебаниям эхо-сигнала. Рыба может обладать обоими этими паттернами, потому что она имеет большой размер в одном направлении и гораздо меньший размер под прямым углом к нему, но на практике мы обычно имеем дело только с небольшими вариациями спинного аспекта.
Рис. 15.
Присутствие рыбы в «акустическом поле» (окружающие акустические волны) влияет на изменение поля вокруг поверхности рыбы путем добавления так называемого поля возмущения ( возмущение означает сильное беспокойство). Это как если бы поле возмущения возникает от виртуальных источников акустической энергии внутри тела рыбы. Другими словами, рыба, кажется, генерирует излучающую наружу волновую систему, извлекая поток энергии из проходящих падающих волн и повторно излучающий его во всех направлениях.Вокруг поверхности рыбы поле возмущения имеет «волнистость», которая соответствует волнам падающего поля, поэтому, конечно, существует конечное число из длин волн , возникающих в зависимости от длины рыбы. Количество лепестков в диаграмме направленности зависит от размера рыбы в длинах волн , а не от ее абсолютного размера, например. при 38 кГц рыба 40 см имеет 10 длин волн, а при 120 кГц — 32 l. Размер долей в относительной шкале амплитуд определяется размером рыбы.
Хотя существует максимальная возможных амплитуд эхосигналов от любой конкретной рыбы, фактический полученный размер зависит от угла лепестка или лепестков диаграммы направленности, «указывающих» в направлении акустического эхолота. ось, см. рисунок 16.
Рис. 16.
До сих пор обсуждение предполагало, что рыба остается той же формы, но это неверно, форма меняется со временем, когда рыба плавает.Эффект состоит в том, что виртуальные источники в пределах его объема немного изменяют положение, что вызывает другой вид модуляции амплитуды эха. Таким образом, очевидно, что попытка предсказать или смоделировать реакцию рыбы является сложной задачей, поэтому мы должны проводить измерения либо отдельных особей, либо известных количеств, и это обсуждается позже в разделах 4.5 и 4.6. Раздел 2.8 основан на заметках, написанных покойным доктором В. Г. Уэлсби. В следующей главе рассматриваются инструменты, необходимые для акустики рыболовства.
Что такое коэффициент мощности (Cosθ)? Cos fi или Pf Определения и формулы
Определения и формулы коэффициента мощностиВ электротехнике коэффициент мощности относится только и только к цепям переменного тока, т.е. в цепях постоянного тока отсутствует коэффициент мощности (Pf) из-за нуля разность частот и фазовых углов (Φ) между током и напряжением.
Что такое коэффициент мощности?Коэффициент мощности может быть определен тремя следующими определениями и формами.
1). Косинус угла между током и напряжением называется коэффициентом мощности.
Где:
- P = мощность в ваттах
- V = напряжение в вольтах
- I = ток в амперах
- W = активная мощность в ваттах
- VA = полная мощность в вольт-амперах или кВА
- Cosθ = коэффициент мощности
2). Соотношение между сопротивлением и импедансом в цепи переменного тока известно как коэффициент мощности.
Cosθ = R / Z
Где:
- R = Сопротивление в Ом (Ом)
- Z = Импеданс (сопротивление в цепях переменного тока, т.е. X L , X C и R , известное как Индуктивное реактивное сопротивление , емкостное реактивное сопротивление и (сопротивление соответственно) в Ом (Ом)
- Cosθ = Коэффициент мощности
Импеданс «Z» — это полное сопротивление цепи переменного тока, т.е.
Z = √ [R 2 + (X L + X C ) 2 ]
Где:
- X L = 2π f L… L — индуктивность по Генри
- X C = 1 / 2π f C… C — емкость в фарадах
Связанное сообщение: Разница между активной и реактивной мощностью
3). Соотношение между активной мощностью и полной мощностью в вольтах-амперах называется коэффициентом мощности.
- Cosθ = Активная мощность / Кажущаяся мощность Мощность
- Cosθ = P / S
- Cosθ = кВт / кВА
Где мощность кВт = 9045 9045
- 9045 киловатт
- кВА = S = полная мощность в киловольт-амперах или ваттах
- Cosθ = коэффициент мощности
Формула коэффициента мощности в трехфазных цепях переменного тока
Коэффициент мощности Cosθ = P / √3 В L x I L … Линейный ток и напряжение
Коэффициент мощности Cosθ = P / √3 V P x I P … Фазный ток и напряжение
Треугольник коэффициента мощности и примерыПивная аналогия активной или истинной мощности , реактивной мощности, полной мощности и коэффициента мощности.
Аналогия мешка для микросхем истинной или активной мощности , реактивной мощности, полной мощности и коэффициента мощности.
Полезно знать:
В чисто резистивной цепи коэффициент мощности равен 1 из-за нулевой разности фаз (Φ) между током и напряжением.
В чисто емкостной цепи коэффициент мощности является опережающим из-за запаздывающих VAR. То есть напряжение отстает на 90 ° от тока. Другими словами, ток опережает напряжение на 90 ° (ток и напряжение на 90 ° не совпадают по фазе друг с другом, при этом ток идет впереди, а напряжение отстает).
В чисто индуктивной цепи коэффициент мощности отстает из-за опережающих VAR, т.е. напряжение опережает на 90 ° от тока. Другими словами, ток отстает на 90 ° от напряжения (ток и напряжение на 90 ° не совпадают по фазе друг с другом, другие — где напряжение впереди, а ток отстает).
Калькулятор силы тока — Deelat Industrial Australia
Используйте этот калькулятор для определения электрического тока в амперах (A).
Текущий Тип Постоянный токAC — однофазныйAC — трехфазный
Тип напряжения Линия к линии Линия к нейтрали
Как пользоваться калькулятором силы тока
- Выберите тип тока (постоянный ток, переменный ток — однофазный, или переменный — трехфазный)
- Введите мощность в ваттах
- Введите напряжение в вольтах
- (для систем переменного тока) Введите коэффициент мощности
- (только для трехфазного переменного тока) Введите тип напряжения: от линии к линии или от линии к нейтрали
- Нажмите РАССЧИТАТЬ
Преобразование ватт в амперы (система постоянного тока)
Вычислить ток I в амперах (A) можно, разделив мощность P в ваттах (Вт) на напряжение V в вольтах (В):
Преобразование ватт в амперы (однофазная система переменного тока)
Определите фазный ток I в амперах (A), разделив мощность P в ваттах (Вт) на коэффициент мощности PF, умноженный на действующее значение напряжения V в вольтах (В):
(Коэффициент мощности — это отношение реальной мощности, протекающей к нагрузке, к полной мощности в цепи.Значения коэффициента мощности могут находиться в диапазоне от 0 до 1.
Среднеквадратичное значение напряжения — это квадратный корень из среднего за один цикл квадрата мгновенного напряжения.)
Преобразование ватт в амперы (трехфазная система переменного тока)
Линейное напряжение:
Вычислите фазный ток I в амперах (A), разделив мощность P в ваттах (Вт) на квадратный корень из 3-кратного коэффициента мощности PF, умноженного на среднеквадратичное напряжение VL-L между линиями в вольтах (В):
(Коэффициент мощности — это отношение реальной мощности, протекающей к нагрузке, к полной мощности в цепи.Значения коэффициента мощности могут находиться в диапазоне от 0 до 1.
Линейное напряжение — это напряжение, измеренное между любыми двумя линиями в трехфазной цепи.)
Напряжение между фазой и нейтралью:
Определите фазный ток I в амперах (A), разделив мощность P в ваттах (Вт) на 3-кратный коэффициент мощности PF, умноженный на действующее значение напряжения VL-N между фазой и нейтралью в вольтах (В):
(Коэффициент мощности — это отношение реальной мощности, протекающей к нагрузке, к полной мощности в цепи.
