Катушка индуктивности в цепи постоянного тока
Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.
Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.
Это понятно из формулы:
Предположим, что ток iL изменился скачком, то есть:
А значит, что и напряжение в данном случае будет бесконечно велико:
Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.
На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.
Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону.
Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.
Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.
Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн.
Скачать файл Multisim 13.0
Рассчитаем время, за которое ток в цепи достигает установившегося значения:
Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”.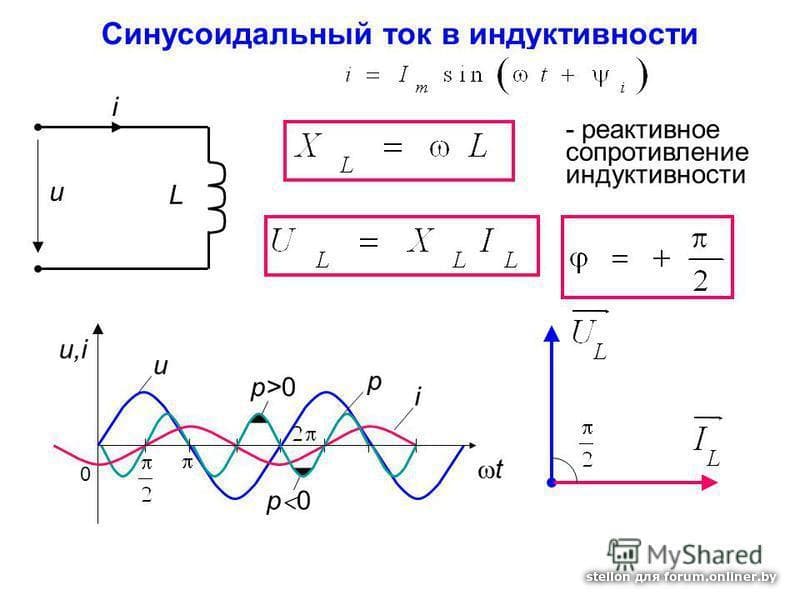 Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.
Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.
Индуктивность и емкость в цепи переменного тока
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
i = Iм sin ωt, (26.8)
u = Uм sin (ϕ + ωt), (26.9)
e = Ɛm sin (ψ + ωt). (26.10)
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению  18):
18):
R=(p0l/S)(1 + at).
В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:
ХL = ωL. (26.11)
(26.11)
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;
Оно обратно пропорционально емкости С и круговой частоте ω;
Хс = 1/ωС. (26.12)
Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока.
Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:
X = XL—XC (26.13)
и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.
В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:
P = IU cos ϕ. (26.14)
(26.14)
Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:
Р = I2R. (26.15)
Из (26. 14) видно, что для увеличения активной мощности
Особенности применения силовых индуктивностей | «ЛЭПКОС», ИЦ «Северо-Западная Лаборатория»
Поскольку технические параметры современных электронных устройств постоянно совершенствуются, для БИС, используемых в таких изделиях, характерно снижение напряжения питания. В этой связи, энергопотребление может уменьшаться, а скорость работы увеличиваться. Однако снижение напряжения источника питания также предполагает более жесткие требования, учитывающие колебания напряжения, что вприводит к необходимости использования высокопроизводительных DC-DC преобразователей. Силовые индуктивности при этом являются важными компонентами, существенно влияющими на эффективность преобразователей.
Компания TDK выпускает широкую линейку силовых индуктивностей. В данной статье рассмотрены эффективные способы применения данных компонентов, а также ключевые особенности при выборе катушек индуктивности в соответствии с требуемыми характеристиками преобразователей постоянного тока.
Несмотря на то, что катушка индуктивности может плавно пропускать постоянный ток, при любом изменении его величины она будет генерировать ЭДС, препятствующую этим колебаниям. Такое явление известно как самоиндукция. При подключении к источнику переменного тока катушка индуктивности оказывает сопротивление проходящему по ней переменному току. Таким образом, если ток прошел через индуктивность, он будет накапливаться в виде энергии, а если процесс передачи тока нарушен, эта энергия будет разряжаться. Данная отличительная особенность эффективно используется в цепях источников питания, в преобразователях постоянного тока.
На рисунке 1 представлена основная схема понижающего преобразователя постоянного тока (диодный выпрямитель).
Сложности в процессе разработки силовых индуктивностей обусловлены изменчивостью характеристик в зависимости от степени воздействия таких факторов как температура и величина тока. Так, например, индуктивность (L) имеет тенденцию к снижению, поскольку величина тока становится больше (характеристика наложения тока DC), а рост температуры, вызванный повышением силы тока, может вызвать изменение как магнитной проницаемости (μ) сердечника, так и индукции насыщения (Bs). Даже при одинаковых значениях индуктивности сопротивление постоянному току (Rdc) будет меняться в зависимости от толщины обмотки и количества витков, вызывающих изменения в степени тепловыделения. Различия в структуре магнитного экрана также могут влиять на шумовые характеристики. Эти параметры имеют сложную компромиссную взаимосвязь, поэтому крайне важно выбрать наиболее подходящую индуктивность для требуемой области применения с учетом эффективности, размеров и стоимости преобразователей постоянного тока.
Ключевой момент: Силовые индуктивности могут быть классифицированы на моточные, многослойные и тонкопленочные в зависимости от различий в методах изготовления, с сердечниками на основе феррита или порошкового сплава. Ферриты характеризуются высокими значениями проницаемости (μ) и индуктивности, в то время как сердечники на основе порошковых материалов имеют высокие значения индукции насыщения, что делает их подходящими для использования при больших величинах тока.
Ключевой момент:
Выделяется два определения номинального тока для силовых индуктивностей: допустимый ток при суперпозиции DC и допустимый ток при возрастании температуры. Если сердечник войдет в насыщение, величина его индуктивности будет снижена.
Рекомендуемая величина максимального тока, который может быть передан без достижения магнитного насыщения, соответствует допустимому току при наложении постоянного тока (пример: падение на 40% от начального значения индуктивности).
Ключевой момент: К основным типам потерь, которые могут вызвать скачок температуры можно отнести: потери в меди, появляющиеся из-за обмотки проводом, а также потери в магнитопроводе.
Потери в меди возникают из-за сопротивления DC (RDC) обмотки и увеличиваются пропорционально величине тока в квадрате. Кроме того, когда частота переменного тока становится выше, существует тенденция концентрации тока в области недалеко от поверхности проводника и увеличения эффективного значения сопротивления (скин-эффект). В высокочастотном диапазоне также добавляются потери в меди, возникающие в результате протекания переменного тока.
Потери в магнитопроводе соответствуют сумме потерь на вихревые токи и на гистерезис. Потери на вихревые токи пропорциональны квадрату частоты, поэтому в высокочастотных областях потери в сердечнике, вызванные потерями на вихревые токи, становятся больше. Одним из ключевых моментов для повышения эффективности является выбор материалов сердечника, характеризующихся низкими потерями даже в высокочастотном диапазоне.
Ключевой момент:
Потери в меди становятся доминирующими в случае подключения умеренной или интенсивной нагрузки, в то время как вклад потерь в магнитопроводе становится существенным уже при включении небольшой нагрузки. Для тока, протекающего через индуктивность при включении умеренной и большой нагрузки, вклад смещения (DC bias current) достаточно велик, в этой связи потери в меди, появляющиеся в результате сопротивления постоянному току (RDC), становятся доминирующими. С другой стороны, при подключении неполной нагрузки тока смещения (DC bias) практически нет. В этой связи, уровень потерь в меди снижается, но поскольку операция переключения с постоянной частотой выполняется даже в режиме ожидания, потери в сердечнике из-за особенностей материала феррита становятся существенными , а эффективность значительно уменьшается (рисунок 3).
В этой связи, уровень потерь в меди снижается, но поскольку операция переключения с постоянной частотой выполняется даже в режиме ожидания, потери в сердечнике из-за особенностей материала феррита становятся существенными , а эффективность значительно уменьшается (рисунок 3).
Ключевой момент: использование компонентов в режиме прерывистого тока влияет на стабильность источников питания.
В силовых индуктивностях, применяемых в понижающих DC-DC преобразователях, будет протекать пульсирующий ток (ΔIL) с формой непрерывных треугольных волн в сочетании с операцией ВКЛ/ВЫКЛ для переключающих элементов (рисунок 4).
В ходе подключения нагрузки от умеренной до интенсивной ΔIL будет накладываться на смещение по постоянному току, поэтому ток индуктивности будет протекать непрерывно (режим непрерывного тока (Iвых > 1 / 2ΔIL)). Однако в преобразователях постоянного тока с диодным выпрямлением при подключении легкой нагрузки, где Iвых < 1/2ΔIL, будут периоды, когда ток индуктивности станет нулевым. В этом состоянии (режим прерывистого тока) ток индуктивности будет периодически прерываться, что, в свою очередь, будет влиять на стабильность источника питания. Кроме того, если катушка индуктивности работает в режиме прерывистого тока, также будет возникать акустический шум. В результате переключения будет генерироваться импульсный сигнал напряжения, что будет способствовать появлению шума.
В этом состоянии (режим прерывистого тока) ток индуктивности будет периодически прерываться, что, в свою очередь, будет влиять на стабильность источника питания. Кроме того, если катушка индуктивности работает в режиме прерывистого тока, также будет возникать акустический шум. В результате переключения будет генерироваться импульсный сигнал напряжения, что будет способствовать появлению шума.
Ключевой момент: Необходимо задавать такую величину индуктивности, чтобы вклад пульсирующего тока составлял 20-30% от номинального тока.
Величина пульсирующего тока связана с индуктивностью. В этой связи, преобразователи постоянного тока с диодным выпрямлением должны быть спроектированы таким образом, чтобы избежать проблем, связанных с работой в режиме прерывистого тока путем ограничения вклада пульсирующего тока. Если предпочтительно применение компонента с небольшим значением индуктивности из-за размеров или стоимости, величина пульсирующего тока станет больше. И наоборот, если требуется уменьшить пульсирующий ток, необходима большая индуктивность, что может привести к недостаткам, связанным с размером или стоимостью, а также вызвать ухудшение характеристик переходного процесса при внезапных изменениях нагрузки. Таким образом, обычно принято указывать такое значение индуктивности, при которой величина пульсирующего тока будет составлять 20-30% от номинального (прерывистый ток будет фиксироваться в области, когда пульсирующий ток будет составлять примерно 10% от номинального).
И наоборот, если требуется уменьшить пульсирующий ток, необходима большая индуктивность, что может привести к недостаткам, связанным с размером или стоимостью, а также вызвать ухудшение характеристик переходного процесса при внезапных изменениях нагрузки. Таким образом, обычно принято указывать такое значение индуктивности, при которой величина пульсирующего тока будет составлять 20-30% от номинального (прерывистый ток будет фиксироваться в области, когда пульсирующий ток будет составлять примерно 10% от номинального).
Ключевой момент: выбор правильного подхода при снижении значения индуктивности может улучшить характеристики отклика нагрузки .
В случае, когда, например, отмечается внезапный рост нагрузки, будет происходить падение выходного напряжения. В ходе последующего восстановления через индуктивность в течение короткого времени может протекать аномально большой пиковый ток для зарядки выходного конденсатора совместно с током нагрузки. Однако, если будет установлено небольшое значение пульсирующего тока, достичь требуемых характеристик переходного процесса для быстрого восстановления после внезапного падения выходного напряжения будет невозможно. Одним из способов решения этой ситуации могло бы стать уменьшение значения индуктивности и, таким образом, увеличение величины пульсирующего тока. Как показано на рисунке 6, выходное напряжение существенно падает, если характеристики отклика нагрузки плохие. В то же время, если значение индуктивности соответствующим образом снижается, и пульсирующий ток увеличивается, изменение величины тока индуктивности становится более существенным, что вызывает снижение вклада падения напряжения и способствует более быстрому восстановлению. Однако при понижении значения индуктивности важно использовать настройку, которая учитывает общий баланс системы.
Однако, если будет установлено небольшое значение пульсирующего тока, достичь требуемых характеристик переходного процесса для быстрого восстановления после внезапного падения выходного напряжения будет невозможно. Одним из способов решения этой ситуации могло бы стать уменьшение значения индуктивности и, таким образом, увеличение величины пульсирующего тока. Как показано на рисунке 6, выходное напряжение существенно падает, если характеристики отклика нагрузки плохие. В то же время, если значение индуктивности соответствующим образом снижается, и пульсирующий ток увеличивается, изменение величины тока индуктивности становится более существенным, что вызывает снижение вклада падения напряжения и способствует более быстрому восстановлению. Однако при понижении значения индуктивности важно использовать настройку, которая учитывает общий баланс системы.
Электричество и магнетизм
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре
Введем коэффициент пропорциональности L
|
|
(8.16) |
Коэффициент пропорциональности L называется индуктивностью контура.
|
Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока. |
Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.
|
В системе СИ единицей измерения индуктивности является генри (Гн)
|
Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.
|
Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции. |
Видео 8. 13. Закон Фарадея. Явление самоиндукции.
13. Закон Фарадея. Явление самоиндукции.
Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.
Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
|
|
(8.17) |
Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков
,
что необходимо учитывать при дифференцировании
Подставляя это выражение в (8.17), получаем для неподвижного контура всреде
|
|
(8. |
Если же индуктивность контура не зависит от силы тока в нём, то имеем
|
|
(8.19) |
Мы приходим к закону самоиндукции. В этом простейшем случае:
|
В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи. |
Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна
где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
|
|
(8.20) |
где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
|
|
(8.21) |
Рис. 8.31. Индуктивность соленоида
При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Ток через индуктивность и напряжение на емкости не может изменяться скачком
Содержание:
Ток через индуктивность и напряжение на емкости не может изменяться скачком
Ток, протекающий через индуктивность, и напряжение на емкости не изменяются внезапно *. Доказательство того, что ток через индуктивность не может резко измениться, основано на примере схемы на рисунке. 293.
- Согласно второму закону Кирхгофа, L ~ + Ri ~ E dt 1, ток I и ЭДС E могут принимать только конечное значение (ns бесконечно велико). Предположим, что
ток я быстро меняется. Людмила Фирмаль
Скачок тока означает, что бесконечно короткий интервал времени A / стремится к нулю, а ток изменяется на конечное значение A /. Также = Ко. x) магнитного поля индукционной катушки также резко изменится. Окончательное приращение энергии магнитного поля и wM может быть выражено как произведение мощности источника энергии P на время A /, в течение которого происходит приращение энергии.
x) магнитного поля индукционной катушки также резко изменится. Окончательное приращение энергии магнитного поля и wM может быть выражено как произведение мощности источника энергии P на время A /, в течение которого происходит приращение энергии.
Следовательно, d / -> o D / Однако ни один из источников энергии не может обеспечить бесконечно большое количество энергии в цепи. Ток, протекающий через L, не может внезапно измениться, но изменяется
напряжение индуктивности, равное быстрому изменению. Людмила Фирмаль
Это не противоречит второму закону Кирхгофа и энергетическим отношениям. Доказательство того, что напряжение на емкости не изменяется внезапно, выполняется так же, как и доказательство исходного положения. а) б) Рисунок 294 Давайте рассмотрим простейшую схему с емкостным сопротивлением (Рисунок 294, а).
Для нее создайте формулу согласно второму закону Кирхгофа. Ri + = E Источником и конечным значением является напряжение емкости. , dt, то = (10.4), при условии, что напряжение u быстро изменяется, левая часть уравнения (10.4) не равна правой стороне.
, dt, то = (10.4), при условии, что напряжение u быстро изменяется, левая часть уравнения (10.4) не равна правой стороне.
Таким образом, предположение о возможности внезапного изменения напряжения на емкости противоречит второму закону Кирхгофа. Можно показать, что предположение о возможности прыжка также противоречит соотношению энергии *. * Это доказательство основано на соотношении энергий и выполняется так же, как доказательство невозможности скачка тока.
* Вы можете только плавно измениться без прыжков. Однако ток, протекающий через емкость, равную, может измениться при прыжке. Это согласуется со вторым законом Кирхгофа и энергетическими отношениями. Из двух основных пунктов, приведенных выше, следуют два закона о исправлении.
Смотрите также:
Индуктивность в автосигнализации
Радиодеталь под названием индуктивность представляет собой простой провод, скрученный в виде спирали или мотка. Поэтому ее часто называют катушкой индуктивности или просто катушкой. Катушки обычно многослойные (то есть провод уложен в несколько слоев), и намотаны на специальный сердечник, который усиливает ее индуктивные свойства.
Катушки обычно многослойные (то есть провод уложен в несколько слоев), и намотаны на специальный сердечник, который усиливает ее индуктивные свойства.
Рисунок 32. Внешний вид катушек индуктивности |
Для постоянного тока катушка является обычным проводником, обладающим только сопротивлением. Однако, совсем по другому через катушку будет проходить ток переменный. Катушка, образно говоря, препятствует любому изменению тока: если ток нарастает, индуктивность будет мешать увеличению тока, а если ток уменьшается — будет стремиться ток сохранить. Понять как работает индуктивность можно на простом примере инерции. Пробуем толкнуть не заведенный автомобиль — это потребует приложения некоторых усилий, так как автомобиль обладает большой массой. Однако, для того, чтобы остановить уже разогнавшийся автомобиль потребуется приложение немалых усилий.
Катушка индуктивности обладает двумя параметрами, на которые следует обратить внимание — это собственно индуктивность, которая измеряется в Генри, и допустимый ток.
12. Единицы индуктивности
1 мГн (один миллигенри) = 0,001 Гн (одна тысячная генри) 1 мкГн (один микрогенри) = 0,000 001 Гн (одна миллионная генри)
От величины индуктивности зависит то, насколько сильно катушка будет сопротивляться изменению тока: чем этот параметр больше, тем сложнее переменному току «преодолеть» катушку, а потом сложнее «остановиться».
На этот параметр оказывают влияние многие факторы: это и количество витков в катушке, и ее диаметр, и размеры, и материал сердечника. На некоторых катушках индуктивности предусмотрена возможность регулировки, для чего сердечник может перемещаться вдоль ее оси.
Рисунок 33. Катушка индуктивности с подстройкой |
Величина индуктивности, как правило, наносится на корпус катушки либо в виде цифробуквенной маркировки, либо в виде цветных полос или точек.
Первые две цифры указывают значение в микрогенри (мкГн, рН), последняя — количество нулей. Следующая за цифрами буква указывает на допуск (насколько реальная индуктивность может отличаться от указанной в маркировке цифры). Например, код 101J обозначает 100 мкГн с допуском ±5%. Если последняя буква не указывается — допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.
Следующая за цифрами буква указывает на допуск (насколько реальная индуктивность может отличаться от указанной в маркировке цифры). Например, код 101J обозначает 100 мкГн с допуском ±5%. Если последняя буква не указывается — допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.
Допуск может обозначаться также другими буквами: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%. Иногда катушки индуктивности маркируются непосредственно в микрогенри.
Цветовая маркировка катушек индуктивностей аналогична маркировке
«полосатых» резисторов: |
Рисунок 34. Расшифровка обозначения катушек индуктивностей |
Допустимый ток катушки определяется в основном диаметром провода, из которого она изготовлена.
Рисунок 35. |
Для переменного тока полное сопротивление катушки индуктивности зависит и от его частоты. Чем выше частота, тем меньше остается времени на преодоление током индуктивного препятствия. Значит, тем меньше тока катушка пропустит Это свойство часто используется в так называемых фильтрах — элементах, отделяющих переменный ток одной частоты от переменного же тока, но другой частоты или диапазона частот
Рисунок 36. Отсечение частот индуктивным фильтром |
Аналогичным образом катушка индуктивности ведет себя не только при переменном токе, но и в момент включения или выключения постоянного. В эти моменты ток постепенно увеличивается с нуля до максимального значения (или уменьшается от максимального значения до нуля), этим он похож на переменный ток. Поэтому зачастую мощные катушки индуктивности (их иногда называют дроссели) устанавливаются на входах питания каких-либо устройств для сглаживания возможных пульсаций тока и защиты оборудования.
В автомобильном электрооборудовании катушки применяются очень широко, например, в катушках зажигания, акустических динамиках, электродвигателях и других устройствах.
|
Урок |
|||
|
1/1 |
Что изучает физика. Физические термины. Наблюдения и опыты. | § 1 — 3, Л № 5, 12 | |
| 2/2 | Физические величины. Измерение физических величин. Погрешность и точность измерений | § 4, 5, упр.1 | |
| 3/3 | Определение цены деления измерительного прибора | § 4, 5 | |
| 4/4 | Физика и техника | § 6, | |
| Первоначальные сведения о строении вещества | |||
| 5/1 | Строение вещества. Молекулы Молекулы |
§ 7, 8 | |
| 6/2 | Определение размеров малых тел | § 7, 8 | |
| 7/3 | Движение молекул. Диффузия в газах, жидкостях и твердых телах | § 9, | |
| 8/4 | Взаимодействие молекул | ||
|
9/5 |
Три состояния вещества | § 11, 12 | |
| 10/6 | Повторение. Контрольная работа №1 «Первоначальные сведения о строении вещества» | § 12 | |
цепей переменного тока | Безграничная физика
Индуктивность
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.
Цели обучения
Опишите свойства индуктора
Основные выводы
Ключевые моменты
- В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
- Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
- Взаимная индуктивность обозначена. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
- Самоиндукция — это действие закона индукции Фарадея устройства на самого себя.
 Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс]. - Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
Ключевые термины
- взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
- самоиндукция : Отношение напряжения к изменению тока в той же цепи.
- индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.
Индуктивность
ОБЗОР
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность). Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).
Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.
Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как
[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружившего самоиндукцию). То есть 1 H = 1 Ом.
То есть 1 H = 1 Ом.
Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]
, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью М.
Большая взаимная индуктивность M, может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля.(Видеть ).
Противоточная намотка : Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.
САМОИНДУКЦИЯ
Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]
, где L — собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
.Обозначение индуктора
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.
СОЛЕНОИДЫ
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L, обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).
Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Цепи RL
Цепь RL состоит из катушки индуктивности и резистора, включенных последовательно или параллельно друг другу, с током, управляемым источником напряжения.{\ frac {- \ text {t}} {\ tau}}) [/ latex]. Конечный ток по прошествии длительного времени будет [латекс] \ текст {I} _0 [/ латекс].
Ключевые термины
- характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, за которое ток затухает с коэффициентом 1 / e.
- индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
Цепи RL
Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.
Обзор
Напомним, что индукция — это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.
Энергия индуктора
Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].
Катушки индуктивности в цепях
Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет потоком, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.
Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещен в положение 2.
Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге повышается до I 0 = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]
— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I 0 = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :
[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],
, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I 0 , так как I = I 0 (1 − e −1 ) = I 0 ( 1−0,368) = 0,632I 0 . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [latex] \ tau [/ latex] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).
Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы добраться до него. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.
Когда переключатель в (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, вызывая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI 0 2 , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I 2 R.{\ frac {- \ text {t}} {\ tau}} [/ latex]
В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I 0 e −1 = 0,368I 0 . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.
Цепь серииRLC: на больших и малых частотах; Фазорная диаграмма
Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.
Цели обучения
Различать поведение цепей серии RLC на больших и малых частотах
Основные выводы
Ключевые моменты
- RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, то при приложении синусоидального напряжения ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
- На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
- На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока с конденсатор. Следовательно, среднеквадратичное значение тока будет выражено как V rms / X C, , а ток опережает напряжение почти на 90 ∘ .
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I среднеквадратичное значение = В действующее значение / Z; I среднеквадратичное значение и В среднеквадратичное значение являются действующими значениями тока и напряжения) и выражения для импеданса Z из:
Цепь RLC серии : Цепь последовательного RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].
Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на 90º по фазе в цепи с катушкой индуктивности, а ток опережает напряжение на 90 ∘ в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.
на больших частотах
На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X L намного больше, чем X C .Если частота достаточно высока, так что X L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять В / X L , а ток отстает от напряжения почти на 90 ∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.
на малых частотах
В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостный член, предполагая, что частота достаточно высока, так что X C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичное значение тока будет выражено как V rms / X C, , а ток опережает напряжение почти на 90 ∘ .
Резисторы в цепях переменного тока
В цепи с резистором и источником питания переменного тока все еще действует закон Ома ( В, = IR ).
Цели обучения
Применить закон Ома для определения силы тока и напряжения в цепи переменного тока
Основные выводы
Ключевые моменты
- При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].
Ключевые термины
- Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.
Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая обслуживает так много наших потребностей. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
Мы изучили закон Ома:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]
, где I, — ток, В, — напряжение, а R, — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, при напряжении переменного тока, определяемом по формуле:
[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]
, где В 0 — пиковое напряжение, а [латекс] \ nu [/ latex] — частота в герцах, ток в цепи задается как:
[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]
В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b).Ток в резисторе чередуется взад и вперед без разницы фаз, как и напряжение возбуждения.
Рассмотрим идеальный резистор, который увеличивает и уменьшает яркость 120 раз в секунду, когда ток постоянно проходит через ноль. 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]
Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]
Конденсаторыв цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.
Цели обучения
Объясните преимущества использования векторного представления
Основные выводы
Ключевые моменты
- Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
- Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
- Среднеквадратичное значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — это емкостное реактивное сопротивление.
Ключевые термины
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.
Конденсаторы в цепях переменного тока с фазорами
Фазор
Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.
Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.
Конденсаторы в цепях переменного тока
Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пиков напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ∘ ». Это показано на.
Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.
Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V max / I max полезно и называется емкостным реактивным сопротивлением (X C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].
Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I , действующее значение в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V rms — это действующее значение напряжения. Обратите внимание, что X C заменяет R в версии закона Ома для постоянного тока.
Фазовое представление
Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Рис. 4 : Векторная диаграмма для цепи переменного тока с конденсатором
Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.
Цели обучения
Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности
Основные выводы
Ключевые моменты
- С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
- Среднеквадратичное значение тока I среднеквадратичное значение через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
- Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- phasor : представление комплексного числа в виде комплексной экспоненты.
Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).
Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I rms через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V rms — среднеквадратичное значение напряжения на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.
Представление векторов
Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.
Фазоры для индукторов в цепях переменного тока
Резонанс в цепях RLC
Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].
Цели обучения
Сравнить резонансные характеристики цепей с высоким и низким сопротивлением
Основные выводы
Ключевые моменты
- Условие резонанса последовательной цепи RLC может быть получено приравниванием X L и X C , так что два противоположных вектора компенсируют друг друга.
- В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I среднеквадратичное значение является максимальным.
- Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.
Ключевые термины
- реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.
Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],
, где I rms и V rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], причем X L большое на высоких частотах и X C большое на низких частотах, представленное как:
[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].
На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I rms .Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X L = X C . Подстановка определений X L и X C дает:
[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].
[латекс] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I rms является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции — это RLC-схема, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик I rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.
Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Мощность
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.
Цели обучения
Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.
Основные выводы
Ключевые моменты
- Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
- На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
- Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.
Ключевые термины
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный
.[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке
Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.
Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I rms ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность
[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]
(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — это ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при разработке эффективного двигателя. На резонансной частоте cosϕ = 1.
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).
Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.
индуктивность | Физика
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы.Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.
Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор.Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что « E 2 индуцированный» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом.Мы выражаем это в форме уравнения как
[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],
, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность М, , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван генри (H) в честь Джозефа Генри.То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],
, где M то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M, может быть, а может и не быть желательной.Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля. (См. Рисунок 2.)
Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство.Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],
, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на рисунке 3.
Рисунок 3.
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока.Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2. Катушка индуктивности 1 H является большой. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1.0 H, через который протекает ток 10 A. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет противодействовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Положительный знак означает это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный свист трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. Рисунок 4.)
Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля.Таким образом, в этом тексте индуктивность L, обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L (Δ I / Δ т ).Приравнивая эти доходности к
[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]
Решение для л дает
[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]
Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A, соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. (Здесь = / , где is — количество катушек, а ℓ — длина соленоида.{2} A} {\ ell} \ text {(соленоид)} \\ [/ latex].
Это самоиндукция соленоида с площадью поперечного сечения А, и длиной . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Пример 1. Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
СтратегияЭто прямое применение [латекса] L = \ frac {{\ mu} _ {0} {N} ^ {2} A} {\ ell} \\ [/ latex], поскольку все величины в уравнении, кроме L известны. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].
ОбсуждениеЭтот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал светофору об изменении цвета.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.
Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)
Понимание индуктивности в реальном мире
Как только ток течет по металлическим проводникам, появляется индуктивность Брюс Аршамбо, доктор философии, заслуженный инженер IBM, IBM,
Research Triangle Park, NC
Концепция индуктивность — одно из наиболее неправильно понимаемых понятий в электротехнике.Такие термины, как «самоиндуктивность», «индуктивность контура», «частичная индуктивность», «взаимная индуктивность» используются без особого внимания к истинной физике, лежащей в основе эффектов и причин индуктивности.
Индуктивность важна при проектировании EMI / EMC, поскольку она является одним из основных ограничивающих факторов в высокочастотной конструкции. Когда есть металл, и ток проходит через этот металл, присутствует индуктивность, которая влияет на ток. На высоких частотах эта собственная индуктивность доминирует над всеми компонентами, дорожками и металлическими поверхностями.Даже конденсаторы и резисторы становятся индукторами.
Полное исследование индуктивности заняло бы как минимум одну целую книгу. Цель этой статьи — помочь читателю лучше понять концепции индуктивности, взаимной индуктивности и частичной индуктивности в том, что касается проектирования EMI / EMC, особенно на печатных платах (ПК).
Где петля?
Одна из первых вещей, которую мы узнали в нашем первом классе схем, — это то, что ток всегда должен возвращаться к своему источнику.Обычно мы сначала изучаем это для цепей постоянного тока, а затем переходим к цепям переменного тока. Однако к тому времени, когда мы начнем проектировать высокоскоростные печатные платы, многие из нас, кажется, забывают этот фундаментальный принцип. Ток всегда должен течь по замкнутому контуру, независимо от частоты. Как разработчик печатных плат, разработчик корпусов или системный разработчик всегда должен задавать вопрос: «Как ток возвращается к своему источнику?» Ток должен течь по замкнутому контуру. Действительно, ток будет течь по замкнутому контуру.Единственный реальный вопрос заключается в том, пойдет ли он по пути, который поможет снизить выбросы EMI, или по пути, который приведет к увеличению выбросов EMI. Гораздо лучше спроектировать путь обратного тока «специально», чем «по ошибке». Без этой преднамеренной конструкции пути обратного тока инженеры также должны спросить себя: «Вам сегодня повезло?»
Когда кто-то говорит об индуктивности переходного отверстия или прямого куска провода, петли нет, значит, нет и индуктивности. В случае переходного отверстия, если нет преднамеренного обратного тока через переходное отверстие, то обратный ток будет распространяться и течь через диэлектрик как ток смещения.Чем дальше проходит ток, тем больше петля и, следовательно, больше индуктивность. Если рядом с сигнальным переходом находится обратное переходное отверстие, то индуктивность изменится из-за изменения площади контура. По мере того, как мы приближаем обратный переходник, площадь контура изменяется, как и индуктивность исходного проходного отверстия. Ясно, что сквозной сигнал сам по себе не может иметь много значений индуктивности. Значение индуктивности контура, в котором переходное отверстие является частью этого контура, определяет «индуктивность переходного отверстия».
Закон Фарадея
Когда ток в контуре изменяется во времени, магнитное поле, связанное с этим током, также изменяется.Когда это изменяющееся магнитное поле прорезает проводник, оно индуцирует напряжение в цепи этого проводника. Это изменение происходит независимо от того, прорезают ли линии магнитного поля другой проводник или тот же проводник, что и исходный ток. Напряжение, индуцированное в однопроводной петле, равно скорости изменения магнитного потока, проходящего через проволочную петлю, во времени. [1], [2] Это описано в законе электромагнитной индукции Фарадея как:
(1)
Часто уравнения, такие как (1), не исследуются тщательно для интуитивного понимания основ физики.Закон Фарадея не так сложен, как может показаться на первый взгляд. Правая часть (1) описывает величину изменяющегося во времени магнитного поля в некоторой области. Левая часть (1) — это определение напряжения (электрического поля вдоль пути). И в этом случае путь представляет собой замкнутый контур. Знак минус с правой стороны указывает на то, что напряжение будет противодействовать потоку тока, который в первую очередь создал магнитное поле. Это противопоставление является основным определением индуктивности. Обратите внимание, что левосторонний интеграл — это интеграл с обратной связью.Также обратите внимание, что правая часть — это величина (изменяющегося во времени) магнитного поля, содержащегося в области. Естественно, чтобы вычислить «площадь», мы должны иметь замкнутую окружность, поэтому обе стороны этого уравнения ясно указывают на то, что для определения индуктивности требуется замкнутый контур. Кроме того, чем больше площадь контура (правая сторона), тем больше тормозящий эффект индуктивности.
Мы можем упростить (1), рассмотрев случай простой квадратной петли (показанной на рисунке 1). Если петля мала по сравнению с длиной волны интересующей частоты, то можно предположить, что магнитный поток постоянен в области A, и уравнение (1) может быть уменьшено до
(2)
Рисунок 1.Квадратная петля.Величину напряжения, индуцированного изменяющимся во времени магнитным полем, можно найти для любой геометрии с помощью уравнения (1) и для простой прямоугольной петли с помощью (2). Опять же ясно, что чем больше площадь в (2), тем больше тормозящая индуктивность.
Теперь, когда мы рассмотрели основное определение индуктивности, мы можем использовать несколько простых уравнений, чтобы найти значение индуктивности на основе физических размеров контура.Предполагая, что площадь петли намного меньше длины волны в интересующем частотном диапазоне, магнитное поле аппроксимируется как постоянное. Примерная индуктивность для нескольких простых форм [3] приведена ниже.
Простая круглая петля
Для простой изолированной токовой петли, где радиус провода r 0 намного меньше, чем радиус петли a , тогда индуктивность петли приблизительно равна
(3)
Если используется несколько витков проволочной петли, то индуктивность просто умножается на количество витков, чтобы найти общую индуктивность числа витков.Обратите внимание на (3), что индуктивность прямо пропорциональна площади контура a , но только минимально зависит от радиуса провода r 0 (из-за функции естественного логарифма). Еще раз, важность площади контура для индуктивности очевидна.
Простая квадратная петля
Для изолированной квадратной петли (с длиной стороны = w ) в свободном пространстве, где радиус провода намного меньше площади петли ( r 0 << w 2 ), индуктивность может быть найдена с помощью
(4)
Простая прямоугольная петля
Для однооборотной прямоугольной петли в свободном пространстве индуктивность может быть найдена из
(5)
где
w = ширина прямоугольника (широкий размер)
h = высота прямоугольника (короткий размер), и
r 0 = Радиус проволоки.
Хотя эти формулы выглядят сложными, их можно легко вычислить с помощью программы для работы с электронными таблицами. Более того, в каждой из этих формул ясно, что площадь контура значительно больше влияет на значение индуктивности, чем размер проводника.
Почему нам важна индуктивность контура?
Одной из основных проблем EMI / EMC является индуктивность, особенно индуктивность компонентов фильтра. Например, конденсаторы используются на печатных платах (PCB) для развязки плоскостей питания / заземления, компонентов фильтра ввода-вывода и других высокочастотных целей.Индуктивность, связанная с физическим подключением конденсатора (установленного вверху / внизу печатной платы) к соответствующим плоскостям, будет преобладать над импедансом конденсатора на высоких частотах и сделает конденсатор неэффективным на высоких частотах. Эта индуктивность должна быть включена в любой анализ.
Для точного расчета индуктивности подключения конденсатора требуется сложная формула. [4] Однако, поскольку индуктивность прямо пропорциональна площади контура, мы можем получить относительную добротность, просто преобразовав эту сложную задачу в простой прямоугольный контур и вычислив площадь прямоугольного контура для каждого варианта.Если один вариант имеет меньшую площадь контура, он будет иметь меньшую индуктивность и будет предпочтительным вариантом конструкции.
На рисунках 2 и 4 показано подключение развязывающего конденсатора с низкой индуктивностью, а на рисунках 3 и 5 показано подключение развязывающего конденсатора с высокой индуктивностью.
На рисунках 2 и 3 площадь контура сильно различается, при этом контур на рисунке 3 значительно больше. В этом примере, где панель питания / заземления находится ближе к низу платы, чем к верху, площадь контура будет меньше (Рисунок 4), а индуктивность соединения будет ниже, если конденсатор будет установлен на задней стороне платы. доска, а не верхняя сторона доски.Обратное было бы верно, если бы пара плоскости питания / заземления находилась рядом с верхней частью печатной платы, как показано на рисунках 2 и 5.
Рисунок 2. Низкоиндуктивное соединение с конденсатором, установленным наверху платы. Рисунок 3. Высокоиндуктивное соединение с конденсатор установлен на верхней части платы. Рисунок 4. Низкоиндуктивное соединение с конденсатором, установленным на нижней части платы. Рисунок 5. Высокоиндуктивное соединение с конденсатором, установленным наверху платы.Таблица 1 показывает некоторые примерные значения индуктивности подключения, связанной с установленным на печатной плате развязывающим конденсатором для некоторых типичных размеров.Более сложная формула более точна, но даже значения простой прямоугольной формулы достаточно точны для большинства приложений.
Таблица 1. Типовые значения индуктивности развязывающего конденсатора.Из уравнения 5 важно отметить, что радиус провода очень мало влияет на индуктивность контура, а высота и ширина (площадь контура) имеют большое влияние на значение индуктивности контура.
Этот тип анализа также применим для определения того, оправдывают ли специальные технологии платы, например, скрытая емкость, затраты на конфигурацию стека плат.Если слой скрытой емкости находится глубоко в плате (ближе к низу), тогда площадь прямоугольной петли между выводами питания / заземления ИС и слоем скрытой емкости будет большой, что сводит к минимуму любые положительные эффекты от слоя скрытой емкости. В качестве альтернативы, если слой скрытой емкости находится рядом с верхом печатной платы, площадь прямоугольного контура, связанная с индуктивностью соединения, мала, в результате чего ИС получает преимущество слоя скрытой емкости без значительной индуктивности соединения.
Взаимная индуктивность
Взаимную индуктивность цепей реального мира часто трудно вычислить, поскольку контуры редко имеют простую геометрию, а другие металлы в окружающей среде будут влиять на поведение полей. Если предположить, что две петли расположены в свободном пространстве (электрически далеко от других проводников), тогда проблема упрощается и может быть сделана разумная оценка. В этих условиях взаимная индуктивность между двумя контурами определяется как
(6)
, где
I 1 = текущий в контуре # 1,
B = магнитный поток, создаваемый током в контуре №1, и
S 2 = поверхность контура №2.
В уравнении (6) магнитный поток от тока в первом контуре интегрируется по поверхности второго контура, чтобы найти взаимную индуктивность. Если петли достаточно малы, чтобы мы могли предположить, что магнитное поле постоянно на лицевой стороне петли, то взаимная индуктивность — это просто количество магнитного потока от первого витка, содержащегося в области второго витка, и деленное на ток в первом шлейфе. Следовательно, очевидно, что взаимная индуктивность определяется размером двух контуров и их ориентацией относительно друг друга.Петли большего размера будут иметь большую взаимную индуктивность. Петли, расположенные ближе друг к другу, будут иметь большую взаимную индуктивность (поскольку магнитный поток от первого витка будет сильнее). Петли с одинаково ориентированными гранями также будут иметь большую взаимную индуктивность (поскольку магнитный поток будет максимальным).
Почему мы заботимся о взаимной индуктивности?
Когда развязывающий конденсатор размещается рядом с выводами питания ИС, область взаимной индуктивности может эффективно снизить индуктивность контура тракта.Чтобы это уменьшение было значительным, конденсатор и ИС должны располагаться близко друг к другу.
На рисунке 6 показан пример ИС и развязывающего конденсатора, установленных на печатной плате. Когда сквозные соединения показаны на рисунке 6, направление тока в двух ближайших друг к другу переходных отверстиях приводит к возникновению магнитного потока в противоположном направлении в области взаимного потока между плоскостями питания / земли, как показано на рисунке 6. Этот эффект противоположной взаимной индуктивности снижает полное сопротивление пути.Это уменьшение общей индуктивности за счет этого эффекта наблюдается только тогда, когда конденсатор расположен очень близко к ИС.
Рисунок 6. Взаимная индуктивность между развязывающим конденсатором и ИС. Частичная индуктивность
Основное определение индуктивности требует наличия тока, протекающего в контуре. Без полного контура не может быть индуктивности. Однако практические соображения заставляют нас обсудить индуктивность части полного токового контура, например индуктивность конденсатора.Идея обсуждения индуктивности только части контура в целом называется частичной индуктивностью. [4], [5] Частичные индуктивности можно объединить, чтобы найти общую индуктивность, используя уравнение (7).
(7)
Почему нам важна частичная индуктивность?
Концепция частичной индуктивности особенно полезна, когда физическая геометрия является сложной или когда ток неоднороден по всему поперечному сечению металла. Например, на рисунке 7 показан конденсатор для поверхностного монтажа (SMT) на печатной плате с переходными отверстиями, дорожками и т. Д.В то время как простая формула прямоугольной петли может использоваться для определения приблизительной индуктивности петли, различные поперечные сечения проводников делают расчет только приблизительным. Концепция частичной индуктивности позволяет найти частичную индуктивность каждого компонента и объединить их в конце, чтобы найти полную индуктивность контура, как в уравнении (8).
Используя частичные индуктивности, общая индуктивность контура будет равна
, где Lp, — частичная индуктивность компонента. Lpm. — это частичная взаимная индуктивность параллельных компонентов.
Обратите внимание, что конструкция может быть проанализирована с возможной целью уменьшения общей индуктивности контура. Каждый из отдельных сегментов может быть изменен (например, путем увеличения диаметра), чтобы определить влияние на конечную индуктивность. С помощью этого анализа можно быстро проанализировать многие конфигурации «что, если».
Рис. 7. Пример геометрии установки развязывающего конденсатора с разбивкой на составляющие частичной индуктивности. Резюме
Основной принцип, согласно которому индуктивность требует, чтобы ток протекал в контуре, является важной концепцией, которую необходимо понять.Это небезосновательно, поскольку ток должен течь по петле. Размер токовой петли определяет величину индуктивности.
Индуктивность является основным строительным блоком в электронных схемах — например. , как только используются металлические проводники и по ним течет ток, возникает индуктивность. Эта индуктивность становится ограничивающим фактором во всех высокочастотных цепях. Например, когда конденсаторы используются в качестве фильтрующих элементов или развязывающих конденсаторов, индуктивность контура, связанная с подключением этого конденсатора к печатной плате, будет ограничивать частотный диапазон, в котором конденсатор является эффективным компонентом.
Также дается краткое обсуждение взаимной индуктивности и частичной индуктивности. Однако идея о том, что для оценки индуктивности требуется замкнутый контур, также верна для расчетов взаимной индуктивности и частичной индуктивности.
Это было очень краткое введение в индуктивность. Более полное изучение этой темы можно найти в справочной литературе.
Ссылки
- J.D. Kraus and K.R. Carver, Electromagnetics , 2nd Edition, McGraw-Hill, 1973
- F.М. Теще, М.В. Ианоз и Т. Карлссон, Методы анализа ЭМС и вычислительные модели , Wiley-Interscience, 1997 г.
- FW Gover, Расчет индуктивности , Dover Publications, NY, 1946 г.
- AE Ruehli, «Расчет индуктивности в сложной интегральной схеме. Окружающая среда », IBM J. Research and Development , 16, pp 470-481, 1972
- CR Paul, Анализ многопроводных линий передачи , Wiley, 1994
Dr.Брюс Аршамбо — заслуженный инженер IBM в IBM в Research Triangle Park, Северная Каролина. Он получил степень BSEE в Университете Нью-Гэмпшира в 1977 году и степень MSEE в Северо-Восточном университете в 1981 году. Он получил докторскую степень в Университете Нью-Гэмпшира в 1997 году. Его докторские исследования были в области прикладной вычислительной электромагнетизма. В 1981 году он присоединился к Digital Equipment Corporation и в течение 1994 года выполнял различные задания: от проектирования и тестирования продуктов EMC / TEMPEST до разработки программных инструментов, связанных с вычислительной электромагнитной совместимостью.В 1994 году он присоединился к SETH Corporation, где продолжил разрабатывать программные инструменты, связанные с вычислительной электромагнитной электромагнитной совместимостью, и использовал их в качестве инженера-консультанта в различных отраслях промышленности. В 1997 году он присоединился к IBM в Роли, Северная Каролина, где он является ведущим инженером EMC, отвечающим за разработку инструментов EMC и их использование в различных продуктах. Во время своей карьеры в ВВС США он отвечал за внутреннюю безопасность связи и проекты исследований и разработок, связанные с TEMPEST / EMC.Аршамбо является автором или соавтором ряда статей в области вычислительной электромагнетизма, в основном применяемых в реальных приложениях EMC. В настоящее время он является членом совета директоров IEEE EMC Society и бывшим членом совета директоров Applied Computational Electromagnetics Society (ACES). В прошлом он был заслуженным лектором IEEE / EMCS и младшим редактором журнала IEEE Transactions по электромагнитной совместимости. Он является автором книги «Проектирование печатных плат для управления электромагнитными помехами в реальном мире» и ведущим автором книги «Справочник по вычислительному моделированию электромагнитных помех и электромагнитной совместимости».”
Важность индуктивности катушки
В этом блоге мы исследуем индуктивность; одно из основных свойств электрической схемы или электронного устройства. Индуктивность определяется как свойство электрической цепи или устройства, которое препятствует изменению тока. Важно отметить, что индуктивность не противодействует току, а скорее противодействует изменению тока, протекающего в цепи.
Единицей индуктивности является генри (Гн), и она зависит от физических свойств цепи, а не от электрических характеристик, поскольку в ней нет тока или напряжения.Кроме того, индуктивность прямо пропорциональна «количеству витков», «площади, окруженной катушкой» и обратно пропорциональна «длине катушки».
Символ, используемый для обозначения индуктивности, — это заглавная буква L. Индуктивность (или, точнее, самоиндукция) катушки может быть найдена с помощью следующего уравнения:
Применяемая формула в электрических цепях:
Обзор процесса индуктивностиЧтобы понять процесс индуктивности и принцип его работы, давайте рассмотрим иллюстрированный источник постоянного тока с переключателем и катушкой (рисунок 1).Когда переключатель замкнут, по цепи течет ток. Здесь мы используем поток электронов, показанный красными стрелками, как направление электронов. Когда мы замыкаем переключатель, ток, протекающий от батареи, увеличивается в каждой катушке. Принимая во внимание правило большого пальца левой руки, ток течет, а магнитный поток течет против часовой стрелки и расширяется наружу. Принимая во внимание Катушку 1 и Катушку 2, как на рисунке; Поток от катушки 1 проходит через катушку 2, создавая индуцированное напряжение.Закон Ленца и закон Фарадея — два закона, применяемые для понимания этого процесса. Индуцированное напряжение всегда будет создавать поток, противоположный исходному потоку, который его вызвал. Таким образом, наше приложенное напряжение пытается направить ток в катушку, а индуцированное напряжение работает против этого. Он не останавливает ток, он просто замедляет его. Если по закону Ома сила тока будет 10 ампер, он не изменится мгновенно от 0 до 10, вместо этого потребуется некоторое время в зависимости от индуктивности, обеспечиваемой индуктором.
Рисунок 1В следующем случае мы попытаемся уменьшить ток, в той же цепи с 10 А, как установлено, магнитный поток связывает все витки в катушке. Когда мы размыкаем переключатель, поток возвращается к исходному проводнику. Движение потока прекращается, когда ток перестает изменяться. Уменьшение магнитного потока на каждом витке катушки проводника вызывает относительное движение между магнитными полями, что приводит к сильному индуцированному напряжению. Действие по уменьшению тока / напряжения до нуля путем удаления приложенного напряжения приводит к непрерывному изменению магнитного потока, который индуцирует напряжение, пытаясь противодействовать причине.Таким образом, схема пытается поддерживать ток, что приводит к задержке в скорости уменьшения тока, а не снижает ее мгновенно. Это называется индуктивным ударом. Происходящий процесс — это просто возвращение энергии обратно в цепь из магнитных полей. Величина индуцируемого напряжения зависит от таких факторов, как величина магнитного потока, количество витков и время.
Разрыв цепи может вызвать очень высокое наведенное напряжение в катушке, так как время очень короткое, а магнитный поток очень быстро спадает.Если нет пути для прохождения этой энергии, мы можем получить дугу через переключатели или дугу рядом с другими подключенными устройствами, что может вызвать повреждения. Таким образом, настоятельно рекомендуется соблюдать некоторые меры предосторожности при обнаружении характеристик индуктивности в электронных схемах.
Профилактические меры по предотвращению дугового разрядаИндуктивный ток, создаваемый в цепи постоянного тока, имеет высокую силу, когда поток, связанный с катушкой, мгновенно падает.Поэтому важно принять превентивные меры для устранения ущерба, предоставив альтернативный путь для энергии. Например, трансформатор тока является высокоиндуктивным устройством, так как у него много витков катушки, и количество витков катушки имеет большое влияние на генерируемый ток (L = µ N2A / l, где N = кол-во поворотов) .
Рисунок 2: Принцип противодействия ЭДСЕсли амперметр, присоединенный к катушке, как показано на рисунке 2, снимается, пока цепь горячая, цепь с высокой индуктивностью прерывается.Разрыв цепи приводит к схлопыванию потока по виткам катушки, создавая чрезвычайно высокое индуцированное напряжение, которое может вызвать электрическую дугу длиной 4-5 дюймов. Эта электрическая дуга может нанести травму человеку, пытающемуся отключить амперметр от цепи.
Это похоже на шунтирующую обмотку двигателя постоянного тока, которая представляет собой еще одну высокоиндуктивную цепь. Шунтирующий двигатель постоянного тока также удовлетворяет всем характеристикам, которые генерируют высокоиндуктивный ток. Шунтирующий двигатель обычно находится под напряжением, и в другую часть двигателя вносятся изменения, чтобы обеспечить альтернативный путь для протекания индуктивного тока.Это сделано для того, чтобы переключение поля шунта могло вызвать серьезные повреждения и сократить срок службы контактов. Даже в небольших катушках, используемых в схемах ПЛК, возникает обратная подача и некоторые повреждения.
Шунтирующий двигательСамый простой способ устранить повреждение, вызванное током обратной связи, — это подключить резистор к катушке индуктивности. Это обеспечивает путь для индуктора, чтобы управлять энергией, но, когда он находится под напряжением в течение более длительного периода, это может быть неэффективным, поскольку все это время будет иметь место потеря мощности на резисторе.Эту проблему можно решить, включив диод последовательно с резистором, чтобы диод блокировал ток во время нормальной работы. Это снижает рассеиваемую мощность на резисторе. Питание подается через резистор только тогда, когда цепь разомкнута, вызывая индуктивный удар.
Помимо использования одного резистора и последовательной комбинации резистор-диод, конденсатор также может устранить повреждения, вызванные индуктивным током. Энергия, генерируемая во время обратной подачи индуктивного тока, рассеивается в конденсаторе, а оставшийся ток течет обратно от конденсатора к катушке индуктивности, тем самым защищая контакты переключателя, а также любые другие соприкасающиеся устройства.Подводя итог, индуктивность — это свойство цепи, которая препятствует изменению тока в этой цепи.
До сих пор мы изучили индуктивность, вызванную цепью постоянного тока, но когда мы посмотрим на индуктивность, вызванную переменным током, который непрерывно изменяется во времени, формируется реактивная индуктивность, зависящая не только от индуктивности катушки, но и также от частоты сигнала переменного тока, как показано на рисунке 3.
Рисунок 3Мы надеемся, что это было полезно для вас, как для технического специалиста, или для студента, приступившего к работе.Если у вас есть какие-либо вопросы о программах по электронике или электромеханику, вы можете связаться с одним из наших консультантов по программе по бесплатному телефону 1-888-553-5333 или по электронной почте [email protected].
Катушки индуктивности могут быть подключены в цепь таким же образом, как и резисторы. При последовательном соединении общая индуктивность складывается из индуктивностей. индукторов, или LT = L1 + L2 + L3 и т. Д. Когда две или более катушки индуктивности соединены параллельно, общая индуктивность , как и сопротивление, включенное параллельно, меньше, чем у самой маленькой катушки индуктивности, или же Суммарная индуктивность последовательно-параллельно включенных индукторов может быть вычисляется путем объединения параллельных индуктивностей и последующего сложения ряда значения. Во всех случаях эти формулы верны, если магнитная поля индукторов не взаимодействуют. Индуктивное реактивное сопротивление Противодействие протеканию тока, которое индуктивности вводят в цепь называется индуктивным реактивным сопротивлением. Обозначение индуктивного сопротивления — XL, и измеряется в омах, как и сопротивление. В любой цепи, в которой есть только сопротивление, выражение для соотношение напряжения и тока — это закон Ома: I = E / R. По аналогии, когда в цепи переменного тока присутствует индуктивность, соотношение между напряжением а ток можно выразить как: Если все остальные значения цепи остаются постоянными, тем больше индуктивность. в катушке, тем больше эффект самоиндукции или противодействия изменение значения тока.С увеличением частоты индуктивная реактивное сопротивление увеличивается, так как чем больше скорость изменения тока, тем больше сопротивление изменению катушки возрастает. Следовательно, индуктивное реактивное сопротивление пропорциональна индуктивности и частоте или,
Решение: Чтобы найти индуктивное сопротивление:
|
Индуктивность в цепях переменного тока
ЗАДАЧИ:
• обсудить свойства индуктивности в цепи переменного тока.
• обсудить индуктивное реактивное сопротивление.
• вычислить значения индуктивного сопротивления и индуктивности.
• обсудить взаимосвязь напряжения и тока в чисто индуктивном схема.
• уметь вычислять значения для катушек индуктивности, подключенных последовательно или параллельно.
• обсудить реактивную мощность (VAR).
• определить добротность катушки.
ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА УСЛОВИЯ
- ток запаздывает по напряжению — соотношение силы тока и напряжения в чистая индуктивная цепь
- импеданс (Z) — общий токоограничивающий эффект в цепи переменного тока
- индуцированное напряжение — напряжение, которое подводится к проводнику при разрезании. линии магнитного потока
- индуктивность (Л) — свойство электрической цепи, при котором напряжение производится резкой магнитных линий
- индуктивное реактивное сопротивление (XL) — токоограничивающий эффект чистого индуктор Качество
- (Q) — отношение индуктивного реактивного сопротивления к сопротивлению
- реактивное сопротивление — свойство цепи, ограничивающее ток с помощью кроме сопротивления
- реактивная мощность (ВАР) — Вольт Ампер Реактивная; часто упоминается как безбатная мощность
———————————
В этом модуле обсуждается влияние индуктивности на цепи переменного тока.Устройство также объясняет, как ограничивается ток в индуктивной цепи. поскольку индуктивность влияет на соотношение напряжения и тока.
ИНДУКТИВНОСТЬ
Индуктивность (L) — один из основных типов нагрузок переменного тока. схемы. Некоторая индуктивность присутствует во всем переменном токе. цепей из-за постоянно меняющегося магнитного поля (рис. 1). Величина индуктивности одного проводника чрезвычайно мала, и в большинстве случаев это не учитывается в схемных расчетах.
Считается, что цепи содержат индуктивность, когда любой тип нагрузки, содержащей катушку. Для цепей, содержащих катушку, индуктивность учитывается при расчетах схемы. Такие нагрузки, как двигатели, трансформаторы, осветительный балласт и дроссели содержат катушки с проводом.
РИС. 1 Постоянно меняющееся магнитное поле индуцирует напряжение в
любой проводник.
РИС. 2 Когда ток течет через катушку, создается магнитное поле.
вокруг катушки.
РИС. 3 По мере уменьшения тока магнитное поле схлопывается.
В разделе 10 обсуждалось, что всякий раз, когда ток проходит через катушка с проволокой — вокруг проволоки создается магнитное поле (фиг. 2). Если величина тока уменьшается, магнитное поле схлопывается (фиг. 3). Вспомните из Раздела 10 несколько фактов, касающихся индуктивности:
1. Когда магнитные линии потока проходят через катушку, индуцируется напряжение. в катушке.
2. Индуцированное напряжение всегда имеет полярность, противоположную приложенному напряжению. Это часто называют встречной ЭДС (CEMF).
3. Величина наведенного напряжения пропорциональна скорости изменения. тока.
4. Катушка индуктивности препятствует изменению тока.
Катушки индуктивности на фиг. 2 и 3 подключены к чередующемуся Напряжение. Поэтому магнитное поле непрерывно увеличивается, уменьшается, и меняет полярность.Поскольку магнитное поле постоянно меняет величину и направление, в катушке постоянно индуцируется напряжение. Этот наведенное напряжение сдвинуто по фазе на 180 ° с приложенным напряжением и всегда против приложенного напряжения (фиг. 4). Поскольку индуцированное напряжение всегда противоположно приложенному напряжению, приложенное напряжение должно преодолеть индуцированное напряжение до того, как ток сможет течь по цепи. Например, предположим, что катушка индуктивности подключена к сети переменного тока напряжением 120 В.Теперь предположим индуктивность индуктора составляет 116 В. Поскольку равная величина приложенного напряжения необходимо использовать для преодоления наведенного напряжения, при этом будет всего 4 В, чтобы протолкнуть ток через сопротивление провода катушки (120 — 116 = 4).
РИС. 4 Приложенное напряжение и индуцированное напряжение сдвинуты по фазе на 180 °.
друг с другом.
РИС. 5 Измерение сопротивления катушки.
РИС. 6 Измерение тока цепи амперметром.
РАСЧЕТ ИНДУЦИРОВАННОГО НАПРЯЖЕНИЯ
Величину наведенного напряжения в катушке индуктивности можно вычислить, если сопротивление длины провода в катушке и величина тока в цепи известны. Для Например, предположим, что омметр используется для измерения фактического количества сопротивление в катушке, и обнаружено, что катушка содержит 6 Ом сопротивления провода (Фиг.5).
Теперь предположим, что катушка подключена к цепи переменного тока 120 В и амперметру. измеряет текущий расход 0.2] = 119: 9 В). Обратитесь к векторам в Разделе 13.
ИНДУКТИВНАЯ РЕАКТИВНОСТЬ
Обратите внимание, что индуцированное напряжение может ограничивать протекание тока через схема аналогична сопротивлению. Это индуцированное напряжение равно не сопротивление, но он может ограничивать поток тока так же, как сопротивление делает. Это свойство ограничения тока индуктивности называется реактивным сопротивлением. и обозначается буквой X. Это реактивное сопротивление обусловлено индуктивностью, поэтому оно называется индуктивным реактивным сопротивлением и обозначается XL, произносится как «X». sub L.»Индуктивное реактивное сопротивление измеряется в омах так же, как сопротивление есть и может быть вычислено, когда значения индуктивности и частоты равны известен. Для определения индуктивного сопротивления можно использовать следующую формулу.
XL = 2πFL
где:
XL = индуктивное реактивное сопротивление
2 = постоянная
пи или π = 3,1416
F = частота в герцах (Гц)
L = индуктивность в генри (Гн)
Индуктивное реактивное сопротивление — это индуцированное напряжение и, следовательно, пропорционально к трем факторам, определяющим индуцированное напряжение:
1.Количество витков провода
2. Напряженность магнитного поля
3. Скорость режущего действия (относительное перемещение индуктора и магнитные линии потока)
РИС. 7 Катушки с более близкими витками создают большую индуктивность, чем
катушки с далеко друг от друга витками.
Определяются количество витков провода и напряженность магнитного поля. по физической конструкции индуктора. Такие факторы, как размер используемого провода, количество витков, насколько близко друг к другу витки, и тип материала сердечника определяют величину индуктивности (в генри, H) катушки (РИС.7). Скорость режущего действия пропорциональна к частоте (Гц). Увеличение частоты вызовет магнитное линии потока, чтобы сократить проводники с большей скоростью, и, таким образом, будет производить более высокое наведенное напряжение или большее индуктивное сопротивление.
РИС. 9 Условные обозначения катушек индуктивности.
СХЕМАТИЧЕСКИЕ СИМВОЛЫ
На схематическом изображении катушки индуктивности изображена катушка с проводом. Несколько символов для катушек индуктивности показаны на фиг.9. Показанные символы с двумя параллельными линиями представляют индукторы с железным сердечником, а символы без параллельных линий представляют индукторы с воздушным сердечником.
ИНДУКТОРЫ, ПОДСОЕДИНЕННЫЕ СЕРИИ
При последовательном включении катушек индуктивности (РИС. 10) общая индуктивность цепи (LT) равна сумме индуктивностей всех катушек индуктивности.
LT = L1 + L2 + L3
Суммарное индуктивное сопротивление (XLT) последовательно соединенных катушек индуктивности равно сумма индуктивных сопротивлений всех катушек индуктивности.
XLT = XL1 + XL2 + XL3
ИНДУКТОРЫ, СОЕДИНЕННЫЕ ПАРАЛЛЕЛЬНО
При параллельном подключении катушек индуктивности (РИС. 11) общая индуктивность можно найти аналогично нахождению полного сопротивления параллельного схема. Обратная величина полной индуктивности равна сумме обратные величины всех катушек индуктивности.
РИС. 10 последовательно соединенных индукторов.
РИС. 11 индукторов, подключенных параллельно.
Формулу произведения на сумму можно также использовать для определения общей индуктивности. параллельных индукторов.
LT = L1 x L2 / L1 + L2
Если значения всех индукторов одинаковы, общая индуктивность может можно найти, разделив индуктивность одной катушки индуктивности на общее количество индукторов.
LT = L / N
По аналогичным формулам можно найти полное индуктивное сопротивление индукторы соединены параллельно.
1 / XLT = 1 / XL1 + 1 / XL2 + 1 / XL3
ОТНОШЕНИЯ НАПРЯЖЕНИЯ И ТОКА В ИНДУКТИВНОЙ ЦЕПИ
РИС. 12 Наведенное напряжение пропорционально скорости изменения
Текущий.
РИС. 13 Никакое напряжение не индуцируется, когда ток не изменяется.
РИС. 14 Ток отстает от приложенного напряжения на 90 °.
В разделе 11 обсуждалось, что когда ток течет через чистую резистивная цепь, ток и напряжение находятся в фазе друг с другом.В чисто индуктивной цепи ток отстает от напряжения на 90 °. Сначала это может показаться невыполнимым условием, пока отношение применяемых учитывается напряжение и наведенное напряжение. Как нынешний и применяемый Напряжение может сдвинуться по фазе на 90 ° друг с другом. сравнивая соотношение тока и наведенного напряжения (фиг. 12). Напомним, что индуцированное напряжение пропорционально скорости изменение силы тока (скорости режущего действия).В начале осциллограммы, ток отображается с максимальным значением в отрицательном направлении. В это время ток не меняется, поэтому индуцированное напряжение равно нулю. Когда ток начинает уменьшаться в значении, магнитное поле создает потоком ток уменьшается или коллапсирует и начинает индуцировать напряжение в катушку, когда она прорезает проводники (РИС. 13).
Наибольшая скорость изменения тока происходит, когда ток проходит от отрицательный, через ноль, и начинает увеличиваться в положительном направлении (РИСУНОК.13). Поскольку ток изменяется с наибольшей скоростью, индуцированная напряжение максимальное.
Когда ток приближается к своему пиковому значению в положительном направлении, скорость изменения уменьшается, вызывая уменьшение наведенного напряжения. Индуцированная напряжение снова будет равно нулю, когда ток достигнет своего пикового значения и магнитное поле перестает расширяться.
Видно, что ток, протекающий через катушку индуктивности, является ведущим индуцированное напряжение на 90 °.
Поскольку индуцированное напряжение сдвинуто по фазе на 180 ° с приложенным напряжением, ток будет отставать от приложенного напряжения на 90 ° (рис. 14).
МОЩНОСТЬ В ИНДУКТИВНОЙ ЦЕПИ
В чисто резистивной цепи истинная мощность или ватты равна произведение напряжения и тока.
Однако в чисто индуктивной цепи не вырабатывается истинная мощность или ватт. Напомним, что напряжение и ток должны быть либо положительными, либо отрицательными. прежде, чем будет произведена настоящая сила.Поскольку напряжение и ток равны 90 ° не совпадают по фазе друг с другом в чистой индуктивной цепи, ток и напряжение будет иметь разную полярность в 50% случаев и в одно и то же время. полярность в 50% случаев. В течение периода времени, когда текущая и напряжения имеют одинаковую полярность, питание на цепь подается в форма создания магнитного поля. Когда ток и напряжение равны противоположной полярности, мощность возвращается в цепь в качестве магнитного поле схлопывается и снова индуцирует напряжение в цепи.2 R потери, потери на вихревые токи и гистерезис убытки.
РИС. 15 Соотношение напряжения и тока в разных частях цикла.
Форма волны тока и напряжения на фиг. 15 было разделено на четыре секции:
A, B, C и D. В течение первого периода времени, обозначенного A, текущий отрицательный, а напряжение положительное. В этот период энергия передается в цепь при схлопывании магнитного поля.В течение второй период времени, раздел B, и напряжение, и ток положительны. Энергия используется для создания магнитного поля. В третьем временном периоде C, ток положительный, а напряжение отрицательное. Сила снова возвращается в схему, когда поле схлопывается. Во время четвертого период времени D, напряжение и ток отрицательны. Сила снова используется для создания магнитного поля. Если количество энергии, используемой для магнитное поле вычитается из возвращаемой мощности, результат будет нулевым.
РЕАКТИВНАЯ МОЩНОСТЬ
Хотя, по сути, истинная мощность не используется, за исключением ранее упомянутых потерь, электрическое измерение, называемое VARs, используется для измерения реактивная мощность в чисто индуктивной цепи. VARs — это аббревиатура для вольт-ампер-реактивных. VAR можно вычислить как ватт, за исключением индуктивного значения заменяются на значения сопротивления в формулах.
ВАр равно количеству тока, протекающего через индуктивную цепь. умноженное на напряжение, приложенное к индуктивной части цепи.2 L x XL
где
EL = напряжение, приложенное к катушке индуктивности
IL = текущий расход через индуктор
XL = индуктивное реактивное сопротивление
Q ИНДУКТОРА
РИС. 16 Катушки индуктивности содержат внутреннее сопротивление.
РИС. 17 Добротность катушки индуктивности — это отношение индуктивного реактивного сопротивления как
по сравнению с сопротивлением. Буква Q означает качество.
До сих пор в этом разделе обычно предполагалось, что индуктор не имеет сопротивления, и это индуктивное реактивное сопротивление является единственным ограничивающим ток фактор.На самом деле это не так. Поскольку индукторы на самом деле являются катушками провода, все они содержат некоторое количество внутреннего сопротивления. Индукторы на самом деле выглядит как катушка, соединенная последовательно с некоторым сопротивлением (РИС. 16). Величина сопротивления по сравнению с индуктивным сопротивлением определяет добротность катушки. Буква Q означает качество.
Катушки индуктивности с более высоким отношением индуктивного реактивного сопротивления к сопротивлению считаются индукторами более высокого качества.Индуктор построен с большим проводом будет иметь низкое сопротивление провода и, следовательно, более высокое Q (фиг.17). Индукторы, состоящие из множества витков небольшого провода, имеют гораздо более высокое сопротивление и, следовательно, более низкое значение Q.
.Чтобы определить добротность катушки индуктивности, разделите индуктивное реактивное сопротивление на сопротивление.
Q = XL / R
РИС. 18 Импеданс катушки представляет собой комбинацию сопротивления провода и индуктивного сопротивления.
реактивное сопротивление.
Хотя индукторы имеют некоторое сопротивление, индукторы с Q = 10 или больше обычно считаются чистыми индукторами.Один раз отношение индуктивного реактивного сопротивления становится в 10 раз больше сопротивления, величина сопротивления считается незначительной. Например, предположим индуктор имеет индуктивное сопротивление 100 Ом и сопротивление провода 10 Ом. Индуктивная реактивная составляющая в цепи находится под углом 90 ° фаза с резистивной составляющей. Эти отношения создают право треугольник (фиг.18). Общий ток ограничивающий эффект катушки индуктивности представляет собой комбинацию индуктивного реактивного сопротивления и сопротивления.Эта сумма токоограничивающий эффект называется импедансом и обозначается буквой Z. Импеданс цепи представлен гипотенузой прямоугольный треугольник, образованный индуктивным сопротивлением и сопротивлением. К вычислить значение импеданса для катушки, индуктивного реактивного сопротивления и сопротивление должно быть добавлено. Поскольку эти два компонента образуют ножки прямоугольный треугольник и импеданс образует гипотенузу, сложение вектора должны быть заняты.
Обратите внимание, что значение полного сопротивления катушки индуктивности составляет всего 0,5. O больше, чем значение индуктивного реактивного сопротивления.
РЕЗЮМЕ
• Наведенное напряжение пропорционально скорости изменения тока.
• Индуцированное напряжение всегда противоположно полярности приложенного напряжения.
• Индуктивное реактивное сопротивление — это противодействующее напряжение, ограничивающее ток, как и сопротивление.
• Индуктивное реактивное сопротивление измеряется в омах.
• Индуктивное реактивное сопротивление пропорционально индуктивности катушки и частота линии.
• Индуктивное реактивное сопротивление обозначается XL.
• Индуктивность измеряется в генри (H) и обозначается буквой. L.
• При последовательном подключении катушек индуктивности общая индуктивность равна сумме всех индукторов.
• При параллельном подключении катушек индуктивности обратная величина индуктивность равна сумме обратных величин всех индукторов.
• Ток отстает от приложенного напряжения на 90 ° в чисто индуктивной цепи.
• Все катушки индуктивности содержат некоторое сопротивление.
• Добротность катушки индуктивности — это отношение индуктивного реактивного сопротивления к сопротивление.
• Катушки индуктивности с добротностью 10 обычно считаются «чистыми» индукторами.
• Чисто индуктивные цепи не содержат истинной мощности или ватт.
• Реактивная мощность измеряется в барах.
• VARs — это сокращение от вольт-ампер-реактивного.
ВИКТОРИНА
1. На сколько градусов не совпадают по фазе ток и напряжение с каждым другой в чисто резистивной цепи?
2. На сколько градусов не совпадают по фазе ток и напряжение с каждым другой в чисто индуктивной цепи?
3. Чему пропорционально индуктивное сопротивление?
4. Четыре катушки индуктивности, каждая с индуктивностью 0.6 H, подключены в ряд. Какая общая индуктивность цепи?
5. Три индуктора подключены параллельно. Индуктор 1 имеет индуктивность 0,06 H; индуктор 2 имеет индуктивность 0,05 Гн; а индуктор 3 имеет индуктивность 0,1 ч. Какова общая индуктивность этой цепи?
6. Если три катушки индуктивности, о которых идет речь 5, были соединены последовательно, что будет индуктивное сопротивление цепи? Предположим, что катушки индуктивности подключен к линии 60 Гц.
7. Катушка индуктивности подключена к линии 240 В, 1000 Гц. Ток в цепи составляет 0,6 А. Какова индуктивность катушки индуктивности?
8. Катушка индуктивности с индуктивностью 3,6 Гн подключена к сети 480 В, 60 Гц. линия. Сколько тока будет протекать в этой цепи?
9. Если частота в вопросе 8 снижена до 50 Гц, сколько тока будет течь в контуре?
10. Катушка индуктивности имеет индуктивное сопротивление 250 Ом при подключении к линия 60 Гц.Каким будет индуктивное сопротивление, если катушка индуктивности подключена на линию 400 Гц?
РЕАЛЬНЫЕ ПРИЛОЖЕНИЯ ДЛЯ МИРА
1. Вы работаете электриком по установке люминесцентных ламп. Ты обратите внимание, что фары были произведены в Европе и что балласты рассчитаны на для работы в сети 50 Гц. Будут ли эти балласты повреждены более чем ток, если они подключены к 60 Гц? Если есть проблема с этими огни, что будет наиболее вероятной причиной неисправности?
2.У вас есть задача заказать замену катушки индуктивности для той, у которой есть стать неисправным. Информация на паспортной табличке закрашена и не читается. Машина, в которой находится индуктор, работает от 480 В при частоте 60 Гц. Другая машина имеет идентичный индуктор в нем, но закрашен и его шильдик. Токоизмерительные клещи показывает ток 18 А, а вольтметр показывает падение напряжения 324 В на катушке индуктивности машины, которая все еще работает.После выключив питание и заблокировав панель, вы отключаете индуктор в работающей машине и измерьте сопротивление провода 1,2 Ом с омметр. Использование идентичного индуктора в действующей машине в качестве пример, какое значение индуктивности следует заказать, и какое будет минимальный рейтинг VAR индуктора? Если вас беспокоит сумма сопротивления провода в индукторе при заказе? Поясните свой ответ.
Катушки индуктивности — практические EE
Индукторы — это устройства, накапливающие электрическую потенциальную энергию в магнитном поле.Они состоят из намотки проволоки и значительно улучшены за счет размещения в середине катушки черного металла.
Символ индуктивности
Символ индуктораОбщие уравнения индуктивности
Напряжение через катушку индуктивности равно индуктивности, умноженной на скорость изменения тока (производная тока по времени).
Это уравнение означает пару важных вещей:
- Ток через катушку индуктивности не может измениться мгновенно, для этого потребуется бесконечное напряжение.Индукторы борются с быстрыми изменениями тока.
- Напряжение на индукторе пропорционально скорости изменения тока через индуктор. Константа пропорциональности — это индуктивность.
- Напряжение на индукторе может изменяться мгновенно.
Катушка индуктивности Реактивное сопротивление = 2 * Pi * Частота в Гц * Индуктивность; Реактивное сопротивление имеет единицы
Ом.- Реактивное сопротивление катушки индуктивности увеличивается с увеличением частоты.Индукторы действуют как разомкнутые цепи для высокочастотных сигналов и действуют как короткие замыкания для низкочастотных сигналов.
- Положительное реактивное сопротивление означает, что напряжение ведет к току (напряжение быстро меняется, ток отстает).
- Для идеального индуктора его сопротивление равно 0, поэтому его полное сопротивление равно ZL = R + jXc = j * (2πfL)
Идеально Индуктор: ; f = частота в Гц, L = индуктивность, j = мнимое число
Правило правой руки
Чтобы понять, почему намотка проволоки создает индуктор, вам нужно знать правило правой руки.
Правило правой рукиПравило правой руки гласит, что если вы поместите правую руку большим пальцем в направлении тока, магнитное поле будет в направлении ваших пальцев, которые изгибаются вокруг оси вашего большого пальца. Итак, теперь представьте проволоку , свернутую в спираль, . Представьте себе ток, протекающий по этому проводу в определенном направлении, а затем представьте магнитное поле, образованное током, протекающим через каждую петлю из провода. Магнитное поле внутри каждой петли проходит одно направление, а магнитное поле снаружи каждой петли — в противоположном направлении.Магнитное поле от каждой петли складывается в общее магнитное поле.
Магнитное поле индуктораКогда вы помещаете железный материал, называемый ферритовым сердечником, в середину витого провода, магнитное поле взаимодействует с ферритовым сердечником и значительно усиливается.
Основные характеристики реальных индукторов
- Индуктивность
- Допуск — точность индуктивности
- Номинальный ток — Существует два типа номинальных значений тока для индукторов.Один — это номинальный ток из-за выделяемого тепла, другой — ток, выше которого ферритовый сердечник насыщается магнитным полем, и индуктивность начинает быстро терять индуктивность. Вы никогда не хотите, чтобы ядро стало насыщенным.
Типы индукторов
Индукторы с воздушным сердечником
- Не используйте ферритовый материал в сердечнике катушки. Вместо этого в сердечнике используется керамический материал для обеспечения механической структуры.
- Имеют относительно низкую индуктивность
- Обычно используются для высокочастотных приложений
Индукторы с ферритовым сердечником
- Намного более высокая индуктивность, чем у индукторов с воздушным сердечником
- Более высокая стоимость из-за ферритового материала
Формы индукторов с ферритовым сердечником
Формы стержней Форма тороида Форма шпульки со сквозным отверстием Форма шпульки для поверхностного монтажаЧип-индукторы
- Устройства поверхностного монтажа (SMD)
- Доступны небольшие размеры с использованием тех же размеров корпуса, что и резисторы SMD
- Относительно низкая индуктивность и низкий номинальный ток
- Обычно используется для радиочастотных (RF) и других высокочастотных фильтров
Ферритовые бусины и сердечники
- Также называется ферритовыми дросселями.
- Доступны в небольших корпусах SMD для последовательного размещения с сигналом или в больших размерах, которые проходят вокруг кабелей.
- Их электромагнитное воздействие не совсем то же, что и у истинного индуктора.Они становятся более устойчивыми к сигналам более высокой частоты.
- Дешевле, чем катушки индуктивности.
- Используется в основном для фильтрации шума в линиях электропередач и для фильтрации шума в кабелях для снижения кондуктивных и излучаемых помех.
Экранированные индукторы
- Экранированные катушки индуктивности имеют ферритовый материал, окружающий спиральный провод, который сохраняет большую часть магнитного поля внутри устройства.
- Экранированные индукторы дороже неэкранированных.
- Экранированные индукторы имеют ряд применений:
- Используйте, когда вам нужно разместить индукторы близко друг к другу, чтобы они не работали как трансформаторы.
- Используется, когда необходимо разместить индуктор рядом с чувствительными сигналами
- Используется для уменьшения излучения индуктора
Общие значения индуктивности
| Стандартные значения индуктивности | |||||||||
| нГн, мкГн | нГн, мкГн | нГн, мкГн | нГн, мкГн | ||||||
| 1.0 | 10 | 100 | 1000 | ||||||
| 1,1 | 11 | 110 | 1100 | ||||||
| 1,2 | 12 | 120 | 1200 | 1300 | |||||
| 1,5 | 15 | 150 | 1500 | ||||||
| 1,6 | 16 | 160 | 1600 | ||||||
| 1,8 | 0 | 20 | 200 | 2000 | |||||
| 2,2 | 22 | 220 | 2200 | ||||||
| 2,4 | 24 | 240 | 2400 | 2700 | |||||
| 3,0 | 30 | 300 | 3000 | ||||||
| 3,3 | 33 | 330 | 3300 | ||||||
| 3,6 | 9 | 39 | 390 | 3900 | |||||
| 4,3 | 43 | 430 | 4300 | ||||||
| 4,7 | 47 | 470 | 47 | 470 | 9571347 | 5100 | |||
| 5,6 | 56 | 560 | 5600 | ||||||
| 6,2 | 62 | 620 | 6200 | ||||||
| 6,8 | |||||||||
| 6,8 | 5 | 75 | 750 | 7500 | |||||
| 8,2 | 82 | 820 | 8200 | ||||||
| 8,7 | 87 | 870 | 9571387 9571387 | 9100 |


 18)
18) Условное изображение катушки индуктивности
Условное изображение катушки индуктивности