Виды резонанса: Виды резонанса — купить в Москве, цены — Мир Антенн

Содержание

Явление резонанса — Основы электроники

Явления резонанса связаны с периодическим колебательным движением электронов в контуре и состоят в том, что электроны в данном колебательном контуре легче всего «раскачиваются» с какой-то определенной частотой, которую мы называем резонансной. С периодическим колебательным движением мы встречаемся повсеместно. Колебания маятника, дрожание струны, движение качелей — все это примеры колебательного движения.

Для примера рассмотрим колебательную систему, изображенную на рисунке 1. Эта система, как мы увидим дальше, имеет много общего с электрическим колебательным контуром. Состоит она из пружины и массивного шара, закрепленного на стержне.

Рисунок 1. Механическая модель колебательного контура. Масса-индуктивность, гибкость-емкость, трение-сопротивление.

Если мы оттянем шар в низ от положения равновесия, то он под действием пружины немедленно устремится обратно; однако приобретя некоторую скорость шар не остановится в точке равновесия, а по инерции проскочит дальше, чем вызовет новую деформацию (сжатие) пружины.

Затем этот процесс повторится в обратном направлении и т. д. Шар будет колебаться в ту и другую сторону до тех пор, пока не израсходуется на трение весь запас энергии, сообщенной пружине при отклонении шара.

Нетрудно заметить, что при колебаниях шара энергия, сообщенная системе, все время переходит из энергии деформации (сжатия и растяжения) пружины в энергию движения шара и обратно. В механике первый вид энергии называется потенциальной энергией, а второй вид — кинетической.

В то время, когда шар находится в одном из крайних положений, он на мгновение останавливается. В этот момент энергия его движения равна нулю. Зато пружина в этот момент очень сильно деформирована: или сжата или растянута; в ней, следовательно, заключено наибольшее количество энергии. В тот же момент, когда шар с наибольшей скоростью проходит через положение равновесия, он обладает наибольшей энергией, но зато энергия пружины в этот момент равна нулю, так как она не сжата и не растянута.

Отклоняя шар на различные расстояния и наблюдая каждый раз за частотой последующих свободных колебаний системы, мы заметим, что частота колебаний системы остается все время одной и той же. Иными словами, она не зависит от величины начального отклонения. Эту частоту мы будем называть собственной частотой колебаний системы.

Если бы мы имели в своем распоряжении не одну такую систему, а несколько, то мы могли бы убедиться в том, что собственная частота свободных колебаний системы уменьшается с увеличением массы шара и увеличивается с увеличением упругости, т. е. с уменьшением гибкости пружины. Эта зависимость может быть обнаружена и на более простом примере с колеблющимися струнами различной толщины и различной степени натяжения.

Если мы пожелаем раскачать шар с наименьшей затратой усилий, то мы, безусловно, постараемся, во-первых, установить строгую периодичность наших толчков, т. е. постараемся, чтобы толчки следовали друг за другом через определенное время, а во-вторых, постараемся, чтобы промежуток времени между толчками равнялся периоду собственных колебаний системы (Рисунок 2).

Рисунок 2. Механическая модель колебательного контура с незатухающими колебаниями. Частота вынужденной силы равна собсвенной частоте системы (резонанс).

Для того чтобы раскачать колебательную систему с наименьшей затратой усилий, нужно частоту вынуждающей силы сделать равной собственной частоте колебания системы. Это правило очень хорошо известно всем нам еще с детского возраста, когда мы его применяли, раскачиваясь на качелях.

Рисунок 3. Явление резонанса на примере качелей.

Итак, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы, амплитуда колебаний становится наибольшей.

Таким образом, необходимо сказать, что совпадение частоты вынуждающей силы с собственной частотой колебаний системы и является резонансом.

За примерами резонанса ходить далеко не нужно. Оконное стекло, дрожащее с определенной частотой каждый раз, когда мимо проезжает трамвай или грузовая машина; дрожание струны музыкального инструмента после того, как мы прикоснулись к соседней струне, настроенной в унисон с первой, и т. п. — все это явления резонанса.

Зарядим конденсатор некоторым количеством электричества (рис.4, а) и замкнем его после этого на катушку индуктивности (рис.4, б). Конденсатор начнет немедленно разряжаться. Через катушку индуктивности потечет разрядный ток, а появление тока в катушке приведет к возникновению магнитного поля вокруг нее. При этом в катушке возникнет ЭДС самоиндукции, которая будет задерживать разряд конденсатора. Когда конденсатор разрядится, то ток в катушке не прекратится, так как он будет теперь поддерживаться ЭДС самоиндукции за счет энергии, запасенной в магнитном поле катушки во время разряда конденсатора. Этот продолжающийся ток перезарядит конденсатор в обратном направлении, т. е. та пластина, которая была прежде положительной, станет отрицательной, и наоборот (рис.4, в).

Рисунок 4. Свободные колебания. Вверху — электрические, внизу — механические.

После этого конденсатор снова начнет разряжаться, снова перезарядится (рис. 4, г, д) и т. д. Колебания тока в контуре будут продолжаться до тех пор, пока вся электрическая энергия, сообщенная контуру при заряде конденсатора, не превратится в тепловую энергию. Это произойдет тем скорее, чем больше активное сопротивление контура.

Итак, разряд конденсатора через катушку индуктивности является колебательным процессом. Во время этого процесса конденсатор несколько раз заряжается и разряжается, энергия поочередно переходит из электрического поля конденсатора в магнитное поле катушки и обратно.

Рисунок 5. Колебания в колебательном контуре.

Колебания тока, имеющие место при этом разряде, носят затухающий характер (рис.6).

Рисунок 6. Затухающие колебания в контуре.

Частота колебаний при выбранных величинах емкости и индуктивности является величиной вполне определенной и называется собственной частотой контура. Собственная частота контура будет тем больше, чем меньше величины емкости и индуктивности контура.

Если в колебательный контур ввести источник переменного тока, частота которого совпадает с собственной частотой контура, то колебания в контуре достигнут наибольшей величины, т. е. будет иметь место явление резонанса.

Между электрическими и механическими колебаниями может быть проведена далеко идущая параллель.

В табл. 1 слева даны электрические величины и явления, а справа аналогичные им величины и явления из области механики применительно к нашей механической модели колебательного контура.

**Аналогия электрических и механических величин**
Электрические величины	Механические величины
Индуктивность колебательного контура	Масса шара;
Емкость колебательного контура	Гибкость пружин
Активное сопротивление контура	Механическое трение
Пластины конденсатора	Пружины
Заряд конденсатора	Деформация (сжатие и растяжение) пружин
Положительный заряд пластин	Сжатие пружины
Отрицательный заряд пластины	Растяжение пружины
Сила тока	Скорость движения шара
Направление тока	Направление движения шара
Электродвижущая сила самоиндукции	Сила инерции шара
Амплитуда (наибольшее мгновенное значение тока)	Амплитуда (наибольшее отклонение шара от положения равновесия)
Частота (число циклов в секунду)	Частота (число колебаний в се¬кунду)
Резонанс (совпадение частоты внешней ЭДС с собственной частотой конура)	Резонанс (совпадение частоты толчков вынуждающей силы с собственной частотой колебаний шара)

Различные моменты электрического колебания и соответствующие им моменты колебания нашей механической модели колебательного контура изображены на рис.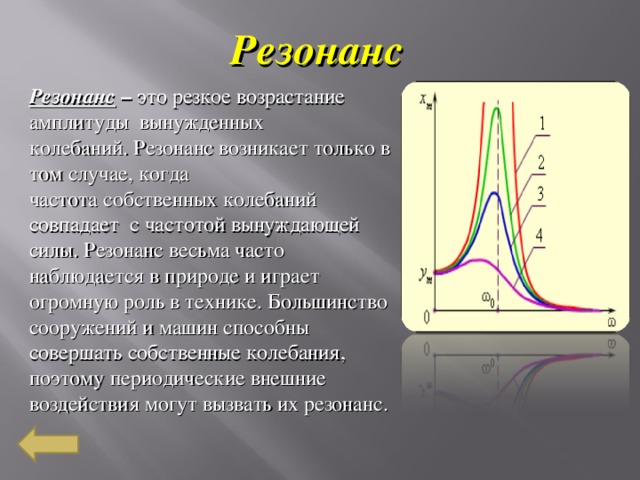 4.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

► Сделать МРТ в Москве

Медэксперт – это уникальное сочетание экспертного уровня, высокого качества и доступной цены. С самого начала Медэксперт был задуман как специализированный центр исключительно для проведения магнитно-резонансной томографии.

Наш принцип – делать только один вид обследования,

но делать его лучше всех!

Такая узкая специализация дает нам возможность сконцентрировать лучшие технические средства, а также профессиональные знания и опыт на одном-единственном направлении. Благодаря этому на сегодняшний день Медэксперт является признанным лидером Москвы в области проведения МРТ-исследований.

Это значит, что, обратившись к нам, вы сможете в полной мере воспользоваться всеми преимуществами этого высокотехнологичного метода диагностики. В центре Медэксперт представлены все основные виды современной магнитно-резонансной томографии (всего более 40):

Где сделать МРТ в Москве?

Центр Медэксперт предлагает следующие преимущества:

Специализированный центр МРТ экспертного уровня, более 40 видов МРТ
Мощный томограф Philips 1,5 Тесла — гарантия высокого качества изображений, позволяющего установить точный диагноз
Специалисты высокого уровня с многолетним опытом в диагностике МРТ — наша гарантия точного описания исследования!
Наши партнеры — Клиника Первого Медицинского Института, Ортоспайн и др. Нам доверяют!
В шаговой доступности от м. Новокузнецкая
Заключения МРТ от 30 минут!

Что такое МРТ-диагностика

Магнитно-резонансная томография (МРТ)– это послойное сканирование тканей с помощью магнитного поля. В результате такого сканирования получаются снимки с определенным шагом (обычно 1-2 мм), которые позволяют построить трехмерное изображение области обследования. Свободно проникая в ткани, магнитное поле не причиняет им никакого вреда. За счет этого МРТ является полностью безопасным и безболезненным методом диагностики. Отсутствие побочных эффектов делает возможным обследование как взрослых, так и детей, а также многократные обследования.

В настоящее время именно магнитно-резонансная томография считается лучшим диагностическим методом при заболеваниях опорно-двигательного аппарата, внутренних органов, кровеносных сосудов. Это объясняется высокой информативностью, достоверностью и детализацией данных, возможностью подробно изучить различные ткани в разных плоскостях, обнаружить даже незначительные по размерам опухоли, повреждения, патологические изменения. К этому остается добавить высокую универсальность процедуры, которая с одинаковым успехом используется для диагностики опухолевых, воспалительных и дегенеративно-дистрофических заболеваний.

МРТ в неврологии
История применения МРТ в неврологии началась в 1990-х годах с появлением томографов мощностью 1,5 Тесла. И сегодня уже почти невозможно представить себе диагностику широкого ряда неврологических заболеваний без МРТ.
Как часто можно делать МРТ?
Магнитно-резонансная томография считается абсолютно безвредным обследованием, поскольку при ее проведении не используется жесткое излучение. Тем не менее, многие задают вопрос, как часто можно делать МРТ?
Как МРТ изменило медицину?
Появление магнитно-резонансной томографии значительно повысило информативность и расширило возможности диагностики. Впервые стало возможно одновременно обследовать различные ткани, что особенно важно при сочетанных и сложных патологиях.

Кабинет магнитно-резонансной томографии

ЧТО ТАКОЕ МАГНИТНО-РЕЗОНАНСНАЯ ТОМОГРАФИЯ

В основе МР-томографии лежит принцип магнитного резонанса ядер водорода. Поскольку вода содержится в органах и тканях человека в значительном количестве, то водород – самый распространенный элемент в организме человека. Исследование происходит следующим образом. Пациента помещают в магнитное поле МР-томографа, после чего ядра атомов водорода в теле человека, которые представляют собой маленькие магнитики, ориентируются по направлению поля. Исследуемую область выбирают, добавляя слабое переменное магнитное поле с помощью, так называемых градиентных катушек. Атомы водорода возбуждаются и генерируют ответный сигнал, который улавливается приёмными катушками. Разные виды тканей (кости, мышцы, и т.п.) содержат разное количество атомов водорода, поэтому они генерируют сигналы с различными характеристиками. Эти сигналы с помощью специального оборудования расшифровываются и происходит построение изображения. Полученные изображения выглядят, как фотографии анатомических срезов различных органов.

ВОЗМОЖНОСТИ МАГНИТНО-РЕЗОНАНСНОЙ ТОМОГРАФИИ

МРТ головного мозга
МРТ позвоночника, спинного мозга
МРТ сосудов головного мозга, шеи (МР-ангиография интракраниальных, экстракраниальных сосудов)
МРТ суставов
МРТ органов брюшной полости
МРТ органов малого таза
МРТ мягких тканей

ДОСТОИНСТВА МАГНИТНО-РЕЗОНАНСНОЙ ТОМГРАФИИ

Отсутствие лучевой нагрузки, что позволяет пациенту без вреда для собственного здоровья проходить данное исследование неограниченное количество раз за короткий промежуток времени в любом возрасте, начиная с младенчества.
Неинвазивность /т.е. без внутреннего вмешательства/ и, следовательно, абсолютно безболезненно и безопасно.
Крайне низкая вероятность осложнений при использовании контрастных препаратов.
Полипроекционность — возможность проводить исследование в трех основных взаимно перпендикулярных плоскостях (аксиальной, фронтальной, сагиттальной), а при необходимости в любой мысленной плоскости.
Высокая межтканевая контрастность.
Высокая разрешающая способность
Правильный диагноз в кратчайшие сроки
Современный наиболее информативный безопасный метод диагностики без лучевой нагрузки на оборудовании экспертного класса

КАК ПРОВОДИТСЯ ИССЛЕДОВАНИЕ

МР-томограф по своему внешнему виду похож на рентгеновский компьютерный томограф; не специалист вряд ли их различит. В процессе исследования стол с пациентом постепенно продвигается внутрь сканера, выполненного в форме тоннеля. При сканировании пациент находится в тоннеле томографа, где достаточно светло и имеется вентилятор, обеспечивающий приток свежего воздуха. Необходимо, чтобы пациент не шевелился, поскольку даже небольшие смещения могут существенно снизить качество получаемых изображений. Длительность диагностического исследования в среднем 20-30 минут.

НАШЕ ОБОРУДОВАНИЕ

Новейший МР-томограф фирмы Дженерал Электрик, производство США, напряженность магнитного поля 1.5Т. Современное оборудование – широкий круг диагностических возможностей.

НАШИ СПЕЦИАЛИСТЫ:

Заведующая кабинетом МРТ — УДАЛОВА СВЕТЛАНА ВЛАДИМИРОВНА, врач-рентгенолог высшей категории.

РОМАНЮХА ИЛЬЯ ВЛАДИМИРОВИЧ, врач-рентгенолог высшей категории

ЩЕРБА ТАТЬЯНА АЛЕКСАНДРОВНА, врач-рентгенолог

Контакты:

Тел. 8 (423) 222-43-50,

Тел. 8 (423) 259-96-05

Часы работы: 8:00-20:00, выходной суббота, воскресенье

Адрес: г.Владивосток, ул,Светланская 38/40

FAQ • Резонансы шагового двигателя, среднечастотный резонанс

Суть явления

Дискретность и периодичность усилий, прикладываемых к ротору шагового двигателя, порождает в шаговом двигателе явление резонанса. Суть его аналогична резонансу в любой другой системе, в т.ч. классического примера с грузом на пружине. Роль «груза» выполняет ротор, роль «пружины» — усилия магнитного поля.
Резонанс — крайне негативное явление, возникающее на всех без исключения ШД. Эффект проявляется в виде внезапного появления гула, вибрации и падения момента на некоторых скоростях. Это может привести к пропуску шагов, потере синхронности или вообще остановке двигателя. Эффект проявляется в том случае, если частота шагов совпадает с собственной резонансной частотой ротора двигателя.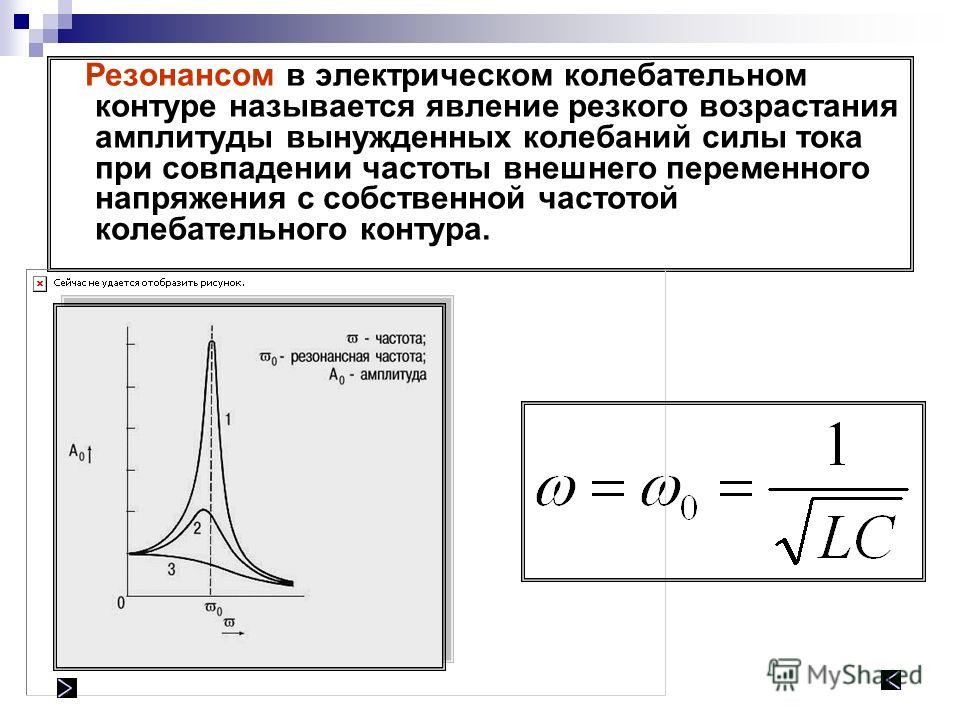

Виды резонанса

При вращении ШД Вы можете столкнуться с двумя типами резонанса (любой резонанс отнимает момент у ШД).

Низкочастотный резонанс. Проявлется в виде вибрации на низких скоростях кращения (~1 об/сек). Вызван резонанс несимметричностью токов в обмотках ШД. Современные драйверы Purelogic имеют механизм устранения низкочастотного резонанса путем выравниваем симметрии(подстройка фазных токов).

Среднечастотный резонанс. Проявляется в виде гула на средних скоростях вращения (6-12 об/сек). Частота, на который возникает и сила резонанса сильно зависит от параметров ШД и механической нагрузки. Собственная частота колебаний ШД зависит от момента инерции ротора (вместе с нагрузкой) и величины магнитного поля. Ввиду сложной конфигурации магнитного поля, резонансная частота ротора зависит от амплитуды колебаний. При уменьшении амплитуды частота растет — больший момент удержания и меньший момент инерции приводят к увеличению резонансной частоты.

Типичные случаи резонанса ШД: ссылка1 ссылка1

Как правило, резонанс ослабевает с увеличением деления шага. Это связано с тем, что ротор после подачи тока в обмотку некоторое время колеблется прежде чем зафиксироваться в конечном положении, и колебания тем сильней, чем больше инерция ротора.

Более мелкие перемещения в микрошаге не требуют длительных разгона-фиксации ротора, и позволяют быстро останавливать его между шагами, что уменьшает негативные последствия резонанса.

Видно, что в полношаговом режиме наблюдаются выбросы и колебания, в то время как в микрошаговом режиме их нет. Однако и в этом режиме график положения ротора отличается от прямой линии. Эта объясняется погрешностью геометрии деталей двигателя. Отсюда вытекает следующее правило:

Крайне не рекомендуется использовать на драйверах режим полного шага и полушага.
На этих режимах резонанс проявляется особенно сильно!

Оптимальные режимы, которые мы рекомендуем, это микрошаг 1:8, 1:16 и 1:32.

Решение

Для борьбы с резонансом можно использовать различные методы, например, демпфирующие элементы типа муфт, но реальный эффект дает только использование микрошага и применение драйверов с подавлением резонанса.

Большинство драйверов Purelogic имеют специально разработанную электронную схему — автоматический компенсатор среднечастотного резонанса. Компенсатор позволяет полностью исключить резонирование ШД и сделать его вращение равномерным и устойчивым во всем диапазоне частот. Компенсатор среднечастотного резонанса не требует настройки.

Контрастирующие вещества в магнитно-резонансной томографии

В основе любого метода визуализации лежит способность глаза отличать участки изображения по их яркости. Контрастность патологического очага по отношению к окружающим тканям зависит от собственных свойств ткани и способа получения изображения на томограммах. В магнитно-резонансной томографии (МРТ) изображение, получаемое на томограммах строится на основе магнитных характеристик тканей, главные из которых — протонная плотность (р) и релаксационные времена T1 и Т2.

На магнитные характеристики объекта при проведении МРТ с контрастом влияют содержание воды, крупных молекул (это в основном белки), ионов и свободных радикалов. Эти соотношения почти всегда нарушаются при патологических состояниях. Так, воспаление сопровождается увеличением количества внутриклеточной и внеклеточной воды, а опухоли — внутриклеточной воды. Вода удлиняет релаксационные времена, белковые молекулы, ионы и радикалы их сокращают.

По-особому ведет себя кровоизлияние на томограммах. Дезоксигемоглобин — диамагнетик. Метгемоглобин действует как парамагнетик, в неразрушенных эритроцитах крови он сокращает релаксационные времена. После разрушения эритроцитов проявляется суперпарамагнитный эффект, и кровь становится яркой на Т1-взвешенных томограммах. Гемосидерин обладает высокой магнитной чувствительностью, приводя к быстрой дефазировке окружающие протоны, кровь выглядит на томограмма темной.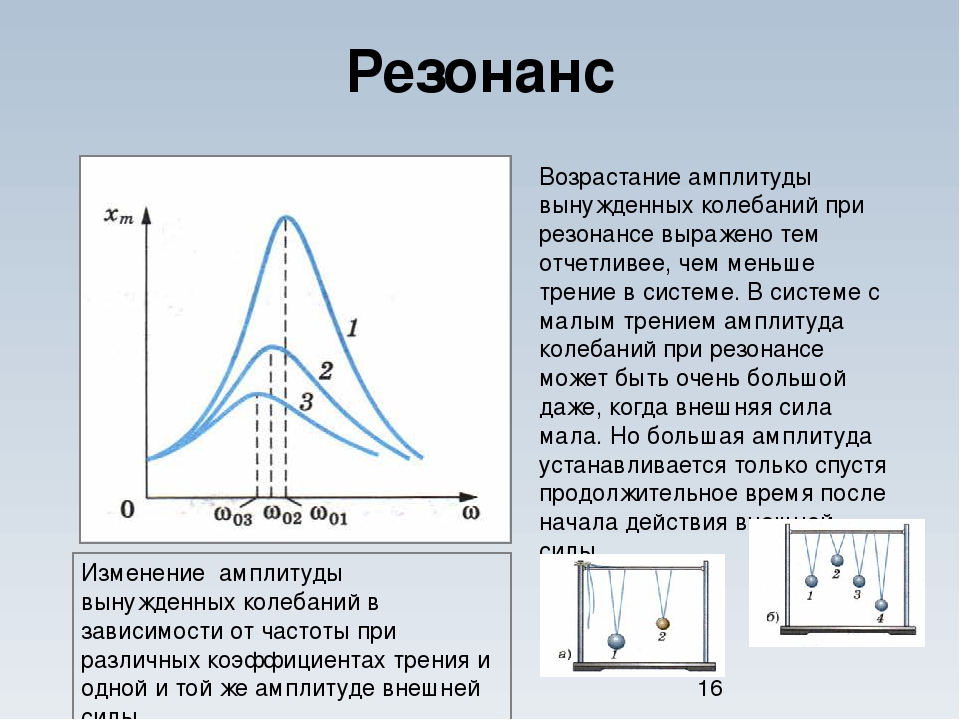

Протонная плотность— число резонирующих протонов в единице объема — мало отличается у тканей в норме и при патологических состояниях. Исключение составляетжировая ткань, имеющая самую высокую протонную плотность и потому высокую интенсивность сигнала, особенно на Т1-взвешенных томограммах. Низкая протонная плотность компактной костной ткани делает ее темной на изображениях любого типа взвешенности.

В большинстве случаев естественной контрастности МР — томограмм достаточно для выявления и характеристики патологического очага. Вместе с тем встречаются ситуации, когда патологический очаг не визуализируется на томограмме вследствие изоинтенсивности или малых размеров. Бывает трудно определить границы патологических изменений при МРТ и оценить внутреннюю структуру. В таких ситуациях помогает диагностика с введением контрастных веществ, т.н. МРТ с контрастным усилением. Кроме того, есть и другие специальные применения контрастных веществ. Точкой приложения магнито-фармацевтики являются релаксационные времена. Контрастные вещества для МР исследований меняют их неспецифически и напрямую. В этом плане они принципиально отличаются от контрастных веществ, применяемых в рентгенологии, которые видны сами ввиду высокой рентгеновской плотности, поэтому, правильнее называть их контрастирующие вещества.

Позитивные контрастные веществаотносятся к группе парамагнетиков. Парамагнетики содержат в качестве активной части ионы с непарными электронами на внешней орбите — Gd³⁺, Mn²⁺, Fe³⁺, Cr³⁺и т.д. Практическое значение при проведении МРТ с контрастом на сегодняшний день имеют соли гадолиния (Gd³⁺), так как остальныеионы более токсичны и малорастворимы.

Гадолинийотносится к редкоземельным элементам из группы лантаноидов. Гадолиний содержит семь непарных электронов, которые преимущественно сокращают время спин-решетчатой релаксации (Т₁). В результате патологический очаг становится ярким при рассмотрении томограммы. Гадолиний в виде простых солей очень токсичен, поэтому он включается в состав хелатов. В таблице приведены основные соединения гадолиния, выпускаемые в качестве контрастных препаратов для МРТ диагностики.

Контрастные вещества, содержащие гадолиний(Gd³⁺)
Название МРКС	Химическое соединение	Сокращенное обозначение	Химическая структура	Заряд	Производитель
Омнискан	Гадодиамид	Gd-DTPA-BMA	Линейная	Неионный	Nycomed Австрия
Магневист	Гадопентетата димеглумин	Gd-DTPA	Линейная	Ионный	Schering Германия
Мультиханс	Гадобената димеглумин	Gd-BOPTA	Линейная	Ионный	Braeco Италия
Примовист	Гадоксетовой кислоты динатриевая соль	Gd-EOB-DPTA	Линейная	Ионный	Байер Шеринг АГ(Германия)
Вазовист	Гадофосвесета тринатриевая соль	Gd-DTPA	Линейная	Ионный	Меллинкродт Медикал Ink США
Проханс	Гадотеридол	Gd-HP -DO3A	Цикличная	Неионный	Braeco Италия
Гадовист	Гадобутрол	Gd-BTDO3A	Цикличная	Неионный	Шеринг АГ(Германия)
Дотарем	Гадотерата меглумин	GdDOTA	Цикличная	Ионный	Guerbet Франция

Принцип действияконтрастных веществ в МРТ диагностике одинаковый, хотя и с некоторыми фармакологическими и фармакокинетическими различиями.

При внутривенном введении контрастные вещества попадают в межклеточное пространство тканей, не задерживаясь в сосудистом русле. Накопление в патологических тканях (кроме ЦНС) зависит от васкуляризации этих образований. Препараты гадолиния в соединении со средними полимерными цепями относительно длительно удерживаются в сосудистом русле и могут применяться для контрастной МР — ангиографии, томографии головного мозгас контрастным усилением.

Контрастирующие вещества на основе гадолиния должны с осторожностью применяться при заболеваниях почек.

В виде жировых эмульсий гадолиний потенциально применим как вещество, контрастирующее желудочно-кишечный тракт.

Негативные контрастные веществасодержат в качестве активной части Fe²⁺ или Fe³⁺. По своему действию железо выступает в качестве суперпарамагнетика. Препарат Endorem применяется для выявления очагового поражения печени (МРТ печени). Для контрастирования желудочно-кишечного тракта служат Lumirem, Gastromark, Abdoscan. В нашем отделении используются только контрастирующие вещества содержащие гадолиний.

Проведение МР исследования с контрастирующим веществом состоит из двух этапов. Вначале проводится МР сканирование соответствующего отдела со стандартными требованиями. Необходимость контрастного усиления определяется по данным именно этого исследования. При согласии пациента и отсутствии противопоказаний врач определяет дозировку контрастирующего вещества и способ его введения. Перед повторным исследованием пациент вывозится из туннеля томографа. В вену локтевого сгиба устанавливается катетер, через который вводится контрастирующее вещество. Внутривенное введение может осуществляться вручную, и с помощью электронного инжектора.

Для автоматического введения контрастирующего веществамы используемдвухголовочный инжектор Optistar LE. Онспециально создан для магнитно-резонансной томографии, и работает в условиях магнитного поля до 3. 0 Тесла.

Рабочая головка и вертикальная стойка с основанием, размещенные рядом с магнитно-резонансным томографом, изготовлены из немагнитных материалов.

Инжектор позволяет осуществлять различные схемы введения контрастирующего вещества. Применяется фронтальная загрузка двух одноразовых шприцов, заполненных контрастирующим препаратом и физиологическим раствором соответственно.

ИнжекторOptiStar LE обеспечивает выполнение инъекции с изменением программируемых параметров: скорость введения, давление, объем контрастирующего препарата, задержка инъекции, режим капельного введения физиологического раствора.

Пациенту запрещается менять положение тела и двигаться во время всего исследования.

Если исследование с введением контрастирующего вещества запланировано, необходимо убедиться в доступности и проходимости поверхностных вен. Если пункция вены вызывает затруднение (был проведён курс химиотерапии, анатомические особенности и т. п.), до МР исследования необходимо позаботиться об установке венозного катетера до исследования. Данную манипуляцию можно осуществить в нашем стационаре.

Два резонанса параметрического контура (обзор)

Былов, Б. Ф.; Виноград, Р. Э.; Гробман, Д. М.; Немыцкий, В. В. Теория показателей Ляпунова и ее приложение в вопросах устойчивости. М.: Наука, 1966. 582 с.

Мандельштамм, Л. И. “Вопросы электрических колебательных систем и радиотехники,” Успехи физических наук, Т. 13, № 2, С. 161–194, 1933. DOI: https://doi.org/10.3367/UFNr.0013.193302a.0161.

Горелик, Г. С. “Резонансные явления в линейных системах с периодически меняющимися параметрами,” Журнал технической физики, Т. 4, № 10, С. 1783–1817, 1934; Т. 5, № 2, С. 196–215, 1935; Т. 5, № 3, С. 490–517, 1935.

Ляпунов, А. М. Собрание сочинений, Т. 2. М.-Л.: Изд. АН СССР, 1956. 472 с.

Якубович, В. А.; Старжинский, В. М. Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения. М.: Наука, 1972. 718 с.

Демидович, Б. П. Лекции по математической теории устойчивости. М.: Наука, 1967. 472 с.

Тафт, В. А. Электрические цепи с переменными параметрами. М.: Энергия, 1968. 328.

Бирюк, Н. Д.; Юргелас, В. В. Основы теории параметрических радиоцепей. Воронеж: ВГУ, 2012. 345 с.

Birjuk, N.; Damgov, V. “Qualitative analysis of the free process in a generalized linear oscillating circuit with periodic parameters. I. Structure of the differential equations and classification of, the free processes in Hamiltonian oscillating circuits,” Аерокосмически изследoвания в България, № 13, С. 59-82, 1997.

Birjuk, N. D.; Damgov, V. N. “Qualitative analysis … Part. 2. Stability of the canonical systems an a generalized linear resonance circuit,” Аерокосмически изследвания в България, № 14, С. 20-30, 1998.

Birjuk, N.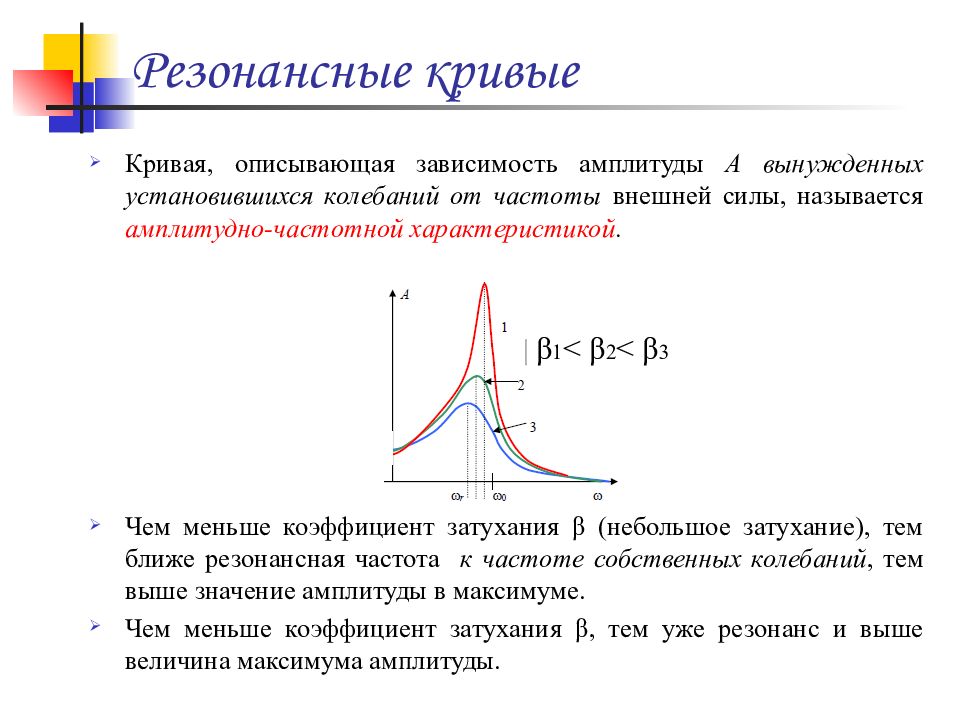 ; Damgov, V. “Qualitative analysis … Part. 3. Analysis of the free processes in piece-wise linear and quasi-harmonic oscillating circuits,” Аерокосмически изследвания в България, № 15, С. 55-63, 1999.

Белоглазов, В. В.; Бирюк, Н. Д.; Юргелас, В. В. “Анализ, свойства и потенциальные возможности параметрического контура. Резонанс,” Известия вузов. Радиоэлектроника, Т. 50, № 6, С. 39–51, 2007. URI: http://radio.kpi.ua/article/view/S0021347007060040.

Белоглазов, В. В.; Бирюк, Н. Д.; Юргелас, В. В. “Анализ свободных процессов в параметрическом контуре методом обобщенных характеристических уравнений,” Известия вузов. Радиоэлектроника, Т. 53, № 5, С. 32–40, 2010. URI: http://radio.kpi.ua/article/view/S0021347010050043.

Бирюк, Н. Д.; Хорпяков, О. С. “Резонанс по Мандельштаму параметрического контура,” Вестник ВГУ. Серия: Физика. Математика, № 1, С. 23–33, 2017. URI: https://elibrary.ru/item. asp?id=28989672.

Бирюк, Н. Д.; Короткова, Т. Н.; Хорпяков, О. С. “Процессы в параметрических радиоцепях, как обобщение процессов в стационарных радиоцепях,” Вестник ВГУ. Серия: Физика. Математика, № 1, С. 5–14, 2019. URI: https://elibrary.ru/item.asp?id=37285745.

Шаповалов, Ю. I. Символьний аналiз лiнiйних електричних кiл у частотній областi. Постiйнi та змiннi параметри. Львiв: Видавництво Львiвськоi полiтехнiки, 2014. 321 с.

Перов, А. И.; Коструб, И. Д. “Об ограниченных решениях слабо нелинейных векторно-матричных дифференциальных уравнений n-го порядка,” Сибирский математический журнал, Т. 57, № 4, С. 830–849, 2016. URI: http://mi.mathnet.ru/smj2787.

Финогенко, И. А. “Принцип инвариантности для неавтономных дифференциальных уравнений с разрывными правыми частями,” Сибирский математический журнал, Т. 57, № 4, С. 913–927, 2016. URI: http://mi.mathnet.ru/smj2792.

Катаев, Д. Е.; Ядыкин, И. Б. “О решении матричных дифференциальных уравнений Ляпунова частотным методом,” Известия РАН. Теория и системы управления, № 6, С. 3–15, 2016. DOI: https://doi.org/10.7868/S0002338816050061.

Лапин, А. А.; Желтиков, А. М. “Октавный фазовый синхронизм для оптического параметрического усиления однопериодных импульсов среднего инфракрасного диапазона,” Письма в ЖЭТФ, Т. 103, № 3, С. 184–188, 2016. URI: http://www.jetpletters.ac.ru/ps/2109/article_31690.shtml.

Сазонов, Л. И. “О существовании периодических решений у ОДУ в банаховом пространстве с высокочастотными слагаемыми,” Математические заметки, Т. 100, № 6, С. 900–910, 2016. DOI: https://doi.org/10.4213/mzm10548.

Шкаликов, А. Л.; Трунк, К. “Об устойчивости, замкнутости и самосопряженности для 2×2 оператор-матриц,” Математические заметки, Т. 100, № 6, С. 932–938, 2016. DOI: https://doi. org/10.4213/mzm11305.

Мирзоев, К. А.; Конечная, Н. Н. “Об асимптотике решений одного класса линейных дифференциальных уравнений с негладкими коэффициентами,” Математические заметки, Т. 100, № 2, С. 312–317, 2016. DOI: https://doi.org/10.4213/mzm11203.

Калитин, Б. С. “К прямому методу Ляпунова для полудинамических систем,” Математические заметки, Т. 100, № 4, С. 531–543, 2016. DOI: https://doi.org/10.4213/mzm11007.

Артамонов, Н. В. “О разрешимости системы прямых-обратных линейных уравнений с неограниченными операторными коэффициентами,” Математические заметки, Т. 100, № 5, С. 762–765, 2016. DOI: https://doi.org/10.4213/mzm11355.

Бессонов, Д. А.; Любимов, В. Н.; Альшиц, В. И. “Акустический резонанс в тетрагональных и кубических кристаллах,” Известия РАН. Серия физическая, Т. 80, № 12, С. 1720–1728, 2016. DOI: https://doi.org/10.7868/S0367676516080056.

Ganti, R. K.; Haenggi, M. “Asymptotics and approximation of the SIR distribution in general cellular networks,” IEEE Trans. Wireless Commun., Vol. 15, No. 3, p. 2130-2143, 2016. DOI: https://doi.org/10.1109/TWC.2015.2498926.

Kostic, Marco. “Asymptotically almost periodic solutions of fractional relaxation inclusions with Caputo derivatives,” Publications de L’institut mathematique, Vol. 104, No. 118, p. 23-41, 2018.

Onitsuka, M. “Uniform asymptotic stability of damped linear oscillators with variable parameters,” Appl. Math. Comput., Vol. 2018, No. 4, p. 1436-1442, 2011. DOI: https://doi.org/10.1016/j.amc.2011.06.025.

Smith, R. A. “Asymptotic stability of x″ + a(t)x′ + x = 0,” Quarter. J. Math., Vol. 12, No. 1, p. 123-126, 1961. DOI: https://doi.org/10.1093/qmath/12.1.123.

Sugie, J.; Onitsuka, M. “Integral conditions on the uniform asymptotic stability for two-dimensional linear systems with time-varying coefficients,” Proc. dot + TX + Q(X) = 0 in Rⁿ,” Proc. Edinburgh Math. Soc., Vol. 45, No. 3, p. 601-615, 2002. DOI: https://doi.org/10.1017/S0013091501000281.

Zalar, B.; Mencinger, M. “Near-idempotents, near-nilpotents and stability of critical points for Riccati equations,” Glasnik Matematicki, Vol. 53, No. 2, p. 331-342, 2018. DOI: https://doi.org/10.3336/gm.53.2.06.

Onitsuka, M.; Tanaka, S. “Box-counting dimension of solution curves for a class of two-dimensional nonautonomous linear differential systems,” Math. Commun., Vol. 23, No. 1, p. 43-60, 2018. URI: http://www.mathos.unios.hr/mc/index.php/mc/article/view/2334.

Onitsuka, M. “Non-uniform asymptotic stability for the damped linear oscillator,” Nonlinear Analysis: Theory, Methods, Appl., Vol. 72, No. 3-4, p. 1266-1274, 2010. DOI: https://doi.org/10.1016/j.na.2009.08.010.

Duc, L. H.; Ilchmann, A.; Siegmund, S.; Taraba, P. “On stability of linear time-varying second-order differential equations,” Quarter. Appl. Math., Vol. 64, No. 1, p. 137-151, 2006. URI: https://www.jstor.org/stable/43638716.

Kwong, M. K.; Pasic, M.; Wong, J. S. W. “Rectifiable oscillations in second-order linear differential equations,” J. Differential Equations, Vol. 245, No. 8, p. 2333-2351, 2008. DOI: https://doi.org/10.1016/j.jde.2008.05.016.

Zaouche, E. “Uniqueness of solution in a rectangular domain of an evolution dam problem with heterogeneous coefficients,” Electron. J. Differential Equations, Vol. 2018, No. 169, p. 1-17, 2018. URI: https://ejde.math.txstate.edu/Volumes/2018/169/abstr.html.

Wang, G.; Ahmad, B.; Zhang, L.; Nieto, J. J. “Comments on the concept of existence of solution for impulsive fractional differential equations,” Commun. Nounlinear Sci. Numer. Simul., Vol. 19, No. 3, p. 401-403, 2014. DOI: https://doi.org/10.1016/j.cnsns.2013.04.003.

Канторович, Л. В.; Крылов, В. И. Приближенные методы высшего анализа. М.-Л.: Госфизматиздат, 1962. 708 с.

Zemliak, A. “Analysis of the Lyapunov function characteristics for the minimal-time design strategy,” WSEAS Trans. Circuit Syst., Vol. 6, No. 1, p. 110-116, 2007.

Земляк, А. М. “Сравнительный анализ функции Ляпунова различных стратегий проектирования аналоговых цепей,” Известия вузов. Радиоэлектроника, T. 51, № 5, С. 3–11, 2008. URI: http://radio.kpi.ua/article/view/S0021347008050014.

Земляк, А. М. “Структура минимальной по времени стратегии оптимизации аналоговых цепей,” Известия вузов. Радиоэлектроника, T. 52, № 1, С. 47–56, 2009. URI: http://radio.kpi.ua/article/view/S0021347009010051.

Земляк, А. М. “Сравнение различных стратегий оптимизации цепей на основе функции Ляпунова,” Известия вузов. Радиоэлектроника, T. 54, № 7, С. 43–50, 2011. DOI: https://doi.org/10.20535/S0021347011070065.

Земляк, А. М. “Структура квазиоптимального по времени алгоритма проектирования аналоговых цепей,” Известия вузов. Радиоэлектроника, T. 55, № 11, С. 40–49, 2012. DOI: https://doi.org/10.20535/S0021347012110052.

Zemliak, A. “Analog circuit optimization on basis of control theory approach,” COMPEL: Int. J. Computation Math. Electrical Electronic Eng., Vol. 33, No. 6, p. 2180-2204, 2014. DOI: http://dx.doi.org/10.1108/compel-10-2013-0324.

Zemliak, A.; Markina, T. “Behaviour of Lyapunov’s function for different strategies of circuit optimisation,” Int. J. Electronics, Vol. 102, No. 4, p. 619-634, 2015. DOI: https://doi.org/10.1080/00207217.2014.936046.

Земляк, А. М. “Применение принципа максимума для оптимизации цепей,” Известия вузов. Радиоэлектроника, T. 60, № 6, С. 353–364, 2017. DOI: http://dx.doi.org/10.20535/S002134701706005X.

Ковалев, М. Я. “Абсолютная устойчивость в задачах оптимального выбора с фиксированным прошлым,” Доклады Акад. Наук Белоруси, Т. 62, № 2, C. 147–150, 2018. DOI: https://doi.org/10.29235/1561-8323-2018-62-2-147-150.

Дмитричев, А. С.; Захаров, Д. Г.; Некоркин, В. И. “О глобальной устойчивости синхронного режима в хаб-кластерах энергосетей,” Известия вузов. Радиофизика, T. 60, № 6, С. 564–571, 2017. URI: https://radiophysics.unn.ru/issues/2017/6/564.

Bengochea, Gabriel; Verde-Star, Luis; Ortigueira, Manuel. “Operational method for the solution of ordinary differential equations using Hermite series,” Math. Commun., Vol. 23, No. 2, p. 279-293, 2018. URI: http://www.mathos.unios.hr/mc/index.php/mc/article/view/2510.

Что такое резонанс в физике кратко. Что такое резонанс — его виды (звуковой, когнитивный), а также польза и опасность резонанса.

Что такое явление резонанса: частота колебаний
С каждым маленьким усилием, которое ты проявляешь на пути, чтобы приблизиться к Божеству, Божество проявляет гораздо большее усилие, чтобы приблизиться к тебе.
Х.А. Ливрага
Резонанс подобен айсбергу. В целом он представляет собой универсальный закон (например, Тесла считал закон резонанса наиболее общим природным законом). Но нашему взору открыта лишь малая его часть. Сюда относится практически весь спектр ассоциаций, связанных со словом «резонанс». Это и маятники на общей нити, и посуда, дребезжащая в шкафу в ответ на проехавший по улице трамвай, и раскачивание качелей, и питерский мост, рухнувший от строевого шага прошедшей по нему роты солдат, и лазерная генерация и т.д.
Что же таят глубины и как нам об этом узнать? Во-первых, можно подождать, пока усилиями науки кусочек подводной части покажется над поверхностью. Этот способ работает, поскольку навстречу усилиям неутомимых исследователей айсберг-резонанс действительно всплывает. И с каждым днем открывает нам все новые и новые грани. Это и магнитно-резонансная томография — «нобелевский лауреат» 2003 г., и биорезонанс с многочисленными сферами его практического применения (гомеопатия, акупунктура, диагностика по Фоллю и методу Кирлиан и др.), и многое другое. Во-вторых, подводную часть айсберга можно мельком увидеть самому, нырнув в глубину какого-либо явления вне или внутри себя. Но когда мы выныриваем на поверхность, мы сталкиваемся с неизбежной трудностью адекватного и понятного для других описания пережитого нами. И тогда мы либо оставляем свой опыт при себе, либо пробуем перевести его на универсальный язык — образный, символический язык сказаний, мифов и притч или язык науки. И в том и в другом случае мы проводим параллель с уже известным, принятым и понятным, призывая на помощь действенное орудие мысли — принцип аналогий. Например, в ситуации, когда мы понимаем друг друга без слов, когда ощущаем мысли и чувства друга, невзирая на расстояние и время, разделяющие нас, мы можем сказать: мы на одной волне, мы в резонансе. И принцип аналогий тоже резонанс — согласие, созвучие, соответствие принципов и законов, применимых ко многим планам проявления жизни: «Как наверху, так и внизу, как внизу, так и наверху».
Ричард Гербер называет резонанс «ключом к пониманию и управлению любой системой, который откроет дверь в невидимый мир жизненных процессов». Что такое ключ? Это то, что открывает смысл происходящего вовне и внутри нас. Это то, что помогает подойти к исследованию неизвестного не только с вопросами, что и как происходит, но и почему и зачем. Может быть, есть резон взглянуть на физику резонанса в надежде отыскать в ней подобный ключ (случайно ли слово «резон» означает «разумный довод», «смысл»)? Ключ к пониманию и управлению не любой системой. Ключ к пониманию и управлению собой. Итак, в добрый путь исследования подводной части айсберга-резонанса, а заодно и нас самих. Ведь человек подобен айсбергу. И все, что мы знаем о себе, есть лишь крошечная часть нашей истинной природы (ученые, например, считают, что в нашей повседневной жизни мы задействуем всего 4% возможностей нашего мозга).
«Познай себя, и ты познаешь Вселенную и Богов».
Резонанс: что, как и зачем
Все связи между явлениями устанавливаются исключительно путем разного рода простых и сложных резонансов — согласованных вибраций физических систем.
Н. Тесла
Резонанс (от лат. resono — «звучу в ответ, откликаюсь») — это:
1) резкое увеличение:
амплитуды механических (звуковых) колебаний под влиянием внешних воздействий, когда частота собственных колебаний системы совпадает с частотой колебаний внешнего воздействия, — механический (акустический) резонанс;
силы тока в контуре при приближении частоты внешнего воздействия к собственной частоте колебаний контура, — электрический резонанс;
числа поглощаемых системой фотонов, вызывающих квантовые переходы на более высокий энергетический уровень, при совпадении энергии фотона с разностью энергий двух энергетических уровней, — квантовый резонанс;
Условия резонанса
Условие первое: «мы не одни». Человек, хочет он того или нет, никогда не существует сам по себе, никогда не пребывает в изоляции. Человек непрерывно взаимодействует с широчайшим спектром всевозможных существ и явлений, которые воздействуют на него. Когда такое взаимодействие становится резонансом?
Условие второе: его нам подсказывает значение слова «резонанс». Резонанс наблюдается только тогда, когда нечто в нас соответствует, гармонирует, согласуется с воздействием извне и откликается на него, когда этому воздействию есть за что зацепиться. Это означает, что наша внутренняя природа подобна природе, окружающей нас, — «человек есть микрокосм Макрокосма». На чем основывается это подобие, что в нас и вне нас вступает во взаимодействие?
Условие третье: «покоя нет, все движется, вращаясь». Все внутри и вне нас пронизано различными вибрациями — механическими, акустическими, электромагнитными и др. Даже в самом простом одноклеточном организме колебания происходят на субатомных, атомных, молекулярных, субклеточных и клеточных уровнях. А уж наши тела — воистину многоуровневые ансамбли вибрирующих частиц, от атомов до органов и тканей. Например, молекулы ДНК и мембраны клеток могут совершать колебания в радиоволновом диапазоне частот. Органы тоже вибрируют с характерной для большинства людей частотой (сердце и мускулатура внутренних органов — 7 Гц; альфа-режим работы мозга — 4-6 Гц, бета-режим — 20-30 Гц). И то, что мы воспринимаем извне с помощью органов чувств (слух — колебания воздуха, зрение — электромагнитные колебания в видимом диапазоне, осязание — механические и тепловые колебания и т. д.), и то, что излучаем вовне (мысли, эмоции, слова, действия), — все есть вибрации, различные по характеру и интенсивности. Вибрационную природу раскачивающихся качелей или звучащей струны мы воспринимаем непосредственно; света и тепла — с помощью специальных приборов; а мыслей и эмоций не воспринимаем вовсе, поскольку скорость их вибраций выходит за пределы воспринимающей способности наших органов чувств.
От третьего условия легко подойти к значению резонанса как закона гармоничного объединения, рождения Целого. Человек — система сложная, состоящая из астрономического количества частей, больших и малых, вибрирующих с периодом от долей секунды (молекулярные осцилляции, потоки ионов и т. д.) до нескольких лет (гормональные). Но несмотря на такое обилие составляющих частей, благодаря их резонансной синхронизации наш организм представляет собой единое целое. Человек как целое является частью более глобального Целого — природы, общества, человечества. И взаимодействует как с самим Целым, так и с другими полноправными его частями. Взаимодействие это тем успешнее, чем больше деятельность человека находится в гармонии, в согласии с законами существования целого. Мы не можем не быть частью целого. Мы можем стать негармоничной его частью, противопоставляющей себя остальным, подобно раковой клетке, но эта оппозиция, в конце концов, скажется на нас же, на нашем здоровье на всех планах (даже раковая клетка, убивая организм, лишает будущего и саму себя). Ведь здоровье — это гармония, согласие, соответствие внешнего и внутреннего, целого и его части. В современном русском языке слово «целый» означает «такой, от которого ничего не убавлено, не отделено», а исходно это слово означало «здоровый».
Частоты э/м волн:
102-108 Гц — радиоволны (20-2х104 Гц — слышимый звук)
109-1011 Гц — радиоволны СВЧ
1013-1014 Гц — инфракрасный свет (тепло)
1015 Гц — видимый свет
1015-1016 Гц — ультрафиолетовый свет
1017-1020 Гц — рентгеновское излучение
1020-1022 Гц — гамма-излучение
Резонансное объединение частей в единое целое происходит по принципу «минимума энергии»: каждому из участников общего дела, находящихся в резонансе (будь то маятники на общей нити, органы в организме или люди, объединенные доброй волей и благородной целью), для выполнения собственной работы требуется меньше энергии, чем в случае работы по отдельности. Это не значит, что каждая часть работает вполсилы. Это значит, что группа людей, работая с полной отдачей, способна совершать то, на что каждый в отдельности никогда бы не отважился. Это значит, что свойства целого качественно превосходят простую сумму свойств слагающих его частей.
Резонанс служит индикатором свойств, внутренне присущих объекту, и позволяет выявить даже очень слабые колебания. Например, если два музыкальных инструмента настроены одинаково и на одном из них начать играть, то другой тоже зазвучит. На этом свойстве основаны резонансные методы исследования веществ и процессов, происходящих в живом организме. Отсюда следует важный вывод: выявить и усилить с помощью резонанса можно лишь те свойства объекта, которые в нем уже существуют. При этом воздействия отнюдь не должны быть интенсивными, энергетически мощными. Особенно на стадии, когда объект к ним особенно восприимчив. Так, нужное слово, сказанное в нужное время, способно сотворить чудо. И многие судьбоносные, поворотные моменты в нашей жизни есть следствия подобного рода резонансов.
Резонанс — ключ к пониманию и управлению собой
Подобное притягивает подобное. Или: с кем поведешься — так тебе и надо.
Человек одновременно подвергается влиянию «внешней среды» и сам влияет на нее. Человек, с одной стороны, является системой, в которой может быть возбужден резонанс, с другой — способен выступать в роли внешней силы, вызывающей резонанс в других. Происходит ли все это само собой, без сознательного контроля со стороны человека? Отчасти да. Особенно это касается широкого спектра электромагнитных взаимодействий человека и окружающего пространства. А вот с мыслями, эмоциями и их словесным выражением дело обстоит иначе. То, что человек несет ответственность за свои поступки, признать нетрудно. Но, согласно карме, которая не дремлет, к «поступкам» следует отнести не только физические действия, но и слова, эмоции и мысли. Конечно, мы не можем отвечать за поступки всех тех, кто воздействует на нас! Но эти воздействия рождают в нас отклик (дословный перевод слова «резонанс»), нашу собственную реакцию, которая, проявляясь вовне, становится «поступком», за последствия которого мы уже отвечаем. Получается «цепная реакция»: воздействие — отклик = воздействие — отклик = воздействие… Иначе это можно назвать цепью акций и реакций, причин и следствий. Иногда подобная цепь становится яркой иллюстрацией принципа «что посеешь, то и пожнешь». Например: сосед-начальник отругал папу; папа «поделился» раздражением с мамой; мама сгоряча шлепнула сына; сын пнул собаку. А собака, выйдя на прогулку, укусила… соседа! К счастью, «эстафеты» радости, добра, благодарности тоже существуют… Какому отклику мы дадим зеленый свет, а какой оставим при себе (или не породим вовсе), зависит только от нас. А в идеале — «ненависть не побеждается ненавистью, но любовью» (Будда).
Ответственность — штука нелегкая. Гораздо приятнее искать причину своих бед вне и считать себя невинной жертвой чьего-то дурного влияния. Но закон резонанса неумолим: любое воздействие лишь выявляет скрытое в нас. «Проблемы» не внешние, они в нас самих. Например, заболел человек. Почему? Потому что на него напали «враги» — вирусы, микробы, аллергены, канцерогены и пр.? Тактика предупреждения-лечения болезни при таком подходе очевидна: от врага надо всеми силами защищаться, а уж если он проник, то немедленно уничтожать. Но всегда ли такой подход оправдан? Есть ли альтернатива? Есть, и уходит она корнями в глубокую древность. Суть ее в том, что все внешние «враги» способны поразить только того, кто уже готов заболеть. А значит, главная причина болезни — в самом человеке. «Если вибрации злого духа-возбудителя болезни и человека совпадут — человек заболевает» (Аюрведа). И чтобы выздороветь, усилия человека в познании этой причины и в изменении себя и медицинская помощь извне должны идти навстречу друг другу.
Резонанс внутреннего и внешнего лежит в основе восприятия информации, исследования неизвестного, открытий и озарений. Таинство познания не происходит на пустом месте. Идеи витают в воздухе, но уловить их способен лишь тот, кто настроен на их восприятие. Открытие тайны — это Отклик знания на Зов усилий исследователя. Великие открытия совершают единицы, маленькие открытия сопутствуют каждому из нас. И всегда им предшествует поиск, всегда новое знание приходит на плодородную почву, удобренную знанием, уже принятым и примененным нами. Недаром говорят, что любая новая информация должна содержать долю (30-50%) известного. Только тогда она будет понята. Ведь резонанс с известным усиливает способность к восприятию нового.
Закон «подобное притягивает подобное» справедлив и в сфере взаимоотношений. Например, если нас в ком-то что-то раздражает, это верный признак того, что это качество мы носим в себе. И всю ту энергию негодования, которую привыкли изливать на провинившегося, мы можем направить на поиск соответствующего качества и его преодоление. Поэтому одним из критериев нравственной чистоты человека служат его доброта и терпимость к другим.
В жизни бывают периоды, когда человек ни с кем не находит общего языка, не может вписаться ни в один коллектив. При этом он либо пассивно ждет, когда шаги навстречу сделают другие, либо агрессивно вторгается на чужую территорию. Представим себе сложившийся коллектив оркестра и музыканта, инструмент которого расстроен. А музыкант или ждет, пока инструмент настроится сам собой, или вовсе не желает ничего менять, полагая, что только его инструмент и настроен единственно верно. Понятно, что партия этого музыканта будет в явном диссонансе с общим звучанием оркестра и дирижер будет вынужден принять меры. Что сделает музыкант? Утвердится в своей оппозиции к враждебному миру или… настроит свой инструмент в унисон с оркестром?
Мысли и чувства человека подобны инструменту. Как его настроить? Найти такой «инструмент», в гармоничности звучания которого мы не сомневаемся, чья музыка жизни пробуждает в нас стремление следовать ему. Это может быть реальный человек или герой кинофильмов, романов, легенд и мифов. И если его пример вызывает в нас резонанс, значит, в нашей душе есть хотя бы одна струна, настроенная в унисон с душой героя. «Способность восхищаться означает способность достигать, а любовь и почтение к великим означает, что человек способен дорасти до них» (А. Безант). И не беда, если в нас это вдохновляющее качество еще не проявилось сполна, если звучание нашего инструмента еще далеко не идеально. Главное, что мы хотим его достичь, что мы нашли и услышали в себе ту струну, по которой постепенно, усилие за усилием, мы будем настраивать наш инструмент. И его все более и более гармоничное звучание будет задевать соответствующие струны в душах других людей.
Человек, шаг за шагом, ступень за ступенью познающий себя, идет навстречу собственной судьбе, учится откликаться на ее Зов и становится Зовом для других. Каждое усилие, каждая победа над собой, каждый верный шаг на этом пути приближают Встречу-Резонанс человека и его Предназначения. Резонанс, который предоставляет шанс увидеть следующую ступень, а также радость и силы для ее достижения. «Каждый твой шаг на пути заставляет тот горизонт, к которому ты идешь, отодвинуться еще на шаг дальше. Когда перед тобой открывается одно таинство, это можно сравнить с силой трамплина, подбрасывающего тебя к другому таинству, еще более высокому и сокровенному… и так постоянно» (Х.А. Ливрага).
Природа стандартного камертона
(по Б.В. Гладкову)
Издавна прослеживается удивительная приверженность музыкантов звуковому сигналу, у которого частота колебаний основного тона равна 440 Гц (или близка к ней). Этот сигнал возведен в ранг стандартного международного камертона, предназначенного для настройки всех музыкальных инструментов. Стандартному камертону придано значение ноты «ля» в первой октаве музыкального звукоряда. Так почему же именно этот звук, а не какой-либо другой?
«Существует легенда, что в незапамятные времена около древнеегипетского города Фивы каждое утро на рассвете этот звук издавала огромная статуя, известная под именем колосса Мемнона, и фивские музыканты приходили к ней настраивать свои инструменты. Колосс Мемнона перестал звучать в начале нашей эры, и проверить истинность легенды сейчас невозможно» (Г.Е. Шилов).
С другой стороны, сравнительно недавно было установлено, что первый крик новорожденного, возвещающий о перемене «места жительства», оказался почти одинаковым по своей высоте (или частоте звукового сигнала) у всех особей независимо от пола и расы. С разбросом порядка -3% значение сигнала на частотной шкале соответствует 440 Гц (нота ля). В частности, об этом пишет болгарский фониатр Иван Максимов. Вероятно, этот звук стал исполнять роль опорного, поскольку соответствует первому крику новорожденного. Но тогда остается вопрос: а почему новорожденный издает именно этот звук? И имеет ли под собой почву легенда о колоссе Мемнона?
В индийской классической музыке известен такой факт: если поместить ситар в пустой комнате в углу, а напротив искусный музыкант-ситарист станет играть, то другой ситар начнет вибрировать с той же частотой, что и первый, повторяя мелодию. Но это происходит только в том случае, если музыкант высокого класса. Певец силой голоса может разбить вдребезги бокал при условии, что взятая нота точно соответствует частотным характеристикам этого бокала.
В.И. Черепанов. Резонансные методы исследования вещества
Человек в резонансе с Землей: частота сердечных сокращений в среднем составляет 70 ударов в минуту — 7 Гц (1 Гц — 1 колебание в секунду). Частота «пульса» Земли составляет около 7,5 Гц (согласно Н. Тесле).
Резонансные методы исследования вещества — наиболее чувствительные и точные. Они нашли широкое применение в физике, химии, биологии и медицине. Каждое вещество имеет свой, характерный только для него частотный или энергетический спектр. Этот набор частот служит визитной карточкой вещества, изучая которую можно распознать химический состав, структуру, симметрию, характер внутренних взаимодействий (электрических, магнитных и т.д.) между структурными единицами вещества и другие его характеристики.
Теория резонанса в химии, предложенная в 30-е гг. XX в. Л. Полингом, позволяет судить об эквивалентности тех или иных связей и структурных элементов в молекулах, об их симметрии, стабильности и реакционной способности. В рамках теории резонанса были введены такие широко используемые в настоящее время представления, как одно- и трех-электронные связи, гибридизация связевых орбиталей, сверхсопряжение, а также представление о частично ионном характере ковалентных связей между различными атомами.
Все, что происходит на плане материи, есть лишь отражение в плотной материи происходящего на высших планах, и мы всегда можем найти опору для своего хромающего воображения, изучая развитие на физическом плане.
А. Безант
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Всякая мех-ая упругая система имеет собственную частоту колебаний. Если какая-либо сила выведет эту систему из равновесия, а затем перестанет действовать, то система будет некоторое время колебаться около своего положения равновесия. Частота этих колебаний и называется собственной частотой колебаний системы. Скорость её затухания зависит от упругих свойств и массы, от сил трения и не зависит от силы, вызвавшей колебания.
Если сила, выводящая мех систему из равновесия, будет меняться с частотой, равной частоте собственной частотой колебаний, то на деформацию одного периода будет накладываться деформация следующего периода и система будет раскачиваться со всё возрастающей амплитудой, теоретически до бесконечности. Естественно, что конструкция не сможет противостоять такой всё возрастающей деформации и будет разрушаться.
Совпадение частоты собственных колебаний с частотой изменения электродинамической силы называется механическим резонансом .
Полный резонанс наблюдается при точном совпадении частоты колебаний силы с частотой собственных колебаний конструкции и равных положительных и отрицательных амплитудах, частичный — при неполном совпадении частот и неравных амплитудах.
Для избежания мех резонанса необходимо, чтобы частота собственных колебаний конструкции отличалась от частоты изменения электродинамической силы. Лучше, когда частота собственных колебаний лежит ниже частоты изменения силы. Подбор требуемой частоты собственных колебаний можно производить различными способами. Для шин, например, — изменением длины свободного пролёта
В случае, когда частота переменной составляющей ЭДУ близка к собственной частоте механических колебаний, даже при сравнительно небольших усилиях возможно разрушение аппарата вследствие явлений резонанса.
Шины под воздействием ЭДУ совершают вынужденные колебания в виде стоячих волн. Если частота свободных колебаний выше 200 Гц, то расчёт усилий производится для статического режима без учёта резонанса.
Если частота свободных колебаний шины при конструировании стремятся исключить возможность резонанса за счёт выбора длины свободного пролета шины.
При гибком креплении шины собственная частота механических колебаний снижается. Энергия ЭДУ частично тратится на деформацию токоведущих частей, частично на перемещение их и связанных с ним гибких креплений. При этом мех. Напряжения в материале шин уменьшаются
Мы часто слышим слово резонанс: «общественный резонанс», «событие, вызвавшее резонанс», «резонансная частота». Вполне привычные и обыденные фразы. Но можете ли вы точно сказать, что такое резонанс?
Если ответ отскочил у вас от зубов, мы вами по-настоящему гордимся! Ну а если тема «резонанс в физике» вызывает вопросы, то советуем прочесть нашу статью, где мы подробно, понятно и кратко расскажем о таком явлении как резонанс.
Прежде, чем говорить о резонансе, нужно разобраться с тем, что такое колебания и их частота.
Колебания и частота
Колебания – процесс изменения состояний системы, повторяющийся во времени и происходящий вокруг точки равновесия.
Простейший пример колебаний — катание на качелях. Мы приводим его не зря, этот пример еще пригодится нам для понимания сути явления резонанса в дальнейшем.
Резонанс может наступить только там, где есть колебания. И не важно, какие это колебания – колебания электрического напряжения, звуковые колебания, или просто механические колебания.
На рисунке ниже опишем, какими могут быть колебания.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Колебания характеризуются амплитудой и частотой. Для уже упомянутых выше качелей амплитуда колебаний — это максимальная высота, на которую взлетают качели. Также мы можем раскачивать качели медленно или быстро. В зависимости от этого будет меняться частота колебаний.
Частота колебаний (измеряется в Герцах) — это количество колебаний в единицу времени. 1 Герц — это одно колебание за одну секунду.
Когда мы раскачиваем качели, периодически раскачивая систему с определенной силой (в данном случае качели – это колебательная система), она совершает вынужденные колебания. Увеличения амплитуды колебаний можно добиться, если воздействовать на эту систему определенным образом.
Толкая качели в определенный момент и с определенной периодичностью можно довольно сильно раскачать их, прилагая совсем немного усилий.Это и будет резонанс: частота наших воздействий совпадает с частотой колебаний качелей и амплитуда колебаний увеличивается.

Суть явления резонанса
Резонанс в физике – это частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы.
Суть явления резонанса в физике состоит в том, что амплитуда колебаний резко возрастает при совпадении частоты воздействия на систему с собственной частотой системы.
Известны случаи, когда мост, по которому маршировали солдаты, входил в резонанс от строевого шага, раскачивался и разрушался. Кстати, именно поэтому сейчас при переходе через мост солдатам положено идти вольным шагом, а не в ногу.
Примеры резонанса
Явление резонанса наблюдается в самых разных физических процессах. Например, звуковой резонанс. Возьмём гитару. Само по себе звучание струн гитары будет тихим и почти неслышным. Однако струны неспроста устанавливают над корпусом – резонатором. Попав внутрь корпуса, звук от колебаний струны усиливается, а тот, кто держит гитару, может почувствовать, как она начинает слегка «трястись», вибрировать от ударов по струнам. Иными словами, резонировать.
Еще один пример наблюдения резонанса, с которым мы сталкиваемся — круги на воде. Если кинуть в воду два камня, попутные волны от них встретятся и увеличатся.
Действие микроволновки также основано на резонансе. В данном случае резонанс происходит в молекулах воды, которые поглощают излучение СВЧ (2,450 ГГц). Как следствие, молекулы входят в резонанс, колеблются сильнее, а температура пищи повышается.

Резонанс может быть как полезным, так и приносящим вред явлением. А прочтение статьи, как и помощь нашего студенческого сервиса в трудных учебных ситуациях, принесет вам только пользу. Если в ходе выполнения курсовой вам понадобится разобраться с физикой магнитного резонанса, можете смело обращаться в нашу компанию за быстрой и квалифицированной помощью.
Напоследок предлагаем посмотреть видео на тему «резонанс» и убедиться в том, что наука может быть увлекательной и интересной. Наш сервис поможет с любой работой: от реферата «Сеть интернет и киберпреступность» до курсовой по физике колебаний или эссе по литературе.
Прежде чем приступить к знакомству с явлениями резонанса, следует изучить физические термины, связанные с ним. Их не так много, поэтому запомнить и понять их смысл будет несложно. Итак, обо всем по порядку.
Что такое амплитуда и частота движения?
Представьте обычный двор, где на качелях сидит ребенок и машет ножками, чтобы раскачаться. В момент, когда ему удается раскачать качели и они достигают из одной стороны в другую, можно подсчитать амплитуду и частоту движения.
Амплитуда — это наибольшая длина отклонения от точки, где тело находилось в положении равновесия. Если брать наш пример качелей, то амплитудой можно считать наивысшую точку, до которой раскачался ребенок.
А частота — это количество колебаний или колебательных движений в единицу времени. Измеряется частота в Герцах (1 Гц = 1 колебание в секунду). Возвратимся к нашим качелям: если ребенок проходит за 1 секунду только половину всей длины качания, то его частота будет равна 0,5 Гц.
Как частота связана с явлением резонанса?
Мы уже выяснили, что частота характеризует число колебаний предмета в одну секунду. Представьте теперь, что слабо качающемуся ребенку взрослый человек помогает раскачаться, раз за разом подталкивая качели. При этом данные толчки также имеют свою частоту, которая будет усиливать либо уменьшать амплитуду качания системы «качели-ребенок».
Допустим, взрослый толкает качели в то время, когда они движутся навстречу к нему, в таком случае частота не будет увеличивать амлитуду движения То есть сторонняя сила (в данном случае толчки) не будет способствовать усиления колебания системы.
В случае если частота, с которой взрослый раскачивает ребенка, будет численно равна самой частоте колебания качелей, может возникнуть являение резонанса. Другими словами, пример резонанса — это совпадение частоты самой системы с частотой вынужденных колебаний. Логично представить, что частота и резонанс взаимосвязаны.
Где можно наблюдать пример резонанса?
Важно понимать, что примеры проявления резонанса встречаются практически во всех сферах физики, начиная от звуковых волн и заканчивая электричеством. Смысл резонанса заключается в том, что когда частота вынуждающей силы равна собственной частоте системы, то в этот момент достигает наивысшего значения.
Следующий пример резонанса даст понимание сути. Допустим, вы шагаете по тонкой доске, перекинутой через речку. Когда частота ваших шагов совпадет с частотой или периодом всей системы (доска-человек), то доска начинает сильно колебаться (гнуться вниз и вверх). Если вы продолжите двигаться такими же шагами, то резонанс вызовет сильную амплитуду колебания доски, которая выходит за пределы допустимого значения системы и это в конечном счете приведет к неминуемой поломке мостика.
Существуют также те сферы физики, где можно использовать такое явление, как полезный резонанс. Примеры могут удивить вас, ведь обычно мы используем его интуитивно, даже не догадываясь о научной стороне вопроса. Так, например, мы используем резонанс, когда пытаемся вытащить машину из ямы. Вспомните, ведь легче всего достичь результат только тогда, когда толкаешь машину в момент ее движения вперед. Этот пример резонанса усиливает амплитуду движения, тем самым помогая вытащить машину.
Примеры вредного резонанса
Сложно сказать, какой резонанс в нашей жизни встречается больше: хороший или же наносящий нам вред. Истории известно немалое количество ужасающих последствий явления резонанса. Вот самые известные события, на которых можно наблюдать пример резонанса.
Во Франции, в городе Анжера, в 1750 году отряд солдат шел в ногу через цепной мост. Когда частота их шагов совпала с частотой моста, размахи колебаний (амплитуда) резко увеличились. Наступил резонанс, и цепи оборвались, а мост обрушился в реку.
Бывали случаи, когда в деревнях дом был разрушен из-за проезжающего по главной дороге грузового автомобиля.
Как видите, резонанс может иметь весьма опасные последствия, вот почему инженерам следует тщательно изучать свойства строительных объектов и правильно вычислять их частоты колебаний.
Полезный резонанс
Резонанс не ограничивается только плачевными последствиями. При внимательном изучении окружающего мира можно наблюдать множество хороших и выгодных для человека результатов резонанса. Вот один яркий пример резонанса, позвляющий получать людям эстетическое удовольствие.
Устройсто многих музыкальных инструментов работает по принципу резонанса. Возьмем скрипку: корпус и струна образуют единую колебательную систему, внутри которой имеется штифт. Именно через него передаются частоты колебаний из верхней деки в нижнюю. Когда лютьер водит смычком по струне, то последняя, подобно стреле, побеждает своей трение канифольной поверхности и летит в обратную сторону (начинает движение в противоположную область). Возникает резонанс, который передается в корпус. А внутри его есть специальные отверстия — эфы, сквозь которые резонанс выводится наружу. Именно таким образом он контролируется во многих струнных инструментах (гитара, арфа, виолончель и др).
Слово «резонанс» используется людьми каждый день в самых разных значениях. Его произносят политики и телеведущие, пишут в своих работах ученые и изучают на уроках школьники. У этого слова есть несколько значений, относящихся к разным областям человеческой деятельности.
Откуда взялось слово резонанс
Все мы узнаем, что такое резонанс впервые из курса школьной физики. В научных словарях этому термину дается подробное объяснение с точки зрения механики, электромагнитных излучений, оптики, акустики и астрофизики.
С технической точки зрения резонанс — это явление отклика колебательной системы не внешнее воздействие. При совпадении периодов воздействия и отклика системы возникает резонанс — резкое увеличение амплитуды рассматриваемых колебаний.
Простейший пример механического резонанса приводит в своих работах средневековый ученый Торичелли. Точное определение явления резонанса дано Галилео Галилеем в работе о маятниках и звучании музыкальных струн. Что такое электромагнитный резонанс, объяснил в 1808 году Джеймс Максвелл, основоположник современной электродинамики.
Узнать, что такое «резонанс» можно не только в Википедии, но в таких справочных изданиях:
учебники физики за 7-11 классы;
физическая энциклопедия;
научно-технический энциклопедический словарь;
словарь иностранных слов русского языка;
философская энциклопедия.
Резонанс в полемике и риторике
Еще одно значение слово «резонанс» приобрели в сфере общественных наук. Этим словом называют отклик общественности на некоторое явление в жизни людей, определенное высказывание, происшествие. Как правило, слово «резонанс» используют, когда нечто вызывает у многих людей одновременно схожую и очень яркую реакцию. Известно даже общеупотребимое выражение «широкий общественный резонанс», которое является речевым штампом. В собственной речи, письменной или устной, его лучше избегать.
В философском словаре резонанс трактуется как понятие, имеющее переносное значение и понимаемое как согласие или единомыслие двух людей, двух душ в сострадании, симпатии или антипатии, сочувствии или возмущении.
В значении «сильный отклик», «единодушная оценка» слово резонанс очень любят использовать политики, ораторы, дикторы. Оно помогает передать эмоциональный подъем, единодушный порыв, подчеркнуть значимость происходящего.
Где мы встречаемся с резонансом
В прямом смысле слово резонанс стоит употреблять в отношении множества естественных процессов, происходящих вокруг нас. Все дети, которые катаются на обычных качелях или каруселях на детской площадке, эксплуатируют механический резонанс.
Хозяйки, разогревая пищу в микроволновке, используют электромагнитный резонанс. На принципах резонанса построена теле- и радиовещательная сеть, работа мобильных телефонов и wifi для интернета.
Звуковой резонанс позволяет нам наслаждаться музыкой или баловаться эхом в горах и закрытых помещениях, где стены не имеют достаточной звукоизоляции. На принципе акустического резонанса построена работа эхолотов и многих других измерительных приборов.
Чем опасен резонанс
В естественно-научном смысле резонанс как явление может быть не только полезен человеку, но и опасен. Самый яркий пример — строительство.
При конструировании зданий и сооружений расчеты конструкций на резонанс строго необходимы. Так просчитываются все высотные сооружения, башни, опоры ЛЭП, передающие и принимающие антенны, а также высотные здания, которые входят в резонанс с ветрами на большой высоте.
На резонанс обязательно проверяются все мосты и протяженные объекты. В 2010 году весь интернет облетело видео моста через Волгу, который пошел волной как шелковая лента. Результаты расследования показали, что конструкции моста вошли в резонанс с ветром.
Аналогичный случай произошел в США. 7 ноября 1940 года разрушился один из пролетов висячего Такомского моста, расположенного в штате Вашингтон. Еще при строительстве специалисты отмечали колебания полотна моста, связанные с ветром и низкой высотой опор. В результате обрушения были проведены многочисленные исследования и расчеты, ставшие основой для технологий современного мостостроения. В среде специалистов возник даже термин «Такомский мост», означающий ненадлежащее качество строительных расчетов.
С резонансом каждый из нас сталкивается ежедневно. Об этом явлении необходимо помнить в повседневной жизни, вздумав раскачаться на пешеходном мосту или отправляя металлическую посуду в микроволновку (это запрещено правилами). А само слово «резонанс» можно использовать в своей речи для ее украшения и усиления впечатления от сказанного вами.
Резонанс
: определение, типы, частота и примеры
Обновлено 5 декабря 2019 г.
Ли Джонсон
Всем известен старый образ, когда мощный оперный певец бьет нужную ноту, а хрустальное стекло разбивается от шума, но так ли это? действительно возможно? Ситуация может показаться надуманной, как что-то, что вы с большей вероятностью увидите в фильмах или мультфильмах, чем в реальной жизни.
Фактически, явление резонанса означает, что это технически возможно в реальной жизни, независимо от того, создается ли резонансная частота (та, которая соответствует собственной частоте стекла) чьим-то голосом или одним или несколькими музыкальными инструментами.
Изучение резонанса дает вам понимание того, как работает звук, принципов, лежащих в основе многих музыкальных инструментов, и того, как увеличить или уменьшить движение в механической системе, такой как качели или веревочный мост.
Определение резонанса
Слово резонанс первоначально происходит от латинского резонанса , что означает «эхо», и оно тесно связано с резонансом, что означает возвращение эха или «звук снова». Эти два определения уже относятся к звуковым волнам и дают вам общее представление о значении этого слова в физике.
Однако, более конкретно, определение резонанса в физике — это когда частота внешнего колебания или вибрации совпадает с собственной частотой объекта (или полости) и в результате либо заставляет его вибрировать, либо увеличивает его амплитуду колебаний. .
В механических системах под резонансом понимается усиление, усиление или продление звука или других вибраций. Как и в приведенном выше определении, это требует приложения внешней периодической силы с частотой, равной собственной частоте движения объекта, которую иногда называют резонансной частотой.
Все объекты имеют собственную частоту или резонансную частоту, которую вы можете представить как частоту, на которой объект «любит» вибрировать. Например, если вы постучите ногтем по хрустальному стеклу, он начнет вибрировать на своей резонансной частоте и будет издавать «звон» с соответствующей высотой звука. Частота вибрации зависит от физических свойств объекта, и вы можете довольно хорошо предсказать это для некоторых вещей, таких как натянутая струна.
Примеры резонанса — Звуковой резонанс
Изучение некоторых примеров резонанса поможет вам понять различные формы резонанса, с которыми вы сталкиваетесь в повседневной жизни.Самый распространенный и простой пример — звуковые волны, потому что, когда вы вибрируете голосовые связки на нужной частоте (для полости горла и рта), вы можете воспроизводить тоны речи и музыкальные тона, которые могут слышать другие люди.
Вибрация ваших голосовых связок создает звуковые волны, которые на самом деле представляют собой волны давления в воздухе, состоящие из чередующихся сжатых участков (с плотностью выше средней) и разрежений (с плотностью ниже средней).
Большинство музыкальных инструментов работают одинаково.Например, в медном инструменте вибрация губ игрока относительно мундштука создает начальную вибрацию, и когда она совпадает с резонансной частотой (или кратной ей) для размера трубы, в которую он или она дует, возникает резонанс, и амплитуда колебаний заметно увеличивается и дает слышимый тон.
В деревянных духовых инструментах есть «трость», которая вибрирует, когда над ней проходит воздух, и снова тот же самый процесс резонанса и усиления превращает эту небольшую вибрацию в слышимый музыкальный тон.Струнные инструменты, такие как гитара, немного отличаются, но струны имеют резонансную частоту вибрации, а производимые звуковые волны резонируют в полости (например, в пространстве в корпусе акустической гитары), делая шум громче.
Более простой пример: вы уронили инструмент или тарелку на землю. Звук возникает из-за того, что инструмент или пластина вибрируют на своей резонансной частоте. Этот более простой способ генерации звука используется тщательно разработанными камертонами, которые сконструированы таким образом, чтобы воспроизводить определенную высоту звука в качестве собственной частоты, на которую музыканты могут затем настраивать свои инструменты.
Примеры резонанса — Механический резонанс
Хотя резонанс обычно используется для обозначения звуковых волн, механический резонанс в некотором смысле легче понять. Простой пример — ребенок впервые учится качать качели. Колебательное движение качелей имеет собственную частоту, и когда ребенок учится толкать (то есть прикладывать периодическую силу) с собственной частотой качелей, его толчки становятся намного более эффективными. В результате этого амплитуда колебаний качелей увеличивается, и человек, сидящий на них, с каждым разом становится все выше.
Однако попадание в собственную частоту объекта не всегда хорошо. Например, солдаты, идущие по веревочному мосту в унисон, могут заставить его выйти из-под контроля и, возможно, даже упасть, если они наступят на его собственную частоту. В подобных случаях генерал может попросить их «сломать ступеньку», чтобы они не применяли периодическую силу с собственной частотой моста.
Даже более стабильные конструкции мостов имеют резонансные частоты, но это вызывает проблемы только в редких случаях (например, с Бротонским подвесным мостом, мостом в Англии, который рухнул в 1831 году, предположительно из-за солдат, шагающих по мосту).
Аналоговые часы также зависят от механического резонанса и собственной частоты компонента, чтобы отследить время. Например, маятниковые часы используют собственную частоту колебаний маятника, чтобы отсчитывать время, а балансовое колесо работает по тому же основному принципу. Даже часы на кварцевом кристалле зависят от резонансной частоты, но в этом случае кристалл регулирует колебания от электронного генератора, что приводит к значительному повышению точности по сравнению с более простыми конструкциями.
Другие примеры резонанса
Есть много других форм резонанса, и все они работают по одному и тому же основному принципу.Два других примера резонанса, с которыми вы будете знакомы, связаны с электромагнитными колебаниями, а не с механическими. Во-первых, ваша микроволновая печь.
Волны, создаваемые микроволновой печью, выделяют тепло в вашей пище, потому что их частота совпадает с резонансной частотой молекул внутри продукта (например, молекул воды и жира), что заставляет их колебаться и впоследствии выделять энергию в виде тепла.
Другой пример — антенна для вашего телевизора или даже радиоантенна.Эти устройства предназначены для максимального поглощения электромагнитного излучения, и когда вы «настраиваете» антенну на определенную частоту, вы регулируете резонансную частоту устройства. Когда частота антенны совпадает с частотой входящего сигнала, она резонирует, и ваш телевизор или радио «улавливает» сигнал.
Так как же ломается кристалл?
Теперь, когда вы понимаете ключевые моменты определения резонанса и того, что такое резонансная частота, вы можете понять классический пример певца, которому удалось разбить хрустальное стекло, напевая с правильной тональностью.Стекло имеет резонансную частоту, и если певец издает звук с совпадающей частотой, стакан начинает вибрировать. Это называется симпатической вибрацией , потому что до того, как певец издал звук, стекло было совершенно неподвижным.
Сначала в стекле может быть небольшая вибрация, но для того, чтобы заставить его разбиться, требуется длительная и громкая нота на нужной частоте. Если певец может это сделать, амплитуда колебаний стекла увеличивается и в конечном итоге начинает нарушать структурную целостность стекла.Только в этот момент — когда нота выдерживается достаточно долго, чтобы вибрация стекла достигла максимальной амплитуды, которую оно может выдерживать, — стекло действительно разбивается.
Резонансные формы — Chemistry LibreTexts
Последнее обновление
Сохранить как PDF
Введение
Общие примеры
Рисование форм резонанса
Полезные советы
Внешние ссылки
Ссылки
Проблемы

Резонансная форма — это еще один способ рисования точечной структуры Льюиса для данного соединения.Эквивалентные структуры Льюиса называются резонансными формами. Они используются, когда есть более одного способа разместить двойные связи и неподеленные пары на атомах. Резонансные структуры возникают, когда существует более одного способа нарисовать точечную диаграмму Льюиса, удовлетворяющую правилу октетов . Помните, что правило октетов заключается в том, что атом получает, теряет или делится электронами, так что внешняя электронная оболочка имеет восемь электронов. Мы рисуем их, когда одна конструкция неточно отображает реальную структуру.

Введение

Есть несколько основных принципов теории резонанса.Структуры первого резонанса не реальны, они просто показывают возможные структуры соединения. Резонансные структуры не находятся в равновесии друг с другом. Резонансные структуры не являются изомерами. Изомеры имеют разное расположение атомов и электронов. Формы резонанса отличаются только расположением электронов.

Резонансные структуры лучше отражают точечную структуру Льюиса, потому что они ясно показывают связь в молекулах. Не все резонансные структуры одинаковы, некоторые из них лучше других.Лучшие из них имеют минимальные формальные заряды, отрицательные формальные заряды являются наиболее электроотрицательными атомами, а связь в структуре максимальна. Чем больше резонансных форм имеет молекула, тем она стабильнее. Они нарисованы с двухсторонней стрелкой между ними, чтобы показать, что реальная структура находится где-то между резонансными структурами. В этих структурах использовались изогнутые стрелки, чтобы показать движение электронов в одной резонансной форме к другой.

Формальные заряды используются в химии для определения местоположения заряда в молекуле и определения того, насколько хорошей будет структура Льюиса.Помните, что лучшая резонансная структура — это структура с наименьшим формальным зарядом. Вот почему официальные обвинения очень важны. Атомы, у которых отсутствует один или несколько электронов, будут иметь положительный заряд. Атом с множеством электронов будет иметь отрицательный заряд. Присвоение атому формальных зарядов очень полезно в резонансных формах.

Формальный заряд рассчитывается с использованием этого формата:

# валентных электронов- (# несвязывающие электроны + 1/2 # связывающие электроны)

Изогнутая стрелка используется для отображения размещения электронов между атомами.Конец стрелки начинается у источника электронов, а острие указывает туда, где будет электрон. Убедитесь, что стрелки четкие, включая одинарную и половинную стрелку. Читатель должен знать поток электронов.

Общие примеры

Бензол обычно встречается в органической химии и имеет резонансную форму. Бензол имеет две резонансные структуры, показывающие размещение облигаций.

Другой пример резонанса — озон. Озон представлен двумя разными структурами Льюиса.Разница между двумя структурами заключается в расположении двойной связи.

Рисование резонансных форм

Есть несколько вещей, которые следует проверить до и после рисования резонансных форм. Сначала узнайте, где находятся несвязывающие электроны, отслеживайте формальные заряды на атомах и не разрывайте сигма-связи. Наконец, после рисования резонансной формы убедитесь, что все атомы имеют восемь электронов на внешней оболочке. Их проверка упростит рисование резонансных форм.

При рисовании резонансной структуры необходимо соблюдать три правила, чтобы структура была правильной:

Движутся только электроны, а ядра атомов никогда не движутся.
Только электроны, которые могут двигаться, — это пи-электроны, одиночные неспаренные электроны и неподеленные парные электроны.
Общее количество электронов в молекуле не меняется, равно как и количество спаренных и неспаренных электронов.

Подходы к перемещению электронов заключаются в перемещении пи-электронов к положительному заряду или к другой пи-связи.Переместите одиночный несвязывающий электрон к пи-связи. Переместите электроны неподеленной пары к пи-связи, и когда электроны могут двигаться более чем в одном направлении, переместите их к более электроотрицательному атому.

Полезные советы

Две резонансные структуры различаются расположением кратных связей и несвязывающего электрона. Размещение атомов и одинарных связей всегда остается неизменным.
Они должны иметь смысл и соглашаться с правилами. Водороды должны иметь два электрона, а элементы во втором ряду не могут иметь более 8 электронов.Если это так, то резонансная структура недействительна. Всегда смотрите на расположение стрелок, чтобы убедиться, что они совпадают.
Электроны движутся к sp ² гибридизированному атому. Гибридизированный атом sp ² представляет собой либо углерод с двойной связью, либо углерод с положительным зарядом, либо неспаренный электрон. Электроны не движутся к гибридизированному углероду sp ³, потому что для электронов нет места.

После построения резонансных структур проверьте чистый заряд всех структур.Например, если структура имеет чистый заряд +1, то все остальные структуры также должны иметь чистый заряд +1. В противном случае структура неправильная. Всегда проверяйте чистую плату после каждой постройки. Эти важные детали могут обеспечить успех в рисовании любой резонансной структуры.

Ссылки

Макмерри, Джон М. Органическая химия Биологический подход . N.p .: Thomson, 2007.

Problems

Заполните все неподеленные пары электронов и идентифицируйте любые электроны пи-связи.

3)
Заполните все неподеленные пары электронов и идентифицируйте любые электроны пи-связи.

9 повседневных примеров резонанса — StudiousGuy

Вы когда-нибудь задумывались, как радио выбирает определенные частоты, чтобы вы могли включить ваш любимый канал, или почему на концерте оркестра разбивается стекло? Вы когда-нибудь чувствовали, что мост вибрирует, когда вы идете по нему? Как вы думаете, почему вы попадаете в такие ситуации? Ответ кроется в явлении резонанса.

Резонанс — это явление, при котором внешняя сила и вибрирующая система заставляют другую систему вокруг себя вибрировать с большей амплитудой при определенной рабочей частоте. Частота, при которой второе тело начинает колебаться или вибрировать с большей амплитудой, называется резонансной частотой тела.

Давайте посмотрим на примеры резонанса, которые встречаются в нашей повседневной жизни.

1. Качели
Детские качели — один из хорошо известных примеров резонанса.Когда мы толкаем качели, они начинают двигаться вперед и назад. Если дать замаху серию регулярных толчков, можно построить его движение. Человек, который толкает тетиву, должен синхронизировать время взмаха. Толкатель должен синхронизироваться с временем качания. Это приводит к увеличению амплитуды качания, чтобы достичь большего. Когда качели достигают собственной частоты колебаний, легкое нажатие на качели помогает сохранить его амплитуду из-за резонанса.Мы называем это синхронизированное движение «Резонансом». Но, если толчок нерегулярный, качели почти не будут вибрировать, и это несинхронизированное движение никогда не приведет к резонансу, и колебание не будет увеличиваться.
2. Гитара
Гитара производит звук исключительно за счет вибрации. В акустической гитаре, когда вы дергаете струну, она вибрирует и передает звуковую энергию в полый деревянный корпус гитары, заставляя ее (и воздух внутри) резонировать и усиливая звук (делая его значительно громче).
В то время как в электрогитаре, когда музыкант ударяет по струне, она колеблется, и электромагнитное устройство в гитаре превращает это колебание в электрический сигнал, который отправляется на усилитель. Усилитель посылает колебания на динамик. Если частота динамиков соответствует вибрации гитары, это приводит к звуку, который называется звуковой обратной связью.
3. Маятник
Маятник работает по тому же принципу, что и качели.Если мы толкаем маятник, он будет двигаться вперед и назад. Продолжительное нажатие через равные промежутки времени вызовет увеличение движения маятника. Если маятник регулярно толкают, его движение может быть значительно увеличено.
4. Певица разбивает бокал для вина
Вы когда-нибудь видели или слышали о разбивании бокала в оркестре? Если да, то это все из-за явления резонанса. Собственная частота стекла или любого другого предмета определяется его формой и составом.Если голос певца попадает на резонансную частоту бокала с вином, происходит передача энергии. Однако полная передача энергии может вызвать разбитие стекла.
5. Мост
Группу солдат во время марша по мосту очень часто просят ломать ступеньки. Их ритмичный марш может вызвать экстремальные вибрации на собственной частоте моста. Если их синхронизированные шаги резонируют с собственной частотой моста, это может расшатать мост.Таким образом, при проектировании таких конструкций инженеры следят за тем, чтобы резонансные частоты компонентов отличались от резонансных частот других колеблющихся компонентов. Самым большим примером того же является Tacoma Bridge Collapse , в котором частота воздушного потока совпадала с частотой моста, что приводило к его разрушению.
6. Музыкальная система, играющая в высоком тяжелом ритме
Вы когда-нибудь замечали, что стены и мебель вашего дома вибрируют, когда вы играете музыку в тяжелом ритме? Это связано с тем, что собственная частота мебели резонирует с частотой звука музыки и, следовательно, заставляет их вибрировать.
7. Пение в душе
Люди, которые не очень хорошо поют, звучат намного лучше во время пения в душе, потому что излучаемые чистые ноты резонируют в душевой кабине. Санузел закрытый и иногда небольшой; когда вы поете, звуковые волны чаще ударяют о стены, заставляя стену вибрировать, поскольку стены параллельны друг другу. Отраженные звуки ударяются друг о друга, заставляя стену вибрировать с вашей собственной частотой, и передается более громкий звук.
8. Радио
Когда мы поворачиваем ручку радио на наш любимый канал, мы меняем собственную частоту приемника. Тогда собственная частота приемника совпадает с частотой передачи радиостанции. Когда две частоты совпадают, происходит передача энергии, и мы слушаем выбранный канал.
9. Микроволновая печь
Пища быстро нагревается в микроволновой печи из-за резонанса.Излучение, испускаемое микроволновой печью, имеет определенную длину волны и частоту. И, как и все другие объекты, молекулы воды и жира также имеют резонансную частоту. На определенной частоте молекулы поглощают длины волн и начинают вибрировать, вызывая приготовление и нагрев пищи.
Учебное пособие по физике: Резонанс
Цель урока 11 учебного курса по физике — развить понимание природы, свойств, поведения и математики звука и применить это понимание к анализу музыки и музыкальных инструментов.До сих пор в этом модуле принципы звуковых волн применялись к обсуждению ударов, музыкальных интервалов, акустики концертного зала, различий между шумом и музыкой, а также воспроизведения звука музыкальными инструментами. В Уроке 5 основное внимание будет уделено применению математических соотношений и концепций стоячей волны к музыкальным инструментам. Будут исследованы три основные категории инструментов: инструменты с вибрирующими струнами (которые будут включать струны гитары, струны скрипки и струны фортепиано), инструменты с открытой воздушной колонной (которые будут включать медные инструменты, такие как тромбон, и деревянные духовые инструменты, такие как флейта и блок-флейта), а также инструменты с воздушной колонной закрытого типа (которые будут включать в себя органную трубу и флаконы оркестра поп-флаконов ).Четвертая категория — вибромеханические системы (в которую входят все ударные инструменты) — обсуждаться не будет. Эти категории инструментов могут быть необычными для некоторых; они основаны на общности их моделей стоячих волн и математических соотношениях между частотами, производимыми инструментами.
Резонанс
Как упоминалось в Уроке 4, музыкальные инструменты приводятся в колебательное движение с их естественной частотой, когда человек ударяет, ударяет, звенит, щиплет или как-то мешает объекту.Каждая собственная частота объекта связана с одним из множества паттернов стоячих волн, с помощью которых этот объект может вибрировать. Собственные частоты музыкального инструмента иногда называют гармониками инструмента. Инструмент можно заставить вибрировать на одной из своих гармоник (с одной из его моделей стоячих волн), если другой взаимосвязанный объект толкает его с одной из этих частот. Это известно как резонанс — когда один объект вибрирует с той же собственной частотой, что и второй объект, заставляет этот второй объект совершать колебательные движения.
Слово «резонанс» происходит от латинского и означает «звучать» — звучать вместе с громким звуком. Резонанс — частая причина звукоизвлечения музыкальных инструментов. Одна из наших лучших моделей резонанса в музыкальном инструменте — это резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и вызываемая вибрацией с помощью камертона. Камертон — это объект, который заставил воздух внутри резонансной трубки войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые сталкиваются с отверстием резонансной трубки.Эти падающие звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Таким образом, если частота, на которой вибрирует камертон, не идентична одной из собственных частот воздушного столба внутри резонансной трубки, резонанса не произойдет, и два объекта не будут издавать звук вместе с громким звуком.Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха. Как мы узнали ранее, увеличение длины колебательной системы (здесь воздух в трубке) увеличивает длину волны и снижает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, повышая и понижая уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон.Когда согласование достигается, камертон заставляет столб воздуха внутри резонансной трубки вибрировать на собственной частоте, и достигается резонанс. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.

Еще одна распространенная физическая демонстрация, которая служит отличной моделью резонанса, — это знаменитая демонстрация «поющего жезла». В центре держится длинный полый алюминиевый стержень. Будучи профессиональным музыкантом, учитель достает канифольный пакет, чтобы подготовиться к мероприятию.Затем с большим энтузиазмом он / она медленно проводит рукой по алюминиевому стержню, заставляя его издавать громкий звук. Это пример резонанса. Когда рука скользит по поверхности алюминиевого стержня, трение между рукой и стержнем вызывает колебания алюминия. Колебания алюминия заставляют воздушный столб внутри стержня колебаться с собственной частотой. Соответствие колебаний столба воздуха одной из собственных частот поющего стержня вызывает резонанс.Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Знакомый шум моря , который слышен, когда морская ракушка подносится к уху, также объясняется резонансом. Даже в кажущейся тихой комнате есть звуковые волны с разными частотами. Эти звуки в основном неслышны из-за их низкой интенсивности. Этот так называемый фоновый шум наполняет морскую ракушку, вызывая вибрацию внутри ракушки.Но у морской ракушки есть набор собственных частот, на которых она будет вибрировать. Если одна из частот в комнате заставляет воздух внутри ракушки вибрировать с собственной частотой, возникает резонансная ситуация. И всегда результатом резонанса является сильная вибрация, то есть громкий звук. На самом деле звук достаточно громкий, чтобы его можно было услышать. Поэтому в следующий раз, когда вы услышите звук моря в морской раковине, помните, что все, что вы слышите, — это усиление одной из множества фоновых частот в комнате.
Резонансные и музыкальные инструменты
Музыкальные инструменты воспроизводят выбранные звуки таким же образом. Медные инструменты обычно состоят из мундштука, прикрепленного к длинной трубке, наполненной воздухом. Трубку часто изгибают, чтобы уменьшить размер инструмента. Металлическая трубка служит лишь контейнером для столба воздуха. Именно вибрации этой колонны производят звуки, которые мы слышим.Длину вибрирующего столба воздуха внутри трубки можно регулировать, сдвигая трубку для увеличения и уменьшения ее длины или открывая и закрывая отверстия, расположенные вдоль трубки, чтобы контролировать, где воздух входит и выходит из трубки. Медные духовые инструменты включают в себя вдувание воздуха в мундштук. Вибрации губ относительно мундштука создают диапазон частот. Одна из частот в диапазоне частот соответствует одной из собственных частот воздушного столба внутри медного инструмента.Это заставляет воздух внутри колонны испытывать резонансные колебания. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.
Деревянные духовые инструменты работают аналогичным образом. Только источником вибраций являются не губы музыканта, соприкасающиеся с мундштуком, а вибрация трости или деревянной полоски. Работа деревянных духовых инструментов часто моделируется на уроках физики с помощью пластиковой соломинки. Концы соломки обрезаются ножницами, образуя конический язычок .Когда воздух проходит через тростник, тростник вибрирует, создавая турбулентность с диапазоном частот колебаний. Когда частота вибрации язычка совпадает с частотой вибрации столба воздуха в соломе, возникает резонанс. И еще раз, результатом резонанса является сильная вибрация — язычок и столб воздуха излучаются вместе, создавая громкий звук. Как будто этого было недостаточно, длину соломинки обычно сокращают, отрезая небольшие кусочки от противоположного конца. По мере того как соломинка (и столб воздуха, который в ней содержится) укорачивается, длина волны уменьшается, а частота увеличивается.По мере укорачивания соломы наблюдаются все более высокие шаги. Деревянные духовые инструменты издают звуки, похожие на соломенную демонстрацию. Вибрирующий язычок заставляет столб воздуха вибрировать на одной из собственных частот. Только для духовых инструментов длина столба воздуха регулируется путем открытия и закрытия отверстий в металлической трубе (поскольку трубы немного трудно разрезать и их слишком дорого заменять каждый раз, когда их разрезают).
Резонанс — причина образования звука в музыкальных инструментах.В оставшейся части Урока 5 математика стоячих волн будет применена для понимания того, как резонирующие струны и воздушные колонны создают свои определенные частоты.

Resonance — Репетитор по органической химии

Вы сможете загрузить видеозаметки и получить доступ к практическим вопросам, когда начнете свое членство на сайте.
Подписка на курс органической химии
Под резонансом в органической химии мы понимаем взаимодействие нескольких p-орбиталей, образующих длинную π-связь, охватывающую несколько атомов. Случай простой π-связи является результатом взаимодействия двух p-орбиталей, соединяющих два атома. Однако бывают ситуации, когда три или более орбиталей могут взаимодействовать, создавая гораздо более длинную и более сложную систему орбитального взаимодействия.
Есть 4 типа резонанса, которые вам нужно знать в рамках вашего курса органической химии.
Тип 1. Взаимодействие пустой p-орбитали и соседней пары электронов. Обычно это приводит к структуре, аналогичной простой π-связи.
Тип 2. Взаимодействие между пустой орбиталью и π-связью. Это были бы примеры аллильных и бензильных систем.
Тип 3. Электронная пара и соседняя π-связь образуют аллильные или бензильные анионы. Мы не собираемся уделять столько внимания анионам в органической химии, сколько катионам.Однако они очень важны для определенных типов реакционной способности, в частности, для кислотно-щелочной химии.
Тип 4. Две (или более) π-связи, взаимодействующие друг с другом. Мы будем говорить об этих взаимодействиях более подробно, когда будем обсуждать сопряженную систему. Хотя все приведенные выше примеры, строго говоря, являются сопряженными, мы будем называть множественные π-связи, участвующие в резонансе, только «сопряженной системой» из-за их особых химических свойств.
Резонанс — одна из самых важных тем в органической химии связывания. Это объяснит хорошие 3/4 реактивности в курсе, так что это чрезвычайно важная тема для освоения. Давайте рассмотрим эти типы резонанса более подробно.
Три типа резонанса
Следующее взято из Тайны эфира:
Резонанс
Распределенная частота равна резонансу. Просмотр резонанса только в одном измерении частоты подобен области просмотра только в одном измерении длины.2} \ tag {6.39} \]
Современная физика не измеряет емкость и индуктивность как квадратные корни, но уравнение резонанса обычно выражается как:
\ [F = \ frac {1} {{2 \ pi \ sqrt {LC}}} \ tag {6.40} \]
где \ (F \) — «резонансная частота», \ (L \) — индуктивность, а \ (C \) — емкость. («Резонансная частота» избыточна и неверна. Это все равно, что сказать «длина поверхности».) Уравнение (6.40) теряет большую часть своего смысла, поскольку кажется, что измерения индуктивности и емкости являются квадратными корнями и выражают резонанс в терминах частоты.Как будто современная физика еще не открыла единицу резонанса.
Чтобы сделать расчет резонанса совместимым с остальной физикой, правильное выражение должно было бы сохранить естественные измерения индуктивности и емкости и записать результат в виде квадрата частоты. В модели физики эфира уравнение (6.41) возникает как уравнение (6.40), отличное от уравнения резонанса Стандартной модели.
\ [rson = \ frac {1} {{4 \ pi \ cdot indc \ cdot capc}} \ tag {6.41} \]
Уравнение (6.2} \ cdot indc \ cdot capc}} \ tag {6.44} \]
Уравнения (6.42) — (6.44) связаны таким образом, что:
\ [rson1 + rson2 = rson3 \ tag {6.45} \]
Уравнение rson1 идентично уравнению стандартной модели для резонанса (6.40) и связано с наивысшим потенциалом. Уравнение rson3 представляет собой истинный резонанс индуктивно-емкостной цепи и идентично уравнению (6.41). Оба уравнения rson2 и rson3 резонируют с потенциалом вблизи нуля.
Единица измерения резонанса указывает на то, что резонанс должен измеряться как распределенная величина, чтобы мы могли получить правильное значение.Конструкция настоящего измерительного оборудования позволяет измерять резонанс только в одном измерении частоты.
Поскольку знакомство с временной областью существует на макроуровне существования, современная физика также измеряет квантовую область во временной области. Время, обратное величине, — это частота, а не резонанс. То, что современная физика не признает резонанс как распределенную единицу, является серьезной ошибкой.
Квантовая область существует в пятимерном пространственном резонансе в противоположность четырехмерному пространству-времени.Если физики хотят правильно понять квантовое существование, мы должны разработать измерительное оборудование для измерения непосредственно в резонансной области. В настоящее время анализ Фурье пытается учесть этот недостаток путем математического преобразования измерений во временной области в данные частотной области.
6.2. Резонанс | Органическая химия 1: Открытый учебник
Начните с просмотра этого видео:

Если бы мы изобразили структуру ароматической молекулы, такой как 1,2-диметилбензол, мы могли бы нарисовать двойные связи двумя способами:
Какой путь правильный? На этот вопрос есть два простых ответа: «оба» и «ни один».Оба способа рисования молекулы являются одинаково приемлемыми приближениями к картине связывания молекулы, но ни один из них сам по себе не является точной картиной делокализованных пи-связей. Однако два альтернативных чертежа, , если рассматривать их вместе , дают гораздо более точную картину, чем любой из них по отдельности. Это потому, что вместе они подразумевают, что углерод-углеродные связи не являются двойными связями, не одинарными связями, а примерно посередине между ними.
Эти два рисунка являются примером того, что в органической химии называется вкладчиками резонанса : две или более различных структур Льюиса, изображающие одну и ту же молекулу или ион, которые, если их рассматривать вместе, лучше справляются с аппроксимацией делокализованных пи-связей, чем любая отдельная структура.По соглашению, участники резонанса связаны двухсторонней стрелкой и иногда заключаются в скобки:
Чтобы упростить визуализацию разницы между двумя составляющими резонанса, часто используются маленькие изогнутые стрелки. Каждая из этих стрелок изображает «движение» двух пи-электронов. Через несколько глав, когда мы начнем изучать органические реакции — процесс, в котором электронная плотность смещается и ковалентные связи между атомами разрываются и образуются, — это «обозначение изогнутой стрелки» станет чрезвычайно важным для описания движения электронов.Однако при рисовании вкладчиков резонанса это «движение» электрона происходит только в нашем сознании, когда мы пытаемся визуализировать делокализованные пи-связи. Тем не менее, использование обозначения изогнутой стрелкой — важный навык, который вам нужно будет развить при рисовании вкладчиков резонанса.
Изображение бензола с использованием двух вкладчиков резонанса A и B на рисунке выше не , а не подразумевает, что молекула в один момент выглядит как структура A, а в следующий момент смещается, чтобы выглядеть как структура B.Скорее, во все моменты молекула представляет собой комбинацию или резонанс гибрид как A, так и B.
Осторожно ! Очень важно понимать, что при рисовании двух (или более) участников резонанса мы не рисуем две разные молекулы: это просто разных изображений одной и той же молекулы . Кроме того, двунаправленная резонансная стрелка НЕ означает, что произошла химическая реакция.
Обычно производные бензола (и фенильные группы, когда бензольное кольцо включено в более крупную органическую структуру) изображаются только с одним вкладчиком резонанса, и предполагается, что читатель понимает, что подразумевается резонансная гибридизация.Это соглашение, которое будет использоваться по большей части в этой книге. В других книгах или статьях вы можете иногда увидеть бензол или фенильную группу, нарисованную кружком внутри шестиугольника, сплошным или пунктирным, как способ рисования резонансного гибрида.
Резонансные участники карбоксилатной группы
Условие рисования двух или более участников резонанса для аппроксимации единой структуры может показаться вам немного неуклюжим на данном этапе, но по мере того, как вы приобретете опыт, вы увидите, что эта практика на самом деле очень полезна при обсуждении способа, которым пользуются многие функциональные группы. реагировать.Теперь давайте рассмотрим карбоксилат-ион (сопряженное основание карбоновой кислоты). В качестве нашего примера мы будем использовать формиат, простейшую из возможных карбоксилатсодержащих молекул. Конъюгированная кислота с формиатом представляет собой муравьиную кислоту, которая вызывает болезненное укус, которое вы чувствуете, если когда-либо были укушены муравьем.
Обычно вы видите карбоксилатные группы, нарисованные одной двойной связью углерод-кислород и одной одинарной связью углерод-кислород с отрицательным формальным зарядом, расположенным на одинарном кислороде.На самом деле, однако, две углеродно-кислородные связи имеют одинаковую длину, и хотя действительно существует общий отрицательный формальный заряд на группе, он поровну распределяется между двумя атомами кислорода. Следовательно, карбоксилат может быть более точно описан парой вкладчиков резонанса. В качестве альтернативы можно использовать единую структуру с пунктирной линией, изображающей резонансно-делокализованную пи-связь и отрицательный заряд, расположенный между двумя атомами кислорода.
Давайте посмотрим, сможем ли мы соотнести эти условные обозначения на чертежах с теорией валентных связей, описывающей связь в карбоксилатной группе.Мы знаем, что углерод должен быть sp ² -гибридизованным (валентные углы близки к 120 °, а молекула плоская), и мы будем рассматривать оба атома кислорода как sp ² -гибридизованные. Обе углерод-кислородные сигма-связи, таким образом, образуются в результате перекрывания углеродных sp ² орбиталей и кислородных sp ² орбиталей.
Кроме того, углерод и оба атома кислорода имеют негибридизированную орбиталь 2 p _z, расположенную перпендикулярно плоскости сигма-связей.Эти три орбитали 2 p _z параллельны друг другу и могут перекрываться бок о бок, образуя делокализованную пи-связь.
Вкладчик резонанса A показывает, что кислород № 1 разделяет пару электронов с углеродом в пи-связи, а кислород № 2 удерживает неподеленную пару электронов на своей орбитали 2 p _z. Вкладчик резонанса B, с другой стороны, показывает, что кислород № 2 участвует в пи-связи с углеродом, а кислород № 1 удерживает неподеленную пару на своей орбитали 2 p _z.В целом, ситуация представляет собой одну из трех параллельных, перекрывающихся 2p _z орбиталей, разделяющих четыре делокализованных пи-электрона . Поскольку существует на один электрон больше, чем 2 p _z орбиталей, система имеет общий заряд -1. Это тот вид трехмерного изображения, для аппроксимации которого используются участники резонанса, и как только вы немного попрактикуетесь, вы сможете быстро визуализировать перекрывающиеся орбитали 2 p _z и делокализованные пи-электроны всякий раз, когда вы видите, что используются резонансные структуры.В этом тексте карбоксилатные группы обычно изображаются с указанием только одного участника резонанса для простоты, но вы всегда должны иметь в виду, что две связи C-O равны, и что отрицательный заряд делокализован по обоим атомам кислорода.
Упражнение
Для formate есть третий резонансный участник (который, как мы скоро узнаем, считается «второстепенным»). Нарисуйте этот вкладчик резонанса.
Вот еще один пример, на этот раз с карбокатионом.Напомним из раздела 2.1. что карбокатионы sp ² -гибридизованы, с пустой орбиталью 2p , ориентированной перпендикулярно плоскости, образованной тремя сигма-связями. Если карбокатион примыкает к двойной связи, то три орбитали 2p могут перекрываться и разделять два пи-электрона — еще один вид сопряженной пи-системы, в которой положительный заряд разделяется на два атома углерода.
Упражнения
1. Изобразите составляющие резонанса, которые соответствуют изогнутым стрелкам движения двух электронов в выражениях резонанса ниже.
2. В каждом выражении резонанса нарисуйте изогнутые стрелки движения двух электронов на левом участнике, который показывает, как мы добираемся до правого участника. Обязательно укажите официальные сборы.
Показать решение
Некоторые общие шаблоны для резонанса
Если вы изучите большое количество примеров резонанса, вы начнете замечать, что они почти всегда совпадают с определенными общими паттернами, которых всего четыре. Из них две относятся к незаряженным структурам, а две — к заряженным, как видно на рисунке:
Они перечислены как типы I-IV, но эти термины не используются вне данного учебника! Наиболее важными являются типы III и IV, где резонанс используется для разделения или «делокализации» заряда вокруг структуры для стабилизации структуры.В более сложных случаях оба типа могут возникать одновременно.
Резонанс типа III наблюдается только при положительном заряде и обычно включает положительный заряд кислорода или азота, разделяемый на углерод; форма карбокатиона имеет только шесть валентных электронов на углероде, поэтому это менее стабильная форма, чем основная форма (которая имеет полные октеты).

Явление резонанса — Основы электроники

Похожие материалы:

Добавить комментарий

► Сделать МРТ в Москве

Где сделать МРТ в Москве?

Что такое МРТ-диагностика

Кабинет магнитно-резонансной томографии

FAQ • Резонансы шагового двигателя, среднечастотный резонанс

Суть явления

Виды резонанса

Решение

Контрастирующие вещества в магнитно-резонансной томографии

Два резонанса параметрического контура (обзор)

Что такое резонанс в физике кратко. Что такое резонанс — его виды (звуковой, когнитивный), а также польза и опасность резонанса.

Колебания и частота

Суть явления резонанса

Примеры резонанса

Что такое амплитуда и частота движения?

Как частота связана с явлением резонанса?

Где можно наблюдать пример резонанса?

Примеры вредного резонанса

Полезный резонанс

Откуда взялось слово резонанс

Резонанс в полемике и риторике

Где мы встречаемся с резонансом

Чем опасен резонанс

: определение, типы, частота и примеры

Определение резонанса

Примеры резонанса — Звуковой резонанс

Примеры резонанса — Механический резонанс

Другие примеры резонанса

Так как же ломается кристалл?

Резонансные формы — Chemistry LibreTexts

Введение

Общие примеры

Рисование резонансных форм

Полезные советы

Ссылки

Problems

9 повседневных примеров резонанса — StudiousGuy

Учебное пособие по физике: Резонанс

Resonance — Репетитор по органической химии

Подписка на курс органической химии

Три типа резонанса

Резонанс

6.2. Резонанс | Органическая химия 1: Открытый учебник

Резонансные участники карбоксилатной группы

Упражнение

Упражнения

Некоторые общие шаблоны для резонанса

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ