Вторая гармоника частоты: Общая физика. Оптика и волны

Вторая гармоника частоты

Четырехволновое смешение, доминирующий параметрический процесс в волоконных световодах, генерирует спектральные боковые полосы, отстоящие от частоты накачки вплоть до Во многих экспериментах [] при накачке волоконного световода мощными импульсами на длине волны 1,06 мкм спектр выходного излучения простирался в видимую и ультрафиолетовую области. Генерация спектральных компонент в этих областях обусловлена смешиванием двух или нескольких волн с частотами, сумма которых равна частоте генерируемой волны. Так, взаимодействие двух волн с частотами может приводить к генерации вторых гармоник третьих гармоник и суммарных частот вида Генерация таких частот, как вызывается параметрическими процессами третьего порядка, обусловленными Эффективность преобразования довольно низка, поскольку обычно для таких параметрических процессов трудно достичь фазового синхронизма. В эксперименте [50] частоты третьих гармоник и суммарные частоты генерировались в результате смешивания входной волны накачки и стоксовой волны ВКР с длинами волн соответственно 1,06 и 1,12 мкм.

Двухметровый отрезок световода имел эллиптическую сердцевину и накачивался импульсами пиковой мощности 5 кВт.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Проблемы высших гармоник в современных системах электропитания
• Доказано: В электросетях существуют высшие гармоники с частотами свыше 2 кГц
• Негативное воздействие токов высших гармоник на элементы системы электроснабжения
• Гармоники тока и напряжения в электросетях
• Энергетические системы — Гармоники высшего порядка
• Справочник химика 21
• Активный фильтр гармоник как средство повышения качества электрической энергии
• Особенности тестирования проигрывателей оптических дисков
• Гармоники в электрических сетях, причины, влияние, методы борьбы

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 432 Гц Частоты Счастья — Музыка Погружает в Состояние Блаженства — Райские Сферы — Нектар Для Души

Проблемы высших гармоник в современных системах электропитания

За последние 3 года центр электромагнитной безопасности исследовал в Москве состояние систем электроснабжения в крупнейших зданиях, имеющих сети с сотнями и тысячами компьютеров. Анализ собственных данных и зарубежных публикаций, привели специалистов к выводу, что Россия столкнулась с новой серьезнейшей проблемой.

При превышении указанного предела появляются различные проблемы в эксплуатации. Аналогичная проблема возникает при наличии нелинейных нагрузок типа полупроводниковых [9]. Реальная часто встречающаяся форма напряжения показана на рис. Высшие гармоники тока кратные трем то есть 3, 9, 15, 21 и т.

В сбалансированной симметричной трехфазной системе гармонические синусоидальные токи во всех трех фазах сдвинуты на градусов по отношению друг к другу, и в результате сумма токов в нейтральном проводнике равна нулю. Следовательно, не возникает и падения напряжения на проводнике нейтрали в кабеле. Это утверждение остается справедливым для большинства гармоник. Однако некоторые из них имеют направление вращения вектора тока в ту же сторону, что и основная гармоника первая, «фундаментальная», то есть 50 Гц , то есть они имеют прямую последовательность.

Другие же вращаются в обратном направлении и, таким образом, имеют обратную последовательность. Это не относится к гармоникам, кратным третьей.

В трехфазных цепях они сдвинуты на градусов друг к другу, совпадают по фазе и образуют нулевую последовательность. Нечетные гармоники, кратные третьей, суммируются в проводнике нейтрали. В результате, с учетом того, что они составляют большую долю в действующем значении фазных токов, общий ток в нейтрали может превышать фазные токи.

Гармоники, кратные третьей, приводят к падениям напряжения как в нейтрали, так и в фазных проводниках, вызывая искажения формы напряжения на других нагрузках, подключенных к этой сети [6].

Активный ток Ia совпадает по фазе а напряжением сети.

Реактивный ток Ir сдвинут на 90 градусов относительно активного или же отстает при индуктивной нагрузки и опережает для емкостной нагрузки. Полный ток It — результирующий первых двух составляющих, протекающий от источника к потребителю.

Среднее значение реактивной мощности Q за период равно нулю, так как за это время синусоидальное напряжение меняет направление четыре раза.

Искажение формы синусоиды и возникновение гармоник приводит к серьезным техническим и эконмическим последствиям. На рис. Циркуляция реактивной мощности Q по распределительной сети увеличивает потребляемый ток и вызывает:.

Поэтому, рекомендуется производить реактивную мощность как можно ближе к нагрузкам, чтобы избежать её потребление из сети. Чтобы выработать и поставить реактивную мощность индуктивным потребителям, используются конденсаторы. Гармонические искажения напряжений и токов возникают из-за наличия в сетях элементов или оборудования с нелинейной вольт-амперной характеристикой.

Источники искажения синусоидального напряжения могут быть сгруппированы по основным типам. Современные осветительные системы обладают рядом свойств, вредно влияющих на питающую сеть и подключаемые к ней устройства. Наиболее важными из этих свойств являются гармонические искажения потребляемого из сети тока и низкий коэффициент мощности.

Наиболее серьезные нарушения из-за больших амплитуд гармоник в электрической сети получаются при работе мощных управляемых вентильных преобразователей. При этом порядок высших гармонических составляющих тока и напряжения в сети определяется по формуле.

Гармоники, генерируемые нелинейной нагрузкой, создают дополнительные потери в трансформаторах. Гармоники напряжения вызывают в трансформаторах увеличение потерь на гистерезис и потерь, связанных с вихревыми токами в стали, а так же потерь в обмотках. Сокращается также срок службы изоляции. Эти потери могут привести к значительным потерям энергии и быть причиной выхода из строя трансформаторов вследствие перегрева.

Протекание по обмоткам трансформатора несинусоидальных токов, вследствие поверхностного эффекта и эффекта близости, приводит к увеличению активного сопротивления обмоток трансформатора и, как следствие, к дополнительному нагреву.

Срок службы трансформатора зависит от нагрева его частей и не позволяет при несинусоидальном токе использовать трансформатор на всю его номинальную мощность, ее приходится занижать. Кроме того, высокочастотные гармоники тока — это причина появления вихревых токов в обмотках трансформатора, что вызывает дополнительные потери мощности и перегрев трансформатора. Сокращение срока службы электрооборудования из-за интенсификации теплового и электрического старения изоляции.

При рабочих температурах в изоляционных материалах протекают химические реакции, приводящие к постепенному изменению их изоляционных и механических свойств. С ростом температуры эти процессы ускоряются, сокращая срок службы оборудования. В конденсаторах потери энергии пропорциональны частоте, поэтому несинусоидальный ток приводит к их дополнительному нагреву. В электрических машинах токи нулевой последовательности создают дополнительное подмагничивание стали, что приводит к ухудшению их характеристик и дополнительному нагреву сердечников статоры асинхронных двигателей, магнитопроводы трансформаторов.

Сущность электрического старения состоит в возникновении так называемых частичных разрядов, которые распространяются лишь на часть изоляционного промежутка, например, частичные разряды в газовых включениях. Частичные разряды связаны с рассеянием энергии, следствием которого является электрическое, механическое и химическое воздействия на окружающий диэлектрик.

В результате развиваются местные дефекты в изоляции, что приводит к сокращению срока службы. Возможен перегрев и разрушение нулевых рабочих проводников кабельных линий вследствие их перегрузки токами третьей гармоники. Это происходит тогда, когда токи в нулевых рабочих проводниках значительно превосходят токи фазных проводников, а защита от токовых перегрузок в цепях нулевых проводников не предусмотрена п.

Отметим также ускоренное старение изоляции при повышении рабочей температуре токонесущих проводников. Нулевой рабочий проводник не защищен от перегрева автоматическими выключателями либо предохранителями п.

Следовательно, ток в нулевом рабочем проводнике не мог превосходить ток в наиболее нагруженной фазе, то есть защита на фазных проводниках одновременно защищала от перегрева и нулевой рабочий проводник. Поэтому при определении длительно допустимых токов по условиям нагрева проводов и кабелей нулевой рабочий проводник четырехпроводной системы трехфазного тока, заземляющие и нулевые защитные проводники в расчет не принимаются п.

В кабельных линиях гармоники напряжения увеличивают воздействие на диэлектрик пропорционально увеличению максимального значения амплитуды. Это, в свою очередь, увеличивает число повреждений кабеля и стоимость ремонтов. В случае нелинейных электропотребителей токи в нулевых рабочих проводниках превышают фазные предельно — в 1,73 раза, когда ширина импульса тока равна 60 электрическим градусам.

Поэтому значения длительно допустимых токов, приведенных в таблицах 1. На корпусах электрооборудования, подключенного к нулевому проводу, могут возникать напряжения, оказывающие при прикосновении раздражающее влияние на человека. Все сказанное в равной мере относится и к шинопроводам. В ПУЭ еще не прописаны количественные данные по неравномерности распределения токов по шинам по фазам и по величинам допустимых гармоник. При наличии высших гармоник в электрических цепях со сосредоточенными и распределенными параметрами, какими могут быть представлены блоки, узлы и распределительные сети системы электропитания, возникает опасность появления резонансных явлений.

При возникновении резонансного или близкого к нему режима на какой-либо высшей гармонике тока или напряжения эта составляющая оказывается больше, чем амплитудное значение первой гармоники тока напряжения на тех же участках цепи. Это отрицательным образом может отразиться на работоспособности отдельных элементов и узлов системы. Гармоники могут нарушать работу устройств защиты или ухудшать их характеристики.

Характер нарушения зависит от принципа работы устройства. Цифровые реле и алгоритмы , основанные на анализе выборки данных или точки пересечения нуля, особенно чувствительны к гармоникам. Чаще всего изменения характеристик несущественны. Однако увеличение доли мощных преобразователей в сетях может в будущем изменить ситуацию. Проблемы, возникающие из-за гармоник, различны для нормальных и аварийных режимов и ниже рассмотрены отдельно. Происходит ложное срабатывание предохранителей и автоматических выключателей вследствие дополнительного нагрева внутренних элементов защитных устройств.

Этот процесс обусловлен протеканием несинусоидальных токов и, следовательно, действием поверхностного эффекта и эффекта близости. Снижение уровня выпрямленного напряжения.

Деформация синусоиды питающего напряжения приводит к снижению значения амплитуды входного напряжения, вследствие этого снижается напряжение на конденсаторе рис. Высшие гармонические составляющие в токах нелинейных электропотребителей приводят к негативным, а иногда и катастрофическим последствиям.

Измерительные устройства обычно калибруются при чисто синусоидальном напряжении и увеличивают погрешность при наличии высших гармоник. Величина и направление гармоник являются важными факторами, так как знак погрешности определяется направлением гармоник. Погрешности измерения, вызываемые гармониками, сильно зависят от типа измерительной аппаратуры. Такие потребители оказываются автоматически наказанными за внесение искажений в сеть, поэтому в их собственных интересах установить соответствующие средства для подавления этих искажений.

Снижение несинусоидальности напряжения обеспечивается или рациональным построением схемы электрической сети предприятия, при которой коэффициент перекручивания кривой напряжения будет в допустимых границах, или применением специальных схем нелинейных нагрузок, а также корректирующих устройств. На практике, как правило, соединят разные методы [7]. Наиболее эффективными средствами борьбы с гармониками, очевидно, являются те, которые предотвращают явления, генерирующие гармоники. В частности, во вращающихся машинах число, форма и распределение пазов должны быть подобраны так, чтобы уничтожить по крайней мере гармоники низкого порядка это хорошо удалось сделать в отношении гармоник 3, 5 и 7-го порядков, несколько хуже — гармоник выше 7-го порядка, а гармоники выше го порядка имеют незначительные коэффициенты.

Подобные конструктивные меры не всегда экономичны, поэтому следует искать оптимальное соотношение между стоимостью аппарата и потерями, вызываемыми гармониками. Это, в частности, относится к трансформаторам, в которых при желании избавиться от гармоник не превосходя, однако, порога насыщения надо было бы значительно увеличить сечение сердечников и ярма, а следовательно, вес и стоимость этих аппаратов. Имеются и такие аппараты, в которых нельзя уменьшить гармоники конструктивными средствами например, в выпрямителях, металлических ртутных выпрямителях.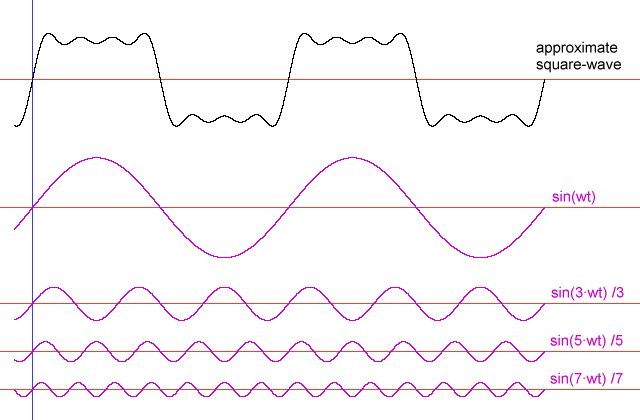

При этом между аппаратом и системой необходимо располагать устройство, способное помешать гармоникам распространиться в систему.

Это устройство является фильтром , иногда состоящим из конденсаторов, иногда образованным сочетанием емкостных и индуктивных сопротивлений, включенных последовательно и параллельно таким образом, чтобы получить полосу пропускания необходимой ширины. Фильтры, включаемые параллельно, представляют собой цепи с большой полной проводимостью, поглощающие мощности гармоник. Они могут быть дополнены другими фильтрами, включаемыми последовательно в систему и образующими фильтрыпробки.

В передачах постоянного тока необходимо установить фильтры, чтобы ограничить доступ в систему гармоник. Для люминесцентных ламп большой мощности применяются устройства компаундирования, представляющие собой фильтр гармоник. Для конденсаторных батарей, которые весьма чувствительны к перегрузкам гармониками, возможно применение последовательно включаемых индуктивностей для создания таким образом низкочастотного фильтра; На практике процент гармоник напряжений, существующих в системе, почти всегда достаточно мал и не вызывает опасного нагрева конденсаторных батарей при отсутствии других резонансных явлений [1].

Учитывая, что большинство офисов располагается в зданиях, не рассчитанных на значительный рост нелинейных нагрузок, необходим особый подход к эксплуатации систем электроснабжения этих построек.

Действия по предупреждению негативного воздействия высших гармоник:. В первую очередь необходимо добиться, насколько это возможно, сбалансированности нагрузок по фазам. При этом обеспечивается минимальный ток в проводнике нейтрали и минимальное содержание гармоник в выходном напряжении ИБП. Соответствующие схемы контроля и управления в ИБП будут поддерживать номинальное действующее значение выходного напряжения, в то же самое время стремясь обеспечить его синусоидальную форму.

Не всегда возможно одновременно выполнить обе эти функции. Применение последовательно включенных линейных дросселей в ряде случаев не позволяет уменьшить гармонические искажения тока до желаемых пределов. В этом случае целесообразно применение пассивных LC-фильтров, настроенных на определенный порядок гармоник.

Доказано: В электросетях существуют высшие гармоники с частотами свыше 2 кГц

Причины искажения: постоянные и непостоянные нелинейные нагрузки работа выпрямителей, преобразователей частоты, трансформаторов разовое включение большого потребителя, например сварочного автомата или станка , цикличные нагрузки крупный потребитель подключается в определенное время суток к сети , пиковые нагрузки при массовом потреблении электроэнергии. Часто причиной возникновения гармонических колебаний по напряжению является изношенность оборудования в энергогенерирующей отрасли и распределительных сетях в основном, это старые ТП и сети с малым пределом потребления. В таких случаях необходимо применять меры по устранению токовых искажений. По сути, гармоники — это токи-паразиты, которые оборудование не может потребить или потребляет частично с негативным эффектом. В электродвигателях они являются причиной вибраций, в различных сетях приводят к перегреву, а если гармоника ниже чем номинальный синусоидальный ток необходимый для работы электротехники, то в сервоприводах, автоматических выключателях и другом оборудовании они могут вызывать ложные срабатывания. Большая проблема — преждевременное старение электроизоляции в сетях с обилием гармоник.

Что собой представляют гармоники в электрических сетях и чем они представить как сумму сигналов различной частоты и величины.

Негативное воздействие токов высших гармоник на элементы системы электроснабжения

За последние 3 года центр электромагнитной безопасности исследовал в Москве состояние систем электроснабжения в крупнейших зданиях, имеющих сети с сотнями и тысячами компьютеров. Анализ собственных данных и зарубежных публикаций, привели специалистов к выводу, что Россия столкнулась с новой серьезнейшей проблемой. При превышении указанного предела появляются различные проблемы в эксплуатации. Аналогичная проблема возникает при наличии нелинейных нагрузок типа полупроводниковых [9]. Реальная часто встречающаяся форма напряжения показана на рис. Высшие гармоники тока кратные трем то есть 3, 9, 15, 21 и т. В сбалансированной симметричной трехфазной системе гармонические синусоидальные токи во всех трех фазах сдвинуты на градусов по отношению друг к другу, и в результате сумма токов в нейтральном проводнике равна нулю. Следовательно, не возникает и падения напряжения на проводнике нейтрали в кабеле. Это утверждение остается справедливым для большинства гармоник.

Гармоники тока и напряжения в электросетях

Отправьте статью сегодня! Журнал выйдет 19 октября , печатный экземпляр отправим 23 октября. Дата публикации : Статья просмотрена: раз.

Большая часть компьютерного и офисного оборудования представляет собой нелинейную электрическую нагрузку, что создает искажения в питающей сети. Суммарный эффект этих нагрузок выражается в искажении напряжения, которое воздействует на другое оборудование, получающее электропитание от того же источника.

Энергетические системы — Гармоники высшего порядка

Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Войти Регистрация. Гармонические колебания Математика , Визуализация данных На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов ЦОС , но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить. АЧХ шума. Лично мне после прочтения этих статей например, этой не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.

Справочник химика 21

Колебания камерюна издают один звук базовой частоты А. Более сложные звуковые колебания возникают, когда одновременно звучат два камертона В Основной тон колеблющегося столба воздуха во флейте изменяется под воздействием призвуков с более короткой длиной волны, которые дополняют основной тон С. Деревянные духовые инструменты имеют более гнусавый звук из-за взаимодействия всех этих различных частот, слышимых одновременно D. Научно-технический энциклопедический словарь. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А. Спектр звуковой.

Вторая (тканевая) гармоника (Second Harmonic, Tissue Harmonic Удвоение частоты ультразвука связана с нелинейностью его.

Активный фильтр гармоник как средство повышения качества электрической энергии

Это частный случай нелинейного сложения частот излучения. В этом опыте излучение, генерируемое рубиновым лазером, фокусировалось в кристалл кварца. Выходное излучение разворачивали в спектр при помощи дисперсионной призмы и фокусировали на фотопластинку.

Особенности тестирования проигрывателей оптических дисков

Авторы: К. Замула, Ю. Соколов, А. На сегодняшний день большинство энергоснабжающих организаций не обладают необходимым оборудованием, обеспечивающим в автоматическом режиме требуемого уровня содержания высших гармоник в сетях.

Присутствие гармоник говорит об искаженной форме тока или напряжения.

Гармоники в электрических сетях, причины, влияние, методы борьбы

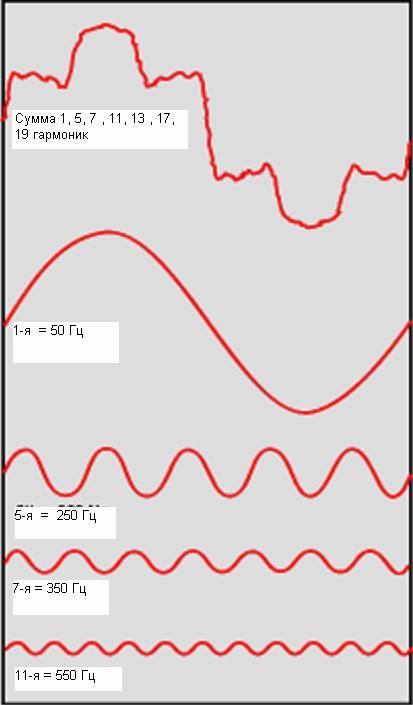
Содержание: Определение гармоник Источники помех Последствия гармонических помех. Эти зазубрины и всплески и вызваны гармониками. Мы попытаемся рассказать об этом явлении простыми словами. Изображенный выше график можно представить как сумму сигналов различной частоты и величины. Если всё это сложить, то в результате получится именно такой сигнал.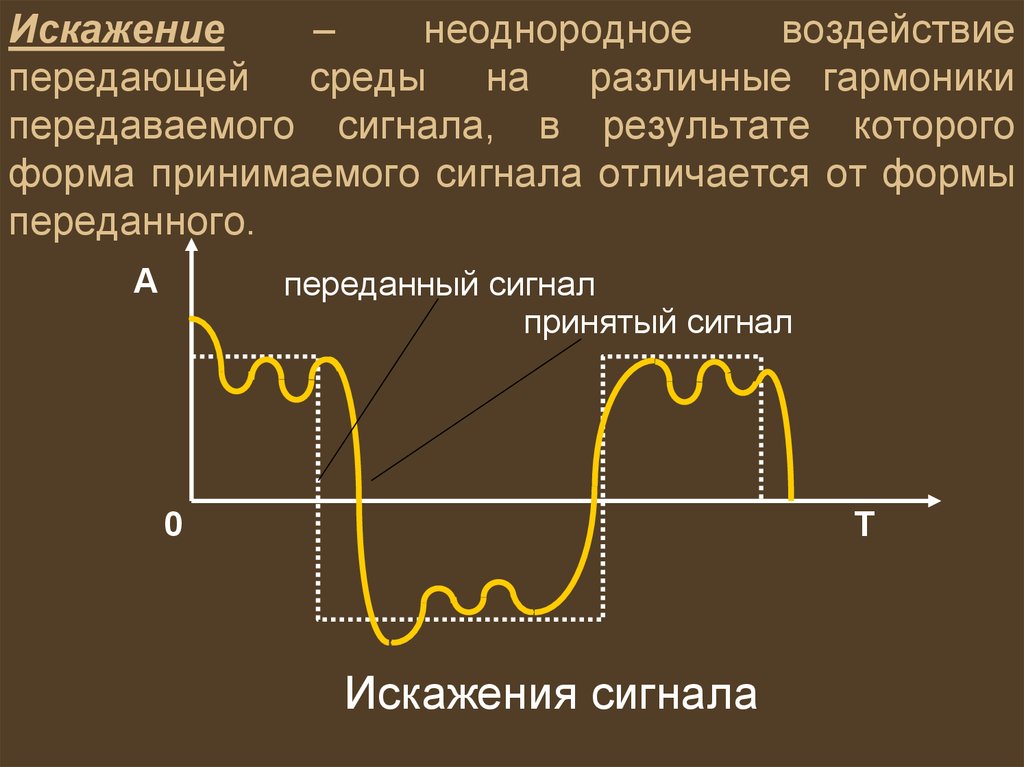

Спектры периодических сигналов. Периодическим сигналом током или напряжением называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T , который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой.

Механические ослабления | Спектральная вибродиагностика

Русов В.А.

«Диагностика дефектов вращающегося оборудования по вибрационным сигналам» 2012 г.

3.2. Дефекты оборудования уровня «механизм»

Это обобщенное название целого ряда специфических дефектов оборудования, имеющих различную причину возникновения, локализацию и по-разному влияющих на состояние агрегатов. Достаточно часто под термином «механическое ослабление» понимается сумма нескольких различных дефектов, имеющихся в конструкции, или являющихся следствием особенностей эксплуатации.

Все разнообразие проявлений ослабления связей между элементами механизмов и агрегатов имеет ниже общее название «механические ослабления» по одной простой причине — в спектрах вибросигналов все они дают качественно примерно одинаковые картины.

Механические ослабления довольно часто характеризуют вторым термином, применяемым на практике для обозначения таких дефектов, это слово «люфт», понятное всем сотрудникам механических служб. Мы не используем в данном разделе этот термин в качестве основного только по одной причине – он не охватывает все возможные проявления механических ослаблений.

Возникновение механических ослаблений автоматически приводит к тому, что в процессе работы контролируемого оборудования, по тем или иным причинам, возникают соударения деталей или элементов агрегатов, между которыми ослабли механические связи. Соударения могут происходить как между элементами на вращающемся роторе, так и между неподвижными элементами механизмов, фундамента, а также между подвижными (вращающимися) и неподвижными частями агрегата.

В любом случае, для проявления механических ослаблений в вибрационных сигналах, должны существовать динамические факторы, приводящие к усилиям, заставляющим элементы перемещаться, и соударяться друг с другом. При отсутствии таких возбуждающих сил механические ослабления в конструкции могут не проявляться.

Мы уже выше рассматривали практические случаи, в которых возбуждающие силы были обусловлены наличием в контролируемом агрегате других дефектов, например, небаланса или расцентровки. Если эти «первичные» дефекты устранялись, то и проявления механических ослаблений в спектрах вибрационных сигналов исчезали. Это вполне понятно, ведь исчезали возбуждающие силы.

Механические ослабления не всегда являются «вторичным» дефектом во вращающемся оборудовании, диагностируемым при наличии возмущающих конструкцию «первичных» дефектов. Достаточно часто и механические ослабления сами являются «первичным» дефектом, всегда вызывающим увеличение вибрации агрегата. Особенно часто это случается в механизмах возвратно — поступательного принципа действия или имеющих такие узлы. Знакопеременные нагрузки – наиболее часто встречающаяся причина появления вибраций от механических ослаблений в различных механизмах.

3.2.3.1. Общие вопросы диагностики ослаблений

Происхождение механических ослаблений во вращающемся оборудовании весьма многообразно, связано с большим количеством различных параметров конструкции, монтажа и эксплуатации. В целом все обилие механических ослаблений можно разделить на две большие группы:

• Механические ослабления, являющиеся дефектом изготовления, сборки и монтажа вращающегося оборудования. К ослаблениям этой группы следует относить всевозможные чрезмерно свободные посадки деталей вращающихся роторов, сопряженные с наличием нелинейностей типа «люфт». Ослабления такого типа могут иметь место в опорных подшипниках любого типа, соединительных муфтах, в элементах самих механизмов, в опорных фундаментах и даже конструкциях зданий.
• Механические ослабления, являющиеся результатом естественного износа элементов конструкции агрегата, следствием аварийного и внезапного разрушения  элементов конструкции. Ослабления могут возникать при неправильной эксплуатации оборудования, нарушении режимов работы. В эту же группу следует относить всевозможные трещины и дефекты в конструкции и фундаменте, возникшие в процессе эксплуатации контролируемого оборудования.

Деление причин возникновения механических ослаблений на эти две группы является достаточно условным. И в том, и в другом случаях характерные признаки дефекта в спектре  вибросигнала, примерно одинаковы. Важно, что эта диагностическая похожесть наблюдается в спектрах вибрационных сигналов, как в качественном, так и в количественном соотношении.  Просто таким делением хотелось еще раз подчеркнуть, что реальные причины возникновения механических ослаблений значительно различаются.

Форма временного вибросигнала при механических ослаблениях содержит в себе значительную нестационарную, непериодическую компоненту, которая приводит к тому, что даже от оборота к обороту форма сигнала может сильно меняться. По форме временного сигнала проводить диагностику механического ослабления достаточно сложно, так как она часто непостоянна, имеет случайные пики и сдвиги. На временном сигнале имеется большое количество пиков от соударений, которые носят, на первый взгляд, хаотический характер. Такая форма временного сигнала обычно сопровождает все дефекты типа «механическое ослабление» или «люфт».

Причина изменчивости формы вибрационного сигнала при механических ослаблениях легко объяснима. Самой простейшей моделью возникновения этой особенности является всем известная «важная прикладная процедура — перемешивание чайной ложкой сахара в стакане», это упрощенная до предела модель механического ослабления. Проводя этот «практический» эксперимент читатель легко убедится, что удары ложкой о стенки стакана каждый раз будут происходить в разных, всегда случайных точках. Ударов возникает много, места ударов различны, интервал времени между ударами может тоже сильно различаться. Соответствующий вид будет иметь и временной вибросигнал в этом эксперименте — очень сильна будет нестационарная компонента вибросигнала. Хотелось бы предложить читателю запомнить издаваемый при таком, достаточно быстром, помешивании звук — в практике диагностики механических ослаблений с ним можно встретиться достаточно часто.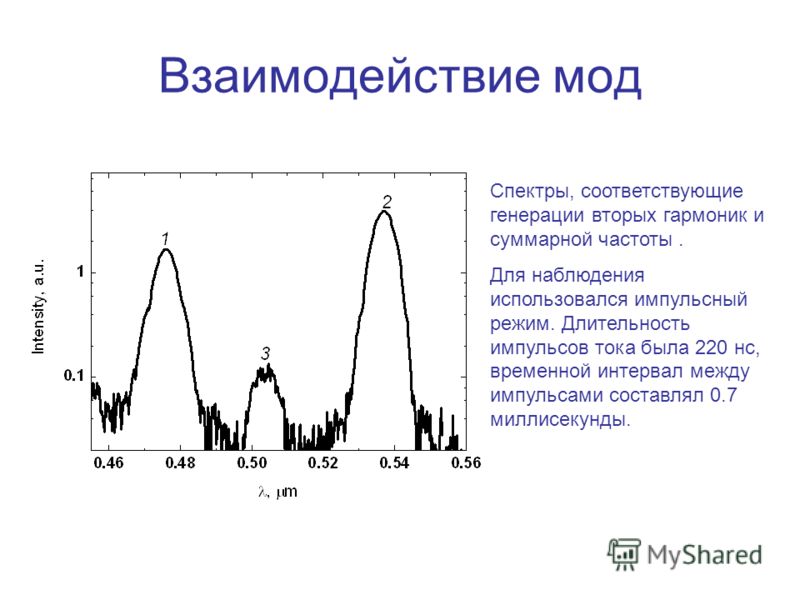

Пространственная ориентация направления механических ослаблений, чаще всего это радиальное или осевое направление, обычно приводит к тому, что характер и интенсивность вибрации по различным направлениям измерения вибрации на опорных подшипниках, например в вертикальном и поперечном направлениях, может сильно различаться. Это следует всегда помнить, и при возможности не жалеть времени на измерение вибрации во многих направлениях имея конечной целью построение «розы вибраций». Ее помощь в диагностике ориентации ослаблений, как и в диагностике расцентровки, обычно незаменима.

Имеющие место при механическом ослаблении множественные нестационарные соударения элементов обычно приводят к появлению в спектре вибросигнала большого количества сильно выраженных гармоник оборотной частоты вращения ротора. Их число может доходить до 10 и даже более. Причем важно, что количество этих гармоник в спектре, и их амплитуда, может сильно изменяться, часто при неизменной величине самого механического ослабления. Пример вибрационного сигнала и спектра, при механическом ослаблении, приведен на рисунке 3.2.3.1.

Этому есть объяснение, основанное на анализе физических процессов при знакопеременных нагрузках на зону с механическим ослаблением. Попробуем дать его максимально просто, насколько это возможно, для чего рассмотрим самые основные особенности формирования вибросигнала, и его спектра при таком дефекте:

• Количество соударений ослабленных элементов конструкции агрегата друг о друга, приходящихся на один оборот ротора, обычно бывает достаточно большим. Как мы уже отмечали, от оборота к обороту это количество может изменяться в некоторых пределах, до ± 30%.
• В самом простейшем приближении количество соударений на один оборот связано с величиной перемещающихся масс, и приложенными усилиями. Реально эта величина обратно пропорциональна интервалу времени между двумя соударениями масс. Вполне очевидно, что эта величина, как и количество соударений на один оборот, является переменной.
• Будем считать, что динамические усилия, возникающие при всех соударениях между элементами конструкции, имеют примерно одинаковую силу. Это допущение также не далеко от сути реальных процессов, имеющих место при дефектах типа «люфт».

В силу особенностей работы FFT (функция быстрого преобразования Фурье, предназначенная для получения спектра вибросигнала), максимальную амплитуду в спектре будут иметь те гармоники, которые связаны с соударениями, наиболее часто повторяющимися в процессе вращения вала агрегата.

«Пропусков» в гармоническом ряду этих целых гармоник оборотной частоты почти не бывает, присутствуют все гармоники подряд. Амплитуда гармоник по мере роста номера гармоники может постепенно уменьшаться, но никогда не растет. Иногда амплитуда гармоник примерно стабильна до 5 — 7 гармоники, а затем начинает примерно монотонно убывать.

Причины возникновения в спектре только «целых» гармоник вполне объяснимы. Для корректного частотного математического описания достаточно случайных соударений, в спектре сигнала приходится использовать много гармоник различной частоты, захватывающих достаточно широкий частотный спектр. Но поскольку все соударения, так или иначе, связаны с частотой вращения ротора, почти все гармоники в спектре являются синхронными и «целыми по номеру».

Иногда вблизи одной гармоники, являющейся основной в процессах соударений, происходит поднятие спектра или просто уширение гармоники. Это уширение обозначает сосредоточение мощности ударов в одной частотной полосе и вызывается наличием несинхронных компонент в вибросигнале.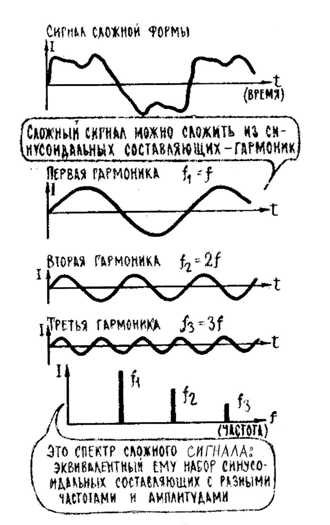 Несинхронные компоненты имеют частоту, близкую к частоте основной гармоники процесса. Например, эта гармоника может быть связана с числом пальцев в дефектной пальцевой муфте, имеющей сильный износ или даже механический дефект. Или это число лопаток дефектного колеса насоса. Такая «уширенная» гармоника часто имеет в спектре вибросигнала свое семейство гармоник. Для примера, при дефекте посадки на вал рабочего колеса насоса с шестью лопатками наибольшую амплитуду в спектре будут иметь шестая и двенадцатая гармоники оборотной частоты ротора.

Механическое ослабление, особенно в неподвижных конструкциях, часто всего носит направленный, векторный характер. По этой причине оно в различной степени проявляется при проведении измерений вибрации в различных направлениях. «Набор гармоник» в вибросигналах, измеренных «на фундаменте» в направлениях разных осей агрегата, часто бывает различен.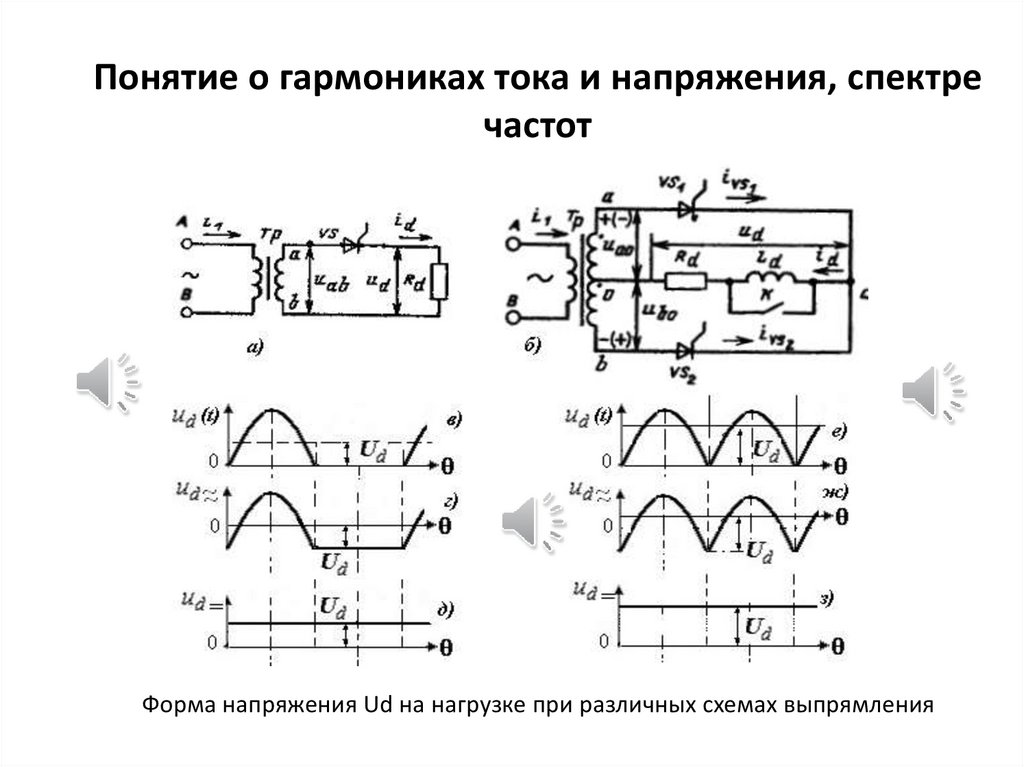 Спектральная картина, свойственная механическому ослаблению, наиболее сильна в том направлении, в котором суммарная мощность «целых» гармоник максимальна.

Часто полезным для диагностики данного дефекта является обычное прослушивание ухом вибраций подшипника или корпуса механизма, на который имеется подозрение на наличие механического ослабления. Прослушивание желательно проводить как можно ближе к той точке, где подозревается ослабление Для проведения прослушивания лучше всего использовать обычную сухую деревянную палочку или дощечку достаточных размеров. Эффективность диагностики механических ослаблений при помощи процедуры «прослушивания» достаточно высока и ей не следует пренебрегать.

Все соударения от имеющегося механического ослабления прекрасно слышны ухом через «деревянный зонд», и тот, кто хотя бы раз их слышал, никогда уже ни с какой другой причиной повышенной вибрации не спутает. Как уже говорилось выше, по звуку вибрация от механического ослабления во многом похожа на процесс перемешивания чайной ложечкой в пустом стакане без воды, а может быть и с водой, та или иная аналогия определяется особенностями конструкции агрегата.

В заключение по общим особенностям диагностирования дефекта «механические ослабления» можно сказать следующее. Этот дефект наиболее «страшно» проявляется в спектре вибросигнала. Появление «развесистого» букета целочисленных гармоник часто вызывает у начинающего диагноста очень тяжелое состояние, близкое к паническому. Ему кажется, что наличие многих гармоник обозначает наличие большого количества дефектов в контролируемом агрегате. Самым сложным является то, что диагносту кажется, что для ничего все непонятно. Лихорадочные поиски характерных особенностей агрегата, чтобы как-то связать частоты гармоник с конструктивными параметрами агрегата кончаются ничем. Все плохо! На самом деле это банальное ослабление связей между элементами конструкции, правда, это не обозначает, что оно не опасно для дальнейшей эксплуатации оборудования.

Задача диагноста, сразу сказать об этом дефекте. Можно долго рассуждать, например, о соотношении амплитуд пятой и восьмой гармоник, но никакого практического смысла это не имеет. Максимум того, что может сделать диагност, так это попытаться уточнить место возникновения этого ослабления, чем он в значительной степени поможет предстоящей работе ремонтных служб предприятия. Но делать это придется ему чаще всего не при помощи анализа спектров вибросигналов, а другими, более простыми и понятными методами, имеющимися в арсенале вибрационной диагностики.

В заключение по описанию общих вопросов диагностики механических ослаблений в агрегате скажем, что он во многом перекликается с диагностикой состояния и поиском дефектов фундаментов, описанной в разделе 3. 3.2. Для получения дополнительной информации о диагностике механических ослаблений советуем внимательно причитать и этот раздел настоящего руководства. В нем вы тоже можно ознакомиться с полезной для процедуры диагностики информацией.

Ниже приведена информация о некоторых «стандартных» механических ослаблениях, диагностируемых по вибрационным параметрам.

3.2.3.2. Ослабление посадки элементов механизма на валу

Это самый известный и широко распространенный в практике тип дефекта, связанный с наличием механических ослаблений в оборудовании. Он может возникать по различным причинам, но заключается в одном и том же — в ослаблении посадки различных элементов конструкции ротора на валу.

Этот же дефект в оборудовании достаточно часто диагностируется из-за увеличения зазоров в опорных подшипниках. В случае использования подшипников скольжения это бывает при увеличении рабочего зазора, а в подшипниках качения дефект проявляется при повышенном износе поверхностей качения, или же при ослабленной посадке обоймы подшипника в опоре, или же на валу.

Очень часто вибрационные признаки механического ослабления в диагностируемых вращающихся агрегатах может возникать при неплотной посадке соединительных полумуфт на валах, возникающей при износах и нарушениях технологии монтажа. Возможно влияние зазора, часто имеющего место между полумуфтами.

Специфическое механическое ослабление может возникать в оборудовании по абсолютно разным причинам. Например, оно может возникать в высоковольтных синхронных машинах. Причиной возникновения дефекта может быть неплотная посадка магнитной системы возбудителя, смонтированного на свободном конце ротора.

Всем этим, внешне различным причинам повышенной вибрации, всем типам механических ослаблений, обычно соответствует одинаковый и очень характерный спектр вибросигнала, имеющий в своем составе большое количество гармоник с целым номером. Как мы уже говорили, амплитуды этих гармоник какой-либо прямой связи с параметрами контролируемого механизма обычно не имеют.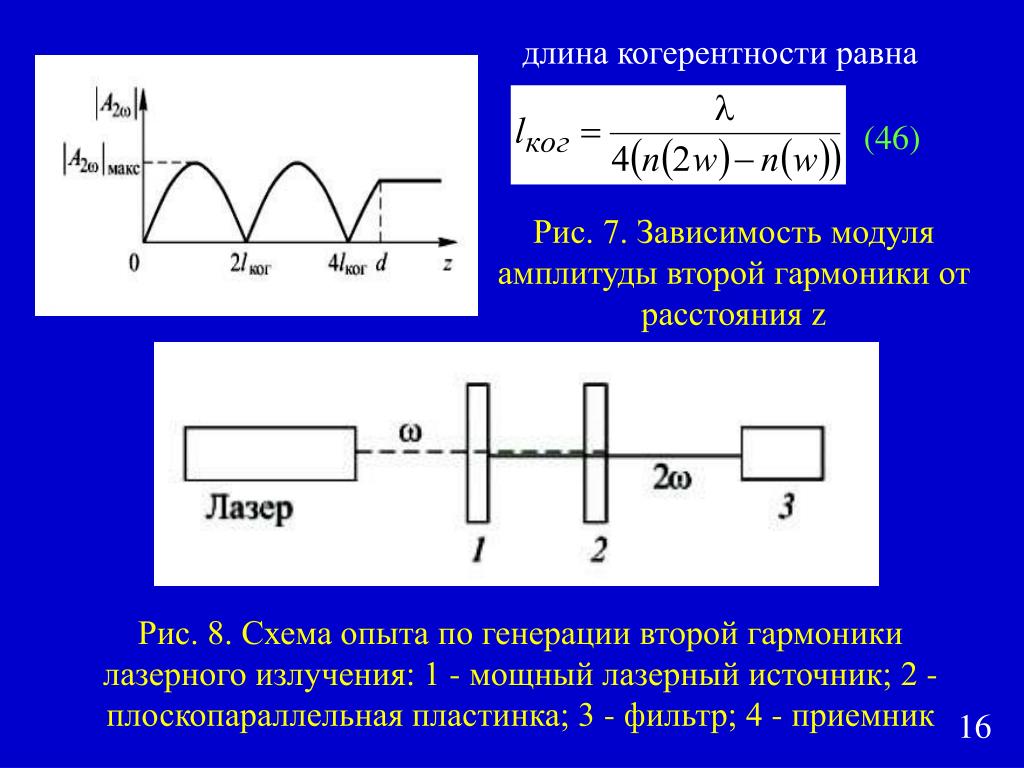

Общее количество «целых» гармоник в спектре велико, не менее десяти, но гармоники с «дробным номером», кратные 0,5 от оборотной частоты, при таком дефекте встречаются достаточно редко.

3.2.3.3. Механические ослабления – трещины в агрегате

Дробные гармоники появляются в спектре вибрационного сигнала в том случае, когда ослабление полностью определяется, или же обязательно сопровождается, наличием трещин в агрегате, или в фундаменте.

Появление дробных гармоник в спектре при таком дефекте объяснить не очень просто, как с использованием математического аппарата, так и без него. Самым сложным является объяснение физического смысла дробных гармоник с номером 1,5 и выше. Гармонику с номером 0,5 от оборотной еще можно как-то представить и объяснить, а вот гармонику, например, с номером 3,5 от оборотной даже и представить сложно. Каким должен быть динамический процесс в механизме, чтобы он продолжался ровно 3,5 раза на один оборот ротора, а затем повторялся. Достаточно сложно объяснить возникновение такой гармоники в спектре вибрационного сигнала. В этом случае действует афоризм, что «сложно объяснить сложное легко, но просто объяснить сложное сложно». Мы попытаемся это сделать, как нам кажется, максимально просто.

С физической точки зрения самое главное объяснить возникновение в механизме дробной гармоники с номером 0,5 от оборотной. Эта гармоника соответствует вибрационным процессам в оборудовании, частота которых не укладывается ровно в один оборот ротора, а занимают два оборота. Чаще всего это процессы, когда в течение одного оборота ротора на подшипники действует сила одного знака, а течение другого оборота на них воздействует сила другого знака.

Так бывает иногда, например, когда трещина располагается на вращающемся роторе, и периодически то «открывается», в течение одного оборота, то «закрывается», в течение другого оборота. Таким образом, в спектре вибрации возникает гармоника с кратностью частоты, равной 0,5 от оборотной частоты. Такое может также происходить при наличии ослаблений (трещин) в конструкции и фундаменте агрегата.

Именно трещины характеризуются дробными гармониками в спектре вибрационного сигнала. Вообще следует с большим подозрением относиться к таким гармоникам, пусть даже небольшой амплитуды. Их появление обычно предшествует возникновению достаточно больших проблем в оборудовании.

Дальше все объяснить немного проще. Поскольку, кроме трещины мы имеем в агрегате и механическое ослабление (на самом деле это одно, и тоже), то возникшая в агрегате вибрация с основной частотой в 0,5*F₁, будет также создавать свое семейство гармоник, как и оборотная гармоника, базовая для своего семейства целых гармоник. Созданию семейства дробных гармоник в спектре будет способствовать наличие механических ослаблений в механизме.

Частоты «целых» гармоник от частоты 0,5 будут равны 1,0, 1,5, 2,0, 2,5 от оборотной частоты вращения ротора агрегата. Это не оговорка, потому что, являясь целыми относительно базовой гармоники 0,5, они будут являться «дробными» гармониками относительно оборотной частоты агрегата. На «целых» частотах эти гармоники сольются с целыми гармониками оборотной частоты, и мы их при этом не заметим, будет иметь место некоторое увеличение амплитуды, и только. На дробных частотах эти гармоники будут выглядеть обособлено, и будут заметны.

Такие процессы чаще всего возникают в оборудовании при наличии дефектов типа «трещина», «люфт», ну и при некоторых типах механических ослаблений. Такое достаточно часто бывает при наличии трещин в фундаментах.

На рисунке 3.2.3.3. приведен пример спектра вибросигнала, зарегистрированного на подшипниках ротора насоса, вращающегося с частотой 3000 оборотов в минуту. Механическое ослабление в этом агрегате возникло из-за увеличенного зазора в подшипнике скольжения. К картине общего механического ослабления добавились вибрационные признаки наличия трещины на лапе подшипниковой стойки насоса.

Общее число целых гармоник на таком спектре, как и при обычном ослаблении, может достигать до 7 — 10, причем в таком спектре могут быть два — три «пропуска» целых по номеру гармоник оборотной частоты. Например, не будет пятой и седьмой гармоник, как это показано в приведенном примере, на рисунке 3.2.3.3.

Максимальной на приведенном спектре является вторая гармоника оборотной частоты, что не является обязательным при таком типе дефекта оборудования. На приведенном спектре вибросигнала есть также три пика дробных гармоник с кратностью 0,5, т.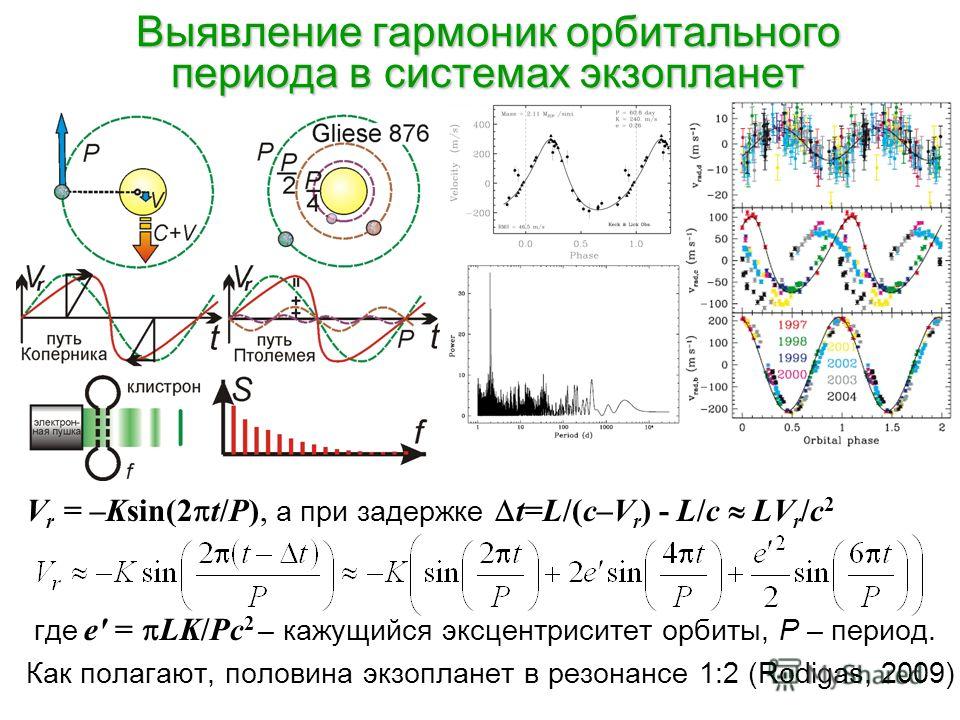 е. с частотами 25 и 75 Гц. Следуя несколько другой терминологии, это есть одна субгармоника (с частотой, меньше оборотной), и две гармоники с дробным номером, кратным коэффициенту 0,5. Такая терминология в обозначении нецелых гармоник в спектре, также встречается на практике, и в литературе.

 Достаточно часто на спектрах вибрационных сигналов, при наличии трещины, могут быть обнаружены несколько дробных гармоник или субгармоник, с частотной кратностью к оборотной частоте вращения вала, равной значению 1/3. Понятно, что основной гармоникой, «главой семейства, в этом случае является гармоника с частотой 0,33 от оборотной. Она наводится усилиями, один полный цикл действия которых равняется трем оборотам ротора. Все остальные гармоники такой кратности возникают в спектре за счет наличия в агрегате механического ослабления любой природы возникновения.

Это тоже очень опасные для последующей эксплуатации агрегата гармоники, они обычно предвещают очень серьезные проблемы в ближайшем будущем.

Своеобразно проявляется механическое ослабление (трещина) в фундаменте агрегата. На рисунке 3.2.3.4. приведен спектр виброскорости вибрационного сигнала для такого случая. Основным признаком наличия трещины в фундаменте на этом спектре являются два элемента.

Во-первых, это наличие одной гармоники с кратностью 0,33, причем, что является отличием от трещины в механизме, она не имеет своего «развитого» семейства кратных гармоник. Причина отсутствия кратных гармоник достаточно проста, в этом случае нет признаков механического ослабления в механизме, а это значит, что в получаемом спектре не будет кратных гармоник этой частоты, впрочем, как и гармоник оборотной частоты.

Во-вторых, ниже (по частоте) гармоники с кратностью 0,33 имеется локальное поднятие на спектре, имеющее максимум в районе 7 – 10 герц. Если бы это поднятие было до нулевой частоты в спектре, причем с уменьшением частоты амплитуды росли, то это бы говорило, чаще всего, о низком качестве используемой виброизмерительной аппаратуры. В данном случае это говорит о дефекте в фундаменте. Достаточно трудно объяснить это с логической точки зрения, но так чаще всего бывает на практике. Поднятие на спектре в зоне низких частот говорит о наличии дефекта в фундаменте.

Последнее замечание по данному разделу. Форма временного сигнала при наличии трещины в агрегате, и в фундаменте, является нестационарной, и нестабильной. Она имеет в своем составе много различных, неявно выраженных пиков от внутренних динамических ударов, следующих хаотично, без очевидной связи между собой. Вполне понятно, что такой временной сигнал, по своей форме, мало пригоден для диагностики механических ослаблений и трещин в оборудовании.

3.2.3.4. Ослабление в агрегатах с вертикальной осью

В оборудовании, в котором рабочий вал расположен горизонтально, справедливы все вышеописанные диагностические правила. Чаще всего механическое ослабление проявляется в вибрации и может быть выявлено персоналом только тогда, когда в агрегате есть неуравновешенные динамические силы. Эти силы могут быть вызваны другими дефектами, например небалансом, расцентровкой и т. д. Мы называем их динамическими дефектами первого типа.

Если же возмущающей силы в работающем агрегате нет, то механическое ослабление, и даже трещина, может и не проявляться в спектре вибрации. В этом случае дефект спектральными методами диагностировать нельзя.

Иначе дело обстоит в агрегатах с вертикальным направлением вала. В таких случаях если в агрегате есть механическое ослабление — то оно будет проявляться в спектре вибрации практически всегда.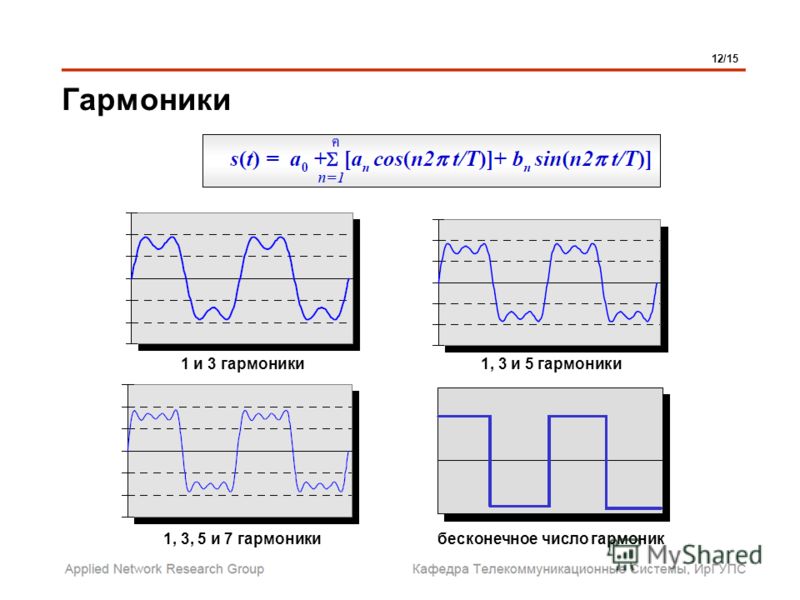 Причина этого явления проста — в агрегате с горизонтальным валом ротор прижат к подшипнику собственным весом, что является стабилизирующим фактором, требующим для возбуждения вибраций значительной возбуждающей силы, соизмеримой с весом ротора. При вертикальном расположении ротора агрегата для возбуждения вибраций достаточно очень небольших усилий. В наибольшей мере все это относиться к вертикальным насосам с длинным промежуточным валом.

У этого явления есть обратная сторона. В агрегатах с вертикальным валом механические ослабления проявляются в спектре вибрационных сигналов очень сильно. Поэтому есть достаточно высокая вероятность в переоценке степени возникновения механических ослаблений в агрегатах с вертикальным валом.

 

основных и гармонических частот — Teach Me Audio

Музыкальные звуки состоят из основной частоты, гармоник и обертонов.

• Основная частота
• Гармоники
• обертонов
• Результирующий тембр

Основная частота

Самая низкая частота любого вибрирующего объекта называется основной частотой . Основная частота придает звуку самый сильный слышимый высота тона ссылка — это преобладающая частота в любом сложном сигнале.

Синусоидальная волна является самой простой из всех форм волны и содержит только одну основную частоту и не содержит гармоник, обертонов или частичных составляющих.

Практически все музыкальные звуки имеют волны, бесконечно более сложные, чем синусоида. Именно добавление к волне гармоник и обертонов позволяет различать разные звуки и инструменты; тембр.

Гармоники

Гармоника является одним из восходящих рядов звуковых компонентов, которые звучат выше слышимой основной частоты.

Гармоники более высокой частоты, которые звучат выше основной, составляют гармонический спектр звука. Гармоники бывает трудно отчетливо воспринимать как отдельные компоненты, тем не менее, они есть.

Гармоники имеют меньшую амплитуду  , чем основная частота.

Гармоники – это целые кратные основной частоты. Например, если основная частота равна 50 Гц (также известная как первая гармоника), то второй гармоникой будет 100 Гц (50 * 2 = 100 Гц), третьей гармоникой будет 150 Гц  (50 * 3 = 150 Гц) и так далее.

Рисунок 1 – Гармоники

Обертоны

Обертоны — это частоты волны, которые выше, но не имеет прямого отношения к , основной частоте.

Результирующий тембр

Два тона, воспроизводимые разными инструментами, могут иметь одну и ту же основную частоту и, следовательно, одинаковую высоту тона, например нота до, но звучать очень по-разному из-за наличия разного количества гармоник и обертонов.

Это присутствие гармоник и обертонов в звуковой волне, что помогает производить звук уникальный звук.

Тембр описывает те характеристики звука, которые позволяют уху различать звуки, имеющие одинаковую основную высоту .

Именно по тембру мы можем отличить один инструмент от другого, например, пианино, играемое в ноте C3, звучит иначе, чем гитара, играющая в ноте C3.

Тембр часто описывается субъективно, например, тростниковый или золотой.

Обновлено 6 мая 2020 г.

Частоты гармоник

Краткое описание

Введение

Термин «гармоники» относится к основной частоте сигнала. Прежде чем узнать о гармониках, мы должны быть знакомы с некоторыми концепциями волновых форм. Давайте обсудим темы Собственная частота и вынужденная частота.

[адсенс1]

Собственная частота

Когда тело свободно колеблется без приложения к нему внешних сил, то такие колебания называются «собственными колебаниями».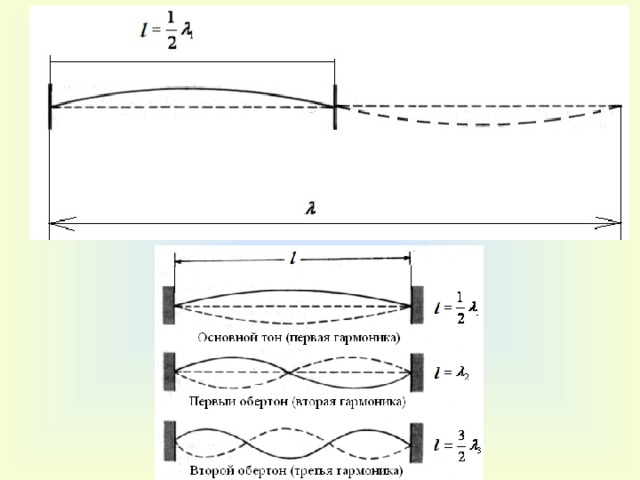 Частота, на которой происходят собственные колебания, называется «естественной частотой».

Вынужденная частота

Когда тело колеблется под действием внешней периодической силы, колебания называются «Вынужденными колебаниями». Частота вынужденных колебаний называется «Вынужденной частотой».

Прогрессивные волны

Когда волна непрерывно движется вперед в среде, не отражаясь ни в одной точке пути, это называется «прогрессивной волной».

Стоячие волны

Когда две прогрессивные волны одинаковой частоты и амплитуды проходят через среду в противоположных направлениях, они накладываются друг на друга. Наложенная волна называется «Стоячая волна». В стоячих волнах мы находим узлы и пучности.

Вернуться к началу

 Основная частота

Определяется как самая низкая частота периодического сигнала. Обычно обозначается буквой «f». Другими словами, самая низкая резонансная частота вибрирующего объекта называется «основной частотой».

Наверх

Что такое гармоника?

Гармоника – это частота, кратная основной частоте. Вынужденные резонансные колебания объекта вызывают появление стоячих волн. На собственной частоте он образует стоячую волну. Эти паттерны создаются на определенных частотах, они называются «Гармонические частоты» или «Гармоники».

Звук, издаваемый формой волны на ее гармонической частоте, очень чистый, а на других частотах возникает шум, и мы не можем слышать чистый звук волн.

[адсенс2]

Гармоники могут возникать в волнах любой формы, но чаще всего они встречаются только в синусоидальных волнах. Несинусоидальные формы волны, такие как треугольные и пилообразные формы волны, создаются путем сложения частот гармоник. Слово «гармоника» обычно используется для описания искажений, вызванных различными нежелательными частотами, называемыми «шумом», синусоидальной волны.

В каждой гармонике мы находим две позиции, это узлы и антиузлы.

Узел

Узлы — это точки, которые кажутся все еще стоящими вдоль среды. У них нет смещения. Поэтому их называют точками, также называемыми узлами.

Пучности

Частицы, которые претерпевают максимальное смещение между двумя точками. Две точки являются узлами. Здесь один узел положительный, а другой отрицательный. Узлы и пучности показаны на рисунке ниже.

Узлы и пучности встречаются в форме волны. Таким образом, волны имеют в себе гармоническую частоту. Основная частота – это наименьшая частота гармоники. Следовательно, между ними возникает только одна пучность. Этот Antinode является средним из двух узлов. Отсюда мы можем сказать, что гитарная струна производит самую большую длину волны и самую низкую частоту.

Самая низкая частота, воспроизводимая любым инструментом, называется основной частотой. Это также известно как «первая гармоника» волны. Говоря словами о основной частоте, мы можем сказать, что гармоники — это целые кратные основной частоты.

Пример: f, 2f, 3f, 4f и т. д. — это гармоники.

Из-за множества целых чисел основной частоты у нас будет n гармоник, таких как 1-я гармоника, 2-я гармоника, 3-я гармоника и т. д.

Первая гармоника

Как мы обсуждали ранее, основная частота также называется первой гармоникой. В первой гармонике у нас есть два узла и один антиузел.

Вторая гармоника

Вторая гармоника состоит из 3 узлов и двух пучностей. Если мы установим узел между двумя узлами первой гармоники, мы можем получить вторую гармонику. В первой гармонике второй узел будет между двумя узлами, первым и последним.

Третья гармоника

Для третьей гармоники, если узел сохраняется на обоих концах жала, результирующая волновая картина состоит из четырех узлов и 3 пучностей. Это означает, что форма волны на третьей гармонике имеет полный синусоидальный период волны и один полупериод. Диаграмма показана ниже.

Наблюдая за приведенным выше обсуждением, мы можем сказать, что числа пучностей равны целым кратным конкретных гармоник. т. е. для 1-й гармоники имеем 1 пучность, для 2-й гармоники 2 пучности и т. д.
Частоты гармоник можно рассчитать по формуле:

Скорость = частота x длина волны мы можем рассчитать гармоническую частоту. В волнах есть два типа гармоник: четные гармоники и нечетные гармоники. Например, цилиндр с обеими открытыми сторонами будет вибрировать как на четных, так и на нечетных гармониках, а цилиндр с одной закрытой стороной будет вибрировать только на нечетных гармониках.

Вернуться к началу

Характеристики гармоник

Большинство колебаний, которые мы слышим, вызваны гармониками. Например, музыка звучит как гитара, скрипка и даже человеческий голос. Гармоники также называются гармоническими парциальными. Характеристики гармоник будут зависеть от колебаний прибора или формы волны.

Таким образом, обычно колебания являются причиной возникновения гармоник. Осциллятор — это не что иное, как движущийся или вибрирующий инструмент. Частичные гармоники будут давать другую частоту, чем полные гармоники. Но точная гармоническая частота будет производиться инструментами большой длины и тонкой проводки.

Они воспроизводят ровно одну гармонику. Частоты, кратные целым числам основной частоты, называются гармоническими частотами.

Человеческое ухо не может отчетливо слышать все гармоники. Частоты, отличные от частот гармоник, называются негармоническими частотами. При этом многие гармоники объединяются в звук. Негармоничные звуки слышны человеческому уху.

Пример: Первый: Наш школьный звонок и церковный звонок мы видим регулярно. Во-вторых, старинные поющие чаши — еще один пример, который вибрирует только на гармонических частотах. Другим важным характерным свойством гармоник является то, что все гармоники являются периодическими на основной частоте, и тогда сумма гармоник также периодична на основной частоте.

Вернуться к началу

Гармоники и обертоны

Частота выше основной частоты называется «обертоном». Обычно обертоны существуют в музыкальных инструментах. Овертона будут зависеть от тембра музыкального инструмента. Поскольку тон будет отличаться от одного музыкального инструмента к другому, появление обертонов также будет отличаться. Смешивая/сочетая обертоны, мы можем получить основной тон инструмента.

Обратите внимание на вышеупомянутые звуковые выходы, воспроизводимые различными инструментами, скрипкой и фортепиано. У них одинаковая частота, поэтому у них одна и та же нота, их обертоны разные, и в конечном счете их звуки тоже разные. Это означает, что обертоны инструмента могут влиять на его звучание. Зубчатая форма волны скрипки означает более резкий звук, в то время как фортепиано производит более чистый звук, близкий к синусоиде.

Вернуться к началу

Отношение длины волны к длине

Чтобы получить отношение длины к длине волны, мы снова увидим все гармоники. То есть первая, вторая, третья гармоники. Все мы знаем, что длина волны синусоиды равна «лямбда». Гармоники также представлены в виде синусоид. Вычислим

Из первой гармоники

Итак, в первой гармонике два конца струны фиксированы, они называются узлами. И когда есть вибрации, проволока движется вверх и вниз, создавая пучность. Так что эта фигура похожа на полусинусоиду. Таким образом, половина длины волны

 

Из второй гармоники

Во второй гармонике две пучности, поэтому есть две петли. Из первой гармоники мы уже вычислили, что одна петля равна половине длины волны. Таким образом, здесь две петли составляют одну длину волны.

От третьей гармоники

В движении третьей гармоники есть три петли, и каждая петля состоит из одной половины длины волны. Таким образом, сумма всех трех петель составляет 3/2 лямбда

Из всех этих гармоник мы можем сказать, что для 1-й гармоники имеем одну пучность, для второй гармоники 2 пучности, для третьей гармоники 3 пучности. Таким образом, для n-й гармоники имеется n пучностей.

Таким образом, выведя формулу для отношения длины к длине волны, мы получим

L=n/2 длины волны

Кроме того, мы можем записать эти формулы, как показано ниже

Для 1-й гармоники: L=1/2-лямбда

Для 2-й гармоники: 2L=2/2-лямбда

Для 3-й гармоники: 3L=3/2-лямбда

Аналогично для n-й гармоники: nL=n/2-лямбда Где ‘n’ — целое число.

Соотношение длины и длины волны в гармониках, а также математическое соотношение, также представленное ниже в табличном формате

L=n/2 (лямбда)

Вернуться к началу

Недостатки гармоник

• Гармоники влияют на работу энергосистем. Недостатки гармоник перечислены ниже.
• Гармоники ухудшают качество электроснабжения в распределительной сети. Это может вызвать несколько негативных последствий.
• Гармоники могут привести к увеличению эффективного среднеквадратичного тока, что приведет к потере мощности в системе распределения.
• Совокупное увеличение третьей гармоники вызовет перегрузку в нейтральных проводниках.
• Гармоники вызывают увеличение уровня шума электрического сигнала.
• Гармоники могут возмущать напряжение питания, вызывая неправильную работу чувствительных нагрузок.
• Гармоника вызывает помехи в линиях связи и телефонных линиях.
• Они влияют на резонанс между индуктивностью источника питания и уровнем емкости конденсаторов коэффициента мощности.

Вкратце, гармоники вызывают следующие ошибки в энергосистеме и телекоммуникационных системах.

• Оборудование для обогрева
• Неисправность оборудования
• Отказ оборудования
• Помехи связи
• Неисправность предохранителя и прерывателя
• Проблемы с процессом
• Нагрев проводника.

Вернуться к началу

Гармоники Пример

Мы уже знаем, что в нашей повседневной жизни мы сталкиваемся со многими частотами гармоник, здесь мы видим несколько примеров для гармоник

 Пример 

Многие осцилляторы, такие как щипковая гитарная струна, будут колебаться на многих частотах, но они не являются гармониками, их обычно называют частичными гармониками. Поэтому, когда мы возьмем длинный и тонкий осциллятор, частоты будут находиться в гармоническом диапазоне. Чтобы узнать точное положение возникновения гармоник, в первую очередь мы должны вычислить основную частоту формы волны.