«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
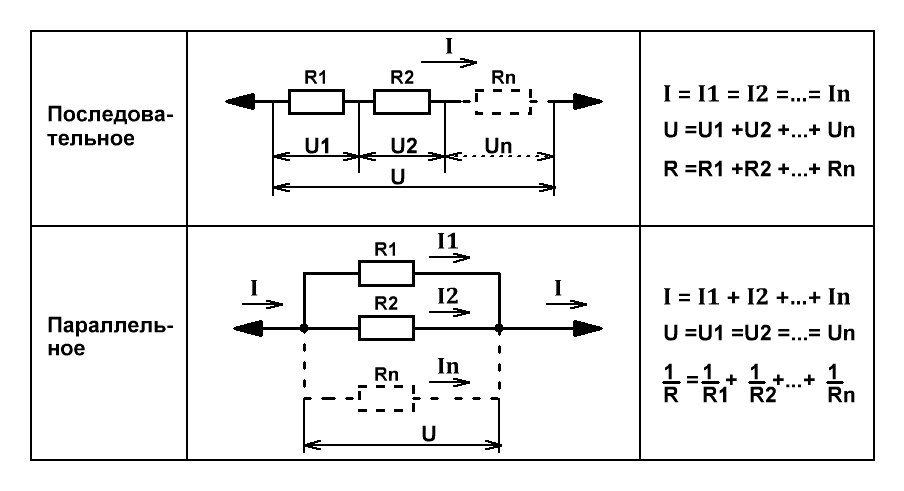
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность,
а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную
зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2 +….+ Сn и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln и
1/С = 1/С1+ 1/С2+…+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор — пассивный элемент, присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
- Постоянные.
- Переменные.
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
- Последовательное.
- Параллельное.
- Смешанное.
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно. Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно. То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов. Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Онлайн-калькулятор маркировки SMD резисторов
Представляем простой и удобный калькулятор сопротивлений SMD резисторов. Чтобы узнать номинал своего резистора, введите его код в черное поле:
Наш калькулятор позволяет определять сопротивление SMD резисторов, маркированных по стандарту EIA-96, по которому на корпус наносится 3 или 4 цифры, либо 2 цифры и 1 буква.
Обозначения маркировок SMD резисторов
При использовании маркировки с тремя или четырьмя цифрами, первые 2 или 3 из которых обозначают количественное значение сопротивления резистора, а последняя — показатель множителя. Множитель равен степени, в которую необходимо возвести количество, чтобы получить итоговый номинал.
Приведем нескольлко примеров определения номинала SMD резистора, исходя из его маркировки:
- 473 = 47kΩ ± 5%
- 103 = 10kΩ ± 5%
- 312 = 3.1kΩ ± 5%
- 106 = 10MΩ ± 5%
При маркировке сопротивлений менее 10Ω используется Буква R. Она указывает на положене десятичной точки деления:
- 0R5 = 0.5Ω
- 0R3 = 0.3Ω
- 0R7 = 0.7kΩ
У высокоточных резисторов, показатель погрешности которых составляет 1%, буква ставится в конце номинала и является множителем. Две цифры в начале обозначают код, по которому определяется сопротивление:
- 92Z = 0.89Ω ± 1%
- 32D = 210kΩ ± 1%
- 24E = 1.74MΩ ± 1%
Где купить недорогие резисторы?
Заходите в наш интернет-магазин, там большой выбор недорогих резисторов с быстрой доставкой по России и СНГ.
Вольтик.ру — это более 800 товаров для мейкеров, радиолюбителей и инженеров.В магазине представлены:
И многое-многое другое!
Рекомендуем ознакомиться с другими тематическими материалами
При последовательном соединении резисторов конец одного из них соединяется с началом следующего. В такой схеме через все резистивные элементы протекает одинаковый ток I, но падение напряжения на каждом из них пропорционально величине сопротивления. Для расчета электрических величин в схемах используется сложение сопротивлений всех элементов в последовательной цепи для получения суммарной величины, как показано на рисунке:
Последовательное соединение резисторовДанный онлайн калькулятор позволяет выполнять расчет суммарного сопротивления для последовательно соединенных элементов цепи.
Чтобы воспользоваться калькулятором расчета вам необходимо:
- В окошке «количество резисторов» укажите число последовательно соединенных элементов, в данном случае, в схеме представлено три резистора, но может быть и другое количество;
- После этого в поле ниже появится несколько окошек, в которые вам необходимо внести значение сопротивления каждого резистора, к примеру, 10, 20 и 45 Ом;
- Нажмите кнопку «рассчитать» и в окошке «сопротивление» вы получите значение сопротивления в 75 Ом.
Для перехода к расчету следующей цепи или при необходимости подобрать другие элементы, нажмите кнопку «сбросить», чтобы обнулить значение последовательно включенных элементов калькулятора.
В работе калькулятора для определения сопротивления цепи последовательно соединенных резисторов используется принцип арифметического сложения. Поэтому формулу для определения суммарного значения можно представить следующим образом:
Rсум = R1 + R2 + R3 +…+ Rn
Где,
- Rсум — суммарное сопротивление последовательно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.
Так как в рассматриваемом примере включено только три элемента, то формула примет такой вид:
Rсум = R1 + R2 + R3
Подставив значение омического сопротивления каждого из элементов, получим:
Rсум = 10 + 20 + 45 = 75 Ом
Использование калькулятора для вычисления суммарного сопротивления в цепи последовательно соединенных резисторов наиболее актуально для схем с большим количеством элементов и дробными величинами.
Следует отметить, если вам известно омическое сопротивление каждого элемента в разных единицах измерения (Ом, кОм, МОм), то их следует привести к одной, к примеру, к Омам, так как калькулятор выполняет расчет для всех резисторов в одинаковой единице.
Соединение резисторов ⋆ diodov.net
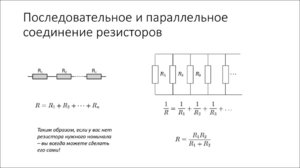
Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
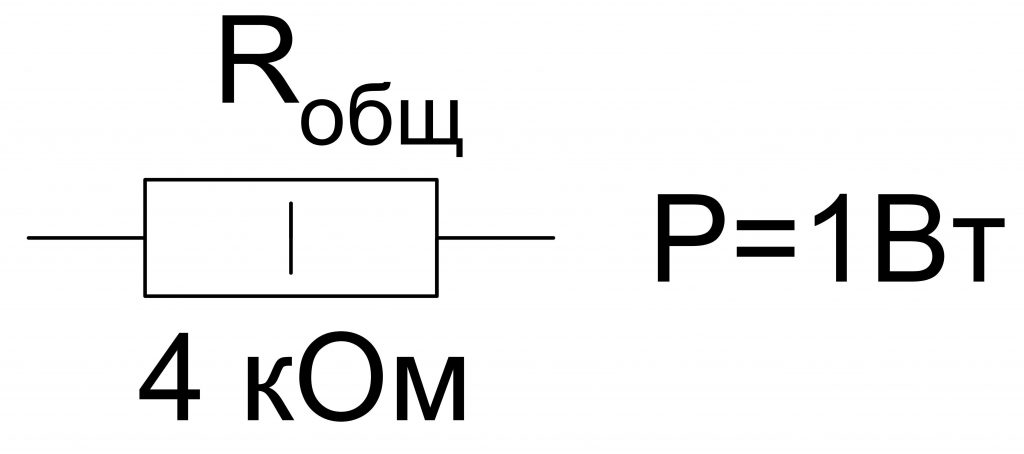
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.
Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.
В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
Параллельное соединение резисторов
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.
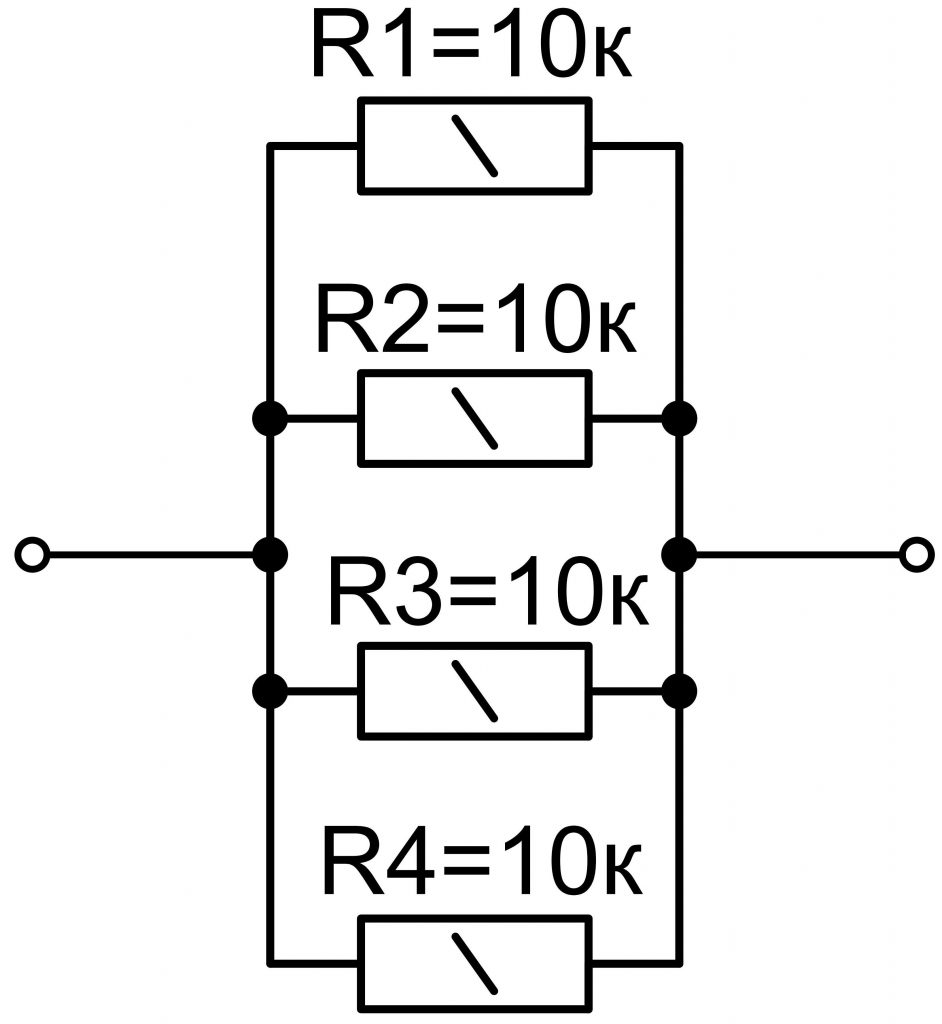
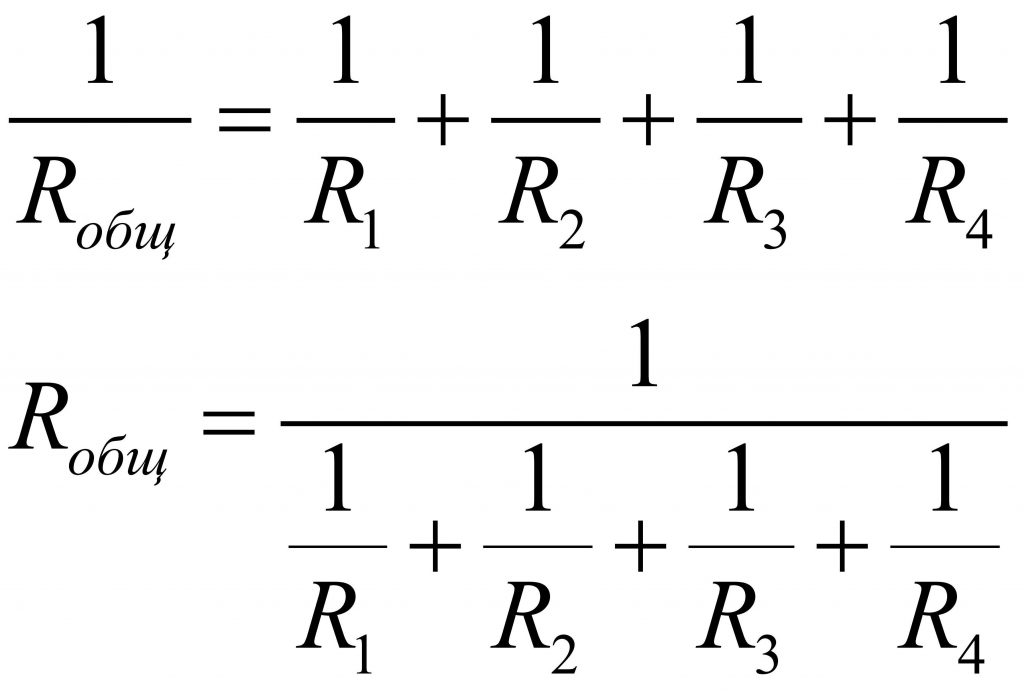
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R, то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм, тогда
Rобщ = 10 кОм/4 = 2,5 кОм.
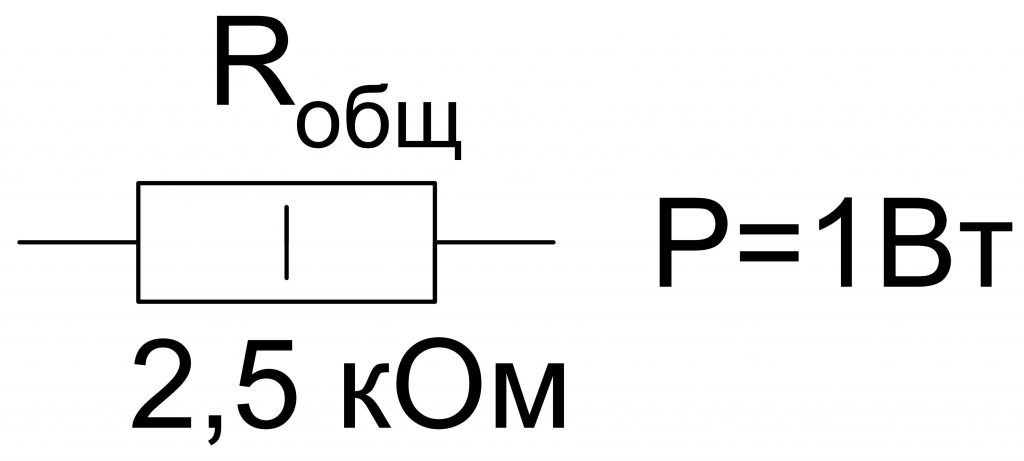
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторов
Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.
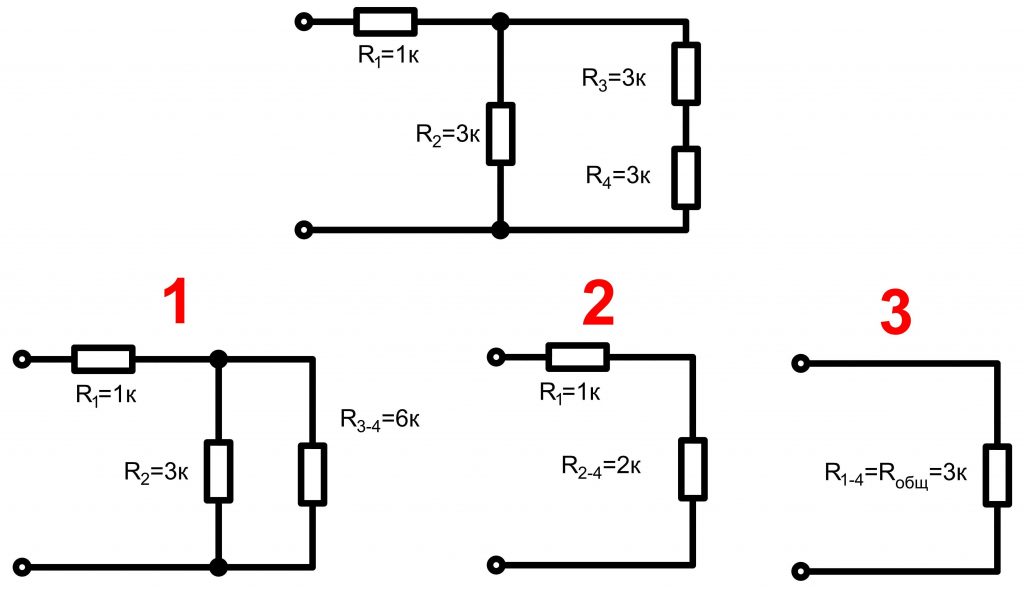
Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.
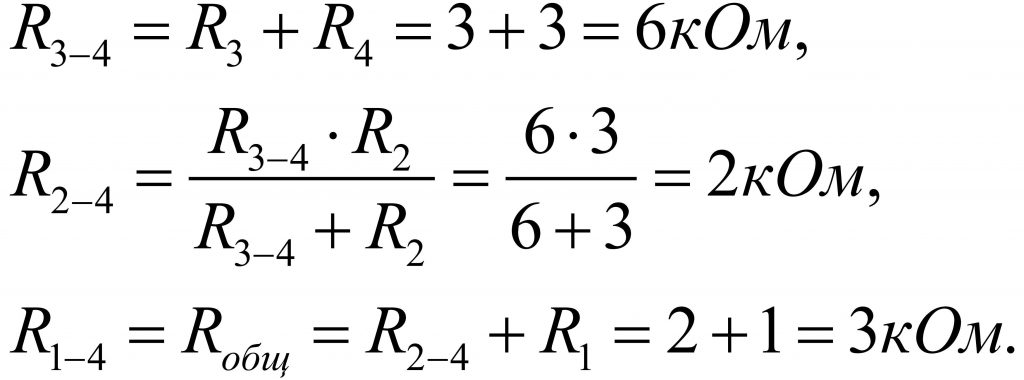
Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.
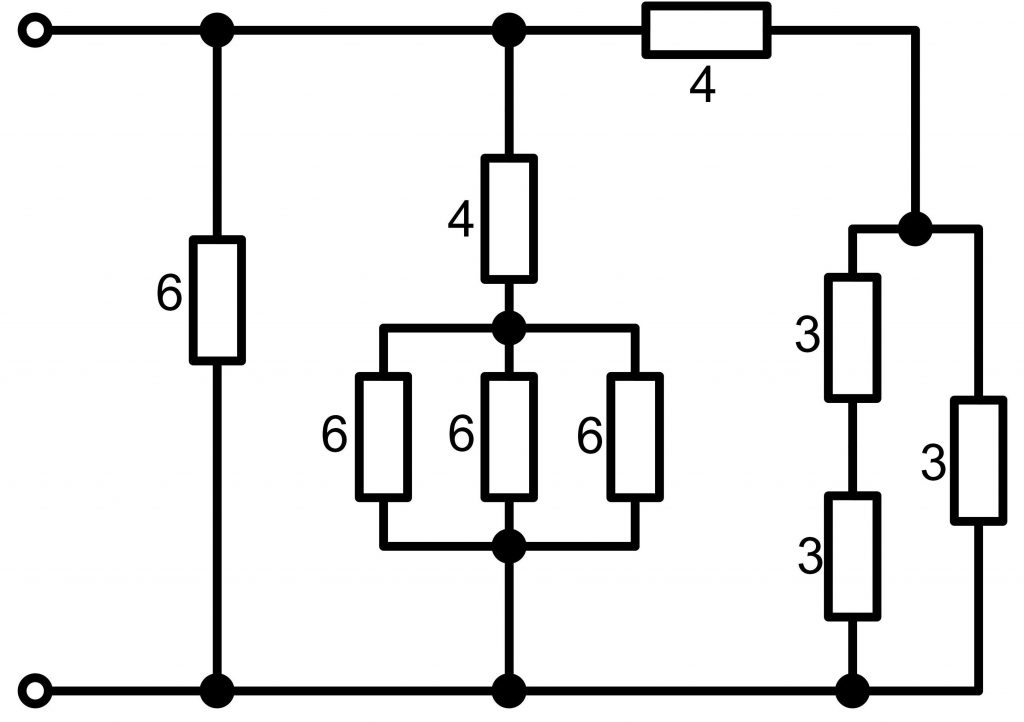
Правильный ответ: 2 ома.
Еще статьи по данной теме
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Видео: Последовательное и параллельное соединение проводников
Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
причем :
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
причем:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
R(общ)=R1\n.
причем :
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Этот калькулятор может решить другие математические задачи. Этот калькулятор можно использовать для рабочих задач. Например, «А» может покрасить комнату за 5 часов, а ‘B’ — покрасить комнату за 6 часов. Если они оба работают вместе, сколько времени займет работа? Введите 5 и 6 как если бы они были резисторами и получили ваш ответ. Этот калькулятор можно использовать для задач «заполнения». Например, одна труба может заполнить воду резервуар за 5 часов, в то время как другая труба может заполнить тот же резервуар за 6 часов. Если обе трубы работают одновременно …….. хммм кажется до боли знакомым с другой проблемой, не так ли? Удачи в твоих математических задачах. Числа отображаются в научной записи с количеством Значимые цифры вы указываете. Для удобства чтения числа между .001 и 1000 будет , а не в научной нотации, но все равно будет иметь такую же точность. Вы можете изменить количество значащих цифр, отображаемых изменить номер в поле выше. Большинство браузеров, будут отображать ответы правильно, но если вы не видите ответов, введите ноль в поле выше, которое будет Устраните все форматирование, но, по крайней мере, вы увидите ответы. Вернуться на главную страницу Copyright © 1999 — 1728 Программные Системы | ||
Калькулятор
Ниже приведены инструменты для расчета значения и допуска в омах на основе цветовых кодов резисторов, общего сопротивления группы резисторов, включенных параллельно или последовательно, а также сопротивления проводника на основе размера и проводимости.
Резистор калькулятор кодов цвета
Используйте этот калькулятор, чтобы узнать значение ома и допуск на основе цветовых кодов резистора.
 |
Параллельный резисторный калькулятор
Укажите все значения сопротивления параллельно, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы определить общее сопротивление.
Резисторы в последовательном калькуляторе
Укажите все значения сопротивления последовательно, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы определить общее сопротивление.
Сопротивление проводника
Используйте следующее для расчета сопротивления проводника. Этот калькулятор предполагает, что проводник круглый.
Законодательный калькуляторРезистор
Цветовой код
Электронный цветовой код — это код, который используется для указания номинальных характеристик определенных электрических компонентов, таких как сопротивление в омах резистора.Электронные цветовые коды также используются для оценки конденсаторов, катушек индуктивности, диодов и других электронных компонентов, но чаще всего используются для резисторов. Только резисторы адресованы этим калькулятором.
Как работает цветовое кодирование:
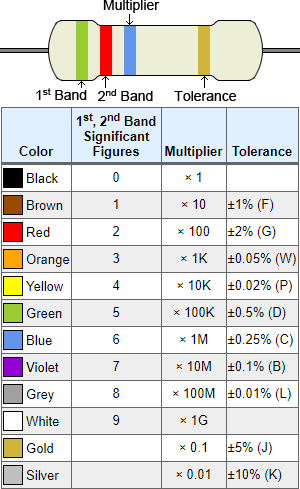
Цветовое кодирование для резисторов является международным стандартом, который определен в МЭК 60062. Цветовой код резистора, показанный в таблице ниже, включает различные цвета, которые представляют значащие цифры, множитель, допуск, надежность и температурный коэффициент.К какому из этих цветов относится цвет, зависит от положения цветовой полосы на резисторе. В типичном четырехполосном резисторе имеется промежуток между третьей и четвертой полосой, чтобы указать, как должен считываться резистор (слева направо, с одиночной полосой после интервала, являющейся самой правой полосой). В приведенном ниже объяснении будет использоваться четырехполосный резистор (тот, который конкретно показан ниже). Другие возможные варианты резисторов будут описаны позже.
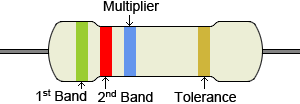
Значимая составляющая фигуры:
В типичном четырехполосном резисторе первая и вторая полосы представляют значимые цифры.Для этого примера обратитесь к рисунку выше с зеленой, красной, синей и золотой полосой. Используя приведенную ниже таблицу, зеленая полоса представляет число 5, а красная полоса — 2.
Множитель:
Третья синяя полоса — множитель. Таким образом, используя таблицу, множитель составляет 1 000 000. Этот множитель умножается на значащие цифры, определенные из предыдущих полос, в данном случае 52, что приводит к значению 52 000 000 Ом или 52 МОм.
Допуск:
Четвертая полоса присутствует не всегда, но когда она есть, представляет собой допуск.Это процент, на который значение резистора может меняться. Золотая полоса в этом примере показывает допуск ± 5%, который можно обозначить буквой J. Это означает, что значение 52 МОм может изменяться на 5% в любом направлении, поэтому значение резистора составляет 49,4 МОм. 54,6 МОм.
Надежность, температурный коэффициент и другие вариации:
Кодированные компоненты имеют как минимум три полосы: две значимые полосы цифр и множитель, но возможны и другие варианты.Например, компоненты, изготовленные по военным спецификациям, обычно представляют собой четырехполосные резисторы, которые могут иметь пятую полосу, которая указывает на надежность резистора с точки зрения процента отказов на 1000 часов работы. Также возможно иметь диапазон 5 th , который является температурным коэффициентом, который указывает на изменение сопротивления компонента в зависимости от температуры окружающей среды в пересчете на ppm / K.
Чаще всего существуют пятиполосные резисторы, более точные из-за третьего значащего диапазона цифр.Это смещает положение множителя и диапазона допусков в положение 4 th и 5 th по сравнению с типичным четырехполосным резистором.
На самых точных резисторах может присутствовать полоса 6 тыс. . Первые три полосы будут значимыми полосами цифр, 4 -й — множителем, 5 -й — допуском, а 6 -й — либо надежностью, либо температурным коэффициентом. Есть и другие возможные варианты, но это некоторые из наиболее распространенных конфигураций.
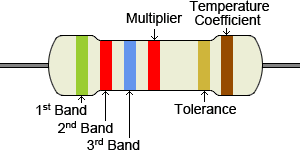
| Цвет | 1 st , 2 и , 3 и Значимые цифры диапазона | Множитель | Допуск | Температурный коэффициент |
| Черный | 0 | × 1 | 250 ppm / K (U) | |
| Коричневый | 1 | × 10 | ± 1% (F) | 100 ppm / K (S) |
| Красный | 2 | × 100 | ± 2% (G) | 50 ppm / K (R) |
| Оранжевый | 3 | × 1K | ± 0.05% (Ш) | 15 ppm / K (P) |
| Желтый | 4 | × 10К | ± 0,02% (P) | 25 ppm / K (Q) |
| Зеленый | 5 | × 100К | ± 0,5% (D) | 20 ppm / K (Z) |
| Синий | 6 | × 1M | ± 0.25% (С) | 10 ppm / K (Z) |
| Фиолетовый | 7 | × 10М | ± 0,1% (В) | 5 промилле / К (М) |
| Серый | 8 | × 100М | ± 0,01% (л) | 1 ppm / K (K) |
| Белый | 9 | × 1G | ||
| Золото | × 0.1 | ± 5% (Дж) | ||
| Серебро | × 0,01 | ± 10% (К) | ||
| Нет | ± 20% (М) |
Резисторы — это элементы схемы, которые придают электрическое сопротивление.Хотя схемы могут быть очень сложными, и существует множество различных способов, которыми резисторы могут быть расположены в цепи, резисторы в сложных цепях обычно могут быть разбиты и классифицированы как соединенные последовательно или параллельно.
Резистор параллельно:
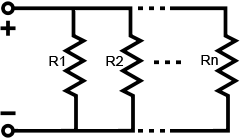
Общее сопротивление параллельных резисторов равно обратной величине суммы обратных величин каждого отдельного резистора. Обратитесь к уравнению ниже для уточнения:
| R всего = |
| |||||||||||||||||||||||||
Резистор в серии:
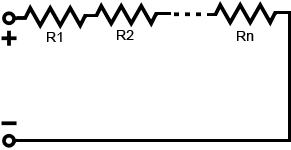
Общее сопротивление параллельных резисторов — это просто сумма сопротивлений каждого резистора. Обратитесь к уравнению ниже для уточнения:
R всего = R 1 + R 2 + R 3 … + R n
Сопротивление проводника:
Где:
L — длина проводника
А — площадь поперечного сечения проводника
С — проводимость материала