Расчет мощности электических ТЭНов
Оптимальным источником энергии, для нагрева испарительной емкости, является квартирная электрическая сеть, напряжением 220 В. Можно просто использовать для этих целей бытовую электроплиту. Но, при нагреве на электроплите, много энергии расходуется на бесполезный нагрев самой плиты, а также излучается во внешнюю среду, от нагревательного элемента, не совершая при этом, полезной работы. Эта, понапрасну затрачиваемая энергия, может достигать приличных значений — до 30-50 %, от общей затраченной мощности на нагрев куба. Поэтому использование обычных электроплит, является нерациональным с точки зрения экономии. Ведь за каждый лишний киловатт энергии, приходится платить. Наиболее эффективно использовать врезанные в испарительную емкость эл. ТЭНы. При таком исполнении, вся энергия расходуется только на нагрев куба + излучение от его стенок вовне. Стенки куба, для уменьшения тепловых потерь, необходимо теплоизолировать. Ведь затраты на излучение тепла, от стенок самого куба могут так же, составлять до 20 и более процентов, от всей затрачиваемой мощности, в зависимости от его размеров.
Поэтому мощность 1-го ТЭНа, может не соответствовать по параметрам, для нагрева куба и быть больше или меньше. В таких случаях, для получения необходимой мощности нагрева, можно использовать несколько ТЭНов, соединенных последовательно или последовательно-параллельно. Коммутируя различные комбинации соединения ТЭНов, переключателем от бытовой эл. плиты, можно получать различную мощность. Например имея восемь врезанных ТЭНов, по 1.25 кВт каждый, в зависимости от комбинации включения, можно получить следующую мощность.
- 625 Вт
- 933 Вт
- 1,25 кВт
- 1,6 кВт
- 1,8 кВт
- 2,5 кВт
Такого диапазона вполне хватит для регулировки и поддержания нужной температуры при перегонке и ректификации. Но можно получить и иную мощность, добавив количество режимов переключения и используя различные комбинации включения.
Но можно получить и иную мощность, добавив количество режимов переключения и используя различные комбинации включения.
Последовательное соединение 2-х ТЭНов по 1.25 кВт и подключение их к сети 220В, в сумме дает 625 Вт. Параллельное соединение, в сумме дает 2.5 кВт.
Рассчитать можно по следующей формуле.
Мы знаем напряжение, действующее в сети, это 220В. Далее мы так же знаем мощность ТЭН, выбитую на его поверхности допустим это 1,25 кВт, значит, нам нужно узнать силу тока, протекающую в этой цепи. Силу тока, зная напряжение и мощность, узнаем из следующей формулы.
Сила тока = мощность, деленная на напряжение в сети.
Записывается она так:
Где I — сила тока в амперах.
P — мощность в ваттах.
U — напряжение в вольтах.
При подсчете нужно мощность, указанную на корпусе ТЭН в кВт, перевести в ватты.
1,25 кВт = 1250Вт. Подставляем известные значения в эту формулу и получаем силу тока.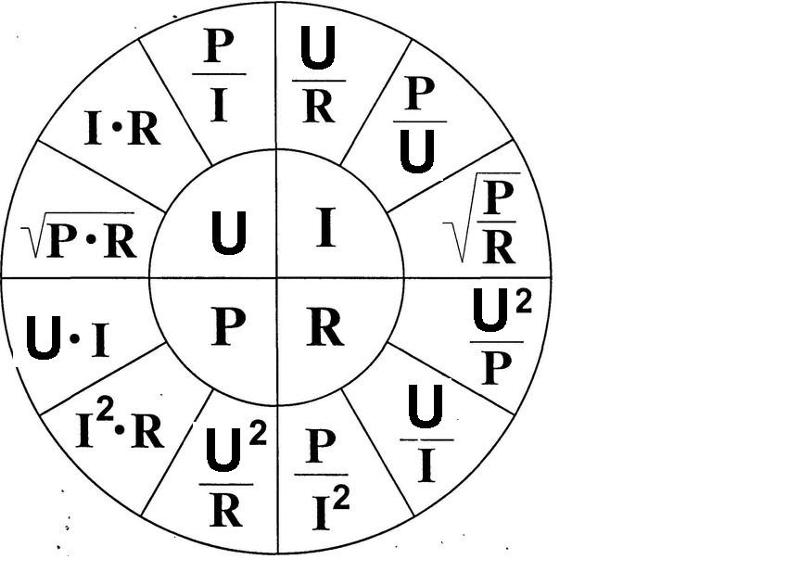
I = 1250Вт / 220 = 5,681 А
Далее зная силу тока подсчитываем сопротивление ТЭНа, по следующей формуле.
R = U / I, где
R — сопротивление в Омах
U — напряжение в вольтах
I — сила тока в амперах
Подставляем известные значения в формулу и узнаем сопротивление 1 ТЭНа.
R = 220 / 5.681 = 38,725 Ом.
Далее подсчитываем общее сопротивление всех последовательно соединенных ТЭНов. Общее сопротивление равно сумме всех сопротивлений, соединенных последовательно ТЭНов
Rобщ = R1+ R2 + R3 и т.д.
Таким образом, два последовательно соединенных ТЭНа, имеют сопротивление равное 77,45 Ом. Теперь нетрудно подсчитать мощность выделяемую этими двумя ТЭНами.
P = U2 / R где,
P — мощность в ваттах
U2— напряжение в квадрате, в вольтах
R — общее сопротивление всех посл. соед. ТЭНов
соед. ТЭНов
P = 624,919 Вт, округляем до значения 625 Вт.
Далее при необходимости можно подсчитать мощность любого количества последовательно соединенных ТЭНов, или ориентироваться на таблицу.
Таблица 1.1. Значения для последовательного соединения ТЭНов при напряжении 220В.
| Кол-во ТЭН | Мощность (Вт) | Сопротивление (Ом) | Сила тока (А) |
| 1 | 1250 | 38,8 | 5,7 |
| 2 | 625 | 77,5 | 2,8 |
| 3 | 416 | 116,2 | 1,9 |
| 4 | 312 | 154,9 | 1,4 |
| 5 | 250 | 193,6 | 1,1 |
| 6 | 208 | 232,4 | 0,9 |
| 7 | 178 | 271 | 0,8 |
| 8 | 156 | 309,8 | 0,7 |
Таблица 1. 2. Значения для параллельного соединения ТЭНов при напряжении 220В.
2. Значения для параллельного соединения ТЭНов при напряжении 220В.
| Кол-во ТЭН | Мощность (Вт) | Сопротивление (Ом) | Сила тока (А) |
| 2 | 2500 | 19,4 | 11,4 |
| 3 | 3750 | 12,9 | 17 |
| 4 | 5000 | 9,7 | 22,7 |
| 6250 | 7,7 | 28,4 | |
| 6 | 7500 | 6,5 | 34 |
| 7 | 8750 | 5,5 | 39,8 |
| 8 | 10000 | 4,8 | 45,5 |
Еще один немаловажный плюс, который дает последовательное соединение ТЭНов, это уменьшенный в несколько раз протекающий через них ток, и соответственно малый нагрев корпуса нагревательного элемента, тем самым не допускается пригорание браги во время перегонки и не привносит неприятного дополнительного вкуса и запаха в конечный продукт. Так же ресурс работы ТЭНов, при таком включении, будет практически вечным.
Так же ресурс работы ТЭНов, при таком включении, будет практически вечным.
Расчеты выполнены для ТЭНов, мощностью 1.25 кВт. Для ТЭНов другой мощности, общую мощность нужно пересчитать согласно закона Ома, пользуясь выше приведенными формулами.
Калькулятор зависимости силы тока от напряжения и сопротивления. Ом
Все источники питания рассчитаны на предельную нагрузку (на определенную мощность).
По сути любой источник энергии имеет определенное напряжение на выходе, а так же определенную допустимую силу тока. При превышении максимальной силы тока (мощности) источник питания может сгореть.
Давайте представим, что у нас есть источник питания с напряжением 12 Вольт и с допустимой силой тока в 1 Ампер.
Если подключим к такому источнику нагрузку в виде сопротивления 24 Ома, через чем будет протекать ток равный ½ максимально допустимого тока — тоесть 0,5 Ампера.
Если параллельно мы подключим еще одно сопротивление 24 Ома сила тока достигнет максимально допустимой в 1 Ампер.
Схема зависимости силы тока от сопротивления нагрузки
Подключив еще одно сопротивление параллельно к источнику питания через цепь будет протекать ток в 1,5 раза больше допустимого. При такой нагрузке в источнике питания скорее всего сгорит предохранитель, возможно такой источник питания даже сгорит сам в условиях перегрузки.
По сути тоже самое происходит когда вы подключаете низкоомную нагрузку к усилителю. Если вы подключите к усилителю нагрузку (скажем динамик) с сопротивлением меньше, чем заявленная в характеристиках усилителя, он может сгореть. Тоже самое произойдет, если вы подключите несколько динамиков параллельно, тем самым увеличив силу тока а значит и мощность.
Сопротивление нагрузки может служить инструментом регулировки выходной мощности усилителя. Чем меньше сопротивление нагрузки тем больший будет протекать через него, а значит и мощность будет больше. Не забываейте, что нельзя допускать понижения сопротивления ниже заявленных параметров усилителя .
Пример расчета зависимости силы тока от сопротивления проводника или потребителя (нагрузки)
Так как основные примеры электроники мы рассматриваем на примерах автозвука…. Давайте предположим, что у нас есть усилитель мощностью 100 Ватт (мощность мы разберем более подробно чуть позже) и он рассчитан на минимальное сопротивление 4 Ома.
Это означает, что усилитель может генерировать мощность до 100 Ватт на нагрузку в 4 Ома, и если сопротивление нагрузки будет меньше, вполне вероятно он сгорит.
Для того что бы достичь мощности в 100 Ватт на 5 Ома через цепь нагрузки должен протекать ток в 5 Ампер.
Для того что бы такой ток протекал через нагрузку 4 Ома, необходимо создать разность потенциалов (напряжение) на контактах динамика в 20 Вольт. (то есть при максимальной мощности, напряжение на контактах динамика будет равно 20 Вольт).
Пусть множество этих цифр не сбивает вас с толку, мы ниже более подробно рассмотрим все определения.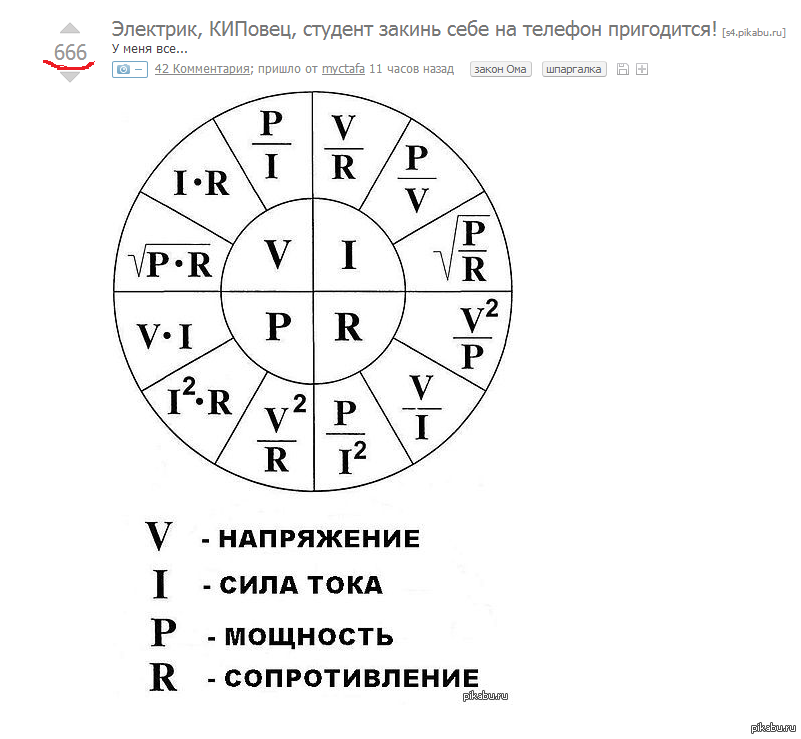
Ниже приведен калькулятор который рассчитывает силу тока в зависимости от напряжения и сопротивления.
Калькулятор зависимости силы тока от напряжения и сопротивления.
Если вы введете наши исходные данные 20 Вольт и 4 Ома в исходные параметры, вы увидите в результатах калькулятора что через нагрузку будет протекать ток в 5 Ампер. Если вы уменьшите сопротивление до 2 Ом, сила тока увеличится вдвое. Но как мы помним максимальная допустимая сила тока для нашего усилителя 5 Ампер и более низкое сопротивление нагрузки приведет к повышению силы тока, а это может повредить ваш усилитель.
Используйте этот калькулятор для расчета силы тока протекающего через нагрузку.
— Калькулятор наглядно продемонстрирует вам как напряжение приложенное к нагрузке, а так же сопротивление нагрузки, влияет на ток протекающий в цепи
— вы можете отдельно менять Вольтаж и сопротивление
— обратите внимание, что увеличение силы тока обычно связано с увеличением приложенного напряжения и УМЕНЬШЕНИЕМ сопротивления.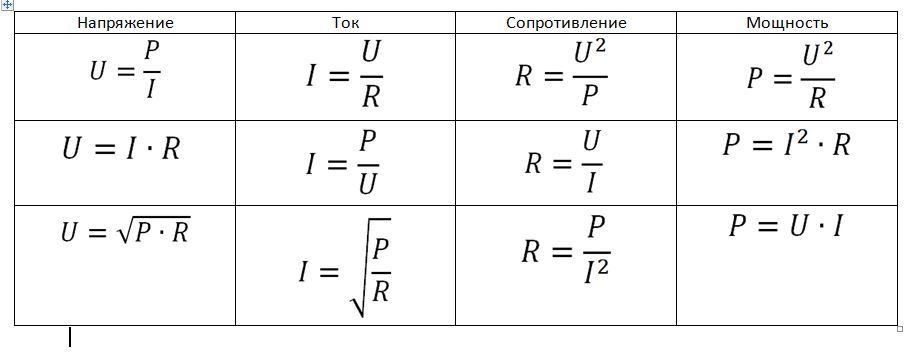
Понижение силы тока связано обычно с понижением напряжения и УВЕЛИЧЕНИЕМ сопротивления.
п.с. Когда вы покупаете динамики для вашей аудиосистемы вы должны знать минимальное сопротивление на которое рассчитан ваш усилитель, что бы получить от него максимальную мощность. Зная параметры усилителя вы можете точно выбрать правильный динамик (как с одной катушкой так и с двумя — помните о параллельном и последовательном соединении).
!!! Помните что Ом это единица выражающая сопротивление нагрузки протеканию электрического тока.
Формула мощности электрического тока. Как узнать, найти, вычислить, рассчитать мощность.
Электрическая мощность является одной из наиболее важных и значимых характеристик, которая показывает величину, силу той электротехники, систем, цепей, что работают, выполняя ту или иную функцию. Естественно, как и любая другая физическая величина электрическая мощность должна иметь свою меру, благодаря которой появляется возможность ее рассчитывать, делая заведомо точные, экономичные, эффективные устройства, системы и т. д. Для расчетов существуют определенные формулы, по которым и находятся нужные значения мощности.
д. Для расчетов существуют определенные формулы, по которым и находятся нужные значения мощности.
Формула мощности тока (электрического) достаточно проста и выражается как произведение напряжения на силу тока. То есть, чтобы найти электрическую мощность достаточно просто напряжение умножить на ток. Если воспользоваться законом ома, то ее можно найти и через сопротивление. В этом случае электрическая мощность будет равна силе тока в квадрате умноженный на сопротивление или же напряжение в квадрате деленное на сопротивление.
Напомню, что при использовании формул подразумевается применение основных единиц измерения физических величин. В нашем случае основными единицами будут:
Электрическая мощность — Ватт;
Сила тока — Ампер;
Напряжение — Вольт;
Сопротивление — Ом.
Исходя из этого формула мощности электрического тока будет звучать так — 1 Ватт равен 1 Вольт умноженный на 1 Ампер. Думаю вы смысл поняли. Меньшими единицами измерения мощности является милливатты (1000 мВт = 1 Вт), большими единицами являются киловатты и мегаватты (1 кВт = 1000 Вт, 1 МВт = 1000 000 Вт). Милливатты это достаточно маленькая мощность, ее используют в электронике, радиотехнике. К примеру мощность слухового аппарата измеряется именно в милливаттах. Мощность в ваттах можно встретить в звуковых усилителях, у небольших блоках питания, мини электродвигателях. Киловатты это мощность, которая часто встречается в бытовых и технических устройствах (электрочайники, электродвигатели, обогреватели и т.д.). Мегаватты это уже достаточно большая мощность, ее можно встретить на электроподстанциях, электростанциях, у потребителях электроэнергии размером с город и т.д.
Милливатты это достаточно маленькая мощность, ее используют в электронике, радиотехнике. К примеру мощность слухового аппарата измеряется именно в милливаттах. Мощность в ваттах можно встретить в звуковых усилителях, у небольших блоках питания, мини электродвигателях. Киловатты это мощность, которая часто встречается в бытовых и технических устройствах (электрочайники, электродвигатели, обогреватели и т.д.). Мегаватты это уже достаточно большая мощность, ее можно встретить на электроподстанциях, электростанциях, у потребителях электроэнергии размером с город и т.д.
Если говорить о формуле более научной, которая электрическую мощность тока выражает через работу и время, то она будет звучать так — электрическая мощность равна отношению работы тока на участке цепи ко времени, в течении которого совершается эта работа.
То есть, работа деленная на время будет определять мощность. Кроме этого часто путают такие величины как ватты и ватт-час. В ваттах измеряется электрическая мощность — скорость изменения энергии (передачи, преобразования, потребления). А ватт-час являются единицей измерения самой энергии (работы). В ватт-часах выражается энергия, произведенная (переданная, преобразованная, потребленной) за определенное время.
Мощность также разделяется на активную и реактивную. Активная мощность — часть полной мощности, что удалось передать в нагрузку за период переменного тока. Она равна произведению действующих значений напряжения и тока на cosφ (косинус угла сдвига фаз между ними). Электрическая мощность, что не была передана в нагрузку, а привела к некоторым потерям (на излучение, нагрев) называется реактивной мощностью. Она равна произведению действующих значений напряжения и тока на sinφ (синус угла сдвига фаз между ними).
P.S. Электрическая мощность является одной из главных величин и характеристик, используемые в электротехнике. Именно ее мы узнаем при покупки того или иного электрического устройства. Ведь она определяет силу, с которой электротехника может работать. К примеру электродрель. Если мы купим дрель недостаточной мощности, то она просто не сможет обеспечить нам нормальную работу при сверлении. Хотя гнаться за слишком большой мощностью также не следует, ведь это ведет к излишней трате электроэнергии, за которую вы будете платить. Так что у всего должна быть своя мера и мощность.
Хотя гнаться за слишком большой мощностью также не следует, ведь это ведет к излишней трате электроэнергии, за которую вы будете платить. Так что у всего должна быть своя мера и мощность.
Расчет мощности при параллельном соединении
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
- P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
- P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
- P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при паралл ельном соединение
При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.

- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P1 = U 2 /R1 = 100 2 /200 = 50 Вт; P2 = U 2 /R2 = 100 2 /100 = 100 Вт; P3 = U 2 /R3 = 100 2 /51 = 195,9 Вт; P4 = U 2 /R4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).

- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.

- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).

- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединениеПри таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Следствием первых двух правил будет являться третье правило.
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа токаПоследовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность токаПри рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторовПри последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводниковВ электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.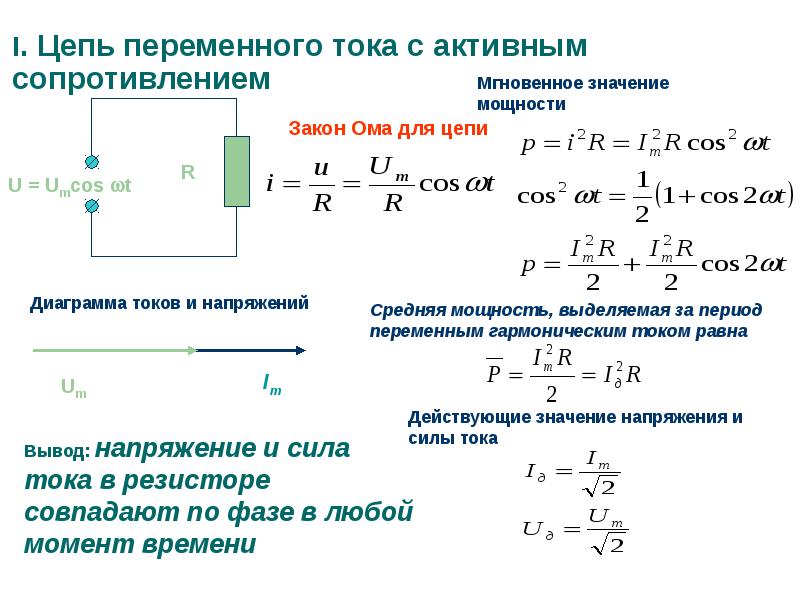
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Расчет мощности последовательного соединения
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка.
Выполняется для металлов и электролитов.
Закон Джоуля – Ленца.
Дж. Джоуль (1841—1843) Э. X. Ленц (1842—1843) независимо друг от друга экспериментально установили
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:
Работа и мощность электрического тока.
Работа электрического тока:
Мощность электрического тока (работа в единицу времени):
В электричестве иногда применяется внесистемная единица работы – кВт .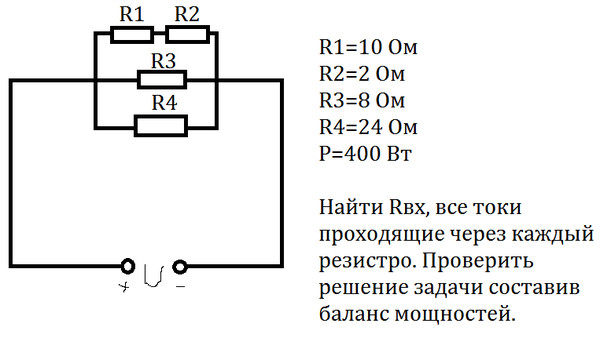 ч (киловатт-час).
ч (киловатт-час).
1 кВт . ч = 3,6 . 10 6 Дж.
Виды соединения проводников.
Последовательное соединение.
1. Сила тока во всех последовательно соединенных участках цепи одинакова:
I1=I2=I3=. =In=.
2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:
U=U1+U2+. +Un+.
3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:
R=R1+R2+. +Rn+.
Если все сопротивления в цепи одинаковы, то:
R=R1 . N
N
При последовательном соединении общее сопротивление увеличивается (больше большего).
Параллельное соединение.
1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.
2. Напряжение на всех параллельно соединенных участках цепи одинаково:
U1=U2=U3=. =Un=.
3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то:
При параллельном соединении общее сопротивление уменьшается (меньше меньшего).
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:
5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:
Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. силы тока во всех участках одинаковы, то: U1:U2. Un. = R1:R2. Rn.
Для двух резисторов: – чем больше сопротивление, тем больше напряжение.
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:
A=A1+A2+. +An+.
т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
+Pn+.
6. Т.к. напряжения на всех участках одинаковы, то:
Для двух резисторов: – чем больше сопротивление, тем меньше сила тока.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединениеПри таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
ПрименениеПоследовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой.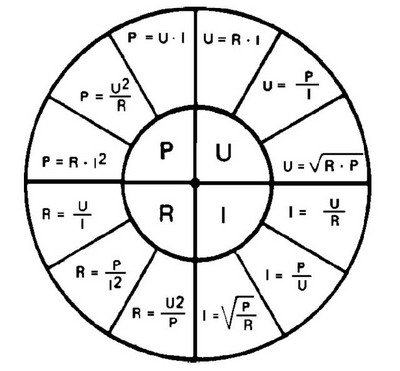 Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединениеВ этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
ПрименениеЕсли рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Работа токаПоследовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность токаПри рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Влияние схемы соединения на новогоднюю гирляндуПосле перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторовПри последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводниковВ электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
“>
Мощность при параллельном и последовательном соединении резисторов
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Мощность при последовательном соединение
При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять I = U/R = 100/390 = 0,256 A. На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I2 x R = 0,2562 x 390 = 25,55 Вт.
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
- P1 = I2 x R1 = 0,2562 x 200 = 13,11 Вт;
- P2 = I2 x R2 = 0,2562 x 100 = 6,55 Вт;
- P3 = I2 x R3 = 0,2562 x 51 = 3,34 Вт;
- P4 = I2 x R4 = 0,2562 x 39 = 2,55 Вт.
Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.
Мощность при параллельном соединение
При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.
Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:
- 1/R = 1/R1+1/R2+1/R3+1/R4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
- Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
- Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
- Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом: P = I2 x R = 6,0242 x 16,6 = 602,3 Вт.

- Расчет силы тока для каждого резистора выполняется по формулам: I1 = U/R1 = 100/200 = 0,5A; I2 = U/R2 = 100/100 = 1A; I3 = U/R3 = 100/51 = 1,96A; I4 = U/R4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов: P1 = U2/R1 = 1002/200 = 50 Вт; P2 = U2/R2 = 1002/100 = 100 Вт; P3 = U2/R3 = 1002/51 = 195,9 Вт; P4 = U2/R4 = 1002/39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р1+Р2+Р3+Р4 = 50+100+195,9+256,4 = 602,3 Вт.
Таким образом, мощность при последовательном и параллельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.
Онлайн расчёт мощности, выделяющейся в форме тепла в электрическом проводнике
Данный калькулятор будет полезен тем, кто решил сделать электрический обогреватель своими руками.Например, в случае, если вы решили сделать электрический подогрев руля на легковом автомобиле с напряжением питания 12 вольт.
Как это выглядит? Берётся нихромовая проволока (продаётся в хозяйственном магазине, вы её наверняка видели в электроплитках), она обматывается вокруг рулевого колеса, а её концы присоединяются, например, к питанию звукового сигнала или к прикуривателю.
В примере вы можете видеть расчёт для нихромовой проволоки сечением 0,6 кв. мм. и длиной 2 м. В провод нужно также вставить предохранитель с допустимым током 5-10 ампер. 2 * R
2 * R
R = ρ * L / S, то есть удельное сопротивление, умноженное на длину носителя, делённое на площадь сечения. Таблица основных удельных сопротивлений металлов и сплавов (в омах) — под калькулятором.
Первая часть калькулятора позволяет определить выделяющуюся мощность, а вторая — рассчитать температуру и время нагрева проводника, а также ток, который необходим для поддержания заданной температуры.
Поскольку проводник может находиться в разных средах (в воде, в воздухе, на какой-то поверхности и т.п.), то вторая часть — довольно приблизительна, так как определённое количество тепла будет уходить с теплообменом. Но для общего понимания — нормально.
По поводу нормального тока — он рассчитан для справки. Если вы питаете обогреватель не от сети, а от стационарного источника, то для него существует некий нормальный ток, при котором аккумулятор дольше проживёт и будет отдавать максимальную ёмкость. Величина этого тока очень сильно отличается в зависимости от технологии изготовления источника и может быть и 0,1 от ёмкости, и 0,3, и 10, и 20, и 30. Обозначается это символом С. Например, если на аккумуляторе указано 10С, а сам он ёмкостью 10А, значит, он может отдавать ток в 100 ампер.
Обозначается это символом С. Например, если на аккумуляторе указано 10С, а сам он ёмкостью 10А, значит, он может отдавать ток в 100 ампер.
Из Википедии:https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление | |
| Серебро | 0,015…0,0162 |
| Медь | 0,01724…0,018 |
| Золото | 0,02 |
| Алюминий | 0,0262…0,0295 |
| Иридий | 0,05 |
| Молибден | 0,05 |
| Вольфрам | 0,053…0,055 |
| Цинк | 0,06 |
| Никель | 0,09 |
| Железо | 0,10 |
| Платина | 0,11 |
| Олово | 0,12 |
| Свинец | 0,217…0,227 |
| Титан | 0,5562…0,7837 |
| Висмут | 1,20 |
| Сталь | 0,103…0,137 |
| Никелин | 0,42 |
| Константан | 0,50 |
| Манганин | 0,43…0,51 |
| Нихром | 1,05…1,4 |
| Фехраль | 1,15…1,35 |
| Хромаль | 1,3…1,5 |
| Латунь | 0,025…0,108 |
| Бронза | 0,095…0,1 |
Из данных программы «Начала электроники» | |
| Висмут | 1,2000 |
| Нихром | 1,0000 |
| Константан | 0,4900 |
| Манганин | 0,4400 |
| Свинец | 0,2060 |
| Олово | 0,1140 |
| Платина | 0,1050 |
| Железо | 0,0980 |
| Латунь | 0,0800 |
| Никель | 0,0724 |
| Цинк | 0,0592 |
| Молибден | 0,0560 |
| Фольфрам | 0,0550 |
| Алюминий | 0,0282 |
| Золото | 0,0242 |
| Медь | 0,0172 |
| Серебро | 0,0162 |
Со страницы http://bourabai. | |
| Серебро | 0,02 |
| Медь | 0,02 |
| Золото | 0,02 |
| Латунь | 0,025… 0,108 |
| Алюминий | 0,03 |
| Натрий | 0,05 |
| Иридий | 0,05 |
| Вольфрам | 0,05 |
| Цинк | 0,05 |
| Молибден | 0,06 |
| Никель | 0,09 |
| Бронза | 0,095… 0,1 |
| Железо | 0,10 |
| Сталь | 0,103… 0,137 |
| Олово | 0,12 |
| Свинец | 0,22 |
| Никелин (сплав меди, никеля и цинка) | 0,42 |
| Манганин (сплав меди, никеля и марганца) | 0,43… 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,50 |
| Титан | 0,60 |
| Ртуть | 0,94 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05… 1,4 |
| Фехраль | 1,15… 1,35 |
| Висмут | 1,20 |
| Хромаль | 1,3… 1,5 |
Ома с калькулятором
Закон Ома Есть 2 основные формулы, которые помогут вам понять взаимосвязь между током, напряжением, сопротивлением и мощностью. Если у вас есть какие-либо два параметра, вы можете рассчитать два других параметра.
Если у вас есть какие-либо два параметра, вы можете рассчитать два других параметра.
| ЗАКОН ОМА | |||
| БАЗОВЫЕ ФОРМУЛЫ | P = I * E | E = I * R | |
| НАЙТИ НАПРЯЖЕНИЕ | E = P / I | E = I * R | E = SQR (P * R) |
| НАЙТИ ТЕКУЩИЙ | I = P / E | I = E / R | I = SQR (P / R) |
| НАЙТИ ВЛАСТЬ | P = I * E | P = E 2 /Р | P = I 2 *Р |
| НАЙТИ СОПРОТИВЛЕНИЕ | R = E 2 /П | R = E / I | R = P / I 2 |
| P = мощность в ваттах E = электродвижущая сила в вольтах I = электрический ток в амперах R = электрическое сопротивление в омах SQR = квадратный корень |
| Примечание: Я использую букву «E» для обозначения напряжения большую часть времени, но иногда вы увидите, что для обозначения напряжения используется буква «V».  Не позволяйте этому сбивать вас с толку. Не позволяйте этому сбивать вас с толку. |
Краткий курс повышения квалификации
Изменение сопротивления:
На следующей диаграмме вы можете видеть, что единственная разница между диаграммами слева и диаграммами справа — это сопротивление в каждой «системе». Сопротивление в кране соответствует величине открытия клапана. В проводе сопротивление равно размеру отверстия * в отрезке провода. Вы можете видеть, что напряжение / давление одинаковы как для левого, так и для правого примеров.Что вы должны отметить на этой диаграмме, так это … При прочих равных, если есть увеличение сопротивления, ток будет уменьшаться. Вы можете видеть, что ток в крайнем правом проводе составляет половину тока в крайнем левом проводе. Это потому, что крайний правый провод имеет половину площади, через которую проходят электроны.
* Обратите внимание, что размер «отверстия» аналогичен сопротивлению. В реальном куске провода нет физических ограничений.
По формуле:
I = E / R
Вы можете видеть, что ток обратно пропорционален сопротивлению в цепи.
А для тех, кто более графичен …
Изменение напряжения:
На следующей диаграмме вы можете видеть, что сопротивление во всех системах одинаковое. На этот раз мы изменили напряжение / давление. Вы можете видеть, что повышенное напряжение вызывает увеличение тока, даже если сопротивление в левой и правой системах одинаково.
С помощью формулы:
I = E / R
Вы можете видеть, что ток прямо пропорционален напряжению, приложенному к сопротивлению.
Ну, теперь, когда это до смерти объяснили, перейдем к математике!
Математический пример:
В следующем примере мы знаем, что у нас есть 12 вольт, приложенных к резистору 10 Ом. Если вы хотите узнать, сколько мощности рассеивается на резисторе 10 Ом, используйте формулу:
P = E 2 / R
P = 12 2 /10
P = 144/10.
P = 14,4 Вт
Рассеиваемая мощность на резисторе 14.4 Вт.
Если вы хотите узнать, какой ток протекает через резистор, вы должны использовать формулу:
I = E / R
I = 12/10
I = 1,2 ампера
Ток через резистор 1,2 ампера.
Если вам нужно больше примеров, страница с резисторами приносит больше удовольствия, чем бочка с обезьянами.
Если вы хотите попробовать несколько самостоятельно, приведенные ниже калькуляторы позволят вам проверить свои математические данные.
Найти: рассеиваемая мощность и ток в зависимости от сопротивления и приложенного напряжения.
Важное примечание о демонстрациях Flash / графике на этом сайте … Власти посчитали, что Flash-контент на веб-страницах слишком опасен для использования обычным пользователем Интернета, и вскоре вся его поддержка будет устранено (большая часть доступа к Flash была прекращена 1-1-2021). Это означает, что ни один современный браузер по умолчанию не отображает ни одной из этих демонстраций. На данный момент исправление заключается в загрузке расширения Ruffle для вашего браузера.
Веб-сайт Ruffle. Напишите мне, пожалуйста, (babin_perry @ yahoo.com), чтобы сообщить мне, подходит ли вам Ruffle и какой браузер вы используете.
Это означает, что ни один современный браузер по умолчанию не отображает ни одной из этих демонстраций. На данный момент исправление заключается в загрузке расширения Ruffle для вашего браузера.
Веб-сайт Ruffle. Напишите мне, пожалуйста, (babin_perry @ yahoo.com), чтобы сообщить мне, подходит ли вам Ruffle и какой браузер вы используете.
Альтернативой Ruffle является другой браузер Maxthon 4.9.5.1000. Для получения дополнительных сведений о проблеме с Flash и Maxthon (стандартном и переносном) щелкните ЗДЕСЬ.
Георг Симон Ом:
Георг Симон Ом был немецким физиком, который жил с 1789 по 1854 год. Он обнаружил взаимосвязь между напряжением, током и сопротивлением в проводнике с постоянной температурой (постоянная температура важна, потому что сопротивление изменяется с температурой, а закон Ома не действует). не занимаюсь изменением температуры / сопротивления).Он обнаружил, что при постоянном сопротивлении напряжение и ток прямо пропорциональны (как мы показали на графике выше). Это соотношение может быть выражено как V = IR, где V — напряжение, приложенное к сопротивлению, I — ток, протекающий через сопротивление, а R — сопротивление в омах.
Это соотношение может быть выражено как V = IR, где V — напряжение, приложенное к сопротивлению, I — ток, протекающий через сопротивление, а R — сопротивление в омах.
Джеймс Ватт:
Джеймс Ватт был шотландским изобретателем, который жил с 1736 по 1819 год. Единица измерения мощности, ватт, была названа в его честь.
Джеймс Прескотт Джоуль:
Джеймс Прескотт Джоуль был английским физиком, который жил с 1818 по 1889 год.Он обнаружил взаимосвязь между мощностью, рассеиваемой в резисторе, и током, протекающим через резистор. Это соотношение может быть представлено формулой P = I ² R, где P — рассеиваемая мощность в ваттах, I — ток в амперах, R — сопротивление в омах. Ому обычно приписывают формулы, которые выражают взаимосвязь между мощностью, током, сопротивлением и напряжением, но, вероятно, следует отдать должное Джоулям.
«Джоуль» как единица измерения:
«Джоуль» представляет собой количество энергии, используемое, когда 1 ватт рассеивается в течение 1 секунды (или 1 ватт-секунды).
Мощность цепи — AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать падение напряжения и потерю мощности в проводах
Вы должны рассматривать провод как еще один последовательно включенный резистор. Вместо этого сопротивление \ $ \ text {R} _ {\ text {load}} \ $ подключено к источнику питания с напряжением \ $ \ text {V} \ $…
Вы должны увидеть это так: сопротивление \ $ \ text {R} _ {\ text {load}} \ $, подключенное к через два провода с сопротивлением \ $ \ text {R} _ {\ text {wire}} \ $ на блок питания с напряжением \ $ \ text {V} \ $:
Теперь мы можем использовать \ $ \ text {V} = \ text {I} \ cdot {} \ text {R} \ $, где \ $ \ text {V} \ $ означает напряжение, \ $ \ text {I} \ $ для тока и \ $ \ text {R} \ $ для сопротивления.
Пример
Предположим, что напряжение, приложенное к цепи, равно \ $ 5 \ text {V} \ $.\ $ \ text {R} _ {\ text {load}} \ $ равно \ $ 250 \ Omega \ $, а сопротивление \ $ \ text {R} _ {\ text {wire}} \ $ равно \ $ 2.5 \ Omega \ $ (если вы не знаете сопротивление провода, см. ниже в разделе «Расчет сопротивления провода»). Сначала мы вычисляем ток в цепи, используя \ $ \ text {I} = \ dfrac {\ text {V}} {\ text {R}} \ $: \ $ \ text {I} = \ dfrac {5 } {250 + 2 \ cdot2.5} = \ dfrac {5} {255} = 0,01961 \ text {A} = 19,61 \ text {mA} \
$Теперь мы хотим узнать, какое падение напряжения на одном куске провода используется \ $ \ text {V} = \ text {I} \ cdot {} \ text {R} \ $: \ $ \ text {V} = 0.01961 \ cdot2.5 = 0,049025 В = 49,025 \ text {мВ} \
долл. СШАТаким же образом мы можем рассчитать напряжение в \ $ \ text {R} _ {\ text {load}} \ $: \ $ \ text {V} = 0.01961 \ cdot250 = 4.9025 \ text {V} \ $
Ожидание потери напряжения
Что, если нам действительно нужно напряжение \ $ 5 \ text {V} \ $ over \ $ \ text {R} _ {\ text {load}} \ $? Нам нужно будет изменить напряжение \ $ \ text {V} \ $ от источника питания, чтобы напряжение выше \ $ \ text {R} _ {\ text {load}} \ $ стало \ $ 5 \ text {V } \ $.
Сначала мы вычисляем ток через \ $ \ text {R} _ {\ text {load}} \ $: \ $ \ text {I} _ {\ text {load}} = \ dfrac {\ text {V} _ {\ text {load}}} {\ text {R} _ {\ text {load}}} = \ dfrac {5} {250} = 0.02 \ text {A} = 20 \ text {mA} \
$Поскольку мы говорим о последовательном сопротивлении, ток во всей цепи одинаков. Следовательно, ток, который должен дать источник питания, \ $ \ text {I} \ $, равен \ $ \ text {I} _ {\ text {load}} \ $. Нам уже известно полное сопротивление цепи: \ $ \ text {R} = 250 + 2 \ cdot2.5 = 255 \ Omega \ $. Теперь мы можем рассчитать необходимое напряжение питания, используя \ $ \ text {V} = \ text {I} \ cdot {} \ text {R} \ $: \ $ \ text {V} = 0.02 \ cdot255 = 5.1 \ text { V} \ $
Что, если мы хотим знать, сколько мощности теряется в проводах? Обычно мы используем \ $ \ text {P} = \ text {V} \ cdot {} \ text {I} \ $, где \ $ \ text {P} \ $ означает мощность, \ $ \ text {V} \ $ для напряжения и \ $ \ text {I} \ $ для тока.
Итак, единственное, что нам нужно сделать, это ввести правильные значения в формулу.
Пример
Мы снова используем блок питания \ $ 5 \ text {V} \ $ с \ $ 250 \ Omega \ $ \ $ \ text {R} _ {\ text {load}} \ $ и двумя проводами \ $ 2.5 \ Omega \ $ каждый. Падение напряжения на одном куске провода, как вычислено выше, составляет \ $ 0,049025 \ text {V} \ $. Ток в цепи был \ $ 0.01961 \ text {A} \ $.
Теперь мы можем рассчитать потери мощности в одном проводе: \ $ \ text {P} _ {\ text {wire}} = 0.049025 \ cdot0.01961 = 0.00096138 \ text {W} = 0.96138 \ text {mW} \
$Во многих случаях нам известна длина провода \ $ l \ $ и AWG (американский калибр проводов) провода, но не сопротивление. Однако рассчитать сопротивление легко.
В Википедии есть список доступных здесь спецификаций AWG, который включает сопротивление на метр в Ом на километр или в миллиОм на метр. У них также есть это за килофуты или футы.
Мы можем вычислить сопротивление провода \ $ \ text {R} _ {\ text {wire}} \ $, умножив длину провода на сопротивление на метр.
Пример
У нас есть \ $ 500 \ text {m} \ $ провода 20AWG. Какое будет общее сопротивление?
\ $ \ text {R} _ {\ text {wire}} = 0.5 \ text {km} \ cdot 33.31 \ Omega / \ text {km} = 16.655 \ Omega \ $
РЕАКТИВНАЯ МОЩНОСТЬ — прикладное промышленное электричество
Рисунок 6.1 Чисто резистивная цепь переменного тока: напряжение и ток резистора совпадают по фазе.Если бы мы изобразили ток и напряжение для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)
Рисунок 6.2 Напряжение и ток «синфазны» для резистивной цепи.Поскольку резистор просто и напрямую сопротивляется протеканию тока в любое время, форма волны падения напряжения на резисторе точно совпадает по фазе с формой волны тока через него. Мы можем посмотреть в любой момент времени вдоль горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «снимок», показывающий значения волны, упоминается как мгновенных значений , что означает значения при этом момент времени ).Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Аналогичным образом, в момент времени, когда ток через резистор находится на своем положительном пике, напряжение на резисторе также находится на своем положительном пике, и так далее. В любой момент времени на волнах закон Ома справедлив для мгновенных значений напряжения и тока.
Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)
Рисунок 6.3 Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительная.Резисторы и катушки индуктивности
Катушки индуктивности ведут себя иначе, чем резисторы. В то время как резисторы просто препятствуют прохождению тока через них (снижая напряжение, прямо пропорциональное току), индукторы противодействуют изменениям тока через них, понижая напряжение, прямо пропорциональное скорости изменения тока. В соответствии с законом Ленца , это индуцированное напряжение всегда имеет такую полярность, чтобы поддерживать ток на его текущем уровне.То есть, если ток увеличивается по величине, индуцированное напряжение будет «противодействовать» току; если ток уменьшается, полярность изменится на противоположную и «подтолкнет» ток, чтобы противодействовать уменьшению. Это противодействие текущему изменению называется реактивным сопротивлением , а не сопротивлением . Выражаясь математически, соотношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:
[латекс] e = L \ frac {d_i} {d_t} [/ латекс]
Переменный ток в простой индуктивной цепи
Выражение di / dt — это выражение из расчетов, означающее скорость изменения мгновенного тока (i) во времени в амперах в секунду.Индуктивность (L) измеряется в Генри, а мгновенное напряжение (е), конечно, выражается в вольтах. Иногда вы можете встретить скорость мгновенного напряжения, выраженную как «v» вместо «e» (v = L di / dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:
Рисунок 6.4 Чистая индуктивная цепь: ток индуктора отстает от напряжения индуктора на 90 °.Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее на . Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток достигает пика (нулевое изменение или наклон уровня на синусоидальной волне тока), а мгновенное напряжение находится на пике везде, где мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, сдвинутой по фазе на 90 ° с волной тока. Глядя на график, кажется, что волна напряжения имеет «фору» по сравнению с волной тока; напряжение «опережает» ток, а ток «отстает» от напряжения.
Ток отстает от напряжения на 90 ° в чисто индуктивной цепи.
Все становится еще интереснее, когда мы строим график мощности для этой схемы:
Рисунок 6.6 В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p = ie), мощность равна нулю, когда мгновенный ток или напряжение равно нулю. Если мгновенный ток и напряжение положительные (над линией), мощность положительная. Как и в случае с резистором, мощность также положительна, когда мгновенные ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90 °, бывают моменты, когда одна из них положительна, а другая — отрицательна, что приводит к одинаково частым появлениям отрицательной мгновенной мощности .
Что такое отрицательная сила?
Но что означает отрицательная мощность ? Это означает, что катушка индуктивности возвращает мощность в цепь, в то время как положительная мощность означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности с течением времени, индуктор возвращает обратно в цепь столько же энергии, сколько потребляет в течение полного цикла. В практическом смысле это означает, что реактивное сопротивление катушки индуктивности рассеивает нулевую полезную энергию, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, у которых нет сопротивления провода.
Реактивное сопротивление в зависимости от сопротивления
Противодействие катушки индуктивности изменению тока означает противодействие переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току аналогично сопротивлению, но отличается тем, что всегда приводит к сдвигу фаз между током и напряжением и рассеивает нулевую мощность. Из-за различий он имеет другое название: реактивное сопротивление .Реактивное сопротивление по переменному току выражается в омах, как и сопротивление, за исключением того, что его математическим символом является X вместо R. Чтобы быть конкретным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X L .
Так как напряжение на катушках индуктивности падает пропорционально скорости изменения тока, они будут снижать большее напряжение при более быстром изменении тока и меньшее напряжение при более медленном изменении тока. Это означает, что реактивное сопротивление в Ом для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула для определения реактивного сопротивления выглядит следующим образом:
[латекс] X_L = 2πfL [/ латекс]
Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, он проявит реактивные сопротивления, указанные в таблице ниже.
Реактивное сопротивление индуктора 10 мГн:
| Частота (Герцы) | Реактивное сопротивление (Ом) |
| 60 | 3.7699 |
| 120 | 7,5398 |
| 2500 | 157.0796 |
В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение. Это количество радиан в секунду, на которое «вращается» переменный ток, если вы представите себе один цикл переменного тока, представляющий вращение полного круга. радиан — это единица измерения угла: в одном полном круге 2π радиана, так же как в полном круге 360 °.Если генератор переменного тока является двухполюсным, он будет производить один цикл на каждый полный оборот вала, что составляет каждые 2π радиан или 360 °. Если эту константу 2π умножить на частоту в герцах (циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.
Угловая скорость в системах переменного тока
Угловая скорость может быть представлена выражением 2πf или ее собственным символом — строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формула реактивного сопротивления X L = 2πfL также может быть записана как X L = ωL.
Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро колеблются колебания переменного тока, полный цикл равен 2π радиан. Это не обязательно соответствует фактической скорости вала генератора переменного тока. Если генератор имеет более двух полюсов, угловая скорость будет кратной скорости вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.
Как бы мы ни выразили угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в катушке индуктивности. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока катушка индуктивности будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Пример схемы показан здесь:
Индуктивное сопротивление(Индуктивное сопротивление индуктора 10 мГн при 60 Гц)
[латекс] X_L = 3,7600 Ом [/ латекс]
[латекс] I_ {X_ {L}} = \ frac {E} {X} [/ латекс]
[латекс] = \ frac {10 В} {3,7600 Ом} [/ латекс]
[латекс] \ mathbf {= 2.6526A} [/ латекс]
Фазовые углы
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг + 90 ° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что сопротивление катушки индуктивности току также имеет фазовый угол:
[латекс] \ text {Opposition} = \ frac {\ text {Voltage}} {\ text {Current}} [/ latex]
[латекс] \ text {Opposition} = \ frac {10 V \ angle \ text {90 °}} {2.6526A \ angle \ text {90 °}} [/ латекс]
[латекс] \ begin {align} \ text {Opposition} = & 3.7699 \ Omega \ angle \ text {90 °} \\ \ text {или} & 0 + j3.7699 \ Omega \ end {align} [/ latex]
Математически мы говорим, что фазовый угол сопротивления катушки индуктивности току равен 90 °, что означает, что сопротивление катушки индуктивности току является положительной мнимой величиной. Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют. Будет полезно представить любую оппозицию компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.
- Индуктивное реактивное сопротивление — это противодействие, которое индуктор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
- Индуктивное реактивное сопротивление можно рассчитать по следующей формуле: X L = 2πfL
- Угловая скорость цепи переменного тока — это еще один способ выразить ее частоту в единицах электрических радиан в секунду вместо циклов в секунду.Его символизирует строчная греческая буква «омега» или ω.
- Индуктивное реактивное сопротивление увеличивается с увеличением частоты . Другими словами, чем выше частота, тем сильнее он противодействует потоку электронов переменного тока.
Возьмем эту схему в качестве примера для работы:
Цепь индуктивности последовательного резистора: ток отстает от приложенного напряжения от 0 ° до 90 °.
Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а катушка индуктивности — 3.Реактивное сопротивление 7699 Ом на переменный ток при 60 Гц.
Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности — мнимым числом (3,7699 Ом ∠ 90 ° или 0 + j3,7699 Ом), комбинированный эффект двух компонентов будет противодействовать току, равному комплексной сумме двух чисел.
Это комбинированное противодействие будет векторной комбинацией сопротивления и реактивного сопротивления. Чтобы выразить это противопоставление лаконично, нам нужен более полный термин для обозначения сопротивления току, чем просто сопротивление или реактивное сопротивление.
Этот термин называется импедансом , его символ — Z, и он также выражается в омах, как сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:
Сопротивление по закону Ома
Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:
На самом деле, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E = IR), так же как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление, отдельно или в комбинации (последовательно / параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока.
Чтобы рассчитать ток в приведенной выше схеме, нам сначала нужно задать опорный фазовый угол для источника напряжения, который обычно принимается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0 ° и + 90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока).
Как и в чисто индуктивной схеме, волна тока отстает от волны напряжения (источника), хотя на этот раз запаздывание не так велико: всего 37,016 ° по сравнению с полными 90 °, как в случае чисто индуктивного схема.
Ток отстает от напряжения в последовательной цепи L-R.
Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось.Напряжение на резисторе синфазно (сдвиг 0 °) с током через него, а напряжение на катушке индуктивности на + 90 ° не совпадает по фазе с током, проходящим через него. Мы можем проверить это математически:
Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора).
Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через катушку индуктивности имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °. Это говорит нам о том, что E и I все еще не совпадают по фазе на 90 ° (только для катушки индуктивности).
Используйте закон Кирхгофа о напряжении
Мы также можем математически доказать, что эти комплексные значения в сумме составляют общее напряжение, как и предсказывает закон напряжения Кирхгофа:
Давайте возьмем те же компоненты для нашей схемы последовательного примера и соединим их параллельно:
Рисунок 6.7 Параллельная цепь R-L.Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.2 Таблица анализа импеданса 1Единственная разница в нашей методике анализа на этот раз состоит в том, что мы будем применять правила для параллельных цепей вместо правил для последовательных цепей.Принцип такой же, как и для DC. Мы знаем, что напряжение равномерно распределяется между всеми компонентами в параллельной цепи, поэтому мы можем передать значение общего напряжения (10 вольт 0 °) на все столбцы компонентов:
Таблица 6.3. Таблица анализа импеданса 2Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:
Таблица 6.4 Таблица анализа импеданса 3Так же, как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току все еще сохраняется для переменного тока, как и для постоянного тока):
Таблица 6.5 Таблица анализа импеданса 4Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Между прочим, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений.
[латекс] \ tag {6.1} Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [ / латекс]
Единственная проблема с использованием этой формулы состоит в том, что она обычно требует большого количества нажатий клавиш калькулятора.И если вы полны решимости использовать формулу, подобную этой «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается. Независимо от того, каким способом вы рассчитываете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:
Таблица 6.6 Таблица анализа импеданса 5- Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, чтобы сформировать общий импеданс, используя обратную формулу.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме!
[латекс] Z_ {parallel} = \ frac {1} {(\ frac {1} {Z1} + \ frac {1} {Z2} +… \ Frac {1} {Zn})} [/ латекс]
- Закон Ома для цепей переменного тока:
[латекс] E = {I} {Z} [/ латекс]; [латекс] I = \ frac {E} {Z} [/ latex]; [латекс] Z = \ frac {E} {I} [/ latex]
- Когда резисторы и катушки индуктивности смешаны вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и + 90 °.Ток в цепи будет иметь фазовый угол от 0 ° до -90 °.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противодействие переменному току строго основано на индуктивной реакции на изменения тока, а не на трении электронов, как в случае с резистивными компонентами.Однако индукторы не так чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, и мы знаем, что все проволоки обладают некоторой измеримой величиной сопротивления (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было подключено последовательно с идеальной индуктивностью катушки, например:
Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.
Следовательно, полное сопротивление любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и индуктивного реактивного сопротивления.
Эту проблему усугубляет то, что называется скин-эффектом , который представляет собой тенденцию переменного тока проходить через внешние области поперечного сечения проводника, а не через середину. Когда электроны движутся в одном направлении (постоянный ток), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, меняющие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения. Скин-эффект становится более выраженным с увеличением частоты.
Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается к катушке индуктивности и поэтому проявляется в виде сопротивления (рассеяния мощности) в цепи.
Помимо резистивных потерь в проводе и излучения, в индукторах с железным сердечником действуют и другие эффекты, которые проявляются как дополнительное сопротивление между выводами.Когда на индуктор подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи в железном сердечнике, известные как вихревые токи , . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление, обеспечиваемое железом, который не так хорош в качестве проводника, как медь. Вихретоковым потерям в первую очередь противодействуют, разделив железный сердечник на множество тонких листов (пластин), каждый из которых отделен от другого тонким слоем электроизоляционного лака.Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого не будет (или будет очень мало) резистивных потерь.
Как и следовало ожидать, потери на вихревые токи в металлических сердечниках индуктора проявляются в виде тепла. Эффект более выражен на более высоких частотах и может быть настолько сильным, что иногда его используют в производственных процессах для нагрева металлических предметов! Фактически, этот процесс «индукционного нагрева» часто используется в процессах литья металлов высокой чистоты, где металлические элементы и сплавы должны нагреваться в вакууме, чтобы избежать загрязнения воздухом, и, таким образом, там, где стандартная технология нагрева сжиганием была бы бесполезной.Это «бесконтактная» технология, когда нагретое вещество не должно касаться катушки (катушек), создающей магнитное поле.
В высокочастотной среде вихревые токи могут возникать даже в поперечном сечении самого провода, что способствует дополнительным резистивным эффектам. Чтобы противодействовать этой тенденции, можно использовать специальный провод, сделанный из очень тонких, индивидуально изолированных жил, который называется Litz wire (сокращенно от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.
Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля индуктора, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействовать этому эффекту лучше всего за счет правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, генерируемой в каждом цикле.
В целом паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:
Рисунок 6.9 Эквивалентная схема реального индуктора с потерями на скин-эффект, излучение, вихревые токи и гистерезис.
Следует отметить, что скин-эффект и потери на излучение применимы к прямым отрезкам провода в цепи переменного тока так же хорошо, как и к спиральному проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах они могут быть довольно большими. Например, антенна радиопередатчика спроектирована специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.
Конденсаторы Vs. Резисторы
Конденсаторы не ведут себя так же, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения является другой формой реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.
Характеристики цепи конденсатора
Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе как таковое:
[латекс] i = C \ frac {d_e} {d_t} [/ латекс]
Выражение de / dt — это выражение из расчетов, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду. Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.Иногда скорость мгновенного изменения напряжения с течением времени выражается как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:
Рисунок 6.10 Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °
Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.11 Формы сигналов чисто емкостной цепи.
Помните, что ток через конденсатор — это реакция на изменение напряжения на нем на . Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение находится на пике (нулевое изменение или наклон уровня на синусоидальной волне напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение имеет максимальное изменение (точки самый крутой наклон на волне напряжения, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, которая на -90 ° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Рисунок 6.12 Напряжение отстает от тока на 90 ° в чисто емкостной цепи.
Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:
Рисунок 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой схемой индуктивности, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительной и отрицательной полярностью. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения означает сопротивление переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой данной величины переменного напряжения на данной частоте конденсатор данного размера будет «проводить» определенную величину переменного тока. Так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , обеспечиваемого конденсатором. Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или, если точнее, X C ).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. . Это означает, что реактивное сопротивление в Ом для любого конденсатора составляет обратно пропорционально частоте переменного тока.
[латекс] X_C = \ frac {1} {2πfC} [/ латекс]
Реактивное сопротивление конденсатора 100 мкФ:| Частота (Герцы) | Реактивное сопротивление (Ом) |
| 60 | 26.5258 |
| 120 | 13,2629 |
| 2500 | 0,6366 |
Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления. Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Катушки индуктивности противодействуют более быстрому изменению токов, создавая большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения, допуская большие токи.
Как и в случае с индукторами, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение X C = 1 / (2πfC) также может быть записано как X C = 1 / (ωC), с приведением ω в единицах радиан в секунду .
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
[латекс] X_C = 26,5258 Ом [/ латекс]
[латекс] I = \ frac {E} {X} [/ латекс]
[латекс] I = \ frac {10} {26,5258 Ом} [/ латекс]
[латекс] I = 0,3770A [/ латекс]
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению.Если мы математически представим эти фазовые углы напряжения и тока, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
Напряжение в конденсаторе отстает от тока на 90 °.
Математически мы говорим, что фазовый угол сопротивления конденсатора току составляет -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше). Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют.Будет полезно представить любую оппозицию компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
- Емкостное реактивное сопротивление — это противодействие, которое конденсатор предлагает переменному току из-за его сдвинутого по фазе накопления и высвобождения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
- Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
- Емкостное реактивное сопротивление уменьшается с увеличением частоты.Другими словами, чем выше частота, тем меньше он противодействует (тем больше «проводит») переменному току.
Используя компоненты с одинаковыми значениями в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:
Рисунок 6.14 Параллельная цепь RC.
Параллельный резистор и конденсатор
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.7Теперь это параллельная схема, и мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт 0 °) во все столбцы:
Таблица 6.8 Расчетпо закону Ома
Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через конденсатор:
Таблица 6.9Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):
Таблица 6.10Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле. И снова формула параллельного импеданса выглядит так:
[латекс] Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [/ латекс]
Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:
- Импедансами (Z) управляют так же, как сопротивлениями (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, чтобы сформировать общий импеданс, используя обратную формулу. Только не забудьте
- выполнять все вычисления в сложной (не скалярной) форме! ZTotal = 1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
- Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
- Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
(Следующий раздел был адаптирован из: Уроки электрических цепей, Том II, Глава 5 — Реактивное сопротивление и импеданс — R, L и C)
Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.
Сопротивление
Это по сути трение против потока тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).
Реактивное сопротивление
Это по сути инерция против тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).
Импеданс
Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° не в фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.
Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.
Рис. 6.15. Идеальный резистор, катушка индуктивности и конденсатор.Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток всегда находятся в фазе , поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.
Полные сопротивления переменного тока ведут себя аналогично сопротивлениям в цепях постоянного тока: они добавляются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:
Закон Ома для цепи переменного тока
[латекс] \ begin {align} \ tag {6.2} \ text {E} & = {I} {Z} \\ \ text {I} & = \ frac {E} {Z} \\ \ text {Z } & = \ frac {E} {I} \ end {align} [/ latex]
Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:
Рисунок 6.16 Пример параллельной схемы R, L и C.Импеданс в параллельных компонентах
Тот факт, что эти компоненты соединены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.
Рисунок 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими значения компонентов.Со всеми значениями компонентов, выраженными как импедансы (Z), мы можем настроить таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательного.
Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести цифру для общего напряжения во все столбцы компонентов в таблице:
Значения компонентов в таблице 6.11 выражаются в виде импеданса изображения 2Теперь мы можем применить закон Ома (I = E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:
Таблица 6.12. Значения компонентов выражаются как изображение импеданса 3Расчет полного тока и полного импеданса
Существует две стратегии расчета полного тока и полного сопротивления.Во-первых, мы можем рассчитать общий импеданс из всех отдельных параллельных сопротивлений (Z Total = 1 / (1 / Z R + 1 / Z L + 1 / Z C ), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I = E / Z).
Тем не менее, работа с уравнением параллельного импеданса с комплексными числами — непростая задача, учитывая все взаимные колебания (1 / Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать индивидуальные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).Второй способ рассчитать общий ток и полное сопротивление — сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи — переменный или постоянный — равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z = E / I).
Таблица 6.13 Расчет общего тока и полного импедансаЛюбой из методов, выполненный должным образом, даст правильные ответы.
За заметным исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты для цепей постоянного тока.Единственное существенное отличие состоит в том, что в расчетах переменного тока используются комплексные величины, в то время как в расчетах постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, остаются верными для переменного тока, когда напряжение, ток и импеданс выражаются комплексными числами. Те же стратегии поиска и устранения неисправностей, которые применяются в цепях постоянного тока, справедливы и для переменного тока, хотя с переменным током, безусловно, может быть труднее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.
Power — это отдельная тема, которая будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и высвобождается, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.
При анализе цепи переменного тока первым шагом в анализе является преобразование всех значений компонентов резистора, катушки индуктивности и конденсатора в импедансы (Z) в зависимости от частоты источника питания.После этого выполните те же шаги и стратегии, которые были изучены для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I = E / Z; и Z = E / I
Помните, что только рассчитанные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольные обозначения — это просто полезный инструмент для сложения и вычитания сложных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеренного напряжения или тока, а угол напрямую связан с фазовым сдвигом в градусах, является наиболее практичным способом выражения сложных величин для анализа схем.
Электроэнергия — Веб-формулы
Электрическая мощность определяется по формуле:P = V · I
Где V — напряжение, а I — ток.
Соответствующие единицы:
ватт (Вт) = вольт (В) · ампер (A)
Мощность также можно определить по следующим формулам:
P = I 2 · R ↔ R = P / I 2 ↔ I R )
P = V 2 / R ↔ R = V
Подробнее о Electric Power 9000 3
Электроэнергия определяется как скорость, с которой работа выполняется источником эл.м.ф. в поддержании тока в электрической цепи. Практическая единица мощности — киловатт и лошадиные силы; где 1 киловатт = 100 ватт и 1 л.с. = 746 ватт.
Если сопротивления (например, электрические приборы) соединены последовательно, ток через каждое сопротивление будет одинаковым. Тогда мощность электрического прибора, P α R и P α V (поскольку V = IR), это означает, что в комбинации сопротивлений серии разность потенциалов и потребляемая мощность будут больше при большем сопротивлении .
Если сопротивления ( i.е. электроприборов) подключены параллельно, разность потенциалов на каждом приборе одинакова. Тогда P α 1 / R и I α 1 / R (как V = IR), что означает, что в параллельных комбинациях сопротивлений потребляемый ток и мощность будут больше при меньшем сопротивлении.
Для данного напряжения В, , если сопротивление изменяется с R на ( R / n ), а потребляемая мощность изменяется с P на nP , затем согласно P = V 2 / R , имеем:
P = V 2 / (R / n)) = n (V 2 / R) = nP, где R = R / n и P = nP
Когда приборы питания P 1 , P 2 , P 3 … P n включены последовательно с источником напряжения, эффективная потребляемая мощность ( P s ) определяется по формуле:
1/ P s = 1 / P 1 + 1 / P 2 + 1 / P 3 +… + 1 / P n
Для n приборов, каждый из сопротивление R , последовательно соединены с источником напряжения В, рассеиваемая мощность P с тогда определяется как:
(1) P с = В 2 / n R
Когда приборы питания
P 1 , P 2 , P 3 … P n подключены параллельно к источнику напряжения, эффективная мощность потреблено ( P p ) затем определяется следующим образом:P s = P 1 + P 2 + P 3 +… + P n
909 Для устройств n , каждое с равным сопротивлением R , подключенных параллельно к источнику напряжения В , рассеиваемая мощность тогда определяется как:
(2) P p = В 2 / ( R / n) = n V 2 / R
Из (1) и (2) мы имеем P p / P s = n 2 или просто записываем как : P P = n 2 P s .
В соответствии с приведенными выше формулами мы можем объяснить, что:
При группировании лампочек серии по заданному источнику напряжения лампа большей мощности будет давать меньшую яркость и будет иметь меньший потенциал сопротивления, но тот же ток , тогда как в параллельном группировке лампочек по данному источнику напряжения лампа большей мощности даст большую яркость и позволит большему току проходить через нее, но будет иметь меньшее сопротивление и такую же разность потенциалов на нем.
Электроэнергия
Электроэнергия определяется как общая выполненная работа или энергия, поставленная источником ЭДС. при поддержании тока в электрической цепи в течение заданного времени:
Электрическая энергия = электрическая мощность × время = P × t
Таким образом, формула для электрической энергии имеет вид:
Электрическая энергия = P × т = V × I × т = I 2 × R × т = V 2 т / R
S.I единица электрической энергии — джоуль (обозначается Дж), где 1 джоуль = 1 ватт × 1 секунда = 1 вольт × 1 ампер × 1 секунда
Коммерческая единица электрической энергии — киловатт-час ( кВт · ч, ), где 1 кВтч = 1000 Вт h = 3,6 × 10 6 J = одна единица потребляемой электроэнергии .
Количество единиц потребляемой электроэнергии равно n = (общая мощность × время в часе) / 1000
Стоимость потребления электроэнергии в доме = количество.единиц потребленной электроэнергии × количество на одну единицу электроэнергии.
Теорема о максимальной мощности
В ней говорится, что выходная мощность источника тока максимальна, когда внутреннее сопротивление источника равно внешнему сопротивлению в цепи. Итак, если R — внешнее сопротивление цепи, а r — внутреннее сопротивление источника тока (то есть батареи), то выходная мощность максимальна, когда R = R.
Эта теорема применима ко всем типам источников ЭДС. и связан с выходной мощностью, а НЕ с рассеиваемой мощностью.
Если E — применяемая ЭДС. источника ЭДС. т.е. . батарея с внутренним сопротивлением r и R — внешнее сопротивление, тогда ток в цепи определяется как:
I = E / (R + r)
При максимальной выходной мощности R = r , поэтому имеем:
I = E / (r + r) = E / (2r)
и
максимальная выходная мощность:
P max = I 2 r = E 2 / (4r)
При коротком замыкании аккумулятора мощность равна нулю.В этом случае вся мощность батареи рассеивается внутри батареи из-за ее внутреннего сопротивления. Таким образом, мощность, рассеиваемая внутри батареи, определяется как: P = ( E / r) 2 × r = E 2 / r
КПД источника ЭДС.
КПД источника ЭДС. определяется как отношение выходной мощности (, т. е. , мощность на внешнем сопротивлении цепи, к входной мощности (т. е.мощность, потребляемая от источника ЭДС). Итак,
Где V = падение потенциала на внешнем сопротивлении R,
E = E.M.F. источника тока,
I = ток в цепи.
Если r — внутреннее сопротивление источника ЭДС, тогда
В = IR и E = I (R + r )
или
Когда мощность, полученная от источника, максимальная, тогда R = р. В данной ситуации имеем:
Таким образом максимальная эффективность источника эл.м.ф. составляет 50%. Это означает, что для элемента только половина общей мощности, потребляемой элементом, используется для полезных целей, тогда как другая половина рассеивается внутри элемента.
Пример 1:
Лифт должен поднимать 1000 кг на расстояние 100 м со скоростью 4 м / с. Какую в среднем мощность оказывает лифт во время этой поездки?
Решение:
Работу, проделанную лифтом на 100 метров, легко вычислить:
W = mgh = (1000) (9.8) (100) = 9,8 × 10 5 Джоулей.
Общее время поездки можно рассчитать по скорости лифта:
t = x / v = 100 м / 4 м / с = 25 с .
Таким образом, средняя мощность определяется по формуле: P = Вт / t = 9,8 × 10 5 / 25s = 3,9 × 10 4 Вт, или 39 кВт.
Пример 2:
Считается, что объект в свободном падении достиг конечной скорости , если сопротивление воздуха становится достаточно сильным, чтобы противодействовать всему ускорению свободного падения, в результате чего объект падает с постоянной скоростью.Точное значение конечной скорости зависит от формы объекта, но для многих объектов оно может быть оценено на уровне 100 м / с. Когда объект весом 10 кг достиг предельной скорости, какую силу сопротивление воздуха оказывает на объект?
Решение: Для решения этой задачи мы будем использовать уравнение P = Fv cos θ , Вместо обычного уравнения мощности, поскольку нам дана скорость объекта. Нам просто нужно вычислить силу, прилагаемую к объекту сопротивлением воздуха, и угол между силой и скоростью объекта.Поскольку объект достиг постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Поскольку на объект действуют только две силы: сила тяжести и сопротивление воздуха, сопротивление воздуха должно быть равным по величине и противоположным по направлению силе тяжести. Таким образом, F a = — F G = мг = 98 N, направленным вверх. Таким образом, сила, прилагаемая сопротивлением воздуха, антипараллельна скорости объекта. Таким образом:
P = Fv cos θ = (98) (100) (cos180) = — 9800 Вт
Пример 3: Мощность двигателя насоса составляет 4 кВт.Сколько воды в кг / мин он может поднять на высоту 20 м? (g = 10 м / с 2 )
Решение:
Заданная мощность двигателя P = 4KW = 4000 Вт
Если масса воды, поднятая за одну секунду, = m кг.
Общая работа, выполненная при подъеме воды, W = mgh
Мощность P = Вт / т, но t = 1 минута = 60 сек.
4000 = mgh / 60
4000 = (m × 10 × 20) / 60
m = 1200 кг.
Пример 4 : Когда вода течет по трубе, ее скорость изменяется на 5%, найти изменение силы воды?
Решение: Мощность = Сила × Скорость = Скорость изменения количества движения × скорость = {(масса / время) × скорость} x скорость = {(adv) × v} × v = adv 3 , где a — площадь поперечного сечения, d — плотность воды, а v — скорость потока воды.
Следовательно, Сила воды прямо пропорциональна кубу скорости воды, поэтому пусть
P = Kv 3 (k — постоянная величина, равная ad.)
Ведение журнала с обеих сторон
log P = 3log v + log k
Дифференциация с обеих сторон
dP / P = 3.dv / v
процентное изменение мощности, dP / P × 100 = 3 × 5% = 15%.
Пример 5 : Кинетическая энергия выбрасываемой воды из плотины используется для вращения турбины. Труба, по которой устремляется вода — 2.4 метра и его скорость 12 м / сек. Предполагая, что вся кинетическая энергия воды используется для вращения турбины, вычислите производимый ток, если эффективность динамо-машины составляет 60% и станция передает мощность 240 кВ. Плотность воды = 10 3 кг / м 3 .
Решение: Учитывая, что
r = радиус трубы = 1,2 м, средняя скорость воды v = 12 м / с
V = 240 кВ = 240 × 10 3 вольт, плотность воды p = 10 3 кг / м 3 .
Теперь кинетическая энергия текущей воды в секунду, т.е.
Power P = (1/2) (массовый расход в секунду) × v 2
= (1/2) pr 2 (л / т) rv 2
= (1/2) pr 2 rv 3
= (1/2) 3,14 × (1,2) 2 × 10 3 × (12) 3 Вт
= 3,9 x 10 6 Вт
Ток в кабелях передачи определяется по формуле:
ток = выходная мощность / напряжение
= (60% мощности P) / (240 × 1000)
= [(60/100) × 3.9 × 10 6 ] / (240 × 1000) = 9,75 A
Закон Ома
Закон Ома Главная | Карта | Проекты | Строительство | Пайка | Исследование | Компоненты | 555 | Символы | FAQ | Ссылки Следующая страница: Мощность и энергия
См. Также: Напряжение и ток | Сопротивление |
Резисторы
Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между напряжением (V), током (I) и сопротивлением (R). Это можно записать тремя способами:
| где: | В = напряжение в вольтах (В) I = ток в амперах (А) R = сопротивление в Ом () | или: | В = напряжение в вольтах (В) I = ток в миллиамперах (мА) R = сопротивление в кОм (к) |
Уравнения закона Ома работают, если вы используете V, A и , или если вы используете В, мА и k. Вы не должны смешивать эти наборы единиц в уравнениях, поэтому вам может потребоваться преобразование между mA и A или k и .
Треугольник ВИР
| V I R |
| Закон Ома треугольник |
Запишите V, I и R в треугольнике, как в желтом поле справа.
- Для расчета напряжения, В : поместите палец на V,
это оставляет вас с I R, поэтому уравнение V = I × R - Чтобы рассчитать ток , I : положите палец на I,
это оставляет вас с V над R, поэтому уравнение I = V / R - Чтобы рассчитать сопротивление , R : поместите палец на R,
это оставляет вас с V над I, поэтому уравнение R = V / I
Расчет по закону Ома
Используйте этот метод для проведения расчетов:- Запишите Значения , при необходимости конвертируя единицы.
- Выберите необходимое уравнение Equation (используйте треугольник VIR).
- Подставьте чисел в уравнение и вычислите ответ.
Это должно быть V ery E asy N ow!
Следующая страница: Power and Energy | Изучение электроники
© Джон Хьюс 2007, Клуб электроники, www.kpsec.freeuk.com
Этот сайт был взломан с использованием ПРОБНОЙ версии WebWhacker.Это сообщение не появляется на лицензированной копии WebWhacker.
ПИТАНИЕ В КОМБИНИРОВАННЫХ ЦЕПЯХ
Как вы подсчитали ранее, общая мощность, потребляемая последовательной или параллельной цепью, равна сумме мощности, потребляемой каждым из компонентов цепи. То же самое и с комбинированной схемой. Часто предоставляется только один параметр (например, сопротивление, напряжение или ток). Ваша задача — уменьшить и объединить различные сопротивления, чтобы найти второй параметр.
Часто для этого требуется систематическое уменьшение цепи до единственного эквивалентного значения сопротивления. Затем вы работаете в обратном направлении, чтобы получить недостающие значения для различных компонентов, используя закон Ома. Помните, что вы не можете найти мощность, пока не получите два из трех параметров для каждого из компонентов. Общая мощность получается путем сложения всех индивидуальных мощностей каждого из компонентов.
Рассчитайте мощность, рассеиваемую каждым компонентом, и общую мощность комбинированной схемы, показанной на Рисунке 6–33.Первый шаг — просмотреть схему, проанализировать, что известно, а что неизвестно, и сравнить то, что вы видите, с тем, что вы решаете.
На рис. 6–33 нет компонентов с двумя значениями, с которыми можно работать. Это означает, что вам придется начать с объединения компонентов схемы, чтобы найти необходимую вторую переменную.
Вы можете использовать уравнение P T = E T × I T для расчета полной мощности.Однако на рис. 6–33 нет значения для I T . Поэтому первый шаг — найти I T . Чтобы вычислить значение I T , вам необходимо значение общего сопротивления (R T ). Зная R T , вы можете рассчитать I T по следующей формуле:
Чтобы вычислить R T в этой схеме, вы начнете с объединения резисторов R 2 и R 3 :
Просто для проверки мы могли бы использовать предполагаемое напряжение для резисторов 100 Ом и 200 Ом, включенных параллельно.В качестве примера возьмем параллельное напряжение 400 В.
Резистор 100 Ом допускает 4 А, а резистор 200 Ом допускает 2 А, всего 6 А. Эти 6 А будут общим током при приложенном 400 В. Таким образом,
Второй шаг — уменьшить последовательный резистор R 1 и эквивалентный резистор R 2,3 до одного значения. Это дает R T . Поскольку это последовательная схема, R T вычисляется путем сложения последовательных элементов:
Теперь, когда у вас есть напряжение источника E T 100 В и общее сопротивление R T , вы можете вычислить общий ток (I T ), используя следующую формулу:
Теперь у вас есть все три параметра эквивалентной схемы.С помощью этих значений можно найти общую мощность для цепи P T и мощность, потребляемую каждым из компонентов схемы R 1 , R 2 и R 3 . Сначала вы решаете общую мощность цепи (P T ), используя следующую формулу:
Теперь у вас есть необходимая информация для расчета индивидуальных потерь мощности, начиная с R 1 . Поскольку в последовательной цепи ток одинаков во всей цепи, и поскольку вам известен общий ток I T , ток в R 1 и R 2,3 можно рассчитать как:
Теперь у вас есть ток и сопротивление для R 1 , и, таким образом, вы можете рассчитать мощность, потребляемую R 1 , используя следующую формулу:
Есть несколько способов рассчитать мощность, рассеиваемую R 2 и R 3 .Поскольку вам известен ток через параллельную ветвь R 2,3 и эквивалентное сопротивление R 2,3 (вычисленное ранее в задаче), вы можете рассчитать напряжение на этой ветви, используя закон Ома. Используйте следующую формулу:
Поскольку это параллельная ветвь, вы знаете, что напряжение одинаково как на R 2 , так и на R 3 :
Теперь у вас есть падение напряжения и сопротивление R 2 и R 3 , и вы можете рассчитать мощность, рассеиваемую каждым из этих компонентов, используя следующие формулы:
Вы выполнили все расчеты, необходимые для определения общей мощности и мощности, потребляемой отдельными компонентами, составляющими схему на Рисунке 6–33.Вы должны проверить свои расчеты, добавив отдельные рассеиваемые мощности и сравнив их с общей мощностью, рассчитанной ранее:
Ранее вы рассчитали P T как 0,316 × 100 = 31,6 Вт. Небольшая ошибка вызвана округлением десятичных знаков во время вычислений.
ЦЕПИ С ИЗВЕСТНЫМ ИСПОЛЬЗОВАНИЕМ ЭНЕРГИИ
Цепи, над которыми вы будете работать в своей работе, часто имеют известные значения мощности и напряжения. Один из аспектов, который вам необходимо принять во внимание, — это реальная потребляемая мощность для цепей с компонентами, которые уже рассчитаны.Например, посмотрите на рис. 6–34.
В этой схеме три лампы подключены к источнику питания с помощью медного провода №16 американского калибра (AWG) длиной 300 футов.
Из рисунка видно, что каждая лампа рассчитана на 25 Вт и что лампы подключаются параллельно. Когда вы смотрите на такую схему, вы должны обязательно принять во внимание все параметры схемы. Электрик, установивший лампы, подсчитал, что лампы потребляют 0.5 А на каждый при 50 В, что делает общий ток цепи суммой тока в отдельных ветвях (т. Е. 1,5 А). Следующие формулы подтверждают расчеты электрика. Для расчета силы тока отдельных ламп (общий ток складывается из всех трех ламп):
Кажется, все в порядке. Однако посмотрите на схему еще раз. Нагрузка, все три лампы, находится на расстоянии 300 футов от источника напряжения. Из предыдущих глав вы знаете, что все проводники, даже медные, имеют некоторое сопротивление.Вы также знаете, что чем длиннее провод, тем выше сопротивление: медь # 16 AWG имеет сопротивление 4,99 Ом на 1000 футов. Эта информация получена из NEC ® и применима к семисковому проводнику при температуре 75 ° C. Обратите внимание, что это значение немного отличается от значения, приведенного в предыдущей главе. Это связано с тем, что значение в этой таблице относится к одножильному, а не многожильному проводу. Просмотрите другие размеры проводов, чтобы узнать, какое сопротивление они имеют на тысячу футов проводника.Учтите, что чем крупнее проводник, тем меньше значение сопротивления. Тот факт, что нагрузка находится на расстоянии 300 футов от источника питания, означает, что при расчетах необходимо учитывать сопротивление медного проводника №16, идущего к лампам и возвращающегося от них. Поскольку в проводниках, питающих осветительную нагрузку, существует сопротивление, при расчетах для этой схемы необходимо учитывать и другие факторы.
Изучите рисунок 6–35. Эта схема была перерисована, чтобы представить все сопротивления, которые необходимо учитывать в схеме при выполнении расчетов.Номинальная мощность лампы — это количество энергии, которое лампа рассеивает при приложенном номинальном напряжении. Поскольку номинальное напряжение не будет применяться из-за падения напряжения на проводе, вам необходимо знать сопротивления ламп, чтобы вы могли решить эту схему как комбинированную схему, используя методы, которые вы изучили в этой и предыдущих главах. Поскольку лампы рассчитаны на 25 Вт при 50 В, вы можете рассчитать значение сопротивления лампы следующим образом:
Обратите внимание, что это сопротивление каждой отдельной лампы.Чтобы полностью проанализировать эту схему, нужно также знать сопротивление провода, питающего лампы. Исходя из того, что сопротивление провода # 16 AWG составляет 4,99 Ом на 1000 футов провода, вы можете рассчитать общее сопротивление как:
Помните, в этой цепи 300 футов провода, идущего к лампам, и 300 футов провода, идущего от ламп. Необходимо учитывать оба расстояния. На Рис. 6–36 показана полная схема со всеми включенными сопротивлениями.
Это комбинированная схема, которую можно уменьшить с помощью методов, которые вы изучили.Начнем с расчета сопротивления трех параллельно включенных ламп, R Все лампы :
Схема теперь сведена к простой последовательной схеме с двумя отрезками медного провода и параллельным комбинированным сопротивлением ламп. Общее сопротивление складывается из трех элементов серии:
Общий ток рассчитывается как:
Обратите внимание, что значение, рассчитанное электриком, устанавливающим этот проект (1.5 A) отличается от рассчитанного ранее значения. Уменьшение тока вызвано дополнительным сопротивлением провода. Теперь узнаем, какое напряжение на самом деле подается на лампы. Мы знаем, что полный ток для этой цепи на самом деле составляет 1,38 А, и мы знаем, что эквивалентное сопротивление для ламп, включенных последовательно с сопротивлением, равно 33,33. Используя закон Ома, мы можем легко рассчитать напряжение на лампах следующим образом:
Это означает, что мы потеряли (упали) на проводах 4 В.В процентах это:
Такое падение является чрезмерным. Максимальные падения напряжения обычно не должны превышать 3%. Лампы не рассеивают мощность, на которую они рассчитаны. Другими словами, вместо ламп, фактически обеспечивающих свет в соответствии с их проектными параметрами, теперь огни будут работать в соответствии с фактическими параметрами установки. Посмотрим, как на самом деле влияют параметры установки на лампы. Поскольку теперь мы знаем, что установка питает лампы напряжением 46 В, мы можем пересчитать фактическую мощность ламп следующим образом:
Эта схема с учетом сопротивления проводников в действительности потеряла примерно 15% мощности лампы.Это:
Как видите, при проектировании установки необходимо учитывать всю схему. Все компоненты сопротивления в комбинированной цепи потребляют мощность, и это необходимо учитывать. Взгляните на сопротивление проводов и посмотрите, сколько энергии потребляет их сопротивление. Поскольку вы уже рассчитали ток и сопротивление проводников, вы можете легко рассчитать мощность, потребляемую проводниками, по следующей формуле:
Обратите внимание на множитель 2.Есть два проводника, и вы должны учитывать их обоих. Предыдущий расчет показывает, что из всей мощности, потребляемой установкой, часть этой мощности (5,69 Вт) потребляется проводниками и теряется в виде тепла. Не принимая во внимание потерю мощности в проводниках, фактическая схема не работала с оптимальной проектной эффективностью, фактическая мощность лампы была снижена, а проводники потребляли мощность, которая терялась в виде тепла. Всего этого можно было избежать или уменьшить, выбрав провод большего диаметра.
В последовательных и параллельных цепях, особенно в цепях с длинными проводниками или проводниками малого диаметра (например, пожарная сигнализация или акустические системы), вы должны учитывать падение напряжения и потери мощности из-за сопротивления проводника.
Другой пример проблемы обрыва линии и потери линии — использование цепей пожарной сигнализации. В цепях мониторинга, где в зоне защиты находится много тепловых датчиков или датчиков дыма, на двух проводниках, идущих от датчика к датчику, будет пропадание линии.В схемах уведомления (рис. 6–37) все чувствительные элементы включены параллельно через два параллельных проводника. Обычно датчики имеют разомкнутую связь с параллельной цепью.
Контроль цепи осуществляется путем размещения резистора между линейными проводниками в самом конце цепи. Этот резистор называется оконечным резистором. Его цель — позволить небольшому количеству тока течь по отрицательному проводнику до конца, через резистор и обратно к источнику.

 ru/toe/resistance.htm
ru/toe/resistance.htm