формулы, таблицы, примеры расчетов, правила выбора сечения проводов
Умение правильно выбрать сечение кабеля со временем может пригодиться каждому, и для этого необязательно быть квалифицированным электриком. Неверно рассчитав кабель, можно подвергнуть себя и своё имущество серьёзному риску — чересчур тонкие провода будут сильно греться, что может привести к появлению возгорания.
Для чего нужен расчёт сечения кабеля
В главную очередь, проведение этой несильно сложной процедуры необходимо для обеспечения безопасности как самого помещения, так и находящихся в нём людей. На сегодня человечеством не изобретено более удобного метода распределения и доставки электрической энергии до потребителя, как по проводам. Людям практически ежедневно необходимы услуги электрика — кто-то нуждается в подключении розетки, кому-то необходимо установить светильник и т. д. Из этого выходит, что с операцией подбора требуемого сечения связана даже такая, казалось бы, незначительная процедура, как установка нового светильника.
Несоблюдение норм может привести к нарушению целостности проводки, что нередко становится причиной короткого замыкания или даже поражения электрическим током.
Если при выборе сечения кабеля допустить ошибку, и приобрести кабель с меньшей площадью проводника, то это приведёт к постоянному нагреву кабеля, что станет причиной разрушения его изоляции. Естественно, все это негативно влияет на продолжительность эксплуатации проводки — нередки случаи, когда через месяц после успешного монтажа электропроводка переставала работать, и требовалось вмешательство специалиста.
Следует помнить, что от правильно подобранного значения сечения кабеля напрямую зависит электро и пожаробезопасность в здании, а значит, и жизнь самих жильцов.
Конечно, каждый собственник желает как можно больше сэкономить, но не стоит делать это ценой своей жизни, ставя её под угрозу — ведь в результате короткого замыкания может случиться пожар, который вполне может уничтожить все имущество.
Во избежание этого, перед началом электромонтажных работ следует подобрать кабель оптимального сечения. Для подбора необходимо учитывать несколько факторов:
- общее количество электротехнических устройств, находящихся в помещении;
- совокупную мощность всех приборов и потребляемую ими нагрузку. К полученному значению следует добавить «про запас» 20–30%;
- затем, путём нехитрых математических расчётов, перевести полученное значение в сечение провода, учитывая при этом материал проводника.
Внимание! Ввиду более низкой электропроводимости, провода с алюминиевыми жилами должны приобретаться с большим сечением, нежели медные.
Что влияет на нагрев проводов
Если во время эксплуатации бытовых приборов нагревается проводка, то следует незамедлительно принять все необходимые меры для устранения этой проблемы. Факторов, влияющих на нагрев проводов, существует немало, но к основным можно отнести следующие:
- Недостаточная площадь сечения кабеля.
 Выражаясь доступным языком, можно сказать так — чем толще будут у кабеля жилы, тем больший ток он может передавать, не греясь при этом. Величина этого значения указывается в маркировке кабельной продукции. Также можно измерить сечение самостоятельно при помощи штангенциркуля (следует убедиться, что провод не находится под напряжением) или по марке провода.
Выражаясь доступным языком, можно сказать так — чем толще будут у кабеля жилы, тем больший ток он может передавать, не греясь при этом. Величина этого значения указывается в маркировке кабельной продукции. Также можно измерить сечение самостоятельно при помощи штангенциркуля (следует убедиться, что провод не находится под напряжением) или по марке провода. - Материал, из которого изготовлен провод. Медные жилы лучше передают напряжение до потребителя, и обладают меньшим сопротивлением, по сравнению с алюминиевыми. Естественно, они меньше греются.
- Тип жил. Кабель может быть одножильным (жила состоит из одного толстого стержня) или многожильным (жила состоит из большого числа маленьких проводков). Многожильный кабель более гибкий, но существенно уступает одножильному по допустимой силе передаваемого тока.
- Способ укладки кабеля. Плотно уложенные провода, находящиеся при этом в трубе, греются ощутимо сильнее, нежели открытая проводка.

- Материал и качество изоляции. Недорогие провода, как правило, имеют изоляцию низкого качества, что отрицательно сказывается на их устойчивости к воздействию высоких температур.
Как делается расчёт потребляемой мощности
Рассчитать приблизительное сечение кабеля можно и самостоятельно — необязательно прибегать к помощи квалифицированного специалиста. Полученные в результате расчётов данные можно использовать для покупки провода, однако, сами электромонтажные работы следует доверять только опытному человеку.
Последовательность действий при расчёте сечения такова:
- Составляется подробный список всех находящихся в помещении электрических приборов.
- Устанавливаются паспортные данные потребляемой мощности всех найденных устройств, после чего определяется непрерывность работы того или иного оборудования.
- Выявив значение потребляемой мощности от устройств, работающих постоянно, следует суммировать это значение, добавив к нему коэффициент, равный значению периодически включающийся электроприборов (то есть, если прибор будет работать всего 30% времени, то следует прибавить треть от его мощности).

- Далее ищем полученные значения в специальной таблице расчёта сечения провода. Для большей гарантии рекомендуется к полученному значению потребляемой мощности добавить 10-15%.
Для определения необходимых вычислений по подбору сечения кабелей электропроводки согласно их мощности внутри сети важно использовать данные о количестве электрической энергии, потребляемой устройствами и приборами тока.
На этом этапе необходимо учесть очень важный момент – данные электропотребляемых приборов дают не точное, а приближенное, усредненное значение. Поэтому к такой отметке необходимо добавлять около 5% от параметров, указанных компанией-производителем оборудования.
Большинство далеко не самых компетентных и квалифицированных электриков уверены в одной простой истине – для того, чтобы правильно провести электрические провода для источников освещения (к примеру, для светильников), необходимо брать провода с сечением, равным 0,5 мм², для люстр – 1,5 мм², а для розеток – 2,5 мм².
Об этом думают и так считают только некомпетентные электрики. Но что, если, например, в одном помещении одновременно работают микроволновка, чайник, холодильник и освещение, для которых нужны провода с разным сечением? Это может привести, к самым разным ситуациям: короткому замыканию, быстрой порче проводки и изоляционного слоя, а также к возгоранию (это редкий случай, но все же возможный).
Точно такая же не самая приятная ситуация может произойти, если человек будет подключать к одной и той же розетке мультиварку, кофеварку и, допустим, стиральную машину.
Особенности расчёта мощности скрытой проводки
Если проектной документацией подразумевается использование скрытой проводки, то необходимо приобретать кабельную продукцию «с запасом» — к полученному значению сечения кабеля следует прибавить порядка 20–30%. Это делается во избежание нагрева кабеля в процессе эксплуатации. Дело в том, что в условиях стеснённого пространства и отсутствия доступа воздуха нагрев кабеля происходит значительно интенсивнее, чем при монтаже открытой проводки. Если же в закрытых каналах предусматривается укладка не одного кабеля, а сразу нескольких, то следует увеличить сечение каждого провода не менее чем на 40%. Также не рекомендуется плотно укладывать различные провода — в идеале каждый кабель должен находиться гофротрубе, обеспечивающей его дополнительную защиту.
Дело в том, что в условиях стеснённого пространства и отсутствия доступа воздуха нагрев кабеля происходит значительно интенсивнее, чем при монтаже открытой проводки. Если же в закрытых каналах предусматривается укладка не одного кабеля, а сразу нескольких, то следует увеличить сечение каждого провода не менее чем на 40%. Также не рекомендуется плотно укладывать различные провода — в идеале каждый кабель должен находиться гофротрубе, обеспечивающей его дополнительную защиту.
Важно! Именно по значению потребляемой мощности профессиональные электрики ориентируются при выборе сечения кабеля, и только такой способ является корректным.
Как рассчитать сечения кабеля по мощности
При достаточном значении сечения кабеля электрический ток будет проходить до потребителя, не вызывая нагрева. Почему происходит нагрев? Постараемся объяснить максимально доступно. К примеру, в розетку включён чайник потребляемой мощностью 2 киловатта, но идущий к розетке провод может передать для него ток мощностью только 1 киловатт.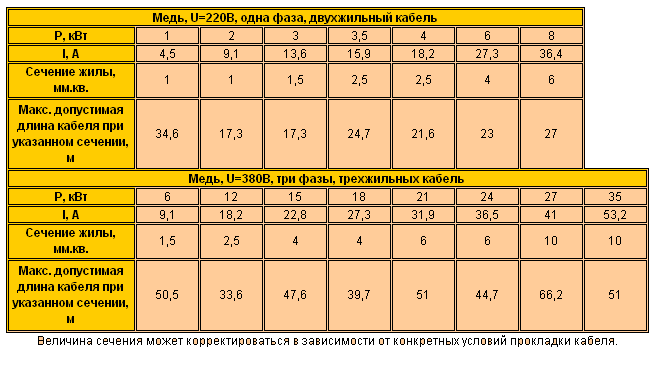 Пропускная способность кабеля связана с сопротивлением проводника — чем оно больше, тем меньший ток может передаваться по проводу. В результате высокого сопротивления в проводке и происходит нагрев кабеля, постепенно разрушающий изоляцию.
Пропускная способность кабеля связана с сопротивлением проводника — чем оно больше, тем меньший ток может передаваться по проводу. В результате высокого сопротивления в проводке и происходит нагрев кабеля, постепенно разрушающий изоляцию.
При соответствующем сечении электрический ток доходит до потребителя в полном объёме, и нагревание провода не происходит. Поэтому, проектируя электропроводку, следует учитывать потребляемую мощность каждого электрического прибора. Это значение можно узнать из технического паспорта на электроприбор или из наклеенной на нём этикетки. Суммируя максимальные значения и используя нехитрую формулу:
I=(P1+P2+…+Pn)/220
и получаем значение общей силы тока.
Pn обозначает указанную в паспорте мощность электроприбора, 220 — номинальный вольтаж.
Для трехфазной системы (380 В) формула выглядит так:
I=(P1+P2+….+Pn)/√3/380.
Полученное значение I измеряется в Амперах, и на основании него и подбирается соответствующее сечение кабеля.
Известно, что пропускная способность медного кабеля составляет 10 А/мм, для алюминиевого кабеля значение пропускной способности составляет 8 А/мм.
Для того чтоб рассчитать сечение кабеля нужно величину тока разделить на 8 или 10, в зависимости от вида кабеля. Полученный результат и будет размером сечения кабеля.
Например рассчитаем величину сечения кабеля для подключения стиральной машины, потребляемая мощность которой составляет 2400 Вт.
I=2400 Вт/220 В=10,91 А, округлив получаем 11 А.
Дальше, чтоб увеличить запас прочности, согласно правилу «пяти ампер» к полученному значению силы тока нужно прибавить еще 5 А:
11 А+5 А=16 А.
Если учитывать, что в квартирах используют трехжильные кабеля и посмотреть по таблице, то к 16 А близкое значение 19 А, поэтому для установки стиральной машины потребуется провод, сечение которого не меньше 2 мм².
Таблица сечения кабеля относительно величины силы тока
| Сечение токо- прово- дящей жилы(мм2) | Ток(А), для проводов, проложенных | |||||
|---|---|---|---|---|---|---|
| Откры- то | в одной трубе | |||||
| двух одно- жильных | трех одно- жильных | четырех одно- жильных | одного двух- жильного | одного трех- жильного | ||
| 0,5 | 11 | — | — | — | — | — |
| 0,75 | 15 | — | — | — | — | — |
| 1 | 17 | 16 | 15 | 14 | 15 | 14 |
| 1,2 | 20 | 18 | 16 | 15 | 16 | 14,5 |
| 1,5 | 23 | 19 | 17 | 16 | 18 | 15 |
| 2 | 26 | 24 | 22 | 20 | 23 | 19 |
| 2,5 | 30 | 27 | 25 | 25 | 25 | 21 |
| 3 | 34 | 32 | 28 | 26 | 28 | 24 |
| 4 | 41 | 38 | 35 | 30 | 32 | 27 |
| 5 | 46 | 42 | 39 | 34 | 37 | 31 |
| 6 | 50 | 46 | 42 | 40 | 40 | 34 |
| 8 | 62 | 54 | 51 | 46 | 48 | 43 |
| 10 | 80 | 70 | 60 | 50 | 55 | 50 |
| 16 | 100 | 85 | 80 | 75 | 80 | 70 |
| 25 | 140 | 115 | 100 | 90 | 100 | 85 |
| 35 | 170 | 135 | 125 | 115 | 125 | 100 |
| 50 | 215 | 185 | 170 | 150 | 160 | 135 |
| 70 | 270 | 225 | 210 | 185 | 195 | 175 |
| 95 | 330 | 275 | 255 | 225 | 245 | 215 |
| 120 | 385 | 315 | 290 | 260 | 295 | 250 |
| 150 | 440 | 360 | 330 | — | — | — |
| 185 | 510 | — | — | — | — | — |
| 240 | 605 | — | — | — | — | — |
| 300 | 695 | — | — | — | — | — |
| 400 | 830 | — | — | — | — | — |
Как выбрать сечения проводника
Существует ещё несколько критериев, которым должно соответствовать сечение используемых проводов:
- Длина кабеля.

- Тип используемых проводов. В бытовом электроснабжении используются 2 типа проводников — на основе меди или алюминия. Медные провода качественнее и обладают меньшим сопротивлением, но зато алюминиевые дешевле. При полном соответствии нормам, алюминиевая проводка справляется со своими задачами не хуже медной, так что необходимо тщательно взвесить свой выбор перед покупкой провода.
- Конфигурация электрощита. Если все провода, питающие потребителей, подключены к одному автомату, то именно он и будет являться слабым местом в системе.
 Сильная нагрузка приведёт к нагреву клеммных колодок, а несоблюдение номинала к его постоянному срабатыванию. Рекомендуется разделять электропроводку на несколько «лучей» с установкой отдельного автомата.
Сильная нагрузка приведёт к нагреву клеммных колодок, а несоблюдение номинала к его постоянному срабатыванию. Рекомендуется разделять электропроводку на несколько «лучей» с установкой отдельного автомата.
Для того, чтобы определить точные данные для выбора сечения кабелей электрической проводки, необходимо учитывать любые, даже самые незначительные параметры, такие как:
- Вид и тип изоляции электрической проводки;
- Длина участков;
- Способы и варианты прокладки;
- Особенности температурного режима;
- Уровень и процент влажности;
- Максимально возможная величина перегрева;
- Разница в мощностях всех приемников тока, относящихся к одной и той же группе. Все эти и многие другие показатели позволяют значительно увеличить эффективность и пользу от использования энергии в любых масштабах. Кроме того, правильные расчеты помогут избежать случаев перегревания или быстрого истирания изоляционного слоя.
Для того, чтобы правильно определить оптимальное кабельное сечение для любых человеческих бытовых нужд, необходимо во всех общих случаях использовать стандартизированные следующие правила:
- для всех розеток, которые будут монтироваться в квартире, необходимо использовать провода с соответствующим сечением в 3,5 мм²;
- для всех элементов точечного освещения необходимо использовать кабеля электрической проводки с сечением в 1,5 мм²;
- что же касается приборов повышенной мощности, то для них следует использовать кабеля с сечением в 4-6 мм².

Если в процессе монтажа или расчетов возникают некоторые сомнения, лучше не действовать вслепую. Идеальным вариантом будет обратиться к соответствующей таблице расчетов и стандартов.
Таблица сечения медного кабеля
| Сечение жил, проводящих ток (мм) | Медные жилы проводов и кабелей | |||
| Напряжение 220 В | Напряжение 380 В | |||
| Ток (А) | Мощность (кВТ) | Ток (А) | Мощность (кВТ) | |
| 1,5 | 19 | 4,1 | 16 | 10,5 |
| 2,5 | 27 | 5,9 | 25 | 16,5 |
| 4 | 38 | 8,3 | 30 | 19,8 |
| 6 | 46 | 10,1 | 40 | 26,4 |
| 10 | 70 | 15,4 | 50 | 33 |
| 16 | 80 | 18,7 | 75 | 49,5 |
| 25 | 115 | 25,3 | 90 | 59,4 |
| 35 | 135 | 29,7 | 115 | 75,9 |
| 50 | 175 | 38,5 | 145 | 95,7 |
| 70 | 215 | 47,3 | 180 | 118,8 |
| 95 | 265 | 57,2 | 220 | 145,2 |
| 120 | 300 | 66 | 260 | 171,6 |
Таблица сечения алюминиевого кабеля
| Сечение жил, проводящих ток (мм) | Алюминиевые жилы проводов и кабелей | |||
| Напряжение 220 В | Напряжение 380 В | |||
| Ток (А) | Мощность (кВТ) | Ток (А) | Мощность (кВТ) | |
| 2,5 | 22 | 4,4 | 19 | 12,5 |
| 4 | 28 | 6,1 | 23 | 15,1 |
| 6 | 36 | 7,9 | 30 | 19,8 |
| 10 | 50 | 11 | 39 | 25,7 |
| 16 | 60 | 13,2 | 55 | 36,3 |
| 25 | 85 | 18,7 | 70 | 46,2 |
| 35 | 100 | 22 | 85 | 56,1 |
| 50 | 135 | 29,7 | 110 | 72,6 |
| 70 | 165 | 36,3 | 140 | 92,4 |
| 95 | 200 | 44 | 170 | 112,2 |
| 120 | 230 | 50,6 | 200 | 132 |
От верно подобранного сечения кабеля напрямую зависит безопасность объекта — поэтому необходимо подойти к процедуре выбора со всей ответственностью. Рекомендуется также проконсультироваться со специалистами перед приобретением проводов — опытный электрик подскажет наиболее оптимальный вариант.
Рекомендуется также проконсультироваться со специалистами перед приобретением проводов — опытный электрик подскажет наиболее оптимальный вариант.
Экономия при покупке часто выходит боком — нередко владельцы квартир или домов приобретают алюминиевый кабель взамен медного, не учитывая тот факт, что его сечение должно быть больше. В итоге смонтированная электропроводка сильно греется, и в течение достаточно малого времени требуется полная замена проводов, что не слабо ударит по кошельку собственника жилья. К тому же, это ещё и чрезвычайно опасно — многие любители сэкономить остались в итоге без крыши над головой.
Если возникли сомнения в собственных силах, рекомендуется обратиться к специалисту — только в этом случае можно гарантировать безопасность для жильцов и продолжительность работы новой электропроводки.
Расчет сечения кабеля. По мощности, току, длине | Техно 206
Как рассчитать кабель по току, напряжению и длине.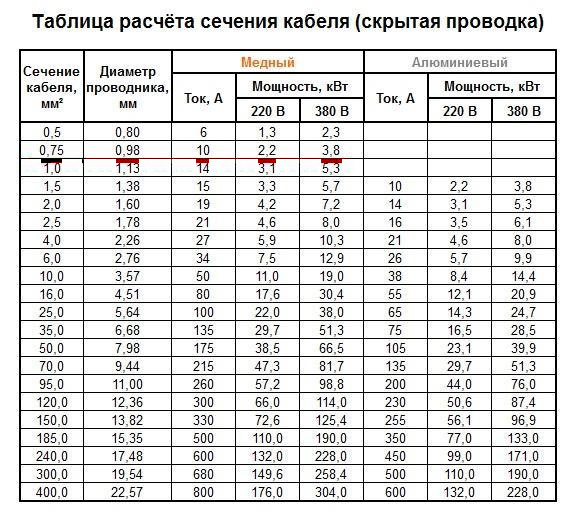 Кабели, как известно, бывают разного сечения, материала и с разным количеством жил. Какой из них надо выбрать, чтобы не переплачивать, и одновременно обеспечить безопасную стабильную работу всех электроприборов в доме. Для этого необходимо произвести расчет кабеля. Расчет сечения проводят, зная мощность приборов, питающихся от сети, и ток, который будет проходить по кабелю. Необходимо также знать несколько других параметров проводки.
Кабели, как известно, бывают разного сечения, материала и с разным количеством жил. Какой из них надо выбрать, чтобы не переплачивать, и одновременно обеспечить безопасную стабильную работу всех электроприборов в доме. Для этого необходимо произвести расчет кабеля. Расчет сечения проводят, зная мощность приборов, питающихся от сети, и ток, который будет проходить по кабелю. Необходимо также знать несколько других параметров проводки.
Основные правила
При прокладке электросетей в жилых домах, гаражах, квартирах чаще всего используют кабель с резиновой или ПВХ изоляцией, рассчитанный на напряжение не более 1 кВ. Существуют марки, которые можно применять на открытом воздухе, в помещениях, в стенах (штробах) и трубах. Обычно это кабель ВВГ или АВВГ с разной площадью сечения и количеством жил.
Применяют также провода ПВС и шнуры ШВВП для подсоединения электрических приборов.
После расчета выбирается максимально допустимое значение сечения из ряда марок кабеля.
Основные рекомендации по выбору сечения находятся в Правилах устройства электроустановок (ПУЭ). Выпущено 6-е и 7-е издания, в которых подробно описывается, как прокладывать кабели и провода, устанавливать защиту, распределяющие устройства и другие важные моменты.
За нарушение правил предусмотрены административные штрафы. Но самое главное состоит в том, что нарушение правил может привести к выходу из строя электроприборов, возгоранию проводки и серьезным пожарам. Ущерб от пожара измеряется порой не денежной суммой, а человеческими жертвами.
Важность правильного выбора сечения
Почему расчет сечения кабеля так важен? Чтобы ответить, надо вспомнить школьные уроки физики.
Ток протекает по проводам и нагревает их. Чем сильнее мощность, тем больше нагрев. Активная мощность тока вычисляют по формуле:
P=U*I* cos φ=I²*R
R – активное сопротивление.
Как видно, мощность зависит от силы тока и сопротивления. Чем больше сопротивление, тем больше выделяется тепла, то есть тем сильнее провода нагреваются. Аналогично для тока. Чем он больше, тем больше греется проводник.
Сопротивление в свою очередь зависит от материала проводника, его длины и площади поперечного сечения.
R=ρ*l/Sρ – удельное сопротивление;
l – длина проводника;
S– площадь поперечного сечения.
Видно, что чем меньше площадь, тем больше сопротивление. А чем больше сопротивление, тем проводник сильнее нагревается.
Площадь рассчитывается по формуле:
S=π*d²/4d – диаметр.
Не стоит также забывать удельное сопротивление. Оно зависит от материала, из которого сделаны провода. Удельное сопротивление алюминия больше, чем меди. Значит, при одинаковой площади сильнее нагреваться будет алюминий. Сразу становится понятно, почему алюминиевые провода рекомендуют брать большего сечения, чем медные.
Значит, при одинаковой площади сильнее нагреваться будет алюминий. Сразу становится понятно, почему алюминиевые провода рекомендуют брать большего сечения, чем медные.
Чтобы каждый раз не вдаваться в длинный расчет сечения кабеля, были разработаны нормы выбора сечения проводов в таблицах.
Расчет сечения провода по мощности и токуРасчет сечения провода зависит от суммарной мощности, потребляемой электрическими приборами в квартире. Ее можно рассчитать индивидуально, или воспользоваться средними характеристиками.
Для точности расчетов составляют структурную схему, на которой изображены приборы. Узнать мощность каждого можно из инструкции или прочитать на этикетке. Наибольшая мощность у электрических печек, бойлеров, кондиционеров. Суммарная цифра должна получиться в диапазоне приблизительно 5-15 кВт.
Зная мощность, по формуле определяют номинальную силу тока:
I=(P*K)/(U*cos φ)P – мощность в ваттах
U=220 Вольт
K=0,75 – коэффициент одновременного включения;
cos φ=1 для бытовых электроприборов;
Если сеть трехфазная, то применяют другую формулу:
I=P/(U*√3*cos φ)U=380 Вольт
Рассчитав ток, надо воспользоваться таблицами, которые представлены в ПУЭ, и определить сечение провода. В таблицах указан допустимый длительный ток для медных и алюминиевых проводов с изоляцией различного типа. Округление всегда производят в большую сторону, чтобы был запас.
В таблицах указан допустимый длительный ток для медных и алюминиевых проводов с изоляцией различного типа. Округление всегда производят в большую сторону, чтобы был запас.
Можно также обратиться к таблицам, в которых сечение рекомендуют определять только по мощности.
Разработаны специальные калькуляторы, по которым определяют сечение, зная потребляемую мощность, фазность сети и протяженность кабельной линии. Следует обращать внимание на условия прокладки (в трубе или на открытом воздухе).
Влияние длины проводки на выбор кабеляЕсли кабель очень длинный, то возникают дополнительные ограничения по выбору сечения, так как на протяженном участке происходят потери напряжения, которые в свою очередь приводят к дополнительному нагреву. Для расчета потерь напряжения используют понятие «момент нагрузки». Его определяют как произведение мощности в киловаттах на длину в метрах. Далее смотрят значение потерь в таблицах. Например, если потребляемая мощность составляет 2 кВт, а длина кабеля 40 м, то момент равняется 80 кВт*м. Для медного кабеля сечением 2,5 мм². это означает, что потери напряжения составляют 2-3%.
Например, если потребляемая мощность составляет 2 кВт, а длина кабеля 40 м, то момент равняется 80 кВт*м. Для медного кабеля сечением 2,5 мм². это означает, что потери напряжения составляют 2-3%.
Если потери будут превышать 5%, то необходимо брать сечение с запасом, больше рекомендованного к использованию при заданном токе.
Расчетные таблицы предусмотрены отдельно для однофазной и трехфазной сети. Для трехфазной момент нагрузки увеличивается, так как мощность нагрузки распределяется по трем фазам. Следовательно, потери уменьшаются, и влияние длины уменьшается.
Потери напряжения важны для низковольтных приборов, в частности, газоразрядных ламп. Если напряжение питания составляет 12 В, то при потерях 3% для сети 220 В падение будет мало заметно, а для низковольтной лампы оно уменьшится почти вдвое. Поэтому важно размещать пускорегулирующие устройства максимально близко к таким лампам.
Расчет потерь напряжения выполняется следующим образом:
∆U = (P∙r0+Q∙x0)∙L/ UнP — активная мощность, Вт.
Q — реактивная мощность, Вт.
r0 — активное сопротивление линии, Ом/м.
x0 — реактивное сопротивление линии, Ом/м.
Uн – номинальное напряжение, В. (оно указывается в характеристиках электроприборов).
L — длинна линии, м.
Ну а если попроще для бытовых условий:
ΔU=I*RR – сопротивление кабеля, рассчитывается по известной формуле R=ρ*l/S;
I – сила тока, находят из закона Ома;
Допустим, у нас получилось, что I=4000 Вт/220 В=18,2 А.
Сопротивление одной жилы медного провода длиной 20 м и площадью 1,5 мм кв. составило R=0,23 Ом. Суммарное сопротивление двух жил равняется 0,46 Ом.
Тогда ΔU=18,2*0,46=8,37 В
В процентном соотношении
8,37*100/220=3,8%
На длинных линиях от перегрузок и коротких замыканий устанавливают автоматические выключатели с тепловыми и электромагнитными расцепителями.
формулы и таблицы ⋆ Прорабофф.рф
Выбор сечения кабеля мощности необходим при проведении проводки в помещение. Начинать этот процесс лучше с детального плана и полных расчетов до покупки нужных материалов.
Их в магазинах огромное разнообразие. Сначала требуется провести расчет сечения кабеля по нагрузке. Даже при самых тщательных измерениях, он все равно будет приблизительным.
При том, что заранее продуманы все осветительные приборы и их мощность, учтена вся бытовая техника, общее значение их мощности будет усредненным. К полученной цифре лучше прибавить еще процентов 5 на всякий случай.
Поэтому большинство людей считают, что этих показателей хватит для выбора стандартного медного кабеля:
- 0,5мм2 для кабелей для точечных светильников, установленных в доме.
- 1,5мм2 станет достойным выбором для проводов у люстр.
- 2,5мм2 подходит для проводов розеток.
С точки зрения бытового потребления энергии с учетом всех электроприборов, эти размеры выглядят приемлемо. Так считается, пока, например, на кухне не включатся в одно время холодильник, микроволновка, электрочайник и тостер. Результат может стать плачевным. Сечение кабеля и мощность нагрузки тесно взаимосвязаны.
Так считается, пока, например, на кухне не включатся в одно время холодильник, микроволновка, электрочайник и тостер. Результат может стать плачевным. Сечение кабеля и мощность нагрузки тесно взаимосвязаны.
При проведении проводки требуется учитывать расчет сечения кабеля по диаметру жилы провода. Не всегда указания на маркировке покупаемого провода бывают правдивой. Для избегания домашних «аварий» в дальнейшем, лучше самим произвести расчет. Существует несколько достаточно простых способов.
- Воспользоваться специальными измерительными инструментами – электронным микрометром или штангенциркулем. Этот способ быстрый, но требует затрат на эти приборы.
- «Дедовский» метод при наличии карандаша, провода и линейки. Кабель зачищается и плотными витками наматывается на карандаш. Затем измеряется длина намотки и делится на количество жил. Витков обязано быть минимум 15 для лучшей точности.
- Применение готовых расчетов сечения кабеля по диаметру жил в таблицах.

Важно помнить: расчет ведется только по диаметру открытой жилы. Провод вполне может выглядеть должного размера за счет изоляции.
При выборе кабеля для применения в бытовых целях стоит учитывать расчет сечения кабеля по длине. Для этого заранее ставятся отметины на поверхности во всех точках, где будут розетки, включатели, светильники и остальное. Делаются обмеры расстояния, и кабель режется исходя из них, но с хорошим запасом.
Формула расчета сечения кабеля состоит из внесения данных длины, площади его сечения и удельного сопротивления проводника. Затем следует рассчитать данные токов, поделив суммарную мощность нагрузки на размер напряжения в сети. Далее рассчитывается вероятная величина понижения напряжения. После этого оценивается размер уменьшения напряжения к номинальному напряжению в сети в процентном соотношении, и выбирается сечение провода, не превышающий 5 процентный рубеж.
Формула по силе тока – I= P/U x cosф. В этой формуле I – сила тока (Ампер) P – суммарное показание мощности (Ватт) U – сила напряжения (В) cosф – показатель, равный единице.![]()
При показателе общей суммарной мощности потребителей в 3,8кВт, их надо разделить на 220Вольт. Получится 17,3 Ампера. Определяясь по данным таблицы ПУЭ, выбор сечения кабеля из меди или алюминия найти легко. С показателем силы тока в 17,3 (А) сечение медного кабеля составляет 1,5мм2.
Сечение кабеля и мощность – таблица представлена в статье. Это общедоступная таблица расчета сечения кабеля по мощности.
Сечение кабеля для ввода в дом или квартиру
Как уже говорилось выше, после подсчетов всей нагрузки и выбора провода по его составу, можно проводить последние вычисления: сечение вводного кабеля в квартиру. Возьмем за пример квартиру из двух комнат, в которой вся нагрузка распределяется на силовую и осветительную. Главная силовая нагрузка – это, обычно, розетки в ванной и на кухне. Именно здесь расположено большинство бытовых приборов – бойлер, стиральная машинка, микроволновки, холодильник и множество мелких помощников по хозяйству.
Для этой группы розеток выберем провод с сечением 2,5мм2. Это допустимое сечение кабеля при условии, что нагрузка распределяется на несколько розеток. В случае использования всех приборов в одной розетке, такое сечение категорически не подходит. В такой ситуации требуется максимальное сечение кабеля до 6мм2.
Окончательный вывод о размере сечения кабеля можно делать только после всех расчетов. Например, в комнатах на все розетки идет малое распределение нагрузки и там сечение провода допускает 1,5мм2.
Следует помнить, раз нагрузка в помещениях квартиры разная, значит покупать провод необходимо с разным сечением.
Самая большая нагрузка в квартире идет на вводном участке, поэтому там сечение так же должно быто максимальным – 4-6мм2. При расчетах желательно опираться на данные в ПУЭ, но там они часто завышены. Рассмотрим на примере, какое сечение кабеля для электроплиты требуется, а какое рекомендуется.
Электроплита относится к категории силовой нагрузки и по стандарту ей вполне подойдет кабель с сечением 2,5мм2. Но в ПУЭ эти показатели завышены, с целью обезопасить жилое помещение от электрических аварий.
Но в ПУЭ эти показатели завышены, с целью обезопасить жилое помещение от электрических аварий.
Что учитывается при подключении электроплиты:
- Во-первых, показатели инструкции к прибору и рекомендации ПУЭ. Владельца чудо техники ожидают повышенные денежные затраты, если к электроприбору, имеющему силовые показатели сечения 2,5мм2 поставить провода с увеличенным сечением 6мм2, рекомендуемые ПУЭ. При этом переплата составит 50-70% от цены кабеля с сечением 2,5мм2.
- Во-вторых, требуется проверить электросчетчик. Нужно, чтобы вводный в квартиру кабель был обязательно трехжильным. Он в обязательном порядке обязан быть 6мм2 по меди.
- В-третьих, проверяется автоматический вводный выключатель. Номинальный ток в нем должен быть 45-50 Ампер.
- В-четвертых, нужно позаботиться об устройстве защитного отключения.
- В-пятых, правильно выбрать силовую розетку. При однофазовом подключении электроплиты, она должна быть на 25-32 Ампера и с тремя контактами.

И только после всех перечисленных действий стоит приступать к выбору кабеля. Его сечение по меди не должно быть ниже 4мм2.
Установление проводки в квартире или доме требует высокого профессионализма. Вопрос о том, чтобы сделать все своими руками не должен даже подниматься, если владелец помещения не имеет нужного образования и годы практики.
Мало построить дом или сделать капитальный ремонт в квартире. Электропроводка – это важнейшая часть при проектировании здания. Именно она делает помещение пригодным для жилья, давая ему освещение, тепло и необходимые для жизни коммуникации. Установленная проводка может стать помощником для владельца помещения, а может быть его серьезной проблемой. Следует тщательно изучить, как правильно рассчитать сечение кабеля, сколько его нужно, а еще лучше, доверить это специалистам. Слишком тонкая и опасная для жизни наука – электропроводка.
Расчет сечения кабеля по току — используем калькуляторы и таблицы для расчета
При ремонте и проектировании электрооборудования появляется необходимость правильно выбирать провода. Можно воспользоваться специальным калькулятором или справочником. Но для этого необходимо знать параметры нагрузки и особенности прокладки кабеля.
Можно воспользоваться специальным калькулятором или справочником. Но для этого необходимо знать параметры нагрузки и особенности прокладки кабеля.
Блок: 1/6 | Кол-во символов: 248
Источник: https://odinelectric.ru/wiring/kak-rasschitat-neobhodimoe-sechenie-provoda-po-moshhnosti-nagruzki
Для чего учиться делать расчеты?
Прежде всего, осуществление таких математических действий требуется для обеспечения безопасности помещения. Любой кабель или провод являются основными средствами для передачи и распределения тока, подводящего к электрическим приборам.
Практически каждый день, электрику необходимо подключить где-то электрическую кухонную плиту, починить розетку, установить новый светильник. Одним словом, необходимость произвести расчет сечения провода обусловлено обеспечением постоянного притока электроэнергии и избежание различных неприятных ситуаций, которые включают в себя некоторые повреждения в самой электрической проводке.
Если осуществить подключение прибора по кабелю и сечение выбранных проводов будет небольшим, неспособным в нужных объемах обеспечивать нормальное функционирование прибора, в таком случае сам кабель будет перегреваться, что, в свою очередь, приводит к медленному разрушению изоляции. Как следствие возможного возникновения короткого замыкания. В результате снижения надежности и срока службы эксплуатации электропроводки в помещении резко упадет или, более того, исчезнет, то есть сгорит.
Следует отметить, что правильный выбор сечения провода обеспечивает пожаробезопасность и электробезопасность в помещении.
Наиболее распространенной бытовой ситуацией, на сегодняшний день, является попытка сэкономить на стоимости провода, что неизбежно приводит к возникновению коротких замыканий или пожаров.
Именно по этой причине, перед тем как осуществлять электрическую проводку кабеля, выбрать сечение используемых проводов по всей квартире необходимо определить:
- количество бытовых приборов, которые будут находиться в квартире;
- суммарную мощность и потребляемую нагрузку приборов с учетом небольшого запаса;
- осуществить математические расчеты;
- определить тип и сечение необходимых проводов.

Блок: 2/6 | Кол-во символов: 1841
Источник: https://220.guru/electroprovodka/provoda-kabeli/raschet-secheniya-po-moshhnosti.html
Если покупаете провод и замеряете его диаметр, то не забудьте, что площадь рассчитывается по формуле:
S=π*d²/4
d – диаметр.
Не стоит также забывать удельное сопротивление. Оно зависит от материала, из которого сделаны провода. Удельное сопротивление алюминия больше, чем меди. Значит, при одинаковой площади сильнее нагреваться будет алюминий. Сразу становится понятно, почему алюминиевые провода рекомендуют брать большего сечения, чем медные.
Чтобы каждый раз не вдаваться в длинный расчет сечения кабеля, были разработаны нормы выбора сечения проводов в таблицах.
Расчет сечения провода по мощности и токуРасчет сечения провода зависит от суммарной мощности, потребляемой электрическими приборами в квартире. Ее можно рассчитать индивидуально, или воспользоваться средними характеристиками.
Для точности расчетов составляют структурную схему, на которой изображены приборы. Узнать мощность каждого можно из инструкции или прочитать на этикетке. Наибольшая мощность у электрических печек, бойлеров, кондиционеров. Суммарная цифра должна получиться в диапазоне приблизительно 5-15 кВт.
Блок: 2/4 | Кол-во символов: 1080
Источник: https://electrosam.ru/glavnaja/jelektrotehnika/raschjoty/raschet-secheniia-kabelia/
Что влияет на нагрев проводов
Если во время эксплуатации бытовых приборов нагревается проводка, то следует незамедлительно принять все необходимые меры для устранения этой проблемы. Факторов, влияющих на нагрев проводов, существует немало, но к основным можно отнести следующие:
- Недостаточная площадь сечения кабеля. Выражаясь доступным языком, можно сказать так — чем толще будут у кабеля жилы, тем больший ток он может передавать, не греясь при этом. Величина этого значения указывается в маркировке кабельной продукции.
 Также можно измерить сечение самостоятельно при помощи штангенциркуля (следует убедиться, что провод не находится под напряжением) или по марке провода.
Также можно измерить сечение самостоятельно при помощи штангенциркуля (следует убедиться, что провод не находится под напряжением) или по марке провода. - Материал, из которого изготовлен провод. Медные жилы лучше передают напряжение до потребителя, и обладают меньшим сопротивлением, по сравнению с алюминиевыми. Естественно, они меньше греются.
- Тип жил. Кабель может быть одножильным (жила состоит из одного толстого стержня) или многожильным (жила состоит из большого числа маленьких проводков). Многожильный кабель более гибкий, но существенно уступает одножильному по допустимой силе передаваемого тока.
- Способ укладки кабеля. Плотно уложенные провода, находящиеся при этом в трубе, греются ощутимо сильнее, нежели открытая проводка.
- Материал и качество изоляции. Недорогие провода, как правило, имеют изоляцию низкого качества, что отрицательно сказывается на их устойчивости к воздействию высоких температур.

Блок: 3/7 | Кол-во символов: 1434
Источник: http://remontnichok.ru/elektrichestvo/raschet-secheniya-kabelya-po-moshchnosti-prakticheskie-sovety-ot-professionalov
Зная мощность, по формуле определяют номинальную силу тока:
I=(PK)/(Ucos φ)
P – мощность в ваттах
U=220 Вольт
K=0,75 – коэффициент одновременного включения;
cos φ=1 для бытовых электроприборов;
Если сеть трехфазная, то применяют другую формулу:
I=P/(U√3cos φ)
U=380 Вольт
Рассчитав ток, надо воспользоваться таблицами, которые представлены в ПУЭ, и определить сечение провода. В таблицах указан допустимый длительный ток для медных и алюминиевых проводов с изоляцией различного типа. Округление всегда производят в большую сторону, чтобы был запас.
Можно также обратиться к таблицам, в которых сечение рекомендуют определять только по мощности.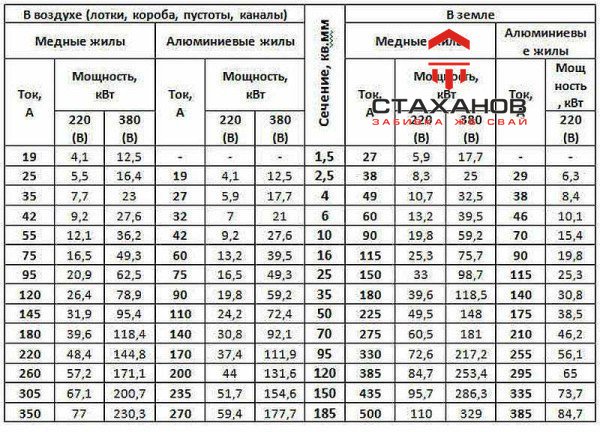
Разработаны специальные калькуляторы, по которым определяют сечение, зная потребляемую мощность, фазность сети и протяженность кабельной линии. Следует обращать внимание на условия прокладки (в трубе или на открытом воздухе).
Влияние длины проводки на выбор кабеляЕсли кабель очень длинный, то возникают дополнительные ограничения по выбору сечения, так как на протяженном участке происходят потери напряжения, которые в свою очередь приводят к дополнительному нагреву. Для расчета потерь напряжения используют понятие «момент нагрузки». Его определяют как произведение мощности в киловаттах на длину в метрах. Далее смотрят значение потерь в таблицах. Например, если потребляемая мощность составляет 2 кВт, а длина кабеля 40 м, то момент равняется 80 кВт*м. Для медного кабеля сечением 2,5 мм кв. это означает, что потери напряжения составляют 2-3%.
Если потери будут превышать 5%, то необходимо брать сечение с запасом, больше рекомендованного к использованию при заданном токе.
Расчетные таблицы предусмотрены отдельно для однофазной и трехфазной сети. Для трехфазной момент нагрузки увеличивается, так как мощность нагрузки распределяется по трем фазам. Следовательно, потери уменьшаются, и влияние длины уменьшается.
Потери напряжения важны для низковольтных приборов, в частности, газоразрядных ламп. Если напряжение питания составляет 12 В, то при потерях 3% для сети 220 В падение будет мало заметно, а для низковольтной лампы оно уменьшится почти вдвое. Поэтому важно размещать пускорегулирующие устройства максимально близко к таким лампам.
Блок: 3/4 | Кол-во символов: 2180
Источник: https://electrosam.ru/glavnaja/jelektrotehnika/raschjoty/raschet-secheniia-kabelia/
А для чего вообще необходимо рассчитывать сечение проводов? Нельзя ли ограничиться подбором «на глаз»?
Нет, нельзя, так как совсем несложно впасть в две крайности:
- Проводник недостаточного сечения начинает сильно перегреваться.
 Это ведет к оплавлению изоляции проводки, созданию условий для самовозгорания, для коротких замыканий. Все это становится причиной разрушительных пожаров, часто сопровождающихся человеческими трагедиями.
Это ведет к оплавлению изоляции проводки, созданию условий для самовозгорания, для коротких замыканий. Все это становится причиной разрушительных пожаров, часто сопровождающихся человеческими трагедиями. - Проводники избыточного диаметра, безусловно, такими опасностями не грозят. Но зато они и существенно дороже (особенно если разговор идет о медных кабелях), и не столь удобны в работе. Получаются совершенно неоправданные материальные и трудовые затраты.
Так что руководствоваться следует принципом разумной достаточности. Тем более что произвести необходимые вычисления – по силам каждому, кто хоть немного разбирается в азах математики и физики.
Для начала вспомним некоторые понятия, многим, наверное, и без того хорошо известные. Но просто для того, чтобы в дальнейшем изложении не появилось разночтений.
Провода одножильные и многожильныеС этим вопросом часто бывает путаница, в том числе в статьях, опубликованных на интернет-сайтах.
Итак, в качестве проводника в проводах и кабелях может использоваться одна проволока — с точки зрения электрической проводимости — это оптимальный вариант.
Но для достижения гибкости кабельной продукции приходится использовать более сложные конструкции – множество тонких проволочек, обычно скрученных при этом в «косичку». Чем больше таких проволочек – тем более гибким получается проводник.
Однако, это не следует путать с многожильностью провода. Под отдельной жилой подразумевается именно отдельный проводник. Чтобы стало понятнее – смотрим на иллюстрацию.
На картинке ниже – примеры одножильного провода. Просто с левой стороны – жесткий однопроволочный, а с правой – более гибкий многопроволочный вариант.
И слева, и справа — это одножильный провод.
Если провод (кабель) конструктивно совмещает два изолированных друг от друга проводника или больше, он становится двухжильным, трехжильным и т.п. Но он также может оставаться одно- или многопроволочным.
Двухжильный многопроволочный провод
Аналогичная ситуация и с кабелями. По определению, кабель – это конструкция из нескольких изолированных друг от друга проводников, заключенных в общую изолирующую и защитную оболочку. А вот проводники также могут быть одно- или многопроволочными.
Трехжильные силовые кабели – с однопроволочными или многопроволочными жилами
Жесткие однопроволочные изделия хороши для неподвижных участков проводки, например, вмуровываемых в стены. Многопроволочные провода и кабели отлично подходят для тех участков, где бывает нужна подвижность — типичным примером являются шнуры питания бытовой техники и осветительных приборов.
Итак, все последующие расчеты будут вестись для сечения жилы провода или кабеля.
При оценке условий расположения проводов в дальнейшем могут быть варианты, когда придется представлять разницу, например, между тремя одножильными проводами, протянутыми в одной трубе, или одним трехжильным кабелем.
Диаметр и площадь поперечного сечения проводаДва взаимосвязанных параметра, которые порой по неопытности путают. Смотрим на схему – по ней все станет понятно.
Слева – диаметр проводника (жилы), измеряется в миллиметрах. Справа – площадь поперечного сечения проводника, измеряется в мм².
Во всех справочника обычно используется параметр сечения, так как именно по этому критерию производится классификация различных марок проводов и кабелей.
Но это хорошо, если известна марка кабеля (провода). Если нет, то сечение остается подсчитать, опираясь на диаметр, который можно измерить штангенциркулем или микрометром.
Диаметр жилы (проволоки) поддается обычному измерению. Площадь сечения – только расчёту.
Формулу площади круга должны, наверное, помнить все. Но тем не менее – приведем ее на всякий случай.
Sc = π × d² / 4 ≈ 3.14 × d² / 4 ≈ 0.785 × d²
Знак «примерно равно» применен только потому, что взято округление числа π до сотых, всем известное значение π ≈ 3,14. Но в нашем случае такой точности – более чем достаточно!
Это формула сечения однопроволочного проводника. А если нужно найти сечение неизвестного провода, с многопроволочной жилой?
Тоже ничего сложного. Жила распушается, чтобы появилась возможность подсчитать количество проволочек в «косичке». И останется только микрометром или штангенциркулем промерить диаметр одной проволочки.
Sc = n × π × d² / 4 ≈ n × 3.14 × d² / 4 ≈ 0.785 × n × d²
где n – это количество проволочек в одной жиле.
Калькулятор пересчёта диаметра проводника в площадь его поперечного сеченияПерейти к расчётам
Основные электрические параметры цепиПри проведении расчетов нам могут понадобиться формулы, показывающими взаимосвязь между основными электрическими параметрами.
I = U / R
I — сила тока, ампер, А.
U — напряжение (разность потенциалов), вольт, В.
R — электрическое сопротивление, ом, Ом.
Из этой формулы несложно вывести другие:
U = I × R
R = U / I
- Теперь обратимся к мощности электрического тока.
Для начала – работа, выполняемая электрическим током. Она равна произведению силы тока на напряжение и на длительность промежутка времени, в течение которого она выполнялась.
А = I × U × Δt
А — работа электрического тока, джоулей, Дж.
Δt — длительность периода, секунд, с.
Но более наглядной величиной всегда является мощность, то есть показатель работы, выполненной за единицу времени, например, секунду.
P = A / Δt = I × U × Δt / Δt = I × U
P — мощность электрического тока, джоулей в секунду или ватт, Вт.
- Отсюда напрашивается целый каскад производных формул, описывающих взаимосвязи напряжения, силы тока, сопротивления и мощности между собой. Чтобы не перечислять все формулы «в столбик», можно привести хорошо понятное графическое их представление.
Графическое представление формул взаимосвязей основных электрических параметров.
- Вернемся к сопротивлению проводника. Как оно выражается через ток и напряжение – мы уже знаем.
Но оно в первую очередь зависит от материала изготовления проводника и его геометрических размеров. Описывается эта зависимость следующей формулой:
R = ρ × L / S
ρ — удельное сопротивление материала, из которого изготовлен проводник. Показывает, какое сопротивление имеет проводник длиной 1 метр с площадью поперечного сечения 1 мм².
Как правило, на практике в электротехнике чаще всего встречаются алюминий и медь. Реже применяются стальные проводники, но обычно – лишь в качестве каких-то токонесущих деталей электротехнической арматуры.
Для алюминия удельное сопротивление равно 0,029 Ом×м, у меди оно пониже – 0,0175 Ом×м.
L — длина линии (участка цепи) метров, м.
S — площадь поперечного сечения проводника, мм²
Эти соотношения полезно знать, так как иногда приходится оценивать собственные резистивные потери мощности на линиях большой протяженности.
- Акцентируем внимание еще на одном взаимоотношении, которое, в принципе, уже было рассмотрено выше. Это – количество тепла, выделяемое проводником при прохождении по нему электрического тока. Описывается уравнением Джоуля-Ленца.
Q = I² × R × Δt
Как видно, нагрев проводника (Q) лежит в квадратичной зависимости от силы тока (I) и от сопротивления (R). Понятно, что при всех остальных равных параметрах медный провод будет иметь более низкое сопротивление, нежели алюминиевый, то есть при одинаковой нагрузке греться станет существенно меньше.
Так оно и есть – это будет очень хорошо заметно дальше, при работе с таблицами.
- Можно еще вспомнить понятие плотности тока. Здесь все относительно просто – это количество ампер на единицу площади сечения проводника. Этот термин будет задействован в одном из способов оценки проводки.
Далеко не все их показанных формул и определений понадобятся для правильного подбора сечения проводника. Но зато они помогают более «рельефно» представить взаимосвязи между разными величинами.
Материалы изготовления проводкиОб этом уже вкратце говорилось – в подавляющем большинстве случаев используются медь и алюминий. Провода из иных металлов и сплавов если и встречаются, то имеют очень узкую специализацию.
Медь выигрывает у алюминия практически по всем статьям!
Сравнение меди и алюминия практически по всем статьям показывает ее преимущество.
- Удельное сопротивление даже просто в «чистом виде» у меди практически в полтора раза ниже.
- Оба этих металла от контакта с кислородом покрываются тонким слоем окислов. Однако, к меди этот слой практически не становится препятствием для токопроводимости. То есть в местах контактных соединений особых проблем не возникает (низкое переходное сопротивление).
А вот окислы алюминия по своим качествам близки к диэлектрикам. И проводимость обеспечивается только тем, что этот слой очень тонок. В местах механических контактов проблем значительно больше. Поэтому рекомендуется зачистка проводников, а также использование специальных смазок, предотвращающих поверхностную коррозию алюминия.
- Медь прочнее алюминия. Она в меру пластична, что позволяет достигать надёжных контактов при обжиме. Сломать медный проводник механическим воздействием – довольно сложно.
Переломить же алюминиевый провод можно буквально через несколько изгибов по одному месту. Недостаток упругости этого металла (слишком уж высокая пластичность) приводит к тому, что после выполнения скруток или обжима в клеммах, то есть при стабилизировавшейся механической нагрузке, алюминий продолжает «течь». А это значит, что надежность механических контактных соединений всегда постоянно снижается и требует регулярной подтяжки.
- Оптимальный вариант контактов для любого металла – это сварка или пайка. Но и по этим позициям медь впереди. Произвести пайку меди можно, не прибегая к каким-то сложным технологическим приёмам. Пайка или сварка алюминия требует использования специальных припоев и флюсов, и неопытному человеку выполнить эту операцию – крайне затруднительно.
- Единственные позиции, по которым алюминий обходит медь – он втрое легче и значительно дешевле. Этим и объясняется его широкое использование в эпоху массового городского многоэтажного строительства. Сейчас же по действующим СНиП в качестве проводки в жилых домах должна использоваться исключительно медь.
Блок: 2/5 | Кол-во символов: 10156
Источник: https://stroyday.ru/stroitelstvo-doma/elektroxozyajstvo/raschet-secheniya-kabelya-po-toku.html
Как делается приблизительный расчет потребляемой мощности?
Для того что бы узнать как определить сечение провода по мощности необходимо выполнить ряд последовательных действий:
- Делаем полный список используемых электрических приборов в данном помещении.
- Определить общую потребляемую мощность всего оборудования, которое находится в помещении. Для этого берем лист, на котором отмечен весь список приборов и помечаем напротив каждого его потребляемую мощность. Определить это значение возможно, сняв показания с этикетки на каждом приборе или изучить листок-вкладыш от техники.
- Суммируем все полученные значения.
- Определяем какие приборы будут находиться в непрерывной работе, сколько единиц в периодичной и число редко используемых. Такие мероприятия необходимы для расчета более точного значения сечение всех проводов.
- Суммируем мощность постоянно работающих приборов и периодически включающих. Определяем приблизительное время работы проводки с такой нагрузкой (если коэффициент работы составляет 70%, то при дальнейших расчетах необходимо брать значение 0,7).
- Делаем расчет сечения кабеля по мощности. Для этого общую мощность потребляемой энергии делим на коэффициент работы сети и получаем требуемое значение мощности провода. Используя специальную таблицу проводов, определяем сечение жил.
Чтоб определить точный расчет сечения кабеля по мощности в сети необходимо использовать данные о потреблении приборами тока с усредненного подсчета. Однако, следует учесть, что данные на приборах зачатую проставляются среднего значения. Поэтому к этой цифре следует сразу добавить 5 % от полного значения.
Некоторые электрики полагают, что для проведения проводов освещения точечных светильников вполне достаточно сечение кабеля 0, 5 мм², для люстр – 1,5 мм², розеток – 2,5 мм².
Только нерадивый специалист станет утверждать, что реализация такой электрической схемы и сечения купленных проводов смотрятся вполне приемлемыми для использования в бытовых целях. Однако, как же вам быть, если, к примеру, на кухне включили одновременно холодильник, чайник электрический, телевизор и микроволновку?
Такая же неприятная ситуация произойдет с вами если в одну розетку включите одновременно кофеварку, стиральную машину и мультиварку.
Блок: 4/6 | Кол-во символов: 2230
Источник: https://220.guru/electroprovodka/provoda-kabeli/raschet-secheniya-po-moshhnosti.html
Любой проводник обладает собственным сопротивлением – об этом мы говорили в самом начале статьи, когда приводили значения удельного сопротивления материалов, меди и алюминия.
Оба этих металла обладают весьма достойной проводимостью, и на участках небольшой протяженности собственное сопротивление линии не оказывает сколь-нибудь значимого влияния на общие параметры цепи. Но если планируется прокладка линии большой протяженности, или, например, изготавливается удлинитель-переноска большой длины для работы на значительном удалении от дома, то собственное сопротивление желательно просчитать, и сравнить вызываемое им падение напряжения с напряжением питания. Если падение напряжения получается более 5% от номинала напряжения в цепи, правила эксплуатации электроустановок предписывают брать кабель с жилами большего сечения.
Например, изготавливается переноска для сварочного инвертора. Если сопротивление самого кабеля будет чрезмерным, провода под нагрузкой будут сильно перегреваться, а напряжения и вовсе может оказаться недостаточно для корректной работы аппарата.
Собственное сопротивление кабеля можно вычислить по формуле:
Rk = 2 × ρ × L / S
Rk — собственное сопротивление кабеля (линии), Ом;
2 — длина кабеля удваивается, так как учитывается весь путь прохождения тока, то есть «туда и обратно»;
ρ — удельное сопротивление материала жил кабеля;
L — длина кабеля, м;
S — площадь поперечного сечения жилы, мм².
Предполагается, что нам уже известно, с каким током придется иметь дело при подключении нагрузки — об этом уже не раз рассказывалось в настоящей статье.
Зная силу тока, несложно по закону Ома вычислить падение напряжения, а затем сравнить его с номиналом.
Ur = Rk × I
ΔU (%) = (Ur / Uном) × 100
Если проверочный результат получается более 5%, то следует увеличить сечение жил кабеля на один шаг.
Быстро провести такую проверку поможет еще один онлайн-калькулятор. Дополнительных пояснений он, думается, не потребует.
Калькулятор проверки падения напряжения на линии большой протяженностиПерейти к расчётам
Как уже говорилось, при значении до 5% можно ничего не менять. Если получается больше – увеличивается сечение жилы кабеля, также с последующей проверкой.
* * * * * * *
Итак, были рассмотрены основные вопросы, касающиеся необходимого сечения кабеля в зависимости от планируемой нагрузки на него. Читатель волен выбрать любой из предлагаемых способов расчета, какой ему больше понравится.
Завершим статью видеосюжетом на эту же тему.
Блок: 4/5 | Кол-во символов: 2523
Источник: https://stroyday.ru/stroitelstvo-doma/elektroxozyajstvo/raschet-secheniya-kabelya-po-toku.html
Расчет сечения кабеля по мощности и длине
Длина кабеля влияет на потерю напряжения. Таким образом, на конце проводника напряжение может уменьшится и оказаться недостаточным для работы электроприбора. Для бытовых электросетей этими потерями можно пренебречь. Достаточно будет взять кабель на 10-15 см длиннее. Этот запас израсходуется на коммутацию и подключение. Если концы провода подсоединяются к щитку, то запасная длина должна быть еще больше, т. к. будут подключаться защитные автоматы.
При укладке кабеля на большие расстояния приходиться учитывать падение напряжения. Каждый проводник характеризуется электрическим сопротивлением. На данный параметр влияют:
- Длина провода, единица измерения – м. При её увеличении растут потери.
- Площадь поперечного сечения, измеряется в мм². При ее увеличении падение напряжения уменьшается.
- Удельное сопротивление материала (справочное значение). Показывает сопротивление провода, размеры которого 1 квадратный миллиметр на 1 метр.
Падение напряжения численно равняется произведению сопротивления и тока. Допустимо, чтобы указанная величина не превышала 5%. В противном случае надо брать кабель большего сечения. Алгоритм расчета сечения провода по максимальной мощности и длине:
- В зависимости от мощности P, напряжения U и коэффициента cosф находим ток по формуле: I=P/(U*cosф). Для электросетей, которые используются в быту, cosф = 1. В промышленности cosф рассчитывают как отношение активной мощности к полной. Последняя состоит из активной и реактивной мощностей.
- С помощью таблиц ПУЭ определяют сечение провода по току.
- Рассчитываем сопротивление проводника по формуле: Rо=ρ*l/S, где ρ – удельное сопротивление материала, l – длина проводника, S – площадь поперечного сечения. Необходимо учесть ток факт, что ток идет по кабелю не только в одну сторону, но и обратно. Поэтому общее сопротивление: R = Rо*2.
- Находим падение напряжения из соотношения: ΔU=I*R.
- Определяем падение напряжения в процентах: ΔU/U. Если полученное значение превышает 5%, тогда выбираем из справочника ближайшее большее поперечное сечение проводника.
Блок: 5/6 | Кол-во символов: 2060
Источник: https://odinelectric.ru/wiring/kak-rasschitat-neobhodimoe-sechenie-provoda-po-moshhnosti-nagruzki
Блок: 5/5 | Кол-во символов: 63
Источник: https://stroyday.ru/stroitelstvo-doma/elektroxozyajstvo/raschet-secheniya-kabelya-po-toku.html
Выводы и полезное видео по теме
Расчет сечения проводника по формулам:
Рекомендации специалистов по подбору кабельно-проводниковой продукции:
Приведенные расчёты справедливы для медных и алюминиевых проводников промышленного назначения. Для других типов проводников предварительно рассчитывается полная теплоотдача.
На основе этих данных производится расчет максимального тока способного протекать по проводнику, не вызывая чрезмерного нагрева.
Если остались какие-либо вопросы по методике расчета сечения кабеля или есть желание поделиться личным опытом, пожалуйста, оставляйте к этой статье. Блок для отзывов расположен ниже.
Блок: 6/6 | Кол-во символов: 625
Источник: https://sovet-ingenera.com/elektrika/provodka/raschyot-secheniya-kabelya.html
Как осуществить правильный выбор сечения проводника?
Для точного определения максимальной мощности следует знать потребляемый ток и вид фазы (одно- или трехфазная сеть).
Для однофазной сети суммарная мощность будет равна Р= 220*I*1,3, где I— это потребляемый суммарный ток.
Для трехфазной сети расчет осуществляется немного по-иному: Р= √3*380* I*1,3.
Однако, необходимо учесть, что сечение используемых проводов должно соответствовать критериям:
- длину токоведущей линии;
- способ реализации электропроводки;
- общие характеристики автомата.
Правильно подобранное сечение используемых проводов – это самый важный критерий для осуществления и прокладки надежной проводки в помещении. Всем известно, что только скупой платит дважды, и не только за кабель, но и за весь ремонт в целом.
Блок: 6/6 | Кол-во символов: 808
Источник: https://220.guru/electroprovodka/provoda-kabeli/raschet-secheniya-po-moshhnosti.html
Количество использованных доноров: 6
Информация по каждому донору:
- https://220.guru/electroprovodka/provoda-kabeli/raschet-secheniya-po-moshhnosti.html: использовано 3 блоков из 6, кол-во символов 4879 (18%)
- http://remontnichok.ru/elektrichestvo/raschet-secheniya-kabelya-po-moshchnosti-prakticheskie-sovety-ot-professionalov: использовано 1 блоков из 7, кол-во символов 1434 (5%)
- https://odinelectric.ru/wiring/kak-rasschitat-neobhodimoe-sechenie-provoda-po-moshhnosti-nagruzki: использовано 3 блоков из 6, кол-во символов 3135 (12%)
- https://stroyday.ru/stroitelstvo-doma/elektroxozyajstvo/raschet-secheniya-kabelya-po-toku.html: использовано 3 блоков из 5, кол-во символов 12742 (47%)
- https://sovet-ingenera.com/elektrika/provodka/raschyot-secheniya-kabelya.html: использовано 2 блоков из 6, кол-во символов 1498 (6%)
- https://electrosam.ru/glavnaja/jelektrotehnika/raschjoty/raschet-secheniia-kabelia/: использовано 2 блоков из 4, кол-во символов 3260 (12%)
Источник: m-strana.ru
|
Высший уровень: сопротивление и площадь поперечного сечения — Расчет сопротивления — CCEA — Редакция GCSE Physics (Single Science) — CCEA
Второй эксперимент может быть проведен для экспериментального исследования того, как сопротивление металлического проводника при постоянной температуре зависит от площадь поперечного сечения.
Описанный выше эксперимент повторяется, но с шестью равными отрезками константановой проволоки разной толщины.
Запишите напряжение, ток и диаметр провода, d (поставляется производителем).2} {4} \)).
Постройте график зависимости сопротивления R в Ом по оси y от площади поперечного сечения A в мм2 по оси x.
Проведите линию наилучшего соответствия.
Из графика видно, что с увеличением площади поперечного сечения A сопротивление R уменьшается.
Более толстая проволока имеет меньшее сопротивление, чем тонкая.
Более подробное исследование показывает, что сопротивление и площадь поперечного сечения обратно пропорциональны.
Если вы удвоите площадь поперечного сечения, вы получите половину сопротивления провода.
Последний эксперимент может быть проведен для экспериментального исследования того, как сопротивление металлического проводника при постоянной температуре зависит от материала проводника.
Эксперимент повторяется снова, но с шестью проволоками из разных материалов одинаковой длины и толщины.
Запишите напряжение, ток и вычислите сопротивление.
Сравнение результатов в таблице показывает, что провода из разных материалов имеют разное сопротивление.
Ключевой момент
Сопротивление металлического проводника при постоянной температуре зависит от:
- Длина l.Сопротивление прямо пропорционально длине.
- Площадь поперечного сечения A. Сопротивление обратно пропорционально площади поперечного сечения.
- Материал проводника.
Сопротивление увеличивается как:
- длина провода увеличивается;
- толщина проволоки уменьшается.
Электрический ток течет, когда свободные электроны движутся в одном направлении через проводник, например металлический провод.
Движущиеся электроны могут сталкиваться с ионами металла.
Это затрудняет прохождение тока и вызывает сопротивление.
Сопротивление длинного провода больше, чем сопротивление короткого провода, потому что электроны сталкиваются с большим количеством ионов по мере их прохождения.
Сопротивление и длина провода прямо пропорциональны.
Сопротивление тонкой проволоки больше, чем сопротивление толстой проволоки, потому что у тонкой проволоки меньше зазоров, через которые могут пройти свободные электроны.
Сопротивление и площадь поперечного сечения провода обратно пропорциональны.
Сечения рассеяния — обзор
§126. Формула Бора
Сечение рассеяния может быть вычислено в общем виде в очень важном случае, а именно в том случае, когда поле рассеяния можно рассматривать как возмущение. два условия
(126,1) | U | ≪ℏ2 / ma2.
и
(126.2) | U | ≪ℏv / a = (2 / ma2) ka
, a — дальность действия поля U ( r ) и U — порядок величины поля в диапазоне, где это значимо. Когда первое условие выполнено, приближение справедливо для всех скоростей; второе условие показывает, что оно всегда применимо для достаточно быстрых частиц.
В соответствии с §45, ищем волновую функцию в виде ψ = ψ (0) + ψ (1) , где ψ (0) = e i k.r соответствует падающей частице, имеющей волновой вектор k = p /. Тогда из формулы (45.3) имеем
(126.3) ψ (1) (x, y, z) = — m2πℏ2∫U (x ′, y ′, z ′) ei (k · r ′ + kR) dV ′ Р.
Взяв начало координат в центре рассеяния, введем радиус-вектор R 0 от начала координат до точки, где требуется значение ψ (1) , и обозначим n ′ единичный вектор. по R 0 . Пусть радиус-вектор элемента объема d V ′ равен r ′; тогда R = R 0 — r ′.На больших расстояниях от центра R 0 ≫ r ′, так что
R = | R0-r ′ | ≈R0-r ′ · n ′.
Подставляя это в (126.3), мы получаем следующее асимптотическое выражение для ψ (1) :
ψ (1) ≈-m2πℏ2eikR0R0∫U (r ′) ei (kk ′) · r′dV ′
(где k ′ = k n ′ — волновой вектор частицы после рассеяния). Сравнивая это с амплитудой рассеяния, определяемой формулой (123.3), находим для последней выражение
(126.4) f = -m2πℏ2∫Ue-iq · rdV,
, где мы переименовали переменную интегрирования и ввели вектор
(126,5) q = k′-k,
, абсолютная величина которого равна
(126,6) q = 2ksin12θ,
θ — это угол между k и k ′, то есть угол рассеяния.
Наконец, возведя в квадрат модуль амплитуды рассеяния, мы имеем следующее выражение для сечения рассеяния на элемент телесного угла d o :
(126.7) dσ = m24π2ℏ2 | ∫Ue-iq.rdV | 2do.
Мы видим, что рассеяние с изменением импульса ℏ q определяется квадратом модуля соответствующей фурье-компоненты поля U . Формула (126,7) впервые была получена М. Борном (1926 г.). В теории столкновений рассматриваемое здесь приближение часто называют Борновским приближением .
Можно отметить, что в этом приближении соотношение
(126.8) f (k, k ′) = f ∗ (k ′, k)
выполняется между амплитудами прямого и обратного процессов рассеяния, i .е. процессы, отличающиеся сменой начального и конечного импульсов без изменения знака, например, при обращении времени. Таким образом, в рассеянии появляется еще одно свойство симметрии, помимо теоремы взаимности (125.12). Это свойство тесно связано с малостью амплитуд рассеяния в теории возмущений и непосредственно следует из условия унитарности (125.8), если пренебречь интегральным членом, квадратичным по f . †
Формула (126.7) также может быть получена следующим образом: другой метод (который, однако, не определяет фазу амплитуды рассеяния).Начать можно с общей формулы (43.1), согласно которой вероятность перехода между состояниями непрерывного спектра определяется выражением
dwfi = (2π / ℏ) | Ufi | 2δ (Ef-Ei) dνf.
В рассматриваемом случае мы должны применить эту формулу к переходу из состояния падающей частицы с импульсом p в состояние частицы с импульсом p ′, рассеянной в элемент телесного угла d o ′. В качестве интервала состояний dν f можно взять d 3 p ′ / (2πℏ) 3 .Подставляя разность конечной и начальной энергий
Ef-Ei = (p′2-p2) / 2m,
, получаем
(126.9) dwP′P = (4πm / ℏ) | UP′P2δ (p ′ 2-p2) d3p ′ / (2πℏ) 3.
Волновые функции падающих и рассеянных частиц представляют собой плоские волны. Поскольку за интервал состояний dν f мы взяли элемент пространства p / 2πℏ, конечная волновая функция должна быть нормирована дельта-функцией p / 2πℏ:
(126.10) ψP ′ = e (i / ℏ) p ′.р.
Нормируем начальную волновую функцию на единицу плотности тока:
(126,11) ψP = √ (m / p) e (i / ℏ) p′.r.
Тогда (126.9) будет иметь размеры площади, а — дифференциальное сечение рассеяния.
Наличие дельта-функции в формуле (126.9) означает, что p ′ = p , т.е. абсолютная величина импульса не меняется, как и должно быть при упругом рассеянии. Мы можем удалить дельта-функцию, перейдя к сферическим координатам в импульсном пространстве (т.е. путем замены d 3 p ′ на p’2dp’do ‘= 12p’d (p’2) do’ |) и интегрирования более p ′ 2 . Интегрирование сводится к замене p ′ на p в подынтегральном выражении, и мы получаем
dσ = (mp / 4π2ℏ4) | ∫ψP ′ * UψPdV | 2do ′.
Подставляя функции (126.10), (126.11), мы еще раз приходим к окончательному выражению (126.7).
В форме (126.7) эта формула применима к рассеянию в поле U ( x, y, z ), которое является любой функцией координат, а не только функцией r .Однако в случае центрального поля U ( r ) эта формула может быть дополнительно преобразована. В интеграле
∫U (r) e-iq.rdV
мы используем сферические пространственные координаты r , θ, φ с полярной осью в направлении вектора q , обозначая полярный угол как θ отличить его от угла рассеяния θ. Можно выполнить интегрирование по v и φ, и мы получим
∫0∞∫02π∫0πU (r) eiqrcosϑr2sinϑdϑdφdr = 4π∫0∞U (r) sinqrqr dr.
Подставляя это выражение в (126.4), получаем следующую формулу для амплитуды рассеяния в центрально-симметричном поле:
(126.12) f = -2mℏ2∫0∞U (r) sinqrqrdr.
Для θ = 0 (т. Е. q = 0) интеграл расходится, когда U ( r ) убывает на бесконечности не быстрее, чем 1/ r 3 (в соответствии с общими результатами §124).
Обращаем внимание на следующий интересный факт.Импульс частицы p и угол рассеяния θ входят в (126,12) только через q . Таким образом, в борновском приближении сечение рассеяния зависит от p и θ только в комбинации psin12θ.
Возвращаясь к случаю произвольных полей U ( x, y, z ), рассмотрим предельные случаи малых скоростей ( ка, ≪ 1) и больших скоростей ( ка, 1). Для малых скоростей можно положить e — i q.r ≈ 1 дюйм (126,4), так что
(126,13) f = -m2πℏ2∫UdV,
, а если U = U ( r ),
(126,14) f = -2mℏ2 ∫0∞U (r) r2dr.
Здесь рассеяние изотропно и не зависит от скорости в соответствии с общими результатами § 132.
В противоположном предельном случае высоких скоростей рассеяние заметно анизотропно и в основном вперед в узком конусе с углом Δθ ∼ 1/ ka ; поскольку вне этого конуса величина q велика, коэффициент e — i q.r — быстро меняющаяся функция, и интеграл ее произведения с медленно меняющейся функцией U почти равен нулю.
Закон убывания для больших q не универсален и зависит от конкретной формы поля. Если поле U ( r ) имеет сингулярность при r = 0 или при любом другом действительном значении r , интеграл (126,12) в основном определяется диапазоном вблизи особой точки, а крест -сечение убывает по степенному закону.То же самое относится к случаю, когда функция U ( r ) не имеет сингулярности, но не является четной функцией; здесь область около r = 0 является наиболее важной в интеграле. Если U ( r ) является четной функцией r , однако, интегрирование может быть формально расширено до отрицательных значений r , то есть вдоль всей действительной оси переменной r , после чего (если U ( r ) не имеет сингулярности на действительной оси) путь интегрирования может быть перемещен в комплексную плоскость до тех пор, пока он не встретится с ближайшей комплексной сингулярностью.Тогда при больших q интеграл будет убывать экспоненциально. Однако следует иметь в виду, что приближение Борна в общем случае неадекватно для вычисления этой экспоненциально малой величины (см. Также §131).
Хотя значение дифференциального сечения рассеяния внутри конуса Δθ ∼ 1/ ka не сильно зависит от скорости, полное сечение рассеяния (если предположить, что интеграл dσ действительно сходится) уменьшается при высоких энергиях. из-за уменьшения угла конуса пропорционально телесному углу конуса, т.е.е. как (Δθ) 2 ∼ 1/ k 2 a 2 , или наоборот, как энергия.
Во многих физических приложениях теории столкновений величина, описывающая рассеяние, является интегралом
(126,15) σtr = ∫ (1-cosθ) dσ,
часто называется транспортным сечением . Рассуждения, аналогичные приведенным выше, показывают, что при высоких скоростях эта величина обратно пропорциональна квадрату энергии.
ПРОБЛЕМЫ
Проблема 1.Определите в борновском приближении сечение рассеяния для сферической потенциальной ямы: U = — U 0 для r < a, U = 0 для r > a .
Решение. Вычисление интеграла в (126.12) дает
dσ = 4a2 (mU0a2ℏ2) 2 (sinqa-qacosqa2) (qa) 6do.
Интегрирование по всем углам (которое удобно осуществить, используя переменную q = 2ksin12θ и заменяя d o на 2π q d q / k 2 ) дает полное сечение рассеяния
σ = 2πk2 (mU0a2ℏ2) 2 [1-1 (2ka2) + sin4ka (2ka) 3-sin22ka (2ka) 4].
В предельных случаях эта формула дает
σ = 16πa29 (mU0a2ℏ2) 2forka≪1, σ = 2πk2 (mU0a2ℏ2) 2forka≫1.
Задача 2. То же, что и задача 1, но в поле U = Uoe − r2 / a2.
Решение. Расчет удобно производить по формуле (126.7), принимая направление q вдоль одной из осей координат. Результат:
dσ = 14πa2 (mU0a2ℏ2) 2e-q2a2 / 2do,
, а полное сечение составляет
σ = π22k2 (mU0a2ℏ2) 2 (1-e-2k2a2).
Условие применимости этих формул задается неравенствами (126.1), (126.2) с U 0 вместо U . Формула для dσ также неприменима, если показатель степени велик по абсолютной величине. †
Задача 3. То же, что и задача 1, но в поле U = (α / r) e − r / a.
Решение. Вычисление интеграла в (126.12) дает
dσ = 4a2 (αmaℏ2) 2do (q2a2 + 1) 2.
Полное сечение
σ = 16πa2 (αmaℏ2) 214k2a2 + 1.
Условие применимости этих формул находится из (126.1) и (126.2) с α / a вместо U : α ma / ℏ 2 ≪ 1 или α / ℏ v ≪ 1.
Задача 4. Определить фазы δ l для рассеяния в центрально-симметричном поле для случая, соответствующего борновскому приближению.
Решение. Для радиальной волновой функции χ = rR для движения в поле U ( r ) и для функции χ (0) для свободного движения имеем уравнения (см. (32.10))
χ ″ + [k2-l (l + 1) r2-2mℏ2U] χ = 0, χ (0) ″ + [k2-l (l + 1) r2] χ (0) = 0 ·
Умножая первое уравнение на χ (0) , второе на χ и вычитая с последующим интегрированием по r (используя граничное условие χ = 0 при r = 0), получаем
χ ′ (r) χ (0) (r) -χ (r) χ (0) ′ (r) = 2mℏ2∫0rUχχ (0) dr.
Что касается U как возмущения, мы можем положить χ ≈ χ (0) справа от меня. При r → ∞ асимптотические выражения (33.12), (33.20) можно использовать в левой части, а в интеграл подставим точное выражение (33.10). Результат:
sinδl≈δl = -πmℏ2∫0∞U (r) [Jl + 1/2 (kr)] 2r dr.
Эту формулу можно также получить прямым разложением амплитуды борновского рассеяния (126,4) по полиномам Лежандра в соответствии с (123.11) (для малых δ l ).
Задача 5. Определить в борновском приближении полное сечение рассеяния в поле U = α / ( r 2 + a 2 ) n ′ 2 с n > 2, для быстрых частиц ( ка ≫ 1).
Решение. Мы увидим, что в этом случае в этом рассеянии преобладают парциальные амплитуды с большими угловыми моментами l . Таким образом, поперечное сечение можно рассчитать по формуле (123.11), заменив суммирование по · интегрированием; в борновском приближении все δ l ≪ 1, так что
(1) σ≈4πk2∫0∞2lδl2dl.
Фазы δ l с большим l рассчитываются по (124.1):
δl = -αmℏ2∫l / k∞dr (r2 + a2) n / 2 (k2-l2 / r2) 1/2.
Путем замены r 2 + a 2 = ( a 2 + l 2 / k 2 ) / ξ интеграл приводится к знакомая форма Эйлера, и результат:
(2) δl = -mαkn-22ℏ2 (a2k2 + l2) (n-1) / 2Γ (12) Γ (12n-12) Γ (12n).
Интеграл (1) определяется диапазоном l ∼ ak ≫ 1, и это подтверждает сделанное предположение.Вычисление интеграла дает результат
(3) σ = π2n-2 [Γ (12n-12) Γ (12n)] 2 (mαkℏ2an-2) 2.
Согласно (126.2) условие выполнения борновского приближения в этом случае составляет м α / ℏ 2 ka n −1 ≪ 1. Обратите внимание на зависимость σ ∼ k −2 , что соответствует общему утверждению, сделанному выше.
Задача 6. Определить в борновском приближении амплитуду рассеяния в двумерном случае поля U = U ( x, z ) с потоком частиц, падающим вдоль оси z .
Решение. Используя вторую сноску к §45 и известное асимптотическое выражение функции Ганкеля
δ0 (1) (u) ≈√2πuei (u-π / 4) при u → ∞,
находим для поправки на волну функция на больших расстояниях R 0 от оси поля (ось y ) выражение
ψ (1) ≈f (θ) √R0eikR0,
где амплитуда рассеяния равна
f (θ ) = — mℏ2√ (2πk) eiπ / 4∫U (ρ) e-iq.pd2ρ,
с ρ = ( x, z ) двумерным радиус-вектором, d 2 ρ = d x d z 〉 и θ угол рассеяния в плоскости xz .В двумерном случае амплитуда рассеяния имеет размерность корня квадратного из длины, а сечение рассеяния dσ = | f | 2 dθ длина.
5.1 Поток | Мониторинг и оценка
Что такое сток и почему он важен?Поток или расход воды — это объем воды, который движется над заданной точкой за фиксированный период времени. Часто выражается в кубических футах в секунду ( 3 футов в секунду).
Расход ручья напрямую зависит от количества воды, уходящей с водораздела в русло ручья. Он зависит от погоды, увеличивается во время ливней и уменьшается в засушливые периоды. Он также меняется в разные сезоны года, снижаясь в летние месяцы, когда интенсивность испарения высока и прибрежная растительность активно растет и удаляет воду с земли. Август и сентябрь — обычно месяцы самого низкого стока для большинства ручьев и рек на большей части страны.
Забор воды для целей орошения может серьезно истощить сток воды, как и промышленный забор воды. Плотины, используемые для выработки электроэнергии, особенно сооружения, предназначенные для выработки электроэнергии в периоды пиковой потребности, часто блокируют течение потока, а затем выпускают его в виде скачка.
Расход — это функция объема и скорости воды. Это важно из-за своего воздействия на качество воды, а также на живые организмы и среду обитания в ручье. Крупные реки с быстрым течением могут получать сбросы загрязняющих веществ и подвергаться незначительному воздействию, в то время как небольшие реки обладают меньшей способностью разбавлять и разлагать отходы.
Скорость потока, которая увеличивается по мере увеличения объема воды в ручье, определяет виды организмов, которые могут жить в ручье (некоторым нужны участки с быстрым течением, другим нужны тихие бассейны). Это также влияет на количество ила и наносов, переносимых ручьем. Осадок, внесенный в тихие, медленно текущие потоки, быстро оседает на дно ручья. Быстро движущиеся потоки дольше удерживают осадок во взвешенном состоянии в толще воды. Наконец, быстро движущиеся потоки обычно имеют более высокий уровень растворенного кислорода, чем медленные потоки, потому что они лучше аэрируются.
В этом разделе описан один метод оценки потока в определенной области или на участке потока. Он адаптирован на основе методов, используемых несколькими программами мониторинга добровольцами, и использует поплавок (такой объект, как апельсин, мяч для пинг-понга, сосновая шишка и т. Д.) Для измерения скорости потока. Расчет расхода включает решение уравнения, которое исследует взаимосвязь между несколькими переменными, включая площадь поперечного сечения потока, длину потока и скорость воды. Один из способов измерения расхода — решить следующее уравнение:
| Расход = ALC / T | ||
| Где: | ||
| А | = | Средняя площадь поперечного сечения ручья (ширина ручья, умноженная на среднюю глубину воды). |
| л | = | Измеренная длина участка реки (обычно 20 футов) |
| С | = | Коэффициент или поправочный коэффициент (0,8 для потоков с каменистым дном или 0,9 для потоков с илистым дном). Это позволяет вам скорректировать тот факт, что вода на поверхности движется быстрее, чем у дна ручья из-за сопротивления гравия, булыжника и т. Д. Умножение скорости на поверхности на поправочный коэффициент уменьшает значение и дает более точную оценку общей протяженности потока. скорость. |
| т | = | Время в секундах, за которое поплавок проходит длину L |
Задача 1 Подготовиться перед выездом на место отбора проб
См. Раздел 2.3 — Меры безопасности для получения подробной информации о подтверждении даты и времени отбора проб, соображениях безопасности, проверке расходных материалов, а также проверке погоды и направления. В дополнение к стандартному оборудованию для отбора проб и одежде, при измерении и расчете расхода, необходимо включать следующее оборудование:
- Шар из прочной струны, четыре колья и молоток для забивания кольев в землю.Трос будет натянут по ширине ручья перпендикулярно берегу в двух местах. Ставки заключаются в том, чтобы закрепить веревку на каждом берегу, чтобы сформировать линию разреза.
- Рулетка (минимум 20 футов)
- Водонепроницаемая линейка или другой прибор для измерения глубины воды
- Хомуты (для обозначения интервалов на нити линии трансекты)
- Апельсин и рыболовная сеть (чтобы вычерпать апельсин из ручья)
- Секундомер (или часы с секундной стрелкой)
- Калькулятор (опционально)
Задача 2 Выберите участок потока
| Рисунок 5.4 Схема трансекты 20 футов |
Участок ручья, выбранный для измерения расхода, должен быть прямым (без изгибов), глубиной не менее 6 дюймов и не должен содержать участков с медленной водой, таких как бассейн. Идеально подходят беспрепятственные перекаты или беговые дорожки. Выбранная длина будет равна L при решении уравнения потока. Двадцать футов — стандартная длина, используемая во многих программах. Измерьте свою длину и отметьте верхний и нижний конец, проведя линию разреза поперек ручья перпендикулярно берегу, используя веревку и колья (рис.5.4). Трос должен быть натянут и находиться у поверхности воды. Трансект выше по течению — это разрез №1, а нижний по течению — разрез №2.
Задача 3 Рассчитать среднюю площадь поперечного сечения
Площадь поперечного сечения (A в формуле) — произведение ширины ручья на среднюю глубину воды. Чтобы рассчитать среднюю площадь поперечного сечения для охвата исследуемого ручья, добровольцы должны определить площадь поперечного сечения для каждой трансекты, сложить результаты вместе, а затем разделить на 2, чтобы определить среднюю площадь поперечного сечения для участка протока.
Для измерения площади поперечного сечения:
Рисунок 5.5
Поперечный разрез для измерения ширины и глубины потока- Определите среднюю глубину вдоль трансекты, отметив равные интервалы вдоль струны с помощью скрученных стяжек. Интервалы могут составлять одну четвертую, половину или три четверти расстояния через ручей.Измерьте глубину воды в каждой точке интервала (рис. 5.5). Чтобы вычислить среднюю глубину для каждого разреза, разделите сумму трех измерений глубины на 4. (Вы делите на 4 вместо 3, потому что вам нужно учитывать нулевые глубины, которые встречаются на берегах). В примере, показанном на Рисунке 5.6. , средняя глубина трансекты № 1 составляет 0,575 футов, а средняя глубина трансекты № 2 составляет 0,625 футов.
- Определите ширину каждого разреза, измерив расстояние от береговой линии до береговой линии.Просто сложите все интервалы ширины для каждого разреза, чтобы определить его ширину. В примере на Рисунке 5.6 ширина трансекты № 1 составляет 8 футов, а ширина трансекты № 2 — 10 футов.
- Рассчитайте площадь поперечного сечения каждого разреза, умножив ширину на среднюю глубину. Пример, приведенный на Рисунке 5.6, показывает, что средняя площадь поперечного сечения трансекты № 1 составляет 4,60 квадратных футов, а средняя площадь поперечного сечения трансекты № 2 составляет 6,25 квадратных футов.
- Чтобы определить среднюю площадь поперечного сечения всего участка ручья (A в формуле), сложите среднюю площадь поперечного сечения каждой трансекты и затем разделите на 2.Средняя площадь поперечного сечения ручья на Рисунке 5.6 составляет 5,42 квадратных футов.
Задача 4 Измерение времени в пути
Добровольцы должны отсчитывать с помощью секундомера, сколько времени требуется апельсину (или другому объекту), чтобы проплыть от верхнего к нижнему разрезу. Апельсин — хороший объект для использования, потому что он обладает достаточной плавучестью, чтобы плавать чуть ниже поверхности воды. Именно в этом положении обычно наблюдается максимальная скорость.
Доброволец, который пропускает апельсин на разрезе выше по течению, должен расположить его так, чтобы он тек в самое быстрое течение.Часы останавливаются, когда оранжевый полностью проходит под линией разреза вниз по течению. Оказавшись под линией трансекты, апельсин можно вычерпать из воды с помощью рыболовной сети. Это измерение «времени в пути» должно быть проведено не менее трех раз, а результаты усреднены — чем больше испытаний вы проведете, тем точнее будут ваши результаты. Усредненные результаты равны T в формуле. Рекомендуется размещать апельсин на разных расстояниях от берега, чтобы получить различные оценки скорости.Вы должны отказаться от любых попыток поплавка, если объект зависает в потоке (булыжниками, корнями, обломками и т. Д.).
Задача 5 Рассчитать расход
Напомним, что расход можно рассчитать по формуле:
Продолжая пример на рис. 5.6. скажем, среднее время прохождения апельсина между трансектом №1 и №2 составляет 15 секунд, а дно ручья было каменистым. Расчет расхода:
| Где: | ||
| А | = | 5.42 фут2 |
| л | = | 20 футов |
| С | = | 0,8 (коэффициент для каменистого течения) |
| т | = | 15 секунд |
| Расход = 15 секунд (5,42 футов 2 ) (20 футов) (0,8) / 15 секунд. | ||
| Расход = 86,72 фута 3 /15 сек. | ||
| Расход = 5,78 фут3 / сек. |
Задача 6 Записать поток в форму данных
На следующей странице волонтеры могут использовать форму для расчета расхода ручья.
СсылкиФонд Adopt-A-Stream. Полевое руководство: Инвентаризация водосборов и методы мониторинга водотоков, Тома Мердока и Марты Чео. 1996. Эверетт, Вашингтон.
Mitchell, M.K., and W. Stapp. Полевое руководство по мониторингу качества воды. 5 th Edition. Принтеры Thompson Shore.
Миссури Стрим Команды. Добровольный мониторинг качества воды. Департамент природных ресурсов штата Миссури, P.O. Box 176, Джефферсон-Сити, Миссури 65102.
Форма данных для расчета расхода (PDF, 82,8 КБ)
Вам понадобится Adobe Acrobat Reader для просмотра файлов Adobe PDF на этой странице. См. Страницу EPA в формате PDF для получения дополнительной информации о получении и использовании бесплатного Acrobat Reader.Механика материалов: кручение »Механика тонких конструкций
Деформация при кручении
Крутящий момент — это момент, который скручивает структуру.В отличие от осевых нагрузок, которые создают равномерное или среднее напряжение по поперечному сечению объекта, крутящий момент создает распределение напряжения по поперечному сечению. Для простоты мы сосредоточимся на структурах с круглым поперечным сечением, часто называемых стержнями или валами. Когда к конструкции приложен крутящий момент, она будет закручиваться по длинной оси стержня, а ее поперечное сечение остается круглым.
Чтобы представить себе, о чем я говорю, представьте, что поперечное сечение стержня представляет собой часы с часовой стрелкой.Когда крутящий момент не применяется, часовая стрелка находится в положении «12 часов». Когда к стержню прилагается крутящий момент, он будет вращаться, и часовая стрелка повернется по часовой стрелке в новое положение (скажем, на 2 часа). Угол между 2 и 12 часами называется углом поворота и обычно обозначается греческим символом фи . Этот угол позволяет определить деформацию сдвига в любой точке поперечного сечения.
Прежде чем мы углубимся в детали этого уравнения, важно отметить, что, поскольку мы обсуждаем только круглые сечения , мы перешли с декартовых координат на цилиндрические.Отсюда и возник греческий символ rho — он обозначает расстояние по поперечному сечению, где rho = 0 в центре и rho = c на внешнем крае стержня.
Мы можем сразу узнать несколько вещей из этого уравнения. Первое может быть очевидным: чем больше угол скручивания, тем больше деформация сдвига (как и раньше, обозначается греческим символом gamma ). Во-вторых, и это большая разница между осевыми нагруженными конструкциями и нагруженными крутящим моментом, деформация сдвига неоднородна по поперечному сечению.Он равен нулю в центре скрученного стержня и имеет максимальное значение на краю стержня. Наконец, чем длиннее стержень, тем меньше деформация сдвига.
До сих пор мы сосредоточили свое внимание на смещениях и деформациях. Чтобы обсудить напряжение внутри скрученного стержня, нам нужно знать, как связаны крутящий момент и напряжение . Поскольку скручивание вызывает деформацию сдвига, мы ожидаем, что крутящий момент будет прикладывать напряжение сдвига . Взаимосвязь между крутящим моментом и напряжением сдвига подробно описана в разделе 5.2 вашего учебника, и получается следующее соотношение:
В этом уравнении J обозначает второй полярный момент площади поперечного сечения. Иногда это называют «вторым моментом инерции», но поскольку это уже имеет хорошо установленное значение в отношении динамического движения объектов, давайте не будем здесь путать вещи. Мы обсудим моменты площади более подробно позже, но они принимают очень простую форму для круглых поперечных сечений:
(Примечание: это одно и то же уравнение — твердые стержни имеют внутренний радиус c i = 0).
Теперь у нас есть уравнения для нашей деформации сдвига и напряжения сдвига, все, что осталось сделать, это использовать закон Гука для сдвига, чтобы увидеть, как они связаны. Закон Гука позволяет нам записать красивое уравнение для угла скручивания — очень удобную вещь для измерения в лаборатории или в полевых условиях.
И, как мы видели для осевых смещений , мы можем использовать суперпозицию и для наших сдвиговых деформаций :
Это окончательное уравнение позволяет разделить крутящие моменты, приложенные к разным частям одной и той же конструкции.Давайте решим проблему и посмотрим, понимаем ли мы, что происходит с крутильными деформациями.
Трансмиссия
Одним из наиболее распространенных примеров кручения в инженерном проектировании является мощность, генерируемая трансмиссионными валами. Мы можем быстро понять, как скручивание генерирует мощность, просто выполнив простой анализ размеров. Мощность измеряется в единицах: Вт [Вт] , а 1 Вт = 1 Н · м · с -1 . В начале этого раздела мы отметили, что крутящий момент представляет собой крутящую пару, что означает, что он имеет единицы силы, умноженные на расстояние, или [Н · м].Итак, при осмотре, чтобы генерировать мощность с крутящим моментом, нам нужно что-то, что происходит с заданной частотой f , поскольку частота имеет единицы Герц [Гц] или [s -1 ]. Таким образом, мощность на оборот (2 * пи) круглого стержня равна приложенному крутящему моменту, умноженному на частоту вращения, или:
В крайней правой части уравнения мы использовали соотношение, согласно которому угловая скорость, обозначаемая греческой буквой омега , равна частоте, умноженной на 2pi.
Статически неопределимые задачи
Одно уравнение, два неизвестных… мы шли по этому пути, прежде чем понадобилось что-то еще. Хотя тип нагружения и деформации различны, статически неопределенные задачи , связанные с скручиванием стержней, решаются точно так же, как и с осевыми нагруженными конструкциями. Начнем со схемы свободного тела скрученного стержня. Возьмем, к примеру, стержень на рисунке ниже, застрявший между двумя стенами.
Сразу после осмотра вы должны заметить, что стержень прикреплен к двум стенкам, тогда как для статического равновесия требуется только одна. Больше опор, чем необходимо: статическая неопределенность . Статическая неопределенность означает: нарисуйте диаграмму свободного тела, просуммируйте силы в направлении x —, и вы получите одно уравнение с двумя неизвестными силами реакции. Итак, нам нужно учитывать наши деформации — для кручения это означает, что давайте обратимся к нашему уравнению, которое описывает суперпозицию углов закручивания.Для этого уравнения мы должны отметить, что половина стержня сплошная, а другая половина — полая, что влияет на то, как мы вычисляем J для каждой половины. Самое главное, мы должны спросить себя: «Что мы знаем о деформации?» Ну, так как стержень прилипает к стене краем, скручивание в точках A и B должно быть равно нулю (точно так же, как смещение в последнем разделе). Посмотрите, сможете ли вы решить остальную проблему самостоятельно: каков крутящий момент в каждой половине стержня?
(ответ: Т а = 51.7 фунт-фут & T b = 38,3 фунт-фут).
СводкаВ этом уроке мы узнали про крутящий момент и торсионный . Этот другой тип нагрузки создает неравномерное распределение напряжений по поперечному сечению стержня — от нуля в центре до максимального значения на краю. На основе этого анализа мы можем установить взаимосвязь между углом скручивания в любой точке вдоль стержня и деформацией сдвига внутри всего стержня.Используя закон Гука, мы можем связать эту деформацию с напряжением внутри стержня. Мы также использовали метод анализа размеров для определения мощности, генерируемой трансмиссионным валом (т. Е. Стержнем), который вращается с заданной частотой под действием приложенного крутящего момента. Наконец, мы показали, что проблемы с кручением также часто являются статически неопределенными , и даже несмотря на то, что нагрузка и деформация различаются, метод, который мы установили в последнем разделе для решения задач с осевой нагрузкой, является той же методикой для решения задач с крутящим моментом.
Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.
Анализ мощности для поперечных и продольных исследований
Психиатрия Шанхайской арки. 2013 Aug; 25 (4): 259–262.
, 1 , 2 , *, 1 , 1 , 3 , 1 , 2 , 4 и 1 , 2 , 5 , *Naiji LU
1 Департамент биостатистики, Медицинский центр Университета Рочестера, Рочестер, штат Нью-Йорк, США
2 Сеть комплексных услуг для ветеранов 2 Центр передового опыта по предотвращению самоубийств, Медицинский центр Канандайгуа, штат Вирджиния, Канандайгуа, штат Нью-Йорк, США
Yu HAN
1 Департамент биостатистики, Медицинский центр Университета Рочестера, Рочестер, штат Нью-Йорк, США
Тиан ЧЕН
1 Департамент биостатистики, Медицинский центр Университета Рочестера, Рочестер, Нью-Йорк, США
Дуглас Д.GUNZLER
3 Школа медицины, Университет Кейс Вестерн Резерв, Центр исследований и политики в области здравоохранения, Медицинский центр MetroHealth, Кливленд, Огайо, США
Yinglin XIA
1 Департамент биостатистики, Медицинский центр Университета Рочестера , Рочестер, штат Нью-Йорк, США
2 Сеть интегрированных услуг для ветеранов 2 Центр передового опыта по предотвращению самоубийств, Медицинский центр Канандаигуа, Канандайгуа, штат Нью-Йорк, США
Джулия Ю.LIN
4 Координационный центр программы совместных исследований Министерства по делам ветеранов США, Система здравоохранения Пало-Альто, штат Вирджиния, Пало-Альто, Калифорния, США
Xin M. TU
1 Департамент биостатистики, Медицинский центр Университета Рочестера , Рочестер, штат Нью-Йорк, США
2 Сеть комплексных услуг для ветеранов 2 Центр передового опыта по предотвращению самоубийств, Медицинский центр Канандаигуа, штат Нью-Йорк, США
5 Департамент психиатрии, Медицинский центр Университета Рочестера, Рочестер, Нью-Йорк, США
1 Департамент биостатистики, Медицинский центр Университета Рочестера, Рочестер, штат Нью-Йорк, США
2 Сеть интегрированных услуг для ветеранов 2 Центр передового опыта по предотвращению самоубийств, Медицинский центр Канандаигуа, штат Нью-Йорк, США
3 Медицинский факультет Университета Кейс Вестерн Резерв, Центр исследований и политики в области здравоохранения, MetroHeal th Medical Center, Кливленд, Огайо, США
4 Координационный центр программы совместных исследований Департамента по делам ветеранов США, Пало-Альто, штат Вирджиния, Система здравоохранения, Пало-Альто, Калифорния, США
5 Департамент психиатрии, Рочестерский университет Медицинский центр, Рочестер, Нью-Йорк, США
Авторское право © 2013 г., редакция Шанхайского архива психиатрии Эта статья цитируется в других статьях в PMC.1. Введение
Оценка мощности и размера выборки является важным компонентом разработки и планирования современных научных исследований. Он предоставляет информацию для оценки осуществимости исследования по выявлению эффектов лечения и для оценки ресурсов, необходимых для проведения проекта. В этом руководстве обсуждаются основные концепции анализа мощности и основные различия между проверкой гипотез и анализом мощности. Мы также обсуждаем преимущества продольных исследований по сравнению с поперечными исследованиями и статистические вопросы, возникающие при разработке таких исследований.Эти моменты проиллюстрированы рядом примеров.
2. Проверка гипотез, выборочное распределение и мощность
В большинстве исследований у нас нет доступа ко всей представляющей интерес популяции из-за чрезмерно высокой стоимости идентификации и оценки каждого субъекта в популяции. Чтобы преодолеть это ограничение, мы делаем выводы об особенностях, представляющих интерес для нашей популяции, таких как средний доход или распространенность злоупотребления алкоголем, на основе относительно небольшой группы субъектов или выборки из исследуемой популяции.Такая представляющая интерес особенность называется параметром , который часто остается незамеченным, если не оценивается каждый субъект в популяции. Однако мы можем наблюдать оценку параметра в исследуемой выборке; эта величина называется статистикой . Поскольку значение статистики основано на конкретной выборке, оно обычно отличается от значения параметра для генеральной совокупности в целом. Статистический анализ использует информацию из статистики, чтобы сделать выводы о параметре.
Например, предположим, что нас интересует распространенность большой депрессии в городе с населением в один миллион человек. Параметр π — это распространенность большой депрессии. Взяв случайную выборку населения, мы можем вычислить статистику p, долю субъектов с большой депрессией в выборке. Размер выборки n обычно довольно мал по сравнению с размером генеральной совокупности. Статистика p, скорее всего, не будет равна параметру π, потому что p основывается на выборке и, следовательно, будет варьироваться от выборки к выборке.Разброс, на который p отклоняется от π при повторной выборке, называется ошибкой выборки . Пока n меньше 1 000 000, всегда будет некоторая ошибка выборки. Хотя мы не знаем точно, насколько велика эта ошибка для конкретной выборки, мы можем охарактеризовать ошибки выборки повторных выборок с помощью распределения выборки статистики . В приведенном выше примере распространенности большой депрессии поведение оценки p может быть охарактеризовано биномиальным распределением.Распределение, скорее всего, будет иметь пик около истинного значения параметра по мере увеличения размера выборки n , то есть чем больше размер выборки n , тем меньше ошибка выборки.
Если мы хотим иметь более точные оценки параметра, нам нужно иметь достаточно большое значение n , чтобы ошибка выборки была достаточно маленькой. Если n слишком мало, оценка будет слишком неточной, чтобы быть полезной. С другой стороны, существует также точка уменьшения отдачи, за которой увеличение n обеспечивает небольшую дополнительную точность.
Анализ мощности помогает найти размер выборки, обеспечивающий желаемый уровень точности. Хотя вопросы исследования разнятся, анализ данных и мощности основан на проверке статистических гипотез . Статистическая гипотеза выражает нашу веру в интересующий параметр в форме, которую можно исследовать с помощью статистического анализа. Например, в примере с большой депрессией, если мы считаем, что распространенность большой депрессии в данной конкретной группе населения превышает средний показатель по стране, составляющий 6%, мы можем выразить это убеждение в форме нулевой гипотезы ( H 0 ) и альтернативная гипотеза ( H a ):
Статистический анализ оценивает вероятность наблюдения данных, полученных нами из выборки, если нулевая гипотеза H 0 была верной.Если для нас очень маловероятно наблюдать данные, которые у нас есть, если H 0 было истинным, то мы отклоняем H 0 .
Таким образом, существует четыре возможных результата принятия решения при проверке статистической гипотезы, как показано в таблице ниже.
Результаты решения проверки гипотез
| Истина | Решение | |
|---|---|---|
| Не отклонять H 0 | Отклонить H 0 | |
| H 0 истина | Правильное решение | Ошибка I типа α |
| H 0 ложь | Ошибка II типа β | Правильное решение |
Есть два типа ошибок, связанных с решением отклонить и не отклонять нулевую гипотезу H 0 .Ошибка типа I α фиксируется, если мы отклоняем H 0 , когда H 0 истинно; ошибка типа II β возникает, когда мы не можем отклонить H 0 , когда H 0 ложно. Как правило, α (риск совершения ошибки типа I) устанавливается равным 0,05. Статистическая мощность для обнаружения определенного отклонения от H 0 (вычисляется как 1 – β) обычно устанавливается на 0.80 и выше; таким образом β (риск совершения ошибки типа II) установлен равным 0,20 или меньше.
3. Разница между проверкой гипотез и анализом мощности
3.1. Проверка гипотез
В большинстве случаев проверки гипотез нас интересует, есть ли доказательства против H 0 на основе уровня статистической значимости . Рассмотрим исследование, в котором сравниваются две группы по некоторому интересующему результату и . Если μ1 и μ2 обозначают средние значения y для групп 1 и 2 в популяции, можно было бы сделать следующие гипотезы:
В приведенном выше примере разница между двумя средними согласно альтернативной гипотезе H a составляет не указано, поскольку при проверке гипотез мы пытаемся определить, есть ли доказательства для отклонения H 0 .Вывод о H 0 основан на распределении статистики, d = y¯1 + y¯2 , где y¯1 и y¯2 — средние значения результата y, наблюдаемого в исследуемой выборке. Уровень статистической значимости обозначается значением p , которое представляет собой вероятность наблюдения наших данных или что-то более экстремальное, если значение H 0 было истинным. На практике порог отклонения нуля обычно составляет α = 0,05 или α = 0,01 для крупных исследований, а нулевая гипотеза отклоняется, если значение p <α.
Обратите внимание, что направление действия не указано в двухсторонней альтернативе H a выше; то есть мы не указываем, больше или меньше среднее значение для группы 1, чем среднее значение для группы 2. Если мы предположим направление воздействия, односторонний Можно использовать H и . Например:
3.2. Анализ мощности
В отличие от проверки гипотез, при выполнении анализа мощности необходимо полностью учитывать как нулевую гипотезу H 0 , так и альтернативную гипотезу H a .Обычными целями проведения анализа мощности являются (а) оценка минимального размера выборки, необходимого в предлагаемом исследовании для обнаружения эффекта определенной величины на заданном уровне статистической мощности, или (б) определение уровня статистической мощности в завершенное исследование для обнаружения эффекта определенной величины с учетом размера выборки в исследовании. В приведенном выше примере, чтобы оценить минимальный необходимый размер выборки или вычислить статистическую мощность, мы должны указать значение для δ = μ 1 -μ 2 , разность между двумя средними значениями группы, которую мы хотим обнаружить. под H .
В анализе мощности эффекты часто указываются в терминах размеров эффекта , а не в терминах абсолютной величины предполагаемого эффекта, потому что величина эффекта зависит от того, как определяется результат (т. Е. Какой тип мер используются) и не учитывает изменчивость таких показателей результатов в исследуемой популяции. Например, если результатом и является масса тела, она может быть альтернативно измерена в фунтах или килограммах, разница между средними значениями двух групп может быть выражена в 11 фунтов или 5 килограммов.Чтобы устранить зависимость от типа используемой меры и учесть вариабельность результатов в исследуемой популяции, размер эффекта — как стандартизованная мера разницы между группами — часто используется для количественной оценки предполагаемого эффекта:
где σ 1 2 и σ 2 2 обозначают дисперсию результатов в двух группах. В отличие от разности δ = μ 1 -μ 2 , величина эффекта является инвариантной величиной , то есть остается неизменной независимо от используемого масштаба.
Обратите внимание, что величина эффекта различается для разных аналитических моделей. Например, в регрессионном анализе величина эффекта обычно основывается на изменении R 2 , показателя степени изменчивости в ответной (зависимой) переменной, которая объясняется независимыми (независимыми) переменными. Независимо от таких различий, величина эффекта является безразмерной величиной.
4. Примеры анализа мощности
4.1. Пример 1
Рассмотрим еще раз гипотезу, чтобы проверить разницу в средних результатах между двумя группами:
или эквивалент, если указан в размере эффекта:
Мощность вычисляется на основе выборочного распределения статистики разности, d = y¯1 + y¯2.
Для расчета мощности мы можем указать n 1 , n 2 , μ 1 , μ 2 , σ 1 и σ 2 . Например, если n 1 = n 2 = 50, μ 1 = 0,2, μ 2 = 1,1 и σ 1 = σ 2 = 1,6, то мощность = 80%. В качестве альтернативы мы можем указать разницу в величине эффекта, размер эффекта = 1,1-0,21,6 = 0,56, чтобы получить ту же мощность = 80%.
4.2. Пример 2
Рассмотрим модель линейной регрессии для переменной ответа (результата), которая является непрерывной с m независимыми (независимыми) переменными в модели.Наиболее распространенная гипотеза заключается в том, объясняют ли объясняющие переменные совместно вариабельность переменной ответа. Мощность основана на выборке F -распределение статистики, измеряющей силу линейной зависимости между откликом и независимыми переменными, и является функцией m , R 2 (размер эффекта) и размер выборки n .
Если m = 5, нам нужен размер выборки n = 100, чтобы обнаружить увеличение на 0.12 дюймов R 2 при мощности 80% и α = 0,05. Обратите внимание, что R также называется коэффициентом множественной корреляции или коэффициентом множественного определения .
4.3. Пример 3
Рассмотрим модель логистической регрессии для оценки факторов риска самоубийства. Во-первых, рассмотрим случай только с одним фактором риска, таким как большая депрессия (предиктор). Размер выборки является функцией общего уровня самоубийств π в исследуемой популяции, отношения шансов для фактора риска и уровня статистической мощности.В таблице ниже показаны оценки размера выборки в зависимости от этих параметров с α = 0,05 и мощностью = 80%. Как показано в таблице, если π = 0,5, размер выборки n = 272 необходим для определения отношения шансов 2,0 для переменной риска (большая депрессия) в логистической модели.
Размеры выборки должны иметь мощность 80%, чтобы обнаруживать разные отношения шансов на двух разных уровнях распространенности (π) целевой переменной, представляющей интерес
| π | Отношение шансов | ||||||
|---|---|---|---|---|---|---|---|
| 0.6 | 0,8 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | |
| 0,2 | 892 | 4228 | 5601 | 1579 | 783 | 487 | 342 |
| 0,5 | 492 | 2532 | 3788 | 1120 | 579 | 374 | 272 |
Во многих исследованиях мы рассматриваем несколько факторов риска или один фактор риска, влияющий на другие коварианты.В этом случае мы сначала рассчитываем размер выборки, необходимый для интересующей переменной риска, а затем корректируем его с учетом наличия других переменных риска (ковариат).
В случае большой депрессии как фактора риска самоубийства с одним фактором риска, если мы дополнительно учитываем другие ковариаты, такие как возраст и пол, в модели логистической регрессии, необходимый размер выборки получается путем деления полученного размера выборки. из модели с одним фактором риска на 1- R 2 , где R 2 — из регрессионной модели с интересующим фактором риска в качестве зависимой переменной и другими ковариантами в качестве независимых переменных.В случае, когда π = 0,5, если R 2 = 0,3 для модели логистической регрессии с большой депрессией в качестве зависимой переменной и возрастом и полом в качестве независимых переменных, тогда 2721-0,3 = 389 — это размер выборки, необходимый для определить отношение шансов 2,0 для большой депрессии при прогнозировании самоубийства с поправкой на возраст и пол. Таким образом, требуется больший размер выборки при контроле других ковариат в модели, а увеличение необходимого размера выборки тем больше, когда корреляция между интересующей переменной риска и другими ковариатами выше.
4.4. Пример 4
Рассмотрим исследование злоупотребления наркотиками, в котором сравниваются конфликты между родителями и родительское поведение родителей из семей с отцом, злоупотребляющим наркотиками (DA), с таковым в семьях с отцом, злоупотребляющим алкоголем (AA). Каждый участник исследования оценивается в трех временных точках. Для таких лонгитюдных исследований мощность является функцией корреляции внутри субъекта ρ, то есть корреляции между повторными измерениями внутри участника. Существует множество структур данных, которые можно использовать для оценки этой внутрипредметной корреляции; подробности этого можно найти в статье Дженнриха и Шлухтера.[1]
Необходимые размеры выборки для полных данных (и 15% отсутствующих данных) для выявления различий в интересующем исходе между двумя группами (α = 0,05; β = 0,20), когда результат оценивается повторно и существуют разные уровни внутри субъекта корреляция
| количество постбазовых оценок | внутрипредметная корреляция ρ | ||||
|---|---|---|---|---|---|
| 0,1 | 0,3 | 0,5 | 0,7 | 0.9 | |
| два | 52 (61) | 68 (80) | 84 (98) | 102 (120) | 118 (138) |
| четыре | 36 (42) | 56 (65) | 76 (89) | 96 (112) | 116 (136) |
Как видно из вышеприведенной таблицы, размеры выборки, необходимые для обнаружения желаемого размера эффекта, увеличивались по мере приближения ρ к 1 и уменьшались по мере приближения ρ к 0.Размер выборки также зависит от количества оценок после исходного уровня, при этом требуется меньший размер выборки, когда оценок больше. В крайнем случае, когда ρ = 0 (нет связи между повторной оценкой внутри участника) или ρ = 1 (повторные оценки внутри участника дают идентичные данные), повторяющиеся результаты становятся полностью независимыми (как если бы они были получены от других физических лиц) или дублирующий (не предоставляющий дополнительной информации).
Когда ρ = 1, все повторные оценки внутри участника идентичны друг другу, и, таким образом, дополнительные оценки не дают никакой новой информации.Для сравнения, когда ρ 1, продольные исследования всегда обеспечивают большую статистическую мощность, чем их поперечные аналоги. Кроме того, требуемый размер выборки меньше, когда р приближается к 0, потому что повторные измерения менее похожи друг на друга и предоставляют дополнительную информацию об участниках. Чтобы обеспечить достаточно небольшие корреляции внутри субъектов, исследователи должны избегать слишком близкого по времени планирования оценок после исходных данных.
На практике отсутствие данных неизбежно.Поскольку большинство коммерческих статистических пакетов не учитывают недостающие данные, нам необходимо выполнить корректировку, чтобы учесть их влияние на мощность. Один из способов сделать это (показанный в таблице) — увеличить предполагаемый размер выборки. Например, если ожидается, что 15% данных будет отсутствовать при каждом последующем посещении, а n — это предполагаемый размер выборки, необходимый в предположении полноты данных, мы увеличиваем размер выборки n ‘= n / ( 1-15%). Как видно из таблицы, отсутствующие данные могут иметь значительное влияние на предполагаемый размер необходимой выборки, поэтому важно иметь хорошие оценки ожидаемого количества недостающих данных при оценке требуемого размера выборки для предлагаемого исследования.Не менее важно попытаться уменьшить количество недостающих данных в ходе исследования, чтобы повысить статистическую мощность результатов.
5. Пакеты программного обеспечения
Для анализа мощности можно использовать различные пакеты статистического программного обеспечения. Хотя популярные пакеты анализа данных, такие как R [2] и SAS [3], могут использоваться для анализа мощности, их применение несколько ограничено, поэтому часто необходимо использовать более специализированные пакеты программного обеспечения для анализа мощности. Мы использовали PASS 11 [4] для всех примеров в этой статье.Как отмечалось ранее, большинство пакетов не учитывают недостающие данные для планов продольных исследований, поэтому для учета недостающих данных необходимы специальные корректировки.
6. Обсуждение
Мы обсудили анализ мощности для ряда статистических моделей. Хотя разные статистические модели требуют разных методов и входных параметров для анализа мощности, цели анализа одинаковы: либо (а) определить способность обнаруживать определенный размер эффекта (и отклонить нулевую гипотезу) для данного размера выборки, или (b) для оценки размера выборки, необходимого для обнаружения определенного размера эффекта (и отклонения нулевой гипотезы) при заданной мощности.Анализ мощности для лонгитюдных исследований сложен, потому что внутрипредметная корреляция, количество повторных оценок и уровень недостающих данных могут повлиять на оценки требуемых размеров выборки.
При проведении анализа мощности необходимо указать желаемую величину эффекта, то есть минимальную величину стандартизированной разницы между группами, которая будет считаться релевантной или важной. Существует два общих подхода к определению величины эффекта, используемого при проведении анализов мощности: использование «клинически значимой» разницы; и использовать информацию из опубликованных исследований или пилотных данных о величине различия, которое является общим или считается важным.При использовании второго подхода следует помнить о размерах выборки в предыдущих исследованиях, поскольку сообщаемые средние значения, стандартные отклонения и размеры эффекта могут быть весьма различными, особенно для небольших исследований. И предыдущие отчеты могут быть сосредоточены на разных когортах населения или использовать дизайн исследований, отличный от тех, которые предназначены для интересующего исследования, поэтому использование предыдущих оценок в предлагаемом исследовании может быть нецелесообразным. Кроме того, учитывая, что исследования с большей величиной эффекта с большей вероятностью достигнут статистической значимости и, следовательно, с большей вероятностью будут опубликованы, оценки из опубликованных исследований могут переоценить истинный размер эффекта.
Выражение признательности
Это исследование частично поддержано Клиническим и трансляционным научным сообществом Кливленда, UL1TR000439, и Университетом Рочестера, 5-27607, Национальным институтом здравоохранения.
Биография
Найджи Лу получил докторскую степень. закончил математический факультет Университета Рочестера в 2007 году, защитив диссертацию на тему «Ветвящийся процесс». В настоящее время он является доцентом-исследователем кафедры биостатистики и вычислительной биологии в Медицинском центре Университета Рочестера.Научные интересы доктора Лу включают анализ социальных сетей, продольный анализ данных, модели без распределения, надежную статистику, модели причинно-следственных связей и модели структурных уравнений в применении к крупным комплексным клиническим испытаниям в психосоциальных исследованиях.
Сноски
Конфликт интересов: Авторы сообщают об отсутствии конфликта интересов, связанного с этой рукописью.
Ссылки
1. Jennrich RI, Schluchter MD. Несбалансированные модели повторных измерений со структурированными ковариационными матрицами.Биометрия. 1986; 42: 805–820. [PubMed] [Google Scholar] 2. R Core Team. R: Язык и среда для статистических вычислений. Вена (Австрия): Фонд R для статистических вычислений; 2012. ISBN 3-1-07-0, URL http://www.R-project.org/ [Google Scholar] 3. Castelloe JM. Вычисления размера выборки и анализ мощности с помощью системы SAS. Материалы Двадцать пятой ежегодной международной конференции SAS Users GroupM; 9-12 апреля 2000 г .; Индианаполис, Индиана, США. Кэри, Северная Каролина: SAS Institute Inc .; Документ 265-25.[Google Scholar] 4. Hintze J. PASS 11. Кейсвилл, Юта, США: NCSS, LLC; 2011. [Google Scholar]6.1.1: Сечение столкновений — Chemistry LibreTexts
Сечение столкновений — это «эффективная площадь», которая количественно определяет вероятность события рассеяния, когда случайный вид поражает целевой вид. В приближении твердого объекта поперечное сечение — это площадь обычного геометрического поперечного сечения. Сечения столкновения обычно обозначаются σ и измеряются в единицах площади.
Введение
Атомы и молекулы могут перемещаться в пространстве и сталкиваться друг с другом. При соблюдении определенных условий столкновения происходит химическая реакция и образуется продукт. Однако иногда частицы могут подбираться очень близко друг к другу, но не ударяются. Мы можем использовать сечение столкновения, чтобы определить, насколько большим должно быть расстояние между двумя частицами, чтобы произошло столкновение.
Необходимо сделать несколько предположений:
- Все частицы движутся в пространстве линейно
- Все частицы представляют собой твердые сферы
- В столкновении участвуют только две частицы
Сечение столкновения определяется как область вокруг частицы, в которой должен находиться центр другой частицы, чтобы произошло столкновение.2} \]
Столкновение происходит, когда расстояние между центрами двух молекул реагентов меньше суммы радиусов этих молекул, как показано на рисунке \ (\ PageIndex {2} \). Сечение столкновения описывает область вокруг единственного реагента. Для возникновения реакции столкновения центр одного реагента должен находиться в пределах поперечного сечения столкновения соответствующего реагента.
Рисунок \ (\ PageIndex {2} \): Расстояние меньше радиусов \ (A \) и \ (B \), поэтому столкновения не происходит.2 \ nonumber \]Хотя сечение столкновения частицы можно вычислить, оно обычно не используется само по себе (Таблица \ (\ PageIndex {1} \)). Вместо этого это компонент более сложных теорий, таких как частота столкновений и теория столкновений.
| Молекула | Поперечное сечение (нм 2 ) |
|---|---|
| Ar | 0.36 |
| C 2 H 4 | 0,64 |
| C 6 H 6 | 0,88 |
| CH 4 | 0,46 |
| Класс 2 | 0,93 |
| CO 2 | 0,52 |
| H 2 | 0.27 |
| He | 0,21 |
| N 2 | 0,43 |
| Ne | 0,24 |
| О 2 | 0,40 |
| СО 2 | 0,58 |
А что, если бы частицы были разного размера и радиуса? Член \ (2r \) в уравнении \ (\ ref {SameEq} \) на самом деле является суммой радиуса каждой молекулы (т.е.2 \]
Упражнение \ (\ PageIndex {1A} \)
\ (H_2 + O_2 \ стрелка вправо H_2O \). Радиус кислорода 4,8 х 10 -11 м. Каково столкновительное сечение этой реакции? (Подсказка: предположите, что радиус молекулы — это просто сумма ее атомов.)
- Ответ
Радиус H 2 равен 2 (r H ) = 1,06 x 10 -10 м. Радиус O 2 равен 2 (r O ) = 9.{-19} \]
Упражнение \ (\ PageIndex {1B} \)
\ (N_2 + O_2 \ стрелка вправо N_2O \). Радиус азота 5,6 х 10 -11 м. Если расстояние между двумя центрами составляет 2,00 x 10 -19 м, существует ли столкновение между двумя молекулами?
- Ответ
Да, коллизия есть. Радиус N 2 равен 2 (r N ) = 1,12 x 10 -10 м. Радиус O 2 равен 2 (r O ) = 9.{-19} \] 1,36 x 10 -11 м — это наибольшее расстояние, на котором две молекулы могут быть, но все же сталкиваются. Поскольку 2,00 x 10 -11 м больше, чем это расстояние, центр одной молекулы не находится в поперечном сечении столкновения другой молекулы. Следовательно, столкновения не происходит. Молекулы слишком далеко друг от друга.
Упражнение \ (\ PageIndex {1C} \)
\ (F + F \ rightarrow F_2 \) Центры двух атомов находятся на расстоянии 3,50 x 10 -20 м друг от друга.{-20} \] Молекулы должны быть ближе 1,28 x 10 -20 м.
Макроскопическое сечение | Определение и примеры
Макроскопическое сечение представляет собой эффективную целевую площадь всех ядер , содержащихся в объеме материала (такого как топливная таблетка). Единицы указаны в см -1 . Это вероятность нейтронно-ядерного взаимодействия на сантиметр пути нейтрона. Коды обычно используют эти данные для анализа и проектирования активной зоны реактора.Эти коды основаны на предварительно рассчитанных гомогенизированных макроскопических сечениях сборки .Макроскопическое поперечное сечение
Разница между микроскопическим поперечным сечением и макроскопическим поперечным сечением очень важна и переформулирована для ясности. Микроскопическое поперечное сечение представляет собой эффективную площадь мишени одиночного ядра-мишени для падающей частицы. Единицы представлены в коровниках или см 2 .
В то время как макроскопическое сечение представляет собой эффективную площадь мишени для всех ядер , содержащихся в объеме материала, единицы даны в см -1 .
Макроскопическое поперечное сечение получается из микроскопического поперечного сечения и плотности атомных номеров :
Σ = σ.N
Здесь σ , имеющее единицы измерения m 2 , равно микроскопический разрез.Поскольку единицы N (плотности ядер) — это ядра / м 3 , макроскопическое сечение Σ имеет единицы измерения -1 м. Таким образом, это неправильное название, потому что это неправильная единица измерения поперечных сечений. В терминах Σ t (полное сечение) уравнение для интенсивности нейтронного пучка можно записать как
-dI = N.σ.Σ t .dx
Разделив это выражение по I (x) дает
-dΙ (x) / I (x) = Σ t .dx
Поскольку dI (x) — это количество нейтронов, которые сталкиваются в dx, величина — dΙ ( x) / I (x) представляет собой вероятность того, что нейтрон, который выжил, не столкнувшись до x, столкнется в следующем слое dx.Отсюда следует, что вероятность P (x) того, что нейтрон пройдет расстояние x без какого-либо взаимодействия в веществе, которое характеризует Σt, составляет:
P (x) = e -Σ t .x
Мы можем получить вероятность того, что нейтрон совершит свое первое столкновение в dx из этого уравнения . Это будет количество P (x) dx . Предположим, что вероятность первого столкновения в dx не зависит от его истории. В этом случае требуемый результат будет равен вероятности того, что нейтрон доживет до слоя x без какого-либо взаимодействия (~ Σ t dx), умноженной на вероятность того, что нейтрон будет взаимодействовать в дополнительном слое dx (т.е.е., ~ e -Σ t . x ).
P (x) dx = Σ t dx. e -Σ t .x = Σ t e -Σ t .x dx
Средний свободный пробег
Из уравнения для вероятности первого столкновения в dx, мы можно вычислить длину свободного пробега , пройденного нейтроном между двумя столкновениями. Символом λ обычно обозначается эта величина . Оно равно среднему значению x, расстояния, пройденного нейтроном без какого-либо взаимодействия, по распределению вероятности взаимодействия.
, где можно различить λ s , λ a , λ f и т. Д. Эта величина также известна как длина релаксации , потому что это расстояние, на котором интенсивность нейтронов которые не вызвали реакции, уменьшилось в е.
Для материалов с высоким поперечным сечением поглощения длина свободного пробега составляет очень короткая, и поглощение нейтронов происходит в основном на поверхности материала .Это поверхностное поглощение называется самоэкранированием , потому что внешние слои атомов экранируют внутренние слои.
Макроскопическое сечение смесей и молекул
Большинство материалов состоит из нескольких химических элементов и соединений. Большинство химических элементов содержат несколько изотопов этих элементов (например, гадолиний с его шестью стабильными изотопами). По этой причине большинство материалов имеют много поперечных сечений. Следовательно, чтобы включить все изотопы в данном материале, необходимо определить макроскопическое сечение для каждого изотопа, а затем просуммировать все отдельные макроскопические сечения.
В этом разделе оба фактора (различные атомные плотности и сечения ) будут учитываться при вычислении макроскопического сечения смесей .
Сначала рассмотрим число Авогадро N 0 = 6,022 x 10 23 , которое представляет собой количество частиц (молекул, атомов), содержащихся в количестве вещества, указанном на один моль. Таким образом, если M представляет собой молекулярную массу , соотношение N 0 / M равно количеству молекул в 1 г смеси.Число молекул на см 3 в материале с плотностью ρ и макроскопическое сечение для смесей задаются следующими уравнениями:
N i = ρ i .N 0 / M i
Рассеяние медленных нейтронов на молекулах больше, чем на свободных ядрах.
Обратите внимание, что в некоторых случаях поперечное сечение молекулы не равно сумме поперечных сечений ее отдельных ядер .Например, сечение упругого рассеяния нейтронов водой имеет аномалии для тепловых нейтронов. Это происходит потому, что кинетическая энергия падающего нейтрона порядка или меньше энергии химической связи . Следовательно, рассеяние медленных нейтронов на воде (H 2 O) больше, чем на свободных ядрах (2H + O).
Пример — Макроскопическое поперечное сечение карбида бора в регулирующих стержнях
Регулирующий стержень обычно содержит твердый карбид бора с природным бором.Природный бор состоит в основном из двух стабильных изотопов: 11 B (80,1%) и 10 B (19,9%). Карбид бора имеет плотность 2,52 г / см 3 .Определите полное макроскопическое сечение и длину свободного пробега .
Плотность:
M B = 10,8
M C = 12
M Смесь = 4 x 10,8 + 1 x 12 г / моль
N B4C = ρ. N a / M Смесь
= (2.52 г / см 3 ) x (6,02 × 10 23 ядер / моль) / (4 x 10,8 + 1 × 12 г / моль)
= 2,75 × 10 22 молекул B4C / см 3
N B = 4 x 2,75 × 10 22 атомов бора / см 3
N C = 1 x 2,75 × 10 22 атомов углерода / см 3
N B10 = 0,199 × 4 × 2,75 × 10 22 = 2,18 × 10 22 атомов 10 Б / см 3
N B11 = 0.801 × 4 × 2,75 × 10 22 = 8,80 × 10 22 атомов 11B / см 3
N C = 2,75 × 10 22 атомов 12C / см 3
микроскопический поперечные сечения
σ t 10B = 3843 b из которых σ (n, alpha) 10B = 3840 b
σ t 11B = 5.07 b
σ t 12C = 5.01 b
макроскопическое сечение
Σ t B4C = 3843 × 10 -24 x 2.18 × 10 22 + 5,07 × 10 -24 x 8,80 × 10 22 + 5,01 × 10 -24 x 2,75 × 10 22
= 83,7 + 0,45 + 0,14 = 84,3 см -1
средняя длина свободного пробега
λ t = 1 / Σ t B4C = 0,012 см = 0,12 мм (сравните с диаметром гранул B4C в управляющих стержнях, который может составлять около 7 мм )
λ a ≈ 0,12 мм
“Пример
Было написано, что макроскопическое сечение получено из микроскопического сечения и плотности атомного числа (N) :Σ = σ.N
В этом уравнении плотность атомного числа играет решающую роль в качестве микроскопического поперечного сечения. В активной зоне реактора можно изменять атомную плотность некоторых материалов (например, воды в качестве замедлителя), что приводит к определенным изменениям реактивности . Чтобы понять природу этих изменений реактивности , мы должны понимать термин атомная плотность числа.
См. Теорию: Плотность атомного числа.
В большинстве реакторов PWR используется урановое топливо , которое имеет форму диоксида урана (UO 2 ).Обычно топливо имеет обогащение ω 235 = 4% [граммы 235 U на грамм урана] изотопа 235 U.
Рассчитайте плотность атомного числа 235 U (N235U ), когда:
- молекулярная масса обогащенного урана M UO2 = 237,9 + 32 = 269,9 г / моль
- плотность урана ⍴ UO2 = 10,5 г / см 3
N UO2 = ⍴ UO2 .N A / M UO2
N UO2 = (10,5 г / см 3 ) x (6,02 × 10 23 ядер / моль) / 269,9
N UO2 = 2,34 x 10 22 молекул UO2 / см 3
N U = 1 x 2,34 × 10 22 атомов урана / см 3
N O = 2 x 2,34 × 10 22 атомов оксида / см 3
N 235U = ω 235 .N A .⍴ UO2 / M 235U x (M U / M UO2 )
N 235U = 0,04 x 6,02 × 10 23 x 10,5 / 235 x 237,9 / 269,9 = 9,48 x 10 20 атомов 235U / см 3
Ссылки:
Ядерная и реакторная физика:- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading , Массачусетс (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную инженерию, 3-е изд., Прентис-Холл, 2001, ISBN: 0-201-82498-1.
- У. М. Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Glasstone, Сесонске. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4-е издание, 1994 г., ISBN: 978-0412985317
- W.S.C. Уильямс. Ядерная физика и физика элементарных частиц. Кларендон Пресс; 1 издание, 1991 г., ISBN: 978-0198520467
- Г. Р. Кипин. Физика ядерной кинетики. Аддисон-Уэсли Паб. Co; 1-е издание, 1965 г.
- Роберт Рид Берн, Введение в эксплуатацию ядерных реакторов, 1988 г.
- Министерство энергетики, ядерной физики и теории реакторов США. Справочник DOE по основам, том 1 и 2. Январь 1993 г.
Advanced Reactor Physics:
- KO Ott, WA Bezella, Introductory Nuclear Reactor Statics, Американское ядерное общество, пересмотренное издание (1989), 1989, ISBN: 0-894-48033-2.
