Снятие энергии с резонанса: схемы, инструкции, описание, как собрать

Рассказ разработчика о генераторе свободной энергии

Автор видео канала “Vasili Ivanov” разработчик, который специализируется в области свободной энергии. Закончил делать катушку трансформатора-генератора. Она трехсекционная, в каждой секции по 465 витков.

Первая секция проводам 0,5 мм. Вторая 0,45 мм, и третья 0,35. В одной части расположится узел напряженности, в другой – кучность тока. Индуктивность конструкция получилась большая через 17,54 миллигенри. По секциям: 5,66; 4,77; 5,65. Общий резонанс 65,6 килогерц.

Для поиска волнового резонанса сделал временной индуктор, который разместил над первой секцией. Здесь будет возбуждение все катушки от генератора. Осциллограф подключил, периодически последовательно проверял резонанс разных секций и общий.

Получилась такая картина резонанса по секциям.

Резонансы правильные, то есть гармоники четко прослеживаются.

Прогонял по всем частотам катушку до 15 Мгц. Смотрел, чем такая многослойная намотка дышит. Услышал много критики, что волнового резонанса при многослойном волноводе не будет. Что не определить, где узел напряжение будет и так далее. Но ничего такого не увидел. Проверял и настраивал классический трансформатор Теслы, всё тоже самое. Открыл для себя неожиданно незапланированный эффект, когда когда ушёл на низкие частоты. На частоте 5 килогерц получился такой сигнал на осциллографе. Нижний щуп подключен к выходу генератора на два вывода индуктора. Видим, как генератор работает по возбуждению катушки.

Интересуют 2 и 3 секции. Узел напряжение будет на 3 и 2 секциях. Поэтому все работы по съем энергии будут в этой области.

Что мы наблюдаем? Говорят: откуда берётся свободная энергия? Отвечаем. Работа индуктора по частоте и фазе сигнала совпадают полностью. Если переместить сигнал индуктор наверх, то получится такая картина.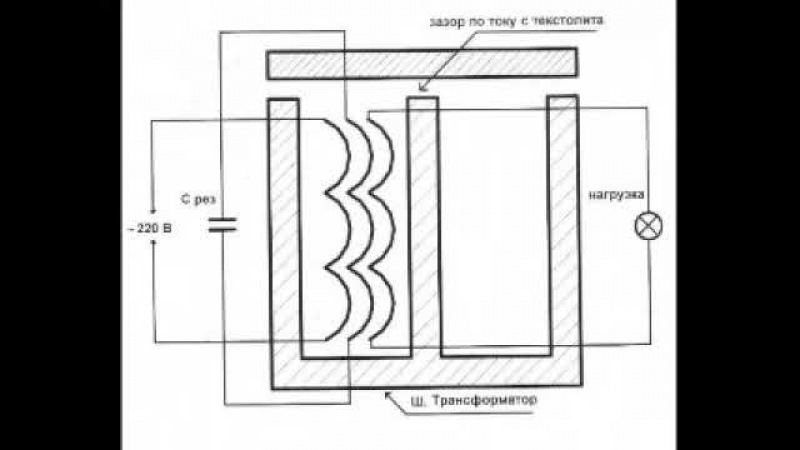

Что мы наблюдаем? Идет удар импульса генератора по катушке. Колебания пошли на затухание. А что мы видим в секции, в обмотке? Там идёт возрастание. На первый импульс пришелся удар, и пошёл затухать. А в секции 3 импульса получили прибавку энергии. На фоне затухания колебания меандра. Затем эти четыре пика идут на убывание, а на трех ровный сигнал. В то время, как возбуждение индуктора по амплитуде уменьшается. И потом снова: удар импульса и опять идет возрастание колебаний. Мы имеем на этом этапе свободную энергию. Так как удары импульса вызывают свободные колебания с возрастающей амплитудой. Если мы теперь поменяем секции, получаем аналогичную картину.

Удар – происходит сразу снижение амплитуды меандра. В то время, как в 3 секции сигнал возрастает.
Появилась почва для мыслей: на какой же частоте работать и откуда добывать эту свободную энергию? Как найти узел напряжение при такой многослойной намотке? Он будет на 3 секции. Такие итоги поиска резонансных частот.

Один из комментариев под видео на YouTube

Михаил Незнаю:
Для размышления. Из личного опыта. Я намотал конденсатор в виде катушки из двух алюминиевых полос по 25 мм, по 50 витков каждая (примерно) это около 6 м, на сердечнике от твс, а контакты вывел как бы бифилярно – начало одной обкладки и конец другой.. Емкость такой катушки-конденсатора получилась около 50 нф. Эту катушку-конденсатор подключить к индуктивности, что бы получить параллельный колебательный контур. Получилось зажечь лампочку на вторичной обмотке, при этом ставил цель создать магнитный поток в сердечнике, не за счет тока, а за счет статического электричества (видимо холодного электричества), а раз это так, то зарядом этого “конденсатора” можно воспользоваться многократно получая на выходе больше затраченного… Сейчас жду трансформаторное масло, что бы проверить работу от искровика в резонансном контуре, т.к. у такой “катушки” емкость и мощность, как я понял, годится только при высоком потенциале.

Волновой резонанс, генерируемый многослойной катушкой

Мастер снял видеоролик о волновом резонансе многослойной катушки, которая будет использоваться в резонансном трансформаторе для получения свободной энергии. Катушка моталась из расчёта рабочей частоты 288 кгц.

Длина волны 1041,6 м. 1 четверть, соответственно, 260 м. Это уложилось в 1385 витков. Намотал секциями по 462 витка.

Проверка будет проводиться датчиками напряжения и магнитного поля. В схеме опыта 2 датчика: датчик тока на земляном конце. И второй на горячем конце. На осциллографе верхний луч на горячем, нижний на холодном. Аккумулятор, узел коммутации. Включаем. Только потребление порядка 3 ампер. На фото сигналы датчика.

При такой противофазе сигналов только горячего и холодного концов появился волновой резонанс на частоте 154 килогерц.

Высокое напряжение внутри катушки. Что же образовалась внутри? Датчик напряжения на расстоянии 10 и 12 сантиметров мощно светится.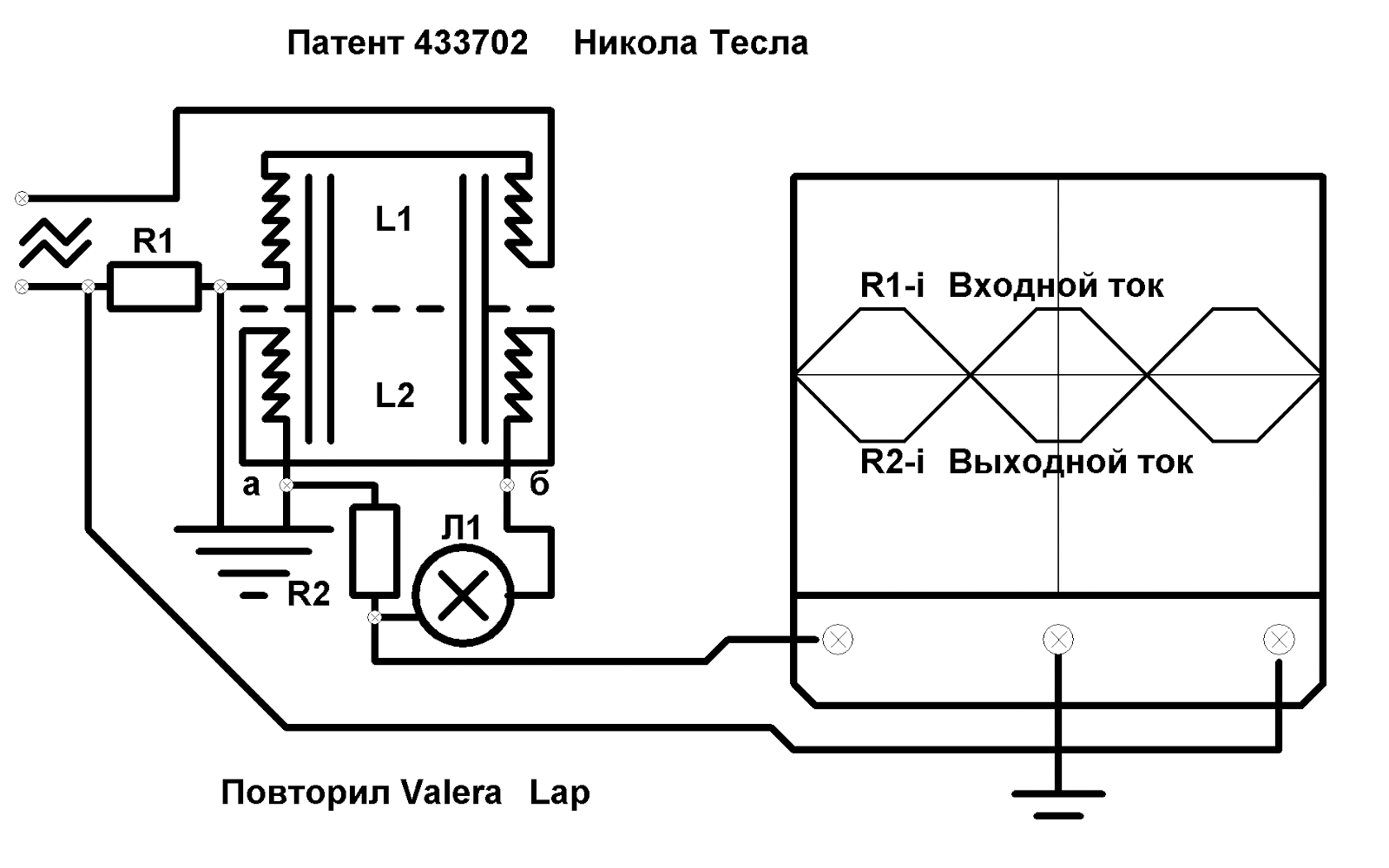 Это происходит именно на 3 секции.

В результате сложения волн здесь образовался узел. Теперь смотрим датчик магнитного поля. Он должен светиться по всей катушке при волновом резонансе. Это так и есть.

На узле при расстоянии 1,5 – 2 см максимально яркость свечения. То есть катушку съёма надо ставить на этом расстоянии. Таким образом можно с помощью датчика определять радиус магнитного поля на разных участках катушки.
Обмотка нагревается, буквально за несколько минут 3 секции становится горячей.

Если выбирать частоту от резонансной в другую сторону, смотрим, что на катушке. Датчик не светится. То есть падающая и отраженная волна здесь не складываются. Резонанса при этой частоте нет. Если вращать новое регулятор частоты, чтобы сигналы датчиков находились в противофазе, загорается лампа, появляется зебра и снова такое поле напряженности.
Чтобы работать с этой намоткой, инженер изготовил катушку съема здесь пока 40 м.

Сильно отличается частота волнового резонанса от теоретической. По идее должно быть около 1 Мгца, но из-за того, что такой многослойный пирог, частота получилось совсем другая – 154 килогерц.

Другие видео автора:
https://www.youtube.com/channel/UCS01B9OLC57Ipp8XUTPmbEA/videos?disable_polymer=1

Как работала Башня Тесла по передаче энергии — собственное «расследование»

Несколько лет назад мы – авторы данного материала – изрядно покопавшись в патентах, дневниках и лекциях Н.Теслы (благо, образование позволяло) пришли к выводу, что пресловутая Башня Тесла по передаче энергии не «фейк», а вполне рабочая конструкция.

В результате нескольких лет исследований, размышлений, изучения первоисточников, сопоставления данных, формирования и отсеивания гипотез и т.п. – появилась красивая и, по сути, простая модель, которая строго вписалась в классическую физику и была подтверждена численным моделированием в пакете Ansoft HFSS. С момента начала проекта, мы провели некоторое количество дискуссий в различных сообществах, где от нас требовали «статью для технарей» — в результате появился данный материал.

Этот материал не является строгой теорией (т.е. теорией, учитывающей все возможные аспекты работы Башни Теслы). Тем не менее, мы постарались достаточно полно осветить предлагаемую концепцию и привести адекватные численные оценки основных характеристик процесса. Так что, если Вам интересно разобраться в модели и поучаствовать в конструктивной дискуссии – приглашаем ознакомиться с материалами.

Итак, в нашей науч-поп статье изложено начало концепции – по сути, отправная точка исследований (на формулирование которой, к слову, потребовалось изрядное кол-во времени).

Можно в нескольких предложениях описать суть поста ниже, с пометкой «внимание — не для специалистов». Тогда суть можно было бы сформулировать так: Башня создает резонанс токов–напряжений в длинной линии, где в качестве длинной линии (проводника, одним концом подсоединенного к задающему генератору – т.е. к Башне) берется вся Земля. Сопротивление Земли оказывается крошечным (почему — разобрано ниже). Потери от ЭМ излучения также не носят драматических последствий, т. к. “спасает” ионосфера, от которой отлично отражается низкочастотное ЭМ–излучение, а отразившись – взаимодействует с Землей, снова переходя в токи в длинной линии – Земле (модель волновода). И возникает устойчивая картина стоячих волн токов–напряжений–зарядов в земле, сопровождаемая слабым ЭМ–излучением между землей и ионосферой.

Начали мы с того, что досконально изучили режим работы Башни Тесла следуя его записям и патентам. А из этого уже родилось понимание – какие физ-процессы может вызывать такое устройство в планете Земля, и из этого понимания – возникла уверенность, что передача энергии предложенным (и апробированным) Теслой путем вполне возможна. При этом, мы отталкиваемся от того, что в патенте Теслы присутствует вся полнота описания и нет «скрытых/спрятанных» параметров/процессов. Так что “идеи”, активно муссируемые желтой прессой и СМИ – о том, что Тесла с помощью своей Башни пытался “качать энергию эфира”, использовать “радиантную энергию” и т.п. – полагаем являются лишь фантазиями журналистов, далеких от физики. По нашему мнению, работа Башни полностью укладывается в известные физические законы, не требует привлечения каких бы то ни было новых концепций или физических эффектов, и в этом смысле наша работа (и будущий планируемый эксперимент) носит сугубо прикладной характер – а не характер фундаментальных исследований. Если материал ниже сложен для понимания, то можно ознакомиться со статьей по ссылке выше (она написана для гуманитариев, и содержит ряд неточностей, граничащих с некорректностью, но дает хорошее качественное понимание).

За сим, приступим.

Башня Тесла: характеристики работы

Если отсечь все невозможное, то Башня Тесла (за вычетом не существенных здесь технических нюансов) есть не что иное, как заземленный одним концом спиральный четвертьволновой резонатор (характеризующийся распределенными параметрами), с дополнительной ёмкостью на верхнем конце спирали. Этот резонатор раскачивается задающим генератором (синусоидальный сигнал, частота ниже 20 кГц — если исходить из патентов Тесла, US787412 и US1119732).

Иначе говоря, принципиальная схема башни выглядит следующим образом:

Слева показана физическая уединенная ёмкость на вершине башни (дополнительная к собственной ёмкости катушки), справа – условная эквивалентная схема, где отдельно подчеркнуто, что ёмкость – уединенная, т.е. формально – ёмкость между Башней и бесконечностью, а не между Башней и Землей (т.к. в противном случае получим банальный LC-контур, замкнутый через землю). Для того чтобы минимизировать паразитную ёмкость между башней и землей — т.е. замыкание LC-контура Башни через землю — очевидно, необходимо поднять уединенную ёмкость от грунта (простая оценка показывает, что достаточно поднять ёмкость на высоту, равную нескольким средним диаметрам такой ёмкости — при выполнении такого условия, ёмкость между Башней и Землей уменьшится до значения сопоставимого с собственной уединенной ёмкости Башни).

Как известно из классической электротехники, в режиме резонанса такого резонатора ёмкостное и индуктивное сопротивления взаимно компенсируют друг друга, так что генератор “видит” только активное сопротивление резонатора. В спирали возникает стоячая волна – с узлом напряжения в точке генератора, и пучностью тока там же (при этом на конце резонатора наоборот – пучность напряжения и узел тока). Подробную аналитическую теорию работы такого резонатора можно посмотреть например вот здесь. Если материал по этой ссылке сложен для понимания – то можно упростить без потери сущности: спиральный резонатор такого рода это не что иное как просто четвертьволновая длинная линия, свернутая в спираль – т.е. как и в “вытянутой” длиной линии, в таком резонаторе на резонансной частоте будет существовать стоячая волна токов-напряжений, с узлом напряжения на одном конце линии, и узлом тока – на противоположном конце линии; существенное отличие от “вытянутой” длинной линии – только в усиленной индуктивной и ёмкостной связи между соседними участками такой линии в силу их геометрической близости в спиральной конфигурации, что немного (не в разы) — меняет резонансную частоту и скорость распространения волны вдоль линии.

На рисунке — стоячие волны в длинной линии. Распределение волн: а – напряжения; б – тока в однопроводниковой линии в различные моменты времени (иллюстрация с сайта)

Иначе говоря, Башня является буфером заряда – уединенной ёмкостью, в которую задающий силовой генератор “гоняет” заряд из земли.

При этом, ЭМ-излучение в смысле радиоволн (т.е. поле в дальней, волновой зоне Башни) для нашего диапазона рабочих параметров – фактически отсутствует. Покажем это.

В радиофизике есть понятие спиральных антенн, которое, на первый взгляд, можно соотнести с таким спиральным резонатором. Однако, в отличие от антенн, электрическая длина витка Башни на 3-5 порядков меньше длины волны (т.е. кол-во витков исчисляется тысячами – при том, что вся длина обмотки примерно равна четверти длины волны). При этом, бОльшая часть токов (пучность тока) сосредоточена в нижней половине башни. Иначе говоря, в смысле внешнего ЭМ-излучения, такая структура работает как обычная классическая сосредоточенная индуктивность. Т.е. обычный магнитный диполь.

Известна формула, задающее сопротивление излучения электрически короткой магнитной рамки (магнитного диполя) с длиной волны λ (сопротивление излучения характеризует потери проводника на излучение ЭМ-волн — т.е. потери энергии тока на излучение рассматриваются как формальное активное сопротивление, потери на котором равны потерям на излучения):

(формула 4.30 по ссылке выше)

Где эквивалентная длина диполя l_э связана с радиусом «а» рамки соотношением:

Для случая N витков формула домножается на коэффициент N² (из очевидных соображений – плотность энергии излучения пропорциональна квадрату амплитуды поля рамки, т.е. квадрату кол-ва витков в рамке).

Итого,

Подставляя наши параметры (частота 10 кГц, т.е. длина волны 30 000 м, радиус катушки – пусть 2 метра, длина обмотки – 10 км, кол-во витков около 800) получаем сопротивление излучения равное 390 наноом. Что пренебрежимо мало по сравнению с потерями на активном сопротивлении системы (составляющем, как минимум, единицы Ом).

Но, помимо тангенциальной составляющей тока в таком резонаторе, есть и осевая компонента (результирующий вертикальный ток) благодаря которой Башня дает, в том числе, излучение обычного короткого электрического диполя, для которого сопротивление излучения связано с длиной диполя l и длиной волны λ как:

(формула 4.27 по ссылке выше)

Таким образом, сопротивление излучения (относительно тока, идущего через генератор) для вертикальной компоненты тока и для наших параметров (высоте башни в десятки метров – пусть будет 30 метров для конкретики, и частоты в 10 кГц) можно оценить примерно в 1 миллиОма.

В итоге видим, что оба вида излучения (и от тангенциальной, и от осевой составляющих тока) пренебрежимо малы относительно потерь на активном сопротивлении контура, при том что это оценки сверху (т.к. для них величина тока полагается одинаковой на всём протяжении обмотки катушки, в то время как на самом деле ток падает по синусу – и на “горячем конце” катушки имеется узел тока – т. е. ноль тока, и реальное излучение будет в разы меньше оценок выше). Так что любые идеи о том, что Башня работает как антенна – не имеют под собой абсолютно никаких оснований (во всяком случае, до тех пор, пока мы следуем патентам Теслы, а не занимаемся фантазированием). Башня не является антенной в классическом понимании – её радиоизлучение (те. ЭМ-поле в дальней, волновой зоне) пренебрежимо мало, и всё что она позволяет делать – это быть эффективным накопителем для заряда, который генератор заводит-выводит из почвы на частоте работы генератора. Так что “гениальные” возражения вида “у вас обычная спиральная антенна – КПД передачи энергии будет ниже плинтуса”, и прочие “аргументы” исходящие из радиоизлучения такой структуры – лишь демонстрируют полное непонимание оппонентом самых базовых концепций радиофизики.

С Башней разобрались, теперь идем к Земле

Для простоты, начнем с элементарных аналогий – от которых постепенно перейдем к итоговой концепции.

Пусть у нас есть электрически-длинный проводник с разрывом на одном конце, заземленный вторым концом через источник переменного напряжения (электрически длинный — означает, что длина проводника сопоставима/больше длины волны от генератора, исходя из частоты генератора и скорости распространения волны — близкой к скорости света в вакууме):

В такой длинной линии, в случае если потери в линии малы – возникает стоячая волны токов-напряжений (т. е. суперпозиция падающих волн от генератора и волн, отраженных от свободного конца длинной линии). Характерным примером таких линий и таких волн являются обычные электрические вибраторы (то бишь классические антенны), как показано на рисунке ниже.

Распределение тока в симметричных вибраторах различной длины.

Суть стоячих волн в длинной линии достаточно простая для понимания. Можно мысленно разбить весь проводник на отрезки в половину длины волны. Каждый такой отрезок является ёмкостью (т.к. у проводника есть распределенная вдоль него ёмкость) и индуктивностью (аналогично). Соответственно стоячие волны это не что иное как волны токов, заряжающих такие ёмкости — т.е. энергия в такой стоячей волне попеременно запасается то в виде заряда, распределенного вдоль проводника (по синусу) — и в этот момент токи равны нулю, то в виде токов распределенных вдоль проводника (так же по синусу) — и в этот момент поверхностная плотность зарядов вдоль проводника равна нулю. Что по сути повторяет режим работы обычной LC-цепи (катушка индуктивности последовательно соединенная с ёмкостью-конденсатором), но только с учетом распределенного характера ёмкости и индуктивности. Токи в полуволне «стекаются» к центру такого выделенного отрезка — создавая пучность напряжения (т.е. появление поверхностного заряда на проводнике), а в соседнем отрезке «растекаются» от аналогичного центра — создавая заряд противоположного знака, далее этот процесс повторяется (в противоположную сторону — создавая противоположные по знаку заряды на поверхности проводника). Разумеется вышесказанное относится к идеальной линии (без потерь) разомкнутой на конце, в реальной линии с потерями (и/или линии с нагрузкой на конце) процессы несколько сложнее — но принципиальная суть от этого не меняется.

Если переходить к элементарным механическим аналогиям, то наиболее близким процессом будут волны сжатия-растяжения в длинной пружине, возникающие в том случае когда такую пружину (лежащую на опоре с нулевым трением) начинают качать туда-сюда вдоль оси пружины на одном из концов пружины — при закрепленном втором конце. При этом току — соответствует скорость движения соответствующего участка пружины, а напряжению — соответствует степень сжатия пружины.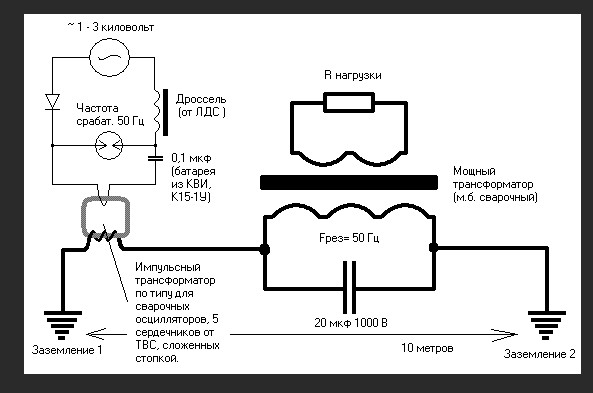 Т.е. в какой-то момент времени все участки пружины будут иметь нулевую скорость — а степень растяжения пружины будет меняться по синусу вдоль ней (эдакие чередующиеся сгустки и разряжения) — чему соответствует нулевой ток в стоячей волне и одновременно максимум напряжения (т.е. максимум поверхностной плотности заряда на проводнике), а в другой момент времени — через четверть периода колебания — наоборот вся пружина будет не деформированной, но мгновенная скорость её участков будет изменяться по синусу вдоль оси пружины (чему соответствует момент нулевой плотности заряда вдоль проводника длинной линии — но максимуму тока в нем).

Потери для такой ситуации в целом можно разделить на 2 составляющих: омические потери, и потери на излучение.
В случае большой длины проводника, и его малом омическом сопротивлении, основной вклад в потери будет давать излучение (т.е. сопротивление излучения).

Как известно, если окружить такую линию заземленным проводящим экраном, то потери на излучение будут нивелированы, и такая структура носит название коаксиального волновода – причем, в нашем примере, волна в таком коаксиальном волноводе будет существовать в виде ТЕМ-моды (портом возбуждения при этом, по сути, является генератор, подключенный через землю — к внутреннему и внешнему проводникам волновода).

По сути, режим ТЕМ-моды можно трактовать, как режим индуктивной связи внутреннего и внешнего проводников волновода через поле ближней зоны токов на этих проводниках (изменение тока на внутренней жиле — вызывает соответственно ЭДС на внешнем экране, причем наведенный на внешнем экране ток направлен против изменения тока на внутренней жиле — т.е. по сути обычная индукция в ближнем поле тока), так что поперечные потоки энергии не просто нулевые в среднем по времени (как для ТЕ или ТМ мод), но нулевые в любой момент времени. Не происходит переотражений от границ волновода – поток энергии носит только продольный характер (т.е. направлен вдоль оси, и соответственно вектор Пойнтинга направлен так же строго параллельно направлению распространения волны – вдоль оси такого коаксиального резонатора).

Поэтому режим ТЕМ-моды в коаксиальном волноводе характеризуется хорошими параметрами (относительно режимов ТЕ или ТМ мод) в части передачи энергии и в части малости коэффициента затухания волны в волноводе, и при необходимости передачи энергии по коаксиальному волноводу – как правило, стремятся использовать именно режим ТЕМ-моды.

Однако, даже если мы удалим заземление внешнего экрана такого волновода, по всей длине экрана кроме его концевых участков – экран будет отлично выполнять свою функцию.

Ведь такой экран в любом случае есть длинная линия, в качествен генератора для которой выступает ЭДС от переменного тока на внутреннем проводнике-жиле. И только на краях экрана – в силу очень малой ёмкости таких краев, будет существовать некоторая пучность напряжения, а на всей остальной длине такого экрана – он будет нормально функционировать. Что подтверждается элементарным моделированием в HFSS.

Далее, что будет, если мы не просто уберем заземление внешнего экрана – но “замкнем” края как показано на рисунке ниже (так что внешний экран станет этакой “капсулой”)? Ответ вполне ясен – эта ситуация не будет отличаться от рассмотренной выше. Экран будет работать по всей длине, а на таких вот окончаниях внешней “капсулы” – будут пучности напряжений (и узлы тока соответственно).

Далее, если внутренний и внешний проводники сделать уже в виде сфер – то мы придем к общей модели предполагаемого эксперимента (пропорции на рисунке, разумеется, не соблюдены):

Как не трудно догадаться, внутренняя проводящая сфера – это Земля, внешняя проводящая сфера – это верхние слои атмосферы (в основном ионосфера). А общая геометрия такого резонатора – это обычный концентрический сферический резонатор (в котором говорить про ТЕМ моду, в строгом смысле – уже нельзя, т.к. в нем существуют только ТЕ и ТМ моды), только с немного необычным способом возбуждения ТМ-моды (т.е. порт возбуждения – не связывает между собой внешнюю и внутреннюю обкладки, как это делается в «классической» электротехнике).

Хотя, в силу переменного сечения внутреннего и внешнего проводников, амплитуды стоячих волн токов и напряжений будут уменьшаться по мере удаления от генератора, общая суть при этом остается той же самой – ТЕМ мода коаксиального (или же ТМ-мода сферического) резонатора, возбуждаемая соответствующим источником (Башней Тесла).

На первый взгляд, идея странная: известно, что проводимость грунта Земли, и ионосферы (в ясный день на освещенной стороне) около 0.001 См/м (плюс-минус порядок), в то время как проводимость например меди – около 58 000 000 См/м. Однако, давайте посмотрим на этот вопрос исходя из численных оценок, а не из интуитивных соображений. И для начала разберемся с сопротивлением грунта Земли. Общая мысль состоит в том, что с точки зрения процессов протекания тока, деление на диэлектрики, полупроводники и проводники – достаточно условно по своей сути, т.к. при достаточно большом сечении диэлектрика – он становится вполне хорошим проводником (т.е. обладает малым итоговым сопротивлением).
Как известно, при достаточной толщине проводника, ток имеет существенное значение только на некоторой глубине, называемой глубиной скин-слоя, которая рассчитывается по формуле:

Где — удельное сопротивление, — относительная магнитная проницаемость, — частота.

Разумеется, это упрощенная формула, применимая для проводника, а не диэлектрика – однако на наших сверхнизких частотах потери связанные с диэлектрической проницаемостью грунта — малы, так что в качестве оценки – такая формула вполне применима.

Для диапазона частот 1-10 кГц, и диапазона проводимостей 0.001-0.00001 См/м глубина скин-слоя лежит в диапазоне от сотни метров до нескольких километров. При этом, чем ниже будет частота – тем больше толщина скин-слоя, т.е. тем меньше омические потери в планетарном резонансе (обратно пропорционально корню из частоты).

Таким образом, мы приходим к выводу, что, рассматривая чисто активное сопротивление Земли (как шара из грунта, т.е. материала имеющего проводимость на уровне 0.01-0.0001 См/м), и подразумевая диапазон частот не ниже 1 кГц (т.к. еще меньшие частоты не реализуемы с практической точки зрения — исходя из требуемых технических параметров Башни Тесла) необходимо ограничиться километровым слоем. Отметим, что Тесла, видимо, не вполне отдавал себе в этом отчет – и искренне полагал, что токи от его установки идут вглубь земли (а не бегут по поверхности оной), как это указано в нашей научно-популярной статье. Согласно современным данным по электродинамике – этого, разумеется, не может быть.

Сопротивление между двумя стержнями, погруженными в плохо проводящую среду (например в грунт) задается формулой:

Где

Здесь L – длина стержней, D – расстояние между ними, r1 – радиус сечения стержней, — удельная проводимостью среды.

Интересно отметить, что исходя из этой формулы, начиная с расстояния между стержнями много большего длины стержней – сопротивление между стержнями фактически становится константой (перестает расти по мере роста расстояния).

Так, например, для двух стержней длиной 30м, диаметром 0.2 м, и проводимости грунта около 0.04 См/м (что корректно для верхних слоев почвы) характерное сопротивление (между ними) лежит в диапазоне 1-3 Ом – начиная с расстояния в метры, и далее (без ограничения дальности расстояния) остается таковым при любом увеличении расстояния между стержнями. Так что идея о том, что Земля – плохой проводник (как объект в целом) – это, разумеется, интуитивное заблуждение, и будь так – заземление просто не имело бы смысла.

Так же особенностью данной формулы является тот факт, что начиная с некоторой длины стержней – дальнейший рост длины стержня не приводит к заметному уменьшению сопротивления между стержнями (т.е. иначе говоря, итоговое сопротивление между приёмником и передатчиком – слабо зависит от глубины скин-слоя). Что в целом является известным фактов в части заземляющих систем (данный характерный график взят с этой страницы).

Таким образом, у нас есть все основания для оптимизма по части сопротивления всей поверхности Земли.

Сделаем теперь более строгие оценки

Постоянная затухания, характеризующая потери на стенках волновода в силу активного сопротивления, для ТЕМ-моды коаксиального волновода

(к которому близка большая, центральная часть Земли-резонатора как показано на рисунке выше) задается формулой (см. например тут):

где R_s1 и R_s2 — поверхностные сопротивления металла внутреннего и внешнего цилиндров волновода, которые можно определить по формуле:

Здесь мю – это абсолютная магнитная проницаемость (для подавляющей части поверхностного грунта – это соответственно просто магнитная постоянная).

Сразу отметим, что под корнем стоит отношение частоты и проводимости – т.е. меньшая по сравнению с металлами проводимость во многом компенсируется килогерцевым диапазоном частот (в то время как коаксиальные волноводы применяют для частот в гигагерцы), а то что отношение стоит под знаком корня – еще больше “улучшает” ситуацию. Итого, для наших параметров (f=3 кГц, и σ=0.01 См/м получаем величину в 1.06 Ом) характерная величина поверхностного сопротивления (и земли и ионосферы) порядка одного Ома, плюс-минус порядок.

Один Ом – это, казалось бы, всё еще достаточно большая величина. Однако, добротность объемного резонатора пропорциональна его линейным размерам (т.к. кол-во энергии в резонаторе пропорционально объему оного, а потери – пропорциональны площади стенок резонатора). Что находит отражение в формуле в числителе. Радиусы D и d в нашем случае имеют колоссальное значение (D=6 600 000 м, d = 6 400 000 м,), что с лихвой перекрывает относительно большую величину поверхностной проводимости стенок волновода, так что постоянная затухании для наших параметров может быть оценена по формулам выше как 10^-8-10^-9 1/м.

В реальности, бОльшая часть поверхности планеты покрыта хорошим электролитом (соленая океаническая вода) – т.е. данная оценка это оценка сверху.

Постоянная затухания равная 10^-9 означает, что за всю длину пути «x» волны до противоположной точки Земного Шара (примерно 20 000 км) амплитуда волны упадет на величину =2%.

Чему соответствует крайне высокая добротность резонатора Земля-Ионосфера (на порядки выше, чем сотня) для такой моды, в отличие от механизма распространения обычных радиоволн через переотражение от границ земли-ионосферы. И даже ухудшение оценочной проводимости на 1-3 порядка (что имеет смысл для ионосферы) не приводит к фатальным последствиям в части самой возможности существования такого резонанса.

Мы убедились, что в принципе, искомый резонанс (исходя из фактических параметров резонатора) может иметь место, хотя реальная добротность такого резонанса может иметь вилку примерно в 2-3 порядка (но даже при самом худшем сочетании параметров – не должна быть ниже сотни).

Аналогичные оценки возможной высокой добротности ТМ-мод в резонаторе Земля-ионосфера даны в работе М.В. Давидовича – “моды многослойного концентрического сферического резонатора”.

Если говорить про строгий подход, то разумеется необходимо рассматривать полноценный концентрический резонатор в режиме ТМ-мод (например, неплохой обзор по этому вопросу можно найти по этой ссылке, для интересующихся более глубокими теоретическими аспектами — можно порекомендовать вот эту и вот эту работы).

Первые гармоники нулевой ТМ-моды – соответствуют явлению т.н. резонанса Шумана. Однако, если говорить про частоты в районе нескольких килогерц, то помимо нулевой моды – так же будут возбуждаться и следующие за ней моды (для 10 кГц – это номера мод в диапазоне 0-6).

Действительно, из формулы

для первой моды – низшая гармоника будет иметь частоту около 1.5 кГц, для второй моды – 3 кГц, и т.п.

При этом, как следует из формулы задающей частоты гармоник для каждой из таких мод, начиная с первой моды и далее – “плотность” расположения гармоник по частотной оси крайне велика (если для нулевой моды гармоники идут с шагом порядка 10 Гц, то для остальных мод попадающих в диапазон ниже 10 кГц – с шагом порядка 0.01-0.1 Гц). Так что, осуществляя возбуждение ТМ-мод такого резонатора на частотах в диапазоне нескольких килогерц, по сути невозможно говорить о какой-то конкретной моде/гармонике: итоговая картина стоячих волн будет соответствовать чрезвычайно большому количеству гармоник, сразу для нескольких мод. Что принципиально отличает такой резонанс от резонанса Шумана.

Есть и другое принципиальное отличие. Как известно (например, см. здесь – стр. 8), для пассивного резонатора, добротность гармоник растет с ростом частоты – примерно пропорционально корню из оной. Однако, резонатор Земля-ионосфера не является пассивным. В самом деле, электрическая машина Земли поддерживает примерно постоянную разность потенциалов между обкладками планетарного конденсатора (грунт-атмосфера). В случае удара молнии, данный потенциал уменьшается – однако восстанавливается за характерное время измеряемое секундами, при этом характерная плотность тока дозарядки – составляет порядка 0.1-1 ампера (стр. 6-8) на квадратный километр. Иначе говоря, Земля работает по сути как источник ЭДС, выравнивающий (впрочем, весьма медленно) разность потенциалов на некоем среднем уровне. Очевидно, что в случае сверх-низкочастотных колебаний, соответствующих резонансу Шумана (первые гармоники нулевой ТМ-моды резонатора), наличие такого источника ЭДС приводит к резкому ухудшению добротности резонанса: в случае отклонения потенциала от среднего уровня, этот источник ЭДС стремится скомпенсировать отклонение, что означает активное подавление ТМ-моды – а учитывая планетарные масштабы явления, это подавление может носить значительный характер. К сожалению, данный фактор не учитывает ни в одной из известных нам моделей резонанса ТМ-мод в резонаторе Земля-ионосфера – и причины этого понятны: до сих пор нет единой однозначной модели механизма возникновения этого источника ЭДС, и более того – как и всякие явления связанные с атмосферным электричеством, данный механизм существенно нелинеен, так что сколь-нибудь адекватное моделирование (учет) этого фактора для ТМ-мод резонатора пока не возможен – не достаточно данных.

Тем не менее, известны данные по добротности первых гармоник нулевой ТМ-моды резонатора Земля-ионосфера (данные свежие – 2011 год):

Из этих данных видно, что с ростом номера гармоники – фактическая добротность растет быстрее, чем корень из частоты (т.е. быстрее, чем для пассивного резонатора). Учитывая относительную “медленность” механизма дозарядки планетарного конденсатора, именно для низших гармоник нулевой моды данный механизм будет оказывать наиболее сильное влияние – т.к. с ростом частоты можно ожидать роста добротности резонанса с существенно большей скоростью, нежели корень из частоты.

Интересно отметить, что в 2011 году (что отражено в данных по ссылке выше) были обнаружены токи в ионосфере (соответствующие резонансу Шумана) на высотах (400-800 км), для которых все известные предыдущие модели давали полное отсутствие таких токов. Де-факто, существующие модели проводимости ионосферы оказались некорректными – и их нельзя использовать для построения моделей резонанса ТМ-мод в резонаторе Земля-Ионосфера.

Таким образом, есть основания для проведения прямых замеров добротности итогового резонанса на частотах в несколько килогерц – как исходя из теоретических предпосылок, так и исходя из фактических результатов, полученных Теслой. Прямой же аналитический (или численный) расчет невозможен – слишком сложным и плохо известным объектом является Земля сразу в большом кол-ве своих параметров/характеристик.

Предлагаемая же схема эксперимента фактически не имеет отношения ни к резонансу Шумана (принципиально другие добротности, а так же дополнительные ТМ-моды и гармоники резонанса), ни к передаче энергии радиоволнами (т.е. волнами ЭМ-поля дальней волновой зоны обычных радиоизлучателей) — о чем прямо и заявлял Тесла.

Разумеется, как уже упоминалось выше, поскольку сечение резонатора не является постоянным, то и волновое сопротивление (задающее отношение напряжения в линии — к току в ней же) будет так же переменным: максимум напряжения будет иметь место на пучностях вблизи от башни (и противоположного конца планеты), минимум – на “экваторе” от Башни, что подтверждается численным расчетом в HFSS (и соответствующими аналитическими формулами например для нулевой ТМ-моды такого резонатора).

На рисунке приведено распределение амплитуд электрического E и магнитного B полей для первых 3-х гармоник нулевой ТМ-моды резонатора Земля-ионосфера.

“Заземление” для резонатора Земля-Ионосфера

Откуда мы возьмем “заземление”, к которому подключается генератор для накачки такого резонатора на ранее приведенном рисунке?

Ответ прост – поскольку мы ранее уже провели анализ работы Башни Тесла. С точки зрения генератор, Башня Тесла с практической точки зрения ничем не отличается от некоей внешней земли (подключенной через активное сопротивление Башни). Т.к. генератор “видит” только активное сопротивление башни, но никак не реагирует на величину заряда, накопленного на башне (ибо ёмкостное и индуктивное сопротивления в режиме резонанса – компенсируют друг друга) — иначе говоря, для генератора башня это и есть “заземление” через сопротивление, равное активному сопротивлению башни.

Разумеется, как уже отмечалось выше, такой заряд вызывает перераспределение зарядов в грунте в окрестности от Башни – но чем выше поднят накопитель заряда Башни, тем менее значим этот фактор (т.к. уменьшается ёмкость Башня-Земля). Достаточно поднять накопитель заряда на высоту заметно большую, чем размер накопителя – чтобы Башня Тесла стала действительно “внешней землей” для задающего генератора (т.е. достаточно минимизировать ёмкость между башней и землей — так, чтобы собственная уединенная ёмкость Башни стала хотя-бы одного порядка с ёмкостью Башня-Земля).

КПД передачи энергии

После установления по всей планете стоячих волн напряжений и токов (при этом токи будут иметь крайне малую амплитуду – в отличие от напряжений) возможно эффективное снятие этой энергии аналогичной системой (Башней – но уже без генератора). Физ-процессы при работе приёмника характеризуются созданием связи между резонансными контурами (башни-приёмника), что позволяет получать высокий КПД передачи даже при крайне низком коэффициенте связи источника и приёмника (строго в соответствии с классической электротехникой).

Рассмотрим данный вопрос подробнее.

В случае расположения приёмника (т.е. аналогичного контура) в пучности напряжения (и узле тока) итоговой стоячей волны, переменный потенциал поверхности будет являться источником ЭДС для приёмника. При этом, в приёмнике будет возбужден резонанс – полностью аналогичный резонансу в источнике, соответственно приёмник будет генерировать стоячую волну так же полностью аналогично источнику. При этом, поскольку приёмник расположен в пучности напряжения (и узле тока), то генерируемая им волна будет, очевидно, создавать дополнительную нагрузку на источник – тем самым создавая систему в виде т.н. резонансных связанных контуров (беглый обзор по этому вопросу можно найти здесь и здесь). Действительно, в пучности напряжения внешней волны – приёмник имеет узел напряжения (и пучность тока), и работает на той же частоте, т.е. в области расположения источника – приёмник будет создавать пучность напряжения (и узел тока), которую источник и будет “видеть” как дополнительную нагрузку. Что отлично видно на видео (соответствующего моделировании в HFSS).

На видео, и на рисунке выше – источник расположен в левой верхней области, область расположения приёмника выделена в правой около-центральной части. Видно, что в области приёмника постоянный минимум поля – что и означает эффективную откачку энергии из планетарного резонанса. Так же хорошо видна интерференционная картина волн, испускаемых приёмником и источником.

Для такого рода систем (т.е. резонансных связанных контуров), КПД передачи энергии определяется произведением коэффициента связи систем k и их добротности Q. Коэффициент связи — это, грубо говоря, коэффициент, определяющий — какую часть энергии резонанса контура-источника «видит» контур-приёмник. Например, для близко расположенных катушек индуктивности (особенно если они намотаны на одном сердечнике) коэффициент связи стремится к единице, и падает по мере разнесения катушек (т.к. по мере такого разнесения — падает ЭДС, наводимая катушками друг в друге). Типичный график зависимости КПД от произведения коэффициента связи на добротность – приведен ниже (взят из документа по ссылке выше):

Физический смысл этой зависимости очевиден: даже если за один период колебаний приёмник «забирает» лишь малый процент энергии источника, но за этот же период (в силу высокой добротности резонанса) потери энергии в суммарном резонансе малы – то КПД передачи (определяющий отношение переданной и рассеянной энергий) будет высоким. Т.е. для высокого КПД передачи в общем случае не требуется высокий коэффициент связи контуров — большая добротность резонанса может компенсировать малость коэффициента связи.

Оценим коэффициент связи между источником и приёмником – в предположении высокой добротности резонатора Земля-ионосфера (для чего, как указывалось выше – есть все основания).

Пусть частота — 10 кГц. Это значит, что Земля поделена на «кольца» шириной 30 км, коих соответственно на длину половины периметра — приходится около 700. Ёмкость Земли как уединенного проводника — около 700 мкФ. Пусть ток в Башне (источнике) — 1 кА (это соответствует мощности генератора как минимум в несколько мегаватт). Для длинной линии-Земли, наши «кольца» — это параллельные ёмкости. Т.е. ёмкость, приходящуюся на одну длину волны в районе «экватора» от башни — можно оценить в c1=1 мкФ (700 мкФ/700 волн). Что при токе в 1 кА (идущем на подзаряд каждой из таких ёмкостей) дает напряжение около 15 кВ (по стандартной формуле U=I*Rc=I/(c1*w) ). Всё поле (для ТМ-моды) сосредоточено примерно на длине, равной половине длины волны (перпендикулярно грунту), как это следует из моделирования в HFSS (и/или из соответствующих аналитических формул на которые приводились ссылки выше). Для 10 кГц — это 15 км.

Что означает напряженность поля около грунта — всего один вольт на метр (при фоновой напряженности вертикальной составляющей поля — около 130 вольт на метр). Это — «на экваторе», а в ближайших к башне пучностях (т.к. ёмкость меньше на 1-2 порядка) будет соответственно на 1-2 порядка больше. Т.е. башня-приёмник «увидит» напряжение в сотню киловольт (и напряженность поля будет около 10 в/м) — если расположена на дистанции в десятки км от источника. В данной ситуации — переменный потенциал грунта велик, но напряженность поля — мала, ибо поле распределено вертикально на большой дистанции — в десятки км (что вполне позволяет говорить даже при гигаватную мощность передатчика — так чтобы не выходить за фоновый уровень напряженности поля около поверхности Земли). В случае если мы говорим про «экватор», при указанных параметрах, и итоговом резонансном напряжении в источнике, например, в мегавольт (а на экваторе, как следует из оценки выше, в 10 киловольт) — коэффициент связи, соответственно, около 1% (и десятки % на дистанции в десятки км от источника), т.к. коэффициент связи можно определить как отношение напряжений на индуктивности приёмника (при разомкнутом контуре приёмника) – и работающего источника (разумеется, при одинаковых параметрах приёмника и источника). Исходя из возможной добротности резонанса в районе нескольких сотен, такой коэффициент связи означает КПД передачи как минимум в десятки % — для экватора, и вполне может дать цифру выше 90% — для дистанции в десятки км (что соответствует заявлениям, сделанным Тесла по соответствующим экспериментам). Однако, в силу проблем с моделирование и расчетом реальной добротности резонанса, пытаться сделать более точные оценки, по сути, смысла нет (по большому счету, всё зависит от реальной добротности резонанатора-Земли, и резонатора-башни – моделирование же может дать ошибки в порядки). Так что единственный адекватный вариант – это постановка полномасштабного эксперимента — для чего, очевидно, необходимо построить полный аналог башни Тесла. Это позволит как воспроизвести «ту самую Башню Тесла» и «тот самый эксперимент», так и расставить все «точки над и» в вопроса КПД передачи для больших расстояний. В то же время, у нас нет никаких сомнений в высоком КПД передачи для конфигурации эксперимента, соответствующей параметрам исходных экспериментов Тесла (т.е. для расстояния в сотню километров), что в любом случае интересно с практической точки зрения.

Дополнительные соображения

Помимо собственно патентов, посвященных Башне, Тесла так же запатентовал устройство для детекции стоячих волн напряжений в грунте, возникающих вследствие удара молний. Данное устройство описано в патенте US787412 . Суть данного детектора, переводя на современный язык — состоит в организации т.н. синхронного детектора (или lock-in amplifier). Вот что написано по этому поводу в википедии:

The lock-in amplifier is commonly believed to be invented by Princeton University physicist Robert H. Dicke who founded the company Princeton Applied Research (PAR) to market the product. However, in an interview with Martin Harwit, Dicke claims that even though he is often credited with the invention of the device, he believes he read about it in a review of scientific equipment written by Walter C Michels, a professor at Bryn Mawr College. This was probably a 1941 paper by Michels and Curtis, which in turn cites a 1934 paper by C. R. Cosens.

Очевидно, как и многие другие идеи и патенты Теслы по которым он объективно имел приоритет — его современники не разобрались в том, что и как делал Тесла, так что приоритет относят не к нему и датируют датой на пару — тройку десятилетий позже. Однако внимательный анализ устройства по детекции стоячих волн, использованного Теслой, не оставляет никаких сомнений в том, что приоритет изобретения синхронного детектора принадлежит именно Тесле.

В самом деле, суть устройства использованного Теслой состояла в том, что на заданной частоте (и заданной скважности — см. патент) он создавал поочередное замыкание одного из контактов конденсатора-накопителя с грунтом (в это время второй контакт конденсатора находился «в воздухе»), чисто механическим способом — используя скользящие контакты на соответствующем барабане (F на рисунке ниже).

Таким образом, при условии совпадения частоты стоячей волны в грунте, и частоты замыкания контактов в приёмнике, конденсатор Т постепенно накапливал заряд — а затем принудительно разряжался через приёмник R (позволяющий регистрировать ток разряда такого конденсатора-накопителя). Что в явном виде и является логикой синхронного детектора. При этом, поскольку длина проводов соединяющих конденсатор с грунтом — была много меньше длины волны, то говорить об ЭМ-наводках на такие провода (от ударов молний) не приходится — они будут ничтожными.

Вот что писал по этому поводу сам Тесла — и с чего начался его путь в этой области:

The date I shall never forget — when I obtained the first decisive experimental evidence of a truth of overwhelming importance for the advancement of humanity. A dense mass of strongly charged clouds gathered in the west and towards the evening a violent storm broke loose which, after spending its fury in the mountains, was driven away with great velocity over the plains. Heavy and long persisting arcs formed almost in regular time intervals. My observations were now greatly facilitated and rendered more accurate by the experiences already gained. I was able to handle my instruments quickly and I was prepared. The recording apparatus being properly adjusted, its indications became fainter and fainter with the increasing distance of the storm until they ceased altogether. I was watching in eager expectation. Surely enough, in a little while the indications again began, grew stronger and stronger and, after passing thru a maximum, gradually decreased and ceased once more. Many times, in regularly recurring intervals, the same actions were repeated until the storm, which, as evident from simple computations, was moving with nearly constant speed, had retreated to a distance of about three hundred kilometers. Not did these strange actions stop then, but continued to manifest themselves with undiminished force. Subsequently, similar observations were also made by my assistant, Mr. Fritz Lowenstein, and shortly afterwards several admirable opportunities presented themselves which brought out still more forcibly and unmistakably, the true nature of the wonderful phenomenon. No doubt whatever remained: I was observing stationary waves.

Исходя из фактического устройства детектора, нет никаких сомнений в том, что факт работы такого детектора — а именно, периодическое синусоидальное изменение амплитуды энергетики процесса по мере хода и удаления грозы (на сотни миль), регистрируемого детектором — однозначно свидетельствовал именно о стоячих волнах напряжения на грунте Земли, что и было для Тесла отправной точкой его исследований.

По совокупности информации, приведенной выше — есть все основания для постановки полномасштабного эксперимента с целью окончательного подтверждения работоспособности Башни Тесла.

Если представленный материал слишком сложен для понимания — то более «гуманитарное» изложение (местами граничащее с некорректностью, но дающее хорошее понимание того, что мы собираемся сделать в плане эксперимента) можно найти, например, по этой ссылке.

Авторы: Сергей Плеханов, Леонид Плеханов

F.A.Q.

Ниже — список наиболее часто задаваемых вопросов, с ответами. Если у Вас есть вопрос — пожалуйста, прежде чем задавать его, убедитесь, что его нет в списке ниже, либо приведите аргументацию — почему приведенный ниже ответ на такой вопрос является неубедительным.

• Если эта идея рабочая — то не убьют ли токи в грунте земли всё живое что там есть?
Таких рисков нет. Просто потому, что плотность тока в поверхностном слое Земли будет мизерная (возьмем 2 килоампера в Башне, и распределим такой ток по периметру в 20 000 км длиной, и 100 метров глубиной; получим плотность тока — порядка 1 мкА на квадратный метр, что не ощутит ни один живой организм). Т.е. большой переменный внешний потенциал от заряда на грунте (киловольты и выше) — сочетается с очень малыми токам, и одновременно вертикальная составляющая напряженности электрического поля около грунта — мала (много меньше фоновой величины в 130 вольт на метр). По мере роста высоты — напряженность поля (и без того малая) будет падать, так что самолетам и спутникам -) тоже ничего не грозит.

• Вы делаете планетарную микроволновку.
К механизму нагрева вещества микроволновым излучением процессы связанные с Башней Тесла не имеют абсолютно никакого отношения. Омические потери, разумеется, будут — но даже гигаватт, распределенный на площадь всей планеты — это все равно, что спичкой греть море.

• У вас модель в HFSS некорректная — вы взяли две сферы из металла и конечно получили ТМ-моду.
Нет, мы не брали сферы из проводников — а честно заложили проводимости грунта и ионосферы, исходя из их табличных значений. Соответственно и размер модели — большой (чтобы благодаря площади сечения диэлектрика-грунта, его можно было рассматривать как проводник).

• Понятно, что ТМ-моду можно возбудить. Но как на практике можно пробросить порт от грунта до ионосферы?
А этого и не надо делать — см. в статье выше. Достаточно подключения генератора только к грунту, остальное будет автоматически наведено переменными токами в окрестности Башни. Т.е. формально можно считать антенной — круговую область грунта около башни, с радиусом порядка длины волны.

• Земля — диэлектрик, так что ток не проводит, и ничего не получится.
Грунт отлично проводит ток, см выше. На заре ЖД индустрии обратным проводником служила как раз Земля, и совершенно замечательно работала в качестве такового (не внося сколь-нибудь заметного сопротивления). К тому же, будь грунт в целом — плохим проводником, обычное заземление было бы бесполезно (т.е. не работало бы — а практика показывает обратное).

• У вас обычная радиоантенна, КПД передачи будет ничтожным.
Как показано выше, к радиоантеннам Башня не имеет ни малейшего отношения — т.к. собственно радиоизлучение у неё в практическом смысле — отсутствует (т.е. оно на очень много порядков меньше потерь на омическое сопротивление Башни).

• Чем это всё отличается от Шумана? Обычный резонанс Шумана, все это знают и поэтому идея не работоспособна. И ничего нового в этом нет.
Резонанс Шумана — это не резонанс конкретной моды, а явление шума на первых гармониках нулевой ТМ-моды, связанное с наличием импульсной накачки резонатора Земля-Ионосфера на частоте около первой моды (10 Гц — т.к. в среднем в секунду происходит около 40-50 разрядов молний, из которых по статистике только 20%-25% бьют в землю), и с тем фактом что средняя частота разрядов распределена по поверхности планеты не равномерно (с характерным масштабом неоднородности такого распределения — порядка длины волны первых гармоник). Иначе говоря, шум резонанса Шумана — связан с наличием (хотя и слабой) пространственно-временной когерентности ударов молний. Т.е. если бы молнии били равномерно по всей поверхности — резонанса Шумана (т.е. шума на частотах первых гармоник) не было бы. Или если бы средняя частота удара молний была бы не 10 Гц, а 10 кГц, то максимум энергии был бы совершенно на других гармониках/модах. Кроме того, в резонансе Шумана возбуждается только нулевая ТМ-мода, а для наших частот — будут активно участвовать и следующие моды. Таким образом, хотя косвенная связь с резонансом Шумана и есть — но наш случай это не резонанс Шумана. Принципиально новых физических эффектов мы действительно не предлагаем – всё строго в рамках того, что уже давно известно в соответствующих разделах физики. Мы лишь “склеили” известные знания в объяснение работоспособности Башни Тесла.

• Добротность резонанса будет низкой — потому как у вас, по сути, Шуман, так что стоячей волны не получится, будет бегущая волна с большим затуханием.
Не верно, во-первых у нас не Шуман — см. вопросы выше, во-вторых даже для первых гармоник нулевой ТМ-моды (т.е. для резонанса Шумана) добротность доходит до 10-ки (см. пруфы выше), что означает время затухания энергии в несколько десятых секунды — т.е. очень много. И согласно фактически экспериментальным данным, добротность с ростом номера гармоники (т.е. с ростом частоты) — растет, причем быстрее, чем корень из частоты. Так что стоячая волна — будет, и ожидаемая добротность на нашем диапазоне частот составляет как минимум несколько сотен.

• Если в грунте будут проводники электрически-длинные относительно длины волны — у вас волна будет на них концентрироваться и затухать.
Не верно, проводники в грунте (например, трубы систем отопления и т.п.) означают локально улучшенную проводимость грунта, что приведет только к возрастанию добротности резонанса — т.е. увеличению КПД передачи энергии. Реально в качестве такого «оттягивающего» проводника может работать только проводник достаточной длины, находящийся не в грунте, но — заземленный одним концом. Таковых не наблюдается (провода линий ЛЭП, при том что они достаточной длины, разумеется не заземлены — т.е «не видят» переменного потенциала грунта, а наводки от внешнего поля грунта буду слабы — т.к. мала напряженность поля, см. выше — велик только переменный потенциал самого грунта, но не поле от такого потенциала).

• При таком подходе невозможна адресная доставка энергии, так что в такой технологии — даже если она заработает — нет никакого смысла.
Можно идти не путем адресной доставки, а путем контроля доставки. Любой приёмник будет генерировать волну, которую можно элементарно засечь. Для отбора сколь-нибудь высокого по плотности потока энергии — потребуется очень хорошее заземление и высокодобротный приёмник (т.е. фундаментальная и дорогая конструкция). Так что делать фундаментальную конструкцию, для того чтобы её функционирование было пресечено на следующий день — экономически не целесообразно.

• А вы не боитесь, что создадите второй Тунгусский метеорит? Можно ли как-то защититься от поля, создаваемого установкой?
Нет, не боимся. Чтобы всерьез об этом говорить, надо иметь четкую модель того что такое тунгусский метеорит и как его вызвать Башней. У нас такой модели нет. Если же есть острое параноидальное желание защититься от поля, создаваемого стоячей волной – то, разумеется, это можно сделать (например — заглубив объект под землю, т.е. по сути просто хорошо заземлив всю его внешнюю поверхность – что просто и недорого, либо же поставив отдельный приёмник — снимающий и отводящий энергию при достижении некоего порога плотности энергии).

• Вы не учли возможную электрохимию при протекании тока в грунте.
Да, разумеется. Как только вы дадите нам подробную карту (с разрешением хотя-бы в километр) электрохимических свойств грунта всех материков Земли (на глубину хотя-бы в 100 метров) — мы непременно учтем это в модели. Но в обозримом будущем таких данных не предвидится.

• Вы влезете в диапазон СДВ-связи, и/или связи подлодок, и «за вами придут».
Во первых, отдельный чистый синус — не сможет нарушить связь (т.е. фильтруется совершенно элементарно). Во вторых, при высоком значении переменного потенциала грунта Земли, напряженность поля будет малой (в силу достаточно большой области распределения поля в вертикальном направлении). В третьих, эксперимент разумеется нужно проводить под эгидой одного из НИИ, в этом случае соответствующие «разрешения» на эксперимент — проблемой не станут.

• Как будет сказываться факт работы нескольких башен/приёмников одновременно?
Никак. Если частоты башен одинаковы — то итоговая стоячая волна будет просто несколько более сложной формы (как результат интерференции волн от нескольких башен), чем от одной Башни — что никак не скажется на работоспособности системы. Если же частоты разные — то в силу очень высокой добротности контуров (у источника и приёмника), частотная избирательность контуров будет огромной, т.е. башни по сути просто «не будут видеть» никаких частот кроме собственной. Т.е. суммарное поле в резонаторе Земля-ионосфера будет существовать в форме биения частоты, но на работе системы это никак не скажется.

• Не возникнет ли большого шагового напряжения — аналогично тому как это происходит при падении на грунт оборванного конца ЛЭП?
Нет, не возникнет. Если, например, взять амплитуду переменного потенциала грунта в пучности напряжения стоячей волны равную 15 киловольт, и длину волны в 30 000 м (что соответствует частоте 10 кГц, и мощности источника много больше мегаватта), то это даст «шаговое напряжение» (т.е. градиент потенциала вдоль поверхности земли) около 2 вольта на метр. Что совершенно безопасно. Основное отличие от обрыва провода ЛЭП в том, что площадь контакта провода ЛЭП с грунтом минимальна — что дает очень большое сопротивление заземления. В результате подавляющая часть напряжения падает на небольшой (короткой) окрестности от конца провода, что и приводит к высокому шаговому напряжению для такого случая. В случае же стоячей волны от Башни Тесла, «область локализации» напряжения очень велика (половина длины волны — т.е. десятки км), так что шаговое напряжение — мало.

//———————————————————————————//
UPDATE 2017.02.26:
Поскольку практическая реализация исходной идеи оказалась значительно сложнее первоначальных ожиданий, и в теорчасти и в плане проведения проверочных экспериментов, то этот проект находится на паузе.

Мы решили сфокусироваться на более прикладных аспектах применения технологии дистанционной беспроводной передачи электроэнергии. Два года назад мы стали компанией в США, и за это время прошли большой путь развития — налаживание бизнес контактов, получение инвестиций, договоренности по пилотным проектам и т.п. В настоящий момент мы сфокусировали свои усилия на cоздании и внедрении в массовую коммерческую эксплуатацию промышленной системы для подзарядки дронов на лету. Суть системы та же что и в статье выше, резонансные связанные контуры. Было сделано несколько прототипов с последовательным наращиванием уровня мощности/КПД/дистанции и достигнуты серьезные результаты. Видео полета большого дрона, полностью запитанного посредством беспроводной передачи энергии, можно найти по этой ссылке.

Для реализации этой (и не только) задачи мы открываем инженерный офис в России (100% дочернее предприятие головной корпорации) и набираем в команду инженеров имеющих хороший практический опыт в области силовой импульсной схемотехники, от проектирования до сборки и отладки железа. Т.е. нужны руки из плеч, большой опыт и активная позиция в проекте — готовность разбираться с непонятным, и самостоятельно формулировать/решать нестандартные/нетривиальные задачи в русле основного направления проекта. Дополнительным плюсом является умение программировать контроллеры, знание тепловых расчетов, опыт работы с вопросами электромагнитной совместимости, знание ограничений по госрегулированию в области радиоизлучения на диапазон 10-100 кГц в США/Европе, опыт прохождения сертификации по FCC.

Работа в проекте будет крайне насыщенной и интересной т.к. решаемые задачи далеки от областей имеющих устоявшиеся решения. Режим работы — фуллтайм, в дружном коллективе, с конкурентной зарплатой и хорошим техническим обеспечением. Дислокация — Москва/ближнее подмосковье.

Если Вы соответствует описанным выше требованиям и у вас есть желание работать в таком проекте, то пишите в личку, с радостью пообщаемся, расскажем все подробности и с узнаем о ваших достижениях и увлечениях. В комментах по этой теме ничего отвечать не буду дабы не начинался холивар.

Методы измерения электрического колебательного контура

Эффект резонанса находит своё применение в решении различных технических задач. Одной из таких задач была симуляция резонанса вибростенда электрическим колебательным контуром. Подбор элементов для колебательного контура осуществляется с целью добиться резонанса на заданной частоте с заданной добротностью. Резонансная частота и добротность определяются по нижеприведённым формулам. Для подтверждения расчетной частоты резонанса или добротности требуются практические методы с использованием измерительных приборов. Преимущество виртуальной лаборатории ZETLab в том, что она содержит в себе широкий спектр программ для различных измерений, которые можно использовать для проверки теоретических расчетов.

Принципиальная схема последовательного колебательного контура

Параметры схемы, приведённой на рисунке 1, вычисляются по следующим формулам:

Резонансная частота электрического колебательного контура

Добротность электрического колебательного контура

Примечание: в формулы для расчета подставляются не паспортные данные элементов (по которым их возможно выбирали), а реальные, которые были измерены с помощью соответствующих измерительных приборов.

Теоретический расчет

R=16 Ом,
L=18 мГн,
C=1,75 мкФ

Резонансная частота

Добротность

Программа «Измерение АЧХ (8 каналов)»

График АЧХ электрического резонансного контура

Измерение добротности по графику АЧХ

По графику АЧХ колебательного контура определяем частоту резонанса курсорными измерениями: f₀ = 847 Гц.

Добротность электрического колебательного контура обратно пропорциональна разности относительных частот, соответствующих значениям относительного напряжения 1/√2 (относительно резонансной частоты и резонансного напряжения):

Кроме того добротность может быть вычислена как отношение напряжения в пике резонанса к входному напряжению.

На частоте менее 10% от резонансной частоты напряжение на конденсаторе будет составлять более 99% от входного напряжения. Соответственно ошибка, которую внесёт метод вычисления добротности, составит менее 1%.

Программа «Измерение АЧХ-ФЧХ (4 канала)»

Как известно из радиотехники, полосу пропускания колебательного контура можно найти из частотных характеристик, отмечая граничные частоты, по уровню 1/v2 от максимума модуля амплитудной характеристики для последовательного колебательного контура или максимума сопротивления для параллельного контура. Можно также измерить полосу пропускания резонатора по фазово-частотной характеристике электрического импеданса как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Отношение резонансной частоты к ширине полосы пропускания есть добротность колебательной системы.

Гафики измеренных АЧХ и ФЧХ

f₀ = 845,3 Гц

Измерение добротности по АЧХ

АЧХ: f₂=898,5 Гц ФЧХ: f₂=903,3 Гц

АЧХ: f₁=739 Гц ФЧХ: f₁=738 Гц

Измерение добротности по ФЧХ

Модальный анализ

Измерение резонанса с помощью программы «Модальный анализ»

Затухающие колебания на выходе электрического колебательного контура

Если на вход системы подать дельта-импульс, то на выходе будет импульсная характеристика системы. Дельта-импульс эмулируется радио-импульсом высокой частоты с 0 периодов (полуволна).

Характеристики колебательного контура:

τ — время релаксации колебаний — время, в течение которого амплитуда колебаний уменьшится в e раз.
λ — логарифмический декремент затухания — логарифм отношения двух последовательных амплитуд колебаний.
Q — добротность контура — отношение энергии запасённой в контуре к убыли энергии за один период колебаний умноженное на 2π.

Взаимный узкополосный спектр, передаточная функция h2

Вычисления по взаимному узкополосному спектру:

Вычисления по переходной характеристике:

Взаимный узкополосный спектр генератора и измерительного канала

Корреляционная функция (белый шум и радиоимпульс)

Корреляционная функция сигнала генератора и выхода колебательного контура

U₁=48,922 мВ·g

U₂=24,297 мВ·g

U₃=12,513 мВ·g

U₄=6,498 мВ·g

Узкополосный спектр

Применяя те же самые формулы, что и для АЧХ находим характеристики системы:

Узкополосный спектр широкополосного шума с усреднением за 600 секунд

Проведение виброиспытаний на системе с резонансом

Узкополосный спектр широкополосного шума с усреднением за 600 секунд

Узкополосный спектр широкополосного шума с усреднением за 600 секунд

Результаты, полученные в ходе испытаний:

Финал конкурса «УМНИК Энерджинет»

Темы трека:
1.    Программно-аппаратные средства удаленного доступа к электроприемникам потребителей электроэнергии для дистанционного управления их нагрузкой в рамках практик управления спросом (demand response).
2.    Алгоритмы управления агрегированными множествами электроприемников потребителей электроэнергии для реализации практик управления спросом (demand response).
3.    Компактные твердотельные трансформаторы для распределительных электрических сетей напряжением 0,4 кВ.
4.    Силовые преобразовательные устройства управления потоками мощности (энергетические роутеры) для электрических сетей 0,4 кВ.
5.    Компоненты систем электроснабжения коммерческих и бытовых потребителей на основе сетей постоянного тока.
6.    Алгоритмы обеспечения статической и динамической устойчивости в энергосистемах и электрических сетях с электронной генерацией (источниками энергии, подключенными через инверторы).
7.    Высокоэффективные возобновляемые источники энергии (ВИЭ) и средства повышения эффективности использования ВИЭ.
8.    Адаптивное энергоэффективное управление освещением, отоплением и другими энергопотребляющими инженерными системами.
9.    «Быстрая» зарядка электрического транспорта, поддерживающая возможность выдачи электроэнергии в сеть (V2G).
10.    Беспроводная зарядка электроприемников (цифровой техники, дронов) мощностью не менее 200 Вт и выше с КПД выше 90%.
11.    Средства создания цифровых моделей («цифровых двойников») потребителей электроэнергии, обеспечивающих возможность многофакторного анализа и прогнозирования их электропотребления.
12.    Портативные источники энергии, не требующие предварительной зарядки, мощностью не менее 100 Вт.
13.    Управление распределенными энергетическими ресурсами (накопителями электроэнергии, генераторами малой мощности) для формирования виртуальных электростанций (VPP/VESS).
14.    Управление накопителями электроэнергии у конечных потребителей, обеспечивающими снижение расходов на электроснабжение.
15.    Расчетные, платежные и биллинговые средства на основе технологии распределенных реестров.
16.    Программные средства оптимального выбора характеристик систем накопления электроэнергии для промышленных и коммерческих потребителей.
17.    Анализ вклада электроприемников в потребление для электрических сетей 0,4 кВ (средства дезагрегации электропотребления).
18.    Технические решения для реконструкции котельных с переводом в режим совмещенной генерации электрической энергии и тепла (когенерации), а также, опционально, холода (тригенерации)
19.    Энергоустановки для производства электрической и тепловой энергии на основе топливных элементов для стационарного применения.
20.    Снятие ограничений мощности парогазовых установок ТЭС при изменении температуры окружающего воздуха.
21.    Снижение температуры охлаждающей (циркуляционной) воды водохранилища, направленное на углубление вакуума в конденсаторах паровых турбин ТЭС.
22.    Технические решения по глубокой утилизации тепла уходящих газов ТЭС.
23.    СКМ-системы для энергосбытовых компаний, обеспечивающие сбор, систематизацию и программную аналитику данных о клиентах с привлечением технологий слабого искусственного интеллекта.
24.    Цифровые системы для энергосбытовых компаний, обеспечивающие возможность работы в режиме мультисервисных компаний в жилищно-коммунальном секторе.
25.    Системы и компоненты систем «умного» дома.
26.    Средства цифрового коммерческого учета электроэнергии.
27.    Новые способы передачи электроэнергии: беспроводные, резонансные, пакетные и другие нетрадиционные виды транспорта энергии.
28.    Прогнозирование доступного резерва мощности электрического оборудования со стохастическим поведением (электромобилей, общественного электрического транспорта и бытовой нагрузки)
29.    Оптимальное погодозависимое управление температурным режимом передачи энергии по тепловым сетям.
30.    Алгоритмы работы релейной защиты и противоаварийной автоматики для электросетевого комплекса и изолированных microgrid с большой долей электронной генерации.
 

Как позаботиться об отношениях: резонанс и энергия

Сумма от 95 до 125 баллов. Ваша зеркальная система работает правильно. Ваши отношения не требуют больших эмоциональных затрат, и вам с друзьями не приходится тратить много времени на самопрезентацию. В большинстве случаев вы понимаете окружающих и чувствуете, что близкие люди видят вашу истинную сущность.

Сумма от 70 до 94 баллов. Иногда вы приводите людей в замешательство. Время от времени у вас создается впечатление, что важные для вас люди не понимают вас, а вы, в свою очередь, неверно истолковываете намерения или реакцию окружающих, причем это происходит чаще, чем вам хотелось бы.

Сумма менее 70 баллов. По всей вероятности, люди для вас – загадка. Возможно, вы часто ловите себя на том, что, в недоумении качая головой, говорите друзьям и коллегам: «Я просто тебя не понимаю!» Некоторые люди с такой низкой оценкой чрезмерно подозрительны; другие ведут себя слишком простодушно, наивно полагая, что у окружающих всегда самые чистые помыслы. Ваши намерения тоже интерпретируют неправильно: когда вы проявляете доброжелательность, вас обвиняют в том, что вы ведете себя слишком заискивающе или навязчиво, или что вы посылаете сигналы, свидетельствующие о вашем романтическом интересе, хотя на самом деле вы не планировали этого делать. Все эти чувства вызывают у вас ощущение дискомфорта и подавленности.

«E» — «энергия»: дофаминовая система вознаграждения

Дофамин – это нейромедиатор удовольствия. В идеале нейронные пути дофаминовой системы вознаграждения должны быть связаны со здоровыми отношениями; в таком случае контакты с окружающими вызывают ощущение энергии. Но если отношения вас опустошают, парализуют и делают несчастными, вы можете обратиться к другим источникам получения дофамина, таким как еда, алкоголь, наркотики, бессмысленный секс и другие формы зависимости. Один из способов избавиться от вредных привычек и пагубных пристрастий – перенастроить свои дофаминовые пути на получение удовольствия от здоровых отношений, а не от вредных привычек.

Для того чтобы оценить работу нейронного пути энергии, ответьте, как часто следующие 4 утверждения соответствуют истине в случае каждого из пяти важных для вас людей. Оцените утверждения по шкале от 1 до 5 баллов: 1 = никогда; 2 = редко или крайне редко; 3 = время от времени; 4 = достаточно часто; 5 = в большинстве случаев.

1. Отношения с этим человеком помогают мне добиваться большего в жизни
2. Мне нравится проводить время с этим человеком
3. Смех — это один из аспектов отношений с этим человеком
4. Благодаря общению с этим человеком я заряжаюсь энергией

Подсчитайте сумму баллов во всех ответах на эти утверждения. Максимальная оценка составляет 100 баллов (четыре утверждения с максимальным количеством баллов 25 по каждому: 5 максимальных баллов х 5 отношений).

Теория и механизмы демпфирования в механике конструкций

Если ударить по стеклянной или металлической чаше, то она будет издавать затухающий со временем звон. В мире без демпфирования этот звон продолжался бы вечно. В реальности же, благодаря нескольким физическим процессам, кинетическая энергия и (потенциальная) энергия упругой деформации чаши переходят в другие формы энергии. В этой статье мы обсудим, как описывать демпфирование в моделях и какие физические явления его вызывают затухание в вибрирующих механических системах.

Как математически описывается демпфирование?

Есть несколько математических подходов к описанию и учету демпфирования. Давайте кратко резюмируем самые популярные из них.

Самое заметное проявления демпфирования — падение (затухание) амплитуды свободных колебаний со временем, как, например, в случае с «поющей» чашей. Скорость ослабления амплитуды зависит от того, насколько большое демпфирование в системе. Обычно амплитуда колебаний экспоненциально затухает со временем. В таком случае потери энергии за период пропорциональны амплитуде колебаний (на этом периоде).

Классическая «поющая» чаша.\prime} = \eta

Угол потерь δ определяет фазовый сдвиг между напряжением и деформацией.

Демпфирование, заданное через коэффициент гистерезисных потерь, несколько отличается от случая вязкого демпфирования. Гистерезисные потери пропорциональны амплитуде смещений, а вязкое демпфирование пропорционально скорости. Таким образом, эти величины невозможно однозначно связать друг с другом.

На рисунке ниже сравнивается отклик системы с одной степенью свободы при использовании двух разных моделей демпфирования. Можно заметить, что модель вязкого демпфирования предсказывает более сильное затухание на частотах выше резонансной по сравнению с моделью через коэффициент гистерезисных потерь и более слабое затухание на частотах ниже резонансной.

Сравнение динамического отклика для модели вязкого демпфирования (сплошные линии) и для модели через коэффициент гистерезисных потерь (пунктирные линии).

Обычно на резонансной частоте выполняется следубщее соотношение между указанными критериями: \eta \approx 2 \zeta.\prime} = \dfrac{D}

{2 \pi W_s}

Это определение через рассеянную энергию можно использовать, даже если петля гистерезиса не выглядит как идеальный эллипс; достаточно лишь иметь возможность определить две эти энергетических величины.

Источники демпфирования

Физических механизмов демпфирования огромное множество. Во всех естественных процессах энергия так или иначе рассеивается.

Внутренние потери в материале

Во всех реальных материалах энергия рассеивается при деформации. Можно считать это разновидностью внутреннего трения. Обратите внимание, что кривая нагружения для полного периода не укладывается на идеально прямую линию. Она больше похожа на вытянутый эллипс.

Обычно для описания демпфирования в материале применяется модель через коэффициент гистерезисных потерь, так как на опыте оказывается, что потери энергии за период слабо зависят от частоты и амплитуды. При этом математическое описание в модели коэффициента потерь основано на комплексных величинах, то есть подразумевает только случай гармонических колебаний. Поэтому эту модель демпфирования можно использовать только для исследований в частотной области.

Коэффициенты гистерезисных потерь в материале могут сильно различаться в зависимости от точного состава материала и источников данных, которыми вы пользуетесь. В таблице ниже приведены некоторые грубые оценки.

Материал	Коэффициент гистерезисных потерь η
Алюминий	0.0001–0.02
Бетон	0.02–0.05
Медь	0.001–0.05
Стекло	0.0001–0.005
Резина	0.05–2
Сталь	0.0001–0.01

Коэффициенты потерь и схожие модели демпфирования используются, если физические механизмы затухания в материале неизвестны или не важны в контексте рассматриваемой задачи. В некоторых моделях материала, например, в вязкоупругих материалах, рассеивание энергии изначально заложено в математическую модель.

Трение в соединениях

Конструкции часто соединяются болтами или другими типами креплений. Если при колебаниях соединенные поверхности двигаются относительно друг друга, энергия рассеивается через трение. Если величина силы трения не меняется за период, потери энергии за период слабо зависят от частоты. В этом смысле трение схоже с внутренними потерями в материале.

Болтовые соединения широко распространены в задачах механики конструкций. Величина рассеиваемой в болтовых соединениях энергии может сильно зависеть от конструкции. Если важно снизить потери, болты должны плотно прилегать друг к другу и быть хорошо затянуты, чтобы уменьшить макроскопическое проскальзывание между поверхностями.

Излучение звука

Вибрирующая поверхность будет приводить в движение окружающий воздух (или другую среду) и испускать звуковые (акустические) волны. Эти волны уносят часть энергии, из-за чего конструкция теряет энергию.

Излучение звука преобразователем типа Tonpilz.

Анкерные потери

Часто небольшой компонент крепится к большой конструкции (основанию/подложке), которая не включается в расчетную модель. Когда деталь вибрирует, в несущей конструкции возникают упругие волны, также являющимися источником рассеяния энергии. В контексте микроэлектромеханических систем (МЭМС), этот эффект называют анкерные потери (anchor losses).

Термоупругое демпфирование

Даже если в процессе совершенно упругой деформаций энергия не рассеивается, деформация материала слегка изменяет его температуру. Локальное растяжение приводит к снижению температуры, а сжатие — к нагреву.

Это принципиально обратимый процесс, так что при снятии напряжения температура вернется к исходному значению. Однако часто в поле напряжения есть ненулевые градиенты, которым соответствуют градиенты распределения температуры. Они вызывают тепловые потоки от теплых областей к холодным. Когда по ходу цикла нагружения напряжение «убирают», распределение температуры уже отличается от того, что было при нагрузке. Поэтому локальный возврат к исходному состоянию невозможен. Это приводит к рассеиванию энергии.

Термоупругое демпфирование (thermoelastic damping) важно при исследовании высокочастотных колебаний на малых масштабах. Например, оно может значительно снизить добротность микроэлектромеханических резонаторов.

Демпферы и гасители

Иногда в конструкцию включают специализированные выделенные гасители колебаний, например, рессоры в подвеске колес.

Рессоры. Автор изображения — Avsar Aras, собственное произведение. Доступно по лицензии CC BY-SA 3.0 на Викискладе.

Естественно, такие компоненты сильно влияют на суммарное демпфирование, по крайней мере, для некоторых мод колебаний.

Сейсмогасители

Особое внимание искуственному демпфированию колебаний уделяется при строительстве в сейсмоопасных районах. Чрезвычайно важно снизить амплитуду колебаний в зданиях при землетрясении. При этом гасители могут как изолировать здание от фундамента, так и рассеивать энергию.

Сейсмогасители в общественном здании. Изображение предоставлено Shustov — собственное произведение. Доступно по лицензии CC BY-SA 3.0 на Викискладе.

Продолжение

Во второй части данной серии вы сможете найти информацию о том, как задавать демпфирование в COMSOL Multiphysics®.

Последовательный колебательный контур | Резонанс напряжений

Последовательный колебательный контур обозначение на схеме

Последовательный колебательный контур – это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.

Идеальный последовательный колебательный контур

 На схемах идеальный последовательный колебательный контур обозначается вот так:

где

L – индуктивность, Гн

С – емкость, Ф

Реальный последовательный колебательный контур

Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:

R  – это суммарное сопротивление потерь катушки и конденсатора

L – собственно сама индуктивность катушки

С – собственно сама емкость конденсатора

Принцип работы последовательного колебательного контура

Генератор частоты и последовательный колебательный контур

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор (Ген)у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R – это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно “прячется” внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш , а также снимая осциллограмму с самого генератора U_ГЕН.

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

[quads id=1]

Влияние частоты генератора на сопротивление колебательного контура

В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма – это напряжение с генератора частоты, а желтая осциллограмма – отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600  Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Резонанс последовательного колебательного контура

Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:

Это явление носит название резонанса.

Не будем углубляться  в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.

Как вы помните, если у нас сопротивление  становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.

Формула Томсона (резонанса) для последовательного колебательного контура

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

[quads id=1]

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как  среднеквадратичное напряжение  будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Добротность последовательного колебательного контура

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R – сопротивление потерь в контуре, Ом

L – индуктивность, Генри

С – емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура – это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Видео на тему “Как работает колебательный контур. Резонанс”:

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса – индуктивную составляющую тока.

вынужденных колебаний и резонанса | Физика

Цели обучения

К концу этого раздела вы сможете:

• Наблюдайте за резонансом гребного мяча на струне.
• Наблюдать за амплитудой затухающего гармонического осциллятора.

Рис. 1. Вы можете вызвать вибрацию струн пианино, просто создав звуковые волны своим голосом. (Источник: Мэтт Биллингс, Flickr)

Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту с отключенными демпферами.Он пропоет вам ту же ноту — струны, имеющие те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Ваш голос и струны пианино — хороший пример того факта, что объекты — в данном случае струны пианино — можно заставить колебаться, но лучше всего они колеблются на своей собственной частоте. В этом разделе мы кратко рассмотрим применение периодической движущей силы , действующей на простой гармонический осциллятор. Движущая сила вводит энергию в систему с определенной частотой, не обязательно такой же, как собственная частота системы.Собственная частота — это частота, на которой система будет колебаться, если бы не было движения и демпфирующей силы.

Большинство из нас играли с игрушками, в которых использовался объект, поддерживаемый на резинке, что-то вроде шарика, подвешенного к пальцу на рисунке 2. Представьте, что палец на рисунке — это ваш палец. Сначала вы держите палец ровно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе.Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете. Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом . Говорят, что система, работающая на собственной частоте, резонирует с . По мере того, как частота возбуждения постепенно становится выше резонансной или собственной частоты, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.

Рис. 2. Шарик на резинке перемещается в ответ на палец, поддерживающий его. Если палец движется с собственной частотой f0 мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он реагирует колебаниями с меньшей амплитудой.

На рис. 3 показан график зависимости амплитуды затухающего гармонического осциллятора от частоты движущей им периодической силы.На графике есть три кривые, каждая из которых представляет разную величину демпфирования. Все три кривые достигают пика в точке, где частота движущей силы равна собственной частоте гармонического осциллятора. Самый высокий пик или самый высокий отклик — для наименьшего количества демпфирования, потому что демпфирующая сила снимает меньше энергии.

Рис. 3. Амплитуда гармонического осциллятора как функция частоты движущей силы. Кривые представляют один и тот же генератор с одинаковой собственной частотой, но с разной степенью демпфирования.Резонанс возникает, когда частота возбуждения равна собственной частоте, а наибольший отклик — при наименьшем затухании. Самый узкий ответ также соответствует наименьшему демпфированию.

Интересно, что ширина резонансных кривых, показанных на рисунке 3, зависит от затухания: чем меньше затухание, тем уже резонанс. Суть в том, что если вы хотите, чтобы управляемый генератор резонировал на очень определенной частоте, вам нужно как можно меньше демпфирования. Небольшое демпфирование характерно для струн фортепиано и многих других музыкальных инструментов.И наоборот, если вам нужны колебания малой амплитуды, например, в системе подвески автомобиля, вам нужно сильное демпфирование. Сильное демпфирование снижает амплитуду, но компромисс заключается в том, что система реагирует на большем количестве частот.

Эти особенности управляемых гармонических генераторов применимы к огромному количеству систем. Например, когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на радиовещательной (движущей) частоте желаемой радиостанции. Чем более избирательно радио различает станции, тем меньше его демпфирование.Магнитно-резонансная томография (МРТ) — широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать приходящими радиоволнами (порядка 100 МГц). Ребенок на качелях приводится в движение родителями на собственной частоте качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.

Рис. 4. В 1940 году обрушился мост через Такома в штате Вашингтон.Сильный поперечный ветер приводил мост к колебаниям на его резонансной частоте. Демпфирование уменьшалось, когда опорные тросы разрывались и начинали скользить по опорам, что увеличивало амплитуду до разрушения конструкции (кредит: PRI’s Studio 360, через Flickr)

Неровности и гравийные дороги доказывают, что даже система подвески автомобиля не застрахована от резонанса. Несмотря на тщательно спроектированные амортизаторы, которые обычно преобразуют механическую энергию в тепловую почти так же быстро, как она приходит, лежачие полицейские по-прежнему вызывают колебания большой амплитуды.На гравийных дорогах с рифленым покрытием вы, возможно, заметили, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности вообще можно не почувствовать. На рисунке 4 показана фотография известного примера (моста Tacoma Narrows Bridge) деструктивного воздействия возбужденного гармонического колебания. Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.

В нашем организме полость грудной клетки является ярким примером системы, находящейся в резонансе.Диафрагма и грудная стенка вызывают колебания грудной полости, в результате чего легкие раздуваются и сдуваются. Система критически демпфирована, и мышечная диафрагма колеблется с резонансным значением для системы, что делает ее высокоэффективной.

Проверьте свое понимание

В известном фокусе исполнитель поет ноту в сторону хрусталя, пока стекло не разобьется. Объясните, почему этот трюк работает, с точки зрения резонанса и собственной частоты.

Решение

Исполнитель должен петь ноту, соответствующую собственной частоте стекла.Когда звуковая волна направлена ​​на стекло, стекло резонирует с той же частотой, что и звуковая волна. Когда в систему вводится достаточно энергии, стекло начинает вибрировать и в конечном итоге разбивается.

Сводка раздела

• Собственная частота системы — это частота, с которой система будет колебаться, если на нее не действуют движущие или демпфирующие силы.
• Периодическая сила, управляющая гармоническим осциллятором на его собственной частоте, вызывает резонанс.Говорят, что система резонирует.
• Чем меньше демпфирование в системе, тем выше амплитуда вынужденных колебаний вблизи резонанса. Чем больше демпфирование у системы, тем более широкий отклик она имеет на изменение частот движения.

Концептуальные вопросы

1. Почему солдатам обычно приказывают «шагать шагом» (идти не в ногу) через мост?

Задачи и упражнения

1. Сколько энергии должны рассеять амортизаторы автомобиля массой 1200 кг, чтобы погасить отскок, изначально имеющий скорость 0.800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.
2. Если у автомобиля есть система подвески с силовой постоянной 5,00 × 10 ⁴ Н / м, сколько энергии должны отводить амортизаторы автомобиля, чтобы гасить колебания, начиная с максимального смещения 0,0750 м?
3. (a) Насколько пружина с силовой константой 40,0 Н / м будет растянута объектом массой 0,500 кг, когда она неподвижно подвешена на пружине? (б) Рассчитайте уменьшение гравитационной потенциальной энергии 0.Объект весом 500 кг, когда он спускается на это расстояние. (c) Часть этой гравитационной энергии уходит в пружину. Вычислите энергию, запасенную в пружине на этом участке, и сравните ее с потенциальной энергией гравитации. Объясните, куда может уйти остальная энергия.
4. Предположим, у вас есть объект весом 0,750 кг на горизонтальной поверхности, соединенный с пружиной, имеющей силовую постоянную 150 Н / м. Между объектом и поверхностью существует простое трение со статическим коэффициентом трения μ _s = 0.100. а) Как далеко можно растянуть пружину без перемещения груза? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения составляет μ _k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, что он начинается с максимальной амплитуды.
5. Инженерное приложение. Подвесной мост колеблется с постоянной эффективной силы 1,00 × 10 ⁸ Н / м. (а) Сколько энергии нужно, чтобы заставить его колебаться с амплитудой 0.100 м? (b) Если солдаты маршируют по мосту с частотой, равной собственной частоте моста, и каждую секунду передают 1,00 × 10 ⁴ Дж энергии, сколько времени потребуется, чтобы колебания моста достигли амплитуды от 0,100 м до 0,500 м. .

Глоссарий

собственная частота: частота, с которой система будет колебаться, если бы не было движения и демпфирующих сил

резонанс: явление возбуждения системы с частотой, равной собственной частоте системы

резонирует: система работает на собственной частоте

Избранные решения проблем и упражнения

1.384 Дж

3. (а). 0,123 м; (б). −0,600 Дж; (с). 0,300 Дж. Остальная энергия может уйти в тепло из-за трения и других демпфирующих сил.

5. (а) 5.00 × 10 ⁵ Дж; (б) 1.20 × 10 ³ с

Резонанс — энергия, частота, колебания и движение

Есть много случаев, когда мы хотим добавить энергии к движению объекта, который колеблется. Чтобы эта передача была эффективной, колебания и источник новой энергии должны быть «согласованы» очень специфическим образом.Когда это совпадение происходит, мы говорим, что колебание и источник находятся в резонансе.

Простой пример колебания, который мы все видели, — это ребенок на качелях на игровой площадке. Движение начинается, когда кто-то переводит качели в положение, удаленное от точки устойчивого равновесия, и отпускает их. Затем ребенок движется вперед и назад, но постепенно замедляется, поскольку энергия движения теряется из-за трения в суставе, где веревка или цепь качелей прикреплены к его опоре.Конечно, ребенок хочет двигаться дальше, обычно выше и быстрее, а это требует дополнительных усилий. Этого легко добиться, нажимая на качели, но все мы по опыту знаем, что время имеет решающее значение. Даже небольшой толчок может эффективно добавить энергии, если он происходит как раз в тот момент, когда качели переместились в свое наивысшее положение и начинают возвращаться к точке устойчивого равновесия. Если толчок происходит слишком поздно, не вся энергия толчка добавляется (неэффективно).Хуже того, если толчок произойдет слишком рано, результатом будет замедление качания (удаление энергии вместо ее добавления). Кроме того, очевидно, что толкать в другое время, когда качели отошли в сторону, бесполезно (это выглядит странно, и в любом случае эффективность равна нулю, , поскольку энергия не передается в движение). Уловка состоит в том, чтобы толкать в «нужный» момент при каждом повторении раскачивающего движения. Когда это происходит, толчок взрослого (в данном случае источник энергии) и колебания находятся в резонансе.

Характеристика движения, которая должна согласовываться в резонансе, — это частота . Для любого колебания движение занимает определенное количество раз, , чтобы повториться (его период для одного цикла). Следовательно, в течение каждой секунды (частоты) происходит определенное количество циклов. Частота говорит нам, как часто объект возвращается в положение максимального смещения, и, как мы знаем для качелей, это лучшее место для добавления энергии. Резонанс возникает, когда ритм источника энергии совпадает с естественной характеристической частотой колебаний.По этой причине последнюю часто называют резонансной частотой. Обычно говорят, что источник энергии обеспечивает движущую силу, как в случае, когда требуется толчок, чтобы добавить энергии движению качелей.

В некотором смысле, резонанс — это просто новое название знакомой ситуации. Однако резонанс важен и в других менее очевидных случаях, таких как лазеры и электронные схемы. Особенно интересным примером является микроволновая печь, которая готовит пищу без внешнего нагрева .Даже если такой объект, как книга (или стейк) кажется неподвижным, он состоит из микроскопических атомов , которые колеблются вокруг положений устойчивого равновесия. Эти движения слишком малы, чтобы их можно было увидеть, но мы можем их почувствовать, поскольку температура объекта связана с их амплитудами — чем больше амплитуды, тем горячее объект. Это очень похоже на движение ребенка на качелях, где большая амплитуда означает больше энергии. Если мы сможем добавить энергию движению качелей за счет движущей силы в резонансе, тогда мы сможем очень эффективно добавить энергию (тепло) к стейку.В обычных духовках пищу готовят снаружи, например, путем нагрева молекул воздуха, которые сталкиваются с атомами на поверхности пищи. Однако микроволновая печь использует резонанс для приготовления пищи изнутри.

Молекула воды состоит из одного атома кислорода и двух атомов водорода , которые удерживаются вместе не по прямой линии, а в форме буквы «V». Атом кислорода расположен внизу буквы «V», а атомы водорода — на концах плеч. Неудивительно, что молекулы воды и даже атомы кислорода и водорода внутри них могут колебаться.Однако эксперименты обнаружили особое колебание (на самом деле поворот всей молекулы на на ), что особенно важно. Характерная частота этого колебания находится в том же диапазоне, что и микроволновое электромагнитное излучение типа . Микроволны обычно используются в радаре , поэтому уже была проделана большая работа по разработке надежных, относительно компактных устройств для их производства. Прорыв состоял в осознании того, что хороший стейк (даже плохой) содержит большое количество воды.Если мы поместим стейк в микроволновую печь и включим ее, внутри духовки будут образовываться микроволны на резонансной частоте молекулы воды. Микроволны действуют как движущая сила для добавления энергии, заставляя молекулы колебаться с большей амплитудой. Это нагревает стейк, готовя его изнутри.

Есть много других ситуаций, когда важен резонанс. Например, рок-гитарист должен быть осторожен, играя перед мощным динамиком. Когда струна вибрирует (колеблется) после удара, электромагнитный датчик преобразует это движение в электрический импульс, который затем отправляется на усилитель и далее на динамик.Если звуковая вибрация из динамика (та же частота, что и у колебания струны) совпадает с резонансной частотой корпуса гитары, может возникнуть обратная связь. Собственно, это пример положительной обратной связи. Звук добавляет энергии корпусу гитары, которая также вибрирует; это добавляет энергии струне, чтобы произвести больший электрический сигнал и даже больше звука. Этот паттерн может повторяться до тех пор, пока громкость на этой резонансной частоте не вырастет, чтобы заглушить другие ноты и остальную часть полосы. Точно так же резонанс может иметь разрушительные последствия.Известный случай — это мост Tacoma Narrows Bridge в штате Вашингтон, где ветрам удалось выступить в качестве движущей силы, заставив мост сильно раскачиваться, пока он не рухнул, добавив энергии к колебаниям на резонансной частоте.

Книги

Кларк Дж. Материя и энергия: физика в действии. Нью-Йорк: Oxford University Press, 1994.

Эрлих Р. Переворачивание мира наизнанку и 174 Другие простые демонстрации физики. Princeton, NJ: Princeton University Press, 1990.

Epstein, L.C. Физика мышления: практические уроки критического мышления. 2-е изд. Сан-Франциско: Insight Press, 1994.

5 советов по обнаружению и устранению проблем резонанса

В случае поломки виновником может быть любое количество проблем, но есть одна, которую особенно сложно диагностировать: резонанс .

Резонанс может быть проблемой в любой машине, поскольку физические структуры имеют собственные частоты, которые могут быть возбуждены.Резонанс возникает, когда форсирующая функция возбуждает собственную частоту машины, вызывая чрезмерную вибрацию. Эти чрезмерные вибрации вызывают дополнительную нагрузку на машину, что приводит к снижению надежности, преждевременному выходу из строя и увеличению затрат на техническое обслуживание и детали. Раннее исправление резонанса предотвращает вторичные дефекты, такие как износ подшипников, и структурные дефекты, такие как трещины сварных швов, ослабленные болты и повреждение фундамента.

Если вы знаете, что с вашим активом что-то не так, диагностировать резонанс может быть очень сложно, поскольку он может возникать только в определенные моменты дня — обычно, когда потребность требует, чтобы машина работала на определенных проблемных скоростях.Когда машина не возбуждена, она может нормально работать.

Лучший способ обнаружить и полностью понять влияние резонанса — это постоянно контролировать машину. С увеличением количества машин, работающих на частотно-регулируемых приводах (ЧРП), проблемы резонанса становятся все более распространенными. Классическое обслуживание на основе маршрутов не очень эффективно, потому что есть большая вероятность, что рассматриваемая машина не работает в момент сбора данных. В зависимости от условий эксплуатации вы можете никогда не увидеть возникновения резонанса лично.

Пример резонансной кривой.

Как эффективно обнаружить резонанс?

1. Непрерывная диагностика. Непрерывная диагностика, включая полные спектральные данные и информацию о скорости машины. Непрерывный информационный поток обеспечивает обнаружение возбужденного состояния машины. Информация о скорости позволяет отслеживать форсирующие функции машины. Остаточные силы дисбаланса, связанные с вращающимися валами, являются наиболее вероятными входными факторами для возбуждения резонанса, но энергия вибрации, связанная с любым компонентом машины, также может служить входной.

Сбор полного спектра вибрации позволяет точно отслеживать все эти функции, чтобы можно было полностью понять реакцию машины. Когда форсирующая функция приближается к резонансной частоте, наблюдается резкое увеличение амплитуды, за которым следует резкое уменьшение по мере того, как частота продолжает расти. Более того, непрерывный поток данных позволяет понять количество возбуждений и их продолжительность, поскольку они происходят в течение дня. Знание природы и продолжительности возбужденного состояния позволяет наиболее точно оценить степень тяжести.

2. Тест развертки. Тест развертки — это когда вы вручную проверяете прибор в частотном диапазоне, снимая показания на каждом этапе. Это может отображать реакцию вибрации в зависимости от скорости для легкого обнаружения проблемных частот. Однако не дается никаких сведений о том, как часто машина вызывает резонанс во время нормальной работы.

3. Тест разгона или выбега. Этот метод включает сбор данных за период времени, когда машина либо набирает скорость, либо останавливается.В этом конкретном испытании вибрация вала используется как функция силы, обеспечивающая ввод энергии в систему. Это вызовет резонанс, поскольку вибрация вала преодолеет критическую скорость. Тахометр используется для измерения разности фаз между положением тяжелого пятна ротора и вектором вибрации. Когда машина проходит через резонанс, фаза сдвигается на 90 градусов. Наблюдение за этим сдвигом обеспечивает доказательство резонанса.

4. Ударный тест. Это включает измерение отклика обесточенной машины, когда она ударяется модальным молотком или другим источником широкополосной подводимой энергии.Этот импульсный вход возбуждает все частоты одновременно, и усиление из-за резонанса легко наблюдается.

Из этих методов только непрерывная диагностика может оценить практическую серьезность резонансного состояния. Все машины имеют собственные частоты, и понимание характера отклика — только половина дела. Для возникновения повреждений требуется реальная работа в проблемных условиях, и наблюдение во времени — единственный способ по-настоящему понять это состояние.

Беспроводные датчики Halo контролируют ваши критически важные объекты, регистрируя вибрацию, температуру и магнитные данные. Пользователи видят оповещения и отчеты в реальном времени в веб-приложениях и мобильных приложениях Augury.

Реакция на резонанс

Выбирая между добавлением частоты пропуска к ЧРП и изменением массы / жесткости вашей конструкции, вы должны учитывать физическую природу самой установки. Без предварительной детальной инженерной оценки может быть сложно полностью понять, как система отреагирует на любое данное изменение.

Чтобы обеспечить успех, потратьте некоторое время, прежде чем внедрять исправление , чтобы определить, на чем установлено ваше оборудование, размер и угол расположения трубопроводов и многое другое, поскольку эти факторы будут влиять на реакцию на вибрацию и должны быть оценены в индивидуальном порядке.

1. Частота пропуска. Быстрое решение — использовать частоту пропуска на частотно-регулируемом приводе, чтобы как можно быстрее продвинуть машину через проблемную частоту. Хотя технически это не , исправление , но это недорогое решение проблемы.Использование частоты пропуска означает, что, хотя ваша машина все еще должна будет проходить через отрицательную частоту, она будет делать это быстрее. Требования к процессу могут запрещать пропуски частот, если эти частоты требуются для надлежащей работы оборудования.

2. Изменение массы или жесткости. Другое решение — изменить массу или жесткость системы, чтобы вы изменили местоположение собственной частоты, тем самым сместив частоту в положение за пределами естественного рабочего диапазона машины.Увеличение массы или уменьшение жесткости приводит к снижению собственной частоты. Чтобы изменить жесткость, вам необходимо стабилизировать конструкцию, добавив поперечные распорки, арматуру или другие структурные модификации. В результате собственная частота выйдет за пределы рабочего диапазона.

Чтобы избежать резонансных проблем, следует развернуть непрерывный мониторинг с момента ввода вашего актива в эксплуатацию. Это позволит вам регулярно делать снимки состояния вашей машины и, в частности, определять, сколько времени она проводит в резонансе и какую амплитуду испытывает, если она терпит бедствие.

Вполне возможно, что даже если машина испытывает резонанс, она не может достичь опасного уровня амплитуды. Это одна из причин, по которой непрерывный мониторинг резонанса полезен для определения того, требуется ли и когда исправление для поддержания обычных функций активов.

Резонанс может стать серьезной проблемой для надежности активов и часто остается незамеченным из-за его периодического присутствия на исправной машине. Постоянно отслеживая состояние машины, вы можете избежать ошеломления от этой «не такой тихой» неисправности.

Эффективная передача энергии структурного резонанса от микроволн к ограниченным акустическим колебаниям в вирусах

По изображениям, полученным с помощью просвечивающего электронного микроскопа, люди знали, что вирусы вирусов гриппа представляют собой сферические шары, упаковывающие внутри геномы. Поскольку белок и геном имеют схожие механические свойства ⁸ , для оценки частот диполярных колебаний мы рассматриваем вирион как однородную сферу.

Диполярный режим однородной сферы

Из-за пространственного ограничения не только электронное, но и акустическое квантование энергии наблюдалось в низкоразмерных системах, таких как квантовые точки и нанопроволоки.В 1882 году Лэмб изучил торсионный (TOR) и сфероидальный (SPH) режимы однородной свободной сферы, рассматривая граничное условие отсутствия напряжений на поверхности ¹² . Среди этих режимов режим SPH с допускающей диполярной связью ¹³ и соответствующее уравнение собственных значений может быть выражено как ^14,15 :

, где — сферическая функция Бесселя первого рода, ω — угловая частота колебательная мода, R — радиус наносферы, c _l и c _t — продольная и поперечная скорости звука соответственно.Сравнение между обычно наблюдаемым режимом дыхания и диполярным режимом можно найти в дополнительном онлайн-режиме. Поскольку дипольный режим наносферы не может быть обнаружен с помощью экспериментов по светорассеянию ¹⁶ , он не наблюдался до предыдущего исследования резонансного возбуждения дипольной моды посредством ТГц волны или микроволнового возбуждения ^17,18 , когда ядро и оболочка наносферы имеют постоянное разделение зарядов. После того, как к наносфере было приложено резонансно колеблющееся электрическое поле, между ядром и оболочкой возникло противоположное смещение, которое возбудило колебания дипольной моды.По сравнению с режимами дыхания () и квадраполярности (), дипольный режим () является единственным режимом SPH, который напрямую взаимодействует с электромагнитными волнами, длина которых намного больше, чем размер частицы. В связи с тем, что вирусы обладают постоянным разделением зарядов, в 2009 году было подтверждено, что диполярное взаимодействие с КАВ является механизмом, ответственным за микроволновое резонансное поглощение в вирусах, рассматривая сферические вирусы как свободные гомогенные наночастицы ^8,9 .

На рисунке 1 показано смоделированное поле смещения дипольной моды (рассчитанное методом конечных элементов, COMSOL Multiphysics, COMSOL, Inc.) однородной сферы (массовая плотность и вязкоупругие свойства постоянны по всей сфере). Мы определяем направление относительного смещения дипольной моды как направление z, которое также будет направлением поля приложенных электромагнитных волн, обсуждаемых в следующем разделе. Построив поле смещения плоскости x-z (y = 0) сферы, противоположное смещение между областями ядра и оболочки можно ясно наблюдать на рис. 1 (b). Между тем на рис. 1 (c) показан вид сбоку искажения плоскости x-y сферы в различных положениях z, из которого делается вывод, что максимальное искажение происходит в экваториальной плоскости (z = 0) сферы.На рис. 1 (г) показан вид сверху поля смещения экваториальной плоскости (z = 0). Интересно узнать, что величина усредненного положительного смещения (внутренняя область) в 1,27 раза больше величины усредненного отрицательного смещения (внешняя область), в то время как положительные и отрицательные смещения занимают 42% и 58% площади соответственно. Кроме того, можно обнаружить, что максимальная величина смещения, возникающего либо в самом центре, либо на внешней поверхности экваториальной плоскости, примерно вдвое превышает усредненную величину смещения.

Рисунок 1

( a ) Схема, показывающая однородную сферу и приложенное электрическое поле ( b ) Распределение поля смещения в плоскости xz (y = 0) сферы, ( c ) вид сбоку искажение плоскости xy в различных положениях z и ( d ) вид сверху распределения поля смещения плоскости экватора (z = 0) сферы при возбуждении режима дипольного резонанса.

Модель демпфированной массы-пружины

В этой работе микроволны применялись для возбуждения диполярного резонанса всей структуры вируса.Возбуждая дипольную моду наносферы, ядро ​​и оболочка с противоположным распределением заряда будут двигаться в противоположных направлениях и будут резонировать, как система с амортизированной массой и пружиной ¹⁷ . Наш следующий анализ похож на модель Друде-Лоренца, описывающую взаимодействие легкого атома, которое связывает систему демпфированной массы-пружины с квантово-механическими электронными резонансными переходами. В системе с амортизированной массой и пружиной с учетом приведенной массы ( м * ) сердечника и оболочки в анализе, относительное перемещение смещения может быть показано в следующем уравнении:

, где z — относительное смещение. между сердечником и оболочкой; b — коэффициент демпфирования, связанный с окружающей средой; k — эффективная жесткость пружины этой системы.Предполагая, что z (t) пропорционально exp (i ω t) , можно решить комплексную угловую частоту резонатора как:

Следовательно, скорость затухания колебаний равна мнимой части частоты ( b / 2m * ), что соответствует ω ₀ / 2Q ¹⁹ :

Угловая частота собственного резонанса (ω ₀ ) этой системы составляет ( k / ) ^0,5 . Q — добротность резонатора. Согласно уравнению (4), более сильное демпфирование увеличивает передачу энергии между резонатором и окружающей его средой, что уменьшает ограничение вибрации и приводит к более низкому значению Q . Теперь мы приближаемся к тому, что сферический вирус похож на однородную сферу, но с противоположными и равными зарядами в областях ядра и оболочки. Когда к системе приложено осциллирующее электрическое поле ( cos ) микроволн, вынужденные смещения будут индуцироваться с той же частотой, что и применяемые микроволны.Уравнение движения теперь должно включать силу, индуцированную приложенным электрическим полем ( qE ), где q — это общее количество заряда, распределенного в области ядра и оболочки вируса:

Мы описываем вынужденное смещение as, где A — амплитуда вынужденного смещения, а — фазовая задержка между смещением и приложенным электрическим полем. Решая конкретное решение этого дифференциального уравнения, можно получить фазовую задержку и амплитуду вынужденного колебательного смещения как

и

. Мгновенное потребление энергии этой системой затем описывается следующим уравнением, где v равно скорость колебательного движения ¹⁷ :

Путем интегрирования за один полный цикл можно получить среднее потребление энергии системой:

Тогда сечение поглощения вируса можно получить, задав входной поток мощности как с ²⁰

, где — относительная диэлектрическая проницаемость в системе, а c — скорость света в вакууме.

Порог разрушения вируса

При осциллирующей диполярной вибрации для инактивации вируса наиболее вероятным механизмом является разрушение самой внешней поверхности экваториальной плоскости (z = 0) из-за расположения максимальных искажений, как показано на Рис. 1 (в, г). Для вирусов гриппа это соответствует липидной мембране оболочки. Чтобы оценить максимальное индуцированное напряжение в экваториальной плоскости, мы разделим максимальную индуцированную силу на площадь области оболочки (определяемую направлением движения в приближенной модели) в экваториальной плоскости.Следуя приведенному выше обсуждению, мы обнаружили, что максимальное индуцированное напряжение в два раза превышает среднее значение, а область оболочки покрывает 58% экваториальной плоскости:

Если можно получить требуемый порог напряжения для разрушения вируса, пороговая величина электрического поля падающие микроволны также могут быть получены с помощью:

На рисунке 2 показана пороговая величина падающего электрического поля на разных частотах с разными Q на основе уравнения (12) с фиксированным пороговым значением.Можно заметить, что минимум пороговой величины электрического поля возникает, когда приложенная частота близка к собственной резонансной частоте. Кроме того, фактор качества полости Q играет важную роль. Изменяя значение pH раствора, можно регулировать состояние заряда вирусной поверхности, что влияет на Q вибрации. Например, предыдущие исследования показали, что полость Q сферических вирусов находится в диапазоне 2–10 за счет повышения значения pH раствора с 5.4 по 7,4 ⁸ . При увеличении Q больше энергии может удерживаться внутри резонатора, что приводит к гораздо более низкой пороговой величине микроволнового поля на резонансной частоте.

Рисунок 2

Пороговые величины электрического поля падающих электромагнитных волн для разрушения вируса в зависимости от угловой частоты с различными Q .

Для экспериментального исследования эффективности SRET от микроволн до CAV сферических вирусов был использован вирус гриппа A подтипа h4N2.h4N2 — это подтип вируса гриппа А, вызывающего грипп. Такие вирусы могут инфицировать птиц и млекопитающих и становятся все более распространенными при сезонном гриппе, от которого ежегодно умирает около 6309 человек в Соединенных Штатах, включая пневмонию и грипп, вызывающий ²¹ . Основываясь на предыдущих исследованиях, средняя масса и диаметр вируса h4N2 составляют 161 МДа ²² и 100 нм ²³ . Здесь мы аппроксимируем структуру вируса как наносферу со структурой ядро-оболочка с противоположным распределением заряда.Оболочка (90% от общей массы) содержит липид, нейраминидазу (NA), гемагглютинин (HA) и М-белок. Ядро (10% от общей массы) включает РНК и РНП. Таким образом, приведенная масса ( м * ) вируса составляет 14,5 МДа. Из литературы ²⁴ видно, что сила 400 пН, приложенная к наконечнику АСМ, может разрушить липидную оболочку. Поскольку радиус острия составлял 30 нм ²⁴ , пороговое напряжение разрушения оболочки составляло 0,141 МПа (). Чтобы рассчитать пороговую величину электрического поля для разрушения вируса h4N2 по уравнению (12), некоторые важные параметры, такие как q , Q и ω ₀ исследуемого вируса h4N2, должны быть получены с помощью измерение микроволнового спектра поглощения вирусов.

Как показано на рис. 3 (a), мы покрыли структуру копланарного волновода (CPW) микрофлюидным каналом с зоной восприятия длиной 1,25 мм ( L ), чтобы измерить спектр микроволнового поглощения вирусов. Этот микроволновый микрожидкостный канал может обеспечивать полосу пропускания микроволнового излучения более 40 ГГц. Результаты измерений представлены на рис. 3 (б). Как видно из рисунка, коэффициент поглощения мощности (α) вирусом на резонансной частоте (8,2 ГГц) составлял 21%, а Q был только 1.95 путем измерения полной ширины на половине максимума спектра. Поскольку плотность вирусов ( N ) в растворе составляла 7,510 ¹⁴ м ⁻³ , экспериментальное сечение поглощения вируса на резонансной частоте можно рассчитать с помощью следующего уравнения:

Рисунок 3

( a ) Спроектированная схема CPW для измерения микроволнового спектра, покрытая микрожидкостным каналом. ( b ) Измеренный микроволновый спектр поглощения вирусов h4N2.( c ) Расчетная пороговая величина электрического поля для разрушения вируса в зависимости от частоты микроволн.

Из уравнения (10) теоретическое поперечное сечение поглощения вируса на резонансной частоте составляет:

При установке PBS на 8,2 ГГц как 67,13 ²⁵ , = можно получить, сравнивая уравнение (13) и уравнение (14).

На данный момент получены все параметры для оценки порога электрического поля в уравнении (12). Подставляя порог P _{напряжение} = 0.141 МПа , =, м * = 14,5 МДа, Q = 1,95 и ω ₀ = 2π × 8,22 ГГц в уравнение (12), пороговая величина электрического поля для разрушения вируса при различных частотах СВЧ можно рассчитать. Результат показан на рис. 3 (c). Для сравнения со следующими экспериментами по инактивации наша оценочная пороговая величина электрического поля на частотах 6, 8 и 10 ГГц составляет 103,3, 86,9 и 137,1 В / м соответственно. Минимальный порог возникает около 8 ГГц из-за резонанса, и можно ожидать, что внутреннее напряжение, достаточное для разрушения вируса, будет более эффективно генерироваться более слабым электрическим полем.

В соответствии со стандартом безопасности микроволн IEEE, усредненное в пространстве значение плотности мощности в воздухе в открытом общественном пространстве не должно превышать эквивалентную плотность мощности 100 ( f /3) ^1/5 Вт / м ² на частотах от 3 до 96 ГГц ( f в ГГц) ²⁶ . Это соответствует 115 Вт / м ² на 6 ГГц, 122 Вт / м ² на 8 ГГц и 127 Вт / м ² на 10 ГГц для усредненных значений плотностей мощности в воздухе. Предполагая, что вся микроволновая мощность в воздухе на 100% передается в образец, и принимая диэлектрическую проницаемость воды 71.92 (6 ГГц), 67,4 (8 ГГц) и 63,04 (10 ГГц) ²⁵ для расчета, этот стандарт безопасности соответствует средней величине электрического поля 101 В / м (6 ГГц), 106 В / м (8 ГГц), 110 В / м (10 ГГц) внутри образцов на водной основе. Интересно отметить, что требуемые пороговые величины электрического поля на резонансной частоте (86,9 В / м) для разрушения вирусов h4N2, как показано на рис. 3 (c), находятся в пределах стандарта безопасности микроволн IEEE (106 В / м), что указывает на высокая эффективность SRET, хотя добротность вируса h4N2 невысока.

Прямое наблюдение когерентной передачи энергии в нелинейных микромеханических осцилляторах

Теоретическое описание результатов, показанных на рис. 2, может быть получено с помощью упрощенной модели с условием ИК-излучения 1: 1, учитывающим два связанных затухающих осциллятора: нелинейный осциллятор Дуффинга, связанный с линейным. В этом случае уравнения движения для пространственных степеней свободы x ₁ и x ₂ выражаются как:

, где γ ₁ , γ ₂ являются соответствующие скорости рассеяния, β — нелинейный коэффициент Дуффинга, а Ω ₂ À1 — нормализованная частота несвязанного линейного генератора x ₂ .Два генератора связаны друг с другом с коэффициентами связи J и J ‘. Только нелинейный осциллятор приводится в действие внешней силой обратной связи F _fb для компенсации рассеивания энергии и достижения самоподдерживающихся колебаний. Для положительного коэффициента Дуффинга, β > 0, частота нелинейного осциллятора Ω ₁ может быть увеличена путем увеличения F _fb . Без связи ( J = J ′ = 0) система сводится к двум независимым осцилляторам, с x ₂ асимптотически в состоянии покоя и x ₁ , ведущим себя как самоподдерживающийся нелинейный осциллятор с настраиваемая частота ²⁸ (дополнительное примечание 1).Для конечной связи линейный осциллятор x ₂ теперь может быть возбужден из-за движения ведомого нелинейного осциллятора x ₁ . Когда условие IR достигается, линейный осциллятор приводится в действие резонансно с силой, определяемой муфтой J ‘. Приведенный выше анализ с использованием пространственных степеней свободы эквивалентен модели, описывающей режимы собственных колебаний системы, в которой связь является нелинейной (дополнительное примечание 6).

Стационарные решения уравнения (1) определяют возможные начальные условия эволюции кольца вниз, которое, в свою очередь, регулируется теми же уравнениями, но с F _fb = 0. В случае, когда оба генератора имеют малую скорость рассеяния, мы можем применить метод возмущений для решения уравнения (1) как для установившегося режима, так и для переходной характеристики во время обрыва сигнала ^27,30 (дополнительные примечания 3 и 4). На рисунке 3 показаны численные решения уравнения (1) для малой диссипации, достаточно больших нелинейных коэффициентов Дуффинга, гарантирующих, что амплитуда колебаний находится в пределах нелинейного режима (до 10 ⁻² ), и больших коэффициентов связи (до 10 ⁻⁷ ).Спад энергии с временным разрешением нелинейного осциллятора x ₁ показан на рис. 3а и сравнивается с его затуханием за пределами ИК-диапазона. Представленная выше упрощенная модель качественно воспроизводит экспериментальные результаты рис.2: в ИК-диапазоне и в течение конечного периода времени, t _{когерентный} , осциллятор продолжает колебаться с практически постоянной амплитудой (рис. 3а) и частотой (рис. 3б) после отключения внешнего источника энергии. На рисунке 3c показана соответствующая временная эволюция высокочастотного линейного осциллятора, указывающая на быстрое неэкспоненциальное затухание его амплитуды, достигающее нуля в момент времени t _coherent .Эти результаты указывают на чистую передачу энергии от более высокочастотного линейного осциллятора к основному, поскольку первый затухает со скоростью, намного превышающей скорость экспоненциального затухания, характерную для рассеяния энергии в сторону термостата окружающей среды (пунктирная линия на рис. 3c). . Разница между двумя кривыми на рис. 3c обеспечивает прямую оценку количества энергии, переданной за период t _{когерентный} . Это ясно показывает, что значительная часть энергии перенаправляется к x ₁ вместо того, чтобы рассеиваться в ванне окружающей среды.Для времен, превышающих t _{когерентный} , амплитуда более высокочастотного осциллятора приближается к нулю, а основной начинает свое экспоненциальное затухание к равновесию. В частном случае нашего эксперимента с модовой связью 1: 3 между преимущественно изгибной плоскостной (более низкой частотой) модой и преимущественно крутильной (более высокочастотной) модой более высокочастотная мода действует как резервуар энергии для изгиба в -плоскостной (основной) режим, за счет накопления механической энергии в стационарном состоянии и перевода ее в низкочастотный режим при отключении внешней силы обратной связи до тех пор, пока ее энергия не будет исчерпана.

Рисунок 3: Моделирование отклика нелинейного генератора на вызывной сигнал.

( a ) Смоделированные переходные характеристики спада колебательной амплитуды (то есть огибающая колебательного смещения) однонелинейного осциллятора Дуффинга (синий) и нелинейного осциллятора при внутреннем резонансе (красный). Обратите внимание, что для нелинейного осциллятора в ИК-диапазоне амплитуда колебаний не уменьшается в течение t _{когерентного} после того, как внешнее возбуждение устранено при t = 0.( b ) Смоделированные переходные характеристики мгновенного сдвига частоты Ω ₁ -1 для двух случаев, представленных в a . После устранения внешнего возбуждения мгновенный сдвиг частоты для одиночного нелинейного генератора (синий) экспоненциально спадает к нулю, в то время как для нелинейного генератора в ИК-диапазоне (красный) мгновенная частота остается постоянной до t _{когерентный} . ( c ) Временная эволюция во время отключения высокочастотного линейного генератора ( x ₂ ) в ИК-диапазоне: амплитуда (красная линия) спадает намного быстрее, чем ожидаемое экспоненциальное затухание (пунктирная черная линия), что указывает на более быструю передачу энергии до x ₁ , чем для ванны окружающей среды.Заштрихованная область указывает количество энергии, переданной от x ₂ к x ₁ . ( d ) Зависимость от времени амплитуды основного осциллятора ( x ₁ ) в течение периода t _{когерентный} , обнаруживая небольшие колебания (∼0,1%) вокруг своего начального значения с уменьшающейся частотой. ( e ) Смоделированная разность фаз η между двумя связанными генераторами в течение того же периода времени, что и в d .Он показывает наличие когерентных колебаний около положительного среднего значения η , что указывает на передачу чистой энергии от x ₂ к x ₁ .

Более пристальный взгляд на временную зависимость x ₁ в течение t _{когерентный} показывает когерентные колебания вокруг своего стационарного значения с относительно очень малой амплитудой (∼0,1%) и медленно убывающей частотой ( Рис. 3г). Кроме того, разность фаз между двумя осцилляторами, η , значение которой является постоянным до вызывного сигнала, представляет аналогичные колебания, которые указывают на колебательный поток энергии между двумя осцилляторами (рис.3д). Смоделированные переходные характеристики η показывают, что он колеблется вокруг положительного значения, что означает, что, несмотря на мгновенное направление потока энергии, существует чистый поток энергии от x ₂ до x ₁ . Следовательно, амплитуда x ₂ затухает довольно резко, а амплитуда x ₁ остается в среднем практически постоянной. Этот динамический обмен прекращается, как только линейный осциллятор исчерпывает свою энергию, и с этого момента главный осциллятор ведет себя как одномодовый нелинейный осциллятор.

Хотя наша экспериментальная установка не может напрямую измерить когерентные колебания амплитуды, показанные на рис. 3d, из-за ограничения ширины полосы измерения, мы действительно видим их присутствие в частотном спектре с временным разрешением до и во время t _{когерентный} . На рисунке 4 показано изменение частоты резонатора во времени при переходе от установившегося состояния к выключенному в устройстве, которое приводится в состояние сильного ИК-излучения с большей силой обратной связи F _fb .В установившемся режиме (режим I) мы обнаруживаем две боковые полосы, фланкированные вокруг основного пика в спектре мощности. Во время t _{когерентный} (режим II) обе боковые полосы развиваются в сторону частоты основной изгибной моды в плоскости, сливаясь с ней при t = t _{когерентный} . Когда частота Ω ₁ экспоненциально спадает (режим III), нет никаких признаков боковых полос, потому что нет связи между колебательными модами и, следовательно, нет обмена энергией.Возникновение этих боковых полос является прямым следствием обмена энергией (см. Рис. 3e), значение которого количественно определяет скорость обмена: γ _ex . Для частного случая, представленного на рис. 4а, мы получили частоту Гц, которая почти на три порядка больше, чем собственная скорость затухания каждой из связанных мод (∼1 Гц). Выполняя аналогичные измерения частоты при разных движущих силах, получается линейная корреляция между t _{когерентным} и γ _ex (рис.4а, правая вставка). Данные показывают, что для получения конечного t _{когерентного} требуется γ _ex > 200 Гц, и чем больше γ _ex , тем больше t _{когерентный} .

Рисунок 4: Временная шкала динамики энергообмена при внутреннем резонансе.

( a ) Изменение мгновенной частоты во времени до (режим I) и во время (режим II и III) сигнала вызова. Для t <0, самоподдерживающееся движение управляется линейным сигналом обратной связи с соответствующей фазовой задержкой, вместо использования схемы ФАПЧ, которая использовалась для получения данных, представленных на рис.2. В режиме I есть две боковые полосы, фланкирующие основную установившуюся частоту (64,9 кГц, IR), которые показывают скорость обмена энергией между основной и более высокочастотной модами (спектр с одинарной мощностью показан на левой вставке). В течение t _{когерентного} (режим II) основная частота остается постоянной, а боковые полосы сливаются в направлении пика основной частоты и, наконец, исчезают в конце режима II. Режим III представляет собой нормальный спад для нелинейного осциллятора Дуффинга и, таким образом, не показывает никаких признаков боковых полос.Вставка справа: извлеченный γ _ex нанесен на график против соответствующего t _{когерентного} , показывая линейную корреляцию между ними. Планки погрешностей меньше размера символов. ( b ) Схематическое изображение потока энергии во время t _{когерентного} (режим II): есть чистый поток энергии от высокочастотной крутильной моды к основной моде в плоскости со скоростью γ _ex γ ₁ , γ ₂ .Эта большая разница в скоростях релаксации заставляет основную плоскую моду поддерживать стабильные колебания даже после отключения внешнего источника питания.

Экспериментальные и численные результаты, обсужденные выше, демонстрируют, что связь мод может быть использована для моделирования внутренних релаксационных явлений нелинейных осцилляторов. В частности, когда различные колебательные моды связаны через ИК-излучатель, обмен энергией между модами может происходить на порядки быстрее, чем обмен энергией с внешней ванной (рис.4б). В этих условиях нелинейные резонаторы могут поддерживать в течение конечного периода времени устойчивые колебания без внешнего источника энергии. Представленная в этой работе инженерная концепция рассеяния может быть применена к широкому спектру генераторов MEMS и NEMS, производительность которых ограничена электрическим шумом в цепи обратной связи ³¹ . Резонаторы MEMS и NEMS, колеблющиеся без внешнего питания, должны быть идеальными устройствами для определения предельного предела стабильности, налагаемого термомеханическим шумом ³² .Возможность управления скоростью обмена энергией между связанными модами создает испытательный стенд для проверки теорий термализации нелинейных систем из состояния равновесия ^33,34 и аномального трения в нелинейных резонаторах ^4,35 . В атомарно тонких резонаторах NEMS, где нелинейный динамический отклик может быть легко достигнут ³⁶ , связь мод может иметь значительное влияние на процесс релаксации к равновесию ³⁷ .

Стоит подчеркнуть многообразную роль нелинейности в возникновении изучаемых здесь явлений.Во-первых, нелинейность отвечает за связь между различными режимами колебаний, обеспечивая обмен энергией, определяющий их взаимное влияние. В то же время повышение частоты колебаний по мере увеличения амплитуды вынуждающей силы делает возможным достижение нелинейным осциллятором состояния IR — эффекта, который отсутствует в гармонических осцилляторах. Наконец, наличие интервала когерентности сразу после выключения движущей силы также должно быть приписано нелинейности.Комбинация биений и экспоненциального затухания, характеризующая динамику связанных линейных осцилляторов, на самом деле не может объяснить такую ​​временную стабильность амплитуды колебаний в отсутствие внешнего воздействия.

от качелей до субатомных струн ›Основы Берни (ABC Science)

Основы Берни

Резонанс возникает, когда мы говорим о музыке, искусстве и идеях. Но это ничто по сравнению с тем, насколько широко это проявляется в науке.

Берни Хоббс

Если субатомные струны действительно существуют, они будут накапливать энергию на резонансных частотах, как и все остальное во Вселенной. (Источник: Джули Рамсден / ABC)

Научная версия резонанса стоит за всем, от лазеров до МРТ и мостов, которые вибрируют до смерти *.

Без резонанса у нас не было бы музыки или голосов, весь наш мир был бы прозрачным, и парниковый эффект был бы невозможен.

Так что же такое резонанс и почему он везде?

Резонанс — это способ накопления энергии путем вибрации определенной частоты.И все — все — во Вселенной может резонировать.

Это так же просто, как толкать ребенка на качелях, но чтобы понять резонанс, вам нужно читать такие термины, как частота, вибрация, колебания и Гц, чтобы ваш мозг не затуманивался. (Быстрое прочтение «Вибрации» для начинающих должно предотвратить опускание лобных долей).

Теперь о парне на качелях.

Резонанс и колебания

Дети на качелях говорят «толкни меня», потому что они знают, что с каждым толчком они могут подняться немного выше, если толчки совпадают с качелями.

Этот фундаментальный закон игровой площадки суммирует основы резонанса — если к чему-то добавляется энергия на его резонансной частоте, он может накапливать все больше и больше этой энергии, вибрируя на этой резонансной частоте: это резонирует.

Итак, чтобы что-то резонировало, вам нужно знать его резонансную частоту (частоту, на которой оно естественным образом вибрирует, когда вы добавляете к нему энергию, например, толкая, тыкая или ударяя по нему). Затем вы просто добавляете энергию на этой частоте и наблюдаете, как нарастают вибрации.Мы, естественно, толкаем качели на их резонансной частоте (скажем, каждые три секунды), и они накапливают эту энергию толчка, колеблясь все выше и выше.

Ритмичный толчок со стороны ответственного взрослого — это один из способов добавления энергии с определенной частотой, но это не тот вид спонтанного события, которое действительно возникает в природе. В реальном мире регулярные удары энергии, создающие резонанс, обычно происходят от волн.

Волны на воде, волны давления (включая звуковые волны), электромагнитные (световые) волны — все они источники энергии, которые бывают разных частот, поэтому все они могут вызывать резонанс, толкая другие объекты.А при правильном типе полости, в которой можно отскакивать, волны тоже могут резонировать сами с собой.

Резонансные камеры

Когда волны встречаются с другими волнами, они складываются. Но если они встречаются в какой-то камере, размер которой соответствует их частоте, они могут продолжать складываться (резонировать), создавая одну большую стоячую волну.

Наши голоса приобретают громкость, потому что полости в нашей голове (особенно в гортани) представляют собой резонансные камеры: они имеют правильный размер, чтобы отражать наши звуковые волны, заставляя их резонировать как стоячие волны.

Корпуса музыкальных инструментов также являются резонирующими камерами — гитарная струна или трость кларнета сами по себе не обладают особой привлекательностью.

И резонансные камеры предназначены не только для звуковых волн. Залив правильной формы может вызвать приливный резонанс, что приведет к значительным сдвигам при отливе и приливе. А зеркала на концах лазерной камеры заставляют лазерный свет резонировать в виде высокоэнергетических стоячих волн — это удобно для DVD и удаляет нежелательные волосы и ворсинки.

Напористые звуковые волны и рюмки

Звуковые волны

также могут вызывать резонанс, физически толкая предметы, точно так же, как вы это делаете с качелями.Вот так любому количеству учителей физики и чудаковатому тенору удалось разбить бокал звуком.

Бокалы имеют резонансную частоту в диапазоне нашего слуха — поэтому мы слышим их звон, когда мы по ним стучим. Если вы сыграете ноту, которая соответствует этой частоте, вы можете вызвать резонанс в бокале. Увеличьте громкость (т.е. добавьте больше энергии на резонансной частоте), и стекло будет вибрировать все более и более дико, поскольку оно накапливает все больше и больше энергии. В конце концов, стекло не может выдержать вибрации — бокал разбивается.Еще более впечатляющим будет то, что вы сможете сделать это своим неусиленным голосом, как этот парень из Mythbusters .

Напористые электромагнитные волны

Электромагнитные волны (свет, радиоволны, рентгеновские лучи и т. Д.) Также могут вызывать колебания на их резонансной частоте. Но они влияют только на магнитные или электрически заряженные предметы, такие как электроны, протоны и молекулы. И только если электрические / магнитные поля волны меняются с резонансной частотой для этих частиц.

Резонансные колебания на атомном уровне, подобные этому, стоят за всем, от парникового эффекта и МРТ до нашего видимого мира.

Резонанс и видение

Если вам когда-либо делали МРТ (магнитно-резонансное изображение), вы знаете, что они дают удивительно четкие изображения наших внутренностей. И они делают это, используя простые старые радиоволны, воду и резонанс.

Атомы водорода в воде — это просто протоны, и эти протоны действуют как крошечные магниты.Протоны имеют резонансную частоту, на которой они колеблются при правильных условиях (то есть внутри огромного магнитного поля аппарата МРТ). И эта резонансная частота находится в радиодиапазоне. Итак, когда вы находитесь в аппарате МРТ, радиоволны поражают воду в вашем теле, заставляя протоны (атомы водорода) вибрировать (резонировать) с той же частотой. Вибрирующие протоны излучают собственный радиосигнал, и этот сигнал используется для построения изображения вашей водянистой ноги / мозга / живота. Это магнитно. Это резонанс.Это визуализация.

Резонанс также играет решающую роль в нашей способности видеть — резонирующие электроны ответственны за наш видимый мир. Если вы что-то видите, это потому, что электроны в этом предмете поглощают частоты (цвета) видимого света, которые соответствуют их резонансным частотам, и вибрируют изо всех сил. Атомы, электроны которых не поглощают в видимом диапазоне, для нас невидимы.

Но невидимые предметы — например, углекислый газ — все еще могут ощущать свое присутствие через резонанс.

Парниковый эффект — идея, которая действительно находит отклик …

Двуокись углерода (CO ₂ ) — это парниковый газ, и парниковые газы нагревают нашу атмосферу, потому что их молекулы могут поглощать инфракрасное излучение. Вы совсем не удивитесь, узнав, что они делают это, потому что их резонансные частоты соответствуют некоторым частотам инфракрасного излучения. Выстрел инфракрасного излучения правильной частоты дает CO ₂ , метан, воду и все эти парниковые газы, образующие молекулярную ча-ча-ча.(Вот отличная интерактивная версия этого процесса).

Придется искать повсюду, чтобы найти часть Вселенной, которая не связана с резонансом и не полагается на него. Энергия накапливается в колебаниях резонирующих частот от самых больших галактик до мельчайших субатомных частиц — и за их пределами. Если теория струн верна и субатомные струны действительно существуют, они будут вибрировать на своих резонансных частотах, как и все остальное в этой вселенной … и все остальные.

Спасибо доценту Бену Бухлеру с факультета квантовой науки Австралийского национального университета и профессору Рою Таскеру из Школы науки и здоровья Университета Западного Сиднея.наверх

Опубликовано 16 июня 2014 г.

Электронная почта ABC Science

Используйте эти ссылки в социальных сетях, чтобы поделиться Resonance: от свингов до субатомных струн .

Используйте эту форму, чтобы отправить сообщение «Резонанс: от колебаний к субатомным струнам» кому-нибудь из ваших знакомых:
https://www.abc.net.au/science/articles/2014/06/16/4022877.htm?

Снижение вынужденных колебаний энергосистемы на основе унифицированного регулятора потока мощности

Введение в систему

Как показано на рис.1 система с одной машиной с бесконечной шиной (SMIB) с UPFC, установленным в средней точке, анализируется с использованием модели генератора третьего порядка, чтобы проиллюстрировать влияние UPFC и принцип предлагаемого метода [7]. На рис. 1 E ’- переходная электродвижущая сила, а δ _г — ее фаза; X _d ’- переходное реактивное сопротивление генератора, а X _T — реактивное сопротивление трансформатора; X — реактивное сопротивление линии передачи; V _UPFC и X _UPFC — напряжение стороны шунта UPFC и реактивное сопротивление последовательной стороны UPFC, соответственно; В — напряжение на передающей клемме.{2}}} + D _ {\ text {g}} \ frac {{{\ text {d}} \ Delta \ delta}} {{{\ text {d}} t}} = — \ Delta P _ {\ текст {e}} + \ Delta P _ {\ text {m}} $$

(1)

где δ — угол мощности генератора; ω ₀ — базовая частота; T _J и D _g — инерционная постоянная и коэффициент демпфирования генератора соответственно; ∆ P _e и ∆ P _m — это изменение выходной электромагнитной мощности и механической мощности соответственно.Механическая мощность регулируется губернатором; Помехи от регулятора — частая причина ОС [12].

В модели генератора изменение электромагнитной мощности ∆ P _e приблизительно равно изменению электромагнитного момента ∆ T _e [7]. Изменение электромагнитной мощности определяется выражением (2).

$$ \ Delta P _ {\ text {e}} \ приблизительно \ Delta T _ {\ text {e}} = K \ Delta \ delta + D _ {\ text {e}} \ frac {{{\ text {d }} \ Delta \ delta}} {{{\ text {d}} t}} $$

(2)

, где D _e — коэффициент демпфирования.Исходные значения K и D _e зависят от параметров генератора и его системы возбуждения. Эти значения также связаны с импедансом линии передачи [23].

UPFC устанавливается в средней точке линии передачи. Он может одновременно управлять напряжением локальной шины и сопротивлением цепи. UPFC реализован с использованием двух аналогичных твердотельных преобразователей фазового напряжения (VSC), которые подключены через общий конденсатор промежуточного контура, как показано на рис.1, и каждый преобразователь соединен с трансформатором [24]. UPFC в этом случае разделен на последовательную сторону и сторону шунта. Обе стороны могут быть использованы для смягчения опровержений; соответствующие модели приведены в следующих разделах.

Механизм резонанса

Когда в регуляторе возникает непрерывная синусоидальная помеха с частотой Ом и амплитудой r , можно получить уравнение в форме (3). В (3) D представляет собой общий коэффициент демпфирования.{2}}} + D \ frac {{{\ text {d}} \ Delta \ delta}} {{{\ text {d}} t}} + K \ Delta \ delta = r \ sin \ left ({ \ varOmega t} \ right) $$

(3)

Решение (3) можно разделить на две части, а именно, общее решение и частное решение, которые объединяются для формирования синтезированного отклика системы:

$$ \ Delta \ delta = B \ sin \ left ({\ varOmega t — \ varphi} \ right) + B_ {1} \ left (t \ right) \ cos \ left ({\ omega _ {\ text {d}} t} \ right) + B_ {2} \ left (t \ right) \ sin \ left ({\ omega _ {\ text {d}} t} \ right) $$

(4)

Первый пункт (4) — это установившаяся реакция ОС. φ — начальная фаза этого компонента. Значение максимальной амплитуды B связано с коэффициентом демпфирования D , коэффициентом синхронного крутящего момента K и амплитудой возмущения r . Подробное выражение B приведено в следующем разделе. Частота установившегося отклика равна частоте помехи Ом . Второй и третий пункты — это переходные реакции. ω _d — частота переходных характеристик.Амплитуды переходных характеристик B ₁ ( t ) и B ₂ ( t ) уменьшаются до относительно небольших значений через несколько секунд после начальной точки.

Переходные характеристики можно также классифицировать как свободные колебания, вызванные начальными условиями, и сопровождаемые свободные колебания, вызванные возмущением. На основании теоретического анализа кривые синтезированного ОС имеют вид, показанный на рис. 2. Переходные характеристики 1 и 2 представляют собой свободные колебания и сопровождаемые ими свободные колебания, соответственно.Процесс запуска синтезированного ОС немного отличается от реальной ситуации, поскольку используется идеальный фазовый шаг. Как показано на рис. 2, основным фактором, влияющим на амплитуду ОС, является установившаяся характеристика. Таким образом, сведение к минимуму амплитуды установившегося отклика может эффективно уменьшить FO.

Рис.2

Кривые синтезированного ФО

Влияние коэффициента синхронного момента

Согласно резонансному механизму, резонансная частота равна частоте свободных колебаний без демпфирования.{2}}} + K \ Delta \ delta = 0 $$

(5)

Решая это уравнение, можно определить частоту \ (\ Delta \ delta \); эта частота равна резонансной частоте. В результате имеем

$$ \ omega _ {\ text {n}} = \ sqrt {\ frac {{\ omega_ {0} K}} {{T _ {\ text {J}}}}} $$

(6)

Этот результат показывает, что резонансная частота связана как с коэффициентом синхронного крутящего момента, так и с инерционной постоянной генератора.

Аналогично механической системе, когда частота возмущения близка к резонансной частоте, возмущение оказывает положительное воздействие на систему. Энергия возмущения непрерывно преобразуется в потенциальную энергию системы, вызывая тем самым ОС. Напротив, когда резонансная частота отличается от частоты возмущения, возмущение выполняет отрицательную работу, и колебания затухают. Согласно этой теории, когда коэффициент синхронного крутящего момента изменяется, резонансная частота изменяется, и оптические колебания уменьшаются.{2}}}} \ frac {r} {K} $$

(7)

Основываясь на приведенном выше выводе, когда изменяется коэффициент синхронного крутящего момента, это влияет на состояние резонанса, и амплитуда отклика в установившемся режиме намного меньше. Ожидаемый результат показан на рис. 3. Согласно кривым, реакция в установившемся состоянии уменьшается, а реакции в переходном состоянии остаются. Таким образом, предлагаемый метод идеально подходит для устранения ОС. Метод преобразует ОС в низкочастотные фильтры отрицательного демпфирующего механизма.Проблема ОС не может быть полностью решена с помощью простого управления демпфированием. Однако, преобразовав FO в LFO механизма отрицательного демпфирования, можно эффективно уменьшить колебания с помощью метода управления демпфированием. Когда колебания уменьшаются до небольшого диапазона, стабильность системы может быть гарантирована.

Рис.3

Кривые смягченного синтезированного ФО

Изменение активной мощности и изменение угла мощности имеют соотношение ∆ P = K ∆ δ .Когда частота возмущений фиксирована, соотношение между максимальной амплитудой отклика в установившемся режиме B и коэффициентом синхронного крутящего момента K может быть получено из (7). Кривые взаимосвязи между K и B показаны на рис. 4. Четыре кривые представляют четыре различные частоты возмущений.

Рис. 4

Кривые зависимости между коэффициентом синхронного крутящего момента и максимальной амплитудой мощности FO

Обобщение принципа

Чтобы обобщить предложенный принцип на многомашинную систему, необходимо проанализировать линеаризованный набор уравнений качания.{2}}}} \ hfill \\ \ end {array}} \ right] = \ Delta \ varvec {P} _ {\ text {M}} — \ left [{\ begin {array} {* {20} l} {D_ {1} \ frac {{\ text {d} \ Delta \ delta_ {1}}} {{\ text {d} t}}} \ hfill \\ {D_ {2} \ frac {{\ текст {d} \ Delta \ delta_ {2}}} {{\ text {d} t}}} \ hfill \\ \ vdots \ hfill \\ {D_ {n} \ frac {{{\ text {d}} \ Delta \ delta_ {n}}} {{\ text {d} t}}} \ hfill \\ \ end {array}} \ right] — \ left [{\ begin {array} {* {20} l} {K _ {{\ text {s1}}} \ Delta \ delta_ {1}} \ hfill \\ {K _ {{\ text {s2}}} \ Delta \ delta_ {2}} \ hfill \\ \ vdots \ hfill \\ {K _ {{{\ text {s}} n}} \ Delta \ delta_ {n}} \ hfill \\ \ end {array}} \ right] $$

(8)

, где T _J1 , T _J2 ,…, T _{J n} обозначают инерционные постоянные n мод колебаний; D ₁ , D ₂ ,…, D _n обозначают коэффициенты демпфирования мод колебаний; K _s1 , K _s2 ,…, K _{s n} обозначают коэффициенты синхронного крутящего момента для режимов колебаний; ∆ δ ₁ , ∆ δ ₂ ,…, ∆ δ _n — вариации углов мощности мод колебаний; \ (\ Delta \ varvec {P} _ {\ text {M}} \) — вектор, который представляет мощность возмущения от механической мощности генераторов.