Индуктивности обмоток трансформатора и электромагнитное рассеяние
Дата публикации: .
Категория: Трансформаторы.
Индуктивности обмоток
В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i0 возникают высшие гармоники (смотрите статью «Явления, возникающие при намагничивании магнитопроводов трансформаторов»).
 |
| Рисунок 1. Магнитные потоки трансформатора при одностороннем намагничивании (i1 ≠ 0, i2 = 0) |
При работе трансформатора на ток i0 накладывается ток нагрузки, по отношению к которому ток i0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i0. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.
Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Фс, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).
Пусть поток Фс создается током первичной обмотки i1, когда ток вторичной обмотки i2 = 0. Значения Фс и i1 могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе
| Lс1 = w1 × Фс / i1. | (1) |
Величину Lс1 можно выразить также через магнитное сопротивление магнитопровода
| (2) |
где lk, Sk и µk соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом
| Фc = F1 / Rµc = w1× i1 / Rµc. | (3) |
и после подстановки этого значения Фс в выражение (1) получим
Отметим, что значение Rµc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).
Аналогично индуктивность вторичной обмотки от потока магнитопровода
а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода
| Mс = w1 × w2 / Rµс | (6) |
Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Фс одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина Rµс. Вследствие этого также
| (7) |
Кроме потока Фс, ток первичной обмотки i1 создает также поток Фв1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψв1 и Ψв12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки
Lв1 = Ψв1 / i1
и взаимная индуктивность двух обмоток
Mв12 = Ψв12 / i1.
Точно так же при питании вторичной обмотки током i2 создается поток Фв2, замыкающийся частично по воздуху. Потокосцеплениям Ψв2 и Ψв21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки
Lв2 = Ψв2 / i2
и взаимная индуктивность двух обмоток
Mв21 = Ψв21 / i2.
При этом, согласно принципу взаимности,
Mв12 = Mв21 = Mв
Поля потоков Фв1 и Фв2 имеют гораздо более сложный характер, чем поле потока Фс. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от Lс2 [смотрите соотношение (7)]
| (8) |
Полные собственные индуктивности первичной и вторичной обмоток
| L11 = Lс1 + Lв1; L22 = Lс2 + Lв2, | (9) |
и полная взаимная индуктивность
Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы.
Понятие об электромагнитном рассеянии
Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей
| (11) |
Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1.
Если бы в трансформаторе отсутствовали потоки Фв1 и Фв2, замыкающиеся по воздуху, то L11 = Lc1, L22 = Lc2, M = Mc, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)
Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Фв1 и Фв2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.
Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния
| (12) |
Чем меньше c и чем больше σ, тем больше рассеяние.
Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Фв1 и Фв2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Фв1 и Фв2 обусловливают также явление взаимной индукции, поскольку Mв ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин.
В трансформаторах с ферромагнитным магнитопроводом потоки Фв1 и Фв2 относительно малы.
Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало.
В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 – 0,004.
Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L11, L22 и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
www.electromechanics.ru
Индуктивность трансформатора
Итак, явление взаимной индукции используется в широко распространенных устройствах – трансформаторах.
Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова).
Рассчитаем взаимную индуктивность двух катушек и , намотанных на общий сердечник (рис. 5.5).
Когда в первой катушке идет ток , в сердечнике возникает магнитная индукция и магнитный поток Ф через поперечное сечение S.
Рис. 5.5.
Магнитное поле тороида можно рассчитать по формуле
Через вторую обмотку проходит полный магнитный поток , сцепленный со второй обмоткой:
здесь – потокосцепление, которое можно найти по формуле:
По определению, взаимная индуктивность двух катушек равна:
К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции.
где – сопротивление обмотки.
– делают малым (медные провода) и . Тогда
Во второй обмотке, по аналогии, , отсюда
| , | (5.4.1) |
Если пренебречь потерями, т.е. предположить, что , то
| , | (5.4.2) |
Коэффициент трансформации будет равен:
ens.tpu.ru
Простой расчет трансформатора. Онлайн-калькулятор расчёта по размерам магнитопровода габаритной мощности трансформатора. Ламповый звук hi-end и ретро электроника
Такая методика расчета трансформаторов конечно очень приблизительная но для радиолюбительской практики вполне подходит.
Кроме этого все нижеперечисленные расчеты актуальны только лишь для трансформаторов с Ш-образным сердечником и для работы с током промышленной частоты 50 Гц.
Итак, начнем….
Задача: нужен трансформатор с выходным напряжением 12V и током на вторичной обмотке не менее 1A. (если обмоток несколько то токи складываются).
Мощность вторичной обмотки получается 12V* 1A =12W.
Так как КПД у трансформаторов приблизительно 85%, то мощность забираемая первичкой при работе будет приблизительно в 1,2 раза выше и получится 12W * 1.2 = 14.4W.
Где S- площадь сердечника, P1- мощность первичной обмотки
.
получится 4,93 кв.см. (ну в общем округлим до 5….)
Это необходимая минимальная площадь сердечника. Если есть возможность применить больше-это даже лучше.
Здесь:
W- количество витков,
Ктр- коэффициент трансформации,
Sс- площадь сечения сердечника
.
Так как мы решили взять Ктр=50, то считаем:
W1= 50/5 * 220 = 2200
W2= 50/5 * 12 = 120
где I это ток протекающий через обмотку.
Ах, да…. мы же еще не знаем ток который будет потреблять первичка….
Ну, что же, это тоже не проблема: напряжение мы знаем, мощность тоже, получается:
I1= P1/U1 = 14.4/220 = 0.065A.
Итак:
диаметр провода для первички будет:
D1 = 0,7 * на корень из 0,065 = 0,18 мм.
Для вторичной обмотки:
D2 = 0.7 * на корень из 1 = 0,7 мм.
Вот и весь расчет!
Очень часто для питания радиолюбительских конструкций или для питания готовых устройств требуется понижающий трансформатор. Точный расчёт силового трансформатора очень сложен, но для приблизительного расчёта можно воспользоваться упрощёнными формулами. В этой статье рассмотрим как рассчитать трансформатор, собранный на наиболее часто встречающемся магнитопроводе из Ш-образных пластин.
Для расчёта трансформатора нам нужно знать: желаемое напряжение на вторичной обмотке и ток нагрузки. Ели ток нагрузки не известен, но известна его мощность, то вычислить ток не составит труда — нужно мощность поделить на напряжение на вторичной обмотке.
1. Расчёт тока вторичной обмотки
I2 = 1,5*Iн , где
- I2 — ток во вторичной обмотке, А,
- Iн — ток нагрузки, А.
2. Определение мощности, потребляемой от вторичной обмотки
P2 = U2*I2 , где
- P2 — мощность вторичной обмотки, Вт,
- U2 — напряжение вторичной обмотки, В,
- I2 — ток вторичной обмотки, А.
Если необходимо несколько вторичных обмоток, то считаем мощность каждой обмотки, а затем складываем мощности всех вторичных обмоток и подставляем в следующую формулу.
3. Определение мощности трансформатора
Pт = 1,25*P2 , где
- Рт — общая мощность трансформатора, Вт,
- Р2 — мощность вторичной обмотки, Вт.
4. Расчёт тока первичной обмотки
I1 = Pт/U1 , где
- I1 — ток в первичной обмотке трансформатора, А,
- Pт — мощность трансформатора, Вт,
- U1 — напряжение первичной обмотки, В.
5. Определение необходимого сечения сердечника магнитопровода
S = 1,3*√ Pт , где
Следует заметить, что магнитопровод нужно подбирать так, чтобы отношение ширины сердечника (центральной пластины) магнитопровода к толщине набора было в пределах 1 ÷ 2.
6. Расчёт числа витков в первичной обмотке
W1 = 50*U1/S , где
- W1 — число витков первичной обмотки, шт,
- U1 — напряжение первичной обмотки, В,
- S — площадь сечения сердечника магнитопровода, см² .
7. Расчёт числа витков во вторичной обмотке
W2 = 55* U2/S , где
- W2 — число витков вторичной обмотки, шт,
- U1 — напряжение вторичной обмотки, В,
- S — площадь сечения сердечника магнитопровода, см² .
8. Определение диаметров проводов обмоток трансформатора
d = 0,632* √ I , где
- d — диаметр провода, мм,
- I — ток обмотки, А (соответственно подставляем I1 и I2 для первичной и вторичной обмоток).
Расчёт приведён для медного провода.
9. Проверка заполняемости окон магнитопровода
После подбора пластин магнитопровода следует проверить влезет ли провод на каркас трансформатора.
Sо = 50*Pт , где
- Sо — площадь, занимаемая намотанными проводами, в одном окне магнитопровода, мм 2 ,
- Pт — мощность трансформатора, Вт.
Если площадь окна подобранного магнитопровода больше или равна вычисленной, то провод влезет.
Пластины магнитопровода нужно собирать вперекрышку, как это показано на рисунке вверху.
Магнитопровод следует стянуть обоймой или шпильками с гайками, шпильки необходимо обернуть бумагой или другим изоляционным материалом, чтобы шпильки не замыкали пластины. Если магнитопровод плохо стянут, то он будет гудеть.
Провода следует наматывать равномерно и плотно(иначе могут не влезть). Между каждым рядом надо прокладывать тонкую бумагу или лавсановую плёнку в 1-2 слоя и 3-4 слоя между обмотками.
Для удобства намотки можно сделать простое приспособление, показанное на рисунке:
Состоит устройство из двух фанерных стоек, закреплённых на общем основании и вставленного в них металлического прутка, с одного конца изогнутого в виде ручки. Одной рукой крутим ручку, второй направляем провод, катушку с проводом можно наподобие разместить ещё на одном прутке, но уже без ручки.
tehnodinamika.ru
Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии
le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формулегде ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.

Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
в) трапецеидальное поперечное сечение с острыми кромками
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости

Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.

Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
Таким образом коэффициент С1 и индуктивность L составят
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят

Таким образом коэффициент С1 и индуктивность L составят
На сегодня всё. Продолжение смотри в следующей статье.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Скажи спасибо автору нажми на кнопку социальной сети
www.electronicsblog.ru
51. Взаимная индукция. Трансформаторы. Коэффициент трансформации. Индукция трансформатора
Индуктивности обмоток трансформатора и электромагнитное рассеяние
Индуктивности обмоток
В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i0 возникают высшие гармоники (смотрите статью «Явления, возникающие при намагничивании магнитопроводов трансформаторов»).
 |
| Рисунок 1. Магнитные потоки трансформатора при одностороннем намагничивании (i1 ≠ 0, i2 = 0) |
При работе трансформатора на ток i0 накладывается ток нагрузки, по отношению к которому ток i0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i0. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.
Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Фс, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).
Пусть поток Фс создается током первичной обмотки i1, когда ток вторичной обмотки i2 = 0. Значения Фс и i1 могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе
| Lс1 = w1 × Фс / i1. | (1) |
Величину Lс1 можно выразить также через магнитное сопротивление магнитопровода
| (2) |
где lk, Sk и µk соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом
| Фc = F1 / Rµc = w1× i1 / Rµc. | (3) |
и после подстановки этого значения Фс в выражение (1) получим
Отметим, что значение Rµc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).
Аналогично индуктивность вторичной обмотки от потока магнитопровода
а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода
| Mс = w1 × w2 / Rµс | (6) |
Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Фс одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина Rµс. Вследствие этого также
| (7) |
Кроме потока Фс, ток первичной обмотки i1 создает также поток Фв1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψв1 и Ψв12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки
Lв1 = Ψв1 / i1
и взаимная индуктивность двух обмоток
Mв12 = Ψв12 / i1.
Точно так же при питании вторичной обмотки током i2 создается поток Фв2, замыкающийся частично по воздуху. Потокосцеплениям Ψв2 и Ψв21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки
Lв2 = Ψв2 / i2
и взаимная индуктивность двух обмоток
Mв21 = Ψв21 / i2.
При этом, согласно принципу взаимности,
Mв12 = Mв21 = Mв
Поля потоков Фв1 и Фв2 имеют гораздо более сложный характер, чем поле потока Фс. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от Lс2 [смотрите соотношение (7)]
| (8) |
Полные собственные индуктивности первичной и вторичной обмоток
10i5.ru
|
«Как-то лет в 12 нашёл я старый трансформатор, слегка перемотал его и включил. А тем временем традиционные линейные источники питания на силовых трансформаторах всё чаще стали вытесняться своими импульсными
коллегами. Наиболее популярными среди радиолюбителей стали сетевые источники питания, собранные на микросхемах IR2153 и IR2155, которые
представляют из себя самотактируемые высоковольтные драйверы, позволяющие получать полумостовые импульсные блоки питания
мощностью до 1,5 кВт с минимальной обвязкой. Для наших высокотоковых дел лучше всего применять трансформаторы с тороидальным магнитопроводом.
В сравнении с другими сердечниками они имеют меньший вес и габариты, а также отличаются лучшими условиями охлаждения обмоток и
повышенным КПД. По сути дела, умных статей в сети на предмет расчёта импульсных трансформаторов великое множество, с картинками, формулами, таблицами и прочими авторитетными причиндалами. Наблюдаются в свободном доступе и многочисленные онлайн-калькуляторы на интересующую нас тематику. И снизошла б на нас благодать неземная, кабы вся полученная информация сложилась в наших любознательных головах в единое большое целое. Вот и гуляют по сети идентичные радиолюбительские схемы импульсных блоков питания на IR2153 с идентичными заявленными характеристиками,
трансформаторами на одних и тех же кольцах, но радикально не идентичным количеством витков первичных обмоток трансформаторов. А для лучшего восприятия сказанного, приведу типовую схему источника питания на IR2153, не обременённую ни устройством защиты, ни какими-либо другими излишествами.
Схема проверена временем и многочисленными опытами изрядно пощипанных током, неустрашимых радиолюбителей, так что не работать в ней — просто нечему. Ну и наконец, переходим к расчёту импульсного трансформатора. Мотать его будем на бюджетных низкочастотных ферритовых кольцах отечественного производителя 2000НМ или импортных — EPCOS N87, а для начала определимся с габаритной мощностью тороидального ферритового магнитопровода. Концепция выбора габаритной мощности с запасом в 10% от максимальной мощности в нагрузке, заложенная в режимы
автоматического подбора сердечника в большинстве калькуляторов, хотя и не противоречит теоретическим расчётам, учитывающим высокий КПД
импульсного трансформатора, но всё же наводит на грустную мысль о ненадлежащей надёжности и возможной скорой кончине полученного
моточного изделия. Расчёты поведём исходя из частоты работы преобразователя IR2153, равной 50 кГц. Почему именно такой? Параметры первичной обмотки трансформатора рассчитаем при помощи программы Lite-CalcIT, позволяющей, на мой взгляд, вполне
адекватно оценить как размер сердечника, так и количество витков первичной обмотки.
Как следует мотать первичную обмотку трансформатора?
Если используются кольца 2000НМ отечественного производителя, то для начала — посредством наждачной бумаги скругляем наружные острые грани до состояния, приведённого на Рис.2 а). Далее на кольцо следует намотать термостойкую изоляционную прокладку (Рис.2 б). В качестве изоляционного материала можно выбрать лакоткань, стеклолакоткань, киперную ленту, или сантехническую фторопластовую ленту. Для буржуйских колец фирмы EPCOS первые два пункта практической ценности не имеют. Настало время намотать однослойную обмотку «виток к витку» (Рис.2 в). Обмотка должна быть равномерно распределена по периметру магнитопровода — это важно! Если в закромах радиолюбительского хозяйства не завалялся обмоточный провод необходимого диаметра, то обмотку можно намотать сразу в два, или несколько проводов меньшего диаметра (Рис.2 г). Не забываем, что зависимость тока от диаметра квадратичная и если, к примеру, нам надо заменить провод диаметром 1мм, то это будет не два провода по 0,5мм, а четыре (или два провода по 0,7мм). Ну и для завершения первичного процесса поверх первичной обмотки трансформатора наматываем межобмоточную прокладку — пару слоёв лакоткани или другой изолирующей ленты (Рис.2 д). А вот теперь мы плавно переходим к выполнению второй части упражнения. Теперь, что касается диаметра провода вторичной обмотки трансформатора. Диаметр этот достаточно просто вычисляется по формуле: И в завершении приведу незамысловатый калькулятор для расчёта параметров вторичной обмотки импульсного трансформатора. Точно так же, как и в случае с первичной обмоткой — вторичная должна быть как можно более равномерно распределена по периметру магнитопровода.
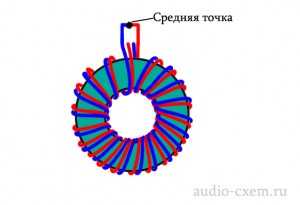
При необходимости поиметь двуполярный источник питания, обе обмотки следует мотать одновременно, затем присовокупить начало одной обмотки к концу другой, а уже потом направить это соединение, в зависимости от личных пристрастий — к земле, средней точке, общей шине, корпусу, или совсем на худой конец — к GND-у. Ну что ж, с трансформатором определились, пора озадачиться полным джентльменским набором настоящего мужчины — плавками
с меховым гульфиком, а главное, непосредственно импульсным блоком питания, оснащённым такими значимыми прибамбасами, как устройства
мягкого пуска и защиты от токовых перегрузок и КЗ.
|
vpayaem.ru
Выходной трансформатор — почти просто, но не дешево
Введение
Вокруг выходных трансформаторов для ламповых усилителей в последние годы создан некий ореол мистики и таинственности, знания, доступного лишь избранным. Отчасти так и есть, однако… Методики инженерного расчета трансформаторов были разработаны более полувека назад и за эти годы претерпели несущественные изменения лишь в части использования новых магнитных материалов более высокого качества [1]. Основные же принципы и расчетные соотношения остались прежними. Законы физики не изменяются за полста лет…
Расчёт параметров выходного трансформатора
Исходные данные для расчета трансформатора определяются в процессе расчета оконечного каскада усилителя. Ими являются — выходная мощность, приведенное сопротивление нагрузки в цепи анода, индуктивность первичной обмотки и индуктивность рассеяния трансформатора [2].
Определение необходимых размеров магнитопровода
Первоначально надо определить требуемый габарит магнитопровода. Пригодность имеющегося железа можно ориентировочно оценить по условию:
где Vc — активный объем стали;
L1 — расчетная индуктивность первичной обмотки, Гн;
UA — амплитуда напряжения на зажимах первичной обмотки, В;
FH — нижняя граничная частота, Гц;
Bmax — максимальная амплитуда магнитной индукции, Гс.
S — площадь сечения магнитопровода, см2;
lC — средняя длина магнитной силовой линии, см.
Для броневого магнитопровода средняя длина магнитной силовой линии рассчитывается, как:
А для стержневого:
где обозначения соответствуют принятым на Рис. 1.


Рис. 1 Основные размеры магнитопроводов
При оценке габаритов магнитопровода величину Вmax следует ориентировочно принять равной 7000 — 8000 Гс для пластинчатых и 10000 Гc для витых разрезных наборов железа.
Экспериментальное определени индукции трансформатора
Для дальнейших расчетов максимальное значение индукции Вmax желательно определить экспериментально на выбранном железе. С этой целью на каркас трансформатора наматывается пробная обмотка в 100 витков и включается в схему по Рис. 2. Магнитопровод при этом должен быть собран без зазора. Плавно увеличивая напряжение на обмотке с помощью ЛАТРа, наблюдают форму тока через нее. В момент появления заметных на глаз искажений формы синусоиды фиксируют напряжение на обмотке (показания прибора V1).

Рис. 2 Схема для измерения максимальной индукции в магнитопроводе
Затем допустимое значение индукции рассчитывают по формуле:
где U1 — показания прибора, В;
S — площадь сечения магнитопровода, см2 (чистого железа).
Определение коэффициента трансформации
Расчет конструктивных данных начинают с определения коэффициента трансформации, который, при заданной величине сопротивления нагрузки усилителя, обеспечит расчетную величину анодной нагрузки выходной лампы.
где n — коэффициент трансформации;
N1 — число витков первичной обмотки;
N2 — число витков вторичной обмотки;
RA — расчетная величина сопротивления анодной нагрузки лампы, Ом;
RH — сопротивление нагрузки усилителя, Ом;
К — КПД трансформатора.
Величина КПД однотактных трансформаторов на мощности 5 — 30 Вт обычно лежит в пределах 0,8 — 0,9. За значение сопротивления нагрузки усилителя желательно принять величину, равную:
где Rном — номинальное сопротивление акустической системы;
Rmin — минимальное сопротивление акустической системы в рабочем диапазоне частот.
Такая величина является компромиссной с точки зрения обеспечения как расчетного сопротивления анодной нагрузки лампы в номинальных условиях с одной стороны, так и коэффициента демпфирования с другой.
Расчёт числа витков первичной обмотки
Число витков первичной обмотки вычисляется из условия непревышения максимально допустимого значения индукции в магнитопроводе:
где U1M — максимальная амплитуда напряжения на зажимах первичной обмотки, В;
ВМП — максимально допустимая амплитуда переменной составляющей индукции, Гс.
где ВM — изморенное ранее значение максимальной индукции, Гс.
Опыт расчета и изготовления значительного количества разнообразных трансформаторов (как выходных, так и межкаскадных) позволяет сделать вывод, что значение ВМП не должно превышать 3500 — 4000 Гс для пластинчатых магнитопроводов (шихтованных) и 5000 Гс для витых разрезных (ленточных). Следует отметить, что витые сердечники, несмотря на более высокие качественные параметры в силовых трансформаторах, несколько уступают пластинчатым для применения в выходных. Искажения сигнала, вносимые трансформатором из-за нелинейности характеристики В/Н при использовании витых магнитопроводов проявляются при меньших значениях индукции, хотя, после появления, нарастают медленнее.
Это явление объясняется тем, что магнитный поток концентрируется во внутренних витках магнитопровода, где длина силовой линии короче. В результате сердечник постепенно насыщается, начиная от внутренних слоев и заканчивая внешними. Внутренние слои оказываются насыщенными гораздо раньше внешних, что проявляется в виде небольшого искривления характеристики намагничивания железа даже при средней индукции 4000 — 6000 Гс. Более высокое качество железа витых сердечников несколько смягчает этот эффект, но полностью устранить не может.
Количество витков первичной обмотки можно определить и по другой формуле, исходя из условия обеспечения расчетной индуктивности:
где L1 требуемая индуктивность обмотки, Гн;
m — магнитная проницаемость материала сердечника при заданных ампер-витках постоянного подмагничивания.
Однако, практика показывает, что расчет по формуле (10) приводит к заниженному числу витков по сравнению с (8), а это недопустимо из-за резкого роста искажений на низких частотах вследствие насыщения магнитопровода.
Только при высокой нижней граничной частоте (более 100 — 150 Гц) формула (10) дает большее значение числа витков. Кроме того, она неудобна тем, что в расчет входит величина m , зависящая от ампер-витков постоянного подмагничивания, определить которую до экспериментального изготовления трансформатора можно лишь приблизительно по графикам соответствующих зависимостей [1], [3], [4].
Расчёт числа витков вторичной обмотки
Число витков вторичной обмотки рассчитывается как:
Расчёт диаметра провода
Диаметр провода (чистой меди) первичной обмотки:
Формула (13a) справедлива для расчета средней длины витка на броневом сердечнике (Рис. 1а), а формула (13b) — на стрежневом (Рис. Ч в), величина dk (см) — толщина материала каркаса.
Диаметр провода вторичной обмотки:
Если вторичная обмотка состоит из нескольких параллельно соединенных секций, то диаметр провода секции рассчитывают как:
Размещение обмоток трансформатора
После расчета обмотки необходимо проверить их размещение в окне магнитопровода. Наилучшим считается такое размещение, когда и первичная и вторичная обмотки укладываются в целое число слоев и полностью заполняют окно магнитопровода. Для достижения такого результата допустимо варьировать число витков и диаметр провода обмоток в небольших пределах (до _* 10%).
Заполнение окна магнитопроводаможно проверить по формулам:
где A1 , А2, Aиз — толщины первичной обмотки , вторичной обмотки и межобмоточной изоляции;
р1, р2 — число слоев первичной и вторичной обмоток;
d`1, d`2 -диаметры проводов с изоляцией первичной и вторичной обмоток;
dиз — толщина межслойной изоляции.
Индуктивность рассеяния трансформатора достаточной точностью определяется по формуле;
где l0 — средняя длина витка, см;
h’ — высота намотки слоя, см;
к — количество секций.
Для получения расчетной величины индуктивности рассеяния, обмотки трансформатора в большинстве случаев необходимо секционировать. Наиболее просто и эффективно выполнить послойное

Рис. 3 Пример размещения обмоток в окне магнитопровода (цилиндрическое секционирование)
(цилиндрическое) секционирование, когда обмотки наматываются на каркас частями, а в конце соединяются последовательно или параллельно. Чаще всего применяют последовательное включение секций первичной обмотки и параллельное — вторичной. Суммарное число секций первичной и вторичной k должно быть таким, чтобы индуктивность рассеяния LS, вычисленная по (17), не превышала найденную при электрическом расчете оконечного каскада. Один из вариантов размещения секций на каркасе приведен на Рис. 3. Необходимо помнить, что общее число секций первичной и вторичной обмотки должно быть нечетным, а крайние секции (т.е. непосредственно лежащая на каркасе и внешняя) должны принадлежать одной обмотке и иметь половинное число витков по отношению к внутренним секциям той же обмотки. Только в этом случае выполняется условие компенсации полей рассеяния соседних секций и индуктивность рассеяния будет соответствовать расчетной.
Если обмотка распределена на двух катушках (стержневые трансформаторы), то секции ее должны чередоваться от одной катушки к другой.
Это условие относится и к двухтактным трансформаторам, где обмотки каждого плеча обязательно должны иметь одинаковое число секций на одном и на другом стержнях магнитопровода.
Определение величины немагнитного зазора
Неотъемлемой конструктивной особенностью трансформатора выходного однотактного каскада является немагнитный зазор между частями магнитопровода. При его отсутствии постоянная составляющая анодного тока выходной лампы, протекающая через первичную обмотку, вызывает насыщение железа и, как следствие, происходит катастрофическое падение магнитной проницаемости и возрастание искажений, вносимых трансформатором. Зазор не позволяет магнитопроводу войти в насыщение от постоянного подмагничивания (поскольку он эквивалентен многократному увеличению длины магнитной силовой линии для постоянной составляющей магнитного потока) и, в то же время, не влечет за собой драматического снижения величины m . Оптимальным является такой немагнитный зазор, при котором индукция, соответствующая постоянной составляющей магнитного потока, находилась бы примерно на середине линейной части характеристики намагничивания. Для наиболее распространенных типов электротехнической стали величина зазора может быть ориентировочно определена по формуле:
I0 — ток постоянного подмагничивания, А;
lC — длина силовой линии, см.
Более точно величину зазора подгоняют экспериментально при номинальном токе подмагничивания, исходя из условий получения наибольшей выходной мощности на нижней граничной частоте и минимальных искажении при половине номинальной выходной мощности на той же частоте сигнала.
Поскольку теоретический расчет оптимального зазора достаточно сложен и требует значительного количества экспериментальных данных о качестве применяемого железа, то представляется более целесообразным использовать практический подбор зазора в готовом трансформаторе.
Паразитные ёмкости и методы борьбы с ними
В заключение следует обратить внимание на такие неприятные и неизбежные явления, как межобмоточная и распределенная емкости трансформатора. Совместно с индуктивностями обмоток (или их частями) и индуктивностями рассеяния, они образуют паразитные колебательные контуры, резонирующие в области верхних звуковых и ультразвуковых частот. Эти резонансы искажают частотную и фазовую характеристики трансформатора (набег фазы из-за распределенной емкости плохо сконструированного трансформатора на высших частотах может достигать 400° — 7000° и, кроме того, быть немонотонным). Радикального средства борьбы с этими явлениями нет, но уменьшить их можно следующими способами:
- Равномерной плотной укладкой (виток к витку) обмоток трансформатора.
- Использованием межслойной изоляции внутри секций каждой обмотки (бумага 0,05 — 0,1 мм).
- Увеличение толщины межобмоточной изоляции (что несколько уменьшает коэффициент заполнения окна, зато существенно снижает междуобмоточную емкость).
- Использование магнитопровода расчетного размера. (Увеличение габаритов трансформатора против необходимого введет к росту указанных емкостей, а увеличение длины витка — к росту Ls).
- Укладка расчетного числа секций (непомерное увлечение секционированием резко увеличивает междуобмоточную емкость).
Пропитка катушки трансформатора различными компаундами имеет как достоинства, так и недостатки. К первым относится увеличение механической прочности и снижение резонансов конструкции. Ко вторым — увеличение паразитных емкостей и снижение частот паразитных электрических резонансов вплоть до звукового диапазона. Решение о пропитке трансформатора должно приниматься только после тщательного анализа всех «за» и «против».
Заключение
И, наконец, хотелось бы напомнить, что выходной трансформатор — это клубок компромиссов. Не следует гнаться за идеальными параметрами и огромной массой: в 99% случаев улучшение одного параметра ведет к ухудшению нескольких других. Излишнее количество секций увеличивает межобмоточную емкость; излишнее число витков — индуктивность рассеяния и активное сопротивление. Таких примеров множество. При расчете задавайтесь разумными исходными параметрами и не делайте из трансформатора противовес для башенного крана. Не требуйте от трансформатора невозможного, но разумно используйте то, что он может предоставить.
Литература
- Цыкни Г.С. Трансформаторы низкой частоты. М., Связьиздат, 1955.
- Андронников Д.В. «Три электрода в один такт». «Вестник А.Р.А.» No. 3, 1998 г.
- Войшвилло Г.В. Усилители низкой частоты на электронных лампах. Изд. 2.
- Белопольский И.И. Электропитание радиоаппаратуры. М., Энергия, 1965.
- Лукачер. Расчет выходных трансформаторов, ж. Радиофронт No. 22 1935.
vt-tech.eu





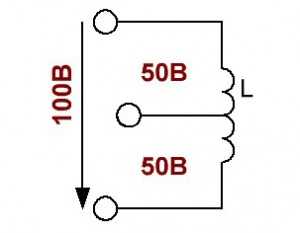
 Количество вторичных обмоток ограничено только размерами магнитопровода.
При этом суммарная величина снимаемых с обмоток мощностей
не должна превышать расчётную мощность трансформатора.
Количество вторичных обмоток ограничено только размерами магнитопровода.
При этом суммарная величина снимаемых с обмоток мощностей
не должна превышать расчётную мощность трансформатора.